MATEMAT K SORU BANKASI
|
|
|
- Çağatay Baykara
- 8 yıl önce
- İzleme sayısı:
Transkript
1 LYS MATEMAT K SORU BANKASI 14 KONU ÖZET 118 KONU TEST TOPLAM 2320 SORU
2 TEŞEKKÜR Kitaba emeği geçen değerli Zafer Dershaneleri öğretmenlerine ve de dizgisinden baskısına kadar kitaba emek veren tüm çalışanlara teşekkür ederim. Ali DEMİR Zafer Yayınları Kurucusu COPYRIGHT ZAFER E T M VE Ö RET M L M TED fi RKET BU K TAP ZAFER DERSHANELER YAYINIDIR. HER HAKKI SAKLIDIR. K TAPTAK TESTLER VE SORULAR AYNEN YA DA DE fit R LEREK YAYIMLANAMAZ. YEN MÜFREDATA TÜMÜYLE UYGUN ANKARA Dizgi Grafik Zehra BÜLBÜL Muharrem ÇEL K Mevsimben TEM ZER Tolga YURDASAH P ISBN
3
4 İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır, parlayacak; O benimdir, o benim milletimindir ancak. Çatma, kurban olayım, çehreni ey nazlı hilâl! Kahraman ırkıma bir gül! Ne bu şiddet, bu celâl? Sana olmaz dökülen kanlarımız sonra helâl... Hakkıdır, Hakk'a tapan, milletimin istiklâl! Ben ezelden beridir hür yaşadım, hür yaşarım. Hangi çılgın bana zincir vuracakmış? Şaşarım! Kükremiş sel gibiyim, bendimi çiğner, aşarım. Yırtarım dağları, enginlere sığmam, taşarım. Garbın âfâkını sarmışsa çelik zırhlı duvar, Benim iman dolu göğsüm gibi serhaddim var. Ulusun, korkma! Nasıl böyle bir imanı boğar, "Medeniyet!" dediğin tek dişi kalmış canavar? Arkadaş! Yurduma alçakları uğratma, sakın. Siper et gövdeni, dursun bu hayâsızca akın. Doğacaktır sana va'dettiği günler Hakk'ın... Kim bilir, belki yarın, belki yarından da yakın. Bastığın yerleri "toprak!" diyerek geçme, tanı: Düşün altındaki binlerce kefensiz yatanı. Sen şehit oğlusun, incitme, yazıktır, atanı: Verme, dünyaları alsan da, bu cennet vatanı. Kim bu cennet vatanın uğruna olmaz ki fedâ? Şühedâ fışkıracak toprağı sıksan, şühedâ! Cânı, cânânı, bütün varımı alsın da Hüdâ, Etmesin tek vatanımdan beni dünyada cüdâ. Ruhumun senden, İlâhi, şudur ancak emeli: Değmesin mabedimin göğsüne nâmahrem eli. Bu ezanlar ki şahadetleri dinin temeli Ebedî yurdumun üstünde benim inlemeli. O zaman vecd ile bin secde eder varsa taşım, Her cerîhamdan, İlâhi, boşanıp kanlı yaşım, Fışkırır ruh ı mücerred gibi yerden na'şım. O zaman yükselerek arşa değer belki başım. Dalgalan sen de şafaklar gibi ey şanlı hîlâl! Olsun artık dökülen kanlarımın hepsi helâl. Ebediyen sana yok, ırkıma yok izmihlâl: Hakkıdır, hür yaşamış, bayrağımın hürriyet; Hakkıdır, Hakk'a tapan, milletimin istiklâl! Mehmet Âkif Ersoy
5 10. YIL MARŞI Çıktık açık alınla on yılda her savaştan; On yılda on beş milyon genç yarattık her yaştan; Başta bütün dünyanın saydığı başkumandan, Demir ağlarla ördük anayurdu dört baştan. Türk'üz: Cumhuriyet'in göğsümüz tunç siperi; Türk'e durmak yaraşmaz, Türk önde, Türk ileri! Bir hızda kötülüğü, geriliği boğarız, Karanlığın üstüne güneş gibi doğarız. Türk'üz, bütün başlardan üstün olan başlarız; Tarihten önce vardık, tarihten sonra varız. Türk'üz: Cumhuriyet'in göğsümüz tunç siperi; Türk'e durmak yaraşmaz, Türk önde, Türk ileri! Çizerek kanımızla öz yurdun haritasını, Dindirdik memleketin yıllar süren yasını; Bütünledik her yönden istiklâl kavgasını... Bütün dünya öğrendi Türklüğü saymasını! Türk'üz: Cumhuriyet'in göğsümüz tunç siperi; Türk'e durmak yaraşmaz, Türk önde, Türk ileri! Örnektir milletlere açtığımız yeni iz; İmtiyazsız, sınıfsız, kaynaşmış bir kitleyiz: Uyduk görüşte bilgiye, gidişte ülküye biz. Tersine dönse dünya yolumuzdan dönmeyiz. Türk'üz: Cumhuriyet'in göğsümüz tunç siperi; Türk'e durmak yaraşmaz, Türk önde, Türk ileri! Söz: Behçet Kemal Çağlar, Faruk Nafiz Çamlıbel Müzik: Cemal Reşit Rey
6
7 Sevgili Ö renciler, Amac n z, üniversite s nav n kazanmak, üniversiteli olmak. Bu nedenle, yaflam n z n önemli bir dönüm noktas nda bulunuyorsunuz. Böylesi bir noktada, üniversitenin herhangi bir ö retim program n rastgele tercih edip kazanman n ötesinde, istedi iniz ö retim program na girmeyi temel amaç k lman z gerekiyor. Çünkü tercih edip kazanaca n z üniversite ö retim program, bir bak ma gelece inizi belirleyecektir. Ancak, flu da biliniyor ki, ülkemizde, her ö rencinin istedi i üniversite ö retim program na girmesi bir yana, üniversite s navlar n kazanmas ve üniversiteli olmas art k kolay de il. Sorun, üniversite s navlar na baflvuran aday say s n n yüz binleri bulmas ndan; buna karfl l k üniversite ö retim programlar ndaki kontenjanlar n s n rl l ndan kaynaklan yor. Bu durumda, yüz binlerin aras ndan s yr l p öne ç karak üniversite s navlar nda baflar l olabilmenin birtak m koflullar yla karfl karfl yas n z demektir. Birinci koflul, yetene inize uygun, baflar n zla orant l üniversite ö retim programlar n sa l kl bir biçimde seçmektir. kinci koflul, düzenli, disiplinli, verimli bir çal flma temposu tutturmakt r. Üçüncü koflul, üniversite s navlar na haz rl k amac yla ç kar lan ciddi yay nlarla çal flman z destekleyip sürdürmektir. Zafer Yay nlar, çal flmalar n z desteklemek amac yla, özgün, titiz, yo un çal flma ürünü olan ve yeni sisteme tamamiyle uygun yeni serisini hizmetinize sunmaktan gurur duymaktad r. Elinizdeki LYS Matematik Soru Bankas bu amaca hizmet eden ve sizlerin bu yöndeki gereksiniminizi karfl layacak yönde haz rlanm fl yetkin bir baflvuru kayna d r. LYS Matematik Soru Bankas kitab Lisans Yerlefltirme S nav nda yer alaca düflünülen konulardan ç kabilecek, zorluk katsay s LYS'ye uygun özgün sorular içermektedir. fiimdiye de in yay mlanan soru bankalar ndan nitelikçe çok daha üstün olan bu kitap on dört bölümden oluflmaktad r. Her bölümde, test sorular na geçilmeden önce, o bölüme iliflkin bilgi alan n n temel çizgileriyle, karakteristik özellikleriyle gözden geçirilmesini sa layan konu özetleri yer almaktad r. Özenle haz rlanan bu konu özetlerinin ayr nt lardan s yr lm fl fakat konunun özünü yakalayan metinler olmalar büyük önem tafl maktad r. Konu özetlerini bu yönleriyle de erlendirmek gerekir. Konu özetlerinin d fl nda, her bölüm, konuyu hiç boflluk b rakmaks z n alt bölümlerine ayr lm fl ve konular hiyerarflik olarak tarayan sorulardan oluflmufl, geçerlili i ve güvenirlili i s nanm fl, yeterli say da testlerle tamamlanm flt r. Gerek konu özetleri gerekse konu testleri kapsam ve nitelik aç s ndan s nav sistemindeki de ifliklikler, ÖSYM standartlar dikkate al narak haz rlanm flt r. Bu kitaptan yararlanarak yapaca n z al flt rmalar, daha önce ö rendi iniz kavramlar n, terimlerin, zihninizde somut biçimler kazanmas n, giderek daha da netleflmesini sa layacakt r. Tüm sorular eksiksiz çözdü ünüzde, eminim, kendinizi LYS'deki Matematik sorular n çözmeye haz r hissedeceksiniz. Okuldan üniversiteye uzanan bu yolda, tüm ö rencilerimize baflar lar diliyorum. Ankara ALİ DEMİR Zafer Yayınları Kurucusu
8 Ç NDEK LER 1. BÖLÜM : POL NOMLAR TEST BÖLÜM : ÖZDEfiL KLER VE ÇARPANLARA AYIRMA...35 TEST BÖLÜM : PERMÜTASYON, KOMB NASYON, B NOM, OLASILIK VE STAT ST K TEST BÖLÜM : K NC DERECEDEN DENKLEMLER, Efi TS ZL KLER VE FONKS YONLAR TEST BÖLÜM : TR GONOMETR TEST BÖLÜM : KARMAfiIK SAYILAR TEST BÖLÜM : LOGAR TMA TEST BÖLÜM : TOPLAM VE ÇARPIM S MGES TEST BÖLÜM : D Z LER TEST BÖLÜM : MATR S VE DETERM NANT TEST BÖLÜM : ÖZEL TANIMLI FONKS YONLAR TEST BÖLÜM : L M T VE SÜREKL L K TEST BÖLÜM : TÜREV VE UYGULAMALARI TEST BÖLÜM : NTEGRAL TEST
9 Polinomlar / Bölüm 1 9 POLİNOMLAR BÖLÜM 1 TANIM : P(x)=a n x n +a n 1 x n a 3 x 3 +a 2 x 2 +a 1 x+a 0 a 0, a 1, a 2, a 3,..., a n R ve n N olmak üzere, Q(x)=b n x n + b n 1 x n b 3 x 3 +b 2 x 2 +b 1 x+b 0 P(x)=a n x n +a n 1 x n a 3 x 3 +a 2 x 2 +a 1 x+a 0 ifadesine polinomları için, reel katsayılı POLİNOM de nir. a 0, a 1, a 2,..., a n sayılarına KATSAYILAR, a n e BAŞKATSAYI ve a 0 a SABİT TERİM denir. a 0, a 1 x, a 2 x 2,..., a n x n ifadelerine polinomun TERİMLERİ denir. Bir polinomda her terimdeki x lerin üsleri içe - risindeki en büyük değere (doğal sayıya) polinomun DERECESİ denir. Yalnız bir sayıdan (sıfır hariç) oluşan polinoma sabit polinom denir. Sabit polinomun derecesi 0 dır. Bir polinom yal nızca 0 (sıfır) dan oluşuyorsa buna sıfır polinomu denir. Sıfır polinomunun derecesi belirsizdir. P(x)=Q(x) a n = b n, a n 1 =b n 1,..., a 3 = b 3, a 2 = b 2, a 1 = b 1, a 0 = b 0 dır. POLİNOMLARDA TOPLAMA ve ÇIKARMA : İki polinom toplanırken veya çıkarılırken aynı dereceden terimler kendi aralarında toplanır veya çıkarılır. P(x) = a n x n + a n 1 x n a m x m +a m 1 x m a 2 x 2 + a 1 x + a 0 ve Q(x) = b m x m + b m 1 x m b 2 x 2 + b 1 x + b 0 P(Q(X)) VERİLDİĞİNDE P(x) i BULMAK : (Q o Q 1 )(x) = I(x) = x olacağından P(x) = P( Q(Q 1 (x) ) biçiminde bulunur. POLİNOMDA EŞİTLİK : Dereceleri eşit iki polinomun aynı dereceden terimlerinin katsayıları birbirine eşit ise, bu iki po linom eşittir. olsun (n > m) P(x) ± Q(x)=a n x n +a n 1 x n (a m ± b m )x m + (a m 1 ± b m 1 ).x m (a 2 ± b 2 )x 2 +(a 1 ±b 1 )x+(a 0 ± b 0 ) POLİNOMLARDA ÇARPMA : İki polinomun çarpımında birinci polinomun her terimi ile ikinci polinomun her terimi çarpılır. İki polinomun çarpımının derecesi, polinomla rın dereceleri toplamına eşittir. dpx [ ( ). Qx ( )] = dpx ( ( )) + dqx ( ( ))
10 10 POLİNOMLARDA BÖLME : Bölüm 1 / Polinomlar c) P(x) polinomunun (x a) m ile bö lünebilmesi : P(x) bölünen, Q(x) bölen, B(x) bölüm ve K(x) kalan ise, Px ( ) = Qx ( ). Bx ( ) + Kx ( ) dir. P(x) polinomunun (x a) m ile tam bölünebilmesi için P(x) polinomu, P(x) in birinci, ikinci,..., m 1 inci türevinde x = a konulduğunda sıfır olmalıdır. K(x) in derecesi daima Q(x) in derecesin den küçüktür.iki polinomun bölümünde, bölümün derecesi, bölünenin derecesi ile bölenin derecesi farkına eşittir. dbx ( ( )) = dpx ( ( )) dqx ( ( )) KALAN BULMA : a) P(x) polinomunun x a ile bölü münden kalan : d) P(x) polinomunun x a ve x b ile bölümünden kalanlar verildiğinde (x a).(x b) bulma : çarpımı ile bölü münden ka lanı P(x) polinomunun x a ile bölü münden kalan k 1 ve x b ile bölümünden kalan k 2 olsun. P(x) polinomunun (x a) (x b) çarpımına bölümünden kalan, K(x) = mx + n ise Ka ( ) = ma. + n= k1 4 denklem sisteminin çözümünden m ve n Kb ( ) = mb+ n= k2 bulunur. P(x) polinomunun x a ile bölü münden kalan x a=0 denkleminin kökünü P(x) polinomunda x yerine yazarak bulunur. Yani, Kalan=P(a) dır. NOT P(x) = a n x n + a n 1 x n a 0 polinomunda katsayıların toplamını bulmak için x yerine 1, sabit terimi bulmak için x yerine 0 yazılır. b) P(x) polinomunun x n a ile bölümünden kalan: Katsayılar toplamı : P(1) = a n + a n a 0 Sabit terim : P(0) = a 0 Çift dereceli terimlerin P( 1) + P( 1) = katsayılarının toplamı 2 P(x) polinomunun x n a ile bölü münden kalan, polinomda her x n yerine a yazıla rak bulunur. Tek dereceli terimlerin katsayıla rının toplamı = P( 1) P( 1) 2
11 Polinomlar / Bölüm 1 11 TEST POLİNOMLAR 1 1. x R ve n N olmak üzere, aşağıdakilerden hangisi daima bir polinom belirtir? A) P(x) = 3x n + 1 2x n 2 + x P(x) = 4x n 5 n+ 2 3x 1 olduğuna göre, P(x) polinomunun derecesi aşağıdakiler den hangisine eşittir? B) C) D) 2n n Px ( ) = x + 3x3 + 1 n n 2 Px ( ) = 2x + 3x 3 3 Px ( ) x x n + 1 = + 5 A) 1 B) 2 C) 3 D) 4 E) 5 E) Px ( ) = 5 x n Px ( ) = xk + 1 3xk polinomunun derecesi en fazla kaç olabilir? a+ 1 P(x) = 3x 5x a 3 polinomunun derecesi en fazla kaç olabilir? A) 3 B) 5 C) 7 D) 10 E) 14 A) 6 B) 9 C) 10 D) 11 E) a + 7 Px ( ) = 3x a 2a + x + 7 polinomunun de recesi kaçtır? 3a a + 1 P(x) = x + 2x 2 x + 2 eşitliği bir polinom olduğuna göre, a nın tam sayı değerleri top lamı kaçtır? A) 6 B) 12 C) 14 D) 15 E) 18 A) 6 B) 4 C) 2 D) 2 E) 4
12 12 7. P b 4 x 3 l = 2.x 24 3.x olduğuna göre, P(x) polinomunun derecesi kaçtır? A) 12 B) 18 C) 24 D) 32 E) 48 Bölüm 1 / Polinomlar 11. P(x) ve Q(x) polinomları için; dp > 2 ( x). Qx b 3 lh= 17 R V S Qb 2 x l W S W d = 1 S xpx. ( ) W T X olduğuna göre, d[p(x) + Q(x)] kaçtır? A) 12 B) 7 C) 6 D) 4 E) 3 8. P(x) = 2x n+1 3x 4 n + 6 polinomlarında derecesi en büyük olanının derecesi aşağıdakilerden hangisidir? A) 3 B) 4 C) 5 D) 6 E) P(x) ve Q(x) birer polinom ve P(x). Q(x) polinomunun derecesi 5 tir. P(x) polinomunun Q(x) polinomuna bölümünden elde edilen bö lüm polinomu nun derecesi 3 olmak üzere, 3.P(x) 2.Q(x) polinomunun derecesi kaçtır? A) 4 B) 3 C) 2 D) 1 E) 0 n P(x) = 9.x n 6 n x + 5 polinomunun de recesi kaçtır? A) 2 B) 3 C) 4 D) 5 E) P(x), Q(x) birer polinom ve P(x). Q(x) dere cesi 9 dur. x 2. Q(x) polinomu P(x) polinomu ile bölündüğünde bölümün derecesi 5 olduğuna göre, P(x) + Q(x) in derecesi kaçtır? A) 9 B) 8 C) 7 D) 6 E) P(x) ve Q(x) iki polinom, P(x). Q(x) polinomunun derecesi 9, xpx ( ( 1)) 2 R(x) = polinomun derecesi 7 Qx ( ) olduğuna göre, [ P(x) Q(x) ] polinomunun derecesi kaçtır? 14. P(x), Q(x) birer polinom olmak üzere, dbp( x 2 ) l = 5 ve d(p(x). Q(x)) = 7 dqx ( ( )) olduğuna göre, d (P(x) Q(2x)) kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 A) 3 B) 4 C) 5 D) 6 E) 7
13 Polinomlar / Bölüm P(x), Q(x) birer polinom, P 2 (x). Q(x) ifade sinin derecesi 8 dir. P(x) polinomu Q(x) ile bölündüğünde bölümün derecesi 1 olduğuna göre, Q(x) polinomunun derecesi kaçtır? 18. (x 4 ax 3 + 3x 5) (ax 3 x 2 + 4x + 2) çarpımı yapıldığında x 4 lü terimin bulun ma ması için a kaç olmalıdır? A) 2 B) 3 C) 4 D) 5 E) 6 A) 2 B) 1 C) 0 D) 1 E) P(x, y) = x (n2 ). y n + xy 3 7 polinomunun derecesi 6 olduğuna göre, P( 2, 2) kaçtır? 19. P(x) = (x 3 2x 2 + x 5) (ax 2 + x 4) oldu ğuna göre, P(x) polinomunun x 4 lü te riminin katsayısının 5 olması için a ne ol malıdır? A) 33 B) 37 C) 41 D) 45 E) 51 A) 2 B) 1 C) 0 D) 1 E) P(x) = (x 2 2) 5 + (3x + 1) 4 polinomunun te rim sayısı kaçtır? 20. (4x 4 + 3x 3 2x 2 + 5) (3x 3 + 4x 2 6x + 2) çarpımı yapıldığında, x 5 in katsayısı kaç olur? A) 5 B) 6 C) 8 D) 10 E) 11 A) 26 B) 18 C) 16 D) 14 E) 12 1.D 2.C 3.C 4.C 5.D 6.C 7.D 8.C 8. 9.B 10.A 11.D 12.A 13.D 14.C 14.C 15.A 16.C 16.B 17.C 18.E 19.E 20.B
14 14 Bölüm 1 / Polinomlar TEST POLİNOMLAR n 3 n + 2 Px ( ) = 2x + 3x + 3 ifadesi reel katsayılı bir polinom olduğuna göre, P(x) polinomunun derecesi en çok kaçtır? A) 12 B) 13 C) 15 D) 16 E) P(x) = (a 1)x 3 (b 2)x + a. b + 3 polinomu sabit polinom olduğuna göre, P(1907) kaçtır? A) 1907 B) 10 C) 7 D) 5 E) 1 2. P(x) = (n 2) x 3 2x 2 + 3x + 1 polinomunun çarpanlarından biri (x + 1) olduğuna göre, n kaçtır? A) 3 B) 2 C) 2 D) 3 E) 4 5. P(x + 1) + P(x 2) = 5x + 8 olduğuna göre, P(2) P(1) farkı kaçtır? A) 5 B) 4 C) 5 D) 2 E) dep: P 2 ( x). Q( x 3 ) D = 10 Px ( ) der> Qx H= 5 ( ) olduğuna göre, der[p(x) Q(x)] kaçtır? A) 6 B) 5 C) 4 D) 3 E) 2 6. P(x) = 3x 3 12x Q(x) = (x 2 1) (x 1). a + bx 2 + cx + d polinomları veriliyor. P(x) = Q(x) olduğuna göre, a + b + c + d toplamı kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5
15 Polinomlar / Bölüm P(x) = 2ax 2 + 3x + a polinomunun katsayılar toplamı 12 olduğuna göre, a kaçtır? A) 8 B) 7 C) 4 D) 3 E) P(x) = x 12 3x x polinomunun x ile bölümünden kalan aşağıdakilerden hangisidir? A) 3x + 2 B) 3x 1 C) 2x 2 D) x + 2 E) x 1 8. x sayı tabanı olmak üzere, P(x) = (1331) x polinomunun (x 4) ile bölümünden kalan kaçtır? A) 4 B) 17 C) 98 D) 118 E) P(x + 1) = (x 1) 3 3(x 1) 2 + 3x + 6 olduğuna göre, Pb l kaçtır? A) 6 3 B) 9 C) 10 D) 12 E) n > 1 olmak üzere, P(x) = (x 1) 2n (1 x) 2n+1 + 2x + 3 polinomunun (x 2) ile bölümünden kalan kaçtır? A) 9 B) 8 C) 7 D) 6 E) P(x) ve Q(x) polinomları için P(x 1) = (x 2 + 1). Q(x + 1) + 2x 3 olduğu biliniyor. Q(x) in (x 3) ile bölümünden kalan 2 olduğuna göre P(x + 4) ün x + 3 ile bölümünden kalan kaçtır? A) 12 B) 11 C) 10 D) 9 E) P(x) polinomunun (x + 1) 3 ile bölümünden kalan x 2 + x 4 tür. P(x) polinomunun (x + 1) ile bölümünden kalan kaçtır? A) 4 B) 1 C) 4 D) 7 E) P(x) = (x + 1). Q(x) + 5 Q(x) = (x 1). K(x) + 2 dir. P(x) polinomunun x 2 1 ile bölümünden kalan aşağıdakilerden hangisidir? A) x + 1 B) 2x 1 C) 2x + 1 D) x + 7 E) 2x + 7
16 (x + 2). P(x + 1) = 2x 3 + mx 2 + 9x + 6 eşitliğini sağlayan P(x) polinomunun x + 1 ile bölümünden kalan kaçtır? A) 5 B) 7 C) 9 D) 11 E) Pe 3 x o = 2 x 2 Pe x veriliyor. 9 o Buna göre, P 1 e 3 o Bölüm 1 / Polinomlar değeri kaçtır? A) 12 B) 10 C) 8 D) 6 E) P(x) polinomu (x 2) ve (x + 1) ile bölündüğünde sırasıyla 6 ve 3 kalanlarını veriyor. P(x) polinomu x 2 x 2 ile bölündüğünde kalan aşağıdakilerden hangisidir? A) x + 4 B) x + 2 C) x 1 D) 2x 1 E) 2x x 5 A B C 3 = + + x x x 1 x + 1 x olduğuna göre, A. B. C çarpımı kaçtır? A) 32 B) 30 C) 24 D) 20 E) a N olmak üzere, P(x) = x 3a + 2x 2a 7x a + 1 polinomunun x a + 1 ile bölümünden kalan kaçtır? 20. P(Q(x + 1)) = x 2 + 2x + 7 polinomu için Q(x 1) polinomunun x + 2 ile bölümünden kalan 7 olduğuna göre, P(x + 2) polino munun x 5 ile bölümünden kalan kaçtır? A) 6 B) 7 C) 8 D) 9 E) 10 A) 16 B) 15 C) 13 D) 11 E) 9 1.E 2.C 3.B 4.D 5.C 6.A 7.D 8.E 9.A 10.C 11.A 12.E 13.B 14.C 14.E 15.A 16.B 16.A 17.D 18.E 19.B 20.B
17 Polinomlar / Bölüm 1 17 TEST POLİNOMLAR x 4 3x 2 + 7x = (x+2). Q(x) + 6 eşitliğini sağlayan Q(x) polinomunun kat sayıları toplamı aşağıdakilerden hangisidir? 4. (x+1). P(x) = 2x 3 + 4x 2 + m eşitliğindeki P(x) polinomunun katsayıları toplamı kaçtır? A) 4 B) 1 C) 0 D) 3 E) 7 A) 2 B) 1 C) 0 D) 1 E) 2 2. P(x) bir polinom ve x IR için P(x + 1) = 2x 3 + bx 2 6x + 2 olduğuna göre, P(x) polinomunun katsayılar toplamı kaçtır? 5. (x + 3). Q(x) + 3 = 2x 3 + 3x 2 10x eşitliğini sağlayan Q(x) polinomunda x in, kuvveti çift olan terimlerinin katsayıları toplamı kaçtır? A) 0 B) 1 C) 2 D) 3 E) 5 A) 2 B) 1 C) 0 D) 1 E) 2 3. P(x, y) = (3x 2 y xy 2 + 2) m+1 polinomunun katsayıları toplamı 256 olduğuna göre, m kaç tır? A) 0 B) 2 C) 3 D) 4 E) 5 6. P(x, y) = (5x 3 y + 3x 2 y 4) n+3 iki değişkenli polinomunun açılımı yapıldığında, katsayıların toplamı 64 oluyor. Buna göre, n nin değeri kaçtır? A) 0 B) 1 C) 2 D) 3 E) 4
18 18 7. P(x, y) = ( 2x + y 1) n 1 olmak üzere, P(x, y) polinomunun kat sayıları toplamı 32 olduğuna göre, n kaçtır? A) 2 B) 3 C) 5 D) 6 E) 7 Bölüm 1 / Polinomlar 11. P(x) = 2x 3 + bx 2 + cx + 30 ve bir Q(x) polinomu için Q(x 1) = (2x 5) (x 2 7x 4) P(x) = Q(x) olduğuna göre, b+c toplamı aşağıdakilerden hangisine eşittir? A) 18 B) 16 C) 12 D) 4 E) 6 8. P(x) = (x 2 +2x) 3 polinomunda çift dereceli terimle rinin katsayılar toplamı A ve tek dereceli te rimlerin katsayılar toplamı B olduğuna göre, 2A B kaçtır? 12. P(x) = (x 2 + 2x) 3, Q(x) = x 6 + ax 5 + bx 4 + 8x 3 P(x) = Q(x) ve olduğuna göre, 2a+b toplamı kaçtır? A) 8 B) 9 C) 12 D) 16 E) 20 A) 23 B) 24 C) 25 D) 26 E) P(x) = x 3 mx 2 7x + n 4 polinomu 9. 5x 5=A.(x 2).(x+1)+B(x 2).x+C(x 1).(x + 1) olduğuna göre, 4. A + 3. B + 8. C toplamı kaçtır? Q(x) = (x 1). (x 2 + 3x 4) 1 polinomuna eşit olduğuna göre, n kaçtır? A) 20 B) 18 C) 15 D) 12 E) 8 A) 4 B) 5 C) 6 D) 7 E) P(x) = 4x 8 + 8x 5 ax x 3 + cx Q(x) = (2x 5 + x 3 + 3x + 12) (2x 3 x + 4) P(x) = Q(x) olduğuna göre, a+c toplamı aşağıdakilerden hangisine eşittir? A) 12 B) 8 C) 4 D) 2 E) P(x) = 5x 4 3x 3 + 2x 2 x + 6 ve Q(x) = 2x 6 + 3x 5 4x 4 + 5x 3 6x polinomlarının çarpımında x 7 li terimin katsayısı kaçtır? A) 60 B) 52 C) 45 D) 33 E) 27
19 Polinomlar / Bölüm P(x) = 5x 4 4x 3 +7x 2 8x 16 polinomunun x + 1 ile bölümünden kalan kaçtır? A) 8 B) 6 C) 4 D) 4 E) P(x) = 2x 2 4x + 5 polinomunun x 2 x 1 ile bölümünden kalan nedir? A) 2x + 7 B) 2x 7 C) 3x + 11 D) 3x + 11 E) 4x P(x) = 4x 3 3x a polinomunun x 1 ile bölümünden kalan 5 olduğuna göre, a kaçtır? A) 7 B) 8 C) 9 D) 10 E) P(x) = 5x 3 + ax 2 bx + 5 polinomunun x ile bölümünden kalan 5x 2 4x + c olduğuna göre, a + b + c toplamı kaçtır? A) 14 B) 9 C) 5 D) 4 E) P(x) = 3x 3 + 2x 2 x + 7 polinomumun x 2 2 ile bölümünden kalan nedir? A) 6x + 7 B) 5x + 11 C) 4x 7 D) 3x + 7 E) 2x P(x) = 2x 3 kx 2 + c 4 polinomu x 2 + x ile tam bölündüğüne göre, bu polinomun x + 2 ile bölümünden kalan c nin kaç katıdır? A) 4 B) 2 C) 1 D) 1 E) 2 1.C 2.C 3.C 4.E 5.D 6.A 7.D 8.C 9.A 10.B 11.A 12.B 13.D 14.C 15.A 16.B 16.E 17.B 18.A 19.D 20.E
20 20 Bölüm 1 / Polinomlar TEST POLİNOMLAR 4 1. P(x) = x 3 3x 2 +3x 1 olmak üzere, Pb l aşağıda kilerden hangisine eşittir? 4. P(x) = 2x 2. Q(x 1) + 3x + 1 ifadesinde P(x) ve Q(x) birer polinomdur. Buna göre, P(3) 10 Q(2) kaçtır? A) 8 B) 4 C) 0 D) 2 E) 4 A) 14 B) 15 C) 16 D) 17 E) P(x) bir polinom olmak üzere, 2P( x) = 3P(x) 5x olduğuna göre, P(1) kaçtır? 5. P(2x + 3) + P(x + 1) = 3x 2 + 2x 2 polinomu verili yor. P(x) polinomunun sabit terimi 2 olduğuna göre, kat sayıları toplamı kaçtır? A) 4 B) 3 C) 2 D) 2 E) 4 A) 1 B) 0 C) 1 D) 2 E) 3 3. P(x+1) + P(x 1) = 2x 2 + 4x 6 olduğuna göre, P(0) aşağıdakilerden hangisidir? 6. P( 3x 2) = 2x 4 x 2 1 olduğuna göre, P(x) polino munun kat sayılarının toplamı kaçtır? A) 4 B) 2 C) 0 D) 2 E) 4 A) 2 B) 1 C) 0 D) 1 E) 2
9. SINIF MATEMAT K (SORU BANKASI) 7 BÖLÜM 105 KONU TEST 1970 SORU
 9. SINIF MATEMAT K (SORU BANKASI) Mehmet ÖZBEK brahim ORAK 7 BÖLÜM 105 KONU TEST 1970 SORU TEŞEKKÜR Bu kitabın hazırlanmasında emeğini hiç esirgemeyen Mehmet Özbek ve İbrahim Orak ile Zafer Dershaneleri
9. SINIF MATEMAT K (SORU BANKASI) Mehmet ÖZBEK brahim ORAK 7 BÖLÜM 105 KONU TEST 1970 SORU TEŞEKKÜR Bu kitabın hazırlanmasında emeğini hiç esirgemeyen Mehmet Özbek ve İbrahim Orak ile Zafer Dershaneleri
MateMito AKILLI MATEMATİK ATÖLYEM
 ATÖLYE BİLGİSİ! MateMito AKILLI MATEMATİK ATÖLYEM Artık matematikten korkmuyorum. Artık matematiği çok seviyorum. Artık matematik dersinde daha pratiğim. Artık matematik dersinde ustalaşıyorum. 7 Artık
ATÖLYE BİLGİSİ! MateMito AKILLI MATEMATİK ATÖLYEM Artık matematikten korkmuyorum. Artık matematiği çok seviyorum. Artık matematik dersinde daha pratiğim. Artık matematik dersinde ustalaşıyorum. 7 Artık
Mustafa Kemal ATATÜRK
 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini ve daha sonrada istiklal ve istikballerini kaybederler. Mustafa Kemal ATATÜRK İSTİKLÂL MARŞI
Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini ve daha sonrada istiklal ve istikballerini kaybederler. Mustafa Kemal ATATÜRK İSTİKLÂL MARŞI
İSTİKLÂL MARŞI. Mehmet Akif ERSOY
 İSTİKLÂL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır, parlayacak; O benimdir, o benim milletimindir ancak. Çatma, kurban
İSTİKLÂL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır, parlayacak; O benimdir, o benim milletimindir ancak. Çatma, kurban
YGS TEMEL MATEMAT K SORU BANKASI MATEMAT K GEOMETR KONU ÖZETLER KONU TESTLER DENEME SINAVI
 YGS TEMEL MATEMAT K SORU BANKASI MATEMAT K GEOMETR KONU ÖZETLER KONU TESTLER DENEME SINAVI TEŞEKKÜR Kitabın hazırlanmasında emeğini hiç esirgemeden çok titiz çalışarak güzel bir eser ortaya koyan başta
YGS TEMEL MATEMAT K SORU BANKASI MATEMAT K GEOMETR KONU ÖZETLER KONU TESTLER DENEME SINAVI TEŞEKKÜR Kitabın hazırlanmasında emeğini hiç esirgemeden çok titiz çalışarak güzel bir eser ortaya koyan başta
TANIM : a, a, a, a,..., a R ve n N olmak üzere,
 MATEMAT K TANIM : a, a, a, a,..., a R ve n N olmak üzere, 0 1 2 3 n P(x) = a x n a x n 1... a x 3 a x 2 a x n n 1 3 2 1 a ifadesine reel katsay l POL NOM denir. 0 a, a, a,..., a say lar na KATSAYILAR,
MATEMAT K TANIM : a, a, a, a,..., a R ve n N olmak üzere, 0 1 2 3 n P(x) = a x n a x n 1... a x 3 a x 2 a x n n 1 3 2 1 a ifadesine reel katsay l POL NOM denir. 0 a, a, a,..., a say lar na KATSAYILAR,
KKTC MİLLİ EĞİTİM VE KÜLTÜR BAKANLIĞI YAYINIDIR
 Yazı ve Araştırma Kurulu Başkan Dr. İsmail Ertunç Özatenç Üyeler Uzm. Duygu Geylan Nazife Uçar Aysun Candan Özada Resimleyen Celal Deniz Grafik Tasarım Aziz Ener Düzeltme Meltem Tekin Okuyucular Yrd. Doç.
Yazı ve Araştırma Kurulu Başkan Dr. İsmail Ertunç Özatenç Üyeler Uzm. Duygu Geylan Nazife Uçar Aysun Candan Özada Resimleyen Celal Deniz Grafik Tasarım Aziz Ener Düzeltme Meltem Tekin Okuyucular Yrd. Doç.
Bu kitapta neler var?
 Bu kitapta neler var? Akıllı ve Eğlenceli >> Pekiştirici Etkinlikler Tam Ölçen ve Bilgilerinizi Derinlemesine Sorgulayan >> Ünite Testleri Artıbir >> Sınav Özel Soruları Kazanım Odaklı >> Konu Testleri
Bu kitapta neler var? Akıllı ve Eğlenceli >> Pekiştirici Etkinlikler Tam Ölçen ve Bilgilerinizi Derinlemesine Sorgulayan >> Ünite Testleri Artıbir >> Sınav Özel Soruları Kazanım Odaklı >> Konu Testleri
İSTİKLÂL MARŞI. Mehmet Akif Ersoy
 İSTİKLÂL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır, parlayacak; O benimdir, o benim milletimindir ancak. Çatma, kurban
İSTİKLÂL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır, parlayacak; O benimdir, o benim milletimindir ancak. Çatma, kurban
Bu kitapta neler var?
 Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Hadi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Hadi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
T.C. BURDUR VALİLİĞİ İl Milli Eğitim Müdürlüğü...İİÇE MİLLİ EĞİTİM MÜDÜRLÜĞÜNE...MÜDÜRLÜĞÜNE...BÖLÜMÜNE
 T.C. BURDUR VALİLİĞİ İl Milli Eğitim Müdürlüğü Sayı : 39958266-102-E.8764864 03.09.2015 Konu: Çalışma Takvimi...İİÇE MİLLİ EĞİTİM MÜDÜRLÜĞÜNE...MÜDÜRLÜĞÜNE...BÖLÜMÜNE İlgi : Bakanlığımız Ortaöğretim Genel
T.C. BURDUR VALİLİĞİ İl Milli Eğitim Müdürlüğü Sayı : 39958266-102-E.8764864 03.09.2015 Konu: Çalışma Takvimi...İİÇE MİLLİ EĞİTİM MÜDÜRLÜĞÜNE...MÜDÜRLÜĞÜNE...BÖLÜMÜNE İlgi : Bakanlığımız Ortaöğretim Genel
biçimindeki ifadelere iki değişkenli polinomlar denir. Bu polinomda aynı terimdeki değişkenlerin üsleri toplamından en büyük olanına polinomun dereces
 TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
UETD Genelmerkez Gençlik Kolları Mart 2014 Faaliyet Raporu
 UETD Genelmerkez Gençlik Kolları Mart 2014 Faaliyet Raporu GK Faaliyet Raporu Mart 2014 2 UETD Gençlik Kolları olarak düzenleyeceğimiz Birinci Gençlik Makale Yarışması. Konu Demokrasi ve Değerlerimiz.
UETD Genelmerkez Gençlik Kolları Mart 2014 Faaliyet Raporu GK Faaliyet Raporu Mart 2014 2 UETD Gençlik Kolları olarak düzenleyeceğimiz Birinci Gençlik Makale Yarışması. Konu Demokrasi ve Değerlerimiz.
T.C KÖRFEZ KAYMAKAMLIĞI Körfez Anadolu Öğretmen Lisesi BRİFİNG DOSYASI
 T.C KÖRFEZ KAYMAKAMLIĞI Körfez Anadolu Öğretmen Lisesi BRİFİNG DOSYASI KASIM 2014 1 Korkma, sönmez bu şafaklarda yüzen al sancak Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır
T.C KÖRFEZ KAYMAKAMLIĞI Körfez Anadolu Öğretmen Lisesi BRİFİNG DOSYASI KASIM 2014 1 Korkma, sönmez bu şafaklarda yüzen al sancak Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır
matematik LYS SORU BANKASI KONU ÖZETLERİ KONU ALT BÖLÜM TESTLERİ GERİ BESLEME TESTLERİ Süleyman ERTEKİN Öğrenci Kitaplığı
 matematik SORU BANKASI Süleyman ERTEKİN LYS KONU ALT BÖLÜM TESTLERİ GERİ BESLEME TESTLERİ KONU ÖZETLERİ Öğrenci Kitaplığı SORU BANKASI matematik LYS EDAM Öğrenci Kitaplığı 18 EDAM ın yazılı izni olmaksızın,
matematik SORU BANKASI Süleyman ERTEKİN LYS KONU ALT BÖLÜM TESTLERİ GERİ BESLEME TESTLERİ KONU ÖZETLERİ Öğrenci Kitaplığı SORU BANKASI matematik LYS EDAM Öğrenci Kitaplığı 18 EDAM ın yazılı izni olmaksızın,
POL NOMLAR. Polinomlar
 POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
Bu kitapta neler var?
 Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Hadi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Hadi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Örnek...4 : P(x) = 3x + 2 ve Q(x)= x 2 +4x -3 polinomları için a) P(x). Q(x) b)x.p(x) 2.Q(x) işlem lerini ya pınız.
 POLİNOMLARDA Polinomlarda To plama ve Çıkarma P(x) ve Q(x) iki polinom olsun. P(x) + Q(x) veya P(x) Q(x) işlemi yapılırken eşit dereceli terimlerin katsayıları işlemine göre toplanır veya çıkarılır. Örnek...1
POLİNOMLARDA Polinomlarda To plama ve Çıkarma P(x) ve Q(x) iki polinom olsun. P(x) + Q(x) veya P(x) Q(x) işlemi yapılırken eşit dereceli terimlerin katsayıları işlemine göre toplanır veya çıkarılır. Örnek...1
T.C. İSTANBUL VALİLİĞİ İL MİLLİ EĞİTİM MÜDÜRLÜĞÜ
 T.C. İSTANBUL VALİLİĞİ İL MİLLİ EĞİTİM MÜDÜRLÜĞÜ KADIKÖY GAZİ MUSTAFA KEMAL PAŞA ORTAOKULU 2015/2016 EĞİTİM ÖĞRETİM YILI BRİFİNG DOSYASI İSTİKLAL MARŞI Korkma! Sönmez bu şafaklarda yüzen al sancak, Sönmeden
T.C. İSTANBUL VALİLİĞİ İL MİLLİ EĞİTİM MÜDÜRLÜĞÜ KADIKÖY GAZİ MUSTAFA KEMAL PAŞA ORTAOKULU 2015/2016 EĞİTİM ÖĞRETİM YILI BRİFİNG DOSYASI İSTİKLAL MARŞI Korkma! Sönmez bu şafaklarda yüzen al sancak, Sönmeden
Örnek...3 : P(x+4)=x 7 +6.x 6 +2x 3 polinomu için P(2) kaçtır? Örnek...4 : P(2x 1) = x 2 olduğuna göre, P(3)+P(5) kaçtır? Örnek...
 POLİNOMLAR n N, a n, a n 1, a n 2,a 1,a 0 R ve a n 0 olmak üzere, a n x n +a n 1 x n 1 +a n 2 x n 2 +...+a 1 x+a 0 ifadesine x in bir polinomu denir ve genellikle bu ifade P(x),Q(x) gibi bir ifadeye eşitlenerek
POLİNOMLAR n N, a n, a n 1, a n 2,a 1,a 0 R ve a n 0 olmak üzere, a n x n +a n 1 x n 1 +a n 2 x n 2 +...+a 1 x+a 0 ifadesine x in bir polinomu denir ve genellikle bu ifade P(x),Q(x) gibi bir ifadeye eşitlenerek
2. Matematiksel kavramları organize bir şekilde sunarak, bu kavramları içselleştirmenizi sağlayacak pedagojik bir alt yapı ile yazılmıştır.
 Sevgili Öğrenciler, Matematik ilköğretimden üniversiteye kadar çoğu öğrencinin korkulu rüyası olmuştur. Buna karşılık, istediğiniz üniversitede okuyabilmeniz büyük ölçüde YGS ve LYS'de matematik testinde
Sevgili Öğrenciler, Matematik ilköğretimden üniversiteye kadar çoğu öğrencinin korkulu rüyası olmuştur. Buna karşılık, istediğiniz üniversitede okuyabilmeniz büyük ölçüde YGS ve LYS'de matematik testinde
Dr. Kemal Akkan BATMAN
 Dr. Kemal Akkan BATMAN (Komisyon Başkanı) Dr. Ayer BURKE Diren CİVA GÜNER Mevhibe B. HOCAOĞLU Salih SARPTEN Ömer ÖZKAN Bu kitap, Milli Eğitim ve Kültür Bakanlığı, Talim Terbiye Dairesi tarafından ortaokullarda
Dr. Kemal Akkan BATMAN (Komisyon Başkanı) Dr. Ayer BURKE Diren CİVA GÜNER Mevhibe B. HOCAOĞLU Salih SARPTEN Ömer ÖZKAN Bu kitap, Milli Eğitim ve Kültür Bakanlığı, Talim Terbiye Dairesi tarafından ortaokullarda
Polinomlar. Rüstem YILMAZ
 Polinomlar Rüstem YILMAZ 546 550 86 48 matematikklinigi@gmail.com 26 Aralık 2016 0.1 Tanımı a, b, c, d reel sayılar ve n N olmak üzere, P (x) = ax n + bx n 1 + + cx + d ifadesine reel katsayılı ve bir
Polinomlar Rüstem YILMAZ 546 550 86 48 matematikklinigi@gmail.com 26 Aralık 2016 0.1 Tanımı a, b, c, d reel sayılar ve n N olmak üzere, P (x) = ax n + bx n 1 + + cx + d ifadesine reel katsayılı ve bir
Bu kitapta neler var?
 Bu kitapta neler var? Akıllı ve Eğlenceli >> Pekiştirici Etkinlikler Tam Ölçen ve Bilgilerinizi Derinlemesine Sorgulayan >> Ünite Testleri Artıbir >> Sınav Özel Soruları Kazanım Odaklı >> Konu Testleri
Bu kitapta neler var? Akıllı ve Eğlenceli >> Pekiştirici Etkinlikler Tam Ölçen ve Bilgilerinizi Derinlemesine Sorgulayan >> Ünite Testleri Artıbir >> Sınav Özel Soruları Kazanım Odaklı >> Konu Testleri
POLİNOMLAR Test I m P x 3 2x x 4x. P x x 5 II. III. A) 13 B) 12 C) 11 D) 10 E) 9
 POLİNOMLAR Test -. I. P x x 5 II. III. P x x P x ifadelerinden hangileri polinom belirtir? 6. P x x x x 7 polinomunun katsayılar toplamı A) B) C) D) 0 E) 9 A) Yalnız I B) Yalnız II C) I ve II D) I ve III
POLİNOMLAR Test -. I. P x x 5 II. III. P x x P x ifadelerinden hangileri polinom belirtir? 6. P x x x x 7 polinomunun katsayılar toplamı A) B) C) D) 0 E) 9 A) Yalnız I B) Yalnız II C) I ve II D) I ve III
Bu kitapta neler var?
 Bu kitapta neler var? Akıllı ve Eğlenceli >> Pekiştirici Etkinlikler Tam Ölçen ve Bilgilerinizi Derinlemesine Sorgulayan >> Ünite Testleri Artıbir >> Sınav Özel Soruları Kazanım Odaklı >> Konu Testleri
Bu kitapta neler var? Akıllı ve Eğlenceli >> Pekiştirici Etkinlikler Tam Ölçen ve Bilgilerinizi Derinlemesine Sorgulayan >> Ünite Testleri Artıbir >> Sınav Özel Soruları Kazanım Odaklı >> Konu Testleri
AAA AYŞE HASAN TÜRKMEN ORTAOKULU MÜDÜRLÜĞÜ YILLIK FAALİYET PLANI
 2015-2016 YILLIK FAALİYET PLANI 1 T.C. KEMALPAŞA KAYMAKAMLIĞI Ayşe Hasan Türkmen Ortaokulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
2015-2016 YILLIK FAALİYET PLANI 1 T.C. KEMALPAŞA KAYMAKAMLIĞI Ayşe Hasan Türkmen Ortaokulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
1.BÖLÜM SORU SORU. (x 1) (x 3) = A + B. x 3 ise, d(p(x)) ve d(q(x)) polinomlar n derecelerini göstermek. A. B çarp m kaçt r?
 1.BÖLÜM MATEMAT K Derginin bu say s nda Polinomlar konusunda çözümlü sorular yer almaktad r. Bu konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü
1.BÖLÜM MATEMAT K Derginin bu say s nda Polinomlar konusunda çözümlü sorular yer almaktad r. Bu konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü
5. P(x). Q(x) polinomunun derecesi 9, P(x) Q(x) 7. P(x) = (3m 1)x 3 4x 2 (n + 1) x+ k ve. Q(x) = 17x 3
 , 006 MC Cebir Notları Gökhan DEMĐR, gdemir@yahoo.com.tr Polinomlar TEST I 1. Aşağıdakilerden hangisi bir polinomdur? A) = 4 x5 4x 4 5 + 7 x 4 5.. polinomunun derecesi 9, polinomunun derecesi 5 olduğuna
, 006 MC Cebir Notları Gökhan DEMĐR, gdemir@yahoo.com.tr Polinomlar TEST I 1. Aşağıdakilerden hangisi bir polinomdur? A) = 4 x5 4x 4 5 + 7 x 4 5.. polinomunun derecesi 9, polinomunun derecesi 5 olduğuna
10 SINIF MATEMATİK. Polinomlar Çarpanlara Ayırma İkinci Dereceden Bir Bilinmeyenli Denklemler
 10 SINIF MATEMATİK Polinomlar Çarpanlara Ayırma İkinci Dereceden Bir Bilinmeyenli Denklemler YAYIN KOORDİNATÖRÜ Oğuz GÜMÜŞ EDİTÖR Hazal ÖZNAR - Uğurcan AYDIN DİZGİ Muhammed KARATAŞ SAYFA TASARIM - KAPAK
10 SINIF MATEMATİK Polinomlar Çarpanlara Ayırma İkinci Dereceden Bir Bilinmeyenli Denklemler YAYIN KOORDİNATÖRÜ Oğuz GÜMÜŞ EDİTÖR Hazal ÖZNAR - Uğurcan AYDIN DİZGİ Muhammed KARATAŞ SAYFA TASARIM - KAPAK
İSTİKLÂL MARŞI NA DİLBİLİMSEL BİR YAKLAŞIM
 İSTİKLÂL MARŞI NA DİLBİLİMSEL BİR AKLAŞIM * Arş.Gör. Eyup Sertaç AAZ Kafkas Üniversitesi Fen Edebiyat Fakültesi Türk Dili ve Edebiyatı Bölümü ÖZET Dünyada hemen her milletin bir milli marşı bulunmaktadır.
İSTİKLÂL MARŞI NA DİLBİLİMSEL BİR AKLAŞIM * Arş.Gör. Eyup Sertaç AAZ Kafkas Üniversitesi Fen Edebiyat Fakültesi Türk Dili ve Edebiyatı Bölümü ÖZET Dünyada hemen her milletin bir milli marşı bulunmaktadır.
Gelecek için hazırlanan vatan evlâtlarına, hiçbir güçlük karşısında yılmayarak tam bir sabır ve metanetle çalışmalarını ve öğrenim gören
 Gelecek için hazırlanan vatan evlâtlarına, hiçbir güçlük karşısında yılmayarak tam bir sabır ve metanetle çalışmalarını ve öğrenim gören çocuklarımızın ana ve babalarına da yavrularının öğreniminin tamamlanması
Gelecek için hazırlanan vatan evlâtlarına, hiçbir güçlük karşısında yılmayarak tam bir sabır ve metanetle çalışmalarını ve öğrenim gören çocuklarımızın ana ve babalarına da yavrularının öğreniminin tamamlanması
POLİNOMLARIN TANIMI. ÖĞRENCİNİN ADI SOYADI: KONU: POLİNOMLAR NUMARASI: SINIFI:
 ÖĞRENCİNİN ADI SOYADI: Dersin Adı POLİNOMLARIN TANIMI 1. Aşağıdaki fonksiyonlardan polinom belirtir? I. Dersin Konusu 1 5. P x x n 1 7 x 4 n 5 ifadesi bir polinom belirttiğine göre, bu polinomun derecesi
ÖĞRENCİNİN ADI SOYADI: Dersin Adı POLİNOMLARIN TANIMI 1. Aşağıdaki fonksiyonlardan polinom belirtir? I. Dersin Konusu 1 5. P x x n 1 7 x 4 n 5 ifadesi bir polinom belirttiğine göre, bu polinomun derecesi
İstiklal Marşının Kabulü
 İstiklal Marşının Kabulü TBMM nin açtığı yarışmaya katılan 724 şiir arasından 12 Mart 1921 de Mehmet Akif Ersoy'un şiiri kabul edildi. Türk Kurtuluş Savaşı'nın başlarında, İstiklâl Harbi'nin milli bir
İstiklal Marşının Kabulü TBMM nin açtığı yarışmaya katılan 724 şiir arasından 12 Mart 1921 de Mehmet Akif Ersoy'un şiiri kabul edildi. Türk Kurtuluş Savaşı'nın başlarında, İstiklâl Harbi'nin milli bir
Bu kitapta neler var?
 Bu kitapta neler var? Anlaşılması Kolay >> Çözümlü ler Tam Ölçen ve Bilgilerinizi Derinlemesine Sorgulayan >> Ünite Testleri Artıbir >> Sınav Özel Soruları Kazanım Odaklı >> Konu Testleri Yeni Sisteme
Bu kitapta neler var? Anlaşılması Kolay >> Çözümlü ler Tam Ölçen ve Bilgilerinizi Derinlemesine Sorgulayan >> Ünite Testleri Artıbir >> Sınav Özel Soruları Kazanım Odaklı >> Konu Testleri Yeni Sisteme
Kiraz Öğretmen Evi ve Akşam Sanat Okulu Müdürlüğü YILLIK FAALİYET PLANI
 2015-2016 YILLIK FAALİYET PLANI 1 T.C. KİRAZ KAYMAKAMLIĞI Kiraz Öğretmenevi ve ASO Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
2015-2016 YILLIK FAALİYET PLANI 1 T.C. KİRAZ KAYMAKAMLIĞI Kiraz Öğretmenevi ve ASO Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
KONU: Polinomlarda Bölme İşlemi. 6. P x x x 1
 ÖĞRENCİNİN ADI SOYADI: NUMARASI: Dersin Adı SINIFI: KONU: Polinomlarda Bölme İşlemi Dersin Konusu 1. Px 4 x x polinomunun x 1 ile bölümünden kalan A) 0 B) 1 C) D) 4 E) 6. Px x x 1 polinomunun x + 1 ile
ÖĞRENCİNİN ADI SOYADI: NUMARASI: Dersin Adı SINIFI: KONU: Polinomlarda Bölme İşlemi Dersin Konusu 1. Px 4 x x polinomunun x 1 ile bölümünden kalan A) 0 B) 1 C) D) 4 E) 6. Px x x 1 polinomunun x + 1 ile
Bu kitapta neler var?
 Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
BAĞYURDU KAZIM DİRİK ORTAOKULU Müdürlüğü YILLIK FAALİYET PLANI
 2015-2016 YILLIK FAALİYET PLANI 1 T.C. KEMALPAŞA KAYMAKAMLIĞI B.Kazım Dirik Ortaokulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
2015-2016 YILLIK FAALİYET PLANI 1 T.C. KEMALPAŞA KAYMAKAMLIĞI B.Kazım Dirik Ortaokulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
Bu kitapta neler var?
 Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Sunum ve Sistematik. Bu başlıklar altında uygulamalar yaparak öğrenciye yorum, analiz, sentez yetisinin geliştirilmesi hedeflenmiştir.
 Sunum ve Sistematik 1. BÖLÜM: POLİNOMLAR ALIŞTIRMALAR Bu başlık altında her bölüm kazanımlara ayrılmış, kazanımlar tek tek çözümlü temel alıştırmalar ve sorular ile taranmıştır. Özellikle bu kısmın sınıf
Sunum ve Sistematik 1. BÖLÜM: POLİNOMLAR ALIŞTIRMALAR Bu başlık altında her bölüm kazanımlara ayrılmış, kazanımlar tek tek çözümlü temel alıştırmalar ve sorular ile taranmıştır. Özellikle bu kısmın sınıf
ünite12 POLİNOMLAR Polinomlar
 ünite1 POOM = 1 Polinomlar 0 1 1. şağıdakilerden hangileri bir polinom değildir?. x 4 + 3. x 3 3x 5 +. x 6 1 V. x 4 1 + V. 5x 1 8 POOM POOM 5. P(x) = (a )x + (b + 3)x + ab 1 polinomu sabit bir polinom
ünite1 POOM = 1 Polinomlar 0 1 1. şağıdakilerden hangileri bir polinom değildir?. x 4 + 3. x 3 3x 5 +. x 6 1 V. x 4 1 + V. 5x 1 8 POOM POOM 5. P(x) = (a )x + (b + 3)x + ab 1 polinomu sabit bir polinom
Rafet ÖZTÜRK. Üniteye Hazırlık
 Rafet ÖZTÜRK Bu kitap Talim ve Terbiye Kurulu Başkanlığı nın 18/12/2009 tarih ve 261 sayılı Kurul Kararı ile 2010-2011 öğretim yılından itibaren 5 (beş) yıl süre ile Ders Kitabı olarak kabul edilmiştir.
Rafet ÖZTÜRK Bu kitap Talim ve Terbiye Kurulu Başkanlığı nın 18/12/2009 tarih ve 261 sayılı Kurul Kararı ile 2010-2011 öğretim yılından itibaren 5 (beş) yıl süre ile Ders Kitabı olarak kabul edilmiştir.
EĞİTİM VE ÖĞRETİM YILI
 T.C. BANDIRMA KAYMAKAMLIĞI Şehit Öğretmen Mustafa Boz Özel Eğitim Mesleki Eğitim Merkezi 2015-2016 EĞİTİM VE ÖĞRETİM YILI İLİ İLÇESİ OKUL/KURUM ADI : BALIKESİR : Bandırma : (748900) Şehit Öğretmen Mustafa
T.C. BANDIRMA KAYMAKAMLIĞI Şehit Öğretmen Mustafa Boz Özel Eğitim Mesleki Eğitim Merkezi 2015-2016 EĞİTİM VE ÖĞRETİM YILI İLİ İLÇESİ OKUL/KURUM ADI : BALIKESİR : Bandırma : (748900) Şehit Öğretmen Mustafa
Mehmet ŞAHİN. www.mehmetsahinkitaplari.org
 0. Sınıf M AT E M AT İ K Mehmet ŞAHİN www.mehmetsahinkitaplari.org M.E.B Talim ve Terbiye Kurulu Başkanlığı nın 0..009 tarih ve 4 sayılı kararı ve 00-0 öğretim yılından itibaren uygulanacak programa göre
0. Sınıf M AT E M AT İ K Mehmet ŞAHİN www.mehmetsahinkitaplari.org M.E.B Talim ve Terbiye Kurulu Başkanlığı nın 0..009 tarih ve 4 sayılı kararı ve 00-0 öğretim yılından itibaren uygulanacak programa göre
Mustafa Sezer PEHLİVAN. Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü
 * Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
* Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
STRATEJİK PLANI
 2011-2014 STRATEJİK PLANI ELAZIĞ CEMİL MERİÇ FEN LİSESİ 2011,ELAZIĞ Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini ve daha sonrada istiklal
2011-2014 STRATEJİK PLANI ELAZIĞ CEMİL MERİÇ FEN LİSESİ 2011,ELAZIĞ Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini ve daha sonrada istiklal
PROTOKOL ÇELENK SUNMA SIRASI İSTİKLÂL MARŞI
 PROTOKOL ÇELENK SUNMA SIRASI İSTİKLÂL MARŞI Kaymakamlık Garnizon Komutanlığı Belediye Başkanlığı Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin
PROTOKOL ÇELENK SUNMA SIRASI İSTİKLÂL MARŞI Kaymakamlık Garnizon Komutanlığı Belediye Başkanlığı Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin
YAHŞİHAN HALK EĞİTİM MERKEZİ MÜDÜRLÜĞÜ (Brifing Dosyası) T.C. YAHŞİHAN KAYMAKAMLIĞI HALK EĞİTİMİ MERKEZİ MÜDÜRLÜĞÜ BRİFİNG DOSYASI
 T.C. YAHŞİHAN KAYMAKAMLIĞI HALK EĞİTİMİ MERKEZİ MÜDÜRLÜĞÜ BRİFİNG DOSYASI 2012 2013 1 İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin
T.C. YAHŞİHAN KAYMAKAMLIĞI HALK EĞİTİMİ MERKEZİ MÜDÜRLÜĞÜ BRİFİNG DOSYASI 2012 2013 1 İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin
Bu kitapta neler var?
 Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Yeşilköy Anadolu Lisesi
 Yeşilköy Anadolu Lisesi TANIM (KONUYA GİRİŞ) a, b, c gerçel sayı ve a ¹ 0 olmak üzere, ax 2 + bx + c = 0 biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir. Bu açık önermeyi
Yeşilköy Anadolu Lisesi TANIM (KONUYA GİRİŞ) a, b, c gerçel sayı ve a ¹ 0 olmak üzere, ax 2 + bx + c = 0 biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir. Bu açık önermeyi
Refet Bele Anaokulu Müdürlüğü YILLIK FAALİYET PLANI
 2017-2018 YILLIK FAALİYET PLANI 1 T.C. KARABAĞLAR KAYMAKAMLIĞI Refet Bele Anaokulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
2017-2018 YILLIK FAALİYET PLANI 1 T.C. KARABAĞLAR KAYMAKAMLIĞI Refet Bele Anaokulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
POLİNOMLAR. Polinomlar. Konu Kavrama Çalışması
 POLİNOMLAR Polinomlar f: A B biçiminde tanımlanmış f(x) fonksiyonunda, A kümesi tanım kümesi ve B kümesi değer kümesidir. Fonksiyonlarda, fonksiyonu tanımsız yapan değerler tanım kümesinde yer alamaz.
POLİNOMLAR Polinomlar f: A B biçiminde tanımlanmış f(x) fonksiyonunda, A kümesi tanım kümesi ve B kümesi değer kümesidir. Fonksiyonlarda, fonksiyonu tanımsız yapan değerler tanım kümesinde yer alamaz.
Karşıyaka İlçe Milli Eğitim Müdürlüğü KARŞIYAKA ÖZEL EĞİTİM MESLEKİ EĞİTİM MERKEZİ (OKULU) YILLIK FAALİYET PLANI
 KARŞIYAKA ÖZEL EĞİTİM MESLEKİ EĞİTİM MERKEZİ (OKULU) YILLIK FAALİYET PLANI 1 T.C. KARŞIYAKA KAYMAKAMLIĞI KARŞIYAKA ÖZEL EĞİTİM MESLEKİ EĞİTİM MERKEZİ (OKULU) 2 Çalışmadan, yorulmadan, üretmeden, rahat
KARŞIYAKA ÖZEL EĞİTİM MESLEKİ EĞİTİM MERKEZİ (OKULU) YILLIK FAALİYET PLANI 1 T.C. KARŞIYAKA KAYMAKAMLIĞI KARŞIYAKA ÖZEL EĞİTİM MESLEKİ EĞİTİM MERKEZİ (OKULU) 2 Çalışmadan, yorulmadan, üretmeden, rahat
(m+2) +5<0. 7/m+3 + EŞİTSİZLİKLER A. TANIM
 EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
1. BÖLÜM Polinomlar BÖLÜM II. Dereceden Denklemler BÖLÜM II. Dereceden Eşitsizlikler BÖLÜM Parabol
 ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
Konak Halk Eğitimi Merkezi ve Akşam Sanat Okulu Müdürlüğü YILLIK FAALİYET PLANI
 2017-2018 YILLIK FAALİYET PLANI 1 T.C. KONAK KAYMAKAMLIĞI Konak Halk Eğitimi Merkezi ve Akşam Sanat Okulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini,
2017-2018 YILLIK FAALİYET PLANI 1 T.C. KONAK KAYMAKAMLIĞI Konak Halk Eğitimi Merkezi ve Akşam Sanat Okulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini,
İKİNCİ DERECEDEN DENKLEMLER
 İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
YGS KİMYA. Emine ULUTAŞ Gülay ÖZMEN KONU ANLATIMI ÇÖZÜMLÜ SORULAR ÇÖZÜMLÜ TESTLER KONU TESTLER
 YGS KİMYA Emine ULUTAŞ Gülay ÖZMEN KONU ANLATIMI ÇÖZÜMLÜ SORULAR ÇÖZÜMLÜ TESTLER KONU TESTLER ZAFER YAYINLARI TEŞEKKÜR Bu kitabın hazırlanmasında emeğini hiç esirgemeyen başta Emine ULUTAŞ a, ve Gülay
YGS KİMYA Emine ULUTAŞ Gülay ÖZMEN KONU ANLATIMI ÇÖZÜMLÜ SORULAR ÇÖZÜMLÜ TESTLER KONU TESTLER ZAFER YAYINLARI TEŞEKKÜR Bu kitabın hazırlanmasında emeğini hiç esirgemeyen başta Emine ULUTAŞ a, ve Gülay
Mil li Eği tim Ba kan lı ğı Ta lim ve Ter bi ye Ku ru lu Baş kan lı ğı nın ta rih ve 121 sa yı lı ka ra rı ile ka bul edi len ve
 Mil li Eği tim Ba kan lı ğı Ta lim ve Ter bi ye Ku ru lu Baş kan lı ğı nın.08.0 ta rih ve sa yı lı ka ra rı ile ka bul edi len ve 0-0 Öğ re tim Yı lın dan iti ba ren uy gu lana cak olan prog ra ma gö re
Mil li Eği tim Ba kan lı ğı Ta lim ve Ter bi ye Ku ru lu Baş kan lı ğı nın.08.0 ta rih ve sa yı lı ka ra rı ile ka bul edi len ve 0-0 Öğ re tim Yı lın dan iti ba ren uy gu lana cak olan prog ra ma gö re
ARTVİN/MERKEZ. HALK EĞİTİMİ MERKEZİ ve ASO MÜDÜRLÜĞÜ BRİFİNG DOSYASI
 ARTVİN/MERKEZ HALK EĞİTİMİ MERKEZİ ve ASO MÜDÜRLÜĞÜ BRİFİNG DOSYASI 1 İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır,
ARTVİN/MERKEZ HALK EĞİTİMİ MERKEZİ ve ASO MÜDÜRLÜĞÜ BRİFİNG DOSYASI 1 İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin yıldızıdır,
ÜN TE II L M T. Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler
 ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
Atakent Anadolu Lisesi Müdürlüğü YILLIK FAALİYET PLANI
 2015-2016 YILLIK FAALİYET PLANI 1 T.C. KARŞIYAKA KAYMAKAMLIĞI Atakent Anadolu Lisesi Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
2015-2016 YILLIK FAALİYET PLANI 1 T.C. KARŞIYAKA KAYMAKAMLIĞI Atakent Anadolu Lisesi Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini, sonra hürriyetlerini
T.C. DİYADİN KAYMAKAMLIĞI İlçe Milli Eğitim Müdürlüğü Öğretmenevi ve Akşam Sanat Okulu Müdürlüğü STRATEJİK PLAN (2015-2019)
 T.C. DİYADİN KAYMAKAMLIĞI İlçe Milli Eğitim Müdürlüğü Öğretmenevi ve Akşam Sanat Okulu Müdürlüğü STRATEJİK PLAN (2015-2019) 2015 Millete efendilik yoktur. Hizmet vardır. Bu millete hizmet eden onun efendisi
T.C. DİYADİN KAYMAKAMLIĞI İlçe Milli Eğitim Müdürlüğü Öğretmenevi ve Akşam Sanat Okulu Müdürlüğü STRATEJİK PLAN (2015-2019) 2015 Millete efendilik yoktur. Hizmet vardır. Bu millete hizmet eden onun efendisi
İZMİR ÖZEL EĞİTİM İŞ UYGULAMA MERKEZİ ( OKULU ) MÜDÜRLÜĞÜ YILLIK FAALİYET PLANI
 2015-2016 YILLIK FAALİYET PLANI 1 T.C. KARŞIYAKA KAYMAKAMLIĞI İzmir Özel Eğitim İş Uygulama Merkezi (Okulu)Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini,
2015-2016 YILLIK FAALİYET PLANI 1 T.C. KARŞIYAKA KAYMAKAMLIĞI İzmir Özel Eğitim İş Uygulama Merkezi (Okulu)Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini,
PENDİK ANADOLU İMAM HATİP LİSESİ EĞİTİM VE ÖĞRETİM YILI 10.SINIF MATEMATİK DERSİ YILLIK PLANI
 PENDİK ANADOLU İMAM HATİP LİSESİ 0-0 EĞİTİM VE ÖĞRETİM YILI 0.SINIF MATEMATİK DERSİ YILLIK PLANI EYLÜL EKİM. Gerçek katsayılı ve tek değişkenli polinomu kavram olarak örneklerle açıklar, polinomun derecesini,
PENDİK ANADOLU İMAM HATİP LİSESİ 0-0 EĞİTİM VE ÖĞRETİM YILI 0.SINIF MATEMATİK DERSİ YILLIK PLANI EYLÜL EKİM. Gerçek katsayılı ve tek değişkenli polinomu kavram olarak örneklerle açıklar, polinomun derecesini,
Dünyanın kaderi TAMLAYAN TAMLANAN
 İSİM TAMLAMALARI Dünyanın kaderi TAMLAYAN TAMLANAN Dönüklü kasabası At kuyruğu Evin yanı Demir kapı Arkadaşımın arkadaşının arkadaşı İSİM TAMLAMASININ TÜRLERİ 1. Hem tamlayanı hem tamlananı ek alan isim
İSİM TAMLAMALARI Dünyanın kaderi TAMLAYAN TAMLANAN Dönüklü kasabası At kuyruğu Evin yanı Demir kapı Arkadaşımın arkadaşının arkadaşı İSİM TAMLAMASININ TÜRLERİ 1. Hem tamlayanı hem tamlananı ek alan isim
ZEYTİNBURNU İMKB KIZ TEKNİK VE MESLEK LİSESİ BRİFİNG DOSYASI 2012-2013
 ZEYTİNBURNU İMKB KIZ TEKNİK VE MESLEK LİSESİ BRİFİNG DOSYASI 2012-2013 - 1 - İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin
ZEYTİNBURNU İMKB KIZ TEKNİK VE MESLEK LİSESİ BRİFİNG DOSYASI 2012-2013 - 1 - İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim milletimin
1. SINIF MATEMATİK KİTABI 2
 . SINIF MATEMATİK KİTABI Adı - Soyadı :...... Sınıfı :... Okulu :... K K T C MİLLİ EĞİTİM VE KÜLTÜR BAKANLIĞI YAYINIDIR. Milli Eğitim ve Kültür Bakanlığı Talim Terbiye Dairesi, bu kitabın ilkokul. sınıflarda
. SINIF MATEMATİK KİTABI Adı - Soyadı :...... Sınıfı :... Okulu :... K K T C MİLLİ EĞİTİM VE KÜLTÜR BAKANLIĞI YAYINIDIR. Milli Eğitim ve Kültür Bakanlığı Talim Terbiye Dairesi, bu kitabın ilkokul. sınıflarda
SOSYAL BİLGİLER (COĞRAFYA)
 KKTC MİLLİ EĞİTİM VE KÜLTÜR BAKANLIĞI SOSYAL BİLGİLER (COĞRAFYA) 7 1. Baskı AĞUSTOS 2006 KKTC MİLLİ EĞİTİM VE KÜLTÜR BAKANLIĞI YAYINIDIR Başkan Dr. İsmail Ertunç Özatenç Üyeler Uzm. Sibel Kutoğlu Uzm.
KKTC MİLLİ EĞİTİM VE KÜLTÜR BAKANLIĞI SOSYAL BİLGİLER (COĞRAFYA) 7 1. Baskı AĞUSTOS 2006 KKTC MİLLİ EĞİTİM VE KÜLTÜR BAKANLIĞI YAYINIDIR Başkan Dr. İsmail Ertunç Özatenç Üyeler Uzm. Sibel Kutoğlu Uzm.
STRATEJÝK PLANI 2011-2014
 i i T.C. KARABÜK VALÝLÝÐÝ TEKNÝK VE ENDÜSTRÝ MESLEK LÝSESÝ E n d ü s t r i M e s e v KARABÜK l e k k L n s k e T K a r a b k ü s i e STRATEJÝK PLANI 0-04 KARABÜK - 00 ÝSTÝKLÂL MARÞI Korkma, sönmez bu þafaklarda
i i T.C. KARABÜK VALÝLÝÐÝ TEKNÝK VE ENDÜSTRÝ MESLEK LÝSESÝ E n d ü s t r i M e s e v KARABÜK l e k k L n s k e T K a r a b k ü s i e STRATEJÝK PLANI 0-04 KARABÜK - 00 ÝSTÝKLÂL MARÞI Korkma, sönmez bu þafaklarda
Örnek...1 : Örnek...5 : n bir pozitif tamsayı ise i 4 n + 2 +i 8 n + 1 2 +i 2 0 n + 6 =?
 KARMAŞIK SAYILAR Karmaşık saılar x 2 + 1 = 0 biçimindeki denklemlerin çözümünü apabilmek için tanım lanm ıştır. Örnek...2 : Toplamları 6 ve çarpımları 34 olan iki saı bulunuz. a ve b birer reel saı ve
KARMAŞIK SAYILAR Karmaşık saılar x 2 + 1 = 0 biçimindeki denklemlerin çözümünü apabilmek için tanım lanm ıştır. Örnek...2 : Toplamları 6 ve çarpımları 34 olan iki saı bulunuz. a ve b birer reel saı ve
Semiha İrfan Çalı Mesleki ve Teknik Anadolu Lisesi Müdürlüğü YILLIK FAALİYET PLANI
 2017-2018 YILLIK FAALİYET PLANI 1 T.C. SEFERİHİSAR KAYMAKAMLIĞI Semiha İrfan Çalı Mesleki ve Teknik Anadolu Lisesi Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini,
2017-2018 YILLIK FAALİYET PLANI 1 T.C. SEFERİHİSAR KAYMAKAMLIĞI Semiha İrfan Çalı Mesleki ve Teknik Anadolu Lisesi Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini,
7. ( ) ( ) ( ) A)11 B)12 C)13 D)14 E)15 8. ( ) çarpanı A) 2 B) 1 C) 0 D)1 E) 2 A)1 B) 2 C)3 D) 4 E)5 10. ( ) (B) A) 9 B)10 C)11 D)12 E)13 11.
 1. POLİNOMLAR 6 ( + + 6 ) ( + + ) çarpımında lü terimin katsayısı A)16 B)18 C) 0 D) E) 6. P( ) polinomunun 6 + ile bölümünden elde edilen bölüm ve kalan P in derecesi en polinomları eşit olmaktadır. (
1. POLİNOMLAR 6 ( + + 6 ) ( + + ) çarpımında lü terimin katsayısı A)16 B)18 C) 0 D) E) 6. P( ) polinomunun 6 + ile bölümünden elde edilen bölüm ve kalan P in derecesi en polinomları eşit olmaktadır. (
Bu kitapta neler var?
 Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
ÖĞRENCİ GÖZÜYLE 15 TEMMUZ
 ÖĞRENCİ GÖZÜYLE 15 TEMMUZ ÖĞRENCİ GÖZÜYLE 15 TEMMUZ 15 Temmuz Konulu; Resim Yarışması İLKOKUL ÖĞRENCİLERİ ARASI ORTAOKUL ÖĞRENCİLERİ ARASI 15 Temmuz Konulu; Şiir Yarışması ORTAOKUL ÖĞRENCİLERİ ARASI LİSE
ÖĞRENCİ GÖZÜYLE 15 TEMMUZ ÖĞRENCİ GÖZÜYLE 15 TEMMUZ 15 Temmuz Konulu; Resim Yarışması İLKOKUL ÖĞRENCİLERİ ARASI ORTAOKUL ÖĞRENCİLERİ ARASI 15 Temmuz Konulu; Şiir Yarışması ORTAOKUL ÖĞRENCİLERİ ARASI LİSE
İS T İK L Â L MARŞI V E A N LA M I*
 İS T İK L Â L MARŞI V E A N LA M I* Zehra KAVCAR** Bağımsızlık ve özgürlük, toplumların en çok değer verdiği kavramların başında gelir. Çünkü bu değerler, ulus olmanın iik koşuludur. Bağımsız devletler,
İS T İK L Â L MARŞI V E A N LA M I* Zehra KAVCAR** Bağımsızlık ve özgürlük, toplumların en çok değer verdiği kavramların başında gelir. Çünkü bu değerler, ulus olmanın iik koşuludur. Bağımsız devletler,
TEKİRDAĞ SOSYAL BİLİMLER LİSESİ 10. SINIF MATEMATİK DERSİ YILLIK PLANI
 9 Eylül- Eylül 0-07 TEKİRDAĞ SOSYAL BİLİMLER LİSESİ 0. SINIF MATEMATİK DERSİ YILLIK PLANI Veri, Sayma ve Sayma. Olayların gerçekleşme sayısını toplama ve çarpma prensiplerini kullanarak hesaplar. Sıralama
9 Eylül- Eylül 0-07 TEKİRDAĞ SOSYAL BİLİMLER LİSESİ 0. SINIF MATEMATİK DERSİ YILLIK PLANI Veri, Sayma ve Sayma. Olayların gerçekleşme sayısını toplama ve çarpma prensiplerini kullanarak hesaplar. Sıralama
TAMSAYILAR. 9www.unkapani.com.tr. Z = {.., -3, -2, -1, 0, 1, 2, 3, } kümesinin her bir elemanına. a, b, c birer tamsayı olmak üzere, Burada,
 TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
T.C. DARICA KAYMAKAMLIĞI İlçe Milli Eğitim Müdürlüğü DARICA ASLAN ÇİMENTO İLKOKULU BRİFİNG DOSYASI
 T.C. DARICA KAYMAKAMLIĞI İlçe Milli Eğitim Müdürlüğü DARICA ASLAN ÇİMENTO İLKOKULU BRİFİNG DOSYASI KOCAELİ 2013 2014 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini,
T.C. DARICA KAYMAKAMLIĞI İlçe Milli Eğitim Müdürlüğü DARICA ASLAN ÇİMENTO İLKOKULU BRİFİNG DOSYASI KOCAELİ 2013 2014 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen toplumlar, önce haysiyetlerini,
Selçuk Yaşar Alaybey Ortaokulu Müdürlüğü YILLIK FAALİYET PLANI
 2015-2016 YILLIK FAALİYET PLANI 1 Selçuk Yaşar Alaybey Ortaokulu Müdürlüğü T.C. KARŞIYAKA KAYMAKAMLIĞI Selçuk Yaşar aşar Alaybey Ortaokulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen
2015-2016 YILLIK FAALİYET PLANI 1 Selçuk Yaşar Alaybey Ortaokulu Müdürlüğü T.C. KARŞIYAKA KAYMAKAMLIĞI Selçuk Yaşar aşar Alaybey Ortaokulu Müdürlüğü 2 Çalışmadan, yorulmadan, üretmeden, rahat yaşamak isteyen
Türkçe. 6. Sınıf. Ali PEHLİVAN. Okula Yardımcı, Sınavlara Hazırlık. Konu Anlatımı Konu Etkinlikleri Konu Testleri Yazılıya Hazırlık Çalışmaları
 Okula Yardımcı, Sınavlara Hazırlık 6. Sınıf Türkçe Konu Anlatımı Konu Etkinlikleri Konu Testleri Yazılıya Hazırlık Çalışmaları Ali PEHLİVAN PALME YAYINCILIK Ankara, 2014 1 PALME YAYINLARI: 904 6. Sınıf
Okula Yardımcı, Sınavlara Hazırlık 6. Sınıf Türkçe Konu Anlatımı Konu Etkinlikleri Konu Testleri Yazılıya Hazırlık Çalışmaları Ali PEHLİVAN PALME YAYINCILIK Ankara, 2014 1 PALME YAYINLARI: 904 6. Sınıf
Buna göre, eşitliği yazılabilir. sayılara rasyonel sayılar denir ve Q ile gösterilir. , -, 2 2 = 1. sayıdır. 2, 3, 5 birer irrasyonel sayıdır.
 TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
BÝREY DERSHANELERÝ SINIF ÝÇÝ DERS ANLATIM FÖYÜ MATEMATÝK - II
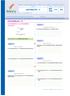 BÝREY DERSHANELERÝ SINIF ÝÇÝ DERS ANLATIM FÖYÜ DERSHANELERÝ Konu Ders Adý Bölüm Sýnav DAF No MATEMATÝK - II POLÝNOMLAR - IV MF TM LYS1 04 Ders anlatým föyleri öðrenci tarafýndan dersten sonra tekrar çalýþýlmalýdýr
BÝREY DERSHANELERÝ SINIF ÝÇÝ DERS ANLATIM FÖYÜ DERSHANELERÝ Konu Ders Adý Bölüm Sýnav DAF No MATEMATÝK - II POLÝNOMLAR - IV MF TM LYS1 04 Ders anlatým föyleri öðrenci tarafýndan dersten sonra tekrar çalýþýlmalýdýr
Bu kitapta neler var?
 Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET MEB TTKB NİN UYGULADIĞI 10 KÖK DEĞER FASİKÜLLERİMİZDE İŞLENMİŞTİR. EVLE OKUL BiR ARADA ATU
 Türkiye de ilk defa EVLE OKUL BiR ARADA ATU MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ÖZGÜN KONU ANLATIMI DEĞERLENDİRME SORULARI SINIF İÇİ UYGULAMALAR MEB TTKB NİN UYGULADIĞI 10 KÖK DEĞER FASİKÜLLERİMİZDE
Türkiye de ilk defa EVLE OKUL BiR ARADA ATU MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ÖZGÜN KONU ANLATIMI DEĞERLENDİRME SORULARI SINIF İÇİ UYGULAMALAR MEB TTKB NİN UYGULADIĞI 10 KÖK DEĞER FASİKÜLLERİMİZDE
Mehmet Âkif Ersoy un Hayatı ve İstiklâl Marşı
 1 Mehmet Akif Ersoy u Anma Programı İle İlgili Konferans Adıyaman Üniversitesi Vehbi Koç Konferans Salonu 12.03.2015 Saat: 10:00 Mehmet Âkif Ersoy un Hayatı ve İstiklâl Marşı Mustafa KARABULUT 1 1. Giriş
1 Mehmet Akif Ersoy u Anma Programı İle İlgili Konferans Adıyaman Üniversitesi Vehbi Koç Konferans Salonu 12.03.2015 Saat: 10:00 Mehmet Âkif Ersoy un Hayatı ve İstiklâl Marşı Mustafa KARABULUT 1 1. Giriş
önce biz sorduk KPSS Soruda 92 soru GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ SORU BANKASI TAMAMI ÇÖZÜMLÜ Eğitimde
 KPSS 2017 önce biz sorduk 120 Soruda 92 soru GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ SORU BANKASI TAMAMI ÇÖZÜMLÜ Eğitimde 30. yıl Editör Kenan Osmanoğlu - Kerem Köker Yazar Komisyon KPSS Matematik-Geometri
KPSS 2017 önce biz sorduk 120 Soruda 92 soru GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ SORU BANKASI TAMAMI ÇÖZÜMLÜ Eğitimde 30. yıl Editör Kenan Osmanoğlu - Kerem Köker Yazar Komisyon KPSS Matematik-Geometri
ÜNİTE: RASYONEL SAYILAR KONU: Rasyonel Sayılar Kümesinde Çıkarma İşlemi
 ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
KE00-SS.08YT05 DOĞAL SAYILAR ve TAM SAYILAR I
 Üniversite Hazırlık / YGS Kolay Temel Matematik 0 KE00-SS.08YT05 DOĞAL SAYILAR ve TAM SAYILAR I. 8 ( 3 + ) A) 7 B) 8 C) 9 D) 0 E) 6. 3! 3 ( 3 3)": ( 3) A) B) 0 C) D) E) 3. 7 3. + 5 A) 6 B) 7 C) 8 D) 0
Üniversite Hazırlık / YGS Kolay Temel Matematik 0 KE00-SS.08YT05 DOĞAL SAYILAR ve TAM SAYILAR I. 8 ( 3 + ) A) 7 B) 8 C) 9 D) 0 E) 6. 3! 3 ( 3 3)": ( 3) A) B) 0 C) D) E) 3. 7 3. + 5 A) 6 B) 7 C) 8 D) 0
önce biz sorduk KPSS Soruda 31 soru ÖABT LİSE MATEMATİK TAMAMI ÇÖZÜMLÜ SORU BANKASI Eğitimde
 KPSS 2017 önce biz sorduk 50 Soruda 31 soru ÖABT LİSE MATEMATİK TAMAMI ÇÖZÜMLÜ SORU BANKASI Eğitimde 30. yıl Komisyon ÖABT LİSE MATEMATİK ÖĞRETMENLİĞİ SORU BANKASI ISBN 978-605-318-684-7 Kitapta yer alan
KPSS 2017 önce biz sorduk 50 Soruda 31 soru ÖABT LİSE MATEMATİK TAMAMI ÇÖZÜMLÜ SORU BANKASI Eğitimde 30. yıl Komisyon ÖABT LİSE MATEMATİK ÖĞRETMENLİĞİ SORU BANKASI ISBN 978-605-318-684-7 Kitapta yer alan
Bu kitapta neler var?
 Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
Bu kitapta neler var? Her bölümün başında kısa, pratik bilgilerle konuyu kavramanızı hedefleyen >> Haydi Öğrenelim Yol gösteren, öğretici >> Çözümlü Sorular Eğlenerek çözeceğiniz pekiştirici etkinlikler
T.C. BEYOĞLU KAYMAKAMLIĞI Özel Saint Benoit Fransız Lisesi 2010-2014 STRATEJİK PLAN İSTANBUL
 T.C. BEYOĞLU KAYMAKAMLIĞI Özel Saint Benoit Fransız Lisesi -2014 STRATEJİK PLAN İSTANBUL İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim
T.C. BEYOĞLU KAYMAKAMLIĞI Özel Saint Benoit Fransız Lisesi -2014 STRATEJİK PLAN İSTANBUL İSTİKLAL MARŞI Korkma, sönmez bu şafaklarda yüzen al sancak; Sönmeden yurdumun üstünde tüten en son ocak. O benim
LYS K MYA KONU ANLATIMI ÇÖZÜMLÜ SORULAR ÇÖZÜMLÜ TESTLER KONU TESTLER
 LYS K MYA KONU ANLATIMI LÜ SORULAR LÜ TESTLER KONU TESTLER ZAFER YAYINLARI TEŞEKKÜR Kitaba emeği geçen değerli Zafer Dershaneleri öğretmenlerine ve de dizgisinden baskısına kadar kitaba emek veren tüm
LYS K MYA KONU ANLATIMI LÜ SORULAR LÜ TESTLER KONU TESTLER ZAFER YAYINLARI TEŞEKKÜR Kitaba emeği geçen değerli Zafer Dershaneleri öğretmenlerine ve de dizgisinden baskısına kadar kitaba emek veren tüm
kpss Önce biz sorduk 50 Soruda SORU Güncellenmiş Yeni Baskı ÖABT İLKÖĞRETİM MATEMATİK Tamamı Çözümlü SORU BANKASI
 Önce biz sorduk kpss 2 0 1 8 50 Soruda 30 SORU Güncellenmiş Yeni Baskı ÖABT İLKÖĞRETİM MATEMATİK Tamamı Çözümlü SORU BANKASI Komisyon ÖABT İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ SORU BANKASI ISBN 978-605-318-952-7
Önce biz sorduk kpss 2 0 1 8 50 Soruda 30 SORU Güncellenmiş Yeni Baskı ÖABT İLKÖĞRETİM MATEMATİK Tamamı Çözümlü SORU BANKASI Komisyon ÖABT İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ SORU BANKASI ISBN 978-605-318-952-7
Denklemler İkinci Dereceden Denklemler. İkinci dereceden Bir Bilinmeyenli Denklemler. a,b,c IR ve a 0 olmak üzere,
 Bölüm 33 Denklemler 33.1 İkinci Dereceden Denklemler İkinci dereceden Bir Bilinmeyenli Denklemler a,b,c IR ve a 0 olmak üzere, ax 2 + bx + c = 0 biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli
Bölüm 33 Denklemler 33.1 İkinci Dereceden Denklemler İkinci dereceden Bir Bilinmeyenli Denklemler a,b,c IR ve a 0 olmak üzere, ax 2 + bx + c = 0 biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli
KPSS ÖABT İLKÖĞRETİM MATEMATİK. Tamamı Çözümlü SORU BANKASI. 50 soruda SORU
 KPSS ÖABT 09 İLKÖĞRETİM MATEMATİK Tamamı Çözümlü SORU BANKASI 50 soruda SORU Komisyon ÖABT İLKÖĞRETİM MATEMATİK TAMAMI ÇÖZÜMLÜ SORU BANKASI ISBN 978-605--9-6 Kitapta yer alan bölümlerin tüm sorumluluğu
KPSS ÖABT 09 İLKÖĞRETİM MATEMATİK Tamamı Çözümlü SORU BANKASI 50 soruda SORU Komisyon ÖABT İLKÖĞRETİM MATEMATİK TAMAMI ÇÖZÜMLÜ SORU BANKASI ISBN 978-605--9-6 Kitapta yer alan bölümlerin tüm sorumluluğu
YGS - LYS SAYILAR KONU ÖZETLİ ÇÖZÜMLÜ SORU BANKASI
 YGS - LYS SAYILAR KONU ÖZETLİ LÜ SORU BANKASI ANKARA ÖN SÖZ Sevgili Öğrenciler, ÖSYM nin son yıllarda yaptığı sınavlardaki matematik sorularının eski sınav sorularından çok farklı olduğu herkes tarafından
YGS - LYS SAYILAR KONU ÖZETLİ LÜ SORU BANKASI ANKARA ÖN SÖZ Sevgili Öğrenciler, ÖSYM nin son yıllarda yaptığı sınavlardaki matematik sorularının eski sınav sorularından çok farklı olduğu herkes tarafından
Başlayanlara AKTİF MATEMATİK
 KPSS - YGS - DGS - ALES Adayları için ve 9. sınıfa destek 0 dan Başlayanlara AKTİF MATEMATİK MEHMET KOÇ ÖNSÖZ Matematikten korkuyorum, şimdiye kadar hiç matematik çözemedim, matematik korkulu rüyam! bu
KPSS - YGS - DGS - ALES Adayları için ve 9. sınıfa destek 0 dan Başlayanlara AKTİF MATEMATİK MEHMET KOÇ ÖNSÖZ Matematikten korkuyorum, şimdiye kadar hiç matematik çözemedim, matematik korkulu rüyam! bu
YAZILI SINAV SORU ÖRNEKLERİ MATEMATİK
 YAZILI SINAV SORU ÖRNEKLERİ MATEMATİK SORU 1: Aşağıdaki grafik, bir okuldaki spor yarışmasına katılan öğrencilerin yaşa göre dağılışını göstermektedir. Öğrenci sayısı 5 3 9 10 1 14 Yaş 1.1: Yukarıdaki
YAZILI SINAV SORU ÖRNEKLERİ MATEMATİK SORU 1: Aşağıdaki grafik, bir okuldaki spor yarışmasına katılan öğrencilerin yaşa göre dağılışını göstermektedir. Öğrenci sayısı 5 3 9 10 1 14 Yaş 1.1: Yukarıdaki
