MINKOWSKI 4-UZAYINDA JET YAPILAR VE MEKANİK SİSTEMLER
|
|
|
- Kudret Isler
- 8 yıl önce
- İzleme sayısı:
Transkript
1 PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MINKOWSKI -UZAYINDA JET YAPILAR VE MEKANİK SİSTEMLER YÜKSEK LİSANS TEZİ Smge DAĞLI Anablm Dalı Matematk Anablm Dalı Programı Geometr Tez Danışmanı Yrd. Doç. Dr. Cansel AYCAN Hazran-0
2
3
4 ÖNSÖZ Bu tez çalıģması, Pamukkale Ünverstes Fen Blmler Ensttüsü Matematk Anablm Dalı Yüksek Lsans programında yapılmıģtır. Bu çalıģmada, dferansyel geometrk kavramlardan jet demet yapıları ele alınarak, son yıllarda matematksel fzkte fzksel uygulamaları açısından önem kazanan Mnkowsk uzayı üzernde, geometrk teknklern kullanımı açısından özel br konu olan analtk mekanktek Lagrangan ve Hamltonan enerj sstemler ncelenmģtr. Bu çalıģmaya baģlamamda bana katkıda bulunan, yardım ve eleģtrlern esrgemeyen değerl hocalarım; danıģmanım Y.Doç. Dr. Cansel AYCAN, Y.Doç. Dr. ġevket CĠVELEK, Y.Doç. Dr. Mustafa AġCI, Doç. Dr. AyĢegül DAġCIOĞLU a teģekkürü br borç blrm. Ayrıca çalıģmalarım esnasında benden madd ve manev desteklern esrgemeyen alem ve değerl arkadaģlarıma teģekkürlerm sunarım. Hazran, 0 Smge DAĞLI
5 İÇİNDEKİLER ÖZET... v SUMMARY... v. GİRİŞ.... HERMANN MINKOWSKI.... TARĠHÇE.... TEMEL KAVRAMLAR Demet Yapıları Euler-Lagrange ve Hamlton sstemler Lorentz- Mnkowsk Uzay.... MINKOWSKI -UZAYINDA EULER-LAGRANGE MEKANİK SİSTEMLER Euler-Lagrange Sstemler...5. Uygulamalar Hels Örneğ Çember Örneğ MINKOWSKI -UZAYINDA HAMİLTON MEKANİK SİSTEMLER.... Hamlton Sstemler.... Uygulamalar Hels Örneğ Çember Örneğ... 5.SONUÇ VE DEĞERLENDİRME KAYNAKLAR Sayfa v
6 ŞEKİL LİSTESİ Şekller. IĢık kon.... Tme kon.... Hels eğrs.... Çember eğrler... 8 v
7 SEMBOL LİSTESİ Mnkowsk -uzayı Demet Brnc Jet Demet Mnkowsk Brnc Jet Demet Tanjant Demet Kotanjant Demet Lagrange Enerj Fonksyonu Hamlton Enerj Fonksyonu v
8 ÖZET MİNKOWSKİ -UZAYINDA MEKANİK SİSTEMLER Bu çalıģma dört bölümden oluģmaktadır. Ġlk bölümde, konunun kısa br tarhçes sunulmuģtur. Bu kısımda öncelkle Mnkowsk nn hayatı, çalıģmaları ve bu çalıģmaların genel özellkler anlatılmıģtır. Daha sonra Mnkowsk uzay-zaman konusunun geometrk ve fzksel özellkler sunulmuģtur. Ayrıca, çalıģmamızın sonrak bölümlernde kullanılacak olan jet demet yapılarının elde edlģ ve geometrk özellkler de ncelenmģtr. Ġknc bölümde se Mnkowsk -uzayı üzernde jet demet yapısı kurulmuģtur. Bu yapının anlaģılablmes çn gerekl olan tüm geometrk özellkler ayrı ayrı ncelenmģtr. Üçüncü bölümde, knc bölümde elde edlen Mnkowsk jet demet yapısı üzernde Lagrange mekank sstemler kurulmuģtur. Bu sstemden elde edlen dferansyel denklemler çözümlenerek Lagrange enerj denklem üretlmģtr. Daha sonra fzksel yorumun yapılablmes çn bu bölümde yapılan çalıģmaya örnekler verlmģtr. Bu mekank örneklern çözümünde, enerj denklemlernn çözümü yapılmıģ, gerekl grafkler çzlmģ ve çözüm fonksyonunun fzksel yorumlarına değnlmģtr. Dördüncü bölümde se, knc bölümde elde edlen Mnkowsk jet demet yapısı çn Hamlton mekank sstemler kurulmuģtur. Burada elde edlen dferansyel denklemler çözümlenerek Hamlton enerj denklemlerne ulaģılmıģtır. Böylece, bu örnekler yardımıyla Hamlton enerj yapıları hakkında geometrk ve fzksel yorum yapılablmģtr. Anahtar Kelmeler Mnkowsk uzay-zaman, jet demet yapısı, Euler-Lagrange enerj sstemler, Hamlton enerj sstemler. v
9 SUMMARY MECHANICAL SYSTEMS ON MINKOWSKI -SPACE Ths study consst of four sectons. In the frst secton, the short hstory of ths subject s presented. In ths secton frstly, Mnkowsk s lfe tme, studes and the general propertes of ths studes have been mentoned. Then, the physcal and geometrc propertes of Mnkowsk space tme have been gven. In addton to, defntons and geometrcal propertes of jet bundle structures whch wll be used on followng sectons are examned. In the second secton, the jet bundle structure s set up on Mnkowsk -space. For understandng ths mathematcal structure, all requred geometrcal propertes are nvestgated separately. In the thrd secton, Lagrangan mechancal systems s obtaned for Mnkowsk jet bundle whch s denoted n the second secton. The Lagrangan energy functon s produced wth solvng dfferantal equatons whch s obtaned from ths system. Then, some examples are gven for physcal comment. In solvng of these mechanc examples, the soluton of energy equatons have been obtaned, geometrcal tables are drawn and the physcal comments of ths solvng functon are mentoned. In the fourth secton, Hamltonan mechancal systems s obtaned for Mnkowsk jet bundle whch s denoted n the second secton. The Hamltonan energy functon s produced wth solvng calculated dfferantal equatons whch s obtaned n ths secton. So, the geometrc and physcal comments can be explaned about the Hamltonan structure wth ths examples. Keywords Mnkowsk space-tme, jet bundle structure, Euler-Lagrange energy systems, Hamlton energy systems. v
10 G IR IŞ. HERMANN MINKOWSKI Ltvanya l br matematkç olan Hermann Mnkowsk (86-909), 86 y l nda Aleksotas da do¼gdu. 896 le 90 y llar aras nda Zürh Federal Polteknk Okulunda ve ölünceye kadar da Göttngen Ünverstesnde profesörlük yapt. 88 y l nda, tam katsay l knc dereceden şekller kuram n n temeller üstüne nceleme yaz s yla Fen Akademsnn büyük matematk ödülünü ald. Eucldes olmayan geometryle kar şt r lmamas gereken br say lar geometrs kurarak say lar kuram na baz geometrk kavramlar getrd. Sonunda özel br metrkle donat lm ş dört boyutlu özel br uzaya başvurarak, Ensten n k s tl ba¼gl l k kuram n n, bugün klask say lan geometrk br yorumunu verd. Buna Mnkowsk uzay zaman denr. Say lar geometrs sml ktab, 896 y l nda bas ld. 907 y l nda Dophantus Yaklaş mlar adl eser yay nlad. Çal şmalar adl yap t n n da 9 y l nda ç kt ¼g blnmektedr. Kends, 909 y l nda Göttngen de öldü.. TAR IHÇE Tarh boyunca, blmn temel problem, mümkün oldu¼gu kadar do¼gay y br şeklde anlayablmek ve aç klayablmektr. Bunu başarablmes çnde elnde yeter kadar matematksel donan m mevcut olmas gerekmektedr. Boyut ve ekstra boyut kavram temel olarak, zorunluluk veya key uygulamalar sonucu ortaya ç kan zksel ncelklerdr. Mnkowsk uzay-zaman geometrsnn do¼gum y l 905 olarak blnr. 909 y l nda, Mnkowsk, Maxwell n Elektrodnam¼g le Ensten n Özel Rölatvte teorlernden lham alarak, do¼gan n, bld¼gmz üç boyutuna ek olarak dördüncü br boyut yard m yla tasvr edleblece¼gn belrtmştr. Ntekm Ensten 95 y l nda yay nlad ¼g Genel Rölatvte Teorsyle, Mnkowsk nn bu ddas n genelleştrerek uzay-zaman kavram le do¼gay - boyutlu ( -uzay + -zaman ) tasvr etmştr. Böylece Mnkowsk ve Ensten taraf ndan başlat lan boyut say s yla oynama le evrenmz anlama kr günümüze kadar
11 artan br vme le zkçler taraf ndan farkl teorlerde farkl boyut say s le karş m za ç kmaktad r. Bu se zksel olaylar belrl baz lkelern çerçeves çnde kesn br geometrk termnoloj yard m yla ncelemeye uygun ve toplay c, brleştrc matematk br modelden başka br şey de¼gldr. Bu geometrk modele göre, göz önüne al nan dört boyutlu uzay (yan bu uzay - zaman) zksel olaylara yatakl k eden br katman olarak düşünüleblr. Ensten n 905 y l nda yay nlad ¼g özel görelk kuram na göre. Fzk yasalar her türlü referans noktas ndan ba¼g ms zd r.. Iş k h z uzayda sabttr ve gözlem yapanlar n h z ndan ba¼g ms zd r. Ilkne göre evrenn her yernde zk yasalar ayn d r. Ikncsne göre h z n z ne olursa olsun ş k h z n hep ayn ölçersnz. Bu durumda dyeblrz k ş ¼g n h z n n bzm h z m zdan etklenmemes nsan sa¼gduyusu le ba¼gdaşmamaktad r. Bu br yan lsamad r. Mnkowsk uzay özel br metrk sayesnde gelştrlmş olan br uzay bçmdr. Mnkowsk uzay-zaman olarak an lmas ndak en büyük etken se klask boyuttan oluşan ve her türlü vektörün boyunu bu üç boyutta tan mlayan klask uzay kavram na br de zaman eklemesyle lşkldr. Daha anlaş l r olacak olursa bu uzayda br vektörün boyu yaln zca x,y,z nn kends le belrlenmez, buna br de c.t denlen ve ş ¼g n ald ¼g yol da eklenr.[6] Mnkowsk uzay n n pek çok yarar olmuştur. Özel görell¼ge göre ş k, br kon bçmnde yol alacakt r. O nedenle blg ded¼gmz ve en h zl ş kla beraber aktar lan her türlü şey bu konnn çnde yer alacakt r. Ancak genel görellkte bu kon do¼gal formunu kaybederek br hperbolü and racak br bçmde br kon oluşturacakt r. Aşa¼g dak şeklde altta ve üstte, göreblece¼gnz k kon var. Bu k konden üsttek, a olay n n gelece¼gnde olmas mümkün olaylar, alttak kon se, a olay n n geçmşnde olmas mümkün olmuş olaylar gösteryor. Tam kesşm noktalar se a olay n temsl edyor. şekl
12 Yukar dak konnn kenarlar ş k h z n temsl edyor, herhang br şey ş k h z n geçemeyece¼g çn, gelece¼gndek htmaller o konnn d ş na ç kam yor. Yan o konnn d ş nda olan hç br şeyn bzm gelece¼gmzde yer yok denleblr. Blmekteyz k objeler uzay çnde lerlerler, ama ayn zamanda zaman çnde de lerlerler. Hç br şeklde hareket etmesenz ble, çnde bulundu¼gunuz ortamda mevcut objelerle brlkte, zaman çnde hareket halndesnz. Uzay çnde hareket etmeyeblrsnz ama, her zaman, zaman çnde hareket etmek zorundas n z. O halde zaman kullan lan br de¼gerdr. Her tepkleşmeye, her sürece zaman da kat l r. Onsuz hçbr şey gerçeklemez. Zaman ayr ca uzay dokusunun ö¼gelernden brdr. Zaman ş k h z na ndeksled¼gmz zaman ortaya lgnç gözlemler ç kmaktad r. Zaman görellk kazanmakta ve uzay genşlemekte ve daralmaktad r. Hareket ne kadar ş k h z na yak nsa, uzay o kadar genşlemektedr. Ayr ca; 87 de F.Klen, Erlanger Program olarak blnen çal şmas nda geometrlern grup etks alt nda nceleneblece¼gn fade etmştr. Bu ba¼glamda Ökld geometrs, Ökld grubu, A n geometrs, A n grubu alt nda, nokta, e¼gr ve yüzeylern ortogonal ve a n dönüşümler alt nda korunan özelklernn, nvaryantlar n n araşt r lablece¼gn ve önemn belrtmştr. Bu durum F.Klen n fade ett¼g anlamda, Mnkowsk uzay-zaman geometrsn ortaya ç karan grup etks alt nda nokta, e¼gr ve yüzeylern nvaryantlar n bulma problemn ortaya ç karm şt r. D¼ger taraftan bu geometr çn matematksel ve zksel yap lara at çal şmalar da yap lm şt r. O(,) olarak ncelenen ortogonal grup, Mnkowsk uzayzaman geometrsn etkleyen grup anlam nda al n r. Bu grup G.L. Naber n The Geometry of Mnkowsk Space-tme ktab nda Genel Lorentz Grubu olarak adland r lm şt r. Invaryantlar teors le lgl çal şmalara se y llar aras nda başlanm şt r. 890 y l nda Hlbert, nvaryantlar teors le lgl temel çal şmalar yapm şt r. Invaryantlara at baz farkl çal şmalar J.A.Deudonne n Invarant Theory, D.Hlbert n Theory Of Algebrac Invarants, D.Khadjev n An Applcaton Of Invarant Theory To D erantal Geometry, T.A.Sprnger n Invarant Theory, H.Weyl n The Classcal Groups, Ther Invarants And Representatons eserlernde yer almaktad r. 988 y l nda D.Khadjev ktab nda ve R.Arpov makalelernde Ökld grubu çn noktalar n üreteçler yard m yla denklk problem ve yörünge problemn ncelemştr. [7; ; 5] Kuantum mekan¼gnn temeller se 0. yüzy l n lk yar s nda Max Planck, Albert Ensten, Nels Bohr, Werner Hesenberg, Erwn Schrödnger, Max Born, John von Neumann, Paul Drac, Wolfgang Paul gb blm adamlar nca at lm şt r. Belrszlk lkes, ant madde, Planck sabt, kara csm ş n m, dalga kuram, alan teorler gb kavram ve kuramlar bu alanda gelştrlmş ve klask z¼gn de¼gştrl-
13 mesne sebep olmuştur. Yan s ra, Lagrange formalzm 788 y l nda Frans z zkç Joseph Lose Lagrange taraf ndan oluşturulmuştur. Hamlton formalzm se 8 y l nda Irlandal br zkç olan Wllam Rowan Hamlton taraf ndan oluşturulmuştur. Hamlton formalzmn anlamak Lagrange a göre daha basttr. Çünkü H=T+V yan toplam mekank enerj knetk enerj le potansyel enerjnn toplam d r. [5] Toplam enerj de do¼gada dama korunur ve sabttr. Lagrangan se enerj gb korunumlu br ncelk yerne varyasyon prensb (en küçük etk prensb) le tan mlan r. Hamlton denklemler. mertebeden dferansyel denklemlerdr ve bu nedenle. dereceden Lagrange denklemlern çözmekten daha kolayd r. Br d¼ger avantaj se sstem br smetrye sahpse Hamltonan de momentum korunumludur. Lagrangan da se momentum korunumlu olsada tüm genelleşmş h zlar Lagrangan da mevcuttur. Yan n boyutlu br sstemn Lagrangan n çözmek zorunda kal r z. Lagrange ve Hamlton formalzm 9. yy. sonlar ndan tbaren Klask mekan¼gn ve Kuantum mekan¼g teorlernn kullan m nda ve daha detayl anlaş lmas nda temel br yere sahptr. 0. yy. da özellkle 980 den sonra, smplektk manfold, smplektk topoloj ve kotanjant demet kavramlar n n, özellkle bundle ve jet bundle yap lar n matematkçler taraf ndan kullan lmas n n artmas le klask mekankte yap lan çal şmalar artm şt r. Özellkle 900 lu y llarda yüksek mertebeden türevleneblme le lgl çal şmalar n başlamas le jet manfold yap lar oluşturulmaya başlanm şt r. 90 da F.Bopp, M.Ostrogransky ve B. Podolksy bu çal şmalar z¼ge uyarlam şlard r. Geometrk denklklern z¼ge uygulamalar, tanjant ve kotanjant demetlern mekankte çal şmalar ve alan teorde özel lf demetlernde konneksyonlar n kullan m le devam etmştr. Bu çal şmalar Lagrangan ve Hamltonan yap lar n temelnde öneml yer tutar. 950 de Ch. Ehresman lk jet çal şmalar n başlatm şt r. 980 l y llarda D. J. Saunders, B.A.Kupperschmdt bu konu le lgl çal şmalara devam etmşlerdr. Bunun yan s ra 970 lerde K. Yano, S. Ishhara se tanjant ve kotanjant demetlerle lgl öneml çal şmalarda bulunmuşlard r. Son zamanlarda G. Sardanashvly, bzm de bu çal şmam zda kulland ¼g m z matemat¼gn teork z¼ge uygulamalar üzerne çal şmalar yapm şt r. [8; 9; 0; ; ] Bu blgler ş ¼g nda, C. Aycan jet demet yap lar üzernde Lagrangan ve Hamltonan sstemlern doktora tez olarak ncelemştr.[] Bu çal şma le yukar da belrtt¼gmz ktap ve makalelern ncelenmes sonucunda, öncelkle Mnkowsk -uzay n n jet yap lar oluşturulmuş, daha sonra benzer şeklde bu çal şmada Mnkowsk -uzay n n jet demet yap lar da elde edlerek üzerndek mekank sstemler ncelenmştr. Ş. Cvelek se demet yap lar n tan tarak, bu enerj denklemlernn brnc mertebeden yükseltmelern elde etmştr. []
14 . TEMEL KAVRAMLAR Bu bölümde, lerk bölümlerde kullan lacak olan demet yap s, mekank sstemler, Lagrange ve Hamlton enerj denklemler le Mnkowsk uzay n n temel yap lar tan mlanm şt r... DEMET YAPILARI Bu bölümde, dferansyel geometrde öneml br yere sahp olan manfold yap s üzernde demet yap s n n nas l oluşturulaca¼g ele al nm şt r. Tan m. E ve M, C -manfoldlar, E! M br C -dönüşüm olsun. E¼ger br örten submerson se, (E; ; M) üçlüsüne br l manfold denr. Br (E; ; M) l manfoldunda, E ye total uzay, M ye taban uzay, ye projeksyon ve her br p M noktas çn E nn (p) altcümlesne de p üzerndek lf denr.[; ] Tan m. Br l manfold (E; ; M), boym = m; boye = m+n ve U E aç k alt cümles üzernde br koordnat sstem, y U! R m+n olsun. pr R m+n! R m olmak üzere, a; b U ve (a) = (b) = p ) pr (y (a)) = pr (y (b)) önermes do¼gru se, y ye br uyarlanm ş koordnat sstem denr.[] Tan m. Br l manfold (E; ; M) ve br C -manfold F olmak üzere, e¼ger t E! M F dönüşümü pr t = olacak şeklde br d eomor zm se (F; t) klsne nn model l ve en az ndan br trvalzasyona sahp (E; ; M) l manfolduna da trval l manfold denr.[] Tan m. Br l manfold (E; ; M) ve p M olsun. F p br C -manfold, p nn br komşulu¼gu W p ve t p (W p )! W p F p 5
15 dönüşümü pr t p = j (W p) şart n sa¼glayan br d eomor zm se o zaman (W p ; t p ; F p ) üçlüsüne p nn komşulu¼gunda nn br lokal trvalzasyonu ve taban uzay n her br noktas cvar nda en az br lokal trvalzasyona sahp br (E; ; M) l manfolduna da lokal trval l manfold veya demet denr.[] Tan m.5 M ve N, C -manfoldlar, ' M! N br C -dönüşüm, p M ve br V p T p M tanjant vektörüne p noktas nda te¼get olan br e¼gr I R! M olsun. Bu durumda, ' j p (V p ) = W '(p) T '(p) N tanjant vektörü, ' I R! N e¼grsne ' (p) noktas nda te¼get olan br tanjant vektör olmak üzere ' j p T p M! T '(p) N le tan mlanan dönüşüme ' nn p M noktas ndak türev dönüşümü denr.[] Bu durumda, T E! T M, nn türev dönüşümü olmak üzere, = (T E; ; T M) üçlüsü br demet olup; ye nn tanjant demet denr. Tan m.6 (E; ; M) br l manfold ve ' M! E br dönüşüm olsun. E¼ger ' = d M koşulu gerçeklenyorsa, ' ye nn br kest denr ve nn tüm kestlernn cümles () le gösterlr.[] Tan m.7 (E; ; M) br demet ve p M olsun., ' p () kestler, p noktas nda (p) = ' (p) ve (p) cvar nda (x ; u ) uyarlanm ş koordnat sstemnde j p = ' j p m; n x x se brnc mertebeden denklem olarak tan mlan r. y çeren denklk s n ar na n n p noktas ndak brnc jet denr ve Jp le gösterlr. Buna göre, J p p M; p () (.) cümlesne demetnn brnc jet manfoldu denr ve J le gösterlr.[; 9] Tan m.8 (E; ; M) br demet ve (U; u), u = (x ; u ) olmak üzere E ü- zernde uyarlanm ş koordnat sstem olsun. Bu durumda J üzernde (U ; u ) ndrgenmş koordnat sstem, U = Jp (p) U u = (x ; u ; u ) 6
16 le tan ml olup burada x J p = x (p); u J p = u ( (p)) ve yen mn-adet u U! R fonksyonlar se, u (J p ) = ' x j p (.) şeklnde belrldr.bu şeklde fade edlen yen u koordnatlar türevsel koordnatlar olarak adland r l r.[].. EULER-LAGRANGE VE HAM ILTON DENKLEMLER I Bu bölümde Euler-Lagrange ve Hamlton denklemler le lgl temel kavramlar verlecektr. Tan m.9 m boyutlu br manfold M ve M nn tanjant demet T M olsun. T M üzernde J = 0 eştl¼gn sa¼glayan ve rankj = m le verlen (; ) tpnden J tensör alan na yaklaş k tanjant yap denr. M manfoldu üzernde lokal koordnatlar (x ), m ve T M üzernde lokal koordnatlar (x ; x ) olmak üzere T M üzernde J yaklaş k tanjant yap s, J = x x, J x = 0 (.) olarak tan mlan r.[] Tan m.0 m boyutlu br manfold M ve M nn tanjant demet T M olsun. T M üzerndek br vektör alan na M üzernde semspray denr. Bu durumda " semspray lokal olarak; " = x + " x x (.) le verlr. Burada " fonksyonlar " = " (x ; x ) olarak tan ml d r. Bu durumda, M manfoldu üzernde verlen br e¼grs e¼ger " nn br ntegral e¼grs oluyorsa, bu e¼grye " nn br çözümü denr.[] Tan m. J, m boyutlu br M manfoldunun tanjant demet üzernde br yaklaş k tanjant yap olsun. Bu durumda T M üzernde lokal koordnatlar (x ; x ), m ve " = x + " x x vektör alan M üzernde semspray olmak üzere V = J" = x x (.5) 7
17 le verlen V vektör alan na Louvlle vektör alan denr.[] Buna göre, T M üzernde tan ml " vektör alan n n br semspray olmas çn gerek ve yeter şart J" = V olmas d r. [6] Tan m. M manfoldunun tanjant demet T M üzerndek p-formlar n cümles p (T M) ve T M üzerndek vektör alanlar n n cümles (T M) olsun. J f = 0; f C (T M) px J f(x ; ; X p ) = w(x ; ; JX ; X p ); w p (T M); X ; ; X p (T M) = (.6) olarak tan ml J fonksyonuna düşey türev denr. [] Burada, J (dx ) = 0; J (d x ) = dx olur. Ayr ca w p (T M) p-formu, w = X w ;; p dx dx p << p şeklnde tan ml d r ve dferansyel se dw = X dw ;; p dx dx p << p olarak fade edlen p + -formdur.[] p + -formlar n cümlesn de p+ (T M) olarak gösterrsek d j p (T M)! p+ (T M) olacak şeklde d j = [ j d; d] = j d d j (.7) le tan ml d j fonksyonuna düşey dferansyel denr. 8X (M) vektör alan le w p-formunun X w ç çarp m aşa¼g dak şartlar sa¼glayan br p -formdur. ) X w = 0; e¼ger p = 0 se; ) X w = w(x); e¼ger p = se; ) X w(y ; ; Y p ) = w (X; Y ; ; Y p ) ; e¼ger Y ; ; Y p (M) se; 8
18 bu durumda X w p (M) olur.[8] Tan m. M, m boyutlu br manfold ve M nn T M tanjant demet üzernde br -form olsun. E¼ger maksmal rankl br kapal -form se, (M; ) klsne smplektk manfold denr. T M üzernde L = dd J L -formu smplektk se, bu durumda T M üzernde tan ml L T M! R fonksyonu regüler yada non-dejeneredr denr.[; 5] Tan m. M, m boyutlu br manfold ve T M tanjant demet olsun. L T M! R br C -fonksyon olmak üzere, T M üzerndek L = dd J L le tan ml kapal -formu çn E L = V L L eştl¼gne L le brleşen enerj fonksyonu ve L ye de T M tanjant demet üzerndek Lagrange fonksyonu denr. T M se M kon gürasyon manfoldunun h z uzay olarak adland r l r.[] Tan m.5 (M; ) smplektk manfold olmak üzere, L regüler Lagrange fonksyonuna karş l k gelen ve E L = V L L eştl¼g le belrl olan enerj fonksyonuna Hamlton enerj fonksyonu denr ve H M! R le gösterlr. M smplektk manfoldunun koordnatlar se (x ; x ) olmak üzere, M üzernde X H = H x x H x x (.8) olarak tan ml vektör alan na Hamlton vektör alan denr.[] Tan m.6 (M; ) smplektk manfoldu üzernde H Hamlton enerj fonksyonu, X H Hamlton vektör alan olmak üzere; XH = dh (.9) denklemne Hamlton sstemlernn smplektk (esas) formu yada Hamlton sstemler dnamk denklem denr. Bu denklemde L = dd J L -form ve " br semspray kullan larak elde edlen " L = de L denklemne Lagrange sstemler çn dnamk denklem ad verlr.[] Teorem. " L = de L denklemn sa¼glayan br tek " semspray vard r.[8] Tan m.7 " L = de L denklemn sa¼glayan br tek " semspray varsa E L ye L T M! R fonksyonu çn Euler-Lagrange vektör alan denr. Bu koşulu sa¼glayan L fonksyonuna da Lagrange enerj fonksyonu denr. Burada, E L = x + " x x (.0) le tan ml vektör alan d r ve " fonksyonlar " = " (x ; x ) le belrldr. 9
19 " L = de L eştl¼gn çözümüyle elde edlen d L L dt x = 0 (.) x denklemne de Euler-Lagrange enerj denklem denr.[; 5; 6; 7] Zamana ba¼gl Lagrange sstemlern oluşturmak çn jet manfoldlardan yararlan l r. R br boyutlu ökld uzay olmak üzere J (R; M) = T M zomor zm blnmektedr. T M nn koordnatlar (x ; x ), R nn koordnat se (t) olmak üzere J (R; M) üzerndek uyarlanm ş koordnat sstem (t; x ; x ) olur. Zamana ba¼gl durumda yukar da verlen Lagrange fonksyonu L J (R; M)! R tan ml C - dönüşümüdür. Ayr ca, bu jet manfold üzernde J = 0 eştl¼gn sa¼glayan ve rankj = m le verlen (; ) tpnden tensör alan zamana ba¼gl yaklaş k tanjant yap olarak tan mlan r. V br Louvlle vektör alan olmak üzere, yaklaş k tanjant yap ; J = V; J = t x x ; J x = 0 (.) koşullar n sa¼glamal d r.[8] Zamana ba¼gl durumda " semspray lokal olarak " = t + x + " x x (" = " (t; x ; x ), m) (.) şeklnde fade edlr. Tan m.8 L J (R; M)! R zamana ba¼gl Lagrange fonksyonu olsun. J (R; M) üzernde, -formuna Poncare-Cartan -formu ve -formuna Poncare-Cartan -formu denr. Buna göre J (R; M) manfoldu üzernde L = d J L + Ldt (.) L = dd J L + dl ^ dt (.5) " L = 0; " dt = (.6) denklemlern sa¼glayan br tek E L vektör alan vard r, buna zamana ba¼gl Euler- Lagrange vektör alan denr. (J (R; M); L ; E L ) üçlüsüne de zamana ba¼gl Lagrange sstem denr.[8]..6 denklemlernn çözümü le elde edlen d L L dt x = 0 (.7) x 0
20 denklemne zamana ba¼gl Euler-Lagrange enerj denklem denr.[; 0] Burada dkkat edlrse; zamana ba¼gl olan durumda elde edlen.7 Euler- Lagrange denklem le zamana ba¼gl olmayan durumda elde edlen Euler-Lagrange denklem. ayn ç kar. O halde, jet demet yap s nda çal şmak Lagrange enerj denklemlernn genel yap s n de¼gştrmez, fakat zaman parametres çal şmaya dahl edlece¼g çn zksel ve mekank uygulamalar aç s ndan elverşl olur. Tan m.9 T M kotanjant demetnn uyarlanm ş koordnatlar (x ; x ) olmak üzere, M = x dx (.8) olarak tan ml -formuna Louvlle form denr. Buna ba¼gl olarak T M üzernde, M = d M = dx ^ d x (.9) smplektk formu kanonk smplektk form olarak adland r l r.[; 8; 9] Tan m.0 (M; ) smplektk manfold ve H M! R, M üzernde tan ml Hamlton fonksyonu olsun. XH = dh denklemn sa¼glayan br tek X H vektör alan na, H Hamlton enerj fonksyonu le brleşen Hamlton vektör alan denr. Böylece, XH = dh (.0) smplektk formu kullanarak, x t = H x, x t = H x (.) denklemler elde edlr. Bu denklemlere Hamlton denklemler denr.[] Zamana ba¼gl Hamlton sstemler aşa¼g dak şeklde fade edlecektr. Tan m. (M; ) smplektk manfold ve H M! R, M üzernde tan ml Hamlton fonksyonu olsun. XHt = dh t denklemn sa¼glayan br tek X Ht vektör alan na, zamana ba¼gl Hamlton vektör alan denr. Böylece; X Ht lokal olarak X Ht = t + H t x x H t x x (.) şeklnde fade edlr.[5] I = ( ; )! R M, > 0 çn X Ht vektör alan n n br ntegral e¼grs olsun. Böylece, (t) = (t; x (t) ; x (t)) (.)
21 ve ayr ca, X Ht nn br ntegral e¼grs oldu¼gundan olur. Bu durumda smplektk formu kullan larak (t) = X Ht ( (t)) = t + X t (x (t) ; x (t)) XHt = dh t x t = H x, x t = H x (.) denklemler elde edlr. Bu denklemlere zamana ba¼gl Hamlton denklemler denr.[].. LORENTZ-M INKOWSK I UZAYI Bu bölümde çal şmam z n temel konumunu oluşturan Mnkowsk -uzay le lgl temel geometrk ve cebrsel özellkler verlmştr. Tan m. V sonlu boyutlu reel vektör uzay olsun. h ; V V! R (.5) b-lneer fonksyonu 8v; w V çn hv; w = hw; v özell¼gn sa¼glayan h ; ye V üzernde br smetrk b-lneer form denr. V, vektör uzay üzernde br smetrk b-lneer form h ; olmak üzere; )8! v V,! v 6= 0 çn h! v ;! v > 0 se h ; b-lneer formu poztf tan ml, )8! v V,! v 6= 0 çn h! v ;! v < 0 se h ; b-lneer formu negatf tan ml, ) 8! v V,! v 6= 0 çn h! v ;! v 0 se h ; b-lneer formu yar -poztf tan ml, v)8! v V,! v 6= 0 çn h! v ;! v 0 se h ; b-lneer formu yar -negatf tan ml, v)8! v V, h! v ;! v = 0 çn! v = 0 oluyorsa h ; b-lneer formuna non-dejenere,aks halde dejenere denr.[5] Tan m. h ;, V üzernde smetrk b-lneer form ve W da V nn br altuzay olsun. h ; nn W üzernde k s tlan ş h ; W olmak üzere
22 h ; W W W! R negatf tan ml olacak şeklde en büyük boyutlu W altuzay n n boyutuna h ; smetrk b-lneer formun ndeks denr. E¼ger h ; nn ndeks v se 0 v boyv dr.[] Tan m. M, türevleneblr (C -s n f ndan) manfold ve h ; (M) (M)! C (M; R) (! x ;! y )! h! x ;! y şeklnde tan mlanan smetrk, b-lneer ve non-dejenere metrk fonksyonuna M üzernde br metrk tensör denr. Bu metrk tensörün ndeks M manfoldunun ndeks olarak fade edlr. M br C -s n f ndan manfold olmak üzere, (M) de tan ml h ; fonksyonu, M nn her br tanjant uzay na br ç çarp m ndrger, öylek;! X ;! Y (M) ve p M çn,! X p ;! Y p T M (p) dr. Böylece ç çarp m h ; T M (p)! T M (p)! R smetrk b-lneer, non-dejenere dönüşüm tan mlayan h ; üzernde br metrk tensör denr.[] p fonksyonuna T M (p) Tan m.5 M br C -s n f ndan manfold ve h ; de M üzernde sabt ndeksl br metrk tensör olmak üzere (M; h ; ) klsne br yar -Remann manfoldu denr. M nn ndeks v olmak üzere 0 v n = boym çn, v = 0 se M nn br Remann manfoldu, v = ve n durumunda se M ye Lorentz manfoldu denr.[] Tan m.6 R, -boyutlu standart reel vektör uzay üzernde 8p R ve V p ; W p T p (R ) olmak üzere hv p ; W p = v w + v w + v w + v w (.6) eştl¼gyle verlen v-ndeksl metrk tensörle elde edlen uzaya yar -Ökldyen uzay denr ve RV le gösterlr. Burada s ras yla v ve w ler V p ve W p tanjant vektörlernn bleşenlerdr. []
23 Özel olarak v = ve n durumunda se E, -boyutlu Mnkowsk uzay ad n al r. Metrk tensör se Lorentz metr¼g olarak adland r l r.[] Tan m.7! X = ( ; ; ; ) E olsun. E¼ger, D!X! E ) ; X < 0 se! X tmelke vektör, D!X! E ) ; X > 0 veya! X = 0 se! X spacelke vektör, D!X! E ) ; X = 0 ve! X 6= 0 se! X null vektör olarak fade edlr.[] Tan m.8 E Mnkowsk -uzay n n bütün tmelke vektörlern kümes olsun. Böylece 8u çn C (! u ) = f! h! u ;! x < 0g =! E g (x u; x u) < 0 (.7) bçmnde tan mlanan C (! u ) kümesne u yu çeren E ün tme-kons denr.[] τ z C ışık kons x Space lke y Tme lke Lght lke şekl Teorem. E Mnkowsk -uzay nda! x ve! y tmelke vektörler ayn tmekonsnn eleman se h! x ;! y = k! x k k! y k cosh (.8) olacak şeklde br tek 0 reel say s vard r. Yukar dak verlen reel say s na! x ve! y tmelke vektörler aras ndak Lorentz tmelke aç denr.[; ]
24 MINKOWSKI -UZAYINDA EULER-LAGRANGE MEKAN IK S ISTEM- LER Teork zkte Mnkowsk -uzay, -boyutlu Ökld uzay na -zaman parametres eklenerek tan mlanan uzayd r. Bu sebeple ço¼gunlukla Ökld uzay le zomorf olarak da kabul edlr. Br Ökldyen uzay n smetr grubu Ökldyen grup olarak adland r l r ve Mnkowsk uzay çn br Poncare grubudur. Mnkowsk uzay Poncare grubun homojen uzay olarak br a n uzayd r. Dolay s yla n çn n boyutlu Mnkowsk uzay, n reel boyutlu br vektör uzay d r. n boyutlu reel uzay n geometrk olarak C - manfold yap s na da sahp oldu¼gu aşkard r. Bu bölümde öncelkle çal şmam z n temel alan n oluşturan Euler-Lagrange mekank sstemlern nceleyece¼gz.. EULER-LAGRANGE S ISTEMLER.. de tan mlanan (E; ; M) demetn ele alal m. Burada E total manfold, M baz manfold olarak kabul edlmşt. Ayr ca, E ve M brer C - manfoldlard r. Mnkowsk geometrsnde çal ş rken key br M manfoldu çn demet yap s oluşturmak zksel uygulamalar aç s ndan elverşl de¼gldr. Çünkü, bu kullan mda jet demet yap s tan mlan rken oluşturulan türevsel koordnatlar n genel br durumu söz konusu olur. Bu se zksel yorumlar güçleştrr. Ayr ca, zksel yorumlamlarda genel olarak -boyutlu uzay yap s le zaman parametres kullan m daha yayg nd r. Bu sebeple oluşturaca¼g m z demet yap s n n baz manfoldunu br boyutlu reel uzay R olarak kabul edece¼gz. Bu kabulün başka br avantaj se bu uzayda tan mlayaca¼g m z koordnat zaman parametres olarak kabul edeblmemzdr. Zaten mekank sstemler üzerne yap lan çal şmalar n uygulamalar nda baz uzay olarak reel uzay n al nmas s kl kla terch edlmektedr. O halde Mnkowsk demet yap s n kurmak çn total manfoldu da çal şmam z gereken uzay yap s olarak seçmelyz. Yan, Mnkowsk uzay n n yukar da verd¼gmz aç klamaya dayal olarak kabul edlen manfold yap s n kullanmal y z. O halde, (E; ; R) n br demet oldu¼gunu görelm. Demet yap s çn öncelkle trval yap y oluşturmak gerekr. Bunun çn gerekl olan ve bölüm.. de tan mlanan komütatf dyagram aşa¼g dak şeklde fade edlrse; E! E # # R R I! R R (.) 5
25 burada br zomor zm, R örten submersyon ve I R özdeşlk dönüşümü olmak üzere olur. D¼ger br fadeyle = I R R I R = R oldu¼gundan. dyagram komütatftr. Sonuç olarak dferansyelleneblr br dönüşümdür. Böylece, (E ; ; R) br demet yap s oluşturur. Şmd (E ; ; R) demetn alal m. Bu demet üzerndek jet demet yap s n J E olarak tan mlayal m. Bu durumda jet demetn koordnatlar aşa¼g dak şeklde fade edlecektr. E n koordnatlar ( ; ; ; ) ve R nn koordnat (t) olmak üzere, J E n koordnatlar (t; ; ; ; ; ; ; ; ) (.) şeklnde tan mlan r. Burada, jet demet yap s ndan gelen ( x ) türevsel koordnatlar aşa¼g dak şeklde fade edlr. = d dt ; = d dt ; = d dt ; = d dt (.) () kest se, R! E t! (t) olarak belrldr ve = d R sa¼glan r. (U; u) ndrgenmş koordnat sstemn de, U = J p (p) U u = (t; x ; x ) olarak tan mlar z. Buna ba¼gl olarak, bu koordnatlar çn t J p = tj p ; x J p = x ( (p)) eştlkler geçerl olup, yen tan mlanan -adet x U! R fonksyonlar göz önüne al nd ¼g nda, x (Jp ) = t j p; (.) eştl¼g vard r. Böylece, Mnkowsk uzay çn jet demet yap s oluşturulmuş olur. Şmd, oluşturdu¼gumuz bu demet yap s üzernde bölüm.. de verlen mekank sstemler oluştural m. Bunun çn öncelkle en temel geometrk yap 6
26 olan ve. de verlen yaklaş k tanjant yap n n varl ¼g n ve matematksel fadesn görmemz gerekr. Buna göre, E üzerndek jet demet çn yaklaş k tanjant yap, J T J E! T J E şeklnde fade edlen br dönüşüm olup, J = 0 koşulunu sa¼glayan (; ) tpnden tensör alan olmal d r.o halde, J E demet üzerndek tan mlanan koordnat sstemn kullanarak aşa¼g dak şeklde yaklaş k tanjant yap y oluşturablrz. alan J = J ; = ; J J = = J x = J x = J x = J x = 0 J = t x + x + x + x Dkkat edlrse J = 0 koşulu sa¼glan r. Yukar da aç k fades verlen J tensör J = ( d x dt) + (d + dt) + (d + dt) + (d + dt) x x elde edlr. Bundan sonra elde edlecek geometrk yap lar, koordnat fonksyonlar n n çoklu¼gu aç s ndan uygun br düzenleme le formülze edeblmek çn notasyonlar kullanaca¼g z. Mnkowsk metr¼gnden gelen negatf termn bu düzenleme çersnde korunablmes çn, negatf ve poztf termler betmleyen notasyonlar belrleyece¼gz. Buna göre J yaklaş k tanjant yap k saca, olmak üzere ( ; = = ; = ; ; X J = (dx x dt) x = (.5) 7
27 şeklnde fade edleblr. Bu se yne (; ) tpnden tensör alan n gösterr. Bu durumda, bölüm.. de tan mlanan ve aç k fades. le gösterlen semspray bu bölümde kullan lan jet demet yap s üzernde aşa¼g dak şeklde fade edlr; " = t " x + " x + " x + " x K saca, " = X t + = x + " x x (.6) şeklndedr. Bu semsprayn yaklaş k tanjant yap üzerndek de¼ger al narak elde edlen Louvlle vektör alan se; V = = X + x = + + x x (.7) şeklnde belrlenr. Mekank sstemler çn enerj denklemlernn elde edlmesnde kullan lan ve bölüm.. de. le verlen Poncare-Cartan -formu,.5 le verlen Poncare- Cartan -formu tan mlayablmemz çn öncelkle dferansyel operatörü Mnkowsk jet demet yap s n n koordnatlar le fade etmemz gerekr. O halde d dferansyel operatörü d = t dt d + d + d + d K saca, x d x + x d x + x d x + d d = t dt + X dx + x x d x = (.8) 8
28 olarak tan mlan r. Buna göre, Mnkowsk jet demet yap s n n koordnatlar le Poncare-Cartan -formu bölüm.. dek şlemlere benzer olarak aşa¼g dak bçmde elde edlr. L = d J L + Ldt = L x dt + L x dt + L x dt + L x dt L x d + L x d + L x d + L x d + Ldt Bu eştlk k saca, L = X L x x dt + L x dx + Ldt = (.9) şeklnde fade edleblr. Cartan -form elde edlr. Bu -formun tekrar dferansyellenmes le Poncare- L = dd J L + dl ^ dt = (d ^ dt) t x + L + (d ^ dt) + x t x x + x + x + L + (d ^ dt) + x t x x + x + x + L 9
29 + (d ^ dt) + x t x x + x + x + L + (d x ^ dt) x + (d x ^ dt) + (d x ^ dt) + (d x ^ dt) + (d ^ d ) x + x + x + x + x + x + x + x + x + L x +(d ^ d ) x + L x + L x + x + L x x + L x + (d ^ d ) + (d ^ d ) x + L x +(d ^ d ) x + L x +(d ^ d ) x + L x x + L x + (d ^ d x ) + (d ^ d x ) + (d ^ d x ) + (d ^ d x ) x + (d ^ d x ) + (d ^ d x ) + (d ^ d x ) + (d ^ d x ) x + (d ^ d x ) + (d ^ d x ) 0
30 + (d ^ d x ) + (d ^ d x ) x + (d ^ d x ) + (d ^ d x ) + (d ^ d x ) + (d ^ d x ) x bulunur. K saca, = j = 8 >< j = > ( ; = ; = ; ; ; = j = ; ve = j ; ve 6= j j = ( 0; = j ; 6= j notasyonlar kullan larak L = + " X ("(dx ^ dt) = + P (d x ^ dt) ;j= P j x j j= (d x ^ d x j ) j!# P t x + j x j j= x x j!# L x + x j x + L x ) + (dx ^ dx j ) x x j j x x j + L (.0) eştl¼g le fade edlen -forma Poncare Cartan -formu denr. Bölüm.. de.6 da verlen " = (") = 0 denklemnn çözümlernn Euler-Lagrange enerj denklemn verd¼gn blyoruz. Buna göre, yukar da tan mlad ¼g m z geometrk yap lar kullanarak bu denklem çözdü¼gümüz taktrde, elde
31 edlen çözüm, Mnkowsk jet demet üzernde Euler-Lagrange denklemn verr. Dolay s yla bu çözüm çn gerekl olan şlemler yaparsak, " = (") = ( L t + L x + x + x + +" x + " x + " x + " x )d ( t x + x + x + x + L x + x + x + " x " x " x x " x x )d ( t x + x + x + x + L x + x + x + " x x " x " x " x x )d ( t x + x + x + x + L x + x + x + " x x " x x " x " )d
32 ( x x x )d ( x x x + x + x + x + L + x + x + x + x )d ( x x x + x + x + x + L + x + x + x + x )d ( x x x + x + x + x + L x + x + x + x + x )d +( t x + x + + x + L t + x x + x + x + L t x + x x + L x + t x + x + L
33 " x + " +" x " x + " x + " x +" x + " x " +" " x + " x + " x + " x + " +" x + " L L L x + " x + " x )dt eştl¼g elde edlr. K saca, " = (") = ( P P x t x + = = x P x j j=! P + " j x x j x j= x j P + L L x x + " = x L + " x dt + ( P = t x L P x + " j ;j= x x + j j x x x j + P ;j= j x j ) ( dx x j x P ;j= j x j x x + j x j x x j ) d x şeklnde fade edleblr. Bulunan denklem homojen br dferansyel denklemdr. Dolay s yla elde edlen bu denklemde her dferansyel termn katsay s s f ra eşt olmal d r. Bu eştl¼gn kurulmas le aşa¼g dak denklem sstem elde edlr.
34 ) t x + ( L + L x + L x + L x + L) +( x + x + L L L L x (" x + " x + " x + " x ) = 0 ) t ( L + L x + L x + L x + L) +( x + x + + x x + L L L L (" + " + " + " ) = 0 ) t ( L + L x + L x + L x + L) +( x + x + + x x + L L L L (" x + " x + " x + " x ) = 0 ) t ( L + L x + L x + L x + L) +( x + x + + x x + L L L L (" x + " x + " x + " x ) = 0 5) + x + x + x + L + + x + x + L = 0 6) x L 5
35 x x x x L = 0 7) x x x x x L L = 0 8) x x x x x L L = 0 9) t x + x + x + x + L t x + x + x + x + L t x + x + x + x + L t x + x + x + x + L " x + " x + " x + " " x + " x + " x + " " x + " x + " x + " " x + " x + " x + " x L L L +" x + " x + " x = 0 6
36 denklem sstem elde edlr. K saca, ) t x + L P = x L + L x P x " L = x + P =;j= j xj x x j x j x = 0 ) t L P = x L + L x + P x = " L x P =;j= j xj x x j x j x = 0 ) t L P = x L + L x + P x = " L x P =;j= j xj x x j x j x = 0 ) t L P = x L + L x + P x = " L x P =;j= j xj x x j x j x = 0 5) P x = x L + L x + P x L x = x L = 0 6) P x = x L + L x P x L x = + L x = 0 7) 8) P x = P x = x L x L + L x + L x + P x + P x L x = L x = + L x + L x = 0 = 0 7
37 9) ( P P x t x + = = x P + L L x x + " = x P x j j=! P + " j x x j x j= L + " x = 0 x j (.) şeklnde yaz lablr. Euler-Lagrange enerj denklemnn elde edleblmes çn. dek k sm türevl denklem sstem çözümlenmeldr.. non-lneer br denklem sstemdr. Dolay s yla, br özel kabul alt nda çözümü mümkündür.bu nedenle arad ¼g m z çözüm çn özel olarak, " = ; " = ; " = ; " = (.) kabulünü yapal m. Bu kabulü yaparken dkkat ett¼gmz husus, Mnkowsk metr- ¼gnde lk termn negatf al nmas sebebyle ve çal şmam zda bu metrk kullan ld ¼g çn burada da lk termn negatf olmas d r. Bunun d ş nda, katsay fonksyonlar olan " ler hem t hem de x koordnat fonksyonlar n çermeldr. Türevsel koordnatlar n t ve x koordnatlar na ba¼gl oldu¼gunu bld¼gmze göre, katsay fonksyonlar n n yerne özel olarak türevsel koordnatlar kullanmam z uygun olur. kabul alt nda yukar dak denklem sstemnn ortak çözümü ncelenecektr. Yne metr¼gn negatf tan ml l k özell¼gn dkkate alarak çözüm yap lmal d r. Bulunan çözüm se.7 le verlen herhang br demet üzernde elde edlmş olan Euler- Lagrange denklemnn genel yap s le örtüşmeldr. Yap lan gerekl ncelemeler ve şlemler sonucunda aşa¼g da verlen ortak çözümün en elverşl çözüm oldu¼gu görülmüştür. Buna göre, Bu () () () () + x (5) (6) (7) (8) + (9) = 0 ortak çözümünü yapar z. Gerekl hesaplamalar tamamland ¼g nda aşa¼g da verlen homojen dferansyel denklem elde edlr. t t t t x + x + x + 8 x + L
38 x + x + x + x + L x + x + x + x + L x + x + x + x + L + x + x x + x + x x + x + x + x + x + x + x + x + x + + x L x + L x + L x = 0 (.) Sonuçta, bulunan bu denklem, elde edlmes stenlen Euler-Lagrange denklemnn aç k haldr. Böylece çözüm tamamlanm ş olur. K saca, = ; = ; = ; ; olmak üzere Mnkowsk jet demet yap s üzernde Euler-Lagrange enerj denklem aşa¼g dak şeklde fade edlr. 9
39 t! X L x = x! X L + x + = x X L x x = + X = L x! X L x j + x j j= L x x! X L x x = + + X =! X L x = x X L x = 0 x = L x x!! X L x j j= x j (.).7 de verlen denklem le bu denklemn brnc ve sonuncu termler benzerdr. Sadece özel kabulümüzden kaynaklanan katsay fonksyonlar m z eklenmştr. Bu fonksyonlar daha da özelleştrp, örne¼gn br sabt de¼gern alsayd k bu katsay lar oluşmazd. Aradak termler kullan lan metr¼gn negatf tan ml olmas ndan dolay oluşur..7 de metrk poztf oldu¼gundan bu termler sadeleşmeyle ortadan kalkar. Sonuç olarak. eştl¼g Mnkowsk uzay nda Euler-Lagrange enerj denklemn fade eder.. UYGULAMALAR Bu k s mda. le verlen Euler-Lagrange enerj denklemnn baz yüzeyler üzernde ncelenmesne dar örnekler verlmştr. Burada amaç, enerj fonksyonunu t zaman ve x konum de¼gerne göre elde ederek, enerj de¼gern hesaplamakt r. Bu sayede oluşan hareket ve hareket esnas nda ortaya ç kan enerj çn matematksel hesaplaman n yan s ra zksel yorum da yap lablr. Böylece çal şmam z teork zkte kullan lan matematksel kavramlar daha somut hale getrr. Ayr ca dferansyel denklemlern çözümü, enerj fonksyonunun bulunmas n n yan s ra bu fonksyon le hareketn her aşamas nda ortaya ç kan enerj de¼gern hesaplamay avantajl k lar... Örnek (HEL IS ÖRNE ¼G I) Mnkowsk zaman-kon üzernde () = (t; r snh u; r cosh u sn ; r cosh u cos ) (.5) 0
40 helsn alal m. [] Bu hels e¼grsn aşa¼g dak gra kle göstereblrz. m null tme lke space lke future past helx şekl Şekl- de uzayda al nan hareketl br m parçac ¼g n n Mnkowsk zaman kon üzerne düştükten sonra, kon çnde kalan hels e¼grs üzerndek hareketn görmekteyz. Zaman kon d ş nda kalan e¼grler space-lke e¼gr olarak tan mlan r. Dolay s yla parçac ¼g n kon üzerne düşene kadar yapt ¼g hareket space-lke br e¼gr üzernde olmal d r. Kon kabu¼guna de¼gd¼g anda, hareketl csm null br vektör üzerne düşmüş olur. Zaman konnn çnde kalan e¼grler tme-lke e¼grdr. m parçac ¼g kon çnde hareketne devam ederse, bu hareketn do¼grultu ve büyüklü¼günü oluşturan vektörler brer tme-lke vektör olmal d r. Bzm esas çal şma alan m z kon çnde oluşan hareket oldu¼gundan, sadece tme-lke vektörler le çal şmam z gerekt¼g aç kt r. Dolay s yla, hels e¼grsne herhang br noktadak te¼get vektörün tme-lke olmas ncelend¼gnde e¼grnn parametrzasyon de¼gerler çn baz şartlar oluşur. Elde edlen bu koşullar çal şmam zdak temel kavramlar n do¼grulu¼gu le uyuşmaktad r. Ayr ca çözüm de¼gerlermz üzernde de hareketn oluşumu aç s ndan baz s n rlamalar getrr. Bu s n rlaman n olmas da hareketn tme kon le s n rl olmas ve konnn gelecek k sm ndan geçmşe do¼gru oluşmas aç s ndan do¼gald r. D¼ger yandan uzaydak hareketn, yan space-lke e¼gr üzernde oluşan hareketn zaman aral ¼g le tme kon çnde oluşan hareketn zaman aral ¼g farkl al nablr. Bunun sebeb zksel anlamda yer çekmnden kaynaklanan uzay ve dünyadak hareketlerde oluşan zamandak farkl l kt r. Bu k kavram her ne kadar brbrne ba¼gl olablse de matematksel olarak k ayr parametre le tan mlanablrler. O halde, bu çal şmada uzay zaman s ve tme kon çnde geçen zaman t parametres le fade edelm. Şmd, al nan hels e¼grs çn jetler tan mlayal m. Jet manfold yap s n kurmak çn öncelkle koordnat sstemn oluşturmal y z. Brnc jetlern e¼grnn
41 te¼get vektörler le çak ş k oldu¼gunu blyoruz. Bu nedenle hels e¼grsnn brnc türevn alarak bze gerekl olan jet koordnat sstemn elde ederz. O halde, bu koordnatlar aşa¼g dak şeklde belrlenr; s; t; r snh u; r cosh u sn ; r cosh u cos ; t; r snh u; r cosh u sn ; r cosh u cos! (.6) Burada türevsel koordnatlarda kullan lan t ve r parametreler t = dt ds ; r = dr ds (.7) le belrldr. Hels çn aç s sabt kalaca¼g ndan bu parametre çn türev söz konusu de¼gldr. D¼ger yandan hels e¼grsnn tme-lke br e¼gr olmas gerekt¼gn fade etmştk. O halde, 0 ; 0 < 0 olmal d r, ayr ca k tme-lke vektör aras ndak aç oldu¼gunda.8 eştl¼g sa¼glan r. 0 () = (0; ru cosh u; ru snh u sn + r cosh u cos ; ru snh u cos r cosh u sn ) oldu¼guna göre yukar dak.8 eştl¼g dkkate al n rsa D 0 ; 0E = r cosh u u elde edlr. Burada.6 le verlen metr¼g kullan rken 0 () h z vektöründek brnc term hmal ederz. Bunun sebeb, çal şmam zda brnc koordnat zamana karş l k geld¼g çn, burada da bu koordnat s f r oldu¼gundan zksel olarak br anlams zl kla karş laş r z. Bu nedenle h z vektörünü tan mlarken vektörü zamandan ayr tutup, konum de¼gerlerne ba¼gl kalaca¼g n gözönüne al r z. Bu nedenle.6 dek metr¼g dkkate ald ¼g m zda ve 0 ; 0 < 0 olaca¼g çn u < cosh u < u koşulu alt nda çözüm vard r..6 le fade edlen jet koordnatlar. Lagrange enerj denklemnde yerne yaz l rsa hels e¼grs üzernde tan mlad ¼g m z hareketn Euler-Lagrange enerj denklemn elde ederz. Böylece, t L s t r snh u s r snh u r cosh u sn s r cosh u sn
42 r cosh u cos s r cosh u cos t L t t + t r snh u t r snh u + t r cosh u sn t r cosh u sn + t r cosh u cos t r cosh u cos + t L t t r snh u r snh u t + ( r snh u) r snh u r snh u + r snh u r cosh u sn r snh u r cosh u sn + r snh u r cosh u cos r snh u r cosh u cos + r L snh u r snh u t r cosh u sn r cosh u sn t + r snh u r cosh u sn r cosh u sn r snh u + ( r cosh u sn ) r cosh u sn r cosh u sn + r cosh u sn r cosh u cos r cosh u sn r cosh u cos + r L cosh u sn r cosh u sn t r cosh u cos r cosh u cos t + r snh u r cosh u cos r cosh u cos r snh u + r cosh u sn r cosh u cos r cosh u sn r cosh u sn + ( r cosh u cos ) r cosh u cos r cosh u cos + r L cosh u cos r cosh u cos
43 + t L t t + t r snh u t r snh u + ( r snh u) r snh u r snh u + r snh u r cosh u sn r snh u r cosh u sn + r snh u r cosh u cos r snh u r cosh u cos + t r cosh u sn r cosh u sn t + r snh u r cosh u sn r cosh u sn r snh u + ( r cosh u sn ) r cosh u sn r cosh u sn + r cosh u sn r cosh u cos r cosh u sn r cosh u cos + t r cosh u cos t r cosh u cos + r snh u r cosh u cos r snh u r cosh u cos + r cosh u sn r cosh u cos r cosh u sn r cosh u cos + ( r cosh u cos ) r cosh u cos r cosh u cos t r snh u t r snh u t r cosh u sn t r cosh u sn t r cosh u cos t r cosh u cos + r L cosh u cos r cosh u cos + r L snh u r snh u + r L cosh u sn r cosh u sn = 0
44 Euler-Lagrange enerj denklem elde edlr. Gerekl sadeleştrmeler yaparak denklem düzenled¼gmzde, t L s t r L s r t L t t + t r L t r + t L t t r L r t + 9 r r r + r L r + t L t t + t r L r t + 9 r r r t r L r t + 6 r L r = 0 (.8) denklem elde edlr. Burada s ve t zaman de¼gerler brbrlerne ba¼gl kabul edlmştr. Yan, dt ds olur. Böylece, t = ks eştl¼g elde edlr. = k(sbt) (.9).8 denklem non-lneer br denklem oldu¼gundan ancak özel koşul alt nda çözüleblr. Burada t = t(s); L = L(t; s) oldu¼guna göre özel koşulu al rken öncelkle türevsel koordnatlar kullanmay terch ederz. Buna göre dl d r = ) L = r (.0) dl d t = ) L = t (.) koşullar n n varl ¼g n kabul edelm. Bu koşullar.8 de yerne yazarsak dt L ds t + dr L ds r + 6dr L ds r = 0 denklemn elde ederz. Bu denklemn düzenlenmes le L s + L s + 6 r L r = 0 eştl¼g bulunur. Yukar dak koşullar n tekrar kullan m ve sadeleştrme le 5
45 ) r + L s = 0 ) dr ds + L r r s = 0 ) dr + L = 0 ds r eştl¼g elde edlr. Burada dr 6= 0 oldu¼gundan ds olmal d r. Böylece, L r = L = r (.) enerj fonksyonu elde edlr. D¼ger taraftan,.0 ve. eştlklern eştlersek, r = r olaca¼g ndan, dr ds = r ) r = e s t ) r = e k (.) elde edlr. Buldu¼gumuz. yar çap fonksyonunu. enerj fonksyonunda yerne yazarsak, t L = e k (sbt) (.) 6
46 bulunur.. eştl¼g hels e¼grs çn Euler-Lagrange enerj fonksyonudur. Kabulümüze uygun olarak temel parametrenn zaman oldu¼gunu görürüz. Demek k hareket ve hareketn oluşturdu¼gu enerj zamana ba¼gl olarak de¼ger al r. Burada dt = k eştl¼g le belrl olan k y bulmak çn aşa¼g dak yol zlenr. ds Dünya zaman le Mnkowsk uzay zaman aras ndak oran k oldu¼guna göre, hareketl csmn dünyadak h z n n Mnkowsk uzay ndak h z na oran da k olmal d r. Buna göre, (t) = (t; r snh u; r cosh u sn ; r cosh u cos ) hels e¼grsn gözönüne ald ¼g m zda Ökld uzay nda bu e¼gr boyunca hareket eden csmn h z d dt = ; dr dr dr snh u; cosh u sn ; cosh u cos dt dt dt eştl¼gnden s d d dt = dt ; d s = + dt dr cosh u dt elde edlr. Benzer şeklde Mnkowsk uzay ndak h z se d dt ds = ds ; dr dr dr snh u; cosh u sn ; cosh u cos ds ds ds olur ve s d d ds = ds ; d s dr = cosh u k ds ds h z de¼ger bulunur. O halde bu eştlkler oranlad ¼g m zda, k oran n n korunaca¼g n bld¼gmze göre aşa¼g dak eştl¼g yazablrz. d dt d ds = s dr + cosh u dt s dr = k (.5) cosh u k ds 7
47 Burada. le belrl olan yar çap fonksyonunda t ve s ye göre türevler gözönüne al r ve yerne yazarsak, r + 9 k e t k cosh u r 9 e s cosh u k = k bulunur. Gerekl düzenlemeler yaparak k oran le t zaman aras nda varolan ba¼g nt y aşa¼g dak şeklde elde ederz. t = k ln k ( + k ) 9 (k ) cosh u (.6).. Örnek (ÇEMBER ÖRNE ¼G I) Mnkowsk zaman-kon üzernde () = (t; r cos ; r sn ; u) (.7) çembern alal m. m null space lke future past tme lke crcle e m r tme lke şekl Şekl- de uzayda al nan hareketl br m parçac ¼g n n Mnkowsk zaman kon üzerne düştükten sonra, kon çnde kalan çember e¼grler üzerndek hareketn 8
48 görmekteyz. Bu örnekte de hels örne¼gndekne benzer br hareket düşünmekteyz. Bu nedenle hels örne¼gnde ald ¼g m z e¼gr tpler burada da geçerldr. Yaln z m csm burada helsten farkl olarak çember e¼grlerne bell br noktada de¼gecek şeklde düşme yapar. Bu düşme esnas nda çemberlern yar çaplar n n zamana ba¼gl olarak de¼gşece¼g aç kt r. Bu de¼gşm hels örne¼gnde oldu¼gu gb enerjnn zamana ba¼gl olmas n gerektrr. Bunun yan s ra,bu çal şmada uzay zaman s ve tme kon çnde geçen zaman t parametres olmak üzere, bu zaman de¼gerler aras nda yne belrl br oran olmal d r. Şmd al nan çember e¼grs çn jetler tan mlayal m. Brnc jetlern e¼grnn te¼get vektörler le çak ş k oldu¼gunu bld¼gmze göre, çember e¼grsnn brnc türevn alarak bze gerekl olan jet koordnat sstemn elde ederz. O halde, jet koordnatlar aşa¼g dak şeklde belrlenr; s; t; r cos ; r sn ; u; t; r cos ; r sn ; 0 (.8) Burada türevsel koordnatlarda kullan lan t ve r parametreler.7 de verld¼g şeklde belrldr. m csmnn düşme hareketnn bell br noktada oldu¼gunu kabul ett¼gmz çn, bu noktan n ve zdüşümlernn, çemberlern asal eksenler le yapt ¼g aç s n n sabt kalaca¼g n kabul edeblrz. Dolay s yla parametres çn zamana göre türev söz konusu de¼gldr. D¼ger yandan çember e¼grs br tme-lke br e¼gr oldu¼gundan 0 ; 0 < 0 olmal d r. 0 () = (0; r sn ; r cos ; 0) oldu¼gundan yan sn < 0 80 < < 60 koşulu sa¼glanmal d r. Bu se şekl- de görülmektedr. 90 < < 80 (.9).8 jet koordnatlar n. enerj denklemnde yerne yazarsak, t L st r cos s r cos r sn s r sn 9
49 t L t t + t r cos t r cos + t r sn t r cos + t L t t r cos r cos t + ( r cos ) r cos r cos + r cos r sn r cos r sn + r L cos r cos t r sn r sn t + r cos r sn r cos r sn + ( r sn ) r sn r sn + r L sn r sn + t L t t +t r cos r cos t + ( r cos ) r cos r cos + r cos r sn r cos r sn + t r sn r sn t + r cos r sn r cos r sn + ( r sn ) r sn r sn t r cos t r cos t r sn t r sn + r L cos r cos + r L sn r sn = 0 Euler-Lagrange enerj denklemn elde ederz. Bu denklem düzenled¼gmzde, t L s t r L s r t L t t + t r L t r + t L t t r L r t + r r r + r L r + t L t t + t r L r t + r r r t r L r t + r L r = 0 (.0) elde edlr. Burada s ve t brbrne ba¼gl oldu¼gundan,.9 eştl¼gn gözönüne ald ¼g m zda t = ks olur. Elde edlen bu denklem yne non-lneer br denklem oldu¼gundan özel koşul alt nda çözüme gderz. Bu örnekte de.0 ve. koşullar n aynen kabul edelm. Bu koşullar le denklem yenden düzenlersek, dt L ds t + dr L ds r + dr L ds r = 0 0
50 ) L s + L s + r L r = 0 ) r + L s = 0 ) dr ds + L r r s = 0 ) dr + L = 0 ds r eştl¼g elde edlr. Burada dr ds 6= 0 olaca¼g ndan L r = bulunur. Bu eştl¼gn çözümü le L = r (.) Euler-Lagrange fonksyonu elde edlr. D¼ger taraftan,.0 ve. den r = r olaca¼g çn, dr ds = r ) r = e s
51 ) r = e t k (.) yar çap fonksyonu elde edlr. O halde çember e¼grs çn Euler-Lagrange fonksyonu, t L = e k (sbt) (.) olarak belrlenr. Kabulümüze uygun olarak yne temel parametrenn zaman oldu¼gunu görürüz. Demek k çember üzernde de hareket ve hareketn oluşturdu¼gu enerj zamana ba¼gl olarak de¼ger al r. Burada da dt = k eştl¼g le belrl olan k y bulmak çn yukar dak örne¼ge ds benzer yol zlenr. (t) = (t; r cos ; r sn ; u) çember e¼grsn gözönüne ald ¼g m zda Ökld uzay nda bu e¼gr boyunca hareket eden csmn h z türev hesaplanarak d dt = ; dr dr cos ; sn ; 0 dt dt s d d dt = dt ; d s = + dt dr dt de¼ger le elde edlr. Benzer şeklde Mnkowsk uzay ndak h z se, Mnkowsk zamana göre türev al narak, d dt ds = ds ; dr dr cos ; sn ; 0 ds ds s d d ds = ds ; d s dr = k ds ds bulunur. O halde bu eştlkler oranlad ¼g m zda,
52 d dt d ds = s dr + dt s dr = k (.) k ds eştl¼g elde edlr. Burada. le belrl olan yar çap fonksyonunun t ve s ye göre türevlern gözönüne al r ve yerne yazarsak, r + 6 9k e 8t k r = k 6 9 e 8 s k eştl¼g bulunur. Burada gerekl düzenlemeler yapt ¼g m zda, t = k 9k 8 ln ( + k ) 6 (k ) k oran le t zaman aras ndak ba¼g nt elde edlr. (.5)
53 MINKOWSKI -UZAYINDA HAMILTON MEKAN IK S ISTEMLER Bu bölümde analtk mekan¼gn öneml konular ndan br d¼ger olan Hamlton mekank sstemlern nceleyece¼gz. Öncelkle bölüm- de verlen Mnkowsk jet demet yap s üzernde, Hamlton enerj denklemn elde etmek çn gerekl geometrk yap lar tan mlayaca¼g z. Daha sonra bulunan enerj denklemnn baz örnekler üzernde uygulamalar n gösterece¼gz.. HAMILTON S ISTEMLER Bölüm. de tan mlad ¼g m z Mnkowsk jet demet J E ü ele alal m. Bu demet yap s üzerndek ndrgenmş koordnat sstem. le belrlenmştr. Hatta jet demet yap s ndan gelen türevsel koordnatlar burada da. le ayn bçmde fade edlr. Buna göre, verlen koordnat sstem kullan larak bölüm.. de herhang br demet üzernde tan ml olan Hamlton mekank sstemlern Mnkowsk jet demet yap s üzernde oluşturablrz. Aşa¼g da s ras yla bu geometrk yap lar tan mlanm şt r. Bölüm. de Mnkowsk- uzay n n Ökld uzay na eş de¼ger oldu¼gunu, dolay s yla br manfold yap s na sahp oldu¼gunu belrtmştk. Buna göre Mnkowsk- uzay üzernde br kotanjant manfold yap s n n da var oldu¼gu aç kt r. Bu kotanjant yap le burada da.8 le verlen Louvlle form tan mlanablr. O halde, Mnkowsk jet demet yap s üzernde Louvlle form = x d + x d + x d + x d X = x dx = (.) eştl¼g le fade edlr..8 le tan mlanan dferansyel operatör kullan larak elde edlen = d kanonk smplektk formu aşa¼g dak bçmdedr. = d ^ d x + d ^ d x + d ^ d x + d ^ d X = dx ^ d x = (.)
6. NORMAL ALT GRUPLAR
 6. ORMAL ALT GRUPLAR G br grup ve olsun. 5. Bölümden çn eştlğnn her zaman doğru olamayacağını blyoruz. Fakat bu özellğ sağlayan gruplar, grup teorsnde öneml rol oynamaktadır. Bu bölümde bu tür grupları
6. ORMAL ALT GRUPLAR G br grup ve olsun. 5. Bölümden çn eştlğnn her zaman doğru olamayacağını blyoruz. Fakat bu özellğ sağlayan gruplar, grup teorsnde öneml rol oynamaktadır. Bu bölümde bu tür grupları
Üç Boyutlu Yapı-Zemin Etkileşimi Problemlerinin Kuadratik Sonlu Elemanlar ve Sonsuz Elemanlar Kullanılarak Çözümü
 ECAS Uluslararası Yapı ve Deprem Mühendslğ Sempozyumu, Ekm, Orta Doğu Teknk Ünverstes, Ankara, Türkye Üç Boyutlu Yapı-Zemn Etkleşm Problemlernn Kuadratk Sonlu Elemanlar ve Sonsuz Elemanlar Kullanılarak
ECAS Uluslararası Yapı ve Deprem Mühendslğ Sempozyumu, Ekm, Orta Doğu Teknk Ünverstes, Ankara, Türkye Üç Boyutlu Yapı-Zemn Etkleşm Problemlernn Kuadratk Sonlu Elemanlar ve Sonsuz Elemanlar Kullanılarak
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeler http://ocm.mt.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında blg almak çn http://ocm.mt.edu/terms veya http://tuba.açık ders.org.tr adresn zyaret ednz. 18.102
MIT Açık Ders Malzemeler http://ocm.mt.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında blg almak çn http://ocm.mt.edu/terms veya http://tuba.açık ders.org.tr adresn zyaret ednz. 18.102
Deney No: 2. Sıvı Seviye Kontrol Deneyi. SAKARYA ÜNİVERSİTESİ Dijital Kontrol Laboratuvar Deney Föyü Deneyin Amacı
 SRY ÜNİVERSİESİ Djtal ontrol Laboratuvar Deney Föyü Deney No: 2 Sıvı Sevye ontrol Deney 2.. Deneyn macı Bu deneyn amacı, doğrusal olmayan sıvı sevye sstemnn belrlenen br çalışma noktası cvarında doğrusallaştırılmış
SRY ÜNİVERSİESİ Djtal ontrol Laboratuvar Deney Föyü Deney No: 2 Sıvı Sevye ontrol Deney 2.. Deneyn macı Bu deneyn amacı, doğrusal olmayan sıvı sevye sstemnn belrlenen br çalışma noktası cvarında doğrusallaştırılmış
uzayında vektörler olarak iç çarpımlarına eşittir. Bu iç çarpım simetrik ve hem w I T s formuna karşılık gelir. Buna p u v u v v v
 1. Temel Form: Brnc temel form geometrk olarak yüzeyn çnde blndğ zayına gtmeden yüzey üzernde ölçme yamamızı sağlar. (Eğrlern znlğ, teğet ektörlern açıları, bölgelern alanları gb) S üzerndek ç çarım, br
1. Temel Form: Brnc temel form geometrk olarak yüzeyn çnde blndğ zayına gtmeden yüzey üzernde ölçme yamamızı sağlar. (Eğrlern znlğ, teğet ektörlern açıları, bölgelern alanları gb) S üzerndek ç çarım, br
VANTİLATÖR TASARIMI. Şekil 1. Merkezkaç vantilatör tipleri
 563 VANTİLATÖR TASARIMI Fuat Hakan DOLAY Cem PARMAKSIZOĞLU ÖZET Bu çalışmada merkezkaç ve eksenel vantlatör tpler çn gelştrlmş olan matematksel modeln çözümünü sağlayan br blgsayar programı hazırlanmıştır.
563 VANTİLATÖR TASARIMI Fuat Hakan DOLAY Cem PARMAKSIZOĞLU ÖZET Bu çalışmada merkezkaç ve eksenel vantlatör tpler çn gelştrlmş olan matematksel modeln çözümünü sağlayan br blgsayar programı hazırlanmıştır.
5.3. Tekne Yüzeylerinin Matematiksel Temsili
 5.3. Tekne Yüzeylernn atematksel Temsl atematksel yüzey temslnde lk öneml çalışmalar Coons (53) tarafından gerçekleştrlmştr. Ferguson yüzeylernn gelştrlmş hal olan Coons yüzeylernde tüm sınır eğrler çn
5.3. Tekne Yüzeylernn atematksel Temsl atematksel yüzey temslnde lk öneml çalışmalar Coons (53) tarafından gerçekleştrlmştr. Ferguson yüzeylernn gelştrlmş hal olan Coons yüzeylernde tüm sınır eğrler çn
4.5. SOĞUTMA KULELERİNİN BOYUTLANDIRILMASI İÇİN BİR ANALIZ
 Ünsal M.; Varol, A.: Soğutma Kulelernn Boyutlandırılması İçn Br Kuramsal 8 Mayıs 990, S: 8-85, Adana 4.5. SOĞUTMA KULELERİNİN BOYUTLANDIRILMASI İÇİN BİR ANALIZ Asaf Varol Fırat Ünverstes, Teknk Eğtm Fakültes,
Ünsal M.; Varol, A.: Soğutma Kulelernn Boyutlandırılması İçn Br Kuramsal 8 Mayıs 990, S: 8-85, Adana 4.5. SOĞUTMA KULELERİNİN BOYUTLANDIRILMASI İÇİN BİR ANALIZ Asaf Varol Fırat Ünverstes, Teknk Eğtm Fakültes,
bir yol oluşturmaktadır. Yine i 2 , de bir yol oluşturmaktadır. Şekil.DT.1. Temel terimlerin incelenmesi için örnek devre
 Devre Analz Teknkler DEE AAĐZ TEKĐKEĐ Bu zamana kadar kullandığımız Krchoffun kanunları ve Ohm kanunu devre problemlern çözmek çn gerekl ve yeterl olan eştlkler sağladılar. Fakat bu kanunları kullanarak
Devre Analz Teknkler DEE AAĐZ TEKĐKEĐ Bu zamana kadar kullandığımız Krchoffun kanunları ve Ohm kanunu devre problemlern çözmek çn gerekl ve yeterl olan eştlkler sağladılar. Fakat bu kanunları kullanarak
2 Mayıs 1995. ELEKTRONİK DEVRELERİ I Kontrol ve Bilgisayar Bölümü Yıl içi Sınavı Not: Not ve kitap kullanılabilir. Süre İKİ saattir. Soru 1.
 ELEKONİK DEELEİ I Kntrl ve Blgsayar Bölümü Yıl ç Sınavı Nt: Nt ve ktap kullanılablr. Süre İKİ saattr. Sru.- r 00k 5k 5k 00Ω 5 6 k8 k6 7 k 8 y k5 0kΩ Mayıs 995 Şekl. Şekl-. de kullanılan tranzstrlar çn
ELEKONİK DEELEİ I Kntrl ve Blgsayar Bölümü Yıl ç Sınavı Nt: Nt ve ktap kullanılablr. Süre İKİ saattr. Sru.- r 00k 5k 5k 00Ω 5 6 k8 k6 7 k 8 y k5 0kΩ Mayıs 995 Şekl. Şekl-. de kullanılan tranzstrlar çn
Bir H Hilbert uzay üzerinde herhangi bir kompakt simetrik T operatörü için,
 Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
YAYILI YÜK İLE YÜKLENMİŞ YAPI KİRİŞLERİNDE GÖÇME YÜKÜ HESABI. Perihan (Karakulak) EFE
 BAÜ Fen Bl. Enst. Dergs (6).8. YAYII YÜK İE YÜKENİŞ YAPI KİRİŞERİNDE GÖÇE YÜKÜ HESABI Perhan (Karakulak) EFE Balıkesr Ünverstes ühendslk marlık Fakültes İnşaat üh. Bölümü Balıkesr, TÜRKİYE ÖZET Yapılar
BAÜ Fen Bl. Enst. Dergs (6).8. YAYII YÜK İE YÜKENİŞ YAPI KİRİŞERİNDE GÖÇE YÜKÜ HESABI Perhan (Karakulak) EFE Balıkesr Ünverstes ühendslk marlık Fakültes İnşaat üh. Bölümü Balıkesr, TÜRKİYE ÖZET Yapılar
VEKTÖRLER VE VEKTÖREL IŞLEMLER
 VEKTÖRLER VE VEKTÖREL IŞLEMLER 1 2.1 Tanımlar Skaler büyüklük: Sadece şddet bulunan büyüklükler (örn: uzunluk, zaman, kütle, hacm, enerj, yoğunluk) Br harf le sembolze edleblr. (örn: kütle: m) Şddet :
VEKTÖRLER VE VEKTÖREL IŞLEMLER 1 2.1 Tanımlar Skaler büyüklük: Sadece şddet bulunan büyüklükler (örn: uzunluk, zaman, kütle, hacm, enerj, yoğunluk) Br harf le sembolze edleblr. (örn: kütle: m) Şddet :
ROBİNSON PROJEKSİYONU
 ROBİNSON PROJEKSİYONU Cengzhan İPBÜKER ÖZET Tüm yerkürey kapsayan dünya hartalarının yapımı çn, kartografk lteratürde özel br öneme sahp olan Robnson projeksyonu dk koordnatlarının hesabı brçok araştırmacı
ROBİNSON PROJEKSİYONU Cengzhan İPBÜKER ÖZET Tüm yerkürey kapsayan dünya hartalarının yapımı çn, kartografk lteratürde özel br öneme sahp olan Robnson projeksyonu dk koordnatlarının hesabı brçok araştırmacı
1. KEYNESÇİ PARA TALEBİ TEORİSİ
 DERS NOTU 07 KEYNESÇİ PARA TALEBİ TEORİSİ, LM EĞRİSİ VE PARA TALEBİ FAİZ ESNEKLİĞİ Bugünk dersn çerğ: 1. KEYNESÇİ PARA TALEBİ TEORİSİ... 1 1.1 İŞLEMLER (MUAMELELER) TALEBİ... 2 1.2 ÖNLEM (İHTİYAT) TALEBİ...
DERS NOTU 07 KEYNESÇİ PARA TALEBİ TEORİSİ, LM EĞRİSİ VE PARA TALEBİ FAİZ ESNEKLİĞİ Bugünk dersn çerğ: 1. KEYNESÇİ PARA TALEBİ TEORİSİ... 1 1.1 İŞLEMLER (MUAMELELER) TALEBİ... 2 1.2 ÖNLEM (İHTİYAT) TALEBİ...
Adi Diferansiyel Denklemler NÜMERİK ANALİZ. Adi Diferansiyel Denklemler. Adi Diferansiyel Denklemler
 6.4.7 NÜMERİK ANALİZ Yrd. Doç. Dr. Hatce ÇITAKOĞLU 6 Müendslk sstemlernn analznde ve ugulamalı dsplnlerde türev çeren dferansel denklemlern analtk çözümü büük öneme saptr. Sınır değer ve/vea başlangıç
6.4.7 NÜMERİK ANALİZ Yrd. Doç. Dr. Hatce ÇITAKOĞLU 6 Müendslk sstemlernn analznde ve ugulamalı dsplnlerde türev çeren dferansel denklemlern analtk çözümü büük öneme saptr. Sınır değer ve/vea başlangıç
Sürekli Olasılık Dağılım (Birikimli- Kümülatif)Fonksiyonu. Yrd. Doç. Dr. Tijen ÖVER ÖZÇELİK
 Sürekl Olasılık Dağılım Brkml- KümülatFonksyonu Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr Sürekl olasılık onksyonları X değşken - ;+ aralığında tanımlanmış br sürekl rassal değşken olsun. Aşağıdak
Sürekl Olasılık Dağılım Brkml- KümülatFonksyonu Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr Sürekl olasılık onksyonları X değşken - ;+ aralığında tanımlanmış br sürekl rassal değşken olsun. Aşağıdak
fonksiyonu, her x 6= 1 reel say s için tan ml d r. (x 1)(x+1) = = x + 1 yaz labilir. Bu da; f (x) = L
 Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
ÇOKLU REGRESYON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESYON ÇÖZÜMLEMESİ,REGRES-YON KATSAYILARININ YORUMU
 6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
dir. Bir başka deyişle bir olayın olasılığı, uygun sonuçların sayısının örnek uzaydaki tüm sonuçların sayısına oranıdır.
 BÖLÜM 3 OLASILIK HESABI 3.. Br Olayın Olasılığı Tanım 3... Br olayın brbrnden ayrık ve ortaya çıkma şansı eşt n mümkün sonucundan m tanes br A olayına uygun se, A olayının P(A) le gösterlen olasılığı P(A)
BÖLÜM 3 OLASILIK HESABI 3.. Br Olayın Olasılığı Tanım 3... Br olayın brbrnden ayrık ve ortaya çıkma şansı eşt n mümkün sonucundan m tanes br A olayına uygun se, A olayının P(A) le gösterlen olasılığı P(A)
Sistemde kullanılan baralar, klasik anlamda üç ana grupta toplanabilir :
 5 9. BÖLÜM YÜK AKIŞI (GÜÇ AKIŞI) 9.. Grş İletm sstemlernn analzlernde, bara sayısı arttıkça artan karmaşıklıkları yenmek çn sstemn matematksel modellenmesnde kolaylık getrc bazı yöntemler gelştrlmştr.
5 9. BÖLÜM YÜK AKIŞI (GÜÇ AKIŞI) 9.. Grş İletm sstemlernn analzlernde, bara sayısı arttıkça artan karmaşıklıkları yenmek çn sstemn matematksel modellenmesnde kolaylık getrc bazı yöntemler gelştrlmştr.
GRUPLARDA VE YARIGRUPLARDA ETKİNLİK(EFFICIENCY) The Efficiency Of Groups And Semigroups *
 GRUPLARDA VE YARIGRUPLARDA ETKİNLİK(EFFICIENCY The Effcency Of Groups And Semgroups * Özer CAN Matematk Ana Blm Dalı Blal VATANSEVER Matematk Ana Blm Dalı ÖZET Bu çalışmada öncelkle gruplarda, yarıgruplarda,
GRUPLARDA VE YARIGRUPLARDA ETKİNLİK(EFFICIENCY The Effcency Of Groups And Semgroups * Özer CAN Matematk Ana Blm Dalı Blal VATANSEVER Matematk Ana Blm Dalı ÖZET Bu çalışmada öncelkle gruplarda, yarıgruplarda,
2. Topolojik Uzaylarda Ba¼glant l l k Ba¼glant l Topolojik Uzaylar. Tan m (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k
 2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
NÜMER IK ANAL IZ. Nuri ÖZALP FONKS IYONLARA YAKLAŞIM. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
MOD SÜPERPOZİSYONU İLE ZAMAN TANIM ALANINDA ÇÖZÜM
 Nur ÖZHENEKCİ O SÜPERPOZİSYONU İLE ZAAN ANI ALANINA ÇÖZÜ Aşağıda açılanaca olan ortogonall özelllernn sağlandığı yapılar çn, zaman tanım alanında çözüm, her mod çn ayrı ayrı yapılıp daha sonra bu modal
Nur ÖZHENEKCİ O SÜPERPOZİSYONU İLE ZAAN ANI ALANINA ÇÖZÜ Aşağıda açılanaca olan ortogonall özelllernn sağlandığı yapılar çn, zaman tanım alanında çözüm, her mod çn ayrı ayrı yapılıp daha sonra bu modal
ENERJİ. Isı Enerjisi. Genel Enerji Denklemi. Yrd. Doç. Dr. Atilla EVCİN Afyon Kocatepe Üniversitesi 2007
 Yrd. Doç. Dr. Atlla EVİN Afyon Kocatepe Ünverstes 007 ENERJİ Maddenn fzksel ve kmyasal hal değşm m le brlkte dama enerj değşm m de söz s z konusudur. Enerj değşmler mler lke olarak Termodnamğn Brnc Yasasına
Yrd. Doç. Dr. Atlla EVİN Afyon Kocatepe Ünverstes 007 ENERJİ Maddenn fzksel ve kmyasal hal değşm m le brlkte dama enerj değşm m de söz s z konusudur. Enerj değşmler mler lke olarak Termodnamğn Brnc Yasasına
X, R, p, np, c, u ve diğer kontrol diyagramları istatistiksel kalite kontrol diyagramlarının
 1 DİĞER ÖZEL İSTATİSTİKSEL KALİTE KONTROL DİYAGRAMLARI X, R, p, np, c, u ve dğer kontrol dyagramları statstksel kalte kontrol dyagramlarının temel teknkler olup en çok kullanılanlarıdır. Bu teknkler ell
1 DİĞER ÖZEL İSTATİSTİKSEL KALİTE KONTROL DİYAGRAMLARI X, R, p, np, c, u ve dğer kontrol dyagramları statstksel kalte kontrol dyagramlarının temel teknkler olup en çok kullanılanlarıdır. Bu teknkler ell
1.3. Normal Uzaylar. Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak. baz temel özellikleri incelenecektir.
 1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
KARMAŞIK SAYILAR. Derse giriş için tıklayın...
 KARMAŞIK SAYILAR Derse grş çn tıklayın A Tanım B nn Kuvvetler C İk Karmaşık Sayının Eştlğ D Br Karmaşık Sayının Eşlenğ E Karmaşık Sayılarda Dört İşlem Toplama - Çıkarma Çarpma Bölme F Karmaşık Dülem ve
KARMAŞIK SAYILAR Derse grş çn tıklayın A Tanım B nn Kuvvetler C İk Karmaşık Sayının Eştlğ D Br Karmaşık Sayının Eşlenğ E Karmaşık Sayılarda Dört İşlem Toplama - Çıkarma Çarpma Bölme F Karmaşık Dülem ve
Standart Model (SM) Lagrange Yoğunluğu. u, d, c, s, t, b. e,, Şimdilik nötrinoları kütlesiz Kabul edeceğiz. Kuark çiftlerini gösterelim.
 SM de yer alacak fermyonlar Standart Model (SM) agrange Yoğunluğu u s t d c b u, d, c, s, t, b e e e,, Şmdlk nötrnoları kütlesz Kabul edeceğz. Kuark çftlern gösterelm. u, c ve t y u (=1,,) olarak gösterelm.
SM de yer alacak fermyonlar Standart Model (SM) agrange Yoğunluğu u s t d c b u, d, c, s, t, b e e e,, Şmdlk nötrnoları kütlesz Kabul edeceğz. Kuark çftlern gösterelm. u, c ve t y u (=1,,) olarak gösterelm.
III - ELEKTROMAGNETİK GENELLEŞTİRME
 3 - EEKTROMAGNETİK GENEEŞTİRME.A ) AGRANGE ORMAİZMİ Dnamğn agrange medu le yenden frmüle edlmes, genelleşrlmş krdna ssemlernn kullanılmasına mkan anır. Yen krdnaların ye larak ble dk lmaları gerekmez.
3 - EEKTROMAGNETİK GENEEŞTİRME.A ) AGRANGE ORMAİZMİ Dnamğn agrange medu le yenden frmüle edlmes, genelleşrlmş krdna ssemlernn kullanılmasına mkan anır. Yen krdnaların ye larak ble dk lmaları gerekmez.
BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER İki Boyutlu Rasgele Değişkenler
 BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER 5.. İk Boyutlu Rasgele Değşkenler Br deney yapıldığında, aynı deneyle lgl brçok rasgele değşkenn aynı andak durumunu düşünmek gerekeblr. Böyle durumlarda
BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER 5.. İk Boyutlu Rasgele Değşkenler Br deney yapıldığında, aynı deneyle lgl brçok rasgele değşkenn aynı andak durumunu düşünmek gerekeblr. Böyle durumlarda
TALEP TAHMİNLERİ. Y.Doç.Dr. Alpagut YAVUZ
 TALEP TAHMİNLERİ Y.Doç.Dr. Alpagut YAVUZ Yöetm e temel foksyolarıda br ola plalama, e kaba taımıyla, şletme geleceğe yöelk alıa kararları br bleşkesdr. Geleceğe yöelk alıa kararları başarısı yöetcler yaptıkları
TALEP TAHMİNLERİ Y.Doç.Dr. Alpagut YAVUZ Yöetm e temel foksyolarıda br ola plalama, e kaba taımıyla, şletme geleceğe yöelk alıa kararları br bleşkesdr. Geleceğe yöelk alıa kararları başarısı yöetcler yaptıkları
NÜMER IK ANAL IZ. Nuri ÖZALP. Sabit Nokta ve Fonksiyonel Yineleme. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
RİJİT CİSİMLERİN DÜZLEMSEL KİNETİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNETİĞİ Rjt csmn knetğ, csme etk eden kuvvetler le csmn şekl, kütles ve bu kuvvetlern yarattığı hareket arasındak bağıntıları nceler. Parçacığın knetğ konusunda csm yalnızca
RİJİT CİSİMLERİN DÜZLEMSEL KİNETİĞİ Rjt csmn knetğ, csme etk eden kuvvetler le csmn şekl, kütles ve bu kuvvetlern yarattığı hareket arasındak bağıntıları nceler. Parçacığın knetğ konusunda csm yalnızca
BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY - 8
 BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK - 402 MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY - 8 FARKLI YÜZEY ÖZELLİKLERİNE SAHİP PLAKALARIN ISIL IŞINIM YAYMA ORANLARININ HESAPLANMASI BAŞKENT ÜNİVERSİTESİ
BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK - 402 MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY - 8 FARKLI YÜZEY ÖZELLİKLERİNE SAHİP PLAKALARIN ISIL IŞINIM YAYMA ORANLARININ HESAPLANMASI BAŞKENT ÜNİVERSİTESİ
UYUM ĐYĐLĐĞĐ TESTĐ. 2 -n olup. nin dağılımı χ dir ve sd = (k-1-p) dir. Burada k = sınıf sayısı, p = tahmin edilen parametre sayısıdır.
 UYUM ĐYĐLĐĞĐ TESTĐ Posson: H o: Ver Posson dağılıma sahp br ktleden gelmektedr. H a : Ver Posson dağılıma sahp br ktleden gelmemektedr. Böyle br hpotez test edeblmek çn, önce Posson dağılım parametres
UYUM ĐYĐLĐĞĐ TESTĐ Posson: H o: Ver Posson dağılıma sahp br ktleden gelmektedr. H a : Ver Posson dağılıma sahp br ktleden gelmemektedr. Böyle br hpotez test edeblmek çn, önce Posson dağılım parametres
kadar ( i. kaynağın gölge fiyatı kadar) olmalıdır.
 KONU : DUAL MODELİN EKONOMİK YORUMU Br prmal-dual model lşks P : max Z cx D: mn Z bv AX b AV c X 0 V 0 bçmnde tanımlı olsun. Prmal modeln en y temel B ve buna lşkn fyat vektörü c B olsun. Z B B BB c X
KONU : DUAL MODELİN EKONOMİK YORUMU Br prmal-dual model lşks P : max Z cx D: mn Z bv AX b AV c X 0 V 0 bçmnde tanımlı olsun. Prmal modeln en y temel B ve buna lşkn fyat vektörü c B olsun. Z B B BB c X
PROJE SEÇİMİ VE KAYNAK PLANLAMASI İÇİN BİR ALGORİTMA AN ALGORITHM FOR PROJECT SELECTION AND RESOURCE PLANNING
 Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Clt 3, Sayı:2, 2001 PROJE SEÇİMİ VE KAYAK PLALAMASI İÇİ BİR ALGORİTMA lgün MORALI 1 C. Cengz ÇELİKOĞLU 2 ÖZ Kaynak tahss problemler koşullara bağlı olarak
Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Clt 3, Sayı:2, 2001 PROJE SEÇİMİ VE KAYAK PLALAMASI İÇİ BİR ALGORİTMA lgün MORALI 1 C. Cengz ÇELİKOĞLU 2 ÖZ Kaynak tahss problemler koşullara bağlı olarak
TEMEL DEVRE KAVRAMLARI VE KANUNLARI
 TDK Temel Devre Kavramları ve Kanunları /0 TEMEL DEVRE KAVRAMLARI VE KANUNLARI GĐRĐŞ: Devre analz gerçek hayatta var olan fzksel elemanların matematksel olarak modellenerek gerçekte olması gereken sonuçların
TDK Temel Devre Kavramları ve Kanunları /0 TEMEL DEVRE KAVRAMLARI VE KANUNLARI GĐRĐŞ: Devre analz gerçek hayatta var olan fzksel elemanların matematksel olarak modellenerek gerçekte olması gereken sonuçların
AZIRBAYCAN HALK MÜZİGİ MAKAMLARıNDAN RAST MAKAMıNıN İNCILINMESi
 AZIRBAYCAN HALK MÜZİGİ MAKAMLARıNDAN RAST MAKAMıNıN İNCILINMES Arş. Gör. Yavuz ŞEN* Türl< müzğnde bast mal
AZIRBAYCAN HALK MÜZİGİ MAKAMLARıNDAN RAST MAKAMıNıN İNCILINMES Arş. Gör. Yavuz ŞEN* Türl< müzğnde bast mal
2009 Kasım. www.guven-kutay.ch FRENLER GENEL 40-4. M. Güven KUTAY. 40-4-frenler-genel.doc
 009 Kasım FRENLER GENEL 40-4. Güven KUTAY 40-4-frenler-genel.doc İ Ç İ N D E K İ L E R 4 enler... 4.3 4. en çeştler... 4.3 4.3 ende moment hesabı... 4.4 4.3.1 Kaba hesaplama... 4.4 4.3. Detaylı hesaplama...
009 Kasım FRENLER GENEL 40-4. Güven KUTAY 40-4-frenler-genel.doc İ Ç İ N D E K İ L E R 4 enler... 4.3 4. en çeştler... 4.3 4.3 ende moment hesabı... 4.4 4.3.1 Kaba hesaplama... 4.4 4.3. Detaylı hesaplama...
( ) 3.1 Özet ve Motivasyon. v = G v v Operasyonel Amplifikatör (Op-Amp) Deneyin Amacı. deney 3
 Yıldız Teknk Ünverstes Elektrk Mühendslğ Bölümü Deneyn Amacı İşlemsel kuvvetlendrcnn çalışma prensbnn anlaşılması le çeştl OP AMP devrelernn uygulanması ve ncelenmes. Özet ve Motvasyon.. Operasyonel Amplfkatör
Yıldız Teknk Ünverstes Elektrk Mühendslğ Bölümü Deneyn Amacı İşlemsel kuvvetlendrcnn çalışma prensbnn anlaşılması le çeştl OP AMP devrelernn uygulanması ve ncelenmes. Özet ve Motvasyon.. Operasyonel Amplfkatör
Direct Decomposition of A Finitely-Generated Module Over a Principal Ideal Domain *
 BİR ESAS İDEAL BÖLGESİ ÜZERİNDEKİ SONLU DOĞURULMUŞ BİR MODÜLÜN DİREK PARÇALANIŞI * Drec Decompoon of A Fnely-Generaed Module Over a Prncpal Ideal Doman * Zeynep YAPTI Fen Blmler Enüü Maemak Anablm Dalı
BİR ESAS İDEAL BÖLGESİ ÜZERİNDEKİ SONLU DOĞURULMUŞ BİR MODÜLÜN DİREK PARÇALANIŞI * Drec Decompoon of A Fnely-Generaed Module Over a Prncpal Ideal Doman * Zeynep YAPTI Fen Blmler Enüü Maemak Anablm Dalı
Ercan Kahya. Hidrolik. B.M. Sümer, İ.Ünsal, M. Bayazıt, Birsen Yayınevi, 2007, İstanbul
 Ercan Kahya 1 Hdrolk. B.M. Sümer, İ.Ünsal, M. Bayazıt, Brsen Yayınev, 007, İstanbul se se da Brm kanal küçük gen kestl br kanalda, 1.14. KANAL EGIMI TANIMLARI Brm kanal genşlğnden geçen deb q se, bu q
Ercan Kahya 1 Hdrolk. B.M. Sümer, İ.Ünsal, M. Bayazıt, Brsen Yayınev, 007, İstanbul se se da Brm kanal küçük gen kestl br kanalda, 1.14. KANAL EGIMI TANIMLARI Brm kanal genşlğnden geçen deb q se, bu q
Şek. 1 () t e bağlayan diferansiyel denklemi elde ediniz. (5p) H s
 YTÜ EEKTONİK VE HABEEŞME MÜHENDİSİĞİ BÖÜMÜ DEVEE VE SİSTEME ANABİİM DAI DEVE VE SİSTEM ANAİZİ DESİ. VİZE_ÇÖZÜMEİ Soru : Şekl dek derey göz önüne alarak k t t Şek. a) () t ı k () t e bağlayan dferansyel
YTÜ EEKTONİK VE HABEEŞME MÜHENDİSİĞİ BÖÜMÜ DEVEE VE SİSTEME ANABİİM DAI DEVE VE SİSTEM ANAİZİ DESİ. VİZE_ÇÖZÜMEİ Soru : Şekl dek derey göz önüne alarak k t t Şek. a) () t ı k () t e bağlayan dferansyel
PÜRÜZLÜ AÇIK KANAL AKIMLARINDA DEBİ HESABI İÇİN ENTROPY YÖNTEMİNİN KULLANILMASI
 PÜRÜZLÜ AÇIK KANAL AKIMLARINDA DEBİ HESABI İÇİN ENTROPY YÖNTEMİNİN KULLANILMASI Mehmet ARDIÇLIOĞLU *, Galp Seçkn ** ve Özgür Öztürk * * Ercyes Ünverstes, Mühendslk Fakültes, İnşaat Mühendslğ Bölümü Kayser
PÜRÜZLÜ AÇIK KANAL AKIMLARINDA DEBİ HESABI İÇİN ENTROPY YÖNTEMİNİN KULLANILMASI Mehmet ARDIÇLIOĞLU *, Galp Seçkn ** ve Özgür Öztürk * * Ercyes Ünverstes, Mühendslk Fakültes, İnşaat Mühendslğ Bölümü Kayser
Fizik 101: Ders 19 Gündem
 Fzk 101: Ders 19 Gündem Açısal Momentum: Tanım & Türetmeler Anlamı nedr? Sabt br eksen etrafında dönme L = I Örnek: 2 dsk Dönen skemlede br öğrenc Serbest hareket eden br csmn açısal momentumu Değneğe
Fzk 101: Ders 19 Gündem Açısal Momentum: Tanım & Türetmeler Anlamı nedr? Sabt br eksen etrafında dönme L = I Örnek: 2 dsk Dönen skemlede br öğrenc Serbest hareket eden br csmn açısal momentumu Değneğe
ALTERNATİF AKIM DEVRE YÖNTEM VE TEOREMLER İLE ÇÖZÜMÜ
 BÖLÜM 6 ALTERNATİF AKIM DEVRE ÖNTEM VE TEOREMLER İLE ÇÖZÜMÜ 6. ÇEVRE AKIMLAR ÖNTEMİ 6. SÜPERPOZİSON TEOREMİ 6. DÜĞÜM GERİLİMLER ÖNTEMİ 6.4 THEVENİN TEOREMİ 6.5 NORTON TEOREMİ Tpak GİRİŞ Alternatf akımın
BÖLÜM 6 ALTERNATİF AKIM DEVRE ÖNTEM VE TEOREMLER İLE ÇÖZÜMÜ 6. ÇEVRE AKIMLAR ÖNTEMİ 6. SÜPERPOZİSON TEOREMİ 6. DÜĞÜM GERİLİMLER ÖNTEMİ 6.4 THEVENİN TEOREMİ 6.5 NORTON TEOREMİ Tpak GİRİŞ Alternatf akımın
2.7 Bezier eğrileri, B-spline eğrileri
 .7 Bezer eğrler, B-splne eğrler Bezer eğrler ve B-splne eğrler blgsaar grafklernde ve Blgsaar Destekl Tasarım (CAD) ugulamalarında çok kullanılmaktadır.. B-splne eğrler sadece br grup ver noktası çn tanımlanan
.7 Bezer eğrler, B-splne eğrler Bezer eğrler ve B-splne eğrler blgsaar grafklernde ve Blgsaar Destekl Tasarım (CAD) ugulamalarında çok kullanılmaktadır.. B-splne eğrler sadece br grup ver noktası çn tanımlanan
ADIYAMAN ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI YÜKSEK LİSANS TEZİ SOFT KÜMELER VE BAZI SOFT CEBİRSEL YAPILAR.
 ADIYAMAN ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI YÜKSEK LİSANS TEZİ SOFT KÜMELER VE BAZI SOFT CEBİRSEL YAPILAR Ebubekr İNAN DANIŞMAN Yrd. Doç. Dr. Mehmet Al ÖZTÜRK ADIYAMAN 2011 Her
ADIYAMAN ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI YÜKSEK LİSANS TEZİ SOFT KÜMELER VE BAZI SOFT CEBİRSEL YAPILAR Ebubekr İNAN DANIŞMAN Yrd. Doç. Dr. Mehmet Al ÖZTÜRK ADIYAMAN 2011 Her
ELEKTRİK DEVRE TEMELLERİ
 ELEKTRİK DEVRE TEMELLERİ Öğretm üyes: Doç. Dr. S. Özoğuz Tel: 85 36 9 e-posta: serdar@ehb.tu.edu.tr Ders saat: Pazartes,.-3. / D-4 İçndekler. Dere teors, toplu parametrel dereler, Krchhoff un gerlm e akım
ELEKTRİK DEVRE TEMELLERİ Öğretm üyes: Doç. Dr. S. Özoğuz Tel: 85 36 9 e-posta: serdar@ehb.tu.edu.tr Ders saat: Pazartes,.-3. / D-4 İçndekler. Dere teors, toplu parametrel dereler, Krchhoff un gerlm e akım
ÜN TE II L M T. Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler
 ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
Fumonic 3 radio net kablosuz duman dedektörü. Kiracılar ve mülk sahipleri için bilgi
 Fumonc 3 rado net kablosuz duman dedektörü Kracılar ve mülk sahpler çn blg Tebrk ederz! Darenze akıllı fumonc 3 rado net duman dedektörler monte edlmştr. Bu şeklde ev sahbnz yasal donanım yükümlülüğünü
Fumonc 3 rado net kablosuz duman dedektörü Kracılar ve mülk sahpler çn blg Tebrk ederz! Darenze akıllı fumonc 3 rado net duman dedektörler monte edlmştr. Bu şeklde ev sahbnz yasal donanım yükümlülüğünü
6 Devirli Kodlar. 6.1 Temel Tan mlar
 6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
DENEY 2: PROTOBOARD TANITIMI VE DEVRE KURMA
 A. DENEYİN AMACI : Protoboard kullanımını öğrenmek ve protoboard üzerinde basit direnç devreleri kurmak. B. KULLANILACAK ARAÇ VE MALZEMELER : 1. DC güç kaynağı, 2. Multimetre, 3. Protoboard, 4. Değişik
A. DENEYİN AMACI : Protoboard kullanımını öğrenmek ve protoboard üzerinde basit direnç devreleri kurmak. B. KULLANILACAK ARAÇ VE MALZEMELER : 1. DC güç kaynağı, 2. Multimetre, 3. Protoboard, 4. Değişik
Korelasyon ve Regresyon
 Korelasyon ve Regresyon 1 Korelasyon Analz İk değşken arasında lşk olup olmadığını belrlemek çn yapılan analze korelasyon analz denr. Korelasyon; doğrusal yada doğrusal olmayan dye kye ayrılır. Korelasyon
Korelasyon ve Regresyon 1 Korelasyon Analz İk değşken arasında lşk olup olmadığını belrlemek çn yapılan analze korelasyon analz denr. Korelasyon; doğrusal yada doğrusal olmayan dye kye ayrılır. Korelasyon
Fen ve Mühendislik için Fizik 1 Ders Notları: Doç.Dr. Ahmet CANSIZ
 9. ÇİZGİSEL (OĞRUSAL) OENTU VE ÇARPIŞALAR 9. Kütle erkez Ssten kütle erkeznn yern ssten ortalaa konuu olarak düşüneblrz. y Δ Δ x x + x = + Teraz antığı le düşünürsek aşağıdak bağıntıyı yazablrz: Δ= x e
9. ÇİZGİSEL (OĞRUSAL) OENTU VE ÇARPIŞALAR 9. Kütle erkez Ssten kütle erkeznn yern ssten ortalaa konuu olarak düşüneblrz. y Δ Δ x x + x = + Teraz antığı le düşünürsek aşağıdak bağıntıyı yazablrz: Δ= x e
Akköse, Ateş, Adanur. Matris Yöntemleri ile dış etkilerden meydana gelen uç kuvvetlerinin ve uç yerdeğiştirmelerinin belirlenmesinde;
 MATRİS ÖNTEMER 1. GİRİŞ Matrs öntemler; gerçek sürekl apının erne, matrs bçmnde ade edleblen blnen atalet (elemslk) ve elastklk öellklerne sahp sonl büüklüktek apısal elemanlardan olşan matematksel br
MATRİS ÖNTEMER 1. GİRİŞ Matrs öntemler; gerçek sürekl apının erne, matrs bçmnde ade edleblen blnen atalet (elemslk) ve elastklk öellklerne sahp sonl büüklüktek apısal elemanlardan olşan matematksel br
Doğru Önermeler, Yanlış Önermeler 1 Ali Nesin
 Doğru Önermeler, Yanlış Önermeler Al Nesn Bu yazıda 6 mantık sorusu sorup yanıtlayacağız. Brnc Blmece. Yargıç karar recek. Mahkeme tutanaklarından şu blgler çıkıyor: Eğer A suçsuzsa, hem B hem C suçlu.
Doğru Önermeler, Yanlış Önermeler Al Nesn Bu yazıda 6 mantık sorusu sorup yanıtlayacağız. Brnc Blmece. Yargıç karar recek. Mahkeme tutanaklarından şu blgler çıkıyor: Eğer A suçsuzsa, hem B hem C suçlu.
ÖRNEK SET 5 - MBM 211 Malzeme Termodinamiği I
 ÖRNE SE 5 - MBM Malzeme ermdnamğ I 5 ºC de ve sabt basınç altında, metan gazının su buharı le reaksynunun standart Gbbs serbest enerjs değşmn hesaplayın. Çözüm C O( ( ( G S S S g 98 98 98 98 98 98 98 Madde
ÖRNE SE 5 - MBM Malzeme ermdnamğ I 5 ºC de ve sabt basınç altında, metan gazının su buharı le reaksynunun standart Gbbs serbest enerjs değşmn hesaplayın. Çözüm C O( ( ( G S S S g 98 98 98 98 98 98 98 Madde
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ. Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 2012
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
Fizik 101: Ders 15 Ajanda
 zk 101: Ders 15 Ajanda İk boyutta elastk çarpışma Örnekler (nükleer saçılma, blardo) Impulse ve ortalama kuvvet İk boyutta csmn elastk çarpışması Önces Sonrası m 1 v 1, m 1 v 1, KM KM V KM V KM m v, m
zk 101: Ders 15 Ajanda İk boyutta elastk çarpışma Örnekler (nükleer saçılma, blardo) Impulse ve ortalama kuvvet İk boyutta csmn elastk çarpışması Önces Sonrası m 1 v 1, m 1 v 1, KM KM V KM V KM m v, m
17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A
 AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
JFM316 Elektrik Yöntemler ( Doğru Akım Özdirenç Yöntemi)
 JFM316 Elektrk Yöntemler ( Doğru Akım Özdrenç Yöntem) yeryüzünde oluşturacağı gerlm değerler hesaplanablr. Daha sonra aşağıdak formül kullanılarak görünür özdrenç hesaplanır. a K I K 2 1 1 1 1 AM BM AN
JFM316 Elektrk Yöntemler ( Doğru Akım Özdrenç Yöntem) yeryüzünde oluşturacağı gerlm değerler hesaplanablr. Daha sonra aşağıdak formül kullanılarak görünür özdrenç hesaplanır. a K I K 2 1 1 1 1 AM BM AN
Ç NDEK LER. Bölüm 4: Üslü Say lar...44 Üslü fadeler...44 Al t rmalar...47 Test Sorular...49
 Ç NDEK LER Bölüm1: Say Sistemleri...1 Say Sistemi...2 Desimal (Onluk) Say Sistemi...2 Say Basamaklar ve Taban...4 Binary ( kilik) Say Sistemi...4 Oktal (Sekizlik) Say Sistemi...7 Heksadesimal (Onalt l
Ç NDEK LER Bölüm1: Say Sistemleri...1 Say Sistemi...2 Desimal (Onluk) Say Sistemi...2 Say Basamaklar ve Taban...4 Binary ( kilik) Say Sistemi...4 Oktal (Sekizlik) Say Sistemi...7 Heksadesimal (Onalt l
TEST - 1 ELEKTROMANYET K NDÜKS YON
 EETET DÜS TEST - y 3 x magnetk ak Φ z S enz kanununa göre: Tel çerçeve +x yönünde çeklrse, tel çerçevede den ye do ru ndksyon - S kutuplar karfl l kl olarak brbrne yaklaflt r l rsa, m knat slar aras ndak
EETET DÜS TEST - y 3 x magnetk ak Φ z S enz kanununa göre: Tel çerçeve +x yönünde çeklrse, tel çerçevede den ye do ru ndksyon - S kutuplar karfl l kl olarak brbrne yaklaflt r l rsa, m knat slar aras ndak
Makine Öğrenmesi 10. hafta
 Makne Öğrenmes 0. hafta Lagrange Optmzasonu Destek Vektör Maknes (SVM) Karesel (Quadratc) Programlama Optmzason Blmsel term olarak dlmze geçmş olsa da bazen en leme termle karşılık bulur. Matematktek en
Makne Öğrenmes 0. hafta Lagrange Optmzasonu Destek Vektör Maknes (SVM) Karesel (Quadratc) Programlama Optmzason Blmsel term olarak dlmze geçmş olsa da bazen en leme termle karşılık bulur. Matematktek en
Bulanık Mantık ile Hesaplanan Geoid Yüksekliğine Nokta Yüksekliklerinin Etkisi
 Harta Teknolojler Elektronk Dergs Clt: 5, No: 1, 2013 (61-67) Electronc Journal of Map Technologes Vol: 5, No: 1, 2013 (61-67) TEKNOLOJİK ARAŞTIRMALAR www.teknolojkarastrmalar.com e-issn: 1309-3983 Makale
Harta Teknolojler Elektronk Dergs Clt: 5, No: 1, 2013 (61-67) Electronc Journal of Map Technologes Vol: 5, No: 1, 2013 (61-67) TEKNOLOJİK ARAŞTIRMALAR www.teknolojkarastrmalar.com e-issn: 1309-3983 Makale
FLYBACK DÖNÜŞTÜRÜCÜ TASARIMI VE ANALİZİ
 FLYBACK DÖNÜŞTÜRÜCÜ TASARIMI VE ANALİZİ 1 Nasır Çoruh, Tarık Erfdan, 3 Satılmış Ürgün, 4 Semra Öztürk 1,,4 Kocael Ünverstes Elektrk Mühendslğ Bölümü 3 Kocael Ünverstes Svl Havacılık Yüksekokulu ncoruh@kocael.edu.tr,
FLYBACK DÖNÜŞTÜRÜCÜ TASARIMI VE ANALİZİ 1 Nasır Çoruh, Tarık Erfdan, 3 Satılmış Ürgün, 4 Semra Öztürk 1,,4 Kocael Ünverstes Elektrk Mühendslğ Bölümü 3 Kocael Ünverstes Svl Havacılık Yüksekokulu ncoruh@kocael.edu.tr,
Fizik 101: Ders 20. Ajanda
 Fzk 101: Ders 20 = I konusunda yorumlar Ajanda Br sstemn açısal momentumu çn genel fade Kayan krş örneğ Açısal momentum vektörü Bsklet teker ve döner skemle Jroskobk hareket Hareketl dönme hakkında yorum
Fzk 101: Ders 20 = I konusunda yorumlar Ajanda Br sstemn açısal momentumu çn genel fade Kayan krş örneğ Açısal momentum vektörü Bsklet teker ve döner skemle Jroskobk hareket Hareketl dönme hakkında yorum
OLASILIĞA GİRİŞ. Biyoistatistik (Ders 7: Olasılık) OLASILIK, TIP ve GÜNLÜK YAŞAMDA KULLANIMI
 OLASILIĞA GİRİŞ Yrd. Doç. Dr. Ünal ERKORKMAZ Sakarya Ünverstes Tıp Fakültes Byostatstk Anablm Dalı uerkorkmaz@sakarya.edu.tr OLASILIK, TIP ve GÜNLÜK YAŞAMDA KULLANIMI Br olayındoğal koşullar altında toplumda
OLASILIĞA GİRİŞ Yrd. Doç. Dr. Ünal ERKORKMAZ Sakarya Ünverstes Tıp Fakültes Byostatstk Anablm Dalı uerkorkmaz@sakarya.edu.tr OLASILIK, TIP ve GÜNLÜK YAŞAMDA KULLANIMI Br olayındoğal koşullar altında toplumda
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I
 DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
SPOR BİYOMEKANİĞİNDE MODELLEME ve KARŞILAŞILAN SORUNLAR
 SPOR BİYOMEKANİĞİNDE MODELLEME ve KARŞILAŞILAN SORUNLAR SERDAR ARITAN serdar.artan@hacettepe.edu.tr Byomekank Araştırma Grubu www.bomech.hacettepe.edu.tr Spor Blmler ve Teknolojs Yüksekokulu www.sbt.hacettepe.edu.tr
SPOR BİYOMEKANİĞİNDE MODELLEME ve KARŞILAŞILAN SORUNLAR SERDAR ARITAN serdar.artan@hacettepe.edu.tr Byomekank Araştırma Grubu www.bomech.hacettepe.edu.tr Spor Blmler ve Teknolojs Yüksekokulu www.sbt.hacettepe.edu.tr
TEKNOLOJİ, PİYASA REKABETİ VE REFAH
 TEKNOLOJİ, PİYASA REKABETİ VE REFAH Dr Türkmen Göksel Ankara Ünverstes Syasal Blgler Fakültes Özet Bu makalede teknoloj sevyesnn pyasa rekabet ve refah sevyes üzerndek etkler matematksel br model le ncelenecektr
TEKNOLOJİ, PİYASA REKABETİ VE REFAH Dr Türkmen Göksel Ankara Ünverstes Syasal Blgler Fakültes Özet Bu makalede teknoloj sevyesnn pyasa rekabet ve refah sevyes üzerndek etkler matematksel br model le ncelenecektr
DOĞRUSAL OLMAYAN PROGRAMLAMA -III- Çok değişkenli doğrusal olmayan karar modelinin çözümü
 DOĞRUSAL OLMAYAN PROGRAMLAMA -III- Çok değşkenl doğrusal olmayan karar modelnn çözümü Hazırlayan Doç. Dr. Nl ARAS Anadolu Ünverstes, Endüstr Mühendslğ Bölümü İST8 Yöneylem Araştırması Ders - Öğretm Yılı
DOĞRUSAL OLMAYAN PROGRAMLAMA -III- Çok değşkenl doğrusal olmayan karar modelnn çözümü Hazırlayan Doç. Dr. Nl ARAS Anadolu Ünverstes, Endüstr Mühendslğ Bölümü İST8 Yöneylem Araştırması Ders - Öğretm Yılı
SORULAR. 1. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim. 1 n sin. lim. q 1 x 1+x
 SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
ITAP Fizik Olimpiyat Okulu
 Eylül Deneme Sınavı (Prof.Dr.Ventsslav Dmtrov) Konu: Elektrk Devrelernde İndüktans Soru. Şekldek gösterlen devrede lk anda K ve K anahtarları açıktır. K anahtarı kapatılıyor ve kondansatörün gerlm U ε/
Eylül Deneme Sınavı (Prof.Dr.Ventsslav Dmtrov) Konu: Elektrk Devrelernde İndüktans Soru. Şekldek gösterlen devrede lk anda K ve K anahtarları açıktır. K anahtarı kapatılıyor ve kondansatörün gerlm U ε/
Basel II Geçiş Süreci Sıkça Sorulan Sorular
 Basel II Geçş Sürec Sıkça Sorulan Sorular Soru No: 71 Cevaplanma Tarh: 06.03.2012 İlgl Hüküm: --- Konu: Gayrmenkul İpoteğyle Temnatlandırılmış Alacaklar İçn KR510AS Formunun Doldurulmasına İlşkn Örnek
Basel II Geçş Sürec Sıkça Sorulan Sorular Soru No: 71 Cevaplanma Tarh: 06.03.2012 İlgl Hüküm: --- Konu: Gayrmenkul İpoteğyle Temnatlandırılmış Alacaklar İçn KR510AS Formunun Doldurulmasına İlşkn Örnek
OPERATÖRLER BÖLÜM 4. 4.1 Giriş. 4.2. Aritmetik Operatörler
 BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
Doğrusal Korelasyon ve Regresyon
 Doğrusal Korelasyon ve Regresyon En az k değşken arasındak lşknn ncelenmesne korelasyon denr. Kşlern boyları le ağırlıkları, gelr le gder, öğrenclern çalıştıkları süre le aldıkları not, tarlaya atılan
Doğrusal Korelasyon ve Regresyon En az k değşken arasındak lşknn ncelenmesne korelasyon denr. Kşlern boyları le ağırlıkları, gelr le gder, öğrenclern çalıştıkları süre le aldıkları not, tarlaya atılan
MONTE CARLO SİMÜLASYON METODU VE MCNP KOD SİSTEMİ MONTE CARLO SIMULATION METHOD AND MCNP CODE SYSTEM
 Ekm 26 Clt:14 No:2 Kastamonu Eğtm Dergs 545-556 MONTE CARLO SİMÜLASYON METODU VE MCNP KOD SİSTEMİ Özet Aybaba HANÇERLİOĞULLARI Kastamonu Ünverstes, Fen-Edebyat Fakültes, Fzk Bölümü, Kastamonu. Monte Carlo
Ekm 26 Clt:14 No:2 Kastamonu Eğtm Dergs 545-556 MONTE CARLO SİMÜLASYON METODU VE MCNP KOD SİSTEMİ Özet Aybaba HANÇERLİOĞULLARI Kastamonu Ünverstes, Fen-Edebyat Fakültes, Fzk Bölümü, Kastamonu. Monte Carlo
TEKNOLOJİ BAĞIMLI YAŞAMIN MATEMATİKSEL DESENLERİ-I
 TEKNOLOJİ BAĞIMLI YAŞAMIN MATEMATİKSEL DESENLERİ-I Fevz ÜNLÜ *, Esra DALAN YILDIRIM **,Şule AYAR *** ÖZET: Evren her an nano-önces, nano, mkro, normal, makro ve makro-ötes gözler le gözlemlermze açıktır.
TEKNOLOJİ BAĞIMLI YAŞAMIN MATEMATİKSEL DESENLERİ-I Fevz ÜNLÜ *, Esra DALAN YILDIRIM **,Şule AYAR *** ÖZET: Evren her an nano-önces, nano, mkro, normal, makro ve makro-ötes gözler le gözlemlermze açıktır.
BĐSĐKLET FREN SĐSTEMĐNDE KABLO BAĞLANTI AÇISININ MEKANĐK VERĐME ETKĐSĐNĐN ĐNCELENMESĐ
 tasarım BĐSĐKLET FREN SĐSTEMĐNDE KABLO BAĞLANTI AÇISININ MEKANĐK VERĐME ETKĐSĐNĐN ĐNCELENMESĐ Nihat GEMALMAYAN Y. Doç. Dr., Gazi Üniversitesi, Makina Mühendisliği Bölümü Hüseyin ĐNCEÇAM Gazi Üniversitesi,
tasarım BĐSĐKLET FREN SĐSTEMĐNDE KABLO BAĞLANTI AÇISININ MEKANĐK VERĐME ETKĐSĐNĐN ĐNCELENMESĐ Nihat GEMALMAYAN Y. Doç. Dr., Gazi Üniversitesi, Makina Mühendisliği Bölümü Hüseyin ĐNCEÇAM Gazi Üniversitesi,
Tanımlayıcı İstatistikler
 Taımlayıcı İstatstkler Br veya brde azla dağılışı karşılaştırmak ç kullaıla ve ayrıca örek verlerde hareket le rekas dağılışlarıı sayısal olarak özetleye değerlere taımlayıcı statstkler der. Aalzlerde
Taımlayıcı İstatstkler Br veya brde azla dağılışı karşılaştırmak ç kullaıla ve ayrıca örek verlerde hareket le rekas dağılışlarıı sayısal olarak özetleye değerlere taımlayıcı statstkler der. Aalzlerde
HİPERSTATİK SİSTEMLER
 HİPERSTATİK SİSTELER Tanım: Bütün kest zorlarını ve bunlara bağlı olarak şekl değştrmelern ve yer değştrmelern hesabı çn denge denklemlernn yeterl olmadığı sstemlere Hperstatk Sstemler denr. Hperstatk
HİPERSTATİK SİSTELER Tanım: Bütün kest zorlarını ve bunlara bağlı olarak şekl değştrmelern ve yer değştrmelern hesabı çn denge denklemlernn yeterl olmadığı sstemlere Hperstatk Sstemler denr. Hperstatk
Belirtilen kapasitede son kata aittir
 TE Sers Elektrkl Vnçler 00 kg le, ton aras kapastelerde Her türlü kald rma, çekme uygulamas çn, tona kadar standart modeller mevcuttur. Dayan kl l k ve büyük sar m kapastes le genfl br uygulama alan nda
TE Sers Elektrkl Vnçler 00 kg le, ton aras kapastelerde Her türlü kald rma, çekme uygulamas çn, tona kadar standart modeller mevcuttur. Dayan kl l k ve büyük sar m kapastes le genfl br uygulama alan nda
BORULARDA, BORU BAĞLANTI ELEMANLARINDA VE GEÇİŞ BORULARINDA ENERJİ KAYIPLARI
 547 BORULARDA, BORU BAĞLANTI ELEMANLARINDA VE GEÇİŞ BORULARINDA ENERJİ KAYIPLARI Mehmet ATILGAN Harun Kemal ÖZTÜRK ÖZET Boru akış problemlernn çözümünde göz önünde bulundurulması gereken unsurlardan en
547 BORULARDA, BORU BAĞLANTI ELEMANLARINDA VE GEÇİŞ BORULARINDA ENERJİ KAYIPLARI Mehmet ATILGAN Harun Kemal ÖZTÜRK ÖZET Boru akış problemlernn çözümünde göz önünde bulundurulması gereken unsurlardan en
AKDEN IZ ÜN IVERS ITES I 21. ULUSAL ANTALYA MATEMAT IK OL IMP IYATI SORULARI
 KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
(z z 0 ) n. n=1. Z f (z) dz = 2ib 1
 0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
Deprem Tepkisinin Sayısal Metotlar ile Değerlendirilmesi (Newmark-Beta Metodu) Deprem Mühendisliğine Giriş Dersi Doç. Dr.
 Deprem Tepksnn Sayısal Metotlar le Değerlendrlmes (Newmark-Beta Metodu) Sunum Anahat Grş Sayısal Metotlar Motvasyon Tahrk Fonksyonunun Parçalı Lneer Interpolasyonu (Pecewse Lnear Interpolaton of Exctaton
Deprem Tepksnn Sayısal Metotlar le Değerlendrlmes (Newmark-Beta Metodu) Sunum Anahat Grş Sayısal Metotlar Motvasyon Tahrk Fonksyonunun Parçalı Lneer Interpolasyonu (Pecewse Lnear Interpolaton of Exctaton
PARÇALI DOĞRUSAL REGRESYON
 HAFTA 4 PARÇALI DOĞRUSAL REGRESYO Gölge değşkenn br başka kullanımını açıklamak çn varsayımsal br şrketn satış temslclerne nasıl ödeme yaptığı ele alınsın. Satış prmleryle satış hacm Arasındak varsayımsal
HAFTA 4 PARÇALI DOĞRUSAL REGRESYO Gölge değşkenn br başka kullanımını açıklamak çn varsayımsal br şrketn satış temslclerne nasıl ödeme yaptığı ele alınsın. Satış prmleryle satış hacm Arasındak varsayımsal
ÖZET Yüksek Lsans Tez KUANTUM KANONİK DÖNÜŞÜMLER Şeyda ERAZ Ankara Ünverstes Fen Blmler Ensttüsü Fzk Anablm Dalı Danışman: Doç. Dr. Adnan TEĞMEN Bu te
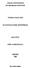 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ KUANTUM KANONİK DÖNÜŞÜMLER Şeyda ERAZ FİZİK ANABİLİM DALI ANKARA 008 Her hakkı saklıdır ÖZET Yüksek Lsans Tez KUANTUM KANONİK DÖNÜŞÜMLER Şeyda
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ KUANTUM KANONİK DÖNÜŞÜMLER Şeyda ERAZ FİZİK ANABİLİM DALI ANKARA 008 Her hakkı saklıdır ÖZET Yüksek Lsans Tez KUANTUM KANONİK DÖNÜŞÜMLER Şeyda
Calculating the Index of Refraction of Air
 Ankara Unversty Faculty o Engneerng Optcs Lab IV Sprng 2009 Calculatng the Index o Reracton o Ar Lab Group: 1 Teoman Soygül Snan Tarakçı Seval Cbcel Muhammed Karakaya March 3, 2009 Havanın Kırılma Đndsnn
Ankara Unversty Faculty o Engneerng Optcs Lab IV Sprng 2009 Calculatng the Index o Reracton o Ar Lab Group: 1 Teoman Soygül Snan Tarakçı Seval Cbcel Muhammed Karakaya March 3, 2009 Havanın Kırılma Đndsnn
NÜMER IK ANAL IZ. Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
DOĞRUSAL HEDEF PROGRAMLAMA İLE BÜTÇELEME. Hazırlayan: Ozan Kocadağlı Danışman: Prof. Dr. Nalan Cinemre
 1 DOĞRUSAL HEDEF PROGRAMLAMA İLE BÜTÇELEME Hazırlayan: Ozan Kocadağlı Danışman: Prof. Dr. Nalan Cnemre 2 BİRİNCİ BÖLÜM HEDEF PROGRAMLAMA 1.1 Grş Karar problemler amaç sayısına göre tek amaçlı ve çok amaçlı
1 DOĞRUSAL HEDEF PROGRAMLAMA İLE BÜTÇELEME Hazırlayan: Ozan Kocadağlı Danışman: Prof. Dr. Nalan Cnemre 2 BİRİNCİ BÖLÜM HEDEF PROGRAMLAMA 1.1 Grş Karar problemler amaç sayısına göre tek amaçlı ve çok amaçlı
Ercan Kahya. Hidrolik. B.M. Sümer, İ.Ünsal, M. Bayazıt, Birsen Yayınevi, 2007, İstanbul
 Ercan Kaha 1 Hdrolk. B.M. Sümer, İ.Ünsal, M. Baazıt, Brsen Yaınev, 2007, İstanbul BÖLÜM 12 AÇIK KANALLARDA AKIM: ÜNİFORM OLMAYAN AKIMLAR 12.1 GİRİŞ - --- --.;! Baraj sonrak su üze öncek su üze.. Vnfom
Ercan Kaha 1 Hdrolk. B.M. Sümer, İ.Ünsal, M. Baazıt, Brsen Yaınev, 2007, İstanbul BÖLÜM 12 AÇIK KANALLARDA AKIM: ÜNİFORM OLMAYAN AKIMLAR 12.1 GİRİŞ - --- --.;! Baraj sonrak su üze öncek su üze.. Vnfom
AĞIRLIKLI KALANLAR YÖNTEMİ VE BAZI UYGULAMALARI
 AĞIRLIKLI KALALAR YÖTEMİ VE BAZI UYGULAMALARI Pamukkale Ünverstes Fen Blmler Ensttüsü Yüksek Lsans Tez Matematk Anablm Dalı Mukaddes ÖKTE Danışman: Doç. Dr. Uğur YÜCEL Temmuz DEİZLİ TEŞEKKÜR Bu çalışmanın
AĞIRLIKLI KALALAR YÖTEMİ VE BAZI UYGULAMALARI Pamukkale Ünverstes Fen Blmler Ensttüsü Yüksek Lsans Tez Matematk Anablm Dalı Mukaddes ÖKTE Danışman: Doç. Dr. Uğur YÜCEL Temmuz DEİZLİ TEŞEKKÜR Bu çalışmanın
QKUIAN. SAĞLIK BAKANLIĞI_ KAMU HASTANELERİ KURUMU Trabzon Ili Kamu Hastaneleri Birliği Genel Sekreterliği Kanuni Eğitim ve Araştırma Hastanesi
 V tsttşfaktör T.C. SAĞLIK BAKANLIĞI KAMU HASTANELERİ KURUMU Trabzon Il Kamu Hastaneler Brlğ Genel Sekreterlğ Kanun Eğtm ve Araştırma Hastanes Sayı ı 23618724/?ı C.. Y** 08/10/2015 Konu : Yaklaşık Malyet
V tsttşfaktör T.C. SAĞLIK BAKANLIĞI KAMU HASTANELERİ KURUMU Trabzon Il Kamu Hastaneler Brlğ Genel Sekreterlğ Kanun Eğtm ve Araştırma Hastanes Sayı ı 23618724/?ı C.. Y** 08/10/2015 Konu : Yaklaşık Malyet
YAPILARIN ENERJİ ESASLI TASARIMI İÇİN BİR HESAP YÖNTEMİ
 YAPILARI EERJİ ESASLI TASARIMI İÇİ BİR HESAP YÖTEMİ Araş. Gör. Onur MERTER Araş. Gör. Özgür BOZDAĞ Prof. Dr. Mustafa DÜZGÜ Dokuz Eylül Ünverstes Dokuz Eylül Ünverstes Dokuz Eylül Ünverstes Fen Blmler Ensttüsü
YAPILARI EERJİ ESASLI TASARIMI İÇİ BİR HESAP YÖTEMİ Araş. Gör. Onur MERTER Araş. Gör. Özgür BOZDAĞ Prof. Dr. Mustafa DÜZGÜ Dokuz Eylül Ünverstes Dokuz Eylül Ünverstes Dokuz Eylül Ünverstes Fen Blmler Ensttüsü
