Halk Sağlığı Açısından Temel Biyoistatistik İlke ve Kavramlar
|
|
|
- Ediz Köse
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Halk Sağlığı Açısından Temel Biyoistatistik İlke ve Kavramlar Prof. Dr. Ahmet SALTIK Ankara Üniversitesi Tıp Fakültesi Halk Sağlığı Anabilim Dalı Aralık 2014 / Ankara
2 2
3 Amaçlar ve öğrenim hedefleri Günümüz sağlık çalışanlarının, sayısal yöntemler ile barışık, hatta alışık olması.. Makale okur-yazarı olabilme.. DSÖ nün istemine koşut olarak, çalışılan bölgedeki sağlık sorunlarını doğru ve yerinde belirleyebilme.. Ders ile öğrencilerin, Halk Sağlığı bilimlerinde Biyoistatistiğin yerini ve önemini kavramaları ve buna uygun davranmaları hedeflenmektedir. 3
4 History of Patient-based Assessment B.C. Collection of vital statistics in ancient Greece and Egypt? Mid-1600s Growth of vital statistics in England Mid-to-late 1800s Health interview surveys Health survey content expanded to include the duration of illness and related disability or dysfunction Prof. Albert I. Wertheimer, Temple University, USA. 4
5 History of Patient-based Assessment Cont d Early 1900s Appearance of psychometric techniques that included traditional approaches, such as those associated with Thurstone, Likert, and Guttman 1930s More positive definitions of health appeared, possibly first in measures commissioned by the health organization of the league of nations, which included health and vitality among the set of indicators 5
6 History of Patient-based Assessment Cont d 1940s Health Opinion Survey used to screen recruits for mental fitness during World War II. Utility assessment based on work on mathematical decision theory appeared Karnofsky Performance Status Scale developed for use with cancer patients World Health Organization s constitution offered definition of health as a state of complete physical, mental, and social well-being and not merely the absence of disease or infirmity. 6
7 History of Patient-based Assessment Cont d 1950s Shift toward measures that included positive feelings of well-being. Different dimensions of general health perceptions identified, including the time-bound and relation to others. 1960s Definition of physical health expanded in many measures to include intermediate activities of daily living in addition to the most basic self-care Psychometric approaches were first applied to health measurement. 7
8 History of Patient-based Assessment Cont d 1960s cont d Landmark studies include the 1963 study by Katz and colleagues who used Guttman scalogram analysis to construct the Index Activities of Daily Living to monitor results or rehabilitative care for elderly patients 1970s Most physical health measures expanded the range of measurement to consider performance of or capacity to perform strenuous physical activities Measures of overall mental health began to tap both psychological distress and well-being 8
9 History of Patient-based Assessment Cont d 1970s cont d Psychometric methods of enumerating general health perceptions measures became more common Ware and colleagues employed Likert s method of summated ratings to construct a variety of measures, including the General Health Perceptions Questionnaire, the Mental Health Inventory, and other general and mental health measures used in the Health Insurance Experiment ( ) and in the Medical Outcomes Study ( ) 9
10 History of Patient-based Assessment Cont d 1970s cont d Earliest applications of utility assessment and QALYs to health measurement appeared in work by Fanshel and Bush and by Torrance. Documented inclusion of health-related quality of life measures in clinical trials and research dates to the early 1970s. Study by Nagi of the Independent Living Index Bergner and colleagues used Thurstone s methods of equal-appearing intervals to construct the Sickness Impact Profile. 10
11 History of Patient-based Assessment Cont d 1970s to mid-1980s Social aspects of functioning and well-being tended to be measured distinctly from mental and physical aspects Omnibus Budget Reconciliation Act creates the Agency for Health Care Policy and Research which funds research to monitor patient-based assessments. 11
12 History of Patient-based Assessment Cont d Early 1990s New psychometric models based on Rasch s Item Response Theory test measures of pain and functioning in assessing rehabilitative care n physical functioning in general populations. Mid-1990s Comprehensive overall health measures include physical functioning; health-related limitations in social and role functioning; bodily pain; energy and fatigue; and general health perceptions. 12
13 History of Patient-based Assessment Cont d Mid-1990s cont d Content of the most recent questionnaires suggest that sleep and sexual functioning are becoming accepted parts of this comprehensive model of overall health. Research underway to conceptualize and enumerate children s health. 13
14 Neden Biyoistatistik? Geleceğin hekimleri araştırıcı, sorgulayıcı kişiler olmalıdır. Bu, Biyoistatistik siz olanaksız.. Biyoistatistik bilgisi olmadan araştırma yapmak, yapılmış araştırmaları anlamak yorumlamak ve doğru değerlendirebilmek de olanaksız.. Matematiksel düşünme yaşamın temeli, evrenin temel yasası matematik.. Tıp ve sağlık bilimleri Biyomatematiğin tam da ortasında.. 14
15 Neden Biyoistatistik? Dünya Sağlık Örgütü ne göre; bir hekim, bulunduğu bölgedeki sağlık sorunlarını belirleyebilmelidir. Hekimin bunu yapabilmesi için, temel Biyoistatistik bilgisi ve uygulama becerisi olması gereklidir. DSÖ bu amaçla, tıp fakülteleri için mezuniyet öncesi eğitimde çekirdek bir Biyoistatistik müfredatı önermiştir. 15
16 Bilimsel araştırmaların kuralları Başlamadan önce: Yerel Etik Kurul onayı gerek. Ülke genelinde araştırmalarda Sağlık Bakanlığı Etik Kurulu nun izni alınmalı. Bildiri veya yayın aşamasında: Helsinki Biyomedikal Araştırma Etik Kuralları na uygunluk zorunludur.. Klinik Araştırmalar Yönetmeliği Helsinki Bildirgesi ne gönderme (atıf) yaparak içselleştiriyor. Araştırma verilerinin her zaman ulaşılabilirliği, araştırmanın yinelenebilirliği, tutarlılığı gereklidir. Akreditasyon kurumları önemli.. Türkiye de Türk Akreditasyon Kurumu TÜRKAK var. 16
17 Bilimsel araştırmaların kuralları ABD de FDA (Food and Drug Administration) ve NIOSH, AB de OSHA ve EFSA Üniversite laboratuvarları TÜBİTAK laboratuvarları Refik Saydam Ulusal Referans Lab. Gıda Tarım ve Hayvancılık Bakanlığı Ulusal Gıda Referans Laboratuvarı Adli Tıp Kurumu.. gibi 17
18 Dünyada her şey için, uygarlık için, yaşam için, başarı için, en gerçek yol gösterici bilimdir, tekniktir. Bilim ve tekniğin dışında yol gösterici aramak aymazlıktır, cehalettir, sapkınlıktır. Gazi Mustafa Kemal A T A T Ü R K ( , Samsun Ögretmenleriyle Konuşma) 18
19 Bilim adamlığı nedir? Bilim adamlığı bir meslek değil; bir yaşam biçimidir. Prof. Dr. Cahit ARF Arf Teoremi bulucusu 19
20 Bilim ve teknoloji üretme yükümü.. Bilgi ve onun ürünü olan teknolojiyi üret(e)meyen milletler, bağımsızlıklarını, dolayısıyla mutluluklarını yitirirler. Prof. Dr. Cahit ARF Arf Teoremi bulucusu 20
21 Uygulayıcı ya da Bilim İnsanı Olmak.. Prof. Dr. Lowe, C.R. Kardif Üniversitesi, 1962 Günümüzde biyolojik ve tıpsal sorunları yansız ve eleştirel bir düşünce içinde, sayısal temellere göre değerlendirmeye alışmamış bir hekim, bir sağlık çalışanı, bir bilimin temsilcisi değil; ancak bir sanatın uygulayıcısıdır. 21
22 Lord WT Kelvin.. Gözlemlerinizi sayılarla dile getiremiyorsanız bilginiz geçersizdir. demektedir. O halde; sayısal anlatım çok önemlidir. Bunun için İse ölçüm yapabilmek gereklidir. KELVİN, Lord William Thomson ( ) 22
23 Galileo Galilei ( ) Sayamadığınız, ölçemediğiniz hesaplayamadığınız olayları tanıyamazsınız. Çağdaş bilim, şanlı Galileo Galilei'nin, olayların nasıl olduğunu açıklamak için çalışıp, bugün bilimsel araştırmanın temeli olan kontrollü deney i kullanmasıyla doğdu. 23
24 Aristo dan G. Galilei ye.. Aristo (M.Ö ), belli ilkelerden başlayıp, usavurma yoluyla temel gerçeklere, deney ya da gözleme değinmeksizin (!?) varılabileceğine inanırdı. Bilim dünyasını yıl ketledi bu aforizmalarıyla. Deneysel ve gözlemsel bilimsel sürece varmak hiç de öyle kolay olmadı. Aristo ya göre biliminin amacı, olayların "niçin oluştuğunu açıklamaktı!? Çağdaş bilim, şanlı Galileo Galilei'nin, olayların nasıl olduğunu açıklamak için çalışıp, bugün bilimsel araştırmanın temeli olan kontrollü deney i kullanmasıyla doğdu. En bedbaht millet, kaleleri ayakta olup da ahlakı harabe olan millettir. sözü de Aristo nundur.. 24
25 25 Not everything that can be counted counts and not everything that counts can be counted. Albert Einstein "More the knowledge lesser the Ego, lesser the knowledge, more the Ego" «Sayılabilen her şey önemli değildir ve önemli olan her şey de sayılmış olamaz.»
26 Halk sağlığı uygulamasının ve politikalarının dayandığı temel, araştırma olmalıdır. Geçmişte olduğu gibi iyi araştırma, başarılı yönetsel uygulamaların temelidir. Özellikle Epidemiyolojik araştırmalar hastalık için risklerin belirlenmesinde ve gerekli önlemlerin sağlanmasına yardım eder ve bu tür niceliksel ve niteliksel araştırma ve uygulama çalışmaları yararlı bilgiler sağlar. EUPHA - Europan Public Health Association, The Future of Public Health in Europa: Towords a More Active Partnership with WHO/EURO. European Journal of Public Health, 2006;Vol. 16, No. 2,
27 Kimi kez sayarak dönüşüm yapar ve ölçeriz.. Örn. menopoz ölçüm eşeli.. 0= Hiç Yok 1= Hafif 2= Orta 3= Şiddetli 4= Çok Şiddetli MRS Psikolojik Puanlar (I) 1,2,3 MRS Somatik Puanlar (II) 4,5,6,7,11 MRS Ürojinekolojik Puanlar (III) 8,9,10 MRS Toplam Puanlar I,II,III 27
28 Kupperman İndeksi hesaplaması (ağırlıklı eşel) Ateş basması X 4 Parestezi X 2 Uykusuzluk X 2 Sinirlilik X 2 Depresyon X 1 Vertigo X 1 Yorgunluk X 1 Atralji / Miyalji X 1 Baş ağrısı X 1 Çarpıntı X 1 Karıncalanma X 1 KPI toplam puanı 0= Yok 1= Hafif 2= Orta 3= Şiddetli 28
29 Yıl içinde gündüz süresi sinüzoidal.. FROM DATA TO MODEL 29
30 Bilimin temel varsayımları.. Kendi dışımızda bir olgular dünyası vardır. Nedensiz olgu yoktur ve nedenler doğanın içindedir. Olgular düzenli ilişki içindedirler. Dünya gelişigüzel değildir; tutarlıdır ve kapristen uzaktır. Dünya bilim için anlaşılabilir dir. Bu dünyayı / evreni bilme ve anlama insanlar için değerli bir uğraştır. Eğer böyle değilse; bilim, yaşamı anlama çabası olarak gerekçesini yitirir. 30
31 Bilimsel araştırma kolay mı? Bilimsel araştırma; her adımı tuzaklarla dolu kıldan ince, kılıçtan keskin bir bilim ve sanattır. Dr. Ahmet Saltık 31
32 Bilimsel Sürecin Basamakları - 1 Karl Pearson'dan John Dewey uyarlaması ile bu aşamalar şöyle sıralanabilir : Güçlük yaratan bir durumun ayırdedilmesi Durum içindeki sorun un anlaşılıp, tanımlanması. Belki li çözümlerin incelenerek denenceler in (hipotezlerin) belirlenmesi. Denence nin uygulanması veya denenmesiyle ulaşılacak sorunların gereğince değişikliğe uğratılması. 32
33 Bilimsel Sürecin Basamakları - 2 Dolayısıyla bilimsel yöntem ya da süreç Kuralcı (Normatif) özlüdür. O halde bu basamaklarda ilerleyebilmek için bilim insanı; Gözler Ölçer Bulgu ve verilerini sınıflar Vardama yapar (Endüksiyon, Dedüksiyon, Öteleme, Ulama) Yordar (kestirimde bulunur) İletişim kurar Olmuşu ya da olacağı betimler, ilişkileri açıklar.. 33
34 Bilimsel Sürecin Basamakları - 3 Kuralcı (Normatif) yapısıyla biliminin istikrarlı ögesi olan bilimsel yöntem; Kendini düzelticidir : Kendini sınar Vargılarını gerektiğinde değiştirir. Bilgisi Güvenilir ve Geçerlidir ama; mutlak ve değişmez değildir. Böylece Bilim, asıl gücünü Yöntem'inde bulur. 34
35 Bilimsel Sürecin Basamakları - 4 Bu sayede de Doğal ve Toplumsal olaylar ve koşullar denetim altına alınabilir. Bu amaçla Ölçme yapabilmek gerekir. Çünkü varolan her şey bir miktar la vardır. O halde bulguların Niceliği (miktarı) de önemlidir, Niteliği (kalitesi) gibi.. Öyleyse Ölçme kaçınılmazdır! Ölçme tekniğinin düzeyi, o bilim dalının gelişme derecesini de yansıtır. Hatta, Ölçümbilim (Metroloji) adıyla yeni bir bilim dalı geliş(tiril)miştir. 35
36 Bilimsel Sürecin Basamakları - 5 Ancak; bilimsel yöntem ve bilimsel tutumun gerektirdiği davranışlar vazgeçilmez önkoşullardır. Aristo ve Bacon'a göre bilimsel süreçte aşamalar şöyledir : 1. Gözlem 2. Varsayım kurma 3. Doğrulama 4. Genelleme Bu 4 aşamaya ya da adıma, Bilimsel süreç 4 lüsü (Quartet'i) de denir. 36
37 Bilimsel araştırma çok pahalı! Araştırma gereçlerinin yüksek fiyatlı oluşu yoksul ülkelerin kıt kaynaklarını çok zorluyor.. Batı'daki araştırmacılar bütçe kısıtlamalarından yakınırken, görece yoksul ülkelerdeki meslektaşları laboratuvar gereçleri edinmek için aşırı yüksek bedeller ödüyor. Görece yoksul ülkelerdeki bilim insanları, aynı gereci edinmek için varlıklı ülkelerdeki meslektaşlarından %70 daha çok para ödemek zorunda. Dolayısıyla yöntem hatası yapmamalıyız. Dünyanın geri kalanı için ufukta bir rahatlama gözükmüyor. Bu durum araştırmacıları düş kırıklığına uğratmayı sürdürüyor. ( v428/n6982/index.html, ) 37
38 38
39 ARAŞTIRMA YÖNTEMLERİ PİRAMİDİ Randomize kontrollü çift kör çalışmalar Randomize kontrollü çalışmalar (RCT) Ko h o r t ç a l ı ş m a l a r ı O l g u - ko ntro l ç a l ı ş m a l a r ı O l g u s e r i l e r i O l g u s u n u l a r ı D ü ş ü n c e l e r, Edito r ya l ya z ı l a r Metaanaliz ve Sistematik Derlemeler H ay va n A ra ş t ı r m a l a r ı I n v i t r o A r a ş t ı r m a l a r 39
40 RANDOMİZE KONTROLLÜ ARAŞTIRMA (RKA) SONUÇLARI AÇISINDAN, TIPSAL KARARLAR OLUŞTURMADA, EN ÜST DÜZEYDE GÜVENİLİR KANIT ÜRETEN ARAŞTIRMA TİPİ RANDOMİZASYON, İLERİ YÖNELİK KLİNİK ÇALIŞMALARDA, FARKLI TIPSAL GİRİŞİMLERİN ETKİLERİNİ HATASIZ ORTAYA KOYABİLMEK AMACI İLE, DEĞERLENDİRİLEN SAĞALTIM TİPİ DIŞINDAKİ, KONU EDİNİLEN TIPSAL SONUÇ AÇISINDAN ETKİLİ OLABİLECEK ÖZELLİKLERİN (PROGNOSTİK FAKTÖR), YARGILAMA KÜMELERİNE EŞDÜZEYLİ DAĞILIMINI SAĞLAMAK AMACI İLE KULLANILAN YÖNTEMDİR... BÖYLECE RANDOMİZASYON ; BİLİNEN VE BİLİNMEYEN RİSK ÖGELERİ AÇISINDAN ÇALIŞMA KÜMELERİNİ KIYASLANIR DURUMA GETİRMEYİ ve SONUÇ YARGILARIN GÜVENİLİR OLARAK ELDESİNİ HEDEFLER... CALAY, PURİSA, ŞENOCAK 40
41 41 RANDOMİZE KONTROLLÜ ARAŞTIRMA (RKA) SONUÇLARI AÇISINDAN, TIPSAL KARARLAR OLUŞTURMADA, EN ÜST DÜZEYDE GÜVENİLİR KANIT ÜRETEN ARAŞTIRMA TİPİ GERÇEKLEŞTİRİLMESİ ZOR... KALİTELİ GERÇEKLEŞTİRİLMESİ ZOR... BİLİMSEL KALİTE ÖLÇÜM DİZGELERİNDE, OLUMLU SONUÇLAR ALMALARI BEKLENİR.. BELLİ ÖZELLİKTE/ KONUDA ARAŞTIRMALARIN ÖZGÜN YÖNTEMBİLİMSEL YAPILANMALARINI ORTAYA KOYABİLİR.. ŞENOCAK, UYSAL, SÜT, KÖKSALAN
42 Hatanın kaynağı önemli mi? Bilimsel araştırmalarda yanılgıya bilerek ya da bilmeyerek düşülmesi, sonucu değiştirmez. Gerçek ten aynı derecede uzaklaşılmış olur. Dolayısıyla, Türkiye gibi dar kaynaklı bir ülkede, eldeki sınırlı kaynakların uygun bilimsel yöntemlerle değerlendirilerek, bilimsel yanılgıya düşülmemesi beklenir. Alan bilgisi yeterli değildir. Bilimsel araştırma Yöntembilim i bilgisi ve uygulama becerisi son derece önemlidir. Köklü bir Biyoistatistik ve Epidemiyoloji eğitimi kaçınılmazdır. Dolayısıyla mutlaka takım (ekip) çalışması gereklidir.. 42
43 Duyarlı, Doğru Ölçüm Yapabilmek.. Ölçüm, öznellikten nesnelliğe geçiş sürecidir. Zaman ilerledikçe sayısal veriler giderek artıyor. Çünkü daha çok ve duyarlı ölçüm yapılabiliyor. Eskiden karaciğer büyüklüğü parmakla değerlendirilirken şimdi ultrason sayesinde ml olarak büyüklük ölçümleri yapılabiliyor. Eskiden ateş elle bakılırken, şimdi ateşi ölçen analog ve sayısal (dijital) derecelerimiz var vb m, gm, Litre.. düzeyine erişebildik! 43
44 Ultra Ölçüm Yapabilmek.. Endokrinolojide hormon düzeyleri pikogramla (10-12 ) ölçülüyor. Femto, Atto gm ı ölçüyoruz! Bu örnekler bize, bugün için anlayamadığımız kimi olayları da ileride açıklayabileceğimizi gösterir. Ölçüm yeteneğimiz geliştikçe, mikro evrenleri daha yakından tanıyabiliyoruz. Ölçüm yeteneğimiz sayesindedir ki, plazmadaki kozmik endokrin dalgalanmaları sayısal olarak belirleyebiliyor, endokrin patolojileri tanılıyoruz. 44
45 F.Galton un yalın deneyi.. Nohutlar bir elekten sabit genlik ile salınarak geçirilirse, biriktikleri kapta nasıl yığışır? Bu sorunun yanıtını Aristo nun önerdiği gibi yanıtlarsak; Gerçek, düşünerek ve sezgi ile bulunabilir... Sezgi ile çabalayalım bakalım, herkes nasıl bir şekil çizecek? Yoksa GÖZLEM ve DENEY i sezgilerimizin önüne mi alacağız? Gerçeğe ulaşmanın tek yolu, us ve deneysel-gözlemsel bilim! 45
46 Sezgi her şeye çözüm mü? Herkes, Galton un düzeneğinde elenen nohutların birikimini değişik biçimde çiziyor. Çünkü herkesin sezgisi öznel dir.. Aristo, bu mantıkla 1000 yıl, bilimi deneye ve gözleme kapatmıştır. Oysa bilim genel ve nesnel dir. 46
47 Sezgi her şeye çözüm mü? Bilim, mutlaka, yinelenebilir deney-gözleme dayalı olmak, kendini doğrulamak ya da yalanlamak zorundadır. İçerik; bilimin yalnız bugün geçerli göreceli gerçeği, zamanla değişime zorunludur. Bunu sağlayacak olan, araştırma yöntembilimidir (Metodoloji). Yani Epidemiyoloji dir, Biyoistatistik tir.. 47
48 Galton un nohutları, Çan Eğrisi çizdi! -3 SS -2 SS -1 SS X +1 SS 2 SS +3 SS Standart normal dağılım, Çan eğrisi (bell shape) gibidir. Deneyle ortaya konmuştur.. Kuramsal hesapları ardından geliştirilmiştir. Ortalamanın (X) çevresinde ± 1, 2 ve 3 St. sp. gösterilmektedir. 48
49 Ortalaması µ, standart sapması σ olan standart normal dağılım.. Gauss eğrisi.. Evrenden elde edilen normal dağılım 49
50 Ortalaması X, standart sapması SD olan, evrenden çekilen bir örnekten elde edilen normal dağılım. Örnekten elde edilen normal dağılım 50
51 Ortalaması 100 ve standart sapması 10 olan Normal Dağılım Eğrisi µ=100 ve σ = 10 olan bu normal dağılım eğrisinde, ± 1 st. sp. sınırları içinde, bir başka deyimle arasında, incelenen kişilerin % 68 i yer alır. Ya da bu böyle ise dağılım normaldir. 51
52 Standart Normal Dağılım ± 1 SD içinde, kümenin % sı, ± 2 SD içinde, kümenin % ü, ± 3 SD içinde ise kümenin % ü yer alır.. Tersinden söylenir ise, bir ana kütleden (evrenden) çekilen örneklemde bireylerin ölçümlerinin dağılımı aritmetik ortalama çevresinde böylesine dağılıyorsa, o ölçüde kuramsal normal dağılım a yakındır. Yüksek varyasyonlu dağılımlarda aritmetik ortalama dağılımı temsil yeteneğini yitirir. Böylesi durumlarda yine de ortalama verilecekse; Geometrik, Harmonik, Kareler, Kübik, Ters (1/X), Logaritmik vb. ortalamalar alınır. Ortalama; n, SD ve % 95 GA değeriyle verilmelidir. 52
53 S( X ) k i 1 ( X ) i X 2 İzlendiği gibi, Galton Modeline de uyan standart bir Normal Dağılımda, ortalamanın ±1 SD sağ ve solunda kalan çizgi altındaki alan % 68.26; ±2 SD sağ ve solunda % ve ±3 SD sağ ve solunda % tür. Standart Normal Dağılım (z dağılımı) 53
54 Tam Simetrik Normal Dağılım Aritmetik Ortalama (mean), Ortanca (median) ve Tepe (mode; en sık gözlenen değer) değerinin örtüştüğü ideal, tam simetrik normal dağılım eğrisi.. 54
55 Standart sapma (St. deviation, SD, SS) Bir dağılımda yer alan birey lerin, ölçümlerinin, küme ortalamasından gösterdiği sapmanın, bir tür standardize edilmiş biçimidir. Her ölçüm için ayrı ayrı ortalamadan sapma mı verelim, tek standart değer mi hesaplayalım? Pratikte gerçek sapmalar kullanılarak SS hesaplanır, standartlaştırılmış tek bir sonuç verilir : Bu standart sapmadır (SS, SD). Birçok üründe SS değeri vardır. Örn. bir çikolatada 40 ± 2 gm (SS) yazılması gibi.. 55
56 56 Standart Sapma nın büyümesi.. Dağılım genişliği (maks-min, range) büyüdükçe dağılım yaygınlaşır; bir başka anlatımla varyasyon yüksektir. Örn. dar olan dağılımda sınav notları, sözgelimi arasındayken, geniş dağılımda arasındadır.
57 Ortalamaları farklı, standart sapmaları aynı olan 3 Normal dağılım eğrisi 57
58 _ Ortalamaları aynı (X=55), standart sapmaları farklı 3 normal dağılım eğrisi.. Aritmetik ortalamalar çok yanıltıcı olabilirler. Örn. ülkemizde kişi başına yıllık gelir (pc/pa) ortalama 10 bin $ dır. Ancak uç değerler vardır; birkaç yüz $ gelirli milyonlarla onbinlerce $ gelirli bir avuç varsıl
59 Değişik normal dağılım eğrileri.. 59
60 Dark blue is less than one standard deviation from the mean. For the normal distribution, this accounts for about 68% of the set (dark blue) while two standard deviations from the mean (medium and dark blue) account for about 95% and three standard deviations (light, medium, and dark blue) account for about 99.7%. 60
61 S a ğ a S o l a Ç a r p ı k v e T a m S i m e t r i k D a ğ ı l ı m 61
62 Standart Sapma nın Ölçüsü Ne Olmalı? Çok küçük (görece!) olarak hedeflenen bir standart sapma, maliyeti artırır. Ancak çok ince ve önemli ayar gerektiren malzemeler, toksik maddeler ve süreçler için SS çok önemlidir. Bu durumda da maliyet-yarar arasında optimum denge kurulmalıdır. 62
63 St. sapma için örnekler... Yarım litre bira şişesinde 500 ± 5 cc, Yağ tenekelerinde 5 lt ± 30 cc, Morfin ampulünde 1 cc ± 0.1 cc, Floresan lambalarda 120 cm ± 0.1 cm.. gibi St. sapma rakamları verilebilir. Her türlü üründe malzemenin oylumu, boyutları vb. üreten makinenin özelliklerine göre, öngörülen standartlara göre uygun sapmalarla üretim yapılır. St. sapmanın sıfır kılınması hedeflenmez. Bu maliyeti çok artırır ve gerekmeyebilir de.. Kabul edilebilir bir düzeyle yetinilir. Bu yüzden ulusal, uluslar arası Standart Kurumları bu alt ve üst sınırları koyarlar. Örn. ülkemizde TSE, ABD de ANSI, AB de CE, Dünyada ISO gibi. 63
64 Standartların Gereği Yaşamda pek çok temel alanda standartlar kaçınılmazdır. Türkiye de bu standartları, Türk Standartları Enstitüsü koyar. Şırıngalarla iğneleri, kanüller, sondalar, ilaç dozları, lab. tartaçları ve analizörler, kalem uçları, ayakkabı numaraları, giysi ölçüleri, ampuller, tüp kafaları, oto lastikleri, vidalar, somunlar, protezler.. tanımlanan standarda uymalıdır. 64
65 Sağa, sola çarpık dağılım eğrileri Yoksul insanların hemoglobini değerlendirildiğinde, çarpık bir dağılım eğrisi ile karşılaşılır. Çünkü bu insanlarda anemi yaygındır; eğri normal dağılıma uygun çıkarsa; hatalı olarak, düşük bir anemi oranına ulaştık.. demektir. Benzer tarama herhangi bir yörede gebeemziren kadınlar için yinelendiğinde, aynı biçimde, çarpık dağılım eğrileri ile karşılaşılır. Tersine; polistemia rubra hastalarında, yüksek Hb değerlerinin çokluğuna bağlı çarpılma olur.. 65
66 66 Pozitif Çarpık (Skewed) Dağılım Bu dağılım, başarısız geçen bir sınav, düşük Hb değerlerinin saptandığı yüksek düzeyde anemik bir küme, çok balık tüketen bir toplumda tiroid bezi kitlesi vb. örnekler için uygundur.. Özetle dağılımda küçük değerler egemendir, yoğunluktadır. İzleyen dağılımda ise durum tersinedir..
67 Negatif Çarpık (Skewed) Dağılım Bu dağılım, başarılı geçen bir sınav, yüksek Hb değerlerinin saptandığı bir küme, çok az iyot alan bir toplumda tiroid bezi kitlesi vb. örnekler için uygundur.. Özetle dağılımda büyük değerler çoktur. Bir başka anlatımla, rekorların kırıldığı bir olimpiyat, çok gollü bir lig, son yıllarda yüksek çıkan enflasyon değerleri, yüksek ortalama kur.. değerlerini temsil etmektedir.. 67
68 Neden-Sonuç Bağıntısı-1 Bir başka örnek olarak, asbestli işlerde çalışanlarda gözlenen akciğer kanseri sorunu sunulabilir. Asbestle karşılaşanlarda artmış bir akciğer kanseri insidensi söz konusu ise, bunun ardından, sorunun nedenlerinin araştırılması gündeme gelir. Asbest lifleri ve yüksek akciğer kanseri morbidite / mortalitesi, saptamanın 2 temel tanımlayıcı öğesidir. 68
69 Neden-Sonuç Bağıntısı-2 İki olay bir arada (ko-egzistans) olsa, hatta birlikte değişim (ko-varyasyon) gösterse bile, aralarında bir neden-sonuç ilişkisi ileri sürmek henüz olanaklı değildir. Her 2 sini de koşullayan, birlikte bulunan ancak fark edil(e)meyen başka birtakım etmenlerin de varlığı olasıdır. Örn. asbeste sunuk (asbestle karşılaşan, maruz kalan) insanlar aynı zamanda, toplumun öbür kesimlerine göre çok yüksek düzeyde sigara içiyor olabilirler
70 Neden-Sonuç Bağıntısı.. Bu aşamada çözümleyici (analitik) epidemiyoloji devreye girmektedir. İzlenecek 2 temel strateji vardır. Her ikisinde de amaç aynıdır. İki olay arasında bir neden-sonuç ilişkisi (birincil ilişki, causality) var mıdır; varsa bu ilişki nasıl kanıtlanabilir; yoksa nasıl reddedilebilir? Karl Popper in Yanlışlamacı Kuram ı bağlamında, ilişkinin-bağın ancak reddedilemeyişi karşısında kabulü gibi dolaylı bir yöntem izlenmektedir. Dolayısıyla temel denence (sayıltı, hipotez); 70
71 Karl Popper in Yanlışlamacı Kuram ı Bu aşamada çözümleyici (analitik) epidemiyoloji devreye girmektedir. İzlenecek 2 temel strateji vardır. Her ikisinde de amaç aynıdır. İki olay arasında bir neden-sonuç ilişkisi (birincil ilişki, causality) var mıdır; varsa bu ilişki nasıl kanıtlanabilir; yoksa nasıl reddedilebilir? Karl Popper in Yanlışlamacı Kuram ı bağlamında, ilişkinin-bağın ancak reddedilemeyişi karşısında kabulü gibi dolaylı bir yöntem izlenmektedir. Dolayısıyla temel denence (sayıltı, hipotez); 2 değişken ilişkisizdir. biçiminde kurulmakta, ancak bu reddedilirse ilişki kabul edilmektedir. 71
72 B i r a z g ü l e l i m 72
73 Aritmetik Ortalamanın Yanıltıcılığı 80 milyonun yarısı her gün 1 piliç, öteki yarısı da her gün 1 ekmek yiyorsa; bundan, herkes günde yarım piliç ile yarım ekmek yiyor sonucu çıkar mı? Dünya geliri adil paylaşılacak olsa, kişi başına $ düşmektedir! Oysa dünya insanlarının yarısı günde 2, yılda 750 $ dan az bir para ile yaşamak = sürünmek zorunda bırakılmıştır. 73
74 U y g u n Ö r n e k l e m.. Bilimsel araştırmada belki de ilk adım, uygun örneklem dir. Çayın şekerinin tadına bakmak da bir örneklemedir. Ancak bu davranış, şeker karıştırıldıktan sonra yapılır. Amaç birörnekliği (türdeşliği, homojenliği) sağlamaktır. Bu yapılırsa, minik bir çay kaşığı ile tadına bakma başarılıdır. 74
75 Çorbadan örnek alma.. Bir çorba hazırlarken, her şeyini koyup iyice karıştırdıktan sonra (birörnek kılma) tadına bakıyoruz. Yani, uygun örneklem için evreni hazırlıyoruz. Böyle yaparsak, bir çorba kaşığının ucu kadar örnekle, tüm tencere (evren) hakkında geçerli bir karara varıyoruz. Oysa bunu yapmazsak birkaç kepçe de içsek, çorbanın tadı hakkında geçerli bir yargı üretemeyiz. Açıktır ki, örneklemi büyütmek her durumda onun temsil yeteneğini aynı oranda artırmaz. 75
76 Bir örnek üzerinde ilerleyelim.. Tıp fakültesinin 1200 öğrencisinin açlık kan şekerine (AKŞ) bakalım.. Tüm evren mi çalışmaya alınacak? Ya da kaç kişi seçilecek? Bu seçim nasıl, hangi yöntemle yapılacak? Nasıl bir ÖRNEKLEME yöntemi izlemeliyiz? Örneklem in (Sample) temsil gücü nasıl sağlanır? Verileri genellerken evrenimizle sınırlıyız! 76
77 Örnekleme (sampling) 1200 kişilik ana kütleden, evrenin % 10 unu çekelim öğrenci eder. Bu 120 kişi nasıl seçilecektir? Ana küme katmanlanmalı dır. yaşa, sınıfa, cinsiyete.. göre vb. tabakalanmalıdır. Katman niteliği, bağımlı değişkene göre ayrı ayrıdır. Kimi kez ırk, sosyo-ekonomik durum vb. katmanlamada (stratifying) kullanılır. 77
78 78 Ö r n e k l e m e (sampling) Bu örnekte de evren, katmanlama (tabakalama), ağırlıklandırma ile örneklemin türdeşliği (homojenliği) sağlanmış olur. Birörneklik, ana kitledeki bireylerin örnekleme çıkma olasılıklarını eşitlemiş olmaktadır. Bu koşulla rastgele / random örnekleme yapılabilecektir. Bireylerin örneğe çıkma şansları eşitlenmediğinde, örneklem gelişigüzel dir RASTGELE (random) olması gerekir. Gelişigüzel örneklem, genellikle örneklem sayılmaz!
79 Örnek (sample) İnceleyeceğimiz evreni temsil ettiği düşünülen, optimum büyüklük ve uygun bileşimde olan evrenin (ana kitle) bir minyatürü olmalıdır. Böylece, evreni incelemek yerine seçilen küme incelenir; para, zaman, emek yitiği önlenir. Örneklemin optimal büyüklüğü, maliyet-zaman çözümlemeleri ile belirlenebilir. Uygun=temsil yetenekli örneklemle çalışmak, bilimsel, etik ve ekonomik bir yükümlülüktür. (Biyo)İstatistik, özünde yığınlarla çalışır.. 79
80 Örneği Optimum büyüklükte kılma Örneklemin temsil yeteneği için, öngörülen bir güven düzeyi konmalıdır. Optimum örneklem büyüklüğünü öngörmek için matematik formüller vardır; kullanılmalıdır.. Araştırmanın tipine göre (alan, klinik..) örnek çekme yöntemi ve örnek büyüklüğü değişim gösterir. DSÖ nün, yayınladığı bir rehber kitap vardır; yararlanılmalıdır. Örneklemin temsil yeteneği, büyüklüğüyle doğrusal ilişkili değildir. Bileşimi de önemlidir. 80
81 Tuzlu Küme! Çalışmalarda kimi zaman, normali çok aşan oranlar bulunur. Örn. bir bölgede % Talasemi taşıyıcılığı (trait) saptanmıştır. Acaba bu durum doğal mıdır, gerçek midir? Yoksa, Tuzlu küme ye rastlandığı, iyi örneklem çekil(e)mediği için mi böyledir? Peynirin ya da yemeğin tuzlu yanı mıdır? 81
82 Bir Biyoistatistik deneyi yapalım.. Ana kümeden 10 kez örnek çeksek ve aşağıdaki ortalamaları bulsak.. % 10, 120 kişi, % 10, 120 kişi, % 10, 120 kişi, % 10, 120 kişi, % 10, 120 kişi, % 10, 120 kişi, % 10, 120 kişi, % 10, 120 kişi, % 10, 120 kişi, % 10, 120 kişi, Görüldüğü gibi her örneklemde farklı ortalamalar çıkmıştır. Hangisi gerçek evren ortalamasıdır? Örneklem ortalamaları doğal bir varyasyon göstermektedir. Örneklem hatasının kaynağı bu varyasyondur. Toplam 1200, ortalamaların ortalaması µ = X 1 +X X 10 /
83 Standart Hata = Örneklemin hatası! Her örneklem, kendi evrenini ancak, hesaplanabilen bir yanılgı payı ile temsil eder. Bu yanılgı payına standart hata (S e )denir. Standart hata örneklem hatasıdır; h a t a s ı z ö r n e k l e m o l m a z. Standart hata arttıkça, örneklemin evreni temsil gücünün azaldığı düşünülür. Bu hata sayısal olarak hesaplanabilir. Örneklem yoksa, standart hata = örneklem hatası da -doğallıkla - yoktur. Ancak örneklem hatası dışında da hata (Bias) hep olanaklıdır. 83
84 Standart Sapma (SS) Ne Zaman Sıfır Olur? Dağılımda değişken ölçüm / sayım değerleri (varyasyon) yoksa SS da yoktur. B i r ö y k ü : Yunus Emre, öğretmeni Taptuk Emre nin yanında eğitim alırken, eve getirdiği odunların hepsi aynı boy, aynı en ve biçimde imiş.. Yani SS sı sıfır olan. Uygulamada bu olanaklı değildir. Hiç kimsenin kan şekeri, Hb değeri, boyu vb. tıpatıp aynı değildir. Dolayısıyla evrenin tümü de incelense, bir SS mutlaka olacaktır. Biyolojik varyasyonu saklı tutarak SS yı azaltmanın yolu; güvenilirgeçerli gözlem (=ölçüm - sayım) ve kayıttır. 84
85 Standart hata ve standart sapma ilişkisi Standart Hata = Standart Sapma Vn Standart Hata, örneklemden kaynaklanır. Ancak, her evrenin, bir başka evrenin alt kümesi olduğu da unutulmamalıdır. Kimi zaman araştırmacılar, standart sapmayı çok yüksek bulunca n in kareköküne bölerek standart hatayı kullanırlar. Ancak, ortalamanın önüne yazılan ne ise, o mutlaka belirtilmelidir. Yüksek standart sapma, çok anlamlı da olabilir. 85
86 SE & The Confidence Interval Sometimes, a confidence interval may be computed from theory alone. For instance, means of large, random samples tend to be unbiased and normally distributed. Therefore, the 95 % Confidence Interval (95 % CI) for any such mean is just m ± 1.96 SE, where m is the observed mean and SE is the standard error of the mean, as given by the equation below where σ is the population standard deviation for the data and n is the sample size. 86
87 Örneklem yanılgısı.. Hipotez testlerinde test sonucunda yokluk hipotezi ya kabul ya da reddedilir. Yokluk hipotezinin kabul ya da reddedilmesi, hipotezin gerçek durumuna göre Tip I ya da Tip II hataya düşülmesine neden olur. Evrenin tümü yerine örneklem üzerinde yapılacak çalışmalarda bu hatalar kaçınılmazdır. Ancak yeterli sayıda deneğin çalışmaya alınması ile hata oranları belli bir düzeye indirgenebilir. 87
88 Örneklem büyüklüğü.. Klinik çalışmalarda örneklem büyüklüğünün hesabında gerek duyulan parametreler : Çalışmanın deseni, Önemlilik düzeyi, Güç, En küçük önemli klinik farklılık, Kullanılacak hipotez testidir. 88
89 Evren Örnek(lem) Çekimi 89
90 Örneklem büyüklüğü.. Örneklem büyüklüğü, 3 temel nedenden dolayı önem taşır : 1. Ekonomik gerekçeler 2. Etik sorunlar 3. Bilimsel geçerlilik 90
91 Standart Sapma (SS) Ne Zaman Sıfır Olur? Sensus (=tam sayım, tam alım) yapılsa da (örneğimizdeki 1200 öğrenci) sonuçların ortalamasının bir standart sapması olur. Çünkü herkesin değeri birbirinden, doğal biyolojik varyasyon gereği farklıdır (örnekteki AKŞ gibi). Ancak değerler belli bir aralık (range) içinde dalgalanır. Fizyolojik / Patolojik ayrımında SS dan çok yararlanılır. 91
92 Bilimin işlevi : Standart koyma.. Yığınlar, genellikle kendi ortalaması ve kendi ölçümleri içinde değerlendirilmektedir. IQ, BKİ, bel / kalça oranı, kan basıncı, Hb, AKŞ, boy, enflasyon hızı.. vb. ölçümler, normal dağılıma uydukları varsayılarak incelenmektedir. Elbette Binom, Poisson, Fisher, Pearson, Weibull gibi dağılımlar da vardır. Fakat çoğu biyolojik, sosyolojik.. özellik, ölçülebiliyorsa normal dağılır. Fizyolojik norm, normal, standartlar; uzun yığın çalışmaları ve biyo-matematik desteğiyle konabilmektedir ve zamanla değişime açıktır : Evrim sonucu, müdahale, yeni bilgi üretimiyle. 92
93 Bilimin işlevi : Norm koyma.. Kategorik olarak (bir eşik değer atayarak) ya da alt kümenin veya evrenin ortalamasına dayanarak ± 2 st. sapma değerlerinin dışındakiler patolojik / anormal, aradakiler normal olarak kabul edilir. Sınır, geçiş (border) değerler de tanınabilir. Ancak bilgilerimiz arttıkça sınırlar gözden geçirilir. Örn. kan basıncı normal değerleri sürekli aşağı çekilmektedir
94 Norm koyma : PSA örneği Varyasyonu çok yüksek bulunan bir kümede, diyelim ki PSA (prostat spesifik antijen) değerlerinde; bu maddenin kadın-erkek ayrılarak ölçülmesi ile kadınlarda bulunacak sıfır değeri çok anlamlı olur. Söz konusu antijenin önce «erkeklere» sonra da «prostata ait» olduğu giderek anlaşılır. 94
95 Norm koyma : PSA örneği Yaşla ilişkisi de, hâlâ süren yüksek varyasyonla kurulur. PSA çocuk ve gençlerde çok düşük, yaşlılarda yüksek olduğundan, sonunda prostat tümörü için bir belirteç (marker) işlevi, Biyoistatistik, Epidemiyoloji ve Kliniğin (alan bilgisinin) ortak çabasıyla aydınlatılır. 95
96 Referanstan sapmanın irdelenmesi Doğru çizgisi (accuracy line) AKŞ Üst sınır Alt sınır 96 Referans değer 100 birim ise, hangi alt ve üst sınırı koyarak gerisini anormal, kabul edilemez sayacağız? NORM koyma, normal i tanımlama o denli kolay mı? Referans ölçüm; laboratuvar, yöntem, kişi ya da gözlem; kategorik sınırlarla bunu yapabileceği gibi, çan eğrisinden yararlanarak, ±2 st. sapma sınırlarını normal olarak belirleyebilir. Bu durumda ölçümlerin % 95 i a priori (baştan) normal kabul edilmiş olur. Bilim- Matematiksiz soluk alamaz.
97 F D A H a k k ı n d a... Bitkisel, hayvansal ya da sentetik bir formülasyonun ilaç durumuna gelmesi 10 yılı bulan Faz 1-4 deneylerini gerektirir ve yaklaşık milyon $ a malolur. İlaç firmaları, akredite kurumların raporu ile FDA ya ruhsat için başvurur. FDA bu raporları inceler, gerekirse yineler, yineletir ve sonucunda bu ilaç ya da besin maddesinin kullanılabilir izin belgesi ni verir. Ayrıca FDA, referans laboratuvar olarak, ölçmesi için ülkedeki tüm laboratuvarlara kimi maddeler yollar.. Belirlediği üst ve alt sınırların dışında değer verenleri uyarır, lisanslarını askıya alır ya da iptal eder. Bu süreçlerde çok yoğun olarak Temel Biyoistatistik yöntemleri kullanır.. 97
98 E 2 Serum Düzeyleri pmol/l Bilimin evrensel işlevine hatalı ve kötü bir örnek.. Ne yazık ki seyrek de değil! tarama aylar Implanon N = Norplant N = (Croxatto and Mäkäräinen. Contraception 1998; 58: 91S-97S) 98
99 Yöneylem Araştırması (Operational research) 1. Dünya Paylaşım Savaşı sonrasında İngilizler,..yanmış ve yıkılmış durumdan nasıl çıkabiliriz.. diye düşünürken, kimi araştırmalar yaptılar. Sayısal karar verme teknikleri (quantitative decision making procedures) bu biçimde gelişti ve Yöneylem Araştırmaları sıkça uygulanmaya başladı. 99
100 Yöneylem Araştırmaları Türkiye de de Hastalık Yükü (Burden of Disease - DALY) kavramı sıkça konuşulmaya başlandı. Örn. ülkede böbrek aktarımı için bekleyen hastaların ne kadarı transplantasyona gitmeli? Eldeki dar kaynakların en uygun kullanılması için hangisi, ne ölçüde maliyet-etkili? Biyoistatistik, klinik karar verme süreçlerinde sayısal temelli, yerinde, nesnel karar üretmede son derece yararlı, vazgeçilmez işlevdedir. 100
101 101 B i r u y g u l a m a... Bir TSM hekimi, bölgesinde 2 köyün sularında serbest klor (SK) ölçümü yapıyor ve 0-6 yaş çocuklarda ishal atak hızı (İAH) hesaplıyor.. 1. köyde, SK u 0.5 ppm, İAH nı 1.8; 2. köyde bu verileri sırasıyla 1 ppm ve 2.4 olarak buluyor.. Soru : İAH ları birbirinden anlamlı (signifikan) olarak farklı mı yoksa rastlantısal mıdır? Farksızlık (H o hipotezi) : İAH ları farksızdır. Seçenek hipotez (H 1 - H A, ) : İAH ları farklıdır.
102 HİPOTEZ (sayıltı, denence, sınanca, varsayım) Deneme sonucunda sınanacak hipotezlerden en önemlisi, işlem kümeleri arasındaki farkın rastlantıdan ileri gelip gelmediğidir. H 0 H : i : 1 i i i 102
103 BİLİMSEL TUTUM, BİLİM ADAMLIĞI.. Bilim toplum, insan içindir; salt bilim için değildir. İnsan gönencinin aracıdır. Bilim insanı donanıktır, yaratıcı olmak zorundadır. Yansız, önyargısızdır; ama vardığı bilimsel sonuçların da kellesi pahasına yandaşıdır. (Prof. Server Tanilli, Uygarlık Tarihi) Nesneldir. Beklentisi yoktur, eriştiği bilimsel sonuçla kendini bağlı sayar. Açık fikirli / bilimin varsayımlarına saygılıdır. Ne denli akla yatkın olsa da, her tür dogmadan uzaktır. 103
104 Hangi İstatistik Tekniği Kullanmalı? Bu tür soruları yanıtlayabilmek için çeşitli istatistiksel yöntemler vardır ve sonucunda bir test istatistiği (t, U, Z, 2 vb.) ve bir de p değeri (probabilite = olasılık) elde edilir. Örnekteki soruyu yanıtlamak içinse, 2 yüzde arası fark testi ni kullanırız. Bu test sonucu test istatistiği olarak t ve bir p değeri hesaplanır. Kimi istatistik analizlerde, karşılaştırmalarda salt p değeri de verilebilmektedir. Bilgisayarlar günümüzde p nin sayısal eşitini vermektedir. 104
105 p değeri ve Tip 1 Hata.. t=2.12, p=0.121 olarak bulunursa yorum ne olurdu? Burada p> 0.05 tir ve H 0 kabul edilmezse, düşülecek yanılgı % 12.1 düzeyindedir! Dolayısıyla 2 İAH birbirinden istatistiksel olarak farklı değildir; suda SK düzeyinden bağımsızdır. Yani farksızlık hipotezi olan H 0 kabul, farklılık hipotezi olan H 1 reddedilir. Tersi yapılırsa (Tip 1 hata), gerçekte doğada, toplumda bulunmayan bir ilişki, hatalı (bias lı) biçimde kurulmuş olur. Oysa bu verilerle gerçekte SK ve İAH ilişkisizdir.. 105
106 p değeri ve Tip 2 hata.. Diyelim ki, t=4.72, p=0.024 bulunursa, yorum ne olacaktır? p<0.05 olduğundan, bulunan iki değer (İAH) birbirinden istatistiksel bakımdan farklıdır. Yani farksızlık hipotezi olan H 0 reddedilir. Bu durumda düşülebilecek hata p=0.024 (% 2.4) düzeyindedir ve kabul edilebilecek yanılgı boyutundadır. İstatistiksel yanılgı, % 5 e dek tolerans kabul görmektedir.. Bu p ile H 0 ın kabulü ise, 1-p = % 97.6 düzeyinde hata (Tip 2 hata) demektir ki, kabulü olanaksızdır! 106
107 Şu ünlü p değeri.. Dikkat edilirse, SK düzeyinin yüksek olduğu Sağlık Ocağı nda, öbüründen daha büyük bir İAH saptanmıştır. Bu saptama anlamlı ve yanlış etiketleme (tagging) değilse, güvenli ise, çok değerlidir. İAH, SK ölçümleri ters ilişkilidir. Nedenlerini aramak gerekir. Bu örnekte uygun bir p ile H 0 reddedilir ve H 1 (H A ) kabul edilirse, bu kez, kurulacak ilişkinin yönü büyük önem kazanır. 107
108 Şu ünlü p değeri.. Dikkat : SK düzeyi ile İAH doğru orantılıdır! SK düzeyinin artışına karşılık İAH da artmaktadır. Ölçüm, gözlem, etiketleme.. her şey doğru ise; bu sonuç çok değerlidir. Burada, klasik bir koşullanma ile, bulunan ilişki, dikkat edilmeden, yön bakımından yanlış değerlendirilerek artan SK düzeyinin İAH larını azalttığı yargısına - çıkarımına (statistical inference; istatistiksel çıkarsama) varmak, bir başka ciddi bilimsel yanılgıdır: Tip 3 (θ) Hata.. Gerçekten her adım tuzaklarla dolu değil mi? 108
109 Hipotez Testinde Kullanılan Kararlar ve Hatalar Çapraz seçenekler Karar (Contingency options) H 0 red H 0 reddedilemez Gerçek Durum H 0 doğru H 0 yanlış Yanlış Karar Tip 1 hata (α hata) Doğru karar (Testin Gücü) 1-β Doğru karar 1- α Yanlış Karar Tip 2 hata (β hata) 109
110 Nasrettin Hoca dan bir fıkra.. Nasrettin Hoca bir gün almış sazı eline.. Bir eli bir perde de sabit, öbürü ile tellere monoton vurup duruyor.. Hoca nın eşi sorar : - Hoca Efendi, benim bildiğim o el aşağı-yukarı gezer durur, seninki gibi bir yerde yapışıp kalmaz.. Hazır yanıt Hoca : - Hanım, onlar benim tuttuğum yeri arıyorlar!.. Notanın yeri sabit bir «nokta» değil; nota perdesi, bir «aralık» tır. Bilim sıklıkla aralık kestirimi yapar. Noktasal kestirim, belirleme, norm.. güçtür. 110
111 Nota perdesinden Güven Aralığı na Evrenin ya da örneklenen alt kümelerinin ortalama, oran, hız gibi parametrelerinin noktasal, kesin, tek bir değer olarak belirlenmesi çoğu kez «oldukça» güçtür. Bu bakımdan, belirli bir sayısal aralık (range, marj) olarak belirleme yapılır. Söz konusu kestirim için güven aralığı (GA) da verilir. % 90, genellikle % 95, % 99 veya serek olarak % 99.9 düzeyinde.. _ 1200 tıp öğrencisinin AKŞ ortalaması (X) şöyle gösterilmelidir : 105 ± 4.4 (% 95 GA : ) Yorum : Bu kümeden 100 kez örneklem çekilip AKŞ ortalaması hesaplansa, 95 kezinde bu ortalamalar, % 95 GA sınırları içinde kalacaktır.. 111
112 Güven Aralığı (Confidence interval) Bir çalışmanın yinelenebilirliğini (repeatability), kabul edilebilir sapmalar taşıdığını gösterir. Notalar, saz / gitar perdeleri.. bir aralığa örnektir. Bu aralıkta nereye basılsa yakın ses çıkar. Bu da onların güven aralığıdır. Kilo kestirimi yapılsa; Ben kaç kiloyum? kg arasında.. yanıtı, görece dar güven aralığına uygun bir örnektir. 112
113 Güven Aralığı (Confidence interval) Tartım kg arası.. dense, çok geniş bir güven aralığı içerir. Yanılma payı çok düşüktür ancak, bu denli geniş bir aralık kestirimi nin değeri yoktur.. Amaç, doğru noktasal değeri içeren, yeterince dar bir aralık hesaplamaktır. Noktasal kestirim çok güçtür ve yanılma payı oldukça yüksektir. Tartı örneğinden devamla, Bana 75 kilosunuz.. denirse ve büyük bir olasılıkla değilse, yanılmış olunur. 113
114 % 95 GA (95 % CI) Evrenden çekilen örneklem sonucu kestirimleri (oran veya ortalama), % 95 olasılıkla ( ) aralıkta bir değerdir. 114 Evrende doğumsal kalça displazisi (DKD) ne orandadır? Diyelim bu prevalans % 2 dir. Çekeceğimiz örneklerle bu değeri noktasal olarak kestirimimiz birçok nedenle pek güçtür. Dolayısıyla bu değeri içinde barındıran bir aralık bulmaya çalışırız.. Bilmediğimiz evren oranı P yi, örnek oranı p ile kestirmeye çalışırız. % 95 GA sınırlarını % 3-5 bulduysak; 100 örneklem yapılsa, 95 inde bu sınırlarda kalan bir oran bulacağız.. demektir.
115 Güven Aralığı (Confidence interval) Örneklemden hesaplanan, çekildiği evrenin incelenen parametresinin noktasal (point) değerini % olasılıkla (% 90, % 95, % 99, % 99.9 düzeyi seçilebilir) içinde barındıran bir aralık (interval) kestirimidir. Oran, hız (prevalans, insidens..) Ortalama Göreli risk (RR), Olasılık oranı (OR) gibi evren parametreleri için bir değerler aralığı belirlenir. 115
116 Doğrusal (Lineer) regresyon modeli.. 116
117 Değişkenler arasındaki ilişkiler her zaman bire bir yalın olmayıp, karmaşık ve çok etmenlidirler Tutum Eğitim Sosyal Ahlak Kültür Deneyimler Yaş Cinsellik Koşullar Önyargılar Fizik Yapı Benlik algısı Partner Tıp ve sağlık bilimlerinin (Biyomedikal bilimler) inceleme konuları çok değişkenlidir. Uygun analiz gereklidir..
118 Üstel fonksiyon ile Prostat Ca riski hesaplama.. Yandaki grafikte 'serbest PSA' değerinin' toplam PSA' içindeki oranına (Y) göre prostat kanseri riski % olarak görülüyor. Bu oran büyüdükçe, basit bir üstel fonksiyonla gösterebileceğimiz Kanser riski azalıyor: Risk = e -10 Y (serbest PSA / toplam PSA) = Y = 0,30 ise " prostat kanseri riski yaklaşık 0,05 tir (%5). (Prof. Dr. D. Ali Ercan, ) 118
119 Biyoistatistik ve Epidemiyoloji İlişkisi Biyoistatistik, tıp ve sağlık bilimlerinde, sayım ya da ölçüme dayalı sayısal verilerin incelenmesi, karşılaştırılması ve matematiksel analizle değerlendirilmesi (statistical inference) olanağını verir. Piliç - ekmek örneğinde olduğu gibi, sayısal analizlere biyolojik, sosyal, tıbbi türlü anlam yükleyip yorumlayacak olan Epidemiyoloji dir. 119
120 Biyoistatistik ve Epidemiyoloji İlişkisi Depremler sonrasında, doğumlar artıyorsa, bundan doğrudan deprem mi sorumludur? Aradaki ilişki, bağ Birincil mi, İkincil midir? Burada sorun epidemiyolojik sağduyu (epidemiological commonsense) ile çözülür. Tüm tıp ve sağlık bilimlerinde (Biyomedikal Bilimler), yeterince Biyoistatistik ve Epidemiyoloji bilen uzmanlar ile takım (ekip) çalışması kaçınılmazdır.. 120
121 Biyoistatistik ve Epidemiyoloji İlişkisi Biyoistatistik, değişkenler arasında sayısal ilişkileri irdeler. Bu değişkenlerin biyolojik, sosyal, psikolojik, ekonomik.. yükü / türü / anlamı ile ilgilenmez.. Erişilen sayısal sonuçları anlamlandıracak olan, Epidemiyoloji dir. Klinikte de, alanda da, her yerde.. 121
122 Araştırma Aşamasına Göre Yan Tutma / Bias Sınıflaması Dorak (2005), Sackett sınıflamasını temel alarak, klinik bir denemeyi (trial) yanlılığın oluşabileceği 7 aşamaya ayırmış ve 18 alt başlıkta 103 yanlılık (bias) türü tanımlamıştır! 1. Literatür incelemede 2. Çalışma düzeninde 3. Çalışmanın yürütülmesi sırasında 4. Veri toplama sürecinde 5. Veri çözümlemesinde (analizde) 6. Sonuçların yorumlanmasında 7. Yayın sürecinde 122
123 Etki Karışımı (Confounding) Literatürde, rastgele hata ve sistematik hataya ek olarak, kimi kez Etki Karışımı da 3. bir hata kaynağı olarak yer almaktadır. Etki karışımı, çalışılan sunuk (maruz) kalmanın sonuç üzerine etkisinin, sonuç için bağımsız bir risk etmeni ve sunuk (maruz) kalmayla ilişkili 3. bir etmenle karışımıdır. 123
124 Etki Karışımı (Confounding) Etki karışımı, kestirilen ilişkinin doğru etki ile aynı olmamasına neden olur. Etki karışımı, doğru ilişkinin çok ya da eksik kestirimine neden olabilir; hatta gözlenen etkinin yönünü bile değiştirebilir. Etki karıştırıcılar, pozitif veya negatif olabilir. Pozitif etki karıştırıcılar bir ilişkinin aşkın (fazla) kestirimine, negatif etki karıştırıcılar ise düşük (eksik) kestirimine neden olurlar. 124
125 Etki Karıştırıcı (Confounder) Etki karışımının tipik örneği, alkol tüketimi ve akciğer ca arasındaki ilk ilişkidir. Buradaki etki karıştıran, alkol kullanımıyla ilişkili ve akciğer ca için bağımsız bir risk etmeni olan sigara içimidir. 125
126 Etki Karışımı (Confounding) Etki karışımı, yanlılığa (Biasa) benzerdir ve genellikle birbirine karıştırılır. Kimi kez, yanlılık tipleri içinde bile sayılır. Ama Yanlılık, bir denemenin planlanmasındaki veya bir değişkenin ölçümündeki hatayı içerirken; etki karışımı, doğru planlanmış bir denemenin veya doğru olabilecek bir ölçümün Biyoistatistik modellemede yanlış kullanılmasından dolayı sonuçların hatalı olmasına neden olur. Doğru model geliştirilirse, hata yerine bilgi kaynağıdır. 126
127 Örneklem büyüklüğü hesabı ve süreçte değişimi!! Randomizasyon ve ayrıntıları!? Körleme!!? Biyoistatistiksel değerlendirmenin genellikle basit, çift değişkenli yargılamalarla gerçekleştirilmiş olması!? ve derinlemesine irdeleme eksikliği 127 ŞENOCAK, SÜT, UYSAL
128 B i r i k i m l i i n s i d e n s Cumulative incidence is a measure of frequency, as in epidemiology, where it is a measure of disease frequency during a period of time. Cumulative incidence is the incidence calculated using a period of time during which all of the individuals in the population are considered to be at risk for the outcome. It is sometimes referred to as the incidence proportion or the attack rate. Cumulative incidence is calculated by the number of new cases during a period divided by the number of people at risk in the population at the beginning of the study. It may also be calculated by the incidence rate multiplied by duration. 128
129 İnsidens, çoğunlukla İleriye Dönük (prospektif) araştırmalardan elde edilir. Geriye Dönük bir çalışmadan insidens hesaplayabilmek için, toplumla ilgili kayıtlar «tam ve doğru» olmalıdır. İleriye Yönelik (prospektif) çalışmalarda kaçınılmaz denek yitikleri (drop out) nedeniyle, insidens hızı yerine insidens yoğunluğu kullanılması gerekir. Bu ölçütte pay (nominator) değişmemekte, payda (de-nominator) her deneğin izleme katkısı (kişi-süre) biçiminde oluşmaktadır. Kontraseptif yöntemlerin etkinlik irdelemesinde kullanılan Pearl İndeksi tipik bir örnektir
130 Yaşanmış bir olay.. Bir tarihte Elazığ Ruh ve Sinir Hastalıkları Hastanesi nden bir miktar hasta kaçmıştır.. Başhekim (Dr. Mutemit Yazıcı), kaçanları bulmak için, dahice bir yol izler. Beyaz önlükleriyle bir bölüm hastane çalışanını alıp, kent merkezine inerler.. Trencilik oynarlar. Ben lokomotifim.. der, sağlık ekibini arka arkaya dizerek, birkaç ana caddeyi dolaştırır. Gözü kuyrukta olan Başhekim, bir de bakar ki, epey insan - hasta katara katılmış!... Kuyruk «yeterince» uzayınca, Lokomotif Başhekim katarı hastaneye çeker. Yeni hastalar bulunmuştur. Yaratıcı zekânın, polisiye yöntemler yerine, akıllıca, Epidemiyolojik olgu bulma» ya (depistaj) katkısı.. 130
131 S AY I L A R I N G İ Z E M İ 1 x = 9 12 x = x = x = x = x = x = x = x =
132 Biyoistatistiği yaşamınızda kullanmalısınız.. Ders bitmiştir, ilginiz için teşekkür ederiz... Soru ve katkılarınızı bekliyoruz... Dosyayı web sitemizden indirebilirsiniz
133
134 Eğitim yönlendiriciniz; Katılım, katkı ve sabrınız için içtenlikle teşekkür eder.. Sizleri sevgi ve saygı ile selamlar.. Dosya, güncel olarak web sitemizden indirilebilir.. Dr. Ahmet SALTIK - AÜTF 134
Halk Sağlığı Açısından Temel Biyoistatistik İlke ve Kavramlar
 Halk Sağlığı Açısından Temel Biyoistatistik İlke ve Kavramlar Prof. Dr. Ahmet SALTIK www.ahmetsaltik.net Ankara Üniversitesi Tıp Fakültesi Halk Sağlığı Anabilim Dalı Aralık 2014 / Ankara 2 Amaçlar ve öğrenim
Halk Sağlığı Açısından Temel Biyoistatistik İlke ve Kavramlar Prof. Dr. Ahmet SALTIK www.ahmetsaltik.net Ankara Üniversitesi Tıp Fakültesi Halk Sağlığı Anabilim Dalı Aralık 2014 / Ankara 2 Amaçlar ve öğrenim
BKİ farkı Standart Sapması (kg/m 2 ) A B BKİ farkı Ortalaması (kg/m 2 )
 4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
Halk Sağlığı Açısından Temel Biyoistatistik İlke ve Kavramlar
 Halk Sağlığı Açısından Temel Biyoistatistik İlke ve Kavramlar Prof. Dr. Ahmet SALTIK www.ahmetsaltik.net Ankara Üniversitesi Tıp Fakültesi Halk Sağlığı Anabilim Dalı Aralık 2014 / Ankara 2 Amaçlar ve öğrenim
Halk Sağlığı Açısından Temel Biyoistatistik İlke ve Kavramlar Prof. Dr. Ahmet SALTIK www.ahmetsaltik.net Ankara Üniversitesi Tıp Fakültesi Halk Sağlığı Anabilim Dalı Aralık 2014 / Ankara 2 Amaçlar ve öğrenim
HOŞ GELDİNİZ Prof. 1
 HOŞ GELDİNİZ.. 13.05.2012 www.ahmetsaltik.net Prof. 1 Epidemiyoloji ve Biyoistatistik İlişkisi Dr. Ahmet SALTIK AÜTF Halk Sağlığı Anabilim Dalı www.ahmetsaltik.net profsaltik@gmail.com 2011-12 Ders Yılı
HOŞ GELDİNİZ.. 13.05.2012 www.ahmetsaltik.net Prof. 1 Epidemiyoloji ve Biyoistatistik İlişkisi Dr. Ahmet SALTIK AÜTF Halk Sağlığı Anabilim Dalı www.ahmetsaltik.net profsaltik@gmail.com 2011-12 Ders Yılı
HOŞ GELDİNİZ.. 29.04.2015 www.ahmetsaltik.net Prof. SALTIK 1
 HOŞ GELDİNİZ.. 29.04.2015 www.ahmetsaltik.net Prof. SALTIK 1 Epidemiyoloji ve Biyoistatistik İlişkisi Dr. Ahmet SALTIK AÜTF Halk Sağlığı Anabilim Dalı www.ahmetsaltik.net profsaltik@gmail.com 2014-15 Ders
HOŞ GELDİNİZ.. 29.04.2015 www.ahmetsaltik.net Prof. SALTIK 1 Epidemiyoloji ve Biyoistatistik İlişkisi Dr. Ahmet SALTIK AÜTF Halk Sağlığı Anabilim Dalı www.ahmetsaltik.net profsaltik@gmail.com 2014-15 Ders
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI. Yrd. Doç. Dr. Emre ATILGAN
 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
Temel İstatistik. Y.Doç.Dr. İbrahim Turan Mart Tanımlayıcı İstatistik. Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri
 Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
YANLILIK. Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır.
 AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
Oluşturulan evren listesinden örnekleme birimlerinin seçkisiz olarak çekilmesidir
 Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
İki Ortalama Arasındaki Farkın Önemlilik Testi (Student s t Test) Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı
 İki Ortalama Arasındaki Farkın Önemlilik Testi (Student s t Test) Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı İki Ortalama Arasındaki Farkın Önemlilik Testi (Student s t test) Ölçümle
İki Ortalama Arasındaki Farkın Önemlilik Testi (Student s t Test) Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı İki Ortalama Arasındaki Farkın Önemlilik Testi (Student s t test) Ölçümle
Örneklem Dağılımları & Hipotez Testleri Örneklem Dağılımı
 Örneklem Dağılımları & Hipotez Testleri Örneklem Dağılımı Ortalama veya korelasyon gibi istatistiklerin dağılımıdır Çıkarımsal istatistikte örneklem dağılımı temel fikirlerden biridir. Çıkarımsal istatistik
Örneklem Dağılımları & Hipotez Testleri Örneklem Dağılımı Ortalama veya korelasyon gibi istatistiklerin dağılımıdır Çıkarımsal istatistikte örneklem dağılımı temel fikirlerden biridir. Çıkarımsal istatistik
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK. Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005
 KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ
 1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
SÜREKLĠ OLASILIK DAĞILIMLARI
 SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
Hipotez Testlerine Giriş. Hipotez Testlerine Giriş
 Hipotez Testlerine Giriş Hipotez Testlerine Giriş Hipotez Testlerine Giriş Gözlem ya da deneme sonucu elde edilmiş sonuçların, raslantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel
Hipotez Testlerine Giriş Hipotez Testlerine Giriş Hipotez Testlerine Giriş Gözlem ya da deneme sonucu elde edilmiş sonuçların, raslantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel
16.05.2012 www.ahmetsaltik.net 1 HOŞ GELDİNİZ..
 16.05.2012 www.ahmetsaltik.net 1 HOŞ GELDİNİZ.. Biyoistatistik Çözümleme -Analiz- Sonuçlarının Yorumlanması Dr. Ahmet SALTIK AÜTF Halk Sağlığı Anabilim Dalı www.ahmetsaltik.net 16.05.2012 www.ahmetsaltik.net
16.05.2012 www.ahmetsaltik.net 1 HOŞ GELDİNİZ.. Biyoistatistik Çözümleme -Analiz- Sonuçlarının Yorumlanması Dr. Ahmet SALTIK AÜTF Halk Sağlığı Anabilim Dalı www.ahmetsaltik.net 16.05.2012 www.ahmetsaltik.net
BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ
 1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER
 NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER A) Normal Dağılım ile İlgili Sorular Sayfa /4 Hamileler ile ilgili bir araştırmada, bu grubun hemoglobin değerlerinin normal dağılım gösterdiği
NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER A) Normal Dağılım ile İlgili Sorular Sayfa /4 Hamileler ile ilgili bir araştırmada, bu grubun hemoglobin değerlerinin normal dağılım gösterdiği
BİYOİSTATİSTİK. Uygulama 4. Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Uygulama 4 Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Güven Aralıkları 2 Güven Aralıkları
BİYOİSTATİSTİK Uygulama 4 Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Güven Aralıkları 2 Güven Aralıkları
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri. BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014
 Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
EVREN, ÖRNEK, TEMSİLİYET. Prof. Mustafa Necmi İlhan
 EVREN, ÖRNEK, TEMSİLİYET Prof. Mustafa Necmi İlhan MD, PhD, PhD, MBA Gazi Üniversitesi Tıp Fakültesi Halk Sağlığı AbD mnilhan@gazi.edu.tr 1 Neden Araştırma Yaparız? Bilimsel gerçeğe ulaşmak Bilinenlerin
EVREN, ÖRNEK, TEMSİLİYET Prof. Mustafa Necmi İlhan MD, PhD, PhD, MBA Gazi Üniversitesi Tıp Fakültesi Halk Sağlığı AbD mnilhan@gazi.edu.tr 1 Neden Araştırma Yaparız? Bilimsel gerçeğe ulaşmak Bilinenlerin
OLASILIK ve KURAMSAL DAĞILIMLAR
 OLASILIK ve KURAMSAL DAĞILIMLAR Kuramsal Dağılımlar İstatistiksel çözümlemelerde; değişkenlerimizin dağılma özellikleri, çözümleme yönteminin seçimi ve sonuçlarının yorumlanmasında önemlidir. Dağılma özelliklerine
OLASILIK ve KURAMSAL DAĞILIMLAR Kuramsal Dağılımlar İstatistiksel çözümlemelerde; değişkenlerimizin dağılma özellikleri, çözümleme yönteminin seçimi ve sonuçlarının yorumlanmasında önemlidir. Dağılma özelliklerine
rasgele değişkeninin olasılık yoğunluk fonksiyonu,
 3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
Konum ve Dağılım Ölçüleri. BBY606 Araştırma Yöntemleri Güleda Doğan
 Konum ve Dağılım Ölçüleri BBY606 Araştırma Yöntemleri Güleda Doğan Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl? Yakın, uzak? Sıklık dağılımlarının karşılaştırılması
Konum ve Dağılım Ölçüleri BBY606 Araştırma Yöntemleri Güleda Doğan Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl? Yakın, uzak? Sıklık dağılımlarının karşılaştırılması
Örneklemden elde edilen parametreler üzerinden kitle parametreleri tahmin edilmek istenmektedir.
 ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
Kazanımlar. Z puanları yerine T istatistiğini ne. zaman kullanacağını bilmek. t istatistiği ile hipotez test etmek
 T testi Kazanımlar Z puanları yerine T istatistiğini ne 1 zaman kullanacağını bilmek 2 t istatistiği ile hipotez test etmek 3 Cohen ind sini ve etki büyüklüğünü hesaplamak 1 9.1 T İstatistiği: zalternatifi
T testi Kazanımlar Z puanları yerine T istatistiğini ne 1 zaman kullanacağını bilmek 2 t istatistiği ile hipotez test etmek 3 Cohen ind sini ve etki büyüklüğünü hesaplamak 1 9.1 T İstatistiği: zalternatifi
ORTALAMA ÖLÇÜLERİ. Ünite 6. Öğr. Gör. Ali Onur CERRAH
 ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
BİYOİSTATİSTİK Uygulama 4 Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Uygulama 4 Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Örnek Senaryo İmplant üreten İMPLANTDENT
BİYOİSTATİSTİK Uygulama 4 Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Örnek Senaryo İmplant üreten İMPLANTDENT
26.12.2013. Farklı iki ilaç(a,b) kullanan iki grupta kan pıhtılaşma zamanları farklı mıdır?
 26.2.23 Gözlem ya da deneme sonucu elde edilmiş sonuçların, raslantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HĐPOTEZ TESTLERĐ denir. Sonuçların raslantıya bağlı olup
26.2.23 Gözlem ya da deneme sonucu elde edilmiş sonuçların, raslantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HĐPOTEZ TESTLERĐ denir. Sonuçların raslantıya bağlı olup
İSTATİSTİK MHN3120 Malzeme Mühendisliği
 İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :emre.yalamac@cbu.edu.tr YARDIMCI KAYNAKLAR Mühendiler
İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :emre.yalamac@cbu.edu.tr YARDIMCI KAYNAKLAR Mühendiler
GÜVEN ARALIKLARI ve İSTATİSTİKSEL ANLAMLILIK. Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı
 GÜVEN ARALIKLARI ve İSTATİSTİKSEL ANLAMLILIK Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Kestirim Pratikte kitle parametrelerinin doğrudan hesaplamak olanaklı değildir. Bunun yerine
GÜVEN ARALIKLARI ve İSTATİSTİKSEL ANLAMLILIK Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Kestirim Pratikte kitle parametrelerinin doğrudan hesaplamak olanaklı değildir. Bunun yerine
Olgu-kontrol araştırmalarının analizi ve değerlendirilmesi. Raika Durusoy
 Olgu-kontrol araştırmalarının analizi ve değerlendirilmesi Raika Durusoy 1 Olgu-kontrol araştırmaları Belli bir hastalığı olan ( olgu ) ve olmayan ( kontrol ) bireyler belirlenir Her iki grubun bir etkene
Olgu-kontrol araştırmalarının analizi ve değerlendirilmesi Raika Durusoy 1 Olgu-kontrol araştırmaları Belli bir hastalığı olan ( olgu ) ve olmayan ( kontrol ) bireyler belirlenir Her iki grubun bir etkene
Olasılık ve Normal Dağılım
 Olasılık ve Normal Dağılım P = 0 İmkansız P =.5 Yarı yarıya P = 1 Kesin Yazı-Tura 1.5 2 1.5 2.5.5.25 Para atışı 10 kere tekrarlandığında Yazı Sayısı f % 0 3 30 1 6 60 2 1 10 Toplam 10 100 Atış 1000 kere
Olasılık ve Normal Dağılım P = 0 İmkansız P =.5 Yarı yarıya P = 1 Kesin Yazı-Tura 1.5 2 1.5 2.5.5.25 Para atışı 10 kere tekrarlandığında Yazı Sayısı f % 0 3 30 1 6 60 2 1 10 Toplam 10 100 Atış 1000 kere
ARAŞTIRMA TÜRLERİ R. ALPAR
 ARAŞTIRMA TÜRLERİ R. ALPAR ARAŞTIRMA TÜRLERİ Araştırmanın yapılacağı yer, amaç, kapsadığı zaman ve veri toplama biçimine göre değişik biçimlerde sınıflandırılabilir. Araştırmanın kapsadığı zamana göre:
ARAŞTIRMA TÜRLERİ R. ALPAR ARAŞTIRMA TÜRLERİ Araştırmanın yapılacağı yer, amaç, kapsadığı zaman ve veri toplama biçimine göre değişik biçimlerde sınıflandırılabilir. Araştırmanın kapsadığı zamana göre:
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
İstatistik. Temel Kavramlar Dr. Seher Yalçın 1
 İstatistik Temel Kavramlar 26.12.2016 Dr. Seher Yalçın 1 Evren (Kitle/Yığın/Popülasyon) Herhangi bir gözlem ya da inceleme kapsamına giren obje ya da bireylerin oluşturduğu bütüne ya da gruba Evren veya
İstatistik Temel Kavramlar 26.12.2016 Dr. Seher Yalçın 1 Evren (Kitle/Yığın/Popülasyon) Herhangi bir gözlem ya da inceleme kapsamına giren obje ya da bireylerin oluşturduğu bütüne ya da gruba Evren veya
BİYOİSTATİSTİK Örnekleme ve Örnekleme Yöntemleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Örnekleme ve Örnekleme Yöntemleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Araştırmalarda
BİYOİSTATİSTİK Örnekleme ve Örnekleme Yöntemleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Araştırmalarda
Temel ve Uygulamalı Araştırmalar için Araştırma Süreci
 BÖLÜM 8 ÖRNEKLEME Temel ve Uygulamalı Araştırmalar için Araştırma Süreci 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
BÖLÜM 8 ÖRNEKLEME Temel ve Uygulamalı Araştırmalar için Araştırma Süreci 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
BÖLÜM 13 HİPOTEZ TESTİ
 1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ
 BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ DÖNEM I-I. DERS KURULU Konu: Bilimsel yöntem ve istatistik Amaç: Biyoistatistiğin tıptaki önemini kavrar ve sonraki dersler için gerekli terminolojiye hakim olur.
BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ DÖNEM I-I. DERS KURULU Konu: Bilimsel yöntem ve istatistik Amaç: Biyoistatistiğin tıptaki önemini kavrar ve sonraki dersler için gerekli terminolojiye hakim olur.
Temel ve Uygulamalı Araştırmalar için Araştırma Süreci
 BÖLÜM 8 ÖRNEKLEME Temel ve Uygulamalı Araştırmalar için Araştırma Süreci 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
BÖLÜM 8 ÖRNEKLEME Temel ve Uygulamalı Araştırmalar için Araştırma Süreci 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
T.C. MUĞLA SITKI KOÇMAN ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ
 T.C. MUĞLA SITKI KOÇMAN ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ TEZ ÖNERİSİ HAZIRLAMA KILAVUZU MART, 2017 MUĞLA T.C. MUĞLA SITKI KOÇMAN ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ.... ANABİLİM DALI.... BİLİM
T.C. MUĞLA SITKI KOÇMAN ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ TEZ ÖNERİSİ HAZIRLAMA KILAVUZU MART, 2017 MUĞLA T.C. MUĞLA SITKI KOÇMAN ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ.... ANABİLİM DALI.... BİLİM
BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ
 BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ İŞTİRME Araştırma rma SüreciS 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ İŞTİRME Araştırma rma SüreciS 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
LOJİSTİK REGRESYON ANALİZİ
 LOJİSTİK REGRESYON ANALİZİ Lojistik Regresyon Analizini daha kolay izleyebilmek için bazı terimleri tanımlayalım: 1. Değişken (incelenen özellik): Bireyden bireye farklı değerler alabilen özellik, fenomen
LOJİSTİK REGRESYON ANALİZİ Lojistik Regresyon Analizini daha kolay izleyebilmek için bazı terimleri tanımlayalım: 1. Değişken (incelenen özellik): Bireyden bireye farklı değerler alabilen özellik, fenomen
BİYOİSTATİSTİK Bazı Olasılık Dağılışları Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Bazı Olasılık Dağılışları Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Uygulamalı bilim
BİYOİSTATİSTİK Bazı Olasılık Dağılışları Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Uygulamalı bilim
Üretim Süreci: Girdi İşlem Ürün (Sonuç) Araştırma Süreci: Hangi alanda olursa olsun araştırma bir BİLGİ ye ulaşma sürecidir.
 BİYOİSTATİSTİK Üretim Süreci: Girdi İşlem Ürün (Sonuç) Araştırma Süreci: Hangi alanda olursa olsun araştırma bir BİLGİ ye ulaşma sürecidir. Veri Analiz Bilgi El ile ya da birtakım bilgisayar programları
BİYOİSTATİSTİK Üretim Süreci: Girdi İşlem Ürün (Sonuç) Araştırma Süreci: Hangi alanda olursa olsun araştırma bir BİLGİ ye ulaşma sürecidir. Veri Analiz Bilgi El ile ya da birtakım bilgisayar programları
Ders 9: Kitle Ortalaması ve Varyansı için Tahmin
 Ders 9: Kitle Ortalaması ve Varyansı için Tahmin Kitle ve Örneklem Örneklem Dağılımı Nokta Tahmini Tahmin Edicilerin Özellikleri Kitle ortalaması için Aralık Tahmini Kitle Standart Sapması için Aralık
Ders 9: Kitle Ortalaması ve Varyansı için Tahmin Kitle ve Örneklem Örneklem Dağılımı Nokta Tahmini Tahmin Edicilerin Özellikleri Kitle ortalaması için Aralık Tahmini Kitle Standart Sapması için Aralık
Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II
 Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II İstatistik Nedir? İstatistik kelimesi farklı anlamlar taşımaktadır. Bunlar; Genel anlamda; üretim, tüketim, nüfus, sağlık, eğitim, tarım,
Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II İstatistik Nedir? İstatistik kelimesi farklı anlamlar taşımaktadır. Bunlar; Genel anlamda; üretim, tüketim, nüfus, sağlık, eğitim, tarım,
BİYOİSTATİSTİK Sağlık Alanına Özel İstatistiksel Yöntemler Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Sağlık Alanına Özel İstatistiksel Yöntemler Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr
BİYOİSTATİSTİK Sağlık Alanına Özel İstatistiksel Yöntemler Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
DEĞERLENDİRME ARASINDAKİ İLİŞKİLER... 1
 İÇİNDEKİLER ÖNSÖZ... xxii BÖLÜM 1 - ÖĞRENME, ÖĞRETİM VE DEĞERLENDİRME ARASINDAKİ İLİŞKİLER... 1 EĞİTİM SÜRECİ VE ÖĞRENME... 2 Öğrenme ve Bilişsel Yaklaşım... 3 Bilişsel Yaklaşımın Eğitimdeki Genel Sonuçları...
İÇİNDEKİLER ÖNSÖZ... xxii BÖLÜM 1 - ÖĞRENME, ÖĞRETİM VE DEĞERLENDİRME ARASINDAKİ İLİŞKİLER... 1 EĞİTİM SÜRECİ VE ÖĞRENME... 2 Öğrenme ve Bilişsel Yaklaşım... 3 Bilişsel Yaklaşımın Eğitimdeki Genel Sonuçları...
Nokta ve Aralık Tahmini Merkezi Limit Teoremi Örneklem Dağılımı Hipotez Testlerine Giriş
 Nokta ve Aralık Tahmini Merkezi Limit Teoremi Örneklem Dağılımı Hipotez Testlerine Giriş Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Nokta Tahmini
Nokta ve Aralık Tahmini Merkezi Limit Teoremi Örneklem Dağılımı Hipotez Testlerine Giriş Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Nokta Tahmini
Kestirim (Tahmin) Bilimsel çalışmaların amacı, örneklem değerinden evren değerlerinin kestirilmesidir.
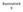 Biyoistatistik 9 Kestirim (Tahmin) Bilimsel çalışmaların amacı, örneklem değerinden evren değerlerinin kestirilmesidir. Evren parametrelerinin kestirilmesi (tahmini) için: 1. Hipotez testleri 2. Güven
Biyoistatistik 9 Kestirim (Tahmin) Bilimsel çalışmaların amacı, örneklem değerinden evren değerlerinin kestirilmesidir. Evren parametrelerinin kestirilmesi (tahmini) için: 1. Hipotez testleri 2. Güven
BÖLÜM 12 STUDENT T DAĞILIMI
 1 BÖLÜM 12 STUDENT T DAĞILIMI 'Student t dağılımı' ya da kısaca 't dağılımı'; normal dağılım ve Z dağılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
1 BÖLÜM 12 STUDENT T DAĞILIMI 'Student t dağılımı' ya da kısaca 't dağılımı'; normal dağılım ve Z dağılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
TEMEL KAVRAMLAR. BS503 ARAŞTIRMA YÖNTEMLERİ 1. seminer PROF. DR. SALİH OFLUOĞLU MSGSÜ ENFORMATİK BÖLÜMÜ BİLGİSAYAR ORTAMINDA SANAT VE TASARIM 1
 TEMEL KAVRAMLAR 1. seminer PROF. DR. SALİH OFLUOĞLU MSGSÜ ENFORMATİK BÖLÜMÜ BİLGİSAYAR ORTAMINDA SANAT VE TASARIM 1 ARAŞTIRMA Neden araştırma yapılır? Araştırma sorularına yanıt bulmak Araştırma problemlerinin
TEMEL KAVRAMLAR 1. seminer PROF. DR. SALİH OFLUOĞLU MSGSÜ ENFORMATİK BÖLÜMÜ BİLGİSAYAR ORTAMINDA SANAT VE TASARIM 1 ARAŞTIRMA Neden araştırma yapılır? Araştırma sorularına yanıt bulmak Araştırma problemlerinin
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
TEMEL İSTATİSTİK BİLGİSİ. İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar
 TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
Olasılık Teorisi ve İstatistik (MATH392) Ders Detayları
 Olasılık Teorisi ve İstatistik (MATH392) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Olasılık Teorisi ve İstatistik MATH392 Güz 4 0 0 4 7 Ön Koşul Ders(ler)i
Olasılık Teorisi ve İstatistik (MATH392) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Olasılık Teorisi ve İstatistik MATH392 Güz 4 0 0 4 7 Ön Koşul Ders(ler)i
Toplum ve Örnek. Temel Araştırma Düzenleri. Doç. Dr. Ertuğrul ÇOLAK. Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı
 Toplum ve Örnek Temel Araştırma Düzenleri Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Toplum ve Örnek İstatistik, toplumdan kurallara uygun olarak,
Toplum ve Örnek Temel Araştırma Düzenleri Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Toplum ve Örnek İstatistik, toplumdan kurallara uygun olarak,
K-S Testi hipotezde ileri sürülen dağılımla örnek yığılmalı dağılım fonksiyonunun karşılaştırılması ile yapılır.
 İstatistiksel güven aralıkları uygulamalarında normallik (normal dağılıma uygunluk) oldukça önemlidir. Kullanılan parametrik istatistiksel tekniklerin geçerli olabilmesi için populasyon şans değişkeninin
İstatistiksel güven aralıkları uygulamalarında normallik (normal dağılıma uygunluk) oldukça önemlidir. Kullanılan parametrik istatistiksel tekniklerin geçerli olabilmesi için populasyon şans değişkeninin
Projede istatistik analiz planı
 Projede istatistik analiz planı Prof Dr Belgin Ünal Analiz planı Proje yazımı sırasında oluşturulur Araştırmanın /projenin amaçları doğrultusunda kurgulanmalıdır. Araştırmanın yanıtlamayı planladığı sorular
Projede istatistik analiz planı Prof Dr Belgin Ünal Analiz planı Proje yazımı sırasında oluşturulur Araştırmanın /projenin amaçları doğrultusunda kurgulanmalıdır. Araştırmanın yanıtlamayı planladığı sorular
Copyright 2004 Pearson Education, Inc. Slide 1
 Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
 A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
UYGUN HİPOTEZ TESTİNİN SEÇİMİ. Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı
 UYGUN HİPOTEZ TESTİNİN SEÇİMİ Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı ÖNEMLİLİK (Hipotez) TESTLERİ ü Önemlilik testleri, araştırma sonucunda elde edilen değerlerin ya da varılan
UYGUN HİPOTEZ TESTİNİN SEÇİMİ Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı ÖNEMLİLİK (Hipotez) TESTLERİ ü Önemlilik testleri, araştırma sonucunda elde edilen değerlerin ya da varılan
Olasılık ve İstatistiğe Giriş-II (STAT 202) Ders Detayları
 Olasılık ve İstatistiğe Giriş-II (STAT 202) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Olasılık ve İstatistiğe Giriş-II STAT 202 Bahar 3 0 0 3 5 Ön Koşul
Olasılık ve İstatistiğe Giriş-II (STAT 202) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Olasılık ve İstatistiğe Giriş-II STAT 202 Bahar 3 0 0 3 5 Ön Koşul
BS503 BİLİMSEL NEDENSELLİK VE YAZIM
 Temel Kavramlar 1. Seminer BS503 BİLİMSEL NEDENSELLİK VE YAZIM MSGSÜ Enformatik Bölümü BST/MKE Y. Lisans Programları PROF. DR. SALİH OFLUOĞLU Araştırma Neden araştırma yapılır? Belirli bir alanda: varolan
Temel Kavramlar 1. Seminer BS503 BİLİMSEL NEDENSELLİK VE YAZIM MSGSÜ Enformatik Bölümü BST/MKE Y. Lisans Programları PROF. DR. SALİH OFLUOĞLU Araştırma Neden araştırma yapılır? Belirli bir alanda: varolan
TOPRAKTA PH TAYİNİ YETERLİLİK TESTİ RAPORU TÜBİTAK ULUSAL METROLOJİ ENSTİTÜSÜ REFERANS MALZEMELERI LABORATUVARI. Rapor No: KAR-G3RM-400.2014.
 TOPRAKTA PH TAYİNİ YETERLİLİK TESTİ RAPORU TÜBİTAK ULUSAL METROLOJİ ENSTİTÜSÜ REFERANS MALZEMELERI LABORATUVARI Rapor No: KAR-G3RM-400.2014.02 Koordinatör: Dr. Fatma AKÇADAĞ 24 Aralık 2014 Gebze/KOCAELİ
TOPRAKTA PH TAYİNİ YETERLİLİK TESTİ RAPORU TÜBİTAK ULUSAL METROLOJİ ENSTİTÜSÜ REFERANS MALZEMELERI LABORATUVARI Rapor No: KAR-G3RM-400.2014.02 Koordinatör: Dr. Fatma AKÇADAĞ 24 Aralık 2014 Gebze/KOCAELİ
TANIMLAYICI İSTATİSTİKLER
 TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
Özgün Problem Çözme Becerileri
 Özgün Problem Çözme Becerileri Research Agenda for General Practice / Family Medicine and Primary Health Care in Europe; Specific Problem Solving Skills ANKARA ÜNİVERSİTESİ TIP FAKÜLTESİ AİLE HEKİMLİĞİ
Özgün Problem Çözme Becerileri Research Agenda for General Practice / Family Medicine and Primary Health Care in Europe; Specific Problem Solving Skills ANKARA ÜNİVERSİTESİ TIP FAKÜLTESİ AİLE HEKİMLİĞİ
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5
 Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
Deneysel Araştırma Modelleri. Dr. Şebnem Bozkurt Bartın Devlet Hastanesi
 Deneysel Araştırma Modelleri Dr. Şebnem Bozkurt Bartın Devlet Hastanesi Deney Nedir? Deney yapan kişi tarafından bir yada daha çok değişkene müdahale edilerek bu müdahalenin başka bir değişkene etkisini
Deneysel Araştırma Modelleri Dr. Şebnem Bozkurt Bartın Devlet Hastanesi Deney Nedir? Deney yapan kişi tarafından bir yada daha çok değişkene müdahale edilerek bu müdahalenin başka bir değişkene etkisini
 0.04.03 Standart Hata İstatistikte hesaplanan her istatistik değerin mutlaka hatası da hesaplanmalıdır. Çünkü hesaplanan istatistikler, tahmini bir değer olduğu için mutlaka hataları da vardır. Standart
0.04.03 Standart Hata İstatistikte hesaplanan her istatistik değerin mutlaka hatası da hesaplanmalıdır. Çünkü hesaplanan istatistikler, tahmini bir değer olduğu için mutlaka hataları da vardır. Standart
RİSK ÖLÇÜLERİ. Yrd.Doç.Dr. Selçuk Korkmaz Trakya Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı. Turcosa Analitik Çözümlemeler
 RİSK ÖLÇÜLERİ Yrd.Doç.Dr. Selçuk Korkmaz Trakya Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Turcosa Analitik Çözümlemeler selcukorkmaz@gmail.com ÇOCUK NEFROLOJİ DERNEĞİ BİYOİSTATİSTİK EĞİTİMİ
RİSK ÖLÇÜLERİ Yrd.Doç.Dr. Selçuk Korkmaz Trakya Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Turcosa Analitik Çözümlemeler selcukorkmaz@gmail.com ÇOCUK NEFROLOJİ DERNEĞİ BİYOİSTATİSTİK EĞİTİMİ
Faktöriyel: 1'den n'ye kadar olan tüm pozitif tamsayıların çarpımına, biçiminde gösterilir. Aynca; 0! = 1 ve 1!=1 1 dir. [Bunlar kabul değildir,
 14. Binom ve Poisson olasılık dağılımları Faktöriyeller ve kombinasyonlar Faktöriyel: 1'den n'ye kadar olan tüm pozitif tamsayıların çarpımına, n! denir ve n! = 1.2.3...(n-2).(n-l).n biçiminde gösterilir.
14. Binom ve Poisson olasılık dağılımları Faktöriyeller ve kombinasyonlar Faktöriyel: 1'den n'ye kadar olan tüm pozitif tamsayıların çarpımına, n! denir ve n! = 1.2.3...(n-2).(n-l).n biçiminde gösterilir.
BİYOİSTATİSTİK Korelasyon Analizi Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Korelasyon Analizi Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Bir değişkenin değerinin,
BİYOİSTATİSTİK Korelasyon Analizi Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Bir değişkenin değerinin,
1. BETİMSEL ARAŞTIRMALAR
 ARAŞTIRMA MODELLERİ 1. BETİMSEL ARAŞTIRMALAR A. BETİMLEME (KAMUOYU) ARAŞTIRMALARI Bir survey yöntemi olan betimleme yöntemi, grupla ilgili, genişliğine bir çalışmadır. Bu tür araştırmalar, çok sayıda
ARAŞTIRMA MODELLERİ 1. BETİMSEL ARAŞTIRMALAR A. BETİMLEME (KAMUOYU) ARAŞTIRMALARI Bir survey yöntemi olan betimleme yöntemi, grupla ilgili, genişliğine bir çalışmadır. Bu tür araştırmalar, çok sayıda
KANITA DAYALI LABORATUVAR TIBBI İLE İLİŞKİLİ HESAPLAMALAR. Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005
 KANITA DAYALI LABORATUVAR TIBBI İLE İLİŞKİLİ HESAPLAMALAR Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Kanıta dayalı tıp Kanıta dayalı tıp, hekimlerin günlük kararlarını, mevcut en iyi kanıtın ışığında,
KANITA DAYALI LABORATUVAR TIBBI İLE İLİŞKİLİ HESAPLAMALAR Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Kanıta dayalı tıp Kanıta dayalı tıp, hekimlerin günlük kararlarını, mevcut en iyi kanıtın ışığında,
BİR ÖRNEKLEM İÇİN T TESTİ İLİŞKİSİZ ÖRNEKLEMLER İÇİN T-TESTİ
 1 BİR ÖRNEKLEM İÇİN T TESTİ İLİŞKİSİZ ÖRNEKLEMLER İÇİN T-TESTİ 2 BİR ÖRNEKLEM İÇİN T TESTİ 3 Ölçüm ortalamasını bir norm değer ile karşılaştırma (BİR ÖRNEKLEM İÇİN T TESTİ) Bir çocuk bakımevinde barındırılan
1 BİR ÖRNEKLEM İÇİN T TESTİ İLİŞKİSİZ ÖRNEKLEMLER İÇİN T-TESTİ 2 BİR ÖRNEKLEM İÇİN T TESTİ 3 Ölçüm ortalamasını bir norm değer ile karşılaştırma (BİR ÖRNEKLEM İÇİN T TESTİ) Bir çocuk bakımevinde barındırılan
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
Sağlık Bakımıyla İlişkili İnfeksiyonların Epidemiyolojisinde Temel Tanımlar
 Sağlık Bakımıyla İlişkili İnfeksiyonların Epidemiyolojisinde Temel Tanımlar Dr. Alpay AZAP Ankara Üniversitesi Tıp Fakültesi Enfeksiyon Hastalıkları ve Klinik Mikr. AD. Epidemiyoloji Nedir? Sağlıkla ilgili
Sağlık Bakımıyla İlişkili İnfeksiyonların Epidemiyolojisinde Temel Tanımlar Dr. Alpay AZAP Ankara Üniversitesi Tıp Fakültesi Enfeksiyon Hastalıkları ve Klinik Mikr. AD. Epidemiyoloji Nedir? Sağlıkla ilgili
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI Tanım
 2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
HİPOTEZ TESTLERİ. Yrd. Doç. Dr. Emre ATILGAN
 HİPOTEZ TESTLERİ Yrd. Doç. Dr. Emre ATILGAN Hipotez Nedir? HİPOTEZ: parametre hakkındaki bir inanıştır. Parametre hakkındaki inanışı test etmek için hipotez testi yapılır. Hipotez testleri sayesinde örneklemden
HİPOTEZ TESTLERİ Yrd. Doç. Dr. Emre ATILGAN Hipotez Nedir? HİPOTEZ: parametre hakkındaki bir inanıştır. Parametre hakkındaki inanışı test etmek için hipotez testi yapılır. Hipotez testleri sayesinde örneklemden
Student t Testi. Doç. Dr. Ertuğrul ÇOLAK. Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı
 Student t Testi Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Konu Başlıkları Tek örnek t testi SPSS de tek örnek t testi uygulaması Bağımsız iki örnek
Student t Testi Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Konu Başlıkları Tek örnek t testi SPSS de tek örnek t testi uygulaması Bağımsız iki örnek
Hatalar Bilgisi ve İstatistik Ders Kodu: Kredi: 3 / ECTS: 5
 Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Ortalamaların karşılaştırılması
 Parametrik ve Parametrik Olmayan Testler Ortalamaların karşılaştırılması t testleri, ANOVA Mann-Whitney U Testi Wilcoxon İşaretli Sıra Testi Kruskal Wallis Testi BBY606 Araştırma Yöntemleri Güleda Doğan
Parametrik ve Parametrik Olmayan Testler Ortalamaların karşılaştırılması t testleri, ANOVA Mann-Whitney U Testi Wilcoxon İşaretli Sıra Testi Kruskal Wallis Testi BBY606 Araştırma Yöntemleri Güleda Doğan
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ
 DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati (T+U+L) Kredi AKTS OLASILIK VE İSTATİSTİK FEB-222 2/ 2.YY 3+0+0 3 3 Dersin Dili Dersin Seviyesi
DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati (T+U+L) Kredi AKTS OLASILIK VE İSTATİSTİK FEB-222 2/ 2.YY 3+0+0 3 3 Dersin Dili Dersin Seviyesi
Değişken Türleri, Tanımlayıcı İstatistikler ve Normal Dağılım. Dr. Deniz Özel Erkan
 Değişken Türleri, Tanımlayıcı İstatistikler ve Normal Dağılım Dr. Deniz Özel Erkan Evren Parametre Örneklem Çıkarım Veri İstatistik İstatistik Tanımlayıcı (Descriptive) Çıkarımsal (Inferential) Özetleme
Değişken Türleri, Tanımlayıcı İstatistikler ve Normal Dağılım Dr. Deniz Özel Erkan Evren Parametre Örneklem Çıkarım Veri İstatistik İstatistik Tanımlayıcı (Descriptive) Çıkarımsal (Inferential) Özetleme
SÜREKLİ RASSAL DEĞİŞKENLER
 SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
Test Tekrarının Objektif Olarak Değerlendirilmesi. Abdurrahman Coşkun Acıbadem Üniversitesi, Tıp Fakültesi, Tıbbi Biyokimya Anabilim Dalı
 Test Tekrarının Objektif Olarak Değerlendirilmesi Abdurrahman Coşkun Acıbadem Üniversitesi, Tıp Fakültesi, Tıbbi Biyokimya Anabilim Dalı Sunum Planı Test Tekrarı Nedenleri Aynı Cihazla Yapılan Tekrarlı
Test Tekrarının Objektif Olarak Değerlendirilmesi Abdurrahman Coşkun Acıbadem Üniversitesi, Tıp Fakültesi, Tıbbi Biyokimya Anabilim Dalı Sunum Planı Test Tekrarı Nedenleri Aynı Cihazla Yapılan Tekrarlı
İSTATİSTİK HAFTA. ÖRNEKLEME METOTLARI ve ÖRNEKLEM BÜYÜKLÜĞÜNÜN TESPİTİ
 ÖRNEKLEME METOTLARI ve ÖRNEKLEM BÜYÜKLÜĞÜNÜN TESPİTİ HEDEFLER Bu üniteyi çalıştıktan sonra; Örneklemenin niçin ve nasıl yapılacağını öğreneceksiniz. Temel Örnekleme metotlarını öğreneceksiniz. Örneklem
ÖRNEKLEME METOTLARI ve ÖRNEKLEM BÜYÜKLÜĞÜNÜN TESPİTİ HEDEFLER Bu üniteyi çalıştıktan sonra; Örneklemenin niçin ve nasıl yapılacağını öğreneceksiniz. Temel Örnekleme metotlarını öğreneceksiniz. Örneklem
TANI TESTLERINE GIRIŞ & ROC ANALİZİ
 TANI TESTLERINE GIRIŞ & ROC ANALİZİ Yrd.Doç.Dr. Selçuk Korkmaz Trakya Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Turcosa Analitik Çözümlemeler selcukorkmaz@gmail.com ÇOCUK NEFROLOJİ DERNEĞİ
TANI TESTLERINE GIRIŞ & ROC ANALİZİ Yrd.Doç.Dr. Selçuk Korkmaz Trakya Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Turcosa Analitik Çözümlemeler selcukorkmaz@gmail.com ÇOCUK NEFROLOJİ DERNEĞİ
Prof.Dr. Rian Dişçi İ.Ü.Onkoloji Enstitüsü Kanser Epidemiyolojisi ve Biyoistatistik Bilim Dalı
 SAĞKALIM (SÜRVİ) ANALİZİ Prof.Dr. Rian Dişçi İ.Ü.Onkoloji Enstitüsü Kanser Epidemiyolojisi ve Biyoistatistik Bilim Dalı Amaç Tedaviden sonra hastaların beklenen yaşam sürelerinin tahmin edilmesi, genel
SAĞKALIM (SÜRVİ) ANALİZİ Prof.Dr. Rian Dişçi İ.Ü.Onkoloji Enstitüsü Kanser Epidemiyolojisi ve Biyoistatistik Bilim Dalı Amaç Tedaviden sonra hastaların beklenen yaşam sürelerinin tahmin edilmesi, genel
Sık kullanılan istatistiksel yöntemler ve yorumlama. Doç. Dr. Seval KUL Gaziantep Üniversitesi Tıp Fakültesi
 Sık kullanılan istatistiksel yöntemler ve yorumlama Doç. Dr. Seval KUL Gaziantep Üniversitesi Tıp Fakültesi Biyoistatistik AD Bşk. 1 Hakkımda 2 Hedef: Katılımcılar modülün sonunda temel istatistiksel yöntemler
Sık kullanılan istatistiksel yöntemler ve yorumlama Doç. Dr. Seval KUL Gaziantep Üniversitesi Tıp Fakültesi Biyoistatistik AD Bşk. 1 Hakkımda 2 Hedef: Katılımcılar modülün sonunda temel istatistiksel yöntemler
SAKARYA ÜNİVERSİTESİ EĞİTİM FAKÜLTESİ DÖRDÜNCÜ SINIF ÖĞRENCİLERİNİN ÖĞRETMENLİK MESLEĞİNE KARŞI TUTUMLARI
 SAKARYA ÜNİVERSİTESİ EĞİTİM FAKÜLTESİ DÖRDÜNCÜ SINIF ÖĞRENCİLERİNİN ÖĞRETMENLİK MESLEĞİNE KARŞI TUTUMLARI Arş.Gör. Duygu GÜR ERDOĞAN Sakarya Üniversitesi Eğitim Fakültesi dgur@sakarya.edu.tr Arş.Gör. Demet
SAKARYA ÜNİVERSİTESİ EĞİTİM FAKÜLTESİ DÖRDÜNCÜ SINIF ÖĞRENCİLERİNİN ÖĞRETMENLİK MESLEĞİNE KARŞI TUTUMLARI Arş.Gör. Duygu GÜR ERDOĞAN Sakarya Üniversitesi Eğitim Fakültesi dgur@sakarya.edu.tr Arş.Gör. Demet
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI
 ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
