O ZBEKSTAN RESPUBLİKASI JOQARI HA M ORTA ARNAWLI BİLİM MİNİSTRLİGİ BERDAQ ATINDA I QARAQALPAQ MA MLEKETLİK UNİVERSİTETİ. Matematika fakulteti
|
|
|
- Duygu Kılıç
- 5 yıl önce
- İzleme sayısı:
Transkript
1 O ZBEKSTAN RESPUBLİKASI JOQARI HA M ORTA ARNAWLI BİLİM MİNİSTRLİGİ BERDAQ ATINDA I QARAQALPAQ MA MLEKETLİK UNİVERSİTETİ Mateatika fakulteti «Algeba h a diffeetsiallıq te leele» kafedası Mateatika qa igeligii 3-kus studetlei ushı «Ulıwa algeba» a i boyısha LEKTsİYaLAR TEKSTİ Du zge: dots. Tajetdiov S. dots. Allabegeov H. NO KİS-008 j
2 -lektsiya. Guala teoiyasıa ayıı ag lıwatla Ege G ko ligii eleetleii qa lege ta tilege ( a, b) jubıa qaday da bi (9) sa ykesligi boyısha usı ko likti bi a isli aıqlag a c eleeti qoyılsa - bul jag dayda a * b = c de jazıladı - oda G ko ligide 9 bialıq oeatsiyası beilge deliedi. Ege G ko ligide 9 bialıq oeatsiyası beilge bolı, ol to edegi u sh sha tti qaaatladısa: ) Qa lege a, b, c G ushı ( a * b) * c = a * ( b * c) ) Qa lege a G ushı e G : a * e = e * a = a 3) g G g G : g * g = g * g = e G ko ligi usı 9 bialıq oeatsiyasıa qaata gua de ataladı. Ege qa lege a, b, c G ushı a * b = b * a bolsa G guası abellik gua de ataladı. G ko ligii quwatlılıg ı G guasıı ta tibi de ataladı h a ol G de belgileedi. a = e bolatug ıday e kishi N saı a eleetii ta tibi de ataladı h a ol a de belgileedi. a eleetie jasalg a gua usı eleette jasalg a tsikllik gua de ataladı h a ol гр ( a) =< a > de belgileedi. Soda ) { } boladı. гр ( a = a Z boladı. гр a) = a ( te ligi oılı G guasıı H u les guası boyısha o h a sol qo sılas G : H de belgileedi. klasslaıı saı bidey boladı h a bul sa Lagaj teoeası: bul jede G <. G H G : H =, Ege H <G h a g G, h H ushı g hg H bolsa H u les guası G guasıı oal u les guası de ataladı h a ol H <G de belgileedi. Joqaıdag ı sha t g G ushı gh = Hg sha tie te ku shli. Ege H <G bolsa { gh g G} ko ligi H g H g g H de g = beilge bialıq oeatsiyag a qaata gua du zedi. Bul gua G guasıı H oal u les guası boyısha faktoguası de ataladı h a ol G /H de belgileedi. Ege G : H = bolsa H < G boladı. Ege H <G, N <G bolsa H N <G boladı. G /[ G, G ] guası abellik gua boladı, bul jede [ G, G ] G ı koutatı. Meyli f : G G sa wlelediiwi G guasıı G guasıa sa wlelediiwi bolsı. Ege f ( ab) = f ( a) f ( b) a, b G bolsa f sa wlelediiwi G guasıı G guasıa gooofizi de ataladı. Ege a b f ( a) f ( b) sha ti oılasa f ooofiz de, al f ( G ) = G sha ti oılasa f eiofiz de ataladı. Bi waqıttı o zide h a
3 ooofiz h a eiofiz bolg a gooofiz izoofiz de ataladı. Bul jag dayda G ~G de jazıladı. Kef = { a G f ( a) = e } ko ligi f gooofizii yadosı de ataladı. Buda Kef < G boladı. Beilge A < G, B < G ushı A B = { e}, AB = G bolsa G guası A h a B u les gualaıı tuwı ko beyesi de ataladı h a ol G = A B de belgileedi. Ege G = G G... G bolsa G = G G... G boladı. Ege G = A B h a G = A B bolsa h a B B bolsa, oda B = B sha ti oılaatug ılıg ı keli shıg adı. -lektsiya. Shekli abellik gualadı du zilisi Teoea: Ha qaday shekli abellik -gua tsikllik gualadı tuwı ko beyesi boladı. Teoea: Ege shekli abellik -gua A ushı A = A... A = B... B s bolsa = s boladı h a A i = B j boladı. Salda: Ta tibi ge te bolg a izoof ees abellik gualadı saı h = , h,...,, jikleiwleii saıa te boladı. Tiykag ı teoea: Qa lege shekli abellik gua A ialıq tsikllik u les gualadı tuwı ko beyesi boladı. Qa lege eki jikleiwde bidey ta tili ko beytiwshiledi saı bidey boladı. Mısal etide ta tibi 6 h a 36 g a te bolg a balıq abellik gualadı aıqlayıq: 4 ) A = 6 =, (4) = 5, Z 6, Z 8 Z, Z 4 Z 4, Z 4 Z Z, ) A = 36 = 3 Eleeta bo liwshile 4 Z 9 ~ Z 36Z 4, 9 Z Z 9 Z 8 Z,, 9 4 Z 3 Z 3 ~ Z Z 3 4, 3, 3 Z Z 3 Z 3 ~ Z 6 Z 6,, 3, 3 Z Z Z İvaiat faktola 3, 6 8,, 3 6, 6 3) Ege A A B B ~, A < h a B < bolsa A ~ B boladı. 3
4 4) Ege A B, C sha ti oılasa, oda, shekli abellik guala bolsa h a A C ~ B C A ~ B sha ti de oılaadı. 4
5 3-lektsiya. Shekli guala ushı silovtı -shi h a -shi teoealaı Meyli G = bolsı, bul jede - a iwayı sa h a N, (, ) =. Soda G, = u les guası G guasıı silovlıq - u les guası de ataladı. Teoea (Silov): Silovlıq - u les guala ba boladı. P u les gualaı G guasıı Teoea (Silov): Meyli P h a qa lege eki silovlıq u les gualaı bolsı. Soda P = apa bolatug ıday a G eleeti ba boladı. deek balıq silovlıq -u les guala o z-aa tu yiles boladı. Da liyllew: Meyli P u les guası G guasıı silovlıq u les P G guasıı qa lege -u les guası bolsı. guası bolsı. Meyli Soda P ge qaata qa lege obitaı uzılıg ı qaldıqsız bo ledi: G = = = G P k = P P / k + + k =, k saı k bul jede k,,... obitaladı uzılıg ı (, ) = bolg aı ushı h esh k bolasa bi obitaı uzılıg ı i = boladı, yag ıy P ap = ap () boladı, bul jede a = g i G qaday da bi eleet () di P apa = apa de jazı biz P apa () ge iye bolaız, sebebi apa - gua. Daa jag dayda, ege P - silovlıq - u les gua bolsa, P = boladı, soı ushı () foulada P = apa ekeligi keli shıg adı...., 5
6 4-lektsiya. Silovtı 3-shi teoeası Teoea 3 (Silov): G guasıı u les gualaıı saı to edegi te likle oılı ( G : N ( P)) N = h a N (od ) Da liyllew: Da liylleiwi N = ( G : N ( P)) -teoeada h a guasıı obitasıı uzılıg ı h aqqıdag ı tastıyıqlawda keli shıg adı. s Meyli edi G = t, s, h a (s ) s N ushı H N saı G guasıı ta tibi ke te bolg a balıq u les gualaıı saı bolsı. N ( s) (od ) N = N h a ( ) bolatug ılıg ı ko seteyik. Meyli Ω = { M G M s = } bolsı. Soda Ω = Ωi, Ωi = ( G : G i i boladı. Bua G = Ω i (od t ) s Ω. (3) Ωi = t Bul salıstıalıqtı to edegishe de jazıwg a boladı: G Ωi t N ( s)(od t ). s (4) Ωi = t Ege bul jede G guası ushı ta tibi s t ke te bolg a tsikllik guaı alsaq, oda N ( s, G ) = boladı. Soı ushı G s t (od t ) boladı. (4) h a (5) salıstıalıqladı she ta elei bidey bolg aı ushı t tn ( s)(od t ) ekeligi keli shıg adı. Deek ( s) (od ) N. Teoea da lilledi. ) G (5) 5-lektsiya. Koltsola teoiyasıa ayıı ag lıwatla Ege K ko ligide + h a 9 bialıq oeatsiyalaı aıqlag a bolı, ola to edegi u sh sha tti qaaatladısa: ) ( K, + ) abellik gua 6
7 ) a, b, c K ushı ( ab ) c = a( bc) 3) a, b, c K ushı ( a + b) c = ac + bc a( b + c) = ab + ac oda K ko ligi koltso de ataladı h a ol ( K, +, ) de belgileedi. Ege a, b K ushı ab = ba bolsa K koutativ koltso de ataladı. Ege L K h a x, y L x y L h a xy L sha tlei oılasa L u les ko ligi K koltsosıı u les koltsosı de ataladı. Ege a 0 h a b 0 bolı ab = 0 bolsa a h a b eleetlei K koltsosıdag ı oldi bo liwshilei de ataladı. Meyli bizge K koltsosıı K koltsosıa bolg a f : K K sa wlelediiwi beilge bolsı. Ege f ( ab) = f ( a) f ( b) h a f ( a + b) = f ( a) + f ( b) bolsa f sa wlelediiwi K koltsosıı K koltsosıa gooofizi de ataladı. Ege a b f ( a) f ( b) bolsa f ooofiz de h a f ( K ) = K bolsa f eiofiz de ataladı. Bi waqıttı o zide h a ooofiz h a eiofiz bolg a gooofiz izoofiz de ataladı. Bul jag dayda K h a K koltsolaı izoof koltsola de ataladı, bul K ~ K de jazıladı. Kef = { a K f ( a) = o } K u les ko ligi f gooofizii yadosı de ataladı. Kef u les ko ligi K ı u les koltsosı boladı. Ege K ı u les koltsosı L KL L h a LK L sha tlei qaaatladısa oda ol K koltsosıı idealı de ataladı. Bul jag dayda L< K de jazıladı. Kef u les koltsosı K da ideal boladı. Meyli edi L K koltsosıı idealı bolsı. Soda { a + L a K } qo sılas klassla ko ligi ( a + L ) + ( b + L ) = a + b + L ( a + L )( b + L ) = ab + L de beilge qosıw h a ko beytiw oeatsiyalaıa qaata koltso du zedi. Bul koltso K koltsosıı L idealı boyısha faktokoltsosı de ataladı h a ol K /L de belgileedi. Ege f : K K eiofiz bolsa, oda f / Kef ~ K boladı. Ege Kef = {0} bolsa f ooofiz boladı h a keisishe. Nolde o zgeshe bilik eleetke iye bolg a h a o zii qa lege 0 eleeti ushı kei eleetke iye bolg a K koutativ koltsosı ayda de ataladı. P \ {0} ko ligi ege P ayda bolsa ultilikativ gua du zedi. Z = Z / Z faktokoltsosı a iwayı sa bolg ada h a tek soda g aa ayda boladı. Bul ayda oduli boyısha qaldıqla aydaı de ataladı. Ege e = 0 bolsa (e bilik eleet), oda buday atual salaıı e kishisi P aydaıı xaakteistikası de ataladı. Bul 7
8 sa a iwayı sa boladı. Q aydaı xaakteistikası 0 ge, al xaakteistikası g a te boladı. Z aydaıı 6-lektsiya. Faktoial koltsola K eleeti kei eleette iye bolasa h a Ege K koltsosıı = ab, a, b kei eleetke iye ees eleetle, tu ide ko setilese oda ol a iwayı eleet de ataladı. Maydada a iwayı eleet bolaydı. Aıqlaa: Ege oldi bo liwshilei bolag a K koltsosıı qa lege a 0 eleeti a = u... tu ide jazılsa, bul jede u kei eleetke iye eleet,... s - a iwayı eleetle h a ege a = v... s bolsa = s h a q = u,... q = u, bul jede u... u - kei eleetke iye eleetle bolsa, oda K faktoial koltso de ataladı. Teoea: Noldi bo liwshilei joq koutativ koltso K faktoial bolıwı ushı oda qa lege a iwayı eleeti ege ol ab ı bo lse, oda ol a h a b eleetleii h esh bolasa biewi bo letug ı bolıwı za u h a jeteli. Da liyllew: Meyli ab = c bolsı. Ege a = ai, b = b j, c = c k bolsa, bul jede a ib j, c k a iwayı eleetle. a i b j = c k da ı a yaasa b eleetleii biewi bo letug ılıg ı keli shıg adı. Meyli edi / ab / a yaasa / b bolsı. İduktsiya boyısha eyli ko beytiwshile saı bolg a eleetledi alayıq. Meyli edi + + a = i = j, i = i = bolsı. Oda + eleeti,..., + eleetleii h esh bolasa biewi bo liwi keek. Deek, = u i j i = j = yag ıy teoea oıladı. Teoeadag ı balıq sha tle za u ekeligi ko setiw qıyı ees. Teoea da liylledi 7-lektsiya. Evklid koltsolaı 8
9 Aıqlaa: Meyli K oldi bo liwshilei bolag a koutativ koltso bolsı. Ege * δ : K \ {0} = K N {0} sa wlelediiwi ba bolı ol ( E) δ ( ab) δ ( a) a, b 0 ( E ) a, b K, b 0 q, K a = qb + ; δ ( ) < δ ( b) yaasa = 0 sha tlei qaaatladısa, oda K koltsosı Evklid koltsosı de ataladı. δ ( a) = a, a Z h a δ ( a) = dega, a = a( x ) P( x ) de alı biz Z, P( x ) koltsolaı Evklid koltsolaı bolatug ılıg ı ko eiz. Meyli edi a, b K h a a 0, b 0 bolsı. Soda a = q... k b = q = q... b +, ,, k..., δ ( δ ( δ (..., ) < δ (... ) < δ ( b) ) < δ (... δ (... ), ), ) < δ ( = 0. k k + k k + boladı. Soda k = HOD ( a, b) boladı. Teoea: K Evklid koltsosıdag ı qa lege HOK g a iye HOD ( a, b) = au + bv. Deek ( a, b) = u, v K, au + bv = Salda: Meyli K Evklid koltsosı h a a b, Ege HOD ( a, b) = h a ( a, c) = Ege = q = q + k k 3 k... k ), a, b eleetlei HOD h a, c K bolsı. Soda (i ). HOD bolsa HOD ( a, b, c) =.( ii ). a / bc h a HOD ( a, b) = bolsa a / c. Ege b / a, c / a h a HOD ( b, c) = bolsa bc / a. Teoea: K Evklid koltsosıı qa lege a 0 eleeti ko beytiwshilege jikleedi: a = ubb... b s Teoea: Qa lege Evklid koltsosı faktoial koltso boladı. Salda: Z h a P (x ) koltsolaı faktoial koltsola. 9
10 8-lektsiya. A iwayı h a aksial idealla Aıqlaa: Ege ab ko beyesi bo lge qa lege eleet h esh bolasa a h a b eleetleii biewi bolsa, oda P idealı a iwayı ideal de ataladı. Aıqlaa: K koltsosıı J idealı ksial ideal de ataladı, ege T J bolsa oda T = K yaasa T = J ekeligi keli shıqsa. Teoea: Ege K Evklid koltsosıı eleeti bolsa, oda - a iwayı eleet K aksial ideal. Da liyllew: Meyli K a iwayı eleet bolsı h a K T K, T < K bolsı. Oda T = ak h a T bolg aı ushı = ab boladı, bul jede a h a b eleetleii biewi kei eleetke iye. Ege a V (K ) bolsa T = ak = K. Ege b V (K ) bolsa T = ak = abk = K. Keisishe eyli K aksial ideal bolsı h a = ab, a V (K ) bolsı. Oda ak K h a K < ak K = ak a = u = abu bu = b V ( K ) -a iwayı eleet. Teoea da lilledi. Salda: Qa lege = 4 k + a iwayı saı = +,, Z tu ide ko setiledi. Teoea: t = +,, Z t ı a iwayı saladı da ejesi ko iiside h a bi a iwayı sa = 4k ju ko setkishke iye. Da lillew: Haqıyqatıda da HOD (, ) = h a / + bolsa = 4 k + ekeligi ko setiw jetkilikli. Biaq HOD (, ) =, = 4 (od ), + 0(od ) (od ) 0 (od ) ( / 0(od ) 4 Deek s Z : s (od ), s (od ). Yag ıy * Z = h a ol 4 ke bo liedi. Deek = 4k = 4k +. Teoea da lilledi. 9-lektsiya. İdealladı tuwı qosıdısı Meyli J h a oeatsiyala aıqlaadı: J h a J ideallaıı qosıdısı J + J = { x + x x J, x J kesisesi ) J - K koltsosıı ideallaı bolsı. Soda to edegi } =.
11 J J = { x x J h a x J } h a ko beyesi JJ = { x i x i x ki J k } J J. i Teoea: Ege e K h a J + J k = K, k =,...,, J, J,..., J idealla, bolsa J + J J... J = K = J + JJ... J boladı. Da liyllew: J J... J J J... J bolg aı ushı J J J... J = K ekeligi ko setiw jetkilikli, = bul oılı. = de = = ( x + y )( x + y ) = x + y y, x, x, x J h a y i J i. Deek J + JJ h a J Qalg a jag ı saı boyısha iduktsiyada keli shıg adı. Meyli edi K,..., K - koltsola bolsı. K = K... K - dekat ko beye. Meyli ( x,..., x ) + ( y,..., y ( x,..., x ) ( y,..., y K = K... K ) = ( x ) = ( x y + y,..., x,..., x y + y ); bolsı. Oda koltsosı K i koltsolaıı sıtqı tuwı qosıdısı de ataladı. Meyli edi J J K koltsosıı ideallaı bolsı. Ege K = J J h a J k J j = 0, i k bolsa j k K = J... J koltsosı o zii J k ideallaıı ishki tuwı qosıdısı de ataladı. Koltsoladı sıtqı h a ishki tuwı qosıdılaı o z-aa izoof koltsola (idealla) boladı. Soı ushı oladı ekewi de bidey belgileedi h a ol qısqasha koltsoladı (idealladı ) tuwı qosıdısı de ataladı. Yag ıy (ishki tuwı qosıdı) ~ (sıtqı tuwı qosıdı). ); 0-lektsiya. Aalas teoeala ) Meyli... ; Z = Z / Z ( ) ~ i Z... Z Z bolsı. Soda ( ii ) U ( Z ) ~ ( U Z )... U ( boladı. = h a U Z ) = Z \ {0} Z ) (
12 ) Meyli N bolsı. Soda (i ) ege U Z ) tsikllik gua boladı. ii ) U ( Z ) h a Z ) a iwayı sa bolsa ( ( U ( tsikllik guala boladı h a U ( Z ) = h a U ( Z ) = boladı. 3) U ( Z ) tsikllik gua bolıwı ushı > saı,4, yaasa bolıwı keek, bul jede - taq a iwayı sa. eleeti a iwayı eleet bolıwı ushı 4) K faktoial koltsosıı 0 K / K faktokoltsosı u tililik oblastı bolıwı za u h a jeteli. 5) Meyli a iwayı sa bolsı h a K koutativ koltso bolsı, e K h a x = 0 x K sha ti oılası. Oda ( x + y ) = x + y, =,,... Ko sete: boyısha iduktsiyaı h a bioial koeffitsietle C k, 0 < k <, a iwayı saı bo lietug ı-lıg ı aydalaı. 6) Ege K koltsosı bilik eleette iye bolsa K / L faktokoltsosı da bilik eleetke iye bolatug ılıg ı ko seti. Sheshii: Meyli e K K koltsosıı bilik eleeti bolsı. Soda ( a + L )( e + L ) = ( e + L )( a + L ) = a + L. Deek e + L K / L - bilik eleet. 7) Meyli Q -atsioal sala ko ligi bolsı. Q ( ) h a Q ( 5) ke eytiilge aydalaı izoof bolaa? (Juwa: bolaydı). 8) Meyli - a iwayı sa h a Z bolsı. Ege (, ) = bolatug ılıg ı da lille. * Da lillew: Z \ {0} (od ) bolsa Z = ultilikativ guasıı ta tibi te. Lagaj teoeası boyısha saı eleetii ta tibie qaldıqsız bo liedi. Deek = ( ) =, yag ıy = 0, deek (od ). 9) To edegiledi da lille (Silov teoeası aydalaı ) Ko sete: GL (, Z SL (, Z GL h a ) = ( ) SL (, Z ge * Z guasıı qa lege ), ) = ( ). SL gualaıı qa siyetleie aydalaı.
13 H -lektsiya. Guaı jasawshı ko ligi Meyli bizge G guasıı M u les ko ligi beilge bolsı. Soda = H u les gua boladı h a ol M u les ko ligi o z ishie I i H i M H i G alatug ı u les gualadı e kishisi (iialı) boladı. Aıqlaa: H IH i H i M H i G ko ligie jasalg a u les guası de ataladı h a ol гр (M ) belgileedi. Teoea: = u les guası G guasıı M u les H = de гр ( M ) = { tt... t t i M ямаса t i M, N }, yag ıy M u les ko ligie jasalg a u les gua usı M ko lgii eleetleii yaasa oladı kei eleetleii balıq shekli sadag ı ko beyeleie tuadı. Da lillew: Ege {}= H de belgilesek, H гр (M ) ekeligi tu siikli. Edi гр ( M ) H ekeligi da lillew ushı H tı u les gua ekeligi da lillew jetkilikli, sebebi H u les ko ligi M ı balıq eleetlei o z ishie aladı. Bul jede ( t, t... t ) = t... t t te ligi u lke ol oyaydı. k Daa jag dayda, ege M = {a} bolsa гр ( M ) = гр ( a) = { a k Z } tsikllik guası keli shıg adı. Ege oeatsiya qosıw bolsa гр ( a) = { k a k Z } boladı. Mısal-: Z = гр () = гр ( ) boladı Z гр( ), ± Z гр({,3}) гр ({, 4}) = гр ( Mısal-: = ) boladı, sebebi (, 3)= h a (, 4) =. Ege M = { a, a,..., a } bolsa гр (M ) u les guası shekli jasalg a u les gua deliedi h a ol гр ( a, a,..., a ) de te belgileedi. Soawla h a shııg ıwla. Z = гр (3, 7) ekeligi ko seti. k. Ege гр ( a) = { a 0 k ekeligi da lille. a = bolsa } = { e, a, a,... a ] 3
14 -lektsiya. Gualadı gooofizlei. Aıqlaa-: Meyli bizge f : G G sa wlelediiwi beilge bolsı, bul jede G h a G - guala. Ege f ( a * b) = f ( a) f ( b) bolsa, bul jede G = ( G, *), G = ( G, 0), oda f sa wlelediiwi G guasıı G guasıa gooofizi de de ataladı. a) Ege a b f ( a) f ( b) bolsa f gooofizi ooofiz de ataladı. v) Ege f ( G ) = G bolsa f -gooofiz eiofiz de ataladı. s) Ege f ooofiz h a eiofiz bolsa, oda ol izoofiz de ataladı. Bul jag dayda G ~ G de jazıladı. Mısal: Meyli R + - o h aqıyqıy sala, al R - balıq h aqıyqıy sala gualaı bolsı. Soda de beilge sa wlelediiw + izofizi bolatug ılıg ı teksei ko iw qıyı ees. Aıqlaa -: Meyli bizge gualadı f : R + R f ( a) = la R ultilikativ guasıı R additiv guasıa f : G G Kef = a G f ( a) = e } G gooofizi beilge bolsı. Soda { u les ko ligi f gooofizii yadosı de ataladı. Teoea-: Ke f G boladı Da lillew: a Kef bolsa f ( a ) = ( f ( a)) = ( e ) = e h a f ( e) = e bolatug ılıg ı teksei ko iw qıyı ees. h aqıyqatıda da h a f f ( e) = f ( a a ) = f ( a) f ( a ) f ( a ) = ( f ( a)) ( e) = f f f ( a a) = f ( a) = f ( a e) = f ( a) = f ( e a) = f a G ( a ) f ( a) f ( e) f 4 ( a) ( e) f ( e) = e G ( a) Soawla h a shııg ıwla. f : Z Z, f ( ) = k + Z sa wlelediiwii gooofiz bolatug ılıg ı ko seti.. Gualadı gooofizide shekli h a abellik gualadı obazlaı sa ykes shekli h a abellik guala bolatug ılıg ı ko seti
15 3-lektsiya. Tsikllik guala h a oladı klassifikatsiyası Aıqlaa: гр ( a) = { a Z ] guası a eleetie jasalg a tsikllik gua de ataladı. Z = гр () = гр ( ) Mısalla: Z = Z / Z = гр ( + Z ). Bul jede Z = = = h a Z = + Z =. Teoea-: Balıq sheksiz tsikllik guala o z-aa izoof boladı h a oladı balıg ı da Z = гр () guasıa izoof. Da lillew: Meyli bizge G = гр ( a), G = a = sheksiz tsikllik guası beilge bolsı. f : G Z Soda f ( a ) = de beilge f sa wlelediiwii izlege izoofiz boltaug ılıg ı da lillew a sat. Teoea-: Balıq ta tibi ge te bolg a tsikllik guala o z-aa izoof boladı h a oladı balıg ı da Z = Z / Z = гр ( + Z ) guasıa izoof boladı. Da lillew: Meyli bizge G = гр ( a), G = a = tsikllik guası beilge bolsı. Soda f f : G ( a k Z ) = k + Z, 0 k sa wlelediiwdi izlege izoofiz bolatug ılıg ı da lillew a sat. Teoea-3: { } koleks sala ko ligi ko beytiw oeatsiyasıa qaata ta tibi ge te bolg a tsikllik gua boladı. o o kπ kπ Da lillew: = coso + i sio = cos + i si, 0 k boladı. Bul jede { π π } = гр cos + i si, Soawla h a shııg ıwla { 3 guasıı balıq eleetlei ko seti. }, ekeligi da lillew a sat. 5
16 . гр ( a), a = 5, guasıı balıq eleetlei ko seti. 4-lektsiya. İgeles klassla. Lagaj teoeası Aıqlaa: Meyli H G bolsı. Soda Hg = { hg h H } h a gh = { gh h H } ko ligiklei G guasıı H u les guası boyısha sa ykes o h a sol igeles klasslaı de ataladı. ( g eleeti ee aıqlag a). Teoea-: h a qıylı o (sol) igeles klassla o z-aa kesiseydi h a G guası ko lik etide oladı biikesi boladı: G = UHg = U gh. g G g G Teoea-: G guasıı H u les guası boyısha o h a sol igeles klasslaıı saı, yag ıy { Hg g G ] h a { gh g G ] ko likleii eleetle saı bidey boladı (bul sa H u les guasıı G guasıdag ı ideksi de ataladı, ol G : H de belgileedi). Teoea-3: (Lagaj): Meyli H G bolsı. Soda G = H G : H, yag ıy shekli guaı ta tibi oı qa lege u les guasıı ta tibie qaldıqsız bo liedi. Bul teoeaı da lilleiwi teoea h a de h a to edegi sızılada keli shıg adı: Bul sızılada h a bi bo li bi igeles klasstı a latadı. Bizi ısalıızda G guasıı H u les guası boyısha igeles klassla saı 0 g a te boladı. Soawla h a shııg ıwla Z guasıı 5 Z u les guası boyısha balıq igeles klasslaı tabı.. Ta tibi 4 ge te bolg a guaı ta tibi 5 ke te bolg a u les guası bolaa? 6
17 g 5-lektsiya. Noal u les guala. Faktoguala H G h a balıq g G, h H eleetlei ushı Aıqlaa: Ege hg H bolsa, H u les guası G guasıı oal u les guası de H < G. H < G gh = Hg g G yag ıy H u les guası ataladı, jazılıwı Teoea-: oal u les gua bolıwı ushı ol boyısha qa lege o h a sol igeles klass o z-aa te bolıwı keek. Da lillew: g hg H, g G g h Hg gh Hg. gh Hg. g hg H, g G hg gh Hg gh Deek gh = Hg eke. Ege gh = Hg g G bolsa = g gh g Hg H = g Hg g hg H g G, h H H G. Ege H G bolsa { gh g G ] igeles klassla ko ligi g H g H = gg H de aıqlag a oeatsiyag a qaata gua boladı. Bul jede bilik eleet H qa te h a ( gh ) = g H.. Aıqlaa: G = { gh g G} H guası G guasıı H u les guası boyısha faktoguası de ataladı. Teoea-: f : G G gooofizii yadosı G guasıda oal u les gua boladı, yag ıy Ke G. Kef = { a G f ( a) = e } Da lillew: f ( g hg ) = f ( g ) f ( h) f ( g ) = ( f g hg Ke f. Yag ıy Ke f G. Teoea-3: f G G ~ f ( G ) Ke f Bua G boladı. ( g )) f ( g ) = e : gualadı gooofizi bolsa Soawla h a shııg ıwla. Abellik guaı qa lege u les guası oı oal u les guası bolatug ılıg ı ko seti. Z Z gooofizii yadosı tabı. 5Z G : H = bolsa H G ekeligi da lille. 3. Ege 7
18 6-lektsiya. Mayda. Shekli aydala Koutativ koltso. Bilik h a kei eleet. Z aydaı Aıqlaa-. Nolde o zgeshe bilik eleetke iye bolg a h a o zii olde o zgeshe qa lege eleeti ushı kei eleetke iye bolg a koutativ koltso ayda de ataladı. Mısalla: -aydala. Z -ayda ees. Q,R, C Aıqlaa-. Maydaı o zi de ayda bolatug ı u les koltsosı usı aydaı u les aydaı de ataladı. Mısalla: Q aydaı R di, al R aydaı C ı u les aydaı boladı. Teoea-. Maydaı qa lege sadag ı u les aydalaıı kesisesi de usı aydaı u les aydaı boladı. Maydada oldi bo liwshilei bolaydı, sebebi kei eleetke iye eleet oldi bo liwshisi bolaydı. Ege P ayda bolsa P \{0} u les ko ligi ko beytiw oeatsiyasıa qaata gua du zedi, bul gua P aydaıı ultilikativ guası de ataladı. oduli boyısha qaldıqla klasslaıı koltsosı qaayıq: Z = { 0,,,..., } Teoea-. Z koltsosı = a iwayı sa bolg ada h a tek soda g aa ayda boladı. Haqıyqatıda da, ege 0 ko ligii balıq eleetlei s dı ko beyti s bolsa, yag ıy {,,..., } s bolsa biz { s,s,..., s ( )} Z i 0 eleetie basqa balıq ko ligie iye bolaız. Bul ko likti eleetleie tuatug ılıg ı teksei ko iw qıyı ees. Deek s = bolatug ıday eleeti ba boladı, yag ıy = ( s ) Z eke, yag ıy Z ayda eke. Egede = s t, < s < bolsa 0 = = s t boladı, yag ıy s h a t eleetlei oldi bo liwshilei bola edi, biaq bul u ki ees. Soawla h a shııg ıwla. { a + b a, b Q} ko ligi ayda bolaa?. 7 \{0} Z guasıdag ı 5 eleetii ta tibi tabı. 8
19 7-lektsiya. Maydaı xaakteistikası. A iwayı aydala Maydaı xaakteistikası. A iwayı ayda. Q h a aydalaı. Aıqlaa-: Meyli P aydaı h a oı bilik eleeti e beilge bolsı. P aydaıı xaakteistikası de e = 0 bolatug ı e kishi 0 u ti saıa aytıladı h a ege 0 bolsa, oda ol sha tli tu de a iwayı sa boladı. Mısalla: Ratsioal sala aydaı Q di xaakteistikası 0 (ol) ge, al Z aydaıı xaakteistikası g a te. Aıqlaa-: O zie o zgeshe u les aydag a iye bolag a ayda a iwayı ayda de ataladı. Toea-: Ratsioal sala aydaı Z -a iwayı ayda. Teoea-: qa lege -a iwayı saı ushı Z aydaı-a iwayı ayda. Teoea-3: qa lege ayda a iwayı u les aydag a iye. Ege aydaı xaakteistikası 0 ge te bolsa bul a iwayı u les ayda atsioal sala aydaı Q ge, al ege xaakteistikası g a te bolsa bul a iwayı u les ayda Z g a izoof boladı. Teoea-4: Xaakteistikası g a te bolg a aydada bideyligi oılı boladı. ( x + y ) = x + y ( N Soawla h a shııg ıwla ) eleette tuatug ı aydada x = x bideyligi da lille. ) Qa lege aydada tek bi g aa a iwayı u les ayda ba boladı. ) Z 9
20 8-lektsiya. Modulle h a oladı gooofizlei. Modul. u les odul. Modulledi gooofizlei. Shekli jasalg a odul. Eikli odul. Aıqlaa : Meyli K -bilik eleetie iye assotsiativ koltso h a V qosıwg a qaata abellik gua bolsı. Ege K V V, ( x, v ) xv sa wlelediiwi ba bolı, ol qa lege x, y K h a u, v V ushı I. x ( u + v ) = xu + xv II. ( x + y ) v = xv + yv III. ( xy ) v = x ( yv ) IV. v = v sha tlei qaaatladısa, oda V sol K -odul yaasa K koltsosı u stide sol odul de ataladı. Aıqlaa-: Meyli V -K -odul bolsı. Ege U V bolı x K, u U ushı xu U bolsa oda U V odulii u les oduli de ataladı. Aıqlaa-3: Meyli U h a K sa wlelediiwi f ( u + u ) = f ( u) + f ( u V -odulle bolsı. Ege f : U V ) f ( xu ) = xf ( u) sha tlei qaaatladısa, oda f sa wlelediiwi U odulii V odulie gooofizi de ataladı. Teoea-: Meyli f : U V odulledi gooofizi bolsı. Soda Ke f = { u U f ( u) = 0} U odulii, al I f V odulii u les odullei boladı. Aıqlaa-4: Meyli U V odulii u les oduli bolsı. Soda V / U = { v + U v V } faktoodul (abellik additiv guaı faktoguası) de ataladı, bul jede x ( v + U ) = xv + U. Teoea-: Ege V i le V odulii u les odullei bolsa, oda IV i i de V u les oduli boladı. Aıqla-5: IV i v i M u les oduli odul de ataladı h a ol x t x k t k, x i K, t i M eleetleie tuadı. Aıqlaa-6: K V = xv x K }; v V jasalg a tsikllik odul de ataladı. M V ko ligie jasalg a u les { u les oduli v eleetie 0
21 Aıqlaa-7: ataladı V = kv kv oduli shekli jasalg a odul de Soawla h a shııg ıwla ) qa lege abellik gua A Z -odul bolatug ılıg ı ko seti ) P aydaı u stidegi V vektolıq ke isligii P-odul bolatug ılıg ı ko seti. 9-lektsiya. Shekli jasalg a odulle Tsikllik odulle. Jasawshı eleetle. Eikli odulle Meyli K koltsosı u stidegi V oduli beilge bolsı. Aıqlaa-. v V eleeti ee jasalg a odul, yag ıy Kv = { xv x K } oduli v eleeti ee jasalg a tsikllik odul de ataladı. Aıqlaa-. Tsikllik odulledi shekli sadag ı qosıdısı, yag ıy Kv Kv v oduli shekli jasalg a odul de ataladı. oduldi jasawshı eleetlei de ataladı.,...., v V eleetlei bul Aıqlaa-3. Ege V odulii qa lege eleeti v v = x v x v, v i V, x i K v,....,v tu ide bi a isli ko setilse, oda V oduli eleetleie jasalg a eikli odul de ataladı. Teoea-. Meyli K oldi bo liwshileie iye bolag a koltso bolsı. Ege K koltsosı u stidegi V odul u,..., u h a { } { v,..., v } = boladı. sistealaı ee jasalg a eikli odul bolsa, oda Teoea-. Ha bi shekli jasalg a odul qadayda bi shekli jasalg a eikli oduldi gooof obazı boladı. Teoea-3. Eikli oduldi qa lege u les oduli de eikli odul boladı (oı jasawshı eleetleii saı oduldi jasawshı eleetleii saıa ası keteydi). Teoea-4. Bas idealla koltsosı u stidegi qa lege shekli jasalg a oduldi u les oduli de shekli jasalg a odul boladı.
22 Soawla h a shııg ıwla. Z koltsosı u stidegi abellik gua odul bolaa?. R aydaı u stidegi sızıqlı ke islik odul bolaa?
23 0-lektsiya. Maydala u stide algebala. Veddeba teoeası Mayda u stidegi algeba. Algebaı o lshei h a oayı. u les algeba. Algebaladı gooofizlei. Assotsiativ algeba. Veddeba teoeası. Aıqlaa-: P aydaı u stidegi A algebası de ( A, +, ) koltsosıa h a P u stidegi A vektolıq ke isligie tuatug ı julıqqa aytıladı. (yag ıy A koltsosı P u stidegi ke islik boladı), bul jede λ ( xy ) = ( λ x ) y = x ( λ y ), x, y A, λ P sha ti oılaıwı keek. Aıqlaa-: Ege A koltsosı assotsiativ koltso bolsa oda A algebası assotsiativ algeba de ataladı. Aıqlaa-3: A ı o lshei de P u stidegi vektolıq ke islik A ı o lsheie aytıladı. Aıqlaa-4: A algebasıı B u les algebası de A koltsosıı u les koltsosı h a A ke isligii u les ke isligi bolatug ı B g a aytıladı. Teoea-: U les algebaladı kesisesi de u les algeba boladı. Aıqlaa-5: A I A i u les algebasıa aytıladı, bul jede i A M i M u les ko ligie jasalg a u les algeba de A le- A ı u les algebalaı. Aıqlaa-6: A algebasıı B algebasıa gooofizi de A koltsosıı B koltsosıa gooofizie aytıladı, bul gooofiz P- sızıqlı tu lediiw bolıwı keek. Aıqlaa-7: A algebasıı oayı Z (A ) de { a A ax = xa x A} ko ligie aytıladı. Teoea-: A algebasıı oayı Z (A ) usı A algebasıı u les algebası boladı. Teoea-3: (Veddeba). Bo liw oılaatug ı qa lege shekli assotsiativ koltso koutativ boladı. Salda: Bo liw oılaatug ı qa lege shekli assotsiativ koltso ayda boladı. Soawla h a shııg ıwla ) Algebaı idealı h a faktoalgebası dege e? ) (P) te bolg a algeba bolatug ılıg ı ko seti M atitsala ko ligii P aydaı u stidegi h a o lshei qa 3
24 A debiyatla [] Kostiki A.İ. Vvedeie v algebu. M., «Nauka» 977. [] Kuosh A.G. Kus vısshey algebı. M., «Nauka» 963. [3] Faddeev D.K. Lektsii o algebe. M., «Nauka» 984. [4] Skoyakov L.A. Eleetı algebı. M., «Nauka» 980. [5] Nazaov R.N., Toshulatov B.T., Dusubetov A.D. Algeba va sola azaiyasi, I qis, T., «Uqituvchi» 993 [6] Nazaov R.N., Toshulatov B.T., Dusubetov A.D. Algeba va sola azaiyasi, II qis, T., «Uqituvchi» 995. [7] Tajetdiov S. «Guala h a koltsola teoiyası u yeiwge etodikalıq ko setele». No kis,
25 A debiyatla [] Kostiki A.İ. Vvedeie v algebu. M., «Nauka» 977. [] Kagaolov M.İ., Mezlyakov Yu.İ. Osovı teoii gu. M., «Nauka» 977. [3] Va de Vayae. Algeba. M., «Nauka» 980. [4] Nazaov R.N., Toshulatov B.T., Dusubetov A.D. Algeba va sola azaiyasi, I-II qisla, T., «Uqituvchi» 993. [5] Djieuatov U.Tajetdiov S. Algeba kusı boyısha laboatoiyalıq juısla h a oladı oılawg a etodikalıq ko setele. QMU basaxaası, 995. [6] Tajetdiov S. «Guala h a koltsola teoiyası u yeiwge etodikalıq ko setele». No kis, 004,,5 b.t. 5
FUNKTSIONAL ANALIZDIN QOSIMSHA BAPLARI
 O zeist Resulisı joqrı h ort rwlı ililediriw iistrligi QARAQALPAQ MA MLEKETLIK UNIVERSITETI Futsiolliq liz edrsı FUNKTSIONAL ANALIZDIN QOSIMSHA BAPLARI LEKTSİYA TEKSTLERİ Du ziwshi: ss S Tlewurtov No is-8
O zeist Resulisı joqrı h ort rwlı ililediriw iistrligi QARAQALPAQ MA MLEKETLIK UNIVERSITETI Futsiolliq liz edrsı FUNKTSIONAL ANALIZDIN QOSIMSHA BAPLARI LEKTSİYA TEKSTLERİ Du ziwshi: ss S Tlewurtov No is-8
!"! # $%!&'!#!!' ' ( -./01 2!" 3 &' % () !"#$% &' ()*+, -./ :; )* < )*/04 56=> / & )*FGHIJK LMNOD &PQRS1TU )*V / &WXY
 !"! # $%!&'!#!!' ' ( -./01 2!" 3 &' % ()45 6789!"#$% &' ()*+, -./01 234 567 89:; )* < )*/04 56=> 7+?@ABC$DE / & )*FGHIJK LMNOD &PQRS1TU )*V / &WXY / @N )* / NZ)*V[\ ]^_`a:bsc? DE ()* 89E DE 56 ),!"#$%!&',,:-;
!"! # $%!&'!#!!' ' ( -./01 2!" 3 &' % ()45 6789!"#$% &' ()*+, -./01 234 567 89:; )* < )*/04 56=> 7+?@ABC$DE / & )*FGHIJK LMNOD &PQRS1TU )*V / &WXY / @N )* / NZ)*V[\ ]^_`a:bsc? DE ()* 89E DE 56 ),!"#$%!&',,:-;
B T A n a l o g T r a n s m i t t e r. T e k n i k K ı l a v u z u. R e v 1. 2
 B T - 111 A n a l o g T r a n s m i t t e r T e k n i k K ı l a v u z u R e v 1. 2 1. Ö N G Ö R Ü N Ü M, Ü S T Ü N L Ü K L E R İ VE Ö Z E L L İ K L E R İ M i k r o k o n t r o l ö r t a b a n l ı BT- 111
B T - 111 A n a l o g T r a n s m i t t e r T e k n i k K ı l a v u z u R e v 1. 2 1. Ö N G Ö R Ü N Ü M, Ü S T Ü N L Ü K L E R İ VE Ö Z E L L İ K L E R İ M i k r o k o n t r o l ö r t a b a n l ı BT- 111
BİRİNCİ BÖLÜM ÇÖZÜMLÜ PRATİK ÇALIŞMALARI
 İÇİNDEKİLER ÖNSÖZ... VII İÇİNDEKİLER... IX BİRİNCİ BÖLÜM ÇÖZÜMLÜ PRATİK ÇALIŞMALARI PRATİK ÇALIŞMA -... Adi şi ket E ek se a e PRATİK ÇALIŞMA -... Adi şi ket Se a e tü le i PRATİK ÇALIŞMA -... Kollektif
İÇİNDEKİLER ÖNSÖZ... VII İÇİNDEKİLER... IX BİRİNCİ BÖLÜM ÇÖZÜMLÜ PRATİK ÇALIŞMALARI PRATİK ÇALIŞMA -... Adi şi ket E ek se a e PRATİK ÇALIŞMA -... Adi şi ket Se a e tü le i PRATİK ÇALIŞMA -... Kollektif
 Ş Ş Ğ ç ğ ğ ş ş ö ç ö ş ç ş ğ ş ş ş ğ ş ş ö ö ş ö ş ş ş ö ş ç ö ğ ş ğ ş ö İ ç ş ö ö ö ş ğ Ö Ü Ç ç ğ İ İŞ İ Ğ Ö İ İ ç Ç ö İ ğ İ İ ş ğ ç ş ö ş ğ ğ ş İ ş Ş ğ ç ğ ş İ ş ğ İ ç İŞ ç ö ş ç ğ ö ş ç ş ğ ç ş ş ş
Ş Ş Ğ ç ğ ğ ş ş ö ç ö ş ç ş ğ ş ş ş ğ ş ş ö ö ş ö ş ş ş ö ş ç ö ğ ş ğ ş ö İ ç ş ö ö ö ş ğ Ö Ü Ç ç ğ İ İŞ İ Ğ Ö İ İ ç Ç ö İ ğ İ İ ş ğ ç ş ö ş ğ ğ ş İ ş Ş ğ ç ğ ş İ ş ğ İ ç İŞ ç ö ş ç ğ ö ş ç ş ğ ç ş ş ş
H A S T A N E E N F E K S İY O N L A R IN I Ö NLEM E. E L İF C O Ş K U N E n fe k s iy o n K o n tr o l H e m ş ir e s i
 H A S T A N E E N F E K S İY O N L A R IN I Ö NLEM E E L İF C O Ş K U N E n fe k s iy o n K o n tr o l H e m ş ir e s i H ip o k r a t (M.Ö. 4 6 0-3 7 0 ) Ö n c e lik le z a r a r v e r m e 2 F lo r e
H A S T A N E E N F E K S İY O N L A R IN I Ö NLEM E E L İF C O Ş K U N E n fe k s iy o n K o n tr o l H e m ş ir e s i H ip o k r a t (M.Ö. 4 6 0-3 7 0 ) Ö n c e lik le z a r a r v e r m e 2 F lo r e
3-P C ile h a b e r le şm e y e u y g u n b ir a r a b ir im. (IS A, P C I, U S B g ib i )
 M O D E M N E D İR : M o d u la to r -D e m o d u la to r k e lim e le r in in k ıs a ltm a s ı M O D E M. Y a n i v e r ile r i s e s s in y a lle r in e s e s s in y a lle r in i v e r ile r e d ö n
M O D E M N E D İR : M o d u la to r -D e m o d u la to r k e lim e le r in in k ıs a ltm a s ı M O D E M. Y a n i v e r ile r i s e s s in y a lle r in e s e s s in y a lle r in i v e r ile r e d ö n
Kitap. x ve y birer tam sayı olmak üzere, (5x- 1) bir çift sayı, (7y + 5) bir tek sayı oldu una göre, a aıdakilerden hangisi çift sayıdır? x.
 Oı ıo o MATEMATK a Ders Föü '. o Yoyın orı _ - Effectve rııoaoa Ktap Ortaö retm Aanr MF eıs a o Bu ktapcı ın her hakkı sakıdır. Tüm hakarı es Yayınarı'na attr. Kısmen de otse at nı yapıamaz. Metn ve sorutar.
Oı ıo o MATEMATK a Ders Föü '. o Yoyın orı _ - Effectve rııoaoa Ktap Ortaö retm Aanr MF eıs a o Bu ktapcı ın her hakkı sakıdır. Tüm hakarı es Yayınarı'na attr. Kısmen de otse at nı yapıamaz. Metn ve sorutar.
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
 1. BÖÜM A DAGAARI MDE SRU - 1 DEİ SRUARIN ÇÖZÜMERİ 1. 5. T x x x uvvet vektörüü degede uzaklaşa ucu ile hız vektörüü ları çakışık olalıdır. Bua göre şeklide. Dal ga la rı ge li ği de ge ok ta sı a ola
1. BÖÜM A DAGAARI MDE SRU - 1 DEİ SRUARIN ÇÖZÜMERİ 1. 5. T x x x uvvet vektörüü degede uzaklaşa ucu ile hız vektörüü ları çakışık olalıdır. Bua göre şeklide. Dal ga la rı ge li ği de ge ok ta sı a ola
ab H bulunur. Şu halde önceki önermenin i) koşulu da sağlanır ve H G bulunur.
 3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
T.C. Sıra No Aday No Kimlik No Ad Soyad Lisans Lisans Puanı Mülakat Puanı Nihai Ortalama
 T.C. Sıra No Aday No Kimlik No Ad Soyad Lisans Lisans Puanı Mülakat Puanı Nihai Ortalama 1 A370094 58*******92 MU*** KA*** SAĞLIK YÖNETİMİ, LİSANS TAMAMLAMA 94.50 94,5 PROGRAMI, 2 A372539 71*******12 NU***
T.C. Sıra No Aday No Kimlik No Ad Soyad Lisans Lisans Puanı Mülakat Puanı Nihai Ortalama 1 A370094 58*******92 MU*** KA*** SAĞLIK YÖNETİMİ, LİSANS TAMAMLAMA 94.50 94,5 PROGRAMI, 2 A372539 71*******12 NU***
A)22 B)24 C)zo D)za E)so
 üçrırın çıorty 1 1. bir üçgen _...-\ _,.-..\ m() : m() Io1 = 2.. Ia1 = 4.. I + ; = 9.1n 4. 6 üçgeninde [] dı açıortay n1 = 4., IR1 = 6.. l = 12 m 2 x Yukarıdakiverilere göre, = x kaç m dir? )ı )4 )5 )6
üçrırın çıorty 1 1. bir üçgen _...-\ _,.-..\ m() : m() Io1 = 2.. Ia1 = 4.. I + ; = 9.1n 4. 6 üçgeninde [] dı açıortay n1 = 4., IR1 = 6.. l = 12 m 2 x Yukarıdakiverilere göre, = x kaç m dir? )ı )4 )5 )6
BAĞIL HAREKET. 4. kuzey. Şekilde görüldüğü gibi, K aracındaki gözlemci L yi doğuya, M yi güneye, N yi güneybatıya doğru gidiyormuş gibi görür.
 AIŞTIRAAR BÖÜ BAĞI HAREET ÇÖZÜER BAĞI HAREET 1 4 N N =v =0 Şekilde görüldüğü gibi, aracındaki gözlemci yi doğuya, yi e, N yi batıya doğru gidiyormuş gibi görür = = = 0 olur ( aracı duruyor) =v = aracı
AIŞTIRAAR BÖÜ BAĞI HAREET ÇÖZÜER BAĞI HAREET 1 4 N N =v =0 Şekilde görüldüğü gibi, aracındaki gözlemci yi doğuya, yi e, N yi batıya doğru gidiyormuş gibi görür = = = 0 olur ( aracı duruyor) =v = aracı
3. Telin kesit alanı, 4. lsıtılan telin diren ci, R = R o. 5. Devreden geçen proton sayısı, q = (N e. 6. X ve Y ilet ken le ri nin di renç le ri,
 . ÖÜ EETİ ODE SOU - DEİ SOUN ÇÖZÜEİ. Teln kest alanı, 400 mm 4.0 4 m. a a a a n boyu,, a n kest alanı, a.a a a a Teln drenc se, ρ., 500 4.0 6. 4 5 Ω dur. 40. Telden geçen akım, ohm kanunundan, 40 48 amper
. ÖÜ EETİ ODE SOU - DEİ SOUN ÇÖZÜEİ. Teln kest alanı, 400 mm 4.0 4 m. a a a a n boyu,, a n kest alanı, a.a a a a Teln drenc se, ρ., 500 4.0 6. 4 5 Ω dur. 40. Telden geçen akım, ohm kanunundan, 40 48 amper
BAĞIL HAREKET BÖLÜM 2. Alıştırmalar. Bağıl Hareket ÇÖZÜMLER. 4. kuzey
 BAĞI HAREET BÖÜ Alıştırmalar ÇÖZÜER Bağıl Hareket 1 4 batı =v =0 doğu Şekilde görüldüğü gibi, aracındaki gözlemci yi doğuya, yi e, yi batıya doğru gidiyormuş gibi görür = = = 0 olur ( aracı duruyor) aracı
BAĞI HAREET BÖÜ Alıştırmalar ÇÖZÜER Bağıl Hareket 1 4 batı =v =0 doğu Şekilde görüldüğü gibi, aracındaki gözlemci yi doğuya, yi e, yi batıya doğru gidiyormuş gibi görür = = = 0 olur ( aracı duruyor) aracı
Ö Ö Ü İ ö Ü Ş ö Ğ Ğ Ğ Ö Ö Ü Ö İ Ö Ç Ğ Ğ ö Ö Ğ Ö Ü Ç Ö ÜĞÜ Ö ÜĞÜ Ü Ğ ö İ ö Ğ Ğ Ğ ö Ü Ü Ğ Ğ ö Ü Ğ ö Ü ö ö Ü Ö ö Ü ö ĞÜ ö ÜĞÜ Ü Ü Ö ö ö ö Ğ öi Ğ Ç ö Ö Ü
 Ğ Ğ Ğ Ğ İ Ğ Ş Ğ Ş Ö Ü İ ğ İ Ö ö Ğ Ş İ Ş Ö Ü Ş Ş Ü Ö Ş Ş ğ Ş İ ğ Ö Ö Ü İ ö Ü Ş ö Ğ Ğ Ğ Ö Ö Ü Ö İ Ö Ç Ğ Ğ ö Ö Ğ Ö Ü Ç Ö ÜĞÜ Ö ÜĞÜ Ü Ğ ö İ ö Ğ Ğ Ğ ö Ü Ü Ğ Ğ ö Ü Ğ ö Ü ö ö Ü Ö ö Ü ö ĞÜ ö ÜĞÜ Ü Ü Ö ö ö ö Ğ
Ğ Ğ Ğ Ğ İ Ğ Ş Ğ Ş Ö Ü İ ğ İ Ö ö Ğ Ş İ Ş Ö Ü Ş Ş Ü Ö Ş Ş ğ Ş İ ğ Ö Ö Ü İ ö Ü Ş ö Ğ Ğ Ğ Ö Ö Ü Ö İ Ö Ç Ğ Ğ ö Ö Ğ Ö Ü Ç Ö ÜĞÜ Ö ÜĞÜ Ü Ğ ö İ ö Ğ Ğ Ğ ö Ü Ü Ğ Ğ ö Ü Ğ ö Ü ö ö Ü Ö ö Ü ö ĞÜ ö ÜĞÜ Ü Ü Ö ö ö ö Ğ
İTME VE MOMENTUM. 1. P i
 7 BÖÜM İTME E MOMENTUM AIŞTIRMAAR ÇÖZÜMER İTME E MOMENTUM P i 0/s kg P s 0/s kg x +x düzle a Du va rın cis e u gu la dı ğı it e, o en tu de ği şi i ne eşit tir P i i 0 0 kg/s P s s ( 0 0 kg/s it e P P
7 BÖÜM İTME E MOMENTUM AIŞTIRMAAR ÇÖZÜMER İTME E MOMENTUM P i 0/s kg P s 0/s kg x +x düzle a Du va rın cis e u gu la dı ğı it e, o en tu de ği şi i ne eşit tir P i i 0 0 kg/s P s s ( 0 0 kg/s it e P P
ORTA ANADOLU İHRACATÇI BİRLİKLERİ GENEL SEKRETERLİĞİ
 ORTA ANADOLU İHRACATÇI BİRLİKLERİ GENEL SEKRETERLİĞİ Sayı: 70430465-TİM.OAİB.GSK.ARG1.2017/1403-26723 Ankara, 06/12/2017 Konu: Yönetmelikler SİRKÜLER (MAKİNE/2017) Bilim, Sanayi ve Teknoloji Bakanlığı
ORTA ANADOLU İHRACATÇI BİRLİKLERİ GENEL SEKRETERLİĞİ Sayı: 70430465-TİM.OAİB.GSK.ARG1.2017/1403-26723 Ankara, 06/12/2017 Konu: Yönetmelikler SİRKÜLER (MAKİNE/2017) Bilim, Sanayi ve Teknoloji Bakanlığı
ÖĞRETİM) PR. ÖĞRETİM) ÖĞRETİM) ÖĞRETİM) 46*******5 ME*** YI*** İŞLETME PR. (AÇIKÖĞRETİM) ,000 83,9500 Kazandı
 MUHASEBE VE DENETİM,TEZSİZ YÜKSEK LİSANS PROGRAMI, (İKİNCİ 1-19 EĞİTİM-ÖĞRETİM YILI GÜZ YARIYILI YERLEŞTİRME RAPORU 1 A3 3******* İB*** KE*** 93. 95, 9, Kazandı A77 *******5 ULUSLARARASI TİCARET VE FİNANSMAN
MUHASEBE VE DENETİM,TEZSİZ YÜKSEK LİSANS PROGRAMI, (İKİNCİ 1-19 EĞİTİM-ÖĞRETİM YILI GÜZ YARIYILI YERLEŞTİRME RAPORU 1 A3 3******* İB*** KE*** 93. 95, 9, Kazandı A77 *******5 ULUSLARARASI TİCARET VE FİNANSMAN
4. f ( x ) = x m x + m. Cevap C. m açılımındaki bir terim, x. 5. cx 3 + Cevap D. 6. x 2 + ( a + 4 ) x + 3a + 3 ifadesinin tam kare olması için
 Deneme - / YT / MT MTMTİ DNMSİ Çözümle. < n < 0. f ( ) m + m p ve q asal saıla olmak üzee, n p. q vea p şeklinde olmalıdı. n {.,.,. 7,.,.,. 7,. 9,.,. 9,.,. 7,.,.,. 7,. 9,. 7,.,, } 9 tane bulunu.. { 7,,,
Deneme - / YT / MT MTMTİ DNMSİ Çözümle. < n < 0. f ( ) m + m p ve q asal saıla olmak üzee, n p. q vea p şeklinde olmalıdı. n {.,.,. 7,.,.,. 7,. 9,.,. 9,.,. 7,.,.,. 7,. 9,. 7,.,, } 9 tane bulunu.. { 7,,,
- 10. (r) HARFİ ÇALIŞMA SAYFALARI HAZIRLAYAN: ABDULLAH BÜYÜKYILDIZ 1
 - 10 () HAFİ ÇALIŞMA SAYFALAI HAZILAYAN: ABDULLAH BÜYÜKYILDIZ 1 () HAFİ ÇALIŞMA SAYFALAI HAZILAYAN: ABDULLAH BÜYÜKYILDIZ 2 () HAFİ ÇALIŞMA SAYFALAI HAZILAYAN: ABDULLAH BÜYÜKYILDIZ 3 () HAFİ ÇALIŞMA SAYFALAI
- 10 () HAFİ ÇALIŞMA SAYFALAI HAZILAYAN: ABDULLAH BÜYÜKYILDIZ 1 () HAFİ ÇALIŞMA SAYFALAI HAZILAYAN: ABDULLAH BÜYÜKYILDIZ 2 () HAFİ ÇALIŞMA SAYFALAI HAZILAYAN: ABDULLAH BÜYÜKYILDIZ 3 () HAFİ ÇALIŞMA SAYFALAI
ÇEMBER SIVAMALI FANLAR
 Ocak / 0 HAVA ÜFLEME YÖNÜ «"V" "A"» W SERİSİ FAN TİPİ ( Kare Davlumbaz ) S SERİSİ FAN TİPİ ebmpapst AKSİYEL FANLAR «"V" SS50-AH0-0 SE300-AS7-37 SE350-AN0-50 S6E350-AN-0 SE00-AP0- S6E00-AP-7 SE50-AP0-06
Ocak / 0 HAVA ÜFLEME YÖNÜ «"V" "A"» W SERİSİ FAN TİPİ ( Kare Davlumbaz ) S SERİSİ FAN TİPİ ebmpapst AKSİYEL FANLAR «"V" SS50-AH0-0 SE300-AS7-37 SE350-AN0-50 S6E350-AN-0 SE00-AP0- S6E00-AP-7 SE50-AP0-06
ELEKTROSTATİK. 3. K kü re si ön ce L ye do kun - du rul du ğun da top lam yü kü ya rı çap la rıy la doğ ru oran tı lı ola rak pay la şır lar.
 . BÖÜ EETROSTATİ AIŞTIRAAR ÇÖÜER EETROSTATİ. 3 olu. 3. kü e si ön ce ye o kun - u ul u ğun a top lam yü kü ya çap la y la oğ u oan t l ola ak pay la ş la. top 3 olu. Bu u um a, 3 6 ve olu. Da ha son a
. BÖÜ EETROSTATİ AIŞTIRAAR ÇÖÜER EETROSTATİ. 3 olu. 3. kü e si ön ce ye o kun - u ul u ğun a top lam yü kü ya çap la y la oğ u oan t l ola ak pay la ş la. top 3 olu. Bu u um a, 3 6 ve olu. Da ha son a
Sıra No Aday No Kimlik No Ad Soyad Lisans Lisans Puanı Mülakat Puanı Nihai Ortalama Durum
 1 A3719 3*******1 İŞLETME (İNGİLİZCE), LİSANS BE*** İL*** 7.1 95,,55 Kazandı A37793 33******* EB*** ŞE*** İNSAN KAYNAKLARI YÖNETİMİ PR.. 9, 5,3 Kazandı 3 A33 17*******5 SE*** YÜ*** PSİKOLOJİ PR.. 5, 3,9
1 A3719 3*******1 İŞLETME (İNGİLİZCE), LİSANS BE*** İL*** 7.1 95,,55 Kazandı A37793 33******* EB*** ŞE*** İNSAN KAYNAKLARI YÖNETİMİ PR.. 9, 5,3 Kazandı 3 A33 17*******5 SE*** YÜ*** PSİKOLOJİ PR.. 5, 3,9
- 1 - 3 4v A) 450 B) 500 C) 550 D) 600 E) 650
 - -. Bi cisi uzunutai younu sabit hızı ie at eteye başıyo. Cisi youn yaısını at ettiğinde hızını yaıya düşüüp aan youn yaısını at ettiğinde yine hızını yaıya düşüetedi. Cisi aan youn yaısını gittiğinde
- -. Bi cisi uzunutai younu sabit hızı ie at eteye başıyo. Cisi youn yaısını at ettiğinde hızını yaıya düşüüp aan youn yaısını at ettiğinde yine hızını yaıya düşüetedi. Cisi aan youn yaısını gittiğinde
- ~ - p.:, o... :ı> .~ ~ 3. ~... c: (1) ::ı 3 ..., < ... "O ~ rı ;!. o tı) l"li. ... '< j ;ı;. r ~ v:ı ~ ...
 Q. :,. [ ;::l (JQ l O'Q (h ::: ;:,;' (JQ tı) l"li!t "'I N p.:,,, : ") r ti 8 cr'5 r.! :,;.. Q. ı;ıı,. r r (/) tn.{/),, < ) rı, ff ı ı r ı "' ı :: ı,,,, ;:,;', ı (li p.:, p.:, ::! l"li ti" p.:,,(/),,{j)..
Q. :,. [ ;::l (JQ l O'Q (h ::: ;:,;' (JQ tı) l"li!t "'I N p.:,,, : ") r ti 8 cr'5 r.! :,;.. Q. ı;ıı,. r r (/) tn.{/),, < ) rı, ff ı ı r ı "' ı :: ı,,,, ;:,;', ı (li p.:, p.:, ::! l"li ti" p.:,,(/),,{j)..
İŞ, GÜÇ, ENERJİ BÖLÜM 8
 İŞ, GÜÇ, EERJİ BÖÜ 8 ODE SORU DE SORUARI ÇÖZÜER 5 Cise eti eden sür- tüne uvveti, IFI0 ür F α F T W (F ür ) (Fcosα (g Fsinα)) düzle Ya pı lan net iş de ğe ri α, ve ütleye bağ lı dır G düzle 00,5 G0 0 I
İŞ, GÜÇ, EERJİ BÖÜ 8 ODE SORU DE SORUARI ÇÖZÜER 5 Cise eti eden sür- tüne uvveti, IFI0 ür F α F T W (F ür ) (Fcosα (g Fsinα)) düzle Ya pı lan net iş de ğe ri α, ve ütleye bağ lı dır G düzle 00,5 G0 0 I
Açıldı göklerin bâbı
 Dük Açıdı gök bbı Rast-Ih Âm Atş 8 A çı dı gök b bı O ha t m hac o du 5 A ı cü d v t Mv Muham M ço du 9 A ı çü gök gç t O hu u a ço du 13 (So) A ı cü d v t Mv Muham M ço du Sof 4 B vşm Hc-Ih Âm Atş 8 6
Dük Açıdı gök bbı Rast-Ih Âm Atş 8 A çı dı gök b bı O ha t m hac o du 5 A ı cü d v t Mv Muham M ço du 9 A ı çü gök gç t O hu u a ço du 13 (So) A ı cü d v t Mv Muham M ço du Sof 4 B vşm Hc-Ih Âm Atş 8 6
GAZ BASINCI. 1. Cıva seviyesine göre ba- sınç eşitliği yazılırsa, + h.d cıva
 . BÖÜ GZ BSINCI IŞTIRR ÇÖZÜER GZ BSINCI 1. Cıva seviyesine göre ba- sınç eşitliği yazılırsa, P +.d cıva.g Düzenek yeterince yüksek bir yere göre götürülünce azalacağından, 4. Y P zalır zalır ve nok ta
. BÖÜ GZ BSINCI IŞTIRR ÇÖZÜER GZ BSINCI 1. Cıva seviyesine göre ba- sınç eşitliği yazılırsa, P +.d cıva.g Düzenek yeterince yüksek bir yere göre götürülünce azalacağından, 4. Y P zalır zalır ve nok ta
 ş ç ö ç ç ş ş ö ş ş ç ö ö ş ç ç ş ö ö ö ş ş ş ş ş ş ş ö ö ç ç ç ş ş ö ş ö ö ş ö ö ö ş ö ş Ö Ü Ç ö ö Ğ ş ş ö Ö ö ç Ğ ş ş ö Ö ş ş şş ö ş ç ç ö ö ç ş ç ç ç Ö ç ç Ö ç ç ş ş Ö ç ö ş Ö ş ç ç ö ş ö ö ş ö ç ç
ş ç ö ç ç ş ş ö ş ş ç ö ö ş ç ç ş ö ö ö ş ş ş ş ş ş ş ö ö ç ç ç ş ş ö ş ö ö ş ö ö ö ş ö ş Ö Ü Ç ö ö Ğ ş ş ö Ö ö ç Ğ ş ş ö Ö ş ş şş ö ş ç ç ö ö ç ş ç ç ç Ö ç ç Ö ç ç ş ş Ö ç ö ş Ö ş ç ç ö ş ö ö ş ö ç ç
KURUMSAL İŞ ÇÖZÜMLERİNDE 19 YILLIK DENEYİM. Tek Elden Teknoloji
 KURUMSAL İŞ ÇÖZÜMLERİNDE 19 YILLIK DENEYİM Tek Elden Teknoloji SİSBİM HAKKINDA Farklı sektör ve ölçekten firmalara tüm teknolojik alt yapıları ile ilgili kurumsal yazılım ve donanım çözümleri sunan IT
KURUMSAL İŞ ÇÖZÜMLERİNDE 19 YILLIK DENEYİM Tek Elden Teknoloji SİSBİM HAKKINDA Farklı sektör ve ölçekten firmalara tüm teknolojik alt yapıları ile ilgili kurumsal yazılım ve donanım çözümleri sunan IT
T.C. EBELİK, LİSANS PROGRAMI, (ÖRGÜN ÖĞRETİM) EBELİK, LİSANS PROGRAMI, (ÖRGÜN ÖĞRETİM)
 T.C. Sıra No Aday No Kimlik No Ad Soyad Lisans Lisans Puanı Mülakat Puanı Nihai Ortalama BHP EBELİK, TEZSİZ YÜKSEK LİSANS PROGRAMI, (İKİNCİ (* Bu programda mülakat sınavını kazanan öğrenci sayısı 7'nin
T.C. Sıra No Aday No Kimlik No Ad Soyad Lisans Lisans Puanı Mülakat Puanı Nihai Ortalama BHP EBELİK, TEZSİZ YÜKSEK LİSANS PROGRAMI, (İKİNCİ (* Bu programda mülakat sınavını kazanan öğrenci sayısı 7'nin
S4 u(x, y) = ln ( sin y. S5 u(x, y) = 2α 2 sec(α(x 4α 2 t)) fonksiyonunun
 Kısmi Türevli Denklemler Problem Seti-I S1 u = u(x, y ve a, b, c R olmak uzere, ξ = ax + by ve η = bx ay degisken degistirmesi yaparak n cozunuz. au x + bu y + cy = 0 S2 Aşa gidaki denklemleri Adi Diferensiyel
Kısmi Türevli Denklemler Problem Seti-I S1 u = u(x, y ve a, b, c R olmak uzere, ξ = ax + by ve η = bx ay degisken degistirmesi yaparak n cozunuz. au x + bu y + cy = 0 S2 Aşa gidaki denklemleri Adi Diferensiyel
TÜRK DİLİ VE EDEBİYATI PR. (İNGİLİZCE) TARİH PR. (İNGİLİZCE) (TAM BURSLU) SOSYAL BİLGİLER ÖĞRETMENLİĞİ PR.
 Aday Kimlik Ad Soyad Sınav Lisans Lisans 1 A233139 2 A234223 3 A234363 4 A2712 5 A223251 6 A227829 7 A232737 8 A228288 9 A232288 A2596 11 A234425 12 A233457 13 A227794 ******* 36 19******* 90 ******* 46
Aday Kimlik Ad Soyad Sınav Lisans Lisans 1 A233139 2 A234223 3 A234363 4 A2712 5 A223251 6 A227829 7 A232737 8 A228288 9 A232288 A2596 11 A234425 12 A233457 13 A227794 ******* 36 19******* 90 ******* 46
AĞUSTOS / 2017 AYI İTİBARİYLE K TÜRÜ YETKİ BELGESİ SÜRESİ BİTECEK FİRMALAR
 AĞUSTOS / 2017 AYI İTİBARİYLE K TÜRÜ YETKİ BELGESİ SÜRESİ BİTECEK FİRMALAR SIR A NO U -N ET NO FİRM A Ü N VANI BELGE TÜ RÜ BELG E G E Ç ER LİLİK TA R İH İ 1 47894 E R H A LLA R D.Ç SA N. T İC.A.Ş K İ 2
AĞUSTOS / 2017 AYI İTİBARİYLE K TÜRÜ YETKİ BELGESİ SÜRESİ BİTECEK FİRMALAR SIR A NO U -N ET NO FİRM A Ü N VANI BELGE TÜ RÜ BELG E G E Ç ER LİLİK TA R İH İ 1 47894 E R H A LLA R D.Ç SA N. T İC.A.Ş K İ 2
R DEVRESİ L DEVRESİ C DEVRESİ
 6 BÖÜM ATENATİF AKIM AIŞTIMAA - ÇÖÜME DEESİ DEESİ DEESİ f 80 4 A olu 0 snωt snπft 4vsnπ50t 4vsn00πt olu Akıın zaanla dğş dnklndn, (t) snft sn50 400 sn 4 v A olu Gln aksu dğ, 0v 0v olu Gl dnkl, (t) snft
6 BÖÜM ATENATİF AKIM AIŞTIMAA - ÇÖÜME DEESİ DEESİ DEESİ f 80 4 A olu 0 snωt snπft 4vsnπ50t 4vsn00πt olu Akıın zaanla dğş dnklndn, (t) snft sn50 400 sn 4 v A olu Gln aksu dğ, 0v 0v olu Gl dnkl, (t) snft
ATATÜRK ANADOLU LİSESİ MATEMATİK. Karmaşık Sayılar Üzerine Kısa Çalışmalar
 ATATÜRK ANADOLU LİSESİ MATEMATİK Karmaşık Sayılar Üerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 KARMAŞIK SAYILAR. Karmaşık Sayılar Kavramı Denklemlerin, baı kümelerde çöümleri bulunmamaktadır. x 5 0 denkleminin
ATATÜRK ANADOLU LİSESİ MATEMATİK Karmaşık Sayılar Üerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 KARMAŞIK SAYILAR. Karmaşık Sayılar Kavramı Denklemlerin, baı kümelerde çöümleri bulunmamaktadır. x 5 0 denkleminin
IŞIĞIN KIRILMASI BÖLÜM 27
 ŞĞ RAS BÖÜ 7 ODE SORU DE SORUAR ÇÖZÜER 4 9 = = & = 9 5 = = & = 5 = = = 9 5 3 5 olur,, ortamlarıı kırılma idisleri arasıda > > ilişkisi vardır 5 V ESE YAYAR V V,, ortamlarıı kırılma idisleri arasıda > >
ŞĞ RAS BÖÜ 7 ODE SORU DE SORUAR ÇÖZÜER 4 9 = = & = 9 5 = = & = 5 = = = 9 5 3 5 olur,, ortamlarıı kırılma idisleri arasıda > > ilişkisi vardır 5 V ESE YAYAR V V,, ortamlarıı kırılma idisleri arasıda > >
Örnek...1 : Örnek...5 : n bir pozitif tamsayı ise i 4 n + 2 +i 8 n + 1 2 +i 2 0 n + 6 =?
 KARMAŞIK SAYILAR Karmaşık saılar x 2 + 1 = 0 biçimindeki denklemlerin çözümünü apabilmek için tanım lanm ıştır. Örnek...2 : Toplamları 6 ve çarpımları 34 olan iki saı bulunuz. a ve b birer reel saı ve
KARMAŞIK SAYILAR Karmaşık saılar x 2 + 1 = 0 biçimindeki denklemlerin çözümünü apabilmek için tanım lanm ıştır. Örnek...2 : Toplamları 6 ve çarpımları 34 olan iki saı bulunuz. a ve b birer reel saı ve
Web sitemizden Daima en güncel fiyat listelerine erişebilirsiniz.
 Web sitemizden Daima en güncel fiyat listelerine erişebilirsiniz. Sipariş, bilgi ve teklif talepleriniz için Telefon: +90 () 76 9 Whatsapp: +90 (553) 077 9 www.universalelektrik.com.tr info@universalelektrik.com.tr
Web sitemizden Daima en güncel fiyat listelerine erişebilirsiniz. Sipariş, bilgi ve teklif talepleriniz için Telefon: +90 () 76 9 Whatsapp: +90 (553) 077 9 www.universalelektrik.com.tr info@universalelektrik.com.tr
IŞIK VE GÖLGE BÖLÜM 24
 IŞI VE GÖLGE BÖLÜM 24 MODEL SORU 1 DE SORULARIN ÇÖÜMLER MODEL SORU 2 DE SORULARIN ÇÖÜMLER 1 1 Dünya Ay Günefl 2 2 Bu olay ışı ğın fak lı say am o la a fak lı hız la a yayıl ı ğı nı açık la ya maz Şe kil
IŞI VE GÖLGE BÖLÜM 24 MODEL SORU 1 DE SORULARIN ÇÖÜMLER MODEL SORU 2 DE SORULARIN ÇÖÜMLER 1 1 Dünya Ay Günefl 2 2 Bu olay ışı ğın fak lı say am o la a fak lı hız la a yayıl ı ğı nı açık la ya maz Şe kil
U MK E K A MP Ç IL IK E Ğ T İ M İ İ 2008
 U MK E K A MP Ç I L I K E ĞİT İMİ 2008 K A MP Y E R İ S E Ç İMİ V E Ö ZE L L İK L E R İ (Y A Z OP E R A S Y ON L A R I ) U L A Ş I M İÇ İN A R A Ç V E Y A Y A Y A Y OL U N A Y A K I N OL MA L I D I R.
U MK E K A MP Ç I L I K E ĞİT İMİ 2008 K A MP Y E R İ S E Ç İMİ V E Ö ZE L L İK L E R İ (Y A Z OP E R A S Y ON L A R I ) U L A Ş I M İÇ İN A R A Ç V E Y A Y A Y A Y OL U N A Y A K I N OL MA L I D I R.
1 A MO*** HA*** MEDICINE AND SURGERY Belirsiz Kazandı
 ACİL PEDİATRİ, Sınav 1 A372236 MO*** HA*** MEDICINE AND SURGERY 79.90 0.000 79.9000 Belirsiz Kazandı ANALİTİK KİMYA, 1 A374158 NE*** AL*** APPLIED CHEMISTRY 91.41 0.000 91.4100 Belirsiz Kazandı 2 A374661
ACİL PEDİATRİ, Sınav 1 A372236 MO*** HA*** MEDICINE AND SURGERY 79.90 0.000 79.9000 Belirsiz Kazandı ANALİTİK KİMYA, 1 A374158 NE*** AL*** APPLIED CHEMISTRY 91.41 0.000 91.4100 Belirsiz Kazandı 2 A374661
TEST 1 ÇÖZÜMLER KÜTLE ÇEKİMİ VE KEPLER KANUNLARI
 ES ÇÖZÜE ÜE ÇEİİ E EE ANUNAI O u uydu ezeenin kütlesi yaıçapı ise yüzeyindeki çeki ivesi a ( ) 4 ezeenin dışındaki çeki ivesi a ( ) ezeenin içindeki ve üzeindeki çeki ivesi a d eşitliğinden bulunu ve d
ES ÇÖZÜE ÜE ÇEİİ E EE ANUNAI O u uydu ezeenin kütlesi yaıçapı ise yüzeyindeki çeki ivesi a ( ) 4 ezeenin dışındaki çeki ivesi a ( ) ezeenin içindeki ve üzeindeki çeki ivesi a d eşitliğinden bulunu ve d
TORK VE DENGE BÖLÜM 8 MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ. 4. Kuvvetlerin O noktasına
 BÖÜM 8 R VE DEE MDE SRU - 1 DEİ SRUARI ÇÖZÜMERİ 1 1 yönü (+), yönü ( ) alınırsa kuvvetlerin noktasına torkları, x = d d = d olur evha 1 yönünde, d lik torkla döner d d 1 d 4 uvvetlerin noktasına göre torkların
BÖÜM 8 R VE DEE MDE SRU - 1 DEİ SRUARI ÇÖZÜMERİ 1 1 yönü (+), yönü ( ) alınırsa kuvvetlerin noktasına torkları, x = d d = d olur evha 1 yönünde, d lik torkla döner d d 1 d 4 uvvetlerin noktasına göre torkların
ÖĞRETİM) İŞLETME (İNGİLİZCE), LİSANS Bİ*** KA*** PROGRAMI, (ÖRGÜN ÖĞRETİM)
 MUHASEBE VE DENETİM,TEZSİZ YÜKSEK LİSANS PROGRAMI, (İKİNCİ 17-1 EĞİTİM-ÖĞTETİM YILI BAHAR YARIYILI YERLEŞTİRME RAPORU 1 A17 1******* ES*** FE*** İŞLETME PR. (AÇIK 7.9 1, 9,5 Kazandı A 1*******3 BÜ*** Şİ***
MUHASEBE VE DENETİM,TEZSİZ YÜKSEK LİSANS PROGRAMI, (İKİNCİ 17-1 EĞİTİM-ÖĞTETİM YILI BAHAR YARIYILI YERLEŞTİRME RAPORU 1 A17 1******* ES*** FE*** İŞLETME PR. (AÇIK 7.9 1, 9,5 Kazandı A 1*******3 BÜ*** Şİ***
TORK. τ = 2.6 4.sin30.2 + 2.cos60.4 = 12 4 + 4 = 12 N.m Çubuk ( ) yönde dönme hareketi yapar. τ K. τ = F 1. τ 1. τ 2. τ 3. τ 4. 1. 2.
 AIŞIRMAAR 8 BÖÜM R ÇÖZÜMER R cos N 4N 0 4sin0 N M 5d d N ve 4N luk kuv vet lein çu bu ğa dik bi le şen le i şekil de ki gi bi olu nok ta sı na gö e top lam tok; τ = 6 4sin0 + cos4 = 4 + 4 = Nm Çubuk yönde
AIŞIRMAAR 8 BÖÜM R ÇÖZÜMER R cos N 4N 0 4sin0 N M 5d d N ve 4N luk kuv vet lein çu bu ğa dik bi le şen le i şekil de ki gi bi olu nok ta sı na gö e top lam tok; τ = 6 4sin0 + cos4 = 4 + 4 = Nm Çubuk yönde
Mühendislik Fakültesi Makine Mühendisliği Bölümü 12 Ocak 2012 Perşembe, 17:30
 Zonguldak Karaelmas Üniversitesi 2011-2012 Güz Dönemi Mühendislik Fakültesi Makine Mühendisliği Bölümü 12 Ocak 2012 Perşembe, 17:30 NOT: Kullandığınız formül ve tabloların no.ları ile sayfa numaralarını
Zonguldak Karaelmas Üniversitesi 2011-2012 Güz Dönemi Mühendislik Fakültesi Makine Mühendisliği Bölümü 12 Ocak 2012 Perşembe, 17:30 NOT: Kullandığınız formül ve tabloların no.ları ile sayfa numaralarını
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
 1. BÖÜM A DAGAARI MDE SRU - 1 DEİ SRUARIN ÇÖZÜMERİ 5. T 1. uvvet vektörünün dengeden uzaklaşan ucu ile hız vektörünün ları çakışık olmalıdır. Buna göre şeklinde CEVA C 2. Dal ga la rın gen li ği den ge
1. BÖÜM A DAGAARI MDE SRU - 1 DEİ SRUARIN ÇÖZÜMERİ 5. T 1. uvvet vektörünün dengeden uzaklaşan ucu ile hız vektörünün ları çakışık olmalıdır. Buna göre şeklinde CEVA C 2. Dal ga la rın gen li ği den ge
YEMİNLİ MALİ MÜŞAVİRLERİN BANKALAR KANUNU NUN 46 NCI MADDESİNE GÖRE YAPACAKLARI TASDİKE İLİŞKİN USUL VE ESASLAR HAKKINDA YÖNETMELİK
 YEMİNLİ MALİ MÜŞAVİRLERİN BANKALAR KANUNU NUN 46 NCI MADDESİNE GÖRE YAPACAKLARI TASDİKE İLİŞKİN USUL VE ESASLAR HAKKINDA YÖNETMELİK 13 298 YEMİNLİ MALİ MÜŞAVİRLERİN BANKALAR KANUNU NUN 46 NCI MADDESİNE
YEMİNLİ MALİ MÜŞAVİRLERİN BANKALAR KANUNU NUN 46 NCI MADDESİNE GÖRE YAPACAKLARI TASDİKE İLİŞKİN USUL VE ESASLAR HAKKINDA YÖNETMELİK 13 298 YEMİNLİ MALİ MÜŞAVİRLERİN BANKALAR KANUNU NUN 46 NCI MADDESİNE
YAY DALGALARI. 1. m. 4. y(cm) Şe kil de 25 cm lik kıs mı 2,5 dal ga ya kar şı lık ge lir.
 1. BÖÜM A DAGAARI AIŞTIRMAAR ÇÖZÜMER A DAGAARI 1.. (c) T λ 5c Şe kil de 5 c lik kıs ı,5 dal ga a kar şı lık ge lir. 0 5 (c) Bu du ru da, 5 λ = 5 λ = 10 c Dal ga nın aıla hı zı, 60 V = = = 15 t c/ s Dal
1. BÖÜM A DAGAARI AIŞTIRMAAR ÇÖZÜMER A DAGAARI 1.. (c) T λ 5c Şe kil de 5 c lik kıs ı,5 dal ga a kar şı lık ge lir. 0 5 (c) Bu du ru da, 5 λ = 5 λ = 10 c Dal ga nın aıla hı zı, 60 V = = = 15 t c/ s Dal
'( ) ' ' * ' * 0 %!,# + 1 2 +!"". 1.3%4&.%%!3%.#%+ * #4+!"",!"",/#4!3! * + + ' 5 67 - ' ##!""8!""8/#4%," * + + ' 9" -
 !"#" #$!%!"## &#!"## ( ) + %!,#+ - + -!"". &#/#!/!""%!"".!""% 0 %!,# + 1 2 +!"". 1.3%4&.%%!3%.#%+ #4+!"",!"",/#4!3! + + 5 67 - ##!""8!""8/#4%," + + 9" - : ; ","#!"#" < 1= 1 2 += 1.3 %%!3 += - 9" :.""8
!"#" #$!%!"## &#!"## ( ) + %!,#+ - + -!"". &#/#!/!""%!"".!""% 0 %!,# + 1 2 +!"". 1.3%4&.%%!3%.#%+ #4+!"",!"",/#4!3! + + 5 67 - ##!""8!""8/#4%," + + 9" - : ; ","#!"#" < 1= 1 2 += 1.3 %%!3 += - 9" :.""8
Rehber içerisinde yer alan ve mavi özel alanlarla gösterilen NOT bölümleri yapacağınız işlemlerde size kolaylık sağlayacak ipuçları niteliğindedir.
 Y a y ı n a H a z ı r l a y aan l: i RAS L A N E -P o s t a : m e @ a r s l a n i a. c o m W o r d P r e s s R e h b e r i n i n T ü m H a k l a rwı o r d P r e s s T ü r k i y ey e A i t t i r. B u r
Y a y ı n a H a z ı r l a y aan l: i RAS L A N E -P o s t a : m e @ a r s l a n i a. c o m W o r d P r e s s R e h b e r i n i n T ü m H a k l a rwı o r d P r e s s T ü r k i y ey e A i t t i r. B u r
IŞIĞIN KIRILMASI. 1. Ortamların kırılma indisleri n K. , n M. , n L. arasındaki ilişki aşağıdaki gibidir. > n L. > n K. n M. > n M. n L. n K.
 BÖÜ ŞĞ RAS AŞTRAAR ÇÖZÜER ŞĞ RAS Ortamları kırılma dsler,, arasıdak lşk aşağıdak gbdr 9 > > > > > > 6 0 > > > > > > 7 > > > > > > 0 7 0 0 > > > > > 76 OPTİ 7 0 0 > > > > > > 0 θ θ > > > > > > 9 0 O > >
BÖÜ ŞĞ RAS AŞTRAAR ÇÖZÜER ŞĞ RAS Ortamları kırılma dsler,, arasıdak lşk aşağıdak gbdr 9 > > > > > > 6 0 > > > > > > 7 > > > > > > 0 7 0 0 > > > > > 76 OPTİ 7 0 0 > > > > > > 0 θ θ > > > > > > 9 0 O > >
L E K TS I YA T E K S T L E R I
 O ZBEKSTAN RESPUBLIKASI JOQARI HA M ORTA ARNAWLI BILIMLENDIRIW MINISTRLIGI BERDAQ ATINDAG I QARAQALPAQ MA MLEKETLIK UNIVERSITETI «A meliy matematika ha m informatika» kafedrası «WEB TEXNOLOGIYALAR» pa
O ZBEKSTAN RESPUBLIKASI JOQARI HA M ORTA ARNAWLI BILIMLENDIRIW MINISTRLIGI BERDAQ ATINDAG I QARAQALPAQ MA MLEKETLIK UNIVERSITETI «A meliy matematika ha m informatika» kafedrası «WEB TEXNOLOGIYALAR» pa
E M İN E K O Ç A L R İZ E M E R K E Z G Ü L E N D E R E R G E N R İZ E M E R K E Z A Y Ş E D Ü Z G Ü N R İZ E M E R K E Z
 K U R A SIR A A D I S O Y A D I i p y 51 5 9 9 E M İN E K O Ç A L R İZ E M E R K E Z 52 1038 G Ü L E N D E R E R G E N R İZ E M E R K E Z 53 179 A Y Ş E D Ü Z G Ü N R İZ E M E R K E Z 54 1316 H A T İÇ
K U R A SIR A A D I S O Y A D I i p y 51 5 9 9 E M İN E K O Ç A L R İZ E M E R K E Z 52 1038 G Ü L E N D E R E R G E N R İZ E M E R K E Z 53 179 A Y Ş E D Ü Z G Ü N R İZ E M E R K E Z 54 1316 H A T İÇ
Saat B-Başkent li Olmak BL2-Bölümüm GS2-Genç Sağlığı (Prof. Dr. İhsan Doğramacı Konferans Salonu)
 Şube 2 (250 öğrenci) 9.30 B-Başkent li Olmak BL2-Bölümüm 13.00 GS2-Genç Sağlığı Konferans 14.00 Bİ2-Bilişim Hizmetleri Konferans PDR1-Seminer: Üniversite Yaşamına Uyum (Avni Akyol Konferans K2-Kütüphanem-
Şube 2 (250 öğrenci) 9.30 B-Başkent li Olmak BL2-Bölümüm 13.00 GS2-Genç Sağlığı Konferans 14.00 Bİ2-Bilişim Hizmetleri Konferans PDR1-Seminer: Üniversite Yaşamına Uyum (Avni Akyol Konferans K2-Kütüphanem-
STAJ ARA DÖNEM DEĞERLENDİRMESİ AYRINTILI SINAV KONULARI
 22 STAJ ARA DÖNEM DEĞERLENDİRMESİ AYRINTILI SINAV KONULARI 406 A GRUBU STAJ ARA DÖNEM DEĞERLENDİRMESİ AYRINTILI SINAV KONULARI 22 A GRU BU STAJ ARA DÖ NEM DE ER LEN D R ME S AY RIN TI LI SI NAV KO NU LA
22 STAJ ARA DÖNEM DEĞERLENDİRMESİ AYRINTILI SINAV KONULARI 406 A GRUBU STAJ ARA DÖNEM DEĞERLENDİRMESİ AYRINTILI SINAV KONULARI 22 A GRU BU STAJ ARA DÖ NEM DE ER LEN D R ME S AY RIN TI LI SI NAV KO NU LA
ANATOMİ(İSTANBUL TIP), TEZLİ YÜKSEK LİSANS PROGRAMI, (ÖRGÜN ÖĞRETİM) BESİN HİJYENİ VE TEKNOLOJİSİ, TEZLİ YÜKSEK LİSANS PROGRAMI, (ÖRGÜN ÖĞRETİM)
 ANATOMİ(İSTANBUL TIP), PROGRAMI, 1 A99318 2 A101012 P4******* 65 Sınav SI*** MA*** Psikoloji 86.05 0.000 0.0000 Belirsiz Kazandı BA*** FE*** JOURNALISM AND COMMUNICATION RADIO TELEVISION JOUR BESİN HİJYENİ
ANATOMİ(İSTANBUL TIP), PROGRAMI, 1 A99318 2 A101012 P4******* 65 Sınav SI*** MA*** Psikoloji 86.05 0.000 0.0000 Belirsiz Kazandı BA*** FE*** JOURNALISM AND COMMUNICATION RADIO TELEVISION JOUR BESİN HİJYENİ
O`ZBEKSTAN RESPUBLIKASI JOQARI HA`M ORTA ARNAWLI BILIMLENDIRIW MINISTRLIGI. Berdaq atıındag`ı Qaraqalpaq Ma`mleketlik Universiteti
 O`ZBEKSTAN RESPUBLIKASI JOQARI HA`M ORTA ARNAWLI BILIMLENDIRIW MINISTRLIGI Berdaq atııdag`ı Qaraqalpaq Ma`mleetl Uverstet Eooma faul tet ursı boyısha letsyalar test du zwsh Sadov T. No`s-008 Tema. Pa``
O`ZBEKSTAN RESPUBLIKASI JOQARI HA`M ORTA ARNAWLI BILIMLENDIRIW MINISTRLIGI Berdaq atııdag`ı Qaraqalpaq Ma`mleetl Uverstet Eooma faul tet ursı boyısha letsyalar test du zwsh Sadov T. No`s-008 Tema. Pa``
Sistem-atik Membran Kapak Sipariş Takip ve Üretim Takip Sistemi;
 S i s t e m - a t i k M e m b r a n K a p a k S i p a r i T a k i p v e Ü r e t i m T a k i p S i s t e m i ; T ü r k i y e l d e b i r i l k o l a r a k, t a m a m e n m e m b r a n k a p a k ü r e t
S i s t e m - a t i k M e m b r a n K a p a k S i p a r i T a k i p v e Ü r e t i m T a k i p S i s t e m i ; T ü r k i y e l d e b i r i l k o l a r a k, t a m a m e n m e m b r a n k a p a k ü r e t
VEKTÖRLER. 1. Ve ri len kuv vet le ri bi le şen le ri ne ayı rır sak, x y. kuv vet le ri ( 1) ile çar pı lıp top lanır. ve F 3
 ALIŞTIMALA. BÖLÜM VETÖLE ÇÖZÜMLE VETÖLE. Ve ri len kuv vet le ri bi le şen le ri ne ayı rır sak, x y : 0 : 4. ve kuv vet le ri ( ) ile çar pı lıp top lanır sa, kuv ve ti el de edi lir. x y : 0 : 4 : 0
ALIŞTIMALA. BÖLÜM VETÖLE ÇÖZÜMLE VETÖLE. Ve ri len kuv vet le ri bi le şen le ri ne ayı rır sak, x y : 0 : 4. ve kuv vet le ri ( ) ile çar pı lıp top lanır sa, kuv ve ti el de edi lir. x y : 0 : 4 : 0
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
 BÖÜ ŞĞ RAS DE SRU - DEİ SRUAR ÇÖZÜERİ Sell bağıtısıda, si si olur i i sıvısı 0 0 sıvısıı ışığı kırma idisi, h si h si si si0 yasıya ıflı k r la ıflı c si ic h si ih c si 0 si c olur c 0 r cam olur δ açısı,
BÖÜ ŞĞ RAS DE SRU - DEİ SRUAR ÇÖZÜERİ Sell bağıtısıda, si si olur i i sıvısı 0 0 sıvısıı ışığı kırma idisi, h si h si si si0 yasıya ıflı k r la ıflı c si ic h si ih c si 0 si c olur c 0 r cam olur δ açısı,
LYS1 / 3.DENEME MATEMATİK TESTİ ÇÖZÜMLERİ
 . `n 5j- `n- j - n - n vey n- n n 8. 8 8 LYS /.NM MTMTİK TSTİ ÇÖZÜMLRİ evp: evp:. - f p$ f - p f p 9 - - 5! 5 -! 5 5 5. 8... 5 5. 5.. y 8 8 5 5... z < y < z _. ` j. $ ` j ` ise y. ` j y $ ` j ` j yk. `
. `n 5j- `n- j - n - n vey n- n n 8. 8 8 LYS /.NM MTMTİK TSTİ ÇÖZÜMLRİ evp: evp:. - f p$ f - p f p 9 - - 5! 5 -! 5 5 5. 8... 5 5. 5.. y 8 8 5 5... z < y < z _. ` j. $ ` j ` ise y. ` j y $ ` j ` j yk. `
Dönerek Öteleme Hareketi ve Açısal Momentum
 6 Döneek Ötelee Haeketi e Açısal Moentu Test 'in Çözülei.. R L P N yatay M Çebe üzeindeki bi noktanın yee göe hızı, o noktanın ekeze göe çizgisel hızı ile çebein ötelee hızının ektöel toplaına eşitti.
6 Döneek Ötelee Haeketi e Açısal Moentu Test 'in Çözülei.. R L P N yatay M Çebe üzeindeki bi noktanın yee göe hızı, o noktanın ekeze göe çizgisel hızı ile çebein ötelee hızının ektöel toplaına eşitti.
EK - 4 : SPOR EĞİTİM UZMANI İL / İLÇE POZİSYON DAĞILIMI
 K - 4 : T Y K 5 TV HV YH TV TV K CYH TV BK KT TV H K TV VT TV YF TV G T 3 TV T Y Y K Y Y K 3 Y B Y B Y KH Y Y GG Y GCK Y GB Y Y KC Y KHT Y K Y CK Y K Y T Y KYCK FYKH FYKH K 3 Y FYKH BV Y K FYKH Y Y Y FYKH
K - 4 : T Y K 5 TV HV YH TV TV K CYH TV BK KT TV H K TV VT TV YF TV G T 3 TV T Y Y K Y Y K 3 Y B Y B Y KH Y Y GG Y GCK Y GB Y Y KC Y KHT Y K Y CK Y K Y T Y KYCK FYKH FYKH K 3 Y FYKH BV Y K FYKH Y Y Y FYKH
sâfe « & AyM S S iiî (} & (fitli (p/iv» m p S» c sş> g&> H ı P Yevmiye No. Cilt No. Sahife No. Sıra No. «M» Geldisi Tarihi Gittisi a ' ; ^?
 (p/iv m p S (. vo i- o & j r*7) f\ 4 gvn S?5> (} & c sş> g&> ı 1 1 Geldisi S t? Sicilirış, (fitli V &rj i 6 i 18.03.2011 Gittisi S S iiî NOT: ' Mülkiyetin gayri ayni h a Miti 1 ^ e tmçfâjnjitfryûtîfyıas
(p/iv m p S (. vo i- o & j r*7) f\ 4 gvn S?5> (} & c sş> g&> ı 1 1 Geldisi S t? Sicilirış, (fitli V &rj i 6 i 18.03.2011 Gittisi S S iiî NOT: ' Mülkiyetin gayri ayni h a Miti 1 ^ e tmçfâjnjitfryûtîfyıas
( ) ( ) ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. Cevap D. Cevap C. noktası y ekseni üzerinde ise, a + 4 = 0 A 0, 5 = 1+
 ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. a+ = b 4. a = b 0+ a b a b = b a+ b = 0. A ( a + 4, a) noktası y ekseni üzerinde ise, ( + ) a + 4 = 0 A 0, 5 a = 4 B b, b 0 noktası x ekseni
ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. a+ = b 4. a = b 0+ a b a b = b a+ b = 0. A ( a + 4, a) noktası y ekseni üzerinde ise, ( + ) a + 4 = 0 A 0, 5 a = 4 B b, b 0 noktası x ekseni
4. x. y = y xy y = 0. Cevap D. 5. a + b = 13. a 2 + 2ab + 2bc c 2 + b 2 b 2 = ( a + b ) 2 ( b c ) 2. Cevap D. 7. x ve y aralarında asal olduğuna göre,
 Deneme - / Mat MATEMATİK DENEMESİ Çözümler. a, b, c 0 0 a > b ( Payları eşit olan kesirlerden paydası büyük olan daha küçüktür. ) c > a ( Paydaları eşit olan kesirlerden payı büyük olan daha büyüktür.
Deneme - / Mat MATEMATİK DENEMESİ Çözümler. a, b, c 0 0 a > b ( Payları eşit olan kesirlerden paydası büyük olan daha küçüktür. ) c > a ( Paydaları eşit olan kesirlerden payı büyük olan daha büyüktür.
5. ( 8! ) 2 ( 6! ) 2 = ( 8! 6! ). ( 8! + 6! ) Cevap E. 6. Büyük boy kutu = 8 tane. Cevap A dakika = 3 saat 15 dakika olup Göksu, ilk 3 saatte
 Deneme - / Mat MTEMTİK DENEMESİ Çözümle. 7 7 7, 0, 7, + + = + + 03, 00,, 3 0 0 7 0 0 7 =. +. +. 3 = + + = 0 bulunu.. Pa ve padaa eklenecek saı olsun. a- b+ b =- a+ b+ a & a - ab+ a =-ab-b -b & a + b =
Deneme - / Mat MTEMTİK DENEMESİ Çözümle. 7 7 7, 0, 7, + + = + + 03, 00,, 3 0 0 7 0 0 7 =. +. +. 3 = + + = 0 bulunu.. Pa ve padaa eklenecek saı olsun. a- b+ b =- a+ b+ a & a - ab+ a =-ab-b -b & a + b =
π a) = cosa Öğrenci Seçme Sınavı (Öss) / 17 Haziran 2007 Matematik II Soruları ve Çözümleri
 Öğrenci Seçme Sınavı (Öss) 7 Haziran 7 Matematik II Soruları ve Çözümleri. Karmaşık sayılar kümesi üzerinde * işlemi, Z * Z Z + Z + Z Z biçiminde tanımlanıyor. Buna göre, ( i) * ( + i) işleminin sonucu
Öğrenci Seçme Sınavı (Öss) 7 Haziran 7 Matematik II Soruları ve Çözümleri. Karmaşık sayılar kümesi üzerinde * işlemi, Z * Z Z + Z + Z Z biçiminde tanımlanıyor. Buna göre, ( i) * ( + i) işleminin sonucu
T.C. İSTANBUL GELİŞİM ÜNİVERSİTESİ AKADEMİK YILI YABANCI DİLLER YÜKSEKOKULU MÜDÜRLÜĞÜ YABANCI DİLLER BÖLÜMÜ 2.KUR ŞUBELENDİRME LİSTESİ
 AA İ ÜÜÜĞÜ ÖĞ.. A A AÜ ÖÜ Ş 1 170308019 İ AÇÖ İŞ 2 170512903 A AÇ AĞ İİİ Şİİ 3 170314013 AŞA İĞ İİ 4 170308905 A İAİ A AŞ İŞ 5 170813017 ÜŞ Aİ 6 170163093 A İİ 7 170512031 İ ÇA AĞ İİİ Şİİ 8 170308011 A
AA İ ÜÜÜĞÜ ÖĞ.. A A AÜ ÖÜ Ş 1 170308019 İ AÇÖ İŞ 2 170512903 A AÇ AĞ İİİ Şİİ 3 170314013 AŞA İĞ İİ 4 170308905 A İAİ A AŞ İŞ 5 170813017 ÜŞ Aİ 6 170163093 A İİ 7 170512031 İ ÇA AĞ İİİ Şİİ 8 170308011 A
KE00-SS.08YT05 DOĞAL SAYILAR ve TAM SAYILAR I
 Üniversite Hazırlık / YGS Kolay Temel Matematik 0 KE00-SS.08YT05 DOĞAL SAYILAR ve TAM SAYILAR I. 8 ( 3 + ) A) 7 B) 8 C) 9 D) 0 E) 6. 3! 3 ( 3 3)": ( 3) A) B) 0 C) D) E) 3. 7 3. + 5 A) 6 B) 7 C) 8 D) 0
Üniversite Hazırlık / YGS Kolay Temel Matematik 0 KE00-SS.08YT05 DOĞAL SAYILAR ve TAM SAYILAR I. 8 ( 3 + ) A) 7 B) 8 C) 9 D) 0 E) 6. 3! 3 ( 3 3)": ( 3) A) B) 0 C) D) E) 3. 7 3. + 5 A) 6 B) 7 C) 8 D) 0
DUAL KUATERNİYONLAR ÜZERİNDE SİMPLEKTİK GEOMETRİ E. ATA
 DÜ Fe Blmle Esttüsü Degs Dual Kuateyola 6. Sayı (Em l004) Üzede Smlet Geomet DUAL KUATERNİYONLAR ÜZERİNDE SİMLEKTİK GEOMETRİ E. ATA Özet Bu maalede dual uateyola üzede smlet gu, smlet etö uzayı e smlet
DÜ Fe Blmle Esttüsü Degs Dual Kuateyola 6. Sayı (Em l004) Üzede Smlet Geomet DUAL KUATERNİYONLAR ÜZERİNDE SİMLEKTİK GEOMETRİ E. ATA Özet Bu maalede dual uateyola üzede smlet gu, smlet etö uzayı e smlet
Reference:C:\0\43_01_01_PV_320kN_18m_00_Giris.xmcd Reference:C:\0\43_01_01_PV_320kN_18m_01_Kiris_ve_UB_Genel.xmcd L C L K. e L. o OA L 1 L OA.
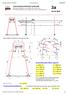 Deve bounlu portal vinçte onak aak Reference:C:\\43 PV_32_8 Giri.xcd Reference:C:\\43 PV_32_8 Kiri_ve_UB_Genel.xcd 3a Onak Aak G H L A L C LAA L K LCC hk C D A C Bütün değerler kontrükion reinden alınıştır.
Deve bounlu portal vinçte onak aak Reference:C:\\43 PV_32_8 Giri.xcd Reference:C:\\43 PV_32_8 Kiri_ve_UB_Genel.xcd 3a Onak Aak G H L A L C LAA L K LCC hk C D A C Bütün değerler kontrükion reinden alınıştır.
e e ex α := e α α +1,
 s t a n b u l K ü l t ü r Ü n i v e r s i t e s i Matematik - Bilgisayar Bölümü MC 886 ntegral Denklemler... Yßliçi Sßnavß CEVAPLAR Talimatlar: Sßnav süresi 9 dakikadßr. lk dakika sßnav salonunu terk etmeyiniz.
s t a n b u l K ü l t ü r Ü n i v e r s i t e s i Matematik - Bilgisayar Bölümü MC 886 ntegral Denklemler... Yßliçi Sßnavß CEVAPLAR Talimatlar: Sßnav süresi 9 dakikadßr. lk dakika sßnav salonunu terk etmeyiniz.
FZM450 Elektro-Optik. 7.Hafta. Fresnel Eşitlikleri
 FZM45 leko-ok 7.Hafa Feel şlkle 28 HSaı 1 7. Hafa De İçeğ Feel şlkle Yaıma Kıılma lekomayek dalgaı dalga özellkle kullaaak ışığı faklı kıılma de ah yüzeydek davaışı celeecek 28 HSaı 2 Feel şlkle-1 Şekldek
FZM45 leko-ok 7.Hafa Feel şlkle 28 HSaı 1 7. Hafa De İçeğ Feel şlkle Yaıma Kıılma lekomayek dalgaı dalga özellkle kullaaak ışığı faklı kıılma de ah yüzeydek davaışı celeecek 28 HSaı 2 Feel şlkle-1 Şekldek
6fr. dub 6=. REz. z. a. =f, 8Bt' s o) 3 o. z=' c 3. o a. o o o ) s6: .c) N (o. N ql O:D O:A -<5 O: -{ o, o o (, -{ -< O:p. <r- - m. E.
 L/ U,,.1 ) (, {
L/ U,,.1 ) (, {
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
 ÖLÜ ÜRESEL YNLR OEL SORU - Eİ SORULRN ÇÖZÜLERİ a a a d Şe kil de ö rül dü ğü i bi, ve şk şn la r yans ma lar so nu u ken di üze rin den e ri dö ner CEVP Şekilde örüldüğü ibi, aynalar arasndaki d uzaklğ,
ÖLÜ ÜRESEL YNLR OEL SORU - Eİ SORULRN ÇÖZÜLERİ a a a d Şe kil de ö rül dü ğü i bi, ve şk şn la r yans ma lar so nu u ken di üze rin den e ri dö ner CEVP Şekilde örüldüğü ibi, aynalar arasndaki d uzaklğ,
C L A S S N O T E S SİNYALLER. Sinyaller & Sistemler Sinyaller Dr.Aşkın Demirkol
 Sinyaller & Sisemler Sinyaller Dr.Aşkın Demirkol SİNYALLER Elekriki açıdan enerjisi ve frekansı olan dalga işare olarak anımlanır. Alernaif olarak kodlanmış sinyal/işare de uygun bir anım olabilir. s (
Sinyaller & Sisemler Sinyaller Dr.Aşkın Demirkol SİNYALLER Elekriki açıdan enerjisi ve frekansı olan dalga işare olarak anımlanır. Alernaif olarak kodlanmış sinyal/işare de uygun bir anım olabilir. s (
LAMBALAR BÖLÜM X 6. X MODEL SORU 1 DEK SORULARIN ÇÖZÜMLER. K anahtarı açık iken: Z ve T lambaları yanar. X ve Y lambaları = 2 dir.
 ÖÜ 0 ODE SOU 1 DE SOUN ÇÖÜE anahtarı açık ken: ve lambaları yanar. ve lambaları yanmaz. N 1 = dr. 1. 3 1 4 5 6 al nız lam ba sı nın yan ma sı çn 4 ve 6 no lu anah tar lar ka pa tıl ma lı dır. CE VP. U
ÖÜ 0 ODE SOU 1 DE SOUN ÇÖÜE anahtarı açık ken: ve lambaları yanar. ve lambaları yanmaz. N 1 = dr. 1. 3 1 4 5 6 al nız lam ba sı nın yan ma sı çn 4 ve 6 no lu anah tar lar ka pa tıl ma lı dır. CE VP. U
VEKTÖRLER BÖLÜM 1 MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
 BÖÜ 1 VETÖE ODE SOU - 1 DEİ SOUAI ÇÖZÜEİ ODE SOU - DEİ SOUAI ÇÖZÜEİ 1. Bir vektörün tersi doğrultu ve büyüklüğü aynı yalnızca yönü ters olan vektördür:. = olacağından, I. eşitlik yanlıştır. II. eşitlik
BÖÜ 1 VETÖE ODE SOU - 1 DEİ SOUAI ÇÖZÜEİ ODE SOU - DEİ SOUAI ÇÖZÜEİ 1. Bir vektörün tersi doğrultu ve büyüklüğü aynı yalnızca yönü ters olan vektördür:. = olacağından, I. eşitlik yanlıştır. II. eşitlik
FEN - EDEBİYAT FAKÜLTESİ KİMYA BÖLÜMÜ DERSLERİ VE SERVİS DERSLERİ EĞİTİM-ÖĞRETİM YILI GÜZ YARIYILI DERS PROGRAMI
 PAZARTESİ 08.30-09.15 Genel Kimya Lab. (F.Y.)(MBG) Genel Kimya Lab. (F.Y.)(MBG) Genel Kimya Lab. (S.I.) (EEM.1.Ö.) Seçmeli II (O.T.) Genel Kimya Lab. (S.I.) (EEM.1.Ö.) Seçmeli II (O.T.) Genel Kimya Lab.
PAZARTESİ 08.30-09.15 Genel Kimya Lab. (F.Y.)(MBG) Genel Kimya Lab. (F.Y.)(MBG) Genel Kimya Lab. (S.I.) (EEM.1.Ö.) Seçmeli II (O.T.) Genel Kimya Lab. (S.I.) (EEM.1.Ö.) Seçmeli II (O.T.) Genel Kimya Lab.
GELECEĞİ DÜŞÜNEN ÇEVREYE SAYGILI % 70. tasarruf. Sokak, Park ve Bahçelerinizi Daha Az Ödeyerek Daha İyi Aydınlatmak Mümkün
 www.urlsolar.com S L D-S K -6 0 W ile 1 5 0 W St an d art S o kak L a m ba sı F iya t K arşılaşt ırm a sı kw h Ü c reti Yıllık Tü ke tim Ü cre ti Y ıllık T ü ketim Fa rkı kw Sa at G ü n A y Stan d art
www.urlsolar.com S L D-S K -6 0 W ile 1 5 0 W St an d art S o kak L a m ba sı F iya t K arşılaşt ırm a sı kw h Ü c reti Yıllık Tü ke tim Ü cre ti Y ıllık T ü ketim Fa rkı kw Sa at G ü n A y Stan d art
YENİ ORTAÖĞRETİM MATEMATİK PROGRAMINA UYGUNDUR. YGS MATEMATİK 4. KİTAP MERVE ÇELENK FİKRET ÇELENK
 YENİ ORTAÖĞRETİM MATEMATİK PROGRAMINA UYGUNDUR. YGS MATEMATİK 4. KİTAP MERVE ÇELENK FİKRET ÇELENK İÇİNDEKİLER Çarpanlara Ayırma 5 52 Polinomlar 53 100 İkinci Dereceden Denklemler 101 120 Karmaşık Sayılar
YENİ ORTAÖĞRETİM MATEMATİK PROGRAMINA UYGUNDUR. YGS MATEMATİK 4. KİTAP MERVE ÇELENK FİKRET ÇELENK İÇİNDEKİLER Çarpanlara Ayırma 5 52 Polinomlar 53 100 İkinci Dereceden Denklemler 101 120 Karmaşık Sayılar
MADDE VE ÖZELLİKLERİ
 BÖÜM 1 MADDE VE ÖZEİERİ MODE SORU - 1 DEİ SORUARIN ÇÖZÜMERİ MODE SORU - DEİ SORUARIN ÇÖZÜMERİ 1. atıların belirli bir şekilleri vardır. Tanecikler birbirlerini çeker. Sıvı moleküllerinin birbirleri üzerinden
BÖÜM 1 MADDE VE ÖZEİERİ MODE SORU - 1 DEİ SORUARIN ÇÖZÜMERİ MODE SORU - DEİ SORUARIN ÇÖZÜMERİ 1. atıların belirli bir şekilleri vardır. Tanecikler birbirlerini çeker. Sıvı moleküllerinin birbirleri üzerinden
n adffiuzcun NihatM^. Alankent Mah.Muh. uye TARiH-i, 22tost2o't7 KARARIN : l]ye nfl' NUMARASI : ou/(a{nale Muh
![n adffiuzcun NihatM^. Alankent Mah.Muh. uye TARiH-i, 22tost2o't7 KARARIN : l]ye nfl' NUMARASI : ou/(a{nale Muh n adffiuzcun NihatM^. Alankent Mah.Muh. uye TARiH-i, 22tost2o't7 KARARIN : l]ye nfl' NUMARASI : ou/(a{nale Muh](/thumbs/94/118844353.jpg) KABATA$ LES ASGAR LQUDE ARSA BRM DEGER TAKD R KM SYU BA$KALTG KARAR : TARH, s' UMARAS : 111 Tkd Ksynu e Beledye Bkn Ykup YLMAZ Bknh$nd Beledye Ml Hele MUdUTU Sel TECM, Beledye en le MUdU Vekl Ede CDEL,
KABATA$ LES ASGAR LQUDE ARSA BRM DEGER TAKD R KM SYU BA$KALTG KARAR : TARH, s' UMARAS : 111 Tkd Ksynu e Beledye Bkn Ykup YLMAZ Bknh$nd Beledye Ml Hele MUdUTU Sel TECM, Beledye en le MUdU Vekl Ede CDEL,
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
 ÖLÜ ÜRESEL YNLR OEL SORU - Eİ SORULRN ÇÖZÜLERİ 4 a a a d Şe kil de ö rül dü ğü i bi, ve ışık ışın la rı yansı ma lar so nu u ken di üze rin den e ri dö ner CEVP Şekilde örüldüğü ibi, aynalar arasındaki
ÖLÜ ÜRESEL YNLR OEL SORU - Eİ SORULRN ÇÖZÜLERİ 4 a a a d Şe kil de ö rül dü ğü i bi, ve ışık ışın la rı yansı ma lar so nu u ken di üze rin den e ri dö ner CEVP Şekilde örüldüğü ibi, aynalar arasındaki
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocm.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocm.mit.edu/terms veya http://tuba.açık ders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocm.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocm.mit.edu/terms veya http://tuba.açık ders.org.tr adresini ziyaret
KATI BASINCI BÖLÜM 1. Alıştırmalar. Katı Basıncı ÇÖZÜMLER. 3. Cis min ağır lı ğı G ise, olur. Kap ters çev ril di ğinde ze mi ne ya pı lan ba sınç,
 TI BSINCI BÖÜM lıştırmalar ÇÖZÜMER atı Basıncı Cis min ağır lı ğı ise, r de: I r( r) 40 & 60rr 4rr ap ters çev ril di ğinde ze mi ne ya pı lan ba sınç, ı rr 60rr rr 60 Nm / r zemin r r zemin I de: sis
TI BSINCI BÖÜM lıştırmalar ÇÖZÜMER atı Basıncı Cis min ağır lı ğı ise, r de: I r( r) 40 & 60rr 4rr ap ters çev ril di ğinde ze mi ne ya pı lan ba sınç, ı rr 60rr rr 60 Nm / r zemin r r zemin I de: sis
7. Sınıf MATEMATİK TAM SAYILARLA ÇARPMA VE BÖLME İŞLEMLERİ 1. I. ( 15) ( 1) 5. ( 125) : ( 25) 5 6. (+ 9) = (+ 14)
 7. Sınıf MATEMATİK TAM SAYILARLA ÇARPMA VE BÖLME İŞLEMLERİ TEST 1 1. I. (15) (1) II. (1) (6) III. (+8) (1) IV. (10) (1) Yukarıda verilen işlemlerden kaç tanesinin sonucu pozitiftir? A) 4 B) 3 C) 2 D) 1
7. Sınıf MATEMATİK TAM SAYILARLA ÇARPMA VE BÖLME İŞLEMLERİ TEST 1 1. I. (15) (1) II. (1) (6) III. (+8) (1) IV. (10) (1) Yukarıda verilen işlemlerden kaç tanesinin sonucu pozitiftir? A) 4 B) 3 C) 2 D) 1
GAZ BASINCI BÖLÜM P Y 3. P K. 2. I. durumda: 5. Tüp F kuvveti ile h kadar MODEL SORU 1 DEK SORULARIN ÇÖZÜMLER = P L = 5P.
 GZ BSINCI BÖÜ 15 ODE SORU 1 DE SORURIN ÇÖZÜER 3. P P 5P olur. 3P. 1. 2 2 d 3 P + 2d 5P 3P + 2dg 2P 2dg P dg olur. P P + 3dg 5P + 3P 8lur. P P P s d Z s 3d 2 ve larının basınçları yazılıp oranlanırsa; P
GZ BSINCI BÖÜ 15 ODE SORU 1 DE SORURIN ÇÖZÜER 3. P P 5P olur. 3P. 1. 2 2 d 3 P + 2d 5P 3P + 2dg 2P 2dg P dg olur. P P + 3dg 5P + 3P 8lur. P P P s d Z s 3d 2 ve larının basınçları yazılıp oranlanırsa; P
O zbekstan Respubikasi Awil ham suw xojalig I Minstrlingi. Tashkent ma mleketlik agrar universiteti No kis filiali Zootexniya fakulteti
 O zbekstan Respubikasi Awil ham suw xojalig I Minstrlingi Tashkent ma mleketlik agrar universiteti No kis filiali Zootexniya fakulteti Zootexniya ta lim bag dari Haywanlar fiziologiyasi paninen O Z BETINSHE
O zbekstan Respubikasi Awil ham suw xojalig I Minstrlingi Tashkent ma mleketlik agrar universiteti No kis filiali Zootexniya fakulteti Zootexniya ta lim bag dari Haywanlar fiziologiyasi paninen O Z BETINSHE
ÖNSÖZ... İÇİNDEKİLER... KISALTMALAR...
 İÇİNDEKİLER ÖNSÖZ... İÇİNDEKİLER... KISALTMALAR... BİRİNCİ BÖLÜM KAVRAMLAR I. ANAYASA HUKUKU... A. A a asa Hukuku u Ta ı ı... B. A a asa Hukuku u Ko usu... II. ANAYASA KAVRAMI... A. Te i oloji... B. A
İÇİNDEKİLER ÖNSÖZ... İÇİNDEKİLER... KISALTMALAR... BİRİNCİ BÖLÜM KAVRAMLAR I. ANAYASA HUKUKU... A. A a asa Hukuku u Ta ı ı... B. A a asa Hukuku u Ko usu... II. ANAYASA KAVRAMI... A. Te i oloji... B. A
PROGRAMI, (ÖRGÜN ÖĞRETİM) NEW PALTZ) (ÜCRETLİ) ÖĞRETİM) ÖĞRETİM)
 1 A377 13******* ENDÜSTRİ MÜHENDİSLİĞİ, LİSANS MU*** SÜ*** PROGRAMI, (ÖRGÜN 91. 1, 95, Kazandı A373 *******1 EKONOMİ PR. (İNGİLİZCE) (UOLP-SUNY FE*** KA*** NEW PALTZ) (ÜCRETLİ).3 1, 9,15 Kazandı 3 A3797
1 A377 13******* ENDÜSTRİ MÜHENDİSLİĞİ, LİSANS MU*** SÜ*** PROGRAMI, (ÖRGÜN 91. 1, 95, Kazandı A373 *******1 EKONOMİ PR. (İNGİLİZCE) (UOLP-SUNY FE*** KA*** NEW PALTZ) (ÜCRETLİ).3 1, 9,15 Kazandı 3 A3797
 http://www.kap.gov.tr/api/bildirim.aspx?id=343204&imza=imzali Page 1 of 1 06.03.2014 İmzasız Görüntüle Ek dosyalar SODA SANAYİİ A.Ş. / SODA, 2014 [SISE] 06.03.2014 18:39:15 Genel Kurul Toplantısı Çağrısı
http://www.kap.gov.tr/api/bildirim.aspx?id=343204&imza=imzali Page 1 of 1 06.03.2014 İmzasız Görüntüle Ek dosyalar SODA SANAYİİ A.Ş. / SODA, 2014 [SISE] 06.03.2014 18:39:15 Genel Kurul Toplantısı Çağrısı
ya kın ol ma yı is ter dim. Gü neş le ısı nan top rak üze rinde ki çat lak la rı da ha net gö rür düm o za man. Bel ki de ka rın ca la rı hat ta yağ
 SAKARKÖY Uzun boy lu bir can lı ol ma yı ben is te me dim. Ben, doğ du ğum da da böy ley dim. Za man la da ha da uzadım üs te lik. Bü yü düm. Ben bü yü dük çe di ğer can lılar kı sal dı lar, kü çül dü
SAKARKÖY Uzun boy lu bir can lı ol ma yı ben is te me dim. Ben, doğ du ğum da da böy ley dim. Za man la da ha da uzadım üs te lik. Bü yü düm. Ben bü yü dük çe di ğer can lılar kı sal dı lar, kü çül dü


 Iilil"lğI,IğUj h EGE IP_Ij :bejtsempo&umu ivgnsirrsi su nnleri pn
Iilil"lğI,IğUj h EGE IP_Ij :bejtsempo&umu ivgnsirrsi su nnleri pn