T.C. İSTANBUL KÜLTÜR ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DÜŞÜK MANYETİK ALANA SAHİP NÖTRON YILDIZLARI ÇEVRESİNDEKİ DİSKLER YÜKSEK LİSANS TEZİ
|
|
|
- Serkan Durmaz
- 8 yıl önce
- İzleme sayısı:
Transkript
1 T.C. İSTANBUL KÜLTÜR ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DÜŞÜK MANYETİK ALANA SAHİP NÖTRON YILDIZLARI ÇEVRESİNDEKİ DİSKLER YÜKSEK LİSANS TEZİ Onur ÇATMABACAK Anabilim Dalı: Fiik Programı: Fiik Te Danışmanı: Doç. Dr. M. Hakan ERKUT HAZİRAN 2014
2 T.C. İSTANBUL KÜLTÜR ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DÜŞÜK MANYETİK ALANA SAHİP NÖTRON YILDIZLARI ÇEVRESİNDEKİ DİSKLER YÜKSEK LİSANS TEZİ Onur ÇATMABACAK Anabilim Dalı: Fiik Programı: Fiik Te Danışmanı: Doç. Dr. M. Hakan ERKUT HAZİRAN 2014
3 T.C. İSTANBUL KÜLTÜR ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DÜŞÜK MANYETİK ALANA SAHİP NÖTRON YILDIZLARI ÇEVRESİNDEKİ DİSKLER YÜKSEK LİSANS TEZİ Onur ÇATMABACAK Anabilim Dalı: Fiik Programı: Fiik Te Danışmanı: Doç. Dr. M. Hakan ERKUT HAZİRAN 2014
4 ÖNSÖZ 4 senedir överisi, sabrı, bilimsel ve mental rehberliği ile bir yol gösterici ve çalışma arkadaşından çok daha falası olan ve bugünlere gelebilmemde en büyük rolü oynayan danışmanım Doç. Dr. Mehmet Hakan ERKUT a, değerli yorumları, teim üerindeki düeltmeleri ve benim için ayırdıkları vakit için te jürimin asıl üyeleri Yrd. Doç. Dr. Emre IŞIK ve Prof. Dr. Mehmet Ali ALPAR a ve yedek üyesi Yrd. Doç. Dr. Gülce ÖĞRÜÇ YILDIZ a, kardeşim ve yeni çalışma arkadaşım Önder ÇATMABACAK a ve adını sayamadığım / saymayı unuttuğum sayılı insanlara ne kadar teşekkür etsem adır. Hairan 2014 Onur ÇATMABACAK i
5 İçindekiler Sembol Listesi Figür Listesi Tablo Listesi ÖZET ABSTRACT iii viii ix x xi 1 GİRİŞ 1 2 YIĞIŞMA DİSKİNİN İNCELENMESİ Tipik Disk Parametrelerini Kullanarak kh QPO Frekanslarının Elde Edilmesi Genel Disk Çöümlerinin Elde Edilmesi Paralel İ Probleminin Açıklanması SONUÇLAR VE TARTIŞMA 32 A KORUNUM EŞİTLİKLERİ 34 A.1 Kütle Korunumu A.2 Momentum Korunumu A.3 Enerji Korunumu B KORUNUM DENKLEMLERİNİN BOYUTSUZLAŞTIRILMASI 41 B.1 Navier-Stokes Denkleminin Boyutsulaştırılması B.2 Süreklilik Eşitiliğinin Boyutsulaştırılması B.3 Enerji Denkleminin Boyutsulaştırılması C DİSK ÇÖZÜMLERİ 46 C.1 C Bölgesi Çöümü C.2 B Bölgesi Çöümü ii
6 C.3 A Bölgesi Çöümü C.4 Sınır Bölgesi Çöümü C.5 GPD ve RPD Bölgeler İçin İç Disk Çöümlerinin Elde Edilmesi Kaynakça 62 iii
7 Sembol Listesi Latin Sembolleri Ṁ ṁ B C c c s d F f G H L x M M M A n P p Q v : Yığışma diskinin kütle aktarım hıı : Boyutsu kütle aktarım hıı : Nötron yıldıının manyetik alanı : Açısal momentum transferi verimlilik katsayısı boyutsu) : Işık hıı : Ses hıı : Nötron yıldıı kaynaklarının uaklığı : Işınım akısı : Nötron yıldıı kaynaklarının X-ışın akısı : Kütleçekimsel sabit : Disk yarı kalınlığı : X-ışın ışınım gücü : Nötron yıldıının kütlesi : Güneş kütlesi : Bir mol gaın kütlesi : Mol : Düşey yönde integre edilmiş basınç : Basınç : Birim hacimdeki visko enerji kayıp oranı iv
8 R r R r A r co r in S a S a T v r x y : Genişletilmiş radyal koordinat : Silindirik koordinatlarda radyal yön bileşeni : Nötron yıldıının yarıçapı : Alfven yarıçapı : Yığışma diskinin, nötron yıldıı ile aynı hıda döndüğü disk yarıçapı : Dskin tipik en iç yarıçap değeri : X-ışın renk-renk diyagramının konum parametresi : X-ışın renk-renk diyagramının konum parametresi : Sıcaklığı : Radyal sürüklenme hıı : Boyutsu fit sabiti : Boyutsu fit sabiti : Silindirik koordinatlarda düşey yön bileşeni Kısaltmalar GP D QP O RP D : Ga basıncı baskın : Kuai periyodik salınım : Radyasyon basıncı baskın Yunan Sembolleri α α BL β g β r ɛ ɛ Γ : Dış diskteki viskoite katsayısı : Sınır bölgesi boyutsu vikosite katsayısı : Ga basıncının radyasyon basıncına oranı : Radyasyon basıncının ga basıncına oranı : Disk kalınlığı parametresi : Disk yarı kalınlığının diskin en iç yarıçapına oranı : Kütle çekimsel potansiyel v
9 γ κ κ es κ ff : Adiabatik indeks : Yığışma diskinin radyal episiklik frekansı : Elektron saçılma opaklığı : Serbest-serbest opaklık µ : Boyutsu katsayı ν ν 1 ν 2 ν b ν ν QP O Ω ω ω Ω K Φ ρ Σ σ SB τ : Vikosite : Alt kuai periyodik salınım frekansı : Üst kuai periyodik salınım frekansı : Milisaniye pulsarlarının patlama salınım frekansı : Milisaniye pulsarlarının dönme frekansı : Kuai periyodik salınım frekansı : Yığışma diskinin açısal dönme frekansı : En iç diskteki maddenin açısal dönme hıının Kepler dönme hıına oranı : Nötron yıldıının dönme hıının en iç diskteki Kepler hıına oranı : Kepler açısal dönme frekansı : Silindirik koordinatlarda açısal yön bileşeni : Hacimsel kütle yoğunluğu : Yüeysel madde yoğunluğu : Stefan-Boltmann sabiti : Gerçek emilime göre optik derinlik Alt İndisler 0 : Durağan durum Φ gas in : Açısal yön bileşeni : Ga basıncının baskın olduğu durum : İç disk vi
10 out r rad t : Dış disk : Radyal yön bileşeni : Radyasyon basıncının baskın olduğu durum : Tipik değer : Düşey yön bileşeni vii
11 Şekil Listesi 1.1 Birincil yıldıın nötron yıldıı) üstüne ikincil yıldıdan madde aktarımı ile disk oluşumu Kilohert QPO gölemlenmiş NSLMXB kaynakları için kh QPO - parlaklık ilişkisi U kaynağı için kh QPO - X-ışın akısı grafiği U kaynağı için 2-16 kev enerji aralığındaki fotonların X-ışın renk-renk diyagramı poisyonunun ilediği yol ve frekans k.g. X-ışın renk-renk diyagramı poisyonu ilişkisi Mende&Belloni-2007 de Tablo 1 de yer alan kaynakların fark frekanslarının dönme frekansına oranının dönme frekansıyla olan ilişkisi GPD genel durağan durum disk çöümleri örnekleri RPD genel durağan durum disk çöümleri örnekleri 1. Tip) RPD genel durağan durum disk çöümleri örnekleri 2. Tip) Radyal episiklik frekans çöümündeki serbest parametrelerin alt kh QPO frekansları üerindeki etkisi U , 4U , 4U ve Aql X-1 nötron yıldıı kaynaklarından gölemlenmiş kh QPO - X-ışın akısı ilişkisi Şekil 2.5 üerinden alınan verilerin teorik modelimi çerçevesinde yeniden oluşturulması kh QPO frekanslarını tekrardan üretmek için salındırılan disk kalınlık parametresinin kütle aktarım hıı ile değişimi kaynağın kh QPO - S a ilişkisi Şekil 2.8 verilerinin modelimi çerçevesinde simülasyonu viii
12 Tablo Listesi 2.1 GPD ve RPD rejimlerinde diskteki temel parametrelerin tipik değerleri M, 10 km yarıçaplı örnek bir yıldı için tipik değer parametreleri üerinden yapılan taramada kh QPO frekanslarının elde edilebildiği frekans aralıkları ix
13 ÖZET Bu çalışmanın konusu düşük manyetik alana sahip nötron yıldılarının çevresindeki disklerin incelenmesidir. Hedef, düşük manyetik alana sahip nötron yıldılarının çevresindeki disklerin çalışılması ile bu tip sistemlerin gölemlerine fiiksel olarak tutarlı bir model çerçevesinde muhtemel cevaplar üretmektir. Düşük manyetik alana sahip düşük kütleli nötron yıldıı çiftlerinin çevresindeki disklerin incelenmesi, yüksek yoğunluktaki yıldı fiiğinin anlaşılması açısından önem taşımaktadır. Belirli varsayımlar ve fiiksel sınırlamalar altında, yığışma diskleri ga basıncının veya radyasyon basıncının baskın olduğu iki farklı rejimde incelenebilir. Bu tede 70 li yılların başında yapılan öncü çalışmalarda elde edilen durağan durum disk çöümleri en iç diskteki Kepler olmayan bir sınır tabakasının varlığı hesaba katılarak kullanılmış ve birleşik disk çöümleri elde edilmiştir. Birleşik disk çöümlerinde ele alınan iç disk sınır tabakaları uygun fiiksel koşullar altında ve Sınır Bölgesi Modeli Boundary Region Model, BRM) [Alpar ve Psaltis, 2008, Erkut v.d., 2008] çerçevesinde nötron yıldıı kaynaklarında gölemlenen kh kuai-periyodik salınım quasi-periodic oscillation, QPO) frekanslarının X-ışın akısı ile olan korelasyonunu açıklamak için kullanılmıştır. Çalışma nötron yıldıı düşük kütleli X-ışın çiftlerindeki Neutron star low-mass X-ray binaries, NSLMXBs) kh kuai periyodik salınım Quasi-Periodic Oscillation, QPO) frekansları ile X-ışın akısı arasındaki büyük aman ölçeklerinde gölemlenen paralel ilerin, Sınır Bölgesi Modeli kapsamında belirli varsayımlar ve fiiksel sınırlandırmalar altında açıklanabileceğini göstermiştir. Bu te çalışmasında elde edilen veriler ileride incelenen kaynakların kütle, yarıçap ve manyetik alan değerlerinin tahmini hakında yapılacak çalışmaya temel oluşturacaktır. Anahtar kelimeler: nötron yıldıı, yığışma diski, Sınır Bölgesi Modeli. x
14 ABSTRACT This study deals with accretion disks around weakly magnetied neutron stars. In this work we aim to come up with possible explanations for observational phenomena within a physically plausible model by studying accretion disks around weakly magnetied neutron stars. Investigating accretion disks around weakly magnetied neutron stars is important for studying and understanding the physics of neutron stars. Under reasonable assumptions and physical constraints, accretion disks can be examined using two different regimes: Gas pressure dominated or radiation pressure dominated. In this thesis, eroth order disk solutions which were also obtained in the early 70 s [Shakura ve Sunyaev, 1973] are employed while taking into account the existence of a non-keplerian boundary layer in the innermost region of the disk and unified disk solutions are found. Boundary layers which define the innermost disk boundary condition for physically plausible unified disk solutions are used to explain the correlation between kh quasi-periodic oscillation QPO) frequencies observed in neutron star low-mass X-ray binaries and the X-ray flux in accordance with the Boundary Region Model BRM) [Alpar ve Psaltis, 2008, Erkut v.d., 2008]. This study has revealed that the parallel tracks phenomena observed with long timescales for the correlation between kh QPO frequencies and the X-ray flux of the neutron stars in low-mass X-ray binaries can be explained within the frame of the BRM under plausible assumptions and self-consistent physical constraints. The model data obtained in this thesis can be used in a subsequent work to determine the masses, radii and magnetic field strengths of the neutron stars in LMXB systems we studied. Key Words: neutron stars, accretion disks, Boundary Region Model. xi
15 Bölüm 1 GİRİŞ Anakol evresindeki yıldılar kütleçekimsel çökmeyi dengeleyebilmek için çekirdek lerinde nükleer tepkime yolu ile hidrojen yakarak, ürettikleri toplam termal basınç sayesinde iç ve dış tabakalarını denge durumunda tutarlar. Çekirdeklerindeki hidrojenin büyük bir bölümünü tükettikleri aman, helyum yakarak karbon üretimine başlarlar ve Hertsprung-Russell diagramında anakol evresinden kırmıı dev evresine geçerler. Kütlesi yaklaşık olarak 8 Güneş kütlesinden M ) büyük olan yıldılar için anakoldan ayrılmak için gereken süre yaklaşık olarak sene iken daha düşük kütleli yıldılar için sene civarındadır. Kısacası büyük kütleli yıldıların ömürleri kısa olur. Bu süreçte çekirdeğe yakın dış bölgelerdeki hidrojen ve helyumu da nükleer tepkimelerle yakmaya başlayan yıldıın iç ve dış tabakaları arasında basınç gradientleri büyümeye başlar ve yıldı şişer. Düşük kütleli yıldılarda helyumun tamamı karbona dönüştürüldüğü aman yıldı karbonu yakabilecek merke sıcaklıklara erişemediği için nükleer tepkimeler ile yanmakta olan çekirdeğe yakın dış katmanların radyasyon basıncı etkisiyle yıldı arfını en dış tabakalarını) uaya atar geegen nebulası). Büyük kütleli yıldılarda ise 10 9 K civarında artık karbondan daha ağır elementler üretilmeye başlanır ve yıldı tekrar şişer. Bu süreç çekirdekte demir elementinin üretimine kadar devam eder. En son safhada çekirdeğin üerine çöken dış tabakalar çekirdeğe çarparak büyük bir şok dalgası oluştururlar ve süpernova patlaması ile yıldı kendini uaya dağıtır. Yıldıın kalan çekirdek kısmının kütlesi 3.0 M nin üstünde ise kara delik evresine kadar çökmeye devam edecektir. Eğer çekirdek kütlesi M 3.0M limiti dahilinde ise; yüksek basınç altında çekirdekteki protonlar elektronlar ile tepkimeye girerek ortamı nötronca engin hale getirirler. Çekirdek kütleçekimsel çökmeyi, Pauli dışlama ilkesine göre dejenere nötron basıncı ile dengeleyen bir nötron yıldıı olmuştur artık. Nötron yıldıı yaşamına iole bir yıldı olarak başlamış ise sahip olduğu termal enerjisi ve dönme kinetik enerjisinden sağladığı enerji ile elektromanyetik tayfın farklı dalga boylarında ışıma yaparak soğur ve yavaşlar. Eğer nötron yıldıı bir anakol ya da geç anakol yıldıı ile ikili bir sistem oluşturmuş ve üerine komşu yıldıdan kütle yığıştırıyor 1
16 ise, nötron yıldıı yaşamına yüksek enerjilerde X-ışını, Gama ışını) ışıma yapan aktif bir cisim olarak devam eder. Bir beya cüce ile bir geç tip normal yıldıın oluşturduğu ikili sistemde beya cücenin üerine kütle aktarımı ile madde birikmesi sonucu, beya cüce yıldıın kütlesinin Chandrasekhar kritik kütle limitini aşması mümkündür. Kritik kütlenin aşılması ile gerçekleşen Tip 1 süpernova olarak da bilinen bir patlama sonucu, beya cüce nötron yıldıına dönüşebilir. Bir nötron yıldıı veya karadelik içeren yıldı çiftleri kendi aralarında yoğun yıldıa madde aktaran normal yıldıın kütlesine göre 3 e ayrılırlar: Yüksek kütleli X-ışın çiftleri High Mass X-ray Binaries, HMXBs), orta kütleli X-ışın çiftleri Intermediate Mass X-ray Binaries, IMXBs) ve düşük kütleli X-ışın çiftleri Low Mass X-ray Binaries, LMXBs). Yüksek kütleli X-ışın çiftleri genç sistemler olup, O veya B sınıfında bir yıldıla bir yoğun yıldıdan kara delik veya nötron yıldıı) oluşur. Kütle aktarımı ikincil yıldıdan yoğun cisme yıldı rügarları ile gerçekleşir. Orta kütleli X-ışın çiftlerinde ikincil yıldı bir önceki sisteme göre daha düşük kütleli bir yıldıdır 3.0M ) ve kütle aktarımı Roche lobunu doldurması ve yıldı rügarları ile gerçekleşir. Düşük kütleli X-ışın çiftlerinde yoğun yıldıa kara delik veya nötron yıldıı) madde aktaran normal yıldı düşük kütleli 1.0M ) olup çoğunlukla G, K, M tayfsal sınıftan bir yıldıdır [Ghosh, 2007]. Düşük kütleli X-ışın çiftlerinde anakol veya geç anakol evresinde olan ikincil yıldı yukarıda bahsedildiği üere yaşamının sonraki aşamalarında anakoldan ayrılmaya başlaması ile birlikte kırmıı dev evresine geçer. Bu evrede yıldı şişerek Roche lobunu doldurur. İkincil yıldıın dış katmanlarındaki gaın bir kısmı, iki yıldı arasında kütle çekimsel kuvvetlerin dengelendiği Lagrange noktasından birincil yıldıın nötron yıldıı veya karadelik) üstüne akmaya başlar. Şekil 1.1 de gösterildiği üere Roche lobunu doldurarak Lagrange noktasından birincil yıldı üerine akan ga yoğun yıldıın kütle çekimi altında girdiği yörüngelerde viskoite sayesinde sahip olduğu açısal momentumunu dış yörüngelere taşıması, böylece yoğun cisme doğru akması sonucu bir yığışma diski oluşturur. İkincil yıldıdan aktarılan ve Lagrange noktasından geçen maddenin disk ile temas noktasında parlak bir bölge oluşur. Dış diskteki bu bölge yüksek madde akış oranlarında disk parlaklığının yüksek olması sebebiyle göreceli belirgin olmamakla birlikte düşük madde aktarımı sö konusu olduğunda disk parlaklığı göreceli olarak daha a olacağından oldukça belirgindir. 2
17 eş yıldı diskin üerine düşen ga tıkı nesne beya cüce, nötron yıldıı veya kara delik) diskten gelen radyasyon yığışma diski Şekil 1.1: Birincil yıldıın nötron yıldıı) üstüne ikincil yıldıdan madde aktarımı ile disk oluşumu. Kütle aktarım disklerinin fiiğinin açıklanmasında öncü çalışmalara 1960 ların sonları 1970 lerin başlarında rastlanmaktadır [Zel dovich ve Shakura, 1969, Pringle ve Rees, 1972, Shakura ve Sunyaev, 1973]. Çoğu durumda kütle aktarım disk kalınlığının disk boyunca her yörüngede yoğun cisme olan radyal uaklığa göre yeterince küçük olduğu varsayılır İnce disk yaklaşımı). Böylece disk kalınlığı boyunca ortalama üerinden diskin 2 boyutta çalışılması ve anlaşılması daha kolay olur [Frank v.d., 2002]. Disk fiiğinin detaylı çalışılması; nötron yıldıının yüksek kütleçekimi altında, aman ölçeği milisaniye mertebesinde olan içdiskteki maddenin dinamiğinin yıldıın karakteristik öellikleri kütle, yarıçap, manyetik alan vs...) hakkında bilgi taşıması sebebiyle önemlidir yılında Rossi X-ışın Zamanlama Kaşifi Rossi X-ray Timing Explorer, RXTE) uydusunun uaya fırlatılması ile milisaniye aman ölçeğindeki kuai-periyodik salınımlar Quasi-Periodic Oscillations, QPOs) [van der Klis v.d., 1996a] ve patlama salınımları burst oscillations) olarak bilinen X-ışın patlamaları sırasında ortaya çıkan atmaların pulsations) keşfi [Strohmayer v.d., 1996] mümkün oldu. Patlama salınımları nötron yıldıı düşük kütleli X-ışın çiftlerindeki X-ışın patlamalarının yükselme ve kuyruk kısımlarında görülen kısa ömürlü neredeyse birebir uyumlu atmalardır [Mende ve Belloni, 2007]. Kütle aktarımı yapan milisaniye pulsarlarının keşfi [Wijnands ve van der Klis, 1998b] ile patlama salınımlarının ölçülmesi daha da bir önem kaandı. Bu tipte keşfedilen ilk pulsar olan SAX J in patlama salınımlarının [Wijnands ve van der Klis, 2003] pulsarın ölçülen dönme frekansı ile aynı olduğunun görülmesi, nötron yıldılarının dönme frekanslarının patlama salınımlarının frekanslarından öğrenilmesini sağladı. Düşük kütleli nötron yıldıı X-ışın çiftlerinin güç tayfında kh frekans aralığında beliren QPO lar aman bağımlı ve güç tayfındaki diğer yapılara göre göreceli olarak dar ve belirgin yapılardır. Bu salınımların frekans aralığının nötron yıldıı çevresindeki yığışma diskinin iç bölgesindeki maddenin, yüksek kütleçekimsel 3
18 alan altında milisaniye ölçeğindeki dönme hareketi ile belirlendiği düşünülmektedir [van der Klis, 2000]. Nötron yıldıı LMXB lerinde NSLMXBs) 2-50 kev enerji bandında ölçülen X-ışın parlaklıklarında bir kaynaktan diğerine 100 kata kadar farklar olmasına rağmen, bugüne kadar RXTE ile kh QPO frekansları ölçülmüş 19 kaynakta yaklaşık H aralığında yüksek frekanslı QPO lara rastlanmıştır. Çoğunlukla çiftler halinde gölemlenen kh QPO frekanslarının düşük olanı ν 1 ve yüksek olanı ν 2 oldukça geniş bir frekans aralığında varlık gösterirler. Şekil 1.2: Kilohert QPO gölemlenmiş NSLMXB kaynakları için kh QPO - parlaklık ilişkisi. Kilohert QPO-parlaklık korelasyonları küçük aman ölçeklerinde birkaç saat ile birkaç gün) doğrusal orantı göstermekle birlikte aynı kaynak veya kaynaklar arası gölemler ele alındığında herhangi bir korelasyon görülememektedir [Ford v.d., 2000]. Örneğin 4U kaynağının yüksek QPO frekansı, ν 2, 449±20 H ile 1339±4 H aralığındadır [van Straaten v.d., 2000]. Hektohert mertebesinde salınım yapan karadelik kaynaklarında ν 1 ve ν 2 arasında görülen yaklaşık 3:2 oranının aksine NSLMXB lerde böyle bir öel oran gölemlenmemiştir. Bununla birlikte kh QPO gösteren NSLMXB ler de QPO gösteren karadelik LMXB lerine göre sayıca fala ve çeşitlidir. Çoğunluğu sürekli kaynaklar olmakla birlikte 4U [Berger v.d., 1996][Mende v.d., 1998], Aql X-1 [Zhang v.d., 1998a] ve XTE J [Homan v.d., 1999][Tomsick v.d., 1999] gibi sınır kaynaklarına da rastlanmaktadır. Z ve Atoll kaynaklar olmak üere tayfsal öelliklerine göre iki sınıfa ayrılan NSLMXB lerde, Z kaynaklarında kh QPO lar güç tayfında daha geniştir ve küçük rms root mean square, karelerinin ortalama karekökü) kesirlerinde görülmelerine ve kütle aktarım oranlarında 100 kata varan fark olmasına örneğin 4U [Strohmayer v.d., 1996], 4U [Mende v.d., 1999]) rağmen bu farklı tipte kaynakların kh QPO - parlaklık ilişkileri hemen hemen aynıdır [Ford v.d., 2000]. Bu da göstermektedir ki X-ışın parlaklığı tek başına QPO salınımlarını belirlememektedir. 4
19 Şekil 1.3: 4U kaynağı için kh QPO - X-ışın akısı grafiği. 4U kaynağı için düşük kh QPO frekansı k.g kev enerji bandında X-ışın foton akısı arasındaki ilişki. Sadece çift olarak gölemlenen QPO datalarının düşük frekansları kullanılmıştır. [Mende v.d., 1999] Şekil 1.2 ve Şekil 1.3 de de görüldüğü üere kh QPO frekans değerleri yaklaşık aynı değerlerde geinirken, X-ışın parlaklığı çok geniş bir aralıkta değişim göstermektedir. Bütün kaynakların gölemlenen en yüksek üst kh QPO frekansları H aralığında değişmektedir. Bu gölemsel öelliğe sebep olabilecek nedenler arasında kararlı en iç yörüngedeki maddenin dönme frekanslarının kh QPO frekanslarını sınırlayabileceği fikri ön plana çıkmaktadır [Zhang v.d., 1997]. Üst kh QPO frekanslarına bener bir şekilde alt frekansların da belli bir minimum değer ile sınırlandığı görülmektedir. Nötron yıldıı LMXB lerinde yeterince küçük aman ölçeklerinde birkaç saat) görülen ν QP O L x korelasyonu daha büyük aman ölçeklerinde günler) boulmakta ve ν QP O L x düleminde paralel iler oluşturmaktadır. Böyle paralel iler hem kaynak başına hem de farklı parlaklık mertebelerindeki pek çok kaynak için gölemlenmiştir [Ford v.d., 2000]. Kilohert QPO ları üreten fiiksel mekanimanın parametreleri bener aralıklarda frekans üretecek şekilde değişiyor olabilir. Ayrıca frekansların X-ışın parlaklığının yanısıra nötron yıldıının dönme frekansı, kütlesi, yarıçapı ve manyetik alanı gibi niceliklerin en a birine daha bağlı olması da geniş aman ölçeklerinde gölemlenen davranışa yol açabilir. 5
20 a b Şekil 1.4: 4U kaynağı için 2-16 kev enerji aralığındaki fotonların X-ışın renk-renk diyagramı poisyonunun ilediği yol ve frekans k.g. X-ışın renk-renk diyagramı poisyonu ilişkisi a) Orta ada ve aşağı mu bölgesinden orta ada ve yukarı mu bölgesine kadar görülen içi dolu noktalarla belirtilmiş datalar kh QPO frekanslarını göstermektedir [Mende v.d., 1999]. b) Grafiğin sağ üst tarafında iki çigi halinde alt ve üst kh QPO frekanslarının ν 1 ve ν 2 ) konum parametresi ile olan ilişkisi görülmektedir. [Mende v.d., 1999] Şekil 1.4 te, Şekil 1.3 te 2-16 kev enerji bandında gölemlenen paralel i verilerinde, 9-16 kev enerji bandındaki fotonların 9-6 kev enerji bandında gölemlenen fotonlara oranına sert renk Hard Color), 9-6 kev enerji bandındaki footnların 6-2 kev enerji bandındaki fotonlara oranına yumuşak renk Soft Color) tanımlaması yapılmıştır. İçi dolu olan data noktaları çift olarak gölemlenmiş kh QPO frekanslarından alt kh QPO frekanslarını göstermektedir. İçi boş olan data noktalarında kh QPO frekansı gölemlenmemiştir. Şekil 1.4 te ada bölgesinden Island state) üst mu bölgesine Upper banana state) gidildikçe X-ışın akısı artmaktadır. Bu tanımlama altında Şekil 1.4 kh QPO frekanslarının daha çok sert renkli fotonlardan yumuşak renkli fotonlara sınır sırasında gölemlendiğini ortaya koymaktadır. NSLMXB lerinde kh QPO frekansları ile X-ışın parlaklığı arasında büyük aman ölçeklerinde belirli bir korelasyon olmamasına karşın frekans ve X-ışın renk-renk diyagramında kaynağın poisyonu S a arasında Şekil 1.4 de gösterildiği üere doğrusal bir ilişki vardır. S a konum parametresi X-ışın renk-renk diyagramında ada bölgesinden island state) mu bölgesine banana state) doğru ilerledikçe kh QPO frekanslarında artış gölemlenmektedir. Orta ada moderate island) ve aşağı mu lower banana) bölgelerinde ortaya çıkmaya başlayan QPO lar uç ada extreme island) ve yukarı mu upper banana) bölgelerinde kaybolurlar [Hasinger ve van der Klis, 1989]. Atoll kaynaklarda kütle aktarım oranının X-ışın renk-renk diyagramı poisyonu, S a, ile birlikte monoton olarak arttığı düşünülmektedir [Hasinger ve van der Klis, 1989]. 6
21 Şekil 1.5: Mende&Belloni-2007 de Tablo 1 de yer alan kaynakların fark frekanslarının dönme frekansına oranının dönme frekansıyla olan ilişkisi. Daha öncelerden savunulan yavaş ve hılı dönen kaynaklar için ortaya atılmış fark frekansı k.g. dönme frekansı korelasyonunun aksine basamak fonksiyonu yerine daha sürekli bir dağılım ilemektedir. [Mende ve Belloni, 2007] Aynı durumda X-ışın sayma oranı da X-ray count rate) kütle aktarım oranını aynı i boyunca takip eder [van der Klis v.d., 1990][van der Klis, 1994][Prins ve van der Klis, 1997]. X-ışın sayma oranının aksine kilohert QPO ların S a parametresi ile korelasyon göstermesi kh QPO frekanslarının toplam kütle aktarımı oranıyla monoton değiştiğini söyler. Z kaynaklarında da bener sonuçlara ulaşılmıştır [Wijnands v.d., 1997]. Yukarıda bahsedilen sebeplerden ötürü Atoll kaynaklarda X-ışın akısından bağımsı X-ışın renk-renk diyagramlarının poisyonu tayfsal değişimleri parametrie etmekte oldukça başarılıdır. Karacisim akısı blackbody flux) [Ford v.d., 1997b], iki bileşenli tayfsal modelde üs-kanunu eğimi de power-law slope) tayfsal poisyonu X-ışın akısından daha iyi tanımlamaktadır [Kaaret v.d., 1998]. NSLMXB lerin güç tayfında kh QPO lara ek olarak görülen patlama salınımları, ν b, nötron yıldıı kaynaklarının dönme hıına oldukça yakındır ve aynı kaynak için her patlamada fala değişmeden aynı kalır [Strohmayer v.d., 1998]. Kütle aktarımı yapan milisaniye pulsarlarında patlama salınımlarının, ν b, pulsarın dönme frekansıyla, ν, neredeyse aynı olduğunun, ν b ν, bulunması patlama salınım frekansı bilinen diğer nötron yıldıı kaynakları için de dönme frekansının kestirilmesini sağladı [van der 7
22 Klis, 2000]. Çift kh QPO ların fark frekansları H aralığında olup frekanslar arttıkça aalırlar. Öncü gölemlerde fark frekansının patlama salınımı değerlerine yakın bulunması Sonik-Nokta Atma Frekansı Sonic-Point Beat Frequency Model, SFBFM) [Miller v.d., 1998] modelinin ortaya çıkmasını sağladı. Gölemsel verilerin artmasıyla 400 H üerinde dönme hıına sahip kaynakların fark frekanslarının patlama salınımı frekansının ve dolayısıyla yıldı dönme frekansının yarısına eşit olduğunun görülmesi varolan modellerde düeltme yapılmasını gerekirdi [van der Klis, 2000, Wijnands ve van der Klis, 2003]. Daha sonraları gölemsel verilerin detaylı analii ile fark frekansının kh QPO frekansları arttıkça aaldığı ortaya konuldu. Bu sonuç beraberinde Rölativistik Yalpalama Modeli Relativistic Precession Model) [Stella ve Vietri, 1998][Stella ve Vietri, 1999] ve Sınır Bölgesi Modeli Boundary Region Model) [Erkut v.d., 2008, Alpar ve Psaltis, 2008] gibi yeni modelleri getirdi. Nötron yıldıı kaynakları artık dönme hılarına göre yavaş dönenler slow rotators ν b < 400H) ve hılı dönenler fast rotators ν b 400H) olarak iki sınıfa ayrıştırıldı [van der Klis, 2006]. Bu kısıtlamalara uymayan kaynakların ortaya çıkması ile nötron yıldıı dönme frekanslarında veya yarısına eşit fark frekanslarının yerine sürekli dağılıma sahip olabileceğini tartışan çalışmalar yapıldı [Mende ve Belloni, 2007]. Bugün biliyoru ki kh QPO frekansları gölemlenmiş nötron yıldıı kaynaklarının neredeyse yarısının fark frekansları nötron yıldıının dönme frekansının üerinde veya yarı değerinin altındadır. Nötron yıldıı LMXB lerinde X-ışın güç tayflarında H frekans aralığında gölemlenen kh QPO ların gölemsel öellikleri, bu salınımların kaynağı olarak yığışma disklerinin en iç bölgesini işaret etmektedir [Erkut v.d., 2008]. Sınır Bölgesi Modeli [Erkut v.d., 2008, Alpar ve Psaltis, 2008] dahilinde kütle yığışma diski ile yıldı manyetosferinin etkileşimi sonucu belirlenen bu sınır sınır) bölgesinin dışında diskin açısal hıı Kepler dönüş hıları ile oldukça iyi tasvir edilebilmektedir. Dış disk bölgelerinde hidrodinamik düeltmelerin yörünge açısal frekansları üerindeki etkisi göardı edilebilinecek kadar önemsidir. Basit olmasına rağmen QPO frekanslarının sadece test parçacığı frekansları ile ifade edilmesi baı eksiklikleri beraberinde getirir. Öncelikle QPO frekanslarının uyarılmasının/yükseltgenmesinin beklendiği sınır bölgesinde dinamik salınım frekansları test parçacığı frekansları değildir. Sınır bölgesinde visko ve manyetik kuvvetler yörüngesel frekansların Kepler değerinden sapmasına yol açar [Erkut ve Alpar, 2004]. Kepler olmayan dönme frekansları disk akışkanının komşu halkaları arasında ki visko ve akustik etkileşimlerin bir sonucu olarak ortaya çıkmaktadır. Nötron yıldıı LMXB lerinin ayıf manyetik alanı nedeniyle sınır bölgesinin yıldı yüeyine yakın olması, QPO frekanslarının diskin en iç bölgesindeki maddenin dinamiği ile belirlenen aman ölçeklerinde X-ışın yayınımında i bırakabilmesini olanaklı hale getirir [Erkut ve Alpar, 2004]. Nötron yıldıının dönüş hıına bağlı olarak diskin en iç bölgesinin karakteristik yapısı Kepler altı veya Kepler üstü akışkan olarak belirlenebilir 8
23 [Erkut, 2014]. Sınır bölgesinde visko, manyetik, basınç ve radyatif kuvvetlerin kütle çekimi ile karşılaştırılabilir büyüklüklere gelmeleriyle akışkan elementlerinin yörüngesel frekansları değişime uğrar. Büyük ölçekli manyetik alanın mevcut olmadığı nötron yıldıı LMXB leri gibi sistemlerde dahi küçük ölçekli çalkantılı manyetik alanlar sayesinde ortaya çıkan Maxwell stresleri en iç diskteki dinamik frekansları etkileyebilir [Hawley ve Krolik, 2001]. Ek olarak iç diskte manyetik frenlemeye bağlı olarak merkekaç desteğinin ayıflamasıyla diskteki madde radyal yönde ivmelenebilir. Radyal sürüklenme hıındaki ani artışa yüey yoğunluğundaki aalma eşlik eder. Sonuçta düşey olarak integre edilmiş dinamik viskoite minimum değerine ulaşır [Erkut ve Alpar, 2004]. Yukarıda bahsedilen sebeplerle sınır koşulları ve manyetik alanın yapısından bağımsı olarak sınır bölgesinde belirli bir yarıçapta yüey yoğunluğu ve radyal sürüklenme hıı gibi disk niceliklerinde büyük değişimler olması kaçınılmadır. İç disk sınır bölgesinde [Erkut, 2014] Kepler değerinden sapma göstermesi beklenen açısal frekansın gradyentinin poitif olduğu durumda κ = [ 2Ω 2Ω + r dω )] 1/2 1.1) dr ile ifade edilen ve diskteki maddenin radyal yöndeki hareketi sonucu meydana gelen türbülanslarla oluşan radyal episiklik frekans diskteki en büyük dinamik frekans olur. Bu sebeple diskin en iç bölgelerinde yüksek frekanslı salınım modları radyal episiklik frekans, κ, ile belirlenir [Alpar ve Psaltis, 2008]. Radyal episiklik frekansın açısal frekans, Ω, ile oluşturduğu frekans bandlarının ortaya çıktığı sınır bölgesi disk manyetosfer sınırında oluştuğundan, diskin yarıçapının yıldıın kütlesi, yarıçapı, manyetik alanı ve diskte birim amanda akmakta olan kütle miktarının fonksiyonu olan Alfvén yarıçapı, bir başka deyişle, r A = GM ) 1/7 Ṁ 2/7 B R 3 ) 4/7 1.2) ile belirlenmesi beklenir. Diskten nötron yıldıı üerine madde akışı, sınır bölgesinde manyetik frenleme ile karşılaşan madde Alfvén yarıçapından data öteye gideme. Dolayısıyla sınır bölgesinde nötron yıldıının manyetik alan çigilerini takip ederek nötron yıldıının manyetik kutuplarından yıldıın üerine akması ile gerçekleşir. Diskin iç yarıçapı yığışma diskinin ve yıldıın fiiksel parametrelerine bağlılık gösterdiğinden, nötron yıldıı LMXB lerinin kh QPO gölemleri nötron yıldıının ve etrafındaki yığışma diskinin fiiği hakkında bie önemli ipuçları verebilir. Bu tede 4U , 4U , 4U ve Aql X-1 nötron yıldıı LMXB lerinden gölemlenen QPO frekansı-parlaklık ilişkisi temel alınarak, Sınır Bölgesi Modeli kapsamında radyasyon basıncının hakim olduğu, ince sınır bölgesine sahip geometrik olarak ince optik olarak kalın yığışma disklerinin en iç bölgesinde QPO ların gölemsel öelliklerini verecek fiiksel koşullar incelenecektir. Diskin fiiksel öellikleri 9
24 temel alınarak çalışılan dört nötron yıldıı kaynağının kütle, yarıçap ve manyetik alan gibi karakteristik öellikleri hakkında öngörülerde bulunulacaktır [Alpar ve Psaltis, 2008]. 10
25 Bölüm 2 YIĞIŞMA DİSKİNİN İNCELENMESİ Bu bölümde nötron yıldıı LMXB lerinin etrafındaki yığışma diskinin en iç sınır bölgesi ele alınarak, kh QPO frekansları ve X-ışın akısı arasında gölemlenmiş korelasyonlar Sınır Bölgesi Modeli çerçevesinde açıklanmaya çalışılacaktır. Analiimi yığışma diskinin fiiksel parametrelerinin çok hılı değişim gösterdiği geometrik olarak ince sınır bölgeleri ile sınırlı olacaktır. Yığışma diski ve nötron yıldıının önemli fiiksel parametreleri için tipik değerleri tartışacağımı bu bölümde, öngörülmüş fiiksel kısıtlamalar çerçevesinde kh QPO lar için gölemlenmiş frekans aralığını diskteki dinamik frekanslar olan radyal episiklik frekans ve açısal frekans ile elde edeceği. Daha sonra kh QPO frekanslarını elde ettiğimi Kepler olmayan iç disk dar sınır bölgeleri ile Kepler dönme profiline sahip dış disk bölgelerini birbirine bağlayan durağan durum birleşik unified) disk çöümlerini vereceği. Son olarak ta iç disk sınır bölgesindeki serbest parametrelerin QPO frekansları üerinde oynadığı rolü inceleyerek, kh QPO ve X-ışın akısı arasındaki korelasyonlara olası açıklamalar getirmeye çalışacağı. 2.1 Tipik Disk Parametrelerini Kullanarak kh QPO Frekanslarının Elde Edilmesi Dar sınır bölgesine sahip yığışma diskleri baı sınırlamalar altında incelenecektir. Öncelikle incelenecek yığışma disklerinin iç bölgelerinde ga basıncının baskın Gas pressure dominated, GPD) veya radyasyon basıncının baskın Radiation pressure dominated, RPD) olduğu iki farklı basınç rejiminin incelenmesi mümkündür. Yığışma diski için kullanılacak fiiksel sınırlamalar aşağıdaki gibidir: 1. kh QPO frekanslarını barındıracak olan diskin en iç bölgesinde her iki tip 11
26 basınç rejiminde de basınçların birbirlerine oranları 10 dan büyüktür GPD için p t,gpd /p t,rpd > 10, RPD için p t,rpd /p t,gpd > 10). 2. Disk ortamı optik olarak kalındır Gerçek emilime göre optik derinlikτ t > 1). 3. Disk yapısı geometrik olarak incedir H t /r in < 0.1) 4. Diskteki dinamik frekanslar gölemler temel alınarak H aralığı ile sınırlandırılmıştır [Ford v.d., 2000]. Yukarıda sıralanmış olan fiiksel sınırlamalar altında diskin en iç yarıçapı manyetik basınç ve maddenin çarpma basıncı arasındaki denge, bir başka deyişle yani Alfvén yarıçapı ile belirlenmektedir. Temel fiiksel tipik disk parametreleri Tablo 2.1 de verilen eşitliklerle ifade edildiğinden dolayı diskin en iç yarıçapının tayini diğer parametreleri de etkilemektedir. Tablodaki eşitliklerde r in yığışma diskinin en iç yarıçapını, r A Alfvén yarıçapını, M, R, ve B sırasıyla nötron yıldıının kütlesi, yarıçapı ve manyetik alanını, Ω r in ) diskin en iç yarıçapındaki maddenin dönme hıını, Ω K diskteki maddenin Kepler dönme hıını, ν b nötron yıldıının patlama salınım frekansını, parante içindeki r in değerleri parametrelerin diskin en iç yarıçapındaki değerini, k gölemlenen kh QPO fark frekansları ile modelin tutarlılığını sağlayan serbest ölçeklendirme parametresini ν < 400 H için k 1 ve ν > 400 H için k 0.5), ω nötron yıldıının dönme frekansının en iç diskteki Kepler frekansına oranı olan hılılık parametresini, ω iç disk yarıçapında maddenin dönme frekansının aynı yarıçaptaki Kepler frekansına oranını, κ r in ) diskin radyal episiklik frekansını, H t diskin tipik yarı kalınlığını, c s,t diskteki ses hıını, Σ t diskin yüey kütle yoğunluğunu, Ṁ t birim amanda diskten nötron yıldıı üerine akan madde miktarını, v r,t diskteki maddenin radyal yönde sürüklenme hıını, ρ t diskin hacimsel kütle yoğunluğunu, p t basıncı, T t sıcaklığı, κ ff,t ve κ es sırasıyla serbest-serbest ve elektron saçılma opaklığını, τ diskteki gerçek optik derinliği göstermektedir. Dış diskteki vikosite diskin herhangi bir yarı kalınlığında oluşabilecek en büyük türbülans ile orantılı olacak şekilde tanımlanmıştır Bakını α modeli [Shakura ve Sunyaev, 1973]). İç diskteki vikosite de aynı tanımlama altında sınır bölgesinde oluşabilecek türbülans ile orantılı olacak şekilde tanımlanmıştır. İç ve dış disklerdeki vikositelerin diskteki termal difüyon gö önünde bulundurularak birbirlerine yakın mertebelerde olacakları varsayımı yapılmıştır. Sonuç olarak dış diskteki vikosite için α, sınır bölgesindeki vikosite için α BL boyutsu oran katsayıları tanımlanmıştır. Yığışma diskindeki maddenin dönme hareketine ek olarak radyal yöndeki salınımlarına karşılık gelen episiklik frekans ile maddenin açısal dönme frekansı birlikte diskin en iç bölgesinde ortaya çıkmasını beklediğimi çift kh QPO frekanslarını oluşturmaya adaydırlar. Olası frekans çiftleri olan [κ Ω, κ] ve [κ, κ + Ω] bandları için Tablo 2.2 de gösterilen anali yapılmıştır fakat [κ, κ + Ω] frekans bandı için kh mertebesinde 12
27 gölemlenen QPO frekanslarını üretmek için kullanılan sınır bölgesi vikosite katsayısı α BL, 1 mertebesinin üerinde olduğundan dolayı analilerimide [κ Ω, κ] frekans bandı kullanılacaktır. Ancak [κ, κ + Ω] çifti için de bener sonuçları elde etmek mümkündür. GPD RPD r in r A = GM ) 1/7 2/7 M t B R ) 4/7 Ω K r in ) = GM /rin) 3 1/2 Ω = 2πν = 2πν burst Ω r in ) = kω ω = Ω r in ) /Ω K r in ) ω = ω/k κ r in ) = 2Ω r in ) [2Ω r in ) + r in dω r) /dr) r=rin ] H t = εr in c s,t = Ω K r in ) H t Σ t = Ṁt/ 2πH t c s,t µ) v r,t = Ṁt/ 2πΣ t r in ) ρ t = Σ t /2H t p t = ρ t c 2 s a = 4σ SB /c p t,gas = nr G T t,gas / γv ) = ρ t c 2 s,t p t,rad = att,rad 4 /3 = ρ tc 2 s,t T t,gas = M A c 2 S,t / γr G) T t,rad = [ 3ρ t c 2 S,t /a] 1/4 κ ff,t = 0.11ρ t T 7/2 t,gas /m p κ ff,t = 0.11ρ t T 7/2 t,rad /m p κ es = 0.4 τ t = κ ff,t κ ff,t + κ es )Σ t τ t = κ ff,t κ ff,t + κ es )Σ t Tablo 2.1: GPD ve RPD rejimlerinde diskteki temel parametrelerin tipik değerleri. Burada ν = ν burst alınmıştır [Mende ve Belloni, 2007]. Yukarıda bahsedilen fiiksel sınırlamalar altında Tablo 2.1 de verilen eşitlikler ile disk iç yarıçapındaki κ r in ) /2π ve κ r in ) Ω r in )) /2π frekans bandlarını kullanarak kh QPO salınımlarını H frekans aralığında 1.4 Güneş kütlesinde 10 km yarıçaplı örnek bir yıldı için aşağıdaki parametre aralıklarında elde ettik. Bener bir şekilde κ r in ) /2π ve κ r in ) + Ω r in )) /2π frekans bandları ile de kh QPO frekansları elde edilebilmektedir. Hakkında kesin bir bilgiye sahip olmadığımı ama 1 mertebesinde 0.5 α BL 5.0) olmasını beklediğimi sınır bölgesi viskoite katsayısının, κ r in ) /2π ve κ r in ) + Ω r in )) /2π bandları için 10 ve yukarı mertebede değerler almasndan dolayı bu tede sadece κ r in ) /2π ve κ r in ) Ω r in )) /2π frekans bandlarına ait analilere yer vereceği. Kütle aktarım oranını g/s, manyetik alan değerini G, sınır bölgesi viskoite katsayısını , fark frekansını H aralıklarında tarayarak Tablo 2.2 de verilen değer aralıklarında, NSLMXB lerde gölemlenen frekans aralığı olan H aralığında kh QPO lar elde ettik. 13
28 Alt Değer Üst Değer Kütle aktarım oranı GPD) g/s g/s Kütle aktarım oranı RPD) g/s g/s Manyetik alan 10 8 G 10 9 G α BL Fark frekansı 200 H 400H kh QPO frekans aralığı 200H 1300H Tablo 2.2: 1.4M, 10 km yarıçaplı örnek bir yıldı için tipik değer parametreleri üerinden yapılan taramada kh QPO frekanslarının elde edilebildiği frekans aralıkları. 2.2 Genel Disk Çöümlerinin Elde Edilmesi Bölüm 2.1 de sıralanan fiiksel sınırlamalar altında ince disk yaklaşımı ile tutarlı gölemlenmiş frekans aralığında kh QPO frekanslarını elde ederken taranacak tipik disk parametrelerini tanıttık. Bu bölümde kh QPO frekansları içerebilecek fiiksel olarak tutarlı geometrik olarak ince diskler için klasik durağan durum dış disk çöümlerinin [Shakura ve Sunyaev, 1973] yanı sıra Kepler olmayan iç diskin de radyal bağımlı durağan durum çöümlerini bulup, bu çöümleri iç diskte Denk Asimtotik Açılımlar Matched Asymptotic Expansion, MAE) [Bender ve Orsag, 1978] metodunu kullanarak birleştirip Bölüm 2.1 de bahsedilen diskler için sürekli disk çöümleri olduğunu göstereceği. Disk çöümlerine sırasıyla diskin kütle, momentum ve enerji korunum eşitliklerini yaarak başlıyoru. Korunum eşitliklerinin çıkarılışları ve denklemlerin çöümlerindeki ara adımlar detaylı olarak EK kısmında verilecektir. Korunum denklemleri ve ρ t +. ρ v ) = 0, 2.1) ρ v t + ρ v. ) v = ρ Γ p +. ν, 2.2) ρ ɛ t + ρ v. ɛ = p. v. F + Q v 2.3) şeklinde yaılabilir. Burada ɛ enerji yoğunluğunu, ν visko stres tensörünü, Γ kütle çekimsel potansiyeli, F ışınım akısını, Q v birim hacimdeki visko enerji kayıp oranını ifade etmektedir. Geriye kalan terimler ise önceki bölümlerdeki tanımlarını korumaktadır. Dış disk çöümlerinin elde edilmesi için 1. Disk ortamı optik olarak kalındır τ > 1) ve radyasyon transferi için difüyon yaklaşımı varsayılacaktır. Opaklık değeri hem Thomson opaklığına hem de 14
29 Elektron Saçılma opaklığı gö önünde bulundurularak gerçek opaklık olarak hesaplanacaktır [Shakura ve Sunyaev, 1973]. 2. Disk eksen simetrik kabul edilecektir /φ = 0). 3. Disk yapısı durağan durum altında incelenecektir /t = 0). 4. Viskoite mevcuttur fakat baskın visko streslerin ν rφ bileşeni hariç geri kalanları ihmal edilecektir ν rφ 0). Yukarıdaki varsayımlar altında korunum denklemlerini silindirik koordinatlara göre r, φ ve bileşenlerine ayrıştırıyoru. Bileşenlerine ayrılmış korunum denklemleri 1 r r rρv r) + ρv ) = 0, 2.4) ) 3/ , 2.5) v r v r r + v v r Ω2 r = 1 p ρ r GM r 2 r 2 ve v v r + v v = 1 ρ v r r p GM ) 3/ , 2.6) r 3 r 2 r 2 Ω ) Ω + v r = 1 ρνr 3 Ω ) ρr 3 r r 2.7) [ ] T ρc v v r r + v T [ 1 = p r r rv r) + v F + ρνr2 Ω r ) 2 ] 1 r r rf r ) 2.8) şeklinde ifade edilir. Burada v r ve v sırasıyla r ve yönlerindeki hı bileşenleri, Ω açısal hı, C v sabit hacimde birim kütle başına öısı, F r ve F r ve yönlerinde ışınımsal enerji akıları, ν kinematik viskoite, a radyasyon basıncı sabiti, ρ hacimsel madde yoğunluğu, T sıcaklık, p basınç, Ṁ diskteki kütle akış hııdır. Geriye kalan terimler genel anlamlarında kullanılmışlardır. Disk boyunca kütle akışı sabittir. Eşitlikler boyutlu denklemler olup çalışmamıdaki tipik değerlere göre boyutsulaştırılarak incelenmesi ve çalışılması daha kolay eşitlikler haline getirilecektir. Hılar ses hıı, basınç ise ρ t c 2 s tipik basınç terimi ba alınarak boyutsulaştırılacaktır. Ölçek olarak radyal uunluk r t = r in, koordinatında uunluk H t olarak seçilmiştir. Notasyonda kolaylık olması açısından EK te ~ ile belirtilmiş olan boyutsu parametrelerimiden ~ işaretini kaldırarak yaıyoru ve dış disk çöümlerine geçiyoru. Bu noktadan sonra 15
30 durağan durum standard dış disk çöümlerini elde etmek amaçlı kullanacağımı denklem seti boyutsudur. Aşağıdaki iki ek varsayıma [Regev, 1983] göre boyutsulaştırılmış disk denklemleri eşitlikleri ile verilmektedir. Disk geometrik olarak incedir, H t /r in 1. Diskteki viskoite çalkantılı olup, α modeli ile verilmektedir, ν = αc s H [Shakura ve Sunyaev, 1973]. ɛ 2 v r v r r + ɛv r Ω2 r = 1 p ɛ2 ρ r 1 r ɛ2 2 r, 2.9) 2 v ɛv r r + v v = 1 ρ p r ɛ2 3 r 5, 2.10) ɛ v r r 2 Ω ) Ω + v r 2 r = 1 αɛ2 νρr 2 Ω ), 2.11) ρr 3 r r ɛ 1 r r rρv r) + ρv ) = 0, 2.12) ve rσv r = ɛµṁ 2.13) ) T β g ρc v ɛv r r + v T [ = p η ɛ 1 r [ ɛ 2 1 r r rv r) + v r rf r ) + F ] ) 2 Ω + ανρr 2 r ]. 2.14) Diskin geometrik olarak ince olması görüldüğü üere denklemlerimie yeni bir parametre olan ɛ parametresinin girişini sağlamıştır ɛ = H t /r in 1). Boyutsulaştırılmış niceliklerimiden yeni katsayılar gelmektedir. Bunlardan ga basıncı, radyasyon basıncı, ve bu basınçların tipik basınç değerlerine oranı olan β g ve β r η = βλ, λ = 4c/c s κρh)) sayılabilir. Durağan durum dış disk çöümlerini bulmak için temel disk parametrelerine Ω = Ω 0 + ɛω 1 + ɛ 2 Ω ) şeklinde pertürbatif açılım uyguluyoru ve diskin dış bölgeleri için sıfırıncı mertebeden durağan durum çöümlerini elde ediyoru Bkn EK C). Diskin en dış bölgesi olan C bölgesinde ga basıncı radyasyon basıncına, serbest-serbest opaklık ise elektron saçılma opaklığına baskındır p t,gpd p t,rpd, κ ff,t κ es ). C bölgesi durağan durum standard disk çöümleri; 16
31 Ω out r) = r 3/2, 2.16) ) µ 2 1/10 T out r) = α 1/5 Ṁ 3/10 r 3/4 1 Cr 1/2) 3/10, 2.17) 3η Σ out r) = 2 µ7/10 η 1/10 3 9/10 α 4/5 Ṁ 7/10 r 3/4 1 Cr 1/2) 7/10, 2.18) p out r) = 2 µ9/10 3 α 1 Ṁr 3/2 1 Cr 1/2), 2.19) ) µ 2 1/20 c s,out r) = α 1/10 Ṁ 3/20 r 3/8 1 Cr 1/2) 3/20, 2.20) 3η ) µ 2 1/20 H out r) = α 1/10 Ṁ 3/20 r 3/4 1 Cr 1/2) 3/20, 2.21) 3η ve ρ out r) = µ3/5 η 3/ /20 α 7/10 Ṁ 11/20 r 3/2 1 Cr 1/2) 11/ ) v r,out r) = 39/10 µ 3/10 2η 1/10 α 4/5 Ṁ 3/10 r 1/4 1 Cr 1/2) 7/ ) şeklindedir. Burada C katsayısı açısal momentum transferinin verimliliği katsayısı olup korunum denklemlerinin integre edilmesi ile gelen boyutsu bir katsayıdır. B bölgesi diskin orta bölgesi olmakla beraber ga basıncı radyasyon basıncına, elektron saçılma opaklığı ise serbest-serbest opaklığa baskındırp t,gpd p t,rpd, κ es κ ff,t ). B bölgesi durağan durum standard disk çöümleri; Ω out r) = r 3/2, 2.24) ) µ 2 1/5 T out r) = α 1/5 Ṁ 2/5 r 9/10 1 Cr 1/2) 2/5, 2.25) 2η Σ out r) = 26/5 µ 3/5 η 1/5 α 4/5 Ṁ 3/5 r 3/5 1 Cr 1/2) 3/5, 2.26) 3 p out r) = 21/10 µ 4/5 η 1/10 α 9/10 Ṁ 4/5 r 51/20 1 Cr 1/2) 4/5, 2.27) 3 17
32 ) µ 2 1/10 c s,out r) = α 1/10 Ṁ 1/5 r 9/20 1 Cr 1/2) 1/5, 2.28) 2η ) µ 2 1/10 H out r) = α 1/10 Ṁ 1/5 r 21/20 1 Cr 1/2) 1/5, 2.29) 2η ve ρ out r) = 23/10 µ 2/5 η 3/10 α 7/10 Ṁ 2/5 r 33/20 1 Cr 1/2) 2/ ) ) µ 2 1/5 v r,out r) = 3 α 4/5 Ṁ 2/5 r 2/5 1 Cr 1/2) 3/5 2η 2.31) şeklindedir. A bölgesi diskin en iç bölgesidir ve radyasyon basıncı ga basıncına, elektron saçılma opaklığı ise serbest-serbest opaklığa göre baskındır p t,rpd p t,gpd κ es κ ff,t ). A bölgesi durağan durum standard disk çöümleri; Ω out r) = r 3/2, 2.32) T out r) = ) 1/4 2η α 1/4 r 3/8, 2.33) 9 ρ out r) = 8η3 81µ 2 α 1 Ṁ 2 r 3/2 1 Cr 1/2) 2, 2.34) Σ out r) = 8η2 27µ α 1 Ṁ 1 r 3/2 1 Cr 1/2) 1, 2.35) H out r) = 3µ 2η Ṁ 1 Cr 1/2), 2.36) c s,out r) = 3µ 2η Ṁr3/2 1 Cr 1/2), 2.37) ve p out r) = 2µ 3 α 1 Ṁr 3/2 1 Cr 1/2) 2.38) v r,out r) = 27µ2 8η 2 αṁ 2 r 5/2 1 Cr 1/2) 2.39) şeklindedir. En iç diskte Kepler olmayan sınır bölgesi ya da sınır tabakasındaki basınç, açısal hı, sıcaklık ve ışınım akısı gradientlerini belirleyebilmek için eşitlikler için pertürbatif açılımlar aracılığıyla sıfırıncı mertebeden çöümler arıyoru. Daha 18
33 sonra geometrik olarak ince disk varsayımımıa uygun olarak denklemlerimii, düşey yönde integre ederek disk parametrelerinin yönündeki ortalamasını alıyoru. Düşey yönde integre edilmiş basınç ifadesi P = ˆ H H pd = 2Hp 2.40) diferansiyel denklem setimide görülebilir. Sınır bölgesi diskin en iç yarıçapına oranla çok daha ince bir bölge olduğundan dolayı, dış disk çöümlerinde kullanmış olduğumu radyal koordinatı r = 1 + δ ε) R olarak genişletiyoru. Bu sayede sınır bölgesinde disk parametrelerindeki ani değişimleri daha rahat gölemleme imkanı elde etmiş olacağı. Radyal momentum denklemine göre δ ε) = ε 2 seçiyoru. Momentum korunumunun r ve φ bileşenleri ve enerji korunumuna ek olarak ışınım akısının tanımı ile birlikte sınır bölgesindeki fiiksel nicelikler için çöülmesi gereken sıradan diferansiyel denklem seti aşağıdaki gibi yaılabilir: dp dr = Σ Ω 2 1 ), 2.41) ve d 2 Ω dr + 1 dω 2 α BL dr dφ dr = µṁα BL 2η = 0, 2.42) dω dr ) ) dt dr = 1 2 κσt 4 Φ. 2.44) Yukarıdaki denklem seti kullanılarak GPD ve RPD rejimlerinde sınır koşulları dikkate alındığında kh QPO frekans bandlarımıı oluşturacak diskin serbest salınım frekansları, denklem 2.42 nin çöümü olan Ω in R) = 1 1 ω) exp R ) α BL 2.45) ifadesine bağlı olarak analitik, geriye kalan disk parametrelerinin çöümleri ise nümerik hesaplanacaktır. Şekil 2.1, 2.2 ve 2.3 te GPD ve RPD rejimlerinde durağan durum birleşik disk çöümlerinden örnekler görülmektedir. Sınır bölgesi diferansiyel denklem setinin RPD rejimi için olan çöümünde iki farklı sayısal çöümün varolduğu görülmüştür. RPD rejiminde sınır bölgesinden diskin iç yarıçapına doğru gidildikçe disk parametrelerinde çöümlere bağlı olarak artış veya aalma görülebilir. 19
34 T log1+r) Σ log1+r) ω=ω/ω K r in ) log1+r) Şekil 2.1: GPD genel durağan durum disk çöümleri örnekleri. Şekil 2.1 GPD rejiminde sırasıyla durağan durum genel sıcaklık, yüey yoğunluğu, açısal hı çöümlerini göstermektedir. Nötron yıldıının kütlesi 1.4M, yarıçapı 10 km, manyetik alanı 2.86x10 8 G, sıcaklığın tipik değeri 1.5x10 7 K, yüey yoğunluğunun tipik değeri 5.3x10 5 g/cm 2, açısal dönme frekansının tipik değeri 322 H, gas basıncının radyasyom basıncına oranı 14.83, gerçek optik derinlik yaklaşık olarak 2000, dış disk vikosite katsayısı , sınır bölgesi vikosite katsayısı 17, dış disk çöümlerinden gelen C katsayısı olup yıldı üerine saniyede akan tipik kütle miktarı 2x10 17 g/s, disk iç yarıçapı 3.57x10 6 cm, en iç diskin dönme hıının Kepler dönme hıına oranı 0.93 tür. Yıldıın dönme frekansı ν = 300 H dir. 20
35 T log1+r) Σ log1+r) ω=ω/ω K r in ) log1+r) Şekil 2.2: RPD genel durağan durum disk çöümleri örnekleri 1. Tip). Şekil 2.1 RPD rejiminde sırasıyla durağan durum genel sıcaklık, yüey yoğunluğu, açısal hı çöümlerini göstermektedir. Nötron yıldıının kütlesi 1.4M, yarıçapı 10 km, manyetik alanı 6.5x10 8 G, sıcaklığın tipik değeri 3.87x10 7 K, yüey yoğunluğunun tipik değeri 5.9x10 3 g/cm 2, açısal dönme frekansının tipik değeri 428 H, gas basıncının radyasyom basıncına oranı 80, gerçek optik derinlik yaklaşık olarak 5, dış disk vikosite katsayısı 0.097, sınır bölgesi vikosite katsayısı 1, dış disk çöümlerinden gelen C katsayısı 0.81 olup yıldı üerine saniyede akan tipik kütle miktarı 2x10 17 g/s, disk iç yarıçapı 2.95x10 6 cm, en iç diskin dönme hıının Kepler dönme hıına oranı 0.7 dir. Yıldıın dönme frekansı ν = 300 H dir. 21
36 T log1+r) Σ log1+r) ω=ω/ω K r in ) log1+r) Şekil 2.3: RPD genel durağan durum disk çöümleri örnekleri 2. Tip). Şekil 2.1 RPD rejiminde sırasıyla durağan durum genel sıcaklık, yüey yoğunluğu, açısal hı çöümlerini göstermektedir. Nötron yıldıının kütlesi 1.4M, yarıçapı 10 km, manyetik alanı 6.5x10 8 G, sıcaklığın tipik değeri 3.87x10 7 K, yüey yoğunluğunun tipik değeri 5.9x10 3 g/cm 2, açısal dönme frekansının tipik değeri 428 H, gas basıncının radyasyom basıncına oranı 80, gerçek optik derinlik yaklaşık olarak 5, dış disk vikosite katsayısı 0.096, sınır bölgesi vikosite katsayısı 1, dış disk çöümlerinden gelen C katsayısı 0.89 olup yıldı üerine saniyede akan tipik kütle miktarı 2x10 17 g/s, disk iç yarıçapı 2.95x10 6 cm, en iç diskin dönme hıının Kepler dönme hıına oranı 0.7 dir. Yıldıın dönme frekansı ν = 300 H dir. 22
37 2.3 Paralel İ Probleminin Açıklanması Paralel i probleminin açıklanmasına Bölüm 2.2 de elde ettiğimi durağan durum standard disk çöümlerindeki Kepler olmayan sınır bölgesi dönme frekansı eşitlik 2.45) ile belirlenen radyal episiklik frekans ifadesindeki serbest parametrelerin kh QPO frekanslarına nasıl etki ettiğini inceleyerek başlayacağı. Eşitlik 2.45 i Eşitlik 1.1 de yerine koyup [ κ r in ) = Ω K r in ) 2ω 2ω ω )] 1/2 2.46) α BL ε 2 radyal episiklik frekansı için diskin en iç yarıçapındaki çöümü elde etmiş oluyoru. Bu çöüm fark frekansı olan Ω r in ) ile birlikte bie kh QPO çiftlerimii verecektir. Eşitlik 2.46 içerisindeki ε ve α BL gibi serbest parametrelerdeki değişimlerin frekanslar üerindeki etkisini Şekil 2.4 te görmektesini ν ν a M/10 18 g/s M/10 18 g/s b 800 ν c M/10 18 g/s Şekil 2.4: Radyal episiklik frekans çöümündeki serbest parametrelerin alt kh QPO frekansları üerindeki etkisi. Serbest parametrelerin a) sabit olduğu α BL = 30, ε = 0.08, b) aaldığı α BL = [50, 40], ε = [0.08, 0.07] ve c) arttığı α BL = [40, 50], ε = [0.07, 0.08] durumlarda, serbest parametrelerin Ṁ arttıkça alt kh QPO frekansları üerindeki etkisini görmektesini. Serbest parametrelerin kh QPO frekansları üerindeki etkisi sonucu yakaladığımı eğilim öellikle Şekil 2.5 te verilen 4U nötron yıldıı kaynağının gölemlenmiş kh QPO - X-ışın akısı korelasyonuna oldukça benemektedir. 23
38 Şekil 2.5: 4U , 4U , 4U ve Aql X-1 nötron yıldıı kaynaklarından gölemlenmiş kh QPO - X-ışın akısı ilişkisi. Ayrı renklerle gösterilen datalar ayrı gölem amanlarına karşılık gelmektedir. İlginç bir ayrıntı da en geniş X-ışın foton akısı aralığına sahip 4U kaynağının bener X-ışın foton akısı aralıklarında diğer kaynakların davranışlarını taklit edebiliyor olmasıdır. Aql X-1 hariç diğer bütün kaynaklardaki kh QPO frekans verileri alt kh QPO frekanslarıdır. Aql X-1 kaynağının kh QPO frekansları çift olarak gölemlenememiştir [Mende, 2000]. Şekil 2.5 te gösterilen paralel i olayını detaylı açıklamak için şekil üerinden QPO frekans verileri toplanmıştır. X-ışın foton akısı dolayısıyla X-ışın akısı parlaklığa 4πd 2 f = L x GM Ṁ R 2.47) şeklinde bağlı olduğundan X-ışın akısı ve kütle aktarım hıı arasında f Ṁ 2.48) ilişkisi vardır. Bu ilişkiye dayanarak X-ışın akılarının kütle aktarım hıı ile orantılı 24
39 olması beklenir. Kaynakların uaklık ölçümleri ortak değerler veremediğinden yapılan çalışmalar arasındaki farklılıklar X-ışın parlaklığı için önemli olabilmektedir. Bu çalışmada göstereceğimi örneklerde her kaynak için kütleyi 1.4M, yarıçapı 10 km aldık. Kütle aktarım hıını ise Şekil 2.5 te en geniş X-ışın foton akısı aralığında gölemlenen 4U kaynağını temel alarak, X-ışın foton akısındaki 400 değerini kütle aktarım hıında g/s ye denk gelecek şekilde orantı 2.48 ye göre modelledik. Diğer kaynaklar içinde bu ilişkiyi göönünde bulundurarak kütle aktarım hılarını hesapladık. Burada açısal dönme hıı çöümünden gelen α BL ve ε 2 çarpımına tek bir serbest gibi davranmayacak ve ayrı tutacak olmamı, α BL katsayısı hakkında bilgimi olmaması ve modelimi çerçevesinde bu katsayı ile ilgili bir açıklama getiremeyecek olmamı fakat disk kalınlık parametresinin kütle aktarım hıı ile nasıl değiştiğini modelleyebilecek olmamıdan kaynaklanmaktadır. Eşitlik 2.46 deki iki serbest paramet remiden sınır bölgesi vikosite katsayısı hakkında herhangi bilgimi olmamasından ötürü bu değişkeni 1 mertebesinde bir sabit alarak frekanslar üerindeki etkisini en aa düşüreceği. Öte yandan disk kalınlık parametresini ince disk yaklaşımına uygun olması için 0.1 in altında salındırarak ve hılılık parametresini Kepler altı sınır bölgesi ile tutarlı olmak amacıyla 1 in altında tutarak, Şekil 2.5 üerinden topladığımı veriyi örnek kaynaklarımı için tekrardan elde etmeye çalışacağı. Gölemlenmiş frekans - X-ışın foton akısı ilişkisini teorik olarak modelleme sürecine radyal episiklik frekansı veren eşitlik 2.46 i aşağıdaki gibi hatırlayarak başlıyoru. [ κ r in ) = Ω K r in ) 2ω 2ω ω )] 1/2 α BL ε 2 Elimide Şekil 2.5 teki her veri noktası için frekans ve kütle aktarım hıı değerleri bulunmaktadır. Örnek nötron yıldıımı için kütle ve yarıçap değerlerimi seçilmişti. Mümkün olan en küçük sınır bölgesi vikosite katsayısı α BL ve uygun bir manyetik alan için en iç yarıçapı hesaplayabiliri. Dolayısıyla Kepler dönme hıı ve hılılık parametresinin ne olduğunu hesaplayabiliri. Artık elimide bilinmeyen olarak kalan tek parametre disk kalınlık parametresidir. Disk kalınlık parametresini modelimi dahilinde her veri noktası için tek tek hesapladıktan sonra, disk kalınlık parametresi ve hılılık parametresinin üst sınır koşulları ε < 0.1 ve ω < 1.0 gö önünde bulundurularak bütün veri noktalarını tek tek kopyalayabilecek uygun parametre değerleri bulunabilmektedir. Burada örnek teşkil etmesi açısından X-ışın foton akısı oran 2.48 ye göre g/s ile ölçeklendirilmiştir. Aynı işlemler daha düşük ve daha yüksek kütle aktarım oranları için de tekrarlanabilir. 25
40 ν U U ν U Aql X m m Şekil 2.6: Şekil 2.5 üerinden alınan verilerin teorik modelimi çerçevesinde yeniden oluşturulması. Paralel i verileri X-ışın akısı yerine kütle aktarım hıının fonksiyonu olarak, alt kh QPO frekansları için disk kalınlık parametresinin, ε, teorik modelimi kapsamında salındırılması ile tekrardan oluşturuldu ṁ = Ṁ/1018 g/s). Şekil 2.6 nın yeniden oluşturulması sürecinde salındırılan disk kalınlık parametresinin öngörülen kütle aktarım hıı aralığında nasıl değiştiğini Şekil 2.7 de görebilirsini. Dü çigi ile gösterilen fit fonksiyonu [Shakura and Sunyaev, 1973] radyasyon basıncının baskın olduğu A bölgesinde yarı disk kalınlığı çöümü olan eşitlik 2.36 ile verilen yarı disk kalınlığının disk iç yarıçapındaki değeri ile elde edilmiştir. Ölçek parametreleri a ve H 0 kullanılarak H t = ah ss ± H ) yaılabilir. Burada ṁ = Ṁ/ 1018 g/s) ve r A,18 = r A Ṁ=10 18 g/s tanımlamaları altında A bölgesi yarı disk kalınlığının boyutlu ifadesi 26
41 H ss = 3 κ T 8π c Ṁ Ṁ 18 = 3 κ T 8π c ṁṁ18 ) Ṁ 18 [ [ 1 C 1 C rin r Sch rin r Sch ) 1/2 ] ) 1/2 ] 2.50) olup, diskin en iç yarıçapı r in = GM ) 1/7 Ṁ 2/7 B R ) 4/7 = GM ) 1/7 ṁ 2/7 Ṁ 2/7 18 B R ) 4/7 = r A,18 ṁ 2/7 2.51) şeklinde yaılarak ε için için fit fonksiyonu boyutsu tipik kütle yığışma hıı ṁ cinsinden ε = H t r in = aaṁ 9/7 abṁ 10/7 ± H 0 r A,18 ṁ 2/7 2.52) olarak yaılabilir. Böylece disk kalınlığının kütle aktarımı ile değişimi modellemiş oluyoru. 27
42 U U a=0.26 H 0 =0.8 km C=0.88 a=7.8 H 0 =-7.75 km C=0.814 ε U Aql X-1 a=3.97 H 0 =-1.68 km C= a=13.56 H 0 =-12.8 km C= ṁ Şekil 2.7: kh QPO frekanslarını tekrardan üretmek için salındırılan disk kalınlık parametresinin kütle aktarım hıı ile değişimi. Şekil 2.5 te paralel i verilerini tekrardan oluşturmak için salındırdığımı disk kalınlık parametresinin kütle aktarım hıı ile değişimine radyasyon basıncının dominant olduğu disk yarı kalınlığı çöümünü kullanarak fiiksel fit yaptık. Şekil 2.7 de, Şekil 2.6 dan toplanan kh QPO verilerini Şekil 2.5 te modelimi kapsamında tekrardan elde ederken kullandığımı disk kalınlık parametresi değerlerinin, diskteki kütle aktarım hıına bağlı değişimi görülmektedir. Disk kalınlık parametresi standart disk çöümlerinden gelen eşitlik 2.52 ün tahmin ettiği eğilimde değişmektedir. Bu sonuç kh QPO frekansları ile X-ışın akısı arasında büyük aman ölçeklerinde belirli bir korelasyon olmamasına dair getirdiğimi olası açıklama olan büyük aman ölçeklerindeki gölemlerde kh QPO frekanslarının diskteki kütle aktarım hıının dışında ikinci bir parametreye de bağlılık gösterebileceğini desteklemektedir. Nötron yıldıı LMXB lerinin amanlama ve parlaklık korelasyonlarına muhtemel açıklamalar getirdikten sonra sırada bu kaynakların amanlama öelliklerinin tayfsal öelliklerle 28
43 olan ilişkisine bakacağı. a b c d Şekil 2.8: 4 kaynağın kh QPO - S a ilişkisi. Şekil 2.8 de a) 4U [Mende v.d., 1999], b) 4U [Di Salvo v.d., 2003], c) 4U [Mende ve van der Klis, 1999], d) Aql X-1 [Reig v.d., 2000] kaynaklarının kh QPO k.g. X-ışın renk-renk diyagramı poisyon parametresi arasındaki lineer korelasyonunu görmektesini. Şekil 1.5 te 4U kaynağı için belirtildiği üere alt ve üst kh QPO frekansları ile, X-ışın renk-renk diyagramının konum parametresi S a arasında korelasyon vardır. Bu ilişkiye modelimi dahilinde olası bir açıklama getirmek için kh QPO frekanslarımıın değerlerini belirleyen eşitlik 2.46 yı aşağıda gösterildiği üere iki kısma ayırıyoru. Öncelikle Ω K r in ) = GM r in ) 1/2 = GM ) 5/7 Ṁ 3/7 B R ) 6/7, 2.53) ve ν ν burst = GM r 3 co 2.54) 29
Yıldızların: Farklı renkleri vardır. Bu, onların farklı sıcaklıklarda olduklarını gösterir. Daha sıcak yıldızlar, ömürlerini daha hızlı tüketirler.
 Yıldızların Hayatı Yıldızların: Farklı renkleri vardır Bu, onların farklı sıcaklıklarda olduklarını gösterir Daha sıcak yıldızlar, ömürlerini daha hızlı tüketirler. Yıldız Oluşum Bölgeleri Evren, yıldız
Yıldızların Hayatı Yıldızların: Farklı renkleri vardır Bu, onların farklı sıcaklıklarda olduklarını gösterir Daha sıcak yıldızlar, ömürlerini daha hızlı tüketirler. Yıldız Oluşum Bölgeleri Evren, yıldız
İZOKRONLAR İLE YAŞ TAYİNİ NURTEN FİLİZ
 T.C. ÇANAKKALE ONSEKİZ MART ÜNIVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ FİZİK ANABİLİM DALI YÜKSEK LİSANS SEMİNERİ İZOKRONLAR İLE YAŞ TAYİNİ NURTEN FİLİZ DANIŞMAN Prof. Dr. Zeki EKER İzokronlar ile Yaş Tayini
T.C. ÇANAKKALE ONSEKİZ MART ÜNIVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ FİZİK ANABİLİM DALI YÜKSEK LİSANS SEMİNERİ İZOKRONLAR İLE YAŞ TAYİNİ NURTEN FİLİZ DANIŞMAN Prof. Dr. Zeki EKER İzokronlar ile Yaş Tayini
BEYAZ CÜCELER, C CELER, NÖTRON YILDIZLARI VE KARADELİKLER
 BEYAZ CÜCELER, C CELER, NÖTRON YILDIZLARI VE KARADELİKLER KLER BEYAZ CÜCELER, NÖTRON YILDIZLARI VE KARADELİKLER, EVRİMLERİNİN SON SAFHALARINDA OLAN YILDIZLARDIR. BİR YILDIZ ANAKOLDAKİ EVRİMİ BOYUNCA, ÇEKİRDEĞİNDEKİ
BEYAZ CÜCELER, C CELER, NÖTRON YILDIZLARI VE KARADELİKLER KLER BEYAZ CÜCELER, NÖTRON YILDIZLARI VE KARADELİKLER, EVRİMLERİNİN SON SAFHALARINDA OLAN YILDIZLARDIR. BİR YILDIZ ANAKOLDAKİ EVRİMİ BOYUNCA, ÇEKİRDEĞİNDEKİ
GÜNEŞİMİZ. Ankara Üniversitesi Kreiken Rasathanesi
 GÜNEŞİMİZ Ankara Üniversitesi Kreiken Rasathanesi Genel Özellikleri Çapı ~ 700000 km Yer in çapının 109 katı Kütlesi: 1.99x10 33 gram Yer in kütlesinin 333000 katı Gaz yapılıdır (Ort. yoğunluk = 1.4 g/cm
GÜNEŞİMİZ Ankara Üniversitesi Kreiken Rasathanesi Genel Özellikleri Çapı ~ 700000 km Yer in çapının 109 katı Kütlesi: 1.99x10 33 gram Yer in kütlesinin 333000 katı Gaz yapılıdır (Ort. yoğunluk = 1.4 g/cm
AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DOKÜMANI
 AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DOKÜMANI Öğrenci Numarası: I. / II. Öğretim: Adı Soyadı: İmza: HAFTA 10 1. KONU: YILDIZ EVRİMİ 2. İÇERİK Yıldız Oluşumu Virial Teoremi, Jeans Kütlesi Zaman
AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DOKÜMANI Öğrenci Numarası: I. / II. Öğretim: Adı Soyadı: İmza: HAFTA 10 1. KONU: YILDIZ EVRİMİ 2. İÇERİK Yıldız Oluşumu Virial Teoremi, Jeans Kütlesi Zaman
Düşük Kütleli X-ışını Çiftlerindeki X-ışını Atarcalarının Zamanlama Özellikleri. Sıtkı Çağdaş İnam Başkent Üniversitesi
 Düşük Kütleli X-ışını Çiftlerindeki X-ışını Atarcalarının Zamanlama Özellikleri Sıtkı Çağdaş İnam Başkent Üniversitesi «X-ışını Atarcası İçeren Düşük Kütleli X-ışını Çifti» Eş Yıldız ( 1M ) X-ışını Atarcası
Düşük Kütleli X-ışını Çiftlerindeki X-ışını Atarcalarının Zamanlama Özellikleri Sıtkı Çağdaş İnam Başkent Üniversitesi «X-ışını Atarcası İçeren Düşük Kütleli X-ışını Çifti» Eş Yıldız ( 1M ) X-ışını Atarcası
Yıldızların Yapısı ve Evrimi. Anakol Sonrası Evrim
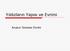 Yıldızların Yapısı ve Evrimi Anakol Sonrası Evrim Anakol Evriminin Sonu Anakolda yıldız hidrostatik dengede ve çekirdekte hidrojenini yakıp helyuma çevirecek yeterli sıcaklığa sahip. Şimdi yıldız kimyasal
Yıldızların Yapısı ve Evrimi Anakol Sonrası Evrim Anakol Evriminin Sonu Anakolda yıldız hidrostatik dengede ve çekirdekte hidrojenini yakıp helyuma çevirecek yeterli sıcaklığa sahip. Şimdi yıldız kimyasal
TAŞINIMIN FİZİKSEL MEKANİZMASI
 BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
Yıldızlara gidemeyiz; sadece onlardan gelen ışınımı teleskopların yardımıyla gözleyebilir ve çözümleyebiliriz.
 Yıldızlara gidemeyiz; sadece onlardan gelen ışınımı teleskopların yardımıyla gözleyebilir ve çözümleyebiliriz. Işık genellikle titreşen elektromanyetik dalga olarak düşünülür; bu suda ilerleyen dalgaya
Yıldızlara gidemeyiz; sadece onlardan gelen ışınımı teleskopların yardımıyla gözleyebilir ve çözümleyebiliriz. Işık genellikle titreşen elektromanyetik dalga olarak düşünülür; bu suda ilerleyen dalgaya
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
Fen ve Mühendislik Bilimleri için Fizik
 Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Genç Nötron Yıldızlarının Yayılma Diskleriyle Evrimi
 Genç Nötron Yıldızlarının Yayılma Diskleriyle Evrimi Ünal Ertan, Şirin Çalışkan, Onur Benli, M.Ali Alpar Sabancı Üniversitesi UAK 2015 (2-6 Şubat 2015, ODTÜ, Ankara) GENÇ NÖTRON YILDIZI SİSTEMLERİ : -
Genç Nötron Yıldızlarının Yayılma Diskleriyle Evrimi Ünal Ertan, Şirin Çalışkan, Onur Benli, M.Ali Alpar Sabancı Üniversitesi UAK 2015 (2-6 Şubat 2015, ODTÜ, Ankara) GENÇ NÖTRON YILDIZI SİSTEMLERİ : -
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
Fen ve Mühendislik Bilimleri için Fizik
 Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Kütle Aktarımı Yapan Nötron Yıldızlarının Gözlemsel Özellikleri. Sıtkı Çağdaş İnam Doç.Dr. - Başkent Üniversitesi
 Kütle Aktarımı Yapan Nötron Yıldızlarının Gözlemsel Özellikleri Sıtkı Çağdaş İnam Doç.Dr. - Başkent Üniversitesi KAYNY İçeren Sistem Nötron Yıldızı İçeren X-ışını Çifti Eş Yıldız Nötron Yıldızı UAK 2015-ÇB-S.Ç.İnam
Kütle Aktarımı Yapan Nötron Yıldızlarının Gözlemsel Özellikleri Sıtkı Çağdaş İnam Doç.Dr. - Başkent Üniversitesi KAYNY İçeren Sistem Nötron Yıldızı İçeren X-ışını Çifti Eş Yıldız Nötron Yıldızı UAK 2015-ÇB-S.Ç.İnam
UBT Foton Algılayıcıları Ara Sınav Cevap Anahtarı Tarih: 22 Nisan 2015 Süre: 90 dk. İsim:
 UBT 306 - Foton Algılayıcıları Ara Sınav Cevap Anahtarı Tarih: 22 Nisan 2015 Süre: 90 dk. İsim: 1. (a) (5) Radyoaktivite nedir, tanımlayınız? Bir radyoizotopun aktivitesi (A), izotopun birim zamandaki
UBT 306 - Foton Algılayıcıları Ara Sınav Cevap Anahtarı Tarih: 22 Nisan 2015 Süre: 90 dk. İsim: 1. (a) (5) Radyoaktivite nedir, tanımlayınız? Bir radyoizotopun aktivitesi (A), izotopun birim zamandaki
Newton un ikinci yasası: Bir cisim ivmesi cisim üzerine etki eden toplam kuvvet ile doğru orantılı cismin kütlesi ile ters orantılıdır.
 Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
tayf kara cisim ışınımına
 13. ÇİZGİ OLUŞUMU Yıldızın iç kısımlarından atmosfere doğru akan ışınım, dalga boyunun yaklaşık olarak sürekli bir fonksiyonudur. Çünkü iç bölgede sıcaklık gradyenti (eğimi) küçüktür ve madde ile ışınım
13. ÇİZGİ OLUŞUMU Yıldızın iç kısımlarından atmosfere doğru akan ışınım, dalga boyunun yaklaşık olarak sürekli bir fonksiyonudur. Çünkü iç bölgede sıcaklık gradyenti (eğimi) küçüktür ve madde ile ışınım
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Evrende Var Olan Yıldız Türleri
 Evrende Var Olan Yıldız Türleri Yıldızlar da, evrende var olan her şey, hatta canlı varlıklar gibi türlere ayrılırlar. Yıldız türleri, doğum anındaki kütlesinden tutun da, ömür sürecindeki değişimlere
Evrende Var Olan Yıldız Türleri Yıldızlar da, evrende var olan her şey, hatta canlı varlıklar gibi türlere ayrılırlar. Yıldız türleri, doğum anındaki kütlesinden tutun da, ömür sürecindeki değişimlere
MIT Açık Ders Malzemeleri Fizikokimya II 2008 Bahar
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri Fizikokimya II 2008 Bahar
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
ÇEV-220 Hidrolik. Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT
 ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Türbülanslı Akış Mühendislik uygulamalarında akışların çoğu türbülanslıdır ve bu yüzden türbülansın
ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Türbülanslı Akış Mühendislik uygulamalarında akışların çoğu türbülanslıdır ve bu yüzden türbülansın
DENEY 4 ÇARPIŞMALAR VE LİNEER MOMENTUMUN KORUNUMU
 DENEY 4 ÇARPIŞMALAR VE LİNEER MOMENTUMUN KORUNUMU AMAÇ: Deneyin amacı esnek ve esnek olmayan çarpışmalarda lineer momentum ve kinetik enerji korunumunu incelemektir. GENEL BİLGİLER: Bir nesnenin lineer
DENEY 4 ÇARPIŞMALAR VE LİNEER MOMENTUMUN KORUNUMU AMAÇ: Deneyin amacı esnek ve esnek olmayan çarpışmalarda lineer momentum ve kinetik enerji korunumunu incelemektir. GENEL BİLGİLER: Bir nesnenin lineer
HİDROLİK. Yrd. Doç. Dr. Fatih TOSUNOĞLU
 HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
Fizik 101-Fizik I 2013-2014. Dönme Hareketinin Dinamiği
 -Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
-Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
MIT 8.02, Bahar 2002 Ödev # 6 Çözümler
 Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 6 Çözümler 5 Nisan 2002 Problem 6.1 Dönen Bobin.(Giancoli 29-62) Bobin, yüzü manyetik alana dik olarak başlar (daha bilimsel konuşmak gerekirse,
Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 6 Çözümler 5 Nisan 2002 Problem 6.1 Dönen Bobin.(Giancoli 29-62) Bobin, yüzü manyetik alana dik olarak başlar (daha bilimsel konuşmak gerekirse,
EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ
 EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ Giriş Isı değiştiricileri (eşanjör) değişik tiplerde olup farklı sıcaklıktaki iki akışkan arasında ısı alışverişini temin ederler. Isı değiştiricileri başlıca yüzeyli
EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ Giriş Isı değiştiricileri (eşanjör) değişik tiplerde olup farklı sıcaklıktaki iki akışkan arasında ısı alışverişini temin ederler. Isı değiştiricileri başlıca yüzeyli
X Işın Çiftleri Bir x-ışın çiftinin ışınım özelliklerini belirleyen faktörler
 X Işın Çiftleri X Işın Çiftleri Bir x-ışın çiftinin ışınım özelliklerini belirleyen faktörler Baş yıldızın bir kara delik mi yoksa bir nötron yıldızı mı olduğu Eğer bir nötron yıldızı ise manyetik alanının
X Işın Çiftleri X Işın Çiftleri Bir x-ışın çiftinin ışınım özelliklerini belirleyen faktörler Baş yıldızın bir kara delik mi yoksa bir nötron yıldızı mı olduğu Eğer bir nötron yıldızı ise manyetik alanının
Büyük Patlama ve Evrenin Oluşumu. Test 1 in Çözümleri
 7 Büyük Patlama ve Evrenin Oluşumu 225 Test 1 in Çözümleri 1. Elektrikçe yüksüz parçacıklar olan fotonların kütleleri yoktur. Işık hızıyla hareket ettikleri için atom içerisinde bulunamazlar. Fotonlar
7 Büyük Patlama ve Evrenin Oluşumu 225 Test 1 in Çözümleri 1. Elektrikçe yüksüz parçacıklar olan fotonların kütleleri yoktur. Işık hızıyla hareket ettikleri için atom içerisinde bulunamazlar. Fotonlar
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
SU Lise Yaz Okulu. Samanyolu ve Diğer Gökadalar
 SU Lise Yaz Okulu Samanyolu ve Diğer Gökadalar Samanyolu Gökadamız kendi kütleçekimi al1nda dengeli, milyarlarca yıldız, gaz ve tozdan oluşan bir yapıdır. Biz gökadamızı gökyüzünde bir kolon halinde görürüz.
SU Lise Yaz Okulu Samanyolu ve Diğer Gökadalar Samanyolu Gökadamız kendi kütleçekimi al1nda dengeli, milyarlarca yıldız, gaz ve tozdan oluşan bir yapıdır. Biz gökadamızı gökyüzünde bir kolon halinde görürüz.
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI Tanım
 2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları
 1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları Sol üstte yüzey seftleştirme işlemi uygulanmış bir çelik
1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları Sol üstte yüzey seftleştirme işlemi uygulanmış bir çelik
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
Doç. Dr. Sabri KAYA Erciyes Üni. Müh. Fak. Elektrik-Elektronik Müh. Bölümü. Ders içeriği
 ANTENLER Doç. Dr. Sabri KAYA Erciyes Üni. Müh. Fak. Elektrik-Elektronik Müh. Bölümü Ders içeriği BÖLÜM 1: Antenler BÖLÜM 2: Antenlerin Temel Parametreleri BÖLÜM 3: Lineer Tel Antenler BÖLÜM 4: Halka Antenler
ANTENLER Doç. Dr. Sabri KAYA Erciyes Üni. Müh. Fak. Elektrik-Elektronik Müh. Bölümü Ders içeriği BÖLÜM 1: Antenler BÖLÜM 2: Antenlerin Temel Parametreleri BÖLÜM 3: Lineer Tel Antenler BÖLÜM 4: Halka Antenler
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KİNETİK GAZ KURAMI. Doç. Dr. Faruk GÖKMEŞE Kimya Bölümü Hitit Üniversitesi Fen Edebiyat Fakültesi 1
 Kinetik Gaz Kuramının Varsayımları Boyle, Gay-Lussac ve Avagadro deneyleri tüm ideal gazların aynı davrandığını göstermektedir ve bunları açıklamak üzere kinetik gaz kuramı ortaya atılmıştır. 1. Gazlar
Kinetik Gaz Kuramının Varsayımları Boyle, Gay-Lussac ve Avagadro deneyleri tüm ideal gazların aynı davrandığını göstermektedir ve bunları açıklamak üzere kinetik gaz kuramı ortaya atılmıştır. 1. Gazlar
Akışkanların Dinamiği
 Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DÖKÜMANI
 AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DÖKÜMANI Öğrenci Numarası: I. / II. Öğretim: Adı Soyadı: İmza: HAFTA 08 1. KONU: TAYFSAL GÖZLEM 1 2. İÇERİK Doppler Etkisi Kirchhoff Yasaları Karacisim Işınımı
AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DÖKÜMANI Öğrenci Numarası: I. / II. Öğretim: Adı Soyadı: İmza: HAFTA 08 1. KONU: TAYFSAL GÖZLEM 1 2. İÇERİK Doppler Etkisi Kirchhoff Yasaları Karacisim Işınımı
BAHAR YARIYILI FİZİK 2 DERSİ. Doç. Dr. Hakan YAKUT. Fizik Bölümü
 2015-2016 BAHAR YARIYILI FİZİK 2 DERSİ Doç. Dr. Hakan YAKUT SAÜ Fen Edebiyat Fakültesi Fizik Bölümü Ofis: FEF A Blok, 3. Kat, Oda No: 812, İş tel.: 6092 (+90 264 295 6092) BÖLÜM 7 MANYETİK ALANLAR 2 İÇERİK
2015-2016 BAHAR YARIYILI FİZİK 2 DERSİ Doç. Dr. Hakan YAKUT SAÜ Fen Edebiyat Fakültesi Fizik Bölümü Ofis: FEF A Blok, 3. Kat, Oda No: 812, İş tel.: 6092 (+90 264 295 6092) BÖLÜM 7 MANYETİK ALANLAR 2 İÇERİK
AKDENİZ ÜNİVERSİTESİ. Anten Parametrelerinin Temelleri. Samet YALÇIN
 AKDENİZ ÜNİVERSİTESİ Anten Parametrelerinin Temelleri Samet YALÇIN Anten Parametrelerinin Temelleri GİRİŞ: Bir antenin parametrelerini tanımlayabilmek için anten parametreleri gereklidir. Anten performansından
AKDENİZ ÜNİVERSİTESİ Anten Parametrelerinin Temelleri Samet YALÇIN Anten Parametrelerinin Temelleri GİRİŞ: Bir antenin parametrelerini tanımlayabilmek için anten parametreleri gereklidir. Anten performansından
Kısa İçindekiler. Fizik: İlkeler ve Pratik Cilt 1: 1-21 Bölümleri, Cilt 2: Bölümleri kapsar
 Kısa İçindekiler Fizik: İlkeler ve Pratik Cilt 1: 1-21 Bölümleri, Cilt 2: 22-34 Bölümleri kapsar Bölüm 1 Temeller 1 Bölüm 2 Bir Boyutta Hareket 28 Bölüm 3 İvme 53 Bölüm 4 Momentum 75 Bölüm 5 Enerji 101
Kısa İçindekiler Fizik: İlkeler ve Pratik Cilt 1: 1-21 Bölümleri, Cilt 2: 22-34 Bölümleri kapsar Bölüm 1 Temeller 1 Bölüm 2 Bir Boyutta Hareket 28 Bölüm 3 İvme 53 Bölüm 4 Momentum 75 Bölüm 5 Enerji 101
2.3 Asimptotik Devler Kolu
 2.3 Asimptotik Devler Kolu 2.3.1 Erken Asimptotik dev kolu 2.3.2 Termal pulsasyon yapan Asimptotik dev kolu 2.3.3 Üçüncü karışım ve Karbon yıldızları 2.3.4 s-süreci nükleosentezi 2.3.5 Kütle kaybı ve AGB
2.3 Asimptotik Devler Kolu 2.3.1 Erken Asimptotik dev kolu 2.3.2 Termal pulsasyon yapan Asimptotik dev kolu 2.3.3 Üçüncü karışım ve Karbon yıldızları 2.3.4 s-süreci nükleosentezi 2.3.5 Kütle kaybı ve AGB
Bize En Yakın Yıldız. Defne Üçer 30 Nisan 2011
 Bize En Yakın Yıldız GÜNEŞ Defne Üçer 30 Nisan 2011 Sayılar sayılar Güneş Kütlesi = 300.000 Dünya Kütlesi Güneş çapı = 110 Dünya çapı Güneş yoğunluğu = Dünya yoğunluğu/4 Güneş Uzaklık= 1 Astronomik Birim
Bize En Yakın Yıldız GÜNEŞ Defne Üçer 30 Nisan 2011 Sayılar sayılar Güneş Kütlesi = 300.000 Dünya Kütlesi Güneş çapı = 110 Dünya çapı Güneş yoğunluğu = Dünya yoğunluğu/4 Güneş Uzaklık= 1 Astronomik Birim
Theory Tajik (Tajikistan)
 Q3-1 Büyük Hadron Çarpıştırıcısı Bu probleme başlamadan önce ayrı bir zarfta verilen genel talimatları lütfen okuyunuz. Bu görevde, CERN de bulunan parçacık hızlandırıcısının LHC ( Büyük Hadron Çarpıştırıcısı)
Q3-1 Büyük Hadron Çarpıştırıcısı Bu probleme başlamadan önce ayrı bir zarfta verilen genel talimatları lütfen okuyunuz. Bu görevde, CERN de bulunan parçacık hızlandırıcısının LHC ( Büyük Hadron Çarpıştırıcısı)
AKM 205-BÖLÜM 2-UYGULAMA SORU VE ÇÖZÜMLERİ
 AKM 205-BÖLÜM 2-UYGULAMA SORU VE ÇÖZÜMLERİ 1 Bir otomobil lastiğinin basıncı, lastik içerisindeki havanın sıcaklığına bağlıdır Hava sıcaklığı 25 C iken etkin basınç 210 kpa dır Eğer lastiğin hacmi 0025
AKM 205-BÖLÜM 2-UYGULAMA SORU VE ÇÖZÜMLERİ 1 Bir otomobil lastiğinin basıncı, lastik içerisindeki havanın sıcaklığına bağlıdır Hava sıcaklığı 25 C iken etkin basınç 210 kpa dır Eğer lastiğin hacmi 0025
SU Lise Yaz Okulu. Karanlık Madde
 SU Lise Yaz Okulu Karanlık Madde Gökadamızın kütle dağılımı Diskteki yıldızlar merkez etra0nda Kepler yörüngelerinde dolaş9kları için gökada diskinin Kütlesi yıldızların hareke< incelenerek bulunabilir.
SU Lise Yaz Okulu Karanlık Madde Gökadamızın kütle dağılımı Diskteki yıldızlar merkez etra0nda Kepler yörüngelerinde dolaş9kları için gökada diskinin Kütlesi yıldızların hareke< incelenerek bulunabilir.
4.1 denklemine yakından bakalım. Tanımdan α = dω/dt olduğu bilinmektedir (ω açısal hız). O hâlde eğer cisme etki eden tork sıfır ise;
 Deney No : M3 Deneyin Adı : EYLEMSİZLİK MOMENTİ VE AÇISAL İVMELENME Deneyin Amacı : Dönme hareketinde eylemsizlik momentinin ne demek olduğunu ve nelere bağlı olduğunu deneysel olarak gözlemlemek. Teorik
Deney No : M3 Deneyin Adı : EYLEMSİZLİK MOMENTİ VE AÇISAL İVMELENME Deneyin Amacı : Dönme hareketinde eylemsizlik momentinin ne demek olduğunu ve nelere bağlı olduğunu deneysel olarak gözlemlemek. Teorik
EDUCATIONAL MATERIALS
 PROBLEM SET 1. (2.1) Mükemmel karıştırılmış, sabit hacimli tank, aynı sıvıyı içeren iki giriş akımına sahiptir. Her akımın sıcaklığı ve akış hızı zamanla değişebilir. a) Geçiş işlemini ifade eden dinamik
PROBLEM SET 1. (2.1) Mükemmel karıştırılmış, sabit hacimli tank, aynı sıvıyı içeren iki giriş akımına sahiptir. Her akımın sıcaklığı ve akış hızı zamanla değişebilir. a) Geçiş işlemini ifade eden dinamik
2.2 Alt Devler Kolu, Kırmızı Devler Kolu ve Yatay Kol
 2.2 Alt Devler Kolu, Kırmızı Devler Kolu ve Yatay Kol 2.2.1 Alt devler kolu (ing. Subgiant branch - SGB) 2.2.2 Kırmızı devler kolu (ing. Red giant branch - RGB) 2.2.3 Yatay kol (ing. Horizontal branch
2.2 Alt Devler Kolu, Kırmızı Devler Kolu ve Yatay Kol 2.2.1 Alt devler kolu (ing. Subgiant branch - SGB) 2.2.2 Kırmızı devler kolu (ing. Red giant branch - RGB) 2.2.3 Yatay kol (ing. Horizontal branch
SU Lise Yaz Okulu 2. Ders, biraz (baya) fizik. Dalgalar Elektromanyetik Dalgalar Kuantum mekaniği Tayf Karacisim ışıması
 SU Lise Yaz Okulu 2. Ders, biraz (baya) fizik Dalgalar Elektromanyetik Dalgalar Kuantum mekaniği Tayf Karacisim ışıması Dalga Nedir Enerji taşıyan bir değişimin bir yöne doğru taşınmasına dalga denir.
SU Lise Yaz Okulu 2. Ders, biraz (baya) fizik Dalgalar Elektromanyetik Dalgalar Kuantum mekaniği Tayf Karacisim ışıması Dalga Nedir Enerji taşıyan bir değişimin bir yöne doğru taşınmasına dalga denir.
H-R DİYAGRAMI. Bir yıldızın Hertzsprung-Russell diyagramındaki yeri biliniyorsa, o yıldızın;
 H-R DİYAGRAMI Bir yıldızın Hertzsprung-Russell diyagramındaki yeri biliniyorsa, o yıldızın; Etkin Sıcaklığı Renk ölçeği Tayf Türü Işınım sınıfı Toplam ışınım gücü Mutlak parlaklığı Yüzey çekim ivmesi Uzaklığı
H-R DİYAGRAMI Bir yıldızın Hertzsprung-Russell diyagramındaki yeri biliniyorsa, o yıldızın; Etkin Sıcaklığı Renk ölçeği Tayf Türü Işınım sınıfı Toplam ışınım gücü Mutlak parlaklığı Yüzey çekim ivmesi Uzaklığı
Enerji iş yapabilme kapasitesidir. Kimyacı işi bir süreçten kaynaklanan enerji deyişimi olarak tanımlar.
 Kinetik ve Potansiyel Enerji Enerji iş yapabilme kapasitesidir. Kimyacı işi bir süreçten kaynaklanan enerji deyişimi olarak tanımlar. Işıma veya Güneş Enerjisi Isı Enerjisi Kimyasal Enerji Nükleer Enerji
Kinetik ve Potansiyel Enerji Enerji iş yapabilme kapasitesidir. Kimyacı işi bir süreçten kaynaklanan enerji deyişimi olarak tanımlar. Işıma veya Güneş Enerjisi Isı Enerjisi Kimyasal Enerji Nükleer Enerji
AST404 Gözlemsel Astronomi. Ders 10 : Yıldız Evrimi
 AST404 Gözlemsel Astronomi Ders 10 : Yıldız Evrimi Anakol Öncesi Evrim Yıldızlar yıldızlararası ortamdaki moleküler gaz bulutlarında (yıldız oluşum bölgelerinde) oluşurlar Bir yıldızın evrimi onu oluşturan
AST404 Gözlemsel Astronomi Ders 10 : Yıldız Evrimi Anakol Öncesi Evrim Yıldızlar yıldızlararası ortamdaki moleküler gaz bulutlarında (yıldız oluşum bölgelerinde) oluşurlar Bir yıldızın evrimi onu oluşturan
İ çindekiler. xvii GİRİŞ 1 TEMEL AKIŞKANLAR DİNAMİĞİ BERNOULLİ DENKLEMİ 68 AKIŞKANLAR STATİĞİ 32. xvii
 Last A Head xvii İ çindekiler 1 GİRİŞ 1 1.1 Akışkanların Bazı Karakteristikleri 3 1.2 Boyutlar, Boyutsal Homojenlik ve Birimler 3 1.2.1 Birim Sistemleri 6 1.3 Akışkan Davranışı Analizi 9 1.4 Akışkan Kütle
Last A Head xvii İ çindekiler 1 GİRİŞ 1 1.1 Akışkanların Bazı Karakteristikleri 3 1.2 Boyutlar, Boyutsal Homojenlik ve Birimler 3 1.2.1 Birim Sistemleri 6 1.3 Akışkan Davranışı Analizi 9 1.4 Akışkan Kütle
LİNEER DALGA TEORİSİ. Page 1
 LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
(b) Model ve prototipi eşleştirmek için Reynolds benzerliğini kurmalıyız:
 AKM 205 BÖLÜM 7 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Askeri amaçlı hafif bir paraşüt tasarlanmaktadır. Çapı 7.3 m, deney yükü, paraşüt ve donanım ağırlığı
AKM 205 BÖLÜM 7 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Askeri amaçlı hafif bir paraşüt tasarlanmaktadır. Çapı 7.3 m, deney yükü, paraşüt ve donanım ağırlığı
Gamma Bozunumu
 Gamma Bozunumu Genelde beta ( ) ve alfa ( ) bozunumu sonunda çekirdek uyarılmış haldedir. Uyarılmış çekirdek gamma ( ) salarak temel seviyeye döner. Gamma görünür ışın ve x ışını gibi elektromanyetik radyasyon
Gamma Bozunumu Genelde beta ( ) ve alfa ( ) bozunumu sonunda çekirdek uyarılmış haldedir. Uyarılmış çekirdek gamma ( ) salarak temel seviyeye döner. Gamma görünür ışın ve x ışını gibi elektromanyetik radyasyon
Kütle Aktarımı Yapan İki İlginç X-ışını Atarcası: GX 1+4 ve SXP 1062
 Kütle Aktarımı Yapan İki İlginç X-ışını Atarcası: GX 1+4 ve SXP 1062 Sıtkı Çağdaş İnam 1, Muhammed Miraç Serim 2, Şeyda Şahiner 2, Danjela Çerri- Serim 2, Altan Baykal 2 1 Başkent Üniversitesi Mühendislik
Kütle Aktarımı Yapan İki İlginç X-ışını Atarcası: GX 1+4 ve SXP 1062 Sıtkı Çağdaş İnam 1, Muhammed Miraç Serim 2, Şeyda Şahiner 2, Danjela Çerri- Serim 2, Altan Baykal 2 1 Başkent Üniversitesi Mühendislik
İÇİNDEKİLER -BÖLÜM / 1- -BÖLÜM / 2- -BÖLÜM / 3- GİRİŞ... 1 ÖZEL GÖRELİLİK KUANTUM FİZİĞİ ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ...
 İÇİNDEKİLER ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ... viii -BÖLÜM / 1- GİRİŞ... 1 -BÖLÜM / 2- ÖZEL GÖRELİLİK... 13 2.1. REFERANS SİSTEMLERİ VE GÖRELİLİK... 14 2.2. ÖZEL GÖRELİLİK TEORİSİ... 19 2.2.1. Zaman Ölçümü
İÇİNDEKİLER ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ... viii -BÖLÜM / 1- GİRİŞ... 1 -BÖLÜM / 2- ÖZEL GÖRELİLİK... 13 2.1. REFERANS SİSTEMLERİ VE GÖRELİLİK... 14 2.2. ÖZEL GÖRELİLİK TEORİSİ... 19 2.2.1. Zaman Ölçümü
8.04 Kuantum Fiziği Ders XII
 Enerji ölçümünden sonra Sonucu E i olan enerji ölçümünden sonra parçacık enerji özdurumu u i de olacak ve daha sonraki ardışık tüm enerji ölçümleri E i enerjisini verecektir. Ölçüm yapılmadan önce enerji
Enerji ölçümünden sonra Sonucu E i olan enerji ölçümünden sonra parçacık enerji özdurumu u i de olacak ve daha sonraki ardışık tüm enerji ölçümleri E i enerjisini verecektir. Ölçüm yapılmadan önce enerji
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH
 OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ
 1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ Bohr Modelinin Yetersizlikleri Dalga-Tanecik İkiliği Dalga Mekaniği Kuantum Mekaniği -Orbital Kavramı Kuantum Sayıları Yörünge - Orbital Kavramları
1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ Bohr Modelinin Yetersizlikleri Dalga-Tanecik İkiliği Dalga Mekaniği Kuantum Mekaniği -Orbital Kavramı Kuantum Sayıları Yörünge - Orbital Kavramları
Kadri Yakut 08.03.2012
 Kadri Yakut 08.03.2012 TEŞEKKÜR Lisans Kara Delikler Eser İş (2009-2010) Büyük Kütleli Kara Delikler Birses Debir (2010-2011) Astrofiziksel Kara Deliklerin Kütlelerinin Belirlenmesi Orhan Erece (2010-2011)
Kadri Yakut 08.03.2012 TEŞEKKÜR Lisans Kara Delikler Eser İş (2009-2010) Büyük Kütleli Kara Delikler Birses Debir (2010-2011) Astrofiziksel Kara Deliklerin Kütlelerinin Belirlenmesi Orhan Erece (2010-2011)
T. C. GÜMÜŞHANE ÜNİVERSİTESİ MÜHENDİSLİK VE DOĞA BİLİMLERİ FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE MÜHENDİSLİĞİ DENEYLER 2
 T. C. GÜMÜŞHANE ÜNİVERSİTESİ MÜHENDİSLİK VE DOĞA BİLİMLERİ FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE MÜHENDİSLİĞİ DENEYLER 2 DOĞAL VE ZORLANMIŞ TAŞINIMLA ISI TRANSFERİ DENEYİ ÖĞRENCİ NO: ADI SOYADI:
T. C. GÜMÜŞHANE ÜNİVERSİTESİ MÜHENDİSLİK VE DOĞA BİLİMLERİ FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE MÜHENDİSLİĞİ DENEYLER 2 DOĞAL VE ZORLANMIŞ TAŞINIMLA ISI TRANSFERİ DENEYİ ÖĞRENCİ NO: ADI SOYADI:
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Beyaz cüceler Nötron yıldızları. Emrah Kalemci Sabancı Üniversitesi
 Beyaz cüceler Nötron yıldızları Kara delikler Emrah Kalemci Sabancı Üniversitesi Giriş Küçük yıldızların evrimlerinin sonu: Beyaz Cüce Büyük yıldızların evrimlerinin sonu Süpernova patlamaları Nötron yıldızları
Beyaz cüceler Nötron yıldızları Kara delikler Emrah Kalemci Sabancı Üniversitesi Giriş Küçük yıldızların evrimlerinin sonu: Beyaz Cüce Büyük yıldızların evrimlerinin sonu Süpernova patlamaları Nötron yıldızları
BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK - 402 MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY 4
 BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK - 0 MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY İÇİNDE SABİT SICAKLIKTA SİLİNDİRİK ISITICI BULUNAN DİKDÖRTGEN PRİZMATİK SAC KUTU YÜZEYLERİNDEN ZORLANMIŞ TAŞINIM
BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK - 0 MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY İÇİNDE SABİT SICAKLIKTA SİLİNDİRİK ISITICI BULUNAN DİKDÖRTGEN PRİZMATİK SAC KUTU YÜZEYLERİNDEN ZORLANMIŞ TAŞINIM
GÖKADAMIZ SAMANYOLU GÖKADASI
 GÖKADAMIZ SAMANYOLU GÖKADASI Gökadalar kütle çekimi ile birbirine bağlı yıldızlar, yıldızlararası gaz ve toz, plazma ve karanlık maddeden oluşan düzeneklerdir. Gökadaların barındırdığı birkaç milyon cüce
GÖKADAMIZ SAMANYOLU GÖKADASI Gökadalar kütle çekimi ile birbirine bağlı yıldızlar, yıldızlararası gaz ve toz, plazma ve karanlık maddeden oluşan düzeneklerdir. Gökadaların barındırdığı birkaç milyon cüce
Hareket Kanunları Uygulamaları
 Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
Yıldızlardan Yıldızsılara. Test 1 in Çözümleri
 43 Yıldızlardan Yıldızsılara Test in Çözüleri. Tabloda verilen bilgilerin taaı doğrudur. Ancak bu sınava giren öğrenci III ve V nuaralı doğru bilgileri yanlış işaretleiştir. Bu nedenle sınavdan 60 puan
43 Yıldızlardan Yıldızsılara Test in Çözüleri. Tabloda verilen bilgilerin taaı doğrudur. Ancak bu sınava giren öğrenci III ve V nuaralı doğru bilgileri yanlış işaretleiştir. Bu nedenle sınavdan 60 puan
Potansiyel Engeli: Tünelleme
 Potansiyel Engeli: Tünelleme Şekil I: Bir potansiyel engelinde tünelleme E
Potansiyel Engeli: Tünelleme Şekil I: Bir potansiyel engelinde tünelleme E
Fiz Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi
 Fiz 1011 - Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi Açısal Yerdeğiştirme, Hız ve İvme Dönme Kinematiği: Sabit Açısal İvmeli Dönme Hareketi Açısal ve Doğrusal Nicelikler Dönme Enerjisi Eylemsizlik
Fiz 1011 - Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi Açısal Yerdeğiştirme, Hız ve İvme Dönme Kinematiği: Sabit Açısal İvmeli Dönme Hareketi Açısal ve Doğrusal Nicelikler Dönme Enerjisi Eylemsizlik
OTOMATİK KONTROL. Set noktası (Hedef) + Kontrol edici. Son kontrol elemanı PROSES. Dönüştürücü. Ölçüm elemanı
 OTOMATİK KONTROL Set noktası (Hedef) + - Kontrol edici Dönüştürücü Son kontrol elemanı PROSES Ölçüm elemanı Dönüştürücü Geri Beslemeli( feedback) Kontrol Sistemi Kapalı Devre Blok Diyagramı SON KONTROL
OTOMATİK KONTROL Set noktası (Hedef) + - Kontrol edici Dönüştürücü Son kontrol elemanı PROSES Ölçüm elemanı Dönüştürücü Geri Beslemeli( feedback) Kontrol Sistemi Kapalı Devre Blok Diyagramı SON KONTROL
MAK 308 MAKİNA DİNAMİĞİ Bahar Dr. Nurdan Bilgin
 MAK 308 MAKİNA DİNAMİĞİ 017-018 Bahar Dr. Nurdan Bilgin EŞDEĞER ATALET MOMENTİ Geçen ders, hız ve ivme etki katsayılarını elde ederek; mekanizmanın hareketinin sadece bir bağımsız değişkene bağlı olarak
MAK 308 MAKİNA DİNAMİĞİ 017-018 Bahar Dr. Nurdan Bilgin EŞDEĞER ATALET MOMENTİ Geçen ders, hız ve ivme etki katsayılarını elde ederek; mekanizmanın hareketinin sadece bir bağımsız değişkene bağlı olarak
Fizik 101: Ders 17 Ajanda
 izik 101: Ders 17 Ajanda Dönme hareketi Yön ve sağ el kuralı Rotasyon dinamiği ve tork Örneklerle iş ve enerji Dönme ve Lineer Kinematik Karşılaştırma açısal α sabit 0 t 1 0 0t t lineer a sabit v v at
izik 101: Ders 17 Ajanda Dönme hareketi Yön ve sağ el kuralı Rotasyon dinamiği ve tork Örneklerle iş ve enerji Dönme ve Lineer Kinematik Karşılaştırma açısal α sabit 0 t 1 0 0t t lineer a sabit v v at
Akışkanların Dinamiği
 Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Burada E, x(t) 'nin beklenen değerini göstermektedir. Standart sapma veya sürecin karelerinin ortalamasının karekökü şu şekilde tanımlanabilir.
 DALGA İSAİSİĞİ Dalga teorileri genel olarak açık deni yapılarının tasarımında ortaya çıkan problemlere yanıt bulmak amacıyla kullanılır. Bu teorilerin temelinde, öellikleri bir periyod dan diğer bir periyoda
DALGA İSAİSİĞİ Dalga teorileri genel olarak açık deni yapılarının tasarımında ortaya çıkan problemlere yanıt bulmak amacıyla kullanılır. Bu teorilerin temelinde, öellikleri bir periyod dan diğer bir periyoda
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
AKM 205 BÖLÜM 2 - UYGULAMA SORU VE ÇÖZÜMLERİ. Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut
 AKM 205 BÖLÜM 2 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Bir otomobile lastiğinin basıncı, lastik içerisindeki havanın sıcaklığına bağlıdır. Hava sıcaklığı
AKM 205 BÖLÜM 2 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Bir otomobile lastiğinin basıncı, lastik içerisindeki havanın sıcaklığına bağlıdır. Hava sıcaklığı
Malzeme Bilgisi Prof. Dr. Akgün ALSARAN. Temel kavramlar Atomsal yapı
 Malzeme Bilgisi Prof. Dr. Akgün ALSARAN Temel kavramlar Atomsal yapı İçerik Temel kavramlar Atom modeli Elektron düzeni Periyodik sistem 2 Temel kavramlar Bütün maddeler kimyasal elementlerden oluşur.
Malzeme Bilgisi Prof. Dr. Akgün ALSARAN Temel kavramlar Atomsal yapı İçerik Temel kavramlar Atom modeli Elektron düzeni Periyodik sistem 2 Temel kavramlar Bütün maddeler kimyasal elementlerden oluşur.
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: SORULAR-CEVAPLAR
 MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: 1- (24 Puan) Şekildeki 5.08 cm çaplı 38.1 m uzunluğunda, 15.24 cm çaplı 22.86 m uzunluğunda ve 7.62 cm çaplı
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: 1- (24 Puan) Şekildeki 5.08 cm çaplı 38.1 m uzunluğunda, 15.24 cm çaplı 22.86 m uzunluğunda ve 7.62 cm çaplı
FİZ4001 KATIHAL FİZİĞİ-I
 FİZ4001 KATIHAL FİZİĞİ-I Bölüm 3. Örgü Titreşimleri: Termal, Akustik ve Optik Özellikler Dr. Aytaç Gürhan GÖKÇE Katıhal Fiziği - I Dr. Aytaç Gürhan GÖKÇE 1 Bir Boyutlu İki Atomlu Örgü Titreşimleri M 2
FİZ4001 KATIHAL FİZİĞİ-I Bölüm 3. Örgü Titreşimleri: Termal, Akustik ve Optik Özellikler Dr. Aytaç Gürhan GÖKÇE Katıhal Fiziği - I Dr. Aytaç Gürhan GÖKÇE 1 Bir Boyutlu İki Atomlu Örgü Titreşimleri M 2
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
Yapı Sistemlerinin Hesabı İçin. Matris Metotları. Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL Bahar Yarıyılı
 Yapı Sistemlerinin Hesabı İçin Matris Metotları 2015-2016 Bahar Yarıyılı Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL 1 BÖLÜM VIII YAPI SİSTEMLERİNİN DİNAMİK DIŞ ETKİLERE GÖRE HESABI 2 Bu bölümün hazırlanmasında
Yapı Sistemlerinin Hesabı İçin Matris Metotları 2015-2016 Bahar Yarıyılı Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL 1 BÖLÜM VIII YAPI SİSTEMLERİNİN DİNAMİK DIŞ ETKİLERE GÖRE HESABI 2 Bu bölümün hazırlanmasında
MASSACHUSETTS TEKNOLOJİ ENSTİTÜSÜ Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 1 Salı, Mart 14, :00-12:30
 Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 1 Salı, Mart 14, 2006 11:00-12:30 SOYADI ADI Öğrenci No. Talimat: 1. TÜM ÇABANIZI GÖSTERİN. Tüm cevaplar sınav kitapçığında gösterilmelidir? 2. Bu kapalı bir sınavdır.
Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 1 Salı, Mart 14, 2006 11:00-12:30 SOYADI ADI Öğrenci No. Talimat: 1. TÜM ÇABANIZI GÖSTERİN. Tüm cevaplar sınav kitapçığında gösterilmelidir? 2. Bu kapalı bir sınavdır.
KİNETİK GAZ KURAMI. Doç. Dr. Faruk GÖKMEŞE Kimya Bölümü Hitit Üniversitesi Fen Edebiyat Fakültesi 1
 Kinetik Gaz Kuramından Gazların Isınma Isılarının Bulunması Sabit hacimdeki ısınma ısısı (C v ): Sabit hacimde bulunan bir mol gazın sıcaklığını 1K değiştirmek için gerekli ısı alışverişi. Sabit basınçtaki
Kinetik Gaz Kuramından Gazların Isınma Isılarının Bulunması Sabit hacimdeki ısınma ısısı (C v ): Sabit hacimde bulunan bir mol gazın sıcaklığını 1K değiştirmek için gerekli ısı alışverişi. Sabit basınçtaki
Tek Boyutlu Potansiyeller: Potansiyel eşiği
 Tek Boyutlu Potansiyeller: Potansiyel eşiği Şekil I: V 0 yüksekliğindeki potansiyel eşiği. Parçacık soldan gelmekte olup, enerjisi E dir. Zamandan bağımsız bir durumu analiz ediyoruz ki burada iyi belirlenmiş
Tek Boyutlu Potansiyeller: Potansiyel eşiği Şekil I: V 0 yüksekliğindeki potansiyel eşiği. Parçacık soldan gelmekte olup, enerjisi E dir. Zamandan bağımsız bir durumu analiz ediyoruz ki burada iyi belirlenmiş
O )molekül ağırlığı 18 g/mol ve 1g suyun kapladığı hacimde
 1) Suyun ( H 2 O )molekül ağırlığı 18 g/mol ve 1g suyun kapladığı hacimde 10 6 m 3 olduğuna göre, birbirine komşu su moleküllerinin arasındaki uzaklığı Avagadro sayısını kullanarak hesap ediniz. Moleküllerin
1) Suyun ( H 2 O )molekül ağırlığı 18 g/mol ve 1g suyun kapladığı hacimde 10 6 m 3 olduğuna göre, birbirine komşu su moleküllerinin arasındaki uzaklığı Avagadro sayısını kullanarak hesap ediniz. Moleküllerin
Şekil 6.1 Basit sarkaç
 Deney No : M5 Deney Adı : BASİT SARKAÇ Deneyin Amacı yer çekimi ivmesinin belirlenmesi Teorik Bilgi : Sabit bir noktadan iple sarkıtılan bir cisim basit sarkaç olarak isimlendirilir. : Basit sarkaçta uzunluk
Deney No : M5 Deney Adı : BASİT SARKAÇ Deneyin Amacı yer çekimi ivmesinin belirlenmesi Teorik Bilgi : Sabit bir noktadan iple sarkıtılan bir cisim basit sarkaç olarak isimlendirilir. : Basit sarkaçta uzunluk
TERMODİNAMİĞİN BİRİNCİ YASASI
 İç Enerji Fonksiyonu ve C v Isınma Isısı Kimyasal tepkimelerin olmadığı kapalı sistemlerde kütle yanında molar miktar da sabit kalmaktadır. Madde miktarı n mol olan kapalı bir ideal gaz sistemi düşünelim.
İç Enerji Fonksiyonu ve C v Isınma Isısı Kimyasal tepkimelerin olmadığı kapalı sistemlerde kütle yanında molar miktar da sabit kalmaktadır. Madde miktarı n mol olan kapalı bir ideal gaz sistemi düşünelim.
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü
 Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 7 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 7 Kasım 1999 Saat: 21.50 Problem 7.1 (Ohanian, sayfa 271, problem 55) Bu problem boyunca roket
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 7 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 7 Kasım 1999 Saat: 21.50 Problem 7.1 (Ohanian, sayfa 271, problem 55) Bu problem boyunca roket
Gezegenli Yıldızların Asterosismik İncelenmesi
 Gezegenli Yıldızların Asterosismik İncelenmesi Dr. Cenk KAYHAN Ege Üniversitesi Astronomi ve Uzay Bilimleri İSTEK Belde Okulları Bilim Merkezi 6 Eylül 2018 İçerik Gezegen Keşifleri Titreşim gösteren yıldızlar
Gezegenli Yıldızların Asterosismik İncelenmesi Dr. Cenk KAYHAN Ege Üniversitesi Astronomi ve Uzay Bilimleri İSTEK Belde Okulları Bilim Merkezi 6 Eylül 2018 İçerik Gezegen Keşifleri Titreşim gösteren yıldızlar
Bölüm 4 Zamana Bağlı Isı İletimi
 Heat and Mass Transfer: Fundamentals & Applications Fourth Edition Yunus A. Cengel, Afshin J. Ghajar McGraw-Hill, 2011 Bölüm 4 Zamana Bağlı Isı İletimi Hazırlayan: Yrd.Doç.Dr. Nezaket Parlak Bu Bölümün
Heat and Mass Transfer: Fundamentals & Applications Fourth Edition Yunus A. Cengel, Afshin J. Ghajar McGraw-Hill, 2011 Bölüm 4 Zamana Bağlı Isı İletimi Hazırlayan: Yrd.Doç.Dr. Nezaket Parlak Bu Bölümün
Bölüm 8: Borularda sürtünmeli Akış
 Bölüm 8: Borularda sürtünmeli Akış Laminer ve Türbülanslı Akış Laminer Akış: Çalkantısız akışkan tabakaları ile karakterize edilen çok düzenli akışkan hareketi laminer akış olarak adlandırılır. Türbülanslı
Bölüm 8: Borularda sürtünmeli Akış Laminer ve Türbülanslı Akış Laminer Akış: Çalkantısız akışkan tabakaları ile karakterize edilen çok düzenli akışkan hareketi laminer akış olarak adlandırılır. Türbülanslı
