Bilgisayar sayısistemi, aritmetiği ve hata kaynakları
|
|
|
- Batur Abdil
- 5 yıl önce
- İzleme sayısı:
Transkript
1 Bilgisayar sayısistemi, aritmetiği ve hata kaynakları Temel Kavramlar Erhan Coşkun Karadeniz Teknik Üniversitesi Mart, 2015 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
2 Bilgisayar sayısistemi ve hata Bu bölümde hata kavramı, ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
3 Bilgisayar sayısistemi ve hata Bu bölümde hata kavramı, bilgisayar sayısistemi, aritmetiği ve ilgili hatalar, ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
4 Bilgisayar sayısistemi ve hata Bu bölümde hata kavramı, bilgisayar sayısistemi, aritmetiği ve ilgili hatalar, taban dönüşümleri ve ilgili hatalar ile ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
5 Bilgisayar sayısistemi ve hata Bu bölümde hata kavramı, bilgisayar sayısistemi, aritmetiği ve ilgili hatalar, taban dönüşümleri ve ilgili hatalar ile anlam kaybıhatalarınıinceleyeceğiz. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
6 Hata(mutlak) x ile gösterilen bir büyüklüğün gerçek değeri ile onu temsil eden x f değeri arasındaki fark, gerçek değerin x f ile temsilinde oluşan mutlak hata veya x f deki mutlak hata olarak tanımlanır ve x = x x f notasyonu ile gösterilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
7 Hata(mutlak) x ile gösterilen bir büyüklüğün gerçek değeri ile onu temsil eden x f değeri arasındaki fark, gerçek değerin x f ile temsilinde oluşan mutlak hata veya x f deki mutlak hata olarak tanımlanır ve x = x x f notasyonu ile gösterilir. x = 10.1 birim uzunluğa sahip sahip olan cismin uzunluğu x f = 10 birim olarak ölçülmüşse, bu ölçüm sonucunda oluşan mutlak hata x = 0.1 değerine eşittir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
8 Hata(mutlak) x ile gösterilen bir büyüklüğün gerçek değeri ile onu temsil eden x f değeri arasındaki fark, gerçek değerin x f ile temsilinde oluşan mutlak hata veya x f deki mutlak hata olarak tanımlanır ve x = x x f notasyonu ile gösterilir. x = 10.1 birim uzunluğa sahip sahip olan cismin uzunluğu x f = 10 birim olarak ölçülmüşse, bu ölçüm sonucunda oluşan mutlak hata x = 0.1 değerine eşittir. x = 1.1 birim gerçek uzunluğuna sahip olan başka bir cismin uzunluğu x f = 1 birim olarak ölçülmüşse, bu ölçüm sonucunda oluşan mutlak hata da x = 0.1 değerine sahiptir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
9 Hata(mutlak) x ile gösterilen bir büyüklüğün gerçek değeri ile onu temsil eden x f değeri arasındaki fark, gerçek değerin x f ile temsilinde oluşan mutlak hata veya x f deki mutlak hata olarak tanımlanır ve x = x x f notasyonu ile gösterilir. x = 10.1 birim uzunluğa sahip sahip olan cismin uzunluğu x f = 10 birim olarak ölçülmüşse, bu ölçüm sonucunda oluşan mutlak hata x = 0.1 değerine eşittir. x = 1.1 birim gerçek uzunluğuna sahip olan başka bir cismin uzunluğu x f = 1 birim olarak ölçülmüşse, bu ölçüm sonucunda oluşan mutlak hata da x = 0.1 değerine sahiptir. Ancak ikinci ölçümde daha fazla hata yaptĭgımızıdüşünürüz! ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
10 Hata(bağıl) Hatanın diğer bir ölçüsü ise, yapılan hatanın gerçek değere oranı olarak tanımlanan ve ε b (x) = x/x, x = 0, notasyonu ile göstereceğimiz bağıl hatadır ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
11 Hata(bağıl) Hatanın diğer bir ölçüsü ise, yapılan hatanın gerçek değere oranı olarak tanımlanan ve ε b (x) = x/x, x = 0, notasyonu ile göstereceğimiz bağıl hatadır Buna göre yukarıdaki birinci ölçüm için oluşan bağıl hata ε b (x) = 0.01 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
12 Hata(bağıl) Hatanın diğer bir ölçüsü ise, yapılan hatanın gerçek değere oranı olarak tanımlanan ve ε b (x) = x/x, x = 0, notasyonu ile göstereceğimiz bağıl hatadır Buna göre yukarıdaki birinci ölçüm için oluşan bağıl hata ε b (x) = 0.01 ikincide oluşan hata ise ε b (x) = 0.1 dir ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
13 Hata(bağıl) Hatanın diğer bir ölçüsü ise, yapılan hatanın gerçek değere oranı olarak tanımlanan ve ε b (x) = x/x, x = 0, notasyonu ile göstereceğimiz bağıl hatadır Buna göre yukarıdaki birinci ölçüm için oluşan bağıl hata ε b (x) = 0.01 ikincide oluşan hata ise ε b (x) = 0.1 dir yani ikinci ölçüm sonucu yapılan bağıl hata beklentilerimiz doğrultusunda daha büyüktür. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
14 Hata(bağıl) Hatanın diğer bir ölçüsü ise, yapılan hatanın gerçek değere oranı olarak tanımlanan ve ε b (x) = x/x, x = 0, notasyonu ile göstereceğimiz bağıl hatadır Buna göre yukarıdaki birinci ölçüm için oluşan bağıl hata ε b (x) = 0.01 ikincide oluşan hata ise ε b (x) = 0.1 dir yani ikinci ölçüm sonucu yapılan bağıl hata beklentilerimiz doğrultusunda daha büyüktür. O halde bağıl hata günlük hayatta algıladĭgımız hata ile daha uyumludur. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
15 Yuvarlama hataları Sayısal analiz sürecinde oluşan hataların bir kısmıbilgisayar sayı sistemi ile ilgilidir ve bu tür hatalar genelde yuvarlama hataları olarak bilinirler. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
16 Yuvarlama hataları Sayısal analiz sürecinde oluşan hataların bir kısmıbilgisayar sayı sistemi ile ilgilidir ve bu tür hatalar genelde yuvarlama hataları olarak bilinirler. Örneğin π sayısının bilgisayarda reel bir sayıiçin tahsis edilen alana sĭgdırılmasıiçin belirli basamaktan sonraki basamaklarının ihmal edilmesi ile oluşan hata bir yuvarlama hatasıdır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
17 Yuvarlama hataları Sayısal analiz sürecinde oluşan hataların bir kısmıbilgisayar sayı sistemi ile ilgilidir ve bu tür hatalar genelde yuvarlama hataları olarak bilinirler. Örneğin π sayısının bilgisayarda reel bir sayıiçin tahsis edilen alana sĭgdırılmasıiçin belirli basamaktan sonraki basamaklarının ihmal edilmesi ile oluşan hata bir yuvarlama hatasıdır. 1/3 = gibi her devirli rasyonel sayının sınırlıbilgisayar bellek alanında temsili esnasında bu tür yuvarlama hatalarıkaçınılmazdır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
18 Yuvarlama hataları Sayısal analiz sürecinde oluşan hataların bir kısmıbilgisayar sayı sistemi ile ilgilidir ve bu tür hatalar genelde yuvarlama hataları olarak bilinirler. Örneğin π sayısının bilgisayarda reel bir sayıiçin tahsis edilen alana sĭgdırılmasıiçin belirli basamaktan sonraki basamaklarının ihmal edilmesi ile oluşan hata bir yuvarlama hatasıdır. 1/3 = gibi her devirli rasyonel sayının sınırlıbilgisayar bellek alanında temsili esnasında bu tür yuvarlama hatalarıkaçınılmazdır. Öte yandan 0.1 sayısıikili sistemin devirli bir sayısıdır ve ikili sistem kullanan bilgisayar sisteminde tam olarak temsil edilemez. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
19 Kesme hataları bir fonksiyon yerine n inci dereceden Taylor polinomunun kullanılması(bölüm 3, Taylor polinomlarıve hata) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
20 Kesme hataları bir fonksiyon yerine n inci dereceden Taylor polinomunun kullanılması(bölüm 3, Taylor polinomlarıve hata) interpolasyon polinomu veya basit fonksiyonlarla yaklaşım(bölüm 6, interpolasyon) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
21 Kesme hataları bir fonksiyon yerine n inci dereceden Taylor polinomunun kullanılması(bölüm 3, Taylor polinomlarıve hata) interpolasyon polinomu veya basit fonksiyonlarla yaklaşım(bölüm 6, interpolasyon) sonsuz toplam yerine sonlu bir toplamla integrale yaklaşım(bölüm 7, Sayısal integrasyon), ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
22 Kesme hataları bir fonksiyon yerine n inci dereceden Taylor polinomunun kullanılması(bölüm 3, Taylor polinomlarıve hata) interpolasyon polinomu veya basit fonksiyonlarla yaklaşım(bölüm 6, interpolasyon) sonsuz toplam yerine sonlu bir toplamla integrale yaklaşım(bölüm 7, Sayısal integrasyon), teğet eğimi(türev) yerine kiriş eğimi( Bölüm 8, Sayısal türev) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
23 Kesme hataları bir fonksiyon yerine n inci dereceden Taylor polinomunun kullanılması(bölüm 3, Taylor polinomlarıve hata) interpolasyon polinomu veya basit fonksiyonlarla yaklaşım(bölüm 6, interpolasyon) sonsuz toplam yerine sonlu bir toplamla integrale yaklaşım(bölüm 7, Sayısal integrasyon), teğet eğimi(türev) yerine kiriş eğimi( Bölüm 8, Sayısal türev) diferensiyel denklemlerde türev yerine sayısal türev kullanılması( Bölüm 9-12) durumunda oluşan hatalar kesme hatalarıdır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
24 Sayısal analiz ve hata Sayısal analiz, yuvarlama ve kesme hatalarınıminimize edecek yaklaşımlarıbelirlemeyi amaçlar ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
25 Sayısal analiz ve hata Sayısal analiz, yuvarlama ve kesme hatalarınıminimize edecek yaklaşımlarıbelirlemeyi amaçlar Sayısal analizde amaç yuvarlama hatalarınıkontrol altında tutan ve "makul" düzeyde kesme hatalarıile işlemler yürüten sayısal yöntemler geliştirmek ve problemlerin çözümüne uygulamaktır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
26 Sayısal analiz ve hata Sayısal analiz, yuvarlama ve kesme hatalarınıminimize edecek yaklaşımlarıbelirlemeyi amaçlar Sayısal analizde amaç yuvarlama hatalarınıkontrol altında tutan ve "makul" düzeyde kesme hatalarıile işlemler yürüten sayısal yöntemler geliştirmek ve problemlerin çözümüne uygulamaktır. Sayısal analiz sürecinde oluşabilecek olan yuvarlama hatalarını anlayabilmek için öncelikle bilgisayar sayısistemini ve bu sistem üzerindeki aritmetiği yakından inceleyelim. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
27 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar R, reel sayılar kümesi olmak üzere, bilgisayarlar sadece R f ile göstereceğimiz ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
28 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar R, reel sayılar kümesi olmak üzere, bilgisayarlar sadece R f ile göstereceğimiz R nin sonlu elemanlıbir alt kümesini belleklerinde saklayabilir ve bu sayılarla işlem yapabilirler. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
29 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar R, reel sayılar kümesi olmak üzere, bilgisayarlar sadece R f ile göstereceğimiz R nin sonlu elemanlıbir alt kümesini belleklerinde saklayabilir ve bu sayılarla işlem yapabilirler. Bilgisayarlar tamsayılarıtamsayıformatı(fixed point format) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
30 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar R, reel sayılar kümesi olmak üzere, bilgisayarlar sadece R f ile göstereceğimiz R nin sonlu elemanlıbir alt kümesini belleklerinde saklayabilir ve bu sayılarla işlem yapabilirler. Bilgisayarlar tamsayılarıtamsayıformatı(fixed point format) kesirli sayılarıise kayan nokta formatı(floating point format) adı verilen bir formatta saklarlar. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
31 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bilgisayar belleğinde saklanabilen sıfırdan farklıbir kayan noktalısayı x f = ±q f β e biçiminde ifade edilebilen bir sayıdır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
32 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bilgisayar belleğinde saklanabilen sıfırdan farklıbir kayan noktalısayı x f = ±q f β e biçiminde ifade edilebilen bir sayıdır. Burada q f sonlu basamağa sahip olan ve q f = 0.d 1 d 2...d n biçiminde ifade edilebilen sayının kesir kısmı(mantis veya d 1 = 0 için normalize edilmiş mantis, 0 d i < β, i = 1, 2,..., n) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
33 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bilgisayar belleğinde saklanabilen sıfırdan farklıbir kayan noktalısayı x f = ±q f β e biçiminde ifade edilebilen bir sayıdır. Burada q f sonlu basamağa sahip olan ve q f = 0.d 1 d 2...d n biçiminde ifade edilebilen sayının kesir kısmı(mantis veya d 1 = 0 için normalize edilmiş mantis, 0 d i < β, i = 1, 2,..., n) β ise kullanılan sayısisteminin tabanı(örneğin iki tabanlısistem için β = 2,on tabanlısistem için β = 10 vb) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
34 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bilgisayar belleğinde saklanabilen sıfırdan farklıbir kayan noktalısayı x f = ±q f β e biçiminde ifade edilebilen bir sayıdır. Burada q f sonlu basamağa sahip olan ve q f = 0.d 1 d 2...d n biçiminde ifade edilebilen sayının kesir kısmı(mantis veya d 1 = 0 için normalize edilmiş mantis, 0 d i < β, i = 1, 2,..., n) β ise kullanılan sayısisteminin tabanı(örneğin iki tabanlısistem için β = 2,on tabanlısistem için β = 10 vb) e ise üs olarak adlandırılır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
35 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bilgisayar belleğinde saklanabilen sıfırdan farklıbir kayan noktalısayı x f = ±q f β e biçiminde ifade edilebilen bir sayıdır. Burada q f sonlu basamağa sahip olan ve q f = 0.d 1 d 2...d n biçiminde ifade edilebilen sayının kesir kısmı(mantis veya d 1 = 0 için normalize edilmiş mantis, 0 d i < β, i = 1, 2,..., n) β ise kullanılan sayısisteminin tabanı(örneğin iki tabanlısistem için β = 2,on tabanlısistem için β = 10 vb) e ise üs olarak adlandırılır. Böylece bir kayan noktalısayıyıtanımlayabilmek için işaret, mantis ve üs bilgileri gerekmektedir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
36 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bilgisayar belleğinde saklanabilen sıfırdan farklıbir kayan noktalısayı x f = ±q f β e biçiminde ifade edilebilen bir sayıdır. Burada q f sonlu basamağa sahip olan ve q f = 0.d 1 d 2...d n biçiminde ifade edilebilen sayının kesir kısmı(mantis veya d 1 = 0 için normalize edilmiş mantis, 0 d i < β, i = 1, 2,..., n) β ise kullanılan sayısisteminin tabanı(örneğin iki tabanlısistem için β = 2,on tabanlısistem için β = 10 vb) e ise üs olarak adlandırılır. Böylece bir kayan noktalısayıyıtanımlayabilmek için işaret, mantis ve üs bilgileri gerekmektedir. Mantisdeki noktanın pozisyonu, üs değiştirilmek suretiyle sağa veya sola kaydırılabileceği için kayan noktalısayılar adıverilmektedir = = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
37 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar En genel halde β tabanlısistemde x = ±q β e, q = 0.d 1 d 2 d n 1 d n d n+1, d 1 = 0 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
38 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar En genel halde β tabanlısistemde x = ±q β e, q = 0.d 1 d 2 d n 1 d n d n+1, d 1 = 0 bilgisayar sayısistemi bellek sınırlamalarıdolayısıyla mantisinde en fazla n basamağa izin veriyorsa bu durumda ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
39 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar En genel halde β tabanlısistemde x = ±q β e, q = 0.d 1 d 2 d n 1 d n d n+1, d 1 = 0 bilgisayar sayısistemi bellek sınırlamalarıdolayısıyla mantisinde en fazla n basamağa izin veriyorsa bu durumda { q f = 0.d 1 d 2 d n 1 d n 0 d n+1... < β/2 0.d 1 d 2 d n 1 (d n + 1) d n+1... β/2 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
40 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar En genel halde β tabanlısistemde x = ±q β e, q = 0.d 1 d 2 d n 1 d n d n+1, d 1 = 0 bilgisayar sayısistemi bellek sınırlamalarıdolayısıyla mantisinde en fazla n basamağa izin veriyorsa bu durumda { q f = 0.d 1 d 2 d n 1 d n 0 d n+1... < β/2 0.d 1 d 2 d n 1 (d n + 1) d n+1... β/2 x f = ±q f β e olarak elde edilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
41 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bu durumda x değeri en yakın x f bilgisayar sayısına yuvarlanmış olur ve ε b (x) ise bağıl yuvarlama hatasıdır ve ε b (x) 1 2 β n+1 (1) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
42 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bu durumda x değeri en yakın x f bilgisayar sayısına yuvarlanmış olur ve ε b (x) ise bağıl yuvarlama hatasıdır ve ε b (x) 1 2 β n+1 (1) 1 2 β n+1 sayısına bilgisayar hassasiyeti(machine precision) adıverilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
43 Bilgisayar sayısistemi, aritmetiği ve ilgili hatalar Bu durumda x değeri en yakın x f bilgisayar sayısına yuvarlanmış olur ve ε b (x) ise bağıl yuvarlama hatasıdır ve ε b (x) 1 2 β n+1 (1) 1 2 β n+1 sayısına bilgisayar hassasiyeti(machine precision) adıverilir. >> eps(1) ans = e-016(= 2 52 ) dir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
44 Sanal bir sayısistemi Sanal bir kayan nokta sistemi örneği üzerinde bilgisayar aritmetiği Sanal sistemimizin üs için 1, 0, 1 ve mantis için q = 0.d 1, d 1 = 1,..., 9 değerlerini alabileceğini kabul edelim. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
45 Sanal bir sayısistemi Sanal bir kayan nokta sistemi örneği üzerinde bilgisayar aritmetiği Sanal sistemimizin üs için 1, 0, 1 ve mantis için q = 0.d 1, d 1 = 1,..., 9 değerlerini alabileceğini kabul edelim. Sistemimiz tabloda belirtilen noktalar ve negatifleri ile sıfır noktasından oluşur(toplam 55 nokta!): Table: e(sol sütun) ve Sanal sistem üzerinde kayan noktalıpozitif sayılar ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
46 R f nin özellikleri R f toplama işlemine göre kapalıolmayabilir: Örneğimiz için 5, 6 R f fakat 11 / R f dir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
47 R f nin özellikleri R f toplama işlemine göre kapalıolmayabilir: Örneğimiz için 5, 6 R f fakat 11 / R f dir. R f de belirli değerden küçük olan sonuçlar sıfır olarak kabul edilir(sistemler bu durumu "undeflow" hatasıolarak yorumlarlar): a = 0.01/2 = 0. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
48 R f nin özellikleri R f toplama işlemine göre kapalıolmayabilir: Örneğimiz için 5, 6 R f fakat 11 / R f dir. R f de belirli değerden küçük olan sonuçlar sıfır olarak kabul edilir(sistemler bu durumu "undeflow" hatasıolarak yorumlarlar): a = 0.01/2 = 0. R f de toplama işlemine göre birleşme özelliği geçerli olmayabilir: ( ) + 1 = 2 = 1 = ( ) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
49 Gerçek bir kayan nokta sistemi örneği üzerinde bilgisayar aritmetiği ve hata kaynakları R f sonlu sayıda elemandan oluşur. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
50 Gerçek bir kayan nokta sistemi örneği üzerinde bilgisayar aritmetiği ve hata kaynakları R f sonlu sayıda elemandan oluşur. >> realmax ans =1.7977E ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
51 Gerçek bir kayan nokta sistemi örneği üzerinde bilgisayar aritmetiği ve hata kaynakları R f sonlu sayıda elemandan oluşur. >> realmax ans =1.7977E O halde kullandĭgımız bilgisayar [ E + 308, E + 308] aralĭgıiçerisindeki kayan nokta sayılarından oluşan sonlu bir kümeden ibarettir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
52 Gerçek bir kayan nokta sistemi örneği üzerinde bilgisayar aritmetiği ve hata kaynakları R f sonlu sayıda elemandan oluşur. >> realmax ans =1.7977E O halde kullandĭgımız bilgisayar [ E + 308, E + 308] aralĭgıiçerisindeki kayan nokta sayılarından oluşan sonlu bir kümeden ibarettir. Herhangi bir işlemin sonucunun bu aralĭgın dışarında bir değer üretmesi durumunda sonuç çok büyük sayı(overflow veya inf) hatası olarak yorumlanır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
53 Gerçek bir kayan nokta sistemi örneği üzerinde bilgisayar aritmetiği ve hata kaynakları R f sonlu sayıda elemandan oluşur. >> realmax ans =1.7977E O halde kullandĭgımız bilgisayar [ E + 308, E + 308] aralĭgıiçerisindeki kayan nokta sayılarından oluşan sonlu bir kümeden ibarettir. Herhangi bir işlemin sonucunun bu aralĭgın dışarında bir değer üretmesi durumunda sonuç çok büyük sayı(overflow veya inf) hatası olarak yorumlanır. Örneğin MATLAB/Octave ortamında >> E e292 x = E 308. ans = inf ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
54 Bilgisayar aritmetiği ve hata kaynakları >> x=realmin ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
55 Bilgisayar aritmetiği ve hata kaynakları >> x=realmin Bunlara ilaveten belirsizlik adınıverdiğimiz tanımlıolmayan (0/0, / gibi) bir işlem sonucu ise NaN(Not a Number- sayıdeğil) olarak kabul edilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
56 Bilgisayar aritmetiği ve hata kaynakları >> x=realmin Bunlara ilaveten belirsizlik adınıverdiğimiz tanımlıolmayan (0/0, / gibi) bir işlem sonucu ise NaN(Not a Number- sayıdeğil) olarak kabul edilir. Hiç bir irrasyonel sayı(π, e, 2) veya devirli rasyonel sayır f almaz. de yer ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
57 Bilgisayar aritmetiği ve hata kaynakları Kayan nokta sayısisteminde sayılar sıfır noktasının komşuluğunda daha sıkça serpiştirilmiştir ve sonuç olarak işlemlerin gerçekleştirilme sırasıfarklıyuvarlama hatalarına neden olabilir ve bu durum işlem sonucunu değiştirebilir(toplama işlemine göre birleşme özelliği olmayabilir). ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
58 Bilgisayar aritmetiği ve hata kaynakları Kayan nokta sayısisteminde sayılar sıfır noktasının komşuluğunda daha sıkça serpiştirilmiştir ve sonuç olarak işlemlerin gerçekleştirilme sırasıfarklıyuvarlama hatalarına neden olabilir ve bu durum işlem sonucunu değiştirebilir(toplama işlemine göre birleşme özelliği olmayabilir). Bu sonucu MATLAB/Octave yazılımlarında kullanılan eps() fonksiyonu yardımıyla gözlemleyebiliriz. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
59 Bilgisayar aritmetiği ve hata kaynakları Kayan nokta sayısisteminde sayılar sıfır noktasının komşuluğunda daha sıkça serpiştirilmiştir ve sonuç olarak işlemlerin gerçekleştirilme sırasıfarklıyuvarlama hatalarına neden olabilir ve bu durum işlem sonucunu değiştirebilir(toplama işlemine göre birleşme özelliği olmayabilir). Bu sonucu MATLAB/Octave yazılımlarında kullanılan eps() fonksiyonu yardımıyla gözlemleyebiliriz. Bu fonksiyon eps(x) biçimindeki kullanımıyla, x sayısıile bu sayıya en yakın bilgisayar sistemindeki sayıarasındaki uzaklĭgıverir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
60 x x x f E E E E E E Table: Sayılar ve komşularıarasındaki uzaklık ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
61 Bilgisayar aritmetiği ve hata kaynakları Sıfır komşuluğundaki sayıların birbirlerine çok yakın olmasıve mutlak değerce büyük olan kayan nokta sayılarıarasındaki uzaklĭgın kısmen daha büyük olmasısonucu sayıların küçükten büyüğe veya büyükten küçüğe sıralanarak toplanmasısonucu farklısonuçlar elde edilebilmektedir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
62 Bilgisayar aritmetiği ve hata kaynakları Sıfır komşuluğundaki sayıların birbirlerine çok yakın olmasıve mutlak değerce büyük olan kayan nokta sayılarıarasındaki uzaklĭgın kısmen daha büyük olmasısonucu sayıların küçükten büyüğe veya büyükten küçüğe sıralanarak toplanmasısonucu farklısonuçlar elde edilebilmektedir. Örneğin N i=1 1 i 2 = 1 + 1/ /N 2 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
63 Bilgisayar aritmetiği ve hata kaynakları Sıfır komşuluğundaki sayıların birbirlerine çok yakın olmasıve mutlak değerce büyük olan kayan nokta sayılarıarasındaki uzaklĭgın kısmen daha büyük olmasısonucu sayıların küçükten büyüğe veya büyükten küçüğe sıralanarak toplanmasısonucu farklısonuçlar elde edilebilmektedir. Örneğin N = 1e5 için N i=1 1 i 2 = 1 + 1/ /N 2 top=0; for i=1:n top=top+1/(i*i); end program parçacĭgıçalıştırıldĭgında top = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
64 bilgisayar aritmetiği ve hata kaynakları Şimdi de N i=1 1 (N (i 1)) 2 = 1/N2 + 1/(N 1) /1 2 olarak ifade edilen küçükten büyüğe toplamınıhesaplayalım: ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
65 bilgisayar aritmetiği ve hata kaynakları Şimdi de N i=1 1 (N (i 1)) 2 = 1/N2 + 1/(N 1) /1 2 olarak ifade edilen küçükten büyüğe toplamınıhesaplayalım: top = elde ederiz. Sonuçların farklıolduğunu görüyoruz. i=1 1 i 2 = π2 /6 = olduğu dikkate alınırsa küçükten büyüğe toplamın daha doğru sonuç ürettiğini gözlemleriz. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
66 Bilgisayar aritmetiği ve hata kaynakları Aynınedenden dolayıfarklımertebeden sayılarla gerçekleştirilen işlemlerde büyük hatalar oluşabilir. Bu duruma örnek olarak aşağıdaki işlem sonuçlarınıinceleyelim: ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
67 Bilgisayar aritmetiği ve hata kaynakları Aynınedenden dolayıfarklımertebeden sayılarla gerçekleştirilen işlemlerde büyük hatalar oluşabilir. Bu duruma örnek olarak aşağıdaki işlem sonuçlarınıinceleyelim: İşlem Yaklaşık hata 0 + 5E 324 = E 324 6E 326 1E5 (1 1E 17) = 1E5 1E 12 1E10 (1E16 + 1E 1) = 1E26 1E + 09 Table: Farklımertebeden büyüklüklere sahip sayılarla işlemler ve oluşan hata ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
68 Taban dönüşümleri ve ilgili hatalar İki tabanlısistemden on tabanlısisteme dönüşüm ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
69 Taban dönüşümleri ve ilgili hatalar İki tabanlısistemden on tabanlısisteme dönüşüm (101101) 2 = = = 45. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
70 Taban dönüşümleri ve ilgili hatalar İki tabanlısistemden on tabanlısisteme dönüşüm (101101) 2 = = = 45. ( ) 2 = = 5 + 1/2 + 1/8 = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
71 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
72 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm 1964 = c c c c ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
73 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm 1964 = c c c c = c 0 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
74 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm 1964 = c c c c = c 0 Şimdi ise eşitliğin her iki tarafınıikiye bölerek elde edilen 982 = c c c c 1 ifadesinden de c 1 in 982 nin 2 ye bölümünden elde edilen kalan olduğuna dikkat edelim. Yani 982 = c 1 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
75 Taban dönüşümleri ve ilgili hatalar 1964 = c 0 c 0 = = c 1 c 1 = = c 2 c 2 = = c 3 c 3 = = c 4 c 4 = 0 61 = c 5 c 5 = 1 30 = c 6 c 6 = 0 15 = c 7 c 7 = 1 7 = c 8 c 8 = 1 3 = c 9 c 9 = 1 1 = c 10 c 10 = 1 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
76 Taban dönüşümleri ve ilgili hatalar 1964 = c 0 c 0 = = c 1 c 1 = = c 2 c 2 = = c 3 c 3 = = c 4 c 4 = 0 61 = c 5 c 5 = 1 30 = c 6 c 6 = 0 15 = c 7 c 7 = 1 7 = c 8 c 8 = 1 3 = c 9 c 9 = 1 1 = c 10 c 10 = = ( ) 2 iki tabanlıgösterimi elde edilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
77 Taban dönüşümleri ve ilgili hatalar Kesirli sayıdönüşümleri ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
78 Taban dönüşümleri ve ilgili hatalar Kesirli sayıdönüşümleri Öncelikle [[x]] notasyonu ile x sayısının tam değerini ve {x} ile de kesirli kısmınıgösterelim. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
79 Taban dönüşümleri ve ilgili hatalar Kesirli sayıdönüşümleri Öncelikle [[x]] notasyonu ile x sayısının tam değerini ve {x} ile de kesirli kısmınıgösterelim. A = sayısının ikili sistemdeki gösterimini belirleyiniz. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
80 Taban dönüşümleri ve ilgili hatalar Kesirli sayıdönüşümleri Öncelikle [[x]] notasyonu ile x sayısının tam değerini ve {x} ile de kesirli kısmınıgösterelim. A = sayısının ikili sistemdeki gösterimini belirleyiniz. Onlu sistemde A = = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
81 Taban dönüşümleri ve ilgili hatalar Kesirli sayıdönüşümleri Öncelikle [[x]] notasyonu ile x sayısının tam değerini ve {x} ile de kesirli kısmınıgösterelim. A = sayısının ikili sistemdeki gösterimini belirleyiniz. Onlu sistemde A = = Aynısayıyıiki tabanına göre A = = (0.d 1 d 2 d 3 d 4...) = d d d d 4 2 şeklinde ifade ettiğimizi varsayalım ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
82 Taban dönüşümleri ve ilgili hatalar Kesirli sayıdönüşümleri Öncelikle [[x]] notasyonu ile x sayısının tam değerini ve {x} ile de kesirli kısmınıgösterelim. A = sayısının ikili sistemdeki gösterimini belirleyiniz. Onlu sistemde A = = Aynısayıyıiki tabanına göre A = = (0.d 1 d 2 d 3 d 4...) = d d d d 4 2 şeklinde ifade ettiğimizi varsayalım İfadenin her iki yanını2 ile çarparsak 2A = = d 1 + d d d ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
83 Taban dönüşümleri ve ilgili hatalar Kesirli sayıdönüşümleri Öncelikle [[x]] notasyonu ile x sayısının tam değerini ve {x} ile de kesirli kısmınıgösterelim. A = sayısının ikili sistemdeki gösterimini belirleyiniz. Onlu sistemde A = = Aynısayıyıiki tabanına göre A = = (0.d 1 d 2 d 3 d 4...) = d d d d 4 2 şeklinde ifade ettiğimizi varsayalım İfadenin her iki yanını2 ile çarparsak 2A = = d 1 + d d d Burada d 1 = [[2A]] = 0 ve ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
84 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
85 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm Her iki yanıtekrar 2 ile çarparak 2K 1 = 0.50 = d 2 + d d d 2 = [[2K 1 ]] = 0 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
86 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm Her iki yanıtekrar 2 ile çarparak 2K 1 = 0.50 = d 2 + d d d 2 = [[2K 1 ]] = 0 Benzer biçimde K 2 = {2K 1 } = 0.50 = d_ d K 2 = 1.0 = d 3 + d d 3 = [[2K 2 ]] = 1 ve K 3 = {2K 2 } = 0 elde edilir. Böylece kesir kısmısıfır olana kadar işleme devam ettirilerek elde edilen d i, i = 1, 2,...değerleri kaydedilir. O halde A = = (0.001) 2 iki tabanlıgösterimi elde edilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
87 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
88 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm sayısının iki tabanlıgösterimini elde ediniz ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
89 Taban dönüşümleri ve ilgili hatalar On tabanlısistemden iki tabanlısisteme dönüşüm sayısının iki tabanlıgösterimini elde ediniz Bunun için yapmamız gereken işlem, yukarıdaki iki örneğe ait sonuçlarıbirleştirmektir. On tabanlısistemde = olacak şekilde ifade edildiği gibi, tam ve kesirli kısımlara karşılık gelen iki tabanlıgösterimler de birleştirildiğinde elde edilir = ( ) 2 = ( ) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
90 İkili sistemde sayıların bellek gösterimi: enbüyük ve enküçük pozitif sayılar IEEE754 standartıadıverilen uluslararasıstandarta göre x f gösterilen sayı, 32 bit formatta ile 1 bit(üs işareti) 7 bit(üs) 24 bit ( Mantis) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
91 İkili sistemde sayıların bellek gösterimi: enbüyük ve enküçük pozitif sayılar IEEE754 standartıadıverilen uluslararasıstandarta göre x f gösterilen sayı, 32 bit formatta ile 64 bit formatta ise 1 bit(üs işareti) 7 bit(üs) 24 bit ( Mantis) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
92 İkili sistemde sayıların bellek gösterimi: enbüyük ve enküçük pozitif sayılar IEEE754 standartıadıverilen uluslararasıstandarta göre x f gösterilen sayı, 32 bit formatta ile 64 bit formatta ise 1 bit(üs işareti) 7 bit(üs) 24 bit ( Mantis) 1 bit(üs işareti) 10 bit(üs) 53 bit ( Mantis) bellek alanlarında temsil edilebilir. İşaret bitindeki 0 ise sayının pozitif ve 1 ise negatif olmasıanlamına gelir. Buna göre sayısının 32 bit formatta bellek alanına yerleşimi aşağıdaki gösterildiği gibidir: ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
93 İkili sistemde sayıların bellek gösterimi: enbüyük ve enküçük pozitif sayılar IEEE754 standartıadıverilen uluslararasıstandarta göre x f gösterilen sayı, 32 bit formatta ile 64 bit formatta ise 1 bit(üs işareti) 7 bit(üs) 24 bit ( Mantis) 1 bit(üs işareti) 10 bit(üs) 53 bit ( Mantis) bellek alanlarında temsil edilebilir. İşaret bitindeki 0 ise sayının pozitif ve 1 ise negatif olmasıanlamına gelir. Buna göre sayısının 32 bit formatta bellek alanına yerleşimi aşağıdaki gösterildiği gibidir: burada 0= dır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
94 İkili sistemde 32 bit formatında temsil edilebilecek x f = ±(.d 1 d 2... d 24 ) 2 e sayısınıgöz önüne alalım. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
95 İkili sistemde 32 bit formatında temsil edilebilecek x f = ±(.d 1 d 2... d 24 ) 2 e sayısınıgöz önüne alalım. Pozitif bir sayıiçin 7 bitlik üs alanında ikili sisteme göre temsil edilebilecek en büyük üs e = ( ) 2 = = 127. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
96 Ayrıca d 1 = 0 olmak üzere en büyük mantis değeri ( ) 2 = 1/ / / olup, noktadan önceki ilk rakam 1 olarak kabul edilip, depolanmayarak, ( ) 2 2 olduğu için en büyük pozitif sayı x f = = E + 38 = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
97 Ayrıca d 1 = 0 olmak üzere en büyük mantis değeri ( ) 2 = 1/ / / olup, noktadan önceki ilk rakam 1 olarak kabul edilip, depolanmayarak, ( ) 2 2 olduğu için en büyük pozitif sayı x f = = E + 38 = Benzer olarak en küçük pozitif değer ise üssün alabileceği mutlak değerce en büyük negatif sayıya( 128) karşılık gelir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
98 Negatif tamsayıların ikili sistemdeki gösterimleri: 1 = ( [1]) = = ( [1]) = = (000000[10]) = = (111111[10]) = = (00001[100]) = = (11110[100]) = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
99 Negatif tamsayıların ikili sistemdeki gösterimleri: 127 = ( [1]) = = ( [1]) = = ( ) = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
100 Soldan itibaren ilk 1 sayısına kadar olan ve köşeli parantez içerisine alınan ikili sayıgrubunun sabit bırakılarak, diğerlerinden 1 lerin 0 ve 0 ların 1 yapılarak pozitif bir tamsayının toplama işlemine göre tersinin elde edildiğine dikkat edelim. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
101 Soldan itibaren ilk 1 sayısına kadar olan ve köşeli parantez içerisine alınan ikili sayıgrubunun sabit bırakılarak, diğerlerinden 1 lerin 0 ve 0 ların 1 yapılarak pozitif bir tamsayının toplama işlemine göre tersinin elde edildiğine dikkat edelim. Buna göre 8 bitlik alanda temsil edilebilecek mutlak değerce en büyük negatif sayının 128 olacağıaçıktır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
102 Soldan itibaren ilk 1 sayısına kadar olan ve köşeli parantez içerisine alınan ikili sayıgrubunun sabit bırakılarak, diğerlerinden 1 lerin 0 ve 0 ların 1 yapılarak pozitif bir tamsayının toplama işlemine göre tersinin elde edildiğine dikkat edelim. Buna göre 8 bitlik alanda temsil edilebilecek mutlak değerce en büyük negatif sayının 128 olacağıaçıktır. O halde en küçük pozitif kayan noktalısayı x f = = E 39 = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
103 Negatif tamsayıların ikili sistemdeki gösterimleri: İkili sistemde 64 bit formatında temsil edilebilecek kayan nokta sayısınıgöz önüne alalım. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
104 Negatif tamsayıların ikili sistemdeki gösterimleri: İkili sistemde 64 bit formatında temsil edilebilecek kayan nokta sayısınıgöz önüne alalım. Pozitif bir sayıiçin 11 bitlik üs alanında ikili sisteme göre temsil edilebilecek en büyük üs e = ( ) 2 = 1023 ve en küçük üs ise e = ( ) 2 = 1024 dür. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
105 Negatif tamsayıların ikili sistemdeki gösterimleri: İkili sistemde 64 bit formatında temsil edilebilecek kayan nokta sayısınıgöz önüne alalım. Pozitif bir sayıiçin 11 bitlik üs alanında ikili sisteme göre temsil edilebilecek en büyük üs e = ( ) 2 = 1023 ve en küçük üs ise e = ( ) 2 = 1024 dür. Ayrıca en büyük mantis değeri ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
106 ( ) 2 = 1/ / /2 53 = 1 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
107 ( ) 2 = 1/ / /2 53 = 1 en büyük pozitif kayan noktalısayıise x f = = E olup bu sayının ikili sistemdeki karşılĭgı elde edilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
108 Negatif tamsayıların ikili sistemdeki gösterimleri: Benzer olarak en küçük pozitif değer ise üssün alabileceği mutlak değerce en büyük negatif sayıya( 1024) karşılık gelir ve olup, ikili sistem karşılĭgı x f = = E ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
109 Taban dönüşümü kaynaklıhatalar Bu durumun en açık örneği onlu sistemdeki 0.1sayısıdır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
110 Taban dönüşümü kaynaklıhatalar Bu durumun en açık örneği onlu sistemdeki 0.1sayısıdır. Bu sayının iki tabanlısistemdeki karşılĭgı(0.0 ( 0011 ) ) 2 devirli sayısıdır. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
111 Taban dönüşümü kaynaklıhatalar Bu durumun en açık örneği onlu sistemdeki 0.1sayısıdır. Bu sayının iki tabanlısistemdeki karşılĭgı(0.0 ( 0011 ) ) 2 sayısıdır. devirli Ancak 32 bit formatta bu sayının mantisi için 24 bitlik bir alan tahsis edildiği için bu formattaki gösterimi dir. ( ) 2 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
112 Taban dönüşümü kaynaklıhatalar Bu durumun en açık örneği onlu sistemdeki 0.1sayısıdır. Bu sayının iki tabanlısistemdeki karşılĭgı(0.0 ( 0011 ) ) 2 sayısıdır. devirli Ancak 32 bit formatta bu sayının mantisi için 24 bitlik bir alan tahsis edildiği için bu formattaki gösterimi dir. ( ) 2 bu sayının on tabanlısistemdeki karşılĭgınıhesaplarsak E 002 elde ederiz. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
113 Taban dönüşümü kaynaklıhatalar Bu durumun en açık örneği onlu sistemdeki 0.1sayısıdır. Bu sayının iki tabanlısistemdeki karşılĭgı(0.0 ( 0011 ) ) 2 sayısıdır. devirli Ancak 32 bit formatta bu sayının mantisi için 24 bitlik bir alan tahsis edildiği için bu formattaki gösterimi dir. ( ) 2 bu sayının on tabanlısistemdeki karşılĭgınıhesaplarsak E 002 elde ederiz. Böylece 0.1 sayısının ikili sistemdeki devirli gösterimi, tahsis edilen bellek alana yerleştirilirken atılmasıgereken kısmıönemli bir hataya neden olmuştur. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
114 Taban dönüşümü kaynaklıhatalar >> x = 0.1; ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
115 Taban dönüşümü kaynaklıhatalar >> x = 0.1; >> y = (x + x + x + x + x + x + x + x + x + x) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
116 Taban dönüşümü kaynaklıhatalar >> x = 0.1; >> y = (x + x + x + x + x + x + x + x + x + x) >> z = (1 y) 1E20 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
117 Taban dönüşümü kaynaklıhatalar >> x = 0.1; >> y = (x + x + x + x + x + x + x + x + x + x) >> z = (1 y) 1E20 z = E + 004! ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
118 Anlamlıbasamak kaybıhatası Anlamlıbasamak sayısı: On tabanlısistemde eğer ε b (x) 5 10 k ise x f yaklaşımıx gerçek değerini k 1 anlamlıbasamakla temsil etmektedir denir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
119 Anlamlıbasamak kaybıhatası Anlamlıbasamak sayısı: On tabanlısistemde eğer ε b (x) 5 10 k ise x f yaklaşımıx gerçek değerini k 1 anlamlıbasamakla temsil etmektedir denir. x f = 1.1 yaklaşımıx = 1 değerini 0 anlamlıbasamakla temsil etmektedir, çünkü ε b (x) = < ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
120 Anlamlıbasamak kaybıhatası Anlamlıbasamak sayısı: On tabanlısistemde eğer ε b (x) 5 10 k ise x f yaklaşımıx gerçek değerini k 1 anlamlıbasamakla temsil etmektedir denir. x f = 1.1 yaklaşımıx = 1 değerini 0 anlamlıbasamakla temsil etmektedir, çünkü ε b (x) = < x f = 1.23 yaklaşımıx = 1.2 değerini 1 anlamlıbasamkla temsil etmektedir, çünkü ε b (x) = < ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
121 Anlamlıbasamak kaybıhatası Anlamlıbasamak sayısı: On tabanlısistemde eğer ε b (x) 5 10 k ise x f yaklaşımıx gerçek değerini k 1 anlamlıbasamakla temsil etmektedir denir. x f = 1.1 yaklaşımıx = 1 değerini 0 anlamlıbasamakla temsil etmektedir, çünkü ε b (x) = < x f = 1.23 yaklaşımıx = 1.2 değerini 1 anlamlıbasamkla temsil etmektedir, çünkü ε b (x) = < x f = yaklaşımıx = değerini 2 anlamlıbasamkla temsil etmektedir, çünkü ε b (x) = < ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
122 Anlamlıbasamak kaybıhatası Birbirine eşit olan ve f 1 (x) = 1000(log(x + 1) log(x)) f 2 (x) = 1000log((x + 1)/x) fonksiyonlarınıgöz önüne alalım ve bu fonksiyonların x = noktasındaki değerlerini virgülden sonra altıbasamağa kadar ve yuvarlama prensibine göre çalışan hesaplayıcıda hesaplayarak sonuçları karşılaştıralım. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
123 Anlamlıbasamak kaybıhatası Birbirine eşit olan f 1 (x) = 1000(log(x + 1) log(x)) ve f 2 (x) = 1000log((x + 1)/x) fonksiyonlarınıgöz önüne alalım ve bu fonksiyonların x = noktasındaki değerlerini virgülden sonra altıbasamağa kadar ve yuvarlama prensibine göre çalışan hesaplayıcıda hesaplayarak sonuçları karşılaştıralım. x = ve x 1 = log(x + 1) = dir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
124 Anlamlıbasamak kaybıhatası Birbirine eşit olan f 1 (x) = 1000(log(x + 1) log(x)) ve f 2 (x) = 1000log((x + 1)/x) fonksiyonlarınıgöz önüne alalım ve bu fonksiyonların x = noktasındaki değerlerini virgülden sonra altıbasamağa kadar ve yuvarlama prensibine göre çalışan hesaplayıcıda hesaplayarak sonuçları karşılaştıralım. x = ve x 1 = log(x + 1) = dir. Ancak altıbasamaklıve yuvarlama prensibine göre çalışan hesaplayıcıda x 1 = olarak kabul edilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
125 Anlamlıbasamak kaybıhatası x 2 = log(x) = 5; ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
126 Anlamlıbasamak kaybıhatası x 2 = log(x) = 5; f 1 (x) = 1000(x 1 x 2 ) = 0.004; ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
127 Anlamlıbasamak kaybıhatası x 2 = log(x) = 5; f 1 (x) = 1000(x 1 x 2 ) = 0.004; f 2 (x) = 1000log((x + 1)/x) = = ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
128 Anlamlıbasamak kaybıhatası x 2 = log(x) = 5; f 1 (x) = 1000(x 1 x 2 ) = 0.004; f 2 (x) = 1000log((x + 1)/x) = = Gerçek sonuç ise dir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
129 Anlamlıbasamak kaybıhatası x 2 = log(x) = 5; f 1 (x) = 1000(x 1 x 2 ) = 0.004; f 2 (x) = 1000log((x + 1)/x) = = Gerçek sonuç ise dir. Yuvarlatılmış x 1 değeri 6 anlamlıbasamağa sahipken birbirine çok yakın x 1, x 2 sayılarının farkıx 1 x 2 = olarak elde edilir. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
130 Anlamlıbasamak kaybıhatası x 2 = log(x) = 5; f 1 (x) = 1000(x 1 x 2 ) = 0.004; f 2 (x) = 1000log((x + 1)/x) = = Gerçek sonuç ise dir. Yuvarlatılmış x 1 değeri 6 anlamlıbasamağa sahipken birbirine çok yakın x 1, x 2 sayılarının farkıx 1 x 2 = olarak elde edilir. Bu yaklaşım gerçek fark değeri olan değerini hiçbir anlamlıbasamakla temsil etmez. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
131 Anlamlıbasamak kaybıhatası x 2 = log(x) = 5; f 1 (x) = 1000(x 1 x 2 ) = 0.004; f 2 (x) = 1000log((x + 1)/x) = = Gerçek sonuç ise dir. Yuvarlatılmış x 1 değeri 6 anlamlıbasamağa sahipken birbirine çok yakın x 1, x 2 sayılarının farkıx 1 x 2 = olarak elde edilir. Bu yaklaşım gerçek fark değeri olan değerini hiçbir anlamlıbasamakla temsil etmez. Dolayısıyla fark işlemi anlam basamağıkaybına neden olmuştur ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
132 Alıştırmalar 1 x f = ±q β e, q = 0.d 1 d 2, d 1,2 = 0, 1,..., 5 ;d 1 = 0, β = 10 tabanlı ve e = 1, 0, 1 üs değerlerine sahip bir R f sayısistemi gözönüne alalım ve gerçekleştirilen her işlem sonucunun R f de olmaması durumunda, sistemde bulunan en yakın sayıya yuvarlatıldĭgınıkabul edelim. Buna göre R f nin elemanları(sayıları) nelerdir. R f nin en büyük pozitif ve en küçük pozitif sayılarınelerdir. R f de "overflow veya inf" hatasına neden olabilecek birer işlem tanımlayınız. R f kümesinin toplama işlemine göre kapalılık özelliğini sağlamayabileceğini bir örnekle gösteriniz. R f de toplama işlemine göre birleşme özelliği olamayabileceğini bir örnekle gösteriniz. ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
133 Alıştırmalar 2 (R, +,.) nın yani Reel sayılar kümesinin bilenen skalerle çarpma ve toplama işlemine göre sağladĭgıbaşka hangi özelliklerin (R f, +,.) de geçerli olmayabileceğini düşünüyorsunuz? 3 x f = ±q β e, q = 0.d 1 d 2 d 3, 0 d i < β,formatında yazılabilen kayan noktalısayılara izin veren sanal bir bilgisayar sistemi gözönüne alalım. Buna göre aşağıdaki tabloda verilen β, e değerleri için sistemde temsil edilebilecek en büyük ve en küçük pozitif tamsayıları belirleyiniz. 4 Soru 3 deki R f sayısistemini inceleyerek, hangi tür işlemlerde daha fazla hata oluşabileceğini düşünüyorsunuz? ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
134 Alıştırmalar 5 (R, +,.) nın yani Reel sayılar kümesinin bilenen skalerle çarpma ve toplama işlemine göre sağladĭgıbaşka hangi özelliklerin (R f, +,.) de geçerli olmayabileceğini düşünüyorsunuz? 6 x f = ±q β e, q = 0.d 1 d 2 d 3, 0 d i < β,formatında yazılabilen kayan noktalısayılara izin veren sanal bir bilgisayar sistemi gözönüne alalım. Buna göre aşağıdaki tabloda verilen β, e değerleri için sistemde temsil edilebilecek en büyük ve en küçük pozitif tamsayıları belirleyiniz. 7 Soru 3 deki R f sayısistemini inceleyerek, hangi tür işlemlerde daha fazla hata oluşabileceğini düşünüyorsunuz? ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
135 Alıştırmalar 8 x = 0.d 1 d 2...d n d n+1...d m β e,x f = 0.d 1 d 2...d n β e için ε b (x) = x x f x 1 2 β n+1 olduğunu gösteriniz.(ipucu: Öncelikle x x f {}}{ n adet ( 1 2 β) βe = ( 1 2 β)β n 1 β e = 1 2 βe n olduğunu gözlemleyiniz ayrıca β tabanlısistemde 1/0.1 = β 1 olduğuna dikkat ediniz.) ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
136 Alıştırmalar 9 Aşağıda verilen on tabanlısayıların karşılarında verilen iki tabanlı gösterimlere sahip olduklarınıgösteriniz 3 (11) 2 8 (1000) 2 10 (1010) 2 50 (110010) ( ) 2 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
137 Alıştırmalar 10 Aşağıda verilen iki tabanlısayıların on tabanlıgösterimlerini belirleyiniz (11001) 2 ( ) 2 ( ) 2 (100001) 2 11 Aşağıda verilen kesirli sayıların iki tabanlıgösterimlerinin doğruluğunu kontrol ediniz.1001 üs çizgi notasyonu sayının devirli sayıolduğunu ifade etmektedir. 2.5 (10.1) (11. ( 1001 ) ) (1.01) (1.001) 2 ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
138 Alıştırmalar 12 Onlu tabanda 0.2 sayısı32 bitlik ( ) 2 gösterimine sahiptir. Elde edilen bu ikilik sistem gösterimini on tabanlı sisteme dönüştürdüğümüzde yine 0.2 sayısınıelde ederiz. Bu sonucu kendi işlemlerinizle kontrol ediniz. 13 Bilgisayar sisteminizde 1 ve 2 arasındaki her sayıile bu sayıya en yakın sayı arasındaki mesafenin birbirine eşit olduğunu eps komutu yardımıyla gözlemleyiniz. Buna göre örneğin eps(1) = eps(1.5) = eps(1.8) olmalıdır. 15 Bilgisayar sisteminizde 2 ile 2 den büyük olan en büyük hangi sayı arasında yer alan bütün sayılar birbirine eşit uzaklıktadırlar? ec (Karadeniz Teknik Üniversitesi) Bölüm 2 Mart, / 48
Bilgisayar sayısistemi, aritmetiği ve hata
 Bölüm 2 Bilgisayar sayısistemi, aritmetiği ve hata Sayısal yöntemler için gerekli en temel araçlar bilgisayarlardır, fakat sayısal yöntemler analitik analiz yöntemlerinden alışık olduğumuz reel veya kompleks
Bölüm 2 Bilgisayar sayısistemi, aritmetiği ve hata Sayısal yöntemler için gerekli en temel araçlar bilgisayarlardır, fakat sayısal yöntemler analitik analiz yöntemlerinden alışık olduğumuz reel veya kompleks
Bilgisayar SayıSistemi, Aritmetiği ve Hata
 Bölüm 2 Bilgisayar SayıSistemi, Aritmetiği ve Hata Sayısal yöntemler için gerekli en temel araçlar bilgisayarlardır, ancak bilgisayarlar reel veya kompleks sayılar kümesi yerine, bu kümelerin sonlu sayıda
Bölüm 2 Bilgisayar SayıSistemi, Aritmetiği ve Hata Sayısal yöntemler için gerekli en temel araçlar bilgisayarlardır, ancak bilgisayarlar reel veya kompleks sayılar kümesi yerine, bu kümelerin sonlu sayıda
Hatalar ve Bilgisayar Aritmetiği
 Hatalar ve Bilgisayar Aritmetiği Analitik yollardan çözemediğimiz birçok matematiksel problemi sayısal yöntemlerle bilgisayarlar aracılığı ile çözmeye çalışırız. Bu şekilde Sayısal yöntemler kullanarak
Hatalar ve Bilgisayar Aritmetiği Analitik yollardan çözemediğimiz birçok matematiksel problemi sayısal yöntemlerle bilgisayarlar aracılığı ile çözmeye çalışırız. Bu şekilde Sayısal yöntemler kullanarak
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
Elemanter fonksiyonlarla yaklaşım ve hata
 Elemanter fonksiyonlarla yaklaşım ve hata Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi Matematik Bölümü Kasım, 2018 e 5 Kasım, 2018 1 / 48 Elemanter fonksiyonlarla yaklaşım ve hata
Elemanter fonksiyonlarla yaklaşım ve hata Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi Matematik Bölümü Kasım, 2018 e 5 Kasım, 2018 1 / 48 Elemanter fonksiyonlarla yaklaşım ve hata
RASYONEL SAYILAR. ÖRNEK: Aşağıda verilen eşitliklerde verilmeyen harflere karşılık gelen tamsayıları bulunuz. RASYONEL SAYILAR A =?
 Kazanım : Rasyonel sayıları tanır ve sayı doğrusunda gösterir. RASYONEL SAYILAR a bir tamsayı ve b sıfırdan farklı bir tamsayı olmak üzere a b biçiminde yazılabilen sayılara rasyonel sayılar denir. Rasyonel
Kazanım : Rasyonel sayıları tanır ve sayı doğrusunda gösterir. RASYONEL SAYILAR a bir tamsayı ve b sıfırdan farklı bir tamsayı olmak üzere a b biçiminde yazılabilen sayılara rasyonel sayılar denir. Rasyonel
Algoritmalar ve Programlama. DERS - 2 Yrd. Doç. Dr. Ahmet SERBES
 Algoritmalar ve Programlama DERS - 2 Yrd. Doç. Dr. Ahmet SERBES Programlama Bilgisayara ne yapması gerektiğini, yani onunla konuşmamızı sağlayan dil. Tüm yazılımlar programlama dilleri ile yazılır. 1.
Algoritmalar ve Programlama DERS - 2 Yrd. Doç. Dr. Ahmet SERBES Programlama Bilgisayara ne yapması gerektiğini, yani onunla konuşmamızı sağlayan dil. Tüm yazılımlar programlama dilleri ile yazılır. 1.
SAYILAR SAYI KÜMELERİ
 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif tamsayılar
SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif tamsayılar
SAYILAR SAYI KÜMELERİ
 1 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif
1 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif
Bir işaretli büyüklük sayısında en soldaki basamak bir işaret içerir. Diğer basamaklarda ise sayısal değerin büyüklüğü (mutlak değeri) gösterilir.
 İşaretli Tamsayı Gösterimi 1. İşaretli Büyüklük Bir işaretli büyüklük sayısında en soldaki basamak bir işaret içerir. Diğer basamaklarda ise sayısal değerin büyüklüğü (mutlak değeri) gösterilir. Örnek
İşaretli Tamsayı Gösterimi 1. İşaretli Büyüklük Bir işaretli büyüklük sayısında en soldaki basamak bir işaret içerir. Diğer basamaklarda ise sayısal değerin büyüklüğü (mutlak değeri) gösterilir. Örnek
SAYISAL ANALİZ. 2. Hafta SAYISAL ANALİZDE HATA KAVRAMI VE HATA TÜRLERİ
 SAYISAL ANALİZ 2. Hafta SAYISAL ANALİZDE HATA KAVRAMI VE HATA TÜRLERİ 1 İÇİNDEKİLER 1. de Problem Çözümünde İzlenilecek Adımlar 2. de Hata Kavramı 3. de Hataların Sebepleri 4. Sayısal Hata ve Hata Türleri
SAYISAL ANALİZ 2. Hafta SAYISAL ANALİZDE HATA KAVRAMI VE HATA TÜRLERİ 1 İÇİNDEKİLER 1. de Problem Çözümünde İzlenilecek Adımlar 2. de Hata Kavramı 3. de Hataların Sebepleri 4. Sayısal Hata ve Hata Türleri
2. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 2. HAFTA BLM323 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 2 HATA Sayısal yöntemler analitik çözümlerden farklı olarak
2. HAFTA BLM323 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 2 HATA Sayısal yöntemler analitik çözümlerden farklı olarak
Yüksek basamaktan tek adım Sonlu Fark Yöntemleri
 Bölüm Yüksek basamaktan tek adım Sonlu Fark Yöntemleri Bu bölümde, birinci basamaktan başlangıç değer problemleri için Tek adım (Yamuk, Düzeltilmiş Euler(Heun), Runge-Kutta yöntemlerinin nasıl elde edildikleri,
Bölüm Yüksek basamaktan tek adım Sonlu Fark Yöntemleri Bu bölümde, birinci basamaktan başlangıç değer problemleri için Tek adım (Yamuk, Düzeltilmiş Euler(Heun), Runge-Kutta yöntemlerinin nasıl elde edildikleri,
1. GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G (e ye birim eleman denir) vardır.
 1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
Sayılar Teorisi SAYILAR TEORİSİ VE SAYILAR
 Sayılar Teorisi SAYILAR TEORİSİ VE SAYILAR Sayılar; insanların ilk çağlardan beri ihtiyaç duyduğu bir gereksinim olmuştur; sayılar teorisi de matematiğin en eski alanlarından birisidir. Sayılar teorisi,
Sayılar Teorisi SAYILAR TEORİSİ VE SAYILAR Sayılar; insanların ilk çağlardan beri ihtiyaç duyduğu bir gereksinim olmuştur; sayılar teorisi de matematiğin en eski alanlarından birisidir. Sayılar teorisi,
TEMEL KAVRAMLAR. SAYI KÜMELERİ 1. Doğal Sayılar
 TEMEL KAVRAMLAR Rakam: Sayıları ifade etmeye yarayan sembollere rakam denir. Bu semboller {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarıdır., b ve c birer rakamdır. 15 b = c olduğuna göre, + b + c
TEMEL KAVRAMLAR Rakam: Sayıları ifade etmeye yarayan sembollere rakam denir. Bu semboller {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarıdır., b ve c birer rakamdır. 15 b = c olduğuna göre, + b + c
SAYILAR DOĞAL VE TAM SAYILAR
 1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
Okut. Yüksel YURTAY. İletişim : (264) Sayısal Analiz. Giriş.
 Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
MATEMATİK. Doç Dr Murat ODUNCUOĞLU
 MATEMATİK Doç Dr Murat ODUNCUOĞLU Mesleki Matematik 1 TEMEL KAVRAMLAR RAKAM Sayıları yazmak için kullandığımız işaretlere rakam denir. Sayıları ifade etmeye yarayan sembollere rakam denir. Rakamlar 0,1,2,3,4,5,6,7,8,9
MATEMATİK Doç Dr Murat ODUNCUOĞLU Mesleki Matematik 1 TEMEL KAVRAMLAR RAKAM Sayıları yazmak için kullandığımız işaretlere rakam denir. Sayıları ifade etmeye yarayan sembollere rakam denir. Rakamlar 0,1,2,3,4,5,6,7,8,9
13.Konu Reel sayılar
 13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ
 Giriş ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ Sayısal Analiz Nedir? Mühendislikte ve bilimde, herhangi bir süreci tanımlayan karmaşık denklemlerin
Giriş ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ Sayısal Analiz Nedir? Mühendislikte ve bilimde, herhangi bir süreci tanımlayan karmaşık denklemlerin
Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak
![Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak](/thumbs/17/146647.jpg) 10.Konu İç çarpım uzayları ve özellikleri 10.1. ve üzerinde uzunluk de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor teoreminden dir. 1.Ö.: [ ] ise ( ) ( ) ve ( ) noktaları gözönüne alalım.
10.Konu İç çarpım uzayları ve özellikleri 10.1. ve üzerinde uzunluk de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor teoreminden dir. 1.Ö.: [ ] ise ( ) ( ) ve ( ) noktaları gözönüne alalım.
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAT 302 SOYUT CEBİR II SORULAR. (b) = ise =
 MAT 302 SOYUT CEBİR II SORULAR 1. : bir dönüşüm, olsunlar. a) ( ) = ( ) ( ) b) ( ) ( ) ( ) olduğunu c) ( ) nin eşitliğinin sağlanması için gerekli ve yeterli bir koşulun nin 1 1 olması ile mümkün olduğunu
MAT 302 SOYUT CEBİR II SORULAR 1. : bir dönüşüm, olsunlar. a) ( ) = ( ) ( ) b) ( ) ( ) ( ) olduğunu c) ( ) nin eşitliğinin sağlanması için gerekli ve yeterli bir koşulun nin 1 1 olması ile mümkün olduğunu
Atatürk Anadolu. Temel Kavramlar Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
Lineer Cebir. Doç. Dr. Niyazi ŞAHİN TOBB. İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler
 Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Bu kısımda işlem adı verilen özel bir fonksiyon çeşidini ve işlemlerin önemli özelliklerini inceleyeceğiz.
 Bölüm 3 Gruplar Bu bölümde ilk olarak bir küme üzerinde tanımlı işlem kavramını ele alıp işlemlerin bazı özelliklerini inceleyeceğiz. Daha sonra kümeler ve üzerinde tanımlı işlemlerden oluşan cebirsel
Bölüm 3 Gruplar Bu bölümde ilk olarak bir küme üzerinde tanımlı işlem kavramını ele alıp işlemlerin bazı özelliklerini inceleyeceğiz. Daha sonra kümeler ve üzerinde tanımlı işlemlerden oluşan cebirsel
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
1.GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G. vardır. 3) a G için denir) vardır.
 1.GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G, ) cebirsel yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir. 1) a, b, c G için a ( b c) ( a b) c (Birleşme özelliği)
1.GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G, ) cebirsel yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir. 1) a, b, c G için a ( b c) ( a b) c (Birleşme özelliği)
SAYISAL ELEKTRONİK. Ege Ü. Ege MYO Mekatronik Programı
 SAYISAL ELEKTRONİK Ege Ü. Ege MYO Mekatronik Programı BÖLÜM 2 Sayı Sistemleri İkilik, Onaltılık ve İKO Sayılar İkilik Sayı Sistemi 3 Çoğu dijital sistemler 8, 16, 32, ve 64 bit gibi, 2 nin çift kuvvetleri
SAYISAL ELEKTRONİK Ege Ü. Ege MYO Mekatronik Programı BÖLÜM 2 Sayı Sistemleri İkilik, Onaltılık ve İKO Sayılar İkilik Sayı Sistemi 3 Çoğu dijital sistemler 8, 16, 32, ve 64 bit gibi, 2 nin çift kuvvetleri
Cebir Notları. Gökhan DEMĐR, ÖRNEK : A ve A x A nın bir alt kümesinden A ya her fonksiyona
 , 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Đşlem ĐŞLEM A ve A x A nın bir alt kümesinden A ya her fonksiyona ikili işlem denir. Örneğin toplama, çıkarma, çarpma birer işlemdir. Đşlemler
, 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Đşlem ĐŞLEM A ve A x A nın bir alt kümesinden A ya her fonksiyona ikili işlem denir. Örneğin toplama, çıkarma, çarpma birer işlemdir. Đşlemler
T.C. ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ
 T.C. ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ DERS: CEBİRDEN SEÇME KONULAR KONU: KARDİNAL SAYILAR ÖĞRETİM GÖREVLİLERİ: PROF.DR. NEŞET AYDIN AR.GÖR. DİDEM YEŞİL HAZIRLAYANLAR: DİRENCAN DAĞDEVİREN ELFİYE ESEN
T.C. ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ DERS: CEBİRDEN SEÇME KONULAR KONU: KARDİNAL SAYILAR ÖĞRETİM GÖREVLİLERİ: PROF.DR. NEŞET AYDIN AR.GÖR. DİDEM YEŞİL HAZIRLAYANLAR: DİRENCAN DAĞDEVİREN ELFİYE ESEN
İÇİNDEKİLER ÖNSÖZ Bölüm 1 KÜMELER Bölüm 2 SAYILAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 KÜMELER 11 1.1. Küme 12 1.2. Kümelerin Gösterimi 13 1.3. Boş Küme 13 1.4. Denk Küme 13 1.5. Eşit Kümeler 13 1.6. Alt Küme 13 1.7. Alt Küme Sayısı 14 1.8. Öz Alt Küme 16 1.9.
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 KÜMELER 11 1.1. Küme 12 1.2. Kümelerin Gösterimi 13 1.3. Boş Küme 13 1.4. Denk Küme 13 1.5. Eşit Kümeler 13 1.6. Alt Küme 13 1.7. Alt Küme Sayısı 14 1.8. Öz Alt Küme 16 1.9.
Fatih University- Faculty of Engineering- Electric and Electronic Dept.
 SAYISAL DEVRE TASARIMI EEM122 Ref. Morris MANO & Michael D. CILETTI SAYISAL TASARIM 4. Baskı Fatih University- Faculty of Engineering- Electric and Electronic Dept. SAYISAL DEVRE NEDİR? Mühendisler, elektronik
SAYISAL DEVRE TASARIMI EEM122 Ref. Morris MANO & Michael D. CILETTI SAYISAL TASARIM 4. Baskı Fatih University- Faculty of Engineering- Electric and Electronic Dept. SAYISAL DEVRE NEDİR? Mühendisler, elektronik
ÜNİTE 1: TEMEL KAVRAMLAR
 MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
MATM 133 MATEMATİK LOJİK. Dr. Doç. Çarıyar Aşıralıyev
 MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 5.KONU Cebiresel yapılar; Grup, Halka 1. Matematik yapı 2. Denk yapılar ve eş yapılar 3. Grup 4. Grubun basit özellikleri 5. Bir elemanın kuvvetleri
MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 5.KONU Cebiresel yapılar; Grup, Halka 1. Matematik yapı 2. Denk yapılar ve eş yapılar 3. Grup 4. Grubun basit özellikleri 5. Bir elemanın kuvvetleri
BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES)
 BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES) Lagrange ve Neville yöntemlerinin bazı olumsuz yanları vardır: İşlem sayısı çok fazladır (bazı başka yöntemlere kıyasla) Data setinde bir nokta ilavesi veya çıkartılması
BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES) Lagrange ve Neville yöntemlerinin bazı olumsuz yanları vardır: İşlem sayısı çok fazladır (bazı başka yöntemlere kıyasla) Data setinde bir nokta ilavesi veya çıkartılması
Buna göre, eşitliği yazılabilir. sayılara rasyonel sayılar denir ve Q ile gösterilir. , -, 2 2 = 1. sayıdır. 2, 3, 5 birer irrasyonel sayıdır.
 TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
Rakam : Sayıları yazmaya yarayan sembollere rakam denir.
 A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir.
 Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir. a) Pozitif doğal sayılar: Sıfır olmayan doğal sayılar kümesine Pozitif Doğal
Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir. a) Pozitif doğal sayılar: Sıfır olmayan doğal sayılar kümesine Pozitif Doğal
2012 LYS MATEMATİK SORU VE ÇÖZÜMLERİ Niyazi Kurtoğlu
 .SORU 8 sayı tabanında verilen (5) 8 sayısının sayı tabanında yazılışı nedir?.soru 6 3 3 3 3 4 6 8? 3.SORU 3 ise 5? 5 4.SORU 4 5 olduğuna göre, ( )? 5.SORU (y z) z(y ) y z yz bulunuz. ifadesinin en sade
.SORU 8 sayı tabanında verilen (5) 8 sayısının sayı tabanında yazılışı nedir?.soru 6 3 3 3 3 4 6 8? 3.SORU 3 ise 5? 5 4.SORU 4 5 olduğuna göre, ( )? 5.SORU (y z) z(y ) y z yz bulunuz. ifadesinin en sade
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir?
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
Modül Teori. Modüller. Prof. Dr. Neşet AYDIN. [01/07] Mart Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart / 50
![Modül Teori. Modüller. Prof. Dr. Neşet AYDIN. [01/07] Mart Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart / 50 Modül Teori. Modüller. Prof. Dr. Neşet AYDIN. [01/07] Mart Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart / 50](/thumbs/62/48180402.jpg) Modül Teori Modüller Prof. Dr. Neşet AYDIN ÇOMÜ - Matematik Bölümü [01/07] Mart 2012 Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart 2012 1 / 50 Giriş M bir toplamsal değişmeli
Modül Teori Modüller Prof. Dr. Neşet AYDIN ÇOMÜ - Matematik Bölümü [01/07] Mart 2012 Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart 2012 1 / 50 Giriş M bir toplamsal değişmeli
Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz.
 1 BİR İŞLEMLİ SİSTEMLER Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz. 1.1 İŞLEMLER Bir kümeden kendisine tanımlı olan her fonksiyona birli işlem denir. Örneğin Z
1 BİR İŞLEMLİ SİSTEMLER Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz. 1.1 İŞLEMLER Bir kümeden kendisine tanımlı olan her fonksiyona birli işlem denir. Örneğin Z
MODÜLER ARİTMETİK Test -4
 MODÜLER ARİTMETİK Test -4 1. A doğal sayısının 7 ye bölümündeki kalan 4, B doğal sayısının 7 ye bölümündeki kalan 5 tir. Buna göre, A toplamının 7 ye bölümündeki kalan 3B A) 0 B) 1 C) D) 3 E) 4 5. I. 1
MODÜLER ARİTMETİK Test -4 1. A doğal sayısının 7 ye bölümündeki kalan 4, B doğal sayısının 7 ye bölümündeki kalan 5 tir. Buna göre, A toplamının 7 ye bölümündeki kalan 3B A) 0 B) 1 C) D) 3 E) 4 5. I. 1
8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR
 0 8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR KAREKÖKLÜ SAYI KAVRAMI Karekök ile gösterilir. karekökünün içi negatif bir sayıya eşit olamaz. ÖR: Aşağıda verilen eşitliklere göre x lerin alabileceği değerleri
0 8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR KAREKÖKLÜ SAYI KAVRAMI Karekök ile gösterilir. karekökünün içi negatif bir sayıya eşit olamaz. ÖR: Aşağıda verilen eşitliklere göre x lerin alabileceği değerleri
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
SAYISAL ÇÖZÜMLEME. Yrd.Doç.Dr.Esra Tunç Görmüş. 1.Hafta
 SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
HATA VE HATA KAYNAKLARI...
 İÇİNDEKİLER 1. GİRİŞ... 1 1.1 Giriş... 1 1.2 Sayısal Analizin İlgi Alanı... 2 1.3 Mühendislik Problemlerinin Çözümü ve Sayısal Analiz... 2 1.4 Sayısal Analizde Bilgisayarın Önemi... 7 1.5 Sayısal Çözümün
İÇİNDEKİLER 1. GİRİŞ... 1 1.1 Giriş... 1 1.2 Sayısal Analizin İlgi Alanı... 2 1.3 Mühendislik Problemlerinin Çözümü ve Sayısal Analiz... 2 1.4 Sayısal Analizde Bilgisayarın Önemi... 7 1.5 Sayısal Çözümün
8.Konu Vektör uzayları, Alt Uzaylar
 8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
Lineer Dönüşümler ÜNİTE. Amaçlar. İçindekiler. Yazar Öğr. Grv.Dr. Nevin ORHUN
 Lineer Dönüşümler Yazar Öğr. Grv.Dr. Nevin ORHUN ÜNİTE 7 Amaçlar Bu üniteyi çalıştıktan sonra; Vektör uzayları arasında tanımlanan belli fonksiyonları tanıyacak, özelliklerini öğrenecek, Bir dönüşümün,
Lineer Dönüşümler Yazar Öğr. Grv.Dr. Nevin ORHUN ÜNİTE 7 Amaçlar Bu üniteyi çalıştıktan sonra; Vektör uzayları arasında tanımlanan belli fonksiyonları tanıyacak, özelliklerini öğrenecek, Bir dönüşümün,
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
KPSS MATEMATÝK. SOYUT CEBÝR ( Genel Tekrar Testi-1) N tam sayılar kümesinde i N için, A = 1 i,i 1
 SOYUT CEBÝR ( Genel Tekrar Testi-1) 1. A = { k k Z, < k 4 } 4. N tam sayılar kümesinde i N için, k 1 B = { k Z, 1 k < 1 } k 1 A = 1 i,i 1 i ( ] kümeleri verildiğine göre, aşağıdakilerden hangisi doğrudur?
SOYUT CEBÝR ( Genel Tekrar Testi-1) 1. A = { k k Z, < k 4 } 4. N tam sayılar kümesinde i N için, k 1 B = { k Z, 1 k < 1 } k 1 A = 1 i,i 1 i ( ] kümeleri verildiğine göre, aşağıdakilerden hangisi doğrudur?
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A
 T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
ECEM ERDURU GAMZE SERİN ZEHRA SABUR EMİNE ÖLMEZ. o TAMSAYILAR KONUSU ANLATILMAKTADIR
 ECEM ERDURU GAMZE SERİN ZEHRA SABUR EMİNE ÖLMEZ o TAMSAYILAR KONUSU ANLATILMAKTADIR Sıfırın sağındaki sayılar pozitif tam sayılar, sıfırın solundaki sayılar negatif tam sayılardır. Pozitif tam sayılar,
ECEM ERDURU GAMZE SERİN ZEHRA SABUR EMİNE ÖLMEZ o TAMSAYILAR KONUSU ANLATILMAKTADIR Sıfırın sağındaki sayılar pozitif tam sayılar, sıfırın solundaki sayılar negatif tam sayılardır. Pozitif tam sayılar,
Floating Point (Kayan Noktalı Sayılar)
 Süleyman Demirel Üniversitesi / Mühendislik Fak. / Bilgisayar Mühendisliği Bölümü Floating Point (Kayan Noktalı Sayılar) BIL-304: Bilgisayar Mimarisi Dersi veren öğretim üyesi: Yrd. Doç. Dr. Fatih Gökçe
Süleyman Demirel Üniversitesi / Mühendislik Fak. / Bilgisayar Mühendisliği Bölümü Floating Point (Kayan Noktalı Sayılar) BIL-304: Bilgisayar Mimarisi Dersi veren öğretim üyesi: Yrd. Doç. Dr. Fatih Gökçe
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir? Örnek...4 : Genel terimi w n. Örnek...1 : Örnek...5 : Genel terimi r n
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler değer kümelerine göre adlandırılırlar. Dizinin değer kümesi
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler değer kümelerine göre adlandırılırlar. Dizinin değer kümesi
12-A. Sayılar - 1 TEST
 -A TEST Sayılar -. Birbirinden farklı beş pozitif tam sayının toplamı 0 dur. Bu sayılardan sadece ikisi den büyüktür. Bu sayılardan üç tanesi çift sayıdır. Buna göre bu sayılardan en büyüğü en çok kaç
-A TEST Sayılar -. Birbirinden farklı beş pozitif tam sayının toplamı 0 dur. Bu sayılardan sadece ikisi den büyüktür. Bu sayılardan üç tanesi çift sayıdır. Buna göre bu sayılardan en büyüğü en çok kaç
DERS NOTLARI. Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi
 DERS NOTLARI Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi DERS-2 22.02.2016 Binary Numbers The Computer Number System İkili sayı Sistemi Bilgisayar Sayı Sistemi Sayı sistemleri nesneleri
DERS NOTLARI Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi DERS-2 22.02.2016 Binary Numbers The Computer Number System İkili sayı Sistemi Bilgisayar Sayı Sistemi Sayı sistemleri nesneleri
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Normal Alt Gruplar ve Bölüm Grupları...37
 İÇİNDEKİLER Ön Söz...2 Gruplar...3 Alt Gruplar...9 Simetrik Gruplar...13 Devirli Alt Gruplar...23 Sol ve Sağ Yan Kümeler (Kosetler)...32 Normal Alt Gruplar ve Bölüm Grupları...37 Grup Homomorfizmaları...41
İÇİNDEKİLER Ön Söz...2 Gruplar...3 Alt Gruplar...9 Simetrik Gruplar...13 Devirli Alt Gruplar...23 Sol ve Sağ Yan Kümeler (Kosetler)...32 Normal Alt Gruplar ve Bölüm Grupları...37 Grup Homomorfizmaları...41
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Sayısal Analiz. Prof. Dr. Erhan Coşkun. Karadeniz Teknik Üniversitesi, Fen Fakültesi, Ekim, 2018
 Sayısal Analiz Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi, Matematik Bölümü E-posta:erhan@ktu.edu.tr Ekim, 2018 E. Coşkun (KTÜ) Bölüm 1 Ekim, 2018 1 / 40 Matematiksel Analiz Analitik
Sayısal Analiz Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi, Matematik Bölümü E-posta:erhan@ktu.edu.tr Ekim, 2018 E. Coşkun (KTÜ) Bölüm 1 Ekim, 2018 1 / 40 Matematiksel Analiz Analitik
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
ab H bulunur. Şu halde önceki önermenin i) koşulu da sağlanır ve H G bulunur.
 3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
Temel Kavramlar. (r) Sıfırdan farklı kompleks sayılar kümesi: C. (i) Rasyonel sayılar kümesi: Q = { a b
 Bölüm 1 Temel Kavramlar Bu bölümde bağıntı ve fonksiyon gibi bazı temel kavramlar üzerinde durulacak, tamsayıların bazı özellikleri ele alınacaktır. Bu çalışma boyunca kullanılacak bazı kümelerin gösterimleri
Bölüm 1 Temel Kavramlar Bu bölümde bağıntı ve fonksiyon gibi bazı temel kavramlar üzerinde durulacak, tamsayıların bazı özellikleri ele alınacaktır. Bu çalışma boyunca kullanılacak bazı kümelerin gösterimleri
olsun. Bu halde g g1 g1 g e ve g g2 g2 g e eşitlikleri olur. b G için a b b a değişme özelliği sağlanıyorsa
 1.GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G, ) cebirsel yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir. 1), G de bir ikili işlemdir. 2) a, b, c G için a( bc)
1.GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G, ) cebirsel yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir. 1), G de bir ikili işlemdir. 2) a, b, c G için a( bc)
1. BÖLÜM Mantık BÖLÜM Sayılar BÖLÜM Rasyonel Sayılar BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler
 ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
İÇİNDEKİLER. Bölüm 2 CEBİR 43
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 13 1.1 Doğal Sayılar 15 1.1.1. Tek ve Çift Sayılar 15 1.1.2. Asal Sayılar 15 1.1.3 Doğal Sayıların Özellikleri 15 1.1.4 Doğal Sayılarda Özel Toplamlar 16 1.1.5. Faktöriyel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 13 1.1 Doğal Sayılar 15 1.1.1. Tek ve Çift Sayılar 15 1.1.2. Asal Sayılar 15 1.1.3 Doğal Sayıların Özellikleri 15 1.1.4 Doğal Sayılarda Özel Toplamlar 16 1.1.5. Faktöriyel
12.Konu Rasyonel sayılar
 12.Konu Rasyonel sayılar 1. Rasyonel sayılar 2. Rasyonel sayılar kümesinde toplama ve çarpma 3. Rasyonel sayılar kümesinde çıkarma ve bölme 4. Tam rayonel sayılar 5. Rasyonel sayılar kümesinde sıralama
12.Konu Rasyonel sayılar 1. Rasyonel sayılar 2. Rasyonel sayılar kümesinde toplama ve çarpma 3. Rasyonel sayılar kümesinde çıkarma ve bölme 4. Tam rayonel sayılar 5. Rasyonel sayılar kümesinde sıralama
2 şeklindeki bütün sayılar. 2 irrasyonel sayısı. 2 irrasyonel sayısından elde etmekteyiz. Benzer şekilde 3 irrasyonel sayısı
 1.8.Reel Sayılar Kümesinin Tamlık Özelliği Rasyonel sayılar kümesi ile rasyonel olmayan sayıların kümesi olan irrasyonel sayılar kümesinin birleşimine reel sayılar kümesi denir ve IR ile gösterilir. Buna
1.8.Reel Sayılar Kümesinin Tamlık Özelliği Rasyonel sayılar kümesi ile rasyonel olmayan sayıların kümesi olan irrasyonel sayılar kümesinin birleşimine reel sayılar kümesi denir ve IR ile gösterilir. Buna
TEMEL KAVRAMLAR. a Q a ve b b. a b c 4. a b c 40. 7a 4b 3c. a b c olmak üzere a,b ve pozitif. 2x 3y 5z 84
 N 0,1,,... Sayı kümesine doğal sayı kümesi denir...., 3,, 1,0,1,,3,... sayı kümesine tamsayılar kümesi denir. 1,,3,... saı kümesine sayma sayıları denir.pozitif tamsayılar kümesidir. 15 y z x 3 5 Eşitliğinde
N 0,1,,... Sayı kümesine doğal sayı kümesi denir...., 3,, 1,0,1,,3,... sayı kümesine tamsayılar kümesi denir. 1,,3,... saı kümesine sayma sayıları denir.pozitif tamsayılar kümesidir. 15 y z x 3 5 Eşitliğinde
DENEY 0. Bölüm 1 - Ölçme ve Hata Hesabı
 DENEY 0 Bölüm 1 - Ölçme ve Hata Hesabı Amaç: Ölçüm metodu ve cihazına bağlı hata ve belirsizlikleri anlamak, fiziksel bir niceliği ölçüp hata ve belirsizlikleri tespit etmek, nedenlerini açıklamak. Genel
DENEY 0 Bölüm 1 - Ölçme ve Hata Hesabı Amaç: Ölçüm metodu ve cihazına bağlı hata ve belirsizlikleri anlamak, fiziksel bir niceliği ölçüp hata ve belirsizlikleri tespit etmek, nedenlerini açıklamak. Genel
LĐMĐT ÖSS ÖYS YILLAR SAĞDAN VE SOLDAN LĐMĐT. ÇÖZÜM: x=2 f(x) de yerine yazılır cevap:7
 YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS ÖYS LĐMĐT Tanım : Bir x0 A = [ a,b ] alalım, f: A R ye veya f: A - { x 0 } R ye bir fonksiyon olsun. Terimleri A - { x 0 } kümesine ait ve x
YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS ÖYS LĐMĐT Tanım : Bir x0 A = [ a,b ] alalım, f: A R ye veya f: A - { x 0 } R ye bir fonksiyon olsun. Terimleri A - { x 0 } kümesine ait ve x
10. DİREKT ÇARPIMLAR
 10. DİREKT ÇARPIMLAR Teorem 10.1. H 1,H 2,, H n bir G grubunun alt gruplarının bir ailesi ve H = H 1 H 2 H n olsun. Aşağıdaki ifadeler denktir. a ) dönüşümü altında dır. b) ve olmak üzere her yi tek türlü
10. DİREKT ÇARPIMLAR Teorem 10.1. H 1,H 2,, H n bir G grubunun alt gruplarının bir ailesi ve H = H 1 H 2 H n olsun. Aşağıdaki ifadeler denktir. a ) dönüşümü altında dır. b) ve olmak üzere her yi tek türlü
Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri. 2. Kayan Noktalı Sayı Sistemleri
 2. SAYI SİSTEMLERİ VE KODLAR Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri 2. Kayan Noktalı Sayı Sistemleri 2.1. Sabit Noktalı Sayı Sistemleri 2.1.1. Ondalık Sayı Sistemi Günlük
2. SAYI SİSTEMLERİ VE KODLAR Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri 2. Kayan Noktalı Sayı Sistemleri 2.1. Sabit Noktalı Sayı Sistemleri 2.1.1. Ondalık Sayı Sistemi Günlük
Soru Konu Doğru Yanlış Boş
 YGS - MATEMATİK DENEME- A Soru Konu Doğru Yanlış Boş Mutlak Değerin Sayıya Eşitliği % % Sayılar Akıl Yürütme % % Okek Dikdörtgen Birleştirme % % Kesirlerin Okeki % % Obeb Problemleri % % Obeb Denklemi
YGS - MATEMATİK DENEME- A Soru Konu Doğru Yanlış Boş Mutlak Değerin Sayıya Eşitliği % % Sayılar Akıl Yürütme % % Okek Dikdörtgen Birleştirme % % Kesirlerin Okeki % % Obeb Problemleri % % Obeb Denklemi
İKİNCİ DERECEDEN DENKLEMLER
 İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
ÜNİTE. MATEMATİK-1 Prof.Dr.Ekrem KADIOĞLU İÇİNDEKİLER HEDEFLER SAYI KÜMELERİ. Sayılar Üslü Sayılar Köklü Sayılar Aralıklar Mutlak Değer
 HEDEFLER İÇİNDEKİLER SAYI KÜMELERİ Sayılar Üslü Sayılar Köklü Sayılar Aralıklar Mutlak Değer MATEMATİK-1 Prof.Dr.Ekrem KADIOĞLU Bu üniteyi çalıştıktan sonra; Üslü ve köklü ifadenin, mutlak değerin ne olduğunu
HEDEFLER İÇİNDEKİLER SAYI KÜMELERİ Sayılar Üslü Sayılar Köklü Sayılar Aralıklar Mutlak Değer MATEMATİK-1 Prof.Dr.Ekrem KADIOĞLU Bu üniteyi çalıştıktan sonra; Üslü ve köklü ifadenin, mutlak değerin ne olduğunu
11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler
 11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler 1. Asal sayılar 2. Bir tam sayının bölenleri 3. Modüler aritmetik 4. Bölünebilme kuralları 5. Lineer modüler aritmetik 6. Euler
11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler 1. Asal sayılar 2. Bir tam sayının bölenleri 3. Modüler aritmetik 4. Bölünebilme kuralları 5. Lineer modüler aritmetik 6. Euler
İSTANBUL ATATÜRK FEN LİSESİ MATEMATİK YARIŞMASI /03/ :00 12:00
 İSTANBUL ATATÜRK FEN LİSESİ MATEMATİK YARIŞMASI 2018 25/03/2018-10:00 12:00 Öğrencinin Adı Soyadı: Okulu / Sınıfı : Lütfen tüm bilgileri doğru bir şekilde yazınız. Sınav sonunda kitapçık salon görevlisine
İSTANBUL ATATÜRK FEN LİSESİ MATEMATİK YARIŞMASI 2018 25/03/2018-10:00 12:00 Öğrencinin Adı Soyadı: Okulu / Sınıfı : Lütfen tüm bilgileri doğru bir şekilde yazınız. Sınav sonunda kitapçık salon görevlisine
ÜNİTE: RASYONEL SAYILAR KONU: Rasyonel Sayılar Kümesinde Çıkarma İşlemi
 ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
Giriş MİKROİŞLEMCİ SİSTEMLERİ. Elektronik Öncesi Kuşak. Bilgisayar Tarihi. Elektronik Kuşak. Elektronik Kuşak. Bilgisayar teknolojisindeki gelişme
 Giriş MİKROİŞLEMCİ SİSTEMLERİ Bilgisayar teknolojisindeki gelişme Elektronik öncesi kuşak Elektronik kuşak Mikroişlemci kuşağı Yrd. Doç. Dr. Şule Gündüz Öğüdücü 1 Bilgisayar Tarihi Elektronik Öncesi Kuşak
Giriş MİKROİŞLEMCİ SİSTEMLERİ Bilgisayar teknolojisindeki gelişme Elektronik öncesi kuşak Elektronik kuşak Mikroişlemci kuşağı Yrd. Doç. Dr. Şule Gündüz Öğüdücü 1 Bilgisayar Tarihi Elektronik Öncesi Kuşak
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
VI. OLİMPİYAT SINAVI SORULAR
 SORULAR 1. N sayısı 1998 basamaklı ve tüm basamakları 1 olan bir doğal sayıdır. Buna göre N sayısının virgülden sonraki 1000. basamağı kaçtır? A)0 B)1 C)3 D)6 E) Hiçbiri. n Z olmak üzere, n sayısı n sayısına
SORULAR 1. N sayısı 1998 basamaklı ve tüm basamakları 1 olan bir doğal sayıdır. Buna göre N sayısının virgülden sonraki 1000. basamağı kaçtır? A)0 B)1 C)3 D)6 E) Hiçbiri. n Z olmak üzere, n sayısı n sayısına
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
SAYILARA GİRİŞ. Her şeyden önce temel kavramları bilmeliyiz. Nedir temel kavramlar? Matematik dilinin abc'si olarak tanımlayabiliriz.
 SAYILARA GİRİŞ Her şeyden önce temel kavramları bilmeliyiz. Nedir temel kavramlar? Matematik dilinin abc'si olarak tanımlayabiliriz. Rakamlar {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} On tane rakam bulunmaktadır.
SAYILARA GİRİŞ Her şeyden önce temel kavramları bilmeliyiz. Nedir temel kavramlar? Matematik dilinin abc'si olarak tanımlayabiliriz. Rakamlar {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} On tane rakam bulunmaktadır.
Elemanter Fonksiyonlarla Yaklaşım ve Hata
 Bölüm 5 Elemanter Fonksiyonlarla Yaklaşım ve Hata Bu bölümde önelikle verilen bir ayrık veri kümesi için standart ve ağırlıklıen küçük kareler yöntemi ile en uygun yaklaşım polinomunun nasıl belirleneeğini
Bölüm 5 Elemanter Fonksiyonlarla Yaklaşım ve Hata Bu bölümde önelikle verilen bir ayrık veri kümesi için standart ve ağırlıklıen küçük kareler yöntemi ile en uygun yaklaşım polinomunun nasıl belirleneeğini
BİRİNCİ BÖLÜM SAYILAR
 İÇİNDEKİLER BİRİNCİ BÖLÜM SAYILAR 1.1 Tamsayılarda İşlemler... 2 1.1.1 Tek, Çift ve Ardışık Tamsayılar... 5 1.2 Rasyonel Sayılar... 6 1.2.1 Kesirlerin Birbirine Çevrilmesi... 7 1.2.2 Kesirlerin Genişletilmesi
İÇİNDEKİLER BİRİNCİ BÖLÜM SAYILAR 1.1 Tamsayılarda İşlemler... 2 1.1.1 Tek, Çift ve Ardışık Tamsayılar... 5 1.2 Rasyonel Sayılar... 6 1.2.1 Kesirlerin Birbirine Çevrilmesi... 7 1.2.2 Kesirlerin Genişletilmesi
Sayıtlama Dizgeleri. (a n a n-1 a n1 a n0. b 1 b 2 b m )r. simgesi şu sayıyı temsil eder.
 1 Sayıtlama Dizgeleri Hint-Arap Sayıtlama Dizgesi Sayıları göstermek (temsil etmek) için tarih boyunca türlü simgeler kullanılmıştır. Sümerlerin, Mısırlıların, Romalıların ve diğer uygarlıkların kullandıkları
1 Sayıtlama Dizgeleri Hint-Arap Sayıtlama Dizgesi Sayıları göstermek (temsil etmek) için tarih boyunca türlü simgeler kullanılmıştır. Sümerlerin, Mısırlıların, Romalıların ve diğer uygarlıkların kullandıkları
KAREKÖKLÜ SAYILAR. a) 15 h) 18 b) 32 ı) 49 c) 81 i) 72 d) 27 j) 36 e) 9 k) 121 f) 45 l) 256 g) 25 m) 152
 KAREKÖKLÜ SAYILAR kök sembolü kök derecesi dir 8. sınıfta kök derecesi olan kökleri öğreneceğiz. Bir kökün en küçük derecesi dir. En genel kullanılan ve en küçük kök olduğu için derecesi yazılmaz. Fakat
KAREKÖKLÜ SAYILAR kök sembolü kök derecesi dir 8. sınıfta kök derecesi olan kökleri öğreneceğiz. Bir kökün en küçük derecesi dir. En genel kullanılan ve en küçük kök olduğu için derecesi yazılmaz. Fakat
İç-Çarpım Uzayları ÜNİTE. Amaçlar. İçindekiler. Yazar Öğr. Grv. Dr. Nevin ORHUN
 İç-Çarpım Uzayları Yazar Öğr. Grv. Dr. Nevin ORHUN ÜNİTE Amaçlar Bu üniteyi çalıştıktan sonra; R n, P n (R), M nxn vektör uzaylarında iç çarpım kavramını tanıyacak ve özelliklerini görmüş olacaksınız.
İç-Çarpım Uzayları Yazar Öğr. Grv. Dr. Nevin ORHUN ÜNİTE Amaçlar Bu üniteyi çalıştıktan sonra; R n, P n (R), M nxn vektör uzaylarında iç çarpım kavramını tanıyacak ve özelliklerini görmüş olacaksınız.
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MB5002 NÜMERİK ANALİZ
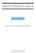 MB500 NÜMERİK ANALİZ Ders Notları Yrd. Doç. Dr. Emel YAVUZ DUMAN İstanbul Kültür Üniversitesi Matematik-Bilgisayar Bölümü c 01, Emel Yavuz Duman Tüm hakkı saklıdır. Bu notlar Örgün Öğretimde Uzaktan Öğretim
MB500 NÜMERİK ANALİZ Ders Notları Yrd. Doç. Dr. Emel YAVUZ DUMAN İstanbul Kültür Üniversitesi Matematik-Bilgisayar Bölümü c 01, Emel Yavuz Duman Tüm hakkı saklıdır. Bu notlar Örgün Öğretimde Uzaktan Öğretim
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
LYS MATEMATİK DENEME - 1
 LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
14.Konu Reel sayılarının topolojisi. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir.
 14.Konu Reel sayılarının topolojisi 1.Teorem: cismi tamdır. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir. 2.Tanım: ve verilsin. nın her komşuluğunda
14.Konu Reel sayılarının topolojisi 1.Teorem: cismi tamdır. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir. 2.Tanım: ve verilsin. nın her komşuluğunda
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular
 Maths@bi 8 3.BÖLÜM Kareköklü Sayılar Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular Kerime ASKER-Abdullah ASKER Matematik Öğretmeni
Maths@bi 8 3.BÖLÜM Kareköklü Sayılar Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular Kerime ASKER-Abdullah ASKER Matematik Öğretmeni
