20. Tanımlar ve temel bağıntılar: İzostatik sistem, hiperstatik sistem Tanımlar ve temel bağıntılar: İzostatik sistem
|
|
|
- Soner Boz
- 5 yıl önce
- İzleme sayısı:
Transkript
1 0 Tanımlar ve temel bağıntılar: İzostatik sistem Kuvvet metodunda eleman iç kuvvetleri ve reaksiyonlar ana bilinmeyenlerdir Bu kuvvetler sistemin düğüm noktalarında yazılan denge denklemlerinden bulunmaya çalışılır Eğer bilinmeyen sayısı kadar denge denklemi varsa bilinmeyenler denge denklemlerinden hesaplanabilir Bu tür sistemlere izostatik sistem denir Örnek 0: Şekil 0 de verilen düzlem kafes sistem çelik borulardan imal edilmiştir Eleman kuvvetlerini, reaksiyonları, elemanların boyca değişimlerini ve düğüm yer değiştirmelerini bulunuz Bu sayısal örnek çözülürken, gerektiğinde, teorik bilgi de verilecektir Yapı çeliğinin elastisite modülü E= 0 8 kn/m Kesit alanı = = Şekil 0 de sistemin verilmiş dış yükler ile hesaplanması istenen eleman iç kuvvetleri ve reaksiyonlar pozitif yönlerinde gösterilmiştir,,,,, : değerleri bilinen düğüm yükleridir, : hesaplanması istenen eleman iç kuvvetleridirbilinmeyenler)!,!,!,! : hesaplanması istenen reaksiyon kuvvetleridir Şekil 0 de sistemin hesaplanması istenen düğüm yer değiştirmeleri, elemanların göreceli yer değiştirmelerielemanın uzama veya kısalma miktarı=şekil değiştirme) ve reaksiyonlar doğrultusundaki göreceli yer değiştirmelerireaksiyonlar doğrultusunda yer değiştirme) gösterilmiştir,,, : Hesaplanması istenen yer değiştirmelerdir, : elemanların hesaplanması istenen göreceli yer değiştirmelerdir boyca uzama veya kısalma miktarı),,, : reaksiyonlar doğrultusunda göreceli yer değiştirmelerdir Mesnet yer değiştiremeyeceği için bunlar sıfırdır, ancak, iş ifadesinin yazılabilmesi için tanımlanmak zorundadır Reaksiyon Dış kuvvet İç kuvveteksenel) çekme pozitif Tanımlanan büyüklükleri matris notasyonunda yazarsak: = Sistemin yük vektörübiliniyor), # & = Sistemin yer değiştirme vektörübilinmiyor) # & =! Sistemin bilinmeyenler vektörü,!! #! & Reaksiyon kuvvetinden yer değiştirme Düğüm yer değiştirmesi Elemanın boyca değişimi=uzama veya kısalma = Sistemin göreceli yer değiştirme vektörübilinmiyor) Dikkat edilirse; ile ve ile iş yapacak şekilde tanımlanmışlardır Statikçe belirli sistem de denir=statically determinate system Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 05-07, Sayfa 60
2 Sistemin denge denklemleri: Sistemin serbestlik derecesi=6 kadar denge denklemi vardır Şimdilik, statik derslerinden bilindiği şekli ile sistemin denge denklemlerini kuralım Bilindiği gibi, her düğümde * =0 ve * =0 olmalıdır İşaret kuralı olarak elemanların eksenel kuvvetini çekme pozitif alalım noktasında denge: x = 0: + CDE45= =0 * =0: 00 GHI45= = 00 noktasında denge: x = 0: CDE45! =0 0707! =0 * =0: GHI45! =0 0707! =0 noktasında denge: x = 0:! =0 * =0:! =0 Bu denklemler matris notasyonunda: Denklem no ! = ! ! 0 6 #, / & #! & #,--/ 0 & 0 Bilinmeyenlerin numaraları noktasında x = 0 ve * =0 koşulu noktasında x = 0 ve * =0 koşulu noktasında x = 0 ve * =0 koşulu 0) Sistemin denge matrisi Sistemin bilinmeyenlerinin vektörü Sistemin yük vektörü 4 = 0) olur 4 ye sistemin denge matrisi, ye sistemin bilinmeyenler vektörü ve ye sistemin yük vektörü denir Denklem sayısını n ile ve bilinmeyenler sayısını m ile gösterirsek; örneğimizde n=6 ve m=6 dır Bilinmeyen sayısı kadar denklem sayısı vardır, sistem izostatiktir Bunun anlamı, bilinmeyenlerin denge denklemlerinden hesaplanabileceğidir 6x6 boyutlu 4 kare matrisi tekil değildir , tersi vardır bilinmeyenleri 0 bağıntısından Gauss indirgeme metodu ile veya 4 nin tersi kullanılarak hesaplanır 4 nin tersini 9 : ile gösterelim: 9 : =4 Ters matrisi Matematica veya Matlab benzeri bir yazılımla hesaplarsak 44! =!! #! &,/ = #, / &,--/ 0 & #,--/ 0 & ; < =0 >? # R =-00 Eleman kuvvetleri R =00 Reaksiyonlar R =00 R =0 00 kn 0) F=44 kn Çekme) 44 kn F = kn 00 kn basınç) Şekil 04: Eleman ve reaksiyon kuvvetleri =9 : 04) bölümde denge denklemlerinin sistematikotomatik) nasıl kurulacağı açıklanacaktır Equilibrium matrix Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 05-07, Sayfa 6
3 Elemanların esneklik matrisi ve göreceli yer değiştirmeleri: Göreceli yer değiştirme elemanın bir ucunun diğer ucuna göre yaptığı yer değiştirmedir Kafes eleman ekseni doğrultusunda sadece uzar veya kısalır O halde göreceli yer değiştirme elemanın boy değiştirme miktarıdır Mukavemet bilgilerini kullanarak ielemanın göreceli yer değiştirmesini bulalım: Mukavemetten bilindiği üzere: K K =L=M = O/Q K dir Buradan R = bulunur Sonlu elemanlarda göreceli yer değiştirme, genelleştirme açısından, N N NQ harfi ile K terimi de S harfi ile gösterilir: = R=S Buradaki NQ Soldaki şekilde sol ucu sabitlenmiştutulmuş) A kesitli bir kafes eleman F eksenel kuvveti ile çekilirse boyu R kadar uzar, sağ uç R kadar yer değiştirir Sabit uç yer değiştiremeyeceğinden R yer değiştirmesine göreceli yer değiştirme denir S = K NQ 05) değerine kafes elemanın esnekliğifleksibilitesi ) denir ve rijitliğin tersidir Birimi uzunluk/kuvvettir, birim kuvvetten oluşan göreceli yer değiştirme anlamındadır S büyüdükçe eleman esnekleşirkolay uzar-kısalır), küçüldükçe rijitleşir S =0 durumunda hiç uzamaz-kısalmazsonsuz rijit), R =0 olur Mesnetler sonsuz rijit olduğundan mesnet kuvvetlerine ait T=< dır i eleman vurgulamak üzere i indisini kulalım: S U = K V N V Q V Kafes elemanın esnekliği 06) U =S U U 07) Kafes elemanın göreceli yer değiştirmesi Kafes elemanda U ve U tek değerdirsadece boyca değişme var) Çerçeve, levha, plak, elemanlarda boyca değişim, dönme gibi birden çok göreceli yer değiştirme vardır Genellik açısından 07 ifadesi matris olarak gösterilir: U =S U U 08) Elemanın esneklik matrisi U ielemanın göreceli yer değişmeleri, S U kare matrisi ielemanın esneklikfleksibilite) matrisi, U ielemanın bilinmeyen kuvvetleridir Sistemin göreceli yer değiştirmeleri ve esneklik matrisi: Sistemin s tane elemanı varsa 08 ifadesi her bir eleman için geçerlidir Bunları topluca 09 daki tek bir matris bağıntısı olarak yazabiliriz Diyagonallerde elemanların esneklik matrisleri var = S =S W =S W W = S # W & Sistemin göreceli yer değiştirmeleri S S = #, / S W & # W & T Sistemin esneklik matrisi Sistemin bilinmeyenleri 09) 00) sistemin göreceli yer değiştirmeleri, mxm boyutundaki S sistemin esneklikfleksibilite) matrisi dır, daha önce tanımlandığı gibi, sistemin bilinmeyen kuvvetlerieleman kuvvetleri ve reaksiyonlar), m bilinmeyen kuvvet sayısıdır Reaksiyon kuvvetleri yönünde yer değiştirme olamayacağı için reaksiyonlara karşılık gelen esneklikler sıfır alınmalıdırmesnet çok rijit olduğu için) Flexibility Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 05-07, Sayfa 6
4 Şimdi sayısal örneğimize geri dönelim, 09 bağıntısını 06 ya göre kuralım: elemanda: R =,Y = 0 Z ]^,= [\ = K = NQ : _ `Z : >a =6 0 /b4 elemanda: R = + =44,Y = 0 Z ]^,= [\ = K = NQ : _ `Z : >a =5 0 /b4 Mesnetlerde: doğrultusunda =0, doğrultusunda =0, doğrultusunda =0, doğrultusunda =0 dır Bu değerler ve 0 den 09 da yerine yazılarak = 0 00 = # & #, / 0& #,--/ 0 & #,------/ 0 & d T =T 0) Sistemin esneklik matrisi Sistemin bilinmeyenleri Sistemin göreceli yer değiştirmeleri Sistemin yer değiştirmeleri: Şekil 0 ve Şekil 0 de görülen,,,, dış yükleri kendi doğrultusunda tanımlı,,,, yer değiştirmeleri ile iş yapar Bu dış kuvvetlerin işidir: e = = g Şekil 0 ve Şekil 0 de görülen,, iç kuvvetleri kendi doğrultusunda tanımlı,,,, göreceli yer değiştirmeleri ile iş yapar Bu iç kuvvetlerin işidir: U = = g e = U, g = g dir 0 ye göre g = g 4 g ve 00 a göre = S olduğundan g 4 g,/ 4 g =S i Sistemin süreklilik koşulu h = g S i olur Buradan 0) olması gerektiği anlaşılır 0 bağıntısına sistemin süreklilik koşulu denir Çünkü sistemin düğümlerindeki yer değiştirmeleri ile elemanlar veya reaksiyonlara ait göreceli yer değiştirmeler arasındaki bir ilişkidir Bu sayısal örnekte 4 kare matrisinin tekil olmadığı , tersinin alınabileceği yukarıda belirtilmişti O halde = 4 g S yazılabilir Bir matrisin transpozunun tersi tersinin transpozuna eşittir: = 4 g S i = 4 g S i 0) 0 e bakıldığında 9 : =4 olduğu görülür Yukarıdaki bağıntıda yerine yazılarak yer değiştirmelerin bağıntısı =9 : g S i Sistemin yer değiştirme vektörü 04) bulunur Örneğimiz için 0 den 9 : matrisi ve 0 den =S vektörü 04 de yerine yazılarak yer değiştirmeler: =9 : g =9 : g S i = = = # & #, / &, / # 0 &,------/ # 0 & ; h < =T j j Sistemin yer değiştirmeleri Compatibility conditions Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 05-07, Sayfa 6
5 0 Tanımlar ve temel bağıntılar: Hiperstatik sistem Kuvvet metodunda eleman iç kuvvetleri ve reaksiyonlar ana bilinmeyenlerdir Bu kuvvetler sistemin düğüm noktalarında yazılan denge denklemlerinden bulunmaya çalışılır Eğer denge denklemi sayısı bilinmeyen sayısından az ise bilinmeyenler sadece denge denklemlerinden hesaplanamaz, ek koşullara gereksinim vardır Bu tür sistemlere Hiperstatik sistem denir Örnek 0: Şekil 05 de verilen düzlem kafes sistem çelik borulardan imal edilmiştir Eleman iç kuvvetlerini, reaksiyonları, eleman boyca değişimlerini ve düğüm yer değiştirmelerini bulunuz Bu sayısal örnek çözülürken, gerektiğinde, teorik bilgi de verilecektir Yapı çeliğinin elastisite modülü E= 0 8 kn/m Kesit alanı = = mm Kesit 6 mm Şekil 06 de sistemin verilmiş dış kuvvetleri ile hesaplanması istenen eleman kuvvetleri ve reaksiyonlar pozitif yönlerinde gösterilmiştir,,, Z : değerleri verilmiş düğüm yükleridir,, : hesaplanması istenen eleman kuvvetleridir!,!,!,!,!,! : hesaplanması istenen reaksiyon kuvvetleridir Şekil 07 de sistemin hesaplanması istenen düğüm yer değiştirmeleri, elemanların göreceli yer değiştirmelerielemanın uzama veya kısalma miktarı) ve reaksiyonlar doğrultusundaki göreceli yer değiştirmelerireaksiyonlar doğrultusunda yer değiştirme) gösterilmiştir,,, Z : Hesaplanması istenen yer değiştirmelerdir,,,`: hesaplanması istenen göreceli yer değiştirmelerdir Bunlardan,, : elemanların göreceli yer değiştirmeleriboyca uzama veya kısalma miktarı),,,,, Z,`: reaksiyonlar doğrultusunda göreceli yer değiştirmedir Reaksiyonlar doğrultusunda U =0 Reaksiyon Tanımlanan büyüklükleri matris notasyonunda yazarsak: = Sistemin yük vektörübiliniyor), # Z & = Sistemin yer değiştirme vektörübilinmiyor) # Z &! =! Sistemin bilinmeyenler vektörü,!!! #! & = Sistemin göreceli yer değiştirme vektörübilinmiyor) Z # `& Statikçe belirsiz sistem de denir Gereğinden çok bağı olan sistem anlamındadır Statically indeterminate, hyperstatic Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 05-07, Sayfa 64 R R Reaksiyon kuvvetinden yer değiştirme 654 kn Şekil 05: Çözülmesi istenen kafes sistem x R P 4 P 6 R P 5 Dış kuvvet P R 4 F F P P Şekil 06: Dış ve iç dış kuvvetler Düğüm yer değiştirmesi P 8 4 R 4 F P 7 79 İç kuvveteksenel) çekme pozitif x Elemanın boyca değişimi=uzama veya kısalma
6 Sistemin denge denklemleri: Sistemin serbestlik derecesi=8 kadar denge denklemi vardır Statik derslerinden bilindiği şekli ile sistemin denge denklemlerini kuralım Her noktada * =0 ve * =0 olmalıdır İşaret kuralı olarak elemanların eksenel kuvvetini çekme pozitif alalım noktasında denge: x = 0: CDE45= = 79 * =0: 654 GHI45 = = 654 noktasında denge: x = 0: CDE45! =0 0707! =0 * =0: GHI45! =0 0707! =0 noktasında denge: x = 0:! =0 * =0:! =0 4 noktasında denge: x = 0:! =0 * =0:! =0 Bu denklemler matris notasyonunda: Denklem no Bilinmeyenlerin numaraları ! ! = ! ! #, /! & 8 #,----/ 0 & #! 0,/ & Sistemin denge matrisi Sistemin bilinmeyenlerinin vektörü Sistemin yük vektörü noktasında x = 0 ve * =0 koşulu noktasında x = 0 ve * =0 koşulu 05) noktasında x = 0 ve * =0 koşulu 4 noktasında x = 0 ve * =0 koşulu 4 = Sistemin denge denklemi 06) Bu denklem sisteminde n=8 denklem, m=9 bilinmeyen var, n<m dir Denklem sayısı çözüm için yeterli değildir, yani sistem hiperstatiktir r=m-n ye hiperstatiklik derecesi denir Çözüm üretebilmek için r tane ek denklem bulmalıyız Çözüm için gerekli olan r tane ek denklemi bulabilmek için biraz matematik ve ek teorik bilgiye ihtiyacımız vardır Sayısal çözüme ara verelim Degree of indeterminacy Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 05-07, Sayfa 65
7 Matematik bilgi: 06 gibi n<m olan) genel doğrusal denklem sisteminin r=m-n kolonu doğrusal bağımlıdır Bir özelinhomojen) ve bir genelhomojen) çözümü vardır : 49 : =k özelinhomojen) çözüm 07) 49 l =0 genelhomojen) çözüm 08) 9 : ve 9 l 07 ve 08 sağlanacak şekilde hesaplanmak kaydı ile 06 daki denge denklemlerini sağlayan vektörübilinmeyenler) =9 : +9 l * 09) dir Buradaki m vektörüne matematikte serbest değişken 4 denilmektedir Serbest değişkenin anlamı şudur: Herhangi bir keyfi değer alabilir, yani m ne olursa olsun 09 çözümü 06 denge denklemlerinde yerine konursa eşitlik daima sağlanır 5 O halde sonsuz sayıda m vektörü, dolayısıyla 09 a göre, sonsuz vektörü vardır Ancak, sistemin tek bir tane vektörüçözümü) vardır Demek ki sonsuz sayıdaki m vektöründen sadece bir tanesi sistemin hem denge denklemlerini ve hem de süreklilik koşullarını sağlar Soru şudur: Hem denge denklemlerini hem de süreklilik koşullarını sağlayan m vektörünü nasıl bulacağız? Sistemin süreklilik koşulu: vektörü hem 06 yı hem de 0 yi sağlamalıdır: 4 g =S i Sistemin süreklilik koşulu 00) Sağdan 9 l g ile her iki tarafı çarpar ve 08 i dikkate alırsak 9,/ g l 4 g =9 g l S i < 0 =9 l g S i 9 l g S i =0 0) 06 denklem sisteminin çözülebilmesi için gerekli ek koşul Olur 09 u yerine yazalım: 9 g l S 9,----/ : +9 l * =0 9 l g S9 : +9 l g S9 l * =0 9 g l S9 l * = 9 g l S9 : Sistemin süreklilik koşulu 0) bulunur * vektörünün rxr boyutlu katsayılar matrisi 9 l g S9 l simetrik ve pozitif tanımlı, det 9 l g S9 l 0 dır O halde, bu denklem sisteminden tek bir * bulunur * süreklilik koşulu sağlanacak şekilde hesaplandığından, 09 da yerine konularak bulunan vektörü de sistemin denge denklemlerini sağlayan çözüm olacaktır Böylece hem denge denklemlerini hem de süreklilik koşullarını sağlayan çözüm bulunmuş olur Doğrusal bağımlılık: 4 matrisinin r tane kolonu diğer n kolon cinsinden ifade edilebilir demektir Bakınız:: Sayfa:6 Matematikte 9: matrisine 4 nin sağ ters matrisiright invers), 9 l matrisine 4 nin çekirdeğikernal, null space) denir Homojen, inhomojen denklem sistemleri ve çözümü hakkında genel bilgi için bakınız: DersNotlarC4B/BDNA0_GenelDenklemSistemleripdf 9: ve 9 l matrislerinin nasıl hesaplanacağı bölümde sayısal örnek ile gösterilecektir 4 Free variable 5 Daima sağlandığını gösterelim: 4 = sağlanması gereken denge denklemi) =9 : +9 l * çözüm) 4q9,------/ : +9 l *r= Hbbs76 stıiıves 4 9 : +49 l * = w < k +0 * = = olur Demek ki * ne olursa olsun 9 çözümü 6 denge denklemini daima sağlar Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 05-07, Sayfa 66
8 Sistemin düğümlerindeki yer değiştirmelerinin hesaplanması: 00 süreklilik bağıntısını soldan 9 : g ile çarpar ve 07 yi dikkate alırsak 9,/ g : 4 g =9 g : S i w =9 : g S i Sistemin yer değiştirme vektörü 0) olur Yorum: Herhangi bir statik sistemin çözümü için yukarıda verilen bağıntıları özetlersek ) 4 = ) 4 9 : =k ) 4 9 l =0 n denklemli ve m bilinmeyenli denge denklemleri özelinhomojen) çözüm genelhomojen) çözüm 4) 9 l g S9 l * = 9 l g S9 : Süreklilik denklemleri 5) =9 : +9 l * 6) =9 : g S i Bilinmeyenlereleman ve reaksiyon kuvvetleri) Yer değiştirmeler şu sonuca varırız: 4,,S : sistemin geometrisinden bilinmektedir Vektörüeleman ve reaksiyon kuvvetleri) hesaplanmak istenmektedir n denklem sayısı, m bilinmeyen sayısı olmak üzere farklı durum sözkonusudur: a) n=m ise sistem izostatiktir : bağıntıdan 9 : =4 ve =9 : kuvvetleri, 6 bağıntıdan yer değiştirmeleri hesaplanır,, 4 ve 5 bağıntılara gerek kalmaz b) n<m ise sistem hiperstatiktir: Hiperstatiklik derecesi r=m-n dir bağıntı nin hesabı için yeterli olmaz, diğer bağıntıların da kullanılması zorunlu olur ve bağıntılarını sağlayan 9 : ve 9 l matrisleri hesaplanır 4 bağıntıdan * vektörü hesaplanır 5 bağıntıdan hesaplanır 6 bağıntıdan yer değiştirmeleri hesaplanır Ancak, ve bağıntılarını sağlayan ; < ve ; m matrislerinin nasıl hesaplanacağını henüz bilmiyoruz bölümd bu matrislerin hesabına yöneliktir c) n>m ise: sistem oynaklabildir), çözüm yoktur Yapı statiği kuvvet metodu ile ilişki: Yapı statiğinden bilindiği gibi, hiperstatik sistemlerin çözümünde oynaklabil) olmayan) bir izostatik esas sistem elle seçilir Sonlu elemanlarda izostatik esas sistem otomatik seçilir *: Hiperstatik bilinmeyenlere, 9 : : =k, * =0 iken izostatik sistemde birim dış yüklerden oluşan iç kuvvetlere, 9 l : =0, * =k iken izostatik sistemde birim hiperstatik yüklerden oluşan iç kuvvetlere, 9 l g S9 l * = 9 l g S9 : : Süreklilik denklemlerine, 9 l g S9 l * y U[ sayılarına karşılık gelir Oynaklabil) sistem: Bağları yetersiz, dengesiz, göçer sistem demektir Örneğin, tek açıklıklı bir kirişin en az bir mesnedi sabit diğer mesnedi kayıcı olmalıdır İki mesnedi de kayıcı ise kiriş kayıp gider Böyle bir sistem inşa edilemez Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 05-07, Sayfa 67
5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi
 5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi u bölümde RITZ metodu eleman bazında uygulanacak, elemanın yer değiştirme fonksiyonu, şekil değiştirme, gerilme bağıntıları, toplam potansiyeli,
5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi u bölümde RITZ metodu eleman bazında uygulanacak, elemanın yer değiştirme fonksiyonu, şekil değiştirme, gerilme bağıntıları, toplam potansiyeli,
6. Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması
 6 Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması 6 Sistemin noktalarında süreklilik koşulu : Her elemanın düğüm noktası aynı zamanda sistemin de düğüm noktası olduğundan, sistemin noktaları
6 Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması 6 Sistemin noktalarında süreklilik koşulu : Her elemanın düğüm noktası aynı zamanda sistemin de düğüm noktası olduğundan, sistemin noktaları
p 2 p Üçgen levha eleman, düzlem şekil değiştirme durumu
 Üçgen levha eleman düzlem şekil değiştirme durumu Üçgen levha eleman düzlem şekil değiştirme durumu İstinat duvarı basınçlı uzun boru tünel ağırlık barajı gibi yapılar düzlem levha gibi davranırlar Uzun
Üçgen levha eleman düzlem şekil değiştirme durumu Üçgen levha eleman düzlem şekil değiştirme durumu İstinat duvarı basınçlı uzun boru tünel ağırlık barajı gibi yapılar düzlem levha gibi davranırlar Uzun
36. Basit kuvvet metodu
 36. Basit kuvvet metodu Basit kuvvet metodu hakkında çok kısa bilgi verilecektir. Basit kuvvet metodunda hiperstatik bilinmeyenlerinin hesaplanmasına, dolayısıyla buna ait denklem sisteminin kurulmasına
36. Basit kuvvet metodu Basit kuvvet metodu hakkında çok kısa bilgi verilecektir. Basit kuvvet metodunda hiperstatik bilinmeyenlerinin hesaplanmasına, dolayısıyla buna ait denklem sisteminin kurulmasına
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
29. Düzlem çerçeve örnek çözümleri
 9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
7. Kafes sistem sayısal örnekleri
 7. Kafes sistem sayısal örnekleri 7. Düzlem kafes sistem sayısal örneği Şekil 7. deki kafes sistem elastisite modülü.. 5 N/mm olan çelik borulardan imal edilmiştir. a noktasındaki kuvvetlerinden oluşan:
7. Kafes sistem sayısal örnekleri 7. Düzlem kafes sistem sayısal örneği Şekil 7. deki kafes sistem elastisite modülü.. 5 N/mm olan çelik borulardan imal edilmiştir. a noktasındaki kuvvetlerinden oluşan:
R 1Y kn R 1X R 1Z R 4Y R 3Y 4 R 4X R 3Z R 3X R 4Z. -90 kn. 80 kn 80 kn R 1Y =10 R 1X =-10 R 4Y =10 R 1Z =0 R 3Y =70 4 R 3X =-70 R 4X =0
 27. Uzay kafes örnek çözümleri Örnek 27.: Şekil 27. de verilen uzay kafes sistem çelik borulardan imal edilecektir. a noktasındaki dış yüklerden oluşan eleman kuvvetleri, reaksiyonlar, gerilmeler ve düğüm
27. Uzay kafes örnek çözümleri Örnek 27.: Şekil 27. de verilen uzay kafes sistem çelik borulardan imal edilecektir. a noktasındaki dış yüklerden oluşan eleman kuvvetleri, reaksiyonlar, gerilmeler ve düğüm
23. Sistem denge denklemlerinin direkt kurulması
 . Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
. Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
4. Sonlu elemanlar yer değiştirme metodu, modelleme, tanımlar
 4. Sonlu Elemanlar Yer Değiştirme Metodu modelleme tanımlar 4. Sonlu elemanlar yer değiştirme metodu modelleme tanımlar. bölümde örneklerle açıklanan RITZ metodu.5. ve.5 bağıntıları yerine kullanılabilen
4. Sonlu Elemanlar Yer Değiştirme Metodu modelleme tanımlar 4. Sonlu elemanlar yer değiştirme metodu modelleme tanımlar. bölümde örneklerle açıklanan RITZ metodu.5. ve.5 bağıntıları yerine kullanılabilen
Hiperstatik sistemlerin çözümünde, yer değiştirmelerin küçük olduğu ve gerilme - şekil değiştirme bağıntılarının lineer olduğu kabul edilmektedir.
 1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
 YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
28. Sürekli kiriş örnek çözümleri
 28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
(, ) = + + yönünde yer değiştirme fonksiyonu
 . Üçgen levha eleman, düzlem gerilme durumu. Üçgen levha eleman, düzlem gerilme durumu Çok katlı yapılardaki deprem perdeleri ve yüksek kirişler düzlem levha gibi davranır. Sağdaki şekilde bir levha sistem
. Üçgen levha eleman, düzlem gerilme durumu. Üçgen levha eleman, düzlem gerilme durumu Çok katlı yapılardaki deprem perdeleri ve yüksek kirişler düzlem levha gibi davranır. Sağdaki şekilde bir levha sistem
33. Üçgen levha-düzlem gerilme örnek çözümleri
 33. Üçgen levha-düzlem gerilme örnek çözümleri Örnek 33.1: Şekil 33.1 deki, kalınlığı 20 cm olan betonarme perdenin malzemesi C25/30 betonudur. Tepe noktasında 1000 kn yatay yük etkimektedir. a) 1 noktasındaki
33. Üçgen levha-düzlem gerilme örnek çözümleri Örnek 33.1: Şekil 33.1 deki, kalınlığı 20 cm olan betonarme perdenin malzemesi C25/30 betonudur. Tepe noktasında 1000 kn yatay yük etkimektedir. a) 1 noktasındaki
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar
 Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
25. SEM2015 programı kullanımı
 25. SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
25. SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
SEM2015 programı kullanımı
 SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Çözebileceği sistemler: Düzlem/uzay kafes: Evet Düzlem/uzay çerçeve:
SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Çözebileceği sistemler: Düzlem/uzay kafes: Evet Düzlem/uzay çerçeve:
34. Dörtgen plak örnek çözümleri
 34. Dörtgen plak örnek çözümleri Örnek 34.1: Teorik çözümü Timoshenko 1 tarafından verilen dört tarafından ankastre ve merkezinde P=100 kn tekil yükü olan kare plağın(şekil 34.1) çözümü 4 farklı model
34. Dörtgen plak örnek çözümleri Örnek 34.1: Teorik çözümü Timoshenko 1 tarafından verilen dört tarafından ankastre ve merkezinde P=100 kn tekil yükü olan kare plağın(şekil 34.1) çözümü 4 farklı model
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım)
 İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
Açı Yöntemi. 1 ql 8. Açı yöntemi olarak adlandırılan denklemlerin oluşturulmasında aşağıda gösterilen işaret kabulü yapılmaktadır.
 çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (3. Hafta)
 TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
Lineer Cebir. Doç. Dr. Niyazi ŞAHİN TOBB. İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler
 Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
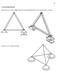 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
Doç. Dr. Bilge DORAN
 Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
SONLU FARKLAR GENEL DENKLEMLER
 SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
25. SEM2015 programı ve kullanımı
 25. SEM2015 programı ve kullanımı Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
25. SEM2015 programı ve kullanımı Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
SONLU ELEMANLAR YÖNTEMİ
 SONLU ELEMANLAR YÖNTEMİ Kurs Kapsamı SONLU ELEMANLAR KAVRAMI SONLU ELEMANLAR FORMULASYONU UYGULAMALARI Sonlu Elemanlar Çözümleri Rijitlik Metodu Esneklik Metodu Karışık Kullanımlar Rijitlik Metodu Kullanılarak
SONLU ELEMANLAR YÖNTEMİ Kurs Kapsamı SONLU ELEMANLAR KAVRAMI SONLU ELEMANLAR FORMULASYONU UYGULAMALARI Sonlu Elemanlar Çözümleri Rijitlik Metodu Esneklik Metodu Karışık Kullanımlar Rijitlik Metodu Kullanılarak
Yapı Sistemlerinde Elverişsiz Yüklemeler:
 Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
MUKAVEMET Öğr. Gör. Fatih KURTULUŞ
 www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
Elastisite Teorisi Düzlem Problemleri için Sonuç 1
 Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
MECHANICS OF MATERIALS
 T E CHAPTER 2 Eksenel MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Yükleme Fatih Alibeyoğlu Eksenel Yükleme Bir önceki bölümde, uygulanan yükler neticesinde ortaya çıkan
T E CHAPTER 2 Eksenel MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Yükleme Fatih Alibeyoğlu Eksenel Yükleme Bir önceki bölümde, uygulanan yükler neticesinde ortaya çıkan
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele
 EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele alınmıştı. Bu bölümde ise, eksenel yüklü elemanların şekil
EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele alınmıştı. Bu bölümde ise, eksenel yüklü elemanların şekil
Yapı Sistemlerinin Hesabı İçin. Matris Metotları. Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL Bahar Yarıyılı
 Yapı Sistemlerinin Hesabı İçin Matris Metotları 05-06 Bahar Yarıyılı Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL BÖLÜM VIII HAREKET DENKLEMİ ZORLANMIŞ TİTREŞİMLER SERBEST TİTREŞİMLER Bu bölümün hazırlanmasında
Yapı Sistemlerinin Hesabı İçin Matris Metotları 05-06 Bahar Yarıyılı Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL BÖLÜM VIII HAREKET DENKLEMİ ZORLANMIŞ TİTREŞİMLER SERBEST TİTREŞİMLER Bu bölümün hazırlanmasında
x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu;
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
30. Uzay çerçeve örnek çözümleri
 . Ua çerçeve örnek çöümleri. Ua çerçeve örnek çöümleri Ua çerçeve eleman sonlu elemanlar metodunun en karmaşık elemanıdır. Bunun nedenleri: ) Her eleman için erel eksen takımı seçilmesi gerekir. Elemanın
. Ua çerçeve örnek çöümleri. Ua çerçeve örnek çöümleri Ua çerçeve eleman sonlu elemanlar metodunun en karmaşık elemanıdır. Bunun nedenleri: ) Her eleman için erel eksen takımı seçilmesi gerekir. Elemanın
KUADRATİK FORM. Tanım: Kuadratik Form. Bir q(x 1,x 2,,x n ) fonksiyonu
 KUADRATİK FORMLAR KUADRATİK FORM Tanım: Kuadratik Form Bir q(x,x,,x n ) fonksiyonu q x : n şeklinde tanımlı ve x i x j bileşenlerinin doğrusal kombinasyonu olan bir fonksiyon ise bir kuadratik formdur.
KUADRATİK FORMLAR KUADRATİK FORM Tanım: Kuadratik Form Bir q(x,x,,x n ) fonksiyonu q x : n şeklinde tanımlı ve x i x j bileşenlerinin doğrusal kombinasyonu olan bir fonksiyon ise bir kuadratik formdur.
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
ÖZDEĞERLER- ÖZVEKTÖRLER
 ÖZDEĞERLER- ÖZVEKTÖRLER GİRİŞ Özdeğerler, bir matrisin orijinal yapısını görmek için kullanılan alternatif bir yoldur. Özdeğer kavramını açıklamak için öncelikle özvektör kavramı ele alınsın. Bazı vektörler
ÖZDEĞERLER- ÖZVEKTÖRLER GİRİŞ Özdeğerler, bir matrisin orijinal yapısını görmek için kullanılan alternatif bir yoldur. Özdeğer kavramını açıklamak için öncelikle özvektör kavramı ele alınsın. Bazı vektörler
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
Lineer Denklem Sistemleri
 Lineer Denklem Sistemleri Yazar Yrd. Doç.Dr. Nezahat ÇETİN ÜNİTE 3 Amaçlar Bu üniteyi çalıştıktan sonra; Lineer Denklem ve Lineer Denklem Sistemleri kavramlarını öğrenecek, Lineer Denklem Sistemlerinin
Lineer Denklem Sistemleri Yazar Yrd. Doç.Dr. Nezahat ÇETİN ÜNİTE 3 Amaçlar Bu üniteyi çalıştıktan sonra; Lineer Denklem ve Lineer Denklem Sistemleri kavramlarını öğrenecek, Lineer Denklem Sistemlerinin
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
T I M U R K A R A Ç AY, H AY D A R E Ş, O R H A N Ö Z E R K A L K U L Ü S N O B E L
 T I M U R K A R A Ç AY, H AY D A R E Ş, O R H A N Ö Z E R K A L K U L Ü S N O B E L 1 Denklemler 1.1 Doğru deklemleri İki noktası bilinen ya da bir noktası ile eğimi bilinen doğruların denklemlerini yazabiliriz.
T I M U R K A R A Ç AY, H AY D A R E Ş, O R H A N Ö Z E R K A L K U L Ü S N O B E L 1 Denklemler 1.1 Doğru deklemleri İki noktası bilinen ya da bir noktası ile eğimi bilinen doğruların denklemlerini yazabiliriz.
Taşkın, Çetin, Abdullayeva 2. ÖZDEŞLİKLER,DENKLEMLER VE EŞİTSİZLİKLER
 MATEMATİK Taşkın, Çetin, Abdullayeva BÖLÜM. ÖZDEŞLİKLER,DENKLEMLER VE EŞİTSİZLİKLER. ÖZDEŞLİKLER İki cebirsel ifade içerdikleri değişkenlerin (veya bilinmeyenlerin) her değeri içinbirbirine eşit oluyorsa,
MATEMATİK Taşkın, Çetin, Abdullayeva BÖLÜM. ÖZDEŞLİKLER,DENKLEMLER VE EŞİTSİZLİKLER. ÖZDEŞLİKLER İki cebirsel ifade içerdikleri değişkenlerin (veya bilinmeyenlerin) her değeri içinbirbirine eşit oluyorsa,
YAPI STATİĞİ II. Hasan KAPLAN. Denizli (İlk Baskı 1999-Gözden Geçirilmekte olan Taslak Kitap)
 YAPI STATİĞİ II Hasan KAPLAN Denizli-3 (İlk Baskı 999-Gözden Geçirilmekte olan Taslak Kitap) Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
YAPI STATİĞİ II Hasan KAPLAN Denizli-3 (İlk Baskı 999-Gözden Geçirilmekte olan Taslak Kitap) Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
STATIK MUKAVEMET. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
35. Karma sistem örnek çözümleri
 35. Karma sistem örnek çözümleri SEM2025 de düzlem kafes ve düzlem çerçeve karma sistem çözülebilir. Bunun dışında, örneğin, aynı sistemde plak, levha veya çerçeve eleman içeren karma sistem çözümü programda
35. Karma sistem örnek çözümleri SEM2025 de düzlem kafes ve düzlem çerçeve karma sistem çözülebilir. Bunun dışında, örneğin, aynı sistemde plak, levha veya çerçeve eleman içeren karma sistem çözümü programda
Özdeğer ve Özvektörler
 Özdeğer ve Özvektörler Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 9 Amaçlar Bu üniteyi çalıştıktan sonra; bir lineer dönüşümün ve bir matrisin özdeğer ve özvektör kavramlarını anlayacak, bir dönüşüm matrisinin
Özdeğer ve Özvektörler Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 9 Amaçlar Bu üniteyi çalıştıktan sonra; bir lineer dönüşümün ve bir matrisin özdeğer ve özvektör kavramlarını anlayacak, bir dönüşüm matrisinin
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Eksenel Yükleme Amaçlar
 Eksenel Yükleme Amaçlar Geçtiğimiz bölümlerde eksenel yüklü elemanlarda oluşan normal gerilme ve normal şekil değiştirme konularını gördük, Bu bölümde ise deformasyonların bulunması ile ilgili bir metot
Eksenel Yükleme Amaçlar Geçtiğimiz bölümlerde eksenel yüklü elemanlarda oluşan normal gerilme ve normal şekil değiştirme konularını gördük, Bu bölümde ise deformasyonların bulunması ile ilgili bir metot
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
Lineer Bağımlılık ve Lineer Bağımsızlık
 Lineer Bağımlılık ve Lineer Bağımsızlık Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 5 Amaçlar Bu üniteyi çalıştıktan sonra; Vektör uzayı ve alt uzay yapısını daha iyi tanıyacak, Bir vektör uzayındaki vektörlerin
Lineer Bağımlılık ve Lineer Bağımsızlık Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 5 Amaçlar Bu üniteyi çalıştıktan sonra; Vektör uzayı ve alt uzay yapısını daha iyi tanıyacak, Bir vektör uzayındaki vektörlerin
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
Kafes Sistemler. Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir.
 KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
AÇI YÖNTEMİ Slope-deflection Method
 SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Tablo 1 Deney esnasında kullanacağımız numunelere ait elastisite modülleri tablosu
 BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN
 Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
TUNCELİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ LİNEER CEBİR DERSİ 2012 GÜZ DÖNEMİ ÇIKMIŞ VİZE,FİNAL VE BÜTÜNLEME SORULARI ÖĞR.GÖR.
 UNCELİ ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ LİNEER CEBİR DERSİ 0 GÜZ DÖNEMİ ÇIKMIŞ VİZE,FİNAL VE BÜÜNLEME SORULARI ÖĞR.GÖR.İNAN ÜNAL www.inanunal.com UNCELİ ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ MAKİNE MÜHENDİSLİĞİ
UNCELİ ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ LİNEER CEBİR DERSİ 0 GÜZ DÖNEMİ ÇIKMIŞ VİZE,FİNAL VE BÜÜNLEME SORULARI ÖĞR.GÖR.İNAN ÜNAL www.inanunal.com UNCELİ ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ MAKİNE MÜHENDİSLİĞİ
YAPI STATİĞİ MESNETLER
 YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
İKİNCİ DERECEDEN DENKLEMLER
 İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
Mukavemet-I. Yrd.Doç.Dr. Akın Ataş
 Mukavemet-I Yrd.Doç.Dr. Akın Ataş Bölüm 5 Eğilmede Kirişlerin Analizi ve Tasarımı Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mukavemet-I Yrd.Doç.Dr. Akın Ataş Bölüm 5 Eğilmede Kirişlerin Analizi ve Tasarımı Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Burulma (Torsion) Amaçlar
 (Torsion) Amaçlar Bu bölümde şaftlara etkiyen burulma kuvvetlerinin etkisi incelenecek. Analiz dairesel kesitli şaftlar için yapılacak. Eleman en kesitinde oluşan gerilme dağılımı ve elemanda oluşan burulma
(Torsion) Amaçlar Bu bölümde şaftlara etkiyen burulma kuvvetlerinin etkisi incelenecek. Analiz dairesel kesitli şaftlar için yapılacak. Eleman en kesitinde oluşan gerilme dağılımı ve elemanda oluşan burulma
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 3- LİNEER DENKLEM SİSTEMLERİNİN ÇÖZÜMÜ Doç. Dr. Ali Rıza YILDIZ 1 LİNEER DENKLEM SİSTEMLERİ Bilimsel ve teknolojik çalışmalarda karşılaşılan matematikle ilgili belli başlı
MAK 210 SAYISAL ANALİZ BÖLÜM 3- LİNEER DENKLEM SİSTEMLERİNİN ÇÖZÜMÜ Doç. Dr. Ali Rıza YILDIZ 1 LİNEER DENKLEM SİSTEMLERİ Bilimsel ve teknolojik çalışmalarda karşılaşılan matematikle ilgili belli başlı
Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir.
 1 DENKLEMLER: Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir. Bir denklemde eşitliği sağlayan(doğrulayan) değerlere; verilen denklemin kökleri veya
1 DENKLEMLER: Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir. Bir denklemde eşitliği sağlayan(doğrulayan) değerlere; verilen denklemin kökleri veya
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme
 Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
 5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor
 3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
Kesit Tesirleri Tekil Kuvvetler
 Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
Lineer Dönüşümler ÜNİTE. Amaçlar. İçindekiler. Yazar Öğr. Grv.Dr. Nevin ORHUN
 Lineer Dönüşümler Yazar Öğr. Grv.Dr. Nevin ORHUN ÜNİTE 7 Amaçlar Bu üniteyi çalıştıktan sonra; Vektör uzayları arasında tanımlanan belli fonksiyonları tanıyacak, özelliklerini öğrenecek, Bir dönüşümün,
Lineer Dönüşümler Yazar Öğr. Grv.Dr. Nevin ORHUN ÜNİTE 7 Amaçlar Bu üniteyi çalıştıktan sonra; Vektör uzayları arasında tanımlanan belli fonksiyonları tanıyacak, özelliklerini öğrenecek, Bir dönüşümün,
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
ÖABT Lineer Cebir KONU TESTİ Matris Cebiri
 ÖB Lineer Cebir KONU ESİ Matris Cebiri. i, j,, i için j i j a j i j a. j i j a. i için j i j a 4 6 j i j a 4 j i j a. 6. 0 0 0 4 0 0 0. 4 6 n 0 0 n 6 Cevap: D Cevap:. I. I I I 0 I 0 0 0..I I I 00 0 0 0
ÖB Lineer Cebir KONU ESİ Matris Cebiri. i, j,, i için j i j a j i j a. j i j a. i için j i j a 4 6 j i j a 4 j i j a. 6. 0 0 0 4 0 0 0. 4 6 n 0 0 n 6 Cevap: D Cevap:. I. I I I 0 I 0 0 0..I I I 00 0 0 0
Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı. Doç.Dr. Bilge Doran
 Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı Dersin Adı : Yapı Mühendisliğinde Bilgisayar Uygulamaları Koordinatörü : Doç.Dr.Bilge DORAN Öğretim Üyeleri/Elemanları: Dr. Sema NOYAN ALACALI,
Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı Dersin Adı : Yapı Mühendisliğinde Bilgisayar Uygulamaları Koordinatörü : Doç.Dr.Bilge DORAN Öğretim Üyeleri/Elemanları: Dr. Sema NOYAN ALACALI,
Dairesel Temellerde Taban Gerilmelerinin ve Kesit Zorlarının Hesabı
 Prof. Dr. Günay Özmen İTÜ İnşaat Fakültesi (Emekli), İstanbul gunozmen@yahoo.com Dairesel Temellerde Taban Gerilmelerinin ve Kesit Zorlarının Hesabı 1. Giriş Zemin taşıma gücü yeter derecede yüksek ya
Prof. Dr. Günay Özmen İTÜ İnşaat Fakültesi (Emekli), İstanbul gunozmen@yahoo.com Dairesel Temellerde Taban Gerilmelerinin ve Kesit Zorlarının Hesabı 1. Giriş Zemin taşıma gücü yeter derecede yüksek ya
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
ÇATI MAKASINA GELEN YÜKLER
 ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta ( ):
 Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Matris Cebiriyle Çoklu Regresyon Modeli
 Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
13. Karakteristik kökler ve özvektörler
 13. Karakteristik kökler ve özvektörler 13.1 Karakteristik kökler 1.Tanım: A nxn tipinde matris olmak üzere parametrisinin n.dereceden bir polinomu olan şeklinde gösterilen polinomuna A matrisin karakteristik
13. Karakteristik kökler ve özvektörler 13.1 Karakteristik kökler 1.Tanım: A nxn tipinde matris olmak üzere parametrisinin n.dereceden bir polinomu olan şeklinde gösterilen polinomuna A matrisin karakteristik
ii) S 2LW 2WH 2LW 2WH S 2WH 2LW S 3( x 1) 5( x 2) 5 3x 3 5x x Maliye Bölümü EKON 103 Matematik I / Mart 2018 Proje 2 CEVAPLAR C.1) C.
 C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
q = 48 kn/m q = 54 kn/m 4 m 5 m 3 m 3 m
 Soru 1) (50 Puan) şağıda verilen sistemin üzerine etkiyen yükler ve konumları şekil üzerinde belirtilmiştir. una ek olarak mesneti cm aşağı yönlü oturmuştur. Tüm kolon ve kirişlerin atalet momenti, elastik
Soru 1) (50 Puan) şağıda verilen sistemin üzerine etkiyen yükler ve konumları şekil üzerinde belirtilmiştir. una ek olarak mesneti cm aşağı yönlü oturmuştur. Tüm kolon ve kirişlerin atalet momenti, elastik
STATİK. Ders_6. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
Kafes Sistemler. Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir.
 Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
x 0 = A(t)x + B(t) (2.1.2)
 ÖLÜM 2 LİNEER SİSTEMLER Genel durumda diferansiyel denklemlerin çözümlerini açık olarak elde etmek veya çözümlerin bazı önemli özelliklerini araştırmak için genel yöntemler yoktur, çoğu zaman denkleme
ÖLÜM 2 LİNEER SİSTEMLER Genel durumda diferansiyel denklemlerin çözümlerini açık olarak elde etmek veya çözümlerin bazı önemli özelliklerini araştırmak için genel yöntemler yoktur, çoğu zaman denkleme
ULUDAĞ ÜNĐVERSĐTESĐ MÜHENDĐSLĐK-MĐMARLIK FAKÜLTESĐ MAKĐNA MÜHENDĐSLĐĞĐ BÖLÜMÜ GENEL MAKĐNE LABORATUARI
 UUDAĞ ÜNĐVRSĐTSĐ MÜNDĐSĐK-MĐMARIK FAKÜTSĐ MAKĐNA MÜNDĐSĐĞĐ BÖÜMÜ GN MAKĐN ABORATUARI STRAĐN GAUG (UZAMA ÖÇR YARDIMI Đ GRĐM ÖÇÜMSĐ DNY GRUBU: ÖĞRNCĐ NO, AD -SOYAD: TSĐM TARĐĐ: DNYĐ YAPTIRAN ÖĞRTĐM MANI:
UUDAĞ ÜNĐVRSĐTSĐ MÜNDĐSĐK-MĐMARIK FAKÜTSĐ MAKĐNA MÜNDĐSĐĞĐ BÖÜMÜ GN MAKĐN ABORATUARI STRAĐN GAUG (UZAMA ÖÇR YARDIMI Đ GRĐM ÖÇÜMSĐ DNY GRUBU: ÖĞRNCĐ NO, AD -SOYAD: TSĐM TARĐĐ: DNYĐ YAPTIRAN ÖĞRTĐM MANI:
Hedefler. Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu
 Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER
 İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER Yapı Elemanları İnşaat Mühendisliği ile ilgili yapı sistemleri üç ayrı tipteki yapı elemanlarının birleşiminden oluşur. 1)Çubuk Elemanlar: İki boyutu üçüncü boyutuna
İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER Yapı Elemanları İnşaat Mühendisliği ile ilgili yapı sistemleri üç ayrı tipteki yapı elemanlarının birleşiminden oluşur. 1)Çubuk Elemanlar: İki boyutu üçüncü boyutuna
Gerilme. Bölüm Hedefleri. Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı
 Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
8. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 8. HAFTA BLM323 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 2 MATRİSLER Matris veya dizey, dikdörtgen bir sayılar tablosu
8. HAFTA BLM323 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 2 MATRİSLER Matris veya dizey, dikdörtgen bir sayılar tablosu
Ayrık Fourier Dönüşümü
 Ayrık Fourier Dönüşümü Tanım: 0 n N 1 aralığında tanımlı N uzunluklu bir dizi x[n] nin AYRIK FOURIER DÖNÜŞÜMÜ (DFT), ayrık zaman Fourier dönüşümü (DTFT) X(e jω ) nın0 ω < 2π aralığında ω k = 2πk/N, k =
Ayrık Fourier Dönüşümü Tanım: 0 n N 1 aralığında tanımlı N uzunluklu bir dizi x[n] nin AYRIK FOURIER DÖNÜŞÜMÜ (DFT), ayrık zaman Fourier dönüşümü (DTFT) X(e jω ) nın0 ω < 2π aralığında ω k = 2πk/N, k =
a) x +3 = 8 b) x -4 = -2 c) x -7 = 4 d) x +5 = 6 e) x +8 = 2 f) x -1= -8 x +3 = 5 denkleminin çözümünü bulunuz.
 Denklemler bilinmeyen - cebirsel ifade - 7 denklem Bir cebirsel ifade bir sonuca eşit oluyorsa buna denklem denir. Bazı denklemlerin çözümü yoktur, bazı denklemlerin sonsuz, bazı denklemlerin bir, iki,
Denklemler bilinmeyen - cebirsel ifade - 7 denklem Bir cebirsel ifade bir sonuca eşit oluyorsa buna denklem denir. Bazı denklemlerin çözümü yoktur, bazı denklemlerin sonsuz, bazı denklemlerin bir, iki,
