BİLDİRİ TAM METİNLERİ e KİTABI
|
|
|
- Adem Açık
- 8 yıl önce
- İzleme sayısı:
Transkript
1 VII. İSTATİSTİK GÜNLERİ SEMPOZYUMU 8 30 Hazran 00 Orta Doğu Teknk Ünverstes Ġstatstk Bölümü BİLDİRİ TAM METİNLERİ e KİTABI Edtörler H. Öztaş AYHAN Ceylan TALU YOZGATLIGİL Yayın: Ankara, Mart 0
2 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ÖNSÖZ 7. Ġstatstk Günler Sempozyumu, 8 30 Hazran 00 tarhler arasında Orta Doğu Teknk Ünverstes, Fen ve Edebyat Fakültes, Ġstatstk Bölümü tarafından, Ankara da ODTÜ Kültür ve Kongre Merkez salonlarında gerçekleģtrlmģtr. Sempozyumda, 4 adet davetl bldr ve 68 adet katkılı bldr baģarı le sunulmuģtur. Sempozyumda sunulan bldrlern br bölümü blmsel hakemlk sürec sonunda bu elektronk Sempozyum Bldrler Ktabı nda yayınlanmıģtır. Sunulan bldrlern dğer br bölümü se, Ġstatstk AraĢtırma Dergs nn bu sempozyum çn planlanan özel sayısında yayınlanmak amacı le blmsel hakemlk sürecne tab tutulmuģlardır. Bzlere bu olanağı sağlayan TÜĠK BaĢkan Vekl sayın Ömer TOPRAK a ve derg edtorü Profesör Feth YILDIRIM ve edtor yardımcısı Yardımcı Doçent Özlem ĠLK e teģekkür ederm. Sempozyum Bldrler Ktabı nda yayınlanmak üzere sunulan bldr tam metnler konunun uzmanı olan hakemler tarafından değerlendrlmģ ve gerekl düzeltmeler elektronk ortamda gerçekleģtrlmģtr. Hakemlk sürecnde yardımlarını esrgemeyen değerl blm nsanlarına teģekkür ederz. Sempozyum blmsel programının çok renkl olmasını çok özel olan davetl konuģmacılarımıza borçluyuz. Kend özel blmsel çalıģma alanlarında dünyada ve ülkemzde öneml söz sahb olan Profesör Orhan GÜVENEN, Profesör Ġ. Burhan TÜRKġEN, Profesör Ġsmhan BAYRAMOĞLU ve Profesör Fkr AKDENĠZ e sempozyuma yaptıkları katkılar nedenyle Ģükranlarımı sunarım. Sempozyumda oturum baģkanı olarak, sempozyum bldrlerne katkıda bulunan tüm meslektaģlarıma da teģekkürlerm sunarım. Bu sempozyumun gerçekleģmesnde değerl desteklern esrgemeyen Rektörümüz Profesör Ahmet ACAR a Ģükranlarımızı sunarız. Ayrıca, bu sempozyumun gerçekleģmesnde değerl görüģleryle katkıda bulunan Sempozyum Onur Kurulu ve Sempozyum Blmsel DanıĢma Kurulu üyelerne teģekkür ederm. Sempozyum hazırlık ve uygulamasının tüm aģamalarında yer alan değerl çalıģma arkadaģlarıma ve özverl çalıģmalarından dolayı Sempozyum Düzenleme Kurulu ve Bölümümüzün tüm dar personelne teģekkür ederm. Sempozyumun baģarılı br Ģeklde sonuçlanmasına katkıda bulunan ODTÜ nn tüm çalıģanlarına ayrıca teģekkür ederm. Sempozyumun gerçekleģmesnde öneml mal desteklern esrgemeyen Türkye Halk Bankası Genel Müdür Yardımcısı Osman ARSLAN ve Tanıtım ve Halkla ĠlĢkler Dares BaĢkanı Yalçın KAYA ya Ģükranlarımı sunuyorum. Sempozyum düzenlemenn tüm aģamalarındak desteklernden dolayı ETĠX Organzasyon ġrket yönetc ve çalıģanlarına teģekkür ederm. Sempozyumun, kapanıģ yemeğnn düzenlenmesnde yaptıkları özverl çalıģmaları nedenyle, Hacettepe Ünverstes Genel Sekreter Profesör Turhan MENTEġ ve Beytepe Akademk Kafeteryası yönetclerne teģekkür ederm. Ġstatstk blm nsanlarının br araya geldğ bu tür sempozyumlar, tecrübel statstkçler le genç akademsyen ve araģtırmacılarımızın brlktelğn sağlamakta ve gençlern motvasyonunu artıran öneml br toplantı olmaktadır. Gelecek yıllarda, bu sempozyumun sürekllğnn, statstkçler çn öneml br blmsel buluģma ortamı olmaya devam etmesn dlyorum. Profesör H. ÖztaĢ AYHAN ODTÜ Ġstatstk Bölümü BaĢkanı 7. ĠGS 00 Düzenleme Kurulu adına ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
3 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 SEMPOZYUM ONUR KURULU Prof. Dr. Ahmet Acar, Orta Doğu Teknk Ünverstes Rektörü Prof. Dr. Cüneyt Can, ODTÜ Fen ve Edebyat Fakültes Dekanı Prof. Dr. Canan Özgen, ODTÜ Fen Blmler Ensttüsü Müdürü SEMPOZYUM DANIġMA KURULU Prof. Dr. Fkr Akdenz, Çukurova Ünverstes Prof. Dr. Soner Gönen, Gaz Ünverstes Prof. Dr. Hüseyn Tatlıdl, Hacettepe Ünverstes Prof. Dr. Serdar Kurt, Dokuz Eylül Ünverstes Prof. Dr. Ömer L. Gebzloğlu, Ankara Ünverstes Doç. Dr. Mehmet Al Cengz, Ondokuz Mayıs Ünverstes SEMPOZYUM DÜZENLEME KURULU Prof. Dr. H. ÖztaĢ Ayhan Prof. Dr. AyĢen Dener Akkaya Doç. Dr. Ġnc Batmaz Doç. Dr. BarıĢ Sürücü Yard.Doç. Dr. Zeynep Kalaylıoğlu Yar.Doç. Dr. Özlem Ġlk Yar.Doç. Dr. B. Burçak BaĢbuğ Erkan Yar.Doç.Dr. Ceylan Talu Yozgatlıgl Yar.Doç.Dr. Vlda Purutçuoğlu Dr. Ayça Dönmez ArĢ.Gör. Span Aslan ArĢ.Gör. Sbel Balcı ArĢ.Gör. Könül Bayramoğlu ArĢ.Gör. Elçn Kartal ArĢ.Gör. Gül Ġnan ArĢ.Gör. Tuğba Erdem ArĢ.Gör. Özgür Asar ArĢ.Gör. Ceyda Yazıcı ArĢ.Gör. Olcay Öztürk ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
4 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ĠÇĠNDEKĠLER NO MAKALE ADI SAYFA AĞIRLIKLI HEDEF PROGRAMLAMA VERĠ ZARFLAMA ANALĠZĠ YÖNTEMĠ -8 ĠLE TÜRKĠYE DEKĠ ĠLLERĠN BAġARIM DEĞERLENDĠRMESĠ H.Hasan ÖRKÇÜ, Hasan BAL ANKARA HAVA KĠRLĠLĠĞĠ ZAMAN SERĠSĠNĠN ÇÖZÜMLENMESĠNDE KLASĠK 9-5 VE BULANIK ZAMAN SERĠLERĠ YAKLAġIMLARININ KARġILAġTIRILMASI Erol EĞRĠOĞLU, Ufuk YOLCU, Ç.Hakan ALADAĞ, V.Rezan USLU 3 BURR XII DAĞILIMININ PARAMETRELERININ ĠLERLEYEN TÜR ĠLK BOZULMA 6-4 SANSÜRLEMEYE DAYALI GÜVEN ARALIKLARI VE GÜVEN BÖLGELERI CoĢkun KUġ, Yunus AKDOĞAN 4 DOGRUSAL OLMAYAN REGRESYONDA BAZI PARAMETRE ARALIK 5-34 TAHMNLEME YONTEMLERNN KIYASLANMASI Atıf EVREN 5 ESENBOĞA, ATATÜRK VE LONDON CITY HAVAALANLARINDAKĠ MEVSĠMSEL HAREKETLĠLĠĞĠN GÖSTERMELĠK DEĞĠġKEN YÖNTEMĠYLE TESPĠT EDĠLMESĠ Denz KONAK, Vlda PURUTÇUOĞLU 6 GAUSS RASTGELE YÜRÜYÜġ SÜRECĠNĠN MAKSĠMUNUN MOMENTLERĠ ĠÇĠN 44-5 YAKLAġIK FORMÜLLER Fkr GÖKPINAR, Tahr KHANĠYEV 7 ĠLERĠ BESLEMELĠ YAPAY SĠNĠR AĞLARI ĠLE ÖNGÖRÜ ĠÇĠN GĠZLĠ TABAKA SAYISI ÜZERĠNE BĠR ARAġTIRMA Faruk ALPASLAN, Ebrucan TĠRĠNG, Erol EĞRĠOĞLU 8 ĠSTATĠSTĠK'TE ENTROPĠYE DAYALI UYUM ÖLÇÜLERĠNĠN DĠĞER UYUM ÖLÇÜLERĠ ĠLE KIYASLANMASI Atıf EVREN 9 L-SIRALI KÜME ÖRNEKLEMESĠ KULLANILARAK YIĞIN ORTALAMASININ TAHMĠN EDĠLMESĠ Nlay AKINCI, Yaprak Arzu ÖZDEMĠR 0 ÖLÇÜM YETERLĠLĠK PARAMETRELERĠNĠN TAHMĠN EDĠCĠLERĠ VE GÜVEN ARALIKLARI Ümt YAMAN, Yunus AKDOĞAN, Ahmet PEKGÖR, CoĢkun KUġ ONDOKUZ MAYIS ÜNĠVERSĠTESĠ TIP FAKÜLTESĠ BEYĠN CERRAHĠSĠ POLĠKLĠNĠĞĠNDE SĠMÜLASYON YARDIMIYLA HASTA BEKLEME SÜRESĠNĠN AZALTILMASI Faruk ALPASLAN, Özge CAĞCAĞ, Erol EĞRĠOĞLU PARETO MÜDAHALELĠ YARI-MARKOV RASTGELE YÜRÜYÜġ SÜREÇĠ ĠÇĠN ASĠMPTOTĠK SONUÇLAR Rovshan ALIYEV, Tülay KESEMEN, Ġhsan ÜNVER 3 RCMARS-SAĞLAMCMARSYÖNTEMĠVESAYISAL BĠRUYGULAMA 0-08 AyĢe ÖZMEN, Gerhard-Wlhelm WEBER, Ġnc BATMAZ 4 SARIMA MODELĠ VE ELMAN YAPAY SĠNĠR AĞININ MELEZ YAKLAġIMI ĠLE 09-4 ANKARAHAVA KALĠTESĠ VERĠLERĠNĠN ÇÖZÜMLENMESĠ ÇağdaĢ Hakan ALADAĞ, Ufuk YOLCU, Erol EĞRĠOĞLU 5 SIRALI KÜME ÖRNEKLEMESĠ TASARIMINDA YIĞIN ORTALAMASINA ĠLĠġKĠN 5- HĠPOTEZTESTĠ Yaprak Arzu ÖZDEMĠR, Fkr GÖKPINAR 6 TLDOLAR DÖVĠZ KURU VERĠLERĠNĠN BULANIK ZAMAN SERĠSĠ YAKLAġIMLARI 3-9 ĠLE ÖNGÖRÜSÜ Cem KOÇAK, Erol EĞRĠOĞLU, Ufuk YOLCU, ÇağdaĢ Hakan ALADAĞ 7 HETEROJEN VARYANS DURUMUNDA ORTALAMALARIN EġĠTLĠĞĠ ĠÇĠN YENĠDEN ÖRNEKLEME TEKNĠKLERĠNE DAYALI BĠR ÇALIġMA Esra YĠĞĠT, Hamza GAMGAM 8 UYARLANMIġ DURBĠN TESTĠ ĠÇĠN PERMÜTASYON TESTĠ VE BĠR SĠMÜLASYON 4-47 ÇALIġMASI Fkr GÖKPINAR, Hülya BAYRAK ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
5 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 AĞIRLIKLI HEDEF PROGRAMLAMA VERĠ ZARFLAMA ANALĠZĠ YÖNTEMĠ ĠLE TÜRKĠYE DEKĠ ĠLLERĠN BAġARIM DEĞERLENDĠRMESĠ H.Hasan ÖRKCÜ * Hasan BAL ** ÖZET Bu çalıģmada, Türkye dek 8 ln baģarım değerlendrmes klask ver zarflama analz (CCR model) ve ağırlıklı hedef programlama ver zarflama analz yöntemler le ncelenmģtr.elde edlen sonuçlar ağırlıklı hedef programlama ver zarflama analz yöntemnn klask ver zarflama analz yöntemne göre daha y br alternatf olduğunu göstermģtr. Anahtar Kelmeler: Ver zarflama analz, hedef programlama, llern etknlğ. EVALUATION FOR PERFORMANCES OF COUNTRIES IN TURKEY BY WEIGHTED GOAL PROGRAMMING DATA ENVELOPMENT ANALYSIS ABSTRACT In ths study, the effcency evaluaton of 8 countres n Turkey was examned by classcal data envelopment analyss (CCR model) and weghted goal programmng data envelopment analyss methods. The obtaned results show that weghted goal programmng data envelopment analyss method s a better alternatve accordng to classcal data envelopment analyss method. Keywords: Data Envelopment Analyss, goal programmng, effcency of countres. GĠRĠġ Karar verme brmlernn (KVB) görel etknlklernn ölçülmes amacı le gelģtrlmģ olan Ver Zarflama Analznn (VZA) uygulamaları gelģtkçe yen problemler de ortaya çıkmıģtır (Adler vd., 00). Brbrne bağlı olan bu problemler zayıf ayırt edleblme gücü problem, gerçekç olmayan ağırlık dağılımı problem ve etkn KVB ler çn ağırlıkların çoklu optmal çözümlere sahp olması problemdr. Zayıf ayırt edleblme gücü problem, çok fazla sayıda brmn etkn olarak değerlendrlmesdr. * AraĢ.Gör.Dr., Gaz Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, 0650 Ankara, hhorkcu@gaz.edu.tr ** Prof.Dr., Gaz Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, 0650 Ankara, hasanbal@gaz.edu.tr ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
6 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Türkye farklı topoğrafya ve klm özellklernn meydana getrdğ en genel le yed coğraf bölgeden oluģmakta ve bu bölgeler arasında ekonomk, sosyal ve kültürel açıdan görel gelģmģlk farklar bulunmaktadır. Görel olarak az gelģmģ yörelern gelģmģlk düzeylernn yükseltlerek, bölgelerarası gelģmģlk farkların azaltılması, ülke genelnde ekonomk büyüme le brlkte sağlıklı br sosyal ve kültürel gelģmenn ve refah dağılımının sağlanması, temel br hedef olarak ele alınmıģtır. Bu hedefe yönelk olarak zlenen ekonomk ve sosyal poltkalar le uygulanan teģvk tedbrlerne ve gösterlen çabalara karģın gelģmedek bölgelerarası dengeszlkler önemn korumaktadır.bu amaçlarla Devlet Planlama TeĢklatı (DPT) ller ve bölgeler sevyesnde performans araģtırmaları yapmaktadır. Bu araģtırmalar br çok değģkenl statstksel analz yöntem olan temel bleģenler analz le yapılmaktadır. Bu çalıģmada, klask VZA yöntemndek zayıf ayırt edleblme problemne seçenek olarak önerlen ağırlıklı hedef programlama model le ülkemzdek 8 ln sosyo-ekonomk baģarım değerlendrmes ele alınmıģtır. Önerlen ağırlıklı hedef programlama model le llern gerçek baģarımları ortaya çıkartılması hedeflenmektedr. VERĠ ZARFLAMA ANALĠZĠ YÖNTEMĠ VZA lk olarak Charnes vd. (978) tarafından, ürettkler mal veya hzmet açısından brbrlerne benzer KVB lern görel etknlklernn ölçülmes amacı le gelģtrlmģ parametrk olmayan br teknktr.bu yöntemn sahp olduğu özellkler kısaca özetlersek; her KVB dek etknszlk mktarını ve kaynaklarını tanımlayablmes, her br KVB nn etknlk değer dğerlerne göre hesaplandığından hesaplanan etknlklern görel etknlkler olması ve değģkenler üzernde herhang br fonksyonel varsayım öne sürmemesdr. VZA da herhang br brmn etknlğ CCR model olarak blnen temel etknlk model le ölçülür (Cooper vd., 000). Grd yönlü CCR model () le verlmektedr. Kısıtlar: z max u y p r rp r s m vx p s m u y v x 0, j,..., n r rj j r () u 0, r,..., s r v 0,,..., m ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
7 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Burada, p etknlk değern, modelnde nds etknlğ hesaplanacak KVB n, z * p n se KVB sayısını, m KVB p x grd sayısını, brm de etkn olmayan olarak değerlendrlecektr. grdler, s y çıktıları, z lgl brmn çıktı sayısını smgelemektedr. () etkn olarak değerlendrlr. Etknlk puanı n altında olan her Klask VZA model olarak da adlandırılan CCR model çok sayıda brm etkn olarak değerlendrr.bu durum brmlern brbrler le karģılaģtırılmalarını, etkn olmayan brmler çn etknlklern gelģtrc poltkalar üretmelern sağlayacak ve bu brmlern referans olarak alablecekler brmler seçmelern zorlaģtırmaktadır. Önerlen hedef programlamaya dayalı VZA yaklaģımı L ve Reeves (999) tarafından önerlen çok ölçütlü VZA yaklaģımına dayanmaktadır ve bu model le Türkye dek 8 ln sosyo-ekonomk baģarımları ncelenmektedr. AĞIRLIKLI HEDEF PROGRAMLAMA VERĠ ZARFLAMA ANALĠZĠ YÖNTEMĠ L ve Reeves (999) üç farklı etknlk ölçütlerne göre yen br etknlk model önermģtr. Bu etknlk ölçütler lgl brme at etknlkten sapmanın mnmum yapılması (etknlğn maksmum yapılması), etknlkten sapmalar toplamının mnmum yapılması ve en büyük etknlk sapmasının mnmum yapılmasıdır.ağırlıklı hedef programlama etknlk modelnde bütün etknlk ölçütlernn aynı öneme sahp olduğu ağırlıklı hedef programlama yöntem ele alınmaktadır.ağırlıklı hedef programlama model le daha brmlern klask CCR modelne göre daha makul br sıralamaları yapılablmektedr. Ağırlıklı hedef programlama VZA yöntem (AGHPVZA) model () le verlmektedr. mn a d d d d + d Kısıtlar: 3 j j m s r v x d d p u y d d s r rp m u y v x d 0, j,,..., n r rj j j r () M d j d 3j d3j 0, j,,..., n u 0, r,,..., s r v 0,,,..., m d 0, j,,..., n j ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 3
8 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 d, d, d, d, d, d 0, j,,..., n 3 j 3 j Bu modelde, ele alınan KVB çn, d ve d hedefnden sırasıyla stenmeyen ve stenen sapmaları, hedefnn br etknlk değernden stenen sapmasını, değģkenler grdlern toplamının br olması d hedefnn br etknlk değernden stenmeyen sapmasını, sapmayı smgelemek üzere ve d 3 j smgelemektedr. değģkenler d d d d d + 3 j + d M d 0, j,,..., n j M d 0, j,,..., n j j değģken ağırlıklı çıktı toplamı değģken ağırlıklı çıktı toplamı d 3 j değģkenler M en büyük hedefnden stenmeyen sapmaları hedefnden stenen sapmaları baģarı fonksyonunda stenmeyen sapmalara eģt ağırlık verlmektedr. Bu modelde amaçlanan bütün stenmeyen sapma değģkenlerne aynı ağırlığı vererek 00). d, d, ve d 3 j sapmalarını mnmum yapmaktır (Bal ve Örkcü, 007; Bal vd. ĠLLERĠN ETKĠNLĠK DEĞERLENDĠRMESĠ Bu bölümde ülkemzdek 8 ln sosyo-ekonomk performansı klask CCR model ve önerlen ağırlıklı hedef programlama VZA yöntemler le ncelenmģtr. Modellern çözümünde WINQSB programından yararlanılmıģtır. VZA da değģkenlern grd ve çıktı olarak ayrılması gerekr. DeğĢkenlern, grd ve çıktı olarak ayrılması brm üzerndek etklerne bağlıdır.retzlaff-roberts (997), grd ve çıktı değģkenler yerne brmler üzernde poztf ve negatf etkl değģkenler kavramını kullanmayı uygun bulmuģtur. ArtıĢı brmn daha y olarak değerlendrlmesn sağlayan değģkenlern poztf etkl, tersne düģüģü brmn daha y olarak değerlendrlmesn sağlayan değģkenlern se negatf etkl olarak alınmasını önermģtr. Çıktı (poztf etkl) değģkenler ve grd (negatf etkl) değģkenler, aģağıda lstelenmģtr. Verler DPT ver tabanından alınmıģtır (DPT, 008). Çıktılar: y : ġehrleģme oranı, : Tarım sektöründe çalıģan nüfusun toplam nüfusa oranı, : Okur-yazar nüfus oranı, y 4 : KĢ baģına düģen mll gelr. y y 3 Grdler : Bebek ölüm oranı, x x : KĢ baģına beledye harcamaları, x : KĢ baģına yatırım harcamaları. 3 ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 4
9 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Klask CCR model le 50 l etkn bulunmuģtur (Adana, Adıyaman, Ağrı, Ankara, Antalya,..., Tekrdağ, Tokat, Kırıkkale, Kls, Osmanye). Buradan llern %6 nn CCR model le etkn olarak değerlendrldğ söyleneblr. Ağırlıklı hedef programlama yaklaģımı le sadece 4 l etkn bulunmuģ ve llern daha makul sıralamaları ve ayrımları sağlanmıģtır. Her k model le de elde edlen etknlk sonuçları ġekl de özetlenmģtr. SONUÇ Elde edlen sonuçlardan, llern sosyo-ekonomk baģarımlarının değerlendrlmesnde ağırlıklı hedef programlama yaklaģımının klask CCR modelne göre çok daha y br seçenek olduğu söyleneblr. CCR model 8 ln yarısından fazlasını etkn olarak değerlendrmģ ve ller sosyo-ekonomk baģarımları bakımından brbrnden sağlıklı br bçmde ayrılamamıģlardır. Ağırlıklı hedef programlamaya yaklaģımı se sadece dört l etkn olarak değerlendrmģ ve dğer llere de makul etknlk değerler atamıģtır. Ağırlıklı hedef programlamanın etkn olarak değerlendrdğ llern Ankara, Bursa, Ġstanbul, Ġzmr olması dkkat çekcdr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 5
10 Kocael Kırşehr Kırklarel Kayser Kastamonu Kars İzmr İstanbul Mersn Isparta Hatay Hakkar Gümüşhane Gresun Gazantep Eskşehr Erzurum Erzncan Elazığ Edrne Dyarbakır Denzl Çorum Çankırı Çanakkale Bursa Burdur Bolu Btls Bngöl Bleck Balıkesr Aydın Artvn Antalya Ankara Amasya Ağrı Afyon Adıyaman Adana VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00,00 CCR ve AGHPVZA Modellernn Etknlk Değerler 0,90 0,80 0,70 Etknlk Değer 0,60 0,50 0,40 CCR AGHPVZA 0,30 0,0 0,0 0,00 İller (Adana-Kocael) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 6
11 Düzce Osmanye Kls Karabük Yalova Iğdır Ardahan Bartın Şırnak Batman Kırıkkale Karaman Bayburt Aksaray Zonguldak Yozgat Van Uşak Şanlıurfa Tuncel Trabzon Tokat Tekrdağ Svas Snop Srt Samsun Sakarya Rze Ordu Nğde Nevşehr Muş Muğla Mardn K.Maraş Mansa Malatya Kütahya Konya VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00,00 CCR ve AGHPVZA Modellernn Etknlk Değerler 0,90 0,80 0,70 Etknlk Değer 0,60 0,50 0,40 CCR AGHPVZA 0,30 0,0 0,0 0,00 İller (Konya-Düzce) ġekl.ccr ve AGHPVZA Modellernn Etknlk Değerler ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 7
12 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 TEġEKKÜR Bu çalıģma TÜBĠTAK Blmsel ve Teknolojk AraĢtırma Projelern Destekleme Programı kapsamında (proje no: 09T337) ve Gaz Ünverstes Blmsel AraĢtırma Projeler Brm tarafından (proje no: 05/009 36) ve kısmen desteklenmģtr. KAYNAKLAR ADLER, N., FRIEDMAN L. ve SINUANY-S.Z. (00), Revew of rankng methods n the data envelopment analyss context, European Journal of Operatonal Research, 40, BAL, H. ve ÖRKCÜ, H.H. (007), A goal programmng approach to weght dsperson n Data Envelopment Analyss, G.U. Journal of Scence, 0(4), 7 5. BAL, H., ÖRKCÜ, H.H. ve ÇELEBĠOĞLU, S. (00), Improvng the dscrmnaton power and weght dsperson n the Data Envelopment Analyss, Computers and Operatons Research, 37(), CHARNES, A., COOPER ve W.W., RHODES, E. (978), The effcency of decson makng unts, European Journal of Operatonal Research,, COOPER, W.W., SEIFORD, L.M. ve TONE, K. (000), Data Envelopment Analyss, Boston USA, Kluwer Academc Publshers. DPT, Uluslar arası Ekonomk Göstergeler, 008. ErĢm: 0 Mart 00. LI, X.B. ve REEVES, G.R. (999), A multple crtera approach to data envelopment analyss, European Journal of Operatonal Research, 5, RETZLAFF-ROBERTS, D.L. (997), A Data Envelopment Analyss approach to Dscrmnant Analyss,Annals of Operatons Research,73, ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 8
13 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ANKARA HAVA KĠRLĠLĠĞĠ ZAMAN SERĠSĠNĠN ÇÖZÜMLENMESĠNDE KLASĠK VE BULANIK ZAMAN SERĠLERĠ YAKLAġIMLARININ KARġILAġTIRILMASI Erol Eğroğlu * Ufuk Yolcu ** Ç. Hakan Aladağ *** V. Rezan Uslu **** ÖZET Bulanık zaman serler yaklaģımları, son yıllarda oldukça yoğun çalıģılmaktadır. Gerçek hayatta karģılaģılan bazı zaman serlernn, gözlemlerndek belrszlk nedenyle bulanık zaman sers olarak ele alınması daha doğrudur. Örneğn hava krllğ verler gün çndek çeģtl zamanlardak ölçümlerde farklı değerlere sahp olmasına rağmen, br zaman sers olarak ele alındığında sadece günlük ortalama değerler dkkate alınmaktadır. Oysa böyle br zaman sersnn gözlemler brçok değer çereblen br bulanık küme olarak alınablr. Bu durumda gözlemler bulanık küme olan zaman serlernn öngörülmes problem ortaya çıkmaktadır. Lteratürde bulanık zaman serlernn öngörülmes çn brçok yöntem önerlmģtr. Bu çalıģmada mevsmsel bulanık zaman serlernn öngörülmesnde kullanılan bazı bulanık zaman sers yaklaģımları, klask mevsmsel zaman sers yaklaģımlarından elde edlen sonuçlarla karģılaģtırılmıģtır. KarĢılaĢtırma Ankara hava krllğ verler üzernden yapılmıģtır. Anahtar kelmeler: Öngörü, Bulanık Zaman Serler, Mevsmsellk A COMPARISON OF TRADITIONAL AND FUZZY TIME SERIES APPROACHES IN ANALYSING THE TIME SERIES OF SULPHUR DIOKSITE VALUES IN ANKARA ABSTRACT Many researchers have recently been workng fuzzy tme seres approaches wth an ncreasngly nterest. It s possble to concern some tme seres data as fuzzy tme seres snce they nclude some type of uncertanty. Often the data of ar polluton s generated as daly averages; however the measurements are changng durng the day. Then we consder the ar polluton data as fuzzy tme seres data by allocatng as f each observaton s actually a fuzzy set. In ths study we ntroduce a seasonal fuzzy tme seres approach. Snce the data of ar polluton n Ankara also contans seasonal behavor t s analyzed by usng ths approach and the results are dscussed comparatvely. Keywords: Forecastng, Fuzzy tme seres, Seasonalty. * Doç. Dr., Ondokuz Mayıs Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, 5539 Samsun, erole@omu.edu.tr(haberleģme Adres) ** AraĢtırma Görevls, Ondokuz Mayıs Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, 5539 Samsun, uyolcu@omu.edu.tr ***Öğretm Görevls Doktor, Hacettepe Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, Ankara, chaladag@gmal.com ****Doç. Dr., Ondokuz Mayıs Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, 5539 Samsun, vruslu@omu.edu.tr ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 9
14 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 GĠRĠġ Bu çalıģma uygulamalı br çalıģma olup, geleneksel yöntemlerden SARIMA (mevsmsel otoregresf bütünleģk hareketl ortalama) ve Wnter Çarpımsal Üstel Düzeltme teknğ le mevsmsel bulanık zaman sers yaklaģımlarından Song (999) un ve Eğroğlu vd (009) nn önerdğ yaklaģımlardan elde edlen öngörü performansları karģılaģtırılmak stenmģtr. Ayrıca mevsmsel bulanık zaman sers yaklaģımları çersnde Eğroğlu vd (009) önerdğ yöntemn öngörü performansını arttırdığını vurgulamayı amaçlamaktadır. Bulanık küme teorsnn Zadeh (965) de ortaya atılması brçok blm alanında yen ve etkn yöntemlern önerlmesne sebep olmuģtur.genel olarak statstk analz yöntemlernde de bulanık küme teorsnn bulanık regresyon, bulanık kümeleme, bulanık zaman sers gb uygulamaları son yıllarda lteratürde yoğun olarak çalıģılmaktadır. Geleneksel zaman serler analzndek doğrusallık, en az 50 gözlem, model varsayımı gb kısıtlamalar araģtırmacıları alternatf zaman serler yaklaģımlarına yöneltmektedr. Son 0 yıl çnde yapay snr ağları ve bulanık zaman sers yaklaģımları getrdkler brçok avantaj ve klask zaman sers kısıtlamalarına sahp olmamaları bu yöntemler daha da cazp hale getrmektedr. Özellkle gözlemler belrszlk çeren veya br zaman brm çnde brden fazla değere sahp olan borsa, sıcaklık, okullara kayıtlı öğrenc sayısı, hava krllğ gb verlern çözümlenmesnde bulanık zaman serler yöntemler terch edleblr. Ġlk olarak Song ve Chssom (993a, 993b) bulanık zaman sers yöntemn önermģlerdr. Chen (996), daha kolay hesaplamalar çeren bulanık mantık lģk tablolarına dayalı br yöntem önermģtr. Huarng ve Yu (006) bulanık lģklern yapay snr ağları le belrlendğ br yöntem önermģlerdr.lteratürde önerlen br çok yöntem brnc dereceden bulanık zaman sers öngörü modellern çermektedr. Ancak brçok zaman sersn, çerdkler yüksek derecel lģkler nedenyle, brnc dereceden modellerle çözümlemek yetersz kalablr.bu nedenle, Chen (00), yüksek derecel bulanık zaman sers öngörü modeln çözümleyen yen br yöntem önermģtr. Chen (00) tarafından önerlen bu yöntemde tüm geckmel değģkenler mevcuttur. Mevsmsel zaman serler çn, bu yöntemde, model derecesnn peryot kadar olması gerektğ açıktır. Ancak bu durum katkısız geckmel değģkenler modele dâhl ederek, modeldek grd sayısını gereksz Ģeklde arttıracaktır. Bununla brlkte, Song (999), peryodu m olan br mevsmsel zaman sersn çözümlemede, F(t-m) geckmel değģkennn grd ve F(t) nn se çıktı olarak alındığı yen br yöntem önermģtr. Bu yöntem de, daha karmaģık lģkler çeren mevsmsel zaman serlern çözümlemede yetersz kalacaktır. Eğroğlu vd. (009) tarafından önerlen yöntem se, yukarıda belrtlen yeterszlkler ortadan kaldırmayı hedeflemektedr.model dereces Box-Jenkns SARIMA yöntem le belrlenr. Böylelkle kısm yüksek derecel, k değģkenl bulanık zaman sers model oluģturulur. Bu yöntemde bulanık lģklern belrlenmes se yapay snr ağları le gerçekleģtrlr. Bu modeln avantajları Ģöyle sıralanablr; ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 0
15 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Yüksek derecel mevsmsel bulanık zaman sers model ortaya koyar. Model dereces sstematk olarak belrlenr Lteratürde MA term çeren lk bulanık zaman sers yöntemdr. Öngörü performansını arttırır. YÖNTEM Bu bölümde uygulamada kullanılan ve Eğroğlu vd. (009) tarafından önerlen yöntemn temeln oluģturan SARIMA modeller ve yapay snr ağları le brlkte temel bulanık zaman sers tanımları verlecektr. SARIMA Modeller Z t, ortalamalı br zaman sers olsun. Bu durumda model; ( s d s D s B ) ( B )( B) ( B ) ( Zt ) ( B) ( B ) a t () Ģeklndedr. SARIMA(p, d, q)(p,d,q) s le fade edlen, mevsmsel otoregresf bütünleģk hareketl ortalama model (SARIMA) çn lk olarak Box-Jenkns (976) br yöntem önermģtr. SARIMA modeller ve Box-Jenkns yöntem çn ayrıntılı blg, Box-Jenkns (976) dan elde edleblr. Yapay Snr Ağları Yapay snr ağları,byolojk snr ağlarını taklt eden sentetk ağlardır. Yapay snr ağları ve byolojk snr ağları arasında hem mmarler hem de yetenekler yönünden büyük farklılıklar vardır (Zurada,99). Yapay snr ağları matematksel br model oluģturur ve genel br fonksyon yaklaģtırıcı olarak blnr (Zhang,998).Yapay snr ağlarının ĢleyĢn yönlendren 3 bleģen mevcuttur, k bunlar, Mmar yapı, öğrenme algortması ve aktvasyon fonksyonudur. Bulanık Zaman Serler Ġlk olarak Song ve Chssom (993a, 993b) tarafından önerlen bulanık zaman sers yaklaģımı le lgl temel kavramlar Ģöyle verleblr; Tanım. Y( t), t...,0,,,... reel değerl zaman sers olsun. Zaman sersne uygun evrensel küme tanımı ve parçalanması yapıldıktan sonra her br reel gözlemn A j bulanık kümlerne dönüģtürülmes sonucu elde edlen yen zaman sers F (t) ye bulanık zaman sers adı verlr. Tanım.Bulanık zaman sers sers öngörü model, F(t) mevsmsellk çerdğnde, brnc dereceden bulanık zaman F( t m) F( t) () Ģeklndedr. Burada, m peryodu fade eder. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
16 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tanım 3.Bulanık zaman sers F(t) etklenmekte se bulanık mantık lģk;, F(t-), F(t-),,F(t-n) geckmel zaman serlernden F( t n),, F( t ), F( t ) F( t) (3) Ģeklnde fade edlr ve n. dereceden bulanık zaman sers öngörü model olarak adlandırılır. EĞRĠOĞLU vd. (009) Tarafından Önerlen YaklaĢım Eğroğlu vd (009) da önerdğ model yapısı le lgl olarak aģağıdak tanım verleblr. Tanım 4.Ġk bulanık zaman sers F(t) ve G(t), olsun. Eğer F( t m ),..., F( t mk ), F( t mk ), G( t n ),..., G( t nl ), G( t nl ) serlernden etklenyor se, bulanık mantık lģk; F(t), bulanık zaman sers geckmel bulanık zaman F( t m ),..., F( t mk ), F( t mk ), G( t n ),..., G( t nl ), G( t nl ) F( t) (4) le fade edlr ve grdler SARIMA model tarafından belrlenen, (k,l) ıncı dereceden kısm k değģkenl bulanık zaman sers öngörü model olarak adlandırılır. Burada, ve n ) j ( j,,.., l tamsayılar olup m... m k,, n... nl Ģeklndedr. m ) (,,.., k Eğroğlu vd. (009) tarafından önerlen bu melez yaklaģımın algortması Ģu Ģeklde özetleneblr. Adım.Zaman sers çn Box-Jenkns (976) prosedürüne göre uygun SARIMA model belrlenr.sarima modelnden elde edlen artıklar hesaplanır. Adım.Zaman sers ve SARIMA dan elde edlen artıklar çn evrensel kümeler ve alt aralıklar tanımlanır. sırasıyla, elmzdek orjnal vernn en küçük ve en büyük gözlemler D mn ve D max olmak üzere Evrensel küme; D poztf k sayıdır. U max ( a t ) Dmn D, D D, Ģeklnde tanımlanablr. Burada Adım 3.Evrensel küme ve alt aralıklara bağlı olarak bulanık kümeler belrlenr. D ve U ve V evrensel kümeler ve parçalanmalarına dayalı olarak değģkenler zaman sers ve artıklar çn aģağıdak gb tanımlanır. A, A,..., A k ve B, B,..., B k dlsel A a A A k a a / u / u / u a a a / u / u / u... a n... a... a n n / u n / u n / u n B b B B k b b / v / v / v b b b / v / v / v... b n... b... b n n / v n / v n / v n (5) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
17 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Burada a j, u parçalanmalarının üyelk değerlerdr, Ģeklnde tanımlanır. Benzer Ģeklde k, ve j n b j, v Ģeklnde tanımlanır. Adım 4.Zaman serler bulanıklaģtırılır. a j 0,, k, ve parçalanmalarının üyelk değerlerdr, b j j n 0, Bulanık zaman sers F(t), SARIMA dan elde edlen bulanık artıklar sers se G(t) le temsl edlr. Adım 5.SARIMA modelnn grdlerne göre modeln dereces nn değerler belrlenr. Örneğn, modeln dereces k 5 ve l ( k, l) ve m,...,m k ve olsun. O halde model, n,...,nl F( t ), F( t ), F( t ), F( t 3), F( t 4), G( t ), G( t ) F( t) (6), Ģeklndedr. Burada F(t), bulanık X t ve m G(t), m, m3, m4 3, m5 4, n, n, bulanık a t dr. olmaktadır ve Adım 6.Bulanık lģkler belrlenr. Bulanık zaman sersne at G( t n ),..., G( t nl ), G( t nl ) F( t m ),..., F( t mk ), F( t mk ), geckmel değģkenler grd, hedef değer se ve bulanık hatalara at F(t), olarak kullanılarak bulanık lģkler oluģturulur. Bu aģamada, ler beslemel yapay snr ağı, verlen grd ve hedef değerlerne göre eğtlr. Adım 7.Öngörüler elde edlr. Verlen modelde yapay snr ağın eğtlmes sonucunda, ağın grdler,, ve hedef F( t k m ),..., F( t k mk ), F( t k mk ) olduğunda ağın çıktısı olarak elde edlen G( t k n ),..., G( t k nl ), G( t k nl ) Fˆ ( t k) bulanık öngörü olacaktır. Adım 8.DurulaĢtırma Ģlem merkezleģtrme yöntem le uygulanır UYGULAMA Yukarıda adım adım verdğmz yöntem, Ankara l merkezne göre yapılan ölçümlerde Mart 994 le Nsan 006 yılları çn elde edlen havadak kükürtdokst (SO) mktarları zaman sers (ANSO) üzerne uygulanmıģtır. Uygulamada Eğroğlu vd (009) da önerlen yöntemde, gzl tabaka brm sayısı le arasında değģtrlmģtr. Evrensel küme parçalanmasındak aralık uzunlukları se zaman sers çn 5, 0, 5, 0 ve artık zaman sers çn 0.0, 0.5, 0.0, 0.5 olarak alınıp 9 farklı durumda çözümleme yapılmıģtır.çözümlemede öngörü performansı hata F(t) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 3
18 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo.Klask ve bulanık zaman sers yaklaģımları le elde edlen öngörüler. Tarh Test Vers SARIMA WMES Song (999) Egroglu vd. (009) Temmuz 005,93 5,40 4, Ağustos 005 7,35 6, 7, Eylül ,6 7,77 4, Ekm ,8 5, 4, Kasım ,97 4, 4, Aralık ,6 46, 46, Ocak ,3 49,80 45, ġubat ,99 44,4 46, Mart ,85 3,96 46, Nsan 006 4,76 8,39 7, HKOK 9,648 7,06,7409 4,5607 OMYH 0,06 0,0035 0,083 0,003 DA 0,5555 0,6666 0,44444 WMES:Wnters Multcaptve Exponental Smootng kareler ortalamasının karakökü (HKOK) açısından en y sonuç, gzl tabaka brm sayısı 8, aralık uzunluğunun zaman sers çn 0 artık zaman sers çn 0.0 olduğu durumda elde edlmģtr. ANSO zaman sersnn (son 0 gözlem) test kümes çn klask ve bulanık zaman serler yaklaģımlarından elde edlen öngörüler aģağıdak Tablo de özetlenmģtr. En y sonucun Eğroğlu vd. (009) da önerlen bulanık zaman sers yaklaģımı le elde edldğ görülmektedr. TARTIġMA Eğroğlu vd. (009) tarafından önerlen yöntemde,k değģkenl bulanık zaman sers model dereces ve grdler Box-Jenkns yöntem yardımı le belrlenmektedr.böylelkle bazı bulanık zaman sers yaklaģımlarındaknn aksne bu belrleme Ģlem sstematk br Ģeklde yapılmaktadır.ayrıca mevsmsel çerk taģıyan zaman serler çn daha doğru öngörüler verebleceğ söyleneblr. KAYNAKLAR BOX, G. E. P., & JENKĠNS, G. M. (976). Tme seres analyss: Forecastng and control. San Francsco, CA: Holdan-Day. CHEN, S. M. (996), Forecastng enrollments based on fuzzy tme-seres, Fuzzy Sets and Systems, 8, CHEN, S.M., Forecastng Enrollments based on hgh-order fuzzy tme seres, Cybernetcs and Systems An Internatonal Journal 33 (00) -6. EĞRĠOĞLU, E., ALADAĞ, Ç.H., YOLCU, U., BAġARAN, M.A., USLU, V.R. (009), A new hybrd approach based on SARIMA and partal hgh order bvarate fuzzy tme seres forecastng model, Expert Systems wth Applcatons, 36, ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 4
19 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 HUARNG, K. and YU, H. K. (006), The applcaton of neural networks to forecast fuzzy tme seres, Physca A, 363, SONG, Q. (999). Seasonal forecastng n fuzzy tme seres. Fuzzy Sets and Systems,07, SONG, Q. and CHISSOM, B.S. (993a), Fuzzy tme seres and ts models, Fuzzy Sets and Systems, 54, SONG, Q. and CHISSOM, B.S. (993b), Forecastng enrollments wth fuzzy tme seres- Part I, Fuzzy Sets and Systems, 54, -0. ZADEH, L. A. (965). Fuzzy Sets. Inform and Control, 8, ZHANG, G. P., PATUWO, B. E., & HU, Y. M. (998).Forecastng wth artfcal neural networks: The state of the art. Internatonal Journal of Forecastng, 4, ZURADA, J. M. (99). Introducton of artfcal neural systems. St. Paul: West Publshng. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 5
20 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 BURR XII DAĞILIMININ PARAMETRELERĠNĠN ĠLERLEYEN TÜR ĠLK BOZULMA SANSÜRLEMEYE DAYALI GÜVEN ARALIKLARI VE GÜVEN BÖLGELERĠ CoĢkun KUġ Yunus AKDOĞAN** ÖZET Bu çalıģmada, Burr XII dağılımının parametrelernn lerleyen tür lk bozulma sansürlü örnekleme dayalı güven aralıkları ve güven bölgeler elde edlmģtr.sonuçları değerlendrmek üzere br uygulama yapılmıģtır. Anahtar kelmeler: Burr XII dağılımı, güven aralığı, ortak güven bölges, en çok olablrlk tahmn edcs, lerleyen tür lk bozulma sansürleme. CONFIDENCE INTERVAL AND CONFIDENCE REGION FOR THE PARAMETERS OF BURR XII DISTRIBUTION BASED ON PROGRESSIVE FIRST FAILURE CENSORED SAMPLE ABSTRACT In ths study, confdence nterval and confdence regon for the parameters of Burr XII dstrbuton based on progressve frst falure censored sample are obtaned. Illustratve example s also gven. Keywords: Burr XII dstrbuton, confdence nterval, confdence regon, maxmum lkelhood estmator, progressve frst falure censorng GĠRĠġ Ġlk kez Burr (94) tarafından önerlen ve le gösterlen k parametrel Burr XII dağılımı, stokastk olayları modellemede çok kullanıģlı olması bakımından son 0 yıl çersnde özel br lg görmüģtür.zmmer ve ark.(998) Burr XII dağılımının güvenlrlk analznde kullanılması hakkında genģ blg vermģ ve stokastk olayları modellemede çok kullanıģlı olduğuna dkkat çekmģlerdr.burr XII dağılımının uygulama alanları le lgl yayımlanmıģ bazı makaleler; klnk denemeler Wngo (983), aktüerya blm Klugman (986) ve elektronk bleģenler Zmmer ve ark.(998) olarak sıralanablr. BurrXII, dağılımına sahp br dağılım fonksyonu X BurrXII, rasgele değģkennn, sırasıyla, olasılık yoğunluk ve * Doç.Dr., Selçuk Ünverstes, Fen Fakültes, Ġstatstk Bölümü, 403 Konya, coskun@selcuk.edu.tr ** ArĢ.Gör., Selçuk Ünverstes, Fen Fakültes, Ġstatstk Bölümü,, 403 Konya, yakdogan@selcuk.edu.tr ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 6
21 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 f Ģeklndedr. ;, x c k x x, x 0, 0, 0 x; c, k x F () () Bu çalıģmada, lerleyen tür lk bozulma sansürlü örneklemler ve bu örneklemlere dayalı Burr XII dağılımının parametrelernn en çok olablrlk tahmn edcler, parametrelern güven aralıkları ve güven bölgeler elde edld. Son olarak elde edlen sonuçlarla lgl uygulama yapıldı. ĠLERLEYEN TÜR ĠLK BOZULMA SANSÜRLÜ ÖRNEKLEM Ġlerleyen tür lk bozulma sansürlenmģ model (Progressve frst falure censorng model) Ģu Ģeklde tanımlanmaktadır: k özdeģ bleģenl brbrnden bağımsız n grubun yaģam testne tab tutulduğu düģünülsün. Testte.,,, m, m n ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 7 bozulma meydana geldğnde, R X : m : n : k bozulmanın meydana geldğ gruptak bleģenler le bozulma meydana gelmeyen sayıda grup testten rasgele çeklsn. Bu Ģeklde elde edlen hacml örnekleme lerleyen tür lk bozulma sansürlü örneklem denr.burada m n m R m bçmndedr ve R, R,, R R sansür R R R Ģeması olarak adlandırılır. X: m: n: k X : m: n: k X m: m: n: k, olasılık yoğunluk fonksyonu(oyf) ve dağılım fonksyonu (df) F olan dağılımdan alınan lerleyen tür lk bozulma sansürlü örneklem olmak üzere nn ortak oyf unu burada X X X R R R : m: n: k : m: n: k m: m: n: k f x x x R R R,,..., X: m: n: k, X: m: n: k,, Xm: m: n: k m m m kr ck f x F x, x x xm c n n R m Ģeklndedr. (3) de R 0,,0 n R R Rm R m, (3) alnırsa lk bozulma sansürlü örneklemn oyf s fonksyonu, alınırsa, lerleyen tür sansürlü sıra statstklernn oyf s, ve R 0,,n m alınırsa sağdan sansürlü sıra statstklernn oyf s elde edlr (Wu ve KuĢ 009). X, X,, X R R R : m: n: k : m: n: k m: m: n: k k k= f, k= aynı zamanda F x dağılımından alınmıģ lerleyen tür sağdan sansürlü örneklem olarak düģünülebleceğnden, lerleyen tür sağdan sansürleme çn elde edlen sonuçlar kolaylıkla lerleyen tür lk bozulma sansürleme çn genģletleblr. Ġlerleyen lk bozulma sansürlü örnekleme, yaģam zamanı analzlernde ver elde etmede öneml br yöntemdr. ÇalıĢan parça dğer br test çn sstemden çeklp, deneyn malyet ve deney süres azaltılablr. Ayrıntılı blg çn Balakrshnan ve Aggarwala ya (000) bakılablr.
22 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 X X X R R R : m: n: k : m: n: k m: m: n: k EN ÇOK OLABĠLĠRLĠK TAHMĠN EDĠCĠSĠ, BurrXII, dağılımına sahp br ktleden alınmıģ lerleyen tür lk bozulma sansürlü örneklem olmak üzere (),() ve (3) kullanılarak sırasıyla olablrlk ve logolablrlk fonksyonu aģağıdak gb elde edlr ( Al Mousa ve Jaheen 00): burada m m m x L, ck exp k R log x x m x m x, log c mlog k log kt x x R : m: n: k, T m R log x parametreler çn olablrlk denklemler m / kt, Ģeklndedr ve c, (3) de tanımlandığı gbdr. ve (4) m m m x x k R x log x log 0 (5) Ģeklndedr. (5) denklemnde parametres yerne (4) denklemndek eģt yazılırsa, parametresne göre lneer olmayan br denklem elde edlr. Elde edlen lneer olmayan denklem Newton-Raphson yöntemyle çözüleblr.daha sonra parametresnn en çok olablrlk tahmn (4) denklemnde yerne konularak parametresnn en çok olablrlk tahmn hesaplanablr. PARAMETRELERĠN ARALIK TAHMĠNĠ Bu bölümde parametres çn güven aralığı, ve parametres çn de güven bölges elde edlmģtr., dağılımına sahp br ktleden alınmıģ lerleyen tür lk bozulma sansürlü örneklem olsun.aģağıdak dönüģüm tanımlansın. X X X R R R : m: n: k : m: n: k m: m: n: k R R : m: n: k : m: n: k BurrXII, Y k log X,,,, m R R R Görüleblr k Y: m: n: k Y: m: n: k Ym : m: n: k, tür sansürlü örneklem olur. AĢağıdak dönüģümü ele alınsın: Üstel dağılımına sahp br ktleden alınmıģ lerleyen ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 8
23 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ny R : m: n: k R R n R Y m n k Y m n k : : : : : : R R n R R R m Y : : : Y : : : m m m m n k m m n k (6) Thomas ve Wlson (97), (6) da tanımlanan genelleģtrlmģ aralıkların (generalzed spacng) bağımsız ve dağılımına sahp olduğunu göstermģtr. Buradan m Üstel dağılımına, R ny: m: n: k m m R R R Y : m: n: k Y: m: n: k dağılımına sahptr. Aynı zamanda açıktır k ve bağımsız rasgele değģkenlerdr. ve rasgele değģkenler m R Y Y m n m Y R R : m: n: k : m: n: k : : : R Y Ģeklnde tanımlansın. m R m n k R : m: n: k AĢağıdak k lemma, yardımcı olacaktır. ve parametrelernn güven aralığı ve güven bölges oluģturmada Lemma., F m, dağılımına, bağımsızdır.(johnson ve ark. 994). dağılımına sahptr. Aynı zamanda, m ve Lemma.Varsayalım k 0 a a v e m R 0,,,, m olsun ve m R log a log a fonksyonu tanımlansın. 0 olmak üzere 007)., nın cdd artan fonksyonudur (Wu ve ark. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 9
24 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 F, yüzdelğ ve, sağ-kuyruk(rght-tal) olasılıklı ve ve serbestlk derecel F dağılımının R R R R X X: m: n: k, X : m: n: k,, X m: m: n: k olsun. Teorem. BurrXII, dağılımına sahp br ktleden alınmıģ R sansür Ģemalı lerleyen tür lk bozulma sansürlü örneklem olsun. O zaman verlen çn parametresnn lık güven aralığı aģağıdak gbdr: burada X X X X R R R : m: n: k : m: n: k m: m: n: k R, F R X,t 00 %, X, F R m, m,,,, 0 m R R R log x: m: n: k nlog x: m: n: k nm log R x: m: n: k t lneer olmayan denklemde nın çözümüdür. Ġspat. Lemma den blyoruz k pvot m R Y ny n m Y R R : m: n: k : m: n: k R : m: n: k m R log R X : m: n: k nlog R X : m: n: k n m log X R : m: n: k F m, dağılımına sahptr. 0 çn F m R log R X : m: n: k nlog R X : m: n: k F m, R m, n m log X : m: n: k olayı X R, F R X, F m, m, olayına denktr. Bu da spatı tamamlar. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 0
25 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00, sağ-kuyruk(rght-tal) olasılıklı ve serbestlk derecel K-kare dağılımının yüzdelğ olsun. ve parametrelernn 00 % lık güven bölges aģağıdak teoremle verlmģtr. R R R Teorem. X: m: n: k X : m: n: k X m: m: n: k BurrXII, dağılımına sahp br ktleden alınmıģ R sansür Ģemalı lerleyen tür lk bozulma sansürlü örneklem olsun. O zaman verlen 0 çn ve parametrelernn lık ortak güven bölges aģağıdak eģtszlklerden belrlenr. 00 %, R R X, F X, F m, m, m m m m R R : m: n: k : m: n: k k R log X k R log X Burada R X,t Ġspat. Lemma den pvot m, Teorem. dek gb tanımlıdır. m m R R Y : m: n: k k R log R X : m: n: k dağılımına sahptr ve den bağımsızdır. P F P Ģeklndedr. Buradan F m, m, m m 0 çn ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
26 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 m R log R X : m: n: k nlog R X: m: n: k P F F m,, n m : m: n: k R m log X m, k R log R X : : : m n k m m Bu se aģağıdak fadeye denktr. R R X, F X, F m, m, m m m m k R log R X : m: n: k k R log R X : m: n: k Bu da spatı tamamlar. UYGULAMA Teorem ve Teorem dek sonuçları örneklendrmek çn R 0,,,0,,0,,0,,0,,0,0,0,,0,,0,0,0 BurrXII, dağılımından k 3 çn sansür Ģemalı lerleyen tür lk bozulma sansürlü örneklem Balakrshnan ve Sandhu nun (995) algortması kullanılarak üretld. Üretlen örneklem aģağıdak tablodadır. Tablo. Üretlen lerleyen tür tp-ii sağdan sansürlü örneklem (4) ve (5) denklemler çözülerek ve parametrelernn en çok olablrlk tahmnler sırasıyla ˆ ve ˆ 0.64 olarak bulunmuģtur. parametresnn lk güven aralığını elde etmek çn gerekl olan yüzdelkler Mntab 3. paket programı kullanılarak aģağıdak gb elde edlmģtr. 95% F , , F , ve F , ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ
27 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Teorem kullanılarak bulunur. parametresnn 95 % lk güven aralığı.33,4.43 Ģeklnde ve parametrelernn 95 % lk ortak güven bölgesn elde etmek çn gerekl olan yüzdelkler Mntab 3. paket programı kullanılarak aģağıdak gb elde edlmģtr. F , 8, F , ve F , ve Teorem kullanılarak ve parametrelernn 95% lk ortak güven bölges aģağıdak gb elde edlr R log R X :0:30:3 3 R log R X :0:30:3 KAYNAKLAR BALAKRISHNAN, N., AGGARWALA, R., (000). Progressve Censorng:Theory, Methods and Applcatons. Brkhauser, Boston BALAKRISHNAN, N., SANDHU, R.A., (995). A smple smulaton algorthm for generatng progressvely Type-II censored sample, Amercan Statstcan 49 () BURR, I. W., 94. Cumulatve frequency functon, Annals Math. Stat., 3, 5-3. JOHNSON, N.L., KOTZ, S., BALAKRISHNAN, N., (994).Contnuous Unvarate Dstrbutons, Volume, nd edton.wley, New York. KLUGMAN, S.A., (986). Loss dstrbutons, Proceedngs of Symposa n Appled Mathematcs: Actuaral Mathematcs, vol. 35, pp KUġ, C., WU, S.-J. (008). Statstcal nference based on progressve frst falure-censored samples from Gompertz dstrbuton, 008 Internatonal Workshop on Appled Probablty, Unversté de Technologe de Compègne, Compègne, France, July 7-0, 008. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 3
28 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 THOMAS, D.R., WILSON W.M., (97). Lnear order statstcs estmaton for the two parameter Webull and Extreme Value dstrbutons from Type-II progressvely censored samples. Technometrcs 4, WANG. F. K., KEATS, J. B., ZIMMER, W. J., (996). Maxmum lkelhood estmaton of the burr XII parameters wth censored and uncensored data.mcroelectron.relab., 36, WINGO, D. R., (983). Maxmum lkelhood methods for fttng the Burr Type XII dstrbuton to lfe test data. Bometrcal J., 5, WU,S.-J.,CHEN,Y.-J., Chang,C.-T. (007). Statstcal nference based on progressvely censored samples wth random removals from the Burr type XII dstrbuton. Journal of Statstcal Computaton and Smulaton,77(),9-7. WU, S.-J., KUġ, C. (009).On the Estmaton Based on Progressve Frst Falure-Censored Sample, Computatonal Statstcs and Data Analyss, 53 (0), ZIMMER, W.J., KEATS, J.B., WANG, F.K. (998). The Burr XII dstrbuton n relablty analyss. J. Qual. Tech. 30, ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 4
29 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 DOĞRUSAL OLMAYAN REGRESYONDA BAZI PARAMETRE ARALIK TAHMĠNLEME YÖNTEMLERĠNĠN KIYASLANMASI Atıf Evren* ÖZET Doğrusal olmayan regresyon modellernde parametrelern aralık tahmnler asmptotk normallk varsayımına dayandırılmaktadır. Ancak bu varsayım çoğu durumda gerçekç olmamaktadır.bu durumda örneklem hacmnn dkkate değer br bçmde büyük olması gerekmektedr. Bununla brlkte doğrusal olmayan vernn elde edlmes yorucu, zaman alıcı ve malyetldr. Çünkü bu tür verler genellkle laboratuvar ortamında elde edlmektedrler. Bu yüzden bootstrap, jackknfe gb yöntemlerle aralık tahmnlerne gdlmektedr. Bu yöntemlere ek olarak ÇebĢev eģtszlğ ya da benzer eģtszlkler le de aralık tahmnlerne gdleblr. Anahtar Kelmeler: Doğrusal olmayan regresyon, parametrk olmayan aralık tahmnler, ÇebĢev eģtszlğ,bootstrap yöntem, Jackknfe yöntem A COMPARISON OF SOME INTERVAL ESTIMATION PROCEDURES IN NONLINEAR REGRESSION ABSTRACT Confdence nterval estmates for the parameters of nonlnear regresson models are based on the assumpton of asymptotc normalty. However ths assumptons may not be not realstc all the tme because asymptotc normalty requres larger sample szes consderably. Large sample szes mean burdensome experences for the scentsts. Because most nonlnear data are generated through expensve and tme consumng experments carred out generally n laboratory condtons. For ths reason other nterval estmaton procedures lke bootstrappng and jackknfe are used qute often. Besdes some probablty nequaltes ncludng Chebyshev's Inequalty can also be used. Keywords: Nonlnear regresson, nterval estmaton, Chebyshev's Inequalty, Bootstrap method, Jackknfe method *Öğretm Üyes, Yard. Doç. Dr., Yıldız Teknk Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, DavutpaĢa Esenler, 340, Ġstanbul, aevren@yldz.edu.tr ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 5
30 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 GĠRĠġ Doğrusal olmayan regresyon modellernde parametrelern aralık tahmnler çn benmsenen asmptotk normallk yaklaģımı çoğu zaman örnek büyüklüklernn yetersz olması nedenyle gerçekç olmamaktadır. Bu çalıģmada doğrusal olmayan modeller çn Bootstrap yöntem, Jackknfe yöntem gb parametrk olmayan aralık bulma yöntemlern benmsemenn yanısıra ÇebĢev türü eģtszlklerden de yararlanılarak parametre aralıkların uzunluklarının düģürülmesne çalıģılacaktır. DOĞRUSAL OLMAYAN REGRESYON MODELLERĠ Doğrusal olmayan br regresyon model Y f ( X, ) Ģeklndedr. Burada. açıklayıcı ya da bağımsız değģkenn gözlem değerler vektörü X xq... X X X q p tane parametre vektörü 0... p ve parametrelern lk tahmn değerler vektörü g g g px... g p olsun. Yne (0) k k 0 (0) g k () () (3) (4) (5) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 6
31 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 (0) Dk Y Y (0) f f ( X, ) (0) Y p k0 f (0) k D (0) k k (0) g (0) denecek olursa Ģu doğrusallaģtırılmıģ regresyon model elde edlr. (6) (7) (8) Y Y (0) p (0) Dk k 0 (0) D (0) (0) k (0) Bu kalıp doğrusal modeller çn kullanılan kalıbın aynısıdır. D türev matrs doğrusal hallerde X matrsnn oynadığı rolü oynamaktadır. Dolayısıyla parametre tahmnler doğrusal hallerle analoj kurularak aģağıdak gb gerçekleģtrlmektedr (Neter vd.,985): b D D ( 0) ( 0) (0) (0) D Y (0) Doğrusal olmayan modellerde parametre tahmn teratf yöntemlerle gerçekleģtrlmektedr. Her terasyon sonucunda parametre tahmnler vektörü =,, çn g g b ( ) ( ) ( ) k k k le revze edlmekte ve ardıģık parametre tahmnler arasındak farklar hmal edleblr br düzeye gelnce terasyonlar sona erdrlmektedr. Hata termler ortalaması sıfıra, varyansı ye eģt bağımsız normal değģkenler olarak kabul edldğnde g nn asmptotk örnekleme dağılımı da yaklaģık olarak normal dağılıģtır. E(g) s g MSEDD ve (4) le bulunan asmptotk varyans-kovaryans matrs, aralık tahmnler ve hpotez testler çn kullanılmaktadır (Huet vd., 996). Doğrusal olmayan regresyonda doğrusal regresyondan farklı olarak dkkate alınması gereken bazı noktalar bulunmaktadır. KarĢılaĢılan bazı sorunlar ve pratk çözüm önerler çn Motulsky ve Chrstopoulos (004)'e bakılablr. Bu zorlukların br kısmı Ģu Ģeklde sıralanablr: (9) (0) () () (3) (4) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 7
32 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ) Doğrusal olmayan modeller çn en küçük kareler (ya da en çok olablrlk) fonksyonu genellkle brden fazla mnmum (en çok olablrlk çn maksmum) noktasına sahptr. ) Doğrusal modellerde kullanılan R-kare gb uyum ylğ le lgl statstkler doğrusal olmayan modeller çn yanıltıcı olablr. Sözgelm doğrusal olan br model çn yeterl sayılan br R-kare değer, doğrusal olmayan modeller çn yetersz kalmaktadır )Doğrusal olmayan regresyonda parametrelern baģlangıç tahmnlern modele dıģsal olarak tanıtmak gerekmektedr. Farklı baģlangıç değerler, farklı (nha) parametre tahmn değerler vereblr. Bu durumu nha parametre tahmnlernn baģlangıç değerlerne olan aģırı bağımlılığı Ģeklnde de fade etmek mümkündür. v) Doğrusal olmayan regresyon modellernde parametre tahmnleycler gözlem değerlernn doğrusal br fonksyonu değldr. Dolayısıyla bağımlı değģkenn ktle dağılımının normal olması, otomatk olarak parametre tahmnleyclernn de normal dağılıma uyacağının garants değldr. Öte yandan asmptotk normallk örnek büyüklüğünün fazla olmasını gerektrmektedr (Seber ve Wld, 989; Bates ve Watts,988). Bu gb durumlarda Bootstrap, Jackknfe gb nonparametrk sayılablecek yöntemlern benmsenmes daha rasyonel olacaktır (Davdson,R., Macknnon, J.G.,993). Yne parametrk olmayan aralık tahmnlernn gerçekleģtrlmesnde ÇebĢev ve benzer eģtszlkler de yararlı olablecektr. X br rastlantı değģken olmak üzere üzere k k P X ÇebĢev ( Bénayme) EĢtszlğ E(X ), Var ( X ) (5)BaĢka Bazı Varyantlar olsun. k br poztf sabt olmak Bazı durumlarda ÇebĢev eģtszlğ le elde edlen aralık çok genģ ve dolayısıyla her zaman Ģlevsel olmamaktadır. Yne de bazen olasılık dağılımına yönelk bazı varsayımlarda bulunularak aralığın uzunluğu daraltılablr.örneğn, X rastlantı değģken tek modlu ve sürekl olsun. E(X ) vevar (X ) se P( X 3 ) 77 / (DasGupta, 008).(6) X X,,..., varyansları da Yne k k X m ÇebĢev EĢtszlğ nn Çok DeğĢkenl Bçm ( X X X değģkenler, ortalamaları sırası le E E( ),..., E( ) ; ve Var k X X ( ), Var ( )..., Var ( X ; ;...; poztf sabtler ve m A, A,..., Am m ) ), olan rastlantı değģkenler olsunlar. olayları da örnek uzay S çersnde m ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 8
33 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 A j X j X j X k E( ) Var ( j j X j ) j=,,,m Ģeklnde tanımlansınlar. Bu durumda Boole EĢtszlğ nden yararlanarak ÇebĢev EĢtszlğnn çok değģkenl versyonu P m m Aj k j j j (Kotz vd. 000). (7) X X,,..., X varyans-kovaryans matrsler de k BaĢka Versyonlar rastlantı değģkenler, ortalamaları sırası le j,,..., olan k tane rastlantı değģken olsun. j sözkonusu varyans-kovaryans matrsnn ters olsun. br sabt olmak üzere k j P X X j j, j k Bootstrap ve Jackknfe k olan ve de olur (Wlks, 96). (8) Bootstrap yöntem aralık tahmnlernde de kullanılan parametrk olmayan br teknktr. Doğrusal olan ya da olmayan regresyon modellernde normallk varsayımının gerçekç olmadığı durumlarda kullanılmaktadır. Brden fazla bootstrap yöntem olmakla brlkte en çok kullanılan bootstrap yöntemn özetlemek gerekrse, regresyon modelnden elde edlen artıklardan adel örnekleme yöntemne göre belrl sayıda artık elde edlmekte ve bu değerler bağımlı değģkene eklenmektedr. Daha sonra bağımlı değģkenn elde edlen yen değerlernden yararlanılarak aynı matematksel kalıba sahp regresyon model oluģturulmakta ve yen parametre tahmn değerler elde edlmektedr. Bu Ģlem çok sayıda tekrar edldğnde, her denemede elde edlen parametre tahmnlernn br sıklık dağılımı oluģmakta ve bu sıklık dağılımlarından hareketle, parametrelern aralık tahmnler yapılmaktadır (Money ve Duval, 993). Jackknfe yöntem se daha çok regresyon denklemnn belrlenmesnde etkl gözlem noktalarının ortaya çıkarılmasında kullanılmaktadır. Bu yönteme göre gözlem setnden her br denemede belrl sayıda gözlem noktası çıkarılmakta ve ger kalanlarla regresyon denklemnn katsayıları tahmn edlmeye çalıģılmaktadır. Bu Ģlem büyük sayılarda ynelendğnde, parametre tahmn değerlernn br sıklık dağılımı oluģmakta ve bu sıklık dağılımından aralık tahmnlernn oluģturulmasında yararlanılmaktadır (Money ve Duval, 993). UYGULAMA Uygulama aģamasında adresnden Rat43 adlı dosyadan alınan ve parametre tahmn zorluk derecesnn yüksek olduğu aģağıdak ver kümes kullanılmıģtır. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 9
34 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo : (X,Y) Değerler X Y X Y Buradak bağımlı değģken Y, kuru soğan tanesnn ağırlığı, bağımsız ya da açıklayıcı değģken X de soğanın büyümes çn geçen süredr. Aynı dosyada ver çn denenen modeln Y=A/[{+exp(B-CX)}^(/D)] olduğu belrtlmektedr. Burada A,B,C ve D modeln parametreler olup, baģlangıç değerler olarak sırasıyla 700, 5, 0.75 ve.3 verlmģtr. Ayrıca yukarıdak denklemn ncelenmesnden X büyük değerler aldıkça Y'nn A parametresne yakınsayacağı öngörüleblr. Bu noktadan yola çıkılarak en büyük X değerne karģılık gelen Y değernn (77), A'nın baģlangıç tahmn değer olarak verlmes dğer B,C ve D parametrelernn baģlangıç değerlernn br olarak alınması ve parametre tahmnlernn gerçekleģtrldğ aralığın -E 9 le E 9 olarak seçlmes halnde de web stesndek sonuçlara oldukça benzer sonuçlar NCSS (Number Cruncher Statstcal Systems) programı yardımı le elde edlmģtr. Bu sonuçları kısaca Ģu Ģeklde özetlemek olasıdır: Tablo :Asmptotk normallk varsayımı altında parametrelern nokta ve aralık tahmnler Yöntem Asmptotk Normallk Parametre Tahmn Standart Hata. %95'lk Alt Sınır % 95'lk Üst Sınır A B C D NCSS çıktısı kalıntıların normal dağıldığını belrtse de örnek büyüklüğünün 5 olması nedenyle bu sonuç htyatla karģılanmalıdır.ġknc olarak Mcrosoft Excel Ver Analz modülü ve NCSS yardımıyla bootstrap yöntem denenmģtr ( N= 00 ).Sonuçlar aģağıdadır: ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 30
35 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo 3:Bootstrap yöntem le parametrelern nokta ve aralık tahmnler Yöntem Bootstap Parametre Tahmn Standart Sapma. %95'lk Alt Sınır % 95'lk Üst Sınır A B C D Üçüncü olarak ver kümesnden her br denemede br gözlem değer atılarak Jackknfe yöntem le parametre tahmnler yenden gerçekleģtrlmģtr. Sonuçlar aģağıdak gbdr: Tablo 4: Jackknfe yöntem le parametrelern nokta ve aralık tahmnler Yöntem Jackknfe Parametre Tahmn Standart Sapma. %95'lk Alt Sınır % 95'lk Üst Sınır A B C D Daha sonra ÇebĢev yöntem le %95'lk aralık tahmnler gerçekleģtrlmģtr(k=4.47). Tablo 5: ÇebĢev eģtszlğ le parametrelern %95 güvenle aralık tahmnler Yöntem ÇebĢev Parametre Tahmn Standart Hata %95'lk Alt Sınır % 95'lk Üst Sınır A B C D Son olarak ÇebĢev EĢtszlğ'nn her dört parametre çn elde edlen aralık tahmnlernn sınır noktaları, lgl parametrelern lk tahmn değer olarak NCSS'e tanıtılmıģ ve bu noktalarda model yenden denenerek regresyon denklemnn katsayılarının bu yen değģklkler karģısında stkrarlı olup olmadığına bakılmıģtır. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 3
36 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo 6: ÇebĢev eģtszlğ le oluģturulan aralıkların kısıt olarak kullanılması le elde edlen parametre tahmnler (ve bu tahmnlern stkrarlı olup olmadığının sınanması) Katsayılar Denenen Değerler ÇebĢev le elde edlen alt sınır ÇebĢev le elde edlen alt sınır Sonuçlar A Benzer noktalara yakınsama B -4 5 Daha y çözüm elde edlemed. C Daha y çözüm elde edlemed. D Daha y çözüm elde edlemed. Yukarıdak tablodan hareketle B,C ve D parametrelernn baģlangıç tahmn değerler le fazla oynanmaması gerektğ düģünülmüģ ve sözkonusu parametrelern NCSS le elde edlen tahmn değerler bu kez de modele brer sabt olarak sokulmuģ ve aģağıdak çıktı elde edlmģtr. Buna göre Y=A/[{+exp( X)}^(/.8)] model denenerek A parametres çn daha düģük standart hatalı br model elde edlmģtr. Özet statstkler Ģöyledr: Tablo 8: Bazı parametrelere kısıtlamalar getrerek (ya da tahmn değerler vererek) parametre uzayının boyutunun azaltılarak daha küçük standart hatalı tahmn edclern aranması Parametre Parametre Tahmn Asmptotk Standart Hata %95'lk Alt Sınır %95'lk Üst Sınır A Bu durumda oluģturulan model Y= ( )/((+EXP( *(X)))^(/.8)) Ģeklndedr ve lgl R-Kare değer de 0.99 olarak bulunmuģtur. SONUÇLAR. Doğrusal olmayan regresyonda parametreler çn aralık tahmnler asmptotk normallğe dayalıdır. Bu bakımdan aralık tahmnne gdlmesnde asmptotk normallk varsayımı yerne Bootstrap, Jackknfe,ÇebĢev eģtszlğ ve benzer yaklaģımları benmsemek özellkle küçük örneklem hacm çn daha doğru olacaktır.. Bootstrap, Jackknfe gb yöntemler blgsayarların yoğun olarak kullanıldığı ve zaman alıcı yöntemlerdr. ÇebĢev ve benzer eģtszlkler kullanmak aralık tahmnlerne gderken kolaylık sağlamaktadır. Yne de bütün bu yöntemler brbrlern destekler br Ģeklde kullanılmalıdır. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 3
37 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI ÇebĢev türü eģtszlklere dayalı aralık tahmnlernn genģ çıkmasında k değerlernn büyüklüğünün yanısıra standart hataların da büyüklüğü br etken olablr. Ancak yne de bu gb yöntemler hç Ģüphesz, Bootstrap, Jackknfe gb yöntemlere göre daha genģ aralık tahmnler vermektedr. 4. Yne de ÇebĢev ve benzer eģtszlklerden yararlanılarak elde edlen aralıkların uç noktalarında modeln stkrarlı olup olmadığı (aynı parametre tahmn değerlerne yakınsayıp yakınsamadığı) test edleblr. Eğer bazı parametre değerler bu tür br stkrarsızlığa neden oluyorsa, bu parametrelern tahmn değerler modele brer sabt olarak dahl edlerek (alacakları değerlere kısıtlar konularak), daha düģük standart hataya sahp baģka (ve daha yalın) modeller elde edleblr. 5. Bunlara ek olarak ÇebĢev eģtszlğnde, dağılıma lģkn ek varsayımlarda bulunarak aralıkları daraltmak mümkündür. 6. Ayrıca lteratürde ÇebĢev eģtszlğnn çok değģkenl bazı versyonları da mevcuttur. Parametre tahmn edclernn aralarındak korelasyonlar dkkate alınarak bazı aralıkların uzunluklarını daraltmak da sözkonusu olablr. 7. Son olarak e Jackknfe yöntemnn özellkle artık analznde (etkl değerlern bulunmasında), Bootstrap yöntemnn de parametre tahmnclernn asmptotk varyanskovaryans matrsnn elde edlmesnde Ģlevsel olduğu, ÇebĢev vb. eģtszlklern se her zaman Ģlevsel olmadığı ama bununla brlkte bulunan parametre tahmnlernn ne kadar stkrarlı olduğunun ncelenmesnde ve almaģık yöntemlern denenmesnde yararlı olableceğ de vurgulanmalıdır. KAYNAKLAR BATES D.M., WATTS D.G.(988), Nonlnear Regresson Analyss and Its Applcatons, New York, John Wley&Sons. DASGUPTA, A.(008), Asymptotc Theory of Statstcs and Probablty, Sprnger Texts n Statstcs, New York, Sprnger DAVIDSON, R., MACKINNON, J.G.(993), Estmaton and Inference n Econometrcs, New York, Oxford Unversty Press. HUET,S., BOUVIER,A., GRUET,M., JOLIVET,E., (996), Statstcal Tools for Nonlnear Regresson: A Practcal Gude wth S-Plus Examples, Sprnger-Verlag, New York, Sprnger Seres n Statstcs. KOTZ,S., BALAKRISHNAN, N., JOHNSON,N.L.(000), Contnuous Multvarate Dstrbutons, Volume : Models and Applcatons, Second Edton, USA, Wley seres n Probablty and Statstcs. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 33
38 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 MOONEY,Z.M.,DUVAL,R.D.(993),Bootstrappng A Nonparametrc Approach to Statstcal Inference, Seres: Quanttatve Applcatons n the Socal Scences,a Sage Unversty Paper, No 95. MOTULSKY, H., CHRISTOPOULOS, A. (004), Fttng Models to Bologcal Data Usng Lnear and Nonlnear Regresson: A Practcal Gude to Curve Fttng, USA, Oxford Unversty Press NETER J., WASSERMAN W., KUTNER M. H. (985), Appled Lnear Statstcal Models, second edton,illnos, Rchard D. Irwn. SEBER G.A.F., WILD C.J.(989), Nonlnear Regresson, USA, John Wley&Sons. WILKS,S.S.(96), Mathematcal Statstcs, Japan,John Wley&Sons Inc. (Doğrusal olmayan regresyon modeller le lgl verler çeren br ste. Steye erģm tarh Mayıs-Hazran 00) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 34
39 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ESENBOĞA, ATATÜRK VE LONDON CITY HAVAALANLARINDAKĠ MEVSĠMSEL HAREKETLĠLĠĞĠN GÖSTERMELĠK DEĞĠġKEN YÖNTEMĠYLE TESPĠT EDĠLMESĠ Denz KONAK* Vlda PURUTÇUOĞLU** ÖZET Göstermelk değģken yöntem özellkle ekonomk verlern analznde kullanılan oldukça yaygın br yöntemdr.bu yöntem, yapay değģkenler ekleyerek, gruplandırılmıģ ntel verlern regresyon modelleryle analzlerne olanak sağlar.bz bu çalıģmada göstermelk değģken yöntemn Atatürk, Esenboğa ve London Cty Havaalanları çn yılları arasındak aylık verler kullanarak olası mevsmsel etkler bulmada ve anlamlı farkların gözlendğ aylar çn sebeplerne yönelk yorumları yapmada kullandık.analzlerde Atatürk Havaalanında anlamlı aylık farkların gözlenmedğ, buna karģın, Esenboğa ve London Cty Havaalanlarında, sırasıyla, eylül ve ekm aylarında anlamlı farkın olduğunu bulduk.bu sonuçların özellkle seçlen havaalanlarındak hava trafğn planlamada faydalı olableceğn düģünmekteyz. Anahtar kelmeler: Mevsmsel etkler, Göstermelk değģken yöntem, Havaalanı hareketllğ DETECTION OF SEASONAL EFFECTS IN ESENBOĞA, ATATÜRK, AND LONDON CITY AIRPORTS BY THE DUMMY VARIABLE METHOD ABSTRACT The dummy varable method s one of the common technques appled, n partcular, n the analyss of the economcal data. Ths method enables the grouped qualtatve data to be analyzed n regresson models by addng artfcal varables. In ths study we have mplemented the dummy varable technque to detect the possble seasonal effects n monthly data of the Atatürk, Esenboğa, and London Cty Arports, and to dscuss the possble reasons of such effects for the sgnfcantly dfferent months. From the analyss we have found that there s not any statstcally sgnfcant month effect for the Atatürk Arport, whereas, there exsts statstcally sgnfcant monthly effects n september and october for the Esenboğa and London Cty Arports, respectvely. We consder that our fndngs can be useful for the organzaton of the ar control n the selected arports. Keywords: Seasonal effects, The dummy varable method, Arcraft movements * Yüksek Lsans Öğrenc, Blkent Ünverstes, Ġktsad ve Ġdar Blmler Fakültes, Ekonom Bölümü, 06800, Ankara, denzkonak@hotmal.com ** Yardımcı Doçent Doktor, Orta Doğu Teknk Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, 0653 Ankara, vpurutcu@metu.edu.tr(haberleģme Adres) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 35
40 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 GĠRĠġ Göstermelk değģken yöntem ntel değģkenlern regresyon modelne eklenmes çn kullanılan ve çok blnen br yöntemdr (Gujarat, 003).Sık kullanımı, ekonomk verlerde görülmektedr.örneğn Gültekn ve Gültekn (983) ve Chen ve ark.(00) Menkul Kıymetler Borsası çn mevsmsel etkler, Asterou ve Kavetsos (006) gelģmekte olan ekonomler çn ocak ayı etks konusunu ncelemģlerdr.koçak (008), Ladray (006) ve Atabek ve ark.(009) ulusal hesaplar serler gb farklı ekonomk verler çn mevsmsel etkler ve takvm etklern ele almıģlardır.bahsedlen alanların dıģında, bu yöntem aslında anlamlı mevsmsel etklern görülebleceğ br çok farklı ver kümesnde de kullanılablr (Green ve Doll, 974). Bz bu çalıģmada göstermelk değģken yöntemn, yılları arasındak Esenboğa, Atatürk ve London Cty Uluslararası Havaalanlarındak uçakların hareketllğn gösteren ver setler üzernde olası mevsmsel etkler saptamak ve etklern nedenlern yorumlayablmek çn kullanmaktayız. Bu amaçla öncelkle çalıģmanın. Bölümünde, kullandığımız ver tanıtılmakta ve analzde kullanılan yöntem anlatılmaktadır. 3. Bölümde uygulamada elde ettğmz sonuçlar sunulmakta, son olarak 4. Bölümde elde edlen bulgular özetlenerek sonuçlar yorumlanmaktadır. VERĠ TANITIMI VE YÖNTEM Zaman sers verler çnde yaygın olan bleģenlerden brs mevsmsel etklerdr (Grenger, 964; Thaler, 987).ÇalıĢmamızda bu etklere sahp olduğunu düģündüğümüz Esenboğa, Atatürk ve London Cty Havaalanlarına at yılları arasındak aylık uçak hareketllklern gösteren zaman sers verler regresyon analz yardımıyla modellenmektedr.çalıģmada kullanılan Esenboğa ve Atatürk Havaalanlarına at verkümes London Cty Havaalanına at verler se nternet stesnden elde edlmģtr. Ver analznde, hem verdek anlamlı mevsmsel etknn olup olmadığını sınamada hem de anlamlı bulunan etknn nereden kaynaklandığını bulmada göstermelk değģken yöntem kullanılmıģtır. Genel anlamda bu yöntemde, bağımlı değģken üzernde etks bulunan her br ntel ver grubu çn, regresyon modelne, at olduğu grup çn, at olmadığı dğer gruplar çn 0 değer alan br yapay değģken ekleme mantığı yer almaktadır (Suts, 957; Asterou, 006, 95). Ntekm bu çalıģmada aylık etklern analznde her br ay çn regresyon modelmze brer adet göstermelk değģken eklenmģtr. Mevsmsel etklern analz çn bu yöntemnn dıģında, Chow Test adlı alternatf br yöntem de kullanılablr. Bu yöntemde se kısaca,göstermelk değģken metodunda olduğu gb tek br regresyon model kullanmak yerne, hafta, ay veya 3 ay gb her br mevsmsel süreç çn ayrı regresyon denklemler kurularak sonuçlar yorumlanır. Fakat burada her model çn farklı bağımlı değģkenlern olması sebebyle model parametrelernn tahmn, ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 36
41 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 hem daha karmaģık hem de hesaplama süres bakımından daha uzundur (Pursell, 970; Salkever, 976).Göstermelk değģken yöntem, Chow Test yöntemne göre daha kolay ve hesaplama aģamasında daha etkl olması sebebyle mevsmsel etklern analznde daha çok terch edlmektedr (Salkever, 976; Pursell, 970; Suts, 957; Karafath, 988). Modeln KuruluĢu Göstermelk değģken yöntemnde, göstermelk değģkenler herhang br regresyon modelne k farklı yolla ekleneblr. Gültekn ve Gültekn (983), Jaffe (989) ve Asterou ve Kavetsos (006) tarafından desteklenen lk yaklaģımda, ncelenen mevsmsel etkler çn kesģm term olmayan ve Denklem () le belrtlen regresyon model kurulur. Y rt = α D t + α D t + α 3 D 3t + +α D t + U t () Denklem () le tanımlanan modelde, U t rassal hata termn, Y rt se r. ay çn aylık hareketllğ fade etmektedr. Dğer yandan α r (r =,..., ), r. ay çn aylık toplam yolcu sayısını ve D rt, r. ay çn, dğer aylar çn 0 değern alan göstermelk değģken göstermektedr.çalıģmamızda uçuģ hareketllğndek mevsmsel etknn anlamlılığını Denklem () le değerlendrrken, her br havaalanı çn ayrı ayrı olmak üzere, H 0 : α = α =...= α =0 formunda kurduğumuz sıfır hpotezne karģılık H : En azından br α r değernn farklı olması alternatf hpotezn test etmekteyz. Bu durumda modelmzdek her br α r değer aylık toplam hareketllğ fade ederken kurduğumuz alternatf hpotezn reddedlmes, seçlen havaalanlarındak uçakların hareketllğnde dkkate değer br mevsmsel etknn olduğu Ģeklnde yorumlanablr. Ayrıca alternatf hpotezn reddedlmes herhang br ay çn özel aylık etknn varolduğunu da gösterr. Eğer böyle br etknn olduğu sonucuna varılırsa, bu etknn hang ayda olduğu Denklem () olarak adlandırılan aģağıdak regresyon model yardımıyla bulunablr. Yrt C + r. Dt + U t () Denklem () le tanımladığımız modelde U t, dğer modelde olduğu gb 0 ortalama ve σ varyansa sahp hata termn göstermektedr. C herhang br aya at özel aylık etky, Y rt se r. ay çn aylık hareketllğ fade etmektedr. Son olarak α r (r=,..., ) belrlenen ay le r. ay arasındak farkı ve D rt, r. ay çn değern alan göstermelk değģken anlatmaktadır. Bu çalıģmada Denklem () y, aylık etklern bulunması durumunda bunun hang aylarda olduğuna bakarak uçuģ hareketllğndek yoğunluğun aslında yaz tatlnde m, ünverstelern dönem tatller, bayram tatller, yılbaģı ya da kıģ dönemde m olduğunu yorumlamada kullanmaktayız. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 37
42 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 UYGULAMA ÇalıĢmada Esenboğa, Atatürk ve London Cty Havaalanlarına at, ġekl de de gösterlen zaman sers verler, Denklem () ve () de verlen regresyon modeller kullanılarak tahmn edlmektedr. Model parametrelernn tahmn genel en az kareler (generalzed least square) metoduyla ve analzler Evews 5.0 paket programı le yapılmıģtır. Bu programın analzler çn seçlme neden se özelkle ekonomk verler değerlendrmede kullanım kolaylığından dolayı yaygın olarak terch edlmesdr. Ancak bu programın, parametre tahmnlernde lglenlen varyans-kovaryans matrsnn ters gerektğ durumlarda kullandığı algortmalarla zaman zaman sngülerlk problemyle karģılaģtığı da blnmektedr. Uçakların hareketllğn gösteren verlerde, öncelkle, aylık anlamlı farklar olup olmadığını test etmek çn Denklem () dek model kullanılmıģtır. Bu analz çn de klask lneer regresyon model varsayımları olan hata termlernn otokorelasyona ve ayrı varyanslılığa (heteroscedastcty) sahp olmamaları durumunun bzm ver kümelermzde uygun olup olmadığı test edlmģtr. Bu testler temelde, hataların normal dağıldığı varsayımına dayanması sebebyle her üç havalanı çn Jarque-Bera test uygulanmıģ, buna alternatf olarak da hataların çarpıklık (skewness) ve basıklık (kurtoss) değerlernn sırasıyla 0 ve 3 e eģt olup olmadıklarına bakılmıģtır. Test sonuçlarından normal dağılım varsayımının Esenboğa ve London Cty Havaalanları çn uygun olduğu gözlenmģtr. Atatürk Havaalanı çn se Temmuz 008 versnn aykırı ver olduğu ve normallk Ģartını bozduğu bulunmuģtur. Bu sebeple öncelkle gözlenen aykırı vernn bulunduğu zamanda havalanındak yoğunluğu etkleyecek özel br olayın olup olmadığı araģtırılmıģ, böylece aracılık (nterventon) analznn uygulanablrlğ değerlendrlmģtr. Aracılık analz, zaman serlernde, sebeb bell olan tek gözleme veya bulunan sebeple serde oluģan yapısal kırılmanın (structural break) olduğu gözlemlerde kullanılan ve bu noktaya/noktalara göre adım (step) veya pulse fonksyon kullanarak yanıtı (response) modellemeye çalıģan br yöntemdr (We, 006). ÇalıĢmamızda, vermzn aracılık analzne uygunluğunu belrlemek çn öncelkle Atatürk Havaalanında belrlenen tarhte özel br olayın varlığı araģtırılmıģ ve yapılan araģtırmada uçuģ yoğunluğunu etkleyeck özel br sebebe rastlanmamıģtır. Bu nedenle aykırı very analzden çıkarmak yerne, bu tek gözlemn kayıp ver olduğu varsayılmıģ ve bu nokta çn EM algortmasıyla (SPSS 6.0 programı yardımıyla) değer tahmn yapılmıģtır. Bulunan değer daha sonra Atatürk Havalanı çn yapılan tüm analzlerde aykırı gözlem yerne kullanılmıģtır. Ntekm kullanılan bu gözlem değeryle ver setnde normallk varsayımının da sağlandığı görülmüģtür. Daha sonra her üç ser çn de serlern otokorelasyon ve ayrı varyanslılık durumları değerlendrlmģtr. Ser korelasyonları çn Breusch Godfrey ve Durbn-Watson testler (Asterou, 006) uygulanmıģ, sağlam br test teknğ olan Breusch Godfrey ve Durbn- Watson nın farklı cevaplar verdğ durumlarda yaygın kullanımı olan ve hata dağılımını göz önünde bulunduran Durbn-Watson test sonuçları dkkate alınmıģtır. Test sonuçları Tablo de gösterlmektedr. Ayrı varyanslılığı kontrol etmek çn se ARCH LM() prosedürü (Asterou, 006) kullanılmıģtır. Tablo de sunulan test statstkler, hataların ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 38
43 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ġekl. Ver set grafkler :0 07:07 08:0 08:07 09:0 09:07 A (a) Esenboğa Havaalanı (b) Atatürk Havaalanı M0 07M07 08M0 08M07 09M0 09M07 M (c) London Cty Havaalanı Esenboğa ve London Cty Havaalanları çn bu varsayımı da karģılamadığını göstermektedr. Hataların bu k varsayımı sağlamaması serlerde beyaz gürültü (whte nose) özellğnn bulunmadığı anlamına geldğ çn serdek olası brm kare (unt root) durumu Phllps-Perron test le kontrol edlmģtr. Sonuçlar üç sernn de durağan hatalara sahp olduğunu göstermektedr. Bu sebeple Denklem () kullanarak yaptığımız parametre tahmnlernde t- statstkler, sadece otokorelasyon ve ayrı varyanslık özellklern göz önünde bulunduran ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 39
44 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Newey-West ayarlanmıģ standard hatalar (Asterou, 006; Asterou ve Kavetsos, 006) kullanılarak yapılmıģtır. Her ay çn bulunan tahmn edcler yne Tablo de sunulmaktadır. Tabloda verlen katsayıların p-değerlerne bakıldığında se Esenboğa ve London Cty Havaalanlarında anlamlı aylık etklern olduğunu gözlenmģtr. Son olarak bulunan modellern sahte (spurous) regresyon olableceğn kontrol etmek amacıyla her havaalanı çn bulunan R ler Durbn-Watson test statstkleryle karģılaģtırılmıģtır. Tablo de verlen R değerler le Durbn-Watson test statstkler serlermzde bu problemn gözlenmedğn, modelmzn bu durumda ser çn uygun br model olarak görülebleceğn göstermektedr. Analzn knc aģaması se bulunan anlamlı farkların, hang aylarda gözlendğn bulmaya yönelktr. Bu amaçla Esenboğa ve London Cty Havaalanları çn Denklem () le ayrı ayrı modelleme yapılmıģtır. Test statstklernden Esenboğa ve London Cty Havaalanları çn uçuģ hareketllğndek değģmn, eylül ve ekm aylarında olduğu gözlenmģtr. Tablo de verlen parametre tahmnlernde C değer her havaalanı çn sadece statstksel olarak anlamlı değģklklern gözlendğ aylar baz alınarak hesaplanmıģ parametre tahmnlern vermektedr. Bu sebeple Esenboğa ve London Cty Havaalanları çn, C değer, sırasıyla, eylül ve ekm aylarına at özel aylık etkler göstermektedr. Ayrıca sonuçlardan, Ġstanbul un stratejk özellğnden dolayı Atatürk Havaalanının dğer havaalanlarına kıyasla her zaman çok daha yoğun br uçuģ trafğne sahp olduğu görülmüģtür (ġekl ). Bu havaalanındak uçuģ hareketllğnn se statstksel olarak aylık fark göstermemes tüm aylar çn havaalanının uluslararası hava trafğndek öneml bağlant noktalarından br olmasıyla açıklanablr. Esenboğa ve London Cty Havaalanları se uluslararası uçuģlara açık olsa da çoğunlukla yurtç seyahatlernde kullanılması sebebyle, dğer aylara göre anlamlı yoğunluğun her k ülkedek yaz tatllernn bttğ, çoğunlukla okulların (ünverste/lse/lköğretm) açıldığı dönemlerde olduğu bulunmuģtur.analzlerde Denklem () de olduğu gb t-statstkler Newey-West ayarlanmıģ standart hatalar kullanılarak hesaplanmıģtır. SONUÇ Bu çalıģmada Esenboğa, Atatürk ve London Cty Havaalanlarındak uçakların hareketllğnde anlamlı br mevsmsel etknn var olup olmadığını göstermelk değģken yöntem le test ettk. Seçlen yöntemn uygulaması lteratürde oldukça yaygın olmasına rağmen uçuģların hareketllğndek mevsmsel etknn saptanması çn kullanılması yen br uygulama alanıdır.analzlermz sonucunda her havaalanı çn de farklı dönemlerde aylık etklern bulunduğunu gösterdk. ÇalıĢmamızın özellkle Türkye nn en büyük k havaalanındak uçuģ trafğne yönelk uzun dönem planlamalarda br ön fkr verebleceğn düģünmekteyz. TEġEKKÜR Yazarlar, çalıģmadak yardımcı yönlendrmelernden dolayı Yrd.Doç.Dr.Ceylan Yozgatlıgl e teģekkür etmektedr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 40
45 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo. Mevsmsel etkler çn test sonuçları Atatürk Havaalanı Esenboğa Havaalanı London Cty Havaalanı Değşken Katsayı t- Katsayı t- Katsayı t-statstğ statstğ statstğ D D D 3 D 4 D 5 D 6 D 7 D 8 D D D D Jarque-Bera (p-value) ARCH LM() (p-value) Durbn- Watson Phlppe-Peron (p-value) R ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 4
46 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo. Anlamlı aylık etkler çn test sonuçları Esenboğa Havaalanı (Eylül) London Cty Havaalanı (Ekm) Değşken Katsayı t- statstğ C Değşken Katsayı t- statstğ C D D D D D D D D D D D D D D D D D D D D D D KAYNAKLAR ASTERIOU, D. (006), Appled Econometrcs, New York: Palgrave Macmllan. ASTERIOU, D. ve KAVETSOS, G. (006), Testng for the exstence of January effect n transton economes, Appled Fnancal Economcs Letters,, ATABEK, A., ATUK, O., ERDOĞAN, E. vesarikaya, C. (009), Mevsmsel modellerde çalıģma günü değsken, TCMB Ekonom Notları, 3. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 4
47 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 CHIEN, C.-C., LEE, C.-F.ve WANG, A.M.L. (00). A note on stock market seasonalty: The mpact of stock prce volatlty on the applcaton of dummy varable regresson model, The Quarterly Revew of Economcs and Fnance, 4, GREEN, R.D. ve DOLL, J.P. (974), Dummy varables and seasonalty-a curo, The Amercan Statstcan, 8, GUJARATI, D.N. (003), Basc Econometrcs, 4 th Edton, New York: Mc Graw Hll. GÜLTEKĠN, M.N. ve GÜLTEKĠN, N.B. (983), Stock market seasonalty: Internatonal evdence, Journal of Fnancal Economcs,, JAFFE, J.F. ve WESTERFIELD, R. (989), Is there a monthly effect n stock market return?,journal of Bankng and Fnance, 3, KARAFIATH, I. (988), Usng dummy varables n the event methodology, The Fnancal Revew, 3, KOÇAK, N.A. (008), Takvm etkler: Ulusal hesaplar uygulaması, 7. Ġstatstk AraĢtırma Sempozyumu Bldr Ktabı, TÜĠK, LADIRAY, D. (006), Calender effects and seasonal adjustments, Proceedng of the Eurostat Workshop. SALKEVER, D.S. (976), The use of dummy varables to compute predctons, predcton errors and confdence ntervals, Journal of the Econometrcs, 4, SUITS, D.B. (957), Use of dummy varables n regresson equatons, Journal of Amercan Statstcal Assocaton, 5, THALER, R.H. (987), Anomales: the January effect, Journal of Economc Perspectves,, WEI, W.W.S. (006), Tme Seres Analyss: Unvarate and Multvarate Methods, th Edton, Pearson Educaton, Inc. USA. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 43
48 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 GAUSS RASTGELE YÜRÜYÜġ SÜRECĠNĠN MAKSĠMUMUNUN MOMENTLERĠ ĠÇĠN YAKLAġIK FORMÜLLER Fkr Gökpınar Tahr Khanyev. GĠRĠġ X, X,.rasgele değģkenler β>0 olmak üzere β beklenen değerl ve varyanslı normal dağılıma sahp olsun. S n = X + + X n, (n=,, ) ve S 0 = 0 olmak üzere Gauss rasgele yürüyüģ (GRYS) sürecnn maksmumu M(β)= maks{s n : n 0} olsun. Amacımız M(β) nın momentler çn yaklaģık formüller elde etmektr. Bu konuda yazılmıģ brçok lgnç çalıģmalar mevcuttur (örneğn, Lotov (996), Korshunov (997), Khanyev ve Mammadova (006), Jannsen ve Leewarden (007a), Jannsen ve Leewarden (007b) vb.). M β ın dağılımı kuyruk teors, rsk teors,stokastk fnans, güvenrlk, matematksel byoloj, çevre gb alanlarda oldukça sık kullanılmaktadır. β=0 durumunda, Lotov (996), GRY sürecnn. basamak yükseklğnn lk üç moment çn 3 terml asmptotk açılım ortaya koymuģlardır. Korshunov (996) Rassal yürüyüģ sürecnn maksmumunun dağılımının kuyruk davranıģları üzerne çalıģmıģlardır. Janssen ve Leeuwarden (007a) β 0 çn maksmum değernn beklenen değer ve varyansı çn zeta fonksyonlar teorsn kullanarak açılımlar elde etmģlerdr.ayrıca Janssen ve Leeuwarden (007b) çalıģmasında sürecn maksmumun kümülantları çn kesn ve asmptotk sonuçlarını genellemģlerdr. Bununla beraber bu asmptotk formüller β nın çok dar br aralığında geçerldr. Özellkle β>0.5 olduğunda asmptotk sonuçlar kesn değerlerden oldukça uzaklaģmaktadır. Bu nedenle bu çalıģmada k amaç gözetlmģtr. Brnc amaç, meta modelleme yöntem le GRY sürecnn maksmumun lk 4 moment çn yaklaģık fadeler elde etmektr. Ġknc amaç se β0 ken Y(β)=βM β rasgele değģkennn dağlımı çn zayıf yakınsama teoremn spatlamaktır. ÇalıĢmada, lmt dağılımın üstel br dağılım olduğu gösterlmģtr.. GAUSS RASGELE YÜRÜYÜġ SÜRECĠNĠN MAKSĠMUMUNUN DAĞILIMI Jannsen ve Leewarden (007b) GRW sürecnn maksmum değernn tüm kümülantları çn kesn br formül vermģtr. Bu formül aģağıdak teorem de verlmģtr. Yardımcı Teorem (Jannsen ve Leewarden, 007b): X, X,. rasgele değģkenler β>0 olmak üzere β beklenen değerl ve varyanslı normal dağılıma sahp olsun. Gauss rasgele yürüyüģ sürecnn maksmumu(m(β)) k.acı kümülantı (J k (β)) çn k=,,... ken aģağıdak kesn fadeler yazılablr. Jk ( ) Ak ( ) Dk ( ) Fk ( ). Ġstatstk Bölümü, Gaz Ünverstes, Ankara EndüstrMühendslğ bölümü TOBB-ETÜ, Ankara ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 44
49 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Burada; Ak F k ( ) ( k)! k, k j k Dk ( ) k j j0 j j kj k j k! k k r / / k r rk r0 j r!(r )...(r k ) 0 ve(x), Remann zeta fonksyonunun x noktasındak değern fade etmektedr. Not: Yardımcı Teorem de verlen kümülantlardan faydalanarak GRW sürecnn maksmumunun Momentler de bulunablr. dek formüldek son term kaldırdığımızda β0 ken asmptotk olarak k J ( ) A ( ) D ( ) o k k k Ģeklnde elde edleblr. Jk ( ) Bell polnomlarından yararlanarak GRY sürecnn maksmumunun M β n. baģlangıç momentler çn asmptotk sonuçlar elde etmek mümkündür. Bu Sonuçlar aģağıdak Teorem de verlmģtr. Teorem :X, X,.rasgele değģkenler β>0 olmak üzere β beklenen değerl ve varyanslı normal dağılıma sahp olsun. Gauss rasgele yürüyüģ sürecnn(grys) maksmumu M(β)'n n.ncı moment E M n ( ) çn aģağıdak asmptotk açılım yazılablr.,, E M ( ) B D ( ), D ( ),... D ( ) n n n! ( ) n o ( )! n n=,,3,... Burada göstermektedr. B D ( ), D ( ),... D ( ) {D (β), D (β), D (β)} kümesnn Bell polnomunu Ġspat: Ak ( ) ( k)! k kenj k (β)= A k (β)+d k (β)+o(β k ) olarak fade edleblr. Bell Polnomlarından faydalanarak, β ya bağlı olarak, kümülantlardan Momentlere geçleblmektedr(comtet, 974,s.60). Tam Bell polnomu B n (x,x, x n ) olmak üzere j j n! x x n(,,... xn)... j j... nj n n B x x xn j! j!... j!!! n! n j n n=,,... Ģeklnde fade edlr(b 0 =). ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 45
50 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Burada Bell Polnomunun değern; n n n n x x x3 x4 x5 xn 3 4 n n n x x x3 x4 x n 3 n3 n3 0 x x x3 xn Bn x, x,..., xn det n x x xn x x n x n x fades kullanarak bulunablr. n.nc moment E(M n (β)), den n e kadar tüm kümülantları Bell polnomunda kullanarak; E(M n (β))=b n (J (β), J (β), J n (β)) Ģeklnde bulunur (Comtet,974). Burada J k (β)= A k (β)+d k (β)+o(β k ) fades kullanarak; E(M n (β)) =B n (A (β)+ D (β), A (β)+d (β),, A n (β)+d n (β))+o() olarak elde edlr. Comtet(974) de Bell Polnomlarının herhang k {a, a, a n } ve {b, b, b n } sers çn; n n B ( a b, a b,..., a b ) B a, a,..., a B b, b,..., b n n n n 0 Ģeklnde fade edleblr olduğunu göstermģtr (Bell polnomumun bnom özellğ). Burada a =A (β) ve b = D (β) alındığında n n n n 0 E M ( ) B A D, A D, A D o n n B n A, A,..., A n B D ( ), D,..., D o elde edlr. Burada j j ( ) A( ) ( n )! A An ( ) Bn A, A,..., An... j j...( n) j!!...!!! ( )! n n j j jn n jn ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 46
51 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 j j ( n )!... n j j...( n) j!!...! ( ) n n j j jn n jn Collns(00) de j j... njn n n olarak verlmģtr. Buradan j j jn... j! j!... j! n,,..., B A A A ( n)! n n n olur. Bu fade yerne konduğunda; n n n ( n )! E M ( ) B D ( ), D,..., D o n 0 n 0 n ( n )! B n D D D o ( ),,..., açılımı elde edlr. Bu açılım aģağıdak Ģeklde yazablrz. E M n n n! ( ) B D, D,... D ( ) n ( )! olarak bulunur. Bu da spatı tamamlar. Sonuç:Y(β)= βm(β) olmak üzere E Y( ) n! dr. n ( ) B D, D,... D! Teorem : X, X,. rasgele değģkenler β>0 olmak üzere β beklenen değerl ve varyanslı normal dağılıma sahp olsun. Bu taktrde, Y(β)= βm(β) rasgele değģkennn dağılımı = x P Y x e olur. parametrel üstel dağılıma zayıf yakınsar. Yan x>0 çn 0 ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 47
52 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Ġspat: Y(β) nn karakterstk fonsyonu; Y t E e () ty ( ). Ģeklndedr. Bu fadey Taylor açılımını kullanarak açarsak (Feller,97); t t t n E M ( ) E M ( )... E M ( )... o()!! n! t t t!!... n! o()!! n! t < ken bu geometrk ser; Y ( ) () t t n olur. ( ) ( t ) fonksyonunun= parametrel üstel dağılımın karakterstk fonksyonu o t olduğu blnmektedr. Dolayısıyla Y(β)= βm(β) rasgele değģkennn dağılımı = parametrel üstel dağılıma zayıf yakınsar. Yan x>0 çn olur. 0 P Y x e 3. GAUSS RASGELE YÜRÜYÜġ SÜRECĠNĠN ĠLK 4 MOMENTĠ ĠÇĠN YAKLAġIK FORMÜLLER Bu bölümde GRY sürecnn maksmum değernn lk 4 moment çn yaklaģık br formül verlecektr. Jannsen ve Leeuwarden(007b) maksmumun kümülantları çn elde ettğ genel br formül sonsuz br serye dayalı olduğu çn hesaplanmasının oldukça zor olduğu görülmektedr. Ayrıca Jannsen&Leeuwarden(007b) elde ettkler asmptotk formüllerde β'ın çok küçük değerler (0<β<0.5) çn geçerllklern korumaktadır. Fakat uygulamada çoğu zaman 0<β<3.3 aralığında değģeblmektedr. Bu da β>0.5 olduğunda yen br yaklaģık formül elde etmey gerektrmektedr. Bu amaçla çeģtl Beta değerler çn MATLAB R009a programını kullanarak β nın hang değer aralığı çn kesn formülle asmptotk formülün aynı değer alıp hang değerden sonra uzaklaģtığını tespt ettk. Elde edlen sonuçlar tablo -4 de verldğ gbdr. Burada ve EM( ) n x EM( ) le sırasıyla M(β)'ın sırasıyla beklenen değernn kesn ve asmptotk formülle hesaplanmasında elde edle edlen sonuçları göstermektedr. Ayrıca E( M ( )) E( M ( )) mutlak hata; EM ( ( )) nsp hatayı göstermektedr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 48
53 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo. Jannsen ve Leewarden(007b) verlen ve oransal farkları EM( ) EM( ) çn asmptotk ve kesn formüller le verlen sonuçlar, nsp β 0,00 0,00 0,030 0,040 0,050 0,060 0,070 0,080 0,090 EM( ) 49,499 4,44 6,095,973 9,498 7,7656 6,5776 5,687 4,995 49,499 4,44 6,095,974 9,4990 7,7657 6,5777 5,6874 4,9955 0,0000 0,0000 0,0000 0,000 0,000 0,000 0,000 0,0003 0,0003 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,0 β 0,00 0,00 0,300 0,400 0,500 0,600 0,700 0,800 0,900 EM( ) 4,440,9657,553 0,7608 0,53 0,3859 0,865 0,60 0,647 4,444,9674,59 0,7674 0,544 0,4007 0,3067 0,44 0,980 0,0004 0,007 0,0037 0,0066 0,003 0,049 0,00 0,064 0,0333 0,0 0,08 0,3 0,87,94 3,85 7,06,0 0,3 β,000,50,500,750,000,50,500,750 3,000 EM( ) 0,64 0,066 0,0347 0,079 0,0090 0,0044 0,000 0,0009 0,0004 0,674 0,99 0,57 0,406 0, ,0 0,44 0,867 0,3344 0,040 0,0637 0,090 0,7 0,584 0,977 0,404 0,858 0,3337 3,47 96,5 6, 683,9 755,37 453,9 776, , ,96 EM( ) EM( ) Tablo. Jannsen ve Leewarden(007b) verlen kümülantlardan elde edlen E M ( ) çn asmptotk ve kesn formüller le verlen sonuçlar, nsp ve oransal farkları β 0,00 0,00 0,030 0,040 0,050 0,060 0,070 0,080 0, ,0780, ,470 98,679 88,6793 9, ,046 7,690 55,5800 EM ( ) 494,0785,07 536,473 98,695 88,683 9,509 94,0487 7,7 55,5834 0,0004 0,0008 0,00 0,006 0,000 0,003 0,007 0,0030 0,0034 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,0 β 0,00 0,00 0,300 0,400 0,500 0,600 0,700 0,800 0,900 EM ( ) 44,4974 9,8957 3,9087,95,060 0,6786 0,439 0,95 0,038 44,50 9,90 3,97,96,67 0,6896 0,4500 0,3054 0,34 0,0037 0,0065 0,0085 0,0099 0,007 0,00 0,008 0,003 0,0096 0,0 0,07 0, 0,5 0,97,6,46 3,50 4,70 β,000,50,500,750,000,50,500,750 3,000 0,436 0,0634 0,09 0,036 0,0063 0,008 0,00 0,0005 0,000 0,5 0,069 0,030 0,04 0,0056 0,005 0,0030 0,0063 0,00 0,0086 0,0057 0,008 0,0005-0,0007-0,0003 0,008 0,0058 0,08 6,00 9,0 9,50 3,5-0,74 -,3 45,5 8, ,05 E M ( ) E M ( ) E M ( ) E M ( ) Tablo -4 tek verlen GRY sürecnn lk dört momentnn maksmumu çn asmptotk ve kesn formüller le verlen sonuçlar arası, mutlak ve Nsç farklarına bakıldığında β= değernden sonra asmptotk ve kesn formüller arasındak oransal fark % y geçmektedr. Özellkle, β> olduğunda nsb hata %3'y aģmaktadır. Bu fark kabul edleblr br durum değldr. Kesn formülde Kümülantların son term zeta ve gamma fonksyonların sonsuz br sers oluģturduğu düģünülürse bu fadey momentlerde kullanmak oldukça zordur bunun yerne bu kesn değerlerle asmptotk değerlern fark değerler üzerne eğr uydurarak daha rahat kullanılablecek br formül oluģturmak gerekr. Burada 4 fonksyon farklı yapı gösterdğnden her br çn farklı fonksyon uydurmak gerekecektr.. Moment çn üstel. Moment çn polnom, 3 ve 4.Moment çn kesrl polnom fonksyon olarak uydurulmuģtur. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 49
54 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo 3. Jannsen ve Leewarden(007b) verlen kümülantlardan elde edlen formüller le verlen sonuçlar, nsp ve oransal farkları E M 3 ( ) çn asmptotk ve kesn β 0,00 0,00 0,030 0,040 0,050 0,060 0,070 0,080 0, , , ,576785, , ,783 05, ,485 96, , , ,636785, , , , ,549 96,4549 0,065 0,0608 0,060 0,0594 0,0587 0,0580 0,0573 0,0566 0,0560 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,0 β 0,00 0,00 0,300 0,400 0,500 0,600 0,700 0,800 0, ,555 74,73 9,594 7,358 3,3533,763 0,966 0,5743 0, , ,33 9,6349 7,3965 3,3870,7558 0,998 0,5965 0,376 0,0553 0,049 0,0434 0,0384 0,0337 0,095 0,057 0,0 0,089 0,0 0,07 0, 0,5,0,7,66 3,86 5,9 β,000,50,500,750,000,50,500,750 3,000 0,99 0,0847 0,034 0,043 0,006 0,005 0,000 0,0004 0,000 0,457 0,0933 0,035 0,0065-0,03-0,03-0,0543-0,085-0,87 0,058 0,0085 0,000-0,0078-0,093-0,0346-0,0553-0,089-0,88 6,88 0,06,95-54,7-37,06-358,6-534,4-095, ,40 E M 3 ( ) E M 3 ( ) E M 3 ( ) E M 3 ( ) E M 3 ( ) E M 3 ( ) Tablo 4. Jannsen ve Leewarden(007b) verlen kümülantlardan elde edlen E M 4 ( ) çn asmptotk ve kesn formüller le verlen sonuçlar, nsp ve oransal farkları β 0,00 0,00 0,030 0,040 0,050 0,060 0,070 0,080 0, , , , , , , , , ,4473 E M 4 ( ) E M 4 ( ) , , , , , , , , ,694,960 6,0767 4,004,968,3469,9330,6375,46,44 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,0 β 0,00 0,00 0,300 0,400 0,500 0,600 0,700 0,800 0,900 3, ,087 7, ,0594,0898 5,0,586,33 0,7479 E M 4 ( ) E M 4 ( ) 4, ,505 7,696 33,534,76 5,3,606,39 0,795,066 0,498 0,93 0,940 0,378 0,00 0,0775 0,060 0,0473 0,0 0,07 0,5 0,59,4,95 3,07 4,5 6,3 β,000,50,500,750,000,50,500,750 3,000 0,440 0,37 0,0488 0,087 0,0073 0,009 0,00 0,0004 0,000 E M 4 ( ) E M 4 ( ) 0,4786 0,589 0,060 0,068 0,0 0,0045-0,009-0,008-0,05 0,0376 0,08 0,03 0,008 0,0048 0,007-0,0030-0,0-0,053 8,5 5,93 6,87 43,3 65,34 57,53-70,95-695,0-696,9 a) Brnc Moment çn yaklaģık formül X, X,.rasgele değģkenler β>0.5 olmak üzere β beklenen değerl ve varyanslı normal dağılıma sahp olsun. Gauss rasgele yürüyüģ sürecnn maksmumu M(β)'n.ncı moment çn yaklaģık formül E M ( ) ( ) B D R R ( ) şeklndedr. Burada 'n tahmn; b / c b /c ˆ R ( ) ae ae ve a = , b =0.634, c =.5, a =0.7545, b =5.863, c =3.88 Ģeklndedr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 50
55 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 b) Ġknc Moment çn yaklaģık formül X, X,. rasgele değģkenler β>0.5 olmak üzere β beklenen değerl ve varyanslı normal dağılıma sahp olsun. Gauss rasgele yürüyüģ sürecnn maksmumu M(β)'n.ncı moment çn yaklaģık formül E M! ( ) B D ( ) B D, D ( ) R ( ) ( ) Ģeklndedr. Burada R ( ) 'n tahmn; R ˆ ( ) p x p x p x p x p x p , ve p = , p = ,p 3 =0.0304,p 4 = , p 5 =0.0476,p 6 = Ģeklndedr. c) Üçüncü Moment çn yaklaģık formül X, X,.rasgele değģkenler β>0.5 olmak üzere β beklenen değerl ve varyanslı normal dağılıma sahp olsun. Gauss rasgele yürüyüģ sürecnn maksmumu M(β) 'n 3.ncı moment çn yaklaģık formül E M 3 3! ( ) B D ( ) B D, D ( ) B D, D, D R3 ( ) ( ) Ģeklndedr. Burada R3 ( ) 'n tahmn; 4 3 px p x p3 x p4 p5 ˆ 3 ( ) x q R x ve p = , p =0.0335, p 3 =0.0348, p 4 =-0.44, p 5 =0.65, q =4.37 Ģeklndedr. d) Dördüncü Moment çn yaklaģık formül X, X,.rasgele değģkenler β>0.5 olmak üzere β beklenen değerl ve varyanslı normal dağılıma sahp olsun. Gauss rasgele yürüyüģ sürecnn maksmumu M(β)'n 4.ncı moment çn yaklaģık formül ! ( ) B D ( ) B D, D ( ) B3 D, D, D3 ( ) B4 D, D, D3, D 4 E M 4 R ( ) ( ) 6 4 Ģeklndedr. Burada 'n tahmn; 4 R 4 ( ) ˆ p x p x p x p x p x p R ( ) x qx q ve p =-0.435, p =.79, p 3 =-7.60, p 4 =.54, p 5 =-4.5, p 6 =9.938, q =67.88, q =.63 Ģeklndedr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 5
56 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Rˆk ların değerler le R k nın kalan termlern değerler arası nsp farkın %0.8 n altında olduğu görülmektedr. Dolayısıyla oluģturulan fonksyonlar bu artık değerler çn uygun olduğu söyleneblr.ayrıca yapılarının kolaylığı nedenyle oldukça kolay br bçmde kullanılablmektedr. KAYNAKLAR Comtet L., 974, Advanced Combnatorcs: The Art of Fnte and Infnte Expansons, Redel, Dordrecht, Holland. Collns B., 00,The role of Bell polynomals n ntegraton, Journal of Computatonal and Appled Mathematcs, Volume 3, Number, June 00, pp. 95-(8) Janssen, A. J. E. M.; van Leeuwaarden, J. S. H. On Lerch's transcendent and the Gaussan random walk. Ann. Appl. Probab. 7 (007), no., Janssen, A. J. E. M.; van Leeuwaarden, J. S. H. Cumulants of the maxmum of the Gaussan random walk. Stochastc Process.Appl. 7 (007), no., Lotov, V.I., 996. On some boundary crossng problems for Gaussan random walks. Ann. Probab. 4 4, pp Khanyev T.A., Mammadova Z.I., (006), On the statonary characterstcs of the extended model of type (s,s) wth Gaussan dstrbuton of summands, Journal of Statstcal Computaton and Smulaton, Vol.76, No.0, p Khorsunov,997, On dstrbuton tal of the maxmum of a random walk, Stochastc Processes and ther Applcatons 7 : ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 5
57 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ĠLERĠ BESLEMELĠ YAPAY SĠNĠR AĞLARI ĠLE ÖNGÖRÜ ĠÇĠN GĠZLĠ TABAKA SAYISI ÜZERĠNE BĠR ARAġTIRMA Prof.Dr.Faruk ALPASLAN, ArĢ.Gör.Ebrucan TĠRĠNG, Doç.Dr.Erol EĞRĠOĞLU Ondokuz Mayıs Ünverstes, Ġstatstk Bölümü, Samsun ÖZET Son yıllarda, zaman sers öngörü problem çn ler beslemel yapay snr ağları baģarılı br Ģeklde uygulanmaktadır. Doğrusal olmayan yapı çeren zaman serlernn modellenmesnde, ARIMA, üstel düzleģtrme gb klask doğrusal zaman sers modeller yetersz kalmaktadır. Zaman sers analz çn brçok doğrusal olmayan zaman sers modeller bulunmasına rağmen hepsnn bell br model varsayımı gerektrmes öneml br engel oluģturmaktadır. Ġler beslemel yapay snr ağlarının hem doğrusallık hem de model varsayımı gb kısıtları yoktur. Lteratürdek brçok çalıģmada ler beslemel yapay snr ağlarında, klask zaman sers yöntemlernden daha doğru öngörüler elde edlmģtr. Brçok avantaja rağmen yapay snr ağları le öngörü çn yapay snr ağlarının bleģenlernn belrlenmes problem halen tam olarak sstematk değldr. Bu çalıģmada öngörü problem çn ler beslemel yapay snr ağı kullanımında, gzl tabaka sayısının belrlenmes ve test kümes uzunluğunun etks üzerne, ĠMKB, Dolar ve Euro zaman sers kullanılarak br araģtırma yapılmıģtır. Anahtar kelmeler:öngörü, Yapay snr ağları, Gzl tabaka sayısı.. GrĢ Ġler beslemel yapay snr ağları (ĠBYSA) brçok avantajı nedenyle zaman sers çözümlemesnde sık kullanılmaya baģlanmıģtır.ġler beslemel yapay snr ağları le zaman sers çözümlemesnde en öneml problem sstematk br yaklaģımın eksklğdr. Ġler beslemel yapay snr ağları le zaman sers çözümlemes çn belrlenmes gereken bleģenler Gzl tabaka sayısı, Çıktı tabakası brm sayısı, Gzl tabaka brm sayısı, Gzl tabaka aktvasyon fonksyonu, Çıktı tabakası aktvasyon fonksyonu, Grd brmlernn seçm, Test kümes uzunluğunun belrlenmesdr. BleĢenlern belrlenmes konusunda lteratürde farklı uygulamalar vardır. 998 yılına kadar mevcut lteratürdek farklı uygulamalar Zhang vd. (998) çalıģmasında özetlenmģtr. Bu çalıģmada gzl tabaka sayısının ve test kümes uzunluğunun belrlenmes üzerne 3 gerçek zaman sers üzernden nceleme yapılmıģtır. Bu problem üzerne lteratür ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 53
58 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 aģağıdak gb özetleneblr. Cybenko (989), Hornk vd. (989) çalıģmalarında tek gzl tabaka kullanmıģ ve tek gzl tabakanın yeterl olacağını savunmuģtur.baron (994), Zhang (994) k gzl tabakanın daha doğru öngörü sonuçları vereceğn savunmuģtur. Lppmann (987) ve Cybenko (988) se kden fazla gzl tabakanın yararlı olmayacağını savunmuģtur. Test kümes uzunluğunun belrlenmes çn lteratürdek çalıģmalarda farklı oranlar alınsa da Zhang vd. (998) de lteratürde genel olarak %0, %5 ve %0 olarak alınmaktadır. Öngörü problem çn ler beslemel yapay snr ağı kullanımında, gzl tabaka sayısının belrlenmes ve test kümes uzunluğunun etks, ĠMKB, Dolar ve Euro zaman sers kullanılarak araģtırılmıģtır.. Ġler Beslemel Yapay Snr Ağları Ġler beslemel yapay snr ağları brçok gerçek hayat problemnn çözümünde baģarıyla kullanılmaktadır.ġler beslemel yapay snr ağlarının öneml br uygulama alanı da zaman serlernn öngörüsüdür.ġler beslemel br yapay snr ağı genel olarak 3 kısımdan oluģmaktadır.ġlk kısım grd tabakası, knc kısım gzl tabaka veya tabakalar ve üçüncü kısım se çıktı tabakasıdır.her tabaka nöron adı verlen elemanlara sahptr. Tabaka ç nöronlar arası bağlantı yoktur, ancak ardı ardına gelen tabakaların nöronları arasında tam bağlantı vardır. Nöronlar arası bağlantıların gücü bu bağlantıların her br le eģleģen ağırlıklarla temsl edlmektedr. Zaman sers öngörü problem çn lteratürde çıktı tabakasında nöron kullanılması le yeterl sonuçlara ulaģılmaktadır. Br gzl tabakanın olduğu ĠBYSA mmars ġekl a da, Ġk gzl tabakanın olduğu ĠBYSA mmars ġekl b de verlmģtr. ġekl. Ġler Beslemel Yapay Snr Ağları Mmarler ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 54
59 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ĠBYSA le zaman sers çözümlemesnde ġekl de verlen mmar kullanılırsa grd tabakasındak nöron sayısı geckmel değģken sayısı kadar olmaktadır. Lteratürde grd tabakasında kaç geckmel değģken kullanılacağı veya gzl tabakalarda kaç nöron olacağı sorusuna deneme yanılma yolu le karar verlmektedr. Yne kaç gzl tabaka kullanılacağı konusunda da genel br sonuç olamamasına rağmen k gzl tabakadan fazlasını kullanmanın gerekl olmadığı Zhang vd. (998) çalıģmasında savunulmaktadır. ĠBYSA le zaman serlernn çözümlenmes konusunda detaylı blg Günay vd. (007) çalıģmasından elde edleblr. 3. ĠMKB, Dolar ve Euro Zaman Serlernn ĠBYSA le Çözümlenmes ĠMKB ndeks, TL/Dolar ve TL/Euro dövz kuru gb ekonomk zaman serler eğrsel ve doğrusal yapıları çeren verlerdr.bu verlern çözümlenmesnde klask eğrsel ve doğrusal zaman sers yaklaģımları yetersz kalmaktadır. Bu tür ekonomk zaman serlernn çözümlenmesnde ĠBYSA kullanımı son yıllarda sık uygulanmaktadır. Ancak ĠBYSA le zaman sers çözümünde bleģenlern belrlenmes çn hala sstematk br yöntem önerlememģtr.bu çalıģmada ĠMKB ndeks, TL/Dolar ve TL/Euro dövz kuru zaman serler ĠBYSA le çözülerek gzl tabaka sayısı ve test kümes uzunluğunun etks araģtırılmıģtır. Her üç vernn çözümlenmesnde tek gzl tabaka ve k gzl tabakalı mmarler kullanılmıģtır. Tek gzl tabaka olduğu durumda gzl tabaka brm sayısı le arasında değģtrlmģ, grd tabakasında kullanılan geckmel değģkenlern sayısı yne le arasında değģtrlmģtr. Böylece tek gzl tabaka olması durumunda 44 farklı mmar ncelenmģtr. Tek gzl tabaka olması durumunda, uygulamada gzl tabaka nöronlarında lojstk, çıktı tabakası nöronlarında doğrusal aktvasyon fonksyonunun kullanıldığı model ( Model ) ve gzl tabaka ve çıktı tabakası nöronlarında lojstk aktvasyon fonksyonunun kullanıldığı model ( Model ) uygulanmıģtır. Böylece tek gzl tabaka durumunda 88 farklı ĠBYSA model her br ser çn denemģtr. Ġk gzl tabakalı mmar kullanıldığında grd tabakası nöron sayısı le arasında, her k gzl tabakadak nöron sayısı le 3 arasında değģtrlerek toplam 08 farklı mmar ncelenmģtr. Model ve Model nn ayrı ayrı uygulanmasıyla ncelenen mmar sayısı 6 olmuģtur. Her br zaman sers çn toplamda 504 farklı ĠBYSA mmars denemģtr. ĠMKB ndeks, TL/Dolar ve TL/Euro zaman serlernn çözümlenmesnden elde edlen sonuçlar sırasıyla Tablo, ve 3 de verlmģtr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 55
60 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Gzl Tabaka Sayısı Tablo.ĠMKB Zaman Sers Ġçn En y Mmarler Ġçn Sonuçlar Test Kümes Uzunluğu Modeller 0% 5% 0% Model 88,546 [-6-] 50,504 [--] 08,396 [4--] Model 6, [6--] 300,48 [-4-] 64,988 [-6-] Model 8,79 [-3--] 68,06 [5---] 84,535 [---] Model 09,694 [4---] 309,879 [3--3-] 75,666 [---] Gzl Tabaka Sayısı Tablo.TL/Dolar Zaman Sers Ġçn En y Mmarler Ġçn Sonuçlar Test Kümes Uzunluğu Modeller 0% 5% 0% Model 0,00989[-8-] 0,039[-8-] 0,037[-8-] Model 0,00966[--] 0,097[-7-] 0,04058[3--] Model 0,0409[8-3--] 0,057[---] 0,03596[0--3-] Model 0,00957[-3--] 0,03538[-3--] 0,03538[-3--] Tablo 3.TL/Euro Zaman Sers Ġçn En y Mmarler Ġçn Sonuçlar Test Kümes Uzunluğu Gzl Tabaka Sayısı Modeller 0% 5% 0% Model 0,0664[-8-] 0,03397[-5-] 0,097[--] Model 0,0797[-7-] 0,0367[-5-] 0,083[-7-] Model 0,0985[-3-3-] 0,03849[-3-3-] 0,03506[--3-] Model 0,0848[-3--] 0,04005[-3--] 0,0[-3--] ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 56
61 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo den görüleceğ gb % 0 test kümes uzunluğunda, gzl tabaka kullanılması daha doğru öngörüler vermektedr. %5 test kümes ve %0 test kümes çn tek gzl tabakanın daha doğru öngörüler verdğ görülmektedr. ĠMKB zaman sers çn uzun dönem öngörü elde etmede tek gzl tabakalı mmarlern, kısa dönem öngörü çn se gzl tabakalı mmarler seçleblr. Tek gzl tabaka kullanıldığında model n model den daha doğru öngörü sonuçları verdğ görülmektedr. Ġk gzl tabaka durumunda se Model nn %0 ve %0 test kümes uzunluğunda daha y sonuçlar verdğ görülmektedr. TL/Dolar zaman sers çn se Tablo ncelenrse %0 ve %5 test kümes uzunluğunda tek gzl tabakalı mmarnn daha y sonuç verdğ %0 test kümes uzunluğunda se gzl tabaka uzunluğunun daha y sonuçlar verdğ söyleneblr. Ayrıca TL/Dolar sers çn Model nn Model e göre daha doğru öngörü sonuçları verdğ söyleneblr. Tablo 3 ncelenrse tek gzl tabaka le daha doğru öngörü sonuçlarına ulaģıldığı açıkça görülmektedr.tek gzl tabakada se Model n model ye göre daha doru öngörüler verdğ söyleneblr. 4. Sonuç ve TartıĢma Bu çalıģmada öngörü problem çn ler beslemel yapay snr ağı kullanımında, gzl tabaka sayısının belrlenmes ve test kümes uzunluğunun etks üzerne, ĠMKB, TL/Dolar ve TL/Euro zaman sers kullanılarak br araģtırma yapılmıģtır. Elde edlen bulgular aģağıdak k maddede özetleneblr. Tek gzl tabakanın genel olarak gzl tabakadan daha y sonuçlar ürettğ yönündedr. Test kümes uzunluğunun değģmesnn öngörü sonuçları üzernde cdd br etksnn olduğu görülmektedr. Her üç serde de test kümes değģm le farklı mmar yapılardan y sonuçlar elde edlmģtr. TL/Dolar ve TL/Euro zaman serlernde grd brm sayısı en y mmarler çn dama olduğu da dkkat çekmektedr. Yne bazı mmar yapılar çn en y snr ağının aynı sayıda grd ve gzl tabaka brm çermektedr. TL/Dolar ve TL/Euro zaman sers k gzl tabakanın ve model nn kullanıldığı durumlarda aynı sayıda grd ve gzl tabaka brmne sahp snr ağları en y sonuçları üretmģtr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 57
62 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI Kaynaklar Barron, A.R., (994). A comment on Neural networks: A revew from a statstcal perspectve. Statstcal Scence 9 (), Cybenko, G., (988). Contnuous Valued Neural Networks wth Two Hdden Layers are Suffcent,Techncal Report, Tuft Unversty. Cybenko, G., (989). Approxmaton by superpostons of a sgmo-dal functon, Mathematcal Control Sgnals Systems, Hornk, K., Stnchcombe, M., Whte, H., (989). Multlayer feedforward networks are unversal approxmators,neural Networks,, Lppmann, R.P., (987). An ntroducton to computng wth neural nets, IEEE ASSP Magazne, Aprl, 4. Zhang, X., (994).Tme seres analyss and predcton by neural Networks,Optmzaton Methods and Software, 4, Zhang, G., Patuwo, B.E. and Hu, Y.M., (998). Forecastng wth artfcal neural networks: The state of the art,internatonal Journal of Forecastng, 4, ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 58
63 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ĠSTATĠSTĠK'TE ENTROPĠYE DAYALI UYUM ÖLÇÜLERĠNĠN DĠĞER UYUM ÖLÇÜLERĠ ĠLE KIYASLANMASI Atıf Evren ÖZET Ġstatstk'te br olasılık ya da görel sıklık dağılımının br dğer dağılıma uygunluğunun test edlmesnde kullanılan bazı ölçüler Kolmogorov-Smrnov statstğ, olablrlk oranı statstğ, k-kare uyum ylğ test, entropye dayalı ölçüler (Kullback-Lebler sapması, Jeffrey sapması), Hellnger sapması, Bhattacharya sapması olarak sıralanablr. Bu çalıģmada ele alınan bazı dağılımların brbrlernden sapması bu ölçüler yardımı le ele alınacak ve bu ölçüler arasında br kıyaslama yapılacaktır. Anahtar Sözcükler: Uyum ylğ ölçüler, görel entrop, Jeffrey sapması,hellnger sapması A COMPARISON BETWEEN GOODNESS OF FIT MEASURES THAT ARE BASED AND THAT ARE NOT BASED ON ENTROPY MEASURES ABSTRACT Some wdely used goodness of ft measures used n statstcs especally for makng comparsons wth a theoretcal and an emprcal dstrbuton are Kolmogorov-Smrnov statstc, lkelhood rato statstc, ch-square goodness-of-ft statstc, measures based on entropy (Kullback-Lebler dvergence, Jeffrey's dvergence), Hellnger dvergence and Bhattacharya dvergence. In ths study the convergence of some probablty dstrbutons to some others wll be nvestgated through these measures. Hence, a comparson between all these measures could be possble. Keywords: Measures for goodness of ft, relatve entropy, Jeffrey's dvergence, Hellnger dvergence GĠRĠġ Uyum ylğ ölçüler, geçerl olduğu düģünülen teork br olasılık dağılımı le gözlenen verlern oluģturacağı görgül (amprk) br dağılımın uyumunun saptanmasında da kullanılmaktadır. Bu konuda önerlen ölçülern bazıları k-kare statstğ, olablrlk oranı statstğ, Kolmogorov- Öğretm Üyes, Yıldız Teknk Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, DavutpaĢa Esenler, 340 Ġstanbul, aevren@yldz.edu.tr ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 59
64 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Smrnov D statstğ, Cramer-Von Mses statstğ, olablrlk oranı, Kullback-Lebler sapması, Jeffrey sapması, Bhattacharya Hellnger sapmalarıdır (Evertt, 006).. Metrk Fonksyonlar ( x, y) adlandırılır: fonksyonu bütün (x,y) değerler çn aģağıdak koģulları yerne getryorsa metrk olarak ) ( x, y) 0, ) ( x, y) ( y, x), 3) ( x, y) 0 Sadece x=y çn 4) ( x, y) ( y, z) ( x, z) (Üçgen eģtszlğ) (Cover & Thomas, 006) Uyum ylğ çn önerlen bazı statstkler metrk olma özellğn taģımazlar. Bu bakımdan bu özellğ tanımayan ölçülern sapma (dvergence) olarak ntelendrlmes daha doğru olacaktır. Bazı çok kullanılan metrkler ve kullanım alanları çn DasGupta(008)'e baģvurulablr... Uyumun Ġylğnn K-Kare ve Olablrlk Oranı Ġstatstkler le Test Edlmes H : ( x) ( x 0 F F 0 x H : ( x) ( x 0 F ) bütün x değerler çn, F x verlmģ ve eldek örneğn brbrn kategork olarak dıģlayan k tane kategorye at olduğu ) düģünülsün. H 0 hpoteznn kabulü altında beklenen sıklıklar e (=,,...,n) olsun. Pearson tarafından önerlen test statstğ, gözlenen sıklıklar da f f e e k () Ģeklndedr. Büyük n değerler çn bu statstğn k- serbestlk derecel br k-kare dağılımına uyduğu blnmektedr (Cramér, 999).Burada testn sağlıklı sonuç vereblmes çn 5 e koģulunun yerne gelmes gerektğn vurgulamak yernde olur (Kanj, 993). ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 60
65 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Multnomal dağılan br anakütlenn k kategorsnn H hpotez altında beklenen olasılıkları 0,,..., k, gözlenen frekansları se f, f,..., f k olsun. Olablrlk fonksyonu L(,,..., ) k k f () H 0 : 0 e n =,,..,k ve ˆ f n olmak üzere olablrlk oranı T L L 0 0, ˆ, ˆ,..., 0 k ˆ k 0 ˆ,..., k f (3) Ģeklndedr. -lnt rastlantı değģkennn olasılık dağılımı yaklaģık olarak k- serbestlk derecel br k-kare dağılımıdır. Bazı statstkçler uyum ylğn belrlemek çn olablrlk oranı statstğ G ln T k f ln 0 ln f n (4) terch etmektedr. (4) le ()'n asmptotk olarak özdeģ olduğunun spatı çn Gbbons& Chakrabort (003,s05-07) 'ye göz atılablr. Agrest(00), H 'ın yanlıģ olması halnde se 0 le G nn n'dek artıģa paralel olarak büyüdükler ve büyük n değerler çn ble brbrne benzer değerlere sahp olmayableceklern belrtmektedr. Agrest, k sabtken ve n artarken 'nn dağılımının G 'nn dağılımına oranla daha hızlı br Ģeklde k-kare dağılımına yakınsadığını ve n/k<5 çn G 'nn br k-kare dağılımı le temsl edlmesnn uygun olmadığını vurgulamaktadır. Örnek büyüklüğünün bu statstklere etks çn Agrest(00, s )'ya baģvurulablr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 6
66 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 H F.3. Kolmogorov-Smrnov Ġk Örneklem Test G : ( x) ( x), : ( x) ( x) ve test statstğ de 0 n A n n H F G n D Maks X F n G ( x) ( x) n (5) Sürekl dağılımların brbrne uygunluğu çn kullanılan bu testn krtk değerler özel tablolar yardımı le elde edlmektedr (Freund & Wllams, 966). Örnek büyüklüğünün küçük olması halnde Kolmogorov-Smrnov test, k-kare testne terch edlmektedr (Conover, 999)..4. Bhattacharya Sapması Olasılık fonksyonları f ve g olan k dağılım arasındak Bhattacharya sapması B. D. cos f ( x) g( x) dx (6) olarak tanımlanmıģtır (Evertt, 006). Ġk dağılım özdeģ olduğunda bu ölçü 0'a eģt olmaktadır..5 Hellnger Sapması. f ( x) g( x) dx (7) olsun. f ve g arasındak Hellnger sapması ( ) Ģeklnde hesaplanmaktadır..6. Cramér-Von Mses Ölçüsü U ) F n( x) F 0( x) df ( x 0 (8) Örnek değerler x x,,..., x küçükten büyüğe sıralandığında ( ( x ) n 0 F sürekl se) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 6
67 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 n n F n n x n statstğ elde edleblr. Burada, x değernden küçük ya da ona eģt olan örnektek brm sayısı ve F n ( x) n olur. Yne gösterleblr. Örnekleme dağılımı tarafından ncelenmģtr.smrnov E( F ( x ) 0 n ) 6n ve 4n 3 Var ( ) 3 80 n (9) oldukları 'dan bağımsız olan 'nn dağılım yasası Smrnov çn n dağılıma sahp olduğunu göstermģtr (Cramér (999), s45). 'nın n'den bağımsız olarak belrl br lmt.7 Freeman-Tukey Ġstatstğ (T) T k o o 4e () Ģeklndedr. Burada k, kategor sayısı, s modeldek parametre sayısı, o.kategorden gelen gözlem sayısı, e, H hpoteznde varsayılan modelden hareketle. kategor çn beklenen 0 gözlem sayısıdır. Bu durumda T statstğ, asmptotk olarak k-s- serbestlk derecel br k-kare dağılımına uymaktadır (Evertt, 006). Upton&Cook( 005), ( ) no'lu denklemn sol tarafını T H 0 le fade edyorlar. Denklemn sağ tarafı se ()'de fade edldğ gbdr. T statstğnn doğru olduğunda yaklaģık olarak k-s serbestlk derecel br k-kare dağılımına uyduğunu belrtyorlar. Tanımlardak bu farklılıkları belrtmek gerekyor.. Entrop Boltzman'a göre br fzksel sstemn entrops, sstemdek düzenszlğn (dsorder) br ölçüsüdür ( Rény, 007a). Br statstksel deneyn entrops, deneyn sonucu le lgl belrszlk mktarının br ölçüsü olarak da kabul edleblr (Reny, 007b). Entrop kavramının dğer bazı uygulama alanları çn Evren(00) nceleneblr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 63
68 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00. Keskl Hallerde Entrop Keskl br örnek uzayı S çnde X rastlantı değģkennn sırası le p, p,..., p n olsun. x x,,..., x değerlern alma olasılıkları n H n p log p (3) Ģeklnde tanımlanan Shannon entrops br statstksel deneyn belrszlğnn br ölçüsüdür. X n entrops, X sonucunu ortaya koyablmek çn gerekl olan mnmum ortalama bt sayısı olarak da görüleblr (Garca, 994). Örnek uzayı S çersnde en büyük entrop, bütün elemanter X x =,,,n UlaĢılablecek maksmum entrop log(n ) olaylarının Ģanslarının eģt olması halnde karģımıza çıkar. H maks olur. Öte yandan X xk (k=,,...,n) çn ) kesn olaysa H=0 olur. Dolayısıyla keskl br olasılık dağılımı çn entrop 0 le log(n) arasında değer alır... Sürekl Dağılımlar çn Entrop Sürekl değģken X n entrops (dferansyel entrop) H ( X ) log( f ( x)) f ( x) dx (4) Ģeklnde olur (Reza, 994)..3. Kullback-Lebler enformasyonu ve görel entrop Görel entrop D( p q) k olasılık dağılımı arasındak sapmanın br ölçüsüdür. Keskl dağılımlar çn Kullback-Lebler sapması (ya da görel entrop) p( x) D ( p q) KL x p( x)log (5) q( x) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 64
69 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 olarak tanımlanmıģtır. Bu konunun daha ayrıntılı ele alınıģı çn Pardo ( 006)'ya bakılablr. Sürekl haller çn de bu sapma benzer Ģeklde tanımlanablr. (5) le (4) arasındak paralellk ncelendğnde Kullback-Lebler sapmasının dağılımının k-kare dağılımı le ncelenebleceğ düģünüleblr. Kullback-Lebler sapması metrk olmanın tüm koģullarını sağlamamaktadır: D KL D ( p q) ( q p) KL (6).4. Kullback-Lebler Sapmasının Smetrk Br Versyonu: Jeffrey Sapması D J( p q) D ( p q) D ( q p) KL KL (7) bçmndedr (Evertt, 006). Jeffrey sapması da metrk değldr ( Kullback, 997). 3. Uyum Ġylğ çn Power Dvergence Ġstatstğ n,. gruba düģen gözlem sayısı, ˆ de bu gruba düģmes öngörülen gözlem sayısı olsun. Bu durumda Cresse&Read tarafından önerlen sapma statstğ( power dvergence statstc) n P. D. S. ( ) n ˆ (8) bçmndedr. Burada sözgelm çn, çn G, çn Freeman-Tukey statstğ, çn Kullback'ın mnmum ayırıcı blg statstğ türetlmektedr (Agrest(00),s). ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 65
70 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Uygulama Tablo: Uygulamadak Kuramsal ve Görgül Dağılımlar (Snedecor&Cochran(969) 'dan alınmıģtır.) Gruplar Gözlenen sıklık (o) Beklenen sıklık (e) Gruplar Gözlenen sıklık (o) Beklenen sıklık (e) A 0. G 36 4 B H C Ġ D J 4 E 39 4 K 0 0. F Toplam Tablo :Tablo dek ver çnuyum Ġylğ Ġstatstkler K-Kare G-Kare Kolmogorov- Smrnov Bhattacharya Hellnger Cramer-Von Mses Freeman- Tukey Kullback- Lebler Jeffrey's Tablo 3: Ġknc Sıklık Dağılımı (Gözlenen ve Beklenen Sıklıklar) Gruplar Gözlenen sıklık (o) Beklenen sıklık (e) Gruplar Gözlenen sıklık (o) Beklenen sıklık (e) A G 36 4 B 3 H C Ġ D 3.4 J 4 E 6 4 K 0 0. F Toplam Tablo 4: Tablo 3 dek ver çn Uyum Ġylğ Ġstatstkler K-Kare G-Kare Kolmogorov- Smrnov Bhattacharya Hellnger Cramer-Von Mses Freeman- Tukey Kullback- Lebler Jeffrey's ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 66
71 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo 5: Uyumun Çok Ġy Olduğu Üçüncü Ver Setnn Gözlenen ve Beklenen Sıklıkları Gruplar Gözlenen sıklık (o) Beklenen sıklık (e) Gruplar Gözlenen sıklık (o) Beklenen sıklık (e) A 0 0. G 4 4 B H 3.4 C Ġ D J E 4 4 K 0 0. F Toplam Tablo 6: Tablo 5 le Ġlgl Uyum Ġylğ Ġstatstkler K-Kare G-Kare Kolmogorov- Smrnov Bhattacharya Hellnger Cramer-Von Mses Freeman- Tukey Kullback- Lebler Jeffrey's E SONUÇ Genel olarak bütün statstkler uyum ylğ arttığında küçük sapma, uyum ylğ azaldığında büyük sapma değerler vermektedr. Bununla brlkte sapmaların büyüklüklernn brbrlernden barz br bçmde farklı olabldkler gözlenmektedr. Bunun sebebnn kullanılan ölçeklern (logartmk değerlern, karel değerlern kullanılması gb) farklı olmasından kaynaklandığı düģünüleblr. Görel entrop, Jeffrey sapması, Freeman-Tukey, kkare, olablrlk oranı gb statstklern dağılım özellkler lteratürde ncelenmģ bulunduğundan, Hellnger sapması, Bhattacharya sapması gb ölçülere oranla avantajlıdırlar. Bütün bunlarla brlkte sürekl br dağılımın keskl hale getrlmes halnde farklı gruplandırma yöntemlernn bu ölçüler nasıl etkleyeceğ de ncelenmeldr. KAYNAKLAR AGRESTI, A.(00), Categorcal Data Analyss, Wley Interscence (Second Edton), Hoboken, New Jersey, s 4 CRAMER,H.(999), Mathematcal Methods of Statstcs, Prnceton Unversty Press, Nneteenth Prntng and Frst Paper Prntng 999, s46-49 CONOVER, W.J.(999), Practcal Nonparametrc Statstcs, Wley Seres n Probablty and Statstcs, Thrd Edton, s 430 COVER, T.M.; THOMAS, J.A.(006) Elements of Informaton Theory, Wley Interscence (Second Edton), Hoboken, New Jersey, s45 ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 67
72 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 DASGUPTA, A.(008), Asymptotc Theory of Statstcs and Probablty, Sprnger Texts n Statstcs, s0- EVERITT,B.S.( 006); The Cambrdge Dctonary of Statstcs, Cambrdge Unversty Press (Thrd Edton), Cambrdge EVREN, A.(00), Entropnn Ġstatstk tek Bazı Uygulamaları, II. Ulusal Konya Ereğl Kemal Akman Meslek Yüksek Okulu Teblğ Günler, 3-4 Mayıs 00 FREUND, J.E., WILLIAMS, F.J.(966), Dctonary/Outlne of Basc Statstcs, Dover Publcatons, NY GARCIA, A.L.(994), Probablty and Random Processes for Electrcal Engneerng, Addson- Wesley Longman (Second Edton), s69 GIBBONS, J.D., CHAKRABORTI, S. (003), Nonparametrc Statstcal Inference, Statstcs: A Dekker Seres of Textbooks and Monographs (Fourth Edton, Revsed and Expanded),Marcel Dekker Inc.,s05-07 KANJI, G.(993), 00 Statstcal Tests, Sage Publcatons, reprnted 995, s KULLBACK, S.(996), Informaton Theory and Statstcs, Dover Publcatons, NY,s6 PARDO, L.(006), Statstcal Inference Based on Dvergence Measures, Chapman&HALL/CRC, s-34 RENYI, A(007a), Probablty Theory, Dover Publcatons, NY, s 554 RENYI, A.(007b), Foundatons of Probablty, Dover Publcatons,NY, s3 REZA,F.M.(994) ; An Introducton to Informaton Theory, Dover Publcatons, NY, s68 SNEDECOR, G.W., COCHRAN, W.G.(969), Statstcal Methods, The Iowa State Unversty Press, Sxth Edton (Thrd Prntng), s6 UPTON, G.; COOK, I. (006); Oxford Dctonary of Statstcs, Oxford Unversty Press (Second edton), NY ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 68
73 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 L-SIRALI KÜME ÖRNEKLEMESĠ KULLANILARAK YIĞIN ORTALAMASININ TAHMĠN EDĠLMESĠ Nlay AKINCI * Yaprak Arzu ÖZDEMĠR ** ÖZET L-sıralı küme örneklemes (LSKÖ), yığın ortalamasını tahmn etmek çn önerlen sıralı küme örneklemes (SKÖ) tasarımlarından brdr. 007 de Al-Saleh tarafından önerlen LSKÖ le, özellkle verde bulunan uç değerlerden etklenmeyen ve smetrk dağılımlar altında yansız br tahmn edcnn elde edlmes mümkündür. Bu çalıģmada, LSKÖ tasarımı le elde edlen yığın ortalamasına lģkn tahmn edcnn, çeģtl dağılımlar ve farklı örnek çapları altında, blnen SKÖ tasarımından elde edlen tahmn edcye göre etknlğ smülasyon çalıģması le ncelenmģtr.ayrıca önerlen dğer SKÖ tasarımlarından elde edlen tahmn edclern de, SKÖ ye göre etknlkler elde edlerek, LSKÖ tasarımının hang dağılımlar altında daha etkn olduğu saptanmaya çalıģılmıģtır. Anahtar kelmeler: L-tahmn edc, Sıralı Küme Örneklemes, Medyan Sıralı Küme Örneklemes, Uç Sıralı Küme Örneklemes, Yüzde Sıralı Küme Örneklemes, Görel Etknlk ESTIMATION OF POPULATION MEAN BY USING L RANKED SET SAMPLING ABSTRACT L-ranked set samplng (LRSS) s one of the ranked set samplng desgns to estmate the populaton mean. LRSS was proposed by Al-Saleh n 007. It s seen that, especally when the data contans outlers, t s possble to obtan an estmator usng LRSS whch s not affected by outlers and unbased n symmetrc dstrbutons. In ths study, the effcency of the populaton mean estmators obtaned by LRSS accordng to the ranked set samplng (RSS) s nvestgated usng smulaton studes at varous dstrbutons and dfferent sample szes. Also, the relatve effcences of estmators obtaned by other proposed RSS desgns are calculated accordng to classcal RSS desgn and determned the dstrbutons where LRSS desgn s more effectve. Keywords:L-estmator, Ranked set samplng, Percentle ranked set samplng, Extreme ranked set samplng, Medan ranked set samplng, Relatve effcency *Öğrenc, Gaz Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, 06 Ankara, akncnlay@gmal.com ** Yrd. Doç. Dr, Gaz Ünverstes, Fen Edebyat Fakültes, Ġstatstk Bölümü, Ankara, yaprak@gaz.edu.tr(haberleģme Adres) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 69
74 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00.GĠRĠġ Sıralı Küme Örneklemes (SKÖ), Bast Tesadüf Örneklemeye (BTÖ) alternatf olarak 95 yılında McIntyre tarafından önerlmģtr. SKÖ, özellkle lglenlen değģken kolay ölçüleblr olmadığı zaman, fakat brmler lglenlen değģken bakımından sıralamak daha kolay olduğunda kullanılır. Bu sıralama görsel yolla veya bazı ucuz ölçüm metotları kullanılarak yapılablr. SKÖ le örnek seçmnde öncelkle lgl yığından seçlen çaplı tesadüfî br örnek, her br n çaplı n kümeye tamamen tesadüfî olarak paylaģtırılır. Böylece brbrnden bağımsız n çaplı n tane küme elde edlmģ olur. Her br kümedek elemanlar kend çnde sıralanarak, kümelern brncsnden lk sıradak brm, kncsnden knc sıradak brm ve bu Ģeklde devam edlerek n. kümeden n. sıradak brm seçlr. SKÖ altında yığın ortalaması nün yansız tahmn edcs n X SKÖ n n X, n () Ģeklnde tanımlanır. Burada, X : n n büyüklüğündek. kümenn. sıra statstğn fade etmektedr. Sıra statstkler bu örnekleme tasarımı altında brbrnden bağımsızdır. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 70 X SKÖ, örnek çapı n aynı kalmak üzere, yığın dağılımı ne olursa olsun BTÖ den elde edlen tahmn edcden daha etkn br tahmn edcdr. Ancak yığının dağılımı blnyorken, tahmn edcnn etknlğn artırmak amacıyla blnen SKÖ le örnek seçm yerne farklı örnek seçmler önerlmģtr. Samaw ve dğerler özellkle tekdüze dağılımın yığın ortalamasını tahmn etmek üzere uç (extreme) SKÖ (USKÖ) n önermģlerdr (Samaw ve dğ., 996). USKÖ de örnek seçm n n çft ya da tek olmasına göre değģr.n çft se; kend çnde sıralanan n brmlk lk (n/) kümeden. sıradak brm, kalan (n/) kümeden se n. sıradak brm seçlr. n tek se; kend çnde sıralanan n brmlk lk ( ) / kümeden. sıradak brm, ( n son ( ) / n n / ). kümeden medyan değer, kümeden se n. sıradak brm seçlr. Örneğe çıkan brmler stenlen hassalıktak br ölçümle lglenlen değģken bakımından ölçülür ve n çaplı uç sıralı küme örneğ elde edlr. Bu tasarım özellkle tekdüze ve tek modlu olmayan smetrk dağılımlar altında SKÖ den daha etkn sonuçlar vermektedr. Muttlak, normal ve üstel dağılımlar çn yığın ortalamasını tahmn etmek üzere medyan SKÖ (MSKÖ) n önermģtr (Muttlak,998). MSKÖ tasarımında örnek seçm n n çft ya da tek olmasına göre değģr.n çft se; kend çnde sıralanan n brmlk lk (n/) kümeden (n/). sıradak brmler ve kalan (n/) kümeden ((n/)+). sıradak brmler seçlr. n tek se; kend çnde sıralanan brmlerden medyan değerler örneğe seçlr. Örneğe çıkan brmler stenlen hassalıktak br ölçümle lglenlen değģken bakımından ölçülür ve n çaplı medyan sıralı küme örneğ elde edlr.mskö le özellkle tek modlu smetrk dağılımlar altında SKÖ den daha etkn
75 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 sonuçlar elde edlmektedr. Muttlak ayrıca yüzde (percentle) SKÖ (YSKÖ) n önermģtr (Muttlak, 003). Bu tasarımda öncelkle 0 ve q=-p olmak üzere br p değer belrlenr ve p örnek seçm Ģlemnde n çft se lk n/ örneğn (p(n+)) nc sıradak brmler ve knc n/ örneğn (q(n+)) nc sıradak brmler örneğe seçlr. n tek se lk (n )/ örneğn (p(n+)) nc sıradak brmler, son (n )/ örneğn (q(n+)) nc sıradak brmler ve kalan örneğn medyanı örneğe seçlr. YSKÖ yığın dağılımı smetrk olduğunda yığın ortalaması çn yansız br tahmn edc vermektedr.ayrıca belrlenen yığın dağılımı altında p değerne bağlı olarak SKÖ ye göre etknlğ değģmektedr.bunun dıģında yen SKÖ, tesadüfî seçme dayalı yen SKÖ, ağırlıklı SKÖ ve L-SKÖ gb tasarımlar da önerlmģtr (Bhoj, 000; L ve ark., 999; Muttlak ve Abu-Dayyeh, 004; Al-Nasser, 007).Ayrıca son yıllarda, örnek seçm Ģlemnn çok aģamalı olarak gerçekleģtğ SKÖ tasarımları da önerlmģtr. Çft SKÖ, çok aģamalı SKÖ, çok aģamalı çeyrek SKÖ bu tasarımlara örnek olarak verleblr (Al-Saleh ve Al-Kadr, 999; Al-Saleh ve Al-Omar, 00; Jeman ve Al-Omar,007). Bu çalıģmada, Al-Nasser tarafından önerlen LSKÖ tasarımı tanıtılacaktır.bu tasarım le yığın ortalaması çn özellkle verdek uç değerlerden etklenmeyen ve smetrk dağılımlar altında yansız br tahmn edcnn elde edlmes mümkündür. LSKÖ nün SKÖ ye göre etknlğn detaylı olarak ncelemek amacıyla, çeģtl dağılımlar ve örnek çapları altında yığın ortalamasına lģkn tahmn edcnn ortalama hata kare(ohk) ve görel etknlk(ge) değer smülasyon yoluyla elde edlmģtr. Ayrıca dğer SKÖ tasarımlarından MSKÖ, USKÖ ve YSKÖ le etknlk bakımından karģılaģtırma yapılarak LSKÖ nün hang dağılımlar altında daha etkn olduğu belrlenmeye çalıģılmıģtır.. L SIRALI KÜME ÖRNEKLEMESĠ ĠLE ÖRNEK SEÇĠMĠ VE YIĞIN ORTALAMASININ TAHMĠNĠ LSKÖ tasarımında örnek seçm Ģlem aģağıdak adımlar zlenerek yapılır. ) Her br n büyüklüğünde, tesadüfî n örnek seçlr. ) Görsel yolla veya ucuz metotlarla, lglenlen değģken göz önüne alınarak brmler sıralanır. Bu sıralamanın hassas ölçümlü sıralama kadar y olduğu varsayılmaktadır. 3) olmak koģuluyla k n. LSKÖ katsayısı seçlr. Burada k, n. ya eģt veya n. dan küçük olan tamsayı değerlernn en büyüğünü fade etmektedr. 4) Ġlk (k+) küme çn (k+). sıradak brmler, son (k+) küme çn (n-k). sıradak brmler ve j=k+,...,n-k-. küme çn se j. sıradak brm seçlr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 7
76 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 5) Örneğe çıkan brmler SKÖ tasarımında olduğu gb stenlen hassalıktak br ölçümle lglenlen değģken bakımından ölçülür ve n çaplı L-sıralı küme örneğ elde edlr. Tablo ve de sırasıyla n=5 ve n=6 ken k= çn seçlen LSKÖ örnekler gösterlmektedr. Tablo. n=5 ve k= çn LSKÖ tasarımı le örneğe seçlen brmler X [,5] X [,5] X [3,5] X [4,5] X [5,5] X [,5] X [,5] X [3,5] X [4,5] X [5,5] X 3[,5] X 3[,5] X 3[3,5] X 3[4,5] X 3[5,5] X 4[,5] X 4[,5] X 4[3,5] X 4[4,5] X 4[5,5] X 5[,5] X 5[,5] X 5[3,5] X 5[4,5] X 5[5,5] Tablo. n=6 ve k= çn LSKÖ tasarımı le örneğe seçlen brmler X [,6] X [,6] X [3,6] X [4,6] X [5,6] X [6,6] X [,6] X [,6] X [3,6] X [4,6] X [5,6] X [6,6] X 3[,6] X 3[,6] X 3[3,6] X 3[4,6] X 3[5,6] X 3[6,6] X 4[,6] X 4[,6] X 4[3,6] X 4[4,6] X 4[5,6] X 4[6,6] X 5[,6] X 5[,6] X 5[3,6] X 5[4,6] X 5[5,6] X 5[6,6] X 6[,6] X 6[,6] X 6[3,6] X 6[4,6] X 6[5,6] X 6[6,6] LSKÖ le seçlen örnekten, yığın ortalamasının tahmn edcs aģağıdak gb tanımlanır. k nk n LSKÖ k n n n k n n l nk X X X X : : : ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 7
77 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 X LSKÖ, smetrk dağılımlar altında yığın ortalamasının yansız br tahmn edcsdr. Ancak smetrk olmayan dağılımlar altında yanlı br tahmn edc olduğundan X LSKÖ nün OHK s OHK X LSKÖ Var( X LSKÖ ) E X LSKÖ Ģeklnde tanımlanır. 3. SĠMÜLASYON ÇALIġMASI Bu bölümde, USKÖ, MSKÖ, YSKÖ ve LSKÖ tasarımlarının SKÖ ye göre GE değerler smülasyon yoluyla ncelenecektr. YSKÖ çn p nn 0.0 ve 0.40 değerler ncelenmģtr. Ayrıca, smetrk dağılımlardan Normal(0,), Laplace(0,0.5) ve Tekdüze(0,) dağılım le smetrk olmayan dağılımlardan Beta(,9), Beta(9,), Üstel() ve Log-normal(0,) dağılımları ele alınmıģtır. Dağılımlar belrlenrken basıklık ve çarpıklık katsayıları dkkate alınmıģtır. Matlab paket programı kullanılarak, her br tasarım çn n=3,4,5,6,0 ve çaplı örnekler seçlerek, tahmn edcnn beklenen değer, OHK s ve SKÖ ye göre GE değerler tekrarlı smülasyon çalıģması le hesaplanmıģtır. GE değer, Var( X ) GE OHK X SKÖ * ( SKÖ) Ģeklnde tanımlanmaktadır. Burada OHK X * ( SKÖ ), dğer SKÖ tasarımlarından (USKÖ, MSKÖ, YSKÖ, LSKÖ) elde edlen tahmn edcnn OHK değern fade etmektedr. Elde edlen sonuçlar Tablo 3-9 arasında verlmektedr. Ayrıca, LSKÖ de n=3,4 çn k=, n=3,4,5,6 çn k=3 değern alması mümkün olmadığından tablolarda lgl kısımlar boģ bırakılmıģtır. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 73
78 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo 3. Normal(0,) dağılımı altında SKÖ tasarımlarından elde edlen tahmn edcnn sapma ve GE değer Örnek çapı n=3 n=4 n=5 n=6 n=0 n= Tasarımlar SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE USKÖ 0,00,00 0,00 0,86 0,00 0,87 0,00 0,76 0,00 0,60 0,00 0,6 MSKÖ 0,00,6 0,00,8 0,00,7 0,00,8 0,00,37 0,00,4 LSKÖ(k=) 0,00,6 0,00,7 0,00,8 0,00,7 0,00,4 0,00,5 LSKÖ(k=) ,00,8 0,00,6 0,00,4 0,00,4 LSKÖ(k=3) ,00,3 0,00,33 YSKÖ(p=0,0) 0,00,00 0,00 0,86 0,00 0,87 0,00 0,75 0,00 0,97 0,00 0,97 YSKÖ(p=0,40) 0,00,6 0,00,8 0,00,9 0,00,8 0,00,3 0,00,38 Tablo 4. Tekdüze(0,) dağılımı altında SKÖ tasarımlarından elde edlen tahmn edcnn sapma ve GE değer Örnek çapı n=3 n=4 n=5 n=6 n=0 n= Tasarımlar SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE USKÖ 0,00,00 0,00,4 0,00, 0,00,56 0,00,8 0,00,97 MSKÖ 0,00 0,83 0,00 0,8 0,00 0,78 0,00 0,78 0,00 0,7 0,00 0,7 LSKÖ(k=) 0,00 0,84 0,00 0,83 0,00 0,87 0,00 0,89 0,00 0,93 0,00 0,94 LSKÖ(k=) ,00 0,78 0,00 0,78 0,00 0,84 0,00 0,87 LSKÖ(k=3) ,00 0,77 0,00 0,79 YSKÖ(p=0,0) 0,00,00 0,00,4 0,00, 0,00,56 0,00, 0,00, YSKÖ(p=0,40) 0,00 0,84 0,00 0,8 0,00 0,86 0,00 0,78 0,00 0,78 0,00 0,74 ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 74
79 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo 5. Laplace (0,0.5) dağılımı altında SKÖ tasarımlarından elde edlen tahmn edcnn sapma ve GE değer Örnek çapı n=3 n=4 n=5 n=6 n=0 n= Tasarımlar SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE USKÖ 0,00,0 0,00 0,69 0,00 0,69 0,00 0,5 0,00 0,36 0,00 0,36 MSKÖ 0,00,83 0,00,9 0,00,45 0,00,55 0,00 3,44 0,00 3,74 LSKÖ(k=) 0,00,8 0,00,90 0,00,8 0,00,76 0,00,57 0,00,53 LSKÖ(k=) ,00,4 0,00,55 0,00,6 0,00,0 LSKÖ(k=3) ,00,86 0,00,75 YSKÖ(p=0,0) 0,00,00 0,00 0,68 0,00 0,69 0,00 0,5 0,00,0 0,00 0,99 YSKÖ(p=0,40) 0,00,8 0,00,90 0,00,83 0,00,54 0,00,74 0,00 3,40 Tablo 6.Üstel() dağılımı altında SKÖ tasarımlarından elde edlen tahmn edcnn sapma ve GE değer Örnek çapı n=3 n=4 n=5 n=6 n=0 n= Tasarımlar SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE USKÖ 0,00,00 0,6 0,63 0,5 0,6 0,3 0,3 0,5 0,09 0,48 0,08 MSKÖ 0,7,35 0,7,9 0,,03 0, 0,88 0,5 0,39 0,6 0,3 LSKÖ(k=) 0,7,35 0,7,9 0,5,0 0,3,5 0,09,07 0,08,07 LSKÖ(k=) ,,0 0, 0,88 0,6 0,7 0,5 0,69 LSKÖ(k=3) , 0,48 0, 0,46 YSKÖ(p=0,0) 0,00,00 0,7 0,6 0,5 0,6 0,3 0,3 0,07 0,87 0,07 0,83 YSKÖ(p=0,40) 0,7,35 0,7,9 0,5,9 0, 0,88 0, 0,5 0,5 0,35 ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 75
80 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo 7. Beta(,9) dağılımı altında SKÖ tasarımlarından elde edlen tahmn edcnn sapma ve GE değer Örnek çapı n=3 n=4 n=5 n=6 n=0 n= Tasarımlar SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE USKÖ 0,00,00 0,0 0,8 0,0 0,80 0,0 0,53 0,03 0,9 0,03 0,8 MSKÖ 0,0, 0,0,0 0,0,03 0,0 0,96 0,0 0,60 0,0 0,5 LSKÖ(k=) 0,0, 0,0, 0,0,07 0,0,05 0,0,0 0,00,0 LSKÖ(k=) ,0,0 0,0 0,96 0,0 0,86 0,0 0,85 LSKÖ(k=3) ,0 0,69 0,0 0,67 YSKÖ(p=0,0) 0,00,00 0,0 0,8 0,0 0,80 0,0 0,53 0,00 0,88 0,00 0,87 YSKÖ(p=0,40) 0,0, 0,0,09 0,0,07 0,0 0,96 0,0 0,7 0,0 0,56 Tablo 8.Beta(9,) dağılımı altında SKÖ tasarımlarından elde edlen tahmn edcnn sapma ve GE değer Örnek çapı n=3 n=4 n=5 n=6 n=0 n= Tasarımlar SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE USKÖ 0,00,00 0,0 0,80 0,0 0,80 0,0 0,53 0,03 0,9 0,03 0,8 MSKÖ 0,0, 0,0,0 0,0,03 0,0 0,96 0,0 0,6 0,0 0,5 LSKÖ(k=) 0,0, 0,0,09 0,0,07 0,0,06 0,0,03 0,00,0 LSKÖ(k=) ,0,03 0,0 0,96 0,0 0,86 0,0 0,84 LSKÖ(k=3) ,0 0,70 0,0 0,67 YSKÖ(p=0,0) 0,00,0 0,0 0,80 0,0 0,80 0,0 0,53 0,00 0,89 0,00 0,86 YSKÖ(p=0,40) 0,0, 0,0,0 0,0,07 0,0 0,96 0,0 0,7 0,0 0,56 ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 76
81 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Tablo 9. Log-normal(0,) dağılımı altında SKÖ tasarımlarından elde edlen tahmn edcnn sapma ve GE değer Örnek çapı n=3 n=4 n=5 n=6 n=0 n= Tasarımlar SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE SAPMA GE USKÖ 0,00,0 0,39 0,5 0,36 0,49 0,74 0,7,9 0,09, 0,09 MSKÖ 0,40,57 0,40,33 0,49,7 0,50,48 0,56 0,67 0,58 0,56 LSKÖ(k=) 0,39,59 0,40,35 0,36,03 0,33,99 0,4,75 0,3,7 LSKÖ(k=) ,50,7 0,49,49 0,40,5 0,38, LSKÖ(k=3) ,50 0,8 0,48 0,77 YSKÖ(p=0,0) 0,00 0,99 0,40 0,5 0,37 0,49 0,74 0,7 0,07,7 0,08,63 YSKÖ(p=0,40) 0,40,59 0,40,34 0,37,0 0,49,49 0,49 0,85 0,55 0,6 Tablo 3-9 ncelendğnde, sapma değerler bakımından USKÖ, MSKÖ, YSKÖ ve LSKÖ tasarımlarından elde edlen tahmn edcsnn smetrk dağılımlar altında sapmasız ken, smetrk olmayan dağılımlar altında sapmalı olduğu görülmektedr. X Tablo 3-9 dan görüldüğü gb, ncelenen smetrk tek modlu dağılımlarda GE değer en yüksek olan tasarım MSKÖ tasarımıdır. YSKÖ (p=0.40) ve LSKÖ (k=) tasarımları da en az MSKÖ tasarımı kadar etkndr. Smetrk tek modlu dağılımlar altında LSKÖ tasarımında k arttıkça etknlk artmaktadır. Bu çalıģmada ncelenen smetrk tek modlu dağılımlar altında MSKÖ tasarımının en yüksek GE değerne sahp olduğu dağılım Laplace (0,0.5) dağılımdır. Laplace (0,0.5) dağılımı ncelenen smetrk tek modlu dağılımlar çnde basıklık katsayısı en yüksek olan dağılımdır. Smetrk tek modlu olmayan Tekdüze(0,) dağılımında se en etkl tasarım USKÖ dür. Smetrk olmayan dağılımlar altında se, en etkl tasarımın LSKÖ(k=) tasarımı olduğu görülmektedr. Smetrk olmayan dağılımlar altında LSKÖ tasarımında k arttıkça etknlk azalmaktadır. Ayrıca n=3,4 ve 5 değerler çn YSKÖ (p=0.40) ve MSKÖ tasarımlarının da etkn olduğu söyleneblr. Bu çalıģmada ncelenen smetrk olmayan dağılımlar altında LSKÖ(k=) ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 77
82 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 tasarımının en yüksek GE değerne sahp olduğu dağılım Log-normal(0,) dağılımdır. Lognormal(0,) dağılımı ncelenen smetrk olmayan dağılımlar çnde basıklık katsayısı en yüksek olan dağılımlardır. Dolayısıyla basıklık katsayısının GE değern etkledğ ve basıklık katsayısı yüksek olan dağılımlarda etknlğn arttığı söyleneblr. Smetrk olmayan dağılımlardan Beta(9,) ve Beta(,9) dağılımları sırasıyla sağa ve sola çarpık dağılımlar olduğundan basıklık katsayıları aynı, çarpıklık katsayıları se mutlak değerce brbrnn aynısıdır. GE değerlerne bakıldığında se sonuçların brbrne çok yakın olduğu görülmektedr. Buradan da dağılımın çarpıklığının GE değer üzernde etkl olmadığı söyleneblr. Sonuç olarak, LSKÖ tasarımı özellkle smetrk olmayan dağılımlar altında, sapmalı br tahmn edc vermesne rağmen örnek çapı arttıkça SKÖ ye göre daha etkn br tahmn edc elde edlmesne mkan vermektedr. Ayrıca smetrk tek modlu dağılımlar altında k arttıkça, smetrk olmayan dağılımlarda se k azaldıkça GE artmaktadır. KAYNAKLAR Al-Nasser, A. D. (007). L-Ranked Set Samplng: A generalzaton procedure for robust vsual samplng. Communcatons n Statstcs-Smulaton and computaton 36, Al-Saleh, M. F., and Al Kadr, M. A:(000). Double ranked set samplng, Statstcs & Probablty Letters, 48: 05-. Al-Saleh M. F. and Al-Omar, A.I. (00) Multstage ranked set samplng, Journal of Statstcal Plannng And Inference, 0: Bhoj, D.S. (000) New ranked set samplng for one-parameter famly of dstrbutons, Bometrcal Journal, 4: Jeman, A. A. and Al-Omar A. I. (007) Multsatge quartle ranked set samples, Pak. J.Statst., 3(): -. L, D., Snha, B.K. and Perron,F. (999). Random selecton n ranked set samplng and ts applcatons, Journal of Statstcal Plannng and Inference,76:85-0. Mclntyre, G.A. (95). A metod of unbased selectve samplng usng ranked sets. Australan Journal of Agrcultural Research, ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 78
83 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Muttlak,H.A. (997). Medan ranked set samplng.. Appled Statstcal Scence, 6(4), Muttlak, H.A. (003). Modfed ranked set samplng. Pakstan Journal of Statstcs 9.3(4): Muttlak,H. A., and Abu-Dayyeh,W. (004). Weghted modfed ranked set samplng methods, Appled Mathematcs and Computaton, 5: Samaw, H., Abu-Dayyeh, W.,Ahmed,M. S. (996). Estmatng the populaton mean usng extreme ranked set samplng. Bometrcal Journal 38: ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 79
84 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ÖLÇÜM YETERLĠLĠK PARAMETRELERĠNĠN TAHMĠN EDĠCĠLERĠ VE GÜVEN ARALIKLARI Ümt YAMAN Yunus AKDOĞAN** Ahmet PEKGÖR*** CoĢkun KUġ**** ÖZET Bu çalıģmada, rasgele ve karma etkl modellerde ölçüm yeterllk parametrelernn tahmn edcler ve güven aralıkları Selçuk Stat programına monte edlmģtr. Ayrıca Selçuk Stat yazılımının çıktıları, Dolezal, Burdck ve Brch (998) n sonuçları le karģılaģtırılmıģtır. Anahtar kelmeler: Güven aralıkları, ölçüm yeterllk parametreler, tekraredleblrlk, tekrarüretleblrlk, varyans analz modeller. ESTIMATORS AND CONFIDENCE INTERVALS FOR MEASUREMENT CAPABILITY PARAMETERS ABSTRACT In ths study, the estmators and confdence ntervals of measurement capablty parameters are assembled to Selçuk Stat software under random and mxed effects models. Also outputs of Selçuk Stat are compared wth results of Dolezal, Burdck and Brch (998). Keywords: Analyss of varance models, confdence nterval, measurement capablty parameters, repeatablty, reproducblty. GĠRĠġ Ölçüm değģkenlğnn tespt edlmes ürün ve süreç değģkenlğn doğru br bçmde gözlemlemek çn gerekldr. Tekraredleblrlk, operatörlern ürünler tekrar tekrar ölçtüğünde hemen hemen aynı değerde ölçeblme kablyetn, Terkrarüretleblrlk, operatörlern brbryle uyum kablyetn göstermek üzere Tekraredleblrlk ve Terkrarüretleblrlk (Repeatablty&Reproducblty, R&R) dğer br deyģle ölçüm (Gauge, gage) analz, ölçüm prosedürünün yeterl olup olmadığını belrlemek çn kullanılır. Ölçüm prosedürü le lgl değģm kaynakları, varyans analz (Analyss of Varance, ANOVA) kullanılarak tespt edleblr. R&R analznde genel olarak kullanılan ANOVA model, operatör ve parça olmak üzere k faktörden(etken) oluģur. R&R analznden önce operatörler ürünler tekrar tekrar ölçerler. Genellkle operatörler, operatörler ktlesnden rasgele seçldğ varsayıldığından ANOVA modelndek faktörler rasgele faktör (random effect) olarak ele alınır. Ne var k süreç * Öğrenc, Selçuk Ünverstes, Fen Fakültes, Ġstatstk Bölümü, 403 Konya, yamanad@mynet.com ** ArĢ.Gör., Selçuk Ünverstes, Fen Fakültes, Ġstatstk Bölümü,, 403 Konya, yakdogan@selcuk.edu.tr ***Öğr.Gör.Dr, Selçuk Ünverstes, Fen Fakültes, Ġstatstk Bölümü, 403 Konya, pekgor@selcuk.edu.tr ****Doç.Dr., Selçuk Ünverstes, Fen Fakültes, Ġstatstk Bölümü, 403 Konya, coskun@selcuk.edu.tr ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 80
85 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 çıktısı ürünler ölçen operatörler özel seçml (fx) faktör de olablr. Örneğn br fabrkadak üretlen parçaları ölçmek çn önceden sthdam edlmģ üç operatöründe ölçüm yapması durumunda operatör faktörü özel seçml olarak ele alınmalıdır. Ölçüm prosesnn yeterl olup olmadığını tespt etmek çn Tekraredleblrlk ve Terkrarüretleblrlk dıģında kullanılan parametrelerden bazıları PTR(Precson-to-Tolerance Rato), (Burdck, Borror ve Montgomery, 003), SNR(Sgnal-to-Nose Rato), (AIAG, 995, Sayfa 3) ve DR(Dscrmnant Rato), (Mader ve ark, 999 ve Wheeler, 99) olarak sıralanablr. Mntab 5 ve NCSS 007 yazılımları, R&R analzn uygulayablmektedrler. Mntab 5, R&R analz çn operatörlern ve parçaların rasgele faktör olarak ele alındığı ANOVA modeln kullanılmasına karģın operatörlern sabt olarak ele alınması durumunda karma model kullanılması çn br seçenek bulunmamaktadır. Mntab 5 yazılımı, ölçüm değģkenlk parametrelernn tahmn değerlern verrken, güven aralıklarını vermemektedr. Ayrıca yukarıda bahsedlen PTR, SNR ve DR parametrelernn güven aralıkları Mntab 5 yazılımında hesaplanmamaktadır. NCSS 007 yazılımında yukarıda bahsedlen güven aralıkları verlmektedr. Bu çalıģmada, ölçüm sstemler analznde kullanılan ölçüm yeterllk parametreler ve bu parametrelern tahmn edcler ve güven aralıkları tanıtılmıģtır. Ayrıca Selçuk Stat paket programına bu tahmn edcler ve güven aralıkları eklenmģ olup Mntab 5 ve NCSS 007 Yazılımlarına karģı üstünlükler tartıģılmıģtır. ÖLÇÜM SĠSTEMLERĠ ANALĠZĠ Tekraredleblrlk ve Tekrarüretleblrlk (Repeatablty &Reproducblty, R&R) dğer br deyģle ölçüm (Gauge, gage) analz ölçüm prosedürünün yeterllğn belrlemek çn kullanılır. Tekraredleblrlk, ölçüm aletnden kaynaklanan değģm, tekrarüretleblrlk, operatörlern ölçme yöntemnden kaynaklanan değģm temsl eder. Ölçüm prosedürü le lgl değģm kaynaklarını elde etmek çn k yöntem kullanılır: Bunlardan lk, uygun varyans bleģenlernn tahmn değernn kullanılmasıyla ANOVA yaklaģımı, dğer de ölçüm değģkenlğnn bleģenlernn standart sapmalarının tahmn çn genģlk metoduna dayalı çzelge algortmadır. Bu çalıģmada, ANOVA yöntem ele alınacaktır. R&R analznde genel olarak kullanılan ANOVA model, operatör ve parça olmak üzere k faktörden oluģur. Genellkle operatörler, operatörler ktlesnden rasgele seçldğ varsayıldığından ANOVA modelnde rasgele faktör (random effect) olarak ele alınır. Operatörler özel seçml faktör olablr. Örneğn br fabrkadak üretlen parçaları ölçmek çn önceden sthdam edlmģ üç operatöründe ölçüm yapması durumunda operatör faktörü özel seçml olarak düģünülmeldr. Bu durumda ölçüm sstemler çalıģmasında karma (mxed effect) model ele alınmalıdır. P, parça faktörü, O, operatör faktörü,, etkleģm faktörü ve hata term olmak üzere R&R analz çn ANOVA model PO,, Y P O PO =,,... p, j =,,...,o k =,,...,r jk j j jk () ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 8
86 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Ģeklnde verlr. Burada, parça sayısı, o, operatör sayısı ve, tekrar sayısıdır. Operatör faktörünün rasgele veya özel seçml olduğu durumlara göre () model rasgele etkl model veya karma etkl model adını almaktadır. p Tablo ve Tablo de Rasgele ve Karma model çn ANOVA tabloları verlmģtr. Tablo. Rasgele etkl ANOVA model çn ANOVA Tablosu DeğĢm Kaynağı Serbestlk D. H.K.0. Beklenen Kareler Ort. F Ġstatst. P O Parça Operatör ParçaOp. PO Tekraredleblrlk p o p o po r S P S O S PO S E r or P PO P r pr O PO O r PO E PO Tablo. Karma Etkl ANOVA model çn ANOVA Tablosu r F= P KTP / KT F O = KTO / KT PO PO F PO = KTPO / KT DeğĢm Kaynağı Serbestlk D. H.K.0. Beklenen Kareler Ort. F Ġstatst. P Parça Operatör O ParçaOp. Tekraredleblrlk P O p o p o po r S P S O S PO S E = or +r + P P PO E o O = pr O j +r PO + o - j= = r + PO E PO E F= P KTP / KT F O = KTO / KT PO PO F PO = KTPO / KT E Ölçüm sstemler analz le lgl ayrıntılı blg çn (AIAG, 995, 00), Horrell (99) ve Croarkn (00) kaynaklarına bakılablr. BAZI ÖLÇÜM YETERLĠLĠK PARAMETRELERĠ VE TAHMĠN EDĠCĠLERĠ Ölçüm R&R analznn (Gauge R&R) amacı, ölçüm sstemnn değģkenlğnn ölçülen parçanın değģkenlğne göre daha az olup olamadığını belrlemektr. Lteratürde ölçüm sstemler çalıģmasında adı geçen brçok parametre ve bu parametrelern fonksyonlarından elde edlmģ parametreler vardır. Bu parametreler süreç ve ölçüm sstem değģkenlğ hakkında blg vermektedr. Rasgele etkl ANOVA model kullanılarak yapılan R&R analznde tekrarüretleblrlk, sırasıyla, tekraredleblrlk ve ve O PO Ģeklnde tanımlanır. Bu durumda toplam ölçüm M O PO ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 8
87 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ve toplam süreç varyansı T P M P O PO ANOVA model ele alındığında yukarıdak verlen tanımlarda alınmalıdır.ptr(precson-to-tolerance Rato) parametres, k M PTR %00 USL LSL bçmnde tanımlanır. Karma O yerne ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 83 o O o Ģeklnde tanımlanır. Burada USL, üst spefkasyon lmt, LSL, alt spefkasyon lmtdr. Ayrıca veya olarak alınır. Selçuk Stat değern ele almaktadır. Bu değerler normal dağılım çn sırasıyla ktlenn en az %99 unu barındıran %95 lk tolerans aralığı sınırları arasındak mesafe ve doğal tolerans aralığı arasındak mesafedr. PTR parametresnn yorumlanmasında faklı görüģler vardır. Montgomery ve Runger (993a) ölçüm sstemnn yeterl olduğunu söyleyeblmek çn PTR parametresnn %0 dan az olması gerektğn vurgulamıģlardır. Bu öner, AIAG Ölçüm Sstemler Analz El Ktabı (995, sayfa 60) nın öners le tutarlıdır. Mader, Prns ve Lambe (999), Wheeler ve Lyday (989) ı referans vererek PTR parametres %0 den fazla olduğu durumda ölçüm sstemnn yetersz olduğunu ler sürmüģlerdr. Son olarak Barrentne (99, sayfa 0) PTR parametres %30 dan fazla olduğu durumda ölçüm sstemnn yetersz olduğunu söylemģtr. Bazı özel durumlarda Montgomery and Runger (993a) ve Mader (999) PTR parametresnn ölçüm yeterllğ konusunda y br katsayı olamayacağını vurgulamıģlardır. Örneğn yüksek yeterllğe sahp teknoloj, ölçüm sstemnden kaynaklanan değģkenlğ tolere edeblr. k 5.5 k 6 k 5.5 Parça hatasının, toplam ölçüm varyansına oranı Ģeklnde tanımlanır. Ölçüm prosedürünün yeterllğ hakkında blg vermes bakımından R&R analznde parametresnn öneml br yer vardır. Parça hatasının, toplam süreç hatasına oranı Ģeklnde tanımlanır. Toplam ölçüm hatasının, toplam süreç hatasına oranı Ģeklnde tanımlanır. P/ M / P P T / M M T P Toplam ölçüm hatasının toplam süreç hatasına göre oranı %0 dan küçükse ölçüm sstem yeterl %0 le %30 arasında se Ģartlı yeterl %30 dan büyükse ölçüm sstem tekrar gözden geçrlmeldr (Kav ve Elevl, 008). (AIAG, 995, sayfa:3) SNR (Sgnal-to-Nose Rato) parametresn veya P parametresne dayalı olarak SNR / P P Ģeklnde tanımlamıģtır. AIAG (995) ölçüm sstemnn yeterl olduğunu söyleyeblmek çn SNR parametresnn 5 den çok olması gerektğn söylemģtr. Bu parametre kategorlern farklı sevyelernn sayısı(the number of dstnct levels of categores) olarak da adlandırılır. Not etmek gerekr k AIAG (990) ölçüm sstemnn yeterl olduğunu söyleyeblmek çn SNR parametresnn 3 den çok olması gerektğn söylemģtr (Dolezal, Burdck, Brch, 998). Ayrıca burada not etmeldr k SNR = olarak tanımlanmıģtır.mntab SNR y ve NCSS 007 SNR y olarak ele almaktadır. j= j
88 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Br baģka parametre Mader, Prns ve Lampe (999) ve Wheeler (99) tarafından önerlen ayırma oranıdır (Dscrmnant Rato) ve DR / P P Ģeklnde tanımlanır. Mader, Prns ve Lampe (999), bu oranın dörtten büyük olmasının, ölçüm sstemnn yeterl olduğunu Ģaret ettğn ler sürmüģlerdr. Burada bahsedlen parametrelern dıģındak parametreler çn Vardeman ve VanValkenburg (999), van den Heuvel ve Trp (00) ve Larsen (00) e bakılablr. ÖLÇÜM YETERLĠLĠK PARAMETRELERĠNĠN GÜVEN ARALIKLARI Montgomery ve Runger (993b), Conors, Merrll ve O Donnell (995), Burdck ve Larsen (997), Vardeman ve VanValkenburg (999), Hamada ve Weerahand (000) ve Chang (00), ölçüm R&R analznde güven aralıklarının önemn vurgulamıģlarıdır. parametresnn tahmn değernn 7 olması, parametrenn gerçek değernn 7 olması anlamına gelmez. Bu durumda, SNR parametresnn 5 den büyük olması ölçüm sstemnn yeterl olduğunu göstermes göz önüne alındığında parametresnn tahmn değernn(7) 5 den büyük olduğundan güvenle ölçüm sstem yeterldr denleblr m? ĠĢte tam bu noktada güven aralığı kavramı önem ortaya çıkmaktadır. parametresnn %95 lk güven aralığının alt sınırı 5 den büyük olduğunda %95 güven sevyesnde ölçüm sstem yeterl denleblr. SNR SNR Selçuk Stat da ve katsayıları ve güven aralıklarının kodları Leva ve Graybll (986) nın metoduna dayalı Chang (00) nn sonuçlarına göre yazılmıģtır. Ġlgl güven aralıkları çn Burdck, Borror ve Montgomery (003) sayfa ye bakılablr. Selçuk Stat yazılımı rasgele model durumunda parametrelernn güven aralıkları çn Burdck ve Larsen (997) n sonuçlarını kullanmaktadır. Yne rasgele modelde ve parametrelernn güven aralıkları çn Chang (00) n sonuçlarını kullanmaktadır. Karma model durumunda se parametrelernn, M P P SNR M SNR P, O,,, M, T,, SNR, PTR SNR,,,,,,, P O M T SNR güven aralıkları çn Dolezal, Burdck, Brch (998) n sonuçlarını kullanmaktadır. AĢağıda Dolezal, Burdck ve Brch (998) n kullandığı verlere dayalı kareler ortalamalarının grlmesyle elde edlen ölçüm yeterllk analz verlmģtr. Burada ver bölges kısmına gerçek ölçümler grlmemģtr. ġekl de Dolezal, Burdck ve Brch (998) sayfa 66 dak kareler ortalamaları grlmģtr ve operatör ve parça rasgele faktör olarak ele alınmıģtır. Verlern orjnal halne ulaģılamadığından analz kareler ortalamaları grlerek yapılmıģtır. ġekl. Selçuk Stat Ölçüm Yeterllk Analz Ara Yüzey Selçuk Stat Program çıktısı ġekl de verlmģtr. Varyans Analz Tablosunda, Kareler Toplamı (K.T.) sütunu ham verlern yerne yazılmasından dolayı 0 yazılmıģtır. Varyans BleĢenler Tablosunda, tekraredleblrlk, tekrarüretleblrlk ve toplam ölçüm varyansı, operatör varyansı, ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 84
89 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 parça varyansı ve toplam süreç varyansı parametrelernn tahmn ve %95 lk güven aralıkları verlmģtr. Ölçüm yeterllk parametreler kısmında se SNR, PTR ve DR parametrelernn tahmn ve %95 lk güven aralıkları verlmģtr. Burada ve verlmesnn sebeb SNR, SNR ve DR tahmn ve güven aralıklarının bu değerlere bağlı olmasıdır. SNR tahmn değer.86 ken %95 lk güven aralığı le.940 arasıdır. SNR değernn 5 den az olması, ölçüm sstemnn yetersz olduğunu gösterdğ göz önüne alındığında SNR n tahmnn.86 olması lk bakıģta ölçüm sstemnn yeterl olmadığını göstermektedr. Dğer taraftan % 95 lk güven aralığının tüm değerler 5 den küçük olduğundan ölçüm sstemnn yeterl olmadığı %95 güven le söyleneblr. PTR alt ve üst tolerans değerler grlmedğnden ġekl de verlen çıktıda yer almamıģtır. M P nn tahmn ve güven aralıkların ġekl. Dolezal, Burdck ve Brch (998) Sayfa 66 da Verlen Kareler Ortalamaları çn Selçuk Stat Çıktısı Tablo 3. Dolezal, Burdck ve Brch (998) n Verdğ Parametre ve Ġlgl Güven Aralıkları Ölçüm varyansları O Rasgele model güven aralığı (0.0,.83) (0.0,.837) (0.089,.9) (0.3, 4.33) Tablo 3, Dolezal, Burdck ve Brch (998) nn sayfa 67 de verdğ parametre ve güven aralıklarını göstermektedr. Tablo 3 tek sonuçlar le ġekl de verlen Selçuk Stat çıktısı le tutarlı olduğu gözükmektedr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 85
90 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Karma Model Durumu AĢağıda Dolezal, Burdck ve Brch (998) n kullandığı verlere dayalı kareler ortalamalarının grlmesyle elde edlen ölçüm yeterllk analz verlmģtr. Burada ver bölges kısmına gerçek ölçümler grlmemģtr. ġekl 3 de Dolezal, Burdck ve Brch (998) sayfa 66 dak kareler ortalamaları (Bkz. Makalede Tablo 3 tek kareler ortalamaları) grlmģtr ve operatör özel seçml ve parça rasgele seçml faktör olarak ele alınmıģtır. Tablo 4. Dolezal, Burdck ve Brch (998) n verdğ parametre ve lgl güven aralıkları Ölçüm varyansları O Karma model güven aralığı (0.07, 0.086) (0.07, 0.097) (0.03, 0.75) (0.86, 4.058) Tablo 4, Dolezal, Burdck ve Brch (998) nn sayfa 67 de verdğ parametre ve güven aralıklarını göstermektedr. Tablo 4 tek değerler le ġekl 3 tek Selçuk Stat çıktısı le tutarlı olduğu gözükmektedr. ġekl 3. Selçuk Stat Ölçüm Yeterllk Analz Ara Yüzey ġekl 4. Dolezal, Burdck ve Brch (998) sayfa 66 da verlen kareler ortalamaları çn Selçuk Stat Çıktısı ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 86
91 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Yukarıda yapılan yorumlar burada da aynı Ģeklde yapılacağından yorum yapılmamıģtır. Burada vurgulanması gereken husus, Selçuk Stat da operatör faktörünün özel seçml olması durumuyla lgl analz yapılablmesne karģın, Mntab 5 ve NCSS 007 de operatör faktörünün özel seçml olması durumuyla lgl analz yapılamamasıdır. SONUÇ Bu çalıģmada, Mntab 5 ve NCSS 007 yazılımlarında analz yapılan Ölçüm R&R analz, lteratürde son çıkan makalelere göre gelģtrlerek Selçuk Stat yazılımına monte edlmģtr. Selçuk Stat Analz sonuçları Mntab 5, NCSS 007 ve lgl makalelerdek sonuçlar karģılaģtırılmıģ ve Selçuk Stat analz sonuçlarının doğruluğu kontrol edlmģtr. Mntab 5 sadece parametrelern tahmn değerlern verrken, Selçuk Stat, NCSS 007 gb ölçüm yeterllk parametrelernn güven aralıklarını da vermektedr. Ayrıca, Mntab 5 yazılımı, operatör faktörünün rasgele olması durumunu ele alırken, Selçuk Stat Operatör faktörünün özel seçml olması durumunu da ele almaktadır. Bu vesle le Selçuk Stat yazılımı, ölçüm sstemler analznde Mntab 5 ve NCSS 007 le yarıģacak düzeye getrlmģtr. KAYNAKLAR Automotve Industry Acton Group, (995), Measurement Systems Analyss, nd cd. Detrat, MI. Automotve Industry Acton Group, (00), Measurement Systems Analyss, 3rd cd. Detrat, MI. BARRENTINE, L.B., (99), Concepts for R&R Studes. ASQC Qualty Prcss, Mlwaukee, WI. BURDICK, R.K., BORROR, C.M., MONTGOMERY, D.C., (003), A Revew of Methods for Measurement Systems Capablty Analyss, Journal of Qualty Technology, 35, BURDICK, R.K., LARSEN, G.A., (997), Confdence Intervals on Measures of Varablty n R&R Studes,Journal of Qualty Technology, 9, CHIANG, A.K.L., (00), A smple General Method for Constructng Confdence Intervals for Functons of Varance Components, Technometrcs 43, CHIANG, A.K.L., (00), Improved Confdence Intervals for a Rato n an R&R Study, Communcatons n Statstcs Smulaton ve Computaton, 3, CROARKIN, C., Edtor (00), Gauge R&R Studes, Secton.4 of the Beta Verson of the Nst /Sematech Engneerng Statstcs Internet Handbook, Located at CONORS, M., MERRILL, K., O DONNELL, B., (995), A Comprehensve Approach to Measurement System Evaluaton, ASA Proceedngs of the Secton on Physcal and Engneerng Scences, DOLEZAL, K.K., BURDICK, R.K., BIRCH, N.J. (998), Analyss of a Two-Factor R&R Study Wth Fxed Operators,Journal of Qualty Technology, 30, ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 87
92 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 HAMADA, M., WEERAHANDI, S., (000), Measurement System Assessment Va Generalzed Inference, Journal of Qualty Technology 3, HORRELL, K., (99), Introducton to Measurement Capablty Analyss, SEMATECH Report A-ENG. KAVI U., ELEVLI S., (008), Art-Craft Sofra Camı Üretm ĠĢletmesnde Ölçüm Sstem Analz Uygulaması, VII. Ulusal Ölçümblm Kongres LARSEN, G., (00), Measurement System Analyss, The Usual Metrcs can be Nonnformatve, Qualty Engneerng 5, LEIVA, R.A., GRAYBILL., F.A., (986), Confdence Intervals for Varance Components n the Balanced Two-Way Model wth Interacton, Communcatons n Statstcs Smulaton and Compulaton 5, MADER, D.P., PRINS, J., LAMPE, R.E., (999), The Economc Inpact of Measurement Error, Qualty Engneerng, MONTGOMERY, D.C., VE RENGER, G.C., (993a), Gauge Capablty and Desgned Experments Part f: Basc Methods, Qualty Engneerng 6, MONTGOMERY, D.C., RUNGER, G.C., (993b), Gauge Capablty Analyss and Desgned Experment, Part II. Expermental Desng Models and Varance Component Estmaton, Qualty Engncerng 6, VAN DEN HEUVEL, E.R., Trp., A., (00), Evaluaton of Measurement Systems wth a Small Number of Observers, Qualty Engncerng 5, VANDERMAN, S.B., VAN VALKENBURG, E.S., (999), Two Way Random-Effects Analyss va Gauge R&R Studes, Technometrcs 4, 0-. WHEELER, D.J., (99), Problems wth Gauge R&R Studes, ASQC Qualty Congress Transactons, WHEELER, D.J., LYDAY, R.W., (989), Evaluatng the Measurement Process. SPC Press, Knoxvlle, TN. ONDOKUZ MAYIS ÜNĠVERSĠTESĠ TIP FAKÜLTESĠ BEYĠN CERRAHĠSĠ POLĠKLĠNĠĞĠNDE SĠMÜLASYON YARDIMIYLA HASTA BEKLEME SÜRESĠNĠN AZALTILMASI ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 88
93 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 Faruk ALPASLAN * Özge CAĞCAĞ ** Erol EĞRĠOĞLU *** ÖZET Son yıllarda sağlık sektöründe smülasyon uygulamaları le lgl çalıģmalarda artıģ görülmektedr. Smülasyon yardımıyla, hastane yatak kapastes araģtırmaları, hasta bekleme sürelernn azaltılması, hastane personel sayısı belrlenmes, cerrah malzeme dağıtım süreçler optmzasyonu gb problemler çözümlenmektedr. Bu çalıģmada Ondokuz Mayıs Ünverstes Tıp Fakültes Beyn Cerrahs Bölümünün smülasyonu gerçekleģtrlerek, resm muayene doktor sayısının artırılması ve polklnk çalıģma saatnn artırılması le hasta bekleme sürelernn azaltılması hedeflenmģtr. Doktor sayısı ve çalıģma saatler üzerne çeģtl senaryolar üretlerek smülasyon sonuçları elde edlmģ ve sonuçlar çeģtl statstksel analzler le değerlendrlmģtr. Anahtar Kelmeler: Benzetm, Kuyruk model, Varyans Analz OPTIMIZATION OF PATIENT WAITING TIME IN ONDOKUZ MAYIS UNIVERSITY DEPARTMENT OF BRAIN SURGERY BY SIMULATION ABSTRACT In recent years, there has been an extensve amount of smulaton appled to the healthcare sector. The many problems such as plannng and management of bed capactes, decreasng of patent watng tme, determne of personal number, dstrbuton of surgcal nstruments processng can be solvable by smulaton. In ths study, Ondokuz Mays Unversty department of bran surgery s smulated for optmze patent watng tme. In the smulaton processng, we ncrease number of assstant doctorsand workng tme. We create varous scenaros for number of doctors and workng tme then we obtan results of smulaton. Fnally, the results of smulaton have been evaluated wth some statstcal analyss methods. Keywords: Smulaton, queung model, analyss of varance. * Prof.Dr., Ġstatstk Bölümü, Ondokuz Mayıs Ünverstes, 5539, Samsun, falpas@omu.edu.tr ** ArĢ.Gör., Ġstatstk Bölümü, Ondokuz Mayıs Ünverstes, 5539, Samsun, ozgecagcag@yahoo.com *** Doç.Dr., Ġstatstk Bölümü, Ondokuz Mayıs Ünverstes, 5539, Samsun, erole@omu.edu.tr GĠRĠġ Hzmet sektörü değģen dünya Ģartlarına ayak uydurmak çn günden güne gelģme göstermektedr. Bu gelģm berabernde planlama ve yönetm alanlarında çeģtl problemler ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 89
94 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ortaya çıkarmaktadır. Oteller de, market, restoran,fabrka ve hastanelerde verlen hzmetler çn gelģtrlen yöntemler artık lteratürde üzernde çalıģılan konular arasında yer almaktadır.bu sektörler arsından üzernde en fazla çalıģma yapılan sağlık sektörüdür. Sağlık sektörü üzernde hızlı değģmelern yaģandığı br sektördür. Sağlık sektöründe üzerne brçok çalıģma yapılmıģ ve yayınlanmıģtır. Bu çalıģmalarda çeģtl yöntemler kullanılmıģtır. Ġlk benzetm uygulamaları hastane sstemlernde modeller oluģturarak kullanılmıģtır. Peter ve Thompson (965) çalıģmasında Grace-New Haven Communty hastanesnn smülayonunu yaparak, hastane yatak ve dğer kaynakların kullanım oranlarını belrlemģ ve alternatfler üretmek suretyle hastanenn yönetm poltkalarını oluģturmaya çalıģmıģlardır. Smth ve Solomon (966) hastane kullanım oranını artırmak çn Lexngton U.S. Publc Health Servce hastanesnde hasta gelģ oranlarının nceleyerek hastaların aylık gelģ oranlarından elde ettğ statstksel dağılıģlardan yararlanarak yönetm poltkaları gelģtrmeye çalıģmıģlardır. Dean (974) nsan kaynakları yönetmyle lglenerek benzetm metodunu kullanarak çalıģanların, meslek grupları ve becerlerne göre planlamasını ve hasta bekleme süresn kısaltmayı amaçlamıģtır. Baesler ve Sepulveda (00) yaptıkları benzetm çalıģmasında kanser tedav merkeznde sstemle lgl dört farklı hedef belrlemģ ve kontrol değģkenlernn en uygununu bulan model gelģtrmģlerdr. Bu dört hedef çn oluģturulan çözüm seçenekler karģılaģtırılmıģ ve %8 - %5 düzeynde br yleģme sağlandığını ortaya koymuģlardır. Çetnkaya vd. (004) çalıģmasında se br hastanenn polklnğnde, Ģ süreçler yenden tasarlanarak veznenn kullanımını arttırmak çn vezne le randevu süreçler brleģtrlmģtr. Ve bu sayede hastanın sstemde kalma süres azaltılmıģ ve doktorların hastaları beklerken kaybettkler boģa zamanda mnmze edlmģtr. Kumar (005) benzetmn hastanede nsan kaynaklarının kullanımının optmzasyonu ve cerrah malzemelern hastane çnde dağıtım sürecnn daha verml hale getrlmesne yardımcı olacağını ve dğer benzer süreçler çnde kullanılableceğn uyguladığı benzetm model le belrtmģtr. Çn de nüfusun fazla olması bazı hastanelerde uzun sürel bekleme kuyruklarını oluģmasına neden olduğu sorunu ortaya konmuģtur. Bunun çn Su ve Yao (006) da var olan bu kuyrukları azaltmak çn benzetm modeln kullanarak br hastanın hastaneye grģyle baģlayan Ģ akıģını ve Ģlem sürelern analz ederek, bu süreçler yenden tasarlayıp farklı yaklaģımlarla karģılaģtırmıģlardır. Ve elde edlen sonuçlarda ortalama kayıt süres 7.4 dakkadan 3.5 dakkaya ndrlerek optmum kayıt süres elde edlmģtr. Ontaro da Cprıono vd. (007) çalıģmasında dz kalça ve protez amelyatları çn hastaların bekleme sürelernn 6 aydan fazla olduğu ve bu bekleme sürenn hastaları amelyat sonrası yleģmelern olumsuz etkledğ ortaya konmuģtur. ÇalıĢmada değģken olarak bölgeden gelen hasta oranları ve cerrah sayıları belrlenmģtr. Cerrah sayıları % arttırıldığında 0 yıl çersnde bekleme süresn azalacağı, bu azalıģla beraber her br bölgedek cerrahların daha etkn dağıtımı le bekleme süresnn daha da azalacağı saptanmıģtır. VanBerkel ve Blake (007) Kanada Nova Scota da Halfax Hastanes Cerrah Klnğnde benzetm model kullanılarak ve hasta bekleme sürelernn analz yapılarak bölüm performansının yanı sıra yen kapaste planları gelģtrlmģtr. Oddoye vd. (007) çalıģmasında smülasyon modeller le br tıbb değerlendrme üntesnn sağlık planını belrlemek çn çalıģma yapılmıģtır. Bu tıbb değerlendrme üntes gereksz hasta grģlern ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 90
95 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 engellemek, hızlı değerlendrme ve hastalara verlen tedavnn kaltesn artırmak çn kurulmuģtur. ONDOKUZ MAYIS ÜNĠVERSĠTESĠ TIP FAKÜLTESĠ BEYĠN CERRAHĠSĠ BÖLÜMÜNÜN SĠMÜLASYONU Doktorların tedav sırasında harcadığı zaman le hastaların ssteme geldkler ve tedav çn bekledkler zamanın elde edlmes çn Beyn cerrahs bölümü 30 gün gözlenp blg toplanmıģtır. Toplanan blglere görehastaların gelģler aģağıda Tablo de verldğ gb görgül dağılımlıdır. Tablo. GelĢler arası sürenn dağılımı Alt sınır Üst sınır Brkml frekans,00 6,4 0,6 6,4 0,85 0,77 0,85 5,8 0,87 5,8 9,7 0,90 9,7 4,4 0,96 4,4 8,57 0,97 8,57 33,00 Ssteme gelen hastalar sekreterlğe grģn yaptırdıktan sonra sstemde muayene olmak çn beklemeye baģlamaktadırlar. Sstemde 6 tane özel doktor ve tane asstan doktor görev yapmaktadır. Hastalar duruma göre özel yada resm muayeney terch etmektedrler. Ssteme gelen hastaların %30-u özel muayeney %70 se resm muayeney terch etmektedrler. Ve bu hastalardan özel muayeney terch edenler %30 oranında. Özel doktora,%30 oranında. Özel doktora ve %0 oranında se dğer 4 doktora muayene olmaktadırlar. Sstemn 30 günlük ncelenmes sonucunda özel doktorlarının tümü çn muayene süresnn 5.0 ortalama ve 5.8 standart sapma le normal dağıldığı, asstan doktorun muayene süresnn se 0.8 ortalama ve 4.45 standart sapma le normal dağılım gösterdğ sonucuna ulaģılmıģtır. Beyn Cerrahs Bölümünde özel veya resm muayeney bekleyen hastalar ayrı olarak kuyruk oluģturmaktadır. Eğer hasta özel muayeney terch etmģse, muayene olmak stedğ doktorun sırasında kuyruğagrmektedr. Eğer hasta resm muayeney seçtyse, asstan doktorun sırasında kuyruğa grmektedr. Beyn Cerrahs Bölümündek görevl doktorların br gün çndek toplam çalıģma süreler 6 saat le sınırlıdır. Beyn cerrahs bölümünün genel ĢleyĢ ġekl de verlmģtr. ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 9
96 VII. ĠSTATĠSTĠK GÜNLERĠ SEMPOZYUMU BĠLDĠRĠLER KĠTABI 00 ġekl. Beyn Cerrahs Servs AkıĢ Dyagramı SĠMÜLASYON SONUÇLARININ ĠSTATĠSTĠKSEL ANALĠZĠ Beyn cerrahs bölümündek asstan sayısını artırdığımızda, hastaların sstemde ortalama bekleme sürerl arasında fark olup olmadığı tek yönlü varyans analz le test edlmģtr. F-test sonucunda p<0.00 olmaktadır. Beyn cerrahs bölümündek asstan doktor sayısının artırılmasının sstemde ortalama bekleme süresnn düģürdüğü sonucuna varılmaktadır. Çoklu karģılaģtırma çn Tamhane test kullanıldığında sstemde asstan, asstan ve 3 asstan doktor olması durumunda hastaların bekleme süresnn anlamlı br Ģeklde farklılaģtığı görülmektedr. Beyn cerrahs bölümünde asstan doktor varken hastaların ortalama bekleme süres 40 dakka cvarında ken, bu süre asstan olduğunda 3 dakkaya ve 3 asstan olması durumunda se dakkaya düģmektedr. Beyn cerrahs bölümündek asstan sayısını artırdığımızda, hastaların kuyrukta ortalama bekleme sürerl arasında fark olup olmadığı tek yönlü varyans analz le test edlmģtr. F-test sonucunda p<0,00 olmaktadır. Beyn cerrahs bölümündek asstan doktor sayısının artırılmasının kuyrukta ortalama bekleme süresnn düģürdüğü sonucuna varılmaktadır. Çoklu karģılaģtırma çn Tamhane test kullanıldığında sstemde asstan, asstan ve 3 asstan doktor olması durumunda hastaların bekleme süresnn anlamlı br Ģeklde farklılaģtığı görülmektedr. asstan doktor varken hastaların kuyrukta ortalama bekleme süres 8 dakka cvarında ken, bu süre asstan olduğunda,5 dakkaya ve 3 asstan olması durumunda se 0,4 dakkaya düģmektedr. Beyn cerrahs bölümündek asstan sayısını artırdığımızda, brnc asstanın ortalama boģ kalma süreler arasında fark olup olmadığı tek yönlü varyans analz le test edlmģtr. P<0.00 olduğundan sstemdek asstan sayısını artırmanın lk asstanın boģ kalma süres üzernde olumlu etk yaptığı söyleneblr. Sstemde asstan doktor var ken ortalama boģ kalma süres 54,6 ORTA DOĞU TEKNĠK ÜNĠVERSĠTESĠ, FEN-EDEBĠYAT FAKÜLTESĠ, ĠSTATĠSTĠK BÖLÜMÜ 9
ÇOKLU REGRESYON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESYON ÇÖZÜMLEMESİ,REGRES-YON KATSAYILARININ YORUMU
 6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
PARÇALI DOĞRUSAL REGRESYON
 HAFTA 4 PARÇALI DOĞRUSAL REGRESYO Gölge değşkenn br başka kullanımını açıklamak çn varsayımsal br şrketn satış temslclerne nasıl ödeme yaptığı ele alınsın. Satış prmleryle satış hacm Arasındak varsayımsal
HAFTA 4 PARÇALI DOĞRUSAL REGRESYO Gölge değşkenn br başka kullanımını açıklamak çn varsayımsal br şrketn satış temslclerne nasıl ödeme yaptığı ele alınsın. Satış prmleryle satış hacm Arasındak varsayımsal
YÖNETİM VE EKONOMİ Yıl:2006 Cilt:13 Sayı:1 Celal Bayar Üniversitesi İ.İ.B.F. MANİSA
 YÖNETİM VE EKONOMİ Yıl:2006 Clt:3 Sayı: Celal Bayar Ünverstes İ.İ.B.F. MANİSA Bulanık Araç Rotalama Problemlerne Br Model Öners ve Br Uygulama Doç. Dr. İbrahm GÜNGÖR Süleyman Demrel Ünverstes, İ.İ.B.F.,
YÖNETİM VE EKONOMİ Yıl:2006 Clt:3 Sayı: Celal Bayar Ünverstes İ.İ.B.F. MANİSA Bulanık Araç Rotalama Problemlerne Br Model Öners ve Br Uygulama Doç. Dr. İbrahm GÜNGÖR Süleyman Demrel Ünverstes, İ.İ.B.F.,
ARAŞTIRMA MAKALESİ/RESEARCH ARTICLE TEK ÇARPIMSAL SİNİR HÜCRELİ YAPAY SİNİR AĞI MODELİNİN EĞİTİMİ İÇİN ABC VE BP YÖNTEMLERİNİN KARŞILAŞTIRILMASI ÖZ
 ANADOLU ÜNİVERSİTESİ Blm ve Teknoloj Dergs A-Uygulamalı Blmler ve Mühendslk Clt: 14 Sayı: 3 013 Sayfa: 315-38 ARAŞTIRMA MAKALESİ/RESEARCH ARTICLE Faruk ALPASLAN 1, Erol EĞRİOĞLU 1, Çağdaş Hakan ALADAĞ,
ANADOLU ÜNİVERSİTESİ Blm ve Teknoloj Dergs A-Uygulamalı Blmler ve Mühendslk Clt: 14 Sayı: 3 013 Sayfa: 315-38 ARAŞTIRMA MAKALESİ/RESEARCH ARTICLE Faruk ALPASLAN 1, Erol EĞRİOĞLU 1, Çağdaş Hakan ALADAĞ,
BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER İki Boyutlu Rasgele Değişkenler
 BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER 5.. İk Boyutlu Rasgele Değşkenler Br deney yapıldığında, aynı deneyle lgl brçok rasgele değşkenn aynı andak durumunu düşünmek gerekeblr. Böyle durumlarda
BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER 5.. İk Boyutlu Rasgele Değşkenler Br deney yapıldığında, aynı deneyle lgl brçok rasgele değşkenn aynı andak durumunu düşünmek gerekeblr. Böyle durumlarda
YGS-1 YGS-2 YGS-3 YGS-4 YGS-5 YGS-6
 2015 OKUL ADI SORU SAYISI TEMEL SOSYAL YGS-1 YGS-2 YGS-3 YGS-4 YGS-5 YGS-6 1 40 26,62 10,91 27,58 22,46 325,218 310,003 355,402 349,084 357,564 344,551 2 40 17,46 10,35 25,77 16,44 275,100 268,374 307,336
2015 OKUL ADI SORU SAYISI TEMEL SOSYAL YGS-1 YGS-2 YGS-3 YGS-4 YGS-5 YGS-6 1 40 26,62 10,91 27,58 22,46 325,218 310,003 355,402 349,084 357,564 344,551 2 40 17,46 10,35 25,77 16,44 275,100 268,374 307,336
Fren Test Cihazları Satış Bayiler. Administrator tarafından yazıldı. Perşembe, 05 Mayıs :26 - Son Güncelleme Pazartesi, 30 Kasım :22
 FDR Adana Fren Test Cihazları FDR Adıyaman Fren Test Cihazları FDR AfyonFren Test Cihazları FDR Ağrı Fren Test Cihazları FDR Amasya Fren Test Cihazları FDR Ankara Fren Test Cihazları FDR Antalya Fren Test
FDR Adana Fren Test Cihazları FDR Adıyaman Fren Test Cihazları FDR AfyonFren Test Cihazları FDR Ağrı Fren Test Cihazları FDR Amasya Fren Test Cihazları FDR Ankara Fren Test Cihazları FDR Antalya Fren Test
ENDÜSTRİNİN DEĞİŞİK İŞ KOLLARINDA İHTİYAÇ DUYULAN ELEMANLARIN YÜKSEK TEKNİK EĞİTİM MEZUNLARINDAN SAĞLANMASINDAKİ BEKLENTİLERİN SINANMASI
 V. Ulusal Üretm Araştırmaları Sempozyumu, İstanbul Tcaret Ünverstes, 5-7 Kasım 5 ENDÜSTRİNİN DEĞİŞİK İŞ KOLLARINDA İHTİYAÇ DUYULAN ELEMANLARIN YÜKSEK TEKNİK EĞİTİM MEZUNLARINDAN SAĞLANMASINDAKİ BEKLENTİLERİN
V. Ulusal Üretm Araştırmaları Sempozyumu, İstanbul Tcaret Ünverstes, 5-7 Kasım 5 ENDÜSTRİNİN DEĞİŞİK İŞ KOLLARINDA İHTİYAÇ DUYULAN ELEMANLARIN YÜKSEK TEKNİK EĞİTİM MEZUNLARINDAN SAĞLANMASINDAKİ BEKLENTİLERİN
Korelasyon ve Regresyon
 Korelasyon ve Regresyon 1 Korelasyon Analz İk değşken arasında lşk olup olmadığını belrlemek çn yapılan analze korelasyon analz denr. Korelasyon; doğrusal yada doğrusal olmayan dye kye ayrılır. Korelasyon
Korelasyon ve Regresyon 1 Korelasyon Analz İk değşken arasında lşk olup olmadığını belrlemek çn yapılan analze korelasyon analz denr. Korelasyon; doğrusal yada doğrusal olmayan dye kye ayrılır. Korelasyon
HAFTA 13. kadın profesörlerin ortalama maaşı E( Y D 1) erkek profesörlerin ortalama maaşı. Kestirim denklemi D : t :
 HAFTA 13 GÖLGE EĞİŞKENLERLE REGRESYON (UMMY VARIABLES) Gölge veya kukla (dummy) değşkenler denen ntel değşkenler, cnsyet, dn, ten reng gb hemen sayısallaştırılamayan ama açıklanan değşkenn davranışını
HAFTA 13 GÖLGE EĞİŞKENLERLE REGRESYON (UMMY VARIABLES) Gölge veya kukla (dummy) değşkenler denen ntel değşkenler, cnsyet, dn, ten reng gb hemen sayısallaştırılamayan ama açıklanan değşkenn davranışını
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 ADRESE DAYALI NÜFUS KAYIT SİSTEMİ (ADNKS) 2014 Yılı Türkiye İstatistik Kurumu 28/01/2015 tarihinde 2014 yılı Adrese Dayalı Kayıt Sistemi Sonuçları haber bültenini yayımladı. 31 Aralık 2014 tarihi itibariyle;
ADRESE DAYALI NÜFUS KAYIT SİSTEMİ (ADNKS) 2014 Yılı Türkiye İstatistik Kurumu 28/01/2015 tarihinde 2014 yılı Adrese Dayalı Kayıt Sistemi Sonuçları haber bültenini yayımladı. 31 Aralık 2014 tarihi itibariyle;
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 ADRESE DAYALI NÜFUS KAYIT SİSTEMİ (ADNKS) 2015 Yılı Türkiye İstatistik Kurumu 28/01/2016 tarihinde 2015 yılı Adrese Dayalı Kayıt Sistemi Sonuçları haber bültenini yayımladı. 31 Aralık 2015 tarihi itibariyle;
ADRESE DAYALI NÜFUS KAYIT SİSTEMİ (ADNKS) 2015 Yılı Türkiye İstatistik Kurumu 28/01/2016 tarihinde 2015 yılı Adrese Dayalı Kayıt Sistemi Sonuçları haber bültenini yayımladı. 31 Aralık 2015 tarihi itibariyle;
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 ADRESE DAYALI NÜFUS KAYIT SİSTEMİ (ADNKS) 2013 Yılı Türkiye İstatistik Kurumu 29/01/2014 tarihinde 2013 yılı Adrese Dayalı Kayıt Sistemi Sonuçları haber bültenini yayımladı. 31 Aralık 2013 tarihi itibariyle;
ADRESE DAYALI NÜFUS KAYIT SİSTEMİ (ADNKS) 2013 Yılı Türkiye İstatistik Kurumu 29/01/2014 tarihinde 2013 yılı Adrese Dayalı Kayıt Sistemi Sonuçları haber bültenini yayımladı. 31 Aralık 2013 tarihi itibariyle;
KARABÜK ÜNİVERSİTESİ PERSONEL DAİRE BAŞKANLIĞI
 KARABÜK ÜNİVERSİTESİ PERSONEL DAİRE BAŞKANLIĞI Yıllara Göre Akademik Personel,İdari Personel ve Öğrenci Sayıları Öğrenci Sayıları Akademik Personel 9.877..79.78 İdari Personel.7..79.. 9 9 9 977 7.99 8.78
KARABÜK ÜNİVERSİTESİ PERSONEL DAİRE BAŞKANLIĞI Yıllara Göre Akademik Personel,İdari Personel ve Öğrenci Sayıları Öğrenci Sayıları Akademik Personel 9.877..79.78 İdari Personel.7..79.. 9 9 9 977 7.99 8.78
3. basamak. Otomobil Kamyonet Motorsiklet
 Tablo-1: İndirim veya artırım uygulanmayan iller için azami primler (TL)* İzmir, Yalova, Erzurum, Kayseri Otomobil 018 614 211 807 686 565 444 Kamyonet 638 110 583 055 897 739 580 Motorsiklet 823 658 494
Tablo-1: İndirim veya artırım uygulanmayan iller için azami primler (TL)* İzmir, Yalova, Erzurum, Kayseri Otomobil 018 614 211 807 686 565 444 Kamyonet 638 110 583 055 897 739 580 Motorsiklet 823 658 494
5.3. Tekne Yüzeylerinin Matematiksel Temsili
 5.3. Tekne Yüzeylernn atematksel Temsl atematksel yüzey temslnde lk öneml çalışmalar Coons (53) tarafından gerçekleştrlmştr. Ferguson yüzeylernn gelştrlmş hal olan Coons yüzeylernde tüm sınır eğrler çn
5.3. Tekne Yüzeylernn atematksel Temsl atematksel yüzey temslnde lk öneml çalışmalar Coons (53) tarafından gerçekleştrlmştr. Ferguson yüzeylernn gelştrlmş hal olan Coons yüzeylernde tüm sınır eğrler çn
İllere ve yıllara göre konut satış sayıları, House sales by provinces and years,
 2013 Ocak Şubat Mart Nisan Mayıs Haziran Temmuz Ağustos Eylül Ekim Kasım Aralık Toplam January February March April May June July August September October November December Total Türkiye 87 444 88 519
2013 Ocak Şubat Mart Nisan Mayıs Haziran Temmuz Ağustos Eylül Ekim Kasım Aralık Toplam January February March April May June July August September October November December Total Türkiye 87 444 88 519
OTO KALORİFER PETEK TEMİZLİĞİ - VİDEO
 OTO KALORİFER PETEK TEMİZLİĞİ - VİDEO Oto Kalorifer Peteği Temizleme Makinası, Araç Kalorifer Petek Temizliği Cihazı. kalorifer peteği nasıl temizlenir, kalorifer peteği temizleme fiyatları, kalorifer
OTO KALORİFER PETEK TEMİZLİĞİ - VİDEO Oto Kalorifer Peteği Temizleme Makinası, Araç Kalorifer Petek Temizliği Cihazı. kalorifer peteği nasıl temizlenir, kalorifer peteği temizleme fiyatları, kalorifer
UYUM ĐYĐLĐĞĐ TESTĐ. 2 -n olup. nin dağılımı χ dir ve sd = (k-1-p) dir. Burada k = sınıf sayısı, p = tahmin edilen parametre sayısıdır.
 UYUM ĐYĐLĐĞĐ TESTĐ Posson: H o: Ver Posson dağılıma sahp br ktleden gelmektedr. H a : Ver Posson dağılıma sahp br ktleden gelmemektedr. Böyle br hpotez test edeblmek çn, önce Posson dağılım parametres
UYUM ĐYĐLĐĞĐ TESTĐ Posson: H o: Ver Posson dağılıma sahp br ktleden gelmektedr. H a : Ver Posson dağılıma sahp br ktleden gelmemektedr. Böyle br hpotez test edeblmek çn, önce Posson dağılım parametres
TABLO-4. LİSANS MEZUNLARININ TERCİH EDEBİLECEĞİ KADROLAR ( EKPSS 2014 )
 7769 MİLLİ EĞİTİM BAKANLIĞI Memur ADANA TÜM İLÇELER Taşra GİH 7 17 4001 7770 MİLLİ EĞİTİM BAKANLIĞI Memur ADIYAMAN TÜM İLÇELER Taşra GİH 7 9 4001 7771 MİLLİ EĞİTİM BAKANLIĞI Memur AFYONKARAHİSAR TÜM İLÇELER
7769 MİLLİ EĞİTİM BAKANLIĞI Memur ADANA TÜM İLÇELER Taşra GİH 7 17 4001 7770 MİLLİ EĞİTİM BAKANLIĞI Memur ADIYAMAN TÜM İLÇELER Taşra GİH 7 9 4001 7771 MİLLİ EĞİTİM BAKANLIĞI Memur AFYONKARAHİSAR TÜM İLÇELER
TABLO-3. ÖNLİSANS MEZUNLARININ TERCİH EDEBİLECEĞİ KADROLAR ( EKPSS 2014 )
 7858 MİLLİ EĞİTİM BAKANLIĞI Memur ADANA TÜM İLÇELER Taşra GİH 10 8 ### 7859 MİLLİ EĞİTİM BAKANLIĞI Memur ADIYAMAN TÜM İLÇELER Taşra GİH 10 4 ### 7860 MİLLİ EĞİTİM BAKANLIĞI Memur AFYONKARAHİSAR TÜM İLÇELER
7858 MİLLİ EĞİTİM BAKANLIĞI Memur ADANA TÜM İLÇELER Taşra GİH 10 8 ### 7859 MİLLİ EĞİTİM BAKANLIĞI Memur ADIYAMAN TÜM İLÇELER Taşra GİH 10 4 ### 7860 MİLLİ EĞİTİM BAKANLIĞI Memur AFYONKARAHİSAR TÜM İLÇELER
İLLERE GÖRE NÜFUS KÜTÜKLERİNE KAYITLI EN ÇOK KULLANILAN 5 KADIN VE ERKEK ADI
 İLLERE GÖRE NÜFUS KÜTÜKLERİNE KAYITLI EN ÇOK KULLANILAN 5 KADIN VE ERKEK ADI İL KADIN ADI ERKEK ADI ADANA ADIYAMAN AFYONKARAHİSAR AKSARAY SULTAN SULTAN İBRAHİM RAMAZAN 1/17 2/17 AMASYA ANKARA ANTALYA ARDAHAN
İLLERE GÖRE NÜFUS KÜTÜKLERİNE KAYITLI EN ÇOK KULLANILAN 5 KADIN VE ERKEK ADI İL KADIN ADI ERKEK ADI ADANA ADIYAMAN AFYONKARAHİSAR AKSARAY SULTAN SULTAN İBRAHİM RAMAZAN 1/17 2/17 AMASYA ANKARA ANTALYA ARDAHAN
Yrd. Doç. Dr. Tahsin KARABULUT
 Yrd. Doç. Dr. Tahsin KARABULUT -İllerin Sosyo-ekonomik gelişmişlik düzeylerinin belirlenmesi amacıyla yapılan bu çalışmada niceliksel bir büyüme anlayışından ziyade, niteliksel bir Sosyo-ekonomik gelişme
Yrd. Doç. Dr. Tahsin KARABULUT -İllerin Sosyo-ekonomik gelişmişlik düzeylerinin belirlenmesi amacıyla yapılan bu çalışmada niceliksel bir büyüme anlayışından ziyade, niteliksel bir Sosyo-ekonomik gelişme
İL ADI UNVAN KODU UNVAN ADI BRANŞ KODU BRANŞ ADI PLANLANAN SAYI ÖĞRENİM DÜZEYİ
 ADANA 8140 BİYOLOG 0 1 LİSANS ADANA 8315 ÇOCUK GELİŞİMCİSİ 0 1 LİSANS ADANA 8225 DİYETİSYEN 0 1 LİSANS ADANA 8155 PSİKOLOG 0 1 LİSANS ADANA 8410 SAĞLIK MEMURU 6000 ÇEVRE SAĞLIĞI 4 LİSE ADANA 8410 SAĞLIK
ADANA 8140 BİYOLOG 0 1 LİSANS ADANA 8315 ÇOCUK GELİŞİMCİSİ 0 1 LİSANS ADANA 8225 DİYETİSYEN 0 1 LİSANS ADANA 8155 PSİKOLOG 0 1 LİSANS ADANA 8410 SAĞLIK MEMURU 6000 ÇEVRE SAĞLIĞI 4 LİSE ADANA 8410 SAĞLIK
Sürekli Olasılık Dağılım (Birikimli- Kümülatif)Fonksiyonu. Yrd. Doç. Dr. Tijen ÖVER ÖZÇELİK
 Sürekl Olasılık Dağılım Brkml- KümülatFonksyonu Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr Sürekl olasılık onksyonları X değşken - ;+ aralığında tanımlanmış br sürekl rassal değşken olsun. Aşağıdak
Sürekl Olasılık Dağılım Brkml- KümülatFonksyonu Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr Sürekl olasılık onksyonları X değşken - ;+ aralığında tanımlanmış br sürekl rassal değşken olsun. Aşağıdak
Yatırım Teşvik Uygulamalarında Bölgeler
 Yatırım Teşvik Uygulamalarında Bölgeler 1. Bölge: Ankara, Antalya, Bursa, Eskişehir, İstanbul, İzmir, Kocaeli, Muğla 2. Bölge: Adana, Aydın, Bolu, Çanakkale (Bozcaada ve Gökçeada İlçeleri Hariç), Denizli,
Yatırım Teşvik Uygulamalarında Bölgeler 1. Bölge: Ankara, Antalya, Bursa, Eskişehir, İstanbul, İzmir, Kocaeli, Muğla 2. Bölge: Adana, Aydın, Bolu, Çanakkale (Bozcaada ve Gökçeada İlçeleri Hariç), Denizli,
kadar ( i. kaynağın gölge fiyatı kadar) olmalıdır.
 KONU : DUAL MODELİN EKONOMİK YORUMU Br prmal-dual model lşks P : max Z cx D: mn Z bv AX b AV c X 0 V 0 bçmnde tanımlı olsun. Prmal modeln en y temel B ve buna lşkn fyat vektörü c B olsun. Z B B BB c X
KONU : DUAL MODELİN EKONOMİK YORUMU Br prmal-dual model lşks P : max Z cx D: mn Z bv AX b AV c X 0 V 0 bçmnde tanımlı olsun. Prmal modeln en y temel B ve buna lşkn fyat vektörü c B olsun. Z B B BB c X
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU EYLÜL 2014 Türkiye İstatistik Kurumu 03/10/2014 tarihinde 2014 yılı Eylül ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU EYLÜL 2014 Türkiye İstatistik Kurumu 03/10/2014 tarihinde 2014 yılı Eylül ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
SEK Tahmincilerinin Arzulanan Özellikleri. SEK Tahmincilerinin Arzulanan Özellikleri. Ekonometri 1 Konu 9 Sürüm 2,0 (Ekim 2011)
 SEK Tahmnclernn Arzulanan Özellkler İk Değşkenl Bağlanım Model SEK Tahmnclernn Arzulanan Özellkler Ekonometr 1 Konu 9 Sürüm 2,0 (Ekm 2011) http://www.ackders.org.tr SEK Tahmnclernn Arzulanan Özellkler
SEK Tahmnclernn Arzulanan Özellkler İk Değşkenl Bağlanım Model SEK Tahmnclernn Arzulanan Özellkler Ekonometr 1 Konu 9 Sürüm 2,0 (Ekm 2011) http://www.ackders.org.tr SEK Tahmnclernn Arzulanan Özellkler
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU MAYIS 2017 Türkiye İstatistik Kurumu 05/06/2017 tarihinde 2017 yılı Mayıs ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU MAYIS 2017 Türkiye İstatistik Kurumu 05/06/2017 tarihinde 2017 yılı Mayıs ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETĠCĠLERĠN FĠYAT BĠLĠNCĠ ÜZERĠNDE ETKĠLĠ OLAN FAKTÖRLERE ĠLĠġKĠN BĠR ĠNCELEME
 Ġstanbul Ünverstes Ġktsat Fakültes Malye AraĢtırma Merkez Konferansları 46. Ser / Yıl 2004 Prof. Dr. Salh Turhan'a Armağan TÜKETĠCĠLERĠN FĠYAT BĠLĠNCĠ ÜZERĠNDE ETKĠLĠ OLAN FAKTÖRLERE ĠLĠġKĠN BĠR ĠNCELEME
Ġstanbul Ünverstes Ġktsat Fakültes Malye AraĢtırma Merkez Konferansları 46. Ser / Yıl 2004 Prof. Dr. Salh Turhan'a Armağan TÜKETĠCĠLERĠN FĠYAT BĠLĠNCĠ ÜZERĠNDE ETKĠLĠ OLAN FAKTÖRLERE ĠLĠġKĠN BĠR ĠNCELEME
YAYILI YÜK İLE YÜKLENMİŞ YAPI KİRİŞLERİNDE GÖÇME YÜKÜ HESABI. Perihan (Karakulak) EFE
 BAÜ Fen Bl. Enst. Dergs (6).8. YAYII YÜK İE YÜKENİŞ YAPI KİRİŞERİNDE GÖÇE YÜKÜ HESABI Perhan (Karakulak) EFE Balıkesr Ünverstes ühendslk marlık Fakültes İnşaat üh. Bölümü Balıkesr, TÜRKİYE ÖZET Yapılar
BAÜ Fen Bl. Enst. Dergs (6).8. YAYII YÜK İE YÜKENİŞ YAPI KİRİŞERİNDE GÖÇE YÜKÜ HESABI Perhan (Karakulak) EFE Balıkesr Ünverstes ühendslk marlık Fakültes İnşaat üh. Bölümü Balıkesr, TÜRKİYE ÖZET Yapılar
Karşılıksız İşlemi Yapılan Çek Sayılarının İllere ve Bölgelere Göre Dağılımı (1) ( 2017 )
 Karşılıksız İşlemi Yapılan Çek Sayılarının İllere ve Bölgelere Göre Dağılımı (1) İller ve Bölgeler (2) Ocak Şubat Mart Nisan Mayıs Haziran Temmuz Ağustos Eylül Ekim Kasım Aralık Toplam İstanbul 18.257
Karşılıksız İşlemi Yapılan Çek Sayılarının İllere ve Bölgelere Göre Dağılımı (1) İller ve Bölgeler (2) Ocak Şubat Mart Nisan Mayıs Haziran Temmuz Ağustos Eylül Ekim Kasım Aralık Toplam İstanbul 18.257
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU HAZİRAN 2014 Türkiye İstatistik Kurumu 03/07/2014 tarihinde 2014 yılı Haziran ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU HAZİRAN 2014 Türkiye İstatistik Kurumu 03/07/2014 tarihinde 2014 yılı Haziran ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU AĞUSTOS 2014 Türkiye İstatistik Kurumu 03/09/2014 tarihinde 2014 yılı Ağustos ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU AĞUSTOS 2014 Türkiye İstatistik Kurumu 03/09/2014 tarihinde 2014 yılı Ağustos ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYATLARI ENDEKSİ (TÜFE) BİLGİ NOTU HAZİRAN 2013 Türkiye İstatistik Kurumu 03/07/2013 tarihinde 2013 yılı Haziran ayı Tüketici Fiyatları Endeksi (TÜFE) haber bültenini yayımladı. 2013 yılı Haziran
TÜKETİCİ FİYATLARI ENDEKSİ (TÜFE) BİLGİ NOTU HAZİRAN 2013 Türkiye İstatistik Kurumu 03/07/2013 tarihinde 2013 yılı Haziran ayı Tüketici Fiyatları Endeksi (TÜFE) haber bültenini yayımladı. 2013 yılı Haziran
LİSTE - II TÜRKİYE HALK SAĞLIĞI KURUMU - TAŞRA
 YER DEĞİŞİKLİĞİ BAŞVURULARI İÇİN İLAN EDİLEN LİSTESİ 1 ADANA BİYOLOG GENEL BÜTÇE 1 1 ADANA EBE GENEL BÜTÇE 6 1 ADANA HEMŞİRE GENEL BÜTÇE 2 1 ADANA SAĞLIK MEMURU ÇEVRE SAĞLIĞI TEKNİSYENİ GENEL BÜTÇE 1 1
YER DEĞİŞİKLİĞİ BAŞVURULARI İÇİN İLAN EDİLEN LİSTESİ 1 ADANA BİYOLOG GENEL BÜTÇE 1 1 ADANA EBE GENEL BÜTÇE 6 1 ADANA HEMŞİRE GENEL BÜTÇE 2 1 ADANA SAĞLIK MEMURU ÇEVRE SAĞLIĞI TEKNİSYENİ GENEL BÜTÇE 1 1
YEREL SEÇİM ANALİZLERİ. Şubat, 2014
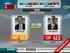 YEREL SEÇİM ANALİZLERİ Şubat, 2014 Partilerin Kazanacağı Belediye Sayıları Partilere Göre 81İlin Yerel Seçimlerde Alınması Muhtemel Oy Oranları # % AK Parti 37 45,7 CHP 9 11,1 MHP 5 6,2 BDP/HDP 8 9,9 Rekabet
YEREL SEÇİM ANALİZLERİ Şubat, 2014 Partilerin Kazanacağı Belediye Sayıları Partilere Göre 81İlin Yerel Seçimlerde Alınması Muhtemel Oy Oranları # % AK Parti 37 45,7 CHP 9 11,1 MHP 5 6,2 BDP/HDP 8 9,9 Rekabet
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU HAZİRAN 2015 Türkiye İstatistik Kurumu 03/07/2015 tarihinde 2015 yılı Haziran ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU HAZİRAN 2015 Türkiye İstatistik Kurumu 03/07/2015 tarihinde 2015 yılı Haziran ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU MAYIS 2016 Türkiye İstatistik Kurumu 03/06/2016 tarihinde 2016 yılı Mayıs ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU MAYIS 2016 Türkiye İstatistik Kurumu 03/06/2016 tarihinde 2016 yılı Mayıs ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
LİSTE - II TÜRKİYE HALK SAĞLIĞI KURUMU - TAŞRA
 1 ADANA EBE 4 1 ADANA SAĞLIK MEMURU RÖNTGEN TEKNİSYENİ 1 1 ADANA SAĞLIK MEMURU TIBBİ SEKRETER 2 2 ADIYAMAN DİYETİSYEN 2 2 ADIYAMAN EBE 2 2 ADIYAMAN HEMŞİRE 1 2 ADIYAMAN SAĞLIK MEMURU TIBBİ SEKRETER 1 2
1 ADANA EBE 4 1 ADANA SAĞLIK MEMURU RÖNTGEN TEKNİSYENİ 1 1 ADANA SAĞLIK MEMURU TIBBİ SEKRETER 2 2 ADIYAMAN DİYETİSYEN 2 2 ADIYAMAN EBE 2 2 ADIYAMAN HEMŞİRE 1 2 ADIYAMAN SAĞLIK MEMURU TIBBİ SEKRETER 1 2
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU EYLÜL 2016 Türkiye İstatistik Kurumu 03/10/2016 tarihinde 2016 yılı Eylül ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU EYLÜL 2016 Türkiye İstatistik Kurumu 03/10/2016 tarihinde 2016 yılı Eylül ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU NİSAN 2014 Türkiye İstatistik Kurumu 05/05/2014 tarihinde 2014 yılı Nisan ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU NİSAN 2014 Türkiye İstatistik Kurumu 05/05/2014 tarihinde 2014 yılı Nisan ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU AĞUSTOS 2015 Türkiye İstatistik Kurumu 03/09/2015 tarihinde 2015 yılı Ağustos ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU AĞUSTOS 2015 Türkiye İstatistik Kurumu 03/09/2015 tarihinde 2015 yılı Ağustos ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU OCAK 2016 Türkiye İstatistik Kurumu 03/02/2016 tarihinde 2016 yılı Ocak ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU OCAK 2016 Türkiye İstatistik Kurumu 03/02/2016 tarihinde 2016 yılı Ocak ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU EKİM 2014 Türkiye İstatistik Kurumu 03/11/2014 tarihinde 2014 yılı Ekim ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU EKİM 2014 Türkiye İstatistik Kurumu 03/11/2014 tarihinde 2014 yılı Ekim ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TAŞRA TEŞKİLATI MÜNHAL TEKNİKER KADROLARI
 ADANA MERKEZ 111918 İL MEM İNŞAAT 1 ADANA MERKEZ 111918 İL MEM ELEKTRİK 2 ADIYAMAN MERKEZ 114014 İL MEM İNŞAAT 1 ADIYAMAN MERKEZ 114014 İL MEM ELEKTRİK 1 AFYONKARAHİSARMERKEZ 114972 İL MEM İNŞAAT 1 AFYONKARAHİSARMERKEZ
ADANA MERKEZ 111918 İL MEM İNŞAAT 1 ADANA MERKEZ 111918 İL MEM ELEKTRİK 2 ADIYAMAN MERKEZ 114014 İL MEM İNŞAAT 1 ADIYAMAN MERKEZ 114014 İL MEM ELEKTRİK 1 AFYONKARAHİSARMERKEZ 114972 İL MEM İNŞAAT 1 AFYONKARAHİSARMERKEZ
Türkiyede ki ĠĢ Kazalarının Yapay Sinir Ağları ile 2025 Yılına Kadar Tahmini
 Türkyede k ĠĢ Kazalarının Yapay Snr Ağları le 2025 Yılına Kadar Tahmn Hüseyn Ceylan ve Murat Avan Kırıkkale Meslek Yüksekokulu, Kırıkkale Ünverstes, Kırıkkale, 71450 Türkye. Kaman Meslek Yüksekokulu, Ah
Türkyede k ĠĢ Kazalarının Yapay Snr Ağları le 2025 Yılına Kadar Tahmn Hüseyn Ceylan ve Murat Avan Kırıkkale Meslek Yüksekokulu, Kırıkkale Ünverstes, Kırıkkale, 71450 Türkye. Kaman Meslek Yüksekokulu, Ah
Bulanık Mantık ile Hesaplanan Geoid Yüksekliğine Nokta Yüksekliklerinin Etkisi
 Harta Teknolojler Elektronk Dergs Clt: 5, No: 1, 2013 (61-67) Electronc Journal of Map Technologes Vol: 5, No: 1, 2013 (61-67) TEKNOLOJİK ARAŞTIRMALAR www.teknolojkarastrmalar.com e-issn: 1309-3983 Makale
Harta Teknolojler Elektronk Dergs Clt: 5, No: 1, 2013 (61-67) Electronc Journal of Map Technologes Vol: 5, No: 1, 2013 (61-67) TEKNOLOJİK ARAŞTIRMALAR www.teknolojkarastrmalar.com e-issn: 1309-3983 Makale
BAYİLER. Administrator tarafından yazıldı. Çarşamba, 18 Nisan :29 - Son Güncelleme Cuma, 03 Mayıs :39
 Federal CNG Dönüşüm Sistemleri olarak, başta Konya olmak üzere Türkiye'nin her bölgesinde ve her ilimizde CNG Dönüşüm Sistemleri konusunda hizmet vermekteyiz. FEDERAL CNG DÖNÜŞÜM SİSTEMLERİ Adana CNG Dönüşüm
Federal CNG Dönüşüm Sistemleri olarak, başta Konya olmak üzere Türkiye'nin her bölgesinde ve her ilimizde CNG Dönüşüm Sistemleri konusunda hizmet vermekteyiz. FEDERAL CNG DÖNÜŞÜM SİSTEMLERİ Adana CNG Dönüşüm
Ulusal Gelişmeler. Büyüme Hızı (%) Türkiye ekonomisi 2017 itibariyle dünyanın 17. Avrupa nın 6. büyük ekonomisidir. a r k a. o r g.
 Ulusal Gelişmeler Büyüme Hızı (%) Türkiye ekonomisi 2017 itibariyle dünyanın 17. Avrupa nın 6. büyük ekonomisidir. %10 veya fazla %6-%10 %3-%6 %0-%3 %0 dan küçük Veri yok Kaynak: TÜİK- Dünya Bankası; *:
Ulusal Gelişmeler Büyüme Hızı (%) Türkiye ekonomisi 2017 itibariyle dünyanın 17. Avrupa nın 6. büyük ekonomisidir. %10 veya fazla %6-%10 %3-%6 %0-%3 %0 dan küçük Veri yok Kaynak: TÜİK- Dünya Bankası; *:
Tek Yönlü Varyans Analizi
 Tek Yönlü Varyan Analz Nedr ve hang durumlarda kullanılır? den fazla grupların karşılaştırılmaı öz konuu e, çok ayıda t-tet nn kullanılmaı, Tp I hatanın artmaına yol açar; Örneğn, eğer 5 grubu kşerl olarak
Tek Yönlü Varyan Analz Nedr ve hang durumlarda kullanılır? den fazla grupların karşılaştırılmaı öz konuu e, çok ayıda t-tet nn kullanılmaı, Tp I hatanın artmaına yol açar; Örneğn, eğer 5 grubu kşerl olarak
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU ARALIK 2014 Türkiye İstatistik Kurumu 05/01/2015 tarihinde 2014 yılı Aralık ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU ARALIK 2014 Türkiye İstatistik Kurumu 05/01/2015 tarihinde 2014 yılı Aralık ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ
 Kİ-KAR TSTLRİ A) Kİ-KAR DAĞILIMI V ÖZLLİKLRİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk gösterp
Kİ-KAR TSTLRİ A) Kİ-KAR DAĞILIMI V ÖZLLİKLRİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk gösterp
Sıklık Tabloları ve Tek Değişkenli Grafikler
 Sıklık Tabloları ve Tek Değşkenl Grafkler Sıklık Tablosu Ver dzsnde yer alan değerlern tekrarlama sayılarını çeren tabloya sıklık tablosu denr. Sıklık Tabloları tek değşken çn marjnal tablo olarak adlandırılır.
Sıklık Tabloları ve Tek Değşkenl Grafkler Sıklık Tablosu Ver dzsnde yer alan değerlern tekrarlama sayılarını çeren tabloya sıklık tablosu denr. Sıklık Tabloları tek değşken çn marjnal tablo olarak adlandırılır.
Kİ-KARE TESTLERİ. şeklinde karesi alındığında, Z i. değerlerinin dağılımı ki-kare dağılımına dönüşür.
 Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk
Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU AĞUSTOS 2016 Türkiye İstatistik Kurumu 05/09/2016 tarihinde 2016 yılı Ağustos ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU AĞUSTOS 2016 Türkiye İstatistik Kurumu 05/09/2016 tarihinde 2016 yılı Ağustos ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
İleri Teknolojili Tıbbi Görüntüleme Cihazları Yoğunluğu. Prepared by: Siemens Turkey Strategy and Business Development, SBD Istanbul, March 2010
 İleri Teknolojili Tıbbi Görüntüleme Cihazları Yoğunluğu Prepared by: Siemens Turkey Strategy and Business Development, SBD Istanbul, March 200 Bilgisayarlı Tomografi milyon kişiye düşen cihaz sayısı İlk
İleri Teknolojili Tıbbi Görüntüleme Cihazları Yoğunluğu Prepared by: Siemens Turkey Strategy and Business Development, SBD Istanbul, March 200 Bilgisayarlı Tomografi milyon kişiye düşen cihaz sayısı İlk
PROJE SEÇİMİ VE KAYNAK PLANLAMASI İÇİN BİR ALGORİTMA AN ALGORITHM FOR PROJECT SELECTION AND RESOURCE PLANNING
 Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Clt 3, Sayı:2, 2001 PROJE SEÇİMİ VE KAYAK PLALAMASI İÇİ BİR ALGORİTMA lgün MORALI 1 C. Cengz ÇELİKOĞLU 2 ÖZ Kaynak tahss problemler koşullara bağlı olarak
Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Clt 3, Sayı:2, 2001 PROJE SEÇİMİ VE KAYAK PLALAMASI İÇİ BİR ALGORİTMA lgün MORALI 1 C. Cengz ÇELİKOĞLU 2 ÖZ Kaynak tahss problemler koşullara bağlı olarak
Kİ KARE ANALİZİ. Doç. Dr. Mehmet AKSARAYLI Ki-Kare Analizleri
 Kİ KAR ANALİZİ 1 Doç. Dr. Mehmet AKSARAYLI www.mehmetaksarayl K-Kare Analzler OLAY 1: Genelde br statstk sınıfında, öğrenclern %60 ının devamlı, %30 unun bazen, %10 unun se çok az derse geldkler düşünülmektedr.
Kİ KAR ANALİZİ 1 Doç. Dr. Mehmet AKSARAYLI www.mehmetaksarayl K-Kare Analzler OLAY 1: Genelde br statstk sınıfında, öğrenclern %60 ının devamlı, %30 unun bazen, %10 unun se çok az derse geldkler düşünülmektedr.
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU KASIM 2016 Türkiye İstatistik Kurumu 05/12/2016 tarihinde 2016 yılı Kasım ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU KASIM 2016 Türkiye İstatistik Kurumu 05/12/2016 tarihinde 2016 yılı Kasım ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU TEMMUZ 2017 Türkiye İstatistik Kurumu 03/08/2017 tarihinde 2017 yılı Temmuz ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU TEMMUZ 2017 Türkiye İstatistik Kurumu 03/08/2017 tarihinde 2017 yılı Temmuz ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 HANEHALKI İŞGÜCÜ İSTATİSTİKLERİ BİLGİ NOTU 2013 Yılı Türkiye İstatistik Kurumu 06/03/2014 tarihinde 2013 yılı Hanehalkı İşgücü İstatistikleri haber bültenini yayımladı. 2013 yılında bir önceki yıla göre;
HANEHALKI İŞGÜCÜ İSTATİSTİKLERİ BİLGİ NOTU 2013 Yılı Türkiye İstatistik Kurumu 06/03/2014 tarihinde 2013 yılı Hanehalkı İşgücü İstatistikleri haber bültenini yayımladı. 2013 yılında bir önceki yıla göre;
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU OCAK 2015 Türkiye İstatistik Kurumu 03/02/2015 tarihinde 2015 yılı Ocak ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU OCAK 2015 Türkiye İstatistik Kurumu 03/02/2015 tarihinde 2015 yılı Ocak ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
Makine Öğrenmesi 10. hafta
 Makne Öğrenmes 0. hafta Lagrange Optmzasonu Destek Vektör Maknes (SVM) Karesel (Quadratc) Programlama Optmzason Blmsel term olarak dlmze geçmş olsa da bazen en leme termle karşılık bulur. Matematktek en
Makne Öğrenmes 0. hafta Lagrange Optmzasonu Destek Vektör Maknes (SVM) Karesel (Quadratc) Programlama Optmzason Blmsel term olarak dlmze geçmş olsa da bazen en leme termle karşılık bulur. Matematktek en
X, R, p, np, c, u ve diğer kontrol diyagramları istatistiksel kalite kontrol diyagramlarının
 1 DİĞER ÖZEL İSTATİSTİKSEL KALİTE KONTROL DİYAGRAMLARI X, R, p, np, c, u ve dğer kontrol dyagramları statstksel kalte kontrol dyagramlarının temel teknkler olup en çok kullanılanlarıdır. Bu teknkler ell
1 DİĞER ÖZEL İSTATİSTİKSEL KALİTE KONTROL DİYAGRAMLARI X, R, p, np, c, u ve dğer kontrol dyagramları statstksel kalte kontrol dyagramlarının temel teknkler olup en çok kullanılanlarıdır. Bu teknkler ell
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU EYLÜL 2015 Türkiye İstatistik Kurumu 05/10/2015 tarihinde 2015 yılı Eylül ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU EYLÜL 2015 Türkiye İstatistik Kurumu 05/10/2015 tarihinde 2015 yılı Eylül ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi (TÜFE)
Kİ-KARE VE KOLMOGOROV SMİRNOV UYGUNLUK TESTLERİNİN SİMULASYON İLE ELDE EDİLEN VERİLER ÜZERİNDE KARŞILAŞTIRILMASI
 C.Ü. İktsad ve İdar Blmler Dergs, Clt 4, Sayı 1, 3 6 Kİ-KARE VE KOLMOGOROV SMİRNOV UYGUNLUK TESTLERİNİN SİMULASYON İLE ELDE EDİLEN VERİLER ÜZERİNDE KARŞILAŞTIRILMASI H. BİRCAN, Y. KARAGÖZ ve Y. KASAPOĞLU
C.Ü. İktsad ve İdar Blmler Dergs, Clt 4, Sayı 1, 3 6 Kİ-KARE VE KOLMOGOROV SMİRNOV UYGUNLUK TESTLERİNİN SİMULASYON İLE ELDE EDİLEN VERİLER ÜZERİNDE KARŞILAŞTIRILMASI H. BİRCAN, Y. KARAGÖZ ve Y. KASAPOĞLU
İZMİR İN EN BÜYÜK SORUNU İŞSİZLİK RAKAMLARININ ANALİZİ
 2015 TEMMUZ- AĞUSTOS EKONOMİK İZMİR İN EN BÜYÜK SORUNU İŞSİZLİK RAKAMLARININ ANALİZİ Erdem ALPTEKİN Türkiye İstatistik Kurumu verilerine göre; 2014 yılında ülkemizde işsizlik oranı % 9,9 seviyesinde gerçekleşti.
2015 TEMMUZ- AĞUSTOS EKONOMİK İZMİR İN EN BÜYÜK SORUNU İŞSİZLİK RAKAMLARININ ANALİZİ Erdem ALPTEKİN Türkiye İstatistik Kurumu verilerine göre; 2014 yılında ülkemizde işsizlik oranı % 9,9 seviyesinde gerçekleşti.
2015 KOCAELİ NÜFUSUNUN BÖLGESEL ANALİZİ TUİK
 0 NÜFUSUNUN BÖLGESEL ANALİZİ TUİK Verilerine Göre Hazırlanmıştır. İLİNİN NÜFUSU.. NÜFUSUNA KAYITLI OLANLAR NDE YAŞAYIP NÜFUS KAYDI BAŞKA İLLERDE OLANLAR.0 %... %. NÜFUSUNUN BÖLGESEL ANALİZİ 0 TUİK Verilerine
0 NÜFUSUNUN BÖLGESEL ANALİZİ TUİK Verilerine Göre Hazırlanmıştır. İLİNİN NÜFUSU.. NÜFUSUNA KAYITLI OLANLAR NDE YAŞAYIP NÜFUS KAYDI BAŞKA İLLERDE OLANLAR.0 %... %. NÜFUSUNUN BÖLGESEL ANALİZİ 0 TUİK Verilerine
Doğrusal Korelasyon ve Regresyon
 Doğrusal Korelasyon ve Regresyon En az k değşken arasındak lşknn ncelenmesne korelasyon denr. Kşlern boyları le ağırlıkları, gelr le gder, öğrenclern çalıştıkları süre le aldıkları not, tarlaya atılan
Doğrusal Korelasyon ve Regresyon En az k değşken arasındak lşknn ncelenmesne korelasyon denr. Kşlern boyları le ağırlıkları, gelr le gder, öğrenclern çalıştıkları süre le aldıkları not, tarlaya atılan
NİTEL TERCİH MODELLERİ
 NİTEL TERCİH MODELLERİ 2300 gözlem sayısı le verlen değşkenler aşağıdak gbdr: calsma: çocuk çalışıyorsa 1, çalışmıyorsa 0 (bağımlı değşken) Anne_egts: Anne eğtm sevyes Baba_egts: Baba eğtm sevyes Kent:
NİTEL TERCİH MODELLERİ 2300 gözlem sayısı le verlen değşkenler aşağıdak gbdr: calsma: çocuk çalışıyorsa 1, çalışmıyorsa 0 (bağımlı değşken) Anne_egts: Anne eğtm sevyes Baba_egts: Baba eğtm sevyes Kent:
BÖLÜM -VII- BÖLGESEL AZALTMA KATSAYILARI
 BÖLÜM -VII- BÖLGESEL AZALTMA KATSAYILARI TMMOB Elektrik Mühendisleri Odası 136 Elektrik, Elektronik ve Bilgisayar Mühendisliği Hizmetleri BÖLGESEL AZALTMA KATSAYILARI 2007 yılı içinde uygulanacak olan
BÖLÜM -VII- BÖLGESEL AZALTMA KATSAYILARI TMMOB Elektrik Mühendisleri Odası 136 Elektrik, Elektronik ve Bilgisayar Mühendisliği Hizmetleri BÖLGESEL AZALTMA KATSAYILARI 2007 yılı içinde uygulanacak olan
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU ARALIK 2015 Türkiye İstatistik Kurumu 04/01/2016 tarihinde 2015 yılı Aralık ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
TÜKETİCİ FİYAT ENDEKSİ (TÜFE) BİLGİ NOTU ARALIK 2015 Türkiye İstatistik Kurumu 04/01/2016 tarihinde 2015 yılı Aralık ayı Tüketici Fiyat Endeksi (TÜFE) haber bültenini yayımladı. Tüketici Fiyat Endeksi
Tüvturk Araç Muayene Gezici Mobil İstasyon Programı
 Tüvturk Araç Muayene Gezici Mobil İstasyon Programı Tüvturk Gezici istasyonlarında ağır vasıtalar (3.5 ton üzeri) hariç tüm motorlu ve motorsuz araçlar için muayene hizmeti verilmektedir. Gezici İstasyon
Tüvturk Araç Muayene Gezici Mobil İstasyon Programı Tüvturk Gezici istasyonlarında ağır vasıtalar (3.5 ton üzeri) hariç tüm motorlu ve motorsuz araçlar için muayene hizmeti verilmektedir. Gezici İstasyon
dir. Bir başka deyişle bir olayın olasılığı, uygun sonuçların sayısının örnek uzaydaki tüm sonuçların sayısına oranıdır.
 BÖLÜM 3 OLASILIK HESABI 3.. Br Olayın Olasılığı Tanım 3... Br olayın brbrnden ayrık ve ortaya çıkma şansı eşt n mümkün sonucundan m tanes br A olayına uygun se, A olayının P(A) le gösterlen olasılığı P(A)
BÖLÜM 3 OLASILIK HESABI 3.. Br Olayın Olasılığı Tanım 3... Br olayın brbrnden ayrık ve ortaya çıkma şansı eşt n mümkün sonucundan m tanes br A olayına uygun se, A olayının P(A) le gösterlen olasılığı P(A)
TAKVİM KARTONLARI 2016 YILI RESMİ TATİL GÜNLERİ
 2016 YILI RESMİ TATİL GÜNLERİ 2016 YILI MÜBAREK GÜN ve GECELER Yılbaşı 1 Ocak Cuma Ulusal Egemenlik ve Çocuk Bayramı 23 Nisan Cumartesi Emek ve Dayanışma Günü 1 Mayıs Pazar Gençlik ve Spor Bayramı 19 Mayıs
2016 YILI RESMİ TATİL GÜNLERİ 2016 YILI MÜBAREK GÜN ve GECELER Yılbaşı 1 Ocak Cuma Ulusal Egemenlik ve Çocuk Bayramı 23 Nisan Cumartesi Emek ve Dayanışma Günü 1 Mayıs Pazar Gençlik ve Spor Bayramı 19 Mayıs
BANKACILIKTA ETKİNLİK VE SERMAYE YAPISININ BANKALARIN ETKİNLİĞİNE ETKİSİ
 BANKACILIKTA ETKİNLİK VE SERMAYE YAPISININ BANKALARIN ETKİNLİĞİNE ETKİSİ Yrd. Doç. Dr. Murat ATAN - Araş. Gör. Gaye KARPAT ÇATALBAŞ 2 ÖZET Bu çalışma, Türk bankacılık sstem çnde faalyet gösteren tcar bankaların
BANKACILIKTA ETKİNLİK VE SERMAYE YAPISININ BANKALARIN ETKİNLİĞİNE ETKİSİ Yrd. Doç. Dr. Murat ATAN - Araş. Gör. Gaye KARPAT ÇATALBAŞ 2 ÖZET Bu çalışma, Türk bankacılık sstem çnde faalyet gösteren tcar bankaların
SAMSUN TİCARET VE SANAYİ ODASI EKONOMİK BÜLTEN
 SAMSUN TİCARET VE SANAYİ ODASI EKONOMİK BÜLTEN ARALIK 2016 Bu eserin tüm telif hakları Samsun Ticaret ve Sanayi Odası na aittir. Samsun Ticaret ve Sanayi Odası nın ismi kaydedilmek koşulu ile alıntı yapmak
SAMSUN TİCARET VE SANAYİ ODASI EKONOMİK BÜLTEN ARALIK 2016 Bu eserin tüm telif hakları Samsun Ticaret ve Sanayi Odası na aittir. Samsun Ticaret ve Sanayi Odası nın ismi kaydedilmek koşulu ile alıntı yapmak
TRANSPORT PROBLEMI için GELIsTIRILMIs VAM YÖNTEMI
 Yönetm, Yl 9, Say 28, Ekm - 1997,5.20-25 TRANSPORT PROBLEMI ÇIN GELIsTIRILMIs VAM YÖNTEMI Dr. Erhan ÖZDEMIR I.Ü. Teknk Blmler M.Y.O. L.GIRIs V AM transport problemlerne en düsük malyetl baslangç çözüm
Yönetm, Yl 9, Say 28, Ekm - 1997,5.20-25 TRANSPORT PROBLEMI ÇIN GELIsTIRILMIs VAM YÖNTEMI Dr. Erhan ÖZDEMIR I.Ü. Teknk Blmler M.Y.O. L.GIRIs V AM transport problemlerne en düsük malyetl baslangç çözüm
Tarım İşletmeleri Genel Müdürlüğü (Personel Daire Bşk.)
 Şube Başkanlıkları 1 NOLU ANKARA ŞUBESİ Mustafa GÜRAN Tarım İşletmeleri Genel Müdürlüğü (Personel Daire Bşk.) Tarım ve Köyişleri Bakanlığı Tel 5366400073 2 NOLU KAHRAMANMARAŞ ŞUBESİ Mustafa Ertan ATALAR
Şube Başkanlıkları 1 NOLU ANKARA ŞUBESİ Mustafa GÜRAN Tarım İşletmeleri Genel Müdürlüğü (Personel Daire Bşk.) Tarım ve Köyişleri Bakanlığı Tel 5366400073 2 NOLU KAHRAMANMARAŞ ŞUBESİ Mustafa Ertan ATALAR
Yığma Yapıların Deprem Güvenliklerinin Arttırılması
 Yığma Yapıların Deprem Güvenliklerinin Arttırılması TÜRKİYE DE YIĞMA BİNALAR İÇİN DEPREMSEL RİSK HARİTASI ELDE EDİLMESİ Yard. Doç. Dr. Ahmet TÜRER & Abdullah DİLSİZ (M.S.) 17.02.2005 AMAÇ & KAPSAM Bu çalışmada,
Yığma Yapıların Deprem Güvenliklerinin Arttırılması TÜRKİYE DE YIĞMA BİNALAR İÇİN DEPREMSEL RİSK HARİTASI ELDE EDİLMESİ Yard. Doç. Dr. Ahmet TÜRER & Abdullah DİLSİZ (M.S.) 17.02.2005 AMAÇ & KAPSAM Bu çalışmada,
Doğal Gaz Sektör Raporu
 GAZBİR HAZİRAN Türkiye Doğal Gaz Dağıtıcıları Birliği Doğal Gaz Sektör Raporu İthalat Haziran ayında yılının aynı ayına göre ülke ithalat miktarında 434 milyon sm3, %13,76 lik bir artış meydana gelmiştir.
GAZBİR HAZİRAN Türkiye Doğal Gaz Dağıtıcıları Birliği Doğal Gaz Sektör Raporu İthalat Haziran ayında yılının aynı ayına göre ülke ithalat miktarında 434 milyon sm3, %13,76 lik bir artış meydana gelmiştir.
KPSS-2014/3 Sağlık Bakanlığı ve Bağlı Kuruluşlarının Sözleşmeli Pozisyonlarına Yerleştirme (Ortaöğretim)
 KURUM ADI KADRO ADI 190160001 SAĞLIK BAKANLIĞI SAĞLIK MEMURU (ADANA TÜM İLÇELER Taşra) 5 0 75,57278 78,51528 190160003 SAĞLIK BAKANLIĞI SAĞLIK MEMURU (ARTVİN TÜM İLÇELER Taşra) 4 0 75,26887 75,34407 190160005
KURUM ADI KADRO ADI 190160001 SAĞLIK BAKANLIĞI SAĞLIK MEMURU (ADANA TÜM İLÇELER Taşra) 5 0 75,57278 78,51528 190160003 SAĞLIK BAKANLIĞI SAĞLIK MEMURU (ARTVİN TÜM İLÇELER Taşra) 4 0 75,26887 75,34407 190160005
Yüksek Dereceli Bulanık Zaman Serisi Yaklaşımı İle Türkiye Enflasyon Öngörüsü
 Yüksek Dereceli Bulanık Zaman Serisi Yaklaşımı İle Türkiye Enflasyon Öngörüsü Vedide Rezan USLU 1 Ufuk YOLCU 2 Erol EĞRİOĞLU 3 Ç.Hakan LDĞ 4 M. lper BŞRN 5 Özet Enflasyon öngörülerinin elde edilmesi önemli
Yüksek Dereceli Bulanık Zaman Serisi Yaklaşımı İle Türkiye Enflasyon Öngörüsü Vedide Rezan USLU 1 Ufuk YOLCU 2 Erol EĞRİOĞLU 3 Ç.Hakan LDĞ 4 M. lper BŞRN 5 Özet Enflasyon öngörülerinin elde edilmesi önemli
VERİ ZARFLAMA ANALİZİ İLE TIBBİ GÖRÜNTÜ, ARŞİV VE İLETİŞİM SİSTEMLERİNİN DEVLET HASTANELERİ PERFORMANSINA ETKİLERİNİN ARAŞTIRILMASI
 Süleyman Demrel Ünverstes Sosyal Blmler Ensttüsü DergsYıl: 2013/1, Sayı:17 Journal of Süleyman Demrel Unversty Insttute of Socal ScencesYear: 2013/1, Number:17 VERİ ZARFLAMA ANALİZİ İLE TIBBİ GÖRÜNTÜ,
Süleyman Demrel Ünverstes Sosyal Blmler Ensttüsü DergsYıl: 2013/1, Sayı:17 Journal of Süleyman Demrel Unversty Insttute of Socal ScencesYear: 2013/1, Number:17 VERİ ZARFLAMA ANALİZİ İLE TIBBİ GÖRÜNTÜ,
HKMO 39. Dönem Çal flma Raporu
 4.8. STAT ST KLER 538 HKMO 39. Dönem Çal flma Raporu Kay t Tarihlerine Göre Üye Say lar / Oranlar Kay t Tarihlerine Göre Grafik Y l: ÜYE SAYISI MERKEZ ADANA ANKARA ANTALYA BURSA D YARBAKIR STANBUL ZM R
4.8. STAT ST KLER 538 HKMO 39. Dönem Çal flma Raporu Kay t Tarihlerine Göre Üye Say lar / Oranlar Kay t Tarihlerine Göre Grafik Y l: ÜYE SAYISI MERKEZ ADANA ANKARA ANTALYA BURSA D YARBAKIR STANBUL ZM R
BİLGİ TEKNOLOJİLERİ VE İLETİŞİM KURULU KARAR. : 2017 Yıllık Kullanım Hakkı Ücretleri. : Yetkilendirme Dairesi Başkanlığının hazırladığı takrir ve
 BİLGİ TEKNOLOJİLERİ VE İLETİŞİM KURULU KARARI Karar Tarihi : 14.12.2016 Karar No : 2016/DK-YED/486 Gündem Konusu : 2017 Yıllık Kullanım Hakkı Ücretleri KARAR ekleri incelenmiştir. : Yetkilendirme Dairesi
BİLGİ TEKNOLOJİLERİ VE İLETİŞİM KURULU KARARI Karar Tarihi : 14.12.2016 Karar No : 2016/DK-YED/486 Gündem Konusu : 2017 Yıllık Kullanım Hakkı Ücretleri KARAR ekleri incelenmiştir. : Yetkilendirme Dairesi
KENTSEL ALANDA ET TALEP ANALİZİ: BATI AKDENİZ BÖLGESİ ÖRNEĞİ. Dr. Ali Rıza AKTAŞ 1 Dr. Selim Adem HATIRLI 2
 Journal of Yasar Unversty 2010 3294-3319 KENTSEL ALANDA ET TALEP ANALİZİ: BATI AKDENİZ BÖLGESİ ÖRNEĞİ Dr. Al Rıza AKTAŞ 1 Dr. Selm Adem HATIRLI 2 ÖZET Bu çalışmada, Batı Akdenz Bölges kent merkezlernde
Journal of Yasar Unversty 2010 3294-3319 KENTSEL ALANDA ET TALEP ANALİZİ: BATI AKDENİZ BÖLGESİ ÖRNEĞİ Dr. Al Rıza AKTAŞ 1 Dr. Selm Adem HATIRLI 2 ÖZET Bu çalışmada, Batı Akdenz Bölges kent merkezlernde
TÜRKİYE ODALAR VE BORSALAR BİRLİĞİ
 Sayfa 1 Gözden Geçirme Notları 2011 Yılı Haziran Ayı TÜFE Göstergeleri TÜİK tarafından tarihinde açıklanan, 2011 yılı Haziran ayı Tüketici Fiyatları Endeksi (TÜFE) haber bültenine göre Endeks; Aylık bazda
Sayfa 1 Gözden Geçirme Notları 2011 Yılı Haziran Ayı TÜFE Göstergeleri TÜİK tarafından tarihinde açıklanan, 2011 yılı Haziran ayı Tüketici Fiyatları Endeksi (TÜFE) haber bültenine göre Endeks; Aylık bazda
Tüvturk Araç Muayene Gezici Mobil İstasyon Programı
 Tüvturk Araç Muayene Gezici Mobil İstasyon Programı Tüvturk Gezici istasyonlarında ağır vasıtalar (3.5 ton üzeri) hariç tüm motorlu ve motorsuz araçlar için muayene hizmeti verilmektedir. Gezici istasyonlar
Tüvturk Araç Muayene Gezici Mobil İstasyon Programı Tüvturk Gezici istasyonlarında ağır vasıtalar (3.5 ton üzeri) hariç tüm motorlu ve motorsuz araçlar için muayene hizmeti verilmektedir. Gezici istasyonlar
Farklı Varyans. Var(u i X i ) = Var(u i ) = E(u i2 ) = σ i2. Eşit Varyans. Hata. Zaman
 Farklı Varyans Var(u X ) = Var(u ) = E(u ) = σ Eşt Varyans Y X Farklı Varyans Hata Var(u X ) = Var(u ) = E(u ) = σ Farklı Varyans Zaman Farklı Varyans le Karşılaşılan Durumlar Kest Verlernde. Kar dağıtım
Farklı Varyans Var(u X ) = Var(u ) = E(u ) = σ Eşt Varyans Y X Farklı Varyans Hata Var(u X ) = Var(u ) = E(u ) = σ Farklı Varyans Zaman Farklı Varyans le Karşılaşılan Durumlar Kest Verlernde. Kar dağıtım
BÖLÜM -VI- BÖLGESEL AZALTMA KATSAYILARI
 BÖLÜM -VI- BÖLGESEL AZALTMA KATSAYILARI 179 180 Elektrik, Elektronik-Biyomedikal-Kontrol Mühendisliği Hizmetleri BÖLGESEL AZALTMA KATSAYILARI (BK) EMO Yönetim Kurulunun 04.11.2017 tarih ve 45/56 sayılı
BÖLÜM -VI- BÖLGESEL AZALTMA KATSAYILARI 179 180 Elektrik, Elektronik-Biyomedikal-Kontrol Mühendisliği Hizmetleri BÖLGESEL AZALTMA KATSAYILARI (BK) EMO Yönetim Kurulunun 04.11.2017 tarih ve 45/56 sayılı
Mart 2012 SAGMER İstatistikleri
 Mart 2012 SAGMER İstatistikleri *Ekli dosyadaki istatistikî veriler, Sigorta Şirketlerinin SBM ye gönderdiği verilerden oluşturulmuştur. Veriler 31 Mart 2012 itibariyle alınmıştır. Tablo 1: Ödeme Yöntemine
Mart 2012 SAGMER İstatistikleri *Ekli dosyadaki istatistikî veriler, Sigorta Şirketlerinin SBM ye gönderdiği verilerden oluşturulmuştur. Veriler 31 Mart 2012 itibariyle alınmıştır. Tablo 1: Ödeme Yöntemine
Ulusal Gelişmeler. Büyüme Hızı (%) a r k a. o r g. t r * II III IV YILLIK I II III IV YILLIK I II III IV YILLIK I II III
 18.01.2019 Ulusal Gelişmeler Büyüme Hızı (%) %10 veya fazla %6-%10 %3-%6 %0-%3 %0 dan küçük Veri yok 2016 2017 2018* 14 II III IV YILLIK I II III IV YILLIK I II III IV YILLIK I II III 12 10 8 6 11,5 4
18.01.2019 Ulusal Gelişmeler Büyüme Hızı (%) %10 veya fazla %6-%10 %3-%6 %0-%3 %0 dan küçük Veri yok 2016 2017 2018* 14 II III IV YILLIK I II III IV YILLIK I II III IV YILLIK I II III 12 10 8 6 11,5 4
LİMANLAR GERİ SAHA KARAYOLU VE DEMİRYOLU BAĞLANTILARI MASTER PLAN ÇALIŞMASI
 T.C. ULAŞTIRMA, DENİZCİLİK VE HABERLEŞME BAKANLIĞI ALTYAPI YATIRIMLARI GENEL MÜDÜRLÜĞÜ LİMANLAR GERİ SAHA KARAYOLU VE DEMİRYOLU BAĞLANTILARI MASTER PLAN ÇALIŞMASI SONUÇ RAPORU-EKLER Mühendislik Anonim
T.C. ULAŞTIRMA, DENİZCİLİK VE HABERLEŞME BAKANLIĞI ALTYAPI YATIRIMLARI GENEL MÜDÜRLÜĞÜ LİMANLAR GERİ SAHA KARAYOLU VE DEMİRYOLU BAĞLANTILARI MASTER PLAN ÇALIŞMASI SONUÇ RAPORU-EKLER Mühendislik Anonim
İŞYERİ EĞİLİM ARAŞTIRMASI 2017
 İŞYERİ EĞİLİM ARAŞTIRMASI 2017 TÜRKİYE İSTATİSTİK KURUMU Neden İşyeri Eğilim Anketi? Kamu hizmetlerinin doğru planlanması ve kamu kaynaklarının etkin olarak kullanılması için güvenilir istatistiklere ihtiyaç
İŞYERİ EĞİLİM ARAŞTIRMASI 2017 TÜRKİYE İSTATİSTİK KURUMU Neden İşyeri Eğilim Anketi? Kamu hizmetlerinin doğru planlanması ve kamu kaynaklarının etkin olarak kullanılması için güvenilir istatistiklere ihtiyaç
Talepte Bulunan PersonelinÜnvanlara Göre Dağılımı
 15/06/2011-05/08/2011 Tarihleri Arasında Başkanlığımız İnternet Sitesinde Yayınlanan "Hizmetiçi Eğitim İhtiyacının Belirlenmesi Anketi"ne Katılan 7.191 Personelin 58.878 Tercihin, "Tercih Edilen Eğitim
15/06/2011-05/08/2011 Tarihleri Arasında Başkanlığımız İnternet Sitesinde Yayınlanan "Hizmetiçi Eğitim İhtiyacının Belirlenmesi Anketi"ne Katılan 7.191 Personelin 58.878 Tercihin, "Tercih Edilen Eğitim
TABLO-1. MERKEZİ YERLEŞTİRMEDEKİ EN KÜÇÜK VE EN BÜYÜK PUANLAR ( ORTAÖĞRETİM MEZUNLARI )
 1573951 3 0 091.496 092.411 HEMŞİRE (BOLU) ABANT İZZET BAYSAL ÜNİVERSİTESİ (Merkez) 1573953 29 0 093.232 096.492 KORUMA VE GÜVENLİK GÖREVLİSİ (ANKARA) ADALET BAKANLIĞI (Merkez) 1573955 11 0 092.813 093.230
1573951 3 0 091.496 092.411 HEMŞİRE (BOLU) ABANT İZZET BAYSAL ÜNİVERSİTESİ (Merkez) 1573953 29 0 093.232 096.492 KORUMA VE GÜVENLİK GÖREVLİSİ (ANKARA) ADALET BAKANLIĞI (Merkez) 1573955 11 0 092.813 093.230
YAŞAM ÇÖZÜMLEMESİNDE AYKIRI DEĞERLER OUTLIERS IN SURVIVAL ANALYSIS
 YAŞAM ÇÖZÜMLEMESİNDE AYKIRI DEĞERLER OUTLIERS IN SURVIVAL ANALYSIS NURAY TUNCER PROF. DR. DURDU KARASOY Tez Danışmanı Hacettepe Ünverstes Lsansüstü Eğtm-Öğretm Yönetmelğnn İstatstk Anablm Dalı İçn Öngördüğü
YAŞAM ÇÖZÜMLEMESİNDE AYKIRI DEĞERLER OUTLIERS IN SURVIVAL ANALYSIS NURAY TUNCER PROF. DR. DURDU KARASOY Tez Danışmanı Hacettepe Ünverstes Lsansüstü Eğtm-Öğretm Yönetmelğnn İstatstk Anablm Dalı İçn Öngördüğü
