YOLCU TALEPLERİ İLE FİLO ROTASI VE UÇUŞ LİsTELERİNE ÇOK AMAÇLI TAMSAYILI AG ALGORİTMASIYLA ÇÖZÜM YAKLAŞıMı VE TÜRK HAVA YOLLARI' NA UYGULANMASI
|
|
|
- Ebru Korkmaz
- 8 yıl önce
- İzleme sayısı:
Transkript
1 YOLCU TALEPLERİ İLE FİLO ROTASI VE UÇUŞ LİsTELERİNE ÇOK AMAÇLI TAMSAYILI AG ALGORİTMASIYLA ÇÖZÜM YAKLAŞıMı VE TÜRK HAVA YOLLARI' NA UYGULANMASI Bir hava yolu şirketi için tilo rotası ve uçuş listeleri pazardaki rekabet gücünü ve servis kalitesini, dolayısıyla da doğrudan doğruya karlılığını etkilemede enönemli unsurlann başında yeralmaktadır. Bu çalışma ile daha iyi bir filo rotası ve uygun zaman tablolarının oluşturulabilmesine yönelik olarak bir model geliştirilmesine yönelik olarak bir model geliştirilmesine ve bunun içinde bir çözüm algoritmasının oluşhrrulmasına çalışılmıştır. Çalışmada yeralan model tamsayılı çoklu ürün akış ağı problemi olarak tasarlanmıştır. Modelin çözüm algoritmasında ise lagragian yaklaşımı, alt gradient yöntemi, ağ simplex metodu, en düşük maliyet akışı algoritması ve akış çözümü algoritmalarından yararlanılarak problemin çözümü gerçekleştirilmiştir. Uygulamaya yönelik olarak gerçekleştirilen çalışma için gerekli veriler THY'dan elde edilmiş ve oldukça uygun sonuçlara ulaşılmıştır. Filo rotası ve uçuş listeleri hava yolu şirketleri için oldukça önemli işleve sahip iki ana problemi oluşhınnaktadır. Normal koşullarda ağ akış teknikleıi pekçok kompleks matematiksel problemin çözüıebilmesi ve tek bir modele dönüştürülebilmesi için yeterli olmaktadır. Ancak, geleneksel yaklaşımlar hem işlemlerde yeralan birbiriyle ilişkili çok sayıda yargıyı ve karar alma işlemini, hem de arz ve talep arasındaki ilişkiyi sistematik olarak doğnıdan yönlendirebilıne ve yönetebilme kapasitesine sahip değillerdir. Bu çalışmanın amacı yolcu talepleri ile uçuş imkanları arasındaki içsel ilişkiyi etkili bir şekilde ortaya çıkararak doğrudan yönetilebilir bir hale getirebilmektir. Filo rotası ve uçuş listelerinin havacılık işlemleri içerisinde son derece kritik iki aktiviteyi oluşturması, özellikle, bu iki faaliyetin uçağın etkili bir şekilde kullanımının, zaman tablolarının oluşturulmasının, uçak bakımının ve mürettebat listesinin oluşturulmasında etkili olmasına yol açmaktadır. Sonuç olarak, tüm bu faaliyetler bir hava yolu şirkcti için pazardaki rckabet gücünü ve scrvis kalitcsini, dolayısıyla da doğrudan doğruya M.Ü. İktisadi ve İdari Bilimler Fakültesi Ekonometri Bölümü Yöneylem Araştımıası Anabilim Dalı Araştımıa Görevlisi.
2 karlılığını etkiiemede son derece önemii bir unsur olarak karşımıza çıkmaktadır. Uçuş listesi işlemi genei oiarak birbiriyle bağiiltı1ı iki aşamadan meydana gelmektedir. Bunlar sırasıyla listenin oluşturulması ve listenin geliştirilmesi aşamasıdır. Oluşturma aşaması proje talebine göre bir taslak zaman tabiosu, pazar payı ve kullanılabiiir hava aianlarının zaman uygunluklarının biraraya getirilmesinden meydana gelmektedir. Bu işlemden sonra, tasiak zaman tabiosu tasarı geliştirme evresi süresince işlem yapılabilirliği, maliyet ve performans kriterlerine göre teste tabi tutulur. Yapılabilirliğin geliştirme evresi süresince test edilmesinde dikkat edilmesi gereken kriterler; filo rotaları, filo büyüklüğü, mürettebat dağılımı ve bakım düzenlemeleridir. Bu aşama sırasında herhangi bir iyileştiıme oluşturma aşamasındaki zaman tablosunun gözden geçirilerek daha da geliştirilmesine etki etmektedir. Uçuş listesi oiuşturma işlemi bu iki aşamanın isteniiene uygun bir zaman tabiosunun eide edilmesine kadar devam etmektedir!. Pek çok hava yolu şirketi filo rotası ve uçuş listesi uygulamalarında deneme yanılma yoiunu kullanmaktadır. Listeniıı oiuşturulması ve geliştirilmesi aşamasını elle tekrar tekrar gerçekleştirme yoiuna gitmektedirier. Bu yaklaşım işlem boyutunun artması durumunda hiç de uygun olmayan sonuçlara neden olabilmektedir. Bu konuda etkiii bir çözüm yakiaşımı Yan ve Young tarafından çoklu fılo rotası ve çoklu duraklı uçuş listesi olarak eie alınmıştır. Yan ve Young yaklaşımı geleneksel deneme yanılma yaklaşımından da etkili ve daha sistematik, mukayeseli iki aşamalı iterasyon probleminin etkili çözümüne yönelik bir matematiksel modei geliştirmesini kapsamaktadır. Buna rağmen bu yöntem de hala planiayıcı personeiin tecrübelerinden hareketle iiksel olarak oiuştumlan zaman tablolarından hareket etmekte ve bunu iki aşama işleminde kullanmaktadır. Genelolarak seyahat talebi kabaca imkanlar ile ilişkilendirilmektedir (örn; uçak büyüklüğü, servis sıklığı ve yol alternatifleri). Yan ve Young'un çalışmasına iiaveten çeşitii hava yolu program modelleri geliştirilmiş olup bunlardan en dikkat çekici olanları Abara'nın sabit uçuş-kalkış zamanları ile filo ataması için tamsayılı doğrusal programiama modeli, Teodorovic ve Kremar-Nozic'in mukayese koşulları altında uçuş sıklıkları üzerine çok amaçlı karar alma modeli, Balakrishııan ve diğerlerinin uzun yol rotaları üzerine karışık tamsayılı programlama modeli ve Han ve diğerlerinin günlük uçak rota ve listesi problemlerinin çözümüne yönelik çoklu ürün ağ akış modeli di? i Yan S, Young RF. A decision support framework for multi-fleet routing and multi-stop flighl seheduling. Transportaıion Research 1996; 3ÜA: Yan S. Approximating redueed eosls under degeneraey in a network flow problem with side eonstraints. Networks 1996;27:
3 Zaman-mesafe ağı tekniği, ulaştınna işlemiyle faaliyet gösteren işletmelerin karlılığını maksimize etmeyi amaçlayan filo rotası ve uçuş listelerinin bir bütün halinde oluşturularak uygulanmasma yöneliktir. Bu model ağ içerisinde yer alan her bir uçak ve yolcunun birlikte optimal bir şekilde yönetilmesini gerektinnektedir. Ayrıca, doğnıdan uçuşlarm, çoklu duraklı uçuşların ve çoklu filoların sistematik bir şekilde idare edilmesini de gerektinnektedir. Modeldeki ana unsurlar fılo-akış zamanı-mesafe ağı, yolcu-akış zamanı-mesafe ağı ve matematiksel fonnülasyonudur 3. Bu tür çalışmalar defalarca zaman-mesafe ağında çoklu fılo rotaları ve uçuş listeleri problemlerine forınülüze edilmiş ve her bir işlem sonucunda çeşitli zaman peıiyodu ve mesafe konumunda uçağın potansiyel hareketlerinin spesifık durumlarını ortaya koymuştur. Modelin oluşturulmasında kullanılan düğüm noktaları ve yaylar ağdaki iki ana kısmı oluştunnaktadır. Her bir düğüm noktası bir hava alanının özel bir zaman dilimi için tasarlanmaktadır. Dizaynın ifadesinde yay'ın gece konaklaması, alanda kalış ve uçuş ayağı gibi bir faaliyeti ifade etmesi gerekmektedir. Yayakışları ağdaki uçağın akışını göstennektedir. Üç farklı yay türünden sözetmek mümkündür. Bunlar 4 ; uçuş ayağı yayı iki farklı hava alanı arasındaki uçuş bağlantısını ifade etmektedir. Tüm muhtemel uçuş ayakları Kabul edilebilir zaman aralıklarında ağa yerleştirilir. Bu yerleştirme işleminde kullanılabilir uygun hava alanları olabildiğince ön planda tutulmak zorundadır. Her bir uçuş ayağı kalkış yapılacak hava alanı, kalkış zamanı, varışın gerçekleşeceği hava alanı, varış zamanı ve işlem maliyeti bilgilerini içennektedir. Bir uçuş ayağı için zaman dilimi uçağın uçuş için hazırlanmasından ve bu uçuş ayağının tamamlanmasına kadar geçen toplam zamanı kapsamaktadır. Bu zaman dilimini kalkıştan önceki araştınna, yakıt alımı, yolcu/bagaj yüklemesi ve havada geçen sure oluştunnaktadır. Yayakışının üst sının bir, alt sınırı ise sıfır dır. Bunlara ilave olarak aynı hava alanı için kalkış aralıkları taşıyıcı işletmelerin işlem isteklerinin düzenlenmesi yoluyla da tasarlanabilir 5. 3 Yan S, Tu Y. Multitleet routing and multistop tlight scheduling for Schedule pemırbation. European Journal of Operational Research 1997;103: Yan S. Approximating reduced costs under degeneracy in a network tlow problem with side constraints. Networks 1996;27: Yan S, Young HF. A decision support framework for multi- tleet routing and multi-s top flight scheduling. Transportation Research 1996; 30A:
4 Alan yayı belirli bir zaman çerçevesi içerisinde bir hava alanında uçakların bekleme ve gece kalışlarını temsil etmektedir. Yay maliyeti, hava alanı vergisi, hava alanı kullanım ödeneği, geçiş kullanımı ödeneği ve bunlarla ilişkili giderlerden meydana gelmektedir. Yayakışının üst limiti şayet kapasite büyükse sınırsız, eğer değilse apron kapasitesi ile sınırlı olup alt limiti ise sıfır dır 6. Döngü yayı fonksiyonu birbirini takip eden iki planlama periyodu arasındaki sürekliliği ifade etmektedir. Döngü yayı, her bir hava alanı için bir süreç diliminin bitişini gelecek süreç diliminin başlangıcına bağlamaktadır. Yayakışının alt ve üst limitleri alan yayına benzer şekilde yay maliyetleri ile sınırlıdır? Zaman-mesafe ağı tekniği yolcu hareketlerinin zaman ve yerleşim açısından uygunluğunu ortaya koymaya çalışmaktadır. Her bir yolcu-akış zamanı-mesafe ağı başlangıç tablosundan oluşturulan özel başlangıç ayrımlarını göstermektedir. Bu ağlar, sistematik olarak filo-akış zamanı-mesafe ağlarından problemin çözümünü kolaylaştırmak için tasarianırlar. Bir düğüm noktası spesifik bir zaman dilimini içerisindeki bir hava alanını temsil etmektedir. Bununla birlikte, bir yay yolcu hareketlerini gösteren bir faaliyet olarak dizayn edilmektedir. Üç farklı yay' dan söz edilebilir. Bunlar s ; Dağıtım yayı yolcuların bir hava alanından bir diğerine uçuş ile taşınması olarak ifade edilmektedir. Ulaştırma zamanı filo-akış zamanı-mesafe ağında ortak uçuşlar için uygun zaman dilimine karşılık gelecek şekilde gerçekleştirilir. Yay maliyeti her bir yolcu için gereken servise 6 Abara J. Applying intcgcr lincar programıning to thc flcc! assignmcnt problcm. lntcrfaccs 1989; 19: Ahuja RK, Magnanti TL, Orlin m. Network flows, theory, algorithms and applications. Englewood Cliffs: Prantice Hall, Teodorovich D. Airline Operations Research. New York: Gordon and Breach Science, 1988.
5 göre değişken maliyetlidir. Yayakışının sınırlıdır. 2-Kalış yayı üst sınırı uçağın kapasitesi ile alt sınırı ise sıfır ile Kalış yayı belirli bir zaman dilimi çerçevesinde bir yolcunun hava alanında kalmasını ifade etmektedir. Yayın maliyeti sıfırdır. Çünkü, pratik olarak hiç bir yolcu zorunlu olmadıkça hava alanında kalmak istememektedir.yayın üst sınırı istasyonun yolcu servis kapasitesi ile sınırlı olup alt sının ise sıfır dır 9 Talep yayı ağdaki uygun başlangıç dağılım çiftlerinin varış ve kalkış istasyonlarını birbirine bağlamaktadır. Yay maliyeti ortalama bilet tutarının negatif değerine eşittir. Yayın üst sınırı başlangıç dağılım çiftlerinin öngörülen talebine bağlı olup, alt sınırı ise sıfırdır. Belirli bir başlangıç dağılım çifti için yolculuk talebi, güncel talep eğilimi, Pazar özellikleri veya taşırnacı firmanın sahip olduğu özelliklere göre çeşitli talep yaylarına ayrılabilirlo. Modelin açıklanmasından önce modelde yer alan sembollerin tanımlanması işlemin anlaşılırlığının sağlanmasına katkıda bulunacaktır. Modelde yer alan semboller aşağıda gösterilmiştir! l. m: ın. filo M: Tüm filoların oluşturduğu küme n: n. başlangıç dağılım çifti N: Tüm başlangıç dağılımlarının oluşturduğu küme Am: m. filo ağındaki tüm yayların oluşturduğu küme B n : n. yolcu ağındaki tüm yayların oluşturduğu küme xit: m. filo ağındaki akış yayı (i,j) Yi/: n. yolcu ağındaki akış yayı C ij m: m. filo ağındaki yay maliyeti 9 PoweIl WB. A review of sensitivity results for linear Networks and a new approximation to reduee the effeets of dcgcneraey. Transportation Sciencc. 1989;23: LO Teodorovieh D. Guberinic S. Optimal dispatching strategy on an airline network after a Schedule perturbation. European Journal Operational Research. 1984;15: ii Yan S, Young HF. A decision support ITamework for multi-fleet routing and mıılti-stop flight schedııling. Transportation Research 1996; 30A:
6 Tt n. yolcu ağındaki yay maliyeti NF nı : m. filo ağındaki tüm düğüm noktalarının oluşturduğu küme NPn: n. yoıcu ağındaki tüm düğüm noktalarının oluşturduğu küme CFm:m. filo ağındaki tüm çevrim yaylarının oluşturduğu küme AFm:ın. filo ağındaki tüm kuııanılabilir uçakların sayısı FF: Tüm uçuş yaylarının oluşturduğu küme Sa: a. istasyondaki uçuş yaylarının oluşturduğu küme Qa: a. istasyondaki uygun uçuş kontenjanı SA: Tüm istasyonların oluşturduğu küme Km:m. filo ağındaki uçak kapasitesi Dijnı: m. filo ağındaki yayakışının üst sınırı D ij n: n. yolcu ağındaki yayakışının üst sınırı Filo akışı ve yolcu akışı ile mesafeye göre düzenlenen ağların oluşturulmasında tam sayılı ağ akış problemi formülasyonundan hareket edilmektedir. Çok sayıda dikkat edilmesi gereken hareket sözkonusudurıı. Buna göre genel algoritma aşağıdaki gibi ifade edilmektedir; (I).Forınülasyon Amaç fonksiyonu: Minimum Z =i i CijXij +i i T,;Yi.~ JTIEM ijea m nen ijeb n Kısıt denklemleri: (1) i Xij- i X~ =0, \:iienf m, \:irnem jenf m kenf m (2) i -v;; - i Yk~= o, \:ii E NP n, \:in E N jenp n kenp n (3) i Xij:::;AF m, \:im E M ijecf m (4) i X:j :::;ı,\:iij E FF JTIEM "Yan S, Tu Y. Multitleet routing and multistop flight scheduling for Schedule perturbation. European Journal of Operational Research 1997; i03:
7 i ix;;~qa,\iaesa memijes, (7) (8) (9) (lo) o~x; ~U;, \iij E Am'\im E M O ~ Yi;' ~ U~, \iij E Bm' \in E N X; E tamsayı, \iij E Am' \im E M Yi; E tamsayı, \iij E B n ' \in E N Model tamsayı ağ akış problemi formülüzasyonundan hareketle oluşturulmuştur. Modeldeki amaç fonksiyonu sistem maliyetinin ıninimizasyonuna yöneliktir. (1) ve (2) no' lu kısıtlar her bir filo/yolcu ağındaki tüm düğüm noktalarında akış muhafazasını sağlamaya yöneliktir. (3) no' lu kısıt kullanılabilir uçak sayısını aşmamak kaydıyla her bir filo için kullanılan uçak sayısını göstermekte, (4) no' lu kısıt her bir uçuşun enfazia bir kere gerçekleştirildiğini, (5) no' lu kısıt her bir istasyonda uygun kontenjanı aşmamak kaydıyla ortalama uçuşları sağlamakta, (6) no' lu kısıt uçak taşıma kapasitesine göre yolcu ulaştırma hacmini göstermekte, (7) ve (8) no' lu kısıtlar tüm kısıtlar altında tüm yayakışlarını tanımlamakta ve (9) ve (10) no' lu kısıtlar ise uçak/yoıcu akışlarının bütünlüğünü sağlamaktadır i 3 Bu çalışma tam sayılı çoklu ürün ağ akış probleminin alt gradient metodu ile lagranja adaptasyonunu içermektedir. Çözüm aşaması ilk olarak yan kısıtlarm lagranjyan problemin oluşturulmasma ve çözülmesine yönelik olarak gevşetilmesini gerektirmektedir. Burada amaç optimal çözümün indirgenmiş sınırını bulmaktır. İkinci olarak da araştırına süresince geliştirilmiş olan sezgisel yaklaşımın optimal çözümün üst sınır değerine ulaşmak için uygulanması söz konusudur. Daha sonra lagrange çarpanlarının tekrarlamnası ve gözden geçirilmesi için spesifık alt gradient metodu alt ve üst sınırların belirlenmesinde kullanılmaktadır. Bu işlem yakınsak çözümün kabul edilmesine veya iterasyon tekrarının " Fisher ML. The lagragian relaxaıion meıhod for solving inleger progranuning problems. ManagemenI Science. 1981;27:1-18
8 belirlenen sayıyı aşmasına kadar devam ettirilir. Çözüm algoritmasının almaktadır i 4. ana kısımları aşağıda yer Alt sınır Alt sınırın araştırılmasında gerçekleştirilen çözüm işlemlerine ait adımlar aşağıda yer almaktadır. Adım.ı. Yan kısıtlar (3-6) UYbrunnegatif olmayan lagrange çarpanları kümesi ile ()l3,)l4,lls ve 116) gevşetilirler ve (i) formülündeki amaç fonksiyonuna ilave edilirler. Bu ilaveyle (Il) nolu formüle ulaşılır. Foımül (II) için optimal amaç değeri formül (I) in alt sınırı haline dönüşüris. (II).Formülasyon Amaç fonksiyonu: Min z= L L CijXij + L LTi;lY;j + L (f.j3m( mem ijea m nen ijeb n mem ijecp m L -AF;nJJ+ L (li4ij(l Xij -1)J+ L(f.Jsa( ijefp mem aes. mem ijes" LL Xij _QaJJ 14 Fishcr ML. TI1C lagragian rclaxation mcthod for solving intcgcr programming problems. Managemcnt Scicnce. 1981;27: Barnhar! C, Johnson EL, Nernhauser GL, Savelsbergh MWP, Vance PH. Branch-and-Price: COlW1IDgeneration for solving hugc intcgcr programs. Operation Research 1998;46:
9 (1) L X~ - L X~~= O,\ii E NF m, \im E M jenf,u kenf,,, (2) L Y;r - L Y~~= O,\ii E NP n, \in E N jenpn kenf m 0 < X m < Um 1-/.. A 1-/ M (7) _ ij - ij' v ıj E rı;' v m E (8) O ~ Y;r ~ U~, \iij E B n, \in E N (9) x~ıe tamsayı, \iij E Am' \im E M (10) Yif E tamsayı, \iij E B n, \in E N Adım.2: Oluşturulan (II)formülü, bağımsız iki ağ grubuna dönüştürülür. Bunlar; filo akış ağı ve yolcu akış ağıdır. Adım.3: Filo akış ağı saf ağ akış problemi olup minimum maliyetli ağ akış problemi olarak karakterize edilebilir. Ağ simpleks yöntemi bu problemin etkin çözümünün bulunmasında kullanılabilir. AdımA: Yolcu akış ağı daima minimum maliyctli ağ akış problcmidir. Bununla birliktc bu problcmlerin her bir ağ için tek bir talep ve arza sahip olmasından dolayı problcmlerin etkili çözümünün eldesi mümkün olmamaktadır bu nedenle sürekli en küçük maliyet akış artış yolu algoritması kullanılabilir. Her bir başlangıç dağılımı çiftleri bu metod da kullanılan her bir bağımsız ağa yüklenir ve her bir ağın maliyeti hesaplanır. Adım.S: Bu iterasyon için indirgenmiş sınır sonuç olarak tüm filo akış ve yoıcu akış ağ maliyetlerinin birleştirilmesiyle elde edilir l6. Üst Sınır Sezgisel yaklaşımın geliştirilmcsiyle bir üst sınır değ'eri elde edilir. Adımlan ise aşağıda yer almaktadır Kennington LL, Helgason RV. Algorithms for network programming. New York: John Wiley, Hane C, Barnhart C, Johnson EL, Marstern R, Nemhauser GL, Sigismondi G. The fleet assignmenı problem:solving a large-scale integerprogram. Mathematical Programming Study 1995;
10 Adım. i:yeni bir yolcu akış ağı oluşturulur. Bu ağdaki her bir dağıtım yayakışları alt sınır araştırına işleminde elde edilen tüm yolcu akış ağlarına ait uygun dağıtım yayakışlarının ortalamasıdır. Adım.2: Oluştunılan yeni yolcu akış ağında dağıtım yayları tanımlanır. Bu tanımlamada uçağın taşıma kapasitesi ihlal edilir. Daha sonra, bozulan yayların ekstra hacimleri en az maliyet akış artışı metodu ile değiştirilmiş algoritma (i) de yer alan (6) no' lu kısıtın tatmin edilmesine kadar aşama aşama artırılır. Adım.3: Her bir fılo akış ağında, her bir uçuş için kullanılan uygun uçak tipine göre dağıtım bilet gelirlerini uçuş maliyetleıine ilave ederek muhtemel karlılık bulunuı.i 8. AdımA: Filo akış ağının uçuş maliyetlerinden oluşan muhtemel net karın ayrılınası ile bir alt problem tarifesi oluşturulur. Amaç, sistem maliyetini minimizasyona yöneliktir. Yan koşullar (1) no' lu formüldeki (3-6) kısıtlarında olduğu üzere aynı olmalıdır. Adım.S: Bu adım süresince alt problemin yan koşullarının gevşetilmesi işleminde lagrange çarpanları uygulanır. Alt problemin ait kısıt çözümü için ise ağ simpleks metodu kullanılır. Adım.6: FOfl1ıül(i) deki (4) no' lu kısıt için en fazla bir defaya mahsus olmak üzere her bir uçuş hizmetinin kısıtları elle değiştirilir. Uçak tipleri ekonomiklik derecesine göre düzenlenir. İlk önce bu yaylar tanımlanır. Tanımlamada diğer ağlardaki benzer uçuşlar mukayese edilerek muhtemel en büyük net kar ve bu uçuş yaylarının sonsuz yay maliyetleri oluşturulur. Daha sonra, yeni ağ akışlarından elde edilen yay maliyetleri ile ağ simpleks metodu kullanılarak tekrar ana ağ çözüıür. Adım. 7: Her bir hava alanı için kullanılabilir alan iniş kontenjanı kısıtı değiştirilir (formül (1) deki (S) no' lu kısıt). Her bir hava alanı için iniş ve kalkışların toplamı bulunur ve alan kontenjanın1l1 herhangi bir nedenle ihlal edilme dunıınu araştırılır. Bu yayakışları m. ağa adapte edilerek tanımlanır (burada m::;uçak tipi sayısı). Bu tanımlamada şayet akış sıfır değil ise maliyet sonsuz olarak ele alnmıaktadır. Daha sonra m. ağ akışları için ağ simpleks metodu uygulanır i9. L8 Camerini PK, Fratta L, MaffıoJi F. On improving rejaxation methods by modified gradient technigues. MathematicaJ Programming Study 1975;3: Clarke LW, Hane CA, Johnson EL, Nemhauser GL. Maintenal1ce and crew consideratioııs in fleet assigııement.lransportation Science 1996;30:249-60
11 Adım.8: Filo hacmi kısıtı değiştirilir (formül (i) deki (3) no' lu kısıt). M. ağdaki döngü yayarkları akışlarının toplamı alınır ve m. ağda m. mo hacminin aşılmasına neden olan uçak sayısı kontrol edilir (forınül (1) deki (AFrn)' göreceli uçuşlar ile düşünülen hava alanları yardımıyla şayet gerekiyorsa kesikli akışları da kapsayacak şekilde bu döngü yayları tanımlanır ve bu döngü yaylarının üst sınırları istenilen limitlere uygun hale getirilir. Daha sonra, m. ağ akışını çözmek için ağ simpleks metodu tekrar uygulanır. Adım.9: tüm ağlar ve hava alanı yer kontenjanlarını incelemek için 7. ve 8. adımlar gerçekleştirilir. Burada filo hacmi kısıtının doyunılmuş olmasına dikkat etmek gerekir. Adım. io: 9. adımda elde edilen filo akış ağı 2. adımda elde edilen yolcu akış ağı ile karşılaştırılarak uygun uçuşların olmaması durumunda yolcu akışları iptal edilir. Adım. i i : Ti.imuçuşlar için uçağın yüklenme durumu ölçüıür. Hali hazırda uygun olup da hizmet vermeyen boş yerlere en az maliyet akış artışı algoritması yardımıyla fazla sayılar dağıtılır. Bu yüklemenin uçağın taşıma kapasitesini ihlal etmemesine dikkat edilir. Bu alt problem için üst sınır çözümü tüm ağlardaki gerçek yay maliyetlerinin filo akış ve yolcu akış ağları ile uygulanmasından elde edilen sistem maliyetlerinin bütünleştirilmesiyle elde edilir. Adım. 12: Şayet bu iterasyonda alt problemin alt ve üst sınırları arasındaki fark kabul edilebilir bir noktada yakınsamıyorsa ve iterasyon sayısı da kabul edilmiş deneme sayısı için önsel limiti aşmamışsa lagrange çarpanları alt gradyant metodu kullanılarak yenilenerek 5. adıma geri dönüıür. İterasyon işlemleri kabul edilebilir bir derecede yakınsak bir sonuç sağlayana ve daha önceden belirlenmiş deneme sayısını aşmayana kadar devam eder. Burada elde edilen uygun çözüm yalnızca alt problemin değilorijinal problemin de uygun çözümüdürü. Lagrange çarpanlarını düzenlemeye yönelik olarak geliştiıilen değiştirilmiş alt gradient metodu bu araştımıaya uygulanarak iterasyon sonuçlarında oldukça uygun yakınsaklık değeıine ulaşılmıştır. Uygulama adımları aşağıda yer almaktadır 21 LO Barnhart C, Johnson EL, Nemhauser GL, Savelsbergh M\VP, Vance PH. Branch-and-Price: column generalion for solving Imge integer programs. Operalion Research ]998;46:3]6-29. LL Chen HK, Chaııg MS, Wang CY. Dynaınic capacitated user-optiınal departure time/route choice problem with time window. European Journal of Operational Research. 200];] 32:603-6 I 8.
12 Adım.2: II no' lu lagrange probleminin optimal çözümü ağ simpleks metodunu ve en düşük maliyet aıtışı algoritması kullanılarak bulunur. Bu işlemde alt sınır olarak Z\IlC) alınır. Şayet çözüm uygun ve tamamen tatmin ediciyse bu çözüm optimal çözümdür. Bu durumda bu adımda işlem durdurulur. Aksi taktirde alt kısıt (ZL) yenilenir. Adım.3:Üst sınırı (Zu(lle» sınır (Zu) yenilenir. bulmak için geliştirilen sezgisel yaklaşımın uygulanarak üst AdımA: Şayet alt sınır (ZL) ile üst sınır (Zu) arasındaki fark spesifik bir tolerans (0) aralığında yer alıyorsa algoritma durdurulur. Bu tolerans aralığı /( ZU - ZL ) / ZU i< e, veya iterasyon çalışmasının limit sayısıdır. Adım.S: ~Lc değiştirilmiş alt gradient metodu vasıtasıyla düzenlenir. Bu yakınsaklığın sağlanmasında yardımcı olınaktadır. Bu çalışmada uygulamaya konu olan araştırma konusunda kullanılan veriler Türk Hava Yolları'na (THY) ait yıllarını kapsayan iç hat uçuş istatistiklerinden ve yıllık faaliyet raporlarından elde edilmiştir. Modelin çözümlenmesinde ise LlNDü paket programından yararlanılmıştır. İşlem adımları sonucunda elde edilen sonuçların her bir uçağa ait rotanın incelenmesinde kullanılamamasından dolayı Ahuja ve diğerleri tarafından geliştirilmiş bir akış analizi yay zincirlerindeki hat akışlarının analizinde kullanılınıştır. Uygulamaya konu olan araştitina THY'na ait 26 iç hat uçuşunu kapsayacak şekilde gerçekleştirilmiş ve bu 26 iç hattın günlük uçuş sayısı ise i60 olarak kabul edilmiştir. Yine 2002 yılına ait verilerden günlük oıtalama taşınan iç hat yolcu sayısı da kişi olarak işleme dahil edilmiştir. Yolcu taşımacılığında kullanı lan uçaklar kendi içerisinde üç ana gruba ayrılmış 22 Baıı MO. Maganti TL, Monma CL, Nemhauser GL. Network routing. Handbooks in Operations Research and Management Scİence 1995;8.
13 ve işlem süreci bu üç ana grup üzerinden gerçekleştirilmiştir. Uçak tipleri ve oluştumlan gmplar hakkındaki genel bilgiler tablo.2 de yer almaktadır. Tüm maliyetler ile ilgili gereken bilgi, işlem ile kısıtlar THY' 111 dan elde edilmiş ve çözüm aşaması boyunca gerçekleştirilen tekrarlama sayısı ise daha önceki konu üzerinde yapılan çalışmalarla paralellik göstermesi açısından 1000 defa ile sınırlandırılmıştır. Uygulamada kullanılan maliyet kavramı tamamen işlem maliyetini kapsamaktadır. Sabit maliyet ve dolaylı maliyetler ise modele dahil edilmemiştir. Bundan dolayı karlılık kavramı bu çalışma için işlem karlılığına karşılık gelmektedir. İşlem karlılığı kısa vadede kar optimizasyonunu, uzun vadede ise mevcut sistemin kalıcılık ve pazar payının artışını sağlamada son derece önemli bir faktör olarak karşımıza çıkmaktadır. Ayrıca, her bir uçuş için planıanan yükleme faktörünün O.Tyi aşmamasına dikkat edilmiştir. Uçuş zamanı, istasyonlar arasındaki mesafe, alan kontenjanları ve alanda kalış zamanı gibi tüm diğer girdi değerleri işlemlerin gerçekleştirilmesi sırasında tutulan istatistiklerden oluşan raporlardan elde edilmiştir. Filo gmbu Uçak tipi Uçak sayısı Yolcu kapasitesi A A A31O B Boeing Boeing Boeing C RJ-l RJ Bu çalışmada filo-akış zamanı-mesafe ağı:2, yolcu-akış zamanı-mesafe ağı ise 12 çalışma katından oluşmaktadır. Bu ağların oluştunılmasında ise 274 düğüm noktası ve 1215 yaydan yararlanılmıştır. Sonuçlar yolculukların %30' unun A (4315), %60' ının B (8631) ve %10' unun da C (1439) filo gmbuyla gerçekleştiıildiğini göstermektedir. Bundan da anlaşılacağı üzere A filo gmbu genelolarak B filo gmpundan daha karlıdır. Buna ilaveten tüm yolcular yolculuklarını kesintisiz uçuş ile durmaksızın gerçekleştirmekte ve transfer işlemi gerçekleşmemektedir. Bunun muhtemel nedeni ise küçük ağ skalası ve kısa uçuş mesafesinden kaynaklanmaktadır. Talep edilen mesafe 410 kın' nin içinde yeralmakta bu da ekonomik olarak katlanılabilir bir dummu ifade etmektedir. Ayrıca model %2.5 lik bir hata payına sahiptir.
14 Uygulamada kullanılan algoritmanın performansının bir problem odaklı heuristik yapıya sahip olmasından dolayı problemin parametrelerinden etkilenmektedir. Performansı değerlendirmek ve çözümde yer alan parametrelerin etkilerini analiz etmek için filo büyüklüğü, talep, uçuş maliyeti ve bilet fiyatları gibi bazı kritik verilerin duyarlılık analizi gerçeki eştirilmiştir. Yapılan bu çalışmadan görülmüştür ki, 12 uçaklı A filosu, 42 uçaklı B filosu ve II uçaklı C filosu ile toplam yurt içi ve yurt dışı yolcu talebi karşılanamamakta bu nedenle de işletme karlı dummda görülmesine rağmen mevcut olan iç ve dış hat pazar payının olması gerekenin çok daha altında bir paya sahip olmaktadır. Bu durum işletmenin rekabet gücünün zaman içerisinde azalmasına ve rakip işletmelerin gelişmesine olanak tanımaktadır. Araştırmadan elde edilen temel noktalardan biri filo büyüklüğünün (A, B, ve c) artırılmasının işletmenin karlılığında bir artışa neden olacağı, bununda şu anki koşullar ile A filosunun 15, B filosunun 44 ve C filosunun ise 13 uçak kapasitesine çıkarılması gerekliliğini ortaya koymaktadır. Bu durumda ulaşılacak karlılık düzeyi şuan ki düzeyinden %18' lik bir artışa neden olacaktır. Ancak buradaki karlılığın uçuş karlılığı ile sınırlandırılmış olduğu unutulmamalıdır. Uygulamada, mevcut talebin hali hazırda karşılanamadığı ve bunun ilerleyen dönemlerde de filo büyüklüğünün artırılmaması durumunda yine karşılanamayacak bir gelişme içerisinde olacağı gözlenmektedir. Genelolarak, talep analizindeki dalgalanmaların (±%25) arasında yer alması durumunda amaç değerleri kabul edilebilir bir değişim göstermektedir. Uçuş maliyeti bu çalışmada yer alan modelin kritik girdi değerini oluşturınaktadır. Uçuş maliyetinin uçuş maliyetinin (±20) arasında tutulabilmesi durumunda amaç değerinde oldukça düşük bir değişiklik gözlemlenmektedir. Ayrıca uçuş maliyeti ile amaç değeri arasında doğnısal bir ilişki söz konusudur.
15 Bilet fiyatı taşıma gelirlerini doğrudan etkileyen bir unsur durumundadır. Bilet fiyatı değerleri ana modele liste fiyatı olarak dahil edilmiştir. Bilet fiyatlarının duyarlılığı da (±%25) arasında incelenmiş, bilet fiyatlarındaki %25 den daha düşük bir artışın %99' luk bir servis oranında, %25 lik bir fıyat indiriminin ise %100' lük bir servis oranına karşılık sabit kaldığı sonucuna ulaşılmıştır. Sonuç olarak tüm senaıyolar için servis oranları benzerdir. Bunun muhtemel nedeni ise bilet tıyatlarının işlem maliyetlerinde göreceli olarak yüksek farklılık göstermesidir. Yapılan testler bilet fiyatındaki % 1 lik bir değişmenin amaç değerinde %1.3' lük bir değişime neden olduğunu ortaya koymaktadır. Bu çalışmada uygulamaya konu olan model ve çözüm algoritınası filo rotası ve uçuş listeleri için etkili bir planlama aracı olarak kullanılmıştır. Bu model ve çözüm algoritması değişiklikleri ana faktörlere simüle edebilmede ve kabul edilebilir sonuçların elde edilmesinde oldukça yardımcı bir roloynamaktadır. Bu ana faktörlerin başında filo büyüklüğü, uçuş maliyeti ve tedarik maliyeti gibi ana kontrol değerleri yer almaktadır. Ayrıca, bu model ve çözüm algoritması gelecek talep, pazardaki esnek fiyat eğilimi, kullanılabilir uçak ve alanlar gibi değişmesi muhtemel kritik çevresel faktörlerin etkisi altmda bir sistemin perforınansının analiz edilebilmesinde de kullanılabilmektedir. Genel olarak model uygulaması son derece geniş tutulabilir. Tablo.2. de uygulamadan elde edilen sonuç değerleri ile senaryolar yer almaktadır. Taşıma şirketleri tüm hava alanı kombinasyonlaıını oluşturarak her bir kombinasyonun karlılığını gerekli istekler çerçevesinde mukayese edebilmektedirler. Bu mukayese işletmelere yeni uçuş imkanlarını tespit etmede son derece faydalı olabilmektedir. Tablo.2 de 26 iç hat hava alanı yer almaktadır. Bu hava alanları sırasıyla; İstanbul, Edremit, İzmir, Denizli, Bodmm, Dalaman, Antalya, Ankara, Konya, Adana, Kayseıi, Samsun, G.Antep, Malatya, Ş.Urfa, Erzincan, Elazığ, Diyarbakır, Trabzon, Erzurum, Muş, Batman, Mardin, Kars, Ağrı ve Van dır. Problem boyutunu 1215 değişken ve 274 kısıt oluştıınnaktadır. Hata aralığı %2.5 düzeyinde olup bu aralıkta çözüm algoritması oldukça iyi sonuç verınektedir. Tablo.2 de yer alan senaryolardan ilki olan SI, ilk on hava alanını, S2, ilk onbir hava alanını içerınekte ve bunu benzer şekilde diğerleri takip etınektedir. Şayet bir hava yolu şirketi S2 senaryosu ile hareket etınek isterse, bu durumda ilk onbir hava alanını işleme dahil etmek durumundadır.
16 Senaryolar Değişken Kısıt Yolcu Sayısı Üst Alt Hata Uçak Sayısı Sayısı Sınır Sınır Aralığı (%) Kombinasyonu Si ,61 2M4B+IC S M6B+1C S M8B+1C S l A+8B+IC S A+10B+2C S6 29J MIOB+IC S MIJB+IC S8 45J A+13B+IC S A+l3B+2C SIO A+i 5B+2C SIL M17B+1C SI ıımi8b+ic Sl MI8B+IC SI ıı A+l9B+IC SI i3a+2ib+lc SI A+22B+IC SI7 II A+22B+2C SI M24B+2C Bu çalışmada en iyi filo rotası ve uçuş listeleri yolculuk talebi ile uçuş arzı arasındaki uyum göz önünde bulundurarak bir matematiksel modelle ifade edilerek en uygun çözümün bulunmasına çalışılmıştır. Bu model hali hazırda kullanılmakta olan ve deneme yanılma yoluyla gerçekleştirilen zaman tablolarından tamamen farklı bir yapıya sahiptir. Model yaklaşımı gerçek anlamda güncelolarak faaliyet gösteren bir hava yolu şirketi (THY) verilerine uygulanmış ve elde edilen sonuçlar bu hava yolu şirketinin mevcut durumuyla karşılaştırılmıştır. Tüm elde edilen ilksel veriler ile sonuç değerleri modelin ve çözüm algoritmasının hava yolu şirketlerinin günlük ıutin planlamalarını yapmada son derece faydalı ve tutarlı sonuçlar vereceği yönündedir. Ayrıca, kullanılan bu model ve çözüm algoritınaslllll1 yalnızca hava yolu şirketleri için değil diğer tüm ulaştırına alanında faaliyet gösteren işletıneiere uygun planlama ve çözüm sağlama konusunda yardımcı olacağı da görülmektedir.
17 Abara J. App1ying integer linear programıning to the fleet assignment problem. Interfaces 1989; 19:20-8. Ahuja RK, Magnanti TL, Orlin JB. Network flows, theory, a1gorithms and app1ications. Eng1ewood Cliffs: Prantice Hall, Ba1akrislınan A, Chien T, Wong R. Selecting aircraft routes for 1ong-hau1 operations: a fonuulation and solution method. Transportation research 1990; 24B: Ball MO, Maganti TL, Monma CL, Nemhauser GL. Network routing. Handbooks in Operations Reseaı"ch and Management Science 1995;8. Bamhart C, Johnson EL, Nemhauser GL, Save1sbergh MWP, Vance PH. Branch-and-Price: column generation for solving huge integer programs. Operation Research 1998;46: Chen HK, Chang MS, Wang CY. Dynamic capacitated user-optima1 departure time/route choice problem with time window. European Journal ofoperationa1 Research. 2001;132: Clarke LW, Hane CA, Jolınson EL, Nemhauser GL. Maintenance and crew considerations in fleet assignement. transportation Science 1996;30: Camerini PK, Fratta L, Maffıoli F. On improving relaxation methods by modified h'tadient technigues. Mathematical Prograınming Study 1975;3:6-25. Fisher ML. The lagragian relaxation method for solving integer programming prob1ems. Management Science. 1981;27:1-18 Hane C, Barnhart C, Johnson EL, Marstern R, Nemhauser GL, Sigismondi G. The fleet assignment problem:so1ving a 1arge-sca1e integer program. Mathematica1 Programming Study 1995; Kennington LL, He1gason RV. A1gorithms for network programming. New York: John Wiley, Powell WB. A review of sensitivity results for linear Networks and a new approximation reduce the effects of degeneracy. Transportation Science. 1989;23: to
18 Teodorovich D, Guberinic S. Optimal dispatching strategy on an airline network after a Schedule perturbation. European Joumal Operational Research. 1984; 15: Teodorovich D, Krcmar-Nozic E. multi criteria model to determine flight frequencies on an airline network under competitive conditions. Transpoıtation Science. 1989;23: Yan S, Young HF. A decision support framework for multi-fleet routing and multi-stop flight schedu1ing. Transportation Research 1996; 3üA: Yan S. Approximating reduced costs under degeneracy in a network flow problem with side constraints. Networks 1996;27: Yan S, Tu Y. Multifleet routing and multistop flight scheduling for Schedule perturbation. European Joumal ofopemtional Reseaı'ch 1997;103:
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ
 ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati Kredi AKTS (T+U+L) ŞEBEKE MODELLERİ EN-413 4/I 3+0+0 3 5 Dersin Dili : İngilizce Dersin Seviyesi : Lisans
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati Kredi AKTS (T+U+L) ŞEBEKE MODELLERİ EN-413 4/I 3+0+0 3 5 Dersin Dili : İngilizce Dersin Seviyesi : Lisans
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
*İlk aşamada, bahsedilen problemin matematiksel modelinin kurulması gerekmektedir. İlgili modelin açık ve kapalı formunu birlikte veriniz.
 Yöneylem Araştırması Proje Ödevi Teslim Tarihi: 04.12.2017 *İlk aşamada, bahsedilen problemin matematiksel modelinin kurulması gerekmektedir. İlgili modelin açık ve kapalı formunu birlikte veriniz. Filo
Yöneylem Araştırması Proje Ödevi Teslim Tarihi: 04.12.2017 *İlk aşamada, bahsedilen problemin matematiksel modelinin kurulması gerekmektedir. İlgili modelin açık ve kapalı formunu birlikte veriniz. Filo
ULUSLARARASI INTERMODAL TAŞIMA AĞINDA OPTIMAL ROTA SEÇİMİ
 III. Ulusal Liman Kongresi doi: 10.18872/DEU.df.ULK.2017.005 ULUSLARARASI INTERMODAL TAŞIMA AĞINDA OPTIMAL ROTA SEÇİMİ ÖZET Melis Özdemir, Berker İnkaya, Bilge Bilgen 1 Globalleşen dünyada taşımacılık
III. Ulusal Liman Kongresi doi: 10.18872/DEU.df.ULK.2017.005 ULUSLARARASI INTERMODAL TAŞIMA AĞINDA OPTIMAL ROTA SEÇİMİ ÖZET Melis Özdemir, Berker İnkaya, Bilge Bilgen 1 Globalleşen dünyada taşımacılık
İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama
 İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama Dr. Özgür Kabak 2016-2017 Güz } Gerçek hayattaki bir çok problem } tam sayılı değişkenlerin ve } doğrusal kısıt ve amaç fonksiyonları ile
İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama Dr. Özgür Kabak 2016-2017 Güz } Gerçek hayattaki bir çok problem } tam sayılı değişkenlerin ve } doğrusal kısıt ve amaç fonksiyonları ile
SİMPLEKS ALGORİTMASI Yapay değişken kullanımı
 Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI Yapay değişken kullanımı Hazırlayan: Doç. Dr. Nil ARAS, 6 AÇIKLAMA Bu sununun
Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI Yapay değişken kullanımı Hazırlayan: Doç. Dr. Nil ARAS, 6 AÇIKLAMA Bu sununun
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
EM302 Yöneylem Araştırması 2. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
Simpleks Yöntemde Duyarlılık Analizleri
 3.2.4. Simpleks Yöntemde Duyarlılık Analizleri Duyarlılık analizinde doğrusal programlama modelinin parametrelerindeki değişikliklerinin optimal çözüm üzerindeki etkileri araştırılmaktadır. Herhangi bir
3.2.4. Simpleks Yöntemde Duyarlılık Analizleri Duyarlılık analizinde doğrusal programlama modelinin parametrelerindeki değişikliklerinin optimal çözüm üzerindeki etkileri araştırılmaktadır. Herhangi bir
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ
 DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
a2 b3 cij: birim başına ulaşım maliyeti xij: taşıma miktarı
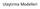 Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
BÖLÜM III: Şebeke Modelleri. Şebeke Kavramları. Şebeke Kavramları. Şebeke Kavramları. Yönlü Şebeke (Directed Network) Dal / ok
 8.0.0 Şebeke Kavramları BÖLÜM III: Şebeke Modelleri Şebeke (Network) Sonlu sayıdaki düğümler kümesiyle, bunlarla bağlantılı oklar (veya dallar) kümesinin oluşturduğu yapı şeklinde tanımlanabilir ve (N,A)
8.0.0 Şebeke Kavramları BÖLÜM III: Şebeke Modelleri Şebeke (Network) Sonlu sayıdaki düğümler kümesiyle, bunlarla bağlantılı oklar (veya dallar) kümesinin oluşturduğu yapı şeklinde tanımlanabilir ve (N,A)
Kalkış Noktası Bağlantı Noktası Varış Noktası
 Kalkış Noktası Bağlantı Noktası Varış Noktası Adana ADANA ANKARA SAMSUN ADANA ANKARA ERZURUM ADANA ANKARA TRABZON ADANA ANKARA BODRUM ADANA ANKARA VAN ADANA ANKARA İZMİR ADANA ANKARA KARS ADANA ANKARA
Kalkış Noktası Bağlantı Noktası Varış Noktası Adana ADANA ANKARA SAMSUN ADANA ANKARA ERZURUM ADANA ANKARA TRABZON ADANA ANKARA BODRUM ADANA ANKARA VAN ADANA ANKARA İZMİR ADANA ANKARA KARS ADANA ANKARA
doğrusal programlama DOĞRUSAL PROGRAMLAMA (GENEL)
 DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
Simpleks Yönteminde Kullanılan İlave Değişkenler (Eşitliğin yönüne göre):
 DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
Genel Graf Üzerinde Mutlak 1-merkez
 Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Yöneylem Araştırması II
 Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü Dr. Özgür Kabak Doğrusal olmayan programlama Tek değişkenli DOP ların çözümü Uç noktaların analizi Altın kesit Araması Çok değişkenli DOP ların
EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü Dr. Özgür Kabak Doğrusal olmayan programlama Tek değişkenli DOP ların çözümü Uç noktaların analizi Altın kesit Araması Çok değişkenli DOP ların
Üstel Öğrenme ve Genel Bozulma Etkili Akış Tipi Çizelgeleme Problemi: Maksimum Tamamlanma Zamanı Minimizasyonu
 Üstel Öğrenme ve Genel Bozulma Etkili Akış Tipi Çizelgeleme Problemi: Maksimum Tamamlanma Zamanı Minimizasyonu Tamer Eren Kırıkkale Üniversitesi, Mühendislik Fakültesi, Endüstri Mühendisliği Bölümü, 71451,
Üstel Öğrenme ve Genel Bozulma Etkili Akış Tipi Çizelgeleme Problemi: Maksimum Tamamlanma Zamanı Minimizasyonu Tamer Eren Kırıkkale Üniversitesi, Mühendislik Fakültesi, Endüstri Mühendisliği Bölümü, 71451,
Yrd.Doç.Dr. Safiye Turgay Doç.Dr. İsmail Erol Fulya Türkmen Abant Izzet Baysal Universitesi
 Lojistik Yönetim Sürecinin Analitik Modeli Ve Sektörel Uygulaması Yrd.Doç.Dr. Safiye Turgay Doç.Dr. İsmail Erol Fulya Türkmen Abant Izzet Baysal Universitesi Giriş İş dünyasında uluslar arası düzeyde rekabetin
Lojistik Yönetim Sürecinin Analitik Modeli Ve Sektörel Uygulaması Yrd.Doç.Dr. Safiye Turgay Doç.Dr. İsmail Erol Fulya Türkmen Abant Izzet Baysal Universitesi Giriş İş dünyasında uluslar arası düzeyde rekabetin
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
Tedarik Zinciri Yönetimi
 Tedarik Zinciri Yönetimi -Tedarik Zinciri Ağı Tasarımı- Yrd. Doç. Dr. Mert TOPOYAN Ağ tasarımı, tedarik zinciri açısından üç karar düzeyini de ilgilendiren ve bu düzeylerde etkisi olan bir konudur. Zincirin
Tedarik Zinciri Yönetimi -Tedarik Zinciri Ağı Tasarımı- Yrd. Doç. Dr. Mert TOPOYAN Ağ tasarımı, tedarik zinciri açısından üç karar düzeyini de ilgilendiren ve bu düzeylerde etkisi olan bir konudur. Zincirin
Montaj Hatti Tasarımı ve Analizi - 5
 Balıkesir Universitesi, Endustri Muhendisligi Bolumu 2017-2018 Bahar Yariyili Montaj Hatti Tasarımı ve Analizi - 5 Yrd. Doç. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr 2 En Erken ve En Gec Istasyon
Balıkesir Universitesi, Endustri Muhendisligi Bolumu 2017-2018 Bahar Yariyili Montaj Hatti Tasarımı ve Analizi - 5 Yrd. Doç. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr 2 En Erken ve En Gec Istasyon
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
ŞEHİR ve HAVAALANI İSİMLERİ KISALTMALARI CITY and AIRPORT NAME CODES. Adıyaman. Antalya
 ŞEHİR ve HAVAALANI İSİMLERİ KISALTMALARI CITY and AIRPORT NAME CODES Adana Adıyaman Ağrı Ankara Antalya Batman Bodrum Bursa Çanakkale Dalaman Denizli Diyarbakır Elazığ Erzincan Erzurum Eskişehir Gaziantep
ŞEHİR ve HAVAALANI İSİMLERİ KISALTMALARI CITY and AIRPORT NAME CODES Adana Adıyaman Ağrı Ankara Antalya Batman Bodrum Bursa Çanakkale Dalaman Denizli Diyarbakır Elazığ Erzincan Erzurum Eskişehir Gaziantep
Doğrusal Programlama. Prof. Dr. Ferit Kemal Sönmez
 Doğrusal Programlama Prof. Dr. Ferit Kemal Sönmez Doğrusal Programlama Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik
Doğrusal Programlama Prof. Dr. Ferit Kemal Sönmez Doğrusal Programlama Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik
SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ
 SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ Doğan EROL Anadolu Üniversitesi Endüstri Mühendisliği Bölümü 1. PROBLEMİN TANIMLANMASI Şekil - 1'de 5 değişik soba borusu için açınım
SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ Doğan EROL Anadolu Üniversitesi Endüstri Mühendisliği Bölümü 1. PROBLEMİN TANIMLANMASI Şekil - 1'de 5 değişik soba borusu için açınım
 KOK KÖMÜRÜ, RAFİNE EDİLMİŞ PETROL ÜRÜNLERİ VE NÜKLEER YAKIT İMALATI Hazırlayan Seher OZAN DÜNDAR Kıdemli Uzman 302 1. SEKTÖRÜN TANIMI Kok kömürü, rafine edilmiş petrol ürünleri ve nükleer yakıt imalatı
KOK KÖMÜRÜ, RAFİNE EDİLMİŞ PETROL ÜRÜNLERİ VE NÜKLEER YAKIT İMALATI Hazırlayan Seher OZAN DÜNDAR Kıdemli Uzman 302 1. SEKTÖRÜN TANIMI Kok kömürü, rafine edilmiş petrol ürünleri ve nükleer yakıt imalatı
Türkiye İletim Sistemi Bağlantı Kapasitesi Raporu ( Dönemi)
 Türkiye İletim Sistemi Bağlantı Kapasitesi Raporu (2016-2026 Dönemi) 13.04.2016 Yönetici Özeti Bu rapor, Türkiye elektrik iletim sistemi mevcut durumu, TEİAŞ tarafından planlanan iletim sistemi yatırımları
Türkiye İletim Sistemi Bağlantı Kapasitesi Raporu (2016-2026 Dönemi) 13.04.2016 Yönetici Özeti Bu rapor, Türkiye elektrik iletim sistemi mevcut durumu, TEİAŞ tarafından planlanan iletim sistemi yatırımları
Şebeke Modelleri (IE 510) Ders Detayları
 Şebeke Modelleri (IE 510) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Şebeke Modelleri IE 510 Her İkisi 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Şebeke Modelleri (IE 510) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Şebeke Modelleri IE 510 Her İkisi 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Montaj Hatti Tasarımı ve Analizi - 8
 Balıkesir Üniversitesi, Endüstri Mühendisliği Bölümü 2017-2018 Bahar Yarıyılı Montaj Hatti Tasarımı ve Analizi - 8 Yrd. Doc. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr Tek Modelli Düz MHD Problemlerinin
Balıkesir Üniversitesi, Endüstri Mühendisliği Bölümü 2017-2018 Bahar Yarıyılı Montaj Hatti Tasarımı ve Analizi - 8 Yrd. Doc. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr Tek Modelli Düz MHD Problemlerinin
Afet Yardım Operasyonlarında CBS Tabanlı Acil Müdahale Sistemi
 Afet Yardım Operasyonlarında CBS Tabanlı Acil Müdahale Sistemi Erdinç Bakır 1, Dr. Onur Demir 1 & Dr. Linet Ozdamar 2 1 Bilg. Müh. Bölümü 2 Sistem ve End. Müh. Bölümü Yeditepe University, Istanbul, Turkey
Afet Yardım Operasyonlarında CBS Tabanlı Acil Müdahale Sistemi Erdinç Bakır 1, Dr. Onur Demir 1 & Dr. Linet Ozdamar 2 1 Bilg. Müh. Bölümü 2 Sistem ve End. Müh. Bölümü Yeditepe University, Istanbul, Turkey
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST328 Yöneylem Araştırması 2 Dersi Bahar Dönemi. Hazırlayan: Doç. Dr.
 Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
ARAÇ ROTALAMA PROBLEMİNE AİT BİR UYGULAMA
 Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Y.2001, C.6, S.1 s.139-155. ARAÇ ROTALAMA PROBLEMİNE AİT BİR UYGULAMA Mehmet ERYAVUZ * Cevriye GENCER ** ÖZET Araç Rotalama Problemi (ARP),
Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Y.2001, C.6, S.1 s.139-155. ARAÇ ROTALAMA PROBLEMİNE AİT BİR UYGULAMA Mehmet ERYAVUZ * Cevriye GENCER ** ÖZET Araç Rotalama Problemi (ARP),
Ulaştırma ve Atama. Konu 2. Ulaştırma Modeli. Doç. Dr. Fazıl GÖKGÖZ
 Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda ürün
Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda ürün
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
LİMANLARININ İŞLEM HACMİ İLE EKİPMAN VE ALTYAPI İLİŞKİSİNİN BELİRLENMESİ. Doç Dr. A. Zafer ACAR Arş. Gör. Pınar GÜROL
 LİMANLARININ İŞLEM HACMİ İLE EKİPMAN VE ALTYAPI İLİŞKİSİNİN BELİRLENMESİ Doç Dr. A. Zafer ACAR Arş. Gör. Pınar GÜROL II. Ulusal Liman Kongresi 5-6 Kasım 2015/ İzmir Global ticarette üretimden tüketime
LİMANLARININ İŞLEM HACMİ İLE EKİPMAN VE ALTYAPI İLİŞKİSİNİN BELİRLENMESİ Doç Dr. A. Zafer ACAR Arş. Gör. Pınar GÜROL II. Ulusal Liman Kongresi 5-6 Kasım 2015/ İzmir Global ticarette üretimden tüketime
 BAŞKA YERDE SINIFLANDIRILMAMIŞ ELEKTRİKLİ MAKİNE VE CİHAZLARIN İMALATI Hazırlayan Birgül OĞUZOĞLU Kıdemli Uzman 540 1. SEKTÖRÜN TANIMI Başka yerde sınıflandırılmamış elektrikli makine ve cihazların imalatı
BAŞKA YERDE SINIFLANDIRILMAMIŞ ELEKTRİKLİ MAKİNE VE CİHAZLARIN İMALATI Hazırlayan Birgül OĞUZOĞLU Kıdemli Uzman 540 1. SEKTÖRÜN TANIMI Başka yerde sınıflandırılmamış elektrikli makine ve cihazların imalatı
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
Bilişim Sistemleri. Modelleme, Analiz ve Tasarım. Yrd. Doç. Dr. Alper GÖKSU
 Bilişim Sistemleri Modelleme, Analiz ve Tasarım Yrd. Doç. Dr. Alper GÖKSU Ders Akışı Hafta 5. İhtiyaç Analizi ve Modelleme II Haftanın Amacı Bilişim sistemleri ihtiyaç analizinin modeli oluşturulmasında,
Bilişim Sistemleri Modelleme, Analiz ve Tasarım Yrd. Doç. Dr. Alper GÖKSU Ders Akışı Hafta 5. İhtiyaç Analizi ve Modelleme II Haftanın Amacı Bilişim sistemleri ihtiyaç analizinin modeli oluşturulmasında,
YATAY UÇUŞ SEYAHAT PERFORMANSI (CRUISE PERFORMANCE)
 YATAY UÇUŞ SEYAHAT PERFORMANSI (CRUISE PERFORMANCE) Yakıt sarfiyatı Ekonomik uçuş Yakıt maliyeti ile zamana bağlı direkt işletme giderleri arasında denge sağlanmalıdır. Özgül Yakıt Sarfiyatı (Specific
YATAY UÇUŞ SEYAHAT PERFORMANSI (CRUISE PERFORMANCE) Yakıt sarfiyatı Ekonomik uçuş Yakıt maliyeti ile zamana bağlı direkt işletme giderleri arasında denge sağlanmalıdır. Özgül Yakıt Sarfiyatı (Specific
EM302 Yöneylem Araştırması 2. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak GAMS Giriş GAMS (The General Algebraic Modeling System) matematiksel proglamlama ve optimizasyon için tasarlanan yüksek seviyeli bir dildir. Giriş dosyası:
EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak GAMS Giriş GAMS (The General Algebraic Modeling System) matematiksel proglamlama ve optimizasyon için tasarlanan yüksek seviyeli bir dildir. Giriş dosyası:
MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ
 SİMPLEKS TABLONUN YORUMU MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ Şu ana kadar verilen bir DP probleminin çözümünü ve çözüm şartlarını inceledik. Eğer orijinal modelin parametrelerinde bazı değişiklikler
SİMPLEKS TABLONUN YORUMU MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ Şu ana kadar verilen bir DP probleminin çözümünü ve çözüm şartlarını inceledik. Eğer orijinal modelin parametrelerinde bazı değişiklikler
ŞEHİR ve HAVAALANI İSİMLERİ KISALTMALARI CITY and AIRPORT NAME CODES. Adıyaman. Antalya
 ŞEHİR ve HAVAALANI İSİMLERİ KISALTMALARI CITY and AIRPORT NAME CODES Adana Adıyaman Ağrı Ankara Antalya Batman Bodrum Bursa Dalaman Denizli Diyarbakır Elazığ Erzincan Erzurum Eskişehir Gaziantep İstanbul
ŞEHİR ve HAVAALANI İSİMLERİ KISALTMALARI CITY and AIRPORT NAME CODES Adana Adıyaman Ağrı Ankara Antalya Batman Bodrum Bursa Dalaman Denizli Diyarbakır Elazığ Erzincan Erzurum Eskişehir Gaziantep İstanbul
NEREDEN AKTARMA NEREYE
 NEREDEN AKTARMA NEREYE Adana Adana Ankara Erzurum Adana Ankara İzmir Adana Ankara Kars Adana Ankara Moskova** Adana Ankara Samsun Adana Ankara Trabzon Adana Ankara Van Adana İstanbul Sabiha Gökçen Amsterdam**
NEREDEN AKTARMA NEREYE Adana Adana Ankara Erzurum Adana Ankara İzmir Adana Ankara Kars Adana Ankara Moskova** Adana Ankara Samsun Adana Ankara Trabzon Adana Ankara Van Adana İstanbul Sabiha Gökçen Amsterdam**
28 C j -Z j /2 0
 3.2.6. Dual Problem ve Ekonomik Yorumu Primal Model Z maks. = 4X 1 + 5X 2 (kar, pb/gün) X 1 + 2X 2 10 6X 1 + 6X 2 36 8X 1 + 4X 2 40 (işgücü, saat/gün) (Hammadde1, kg/gün) (Hammadde2, kg/gün) 4 5 0 0 0
3.2.6. Dual Problem ve Ekonomik Yorumu Primal Model Z maks. = 4X 1 + 5X 2 (kar, pb/gün) X 1 + 2X 2 10 6X 1 + 6X 2 36 8X 1 + 4X 2 40 (işgücü, saat/gün) (Hammadde1, kg/gün) (Hammadde2, kg/gün) 4 5 0 0 0
Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1
 İÇİNDEKİLER Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1 1.1. Yöneticilik / Komutanlık İşlevi ve Gerektirdiği Nitelikler... 2 1.1.1. Yöneticilik / Komutanlık
İÇİNDEKİLER Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1 1.1. Yöneticilik / Komutanlık İşlevi ve Gerektirdiği Nitelikler... 2 1.1.1. Yöneticilik / Komutanlık
YZM ALGORİTMA ANALİZİ VE TASARIM DERS#9: AÇGÖZLÜ ALGORİTMALAR
 YZM 3207- ALGORİTMA ANALİZİ VE TASARIM DERS#9: AÇGÖZLÜ ALGORİTMALAR Aç Gözlü (Hırslı) Algoritmalar (Greedy ) Bozuk para verme problemi Bir kasiyer 48 kuruş para üstünü nasıl verir? 25 kuruş, 10 kuruş,
YZM 3207- ALGORİTMA ANALİZİ VE TASARIM DERS#9: AÇGÖZLÜ ALGORİTMALAR Aç Gözlü (Hırslı) Algoritmalar (Greedy ) Bozuk para verme problemi Bir kasiyer 48 kuruş para üstünü nasıl verir? 25 kuruş, 10 kuruş,
Ankara ya Ana Hava Dağıtım Merkezi (Hub) Olarak Değer Katmak (Developing Ankara as an Aviation Hub)
 Ankara ya Ana Hava Dağıtım Merkezi (Hub) Olarak Değer Katmak (Developing Ankara as an Aviation Hub) Sunum İçeriği Havacılık Sektörüne Genel Bakış Hava İşletmeciliği ve Ana Dağıtım Merkezleri Ankara nın
Ankara ya Ana Hava Dağıtım Merkezi (Hub) Olarak Değer Katmak (Developing Ankara as an Aviation Hub) Sunum İçeriği Havacılık Sektörüne Genel Bakış Hava İşletmeciliği ve Ana Dağıtım Merkezleri Ankara nın
ENGELSİZ HAVAALANI KURULUŞU LİSTESİ
 ENGELSİZ HAVAALANI KURULUŞU LİSTESİ Havaalanlarında engelli ve/veya hareket kabiliyeti kısıtlı yolcuların mağdur edilmemesi ve verilen hizmetlere ilişkin olarak yolculara gerekli tüm kolaylığın sağlanarak,
ENGELSİZ HAVAALANI KURULUŞU LİSTESİ Havaalanlarında engelli ve/veya hareket kabiliyeti kısıtlı yolcuların mağdur edilmemesi ve verilen hizmetlere ilişkin olarak yolculara gerekli tüm kolaylığın sağlanarak,
Devlet Politikaları ve Hizmet Kavramı İlişkisi Getting Technical Support for Enhancement of Institutional Structure in DGRR
 Devlet Politikaları ve Hizmet Kavramı İlişkisi 25.11.2014 Devlet Politikası olarak Hızlı Tren Devlet Hızlı Tren yatırımları yapar: Orta ve uzun mesafede hızlı ve güvenilir taşımacılık yapmak için Hava
Devlet Politikaları ve Hizmet Kavramı İlişkisi 25.11.2014 Devlet Politikası olarak Hızlı Tren Devlet Hızlı Tren yatırımları yapar: Orta ve uzun mesafede hızlı ve güvenilir taşımacılık yapmak için Hava
OYUN TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
Üretim Sistemleri (IE 509) Ders Detayları
 Üretim Sistemleri (IE 509) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Üretim Sistemleri IE 509 Seçmeli 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Üretim Sistemleri (IE 509) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Üretim Sistemleri IE 509 Seçmeli 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
SÜTUN OLUŞTURMA YAKLAŞIMI İLE BİR HAVAYOLU EKİP ÇİZELGELEME UYGULAMASI
 Gazi Üniv. Müh. Mim. Fak. Der. J. Fac. Eng. Arch. Gazi Univ. Cilt 24, No 1, 43-50, 2009 Vol 24, No 1, 43-50, 2009 SÜTUN OLUŞTURMA YAKLAŞIMI İLE BİR HAVAYOLU EKİP ÇİZELGELEME UYGULAMASI Gözde ÇANKAYA ve
Gazi Üniv. Müh. Mim. Fak. Der. J. Fac. Eng. Arch. Gazi Univ. Cilt 24, No 1, 43-50, 2009 Vol 24, No 1, 43-50, 2009 SÜTUN OLUŞTURMA YAKLAŞIMI İLE BİR HAVAYOLU EKİP ÇİZELGELEME UYGULAMASI Gözde ÇANKAYA ve
Türk Hava Yolları Değerlendirme Analizi
 www.alanyatirim.com.tr Türk Hava Yolları Değerlendirme Analizi 25 Temmuz 2018 ÖZET BİLGİLER 1933 yılında kurulan Türk Hava Yolları nın ana faaliyet konusu yurt içi ve yurt dışında yolcu ve kargo hava taşımacılığı
www.alanyatirim.com.tr Türk Hava Yolları Değerlendirme Analizi 25 Temmuz 2018 ÖZET BİLGİLER 1933 yılında kurulan Türk Hava Yolları nın ana faaliyet konusu yurt içi ve yurt dışında yolcu ve kargo hava taşımacılığı
DOĞRUSAL PROGRAMLAMA TEKNİĞİ İLE KÖMÜR DAĞITIM OPTİMİZASYONU COAL DISTRIBUTION OPTIMIZATION BY UTILIZING LINEAR PROGRAMMING
 Eskişehir Osmangazi Üniversitesi Müh.Mim.Fak.Dergisi C.XX, S.1, 2007 Eng&Arch.Fac. Eskişehir Osmangazi University, Vol..XX, No:1, 2007 Makalenin Geliş Tarihi : 17.02.2006 Makalenin Kabul Tarihi : 16.11.2006
Eskişehir Osmangazi Üniversitesi Müh.Mim.Fak.Dergisi C.XX, S.1, 2007 Eng&Arch.Fac. Eskişehir Osmangazi University, Vol..XX, No:1, 2007 Makalenin Geliş Tarihi : 17.02.2006 Makalenin Kabul Tarihi : 16.11.2006
Ulaştırma Problemleri
 Ulaştırma Problemleri Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir. Bu modelde, malların kaynaklardan (fabrika gibi )hedeflere (depo gibi) taşınmasıyla ilgilenir. Buradaki amaç
Ulaştırma Problemleri Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir. Bu modelde, malların kaynaklardan (fabrika gibi )hedeflere (depo gibi) taşınmasıyla ilgilenir. Buradaki amaç
METASEZGİSEL YÖNTEMLER
 METASEZGİSEL YÖNTEMLER Ara sınav - 30% Ödev (Haftalık) - 20% Final (Proje Sunumu) - 50% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn: Zaman çizelgeleme, en kısa yol bulunması,
METASEZGİSEL YÖNTEMLER Ara sınav - 30% Ödev (Haftalık) - 20% Final (Proje Sunumu) - 50% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn: Zaman çizelgeleme, en kısa yol bulunması,
DGridSim Gerçek Zamanlı Veri Grid Simülatörü. Gerçek-Zamanlı Veri Dağıtımı Dokümanı v 1.0.1 01.08.2011
 DGridSim Gerçek Zamanlı Veri Grid Simülatörü Gerçek-Zamanlı Veri Dağıtımı Dokümanı v 1.0.1 01.08.2011 Mustafa Atanak Sefai Tandoğan Doç. Dr. Atakan Doğan 1. Tek Rotadan Veri Dağıtımı 1.1 Gerçek-Zamanlı
DGridSim Gerçek Zamanlı Veri Grid Simülatörü Gerçek-Zamanlı Veri Dağıtımı Dokümanı v 1.0.1 01.08.2011 Mustafa Atanak Sefai Tandoğan Doç. Dr. Atakan Doğan 1. Tek Rotadan Veri Dağıtımı 1.1 Gerçek-Zamanlı
MerSis. Bilgi Teknolojileri Bağımsız Denetim Hizmetleri
 MerSis Bağımsız Denetim Hizmetleri risklerinizin farkında mısınız? bağımsız denetim hizmetlerimiz, kuruluşların Bilgi Teknolojileri ile ilgili risk düzeylerini yansıtan raporların sunulması amacıyla geliştirilmiştir.
MerSis Bağımsız Denetim Hizmetleri risklerinizin farkında mısınız? bağımsız denetim hizmetlerimiz, kuruluşların Bilgi Teknolojileri ile ilgili risk düzeylerini yansıtan raporların sunulması amacıyla geliştirilmiştir.
PLASTİK VE KAUÇUK ÜRÜNLERİ İMALATI Hazırlayan Orkun Levent BOYA Kıdemli Uzman
 PLASTİK VE KAUÇUK ÜRÜNLERİ İMALATI Hazırlayan Orkun Levent BOYA Kıdemli Uzman 364 1. SEKTÖRÜN TANIMI Plastik ve kauçuk ürünleri imalatı ISIC Revize 3 sınıflandırmasına göre, imalat sanayii alt ayrımında
PLASTİK VE KAUÇUK ÜRÜNLERİ İMALATI Hazırlayan Orkun Levent BOYA Kıdemli Uzman 364 1. SEKTÖRÜN TANIMI Plastik ve kauçuk ürünleri imalatı ISIC Revize 3 sınıflandırmasına göre, imalat sanayii alt ayrımında
BÖLGESEL VERİMLİLİK İSTATİSTİKLERİ METAVERİ
 BÖLGESEL VERİMLİLİK İSTATİSTİKLERİ METAVERİ Kapsam Sektörel Kapsam 2003-2008 yılları için Avrupa Topluluğu nda Ekonomik Faaliyetlerin İstatistiki Sınıflaması NACE REV.1.1 e göre; B C D E F G H I J K M
BÖLGESEL VERİMLİLİK İSTATİSTİKLERİ METAVERİ Kapsam Sektörel Kapsam 2003-2008 yılları için Avrupa Topluluğu nda Ekonomik Faaliyetlerin İstatistiki Sınıflaması NACE REV.1.1 e göre; B C D E F G H I J K M
Lojistikte Karar Yönetimi ve Optimizasyon (LOJ 430) Ders Detayları
 Lojistikte Karar Yönetimi ve Optimizasyon (LOJ 430) Ders Detayları Ders Adı Ders Dönemi Ders Uygulama Kodu Saati Saati Laboratuar Kredi AKTS Saati Lojistikte Karar Yönetimi ve Optimizasyon LOJ 430 Her
Lojistikte Karar Yönetimi ve Optimizasyon (LOJ 430) Ders Detayları Ders Adı Ders Dönemi Ders Uygulama Kodu Saati Saati Laboratuar Kredi AKTS Saati Lojistikte Karar Yönetimi ve Optimizasyon LOJ 430 Her
Matematiksel modellerin elemanları
 Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
İstatistik ve Sicil İzleme Dairesi Başkanlığı
 1 İçindekiler Bölüm 1 2004 Yılı Dört Aylık Sonuçlar Bölüm 2 Teyit Sonuçları Bölüm 3 Internet Üzerinden İhale İşlemi Yapan İdarelerin İllerine ve Yapılarına Göre Dağılımları 2 2003 yılında ve 2004 yılının
1 İçindekiler Bölüm 1 2004 Yılı Dört Aylık Sonuçlar Bölüm 2 Teyit Sonuçları Bölüm 3 Internet Üzerinden İhale İşlemi Yapan İdarelerin İllerine ve Yapılarına Göre Dağılımları 2 2003 yılında ve 2004 yılının
İTÜ DERS KATALOG FORMU (COURSE CATALOGUE FORM)
 Dersin Adı Havayolu İşletmeciliği İTÜ DERS KATALOG FORMU (COURSE CATALOGUE FORM) Course Name Airline Management Ders Uygulaması, Saat/Hafta (Course Implementation, Hours/Week) Kodu Yarıyılı Kredisi AKTS
Dersin Adı Havayolu İşletmeciliği İTÜ DERS KATALOG FORMU (COURSE CATALOGUE FORM) Course Name Airline Management Ders Uygulaması, Saat/Hafta (Course Implementation, Hours/Week) Kodu Yarıyılı Kredisi AKTS
TP SORUNLARININ ÇÖZÜMLERİ
 TP SORUNLARININ ÇÖZÜMLERİ (Bu notlar Doç.Dr. Şule Önsel tarafıdan hazırlanmıştır) TP problemlerinin çözümü için başlıca iki yaklaşım vardır. İlk geliştirilen yöntem kesme düzlemleri (cutting planes) olarak
TP SORUNLARININ ÇÖZÜMLERİ (Bu notlar Doç.Dr. Şule Önsel tarafıdan hazırlanmıştır) TP problemlerinin çözümü için başlıca iki yaklaşım vardır. İlk geliştirilen yöntem kesme düzlemleri (cutting planes) olarak
EBEKE MODELLERİ. ebeke Yapısına Giriş. Konu 3
 EBEKE MODELLERİ Konu ebeke Yapısına Giriş Elektriksel yapıların bulunduğu şebekeler Ulaşım sistemi Ulaştırma modeli İstasyonlardan oluşan sistem - Televizy zyon şebekesi ebeke Problemi Bir şebeke problemi
EBEKE MODELLERİ Konu ebeke Yapısına Giriş Elektriksel yapıların bulunduğu şebekeler Ulaşım sistemi Ulaştırma modeli İstasyonlardan oluşan sistem - Televizy zyon şebekesi ebeke Problemi Bir şebeke problemi
Yöneylem Araştırması II (IE 323) Ders Detayları
 Yöneylem Araştırması II (IE 323) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması II IE 323 Güz 3 2 0 4 5.5 Ön Koşul Ders(ler)i IE 222
Yöneylem Araştırması II (IE 323) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması II IE 323 Güz 3 2 0 4 5.5 Ön Koşul Ders(ler)i IE 222
DENİZ HARP OKULU ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ
 DENİZ HARP OKULU ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati (T+U+L) Kredi AKTS YÖNEYLEM ARAŞTIRMA - EN-3 3/ 3+0 3 Dersin Dili : Türkçe Dersin Seviyesi
DENİZ HARP OKULU ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati (T+U+L) Kredi AKTS YÖNEYLEM ARAŞTIRMA - EN-3 3/ 3+0 3 Dersin Dili : Türkçe Dersin Seviyesi
BLM-431 YAPAY ZEKA. Ders-5 Bilgili Arama Yöntemleri. Yrd. Doç. Dr. Ümit ATİLA
 BLM-431 YAPAY ZEKA Ders-5 Bilgili Arama Yöntemleri Yrd. Doç. Dr. Ümit ATİLA umitatila@karabuk.edu.tr http://web.karabuk.edu.tr/umitatilla/ Arama Grafları Eğer arama uzayı ağaç yapısından değil de graf
BLM-431 YAPAY ZEKA Ders-5 Bilgili Arama Yöntemleri Yrd. Doç. Dr. Ümit ATİLA umitatila@karabuk.edu.tr http://web.karabuk.edu.tr/umitatilla/ Arama Grafları Eğer arama uzayı ağaç yapısından değil de graf
Türk-Alman Üniversitesi. Ders Bilgi Formu
 Türk-Alman Üniversitesi Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması WNG301 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta) (saat/hafta) (saat/hafta) 6 2 2 0 Ön Koşullar
Türk-Alman Üniversitesi Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması WNG301 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta) (saat/hafta) (saat/hafta) 6 2 2 0 Ön Koşullar
ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ
 ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ Üretim sistemleri hammaddelerin bitmiş ürüne dönüştürüldükleri sistemlerdir. Bu sistemler için oluşturulacak simülasyon modelleri tamamen üretim sisteminin tipine ve verilecek
ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ Üretim sistemleri hammaddelerin bitmiş ürüne dönüştürüldükleri sistemlerdir. Bu sistemler için oluşturulacak simülasyon modelleri tamamen üretim sisteminin tipine ve verilecek
Kredi Limit Optimizasyonu:
 Kredi Limit Optimizasyonu: «Teorik Değil Pratik" Simge Danışman Analitik Direktörü, Experian EMEA Kar Gelişimi Kredi Limit Optimizasyonu Optimizasyona Genel Bakış Profilleme Modelleme Karar Matrisleri
Kredi Limit Optimizasyonu: «Teorik Değil Pratik" Simge Danışman Analitik Direktörü, Experian EMEA Kar Gelişimi Kredi Limit Optimizasyonu Optimizasyona Genel Bakış Profilleme Modelleme Karar Matrisleri
TAMSAYILI PROGRAMLAMA
 TAMSAYILI PROGRAMLAMA Doğrusal programlama problemlerinde sık sık çözümün tamsayı olması gereken durumlar ile karşılaşılır. Örneğin ele alınan problem masa, sandalye, otomobil vb. üretimlerinin optimum
TAMSAYILI PROGRAMLAMA Doğrusal programlama problemlerinde sık sık çözümün tamsayı olması gereken durumlar ile karşılaşılır. Örneğin ele alınan problem masa, sandalye, otomobil vb. üretimlerinin optimum
2. LOJİSTİK ŞEBEKESİ TASARIMI
 2. LOJİSTİK ŞEBEKESİ TASARIMI Lojistik Şebekesi Tasarımı Lojistikte şebeke planlama prosesi, ürünlerin tedarikçilerden talep noktalarına akacağı sistemin tasarlanmasını içerir. Kamu sektöründe ise aynı
2. LOJİSTİK ŞEBEKESİ TASARIMI Lojistik Şebekesi Tasarımı Lojistikte şebeke planlama prosesi, ürünlerin tedarikçilerden talep noktalarına akacağı sistemin tasarlanmasını içerir. Kamu sektöründe ise aynı
Yöneylem Araştırması I (IE 222) Ders Detayları
 Yöneylem Araştırması I (IE 222) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması I IE 222 Güz 3 2 0 4 5 Ön Koşul Ders(ler)i Math 275 Doğrusal
Yöneylem Araştırması I (IE 222) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması I IE 222 Güz 3 2 0 4 5 Ön Koşul Ders(ler)i Math 275 Doğrusal
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
EKONOMİK GÖSTERGELER BÜLTENİ
 SAYI 12 EKONOMİK GÖSTERGELER BÜLTENİ 2014 2. Çeyrek Yıllar İtibariyle Yatırım Teşvik Belgeli Yatırım Bilgileri YATIRIM TEŞVİK İSTATİSTİKLERİ (ENERJİ YATIRIMLARI HARİÇ) Kaynak: Ekonomi Bakanlığı Bölgemizde
SAYI 12 EKONOMİK GÖSTERGELER BÜLTENİ 2014 2. Çeyrek Yıllar İtibariyle Yatırım Teşvik Belgeli Yatırım Bilgileri YATIRIM TEŞVİK İSTATİSTİKLERİ (ENERJİ YATIRIMLARI HARİÇ) Kaynak: Ekonomi Bakanlığı Bölgemizde
Kavramsal Tasarım - I
 Kavramsal Tasarım - I 25.12.2017 1 Kavramsal Tasarımlar Geliştirme ve Geçerli Kılma 6. Kavramsal Tasarım a. Fonksiyon yapısı b. Metodik kısmi çözümler geliştirme i. Etkileşimli yöntemler ii. Sezgisel (Heuristik)
Kavramsal Tasarım - I 25.12.2017 1 Kavramsal Tasarımlar Geliştirme ve Geçerli Kılma 6. Kavramsal Tasarım a. Fonksiyon yapısı b. Metodik kısmi çözümler geliştirme i. Etkileşimli yöntemler ii. Sezgisel (Heuristik)
Kısıtsız Optimizasyon OPTİMİZASYON Kısıtsız Optimizasyon
 OPTİMİZASYON Bu bölümde çok değişkenli kısıtsız optimizasyon problemlerinin çözüm yöntemleri incelenecektir. Bu bölümde anlatılacak yöntemler, kısıtlı optimizasyon problemlerini de çözebilmektedir. Bunun
OPTİMİZASYON Bu bölümde çok değişkenli kısıtsız optimizasyon problemlerinin çözüm yöntemleri incelenecektir. Bu bölümde anlatılacak yöntemler, kısıtlı optimizasyon problemlerini de çözebilmektedir. Bunun
Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu
 Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması BWL315 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta)
Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması BWL315 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta)
YÖNEYLEM ARAŞTIRMASI - II
 YÖNEYLEM ARAŞTIRMASI - II Araş. Gör. Murat SARI 1/35 I Giriş Biri diğerini izleyen ve karşılıklı etkileri olan bir dizi kararın bütünüyle ele alındığı problemler için geliştirilen karar modelleri ve bunların
YÖNEYLEM ARAŞTIRMASI - II Araş. Gör. Murat SARI 1/35 I Giriş Biri diğerini izleyen ve karşılıklı etkileri olan bir dizi kararın bütünüyle ele alındığı problemler için geliştirilen karar modelleri ve bunların
SEMPOZYUM PROGRAMI. 16 Eylül 2010 Perşembe
 SEMPOZYUM PROGRAMI 16 Eylül 2010 Perşembe KAYIT 9.00 9.45 AÇILIŞ 9.45 11.00 BİLDİRİ SUNUMLARI 11.15 18.45 11.15 13.00 TEDARİK ZİNCİRİ YÖNETİMİ (1) Oturum Salonu : MS213 Oturum Başkanı : Selim ZAİM Düzenli
SEMPOZYUM PROGRAMI 16 Eylül 2010 Perşembe KAYIT 9.00 9.45 AÇILIŞ 9.45 11.00 BİLDİRİ SUNUMLARI 11.15 18.45 11.15 13.00 TEDARİK ZİNCİRİ YÖNETİMİ (1) Oturum Salonu : MS213 Oturum Başkanı : Selim ZAİM Düzenli
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/71 İçerik n Bulunması Kuzey-Batı Köşe Yöntemi En Küçük Maliyetli Göze Yöntemi Sıra / Sütun En Küçüğü Yöntemi Vogel Yaklaşım Metodu (VAM) Optimum Çözümün Bulunması Atlama Taşı
YÖNEYLEM ARAŞTIRMASI - I 1/71 İçerik n Bulunması Kuzey-Batı Köşe Yöntemi En Küçük Maliyetli Göze Yöntemi Sıra / Sütun En Küçüğü Yöntemi Vogel Yaklaşım Metodu (VAM) Optimum Çözümün Bulunması Atlama Taşı
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik (Eşitlik Kısıtlı Türevli Yöntem) Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik (Eşitlik Kısıtlı Türevli Yöntem) Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde
Yükleme Emrinde bulunan belge numarası, kamyon plaka numarası ve şoför adının irsaliyeye taşınması,
 SEVK VE YÜKLEME EMRİ YENİLİKLERİ Amaç ve Fayda Sevk ve Yükleme Emrine bağlı işlemlerde yapılan yenilikler ile; Yükleme Emri oluştururken stok bakiye kontrolü, Yükleme Emri Oluşturulurken stoktan ayrılan
SEVK VE YÜKLEME EMRİ YENİLİKLERİ Amaç ve Fayda Sevk ve Yükleme Emrine bağlı işlemlerde yapılan yenilikler ile; Yükleme Emri oluştururken stok bakiye kontrolü, Yükleme Emri Oluşturulurken stoktan ayrılan
BÜRO, MUHASEBE VE BİLGİ İŞLEM MAKİNELERİ İMALATI Hazırlayan M. Emin KARACA Kıdemli Uzman
 BÜRO, MUHASEBE VE BİLGİ İŞLEM MAKİNELERİ İMALATI Hazırlayan M. Emin KARACA Kıdemli Uzman 516 1. SEKTÖRÜN TANIMI Büro, muhasebe ve bilgi işlem makineleri imalatı ISIC Revize 3 ve NACE Revize 1 sınıflandırmasına
BÜRO, MUHASEBE VE BİLGİ İŞLEM MAKİNELERİ İMALATI Hazırlayan M. Emin KARACA Kıdemli Uzman 516 1. SEKTÖRÜN TANIMI Büro, muhasebe ve bilgi işlem makineleri imalatı ISIC Revize 3 ve NACE Revize 1 sınıflandırmasına
ÖZLEM AYDIN TRAKYA ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ
 YÖNEYLEM ARAŞTIRMASI (OPERATIONAL RESEARCH) ÖZLEM AYDIN TRAKYA ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ SUNUM PLANI Yöneylem araştırmasının Tanımı Tarihçesi Özellikleri Aşamaları Uygulama alanları Yöneylem
YÖNEYLEM ARAŞTIRMASI (OPERATIONAL RESEARCH) ÖZLEM AYDIN TRAKYA ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ SUNUM PLANI Yöneylem araştırmasının Tanımı Tarihçesi Özellikleri Aşamaları Uygulama alanları Yöneylem
FABRİKA ORGANİZASYONU Üretim Planlama ve Yönetimi 2. Uygulama: Sipariş ve Parti Büyüklüğü Hesaplama
 FABRİKA ORGANİZASYONU Üretim Planlama ve Yönetimi 2. Uygulama: Sipariş ve Parti Büyüklüğü Hesaplama Uygulamalar 1. İhtiyaç Hesaplama 2. Sipariş ve Parti Büyüklüğü Hesaplama 3. Dolaşım Akış Çizelgeleme/Terminleme
FABRİKA ORGANİZASYONU Üretim Planlama ve Yönetimi 2. Uygulama: Sipariş ve Parti Büyüklüğü Hesaplama Uygulamalar 1. İhtiyaç Hesaplama 2. Sipariş ve Parti Büyüklüğü Hesaplama 3. Dolaşım Akış Çizelgeleme/Terminleme
TEMEL TANIMLAR. Bir gemiyi tanımlamak için aşağıdaki bilgiler gereklidir: a) Geminin büyüklüğü b) Ana boyutlar c) Tekne form katsayıları
 EME ANIMAR ir gemiyi tanımlamak için aşağıdaki bilgiler gereklidir: a) Geminin büyüklüğü b) Ana byutlar c) ekne frm katsayıları Geminin üyüklüğü: Geminin ağırlığı (Deplasman,Dead Weight naj) Geminin hacimsel
EME ANIMAR ir gemiyi tanımlamak için aşağıdaki bilgiler gereklidir: a) Geminin büyüklüğü b) Ana byutlar c) ekne frm katsayıları Geminin üyüklüğü: Geminin ağırlığı (Deplasman,Dead Weight naj) Geminin hacimsel
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I
 KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
Bulanık Mantık Tabanlı Uçak Modeli Tespiti
 Bulanık Mantık Tabanlı Uçak Modeli Tespiti Hüseyin Fidan, Vildan Çınarlı, Muhammed Uysal, Kadriye Filiz Balbal, Ali Özdemir 1, Ayşegül Alaybeyoğlu 2 1 Celal Bayar Üniversitesi, Matematik Bölümü, Manisa
Bulanık Mantık Tabanlı Uçak Modeli Tespiti Hüseyin Fidan, Vildan Çınarlı, Muhammed Uysal, Kadriye Filiz Balbal, Ali Özdemir 1, Ayşegül Alaybeyoğlu 2 1 Celal Bayar Üniversitesi, Matematik Bölümü, Manisa
Konu 2. Y. Doç. Dr. Fazıl GÖKGÖZ
 Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan kl temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda
Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan kl temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda
Tedarik Zinciri Yönetimi -Bileşenler, Katılımcılar, Kararlar- Yrd. Doç. Dr. Mert TOPOYAN
 Tedarik Zinciri Yönetimi -Bileşenler, Katılımcılar, Kararlar- Yrd. Doç. Dr. Mert TOPOYAN Tedarik Zinciri Bileşenleri Tedarik zincirlerinde üç temel bileșenden söz edilebilir: Aktörler: Tedarik zinciri
Tedarik Zinciri Yönetimi -Bileşenler, Katılımcılar, Kararlar- Yrd. Doç. Dr. Mert TOPOYAN Tedarik Zinciri Bileşenleri Tedarik zincirlerinde üç temel bileșenden söz edilebilir: Aktörler: Tedarik zinciri
T.C. Damla Ok 080401041 Mesutcan Kurt 080401013. 2 Ağustos 2011. Ali Murat Tiryaki
 T.C. ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ MÜHENDİSLİK MİMARLIK FAKÜLTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ UÇAK TAKİP SİSTEMİ Damla Ok 080401041 Mesutcan Kurt 080401013 2 Ağustos 2011 Çanakkale Ali Murat Tiryaki
T.C. ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ MÜHENDİSLİK MİMARLIK FAKÜLTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ UÇAK TAKİP SİSTEMİ Damla Ok 080401041 Mesutcan Kurt 080401013 2 Ağustos 2011 Çanakkale Ali Murat Tiryaki
