olur ki, böylece süre 2t = 2, * olarak bulunmuş olur. Uzaklığı hesaplamak için sürenin yarısı hız ile çarpılmalıdır.
|
|
|
- Bercu Akçatepe
- 8 yıl önce
- İzleme sayısı:
Transkript
1 olur ki, böylece süre 2t = 2, * olarak bulunmuş olur. Uzaklığı hesaplamak için sürenin yarısı hız ile çarpılmalıdır. D = t. C Hız, havanın n kırılma indisine, kırılma indisi de nem, basınç dalganın frekansı ve sıcaklığa bağlı olduğundan gerek geodimetre ve gerekse Tellurometre ile çalışırken her iki istasyonda da meteorolojik etkenlerin tesbitine çalışılır. Kristallerin frekansı da sıcaklığa bağlı olarak değiştiğinden, sıcaklık değişiminden dolayı süreye bir düzeltmenin eklenmesi gerekir. Boşlukta ışığın hızı ,5 Km./s dir., t = 9. 6, Hg = 720 mm. ve bağıl nem % 75 ise, bu şartlar altında ışığın hızı C ,5 * v = = = ,2 Km./s. N 1, olur. Bundan başka yükseklik farkı 0,5 metre doğrulukla ölçülerek, ölçülen D eğik uzaklığı Prof. K. Rinner'in formülü ile izdüşüm yüzeyine indirgenir. R, yarıçap değeri, a açıklığı ile ^ enlemi bilindiğine göre Jordan cetvelinden alınmalıdır. Tellurometrenin Master veya Remote'sinin ağırlığı 12 Kg. dır Bütün takım 35 Kg. ağırlığmdadır. 40 Km. ye kadar olan uzaklıklar ölçülebilir. Ölçü süresi dakika ve ortalama hata ± (5 Cm > ) olarak bildirilmektedir. Oysa 1958 yılında Münich bazı Tellurometre ile ölçülerek uzunluğu S = 8231,86 metre olarak bulunmuştur. Invar telleriyle bulunan değer 8231,846 m. olduğuna göre fark 14 mm. dir. Ayni fark 1962 de Geodimetre 4 A ile yapılan ölçülerin karşılaştırılmasında da elde edilmiştir. Fakat 1959 yılında Geodimetre 2A -128 ile yapılan ölçülerden baz, 8231,879 m. olarak bulunmuştur. Fark 26 mm. dir. Göttingen baz ölçmelerinde kendisiyle birlikte çalıştığım Dr. îng. H. Grope bunu ölçme pratiğinin yetersizliğine vermektedir yılında Danimarka'da bulunan Dostrup bazına bağlı Romovongshoj, I. derece kenarı Geodimetre 2A ile ölçülerek m. ve Tellurometre ile 25084,02 m. olarak bulunmuştur. İnvar telleriyle ölçülmüş bazdan hesaplanan bu kenarın uzunluğu 25084,035 m. dir. Dalgaları yüksekten gönderebilmek için Prof. Höpke (Hannover) nin kullandığı çelik borudan kuleler çok tutunmuştur. 35 m. yüksekliğindeki bir kule bir günde kurulabilmektedir. Kuleler yan gerilmelerin etkisiyle küçük bir dönme hareketi yaptığından, bunun koordinat değerlerine bir tesiri olmamaktadır. 48
2 Ayni prensiple çalışan yeni aletler de yapılmıştır. Geodimetre gibi ışılda çalışan Terrametre adlı bir alet, yine îsveçte Prof. Bjerhammer tarafından düşünülmüştür. Prof. quarts kristalinin çift kırılma özelliğinden faydalanmıştır. Bu alet kısa kenarlar için düşünülmüştür^ Bu alette bütün sistematik hataların tesirlerinin kontrol edilebileceği ileri sürülmektedir. Elektrotope, Distomat, Distometre gibi aletler, Tellurometre gibi elektromagnetik dalgalarla çalışmaktadır. Bunların okuma düzenleri ve hesap karneleri değişiktir. Özellikle Wild firmasının yaptığı Dismat, zaman yerine karşılığı olan uzaklığı doğrudan doğruya vermektedir. Fotosellül kullanmak zorun-luğu olmadığından elektromagnetik dalgalarla çalışan aletler daha ucuza mal olmaktadır. Fakat zamanı veren döner daire ile impulslarm peryotların sabit > tutulması mümkün olamamaktadır. Bu ise elektroniğin geliştirilmesi ve yapı malzemesine ve bu kristallerin verimine bağlıdır. Bu bakımdan elektrooptik aletler şimdilik üstünlüklerini korumaktadırlar. SHOKAN VE HİRAN METOTLAKI ^ Bu metotlarla Kanada da 5. 10^ Km 2, bir alan birkaç yıl içinde ölçülebilmiştır. 190 istasyon kurularak 400 Km. uzunluğunda 500 kenar ölçülmüştür. Hiran metodu ile elde edilen bağıl doğruluk derecesi 1/ dir. Shoran kelimesi kısa menzilli uçuş anlamına gelen Short Range Air Navigation kelimelerinin ilk harflerinden meydana gelmiştir. Hiran kelimesi ise High Aocurate Shoran kelimelerinin ilk harfleriyle yazılmıştır. Yüksek doğruluk dereceli Shoran demektir. Tellurometrede olduğu gibi impuls veren bir elektron tüpü ue yapılır. împulsların frekansı 1,5 KHz dir. Bu impulslar, tüpün meydana getirdiği MHz (\ = 1,5-1 m.) frekanslı! dalgalar tarafından taşınırlar. Bu dalgalar nirengi işaretleri üzerine yerleştirilen 17 m. yüksekliğindeki antenlere çarparak geri dönerler. Zaman ölçüsü, Tellurometrede olduğu gibi ışıklı zaman bazı üzerinde yapılır. Kızdırılmış telin yaydığı elektronlar, Wehnelt silindiri tarafından derlenip toplandıktan sonra anodlardan çekilerek ışıklı ekran üzerine itilirler. Elektronlar ekran üzerine çarpınca ekran ışıldamaya başlar. Saptırıcı plâkların herbfrine faz farkı 90 olan yüksek frekanslı dalgalı. 4»
3 gerilimler tatbik edilerek elektron ışınlarına bir daire çizdirilir, tmpuls konisinin gönderdiği impulslar, gidiş ve dönüşte ekran üzerinde iki çıkıntı meydana ge tirirler AB kenarı ölçülecekse, alet bir uçağa yerleştirilir, ölçme uçağı AB kenarı j üzerinde uçarken sekiz biçiminde bir yörünge çizer. Bu sekizli uçuş 16 defa tekrarlanır. Uzaklık 200 Km. den kısa ise, dışardan uçulur. R; - D,- uzaklık farkları ile çizilen parabolün maksimum değeri uzaklığı verir. Uçuş içeriden yapılmışsa (R; + Dj ) toplamı ile çizilen parabolün minumumu uzaklığı verir. Bu sonucu almak için elektron ışının dönme frekansı 1,5 KHz'e bağlanır ve iki tambur yardımıyla A, B ve C çıkıntıları çakıştırılarak tamburlar okunur. Bu okumalar = 100 Km. nin katı ile kesirlerini verirler. Daha sonra 15 2x1, KHz'e bağlanarak çıkıntılar, özel vidalar yardımıyla çakıştırılıp okumalar yapılır. Bu okumalar da = ıo Km. nin katı ile kesirlerini verirler. 2 X15 x 103 Frekans bu defa 150 KHz'e bağlanarak 1 Km. nin katı ile kesirleri elde edilmiş olur. Okumalar istenilen hızla yapılamayacağından tanburların fotoğrafı çekilir. Elektromagnetik dalgalar atmosferde, ışık gibi kırıldıklarından yarıçapı, dalga boyuna ve meteorolojik şartlara göre, yerin yarıçapının birkaç katı olan bir yay çizerler. \ = 1 m. boyundaki dalgalarla nemli bir havada 500 Km. lik bir uzaklık ölçülüyorsa, yayla kiriş adasındaki fark 15 m. yi bulur. 00.
4 DECCA METODU Bu metot İngiltere'de, gemi seyir ve seferlerini kolaylaştırmak için geliştirilmiştir. Belirli üç merkezden eşit fazlı dalgalar yayınlanır. Bu merkezler arasındaki uzaklık yayınlanan dalgaların tam katı olmalıdır. (\ = v/f) Gemide bulunan elektronik bir alet merkezlerden gelen dalgaların faz farklarını ölçer* Dalgaların ayni fazda ulaştığı. noktalar, bîr hiperbol üzerinde bulunduklarından gemi, iki hiperbolün kesişme noktasında bulunur. Loran metodunda ise, sabit istasyonlar radar yerine sürekli olarak impuls yayarlar. Böylece bütün metotları gözden geçirmiş olduk. 500 Km. ye kadar olan uzaklıklar Shoran veya Hiran metodu ile uçaktan ölçülmektedir. Kutba yakın geniş bölgelerin ve balta girmemiş ormanların alımı bu metotla kısa bir süre içinde yapılabilmektedir. Ancak uçağın ve bazen hedef noktalarının kotu istenilen incelikte tayin edilememektedir. Daha kısa kenarlar (50 Km.) elektrooptik (Geodimetre) veya radyoelektrik t (Tellurometre) metotlarla ölçmektedir. Prof. Höpcke (Hannover) bu metotları kadastro ölçülerine uygulamaya çalışmaktadır. ı Radyoelektrik aletler daha hafif olup (Shoran) da olduğu gibi uçaktan ' da ölçü yapılabilmektedir. Bu aletlerle gece veya gündüz hedefler görünsün veya görünmesin ölçü yapmak mümkündür. Oysa elektrooptik aletlerle, uzak mesafelerin ölçülmesinde ancak geceleri ve görerek çalışılabilmektedir. Buna karşılık ölçü sonuçları, radyoelektirik aletlerde olduğu gibi yansımalar dolayısile zeminin niteliğine bağlı değildir. Radyo dalgaları rüzgârlı bir günde buğday tarlası veya dalgaîı bir su yüzeyi üzerinden geçiyorsa, ölçü yapmak mümkün değildir. Yüksek «foir doğruluk derecesi aranıyorsa elektrooptik metoda öncelik vermek gerekir. Çünkü nemin radyo dalgalarının üzerindeki etkisi ışık dalgalarmmkine oranla 100 kat fazladır. Ayrıca kenar boyunca sıcaklık ve nem gibi atmosfer şartlarının kesinlikle bilinmemesi, doğruluk derecesini yükseltmeye engel teşkil t etmektedir. Ancak kenarın iki ucunda meteorolojik etkenlerin tesbiti ile yetinil-mektedir. Fakat gerektiğinde kenar daha küçük parçalara bölünebilir. İlerde elektroniğin geliştirilmesi veya daha güçlü ışık kaynaklarının bulunması her iki metodun gelişmesine yardım edecektir. Transistörlerin kullanılması Geodimetrelerin bîr kişi tarafından taşınabilir hale gelmesine yardım etmiştir. Laserlerden faydalanmak mümkün olursa, daha uzak mesafelere gündüz rasatları yapılabilecektir. Oysa radyoelektrik aletlerde hem yansıma dolayısile hem de daha büyük antenler gerektiğinden daha uzun dalgalar kullanılamıyacağmdan daha uzun mesafelerin ölçülmesi düşünülmemektedir. Kısa dalgalar ise atmosfer tarafından yutulduğundan uzun mesafelere ulaşmamaktadır. Bu açıklamalara göre herhangibir ölçü işinde metot seçimi, belirtilen bütün bu özellikler göz önünde tutularak yapılmalıdır. Faydalanılan yazarlar 1 Prof. Dr. îng. Gigas (Institut für angewadte Geodaesie, Frankfurt) 2»»» Gercke» y-»»» 3 Dr. Ing. H. Grosse»»»»» 4 Dipl. îng. Kneissel»»»»» 5 Prof. Dr. îng. Kneissel (T.H., Munchen) 6»»» Sigl (T.H.,» ) 1»»» K. Rinner (T.H., Graz ) 8»»» H, Höpcke (T.H., Hannover) Sİ
5 Sayın Hocalarım ve Değerli Meslekdaşlarım : Tertip edilen bu seminerde Geodezi (Geometronix) mühendislerinin dış ülkelerde ve yurdumuzda yetiştirilme nitelikleri ve fonksiyonları hakkında elde ettiğim bilgileri sizlere sunmak benim için mutluluktur. Böyle faydalı bir semineri düzenliyen Sayın oda mensubu arkadaşlarıma teşekkür ederim. Şüphesiz konunun geniş anlam taşıması dolayısile açıklamalarımda noksanlarım olacaktır. Konferansın sonunda tecrübeli hocalarımızdan ye Sayin meslekdaşlarımdan bu hususta bilgilerini esirgemeyeceklerini ümit ederim. >t Konuyu sizlere taktim ederken önce tarihsel gelişme devrelerini ve sonra bugünkü şeklini ele alacağım. 17 inci ve 18 inci yüzyıllar arasında bu mesleğin sahiplerine o zamanki deyimi ile «Mesaha Uzmanı» deniliyordu. Yani ölçü işleri alanında çaba gösteren meslek adamlarının çok çeşitli katagorilerini ihtiva ediyordu. Bu ölçü uzmanlarının teknik işlerde etkili olduğu büyük çalışma alanları : Dünyanın ölçümü (yüksek jeodezi sahası), coğrafik yer tayini, büyük ölçüde nirengi, hassas nivelman, Fotoğrametri, Grevimetri, ve elektronik uzunluk ölçüleri. Bütün bu işler yüksek teorik bilgilere ihtiyaç gösteriyordu. O devrin bu sahada yetişmiş meşhur kimseleri : Fransız matematikçisi Laplace ( ), Lagrange ( ) ve Legendre ( ). Bu üç büyük bilgin bu sahada değerli başarılar sağlamışlardır. Cari - Frederich Gauss ( ) in kılavuzluğuna kadar bu ilim adamları mesleğe önderlik etmişlerdir. Ayrıca bu sahada önderlik eden Alman. Geodezi alimleri F.W. Bessel ( ), J.J. Boeyer ( ) ve F.R. Helmert ( ) idi. (Helmert in yüksek geodezi ve dengelenmeye ait iki ciltlik ders kitabı vardır.) Birinci Cihan harbinden sonra bir çok ilmi topluluklar kuruldu. Bunlar arasında Beynelmilel Jeodezi ve Jeofizik Birliği vardı. (Union Geodesique et Geophisique et Geophisique international) U.G.G.I. Bu birlik 7 dernekden teşekkül ediyordu. Bunlar : Geodezi, Dünyanın iç yapısı, Sismoloji, meteoroloji, arzi miknatisiyet, elektrisite, Fiziki Oşeonogrfi, Volkanolaji ve ilmi Hidroloji dir. (*) «Harita ve Kadastro Semineri» nde yazarı tarafından verilen konferanstır.
6 Uluslararası jeodezi cemiyetinde ilmi çalışmalar milli jeodezi komisyonları tarafından veya memleket ölçü dairelerince yapılırdı. Jeodezi komisyonları üyeleri aslında, jeodezi astronomi profesörleri ve ölçü dairelerinin liderleriydi. Dünya ölçümü yüksek teorik bilgiye ihtiyaç gösterdiğinden bu sahada çalışanlar Geodat adını alır ve bunlar U.G.G.I. ya bağlı dünya memleketlerinde akademi mezunu kimselerdi. Fakat yetiştirilme yolları farklıdır. Meselâ Almanya'da Teknik Üniversitelerde, ölçü mühendisi yetiştirilen diğer memleketlerde, bu ölçü elemanları Geodatların göreceği işleri başaracak nitelikte yetiştirilirler. Geodatlar ekseriya topoğrafik aletler imalinde ödev alırlar. Fransada ölçü uzmanları Paris (Ecole - Polytechnique) te yetiştiriliyordu. Elemanların teknik, bakımdan yetişmeleri (Institute Geographique Nationale) Milli coğrafya enstitüsünde, eskiden Fransız ordusunun askeri coğrafya enstitüsü de şahsi profesörler tarafından temin edilirdi. Bu profesörler sevk ve idare eden memur durumunda Enstitü de çalışırlardı). Keza İngiltere ve Amerika'da Geodat lar - Yüksek Mühendis Okulunda genel bir matematik ve Fizik kültürüne sahip olduktan sonra ilgili memleket ölçü dairelerinde Jeodezi konusuna teorik ve * pratik olarak iyice sahip kılınırlardı. Ölçü uzmanlarının faaliyette bulunduğu» insan hayatının diğer sahalarını gözden geçirirsek, görürüzki, coğrafya, askerlik, Jeoloji, inşaat, kültür mühendisliği, gibi her çeşit işlerde, takeometre, plânçete, ve fotoğrametri yardımı ile topoğrafik ölçüler ve haritalar yapılırdı. îyi haritalar eskiden askeri ihtiyaç için ön safta yer aldığından memleket ölçü dairelerinin sevk ve idaresi askeri şahıslar elinde bulunuyordu. Bugün İnkişaf sahası sivil idareye yönelmiştir. Zira artık harita ve topoğrafik plânlar askeri işlerden ziyade sivil işlerde önemle kullanılmaktadır. Askerlikte ölçü uzmanı görevi, top mevzilerinin ve atış cihazlarının yerlerini tayin etmektir. Bu sahada çalışan ölçü uzmanı topoğraftır. O ayni zamanda fotoğrametri ilede uğraşır. Topoğrafların ve fotoğrametricilerin yetiştirilmesi konusuna dönersek bütün dünya memleketlerinde çeşitli yönleri vardır. 19 uncu yüzyıldan 20 nci yüzyıla geçiş sıralarında Zürich de ki konfederasyon Yüksek Müh. Okulunda yalnız inşaat mühendisliği ile kültür mühendisleri ölçme branşında yetiştiriliyordu. Bu okullarda dengeleme, yüksek jeodezi, astronomi, pratik ve teorik yönden öğretiliyordu senesinde ölçme mühendisliği için hususi bir tahsil plânı yapılmasına teşebbüs edildi. Diğer memleketlerde topoğraflar memleket ölçü dairesinin, meslek mektebinin hususi kollarında yetiştirilmektedir. Bu okulların çoğu konferanslar ve eksersizlerle idare edilmektedirler, öğrenciler daha ziyade pratik yetiştiriliyordu. Bu şekilde yetişen topoğraflar iyi iş yapıyorlardı. Açı ölçümleri, geriden, ilerden kestirmeler, topoğrafik harita yapılması gibi. Fotoğrametrinin topografyada büyük çapta kullanıldığı devirlerde Alman ve isviçreli inşaat mühendisleri yapı yerinin haritasını kendisinin yapmasfc, bu suretle arazinin özelliklerini iyice kavraması istenirdi. İnşaat mühendisleri topoğrafik ölçülerden başka ölçü tekniğini ilgilen diren diğer işlerlede ilgili idiler. Bu işler çok sayıda nokta tesbiti, galeri tesbitleri, sulama, drenaj, petrol boruları, baraj, ve baraj duvarları hidrometrik ölçüler, köprüler yollar ve demiryollarına ait kazı ve dolma, kurplarm arazi üzerinde tesbiti gibi. 08
7 Afrika ve Amerika'nın bir çok yerlerde çalıişmış büyük bağanlar elde etmiş bir inşaat mühendisi olan, Harold, Frank Bîrchal in enteresan bir görüşü : (Modern Surveying for civil Engineers London 1955) adlı kitabında inşaat yapacak mühendisin ölçü detaylarına çok dikkat etmesi lâzımdır. Mesleğinde başarı sağlamak istiyea mühendis ölçünün, büyük bir kismmi bizzat yapmalıdır. Kitabın başka bir yerinde : ölçü bir mühendislik işinin kıymetli bir parçasıdır. Denilmektedir. Mühim olan şey, bir ölçüe ne emek sarf edileceği M ve bu emeğim nasıl kulîanilacağmi bilmektir. ÖÇeüd sıhhat derecesi herşeyin başmda gelmektedir. ölçü mühendisinin, yapılacak inşaatın hususiyetlerini tam olarak kavramaya çalışması lâzımdır. Arazi ölçmesine ait ölçüler, ölçü tekniğini ilgilendiren ilk tarihi işlemlerdir. Pratik geometriyi ilgilendiren bu ijşlemlerden geometri ve matematik doğmuştur. İlk önce tek; tarlaların ölçüsü düşünülüyordu. Mısırda her su basmasından sonra tarla hudutlarım yeni baştan belli etmek gerekiyordu. Şüphesiz bu iş ölçü yapmakla mümkündü. Yapılan ölçüler mülkiyet kadas-'' trosunda yapılan ölçülere benziyordu. Dünyanın her tarafında arazi ölçülmektedir. Bu ölçülerin yapılması köylülerin kültürü ve hükümetin şekli ile de ilgilidir. Yapılan işlem, arazinin ölçülmesi ile geometrik şeklinin tayini ve mülkiyet hakkının teessüsü idi. Mülkiyet hakkının garanti edilmesine, arazi ölçüsüne dayanan vergi kadastrosu '' temel teşkilediyordu. Vergi kadastrosu tapu kütüğüne kayıt edilmekle hâk tesis ediyordu. Bu konulara ait hususlar bütün dünya memleketlerinde birbirlerinden farklı olduğundan ölçü uzmanlarının yetiştirilmesine dair memleketten memlekete farklı görüşler vardır. Bir çok ülkelerde, Yüksek mühendis okullarında Kadastro ölçmeleri, dünya ölçmeleri, topografya ve memleket ölçü işleri öğretilmektedir. ingiltere, Fransa, İtalya ve Amerika'da ölçü elemanlarının yetiştirilmesi : tngiltereîde ölçü elemanı bir kaç sümestir üniversitede yabancı dil matematik, fizik ile birlikte astronomi ve jeodezi gibi mühendislik derslerinin esaslarını öğrenir. Genç eleman esas mesleki yetişmeyi patenti olan bir meslek adamı yanında öğrenir. Bu şahıslar her tarafta itibarı olan (The Royal Institution of Chartered Surveyors) birliğini teşkil ederler. «Landsurveyor» denilen arazi ölfçücüleri yamnda birde (Quantity Surveyors) emlak tahmincileri vardır. Bunlarda ayni derneğe bağlı olarak çalışırlar. Evlere fiat biçerler. : Fransa'da tapu ölçme elemanları hükümetçe kabul edilen bir hususi okul da yetiştiriliyyordu. Pratik yetişmeyi diplomalı mühendisler yamnda öğrenirlerdi. İtalya'da Fransanın takip ettiği metodlara benzer yollar takip etmekte dir. Burada askeri harita dairesi memurlarını tapu ölçüctileri arasından değil Polytchnicumlardan ve Üniversitelerden almaktadırlar.. Bu" okulların mühen dislik bölümlerinde jeodezi ilmi tam olarak öğretilmektedir... 54
8 Amerika'da Pratik yetişme, meslekte çalışanlar yanında öğrenilmektedir. Kadastro ölçme uzmanının yetiştirilmesi! hususunda çeşitlilik gözönüne getirilirse, şu sual ile karşılaşırız. Hangi sistem daha iyidir? Mevcut hal çareleri her ulusun kültürel ve ekonomik durumu ile ilgili olduğundan bu mesele kesin bir şekilde cevaplandırılamaz. Ölçü tekniğinde hatalar teorisi çok önemlidir. Ve Ölçü uzmanına sevk edici bir rehberdir. Bu teorik bilgi ancak yüksek okulda elde edilir. İkinci cihan harbinden sonra Jeodezinin ana kollarından biri olan fotogrametrinin süratle gelişmesi, bütün dünya memleketlerindeki üniversitelerde bu ilim üzerine yeni ders programları yapılmasına lüzum göstermiştir. Avrupada yapılan gözlemlerde : İsviçre, Almanya, Avusturya, İtalya ve Holanda ' daki üniversitelerde geodezi üzerine tahsil ve diploma veren bölümler açılmıştır. Bugün Almanya'da teknik Üniversitelerden Hannover, Karlsnıhe, MîiBich. Stîittgaft, Bonn, West Berlin Institute For Theoritical Study, Üniversite isim-. îerini sayabiliriz. Bu üniversitelerde komple Geodezi ve Fotoğrametri dersleri lf! okutulmakta, Yüksek Mühendis ve Doktora programları verilmektedir. Yine, ftollanda'da, Delft Teknik Üniversitesinde 5 senelik Geodezi Yüksek Mühendisliği veren bir bölüm vardır. Bu bölümle kısmen ilgili Beynelmilel yabancı ve yerli öğrenciler için kurulmuş, ve yalnız havai fotoğrametri üzerine bilhassa pratik bakımdan kuvvetli, teorik olarakta özetlenmiş havai fotoğrametri bilgilerini veren bir senelik, veya muhtelif devreler yetiştiren bir kurs vardır, İsmi ITC. dir (International Training Centre). Yine Avrupa memleketlerinden doğu bloku, Polonya, Çekoslavakya, Yugoslavya Finlandiya, Avusturya ve Rusya Geodezi ve astronomi üzerine, üniversitelerine modern ölçme fakülteleri ilâve etmişlerdir. Matematik ve Fizik ilmine ilâve olarak elektronik, optik, radar, ve elektronik mesafe ölçmelerine önem vermişlerdir. Warsaw ve Moscow Üniversitelerinde Geodezi ve Fotoğrametri fakülteleri vardır. " - Avusturya'da da arazi ölçme mühendisliği üzerine 4 senelik programlı okullar vardır. Kanada Öa modern teknik ölçmeler ve milletlerarası araştırma departmanları birleşerek, Kanada Ölçme Enstitüsünün ve tahsilinin mesuliyetini üzerine almışlardır. Üniversitelerden Laval, Toronto, ve Mc - Gill de ölçme branşları vardır de New - Brunswich Üniversitesi 5 senelik ÖJjçme mühendisliği üzerine bir program yapmıştır. Ve burada Geodezi ve Fotoğrametriye ait bütün kurslar verilmektedir. Amerika'da Geodezi ve Fotoğrametri üzerine hususi kurslar veren yalnız OHIO State Üniversitesidir. İnşaat Mühendisliği Bölümüne bağlı Cornell, Illinois, Perdue Üniversiteleri Geodezi ve Fotoğrametri üzerine Programlar Yapmaktadırlar. Amerika'da Geodezi ve Fotoğrametri dersleri Üniversitelerin bir çoklarında inşaat departmanından verilmekte, bazılarında Jeoloji ve Coğrafya departmanlarında verilmektedir. Amerikadaki üniversitelerden bu branşlarda mezun olanlar eğer master ve Doktora yaptı ise Akademik kariyere veya büyük araştırma projelerine m
9 intisap ederler. Ekserisi de fotoğrametrik ve Jeodezîk iş yapan ticari firmalar ile hükümet işlerinde görev alırlar. Memleketimizde, Geodezi ve Fotoğrametri üzerine ö%me bilgisine haiz elemanlar önceleri Mühendis Okullartnm inşaat branşlarından idi senesine kadar ölçüm işleri inşaat mühendisleri veya dış ülkelerde okumuş Yüksek geodezi mühendisleri tarafından yapılırdı de istanbul Yüksek Teknik okulunda Harita Kadastro Mühendislik Şubesinin açılması ile yurdumuzda da ölçü tekniği ve Geodezi ilmine sahip mesul elemanların yetişmesi sağlanmıştır. Bu gün yurdumuzda bir çok teknik işlerde Kadastro, îmar İskân, İller Bankası, Karayolları, Demiryolları, Su işleri, Belediyeler, Fen ve İmar daireleri, Maden Tetkik Arama ve Serbest ölçme işlerinde bu elemanlar başarı ile çalışmaktadırlar. Teknik Üniversitelerimizde de bu konu ile ilgili modern ölçme dersleri kısmen inşaat mühendislerine öğretilmektedir. Sözlerimi, ünlü Türk Haritacılık Bilgini Amiral Piri Reis'in 16. yüzyılda haritacılara verdiği şu öğütü ile bitiriyorum. : İlini adamları şunu Mlinki!. / Bir harita yapmak için özel bir bilgi gerekir. Rasgele her fen adananın harita yapabileceğini sanma çünkü bir haritadaki her türlü tafsilat, en ince teferruata kadar doğru olmalıdır. Ve gerçeğe aynen uymalıdır. Yanlış harita kabul edilmez. Ayrıca Büyük haritacı merhum üstad Şevki paşa ve merhum değerli ineslekdaşımız Y. Müh. Muhittin Aran'ıda huzurunuzda saygı ile anmayı "bir borç bilirim. Hepinizi saygı ile selâmlarım. REFERANSLAR 1. Brinker, R.C A study of the status of photogrammetry in the Engineering school of the U.S.A. and Canada. Photogrammetric Engineering Vil XVII, No. 3 June C.F- Baeschlin, Zollikan Konferans notlan : a. Mesaha uzmanına uzaktan bir bakış. b. ölçme mesleğinde akademik yetişme zarureti. 3. Turpin, R.D. Some trends in Fhotogrammetric Education in U.S.A. Pho togrammetric Engineering Vol. XXVI No. I March Dean C. Merchant: A survey of Courses Offered in Photogrammetry Photogrammetric Engineering Vol. XXIX No.6 November J.E. Colcord : A new approach to surveying Education Photogrammet ric Engineering Vol. XXIX No. 6 Nov Milton O. Schmidt: Geodetic Engineering Education in West Germany Journal of the Surveying and mapping division proceeding of the Ame rican Society of Civil Engineering. 58
10 Yazan : Prof. Y. Müh, Mehmet Göndoğdîi ÖZGEN t.t.ü. öğretim Üyesi Tesviye eğrileri ile yeryüzü şeklinin belirtilmesinde, tesviye eğrilerini yalnız arazinin biçimini belirten şekil çizgileri olarak mütalâa etmemek lâzımdır. ' Bunların ayrıca konum itibariyle de doğru olmaları, yani, plânın her noktasına ait yükseltinin ardışık iki tesviye eğrisi arasından okunabilmesi de icap etmektedir. Binaenaleyh tesviye eğrilerinin belirli bir presizyon şartını sağlamaları lâzımdır.. Tesviye eğrileri ile belirtilen bir arazi şeklinin presizyonunu mütalâa etmek için,' plân yükseltilerinin karesel ortalama hatasından istifade edilir. Plân yükseltisi olarak, herhangi bir arazi noktasının ardışık iki tesviye eğrisinden enterpolasyon ile elde edilen yükseltisi ifade edilmektedir. Presizyon esas itibariyle, ölçüsü yapılan noktaların sayısına ve seçiliş isabetine, plânın ölçeğine,' kaçınılmayan çizim hatalarına ve tesviye eğrilerinin şekli ile ara uzaklıklarına bağlı olmaktadır. Bu hata kaynaklarını kesin bir formülde toplamak oldukça zor olmakla beraber, ayrıca tatbikat içinde lüzumlu değildir. Çizim ve bilhassa noktalama presizyonu büyük ölçekli plânlarda dahi, ölçme presizyonundan daha yüksek olmadığından, arazi gösterilişinin ölçeği olarak çizim presizyonu alınabilir ve bunun değeri işaretlenen bir nokta için 4. 0,2 mm. dir. Noktaların arasında bulunan alanlar için bu değerin iki katı alınır. O halde ±0.2 mm. değeri, 1:1000 ölçeğindeki bir plânda ±0.2 m. ve tabiatta 0.4 m. ve 1:5000 ölçeğindeki bir plânda, ±1,0 m. ve tabiatta 2,0 m. ye tekabül etmektedir. Tesviye eğrilerinin presizyonu için, arazi noktalarının ölçülmesindeki hatalar ile tesviye eğrilerinin çizilmesindeki sıhhatsizlikler nazarı itibara alınmaktadır. Bir tesviye eğrisinin karesel ortalama yükselti hatasını tahmin etmek için değişik amprik formüller verilmektedir. Avrupa'da, en fazla kullanılan formül Koppe formülüdür. Bunun dışında muhtelif memleketlerde, ölçeklere göre değişik formüller kullanmaktadır. Amerika'da ise formüller ya plânm takeometrik, fotogrametrik... ilâh şeklinde hazırlanış metoduna yahut da arazi klâslarma göre verilmektedir. Kanaatımıza göre bu değişik formül şekilleri için Koppe amprik formülü halen gayeye^ en uygun olanıdır. «7
11 Koppe, a ve b plânın ölçeğine bağlı iki sabit katsayı ve a da arazinin eğimini gösterdiğine göre, bir tesviye eğrisi üzerinde bulunan herhangi bir noktanın karesel ortalama yükselti hatasını m y = _j_ (a + b tg a ) veya yükseklik farkları (h) olan iki tesviye eğrisinin arası 1 ile gösterildiğine göre : m y = 4- (a + b ) 1 şeklinde vermektedir. h Ortalama yükselti hatası, arazi eğimi ile doğru orantılı olarak artmaktadır. - Yükselti hatası, konum hatası olarak da mütalâa edilebilir. Bunun için m ifadesi cotg a ile çarpılır ve bir tesviye eğrisi noktasının karesel ortalama konum hatası olarak m k = -j_ (b + a cotg a ) elde edilir.. '.* Bu formüllerdeki katsayıları tâyin etmek için en basit ve presizyonlu me-, tbd şudur : Plân üzerinde kabil olduğu kadar uniform olarak dağılmış ve değişik eğimde kâfi sayıda nokta, arazide poligon veya takeometrik diziler vasıtasiyle ve tesviye eğrili plâm hazırlamak maksadiyle yapılmış olan ölçmelerden bağımsız olarak, yeniden ölçülür ve köşe noktalarının konum ve yükseltileri tâyin edilir. Hatasız olarak kabul edilen bu ölçmelere istinaden, köşe noktaları,, koordinatlarına göre plâna geçirilir ve yükseltileri tesviye eğrilerinden enterpolasyon ile bulunur. Bu şekilde elde edilen nokta yükseltileri ile arazideki yeni ölçmelerden hesaplanmış olan yükseltiler arasındaki farklar gerçek hatalar olarak mütalâa edilebilir. Ortalama arazi eğimlerine göre bir araya toplanmış farkların ortalama değerleri bir koordinat sisteminde ordinatlar olarak ve bunlara tekabül eden ortalama tg a değerleri de absisler olarak işaret edilir. 8 Bu şekilde elde edilmiş olan nokta serileri arasından, dengeleyen düz bir doğru geçirilir. Bu doğrunun tahminî şekilde geçirilmesi bu iş için gerekli presiz-yonda yapılabilir. Doğrunun denklemi, plân yükseltilerinin aranan karesel ortalama hatasını verir.. 1 : ölçekli haritalar için a = 0,4 ve b = 5 değerleri alınabilir. O takdirde karesel ortalama yükselti hatası ta y = ± (0,4 + 5 tg)a) metre ve hata sınırı da bu değerin takriben 3 katı alınarak fi = ±_ (1, tg a > metre şeklinde yazılabilir. Tesviye eğrili plânların kalitesi için, yalnız geometrik presizyon pek tabii kesin bir kriter değildir. Gerçekten bu şekilde morfolojik doğruluk yani tesviye eğrilerinin doğrultusu, eğriliği ve karşılıklı uzaklıkları hakkında herhangi bir fikir edinilmemektedir. Buna rağmen Koope formülüne göre tesbit edilen hata.sınırının, formülün katsayılarının çok dikkatli seçilmiş olmaları şartile, kifayetli olduğu söylenebilir. Pek tabiî presizyon derecesini artırmak kabildir. Bu ise arazide çalışma maliyetini presizyon artışından daha hızlı artıracaktır. Binaenaleyh işin iktisadî olması île presizyon arasında ortalama bir yol tutmak çok daha uygundur. 5g
12 Kontrol maksadiyle istifade edilen noktaların konumlarına uygun olarak, tesviye eğrili plânların kontrolü değişik yollarla, noktasal, doğrusal ve yüzeysel şekilde yapılabilir. Noktasal kontrol şeklinde, kontrol için lüzumlu noktalar konum ve yükselti bakımından tamamen serbest, fakat kontrol ölçmelerinde konum ve yükseltileri kesin ve kolay bir şekilde ve icap eden presizyonla tayin edebilecek şekilde seçilir. Dolayısiyle bu noktalar, koordinat ve yükseltileri belli sabit noktaların yakınlarında seçilmek suretiyle, kolaylıkla ve kesin olarak tayin edilmeleri imkânı sağlanır. Bu durum sağlanamadığı takdirde, noktalar, koordinatları belli iki sabit nokta arasında geçirilecek bir bağlı poligon yardımiyle tayin edilir. Bu halde poligon köşe noktalarının koordinatları hesaplanır ve bu koordinatlar yardımiyle de noktalar plâna doğru olarak geçirilir. Noktaların yükseltileri nivelman ile tayin edilir. Doğrusal kontrol, düşey yahut yatay kesitler yardımiyle yapılır. Düşey kesitlerin kullanılması halinde, kesitlerin plândaki izleri tesviye eğrilerini takriben dik olarak kesecek şeklide, kesitler arazide alınır. Bu şekildeki bir düşey kesitin, münferit noktalarının koordinatları, iki sabit nokta arasında geçirile-* cek bir poligon dizisi yardımiyle ve yükseltileri de nivelman ile tayin edilir. Yatay kesitlerin kullanılması halinde, arazide münferit tavsiye eğrileri aranır ve bu esnada, tesviye eğrili plânın ölçeğine uygun olacak şekilde, bahis konusu olan tesviye eğrisinin eşit aralıklı münferit noktaları nivelmanla tayin edilir. Noktaların koordinatları, iki sabit nokta arasında geçirilen bir poligon * yardımiyle hesaplanır. Yüzeysel kontrol, bahis konusu alanın tesviye eğrilerini tayin maksadiyle yapılan ölçmeleri bir defa daha, daha dikkatli şekilde ve çok daha fazla sayıda nokta almak suretiyle tekrarlamak suretile yapılır. Bu maksatla, yeniden hazırlanacak plân daha büyük ölçekte çizilir ve sonradan fotoğraf yolu ile asıl plân ölçeğine küçültülür. Kontrol için lâzım gelen noktalar, her iki plânda ölçeğe uygun ve birbirine tamamen intibak eden iki kareler ağının gayet dikkatli bir şekilde geçirilmesi suretiyle, elde edilir. Her iki plânda, kareler ağının köşelerine ait yükseltiler tesviye eğrilerinden elde edilir. Netice olarak, açıklanan metodlardan, en basit ve en presizyonlusu noktasal metoddur. Yüzeysel metod en tafsilâtlısı, fakat buna mukabil diğer iki raetoddan daha düşük presizyonlusudur. Noktasal metodun diğer bir üstünlüğü de, kontrol noktalarının arazinin değişik eğimlerinde kolaylıkla seçilmesidir. Yalnız bu metodun tatbiki için, arazide kâfi miktarda koordinat ve yükseltisi bilinen noktanın mevcut olması şarttır. m
13 İki ve Üçüncü Dereceden kök Hesaplanmasına Dair Yazan :. Müh. Nazmi YILDIZ A. Giriş ÇeşitU vesilelerle sık sık karşılaştığımız karekök ve küpkök alınması, ekseriyetle yorucu ve zaman alıcı hesap işlemlerine ihtiyaç göstermektedir. Bundan kurtulmak için birçok metodlar bulunmuştur. En kolayı karekök Ve küpkök cetvellerinden faydalanmaktır. Kullanılışı gayet kolay olan ve birçok eserlerde bulunan bu cetveller büyük bir boşluğu doldurmaktadırlar. Bazan kökü hesaplanacak sayı oldukça büyük olur ve cetvellerden alınacak netice kâfî hassasiyeti sağlamaz. O zaman daha başka yollar aramak icap eder. İlk olarak okullarda öğrenilen karekök ve küpkök hesaplanması akla gelirse de, iyi netice vermelerine rağmen, bunlar da yorucu ve uzun yollardır. Aşağıda izah edilen hesap metodları bizi sonuca daha kolay götüreceğinden pratikte kullanma sahası bulunmaları beklenebilir. Bunların tatbiki için hemen daima hesap makinelerinden faydalanmak yoluna gidilmektedir. Bugün her meslek dalında hesap makineleri kullanıldığı için önce en çok bahsi geçecek birkaç terimin izahına ihtiyaç duyulmuştur. 60
14 Şekilde basit, bir hesap makinesi genel olarak görülmektedir. Üst kısımdaki U (Umdrehung) bölümü; sayı tablası a, virgül hanesi b ve silme kolu c den ibarettir. E (Einstellung) bölümüne, U bölümündekine ilâveten bir de çevirme kolu f yerleştirilmiştir. R (Resultat) bölümünü meydana getiren kızak, m düğmesi ile sağa sola kaydırılabilmektedir. k kolu R, g kolu E bölümündeki sayıları silmeğe yaramaktadır. B. Karekök Hesaplanması. Karekök hesaplanması için 5 metod vardır : 1. Seriye açma suretiyle karekök alma : Buna T ö p 1 e r metodu da denir. Metod, «ilk n tek sayının toplamı daima n 2 ye eşittir» kaidesine istinat eder. 1 = 12 = ı =2 2 = =32 = =42 = 16v.s. ), ', - Hesap; 1, 3, 5 v.s. gibi bütün tek sayıların birbiri arkasına, karekökü alınacak sayıdan çıkarıldması ile bir çıkarma problemine döner. Büyükçe sayılar virgülden itibaren ikişer ikişer sağ ve sola doğru gruplara ayrılır. Grupların sayısı ile kökün hane sayısı eşittir. f Misal : V 691,69 = 26,3* * Çzüm : Virgülden itibaren sağ ve sola ikişer ikişer ayıralım. Bu suretle 6 91, 69 olur. Makinenin hazırlanması : Sayı, R bölümünün en yüksek hanesine getirilir, bu hane (10) olsun. Kızak tamamen sağa kaydırılır. E ve U bölümlerini 8 haneli kabul edelim. Kök işareti altındaki sayı, virgülden önce ikişer haneli 2 gruptan ibaret olduğundan hesaplanacak sayı da 2 hanelidir. U bölümünde bunun için en yüksek virgül hanesi işaretlenir, bu 6 dır. E bölümü ise 4 üncü virgül hanesine getirilir. Hesap yolu : îlk sayı grubundan, yani 6 dan bütün tek sayılar birbiri arkasına çıkarılır. 1 sayısı E de 6 ncı haneye getirilir ve R deki 6 dan çıkarılır. 3 sayısı E de 6 ncı haneye getirilir ve R deki 6 dan çıkarılır. 5 sayısı çıkarılamıyacağmdan U daki 2 sayısı, aranan sayının ilk rakamıdır. E ye, çıkarılamayan 5 saysı yerine 1 eksiği, yani 4 getirilir. Bu da U daki 2 nin 2 katıdır. Kızak 1 diş sola kaydırılır. E deki 5 inci virgül hanesine tek sayılar 1, 3, 5 v.s. getirilir ve böylece hâsıl olan sayılar R deki sayıdan çıkarılır. 41, 43, 45, 47, 49, 51 sayıları çıkarıldıktan sonra kızaktaki çıkarma işlemi biter. Şimdi U da 26 sayısı bulunmaktadır. Kökün 2 katı, yani 2 X 26 = 52 sayısı, E deki 51 sayısı yerine getirilir, yani 5 inci hanedeki 1 sayısı 2 ye çıkarılır. Kızak tekrar bir diş sola kaydırılır. E deki 4 üncü haneye tek sayılar getirilir (521, 523, 525) ve R deki sayıdan çıkarılır. 525 in çıkarılmasından sonra.. 61
15 R de sıfır kalır.. Kök hesaplanmıştır. Son olarak E deki 4 üncü hanede bulunan rakam 1 arttırılır, böylece 525 sayısı 526 olmuş olur. Neticenin alınması : U da, hesaplanan kök değeri 26,3 bulunmaktadır. Eğer E bölümünde 26,3 ün 2 katı, yani 52,6 varsa hesap doğrudur. Problem : Dik koordinatları bilinen, 2 nokta arasındaki uzaklık 5 = VAY 2 + Ax 2 formülü ile bellidir. Ay = 211,43 AX = 214,12 olsun, s mesa fesinin direkt olarak hesaplanması (Netice: V ,01 93 = 300,92 cm ye yuvarlanmıştır). II. Elle hesaplama metoduna göre karekök hesaplanması Okullarda öğretilen yazılı karekök alma metodunu v on Stein hesap makinesine tatbik etmiştir. Misal : V Çözüm : Sayı ikişer hanelik gruplara bölünür. * Makinenin hazırlanması : Virgül hanesi R(7), U(5), E(2) ye ve sayı R ye getirilir, kızak en sağa kaydırılır. Hesap yolu : îlk çift sayı grubu olan 55 den en yakın tam sayının karesi çıkarılır. Bu ise E deki 5 inci haneye 7 rakamının getirilmesi ve bunun karesinin alınmasıyla olur. Böylece U da 700,0 (5) ve R de bulunur. /.. Kızak bir diş sola kaydırılır. E deki sayının 2 katı alınır ve 14 sayısı 6 ve 5 inci hanelere getirilir. Sonra 665 :14 ^ 4 zihinden hesaplanır ve E deki sayı 144 olacak şekilde değiştirilir. 144 ün 4 defa çıkarılması ile U dam sayı 740,0 ve R deki ise olur. Kızak bir diş daha sola kaydırılır. Aynı iş tekrarlanır. E ye son olarak getirilen 4 sayının 2 katı alınır. Böylece E deki 6,5 ve 4 hanelerindeki sayı 148 olur ve sonra 8916 : 148 ^ 6 zihinden hesaplanarak E ye getirilir nın 6 defa R den çıkarılmasiyle hesap işi biter ve R de sıfır kalır. Son olarak E ye en sonra getirilen 6 sayısının 2 katı alınır ve E deki rakam 1492 yapılır. Neticenin alınması : U da aranan kök 746 bulunmaktadır. Bu sayı, E deki 1492 nin yarısı olduğundan hesap kontrolü sağlanmıştır. Problem : V 41,99 04 = 6,48. III. Yaklaşık bir değerle ve bölme suretiyle karekök hesaplanması (1) Kerl ve Herrmann, tatbikat için uygun yaklaşık metotlar bulunmuşlardır. Bunlardan Herrmann metodu aşağıda izah edilmiştir. Bu metodun, üstünlüğü, hesaplanan karekök değerinin tamamının U bölümünde elde edilmesi ve müteakip hesaplarda tekrar kullanılabilmesidir. Kökün yaklaşık değeri a ve tashih miktarı h ise şu eşitlik daima mevcuttur : 62 (a + h) 2 = & 2 + (2a + h). h (a + h) 2 verilmiştir, Ü bölümünde (a + h) istenmektedir.
16 " ' "'- (a-f hj' 2 "'miktarı R ye getirilir, bundan a 2 çıkarılır ve kalan (a + h) 2 -< a2 ise (2a 4-h) ile bölünür. Bu esnada bölen terim olan (2a + h) nın yaklaşık olarak bilinmesine ihtiyaç vardır. Aranan (a + h) değeri U da elde edilir. Eğer a yaklaşık değeri, kesin kök değerinden '% 3-4 kadar farklı ise pratikte metod kâfi hassasiyeti verir. Misal: V = 123,0 Çözüm : Sayı ikişerlik gruplara ayrılır. Makinenin hazırlanması : Virgül ayan R de 8, U da 5 ve E de 3 e alınır. Sayı R (8) ye, yaklaşık değer a = 120,0 (3) ise E ye getirilir. Hesap yolu: 120nin karesi alınarak R den çıkarılır. U da 120,0(5), R de 729,0 (8) kalır, h tahmin edilir. Bunun için en iyisi R deki sayı sıfıra yaklaşmcaya kadar U daki sayı değiştirilir. Bu miktar 126,0 (5) dir, böylece fark 6 olur ve 2h ya eşittir, h = 3,0. U daki sayının 120,0 ye geri getirilmesinden sonra E ye 2a + )h = 243,0 (3) yerleştirilir, R de kalan 729,0(8) ise 243,0 ile bölünür. Neticenin alınması : Bölme işi biter. U da aranan değer 123,0 (5) bulunmaktadır. Kesin değer de 123,0 tür. Hesaplanan sayı kâfi hassasiyette değilse kök alma işlemi bu metod veya bundan sonra anlatılacak metoda göre tekrarlanabilir..problem : V ,98 24'ün hesaplanması (a = 140,0; h = 2,0. Netice : 142,32263 yani 142,32). * - IV. Yaklaşık bir değer ve çarpma suretiyle karekök hesabı (1) Gene Herrmann tarafından bulunan bu metod, bundan önceki metodla aynıdır, yalnız burada bölüm yerine «çarpma suretiyle bölme» kullanılır. Hesabın başlamasında R boş bırakılır. Önce E ye a getirilir ve R de a 2 teşkil edilir. Tahminen bulunan h dan sonra E ye (2a + h) yerleştirilerek R de karekökü alınacak sayıyı mümkün mertebe doğru elde etmeğe çalışmak lâzımdır. Neticede (a + h) değeri U da meydana gelir. Misal: V ,84 64 = 300,92 Çözüm: Virgül ayarları yapıljır R (8)', U (5), E (3). a = 300 tahmin edilerek E (3) ye getirilir, a 2 alınarak U da 300,0 (5) elde edilir. Kolu çevirdi) Newton, kök almak için en genel şekilde yaklaşık bir metod gösterir. Py'Nnin yaklaşık değeri a ise a ya getirilecek tashihi şöyle bulunur (bak. Matematik ilimler Ansiklopedisi İ Cilt 3a Nr. 10) : N-a p p> _... P. ap- 1 Birkaç kere hesaplanan tashihte tekrarlanan bölmelerden sakınmak için Cauchy (p. 857 = 0 evres 5, p. 433) g yi şöyle hesaplar : g = >a (N - ap ) P.N I..... Burada önceden hesaplanır. P.N ' ; " ". 6 8
17 meğe devam ederek U, 302,0 (5) ye gelince R deki sayı, kök içindekine çok yaklaşmış olur. Bu suretle h takriben 1,0 demektir. U daki değeri 300,0 e geri getirdikten sonra E deki sayı 2a + h = 601,0 (3) e çevrilir. 601, 0 ile R de, verilen ,84 64 e mümkün mertebe yaklaşmağa çalışılır. Neticenin alınması: R de , meydana gelince U da 300,91988 elde edilir. Aranan değeri 300,92 dir. V. Yaklaşık değer ve tashih miktarının hesaplanması ile karekök alma Karekökü alınacak sayı N, yaklaşık değer a, tashih miktarı h ise V~N = & + h N = a 2 + h. (2a + h) - h miktarı 2a ya nisbetle çok küçük olduğundan ekseriya (2a + h) yerine 2a almak maksada yeter. O zaman. N = a 2 + 2a.h - N-a2 h = * 2a Bu da sayfa 4 te verilen Newton formülünden başka birşey değildir, h miktarı kâfi hassasiyetle elde edilmemişse bu sefer yaklaşık değer olarak a + h = A, alınır ve hesap işlemi tekrarlanır, ilk yaklaşık değeri bir sürgülü hesap cetvelinden alınmışsa hesabın tekrarlanmasına ihtiyaç olabilir. *" Misal: N = , Kare cetveli yardımı ile a = 6523 alınır ve , h = = + 0, bulunur. V~N = 6523,742 C. Küpkök Hesaplanması Küpkok hesaplanmasında en çok yaklaşık değerlerden faydalanılır. Bunlardan iki metodu anlatmak yerinde olacaktır. I. Bir Yaklaşık Kare ve Bölme Suretiyle Küpkök Alınması Von Stein'in teklif ettiği gibi kesin çözümler, çok zaman alıcı, ve yorucu olduğundan pratikte elverişli bulunmaz. En çabuk Olarak küpkök cetvelleiiyle netice alınır. Aşağıda anlatılan ve yaklaşık değer yardımı ile kullanılan metod fazla zamana ihtiyaç göstermez. Takribî olarak (a + h)3 = a 2 (a + 3h) yazılabilir, (a + h)3 miktarı, yaklaşık kare olan a 2 ile bölünür ve U da a + 3h elde edilir, 3h veya h hesaplanır. Böylece aranan a + 3h elde edilir, 3h veya h hesaplanır. Böylece aranan a + h kolayca bulunmuş olur. Eğer hassasiyet yetmezse hesap tekrarlanmalıdır, bu sefer yaklaşık değer olarak a + h hesaba sokulur. U
18 Misal : *yj = 234 Çözüm : 3yf ^ 200 tahmin edilir = sayısı E (0) ye, ise R (5) ye getirilir, Bölüm, (5) : (0) = 320,3226 (5) U dadır. 320,...nin 200 den farkı olan 120,3226 run 1/3 ünü 200 e ilâve edersek 200, ,10753 = 240,10753 daha doğru yaklaşık değer elde edilir. Aranan değer 234 olduğundan hassasiyet kâfi bulunmazsa hesap işlemi a = 240 ile tekrarlanır veya bundan sonraki metoda göre devam edilir- Problem : 3^ = 246. II. Bir yaklaşık kare ve çarpım suretiyle küpkök alınması Bir yaklaşık değer yerdımı ve çarpım suretiyle yapılan bir bölme aynı ne- * ticeyi verir. Formül aynıdır..* Misal: Aynıdır. *J = 234. v 1 ' Çözüm :. Yaklaşık: değer olarak bundan, önee bulunan 240,10753 alınır. * Virgül ayarı U (4), E (4) ile 240,10753 değerinin karesi alınır. Böylece R de 57651, (8) meycjana gelir. E (0) ye yaklaşık a2 olarak (yuvar lak sayı) jgetirilir ve R (5) de e en yakın değeri Veren sayı U (5) da 222,24561 olarak elde edilir. Şimdi de 222, ,10753 = 17,86192 ve 1^,86192/3 = -5,95387 teşkil edilir. 240, ,95397 = 234,15356 aranan sayı dır.' Yuvarlak olarak 234 sayısı böylece bulunmuş olur. Literatür 6 H. Wittke : Die Rechenmaschine und ihre Rechentechnik. Eggert - Klietsch : Geodâtische Rechnungen mittels der Rechenmaschine. m.
19 Fotogrametrik Çalışmalarda Para ve Zaman Faktörleri* Çeviren : Y. Müh. Muhlis AKYALI Fotogrametrik çalışmalarda ekonomik faktörler pek büyük bir önem taşırlar. Esasen metodun kabulü içinde bu faktörlerin bidayette lehte olup olmadığı kesin olarak denenmiş olmalıdır. Genel olarak denilebilir ki; metod, en kısa zamanda ve en düşük maliyetle iyi neticeye ulaşması bakımından diğer metodlara üstünlük kazanır ve tercih edilir. Bu, sebepten, fotogrametrik metodiar hızla önem kazanıp sahalarında yerleşmişler ve bu yerleşme, yalnız Topografik harita* yapımında değil diğer arazi çalışmalarında da (yol, sulama, orman, şehircilik...v.s) kendini gös- '' termiştir, Bununla beraber fotogrametrik metodların kullanılışında, ekonomik mülâhazalar için umumi bir beyanda bulunmak ve keza zaman harcanmasını tesbit etmek pek çok faktörlere dayanır. Keyfiyet durumdan duruma da değişir. Fotogrametrik metodla diğer metodları mukayese etmede hususiyle benzer şartlar ele alınır. Havai fatağrametride bu şartlan mukayese etmek, arzi fotoğrametriye göre bir dereceye kadar daha kolaydır. Aşağıda havai fotoğrametri ile yapılan bazı tip haritalar için değişik ameliyelerin ekonomik maliyet yüzdesine ait îsveç ve Alman kaynaklarından derlenmiş bilgiler verilmiştir. I 1/1000 ölçekli Kadastral harita yapımında: Maliyet % Hazırlık : 7 Komple jeodezik şebeke tesisi ve işaretleme : 53 Havai fotoğraf alma ve arazi kaydı : 19 Birinci derece aletle kıymetlendirme t 21 II 1/5000 ölçekli Topografik harita : Hazırlık : 2 Jeodezik arazi çalışması î 15 Havai fotoğraf alımı : 8 Stereoskopik kıymetlendirme : 30 Toplam arazi işi, çizgi ve teksir : 20 (*) B. HALLERT'in 1960 baskılı PHOTOGAMMETRY adlı kitabından. e#;.
20 III 1/ ölçekli fotoğrafik harita yapımında : Havai fotoğraf alımı : 25 Havai nirengi ve kontrol ölçüsü r. 25 İkinci derece aletle kıymetlendirilip harita haline getirme.: 50 IV Ekonomik harita yapımı : (1/10000 ölçekli kontrollü mozaika istinaden her 100 Km 2 için ortalama 4 trigonometrik nokta ve 1/25000 lik havai fotoğrafla) : - Havai fotoğraf hazırlıklar dahil : 12 Kontrol ölçüsü ve Fotoğrametrik geçiş noktası tayini : 7 Düzeltme, mozayik teşkili : 9, Sınırların hakiki durumunu belirtme : 21 Toplam arazi içi çizme dahil : 41 Teksir : 10 Diğer taraftan tecrübe göstermiştir ki; engebeli bir arazinin tesviye eğri-, "- lerini de ihtiva eden bir haritasını yapmakta, zaman bakımından yaklaşık ola-', ft rak şu formül rol oynamaktadır. ' ' ' S ' ' S %\ PD = Hektar/Saat veya (PD = Akre/Saat) Burada S, harita ölçeğinin paydasıdır. Düzeltilmiş ve birleştirilmiş kontrollü mozaikler için ise formül: Akre = Bir İngiliz arazi ölçüsü. s s Pm = Hektar/Saat veya Pm = Akre/saat dır J0 : Kontrolsuz mozaikler için P m formülünde başarı, 5-10 kere daha büyük olabilir. Şurası unutulmamalıdır ki, yukarıdaki bütün değerler normal şartlarda ve büyük bir dikkatle çalışıldığı zaman bize iyi birer sonuç olarak görünürler. Netice olarak, pratik tecrübeler göstermiştir ki : ayni arazi için maliyet mukayesesinde, tam jeodezik metoda nazaran, havai fotogrametri ile % 40 bir tasarruf yapılabilmektedir. Zamandan elde edilen bu mühim tasarruf ise, paraya tahvilen lehe kaydolunmaktadır. %
21 HARİTA VE KADASTRO SEMİNERİ : Geçen devre odamız yönetim kurulunca düzenlenen Birinci Harita ve Kadastro Semineri Şubat 1966 tarihlerinde imar ve îskân Bakanlığı Konferans Salonunda yapılmıştır. Uzun süredir boşluğu hissedilen seminer davetli- 1 ier ve yurdun dört bucağından gelen meslektaşlarımız tarafından ilgi ile izlenmiştir. 11 Şubat Cuma günü saat 14 de başlayan seminerde Yönetim Kurulu Baş kanı Beşir Say'ın açış konuşmasından sonra ilk konuşmacı İ.Y.T.O. öğretim Üyesi Y. Müh. Burhanettin Tansuğ «Fotoğrametrinin Büyük Ölçekli Harita- f lara ve Kadastroya Uygulanması» konusunda bir konferans vermiş ve sonunda birçok meslektaşlarımızın konu ile ilgili sorularını cevaplandırmıştır. Günün ikinci konferansı saat da Harita Genel Müdürlüğü Teknik Muavini Dr. Müh. İslam Erokan tarafından «Türkiye Ana Nirengi Şebekesi» konusunda verilmiştir. Meşedağ ve Avrupa Mebdei ile ilgili sorular ve verilen cevaplar ilginç bir tartışma şeklinde cerayan etmiştir. 12 Şubat 1966 Cumartesi günkü konferansın ilki «Elektro - Magnetik Dal galarla Uzaklık ölçülmesi» konusunda İ.Y.T.O. Öğretim Üyesi Y. Müh. Macit Erbudak tarafından verilmiştir. Uzun süre rahatsızlıktan sonra Sayın Hocamızı tekrar, sıhhatli olarak aramızda görmek 15 yıldanberi yetiştirdiği öğrencilerini ve kendisini tanıyanları son derece sevindirmiş ve kürsüye çıktığında uzun uzun alkışlanmıştır. Konuşmasının başında da hissiyatım «Daha hâlâ bir iş yapa bilmenin zevki içindeyim, bu benim için bir sağlık belgesi oluyor, nefsime olan itimadım artıyor.» şeklinde ifade etmiştir. Konuya, «Konumuz ışık yolunuz ay dınlık olsun» diye başlayan Sayın Hocamız zaman zaman yaptığı nükteler ve 1 verdiği ilgi çekici örneklerle teknik bir konuyu aktüel bir duruma getirmiş ve dinleyiciler tarafından ilgi ile izlenmiştir. Seminerin son konferansını saat 13 de «Harita ve Kadastro Mühendislerinin Dış Ülkelerde ve Yurdumuzda Yetiştirilme Nitelikleri ve Ponksiyonları» konusunda O.D.T.Ü. Müh. Fakültesi öğretim Üyesi Yrd. Prof. Fahrettin Aydın vermiştir. Bu konuda da bir çok sorular sorulmuş, gerek konferansçı ve gerekse hazır bulunan yetkili üyelerimiz tarafından birçok açıklama ve mukayese yapılarak konu aydınlanmıştır.,4».
Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN
 Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN Topografya (Surveying) Nedir? Topografya geleneksel olarak, Dünya yüzeyinin üzerindeki, üstündeki veya altındaki noktalarının rölatif konumlarını belirleyen
Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN Topografya (Surveying) Nedir? Topografya geleneksel olarak, Dünya yüzeyinin üzerindeki, üstündeki veya altındaki noktalarının rölatif konumlarını belirleyen
NÎRENÇİ NOKTALARININ ARANMASI
 NÎRENÇİ NOKTALARININ ARANMASI Yazan ; -.. İsmail Hakkı GÜNEŞ 1, '. ' ' (Ankara) Haritaları yapılmış meskun ve meskun olmayan alanlarda bulunamıyan ve taşları kaybolan nirengilerin yeraltındaki sigorta
NÎRENÇİ NOKTALARININ ARANMASI Yazan ; -.. İsmail Hakkı GÜNEŞ 1, '. ' ' (Ankara) Haritaları yapılmış meskun ve meskun olmayan alanlarda bulunamıyan ve taşları kaybolan nirengilerin yeraltındaki sigorta
KESİTLERİN ÇIKARILMASI
 KESİTLERİN ÇIKARILMASI Karayolu, demiryolu, kanal, yüksek gerilim hattı gibi inşaat işlerinde projelerin hazırlanması, toprak hacminin bulunması amacı ile boyuna ve enine kesitlere ihtiyaç vardır. Boyuna
KESİTLERİN ÇIKARILMASI Karayolu, demiryolu, kanal, yüksek gerilim hattı gibi inşaat işlerinde projelerin hazırlanması, toprak hacminin bulunması amacı ile boyuna ve enine kesitlere ihtiyaç vardır. Boyuna
ÖLÇME BİLGİSİ. PDF created with FinePrint pdffactory trial version http://www.fineprint.com. Tanım
 ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları
 TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Fotogrametride işlem adımları
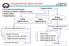 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ
 ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ Doç. Dr. Alper Serdar ANLI 5.Hafta ALANLARIN ÖLÇÜLMESİ Genel bir deyişle herhangi bir arazi parçasının şeklini ve büyüklüğünü belirtecek planın çıkarılabilmesi için gereken
ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ Doç. Dr. Alper Serdar ANLI 5.Hafta ALANLARIN ÖLÇÜLMESİ Genel bir deyişle herhangi bir arazi parçasının şeklini ve büyüklüğünü belirtecek planın çıkarılabilmesi için gereken
TOPOĞRAFYA Takeometri
 TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ
 ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
İnşaat Mühendisliğine Giriş İNŞ-101. Yrd.Doç.Dr. Özgür Lütfi Ertuğrul
 İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ
 Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Uzunluk Ölçümü (Şenaj) Prof.Dr.Mustafa KARAŞAHİN
 Uzunluk Ölçümü (Şenaj) Prof.Dr.Mustafa KARAŞAHİN Uzunlukların Ölçülmesi (Şenaj) Arazide uzunlukların doğru ve hassas bir şekilde ölçülmesi, projelerin doğru hazırlanmasında ve projelerin araziye uygulaması
Uzunluk Ölçümü (Şenaj) Prof.Dr.Mustafa KARAŞAHİN Uzunlukların Ölçülmesi (Şenaj) Arazide uzunlukların doğru ve hassas bir şekilde ölçülmesi, projelerin doğru hazırlanmasında ve projelerin araziye uygulaması
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA. Ölçme Bilgisinin Konusu
 TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
02.04.2012. Düşey mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi
 Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
YÜKSEKLİK ÖLÇÜMÜ. Ölçme Bilgisi Ders Notları
 YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
TOPOĞRAFİK HARİTALAR VE KESİTLER
 TOPOĞRAFİK HARİTALAR VE KESİTLER Prof.Dr. Murat UTKUCU Yrd.Doç.Dr. ŞefikRAMAZANOĞLU TOPOĞRAFİK HARİTALAR VE Haritalar KESİTLER Yeryüzü şekillerini belirli bir yöntem ve ölçek dahilinde plan konumunda gösteren
TOPOĞRAFİK HARİTALAR VE KESİTLER Prof.Dr. Murat UTKUCU Yrd.Doç.Dr. ŞefikRAMAZANOĞLU TOPOĞRAFİK HARİTALAR VE Haritalar KESİTLER Yeryüzü şekillerini belirli bir yöntem ve ölçek dahilinde plan konumunda gösteren
DİK KOORDİNAT SİSTEMİ VE
 Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN
 YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN Yrd. Doç. Dr. Ayhan CEYLAN Yrd. Doç. Dr. İsmail ŞANLIOĞLU 9.3. Nivelman Ağları ve Nivelman Röper Noktası Haritası yapılacak olan arazi üzerinde veya projenin
YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN Yrd. Doç. Dr. Ayhan CEYLAN Yrd. Doç. Dr. İsmail ŞANLIOĞLU 9.3. Nivelman Ağları ve Nivelman Röper Noktası Haritası yapılacak olan arazi üzerinde veya projenin
TEMEL HARİTACILIK BİLGİLERİ. Erkan GÜLER Haziran 2018
 TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
Ölçme Bilgisi ve Kadastro Anabilim Dalı
 ÖLÇME BİLGİSİ Ölçme Bilgisi ve Kadastro Anabilim Dalı Ders Kodu:264 Yrd.Doç.Dr. Muhittin İNAN Anabilim Dalımız "İstanbul Yüksek Orman Mektebi" nin 1934 yılında Ankara Yüksek Ziraat Enstitüsüne bir fakülte
ÖLÇME BİLGİSİ Ölçme Bilgisi ve Kadastro Anabilim Dalı Ders Kodu:264 Yrd.Doç.Dr. Muhittin İNAN Anabilim Dalımız "İstanbul Yüksek Orman Mektebi" nin 1934 yılında Ankara Yüksek Ziraat Enstitüsüne bir fakülte
ANKARA ÜNİVERSİTESİ ZİRAAT FAKÜLTESİ PEYZAJ MİMARLIĞI BÖLÜMÜ ANKARA 2015 PROJE APLİKASYONU
 ANKARA ÜNİVERSİTESİ ZİRAAT FAKÜLTESİ PEYZAJ MİMARLIĞI BÖLÜMÜ ANKARA 2015 PROJE APLİKASYONU Doç. Dr. Aydın ÖZDEMİR Araş. Gör. Pelin ŞAHİN KÖRMEÇLİ 1 PROJE APLİKASYONU NEDİR? Yapılan imar planlarını, yapı
ANKARA ÜNİVERSİTESİ ZİRAAT FAKÜLTESİ PEYZAJ MİMARLIĞI BÖLÜMÜ ANKARA 2015 PROJE APLİKASYONU Doç. Dr. Aydın ÖZDEMİR Araş. Gör. Pelin ŞAHİN KÖRMEÇLİ 1 PROJE APLİKASYONU NEDİR? Yapılan imar planlarını, yapı
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3351 3 4 3 0 0 DERSİN
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3351 3 4 3 0 0 DERSİN
KALINLIK VE DERİNLİK HESAPLAMALARI
 KALINLIK VE DERİNLİK HESAPLAMALARI Herhangi bir düzlem üzerinde doğrultuya dik olmayan düşey bir düzlem üzerinde ölçülen açıdır Görünür eğim açısı her zaman gerçek eğim açısından küçüktür Görünür eğim
KALINLIK VE DERİNLİK HESAPLAMALARI Herhangi bir düzlem üzerinde doğrultuya dik olmayan düşey bir düzlem üzerinde ölçülen açıdır Görünür eğim açısı her zaman gerçek eğim açısından küçüktür Görünür eğim
İNŞAAT MÜHENDİSLİĞİ TEKNİK RESİM DERSİ ÖĞR. GÖR. BERIVAN POLAT
 İNŞAAT MÜHENDİSLİĞİ TEKNİK RESİM DERSİ ÖĞR. GÖR. BERIVAN POLAT Kesit çıkarma ve Merdivenler MERDİVENLER Bir yapıda birbirinden farklı iki seviye arasında muntazam aralıklı, yatay
İNŞAAT MÜHENDİSLİĞİ TEKNİK RESİM DERSİ ÖĞR. GÖR. BERIVAN POLAT Kesit çıkarma ve Merdivenler MERDİVENLER Bir yapıda birbirinden farklı iki seviye arasında muntazam aralıklı, yatay
HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR
 HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR Harita nedir? Yeryüzünün veya bir parçasının belli bir orana göre küçültülerek ve belirli işaretler kullanılarak yatay düzlem üzerinde gösterilmesine harita adı verilir.
HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR Harita nedir? Yeryüzünün veya bir parçasının belli bir orana göre küçültülerek ve belirli işaretler kullanılarak yatay düzlem üzerinde gösterilmesine harita adı verilir.
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ. HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör.
 ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör. Taha Yasin HATAY Trabzon, 2015 UYGULAMA II. NİVO İLE YÜKSEKLİK FARKI ÖLÇÜMÜ UYGULAMANIN
ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör. Taha Yasin HATAY Trabzon, 2015 UYGULAMA II. NİVO İLE YÜKSEKLİK FARKI ÖLÇÜMÜ UYGULAMANIN
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
BOYKESİT Boykesit Tanımı ve Elemanları
 BOYKESİT Boykesit Tanımı ve Elemanları Boykesit yolun geçki ekseni boyunca alınan düşey kesittir. Boykesitte arazi kotlarına Siyah Kot, siyah kotların birleştirilmesi ile elde edilen çizgiye de Siyah Çizgi
BOYKESİT Boykesit Tanımı ve Elemanları Boykesit yolun geçki ekseni boyunca alınan düşey kesittir. Boykesitte arazi kotlarına Siyah Kot, siyah kotların birleştirilmesi ile elde edilen çizgiye de Siyah Çizgi
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
elektromagnetik uzunluk ölçerlerin Iaboratu ar koşullarında kaiibrasyonu
 elektromagnetik uzunluk ölçerlerin Iaboratu ar koşullarında kaiibrasyonu ÖZET Yük. Müh. Uğur DOĞAN -Yük. Müh Özgür GÖR Müh. Aysel ÖZÇEKER Bu çalışmada Yıldız Teknik Üniversitesi İnşaat Fakültesi Jeodezi
elektromagnetik uzunluk ölçerlerin Iaboratu ar koşullarında kaiibrasyonu ÖZET Yük. Müh. Uğur DOĞAN -Yük. Müh Özgür GÖR Müh. Aysel ÖZÇEKER Bu çalışmada Yıldız Teknik Üniversitesi İnşaat Fakültesi Jeodezi
Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1: [2]
![Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1: [2] Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1: [2]](/thumbs/56/37903003.jpg) Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1:4.500.000 [2] 2 25 Şekil 2.23: Orta Akdeniz (İtalya, Adriyatik Denizi, Kuzey Afrika Kıyıları). Ölçek ~ 1:4.500.000 [2] 2 26 Şekil 2.24:
Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1:4.500.000 [2] 2 25 Şekil 2.23: Orta Akdeniz (İtalya, Adriyatik Denizi, Kuzey Afrika Kıyıları). Ölçek ~ 1:4.500.000 [2] 2 26 Şekil 2.24:
Ölçme Bilgisi. Dr. Hasan ÖZ. SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr
 Ölçme Bilgisi Dr. Hasan ÖZ SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr 1 Ölçme Bilgisi; yeryüzünün küçük ya da büyük parçalarının şekil ve büyüklüklerinin ölçülmesi ve elde
Ölçme Bilgisi Dr. Hasan ÖZ SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr 1 Ölçme Bilgisi; yeryüzünün küçük ya da büyük parçalarının şekil ve büyüklüklerinin ölçülmesi ve elde
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI
 ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 2018 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 2018 1.ELEKTRONİK TAKEOMETRELERİN
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
ORMAN YOL AĞI VE TRANSPORT İLİŞKİLERİ Amaç Bu çalışmanın amacı; harita üzerinde bir ormanlık alanın orman yol ağı planlamasının yapılmasıdır.
 ORMAN YOL AĞI VE TRANSPORT İLİŞKİLERİ Amaç Bu çalışmanın amacı; harita üzerinde bir ormanlık alanın orman yol ağı planlamasının yapılmasıdır. Bu çalışmada kullanılacak haritalar, 1/25 000 ölçekli, eş yükselti
ORMAN YOL AĞI VE TRANSPORT İLİŞKİLERİ Amaç Bu çalışmanın amacı; harita üzerinde bir ormanlık alanın orman yol ağı planlamasının yapılmasıdır. Bu çalışmada kullanılacak haritalar, 1/25 000 ölçekli, eş yükselti
2013 YILI SAYISAL HALİHAZIR HARİTA BİRİM FİYATLARI
 İLLER BANKASI ANONİM ŞİRKETİ İHALE DAİRESİ BAŞKANLIĞI 2013 YILI SAYISAL HALİHAZIR HARİTA BİRİM FİYATLARI İLLER BANKASI ANONİM ŞİRKETİ ANKARA - 2013 AÇIKLAMALAR : 1- Bu birim fiyatların kullanıldığı hesaplardaki
İLLER BANKASI ANONİM ŞİRKETİ İHALE DAİRESİ BAŞKANLIĞI 2013 YILI SAYISAL HALİHAZIR HARİTA BİRİM FİYATLARI İLLER BANKASI ANONİM ŞİRKETİ ANKARA - 2013 AÇIKLAMALAR : 1- Bu birim fiyatların kullanıldığı hesaplardaki
ULAŞIM YOLLARINA İLİŞKİN TANIMLAR 1. GEÇKİ( GÜZERGAH) Karayolu, demiryolu gibi ulaşım yollarının yuvarlanma yüzeylerinin ortasından geçtiği
 ULAŞIM YOLLARINA İLİŞKİN TANIMLAR 1. GEÇKİ( GÜZERGAH) Karayolu, demiryolu gibi ulaşım yollarının yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgilerinin topoğrafik harita ya da arazi üzerindeki
ULAŞIM YOLLARINA İLİŞKİN TANIMLAR 1. GEÇKİ( GÜZERGAH) Karayolu, demiryolu gibi ulaşım yollarının yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgilerinin topoğrafik harita ya da arazi üzerindeki
3. Alım için sıklaştırma noktaları (tamamlayıcı nokta, ara ve dizi nirengi),
 ÖLÇME BİLGİSİ 2 DERS NOTLARI YER KONTROL NOKTALARI Genel Bilgi Bir alanın ve üzerindeki örtülerin harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değerleri belli bir takım
ÖLÇME BİLGİSİ 2 DERS NOTLARI YER KONTROL NOKTALARI Genel Bilgi Bir alanın ve üzerindeki örtülerin harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değerleri belli bir takım
HARİTA BİLGİSİ. Produced by M. EKER 1
 HARİTA BİLGİSİ Produced by M. EKER 1 ÖLÇÜ BİRİMLERİ Uzunluk, Alan ve AçıA Ölçü Birimleri Herhangi bir objenin ölçülmesinden, aynı nitelikteki objeden birim olarak belirlenen bir büyüklükle kle kıyaslanmask
HARİTA BİLGİSİ Produced by M. EKER 1 ÖLÇÜ BİRİMLERİ Uzunluk, Alan ve AçıA Ölçü Birimleri Herhangi bir objenin ölçülmesinden, aynı nitelikteki objeden birim olarak belirlenen bir büyüklükle kle kıyaslanmask
TAKEOMETRİ GENEL BİLGİLER
 TAKEOMETRİ GENEL BİLGİLER Optik olarak yatay uzunlukların ve yükseklik farklarının klasik teodolit ve mira kullanılarak bulunması yöntemine takeometri adı verilmektedir. Takeometrik yöntemde amaç, bir
TAKEOMETRİ GENEL BİLGİLER Optik olarak yatay uzunlukların ve yükseklik farklarının klasik teodolit ve mira kullanılarak bulunması yöntemine takeometri adı verilmektedir. Takeometrik yöntemde amaç, bir
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI
 ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 016 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 016 1.ELEKTRONİK TAKEOMETRELERİN
ARAZIDE NOKTALARIN ISARETLENMESI- ARAZI ISLERI
 ARAZIDE NOKTALARIN ISARETLENMESI- ARAZI ISLERI Arazide açi ve uzunluk ölçmelerinin yapilabilmesi için noktalara ve bu noktalarla belirlenen dogrulara gereksinim vardir. Noktalar görünebilir olmali ve arandiklarinda
ARAZIDE NOKTALARIN ISARETLENMESI- ARAZI ISLERI Arazide açi ve uzunluk ölçmelerinin yapilabilmesi için noktalara ve bu noktalarla belirlenen dogrulara gereksinim vardir. Noktalar görünebilir olmali ve arandiklarinda
HARİTA BİLGİSİ ETKİNLİK
 HARİTA Dünya nın tamamının veya bir bölümünün kuş bakışı, küçültülerek bir düzleme aktarılmasıdır. kuşbakışı PLAN... Bir çizimin harita olabilmesi için... KROKİ... PROJEKSİYONLAR: Dünya nın şeklinin geoit
HARİTA Dünya nın tamamının veya bir bölümünün kuş bakışı, küçültülerek bir düzleme aktarılmasıdır. kuşbakışı PLAN... Bir çizimin harita olabilmesi için... KROKİ... PROJEKSİYONLAR: Dünya nın şeklinin geoit
PROJE RAPORU. - Prof. Dr. İrfan ŞİAP - Doç. Dr. Ünal UFUKTEPE
 TÜBİTAK-BİDEB Y.İ.B.O. ÖĞRETMENLERİ(FEN ve TEKNOLOJİ, FİZİK, KİMYA, BİYOLOJİ ve MATEMATİK) PROJE DANIŞMANLIĞI EĞİTİMİ ÇALIŞTAY PROGRAMI 2009-2 PROJE RAPORU PROJENİN ADI: Uzunluk Ölçümlerinde Farklı Bir
TÜBİTAK-BİDEB Y.İ.B.O. ÖĞRETMENLERİ(FEN ve TEKNOLOJİ, FİZİK, KİMYA, BİYOLOJİ ve MATEMATİK) PROJE DANIŞMANLIĞI EĞİTİMİ ÇALIŞTAY PROGRAMI 2009-2 PROJE RAPORU PROJENİN ADI: Uzunluk Ölçümlerinde Farklı Bir
Ölçme Bilgisi DERS 7-8. Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri. Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ )
 Ölçme Bilgisi DERS 7-8 Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için
Ölçme Bilgisi DERS 7-8 Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için
MALZEME ANA BİLİM DALI Malzeme Laboratuvarı Deney Föyü. Deneyin Adı: Malzemelerde Sertlik Deneyi. Deneyin Tarihi:
 Deneyin Adı: Malzemelerde Sertlik Deneyi Deneyin Tarihi:13.03.2014 Deneyin Amacı: Malzemelerin sertliğinin ölçülmesi ve mukavemetleri hakkında bilgi edinilmesi. Teorik Bilgi Sertlik, malzemelerin plastik
Deneyin Adı: Malzemelerde Sertlik Deneyi Deneyin Tarihi:13.03.2014 Deneyin Amacı: Malzemelerin sertliğinin ölçülmesi ve mukavemetleri hakkında bilgi edinilmesi. Teorik Bilgi Sertlik, malzemelerin plastik
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON
 JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
SAKARYA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ ULAŞTIRMA ÇALIŞMA GRUBU 2015-2016 EĞİTİM-ÖĞRETİM DÖNEMİ KARAYOLU MÜHENDİSLİĞİ
 SAKARYA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ ULAŞTIRMA ÇALIŞMA GRUBU 2015-2016 EĞİTİM-ÖĞRETİM DÖNEMİ KARAYOLU MÜHENDİSLİĞİ YOL PROJESİ TASARIM KİTAPÇIĞI PROJE 1. Projenin Tanımı ve İstenenler
SAKARYA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ ULAŞTIRMA ÇALIŞMA GRUBU 2015-2016 EĞİTİM-ÖĞRETİM DÖNEMİ KARAYOLU MÜHENDİSLİĞİ YOL PROJESİ TASARIM KİTAPÇIĞI PROJE 1. Projenin Tanımı ve İstenenler
BAĞLI POLİGON BAĞLI POLİGON
 BAĞLI POLİGON BAĞLI POLİGON 1 BAĞLI POLİGON BAĞLI POLİGON 2 BAĞLI POLİGON BAĞLI POLİGON 6 3 TRİGONOMETRİK NİVELMAN 7 H B - H A = Δh AB = S AB * cotz AB + a t H B = H A + S AB * cotz AB + a - t TRİGONOMETRİK
BAĞLI POLİGON BAĞLI POLİGON 1 BAĞLI POLİGON BAĞLI POLİGON 2 BAĞLI POLİGON BAĞLI POLİGON 6 3 TRİGONOMETRİK NİVELMAN 7 H B - H A = Δh AB = S AB * cotz AB + a t H B = H A + S AB * cotz AB + a - t TRİGONOMETRİK
Hakan AKÇIN* SUNU Ali ihsan ŞEKERTEKİN
 AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ
 YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ Yrd.Doc.Dr. Hüseyin İNCE ÖZET Yol projelerinde yatay kurpta enkesitler arasında yapılacak kübaj hesabında, kurbun eğrilik durumu
YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ Yrd.Doc.Dr. Hüseyin İNCE ÖZET Yol projelerinde yatay kurpta enkesitler arasında yapılacak kübaj hesabında, kurbun eğrilik durumu
İÇİNDEKİLER BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ
 İÇİNDEKİLER II Sayfa No: ÖNSÖZ...I İÇİNDEKİLER...III ŞEKİLLER LİSTESİ...VIII ÇİZELGELER LİSTESİ...XII EKLER LİSTESİ...XIII BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ 1. ÖLÇME TEKNİĞİ VE HARİTA ALMA
İÇİNDEKİLER II Sayfa No: ÖNSÖZ...I İÇİNDEKİLER...III ŞEKİLLER LİSTESİ...VIII ÇİZELGELER LİSTESİ...XII EKLER LİSTESİ...XIII BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ 1. ÖLÇME TEKNİĞİ VE HARİTA ALMA
İÇİNDEKİLER. Çizelgelerin ele alınışı. Uygulamalı Örnekler. Birim metre dikiş başına standart-elektrod miktarının hesabı için çizelgeler
 ELEKTROD SARFİYAT ÇİZELGELERİ İÇİNDEKİLER Kısım A Genel bilgiler Kısım B Çizelgelerin ele alınışı Kısım C Uygulamalı Örnekler Kısım D Birim metre dikiş başına standart-elektrod miktarının hesabı için çizelgeler
ELEKTROD SARFİYAT ÇİZELGELERİ İÇİNDEKİLER Kısım A Genel bilgiler Kısım B Çizelgelerin ele alınışı Kısım C Uygulamalı Örnekler Kısım D Birim metre dikiş başına standart-elektrod miktarının hesabı için çizelgeler
Yükseklik Ölçme (Nivelman) Prof.Dr.Mustafa KARAŞAHİN
 Yükseklik Ölçme (Nivelman) Prof.Dr.Mustafa KARAŞAHİN Yükseklik Ölçümü Arazide, yerleri belli olan noktaların deviz seviyesine göre yüksekliklerinin belirlenmesi işlemidir. Noktalar arasındaki yükseklik
Yükseklik Ölçme (Nivelman) Prof.Dr.Mustafa KARAŞAHİN Yükseklik Ölçümü Arazide, yerleri belli olan noktaların deviz seviyesine göre yüksekliklerinin belirlenmesi işlemidir. Noktalar arasındaki yükseklik
ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ. Doç. Dr. Alper Serdar ANLI. 8. Hafta
 ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ Doç. Dr. Alper Serdar ANLI 8. Hafta DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ Noktaların yükseklikleri düşey ölçmelerle belirlenir.
ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ Doç. Dr. Alper Serdar ANLI 8. Hafta DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ Noktaların yükseklikleri düşey ölçmelerle belirlenir.
PDF created with FinePrint pdffactory trial version Düşey mesafelerin (Yüksekliklerin) Ölçülmesi
 Düşey mesafelerin (Yüksekliklerin) Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen deniz
Düşey mesafelerin (Yüksekliklerin) Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen deniz
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
Yatay Kontrol Noktaları
 Yatay Kontrol Noktaları Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değeri belli olan noktalara ihtiyaç vardır. Bu noktalara yatay
Yatay Kontrol Noktaları Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değeri belli olan noktalara ihtiyaç vardır. Bu noktalara yatay
HARİTA TAPU KADASTRO ALANI ÖĞRETMENLERİMİZ
 ÖĞRETMENLERİMİZ Zekai ERDEN Oğuz KAÇKAR Kudret KAÇMAZ Ercan ŞENGÖR Rıdvan CİVAN Sinan ALKAN Aydın UĞUR Bekir BULUT Çile KAÇKAR Gökhan HASGÜL İdris KUŞDEMİR Rıdvan USLU DALLARI HARİTA DALI Harita mühendisinin
ÖĞRETMENLERİMİZ Zekai ERDEN Oğuz KAÇKAR Kudret KAÇMAZ Ercan ŞENGÖR Rıdvan CİVAN Sinan ALKAN Aydın UĞUR Bekir BULUT Çile KAÇKAR Gökhan HASGÜL İdris KUŞDEMİR Rıdvan USLU DALLARI HARİTA DALI Harita mühendisinin
İÇİNDEKİLER BİRİNCİ BÖLÜM... 1 Genel Hükümler... 1 Amaç... 1 Kapsam... 1 Dayanak... 1 Tanımı... 1 İKİNCİ BÖLÜM...
 İÇİNDEKİLER BİRİNCİ BÖLÜM... 1 Genel Hükümler... 1 Amaç... 1 Kapsam... 1 Dayanak... 1 Tanımı... 1 İKİNCİ BÖLÜM... 2 Fen Adamlarının Gruplandırılması... 2 ÜÇÜNCÜ BÖLÜM... 4 Fen Adamlarının Yetki ve... 4
İÇİNDEKİLER BİRİNCİ BÖLÜM... 1 Genel Hükümler... 1 Amaç... 1 Kapsam... 1 Dayanak... 1 Tanımı... 1 İKİNCİ BÖLÜM... 2 Fen Adamlarının Gruplandırılması... 2 ÜÇÜNCÜ BÖLÜM... 4 Fen Adamlarının Yetki ve... 4
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI
 ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3350)
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3350 3 4 3 0 0 DERSİN
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3350 3 4 3 0 0 DERSİN
ULAŞIM YOLLARINA AİT TANIMLAR
 ULAŞIM YOLLARINA AİT TANIMLAR Geçki: Karayolu, demiryolu gibi ulaştıma yapılarının, yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgisinin harita ya da arazideki izdüşümüdür. Topografik
ULAŞIM YOLLARINA AİT TANIMLAR Geçki: Karayolu, demiryolu gibi ulaştıma yapılarının, yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgisinin harita ya da arazideki izdüşümüdür. Topografik
SATIŞI ÜNiTE ÎLE YAPILAN BAZI MADENLERİN HAKKINDA PRATİK METOD
 SATIŞI ÜNiTE ÎLE YAPILAN BAZI MADENLERİN HAKKINDA PRATİK METOD İKTİSADİLİĞİ Hüsnü KALE. Maden Tetkik ve Arama Enstitüsü, Ankara GİRİŞ Arazi çalışmaları esnasında raslanan ve büyük rezervi olmıyan birçok
SATIŞI ÜNiTE ÎLE YAPILAN BAZI MADENLERİN HAKKINDA PRATİK METOD İKTİSADİLİĞİ Hüsnü KALE. Maden Tetkik ve Arama Enstitüsü, Ankara GİRİŞ Arazi çalışmaları esnasında raslanan ve büyük rezervi olmıyan birçok
ÖLÇME BİLGİSİ. Sunu 1- Yatay Ölçme. Yrd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin YURTSEVEN
 ÖÇME BİGİİ unu - atay Ölçme rd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin URTEVEN COĞRAFİ BİGİ İTEMİNİ OUŞTURABİMEK İÇİN BİGİ TOPAMA ÖNTEMERİ ATA ÖÇMEER (,) ATA AÇIAR VE MEAFEERİN ÖÇÜMEİ ERE ÖÇMEER DÜŞE
ÖÇME BİGİİ unu - atay Ölçme rd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin URTEVEN COĞRAFİ BİGİ İTEMİNİ OUŞTURABİMEK İÇİN BİGİ TOPAMA ÖNTEMERİ ATA ÖÇMEER (,) ATA AÇIAR VE MEAFEERİN ÖÇÜMEİ ERE ÖÇMEER DÜŞE
Öğrenci : İrem DAŞTAN
 BEP Plan Hazırla T.C Yozgat Valiliği Kanuni Sultan Süleyman Özel Eğitim / İlkokul/ Ortaokulu Mesleki Eğitim Merkezi Müdürlüğü Matematik Dersi Bireyselleştirilmiş Eğitim Planı Öğrenci : İrem DAŞTAN Eğitsel
BEP Plan Hazırla T.C Yozgat Valiliği Kanuni Sultan Süleyman Özel Eğitim / İlkokul/ Ortaokulu Mesleki Eğitim Merkezi Müdürlüğü Matematik Dersi Bireyselleştirilmiş Eğitim Planı Öğrenci : İrem DAŞTAN Eğitsel
2 Hata Hesabı. Hata Nedir? Mutlak Hata. Bağıl Hata
 Hata Hesabı Hata Nedir? Herhangi bir fiziksel büyüklüğün ölçülen değeri ile gerçek değeri arasındaki farka hata denir. Ölçülen bir fiziksel büyüklüğün sayısal değeri, yapılan deneysel hatalardan dolayı
Hata Hesabı Hata Nedir? Herhangi bir fiziksel büyüklüğün ölçülen değeri ile gerçek değeri arasındaki farka hata denir. Ölçülen bir fiziksel büyüklüğün sayısal değeri, yapılan deneysel hatalardan dolayı
koşullar nelerdir? sağlamaktadır? 2. Harita ile kroki arasındaki fark nedir?
 1. Bir çizimin harita özelliği taşıması için gerekli koşullar nelerdir? 2. Harita ile kroki arasındaki fark nedir? 3. Haritalar günlük hayatımızda ne gibi kolaylıklar sağlamaktadır? 4. Haritalar hangi
1. Bir çizimin harita özelliği taşıması için gerekli koşullar nelerdir? 2. Harita ile kroki arasındaki fark nedir? 3. Haritalar günlük hayatımızda ne gibi kolaylıklar sağlamaktadır? 4. Haritalar hangi
JEOMORFOLOG TANIM. Günümüzdeki yer şekillerinden elde edilen verilere dayanarak, geçmişteki yer şekillerinin gelecekteki durumunu açıklayan kişidir.
 TANIM Günümüzdeki yer şekillerinden elde edilen verilere dayanarak, geçmişteki yer şekillerinin gelecekteki durumunu açıklayan kişidir. A- GÖREVLER KULLANILAN ARAÇ, GEREÇ VE EKİPMAN Jeomorfologların görevleri
TANIM Günümüzdeki yer şekillerinden elde edilen verilere dayanarak, geçmişteki yer şekillerinin gelecekteki durumunu açıklayan kişidir. A- GÖREVLER KULLANILAN ARAÇ, GEREÇ VE EKİPMAN Jeomorfologların görevleri
ELEKTRO-OPTİK UZUNLUK ÖLÇMELERİNDE DÜZELTMELER VE İNDİRGEMELER
 ELEKTRO-OPTİK UZUNLUK ÖLÇMELERİNDE DÜZELTMELER VE İNDİRGEMELER *ErdalKOÇAK Summary Medium and short range distances are generally measured hy electro-opîical method insurvey sîudies. The aîmospheric correctioııs
ELEKTRO-OPTİK UZUNLUK ÖLÇMELERİNDE DÜZELTMELER VE İNDİRGEMELER *ErdalKOÇAK Summary Medium and short range distances are generally measured hy electro-opîical method insurvey sîudies. The aîmospheric correctioııs
Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik
 Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik 1. Ünite: Geometriden Olasılığa 1. Bölüm: Yansıyan ve Dönen Şekiller, Fraktallar Yansıma, Öteleme, Dönme Fraktallar 2. Bölüm: Üslü Sayılar Tam
Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik 1. Ünite: Geometriden Olasılığa 1. Bölüm: Yansıyan ve Dönen Şekiller, Fraktallar Yansıma, Öteleme, Dönme Fraktallar 2. Bölüm: Üslü Sayılar Tam
MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl
 İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
Kısa Dönemli Amaç Davranışlar Araç Gereçler
 BEP Plan Hazırla T.C Yozgat Valiliği Kanuni Sultan Süleyman Özel Eğitim / İlkokul/ Ortaokulu Mesleki Eğitim Merkezi Müdürlüğü Matematik Dersi Bireyselleştirilmiş Eğitim Planı Öğrenci : Gazi KILIÇ Eğitsel
BEP Plan Hazırla T.C Yozgat Valiliği Kanuni Sultan Süleyman Özel Eğitim / İlkokul/ Ortaokulu Mesleki Eğitim Merkezi Müdürlüğü Matematik Dersi Bireyselleştirilmiş Eğitim Planı Öğrenci : Gazi KILIÇ Eğitsel
KOORDİNATLANDÎRILMIŞ FOTOGRAMETRİK MODELDEN HACİM HESABI
 KOORDİNATLANDÎRILMIŞ FOTOGRAMETRİK MODELDEN HACİM HESABI Dr. Yıhnoz ERKANLI Batı Almanya 1. Genel Yöntem Koordinatlandırılmış fotograrnetrik model kavramı arazi şeklînfn koordinatlarla belirlenmesinde
KOORDİNATLANDÎRILMIŞ FOTOGRAMETRİK MODELDEN HACİM HESABI Dr. Yıhnoz ERKANLI Batı Almanya 1. Genel Yöntem Koordinatlandırılmış fotograrnetrik model kavramı arazi şeklînfn koordinatlarla belirlenmesinde
Doğru ve eğri şeklinde, kesik veya sürekli herhangi bir şekildeki bir başlangıç noktasını bir bitiş (son)
 Çizgiler Çizgi Tipleri ve Uygulamaları Doğru ve eğri şeklinde, kesik veya sürekli herhangi bir şekildeki bir başlangıç noktasını bir bitiş (son) noktası ile birleştiren, uzunluğu ise genişliğinin yarısından
Çizgiler Çizgi Tipleri ve Uygulamaları Doğru ve eğri şeklinde, kesik veya sürekli herhangi bir şekildeki bir başlangıç noktasını bir bitiş (son) noktası ile birleştiren, uzunluğu ise genişliğinin yarısından
PROJE AŞAMALARI : Karayolu Geçkisi (Güzergahı Araştırması, Plan ve Boykesit):
 Bartın Üniversitesi Ad Soyad : Mühendislik Fakültesi Numara : İnşaat Mühendisliği Bölümü Pafta No : KONU : INS36 ULAŞTIRMA II (PROJE) DERSİ P R O J E V E R İ L E R İ /2000 ölçekli tesviye (eşyükselti)
Bartın Üniversitesi Ad Soyad : Mühendislik Fakültesi Numara : İnşaat Mühendisliği Bölümü Pafta No : KONU : INS36 ULAŞTIRMA II (PROJE) DERSİ P R O J E V E R İ L E R İ /2000 ölçekli tesviye (eşyükselti)
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Hataları Ölçme Hatası Herhangi bir ölçme aleti ile yapılan ölçüm sonucu bulunan değer yaklaşık değerdir. Bir büyüklük aynı ölçme
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Hataları Ölçme Hatası Herhangi bir ölçme aleti ile yapılan ölçüm sonucu bulunan değer yaklaşık değerdir. Bir büyüklük aynı ölçme
İNŞAAT MÜHENDİSLİĞİNE GİRİŞ
 İNŞAAT MÜHENDİSLİĞİNE GİRİŞ GİRİŞ Prof.Dr. Zekai Celep İnşaat Mühendisliğine Giriş GİRİŞ 1. Dersin amacı ve kapsamı 2. Askeri mühendislik ve sivil mühendislik 3. Yurdumuzda inşaat mühendisliği 4. İnşaat
İNŞAAT MÜHENDİSLİĞİNE GİRİŞ GİRİŞ Prof.Dr. Zekai Celep İnşaat Mühendisliğine Giriş GİRİŞ 1. Dersin amacı ve kapsamı 2. Askeri mühendislik ve sivil mühendislik 3. Yurdumuzda inşaat mühendisliği 4. İnşaat
ÇATI MAKASINA GELEN YÜKLER
 ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
2016 Yılı Buharlaşma Değerlendirmesi
 2016 Yılı Buharlaşma Değerlendirmesi GİRİŞ Tabiatta suyun hidrolojik çevriminin önemli bir unsurunu teşkil eden buharlaşma, yeryüzünde sıvı ve katı halde değişik şekil ve şartlarda bulunan suyun meteorolojik
2016 Yılı Buharlaşma Değerlendirmesi GİRİŞ Tabiatta suyun hidrolojik çevriminin önemli bir unsurunu teşkil eden buharlaşma, yeryüzünde sıvı ve katı halde değişik şekil ve şartlarda bulunan suyun meteorolojik
M. MARANGOZ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ
 ÖLÇME BİLGİSİ II Poligon İstikşafı ve Yerüstü Tesisleri, Poligon Ölçüsü ve Türleri Yrd. Doç. Dr. Aycan M. MARANGOZ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF120 ÖLÇME BİLGİSİ II DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz
ÖLÇME BİLGİSİ II Poligon İstikşafı ve Yerüstü Tesisleri, Poligon Ölçüsü ve Türleri Yrd. Doç. Dr. Aycan M. MARANGOZ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF120 ÖLÇME BİLGİSİ II DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz
SAYISAL ÇÖZÜMLEME. Yrd.Doç.Dr.Esra Tunç Görmüş. 1.Hafta
 SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
Öğretim Üyesi. Topoğrafya İnşaat Mühendisliği
 Öğretim Üyesi Mehmet Zeki COŞKUN Y. Doç. Dr. İnşaat Fak., Jeodezi ve Fotogrametri Müh. Ölçme Tekniği Anabilim Dalı (212) 285-6573 coskunmeh@itu.edu.tr http://atlas.cc.itu.edu.tr/~coskun Adres Öğrenci görüşme
Öğretim Üyesi Mehmet Zeki COŞKUN Y. Doç. Dr. İnşaat Fak., Jeodezi ve Fotogrametri Müh. Ölçme Tekniği Anabilim Dalı (212) 285-6573 coskunmeh@itu.edu.tr http://atlas.cc.itu.edu.tr/~coskun Adres Öğrenci görüşme
BİREYSELLEŞTİRİLMİŞ MATEMATİK DERSİ EĞİTİM PLANI
 BİREYSELLEŞTİRİLMİŞ MATEMATİK DERSİ EĞİTİM PLANI BEP Hazırlanan Öğrencinin Var Olan Performans Düzeyinin Belirlenmesi Performans Performans düzeyi alanları Akademik beceriler MATEMATİK MATEMATİK - Varlıkları
BİREYSELLEŞTİRİLMİŞ MATEMATİK DERSİ EĞİTİM PLANI BEP Hazırlanan Öğrencinin Var Olan Performans Düzeyinin Belirlenmesi Performans Performans düzeyi alanları Akademik beceriler MATEMATİK MATEMATİK - Varlıkları
Dünya nın şekli. Küre?
 Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
i/leşlerimizle İlgili l\nrıimmn tanıtıyoruz r-^-r-^ ÖL : O J İLLER BANKASI HARİTA DAtEESl REİSLİC!
 i/leşlerimizle İlgili l\nrıimmn tanıtıyoruz r-^-r-^ ÖL : O J İLLER BANKASI HARİTA DAtEESl REİSLİC! s KISA TARİHÇESİ : İlhan Kaya DUMAN Ankara 1933 yılında «Belediyeler Bankası» adıyla kurulan İLLER BANKASI
i/leşlerimizle İlgili l\nrıimmn tanıtıyoruz r-^-r-^ ÖL : O J İLLER BANKASI HARİTA DAtEESl REİSLİC! s KISA TARİHÇESİ : İlhan Kaya DUMAN Ankara 1933 yılında «Belediyeler Bankası» adıyla kurulan İLLER BANKASI
BİTKİ SU TÜKETİMİ 1. Bitkinin Su İhtiyacı
 BİTKİ SU TÜKETİMİ 1. Bitkinin Su İhtiyacı Bitki, yapraklarından sürekli su kaybeder; bünyesindeki su oranını belirli seviyede tutabilmesi için kaybettiği kadar suyu kökleri vasıtasıyıla topraktan almak
BİTKİ SU TÜKETİMİ 1. Bitkinin Su İhtiyacı Bitki, yapraklarından sürekli su kaybeder; bünyesindeki su oranını belirli seviyede tutabilmesi için kaybettiği kadar suyu kökleri vasıtasıyıla topraktan almak
Yapılma Yöntemleri: » Arazi ölçmeleri (Takeometri)» Hava fotoğrafları (Fotoğrametri) TOPOĞRAFİK KONTURLAR
 TOPOĞRAFİK HARİTALAR EŞ YÜKSELTİ EĞRİLERİ TOPOĞRAFİK HARİTALAR Yapılma Yöntemleri:» Arazi ölçmeleri (Takeometri)» Hava fotoğrafları (Fotoğrametri) HARİTALAR ve ENİNE KESİT HARİTALAR Yeryüzü şekillerini
TOPOĞRAFİK HARİTALAR EŞ YÜKSELTİ EĞRİLERİ TOPOĞRAFİK HARİTALAR Yapılma Yöntemleri:» Arazi ölçmeleri (Takeometri)» Hava fotoğrafları (Fotoğrametri) HARİTALAR ve ENİNE KESİT HARİTALAR Yeryüzü şekillerini
İNŞAAT TEKNOLOJİSİ ÖNLİSANS EĞİTİMİNDE HARİTACILIĞIN YERİ. Orhan KURT 1
 İNŞAAT TEKNOLOJİSİ ÖNLİSANS EĞİTİMİNDE HARİTACILIĞIN YERİ Orhan KURT 1 1 Kocaeli Üniversitesi, Mühendislik Fakültesi, Harita Mühendisliği Bölümü, Kocaeli, orhnkrt@gmail.com Özet Bir inşaat teknikeri haritacılık
İNŞAAT TEKNOLOJİSİ ÖNLİSANS EĞİTİMİNDE HARİTACILIĞIN YERİ Orhan KURT 1 1 Kocaeli Üniversitesi, Mühendislik Fakültesi, Harita Mühendisliği Bölümü, Kocaeli, orhnkrt@gmail.com Özet Bir inşaat teknikeri haritacılık
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI
 BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
Bölüm-4. İki Boyutta Hareket
 Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Harita Nedir? Haritaların Sınıflandırılması. Haritayı Oluşturan Unsurlar
 Harita Nedir? Yeryüzünün tamamının veya bir kısmının kuşbakışı görünüşünün belli bir ölçek dahilinde düzleme aktarılmasıyla oluşan çizimlere denir. Haritacılık bilimine kartografya denir. Bir çizimin harita
Harita Nedir? Yeryüzünün tamamının veya bir kısmının kuşbakışı görünüşünün belli bir ölçek dahilinde düzleme aktarılmasıyla oluşan çizimlere denir. Haritacılık bilimine kartografya denir. Bir çizimin harita
