12. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI
|
|
|
- Iskender Karakaş
- 8 yıl önce
- İzleme sayısı:
Transkript
1 12. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Progrmın öğrencilerde geliştirmeyi hedeflediği becerilerle 12. sınıf mtemtik öğretim progrmı ilişkisi Modelleme/Problem çözme Mtemtiksel Süreç Becerileri Akıl Yürütme Mtemtiksel İletişim İlişkilendirme Bilgi ve İletişim Teknolojileri Türev ve integrli modellemede ve problem çözmede kullnm Sentetik, nlitik ve vektörel yklşımlrı geometri problemlerinin çözümünde kullnm Türev ve integrlin ship olduğu özelliklere ilişkin çıkrımlrd bulunm Uzyd doğru ve düzlemleri inceleyerek uzmsl becerilerini geliştirme Türeve, integrle, vektöre, koniklere, uzy geometriye ve sırlmy özgü terim ve sembolleri mtemtiksel düşünceleri ifde etmede kullnm Değişim ornı ile türevi, ln ile integrli, integrl ile türevi ilişkilendirme Anlitik, sentetik ve vektörel yklşımlr rsındki ilişkileri görme Teorik olsılık ile deneysel olsılık rsındki ilişkiyi nlmlndırm Fonksiyonlrın tblo, grfik, cebirsel gösterimleri yrdımıyl limit ve süreklilik uygulmlrı gerçekleştirme Bir fonksiyonun grfiği üzerinde bükeylik ve dönüm noktlrını ve bu noktlrın özelliklerini inceleme Fonksiyonun grfiğiyle x-ekseni rsınd kln sınırlı lnı Riemnn toplmı yrdımıyl belirleme Fonksiyon grfiğini türev yrdımı ile çizme Konikleri oluşturm Uzyd doğru ve düzlemler rsındki ilişkileri belirleme mcıyl bilgi ve iletişim teknolojilerinden yrrlnm 12. sınıft yer ln öğrenme lnlrı rcılığı ile öğrencilerin şğıdki kznımlr ulşmlrı beklenmektedir: Syılr ve Cebir Türev kvrmını değişim ornı ile çıklm, limiti türevi nlmd bir rç olrk kullnm, türevin geometrik yorumu ile mksimum minimum problemlerini ilişkilendirme, türevi kullnrk fonksiyonlrın grfiklerini çizme Belirli integrli, eğri ltınd kln ln ile ilişkilendirme ve uygulmlr ypm, türevle integrl rsınd ilişki kurm ve belirsiz integrl hesplmlrı ypm Geometri Yrıçpı ve merkezi verilen çemberin denklemini elde etme ve ulşıln denklemi kullnrk çemberi inceleme Odklrı verilen hiperbol ve elipsin, doğrultmnı ve odğı verilen prbolün denklemlerini oluşturm Koordint düzleminde doğrulrın vektörel denklemlerini oluşturm ve geometride sentetik, nlitik ve vektörel yklşımlrı uygun durumlrd kullnm Uzyd doğru ve düzlemlerin birbirine göre durumlrını inceleme Dikdörtgenler prizmsı üzerinde uzunluk, çı ve ln hesplmlrı ypm Veri, Sym ve Olsılık Nesnelerin seçilme ve sırlnm syılrı ile ilgili problemleri çözme Olsılık hesbı konusund kıcılık kznm ve teorik olrk hesplnbilen olsılık değerlerinin prtikte ne nlm geleceğini kvrm 43
2 Öğrenme Alnlrı, Üniteler ve Zmn Dğılımı: Bir kznımın işleniş süresi bşt öğrencilerin seviyesi olmk üzere birçok değişkene bğlıdır. Bu nedenle progrmdki kznımlr yönelik şğıd verilen işleniş süreleri kesin olmyıp yklşık olrk verilmiştir. No 12. SINIF İLERİ DÜZEY Ünite/Konulr Kznım Syısı Ders Sti Ağırlık (%) SAYILAR ve CEBİR İD TÜREV İD Limit ve Süreklilik İD Türev İD Türevin Uygulmlrı İD İNTEGRAL İD Belirli ve Belirsiz İntegrl İD Belirli İntegrlin Uygulmlrı GEOMETRİ İD ANALİTİK GEOMETRİ İD Çemberin Anlitik İncelenmesi İD Elips, Hiperbol ve Prbolün Anlitik İncelenmesi İD VEKTÖRLER İD Stndrt Birim Vektörler ve İç Çrpım İD Bir Doğrunun Vektörel Denklemi İD Vektörlerle ilgili Uygulmlr VERİ, SAYMA ve OLASILIK İD SAYMA İD Tekrrlı Permütsyon İD Dönel (Diresel) Permütsyon İD OLASILIK İD Deneysel ve Teorik Olsılık GEOMETRİ İD UZAY GEOMETRİ İD Uzyd Doğru ve Düzlem İD Ktı Cisimler Toplm
3 SAYILAR ve CEBİR İD Türev İD Limit ve Süreklilik Terimler: Bir noktd limit, sğdn limit, soldn limit, süreklilik Sembol ve Gösterimler: lim f(x), lim f(x), lim f(x) + - x " x " x " İD Bir fonksiyonun bir noktdki limiti, soldn limiti ve sğdn limiti kvrmlrını tblo ve grfik kullnrk örneklerle çıklr. [R] Limit kvrmı bir bğımsız değişkenin verilen bir syıy yklşmsındn yol çıkılrk çıklnır. [R] Limit lm işlemi şğıdki durumlrl sınırlndırılır: c! R için lim x " c = c lim x =, lim x = 2 2 x" x" lim 1 3 x = -, lim 1 x " 0 - x " 0 x = x! R için lim - x " x = 2 - lim sin x x = 1 x" 0 lim 2 x - 1 x 2 x " 3 = [R] Bilgi ve iletişim teknolojilerinden yrrlnrk fonksiyonlrın tblo ve grfik gösterimleri yrdımıyl limit uygulmlrı yptırılır. İD Bir fonksiyonun bir noktdki sürekliliği kvrmını çıklr. [R] Fonksiyonun sürekliliği nck tnım kümesindeki noktlrd rştırılır. Örneğin, f(x) = 1/x fonksiyonunun x = 0 noktsındki sürekliliğini trtışmk, x = 0 bu fonksiyonun tnım kümesinde yer lmdığındn nlmsızdır. [R] Fonksiyonun grfiği üzerinde sürekli ve süreksiz olduğu noktlr buldurulur. [R] Bilgi ve iletişim teknolojilerinden yrrlnrk fonksiyonlrın tblo ve grfik gösterimi yrdımıyl süreklilik uygulmlrı yptırılır. 45
4 İD Türev Terimler: Değişim ornı, nlık değişim ornı, türev Sembol ve Gösterimler: f ʹ(x), f ʹʹ (x), dy dx, d2 y dx 2 İD Fizik ve geometri modellerinden yrrlnrk değişim ornı kvrmını çıklr. [R] Anlık değişim ornı kvrmı çıklnrk, nlık değişim ornın türev denildiği belirtilir. [R] Verilen bir fonksiyonun bir noktdki türev değeri ile o noktdki teğetinin eğimi rsındki ilişki incelenir. [R] f(x) = c, f(x) = x 2 fonksiyonlrının türevleri, türev tnımı kullnılrk hespltılır. [R] r!r olmk üzere, f(x) = x r, f(x) = e x, f(x) = :x, f(x) = lnx, f(x) = sinx, f(x) = cosx fonksiyonlrının türevleri kurl olrk verilir. [Q] Ters trigonometrik fonksiyonlrın türevleri verilmez. İD Bir fonksiyonun bir noktd ve bir rlıkt türevli olmsını inceler. [R] Tnım kümesi çıkç belirtilmemiş bir fonksiyonun tnım kümesi olrk, fonksiyonun kurlının geçerli olduğu en geniş küme lınır. [R] Fonksiyonun türevli olmdığı noktlrl grfiği rsınd ilişki kurulur. İD Türevlenebilen iki fonksiyonun toplmının, frkının, çrpımının ve bölümünün türevine it kurllrı çıklr ve bunlrl ilgili uygulmlr ypr. [R] Doğru boyunc hreket eden bir cismin, t zmnı içinde ldığı yol ile t nındki hızı; t nındki hızı ile t nındki ivmesi rsındki ilişki örneklerle incelenir. İD İki fonksiyonun bileşkesinin türevine it kurlı (zincir kurlı) oluşturur ve bunu kullnrk türev hesbı ypr. İD Bir fonksiyonun yüksek mertebeden türevlerini çıklr ve bulur. İD Türevin Uygulmlrı Terimler: Bir fonksiyonun ekstremum noktlrı, dönüm noktsı, bükeylik, simptot, düşey simptot, yty simptot İD Verilen bir fonksiyonun bir noktdki teğet ve normlinin denklemlerini bulur. İD Bir fonksiyonun rtn ve zln olduğu rlıklrı türevinin işretine göre belirler. 46
5 İD Bir fonksiyonun mutlk mksimum ve mutlk minimum, yerel mksimum, yerel minimum noktlrını çıklr ve bir fonksiyonun ekstremum noktlrını türev yrdımıyl belirler. İD Mksimum ve minimum problemlerinin modellenmesi ve çözümünde türevi kullnır. İD Bir fonksiyonun grfiği üzerinde bükeylik ve dönüm noktsı kvrmlrını çıklr. [R] İçbükey ve dışbükey olduğu rlıklr ikinci mertebeden türevin işretiyle ilişkilendirilir, bükeyliğin değiştiği noktlrın dönüm noktsı olduğu belirtilir. [Q] Rolle teoremi ve ortlm değer teoreminden bhsedilmez. İD Fonksiyonlrın grfiğini çizerken türevi kullnır. [R] Asimptot kvrmı çıklnrk sdece düşey simptot ve yty simptot üzerinde durulur. Eğik ve eğri simptotlr girilmez. [R] Grfik çizimleri rsyonel fonksiyonlr ile sınırlı tutulur. İD İntegrl İD Belirli ve Belirsiz İntegrl Terimler: Riemnn toplmı, integrl, integrl sbiti, belirli integrl, belirsiz integrl, kısmi integrsyon, bsit kesirlere yırm yöntemi, integrl hesbın temel teoremi # # Sembol ve Gösterimler: fxdx (), f() xdx b İD Bir fonksiyonun grfiği ile x-ekseni rsınd kln sınırlı bölgenin lnını Riemnn toplmı yrdımıyl thmin eder. [R] Gerçek/gerçekçi hyt durumlrındn hreketle bir fonksiyonun grfiği ile x-ekseni rsınd kln lnın hesplnmsın ihtiyç hissettirilir. [R] Bzı bsit fonksiyonlr (f(x) = x, f(x) = x 2 gibi) için önce fonksiyonun pozitif olduğu rlıklrd Riemnn toplmı yrdımıyl ln thmin edilir, dh sonr fonksiyonun negtif değer ldığı rlıklr için bu yöntem genişletilir. [R] Bir fonksiyonun belirli integrli çıklnır. İD Bir fonksiyonun grfiği ltınd kln lnı veren fonksiyonun türevi ile grfiğin temsil ettiği fonksiyon rsındki ilişkiyi çıklr. [R] Bir fonksiyonun belirsiz integrli çıklnır. 47
6 İD Bir fonksiyonun belirli ve belirsiz integrlleri rsındki ilişkiyi çıklr. b [R] # fxdx () = Fb ()- F () olduğu vurgulnır. İD Bir fonksiyonun bir sbitle çrpımının, iki fonksiyonun toplmının ve frkının belirli integrline it kurllrı oluşturur. [R] Belirli integrlle ilgili şu özellikler verilir: # fxdx () = 0 # # fxdx () = - fxdx () b c b # # # b fxdx () = fxdx () + fxdx () b c İD Belirsiz integrl lm kurllrını türev lm kurllrı yrdımıyl oluşturur. [R] Temel integrl lm kurllrı x n, 1 x, ex, x, cosx, sinx, sec 2 x, csc 2 x fonksiyonlrının integrliyle sınırlndırılır. İD Bir fonksiyonun bir sbitle çrpımının, iki fonksiyonun toplmının ve frkının belirsiz integrline it kurllrı bulur ve bunlrı kullnrk integrl hesbı ypr. İD Belirsiz integrl lm tekniklerini çıklr ve bunlrı kullnrk integrl hesbı ypr. [R] Değişken değiştirme, kısmi integrsyon ve bsit kesirlere yırm teknikleriyle integrl lm uygulmlrı ypılır. [R] Bsit kesirlere yırm tekniği ile integrl lınırken rsyonel fonksiyonlrın integrlleri pydsı lineer çrpnlr yrılbilenlerle sınırlndırılır. İD Belirli İntegrlin Uygulmlrı İD Belirli integrli modellemede ve problem çözmede kullnır. [R] İntegrl ile ln hesbı, doğrusl hreket problemleri vb. durumlr incelenir. [R] İki fonksiyonun grfikleri ve iki düşey doğru rsınd kln sınırlı bölgenin lnının bulunmsı verilir. 48
7 GEOMETRİ İD Anlitik Geometri İD Çemberin Anlitik İncelenmesi Terimler: Merkez, yrıçp, çemberin genel denklemi, çemberin stndrt denklemi, teğet, teğet denklemi, norml, norml denklemi Sembol ve Gösterimler: r, (x ) 2 + (y b) 2 = r 2, x 2 + y 2 + Ax + By + C = 0 İD Merkezi ve yrıçpı verilen çemberin denklemini oluşturur. [R] Çemberin stndrt denklemi yrdımıyl genel denklemi elde edilir: M(, b) merkezli ve r yrıçplı çemberin stndrt denklemi, (x ) 2 + (y b) 2 = r 2 ; genel denklemi x 2 + y 2 + Ax + By + C = 0. İD Denklemleri verilen doğru ile çemberin birbirine göre durumlrını inceler. [R] Doğru ile çemberin vrs kesişim noktlrı bulunur. İD Çember üzerindeki bir noktdn çembere çizilen teğet ve norml denklemlerini oluşturur. İD Elips, Hiperbol ve Prbolün Anlitik İncelenmesi Terimler: Elips, hiperbol, prbol, odk, doğrultmn, sl eksen, yedek eksen, merkez İD Prbol, elips ve hiperbolü tnımlr, stndrt denklemlerini elde eder ve uygulmlr ypr. [R] Prbolün odğı, doğrultmnı, köşesi ve ekseni tnıtılır. [R] Elipsin odklrı, köşeleri, merkezi, sl ekseni ve yedek ekseni tnıtılır. [R] Hiperbolün odklrı, köşeleri, merkezi, sl ve yedek ekseni tnıtılır. İD Vektörler İD Stndrt Birim Vektörler ve İç Çrpım Terimler: Stndrt birim vektör, iki vektörün iç çrpımı, prlel vektörler, dik vektörler izdüşüm, lineer bileşim Sembol ve Gösterimler: e 1, e 2, A#B, A=B, GA, B, (vey A. B), A = (x, y) = x. e 1 + y. e 2 G İD Stndrt birim vektörleri tnımlyrk bir vektörü stndrt birim vektörlerin lineer bileşimi şeklinde yzr. 49
8 İD İki vektörün iç çrpımını çıklr ve iki vektör rsındki çıyı hesplr. [R] İki vektörün iç çrpımı kosinüs teoremi yrdımıyl oluşturulur. [R] İki vektörün prlel ve dik olm durumlrı inceletilir. [R] İç çrpımının özelliklerine yer verilir ve bir vektörün uzunluğu ile iç çrpım iliş kilendirilir. İD Bir vektörün bşk bir vektör üzerine dik izdüşümünü bulur. [R] Vektörler rsındki çının dik, dr vey geniş çı olmsı hllerinde izdüşüm vektörünün yönünün nsıl değiştiği sorgulnır. İD Bir Doğrunun Vektörel Denklemi Terimler: Vektörel denklem, prmetrik denklem, krtezyen denklem x = + m. x Sembol ve Gösterimler: OP = OA + m. 1 V, ) y = b + m. y 1 İD Bir doğrunun vektörel denklemini oluşturur. [R] Bir doğrunun denklemi vektörel olrk gösterilirken şu iki durum incelenir: i) Düzlemde iki noktsı verilen doğrunun denklemi ii) verilen bir vektöre prlel oln ve bir noktdn geçen doğrunun denklemi. [R] Doğru denkleminin vektörel gösterimi ile prmetrik ve krtezyen gösterimleri rsınd ilişki kurdurulur. [R] Bilgi ve iletişim teknolojilerinden yrrlnılbilir. İD Vektörlerle ilgili Uygulmlr İD Vektörel, sentetik ve nlitik yklşımlrı problem çözmede kullnır. 50
9 VERİ, SAYMA ve OLASILIK İD Sym İD Tekrrlı Permütsyon Terimler: Tekrrlı diziliş (permütsyon) İD Sınırlı syıd tekrrlyn nesnelerin dizilişlerini (permütsyonlrını) örneklerle çıklr. [R] En z iki tnesi özdeş oln nesnelerin tüm frklı dizilişlerinin syısı örnekler/ problemler bğlmınd incelenir. Örnek: ANDIRIN kelimesinin hrflerinin yerleri değiştirilerek nlmlı y d nlmsız 7 hrfli kç frklı kelime yzılbilir? İD Dönel (Diresel) Permütsyon Terimler: Dönel (diresel) permütsyon İD Dönel (diresel) permütsyonu örneklerle çıklr. İD Olsılık İD Deneysel ve Teorik Olsılık Terimler: Deneysel olsılık, teorik olsılık İD Deneysel olsılık ile teorik olsılık rsındki ilişkiyi örneklerle çıklr. [R] Simülsyon vb. bilgi ve iletişim teknolojilerinden yrrlnılır. 51
10 GEOMETRİ İD Uzy Geometri İD Uzyd Doğru ve Düzlem Terimler: Temel diklik teoremi, üç dikme teoremi, izdüşüm, uzyd düzlem, uzyd doğru İD Uzyd bir düzlemi belirleyen durumlrı inceler. [R] Bilgi ve iletişim teknolojilerinden yrrlnılbilir. İD Uzyd iki doğru; iki düzlem; bir düzlem ve bir doğrunun birbirlerine göre durumlrını belirler ve uygulmlr ypr. [R] Doğrunun düzleme dik olm durumun vurgu ypılır. [R] Temel diklik teoremine yer verilir. [R] Üç dikme teoremi ile ilgili uygulmlr ypılır. [R] Bilgi ve iletişim teknolojilerinden yrrlnılbilir. İD Uzyd iki düzlem rsındki çıyı belirler. İD Bir şeklin bir düzlem üzerindeki izdüşümünü belirler ve uygulmlr ypr. [R] Uzyd bir doğru ile bir düzlem rsındki çı tnımlnır. [R] Bir doğru prçsının bir düzlem üzerindeki dik izdüşümünün uzunluğu hespltılır. [R] Bir düzlemsel şeklin bir düzlem üzerindeki dik izdüşümünün lnı hespltılır. [R] Aynı düzlemdeki şekiller ile izdüşümüyle oluşn şekiller rsındki ln ve uzunluk ilişkileri nliz ettirilir. İD Ktı Cisimler İD Dikdörtgenler prizmsı üzerinde uzunluk, çı ve ln hesplmlrı ypr. [R] Cisim köşegeni ve yüzey köşegeni incelenir. 52
11 11. SINIF MATEMATİK DERSİ TEMEL DÜZEY ÖĞRETİM PROGRAMI 11 ve 12. Sınıflr Mtemtik Dersi Temel Düzey Öğretim Progrmı öğrencilerin okul sonrsınd mtemtikten günlük yşntılrınd ve iş hytlrınd ktif olrk yrrlnbilmelerini, krrlrınd mtemtiği iyi bir nliz rcı olrk kullnbilmelerini mçlmktdır. Bu kpsmd öğrencilerin 9 ve 10. sınıflrd öğrendikleri bzı kvrm ve ilişkiler günlük yşm temelli problemler rcılığı ile ele lınmktdır. Bu yoll bir üst öğrenim seviyesinde mtemtik ğırlıklı bir progrm tercih etmeyen öğrencilerin günlük yşmd krşılştıklrı problemlerin üstesinden dh etkili bir şekilde gelmeleri öngörülmektedir. Öğrencilerin problem çözme becerilerinin geliştirilmesi progrmın temel hedeflerindendir. Arzulnn bu mçlr ulşılbilmesi için şğıdki hususlr dikkte lınmlıdır: Öğrenciler günlük hytl ilişkili problem durumlrı ile krşı krşıy bırkılmlı, onlr bunlrın üstesinden gelmenin yollrı öğretilmelidir. Tsrlnn gerçek/gerçekçi hyt problemleri öğrencilere, kıl yürütme ve krr vermelerini gerektirecek durumlr brındırmlıdır. Problemler öğrencilerin kültürel çevrelerine uygun, ilelerini ve ykın çevrelerini içine ln gerçek yşm bğlmlrı ile ilişkilendirilmelidir. Derslerde, hyttki olylrdn ve problemlerden bşlnmlı, bzı konu ve kvrmlrın öğrenilmesine bir ihtiyç hissettirilmelidir. Bu çerçevede ilgili kvrmlr problemin çözüm sürecinde irdelenmelidir. Proje tbnlı öğrenme yklşımı rcılığı ile öğrencilerin verileri toplmlrı, düzenlemeleri, nliz etmeleri ve elde ettiği sonuçlrı sınıft sunmlrı sğlnmlıdır. Öğrenme Alnlrı, Üniteler ve Zmn Dğılımı: Bir kznımın işleniş süresi bşt öğrencilerin seviyesi olmk üzere birçok değişkene bğlıdır. Bu nedenle progrmdki kznımlr yönelik şğıd verilen işleniş süreleri kesin olmyıp yklşık olrk verilmiştir. 11. SINIF TEMEL DÜZEY No Ünite/Konulr Kznım Ders Ağırlık Syısı Sti (%) SAYILAR ve CEBİR TD Syı Dizileri TD Bölünebilme TD Bilinçli Tüketici Aritmetiği GEOMETRİ TD Ölçme VERİ ve OLASILIK TD Veri Anlizi TD Olsılık Toplm Sınıf Temel Düzey 53
12 Syılr ve Cebir TD Syı Dizileri TD Syı dizilerini kullnrk gerçek/gerçekçi hyt problemlerini modellerde ve problem çözümünde kullnır. [R] Fiboncci dizisinden, geometrik ve ritmetik dizilerden bhsedilir. [R] Syı dizileri fonksiyon olrk verilir; lt indis kullnılmz. TD Bölünebilme TD İki y d dh fzl doğl syının en büyük ortk bölenini ve en küçük ortk ktını içeren problemleri çözer. [R] 2, 3, 4, 5, 9, 11 ve 6, 15, 18 ile bölünebilme kurllrı verilir. TD Bilinçli Tüketici Aritmetiği TD Gelirleri-giderleri göz önüne lrk birey, ile ve kurum bütçesi oluşturur. [R] Mş, idt, bğış, prim vb. gelirler ve kir, telefon, elektrik, doğlgz, kıyfet, seyht, yiyecek-içecek vb. giderler dikkte lınrk birey, ile, kurum vey bir projenin bütçesi ypılır. TD Yüzde, orn ve orntı kvrmlrını günlük hytt krşılştığı durumlrın nlizinde ve problem çözme sürecinde kullnır. [R] Yüzde hesplmlrınd şğıd verilen bğlmlrdn yrrlnılbilir: Zmnınd ödemeleri ypılmdığınd gecikme bedeli ödenmesi gereken elektrik, su, doğlgz, telefon fturlrı, motorlu tşıtlr vergisi, konut vergisi vb. durumlr, Bir mlın lış fiytı üzerine KDV (frklı ürün/hizmet gruplrınd frklı ornlrd KDV uygulnbilmektedir), özel tüketim vergisi ve kâr eklenmesi, belli bir stış fiytı üzerinden indirim ypılmsı gibi günlük hyt durumlrı, Bsit ve bileşik fiz uygulmlrı içeren problem durumlrı, Vde frkı, enflsyon gibi bireyin günlük yşntısınd sıklıkl krşılştığı kvrmlr, Frklı bnklrın kredi olnklrı inceletilerek istenen şrtlr uyn bnknın belirlenmesi, Ytırımlrın getirilerine yönelik veriler topltılmsı ve ytırımlr içerisinde en iyi olnının belirlenmesi (En iyi ytırımı belirlerken frklı risk fktörleri de trtışılır) Sınıf Temel Düzey
13 [R] Orn ve orntı kvrmlrını içeren problemler oluşturulurken şğıd verilen bğlmlrdn yrrlnılbilir: Frklı ürünlerin birim fiytlrını krşılştırm, Frklı pr birimlerini birbirine çevirme, Frklı syıd kişiler için hzırlnck yemek için kullnılmsı gereken mlzeme miktrı, Arç kullnımı ile ykıt tüketimi rsındki (frklı hızlrd rç sürmenin ykıt tüketimi üzerindeki etkisi dikkte lınrk belli bir rlıkt yol lck oln bir rcın ortlm ykıt tüketiminin hesplnmsı gibi) ilişkileri inceleme, Kütleye vey yş göre ilç dozunun yrlnmsı, dkiky/pkete bğlı telefon ücretleri gibi durumlr, Mirs pylşım problemleri. TD Günlük hytt periyodik olrk tekrr eden durumlrı içeren problemleri çözer. [R] Verilen bir günden belli syıd gün sonr hftnın hngi gününe denk geldiği, yılbşı ve byrm günlerinin yıllr göre değişmesinin hesplnmsı, belli rlıklrl nöbet tutn bir çlışnın tuttuğu nöbet günlerinin nlizi gibi durumlr inceletilir. TD Seyhtlerde mümkün oln lterntifleri krşılştırır. [R] Seyht plnlrını etkileyebilecek kişi syısı, lterntif yollr, hv koşullrı vb. fktörler trtıştırılır. [R] Bir seyht plnı yprk yklşık mliyet nlizi yptırılır. [R] Gidilecek yere ilişkin bir zmn çizelgesi yptırılır. 11. Sınıf Temel Düzey 55
14 Geometri TD Ölçme TD Bir nesnenin belli bir ornd büyütülmüş y d küçültülmüş bir çizimini kullnrk bir mesfe, bir nesnenin çevre uzunluğu, lnı vey hcmi hkkınd çıkrımlrd bulunur. [R] Bir hrit üzerinde cetvelle ölçümler yptırılrk hrit ölçeği yrdımıyl gerçek uzunluklr yklşık olrk buldurulur. [R] Bir nesnenin belli bir ornd büyütülmüş vey küçültülmüş çizimleri kreli kâğıt üzerine çizdirilir. Örneğin öğrencilerden yşdıklrı evin bir plnını kreli kâğıd çizmeleri istenebilir. TD Çevre, ln, yüzey lnı ve hcim ölçmeye yönelik problemleri çözer. [R] Bnyo fynslrının döşenmesi, evin hlılrının yenilenmesi, evin boynmsı, frklı boyutlrdki kutulrı en elverişli şekilde yerleştirme, bir kbın lbileceği sıvı kpsitesinin hesplnmsı gibi örneklere yer verilir. [R] Proje tbnlı öğrenme yklşımındn yrrlnılır. Veri ve Olsılık TD Veri Anlizi TD Gerçek hyt durumlrıyl ilgili bir isttistik problemini çözmek için verileri toplr, düzenler, temsil eder ve yorumlr. [R] Bir veri grubunu temsil edecek en uygun grfik çeşidi üzerinde durulur. Frklı grfik çeşitlerinin kullnımıyl ilgili uygulmlr yptırılır. [R] Proje tbnlı öğrenme yklşımı uygulnır. Projelerin sunumu sırsınd projesini sunn öğrencilerin kullndıklrı grfiklerin, merkezi eğilim ve yyılım ölçülerinin uygun olup olmdığı trtışılır. [R] Özellikle toplumsl duyrlılığı geliştirebilecek çevre bilinci, okum lışknlıklrı gibi konulr bğlmınd verilerin toplnmsı ve nlizi üzerinde durulur. TD Olsılık TD Bsit ve bileşik olylrın olsılıklrını içeren, hytın içinden gerçek/gerçekçi problem durumlrını çözer. [R] Örnek uzy, bir olyın tümleyeni, yrık ve yrık olmyn oly kvrmlrını içeren problemler üzerinde durulur Sınıf Temel Düzey
15 12. SINIF MATEMATİK DERSİ TEMEL DÜZEY ÖĞRETİM PROGRAMI 11 ve 12. Sınıflr Mtemtik Dersi Temel Düzey Öğretim Progrmı öğrencilerin okul sonrsınd mtemtikten günlük yşntılrınd ve iş hytlrınd ktif olrk yrrlnbilmelerini, krrlrınd mtemtiği iyi bir nliz rcı olrk kullnbilmelerini mçlmktdır. Bu kpsmd öğrencilerin 9 ve 10. sınıflrd öğrendikleri bzı kvrm ve ilişkiler günlük yşm temelli problemler rcılığı ile ele lınmktdır. Bu yoll bir üst öğrenim seviyesinde mtemtik ğırlıklı bir progrm tercih etmeyen öğrencilerin günlük yşmd krşılştıklrı problemlerin üstesinden dh etkili bir şekilde gelmeleri öngörülmektedir. Öğrencilerin problem çözme becerilerinin geliştirilmesi progrmın temel hedeflerindendir. Arzulnn bu mçlr ulşılbilmesi için şğıdki hususlr dikkte lınmlıdır: Öğrenciler günlük hytl ilişkili problem durumlrı ile krşı krşıy bırkılmlı, onlr bunlrın üstesinden gelmenin yollrı öğretilmelidir. Tsrlnn gerçek/gerçekçi hyt problemleri öğrencilere, kıl yürütme ve krr vermelerini gerektirecek durumlr brındırmlıdır. Problemler öğrencilerin kültürel çevrelerine uygun, ilelerini ve ykın çevrelerini içine ln gerçek yşm bğlmlrı ile ilişkilendirilmelidir. Derslerde, hyttki olylrdn ve problemlerden bşlnmlı, bzı konu ve kvrmlrın öğrenilmesine bir ihtiyç hissettirilmelidir. Bu çerçevede ilgili kvrmlr problemin çözüm sürecinde irdelenmelidir. Proje tbnlı öğrenme yklşımı rcılığı ile öğrencilerin verileri toplmlrı, düzenlemeleri, nliz etmeleri ve elde ettiği sonuçlrı sınıft sunmlrı sğlnmlıdır. Öğrenme Alnlrı, Üniteler ve Zmn Dğılımı: Bir kznımın işleniş süresi bşt öğrencilerin seviyesi olmk üzere birçok değişkene bğlıdır. Bu nedenle progrmdki kznımlr yönelik şğıd verilen işleniş süreleri kesin olmyıp yklşık olrk verilmiştir. 12. SINIF TEMEL DÜZEY No Ünite/Konulr Kznım Ders Ağırlık Syısı Sti (%) SAYILAR ve CEBİR TD Grfiklerin ve Tblolrın Yorumlnmsı TD Üstel Fonksiyonlr ve Uygulmlr GEOMETRİ TD Ölçme TD Trigonometri ve Uygulmlrı Toplm Sınıf Temel Düzey 57
16 Syılr ve Cebir TD Grfiklerin ve Tblolrın Yorumlnmsı TD Bir grfiğin vey tblonun yorumlnmsını gerektiren problemleri çözer. [R] Grfiklerin hız-zmn, kâr-zrr, nüfus rtışı gibi günlük hyt durumlrın uygun olmsın önem verilir. Bir şehirdeki ylr bğlı hv kirlilik grfiği verilerek hv kirliliğinin rtış vey zlışlrı muhtemel sebeplerle birlikte yorumltılır. [R] Doğrusl grfikler verilerek geleceğe yönelik thminler ve beklentiler trtışılır. [R] Birden fzl grfik bir rd verilir ve kesişim noktlrının nlmı trtışılır. [R] Birimleri verilmeyen bir grfiğin ne olbileceğine yönelik thminler yptırılır ve grfiğe uygun bir senryo yzmlrı istenir. [R] Verilen bir tblonun yorumlnmsı ve geleceğe ilişkin beklentilere yönelik thminler yptırılır ve tbloy uygun bir senryo yzmlrı istenir. [R] Sembolik, grfik vey tblo olrk verilen bir fonksiyonun belli bir rlıktki ortlm değişim hızı (keseninin eğimi, yni f(b) - f() ) hesplttırılır. b- TD Üstel Fonksiyonlr ve Uygulmlrı TD Üstel fonksiyonu tnımlr ve gerçek/gerçekçi hyt durumlrını modellemede ve problem çözmede kullnır. [R] Üstlü ifdelerle ypıln işlemlerin özellikleri htırltılır. [R]!R + -{1} olmk üzere f: R"R +, f(x) = x gibi üstel fonksiyonlrın grfiği çizdirilir. > 1 için rtn fonksiyon, < 1 için zln fonksiyon olduğu frk ettirilir. [R] Nüfus rtışı, bkteri popülsyonu, bileşik fiz, rdyoktif mddelerin bozunumu (yrı ömür), fosil yşlrının tyini, deprem şiddeti (Richter ölçeği) vb. örnekler bğlmınd üstel büyüme/zlm ile modellenebilecek problem durumlrın yer verilir Sınıf Temel Düzey
17 Geometri TD Ölçme TD Dik üçgenleri gerçek/gerçekçi hyt problemlerini çözmede kullnır. [R] Pisgor teoreminin kullnımını gerektiren gerçek hyt problemleri ele lınır. TD Üçgenlerin benzerliğini, gerçek/gerçekçi hyt durumlrını modellemede ve problem çözmede kullnır. [R] Problemler seçilirken uzunluğun, lnın ve hcmin doğrudn ölçümünün mümkün olmdığı hllerde, bunlrın hesplnmsın yer verilir. TD Trigonometri ve Uygulmlrı TD Yönlü çıyı çıklr, çı ölçü birimlerinden derece ile rdynı ilişkilendirir. [R] Derecenin lt birimleri olrk dkikdn bhsedilir. Dünynın eksen eğikliği örnek olrk verilir. [R] Birim çember denklemi verilmeden tnımlnır, çının ess ölçüsünden bhsedilir. TD Trigonometrik fonksiyonlrı birim çember yrdımıyl oluşturur ve grfiklerini çizer. [R] Ylnızc sinüs, kosinüs ve tnjnt fonksiyonlrı incelenir. [R] Trigonometrik fonksiyonlr rsındki temel özdeşlikler, oluşturuln benzer üçgenler yrdımıyl inceletilir. [R] Trigonometrik fonksiyonlrın bölgelere göre işretleri inceletilir. [R] k!z olmk üzere kr!i syılrının trigonometrik değerler i dr çısının trigonometrik değerlerinden yrrlnrk hespltılır. 2 [R] Periyod ve periyodik fonksiyon çıklnır, trigonometrik fonksiyonlrın periyodik olduklrı keşfettirilir. [R] f(x) = sin(bx + c) + k türündeki fonksiyonlrın grfikleri ve ktsyılrının grfik üzerindeki etkileri incelenir. TD Trigonometrik fonksiyonlrı gerçek / gerçekçi hyt durumlrını modellemede ve problem çözmede kullnır. [R] Trigonometrik fonksiyonlrın periyodikliğini içeren problemlere / örneklere (sinüzoidl lterntif kım, ses dlglrı, gece - gündüz uzunluklrı vs.) yer verilir. 12. Sınıf Temel Düzey 59
Kesir Örnek Çözüm. 1. Yandaki şekilde bir TEST - 1. 1. Taralı alanı gösteren. bütün 8 eş parçaya bölünmüş ve bu parçalardan 3 tanesi
 Kesir.. Trlı lnı gösteren kesri bulunuz. kesrini ile genişlettiğimizde elde edilecek kesri bulunuz.. Yndki şekilde bir bütün 8 eş prçy bölünmüş ve bu prçlrdn tnesi trnmıştır. Trlı lnı gösteren kesir syısı
Kesir.. Trlı lnı gösteren kesri bulunuz. kesrini ile genişlettiğimizde elde edilecek kesri bulunuz.. Yndki şekilde bir bütün 8 eş prçy bölünmüş ve bu prçlrdn tnesi trnmıştır. Trlı lnı gösteren kesir syısı
ege yayıncılık Oran Orant Özellikleri TEST : 91 a + 3b a b = 5 2 0,44 0,5 = 0,22 oldu una göre, a + b en az kaçt r? A) 3 B) 11 C) 14 D) 15 E) 16
 Orn Ornt Özellikleri TEST : 91 1. 0,44 0,5 = 0,22 5. + 3 = 5 2 2. 3. 4. oldu un göre, kçt r? A) 0,2 B) 0,25 C) 0,5 D) 0,6 E) 0,75 y = 3 4 + y oldu un göre, y orn kçt r? A) 7 B) 1 C) 1 D) 7 E) 10 oldu un
Orn Ornt Özellikleri TEST : 91 1. 0,44 0,5 = 0,22 5. + 3 = 5 2 2. 3. 4. oldu un göre, kçt r? A) 0,2 B) 0,25 C) 0,5 D) 0,6 E) 0,75 y = 3 4 + y oldu un göre, y orn kçt r? A) 7 B) 1 C) 1 D) 7 E) 10 oldu un
JOVO STEFANOVSKİ NAUM CELAKOSKİ. Sekizyıllık İlköğretim
 JOVO STEFNOVSKİ NUM CELKOSKİ Sekizyıllık İlköğretim Syın Öğrenci! u kitp, ders proğrmınd öngörülen ders mlzemesini öğrenmek için yrdımcı olcktır. Vektörler, öteleme ve dönme hkkınd yeni ilginç bilgiler
JOVO STEFNOVSKİ NUM CELKOSKİ Sekizyıllık İlköğretim Syın Öğrenci! u kitp, ders proğrmınd öngörülen ders mlzemesini öğrenmek için yrdımcı olcktır. Vektörler, öteleme ve dönme hkkınd yeni ilginç bilgiler
BİLİMSEL SÜREÇLERİN KAZANIMINA YÖNELİK BİR PROGRAM ÇALIŞMASI
 BİLİMSEL SÜREÇLERİN KAZANIMINA YÖNELİK BİR PROGRAM ÇALIŞMASI Dilek ARDAÇ, Ebru MUĞALOĞLU Boğziçi Üniversitesi, Eğitim Fkültesi, OFMA Eğitimi Bölümü, İSTANBUL ÖZET: Çlışm bilimsel süreçlerin kznımını mçlyn
BİLİMSEL SÜREÇLERİN KAZANIMINA YÖNELİK BİR PROGRAM ÇALIŞMASI Dilek ARDAÇ, Ebru MUĞALOĞLU Boğziçi Üniversitesi, Eğitim Fkültesi, OFMA Eğitimi Bölümü, İSTANBUL ÖZET: Çlışm bilimsel süreçlerin kznımını mçlyn
Komisyon. ALES EŞİT AĞRILIK ve SAYISAL ADAYLARA TAMAMI ÇÖZÜMLÜ 10 DENEME ISBN 978-605-364-214-5
 Komisyon LES EŞİT ĞRILIK ve SYISL DYLR TMMI ÇÖZÜMLÜ 10 DENEME ISBN 97-605-36-1-5 Kitpt yer ln ölümlerin tüm sorumluluğu yzrın ittir. Pegem kdemi Bu kitın sım, yyın ve stış hklrı Pegem kdemi Yy. Eğt. Dn.
Komisyon LES EŞİT ĞRILIK ve SYISL DYLR TMMI ÇÖZÜMLÜ 10 DENEME ISBN 97-605-36-1-5 Kitpt yer ln ölümlerin tüm sorumluluğu yzrın ittir. Pegem kdemi Bu kitın sım, yyın ve stış hklrı Pegem kdemi Yy. Eğt. Dn.
Yükseköğretime Geçiş Sınavı (Ygs) / 1 Nisan 2012. Matematik Soruları ve Çözümleri
 Yükseköğretime Geçiş Sınvı (Ygs) / Nisn 0 Mtemtik Sorulrı ve Çözümleri. 0,5, işleminin sonuu kçtır? 0,5 0, A) 5 B) 5,5 C) 6 D) 6,5 E) 7 Çözüm 0,5 0,5, 0, 05 50 5.5.4 5.5. 4 4 0 5 .. 4.6 6 işleminin sonuu
Yükseköğretime Geçiş Sınvı (Ygs) / Nisn 0 Mtemtik Sorulrı ve Çözümleri. 0,5, işleminin sonuu kçtır? 0,5 0, A) 5 B) 5,5 C) 6 D) 6,5 E) 7 Çözüm 0,5 0,5, 0, 05 50 5.5.4 5.5. 4 4 0 5 .. 4.6 6 işleminin sonuu
Bahçe Mah. Soğuksu Cad. No:73 MERSİN www.sratanitim.com info@sratnitim.com. Tel :0.324 336 41 24 :0.324 336 41 26 Gsm :0.
 Tnıtım Bhçe Mh. Soğuksu Cd. No:73 MERSİN www.srtnitim.com info@srtnitim.com Tel :0.324 336 41 24 :0.324 336 41 26 Gsm :0.532 592 60 05 çık hvdki prestijiniz 1 Tnıtım ,Büfe Durk Rket 118 x 178 cm Gintbord
Tnıtım Bhçe Mh. Soğuksu Cd. No:73 MERSİN www.srtnitim.com info@srtnitim.com Tel :0.324 336 41 24 :0.324 336 41 26 Gsm :0.532 592 60 05 çık hvdki prestijiniz 1 Tnıtım ,Büfe Durk Rket 118 x 178 cm Gintbord
TEST - 1 KATI BASINCI. I. yarg do rudur. II. yarg yanl flt r. Buna göre, fiekil-i de K ve L cisimlerinin yere yapt klar bas nçlar eflit oldu una göre,
 TI BSINCI TEST - 1 1 1 π dir π Bun göre, 4 > 1 CEV B de ve cisimlerinin e ypt klr s nçlr eflit oldu un göre, SX S Z + 4 8 S Y I II III CEV B Tu llr n X, Y ve Z noktlr n ypt s nç, X S Y S Z S dir Bun göre,
TI BSINCI TEST - 1 1 1 π dir π Bun göre, 4 > 1 CEV B de ve cisimlerinin e ypt klr s nçlr eflit oldu un göre, SX S Z + 4 8 S Y I II III CEV B Tu llr n X, Y ve Z noktlr n ypt s nç, X S Y S Z S dir Bun göre,
PLAJLARDA ÇEVRE BİLİNÇLENDİRME PROJESİ. (19-22 Ağustos 2013 Akyaka)
 PLAJLARDA ÇEVRE BİLİNÇLENDİRME PROJESİ (19-22 Ağustos 213 Akyk) Pljlr Çevre Bilinçlenirme Projesi 19-22 Ağustos trihleri rsın TÜRÇEV Muğl Şuesi ve Akyk Beleiyesi iş irliği ile gerçekleştirili. Proje TÜRÇEV
PLAJLARDA ÇEVRE BİLİNÇLENDİRME PROJESİ (19-22 Ağustos 213 Akyk) Pljlr Çevre Bilinçlenirme Projesi 19-22 Ağustos trihleri rsın TÜRÇEV Muğl Şuesi ve Akyk Beleiyesi iş irliği ile gerçekleştirili. Proje TÜRÇEV
Kontak İbreli Termometreler
 E-mil: Fx: +49 661 6003-607 www.jumo.net www.jumo.co.uk www.jumo.us Veri Syfsı 608523 Syf 1/8 Kontk İbreli Termometreler Özellikler Pnel montj vey ek cihz gibi proses değeri göstergeli sıcklık kontrolörü
E-mil: Fx: +49 661 6003-607 www.jumo.net www.jumo.co.uk www.jumo.us Veri Syfsı 608523 Syf 1/8 Kontk İbreli Termometreler Özellikler Pnel montj vey ek cihz gibi proses değeri göstergeli sıcklık kontrolörü
Ö rendiklerimizi Nerelerde Kullanabiliriz? Alan tahmin etmede kullanabiliriz.
 4.1 Aln Neler Ö renece iz? Geometrik flekillerin lnlr n hesplyc z. Ö rendiklerimizi Nerelerde Kullnbiliriz? Aln thmin etmede kullnbiliriz. Söz Vrl Prlelkenrsl bölge Bir y içinde yklfl k lt metre krelik
4.1 Aln Neler Ö renece iz? Geometrik flekillerin lnlr n hesplyc z. Ö rendiklerimizi Nerelerde Kullnbiliriz? Aln thmin etmede kullnbiliriz. Söz Vrl Prlelkenrsl bölge Bir y içinde yklfl k lt metre krelik
İntegral Uygulamaları
 İntegrl Uygulmlrı Yzr Prof.Dr. Vkıf CAFEROV ÜNİTE Amçlr Bu üniteyi çlıştıktn sonr; düzlemsel ln ve dönel cisimlerin cimlerinin elirli integrl yrdımı ile esplnileceğini, küre, koni ve kesik koninin cim
İntegrl Uygulmlrı Yzr Prof.Dr. Vkıf CAFEROV ÜNİTE Amçlr Bu üniteyi çlıştıktn sonr; düzlemsel ln ve dönel cisimlerin cimlerinin elirli integrl yrdımı ile esplnileceğini, küre, koni ve kesik koninin cim
Do ufl Üniversitesi Matematik Kulübü Fen Liseleri Yar flmas 2005 Soru ve Yan tlar
 Mtemtik ünys, 005 Güz o ufl Ünirsitesi Mtemtik Kulübü en Liseleri Yr flms 005 Soru Yn tlr 1. 005 006 sy s n n 11 e bölümünden kln kçt r? Çözüm: 005 3(mod 11) oldu undn 005 006 3 006 = (3 5 ) 401 3 3 (mod
Mtemtik ünys, 005 Güz o ufl Ünirsitesi Mtemtik Kulübü en Liseleri Yr flms 005 Soru Yn tlr 1. 005 006 sy s n n 11 e bölümünden kln kçt r? Çözüm: 005 3(mod 11) oldu undn 005 006 3 006 = (3 5 ) 401 3 3 (mod
Programın öğrencilerde geliştirmeyi hedeflediği becerilerle 12. sınıf matematik öğretim programı
 Programın öğrencilerde geliştirmeyi hedeflediği becerilerle 12. sınıf matematik öğretim programı ilişkisi Modelleme/Problem çözme Matematiksel Süreç Becerileri Akıl Yürütme Matematiksel İletişim İlişkilendirme
Programın öğrencilerde geliştirmeyi hedeflediği becerilerle 12. sınıf matematik öğretim programı ilişkisi Modelleme/Problem çözme Matematiksel Süreç Becerileri Akıl Yürütme Matematiksel İletişim İlişkilendirme
OKUL DENEYİMİ VE KAYNAŞTIRMA UYGULAMALARI
 OKUL DENEYİMİ VE KAYNAŞTIRMA UYGULAMALARI Uygulm Yönerge Kitpçığı 11.02.2015 ESOGÜ Eğitim Fkültesi Özel Eğitim Bölümü ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ EĞİTİM FAKÜLTESİ ÖZEL EĞİTİM BÖLÜMÜ 2014-2015 BAHAR
OKUL DENEYİMİ VE KAYNAŞTIRMA UYGULAMALARI Uygulm Yönerge Kitpçığı 11.02.2015 ESOGÜ Eğitim Fkültesi Özel Eğitim Bölümü ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ EĞİTİM FAKÜLTESİ ÖZEL EĞİTİM BÖLÜMÜ 2014-2015 BAHAR
12. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI
 9, 10, 11 ve 12. Sınıflr Mtemtik Dersi Öğretim Progrmı 12. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Progrmın öğrencilerde geliştirmeyi hedeflediği ecerilerle 12. sınıf mtemtik öğretim progrmı
9, 10, 11 ve 12. Sınıflr Mtemtik Dersi Öğretim Progrmı 12. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Progrmın öğrencilerde geliştirmeyi hedeflediği ecerilerle 12. sınıf mtemtik öğretim progrmı
KARŞI AKIŞLI SU SOĞUTMA KULESİ BOYUTLANIDIRILMASI
 KARŞI AKIŞI SU SOĞUTMA KUESİ BOYUTANIDIRIMASI Yrd. Doç. Dr. M. Turh Çob Ege Üiversitesi, Mühedislik Fkultesi Mkie Mühedisliği Bölümü turh.cob@ege.edu.tr Özet Bu yzımızd ters kışlı soğutm kulelerii boyut
KARŞI AKIŞI SU SOĞUTMA KUESİ BOYUTANIDIRIMASI Yrd. Doç. Dr. M. Turh Çob Ege Üiversitesi, Mühedislik Fkultesi Mkie Mühedisliği Bölümü turh.cob@ege.edu.tr Özet Bu yzımızd ters kışlı soğutm kulelerii boyut
BÖLÜM 5. MATRİS ve DETERMİNANTLAR 5.1. MATRİSLER. Taşkın, Çetin, Abdullayeva. reel sayılardan oluşan. olmak üzere tüm a.
 MTEMTİK BÖLÜM 5 Tşkın, Çetin, bdullyev MTRİS ve DETERMİNNTLR 5 MTRİSLER Tnım : mni,,, j + olmk üzere tüm ij reel syılrdn oluşn m m n n mn tblosun m x n tipinde bir mtrisi denir ve kısc şeklinde gösterilir
MTEMTİK BÖLÜM 5 Tşkın, Çetin, bdullyev MTRİS ve DETERMİNNTLR 5 MTRİSLER Tnım : mni,,, j + olmk üzere tüm ij reel syılrdn oluşn m m n n mn tblosun m x n tipinde bir mtrisi denir ve kısc şeklinde gösterilir
1.BÖLÜM SORU. (x+3) (4x 2 13) = 3(x+3) denklemini sa layan x de- erlerinin çarp m kaçt r? x+3 kümesi afla dakilerden hangisidir?
 1.BÖLÜM MATEMAT K Derginin u s s nd kinci Dereceden Denklemler, Eflitsizlikler ve Prol konusund çözümlü sorulr er lmktd r. Bu konud, ÖSS de ç kn sorulr n çözümü için gerekli temel ilgileri ve prtik ollr,
1.BÖLÜM MATEMAT K Derginin u s s nd kinci Dereceden Denklemler, Eflitsizlikler ve Prol konusund çözümlü sorulr er lmktd r. Bu konud, ÖSS de ç kn sorulr n çözümü için gerekli temel ilgileri ve prtik ollr,
DERS 1. Sayı Kümeleri ve Koordinatlar
 DERS Syı Kümeleri ve Koordintlr. Kümeler. Mtemtiğin temel kvrmlrındn biri küme kvrmıdır. Okuyucunun küme kvrmın ybncı olmyıp kümelerle ilgili temel işlemleri bildiğini kbul ediyoruz. Bununl berber, kümelerle
DERS Syı Kümeleri ve Koordintlr. Kümeler. Mtemtiğin temel kvrmlrındn biri küme kvrmıdır. Okuyucunun küme kvrmın ybncı olmyıp kümelerle ilgili temel işlemleri bildiğini kbul ediyoruz. Bununl berber, kümelerle
A A A A A TEMEL MATEMAT K TEST. + Bu bölümdeki cevaplar n z cevap ka d ndaki "TEMEL MATEMAT K TEST " bölümüne iflaretleyiniz. 4.
 TEMEL MTEMT K TEST KKT! + u bölümde cevplyc n z soru sy s 40 t r + u bölümdeki cevplr n z cevp k d ndki "TEMEL MTEMT K TEST " bölümüne iflretleyiniz.. ( + )y + = 0 (b ) + 4y 6 = 0 denklem sisteminin çözüm
TEMEL MTEMT K TEST KKT! + u bölümde cevplyc n z soru sy s 40 t r + u bölümdeki cevplr n z cevp k d ndki "TEMEL MTEMT K TEST " bölümüne iflretleyiniz.. ( + )y + = 0 (b ) + 4y 6 = 0 denklem sisteminin çözüm
LKÖ RET M MATEMAT K 8 Ö RETMEN KILAVUZ K TABI. Lokman GÜNDO DU
 LKÖ R M MM K 8 Ö RMN KILVUZ K I Lokmn GÜNO U u kitp, Millî itim knl lim ve erbiye Kurulu flknl n n 8.06.00 trih ve 6 sy l krr yl 0-0 ö retim y l ndn itibren (befl) y l süreyle ders kitb olrk kbul edilmifltir.
LKÖ R M MM K 8 Ö RMN KILVUZ K I Lokmn GÜNO U u kitp, Millî itim knl lim ve erbiye Kurulu flknl n n 8.06.00 trih ve 6 sy l krr yl 0-0 ö retim y l ndn itibren (befl) y l süreyle ders kitb olrk kbul edilmifltir.
ÖLÇME TEKNĠKLERĠ DERSĠ
 1 Konu Ģlıklrı ÖLÇME TEKNĠKLERĠ DERSĠ 1) Ölçme ilgisi İle İlgili çıklmlr 2) sit ölçme letleri 3) Doğrulrın elirtilmesi 4) Uzunluklrın Ölçülmesi 5) ln Hesplrı 6) Thomson Yolu İle ln Hesbı 7) Koordint Yrdımı
1 Konu Ģlıklrı ÖLÇME TEKNĠKLERĠ DERSĠ 1) Ölçme ilgisi İle İlgili çıklmlr 2) sit ölçme letleri 3) Doğrulrın elirtilmesi 4) Uzunluklrın Ölçülmesi 5) ln Hesplrı 6) Thomson Yolu İle ln Hesbı 7) Koordint Yrdımı
EĞİTİM-ÖĞRETİM YILI 12. SINIF İLERİ DÜZEL MATEMATİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ
 KASIM EKİM 2017-2018 EĞİTİM-ÖĞRETİM YILI 12. SINIF İLERİ DÜZEL MATEMATİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ 1 4 TÜREV 12.1.1.1. Bir fonksiyonun bir noktadaki limiti, soldan limiti
KASIM EKİM 2017-2018 EĞİTİM-ÖĞRETİM YILI 12. SINIF İLERİ DÜZEL MATEMATİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ 1 4 TÜREV 12.1.1.1. Bir fonksiyonun bir noktadaki limiti, soldan limiti
Limit. Kapak Konusu: Gerçel Say lar V: Süreklilik ve Limit
 Kpk Konusu: Gerçel S lr V: Süreklilik Limit Limit v = ƒ() Bir bflk örne e bkl m. < c < b olsun. ƒ: [, b] \ {c}, grfi i fl dki gibi oln bir fonksion olsun. Fonksion c nokts nd tn mlnmm fl. Os fonksion c
Kpk Konusu: Gerçel S lr V: Süreklilik Limit Limit v = ƒ() Bir bflk örne e bkl m. < c < b olsun. ƒ: [, b] \ {c}, grfi i fl dki gibi oln bir fonksion olsun. Fonksion c nokts nd tn mlnmm fl. Os fonksion c
TÜRKİYE DE İLLERİN TRAFİK GÜVENLİĞİNİN ANALİTİK HİYERARŞİ PROSESİ (AHP)İLE BELİRLENMESİ
 Ordu Üniv. Bil. Tek. Derg., Cilt:4, Syı:2, 2014,57-69/Ordu Univ. J. Sci. Tech., Vol:4, No:2,2014,57-69 TÜRKİYE DE İLLERİN TRAFİK GÜVENLİĞİNİN ANALİTİK HİYERARŞİ PROSESİ (AHP)İLE BELİRLENMESİ ÖZET Emine
Ordu Üniv. Bil. Tek. Derg., Cilt:4, Syı:2, 2014,57-69/Ordu Univ. J. Sci. Tech., Vol:4, No:2,2014,57-69 TÜRKİYE DE İLLERİN TRAFİK GÜVENLİĞİNİN ANALİTİK HİYERARŞİ PROSESİ (AHP)İLE BELİRLENMESİ ÖZET Emine
İDEAL PERFORMANS DEĞERLENDİRME FORMU TASARIMINDA ANALİTİK HİYERARŞİ YÖNTEMİ YAKLAŞIMI
 Gzi Üniv Müh Mim Fk Der J Fc Eng Arch Gzi Univ Cilt 20, No 1, 95-106, 2005 Vol 20, No 1, 95-106, 2005 İDEAL PERFORMANS DEĞERLENDİRME FORMU TASARIMINDA ANALİTİK HİYERARŞİ YÖNTEMİ YAKLAŞIMI Ergün ERASLAN
Gzi Üniv Müh Mim Fk Der J Fc Eng Arch Gzi Univ Cilt 20, No 1, 95-106, 2005 Vol 20, No 1, 95-106, 2005 İDEAL PERFORMANS DEĞERLENDİRME FORMU TASARIMINDA ANALİTİK HİYERARŞİ YÖNTEMİ YAKLAŞIMI Ergün ERASLAN
2013-2014 EĞİTİM VE ÖĞRETİM YILI TED KDZ EREĞLİ KOLEJİ ORTAOKULU MATEMATİK 8.SINIF ÜNİTELENDİRİLMİŞ YILLIK PLANDIR.
 EYLÜL 2013-201 EĞİTİM VE ÖĞRETİM YILI TED KDZ EREĞLİ KOLEJİ ORTAOKULU MATEMATİK 8.SINIF ÜNİTELENDİRİLMİŞ YILLIK PLANDIR. 9-13 Örüntü ve Süslemeler Dönüşüm Geometrisi 1. Doğru, çokgen ve çember modellerinden
EYLÜL 2013-201 EĞİTİM VE ÖĞRETİM YILI TED KDZ EREĞLİ KOLEJİ ORTAOKULU MATEMATİK 8.SINIF ÜNİTELENDİRİLMİŞ YILLIK PLANDIR. 9-13 Örüntü ve Süslemeler Dönüşüm Geometrisi 1. Doğru, çokgen ve çember modellerinden
Sistem Dinamiği ve Modellemesi. Doğrusal Sistemlerin Sınıflandırılması Doğrusal Sistemlerin Zaman Davranışı
 Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
FONKS YONLAR. Fonksiyon. Fonksiyon Olma Şartları. çözüm. kavrama sorusu. çözüm. kavrama sorusu. çözüm. kavrama sorusu
 FONKS YONLR Fonksion ve o olmn iki küme olsun. krtezen çrp m n n lt kümelerine nt denir. u nt lrdn dki rtlr s lnlr kümesinden kümesine tn mlnm onksion denir. Fonksionlr genelde, g, h gii küçük hrlerle
FONKS YONLR Fonksion ve o olmn iki küme olsun. krtezen çrp m n n lt kümelerine nt denir. u nt lrdn dki rtlr s lnlr kümesinden kümesine tn mlnm onksion denir. Fonksionlr genelde, g, h gii küçük hrlerle
Yrd. Doç. Dr., Süleyman Demirel Üniversitesi, Yalvaç Meslek Yüksek Okulu
 PERSONEL SEÇĐMĐNĐN ANALĐTĐK HĐYERARŞĐ PROSESĐ YÖNTEMĐYLE GERÇEKLEŞTĐRĐLMESĐ ÖZET Orhn ADIGÜZEL Glolleşmenin neden olduğu ilgi ve teknolojideki gelişmeler, işletmeleri ve kurumlrı dh kliteli insn kynğın
PERSONEL SEÇĐMĐNĐN ANALĐTĐK HĐYERARŞĐ PROSESĐ YÖNTEMĐYLE GERÇEKLEŞTĐRĐLMESĐ ÖZET Orhn ADIGÜZEL Glolleşmenin neden olduğu ilgi ve teknolojideki gelişmeler, işletmeleri ve kurumlrı dh kliteli insn kynğın
SORU SORU. ABCDEF... düzgün çokgenin ard fl k köfleleridir. m(ebf) = 12 ise
 GMR erginin bu sy s nd Çokgenler ve örtgenler konusund çözümlü sorulr yer lmktd r. u konud, ÖSS de ç kn sorulr n çözümü için gerekli temel bilgileri ve prtik yollr, sorulr m z n çözümü içinde ht rltmy
GMR erginin bu sy s nd Çokgenler ve örtgenler konusund çözümlü sorulr yer lmktd r. u konud, ÖSS de ç kn sorulr n çözümü için gerekli temel bilgileri ve prtik yollr, sorulr m z n çözümü içinde ht rltmy
Parabol, Elips ve Hiperbol Cebirsel Tan mlar ve Geometrik Çizimler
 Mtemtik Düns, 2005 Yz Kpk Konusu: Konikler Geçen z d, ir koni in denkleminin, düzlemin eksenlerini döndürerek ve öteleerek, 0, c ve ƒ sitleri için, 2 + c 2 = 0, 2 = ƒ, 2 + c 2 = 1, d = 2 içiminde z lilece
Mtemtik Düns, 2005 Yz Kpk Konusu: Konikler Geçen z d, ir koni in denkleminin, düzlemin eksenlerini döndürerek ve öteleerek, 0, c ve ƒ sitleri için, 2 + c 2 = 0, 2 = ƒ, 2 + c 2 = 1, d = 2 içiminde z lilece
TG 12 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
6 2. Bir fonksiyonun bir noktadaki sürekliliği kavramını açıklar. Süreklilik
 AKSARAY KANUNİ ANADOLU İMAM HATİP LİSESİ 201-2017 EĞİTİM ÖĞRETİM YILI MATEMATİK DERSİ 12.SINIFLAR İLERİ DÜZEY ÜNİTELENDİRİLMİŞ YILLIK PLANI AY: TÜREV (70) LİMİT VE SÜREKLİLİK (14) 1. Bir fonksiyonun bir
AKSARAY KANUNİ ANADOLU İMAM HATİP LİSESİ 201-2017 EĞİTİM ÖĞRETİM YILI MATEMATİK DERSİ 12.SINIFLAR İLERİ DÜZEY ÜNİTELENDİRİLMİŞ YILLIK PLANI AY: TÜREV (70) LİMİT VE SÜREKLİLİK (14) 1. Bir fonksiyonun bir
Uzunluklar Ölçme. Çevre. Alan. Zaman Ölçme. S v lar Ölçme. Hacmi Ölçme
 MTEMT K Uzunluklr Ölçme Çevre ln Zmn Ölçme S v lr Ölçme Hcmi Ölçme Temel Kynk 5 Uzunluklr Ölçme UZUNLUKLRI ÖLÇME Çevremizde metre, sntimetre, milimetre vey bunlr n herhngi ikisi ile söyledi imiz uzunluklr
MTEMT K Uzunluklr Ölçme Çevre ln Zmn Ölçme S v lr Ölçme Hcmi Ölçme Temel Kynk 5 Uzunluklr Ölçme UZUNLUKLRI ÖLÇME Çevremizde metre, sntimetre, milimetre vey bunlr n herhngi ikisi ile söyledi imiz uzunluklr
2005 ÖSS BASIN KOPYASI SAYISAL BÖLÜM BU BÖLÜMDE CEVAPLAYACAĞINIZ TOPLAM SORU SAYISI 90 DIR. Matematiksel İlişkilerden Yararlanma Gücü,
 005 ÖSS SIN KPYSI SYISL ÖLÜM İKKT! U ÖLÜME EVPLYĞINIZ TPLM SRU SYISI 90 IR. İlk 45 Soru Son 45 Soru Mtemtiksel İlişkilerden Yrrlnm Gücü, Fen ilimlerindeki Temel Kvrm ve İlkelerle üşünme Gücü ile ilgilidir.
005 ÖSS SIN KPYSI SYISL ÖLÜM İKKT! U ÖLÜME EVPLYĞINIZ TPLM SRU SYISI 90 IR. İlk 45 Soru Son 45 Soru Mtemtiksel İlişkilerden Yrrlnm Gücü, Fen ilimlerindeki Temel Kvrm ve İlkelerle üşünme Gücü ile ilgilidir.
ORAN ORANTI 2 1 3 - - 4 4 2 1 1 2 ÖYS. = = yazılabilir. veya ALIŞTIRMALAR
 YILLAR 00 003 00 00 006 00 008 009 00 0 3 - - ÖYS ORAN ORANTI ve t. t. t.e zılilir. f Or: E z iri sıfır frklı ı iste iki çokluğu ölümüe or eir. Or irimsizir. Ortı : iki ve h fzl orı eşitliğie ortı eir.
YILLAR 00 003 00 00 006 00 008 009 00 0 3 - - ÖYS ORAN ORANTI ve t. t. t.e zılilir. f Or: E z iri sıfır frklı ı iste iki çokluğu ölümüe or eir. Or irimsizir. Ortı : iki ve h fzl orı eşitliğie ortı eir.
KULLANIM KITAPÇIĞI EFL50555OX
 TR KULLANIM KITAPÇIĞI EFL50555OX 2 www.electrolux.com 1x 1x 2x 3x Ø 10 3x Ø 6x70 6x Ø 2,9x9,5 13x Ø 3,5x6,5 1x 1x Type 14 1x 3 4 www.electrolux.com SX BACK R1 FRONT RX R1 ( ) SX BACK Y FRONT RX 3 x Ø 10mm
TR KULLANIM KITAPÇIĞI EFL50555OX 2 www.electrolux.com 1x 1x 2x 3x Ø 10 3x Ø 6x70 6x Ø 2,9x9,5 13x Ø 3,5x6,5 1x 1x Type 14 1x 3 4 www.electrolux.com SX BACK R1 FRONT RX R1 ( ) SX BACK Y FRONT RX 3 x Ø 10mm
İntegralin Uygulamaları
 Bölüm İntegrlin Uygulmlrı. Aln f ve g, [, b] rlığındki her x için f(x) g(x) eşitsizliğini sğlyn sürekli fonksiyonlr olmk üzere y = f(x), y = g(x) eğrileri, x = ve x = b düşey doğrulrı rsındki S bölgesini
Bölüm İntegrlin Uygulmlrı. Aln f ve g, [, b] rlığındki her x için f(x) g(x) eşitsizliğini sğlyn sürekli fonksiyonlr olmk üzere y = f(x), y = g(x) eğrileri, x = ve x = b düşey doğrulrı rsındki S bölgesini
1.BÖLÜM SORU SORU. Reel say larda her a ve b için a 2 b 2 = (a+b) 2 2ab biçiminde bir ifllemi tan mlan yor.
 .BÖLÜM MATEMAT K Derginin u sy s n fllem ve Moüler Aritmetik konusun çözümlü sorulr yer lmkt r. Bu konu, ÖSS e ç kn sorulr n çözümü için gerekli temel ilgileri ve prtik yollr, sorulr m z n çözümü içine
.BÖLÜM MATEMAT K Derginin u sy s n fllem ve Moüler Aritmetik konusun çözümlü sorulr yer lmkt r. Bu konu, ÖSS e ç kn sorulr n çözümü için gerekli temel ilgileri ve prtik yollr, sorulr m z n çözümü içine
EĞİTİM ÖĞRETİM YILI ANADOLU LİSESİ 12.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 12.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. ÜSTEL VE LOGARİTMİK FONKSİYONLAR
08-09 EĞİTİM ÖĞRETİM YILI ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. ÜSTEL VE LOGARİTMİK FONKSİYONLAR
Mustafa YAĞCI, yagcimustafa@yahoo.com Parabolün Tepe Noktası
 Mustf YĞCI www.mustfgci.com.tr, 11 Ceir Notlrı Mustf YĞCI, gcimustf@hoo.com Prolün Tepe Noktsı Ö nce ir prolün tepe noktsı neresidir, onu htırltlım. Kc, prolün rtmktn zlm ve zlmktn rtm geçtiği nokt dieiliriz.
Mustf YĞCI www.mustfgci.com.tr, 11 Ceir Notlrı Mustf YĞCI, gcimustf@hoo.com Prolün Tepe Noktsı Ö nce ir prolün tepe noktsı neresidir, onu htırltlım. Kc, prolün rtmktn zlm ve zlmktn rtm geçtiği nokt dieiliriz.
11. SINIF. No Konular Kazanım Sayısı GEOMETRİ TRİGONOMETRİ Yönlü Açılar Trigonometrik Fonksiyonlar
 11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
Kemalpaşa (İzmir) Kentsel Dış Mekanlarının Yeterliliği Üzerine Bir Araştırma
 Ege Üniv. Zirt Fk. Derg., 2001; 38 (2-3):143-150 ISSN 1018-8851 Kemlpş (İzmir) Kentsel Dış Meknlrının Yeterliliği Üzerine Bir Arştırm Şerif HEPCAN 1 Adnn KAPLAN 2 Erhn KÜÇÜKERBAŞ 3 Bülent ÖZKAN 4 Summry
Ege Üniv. Zirt Fk. Derg., 2001; 38 (2-3):143-150 ISSN 1018-8851 Kemlpş (İzmir) Kentsel Dış Meknlrının Yeterliliği Üzerine Bir Arştırm Şerif HEPCAN 1 Adnn KAPLAN 2 Erhn KÜÇÜKERBAŞ 3 Bülent ÖZKAN 4 Summry
BÖLÜM II B. YENĐ ÇELĐK BĐNALARIN TASARIM ÖRNEKLERĐ ÖRNEK 6 ĐKĐ DOĞRULTUDA SÜNEKLĐK DÜZEYĐ YÜKSEK MERKEZĐ ÇAPRAZ PERDELĐ ÇELĐK BĐNANIN TASARIMI
 BÖLÜM II B. YENĐ ÇELĐK BĐNALARIN TASARIM ÖRNEKLERĐ ÖRNEK 6 ĐKĐ DOĞRULTUDA SÜNEKLĐK DÜZEYĐ YÜKSEK MERKEZĐ ÇAPRAZ PERDELĐ ÇELĐK BĐNANIN TASARIMI 6.1. SĐSTEM... 6/ 6.. YÜKLER... 6/4 6..1. Düşey Yükler...
BÖLÜM II B. YENĐ ÇELĐK BĐNALARIN TASARIM ÖRNEKLERĐ ÖRNEK 6 ĐKĐ DOĞRULTUDA SÜNEKLĐK DÜZEYĐ YÜKSEK MERKEZĐ ÇAPRAZ PERDELĐ ÇELĐK BĐNANIN TASARIMI 6.1. SĐSTEM... 6/ 6.. YÜKLER... 6/4 6..1. Düşey Yükler...
EĞİTİM ÖĞRETİM YILI FEN LİSESİ 12.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 12.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. ÜSTEL VE LOGARİTMİK FONKSİYONLAR
08-09 EĞİTİM ÖĞRETİM YILI FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. ÜSTEL VE LOGARİTMİK FONKSİYONLAR
ÖZEL ÖĞRETİM KURSU MATEMATİK-IV ÇERÇEVE PROGRAMI. 2. KURUMUN ADRESİ : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA
 ÖZEL ÖĞRETİM KURSU MATEMATİK-IV ÇERÇEVE PROGRAMI 1. KURUMUN ADI : Tercih Özel Öğretim Kursu 2. KURUMUN ADRESİ : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA 3. KURUCUNUN ADI : ARTI ÖZEL EĞİTİM ÖĞRETİM
ÖZEL ÖĞRETİM KURSU MATEMATİK-IV ÇERÇEVE PROGRAMI 1. KURUMUN ADI : Tercih Özel Öğretim Kursu 2. KURUMUN ADRESİ : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA 3. KURUCUNUN ADI : ARTI ÖZEL EĞİTİM ÖĞRETİM
Dersin Kodu 1206.1105
 Genel Matematik I Dersin Adı Genel Matematik I Dersin Kodu 1206.1105 Dersin Türü Zorunlu Dersin Seviyesi Dersin AKTS Kredisi 5,00 Haftalık Ders Saati (Kuramsal) 4 Haftalık Uygulama Saati 0 Haftalık Laboratuar
Genel Matematik I Dersin Adı Genel Matematik I Dersin Kodu 1206.1105 Dersin Türü Zorunlu Dersin Seviyesi Dersin AKTS Kredisi 5,00 Haftalık Ders Saati (Kuramsal) 4 Haftalık Uygulama Saati 0 Haftalık Laboratuar
12. SINIF. Ağırlık (%) SAYILAR VE CEBİR ÜSTEL VE LOGARİTMİK FONKSİYONLAR Üstel Fonksiyon 1 8 4
 12. SINIF No Konular Kazanım Sayısı Ders Saati Ağırlık (%) 12.1. ÜSTEL VE LOGARİTMİK FONKSİYONLAR 6 36 17 12.1.1. Üstel Fonksiyon 1 8 4 12.1.2. Logaritma Fonksiyonu 3 18 8 12.1.3 Üstel, Logaritmik Denklemler
12. SINIF No Konular Kazanım Sayısı Ders Saati Ağırlık (%) 12.1. ÜSTEL VE LOGARİTMİK FONKSİYONLAR 6 36 17 12.1.1. Üstel Fonksiyon 1 8 4 12.1.2. Logaritma Fonksiyonu 3 18 8 12.1.3 Üstel, Logaritmik Denklemler
EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
SAYI KÜMELERİ. Örnek...1 :
 SAYILAR SAYI KÜMELERİ RAKAM S yı l r ı i f d e e t m ek i ç i n k u l l n d ı ğ ı m ız 0,,,,,,6,7,8,9 semollerine rkm denir. DOĞAL SAYILAR N={0,,,...,n,...} k üm e s i n e d o ğ l s yı l r k üm e s i d
SAYILAR SAYI KÜMELERİ RAKAM S yı l r ı i f d e e t m ek i ç i n k u l l n d ı ğ ı m ız 0,,,,,,6,7,8,9 semollerine rkm denir. DOĞAL SAYILAR N={0,,,...,n,...} k üm e s i n e d o ğ l s yı l r k üm e s i d
Veri, Sayma ve Olasılık. Test / 30. soru 1. soru 5. soru 2. soru 6. soru 3. soru 7. soru 8. soru 4
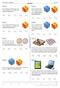 Test / 0 soru soru Bir zr t ld nd üste gelen sy n n tek oldu u ilindi ine göre, sy n n sl sy olm Bir çift zr t ld nd üste gelen sy lr n toplm n n 0 oldu u ilindi ine göre, zrlrdn irinin olm soru soru Bir
Test / 0 soru soru Bir zr t ld nd üste gelen sy n n tek oldu u ilindi ine göre, sy n n sl sy olm Bir çift zr t ld nd üste gelen sy lr n toplm n n 0 oldu u ilindi ine göre, zrlrdn irinin olm soru soru Bir
Tek ve Çift Fonksiyonlar. Özel Tanýmlý Fonksiyonlar. Bir Fonksiyonun En Geniþ Taným Kümesi. 1. Parçalý Fonksiyonlar. 2. Mutlak Deðer Fonksiyonu
 Fonksionlr Konu Özeti. Köklü fonksionlrın en geniş tnım kümesi: f( f( n f( g( fonksionun en geniş tnım kümesi, g( koşulunu sğln noktlr kümesidir. f( f( n f( g( tüm reel sılrd tnımlıdır. fonksionu g( in
Fonksionlr Konu Özeti. Köklü fonksionlrın en geniş tnım kümesi: f( f( n f( g( fonksionun en geniş tnım kümesi, g( koşulunu sğln noktlr kümesidir. f( f( n f( g( tüm reel sılrd tnımlıdır. fonksionu g( in
1. Değişkenler ve Eğriler: Matematiksel Hatırlatma
 DERS NOTU 01 Son Hli Değildir, tslktır: Ekleme ve Düzenlemeler Ypılck BİR SOSYAL BİLİM OLARAK İKTİSAT VE TEMEL KAVRAMLAR 1 Bugünki dersin işleniş plnı: 1. Değişkenler ve Eğriler: Mtemtiksel Htırltm...
DERS NOTU 01 Son Hli Değildir, tslktır: Ekleme ve Düzenlemeler Ypılck BİR SOSYAL BİLİM OLARAK İKTİSAT VE TEMEL KAVRAMLAR 1 Bugünki dersin işleniş plnı: 1. Değişkenler ve Eğriler: Mtemtiksel Htırltm...
14-18 EKİM KURBAN BAYRAMI TATİLİ VE ARA TATİL
 7-11 EKİM SAYILAR RASYONEL SAYILAR 16-227 EYLÜL/1-4 EKİM SAYILAR TAM SAYILARLA İŞLEMLER 9-13 EYLÜL 1. ÜNİTE: TAM SAYILARDAN RASYONEL SAYIL 1. Tam sayılarla toplama ve çıkarma işlemlerini yapar. [!] a-b
7-11 EKİM SAYILAR RASYONEL SAYILAR 16-227 EYLÜL/1-4 EKİM SAYILAR TAM SAYILARLA İŞLEMLER 9-13 EYLÜL 1. ÜNİTE: TAM SAYILARDAN RASYONEL SAYIL 1. Tam sayılarla toplama ve çıkarma işlemlerini yapar. [!] a-b
EĞİTİM ÖĞRETİM YILI. FEN LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
1997 ÖYS A) 30 B) 35 C) 40 D) 45 E) 50. olduğuna göre, k kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5
 7 ÖYS. 0,00 0,00 k 0,00 olduğun göre, k kçtır? 6. Bir ust günde çift ykkbı, bir klf ise günde çift ykkbı ypmktdır. İkisi birlikte, 8 çift ykkbıyı kç günde yprlr? 0 C) 0 D) 0 C) D). (0 ) ( 0) işleminin
7 ÖYS. 0,00 0,00 k 0,00 olduğun göre, k kçtır? 6. Bir ust günde çift ykkbı, bir klf ise günde çift ykkbı ypmktdır. İkisi birlikte, 8 çift ykkbıyı kç günde yprlr? 0 C) 0 D) 0 C) D). (0 ) ( 0) işleminin
TEKNOLOJİK ARAŞTIRMALAR
 www.teknolojikrstirmlr.com ISSN:- Mkine Teknolojileri Elektronik Dergisi 5 () - TEKNOLOJİK ARAŞTIRMALAR Kıs Mkle Sehim Ornın Bğlı Olrk Bir Mil Üzerinde Oluşn Sıcklık Dğılımının Arştırılmsı Vedt SAVAŞ,
www.teknolojikrstirmlr.com ISSN:- Mkine Teknolojileri Elektronik Dergisi 5 () - TEKNOLOJİK ARAŞTIRMALAR Kıs Mkle Sehim Ornın Bğlı Olrk Bir Mil Üzerinde Oluşn Sıcklık Dğılımının Arştırılmsı Vedt SAVAŞ,
SAYIM FORMÜLERİ (31 Mart saat 24 itibarıyla durumu) SAYIM ÇEVRESİ KONUT AİLE (EV HALKI) KİŞİ. Doğum tarihi. Çalışan kişi aile üyesi olarak ikamet eder
 HIRVATİSTAN CUMHURİYETİ DEVLET İSTATİSTİK KURUMU SAYIM FORMÜLERİ (31 Mrt st 24 itibrıyl durumu) Formüler P-1 İşbu formüler kpsmındki bütün bilgiler resmi sır olup sdece isttistik mçl kullnılcktır. 1. Soydı
HIRVATİSTAN CUMHURİYETİ DEVLET İSTATİSTİK KURUMU SAYIM FORMÜLERİ (31 Mrt st 24 itibrıyl durumu) Formüler P-1 İşbu formüler kpsmındki bütün bilgiler resmi sır olup sdece isttistik mçl kullnılcktır. 1. Soydı
Mil li E i tim Ba kan l Ta lim ve Ter bi ye Ku ru lu Bafl kan l n n 30.12.2009 ta rih ve 334 sa y l ka ra r ile ka bul edi len ve 2010-2011 Ö re tim
 Mil li i tim kn l T lim ve Ter bi ye u ru lu fl kn l n n 0..009 t rih ve s y l k r r ile k bul edi len ve 00-0 Ö re tim Y l n dn iti b ren uy gu ln ck oln prog r m gö re h z r ln m flt r. Genel Müdür Temel
Mil li i tim kn l T lim ve Ter bi ye u ru lu fl kn l n n 0..009 t rih ve s y l k r r ile k bul edi len ve 00-0 Ö re tim Y l n dn iti b ren uy gu ln ck oln prog r m gö re h z r ln m flt r. Genel Müdür Temel
LYS 2016 MATEMATİK ÇÖZÜMLERİ
 LYS 06 MATEMATİK ÇÖZÜMLERİ 6.. 5. 5. ( ) 8 6 65 buluruz. 5. 5 5 Doğru Cevp: C Şıkkı 8 7 ()... 9 buluruz. Doğru Cevp : D Şıkkı 9 8 8 9 8 9 8 9 9 9 9 9 8 buluruz. 8 8 8 8 8 Doğru Cevp : A Şıkkı (n )! (n
LYS 06 MATEMATİK ÇÖZÜMLERİ 6.. 5. 5. ( ) 8 6 65 buluruz. 5. 5 5 Doğru Cevp: C Şıkkı 8 7 ()... 9 buluruz. Doğru Cevp : D Şıkkı 9 8 8 9 8 9 8 9 9 9 9 9 8 buluruz. 8 8 8 8 8 Doğru Cevp : A Şıkkı (n )! (n
faydalı motor işletme sahasında her devirdeki muhtemel maksimum güç veya maksimum moment motor işletmesinin tatminkar olduğu devir ve güç sahası
 Motor izyn ve oersyon rmetreleri Motor kullnıcısı çısınn önemli ktörler şunlrır: işletme shsın motor erormnsı işletme shsın motorun ykıt tüketimi ve gereken ykıtın iytı işletme shsın motorun gürültüsü
Motor izyn ve oersyon rmetreleri Motor kullnıcısı çısınn önemli ktörler şunlrır: işletme shsın motor erormnsı işletme shsın motorun ykıt tüketimi ve gereken ykıtın iytı işletme shsın motorun gürültüsü
SORU. m(cdo ) = = 20 olur. OB = OD = OC = r den; m(bco ) = 30, m(dco ) = 20 ve. [AB ile [AD B ve D noktalar nda çembere te ettir.
 GMR eginin bu sy s nd Çembede ç l, Kiiflle ötgeni, e et Kiifl Özelliklei konusund çözümlü soul ye lmktd. u konud, ÖSS de ç kn soul n çözümü için geekli temel bilgilei ptik yoll, soul m z n çözümü içinde
GMR eginin bu sy s nd Çembede ç l, Kiiflle ötgeni, e et Kiifl Özelliklei konusund çözümlü soul ye lmktd. u konud, ÖSS de ç kn soul n çözümü için geekli temel bilgilei ptik yoll, soul m z n çözümü içinde
11. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI
 11. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Programın öğrencilerde geliştirmeyi hedeflediği becerilerle 11. sınıf matematik öğretim programı ilişkisi Modelleme/Problem çözme Matematiksel Süreç
11. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Programın öğrencilerde geliştirmeyi hedeflediği becerilerle 11. sınıf matematik öğretim programı ilişkisi Modelleme/Problem çözme Matematiksel Süreç
VORTEKS TÜPÜNDE AKIŞKAN OLARAK KULLANILAN HAVA İLE OKSİJENİN SOĞUTMA SICAKLIK PERFORMANSLARININ DENEYSEL İNCELENMESİ
 TEKNOLOJİ, Cilt 7, (24), Syı 3, 415-425 TEKNOLOJİ VORTEKS TÜPÜNDE AKIŞKAN OLARAK KULLANILAN HAVA İLE OKSİJENİN SOĞUTMA SICAKLIK PERFORMANSLARININ DENEYSEL İNCELENMESİ ÖZET Hüseyin USTA* Kevser DİNCER**
TEKNOLOJİ, Cilt 7, (24), Syı 3, 415-425 TEKNOLOJİ VORTEKS TÜPÜNDE AKIŞKAN OLARAK KULLANILAN HAVA İLE OKSİJENİN SOĞUTMA SICAKLIK PERFORMANSLARININ DENEYSEL İNCELENMESİ ÖZET Hüseyin USTA* Kevser DİNCER**
Hiperbolde Yolculuk (ve Poncelet Teoremleri)
 Kpk Konusu: oncele Teoremleri Hiperbolde Yolculuk (ve oncele Teoremleri) Bu yz d hiperbolleri ele lc z. Tek bfl n... Yz m zdki her fley. Nzmi lker le Nâz m Terzio lu nun yzd Konikler [fiirkei üreibiye
Kpk Konusu: oncele Teoremleri Hiperbolde Yolculuk (ve oncele Teoremleri) Bu yz d hiperbolleri ele lc z. Tek bfl n... Yz m zdki her fley. Nzmi lker le Nâz m Terzio lu nun yzd Konikler [fiirkei üreibiye
LYS Matemat k Deneme Sınavı
 LYS Mtemtk Deneme Sınvı. İki bsmklı bir sının rkmlrı toplmı dir. Rkmlrı er değiştirdiğinde elde edilen sı, ilk sının sinden fzldır.. Birbirinden frklı tne pozitif tmsının OKEK i olduğun göre, en çok kçtır?
LYS Mtemtk Deneme Sınvı. İki bsmklı bir sının rkmlrı toplmı dir. Rkmlrı er değiştirdiğinde elde edilen sı, ilk sının sinden fzldır.. Birbirinden frklı tne pozitif tmsının OKEK i olduğun göre, en çok kçtır?
1993 ÖYS. 1. Rakamları birbirinden farklı olan üç basamaklı en büyük tek sayı aşağıdakilerden hangisine kalansız bölünebilir?
 ÖYS. Rkmlrı birbirinden frklı oln üç bsmklı en büyük tek syı şğıdkilerden hngisine klnsız bölünebilir? D) 8 E) 7. +b= b olduğun göre, b kçtır? D) 8 E). İki bsmklı, birbirinden frklı pozitif tmsyının toplmı
ÖYS. Rkmlrı birbirinden frklı oln üç bsmklı en büyük tek syı şğıdkilerden hngisine klnsız bölünebilir? D) 8 E) 7. +b= b olduğun göre, b kçtır? D) 8 E). İki bsmklı, birbirinden frklı pozitif tmsyının toplmı
Cevap: Cevap: Cevap: Cevap: Sayfa 1
 1 639 syılı Gı Trım ve Hyvnılık Bknlığının Teşkilt ve Görevleri Hkkın Knun Hükmüne Krrnmeye göre şğıkileren hngisi Hyvnılık Genel Müürlüğünün görevlerinen iri eğilir? ) Hyvnılığı geliştirmek, teşvik etmek
1 639 syılı Gı Trım ve Hyvnılık Bknlığının Teşkilt ve Görevleri Hkkın Knun Hükmüne Krrnmeye göre şğıkileren hngisi Hyvnılık Genel Müürlüğünün görevlerinen iri eğilir? ) Hyvnılığı geliştirmek, teşvik etmek
Ö.Y.S. 1998. MATEMATĐK SORULARI ve ÇÖZÜMLERĐ
 Ö.Y.S. 998 MATEMATĐK SORULARI ve ÇÖZÜMLERĐ. Üç bsmklı bir doğl syısının ktı, iki bsmklı bir y doğl syısın eşittir. 7 Bun göre, y doğl syısı en z kç olbilir? A) B) C) 8 D) E) Çözüm y 7 7y (, en küçük bsmklı,
Ö.Y.S. 998 MATEMATĐK SORULARI ve ÇÖZÜMLERĐ. Üç bsmklı bir doğl syısının ktı, iki bsmklı bir y doğl syısın eşittir. 7 Bun göre, y doğl syısı en z kç olbilir? A) B) C) 8 D) E) Çözüm y 7 7y (, en küçük bsmklı,
RASYONEL SAYILAR KESİR ÇEŞİTLERİ. www.unkapani.com.tr. 1. Basit Kesir. olduğuna göre, a, b tamsayı ve b 0 olmak üzere, a şeklindeki ifadelere
 RASYONEL SAYILAR, tmsyı ve 0 olmk üzere, şeklindeki ifdelere kesir denir. y kesrin pyı, ye kesrin pydsı denir. Örneğin,,,, kesirdir. kesrinde, py kesir çizgisi pyd, 0, 0 ise 0 0 dır.,, 0, syılrı irer 0
RASYONEL SAYILAR, tmsyı ve 0 olmk üzere, şeklindeki ifdelere kesir denir. y kesrin pyı, ye kesrin pydsı denir. Örneğin,,,, kesirdir. kesrinde, py kesir çizgisi pyd, 0, 0 ise 0 0 dır.,, 0, syılrı irer 0
Y = f(x) denklemi ile verilen fonksiyonun diferansiyeli dy = f '(x). dx tir.
 1 İNTEGRAL BİR FONKSİYONUN DİFERANSİYELİ Tanım: f: [a,b] R, x f(x) fonksiyonu (a,b) aralığında türevli olmak üzere, x değişkeninin değişme miktarı x ise f '(x). x ifadesine f(x) fonksiyonunun diferansiyeli
1 İNTEGRAL BİR FONKSİYONUN DİFERANSİYELİ Tanım: f: [a,b] R, x f(x) fonksiyonu (a,b) aralığında türevli olmak üzere, x değişkeninin değişme miktarı x ise f '(x). x ifadesine f(x) fonksiyonunun diferansiyeli
ÇELİK YAPILAR DERS NOTLARI
 ÇELİK YAILAR DERS NOTLARI Skry Üniversitesi Mühendislik Fkültesi İnşt Mühendisliği Bölümü 1- Çeliğin Trihçesi Ülkemizle trihsel ilişkisi Demir : Düşük ornd krbon(c) içerir, yumuşk, ergime noktsı:1500 0
ÇELİK YAILAR DERS NOTLARI Skry Üniversitesi Mühendislik Fkültesi İnşt Mühendisliği Bölümü 1- Çeliğin Trihçesi Ülkemizle trihsel ilişkisi Demir : Düşük ornd krbon(c) içerir, yumuşk, ergime noktsı:1500 0
Ünite Planı Şablonu. Öğretmenin. Fatma BAĞATARHAN Yunus Emre Anadolu Lisesi. Ġnönü Mahallesi. Bingöl. Adı, Soyadı. Okulunun Adı
 Intel Öğretmen Progrmı Ünite Plnı Şlonu Öğretmenin Adı, Soydı Okulunun Adı Okulunun Bulunduğu Mhlle Okulun Bulunduğu Ġl Ftm BAĞATARHAN Yunus Emre Andolu Lisesi Ġnönü Mhllesi Bingöl Ünit Bilgisi Ünite Bşlığı
Intel Öğretmen Progrmı Ünite Plnı Şlonu Öğretmenin Adı, Soydı Okulunun Adı Okulunun Bulunduğu Mhlle Okulun Bulunduğu Ġl Ftm BAĞATARHAN Yunus Emre Andolu Lisesi Ġnönü Mhllesi Bingöl Ünit Bilgisi Ünite Bşlığı
ÇÖZÜMLER. 3. I. Ortam sürtünmesiz ise, a) Di na mi ğin te mel pren si bi sis te me uy gu lan dığın 30 T 1 T 1. II. Ortamın sürtünme katsayısı 0,1 ise,
 BÖÜM DİNAMİ AIŞIRMAAR ÇÖZÜMER DİNAMİ 1 4kg 0N yty M düzle rsınd : rsınd cisin ivesi /s olduğundn cise uygulnn kuvvet, 1 4 0 N olur M rsınd : M rsınd cisin ivesi /s olduğundn cise etki eden sürtüne kuvveti,
BÖÜM DİNAMİ AIŞIRMAAR ÇÖZÜMER DİNAMİ 1 4kg 0N yty M düzle rsınd : rsınd cisin ivesi /s olduğundn cise uygulnn kuvvet, 1 4 0 N olur M rsınd : M rsınd cisin ivesi /s olduğundn cise etki eden sürtüne kuvveti,
MATEMATİK (haftalık ders sayısı 5, yıllık toplam 90 ders saati)
 MATEMATİK (haftalık ders sayısı 5, yıllık toplam 90 ders saati) GİRİŞ XXI. yüzyılda matematik eğitimi yalnız doğa olaylarının araştırmasında ve teknikte değil insan oğlunun mantıklı, eleştirel ve estetik
MATEMATİK (haftalık ders sayısı 5, yıllık toplam 90 ders saati) GİRİŞ XXI. yüzyılda matematik eğitimi yalnız doğa olaylarının araştırmasında ve teknikte değil insan oğlunun mantıklı, eleştirel ve estetik
( x y ) 2 = 3 2, x. y = 5 tir. x 2 + y 2 2xy = 9. x 2 + y 2 = 19 bulunur. Cevap D / 24 / 0 ( mod 8 ) Pikaçu.
 eneme - / YT / MT MTMTİK NMSİ. I. KK (, ) = : Z II. KK (, ) = : Z III. KK ( 8, ) = 7 7 : Z. - - = = ( ) ile. rlrınd sl ise ( ) =,. = tir. + = + = bulunur. evp evp. + / / ( mod 8 ) Pikçu. M n + n n + 8
eneme - / YT / MT MTMTİK NMSİ. I. KK (, ) = : Z II. KK (, ) = : Z III. KK ( 8, ) = 7 7 : Z. - - = = ( ) ile. rlrınd sl ise ( ) =,. = tir. + = + = bulunur. evp evp. + / / ( mod 8 ) Pikçu. M n + n n + 8
TÜREV VE UYGULAMALARI
 TÜREV VE UYGULAMALARI 1-TÜREVİN TANIMI VE GÖSTERİLİŞİ a,b R olmak üzere, f:[a,b] R fonksiyonu verilmiş olsun. x 0 (a,b) için lim x X0 f(x)-f( x 0 ) limiti bir gerçel sayı ise bu limit değerine f fonksiyonunun
TÜREV VE UYGULAMALARI 1-TÜREVİN TANIMI VE GÖSTERİLİŞİ a,b R olmak üzere, f:[a,b] R fonksiyonu verilmiş olsun. x 0 (a,b) için lim x X0 f(x)-f( x 0 ) limiti bir gerçel sayı ise bu limit değerine f fonksiyonunun
LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK-GEOMETRİ SINAVI MATEMATİK TESTİ SORU KİTAPÇIĞI
 LİSANS YERLEŞTİRME SINAVI- MATEMATİK-GEOMETRİ SINAVI MATEMATİK TESTİ SORU KİTAPÇIĞI 09 BU SORU KİTAPÇIĞI LYS- MATEMATİK TESTİ SORULARINI İÇERMEKTEDİR. . Bu testte 0 soru vrdýr. MATEMATİK TESTİ. Cevplrýnýzý,
LİSANS YERLEŞTİRME SINAVI- MATEMATİK-GEOMETRİ SINAVI MATEMATİK TESTİ SORU KİTAPÇIĞI 09 BU SORU KİTAPÇIĞI LYS- MATEMATİK TESTİ SORULARINI İÇERMEKTEDİR. . Bu testte 0 soru vrdýr. MATEMATİK TESTİ. Cevplrýnýzý,
4- SAYISAL İNTEGRAL. c ϵ R olmak üzere F(x) fonksiyonunun türevi f(x) ise ( F (x) = f(x) ); denir. f(x) fonksiyonu [a,b] R için sürekli ise;
![4- SAYISAL İNTEGRAL. c ϵ R olmak üzere F(x) fonksiyonunun türevi f(x) ise ( F (x) = f(x) ); denir. f(x) fonksiyonu [a,b] R için sürekli ise; 4- SAYISAL İNTEGRAL. c ϵ R olmak üzere F(x) fonksiyonunun türevi f(x) ise ( F (x) = f(x) ); denir. f(x) fonksiyonu [a,b] R için sürekli ise;](/thumbs/24/3918052.jpg) 4- SAYISAL İNTEGRAL c ϵ R olmk üzere F() onksiyonunun türevi () ise ( F () = () ); Z ` A d F ` c eşitliğindeki F()+c idesine, () onksiyonunun elirsiz integrli denir. () onksiyonu [,] R için sürekli ise;
4- SAYISAL İNTEGRAL c ϵ R olmk üzere F() onksiyonunun türevi () ise ( F () = () ); Z ` A d F ` c eşitliğindeki F()+c idesine, () onksiyonunun elirsiz integrli denir. () onksiyonu [,] R için sürekli ise;
LYS Matemat k Deneme Sınavı
 LYS Mtemtk Deneme Sınvı 8. sısının pozitif tek tmsı bölenlerinin sısı kçtır? 8. olmk üzere; kesrinin değeri şğıdkilerden hngisi olmz?. (8!) sısının sondn kç bsmğı sıfırdır? 8. ifdesinin sonucu kçtır? (
LYS Mtemtk Deneme Sınvı 8. sısının pozitif tek tmsı bölenlerinin sısı kçtır? 8. olmk üzere; kesrinin değeri şğıdkilerden hngisi olmz?. (8!) sısının sondn kç bsmğı sıfırdır? 8. ifdesinin sonucu kçtır? (
2014 LYS MATEMATİK. P(x) x 2 x 3 polinomunda. 2b a ifade- x lü terimin. olduğuna göre, katsayısı kaçtır? değeri kaçtır? ifadesinin değeri kaçtır? 4.
 04 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. P() polinomunda katsayısı kaçtır? 4 lü terimin. ifadesinin değeri kaçtır? 4. yy y 4y y olduğuna göre, + y toplamının değeri kaçtır?
04 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. P() polinomunda katsayısı kaçtır? 4 lü terimin. ifadesinin değeri kaçtır? 4. yy y 4y y olduğuna göre, + y toplamının değeri kaçtır?
HİPERBOL. Merkezi O noktası olan hiperbole merkezil hiperbol denir. F ve F' noktalarına hiperbolün odakları denir.
 Merkezi Hiperoll HİPERBL Merkezi noktsı oln hiperole merkezil hiperol denir. F ve F' noktlrın hiperolün odklrı denir. dklr rsı uzklık FF' dir. odklr rsı uzklık e sl eksen uzunluğu değerine hiperolün dış
Merkezi Hiperoll HİPERBL Merkezi noktsı oln hiperole merkezil hiperol denir. F ve F' noktlrın hiperolün odklrı denir. dklr rsı uzklık FF' dir. odklr rsı uzklık e sl eksen uzunluğu değerine hiperolün dış
Trigonometri - I. Isınma Hareketleri. 1 Aşağıda verilenleri inceleyiniz. 2 Uygun eşleştirmeleri yapınız. 3 Uygun eşleştirmeleri yapınız.
 Isınm Hreketleri şğıd verilenleri inceleyiniz. Yönlü çı: Trigonometrik irim Çember: Merkezi orjin, yrıçpı br oln çemberdir. O + yön éo Pozitif yönlü (Stin tersi) O yön éo Negtif yönlü (St yönü) O y x Denklemi:
Isınm Hreketleri şğıd verilenleri inceleyiniz. Yönlü çı: Trigonometrik irim Çember: Merkezi orjin, yrıçpı br oln çemberdir. O + yön éo Pozitif yönlü (Stin tersi) O yön éo Negtif yönlü (St yönü) O y x Denklemi:
Belirli ntegral Uygulamalar
 iv CHAPTER 4 Belirli ntegrl Uygulmlr Belirli integrlin b³lc uygulmlr ³unlrdr. (1) Uzunluk () Düzlemsel e rilerin uzunlu u (2) Aln (3) () Düzlemde iki e ri rsnd kln ln (b) Dönel yüzeylerin ln (4) Ortlm
iv CHAPTER 4 Belirli ntegrl Uygulmlr Belirli integrlin b³lc uygulmlr ³unlrdr. (1) Uzunluk () Düzlemsel e rilerin uzunlu u (2) Aln (3) () Düzlemde iki e ri rsnd kln ln (b) Dönel yüzeylerin ln (4) Ortlm
İstatistik I Bazı Matematik Kavramlarının Gözden
 İsttistik I Bzı Mtemtik Kvrmlrının Gözden Geçirilmesi Hüseyin Tştn Ağustos 13, 2006 İçindekiler 1 Toplm İşlemcisi 2 2 Çrpım İşlemcisi 6 3 Türev 7 3.1 Türev Kurllrı.......................... 8 3.1.1 Sbit
İsttistik I Bzı Mtemtik Kvrmlrının Gözden Geçirilmesi Hüseyin Tştn Ağustos 13, 2006 İçindekiler 1 Toplm İşlemcisi 2 2 Çrpım İşlemcisi 6 3 Türev 7 3.1 Türev Kurllrı.......................... 8 3.1.1 Sbit
ANKARA ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ DOKTORA TEZĐ YARI-SONSUZ ZAMAN SKALALARI ÜZERĐNDE STURM-LIOUVILLE OPERATÖRÜ. Adil HUSEYNOV ANKARA 2010
 ANKARA ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ DOKTORA TEZĐ YARI-SONSUZ ZAMAN SKALALARI ÜZERĐNDE STURM-LIOUVILLE OPERATÖRÜ Adil HUSEYNOV MATEMATĐK ANABĐLĐM DALI ANKARA 200 Her hkkı sklıdır ÖZET Doktor Tezi
ANKARA ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ DOKTORA TEZĐ YARI-SONSUZ ZAMAN SKALALARI ÜZERĐNDE STURM-LIOUVILLE OPERATÖRÜ Adil HUSEYNOV MATEMATĐK ANABĐLĐM DALI ANKARA 200 Her hkkı sklıdır ÖZET Doktor Tezi
Anadolu Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2015-2016 Güz Dönemi
 Andolu Üniversitesi Mühendislik Fkültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Plnlmsı 2015-2016 Güz Dönemi 2 Tesis (fcility) Tesis : Belli bir iş için kurulmuş ypı Tesis etmek :
Andolu Üniversitesi Mühendislik Fkültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Plnlmsı 2015-2016 Güz Dönemi 2 Tesis (fcility) Tesis : Belli bir iş için kurulmuş ypı Tesis etmek :
1. x 1 x. Çözüm : (x 1 x. (x 1 x )2 = 3 2 x 2 2x = 1 x + 1 x2 = 9. x x2 = 9 x2 + 1 x2. 2. x + 1 x = 8 ise x 1 x
 MC www.mtemtikclub.com, 006 Cebir Notlrı Çrpnlr Ayırm Gökhn DEMĐR, gdemir3@yhoo.com.tr Đki ifdenin çrpımı ypılırken, sonuc çbuk ulşmk için, bzı özel çrpımlrın eşitini klımızd tutr ve bundn yrrlnırız. Bu
MC www.mtemtikclub.com, 006 Cebir Notlrı Çrpnlr Ayırm Gökhn DEMĐR, gdemir3@yhoo.com.tr Đki ifdenin çrpımı ypılırken, sonuc çbuk ulşmk için, bzı özel çrpımlrın eşitini klımızd tutr ve bundn yrrlnırız. Bu
Mimari Anlatım Teknikleri I (MMR 103) Ders Detayları
 Mimari Anlatım Teknikleri I (MMR 103) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Mimari Anlatım Teknikleri I MMR 103 Güz 2 2 0 3 5 Ön Koşul Ders(ler)i
Mimari Anlatım Teknikleri I (MMR 103) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Mimari Anlatım Teknikleri I MMR 103 Güz 2 2 0 3 5 Ön Koşul Ders(ler)i
Ossmat.com Matematik-Fizik-Kimya-Biyoloji Hakkında Herşey (ana sayfaya git)
 Facebook Fun Sayfamız Twitter Sayfamız Ossmat.com Matematik-Fizik-Kimya-Biyoloji Hakkında Herşey (ana sayfaya git) (adsbygoogle = window.adsbygoogle []).push({}); Çıkmış Soru Çözümlerİ Çözümleri Matematik
Facebook Fun Sayfamız Twitter Sayfamız Ossmat.com Matematik-Fizik-Kimya-Biyoloji Hakkında Herşey (ana sayfaya git) (adsbygoogle = window.adsbygoogle []).push({}); Çıkmış Soru Çözümlerİ Çözümleri Matematik
Matematik. Sosyal Bilgiler
 Matematik 5 Sosyal Bilgiler KUZEY KIBRIS TÜRK CUMHURÝYETÝ MÝLLÝ EÐÝTÝM VE KÜLTÜR BAKANLIÐI TALÝM VE TERBÝYE DAÝRESÝ MÜDÜRLÜÐÜ ÝLKOKUL (TEMEL EÐÝTÝM I. KADEME) MATEMATÝK DERSÝ ÖÐRETÝM PROGRAMI ÇALIÞMA TASLAÐI
Matematik 5 Sosyal Bilgiler KUZEY KIBRIS TÜRK CUMHURÝYETÝ MÝLLÝ EÐÝTÝM VE KÜLTÜR BAKANLIÐI TALÝM VE TERBÝYE DAÝRESÝ MÜDÜRLÜÐÜ ÝLKOKUL (TEMEL EÐÝTÝM I. KADEME) MATEMATÝK DERSÝ ÖÐRETÝM PROGRAMI ÇALIÞMA TASLAÐI
VEKTÖRLER ÜNİTE 5. ÜNİTE 5. ÜNİTE 5. ÜNİTE 5. ÜNİT
 VKTÖRLR ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT VKTÖRLR 1. Kznım : Vektör kvrmını çıklr.. Kznım : İki vektörün toplmını ve vektörün ir gerçek syıyl çrpımını ceirsel ve geometrik olrk gösterir. VKTÖRLR 1.
VKTÖRLR ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT VKTÖRLR 1. Kznım : Vektör kvrmını çıklr.. Kznım : İki vektörün toplmını ve vektörün ir gerçek syıyl çrpımını ceirsel ve geometrik olrk gösterir. VKTÖRLR 1.
Tasarım Psikolojisi (SEÇ356) Ders Detayları
 Tasarım Psikolojisi (SEÇ356) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Tasarım Psikolojisi SEÇ356 Seçmeli 2 0 0 2 5 Ön Koşul Ders(ler)i Dersin Dili
Tasarım Psikolojisi (SEÇ356) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Tasarım Psikolojisi SEÇ356 Seçmeli 2 0 0 2 5 Ön Koşul Ders(ler)i Dersin Dili
YÜKSEKÖĞRETİM KURUMLARI SINAVI MATEMATİK SORU BANKASI ANKARA
 YÜKSEKÖĞRETİM KURUMLARI SINAVI MATEMATİK SORU ANKASI ANKARA İÇİNDEKİLER Fonksionlr... Polinomlr... II. Dereceden Denklemler... 7 II. Dereceden Fonksionlrın Grfiği (Prbol)... 7 Krmşık Sılr... 9 Mntık...
YÜKSEKÖĞRETİM KURUMLARI SINAVI MATEMATİK SORU ANKASI ANKARA İÇİNDEKİLER Fonksionlr... Polinomlr... II. Dereceden Denklemler... 7 II. Dereceden Fonksionlrın Grfiği (Prbol)... 7 Krmşık Sılr... 9 Mntık...
5. a ve b pozitif tamsay lard r say taban olmak üzere,
 1. ve b pozitif tmsy lrd r. + b = 13 oldu un göre, + 3b toplm n n en büyük de eri kçt r? 5. ve b pozitif tmsy lrd r. Yndki bölme iflleminde, n n lbilece i en büyük de er kçt r? b 8 b 8 ) 4 ) 8 ) 34 ) 37
1. ve b pozitif tmsy lrd r. + b = 13 oldu un göre, + 3b toplm n n en büyük de eri kçt r? 5. ve b pozitif tmsy lrd r. Yndki bölme iflleminde, n n lbilece i en büyük de er kçt r? b 8 b 8 ) 4 ) 8 ) 34 ) 37
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal I / 27 Kasım Matematik Sorularının Çözümleri
 Akdemik Personel ve Lisnsüstü Eğitimi Giriş Sınvı ALES / Sonbhr / Syısl I / 7 Ksım 011 Mtemtik Sorulrının Çözümleri 1 1 1 1. 1. + + 1 1. + 3 6 1 3 1 + 3 6 3 1. + + 1 1 1 6+ + 3 1. 1 13 1. 1 13. 5.10 +
Akdemik Personel ve Lisnsüstü Eğitimi Giriş Sınvı ALES / Sonbhr / Syısl I / 7 Ksım 011 Mtemtik Sorulrının Çözümleri 1 1 1 1. 1. + + 1 1. + 3 6 1 3 1 + 3 6 3 1. + + 1 1 1 6+ + 3 1. 1 13 1. 1 13. 5.10 +
1) Öğrenci kendi başına proje yapma becerisini kazanır. 1,3,4 1,2
 DERS BİLGİLERİ Ders Adı Kodu Yarıyılı T+U Saati Ulusal Kredisi AKTS Bitirme Projesi BIL401 7 0+4 2 5 Ön Koşul Dersleri Yok Dersin Dili Dersin Seviyesi Dersin Türü Türkçe Lisans Seçmeli / Yüz Yüze Dersin
DERS BİLGİLERİ Ders Adı Kodu Yarıyılı T+U Saati Ulusal Kredisi AKTS Bitirme Projesi BIL401 7 0+4 2 5 Ön Koşul Dersleri Yok Dersin Dili Dersin Seviyesi Dersin Türü Türkçe Lisans Seçmeli / Yüz Yüze Dersin
BİR SAYININ ÖZÜ VE DÖRT İŞLEM
 ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
