Belirsiz Integraller. 1.1 Ilkel Fonksiyon ve Belirsiz Integral Temel Tan mlar ve Sonuc. lar
|
|
|
- Aygül Hussein
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Ic. indekiler Belirsiz Integraller 3. Ilkel Fonksiyon ve Belirsiz Integral Temel Tan mlar ve Sonuc.lar Temel Integral Alma Yöntemleri De giṣken De giṣtirme Yöntemi K smi Integrasyon Yöntemi Rasyonel Kesirlerin Integrallenmesi Baz Irrasyonel Cebirsel Ifadelerin Integrallenmesi Binom Diferensiyellerinin Integrallenmesi Trigonometrik ifadelerin Integrallenmesi
2
3 Bölüm Belirsiz Integraller Matematikte ve hemen hemen bütün bilim dallar nda verilen bir fonksiyonun türevinin bulunmas iṣleminin tersi olan integral alma, yani, türevi belli olan fonksiyonun kendisinin bulunmas problemi ile karṣ laṣ l r. Bu bölümde analizin en önemli kavramlar ndan biri olan ilkel fonksiyon ve belirsiz integral kavramlar tan mlanacak ve c.eṣitli integral alma yöntemleri incelenecektir.. Ilkel Fonksiyon ve Belirsiz Integral.. Temel Tan mlar ve Sonuc. lar Sonlu veya sonsuz (ac. k, kapal veya yar ac. k) bir I R aral g ve I üzerinde tan ml f; F : I! R fonksiyonlar verilmiṣ olsun. Tan m.. : E ger, F fonksiyonu I üzerinde türevlenebilir ve 8 I ic.in F 0 () f() ise, F () fonksiyonuna f nin I üzerinde ilkel fonksiyonu (veya antitürevi) denir. Not: a; b R; I [a; b] (ya da I [a; ) veya I ( ; b];) durumunda F nin a noktas nda sa gdan ve b noktas nda soldan türevlenebilir 3
4 4 Belirsiz Integraller oldu gu varsay l r. Verilen bir noktada türevli bir fonksiyon bu noktada sürekli oldu guna göre f nin I üzerindeki F ilkel fonksiyonu I üzerinde süreklidir. Örne gin, F () 4 4 ve F () sin fonksiyonlar s ras yla f () 3 ve f () cos fonksiyonlar ninn R üzerinde ilkel fonksiyonlar d r, c.ünkü 8 R ic.in ( 4 4 )0 3 ve (sin ) 0 cos dir. F 3 () p ve F 4 () ln fonksiyonlar s ras yla f 3 () p ve f 4 () fonksiyonlar n n ( ; ) ve (0; +) üzerinde ilkel fonksiyonlar d r, c.ünkü 8 ( ; ) ic.in ( p ) 0 p ve 8 (0; +) ic.in (ln ) 0 dir. Teorem.. : I R üzerinde türevlenebilir iki F; G : I! R fonksiyonlar n n ayn bir f : I! R fonksiyonunun ilkel fonksiyonlar olmas ic. in gerek ve yeter koṣul G() F () fonksiyonunun I üzerinde sabit bir fonksiyon, yani c key bir say olmak üzere 8 I ic.in G() F () + c olmas d r. Ispat: E ger, F : I! R fonksiyonu f nin I üzerinde bir ilkel fonksiyonu, yani 8 I ic.in F 0 () f() ise, c key bir say olmak üzere 8 I ic.in (F () + c) 0 F 0 () f() oldu guna göre F () + c fonksiyonu da f nin I üzerinde bir ilkel fonksiyonudur. E ger, F; G : I! R fonksiyonlar f nin I üzerinde iki ilkel fonksiyonlar, yani 8 I ic.in F 0 () f() G 0 () ise, 8 I ic.in (G() F ()) 0 G 0 () F 0 () f() f() 0 elde ederiz ki buradan G F fonksiyonu I üzerinde sabit bir fonksiyon, yani c key bir say olmak üzere 8 I ic.in G() F () c veya G() F () + c oldu gu anlaṣ l r. Tan m..3 : I R üzerinde tan ml f : I! R fonksiyonunun I üzerindeki tüm ilkel fonksiyonlar s n f na f nin I üzerinde belirsiz integrali denir ve f()d (.) sembolü ile gösterilir. R simgesine integral iṣareti, f() ifadesine integrant ve e de integrasyon de giṣkeni denir.
5 Ilkel Fonksiyon ve Belirsiz Integral 5 E ger, F : I! R fonksiyonu f nin I üzerinde bir ilkel fonksiyonu ise, Teorem.. gere gince c key bir say olmak üzere f()d F () + c (.) olur. Burada, c ye integrasyon sabiti denir. Örne gin, p fonksiyonu ( ; ) üzerinde p fonksiyonunun bir ilkel fonksiyonu oldu guna göre, c key bir say olmak üzere 8 ( p d p + c olur. Not: ; ) ic.in Verilen bir fonksiyonun herhangi bir aral k üzerindeki ilkel fonksiyonunun (veya belirsiz integralinin) varl gi problemi 6. Bölümde incelenecektir. Ṣimdilik belirtelim ki, bir I R aral ginda sürekli her fonksiyonun bu aral k üzerindeki ilkel fonksiyonu (veya belirsiz integrali) vard r (Bkz. Böl.6.4). Örnek..4 : f() sgn fonksiyonunun her I ( ; 0) (veya I (0; +)) aral ginda ilkel fonksiyonunun varl g n ve 0 I olmak üzere her I R aral ginda ilkel fonksiyonunun var olmad g n gösteriniz. C. özüm: Her I ( ; 0) (veya (I (0; +)) üzerinde sgn (sgn ) oldu guna göre, c key bir say olmak üzere 8 I ic.in F () oldu gu ac. kt r. +c (F () +c) fonksiyonu I üzerinde f nin bir ilkel fonksiyonu Ṣimdi a < 0 ve b > 0 olmak üzere f nin [a; b] üzerinde ilkel fonksiyonunun varolmad g n görelim. sgn fonksiyonunun s ras yla [a; 0) ve (0; b] aral klar nda ilkel fonksiyonlar F () + c ve F () + c dir. Burada,c ve c key say lard r. 0 noktas nda tan ml oldu gu varsay lsa bile ( + c ; [a; 0); F () + c ; (0; b]
6 6 Belirsiz Integraller fonksiyonu 0 noktas nda türevli de gildir. Demek ki, f() sgn fonksiyonunun 0 noktas n ic.eren her I R aral g üzerinde ilkel fonksiyonu yoktur. Ṣimdi belirsiz integrallerin aṣa g daki özelliklerini verelim. () ( R f()d) 0 f() veya d( R f()d) f()d: () R df () F () + c: (3) R [f() g()]d R f()d R g()d: (4) Her 6 0 reel say s ic.in [f()]d f()d: (3) ve (4) özellikleri gözönüne al n rsa ve s f rdan farkl herhangi reel say lar olmak üzere [f() + g()]d yaz labilir. f()d + g()d (5) Herhangi bir I R aral g nda F 0 () f() ise a 6 0 ve b herhangi reel say lar olmak üzere f(a + b)d F (a + b) + c a dir. S ralanan bu özelliklerin do gru oldu gu türevle ilgili bilgilere dayanarak ispatlanabilir. Örne gin, (4) özelli ginin do gru oldu gunu gösterelim. () özelli gi gözönüne al narak her iki taraf n türevi al n rsa ( f()]d) 0 ( f()d) 0 ) f() f()
7 Ilkel Fonksiyon ve Belirsiz Integral 7 elde ederiz. 6 0 koṣulunu inceleyelim. E ger, F : I! R fonksiyonu f : I! R nin I üzerinde bir ilkel fonksiyonu ise c key bir say olmak üzere 8 I ic.in R [0f()]d R 0d c; fakat, 0 R f()d 0(F () + c) 0 olur. Böylece 0 durumunda (4) özelli gi genel olarak sa glanamaz. Not: Ṣu ana kadar ifade edilenlerden de anlaṣ laca g gibi (3) ve (4) teki eṣitlikler veya belirsiz integraller ic.eren herhangi iki ifadenin eṣitli gi fonksiyonlardan oluṣan iki kümenin eṣitli gi anlam n taṣ maktad r. (3) özelli gi sa g taraf iki kümenin aritmetik toplam d r. Demek ki, (3) özelli gi f ve g fonksiyonlar n n ilkel fonksiyonlar n n toplam f + g nin bir ilkel fonksiyonu f ve g lerin herhangi ilkel fonksiyonlar n n toplam olmas demektir. E ger, F : I! R (I R) fonksiyonu bir f : I! R fonksiyonunun I üzerinde bir ilkel fonksiyonu, yani 8 I ic.in F 0 () f() ise c key bir say olmak üzere f()d F () + c olacakt r. Demek ki, integrali al nacak ifadenin (integrant n) hangi fonksiyonun türevi oldu gu görülebiliyorsa, bu fonksiyona key bir c sabit say s eklemek suretiyle integral al nm ṣ olur. Buna göre, diferensiyel hesab nda elementer fonksiyonlarla ilgili gördü gümüz temel türev formülleri (Bkz. Böl. 4, Tablo 4.) yard m yla aṣa g daki integral formüllerini tablo halinde yazabiliriz. () R d c ( 6 ): () R d ln j j +c ( 6 0): (3) R a d a + c (a > 0; a 6 ): ln a (4) R e d e + c: (5) R sin d cos + c: (6) R cos d sin + c: (7) R d tan + c ( 6 + n; n ): cos
8 8 Belirsiz Integraller (8) R d sin cot + c ( 6 n; n ): (9) R sinh d cosh + c: (0) R cosh d sinh + c: () R d cosh () R d sinh tanh + c: coth + c ( 6 0): (3) R d + arctan + c arcot + c: (4) R d p arcsin + c arccos + c ( < < ): (5) R d + ln j j +c (j j6 ): (6) R d p + ln( + p + ) + c: (7) R d p ln( + p ) + c (j j> ): Örnek..5 : Aṣa g daki integralleri hesaplay n z. (a) A R (a 0 + a + + a n n )d; (b) A R 4 5 4p +3 d ( > 0); (c) A 3 R ( p ) 3 d ( > 0); (d) (e) A 4 R (3 + 5 ) d; A 5 R sin d; (f) A 6 R cos(a + b)d (a 6 0); (g) A 7 R sin(a + b)d (a 6 0): C. özüm: Verilen integraller integrantlar üzerinde gerekli sadeleṣtirmeler yap larak belirsiz integralin (3) ve (4) özellikleri yard m yla tablo integrallerinin uygulanabilece gi duruma dönüṣtürülerek hesaplan r. (a) A a 0 R d + a R d + + an R n d a 0 + a + + n + a n n+ + c:
9 Ilkel Fonksiyon ve Belirsiz Integral 9 (b) A R ( )d 3 d 5 4 d + 3 d 4 4 4p + 3 ln jj + c: (c) A 3 R ( 3 3 p + 3 ( p ) ( p )d ) 3 3 d 3 3 d + 3 d 3 d p p + c; > 0: (d) A 4 R (3 + :3 :5 + 5 )d 9 d + 5 d + 9 ln 9 + ln ln 5 + c: (e) A 5 R ( cos )d (f) d cos d sin + c: Belirsiz integralin (5) özelli gine göre A 6 sin(a + b) + c a 5 d ve benzer ṣekilde (g) A 7 cos(a + b) + c; a 6 0: a olur. Not: Herhangi bir elementer fonksiyonun türevi de bir elementer fonksiyon oldu gunu Bölüm 4 te inceledik. Baṣka bir deyiṣle, elementer fonksiyonlar
10 0 Belirsiz Integraller s n f nda türev alma iṣlemi kapal l k özelli gine sahiptir. Fakat, bu s n fta söz konusu özellik integral alma iṣlemi ic.in gec.erli de gildir. Yani, baz elementer fonksiyonlar n belirsiz integrali elementer fonksiyon olmayabilir. Örne gin, R e d; R cos( )d; R sin( )d; R d (0 < 6 ); R cos R d; ln sin d; R p k sin (j k j< ) integralleri mevcut olmas na (Bkz. Böl. 5) ra gmen elementer fonksiyonlarla ifade edilemezler. Ileride esas hede miz geliṣtirilmiṣ c.eṣitli integraller alma yöntemleri yard m yla yukar da verdi gimiz tabloyu geniṣletmek olacakt r.. Temel Integral Alma Yöntemleri.. De giṣken De giṣtirme Yöntemi Teorem.. : J R aral g üzerinde tan ml '() (' : J! R) fonksiyonu J üzerinde sürekli türeve sahip bir fonksiyon ve I '(J) olmak üzere F (y)(f : I! R) fonksiyonu f(y) (f : I! R) fonksiyonunun I üzerinde herhangi bir ilkel fonksiyonu olsun. Bu durumda, F ('(t)) (F ' : J! R) fonksiyonu J üzerinde f('()) ' 0 () ((f ')' 0 : J! R) fonksiyonunun bir ilkel fonksiyonudur ve c key bir say olmak üzere f('())' 0 ()d F ('()) + c (.3) eṣitli gi do grudur. Eṣitlik (.3) aṣa g daki gibi iki yönde kullan l r. Birinci Yön: F ('()) + c ['() y dersek] F (y) + c f(y)dy oldu gunu gözönüne al rsak (.3) ten f('())' 0 ()d f(y)dy (.4)
11 Temel Integral Alma Yöntemleri elde edilir. Ikinci Yön: Verilen R f(y)dy integralinde y '() de giṣken de giṣimi yap l rsa, dy ' 0 ()d eṣitli gi gözönüne al nd g nda f(y)dy f('())' 0 ()d (.5) eṣitli gini elde ederiz. (.4) ve (.5) eṣitliklerine, belirsiz integrallerde de giṣken de giṣtirme (veya yerine koyma) formülleri denir. Not: (.4) ve (.5) formüllerinin uygulamalar nda, c. kan sonucu de giṣken de giṣtirmeden önceki ṣekilde ifade etmek gerekti ginden (.4) deki R f(y)dy integrali hesapland ktan sonra y '() dönüṣümü yard m yla tekrar de giṣkenine, (.5) deki R f('())' 0 ()d integrali hesapland ktan sonra y '() fonksiyonunun tersi olan ' (y) dönüṣümü yard m yla tekrar eski y de giṣkenine dönülür. Bu nedenle ' : J! I fonksiyonunun ' : I! J tersi mevcut olmal d r. Örnek.. : Aṣa g daki integralleri hesaplay n z. (a) A R tdt ; (b) A +t R (arctan t) 00 dt; +t (c) A 3 R (5t 6) 00 dt; (d) A 4 R t 5 dt; (3t) + (e) A 5 R dt (k N; t 6 a); (f) A (t a) k 6 R dt (a 6 0); a +t (g) A 7 R p d a (a > 0; j j< a); (h) A 8 R d (a 6 0; 6 a); a (i) A 9 R p d a (j j> a > 0); + (j) A 0 R d p a (jj > a > 0); (k) A R tan d ( 6 + k; k ); (l) A R d ( 6 k) : sin cos
12 Belirsiz Integraller C. özüm: (a) A ( + t ) 0 + t dt [y + t! dy ( + t ) 0 dt] dy y ln j y j + c ( + t ) + c: (b) A arctan t 00 (arctan t) 0 dt [y arctan t! dy (arctan t) 0 dt] y 00 dy y0 0 + c 0 (arctan t)0 + c (c) A 3 (5t 6) 00 (5t 6) 0 dt 5 [y 5t 6! dy (5t 6) 0 dt] y 00 dy y c (5t 6)00 + c: 000 (d) A 4 ((3t) 6 ) t + dy [y (3t) 6! dy ((3t) 6 ) 0 dt] dy 4374 y arctan y + c 4374 arctan (3t)6 + c: (e) A 5 (t a) 0 (t a) dt k [y t a! dy (t a) 0 dt]
13 Temel Integral Alma Yöntemleri 3 dy y k 8 < ln j y j +c; : k ise; + c; k 6 ise: (k )y k 8 < ln j t a j +c; k ise; : + c; k 6 ise: (k )(t a) k (f) A 6 a ( t a )0 + t dt[y t a! dy ( t 0dt] a ) a a dy + y a arctan y + c a arctan t a + c: (g) A 7 ( a p )0 dt[y ( a ) a! dy ( a )0 d] dy p arcsin y + c arcsin( y a ) + c: (h) A 8 a a ( a )0 ( dt[y a ) a! dy ( a )0 d] dy y a ln j + y y j +c a ln j a + a j +c: (i) A 9 ( a )0 p d [y + ( ) a! dy ( a )0 d] a dy p ln(y + p y + ) + c + y (j) A 0 ln( + p + a ) + c: ( a p )0 ( a ) d dy p y ln(y + p y ) + c ln( a + p + a ) + c: (k) A (cos ) 0 cos d[y cos! dy (cos )0 d] dy ln j y j +c ln j cos j +c: y
14 4 Belirsiz Integraller Benzer ṣekilde, ( 6 k; k ) R cot d ln j sin j +c bulunur. cos (l) A (tan ) 0 tan d d [y tan! dy (tan ) 0 d] tan dy ln j y j +c ln j tan j +c y Buradan, d sin ( )0 sin cos d dy ln j tan y j +c sin y cos y ln j tan j +c; 6 k; k d cos ( + )0 sin( + )d dy sin y ln j tan y j +c ln j tan( + 4 ) j +c; 6 + k; k buluruz... K smi Integrasyon Yöntemi Teorem..3 : I R, u; v : I! R fonksiyonlar I üzerinde türevlenebilir ve v()u 0 () fonksiyonun I üzerinde ilkel fonksiyonu var olsun. Bu durumda, u()v 0 () fonksiyonunun da I üzerinde ilkel fonksiyonu vard r ve v()u 0 ()d u()v() v()u 0 ()d (.6) veya (u 0 ()d du ve v 0 ()d dv oldu gundan) udv uv vdu (.7) eṣitli gi do grudur. (.6) veya (.7) formlüne belirsiz integralin k smi integralleme formülü ad verilir.
15 Temel Integral Alma Yöntemleri 5 Not: Uygulamalarda u() ve v() fonksiyonlar n, (.6) veya (.7) deki : integralin hesab : integralin hesab ndan daha kolay olacak bic.imde sec.memiz gerekir. olur. Aṣa g daki durumlarda k smi integrasyon yönteminin kullan lmas uygun. Integrant, ln ; ln '(); arcsin ; arccos ; arctan ; arccot fonksiyonlar ndan herhangi biri ile belli bir v() fonksiyonunun türevinin c.arp m ise, u() olarak ad gec.en fonksiyonlar,dv olarak dv v 0 ()d kabul edilmesi uygun olur.. Integrant, P (); n: dereceden herhangi bir polinom olmak üzere, P ()e ; P () sin, P () cos bic.iminde ise, u() olarak P () ve dv olarak di ger k sm n kabul edilmesi uygun olur. Bu durumda k smi integralleme ardarda n kez uygulan r. 3. Integrant, e a sin(b); e a cos(b); sin(ln ); cos(ln ); vs. bic.iminde ise k smi integralleme iki kez uyguland g nda karṣ m za belli bir katsay ile hesab istenen integral c. kar. Elde edilen bu lineer denklemden hesab istenen integral bulunur. Örnek..4 : Aṣa g daki integralleri hesaplay n z. (a) A R 3 ln d ( R + ); (b) A R arctan d; (c) A 3 R sin(ln )d ( R + ); (d) A 4 R arccos d (j j ); (e) A 5 R arcsin d ( 6 0; j j< ); (f) A 6 R arctan p d ( 0); (g) A 7 R p a d (a R + ; j j a); (h) A 8 R p a d (a R + ; j j a); (i) A 9 R e a cos bd; (j) A 0 R e a sin bd (a 6 0);
16 6 Belirsiz Integraller (k) K n R d +a 4 (n N); (l) I n R d n a +b+c (b 4ac < 0; n N); (m) J n R A+B d (b 4ac < 0; n N); (a +b+c) 4 C. özüm: (a) u ln ; dv 3 d denirse du ln 4 d; v 4 oldu guna göre, (.7) den dolay A 4 4 ln 3 ln d [u ln ; dv 3 d denirse, du d; v 4 oldu guna göre, (.7) den] ln 8 4 ln + 3 d (ln ln + 8 ) + c: (b) u arctan ; dv d denirse, du d + ; v oldu guna göre, A arctan arctan + d d + arctan + arctan + c: (c) u sin(ln ); dv d denirse, du cos(ln )d; v oldu guna göre, (.7) den A 3 sin(ln ) cos(ln )d [u cos(ln ); dv d denirse, du sin(ln )d; v oldu guna göre, (.7) den] sin(ln ) cos(ln ) A 3
17 Temel Integral Alma Yöntemleri 7 Buradan, A 3 (sin(ln ) cos(ln )) + c bulunur. (d) u arccos ; dv d d denirse, du p ; v 3 3 (.7) den [u ; dv p oldu guna göre] (e) den A arccos + 3 d denirse, du d; d v p 3 3 arccos p arccos p arccos 3 3 p d d( ) p p p 9 p d p d( ) q ( ) 3 + c: u arcsin ; dv d denirse, du d p ; v A 5 arcsin d + p olur. Öte yandan, d p oldu guna göre, d q j j ( jj ) d( ) jj q ln ( jj ) oldu guna göre, oldu guna göre, (.7) sgnd(j j) sgnj j q ( jj ) j j + p + c A 5 arcsin + ln j j + p + c:
18 8 Belirsiz Integraller (f) u arctan p d ; dv d denirse, du ; v oldu guna göre, (+) (.7) den dolay A 6 arctan p d p ( + ) arctan p p ( + ) d arctan p p p + arctan + c: (g) u p a ; dv d denirse, du p a bulunur. A 7 p a + p a p a d a p a d + a p a + a arcsin a + c (h) u p a ; dv d denirse, du p A 8 p a p a d p a a p a d a d; v oldu gundan, d p a a d; v oldu gundan, d p a p a A 8 a ln j + p a j p a ) A 8 a ln j + p a j +c bulunur. Benzer ṣekilde, 8a 6 0 ic.in p + a d p + a + a ln j + p + a j +c oldu gu gösterilebilir. (i) u cos(b); dv e a d denirse, du b sin(b)d; v a ea oldu guna göre, (.7) den dolay A 9 a ea cos(b) + b a A 0
19 Temel Integral Alma Yöntemleri 9 olur. u sin(b); dv e a d denirse, du b cos(b)d; v a ea oldu guna göre, (.7) den dolay A 0 a ea sin(b) + b a A 9 denklem sisteminden buluruz. 8 < b A 9 A a 0 a ea cos(b) : b A a 9 + A 0 a ea sin(b) A 9 ea (a cos(b) + b sin(b)) a + b + c; A 0 ea (a sin(b) b cos(b)) a + b (k) u ( +a ) n ; dv d denirse, du n ( +a ) n+ d; v oldu guna göre, (.7) den dolay + c K n ( + a ) + n d n ( + a ) n+ ( + a ) + n + a a d n ( + a ) n+ ( + a ) + nk n n na K n+ ve buradan da K n+ na ( + a ) + n n na K n (.8) buluruz. Örnek..(f) den dolay K d + a a arctan a + c
20 0 Belirsiz Integraller dir. (.8) de n ye ; vs. de gerleri verildi ginde K ; K 3 vs. integralleri hesaplanabilir. Örne gin, d K ( + a ) buluruz. (l) a a K 3 4a 4a + a + a K ( + a ) + ( + a ) + 3 a 3 arctan a + c; 4a K ( + a ) + 3 8a 4 a + b + c a( + b a + c a ) a ( + b I n a n ( + b + a + 3 8a arctan 5 a + c d a ) + 4ac b 4a a ) + 4ac n b 4a oldu guna göre, [t + b ve a d 4ac b denirse] R 4a dt elde edilir. (.8) den a 4 (t +d ) n I n+ dt a n+ (t + d ) n+ t a n+ nd (t + d ) + n n nd dt (t + d ) n olur. Burada,t nin ve d nin de gerleri dikkate al narak gerekli iṣlemler yap ld g nda I n+ a + b a(n ) + n(4ac b ) (a + b + c) n n(4ac b ) I n (.9) formülü elde edilir. n ise I dt a t + d a d arctan t d + c a + b p arctan( p ) + c 4ac b 4ac b
21 Temel Integral Alma Yöntemleri olur. (.9) da n ye ; vs. de gerleri verildi ginde I ; I 3 vs. integralleri hesaplanabilir. Örne gin, n ise d I (a + b + c) a + b 4ac b a + b + c + a 4ac b J a + b 4ac b a + b + c + 4a (4ac b ) p a + b arctan( p 4ac b 4a b ) + c olur. (m) A + B A Ab (a + b) + B oldu gundan, a a A + B J n+ d (a + b + c) n+ A a + b d + (B Ab a (a + b + c) n+ a ) d (a + b + c) n+ A d(a + b + c) d + (B Ab a (a + b + c) n+ a )I n+ (.0) elde edilir. n 0 ise (.0) dan A + B J (a + b + c) d A d(a + b + c) a (a + b + c) + (B Ab a )I A a ln j Ba Ab a + b + c j + a p a + b arctan( p 4ac b ) + c 4ac b olur. n N ise (.0) dan J n+ A na(a + b + c) n + (B Ab a )I n+ (.) elde edilir. (.) de n ye ; vs. de gerleri verildi ginde J ; J 3 vs. integralleri hesaplanabilir. Örne gin, n ic.in (.) den A + B J (a + b + c) d A a(a + b + c) + (B Ab a )I
22 Belirsiz Integraller olur. Burada,I nin az önce bulunan de gerini yerine kor ve gerekli iṣlemleri yaparsak, olur. J + + A a(a + b + c) + Ba Ab a + b a (4ac b )(a + b + c) 4a (4ac b ) p a + b arctan( p 4ac b ) + c 4ac b (Ba Ab)(a + b) A a 4ac b a + b + c (Ba Ab) (4ac b ) p a + b arctan( p 4ac b + c 4ac b..3 Rasyonel Kesirlerin Integrallenmesi P n () a 0 n + a n + + a n + a n (a 0 6 0) ve Q m () b 0 m + b m + + b m + b m (b 0 6 0) s ras yla n. ve m. dereceden reel katsay l polinomlar olmak üzere Qm() P n() kesrine, rasyonel kesir (veya rasyonel fonksiyon) denir. m < n oldu gunda rasyonel kesire düzgün, m n oldu gunda ise düzgün olmayan rasyonel kesir ad verilir. m n oldu gunda polinomlar n bölünmesi kural ile düzgün olmayan Qm() rasyonel kesiri, P P n() m n(), m-n.dereceden, R() ise k. dereceden (k < n) bir polinom olmak üzere Q m() P n() P m n () + R k() bic P n().iminde yaz labilir.buna göre, düzgün olmayan key rasyonel kesrin integrali, belirli bir polinomla bir düzgün rasyonel kesirin integrallerinin toplam bic.iminde gösterilmiṣ olur.bu nedenle ileride yaln zca düzgün rasyonel kesirlerin integrallerinden bahsedece giz. Cebirin temel teoreminden yararlanarak aṣa g daki teoremi ispats z verebiliriz. Teorem..5 : ; ; k ; ; ; l ( + + k + ( + + l ) n) negatif olmayan tam say lar, d ; ; d k ; p ; q ; ; p l ; q l (4q s p s > 0; s ; ; l) reel say lar olmak üzere P n () ( d ) ( d k ) k ( + p + q ) ( + p l + q l ) l (.)
23 Temel Integral Alma Yöntemleri 3 olsun. Bu durumda Qm() P n() düzgün rasyonel kesiri (m < n) Q m () P n () + D() d ( d ) + + D () ( d ) + D() D + D(k) d k ( d k ) + + ( d k ) k + D(k) + A() + B () + + p + q (k) k A() + B () ( + p + q ) + + A () + B () ( + p + q ) + + A(l) + B (l) + A(l) + B (l) + p l + q l ( + p l + q l ) + A (l) l + B (l) l ( + p l + q l ) l (.3) bic.iminde, basit rasyonel kesirler ad verilen kesirlerin toplam ṣeklinde gösterilebilir. Burada, D ; D ; ; D k k ; A ; B ; ; A l l ; B l l Not: (.3) eṣitli gine, Q m() P n() reel say lard r. düzgün rasyonel kesirin basit kesirlere ayr l ṣ denir. Teorem..5 e göre paydas (.) eṣitli gi ile belirlenen Qm() P n() düzgün rasyonel kesrin integrallenmesi D; A ve B sabit say lar olmak üzere D ( d) ( 6 d; N); A + B ( + p + q) (4q p > 0; N) bic.imindeki basit kesirlerin integrallenmesine indirgenmiṣ olur. Bu integrallerin nas l hesapland g n..(l) ve..4(l) den biliyoruz. Q m() P n() ṣeklindeki rasyonel kesirin basit kesirlere ayr l ṣ nda (yani (.3) deki D; A ve B say lar n n bulunmas ic.in) aṣa g daki yöntemler kullan l r. (a) Belirsiz Katsay lar Yöntemi: Bu yönteme göre (.3) eṣitli ginin sa g taraf toplan p paylar eṣitlenir ve in ayn kuvvetlerinin katsay lar eṣitlenerek söz konusu sabitler (reel say lar) ic.in bir lineer denklem sistemi elde edilir. Bu denklem sistemi c.özülerek istenen sabitler bulunur. Örnek..6 : (+)( )( +) kesrini basit kesirlere ay r n z.
24 4 Belirsiz Integraller C. özüm: (+)( )( +) D (+) + D ( ) + A+B ( +) ) D ( )( + ) + D ( + )( + ) + (A + B)( + )( ) elde ederiz.her ikitarafta in ayn kuvvetlerinin katsay lar n birbirine eṣitle yip 0 : D + D B 0 : D + D A + B : D + D + A + B 0 3 : D + D + A 0 denklem sistemi buluruz. Sistemi c.özüp, D 6 ; D 4 5 ; A 3 0 ; B 0 bulur ve verilen kesir ic.in ( + )( )( + ) 6( + ) + 4 5( ) ( + ) ayr l ṣ n elde ederiz. Buna göre, olur. ( + )( )( + ) d 6 Not: d d d ln j j + ln j j ln ( + ) + arctan + c; ( 6 ; 6 ) Örnek..6 dan da görüldü gü gibi genelde rasyonel kesrin basit kesirlere ayr l ṣ (yani, (.3) deki D; A ve B say lar n n bulunmas ) uzun ve yorucudur. Baz durumlarda bu say lar n bulunmas ic.in baṣka yöntemler de kullan l r. (b) d R say s P n () polinomunun katl kökü ve '(d) 6 0 olmak üzere Qm() P n() Qm() olsun. Bu durumda ( ( d) '() d) c.arpana (.3)
25 Temel Integral Alma Yöntemleri 5 ayr l ṣ nda D d + D ( d) + + D ( d) ṣeklinde bir toplam tekabül eder. Q m () P n () Q m () ( a) '() D ( a) + Q m() D '() ( a) '() özdeṣli ginde D say s n öyle sec.elim ki, a say s Q m () D '() in kökü olsun. Bunun ic.in D Qm(a) olmas yeterlidir. '(a) P n () polinomunun tüm kökleri reel ve basit oldu gu durumda (.3) tdeki D say lar n n tümü aṣa g daki gibi kolayca bulunabilir. d ; ; d n reel say lar P n () polinomunun farkl ve basit kökleri oldu gunda (kolayl k ic.in a 0 kabul edilir) Q m () P n () eṣitli ginin her iki taraf n Q m () ( d ) ( d n ) D + + D i + D i + D i+ + + D n d d i d i d i+ D i buluruz. Örne gin, d i ye c.arp p elde edilen eṣitlikte d i yazarsak Q m (d i ) (d i d ) (d i d i )(d i d i+ ) (d i d n ) Q () P 4 () + ( )( + )( + ) D + D + D D 4 eṣitli ginden (d 0; d ; d 3 D D ; d 4 ic.in) Q (d ) (d d )(d d 3 )(d d 4 ) ; Q (d ) (d d )(d d 3 )(d d 4 ) 3 ; d n D 3 D 4 Q (d 3 ) (d 3 d )(d 3 d )(d 3 d 4 ) 6 ; Q (d 4 ) (d 4 d )(d 4 d )(d 4 d 3 ) 3
26 6 Belirsiz Integraller buluruz. Sonuc.ta, ( + )( + )( + ) 3 ( ) 6( + ) + 3( ) olur. Yukar da söylenenlere göre rasyonel kesrin integralini hesaplamak ic.in ṣu yolu takip etmemiz gerekir. () Verilen rasyonel kesir, düzgün de gilse, o bir polinom ile bir düzgün rasyonel kesrin toplam ṣeklinde yaz l r. () Elde edilen düzgün rasyonel kesirde payda basit c.arpanlara ayr l r. (3) Düzgün rasyonel kesir basit kesirlere ayr l r. (4) Ayr l ṣ yap ld g nda elde edilen polinom ve basit kesirler integrallenir. Bilindi gi gibi, polinom ve basit kesirlerin belirsiz integralleri elemanter (rasyonel, logaritmik ve ters trigonometrik )fonksiyonlarla ifade edilebilir. Buna göre, rasyonel kesirlerin integrallenmesi üzerine aṣa g daki teoremi verebiliriz. Teorem..7 : Her rasyonel kesrin paydas s f rdan farkl olan her aral kta elemanter (rasyonel, logaritmik ve ters trigonometrik) fonksiyonlarla ifade edilebilen belirsiz integrali vard r. Ileride esas hede miz irrasyonel, trigonometrik vs. ifadelerin integralinin hesaplanmas problemini rasyonel kesirlerin integrallenmesine dönüṣtürmek olacakt r...4 Baz Irrasyonel Cebirsel Ifadelerin Integrallenmesi a 00 ; a 0 ; a 0 ; ; a 0n herhangi sabit reel say lar olmak üzere P n (; y) a 00 +a 0 +a 0 y+a 0 +a y+a 0 y + +a 0n y n ṣeklindeki fonksiyona ve y
27 Temel Integral Alma Yöntemleri 7 nin kuvvetlerine göre. dereceden polinom ad verilir. P n (; y) ve Q m (; y), ve y ye göre s ras yla n. ve m. derecen iki polinom ise, R(; y) Qm(;y) P n(;y) kesrine ve y ye göre iki de giṣkenli rasyonel fonksiyon (veya rasyonel kesir), R(f(); g()) ifadesine de f ve g nin rasyonel fonksiyonu denir. Örne gin, R(sin ; cos ) sin3 + cos ; sin ve cos in, R(p ; 3p ) p + 3p cos sin + + 3p ; p ve 3p in rasyonel fonksiyonudur. () R R(; y()) d ṣeklinde integraller. Burada,R(; y); ve y y() in bir rasyonel fonksiyonudur. E ger, bu integralde (t) de giṣken de giṣirmesi yap ld g nda ve (t) ve y y((t)), t nin bir rasyonel fonksiyonu oluyorsa, R((t); y((t))) 0 (t) de t nin bir rasyonel fonksiyonu ve R(; y) d R((t); y((t))) 0 t dt olur.bu durumda verilen integral t nin bir rasyonel fonksiyonunun integraline dönüṣtürülür. Aṣa g daki özel durumlar inceliyelim. (a) a; b; c; d reel say lar (ad bc 6 0); n N ve y() n q a+b c+d ol- q sun. Bu durumda, t n a+b c+d yapal m. Buradan, yani a+b c+d tn de giṣken de giṣimi y t; dtn b a ct ; d n 0 (t) dt ndtn (a ct n ) + nct n (dt n b) dt (a ct n ) oldu gundan, R (t) R( dtn b; t) 0 (t) olmak üzere a ct n r a + b R(; n c + d )d R (t) yani, t nin bir R (t) rasyonel fonksiyonun integrali elde edilir. (b) a; b; c reel say lar (a 6 0; b 4ac 6 0) ve y() p a + b + c olsun. Bu durumda, Euler dönüṣümleri denilen aṣa g daki de giṣken
28 8 Belirsiz Integraller de giṣtirmeleri yard m ile I R(; p a + b + c)d integrali rasyonel fonksiyonlar n integraline dönüṣtürülür. () a > 0 ise p a + b + c t + p a (veya t p p a + b + c a) de giṣken de giṣtirimi yap l r. Buradan, t c b+ p ' at (t); d ' 0 (t)dt (' 0 (t) (p ac+bt+ p at ) (b+ p dir), p p a at) + b + c t a t p a' (t) oldu guna göre, I R R (t)dt oldu gu elde edilir.burada, R (t) R(' (t); t p a' (t))' 0 (t), t nin bir rasyonel fonksiyonudur. () c > 0 ise p a + b + c t + p c (veya p p a + b + c t c) de giṣken de giṣtirimi yap l r. Buradan, p ct b ' a t (t), d ' 0 (t)dt, (' 0 (t) (ap c bt+ p ct ) d r), p a (a t ) + b + c t' (t) + p c oldu guna göre, I R R 3 (t)dt oldu gu elde edilir. Burada, R 3 R(' (t); t' (t) + p c)' 0 (t), t nin bir rasyonel fonksiyonudur. (3) b 4ac > 0 ise, a +b+c 0 denkleminin herhangi bir kökü olmak üzere p a + b + c t( ) de giṣken de giṣimi yap l r. Buradan, a( )( ) t ( ) a t ' a t 3 (t); d ' 0 3(t)dt (' 0 3(t) a( )t dir) p a (a t ) + b + c t(' 3 (t) ) a( ) a t ' 4 (t) oldu guna göre, I R R 4 (t)dt elde ederiz. Burada, R 4 (t) R(' 3 (t); ' 4 (t))' 0 3(t), t nin bir rasyonel fonksiyonudur. Not: Baz durumlarda I R R(; p a + b + c)d ṣeklindeki integraller, Euler dönüṣümleri kullan lmadan, daha basit yöntemlerle hesaplanabilir.bunlardan baz lar n görelim. (i) a 6 0; b 4ac 6 0 olmak üzere a + b + c a( + b p 4jaj j4ac a ) + 4ac b 4a oldu guna göre, göre t ( + b ) de giṣken de giṣtirimi yard m yla b j a I integrali, R 5 (u; v); R 6 (u; v); R 7 (u; v) u ve v nin birer rasyonel fonksiyonu olmak üzere R 5 (t; p t )dt; R 6 (t; p t )dt; R 7 (t; p + t )dt
29 Temel Integral Alma Yöntemleri 9 integrallerinden birine dönüṣtürülebilir. Bu integrallerden birincisi t sin u; ikincisi t, üc sinu.üncüsü de t tan u dönüṣümleri ile ileride inceliyece gimiz. R R(sin u; cos u)du bic.imindeki integrallere dönüṣtürülür. R P (ii) p n() ṣeklindeki integraller. Burada, P a +b+c n(); n: dereceden belli bir polinomdur. Q n (); n : dereceden bilinmeyen katsay l bir polinom ve bilinmeyen bir reel say olmak üzere do grulu gu kolayl kla gösterilebilen P n () p a + b + c d Q n (): p a + b + c + d + p (.4) a + b + c eṣitli ginde her iki taraf n türevi al n r, sa g taraf ortak paydaya getirilir, ayn paydal eṣit kesirlerin paylar eṣitlenir, daha sonra da, ayn dereceli terimlerin katsay lar eṣitlenirse Q n () in katsay lar ile say s bulunur.(.4) eṣitli ginin sa g taraf ndaki integral (i) de gördü gümüz yöntemlerle hesaplan r. R d (iii) ( p) np (n N) bic a +b+c.imindeki integraller t de giṣken p de giṣtirimi yard m yla (ii) deki integrale dönüṣtürülür...5 Binom Diferensiyellerinin Integrallenmesi a; b R ve p; q; r Q olmak üzere r (a + b p ) q d ṣeklindeki ifadeye Binom Diferasiyeli, r (a + b p ) q d (.5) bic.imindeki integrallere de Binom Integralleri ad verilir. () q tam say d r, () r+ p tam say d r, (3) r+ p Not: + q tam say d r durumlar nda (.5) tipindeki integraller rasyonel fonksiyonlar n integraline dönüṣtürülür. Birinci durumda k; r ile p nin paydalar n n en
30 30 Belirsiz Integraller küc.ük ortak kat olmak üzere t k ; ikinci durumda n; q nun paydas olmak üzere a + b p t n ; üc.üncü durumda b + a p t n ( n; q nun paydas d r)de giṣken de giṣtirimi yap l r. Örnek..8 : I R d 4p + 4 integralini hesaplay n z. C. özüm: a b ; r 0; p 4; q r+ ve + q 0 4 p 4 4 oldu gundan + 4 t 4 de giṣken de giṣtirimi yap l rsa, t ( + 4 ) 4 ; (t 4 ) 4 ; 4p t + (t 4 ) 4 ; d t 3 (t 4 ) 5 4 dt olur. Bu de gerler 4 integralde yerine yaz l rsa, bulunur. I t dt t 4 ( dt t + 4 ln j + t t j arctan t + c 4p + 4 ln 4 + 4p + 4 dt t + ) 4p + arctan 4 + c Not: P.Chebyskhev göstermiṣtir ki, yaln z ve yaln z q; r+; r+ + q tam p p say lar oldu gu durumlarda (.5) tipindeki integraller rasyonel fonksiyonlar n integrallerine dönüṣtürebilir, yani yaln zca bu durumlarda (.5) tipindeki integraller elementer fonksiyonlarla ifade edilebilir..3 Trigonometrik ifadelerin Integrallenmesi () I R R(sin ; cos )d ṣeklindeki integrallerin hesab. Burada,R(u; v); u ve v nin bir rasyonel fonksiyonudur. Bu integralin hesab ic.in genelde t tan ( 6 (k+); k ) de giṣken de giṣtirmesi yap l r. cos tan + tan t + t ; tan sin + tan t + t ; arctan t; d dt + t
31 Temel Integral Alma Yöntemleri 3 oldu gundan, verilen I integrali t I R( + t ; t + t ) t + t dt ṣeklinde yeni t de giṣkeninin bir rasyonel fonksiyonunun integraline dönüṣtürülür. Baz özel durumlarda baṣka de giṣken de giṣtirmelerin yap lmas daha elveriṣli olur. (a) R( sin ; cos ) R(sin ; cos ) ise t cos ; (b) R(sin ; cos ) R(sin ; cos ) ise t sin ; (c) R( sin ; cos ) R(sin ; cos ) ise t tan ( 6 + k; k ) de giṣken de giṣtirmesi kolayl k sa glar. Not: Her R(u; v) rasyonel ifadesi s ras yla yukar daki (a), (b), (c) özelliklerine sahip R (u; v) R(u; v) R( u; v) ; R (u; v) R 3 (u; v) R( u; v) R( u; v) ; R( u; v) + R(u; v) ; rasyonel ifadelerin toplam ṣeklinde gösterilebilir. () R R(sin ; cos )d veya r(u), u nun bir rasyonel fonksiyonu olmak üzere R r(tan )d ṣeklindeki integrallerin hesab nda t tan de giṣtir mesi kullan l r. (3) R R(sin ; cos ) sin d veya R R(sin ; cos ) cos d ṣeklindeki integ rallerin hesab nda s ras yla t cos veya t sin de giṣken de giṣtirme si kullan l r. (4) R R(tan ; sec )d ( 6 + k; k ) ṣeklindeki integrallerin hesab n
32 3 Belirsiz Integraller da R(tan ; sec ) R(tan ; sec ) ise t tan ; R( tan ; sec ) R(tan ; sec ) ise t sec ; R( tan ; sec ) R(tan ; sec ) ise t tan ; veya t sec de giṣken de giṣtirilmesi kullan l r. (5) R R(cot ; csc )d q ( 6 k; k ) ṣeklindeki integraller cot ; csc + ba g nt lar yard m yla R R(tan ; sec )d tan tan ṣeklindeki integrallere dönüṣtürülür ve 4. deki izlenen yol takip edilir. Örnek.3. : Aṣa g daki intralleri hesaplay n z. (a) I R d ; (b) I sin cos +5 R sin d ; cos (sin +cos ) (c) I 3 R sin d; (d) I 4 cos + cos 7 4 R cos (e) I 5 R cos 3 d : sin 7 cos 4 +sin 4 + sin + d; C. özüm: (a) t tan ; (k ) (k + ); k de giṣken de giṣtirmesi yap ld g nda sin t, cos t ve d dt +t +t +t oldu gundan, dt I () 3t + t + p arctan 3t p + + C k 5 5 p arctan 3 tan p + + C k ; (k + ) 5 5 (k + ); k buluruz. Ilkel fonksiyonun süreklili ginden I (k + ) I (k + ), yani p + C 5 k p + C 5 k+ ya da C k p 5 + C k+ veya C k+ p 5 + C k elde edilir. Buradan, C p 5 + C 0, C C 0 ve herhangi k N ic.in C k K (K ) p 5 + C 0, C k p 5 + C 0 bulunur. Burada, C 0 key sabit bir reel say d r. Öte yandan k < + < (k + ); k
33 Temel Integral Alma Yöntemleri 33! k < + + < k +! [[ ]] oldu gundan, 8 < I : p 5 arctan 3 tan( p )+ 5 + p 5 [[ + lim!(k+) I () k+ p 5 ]] + C; 6 (k + ) ise; ; (k + ) ise: (b) R( sin ; cos ) sin R(sin ; cos ) oldu gundan, t tan ( 6 de giṣtirmesi yap ld g nda ( cos ) ( sin ; cos ) + k; k; k ) de giṣken I () tan d(tan ) + tan ln j + tan j + tan + C bulunur. (c) R( sin ; cos ) ( sin )(cos ) 4 cos + cos 7 R(sin ; cos ) oldu gundan, t cos ( 6 + k; k ) de giṣken de giṣtirmesi yap ld g nda I 3 () tdt 4(t + 3t + 9) 6 tdt (t ) 4 d(t + 3 ) (t + 3 ) d(t + 3) 4 (t + 3 ) 4 4 ln j (t + 3 ) 4 j ln j t t + 7 j +c 4 ln j (cos + 3 ) 4 j ln j cos cos + 7 j +c ( 6 + k; k ) bulunur. cos (d) R( sin ; cos ) cos 4 +sin 4 + sin + R(sin ; cos ) oldu-
34 34 Belirsiz Integraller gundan, t sin de giṣken de giṣtirmesi yap ld g nda d sin I 4 () + sin 4 + ( sin ) + sin dt t p t + p t + t p + dt p 4 p t t t p + dt p 8 p ln sin + sin + p + sin sin + 4 p [arctan(p + ) + arctan( p ] + c bulunur. (e) bulunur. I 5 () R cos d sin [t sin denirse] sin 7 ( t )dt t 7 4 sin 4 (t 7 t 5 )dt 6 t t 4 + c 6 sin 6 + c; 6 k (6) J R R(sinh ; cosh )d ṣeklindeki integrallerin hesab nda t tanh de giṣken de giṣtirmesi yap l r. sinh tanh t ; cosh t +tanh tanh integrali tanh +t t ; arctan ht; d dt t oldu gundan verilen J R(sinh ; cosh ) t R t ; + t dt t t ṣeklinde yeni t de giṣkeninin bir rasyonel fonksiyonunun integraline dönü ṣür. I integralinde oldu gu gibi baz özel durumlarda J integralinin hesab nda aṣa g daki baṣka de giṣken de giṣtirmelerin yap lmas daha elveriṣli olur. (a) R( sinh ; cosh ) R(sinh ; cosh ) ise t cosh ;
35 Temel Integral Alma Yöntemleri 35 (b) R(sinh ; cosh ) R(sinh ; cosh ) ise t sinh ; (c) R( sinh ; cosh ) R(sinh ; cosh ) ise t tanh ; de giṣken de giṣtirmesi kolayl k sa glar. Örnek.3. : Aṣa g daki integralleri hesaplat n z. (a) J R cosh d; 6 0; (b) J sinh 3 R cosh 3 d; (c) J 3 R d ; 6 0; (d) J sinh 4 cosh 4 R tanh 4 d: C. özüm: (a) u cosh ; dv cosh d(sinh ) d denirse sinh 3 sinh 3 du sinh ; v R d(sinh ) oldu guna göre, (.7) den dolay sin h 3 sinh olur. Öte yandan, oldu gundan, J d sinh cosh sinh + d d sinh d(tanh ) tanh sinh cosh dt t ln j t j +c ln j tanh t tan j +c; 6 0 J cosh sinh + ln j tanh j +c; 6 0 bulunur. (b) R(sinh ; cosh ) ( cosh ) 3 R(sinh ; cosh ) oldu gundan, t sinh de giṣken de giṣtirmesi yap lmal d r. Bu durumda, cosh + sinh + t ; cosh d d(sinh ) dt oldu gundan, J cosh cosh d (+t )dt t+ t3 3 +c sinh + 3 sinh3 +c
36 36 Belirsiz Integraller bulunur. (c) R( sinh ; cosh ) ( sinh ) 4 ( cosh ) R(sinh ; cosh ) oldu gundan, t tanh de giṣken de giṣtirmesi yap lmal d r. Bu durumda, ic.in d cos h sinh oldu gundan, bulunur. d(tan h) dt; sinh cosh sinh tanh tanh t t ) sinh 4 ( t ) t 4 t + t 4 J 3 (t 4 t + )dt 3t + 3 t + t + c tanh + coth 3 coth3 + c; 6 0 (d) R( sinh ; cosh ) ( sinh cosh )4 R(sinh ; cosh ) oldu gundan, t tanh de giṣken de giṣtirmesi yap lmal d r. Bu durumda, dt d ( cosh tanh )d ( t )d oldu gundan, bulunur. J 4 tanh 4 d t 4 dt t t 3 t 3 ln j t + t j +c tanh 3 tanh3 + + c ( t + t )dt
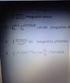
fonksiyonu, her x 6= 1 reel say s için tan ml d r. (x 1)(x+1) = = x + 1 yaz labilir. Bu da; f (x) = L
 Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
mat 103. Çal şma Sorular 1
 mat 0. Çal şma Sorular. FONKS IYONLA. Aşa¼g daki kurallarla verilen fonksiyonlar n gra klerini çiziniz. (a) f() 4 jj (b) f() jj (c) f() 4 jj (ç) f() j j (d) f() j j (e) f() j j (f) f() j j. Aşa¼g daki
mat 0. Çal şma Sorular. FONKS IYONLA. Aşa¼g daki kurallarla verilen fonksiyonlar n gra klerini çiziniz. (a) f() 4 jj (b) f() jj (c) f() 4 jj (ç) f() j j (d) f() j j (e) f() j j (f) f() j j. Aşa¼g daki
SORULAR. 1. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim. 1 n sin. lim. q 1 x 1+x
 SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
ÜN TE II L M T. Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler
 ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
Iki Boyutlu Sabit Katsay l Lineer Homogen Diferensiyel Denklem Sistemleri (Euler Metodu)
 Iki Boyulu Sabi Kasay l Lineer Homogen Diferensiyel Denklem Sisemleri (Euler Meodu) Bu bölümde sabi kasay l, lineer, homogen 8 >< d = a 1x + b 1 y >: dy d = a 2x + b 2 y sisemi ele al nmakad r. Burada
Iki Boyulu Sabi Kasay l Lineer Homogen Diferensiyel Denklem Sisemleri (Euler Meodu) Bu bölümde sabi kasay l, lineer, homogen 8 >< d = a 1x + b 1 y >: dy d = a 2x + b 2 y sisemi ele al nmakad r. Burada
Y = f(x) denklemi ile verilen fonksiyonun diferansiyeli dy = f '(x). dx tir.
 1 İNTEGRAL BİR FONKSİYONUN DİFERANSİYELİ Tanım: f: [a,b] R, x f(x) fonksiyonu (a,b) aralığında türevli olmak üzere, x değişkeninin değişme miktarı x ise f '(x). x ifadesine f(x) fonksiyonunun diferansiyeli
1 İNTEGRAL BİR FONKSİYONUN DİFERANSİYELİ Tanım: f: [a,b] R, x f(x) fonksiyonu (a,b) aralığında türevli olmak üzere, x değişkeninin değişme miktarı x ise f '(x). x ifadesine f(x) fonksiyonunun diferansiyeli
NÜMER IK ANAL IZ. Nuri ÖZALP. Sabit Nokta ve Fonksiyonel Yineleme. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
NÜMER IK ANAL IZ. Nuri ÖZALP FONKS IYONLARA YAKLAŞIM. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
1. GİRİŞ Örnek: Bir doğru boyunca hareket eden bir cismin başlangıç noktasına göre konumu s (metre), zamanın t (saniye) bir fonksiyonu olarak
 DERS: MATEMATİK I MAT0(09) ÜNİTE: TÜREV ve UYGULAMALARI KONU: A. TÜREV. GİRİŞ Bir doğru boyunca hareket eden bir cismin başlangıç noktasına göre konumu s (metre) zamanın t (saniye) bir fonksiyonu olarak
DERS: MATEMATİK I MAT0(09) ÜNİTE: TÜREV ve UYGULAMALARI KONU: A. TÜREV. GİRİŞ Bir doğru boyunca hareket eden bir cismin başlangıç noktasına göre konumu s (metre) zamanın t (saniye) bir fonksiyonu olarak
Bir H Hilbert uzay üzerinde herhangi bir kompakt simetrik T operatörü için,
 Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
(z z 0 ) n. n=1. Z f (z) dz = 2ib 1
 0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI. Analiz. Cilt 2. Ünite 8-14
 ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki olsun. Fonksiyonda meydana gelen artma miktarı
 10.1 Türev Kavramı fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki bir değerine kadar bir artma verildiğinde varılan x = x 0 + noktasında fonksiyonun değeri olsun.
10.1 Türev Kavramı fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki bir değerine kadar bir artma verildiğinde varılan x = x 0 + noktasında fonksiyonun değeri olsun.
NÜMER IK ANAL IZ. Nuri ÖZALP. SAYISAL TÜREV ve INTEGRAL. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP SAYISAL TÜREV ve INTEGRAL Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 1 / 23 1 Say sal Türev ve Richardson
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP SAYISAL TÜREV ve INTEGRAL Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 1 / 23 1 Say sal Türev ve Richardson
6 Devirli Kodlar. 6.1 Temel Tan mlar
 6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
MIT Açık Ders Malzemeleri Kompleks Değişkenli Fonksiyonlar 2008 Güz
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
SDÜ Matematik Bölümü Analiz-IV Final S nav
 Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
2010 oldu¼gundan x 2 = 2010 ve
 ) 444400 say s ndaki rakamlar n yerleri de¼giştirilerek 7 basamakl kaç farkl say yaz labilir? Çözüm : Bu rakamlar n bütün farkl 7 li dizilişlerinin say s 7! olacakt r. Bu dizilişlerin 4!! soldan ilk rakam
) 444400 say s ndaki rakamlar n yerleri de¼giştirilerek 7 basamakl kaç farkl say yaz labilir? Çözüm : Bu rakamlar n bütün farkl 7 li dizilişlerinin say s 7! olacakt r. Bu dizilişlerin 4!! soldan ilk rakam
BÖLÜM 1. stanbul Kültür Üniversitesi. Fonksiyonlar - Özellikleri ve Limit Kavram. ³eklinde tanmlanan fonksiyona Dirichlet fonksiyonu ad verilir.
 BÖLÜM 1 0, Q 1. f() = 1, R/Q, Fonksiyonlar - Özellikleri ve Limit Kavram ³eklinde tanmlanan fonksiyona Dirichlet fonksiyonu ad verilir. Buna göre a³a da verilen tanm bölgeleri altnda görüntü cümlelerini
BÖLÜM 1 0, Q 1. f() = 1, R/Q, Fonksiyonlar - Özellikleri ve Limit Kavram ³eklinde tanmlanan fonksiyona Dirichlet fonksiyonu ad verilir. Buna göre a³a da verilen tanm bölgeleri altnda görüntü cümlelerini
7 TAYLOR SER I GÖSTER IMLER I
 7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
OPERATÖRLER BÖLÜM 4. 4.1 Giriş. 4.2. Aritmetik Operatörler
 BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK (10+10 p.) 2. (15 p.) 3. (7+8 p.) 4. (15+10 p.) 5. (15+10 p.) TOPLAM
 TOBB-ETÜ, MATEMATİK BÖLÜMÜ, GÜZ DÖNEMİ 2014-2015 MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK 2014 Adı Soyadı: No: İMZA: 1. 10+10 p.) 2. 15 p.) 3. 7+8 p.) 4. 15+10 p.) 5. 15+10 p.) TOPLAM 1. a) NOT: Tam
TOBB-ETÜ, MATEMATİK BÖLÜMÜ, GÜZ DÖNEMİ 2014-2015 MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK 2014 Adı Soyadı: No: İMZA: 1. 10+10 p.) 2. 15 p.) 3. 7+8 p.) 4. 15+10 p.) 5. 15+10 p.) TOPLAM 1. a) NOT: Tam
Do ufl Üniversitesi Matematik Kulübü Matematik Bireysel Yar flmas 2004 Soru ve Yan tlar
 o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2004 Soru ve Yan tlar Soru. S f rdan farkl bir a say s için sonsuz ondal klarla oluflan ifadesinin de eri nedir? ise, Soru 2. 0 < < 0 olmak
o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2004 Soru ve Yan tlar Soru. S f rdan farkl bir a say s için sonsuz ondal klarla oluflan ifadesinin de eri nedir? ise, Soru 2. 0 < < 0 olmak
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 1 Denklemlerin Köklerini Bulma Giriş Denklemlerin Köklerini Bulma
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 1 Denklemlerin Köklerini Bulma Giriş Denklemlerin Köklerini Bulma
1998 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
8 LAURENT SER I GÖSTER IMLER I
 8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
POL NOMLAR. Polinomlar
 POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
Diferensiyel Denklemler I Uygulama Notları
 2004 Diferensiyel Denklemler I Uygulama Notları Mustafa Özdemir İçindekiler Temel Bilgiler...................................................................... 2 Tam Diferensiyel Denklemler........................................................4
2004 Diferensiyel Denklemler I Uygulama Notları Mustafa Özdemir İçindekiler Temel Bilgiler...................................................................... 2 Tam Diferensiyel Denklemler........................................................4
2. Topolojik Uzaylarda Ba¼glant l l k Ba¼glant l Topolojik Uzaylar. Tan m (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k
 2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ. Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 2012
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
NÜMER IK ANAL IZ. Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI
 ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI 1 Rassal Değişken Bir deney ya da gözlemin şansa bağlı sonucu bir değişkenin aldığı değer olarak düşünülürse, olasılık ve istatistikte böyle bir
ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI 1 Rassal Değişken Bir deney ya da gözlemin şansa bağlı sonucu bir değişkenin aldığı değer olarak düşünülürse, olasılık ve istatistikte böyle bir
TG 12 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon
 Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon Levent ÖZBEK Fikri ÖZTÜRK Ankara Üniversitesi Fen Fakültesi İstatistik Bölümü Sistem Modelleme ve Simülasyon Laboratuvarı 61 Tandoğan/Ankara
Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon Levent ÖZBEK Fikri ÖZTÜRK Ankara Üniversitesi Fen Fakültesi İstatistik Bölümü Sistem Modelleme ve Simülasyon Laboratuvarı 61 Tandoğan/Ankara
2. (1 + y ) ln(x + y) = yy dif. denk. çözünüz. 3. xy dy y 2 dx = (x + y) 2 e ( y/x) dx dif. denk. çözünüz.
 D DİFERANSİYEL DENKLEMLER ÇALIŞMA SORULARI Fakülte No:................................................... Adı ve Soyadı:................................................. Bölüm:...................................................................
D DİFERANSİYEL DENKLEMLER ÇALIŞMA SORULARI Fakülte No:................................................... Adı ve Soyadı:................................................. Bölüm:...................................................................
1) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir?
 ) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
DENKLEMLER CAUCHY-EULER DENKLEMİ. a n x n dn y dx n + a n 1x n 1 dn 1 y
 SABİT KATSAYILI DENKLEMLERE DÖNÜŞTÜREBİLEN DENKLEMLER Bu bölümde sabit katsayılı diferansiyel denklemlere dönüşebilen değişken katsayılı diferansiyel denklemlerden Cauchy Euler ve Legendre difarensiyel
SABİT KATSAYILI DENKLEMLERE DÖNÜŞTÜREBİLEN DENKLEMLER Bu bölümde sabit katsayılı diferansiyel denklemlere dönüşebilen değişken katsayılı diferansiyel denklemlerden Cauchy Euler ve Legendre difarensiyel
MATEMAT IK-I (SORULAR)
 Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
ıfırdan büyük olan rasyonel sayılara pozitif rasyonel sayılar, sıfırdan küçük rasyonel sayılar da negatif rasyonel sayılar denir.
 1-RASYONEL SAYILAR VE ÖZELLĐKLERĐ A)Rasyonel Sayılar:Birbirine denk olan kesirlerin meydana getirdiği her kümeye rasyonel sayı denir.rasyonel sayıların meydana getirdiği kümelere rasyonel sayılar kümesi
1-RASYONEL SAYILAR VE ÖZELLĐKLERĐ A)Rasyonel Sayılar:Birbirine denk olan kesirlerin meydana getirdiği her kümeye rasyonel sayı denir.rasyonel sayıların meydana getirdiği kümelere rasyonel sayılar kümesi
Baki Karl ¼ga. Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü Ankara/Türkiye
 H IPERBOL IK VE KÜRESEL ÜÇGENLERIN KENAR UZUNLUKLARINA BA ¼GLI ALAN FORMÜLLER I Baki Karl ¼ga karliaga@gazi.edu.tr Murat Savaş msavas@gazi.edu.tr Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü
H IPERBOL IK VE KÜRESEL ÜÇGENLERIN KENAR UZUNLUKLARINA BA ¼GLI ALAN FORMÜLLER I Baki Karl ¼ga karliaga@gazi.edu.tr Murat Savaş msavas@gazi.edu.tr Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü
Math 322 Diferensiyel Denklemler Ders Notları 2012
 1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
TEMEL KAVRAMLAR MATEMAT K. 6. a ve b birer do al say r. a 2 b 2 = 19 oldu una göre, a + 2b toplam kaçt r? (YANIT: 28)
 TEMEL KAVRAMLAR 6. a ve b birer do al say r. a b = 19 oldu una göre, a + b toplam (YANIT: 8) 1. ( 4) ( 1) 6 1 i leminin sonucu (YANIT: ). ( 6) ( 3) ( 4) ( 17) ( 5) :( 11) leminin sonucu (YANIT: 38) 7.
TEMEL KAVRAMLAR 6. a ve b birer do al say r. a b = 19 oldu una göre, a + b toplam (YANIT: 8) 1. ( 4) ( 1) 6 1 i leminin sonucu (YANIT: ). ( 6) ( 3) ( 4) ( 17) ( 5) :( 11) leminin sonucu (YANIT: 38) 7.
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I
 DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
2014 LYS MATEMATİK. P(x) x 2 x 3 polinomunda. 2b a ifade- x lü terimin. olduğuna göre, katsayısı kaçtır? değeri kaçtır? ifadesinin değeri kaçtır? 4.
 04 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. P() polinomunda katsayısı kaçtır? 4 lü terimin. ifadesinin değeri kaçtır? 4. yy y 4y y olduğuna göre, + y toplamının değeri kaçtır?
04 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. P() polinomunda katsayısı kaçtır? 4 lü terimin. ifadesinin değeri kaçtır? 4. yy y 4y y olduğuna göre, + y toplamının değeri kaçtır?
Basit Kafes Sistemler
 YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
1.3. Normal Uzaylar. Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak. baz temel özellikleri incelenecektir.
 1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
Limit. 1.1 Soldan ve Sağdan Yaklaşım. 1.2 Fonksiyonun Limiti
 Bölüm Limit. Soldan ve Sağdan Yaklaşım değişkeni a ya, a dan küçük değerlerle yaklaşıyorsa, bu tür yaklaşıma soldan yaklaşım denir ve a biçiminde gösterilir. değişkeni a ya, a dan büyük değerlerle yaklaşıyorsa,
Bölüm Limit. Soldan ve Sağdan Yaklaşım değişkeni a ya, a dan küçük değerlerle yaklaşıyorsa, bu tür yaklaşıma soldan yaklaşım denir ve a biçiminde gösterilir. değişkeni a ya, a dan büyük değerlerle yaklaşıyorsa,
BİR SAYININ ÖZÜ VE DÖRT İŞLEM
 ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
EEM 202 DENEY 5 SERİ RL DEVRESİ
 SERİ RL DEVRESİ 5.1 Amaçlar i, v, v R ve v L için RMS değerlerini hesaplama Seri RL devresinde voltaj ve empedans üçgenlerini tanımlama Seri RL devresinin empdansının kazanç ve faz karakteristiklerini
SERİ RL DEVRESİ 5.1 Amaçlar i, v, v R ve v L için RMS değerlerini hesaplama Seri RL devresinde voltaj ve empedans üçgenlerini tanımlama Seri RL devresinin empdansının kazanç ve faz karakteristiklerini
LİMİT. lim f(x) = L yazılır. lim. lim x a dır. lim g( clim
 LİMİT I. TANIM:, a yakınındaki değerleri için tanımlı bir onksiyon olsun. Alınan ε> sayısına karşılık -L < ε olacak şekilde -a < δ koşulunu sağlayan δ > sayısı bulunabiliyorsa ;, a ya yaklaşırken, L ye
LİMİT I. TANIM:, a yakınındaki değerleri için tanımlı bir onksiyon olsun. Alınan ε> sayısına karşılık -L < ε olacak şekilde -a < δ koşulunu sağlayan δ > sayısı bulunabiliyorsa ;, a ya yaklaşırken, L ye
Bu yaz girifle gereksinmiyor. Do rudan, kan tlayaca m z
 Yoksulun fians Bu yaz girifle gereksinmiyor. Do rudan, kan tlayaca m z sonuca geçelim: Teorem. Yoksulun zengine karfl flans yoktur. Bu çok bilinen teorem i kan tlayabilmek için her fleyden önce önermeyi
Yoksulun fians Bu yaz girifle gereksinmiyor. Do rudan, kan tlayaca m z sonuca geçelim: Teorem. Yoksulun zengine karfl flans yoktur. Bu çok bilinen teorem i kan tlayabilmek için her fleyden önce önermeyi
Kenan Osmanoğlu / Kerem Köker. KPSS Matematik Konu Anlatımlı ISBN 978-605-318-091-3. Kitapta yer alan bölümlerin tüm sorumluluğu yazarına aittir.
 Kenan Osmanoğlu / Kerem Köker KPSS Matematik Konu Anlatımlı ISBN 97860518091 Kitapta yer alan bölümlerin tüm sorumluluğu yazarına aittir. Pegem Akademi Bu kitabın basım, yayın ve satış hakları Pegem Akademi
Kenan Osmanoğlu / Kerem Köker KPSS Matematik Konu Anlatımlı ISBN 97860518091 Kitapta yer alan bölümlerin tüm sorumluluğu yazarına aittir. Pegem Akademi Bu kitabın basım, yayın ve satış hakları Pegem Akademi
Matematik 1 - Alıştırma 1. i) 2(3x + 5) + 2 = 3(x + 6) 3 j) 8 + 4(2x + 1) = 5(x + 3) + 3
 Matematik 1 - Alıştırma 1 A) Denklemler 1. Dereceden Denklemler 1) Verilen denklemlerdeki bilinmeyeni bulunuz (x =?). a) 4x 6 = x + 4 b) 8x + 5 = 15 x c) 7 4x = 1 6x d) 7x + = e) 5x 1 = 10x + 6 f) 0x =
Matematik 1 - Alıştırma 1 A) Denklemler 1. Dereceden Denklemler 1) Verilen denklemlerdeki bilinmeyeni bulunuz (x =?). a) 4x 6 = x + 4 b) 8x + 5 = 15 x c) 7 4x = 1 6x d) 7x + = e) 5x 1 = 10x + 6 f) 0x =
DERS: MATEMATİK I MAT101(04)
 DERS: MATEMATİK I MAT0(0) ÜNİTE: FONKSİYONLAR KONU:. TRİGONOMETRİK FONKSİYONLAR Öncelikle açı ölçü birimlerine göz atalım: Bilindiği gibi bir tam açının ölçüsü 0 derecedir. Diğer bir açı ölçü birimi de
DERS: MATEMATİK I MAT0(0) ÜNİTE: FONKSİYONLAR KONU:. TRİGONOMETRİK FONKSİYONLAR Öncelikle açı ölçü birimlerine göz atalım: Bilindiği gibi bir tam açının ölçüsü 0 derecedir. Diğer bir açı ölçü birimi de
x e göre türev y sabit kabul edilir. y ye göre türev x sabit kabul edilir.
 TÜREV y= f(x) fonksiyonu [a,b] aralığında tanımlı olsun. Bu aralıktaki bağımsız x değişkenini h kadar arttırdığımızda fonksiyon değeri de buna bağlı olarak değişecektir. Fonksiyondaki artma miktarını değişkendeki
TÜREV y= f(x) fonksiyonu [a,b] aralığında tanımlı olsun. Bu aralıktaki bağımsız x değişkenini h kadar arttırdığımızda fonksiyon değeri de buna bağlı olarak değişecektir. Fonksiyondaki artma miktarını değişkendeki
[ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1
![[ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1 [ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1](/thumbs/96/127250868.jpg) ..3 Ters Trigonometrik Fonksionlar Önceki kesimde belirtilen bütün trigonometrik fonksionlar perodik olduklarından görüntü kümesindeki her değeri sonsuz noktada alırlar. Bölece trigonometrik fonksionlar
..3 Ters Trigonometrik Fonksionlar Önceki kesimde belirtilen bütün trigonometrik fonksionlar perodik olduklarından görüntü kümesindeki her değeri sonsuz noktada alırlar. Bölece trigonometrik fonksionlar
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A
 T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
Diferansiyel denklemler uygulama soruları
 . Aşağıdaki diferansiyel denklemleri sınıflandırınız. a) d y d d + y = 0 b) 5 d dt + 4d + 9 = cos 3t dt Diferansiyel denklemler uygulama soruları 0.0.3 c) u + u [ ) ] d) y + = c d. y + 3 = 0 denkleminin,
. Aşağıdaki diferansiyel denklemleri sınıflandırınız. a) d y d d + y = 0 b) 5 d dt + 4d + 9 = cos 3t dt Diferansiyel denklemler uygulama soruları 0.0.3 c) u + u [ ) ] d) y + = c d. y + 3 = 0 denkleminin,
EK III POTANSİYELİN TANIMLANMASI
 EK III POTANSİYELİN TANIMLANMASI İki vektörün basamaklı (kademeli) çarpımı: Büyüklükte A ve B olan iki vektörünü ele alalım Bunların T= A.B cosθ çarpımı, tanımlama gereğince basamaklıdır. Bu vektörlerden
EK III POTANSİYELİN TANIMLANMASI İki vektörün basamaklı (kademeli) çarpımı: Büyüklükte A ve B olan iki vektörünü ele alalım Bunların T= A.B cosθ çarpımı, tanımlama gereğince basamaklıdır. Bu vektörlerden
İLKÖĞRETİM 6., 7., 8. SINIFLAR MATEMATİK DERSİ MÜFREDAT PROGRAMINDA GEÇEN CEBİR KONULARININ İNCELENMESİ MAT YL 2009 0001
 T.C. ADNAN MENDERES ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİMDALI İLKÖĞRETİM 6., 7., 8. SINIFLAR MATEMATİK DERSİ MÜFREDAT PROGRAMINDA GEÇEN CEBİR KONULARININ İNCELENMESİ MAT YL 2009 0001
T.C. ADNAN MENDERES ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİMDALI İLKÖĞRETİM 6., 7., 8. SINIFLAR MATEMATİK DERSİ MÜFREDAT PROGRAMINDA GEÇEN CEBİR KONULARININ İNCELENMESİ MAT YL 2009 0001
1.BÖLÜM SORU SORU. (x 1) (x 3) = A + B. x 3 ise, d(p(x)) ve d(q(x)) polinomlar n derecelerini göstermek. A. B çarp m kaçt r?
 1.BÖLÜM MATEMAT K Derginin bu say s nda Polinomlar konusunda çözümlü sorular yer almaktad r. Bu konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü
1.BÖLÜM MATEMAT K Derginin bu say s nda Polinomlar konusunda çözümlü sorular yer almaktad r. Bu konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 285 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 285 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
 LYS Y ĞRU MTMTİK TSTİ. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.., y reel sayılar
LYS Y ĞRU MTMTİK TSTİ. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.., y reel sayılar
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
TOBB-ETU, Iktisat Bölümü Macroeconomics II (IKT 234) Ozan Eksi Çal şma Sorular - Cevaplar. 1 Ozan Eksi (TOBB-ETU)
 TOBB-ETU, Iktisat Bölümü Macroeconomics II (IKT 234) Ozan Eksi Çal şma Sorular - Cevaplar 1 1-) (Faizler) Y ll k %10 basit faizden bankaya koyulan 100 tl nin 2 y l sonraki getirisini hesaplay n z? Cevap:
TOBB-ETU, Iktisat Bölümü Macroeconomics II (IKT 234) Ozan Eksi Çal şma Sorular - Cevaplar 1 1-) (Faizler) Y ll k %10 basit faizden bankaya koyulan 100 tl nin 2 y l sonraki getirisini hesaplay n z? Cevap:
1995 ÖYS. a+ =3a a= Cevap:D. Çözüm: Çözüm: Çözüm:
 99 ÖYS. a b c d ve a, b, c, d tek sayılar olmak üzere, abcd dört basamaklı en büyük sayıdır? Bu sayı aşağıdakilerden hangisine kalansız bölünebilir? A) B) 6 C) 9 D) E) a, b, c, d rakamları birbirinden
99 ÖYS. a b c d ve a, b, c, d tek sayılar olmak üzere, abcd dört basamaklı en büyük sayıdır? Bu sayı aşağıdakilerden hangisine kalansız bölünebilir? A) B) 6 C) 9 D) E) a, b, c, d rakamları birbirinden
ANT TÜREV VE NTEGRAL HESAPLAMA YÖNTEMLER
 ANT TÜREV VE NTEGRAL HESAPLAMA YÖNTEMLER 1 TEMEL YÖNTEM VE DE KEN DE T RME Bir kapal aralkta tanmlanm³ olan f ve F fonksiyonlar için e er bu aralkta F () f() ko³ulu sa lanyorsa F fonksiyonu, f fonksiyonunun
ANT TÜREV VE NTEGRAL HESAPLAMA YÖNTEMLER 1 TEMEL YÖNTEM VE DE KEN DE T RME Bir kapal aralkta tanmlanm³ olan f ve F fonksiyonlar için e er bu aralkta F () f() ko³ulu sa lanyorsa F fonksiyonu, f fonksiyonunun
MAT223 AYRIK MATEMATİK
 MAT223 AYRIK MATEMATİK Çizgeler 7. Bölüm Emrah Akyar Anadolu Üniversitesi Fen Fakültesi Matematik Bölümü, ESKİŞEHİR 2014 2015 Öğretim Yılı Çift ve Tek Dereceler Çizgeler Çift ve Tek Dereceler Soru 51 kişinin
MAT223 AYRIK MATEMATİK Çizgeler 7. Bölüm Emrah Akyar Anadolu Üniversitesi Fen Fakültesi Matematik Bölümü, ESKİŞEHİR 2014 2015 Öğretim Yılı Çift ve Tek Dereceler Çizgeler Çift ve Tek Dereceler Soru 51 kişinin
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Türev Uygulamaları. 4.1 Bağımlı Hız
 Bölüm 4 Türev Uygulamaları 4.1 Bağımlı Hız Eğer bir balonun içine hava pompalarsak, balonun hem yarıçapı hem de hacmi artar ve artış hızları birbirine bağımlıdır. Fakat, hacmin artış hızını doğrudan ölçmek
Bölüm 4 Türev Uygulamaları 4.1 Bağımlı Hız Eğer bir balonun içine hava pompalarsak, balonun hem yarıçapı hem de hacmi artar ve artış hızları birbirine bağımlıdır. Fakat, hacmin artış hızını doğrudan ölçmek
28/04/2014 tarihli LYS-1 Matematik-Geometri Testi konu analizi SORU NO LYS 1 MATEMATİK TESTİ KAZANIM NO KAZANIMLAR 1 / 31
 SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 11 32159 Rasyonel sayı kavramını açıklar. 2 12 32151 İki ya da daha çok doğal sayının en büyük ortak bölenini ve en küçük ortak katını bulur.
SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 11 32159 Rasyonel sayı kavramını açıklar. 2 12 32151 İki ya da daha çok doğal sayının en büyük ortak bölenini ve en küçük ortak katını bulur.
2013-2014 EĞİTİM VE ÖĞRETİM YILI TED KDZ EREĞLİ KOLEJİ ORTAOKULU MATEMATİK 8.SINIF ÜNİTELENDİRİLMİŞ YILLIK PLANDIR.
 EYLÜL 2013-201 EĞİTİM VE ÖĞRETİM YILI TED KDZ EREĞLİ KOLEJİ ORTAOKULU MATEMATİK 8.SINIF ÜNİTELENDİRİLMİŞ YILLIK PLANDIR. 9-13 Örüntü ve Süslemeler Dönüşüm Geometrisi 1. Doğru, çokgen ve çember modellerinden
EYLÜL 2013-201 EĞİTİM VE ÖĞRETİM YILI TED KDZ EREĞLİ KOLEJİ ORTAOKULU MATEMATİK 8.SINIF ÜNİTELENDİRİLMİŞ YILLIK PLANDIR. 9-13 Örüntü ve Süslemeler Dönüşüm Geometrisi 1. Doğru, çokgen ve çember modellerinden
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ "A" OLARAK CEVAP KÂĞIDINA İŞARETLEMEYİ UNUTMAYINIZ. SAYISAL BÖLÜM SAYISAL-2 TESTİ
 ALES İlkbahar 007 SAY DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ "A" OLARAK CEVAP KÂĞIDINA İŞARETLEMEYİ UNUTMAYINIZ. SAYISAL BÖLÜM SAYISAL- TESTİ Sınavın bu testinden alacağınız standart puan, Sayısal Ağırlıklı
ALES İlkbahar 007 SAY DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ "A" OLARAK CEVAP KÂĞIDINA İŞARETLEMEYİ UNUTMAYINIZ. SAYISAL BÖLÜM SAYISAL- TESTİ Sınavın bu testinden alacağınız standart puan, Sayısal Ağırlıklı
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
TANIM : a, a, a, a,..., a R ve n N olmak üzere,
 MATEMAT K TANIM : a, a, a, a,..., a R ve n N olmak üzere, 0 1 2 3 n P(x) = a x n a x n 1... a x 3 a x 2 a x n n 1 3 2 1 a ifadesine reel katsay l POL NOM denir. 0 a, a, a,..., a say lar na KATSAYILAR,
MATEMAT K TANIM : a, a, a, a,..., a R ve n N olmak üzere, 0 1 2 3 n P(x) = a x n a x n 1... a x 3 a x 2 a x n n 1 3 2 1 a ifadesine reel katsay l POL NOM denir. 0 a, a, a,..., a say lar na KATSAYILAR,
Ç NDEK LER. Bölüm 4: Üslü Say lar...44 Üslü fadeler...44 Al t rmalar...47 Test Sorular...49
 Ç NDEK LER Bölüm1: Say Sistemleri...1 Say Sistemi...2 Desimal (Onluk) Say Sistemi...2 Say Basamaklar ve Taban...4 Binary ( kilik) Say Sistemi...4 Oktal (Sekizlik) Say Sistemi...7 Heksadesimal (Onalt l
Ç NDEK LER Bölüm1: Say Sistemleri...1 Say Sistemi...2 Desimal (Onluk) Say Sistemi...2 Say Basamaklar ve Taban...4 Binary ( kilik) Say Sistemi...4 Oktal (Sekizlik) Say Sistemi...7 Heksadesimal (Onalt l
(m+2) +5<0. 7/m+3 + EŞİTSİZLİKLER A. TANIM
 EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
n ; = w! =(w 1 ; :::; w n ) (1.2.2) ; :::; + :::
 1. G IR IŞ 1.1. Ön Bilgiler Laplace denklemi, zik ve mühendisli¼gin pekçok alan nda ortaya ç kt ¼g ndan matematikçilerin, mühendislerin ve bilim adamlar n n büyük bir ilgi alan olmuştur. Potansiyel Teorinin
1. G IR IŞ 1.1. Ön Bilgiler Laplace denklemi, zik ve mühendisli¼gin pekçok alan nda ortaya ç kt ¼g ndan matematikçilerin, mühendislerin ve bilim adamlar n n büyük bir ilgi alan olmuştur. Potansiyel Teorinin
ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER
 ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER Şekil-1: BREADBOARD Yukarıda, deneylerde kullandığımız breadboard un şekli görünmektedir. Bu board üzerinde harflerle isimlendirilen satırlar ve numaralarla
ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER Şekil-1: BREADBOARD Yukarıda, deneylerde kullandığımız breadboard un şekli görünmektedir. Bu board üzerinde harflerle isimlendirilen satırlar ve numaralarla
İÇİNDEKİLER. Bölüm 2 CEBİR 43
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 13 1.1 Doğal Sayılar 15 1.1.1. Tek ve Çift Sayılar 15 1.1.2. Asal Sayılar 15 1.1.3 Doğal Sayıların Özellikleri 15 1.1.4 Doğal Sayılarda Özel Toplamlar 16 1.1.5. Faktöriyel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 13 1.1 Doğal Sayılar 15 1.1.1. Tek ve Çift Sayılar 15 1.1.2. Asal Sayılar 15 1.1.3 Doğal Sayıların Özellikleri 15 1.1.4 Doğal Sayılarda Özel Toplamlar 16 1.1.5. Faktöriyel
B02.8 Bölüm Değerlendirmeleri ve Özet
 B02.8 Bölüm Değerlendirmeleri ve Özet 57 Yrd. Doç. Dr. Yakup EMÜL, Bilgisayar Programlama Ders Notları (B02) Şimdiye kadar C programlama dilinin, verileri ekrana yazdırma, kullanıcıdan verileri alma, işlemler
B02.8 Bölüm Değerlendirmeleri ve Özet 57 Yrd. Doç. Dr. Yakup EMÜL, Bilgisayar Programlama Ders Notları (B02) Şimdiye kadar C programlama dilinin, verileri ekrana yazdırma, kullanıcıdan verileri alma, işlemler
0 dan matematik. Bora Arslantürk. çalışma kitabı
 0 dan matematik 0 dan matematik 1 çalışma kitabı Sıfırdan başlanarak matematik ile ilgili sıkıntı yaşayan herkese hitap etmesi, Akıllı renklendirme ile göz yoran değil ayrım yapmayı, istenileni bulmayı
0 dan matematik 0 dan matematik 1 çalışma kitabı Sıfırdan başlanarak matematik ile ilgili sıkıntı yaşayan herkese hitap etmesi, Akıllı renklendirme ile göz yoran değil ayrım yapmayı, istenileni bulmayı
Bu tanım aralığı pozitif tam sayılar olan f(n) fonksiyonunun değişim aralığı n= 1, 2, 3,, n,
 DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
LĐMĐT ÖSS ÖYS YILLAR SAĞDAN VE SOLDAN LĐMĐT. ÇÖZÜM: x=2 f(x) de yerine yazılır cevap:7
 YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS ÖYS LĐMĐT Tanım : Bir x0 A = [ a,b ] alalım, f: A R ye veya f: A - { x 0 } R ye bir fonksiyon olsun. Terimleri A - { x 0 } kümesine ait ve x
YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS ÖYS LĐMĐT Tanım : Bir x0 A = [ a,b ] alalım, f: A R ye veya f: A - { x 0 } R ye bir fonksiyon olsun. Terimleri A - { x 0 } kümesine ait ve x
İÇİNDEKİLER. Ön Söz...2. Adi Diferansiyel Denklemler...3. Birinci Mertebeden ve Birinci Dereceden. Diferansiyel Denklemler...9
 İÇİNDEKİLER Ön Söz... Adi Diferansiyel Denklemler... Birinci Mertebeden ve Birinci Dereceden Diferansiyel Denklemler...9 Homojen Diferansiyel Denklemler...15 Tam Diferansiyel Denklemler...19 Birinci Mertebeden
İÇİNDEKİLER Ön Söz... Adi Diferansiyel Denklemler... Birinci Mertebeden ve Birinci Dereceden Diferansiyel Denklemler...9 Homojen Diferansiyel Denklemler...15 Tam Diferansiyel Denklemler...19 Birinci Mertebeden
1. GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G (e ye birim eleman denir) vardır.
 1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
Kukla Değişkenlerle Bağlanım
 Kukla Değişkenlerle Bağlanım Kukla Değişken Kullanım Şekilleri Ekonometri 1 Konu 29 Sürüm 2,0 (Ekim 2011) UADMK Açık Lisans Bilgisi İşbu belge, Creative Commons Attribution-Non-Commercial ShareAlike 3.0
Kukla Değişkenlerle Bağlanım Kukla Değişken Kullanım Şekilleri Ekonometri 1 Konu 29 Sürüm 2,0 (Ekim 2011) UADMK Açık Lisans Bilgisi İşbu belge, Creative Commons Attribution-Non-Commercial ShareAlike 3.0
Analiz III Ara S nav Sorular 24 Kas m 2010
 Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
YAŞ PROBLEMLERİ Test -1
 YAŞ PROBLEMLERİ Test -1 1. Bugün 36 yaşında olan bir kişinin kaç yıl önceki yaşı, bugünkü yaşının 2 üne eşittir? 3 A) 10 B) 12 C) 14 D) 15 E) 18 5. Begüm 18, Sıla 10 yaşındadır. Buna göre, kaç yıl sonra
YAŞ PROBLEMLERİ Test -1 1. Bugün 36 yaşında olan bir kişinin kaç yıl önceki yaşı, bugünkü yaşının 2 üne eşittir? 3 A) 10 B) 12 C) 14 D) 15 E) 18 5. Begüm 18, Sıla 10 yaşındadır. Buna göre, kaç yıl sonra
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ KAZANIM NO KAZANIMLAR
 2013-2014 PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 12 32173 Üslü İfadeler 2 13 42016 Rasyonel ifade kavramını örneklerle açıklar ve
2013-2014 PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 12 32173 Üslü İfadeler 2 13 42016 Rasyonel ifade kavramını örneklerle açıklar ve
SÜREKLİLİK. 9.1 Süreklilik ve Süreksizlik Kavramları
 SÜREKLİLİK Bu bölümde süreklilik kavramı, süreksizlik, sürekli fonksiyonların özellikleri ile buna ilişkin teoremler örnekler ve grafiklerle açıklanmaktadır. 9.1 Süreklilik ve Süreksizlik Kavramları Tanım
SÜREKLİLİK Bu bölümde süreklilik kavramı, süreksizlik, sürekli fonksiyonların özellikleri ile buna ilişkin teoremler örnekler ve grafiklerle açıklanmaktadır. 9.1 Süreklilik ve Süreksizlik Kavramları Tanım
biçimindeki ifadelere iki değişkenli polinomlar denir. Bu polinomda aynı terimdeki değişkenlerin üsleri toplamından en büyük olanına polinomun dereces
 TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
Ortak Akıl MATEMATİK DENEME SINAVI
 Ortak Akıl LYS MATEMATİK DENEME SINAVI 0505- Ortak Akıl Adem ÇİL Ali Can GÜLLÜ Ayhan YANAĞLIBAŞ Barbaros GÜR Barış DEMİR Celal İŞBİLİR Deniz KARADAĞ Engin POLAT Erhan ERDOĞAN Ersin KESEN Fatih TÜRKMEN
Ortak Akıl LYS MATEMATİK DENEME SINAVI 0505- Ortak Akıl Adem ÇİL Ali Can GÜLLÜ Ayhan YANAĞLIBAŞ Barbaros GÜR Barış DEMİR Celal İŞBİLİR Deniz KARADAĞ Engin POLAT Erhan ERDOĞAN Ersin KESEN Fatih TÜRKMEN
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
DENEY 2: PROTOBOARD TANITIMI VE DEVRE KURMA
 A. DENEYİN AMACI : Protoboard kullanımını öğrenmek ve protoboard üzerinde basit direnç devreleri kurmak. B. KULLANILACAK ARAÇ VE MALZEMELER : 1. DC güç kaynağı, 2. Multimetre, 3. Protoboard, 4. Değişik
A. DENEYİN AMACI : Protoboard kullanımını öğrenmek ve protoboard üzerinde basit direnç devreleri kurmak. B. KULLANILACAK ARAÇ VE MALZEMELER : 1. DC güç kaynağı, 2. Multimetre, 3. Protoboard, 4. Değişik
Örnek...6 : Yandaki bölme işleminde A ve n birer doğal sayıdır. A nın alabileceği en küçük ve en bü yük değerleri bulunu z.
 MODÜLER ARİTMETİK ( BÖLME BÖLÜNEBİLME KURALLARI ÖKLİT ALGORİTMASI DEĞERLENDİRME ) BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...5 : A, B, C birbirinden
MODÜLER ARİTMETİK ( BÖLME BÖLÜNEBİLME KURALLARI ÖKLİT ALGORİTMASI DEĞERLENDİRME ) BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...5 : A, B, C birbirinden
SEYAHAT PERFORMANSI MENZİL
 SEYAHAT PERFORMANSI MENZİL Uçakların ne kadar paralı yükü, hangi mesafeye taşıyabildikleri ve bu esnada ne kadar yakıt harcadıkları en önemli performans göstergelerinden biridir. Bir uçağın kalkış noktasından,
SEYAHAT PERFORMANSI MENZİL Uçakların ne kadar paralı yükü, hangi mesafeye taşıyabildikleri ve bu esnada ne kadar yakıt harcadıkları en önemli performans göstergelerinden biridir. Bir uçağın kalkış noktasından,
12.Konu Rasyonel sayılar
 12.Konu Rasyonel sayılar 1. Rasyonel sayılar 2. Rasyonel sayılar kümesinde toplama ve çarpma 3. Rasyonel sayılar kümesinde çıkarma ve bölme 4. Tam rayonel sayılar 5. Rasyonel sayılar kümesinde sıralama
12.Konu Rasyonel sayılar 1. Rasyonel sayılar 2. Rasyonel sayılar kümesinde toplama ve çarpma 3. Rasyonel sayılar kümesinde çıkarma ve bölme 4. Tam rayonel sayılar 5. Rasyonel sayılar kümesinde sıralama
Elektrik Makinaları I. Senkron Makinalar Stator Sargılarının oluşturduğu Alternatif Alan ve Döner Alan, Sargıda Endüklenen Hareket Gerilimi
 Elektrik Makinaları I Senkron Makinalar Stator Sargılarının oluşturduğu Alternatif Alan ve Döner Alan, Sargıda Endüklenen Hareket Gerilimi Bir fazlı, iki kutuplu bir stator sargısının hava aralığında oluşturduğu
Elektrik Makinaları I Senkron Makinalar Stator Sargılarının oluşturduğu Alternatif Alan ve Döner Alan, Sargıda Endüklenen Hareket Gerilimi Bir fazlı, iki kutuplu bir stator sargısının hava aralığında oluşturduğu
