Farklı Normalizasyon Yöntemlerinin TOPSIS te Karar Verme Sürecine Etkisi
|
|
|
- Umut Gün
- 8 yıl önce
- İzleme sayısı:
Transkript
1 EGE AKADEMİK BAKIŞ / EGE ACADEMIC REVIEW Cilt: 13 Sayı: 2 Nisan 2013 ss Farklı Yöntemlerinin TOPSIS te Karar Verme Sürecine Etkisi The Effects of Different Normalization Methods to Decision Making Process in TOPSIS Aşkın ÖZDAĞOĞLU 1 ÖZET Çok sayıda alternatifin olması durumu bir karar verme problemini ortaya çıkarmaktadır. Bu alternatiflerin karşılaştırılırken de birden çok değerlendirme ölçütünün bir arada incelenmesi kaçınılmaz bir durumdur. Bu tür karar verme problemlerinde kullanılabilen çeşitli çok ölçütlü karar verme yöntemleri mevcuttur. Bazı çok ölçütlü karar verme yöntemlerinin işleyiş aşamalarında ölçüm birimleri birbirinden farklı olan değerlendirme ölçütlerinin birlikte incelenmesini sağlamak amacıyla normalizasyon yöntemleri kullanılmaktadır. Ancak aynı çok ölçütlü karar verme yönteminde farklı normalizasyon yöntemlerinin kullanıldığı da görülmektedir. Bu çalışmanın amacı, çok ölçütlü karar verme yöntemlerinden biri olan TOPSIS yöntemi için tüm normalizasyon yöntemlerinin örnek veri setleri üzerinde denenip sonuçlarının karşılaştırılmasıdır. Anahtar Kelimeler: yöntemleri, çok ölçütlü karar verme, TOPSIS yöntemi. ABSTRACT Existing of many different alternatives has revealed a decision making problem. The analysis of many different evaluation criteria when comparing the alternatives is an inevitable situation. There are various multi criteria decision making methods which can be used in these decision making problems. Normalization methods have been used for analyzing the evaluation criteria which have got different measurement units in some multi criteria decision making methos. However, different normalization methods can be used for the same multi criteria decision making method. The purpose of this study is to compare of the results by trying of all normalization methods in TOPSIS method via sample data sets. Keywords: Normalization methods, multi criteria decision making, TOPSIS method. 1. GİRİŞ İşletmeler karşılaştıkları problemleri çözebilmek için bir çok değerlendirme ölçütünü birlikte göz önüne almak zorundadırlar. Bir karar verme olayından söz edilebilmesi için de elde mevcut çok sayıda alternatiften söz edilmesi gerekmektedir. İşte çok sayıda değerlendirme ölçütünü bir arada göz önüne alarak farklı alternatiflerin karşılaştırılması gerekliliği çok ölçütlü karar verme yöntemlerinin geliştirilmesine yol açmıştır. Karar verme sürecindeki diğer bir sorun da, karar verme süreci üzerinde etkisi olan değerlendirme ölçütlerinin doğal olarak farklı ölçüm birimlerine sahip olabilmesidir. Farklı birimlere sahip olan ölçütleri aynı potada eritebilmek amacıyla çok ölçütlü karar verme yöntemlerinin bazılarının işleyişinde normalizasyon yöntemlerine başvurulmaktadır. Ancak bu normalizasyon yöntemleri doğrusal normalizasyon türleri, vektör normalizasyonu gibi pek çok farklı şekilde uygulanabilmektedir. Farklı çok ölçütlü karar verme yöntemlerinin farklı normalizasyon yöntemlerine başvurmasının yanında aynı çok ölçütlü karar verme yönteminde bile farklı normalizasyon yönteminin tercih edildiği literatürde sıklıkla görülen bir durumdur. İşte bu nedenle, farklı normalizasyon yöntemlerinin çok ölçütlü karar verme yönteminde kullanılması durumunda sonuçların nasıl etkileneceği hakkında bir bilgiye ulaşmak bu çalışmanın çıkış noktasını oluşturmuştur. Bu incelemeyi gerçekleştirmek amacıyla 10 alternatif ve 5 değerlendirme ölçütü içeren 10 farklı veri seti üretilerek bu veri setleri üzerinde çok ölçütlü karar verme yöntemlerinden biri olan TOPSIS ile hesaplamalar gerçekleştirimiştir. Bu hesaplama sürecinde 6 farklı normalizasyon yöntemi aynı veri setleri için kullanılmıştır. Bu çalışmada, ilk olarak normalizasyon yöntemleri açıklanacaktır. yöntemleri hakkında bilgi verilmesinden sonra farklı çok ölçütlü karar verme yöntemleri için hangi normalizasyon yöntemlerinin kullanıldığı konusunda literatürde yer alan çalışmalar hakkında bilgi verilecek, çalışma kapsamında kullanılan TOP- SIS yönteminin işleyişi açıklanacak ve ardından örnek veri setleri üzerinde hesaplamalar açıklanarak sonuçlar karşılaştırılacaktır. 1 Yrd. Doç. Dr., Dokuz Eylül Üniversitesi, İşletme Fakültesi, İşletme Bölümü,askin.ozdagoglu@deu.edu.tr 245
2 Aşkın ÖZDAĞOĞLU 2. NORMALİZASYON YÖNTEMLERİ yöntemleri üç ana başlıkta toplanabilmektedir. * Vektör normalizasyonu, *, * Monoton olmayan normalizasyon. Bu normalizasyon yöntemlerinden doğrusal normalizasyon da farklı şekillerde uygulanabilmektedir. Yöntemlerin uygulanışına ilişkin formüller sunulmadan önce değişkenlerin tanıtılması yerinde olacaktır. Bir çok ölçütlü karar verme probleminde normalizasyon işlemine tabi olacak değişkenler aşağıdaki gibi gösterilsin (Shih vd., 2007: 805). A i :i.alternatif i=1,2,,m C :.değerlendirme ölçütü =1,2,,n x i =.değerlendirme ölçütü açısından i.alternatifin değeri Bu değişkenlere göre oluşan karar matrisi 1 numaralı denklemde gösterilmiştir. A1 x11 x11 x11 x1 n A 2 x21 x22 x23. x 2n D= A 3 x31 x32 x33. x 3n (1) A m xm1 xm2 xm3. x mn yöntemlerinin bu değişkenler doğrultusunda uygulanması Denklem 2-10 aralığında sunulmuştur. Vektör normalizasyonu x i ri =, i=1,2,...,m; =1,2,..., n. (2) m 2 x i= 1 i normalizasyon (1) * ri = xi /( x ) i=1, 2,..., m; =1, 2,..., n; x * =maxi ) (ölçüt için en iyi durum maksimizasyon ise). (3) ri = ( x )/ xi i=1, 2,..., m; =1, 2,..., n; x - =min i ) (ölçüt için en iyi durum minimizasyon ise). (4) normalizasyon (2) * ri = xi /( x ) i=1, 2,..., m; =1, 2,..., n; x * =max i ) (ölçüt için en iyi durum maksimizasyon ise). (5) * ri = 1 xi /( x ) i=1,2,..., m; =1, 2,..., n; x * =max i ) (ölçüt için en iyi durum minimizasyon ise). (6) normalizasyon (3) x ri = x i * x x i=1, 2,...,m; =1,2,...,n;x * =max i ), x - =min i ) (ölçüt için en iyi durum maksimizasyon ise). (7) * x xi ri = * x x i=1, 2,..., m; =1, 2,...,n; x * =max i ), x - =min i ) (ölçüt için en iyi durum minimizasyon ise). (8) normalizasyon (4) xi ri =, i=1, 2,..., m; =1, 2,..., n. (9) m x i= 1 i Monoton olmayan normalizasyon x 0 : ölçütüne ilişkin en uygun değer σ : ölçütüne ilişkin değerlerin standart sapması e x x = (10) 2 z 0 2 i, z σ 3. LİTERATÜR İNCELEMESİ Literatür incelendiğinde çok ölçütlü karar verme yöntemi kullanılarak alternatifler arasında seçim yapılan bir çok çalışma ile karşılaşılmaktadır. TOPSIS yönteminin kullanıldığı çalışmalara bakıldığında çoğunlukla vektör normalizasyonunun tercih edildiği görülmektedir (Peng vd., 2011; Huang ve Huang, 2012; Sun vd., 2011; Sadeghzadeh ve Salehi, 2011; Aalami vd., 2010; Ayala, 2012; Kiran vd., 2011; Lozano-Minguez vd., 2011). Ancak aynı çok ölçütlü karar verme yöntemi içinde normalizasyon (2) olarak açıklanan yöntem (Ouattara vd., 2012) ile normalizasyon (3) olarak açıklanan yöntemin de (Mela vd., 2012; Dai ve Wang, 2011) tercih edildiği görülmektedir. Bu çalışmada örnek veri setleri üzerinde hesaplamalar yapılarak karşılaştırılacak olan TOPSIS için yukarıda açıklandığı üzere bir yöntem birliği bulunmamaktadır. Bu konuda diğer çok ölçütlü karar verme yöntemlerini de inceleyerek yöntem birliğinin bulunmadığını göstermek mümkündür. Örnek vermek gerekirse, EXPROM 2 için doğrusal normalizasyon (3) olarak açıklanan yöntem (Chatteree ve Chakraborty, 2012); COPRAS için doğrusal normalizasyon (4) olarak açıklanan yöntem (Kaklauskas vd., 2010; Kaklauskas vd., 2007); MULTI- MOORA için vektör normalizasyonu (Balezentis vd., 2012; Streimikiene vd., 2012) kullanılan çalışmalara rastlanmıştır. MOORA yöntemi için bazı çalışmalarda doğrusal normalizasyon (4) olarak açıklanan yöntem (Karande ve Chakraborty, 2012); bazılarında ise vektör normalizasyonu (Chakraborty, 2011) kullanıldığı tespit edilmiştir. normalizasyon (1) olarak açıklanan yöntem ile monoton olmayan normalizas- 246
3 Farklı Yöntemlerinin TOPSIS te Karar Verme Sürecine Etkisi yonun kullanıldığı bir çok ölçütlü karar verme yöntemi çalışmasına rastlanamamıştır. Zaten literatürde de monoton olmayan normalizasyon yönteminin diğer normalizasyon yöntemlerine göre çok nadir kullanıldığı ifade edilmektedir (Shih vd., 2007). Yukarıda örnekleri verilen COPRAS, MULTIMOORA ve EXPROM 2 gibi bazı çok ölçütlü karar verme yöntemlerinde kendi içinde bir ortak normalizasyon yönteminin kullanıldığı görülmektedir. Ancak bunun bir nedeni de bahsi geçen yöntemlerin nispeten daha yeni olmaları veya literatürde çok ölçütlü karar verme yöntemi olarak fazla kullanılmamalarıdır. Bu kısımda ELECTRE ve PROMETHEE gibi bazı çok ölçütlü karar verme yöntemlerine değinilmemiştir. Çünkü bu yöntemlerin uygulama adımlarının başında alternatifler arasında ikili karşılaştırmalar yapılmasından dolayı normalizasyon işlemine gerek kalmamaktadır. Ayrıca WSM ve WPM olarak adlandırılan çok ölçütlü karar verme yöntemlerinin gerçekleştirilebilmesi için de karar verme sürecini etkileyen değerlendirme ölçütlerinin aynı ölçüm birimine sahip olmaları ya da ölçeği gibi ortak bir performans değerine göre verilerin sunulması gibi uygulamada çok nadiren karşılaşılabilecek varsayımlar altında çalışma gerekliliklerinden ötürü uygulamada pek kullanılamamaktadırlar. Yukarıda verilen örneklerde görüldüğü üzere kullanılan normalizasyon yöntemi üzerinde bir fikir birliğinin bulunmaması bu çalışmanın hareket nokasını oluşturmuştur. yönteminin verilen karara etkisini görmek üzere 10 alternatif ve 5 değerlendirme ölçütü içeren 10 adet veri seti türetilmiş ve her bir veri seti için TOPSIS yönteminde tüm olası normalizasyon yöntemleri denenerek elde edilen sonuçlar karşılaştırılmıştır. Buna ilave olarak karar verme sürecinde karşılaşılabilecek tüm olası durumları ihtiva etmesi amacıyla 3 numaralı değerlendirme ölçütü için en iyi durumun en düşük değer olması şeklinde düzenleme yapılmıştır. İzleyen bölümde üzerinde deneme yapılacak olan TOPSIS yönteminin işleyişi hakkında bilgi verilecektir. 4. TOPSIS YÖNTEMİ TOPSIS ilk olarak Hwang ve Yoon tarafından geliştirilmiştir. Ölçütlerin tüm en iyi değerlerinin bileşiminden oluşan pozitif ideal çözümlerle, en kötü değerlerinin bileşiminden oluşan negatif ideal çözümlerin olduğu bir çok ölçütlü karar verme problemini çözerken seçilen alternatifin pozitif ideal çözümden en kısa mesafede ve negatif ideal çözümden en uzak mesafede bulunması kavramına dayanmaktadır (Hwang ve Yoon, 1981; Chen ve Tzeng, 2004). Aşağıda TOPSIS yönteminin adımları tanımlanmıştır (Shih vd., 2007). Adım 1. Karar Matrisi (D) oluşturulur. Karar matrisinin satırlarında i,i=1,2,...,m alternatifler, sütunlarında ise,=1,2,...,n ölçütler yer almaktadır. D matrisi karar verici tarafından oluşturulan veri matrisidir. Karar matrisi 11 numaralı denklemdeki gibi gösterilir: x11 x12. x1 n x21 x22. x 2n Di = (11).... xm1 xm2. xmn Adım 2.Normalize karar matrisi (R) oluşturulur. işleminin gerçekleştirilmesinde farklı yöntemler mevcuttur. En sık kullanılanlar vektör normalizasyonu, doğrusal normalizasyon ve monoton olmayan normalizasyondur. normalizasyon içinde farklı yaklaşımlar bulunmaktadır. Normalize edilmiş karar matrisi (R) için vektör normalizasyonu sıklıkla kullanılan bir yöntem olarak ortaya çıkmaktadır. Burada normalize edilmiş karar matrisi (R) için vektör normalizasyonu 12 numaralı denklemde belirtilmiştir. xi ri = i = 1,2,..., m; = 1,2,..., n. m (12) 2 x i= 1 i Burada literatürde incelenen TOPSIS yöntemi kullanılmış olan çalışmalarda çoğunlukla vektör normalizasyonu ile karşılaşıldığından dolayı 12 numaralı denklem olarak vektör normalizasyonu işlemi verilmiştir. Bu çalışmada, belirtilen 12 numaralı denklemin yerine 3-10 numaralı denklemlerin hepsi denenerek sonuçlar incelenecektir. la ilgili bu açıklamanın ardından yöntemin işleyişine geri dönüldüğünde R matrisi denklem 13 gibi elde edilir: r11 r12. r1 n r21 r22. r 2n Ri =.... (13) rm 1 rm 2. rmn Adım 3. Ağırlıklı Normalize Karar Matrisi (Y) oluşturulur. Öncelikle değerlendirme faktörlerine ilişkin ağırlık değerleri (w i n ) belirlenir ( w 1) i= 1 i =. Daha sonra R matrisinin her bir sütunundaki elemanlar ilgili w_i değeri ile çarpılarak Y matrisi oluşturulur. Y matrisidenklem 14 te gösterilmiştir: wr 1 11 wr wr n 1n wr 1 21 wr wr n 2n Yi = (14).... wr 1 m1 wr 2 m2. wr n mn 247
4 Aşkın ÖZDAĞOĞLU Adım 4. Pozitif İdeal (A * ) ve Negatif İdeal (A - ) çözümler oluşturulur. İdeal çözüm setinin oluşturulabilmesi için Y matrisindeki ağırlıklandırılmış ölçütlerin yani sütun değerlerinin en büyükleri (ilgili ölçüt minimizasyon yönlü ise en küçüğü) seçilir. Pozitif ideal çözüm setinin bulunması 15 numaralı denklemde gösterilmiştir. A * ={(max i y i J ),(min i y i J ) } (15) 15 numaralı denklem yardımıyla hesaplanacak olan set 16 numaralı denklemde gösterildiği gibi oluşur. A * ={y 1*,y 2*,,y n*,} (16) Negatif ideal çözüm seti ise, Y matrisindeki ağırlıklandırılmış ölçütlerin, bir başka deyişle, sütun değerlerinin en küçükleri (ilgili değerlendirme faktörü minimizasyon yönlü ise en büyüğü) seçilerek oluşturulur. Negatif ideal çözüm setinin bulunması 17 numaralı denklem ile sağlanmaktadır. A - ={(min i y i J ),(max i y i J ) } (17) 17 numaralı denklem yardımıyla hesaplanacak olan set18 numaralı denklemde gösterilmiştir. A - ={y 1-,y 2-,,y n-,} (18) Her iki formülde de J fayda (maksimizasyon), J ise kayıp (minimizasyon) değerini göstermektedir.gerek pozitif ideal gerekse negatif ideal çözüm seti, ölçüt sayısı yani n elemandan oluşmaktadır. Adım 5. Her alternatifin pozitif ideal çözüm ve negatif ideal çözüme uzaklıkları hesaplanır. TOPSIS yönteminde her bir alternatife ilişkin ölçüt değerinin pozitif ideal ve negatif ideal çözüm setinden uzaklıklarının belirlenmesinde Euclidian Uzaklık Yaklaşımından yararlanılmaktadır. Buradan elde edilen alternatiflere ilişkin uzaklık değerleri ise Pozitif İdeal çözüme uzaklık (S i* ) ve Negatif İdeal çözüme uzaklık (S i- ) olarak adlandırılmaktadır. Pozitif ideal çözüme uzaklık (S i* ) değerinin hesaplanması 19 numaralı denklemde sunulmuştur. * n ( * ) 2 Si = y 1 i y = (19) Negatif ideal çözüme (S i- ) uzaklığın hesaplanması ise 20 numaralı denklemdeki gibidir. n ( ) 2 Si = y 1 i y = (20) * - Burada hesaplanacak S i ve S i sayısı karşılaştırılan alternatif sayısı kadardır. Adım 6. İdeal çözüme göreceli yakınlık değerleri hesaplanır. Her bir alternatifin ideal çözüme göreceli yakınlığının (C i* ) hesaplanmasında pozitif idealden ve negatif idealden uzaklık ölçüleri kullanılmaktadır. Burada kullanılan ölçüt, negatif ideal çözüme uzaklık değerinin pozitif ideal çözüme uzaklık değeri ile negatif ideal çözüme uzaklık değerinin toplamına oranıdır. İdeal çözüme göreceli yakınlık değerinin hesaplanması 21 numaralı denklemde sunulmuştur. * S Ci = S i * i + Si (21) Burada C i* değeri 0 C i* 1 aralığında değer alır ve C i* =1 ilgili alternatifin pozitif ideal çözüm noktasında bulunduğunu, C i* =0 ilgili alternatifin negatif ideal çözüm noktasında bulunduğunu gösterir. 5. UYGULAMA Çalışma kapsamında ilk aşamada 10 alternatif ve 5 değerlendirme ölçütüne göre 10 adet veri seti türetilmiştir. Veri türetme amacıyla Excel 2010 üzerinde RASTGELEARADA formülünden yararlanılmıştır. Modelin tüm olası durumları içermesi amacıyla her bir değerlendirme ölçütü için farklı sayı aralıklarında sayı türetilmiştir. Bu amaçla yazılan formüller Tablo 1 de sunulmuştur. Tablo 1: Veri Türetmede Kullanılan Farklı Formüller Ölçütü Numarası Ölçütü 1 Ölçütü 2 Ölçütü 3 Ölçütü 4 Ölçütü 5 Yazılan Formül =RASTGELEARADA(550;850) =RASTGELEARADA(25;125) =RASTGELEARADA(35;190) =RASTGELEARADA(200;280) =RASTGELEARADA(1040;1300) yöntemleri başlıklı bölümde de açıklandığı üzere modelin olası tüm durumları yansıtabilmesi için 3 numaralı değerlendirme ölçütünün birim üretim zamanı veya maliyet gibi düşük olmasının en iyi durumu gösterdiği düşünülerek hesaplamalar gerçekleştirilmiştir. Tablo 1 de belirtilen formüller yazılarak elde edilen veri setleri Tablo 2 den incelenebilir. Bu veri setleri üzerinde normalizasyon yöntemlerinin etkisini görmek amacıyla 12 numaralı denklemin yerine 3-10 aralığındaki denklemler tek tek denenerek numaralı aralıkta yer alan denklemler kullanılarak TOPSIS yöntemi sonuçları ayrı ayrı hesaplanmıştır. Yöntemlerin işleyişini açıklamak amacıyla ilk veri seti için yapılan işlemler aşağıda açıklanmıştır. İlk olarak 2 numaralı denklem kullanılarak normalize karar matrisi oluşturulur. ölçütü 1 ile alternatif 1 kesişim hücresi değeri için aşağıdaki işlem gerçekleştirilir. 248
5 Farklı Yöntemlerinin TOPSIS te Karar Verme Sürecine Etkisi Veri Seti 1 Veri Seti 2 Veri Seti 3 Veri Seti 4 Veri Seti 5 Veri Seti 6 Ölçütü 1 Tablo 2: Veri Setleri Değerlendirm e Ölçütü 2 Ölçütü 3 Ölçütü 4 Ölçütü 5 En Büyük En Büyük En Küçük En Büyük En Büyük Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif
6 Aşkın ÖZDAĞOĞLU Veri Seti 7 Veri Seti 8 Veri Seti 9 Veri Seti 10 Ölçütü 1 Değerlendirm e Ölçütü Ölçütü 3 Ölçütü 4 Ölçütü 5 En Büyük En Büyük En Küçük En Büyük En Büyük Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif Alternatif ( ) = 0, İşlem tüm değerlere uygulandığında Tablo 3 teki sonuçlara ulaşılmıştır. Tablo 3: Veri Seti 1 için Normalize Karar Matrisi Ölçütü 1 Ölçütü 2 Ölçütü 3 Ölçütü 4 Ölçütü 5 En büyük En büyük En küçük En büyük En büyük Alternatif 1 0, , , , , Alternatif 2 0, , , , , Alternatif 3 0, , , , , Alternatif 4 0, , , , , Alternatif 5 0, , , , , Alternatif 6 0, , , , , Alternatif 7 0, , , , , Alternatif 8 0, , , , , Alternatif 9 0, , , , , Alternatif 10 0, , , , ,
7 Farklı Yöntemlerinin TOPSIS te Karar Verme Sürecine Etkisi Bu değerler ölçüt ağırlıkları ile çarpılarak ağırlıklı normalize karar matrisi oluşturulur. İlk hücre için yapılan işlem aşağıda verilmiştir. 0,2*0,355104=0, Tablo 4: Veri Seti 1 için Ağırlıklı Normalize Karar Matrisi İşlem tüm hücrelere uygulandığında Tablo 4 teki değerler elde edilmiştir. Ölçütü 1 Ölçütü 2 Ölçütü 3 Ölçütü 4 Ölçütü 5 En Büyük En Büyük En Küçük En Büyük En Büyük Alternatif 1 0, , , , , Alternatif 2 0, , , , , Alternatif 3 0, , , , , Alternatif 4 0, , , , , Alternatif 5 0, , , , , Alternatif 6 0, , , , , Alternatif 7 0, , , , , Alternatif 8 0, , , , , Alternatif 9 0, , , , , Alternatif 10 0, , , , , Ardından 15 numaralı denklem ile pozitif ideal çözüm seti bulunmuştur. Burada dikkat edilmesi gereken husus, değerlendirme ölçütü 3 için zaman, maliyet gibi değerin mümkün olduğunca küçük olmasının en iyi durumu göstermesi nedeniyle diğer değerlendirme ölçütlerinden farklı olarak en büyük değil en küçük değerin seçilmesi gerektiğidir. Benzer şekilde 17 numaralı denklem yardımıyla negatif ideal çözüm seti bulunur. Burada da değerlendirme ölçütü 3 için değerin büyük olmasının en kötü durumu göstermesinden dolayı en küçük değer değil en büyük değer seçilmelidir. 15 ve 17 numaralı denklemlerden elde edilen sonuçlar Tablo 5 te sunulmuştur. Pozitif İdeal Çözüm Seti Negatif İdeal Çözüm Seti 19 numaralı denklem kullanılarak her alternatif için pozitif ideal çözüme uzaklık değerleri hesaplanır. İlk alternatif için yapılan işlem aşağıda verilmiştir. 2 2 (0, , ) (0, , ) = 0, numaralı denklem kullanılarak her alternatif için negatif ideal çözüme uzaklık değerleri hesaplanır. İlk alternatif için yapılan işlem aşağıda verilmiştir. Tablo 5: Veri Seti 1 için Pozitif ve Negatif İdeal Çözüm Setleri Değerlendirm Ölçütü 1 Ölçütü 2 e Ölçütü 3 Ölçütü 4 Ölçütü 5 En Büyük En Büyük En Küçük En Büyük En Büyük 2 2 (0, , ) (0, , ) = 0, , , , , , , , , , , Tablo 6: Veri Seti 1 için Pozitif İdeal Çözüm Setine Uzaklık, Negatif İdeal Çözüm Setine Uzaklık ve İdeal Çözüme Göreceli Yakınlık Değerleri Pozitif İdeal Çözüm Setine Uzaklık Son olarak 21 numaralı denklem ile her bir alternatifin ideal çözüme göreceli yakınlık değerleri hesaplanır. İlk alternatif için yapılan işlem aşağıda sunulmuştur. 0, =0, , , İlk veri setine ilişkin pozitif ideal çözüm setine uzaklık, negatif ideal çözüm setine uzaklık ve ideal çözüme göreceli yakınlık değerleri Tablo 6 da verilmiştir. Negatif İdeal Çözüm Setine Uzaklık İdeal Çözüme Göreceli Yakınlık Alternatif 1 0, , , Alternatif 2 0, , , Alternatif 3 0, , , Alternatif 4 0, , , Alternatif 5 0, , , Alternatif 6 0, , , Alternatif 7 0, , , Alternatif 8 0, , , Alternatif 9 0, , , Alternatif 10 0, , ,
8 Aşkın ÖZDAĞOĞLU Farklı normalizasyon yöntemlerinin uygulanması işlem adımlarından ilki olan normalize karar matrisi hesaplamasını değiştirmekte ayrıca bazı normalizasyon yöntemlerinin işleyişine bağlı olarak pozitif ideal çözüm seti ile negatif ideal çözüm setinin bulunmasında farklılık olabilmektedir. Farklılaşan süreçler için örnek hesaplamalar aşağıda sunulmaktadır. normalizasyon (1) için 3 ve 4 numaralı denklemler kullanılarak ilk alternatife ait bazı işlemler aşağıdaki gibi olur. ölçütü 1 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir. 779 = 779 =0, MAK{779;793;769;600;597;565;643;647;846;634} 846 normalizasyon (1), normalleştirme işlemini iki farklı denklemle uygulamakta ve değerin ölçüt 3 gibi küçük olması istendiğinde 4 numaralı denklemin kullanılması gerekmektedir. ölçütü 3 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir. MIN{135;82;178;100;125;73;136;41;111;88} = 41 =0, Bu normalizasyon yöntemi değerin en küçük yada en büyük olmasına göre farklı işlemler kullandığından pozitif ideal çözüm setinin hesaplanmasında değerlendirme ölçütü 3 için de en büyüğün, negatif ideal çözüm setinin hesaplanmasında değerlendirme ölçütü 3 için de en küçüğün belirlenmesine dikkat edilmelidir. normalizasyon (2) için 5 ve 6 numaralı denklemler kullanılarak ilk alternatife ait bazı işlemler aşağıdaki gibi olur. ölçütü 1 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir = =0, MAK{779;793;769;600;597;565;643;647;846;634} 846 normalizasyon (2), normalleştirme işlemini iki farklı denklemle uygulamakta ve değerin ölçüt 3 gibi küçük olması istendiğinde 6 numaralı denklemin kullanılması gerekmektedir. ölçütü 3 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir =0, MAK{135;82;178;100;125;73;136;41;111;88} Bu normalizasyon yöntemi de değerin en küçük yada en büyük olmasına göre farklı işlemler kullandığından pozitif ideal çözüm setinin hesaplanmasında değerlendirme ölçütü 3 için de en büyüğün, negatif ideal çözüm setinin hesaplanmasında değerlendirme ölçütü 3 için de en küçüğün belirlenmesine dikkat edilmelidir. normalizasyon (3) için 7 ve 8 numaralı denklemler kullanılarak ilk alternatife ait bazı işlemler aşağıdaki gibi olur. ölçütü 1 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir. 779-MIN{779;793;769;600;597;565;643;647;846;634} =0, MAK{779;793;769;...;634}-MIN{779;793;769;...;634} normalizasyon (3), normalleştirme işlemini iki farklı denklemle uygulamakta ve değerin ölçüt 3 gibi küçük olması istendiğinde 8 numaralı denklemin kullanılması gerekmektedir. ölçütü 3 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir. MAK{135;82;178;100;125;73;136;41;111;88}-135 =0, MAK{135;82;178;...;88}-MIN{135;82;178;...;88} Bu normalizasyon yöntemi de değerin en küçük yada en büyük olmasına göre farklı işlemler kullandığından pozitif ideal çözüm setinin hesaplanmasında değerlendirme ölçütü 3 için de en büyüğün, negatif ideal çözüm setinin hesaplanmasında değerlendirme ölçütü 3 için de en küçüğün belirlenmesine dikkat edilmelidir. normalizasyon (4) için 9 numaralı denklem kullanılarak ölçütü 1 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir. 779 =0, normalizasyon (4), normalleştirme işlemi için tek bir denklem kullandığından bu işlem ölçüt 3 için de kullanılır. Bu nedenle değerlendirme ölçütü 3 için pozitif ideal çözüm setinin en küçük, negatif ideal çözüm setinin hesaplanmasında ise en büyük değer bulunmalıdır. Monoton olmayan normalizasyon için 10 numaralı denklem kullanılarak ölçütü 1 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir. e 779 MAK 779;793;769;600;597;565;643;647;846;634 2 ( ) STANDARTSAPMA779;793;769;600;597;565;643;647;846;634 2 = 0, ölçütü 3 ile alternatif 1 hücrelerinin kesişimindeki değer için işlem aşağıda verilmiştir. e 135 MN135;82;178;100;125;73;136;41;111;88 2 ( ) STANDARTSAPMA135;82;178;100;125;73;136;41;111;88 2 = 0, Monoton olmayan normalizasyon, normalleştirme işleminde x 0 ile simgelenen en uygun değeri kullandığından pozitif ideal çözüm setinin hesaplanmasında değerlendirme ölçütü 3 için de en büyüğün, negatif ideal çözüm setinin hesaplanmasında değerlendirme ölçütü 3 için de en küçüğün belirlenmesine dikkat edilmelidir. Açıklanan işlemlerin tüm veri setlerine uygulaması sonucunda bulunan ideal çözüme göreceli yakınlık değerleri Tablo 7 de verilmiştir. 252
9 Farklı Yöntemlerinin TOPSIS te Karar Verme Sürecine Etkisi Tablo 7: Tüm Yöntemleri için İdeal Çözüme Göreceli Yakınlık Değerleri Vektörel Veri Seti 6 Veri Seti 5 Veri Seti 4 Veri Seti 3 Veri Seti 2 Veri Seti 1 (1) (2) (3) (4) Monoton Olmayan Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , ,
10 Aşkın ÖZDAĞOĞLU Vektörel (1) (2) (3) (4) Veri Seti 10 Veri Seti 9 Veri Seti 8 Veri Seti 7 Monoton Olmayan Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Alternatif 1 0, , , , , , Alternatif 2 0, , , , , , Alternatif 3 0, , , , , , Alternatif 4 0, , , , , , Alternatif 5 0, , , , , , Alternatif 6 0, , , , , , Alternatif 7 0, , , , , , Alternatif 8 0, , , , , , Alternatif 9 0, , , , , , Alternatif 10 0, , , , , , Elde edilen bu sonuçlar arasındaki ilişkiyi görebilmek amacıyla ikili olarak korelasyon analizleri gerçekleştirilmiştir. Her biri 10 alternatif içeren 10 veri seti üzerinden toplam 100 er adet değer bulunduğundan korelasyon analizi yapmak için yeterli veri mevcuttur. Korelasyon analizi 22 numaralı denklemde gösterilmiştir. nσxy ΣxΣy r = [ nσx Σ ( x)][ nσy Σ ( y)] (22) Bu denklemde yer alan semboller aşağıda açıklanmıştır. x:değişken 1 y:değişken 2 n:örnek hacmi Değişken 1 ve 2 değerleri aralarındaki ilişki düzeyi tespit edilecek olan normalizasyon yöntemlerine göre ideal göreceli çözüme yakınlık değerleridir. 10 farklı alternatif ve veri seti bulunduğundan örnek hacmi 100 olmaktadır. Vektörel normalizasyon ideal çözüme göreceli uzaklık değerlerinin değişken 1 ve doğrusal normalizasyon (1) ideal çözüme göreceli uzaklık değerlerinin değişken 2 olduğu durum için korelasyon hesabı aşağıda sunulmuştur. r = 100(26,019855)-(51,807178)(45,001688) = 0, [100(30,058697) (51,807178) ][100(22, ) (45,001688) ] Bu değerlere ulaşmak için Excel 2010 üzerinde =KORELASYON(DİZİ 1 VERİ ARALIĞI:DİZİ 2 VERİ ARALIĞI) formülü kullanılarak, tüm normalizasyon 254
11 Farklı Yöntemlerinin TOPSIS te Karar Verme Sürecine Etkisi yöntemleri açısından bulunan ideal çözüme göreceli uzaklık değerlerine uygulanması sonucu ulaşılan değerler Tablo 8 de verilmiştir. Tablo 8 de satır ile sütunun kesişiminde yer alan değer ilgili hücrenin bulunduğu satır ve sütundaki normalizasyon yöntemlerinin değişkenleri temsil ettiği korelasyon işleminin sonucunu vermektedir. Örnek vermek gerekirse, vektörel normalizasyon satırı ile doğrusal normalizasyon (1) sütunu kesişimindeki %92,44 değeri vektörelnormalizasyon değişkeni ile doğrusal normalizasyon (1) değişkenlerini içeren korelasyon analizinin sonucudur. Tablo 8: Yöntemlerine göre Sonuçlar Arasındaki Korelasyon (1) (2) (3) (4) Monoton Olmayan Vektörel 92,44% 99,25% 69,31% 99,95% 68,44% (1) 94,06% 71,13% 91,93% 70,76% (2) 73,95% 98,91% 72,71% (3) 68,20% 97,27% (4) 67,38% Korelasyon katsayısı sonuçlar arasındaki ilişkinin gücünü göstermektedir. %0-%25 arası korelasyon değeri ilişkinin çok zayıf olduğunu, %26-%49 arası korelasyon değeri ilişkinin zayıf olduğunu, %50-%69 arası korelasyon değeri ilişkinin orta seviyede olduğunu, %70-%89 arası korelasyon değeri ilişkinin yüksek olduğunu, %90-%100 arası korelasyon değeri ise ilişkinin çok yüksek olduğunu ifade etmektedir (Kalaycı, 2010; 116). Vektör normalizasyon sonuçları incelendiğinde doğrusal normalizasyon (4) olarak adlandırılan yöntem ile elde edilen sonuçlar arası ilişki %99,95 olarak görülmektedir. Bu değer, iki yöntemden elde edilen sonuçların neredeyse aynı olduğunu ifade etmektedir. Yine Vektör normalizasyon sonuçları ve doğrusal normalizasyon (2) olarak adlandırılan yöntem ile elde edilen sonuçlar arası ilişki de %99,25 bulunmuştur ki bu da sonuçların hemen hemen aynı olduğunu göstermektedir. normalizasyon (2) ve doğrusal normalizasyon (4) olarak adlandırılan yöntemler arası ilişki değeri de en yüksek üçüncü değerdir (%98,91). Bu da sonuçların neredeyse birbirine eşit olduğunu göstermektedir. Tablo 4 teki değerler incelendiğinde, monoton olmayan normalizasyon ve doğrusal normalizasyon (3) olarak adlandırılan yöntemlerin diğer normalizasyon yöntemleri ile ilişkisi orta düzeyde kalmakta ve farklı alternatiflerin tercih edilmesi sonucunu doğurabilmektedir. Bu iki yöntemin kendi aralarındaki ilişki düzeyi ise %97,27 ile oldukça yüksektir. Bu ilişki katsayılarına göre normalizasyon yöntemlerini iki ana kategoride toplamak mümkün görünmektedir. Yöntemleri 1. Kategori Vektörel (1) (2) (4) Yöntemleri 2. Kategori (3) Monoton Olmayan Bu çalışmada incelenen TOPSIS yöntemi açısından bakıldığında ilk kategoride yer alan normalizasyon yöntemlerinden herhangi biri ile işlemleri gerçekleştirmek mümkündür. Önemli olan nokta farklı ölçüm birimlerine sahip olan değerlendirme ölçütlerini bir normalizasyon işlemine tabi tutmaktır. Bu gerçekleştirildikten sonra yüzlerce alternatifin aynı anda hızlı bir biçimde tüm değerlendirme ölçütleri açısından bir arada incelenerek karar verilebilmesi mümkündür. Süreç adımları ile ilgili olan diğer önemli nokta ise pozitif ideal çözüm seti hesaplamaları ile negatif ideal çözüm seti hesaplamalarının normalizasyon yöntemine göre uyarlanmasıdır. 12 numaralı denklemde gösterilen vektör normalizasyonu işlemi yerine 3, 4, 5, 6, 7, 8, 10 numaralı denklemlerde gösterilen işlemlerin uygulanması 15 ve 17 numaralı denklemlerin yapısını değiştirecektir. (1), (2), (3) ve Monoton Olmayan yöntemlerinin kullanılması durumunda İdeal çözüm setinin oluşturulabilmesi için Y matrisindeki ağırlıklandırılmış ölçütlerin yani sütun değerlerinin her durumda en büyükleri (ilgili ölçüt minimizasyon yönlü olsa bile) seçilecektir. Çünkü bu normalizasyon yöntemleri en iyi durum olan en küçük değeri göz önüne alarak normalleştirme işlemlerini yapmaktadır. Buna göre pozitif ideal çözüm setinin bulunması için kullanılacak olan 15 numaralı denklemin yeni hali 23 numaralı denklemde gösterilmiştir. {( i i ),( i i )} * ' A = max y J max y J (23) Değişecek olan diğer denklem ise 17 numaralı denklemdir. Negatif ideal çözüm seti ise, Y matrisindeki ağırlıklandırılmış ölçütlerin, bir başka deyişle, sütun değerlerinin en küçükleri (ilgili değerlendirme faktörü minimizasyon yönlü olsa bile) seçilerek oluşturulmalıdır. Buna göre Negatif ideal çözüm setinin bulunması için kullanılacak olan 17 numaralı denklemin yeni hali 24 numaralı denklemde gösterilmiştir. 255
12 Aşkın ÖZDAĞOĞLU ' {(min i i ),(min i i )} A = y J y J (24) Bu denklemlerin uyarlanması dışında süreç aynıdır. Vektörel ile (4) için izlenecek adımlarda ise herhangi bir değişiklik meydana gelmemektedir. 6. SONUÇ İşletmelerin karşı karşıya kaldığı karar verme problemlerinde hemen hemen her durumda birbirlerinden çok farklı ölçüm birimlerine sahip değerlendirme ölçütlerinin bir bütünsellik içinde göz önüne alınması zorunludur. Bu zorunluluk çeşitli çok ölçütlü karar verme yöntemlerinin geliştirilmesine ön ayak olmuştur. Farklı ölçüm birimlerine sahip olan değerlendirme ölçütlerini birlikte inceleyerek alternatifleri karşılaştırmanın bir yolu ikili karşılaştırmaların yapılmasıdır. ELECTRE ve PROMETHEE yöntemleri bu ikili karşılaştırmaları gerçekleştirdiği için karar verme aracı olarak kullanılmaktadırlar. Ancak ikili karşılaştırmaların yapılması alternatiflerin sayısının çok fazla olması durumunda yapılması gereken işlemlerin katlanarak artması ile sonuçlanmakta ve hızlı karar vermenin gerektiği dinamik piyasa koşullarında işletmenin karar vermede gecikmesine yol açabilmektedir. Çok sayıda alternatifi karşılaştırmada ikili karşılaştırmanın dezavantalarını ortadan kaldıran MOORA, TOPSIS, COPRAS gibi yöntemler mevcuttur. Bu yöntemlerde ise ikili karşılaştırmanın yerini normalizasyon işlemleri almaktadır. Literatürde farklı normalizasyon seçenekleri bulunmaktadır. Buna ilave olarak aynı çok ölçütlü karar verme yöntemi için farklı normalizasyon yönteminin kullanıldığı çeşitli çalışmalar mevcuttur. Bu çalışma kapsamında normalizasyon yöntemlerinin çok ölçütlü karar verme yönteminden elde edilen sonuçlara nasıl bir etkide bulunduğunu görmek amacıyla 10 alternatif ve 5 değerlendirme ölçütü içeren 10 farklı veri seti oluşturulmuş ve bu veri setlerine tüm normalizasyon yöntemleri birer birer denenerek sonuçlar korelasyon analizine tabi tutulmuştur. Veri setlerinin gerçek işletme problemlerini daha iyi yansıtabilmesini sağlamak amacıyla veri seti türetilirken farklı sayı aralıklarında ölçekler oluşturulmuş ve olası değişik senaryoları inceleyebilmek için de değerlendirme ölçütlerinden biri açısından en küçük değerin en iyi durumu gösterdiği göz önüne alınarak hesaplamalar gerçekleştirilmiştir. Elde edilen sonuçlar korelasyon analizine tabi tutulduğunda yöntemlerin iki ana kategoride toplandığı görülmektedir. Birinci kategori olarak ifade edilebilecek olan Vektörel, (1), (2) ve (4) yöntemlerinin ikili korelasyon değerlerinin hepsi %90 değerinin üzerindedir. İkinci kategoride kalan (3) ve Monoton Olmayan yöntemleri ise TOPSIS yönteminin oriinal yapısında bulunan vektörel normalizasyon ile karşılaştırıldığında korelasyon değeri düşük kalmaktadır. Bu nedenle ikinci kategori olarak ifade edilen (3) ve Monoton Olmayan yöntemlerinin TOPSIS yöntemi için kullanımı önerilmemektedir. İlk kategoride yer alan, TOPSIS yöntemi ile karar verme sürecinde Vektörel, (1), (2) ve (4) yöntemlerinin herhangi biri TOPSIS yöntemi ile karar verme sürecinde rahatlıkla kullanılabilir. Özellikle (2) ve (4) sonuçları ile vektörel normalizasyon sonuçları ilişki değeri %99 un bile üzerindedir. Burada hatırlanması gereken nokta, (1), (2), (3) ve Monoton Olmayan yöntemlerinin kullanımı durumunda pozitif ideal çözüm seti ile negatif ideal çözüm setinin bulunması için kullanılacak olan denklemlerde bu normalizasyon yöntemlerinin kendi içinde en ideal duruma göre normalleştirme işlemlerini gerçekleştirmesinden dolayı değişikliklerin yapılması gerektiğidir. 256
13 Farklı Yöntemlerinin TOPSIS te Karar Verme Sürecine Etkisi KAYNAKLAR Aalami, H.A.,Moghaddam, M.P. ve Yousefi, G.R. (2010) Modeling and Prioritizing Demand Response Programs in Power Markets Electric Power Systems Research, 80: Ayala, J.G. (2012) Selecting Irrigation Water Pricing Alternatives Using A Multi-Methodological Approach Mathematical And Computer Modelling, 55: Balezentis, A.,Balezentis, T. ve Brauers, W.K.M. (2012) Personnel Selection Based on Computing With Words and Fuzzy MULTIMOORA Expert Systems With Applications, 39: Chakraborty, S. (2011) Applications of The MOORA Method for Decision Making in Manufacturing Environment Int J Adv Manuf Technol, 54: Chatteree, P. Chakraborty, S. (2012) MaterialSelection Using Preferential Ranking Methods Materials And Design, 35: Chen, M.F. ve Tzeng, G.H. (2004) Combining Grey Relation and TOPSIS Concepts For Selecting an Expatriate Host Country Mathematical And Computer Modelling, 40: Dai, L. ve Wang, J. (2011) Evaluation of The Profitability of Power Listed Companies Based on Entropy Improved TOPSIS Method Procedia Engineering, 15: Huang, W. vehuang, Y.Y. (2012) Research on The Performance Evaluation of Chongqing Electric Power Supply Bureaus Based on TOPSIS Energy Procedia, 14: Hwang, C.L. ve Yoon, K. (1981)Multiple Attribute Decision Making, Berlin,Springer-Verlag. Kalaycı, Ş. (2010)SPSS Uygulamalı Çok Değişkenli İstatistik Teknikleri, Ankara, Asil Yayın Dağıtım. Kaklauskas, A., Zavadskas, E.K., Naimaviciene, J.,Krutinis, M.,Plakys, V. ve Venskus, D. (2010) Model For A Complex Analysis of IntelligentBuilt Environment Automationin Construction, 19: Kaklauskas, A.,Zavadskas, E.K. vetrinkunas, V. (2007) A MultipleCriteriaDecisionSupport On- LineSystemFor Construction Engineering Applications of Artificial Intelligence, 20: Karande, P. ve Chakraborty, S. (2012) Application of Multi-Obective Optimization on The Basis of Ratio Analysis (MOORA) Method For Materials Selection Materials And Design, 37: Kiran, C.P.,Clement, S. ve Agrawal, V.P. (2011) Coding, Evaluation and Optimal Selection of A Mechatronic System Expert Systems With Applications, 38: Lozano-Minguez, E., Kolios, A.J. ve Brennan, F.P. (2011) Multi-Criteria Assessment of Offshore Wind Turbine Support Structures Renewable Energy, 36: Mela, K.,Tiainen, T. ve Heinisuo, M. (2012) Comparative Study of Multiple Criteria Decision Making Methods For Building Design Advanced Engineering Informatics. (Baskıda) Ouattara, A., Pibouleau, L., Azzaro-Pantel, C., Domenech, S.,Baudet, P. veyao, B. (2012) Economic And Environmental Strategies For Process Design Computers And Chemical Engineering, 36: Peng, Y., Zhang, Y., Tang, Y. ve Li, S. (2011) An Incident Information Management Framework Based on Data İntegration, Data Mining, And Multi-Criteria Decision Making Decision Support Systems, 51: Sadeghzadeh, K. ve Salehi, M.B. (2011) Mathematical Analysis of Fuel Cell Strategic Technologies Development Solutions in The Automotive Industry by The TOPSIS Multi-Criteria Decision Making Method International Journal Of Hydrogen Energy, 36: Shih, H.S.,Shyur, H.J. ve Lee, E.S. (2007) An Extension of TOPSIS For Group Decision Making Mathematical And Computer Modelling, 45: Streimikiene, D., Balezentis, T., Krisciukaitien, I. vebalezentis, A. (2012) Prioritizing Sustainable Electricity Production Technologies:MCDM Approach Renewable And Sustainable Energy Reviews, 16: Sun, Y.F.,Liang, Z.S., Shan, C.J., Viernstein, H. ve Unger, F. (2011) Comprehensive Evaluation of Natural Antioxidants and Antioxidant Potentials in Ziziphus Juuba Mill. Var. Spinosa (Bunge) Hu Ex H. F. Chou Fruits Based On Geographical Origin By TOPSIS Method Food Chemistry, 124:
14
Normalizasyon Yöntemlerinin Çok Ölçütlü Karar Verme Sürecine Etkisi Moora Yöntemi İncelemesi
 EGE AKADEMİK BAKIŞ / EGE ACADEMIC REVIEW Cilt: 4 Sayı: Nisan 04 ss. 83-94 Normalizasyon Yöntemlerinin Çok lü Karar Verme Sürecine Etkisi Moora Yöntemi İncelemesi The Effects of The Normalization Methods
EGE AKADEMİK BAKIŞ / EGE ACADEMIC REVIEW Cilt: 4 Sayı: Nisan 04 ss. 83-94 Normalizasyon Yöntemlerinin Çok lü Karar Verme Sürecine Etkisi Moora Yöntemi İncelemesi The Effects of The Normalization Methods
Çok Ölçütlü Karar Verme Modellerinde Normalizasyon Tekniklerinin Sonuçlara Etkisi: COPRAS Örneği
 Çok Ölçütlü Karar Verme Modellerinde Normalizasyon Tekniklerinin Sonuçlara Etkisi: COPRAS Örneği Aşkın Özdağoğlu Yrd.Doç.Dr., Dokuz Eylül Üniversitesi İşletme Fakültesi İşletme Bölümü askin.ozdagoglu@deu.edu.tr.
Çok Ölçütlü Karar Verme Modellerinde Normalizasyon Tekniklerinin Sonuçlara Etkisi: COPRAS Örneği Aşkın Özdağoğlu Yrd.Doç.Dr., Dokuz Eylül Üniversitesi İşletme Fakültesi İşletme Bölümü askin.ozdagoglu@deu.edu.tr.
Üretim Yapan İşletmeler için Hidrolik Giyotin Alternatiflerinin TOPSIS Yöntemi ile İncelenmesi
 EGE AKADEMİK BAKIŞ / EGE ACADEMIC REVIEW Cilt: 12 Sayı: 4 Ekim 2012 ss. 549-562 Üretim Yapan İşletmeler için Hidrolik Giyotin Alternatiflerinin TOPSIS Yöntemi ile İncelenmesi Evaluation of Hydraulic Guillotine
EGE AKADEMİK BAKIŞ / EGE ACADEMIC REVIEW Cilt: 12 Sayı: 4 Ekim 2012 ss. 549-562 Üretim Yapan İşletmeler için Hidrolik Giyotin Alternatiflerinin TOPSIS Yöntemi ile İncelenmesi Evaluation of Hydraulic Guillotine
Bu bölümde; Çok ölçütlü karar verme yöntemlerinden biri olan TOPSİS yöntemi anlatılacaktır.
 ÇOK ÖLÇÜTLÜ KARAR VERME TOPSIS (Technique For Order Preference By Similarity To Ideal Solution) PROF. DR. İBRAHİM ÇİL 1 Bu bölümde; Çok ölçütlü karar verme yöntemlerinden biri olan TOPSİS yöntemi anlatılacaktır.
ÇOK ÖLÇÜTLÜ KARAR VERME TOPSIS (Technique For Order Preference By Similarity To Ideal Solution) PROF. DR. İBRAHİM ÇİL 1 Bu bölümde; Çok ölçütlü karar verme yöntemlerinden biri olan TOPSİS yöntemi anlatılacaktır.
TOPSIS yönteminin adımları 5 Adım 1. Normalize karar matrisinin oluşturulması 6 Karar matrisinin normalizasyonu aşağıdaki formül kullanılarak yapılır:
 Giriş 2 TOPSIS Bölüm 5 TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) 1981 yılında Hwang ve Yoon tarafından geliştirilmiştir. Uygulanması basit, ulaşılan sonuçlar çok gerçekçidir.
Giriş 2 TOPSIS Bölüm 5 TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) 1981 yılında Hwang ve Yoon tarafından geliştirilmiştir. Uygulanması basit, ulaşılan sonuçlar çok gerçekçidir.
BİR KONFEKSİYON İŞLETMESİNDE ANAHTAR MÜŞTERİNİN TOPSIS ÇOK KRİTERLİ KARAR VERME METODU KULLANILARAK BELİRLENMESİ
 ÖZET XIII. Uluslararası İzmir Tekstil ve Hazır Giyim Sempozyumu BİR KONFEKSİYON İŞLETMESİNDE ANAHTAR MÜŞTERİNİN TOPSIS ÇOK KRİTERLİ KARAR VERME METODU KULLANILARAK BELİRLENMESİ Eda Acar, Mücella Güner
ÖZET XIII. Uluslararası İzmir Tekstil ve Hazır Giyim Sempozyumu BİR KONFEKSİYON İŞLETMESİNDE ANAHTAR MÜŞTERİNİN TOPSIS ÇOK KRİTERLİ KARAR VERME METODU KULLANILARAK BELİRLENMESİ Eda Acar, Mücella Güner
BULANIK TOPSİS YÖNTEMİYLE TELEFON OPERATÖRLERİNİN DEĞERLENDİRİLMESİ
 BULANIK TOPSİS YÖNTEMİYLE TELEFON OPERATÖRLERİNİN DEĞERLENDİRİLMESİ 1 İpek Nur Erkmen ve 2 Özer Uygun 1 Karabük-Sakarya Ortak Program, Fen Bilimleri Enstitüsü Endüstri Mühendisliği ABD, 2 Sakarya Üniversitesi
BULANIK TOPSİS YÖNTEMİYLE TELEFON OPERATÖRLERİNİN DEĞERLENDİRİLMESİ 1 İpek Nur Erkmen ve 2 Özer Uygun 1 Karabük-Sakarya Ortak Program, Fen Bilimleri Enstitüsü Endüstri Mühendisliği ABD, 2 Sakarya Üniversitesi
Sayı 8 Haziran 2013 ÖZET
 Gümüşhane Üniversitesi Sayı 8 Haziran 2013 Sosyal Bilimler Elektronik Dergisi İMALAT İŞLETMELERİ İÇİN EKSANTRİK PRES ALTERNATİFLERİNİN COPRAS YÖNTEMİ İLE KARŞILAŞTIRILMASI 1 ÖZET İşletmelerin üretim faaliyetlerini
Gümüşhane Üniversitesi Sayı 8 Haziran 2013 Sosyal Bilimler Elektronik Dergisi İMALAT İŞLETMELERİ İÇİN EKSANTRİK PRES ALTERNATİFLERİNİN COPRAS YÖNTEMİ İLE KARŞILAŞTIRILMASI 1 ÖZET İşletmelerin üretim faaliyetlerini
Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997
 Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997 2 Tesis Yer Seçimi Problemi (TYSP) TEK AMAÇLI
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997 2 Tesis Yer Seçimi Problemi (TYSP) TEK AMAÇLI
AHP ANALİTİK HİYERARŞİ PROSESİ AHP AHP. AHP Ölçeği AHP Yönteminin Çözüm Aşamaları
 ANALİTİK HİYERARŞİ PROSESİ 1970 li yıllarda Wharton School of Business da çalışan Thomas L.Saaty tarafından Karmaşık çok kriterli karar verme problemlerinin çözümü için geliştirilmiştir. Tüm kriterler
ANALİTİK HİYERARŞİ PROSESİ 1970 li yıllarda Wharton School of Business da çalışan Thomas L.Saaty tarafından Karmaşık çok kriterli karar verme problemlerinin çözümü için geliştirilmiştir. Tüm kriterler
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
ÇOK ÖLÇÜTLÜ KARAR VERME YÖNTEMLERİ İLE BURSİYER SEÇİMİ: BİR ÖĞRETİM KURUMUNDA UYGULAMA
 Atatürk Üniversitesi İktisadi ve İdari Bilimler Dergisi, Cilt: 26, Sayı: 3-4, 2012 259 ÇOK ÖLÇÜTLÜ KARAR VERME YÖNTEMLERİ İLE BURSİYER SEÇİMİ: BİR ÖĞRETİM KURUMUNDA UYGULAMA Yusuf Alper ABALI (*) Batuhan
Atatürk Üniversitesi İktisadi ve İdari Bilimler Dergisi, Cilt: 26, Sayı: 3-4, 2012 259 ÇOK ÖLÇÜTLÜ KARAR VERME YÖNTEMLERİ İLE BURSİYER SEÇİMİ: BİR ÖĞRETİM KURUMUNDA UYGULAMA Yusuf Alper ABALI (*) Batuhan
BÖLÜM 12 STUDENT T DAĞILIMI
 1 BÖLÜM 12 STUDENT T DAĞILIMI 'Student t dağılımı' ya da kısaca 't dağılımı'; normal dağılım ve Z dağılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
1 BÖLÜM 12 STUDENT T DAĞILIMI 'Student t dağılımı' ya da kısaca 't dağılımı'; normal dağılım ve Z dağılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
Çok Kriterli Karar Verme Teknikleri ile Alt Yüklenici Seçimi: İnşaat Sektöründe Bir Uygulama
 Çok Kriterli Karar Verme Teknikleri ile Alt Yüklenici Hilal AYDIN hilalaydin07@gmail.com betulokul@hotmail.com Yrd. Doç. Dr. Berk AYVAZ İstanbul Ticaret Üniversitesi, Mühendislik ve Tasarım Fakültesi bayvaz@ticaret.edu.tr
Çok Kriterli Karar Verme Teknikleri ile Alt Yüklenici Hilal AYDIN hilalaydin07@gmail.com betulokul@hotmail.com Yrd. Doç. Dr. Berk AYVAZ İstanbul Ticaret Üniversitesi, Mühendislik ve Tasarım Fakültesi bayvaz@ticaret.edu.tr
Dr. Y. İlker TOPCU. Dr. Özgür KABAK web.itu.edu.tr/kabak/
 Dr. Y. İlker TOPCU www.ilkertopcu.net www.ilkertopcu.org www.ilkertopcu.info facebook.com/yitopcu twitter.com/yitopcu instagram.com/yitopcu Dr. Özgür KABAK web.itu.edu.tr/kabak/ ÇOK ÖLÇÜTLÜ KARAR VERME
Dr. Y. İlker TOPCU www.ilkertopcu.net www.ilkertopcu.org www.ilkertopcu.info facebook.com/yitopcu twitter.com/yitopcu instagram.com/yitopcu Dr. Özgür KABAK web.itu.edu.tr/kabak/ ÇOK ÖLÇÜTLÜ KARAR VERME
NETWORK MODELİ İLE AĞ ANALİZİ İÇİN ÇOK KRİTERLİ KARAR VERME YÖNTEMLERİYLE KARŞILAŞTIRMALI ÇÖZÜM
 NETWORK MODELİ İLE AĞ ANALİZİ İÇİN ÇOK KRİTERLİ KARAR VERME YÖNTEMLERİYLE KARŞILAŞTIRMALI ÇÖZÜM Deniz Koçak Gazi Üniversitesi, İktisadi ve İdari Bilimler, Ekonometri Bölümü, Ankara denizkocak36@gmail.com
NETWORK MODELİ İLE AĞ ANALİZİ İÇİN ÇOK KRİTERLİ KARAR VERME YÖNTEMLERİYLE KARŞILAŞTIRMALI ÇÖZÜM Deniz Koçak Gazi Üniversitesi, İktisadi ve İdari Bilimler, Ekonometri Bölümü, Ankara denizkocak36@gmail.com
ÜRETİM FAALİYETİNDE BULUNAN İŞLETMELER İÇİN CNC TORNA TEZGAHI ALTERNATİFLERİNİN VIKOR VE TOPSIS YÖNTEMLERİ İLE KARŞILAŞTIRILMASI
 AİBÜ Sosyal Bilimler Enstitüsü Dergisi, 2014, Cilt:14, Yıl:14, Sayı:2, 14: 37-57 ÜRETİM FAALİYETİNDE BULUNAN İŞLETMELER İÇİN CNC TORNA TEZGAHI ALTERNATİFLERİNİN VIKOR VE TOPSIS YÖNTEMLERİ İLE KARŞILAŞTIRILMASI
AİBÜ Sosyal Bilimler Enstitüsü Dergisi, 2014, Cilt:14, Yıl:14, Sayı:2, 14: 37-57 ÜRETİM FAALİYETİNDE BULUNAN İŞLETMELER İÇİN CNC TORNA TEZGAHI ALTERNATİFLERİNİN VIKOR VE TOPSIS YÖNTEMLERİ İLE KARŞILAŞTIRILMASI
Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN
 Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN Giriş AHP Thomas L.Saaty tarafından 1970'lerde ortaya atılmıştır. Amaç alternatifler arasından en iyisinin seçilmesidir. Subjektif
Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN Giriş AHP Thomas L.Saaty tarafından 1970'lerde ortaya atılmıştır. Amaç alternatifler arasından en iyisinin seçilmesidir. Subjektif
Korelasyon, Korelasyon Türleri ve Regresyon
 Korelasyon, Korelasyon Türleri ve Regresyon İçerik Korelasyon Korelasyon Türleri Korelasyon Katsayısı Regresyon KORELASYON Korelasyon iki ya da daha fazla değişken arasındaki doğrusal ilişkiyi gösterir.
Korelasyon, Korelasyon Türleri ve Regresyon İçerik Korelasyon Korelasyon Türleri Korelasyon Katsayısı Regresyon KORELASYON Korelasyon iki ya da daha fazla değişken arasındaki doğrusal ilişkiyi gösterir.
SATIN ALMA SÜRECİ İÇİN MOORA METODU İLE TEDARİKÇİ SEÇİMİ PROBLEMİ
 SATIN ALMA SÜRECİ İÇİN MOORA METODU İLE TEDARİKÇİ SEÇİMİ PROBLEMİ Gökhan Özçelik 1, H. Ediz Atmaca 2 1 Arş. Gör., Gazi Üniversitesi, Mühendislik Fakültesi, Endüstri Müh. Böl., gokhanozcelik@gazi.edu.tr
SATIN ALMA SÜRECİ İÇİN MOORA METODU İLE TEDARİKÇİ SEÇİMİ PROBLEMİ Gökhan Özçelik 1, H. Ediz Atmaca 2 1 Arş. Gör., Gazi Üniversitesi, Mühendislik Fakültesi, Endüstri Müh. Böl., gokhanozcelik@gazi.edu.tr
SESSION 6B: Bölgesel Ekonomiler II 321
 SESSION 6B: Bölgesel Ekonomiler II 321 Orta Asya Türk Cumhuriyetlerinin Ekonomik Performanslarının TOPSIS Metodu ile Karşılaştırılması Comparison of the Economic Performance of Turkish Republics in Central
SESSION 6B: Bölgesel Ekonomiler II 321 Orta Asya Türk Cumhuriyetlerinin Ekonomik Performanslarının TOPSIS Metodu ile Karşılaştırılması Comparison of the Economic Performance of Turkish Republics in Central
Çok Kriterli Karar Verme Teknikleri İle Performans Değerlendirmesine İlişkin Bir Uygulama
 Social Sciences Research Journal, Volume 4, Issue 2, 176-186 (June 2015), ISSN: 2147-5237 176 Çok Kriterli Karar Verme Teknikleri İle Performans Değerlendirmesine İlişkin Bir Uygulama Meltem Karaatlı,
Social Sciences Research Journal, Volume 4, Issue 2, 176-186 (June 2015), ISSN: 2147-5237 176 Çok Kriterli Karar Verme Teknikleri İle Performans Değerlendirmesine İlişkin Bir Uygulama Meltem Karaatlı,
Eşdeğer Deprem Yüklerinin Dağılım Biçimleri
 Eşdeğer Deprem Yüklerinin Dağılım Biçimleri Prof. Dr. Günay Özmen İTÜ İnşaat Fakültesi (Emekli), İstanbul gunayozmen@hotmail.com 1. Giriş Deprem etkisi altında bulunan ülkelerin deprem yönetmelikleri çeşitli
Eşdeğer Deprem Yüklerinin Dağılım Biçimleri Prof. Dr. Günay Özmen İTÜ İnşaat Fakültesi (Emekli), İstanbul gunayozmen@hotmail.com 1. Giriş Deprem etkisi altında bulunan ülkelerin deprem yönetmelikleri çeşitli
İÇİNDEKİLER. 1. Analitik Hiyerarşi Prosesi(AHP) Yöntemi 2. TOPSİS Yöntemi 3. ENTROPİ Yöntemi 4. MAUT Yöntemi
 İÇİNDEKİLER 1. Analitik Hiyerarşi Prosesi(AHP) Yöntemi 2. TOPSİS Yöntemi 3. ENTROPİ Yöntemi 4. MAUT Yöntemi 1. Analitik Hiyerarşi Prosesi (AHP) Analitik Hiyerarşi Süreci tekniği karmaşık karar problemlerinde
İÇİNDEKİLER 1. Analitik Hiyerarşi Prosesi(AHP) Yöntemi 2. TOPSİS Yöntemi 3. ENTROPİ Yöntemi 4. MAUT Yöntemi 1. Analitik Hiyerarşi Prosesi (AHP) Analitik Hiyerarşi Süreci tekniği karmaşık karar problemlerinde
AHP-VIKOR VE MOORA YÖNTEMLERİNİN DEPO YERİ SEÇİM PROBLEMİNDE UYGULANMASI
 Endüstri Mühendisliði Dergisi Cilt: 25 Sayý: -2 Sayfa: (2-5) Makale AHP-VIKOR VE MOORA YÖNTEMLERİNİN DEPO YERİ SEÇİM PROBLEMİNDE UYGULANMASI Adnan AKTEPE, Süleyman ERSÖZ Kırıkkale Üniversitesi, Endüstri
Endüstri Mühendisliði Dergisi Cilt: 25 Sayý: -2 Sayfa: (2-5) Makale AHP-VIKOR VE MOORA YÖNTEMLERİNİN DEPO YERİ SEÇİM PROBLEMİNDE UYGULANMASI Adnan AKTEPE, Süleyman ERSÖZ Kırıkkale Üniversitesi, Endüstri
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
Gri ilişkisel analiz ile çok kriterli tedarikçi seçimi: Otomotiv sektöründe bir uygulama
 İstanbul Üniversitesi İşletme Fakültesi Dergisi Istanbul University Journal of the School of Business Administration Cilt/Vol:38, Sayı/No:2, 2009, 147-156 ISSN: 1303-1732 - www.ifdergisi.org 2009 Gri ilişkisel
İstanbul Üniversitesi İşletme Fakültesi Dergisi Istanbul University Journal of the School of Business Administration Cilt/Vol:38, Sayı/No:2, 2009, 147-156 ISSN: 1303-1732 - www.ifdergisi.org 2009 Gri ilişkisel
BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ
 1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
MULTIMOORA Yöntemi ile Tehlikeli Atık Miktarı Açısından İllerin Değerlendirilmesi
 MULTIMOORA Yöntemi ile Tehlikeli Atık Miktarı Açısından İllerin Değerlendirilmesi Hande EREN *1, Nuri ÖMÜRBEK 2 1 Süleyman Demirel Üniversitesi, SBE, İşletme ABD, Isparta, Türkiye, hndeeren@gmail.com 2
MULTIMOORA Yöntemi ile Tehlikeli Atık Miktarı Açısından İllerin Değerlendirilmesi Hande EREN *1, Nuri ÖMÜRBEK 2 1 Süleyman Demirel Üniversitesi, SBE, İşletme ABD, Isparta, Türkiye, hndeeren@gmail.com 2
ÇOK KRİTERLİ KARAR VERME TEKNİKLERİ. Dersin Amacı Çok Kriterli Karar Verme Yaklaşımının Genel Yapısı. Dr.Öğr.Üyesi Gökçe BAYSAL TÜRKÖLMEZ
 ÇOK KRİTERLİ KARAR VERME TEKNİKLERİ Dr.Öğr.Üyesi Gökçe BAYSAL TÜRKÖLMEZ Zeleny (1982) multiple criteria decision making kitabına aşağıdaki cümle ile başlar: ıt has become more and more difficult to see
ÇOK KRİTERLİ KARAR VERME TEKNİKLERİ Dr.Öğr.Üyesi Gökçe BAYSAL TÜRKÖLMEZ Zeleny (1982) multiple criteria decision making kitabına aşağıdaki cümle ile başlar: ıt has become more and more difficult to see
ANALİTİK HİYERARŞİ PROSES YÖNTEMİ İLE RÜZGAR TÜRBİN SEÇİMİ. Selçuk Üniversitesi, Mühendislik Mimarlık Fakültesi, Endüstri Mühendisliği Bölümü, KONYA
 S.Ü. Müh. Mim. Fak. Derg., c.25, s.1, 2010 J. Fac.Eng.Arch. Selcuk Univ., v.25, n.1, 2010 ANALİTİK HİYERARŞİ PROSES YÖNTEMİ İLE RÜZGAR TÜRBİN SEÇİMİ Ahmet SARUCAN 1, Mehmet Cabir AKKOYUNLU 2, Aydoğan BAŞ
S.Ü. Müh. Mim. Fak. Derg., c.25, s.1, 2010 J. Fac.Eng.Arch. Selcuk Univ., v.25, n.1, 2010 ANALİTİK HİYERARŞİ PROSES YÖNTEMİ İLE RÜZGAR TÜRBİN SEÇİMİ Ahmet SARUCAN 1, Mehmet Cabir AKKOYUNLU 2, Aydoğan BAŞ
Yard. Doç. Dr. İrfan DELİ. Matematik
 Unvanı Yard. Doç. Dr. Adı Soyadı İrfan DELİ Doğum Yeri ve Tarihi: Çivril/Denizli -- 06.04.1986 Bölüm: E-Posta Matematik irfandeli20@gmail.com, irfandeli@kilis.edu.tr AKADEMİK GELİŞİM ÜNİVERSİTE YIL Lisans
Unvanı Yard. Doç. Dr. Adı Soyadı İrfan DELİ Doğum Yeri ve Tarihi: Çivril/Denizli -- 06.04.1986 Bölüm: E-Posta Matematik irfandeli20@gmail.com, irfandeli@kilis.edu.tr AKADEMİK GELİŞİM ÜNİVERSİTE YIL Lisans
her bir kontrol kriteri (8 adet) için 12 adet bulgu kriteri
 YAZILIM - VIKOR Maçka, tugrulo@itu.edu.tr Özet. ürettikleri uygulama kalitelerinin Technique For Order Preference By Similarity To An Ideal Solution (TOPSIS) ve Vise Kriteriumska Optimizacia I Kompromisno
YAZILIM - VIKOR Maçka, tugrulo@itu.edu.tr Özet. ürettikleri uygulama kalitelerinin Technique For Order Preference By Similarity To An Ideal Solution (TOPSIS) ve Vise Kriteriumska Optimizacia I Kompromisno
Endüstri Mühendisliği - 1. yarıyıl. Academic and Social Orientation. 441000000001101 Fizik I Physics I 3 0 1 4 4 6 TR
 - - - - - Bölüm Seçin - - - - - Gönder Endüstri Mühendisliği - 1. yarıyıl 141000000001101 Akademik ve Sosyal Oryantasyon Academic and Social Orientation 1 0 0 1 0 1 TR 441000000001101 Fizik I Physics I
- - - - - Bölüm Seçin - - - - - Gönder Endüstri Mühendisliği - 1. yarıyıl 141000000001101 Akademik ve Sosyal Oryantasyon Academic and Social Orientation 1 0 0 1 0 1 TR 441000000001101 Fizik I Physics I
REGRESYON ANALİZİ VE UYGULAMA. Yrd. Doç. Dr. Hidayet Takcı
 REGRESYON ANALİZİ VE UYGULAMA Yrd. Doç. Dr. Hidayet Takcı htakci@cumhuriyet.edu.tr Sunum içeriği Bu sunumda; Lojistik regresyon konu anlatımı Basit doğrusal regresyon problem çözümleme Excel yardımıyla
REGRESYON ANALİZİ VE UYGULAMA Yrd. Doç. Dr. Hidayet Takcı htakci@cumhuriyet.edu.tr Sunum içeriği Bu sunumda; Lojistik regresyon konu anlatımı Basit doğrusal regresyon problem çözümleme Excel yardımıyla
BULANIK TOPSIS ALGORİTMASINDA ÜÇGEN BULANIK SAYILAR İLE SATIŞ ELEMANLARININ DEĞERLENDİRİLMESİ ÖZET
 BULANIK TOPSIS ALGORİTMASINDA ÜÇGEN BULANIK SAYILAR İLE SATIŞ ELEMANLARININ DEĞERLENDİRİLMESİ Arş Gör. Burcu AVCI ÖZTÜRK 1 Doç. Dr. Zehra BAŞKAYA 2 ÖZET İşletmelerde satış elemanı seçim süreci bir çok
BULANIK TOPSIS ALGORİTMASINDA ÜÇGEN BULANIK SAYILAR İLE SATIŞ ELEMANLARININ DEĞERLENDİRİLMESİ Arş Gör. Burcu AVCI ÖZTÜRK 1 Doç. Dr. Zehra BAŞKAYA 2 ÖZET İşletmelerde satış elemanı seçim süreci bir çok
a2 b3 cij: birim başına ulaşım maliyeti xij: taşıma miktarı
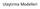 Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
PET ŞİŞE TEDARİKÇİSİ SEÇİMİNDE BULANIK AHP VE BULANIK TOPSIS YAKLAŞIMI * FUZZY AHP AND FUZZY TOPSIS APPROACH TO PET BOTTLE SUPPLIER SELECTION
 Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi Y.202, C.7, S.3, s.35-37. Suleyman Demirel University The Journal of Faculty of Economics and Administrative Sciences Y.202, Vol.7,
Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi Y.202, C.7, S.3, s.35-37. Suleyman Demirel University The Journal of Faculty of Economics and Administrative Sciences Y.202, Vol.7,
AHP (ANALYTIC HIERARCHY PROCESS) YÖNTEMİ VE HAZIR BETON TESİSİ ARAZİ SEÇİMİNDE UYGULAMASI
 AHP (ANALYTIC HIERARCHY PROCESS) YÖNTEMİ VE HAZIR BETON TESİSİ ARAZİ SEÇİMİNDE UYGULAMASI ANALYTIC HIERARCHY PROCESS METHOD AND APPLICATION IN AREA SELECTION OF READY MIXED CONCRETE PLANT ÖZET Ömür TEZCAN*
AHP (ANALYTIC HIERARCHY PROCESS) YÖNTEMİ VE HAZIR BETON TESİSİ ARAZİ SEÇİMİNDE UYGULAMASI ANALYTIC HIERARCHY PROCESS METHOD AND APPLICATION IN AREA SELECTION OF READY MIXED CONCRETE PLANT ÖZET Ömür TEZCAN*
BİR AKARYAKIT İSTASYONU SEÇİMİNDE ELECTRE YÖNTEMİNİN KULLANILMASI
 BİR AKARYAKIT İSTASYONU SEÇİMİNDE ELECTRE YÖNTEMİNİN KULLANILMASI Pınar KILIÇOĞULLARI Burcu ÖZCAN Büşra ERTUĞ Kocaeli Üniversitesi, Mühendislik Fakültesi Endüstri Mühendisliği Bölümü, Veziroğlu Yerleşkesi,
BİR AKARYAKIT İSTASYONU SEÇİMİNDE ELECTRE YÖNTEMİNİN KULLANILMASI Pınar KILIÇOĞULLARI Burcu ÖZCAN Büşra ERTUĞ Kocaeli Üniversitesi, Mühendislik Fakültesi Endüstri Mühendisliği Bölümü, Veziroğlu Yerleşkesi,
Araştırma Makalesi BULANIK ORTAMDA TOPSIS YÖNTEMİ İLE PERSONEL SEÇİMİ: KATILIM BANKACILIĞI SEKTÖRÜNDE BİR UYGULAMA
 Istanbul Commerce University Journal of Science İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi, 15(30), Güz 2016 http://dergipark.gov.tr/ticaretfbd Araştırma Makalesi BULANIK ORTAMDA TOPSIS YÖNTEMİ
Istanbul Commerce University Journal of Science İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi, 15(30), Güz 2016 http://dergipark.gov.tr/ticaretfbd Araştırma Makalesi BULANIK ORTAMDA TOPSIS YÖNTEMİ
OYUN TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
Sigma 2006/3 Araştırma Makalesi / Research Article A SOLUTION PROPOSAL FOR INTERVAL SOLID TRANSPORTATION PROBLEM
 Journal of Engineering and Natural Sciences Mühendislik ve Fen Bilimleri Dergisi Sigma 6/ Araştırma Makalesi / Research Article A SOLUTION PROPOSAL FOR INTERVAL SOLID TRANSPORTATION PROBLEM Fügen TORUNBALCI
Journal of Engineering and Natural Sciences Mühendislik ve Fen Bilimleri Dergisi Sigma 6/ Araştırma Makalesi / Research Article A SOLUTION PROPOSAL FOR INTERVAL SOLID TRANSPORTATION PROBLEM Fügen TORUNBALCI
English for Academic Reading & Speaking I İngilizce Akademik Okuma ve Konuşma I. Introduction to Civil Engineering İnşaat Mühendisliğine Giriş
 T.C. İZMİR KÂTİP ÇELEBİ ÜNİVERSİTESİ MÜHENDİSLİK VE MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 2015-16 GÜZ YARIYILI VE SONRASINDA UYGULANACAK LİSANS PROGRAMI (%100 İNGİLİZCE) BİRİNCİ YIL 1. DÖNEM Ön
T.C. İZMİR KÂTİP ÇELEBİ ÜNİVERSİTESİ MÜHENDİSLİK VE MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 2015-16 GÜZ YARIYILI VE SONRASINDA UYGULANACAK LİSANS PROGRAMI (%100 İNGİLİZCE) BİRİNCİ YIL 1. DÖNEM Ön
FORBES 2OOO LİSTESİNDE YERALAN HAVACILIK SEKTÖRÜNDEKİ ŞİRKETLERİN ENTROPİ, MAUT, COPRAS VE SAW YÖNTEMLERİ İLE ANALİZİ 1
 Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi Y.2018, C.23, S.1, s.257-278. Suleyman Demirel University The Journal of Faculty of Economics and Administrative Sciences Y.2018,
Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi Y.2018, C.23, S.1, s.257-278. Suleyman Demirel University The Journal of Faculty of Economics and Administrative Sciences Y.2018,
Maksimizasyon s.t. İşçilik, saat) (Kil, kg)
 Simplex ile Çözüm Yöntemi Doç. Dr. Fazıl GÖKGÖZ 1 Doğrusal Programlama Modeli Maksimizasyon s.t. İşçilik, saat) (Kil, kg) 2 Doç. Dr. Fazıl GÖKGÖZ Yrd.Doç. Dr. Fazıl GÖKGÖZ 1 Modelin Standard Hali Maksimizasyon
Simplex ile Çözüm Yöntemi Doç. Dr. Fazıl GÖKGÖZ 1 Doğrusal Programlama Modeli Maksimizasyon s.t. İşçilik, saat) (Kil, kg) 2 Doç. Dr. Fazıl GÖKGÖZ Yrd.Doç. Dr. Fazıl GÖKGÖZ 1 Modelin Standard Hali Maksimizasyon
KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI
 KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI Hatice YANIKOĞLU a, Ezgi ÖZKARA a, Mehmet YÜCEER a* İnönü Üniversitesi Mühendislik Fakültesi Kimya Mühendisliği
KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI Hatice YANIKOĞLU a, Ezgi ÖZKARA a, Mehmet YÜCEER a* İnönü Üniversitesi Mühendislik Fakültesi Kimya Mühendisliği
Ön şart D. Kodu Dersin Adı T U L AKTS MAT101. English for Academic Reading & Speaking I İngilizce Akademik Okuma ve Konuşma I
 BİRİNCİ YIL 1. DÖNEM T.C. İZMİR KÂTİP ÇELEBİ ÜNİVERSİTESİ MÜHENDİSLİK VE MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 2015-16 GÜZ YARIYILI VE SONRASINDA UYGULANACAK LİSANS PROGRAMI (%100 İNGİLİZCE) Ön
BİRİNCİ YIL 1. DÖNEM T.C. İZMİR KÂTİP ÇELEBİ ÜNİVERSİTESİ MÜHENDİSLİK VE MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 2015-16 GÜZ YARIYILI VE SONRASINDA UYGULANACAK LİSANS PROGRAMI (%100 İNGİLİZCE) Ön
Dr. Y. İlker TOPCU. Dr. Özgür KABAK web.itu.edu.tr/kabak/
 Dr. Y. İlker TOPCU www.ilkertopcu.net www.ilkertopcu.org www.ilkertopcu.info facebook.com/yitopcu twitter.com/yitopcu instagram.com/yitopcu Dr. Özgür KABAK web.itu.edu.tr/kabak/ Dr. Y. İlker Topcu (www.ilkertopcu.net)
Dr. Y. İlker TOPCU www.ilkertopcu.net www.ilkertopcu.org www.ilkertopcu.info facebook.com/yitopcu twitter.com/yitopcu instagram.com/yitopcu Dr. Özgür KABAK web.itu.edu.tr/kabak/ Dr. Y. İlker Topcu (www.ilkertopcu.net)
ANALİTİK HİYERARŞİ SÜRECİ VE MOORA YÖNTEMLERİNİN PERSONEL SEÇİMİNDE UYGULANMASI
 İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi Yıl: 13 Sayı: 25 Bahar 2014 s. 1-14 ANALİTİK HİYERARŞİ SÜRECİ VE MOORA YÖNTEMLERİNİN PERSONEL SEÇİMİNDE UYGULANMASI Serap TEPE *, Ali GÖRENER Geliş:
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi Yıl: 13 Sayı: 25 Bahar 2014 s. 1-14 ANALİTİK HİYERARŞİ SÜRECİ VE MOORA YÖNTEMLERİNİN PERSONEL SEÇİMİNDE UYGULANMASI Serap TEPE *, Ali GÖRENER Geliş:
DETERM INING THE M OST SUITABL E RENEWEABLE ENERGY RESOURCES USING ANALYTICALNETWORK PROCESS APPROACH
 380 10th International Clean Energy Symposium, 24-26 October 2016, Istanbul, Turkey LE DETERM INING THE M OST SUITABL E RENEWEABLE ENERGY RESOURCES USING ANALYTICALNETWORK PROCESS APPROACH Fatma TARAF
380 10th International Clean Energy Symposium, 24-26 October 2016, Istanbul, Turkey LE DETERM INING THE M OST SUITABL E RENEWEABLE ENERGY RESOURCES USING ANALYTICALNETWORK PROCESS APPROACH Fatma TARAF
İnşaat Yönetiminde Nakliye Aracı Seçiminde Moora Çok Ölçütlü Karar Verme Yöntemi İle Bir Uygulama
 İnşaat Yönetiminde Nakliye Aracı Seçiminde Moora Çok Ölçütlü Karar Verme Yöntemi İle Bir Uygulama Abstract An Application Of Vehicle Selection With Moora Multiple Decision Making Method In Construction
İnşaat Yönetiminde Nakliye Aracı Seçiminde Moora Çok Ölçütlü Karar Verme Yöntemi İle Bir Uygulama Abstract An Application Of Vehicle Selection With Moora Multiple Decision Making Method In Construction
English for Academic Reading & Speaking I İngilizce Akademik Okuma ve Konuşma I. Introduction to Civil Engineering İnşaat Mühendisliğine Giriş
 T.C. İZMİR KÂTİP ÇELEBİ ÜNİVERSİTESİ MÜHENDİSLİK VE MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 2015-16 GÜZ YARIYILI VE SONRASINDA UYGULANACAK LİSANS PROGRAMI (%100 İNGİLİZCE) BİRİNCİ YIL 1. DÖNEM Ön
T.C. İZMİR KÂTİP ÇELEBİ ÜNİVERSİTESİ MÜHENDİSLİK VE MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 2015-16 GÜZ YARIYILI VE SONRASINDA UYGULANACAK LİSANS PROGRAMI (%100 İNGİLİZCE) BİRİNCİ YIL 1. DÖNEM Ön
GAZİOSMANPAŞA ÜNİVERSİTESİ FEN-EDEBİYAT FAKÜLTESİ/MATEMATİK BÖLÜMÜ/MATEMATİK PR.
 İRFAN DELİ YARDIMCI DOÇENT E-Posta Adresi irfandeli@kilis.edu.tr Telefon (İş) Telefon (Cep) Faks Adres 3488142662-1731 3488142663 Kilis 7 aralık üniv. Eğitim fak. kilis/merkez Öğrenim Bilgisi Doktora 2010
İRFAN DELİ YARDIMCI DOÇENT E-Posta Adresi irfandeli@kilis.edu.tr Telefon (İş) Telefon (Cep) Faks Adres 3488142662-1731 3488142663 Kilis 7 aralık üniv. Eğitim fak. kilis/merkez Öğrenim Bilgisi Doktora 2010
28 C j -Z j /2 0
 3.2.6. Dual Problem ve Ekonomik Yorumu Primal Model Z maks. = 4X 1 + 5X 2 (kar, pb/gün) X 1 + 2X 2 10 6X 1 + 6X 2 36 8X 1 + 4X 2 40 (işgücü, saat/gün) (Hammadde1, kg/gün) (Hammadde2, kg/gün) 4 5 0 0 0
3.2.6. Dual Problem ve Ekonomik Yorumu Primal Model Z maks. = 4X 1 + 5X 2 (kar, pb/gün) X 1 + 2X 2 10 6X 1 + 6X 2 36 8X 1 + 4X 2 40 (işgücü, saat/gün) (Hammadde1, kg/gün) (Hammadde2, kg/gün) 4 5 0 0 0
Genel Graf Üzerinde Mutlak 1-merkez
 Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ
 ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ Güven SAĞDIÇ Dokuz Eylül Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik
ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ Güven SAĞDIÇ Dokuz Eylül Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik
MULTIMOORA Yöntemi ile Farklı İllerdeki Organize Sanayi Bölgelerinin Yabancı Yatırımcılar Açısından Optimal Yer Seçimi Olarak Değerlendirilmesi
 Finans Politik & Ekonomik Yorumlar 2017 Cilt: 54 Sayı: 624 T. BULUT 41 Tevfik BULUT 1 MULTIMOORA Yöntemi ile Farklı İllerdeki Organize Sanayi Bölgelerinin Yabancı Yatırımcılar Açısından Optimal Yer Seçimi
Finans Politik & Ekonomik Yorumlar 2017 Cilt: 54 Sayı: 624 T. BULUT 41 Tevfik BULUT 1 MULTIMOORA Yöntemi ile Farklı İllerdeki Organize Sanayi Bölgelerinin Yabancı Yatırımcılar Açısından Optimal Yer Seçimi
PROMETHEE, MOORA VE COPRAS YÖNTEMLERİ İLE ORAN ANALİZİ SONUÇLARININ DEĞERLENDİRİLMESİ: BİR UYGULAMA
 PROMETHEE, MOORA VE COPRAS YÖNTEMLERİ İLE ORAN ANALİZİ SONUÇLARININ DEĞERLENDİRİLMESİ: BİR UYGULAMA EVALUATION OF THE RESULTS OF THE RATE ANALYSIS WITH PROMETHEE, MOORA AND COPRAS METHODS: AN APPLICATION
PROMETHEE, MOORA VE COPRAS YÖNTEMLERİ İLE ORAN ANALİZİ SONUÇLARININ DEĞERLENDİRİLMESİ: BİR UYGULAMA EVALUATION OF THE RESULTS OF THE RATE ANALYSIS WITH PROMETHEE, MOORA AND COPRAS METHODS: AN APPLICATION
KARAR TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 KARAR TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü Karar Ortamları Karar Analizi, alternatiflerin en iyisini seçmek için akılcı bir sürecin kullanılması ile ilgilenir. Seçilen
KARAR TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü Karar Ortamları Karar Analizi, alternatiflerin en iyisini seçmek için akılcı bir sürecin kullanılması ile ilgilenir. Seçilen
MULTIMOORA Yöntemi ile Farklı İllerdeki Organize Sanayi Bölgelerinin Yabancı Yatırımcılar Açısından Optimal Yer Seçimi Olarak Değerlendirilmesi
 Finans Politik & Ekonomik Yorumlar 2017 Cilt: 54 Sayı: 624 T. BULUT 41 Tevfik BULUT 1 MULTIMOORA Yöntemi ile Farklı İllerdeki Organize Sanayi Bölgelerinin Yabancı Yatırımcılar Açısından Optimal Yer Seçimi
Finans Politik & Ekonomik Yorumlar 2017 Cilt: 54 Sayı: 624 T. BULUT 41 Tevfik BULUT 1 MULTIMOORA Yöntemi ile Farklı İllerdeki Organize Sanayi Bölgelerinin Yabancı Yatırımcılar Açısından Optimal Yer Seçimi
MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ
 SİMPLEKS TABLONUN YORUMU MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ Şu ana kadar verilen bir DP probleminin çözümünü ve çözüm şartlarını inceledik. Eğer orijinal modelin parametrelerinde bazı değişiklikler
SİMPLEKS TABLONUN YORUMU MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ Şu ana kadar verilen bir DP probleminin çözümünü ve çözüm şartlarını inceledik. Eğer orijinal modelin parametrelerinde bazı değişiklikler
COURSES OFFERED FOR ERASMUS INCOMING STUDENTS
 COURSES OFFERED FOR ERASMUS INCOMING STUDENTS Department : Computer Engineering 152111001 CALCULUS I 3 2 4 5 152111005 PHYSICS I 3 0 3 3 152111006 PHYSICS I LAB 0 2 1 2 152111007 CHEMISTRY 3 0 3 3 152111008
COURSES OFFERED FOR ERASMUS INCOMING STUDENTS Department : Computer Engineering 152111001 CALCULUS I 3 2 4 5 152111005 PHYSICS I 3 0 3 3 152111006 PHYSICS I LAB 0 2 1 2 152111007 CHEMISTRY 3 0 3 3 152111008
OTOMOTİV SEKTÖRÜNDE FAALİYET GÖSTEREN BİR FİRMADA TEDARİKÇİ SEÇİMİ: AHP-BULANIK AHP VE TOPSIS UYGULAMASI
 BEYKENT ÜNİVERSİTESİ FEN VE MÜHENDİSLİK BİLİMLERİ DERGİSİ Sayı 9(1) 2016, 43 83 OTOMOTİV SEKTÖRÜNDE FAALİYET GÖSTEREN BİR FİRMADA TEDARİKÇİ SEÇİMİ: AHP-BULANIK AHP VE TOPSIS UYGULAMASI Cemil ÇELİK (cemil.celik@kocaeli.edu.tr)
BEYKENT ÜNİVERSİTESİ FEN VE MÜHENDİSLİK BİLİMLERİ DERGİSİ Sayı 9(1) 2016, 43 83 OTOMOTİV SEKTÖRÜNDE FAALİYET GÖSTEREN BİR FİRMADA TEDARİKÇİ SEÇİMİ: AHP-BULANIK AHP VE TOPSIS UYGULAMASI Cemil ÇELİK (cemil.celik@kocaeli.edu.tr)
2001 ve 2008 Yılında Oluşan Krizlerin Faktör Analizi ile Açıklanması
 2001 ve 2008 Yılında Oluşan Krizlerin Faktör Analizi ile Açıklanması Mahmut YARDIMCIOĞLU Özet Genel anlamda krizler ekonominin olağan bir parçası haline gelmiştir. Sıklıkla görülen bu krizlerin istatistiksel
2001 ve 2008 Yılında Oluşan Krizlerin Faktör Analizi ile Açıklanması Mahmut YARDIMCIOĞLU Özet Genel anlamda krizler ekonominin olağan bir parçası haline gelmiştir. Sıklıkla görülen bu krizlerin istatistiksel
VERİ MADENCİLİĞİ (Karar Ağaçları ile Sınıflandırma) Yrd.Doç.Dr. Kadriye ERGÜN
 VERİ MADENCİLİĞİ (Karar Ağaçları ile Sınıflandırma) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Sınıflandırma yöntemleri Karar ağaçları ile sınıflandırma Entropi Kavramı ID3 Algoritması C4.5
VERİ MADENCİLİĞİ (Karar Ağaçları ile Sınıflandırma) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Sınıflandırma yöntemleri Karar ağaçları ile sınıflandırma Entropi Kavramı ID3 Algoritması C4.5
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Simpleks Yönteminde Kullanılan İlave Değişkenler (Eşitliğin yönüne göre):
 DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
Journal of Research in Business & Social Science 5(2) Special Issue, 2016: 71-82
 Journal of Research in Business & Social Science 5(2) Special Issue, 2016: 71-82 İşletme & Sosyal Bilimler Araştırmaları Dergisi IJRBS, CİLT 5 SAYI 2, Özel Sayı ISSN: 2147-4478 Contents available at www.ssbfnet.com/ojs
Journal of Research in Business & Social Science 5(2) Special Issue, 2016: 71-82 İşletme & Sosyal Bilimler Araştırmaları Dergisi IJRBS, CİLT 5 SAYI 2, Özel Sayı ISSN: 2147-4478 Contents available at www.ssbfnet.com/ojs
Standart modellerde öncelikle kısıt denklemleri eşitlik haline çevrilmelidir. Öncelikle ilk kısıta bakalım.
 3. Simpleks Yöntem Doğrusal programlama modelleri grafik yöntem dışında simpleks yöntem adı altında özel bir yöntemle çözülebilir. Bu yöntem Simple Matrix kelimlerinin kısaltmasıdır ve bir çeşit matris
3. Simpleks Yöntem Doğrusal programlama modelleri grafik yöntem dışında simpleks yöntem adı altında özel bir yöntemle çözülebilir. Bu yöntem Simple Matrix kelimlerinin kısaltmasıdır ve bir çeşit matris
ENERJĐ ELDESĐNDE ORTALAMA RÜZGAR HIZI ÖLÇÜM ARALIĞI ve HELLMANN KATSAYISININ ÖNEMĐ: SÖKE ÖRNEĞĐ
 ENERJĐ ELDESĐNDE ORTALAMA RÜZGAR HIZI ÖLÇÜM ARALIĞI ve HELLMANN KATSAYISININ ÖNEMĐ: SÖKE ÖRNEĞĐ Mete ÇUBUKÇU1 mecubuk@hotmail.com Doç. Dr. Aydoğan ÖZDAMAR2 aozdamar@bornova.ege.edu.tr ÖZET 1 Ege Üniversitesi
ENERJĐ ELDESĐNDE ORTALAMA RÜZGAR HIZI ÖLÇÜM ARALIĞI ve HELLMANN KATSAYISININ ÖNEMĐ: SÖKE ÖRNEĞĐ Mete ÇUBUKÇU1 mecubuk@hotmail.com Doç. Dr. Aydoğan ÖZDAMAR2 aozdamar@bornova.ege.edu.tr ÖZET 1 Ege Üniversitesi
Bölüm 3. Tanımlayıcı İstatistikler
 Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
alphanumeric journal The Journal of Operations Research, Statistics, Econometrics and Management Information Systems
 Available online at www.alphanumericjournal.com alphanumeric journal The Journal of Operations Research, Statistics, Econometrics and Management Information Systems Received: September 22, 2017 Accepted:
Available online at www.alphanumericjournal.com alphanumeric journal The Journal of Operations Research, Statistics, Econometrics and Management Information Systems Received: September 22, 2017 Accepted:
3. TAHMİN En Küçük Kareler (EKK) Yöntemi 1
 3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş noktası analizi Oyun kuramı
 Anadolu Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2013-2014 Güz Dönemi Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş
Anadolu Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2013-2014 Güz Dönemi Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş
UZAYSAL VE DOLU GÖVDELİ AŞIKLARIN ÇELİK ÇATI AĞIRLIĞINA ETKİSİNİN İNCELENMESİ
 UZAYSAL VE DOLU GÖVDELİ AŞIKLARIN ÇELİK ÇATI AĞIRLIĞINA ETKİSİNİN İNCELENMESİ Mutlu SEÇER* ve Özgür BOZDAĞ* *Dokuz Eylül Üniv., Müh. Fak., İnşaat Müh. Böl., İzmir ÖZET Bu çalışmada, ülkemizde çelik hal
UZAYSAL VE DOLU GÖVDELİ AŞIKLARIN ÇELİK ÇATI AĞIRLIĞINA ETKİSİNİN İNCELENMESİ Mutlu SEÇER* ve Özgür BOZDAĞ* *Dokuz Eylül Üniv., Müh. Fak., İnşaat Müh. Böl., İzmir ÖZET Bu çalışmada, ülkemizde çelik hal
KORELASYON VE REGRESYON ANALİZİ. Doç. Dr. Bahar TAŞDELEN
 KORELASYON VE REGRESYON ANALİZİ Doç. Dr. Bahar TAŞDELEN Günlük hayattan birkaç örnek Gelişim dönemindeki bir çocuğun boyu ile kilosu arasındaki ilişki Bir ailenin tükettiği günlük ekmek sayısı ile ailenin
KORELASYON VE REGRESYON ANALİZİ Doç. Dr. Bahar TAŞDELEN Günlük hayattan birkaç örnek Gelişim dönemindeki bir çocuğun boyu ile kilosu arasındaki ilişki Bir ailenin tükettiği günlük ekmek sayısı ile ailenin
ÖZGEÇMİŞ 2003 MÜHENDİSLİĞİ İSTANBUL ÜNİVERSİTESİ ÜNİVERSİTESİ
 ÖZGEÇMİŞ 1. Adı Soyadı: İPEK EKER 2. Doğum Tarihi: 31.01.1980 3. Ünvanı: ÖĞRETİM GÖREVLİSİ 4. Öğrenim Durumu: Derece Alan Üniversite Yıl Lisans ENDÜSTRİ İSTANBUL KÜLTÜR 2003 MÜHENDİSLİĞİ ÜNİVERSİTESİ Y.Lisans
ÖZGEÇMİŞ 1. Adı Soyadı: İPEK EKER 2. Doğum Tarihi: 31.01.1980 3. Ünvanı: ÖĞRETİM GÖREVLİSİ 4. Öğrenim Durumu: Derece Alan Üniversite Yıl Lisans ENDÜSTRİ İSTANBUL KÜLTÜR 2003 MÜHENDİSLİĞİ ÜNİVERSİTESİ Y.Lisans
Vol. 4, No. 2, 2017, pp
 Vol. 4, No. 2, 2017, pp. 15-40 PJESS PJESS Karadeniz Ekonomik İşbirliği Üye Ülkelerine İlişkin Etkinlik Analizi: TOPSIS, ARAS ve MOORA Yöntemleriyle Bir Uygulama a An activity analysis on the black sea
Vol. 4, No. 2, 2017, pp. 15-40 PJESS PJESS Karadeniz Ekonomik İşbirliği Üye Ülkelerine İlişkin Etkinlik Analizi: TOPSIS, ARAS ve MOORA Yöntemleriyle Bir Uygulama a An activity analysis on the black sea
ÇOK ÖLÇÜTLÜ KARAR VERME YÖNTEMLERİ İLE SEÇMELİ DERS SEÇİMİ
 ÇOK ÖLÇÜTLÜ KARAR VERME YÖNTEMLERİ İLE SEÇMELİ DERS SEÇİMİ Batuhan Safa Kutlu* Yusuf Alper Abalı** Tamer Eren*** Özet Bu çalışmada amaç çok ölçütlü karar verme yöntemleri kullanılarak öğrencilerin seçmeli
ÇOK ÖLÇÜTLÜ KARAR VERME YÖNTEMLERİ İLE SEÇMELİ DERS SEÇİMİ Batuhan Safa Kutlu* Yusuf Alper Abalı** Tamer Eren*** Özet Bu çalışmada amaç çok ölçütlü karar verme yöntemleri kullanılarak öğrencilerin seçmeli
Ö Z G E Ç M İ Ş. 1. Adı Soyadı: Mustafa GÖÇKEN. 2. Doğum Tarihi: 12 Haziran 1976. 3. Unvanı: Yrd. Doç. Dr. 4. Öğrenim Durumu: Ph.D.
 Ö Z G E Ç M İ Ş 1. Adı Soyadı: Mustafa GÖÇKEN 2. Doğum Tarihi: 12 Haziran 1976 3. Unvanı: Yrd. Doç. Dr. 4. Öğrenim Durumu: Ph.D. Derece Alan Üniversite Yıl Lisans Endüstri Mühendisliği Çukurova Üniversitesi
Ö Z G E Ç M İ Ş 1. Adı Soyadı: Mustafa GÖÇKEN 2. Doğum Tarihi: 12 Haziran 1976 3. Unvanı: Yrd. Doç. Dr. 4. Öğrenim Durumu: Ph.D. Derece Alan Üniversite Yıl Lisans Endüstri Mühendisliği Çukurova Üniversitesi
Temelleri. Doç.Dr.Ali Argun Karacabey
 Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
English for Academic Reading & Speaking I İngilizce Akademik Okuma ve Konuşma I. Introduction to Civil Engineering İnşaat Mühendisliğine Giriş
 T.C. İZMİR KÂTİP ÇELEBİ ÜNİVERSİTESİ MÜHENDİSLİK VE MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 2015-16 GÜZ YARIYILI VE SONRASINDA UYGULANACAK LİSANS PROGRAMI (%100 İNGİLİZCE) BİRİNCİ YIL 1. DÖNEM Ön
T.C. İZMİR KÂTİP ÇELEBİ ÜNİVERSİTESİ MÜHENDİSLİK VE MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 2015-16 GÜZ YARIYILI VE SONRASINDA UYGULANACAK LİSANS PROGRAMI (%100 İNGİLİZCE) BİRİNCİ YIL 1. DÖNEM Ön
Personel Seçimi için Gri Sistem Teori Tabanlı Bütünleşik Bir Yaklaşım
 EGE AKADEMİK BAKIŞ / EGE ACADEMIC REVIEW Cilt: 13 Sayı: 4 Ekim 2013 ss. 461-471 Personel Seçimi için Gri Sistem Teori Tabanlı Bütünleşik Bir Yaklaşım An Integrated Approach Based on Grey System Theory
EGE AKADEMİK BAKIŞ / EGE ACADEMIC REVIEW Cilt: 13 Sayı: 4 Ekim 2013 ss. 461-471 Personel Seçimi için Gri Sistem Teori Tabanlı Bütünleşik Bir Yaklaşım An Integrated Approach Based on Grey System Theory
Öncelikli Sektörlerin Belirlenmesinde AHS-TOPSIS ve AHS-VIKOR Yaklaşımlarının Kullanımı: Rize Organize Sanayi Bölgesi Örneği
 Journal of Yasar University, 2014 9(35) 6099-60xx Öncelikli Sektörlerin Belirlenmesinde AHS-TOPSIS ve AHS-VIKOR Yaklaşımlarının Kullanımı: Rize Organize Sanayi Bölgesi Örneği Using AHP-TOPSIS and AHP-VIKOR
Journal of Yasar University, 2014 9(35) 6099-60xx Öncelikli Sektörlerin Belirlenmesinde AHS-TOPSIS ve AHS-VIKOR Yaklaşımlarının Kullanımı: Rize Organize Sanayi Bölgesi Örneği Using AHP-TOPSIS and AHP-VIKOR
BULANIK AMAÇ KATSAYILI DOĞRUSAL PROGRAMLAMA. Ayşe KURUÜZÜM (*)
 D.E.Ü.İ.İ.B.F. Dergisi Cilt:14, Sayı:1, Yıl:1999, ss:27-36 BULANIK AMAÇ KATSAYILI DOĞRUSAL PROGRAMLAMA Ayşe KURUÜZÜM (*) ÖZET Çalışmada bulanık ( fuzzy ) katsayılı amaç fonksiyonuna sahip doğrusal programlama
D.E.Ü.İ.İ.B.F. Dergisi Cilt:14, Sayı:1, Yıl:1999, ss:27-36 BULANIK AMAÇ KATSAYILI DOĞRUSAL PROGRAMLAMA Ayşe KURUÜZÜM (*) ÖZET Çalışmada bulanık ( fuzzy ) katsayılı amaç fonksiyonuna sahip doğrusal programlama
CRITIC VE EVAMIX YÖNTEMLERİ İLE BİR İŞLETME İÇİN DİZÜSTÜ BİLGİSAYAR SEÇİMİ
 / Şubat 2018 February 2018 www.sosyalarastirmalar.com Issn: 1307-9581 http://dx.doi.org/10.17719/jisr.20185537260 CRITIC VE EVAMIX YÖNTEMLERİ İLE BİR İŞLETME İÇİN DİZÜSTÜ BİLGİSAYAR SEÇİMİ Öz LAPTOP SELECTION
/ Şubat 2018 February 2018 www.sosyalarastirmalar.com Issn: 1307-9581 http://dx.doi.org/10.17719/jisr.20185537260 CRITIC VE EVAMIX YÖNTEMLERİ İLE BİR İŞLETME İÇİN DİZÜSTÜ BİLGİSAYAR SEÇİMİ Öz LAPTOP SELECTION
Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Y.2008, C.13, S.1 s.133-144.
 Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Y.2008, C.13, S.1 s.133-144. ANALİTİK HİYERARŞİ SÜRECİNİN TEDARİKÇİ SEÇİMİNDE UYGULANMASI: OTOMOTİV SEKTÖRÜNDEN BİR ÖRNEK APPLICATION
Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Y.2008, C.13, S.1 s.133-144. ANALİTİK HİYERARŞİ SÜRECİNİN TEDARİKÇİ SEÇİMİNDE UYGULANMASI: OTOMOTİV SEKTÖRÜNDEN BİR ÖRNEK APPLICATION
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
OSPF PROTOKOLÜNÜ KULLANAN ROUTER LARIN MALİYET BİLGİSİNİN BULANIK MANTIKLA BELİRLENMESİ
 OSPF PROTOKOLÜNÜ KULLANAN ROUTER LARIN MALİYET BİLGİSİNİN BULANIK MANTIKLA BELİRLENMESİ Resul KARA Elektronik ve Bilgisayar Eğitimi Bölümü Teknik Eğitim Fakültesi Abant İzzet Baysal Üniversitesi, 81100,
OSPF PROTOKOLÜNÜ KULLANAN ROUTER LARIN MALİYET BİLGİSİNİN BULANIK MANTIKLA BELİRLENMESİ Resul KARA Elektronik ve Bilgisayar Eğitimi Bölümü Teknik Eğitim Fakültesi Abant İzzet Baysal Üniversitesi, 81100,
TCDD İLTİSAK HATLARI PROJELERİNİN DEĞERLENDİRİLMESİNDE UZLAŞIK ÇOK ÖLÇÜTLÜ KARAR VERME YÖNTEMLERİ UYGULAMASI
 Gazi Üniv. Müh. Mim. Fak. Der. Journal of the Faculty of Engineering and Architecture of Gazi University Cilt 31, No 1, 11-0, 016 Vol 31, No 1, 11-0, 016 TCDD İLTİSAK HATLARI PROJELERİNİN DEĞERLENDİRİLMESİNDE
Gazi Üniv. Müh. Mim. Fak. Der. Journal of the Faculty of Engineering and Architecture of Gazi University Cilt 31, No 1, 11-0, 016 Vol 31, No 1, 11-0, 016 TCDD İLTİSAK HATLARI PROJELERİNİN DEĞERLENDİRİLMESİNDE
H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012)
 H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012) Aşağıdaki analizlerde lise öğrencileri veri dosyası kullanılmıştır.
H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012) Aşağıdaki analizlerde lise öğrencileri veri dosyası kullanılmıştır.
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
: Manufacturing Engineering and Management (Link) Üretim Sistemleri/Endüstri Mühendislii Bölümü ne uygun bazı dersler
 : Danimarka : Technical University of Denmark (Link) : Manufacturing Engineering and (Link) Informatics and Mathematical Programming (Link) Production Technology Project System Analysis Statistical Process
: Danimarka : Technical University of Denmark (Link) : Manufacturing Engineering and (Link) Informatics and Mathematical Programming (Link) Production Technology Project System Analysis Statistical Process
Adres : Atılım Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü C Blok No:216 06836 İncek Ankara
 UĞUR BAÇ YARDIMCI DOÇENT E-Posta Adresi : ugur.bac@atilim.edu.tr Telefon (İş) : 3125868759- Telefon (Cep) : Faks : 3125868091 Adres : Atılım Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü
UĞUR BAÇ YARDIMCI DOÇENT E-Posta Adresi : ugur.bac@atilim.edu.tr Telefon (İş) : 3125868759- Telefon (Cep) : Faks : 3125868091 Adres : Atılım Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü
YATAY UÇUŞ SEYAHAT PERFORMANSI (CRUISE PERFORMANCE)
 YATAY UÇUŞ SEYAHAT PERFORMANSI (CRUISE PERFORMANCE) Yakıt sarfiyatı Ekonomik uçuş Yakıt maliyeti ile zamana bağlı direkt işletme giderleri arasında denge sağlanmalıdır. Özgül Yakıt Sarfiyatı (Specific
YATAY UÇUŞ SEYAHAT PERFORMANSI (CRUISE PERFORMANCE) Yakıt sarfiyatı Ekonomik uçuş Yakıt maliyeti ile zamana bağlı direkt işletme giderleri arasında denge sağlanmalıdır. Özgül Yakıt Sarfiyatı (Specific
FONKSİYONLARIN TABLO ŞEKLİNDE HESAPLANMASI
 FONKSİYONLARIN TABLO ŞEKLİNDE HESAPLANMASI Bu kısımda bir fonksiyon değerlerinin tablo şeklinde hesaplanması incelenecektir. İncelenecek fonksiyon y=f(x) şeklinde bir değişenli veya z=f(x,y) şeklinde iki
FONKSİYONLARIN TABLO ŞEKLİNDE HESAPLANMASI Bu kısımda bir fonksiyon değerlerinin tablo şeklinde hesaplanması incelenecektir. İncelenecek fonksiyon y=f(x) şeklinde bir değişenli veya z=f(x,y) şeklinde iki
