Bağımsız Model Blok Dengeleme için Model Oluşturma ve Ön Sayısal Bilgi İşlemleri
|
|
|
- Deniz Peker
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Bağımsız Model Blok Dengeleme için Model Oluşturma ve Ön Sayısal Bilgi İşlemleri Eminnur AYHAN* 1. Giriş Fotogrametrik nirengi çeşitli ölçütlere göre sınıflandırılabilir. Bu ölçütler dengelemede kullanılan birim, veri toplamada kullanılan yöntem ve araçlar olabilir. Son yıllardaki hesaplama araçlarındaki gelişmelere paralel olarak analitik yöntemlere ilgi gittikçe artmaktadır. Analitik yöntemlerin tümünde giriş verileri mono veya stereo komparatör ölçmeleri yardımıyla elde edilen resim koordinatlarıdır. Elde edilen resim koordinatları bilinen tüm hatalardan arındırıldıktan sonra fotogrametrik nirengide kullanılabilir. Bağımsız modellerle blok dengeleme için, tek resim ölçülerinden stereomodelin oluşturulması ve ilgili noktaların model koordinatlarının elde edilmesinde izlenen adımlar şunlardır.. Hazırlık çalışmaları. Ölçme işlemleri. Resim koordinatlarının elde edilişi. Resim koordinatlarına düzeltmelerin getirilişi. Sayısal karşılıklı yöneltme. Model koordinat hesabı 2. ANALİTİK YÖNTEMLERLE MODEL OLUŞTURMA 2.1. Hazırlık Çalışmaları İster analitik, ister analog yöntemde olsun fotogrametrik nirenginin gerçek anlamda gerçekleştirilebilmesi için modeller, kolonlar arasındaki bağlantının çok iyi bir şekilde sağlanmış ve resmler üzerinde yer alan yer kontrol noktalarının kesin olarak belirlenmiş olması gerekir. Bu işlemleri içeren hazırlık çalışmaları, çalışmaların en önemli bir * Dr. (KTÜ) 90
2 kısmını kapsamaktadır Ölçme İşlemleri Bağımsız model blok dengeleme amacıyla resimler üzerinden gerekli bilgilerin alınması çeşitli aletlerle yapılabilir. Bu çalışmada fotogrametrik ölçme aleti olarak monokomparator kullanılmıştır. Komparatordan bilgisayara aktarılan bilgilerin kullanıma hazırlanması için birtakım işlemlerden geçirilmesi gerekir. Elde edilen kayıtlar programlar yardımıyla komparator koordinatları olarak diğer işlemlere hazır duruma getirilebilir Resim Koordinatlarının Elde Edilişi Resim koordinatlarının elde edilebilmesi için rasgele konumda bulunan komparator dik koordinat sistemi ile kalibrasayon raporundan alınan resim koordinat sistemi arasında bir ilişki kurulabilir. Bunun için 6 fotoğrafın bulunduğu blokda çerçeve işaretleri kullanılarak benzerlik dönüşümü ve afin dönüşüm uygulanmıştır. Her iki dönüşüm sonucunda ortak noktalardaki artık hataları gösteren durum Tablo 1' de verilmiştir III. Tablo 1 : Afin ve Benzerlik Dönüşümü Sonuçları 91
3 2.4. Resim Koordinatlarına Getirilecek Düzeltmeler. Başlangıcın Düzeltilmiş Asal Noktaya Alınması ve Film Deformasyonu için Düzeltme. Mercek Distorsiyonu için Düzeltme. Yer Küreselliği için Düzeltme. Atmosferik Kırılma için Düzeltme Başlangıcın Düzeltilmiş Asal Noktaya Alınması ve Film Deformasyonn Emilsiyon ve emilsiyon taşıyıcı film sıcaklık, nem gibi çevre şartları, eskime ve kimyasal işlemler gibi olayların fonksiyonu olarak çok yönlü deformasyonlara uğrarlar. Komparator koordinatlarından resim koordinatlarına dönüşüm sırasında film deformasyonu da giderilmiş olur Mercek Distorsiyonu Fotogrametrik kameralardaki mercekler birden fazla mercekten oluşan sistemlerdir. Bu nedenle görüntü merkezi izdüşüm kuramının belirlediği noktadan farklı bir noktada oluşur. Mercek distorsiyonu radyal (çapsal) ve teğetsel olmak üzere iki kısma ayrılabilir. Odak uzaklığının bir fonksiyonu olarak radyal mercek distorsiyonu, Ar D =r-c tan «. (1) formülü ile ifade edilebilir. Burada, a : Bir ışının kamera ekseni ile yaptığı açı, c : Odak uzaklığı, r : Asal nokta ile görüntü noktası arasındaki uzaklıktır. Radyal mercek distorsiyonu ayrıca sürekil bir fonksiyon yardımıyla da, Ar D = a o r + a^3 + a 2 r 5 + a 3 r 7 + a 4 r şeklinde gösterilebilir. Burada, a : Polinomun bilinmeyen katsayıları, r : Çapsal mesafedeki simetrik çapsal distorsiyondur. 92
4 Radyal mercek distorsiyonu ve onların bileşenleri arasındaki ilişki, şeklinde ifade edilebilir. Ar Ax Ay = = (3) r x y Teğetsel distorsiyon, mercek bileşenlerinin kusurlu merkezlendirilmesi ve bileşik mercek ürünlerindeki diğer kusurlardan dolayı ortaya çıkar. Teğetsel distorsiyonun bileşenleri için, Ax= {P,(r2 + 2x2) + p 2Xy } {l+p 3 r2 + p 4 ı4 +.. } Ay= {2Pıxy + P 2 (fi + 2y 2 ) }{1+P 3 r 2 + P 4 r4 +..} (4) formülleri verilebilir 131. Burada, Pl, P2, P3, P4 : Bilinmeyen katsayılar, x, y : Bir noktanın görüntü koordinatları r : Asal noktadan olan uzaklıktır. Düzeltilmiş resim koordinatları, / Ar D -% x = x - Ax = x _ > (5) / * D 1 y = y - Ay = y \ J formülleriyle bulunabilir Atmosferik Kırılma (Atmospheric Mefraction) Atmosferik kırılma, ışın yolu boyunca olan bütün noktalardaki havanın kırılma oranının bir fonksiyonudur. Kırılma oranı atmosferin bileşimine, basıncına ve sıcaklığına bağlıdır. Yarıçap yönündeki atmosferik kırılmanın etkisi, 93
5 Ar R= K L r + h~ J ifadesi ile hesaplanabilir 151. Bu formüldeki K, 2410 H 2410 h fhj nq. 6 H 2-6H+250 h 2-6h+250H J (7) değerine eşittir. Burada, H (km): Denizden itibaren uçuş yüksekliği h (km) : Ortalama arazi yüksekliğidir. Düzeltilmiş resim koordinatları, / * R \ L r J (8) y = y \ ı şeklinde yazılabilir Yer Küreselliği (Earth Cervatııre) Küçük ölçekli resimlerden oluşan kolonlarda çok büyük bir küresellik hatasından korunmak için analitik çalışmalarda yer küreselliği düzeltmeleri getirilir. Düzeltmeler başlibaşına resimler veya stereo modellerin (kolonlar veya bloklar) herbirine uygulanabilir. Analog çalışmalarda kolonlar veya bloklarla, sayısal çalışmalarda ise resimlerle çalışmak daha uygundur. Jeodezik koordinatların bir referans düzlemine indirgenmiş şekli alındığından düzeltme pozitif yönlüdür. Yer küreselliği, hs3 cs^ Ar K = ( 9 ) 2Rc 2 2Rh2 94
6 formülü ile ifade edilir fil. Burada, h : Arazi nadir noktasından itibaren uçuş yüksekliği, R: Yer yarıçapı, s: Çapsal uzaklık, S : Yer küresi üzerinde nadir noktası ile arazi noktası arasındaki uzaklık, c: odak uzaklığıdır. Denizden itibaren uçuş yüksekliği km Ortalama Arazi Yüksekliği 1.2 km Yer Yarıçapı km Uçuş Yüksekliği k«_ 6 K Sabiti 32.59*10 Değerleri kullanılarak Tablo 2 sonuçları elde edilmiştir III. Tablo 2 : Belirli uzaklıklar için kırılma ve küresellik için bulunan değerler 95
7 Şekil 1 : Eşdüzlemlilik (Coplanarity) Koşulu Resim koordinatlarına gerekli düzeltmeler getirildikten sonra model koordinat sistemine geçebilmek için karşılıklı yöneltme yapılır. Analog karşılıklı yöneltmeye benzer şekilde sayısal işlemlerde de modelde iyi dağılmış en az beş noktaya ihtiyaç vardır ve yapılması gereken bu beş noktadan çıkan ışınların kestirilmesidir/8/. Bu işlemle ilgili olan eşdüzlemlilik (coplanarity condition) koşulu, birden fazla fotoğrafta yer alan aynı noktanın cisim noktasından herbir görüntüye giden görüntü ışınlarının bir düzlem içerisinde yer aldığı görüşüne dayanır 121. Genel eşdüzlemlilik (coplanarity) koşulu, 0 bz -by x [ x' y' - c ] R J -bz 0 bx R 2 y" = 0 by - bx 0 c -I L (10) şeklinde yazılabilir. Sayısal karşılıklı yöneltmede bx önemli değildir. bx 'in etkisi yöneltme elemanlarının bulunması sırasında yok edilebilir. Bu işlem eşdüzlemlilik eşitliğindeki temel matris elemanlarının bx'e bölünmesiyle gerçekleştirilir. 96
8 Harita ve Kadastro Mühendisliği 0 z -J3y. x' y' -c Rj - B Z 0 1 R 2 y" = 0 py c J L J (İD Burada; bx x " bx ile ifade edilir I il, 141. Yöneltme elemanları olarak ya K 2. )p 2 > \^2' J-> Y> z elemanları ya da 1» r 1» 2> ^ 2 > ^ 2 elemanları kullanılarak yöneltme işlemleri yürütülür Sayısal Karşılıklı Yöneltmede Genel İşlemler * v v v v ıs '' e gösterilebilen beş karşılıklı yöneltme elemanı *M» "-2' *^3 ' ^4 ve ^5 seçilir. * 17 î7 ^" î^" î7 y öne l trne bîünıneyenlerinin yaklaşık değerlerini, Ki, K>2, K3, K4, K.5 * AK,, AK 2, AK 3, AK 4 ve AK 5 düzeltmeleri gösterdiği kabu, edihı, * Bilinmeyenler için çoğunlukla ilk yaklaşk değerler Ki = K2 = K3 = K4 = K5 =0 O arak a ı ı mr. (Rİ =I).Rİ ; P.1,0,U ; I yaklaşık değerlerinden oluşturulmuş ortogonal bir matristir. * Modeldeki her nokta için co-planarity eksikliği, -Lj =-c(y- - y i ) formülü ile hesaplanır. * Modeldeki her nokta için yöneltme bilinmeyenlerinin katsayılarından oluşan A matrisi, a ü AK l +a i2 AK 2 +a i3 AK 3 +a i4^k 4 +a i5 AK 5 = - Lj şeklinde oluşturulur. Kullanılmış elemanlara ve eşitliğin doğrusallaştırma 97
9 türüne bağlı olarak ' katsayıları farklı olur. * Karşılıklı yöneltme için en az beş nokta gereklidir. Beşten fazla nokta için dengeleme yapılır. a n a j 2 a 13 a 14 a ı5 AK! : -L { a 21 a 22 a 23 a 24 a 25 A.K 2 -L A'K 3 = -L 3... AK 4 -L 4 ^_ a 51 a 52 a 53 a 54 a 55. AK 5 " -L 5 A AK -L Dengeleme söz konusu olduğunda normal denklemler kurulur. A T AAK=-A T L * Yöneltme bilinmeyenlerinin elde edilmesi için normal denklemler çözülür. (A T A)''A T AAK = - (A 1^)" 1 A T L AK = - (A^-'ATL * Düzeltilmiş yöneltme elemanları hesaplanır. Kı(yeni) = Kı(eski) + AK ı K2(yeni) = K~2(eski) + AK 2 K 5 (yeni) = K 5 (eski) + AK 5 * En uygun sonuç alınana kadar iterasyona devam edilir. * Yöneltme elemanlarının kesin değerleri hesaplanır. * Her bir model için standart sapma ve y paralaksı hesaplanır. Sayısal karşılıklı yöneltmede yöneltme elemanlarına getirilecek düzeltmeler radyandan daha küçük ise iterasyon sona erdirilir. Bu yöntemde bir diğer ölçüt de iterasyon sayısıdır. Yaklaşık düşey resimlerde 3 veya 4 iterasyon sonucunda istenilen sonuç elde edilir. 98
10 Aletlerdeki deneysel karşılıklı yöneltmede iterasyon y paralaksı lofim den daha küçük olduğu zaman durdurulur Model Koordinatlarının Elde Edilmesi (Genel çerçevesiyle) Şekil 2 : Model Koordinat Sistemi Model koordinat sisteminin başlangıcı sol izdüşüm merkezi alınması durumunda model koordinatlarının hesaplanmasındaki adımlar; * Uygun bx değeri seçilir ve by = bxj3 y bz = bx z baz değerleri hesaplanır. * K/îp*rkv»'7İ*»i'i cıı/nı r\iqn 99
11 (x;,y;,z;)iie(x;, y ;,c) ve (x;,y;,z;)iie(x;, y ;, C ) dik koordinat sistemlerinde bir sistemde bilinen koordinatların diğerinde ifadesi bu koordinatların birer ortogonal dönüşüm matrisiyle çarpılması suretiyle elde R R edilir. ' 2 j e dönüklükleri giderilmiş koordinatlar hesaplanır. 1 r 1 r n r o Yj' = R, y'j ve Y;" = R 2 yj' - z U H L Z 'Lİ L C R = I R Genellikle ' ' 2 de son iterasyonla elde edilen yöneltme elemanlarının fonksiyonu olan dönüklük matrisidir. * Her nokta için ölçek faktörleri hesaplanır. 1 - bxz" - bzx" - _ bxz' - bzx H "*** I II II I 5 *-î *"* I II I I I (X Z - X Z ) (X Z - X Z ) * Model koordinatları x i = t \ x ; z i=t ;z; v _t'v' v -tvıhv v -ZLJL^L Y i =t i Y i, i İ tjyj H- by, Yj formülleri ile y paralaksı, Z\y = Yi -Yi şeklinde hesaplanabilir. 3. SONUÇ Komparator koordinatlarından resim koordinatlarına geçişte dört çerçeve noktası kullanılarak projektif dönüşüm uygulanması durumunda artık hatalar sıfır olur. Bu durum kaba hataların kontrol altına alınamaması demektir. Kaba hataların kontrol altına alınmasından dolayı dengeleme tercih edilir. Çalışmada elde edilen sonuçlardan komparator ve resim koordinat sistemleri arasındaki ilişki en iyi afin dönüşüm ile sağlanabilir 100
12 Yapılan çalışmada elde edilen sonuçlardan resim kenarlarına zorunlu kalmadıkça gidilmemesi gerekir. Çünkü bu kısımlarda görüntü bozuk, yer küreselliği söz konusudur. Kısaca bütün resim hataları resim kenarlarına gidildikçe artar. Eşdüzlemliük (coplanarity) eşitliği ile sayısal karşılıklı yöneltme işlemlerinde izdüşüm merkezine indirgenmiş resim koordinatlarının kullanılması durumunda, normal denklem katsayılarının büyüklüğü nisbeten küçük olur ve bundan dolayı büyük kapanma hatalarından kaçınılmış olur. Ayrıca bazı katsayıların hesaplanması da basitleştirilebilir. İlgili resim çiftlerinin analitik karşılıklı yöneltmesi sonucunda oluşan artık paralaks hataları resim kalitesi iyi olan resimlerde 7-8/*m, daha kötü kaliteli resimlerde ise 13-14/* m civarında elde edilmiştir III. Çalışmalarda kullanılacak resimlerin kalitesi de önemli etkenlerden biridir. 4. KAYNAKLAR 1. Amer, F. : Photogrammetric Triangulation Part II Digital Orientation of a Stereomodel and Digital Strip Formation, ITC-Lecture Notes, Ayhan, E. : Dönel Yüzeylerin Yakın Resim Fotogrametrisi Yöntemleriyle Belirlenmesi, Doktora Tezi, KTÜ, Trabzon, Gosh, S.K. : Analytical Photogrammetry, Pergamon Press Inc. N.Y., Koyuncu, D. : Büyük Ölçekli Fotogrametrik Çizgisel Haritaların Güncelleştirilmesinde Fotogrametrik Sayısal Yöntemler, Doktora Tezi, KTÜ, Trabzon, Moffit, H. F. : Photogrammetry, Harper and Rovv, Publishers, Third Edition, Mikail, E.M. New York, Ölücüoğlu, N.: Bağımsız Modellerle Blok Dengeleme için Model Oluşturma ve Ön Sayısal Bilgi İşlemleri, Master Tezi, KTÜ, Trabzon, Yaşayan, A. : Türkiye'de Hava Triyangulasyonu Analiz ve Teklifler, Doktora Tezi, İTÜ İnş. Fak., İstanbul,
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
Fotogrametride işlem adımları
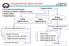 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme)
 FOTOGRAMETRİ FOTOGRAMETRİ Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme) Buna göre ışık yardımı ile ölçme (çizim yapabilme)
FOTOGRAMETRİ FOTOGRAMETRİ Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme) Buna göre ışık yardımı ile ölçme (çizim yapabilme)
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI
 FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI
 FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Fotogrametride Koordinat Sistemleri
 Fotogrametride Koordinat Sistemleri Komparator koordinat sistemi, Resim koordinat sistemi / piksel koordinat sistemi, Model veya çekim koordinat sistemi, Jeodezik koordinat sistemi 08 Ocak 2014 Çarşamba
Fotogrametride Koordinat Sistemleri Komparator koordinat sistemi, Resim koordinat sistemi / piksel koordinat sistemi, Model veya çekim koordinat sistemi, Jeodezik koordinat sistemi 08 Ocak 2014 Çarşamba
GPS/INS Destekli Havai Nirengi
 GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
DİJİTAL FOTOGRAMETRİ. KTÜ Mühendislik Fakültesi Harita Mühendisliği Bölümü. Doç. Dr. Eminnur Ayhan
 DİJİTAL FOTOGRAMETRİ KTÜ Mühendislik Fakültesi Harita Mühendisliği Bölümü Doç. Dr. Eminnur Ayhan Dijital Fotogrametrideki (Raster) Koordinat Sistemleri 1. Piksel koordinat sistemi 2. Görüntü koordinat
DİJİTAL FOTOGRAMETRİ KTÜ Mühendislik Fakültesi Harita Mühendisliği Bölümü Doç. Dr. Eminnur Ayhan Dijital Fotogrametrideki (Raster) Koordinat Sistemleri 1. Piksel koordinat sistemi 2. Görüntü koordinat
Kontrol noktaları (X,Y,Z) Şekil 1- Stereodeğerlendirme ve tek resim değerlendirmesi için kontrol noktaları gereksinimi.
 FOTOGRAMETRİK NİRENGİ 1.GEREKÇE VE TANIM Stereodeğerlendirme yapabilmek için, stereo model alanında, en az üç, olabilirse köşelere gelecek şekilde dört kontrol noktasına gerek vardır. Tek resim değerlendirmesi
FOTOGRAMETRİK NİRENGİ 1.GEREKÇE VE TANIM Stereodeğerlendirme yapabilmek için, stereo model alanında, en az üç, olabilirse köşelere gelecek şekilde dört kontrol noktasına gerek vardır. Tek resim değerlendirmesi
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ
 KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
İnşaat Mühendisliğine Giriş İNŞ-101. Yrd.Doç.Dr. Özgür Lütfi Ertuğrul
 İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
FOTOYORUMLAMA UZAKTAN ALGILAMA
 FOTOYORUMLAMA VE UZAKTAN ALGILAMA (Photointerpretation and Remote Sensing) 1 Ders İçeriği Hava fotoğrafının tanımı Fotogrametrinin geometrik ilkeleri Fotogrametride fotoğrafik temel ilkeler Stereoskopik
FOTOYORUMLAMA VE UZAKTAN ALGILAMA (Photointerpretation and Remote Sensing) 1 Ders İçeriği Hava fotoğrafının tanımı Fotogrametrinin geometrik ilkeleri Fotogrametride fotoğrafik temel ilkeler Stereoskopik
0227130 FOTOGRAMETRİ KAMERA KALİBRASYONU ÖDEV YÖNERGESİ
 0227130 FOTOGRAMETRİ Giriş: KAMERA KALİBRASYONU ÖDEV YÖNERGESİ 0227130 fotogrametri dersini alan öğrencilerin teorik dersleri izlemesinin yanında uygulamalı bir çalışma olan Kamera Kalibrasyonu Ödevi yapması
0227130 FOTOGRAMETRİ Giriş: KAMERA KALİBRASYONU ÖDEV YÖNERGESİ 0227130 fotogrametri dersini alan öğrencilerin teorik dersleri izlemesinin yanında uygulamalı bir çalışma olan Kamera Kalibrasyonu Ödevi yapması
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Aycan M. MARANGOZ
 FOTOGRAMETRİ II GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
FOTOGRAMETRİ II GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
Fotogrametriye Giriş
 ye Giriş 2013-2014, BAHAR YY Fevzi Karslı (Doç. Dr.) Harita Mühendisliği Bölümü 23 Mart 2014 Pazar Ders Planı ve İçeriği 1. Hafta Giriş, dersin kapsamı, kavramlar, kaynaklar. 2. Hafta nin tanımı ve uygulama
ye Giriş 2013-2014, BAHAR YY Fevzi Karslı (Doç. Dr.) Harita Mühendisliği Bölümü 23 Mart 2014 Pazar Ders Planı ve İçeriği 1. Hafta Giriş, dersin kapsamı, kavramlar, kaynaklar. 2. Hafta nin tanımı ve uygulama
Fotogrametriye Giriş
 Fotogrametriye Giriş 2014-2015, Bahar YY Fevzi Karslı (Doç. Dr.) Harita Mühendisliği Bölümü Mühendislik Fakültesi KTÜ 7 Mart 2015 Cumartesi Ders Planı ve İçeriği 1. Hafta Giriş, dersin kapsamı, kavramlar,
Fotogrametriye Giriş 2014-2015, Bahar YY Fevzi Karslı (Doç. Dr.) Harita Mühendisliği Bölümü Mühendislik Fakültesi KTÜ 7 Mart 2015 Cumartesi Ders Planı ve İçeriği 1. Hafta Giriş, dersin kapsamı, kavramlar,
Doç. Dr. Bahadır ERGÜN MİM 466
 MİMARİ FOTOGRAMETRİ Fotogrametri, fiziksel cisimler ve oluşturdukları çevreden yansıyan ışınların şekillendirdiği fotogrametrik görüntülerin ve yaydıkları elektromanyetik enerjilerin kayıt,ölçme ve yorumlama
MİMARİ FOTOGRAMETRİ Fotogrametri, fiziksel cisimler ve oluşturdukları çevreden yansıyan ışınların şekillendirdiği fotogrametrik görüntülerin ve yaydıkları elektromanyetik enerjilerin kayıt,ölçme ve yorumlama
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI
 36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
İÇİNDEKİLER. Ön Söz...2. Noktanın Analitik İncelenmesi...3. Doğrunun Analitiği Analitik Düzlemde Simetri...25
 İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
ÖLÇME BİLGİSİ. PDF created with FinePrint pdffactory trial version http://www.fineprint.com. Tanım
 ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
( m %n' m q >m q J > şekilde şematik olarak gösterilmiştir.
 Diğer Araştırmalar : Bir önceki bölümde açıklanan ilk araştırmaların teorik ve deneysel sonuçlarını sınamak amacı ile, seri halinde yeni teorik ve deneysel araştırmalar yapılmıştır. (Çizelge : IV) de belirtilen
Diğer Araştırmalar : Bir önceki bölümde açıklanan ilk araştırmaların teorik ve deneysel sonuçlarını sınamak amacı ile, seri halinde yeni teorik ve deneysel araştırmalar yapılmıştır. (Çizelge : IV) de belirtilen
AVRASYA ÜNİVERSİTESİ
 Ders Tanıtım Formu Dersin Adı Öğretim Dili FOTOGRAMETRİ Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x) Uzaktan Öğretim( ) Diğer
Ders Tanıtım Formu Dersin Adı Öğretim Dili FOTOGRAMETRİ Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x) Uzaktan Öğretim( ) Diğer
MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl
 İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
Âna nirengi doğrultuları için p = 1 m 2 o Ara nirengi doğrultuları için p a =------------ m\
 4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
23. Sistem denge denklemlerinin direkt kurulması
 . Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
. Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
İçerik Fotogrametrik Üretim 2 Fotogrametri 2 Hava Fotogrametrisi...2 Fotogrametrik Nirengi 3 Ortofoto 4 Fotogrametrik İş Akışı 5 Sayısal Hava
 İçerik Fotogrametrik Üretim 2 Fotogrametri 2 Hava Fotogrametrisi...2 Fotogrametrik Nirengi 3 Ortofoto 4 Fotogrametrik İş Akışı 5 Sayısal Hava Kameralarının Sağlayacağı Faydalar.7 Pramit Oluşturma.10 Kolon
İçerik Fotogrametrik Üretim 2 Fotogrametri 2 Hava Fotogrametrisi...2 Fotogrametrik Nirengi 3 Ortofoto 4 Fotogrametrik İş Akışı 5 Sayısal Hava Kameralarının Sağlayacağı Faydalar.7 Pramit Oluşturma.10 Kolon
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme. Yrd. Doç. Dr. Aycan M. MARANGOZ
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
TOPOĞRAFYA. Ölçme Bilgisinin Konusu
 TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
YILDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT FAKÜLTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ
 YILDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT FAKÜLTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ARAZİ ÇALIŞMASI - 2 UYGULAMA PLANI İSTANBUL, 2018 Dersin Tanıtımı 1) Ders fotogrametri Kamu Ölçmeleri ve Kartografya Anabilim dalları
YILDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT FAKÜLTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ARAZİ ÇALIŞMASI - 2 UYGULAMA PLANI İSTANBUL, 2018 Dersin Tanıtımı 1) Ders fotogrametri Kamu Ölçmeleri ve Kartografya Anabilim dalları
Uygulamada Gauss-Kruger Projeksiyonu
 JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER
 BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
YILDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT FAKÜLTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ FOTOGRAMETRİ ANABİLİM DALI
 YILDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT FAKÜLTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ FOTOGRAMETRİ ANABİLİM DALI Hazırlayan Müh. Uzm. İbrahim ÇETİN İst,2012 PHOTOMOD YAZILIMI İLE 3 BOYUTLU DEĞERLENDİRME 1. Proje Dosyası
YILDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT FAKÜLTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ FOTOGRAMETRİ ANABİLİM DALI Hazırlayan Müh. Uzm. İbrahim ÇETİN İst,2012 PHOTOMOD YAZILIMI İLE 3 BOYUTLU DEĞERLENDİRME 1. Proje Dosyası
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ
 ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3351 3 4 3 0 0 DERSİN
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3351 3 4 3 0 0 DERSİN
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
HAVA FOTOĞRAFLARININ YÖNELTİLMESİNDE GPS/IMU İLE DOĞRUDAN COĞRAFİ KONUMLANDIRMA DOĞRULUĞUNUN ARAŞTIRILMASI
 HAVA FOTOĞRAFLARININ YÖNELTİLMESİNDE GPS/IMU İLE DOĞRUDAN COĞRAFİ KONUMLANDIRMA DOĞRULUĞUNUN ARAŞTIRILMASI A.C. Kiracı, A.Yılmaz, O. Eker, H.H.Maraş L.İşcan Harita Genel Komutanlığı, Fotogrametri Dairesi,
HAVA FOTOĞRAFLARININ YÖNELTİLMESİNDE GPS/IMU İLE DOĞRUDAN COĞRAFİ KONUMLANDIRMA DOĞRULUĞUNUN ARAŞTIRILMASI A.C. Kiracı, A.Yılmaz, O. Eker, H.H.Maraş L.İşcan Harita Genel Komutanlığı, Fotogrametri Dairesi,
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
KUTUPSAL KOORDİNATLAR
 KUTUPSAL KOORDİNATLAR Geometride, bir noktanın konumunu belirtmek için değişik yöntemler uygulanır. Örnek olarak çok kullanılan Kartezyen (Dik ) Koordinat sistemini anımsatarak çalışmamıza başlayalım.
KUTUPSAL KOORDİNATLAR Geometride, bir noktanın konumunu belirtmek için değişik yöntemler uygulanır. Örnek olarak çok kullanılan Kartezyen (Dik ) Koordinat sistemini anımsatarak çalışmamıza başlayalım.
Bilgisayarla Fotogrametrik Görme
 Bilgisayarla Fotogrametrik Görme Dijital Görüntü ve Özellikleri Yrd. Doç. Dr. Mustafa DİHKAN 1 Dijital görüntü ve özellikleri Siyah-beyaz resimler için değer elemanları 0-255 arasındadır. 256 farklı durum
Bilgisayarla Fotogrametrik Görme Dijital Görüntü ve Özellikleri Yrd. Doç. Dr. Mustafa DİHKAN 1 Dijital görüntü ve özellikleri Siyah-beyaz resimler için değer elemanları 0-255 arasındadır. 256 farklı durum
mercek ince kenarlı (yakınsak) mercekler kalın kenarlı (ıraksak) mercekle odak noktası odak uzaklığı
 MERCEKLER Mercekler mikroskoptan gözlüğe, kameralardan teleskoplara kadar pek çok optik araçta kullanılır. Mercekler genelde camdan ya da sert plastikten yapılan en az bir yüzü küresel araçlardır. Cisimlerin
MERCEKLER Mercekler mikroskoptan gözlüğe, kameralardan teleskoplara kadar pek çok optik araçta kullanılır. Mercekler genelde camdan ya da sert plastikten yapılan en az bir yüzü küresel araçlardır. Cisimlerin
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
Harita Projeksiyonları
 Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
Uzaktan Alg ılamaya Giriş Ünite 6 - Görüntü O t r orektifikasyonu
 Uzaktan Algılamaya Giriş Ünite 6 - Görüntü Ortorektifikasyonu Ortorektifikasyon Uydu veya uçak platformları ile elde edilen görüntü verisi günümüzde haritacılık ve CBS için temel girdi kaynağını oluşturmaktadır.
Uzaktan Algılamaya Giriş Ünite 6 - Görüntü Ortorektifikasyonu Ortorektifikasyon Uydu veya uçak platformları ile elde edilen görüntü verisi günümüzde haritacılık ve CBS için temel girdi kaynağını oluşturmaktadır.
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme
 Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar
 Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.
![T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir. T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.](/thumbs/55/35591809.jpg) * = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
* = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
lerin tesirinden hesaplanacak şakul sapması Ölçülen şakul sapmasından çıkartılır :
 lerin tesirinden hesaplanacak şakul sapması Ölçülen şakul sapmasından çıkartılır : 3 (8) formülüne göre elde edilen indirgenmiş A% şakul sapması Md bölümden oluşur : Formülde kıyas düzleminin altındaki
lerin tesirinden hesaplanacak şakul sapması Ölçülen şakul sapmasından çıkartılır : 3 (8) formülüne göre elde edilen indirgenmiş A% şakul sapması Md bölümden oluşur : Formülde kıyas düzleminin altındaki
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI
 BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
Uzay Geriden Kestirme
 Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
7. BÖLÜM İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI .= 1 1 + + Genel: Vektörler bölümünde vektörel iç çarpım;
 İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
FOTOGRAMETRİ DAİRESİ BAŞKANLIĞI FAALIYETLERI
 FOTOGRAMETRİ DAİRESİ BAŞKANLIĞI FAALIYETLERI Fotg.D.Bşk.lığı, yurt içi ve yurt dışı harita üretimi için uydu görüntüsü ve hava fotoğraflarından fotogrametrik yöntemlerle topoğrafya ve insan yapısı detayları
FOTOGRAMETRİ DAİRESİ BAŞKANLIĞI FAALIYETLERI Fotg.D.Bşk.lığı, yurt içi ve yurt dışı harita üretimi için uydu görüntüsü ve hava fotoğraflarından fotogrametrik yöntemlerle topoğrafya ve insan yapısı detayları
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET
 GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
ÇATI MAKASINA GELEN YÜKLER
 ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
GÜZ DÖNEMİ ARASINAV SORULARI. 1. Sayısal çözümleme ve fonksiyonu tanımlayarak kullanıldığı alanları kısaca açıklayınız?
 MAK 05 SAYISAL ÇÖZÜMLEME S Ü L E Y M A N D E M Ġ R E L Ü N Ġ V E R S Ġ T E S Ġ M Ü H E N D Ġ S L Ġ K F A K Ü L T E S Ġ M A K Ġ N A M Ü H E N D Ġ S L Ġ Ğ Ġ B Ö L Ü M Ü I. öğretim II. öğretim A şubesi B
MAK 05 SAYISAL ÇÖZÜMLEME S Ü L E Y M A N D E M Ġ R E L Ü N Ġ V E R S Ġ T E S Ġ M Ü H E N D Ġ S L Ġ K F A K Ü L T E S Ġ M A K Ġ N A M Ü H E N D Ġ S L Ġ Ğ Ġ B Ö L Ü M Ü I. öğretim II. öğretim A şubesi B
Harita Üretimi Dijital Fotogrametri
 FOTOGRAMETRİ DERSİ SLAYTLARI 5 Harita Üretimi Dijital Fotogrametri 2008 2009 BAHAR DÖNEMİ Prof. Dr. Fatmagül BATUK YTÜ 1 Harita Üretimi Haritalar 2 1 Proje bir amacı gerçekleştirmeğe yönelik, başlangıcı
FOTOGRAMETRİ DERSİ SLAYTLARI 5 Harita Üretimi Dijital Fotogrametri 2008 2009 BAHAR DÖNEMİ Prof. Dr. Fatmagül BATUK YTÜ 1 Harita Üretimi Haritalar 2 1 Proje bir amacı gerçekleştirmeğe yönelik, başlangıcı
Dijital (Sayısal) Fotogrametri
 Dijital (Sayısal) Fotogrametri Dijital fotogrametri, cisimlere ait iki boyutlu görüntü ortamından üç boyutlu bilgi sağlayan, sayısal resim veya görüntü ile çalışan fotogrametri bilimidir. Girdi olarak
Dijital (Sayısal) Fotogrametri Dijital fotogrametri, cisimlere ait iki boyutlu görüntü ortamından üç boyutlu bilgi sağlayan, sayısal resim veya görüntü ile çalışan fotogrametri bilimidir. Girdi olarak
YÜKSEKLİK ÖLÇÜMÜ. Ölçme Bilgisi Ders Notları
 YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
1- AYNALI STEREOSKOP UYGULAMASI. X (Uçuş Doğrultusu) H1 H1. 1. resim (sol) 2. resim (sağ) KARTON ÜZERİNDEKİ İŞLEMLER D 1 D 2
 - YNLI STEREOSKO UYGULMSI KRTON ÜZERİNDEKİ İŞLEMLER D D 70 cm 6 cm X (Uçuş Doğrultusu) 00 cm Yukardaki bilgiler karton üzerine çizilir. Kartonun sağ alt köşesine çalışan kişilerin no-adı soadı, resim numaraları,
- YNLI STEREOSKO UYGULMSI KRTON ÜZERİNDEKİ İŞLEMLER D D 70 cm 6 cm X (Uçuş Doğrultusu) 00 cm Yukardaki bilgiler karton üzerine çizilir. Kartonun sağ alt köşesine çalışan kişilerin no-adı soadı, resim numaraları,
DİK KOORDİNAT SİSTEMİ VE
 Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN
 Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
Soru 1: Şekil-1 de görülen düzlem gerilme hali için: b) elemanın saat yönünde 30 0 döndürülmesi ile elde edilen yeni durum için elemana tesir
 Soru 1: Şekil-1 de görülen düzlem gerilme hali için: a) elemanın saat yönünde 30 0 döndürülmesi ile elde edilen yeni durum için elemana tesir eden gerilme bileşenlerini, gerilme dönüşüm denklemlerini kullanarak
Soru 1: Şekil-1 de görülen düzlem gerilme hali için: a) elemanın saat yönünde 30 0 döndürülmesi ile elde edilen yeni durum için elemana tesir eden gerilme bileşenlerini, gerilme dönüşüm denklemlerini kullanarak
Jeodezide Yaklaşım Yöntemleri: Enterpolasyon ve Kollokasyon
 Jeodezide Yöntemleri: ve Lisansüstü Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Fen Bilimleri Enstitüsü e-posta: austun@selcuk.edu.tr Konya, 2007 A. Üstün yöntemleri 1 / 28 Bir soruyu ya
Jeodezide Yöntemleri: ve Lisansüstü Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Fen Bilimleri Enstitüsü e-posta: austun@selcuk.edu.tr Konya, 2007 A. Üstün yöntemleri 1 / 28 Bir soruyu ya
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Mohr Dairesi Düzlem Gerilme
 Mohr Dairesi Düzlem Gerilme Bu bölümde düzlem gerilme dönüşüm denklemlerinin grafiksel bir yöntem ile nasıl uygulanabildiğini göstereceğiz. Böylece dönüşüm denklemlerinin kullanılması daha kolay olacak.
Mohr Dairesi Düzlem Gerilme Bu bölümde düzlem gerilme dönüşüm denklemlerinin grafiksel bir yöntem ile nasıl uygulanabildiğini göstereceğiz. Böylece dönüşüm denklemlerinin kullanılması daha kolay olacak.
Elastisite Teorisi Düzlem Problemleri için Sonuç 1
 Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
İNS1101 MÜHENDİSLİK ÇİZİMİ. Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018
 İNS1101 MÜHENDİSLİK ÇİZİMİ Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 TEKNİK RESİM Teknik resim, teknik elemanların üretim yapabilmeleri için anlatmak istedikleri teknik özelliklerin biçim ve
İNS1101 MÜHENDİSLİK ÇİZİMİ Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 TEKNİK RESİM Teknik resim, teknik elemanların üretim yapabilmeleri için anlatmak istedikleri teknik özelliklerin biçim ve
BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI
 tasarım BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI Nihat GEMALMAYAN, Hüseyin ĐNCEÇAM Gazi Üniversitesi, Makina Mühendisliği Bölümü GĐRĐŞ Đlk bisikletlerde fren sistemi
tasarım BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI Nihat GEMALMAYAN, Hüseyin ĐNCEÇAM Gazi Üniversitesi, Makina Mühendisliği Bölümü GĐRĐŞ Đlk bisikletlerde fren sistemi
YOĞUN GÖRÜNTÜ EŞLEME ALGORİTMALARI İLE ÜRETİLEN YÜKSEK ÇÖZÜNÜRLÜKLÜ SAYISAL YÜZEY MODELİ ÜRETİMİNDE KALİTE DEĞERLENDİRME VE DOĞRULUK ANALİZİ
 YOĞUN GÖRÜNTÜ EŞLEME ALGORİTMALARI İLE ÜRETİLEN YÜKSEK ÇÖZÜNÜRLÜKLÜ SAYISAL YÜZEY MODELİ ÜRETİMİNDE KALİTE DEĞERLENDİRME VE DOĞRULUK ANALİZİ Naci YASTIKLI a, Hüseyin BAYRAKTAR b a Yıldız Teknik Üniversitesi,
YOĞUN GÖRÜNTÜ EŞLEME ALGORİTMALARI İLE ÜRETİLEN YÜKSEK ÇÖZÜNÜRLÜKLÜ SAYISAL YÜZEY MODELİ ÜRETİMİNDE KALİTE DEĞERLENDİRME VE DOĞRULUK ANALİZİ Naci YASTIKLI a, Hüseyin BAYRAKTAR b a Yıldız Teknik Üniversitesi,
Dijital Fotogrametri
 Dijital Fotogrametri 2016-2017, Bahar YY Fevzi Karslı (Prof. Dr.) Harita Mühendisliği Bölümü Mühendislik Fakültesi KTÜ 20 Mart 2017 Pazartesi Ders Planı ve İçeriği 1. Hafta Giriş, dersin kapsamı, kavramlar,
Dijital Fotogrametri 2016-2017, Bahar YY Fevzi Karslı (Prof. Dr.) Harita Mühendisliği Bölümü Mühendislik Fakültesi KTÜ 20 Mart 2017 Pazartesi Ders Planı ve İçeriği 1. Hafta Giriş, dersin kapsamı, kavramlar,
Hava Fotogrametrisi ve Jeodezik Yöntemler ile Sayısal Yükseklik Modeli Üretimi: Erzurum Aksu Köyü Örneği
 TMMOB Harita ve Kadastro Mühendisleri Odası, 16. Türkiye Harita Bilimsel ve Teknik Kurultayı, 3-6 Mayıs 2017, Ankara. Hava Fotogrametrisi ve Jeodezik Yöntemler ile Sayısal Yükseklik Modeli Üretimi: Erzurum
TMMOB Harita ve Kadastro Mühendisleri Odası, 16. Türkiye Harita Bilimsel ve Teknik Kurultayı, 3-6 Mayıs 2017, Ankara. Hava Fotogrametrisi ve Jeodezik Yöntemler ile Sayısal Yükseklik Modeli Üretimi: Erzurum
SAYISAL İŞARET İŞLEME LABORATUARI LAB 5: SONSUZ DÜRTÜ YANITLI (IIR) FİLTRELER
 SAYISAL İŞARET İŞLEME LABORATUARI LAB 5: SONSUZ DÜRTÜ YANITLI (IIR) FİLTRELER Bu bölümde aşağıdaki başlıklar ele alınacaktır. Sonsuz dürtü yanıtlı filtre yapıları: Direkt Şekil-1, Direkt Şekil-II, Kaskad
SAYISAL İŞARET İŞLEME LABORATUARI LAB 5: SONSUZ DÜRTÜ YANITLI (IIR) FİLTRELER Bu bölümde aşağıdaki başlıklar ele alınacaktır. Sonsuz dürtü yanıtlı filtre yapıları: Direkt Şekil-1, Direkt Şekil-II, Kaskad
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
DİJİTAL FOTOGRAMETRİK HARİTA ÜRETİMİ VE TAPU VE KADASTRO ÖRNEĞİ
 Selçuk Üniversitesi Jeodezi ve Fotogrametri Mühendisliği Öğretiminde 30. Yõl Sempozyumu,16-18 Ekim 2002, Konya SUNULMUŞ BİLDİRİ DİJİTAL FOTOGRAMETRİK HARİTA ÜRETİMİ VE TAPU VE KADASTRO ÖRNEĞİ Orhan ERCAN,
Selçuk Üniversitesi Jeodezi ve Fotogrametri Mühendisliği Öğretiminde 30. Yõl Sempozyumu,16-18 Ekim 2002, Konya SUNULMUŞ BİLDİRİ DİJİTAL FOTOGRAMETRİK HARİTA ÜRETİMİ VE TAPU VE KADASTRO ÖRNEĞİ Orhan ERCAN,
MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl
 İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim alı MÜHENİSLİK ÖLÇMELERİ UYGULAMASI (HRT436) 8. Yarıyıl U L K Kredi 3 ECTS 3 UYGULAMA-5 ELEKTRONİK ALETLERİN KALİBRASYONU Prof.r.Engin
İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim alı MÜHENİSLİK ÖLÇMELERİ UYGULAMASI (HRT436) 8. Yarıyıl U L K Kredi 3 ECTS 3 UYGULAMA-5 ELEKTRONİK ALETLERİN KALİBRASYONU Prof.r.Engin
TORNA TEZGAHINDA KESME KUVVETLERİ ANALİZİ
 İMALAT DALI MAKİNE LABORATUVARI II DERSİ TORNA TEZGAHINDA KESME KUVVETLERİ ANALİZİ DENEY RAPORU HAZIRLAYAN Osman OLUK 1030112411 1.Ö. 1.Grup DENEYİN AMACI Torna tezgahı ile işlemede, iş parçasına istenilen
İMALAT DALI MAKİNE LABORATUVARI II DERSİ TORNA TEZGAHINDA KESME KUVVETLERİ ANALİZİ DENEY RAPORU HAZIRLAYAN Osman OLUK 1030112411 1.Ö. 1.Grup DENEYİN AMACI Torna tezgahı ile işlemede, iş parçasına istenilen
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI
 ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 2018 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 2018 1.ELEKTRONİK TAKEOMETRELERİN
