Tanımlayıcı İstatistikler
|
|
|
- Ayşe Niazi
- 7 yıl önce
- İzleme sayısı:
Transkript
1 Dr. Mehmet AKSARAYLI MERKEZİ EĞİLİM ve DEĞİŞKENLİK ÖLÇÜLERİ Ders / Tanımayıcı İstatstker Yer Öçüer (Merkez Eğm Öçüer) Duyarı Ortaamaar Artmetk ort. Tartıı Artmetk Geometrk ort. Kare ort. Harmonk ort. Duyarı Omayan Ort. Mod Medyan Karter Değşkenk Öçüer Değşm Araığı (Range) Standart sapma Varyans Mutak sapma Değşkenk katsayısı Kart sapma katsayısı Ortaama sapma katsayısı Çarpıkık Öçüer Bowey asmetr öçüsü Pearson asmetr öçüsü Basıkık Öçüer Ders /
2 Tanımayıcı statstk: Br gruba at ber değşkenern değerer hakkında bgy özeteyen öçüter: - Merkez eğm öçüter (dağıımın yer gösteren öçüter) - Yayıma öçüter (dağıımın yaygınık öçüter) -Dağıımın şek öçüter Ders / Dağıımın yer gösteren öçüter (merkez eğm öçüter): - Artmetk ortaama (x, µ): Değerer topamı/denek sayısı. - Ortanca (medyan): Dağıımın orta noktasındak değer - Tepe değer (mod): Dağıımda en çok görüen değer -Çeyrek ve yüzdeker (persent): %5-%50- %75 Smetrk (norma) dağıımda artmetk ortaama, ortanca ve tepe değer brbrne eşttr. Ders /4
3 Dağıımın yaygınık öçüter (yayıma öçüter): -Değer araığı (range, w): En büyük değer en küçük değer - Standart sapma (s, σ): Kesnğ tanımar - Varyans (s, σ ) - Varyasyon katsayısı (Coecent o varaton, CV): Standart sapmanın ortaamaya göre % değşm [CV 00 (s/x)] - Standart hata (s/ n) Ders /5 Adı Semboü Bast verer Grupandırımış Verer Artmetk Ortaama X x Medyan (.kart,.çeyrek) Med x n Sıraı gözemerde orta eeman yada orta eemanarın artmetk ortaamasıdır. Mod Mod En çok tekrar eden değer, en sık rastanan değer veya durum. Formüü Sınıandırımış Verer m L+. med Δ L +. Δ +Δ Kuanım Yer Aks geçer omadıkça yer öçüsüdür. Uç değerern buunduğu gözemerde veya aşırı çarpık dağıımarda yada açık uçu sererde kuanıır. Ortaama sözcüğü en çok tekrar eden durumu ade edyorsa ve çarpıkığın öçümesnde. Ders /6
4 İstatstkte Bazı Teme kavramar Range Değşken Ders /7 İstatstkte Bazı Teme kavramar Artmetk ortaama d Sapma d Ders /8 4
5 Standart sapma: σ Br dz öçümün gösterdğ değşmn en güvenr öçüsüdür. Dağıım azaysa standart sapma büyük, dağıım dar aanda se küçüktür. Ders /9 Bast Verer İçn Beş kşnn yaşarı: 4, 6, 0, 8, 4 x Artmetk Ortaama X ( )/5.4 n Sıraı verer: 8, 0, 4, 4, 6 Mod 4 Medyan4 Ders /0 5
6 Grupandırımış Verer İçn 0 bayanın ayakkabı numaraarı: 5, 8, 6, 6, 7, 6, 8, 5, 9, 7, Grup Frekans x Top 0 67 x X 67/06.7 Medyan 0/5,5. Ver 6,5 Moden yüksek r.oan6 Ders / Sınıandırımış Verer İçn Sınıar m m Σ 0-0 dan az den az dan az dan az den az topam X m 65/ Ders / 6
7 Sınıandırımış Verer İçn Sınıar m m Σ 0-0 dan az den az dan az dan az den az topam 5 65 Medyan sınıından br öncek sınıın kümüat rekansı Med L 5 med Medyan sınıının at sınırı med Medyan sınıının rekansı Sını araığı Ders / M e d y a n S ı n ı ı Sınıandırımış Verer İçn Sınıar m m Σ 0-0 dan az den az dan az dan az den az topam 5 65 Δ Mod L mod +. Δ + Δ M o d S ı n ı ı Mod sınıının at sınırı Mod sınııya br öncek sını r. arasındak ark Mod sınııya br sonrak sını r. arasındak ark Ders /4 7
8 Mod Med A.O Ders /5 Sınıar m m Σ den az dan az den az den az dan az topam X m Med Lmed +. med ÖRNEK Δ Mod L mod +. Δ + Δ Ders /6 8
9 L + 4. Med L KARTİLLER +. L + 4. %5 %5 %5 %5 Ders /7 sınıar Σ 0-0 den az dan az dan az den az L Med L L sınıı sınıı sınıı Ders /8 9
10 Br tencere pazarama rmasına bağı çaışan 50 satış personenn ayık tencere satışarı aşağıdak gbdr. Bu verer kuanarak hstogramı çznz, artmetk ortaama, mod, medyan ve karter hesapayarak yorumayınız. sınıar m Σ m Σ topam r Hstogram x X m Ders /9 r Hstogram x %5 %5 %5 %5 Yorumama: : Gözemern % ten daha küçüktür. : Gözemern %5 6. den daha büyüktür. : Gözemern %50 s 5 ten daha küçük, %50 s 5 ten daha büyüktür Mod4.4 A.O5. Ders /0 0
11 sınıar m Σ m Σ topam L Med L + 6. Ders / sınıar m Σ m Σ topam Med L + 5 Mod Δ 4 L Δ + Δ mod 4.4 Ders /
12 DEĞİŞKENLİK ÖLÇÜLERİ Range - Değşm Araığı (R) : Range, br gözem sersnde en büyük gözem e en küçük gözem arasındak arktır. R X max -X mn R X max -X mn + Sürek verer çn Kesk verer çn Ortaama Mutak Sapma (MAD) : Br gözemn ortaamadan ortaama oarak ne kadar saptığının öçüsüdür. Bast verer çn: MAD Grupandırımış verer çn: MAD x x n x x Ders / Standart Sapma : Verern ortaama etraındak dağıımının br öçüsüdür. Bast verer çn: x x - x (x - x ) x 5 / 5 ( x x) s n Ders /4
13 4 Grupandırımış ve sınıandırımış verer çn standart sapma: x x x ( x x ) ( x x ) Top s ( x x) Ders /5 Varyasyon Katsayısı: Standart sapmanın artmetk ortaamanın kaçta kaçı oduğunu gösterr. C V Örnek: Buca ve Asancak çn ger dağıımıya g verer aşağıdak gbdr: s X X s C v Buca Asancak Yorum: Buca dak ger dağıımı Asancak takne göre daha değşkendr. Ders /6
14 Smetrk Dağıım A.O Med Mod Sağa çarpık dağıım A.O > Med > Mod Soa çarpık dağıım A.O < Med < Mod İk modu smetrk dağıım Modu omayan dağıım Tekdüzen dağıım Ders /7 PEARSON ÇARPIKLIK ÖLÇÜSÜ x mod Sk p veya s ( X med) Sk p s Sk p < --- Az çarpık dağıım Sk p > --- Çarpık dağıım Sk p <0 --- Negat çarpıkık Ders /8 4
Merkezi Eğilim (Yer) Ölçüleri
 Merkez Eğlm (Yer) Ölçüler Ver setn tanımlamak üzere kullanılan ve genellkle tüm elemanları dkkate alarak ver setn özetlemek çn kullanılan ölçülerdr. Ver setndek tüm elemanları temsl edeblecek merkez noktasına
Merkez Eğlm (Yer) Ölçüler Ver setn tanımlamak üzere kullanılan ve genellkle tüm elemanları dkkate alarak ver setn özetlemek çn kullanılan ölçülerdr. Ver setndek tüm elemanları temsl edeblecek merkez noktasına
Tanımlayıcı İstatistikler (Descriptive Statistics) Dr. Musa KILIÇ
 Taımlayıcı İstatstkler (Descrptve Statstcs) Dr. Musa KILIÇ TANIMLAYICI ÖRNEK İSTATİSTİKLERİ YER ÖLÇÜLERİ (Frekas dağılışıı abss eksedek durumuu belrtr.) DEĞİŞİM ÖLÇÜLERİ ( Frekas dağılışıı şekl belrtr.).
Taımlayıcı İstatstkler (Descrptve Statstcs) Dr. Musa KILIÇ TANIMLAYICI ÖRNEK İSTATİSTİKLERİ YER ÖLÇÜLERİ (Frekas dağılışıı abss eksedek durumuu belrtr.) DEĞİŞİM ÖLÇÜLERİ ( Frekas dağılışıı şekl belrtr.).
Tanımlayıcı İstatistikler
 Taımlayıcı İstatstkler Br veya brde azla dağılışı karşılaştırmak ç kullaıla ve ayrıca örek verlerde hareket le rekas dağılışlarıı sayısal olarak özetleye değerlere taımlayıcı statstkler der. Aalzlerde
Taımlayıcı İstatstkler Br veya brde azla dağılışı karşılaştırmak ç kullaıla ve ayrıca örek verlerde hareket le rekas dağılışlarıı sayısal olarak özetleye değerlere taımlayıcı statstkler der. Aalzlerde
Asimetri ve Basıklık Ölçüleri Ortalamalara dayanan (Pearson) Kartillere dayanan (Bowley) Momentlere dayanan asimetri ve basıklık ölçüleri
 Asmetr ve Basıklık Ölçüler Ortalamalara dayanan (Pearson) Kartllere dayanan (Bowley) omentlere dayanan asmetr ve basıklık ölçüler Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr III. Asmetr ve Basıklık
Asmetr ve Basıklık Ölçüler Ortalamalara dayanan (Pearson) Kartllere dayanan (Bowley) omentlere dayanan asmetr ve basıklık ölçüler Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr III. Asmetr ve Basıklık
Elektrik Akımı, Potansiyel Fark ve Direnç Testlerinin Çözümleri
 Elektrk Akımı, Potansyel Fark ve Drenç Testlernn Çözümler 1 Test 1 n Çözümü. 1. Soruda verlen akım-potansyel farkı grafğnn eğmnn ters drenc verr. 8 X 5 8 8 Z Ohm kanunu bağıntısıyla verlr. Bu bağın- k
Elektrk Akımı, Potansyel Fark ve Drenç Testlernn Çözümler 1 Test 1 n Çözümü. 1. Soruda verlen akım-potansyel farkı grafğnn eğmnn ters drenc verr. 8 X 5 8 8 Z Ohm kanunu bağıntısıyla verlr. Bu bağın- k
10. SINIF KONU ANLATIMLI. 2. ÜNİTE: ELEKTRİK VE MANYETİZMA 2. Konu ELEKTRİK AKIMI, POTANSİYEL FARK VE DİRENÇ ETKİNLİK ve TEST ÇÖZÜMLERİ
 10. SINIF ONU NTII. ÜNİTE: EETİ E NYETİZ. onu EETİ II, POTNSİYE F E DİENÇ ETİNİ ve TEST ÇÖZÜEİ Ünte Elektrk ve anyetzma 1.. Ünte. onu (Elektrk kımı) nın Çözümler ampul 3. Şekl yenden aşağıdak gb çzeblrz.
10. SINIF ONU NTII. ÜNİTE: EETİ E NYETİZ. onu EETİ II, POTNSİYE F E DİENÇ ETİNİ ve TEST ÇÖZÜEİ Ünte Elektrk ve anyetzma 1.. Ünte. onu (Elektrk kımı) nın Çözümler ampul 3. Şekl yenden aşağıdak gb çzeblrz.
= k. Aritmetik Ortalama. Tanımlayıcı İstatistikler TANIMLAYICI İSTATİSTİKLER. Sınıflanmış Seriler İçin Aritmetik Ortalama
 TANIMLAYICI İSTATİSTİKLER Taımlayıcı İstatstkler MERKEZİ EĞİLİM ÖLÇÜLERİ Dr. Mehmet AKSARAYLI D.E.Ü. İ.İ.B.F..B.F. EKONOMETRİ BÖLÜMÜ mehmet.aksarayl aksarayl@deu.edu.tr Yer Ölçüler (Merkez Eğlm Ölçüler)
TANIMLAYICI İSTATİSTİKLER Taımlayıcı İstatstkler MERKEZİ EĞİLİM ÖLÇÜLERİ Dr. Mehmet AKSARAYLI D.E.Ü. İ.İ.B.F..B.F. EKONOMETRİ BÖLÜMÜ mehmet.aksarayl aksarayl@deu.edu.tr Yer Ölçüler (Merkez Eğlm Ölçüler)
MERKEZİ EĞİLİM ÖLÇÜLERİ
 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlee ver düzeleerek çzelgelerle, graklerle suulması çoğu kez yeterl olmaz. Geel durumu yasıtacak br takım ölçülere gereksm vardır. Bu ölçüler verler yalızca özlü br bçmde belrtmekle
MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlee ver düzeleerek çzelgelerle, graklerle suulması çoğu kez yeterl olmaz. Geel durumu yasıtacak br takım ölçülere gereksm vardır. Bu ölçüler verler yalızca özlü br bçmde belrtmekle
İki veri setinin yapısının karşılaştırılması
 İk ver set yapısıı karşılaştırılması Dağılım: 6,6,6 Ortalama: 6 Medya: 6 Mod: 6 td. apma: 0 Dağılım: 0,6,1 Ortalama: 6 Medya: 6 Mod: çoklu mod td: apma: 6 Amaç: Görüe Ötese Bakablmek Verler değşkelk durumuu
İk ver set yapısıı karşılaştırılması Dağılım: 6,6,6 Ortalama: 6 Medya: 6 Mod: 6 td. apma: 0 Dağılım: 0,6,1 Ortalama: 6 Medya: 6 Mod: çoklu mod td: apma: 6 Amaç: Görüe Ötese Bakablmek Verler değşkelk durumuu
Sıklık Tabloları ve Tek Değişkenli Grafikler
 Sıklık Tabloları ve Tek Değşkenl Grafkler Sıklık Tablosu Ver dzsnde yer alan değerlern tekrarlama sayılarını çeren tabloya sıklık tablosu denr. Sıklık Tabloları tek değşken çn marjnal tablo olarak adlandırılır.
Sıklık Tabloları ve Tek Değşkenl Grafkler Sıklık Tablosu Ver dzsnde yer alan değerlern tekrarlama sayılarını çeren tabloya sıklık tablosu denr. Sıklık Tabloları tek değşken çn marjnal tablo olarak adlandırılır.
SAYISAL ANALİZ. Doç.Dr. Cüneyt BAYILMIŞ. Sayısal Analiz. Doç.Dr. Cüneyt BAYILMIŞ
 SAYISAL ANALİZ Doç.Dr. Cüneyt BAYILMIŞ Doç.Dr. Cüneyt BAYILMIŞ Sayısal Analz SAYISAL ANALİZ SAYISAL TÜREV Numercal Derentaton Doç.Dr. Cüneyt BAYILMIŞ Sayısal Analz İÇİNDEKİLER Sayısal Türev Ger Farklar
SAYISAL ANALİZ Doç.Dr. Cüneyt BAYILMIŞ Doç.Dr. Cüneyt BAYILMIŞ Sayısal Analz SAYISAL ANALİZ SAYISAL TÜREV Numercal Derentaton Doç.Dr. Cüneyt BAYILMIŞ Sayısal Analz İÇİNDEKİLER Sayısal Türev Ger Farklar
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
http://acikogretimx.com
 09 S 0- İstatistik sorularının cevaplanmasında gerekli olabilecek tablolar ve ormüller bu kitapçığın sonunda verilmiştir.. şağıdakilerden hangisi istatistik birimi değildir? ) Doğum B) ile C) Traik kazası
09 S 0- İstatistik sorularının cevaplanmasında gerekli olabilecek tablolar ve ormüller bu kitapçığın sonunda verilmiştir.. şağıdakilerden hangisi istatistik birimi değildir? ) Doğum B) ile C) Traik kazası
Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder.
 Yayılma Ölçütleri Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder. Bir başka ifade ile, bir veri setinin,
Yayılma Ölçütleri Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder. Bir başka ifade ile, bir veri setinin,
YER ÖLÇÜLERİ. Yer ölçüleri, verilerin merkezini veya yığılma noktasını belirleyen istatistiklerdir.
 YER ÖLÇÜLERİ Yer ölçüler, verler merkez veya yığılma oktasıı belrleye statstklerdr. Grafkler bze verler yığılma oktaları hakkıda ö blg vermede yardımcı olurlar. Acak bu değerler gerçek değerler değldr,
YER ÖLÇÜLERİ Yer ölçüler, verler merkez veya yığılma oktasıı belrleye statstklerdr. Grafkler bze verler yığılma oktaları hakkıda ö blg vermede yardımcı olurlar. Acak bu değerler gerçek değerler değldr,
Temel İstatistik. Y.Doç.Dr. İbrahim Turan Mart Tanımlayıcı İstatistik. Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri
 Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
İstatistik Yöntemleri ve Hipotez Testleri
 Sağlık Araştırmalarında Kullanılan Temel İstatistik Yöntemleri ve Hipotez Testleri Yrd. Doç. Dr. Emre ATILGAN BİYOİSTATİSTİK İstatistiğin biyoloji, tıp ve diğer sağlık bilimlerinde kullanımı biyoistatistik
Sağlık Araştırmalarında Kullanılan Temel İstatistik Yöntemleri ve Hipotez Testleri Yrd. Doç. Dr. Emre ATILGAN BİYOİSTATİSTİK İstatistiğin biyoloji, tıp ve diğer sağlık bilimlerinde kullanımı biyoistatistik
2013 SBS (ORTAÖĞRETİME GEÇİŞTE TEK SINAV YENİ SİSTEM)
 2013 SBS (ORTAÖĞRETİME GEÇİŞTE TEK SINAV YENİ SİSTEM) (Şubat 2011-2641 Miî Eğitim Bakanığı Tebiğer Dergisi 113 Değişikikeri ie) 2012-2013 öğretim yıından itibaren 8. sınıfta uyguanacak oan yeni sistemde
2013 SBS (ORTAÖĞRETİME GEÇİŞTE TEK SINAV YENİ SİSTEM) (Şubat 2011-2641 Miî Eğitim Bakanığı Tebiğer Dergisi 113 Değişikikeri ie) 2012-2013 öğretim yıından itibaren 8. sınıfta uyguanacak oan yeni sistemde
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK. Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005
 KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
KOMBİNASYON - PERMÜTASYON Test -1
 KOMİNSYON - PERMÜTSYON Test -. kişi arka arkaya sıralanacaktır. u kişiler kaç farklı sıra oluşturabilir?. kişilik bir sıraya, öğrenci kaç farklı dizilişte yan yana oturabilir?. farklı çatal, farklı kaşık
KOMİNSYON - PERMÜTSYON Test -. kişi arka arkaya sıralanacaktır. u kişiler kaç farklı sıra oluşturabilir?. kişilik bir sıraya, öğrenci kaç farklı dizilişte yan yana oturabilir?. farklı çatal, farklı kaşık
Kütle Merkezi ve Merkezler. Konular: Kütle/Ağırlık merkezleri Merkez kavramı Merkez hesabına yönelik yöntemler
 Kütle Merkez ve Merkezler Konular: Kütle/ğırlık merkezler Merkez kavramı Merkez hesabına önelk öntemler ğırlıklı Ortalama Merkez kavramının brçok ugulama alanı vardır. Öncelkle ağırlıklı ortalama kavramına
Kütle Merkez ve Merkezler Konular: Kütle/ğırlık merkezler Merkez kavramı Merkez hesabına önelk öntemler ğırlıklı Ortalama Merkez kavramının brçok ugulama alanı vardır. Öncelkle ağırlıklı ortalama kavramına
Korelasyon ve Regresyon
 Korelasyon ve Regresyon 1 Korelasyon Analz İk değşken arasında lşk olup olmadığını belrlemek çn yapılan analze korelasyon analz denr. Korelasyon; doğrusal yada doğrusal olmayan dye kye ayrılır. Korelasyon
Korelasyon ve Regresyon 1 Korelasyon Analz İk değşken arasında lşk olup olmadığını belrlemek çn yapılan analze korelasyon analz denr. Korelasyon; doğrusal yada doğrusal olmayan dye kye ayrılır. Korelasyon
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI. Nokta Grafikleri. Ders 2 Minitab da Grafiksel Analiz-II. Nokta Grafikleri İçin Koşullar
 ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Nokta Grafikleri Nokta grafikleri örnek veri dağılımlarını değerlendirmek ve karşılaştırmak için kullanılır. Bir nokta grafiği örneklem verilerini gruplandırır
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Nokta Grafikleri Nokta grafikleri örnek veri dağılımlarını değerlendirmek ve karşılaştırmak için kullanılır. Bir nokta grafiği örneklem verilerini gruplandırır
İSTATİSTİKSEL KALİTE KONTROLDE KULLANILAN TEMEL İSTATİSTİKSEL ÖLÇÜLER (MERKEZİ EĞİLİM VE DAĞILIM ÖLÇÜLERİ)
 İTATİTİKEL KALİTE KOTROLDE KULLAILA TEMEL İTATİTİKEL ÖLÇÜLER (MERKEZİ EĞİLİM VE DAĞILIM ÖLÇÜLERİ) Kalite Mühendisliği kapsamında İstatistik Proses Kontrolde (İPK) kullanılan temel istatistik ölçüler ve
İTATİTİKEL KALİTE KOTROLDE KULLAILA TEMEL İTATİTİKEL ÖLÇÜLER (MERKEZİ EĞİLİM VE DAĞILIM ÖLÇÜLERİ) Kalite Mühendisliği kapsamında İstatistik Proses Kontrolde (İPK) kullanılan temel istatistik ölçüler ve
İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği
 İSTATİSTİK E GİRİŞ TEMEL KAVRAMLAR İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği Elemanlarıl AMAÇ İstatistiğe
İSTATİSTİK E GİRİŞ TEMEL KAVRAMLAR İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği Elemanlarıl AMAÇ İstatistiğe
Mühendislikte İstatistik Yöntemler
 .0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
.0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
GÜÇLENDİRME PERDELERİNDE BOŞLUKLARIN KAPASİTEYE OLAN ETKİSİ
 2. Türkiye Deprem Müendisiği ve Sismooji Konferansı 25-27 Eyü 213 MKÜ HATAY GÜÇLENDİRME PERDELERİNDE BOŞLUKLARIN KAPASİTEYE OLAN ETKİSİ ÖZET: K. Pençereci 1, S. Yıdırım 1, Y.İ. Tonguç 1 1 İnş. Yük. Mü.,Promer
2. Türkiye Deprem Müendisiği ve Sismooji Konferansı 25-27 Eyü 213 MKÜ HATAY GÜÇLENDİRME PERDELERİNDE BOŞLUKLARIN KAPASİTEYE OLAN ETKİSİ ÖZET: K. Pençereci 1, S. Yıdırım 1, Y.İ. Tonguç 1 1 İnş. Yük. Mü.,Promer
6.6. Korelasyon Analizi. : Kitle korelasyon katsayısı
 6.6. Korelasyon Analizi : Kitle korelasyon katsayısı İki ya da daha çok değişken arasındaki ilişkiyi gösterir. Korelasyon çözümlemesinin amacı değişkenler arasındaki ilişkinin derecesini ve yönünü belirlemektir.
6.6. Korelasyon Analizi : Kitle korelasyon katsayısı İki ya da daha çok değişken arasındaki ilişkiyi gösterir. Korelasyon çözümlemesinin amacı değişkenler arasındaki ilişkinin derecesini ve yönünü belirlemektir.
Editörler Yrd.Doç.Dr.Aysen Şimşek Kandemir &Yrd.Doç.Dr.Tahir Benli İSTATİSTİK
 Editörler Yrd.Doç.Dr.Aysen Şimşek Kandemir &Yrd.Doç.Dr.Tahir Benli İSTATİSTİK Yazarlar Yrd.Doç.Dr.Nizamettin Erbaş Yrd.Doç.Dr.Tuğba Altıntaş Dr.Yeliz Sevimli Saitoğlu A. Zehra Çelenli Başaran Azize Sağır
Editörler Yrd.Doç.Dr.Aysen Şimşek Kandemir &Yrd.Doç.Dr.Tahir Benli İSTATİSTİK Yazarlar Yrd.Doç.Dr.Nizamettin Erbaş Yrd.Doç.Dr.Tuğba Altıntaş Dr.Yeliz Sevimli Saitoğlu A. Zehra Çelenli Başaran Azize Sağır
Hipotez Testinin Temelleri
 Hipotez Testleri Hipotez Testinin Temelleri Tanımlar: Hipotez teori, önerme yada birinin araştırdığı bir iddiadır. Boş Hipotez, H 0 popülasyon parametresi ile ilgili şu anda kabul edilen değeri tanımlamaktadır.
Hipotez Testleri Hipotez Testinin Temelleri Tanımlar: Hipotez teori, önerme yada birinin araştırdığı bir iddiadır. Boş Hipotez, H 0 popülasyon parametresi ile ilgili şu anda kabul edilen değeri tanımlamaktadır.
Alsancakıizmir/TÜRKiYE Tel :+90(232)464 30 40 (PBX) Fax:+90(232)464 39 19. Web site : http://www.hlbsaygin.com.lre-posta:mailbox@hlbsaygin.com.
 ID!B Saygın Yemini Mai Müşavirik ve Bağımsız Denetim A.Ş. Rapor N : SYMM 116/1795-184 BÜYÜME AMAÇLI HİsSE SENEDİ EMEKLİLİK YATIRIM FONU'NUN YATIRIM PERFORMANSI KONUSUNDA KAMUYA AÇIKLANAN BİLGİLERE İLİşKİN
ID!B Saygın Yemini Mai Müşavirik ve Bağımsız Denetim A.Ş. Rapor N : SYMM 116/1795-184 BÜYÜME AMAÇLI HİsSE SENEDİ EMEKLİLİK YATIRIM FONU'NUN YATIRIM PERFORMANSI KONUSUNDA KAMUYA AÇIKLANAN BİLGİLERE İLİşKİN
10. ÜNİTE DİRENÇ BAĞLANTILARI VE KİRCHOFF KANUNLARI
 10. ÜNİTE DİRENÇ BAĞLANTILARI VE KİRCHOFF KANUNLARI KONULAR 1. SERİ DEVRE ÖZELLİKLERİ 2. SERİ BAĞLAMA, KİRŞOFUN GERİLİMLER KANUNU 3. PARALEL DEVRE ÖZELLİKLERİ 4. PARALEL BAĞLAMA, KİRŞOF UN AKIMLAR KANUNU
10. ÜNİTE DİRENÇ BAĞLANTILARI VE KİRCHOFF KANUNLARI KONULAR 1. SERİ DEVRE ÖZELLİKLERİ 2. SERİ BAĞLAMA, KİRŞOFUN GERİLİMLER KANUNU 3. PARALEL DEVRE ÖZELLİKLERİ 4. PARALEL BAĞLAMA, KİRŞOF UN AKIMLAR KANUNU
Tanımlayıcı İstatistikler
 TANIMLAYICI İSTATİSTİKLER MERKEZİ EĞİLİM ÖLÇÜLERİ Dr. Mehmet AKSARAYLI D.E.Ü. İ.İ.B.F. EKONOMETRİ BÖLÜMÜ mehmet.aksarayl@deu.edu.tr Taımlayıcı İstatstkler Yer Ölçüler (Merkez Eğlm Ölçüler) Duyarlı Ortalamalar
TANIMLAYICI İSTATİSTİKLER MERKEZİ EĞİLİM ÖLÇÜLERİ Dr. Mehmet AKSARAYLI D.E.Ü. İ.İ.B.F. EKONOMETRİ BÖLÜMÜ mehmet.aksarayl@deu.edu.tr Taımlayıcı İstatstkler Yer Ölçüler (Merkez Eğlm Ölçüler) Duyarlı Ortalamalar
Kİ-KARE TESTLERİ. şeklinde karesi alındığında, Z i. değerlerinin dağılımı ki-kare dağılımına dönüşür.
 Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk
Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk
Kİ KARE ANALİZİ. Doç. Dr. Mehmet AKSARAYLI Ki-Kare Analizleri
 Kİ KAR ANALİZİ 1 Doç. Dr. Mehmet AKSARAYLI www.mehmetaksarayl K-Kare Analzler OLAY 1: Genelde br statstk sınıfında, öğrenclern %60 ının devamlı, %30 unun bazen, %10 unun se çok az derse geldkler düşünülmektedr.
Kİ KAR ANALİZİ 1 Doç. Dr. Mehmet AKSARAYLI www.mehmetaksarayl K-Kare Analzler OLAY 1: Genelde br statstk sınıfında, öğrenclern %60 ının devamlı, %30 unun bazen, %10 unun se çok az derse geldkler düşünülmektedr.
Alıştırma Toleransı -TERMİNOLOJİ
 Alıştırma Toleransı -TERMİNOLOJİ Mil: Dış şekli belirtir. Silindirik olmayan şekilleri de kapsar. Normal Mil (Esas Mil): Bir alıştırma ş sisteminde esas olark seçilen mil. Delik: İç şekli belirtir. Silindirik
Alıştırma Toleransı -TERMİNOLOJİ Mil: Dış şekli belirtir. Silindirik olmayan şekilleri de kapsar. Normal Mil (Esas Mil): Bir alıştırma ş sisteminde esas olark seçilen mil. Delik: İç şekli belirtir. Silindirik
Örnek 2.1: Tablo 1.1 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 BÖLÜM 2. MERKEZİ EĞİLİM ve DAĞILIM ÖLÇÜLERİ Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
BÖLÜM 2. MERKEZİ EĞİLİM ve DAĞILIM ÖLÇÜLERİ Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
BİREYSELLEŞTİRİLMİŞ EĞİTİM PROGRAMI KISA DÖNEMLİ AMAÇLAR (ünite-konu amaçları)
 UZUN DÖNEMLİ AMAÇLAR (yıl sonunda) RİTMİK SAYMALAR BİREYSELLEŞTİRİLMİŞ EĞİTİM PROGRAMI KISA DÖNEMLİ AMAÇLAR (ünite-konu amaçları) 100 e kadar ikişer ritmik sayar. ÖĞRETİMSEL AMAÇLAR BAŞ. BİTİŞ (Kazanımlar)
UZUN DÖNEMLİ AMAÇLAR (yıl sonunda) RİTMİK SAYMALAR BİREYSELLEŞTİRİLMİŞ EĞİTİM PROGRAMI KISA DÖNEMLİ AMAÇLAR (ünite-konu amaçları) 100 e kadar ikişer ritmik sayar. ÖĞRETİMSEL AMAÇLAR BAŞ. BİTİŞ (Kazanımlar)
Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ
 Kİ-KAR TSTLRİ A) Kİ-KAR DAĞILIMI V ÖZLLİKLRİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk gösterp
Kİ-KAR TSTLRİ A) Kİ-KAR DAĞILIMI V ÖZLLİKLRİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk gösterp
8.Hafta. Değişkenlik Ölçüleri. Öğr.Gör.Muhsin ÇELİK. Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek,
 İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
VERİ ANALİZİ GÖRSEL SAYISAL SÖZEL
 VERİ ANALİZİ VERİ ANALİZİ GÖRSEL SAYISAL SÖZEL GÖRSEL ANALİZ ARAÇLARI İKİ BOYUTLU GÖSTERİM GRAFİK RENK Koyuluk/açıklık; Renk kümeleri (soğuk; sıcak) ÇİZGİ Nitelik (sürekli; kesintili vb.) Kalınlık Alan
VERİ ANALİZİ VERİ ANALİZİ GÖRSEL SAYISAL SÖZEL GÖRSEL ANALİZ ARAÇLARI İKİ BOYUTLU GÖSTERİM GRAFİK RENK Koyuluk/açıklık; Renk kümeleri (soğuk; sıcak) ÇİZGİ Nitelik (sürekli; kesintili vb.) Kalınlık Alan
TANIMLAYICI İSTATİSTİKLER
 TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
Merkezi Eğilim Ölçüleri
 Merkezi Eğilim Ölçüleri 1) Parametrik merkezi eğilim ölçüleri Serinin bütün birimlerinden etkilenen merkezi eğilim ölçüleridir. 1) Aritmetik ortalama 2) Geometrik ortalama (G) 3) Harmonik ortalama (H)
Merkezi Eğilim Ölçüleri 1) Parametrik merkezi eğilim ölçüleri Serinin bütün birimlerinden etkilenen merkezi eğilim ölçüleridir. 1) Aritmetik ortalama 2) Geometrik ortalama (G) 3) Harmonik ortalama (H)
Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II
 Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II İstatistik Nedir? İstatistik kelimesi farklı anlamlar taşımaktadır. Bunlar; Genel anlamda; üretim, tüketim, nüfus, sağlık, eğitim, tarım,
Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II İstatistik Nedir? İstatistik kelimesi farklı anlamlar taşımaktadır. Bunlar; Genel anlamda; üretim, tüketim, nüfus, sağlık, eğitim, tarım,
Şekil 2. Azalan f fonksiyonunun grafiği
 3. ÖLÇÜLEBİLİR FONKSİYONLAR SORU 1: f : R R azalan fonksiyon ise f fonksiyonu Borel ölçülebilir midir? ÇÖZÜM 1: Şekil 2. Azalan f fonksiyonunun grafiği α R için f 1 ((α, )) := {x R : f (x) > α} B (R) olduğunu
3. ÖLÇÜLEBİLİR FONKSİYONLAR SORU 1: f : R R azalan fonksiyon ise f fonksiyonu Borel ölçülebilir midir? ÇÖZÜM 1: Şekil 2. Azalan f fonksiyonunun grafiği α R için f 1 ((α, )) := {x R : f (x) > α} B (R) olduğunu
TEST - 1 ELEKTR K AKIMI. ε X = 2V. ε Y = 4V. K anahtar kapal iken: 4R R. i = R R CEVAP B. = 4 Ω dur. R x. I. yarg do rudur.
 EET M TEST - 1 1. 6 1 x Ω dur. 1 1 X anahtar kapal ken: Σ 8. 8. 1 CEP B. yarg do rudur.. 8 voltu gösterr.. yarg yanl flt r. mpermetre 1 amper gösterr.. yarg do rudur. CEP C. X + X 1 1Ω Y Y P. M N P ESEN
EET M TEST - 1 1. 6 1 x Ω dur. 1 1 X anahtar kapal ken: Σ 8. 8. 1 CEP B. yarg do rudur.. 8 voltu gösterr.. yarg yanl flt r. mpermetre 1 amper gösterr.. yarg do rudur. CEP C. X + X 1 1Ω Y Y P. M N P ESEN
1. (10) Makine Elemanlarının zamana göre değişen zorlamalara maruz kalması durumunda, sürekli mukavemet ve zaman mukavemeti nedir? Açıklayınız.
 MAK341 MAKİNA ELEMANLARI I 1. Yarıyıiçi imtihanı 7/03/01 İmtihan müddeti: 90 dakika Ögretim Üyesi: Prof. Dr. Hikmet Kocabaş, Doç. Dr. Cema Baykara 1. (10) Makine Eemanarının zamana göre değişen zoramaara
MAK341 MAKİNA ELEMANLARI I 1. Yarıyıiçi imtihanı 7/03/01 İmtihan müddeti: 90 dakika Ögretim Üyesi: Prof. Dr. Hikmet Kocabaş, Doç. Dr. Cema Baykara 1. (10) Makine Eemanarının zamana göre değişen zoramaara
ÖLÇME VE DEĞERLENDİRME. Antrenörlük Eğitimi 4. Sınıf. Ölçme ve Değerlendirme - Yrd. Doç. Dr. Yetkin Utku KAMUK
 ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
Bölüm 3. Tanımlayıcı İstatistikler
 Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Giriş. Değişkenlik Ölçüleri İSTATİSTİK I. Ders 5 Değişkenlik ve Asimetri Ölçüleri. Değişkenlik. X i ve Y i aşağıdaki gibi iki seri verilmiş olsun:
 Grş İSTATİSTİK I Ders Değşkelk ve Asmetr Ölçüler Ortalamalar, serler karşılaştırılmasıda her zama yeterl ölçüler değldr. Ayı ortalamayı sahp serler arklı dağılım göstereblrler. Bu edele serler karşılaştırılmasıda,
Grş İSTATİSTİK I Ders Değşkelk ve Asmetr Ölçüler Ortalamalar, serler karşılaştırılmasıda her zama yeterl ölçüler değldr. Ayı ortalamayı sahp serler arklı dağılım göstereblrler. Bu edele serler karşılaştırılmasıda,
KPSS AKADEMİ PUANLAR ÜZERİNDE İŞLEM YAPILMASI ÖLÇME VE DEĞERLENDİRME. Ölçme ve değerlendirme ÖLÇME SONUÇLARI ÜZERİNDE İSTATİSTİKSEL İŞLEMLER
 ÖLÇME VE DEĞERLENDİRME Ölçme ve değerlendirme 1 ÖLÇME SONUÇLARI ÜZERİNDE İSTATİSTİKSEL İŞLEMLER KPSS AKADEMİ PUANLAR ÜZERİNDE İŞLEM YAPILMASI PUANLARIN BÜYÜKLÜK SIRASINA KONULMASI 3 Bir testten elde edilen
ÖLÇME VE DEĞERLENDİRME Ölçme ve değerlendirme 1 ÖLÇME SONUÇLARI ÜZERİNDE İSTATİSTİKSEL İŞLEMLER KPSS AKADEMİ PUANLAR ÜZERİNDE İŞLEM YAPILMASI PUANLARIN BÜYÜKLÜK SIRASINA KONULMASI 3 Bir testten elde edilen
Maddenin Ayırtedici Özellikleri
 Maddenin Ayırtedici Özellikleri Bir maddeyi diğer maddelerden ayırmaya yarayan özellikleri Ayırtedici Özellikler denir. Bunlar; Özkütle (Yoğunluk) Erime Noktası Kaynama Noktası Çözünürlük Esneklik İletkenlik
Maddenin Ayırtedici Özellikleri Bir maddeyi diğer maddelerden ayırmaya yarayan özellikleri Ayırtedici Özellikler denir. Bunlar; Özkütle (Yoğunluk) Erime Noktası Kaynama Noktası Çözünürlük Esneklik İletkenlik
10. SINIF KONU ANLATIMLI. 2. ÜNİTE: ELEKTRİK VE MANYETİZMA 3. Konu ELEKTRİK ENERJİSİ VE ELEKTRİKSEL GÜÇ ETKİNLİK ve TEST ÇÖZÜMLERİ
 10. SINIF ONU NTII. ÜNİTE: EETİ E NYETİZ. onu EETİ ENEJİSİ E EETİSE GÜÇ ETİNİ ve TEST ÇÖZÜEİ Ünte Elektrk ve anyetzma. Ünte. onu (Elektrk Enerjs ve Elektrksel Güç) nın Çözümler 1. Noktalama sstemyle Şekl
10. SINIF ONU NTII. ÜNİTE: EETİ E NYETİZ. onu EETİ ENEJİSİ E EETİSE GÜÇ ETİNİ ve TEST ÇÖZÜEİ Ünte Elektrk ve anyetzma. Ünte. onu (Elektrk Enerjs ve Elektrksel Güç) nın Çözümler 1. Noktalama sstemyle Şekl
İstatistik ve Olasılığa Giriş. İstatistik ve Olasılığa Giriş. Ders 3 Verileri Sayısal Ölçütlerle İfade Etme. Verileri Sayısal Ölçütlerle İfade Etme
 İstatistik ve Olasılığa Giriş Robert J. Beaver Barbara M. Beaver William Mendenhall Presentation designed and written by: Barbara M. Beaver İstatistik ve Olasılığa Giriş Ders 3 Verileri Sayısal Ölçütlerle
İstatistik ve Olasılığa Giriş Robert J. Beaver Barbara M. Beaver William Mendenhall Presentation designed and written by: Barbara M. Beaver İstatistik ve Olasılığa Giriş Ders 3 Verileri Sayısal Ölçütlerle
Doğrusal Korelasyon ve Regresyon
 Doğrusal Korelasyon ve Regresyon En az k değşken arasındak lşknn ncelenmesne korelasyon denr. Kşlern boyları le ağırlıkları, gelr le gder, öğrenclern çalıştıkları süre le aldıkları not, tarlaya atılan
Doğrusal Korelasyon ve Regresyon En az k değşken arasındak lşknn ncelenmesne korelasyon denr. Kşlern boyları le ağırlıkları, gelr le gder, öğrenclern çalıştıkları süre le aldıkları not, tarlaya atılan
A A A FEN BİLİMLERİ SINAVI FİZİK TESTİ 1 FİZ (LYS2)
 DİAT! SORU İTAÇIĞINIZIN TÜRÜNÜ A OARA CEVA ÂĞIDINIZA İŞARETEMEİ UNUTMAINIZ. FEN BİİMERİ SINAVI FİZİ TESTİ 1. Bu testte 30 soru vardır.. Cevaplarınızı, cevap kâğıdının Fzk Test çn ayrılan kısına şaretleynz.
DİAT! SORU İTAÇIĞINIZIN TÜRÜNÜ A OARA CEVA ÂĞIDINIZA İŞARETEMEİ UNUTMAINIZ. FEN BİİMERİ SINAVI FİZİ TESTİ 1. Bu testte 30 soru vardır.. Cevaplarınızı, cevap kâğıdının Fzk Test çn ayrılan kısına şaretleynz.
I.BÖLÜM (Toplam 35 soru bulunmaktadır.)
 I.BÖLÜM (Toplam 35 soru bulunmaktadır.) 1. ve B ise aşağıdakilerden hangisi daima doğrudur? )B=B B)B=B )(B) D)(B) E)(B) 5. 19 4 B5 7 Bölme işleminde ve B sıfırdan farklı birer rakam olmak üzere +B kaç
I.BÖLÜM (Toplam 35 soru bulunmaktadır.) 1. ve B ise aşağıdakilerden hangisi daima doğrudur? )B=B B)B=B )(B) D)(B) E)(B) 5. 19 4 B5 7 Bölme işleminde ve B sıfırdan farklı birer rakam olmak üzere +B kaç
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
İSTATİSTİK DERS NOTLARI
 Balıkesr Ünverstes İnşaat Mühendslğ Bölüü uutokkan@balkesr.edu.tr İSTATİSTİK DERS OTLARI Yrd. Doç. Dr. Uut OKKA Hdrolk Anabl Dalı Balıkesr Ünverstes Balıkesr Ünverstes İnşaat Mühendslğ Bölüü İnşaat Mühendslğ
Balıkesr Ünverstes İnşaat Mühendslğ Bölüü uutokkan@balkesr.edu.tr İSTATİSTİK DERS OTLARI Yrd. Doç. Dr. Uut OKKA Hdrolk Anabl Dalı Balıkesr Ünverstes Balıkesr Ünverstes İnşaat Mühendslğ Bölüü İnşaat Mühendslğ
Veride etiket bilgisi yok Denetimsiz öğrenme (unsupervised learning) Neden gereklidir?
 MEH535 Örünü Tanıma 7. Kümeleme (Cluserng) Doç.Dr. M. Kemal GÜLLÜ Elekronk ve Haberleşme Mühendslğ Bölümü web: hp://akademkpersonel.kocael.edu.r/kemalg/ E-posa: kemalg@kocael.edu.r Verde eke blgs yok Denemsz
MEH535 Örünü Tanıma 7. Kümeleme (Cluserng) Doç.Dr. M. Kemal GÜLLÜ Elekronk ve Haberleşme Mühendslğ Bölümü web: hp://akademkpersonel.kocael.edu.r/kemalg/ E-posa: kemalg@kocael.edu.r Verde eke blgs yok Denemsz
1. DERECEDEN İKİ BİLİNMEYENLİ DENKLEMLER
 1. DERECEDEN İKİ BİLİNMEYENLİ DENKLEMLER Örnek...3 : 3 x+ y= 5 2x 3 =2 y s i s t e m i n i s a ğ l a ya n y d e ğ e r i k aç t ır? a, b, c R, a 0, b 0, x v e y d e ğ i şk e n o l m a k ü ze r e, a x+ b
1. DERECEDEN İKİ BİLİNMEYENLİ DENKLEMLER Örnek...3 : 3 x+ y= 5 2x 3 =2 y s i s t e m i n i s a ğ l a ya n y d e ğ e r i k aç t ır? a, b, c R, a 0, b 0, x v e y d e ğ i şk e n o l m a k ü ze r e, a x+ b
Tanımlayıcı İstatistikler
 Taımlayıcı İstatstkler Taımlayıcı İstatstkler br değerler dzs statstksel olarak geel özellkler taımlaya ölçülerdr Taımlayıcı İstatstkler Yer Göstere Ölçüler Yaygılık Ölçüler Yer Göstere Ölçüler Br dağılımı
Taımlayıcı İstatstkler Taımlayıcı İstatstkler br değerler dzs statstksel olarak geel özellkler taımlaya ölçülerdr Taımlayıcı İstatstkler Yer Göstere Ölçüler Yaygılık Ölçüler Yer Göstere Ölçüler Br dağılımı
Merkezi Yığılma ve Dağılım Ölçüleri
 1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
irket Riski (Çeşitlendirilebilir) Hisse Senedi Riski, σ p Piyasa Riski (Çeşitlendirilemez) 10 20 30 40 2,000+ Doç. Dr.
 σ p (%) 35 irket Riski (Çeşitlendirilebilir) Hisse Senedi Riski, σ p 20 0 Piyasa Riski (Çeşitlendirilemez) 10 20 30 40 2,000+ Portföydeki Hisse # Hisse Senedi Piyasa Çeşitlendirilebilir riski = riski +
σ p (%) 35 irket Riski (Çeşitlendirilebilir) Hisse Senedi Riski, σ p 20 0 Piyasa Riski (Çeşitlendirilemez) 10 20 30 40 2,000+ Portföydeki Hisse # Hisse Senedi Piyasa Çeşitlendirilebilir riski = riski +
Özel sektör tasarrufları Hanehalkı Şirketler kesimi Kamu sektörü tasarrufları
 Türkiye Ülke Ekonomik Raporu Özel sektör tasarrufları Hanehalkı Şirketler kesimi Kamu sektörü tasarrufları 1. Tasarruf ve büyüme ilişkisi 2. Tasarruf trendleri 3. Tasarrufun belirleyicileri 4. Mali piyasaların
Türkiye Ülke Ekonomik Raporu Özel sektör tasarrufları Hanehalkı Şirketler kesimi Kamu sektörü tasarrufları 1. Tasarruf ve büyüme ilişkisi 2. Tasarruf trendleri 3. Tasarrufun belirleyicileri 4. Mali piyasaların
3. Bölüm. DA-DA Çevirici Devreler (DC Konvertörler) Doç. Dr. Ersan KABALCI AEK-207 GÜNEŞ ENERJİSİ İLE ELEKTRİK ÜRETİMİ
 3. Bölüm DA-DA Çevirici Devreler (D Konvertörler) Doç. Dr. Ersan KABA AEK-207 GÜNEŞ ENERJİSİ İE EEKTRİK ÜRETİMİ Dönüştürücü Devreler Gücün DA-DA dönüştürülmesi anahtarlamalı tip güç konvertörleri ile yapılır.
3. Bölüm DA-DA Çevirici Devreler (D Konvertörler) Doç. Dr. Ersan KABA AEK-207 GÜNEŞ ENERJİSİ İE EEKTRİK ÜRETİMİ Dönüştürücü Devreler Gücün DA-DA dönüştürülmesi anahtarlamalı tip güç konvertörleri ile yapılır.
Merkezi Eğilim ve Dağılım Ölçüleri
 Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
MUTLAK DEÐER TEST / 1
 MUTLAK DEÐER TEST / 1 1. Aþaðýdaki sayýlardan hangisinin mutlak deðeri en küçüktür? 5. 3 + 6 4 +1 A) 7 B) 19 C) 3 D) 1 E) 4 A) 4 B) 6 C) 8 D) 10 E) 14 2. Aþaðýdaki karþýlaþtýrmalardan hangisi yanlýþtýr?
MUTLAK DEÐER TEST / 1 1. Aþaðýdaki sayýlardan hangisinin mutlak deðeri en küçüktür? 5. 3 + 6 4 +1 A) 7 B) 19 C) 3 D) 1 E) 4 A) 4 B) 6 C) 8 D) 10 E) 14 2. Aþaðýdaki karþýlaþtýrmalardan hangisi yanlýþtýr?
Bölüm 3. Tanımlayıcı İstatistikler
 Bölüm 3 Tanımlayıcı İstatstkler Tanımlayıcı İstatstkler Br ver setn tanımak veya brden fazla ver setn karşılaştırmak çn kullanılan ve ayrıca örnek verlernden hareket le frekans dağılışlarını sayısal olarak
Bölüm 3 Tanımlayıcı İstatstkler Tanımlayıcı İstatstkler Br ver setn tanımak veya brden fazla ver setn karşılaştırmak çn kullanılan ve ayrıca örnek verlernden hareket le frekans dağılışlarını sayısal olarak
13.11.2010 ÖLÇME VE DEĞERLENDĠRMEDE TEMEL ĠSTATĠSTĠKĠ HESAPLAMLAR ĠSTATĠSTĠK? İstatistik, verileri analiz ve organize etmekle uğraşan bir disiplindir.
 13.11. Ġstatistik ĠSTATĠSTĠK? Ölçekler Verilerin Düzenlenmesi Merkezi Eğilim Ölçüleri Dağılım Ölçüleri ĠliĢki Ölçüleri (Korelasyon) Örnek Uygulama ÖLÇME VE DEĞERLENDĠRMEDE TEMEL ĠSTATĠSTĠKĠ HESAPLAMLAR
13.11. Ġstatistik ĠSTATĠSTĠK? Ölçekler Verilerin Düzenlenmesi Merkezi Eğilim Ölçüleri Dağılım Ölçüleri ĠliĢki Ölçüleri (Korelasyon) Örnek Uygulama ÖLÇME VE DEĞERLENDĠRMEDE TEMEL ĠSTATĠSTĠKĠ HESAPLAMLAR
İSTATİSTİK MHN3120 Malzeme Mühendisliği
 İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :emre.yalamac@cbu.edu.tr YARDIMCI KAYNAKLAR Mühendiler
İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :emre.yalamac@cbu.edu.tr YARDIMCI KAYNAKLAR Mühendiler
Fizik 101: Ders 15 Ajanda
 zk 101: Ders 15 Ajanda İk boyutta elastk çarpışma Örnekler (nükleer saçılma, blardo) Impulse ve ortalama kuvvet İk boyutta csmn elastk çarpışması Önces Sonrası m 1 v 1, m 1 v 1, KM KM V KM V KM m v, m
zk 101: Ders 15 Ajanda İk boyutta elastk çarpışma Örnekler (nükleer saçılma, blardo) Impulse ve ortalama kuvvet İk boyutta csmn elastk çarpışması Önces Sonrası m 1 v 1, m 1 v 1, KM KM V KM V KM m v, m
GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL. Frekans Dağılımı Oluşturma Adımları VERİLERİN SUNUMU. Verilerin Özetlenmesi ve Grafikle Gösterilmesi
 VERİLERİN SUNUMU GM-0 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Br çalışadan elde edlen verler ha ver ntelğndedr. Ha verlerden blg ednek zor ve zaan alıcıdır. Ha verler çok karaşık durudadır. Verlern düzenlenes
VERİLERİN SUNUMU GM-0 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Br çalışadan elde edlen verler ha ver ntelğndedr. Ha verlerden blg ednek zor ve zaan alıcıdır. Ha verler çok karaşık durudadır. Verlern düzenlenes
... 2.Adım 3. Adım 4. Adım
 1-.... 2.Adım 3. Adım 4. Adım Yukarıda verilen şekillerdeki üçgen sayısı ile örüntülü bir sayı dizisi oluşturulmuştur. İki basamaklı doğal sayılardan rastgele seçilen bir sayının bu sayı dizisinin elemanı
1-.... 2.Adım 3. Adım 4. Adım Yukarıda verilen şekillerdeki üçgen sayısı ile örüntülü bir sayı dizisi oluşturulmuştur. İki basamaklı doğal sayılardan rastgele seçilen bir sayının bu sayı dizisinin elemanı
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI. Ders 2 Merkezi Eğilim Ölçüleri
 ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ
 TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
Test İstatistikleri AHMET SALİH ŞİMŞEK
 Test İstatistikleri AHMET SALİH ŞİMŞEK İçindekiler Test İstatistikleri Merkezi Eğilim Tepe Değer (Mod) Ortanca (Medyan) Aritmetik Ortalama Merkezi Dağılım Dizi Genişliği (Ranj) Standart Sapma Varyans Çarpıklık
Test İstatistikleri AHMET SALİH ŞİMŞEK İçindekiler Test İstatistikleri Merkezi Eğilim Tepe Değer (Mod) Ortanca (Medyan) Aritmetik Ortalama Merkezi Dağılım Dizi Genişliği (Ranj) Standart Sapma Varyans Çarpıklık
A. Sürüklenme hızı artar. B. Sürüklenme hızı azalır. C. Sürüklenme hızı değişmez. D. Yeterli bilgi yok.
 Q25.1 Farklı yarıçapta iki bakır tel uç uca bağlanıyor ve akım bu tellerden geçiriliyor; Elektronlar büyük yarıçaplı telden küçük yarıçaplı tele geçerken sürüklenme hızı ne olur. A. Sürüklenme hızı artar.
Q25.1 Farklı yarıçapta iki bakır tel uç uca bağlanıyor ve akım bu tellerden geçiriliyor; Elektronlar büyük yarıçaplı telden küçük yarıçaplı tele geçerken sürüklenme hızı ne olur. A. Sürüklenme hızı artar.
5/21/2015. Transistörler
 Transistörler İki polarmalı yüzey temaslı transistörler, teknik ifadelerde BJT ( Bipolar Junction Transistör) olarak adlandırılmaktadır. Transistör birçok elektronik devrede uygulama bulan işaret yükseltme
Transistörler İki polarmalı yüzey temaslı transistörler, teknik ifadelerde BJT ( Bipolar Junction Transistör) olarak adlandırılmaktadır. Transistör birçok elektronik devrede uygulama bulan işaret yükseltme
Bükme sonrasında elde edilmeye çalışılan parça şekli için geri yaylanma durumu dikkate alınmalıdır.
 Bükme Sonrası Geri Yaylanma Bükme işlemi uygulanmış bir malzeme üzerinden bükme yükü kaldırıldığında, d parça bükülmüş haldeki şeklinde d kalmaz. Malzemedeki artık elastikiyet, bükülmüş durumdaki parçanın
Bükme Sonrası Geri Yaylanma Bükme işlemi uygulanmış bir malzeme üzerinden bükme yükü kaldırıldığında, d parça bükülmüş haldeki şeklinde d kalmaz. Malzemedeki artık elastikiyet, bükülmüş durumdaki parçanın
 Türk Deri Hazır Giyim Sektöründeki Küçük Ölçekli İşletmelerin Markalaşma Düzeylerinin Araştırılması Grafik 1. İşletmelerin Sahip Oldukları Marka Sayılarının Dağılımı Grafik 2. İşletmelerin Markalara Sahip
Türk Deri Hazır Giyim Sektöründeki Küçük Ölçekli İşletmelerin Markalaşma Düzeylerinin Araştırılması Grafik 1. İşletmelerin Sahip Oldukları Marka Sayılarının Dağılımı Grafik 2. İşletmelerin Markalara Sahip
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler
 Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
Tanımlayıcı İstatistikler
 Taımlayıcı İstatstkler Br veya brde fazla dağılışı karşılaştırmak ç kullaıla veya ayrıca örek verlerde hareketle frekas dağılışlarıı sayısal olarak düzeleye değerlere taımlayıcı statstkler der. Aalzlede
Taımlayıcı İstatstkler Br veya brde fazla dağılışı karşılaştırmak ç kullaıla veya ayrıca örek verlerde hareketle frekas dağılışlarıı sayısal olarak düzeleye değerlere taımlayıcı statstkler der. Aalzlede
HACİM HESAPLARI. Toprak İşlerinde Karşılaşılan Hacim Hesapları
 03..04 İnşaat Mühendisiği Böümü HACİM HEAPLARI Hacim hesabı, İnşaat Mühendisiğinde apıan toprak işerinin temeini ouşturur. Zira, toprak işeri ödemeeri, hacim (m 3 ) bazında apıır. oprak İşeri ers Notarı
03..04 İnşaat Mühendisiği Böümü HACİM HEAPLARI Hacim hesabı, İnşaat Mühendisiğinde apıan toprak işerinin temeini ouşturur. Zira, toprak işeri ödemeeri, hacim (m 3 ) bazında apıır. oprak İşeri ers Notarı
ORTAOKULU 2014 2015 ÜNİTİLENDİRİLMİŞ YILLIK BİREYSEL DERS PLANI (BEP)
 ORTAOKULU 2014 2015 ÜNİTİLENDİRİLMİŞ YILLIK BİREYSEL DERS PLANI (BEP) AY EYLÜL EKİM SÜRE SINIF:8 DERS: MATEMATİK HAFTA DERS SAATİ UZUN DÖNEMLİ AMAÇ KISA DÖNEMLİ AMAÇ ÖĞRETİMSEL AMAÇLAR AMAÇ 30: Dört basamaklı
ORTAOKULU 2014 2015 ÜNİTİLENDİRİLMİŞ YILLIK BİREYSEL DERS PLANI (BEP) AY EYLÜL EKİM SÜRE SINIF:8 DERS: MATEMATİK HAFTA DERS SAATİ UZUN DÖNEMLİ AMAÇ KISA DÖNEMLİ AMAÇ ÖĞRETİMSEL AMAÇLAR AMAÇ 30: Dört basamaklı
ÇOKLU REGRESYON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESYON ÇÖZÜMLEMESİ,REGRES-YON KATSAYILARININ YORUMU
 6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
ÖRNEK SAYISAL UYGULAMALAR
 ÖRNEK SAYISAL UYGULAMALAR 1-Vidalı kriko: Şekil deki kriko için; Verilenler Vidalı Mil Malzemesi: Ck 45 Vidalı mil konumu: Düşey Somun Malzemesi: Bronz Kaldırılacak en büyük (maksimum) yük: 50.000 N Vida
ÖRNEK SAYISAL UYGULAMALAR 1-Vidalı kriko: Şekil deki kriko için; Verilenler Vidalı Mil Malzemesi: Ck 45 Vidalı mil konumu: Düşey Somun Malzemesi: Bronz Kaldırılacak en büyük (maksimum) yük: 50.000 N Vida
Volkan Karamehmetoğlu
 1 Doğal Sayılar Tanımlar Rakam: Sayıları yazmaya yarayan sembollere denir. {1,2,3,4,5,6,7,8,9} Sayı: Rakamların çokluk belirten ifadesine denir. 365 sayısı 3-6-5 rakamlarından oluşmuştur. 2 Uyarı: Her
1 Doğal Sayılar Tanımlar Rakam: Sayıları yazmaya yarayan sembollere denir. {1,2,3,4,5,6,7,8,9} Sayı: Rakamların çokluk belirten ifadesine denir. 365 sayısı 3-6-5 rakamlarından oluşmuştur. 2 Uyarı: Her
ATATÜRK ÜNĠVERSĠTESĠ UZAKTAN EĞĠTĠM MERKEZĠ
 ATATÜRK ÜNĠVERSĠTESĠ UZAKTAN EĞĠTĠM MERKEZĠ 2009 ATAUZEM ŞABLON 28. HAFTA KONU BAġLIĞI Neler Öğrendik, Bilgilerimizi PekiĢtirelim AMAÇ Biyoistatistik dersinin 15-23. haftalarda öğrenilen konularını tekrarlamak
ATATÜRK ÜNĠVERSĠTESĠ UZAKTAN EĞĠTĠM MERKEZĠ 2009 ATAUZEM ŞABLON 28. HAFTA KONU BAġLIĞI Neler Öğrendik, Bilgilerimizi PekiĢtirelim AMAÇ Biyoistatistik dersinin 15-23. haftalarda öğrenilen konularını tekrarlamak
EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler VERİLERİN DÜZENLENMESİ VERİLERİN DÜZENLENMESİ
 09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
Bölüm 3. Tanımlayıcı İstatistikler
 Bölüm 3 Tanımlayıcı İstatstkler Tanımlayıcı İstatstkler Br ver setn tanımak veya brden fazla ver setn karşılaştırmak çn kullanılan ve örnek verlernden hareket le frekans dağılışlarını sayısal olarak özetleyen
Bölüm 3 Tanımlayıcı İstatstkler Tanımlayıcı İstatstkler Br ver setn tanımak veya brden fazla ver setn karşılaştırmak çn kullanılan ve örnek verlernden hareket le frekans dağılışlarını sayısal olarak özetleyen
8. Sınıf Fen ve Teknoloji. KONU: Sıvılarda ve Gazlarda Basınç
 Sıvılar bulundukları kabın her yerine aynı basıncı uygulamazlar. Katılar zemine basınç uygularken sıvılar kabın her yerine basınç uygularlar. Sıvı basıncı, kapta bulunan sıvının hacmine, kabın şekline
Sıvılar bulundukları kabın her yerine aynı basıncı uygulamazlar. Katılar zemine basınç uygularken sıvılar kabın her yerine basınç uygularlar. Sıvı basıncı, kapta bulunan sıvının hacmine, kabın şekline
DENEY 7: Darbe Kod ve Delta Modülasyonları (PCM, DM)
 DENEY 7: Darbe Kod ve Delta Modülasyonları (PCM, DM) AMAÇ: Darbe Kod (Pulse Code) ve Delta Modülasyonlarının temel işleyişlerinin MATLAB ortamında incelenmesi. ÖN HAZIRLIK 1) Bit, Bps, BER, Kanal, Kanal
DENEY 7: Darbe Kod ve Delta Modülasyonları (PCM, DM) AMAÇ: Darbe Kod (Pulse Code) ve Delta Modülasyonlarının temel işleyişlerinin MATLAB ortamında incelenmesi. ÖN HAZIRLIK 1) Bit, Bps, BER, Kanal, Kanal
Veri Analizi. Isınma Hareketleri. Test İstatistikleri. b) En çok tekrar eden: 7 (mod) c) Açıklık = En büyük En küçük = 10 1 = 9. d)
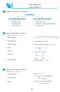 Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
IİSTATIİSTIİK. Mustafa Sezer PEHLI VAN
 IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
KORELASYON VE TEKLİ REGRESYON ANALİZİ-EN KÜÇÜK KARELER YÖNTEMİ
 KORELASYON VE TEKLİ REGRESYON ANALİZİ-EN KÜÇÜK KARELER YÖNTEMİ 1 KORELASYON ANALİZİ İki değişken arasındaki doğrusal ilişkinin gücünü(derecesini) ve yönünü belirlemek için hesaplanan bir sayıdır. Belirli
KORELASYON VE TEKLİ REGRESYON ANALİZİ-EN KÜÇÜK KARELER YÖNTEMİ 1 KORELASYON ANALİZİ İki değişken arasındaki doğrusal ilişkinin gücünü(derecesini) ve yönünü belirlemek için hesaplanan bir sayıdır. Belirli
ELS ELS SEVİYE ŞALTERİ. ELS B10p, ELS B10x, ELS B101x ELS K01, ELS K02, ELS K03 ELS P01, ELS P03, ELS P04 ELS B035, ELS P52, ELS P65 ELS ML2, ELS ML5
 ES Seviye sensörleri tank seviye kontrolü için kullanılmaktadır. Farklı muhafaza bağlantı, malzeme çeşitleri mevcuttur. Çalışma Prensibi: Sıvı seviyesine göre tüp boyunca hareket eden şamandıra içindeki
ES Seviye sensörleri tank seviye kontrolü için kullanılmaktadır. Farklı muhafaza bağlantı, malzeme çeşitleri mevcuttur. Çalışma Prensibi: Sıvı seviyesine göre tüp boyunca hareket eden şamandıra içindeki
Temel Ġstatistik. Tanımlayıcı Ġstatistik. Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri. Y.Doç.Dr. Ġbrahim Turan Mart 2011
 Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
