DOĞRUSAL OLMAYAN PROGRAMLAMA (NLP)
|
|
|
- Esen Şipal
- 7 yıl önce
- İzleme sayısı:
Transkript
1 DOĞRUSAL OLMAYAN PROGRAMLAMA (NLP) 1. Non-lineer kar analizi, 2. Kısıtlı optimizasyon, 3. Yerine koyma (substitution) yöntemi, 4. Lagranj Çarpanları Yöntemi 5. Başabaş Analizleri ve Duyarlılık Testleri KONU 7 Y. Doç. Dr. Fazıl GÖKGÖZ 1 DOĞRUSAL OLMAYAN PROGRAMLAMA (NLP) Lineer programlama; tam sayılı programlama ve hedef programlama gibi alanlarda kullanım alanı bulur. LP özellikle, ulaştırma ve atama problemlerinde başarılıdır. Ancak, gerçek işletme problemlerinde koşullar doğrusal olmayan bir yapı arz ettiğinde; non-lineer fonksiyonların kullanıldığı bir problem çözüm mantığı uygulanmalıdır. Bu düşünce yapısı; NLP çözümüdür. Y. Doç. Dr. Fazıl GÖKGÖZ 2 1
2 Non-Lineer Kar Analizi Başabaş Analizine dayanan bir kar fonksiyonu olsun ve bu fonksiyon Z ile ifade edilsin. Z = v.p C f v.c v Burada, v = satış ş hacmi veya talep miktarı, p = fiyat, C f = sabit maliyet, C v =değişken maliyet Y. Doç. Dr. Fazıl GÖKGÖZ 3 Non-Lineer Kar Analizi Başabaş analizindeki en önemli varsayım satış miktarı veya talebin v fiyattan bağımsız olduğudur. 1,500 Eğim ğ = Ancak, gerçek koşullarda talep ile fiyat arasında yakın bir ilişki bulunur. Western Giyim Şti. nin talep-fiyat ilişkisi lineerdir $ p v = 1, p Y. Doç. Dr. Fazıl GÖKGÖZ 4 2
3 Non-Lineer Kar Analizi Soruda verilen satış hacmi ve fiyat ilişkisini, asıl kar fonksiyonunda yerine koyarsak; Z =v.p C f v.c Kar (Z) v Z = 1,698.8p 24.6p 2 22,000 =(1, p)p C f (1, p)C v =1,500p-24.6p 2 C f 1,500C v +24.6pC v C f = 10,000 $ ve C v =8$ise; p Z = 1,698.8p 24.6p 2 22,000 22,000 $ olur. Y. Doç. Dr. Fazıl GÖKGÖZ 5 Non-Lineer Kar Analizi Z = 1,698.8p 24.6p 2 22,000 1, p Kar (Z) Maksimum Kar Matematiksel işlemlerde; bir eğrinin herhangi bir noktasındaki eğimi, bu fonksiyonun o noktadaki kısmi türevinin alınmasıyla bulunur. Z p 22,000 $ Z = 1,698.8p 24.6p 2 22,000 Eğim = Türev = O Optimal Fiyat p Teorik olarak; bir eğrinin tepe noktasındaki türevi sıfıra eşittir. Y. Doç. Dr. Fazıl GÖKGÖZ 6 3
4 Non-Lineer Kar Analizi Toplam karı maksimize eden; 1) Optimal fiyat; 0 = 1, p 49.2p = 1,696.8 p = $ 2) Optimal satış hacmi; v = 1, p v = 1, (34.49) v=651.6 adet takım elbise Kar (Z) Maksimum Kar 22,000 $ Z = 1,698.8p 24.6p 2 22,000 Eğim = Türev = O Optimal Fiyat p Y. Doç. Dr. Fazıl GÖKGÖZ 7 Non-Lineer Kar Analizi Maksimum Kar-Optimal Fiyat ve Optimal Satış Hacmi Grafiği Kar (Z) 7, $ v = takım elbise Z = 1,698.8p 24.6p 2 22,000 Z = 1,696.8(34.49)-24.6(34.49) 2-22,000 Maksimum Kar Düzeyi 34.49$ p Z= 7,259.45$ 22,000 $ Y. Doç. Dr. Fazıl GÖKGÖZ 8 4
5 Kısıtlandırılmış Optimizasyon Yöntemi Z=v.p C f v.c v Aynı amaç fonskiyonundan yola çıkarak, fiyata dayalı bir model oluşturduk. Z = 1,698.8p 24.6p 2 22,000 Bir önceki bölümde fonksiyonu herhangi bir şekilde sınırlandırmaya tabi tutmadan optimal çözüme ve maksimum kar seviyesine ulaşmıştık. Şöyle ki; fonksiyonu belli bir fiyat düzeyinde sınırlandırmadan analizi gerçekleştirdik. Y. Doç. Dr. Fazıl GÖKGÖZ 9 Kısıtlandırılmış Optimizasyon Yöntemi Grafikte non-lineer fonksiyonu belirli fiyat düzeylerinde sınırlandırlır. Kar (Z) Belirlenen 20$ lık fiyat düzeyinde maksimum kar düzeyi A noktasında gerçekleşir. Bu nokta optimal çözüm noktasıdır. Maksimum Kar A 20$ Optimal Çözüm Noktası p A noktası için gerekli cebirsel işlemler yapıldığı takdirde; maksimum kara 22,000 $ karşılık gelen satış miktarı da belirlenir. Y. Doç. Dr. Fazıl GÖKGÖZ 10 5
6 Kısıtlandırılmış Optimizasyon Yöntemi Bu grafikte ise; 40$ lık bir piyasa fiyatıyla sınırlandırılmış olan bir kar fonksiyonu görülmektedir. Kar (Z) Sınırlandıran fiyatın bulunduğu nokta (C) optimal çözüm değildir, çünkü kendisinden önce fonksiyonun bir tepe noktası (B) bulunmaktadır. Kısaca, çözüm B noktasında gerçekleşir. 22,000 $ B Optimal Çözüm Noktası C 40$ p Y. Doç. Dr. Fazıl GÖKGÖZ 11 Yerine Koyma (Substitution) Yöntemi Bu yöntemde; kısıtlandırılmış eşitlik tek bir değişken için çözülmektedir. LP derslerinde gösterilen; Beaver Creek Şti. örneğini ele alalım. Şirket, kase (X 1 ) ve bardak (X 2 ) üretimi gerçekleştirmektedir. Amaç fonksiyonu; syo Z=a.X 1 + b.x 2 Burada, a ve b ürünlerin kara olan katkı paylarını temsil eder. Y. Doç. Dr. Fazıl GÖKGÖZ 12 6
7 Yerine Koyma (Substitution) Yöntemi Bu defa, amaç fonksiyonunda non-lineer bir ilişki söz konusudur. a = 4 0.1X 1 ve b=5 0.2X 2 olsun. Amaç fonksiyonunda yerlerinde konulduğunda; Z=4X 1-0.1X 12 +5X 2-0.2X 2 2 doğrusal olmayan bir amaç fonksiyonu bulunur. Y. Doç. Dr. Fazıl GÖKGÖZ 13 Yerine Koyma (Substitution) Yöntemi Sorunun orijinal halinde, x 1 +2X 2 = 40 saat gibi bir kısıt bulunur. Kısıtları diğeri cinsinden ifade edilir ve takiben de bulunan kısıt amaç fonsksiyonunda yerine konulursa; x 1 =40-2X 2 Z = 4.(40-2X 2 ) 0.1(40-2X 2 ) 2 +5X 2 0.2X 2 2 Z = 160-8X 2 0.1(1, X 2 +4X 22 )+5X 2 0.2X 2 2 Z = 160-8X X 2 0.4X 22 +5X 2 0.2X 2 2 Z = 13x 2 0.6x 2 2 Y. Doç. Dr. Fazıl GÖKGÖZ 14 7
8 Yerine Koyma (Substitution) Yöntemi Bulunan bu değer, sınırlandırılmamış bir optimizasyon fonksiyonu olduğundan ğ d kısmi türevini i alarak sıfıra eşitlemek suretiyle maksimum kar düzeyi tespit edilir. Z X x 2 0 = x 2 x 2 = 10.8 bardak Y. Doç. Dr. Fazıl GÖKGÖZ 15 Yerine Koyma (Substitution) Yöntemi X 1 ise X 2 kısıt fonksiyonunda yerine konularak bulunur. x 1 +2X 2 =40 x 1 + 2(10.8) = 40 x 1 = 18.4 kase X1 ve X2 optimal değerleri amaç fonksiyonunda yerine konulursa; Z = 4X X X + 5X 2 2 Z = 4(18.4) - 0.1(18.4) 2 + 5(10.8) -0.2(10.8) 2 Z = $ Y. Doç. Dr. Fazıl GÖKGÖZ 16 8
9 Lagranj Çarpanları (ג) Yöntemi Bu yöntemde ise; Lagranj Çarpanı,(ג) amaç fonksiyonundan çıkarılır ve yeni eşitlik bünyesindeki her değişken bazında kısmi türevi alınarak çözülür. Lagranj Çarpanları Yöntemi; genel kabül görmüş bir matematiksel yöntem olup, non-lineer karakteristikli sınırlandırılmış optimizasyon problemlerinin çözümünü sağlar. Bu amaçla, bir önceki örneğimizin üzerinden gideceğiz. Y. Doç. Dr. Fazıl GÖKGÖZ 17 Lagranj Çarpanları (ג) Yöntemi Z=4X 1-0.1X 12 +5X 2-0.2X 2 2 s.t. X 1 +2X 2 =40 İlk aşamada, non-lineer durumdaki fonksiyonun Lagranjiyan Fonksiyonuna (L) dönüştürülür. X 1 +2X 2 40=0 Bu amaçla, kısıtın bulunduğu ifade Lagranj Çarpanı (ג) ile çarpılarak amaç fonsiyonundan çıkarılır. L=4X 1-0.1X 12 +5X 2-0.2X 22 - X )ג 1 +2X 2 40) Y. Doç. Dr. Fazıl GÖKGÖZ 18 9
10 Lagranj Çarpanları (ג) Yöntemi L=4X 1-0.1X 12 +5X 2-0.2X 22 - X )ג 1 +2X 2 40) Elde edilen yeni L fonksiyonu, sırasıyla; X 1, X 2 ve גya ג göre kısmi türevi alınarak sıfıra eşitlenir. Z X1 Z X2 Z ג 1 0.2X 4 2 ג 2-0.4X 2 5 -X 1 2X Y. Doç. Dr. Fazıl GÖKGÖZ 19 Lagranj Çarpanları (ג) Yöntemi Ortak çözüm için elde edilen her denklem sıfıra eşitlenir. = ג 1 0.2X 4 0 =0 ג X 2 -X 1 2X 2 +40=0 Üstteki iki eşitlik incelenirse; en üstte yer alan -2 faktörü ile çarpılarak; =0 ג X 1 = 0 ג X X X 2 =0 Y. Doç. Dr. Fazıl GÖKGÖZ 20 10
11 Lagranj Çarpanları (ג) Yöntemi Türev ile bulunan ve en altta yer alan eşitlik 0.4 faktörü ile çarpılır; -0.4X X = 0 Bir önceki slaytta ulaşılan en son denklem ile toplanır; -0.4X X = X X 2 =0-1.2X =13 X 2 = 10.8 bardak Y. Doç. Dr. Fazıl GÖKGÖZ 21 Lagranj Çarpanları (ג) Yöntemi -X 1 2X = 0 denkleminde d X 2 yerine konulur; -X 1 2(10.8) + 40 = 0 X 1 = 18.3 kase 5 = ג 2-0.4X 2 0 denkleminde X 2 yerine konulur; =0 ג 2 0.4(10.8) = ג Y. Doç. Dr. Fazıl GÖKGÖZ 22 11
12 Lagranj Çarpanları (ג) Yöntemi Tüm kısıtların optimal değerlerine ulaşıldığından dolayı bulunan değerler amaç fonksiyonunda yerine konulur; Z=4X 1-0.1X 12 +5X 2-0.2X 2 2 Z = 4(18.3)- 0.1(18.3) 2 + 5(10.8) - 0.2(10.8) 2 Z = $ Lagranjiyan Fonksiyonu (L) değeri ise; L=4X 1-0.1X 12 +5X 2-0.2X 22 - ) X )ג 1 +2X 2 40) L = 4(18.3) - 0.1(18.3) 2 + 5(10.8) - 0.2(10.8) (0) L = $ Gerek Yerine Koyma (Substution) ve gerekse Lagranj Çarpanları Yöntemlerinde aynı çözüme ulaşılmıştır. Y. Doç. Dr. Fazıl GÖKGÖZ 23 Başa Baş Analizi (Break Even Analysis) İşletmeler belirli maliyetler altında mamül veya hizmet üretirler. Genel olarak maliyetler iki alt grupta toplanır. 1) Sabit Maliyetler (C f ) Bina ve arazi maliyeti, aydınlatma, beyaz yakalı personel ücreti, yönetim giderleri, amortismanlar vb. 2) Değişken Maliyetler (C v ) Hammadde gideri, enerji, direk işçilik, paketleme, stoklama, dağıtım, pazarlama vb. Y. Doç. Dr. Fazıl GÖKGÖZ 24 12
13 Başa Baş Analizi (Break Even Analysis) v = Üretim hacmi TC = Toplam Maliyet Maliyet Sabit Maliyet (C f ) TC = C f +v.c v V (Üretim Hacmi) Y. Doç. Dr. Fazıl GÖKGÖZ 25 Başa Baş Analizi (Break Even Analysis) Maliyet, Gelir Sabit Maliyet (C) f Başabaş noktası V (Üretim Hacmi) Y. Doç. Dr. Fazıl GÖKGÖZ 26 13
14 Başa Baş Analizi (Break Even Analysis) İşletmenin kara geçtiği nokta başabaş üretim düzeyidir. Maliyet, Gelir Kar = Gelirler Maliyetler Kar=p.v C f v.c v Sabit Maliyet (C f) f v Başabaş noktası V (Üretim Hacmi) Y. Doç. Dr. Fazıl GÖKGÖZ 27 Başa Baş Analizi (Break Even Analysis) - Örnek Pha-medical ilaç fabrikasının üretmekte olduğu birağrı kesici ilacın maliyet değerleri ve gelir bilgileri: C v =8 C f = 10,000 p=23 Toplam maliyet fonskiyonunu ve başbaş noktasını belirleyiniz: TC = 10, v TR = Toplam Gelir TR = 23v TR = TC (Başabaş düzeyi) ; Kar = TR - TC Kar = 23v (10, v) = 15v -10,000 = 0 v başabaş = 666 adet (Firma zarar etmemek için en az bu miktarda üretim gerçekleştirmelidir) Y. Doç. Dr. Fazıl GÖKGÖZ 28 14
15 Başa Baş Analizi (Break Even Analysis) - Örnek Pha-medical ilaç fabrikası kapasitesi gereğince 800,000 adet ilaç üretebilmektedir. Firmanın kapasitesini 1,000 maliyet karşılığında 1,200 adede çıkarılması yönündeki öneriye katılıyor musunuz? Firma mevcut kapasitesinin tamamını kullanırsa; Kar 1 = 15v 10,000 Kar 1 = 15(800)-10,000 = 2,000 ; V Başabaş-1 = 10,000/15 = 666 adet Firma kapasite artışınış uygularsa; Kar 2 = 15v 11,000 Kar 2 = 15(1,200)-11,000 = 7,000 ; V Başabaş-2 = 11,000/15 = 733 adet Kar Artışı için; Kar 2 >Kar 1 olduğundan kapasitenin artırılması rasyonel bir karar olur. Y. Doç. Dr. Fazıl GÖKGÖZ 29 Başa Baş Analizi (Break Even Analysis) - Örnek Maliyet, Gelir ( ) Kar 2,000 C f ;10, BBN 666 Kapasite 800 V (Üretim Hacmi) Y. Doç. Dr. Fazıl GÖKGÖZ 30 15
16 Kapasite artışı, kar artışını da beraberinde getireceğinden yeni stratejinin benimsenmesi önerilir. Başa Baş Analizi (Break Even Analysis) C f ; 11,000 Maliyet, Gelir ( ) Yeni Kar 7,000 BBN BBN Kapasite 1,200 V (Üretim Hacmi) Y. Doç. Dr. Fazıl GÖKGÖZ 31 Duyarlılık Analizi (Fiyat Artışı) Genel bir ifadeyle, satış fiyatındaki artış, diğer tüm unsurlar sabit kabul edildiğinde d başabaşb noktası nı (BBN) azaltmaktadır. Maliyet, Gelir (1,000$) Yeni Toplam Gelir Yine aynı örneğimizde; satış fiyatı 23$ dan 30$ seviyesine yükselmiş olsun. Eski Toplam Gelir Toplam Maliyet BBN (Hacim) =C f /(p-c v ) BBN (Hacim) = 10,000/(30-8) f v Sabit Maliyet (C f ) BBN (yeni) BBN (eski) 10,000 $ V (Üretim Hacmi) BBN (Hacim) = Y. Doç. Dr. Fazıl GÖKGÖZ 32 16
17 Duyarlılık Analizi (Değişken Maliyet Değişimi) Genel bir ifadeyle, değişken maliyet düzeyindeki bir artış, diğer tüm unsurlar sabit kabul edildiğinde d başabaş noktası nı (BBN) arttırmaktadır. Aynı örneğimizde; satış fiyatı 30$ olduğunda ve değişken maliyet 12$ a yükseldiğinde; Sabit Maliyet (C f ) Maliyet, Gelir (1,000$) Toplam Gelir Yeni Toplam Maliyet Eski Toplam Maliyet 10,000 $ BBN (Hacim) =C f / (p-c v ) BBN (Hacim) = 10,000/(30-12) BBN (eski) BBN (yeni) V (Üretim Hacmi) BBN (Hacim) = Y. Doç. Dr. Fazıl GÖKGÖZ 33 Duyarlılık Analizi (Sabit Maliyet Değişimi) Genel bir ifadeyle, sabit maliyet düzeyindeki bir artış, diğer tüm unsurlar sabit kabul edildiğinde d başabaş noktası nı (BBN) arttırmaktadır. Aynı örneğimizde; satış fiyatı 30$, değişken maliyet 12$ olduğunda ve sabit maliyet %30 arttığında;. Sabit Maliyet (C f ) Maliyet, Gelir (1,000$) Yeni Toplam Gelir Yeni Toplam Maliyet Eski Toplam Maliyet 13,000 $ 10,000 $ BBN (Hacim) =C f / (p-c v ) BBN (Hacim) = 13,000/(30-12) BBN (eski) BBN (yeni) V (Üretim Hacmi) BBN (Hacim) = Y. Doç. Dr. Fazıl GÖKGÖZ 34 17
18 Bölüm 1 ÖDEV 7 (NLP) Bir tekstil firmasının aylık sabit maliyeti 21,000 $ ve değişken maliyeti ise birim başına 0.45 $ dır. Satış fiyatı 1.3 $ ise; a) Aylık 18,000 birim üretim için toplam maliyet, toplam gelir ve kar düzeyini belirleyiniz. b) Yıllık bazda başabaş noktasını hesaplayınız ve grafik üzerinde gösteriniz. c) Kendi belirleyeceğiniz maliyetler ve satış fiyatı üzerinden duyarlılık analizleri yaparak grafik üzerinde her durumu gösteriniz. Bölüm 2 Bir içecek firmasının aylık sabit maliyeti 12,000 $ ve birim başına değişken maliyeti 17 $ dır. Şirket kar fonksiyonunu ve talep kısıtını aşağıdaki gibi belirlemiştir. Z = vp 12,000 17v s.t. v = p Bu bağlamda, Yerine Koyma ve Lagranj yöntemleriyle ayrı ayrı optimal fiyatı hesaplayınız. Y. Doç. Dr. Fazıl GÖKGÖZ 35 18
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
Maksimizasyon s.t. İşçilik, saat) (Kil, kg)
 Simplex ile Çözüm Yöntemi Doç. Dr. Fazıl GÖKGÖZ 1 Doğrusal Programlama Modeli Maksimizasyon s.t. İşçilik, saat) (Kil, kg) 2 Doç. Dr. Fazıl GÖKGÖZ Yrd.Doç. Dr. Fazıl GÖKGÖZ 1 Modelin Standard Hali Maksimizasyon
Simplex ile Çözüm Yöntemi Doç. Dr. Fazıl GÖKGÖZ 1 Doğrusal Programlama Modeli Maksimizasyon s.t. İşçilik, saat) (Kil, kg) 2 Doç. Dr. Fazıl GÖKGÖZ Yrd.Doç. Dr. Fazıl GÖKGÖZ 1 Modelin Standard Hali Maksimizasyon
Temelleri. Doç.Dr.Ali Argun Karacabey
 Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Çalışma Soruları 1. a) x > 5 b) y < -3 c) xy > 0 d) x 3 < y e) (x-2) 2 + y 2 > 1. ( ) 2x
 Çalışma Soruları. Aşağıdaki denklemleri çözünüz: a) 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: a) 4x > 9 b) x 4
Çalışma Soruları. Aşağıdaki denklemleri çözünüz: a) 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: a) 4x > 9 b) x 4
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
Doğrusal Programlama. Prof. Dr. Ferit Kemal Sönmez
 Doğrusal Programlama Prof. Dr. Ferit Kemal Sönmez Doğrusal Programlama Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik
Doğrusal Programlama Prof. Dr. Ferit Kemal Sönmez Doğrusal Programlama Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik
Karar değişkenlere ilişkin fonksiyonların ve bu fonksiyonlara ilişkin sınırlamaların tanımlanması
 İNŞAAT PROJELERİNİN PROGRAMLAMA, TASARIM VE YAPIM SÜRECİNDE OPTİMİZASYON Doğrusal Optimizasyon Optimizasyon Kuramı (Eniyileme Süreci) Doğrusal Olmayan Optimizasyon Optimizasyon en iyi çözümü bulma sürecidir.
İNŞAAT PROJELERİNİN PROGRAMLAMA, TASARIM VE YAPIM SÜRECİNDE OPTİMİZASYON Doğrusal Optimizasyon Optimizasyon Kuramı (Eniyileme Süreci) Doğrusal Olmayan Optimizasyon Optimizasyon en iyi çözümü bulma sürecidir.
BAŞABAŞ NOKTASI ANALİZİ
 BAŞABAŞ NOKTASI ANALİZİ Herhangi bir işe girişirken, genellikle o iş için harcanacak çaba ve kaynaklarla, o işten sağlanacak fayda karşılaştırılır. Bu karşılaştırmada amaç, kaynaklara (üretim faktörlerine)
BAŞABAŞ NOKTASI ANALİZİ Herhangi bir işe girişirken, genellikle o iş için harcanacak çaba ve kaynaklarla, o işten sağlanacak fayda karşılaştırılır. Bu karşılaştırmada amaç, kaynaklara (üretim faktörlerine)
Çok değişkenli fonksiyonlar. Maksimum- Minimum
 66 Bölüm 6 Ders 06 Çok değişkenli fonksiyonlar. Maksimum- Minimum 6.1 Çözümler:Alıştırmalar 06 Prof.Dr.Haydar Eş Prof.Dr.Timur Karaçay Ön Bilgi: z = f (x, y) fonksiyonu 3-boyutlu uzayda bir yüzeyin denklemidir.
66 Bölüm 6 Ders 06 Çok değişkenli fonksiyonlar. Maksimum- Minimum 6.1 Çözümler:Alıştırmalar 06 Prof.Dr.Haydar Eş Prof.Dr.Timur Karaçay Ön Bilgi: z = f (x, y) fonksiyonu 3-boyutlu uzayda bir yüzeyin denklemidir.
Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli)
 ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS 2 NOTLAR Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli) X, karar değişkenlerinin bir vektörü olsun. z, g 1, g 2,...,g m fonksiyonlardır.
ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS 2 NOTLAR Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli) X, karar değişkenlerinin bir vektörü olsun. z, g 1, g 2,...,g m fonksiyonlardır.
Math 322 Diferensiyel Denklemler Ders Notları 2012
 1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
doğrusal programlama DOĞRUSAL PROGRAMLAMA (GENEL)
 DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
Lineer Programlama. Doğrusal terimi, hem amaç hem de kısıtları temsil eden matematiksel fonksiyonların doğrusal olduğunu gösterir.
 LİNEER PROGRAMLAMA Giriş Uygulamada karşılaşılan birçok optimizasyon problemi kısıtlar içerir. Yani optimizasyon probleminde amaç fonksiyonuna ilave olarak çözümü kısıtlayıcı ek denklemler mevcuttur. Bu
LİNEER PROGRAMLAMA Giriş Uygulamada karşılaşılan birçok optimizasyon problemi kısıtlar içerir. Yani optimizasyon probleminde amaç fonksiyonuna ilave olarak çözümü kısıtlayıcı ek denklemler mevcuttur. Bu
Gazi Üniversitesi, Kimya Mühendisliği Bölümü KM 378 Mühendislik Ekonomisi
 Problem Seti 1 (Arz-Talep) 1. Bir firma, satış fiyatı ile talep arasında D=780$-10p eşitliğini geliştirmiştir. Aylık sabit gider 800$ ve ürün başına değişken gider 30$ dır. Aylık karı maksimum yapmak için
Problem Seti 1 (Arz-Talep) 1. Bir firma, satış fiyatı ile talep arasında D=780$-10p eşitliğini geliştirmiştir. Aylık sabit gider 800$ ve ürün başına değişken gider 30$ dır. Aylık karı maksimum yapmak için
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ
 DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
Ayrık zamanlı sinyaller için de ayrık zamanlı Fourier dönüşümleri kullanılmatadır.
 Bölüm 6 Z-DÖNÜŞÜM Sürekli zamanlı sinyallerin zaman alanından frekans alanına geçişi Fourier ve Laplace dönüşümleri ile mümkün olmaktadır. Laplace, Fourier dönüşümünün daha genel bir şeklidir. Ayrık zamanlı
Bölüm 6 Z-DÖNÜŞÜM Sürekli zamanlı sinyallerin zaman alanından frekans alanına geçişi Fourier ve Laplace dönüşümleri ile mümkün olmaktadır. Laplace, Fourier dönüşümünün daha genel bir şeklidir. Ayrık zamanlı
ĐST 349 Doğrusal Programlama ARA SINAV I 15 Kasım 2006
 ĐST 49 Doğrusal Programlama ARA SINAV I 15 Kasım 006 Adı Soyadı:KEY No: 1. Aşağıdaki problemi grafik yöntemle çözünüz. Đkinci kısıt için marjinal değeri belirleyiniz. Maximize Z X 1 + 4 X subject to: X
ĐST 49 Doğrusal Programlama ARA SINAV I 15 Kasım 006 Adı Soyadı:KEY No: 1. Aşağıdaki problemi grafik yöntemle çözünüz. Đkinci kısıt için marjinal değeri belirleyiniz. Maximize Z X 1 + 4 X subject to: X
Simpleks Yönteminde Kullanılan İlave Değişkenler (Eşitliğin yönüne göre):
 DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
Kübik Spline lar/cubic Splines
 Kübik spline lar önceki metodların aksine bütün data noktalarına tek bir fonksiyon/eğri uydurmaz. Bunun yerine her çift nokta için ayrı ayrı üçüncü dereceden polinomlar uydurur. x i noktasından geçen soldaki
Kübik spline lar önceki metodların aksine bütün data noktalarına tek bir fonksiyon/eğri uydurmaz. Bunun yerine her çift nokta için ayrı ayrı üçüncü dereceden polinomlar uydurur. x i noktasından geçen soldaki
Çalışma Soruları 1. a) x > 5 b) y < -3 c) xy > 0 d) x 3 < y e) (x-2) 2 + y 2 > 1. ( ) 2x
 Çalışma Soruları. Aşağıdaki denklemleri çözünüz: 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: 4x > 9 b) x 4 < - c)
Çalışma Soruları. Aşağıdaki denklemleri çözünüz: 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: 4x > 9 b) x 4 < - c)
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
4.1. Gölge Fiyat Kavramı
 4. Gölge Fiyat Kavramı 4.1. Gölge Fiyat Kavramı Gölge fiyatlar doğrusal programlama modellerinde kısıtlarla açıklanan kaynakların bizim için ne kadar değerli olduklarını gösterirler. Şimdi bir örnek üzerinde
4. Gölge Fiyat Kavramı 4.1. Gölge Fiyat Kavramı Gölge fiyatlar doğrusal programlama modellerinde kısıtlarla açıklanan kaynakların bizim için ne kadar değerli olduklarını gösterirler. Şimdi bir örnek üzerinde
Duyarlılık Analizi, modelde veri olarak kabul edilmiş parametrelerde meydana gelen değişimlerin optimum çözüme etkisinin incelenmesidir.
 ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS IV NOTLAR Bağlayıcı Kısıtlar ve Bağlayıcı Olmayan Kısıtlar: Bağlayıcı Kısıtlar, denklemleri optimum çözüm noktasında kesişen kısıtlardır. Bağlayıcı-Olmayan Kısıtlar,
ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS IV NOTLAR Bağlayıcı Kısıtlar ve Bağlayıcı Olmayan Kısıtlar: Bağlayıcı Kısıtlar, denklemleri optimum çözüm noktasında kesişen kısıtlardır. Bağlayıcı-Olmayan Kısıtlar,
ÇOK KRİTERLİ KARAR VERME HEDEF PROGRAMLAMA
 ÇOK KRİTERLİ KARAR VERME HEDEF PROGRAMLAMA KONU 10 Doç. Dr. Fazıl GÖKGÖZ 1 Genel Bilgiler Lineer programlama kapsamına tek bir amaç fonksiyonu uruma göre maksimize veya minimize eilmekteir. Ancak, gerçek
ÇOK KRİTERLİ KARAR VERME HEDEF PROGRAMLAMA KONU 10 Doç. Dr. Fazıl GÖKGÖZ 1 Genel Bilgiler Lineer programlama kapsamına tek bir amaç fonksiyonu uruma göre maksimize veya minimize eilmekteir. Ancak, gerçek
Cebirsel Fonksiyonlar
 Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
MATEMATİK-II dersi. Bankacılık ve Finans, İşletme, Uluslararası Ticaret. Bölümleri için FİNAL Çalışma Soruları
 MATEMATİK-II dersi Bankacılık ve Finans, İşletme, Uluslararası Ticaret Bölümleri için FİNAL Çalışma Soruları ] e d =? = u d= du du d= udu u u e d= e d= e = edu= e + c= e + c ] e d =? = + = e + c e d e
MATEMATİK-II dersi Bankacılık ve Finans, İşletme, Uluslararası Ticaret Bölümleri için FİNAL Çalışma Soruları ] e d =? = u d= du du d= udu u u e d= e d= e = edu= e + c= e + c ] e d =? = + = e + c e d e
DOĞRUSAL OLMAYAN PROGRAMLAMA -II- Tek değişkenli doğrusal olmayan karar modelinin çözümü
 DOĞRUSAL OLMAYAN PROGRAMLAMA -II- Tek değişkenli doğrusal olmayan karar modelinin çözümü Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi
DOĞRUSAL OLMAYAN PROGRAMLAMA -II- Tek değişkenli doğrusal olmayan karar modelinin çözümü Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi
Bir Doğrusal Programlama Modelinin Genel Yapısı
 Bir Doğrusal Programlama Modelinin Genel Yapısı Amaç Fonksiyonu Kısıtlar M i 1 N Z j 1 N j 1 a C j x j ij x j B i Karar Değişkenleri x j Pozitiflik Koşulu x j >= 0 Bu formülde kullanılan matematik notasyonların
Bir Doğrusal Programlama Modelinin Genel Yapısı Amaç Fonksiyonu Kısıtlar M i 1 N Z j 1 N j 1 a C j x j ij x j B i Karar Değişkenleri x j Pozitiflik Koşulu x j >= 0 Bu formülde kullanılan matematik notasyonların
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
Diferansiyel denklemler uygulama soruları
 . Aşağıdaki diferansiyel denklemleri sınıflandırınız. a) d y d d + y = 0 b) 5 d dt + 4d + 9 = cos 3t dt Diferansiyel denklemler uygulama soruları 0.0.3 c) u + u [ ) ] d) y + = c d. y + 3 = 0 denkleminin,
. Aşağıdaki diferansiyel denklemleri sınıflandırınız. a) d y d d + y = 0 b) 5 d dt + 4d + 9 = cos 3t dt Diferansiyel denklemler uygulama soruları 0.0.3 c) u + u [ ) ] d) y + = c d. y + 3 = 0 denkleminin,
EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü Dr. Özgür Kabak Doğrusal olmayan programlama Tek değişkenli DOP ların çözümü Uç noktaların analizi Altın kesit Araması Çok değişkenli DOP ların
EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü Dr. Özgür Kabak Doğrusal olmayan programlama Tek değişkenli DOP ların çözümü Uç noktaların analizi Altın kesit Araması Çok değişkenli DOP ların
Ödev TeslimTarihi 12.Ocak 2010 KAR PLANLAMASI
 İTÜ Tekstil Teknolojileri ve Tasarımı Fakültesi / Tekstil Mühendisliği Bölümü 2009-2010Öğretim Yılı / Güz Yarıyılı TEK485-MALİYET MUHASEBESİ DERSİ ÖDEV5 (YÖNETİM MUHASEBESİ) 30.Aralık.2009 Ödev TeslimTarihi
İTÜ Tekstil Teknolojileri ve Tasarımı Fakültesi / Tekstil Mühendisliği Bölümü 2009-2010Öğretim Yılı / Güz Yarıyılı TEK485-MALİYET MUHASEBESİ DERSİ ÖDEV5 (YÖNETİM MUHASEBESİ) 30.Aralık.2009 Ödev TeslimTarihi
DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY)
 DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY) 1 DOĞRUSAL PROGRAMLAMADA İKİLİK (DUALİTE-DUALITY) Doğrusal programlama modelleri olarak adlandırılır. Aynı modelin değişik bir düzende oluşturulmasıyla Dual (İkilik)
DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY) 1 DOĞRUSAL PROGRAMLAMADA İKİLİK (DUALİTE-DUALITY) Doğrusal programlama modelleri olarak adlandırılır. Aynı modelin değişik bir düzende oluşturulmasıyla Dual (İkilik)
OPTİMİZASYON TEKNİKLERİ-2. Hafta
 GİRİŞ OPTİMİZASYON TEKNİKLERİ-2. Hafta Mühendislik açısından bir işin tasarlanıp, gerçekleştirilmesi yeterli değildir. İşin en iyi çözüm yöntemiyle en verimli bir şekilde yapılması bir anlam ifade eder.
GİRİŞ OPTİMİZASYON TEKNİKLERİ-2. Hafta Mühendislik açısından bir işin tasarlanıp, gerçekleştirilmesi yeterli değildir. İşin en iyi çözüm yöntemiyle en verimli bir şekilde yapılması bir anlam ifade eder.
2017/3. Dönem Yeminli Mali Müşavirlik Sınavı Yönetim Muhasebesi 20 Kasım 2017 Pazartesi (Sınav Süresi 2 Saat)
 2017/3. Dönem Yeminli Mali Müşavirlik Sınavı Yönetim Muhasebesi 20 Kasım 2017 Pazartesi 18.00 (Sınav Süresi 2 Saat) Sorular -I- SORULAR (10P) 1-İşletmenin tüm bölümleri ve değer zinciri elemanlarının (tedarikçiler,
2017/3. Dönem Yeminli Mali Müşavirlik Sınavı Yönetim Muhasebesi 20 Kasım 2017 Pazartesi 18.00 (Sınav Süresi 2 Saat) Sorular -I- SORULAR (10P) 1-İşletmenin tüm bölümleri ve değer zinciri elemanlarının (tedarikçiler,
GAMS Kullanım Notları
 GAMS Kullanım Notları Dilay Çelebi İstanbul Teknik Üniversitesi 1. Giriş Aşağıdaki DP problemini ele aldığımızı varsayalım. Z min = 4x 1 + 2x 2 + 33x 3 (1) x 1 4x 2 + x 3 12 (2) 9x 1 + 6x 2 = 15 (3) 5x
GAMS Kullanım Notları Dilay Çelebi İstanbul Teknik Üniversitesi 1. Giriş Aşağıdaki DP problemini ele aldığımızı varsayalım. Z min = 4x 1 + 2x 2 + 33x 3 (1) x 1 4x 2 + x 3 12 (2) 9x 1 + 6x 2 = 15 (3) 5x
SAY 203 MİKRO İKTİSAT
 SAY 203 MİKRO İKTİSAT Esneklikler YRD. DOÇ. DR. EMRE ATILGAN SAY 203 MİKRO İKTİSAT - YRD. DOÇ. DR. EMRE ATILGAN 1 ESNEKLİKLER Talep Esneklikleri Talep esneklikleri: Bir malın talebinin talebi etkileyen
SAY 203 MİKRO İKTİSAT Esneklikler YRD. DOÇ. DR. EMRE ATILGAN SAY 203 MİKRO İKTİSAT - YRD. DOÇ. DR. EMRE ATILGAN 1 ESNEKLİKLER Talep Esneklikleri Talep esneklikleri: Bir malın talebinin talebi etkileyen
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
TEKP 409 TEKSTİL TERBİYESİNDE ÜRETİM VE MALİYET HESAPLARI
 T.C. ERCİYES ÜNİVERSİTESİ TEKSTİL MÜHENDİSLİĞİ BÖLÜMÜ 2017-2018 Öğretim Yılı Güz Dönemi TEKP 409 TEKSTİL TERBİYESİNDE ÜRETİM VE MALİYET HESAPLARI Seçmeli Lisans Dersi (2 0 2) Yrd. Doç. Dr. İlhan ÖZEN Erciyes
T.C. ERCİYES ÜNİVERSİTESİ TEKSTİL MÜHENDİSLİĞİ BÖLÜMÜ 2017-2018 Öğretim Yılı Güz Dönemi TEKP 409 TEKSTİL TERBİYESİNDE ÜRETİM VE MALİYET HESAPLARI Seçmeli Lisans Dersi (2 0 2) Yrd. Doç. Dr. İlhan ÖZEN Erciyes
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
Yöneylem Araştırması II
 Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Matematiksel modellerin elemanları
 Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
MAT101 MATEMATİK I BÖLÜM 3 FONKSİYONLAR
 MAT101 MATEMATİK I BÖLÜM 3 FONKSİYONLAR Yrd. Doç. Dr. Furkan BAŞER Ankara Üniversitesi Uygulamalı Bilimler Fakültesi GİRİŞ Fonksiyon kavramı, matematikte en önemli kavramlardan biridir. Temel düzeyin ötesinde
MAT101 MATEMATİK I BÖLÜM 3 FONKSİYONLAR Yrd. Doç. Dr. Furkan BAŞER Ankara Üniversitesi Uygulamalı Bilimler Fakültesi GİRİŞ Fonksiyon kavramı, matematikte en önemli kavramlardan biridir. Temel düzeyin ötesinde
4. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
6. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM. Yazan SAYIN SAN
 6. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM Yazan SAYIN SAN SAN / İKTİSADİ MATEMATİK / 2 A.5. Doğrusal olmayan fonksiyonların eğimi Doğrusal fonksiyonlarda eğim her noktada sabittir
6. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM Yazan SAYIN SAN SAN / İKTİSADİ MATEMATİK / 2 A.5. Doğrusal olmayan fonksiyonların eğimi Doğrusal fonksiyonlarda eğim her noktada sabittir
Modelleme bir sanattan çok bir Bilim olarak tanımlanabilir. Bir model kurucu için en önemli karar model seçiminde ilişkileri belirlemektir.
 MODELLEME MODELLEME Matematik modelleme yaklaşımı sistemlerin daha iyi anlaşılması, analiz edilmesi ve tasarımının etkin ve ekonomik bir yoludur. Modelleme karmaşık parametrelerin belirlenmesi için iyi
MODELLEME MODELLEME Matematik modelleme yaklaşımı sistemlerin daha iyi anlaşılması, analiz edilmesi ve tasarımının etkin ve ekonomik bir yoludur. Modelleme karmaşık parametrelerin belirlenmesi için iyi
Analog Alçak Geçiren Filtre Karakteristikleri
 Analog Alçak Geçiren Filtre Karakteristikleri Analog alçak geçiren bir filtrenin genlik yanıtı H a (jω) aşağıda gösterildiği gibi verilebilir. Ω p : Geçirme bandı kenar frekansı Ω s : Söndürme bandı kenar
Analog Alçak Geçiren Filtre Karakteristikleri Analog alçak geçiren bir filtrenin genlik yanıtı H a (jω) aşağıda gösterildiği gibi verilebilir. Ω p : Geçirme bandı kenar frekansı Ω s : Söndürme bandı kenar
SİSTEMİ YRD.DOÇ. DR. CABBAR VEYSEL BAYSAL ELEKTRIK & ELEKTRONIK YÜK. MÜH.
 EM 420 Yüksek Gerilim Tekniği DÜZLEMSEL ELEKTROT SİSTEMİ YRD.DOÇ. DR. CABBAR VEYSEL BAYSAL ELEKTRIK & ELEKTRONIK YÜK. MÜH. Not: Tüm slaytlar, listelenen ders kaynaklarından alıntı yapılarak ve faydalanılarak
EM 420 Yüksek Gerilim Tekniği DÜZLEMSEL ELEKTROT SİSTEMİ YRD.DOÇ. DR. CABBAR VEYSEL BAYSAL ELEKTRIK & ELEKTRONIK YÜK. MÜH. Not: Tüm slaytlar, listelenen ders kaynaklarından alıntı yapılarak ve faydalanılarak
İÇİNDEKİLER. Bölüm 1 MATEMATİKSEL İKTİSADA GİRİŞ 11 1.1.İktisat Hakkında 12 1.2.İktisatta Grafik ve Matematik Kullanımı 13
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 MATEMATİKSEL İKTİSADA GİRİŞ 11 1.1.İktisat Hakkında 12 1.2.İktisatta Grafik ve Matematik Kullanımı 13 Bölüm 2 STATİK DENGE ANALİZİ 19 2.1 İktisatta Denge Kavramı 20 2.1.1.
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 MATEMATİKSEL İKTİSADA GİRİŞ 11 1.1.İktisat Hakkında 12 1.2.İktisatta Grafik ve Matematik Kullanımı 13 Bölüm 2 STATİK DENGE ANALİZİ 19 2.1 İktisatta Denge Kavramı 20 2.1.1.
EMM3208 Optimizasyon Teknikleri
 2017-2018 Bahar Yarıyılı Balıkesir Üniversitesi Endüstri Mühendisliği Bölümü EMM3208 Optimizasyon Teknikleri (GAMS Kurulumu ve Temel Özellikleri, GAMS ile Modellemeye Giriş) 3 Yrd. Doç. Dr. İbrahim Küçükkoç
2017-2018 Bahar Yarıyılı Balıkesir Üniversitesi Endüstri Mühendisliği Bölümü EMM3208 Optimizasyon Teknikleri (GAMS Kurulumu ve Temel Özellikleri, GAMS ile Modellemeye Giriş) 3 Yrd. Doç. Dr. İbrahim Küçükkoç
a2 b3 cij: birim başına ulaşım maliyeti xij: taşıma miktarı
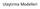 Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Örnek: bir montaj hattı için Dizayn Kapasitesi=100 adet/gün; Etkin Kapasite=80 adet/gün; Gerçek Kapasite=72 adet/gün olarak verildiğinde; Verimlilik=
 1 Kapasite, üretim oranı olarak ölçüldüğünde, gerçek üretim miktarının maksimum üretim miktarına oranı söz konusudur. Maksimum üretim fiziksel yapı ile ilgili olduğundan kolay belirlenebilir. Ancak gerçek
1 Kapasite, üretim oranı olarak ölçüldüğünde, gerçek üretim miktarının maksimum üretim miktarına oranı söz konusudur. Maksimum üretim fiziksel yapı ile ilgili olduğundan kolay belirlenebilir. Ancak gerçek
2018/1. Dönem Yeminli Mali Müşavirlik Sınavı Yönetim Muhasebesi 2 Nisan 2018 Pazartesi (Sınav Süresi 2 Saat)
 2018/1. Dönem Yeminli Mali Müşavirlik Sınavı Yönetim Muhasebesi 2 Nisan 2018 Pazartesi 18.00 (Sınav Süresi 2 Saat) Sorular Soru 1.Batu şirketi tek bir mamulün üretimini gerçekleştirmekte ve yılda 80.000
2018/1. Dönem Yeminli Mali Müşavirlik Sınavı Yönetim Muhasebesi 2 Nisan 2018 Pazartesi 18.00 (Sınav Süresi 2 Saat) Sorular Soru 1.Batu şirketi tek bir mamulün üretimini gerçekleştirmekte ve yılda 80.000
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
TRAKYA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MAKİNA MÜHENDİSLİĞİ ANABİLİM DALI DOKTORA PROGRAMI ŞEKİL TANIMA ÖDEV 2 KONU : DESTEK VEKTÖR MAKİNELERİ
 TRAKYA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MAKİNA MÜHENDİSLİĞİ ANABİLİM DALI DOKTORA PROGRAMI ŞEKİL TANIMA ÖDEV 2 KONU : DESTEK VEKTÖR MAKİNELERİ Kenan KILIÇASLAN Okul No:1098107203 1. DESTEK VEKTÖR MAKİNELER
TRAKYA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MAKİNA MÜHENDİSLİĞİ ANABİLİM DALI DOKTORA PROGRAMI ŞEKİL TANIMA ÖDEV 2 KONU : DESTEK VEKTÖR MAKİNELERİ Kenan KILIÇASLAN Okul No:1098107203 1. DESTEK VEKTÖR MAKİNELER
Genetik Algoritmalar. Bölüm 1. Optimizasyon. Yrd. Doç. Dr. Adem Tuncer E-posta:
 Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: adem.tuncer@yalova.edu.tr Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: adem.tuncer@yalova.edu.tr Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
Ulaştırma ve Atama. Konu 2. Ulaştırma Modeli. Doç. Dr. Fazıl GÖKGÖZ
 Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda ürün
Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda ürün
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik (Eşitlik Kısıtlı Türevli Yöntem) Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik (Eşitlik Kısıtlı Türevli Yöntem) Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde
ÖĞRENME ALANI TEMEL MATEMATİK BÖLÜM TÜREV. ALT ÖĞRENME ALANLARI 1) Türev 2) Türev Uygulamaları TÜREV
 - 1 - ÖĞRENME ALANI TEMEL MATEMATİK BÖLÜM TÜREV ALT ÖĞRENME ALANLARI 1) Türev 2) Türev Uygulamaları TÜREV Kazanım 1 : Türev Kavramını fiziksel ve geometrik uygulamalar yardımıyla açıklar, türevin tanımını
- 1 - ÖĞRENME ALANI TEMEL MATEMATİK BÖLÜM TÜREV ALT ÖĞRENME ALANLARI 1) Türev 2) Türev Uygulamaları TÜREV Kazanım 1 : Türev Kavramını fiziksel ve geometrik uygulamalar yardımıyla açıklar, türevin tanımını
Elemanter fonksiyonlarla yaklaşım ve hata
 Elemanter fonksiyonlarla yaklaşım ve hata Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi Matematik Bölümü Kasım, 2018 e 5 Kasım, 2018 1 / 48 Elemanter fonksiyonlarla yaklaşım ve hata
Elemanter fonksiyonlarla yaklaşım ve hata Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi Matematik Bölümü Kasım, 2018 e 5 Kasım, 2018 1 / 48 Elemanter fonksiyonlarla yaklaşım ve hata
a) x +3 = 8 b) x -4 = -2 c) x -7 = 4 d) x +5 = 6 e) x +8 = 2 f) x -1= -8 x +3 = 5 denkleminin çözümünü bulunuz.
 Denklemler bilinmeyen - cebirsel ifade - 7 denklem Bir cebirsel ifade bir sonuca eşit oluyorsa buna denklem denir. Bazı denklemlerin çözümü yoktur, bazı denklemlerin sonsuz, bazı denklemlerin bir, iki,
Denklemler bilinmeyen - cebirsel ifade - 7 denklem Bir cebirsel ifade bir sonuca eşit oluyorsa buna denklem denir. Bazı denklemlerin çözümü yoktur, bazı denklemlerin sonsuz, bazı denklemlerin bir, iki,
Selçuk Üniversitesi 26 Aralık, 2013 Beyşehir Turizm Fakültesi-Konaklama İşletmeciliği Genel Ekonomi Dr. Alper Sönmez. Soru Seti 3
 Soru Seti 3 1) Q D = 100 2P talep denklemi ve Q S = P 20 arz denklemi verilmiştir. Üretici ve tüketici rantlarını hesaplayınız. Cevap: Öncelikle arz ve talep denklemlerini eşitleyerek denge fiyat ve miktarı
Soru Seti 3 1) Q D = 100 2P talep denklemi ve Q S = P 20 arz denklemi verilmiştir. Üretici ve tüketici rantlarını hesaplayınız. Cevap: Öncelikle arz ve talep denklemlerini eşitleyerek denge fiyat ve miktarı
2015 2016 BAHAR YARIYILI İKTİSADİ MATEMATİK VİZE SORU VE CEVAPLARI 1) Bir mala ait arz ve talep fonksiyonları aşağıdaki gibidir:
 2015 2016 BAHAR YARIYILI İKTİSADİ MATEMATİK VİZE SORU VE CEVAPLARI 1) Bir mala ait arz ve talep fonksiyonları aşağıdaki gibidir: a) Bu malın arz ve talep denklemlerinin grafiklerini çiziniz (5 puan) (DÖÇ.1-).
2015 2016 BAHAR YARIYILI İKTİSADİ MATEMATİK VİZE SORU VE CEVAPLARI 1) Bir mala ait arz ve talep fonksiyonları aşağıdaki gibidir: a) Bu malın arz ve talep denklemlerinin grafiklerini çiziniz (5 puan) (DÖÇ.1-).
Doğrusal Programlamada Grafik Çözüm
 Doğrusal Programlamada Grafik Çözüm doğrusal programlama PROBLEMİN ÇÖZÜLMESİ (OPTİMUM ÇÖZÜM) Farklı yöntemlerle çözülebilir Grafik çözüm (değişken sayısı 2 veya 3 olabilir) Simpleks çözüm Bilgisayar yazılımlarıyla
Doğrusal Programlamada Grafik Çözüm doğrusal programlama PROBLEMİN ÇÖZÜLMESİ (OPTİMUM ÇÖZÜM) Farklı yöntemlerle çözülebilir Grafik çözüm (değişken sayısı 2 veya 3 olabilir) Simpleks çözüm Bilgisayar yazılımlarıyla
Yrd. Doç. Dr. A. Burak İNNER
 Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
Total Contribution. Reduced Cost. X1 37,82 480 18.153,85 0 basic 320 512. X2 22,82 320 7.302,56 0 basic 300 M. Slack or
 HRS şirketi BRN Endüstrileri ile bir anlaşma yapmış ve her ay BRN ye üretebildiği kadar A ürününden sağlamayı garanti etmiştir. HRS de vasıflı ustalar ve çıraklar çalışmaktadır. Bir usta, bir saatte 3
HRS şirketi BRN Endüstrileri ile bir anlaşma yapmış ve her ay BRN ye üretebildiği kadar A ürününden sağlamayı garanti etmiştir. HRS de vasıflı ustalar ve çıraklar çalışmaktadır. Bir usta, bir saatte 3
Ders 10. Prof.Dr.Haydar Eş Prof.Dr.Timur Karaçay. Simpleks Yöntemine Giriş Alıştırmalar 10
 Bölüm 10 Ders 10 Simpleks Yöntemine Giriş 10.1 Alıştırmalar 10 Prof.Dr.Haydar Eş Prof.Dr.Timur Karaçay 197 198 BÖLÜM 10. DERS 10 1. Soru 1 1. Aşağıda verilen simpleks tablolarında temel, temel olmayan,
Bölüm 10 Ders 10 Simpleks Yöntemine Giriş 10.1 Alıştırmalar 10 Prof.Dr.Haydar Eş Prof.Dr.Timur Karaçay 197 198 BÖLÜM 10. DERS 10 1. Soru 1 1. Aşağıda verilen simpleks tablolarında temel, temel olmayan,
Öğr. Gör. Barış Alpaslan
 Dersin Adı DERS ÖĞRETİM PLANI Matematik I Dersin Kodu ECO 05/04 Dersin Türü (Zorunlu, Seçmeli) Dersin Seviyesi (Ön Lisans, Lisans, Yüksek Lisans, Doktora) Dersin AKTS Kredisi 5 Haftalık Ders Saati 3 Haftalık
Dersin Adı DERS ÖĞRETİM PLANI Matematik I Dersin Kodu ECO 05/04 Dersin Türü (Zorunlu, Seçmeli) Dersin Seviyesi (Ön Lisans, Lisans, Yüksek Lisans, Doktora) Dersin AKTS Kredisi 5 Haftalık Ders Saati 3 Haftalık
SONLU FARKLAR GENEL DENKLEMLER
 SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
9. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM. Yazan SAYIN SAN
 9. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM Yazan SAYIN SAN SAN / İKTİSADİ MATEMATİK / 2 A.8. TAM REKABET PİYASALARI A.8.1. Temel Varsayımları Atomisite Koşulu: Piyasada alıcı ve satıcılar,
9. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM Yazan SAYIN SAN SAN / İKTİSADİ MATEMATİK / 2 A.8. TAM REKABET PİYASALARI A.8.1. Temel Varsayımları Atomisite Koşulu: Piyasada alıcı ve satıcılar,
11. HAFTA MÜHENDİSLİK EKONOMİSİ. Başabaş Analiz Yöntemi. Yrd. Doç. Dr. Tahir AKGÜL
 11. HAFTA MÜHENDİSLİK EKONOMİSİ Yrd. Doç. Dr. Tahir AKGÜL Başabaş Analiz Yöntemi BAŞA-BAŞ NOKTASI ANALİZİ Başa-baş noktası, üretim miktarı, maliyet akışları ve satış gelirleri arasındaki ilişkilere dayanarak,
11. HAFTA MÜHENDİSLİK EKONOMİSİ Yrd. Doç. Dr. Tahir AKGÜL Başabaş Analiz Yöntemi BAŞA-BAŞ NOKTASI ANALİZİ Başa-baş noktası, üretim miktarı, maliyet akışları ve satış gelirleri arasındaki ilişkilere dayanarak,
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
biçimindeki ifadelere iki değişkenli polinomlar denir. Bu polinomda aynı terimdeki değişkenlerin üsleri toplamından en büyük olanına polinomun dereces
 TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER
 KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER Örnek 1: Bir boya fabrikası hem iç hem dış boya üretiyor. Boya üretiminde A ve B olmak üzere iki tip hammadde kullanılıyor. Bir günde A hammaddesinden
KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER Örnek 1: Bir boya fabrikası hem iç hem dış boya üretiyor. Boya üretiminde A ve B olmak üzere iki tip hammadde kullanılıyor. Bir günde A hammaddesinden
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
1. Açık Bir Ekonomide Denge Çıktı (Gelir)
 IKTI 2 Mayıs 24 DERS NOTU 5 TOPLAM HARCAMALAR VE DENGE ÇIKTI (3) Dersin içeriği:. AÇIK BİR EKONOMİDE DENGE ÇIKTI (GELİR)... A. DENGE İÇİN SIZINTILAR/ENJEKSİYONLAR YAKLAŞIMI... 5 B. DEVLET HARCAMALARI ÇARPANI...
IKTI 2 Mayıs 24 DERS NOTU 5 TOPLAM HARCAMALAR VE DENGE ÇIKTI (3) Dersin içeriği:. AÇIK BİR EKONOMİDE DENGE ÇIKTI (GELİR)... A. DENGE İÇİN SIZINTILAR/ENJEKSİYONLAR YAKLAŞIMI... 5 B. DEVLET HARCAMALARI ÇARPANI...
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir.
 1 DENKLEMLER: Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir. Bir denklemde eşitliği sağlayan(doğrulayan) değerlere; verilen denklemin kökleri veya
1 DENKLEMLER: Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir. Bir denklemde eşitliği sağlayan(doğrulayan) değerlere; verilen denklemin kökleri veya
Uzayda iki doğrunun ortak dikme doğrusunun denklemi
 Uzayda iki doğrunun ortak dikme doğrusunun denklemi Uzayda verilen d 1 ve d aykırı doğrularının ikisine birden dik olan doğruya ortak dikme doğrusu denir... olmak üzere bu iki doğru denkleminde değilse
Uzayda iki doğrunun ortak dikme doğrusunun denklemi Uzayda verilen d 1 ve d aykırı doğrularının ikisine birden dik olan doğruya ortak dikme doğrusu denir... olmak üzere bu iki doğru denkleminde değilse
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Öğrenim Kazanımları Bu programı başarı ile tamamlayan öğrenci;
 Image not found http://bologna.konya.edu.tr/panel/images/pdflogo.png Ders Adı : Matematik Ders No : 0690230018 Teorik : 4 Pratik : 0 Kredi : 4 ECTS : 4 Ders Bilgileri Ders Türü Öğretim Dili Öğretim Tipi
Image not found http://bologna.konya.edu.tr/panel/images/pdflogo.png Ders Adı : Matematik Ders No : 0690230018 Teorik : 4 Pratik : 0 Kredi : 4 ECTS : 4 Ders Bilgileri Ders Türü Öğretim Dili Öğretim Tipi
ÜNİTE. MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI İÇİNDEKİLER HEDEFLER DOĞRULAR VE PARABOLLER
 HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
Ders İçerik Bilgisi. Karmaşık Sistemlerin Tek Bir Transfer Fonksiyonuna İndirgenmesi
 Dr. Hakan TERZİOĞLU Ders İçerik Bilgisi Karmaşık Sistemlerin Tek Bir Transfer Fonksiyonuna İndirgenmesi 1. Blok Diyagramları İle (GeçenHafta) 2. İşaret Akış Diyagramları İle (Bu Hafta) Sadeleştirme yoluyla
Dr. Hakan TERZİOĞLU Ders İçerik Bilgisi Karmaşık Sistemlerin Tek Bir Transfer Fonksiyonuna İndirgenmesi 1. Blok Diyagramları İle (GeçenHafta) 2. İşaret Akış Diyagramları İle (Bu Hafta) Sadeleştirme yoluyla
MATEMATiKSEL iktisat
 DİKKAT!... BU ÖZET 8 ÜNİTEDİR BU- RADA İLK ÜNİTE GÖSTERİLMEKTEDİR. MATEMATiKSEL iktisat KISA ÖZET KOLAY AOF Kolayaöf.com 0362 233 8723 Sayfa 2 içindekiler 1.ünite-Türev ve Kuralları..3 2.üniteTek Değişkenli
DİKKAT!... BU ÖZET 8 ÜNİTEDİR BU- RADA İLK ÜNİTE GÖSTERİLMEKTEDİR. MATEMATiKSEL iktisat KISA ÖZET KOLAY AOF Kolayaöf.com 0362 233 8723 Sayfa 2 içindekiler 1.ünite-Türev ve Kuralları..3 2.üniteTek Değişkenli
10. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM. Yazan SAYIN SAN
 10. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM Yazan SAYIN SAN SAN / İKTİSADİ MATEMATİK / 2 A.9. TEKEL (MONOPOL) Piyasada bir satıcı ve çok sayıda alıcının bulunmasıdır. Piyasaya başka
10. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM Yazan SAYIN SAN SAN / İKTİSADİ MATEMATİK / 2 A.9. TEKEL (MONOPOL) Piyasada bir satıcı ve çok sayıda alıcının bulunmasıdır. Piyasaya başka
Konu 2. Y. Doç. Dr. Fazıl GÖKGÖZ
 Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan kl temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda
Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan kl temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda
GAMS Kurulumu ve Temel Özellikleri GAMS ile Modellemeye Giriş, Örnek Problemler
 2017-2018 Bahar Yarıyılı Balıkesir Üniversitesi Endüstri Mühendisliği Bölümü GAMS Kurulumu ve Temel Özellikleri GAMS ile Modellemeye Giriş, Örnek Problemler Yrd. Doç. Dr. İbrahim Küçükkoç http://ikucukkoc.baun.edu.tr
2017-2018 Bahar Yarıyılı Balıkesir Üniversitesi Endüstri Mühendisliği Bölümü GAMS Kurulumu ve Temel Özellikleri GAMS ile Modellemeye Giriş, Örnek Problemler Yrd. Doç. Dr. İbrahim Küçükkoç http://ikucukkoc.baun.edu.tr
Zaman kazandıran ipucu: MR eğimi talebin iki katı. Bu her zaman lineer talepte doğru.(bunu geri kalan çözümlerde kullanacağız.)
 Sloan Yönetim Okulu 15.010/15.011 Massachusetts Teknoloji Enstitüsü ÖDEV SETİ #4 ÇÖZÜMLER 1. a. Eğer piyasalar serbest ticarete açıksa tekel piyasaları ayrı tutamaz. Arbitiraj fırsatları P = P1 = P2 anlamına
Sloan Yönetim Okulu 15.010/15.011 Massachusetts Teknoloji Enstitüsü ÖDEV SETİ #4 ÇÖZÜMLER 1. a. Eğer piyasalar serbest ticarete açıksa tekel piyasaları ayrı tutamaz. Arbitiraj fırsatları P = P1 = P2 anlamına
SAYISAL ANALİZ. Doç. Dr. Cüneyt BAYILMIŞ. Sayısal Analiz. Doç.Dr. Cüneyt BAYILMIŞ
 SAYISAL ANALİZ Doç. Dr. Cüneyt BAYILMIŞ 1 SAYISAL ANALİZ 1. Hafta SAYISAL ANALİZE GİRİŞ 2 AMAÇ Mühendislik problemlerinin çözümünde kullanılan sayısal analiz yöntemlerinin algoritmik olarak çözümü ve bu
SAYISAL ANALİZ Doç. Dr. Cüneyt BAYILMIŞ 1 SAYISAL ANALİZ 1. Hafta SAYISAL ANALİZE GİRİŞ 2 AMAÇ Mühendislik problemlerinin çözümünde kullanılan sayısal analiz yöntemlerinin algoritmik olarak çözümü ve bu
EM302 Yöneylem Araştırması 2. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
2016/1.DÖNEM YEMİNLİ MALİ MÜŞAVİRLİK SINAVLARI YÖNETİM MUHASEBESİ 28 Mart 2016-Pazartesi 18:00
 2016/1.DÖNEM YEMİNLİ MALİ MÜŞAVİRLİK SINAVLARI YÖNETİM MUHASEBESİ 28 Mart 2016-Pazartesi 18:00 SORULAR Soru 1 Aşağıdaki kavramları kısaca açıklayınız (25 puan) a. Fırsat maliyeti (5 puan) b. Faaliyet kaldıracı
2016/1.DÖNEM YEMİNLİ MALİ MÜŞAVİRLİK SINAVLARI YÖNETİM MUHASEBESİ 28 Mart 2016-Pazartesi 18:00 SORULAR Soru 1 Aşağıdaki kavramları kısaca açıklayınız (25 puan) a. Fırsat maliyeti (5 puan) b. Faaliyet kaldıracı
Kısıtsız Optimizasyon OPTİMİZASYON Kısıtsız Optimizasyon
 OPTİMİZASYON Bu bölümde çok değişkenli kısıtsız optimizasyon problemlerinin çözüm yöntemleri incelenecektir. Bu bölümde anlatılacak yöntemler, kısıtlı optimizasyon problemlerini de çözebilmektedir. Bunun
OPTİMİZASYON Bu bölümde çok değişkenli kısıtsız optimizasyon problemlerinin çözüm yöntemleri incelenecektir. Bu bölümde anlatılacak yöntemler, kısıtlı optimizasyon problemlerini de çözebilmektedir. Bunun
