TEOG. Kümeler KÜME VE ELEMAN KAVRAMI ÖRNEK KÜMELERİN GÖSTERİMİ ÖRNEK ÖRNEK KÜMENİN ELEMAN SAYISI ÖRNEK 3. ORTAK ÖZELLİK YÖNTEMİ 1.
|
|
|
- Duygu Ayhan
- 7 yıl önce
- İzleme sayısı:
Transkript
1 TEOG ümeler ÜE VE EEN VRI Elemanları belirlenebilen, belirli bir anlam taşıyan canlı ya da cansız varlıkların veya kavramların oluşturduğu topluluğa küme denir. ümeyi oluşturan varlıkların, kavramların her birine kümenin elemanı denir. ümenin elemanları sembolü ile gösterilir. ümenin elemanı olmayanlar ise sembolü kullanılarak gösterilir. a c e b d ir topluluğun küme belirtmesi için;. ümeyi oluşturan elemanların açık ve kesin belli olması gerekir.. ümenin elemanlarının farklı olması gerekir.. ümelerde her eleman bir kez yazılır.. ümeler büyük harf ile adlandırılır. ÜEERİN GÖSTERİİ. İSTE YÖNTEİ ümenin elemanlarının { } sembolü içine elemanlar virgülle ayrılarak açık olarak gösterilmesidir., 5, 7, b, x,,, 0,, 7, elemanlarını kümesinde liste yöntemi ile gösterelim. = {b, x,, 5, 7,,, 0} şeklinde olur. üme oluşturulurken aynı elemanlar bir defa yazılır.. ORT ÖZEİ YÖNTEİ ümenin elemanlarının ortak özelliklerinin küme sembolü içerisinde açık olarak belirtilmesidir. Ortak özellik yönteminde : veya sembolleri kullanılır. u semboller öyleki anlamına gelir. 9 dan küçük doğal sayıların oluşturduğu kümeyi ortak özellik yöntemiyle gösterelim. = {x x, 9 dan küçük} = {x x < 9 ve x N}. ir kümenin elemanlarının yerlerinin değişmesi kümeyi değiştirmez. = {a, b, c, d}={b, c, a, d} ={a, c, b, d}. Her küme ortak özellik yöntemiyle yazılamaz. ÜENİN EEN SYISI ir kümedeki elemanların sayısına kümenin eleman sayısı denir. n tane elamanı bulunan bir kümesinin eleman sayısı s() = n şeklinde gösterilir.. VENN ŞESI YÖNTEİ ümenin elemanlarının kapalı bir düzlemsel bölge içerisinde gösterilmesidir. = {x x, 7 den küçük doğal sayılar} kümesinin eleman sayısı kaçtır? ) 5 ) ) 7 D) 8 7 T E O G TETİ O N U N T I I
2 ÜEER x bir doğal sayı olmak üzere kümesinin elemanları 0 x < 7 aralığındadır. u aralıkta 7 tane doğal sayı vardır. Dolayısıyla kümesinin eleman sayısı s()=7 olur. evap dir. OŞ ÜE Hiç elemanı olmayan kümeye boş küme denir. oş küme veya { } sembolleri ile gösterilir.. { } kümesi boş küme değildir. u küme bir elemanlı bir kümedir. { }. {0} kümesi boş küme değildir. {0} = {x 78 x < 7, x N} kümesinin eleman sayısı kaçtır? ) 0 ) 7 ) 5 D) 78 kümesi dir. Çünkü kümesinin elemanları doğal sayılardır. Doğal sayılar pozitif değerli olduğundan 78 ile 7 arasında bir doğal sayı yoktur. Dolayısıyla kümesinin eleman sayısı 0 dır. evap dır. ÜEERİN RŞIŞTIRISI. DEN ÜEER Eleman sayıları eşit olan kümelere denk kümeler denir. Denk kümeler sembolü ile gösterilir. s() = s() dir. = {x < x, x N} kümesine denk olan küme aşağıdakilerden hangisidir? ) = {a, b,, } ) = {, a,,, b} ) = {,,,, 5, } D) N = {,,, } = {x < x, x N} kümesinin = 5 tane elamanı vardır. Yani s() = 5 dir. s() =, s() = 5, s() =, s(n) = dür. s() = s() = 5 olduğundan ve kümeleri denk kümelerdir. evap dir.. EŞİT ÜEER ütün elemanları aynı olan kümelere eşit kümeler denir. Eşit kümeler = sembolü ile gösterilir. = {çift rakamlar} kümesine eşit olan küme aşağıdakilerden hangisidir? ) ) P S ) D) kümesinin elemanları 0,,,, 8 olur. Dolayısıyla kümesi ile Ş kümesinin elemanları aynı ve eleman sayıları eşit olduğundan ile Ş eşit kümelerdir; yani = Ş dir. evap D dir. R Ş 8 0 Eşit kümeler her zaman denk kümelerdir. Fakat denk kümeler her zaman eşit küme olmayabilir. 8 T E O G TETİ O N U N T I I 8
3 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r. FRI ÜEER azı elemanları aynı olan veya tamamen farklı elemanlardan oluşan kümelere denir. Farklı kümeler sembolü ile gösterilir. Venn Şeması ile gösterelim., şağıda verilen kümelerden hangisi farklı kümelerdir? ) = {a, b, c} = {x, y, z} ) = {ir basamaklı tek sayılar} = {,, 5, 7, 9} ) = {,, O, } = {,,, O} D) = {, a,,, b} = {,,, a, b},, D seçeneklerindeki kümeler aynı elemanlardan oluştuklarından eşit kümelerdir. Fakat seçeneğindeki küme tamamen farklı elemanlardan oluştuklarından farklı kümelerdir. evap dır. T ÜENİN ÖZEİERİ. oş küme her kümenin alt kümesidir.,, herhangi üç küme olsun.,, dir.. Her küme kendisinin alt kümesidir. herhangi bir küme olsun dır.. irbirinin alt kümesi olan iki küme eşittir. ve = dir.. kümesi kümesinin alt kümesi, kümesi de kümesinin alt kümesi ise kümesi kümesinin alt kümesidir. ve dir. ir ümenin lt üme Sayısı. YRI ÜEER Hiç ortak elemanı olmayan kümelere ayrık kümeler denir. n tane elemanı bulunan bir kümenin alt küme sayısı, n tanedir. ve ayrık ise, = dir. T ÜE (ÜE PRÇSI) ve iki küme olsun. kümesinin her elemanı kümesinin de eleman oluyor ise kümesine kümesinin alt kümesi denir. kümesi kümesinin alt kümesi ise şeklinde gösterilir. kümesi kümesinin alt kümesi değilse şeklinde gösterilir. oş kümenin alt küme sayısı dir. elemanlı bir kümenin alt kümelerinin sayısı kaçtır? = {,,,,, } = {,, } kümelerini göz önüne alalım. kümesinin her elemanı kümesinin de elemanı olduğundan dır. ) ) 8 ) D) üme elemanlı olduğundan alt kümelerinin sayısı, = tanedir. evap dir. 9 T E O G TETİ O N U N T I I
4 ÜEER ÖZ T ÜE ir kümenin kendisi dışındaki alt kümelerine o kümenin öz alt kümeleri denir. Öz lt üme Sayısı: n tane elamanı bulunan bir kümenin öz alt küme sayısı, n dir. = {,,,, 5, {a, b}} kümesine göre, aşağıdakilerden hangisi doğrudur? ) lt küme sayısı 7 = 8 tanedir. ) {a, b} dır. ) {,,, a} dır. D) {a, b} dır. oş kümenin öz alt küme sayısı sıfırdır. = {x 0 x 5, x Z} kümesinin öz alt küme sayısı kaçtır? ir kümede elemanlar virgülle ayrıldığından kümesinin elemanları,,,, 5 ve {a, b} olur. O halde; alt küme sayısı = tanedir. {a, b} dır. Çünkü {a, b} dır. {,,, a} dır. Çünkü a dır. {a, b} dır. evap D dir. ) ) ) D) ÜEERDE İŞEER kümesini yazalım. = {0,,,,, 5} kümesinin eleman sayısı dır. kümesinin öz alt küme sayısı, n = = = tanedir. evap dir. Öz alt küme sayısı 7 olan küme kaç elemanlıdır?. ümelerin irleşimi: İki veya daha fazla kümenin tüm elemanlarının oluşturduğu kümeye birleşim kümesi denir. irleşim sembolü ile gösterilir. ve iki küme olsun. ile kümelerinin birleşim kümesi şeklinde gösterilir. kümesinin elemanları veya kümesinin elemanlarıdır. = {x: x veya x } dır. kümesi şekildeki taralı kısımdır. ) 7 ) 8 ) 9 D) 0 üme n elemanlı olsun. Öz alt küme sayısı n = 7 dir. n = 7 n = 8 n = 7 n = 7 dir. evap dır. = {,,, 5} = {, {, 8}, {a, b}} kümelerinin birleşim kümesinin alt küme sayısı kaçtır? ) 9 ) 8 ) 7 D) 5 T E O G TETİ O N U N T I I 0
5 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r = {,,, 5} = {, {, 8}, {a, b}} ise = {,,,, 5, {, 8}, {a, b}} olur. s( ) = 7 olur. nin alt küme sayısı, 7 = 8 dir. evap dir. = {,,, 8, 0} = {,,,, 5, } kümelerinin kesişim kümesinin alt küme sayısı kaçtır? ) ) 8 ) D) irleşimin Özellikleri:. ir kümenin kendisiyle birleşimi yine kendisidir. = dır.. ir kümenin boş küme ile birleşimi yine kendisidir. =, = dir.. irleşim işleminin değişme özelliği vardır. = dır.. irleşim işleminin birleşme özelliği vardır. ( ) = ( ) 5. ir küme ile alt kümesinin birleşimi yine kendisidir., = dir.. İki kümenin birleşimi boş küme ise, kümeler boş kümedir. = ise = ve = dir. ve kümelerinin kesişimi Venn şeması ile gösterirsek; 8 olur. 0 = {,, } dir. s( ) = olur. nin alt küme sayısı = 8 tanedir. evap dir. esişimin Özellikleri:. ir kümenin kendisiyle kesişimi yine kendisidir. = dır. 5. ir kümenin boş küme ile kesişimi boş kümedir.. ümelerin esişimi: İki veya daha fazla kümenin ortak elemanlarının oluşturduğu kümeye kesişim kümesi denir. esişim sembolü ile gösterilir. ve iki küme olsun. ve kümelerinin kesişim kümesi şeklinde gösterilir. kümesinin elemanları ve kümesinin elemanlarıdır. = {x: x ve x } kümesi şekildeki taralı kısımdır. =, =, =. esişim işleminin değişme özelliği vardır. = dır.. esişim işleminin birleşme özelliği vardır. ( ) = ( ) dir. 5. ir küme ile alt kümesinin kesişimi alt kümesine eşittir., = dır.. yrık iki kümenin kesişimi dir. = ise ve ayrık kümelerdir. 7. esişim işleminin birleşim işlemi üzerine dağılma özelliği, birleşim işleminin kesişim işlemi üzerine dağılma özelliği vardır. ( ) = ( ) ( ) ( ) = ( ) ( ) T E O G TETİ O N U N T I I
6 ÜEER. Ortak elemanlar birleşim kümesine bir kez yazılır.. irleşim kümesinin eleman sayısı; kümelerin eleman sayıları toplamından, kesişim kümesinin eleman sayısı çıkarılarak bulunur. ise, s( ) = s() + s() s( ) b c a f g 5 d e 9 h ı Yukarıda verilenlere göre, kümesi aşağıdakilerden hangisidir? ) {e, f, g, h, ı} ) {e, h, ı} ) {f, g} D) {e} kümesi, ve kümelerinin ortak elemanlarından oluşur. = {e} olur. 7 evap D dir. s() = 0, s() = ve kümesinin öz alt küme sayısı 5 ise, kümesinin eleman sayısı kaçtır? ) 8 ) ) D) kümesinin öz alt küme sayısı 5 olduğuna göre, n = 5 n = n = olur. öylece s( ) = bulunur. s( ) = s() + s() s( ) = 0 + = 8 bulunur. evap dır. ve ayrık olmayan iki küme ve s() = s() = olduğuna göre, kümesinin eleman sayısı en çok kaç olur? ) ) 0 ) 9 D) ( ) nin eleman sayısının en çok olabilmesi için kesişim kümesinin eleman sayısı az olmalıdır. ümeler ayrık olmadığından ( ) s( ) = seçilirse s( ) en büyük değerini alır. una göre, s( ) = s() + s() s( ) = + = 9 bulunur. ve iki küme olsun s() = s() = 7 evap dir. olduğuna göre, kümesi en az kaç elemanlı olur? ) ) 7 ) D) 8 I. Yol: s( ) nin eleman sayısının en az olabilmesi için kesişim kümesinde çok eleman bulunmalıdır. u da nin eleman sayısı az olan kümeye eşit olmasıyla mümkün olur. Yani; s( ) = s() = olur. s( ) = s() + s() s( ) II. Yol: = + 7 = 7 bulunur. ümeleri Venn Şeması ile gösterelim. s( ) = s() = 7 olur. evap dir. T E O G TETİ O N U N T I I
7 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r. İki ümenin Farkı: ve herhangi iki küme olmak üzere, nın elemanı olduğu halde nin elemanı olmayan elemanların oluşturduğu kümeye fark kümesi denir \ veya şeklinde gösterilir. \ = {x: x ve x } irleşim kümesinin eleman sayısını fark kümeleri yardımıyla bulabiliriz. s( )=s( \ )+s( \ )+s( ) = {,,, } = {,, 5, } = {, 7, 8} kümelerine göre, ( ) \ kümesi aşağıdakilerden hangisidir? ) {} ) {} ) {, } D) {, 7, 8} = {,,, } {,, 5, } = {, } ( ) \ = {, } \ {, 7, 8} = {, } evap dir. a b Şekilde verilen Venn Şemasına göre, (\) (\) kümesi aşağıdakilerden hangisidir? ) {, a, b} ) {,, } ) {,,, c} D) {,,,, a, b} Venn Şemasına göre \ = {, a, b} \ = {,, } olur. ( \ ) ( \ ) = {, a, b} {,, } e d c = {,,,, a, b} bulunur. evap D dir. ve kümeleri için \ kümesinin alt küme sayısı, kümesinin öz alt küme sayısı 55 olduğuna göre, kümesinin öz alt küme sayısı kaçtır? ) ) 7 ) 5 D) \ kümesinin alt küme sayısı ise, n = n = olur. kümesinin öz alt küme sayısı 55 ise m = 55 m = 5 m = 8 olur. s() = 8 = bulunur. kümesinin öz alt küme sayısı = olur. evap dır. D. Tümleme: Üzerinde işlem yapılan ve tüm kümeleri kapsayan kümeye evrensel küme denir. Evrensel küme E sembolü ile gösterilir. Herhangi bir kümenin dışında kalan ve evrensel kümeye ait olan elemanların oluşturduğu kümeye o kümenin tümleyeni denir. herhangi bir küme olsun. nın tümleyeni ı veya t ile gösterilir. ı = {x x ve x E} E T E O G TETİ O N U N T I I ı
8 ÜEER. ir küme ile bu kümenin tümleyenin eleman sayılarının toplamı evrensel kümenin eleman sayısını verir. s() + s( ı ) = s(e). \ = ı ( ) ve, E evrensel kümesinin alt kümeleri olsun. s(e) = 5 s( ı ) = s( \ ) = s( \ ) = olduğuna göre, nin alt küme sayısı kaçtır? ) 8 ) ) D) \ ( ) ( ) D ( ) D ( \ ) ( \ ) \ ( ) Verilenler Venn Şemasında yerlerine yazılırsa x 9 s(e) = s() + s( ı ) 5 = s() + s() = olur. s() = + x = + x x = bulunur. s( ) = olduğundan alt küme sayısı = bulunur. evap dir. ( ) \ ( ) \ ( ) TRI ÖGE U şağıda Venn Şemalarının altında taralı bölgeye karşılık gelen kümeler yazılmıştır. ÜE PROEERİ ( ) \ üme problemlerinin çözümleri için aşağıdaki bilgileri inceleyiniz.. F V a b c [( ) ( ) ( )] \ ( ) F = Futbol oynayanların kümesi V = Voleybol oynayanların kümesi a = Sadece futbol oynayanların sayısı b = Futbol ve voleybol oynayanların sayısı c = Sadece voleybol oynayanların sayısı a + c = Sadece bir oyun oynayanların sayısı T E O G TETİ O N U N T I I
9 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r. İ F y x z p t s r İ = İngilizce bilenlerin kümesi F = Fransızca bilenlerin kümesi = lmanca bilenlerin kümesi x = Sadece İngilizce bilenlerin sayısı z = Sadece Fransızca bilenlerin sayısı s = Sadece lmanca bilenlerin sayısı t = Üç dil bilenlerin sayısı y + p + r = Sadece iki dil bilenlerin sayısı y + p + r + t = En az iki dil bilenlerin sayısı x + z + s + y + p + r = En fazla iki dil bilenlerin sayısı ir sınıftaki 0 öğrenciden 0 u yalnız matematik dersinden, 7 si yalnız Türkçe dersinden geçmiş, 8 i her iki dersten de kalmıştır. una göre, her iki dersi geçen kaç öğrenci vardır? ) 0 ) 8 ) 5 D) S T İ F Şemada görüldüğü gibi kafilede 58 kişi vardır. evap D dir. ir sınıftaki öğrencilerin tamamını müzik veya sporla ilgilenmektedir. 7 si sadece müzik si sporla, ilgilendiğine göre sınıf mevcudu kaçtır? Yukarıdaki sorunun çözümü için aşağıdaki verilerden hangisine ihtiyaç vardır? ) üzik ve sporla ilgilenmeyen öğrencilerin sayısı ) üzik ve sporla ilgilenen öğrencilerin sayısı ) Yalnızca sporla ilgilenenlerin sayısı D) Veriler yeterlidir. 0 x 7 8 S S = 0 + x S = 5 + x 0 = 5 + x x = 5 evap dir. ir turist kafilesindeki kişi lmanca, kişi İngilizce 9 kişi Fransızca bilmektedir. 7 kişi lmanca ve Fransızca, kişi lmanca ve İngilizce 0 kişi İngilizce ve Fransızca ve kişi her üç dili bilmektedir. una göre, kafilede kaç kişi vardır? 7 Tüm sınıfı venn şeması ile gösterirsek, sınıf mevcudu 7 + = 9 kişidir. Dolayısıyla veriler yeterlidir. aşka bir veriye gerek yoktur. evap D dir. ) ) 0 ) D) T E O G TETİ O N U N T I I
10 ÜEER Ü TEST 7. NR kelimesinin harflerin oluşturduğu kümenin özalt küme sayısı kaçtır? ) 7 ) 5 ) D). = {, {a},, {b, c}} kümesi veriliyor. şağıdakilerden hangisi doğrudur? ) lt küme sayısı dir. ) {b, c} ) a D) {, }. ve boş olmayan iki küme olarak, aşağıdakilerden hangisi, kesinlikle kümesini kapsamaz? ) ) ) \ D) \. s() = s() = olduğuna göre, kümesinin alt küme sayısı en fazla kaç olabilir? ) ) 8 ) D) 8. = [,,, } olduğuna göre, kümesi aşağıdakilerden hangisi olamaz? ) {, } ) {, } ) {,,, } D) { } 9. ve kümelerinin alt kümelerinin toplamı 0 dir. olduğuna göre, aşağıdakilerden hangisi yanlıştır? ) s() = s( ) ) s( \ ) = s() ) s( \ ) = s( ) D) s() =.s(). ir kümenin alt küme sayısı x +, özalt küme sayısı x dir. una göre, bu küme kaç elemanlıdır? ) ) 5 ) D) 5., s( ) =s() + s() olduğuna göre, aşağıdakilerden hangisi kesinlikle yanlıştır? 0. ve denk kümelerdir. S( ) = 7 Olduğuna göre, aşağıdakilerden hangisi, \ kümesinin eleman sayısını bulmak için gerekli değildir? ) s( \ ) = s( \ ) ) s() ) s( \ ) D) s() ) = ) \ = ) = D) \. ir kümenin elemanı sayısı artırılırsa, aşağıdakilerden hangisi gerçekleşir? ) lt küme sayısı artar. ) lt küme sayısı kat artar. ) lt küme sayısı 7 kat artar. D) Özalt küme sayısı 8 artar.. = {a 5 < a <, a Z} = {b b, b N} olduğuna göre, \ kümesi aşağıdakilerden hangisidir? ) ) {, } ) {,,, } D) { 5} T E O G TETİ O N U N T I I
11 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r. ve kümeleri için, s( ) = s() olduğuna göre, aşağıdakilerden hangisi kesinlikle doğrudur? ) = ) = ) \ = D) \ =.. Yandaki şemada bir toplulukta İngilizce, lmanca ve Fransızca bilenler kümesi sırasıyla, I, ve F kümeleri ile gösterilmiş ve her sayı bulunduğu kümenin eleman sayısı göstermektedir. I 5 7 Şemada verilenlere göre, aşağıdakilerden hangileri doğrudur? I. lmanca ve Fransızca bilenlerin sayısı, sadece İngilizce bilenlerin sayısına eşittir. II. Sadece bir dil bilenlerin sayısı, üç dili de bilenlerin sayısının katıdır. III. En az iki dil bilenlerin sayısı 5 tür. IV. lmanca veya Fransızca bilmeyenlerin sayısı 5 tir. F ) I ve II ) III ve IV ) I, II ve IV D) Hepsi. Yukarıdaki şemada taralı olarak verilen küme aşağıdakilerden hangisidir? ) ( ) ) ( ) \ ) [ \ ( )] [ ] D) ( ) \ Ü 7. ir sınıfta bulunan öğrencilerin futbol veya voleybol I. hiç birini oynamayanların sayısı kişi II. sadece birini oynayanların sayısı kişi III. en az birini oynayanların sayısı kişi olduğuna göre, yukarıdaki bilgilerin hangisi verilmezse, sınıfın mevcudu yine de bulunur? ) I ) II ) III D) Hepsi verilmelidir. D a d b h f c g Yukarıdaki şemada verilenlere göre, aşağıdakilerden hangisi yanlıştır? ) D Ü = {f} ) (Ü ) \ D = {b, h, c, g, e} ) (D ) Ü = Ü D) Ü (D ) = {f, h, c} e 8. İngilizce, Türkçe ve Rusça dillerinden en az birini bilenlerin bulunduğu turist kafilesinde, Türkçe bilen herkes İngilizce bilmekte, fakat Rusça bilmemektedir. afilede yalnız iki dil bilenlerin sayısı, yalnız bir dil bilenlerin sayısı olduğuna göre, kafilede kaç kişi bulunmaktadır? ) 5 ) ) 0 D) kişilik bir sınıfta kişi atematikten, 8 kişi Fenden geçerli not almıştır. una göre, her iki dersten geçerli not alan kaç kişi vardır? ) 0 ) ) D) 9. ir sınıftaki öğrencilerin % 0 pop müzik, % 70 rock müzik dinlemektedir. Her iki müzik türünü dinleyenlerin sayısı kişi olduğuna göre, sınıfın mevcudu kaçtır? ) 8 ) 0 ) D) 7 T E O G TETİ O N U N T I I
12 ÜEER ER. {a} ve {b, c} birer elemandır. u yüzden de s() =, = {b, c}, a ve nin birer elemanı olduğuna göre, {, } kümesi nin alt kümesidir. evap D dir.. irleşim kümesi her iki kümenin elemanlarını bulundurduğuna göre, ( ). olursa, = olur ve her küme kendisini kapsar. Dolayısıyla seçeneğinde kesinlik yok. \ kümesi, nın, de olmayan elemanlarından oluştuğuna göre, \ kesinlikle yi kapsamaz. = olursa, \ olur ve her küme kendisini kapsadığına göre, D seçeneğinde kesinlik yok. evap dir. 7. NR kelimesindeki harflerin oluşturduğu küme = {, N,, R] dır. s() = olduğundan özalt küme sayısı = 5 dir. evap dir. 8. kümesinde elemanı bulunmadığına göre, {, } kümesi kümesinin alt kümesi olamaz. evap dır. 9. Toplamları 0 olan, nin kuvvetleri ve olduğuna göre, s() =, s() = s() = s() =. = yani ve ayrık küme olurlarsa s( ) = 5 olur. 5 = evap D dir.. ir kümenin alt küme sayısı, özalt küme sayısından fazladır. x + = x + x = ümenin eleman sayısı n olsun. n = x + = + = 8, n = evap D dir. 5. s( ) = s() + s() s( ) = s() + s() Olduğundan s( ) = 0 = Yani kümeleri ayrık kümelerdir. ve boş olmayan kümeler olduğundan = olamaz. evap dir.. u kümenin eleman sayısı n olursa, alt küme sayısı n olur. Eleman sayısı artırılırsa, alt küme sayısı n+ = n. = 8. n olur. 8. n n = 7. n lt küme sayısı 7 kat artmıştır. evap dir. Şemadan görüldüğü gibi, ve seçeneklerindeki ifadeler doğrudur. Fakat s().s() evap D dir. 0. ve kümeler olduğuna göre, şema aşağıdaki gibidir. a x a verilen: a + x = 7 istenilen: s( \ ) = a seçeneklere baktığımızda, seçeneğindeki bilgiyi, kümelerin denk olmasından elde ederiz. Diğer seçeneklerdeki bilgiler ise s( ) yi bulmak için yeterlidir. evap dır.. ve kümeleri liste yöntemiyle yazarsak, = {,,, 0,, } = {0,,,, } una göre, \ = {,,, } evap dir. T E O G TETİ O N U N T I I 8
13 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r. s( ) = s() olduğuna göre, kümesi, kümesinin alt kümesidir. una göre, seçeneklerden kesinlikle doğru olanı = dir. evap dir. 7. F V x y z. Taralı bölgeyi ikiye ayırırsak. taralı bölge,. taralı bölgeye \ ( ). unların birleşimi [ \ ( )] [ ] dir. evap dir. Yukarıdaki şemada F ve V sırasıyla sınıfta futbol ve voleybol oynayanlar kümesi, x, y, z ve bulundukları kümenin eleman sayısını göstermektedir. Soruda istenilen x + y+ z + toplamıdır. urada x + y + z toplamı en az bir dil bilenlerin sayısını göstermektedir. + = 0 sınıf mevcudu bulunur. O halde sadece birini oynayanların sayısı (x+z) bilgisine gerek kalmıyor. evap dir.. Ü (D ) = {f, c} Fakat D seçeneğinde Ü (D ) = {f, h, c} olarak verilmiştir. evap D dir. 5. = {atematikten geçenler} F = {Fenden geçenler} olmak üzere s( F ) = s() + s(f) s( F) 0 = + 8 s( F) s( F) = evap dir. 8. I R T x z t y Yukarıdaki şemada i, T ve R kafilede İngilizce, Türkçe ve Rusça bilenlerin kümesini göstermektedir. Yalnızca iki dil bilenlerin sayısı x + z = kişi Yalnız bir dil bilenlerin sayısı y + t = kişi afiledeki turist sayısı x + y + z + t = + = 5 kişi evap dır.. I. lmanya Fransızca bilenlerin sayısı + = 5 kişidir. Sadece İngilizce bilenlerin sayısı 5 kişidir. II. Sadece bir dil bilenlerin sayısı = 8 kişidir. I 5 7 Üç dili de bilenlerin sayısı kişidir. 8 =. III. En az iki dil bilenlerin sayısı yalnız iki dil ve yalnız üç dil bilenlerin sayısının toplamına eşittir = 0 IV. lmanca ve ya Fransızca bilmeyenler kümesinin dışında kalanlardır. unların sayısı 5 tir. u durumda I, II ve IV doğru, III yanlıştır. evap dir. F 9 9. P R % 0 % 0 % 0 Şemada P ve R sırasıyla pop müzik ve rock müzik dinleyenler kümesini göstermektedir. % 00 = %0 + %70 % x x = y 0y = 00 y = 0 evap dir. T E O G TETİ O N U N T I I
14 ÜEER EVPI TEST 5. kümesinin özalt küme sayısı, kümesinin alt küme sayısı ve olmak üzere, s( ) nin alabileceği en büyük ve en küçük değerlerin toplamı nedir?. Yandaki taralı bölge aşağıdakiler den hangisi ile ifade edilir? ) 8 ) 0 ) D) 8 ) [( ) / )] ( ) ) ( ) [ / ( )] ) ( ) / D) ( ) /. ={ x: < x 5, x Z} ={ x: x <, x Z} ümeleri veriliyor. kümesinin elemanları toplamı kaçtır? ) 7 ) ) D) 0. = { İ, {R,E}, } = { E,, {R,E}} ümeleri veriliyor. una göre; s( ) s( ) kaçtır? ) ) ) D) 8 7. = {,,, } ümesinin alt kümelerinin kaç tanesinde, bulunur bulunmaz? ) ) 8 ) D). = {, {0},,,, {} } ümesi veriliyor. una göre aşağıdakilerden kaç tanesi doğrudur?.. {0}. {,,,}. {} 5. {} ) ) ) D) 5 8. ve boş olmayan iki küme olmak üzere, s() = s() s( ) + s( ) = 7 olduğuna göre, s() kaçtır? ) ) ) 8 D) 0. s( ) =, kümesinin alt küme sayısı, 8; nin özalt küme sayısı 7 ise s() kaçtır? ) ) 7 ) 8 D) 0 9. = {,,, D, E, F} = {, } kümeleri veriliyor. olacak şekilde ve den farklı kaç tane kümesi yazılabilir? ) ) ) 0 D) T E O G TETİ O N U N T I I 0
15 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r 0. ir dil kursu; İngilizce, lmanca, Fransızca dilini bilenler ve hiçbir dil bilmeyenlerden oluşmaktadır ve aşağıdaki kümelerde rakamlar eleman sayılarını göstermektedir. una göre, aşağıdakilerden hangileri doğrudur?. elemanlı bir kümeye bu elemanlardan farklı x tane eleman katılırsa yeni oluşan kümenin alt küme sayısı; başlangıçtaki kümenin alt küme sayısından kaç fazla olur? ) + x ) (x ) ) x D) ( x ) 5 0. en çok bir dil bilen kişi. en az iki dil bilen 8 kişi. en çok iki dil bilen 8 kişidir; ) ve ) ve ) Yalnız D), ve 5. n elemanlı bir kümenin alt küme sayısıyla, özalt küme sayısının toplamı 7 ise bu kümenin eleman sayısı kaçtır? ) ) 5 ) D) 7. ir geziye katılan 5 kişiden yalnız voleybol oynamak isteyenler her iki oyunu da oynamak isteyenlerden fazla, Futbol oynamak isteyenler de Voleybol oynamak isteyenlerden eksiktir. u gezide 0 kişide hiçbir oyun oynamamaktadır. una göre voleybol oynayan kaç kişi vardır?. ={ ile bölünen iki basamaklı sayılar} ={5 ile bölünen iki basamaklı sayılar} Yukarıda tanımlanan ve kümeleri için kümesinin eleman sayısı kaçtır? ) ) ) 8 D) 0 ) ) 8 ) D) 8 7. = {x: x 9, x Z} kümesinin alt küme sayısı kaçtır? ) 8 ) ) D) 8. 0 kişilik bir sınıfta Gözlüksüz erkekler, gözlüklü kızların katı, Gözlüksüz kızlar, gözlüklü erkeklerden 5 eksiktir. u sınıfta 5 kız varsa, Gözlüklü erkek sayısı kaçtır? ) 0 ) 5 ) 8 D) 0 8. x + x x x x x + 5., ve kümelerinin alt küme sayıları sırasıyla 5,, olduğuna göre, kümesinin özalt küme sayısı kaçtır? ) ) ) D) s[( ) / ] = olduğuna göre, s( ) kaçtır? ) 5 ) 0 ) 5 D) T E O G TETİ O N U N T I I
16 EVPI TEST ÜEER. TTÜR kelimesinin harfler kümesini, TÜRİYE kelimesindeki harfler kümesini oluşturuyorsa aşağıdakilerden hangisi doğrudur? ) \ kümesinin özalt küme sayısı 7 dir. ) s( \ ) = s( \ ) dır. ) ( ) kümesinin alt küme sayısı 5 dır. D) s( \ ) = tür. 8 Yukarıdaki şemaya göre, {,, 7} kümesi aşağıdakilerden hangisidir? ) {( ) \ } ) { \ ( )} ) [ \ ( )] ( \ ) D) [ \ ( )] ( \ ). s() = 7 ve s() = 9 olduğuna göre, s( ) en az kaçtır? ( ) ) ) ) 0 D) 9. \,, kümelerinin alt küme sayıları sırasıyla, 8, olduğuna göre, kümesinin eleman sayısı kaçtır? ) ) 0 ) 9 D) 8. = {,, {, }, a, {a}, {b, c, d}} kümesi ile ilgili verilenlerden kaç tanesi doğrudur? I. s() = 9 II. kümesinin alt küme sayısı tür. III. {a, b} IV. {, } 7. = {, {},, {a}} = {{},{a},,, 5} kümelerine göre kümesi aşağıdakilerden hangisidir? ) {{},, {a}, } ) {{}, } ) {{a}, } D) {, {}, {a}, } ) ) ) D). Taralı bölgeyi gösteren küme aşağıdakilerden hangisidir? ) \( ) ) ( ) \ ) \ ( ) D) ( ) \ 8. s() = 5 s() = 7 olduğuna göre, aşağıdakilerden kaç tanesi daima doğrudur? I. ise s( ) = 7 II. ise s( ) = III. ise nin alt küme sayısı en çok 7 dir. IV. ise nin eleman sayısı en az 8 dir. ) ) ) D) T E O G TETİ O N U N T I I
17 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r 9. s() = s() = D olacak şekilde kaç farklı D kümesi yazılabilir? ) ) ) D). ve kümeleri için, s() = s( \ ) = olduğuna göre, s( ) nin alt küme sayısı en çok kaçtır? ) ) ) D) 0 0. Herkesin Türkçe bildiği 9 kişilik bir sınıfta her üç dili de bilen 7 kişi, lmanca bilen 0 kişi ve İngilizce bilenler yalnız bir dil bilenlerin katı olduğuna göre, Türkçe ve lmanca bilenlerin sayısı için aşağıdakilerden hangisi doğrudur? ) İki basamaklı rakamları farklı en küçük asal sayıdır. ) İki basamaklı en küçük doğal sayıdır. ) İki basamaklı rakamları farklı en küçük doğal sayıdır. D) Yalnızca İngilizce bilenlerin sayısının iki katıdır. 5. \,, \ kümelerinin özalt küme sayıları sırasıyla 7,, tür. s() + s() için aşağıdakilerden hangisi doğrudur? ) sal sayıdır. ) İki basamaklı en küçük doğal sayıdır. ) ir basamaklı en büyük doğal sayıdır. D) İki basamaklı en küçük asal sayıdır.. şağıdakilerden hangisi ya da hangileri kesinlikle yanlıştır? I. Her küme kendisinin alt kümesidir. II. s() = s() = ise = dir. III. oş kümenin özalt küme sayısı dir. IV. oş küme her kümenin alt kümesidir.. s() + s() = s( \ ) = 5 s( \ ) = olduğuna göre, s( ) kaçtır? ) ) ) 8 D) 0 ) Yalnız l ) Yalnız lll ) l ve lll D) ll ve lll 7.. = {,, {}, {}, 5} olduğuna göre, aşağıdakilerden hangisi kümesinin alt kümesidir? ) {,, } ) {, {}, 5} ) {, {}} D) {{}, 5} Şekildeki taralı bölgeye aşağıdaki kümelerden hangisi ilave edilirse,. kümesi rakamlardan, kümesi asal sayılardan oluşmaktadır. una göre, ( \ ) kümesi için aşağıdakilerden hangisi doğrudur? ) 5 elemanlı bir kümedir. ) Özalt küme sayısı 5 dir. ) 5 tane elemanı çift sayıdır. D) tane özalt kümesi vardır. taralı bölgesi elde edilir? ) \ ( ) ) ( ) \ ) ( ) \ D) ( ) \ T E O G TETİ O N U N T I I
18 ÜEER Ç I I Ş S O R U R.. şağıda taralı olarak gösterilen kümelerden hangisi P kümesinde olup, R kümesinde olmayan elemanların kümesidir? ) ) R P P ) D) R P P Şekildeki şemada taralı kısma karşılık gelen kümeler arasındaki işlem aşağıdakilerden hangisinde verilmiştir? ) [ ( )] \ [ ( )] ) ( ) \ ( ) ) \ ( ) D) [( ) )] \ [( ) ] (999 - GS) R R (998 - ÖO). 55 kişilik bir sınıfta her öğrenci futbol veya basketbol oyunlarından en az birini oynamaktadır. Futbol oynayanların sayısı, basketbol oynayanların sayısının katıdır. İki oyunu birden oynayanların sayısı 5 kişi olduğuna göre, futbol oynamayan kaç kişi vardır? ) 8 ) 0 ) D) 5 (000 - ÖO). c a b Şema ile gösterilen kümelerde aşağıda verilen taşıma işlemlerinden hangisi yapılırsa = ve = N olur? ) daki, N ye; deki b, ya ) deki, ye; deki b, N ye ) deki b, ya; deki, N Ye D) deki a, ye; deki, N ye c b N a (999 - GS) 5. Şemadaki T, ve İ harfleri sırasıyla bir sınıftaki Türkçe, atematik ve İngilizce derslerinden geçen öğrencilerin kümelerini göstermektedir. T I 7 7 Sayılar, alt kümelerin eleman sayılarını gösterdiğine göre, aşağıdakilerden hangisi doğrudur? ) u derslerin en az ikisinden geçenlerin sayısı dır. ) Türkçe ve atematikten kalanların sayısı tür. ) atematikten geçenlerin sayısı dir. D) u derslerin sadece birinden geçenlerin sayısı 0 tır. (000 - GS) 9 T E O G TETİ O N U N T I I
19 T E T İ w w w. a k a d e m i v i z y o n. c o m. t r., ve herhangi üç küme olmak üzere, aşağıdaki şemalardan hangisi ve şartına uygun gösterim değildir? 9. şağıda verilen şemalardaki taralı bölgelerden hangisi, ( ) \ kümesinin bir gösterimi değildir? ) ) ) ) ) D) ) D) (00 - ÖO) (000 - GS) 7. a c b 0. a = {,,,5,} ve b = {,5,,7,8}} kümeleri veriliyor. nın alt kümelerinden kaç tanesi nin alt kümelerine eşittir? ) 5 ) ) 8 D) (00 - ÖO) b c 5 + Şemalarla gösterilen, ve kümelerindeki a, b ve c harflerinin yerine aşağıdaki hangi rakamlar yazılırsa, = = olur? a b c ) 5 ) 5 ) 5 D) 5 (000 - ÖO). ir sınıftaki öğrencilerin %70 i matematik, %0 ı Türkçe dersinden başarılı olmuştur. Her iki dersten başarılı olan öğrencilerin sayısı dir. Her iki dersten de başarısız öğrenci olduğuna göre, sınıf mevcudu kaçtır? u problemin çözülebilmesi için, aşağıdakilerden hangisi gereklidir? ) aşka verilere gerek yoktur, mevcut verilerle çözülebilir. ) Her iki dersten başarısız olan öğrencilerin sayısı verilmelidir. ) Her iki dersten de başarısız olanlara ait yüzde verilmelidir. D) Yalnız bir dersten başarılı olan öğrencilerin sayısı verilmelidir. (00 - GS) 8., ve kümeleri yanda şema ile verilmiştir. una göre; 5, aşağıdaki kümelerden hangisinin elemanı değildir? 5 7 ) ( ) \ ) ( ) ) ( ) \ ( ) D) ( ) \ (00 - GS). ir sınıftaki öğrencilerin % 70 i futbol, % 0 ı voleybol oynamaktadır. Hem futbol hem de voleybol oynayanların sayısı dır. u verilere göre, aşağıdakilerden hangisi doğru olur? ) Sınıf mevcudu en az 0 kişidir. ) Sınıf mevcudu en fazla kişidir. ) Sınıf mevcudu kesinlikle 0 kişidir. D) Sınıf mevcudu kesinlikle kişidir. (00 - ÖO) 5 T E O G TETİ O N U N T I I
20 ÜEER. USTF sözcüğünü oluşturan harflerin kümesi, US sözcüğünü oluşturan harflerin kümesi D olsun. una göre, aşağıdakilerden hangileri doğrudur? I. kümesinde olup, D kümesinde olmayan elemanların sayısı tür. II. nin alt kümelerinin sayısı, D nin alt kümelerinin sayısına eşittir. III. D nin alt kümeleri, nin de alt kümeleridir. IV. D nin eleman sayısı, nin eleman sayısına eşittir. ) I ve II ) I ve IV ) II ve III D) III ve IV (00 - GS) 7. s( ) = 8 ve s() = olduğuna göre, aşağıdaki şartlardan hangisinin sağlanması durumunda s() en küçük olur? ) ise ) = ise ) s( \ ) s( \ ) ise D) s( \ ) = ise 8. Şemadaki taralı bölgeler, aşağıdaki kümelerden hangisinin gösterimidir? (00 - ÖO). Şemaya göre, aşağıdaki kümelerden hangisi {} kümesine eşit değildir? ) ( ) \ ) ( \ ) ) ( \ ) \ D) ( ) \ (00 - ÖO) ) \ ( ) ) ( \ ) ) ( \ ) D) ( ) \ (00 - ÖO) 9. Şemadaki \ ( ) kümesinin belirttiği bölge kesilerek çıkartılıyor. 5. Şema ile gösterilen, ve kümelerine göre, aşağıdakilerden hangisi doğrudur? Çıkartılan bölgeyi gösteren şekil aşağıdakilerden hangisidir? ) ) ) = ) \ = ) \ = D) = (00 - GS) ) D). kişilik bir sınıfta kişi matematik dersinden, kişi de hem Türkçe hem matematik dersinden 00 puan almıştır. una göre, aşağıdakilerden hangisi doğrudur? ) 00 puandan az alan öğrencilerin sayısı en fazla tür. ) Yalnız Türkçe den 00 puan alanların sayısı en fazla 8 dir. ) Türkçe den 00 puan alanların sayısı en fazla dır. D) atematik ten 00 puanın altında alan öğrencilerin sayısı en fazla dır. (00 - GS) 0. Şemada verilen, N ve P kümelerine göre, / (P N) kümesi aşağıdakilerden hangisidir? (00 - GS) ) {,, } ) {,,, } ) {,,,, 9} D) {,,,,, 7, 8, 9} (005 - GS) N P T E O G TETİ O N U N T I I
TEST - 1 ÖDEV TESTİ elemanlı alt kümelerinin sayısı 3 elemanlı alt kümelerinin. 1. A = {1, {2}, {1, 2}, 3, Ø} kümesi için aşağıdakilerden
 10 Kümeler ÖDEV TESTİ TEST - 1 6. 5 elemanlı alt kümelerinin sayısı 3 elemanlı alt kümelerinin sayısına eşit olan bir kümenin en az 6 elemanlı kaç alt kümesi vardır? ) 24 ) 28 C) 37 D) 38 E) 42 1. = {1,
10 Kümeler ÖDEV TESTİ TEST - 1 6. 5 elemanlı alt kümelerinin sayısı 3 elemanlı alt kümelerinin sayısına eşit olan bir kümenin en az 6 elemanlı kaç alt kümesi vardır? ) 24 ) 28 C) 37 D) 38 E) 42 1. = {1,
KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 2. ÜNİTE 1. ÜNİT
 KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 2. ÜNİTE 1. ÜNİT Kümelerde Temel Kavramlar 1. Kazanım : Küme kavramını açıklar; liste, Venn şeması ve ortak özellik yöntemleri ile gösterir. 2. Kazanım : Evrensel küme,
KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 2. ÜNİTE 1. ÜNİT Kümelerde Temel Kavramlar 1. Kazanım : Küme kavramını açıklar; liste, Venn şeması ve ortak özellik yöntemleri ile gösterir. 2. Kazanım : Evrensel küme,
1 A IV. a. Kümelerin Gösterimleri-Boş Küme-Denk ve Eşit Kümeler A II. A. a VI. A. b C ) c. 1. A kümesini venn şeması ile gösteriniz.
 Kümelerin Gösterimleri-Boş Küme-Denk ve Eşit Kümeler 1. kümesini venn şeması ile gösteriniz. 6. M kümesine denk olan N kümesini ortak özellik yöntemi ile gösteriniz. 2. B kümesini liste yöntemi ile gösteriniz.
Kümelerin Gösterimleri-Boş Küme-Denk ve Eşit Kümeler 1. kümesini venn şeması ile gösteriniz. 6. M kümesine denk olan N kümesini ortak özellik yöntemi ile gösteriniz. 2. B kümesini liste yöntemi ile gösteriniz.
KÜMELER. İyi tanımlanmış nesneler topluluğuna küme denir. Bir küme, birbirinden farklı nesnelerden oluşur. Bu nesneler somut veya soyut olabilir.
 1 KÜMELER İyi tanımlanmış nesneler topluluğuna küme denir. ir küme, birbirinden farklı nesnelerden oluşur. u nesneler somut veya soyut olabilir. Kümeyi oluşturan nesnelerin her birine eleman(öğe) denir.
1 KÜMELER İyi tanımlanmış nesneler topluluğuna küme denir. ir küme, birbirinden farklı nesnelerden oluşur. u nesneler somut veya soyut olabilir. Kümeyi oluşturan nesnelerin her birine eleman(öğe) denir.
ÜNİTE 11 ÜNİTE 9 MATEMATİK. Kümeler. 1. Bölüm: Kümelerde Temel Kavramlar 2. Bölüm: Kümelerde İşlemler. 9. Sınıf Matematik
 ÜNİTE 11 ÜNİTE Kümeler 1. Bölüm: Kümelerde Temel Kavramlar 2. Bölüm: Kümelerde İşlemler 9 MATEMATİK 1. ÜNİTEDE HEDEFLENEN KAZANIMLAR 1. BÖLÜM: KÜMELERDE TEMEL KAVRAMLAR Kazanım 9.1.1.1: Küme kavramını
ÜNİTE 11 ÜNİTE Kümeler 1. Bölüm: Kümelerde Temel Kavramlar 2. Bölüm: Kümelerde İşlemler 9 MATEMATİK 1. ÜNİTEDE HEDEFLENEN KAZANIMLAR 1. BÖLÜM: KÜMELERDE TEMEL KAVRAMLAR Kazanım 9.1.1.1: Küme kavramını
Starboard dosya aç dosyayı seçerek Andropi teach menu içe aktar dosyayı seçiyoruz nesne olarak seç
 Not: Starboard programında dosya aç kısmından dosyayı seçerek açabilirsiniz. Yazı karakterlerinde bozulma oluyorsa program kapatılıp tekrar açıldığında yazı düzelecektir. Ben yaptığımda düzelmişti. Andropi
Not: Starboard programında dosya aç kısmından dosyayı seçerek açabilirsiniz. Yazı karakterlerinde bozulma oluyorsa program kapatılıp tekrar açıldığında yazı düzelecektir. Ben yaptığımda düzelmişti. Andropi
Cebir Notları. Kümeler. Gökhan DEMĐR, KÜME KAVRAMI
 , 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Kümeler KÜME KVRMI Kümenin tanım yoktur. undan dolayı kümeyi tanıtmaya çalışalım. Küme kavramında bir topluluk, bir kolleksiyon ifadesi vardır.
, 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Kümeler KÜME KVRMI Kümenin tanım yoktur. undan dolayı kümeyi tanıtmaya çalışalım. Küme kavramında bir topluluk, bir kolleksiyon ifadesi vardır.
KÜMELER KÜMELER. Ortak Özellik Yöntemi: Kümenin içindeki elemanlar ortak bir özelliğe yazılır.
 Küme: elirli nesneler topluluğuna küme adını veriyoruz. n iyi sanatçı ( - ) n güzel şarkı ( - ) Sınıftaki en güzel kız ( - ) Sınıftaki mavi gözlü erkekler ( + ) Uçan insanlar ( + ) oş Küme: lemanı olmayan
Küme: elirli nesneler topluluğuna küme adını veriyoruz. n iyi sanatçı ( - ) n güzel şarkı ( - ) Sınıftaki en güzel kız ( - ) Sınıftaki mavi gözlü erkekler ( + ) Uçan insanlar ( + ) oş Küme: lemanı olmayan
KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 1. ÜNİTE 1. ÜNİT
 KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 1. ÜNİTE 1. ÜNİT Kümelerde Temel Kavramlar 1. Kazanım : Küme kavramını açıklar; liste, Venn şeması ve ortak özellik yöntemleri ile gösterir. 2. Kazanım : Evrensel küme,
KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 1. ÜNİTE 1. ÜNİT Kümelerde Temel Kavramlar 1. Kazanım : Küme kavramını açıklar; liste, Venn şeması ve ortak özellik yöntemleri ile gösterir. 2. Kazanım : Evrensel küme,
KÜMELER Test -1. 5. A a,b,c, 1,2, 5. 1. A a,b,c,d 2. A,1,2,3, 1. 7. s(a) = 10 ve s(b) = 7. 4. B x:0 x 40 ve x 5k, k. 8. s(a) = 9 ve s(b) = 4
 KÜMELER Test -1 1. A a,b,c,d kümesi için aşağıdakilerden hangisi yanlıştır? A) A B) a A C) d A D) {a, c} A E) {a} A 5. A a,b,c, 1,2, 5 kümesi için aşağıdakilerden hangisi doğrudur? A) s(a) = 6 B) b A C)
KÜMELER Test -1 1. A a,b,c,d kümesi için aşağıdakilerden hangisi yanlıştır? A) A B) a A C) d A D) {a, c} A E) {a} A 5. A a,b,c, 1,2, 5 kümesi için aşağıdakilerden hangisi doğrudur? A) s(a) = 6 B) b A C)
L İ S E S İ MATEMATİK. Kümeler. Üzerine Kısa Çalışmalar
 MTEMTİK T T Ü R K N D O L U L İ S E S İ M T E M T İ K Üzerine Kısa Çalışmalar KONY \ SELÇUKLU 017 MTEMTİK KÜMELER (CÜMLELER).1 Küme (Cümle) Kavramı Matematiğin dili mantıktır., matematiğin kendisini anlatabilmesini
MTEMTİK T T Ü R K N D O L U L İ S E S İ M T E M T İ K Üzerine Kısa Çalışmalar KONY \ SELÇUKLU 017 MTEMTİK KÜMELER (CÜMLELER).1 Küme (Cümle) Kavramı Matematiğin dili mantıktır., matematiğin kendisini anlatabilmesini
SONUÇ YAYINLARI. 9. Sınıf Kümeler
 9. SINIF SONUÇ YYINLRI 9. Sınıf Kümeler Bu kitabın tamamının ya da bir kısmının, kitabı yayımlayan şirketin önceden izni olmaksızın elektronik, mekanik, fotokopi ya da herhangi bir kayıt sistemiyle çoğaltılması,
9. SINIF SONUÇ YYINLRI 9. Sınıf Kümeler Bu kitabın tamamının ya da bir kısmının, kitabı yayımlayan şirketin önceden izni olmaksızın elektronik, mekanik, fotokopi ya da herhangi bir kayıt sistemiyle çoğaltılması,
Cebir Notları. Kümeler TEST I. Gökhan DEMĐR, gdemir23@yahoo.com.tr. www.matematikclub.com, 2006
 , 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Kümeler TEST I 1. s(a) = 13 s(a \ B) = 7 s(a B) = 23 ise, s(b) nedir? A) 6 B) 7 C) 10 D) 13 E) 16 7. Üç basamaklı 5 ve 7 ile tam bölünebilen,
, 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Kümeler TEST I 1. s(a) = 13 s(a \ B) = 7 s(a B) = 23 ise, s(b) nedir? A) 6 B) 7 C) 10 D) 13 E) 16 7. Üç basamaklı 5 ve 7 ile tam bölünebilen,
5. A ve B gibi iki cümleden A nın bir, B nin iki elemanı A B cümlesinin elemanı değildir. dışında A. 9. A ve B iki kümedir.
 1. KÜMELER 5. A ve B gibi iki cümleden A nın bir, B nin iki elemanı A B cümlesinin elemanı değildir. dışında A B nin alt cümleleri sayısı 63 olduğuna göre, A B cümlesinin alt cümleleri sayısı kaçtır? (51)
1. KÜMELER 5. A ve B gibi iki cümleden A nın bir, B nin iki elemanı A B cümlesinin elemanı değildir. dışında A B nin alt cümleleri sayısı 63 olduğuna göre, A B cümlesinin alt cümleleri sayısı kaçtır? (51)
İçindekiler. 3. Sonlu ve Sonsuz Kümeler Denk ve Eşit Kümeler Kümelerde Birleşim ve Kesişim
 İçindekiler 1. Küme Kavramı...6-7 2. Kümelerin Gösterimi...8-15 3. Sonlu ve Sonsuz Kümeler... 16-17 4. lt Küme Kavramı... 18-27 5. Denk ve şit Kümeler... 28-29 6. Kümelerde irleşim ve Kesişim... 31-41
İçindekiler 1. Küme Kavramı...6-7 2. Kümelerin Gösterimi...8-15 3. Sonlu ve Sonsuz Kümeler... 16-17 4. lt Küme Kavramı... 18-27 5. Denk ve şit Kümeler... 28-29 6. Kümelerde irleşim ve Kesişim... 31-41
YENİ ORTAÖĞRETİM MATEMATİK PROGRAMINA UYGUNDUR. YGS MATEMATİK 3. KİTAP MERVE ÇELENK FİKRET ÇELENK
 YENİ ORTAÖĞRETİM MATEMATİK PROGRAMINA UYGUNDUR. YGS MATEMATİK 3. KİTAP MERVE ÇELENK FİKRET ÇELENK İÇİNDEKİLER Kümeler 5 44 Fonksiyonlar 1 45 88 Fonksiyonlar 2 89 124 Sayma Kuralları 125 140 Faktöriyel
YENİ ORTAÖĞRETİM MATEMATİK PROGRAMINA UYGUNDUR. YGS MATEMATİK 3. KİTAP MERVE ÇELENK FİKRET ÇELENK İÇİNDEKİLER Kümeler 5 44 Fonksiyonlar 1 45 88 Fonksiyonlar 2 89 124 Sayma Kuralları 125 140 Faktöriyel
Her türlü görüş, öneri ve eleştirilerinize açık olduğumu bilmenizi ister çalışmalarınızda ve sınavlarınızda başarılar dilerim.
 Önsöz Değerli Öğrenciler, u fasikül ortaöğretimde başarınızı yükseltmeye, üniversite giriş sınavlarında yüksek puan almanıza yardımcı olmak için özenle hazırlanmıştır. Konular anlamlı bir bütün oluşturacak
Önsöz Değerli Öğrenciler, u fasikül ortaöğretimde başarınızı yükseltmeye, üniversite giriş sınavlarında yüksek puan almanıza yardımcı olmak için özenle hazırlanmıştır. Konular anlamlı bir bütün oluşturacak
A { x 3 x 9, x } kümesinin eleman sayısı A { x : x 1 3,x } kümesinin eleman sayısı KÜMELER
 KÜMELER Küme, nesnelerin iyi tanımlanmış bir listesidir. Kümeyi oluşturan nesnelerin her birine kümenin elemanı denir. Kümeler genellikle A, B, C,... gibi büyük harflerle gösterilir. x nesnesi A kümesinin
KÜMELER Küme, nesnelerin iyi tanımlanmış bir listesidir. Kümeyi oluşturan nesnelerin her birine kümenin elemanı denir. Kümeler genellikle A, B, C,... gibi büyük harflerle gösterilir. x nesnesi A kümesinin
Örnek...1 : Örnek...2 : A = { a, {a}, b, c, {b, d}, d }, B = { {a}, {c, d}, c, d, x, Δ } k ümeleri için s( AUB) kaçtır?
 KÜMELER 2 İKİ KÜMENİN BİRLEŞİMİ A ve B gibi iki kümeden, A' ya veya B' ye ait olan elemanlardan oluşan yeni kümeye A ile B' nin birleşimi denir ve AUB ile gösterilir. Bu gösterim A birleşim B di ye okunur.
KÜMELER 2 İKİ KÜMENİN BİRLEŞİMİ A ve B gibi iki kümeden, A' ya veya B' ye ait olan elemanlardan oluşan yeni kümeye A ile B' nin birleşimi denir ve AUB ile gösterilir. Bu gösterim A birleşim B di ye okunur.
{ x,y x y + 19 = 0, x, y R} = 3 tir. = sonlu kümesinin 32 tane alt kümesinde
 1. Aşağıdaki kümelerden hangisi sonsuz küme belirtir? A) A = { x 4 < x < 36,x N} B) B = { x 19 < x,x asal sayı} C) C = { x x = 5k,0 < x < 100,k Z} D) D = { x x = 5, x Z} E) E = { x x < 19,x N}. A, B ve
1. Aşağıdaki kümelerden hangisi sonsuz küme belirtir? A) A = { x 4 < x < 36,x N} B) B = { x 19 < x,x asal sayı} C) C = { x x = 5k,0 < x < 100,k Z} D) D = { x x = 5, x Z} E) E = { x x < 19,x N}. A, B ve
Örnek...4 : A = { a, b, c, d, {a}, {b,c}} kümesi veriliyor. Aşağıdakilerin doğru mu yanlış mı olduğunu yazınız.
 KÜME KAVRAMI Küme matematiğin tanımsız bir kavramıdır. Ancak kümeyi, iyi tanımlanmış kavram veya nesneler topluluğu diye tarif edebiliriz. Kümeler A, B, X, K,... gibi büyük harflerle gösterilir. Bir kümeyi
KÜME KAVRAMI Küme matematiğin tanımsız bir kavramıdır. Ancak kümeyi, iyi tanımlanmış kavram veya nesneler topluluğu diye tarif edebiliriz. Kümeler A, B, X, K,... gibi büyük harflerle gösterilir. Bir kümeyi
KÜMELER. A = {x : (x in özelliği)} Burada x : ifadesi öyle x lerden oluşur ki diye okunur. Küme oluşturur. Çünkü Kilis in üç tane ilçesi.
 KÜMELER Canlı yada cansız varlıkların oluşturduğu iyi A = {a, b, {a, b, c}} ise, s(a) = 3 tür. tanımlanmış nesneler topluluğuna küme denir. 2. Ortak Özellik Yöntemi Kümenin elemanlarını, daha somut ya
KÜMELER Canlı yada cansız varlıkların oluşturduğu iyi A = {a, b, {a, b, c}} ise, s(a) = 3 tür. tanımlanmış nesneler topluluğuna küme denir. 2. Ortak Özellik Yöntemi Kümenin elemanlarını, daha somut ya
KÜMELER. a. Doğal sayılar b. Elimdeki parmaklar c. Yaşayan dahi insanlar d. Üç ayaklı hayvanlar e.
 1 KÜMELER KÜME KVRMI Modern matematiğin en önemli ve temel öğelerinden biri küme kavramıdır. Kümeler teorisinin dili ve teknikleri matematiğe ve bilimin diğer birçok branşına temel teşkil eder. Kümenin,
1 KÜMELER KÜME KVRMI Modern matematiğin en önemli ve temel öğelerinden biri küme kavramıdır. Kümeler teorisinin dili ve teknikleri matematiğe ve bilimin diğer birçok branşına temel teşkil eder. Kümenin,
A) 4 B) 8 C) 16 D) 32 E) 63. kaçtır?(d) A) 28 B) 44 C) 58 D) 64 E) 79 A) 16 B) 14 C) 12 D) 10 E) 8 8. ( ) veriliyor.a B kümesinin en az iki
 TEST 3 1.={{x},y,{Ø}} kümesi için, aşağıdakilerden kaç tanesi yanlıştır?() i.ø ii.{x} iii.ø iv.{ø} v.{y} ) 1 ) 2 ) 3 D) 4 E) 5 2.Şekildeki taralı küme aşağıdakilerden hangisiyle ifade edilemez? 5. ( Α
TEST 3 1.={{x},y,{Ø}} kümesi için, aşağıdakilerden kaç tanesi yanlıştır?() i.ø ii.{x} iii.ø iv.{ø} v.{y} ) 1 ) 2 ) 3 D) 4 E) 5 2.Şekildeki taralı küme aşağıdakilerden hangisiyle ifade edilemez? 5. ( Α
TEOG. Sayma Sayıları ve Doğal Sayılar ÇÖZÜM ÖRNEK ÇÖZÜM ÖRNEK SAYI BASAMAKLARI VE SAYILARIN ÇÖZÜMLENMESİ 1. DOĞAL SAYILAR.
 TEOG Sayma Sayıları ve Doğal Sayılar 1. DOĞAL SAYILAR 0 dan başlayıp artı sonsuza kadar giden sayılara doğal sayılar denir ve N ile gösterilir. N={0, 1, 2, 3,...,n, n+1,...} a ve b doğal sayılar olmak
TEOG Sayma Sayıları ve Doğal Sayılar 1. DOĞAL SAYILAR 0 dan başlayıp artı sonsuza kadar giden sayılara doğal sayılar denir ve N ile gösterilir. N={0, 1, 2, 3,...,n, n+1,...} a ve b doğal sayılar olmak
İçindekiler. 3. Sonlu ve Sonsuz Kümeler Denk ve Eşit Kümeler Kümelerde Birleşim ve Kesişim
 İçindekiler 1. Küme Kavramı...6-7 2. Kümelerin Gösterimi...8-15 3. Sonlu ve Sonsuz Kümeler... 16-17 4. lt Küme Kavramı... 18-27 5. Denk ve şit Kümeler... 28-29 6. Kümelerde irleşim ve Kesişim... 31-41
İçindekiler 1. Küme Kavramı...6-7 2. Kümelerin Gösterimi...8-15 3. Sonlu ve Sonsuz Kümeler... 16-17 4. lt Küme Kavramı... 18-27 5. Denk ve şit Kümeler... 28-29 6. Kümelerde irleşim ve Kesişim... 31-41
YAZILI ÇALIŞMA TEKNİKLERİ. w w w. g e o m e t r i g o r m e t e k n i k l e r i. c o m. { } : boþ küme demek deðildir. ÇÖZÜMÜ:
 KONU BİLGİSİ 1.KÜME TNIMI VE GÖSTERÝM ÞEKÝLLERÝ Belli özellikleri saðlayan nesneler topluluðuna küme denir. Kümede tüm elemanlar net olmalýdýr. Kümeler büyük harflerle gösterilir. Bir kümede bir eleman
KONU BİLGİSİ 1.KÜME TNIMI VE GÖSTERÝM ÞEKÝLLERÝ Belli özellikleri saðlayan nesneler topluluðuna küme denir. Kümede tüm elemanlar net olmalýdýr. Kümeler büyük harflerle gösterilir. Bir kümede bir eleman
KÜMELER. Kümeler YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 MATEMATĐK ĐM /LYS. UYARI: {φ} ifadesi boş kümeyi göstermez.
 MTEMTĐK ĐM YILLR 00 00 004 005 006 007 008 009 010 011 ÖSS-YGS - 1 - - - - - 1 1 1/1 /LYS KÜMELER TNIM: in tam bir tanımı yoksa da matematikçiler kümeyi; iyi tanımlanmış nesneler topluluğu olarak kabul
MTEMTĐK ĐM YILLR 00 00 004 005 006 007 008 009 010 011 ÖSS-YGS - 1 - - - - - 1 1 1/1 /LYS KÜMELER TNIM: in tam bir tanımı yoksa da matematikçiler kümeyi; iyi tanımlanmış nesneler topluluğu olarak kabul
KÜMELER 05/12/2011 0
 KÜMELER 05/12/2011 0 KÜME NEDİR?... 2 KÜMELERİN ÖZELLİKLERİ... 2 KÜMELERİN GÖSTERİLİŞİ... 2 EŞİT KÜME, DENK KÜME... 3 EŞİT OLMAYAN (FARKLI) KÜMELER... 3 BOŞ KÜME... 3 ALT KÜME - ÖZALT KÜME... 4 KÜMELERDE
KÜMELER 05/12/2011 0 KÜME NEDİR?... 2 KÜMELERİN ÖZELLİKLERİ... 2 KÜMELERİN GÖSTERİLİŞİ... 2 EŞİT KÜME, DENK KÜME... 3 EŞİT OLMAYAN (FARKLI) KÜMELER... 3 BOŞ KÜME... 3 ALT KÜME - ÖZALT KÜME... 4 KÜMELERDE
1. Bir kümenin eleman say s 3 artt r ld nda, alt küme say s 56 artmaktad r.
 1. ir kümenin eleman say s artt r ld nda, alt küme say s 56 artmaktad r. una göre, ilk durumdaki kümenin eleman say - s kaçt r? ) 2 ) ) D) 5 E) 6 6. ve kümelere E evrensel kümesinin alt kümeleri olmak
1. ir kümenin eleman say s artt r ld nda, alt küme say s 56 artmaktad r. una göre, ilk durumdaki kümenin eleman say - s kaçt r? ) 2 ) ) D) 5 E) 6 6. ve kümelere E evrensel kümesinin alt kümeleri olmak
KÜMELER. Küme nesneler topluluğudur. Bu bölümde kümelerle kurulan matematiksel yapıyı tanıtacağız.
 KÜMELER Küme nesneler topluluğudur. u bölümde kümelerle kurulan matematiksel yapıyı tanıtacağız. Küme kavramı matematiğe girmeden önce matematik denilince akla sayılar ve şekiller gelirdi. Kümeler kuramının
KÜMELER Küme nesneler topluluğudur. u bölümde kümelerle kurulan matematiksel yapıyı tanıtacağız. Küme kavramı matematiğe girmeden önce matematik denilince akla sayılar ve şekiller gelirdi. Kümeler kuramının
Dikkat: Bir eleman, her iki kümede de olsa bile sadece bir kez yazılır.
 KÜMELER Kümelerin birleşimi (A B ): Kümelerin bütün elemanlarından oluşur. Kümelerin kesişimi (A B): Kümelerin ortak elemanlarından oluşur. Kümelerin Farkı (A \ B ) veya (A - B ): Birinci kümede olup ikinci
KÜMELER Kümelerin birleşimi (A B ): Kümelerin bütün elemanlarından oluşur. Kümelerin kesişimi (A B): Kümelerin ortak elemanlarından oluşur. Kümelerin Farkı (A \ B ) veya (A - B ): Birinci kümede olup ikinci
Küme Temel Kavramları
 Kümeler Kümeler Küme, matematiksel anlamda tanımsız bir kavramdır. Bu kavram "nesneler topluluğu veya yığını" olarak yorumlanabilir. Bu tanımdaki "nesne" soyut ya da somut bir şeydir; fakat her ne olursa
Kümeler Kümeler Küme, matematiksel anlamda tanımsız bir kavramdır. Bu kavram "nesneler topluluğu veya yığını" olarak yorumlanabilir. Bu tanımdaki "nesne" soyut ya da somut bir şeydir; fakat her ne olursa
1. Ünite - ÜTT. 1. Ünite. Aşağıdaki karşılaştırmalardan hangisi yanlıştır? Aşağıdakilerden hangisi 256 sayısına eşit değildir? 1 57 < < 3 4
 . Ünite - ÜTT. Ünite. şağıdakilerden hangisi 6 sayısına eşit değildir?. şağıdaki karşılaştırmalardan hangisi yanlıştır? < 6 < 3 = 6 3 > 3. ir postacı, her gün tane eve birer adet fatura bırakmaktadır.
. Ünite - ÜTT. Ünite. şağıdakilerden hangisi 6 sayısına eşit değildir?. şağıdaki karşılaştırmalardan hangisi yanlıştır? < 6 < 3 = 6 3 > 3. ir postacı, her gün tane eve birer adet fatura bırakmaktadır.
KÜMELER KÜMELER Kümeler Konu Özeti Konu Testleri (1 6) Kartezyen Çarpım Konu Özeti Konu Testleri (1 6)...
 Sayfa No....................................................................9 - Kümeler Konu Özeti.......................................................... 9 Konu estleri ( 6)...........................................................
Sayfa No....................................................................9 - Kümeler Konu Özeti.......................................................... 9 Konu estleri ( 6)...........................................................
İlter TÜRKMEN, Tolga TANIŞ, Simay AYDIN,
 YAYIN KURULU Hazırlayanlar İlter TÜRKMEN, Tolga TANIŞ, Simay AYDIN, YAYINA HAZIRLAYANLAR KURULU Kurumsal Yayınlar Yönetmeni Saime YILDIRIM Kurumsal Yayınlar Birimi Dizgi & Grafik Mustafa Burak SANK & Ezgi
YAYIN KURULU Hazırlayanlar İlter TÜRKMEN, Tolga TANIŞ, Simay AYDIN, YAYINA HAZIRLAYANLAR KURULU Kurumsal Yayınlar Yönetmeni Saime YILDIRIM Kurumsal Yayınlar Birimi Dizgi & Grafik Mustafa Burak SANK & Ezgi
7. Aşağıda verilen önermelerin değillerini yazınız. a. p: Bazı aylar 30 gündür. p : Bazı aylar 30 gün değildir.
 ADIM 0. Aşağıdaki ifadelerin bir önerme olup olmadığını belirtiniz. a. Asal sayıların hepsi tek sayıdır. önerme b. Türkiye 7 farklı coğrafi bölgeden oluşur. önerme c. Çay içmeye gelen var mı? önerme değil.
ADIM 0. Aşağıdaki ifadelerin bir önerme olup olmadığını belirtiniz. a. Asal sayıların hepsi tek sayıdır. önerme b. Türkiye 7 farklı coğrafi bölgeden oluşur. önerme c. Çay içmeye gelen var mı? önerme değil.
KÜMELER A) 1 B) 2 C) 3 D) 4 E) 5 A) 1 B) 2 C) 3 D) 4 E) 5 A) 30 B) 31 C) 32 D) 33 E) 34 A) 30 B) 25 C) 21 D) 19 E) 17 A) 24 B) 26 C) 28 D) 30 E) 32
 TARAMA TESTİ 1 KÜMELER 1. A= x N : x 6 A B x N : x 8 B \ A aşağıdakikerden hangisidir? A)7,8 B)6,7,8 C)8 D)7 E) 2. A = x N : 2 x 7, B = x N : 2 x 5 olduğuna göre,a \ B nin eleman sayısı kaç? 3. A = x N
TARAMA TESTİ 1 KÜMELER 1. A= x N : x 6 A B x N : x 8 B \ A aşağıdakikerden hangisidir? A)7,8 B)6,7,8 C)8 D)7 E) 2. A = x N : 2 x 7, B = x N : 2 x 5 olduğuna göre,a \ B nin eleman sayısı kaç? 3. A = x N
SAYILAR DOĞAL VE TAM SAYILAR
 1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
TAMSAYILAR. 9www.unkapani.com.tr. Z = {.., -3, -2, -1, 0, 1, 2, 3, } kümesinin her bir elemanına. a, b, c birer tamsayı olmak üzere, Burada,
 TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
1.BÖLÜM ÇÖZÜM SORU. A= {a, b, {a, b}, {c}} kümesi veriliyor. Afla dakilerden kaç tanesi do rudur? I. a A II. {a, b} A III. {c} A IV. {b} A. V.
 1.ÖLÜM MTMT K Derginin bu say s nda Kümeler konusunda çözümlü sorular yer almaktad r. u konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü içinde
1.ÖLÜM MTMT K Derginin bu say s nda Kümeler konusunda çözümlü sorular yer almaktad r. u konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü içinde
9. Sınıf Matemat k Ders İşleme Defter. Altın Kalem Yayınları
 9. Sınıf Matemat k Ders İşleme Defter KÜMELER - 1 Altın Kalem Yayınları Küme: B rb r nden farklı nesneler n oluşturduğu topluluklar küme şekl nde adlandırılır. Kümey oluşturan nesneler n y bel rlenm ş
9. Sınıf Matemat k Ders İşleme Defter KÜMELER - 1 Altın Kalem Yayınları Küme: B rb r nden farklı nesneler n oluşturduğu topluluklar küme şekl nde adlandırılır. Kümey oluşturan nesneler n y bel rlenm ş
ÜNİTE: RASYONEL SAYILAR KONU: Rasyonel Sayılar Kümesinde Çıkarma İşlemi
 ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
Ders 2: Küme Teorisi, Örnek Uzay, Permütasyonlar ve Kombinasyonlar
 Ders 2: Küme Teorisi, Örnek Uzay, Permütasyonlar ve Kombinasyonlar Küme Kavramı Küme İşlemleri Deney, Örnek Uzay, Örnek Nokta ve Olay Kavramları Örnek Noktaları Sayma Permütasyonlar Kombinasyonlar Parçalanmalar
Ders 2: Küme Teorisi, Örnek Uzay, Permütasyonlar ve Kombinasyonlar Küme Kavramı Küme İşlemleri Deney, Örnek Uzay, Örnek Nokta ve Olay Kavramları Örnek Noktaları Sayma Permütasyonlar Kombinasyonlar Parçalanmalar
1. BÖLÜM: KÜMELERDE TEMEL KAVRAMLAR, KÜMELERDE İŞLEMLER BÖLÜM: KARTEZYEN ÇARPIM, KÜME PROBLEMLERİ BÖLÜM: GERÇEK SAYILAR...
 İçindekiler 1. BÖLÜM: KÜMELERDE TEMEL KVRMLR, KÜMELERDE İŞLEMLER... 10. KÜMELERDE TEMEL KVRMLR... 10 B. SONLU, SONSUZ VE BOŞ KÜME... 12 C. KÜMELERİN EŞİTLİĞİ... 14 D. LT KÜME, ÖZ LT KÜME... 14 E. KÜMELERDE
İçindekiler 1. BÖLÜM: KÜMELERDE TEMEL KVRMLR, KÜMELERDE İŞLEMLER... 10. KÜMELERDE TEMEL KVRMLR... 10 B. SONLU, SONSUZ VE BOŞ KÜME... 12 C. KÜMELERİN EŞİTLİĞİ... 14 D. LT KÜME, ÖZ LT KÜME... 14 E. KÜMELERDE
YGS - LYS SAYILAR KONU ÖZETLİ ÇÖZÜMLÜ SORU BANKASI
 YGS - LYS SAYILAR KONU ÖZETLİ LÜ SORU BANKASI ANKARA ÖN SÖZ Sevgili Öğrenciler, ÖSYM nin son yıllarda yaptığı sınavlardaki matematik sorularının eski sınav sorularından çok farklı olduğu herkes tarafından
YGS - LYS SAYILAR KONU ÖZETLİ LÜ SORU BANKASI ANKARA ÖN SÖZ Sevgili Öğrenciler, ÖSYM nin son yıllarda yaptığı sınavlardaki matematik sorularının eski sınav sorularından çok farklı olduğu herkes tarafından
MATEMAT K 1 ÜN TE II KÜMELER
 ÜN TE II KÜMELER 1. TANIM 2. KÜMELER N GÖSTER M a) Liste yöntemi ile gösterimi b) Venn flemas ile gösterimi c) Ortak özelik yöntemi ile gösterimi 3. KÜMELER N KARfiILAfiTIRILMASI a) Kümenin elaman say
ÜN TE II KÜMELER 1. TANIM 2. KÜMELER N GÖSTER M a) Liste yöntemi ile gösterimi b) Venn flemas ile gösterimi c) Ortak özelik yöntemi ile gösterimi 3. KÜMELER N KARfiILAfiTIRILMASI a) Kümenin elaman say
TEMEL SAYMA. Bill Gates
 Bölüm 1 TEMEL SAYMA YÖNTEMLERİ Firmamızın sahip olduğu tek şey insan düş gücüdür. Bill Gates Bu bölümde fazla kuramsal bilgi gerektirmeyen sayma problemleri üzerinde duracağız. Bu tür problemlerde sayma;
Bölüm 1 TEMEL SAYMA YÖNTEMLERİ Firmamızın sahip olduğu tek şey insan düş gücüdür. Bill Gates Bu bölümde fazla kuramsal bilgi gerektirmeyen sayma problemleri üzerinde duracağız. Bu tür problemlerde sayma;
ÜNİTE 1: TEMEL KAVRAMLAR
 MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
TEMEL KAVRAMLAR. SAYI KÜMELERİ 1. Doğal Sayılar
 TEMEL KAVRAMLAR Rakam: Sayıları ifade etmeye yarayan sembollere rakam denir. Bu semboller {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarıdır., b ve c birer rakamdır. 15 b = c olduğuna göre, + b + c
TEMEL KAVRAMLAR Rakam: Sayıları ifade etmeye yarayan sembollere rakam denir. Bu semboller {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarıdır., b ve c birer rakamdır. 15 b = c olduğuna göre, + b + c
Buna göre, eşitliği yazılabilir. sayılara rasyonel sayılar denir ve Q ile gösterilir. , -, 2 2 = 1. sayıdır. 2, 3, 5 birer irrasyonel sayıdır.
 TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
TEMEL KAVRAMLAR Test -1
 TEMEL KAVRAMLAR Test -1 1. 6 ( ) 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 ( 3). ( 8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36:9 18 : 3 A) 1 B) 8 C) D) 4 E) 8 3. (4: 3 + 1):4 A) 3 B) 5
TEMEL KAVRAMLAR Test -1 1. 6 ( ) 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 ( 3). ( 8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36:9 18 : 3 A) 1 B) 8 C) D) 4 E) 8 3. (4: 3 + 1):4 A) 3 B) 5
1. ÜNİTE 2. ÜNİTE 3. ÜNİTE. Bölüm 1 : Üslü Sayılar... 8. Bölüm 2 : Doğal Sayılar... 18. Bölüm 3 : Doğal Sayı Problemleri... 30
 İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
9. SINIF MATEMATİK SORU BANKASI. Sinan YILMAZ Dr. Sefa YILDIZ UĞURLU Ertan GÜLER
 9. SINIF MTEMTİK SORU NKSI Sinan YILMZ r. Sefa YILIZ UĞURLU Ertan GÜLER Nitelik Yayınları /8 9. Sınıf Matematik Soru ankası / Sinan YILMZ - r. Sefa YILIZ UĞURLU - Ertan GÜLER Yayına Hazırlama NİTELİK izgi-grafik
9. SINIF MTEMTİK SORU NKSI Sinan YILMZ r. Sefa YILIZ UĞURLU Ertan GÜLER Nitelik Yayınları /8 9. Sınıf Matematik Soru ankası / Sinan YILMZ - r. Sefa YILIZ UĞURLU - Ertan GÜLER Yayına Hazırlama NİTELİK izgi-grafik
TEMEL SAYMA KURALLARI
 TEMEL SAYMA KURALLARI SAYMA Toplama Yoluyla Sayma A ve B sonlu ve ayrık kümeler olmak üzere, bu iki kümenin birleşiminin eleman sayısı; s(a,b) = s(a) + s(b) dir. Sonlu ve ayrık iki kümenin birleşiminin
TEMEL SAYMA KURALLARI SAYMA Toplama Yoluyla Sayma A ve B sonlu ve ayrık kümeler olmak üzere, bu iki kümenin birleşiminin eleman sayısı; s(a,b) = s(a) + s(b) dir. Sonlu ve ayrık iki kümenin birleşiminin
MODÜLER ARİTMETİK A)1 B)3 C)8 D)11 E)13. TANIM Z tam sayılar kümesinde tanımlı
 MODÜLER ARİTMETİK A)1 B)3 C)8 D)11 E)13 TANIM Z tam sayılar kümesinde tanımlı ={(x,y): x ile y nin farkı n ile tam bölünür} = {(x,y): n x-y, n N + } bağıntısı bir denklik bağıntısıdır. (x,y) ise x y (mod
MODÜLER ARİTMETİK A)1 B)3 C)8 D)11 E)13 TANIM Z tam sayılar kümesinde tanımlı ={(x,y): x ile y nin farkı n ile tam bölünür} = {(x,y): n x-y, n N + } bağıntısı bir denklik bağıntısıdır. (x,y) ise x y (mod
1. BÖLÜM. Sayılarda Temel Kavramlar. Bölme - Bölünebilme - Faktöriyel EBOB - EKOK. Kontrol Noktası 1
 1. BÖLÜM Sayılarda Temel Kavramlar Bölme - Bölünebilme - Faktöriyel EBOB - EKOK Kontrol Noktası 1 Isınma Hareketleri 1 Uygun eşleştirmeleri yapınız. I. {0, 1, 2,..., 9} II. {1, 2, 3,...} III. {0, 1, 2,
1. BÖLÜM Sayılarda Temel Kavramlar Bölme - Bölünebilme - Faktöriyel EBOB - EKOK Kontrol Noktası 1 Isınma Hareketleri 1 Uygun eşleştirmeleri yapınız. I. {0, 1, 2,..., 9} II. {1, 2, 3,...} III. {0, 1, 2,
MateMito AKILLI MATEMATİK DEFTERİ
 Ar tık Matematiği Çok Seveceksiniz! MateMito AKILLI MATEMATİK DEFTERİ Artık matematikten korkmuyorum. Artık matematiği çok seviyorum. Artık az yazarak çok soru çözüyorum. Artık matematikten sıkılmıyorum.
Ar tık Matematiği Çok Seveceksiniz! MateMito AKILLI MATEMATİK DEFTERİ Artık matematikten korkmuyorum. Artık matematiği çok seviyorum. Artık az yazarak çok soru çözüyorum. Artık matematikten sıkılmıyorum.
1) Aşağıdaki varlıklar içerisinde küme oluşturabilecek bir topluluğu yuvarlak içerisine alarak kümenin tarifini yapınız.
 1ÖLÜM KÜMELER KÜMELER TEST 1 1) şağıdaki varlıklar içerisinde küme oluşturabilecek bir topluluğu yuvarlak içerisine alarak kümenin tarifini yapınız..güzelyurt.yeni İskele.Lefkoşa.Gazi Magosa.Girne 2)
1ÖLÜM KÜMELER KÜMELER TEST 1 1) şağıdaki varlıklar içerisinde küme oluşturabilecek bir topluluğu yuvarlak içerisine alarak kümenin tarifini yapınız..güzelyurt.yeni İskele.Lefkoşa.Gazi Magosa.Girne 2)
AYRIK YAPILAR ARŞ. GÖR. SONGÜL KARAKUŞ- FIRAT ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ YAZILIM MÜHENDİSLİĞİ BÖLÜMÜ, ELAZIĞ
 AYRIK YAPILAR P r o f. D r. Ö m e r A k ı n v e Y r d. D o ç. D r. M u r a t Ö z b a y o ğ l u n u n Ç e v i r i E d i t ö r l ü ğ ü n ü ü s t l e n d i ğ i «A y r ı k M a t e m a t i k v e U y g u l a
AYRIK YAPILAR P r o f. D r. Ö m e r A k ı n v e Y r d. D o ç. D r. M u r a t Ö z b a y o ğ l u n u n Ç e v i r i E d i t ö r l ü ğ ü n ü ü s t l e n d i ğ i «A y r ı k M a t e m a t i k v e U y g u l a
ÜNİTE: TAM SAYILAR KONU: Tam Sayılar Kümesinde Çıkarma İşlemi
 ÜNE: AM AYIAR N: am ayılar ümesinde Çıkarma şlemi ÖRNE RAR VE ÇÖZÜMER 1. [(+17) (+25)] + [( 12) (+21)] işleminin sonucu A) 41 B) 25 C) 25 D) 41 Çıkarma işlemi yapılırken çıkanın işareti değişir ve eksilen
ÜNE: AM AYIAR N: am ayılar ümesinde Çıkarma şlemi ÖRNE RAR VE ÇÖZÜMER 1. [(+17) (+25)] + [( 12) (+21)] işleminin sonucu A) 41 B) 25 C) 25 D) 41 Çıkarma işlemi yapılırken çıkanın işareti değişir ve eksilen
MATEMATİK. Doç Dr Murat ODUNCUOĞLU
 MATEMATİK Doç Dr Murat ODUNCUOĞLU Mesleki Matematik 1 TEMEL KAVRAMLAR RAKAM Sayıları yazmak için kullandığımız işaretlere rakam denir. Sayıları ifade etmeye yarayan sembollere rakam denir. Rakamlar 0,1,2,3,4,5,6,7,8,9
MATEMATİK Doç Dr Murat ODUNCUOĞLU Mesleki Matematik 1 TEMEL KAVRAMLAR RAKAM Sayıları yazmak için kullandığımız işaretlere rakam denir. Sayıları ifade etmeye yarayan sembollere rakam denir. Rakamlar 0,1,2,3,4,5,6,7,8,9
MATM 133 MATEMATİK LOJİK. Dr. Doç. Çarıyar Aşıralıyev
 MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 3.KONU Kümeler Teorisi; Küme işlemleri, İkili işlemler 1. Altküme 2. Evrensel Küme 3. Kümelerin Birleşimi 4. Kümelerin Kesişimi 5. Bir Kümenin Tümleyeni
MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 3.KONU Kümeler Teorisi; Küme işlemleri, İkili işlemler 1. Altküme 2. Evrensel Küme 3. Kümelerin Birleşimi 4. Kümelerin Kesişimi 5. Bir Kümenin Tümleyeni
9. Sınıf. Matematik. Soru Bankası. Yeliz ÇELEN
 9. Sınıf Matematik Soru ankası Yeliz ÇELEN opyright Evrensel İletişim Yayın ağıtım San. Tic. Ltd. Şti. u kitabın her hakkı EVRENSEL İLETİŞİM LT. ŞTİ. e aittir. Hangi amaçla olursa olsun, bu kitabın tamamının
9. Sınıf Matematik Soru ankası Yeliz ÇELEN opyright Evrensel İletişim Yayın ağıtım San. Tic. Ltd. Şti. u kitabın her hakkı EVRENSEL İLETİŞİM LT. ŞTİ. e aittir. Hangi amaçla olursa olsun, bu kitabın tamamının
Kartezyen Çarpım Kümesi
 ölüm 1.2 Kümelerde İşlemler Neler Öğreneceğiz? 1.2.4. Kartezyen Çarpım Kümesi Sıralı ikilileri ve iki kümenin kartezyen çarpım kümesini nahtar Terimler Sıralı ikili Kartezyen çarpım aşlarken ir sinema
ölüm 1.2 Kümelerde İşlemler Neler Öğreneceğiz? 1.2.4. Kartezyen Çarpım Kümesi Sıralı ikilileri ve iki kümenin kartezyen çarpım kümesini nahtar Terimler Sıralı ikili Kartezyen çarpım aşlarken ir sinema
PERMÜTASYON, KOMBİNASYON. Örnek: Örnek: Örnek:
 SAYMANIN TEMEL KURALLARI Toplama Kuralı : Sonlu ve ayrık kümelerin eleman sayılarının toplamı, bu kümelerin birleşimlerinin eleman sayısına eşittir. Mesela, sonlu ve ayrık iki küme A ve B olsun. s(a)=
SAYMANIN TEMEL KURALLARI Toplama Kuralı : Sonlu ve ayrık kümelerin eleman sayılarının toplamı, bu kümelerin birleşimlerinin eleman sayısına eşittir. Mesela, sonlu ve ayrık iki küme A ve B olsun. s(a)=
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1
 ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir.
 Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir. a) Pozitif doğal sayılar: Sıfır olmayan doğal sayılar kümesine Pozitif Doğal
Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir. a) Pozitif doğal sayılar: Sıfır olmayan doğal sayılar kümesine Pozitif Doğal
TEMEL KAVRAMLAR. a Q a ve b b. a b c 4. a b c 40. 7a 4b 3c. a b c olmak üzere a,b ve pozitif. 2x 3y 5z 84
 N 0,1,,... Sayı kümesine doğal sayı kümesi denir...., 3,, 1,0,1,,3,... sayı kümesine tamsayılar kümesi denir. 1,,3,... saı kümesine sayma sayıları denir.pozitif tamsayılar kümesidir. 15 y z x 3 5 Eşitliğinde
N 0,1,,... Sayı kümesine doğal sayı kümesi denir...., 3,, 1,0,1,,3,... sayı kümesine tamsayılar kümesi denir. 1,,3,... saı kümesine sayma sayıları denir.pozitif tamsayılar kümesidir. 15 y z x 3 5 Eşitliğinde
1. BÖLÜM Mantık BÖLÜM Sayılar BÖLÜM Rasyonel Sayılar BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler
 ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
6. Ali her gün cebinde kalan parasının (2009) a, b ve c farklı pozitif tamsayılar, 9. x, y, z pozitif gerçek sayılar,
 1. 9 2 x 2 ifadesinin açılımında sabit x terim kaç olur? A) 672 B) 84 C) 1 D) -84.E) -672 6. Ali her gün cebinde kalan parasının %20 sini harcamaktadır. Pazartesi sabahı haftalığını alan Ali ni Salı günü
1. 9 2 x 2 ifadesinin açılımında sabit x terim kaç olur? A) 672 B) 84 C) 1 D) -84.E) -672 6. Ali her gün cebinde kalan parasının %20 sini harcamaktadır. Pazartesi sabahı haftalığını alan Ali ni Salı günü
sayıların kümesi N 1 = { 2i-1: i N } ve tüm çift doğal sayıların kümesi N 2 = { 2i: i N } şeklinde gösterilebilecektir. Hiç elemanı olmayan kümeye
 KÜME AİLELERİ GİRİŞ Bu bölümde, bir çoğu daha önceden bilinen incelememiz için gerekli olan bilgileri vereceğiz. İlerde konular işlenirken karşımıza çıkacak kavram ve bilgileri bize yetecek kadarı ile
KÜME AİLELERİ GİRİŞ Bu bölümde, bir çoğu daha önceden bilinen incelememiz için gerekli olan bilgileri vereceğiz. İlerde konular işlenirken karşımıza çıkacak kavram ve bilgileri bize yetecek kadarı ile
DOĞU AKDENİZ ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ 23. LİSELERARASI MATEMATİK YARIŞMASI
 DOĞU AKDENİZ ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ 23. LİSELERARASI MATEMATİK YARIŞMASI BİREYSEL YARIŞMA SORULARI CEVAPLARI CEVAP KAĞIDI ÜZERİNE YAZINIZ. SORU KİTAPÇIĞINI KARALAMA MAKSATLI KULLANABİLİRSİNİZ 1
DOĞU AKDENİZ ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ 23. LİSELERARASI MATEMATİK YARIŞMASI BİREYSEL YARIŞMA SORULARI CEVAPLARI CEVAP KAĞIDI ÜZERİNE YAZINIZ. SORU KİTAPÇIĞINI KARALAMA MAKSATLI KULLANABİLİRSİNİZ 1
( ) (, ) Kombinasyon. Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir.
 Kombinasyon Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir. n elemanın tüm r li kombinasyonlarının sayısı; (, ) C n r ( ) r n P n, r n!
Kombinasyon Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir. n elemanın tüm r li kombinasyonlarının sayısı; (, ) C n r ( ) r n P n, r n!
Kümenin özellikleri. KÜMELER Burada x : ifadesi öyle x lerden oluşur ki diye okunur. Örnek: Kilis in ilçeleri
 Canlı yada cansız varlıkların oluşturduğu iyi tanımlanmış nesneler topluluğuna küme denir. KÜMELER urada x : ifadesi öyle x lerden oluşur ki diye okunur. iyi tanımlanmış: herkes tarafından kabul edilen
Canlı yada cansız varlıkların oluşturduğu iyi tanımlanmış nesneler topluluğuna küme denir. KÜMELER urada x : ifadesi öyle x lerden oluşur ki diye okunur. iyi tanımlanmış: herkes tarafından kabul edilen
LYS Matemat k Deneme Sınavı
 LYS Matematk Deneme Sınavı. n olmak üzere; n n toplamı ten büük n nin alabileceği tamsaı değerleri kaç tanedir? 9 B) 8 7.,, z reel saılar olmak üzere; ( 8) l 8 l z z aşağıdakilerden hangisidir? B) 8. tabanındaki
LYS Matematk Deneme Sınavı. n olmak üzere; n n toplamı ten büük n nin alabileceği tamsaı değerleri kaç tanedir? 9 B) 8 7.,, z reel saılar olmak üzere; ( 8) l 8 l z z aşağıdakilerden hangisidir? B) 8. tabanındaki
Veri Analizi. Isınma Hareketleri. Test İstatistikleri. b) En çok tekrar eden: 7 (mod) c) Açıklık = En büyük En küçük = 10 1 = 9. d)
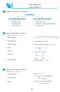 Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
Atatürk Anadolu. Temel Kavramlar Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
6. SINIF GENEL AÇIKLAMA
 6. SINIF GENEL AÇIKLAMA Bu kitapçık 3 bölümden oluşmaktadır. 1. bölümde yer alan 5 sorunun her biri 1, puan değerindedir.. bölümde yer alan 15 sorunun her biri,4 puan değerindedir. 3. bölümde yer alan
6. SINIF GENEL AÇIKLAMA Bu kitapçık 3 bölümden oluşmaktadır. 1. bölümde yer alan 5 sorunun her biri 1, puan değerindedir.. bölümde yer alan 15 sorunun her biri,4 puan değerindedir. 3. bölümde yer alan
ASAL SAYILAR. www.unkapani.com.tr
 ASAL SAYILAR ve kendisinden aşka pozitif öleni olmayan den üyük doğal sayılara asal sayı denir.,, 5, 7,,, 7, 9, sayıları irer asal sayıdır. En küçük asal sayı dir. den aşka çift asal sayı yoktur. den aşka
ASAL SAYILAR ve kendisinden aşka pozitif öleni olmayan den üyük doğal sayılara asal sayı denir.,, 5, 7,,, 7, 9, sayıları irer asal sayıdır. En küçük asal sayı dir. den aşka çift asal sayı yoktur. den aşka
MODÜLER ARİTMETİK. Örnek:
 MODÜLER ARİTMETİK Bir doğal sayının ile bölünmesinden elde edilen kalanlar kümesi { 0,, } dir. ile bölünmesinden elde edilen kalanlar kümesi { 0,,, } tür. Tam sayılar kümesi üzerinde tanımlanan {( x, y)
MODÜLER ARİTMETİK Bir doğal sayının ile bölünmesinden elde edilen kalanlar kümesi { 0,, } dir. ile bölünmesinden elde edilen kalanlar kümesi { 0,,, } tür. Tam sayılar kümesi üzerinde tanımlanan {( x, y)
TABAN ARĠTMETĠĞĠ. ÇÖZÜM (324) 5 = = = = 89 bulunur. Doğru Seçenek C dir.
 TABAN ARĠTMETĠĞĠ Kullandığımız 10 luk sayma sisteminde sayılar {0,1,2,3,4,5,6,7,8,9} kümesinin elemanları (Rakam) kullanılarak yazılır. En büyük elemanı 9 olan, 10 elemanlı bir kümedir. Onluk sistemde;
TABAN ARĠTMETĠĞĠ Kullandığımız 10 luk sayma sisteminde sayılar {0,1,2,3,4,5,6,7,8,9} kümesinin elemanları (Rakam) kullanılarak yazılır. En büyük elemanı 9 olan, 10 elemanlı bir kümedir. Onluk sistemde;
Rakam : Sayıları yazmaya yarayan sembollere rakam denir.
 A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
Kümeler II. KÜMELER. Çözüm A. TANIM. rnek... 3. Çözüm B. KÜMELERÝN GÖSTERÝLMESÝ. rnek... 1. rnek... 2. rnek... 4. 9. Sýnýf / Sayý..
 Kümeler II. KÜMLR. TNIM Küme, bir nesneler topluluðudur. Kümeyi oluþturan nesneler herkes tarafýndan ayný þekilde anlaþýlmalýdýr. Kümeyi oluþturan nesnelerin her birine eleman denir. Kümeyi genel olarak,,
Kümeler II. KÜMLR. TNIM Küme, bir nesneler topluluðudur. Kümeyi oluþturan nesneler herkes tarafýndan ayný þekilde anlaþýlmalýdýr. Kümeyi oluþturan nesnelerin her birine eleman denir. Kümeyi genel olarak,,
Olasılık Kuramı ve İstatistik. Konular Olasılık teorisi ile ilgili temel kavramlar Küme işlemleri Olasılık Aksiyomları
 Olasılık Kuramı ve İstatistik Konular Olasılık teorisi ile ilgili temel kavramlar Küme işlemleri Olasılık Aksiyomları OLASILIK Olasılık teorisi, raslantı ya da kesin olmayan olaylarla ilgilenir. Raslantı
Olasılık Kuramı ve İstatistik Konular Olasılık teorisi ile ilgili temel kavramlar Küme işlemleri Olasılık Aksiyomları OLASILIK Olasılık teorisi, raslantı ya da kesin olmayan olaylarla ilgilenir. Raslantı
2002 ÖSS Soruları. 5. a, b, c, d pozitif tam sayılar ve 123,4 0, ,234 12,34. işleminin sonucu kaçtır?
 00 ÖSS Soruları 3,4.,34 0, 34,34 işleminin sonucu kaçtır? ) 0 ) 0, ) 9,9 ) 0, E),. a, b, c, d pozitif tam sayılar ve a 7 a 4 : = c, : = d b 0 b 4 olduğuna göre, c + d nin alabileceği en küçük değer kaçtır?
00 ÖSS Soruları 3,4.,34 0, 34,34 işleminin sonucu kaçtır? ) 0 ) 0, ) 9,9 ) 0, E),. a, b, c, d pozitif tam sayılar ve a 7 a 4 : = c, : = d b 0 b 4 olduğuna göre, c + d nin alabileceği en küçük değer kaçtır?
MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR
 ATU MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BÖLÜMLERİ AKILLI
ATU MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BÖLÜMLERİ AKILLI
ÖĞRENCİNİN ADI SOYADI: NUMARASI: SINIFI: KONU: Olasılık
 ÖĞRENCİNİN ADI SOYADI: NUMARASI: Dersin Adı SINIFI: KONU: Olasılık Dersin Konusu. Bir kutudaki 7 farklı boncuğun içinden iki tanesi seçiliyor. Buna göre, örneklem uzayının eleman sayısı A) 7 B)! 7. madeni
ÖĞRENCİNİN ADI SOYADI: NUMARASI: Dersin Adı SINIFI: KONU: Olasılık Dersin Konusu. Bir kutudaki 7 farklı boncuğun içinden iki tanesi seçiliyor. Buna göre, örneklem uzayının eleman sayısı A) 7 B)! 7. madeni
Küme temel olarak belli nesnelerin ya da elamanların bir araya gelmesi ile oluşur
 Kümeler Kümeler ve küme işlemleri olasılığın temellerini oluşturmak için çok önemlidir Küme temel olarak belli nesnelerin ya da elamanların bir araya gelmesi ile oluşur Sonlu sayıda, sonsuz sayıda, kesikli
Kümeler Kümeler ve küme işlemleri olasılığın temellerini oluşturmak için çok önemlidir Küme temel olarak belli nesnelerin ya da elamanların bir araya gelmesi ile oluşur Sonlu sayıda, sonsuz sayıda, kesikli
MATEMATİK ADF. Önermeler - I ÜNİTE 1: MANTIK. Önerme. örnek 2. Bir önermenin değili (olumsuzu) örnek 3. Doğruluk Tablosu. örnek 1.
 MATEMATİK ÜNİTE 1: MANTIK Önermeler - I ADF 01 Önerme Doğru ya da yanlış kesin bir hüküm bildiren ifadelere... denir. R Doğru hüküm bildiren önermeye..., Yanlış hüküm bildiren önermeye... denir. R Önermelerin
MATEMATİK ÜNİTE 1: MANTIK Önermeler - I ADF 01 Önerme Doğru ya da yanlış kesin bir hüküm bildiren ifadelere... denir. R Doğru hüküm bildiren önermeye..., Yanlış hüküm bildiren önermeye... denir. R Önermelerin
Matematik. Körfez Yayınları. YGS - LYS Ön Hazırlık
 Matematik R İ T N R Ö SAYISAL K E YGS - LYS Ön Hazırlık Copyright Çağlayan Basım Yayın Dağıtım Ambalaj San. Tic. A.Ş. Bu kitabın tamamının ya da bir kısmının, kitabı yayımlayan şirketin önceden izni olmaksızın
Matematik R İ T N R Ö SAYISAL K E YGS - LYS Ön Hazırlık Copyright Çağlayan Basım Yayın Dağıtım Ambalaj San. Tic. A.Ş. Bu kitabın tamamının ya da bir kısmının, kitabı yayımlayan şirketin önceden izni olmaksızın
2011 YGS MATEMATİK Soruları
 0 YGS MTEMTİK Soruları. + + ) 8 ) 0 ) 6 ) E). a = 6 b = ( a)b olduğuna göre, ifadesinin değeri kaçtır? ) ) 6 ) 9 ) 8 E). (.0 ) ) 0, ) 0, ) 0, ) E) 6. x = y = 8 z = 6 olduğuna göre, aşağıdaki sıralamalardan
0 YGS MTEMTİK Soruları. + + ) 8 ) 0 ) 6 ) E). a = 6 b = ( a)b olduğuna göre, ifadesinin değeri kaçtır? ) ) 6 ) 9 ) 8 E). (.0 ) ) 0, ) 0, ) 0, ) E) 6. x = y = 8 z = 6 olduğuna göre, aşağıdaki sıralamalardan
T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları
 T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu 016-017 Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları 1) 3. [15 3(8: )] 9 =? a) 16 b) 14 c) 0 d) 14 e) 16 6)
T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu 016-017 Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları 1) 3. [15 3(8: )] 9 =? a) 16 b) 14 c) 0 d) 14 e) 16 6)
İKİNCİ DERECEDEN DENKLEMLER
 İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
Ortak Akıl MATEMATİK DENEME SINAVI
 Ortak kıl YGS MTEMTİK ENEME SINVI 1 01511-1 Ortak kıl dem ÇİL li an GÜLLÜ yhan YNĞLIŞ arbaros GÜR arış EMİR eniz KRĞ Ersin KESEN Fatih TÜRKMEN Hatice MNKN Kemal YIN Köksal YİĞİT Muhammet YVUZ Oral YHN
Ortak kıl YGS MTEMTİK ENEME SINVI 1 01511-1 Ortak kıl dem ÇİL li an GÜLLÜ yhan YNĞLIŞ arbaros GÜR arış EMİR eniz KRĞ Ersin KESEN Fatih TÜRKMEN Hatice MNKN Kemal YIN Köksal YİĞİT Muhammet YVUZ Oral YHN
SAYISAL BÖLÜM. 5. a, b, c pozitif tamsayılar, c asal sayı ve. olduğuna göre, aşağıdaki sıralamalardan hangisi doğrudur? 6 E) 1
 SYISL ÖLÜM ĐKKT! U ÖLÜM VPLYĞINIZ TOPLM SORU SYISI 90 IR. Đlk 4 Matematiksel Đlişkilerden Yararlanma Gücü, Son 4 en ilimlerindeki Temel Kavram ve Đlkelerle üşünme Gücü ile ilgilidir. şit ğırlık ÖSS puanınızın
SYISL ÖLÜM ĐKKT! U ÖLÜM VPLYĞINIZ TOPLM SORU SYISI 90 IR. Đlk 4 Matematiksel Đlişkilerden Yararlanma Gücü, Son 4 en ilimlerindeki Temel Kavram ve Đlkelerle üşünme Gücü ile ilgilidir. şit ğırlık ÖSS puanınızın
BMT 206 Ayrık Matematik. Yük. Müh. Köksal GÜNDOĞDU 1
 BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Kümeler Yük. Müh. Köksal GÜNDOĞDU 2 Kümeler Kümeler Ayrık Matematiğin en temel konularından biridir Sayma problemleri için önemli Programlama dillerinin
BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Kümeler Yük. Müh. Köksal GÜNDOĞDU 2 Kümeler Kümeler Ayrık Matematiğin en temel konularından biridir Sayma problemleri için önemli Programlama dillerinin
Olasılık Kavramı. Recep YURTAL. Mühendislikte İstatistik Metotlar. Çukurova Üniversitesi İnşaat Mühendisliği Bölümü
 Olasılık Kavramı Mühendislikte İstatistik Metotlar Çukurova Üniversitesi İnşaat Mühendisliği ölümü OLSILIK KVRMI KÜME KVRMI irlikte ele alınan belirli nesneler topluluğuna küme, Kümede içerilen nesnelere
Olasılık Kavramı Mühendislikte İstatistik Metotlar Çukurova Üniversitesi İnşaat Mühendisliği ölümü OLSILIK KVRMI KÜME KVRMI irlikte ele alınan belirli nesneler topluluğuna küme, Kümede içerilen nesnelere
Ortak Akıl MATEMATİK DENEME SINAVI
 Ortak Akıl YGS MATEMATİK DENEME SINAVI 4 0141- Ortak Akıl Adem ÇİL Ali Can GÜLLÜ Ayhan YANAĞLIBAŞ Barış DEMİR Celal İŞBİLİR Deniz KARADAĞ Engin POLAT Erhan ERDOĞAN Ersin KESEN Fatih TÜRKMEN Hakan BAKIRCI
Ortak Akıl YGS MATEMATİK DENEME SINAVI 4 0141- Ortak Akıl Adem ÇİL Ali Can GÜLLÜ Ayhan YANAĞLIBAŞ Barış DEMİR Celal İŞBİLİR Deniz KARADAĞ Engin POLAT Erhan ERDOĞAN Ersin KESEN Fatih TÜRKMEN Hakan BAKIRCI
