Dünya Kesinlikle Yuvarlak Değildir
|
|
|
- Irmak Esin Kubat
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Dünya Kesinlikle Yuvarlak Değildir (Jeodezinin Bir Ödevi de Dil uyanın Şeklini Belirlemektir) Rudolf SIGL*. - Veli AKARSU İnsanlığın, tüm yaşamının.sürdürdüğü illim ayı tanıma arzusu varoluşundan beri vardır. Jeodezi, insanların \arolduğu bütün alanlar ile yakın ilişkide olmasına karşın, jeodezicilerin çalışmaları \e dünyanın şekli az tanınmaktadır. Jeodezinin bilinen bu açıklığını gidermek amamla Mart 1993 Alman Müzesi Jeodezi, Ölçme ve Harita sergisinin açılışında Prof. Siglln verdiği konferans bu makalenin içeriğini oluşturmaktadır. Bütün jeodezik çalışmaların somut sonucu farklı ölçekteki topografik haritalardır. Haritalar modern bir toplumda \ usanılan mekanın kullanımı ve planlanması için gerekmektedir. Harita, kısaca \eryü/ünün gerçek bir parçasının düzgün geometrik bîr yüzey üzerinde gösterilmesidir Bu tanımla jeodezinin amacı anlatılmaktadır.sözcüğün etimolojik anlamı arazi ölçme ve sınır belirlemektir. Jeodezinin diğer ödevi, tümde ve detayda yerin şeklini belirlemektir. (J/erinde yaşadığımız yeryüzünün jeodezide özel an- Şekil I: Küçük bir bölgenin kartografik çizimi için referans yüzeyi yatay bir düzlemdir. Yer eğriliğinin burada önemi yoktur. Eş potansiyel farkları yükseklik eğrileriyle gösterilir yılında Friedrich Robert Helmert ( )'in bugün de geçerli olan tanımına göre. ieodezi vervüzünün ölçümü ve seklinin belirlenmesi ile uğrasan bir bilim * Bavyera Bilimler Akademisi Matematik ve Doğa Bitimi Bölümü daimi üyesi em. o. Prof. Dr. E. h. Rudolf SIGL'm Kultur &Technik Dergisinin 1/1994 sayısında yayınlanan Almanca makalesinden çeviri iznini alan Yük. Müh. Veli AKARSU tarafından TUrkçeye çevrilmiştir. Makale aynı adla Harita Dergisi Ocak 1997, Sayı: UT de yayımlanmıştır. 80
2 dalıdır. Bu nasıl başarılır? Örneğin; Münih şehir alanının küçük bir bölgesi referans yüzeyi olarak yatay bir düzlem üzerine izdüşurülebilir. Eğer caddeler, binalar ya da işaretli arazi noktaları gibi önemli objeler ölçülür ve bu objelerin X,Y,Z uzay dik koordinatları hesaplanıp referans yüzeyi üzerine dik açılı projeksiyonu yapılırsa gerçeğinin düzlem şekli olan harita elde ediir. X,Y koordinatları objenin konumunu, Z koordinatı da objenin yüksekliğini tanımlar. Projeksiyonda arazi yükseklikleri alışılmış tarzda eş yükseklik eğrileri ile gösterilir. Örneğin; Federal Almanya Cumhuriyeti gibi daha büyük bir sahanın haritası yapılmak istenirse, yer eğriliği etkisi nedeniyle yatay düzlem yerine eğrisel bir referans yüzeyi gerekir. Küre yüzeyi bunun için uygun değildir. Çünkü, yerin deniz yüzeyi ile aynı düzeye getirildiği düşünüldüğünde kutuplarda bir basıklık, ekvatorda ise bir şişkinlik görülecektir. Bu da yerin şeklinin bir küre olmadığını, aksine a ve b gibi iki yan ekseniyle belirlenen bir dönel elipsoit olduğunu göstermektedir. (Şekil 2) Şekil 2 : Daha büyük alanların izdüşümünde ise yeryüzü için öngörülen eğrisel referans yüzeyleri olan küre veya yer elipsoidi gereklidir. Jeodezinin çalışma tarzını kesinlikle etkileyen bir problemde yerin şekliyle olan ilişkisidir. Konum için referans yüzeyi olarak elipsoit uygun olmasına karşın, yükseklikler nasıl gösterilmelidir? Yükseklikler yatay ve düşey kavramlarına bağlıdır; bu nedenle yerin gravite alanı ile bağlantılı bir referans yüzeyi gereklidir. Bununla ilgili olarak şöyle düşünebiliriz: Deniz yüzeyinin, bir dağ gölünün rüzgarsız bir gündeki gibi hiçbir şeyden etkilenmediği düzgün hali düşünülürse, yüzeyin her noktası çekül doğrultusuna, başka bir deyişle kütlesel çekim kuvveti ve yer dönmesinin oluşturduğu merkezkaç kuvvetinin bileşkesi olarak tanımlanan yerçekimi (gravite) kuvvetine diktir. Jeoid olarak adlandırılan, kıtaların altından geçtiği düşünülen ideal bu deniz yüzeyi yüksekliklerin hesabı için özel bir referans yüzeyi olarak alınır. Yeryüzündeki bir noktanın yüksekliği jeoid ve yeryüzü noktası arasındaki çekül doğrultusu boyunca olan uzunluktur. ( Buna aynı zamanda ortometrik yükseklik de denir. (Şekil 3) 81
3 Şekil 3: Konum ve yükseklik için referans yüzeyi olarak elipsoit ve jeoid alınır. Kıta ların altında geçtiği düşünülen tamamen durgun deniz yüzeyinin oluşturduğu şekle jeoid denir. Her iki referans yüzeyi elipsoit ve jeoidden elipsoid; yerin şeklini iyi bir yaklaşımla göstermesine rağmen, jeoid için gravitenin dikkate alınması gerekmektedir. Şekil 4'de ki sayılardan: a yer elipsoidinin büyük yarı ekseninin boyu olup yaklaşık değeri 6378 km'dir. Küçük yarı eksen b ile arasındaki fark yaklaşık olarak 21 km'dir. Böylece graviteyle tanımlanan jeoid ile iyi bir uyum sağlanır. Jeoid yüksekliği ya da ondulasyonu olarak tanımlanan iki yüzey arasındaki fark, genellikle 10 m'den daha küçüktür. Şekil 4 :Elipsoit ve jeoid, geometrik ve fiziksel olarak tanımlanan yer şekilleridir. Yerin çekim kuvveti jeoidin elipsoitten olan farkı bulunurken dikkate alınır. Yeryüzünü ölçümü ve şeklinin belirlenlenmesi çözüm yolu şöyledir: İlk önce yer ölçmesi ile yer elipsoidi ve jeoidi belirlenir, sonrada uygulamalı jeodeziyle yeryüzündeki detay ölçme ve hesaplarının kartografik değerlendirilmesi sonucunda harita elde edilir. Geometrik ve fiziksel olarak tanımlanan yerin şekli XIX. ve XX. yüzyıldaki bilim ve teknolojinin durumuna uymaktadır. İnsanların ilk olarak yerin şeklini ne zaman sorguladıkları kesin olarak bilinmemektedir. Mısır ve Babil uygarlıklarında bilginler yerin küresel şeklini bilmeksizin Astronomi çalışması yaptılar. Homer, yeri bir tarafları askıda 82
4 ve etrafı sıvı ile kaplanmış bir disk sanıyordu. Fakat, Eratosthenes MÖ 3. yüzyılda ilgili merkez açı ile büyük daire yayından yerküresinin yarı çapını belirlemiştir. (Şekil 5) Şekil 5: MÖ II.yüzyılda Eratosthenes yeryüzündeki iki nokta arasındaki b mesafesi ve güneşe gözlem ile ölçülen merkez açı yardımıyla doğru yaklaşım göstererek yer yarı çapını 7300 km olarak hesapladı. Eratosthenes'i yer ölçmenin kurucusu sayabiliriz. Eratosthenos yaklaşık olarak aynı meridyende bulunan Syene (bugünkü Assuan) ve AIexandria arasındaki mesafeyi deve yolculuklarıya elde edilen verilere göre kestirmiş, merkez açıyı da güneşe gözlemler yardımıyla bularak, yer yarıçapını 7300 km olarak hesaplamıştır. Eratosthenos'in düşünüş ve hesaplarının doğruluğu ve günümüz sonuçlarına yaklaşması hayranlık uyandırmaktadır. Eratosthenes ilkesi günümüzde de geçerlidir. Küre yarıçapının belirlenmesi için bir yay ve bu yayın karşısısındaki merkez açı ölçülür. Bu çalışma eskisi gibi yerin şeklinin asiro-jeodezik yöntemle belirlenmesidir. Yerin şeklinin küre olduğu fikri antik öncesi çağda batı kültür çevresinde benimsenmiş ve yakın ortaçağda önemini yitirmiştir. İleri ortaçağda yerin şeklinin küre olduğu yeniden tanınmıştır. Magellan (1480,1521) 1519 yılında ilk olarak dünyanın çevresini yelkenli gemi ile dolaşmaya başlamış ve Juan Sebastioo d'eicano, Magellan'ın ölümünden sonra 1522'de bu turu bitirerek, yerin küresel şeklini herkesin anlayacağı biçiminde kanıtlamıştır. Büyük yükseklikteki uzay uçuşlarında küresel şeklin anlamlı olarak algılanmasını sağlayan bugünkü şekil nesil olmuştur. Hemen hemen 1500 yıl boyunca yerin küresel şekli ve bu küresel şeklin yaklaşık büyüklüğüne ilişkin geçici bilgi, insanların dünya yaşamı ile ilgili ihtiyaçlarından kaynaklanmamıştır. 16. ve 17. yüzyıldan beri değişmiş, fiziksel anlayış nedeniyle gittikçe doğru gözlemlerin yapılması olanağı, elipsoidin yer şekli olarak gösteriminin nedenini açıklamaktadır. Değişikliğin oluşmasını sağlayan neydi.? Nikolaus Kopernikus ( )'ün yapıtı, Ptolemlüs'ün dünya görüşünü düzeltmesi ve güneş merkezli bir dünya görüşüne göre dünyanın yerinin belirlenmesi, 1600'den sonra doğa bilimleri için yeni bir devir açtı. Bu da yer ölçmesine yansımıştır. Yer küreselliğinin şüphe götürmeyen gerçekliği, özellikle yer yarı çapını belirlemek bilimsel ilgi alanına geçti. İlk doğru ölçüler Jean Picard ( ) tarafından XVII. yüzyılın ikinci yarısından itibaren yapıldı. Picard, Paris ve Âmieııs arasındaki meridyen yaylarını ve bunun yanında WiJIebrordıis Snellius'un ( ) denenmiş Triagülasyon (üç-açıyöiîtemi) yöntemini kullanmıştır. Merkez açıyı sabit yıldızlara gözlemlerden coğrafi enlemler farkı olarak türetmiştir. İsaac Nevvton ( ) Picard'ın sonuçlarını çekim yasasına dayandırmıştır. 83
5 NewtoB hidrostatik düşüncesiyle şu sonuçlan çıkartmıştır: Dönen bir yer yuvarı küresel biçimli olmamalı, aksine ekvatorda şişkin ve kutuplarda basık bir elipsoit olmalıdır. Nevvton kutuplardaki basıklığı kestirdiği gibi, aynı zamanda ekvatordan kutuplara yerçekiminin arttığını öne sürmüştür. Bununla yer elipsoitinin belirlenmesi çağı başlatılmış oldu. Elipsoit iki parametreyle belirlenir: Bu parametrelerin hesabı için gereken iki yay uzunluğu ve bu yaylan gören merkez açıları ise astro-jeodezik yöntemle belirlenir. Günümüze kadar belirlenmiş elipsoidlerin en önemlileri Şekil 6'da gösterilmiştirjeodeziciler, elipsoitin iki parametresi olarak büyük yarı eksen a yanında, küçük yarı eksen b yerine genellikle basıklığı, yani x=(a-b):a'yı kullanırlar. Şekil 6 : Astro-Jeodezik olarak belirlenen elipsoitlerin tarihsel sıralaması Yerin kutuplarda basık olduğunu öne süren Newton taraftarları ile, tam doğru olmayan daha doğrusu hatalı ölçülerin değerlendirilebilmesiyle Yer'in kutuplarda sivri, yumurta biçimli olduğu sonucuna varan Giovanni Domenlco Casslni ( ) ve Jacqsıes Cassini ( ) ve Pieıre Loais Moreae de Maupertuis ( )'in yayı ölçmeleri sona erdirdi. George Everestt, George Bidell Alry ve Johra Henry Pratt yerkabuğundaki denge durumu olan isostasi'ye ilişkin ilerlemeleri elipsoitle sağladılar. Friederich Wilhelm Bessel ( ), John Filmore Hayford ( ) ve Feodosij Nikolajewiksch Krasskowskij ( )'in elipsoidleri halen ülke ölçmelerinde hesap yüzeyi olarak kullanılmaktadır. Jeoid belirlemek için gerekli olan gözlemler astronomik olarak belirlenen enlem ve boylam, ayrıca gravite değerleridir. Jeoid devrinim başlama nedeni sadece bilimsel ilgi değil s aksine jeoid bilgisi varsayımı ile ulusal yatay kontrol ağını belirleme talebidir. Jeoid yüzey denklemi kolay ifade edilmeyen karmaşık bir şekildir. Jeoid yüzeyine göre daha basit bir yüzey olan elipsoide göre tek bir noktanın jeoid yüksekliği ancak ölçmelerle elde ediler. (Şekil 7) Yapay yer uydularının jeodeziye yararı; jeoid belirlemenin mevcut 2 yöntemi olan astro-jeodezik ve gravimetrik yöntemlerin uygulanmasında olmuştur. (Şekil 7) 84
6 Şekil 7: Astro-jeodezik jeoid belirleme. Çekül doğrultusu ile elipsoit normali arasındaki doğrultu farkına çekül sapması denir. Çekül doğrultusu sabit yıldızlara astronomik ölçmeler ile belirlenir. Elipsoit normali, elipsoit yüzeyinde konum koordinatları ile bilinir. Astro-jeodezik yöntemle ölçme gerekmektedir. Bu yöntem çok zaman almasından dolayı masraflıdır. Bu yöntemle kıtalarda jeoid belirlemenin avantajı, sadece karada doğru astronomik ölçmelerin yapılabilmesindendir. Buna karşın gravimetrik yöntem daha geçerli ve dünya okyanusları içinde uygulanabilir. Eğer jeoid yüzeyindeki gravite değerleri bilinirse (Şekil 8), tek bir nokta için jeoid yüksekliği de belirlenebilir. Şekil 8: Gravimetrik jeoid belirleme. Yeryüzünün tüm noktalarında gravite değerleri ölçülebilirse tek tek noktalar için jeoid yükseklikleri belirlenebilir. Bu amaçla tüm yeryüzündeki gravitenin ölçülmesi ve jeoid yüzeyine indirgenerek, jeoid dışındaki kütlelerin etkisinin hesap yoluyla çıkartılması gerekmektedir. Gravitenin jeoid yüzeyine indirgenmesine ilişkin temel hesap yöntemleri İngiliz fizikçisi ve matematikçisi George Gabriel Stokes ) tarafından geliştirilmiştir. Gravimetrik yöntemler henüz problemsiz değildir. Şöyle ki : Gravite ölçümü için günümüzde gravite ölçer olmasına karşın, gravite ölçümünde kısmen, ekonomik kısmende politik nedenlerden olayı büyük boşluklar vardır. İkinci olarak yöntemin varsayımlara bağlı olması, yani ölçülen gravite değerlerinin jeoid yüzeyine sayısal olarak indirgenmesi zorunluluğu nedeniyle yer kabuğunun da modellenmesinin gerekliliğidir. Niçin jeodeziciler yükseklik için fiziksel olarak tanımlanan, kıtasal alanlarda görülmeyen,yaklaşılmayan ve de hesaplanmayan bir karmaşık yüzey olan jeoidi referans yüzeyi olarak kullanırlar? Eğer, yerin 85
7 basittir. Yeryuvarı dışındaki potansiyel yüzeyleri bilinirse, her uzay noktasından geçen eş potansiyel yüzeylerine dik olan gravite vektörünün büyüklüğü ve doğrultusu belirlenebilir. Şekil 9: Eş potansiyel yüzeyleri ve gravite alanı. Eğer yerin dışındaki eş potansiyel yüzeyleri bilinirse her uzay noktasından eş potansiyel yüzeylerine dik olan gravite vektörünün büyüklüğü ve doğrultusu belirlenebilir. Birçok jeodezik ölçmeler çekül doğrultusu bilgisini içermektedir. Geometrik olarak tanımlanan bir referans sistemindeki bütün ölçmelerin değerlendirilmesi için çekül doğrultusu bilgisine gereksinim duyulur. Esasında bu zarif yapay yüzeyler normal hayatta da önemli rol oynarlarlar; Örneğin çekül ve su terazisi yardımıyla binaların duvarlarının dikliği ve döşemelerin yataylığının elde edilmesi, eş potansiyel yüzeyleri ile gravite kuvvetine bağlıdır. Klasik yöntemler hem yer elipsoidi hem de jeoid için dikkate değer sonuçlar vermektedir. Bununla beraber geçen 25 yılda yer şeklinin belirlenmesi çalışmaları başarılı görünmektedir. Günümüzde yer elipsoidinin eksenleri ve aynı zamanda evrensel jeoidi ±1 m doğrulukla belirleyebiliyoruz. Bu kesin bilgiye uydular yardımıyla ulaşılmaktadır. Yer çekimine bağlı olarak, yer gravite alanında algılayıcı gibi hareket eden bir uydunun, yer gravite alanındaki yörüngesinin bilinmesi zorunludur. Çünkü yer küreselliğindeki sapmalar ve yer içindeki düzensiz kütle dağılımı nedeniyle, uydu yörüngeleri sabit bölgeli Kepler-Elipsi olmayıp, aksine zamanla bütün yörünge e lemanları kısmen düzgün kısmen de periyodik olarak değişmesinden dolayı gerçek yörünge, kendi eğrilik çemberinde teğet olan elipslerin zarf eğrisidir. Şekil 10: Uydu hareket yörüngeleri deforme olmuş Kepler-Elipsleridir. Gerçek uydu yörüngesi kendi eğrilik çemberinde teğet olan elipslerin bir zarf eğrisidir. Düğüm ve apsid doğrularında önemli bir dönüklüğe sebep olan şey, özellikle yerin 86
8 ekvatordaki şişkinliğini oluşturan kütlesidir.yörünge değişimleri gözlenerek, yerin gravite alanı belirlenir. Yapay yer uydularının jeodeziye yararı gözlemlerden uydu yörüngelerinin tesbitiyle oluşur. Bir P noktasından bir S uydusuna bakılarak doğrultular, uzunluklar, uzunluk değişimleri gözlenirse (Şekil 11), her bir gözlemden P noktasının konumuna, S uydusunun yörüngesine ve yerin gravite alanına ilişkin bilgileri elde edebiliriz. Sekil 11: Dinamik uydu düşüncesinin temel düşüncesi. Yeryüzünde simetrik dağılımlı istasyonlarda, çok sayıda uydu gözlenerek hem gözlem istasyonlarının yer merkezli koordinatları hem de uydu yörüngelerinin ve gravite alanının parametreleri belirlenebilmektedir. Birçok bilinmeyeni araştırırken kullanılan çok sayıda verileri değerlendirebilmek için dinamik yöntemin kullanılması zorunludur. Dinamik uydu yönteminin bir uygulaması da jeoid belirlemedir. Karmaşık yüzeyler iki değişkenli trigonometrik fonksiyonlar olarak tanımlanan küresel fonksiyonlarla gösterilir. Şekil 13'de gösterilen küresel yüzey, düşük derece ve sıradan olan özel bir yüzey, küre harmoniklerivle modellendirilmistir. Şekil 13 : Karmaşık yüzeyler yüzey-küre harmonisi ile tanımlanır. Buradaki yüzey küre harmonisi şekli basit derece ve sıradan olan özel bir fonksiyonla modellendirilmistir. 87
9 Hassas yapılar için daima derece ve sırası büyüyen yeteri kadar birçok küresel yüzey fonksiyonları üst üste çarpılarak ve her yüzeyi temsil eden fonksiyonu sayısal değeri ağırlığı ile çarpılarak, karmaşık yüzeyler pratik olarak gösterilebilirler. Gözlenen uydu yörüngeleri yardımıyla belirlenen bu sayısal değerler ve ağırlıkları, potansiyel sabitleridir. Jeoid yapısı için daha yüksek bir çözüm istenirse bunun için birçok yüzey fonksiyonu kullanılılarak potansiyel sabitlerinin sayısının arttırılması yoluna başvurulur. Son yıllarda, jeoid ile bağlantısı olan yer potansiyel modelleri uydu jeodezisinin dinamik yöntemine göre türetilebilmektedir. Yeni yer potansiyel modeli düşünülmemesine karşın,1981'de Münih Teknik Üniversitesi Uydu Jeodezisi Anabilin» Dalı, GRİM 3'ü hesaplıyarak, Şekil 12'deki yer modelini elde etmiştir. Şekil 12: GRİM 3 jeoidinin basit gösterimi, ortalama yer elipsoidine göre jeoid yüksekliği 10 m aralıklı yükseklik eğrileri ile gösterilmiştir. Bir gariplik :Hint Okyanusunda deniz yüzeyi,ortalama deniz yüzeyi yüksekliğinden yaklaşık 100 m daha düşüktür. 95 uydu gözlem istasyonunda 22 uyduya den fazla ölçmeden elde edilen yer potansiyel modeli yardımıyla, gözlem istasyonlarınınin yer merkezli koordinatları ve 1369 adet potansiyel sabiti belirlenmiştir. Görüldüğü gibi jeoid karmaşık bir yüzeydir. Özellikle Hint Okyanusundaki çöküntü ilgi çekicidir. Burada deniz yüzeyi loom aşağıdadır. Bu çöküntüdeki bir gemi yer merkezine 100 m daha yakındır. Çöküntü terkedildiğinde yaklaşık olarak bir dağa tırmanmak için gereken iş kadar, hiçbir ek işe gereksinim duyulmaz. Çünkü deniz yüzeyi en az yaklaşılan bir eşpotansiyelli yüzeydir. Yani potansiyel enerjisi her yerinde eşit büyüklüktedir. Dinamik yöntem yer elipsoidi için çok doğru değerler sağlamaktadır. Büyük yarı eksen a= km uzunluğu için, <3'=(a-b):a basıklık formülüne göre, basıklık q =1: değerini almaktadır Jeodezîk Referans Sisteminin bu parametreleri çok iyi bilinmektedir ve halen gelişti rilmektedir. 1980'de belirlenen büyük yarı eksen değeri, 1909'da Hayford'un hesapladığı değerden yaklaşık 250 m daha kısadır. (Şekil 14) 88
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları ve Koordinat Sistemleri. Doç. Dr. Senem KOZAMAN
 Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
TOPOĞRAFYA. Ölçme Bilgisinin Konusu
 TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
JEOİD ve JEOİD BELİRLEME
 JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU. Yrd. Doç. Dr. Hüseyin KEMALDERE
 JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
JEODEZİK ÖLÇMELER DERSİ. Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE
 JEODEZİK ÖLÇMELER DERSİ Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM 1. Hafta Ders Notları REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM Referans (Koordinat)
JEODEZİK ÖLÇMELER DERSİ Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM 1. Hafta Ders Notları REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM Referans (Koordinat)
ÖLÇME BİLGİSİ. PDF created with FinePrint pdffactory trial version http://www.fineprint.com. Tanım
 ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ
 HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Konuları_Ders# 5 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ JEODEZİ Yeryuvarının şekil,
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Konuları_Ders# 5 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ JEODEZİ Yeryuvarının şekil,
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
Hakan AKÇIN* SUNU Ali ihsan ŞEKERTEKİN
 AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
BÖLÜM 3: MATEMATİKSEL KARTOGRAFYA - TANIMLAR
 BÖLÜM 3: MATEMATİKEL KARTOGRAFYA - TANIMLAR Türkay Gökgöz (www.yildiz.edu.tr/~gokgoz) 3 İÇİNDEKİLER 3. Bir Haritanın Matematiksel Çatısı... 3-3 3.. Ölçek. 3-3 3... Kesir ölçek 3-3 3... Grafik ölçek.. 3-4
BÖLÜM 3: MATEMATİKEL KARTOGRAFYA - TANIMLAR Türkay Gökgöz (www.yildiz.edu.tr/~gokgoz) 3 İÇİNDEKİLER 3. Bir Haritanın Matematiksel Çatısı... 3-3 3.. Ölçek. 3-3 3... Kesir ölçek 3-3 3... Grafik ölçek.. 3-4
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları
 JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN
 Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN Topografya (Surveying) Nedir? Topografya geleneksel olarak, Dünya yüzeyinin üzerindeki, üstündeki veya altındaki noktalarının rölatif konumlarını belirleyen
Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN Topografya (Surveying) Nedir? Topografya geleneksel olarak, Dünya yüzeyinin üzerindeki, üstündeki veya altındaki noktalarının rölatif konumlarını belirleyen
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI
 ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3351 3 4 3 0 0 DERSİN
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3351 3 4 3 0 0 DERSİN
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ
 ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Dünya nın şekli. Küre?
 Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
TEMEL HARİTACILIK BİLGİLERİ. Erkan GÜLER Haziran 2018
 TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
ÖLÇME BİLGİSİ. Ders Programı ÖLÇME BİLGİSİ ÖLÇME BİLGİSİ. Tanım. ÖLÇME BİLGİSİ Tanım. Tanım
 ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam DOÇ. DR. HAKAN BÜYÜKCANGAZ Bahar 2012 Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi 2. Ölçme Bilgisinde kullanılan
ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam DOÇ. DR. HAKAN BÜYÜKCANGAZ Bahar 2012 Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi 2. Ölçme Bilgisinde kullanılan
EKVATORAL KOORDİNAT SİSTEMİ
 EKVATORAL KOORDİNAT SİSTEMİ Dünya nın yüzeyi üzerindeki bir noktayı belirlemek için enlem ve boylam sistemini kullanıyoruz. Gök küresi üzerinde de Dünya nın kutuplarına ve ekvatoruna dayandırılan ekvatoral
EKVATORAL KOORDİNAT SİSTEMİ Dünya nın yüzeyi üzerindeki bir noktayı belirlemek için enlem ve boylam sistemini kullanıyoruz. Gök küresi üzerinde de Dünya nın kutuplarına ve ekvatoruna dayandırılan ekvatoral
Kış Vaktinde Yaz Saati ve Astronomik Zaman Ölçümleri
 Kış Vaktinde Yaz Saati ve Astronomik Zaman Ölçümleri Yaz saati, kış saati, saatler ileri geri derken, ülkemizde son yıllarda, büyükten küçüğe herkes aslında astronomik bir olguyu konuşuyor. Saat dilimimizin
Kış Vaktinde Yaz Saati ve Astronomik Zaman Ölçümleri Yaz saati, kış saati, saatler ileri geri derken, ülkemizde son yıllarda, büyükten küçüğe herkes aslında astronomik bir olguyu konuşuyor. Saat dilimimizin
DÜNYA NIN ŞEKLİ ve BOYUTLARI
 0 DÜNYA NIN ŞEKLİ ve BOYUTLARI Dünya güneşten koptuktan sonra, kendi ekseni etrafında dönerken, meydana gelen kuvvetle; ekvator kısmı şişkince, kutuplardan basık kendine özgü şeklini almıştır. Bu şekle
0 DÜNYA NIN ŞEKLİ ve BOYUTLARI Dünya güneşten koptuktan sonra, kendi ekseni etrafında dönerken, meydana gelen kuvvetle; ekvator kısmı şişkince, kutuplardan basık kendine özgü şeklini almıştır. Bu şekle
HARİTA DAİRESİ BAŞKANLIĞI. İSTANBUL TKBM HİZMET İÇİ EĞİTİM Temel Jeodezi ve GNSS
 HİZMET İÇİ EĞİTİM MART 2015 İSTANBUL TAPU VE KADASTRO II.BÖLGE MÜDÜRLÜĞÜ SUNUM PLANI 1- Jeodezi 2- Koordinat sistemleri 3- GNSS 3 JEODEZİ Jeodezi; Yeryuvarının şekil, boyut, ve gravite alanı ile zamana
HİZMET İÇİ EĞİTİM MART 2015 İSTANBUL TAPU VE KADASTRO II.BÖLGE MÜDÜRLÜĞÜ SUNUM PLANI 1- Jeodezi 2- Koordinat sistemleri 3- GNSS 3 JEODEZİ Jeodezi; Yeryuvarının şekil, boyut, ve gravite alanı ile zamana
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON
 JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
DÜNYA NIN ŞEKLİ VE HAREKETLERİ
 DÜNYA NIN ŞEKLİ VE HAREKETLERİ YERKÜRE NİN ŞEKLİ Bilim ve teknolojik seviyeye bağlı olarak, İlk Çağ da Dünya mızın şekli, değişik biçimlerde tahmin ediliyordu. Dünya nın çevresi günümüzden yaklaşık 2.200
DÜNYA NIN ŞEKLİ VE HAREKETLERİ YERKÜRE NİN ŞEKLİ Bilim ve teknolojik seviyeye bağlı olarak, İlk Çağ da Dünya mızın şekli, değişik biçimlerde tahmin ediliyordu. Dünya nın çevresi günümüzden yaklaşık 2.200
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
Uygulamada Gauss-Kruger Projeksiyonu
 JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
MADDESEL NOKTANIN EĞRİSEL HAREKETİ
 Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
AVRASYA ÜNİVERSİTESİ
 Ders Tanıtım Formu Dersin Adı Öğretim Dili MATEMATİK JEODEZİ Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x) Uzaktan Öğretim(
Ders Tanıtım Formu Dersin Adı Öğretim Dili MATEMATİK JEODEZİ Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x) Uzaktan Öğretim(
T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.
![T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir. T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.](/thumbs/55/35591809.jpg) * = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
* = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
Coğrafi Bilgi Sistemlerine Giriş. Ünite 3 - Coğrafi Konumlandırma
 Coğrafi Bilgi Sistemlerine Giriş Ünite 3 - Coğrafi Konumlandırma İçerik Giriş Yerkürenin matematiksel modeli Yerküre üzerinde haritalanacak bölgenin matematiksel modeli (datum) GİRİŞ Yeryüzündeki bir mekanın
Coğrafi Bilgi Sistemlerine Giriş Ünite 3 - Coğrafi Konumlandırma İçerik Giriş Yerkürenin matematiksel modeli Yerküre üzerinde haritalanacak bölgenin matematiksel modeli (datum) GİRİŞ Yeryüzündeki bir mekanın
KİTABIN REHBERLİK PLANLAMASI. Bölümler. Bölümlere Ait Konu Kavrama Testleri KONU KAVRAMA TESTİ DOĞA VE İNSAN 1 TEST - 1
 Sunum ve Sistematik SUNUM Sayın Eğitimciler, Sevgili Öğrenciler, ilindiği gibi gerek YGS, gerekse LYS de programlar, sistem ve soru formatları sürekli değişmektedir. Öğrenciler her yıl sürpriz olabilecek
Sunum ve Sistematik SUNUM Sayın Eğitimciler, Sevgili Öğrenciler, ilindiği gibi gerek YGS, gerekse LYS de programlar, sistem ve soru formatları sürekli değişmektedir. Öğrenciler her yıl sürpriz olabilecek
İnşaat Mühendisliğine Giriş İNŞ-101. Yrd.Doç.Dr. Özgür Lütfi Ertuğrul
 İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DÖKÜMANI
 AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DÖKÜMANI Öğrenci Numarası: I. / II. Öğretim: Adı Soyadı: İmza: HAFTA 02 1. KONU: KOORDİNAT SİSTEMLERİ 2. İÇERİK Küresel Koordinat Sistemleri Coğrafi Koordinat
AST404 GÖZLEMSEL ASTRONOMİ HAFTALIK UYGULAMA DÖKÜMANI Öğrenci Numarası: I. / II. Öğretim: Adı Soyadı: İmza: HAFTA 02 1. KONU: KOORDİNAT SİSTEMLERİ 2. İÇERİK Küresel Koordinat Sistemleri Coğrafi Koordinat
Harita Projeksiyonları
 Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
HARİTA BİLGİSİ ETKİNLİK
 HARİTA Dünya nın tamamının veya bir bölümünün kuş bakışı, küçültülerek bir düzleme aktarılmasıdır. kuşbakışı PLAN... Bir çizimin harita olabilmesi için... KROKİ... PROJEKSİYONLAR: Dünya nın şeklinin geoit
HARİTA Dünya nın tamamının veya bir bölümünün kuş bakışı, küçültülerek bir düzleme aktarılmasıdır. kuşbakışı PLAN... Bir çizimin harita olabilmesi için... KROKİ... PROJEKSİYONLAR: Dünya nın şeklinin geoit
CBS. Projeksiyon. CBS Projeksiyon. Prof.Dr. Emin Zeki BAŞKENT. Karadeniz Teknik Üniversitesi Orman Fakültesi 2010, EZB
 Prof.Dr. Emin Zeki BAŞKENT Karadeniz Teknik Üniversitesi Orman Fakültesi Elipsoid şeklindeki dünyanın bir düzlem üzerine indirilmesi ve koordinatlarının matematiksel dönüşümleridir. Harita üç şekilde projeksiyonu
Prof.Dr. Emin Zeki BAŞKENT Karadeniz Teknik Üniversitesi Orman Fakültesi Elipsoid şeklindeki dünyanın bir düzlem üzerine indirilmesi ve koordinatlarının matematiksel dönüşümleridir. Harita üç şekilde projeksiyonu
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
ARAZİ ÖLÇMELERİ. Temel Ödev I: Koordinatları belirli iki nokta arasında ki yatay mesafenin
 Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Datum: Herhangi bir noktanın yatay ve düşey konumunu tanımlamak için başlangıç alınan referans yüzeyidir.
 İçindekiler Projeksiyon ve Dönüşümleri... 1 Dünyanın Şekli ve Referans Yüzeyler... 1 1. Projelsiyon Nedir?... 1 2. Koordinat Sistemleri... 1 3. Coğrafi Koordinat Sistemleri... 2 4. Projeksiyon Koordinat
İçindekiler Projeksiyon ve Dönüşümleri... 1 Dünyanın Şekli ve Referans Yüzeyler... 1 1. Projelsiyon Nedir?... 1 2. Koordinat Sistemleri... 1 3. Coğrafi Koordinat Sistemleri... 2 4. Projeksiyon Koordinat
BÜLENT ECEVİT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT SİSTEMLERİ. Prof.Dr.Rasim Deniz
 BÜLENT ECEVİT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT SİSTEMLERİ Prof.Dr.Rasim Deniz Zonguldak, 2014 YERSEL KOORDİNAT SİSTEMLERİ 1-Genel Yer üzerindeki konumların belirlenmesi
BÜLENT ECEVİT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT SİSTEMLERİ Prof.Dr.Rasim Deniz Zonguldak, 2014 YERSEL KOORDİNAT SİSTEMLERİ 1-Genel Yer üzerindeki konumların belirlenmesi
ARAZİ ÖLÇMELERİ Z P. O α X P. α = yatay açı. ω = düşey açı. µ =eğim açısı. ω + µ = 100 g
 Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
ORMAN VE SU İŞLERİ BAKANLIĞI Su Yönetimi Genel Müdürlüğü Taşkın ve Kuraklık Yönetimi Planlaması Dairesi Başkanlığı. Temel Harita Bilgisi
 ORMAN VE SU İŞLERİ BAKANLIĞI Su Yönetimi Genel Müdürlüğü Taşkın ve Kuraklık Yönetimi Planlaması Dairesi Başkanlığı Temel Harita Bilgisi Harita, yeryüzünün ölçeklendirilmiş ve düzleme aktarılmış bir sunumudur.
ORMAN VE SU İŞLERİ BAKANLIĞI Su Yönetimi Genel Müdürlüğü Taşkın ve Kuraklık Yönetimi Planlaması Dairesi Başkanlığı Temel Harita Bilgisi Harita, yeryüzünün ölçeklendirilmiş ve düzleme aktarılmış bir sunumudur.
Prof. Dr. Ceyhun GÖL. Çankırı Karatekin Üniversitesi Orman Fakültesi Havza Yönetimi Anabilim Dalı
 Jeoloji Prof. Dr. Ceyhun GÖL Çankırı Karatekin Üniversitesi Orman Fakültesi Havza Yönetimi Anabilim Dalı Ders Konuları Jeolojinin tanımı ve tarihçesi Mineraller Güneş sistemi Dünyanın şekli ve hareketleri
Jeoloji Prof. Dr. Ceyhun GÖL Çankırı Karatekin Üniversitesi Orman Fakültesi Havza Yönetimi Anabilim Dalı Ders Konuları Jeolojinin tanımı ve tarihçesi Mineraller Güneş sistemi Dünyanın şekli ve hareketleri
HARİTA. Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir.
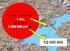 HARİTA BİLGİSİ HARİTA Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir. ÇEŞİTLİ ÖLÇEKLİ HARİTALARIN NUMARALANMA SİSTEMİ
HARİTA BİLGİSİ HARİTA Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir. ÇEŞİTLİ ÖLÇEKLİ HARİTALARIN NUMARALANMA SİSTEMİ
BÖLÜM 1 ÖLÇME BİLGİSİNE GİRİŞ
 BÖLÜM 1 ÖLÇME BİLGİSİNE GİRİŞ Kavramsal Kazanımlar: Yeryuvarının matematiksel ve fiziksel şekli, jeodezik metrolojinin konusu ve ölçü büyüklükleri, belirsizlik ve hata kavramı, koordinat sistemleri ve
BÖLÜM 1 ÖLÇME BİLGİSİNE GİRİŞ Kavramsal Kazanımlar: Yeryuvarının matematiksel ve fiziksel şekli, jeodezik metrolojinin konusu ve ölçü büyüklükleri, belirsizlik ve hata kavramı, koordinat sistemleri ve
31.10.2014. CEV 361 CBS ve UA. Koordinat ve Projeksiyon Sistemleri. Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli
 CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714 km
CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714 km
BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI
 36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
4. SINIF FEN VE TEKNOLOJİ DERSİ II. DÖNEM GEZEGENİMİZ DÜNYA ÜNİTESİ SORU CEVAP ÇALIŞMASI
 4. SINIF FEN VE TEKNOLOJİ DERSİ II. DÖNEM GEZEGENİMİZ DÜNYA ÜNİTESİ SORU CEVAP ÇALIŞMASI 1. Dünya mızın şekli neye benzer? Dünyamızın şekli küreye benzer. 2. Dünya mızın şekli ile ilgili örnekler veriniz.
4. SINIF FEN VE TEKNOLOJİ DERSİ II. DÖNEM GEZEGENİMİZ DÜNYA ÜNİTESİ SORU CEVAP ÇALIŞMASI 1. Dünya mızın şekli neye benzer? Dünyamızın şekli küreye benzer. 2. Dünya mızın şekli ile ilgili örnekler veriniz.
Üç Boyutlu Uzayda Koordinat sistemi
 Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
ARAZİ ÖLÇMELERİ. Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) Dik İnmek. A Dik Çıkmak
 Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) P1 P2 Dik İnmek P3 P4 Dik Çıkmak Şekil 76 Şekil 76 da dik inme ve çıkmaya birer örnek gösterilmiştir. Dik çıkmadan anlaşılması gereken belirlenen bir
Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) P1 P2 Dik İnmek P3 P4 Dik Çıkmak Şekil 76 Şekil 76 da dik inme ve çıkmaya birer örnek gösterilmiştir. Dik çıkmadan anlaşılması gereken belirlenen bir
COĞRAFYA-2 TESTİ. eşittir. B) Gölün alanının ölçek yardımıyla hesaplanabileceğine B) Yerel saati en ileri olan merkez L dir.
 2012 LYS4 / COĞ-2 COĞRAFYA-2 TESTİ 2. M 1. Yukarıdaki Dünya haritasında K, L, M ve N merkezleriyle bu merkezlerden geçen meridyen değerleri verilmiştir. Yukarıda volkanik bir alana ait topoğrafya haritası
2012 LYS4 / COĞ-2 COĞRAFYA-2 TESTİ 2. M 1. Yukarıdaki Dünya haritasında K, L, M ve N merkezleriyle bu merkezlerden geçen meridyen değerleri verilmiştir. Yukarıda volkanik bir alana ait topoğrafya haritası
***Yapılan bir çizimin harita özelliğini gösterebilmesi için çizimin belirli bir ölçek dahilinde yapılması gerekir.
 HARİTA BİLGİSİ Harita Kuşbakışı görünümün Ölçekli Düzleme aktarılmasıdır. ***Yapılan bir çizimin harita özelliğini gösterebilmesi için çizimin belirli bir ölçek dahilinde yapılması gerekir. Kroki Kuşbakışı
HARİTA BİLGİSİ Harita Kuşbakışı görünümün Ölçekli Düzleme aktarılmasıdır. ***Yapılan bir çizimin harita özelliğini gösterebilmesi için çizimin belirli bir ölçek dahilinde yapılması gerekir. Kroki Kuşbakışı
Uzay Geriden Kestirme
 Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
EKVATORAL KOORDİNAT SİSTEMİ_devam. Serap Ak
 EKVATORAL KOORDİNAT SİSTEMİ_devam http://star-www.st-and.ac.uk/~fv/webnotes/chapter5.htm http://star-www.st-and.ac.uk/~fv/webnotes/chapter4.htm Gök küresinde bulunan önemli yıldızların ekvatoral koordinatları
EKVATORAL KOORDİNAT SİSTEMİ_devam http://star-www.st-and.ac.uk/~fv/webnotes/chapter5.htm http://star-www.st-and.ac.uk/~fv/webnotes/chapter4.htm Gök küresinde bulunan önemli yıldızların ekvatoral koordinatları
Alan Hesapları. Şekil 14. Üç kenarı belli üçgen alanı
 lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
Projeksiyon Kavramı. Meridyenler ve paraleller eşitliklere göre düzleme aktarılır. 1) m : harita üzerinde paralelleri çizen yarıçap
 Projeksiyon Kavramı Meridyenler ve paraleller eşitliklere göre düzleme aktarılır. 1) m : harita üzerinde paralelleri çizen yarıçap ) α: harita üzerinde meridyenler arasındaki açıyı ifade eder. m = α =
Projeksiyon Kavramı Meridyenler ve paraleller eşitliklere göre düzleme aktarılır. 1) m : harita üzerinde paralelleri çizen yarıçap ) α: harita üzerinde meridyenler arasındaki açıyı ifade eder. m = α =
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
02.04.2012. Düşey mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi
 Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
HARİTA ve ÖLÇEK HARİTALAR
 Madde ve Özkütle 2 YGS Fizik 1 Bu yazıda ne anlatıyoruz? Coğrafyanın temel konularından biri olan, haritalarla ilgili hazırladığımız bu yazıda harita ve ölçek çeşitlerini basitleştirerek anlattık. Çok
Madde ve Özkütle 2 YGS Fizik 1 Bu yazıda ne anlatıyoruz? Coğrafyanın temel konularından biri olan, haritalarla ilgili hazırladığımız bu yazıda harita ve ölçek çeşitlerini basitleştirerek anlattık. Çok
Test. Yerküre nin Şekli ve Hareketleri BÖLÜM 4
 Yerküre nin Şekli ve Hareketleri 1. Dünya ile ilgili aşağıda verilen bilgilerden yanlış olan hangisidir? A) Dünya, ekseni etrafındaki bir turluk dönüş hareketini 24 saatte tamamlar. B) Dünya ekseni etrafındaki
Yerküre nin Şekli ve Hareketleri 1. Dünya ile ilgili aşağıda verilen bilgilerden yanlış olan hangisidir? A) Dünya, ekseni etrafındaki bir turluk dönüş hareketini 24 saatte tamamlar. B) Dünya ekseni etrafındaki
E.Ömür DEMİRKOL, Mehmet Ali GÜRDAL, Abdullah YILDIRIM
 AVRUPA DATUMU 1950 (EUROPEAN DATUM 1950: ED-50) İLE DÜNYA JEODEZİK SİSTEMİ 1984 (WORLD GEODETIC SYSTEM 1984: WGS84) ARASINDA DATUM (KOORDİNAT) DÖNÜŞÜMÜ VE ASKERİ UYGULAMALARI ÖZET E.Ömür DEMİRKOL, Mehmet
AVRUPA DATUMU 1950 (EUROPEAN DATUM 1950: ED-50) İLE DÜNYA JEODEZİK SİSTEMİ 1984 (WORLD GEODETIC SYSTEM 1984: WGS84) ARASINDA DATUM (KOORDİNAT) DÖNÜŞÜMÜ VE ASKERİ UYGULAMALARI ÖZET E.Ömür DEMİRKOL, Mehmet
HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR
 HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR Harita nedir? Yeryüzünün veya bir parçasının belli bir orana göre küçültülerek ve belirli işaretler kullanılarak yatay düzlem üzerinde gösterilmesine harita adı verilir.
HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR Harita nedir? Yeryüzünün veya bir parçasının belli bir orana göre küçültülerek ve belirli işaretler kullanılarak yatay düzlem üzerinde gösterilmesine harita adı verilir.
Veri toplama- Yersel Yöntemler Donanım
 Veri toplama- Yersel Yöntemler Donanım Data Doç. Dr. Saffet ERDOĞAN 1 Veri toplama -Yersel Yöntemler Optik kamera ve lazer tarayıcılı ölçme robotu Kameradan gerçek zamanlı veri Doç. Dr. Saffet ERDOĞAN
Veri toplama- Yersel Yöntemler Donanım Data Doç. Dr. Saffet ERDOĞAN 1 Veri toplama -Yersel Yöntemler Optik kamera ve lazer tarayıcılı ölçme robotu Kameradan gerçek zamanlı veri Doç. Dr. Saffet ERDOĞAN
ARAZİ ÖLÇMELERİ Z P. O α X P. α = yatay açı. ω = düşey açı. µ =eğim açısı. ω + µ = 100 g
 Trigonometrik Fonksiyonlar ARAZİ ÖLÇMELERİ Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara
Trigonometrik Fonksiyonlar ARAZİ ÖLÇMELERİ Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara
DERSİN ADI: MATEMATİK II MAT II (12) KUTUPSAL KOORDİNATLAR VE UYGULAMALARI 1. KUTUPSAL KOORDİNATLAR 2. EĞRİ ÇİZİMLERİ
 DERSİN ADI: MATEMATİK II MAT II (1) ÜNİTE: KUTUPSAL KOORDİNATLAR VE UYGULAMALARI 1. KUTUPSAL KOORDİNATLAR. EĞRİ ÇİZİMLERİ GEREKLİ ÖN BİLGİLER 1. Trigonometrik fonksiyonlar. İntegral formülleri KONU ANLATIMI
DERSİN ADI: MATEMATİK II MAT II (1) ÜNİTE: KUTUPSAL KOORDİNATLAR VE UYGULAMALARI 1. KUTUPSAL KOORDİNATLAR. EĞRİ ÇİZİMLERİ GEREKLİ ÖN BİLGİLER 1. Trigonometrik fonksiyonlar. İntegral formülleri KONU ANLATIMI
JEODEZİ. Şekil1: Yerin şekli YERİN ŞEKLİ JEOİD
 JEODEZİ Jeodezi, üç boyutlu ve zaman değişkenli uzayda, çekim alanı ile birlikte, yeryuvarının ve öteki gök cisimlerinin ölçülmesi ve haritaya aktarılması ile uğraşan bilim dalıdır. Şekil1: Yerin şekli
JEODEZİ Jeodezi, üç boyutlu ve zaman değişkenli uzayda, çekim alanı ile birlikte, yeryuvarının ve öteki gök cisimlerinin ölçülmesi ve haritaya aktarılması ile uğraşan bilim dalıdır. Şekil1: Yerin şekli
FOTOYORUMLAMA UZAKTAN ALGILAMA
 FOTOYORUMLAMA VE UZAKTAN ALGILAMA (Photointerpretation and Remote Sensing) 1 Ders İçeriği Hava fotoğrafının tanımı Fotogrametrinin geometrik ilkeleri Fotogrametride fotoğrafik temel ilkeler Stereoskopik
FOTOYORUMLAMA VE UZAKTAN ALGILAMA (Photointerpretation and Remote Sensing) 1 Ders İçeriği Hava fotoğrafının tanımı Fotogrametrinin geometrik ilkeleri Fotogrametride fotoğrafik temel ilkeler Stereoskopik
YÜKSEKLİK ÖLÇÜMÜ. Ölçme Bilgisi Ders Notları
 YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ. 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak.
 EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ AMAÇ: 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak. 2. Bu eş potansiyel çizgileri kullanarak elektrik alan çizgilerinin
EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ AMAÇ: 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak. 2. Bu eş potansiyel çizgileri kullanarak elektrik alan çizgilerinin
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
CEV 361 CBS ve UA. Koordinat ve Projeksiyon Sistemleri. Yrd. Doç. Dr. Özgür ZEYDAN Yerin Şekli
 CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Yrd. Doç. Dr. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714
CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Yrd. Doç. Dr. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON
 JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
TOPOĞRAFYA Takeometri
 TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
HARİTA PROJEKSİYONLARI
 1 HARİTA PROJEKSİYONLARI Haritacılık mesleğinin faaliyetlerinden birisi, yeryüzünün bütününün ya da bir parçasının haritasını yapmaktır. Harita denilen şey ise, basit anlamıyla, kapsadığı alandaki çeşitli
1 HARİTA PROJEKSİYONLARI Haritacılık mesleğinin faaliyetlerinden birisi, yeryüzünün bütününün ya da bir parçasının haritasını yapmaktır. Harita denilen şey ise, basit anlamıyla, kapsadığı alandaki çeşitli
Ölçme Bilgisi. Dr. Hasan ÖZ. SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr
 Ölçme Bilgisi Dr. Hasan ÖZ SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr 1 Ölçme Bilgisi; yeryüzünün küçük ya da büyük parçalarının şekil ve büyüklüklerinin ölçülmesi ve elde
Ölçme Bilgisi Dr. Hasan ÖZ SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr 1 Ölçme Bilgisi; yeryüzünün küçük ya da büyük parçalarının şekil ve büyüklüklerinin ölçülmesi ve elde
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (2. Hafta)
 AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
Dünya nın Kütle Hesabı Çılga Misli ve Oktay Yılmaz Çanakkale Onsekiz Mart Üniversitesi, Fizik Bölümü
 Dünya nın Kütle Hesabı Çılga Misli ve Oktay Yılmaz Çanakkale Onsekiz Mart Üniversitesi, Fizik Bölümü Bu çalışma güncel olmamakla birlikte temel fizik yasalarının önemli ve ilk astronomik sonuçlarından
Dünya nın Kütle Hesabı Çılga Misli ve Oktay Yılmaz Çanakkale Onsekiz Mart Üniversitesi, Fizik Bölümü Bu çalışma güncel olmamakla birlikte temel fizik yasalarının önemli ve ilk astronomik sonuçlarından
İÇİNDEKİLER BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ
 İÇİNDEKİLER II Sayfa No: ÖNSÖZ...I İÇİNDEKİLER...III ŞEKİLLER LİSTESİ...VIII ÇİZELGELER LİSTESİ...XII EKLER LİSTESİ...XIII BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ 1. ÖLÇME TEKNİĞİ VE HARİTA ALMA
İÇİNDEKİLER II Sayfa No: ÖNSÖZ...I İÇİNDEKİLER...III ŞEKİLLER LİSTESİ...VIII ÇİZELGELER LİSTESİ...XII EKLER LİSTESİ...XIII BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ 1. ÖLÇME TEKNİĞİ VE HARİTA ALMA
GÜNEY YARIM KÜRESİ İÇİN ŞEKİL
 GÜNEY YARIM KÜRESİ İÇİN ŞEKİL Bu şekilde, gözlemcinin zeniti bundan önceki şekillerdeki gibi yerleştirilir. Bu halde gök ufku şekildeki gibi olur. Güney yarım kürede Q güney kutbu ufkun üzerindedir. O
GÜNEY YARIM KÜRESİ İÇİN ŞEKİL Bu şekilde, gözlemcinin zeniti bundan önceki şekillerdeki gibi yerleştirilir. Bu halde gök ufku şekildeki gibi olur. Güney yarım kürede Q güney kutbu ufkun üzerindedir. O
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
Dünya nın Şekli ve Hareketleri
 Dünya nın Şekli ve Hareketleri YGS Coğrafya 1 Dünya nın Şekli ve Hareketleri Dünya nın Şekli ve Hareketleri başlıklı hazırladığımız bu yazıda, dünyanın şeklinin getirdiği sonuçları; enlem, boylam ve meridyenlerin
Dünya nın Şekli ve Hareketleri YGS Coğrafya 1 Dünya nın Şekli ve Hareketleri Dünya nın Şekli ve Hareketleri başlıklı hazırladığımız bu yazıda, dünyanın şeklinin getirdiği sonuçları; enlem, boylam ve meridyenlerin
GÜNEŞ YÖRÜNGESİ TEMEL ÇİZİMLERİ
 GÜNEŞ YÖRÜNGESİ TEMEL ÇİZİMLERİ için ÖNSÖZ Yeryüzünün herhangi bir noktasında ve yılın herhangi bir gününün istenen bir zamanında, güneşin gökyüzündeki yeri, bilgisayar programları ile elde edilebilmektedir.
GÜNEŞ YÖRÜNGESİ TEMEL ÇİZİMLERİ için ÖNSÖZ Yeryüzünün herhangi bir noktasında ve yılın herhangi bir gününün istenen bir zamanında, güneşin gökyüzündeki yeri, bilgisayar programları ile elde edilebilmektedir.
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
Newton un ikinci yasası: Bir cisim ivmesi cisim üzerine etki eden toplam kuvvet ile doğru orantılı cismin kütlesi ile ters orantılıdır.
 Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
MESLEKİ HESAPLAMALAR
 MESLEKİ HESAPLAMALAR Jeodezi: Yer yuvarı şekil, boyut ve granite alanı ile zamana bağlı değişmelerin üç boyutlu bir koordinat sisteminde tanımlanmasını amaçlayan bir bilim dalıdır. Jeodezinin Bilimsel
MESLEKİ HESAPLAMALAR Jeodezi: Yer yuvarı şekil, boyut ve granite alanı ile zamana bağlı değişmelerin üç boyutlu bir koordinat sisteminde tanımlanmasını amaçlayan bir bilim dalıdır. Jeodezinin Bilimsel
İÇİNDEKİLER. Ön Söz...2. Noktanın Analitik İncelenmesi...3. Doğrunun Analitiği Analitik Düzlemde Simetri...25
 İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
