T.C. Ocak 2013 Konya Her Hakkı Saklıdır
|
|
|
- Özge Balbay
- 8 yıl önce
- İzleme sayısı:
Transkript
1 T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ Gravite Alanı Belirleme Amaçlı Yakın Yer Uyduları İçin Duyarlı Yörünge Belirleme Teknikleri Serkan DOĞANALP DOKTORA TEZİ Harita Mühendisliği Anabilim Dalı Ocak 213 Konya Her Hakkı Saklıdır
2
3 TEZ BİLDİRİMİ Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm. DECLARATION PAGE I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all materials and results that are not original to this work. Serkan DOĞANALP i
4 ÖZET DOKTORA TEZİ Gravite Alanı Belirleme Amaçlı Yakın Yer Uyduları Yörünge Belirleme Teknikleri İçin Duyarlı Serkan DOĞANALP Selçuk Üniversitesi Fen Bilimleri Enstitüsü Harita Mühendisliği Anabilim Dalı Danışman: Doç. Dr. Aydın ÜSTÜN 213, 192 sayfa Jüri Doç. Dr. Aydın ÜSTÜN Prof. Dr. Cevat İNAL Prof. Dr. Galip OTURANÇ Doç. Dr. Cüneyt AYDIN Doç. Dr. Ayhan CEYLAN Yerin gravite alanının olabildiğince yüksek doğruluk ve duyarlıkta belirlenebilmesi açısından yakın yer uydularının (LEO) önemli bir rolü vardır. Söz konusu uyduların duyarlı yörünge (konum) bilgileri gravite alanının uzun dalga boylu bileşenlerini ortaya çıkarır. Bu sayede LEO uydularının son geliştirilen gravite alanı modellerine katkısı fazladır. Gravite alanı belirleme amaçlı gönderilen uydu misyonları CHAMP, GRACE ve GOCE nin GPS ile donatılması sayesinde bu uyduların gerçek yörüngeleri izlenebilmektedir. Uydu yörüngelerinin belirlenmesinde kinematik, dinamik ve indirgenmiş dinamik yöntemler kullanılmaktadır. Bu çalışmada CHAMP, GRACE ve GOCE uydularının duyarlı yörüngeleri kinematik, dinamik ve indirgenmiş dinamik yöntemler kullanılarak belirlenmiştir. Elde edilen yörüngeler birbirleriyle, farklı kurum/enstitülerce yayımlanan yörüngelerle (RSO, GNV1B) ve SLR gözlemleriyle karşılaştırılmış ve yörünge hataları hesaplanmıştır. Ardışık olarak beş günlük uydu yörüngelerinin kinematik ve indirgenmiş dinamik yörüngelerinin arasındaki farklar CHAMP uydusu için 2-5 cm, GRACE uyduları için 2-3 cm ve GOCE için 1-2 cm RMS değerleriyle elde edilmiştir. Ayrıca uydulara ait RD yörüngeler RSO, GNV1B yayınları ile karşılaştırılmıştır. CHAMP için RD-RSO karşılaştırması sonucunda 6-1 cm, GRACE için RD-GNV1B karşılaştırmasında ise 4-6 cm arasında RMS değerleri elde edilmiştir. Bu karşılaştırmalara ek olarak uydulara ait RD yörüngeler SLR gözlemlerinden yararlanılarak kontrol edilmiştir. Buna göre beş gün için CHAMP, GRACE-A, GRACE-B ve GOCE için ortalama RMS değerleri sırasıyla 6.6 cm, 1.5 cm, 9.3 cm ve.9 cm olarak elde edilmiştir. Anahtar kelimeler: Yörünge Belirleme, Kinematik Yörünge Modeli, Dinamik Güç Modeli, Dinamik Yörünge Modeli, İndirgenmiş Yörünge Modeli ii
5 ABSTRACT Ph.D THESIS Precise Orbit Determination for Satellite Gravity Missions in Low Earth Orbiters Serkan DOĞANALP Graduate School Of Natural And Applied Science Of Selcuk University The Degree Of Philosophy in Geomatics Engineering Advisor: Assoc. Prof. Dr. Aydın ÜSTÜN 213, 192 pages Jury Assoc. Prof. Dr. Aydın ÜSTÜN Prof. Dr. Cevat İNAL Prof. Dr. Galip OTURANÇ Assoc. Prof. Dr. Cüneyt AYDIN Assoc. Prof. Dr. Ayhan CEYLAN Low earth orbit (LEO) satellites have a crucial role in terms of the determination of the Earth gravity field with high accuracy and precision as much as possible. Precise orbits of satellites reveal the long wavelength components of the gravity field. Thus, the contribution of LEO satellites to the recently developed gravity field models is significant. The orbits of these satellites can be tracked owing to the fact that satellite missions for gravity field determination such as CHAMP, GRACE and GOCE which are equipped with GPS. Kinematic, dynamic and reduced dynamic models have been used for the determination of the satellite orbits. In this study, the precise orbits of CHAMP, GRACE and GOCE satellites have been determined using these models. The obtained orbits have been compared with each other, the publications of different institutions/agencies (RSO, GNV1B) and SLR observation. Then, orbit errors have been computed. The differences between the consecutive 5-day kinematic and reduced dynamic orbits have been produced. The RMS values are 2-5 cm, 2-3 cm and 1-2 cm for CHAMP, GRACE and GOCE, respectively. Furthermore, RD orbits of the satellites have been compared with RSO and GNV1B orbits. RMS values between 6-1 cm for the CHAMP and 4-6 cm for the GRACE have been reached as the result of RD- RSO comparison and RD-GNV1B comparison, respectively. In addition to these comparisons, RD orbits of the satellites have been validated utilizing the SLR observations. According to this, the mean RMS values for five days are 6.6 cm, 1.5 cm, 9.3 cm and.9 cm for CHAMP, GRACE-A, GRACE-B and GOCE, respectively. Keywords: Orbit Determination, Kinematic Orbit Model, Dynamic Force Field, Dynamic Orbit Model, Reduced Dynamic Orbit Model iii
6 TEŞEKKÜR Doktora çalışmam esnasında olumlu katkılarından dolayı özel insanlara teşekkür etmek istiyorum. Başta doktora tezimin oluşmasında bilgi ve ilgisiyle destek olan, karşılaştığım sorunların çözümünde yol gösterici olan danışman hocam Doç. Dr. Aydın Üstün e, değerli katkılarından dolayı tez izleme komitesi üyeleri Prof. Dr. Cevat İnal ve Prof. Dr. Galip Oturanç hocalarıma teşekkür ederim. Tez çalışmasının belli bir kısmını Avusturya Viyana Teknik Üniversitesi Jeodezi ve Jeofizik Enstitüsü nde tamamladım. Enstitü başkanı Prof. Dr. Harald Schuh, uydu jeodezisi birim başkanı Prof. Dr. Robert Weber ve enstitü bünyesindeki tüm araştırmacılara yakın ilgilerinden dolayı şükranlarımı sunarım. Prof. Weber, geçirdiğim altı aylık burs süresince bilgi ve deneyimlerini benimle paylaştı ve yol gösterici oldu. Kendisine sonsuz teşekkürlerimi sunuyorum. Ayrıca, çalışmamın uygulama aşamasındaki problemlerin çözümü için Bern Üniversitesi araştırmacılarından Dr. Heike Bock a sonsuz teşekkürlerimi sunarım. Tezin yurt dışı çalışmalarına maddi destek sağlayan TÜBİTAK 2214-Yurt Dışı Araştırma Burs Programına ve numaralı proje ile destek veren Selçuk Üniversitesi Bilimsel Araştırma Koordinatörlüğüne teşekkür ederim. Ayrıca akademik hayatın zorluğunu paylaşan, bana her türlü konuda destek veren, çalışmaktan onur ve haz duyduğum sevgili mesai arkadaşlarım ve hocalarıma teşekkür ederim. Özellikle desteklerinden ötürü Arş. Gör. Dr. Fatih İşcan, Arş. Gör. Dr. H. Zahit Selvi, Arş. Gör. Osman S. Kırtıloğlu, Arş. Gör. Sefa Yalvaç ve Arş. Gör. Dr. Mevlüt Yetkin e teşekkür ederim. Bu tezin tamamlanmasında benimle birlikte tüm zorluklara katlanan, çalışmam süresince gösterdikleri sabır ve anlayıştan dolayı teşekkür etmek istediğim çok özel insanlar var. Özellikle her zaman yanımda olan, beni yurt dışında da yalnız bırakmayan sevgili eşim Burcu ya, stresli ve sinirli olduğum anlarda bile beni her zaman rahatlatan aslan parçası oğlum Doruk a ve geçirdiğimiz zor günlerde her zaman arkamda duran aileme ve eşimin ailesine çok teşekkür ediyorum. Bu tezi sizlere ithaf ediyorum. Hayatımda iyi ki varsınız... Serkan DOĞANALP 12 Aralık 212 iv
7 İÇİNDEKİLER TEZ BİLDİRİMİ ÖZET ABSTRACT TEŞEKKÜR İÇİNDEKİLER SİMGELER VE KISALTMALAR i ii iii iv v vii 1 GİRİŞ 1 2 GRAVİTE ALANI BELİRLEMEDE YAKIN YER UYDULARININ ÖNEMİ Temel Kavramlar Yeryuvarının Gravite Alanı ve Küresel Harmonikler Koordinat Sistemleri ve Dönüşümler ICRF ve ITRF arasında dönüşüm Uydu Koordinat Sistemi Gravite Alanı Belirleme Amaçlı Yakın Yer Uyduları CHAMP GRACE GOCE YAKIN YER UYDULARI İÇİN GPS VERİLERİNİN DEĞERLENDİRİLMESİ Uydudan Uyduya İzleme Tekniği GPS Yörünge ve Saatleri LEO Ürünleri GPS Gözlem Modelleri Kod gözlemleri Faz gözlemleri Çift Frekanslı Gözlem Modeli İyonosferden Bağımsız Doğrusal Kombinasyon Değerlendirme Stratejisi DUYARLI YÖRÜNGE BELİRLEME Uydunun Hareket Denklemi ve Kepler Elemanları Kinematik Yörünge Belirleme Dinamik Yörünge Belirleme Dinamik Güç Modeli Yerçekimi ile İlişkili Düzensizlikler Yerçekimi ile İlişkili Olmayan Düzensizlikler İndirgenmiş Dinamik Yörünge Belirleme Uydu Lazer Ölçmeleri v
8 4.6 Duyarlı Yörünge Belirleme Stratejisi SAYISAL UYGULAMA SP3/TLE verileriyle dinamik yörünge belirleme CHAMP Uydusu için DYB İşlemleri GRACE Uyduları için DYB İşlemleri GOCE Uydusu için DYB İşlemleri Uydulara ait ardışık gün çözümleri Tartışma SONUÇ ve ÖNERİLER Sonuçlar Öneriler KAYNAKLAR 155 EKLER 165 A Kepler Efemeris Hesabı 165 B Dinamik Güç Modeli için Kısmi Türevler 168 C Uygulama Sonuçları 171 ÖZGEÇMİŞ 192 vi
9 SİMGELER µ yerçekimi sabiti R yeryuvarının ekvatoral yarıçapı r radyal bileşen θ kutup uzaklığı λ jeosentrik boylam C nm, S nm tam normalleştirilmiş küresel harmonik veya Stokes katsayıları P nm tam normalleştirilmiş bütünleşik Legendre fonksiyonları n, m küresel harmonik açınımının derece ve sırası r, θ, λ küresel koordinatlar x, y, z kartezyen koordinatlar V(r, θ, λ) çekim potansiyeli T bozucu gravite potansiyeli x p,y p kutup hareket bileşenleri W(t) kutup hareket matrisi R(t) yer dönüklük matrisi N(t) nutasyon matrisi P(t) presesyon matrisi α G Greenwich ortalama yıldız zamanı açısı R(t) Radial birim vektör A(t) Along-track birim vektör C(t) Cross-track birim vektör r uydunun konum vektörü ṙ uydunun hız vektörü r uydu konumunun normu Ω açısal hız Ω açısal ivme t GPS zamanı c ışık hızı ( m/sn) ρ u a(t) uydu-alıcı arasındaki geometrik mesafe Pa u(t) sözde uzunluk - pseudorange δ tu (t) uydu saat zamanı ile GPS zamanı arasındaki fark δ ta (t) alıcı saat zamanı ile GPS zamanı arasındaki fark t u a (t) sinyal yol zamanı Ia u(t,f) iyonosferik etki Ta(t) u troposferik etki Ma u(t) diğer etkiler ε u a(t) termal ölçüm gürültüsü ve modellenemeyen diğer etkiler λ taşıyıcı dalga boyu b yeryüzünde iki nokta arasındaki baz uzunluğu (km) σ b baz hatası (m) yörünge hatası (m) σ r vii
10 F m kütleli bir cisme uygulanan bileşke kuvvet vektörü a cismin ölçülen vektörel ivmesi G evrensel çekim sabiti a yörünge elipsinin büyük yarı ekseni e yörünge elipsinin dışmerkezliği veya eksantrisitesi i yörünge düzleminin eğimi Ω çıkış düşümünün boylamı ω günberi uzaklığı veya perige argümanı ν gerçek anomali r bozucu uydu üzerine etki eden tüm bozucu güçlerin toplam vektörü q 1,...,q d dinamik yörünge parametreleri f yerçekimi merkezinden (central gravity term) kaynaklanan ivme f 1 uydu üzerine etki eden güçlerin neden olduğu ivmeler f uydu üzerine etki eden toplam ivme r (t) önsel yörünge p i yörünge parametreleri (p i = 1,...,n) n toplam bilinmeyen yörünge parametre sayısı C D sürüklenme katsayısı A uydunun kesit alanı ρ(r, t) uydu konumundaki atmosferik yoğunluk C sr uydu yüzeyinin yansıtma özelliklerini tanımlayan katsayı AU astronomik birim (AU = m) S Güneş sabitesi (S = w/m 2 ) viii
11 KISALTMALAR AIUB : Astronomical Institute of the University of Berne, Switzerland AS : Anti-Spoofing C/A-code : Coarse-Acquisition, Clear-Access or Civil-Access code (1.23 MHz) CDDIS : Crustal Dynamics Data Information System, NASA, USA CHAMP : CHAllenging Mini-satellite Payload for geophysical research CNES : Centre Nationale d Etudes Spatiale, France CODE : Center for Orbit Determination in Europe CSR : Center for Space Research, Austin, Texas DOP : Dilution Of Precision DORIS : Doppler Orbitography and Radio positioning Integrated by Satellite DOY : Day of Year DYB : Duyarlı Yörünge Belirleme EOP : Earth Orientation Parameters ERP : Earth Rotation Parameter ESA : European Space Agency GEO : Geostationary Earth Orbit/Orbiter GFZ : GeoForschungsZentrum, Potsdam, Germany GLONASS : GLObal NAvigation Satellite System GOCE : Gravity field and steady-state Ocean Circulation Explorer GPS : Küresel konum belirleme sistemi GRACE : Gravity Recovery And Climate Experiment HPF : High-level Processing Facility IBDK : İyonosferden Bağımsız Doğrusal Kombinasyon ICGEM : International Centre for Global Earth Models IERS : International Earth Rotation Service İF : İkili Farklar ICRF : International Celestical Reference Frame IGS : International GPS Service ILRS : International Laser Ranging Service INT : Başlangıç yörünge ISDC : Information System and Data Center ITRF : International Terrestrial Reference Frame JPL : Jet Propulsion Laboratory, Pasadena, California, USA KBR : K/Ka-Band Ranging KIN : Kinematik yörünge LEO : Low Earth Orbit/Orbiter LRR : Laser Retro Reflector MEO : Medium Earth Orbit/Orbiter NASA : National Aeronautics and Space Administration, USA NGS : National Geodetic Survey NIMA : National Imagery and Mapping Agency NPT : Normal Point Data P-code : Precise or Protected code (1.23 MHz) ix
12 POD : Precise Orbit Determination PRN : Pseudo Random Noise PSO : Precise Science Orbit RAC : Radial Along-track Cross-track RD : İndirgenmiş-dinamik yörünge RINEX : Receiver-INdependent EXchange Format RMS : Root-mean-square RSO : Rapid Science Orbit SA : Selective Availability SF : Sıfır Farklar SGG : Satellite Gravity Gradient SLR : Satellite Laser Ranging SOPAC : Scripps Orbit and Permanent Array Center SST : Satellite-to-satellite tracking TEC : Total Electron Content TUM : Technical University of Munich UBKS : Uydu Bazlı Koordinat Sistemi ÜF : Üçlü Farklar UKS : Uydu Koordinat Sistemi VLBI : Very Long Baseline Interferometry x
13 1 1. GİRİŞ Yörüngeye bir uydu fırlatmanın değişik sayıda zorunlu nedenleri vardır. Bilgi iletişim teknolojilerinden askeri amaçlara, doğa olaylarının izlenmesinden bilimsel amaçlara çok geniş bir yelpazede atmosfer, okyanus ve kıtaların büyük ölçekli görüntülerinin elde edilmesi günümüzde kaçınılmaz duruma gelmiştir. Uyduların yoğun olarak kullanıldığı alanların başında jeodezi bilimi gelmektedir. Yeryuvarının şeklini, boyutlarını ve çekim alanını belirlemek, ülke nirengi ağlarını konumlandırmak, yöneltmek veya iyileştirmek, deformasyon izleme ağlarını oluşturmak ve plaka deformasyonlarını belirlemek bu uygulamalardan bazılarıdır. Uydular; yörüngelerinin şekillerine, ağırlıklarına, sağladıkları hizmetlere ve benzeri pek çok ölçüte göre sınıflandırılabilir. Yaygın olarak kullanılan bir sınıflandırma türü ise yeryüzünden olan yüksekliklerine göredir. Buna göre uydular temel olarak üç gruba ayrılabilir: Alçak Yörünge Uyduları (Low Earth Orbit - LEO) Orta Yörünge Uyduları (Medium Earth Orbit- MEO) Yer-durağan (sabit) Yörünge Uyduları (Geostationary Earth Orbit-GEO) LEO uyduları; yeryüzünden yaklaşık 2-2 km arasında değişen yükseklikte konumlanmışlardır. LEO uydularına örnek olarak; gravite alanı belirlemeleri uyduları (CHAMP, GRACE ve GOCE) 4 km, uzaktan algılama uyduları (SPOT, LANDSAT ve ERS) 8-1 km, altimetre uyduları (TOPEX/POSEIDON, ENVISAT ve JASON) 1-15 km arasında yörüngeye yerleştirilmişlerdir (Seeber, 23). LEO uyduları, yörüngede kalabilmek için Newton hareket yasalarına göre oldukça hızlı hareket ederler. Bundan dolayı, yeryüzünde daha dar kapsamlı alanları görürler. Öte yandan, atmosferik etkilere maruz kaldıklarından ömürleri kısadır. MEO uydularının yükseklikleri yaklaşık 5-2 km arasında değişir. Bu grubun bilinen uyduları 2 km yükseklikteki GPS ve GLONASS, 24 km yükseklikteki GALILEO, 6 km yükseklikteki lazer uyduları LAGEOS-1,2 dir (Seeber, 23). GEO uyduları ise genellikle iletişim amaçlıdır. Yörünge yükseklikleri 36 km civarındadır. Ekvator düzleminde yer alırlar ve dönme periyotları yerin dönüş periyoduna eşittir. Dolayısıyla,
14 2 yeryüzündeki bir gözlemciye göre durağan gibi görünür. Yeryuvarının basıklığı ve kitle dağılımındaki düzensizlikler, yapay yer uydularının yörüngelerinde Kepler hareketinden farklı olarak sapmalara neden olur. Yeryuvarının gravite alan bilgisi bu yörünge sapmalarından edinilebilir. Ancak gravite alanı, uydu yörüngesine etkiyen tek kuvvet alanı değildir. Bu kuvvetin yanında yer ve okyanus gelgitleri, atmosferik sürüklenme, diğer gök cisimlerinin (başta güneş ve ay olmak üzere) çekim etkileri, doğrudan ve yerden yansıyan güneş ışınlarının radyasyon basıncından kaynaklanan ivmeler gibi bozucu kuvvetler de bulunmaktadır. Bu nedenle, gravite alanı belirleme çalışmaları için bu bozucu etkileri modellemek ve gözlemlerden arındırmak gerekir. CHAMP, GRACE ve GOCE gibi güncel uydu misyonları jeodezik ve jeodinamik amaçlar doğrultusunda yeryuvarına ait gravite alan bilgisi sağlamaktadır. Uydu izleme verileri ile global gravite alanının uzun dalga boylu bileşenleri hesaplanabilmektedir. Bu üç uydunun hizmete girmesiyle uyduların duyarlı yörünge bilgilerinden, yeryuvarının gravite alanı belirleme çalışmaları ivme kazanmıştır. Bu nedenle, jeodezik amaçlar doğrultusunda LEO uydularının duyarlı yörünge belirleme (DYB) çalışmaları önemini giderek arttırmaktadır. Yörünge belirleme çalışmaları, 4 Ekim 1957 tarihinde SPUTNIK-1 uydusunun gönderilmesiyle birlikte jeodezinin başlıca araştırma konularından biri haline gelmiştir. Öte yandan, 196 lı yıllarda ABD Savunma Bakanlığı tarafından geliştirilen TRANSIT sistemi modern konum belirleme teknolojisinin başlangıcı olarak bu tarihlerde yerini almıştır. Sistemin ana hedefi uçak vb. askeri araçların konumunun belirlenmesine dayanmaktadır den itibaren sistem sivil kullanıma açılarak jeodezik konum belirleme hizmeti sunmuştur. Fakat beklenen konum doğruluğunu karşılayamamıştır. İlerleyen yıllarda TRANSIT sisteminden kazanılan tecrübeyle sürekli gözlem kabiliyeti olan, hava şartlarından etkilenmeyen, küresel anlamda konum belirlemeye olanak veren bir sistem gereksinimi ortaya çıkmıştır. 198 li yıllarda hesaplama ve uzay teknolojisindeki gelişmeye paralel olarak bu gereksinimi karşılayacak GPS sistemi hayata geçirilmiştir (Kahveci ve Yıldız, 212). GPS teknolojisinin hizmete girmesiyle, 198 li yıllarda alçak yörünge uydularına GPS alıcıları yerleştirilmiştir. Böylece uydu üzerindeki alıcı yardımıyla elde edilen GPS sinyali sayesinde uydunun izlenmesi amaçlanmıştır. GPS alıcısı
15 3 taşıyan ilk uydulardan birisi 1984 yılında sadece sözde uzunluk ölçüsü alabilen LANDSAT 5 uydusu olmuştur yılında ise TOPEX/Poseidon uydusunun fırlatılmasıyla GPS alıcıları yardımıyla uyduların DYB çalışmaları fiilen başlamıştır. Bu tarihten itibaren birçok uydunun (CHAMP (2), SAC-C (2), JASON-1 (21), GRACE (22), ICESat (23) ve GOCE (29)) DYB işlemleri için temel veri olarak GPS verileri kullanılmıştır (Bock, 23). LEO uydularının GPS ile donatılması yörünge belirleme işlemlerine farklı bir boyut kazandırmıştır. Bu sayede yörünge bilgileri daha duyarlı bir biçimde belirlenebilmiştir. Gelişen teknolojiye paralel olarak, GPS teknolojisi ve hesaplama yöntemleri de iyileşmiş ve bu iyileşme LEO uydularının konum ve hız kestirim sonuçlarına yansımıştır. DYB işlemlerinde sözü geçen bu yöntemler kinematik, dinamik ve indirgenmiş dinamik yörünge modeli olarak ele alınır (Bock, 23; Bae, 26; Jäggi, 27; Swatschina, 29; Shabanloui, 212). Kinematik yörünge modeli, ayrı bir dış modele yani uyduya etki eden dış kuvvetlere (dinamik güç modeli) ihtiyaç duymadan uydu konumlarının belirlenmesini hedefler. Kinematik yaklaşımın sürekliliği ve kalitesi büyük ölçüde GPS verilerinin kalitesine bağlıdır. GPS gözlemlerindeki ölçü hataları, uygun olmayan uydu geometrisi ve özellikle veri boşlukları bu yaklaşımın kalitesini düşürür. Bundan dolayı, bu dezavantajları ortadan kaldırabilmek için dinamik yaklaşım modeli geliştirilmiştir (Bock, 23; Bae, 26; Jäggi, 27; Swatschina, 29; Shabanloui, 212). Dinamik yörünge modelinde uydu konumu, kinematik modelin tersine uyduya etki eden kuvvetlerin uydu hareket denklemine ilave edilmesiyle belirlenir. Yaklaşımda uydunun önsel bilgilerinin yanında fiziki bilgilerine de (kesit alanı, yörünge yüksekliği, ağırlığı vb.) ihtiyaç duyulur. Kinematik yaklaşımdaki var olan süreksizlik ve veri boşluğu dinamik model için geçerli değildir. Dinamik yaklaşımda model dinamik kuvvetler ile sürekli olarak kurulur. Yaklaşımın başarısı kestirim süresine ve modelleme hatalarına bağlıdır. Kestirim süresinin artması ve LEO uydularının dinamik davranışlarındaki yetersiz bilgiden ötürü yörünge çözümlerinde sapmalar görülür. Bu dezavantajları ortadan kaldırmak için indirgenmiş dinamik model yaklaşımının kullanılması gündeme gelmiştir. SPUTNIK-1 in fırlatılmasını izleyen yıllarda uydu jeodezisinin temelleri, yer
16 4 gravite alanı, uyduya etki eden bozucu kuvvetler ve yörünge modellemenin temelleri gibi konularda ilk çalışmalar ortaya çıkmıştır (Escobal, 1965; Kaula, 1966; King- Hele, 1987; Tapley, 1989). Gelişen teknolojiyle beraber GPS sisteminde yapılan iyileştirmeler, sistemin modernizasyonu, kullanılan ölçü yöntemleri, hata kaynakları vb. bilgiler yörünge belirleme çalışmalarına ışık tutmuştur (Hofmann-Wellenhof ve ark., 1997; Teunissen ve Kleusberg, 1998; Seeber, 23; Leick, 24; Kaplan ve Hegarty, 26; Hofmann-Wellenhof ve ark., 28; Kahveci ve Yıldız, 212). Diğer yandan hesaplama tekniklerindeki iyileşmeler, DYB için kullanılan yöntemleri de geliştirmiş ve yörünge duyarlılığı mümkün olan en iyi duyarlılıkta hesaplanmaya çalışılmıştır. Kullanılan yöntemlerin detaylı bilgisi Bock (23), Bisnath (24), Tapley ve ark. (24), Montenbruck ve ark. (25), Beutler ve ark. (25a,b), Jäggi (27), Prange (211) ve Shabanloui (212) den elde edilebilir. Ayrıca, yörünge belirleme çalışmalarında kullanılan etkili algoritmaların başında stokastik yörünge modeli, diğer bir ifadeyle indirgenmiş dinamik yörünge modeli gelmektedir (Bock ve ark., 22; Jäggi ve ark., 23; Bock ve ark., 25; Jäggi ve ark., 25, 26; Beutler ve ark., 26). DYB çalışmalarında ilk uygulama örnekleri Wu ve ark. (199, 1991) ve Yunck ve ark. (199) nın yayınları ile verilebilir. Bu çalışmalarda dinamik ve indirgenmiş dinamik yaklaşımların GPS gözlemleri yardımıyla TOPEX/Poseidon uydularında bir uygulaması gerçekleştirilmiştir. Sonraki yıllarda LEO uyduları için kinematik ve indirgenmiş dinamik yörünge modeline dayanarak sıfır farklar, ikili farklar ve üçlü farklar yöntemleri kullanılarak LEO uydularının yörüngeleri belirlenmeye çalışılmıştır. Belirlenen yörüngeler birbirleriyle, diğer enstitü/kurumların elde ettiği yörüngelerle ve SLR gözlemleri ile karşılaştırılmış ve yörünge hataları bulunmuştur (Jeongrae, 2; Montenbruck, 2; Kuang ve ark., 21; Bock ve ark., 21; Svehla ve Rothacher, 22; Bobojc ve Drozyner, 23; Svehla ve Rothacher, 23; Hobbs ve Bohn, 26; Bae, 26; Kroes, 26; DongJu ve Bin, 27; Visser ve ark., 29; Swatschina, 29; Li ve ark., 21; Jäggi ve ark., 21, 211). Bu doktora tezinin amacı, uydu verilerinden yararlanarak güncel modelleme teknikleri ile LEO uydularının duyarlı yörüngelerinin dolayısıyla konum ve hızının belirlenmesi ve yörünge kontrollerinin yapılmasıdır. LEO uydularının
17 5 yörünge belirleme işlemleri kinematik, dinamik ve indirgenmiş dinamik model için gerçekleştirilmiştir. Elde edilen yörünge sonuçları birbirleriyle, farklı enstitü/kurumların yayınladığı hassas yörünge dosyalarıyla ve SLR gözlemleriyle karşılaştırılmış ve yörünge hataları ortaya konmuştur. Tezin bölümleri genel olarak şu şekilde özetlenebilir: İkinci bölümde, gravite alanı belirlemede kullanılan yakın yer uyduların karakteristik özellikleri, DYB çalışmalarında kullanılan koordinat sistemleri ve aralarındaki dönüşümler hakkında bilgi verilmiştir. Üçüncü bölümde, uydudan uyduya izleme tekniği, GPS yörünge ve saatleri ve GPS gözlem modelleri hakkında detaylı bilgi verilmiş ve DYB işlemlerinde bu verilerin nasıl kullanılacağı ortaya konmuştur. Dördüncü bölüm, DYB tekniklerinden olan kinematik, dinamik ve indirgenmiş dinamik yöntemler hakkında teorik bilginin yanında modellemede kullanılan matematiksel eşitlikleri içermektedir. Ayrıca, uyduya etki eden kuvvetlerin matematiksel eşitlikleri ve uydu hareket denklemi içerisinde ele alınış biçimleri ayrıntılı olarak açıklanmıştır. Beşinci bölüm, LEO uydularının (CHAMP, GRACE ve GOCE) DYB işlemlerinin gerçekleştirildiği bölümdür. Bu bölümde LEO uydularının bir güne ait çözümleri ayrıntılı bir biçimde gösterilmiş ve nihai çözümler elde edilmiştir. Ayrıca, elde edilen yörüngelerin kontrolü farklı kurum/enstitü sonuçları ve SLR gözlemlerinden yararlanarak yapılmıştır. Son olarak bu bölümde, uydulara ait beşer günlük ardışık çözümler elde edilmiş ve sonuçlar karşılaştırılmıştır. Son bölümde ise, araştırma kapsamında göze çarpan sonuçlar özetlenmiş ve eksik kalan yönler ortaya konulmuştur. Bu bilgiler ışığında da gelecek araştırmalar için önerilerde bulunulmuştur.
18 6 2. GRAVİTE ALANI BELİRLEMEDE YAKIN YER UYDULARININ ÖNEMİ 2.1 Temel Kavramlar Gravite alanının olabildiğince yüksek doğrulukta belirlenmesi jeodezi, jeofizik, oşinografi gibi yer bilimleri için önemlidir. Başta kitle taşınımı olmak üzere yer dinamiği ile ilişkili pek çok doğa olayında gravite alanı anahtar bir rol oynar. Rummel ve ark.(22) na göre aşağıdaki uygulamaların gerçekleştirilmesinde yüksek doğruluklu gravite alanı bilgisine gereksinim duyulur: - farklı datumları birbirlerine bağlamak için global bir referans yükseklik sisteminin tanımlanması, - özellikle yere yakın uyduların hassas yörüngelerinin belirlenmesi, - cm doğruluklu global bir jeoit modelinin oluşturulması, - kutuplardaki buzul miktarlarının ve değişimlerinin kestirilmesi, - yerin çekim alanındaki zamansal değişimlerin izlenmesi ve büyüklüklerinin belirlenmesi, - yeryuvarının geometrik, fiziksel ve jeodinamik parametrelerinin ortaya çıkarılması. Yeryuvarının gravite alanı bilgisinin ortaya çıkarılması için farklı ölçü türleri ve çözüm teknikleri geliştirilmiştir. Ölçü türleri genel olarak yüzey gravite gözlemleri, uydu izleme teknikleri ve uydu radar altimetre verileri biçiminde sınıflandırılabilir. Yeryüzünde gravite gözlemleri, yeryuvarının gravite alanı hakkında en fazla bilgiyi barındırır, fakat uygulamada yerküreye homojen bir dağılım sağlanamadığından yetersiz kalır. Uydu altimetre verileri ise ortalama dinamik deniz yüzeyi topografyasının yeterli bir düzeyde modellenmesi koşuluyla, okyanuslarda ve büyük denizlerde gravite anomalisi ve jeoit bilgisi sağlar. Son olarak uydu izleme verileri, uydular üzerine etki eden yerçekimine ait düzensizliklerin (ivmelerin) ölçülmesinde kullanılır. Yerin çekim alanındaki her uydu, gravite alan bilgisi için birer algılayıcı konumundadır. Bu sayede 199 yılından itibaren gravite alanı
19 7 çözünürlüğünü ve doğruluğunu arttırmak için jeodezik amacı olmayan uyduların bir çoğundan uydu izleme verileri alınmaya başlanmıştır (Liu, 28). Günümüzde yüksek dereceli ve kapsamlı gravite çözümlerine ulaşmak için yukarıda söz edilen üç kaynaktan gelen veri gruplarının bir arada kullanılması gereklidir. Böylece, gravite alanı parametrelerinin, yani küresel harmonik katsayıların ve onların hatalarının belirlenmesi mümkün olacaktır. Bu çözümün anlamlı sonuçlarından biri Lemoine ve ark. (1998) nın geliştirdiği EGM96 (Earth Gravitational Model 1996) jeopotansiyel modelidir. EGM96, NASA, NIMA ve Ohio State Üniversitesi (OSU) işbirliği altında ortaya konulan, yerin gravite alanının küresel harmonik serilerle gösterildiği bir modeldir. Açınımın maksimum derece ve sırası 36 dır. Model, GM = m 3 /s 2 ve a = m jeodezik parametre değerlerini kullanır. EGM96 modeli ile yeryuvarının çekim alanı hakkındaki bilgimiz önemli ölçüde artmıştır. Ancak bu bilgi, jeodezik, oşinografik ve katı yer fiziği gibi çalışmalar için gereksinimleri yeterli seviyede karşılayamamıştır (Rummel ve ark., 22). Yukarıda sözü edilen üç kaynaktan elde edilen verilerin dağılımı ve doğruluğu sınırlı kalmış, yersel gravite verileri gibi uydu izleme verileri de istenen çözüm kalitesini karşılamamıştır. Bu uyduların çoğunun i) sadece kısa aralıklarla yeryüzünden izlenebilmesi, ii) yörünge yüksekliklerinin fazla olmasından dolayı alınan gravite sinyalinin zayıf kalması ve iii) serbest hareketlerinin yerçekimi dışında güneş radyasyon basıncı, atmosferik sürüklenme gibi gravite alanından bağımsız kuvvetlerin etkisi altında kalması ve bu bozucu kuvvetlerin yeterince iyi modellenememesi uydu verilerinin modele katkısını olumsuz etkilemiştir. Bu üç temel problem, gravite alanı belirleme amaçlı alçak yörüngeli (LEO-Low Earth Orbit) yeni nesil uydu misyonlarının (CHAMP, GRACE ve GOCE) hayata geçirilmesinitetiklemiştir(seeber,23;üstün,26a;liu,28). Buproblemlerden ilki, uydudan-uyduya izleme tekniği ile alçak yörüngeli bir LEO uydusu, GPS- GLONASS gibi yüksek yörüngeli bir uydu sistemi tarafından sürekli ve üç boyutta izlenerek, ikincisi ise gravite potansiyelinin türevlerinin gözlemlenebildiği ölçme sistemleri kullanılarak aşılabilir. Son problemin neden olduğu olumsuzluk ise LEO uyduları üzerindeki GPS alıcısı ve ivmeölçer sayesinde elde edilen anlık konum ve gravite alanı ile ilişkili olmayan kuvvet (ivmelenme) bilgisinin uygun biçimde göz
20 8 önüne alınmasıyla ortadan kaldırılabilir (bkz. Bölüm 3). Yer gözlem uyduları yardımıyla gerçekleştirilen tüm uygulamalar, duyarlı yörünge bilgisini kullanır. Eğer bu uyduların gravite alanını belirlemek gibi bir görevi varsa, DYB fazladan bir anlam kazanır. Örneğin, GRACE uydularına ilişkin K-band radar (K-Band Ranging System (KBR)) ölçülerinin, benzer şekilde GOCE ye ilişkin gradyometre (Satellite Gravity Gradiometry (SGG)) verilerinin üç boyutlu uzayda konumlandırılması amacıyla DYB uygulaması gereklidir. Bununla birlikte, bu uydulardaki ivmeölçerler sayesinde, yerçekimine ait olmayan ivmelenmeler de ölçülebildiğinden bütün bu veriler birlikte analiz edilerek gravite alanını modellemek için kullanılabilir (Liu, 28). Uyduların en önemli getirisi, yeryuvarının homojen ve küresel anlamda modellenebilmesi için gereken verinin sağlanmasıdır. Uydunun konum, hız ve yörünge geometrisindeki değişim bu alanın özelliklerinin ortaya çıkarılmasında temel büyüklüklerdir. Bu yüzden jeodezi biliminde DYB çalışmaları, özellikle LEO uydularının yörünge çözümlerine mümkün olan en iyi doğruluk ve duyarlıkta ulaşılması noktasında, giderek önemini arttırmaktadır. DYB tekniklerindeki uygulama çeşitliliği, hem matematiksel araçların hem de yeni sensör türlerinin devreye girmesiyle sürekli genişlemektedir. Sonuç olarak bu bölümde, yeryuvarının gravite alanı ve küresel harmonikler ile gösterimi, referans koordinat sistemleri, sistemler arasındaki dönüşümler, gravite alanı belirleme amaçlı uydu misyonları ölçme değerlendirme teknikleri hakkında temel bilgi verilecektir Yeryuvarının Gravite Alanı ve Küresel Harmonikler Yeryüzündeki bir cisme etki eden merkezkaç ve çekim kuvvetlerinin toplamı gravite kuvveti olarak tanımlanmaktadır. Korunumlu bir kuvvet alanı olarak yeryuvarının çekim alanını belirlemek onun potansiyelini belirlemekle aynı anlama gelir. Bu potansiyel yeryuvarını oluşturan kitlelerin dışında harmonik bir davranış sergilediğinden, gravite alanının gösterimi için genellikle küresel harmonik seriler kullanılır (Kaula, 1966; Heiskanen ve Moritz, 1984; Rummel ve ark., 22; Seeber, 23; Hofmann-Wellenhof ve Moritz, 25). Kitlelerin dışında konumu küresel koordinatlarla belirtilen bir nokta için çekim potansiyeli,
21 9 V(r,θ,λ) = µ R n= ( ) n+1 n R ( C nm cosmλ+ r S nm sinmλ) P nm (cosθ) (2.1) m= seri eşitliğiyle tanımlanır. Eşitlikte geçen parametreler, µ yerçekimi sabiti (G evrensel çekim sabiti ile M yeryuvarının kütlesinin çarpımı) R r θ λ C nm, S nm P nm yeryuvarının ekvatoral yarıçapı radyal bileşen kutup uzaklığı jeosentrik boylam tam normalleştirilmiş küresel harmonik veya Stokes katsayıları tam normalleştirilmiş bütünleşik Legendre polinomları n, m küresel harmonik açınımının derece ve sırasıdır. Yeryuvarının çekim potansiyelinin küresel harmonik fonksiyonlar yardımıyla gösteriminin pratik yararı, çekim potansiyeli ve onun fonksiyonellerinin sayısal uğraşılabilir olmasında yatar. Gravite alanı büyüklükleri, Cnm, Snm katsayıları ile tanımlı yakınsak serilerin değerleri olarak karşımıza çıkar. Bunun için hesap noktasının küresel koordinat sistemindeki koordinatlarına(r, θ ve λ) ihtiyaç duyulur. Küresel koordinatlar ile dik koordinatlar arasındaki ilişki Şekil 2.1 de verilmiştir. z P θ r θ z y x λ rsinθ y x Şekil 2.1. Küresel ve dik koordinatlar
22 1 Şekle göre iki koordinat sistemi arasındaki dönüşüm, x =rsinθcosλ y =rsinθsinλ (2.2) z =rcosθ r = x 2 +y 2 +z 2 θ =tan 1 x2 +y 2 z (2.3) λ =tan 1 y x eşitlikleriyle tanımlıdır. Çekim potansiyeli değerlerinin (2.1) den gerçeğe yakın türetilmesi, küresel harmonik (Stokes) katsayılarının en doğru büyüklükler olarak kestirilmesi anlamına gelir. Küresel harmonik katsayılar yeryuvarının gravite alanı düzensizliklerini yansıtır. Bu durum, bir yapının farklı yoğunluktaki tuğlalarına benzetilebilir. Bundan dolayı bu katsayıların gerçeğe yakın belirlenmesinde global anlamda veri dağılımı ve çözünürlüğü önemli rol oynar. Yüksek dereceler için daha yüksek veri çözünürlüğüne ihtiyaç duyulur. Fakat gerçekte gravite alanı sınırsız veri çözünürlüğüne sahip değildir. Bundan dolayı veri çözünürlüğüne bağlı olarak küresel harmonik açınımın derecesi sonlu bir değerdir. (2.1) in en büyük açınım derecesi (N max ), kürenin yarı-çevre uzunluğunun eldeki verinin açısal çözünürlük değerine ( ϑ) bölünmesiyle elde edilir (Ustun, 211): N max = π ϑ (2.4) Yerkürenin büyüklüğüne bağlı olarak modelin konumsal çözünürlüğünden söz edilmek istenirse λ = 2km N max (2.5) eşitliği kullanılır (Prange, 211). (2.1) için yüksek derece ve sıra ile ilişkili terimlerin hesabında karşılaşılabilecek nümerik problemlerden ötürü genelde tam normalize edilmiş Legendre polinomları kullanılır (Bock, 23; Hofmann-Wellenhof ve Moritz, 25; Jäggi, 27; Swatschina, 29).
23 Koordinat Sistemleri ve Dönüşümler Uydu jeodezisinde, temel olarak iki farklı koordinat sistemi kullanılmaktadır. Bunlar uzay sabit (inertial, space-fixed) ve yer sabit (earth-fixed) sistemlerdir. Uluslararası Yer Dönüklük ve Referans Sistemleri Servisi IERS bu sistemlerin tanım ve gerçekleşmesini uluslararası bir standart olarak kullanıcılara duyurur (IERS, 212). IERS analiz merkezleri VLBI, SLR, LLR, GPS, DORIS gibi uzay jeodezik tekniklerden gelen verileri birleştirerek sonuçları yer dönme parametreleri, Uluslararası Göksel Referans Sistemi (ICRF-International Celestical Reference Frame), Uluslararası Yersel Referans Sistemi (ITRF-International Terrestrial Reference Frame) olarak yayımlar (Kahveci ve Yıldız, 212). Birçok işlem adımına sahip yörünge belirleme için yukarıdakilere ek koordinat sistemlerine ihtiyaç duyulur. Bunlar uydu koordinat sistemi (SCS-Satellite Coordinate System) ve uydu bazlı koordinat sistemi (S/C-Body-Spacecraft Body System) olarak bilinir. Yörünge hesap ve gösterimleri yapılırken adı geçen koordinat sistemleri arasında sık sık dönüşüm yapmak gereklidir. Uydunun hareket denklemi inersiyal referans sistemi olan ICRF sisteminde ifade edilir. Buna karşın IGS tarafından yayımlanan GPS uydu verileri ise ITRF referans sisteminde sunulmaktadır. Ayrıca uyduya ait ölçüler uydu-bazlı sabit sistemde verilirken, hareket denklemlerinde bu ölçülerin kullanılabilmesi için inersiyal sisteme geçiş gereklidir. Bir diğer dönüşüm gerektiren işlem de yörünge kontrolü(orbit validation) ve yörünge hatalarının ifade edilmesi sırasında ortaya çıkar. Gösterim genelde uydu koordinat sisteminin üç bileşeni Radial, Along-Track, Cross-Track üzerinden yapılır (McCarthy, 1996; Swatschina, 29) ICRF ve ITRF arasında dönüşüm Bu dönüşüm işlemi ICRF-ITRF dönüşümü ya da ECI-ECEF dönüşümü adı altında karşımıza çıkar. Günümüz uygulamalarında, ECI nin ICRF, ECEF nin ise ITRF gerçekleşmesi olarak ele alınır. ICRF, kuasar olarak bilinen ekstragalaktik radyo kaynaklarının koordinatları kullanılarak tanımlanmaktadır. Kuasar koordinatları, VLBI (Very Long Baseline Interferometry) ağları olarak bilinen büyük anten dizileri ile yeryüzünden elde edilen gözlemlerden türetilir. Daha sonra bu koordinatlar güneş sistemindeki gök cisimlerinin koordinatları ve optik
24 12 yıldız katalogları ile birleştirilir. Benzer şekilde ITRF nin gerçekleşmesi için SLR, LLR, GPS ve DORIS in yer kontrol ağlarından yararlanılır (Tapley ve ark., 24). ECI sisteminden ECEF sistemine yada ICRF den ITRF sistemine dönüşüm için gerekli matrisler aşağıda verilmiştir. Klasik formülasyon ECI sisteminin J2 deki gerçekleşmesi için tanımlıdır. Uydu hareketi özellikle kutup hareketi (x p,y p ) ve gün uzunluğu ile ilişkili UT1 deki değişim oranına (UT1) duyarlıdır. IERS, uydu gözlemleri ve VLBI verilerinden türetilen Yer Dönüklük Parametrelerini (Earth Orientation Parameters - EOP) dağıtır ve yayımlar. Temel EOP parametreleri (x p,y p ), (UT1) ve düzeltilmiş presesyon ve nutasyon parametreleridir. Bu parametrelerin hesabında atmosferik etki, gelgit vb. doğa olayları göz önüne alınırlar. EOP parametreleri, IERS Bülten B içerisinde düzenli bir şekilde yayımlanır. Bu konu hakkında daha fazla bilgi, farklı uygulama ve gösterimler için McCarthy (1996), Seeber (23), Tapley ve ark. (24), Montenbruck ve ark. (25), Beutler ve ark. (25a) e bakılabilir. Dönüşüm eşitliklerini vermeden önce ECI ve ECEF sistemlerinin kısaca tanıtılması yerinde olacaktır. Yer Merkezli İnersiyal Koordinat Sistemi (ECI) Kartezyen koordinatlarla tanımlı bu sistemin başlangıç noktası yeryuvarının kitle ağırlık merkezidir. Sistemin +Z ekseni yerin dönüş ekseni doğrultusunda kuzey yönünü, +X ekseni ekliptik ile ekvatorun arakesit doğrultusunda ilkbahar noktası yönünü, +Y ekseni sağ el koordinat sistemini oluşturacak ekseni tanımlar. Sistem yerin güneş etrafındaki düzensiz hareketi, presesyon ve nutasyondan dolayı tam anlamıyla inersiyal değildir. Bu sorunun çözümü için koordinat sisteminin eksenlerini belirli bir epoğa göre tanımlamak gereklidir. Bu epok 1 Ocak 2 tarihli 12: UTC zamanındaki J2 olarak adlandırılan epoktur. Yer Merkezli Yer Sabit Koordinat Sistemi (ECEF) ECI koordinat sistemindeki gibi, ECEF de kartezyen koordinatlarla tanımlı olup sistemin başlangıç noktası yerin kitle merkezindedir. +Z ekseni coğrafi kuzey kutbunu gösterir ve 19 ile 195 yılları arasındaki yer dönme ekseninin ortalama konumu ile çakışıktır. +X ekseni ortalama Greenwich meridyeni ve ortalama
25 13 ekvatorun arakesiti ile çakışık olup sıfır derece boylamı doğrultusunda konum alır. +Y ekseni ise sağ el koordinat sistemini oluşturur. ECEF sisteminin gerçekleşmesi yeryüzüne global anlamda dağılmış nokta dizilerine bağlıdır. Bu gerçekleşmeler sonucunda oluşan koordinat sistemlerinden biri WGS84 sistemidir. ECI ve ECEF arasında kaba bir dönüşüm için temel olarak GMST ve kutup hareket bileşenleri (x p,y p )gereklidir. Kesindönüşüm, yerin dönme eksenini belirli peryotlarla devinime zorlayan presesyon ve nutasyon etkilerinin göz önüne alınmasıyla sağlanır. Bu açıklamalar doğrultusunda, ICRF (veya ECI) sisteminde verilen bir konum vektörünün ITRF (veya ECEF) sistemindeki karşılığını bütün etkilerin içinde yer aldığı T(t) dönüşüm matrisi yardımıyla tanımlamak mümkün olur. Dönüşüm matrisi 3x3 boyutlu zaman değişkenli ortogonal bir matris özelliğindedir. Sistemler arasındaki dönüşüm ve zamana bağlı olarak koordinat eksenlerinin uzaydaki konumunu tanımlayan dönüşüm matrisi, r ITRF = T(t)r ICRF (2.6) T(t) = W(t)R(t)N(t)P(t) (2.7) eşitlikleriyle gösterilir. Dönüşüm matrisinin içeriğini W(t) : kutup hareketi, R(t) : yer dönüklük, N(t) : nutasyon ve P(t) : presesyon etkilerini düzenleyen alt matrisler oluşturur. Yörünge belirleme çalışmalarında bozucu etkilerin ortaya çıkarılması için ivmelerin de inersiyal sistemden yermerkezli sisteme dönüşümleri gerekli olacaktır. Bu yüzden (2.6) nın ikinci türevlerinin hesaplanması gereklidir. r ITRF = T(t) r ICRF r ICRF = T T (t) r ITRF (2.8) Dönüşümde kullanılan matrisleri kısaca açıklamak ve matematiksel eşitlikleri vermek yerinde olacaktır.
26 14 Presesyon Matrisi Presesyon, yeryuvarının dönme ekseninin ekliptik eksen etrafındaki devinim hareketi olup peryodu 2577 yıldır. Presesyon, ilkbahar noktasını (ekinoks) ekliptik yörüngesi boyunca yılda 5.3 lik hızla devinime zorlar, buna ekinoks presesyonu veya kısaca presesyon denir. Presesyon hareketini doğuran etkenleri: i) yeryuvarının dönme ekseninin yörünge düzlemine dik olmaması, ii) yeryuvarının kutuplardan basıklığı olarak sıralayabiliriz (Üstün, 26b). Şekil 2.2. Presesyon IAU76 presesyon modeline göre presesyon elemanları aşağıdaki şekilde üç açı ile tanımlanır: ζ = t+.3188t t 3 θ = t.42665t t 3 (2.9) z = t t t 3 Buradaki zaman değişimi (yüzyıllık), t = (JD J2.)(gün) (2.1) eşitliğindenhesaplanır. EşitliktegeçenJ2.(1Ocak2,12 h )başlangıçanından itibaren geçen Jülyen günüdür ve değerine karşılık gelir. Yukarıdaki
27 15 dönüklük elemanlarının her biri bağımsız bir koordinat dönüşümünü işaret eder. Sırasıyla, x, y ve z eksenlerine uygulanacak dönüklük sonucunda P(t) = R z ( z)r y (θ)r z ( ζ) (2.11) cosζcosθcosz sinζsinz sinζcosθcosz cosζsinz sinθcosz P(t) = cosζcosθcosz +sinζsinz sinζcosθcosz +cosζsinz sinθsinz cosζsinθ sinζsinθ cosθ (2.12) toplam presesyon etkisini ifade eden matris ortaya çıkar. Presesyon matrisi ICRF sisteminin J2 anındaki ortalama eksen doğrultularını t gözlem epoğuna taşır. Nutasyon Matrisi Gök kutbunun ekliptik kutup etrafındaki hareketi ekliptik düzlemine paralel ve güneşin çekim doğrultusuna dik yönde gerçekleşir. Güneş yıl içerisinde değişik konumlar aldığından hareketin yönü de zamanla değişir ve periyodik bir görünüm sergiler. Bu periyodik harekete nutasyon adı verilir (Üstün, 26b). Ortalama gün(mean-of-date) sisteminden gerçek gün(true-of-date) sistemine dönüşüm nutasyona bağlıdır. Burada dört açı kullanılır. Bunlar, ekliptiğin ortalama eğiklik açısı ǫ m, ekliptiğin gerçek eğiklik açısı ε t, boylamdaki nutasyon açısı ψ ve ekliptik eğiklikteki nutasyon açısı ε dır. Bu açılar yardımıyla nutasyon matrisi, N(t) = R x ( ε t )R z ( ψ)r x (ε m ) (2.13) N(t) = cos ψ cosε m sin ψ sinε m sin ψ cosε t sin ψ cosε m cosε t cos ψ +sinε m sinε t sinε m cosε t cos ψ cosε m sinε t sinε t sin ψ cosε m sinε t cos ψ sinε m cosε t sinε m sinε t cos ψ +cosε m cosε t (2.14) ile gösterilir (McCarthy, 1996; Seeber, 23; Tapley ve ark., 24; Montenbruck ve
28 16 ark., 25). Ekliptik eğiminin ortalama ve gerçek değerleri ε m = t.59t t 3 ε t =ε m + ε (2.15) eşitliklerinden türetilir. Diğer sayısal büyüklükler McCarthy (1996) da verilmiştir. Yer Dönüklük Matrisi Yerin günlük dönmesi, GMST(Greenwich Mean Sideral Time) olarak bilinen Greenwich ortalama yıldız zamanı açısına (α G ) bağlıdır. Buradan R(t) matrisi sadece z ekseni etrafındaki dönüklük etkisiyle R z (t) = cosα G sinα G sinα G cosα G 1 (2.16) tanımlanır. Bazı durumlarda özellikle ECEF sisteminin dönüklüğüne göre uydu hız vektörü gerekli olduğunda, dönüşüm matrisinin her bir elemanının zamana göre türevi gerekli olacaktır. Bununla beraber R(t) matrisinin zamana göre türevi sonuçlar üzerinde çok etkili olduğundan uygulamada önem teşkil etmektedir. R(t) matrisinin zamana (α G ) göre türevi alındığında sinα G cosα G Ṙ z (t) = α G = cosα G sinα G (2.17) çıkar. Burada α G yerin dönüklük değişimi; başka bir deyişle, açısal hızıdır. Yüksek duyarlık gerektiren uygulamalar için bu hız değeri hesaba dahil edilmelidir. IERS ye göre ortalama hız rad/s dir. Öte yandan GMST değeri
29 17 (radyan biriminde), GMST(UT 1) = T[ T( (2.18) T)] eşitliğinden bulunur (Tapley ve ark., 24). Burada T = UT 1 J2. J2. dan itibaren jülyen günüdür. Yer dönüklük matrisini oluşturmak için bu denkleme ekinoks denklemi olarak bilinen ek düzeltme uygulanmalıdır. Yüksek doğruluk için birkaç milisaniyelik inceliğe kadar inilmelidir (McCarthy, 1996; Tapley ve ark., 24). Sonuç olarak ekinoks denkleminin eklenmesiyle α G = GMST(UT1)+ ψcosε m (2.19) bulunur. Kutup Hareket Matrisi Yerin dönme ekseni sabit değildir ve iki açı (x p,y p ) ECEF sistemine göre dönme ekseninin konumunu tanımlamak için kullanılır. Kutup hareketi bileşenlerinin küçük açılar olması sayesinde dönüşüm matrisi, W(t) = 1 x p 1 y p x p y p 1 (2.2) ile ifade edilebilir. (x p,y p ) radyan biriminde verilir. Şekil 2.3 de tarihinden tarihine kadar kutup hareket matrisini oluşturan kutup gezinmesi bileşenlerinin (x p, y p ) değişimi görülmektedir.
30 YIL y p (").4.2 x p (").2.4 Şekil 2.3. Yıllara göre kutup hareket matris elemanlarının değişimi Uydu Koordinat Sistemi Birçok DYB uygulamasında yörünge karakteristiğini daha kolay ifade edebilmek için uydu koordinat sistemi (UKS) (SCS-Satellite Coordinate System) sistemi tercih edilir. Farklı yörünge sonuçlarını karşılaştırmak ve konumsal hataları göstermek bu sistemin diğer getirileri arasında sayılabilir (Santos, 1995; Tapley ve ark., 24; Swatschina, 29). UKS sisteminin merkezi uydunun kitle merkezi olduğundan, hareketli bir vektör sisteminden söz etmek mümkündür. Uydunun izlediği yörünge boyunca UKS sisteminin eksen yönelimleri değişir (Şekil 2.4). Hareketli bir vektör sistemi olarak, UKS sisteminin koordinat bileşenleri aşağıdaki biçimde oluşturulur. Uydu ile birlikte hareket eden UKS sistemi RAC (Radial, Along-track, Cross-track) veya RTN (Radial, Transverse, Normal) olarak da adlandırılır (Rosborough ve Tapley, 1987; Vallado, 1997, 23):
31 19 Z ICRF v(t) A(t) R(t) C(t) r(t) Uydu yörüngesi Yer Merkezi X ICRF Y ICRF Şekil 2.4. Uydu Koordinat Sistemi (UKS) R(t) = r(t) r(t) = ε xi+ε y j+ε z k A(t) = C(t) R(t) = δ x i+δ y j+δ z k (2.21) C(t) = r(t) ṙ(t) r(t) ṙ(t) = α xi+α y j+α z k (2.21) eşitliklerinden anlaşılacağı üzere koordinat bileşenleri birim vektördür. Burada R(t) (radial) yer merkezinden uydunun kitle merkezine olan birim vektörü, A(t) (along-track) uydu hız vektörünün pozitif doğrultusundaki birim vektörü ve C(t) (cross-track) ise yörünge düzleminin normali olarak tanımlanan birim vektörü ifade eder. Ayrıca A(t) ekseni, hız vektörüne mutlaka paraleldir denemez; aralarında bir miktar kayıklık bulunur. Ancak, yörünge dairesel özellikteyse, bu eksen hız vektörü ile çakışık kabul edilebilir. A(t) ekseninin diğer bir özelliği ise yarıçap vektörüne dolayısıyla radyal bileşene (R(t)) dik olmasıdır. Genel olarak along-track değerleri diğer bileşenlere göre daha büyük değerler alır. Örnek olarak CHAMP uydusunun dinamik değerlendirme sonucundaki koordinatları ile uyduya ait SP3 dosyasında bulunan koordinatlar arasındaki farklar iki farklı koordinat sisteminde gösterilmiştir (Şekil 2.5, Şekil 2.6).
32 2 Şekil 2.5. CHAMP uydusu için kartezyen koordinat sisteminde hataların gösterimi 35 3 Radial Along Cross 25 difference (m) epochs (interval is 6 seconds) Şekil 2.6. CHAMP uydusu için UKS de hataların gösterimi UKS sisteminden ICRF ve ITRF sistemlerine dönüşüm yapmak olanaklıdır. Bu dönüşüm için öncelikle (2.21) den yararlanarak bir dönüşüm matrisi (D(t)) oluşturulur. R(t) ε x ε y ε z i A(t) = δ x δ y δ z j C(t) α x α y α z } {{ } D(t) k (2.22)
33 21 UKS-ICRF ve UKS-ITRF arasındaki dönüşüm için r ICRF = D(t)r UKS (2.23) r UKS = D 1 (t)r ICRF (2.24) r ITRF = T(t)D(t)r UKS (2.25) r UKS = D 1 (t)t T (t)r ITRF (2.26) eşitlikleri kullanılır. Burada T(t) ifadesi eşitlik (2.6) da bahsedilen dönüşüm matrisidir. Uydunun konumunu tanımlayan yörünge verileri çoğunlukla uydunun kitle merkezi ile ifadelendirilir. Bununla birlikte, yörünge belirleme işlemi için gerekli ölçüler genellikle uydu üzerindeki bir donanım vasıtasıyla ölçülür. Fakat bu donanımın konumu tam olarak uydu kitle merkezinde değildir. Bundan dolayı uydu üzerinde bulunan donanımın (anten veya reflektör gibi) konumunun tanımlanması için bir koordinat sistemine daha ihtiyaç duyulur (Xu, 28). Bu koordinat sistemi uydu bazlı koordinat sistemi (UBKS) (satellite (body) fixed coordinate system) olarak isimlendirilir. Sistemin X ekseni uydunun uçuş yönü doğrultusunda, Y ekseni yörünge düzlemine dik olacak şekilde ve Z ekseni yeryuvarının çekim yönü doğrultusunda tanımlanır(wertz, 21; Leick, 24; Xu, 28; Peet, 212). CHAMP uydusuna ait örnek bir gösterim Şekil 2.7 de verilmiştir. DYB Anteni Y(t) KM X(t) v(t) Z(t) KM : Kitle Merkezi DYB : Duyarlı Yörünge Belirleme Şekil 2.7. Uydu Bazlı Koordinat Sistemi (UBKS) Yukarıda da bahsedildiği üzere uydulara ait ölçüler UBKS sisteminde verilmektedir. Çizelge 2.1 de CHAMP, GRACE ve GOCE uydularında bulunan
34 22 GPS alıcıları için kesin koordinatlar verilmiştir (CODE, 212; Swatschina, 29). DYB çalışmalarında GPS alıcılarının faz merkezi kayıklıkları sonuçlar için önemli bir rol oynamaktadır. Bu yüzden hesaplarda mutlaka kullanılması gerekli olan parametrelerdendir. Çizelge 2.1. LEO uydularındaki GPS alıcıları için UBKS de faz merkezi kayıklık değerleri Uydu Adı Tarih ve Saat X (m) Y (m) Z (m) CHAMP GRACE A GRACE B GOCE (POD1) GOCE (POD2) Çizelge 2.1 de verilen değerler uydunun yakıt tüketimine göre zamanla değişim gösterir. GOCE için verilen değerlerin geçerlilik süresi dır. Bu değerlerin güncel halleri Bernese in resmi internet sitesinde yer alan SATELLIT.Ixx dosya içeriğinden edinilebilir. Fakat şu an için bu dosya içerisinde GOCE uydusuna ait bilgi bulunmamaktadır. LEO uydularına benzer şekilde GPS uyduları içinde anten faz merkezi kayıklık değerleri mevcuttur. Bu değerler ise IGS tarafından igsxx.atx dosyaları içerisinde yayımlanır (IGS, 212c). 2.2 Gravite Alanı Belirleme Amaçlı Yakın Yer Uyduları CHAMP 15 Temmuz 2 tarihinde Rus Plesetsk uzay üssünden fırlatılan CHAMP (CHAllenging Minisatellite Payload) gravite alanı belirleme amaçlı olarak fırlatılan alçak-yörüngeli ilk uydu özelliğini taşımaktadır (Şekil 2.8). Uydu görevinin yürütücülüğünü Postdam (Almanya) Yer Araştırmaları Merkezi (GeoForschungsZentrum-GFZ) yapmaktadır. Uydu neredeyse dairesel ve kutba yakın bir yörüngeye, başlangıç yüksekliği 454 km ve eğimi 87.3 olacak şekilde yerleştirilmiştir (GFZ, 212a; ILRS, 212a). Uyduya ait diğer özellikler Çizelge
35 de verilmektedir. Şekil 2.8. CHAMP (GFZ, 212a) Çizelge 2.2. CHAMP uydusunun genel özellikleri ve yörünge bilgileri Parametre Büyüklük Toplam kütle 522 kg Yükseklik 75 mm Toplam boy 8333 mm Genişlik 1621 mm Alan kütle oranı.138m 2 /kg Fırlatma tarihi 15 Temmuz 2 Yerberi (perigee) uzaklığı 477 km Yeröte (apogee) uzaklığı 416 km Eğim (ekvatorla) 87.3 Eksantrisite (e) <.4
36 24 Uydunun başlangıçtaki yörünge yüksekliği atmosferik sürüklenmeden ötürü görev süresinin sonlarına doğru 3 km civarlarına düşecek veya daha da azalacaktır. Atmosferik sürüklenme uydu yüksekliğinde düzenli azalmaya neden olur. Atmosferin yoğunluğuna bağlı olarak uydu bir günde yaklaşık 1 ile 1 metre arasında yükseklik kaybına uğrar (Jäggi, 27). Uydunun başlangıç yörünge yüksekliğinin yaklaşık 454 km seçilmesinin başlıca nedenleri arasında şunlar gösterilmiştir (GFZ, 212a): güneşten kaynaklı şiddetli değişimlere direnç sağlayarak uydu görev süresinin mümkün olduğunca uzatılması, uydunun atmosferin farklı katmanlarından geçerken maruz kaldığı etkilerin belirlenmesi, yeryuvarının manyetik alanının gözlenmesi. Uydu görev süresi başlangıçta beş yıl olarak planlanmış olmasına rağmen 19 Eylül 21 tarihine kadar görevine devam etmiştir. CHAMP uydusu ile gerçekleştirilmek istenen görevler ve bilimsel hedefler şu şekilde sıralanabilir (Seeber, 23; Hofmann-Wellenhof ve Moritz, 25; GFZ, 212a); global gravite alanının haritalanması yani statik yer gravite alanının(ve kısmen zamansal değişimlerinin) uzun-dalga boylu özelliklerinin gerçeğe yakın bir doğrulukla belirlenmesi, global manyetik alanın haritalanması yani yerin başlıca ve kabuk manyetik alanı ve zamansal değişimlerinin belirlenmesi, iyonosfer ve troposfer profilinin ortaya çıkarılması. CHAMP uydusuna, yörünge düzensizliklerini izlemek ve buradan gravite alanını iyileştirmek için BlackJack GPS alıcısı yerleştirilmiştir. STAR ivmeölçer ve bağımsız yıldız sensörleri bu görevin yerine getirilmesinde kullanılan diğer bilimsel donanımlardır. BlackJack GPS alıcısı NASA/JPL tarafından üretilen TRSR (TurboRogue Space Receiver) alıcısının ikinci neslidir (Kuang ve ark., 21). Alıcı çift frekanslı faz ve sözde-uzunluk ölçülerini 16 kanal üzerinden toplar. Uyduda dört adet GPS anteni bulunur. Bu GPS antenlerinin ilki choke ring DYB anteni, diğer ikisi sarmal (helix) antenler ve sonuncusu ise sarmal altimetre antenidir. Alıcı,
37 25 üzerindeki yazılım sayesinde, DYB uygulamaları için maksimum 12 GPS uydusunu izleyebilir. Fakat 22 Mart 21 tarihine kadar yazılım üzerinde birtakım kısıtlamalar yapılarak 7 den fazla uydu izlenmesi engellenmiştir. Daha sonra 5 Mart 22 tarihine kadar 8 uydu ve bu tarihten sonra ise 1 a kadar GPS uydusunun izlenmesine izin verilmiştir (Jäggi, 27; GFZ, 212a). Alıcının STAR(Space Triaxial Accelerometer for Research mission) ivmeölçer ile kombinasyonu CHAMP uydusunun yüksek hassasiyetli yörünge belirlemesine olanak verir. STAR ivmeölçer ONERA (Office National d Etudes et de Recherches Aerospatials) tarafından üretilmiştir (Touboul ve ark., 1998). Gravite alanının modellenebilmesi için gravite alanı ile ilişkili olmayan düzensizlikler (ivmeler) gereklidir. Bundan dolayı atmosferik sürüklenme, albedo, güneş radyasyon basıncı gibi kuvvetlerin yarattığı ivmeler gözlenmeye çalışılır. Bu ivmelerin ölçümü için üç eksenli, yaklaşık m/s 2 çözünürlüğe sahip STAR ivmeölçeri kullanılır. Sistematik etkilerden kaçınmak için ivmeölçer uydunun ağırlık merkezine yerleştirilmiş ve uydunun yönelimi iki yıldız sensörü ile kontrol altına alınmıştır. Uydu üzerindeki diğer bir donanım, GFZ nin geliştirdiği pasif Lazer Retro Reflektör (LRR) dür. LRR, uydunun yer istasyonlarından izlenmesini olanaklı kılar. LRR sayesinde uydu ve yer istasyonları arasındaki mesafe çift yönlü olarak 1-2 cm doğrulukla ölçülür ve bu ölçümler DYB çalışmalarını destekleyici nitelik taşır. Özetle, LRR ekipmanı sayesinde SLR (Satellite Laser Ranging) ölçüleri yapılabilmektedir. SLR tekniği LEO uydularının duyarlı yörünge belirleme işlemi için tamamen bağımsız bir tekniktir. SLR tekniği yörünge sonuçlarının kalibrasyonu veya kontrolü için çok kullanışlı bir yöntemdir ((Bock, 23); bkz. Bölüm 5). Ayrıca uydu üzerinde uydunun yüksek doğrulukta konum bilgisini sağlayan gelişmiş yıldız pusulası (ASC-Advanced Stellar Compass), yerin manyetik alan bileşenlerini ölçmek için manyetometre ve atmosferik ölçmeler için iyon driftölçer bulunmaktadır. Şekil 2.9 ve Şekil 2.1 da uydu üzerindeki tüm donanımlar ve yerleri gösterilmiştir.
38 26 Şekil 2.9. CHAMP uydusu ve donanımının önden görünüşü (GFZ, 212a) Şekil 2.1. CHAMP uydusu ve donanımının arkadan görünüşü (GFZ, 212a) CHAMP uydusu bu detaylı donanımı sayesinde gravite alanının uzundalga boylu bileşenlerinin belirlenmesinde yeni bir devir açmıştır. Daha önce çok sayıda gözlem ve uydudan üretilen GRIM5-S1 ve EGM96S modelleri ile karşılaştırıldığında bir kaç aylık CHAMP yörünge izleme verileriyle belirlenen gravite alanı çözünürlüğünün daha yüksek olduğu görülmektedir. Örneğin EIGEN- 2 modelin çözünürlüğü (yarı-dalga boyu) 55 km olup doğruluk değerleri ise jeoit yüksekliği için 1 cm, gravite anomalisi için.5 mgal dir (Reigber ve ark., 23). Ayrıca CHAMP uydusunun ölçme prensibi uydudan uyduya izleme tekniği yüksek-alçak (SST-hl) moddur (bkz. Bölüm 3.1). Yerin gravite alanı CHAMP uydusunun yörüngesini bozar; böylece, bu bozucu ivmeler yerçekimi potansiyelinin ilk türevleri ile ilişkili bir hal alır. Bu durum, yerin gravite alanının, sayısal yörünge integrasyonu uygulayarak uydu yörünge düzensizliklerinden (ivmelerinden) veya enerjinin korunumu kanunu kullanılarak türetilebileceğini ifade eder (Hofmann- Wellenhof ve Moritz, 25). Sayısal yörünge integrasyonu için Montenbruck ve ark. (25) e enerji korunumu için Jekeli (1999); Sneeuw ve ark. (22) e,
39 27 CHAMP uydusu hakkında detaylı bilgi için Rummel ve ark. (22); Bock (23); Seeber (23); Hofmann-Wellenhof ve Moritz (25); Jäggi (27); GFZ (212a) e bakılabilir GRACE GRACE (Gravity Recovery And Climate Experiment) uydu görevi CHAMP uydusunun devamı niteliğindedir. CHAMP den farklı olarak aynı yörüngede birbirini izleyen ve aralarında 22 km 5 km uzaklık bulunan özdeş iki uydudan oluşmaktadır (Şekil 2.11). Her iki uydu da eş zamanlı olarak 17 Mart 22 tarihinde Rusya Plesetsk uzay üssünden fırlatılmıştır. GRACE misyonu DLR (Deutsches Zentrum für Luft-und Raumfahrt) ve NASA (U.S. National Aeronautics and Space Administration) arasındaki ortak bir projenin ürünüdür. Proje sorumluluğu Texas Üniversitesi Uzay Araştırmaları Merkezine (CSR-Center for Space Research) verilmiştir. CHAMP de olduğu gibi bu uydu misyonunda da gravite potansiyelinin hassas kestirimini elde etmek için yeryuvarını global anlamda saran ve homojen bir şekilde dağılan verilere ihtiyaç duyulur. Bu yüzden GRACE misyonu da kutba yakın ve neredeyse daireseldir. Başlangıç yörünge yüksekliği 5 km civarında ve yörünge eğimi 89 seçilmiştir. Bu yükseklik düzenli bir şekilde 1.1 km/ay oranında azalır. Uyduya ait diğer özellikler Çizelge 2.3 de verilmektedir. CHAMP gibi GRACE uydularının görev süreleri beş yıl olarak planlanmıştır (NASA, 212a; GFZ, 212b; CSR, 212b; ILRS, 212c). Çizelge 2.3. GRACE A-B uydusunun genel özellikleri ve yörünge bilgisi Parametre Büyüklük Toplam kütle kg Yükseklik 3122 mm Toplam boy 1942 mm Genişlik 72 mm Fırlatma tarihi 17 Mart 22 Yerberi (perigee) uzaklığı km Yeröte (apogee) uzaklığı km Eğim (ekvatorla) 89 Eksantrisite (e) <.5
40 28 Şekil GRACE ikiz uydu sistemi (NASA, 212a) GRACE misyonunun amacı yeryuvarının yüksek çözünürlükte global gravite alanını ve bu alandaki zamansal değişimleri belirlemektir. CHAMP uydu görevinde olduğu gibi toplam elektron miktarı haritasının çıkarılmasında da bu uydulardan yararlanılmaktadır (Hofmann-Wellenhof ve Moritz, 25; Jäggi, 27; GFZ, 212b). Bu görevleri yerine getirebilmek için uyduda bulunan donanımlar şunlardır: JPL BlackJack GPS alıcısı SuperSTAR ivmeölçer Otomatik yıldız sensörleri Lazer Retro Reflektör (LRR) Yıldız kamera aksamları (SCA) K/Ka-Band Radar Ölçme sistemi (KBR) Ultra dengeli osilatör (ultra-stable oscillator-uso) JPL BlackJack GPS alıcısı, yıldız sensörleri, LRR donanımları, CHAMP uydusunda bulunan benzer özelliklere sahip aynı donanımlardır. GPS alıcıları 1 uyduya kadar gözlem yapabilir ve SST-hl modda uzunluk ve uzunluk değişimleri
41 29 olarak navigasyon verisi sağlarlar. SuperSTAR, CHAMP de bulunan STAR ivmeölçerin geliştirilmiş modelidir. Ölçülen ivmelerin duyarlılığı radyal ve alongtrack yönünde 1 1 m/s 2 iken cross-track bileşeni için 1 9 m/s 2 dir (Jäggi, 27). SCA donanımı yıldızlara göre uydunun hassas bir biçimde yönlendirmesini sağlar. GRACE uyduları üzerindeki en önemli donanım NASA/JPL tarafından üretilmiş olan K/Ka-Band radar ölçme (KBR-K/Ka-Band Ranging System) sistemidir. Her iki uydu KBR sistemi ile donatılmıştır. KBR sisteminde her uydu iyonosferden bağımsız uzunluk (uydular arasında) ölçmesi için iki frekansta (K-band: 24.5 GHz ve Ka-band: 32.7 GHz) mikrodalga sinyal (taşıyıcı faz) üretir. Sinyaller uydular tarafından karşılıklı olarak gönderilir ve alınır. Böylece uydular arasındaki uzaklık, alınan sinyal ile on-board üretilen sinyalin karşılaştırılmasıyla belirlenmiş olur. Uzaklık değişimi KBR ile mikron düzeyinde ölçülebilmektedir. Ayrıca sözü geçen her iki sinyal aynı USO tarafından üretilmektedir (Seeber, 23; Dunn ve ark., 23; Hofmann-Wellenhof ve Moritz, 25; Üstün, 26a; Jäggi, 27; Liu, 28; Swatschina, 29). Şekil GRACE uydusunun alttan görünüşü (GFZ, 212b)
42 3 Şekil GRACE uydusunun üstten görünüşü (GFZ, 212b) Şekil GRACE uydusunun iç yapısı (GFZ, 212b) GRACE verilerine dayanılarak üretilen gravite alanının çözünürlüğü öncekilere göre daha iyidir. Tapley ve ark. (24) na göre 11 günlük GRACE verileriyle belirlenen GGM1S yer gravite modeli, EGM96 ile karşılaştırılarak global gravite alanındaki iyileşmeler ortaya konmuştur. Ayrıca GRACE uydusunun ölçme prensibi uydudan uyduya izleme tekniği alçak-alçak SST-ll (Satellite-to-Satellite low-low mode) moddur (bkz. Bölüm 3.1). Bu özellik, çok uzun baz (22 km) üzerinden tek boyutlu gradyometre olarak kullanılabilir. Orjinal GRACE gözlemleri iyi bir doğrulukla gravite gradyentlerini türetmek için kullanılabilir (Seeber, 23). Bu konseptin tam tersine GOCE, bir sonraki bölümde anlatıldığı gibi çok kısa bazlar (5 cm) kullanır (Hofmann-Wellenhof ve Moritz, 25).
43 GOCE GOCE (Gravity field and steady-state Ocean Circulation Explorer) görevi Avrupa Uzay Ajansının (ESA Europan Space Agency) Yaşayan Gezegen Programının (Living Planet Programme) çekirdek projesidir. GOCE uydusu gravite alanı belirleme amaçlı gönderilen uydu serisinin sonuncusudur (Şekil 2.15). GOCE uydusunun yörüngesi neredeyse dairesel ve güneş senkronizasyonlu olarak 17 Mart 29 tarihinde Rusya nın Plesetsk üssünden gönderilmiştir. Gravite sinyalinin daha güçlü ve daha hassas olması için uydunun yörünge yüksekliği 25 km seçilmiştir. Uydunun izlenmesi ve kontrolü İsveç te bulunan Kiruna ve Norveç te bulunan Svalbard yer istasyonları yardımıyla ESA/ESOC tarafından yürütülmektedir. GOCE misyonunun temel amacı yer gravite alanının ölçülmesine ve jeoidin mükemmel bir doğruluk ile modellenmesine katkıda bulunmaktır. Beklenen doğruluklar; gravite anomalilerin 1mGal (1 5 ms 2 ), jeoidin 1 2cm duyarlığında belirlenmesi ve 1 km den daha iyi bir konumsal çözünürlüğe ulaşılmasıdır. Şekil GOCE uydusu (ESA/ESOC, 212) GOCE misyonu uydu tarihinde bir ilki başarmıştır. CHAMP ve GRACE misyonlarında olmayan sürüklenmeden bağımsız kontrol (drag-free control) sistemi kullanılmıştır. GOCE uydusunun üzerinde bulunan gelişmiş elektrikli iyon itici güç sistemi (electric ion propulsion system) ile uydu, yeryuvarı atmosferinden arta kalan kalıntılardan tamamen arındırılmış bir halde hareketini sürdürebilmektedir;
44 32 yani, uydu düşük yörünge yüksekliğinde kalmaya ve yerin etrafında serbest düşme (free fall) hareketine devam edebilmektedir. Böylece, gelmiş geçmiş en iyi gravite verilerini elde etmek mümkün hale gelmiştir (ESA, 212). Diğer iki uyduya kıyasla GOCE uydusunun görev süresi 2 ay gibi oldukça kısadır. Uydunun görev süresinin bu kadar kısa olmasının nedenlerinden biri yörünge yüksekliğinden (yaklaşık 25 km) kaynaklanır. Çünkü düşük yörüngelerde atmosferik sürüklenmenin etkisi daha büyüktür. Diğer bir neden ise uydunun görev süresinin iyon iticilerinin yaşam süresine bağlı olmasıdır. GOCE uydusu yaklaşık 5 m uzunluğunda 1 m çapında sekizgen, ince bir uydu görünümündedir. Uydudun diğer fiziksel özellikleri Çizelge 2.4 de verilmektedir (Drinkwater ve ark., 23; Üstün, 26a; ILRS, 212b; ESA, 212; CNES, 212). Çizelge 2.4. GOCE uydusunun genel özellikleri ve yörünge bilgisi Parametre Büyüklük Toplam kütle 11 kg Toplam boy 5 m Fırlatma tarihi 17 Mart 29 Yerberi (perigee) uzaklığı 27 km Yeröte (apogee) uzaklığı 27 km Eğim (ekvatorla) 96.5 CHAMP ve GRACE görevlerinin tersine, yüksek çözünürlüklü gravite alanını belirlemek için GOCE uydusunun kendisi temel bir bilimsel donanım olarak düşünülebilir. GOCE uydusunun üzerinde özellikle iki donanım dikkat çekicidir. Bunlardan ilki uydu gravite gradyometresi (SGG Satellite Gravity Gradiometry) diğeri de bir GNSS alıcısıdır. GNSS alıcısı, Alcatel Alenia Space (önceki adı Laben) tarafından üretilen çift frekanslı Lagrange GPS alıcısıdır. Lagrange GPS alıcısı 1 Hz frekans ile 12 kanal üzerinden faz ve sözde-uzunluk ölçülerini toplar. CHAMP ve GRACE misyonlarının tersine alıcı maksimum 12 GPS uydusunu izleyebilir. Alıcının iki temel görevi vardır. GPS verileri 1 cm hassasiyetinde DYB için kullanılır ki; bu, gravite gradyometresinin konumunu da belirler. Diğer bir görevi ise SSThl tekniğine dayanarak gravite alanının uzun ve orta dalga boyunun özelliklerinin analizine yardımcı olur. Başka bir deyişle, ilk görevinden elde ettiği duyarlı yörünge bilgisinden (yörünge bozulma analizlerinden) gravite bilgisini elde eder (Seeber, 23; Hofmann-Wellenhof ve Moritz, 25; Jäggi, 27).
45 33 Diğer önemli donanım SGG ise oldukça yüksek duyarlılıkta üç çift ivmeölçerden meydana gelir. Bu üç çift ivmeölçer ile üç ana eksen üzerinde gravite gradyentleri ölçülür. Her çift birbirinden yaklaşık 5 cm uzaklıktadır. İvmeölçerler uydunun ağırlık merkezine elmas yapılandırma şeklinde yerleştirilmişlerdir. Böylece her eksen üzerine iki adet ivmeölçer yerleştirilmiş olur. İki ivmeölçer çiftinin herbiri tarafından ölçülen ivmeler arasındaki farklar gerçek gradyometre ölçüleridir ve ölçülen ivme değerlerinin toplamının yarısı uyduya etki eden tüm dış ivmeleri temsil eder (Jäggi, 27). İvmeölçerlerin hassasiyeti 1 12 m/s 2 / Hz dir (Drinkwater ve ark., 27). Tüm üç eksende yerçekimi ivmelerinin farkları ölçülürse, bu ölçüler gravite potansiyelinin ikinci türevlerini (tüm matris elemanlarını) türetmek için kullanılabilir (Liu, 28). GOCE uydusu bu iki donanımdan başka SLR izlemeleri için bir LRR, konum belirleme için yıldız kamerası, iyon iticiler, manyetik torklar ve bazı sensörler ile donatılmıştır. Uydunun iç yapısı ve genel donanımı Şekil 2.16 da verilmektedir. İyon iticiler Zenon tank Nitrojen tank Yıldız sensör Güç kaynağı Manyetik torklar İyon iticilerin kontrol ünitesi Gravite Gradyometre GPS alıcısı Kontrol ünitesi Şekil GOCE uydusunun iç yapısı (ESA/ESOC, 212) Yukarıda da değinildiği üzere GOCE uydusunun yörünge analizlerinden gravite alanının uzun-dalgaboyu bilgisi elde edilirken (SST-hl), uydu gravite gradyometresinden (SGG) kısa-dalgaboyu bilgisi elde edilmektedir. GOCE uydusuna dayalı gravite alanı modelleme çalışmalarında SST-hl ve SGG tekniği birlikte kullanılmaktadır (bkz. Bölüm 3.1).
46 34 3. YAKIN YER UYDULARI İÇİN GPS VERİLERİNİN DEĞERLENDİRİLMESİ GPS (Küresel Konum Belirleme Sistemi-Global Positioning System), ABD Savunma Dairesi tarafından yürütülen ve altı yörünge düzlemine yerleştirilmiş 24 uydudan oluşan uydu bazlı bir radyo navigasyon sistemidir. Yörünge düzlemleri ekvatorla 55 açı yaparlar ve her bir yörünge düzlemi üzerinde eşit sayıda, dört uydu bulunur (Şekil 3.1). GPS yörüngeleri yaklaşık dairesel olup büyük yarı eksen uzunluğu 266 km civarındadır. GPS uydularının yörünge periyodu 11 h 58 m dır. Dolanım süresi bir yıldız gününün yarısına karşılık gelir ve sonuçta her uydu günde iki kez yerin etrafını dolanmış olur (Seeber, 23; Leick, 24; Kaplan ve Hegarty, 26; Kroes, 26; Kahveci ve Yıldız, 212). GPS uydularına göre çok daha alçak yörüngeli LEO uyduları ise yerin çekim etkisini karşılayabilmek için çok daha yüksek yörünge hızına sahip olmalıdırlar km yörünge yüksekliğindeki uydular için dolanım periyodu yaklaşık 9-1 dakikaya karşılık gelir. Buna göre LEO uyduları bir günde kez yerin etrafını dolanabilmektedir. Üzerlerindeki alıcılar sayesinde LEO uydu yörünge davranışları kesintisiz olarak GPS uyduları tarafından izlenebilir. Bu sonuç, başta gravite alanı olmak üzere uydulara etki eden dinamik kuvvetlerin anlaşılmasında büyük önem taşır. Şekil 3.1. GPS uydu yapılandırması (Seeber, 23) GPS tekniğine dayalı DYB çalışmaları günümüzde cm mertebesinde doğruluk üretebilmektedir. Bu bölümde DYB çalışmaları LEO uyduları göz önüne alınarak
47 35 anlatılacaktır. Bunun için öncelikle uydudan uyduya izleme teknikleri, GPS yörüngeleri ve saatleri, GPS gözlem modelleri ayrıntılı olarak açıklanacaktır. 3.1 Uydudan Uyduya İzleme Tekniği GPS sistemindeki modernizasyon çalışmaları, gelişen teknoloji ve özellikle yakın yer uydularında bulunan yüksek duyarlıklı sensörler sayesinde gravite alanı belirleme doğruluğu gün geçtikçe artmaktadır. Son yıllarda gravite alanı belirleme amaçlı uzaya gönderilen söz konusu üç uydu, bu görevin en iyi şekilde gerçekleşmesini üstlenmiştir yılında Sputnik 1 uydusunun gönderilmesinden bu yana uydu teknolojisindeki gelişmelere paralel olarak ölçme tekniklerinde de bir takım önemli gelişmeler yaşanmıştır. Özellikle uydudan uyduya ölçme tekniği (Satelliteto-Satellite Tracking-SST) ve uydu gravite gradyometresi (Satellite Gravity Gradiometry-SGG) en önemlileridir. SST tekniği, yüksek-alçak (SST-hl) ve alçakalçak (SST-ll) olmak üzere iki farklı biçimde uygulanmaktadır (Şekil 3.2). Gravite alanı belirleme amaçlı uydu görevleri hakkında detaylı bilgi Seeber(23); Hofmann- Wellenhof ve Moritz (25); Üstün (26a) ve Shabanloui (212) de bulunabilir. Aşağıda bu gözlem teknikleri hakkında özet bir bilgi verilmektedir. SST - hl SST - ll Kitle Sapması Yeryuvarı Şekil 3.2. Farklı ölçme teknikleri: SST-ll, SST-hl ve SGG SST-hl: Bir LEO uydusunun ivmeleri ölçülür ve gravite potansiyelinin ilk türevleri belirlenir. Alçak yörüngede bulunan bir LEO uydusu GPS, GLONASS veya GALILEO gibi yüksek yörüngede bulunan uydular tarafından üç boyutta kesintisiz olarak izlenir. LEO uyduları üzerinde bulunan GPS alıcısı ve ivmeölçer konum ve
48 36 gravite alanı ile ilişkili olmayan kuvvetleri ölçer. Böylece gözlemlenen artık ivmeler yerçekimi ivmelerine karşılık gelir. SST-ll: İki LEO uydusu arasındaki ivme farkları ölçülür ve gravite potansiyeline ait ilk türevlerin farkları belirlenir. SST-ll modunda aynı alçak yörüngede bulunan iki LEO uydu arasındaki uzaklık değişimi radyo dalgaları (inter satellite link) yardımıyla olabildiğince yüksek duyarlıkta ölçülür ve gravite potansiyelinin birinci türevleri belirlenir. SST-hl tekniğindeki gibi gravite alanı ile ilişkili olmayan kuvvetler ivmeölçer tarafından ölçülür. Sonuç olarak SST-ll modunda iki LEO uydusu arasındaki ivme farkları ölçülmüş olur. SGG: Bir LEO uydusu içerisinde ivme gradyentleri yerinde ölçülür ve gravite potansiyelinin ikinci türevleri belirlenir. LEO uydusunda bulunan gradyometre yardımıyla doğrudan ivme farklarının ölçülmesi anlaşılır. Bu da gravite potansiyelinin ikinci türevlerine (Marussi tensör bileşenleri) karşılık gelir. SST tekniği ile karşılaştırıldığında, bu tekniğin üstünlüğü şöyledir; gravite alanı ile ilişkili olmayan ivmeler uydu içerisinde aynıdır ve böylece fark alma işlemi ortadan kalkar. Yukarıda bahsedilen gravite alanı belirleme amaçlı gönderilen uydu misyonlarından CHAMP uydusu SST-hl tekniğini, GRACE uydusu yörüngeler için SST-ll tekniğini, gravite alanındaki değişimler için SST-hl tekniğini ve GOCE uydusu ise SGG tekniğini kullanır. Ayrıca uydular yardımıyla gravite alanı belirlenirken uydu yüksekliğinin etkisi önemli bir etkendir. Uydudan gelen sinyal ve gürültüleri içeren ölçüler uydu yüksekliğine bağlı olarak (R/r) n+1 oranında etkilenirler. Daha öncede söz edildiği gibi burada R yeryuvarının ekvatoral yarıçapını, r uydu konumunun normunu (r = x 2 +y 2 +z 2 ) ve n çekim potansiyelinin derecesini gösterir. Gravite sinyalinin şiddeti (büyüklüğü) uydu yüksekliği ile ters orantılı olup, yükseklik arttıkça alınan sinyalin şiddeti azalırken gözlemlerdeki gürültü seviyesi artmaktadır. Bu yüzden olabildiğince düşük yörüngeli uydular kullanıldığında alınan sinyal şiddeti yüksek, ölçülerdeki gürültü seviyesi azaltılmış olur. Uydudan uyduya izleme tekniğinin amacı, iki uydu arasındaki uzaklık ve uzaklık değişimini yüksek doğrulukla ölçmektir. Yukarıda da ifade edildiği gibi yüksek-alçak (SST-hl) ve alçak-alçak (SST-ll) izleme tekniklerinin her ikisinde de yakın yer uyduları, yer gravite alanı için birer algılayıcıdır. Söz konusu izleme
49 37 yöntemleri ile bağıl hızlar belirlenir ve bu hızların düzensiz değişimlerinden de gravite bilgisi edinilir. İki uydu arasında uzaklık değişimi için temel gözlem eşitliği aşağıdaki biçimde oluşturulur (Jekeli, 1999; Sneeuw, 2; Jeongrae, 2; Seeber, 23; Austen ve Grafarend, 24; Liu, 28). İnersiyal sistemde 1. uyduya ait konum vektörü r 1, 2. uyduya ait konum vektörü ise r 2 olarak tanımlansın; böylece, uydular arasındaki uzaklık, ρ = (r 2 r 1 ) (r 2 r 1 ) (3.1) uzaklık vektörü, veya r 12 = r 2 r 1 (3.2) r 12 = ρe 12 (3.3) eşitlikleriyle yazılır. doğrultusundaki (line-of-sight) birim vektördür: Burada, e 12, birinci uydudan ikinci uyduya, bakış e 12 = r 2 r 1 r 2 r 1 = r 12 ρ (3.4) Bu durumda uzaklık-oranı (range-rate) gözlemlenebilir uzunluğun türevi, ρ = ṙ 12 e 12 (3.5) elde edilir. Buradaki ṙ 12 terimi iki uyduya ait hızlar arasındaki farkları tanımlar ve ṙ 12 = ṙ 2 ṙ 1 dir. Buna göre, uzaklık-oran-değişimi (range-rate-change), (3.5) in bir kez daha türevinin alınmasıyla, ρ = r 12 e 12 +ṙ 12 ė 12 (3.6) olur. Burada, ė 12 ifadesi ė 12 = d dt (r 12ρ 1 ) = (ṙ 12 ρe 12 )ρ 1 = cρ 1 (3.7)
50 38 olarak yazılabilir. Bu durumda (3.6) eşitliği aşağıdaki biçime dönüşür; ρ = r 12 e 12 +ṙ 12 (ṙ 12 ρe 12 )ρ 1 = r 12 e 12 +[(ṙ 12 ) 2 ( ρ) 2 ]ρ 1 (3.8) SST ölçülerine dayanarak değerlendirme yapılabilmesi için (3.1), (3.5) ve (3.8) in uydu durum vektörlerine göre kısmi türevlerinin hesaplanması gerekir. SST ölçüleri, uzaklık (range), uzaklık-oranı (range-rate) ve uzaklık-oran-değişimi (range-rate-change) veya uzaklık-ivme ölçüsü(range-acceleration) olarak ifade edilir. Uzaklık, sadece konumun bir fonksiyonu olduğundan hıza göre türev değerleri sıfır olur. Bu durumda uzaklığa ait kısmi türevler için: ρ = ( r 1 r 2 r 1 ρ ρ = v 1 ) T ρ = ρ r 2 r 1 ρ v 2 = (3.9) eşitlikleri geçerlidir. Benzer şekilde uzaklık-oranına ait kısmi türevler yazılabilir. (3.9) dan farklı olarak hız ölçüsünün kısmi türevleri, ρ = 1 r 1 ρ (ṙ 12 r 12 ρ ρ)t ρ = ( r 12 v 1 ρ )T ρ = ρ r 2 r 1 ρ = ρ (3.1) v 2 v 1 çıkar. Son olarak uzaklık-oran-değişimine ait kısmi türevler belirlenmelidir. Bu kısmi türevler öncekilere göre biraz daha karmaşık bir görünüm alır(jeongrae, 2). ρ = ( r 12 e 12 ) T + 1 r 1 r 1 ρ (a 2 ρ ρ c 1 ρ c2 e 12 ) T ρ = ( r 12 e 12 ) T 1 r 2 r 2 ρ (a 2 ρ ρ c 1 ρ c2 e 12 ) T ρ = ( r 12 e 12 ) T + 2 v 1 v 1 ρ c2 ρ = ( r 12 e 12 ) T 2 v 2 v 2 ρ c2 (3.11)
51 39 Burada kullanılan a ve c vektörleri aşağıdaki eşitliklerle ifade edilirler: c = ṙ 12 ρe 12 (3.12) a = r 12 (ṙ 12 e 12 )e 12 (3.13) SST metodunun temeli yersel gravite alanı parametreleri ve gözlemler ( ρ, ρ) arasında bir ilişki kurmaktır. Gravite alanı parametreleri küresel harmonik katsayıları C nm ve S nm parametreleri ile temsil edilir. Bu ilişkinin kolay kurulabilmesi için C nm, S nm katsayıları, tek bir parametre, örneğin B n olarak ifade edilebilir. Yaklaşık değerler r s, ṙ s ve ρ s, ρ s, her iki uydunun başlangıç koşullarından elde edilir ve gravite alanı için yaklaşık değer B s n ile gösterilirse, gravite alanı spektrumu B n = B s n + B n, n = 1,...,N. (3.14) eşitliğine indirgenmiş olur. Yukarıda verilen kısmi türevlerden yaralanarak (3.5) ve (3.8) in doğrusallaştırılmasıyla ρ = ρ ρ s = B n (ṙ 12 e 12 ) B n = (e 12 ṙ 12 B n +ρ 1 c r 12 B n ) B n (3.15) ρ = ρ ρ s = B n [( r 12 e 12 +((ṙ 12 ) 2 ( ρ) 2 ))ρ 1 ] B n = (e 12 r 12 B n +2ρ 1 c ṙ 12 B n +ρ 1 (a 2 ρρ 1 c ρ 1 (c) 2 e 12 ) r 12 B n ) B n (3.16) sonuç eşitlikleri bulunur (Seeber, 23). (3.15) ve (3.16), parametre kestirimine konu olacak fonksiyonel model eşitlikleridir ve EKK kestiriminden bilinmeyen B n parametreleri bulunur. Uydu Gravite Gradyometresi Gradyometre uzayda gravite ivmesinin değişimini ölçebilen bir sensördür. V=V(x,y,z) yerçekim potansiyelinin ilk türevleri (g) çekim ivmesini verir (uzayda merkezkaç ivmesinden bağımsız). Gradyometre ile gravite ivmesinin değişimi, yani gravite potansiyelinin ikinci türevleri, başka bir deyişle gravite gradyentleri (gravite
52 4 tensör bileşenleri) ölçülmüş olur. Gravite gradyentleri, gravite vektörünün eksenler boyunca türevleri olarak ifade edilebilir. GOCE uydusunda bulunan gradyometrenin temel prensibi, çok kısa bir baz için(5 cm) ivme farklarının ölçülmesine dayanır. Bir eksen üzerinde 5 cm ile ayrılmış iki ivmeölçer düşünülürse iki adet gözlem denklemi yazılabilir (Seeber, 23; Hofmann-Wellenhof ve Moritz, 25). a 1 = [M+ Ω+ΩΩ] x+f ng a 2 = [M+ Ω+ΩΩ] x+f ng (3.17) Burada a 1 ve a 2, bir eksen üzerinde iki ivmeölçerin ölçülen ivmelerini, M, Marussi tensörünü yani gravite potansiyelinin ikinci türevlerini (gravite gradyent veya Eötvös tensörlerini) M = 2 V x 2 2 V x y 2 V x z 2 V x y 2 V y 2 2 V y z 2 V x z 2 V y z 2 V z 2 V xx V xy V xz = V xy V yy V yz V xz V yz V zz (3.18) temsil eder (ESA, 1999; Bobojc ve Drozyner, 23). Matrise bakıldığında 9 elemanın sadece 5 tanesinin belirlenmesi gereklidir. Çünkü matris simetriktir. Ayrıca Laplace koşuluna göre, matrisin izinin toplamı çekim potansiyeli göz önüne alınırsa sıfır olacaktır (Seeber, 23; Lumley ve ark., 21). V xx +V yy +V zz = (3.19) (3.17) eşitliğinde geçen Ω ifadesi gradyometrenin yönlendirmesini tanımlamak için kullanılan ve açısal hız bileşenlerinden oluşan bir asimetrik matrisi gösterir. Asimetrik matrisin tensörü (ΩΩ) ise simetrik olacaktır. Ω = ω 3 ω 2 ω 3 ω 1 ω 2 ω 1 (3.2) Burada Ω açısal hız, Ω ise açısal ivmeyi temsil eder. (3.17) eşitliğine bakıldığında geriye bilinmeyen iki parametre kalmıştır. Bunlardan ilki x, her bir ivmeölçerden üç koordinat ekseninin kesim noktasına kadar olan vektörü, ikinci f ng ise gravite
53 41 ile ilişkili olmayan tüm etkileri (güneş radyasyon basıncı, atmosferik sürüklenme, albedo vs.) içeren bilinmeyeni temsil eder. Burada amaç Marussi tensörlerini başka ifadeyle gravite potansiyelinin ikinci türevlerini elde etmektir. Bunun için (3.17) eşitliğindeki ivmeler bir kez taraf tarafa toplanıp (ortak mod) bir kez de çıkarılacak (diferansiyel mod) olursa, (a 1 +a 2 )/2 = f ng (3.21) (a 1 a 2 )/2 = [M+ Ω+ΩΩ] x (3.22) sonuç denklemleri bulunur (Seeber, 23; Hofmann-Wellenhof ve Moritz, 25). Ölçülen ivme değerlerinin toplamının yarısı uyduya etki eden tüm dış ivmeleri temsil eder (Eşitlik 3.21, bkz. Sayfa 33). Böylece yerçekimiyle ilişkin olmayan etkiler elde edilmiş olur. Sonuç denklemler elde edilirken kolaylık olması açısından (3.22) eşitliğinde Γ = [M + Ω + ΩΩ] tanımlaması yapılsın. (3.22) de gradyometrenin geometrisinin, yani x in bilindiği kabul edilirse, geriye sadece Γ içindeki gravite gradyentlerinin (M) belirlenmesi kalır. Bunun için öncelikle Γ teriminden ve tranposesinden yararlanarak ortak ve diferansiyel mod uygulaması ile aşağıdaki eşitlikler elde edilir: Γ = [M+ Ω+ΩΩ] (3.23) Γ T = [M Ω+ΩΩ] (3.24) (Γ+Γ T ) = 2M+2ΩΩ (3.25) (Γ Γ T ) = 2 Ω (3.26) (Γ+Γ T )/2 = M+ΩΩ (3.27) (Γ Γ T )/2 = Ω (3.28) Son iki eşitlik (3.27) ve (3.28) yardımıyla çözüm gerçekleştirilir. Öncelikle (3.28) ile Ω açısal ivme değeri, sonrasında ise integrasyon işleminden, Ω(t) = Ω(t )+ t t Ωdt (3.29)
54 42 hesaplanır. Burada, Ω(t ) başlangıç yönelimidir ve yıldız sensörlerinden türetilir. Ω(t) nin karesi ΩΩ ve son olarak (3.27) eşitliğinden gravite gradyent tensörü M = (Γ+Γ T )/2 ΩΩ (3.3) bulunur (Hofmann-Wellenhof ve Moritz, 25). Detaylı bilgi için ESA (1999); Bobojc ve Drozyner (23); Seeber (23); Hofmann-Wellenhof ve Moritz (25); Lumley ve ark. (21) kaynaklarına bakılabilir. 3.2 GPS Yörünge ve Saatleri Hemen hemen her türlü GPS uygulamasının sonuçları GPS yörünge ve saat bilgisine dayanır. GPS uydularının konumları, yer izleme istasyonları tarafından sürekli olarak gözlenir; sonuçlar, yayın ve duyarlı olmak üzere iki adet efemeris (yörünge) bilgisi adı altında yayınlanır. Genel olarak yayın efemerisi izleme istasyonlarında toplanan kod ölçülerinden, duyarlı efemeris bilgisi ise faz ölçülerinden türetilir. Kısa baz uzunluklu diferansiyel GPS uygulamalarında yayın efemerisi yeterli doğruluk sağlarken, bölgesel çalışmalar ve yüksek doğruluk gerektiren uygulamalar için duyarlı efemeris bilgilerinin kullanılması gereklidir. Duyarlı yörünge belirleme çalışmalarında ise yüksek-frekanslı (high-rate) saat ve yörünge bilgileri, doğru sonuç elde etmek için ihtiyaç duyulan başlıca veri türleridir. Bazı araştırma kuruluşları duyarlı yörünge ve saat bilgilerini hesaplayarak internet yoluyla tüm kullanıcılara ücretsiz sunmaktadır. Bunlar arasında NASA JPL (Jet Propulsion Laboratory), NIMA (National Imagery and Mapping Agency), SOPAC (Scripps Orbit and Permanent Array Center), CODE (Center for Orbit Determination in Europe), NGS (National Geodetic Survey) ve IGS (International GNSS Service for Geodynamics) sayılabilir. Adı geçen kuruluşların elde ettikleri ürünler karşılaştırıldığında tutarlı sonuçlar görülmekle birlikte küçük farklılıklar da söz konusudur. Jeodezik literatürde ve uygulamalarda CODE ve IGS ürünlerinin yaygın kullanıma sahip olduğu bilinmektedir. Uluslararası GNSS Servisi (IGS), hassas GPS ve GLONASS ürünleri üretmek için 8 den fazla ülke ve 2 ün üzerinde kurumun katkı sağladığı bir servistir. Servis, GPS izleme istasyonlarından gelen verileri toplayıp uygun formatta arşivler ve farklı
55 43 doğrulukta GPS yörünge ve saat bilgisini kullanıcıya sunar. IGS, ayrıca ITRF sisteminin iyileştirilmesi ve geliştirilmesi, yer dönme parametrelerinin belirlenmesi, deniz seviyesi ve buzullardaki değişimlerin izlenmesi, uydu yörünge bilgilerinin hesaplanması gibi çalışmalar için yüksek doğrulukta veri üretmeyi amaçlayan bir kuruluştur. IGS ürünlerine erişim resmi olarak 1 Ocak 1994 tarihinde başlamıştır. Ürünlerin dağıtımı ücretsiz olarak IGS ile birlikte global ve bölgesel veri merkezleri ile sağlanmaktadır. IGS tarafından sunulan hizmetin gerçekleştirilmesinde aşağıdaki bileşenler anahtar rol oynar (Kouba, 29; IGS, 212d): 35 nin üzerinde çift frekanslı sürekli GPS istasyonundan oluşan global bir ağ (Şekil 3.3). Bazı global veri merkezleri CDDIS(Crustal Dynamics Data Information System, NASA GSFC, USA) IGN (Institut Geographique National, France) SIO (Scripps Institution of Oceanography, USA) KASI (Korean Astronomy and Space Science Institute) Analiz merkezleri CODE, ESOC, GFZ, GRGS, JPL, NOAA, NRCan, SIO, USNO, MIT, GOP-RIGTC Şekil 3.3. IGS global ağı (IGS, 212a)
56 44 Şu anda yukarıda bahsedilen sekiz analiz merkezi, IGS ye ultra-hızlı, hızlı ve sonuç olmak üzere üç türde GPS yörünge ve saat çözümüne katkı sağlamaktadır. IGS tarafından duyarlı GPS yörünge ve saatleri günlük olarak ITRF sisteminde hesaplanır. 2 yılından beri meteorolojik uygulamalarda ve LEO misyonlarını desteklemek için tasarlanmış ultra-hızlı ürünler kullanılabilir hale getirilmiştir. Bu düzenlemeyle birlikte ultra-hızlı ürünler, birçok alanda özellikle gerçek-zamanlı kullanıcılar için yararlı bir hal almıştır. 2 Mayıs 2 tarihinde seçimli doğruluk erişiminin (Selective Availability-SA), ABD Savunma Bakanlığı tarafından kapatılmasıyla konum için beklenen doğruluk artmıştır. 26 Aralık 1999 tarihinden itibaren 5 dakika aralıklı uydu/istasyon saatlerini içeren saat dosyaları (CLK) kullanılmaya başlanmış ve 5 Kasım 2 tarihinden itibaren bu saat dosyaları IGS nin resmi saat ürünü olarak yerini almıştır. Buna göre, IGS-SP3 dosyalarında verilen seçimli doğruluktan bağımsız 15 dakika aralıklı uydu saatlerinin enterpolasyon hatası bir kaç dm seviyesine düşürülebilmiştir (Kouba, 29). Saat enterpolasyon hatalarını cm seviyesine çekebilmek için 14 Ocak 27 (GPS haftası 141) tarihinden itibaren 3 saniye aralıklı IGS sonuç saat dosyaları kullanılmaktadır. Ayrıca bu dosyaların BERNESE, GIPSY, GAMIT gibi akademik GPS yazılım paketleri için değerlendirmelerde kullanılması doğruluğu arttıran önemli bir başka etkendir (Kouba, 29). Yukarıda da bahsedildiği gibi IGS yörünge/saat ürünleri sonuç, hızlı ve ultra-hızlı olarak 5 Kasım 2 (GPS haftası 187) tarihinden itibaren kullanılmaya başlanmıştır. Bu verilere IGS in resmi internet sayfasından ulaşılabilmektedir.
57 45 Şekil 3.4. IGS sonuç yörüngeleri (IGS, 212b) Şekil 3.5. IGS sonuç saatleri (IGS, 212b) Analiz merkezlerinden elde edilen sonuçlar ile IGS sonuç (yörünge ve saat) ürünlerinin karşılaştırılması Şekil 3.4 ve Şekil 3.5 de verilmiştir. Şekillere bakıldığında analiz merkezlerinin sonuç yörüngelerinde uydu konumuna ilişkin RMS değerlerinin günümüze doğru 3 cm den birkaç cm seviyelerine kadar iyileştiği görülebilir. Ayrıca IGS in hızlı (IGR) ürünlerinin de hassasiyetinin iyi olduğu ve özellikle analiz merkezlerinden CODE un ürün doğruluğu göze çarpmaktadır.
58 46 CODE merkezinde üretilen yüksek frekanslı saat (3 sn aralıklı) ve yörünge bilgileri AIUB (Astronomical Institute of the University of Bern) ftp adresinden ücretsiz olarak indirilebilir. Ayrıca BERNESE yazılımı için gerekli dosyaların güncel halleri de kullanıcılara sunulur (CODE, 212). IGS ve CODE ürünleri, özellikleri ve sunucu servisleri Çizelge 3.1 ve Çizelge 3.2 de verilmektedir. Ürünler hakkında daha ayrıntılı bilgiye Beutler ve ark. (27), Kouba (29) ve IGS (212e) kaynaklarından ulaşılabilir. Çizelge 3.1. IGS yörünge ürünleri ve özellikleri Çözüm Tipi Ürün Doğruluk Süre Aralık Sunucu Servisler Yayın efemerisi Yörünge 1 cm Anlık Günlük CDDIS, SOPAC,IGN (Broadcast) Saat 5 ns Ultra Hızlı Yörünge 3 cm 3-9 saat 15 dk. CDDIS, SOPAC,IGN (gözlem) Saat 15 ps IGSCB, KASI Ultra Hızlı Yörünge 5 cm Anlık 15 dk. CDDIS, SOPAC,IGN (kestirim) Saat 3 ns IGSCB, KASI Hızlı Yörünge 2.5 cm saat 15 dk. CDDIS, SOPAC,IGN Saat 75 ps 5 dk. IGSCB, KASI Sonuç Yörünge 2.5 cm gün 15 dk. CDDIS, SOPAC,IGN Saat 75 ps 5 dk./3 sn. IGSCB, KASI Çizelge 3.2. CODE yörünge ürünleri ve özellikleri Çözüm Tipi Ürün Doğruluk Süre Aralık Sunucu Servisler Ultra Hızlı Yörünge < 1 cm Anlık 15 dk. CODE-ftp Hızlı Yörünge < 5 cm 12 saat 15 dk. CODE-ftp Sonuç Yörünge < 5 cm 5-11 gün 15 dk. CODE-ftp, IGS LEO Ürünleri LEO uydularının yörüngelerinin hesaplanması için GPS uydularına ait saat bilgisini içeren duyarlı yörünge dosyaları (EPH/SP3 uzantılı-15 dakika aralıklı), yer dönüklük parametreleri (ERP uzantılı), duyarlı yörüngelerden hesaplanan yüksek frekanslı saat dosyaları (CLK uzantılı-3 sn aralıklı) ve LEO uydularına ait gözlem dosyaları gereklidir. Bu dosyaların ilk üçü IGS analiz merkezi CODE üzerinden veya yukarıda söz edilen merkezlerin birinden edinmek mümkündür. LEO uydularına ait gözlem dosyaları (observation data) ise alıcıdan bağımsız
59 47 RINEX (Receiver INdependent EXchange) formatında GFZ nin bünyesindeki ISDC (Information System and Data Center) veri merkezinden elde edilebilir. Bu hizmetten yararlanmak için üyelik gerekmektedir. CHAMP ve GRACE uydu verileri sistemdeki kullanıcı hesabı (dizini) üzerinden dağıtılır. GOCE uydu verileri Avrupa Uzay Ajansına (Europan Space Agency-ESA) yapılacak proje başvurusunun onaylanmasından sonra erişime açılmaktadır. Veri erişimi için internet tabanlı bir arayüz (Eoli-sa) kullanılır (Şekil 3.6). Şekil 3.6. ESA Eoli-sa programı ve sensör verilerine erişim Atmosfer ve İyonosfer Yörünge ve Gravite Alanı Manyetik ve Elektrik Alanı Level 1 : CH-OG-1-NAV CH-OG-1-SST Level 2 : CH-OG-2-ACC Level 3 : CH-OG-3-PDO CH-OG-3-PDO-champ_drag CH-OG-3-PDO-champ_irvs CH-OG-3-PDO-champ_sao CH-OG-3-PDO-champ_tle CH-OG-3-RSO CH-OG-3-USO Level 4 : CH-OG-4-EGM CH-OG-4-PSO Şekil 3.7. ISDC CHAMP Ürünleri
60 48 ISDC ürünleri için veri yapısı ve dağıtımı, uydu görevlerinde kullanılan sensöre bağımlıdır. Örneğin CHAMP uydusu için ISDC ürün yapısı Şekil 3.7 de verilmektedir (ISDC, 212). Ürün açıklamaları, formatları yardım belgelerinde ayrıntılı olarak açıklanır (ISDC, 212). CHAMP ve GRACE verilerinin uygulamadaki kullanımı Bölüm 5 de detaylı bir biçimde ele alınacaktır. 3.3 GPS Gözlem Modelleri GPS ile konum belirleme işlemi, aslında uydu-alıcı arasındaki uzaklıkları kullanan uzaydan geriden kestirme problemine dayanır. GPS gözlemleri, alınan sinyal ve alıcı tarafından üretilen kopya sinyal arasındaki karşılaştırmayı temel alır. Karşılaştırma işleminden faz farkları ve zaman farkı kullanılarak türetilen uydualıcı uzunlukları ortaya çıkar (Hofmann-Wellenhof ve ark., 28). Konum ve zaman ölçümü için gözlemler dört farklı türde tanımlanır (Seeber, 23): Kod ölçülerinden elde edilen sözde uzunluk (pseudorange) gözlemleri Taşıyıcı fazlar veya taşıyıcı faz farkları Doppler gözlemlerinden türetilen sözde uzunluklar İnterferometrik yöntemle türetilen sinyal yol zamanı gözlemleri Sözde uzunluk, uydu-alıcı arasındaki uzaklığın kesin olmayan değerini nitelemektedir. Sinyalin uydudan çıkış anı ile alıcıya ulaştığı ana kadar geçen zaman farkının (sinyal yol zamanı) ışık hızı ile ölçeklendirilmesi ile bulunur. Bu uzunluk değeri başta alıcı saat hatası olmak üzere atmosferik etkilere bağlı sinyal gecikmesi, sinyal yansıması vb. hataları içermektedir. GPS gözlemleri, uygulamada sadece kod gözlemleri ve taşıyıcı faz gözlemleri olarak sınıflandırılır. Yüksek doğruluk istenen çalışmalar ve bilimsel amaçlı uygulamalarda faz gözlemleri kullanılırken, navigasyon gibi daha düşük doğruluk istenen uygulamalarda ise kod gözlemleri tercih edilir (Kahveci ve Yıldız, 212). Özellikle jeodezik uygulamalar için faz gözlemlerinin kullanımı kaçınılmazdır. Ayrıca sistemin çift frekanslı olması sayesinde, bazı hataları (örn. saat, alıcı, atmosferik) ortadan kaldırmak ya da azaltmak olanaklıdır. Bu gözlemlerin doğrusal kombinasyonları matematiksel olarak daha anlaşılır denklemlerle çalışmayı sağlar.
61 49 Her GPS uydusu L 1 (Link-1) ve L 2 (Link-2) olmak üzere iki frekans yayınlamaktadır MHz olan temel frekansın sırasıyla 154 ve 12 katından L 1 ve L 2 üretilmektedir. Bu durumda 19.5 cm dalga boylu L 1 frekansı MHz, cm dalga boylu L 2 frekansı MHz olarak elde edilir. L 1 ve L 2 frekanslarına, ayrıca yörünge bilgileri, meteorolojik bilgiler, uydu saati düzeltmeleri ve navigasyon mesaj verileri gibi bilgiler modüle edilir. Bu işlem ile her uyduya bağımsız bir PRN (Pseudo Random Noise) kod numarası verilir. Böylelikle tüm uydular aynı frekansları kullanmasına rağmen uydu sinyalleri PRN kodları sayesinde birbirinden ayırt edilebilirler. Modülasyon işleminden sonra L 1 frekansı üzerine iki adet PRN kodu ve navigasyon mesaj verisi eklenmiş olur. Bu PRN kodlarının ilki C/A (Coarse/Acquisition, Clear/Access) kod, ikincisi ise P (Precise/Protected Code) kodudur. L 2 frekansında ise navigasyon mesaj verileri yanında P kod olmak üzere sadece bir adet PRN kodu modüle edilmiştir. P kodu temel frekans olan 1.23 MHz büyüklüğünde, C/A kodu ise temel frekansın onda biri yani 1.23 MHz büyüklüğündedir. Buna göre P kodunun dalga boyu m ve C/A kodunun dalga boyu m dir. Tüm GPS sinyalleri GPS sisteminin zamanı ile ilişkilidir. GPS zamanı yaygın olarak kullanılan bir referans zamanı olarak tanımlanır ve uluslararası atomik zaman TAI ile arasında 19 sn. fark bulunur (McCarthy, 1996). Ayrıca zamanın doğru ölçülmesi için GPS uyduları üzerine ikişer adet ribidyum ve sezyum atomik saati yerleştirilmiştir. GPS nin sinyal yapısı, modernizasyonu ve daha detaylı bilgi için Teunissen ve Kleusberg (1998); Seeber (23); Leick (24); Beutler ve ark. (25a); Kahveci ve Yıldız (212) a bakılabilir Kod gözlemleri Kod gözlemleri kabaca sinyalin yolculuk süresinin ölçümüdür ve aslında alıcıuydu anten faz merkezleri arasındaki uzunluk olarak tanımlanabilir. Hem uydu hem de alıcı üzerinde saat kayıklıkları (clock offset-δ t ) nedeniyle bu uzunluk değeri sözde uzunluk (pseudorange) olarak ifadelendirilir. Eğer uydu ve alıcı saatlerinin GPS saati ile çakışık olduğu ve uydudan çıkan sinyalin herhangi bir atmosferik etkiye maruz kalmadan alıcıya ulaştığı kabul edilirse bu durumda ölçülen sözde uzunluk
62 5 değeri geometrik mesafeye eşit olur ve ρ u a (t) = c(t a(t) t u (t)) (3.31) eşitliği ile ifade edilir (Shabanloui, 212). Denklemdeki t a (t) ifadesi sinyalin alıcıya ulaştığı andaki GPS zamanını, t u (t) sinyalin uydudan çıkış anındaki GPS zamanını, c ışık hızını ve t ise GPS zamanını ifade etmektedir. Ancak yukarıdaki varsayımların gerçekte sağlanması mümkün olmadığından, sözde uzunluk denklemine uydu ve saat hatalarından ileri gelen terimlerin eklenmesi gereklidir. Bu terimler eklendiğinde, P u a (t) = c(t a(t)+δ ta (t) t u (t) δ tu (t)) = c[t a (t) t u (t)]+cδ ta (t) cδ tu (t) (3.32) eşitliği elde edilir. Buradaki c[t a (t) t u (t)] terimi uydu-alıcı arasındaki gerçek geometrik mesafeyi, (t a (t) t u (t)) ifadesi gerçek sinyal yolculuk süresini tanımlar ve kısaca sırasıyla ρ u a (t),tu a (t) olarak gösterilir. Böylece, gerçek geometrik mesafe ρ u a (t) = ctu a (t) olarak elde edilir. Bu tanımlamalarla (3.32) tekrar düzenlenirse, sözde uzunluk için Pa u (t) = ρu a (t)+c[δ t a (t) δ tu (t t u a (t))] (3.33) yazılabilir. (3.32) ve (3.33) eşitliklerinde, δ tu (t) uydu saat zamanı ile GPS zamanı arasındaki farkı (satellite clock offset); δ ta (t) ise alıcı saat zamanı ile GPS zamanı arasındaki farkı (receiver clock offset) temsil etmektedir. (3.33), kod gözleminin temel eşitliğidir. Gerçek gözlem denklemini elde etmek için bu eşitliğe atmosferik etkiler (iyonosfer, troposfer), uydu ve alıcıdan kaynaklanan aletsel düzeltmeler, sinyal yansıma etkisi gibi etkilerin eklenmesi gereklidir. Atmosfer genel olarak iyonosfer ve troposfer olarak iki tabakaya ayrılır. İyonosfer elektron yoğunluğuna sahip olup atmosferin üst tabakasında yer alır ve yaklaşık olarak yer yüzeyinden 7-1 km üstündedir. Troposfer ise atmosferin alt tabakasında yer alır ve yerin yüzeyinden yaklaşık 4 km yüksekliğe kadar uzanır. Bu etkilerin eklenmesiyle kesin kod gözlem denklemi elde edilir (Leick, 24; Beutler ve ark., 25a; Montenbruck ve ark., 25; Beutler ve ark., 27; Hofmann-Wellenhof
63 51 ve ark., 28; Nohutcu, 29; Swatschina, 29): Pa u (t) = ρu a (t)+c[δ t a (t) δ tu (t t u a (t))]+iu a (t,f)+tu a (t)+mu a (t)+εu a (t) (3.34) Burada geçen terimler, c ρ u a(t) P u a (t) δ tu (t) δ ta (t) t u a (t) ışık hızı ( m/sn) uydu-alıcı arasındaki geometrik mesafe sözde uzunluk - pseudorange uydu saat zamanı ile GPS zamanı arasındaki fark alıcı saat zamanı ile GPS zamanı arasındaki fark sinyal yol zamanı Ia u (t,f) iyonosferik etki T u a (t) troposferik etki M u a(t) diğer etkiler ε u a (t) termal ölçüm gürültüsü ve modellenemeyen diğer etkileri ifade eder. İyonosferik etki GPS kod gözlemleri için modellenebilir. İyonosfer için önemli bir parametre, toplam elektron miktarıdır (Total Electron Content - TEC u a(t)). TEC u a (t), uydu-alıcı arasındaki sinyal yolu boyunca m3 deki toplam elektron sayısı olarak tanımlanır (birim: m 2 ) (Montenbruck ve ark., 25; Kaplan ve Hegarty,26;KahveciveYıldız,212). İyonosferiketki(3.35)eşitliğiiletanımlanır. Eşitlikten de görüleceği gibi iyonosferik etki frekansa (f) bağlı olarak değişir. Bu nedenle çift frekanslı alıcılar sayesinde iyonosferden bağımsız doğrusal kombinasyon (ionosphere free lineer combination) kullanılarak iyonosferik etki büyük ölçüde giderilebilir. Frekansa bağımlı iyonosferik gecikme, I u a(t,f) = 4.3 f 2 TECu a(t) (3.35) TEC u a(t) nin fonksiyonu olarak yazılır. GPS sinyalleri uydudan çıktıktan sonra sırasıyla iyonosfer, mezosfer, stratosfer ve troposfer tabakalarında ilerleyerek alıcıya ulaşırlar. Troposfer, iyonosferin aksine elektrik yükü içermez bu yüzden radyo sinyalleri için dağıtıcı bir özelliğe sahip değildir. Sonuç olarak sinyal yayılması, iyonosferdeki gibi frekans bağımlı olmadığından troposfer etkisi kod ve faz ölçülerinde aynı büyüklükte kalır. Ayrıca çift frekanslı alıcıların kullanılmasıyla
64 52 bu etki giderilemez (Tuşat, 23; Kahveci ve Yıldız, 212). Yükseklik açısı düşük uydulardan elde edilen gözlemler troposferik kırılma ve sinyal yansıma etkisine çok daha fazla duyarlıdırlar. Modellenemeyen sistematik hatalar sonuçların kalitesini düşürür. Buna rağmen ufka yakın gözlemler troposferik etkiyi ve istasyon konumlarının düşey bileşenini iyileştirilebilir. Akademik yazılımlarda ufuk düzlemine yakın gözlemleri parametre kestiriminde değerlendirebilmek için uygun bir ağırlık modeli kullanılır. Örneğin Bernese 5.v yazılımı için öngörülen ağırlık modeli w(z) = cos 2 (z) (3.36) eşitliğiyle verilir (Beutler ve ark., 27). Burada z uydunun zenit açısıdır. Troposferik etkinin modellenmesi hakkında daha detaylı bilgi Seeber (23); Leick (24); Montenbruck ve ark. (25); Kaplan ve Hegarty (26); Kroes (26); Beutler ve ark. (27) de bulunabilir. (3.34) de diğer etkiler olarak belirtilen Ma u (t) uydu donanımına ait gecikme (u u a(t)-satellite hardware delay), alıcı donanımına ait gecikme (a u a(t)-receiver hardware delay) ve sinyal yansıma etkisine ait gecikme (s u a (t)-multipath delay) değerlerini içerir (Leick, 24; Kroes, 26; Swatschina, 29): Ma u (t) = uu a (t)+au a (t)+su a (t) (3.37) Kod gözlem denklemleri için geçerli hata kaynaklarının LEO uydularına etkisi Çizelge 3.3 de verilmektedir. Çizelge 3.3. LEO uyduları için kod gözlem denklemindeki terimler ve nominal değerleri (Ramos-Bosch, 28) Parametre Simge Büyüklük Geometrik uzunluk ρ u a 2 km Alıcı saat hatası δ ta < 3 km Uydu saat hatası δ tu < 3 km Troposferik etki Ta u 2-1 m İyonosferik etki Ia u 2-5 m Uydu ve alıcı donanım gecikmesi u u a,au a < 2 m Sinyal yansıma etkisi s u a < 15 m Termal gürültü vd. ε u a 3 m
65 Faz gözlemleri Taşıyıcı dalga faz gözlemleri, gönderilen sinyaldeki tam bir dalga boyunun artık kısmının faz açısını ifade eder. Kod gözlemleri için geçerli eşitlikler benzer şekilde faz gözlemleri için de türetilebilir. Faz gözlemlerinin duyarlılığı yüksek olduğundan yüksek doğruluklu konum ölçmelerinde tercih nedenidir. Faz gözlemi, uydudan yayınlanan sinyal ile alıcı tarafından üretilen sinyal arasındaki fark olarak tanımlanır; tam ve kesirli devir sayılarından oluşur. Ancak, yeryüzündeki alıcı, faz gözlemine ait tam dalga boyu sayısını kestiremez. Yani alıcı açıldığında, uydu-alıcı arasındaki mesafeye karşılık gelen faz farkının sadece kesirli kısımları ölçülürken, tam kısımları belirsiz kalır. Faz gözlem modelinde tam dalga boylarının sayısı bilinmeyen parametre olarak kalır. Bu bilgiler ışığında gözlem modeli, L u a (t) = ρu a (t)+c[δ t a (t) δ tu (t t u a (t))]+iu a (t,f)+λa+tu a (t)+mu a (t)+εu a (t) (3.38) eşitliği ile tanımlanır. Burada λ taşıyıcı dalga boyu, A ise tam sayı belirsizliğidir. Kod gözlemlerinde olduğu gibi faz gözlemlerindeki tüm sistematik hatalar Ma(t) u içerisinde toplanmıştır. Bu ifade kod gözlemlerindeki sistematik etkilere ilave olarak faz wind-up etkisini (wa(t)-phase u wind-up) de içerir. Bu etki alıcı ve verici antenlerin bağıl dönüklüğünden kaynaklanır. Anten dönüklüğünün uydu-alıcı arasındaki mesafe değişimine olan etkisi anlaşılır (Leick, 24; Kroes, 26; Ramos- Bosch, 28; Swatschina, 29). Sistematik hata yaratan tüm belirsizlikler Ma u (t) = uu a (t)+au a (t)+su a (t)+wu a (t) (3.39) eşitliği altında toplanır. Kod ve faz gözlemi arasındaki temel farklılıklar şu şekilde sıralanabilir (Leick, 24; Kahveci ve Yıldız, 212). Faz gözlemlerinde faz başlangıç belirsizliği (ambiguity) kod gözlemlerinde yoktur. Kod gözlemleri mutlak büyüklüklerdir. Gözlemlere iyonosferden dolayı getirilecek düzeltmeler ters işaretlidir. Yani faz gözlemleri için eksi, kod gözlemleri için artı işaretlidir. Daha önce söylendiği gibi, faz ölçüm doğruluğu kod ölçüm doğruluğundan daha yüksektir.
66 54 Kod gözlemlerinde kod chip uzunluğu ile ifade edilirken, faz gözlemlerinde taşıyıcı dalganın dalga boylarının (cycles) sayısı ile ifade edilir. Faz gözlem denklemleri için yukarıda bahsedilen hata kaynaklarının LEO uydularına olan etkisi Çizelge 3.4 de verilmektedir. Çizelge 3.4. LEO uyduları için faz gözlem denklemindeki terimler ve nominal değerleri (Ramos-Bosch, 28) Parametre Simge Etki Miktarı Geometrik uzunluk ρ u a 2 km Alıcı saat farkı δ ta < 3 km Uydu saat farkı δ tu < 3 km Troposferik etki Ta u 2-1 m İyonosferik etki Ia u 2-5 m Uydu ve alıcı donanım gecikmesi u u a,a < 2 m Sinyal yansıma etkisi s L < 2 cm Termal gürültü vd. ε L < 1 cm Faz wind-up w L < 2 cm Belirsizlik terimi λa 2 km Çift Frekanslı Gözlem Modeli CHAMP ve GRACE uydularına JPL tarafından üretilen ve tüm GPS kod (C/A,P 1,P 2 ) ve taşıyıcı faz gözlemlerini (L 1,L 2 ) kaydedebilen BlackJack alıcıları yerleştirilmiştir. Modern bir GPS alıcısı, görüş alanı içerisindeki tüm uydular için her iki frekans içinde taşıyıcı fazları ve sözde uzunlukları üretir (Leick, 24; Swatschina, 29). Bu durumda belirli bir epok için alıcı saat hataları ve yazılım gecikmeleri aynı olarak kabul edilebilir. C/A kodu dışında kod ve taşıyıcı fazlar için çift frekanslı gözlem modeli,
67 55 P 1 (t) = ρ u a (t)+c[δ t a (t) δ tu (t t u a (t))]+i(t,f 1)+T(t)+M P1 (t)+ε P1 (t) (3.4a) P 2 (t) = ρ u a (t)+c[δ t a (t) δ tu (t t u a (t))]+ f2 1 I(t,f f2 2 2 )+T(t)+M P2 (t)+ε P2 (t) (3.4b) L 1 (t) = ρ u a (t)+c[δ t a (t) δ tu (t t u a (t))] I(t,f 1)+λ 1 A 1 +T(t)+M L1 (t)+ε L1 (t) (3.4c) L 2 (t) = ρ u a(t)+c[δ ta (t) δ tu (t t u a(t))] f2 1 I(t,f f2 2 2 )+λ 2 A 2 +T(t)+M L2 (t)+ε L2 (t) (3.4d) eşitlikleri biçiminde yazılabilir. İyonosferik etkinin kod ve faz ölçüleri için ters işaretli yazıldığı görülebilir. (3.4c) ve (3.4d) deki faz belirsizliği terimlerini daha da genişletmek mümkündür: A 1 = N 1 +φ 1 (t ) f 1 δ a (t ) ψ 1 (t )+f 1 δ u (t ) A 2 = N 2 +φ 2 (t ) f 2 δ a (t ) ψ 2 (t )+f 2 δ u (t ) (3.41a) (3.41b) Burada N, ψ(t ) ve φ(t ) sırasıyla başlangıç tam dalga belirsizliği, uydu ve alıcıya ait faz belirsizliklerini gösterir. Söz konusu büyüklükler her iki frekans için ayrı değerlerdir. (3.4) eşitliklerinde geometrik mesafenin ρ u a (t) aynı büyüklükte olduğu varsayılır. Fakat gerçekte bu yaklaşım doğru değildir. Çünkü sinyal yol zamanı herbir frekans için az da olsa farklılık gösterir. Ancak bu farklılık.1µs den daha az bir süreye karşılık gelir ve GPS uydularının konum farklılıklarını mm nin altında etkiler. Diğer hata kaynakları ile karşılaştırıldığında bu etki ihmal edilebilecek bir düzeydedir (Kroes, 26). Stokastik büyüklük ε(t) termal gürültüyü temsil eder. Bu büyüklük için ardışık epok, uydu, frekans ve gözlem türleri arasında korelasyonun bulunmadığı farzedilir. Böylece gözlem vektörü ve kovaryans matrisi,
68 56 P 1 (t) P L SF (t) = 2 (t) L 1 (t) L 2 (t) (ε P1 (t)) 2 (ε C SF (t) = P2 (t)) 2 (ε L1 (t)) 2 (ε L2 (t)) 2 (3.42) (3.43) biçiminde oluşacaktır (Kroes, 26; Swatschina, 29). Bu temel gözlemlere Sıfır Farklar-SF (zero differences or undifferenced) adı verilir. Bu gözlem modeli birçok fark teknikleri için temel eşitliklerdir. Fark eşitlikleri genel olarak tekli (single difference), ikili (double difference) ve üçlü (triple difference) olarak sınıflandırılır. Bu teknik kullanılarak alıcı ve uydu saat hataları, faz başlangıç belirsizliği gibi hatalar elemine edilebilmektedir. Sıfır fark gözlem modeli bu haliyle konum belirleme amaçlı uygulamalarda kullanılamaz. Konum bilgisi orjinal ölçümlerden türetilen doğrusal kombinasyonlar sayesinde elde edilebilir. Bunlardan ilki iyonosfer etkisini hemen hemen ortadan kaldıran iyonosferden bağımsız doğrusal kombinasyondur İyonosferden Bağımsız Doğrusal Kombinasyon Konum belirleme ve veri analizi için geliştirilmiş birçok doğrusal kombinasyon yöntemi bulunmaktadır. Bu kombinasyonlar çift frekanslı gözlem modelinden türetilirler. Burada iyonosfer etkisini ortadan kaldıracak bir kombinasyon tekniğinden bahsedilecektir. Daha önce söz edildiği gibi iyonosferik etki frekansa bağımlıdır. Kod ve faz gözlemleri için iyonosferden bağımsız gözlem modeli P 3 = L 3 = 1 (f 2 f1 2 f2 2 1 P 1 f2 2 P 2) (3.44a) 1 (f f1 2 f2 1 2 L 1 f2 2 L 2) (3.44b) 2
69 57 eşitlikleriyle oluşturulabilir (Beutler ve ark., 27). Burada f 1 = MHz ve f 2 = MHz olduğu dikkate alınırsa eşitlikler, P 3 = 2.546P P 2 L 3 = 2.546L L 2 (3.45a) (3.45b) daha sade bir görünüm alır. (3.44) yaklaşımı (3.4) eşitliklerine uygulanırsa iyonosferik etkilere ait olan parametreler ortadan kalkar ve iyonosferden bağımsız gözlem modeli, (IBDK), P 3 (t) = ρ u a (t)+c[δ t a (t δ tu (t t u a (t))]+t(t)+m P 3 (t)+ε P3 (t) L 3 (t) = ρ u a(t)+c[δ ta (t δ tu (t t u a(t))]+λ 3 A 3 +T(t)+M L3 (t)+ε L3 (t) (3.46a) (3.46b) elde edilir. IBDK kombinasyonu navigasyon ve konum belirleme uygulamalarında sıklıkla kullanılır. Bu tez çalışmasında sıfır farklar ve iyonosferden bağımsız doğrusal kombinasyon (SF+IBDK) kullanılarak duyarlı yörünge bilgileri elde edilecektir. (3.46) eşitliklerinde geçen λ 3 terimi bu doğrusal kombinasyon sonucunda elde edilen dalga boyunu temsil eder. L 1 ve L 2 faz eşitliklerinde bulunan diğer etkiler dikkate alınmaksızın bazı genellemeler yapılırsa, L 1 (t) = ρ u a(t)+c[δ ta (t) δ tu (t t u } {{ a(t))] I(t,f } 1 )+λ 1 A 1 +T(t)+M L1 (t)+ε L1 (t) } {{ } Φ Etkiler L 2 (t) = ρ u a (t)+c[δ t a (t) δ tu (t t u a } {{ (t))] f2 1 I(t,f } f2 2 2 )+λ 2 A 2 +T(t)+M L2 (t)+ε L2 (t) } {{ } Φ Etkiler L 1 = Φ I +λ 1 A 1 L 2 = Φ f2 1 I +λ f2 2 2 A 2 (3.47)
70 58 bulunur. Son eşitlikler (3.44) de yerine konur ve düzenlenirse, 1 L 3 = (f f1 2 f2 1 2 L 1 f2 2 L 2) 2 1 L 3 = (f f1 2 f 1Φ f 2 1I 2 +f1λ A 1 f2φ+f 2 1I 2 f2λ 2 2 A 2 ) 1 L 3 = (Φ(f f1 2 f2 1 2 f2 2 )+f2 1 λ 1A 1 f2 2 λ 2A 2 ) 2 1 L 3 = Φ+ (f f1 2 f 1λ A 1 f2λ 2 2 A 2 ) (3.48) elde edilir. (3.48) eşitliğinin ikinci terimi iyonosferden bağımsız hata terimi (ionosphere-free bias) olarak tanımlanır. Fakat bu terim L 1 ve L 2 faz eşitliklerindeki gibi λ 3 A 3 biçiminde ifade edilmez. Bunun yerine uzun dalga boylu (wide-lane linear combination) ve kısa dalga boylu doğrusal kombinasyonlardan (narrowlane linear combination) yararlanarak türetilir. Kısaca uzun dalga boylu doğrusal kombinasyonda faz belirsizlik terimi için (A WL = A 1 A 2 ) yazılabilir. Eğer A WL nin değeri biliniyorsa iyonosferden bağımsız hata terimi için λ i = c f i eşitliğinden de yararlanarak Bias = 1 (f 2 f1 2 f2 2 1 c f 1 A 1 f 2 2 c f 2 (A 1 A WL )) (3.49a) Bias = 1 (f f1 2 f2 2 1 ca 1 f 2 ca 1 +f 2 ca WL ) (3.49b) Bias = ca 1(f 1 f 2 ) + cf 2A WL f1 2 f2 2 f1 2 f2 2 (3.49c) Bias = 1 +c f 1 +f } {{ 2 f } WL 1 f2 2 c A f 2 A (3.49d) λ 3 elde edilir. Eşitlikten de görüldüğü üzere λ i ile ilgili terimler ortadan kalkmıştır. c, f 1 ve f 2 terimlerinin sayısal değerleri kullanıldığında ve 1MHz = 1 6 sn 1 olduğu göz önüne alındığında λ 3 = cm çıkar. Bu durumda tek bilinmeyen A 1 parametresidir ve buna kısa dalga boylu belirsizlik (narrow-lane ambiguity) adı verilir (Beutler ve ark., 27). IBDK kombinasyonunun kullanılmasıyla iyonosferik etki giderilmiş olur. Bu kombinasyona karşılık gelen kovaryans matrisi halen korelasyonsuz olmasına rağmen, gürültü değerleri yaklaşık 3 kat artar (Kroes, 26; Swatschina, 29).
71 Değerlendirme Stratejisi Yukarıdaki açıklamalar ışığında genel olarak LEO uyduları için şu genellemeler yapılabilir: Troposfer tabakasının yeryüzünden yaklaşık 4 km yükseklikte olduğu ve LEO uydularının yüksekliğinin de yaklaşık 45 km den başladığı (GOCE; 25 km) göz önüne alınırsa, troposferik etkinin Ta u (t) LEO uyduları üzerinde etkisinin olmadığı kolayca anlaşılabilir. Bu yüzden, GPS gözlemlerinde troposferik etki değeri ortadan kalkmış olur. Çizelge 3.3 ve 3.4 e bakıldığında LEO uyduları üzerinde en büyük etkinin iyonosferden kaynaklandığı görülebilir. Bu nedenle, duyarlı yörünge çalışmalarında iyonosferden bağımsız doğrusal kombinasyonun (IBDK) kullanılması yerinde olacaktır. Duyarlı yörünge bilgisi elde etmek için kullanılan verinin kalitesi doğrudan yörünge sonuçlarına yansır. Bundan dolayı, IGS ve CODE merkezlerinde türetilen yüksek-frekanslı saat ve yörünge bilgilerinin kullanımı tercih edilmelidir.
72 6 4. DUYARLI YÖRÜNGE BELİRLEME İlk insan yapımı uzay aracı 1957 yılında fırlatılmasına rağmen, uydu yörüngeleri ikiyüz yıldan beri çalışılan konulardandır. Yerçekimi kanunlarının Newton tarafından ortaya konulmasıyla, bilim adamları güneşin etrafında dolanan gökcisimlerinden sadece birkaçını ve yerin doğal uydusu ayın hareketini izleyebilmişlerdir. Oysa günümüzde, yerin etrafında dolanan sayısız uzay enkazları ile birlikte binlerce insan yapımı uydu bulunmaktadır. Bunların çoğu genellikle 15 km den daha aşağı yükseklikte olup alçak yörünge uyduları (LEO) olarak isimlendirilir (Şekil 4.1). Bunların dışında kalan çoğu uydu yaklaşık 36 km yüksekliktedir ve herhangi bir yer noktasına göre durağan (geostationary-geo) yörüngede dolanırlar. Kuzey yarım küredeki uydu bulutunun güneye göre yoğun oluşu bu nedene dayanmaktadır. Uyduların büyük çoğunluğu telekomünikasyon, konum belirleme, navigasyon ve bilimsel amaçlarla kullanılmaktadır. Şekil 4.1. Kuzey kutbundan bir görünüm (ESA/ESOC, 212) 196 lı yıllarda teknolojinin henüz tam anlamıyla gelişmemesinden ve hesaplama tekniklerinin çok kaba olmasından dolayı yörünge belirleme duyarlığı 1 m civarında seyretmekteydi. 197 li yıllara gelindiğinde duyarlığı kısıtlayıcı alanlarda bir takım iyileşmeler kaydedildi. Özellikle bilgisayar teknolojisine dayalı sayısal analiz tekniklerindeki ilerleme ile uyduya uygulanan güç modellerinin zenginleşmesi ve dolayısıyla yörünge belirleme duyarlığının önce 1 m seviyelerine,
73 lerin sonuna doğru birkaç metreye ulaşması sağlandı. 198 li yıllarda ise yer gravite alanı ve yeryüzeyine etkiyen güç alanları için yeni modeller geliştirilerek önemli adımlar atıldı. Günümüzde ise bu gelişmelerin ışığı altında yapılan iyileştirmeler ve geliştirilen yöntemler ile duyarlık değerleri birkaç cm seviyelerine kadar gerilemiştir (Tapley ve ark., 24). Bu yöntemler genel olarak DYB olarak isimlendirilmektedir. olarak, Konum belirleme uygulamalarında yörünge belirleme işleminin önemi sayısal σ b b = σ r ρ u a (4.1) eşitliği ile ortaya koyulabilir (Beutler ve ark., 27). Burada b yeryüzünde iki nokta arasındaki baz uzunluğunu (km), σ b baz hatasını (m), σ r yörünge hatasını (m) ve ρ u a uydu alıcı arasındaki uzaklığı (km) ifade eder. (4.1) den örneğin bir GPS uydusunun yörünge belirlemesinde yapılacak hata miktarının baz uzunluğuna ne kadar etki ettiği hesaplanabilir. Buna göre 2.5 m lik yörünge hatası 1 km lik bir baz için 124 mm ye kadar çıkabilmektedir. Eğer yörünge.5 m lik bir hata ile belirlenirse hata miktarı aynı baz uzunluğunda 2.5 mm ye kadar gerilemektedir (Çizelge 4.1). Çizelge 4.1. Baz uzunluğuna göre hata miktarları Yörünge Hatası Baz Uzunluğu Baz Hatası (m) (km) (mm) Uydu hareketini birçok bozucu kuvvet etkiler. Bu kuvvetler yerçekimiyle ilişkili ve ilişkisiz olmak üzere sınıflandırılır. Alçak yörüngeli uydular yerin çekim alanından kaynaklanan bozucu etkilere daha duyarlıdır. Tersinden bakıldığında bu durum global gravite alanının modellenmesinde avantaj sağlar. Gravite alanının modellenmesi, gravite ile ilişkili bazı mühendislik problemlerine çözüm bulunması demektir. Ortak bir referans yükseklik sisteminin kurulması jeodezi bilimine
74 62 sağlanabilecek katkılardan ilk akla gelendir. Bu nedenle LEO uyduları jeodezik uygulamalar için ayrı bir önem taşır. Üzerindeki bir ya da birden fazla GPS alıcısı yardımıyla bir uydunun konum ve hız vektörlerinin belirlenmesi, yörünge belirlemede çok kullanışlı, robust ve hızlı bir tekniktir. Başarılı ilk denemeler TOPEX/POSEIDON uydularında gerçekleştirilmiştir. Bundan sonra birçok uyduda söz konusu teknik kullanılmış, paralel olarak matematiksel tekniklerde de iyileşmeler sağlanmıştır. Son on yıllık süreçte LEO uyduları olarak CHAMP, GRACE ve GOCE ye GPS alıcıları yerleştirilerek en gelişmiş DYB uygulamaları gerçekleştirilmiştir. DYB de üç temel yöntem kullanılır. Bunlar; Kinematik veya geometrik Dinamik İndirgenmiş dinamik yörünge belirleme yöntemleri olarak sıralanır. Kinematik veya geometrik yaklaşım ayrı bir dış modele (dinamik güç modeli) ihtiyaç duymadan uydunun yörüngesinin belirlenmesini hedef alır. Yörünge, uydu konumlarının bir zaman serisi olarak temsilidir (Bock ve ark., 25). Gerçek yörünge bilgisi yüksek doğrulukla kestirilen GPS konumlarından elde edilir (Seeber, 23). Kinematik yaklaşımın sürekliliği ve kalitesi büyük ölçüde GPS verilerinin elde edilebilirliğine ve gözlemlerin kalitesine dayanır. GPS gözlemlerindeki ölçü ve ağırlıklandırma hataları, uygun olmayan uydu geometrisi ve veri boşlukları bu yaklaşımın kalitesini düşürür. Bu nedenle kinematik yaklaşımda gözlemler uyuşumsuz ölçülerden mutlaka arındırılmalıdır. Ayrıca GPS uyduları ile karşılaştırıldığında LEO uyduları yaklaşık iki kat daha hızlı hareket eder. Yani geometrileri çok hızlı bir biçimde değişim gösterir. Sonuç olarak kinematik yaklaşım ile iyi ve sürekli bir yörünge elde etmek oldukça zordur (Bae, 26). Bu dezavantajları ortadan kaldırabilmek için dinamik yörünge modeli ortaya atılmıştır. Kinematik yaklaşım nokta tabanlı bir hesaplama ile yörüngeyi belirlerken dinamik yaklaşım yay tabanlı bir hesaplama yapar. Kinematik yaklaşımın aksine dinamik yaklaşımda uyduya etki eden kuvvetler uydu hareket denklemi içerisine ilave edilir. Böylece başlangıç durum vektörü, atmosferik sürüklenme, güneş
75 63 radyasyon basıncı ve yer gravite alanından kaynaklanan ivmeler gibi gravite alanı ile ilişkili olmayan parametreler belirlenir. Kesin yörünge çözümü uydunun başlangıç durum vektörü ile bu bilinmeyen parametrelerin birlikte kestirilmesiyle iyileştirilir. Özetle, önce başlangıç durum vektörü ve diğer dinamik parametreler kestirilir ve buradan hareketle bir sonraki epoktaki durum vektörü, kestirim modelinde dinamik parametreler kullanılarak üretilir. Dinamik yaklaşımda yörünge hataları, kestirim süre uzunluğuna bağlıdır (Bock, 23; Bae, 26). Ayrıca, uydunun önsel yörünge bilgisine ihtiyaç duyulur. Kinematik yaklaşımdaki veri boşluğu ve süreksizlik dinamik model için söz konusu değildir. Çünkü dinamik yaklaşımda model sürekli ve dinamik kuvvetler ile birlikte kurulur. Kötü gözlemler belirlenir ve bunların etkileri giderilir. Böylece, veri kesiklikleri veya boşlukları meydana gelmez; sürekli bir model ortaya çıkar. Aslında, dinamik yaklaşımın doğruluğu kestirim süresinin yanında modelleme hatalarına da bağlıdır denilebilir. Kestirim süresinin artmasının yanısıra özellikle LEO uydularının dinamik davranışları hakkındaki yetersiz bilgiden dolayı dinamik yörünge çözümlerinde sapmalar görülür. Bundan dolayı indirgenmişdinamik model yaklaşımı ortaya atılmıştır (Swatschina, 29). Yukarıda da açıklandığı üzere kinematik yaklaşım doğrudan ölçü hatalarına ve veri boşluklarına duyarlıdır diyebiliriz. Dinamik yaklaşım ise veri boşluklarına rağmen süreklidir fakat dinamik güç modellerine bağlıdır. İndirgenmiş-dinamik yaklaşım bu iki yaklaşımın dezavantajlarını azaltacak ve avantajlarını birleştirecek şekilde tasarlanmıştır. Bu yaklaşımda uydunun dinamik parametrelerine ek parametreler tanımlanır ve sistem çözülür. Ek parametreler önsel model hatalarını azaltmak ya da model eksikliğini gidermek için tanımlanır. Bu deneysel parametrelerin hesaba alınmasında genel olarak literatürde iki yol vardır. İlki anlık hız değişimleri (instantaneous velocity changes) diğeri ise deneysel ivmeler (empirical accelerations) ya da parçalara ayrılmış sabit ivmeler (piecewise constant accelerations) olarak isimlendirilir (Liu, 28). Bu bölümde kinematik, dinamik ve indirgenmiş-dinamik DYB teknikleri üzerinde durulacak ve dinamik güç modeli yani uyduya etki eden kuvvetler hakkında detaylı bilgi ve matematiksel eşitlikler verilecektir. Ayrıca uydunun temel hareket denklemi ve Kepler elemanları ile olan ilişkisi tanımlanacaktır.
76 Uydunun Hareket Denklemi ve Kepler Elemanları Uydunun hareket denklemi Newton un ortaya koyduğu çekim ve ikinci hareket yasasının ortak kullanılmasıyla elde edilir. Newton un ilk kitabı olan Principia adlı eserinde üç hareket yasası şöyle tanımlanır: 1. Her cisim dış güçler tarafından durumu değiştirilmeye zorlanmadıkça ataletini veya düz bir hat boyunca düzenli hareketini sürdürür. 2. Bir cismin hızındaki değişim miktarının (ivme) cismin kütlesiyle çarpımı, hareketi meydana getiren kuvvete eşittir. 3. Her etkiye karşı, eşit ve zıt yönde bir tepki vardır. İkinci hareket yasasının matematiksel gösterimi, F = ma = m r (4.2) ile ifade edilir. Burada F, m kütleli bir cisme uygulanan bileşke kuvvet vektörünü ve a ( r) ise inersiyal (eylemsiz, ataletsiz) bir referans sistemde cismin ölçülen vektörel ivmesini gösterir. Newton un evrensel çekim yasasına göre evrendeki iki cisim birbirlerini aralarındaki uzaklığın karesi ile ters, kütleleri ile doğru orantılı çeker. F = G mm r 2 (4.3) Burada m (uydu) ve M (yer) cisimlerin kütleleri G ise evrensel çekim sabitidir. G nin değeri G = m 3 kg 1 s 2 dir. Bu iki yasa birbirlerine eşitlenir ve eksenlere göre açınımı yapılırsa uydunun temel hareket denklemi, r = GM r 3 r (4.4) bulunur. (4.4) eşitliği uydunun kütlesinin ihmal edildiği, yerin gravite alanının simetrik olduğu ve yerin bir nokta kitle olarak varsayılmasıyla elde edilir. Burada r uydunun yermerkezli konum vektörünü, r konum vektörünün ikinci türevini yani ivmeyi, r ise uydu ve yer arasındaki mesafeyi ifade eder. Hareket denklemi ikinci dereceden üç boyutlu bir diferansiyel denklemdir. Hareket denklemi üzerinden uydunun yörüngesini tanımlamak için altı integrasyon
77 65 sabitine ihtiyaç duyulur. Genel olarak bu altı parametre Kepler yörünge parametreleri veya kısaca Kepler elemanları olarak isimlendirilir (Şekil 4.2). Bu parametreler; z Uydu r ν ω a(1-e) Günberi Ω i x Ekvator Düzlemi Ω y Şekil 4.2. Kepler elemanları a yörünge elipsinin büyük yarı ekseni, e yörünge elipsinin dışmerkezliği veya eksantrisitesi, i yörünge düzleminin eğimi, Ω çıkış düğümünün boylamı, ω günberi uzaklığı veya perige argümanı ve ν gerçek anomali değeri olarak ifade edilir. Uydu yörüngesi Kepler elemanları yardımıyla tanımlanabilir. Bu yöntemde uydunun konum ve hız bileşenleri her epok için ayrı ayrı hesaplanır. Matematiksel eşitlikleri EK A da verilen bu hesaplama tekniğine Kepler efemeris hesabı denir (Swatschina, 29). Yukarıda söz edildiği gibi (4.4) eşitliği, yer gravite alanının homojen olduğu, yerin bir nokta kitle olarak alındığı ve uydu kütlesinin yerin kütlesine göre çok küçük olduğu varsayımından hareketle elde edilir. Fakat, durum gerçekte böyle değildir. Yer gravite alanı homojen bir yapıda olmadığından uydular (özellikle alçak-yörüngeli) üzerindeki çekim etkisi çok düzensizdir. Ayrıca, bu düzensiz etkiye
78 66 gravite alanı ile ilişkili olmayan kuvvetlerde karışır. Bu yüzden temel hareket denklemi (Kepler yörüngesi) gerçek uydu yörüngesinin sadece ilk yaklaşımı olarak kabul edilir (Seeber, 23). 4.2 Kinematik Yörünge Belirleme Kinematik DYB teknikleri sadece GPS gözlemlerinden yararlanarak, her gözlem epoğu için gerçek uydu konumunun kestirilmesi esasına dayanır. Bu yüzden kinematik tekniğin duyarlılığı GPS gözlemlerinin duyarlığına, GPS uydu dağılımına (geometrisine), GPS saat ve yörüngelerinin kalitesine bağlı olarak değişir. Eğer gözlemlerin elde edildiği uyduların sayısı 4 e kadar düşerse bu durumda uydunun konumu istenilen epoklar için belirlenemeyebilir. Bu kinematik yörünge belirleme yönteminin eksik bir yanı olarak göze çarpmaktadır. Böylesi kayıp uydu konumları ve alıcılardan kaynaklanan veri boşluklarına dinamik yörünge belirleme teknikleriyle çözüm getirilebilmektedir. Dinamik yörünge belirlemede uydu yörünge modeli sürekli olarak kurulur ve veri boşluklarından etkilenmez (Bock, 23; Bae, 26). Kinematik yörünge belirleme işlemi bazı değişiklikler ve kestirim teknikleri dışında dinamik ve indirgenmiş-dinamik yörünge belirleme işlemine benzerlikler gösterir. Kinematik yörünge IGS tarafından sağlanan ve duyarlı saat ve efemeris bilgilerini içeren GPS yörüngeleri kullanılarak belirlenir (bkz. Bölüm 3.2). Bu işlem sıfır farklar (SF) (bkz. Bölüm 3.3.3) ve iyonosferden bağımsız kombinasyon kullanılarak yapılır (bkz. Bölüm 3.3.4). Kinematik yörünge belirleme işlemlerinde SF nin alternatifi olarak ikili farklar (İF-double difference) ve üçlü farklar (ÜFtriple difference) yöntemleri de kullanılır. Fakat SF yöntemi hem basit hem de verimli olması açısından tercih edilir. İF ve ÜF yönteminde IGS yer istasyonları ile LEO uydusu arasındaki bazlar kullanılarak çözüme ulaşılır. Bu durum oldukça büyük miktarda GPS gözleminin işleme dahil edilmesi anlamını taşır ve güçlü bilgisayar kapasitesini gerektirir. Yani İF yaklaşımının en belirgin dezavantajı IGS yer istasyonlarından kaynaklı gözlemlerin ve bilinmeyen parametre sayısının çok olmasıdır (Svehla ve Rothacher, 23). Ayrıca bu parametrelere bağlı olarak CPU zamanı (işlem yükü) oldukça artar. Bunun yanında İF yönteminin en önemli avantajı gözlem denklemlerinden tamsayı bilinmeyenlerinin düşürülmesidir. Böylece, LEO yörünge kalitesi iyileştirilebilir. ÜF yaklaşımın sorunlu yanı
79 67 gözlemlerin gürültüsündeki artıştır (Svehla ve Rothacher, 22). Bundan dolayı kinematik yörünge belirlemede genellikle SF yöntemiyle iyonosferden bağımsız doğrusal kombinasyon kullanılması tercih edilir. Şekil 4.3 de kinematik yörünge belirlemenin sıfır, ikili ve üçlü farklar ile nasıl yapılacağına dair bir iş akış örneği verilmiştir (Svehla ve Rothacher, 22). Şekil incelendiğinde IGS nin DYB çalışmalarında çok önemli bir rol oynadığı ve sonuçları doğrudan etkilediği görülebilir. Kinematik DYB LEO GPS alıcısı Faz / Kod LEO Yıldız Sensörü Konum LEO GPS Yörüngeleri IGS ERP parametreleri IGS IGS Ağı Faz / Kod IGS GPS uydu Saatleri IGS IGS Ağı Koordinatlar IGS Troposfer zenit gecikmesi IGS LEO SAAT DOSYASI Kinematik Yörünge SP3 Kinematik Yörünge SP3 Şekil 4.3. Kinematik yörünge belirleme stratejisi (Svehla ve Rothacher, 22) Kinematik yörünge belirleme ile ilgili daha detaylı bilgi Bock ve ark. (21); Svehla ve Rothacher (22); Bock (23); Svehla ve Rothacher (23); Beutler ve ark. (25a,b); Bock ve ark. (25); Beutler ve ark. (26); Jäggi (27); Shabanloui (212) de bulunabilir.
80 Dinamik Yörünge Belirleme Dinamik yörünge belirleme işlemi uydunun hareket denklemine, uydu üzerine etki eden tüm bozucu kuvvetlerin eklenmesiyle elde edilir. Bu durumda(4.4) eşitliği, r = GM r 3 r+ r bozucu (4.5) şeklini alır (Svehla ve Rothacher, 23; Bock, 23; Hobbs ve Bohn, 26; Jäggi, 27; Jäggi ve ark., 21). (4.5) ikinci dereceden doğrusal olmayan bir diferansiyel denklemdir. Burada r bozucu parametresi uydu üzerine etki eden yerçekimi ve yerçekimine ait olmayan tüm bozucu kuvvetlerin toplamını ifade eder ve r bozucu = f 1 (t,r,ṙ,q 1,...,q d ) (4.6) biçiminde tanımlanır. Böylece genişletilmiş hareket denklemi r = GM r 3 r+f 1(t,r,ṙ,q 1,...,q d ) = f +f 1 = f (4.7) olarak yazılır (Jäggi, 27; Jäggi ve ark., 21). Burada t r ṙ q 1,...,q d f f 1 f dinamik zamanı uydunun konumunu uydunun hızını dinamik yörünge parametrelerini yerçekimi merkezinden (central gravity term) kaynaklanan ivmeyi uydu üzerine etki eden kuvvetlerin neden olduğu ivmeleri uydu üzerine etki eden toplam ivmeyi ifade eder. Dinamik yörünge parametreleri veya kısaca dinamik parametreler ya bilinen olarak kabul edilir ya da dengeleme işlemi içerisinde başlangıç koşulları ile birlikte kestirilir (Swatschina, 29). Dinamik parametreler gravite alanı, atmosferik sürüklenme, radyasyon basıncı gibi uydu üzerine etki eden kuvvetlerin neden olduğu bozucu ivmeler olarak tanımlanır. Başlangıç koşulları t epoğunda Kepler elemanlarından
81 69 yararlanarak aşağıdaki biçimde, r(t ) = r(a,e,i,ω,ω,ν;t ) (4.8) ṙ(t ) = ṙ(a,e,i,ω,ω,ν;t ) (4.9) gösterilir. Genel olarak (4.7) den, analitik bir çözüme ulaşmak oldukça karmaşık bir problemdir. Bundan dolayı çözüm nümerik olarak gerçekleştirilir. Çözüm için birçok (Runge-Kutta, ekstrapolasyon, polinom vs.) nümerik yöntem ortaya atılmıştır. Nümerik yöntemler kullanılarak (4.7) nin çözümü gerçekleştirilir ve önsel yörünge (r (t)) elde edilir. Önsel yörünge aynı zamanda GPS kod gözlemlerinin değerlendirilmesinden de elde edilebilir. Böylece dinamik yörünge belirleme işlemi aslında yörünge belirleme işleminden ziyade bir yörünge iyileştirme işlemi gibi düşünülebilir (Svehla ve Rothacher, 23; Jäggi ve ark., 25; Jäggi, 27; Jäggi ve ark., 21). Gerçek yörünge r(t), önsel yörüngedeki r (t) bilinmeyen yörünge parametrelerine (p i = 1,...,n) göre Taylor serisi ile ifade edilirse, r(t) = r (t)+ n i=1 r (t) p i (p i p i ) (4.1) bulunur. Burada, n, toplam bilinmeyen yörünge parametre sayısını ifade eder ve (n = 6+d) toplamında parametreyi içerir. Buradaki altı sayısı konum ve hızlar için başlangıç bilinmeyenini, d ise dinamik parametre sayısını tanımlar. r (t) p i ifadesi p i parametresindeki değişime bağlı yörüngesel değişimi belirtir. Kısmi türevler, varyasyon denklemleri (variational equations) olarak ifade edilen denklemler kullanılarak hesaplanır. Varyasyon denklemleri (4.4) hareket denkleminin kısmi türevlerinden elde edilir (Svehla ve Rothacher, 23; Jäggi, 27). Varyasyon denklemlerinin çözümü için güç modelinin uydu konum ve hızına göre türevleri gerekir (Swatschina, 29). Bu türev eşitliklerinin bir kısmı Ek B de bulunabilir. (4.1) da yörünge parametre düzeltmesi (p i p i ) ve yörünge parametrelerine göre önsel yörüngenin kısmi türevleri biliniyor kabul edilir. (4.1), yörünge belirleme problemi çözümünün doğrusallaştırılmış biçimidir (Jäggi, 27). Alternatif olarak, iyileştirilmiş yörünge güncel parametreler ile birlikte dinamik modelin tekrar sayısal integrasyonu ile elde edilebilir (Jäggi ve ark., 21). Eğer yörünge, bilinmeyen yörünge parametreleri (p i ) ile belirleniyorsa
82 7 dinamik yörünge belirleme, hareket denklemine ek sözde-stokastik parametreler ilave edilip belirleniyorsa bu durumda indirgenmiş-dinamik yörünge belirleme işleminden söz edilir. Dinamik yörünge belirleme işleminde, uyduya etki eden kuvvetlerin modellenmesi ve dinamik güç modelinin kurulması gerekir. Varyasyon Denklemleri Dinamik yörünge modeli, uydu hareket denklemi (4.7) nin özel bir çözümü olarak yörüngeyi başlangıç koşulları ve dinamik parametrelere göre tanımlar. Yörünge belirleme işleminde uydu yörüngesi var olan gözlemlere en iyi uyacak biçimde kestirilir. Bu durumda önsel yörüngenin başlangıç koşulları ve dinamik parametrelere göre kısmi türevleri gereklidir (Jäggi, 27; Swatschina, 29). (4.7) hareket denklemindeki dinamik parametreler veya başlangıç koşullarını tanımlayan parametreleri p i (i = 1,2,...,n) olmak üzere, önsel yörüngenin i. parametreye göre kısmi türevi, z pi (t) = r (t) p i (4.11) şeklinde yazılabilir. (4.11) ile ilgili başlangıç değer problemi, (4.7) hareket denkleminin kısmi türevleri alınarak dinamik güç modelinden elde edilir. Bu sonuç p i parametresinin varyasyon denklemleri, z pi = A z pi +A 1 ż pi + f 1 p i (4.12) olarak tanımlanır. Burada A ve A 1 (3x3) boyutunda olup A [i,k] = f i r,k, A 1[i,k] = f i ṙ,k (4.13) eşitlikleriyle tanımlanır. Burada f i, (4.7) deki toplam ivmenin i. bileşenini, r,k ise (4.7) de yermerkezli konumun k. bileşenini gösterir. Varyasyon denklemi (4.12), p i {a,e,i,ω,ω,ν} için doğrusal, homojen ve z pi (t ), ż pi (t ) başlangıç değerli ikinci dereceden diferansiyel bir denklem sistemi iken p i {q 1,...,q d } içinse homojen olmayan fakat sıfıra eşit başlangıç değerli bir denklem sistemidir. (Jäggi ve ark., 25, 26; Beutler ve ark., 27; Jäggi, 27; Jäggi ve ark., 21). Çizelge 4.2 de başlangıç koşulları ve dinamik parametrelere göre varyasyon denklemleri için
83 71 başlangıç değerleri verilmiştir (Swatschina, 29). Çizelge 4.2. Varyasyon denklemleri için başlangıç koşulları p i z pi,1(t ) z pi,2(t ) z pi,3(t ) ż pi,1(t ) ż pi,2(t ) ż pi,3(t ) p 1 1 p 2 1 p 3 1 p 4 1 p 5 1 p 6 1 q i Yörünge parametreleri (p i ) ile ilgili varyasyon denklemlerinin çözümleri iki şekilde elde edilir. İlki sayısal integrasyon teknikleri diğeri ise ayrıntılı doğrusal kombinasyonlardır. Doğrusal kombinasyonlar sözde stokastik yörünge modeli olarak ele alınır (bkz. Bölüm 4.4). Yörünge parametrelerinin tümü ile birlikte GPS gözlemleri kullanılarak en küçük kareler dengeleme işleminde önsel yörünge parametrelerine (p i ) ait düzeltmeler için nihai bir çözüm sağlanır. Böylece iyileştirilmiş yörünge, (4.1) kullanılarak elde edilir (Jäggi ve ark., 26) Dinamik Güç Modeli Bu bölümde uydular için dinamik güç modeli hakkında detaylı bilgi ve matematiksel eşitlikler verilecektir. Bozucu kuvvetler, genel olarak yerçekimi ile ilgili (gravitational) ve yerçekiminden bağımsız(non-gravitational) ivmeler/düzensizlikler olarak iki kısma ayrılır (Şekil 4.4). Bunlar belirlenirken ek bilgilere gereksinim duyulur. Yerçekimine bağlı ivmeler tamamen uydu konumuna bağlı olarak belirlenirken yerçekiminden bağımsız olanlar uydu ve atmosferik parametrelere göre belirlenir. Dinamik yörünge üzerinde sonuçları yeterli incelikte elde etmek için yörünge ve uydunun karakteristik özellikleri dikkate alınmalıdır (Swatschina, 29). Şekil 4.4 de bu kuvvetlerin sınıflandırılması verilmektedir. Bu kuvvetlerin modellenerek hareket denklemi içerisine konulması ve integrasyonların yapılması ile daha hassas sonuçlar elde edilir.
84 72 Dinamik Güç Modeli Yerçekime Bağlı Düzensizlikler (Gravitational Perturbations) Yerçekimden Bağımsız Düzensizlikler (Non-gravitational Perturbations) - Homojen olmayan yer gravite alanı - Üçüncü cisimlerin (Ay, Güneş) çekim etkisi - Diğer düzensizlikler * Gelgitlerden kaynaklanan (okyanus, kutup ve katıyer) düzensizlikler * Relativistik etkiler - Atmosferik sürüklenme - Güneş'in doğrudan radyasyon basıncı - Albedo - Uydu üzerinde bulunan roket Şekil 4.4. Dinamik güç model bileşenleri Alçak yörünge uyduları üzerine etki eden bozucu kuvvetleri ortaya koymak GPS/GLONASS gibi daha yüksek yörüngede bulunan uydulara göre daha karmaşık bir problemdir. Genel olarak yüksek yörüngedeki uyduların yörünge parametreleri, başlangıç koşulları ve birkaç dinamik parametre ile istenen doğrulukla tanımlanabilir. Fakat LEO uyduları için aynı şeyi söylemek daha zordur (Bock, 23). Çizelge 4.3 de GPS ve LEO uyduları üzerine etki eden kuvvet/ivme değerleri verilmiştir (Seeber, 23; Bock, 23; Cojocaru, 27; Swatschina, 29; Calais, 212). Çizelge 4.3. GPS ve LEO uyduları üzerine etki eden bozucu ivmelerin büyüklüğü İvme GPS (m/s 2 ) LEO (m/s 2 ) Yer gravite alanı iki-cisim terimi (1/r 2 ) Homojen olmayan yer gravite alanı Ayın çekim kuvveti Güneşin çekim kuvveti Yer gravite alanının diğer terimleri Radyasyon basıncı (direkt) Katı yer gelgiti Okyanus gelgiti Atmosferik sürüklenme Albedo
85 73 Çizelge 4.3 incelendiğinde yer gravite alanından kaynaklanan ivme değerinin hem GPS hem de LEO uydusu üzerinde önemli bir etkisi olduğu görülür. Yerin çekim etkisi ile kıyaslandığında, LEO uyduları üzerinde ay ve güneşin çekim etkisi oldukça küçüktür. Yerçekimi ile ilişkili olmayan radyasyon basıncı, temel olarak uydunun alan kütle oranına (area-to-mass ratio) bağlıdır. Atmosferik sürüklenmeden kaynaklanan ivmelenmeyi ise temel olarak uydu yüksekliği, alan kütle oranı, atmosferik yoğunluk bilgisi ve değişimi belirler. Ancak atmosfer yoğunluk bilgisi ve değişimi tam olarak bilinmez, bu yüzden yerin çekiminden bağımsız kuvvetlere göre daha kaba bir büyüklük olarak kalır (Bock, 23) Yerçekimi ile İlişkili Düzensizlikler Yerin Çekim Alanı ve Düzensiz Etkisi Uydu yörüngesindeki düzensizlikler fiziksel jeodezide çok iyi bilinen küresel harmoniklerin seri açılımı, V = µ r ( 1+ n n=1 m= ( ae ) n( Cnm cosmλ+ r S nm sinmλ ) ) Pnm (cosθ) (4.14) ile açıklanır (Seeber, 23; Hofmann-Wellenhof ve Moritz, 25). (4.14) de geçen ilk terim µ/r, homojen bir kürenin potansiyelini temsil eder ve uydu jeodezisinde Kepler hareketi veya Kepler terimi olarak isimlendirilir. Geriye kalan terimler ise bozucu potansiyel olarak ifade edilir (Seeber, 23; Leick, 24; Hofmann-Wellenhof ve Moritz, 25): T = n n=2 m= µa e n r n+1( C nm cosmλ+ S nm sinmλ) P nm (cosθ) (4.15)
86 74 Burada, µ yerçekimi parametresi (GM = km 3 /s 2 ), a e yeryuvarınının ekvatoral yarıçapı, r konum vektörünün normu (r = x 2 +y 2 +z 2 ), λ jeosentrik boylam (λ = arctan(y/x)), ) θ kutup uzaklığı (θ = arctan( x2 +y 2 /z ), P nm C nm, S nm tam normalleştirilmiş bütünleşik Legendre fonksiyonları, tam normalleştirilmiş küresel harmonik katsayılar, n, m küresel harmonik açılımının derece ve sırası, x, y, z ECEF sisteminde kartezyen koordinatları ifade eder. Yerin gravite alanından kaynaklanan ivme değeri, bozucu gravite potansiyelinin gradyentinden türetilir. Hem kartezyen hem de küresel koordinatlar için gradyentler (Leick, 24; Swatschina, 29); r g = xyz T = D rφλ T (4.16) [ T xyz T = x, T y, T ] z (4.17) [ T rφλ T = r, T θ, T ] λ (4.18) olur. Eşitlikte yer alan D matrisi; D = r x r y r z θ x θ y θ z λ x λ y λ z (4.19) şeklinde tanımlanır. Küresel koordinatlara göre bozucu potansiyelin kısmi
87 75 türevleriyse, T r = 1 ( µ max r r)n n=2 T ( µ )n max θ = r n=2 n=2 ( ae ) n(1 n) n ( Cnm cosmλ+ r S nm sinmλ ) Pnm (cosθ) m= ) n n ( ae r m= ( Cnm cosmλ+ S nm sinmλ ) P nm (cosθ) θ T ( µ )n λ = max ( ae ) n n m ( C nm cosmλ+ r r S nm sinmλ ) Pnm (cosθ) m= (4.2) eşitlikleriyle ifade edilir. (4.16) ya göre gravite alanından kaynaklanan bozucu ivmenin bileşenleri aşağıdaki gibi bulunur: ( 1 r gx = r ( 1 r gy = r r gz = T r T r ( 1 T r r ) ( z T 1 r 2 x x 2 +y 2 θ ) z T r 2 x 2 +y 2 θ ( x2 +y 2 ) z + r 2 y ) T θ T x 2 +y 2 λ ( 1 T x 2 +y 2 λ ) y ) x (4.21) Yörünge belirleme uygulamalarında JGM-1, JGM-2 (Nerem ve ark., 1994), JGM-3 (Tapley ve ark., 1996), EGM96 (Lemoine ve ark., 1998), EIGEN1S (Reigber ve ark., 22), EIGEN2 (Reigber ve ark., 23), EIGEN-CHAMP3S (Reigber ve ark., 24), GGM1 (Tapley ve ark., 24), GGM2 (Tapley ve ark., 25), GGMS3 (Tapley ve ark., 27) gibi birçok gravite alan modeli kullanılabilir. Güncel bir modeli kullanmak sonuçların doğruluğu açısından önemlidir. Bir diğer önemli nokta küresel harmonik katsayıların hangi dereceye kadar kullanılması ile ilgilidir. GPS uyduları için 8, LEO uyduları için en az 7 ve daha üzeri açınım derecesi gravite alanından kaynaklı düzensizlikleri belirlemek için yeterli görülür (Bock, 23). Üçüncü Cisimler Uydular üzerinde çekim etkisinden kaynaklı ikinci en büyük etki, üçüncü cisimler olarak ifade edilen Ay ve Güneş in çekim etkileridir. Diğer gezegenlerin etkileri ise genelde ihmal edilebilir düzeydedir (Seeber, 23). Uydu üzerinde Ay ve
88 76 Güneş in çekim etkisi, ( rtb r r tb = GM tb r tb r r ) tb 3 r tb 3 (4.22) uydu ve gök cisimlerinin konumuna bağlı olarak ifade edilir (Seeber, 23; Montenbruck ve ark., 25; Bae, 26; Swatschina, 29). Burada, GM tb Ay ve Güneş e ait çekim sabiti, r tb Ay ve Güneş in yermerkezli konum vektörü, r uydunun yermerkezli konum vektörüdür. Ay ve Güneş için yerçekim etkisi büyüklükleri sırasıyla Ay km 3 s 2 GM tb = (4.23) Güneş km 3 s 2 değerleri sıklıkla kullanılır (Seeber, 23). Ay ve Güneş in koordinatları (efemeris bilgileri) JPL den, iyileştirilmiş efemeris (Development Ephemerides (DE)) ise DE2 ve DE45 den sağlanabilir. Çoğu uygulama için Ay ve Güneş in konumlarının çok yüksek doğrulukla bilinmesine gerek yoktur. Bundan dolayı Montenbruck ve ark. (25) sayfa 7-73 de verilen eşitlikler yardımıyla konum bilgisi düşük doğrulukta hesaplanarak ivme değerleri bulunabilir (Seeber, 23; Montenbruck ve ark., 25; Swatschina, 29). Gelgitler Bu başlık altında katı yer, okyanus ve kutup gelgitleri olmak üzere üç tip gelgitten söz edilecektir. Ay ve Güneş in çekim etkileri yer uyduları üzerinde doğrudan bir güç uygular. Bu güçler aynı zamanda yeryuvarı üzerinde de bir etki bırakır ve bundan dolayı yeryuvarı üzerinde zamana bağlı deformasyona neden olurlar. Yeryuvarının katı kısmı üzerinde oluşan bu küçük periyodik deformasyonlar katı yer gelgitleri olarak isimlendirilir. Benzer şekilde okyanuslar da Ay ve Güneş in hareketlerinden farklı biçimde etkilenirler. Bu ise okyanus gelgitleri olarak adlandırılır (Montenbruck ve ark., 25). Okyanus gelgitleri Ay ve Güneş in dolaylı çekim etkisi olarak değerlendirilir (Seeber, 23). Uydu üzerine etki eden katı yer
89 77 gelgitinden kaynaklanan bozucu ivme, r set = k 2 2 GM tb r 3 tb ( a 5 e 3 15cos 2 θ r ) r 4 r +6cosθr tb r tb (4.24) ile tanımlıdır (Ziebart, 21; Seeber, 23; Combrinck ve Suberlak, 27). Burada, θ; r tb ile r arasındaki açıyı, k 2 ise Love sayısını ifade eder. Love sayısı yerin esnekliğini tanımlayan bir parametredir. Genel olarak k 2 = olarak alınır ve katı yer gelgitlerinin frekanstan bağımsız ve ortalamasını temsil eder (McCarthy, 1996). Katı yer gelgit etkisini açıklamak için küresel harmoniklerden yararlanarak gelgit potansiyeli geliştirilmiştir. Böylece küresel harmonik katsayılarına (C nm,s nm ) bu etkiden kaynaklanan düzeltme terimleri ( C nm, S nm ) ilave edilir. Daha duyarlı çözümler için McCarthy ve Petit (24) e bakılabilir. Katı yer gelgit davranışlarına benzer şekilde okyanus gelgit etkisi küresel harmonik katsayılar (C nm,s nm ) kullanılarak modellenebilir. Katı yer gelgit etkisi ile karşılaştırıldığında okyanus gelgitleri daha küçük genlikli etkilerdir. Uydular üzerindeki okyanus gelgit etkisi düzensiz kıyı şeritleri yüzünden daha karmaşık ve zor modellenir. Son olarak kutup hareketinin merkezkaç etkisi yeryuvarının dış potansiyelinde bir düzensizlik yaratır ve bu düzensizlik kutup gelgiti olarak isimlendirilir. Bu etki kutup hareket bileşenlerine (x p,y p ) bağlı olarak C 21,S 21 jeopotansiyel katsayılarındaki değişimi olarak hesaplanabilir (McCarthy, 1996; McCarthy ve Petit, 24; Swatschina, 29). Sözü geçen gelgitler için detaylı bilgi McCarthy (1996); Seeber (23); McCarthy ve Petit (24); Montenbruck ve ark. (25); Combrinck ve Suberlak (27) de bulunabilir.
90 Yerçekimi ile İlişkili Olmayan Düzensizlikler Atmosferik Sürüklenme Alçak yörüngedeki uydular için atmosfer, yerçekimini içermeyen bozucu nedenler arasında en başta yer alır. Uydular açısından atmosferik etkileri modellemek birçok açıdan oldukça zordur. Atmosferik ortamın değişkenliği ve yoğunluk dağılımı düzensizliği, farklı uydu yüzeylerinin atmosferik gazlarla etkileşimi, sıcaklık, uydu geometri ve hız bilgisinin tam olarak bilinememesi gibi çok değişik olaylar söz konusu zorluğun nedenleri arasındadır (Bock, 23; Swatschina, 29). Diğer atmosferik kuvvetler (kaldırma kuvveti, binormal kuvvetler) ile karşılaştırıldığında LEO uyduları üzerindeki en önemli atmosferik etki sürüklenme etkisidir. Atmosferik sürüklenme, uydunun hareket yönüne karşı bir etki oluşturur. Bundan dolayı uydu zamanla yavaşlar (Montenbruck ve ark., 25). Atmosferik sürüklenmeden kaynaklı ivme, r drag = 1 2 C A ṙ D m ρ(r,t) ṙ 2 ṙ (4.25) ile gösterilir (Seeber, 23; Tapley ve ark., 24; Montenbruck ve ark., 25; Vallado, 25; Beutler ve ark., 25b; Swatschina, 29). Burada, m uydunun kütlesi C D A sürüklenme katsayısı uydunun kesit alanı ρ(r, t) uydu konumundaki atmosferik yoğunluk r, ṙ uydunun konum ve hız vektörünü ifade eder. Kaldırma ve binormal kuvvetler uydunun hareket doğrultusuna dik yönde bir etki yaratırlar; fakat, genelde ihmal edilirler. Bundan dolayı (4.25), gülle (cannonball) modeli olarak tanımlanır. (4.25) de geçen C D sürüklenme katsayısı uydunun yüzey malzemesi ile atmosferin etkileşimini tanımlayan bir katsayıdır ve her bir uydu için özel tanımlanır. Genel olarak bu katsayı aralığında değişen değerler alır ve yörünge belirleme işlemi içerisinde kestirilebilir (Seeber, 23; Montenbruck ve ark., 25; Swatschina, 29). Atmosferik yoğunluk ise uydunun
91 79 yüksekliği, coğrafi konum, zaman, mevsim gibi birçok parametreye bağlı olarak değişiklik gösterir. Uydu yüksekliğine göre bazı yoğunluk değerleri Çizelge 4.4 de verilmiştir (Seeber, 23; Montenbruck ve ark., 25). Çizelge 4.4. Uydu yüksekliğine göre atmosfer yoğunluk değişimi (Seeber, 23; Montenbruck ve ark., 25) Yükseklik Yoğunluk Yükseklik Yoğunluk (km) (g/km 3 ) (km) (g/km 3 ) Çizelge 4.4 e bakıldığında LEO uyduları üzerinde atmosferik etkinin daha büyük değerler aldığı bunun yanında daha yüksek yörüngede bulunan uydular (örneğin GPS) içinse bu etkinin ortadan kalktığı söylenebilir. Genel olarak birçok uygulama için sürüklenme modeli kabul edilebilir bir doğrulukta modellenebilir. Bunlar arasında Harris-Priester modeli (Harris ve Priester, 1962) ve Jacchia 1971 yoğunluk modeli (Jacchia, 1971) en çok bilinenlerdendir (Montenbruck ve ark., 25). Güneşin Radyasyon Basıncı Güneş tarafından sürekli olarak yayılan radyasyon molekülleri uydu üzerinde dolaysız ve dolaylı olmak üzere iki etkiye sebep olur. Uydu ile güneş radyasyonunun etkileşimi sonucunda dolaysız, yeryuvarından yansıması sonucunda ise dolaylı radyasyon basıncı (albedo) ortaya çıkar. Dolaysız radyasyon basıncı modellemesi de atmosferik sürüklenme modellemesine benzer şekilde zorluklar içerir. Modellemenin yapılabilmesi için Güneş ve uydunun konumu, radyasyona maruz kalan uydu kesit alanı ve uydunun yansıtma katsayısı gibi parametrelerin bilinmesi gereklidir. İvme değeri, r srp = C srsaau 2 2cm r r gn r r gn 3 (4.26) eşitliği ile hesaplanabilir (Seeber, 23; Beutler ve ark., 25b; Swatschina, 29). Burada,
92 8 C sr uydu yüzeyinin yansıtma özelliklerini tanımlayan katsayı AU astronomik birim (AU = m) S Güneş sabitesi (S = w/m 2 ) c ışık hızı ( m/sn) A uydu kesit alanı m uydu kütlesi r uydunun yermerkezli konum vektörü r gn Güneş in yermerkezli konum vektörünü ifade eder. (4.26) genel olarak radyasyon basıncı için ilk yaklaşım olarak düşünülür. Daha detaylı deneysel bir yaklaşım GPS uydularında da oldukça kullanılan ve ivmeleri üç yönde ifade eden yaklaşımdır. Detaylı bilgi için Ziebart (21); Bock (23); Swatschina (29) a bakılabilir. Albedo ise uydu üzerinde küçük bir basınca sahip olmasına rağmen kara, deniz ve bulutların zamansal değişimlerinden dolayı oldukça zor modellenen bir kısımdır. Birçok çalışma için dolaysız radyasyon basıncının %1 nundan daha küçük olarak düşünülür. GPS uydularının yörünge kestirimlerinde %1 %2 arasında etkiye sebep olduğundan bu etki GPS uydularında genelde ihmal edilir (Seeber, 23). 4.4 İndirgenmiş Dinamik Yörünge Belirleme Dinamik modelin kalitesi, kurulan güç modeline ve GPS izleme verilerine bağlıdır. Benzer şekilde kinematik modelin kalitesi de GPS ölçümlerinin kalitesine, uydu geometrisine bağlı olarak değişir. Günümüzde LEO uydularına ait GPS izleme verileri sürekli ve yüksek duyarlıkta elde edilebilir ve LEO uydularına etki eden bozucu kuvvetler olabildiğince giderilir. Fakat dinamik modelde kestirim süresi arttıkça modelin duyarlılığı süreye bağlı olarak azalır. Kinematik modelde ise GPS ölçülerindeki veri boşlukları, GPS uydu dağılımı, GPS uydu ve saat bilgisi kalitesi yanında modelin sürekli olmaması model duyarlılığını etkileyen faktörlerdendir. Bu iki yaklaşımın dezavantajlarını giderecek ve GPS ölçme duyarlılığından yararlanılabilecek bir çözüm önerisi olarak indirgenmiş dinamik (reduced-dynamic) yaklaşımı geliştirilmiştir. Bu yaklaşım ardışık Kalman filtreleme tekniğini kullanarak yörünge çözümlerini elde eder. Tekniğin zaman ve ölçü güncellemesi adı altında iki
93 81 önemli adımı bulunur (Yunck ve ark., 199; Wu ve ark., 199, 1991). Yaklaşım sürekli GPS verileri ile dinamik çözümün tekrar düzeltilmesi üzerine kuruludur. Kalman filtreleme tekniğindeki gürültülerin doğru ya da uygun ağırlıklandırılması yöntemin önemli bir aşamasıdır. Gürültü modeli, varyans ve zaman sabiti olmak üzere iki parametre ile tanımlanır. Zaman sabiti büyük ve varyans yaklaşık olarak sıfır olduğunda geometrik bilgiler ortadan yok olur ve model yalnızca dinamik stratejiye bağlı olur. Zaman sabiti sıfır (white-noise) ve varyans yüksek olduğunda ise çözüm büyük ölçüde geometrik verilere bağlı olur (Seeber, 23). (4.7) de dinamik yörünge parametreleri (q 1,...,q d ), analitik bir ivme modeli ile ilişkili olması durumunda deterministik parametreler adını alır. İndirgenmiş dinamik yaklaşımda (4.7) ye deterministik parametreler ile birlikte dengelemeye ek stokastik parametreler ilave edilir. Bu ek parametreler uydunun yörüngesi için çözüm duyarlılığını arttırır. Bu ek parametrelere sözde stokastik parametreler adı verilir. Böylece (4.7), r = GM r 3 r+f 1(t,r,ṙ,q 1,...,q d,p 1,...,p s ) = f (4.27) şeklini alır. İndirgenmiş dinamik model çözümü sözde stokastik parametrelere ve bu parametreler üzerindeki kısıtlamalara bağlıdır (Swatschina, 29). (4.27) deki gibi, dinamik güç modeline ilave edilen çok sayıda sözde stokastik güç modeli geliştirilmiştir (Jäggi, 27). Sözde stokastik parametreler güç alanı eksikliklerin etkisini belli bir ölçüde azaltabilir. Bu yöntemlerden en çok kullanılanları parçalı sabit ivmeler (piecewise constant accelerations), parçalı doğrusal ivmeler (piecewise linear accelerations) ve sözde stokastik sinyaller (pseudo-stochastic pulses) veya anlık hız değişimleridir (instantaneous velocity changes). Bu üç modelleme tekniği de, uydu dinamiklerindeki modelleme eksikliklerini azaltmak için uygundur (Jäggi, 27). Bernese v5. programında LEO uydularının indirgenmiş dinamik yörünge belirleme işlemleri sözde stokastik sinyaller (anlık hız değişimleri) yardımıyla GPSEST modülünde gerçekleştirilir. Sözde stokastik sinyaller radial, along-track ve cross-track bileşenleri üzerinde kurulur ve klasik en küçük kareler dengeleme işleminde bilinmeyen parametre olarak alınır. Her bir sözde stokastik sinyal için bir öncül varyans tanımlanır (Bock, 23). Bu sistem Beutler ve ark. (1994) tarafından
94 82 GPS uydularının yörünge kalitesinin iyileştirilmesi ve güneş radyasyon basıncı modellemesindeki eksiklikleri telafi etmek için tanımlanmıştır. Daha sonrasında çok sayıda sinyalin verimli bir biçimde kurulması yönünden LEO uydularının indirgenmiş dinamik DYB çalışmalarında da etkili olabileceği anlaşılmıştır (Jäggi ve ark., 26). Sözde stokastik sinyaller yönteminin en belirgin özellikleri genel olarak şu başlıklar altında tanımlanır (Beutler ve ark., 25a): Yörünge yayları süreklidir ve diferansiyel denklem sistemleri (hareket denklemi) ile temsil edilir. Sinyaller daha önceden belirlenen yönlerde (RAC) kurulur ve en küçük kareler dengelemesinde parametre olarak dengelemeye dahil edilir. Sinyaller, sıfır ümit değeri ve varyans ile tanımlanır. Hız değişimlerinin (δv) büyüklüğü, yapay gözlem denklemleri (4.28) ve önsel ağırlıklar (4.29) ile kontrol edilir. δv = (4.28) w = σ2 σ 2 δv (4.29) Böylece hız değişimleri, varyans (σδv 2 ) ve ümit değeri sıfır olan rasgele değişkenlerle kısıtlanmış olur. Burada σ, birim ağırlıklı ölçününortalama hatasıdır. Eğer σ δv büyükse ağırlık w küçük olacaktır. Bu durumda hız değişimlerinin (δv) büyük değerler aldığı farz edilir. Eğer σ δv küçükse sadece küçük hız değişimlerinin mümkün olduğu söylenebilir (Beutler ve ark., 25a). Ayrıca, anlık hız değişimlerinin (sözde stokastik parametreler) kurulmasının temel amacı güç modeli eksikliklerinin giderilmesidir. Önceden tanımlanmış e(t i ) (radial, along-track ve cross-track) yönlerindeki t i zamanına ilişkin bir sinyal v i olarak alınırsa, (4.27) deki f 1 içerisinde yer alan p i parametreleri v i sinyallerine eşitlenerek (p i = v i ), v i δ(t t i ) e(t) yazılabilir. Burada δ(t) Dirac ın delta fonksiyonunu temsil eder (Jäggi, 27). Böylece (4.12) ye benzer
95 83 şekilde sistemin varyasyon denklemi z vi = A z vi +A 1 ż vi +δ(t t i ) e(t) (4.3) şeklinde oluşturulur. Fakat p i parametresi hıza bağımlı olmadığından sıfır başlangıç değerleri ile varyasyon denklemi z vi = A z vi +δ(t t i ) e(t) (4.31) daha sade bir biçimde yazılabilir (Jäggi ve ark., 26). z vi, t zamanına ait altı başlangıç koşulunu tanımlayan altı parametreye göre öncül yörüngenin kısmi türevlerinin doğrusal bir kombinasyonu olarak yazılır. Bu durumda (4.31) etkili bir biçimde çözülebilir. Fakat konum vektörü r(t) sürekli elde edilirken, iyileştirilmiş yörüngenin hız vektörü ṙ(t) süreksizlikler içerir. Bu durum yöntemin dezavantajı olarak görülebilir. Bu süreksizlik ise t i sinyal epoklarında gerçekleşir (Beutler ve ark., 1994; Jäggi ve ark., 26; Jäggi, 27). Sözde stokastik yörünge modellemesi için temel eşitlikler, yöntemlerin ayrıntılı tanıtımları ve etkili çözümler Beutler ve ark. (1994); Jäggi ve ark. (23, 25); Beutler ve ark. (25a); Jäggi ve ark. (26); Jäggi (27); Jäggi ve ark. (21) de bulunabilir. 4.5 Uydu Lazer Ölçmeleri Uydu lazer ölçme sistemi (Satellite Laser Ranging), uydu ile yer istasyonu arasındaki uzaklığı ölçmek için geliştirilmiş bir tekniktir. Yer istasyonundan gönderilen lazer sinyali uyduya ulaşır. Uyduda bulunan yansıtıcılar (retroreflectors) yardımıyla bu sinyal tekrar yer istasyonuna iletilir. Böylece sinyalin uyduya gidiş ve gelişi arasındaki zaman farkı ( t) belirlenir. Bu zaman farkının ışık hızı (c) ile ölçeklendirilmesiyle uzunluk elde edilir. Temel gözlem eşitliği d = t 2 c (4.32) olarak ifade edilir (Seeber, 23). Lazer sistemlerinin gelişimi yapay uyduların izlenmesi amacıyla 1961/1962 yıllarında ABD de başlamıştır. Lazer yansıtıcı taşıyan ilk uydu (BEACON EXPLORER-B) 1964 yılında yaklaşık 1 km yükseklik
96 84 ve 8 eğim açısıyla fırlatılmış ve ilk başarılı sinyal 1965 yılında birkaç metre duyarlığında elde edilebilmiştir. Sonraki yıllarda, teknolojinin gelişmesine paralel olarak, lazer ölçme sistemlerindeki gelişmeler çok hızlı bir şekilde ilerlemiş ve uzunluk ölçme duyarlığı birkaç metre seviyelerinden birkaç milimetre seviyelerine kadar iyileştirilmiştir (Seeber, 23). SLR hizmeti Uluslararası Lazer Ölçme Servisi (ILRS) tarafından yürütülmektedir. ILRS, SLR ve LLR verilerini toplar, birleştirir, analiz eder ve kullanıcının hizmetine sunar. Yeryüzüne dağılmış çok sayıda SLR istasyonu vardır (Şekil 4.5). Şekil 4.5. SLR istasyonları (ILRS, 212d) SLR tekniği özellikle jeodezik ve jeodinamik çalışmalara önemli katkıda bulunur. Bunlar kısaca yersel referans sistemi, tektonik plaka hareketleri, yer dönme parametreleri, yeryuvarına ait gelgit hareket modelleri, gravite alanı ve uydu yörüngelerinin belirlenmesi olarak sıralanabilir. Teknik bu kadar önemli katkıyı sağlarken bazı zayıf yönleri de içinde barındırır. Bunlardan en önemlileri; hava şartlarına bağlı olması, yer istasyonlarının yapımı ve sürekliliğinin yüksek maliyet gerektirmesi, GPS, DORIS veya VLBI ile karşılaştırıldığında veri miktarının kısıtlı olması, yeterli ve homojen dağılımlı yer istasyonlarının olmaması sayılabilir (Seeber, 23; Prange, 211; Shabanloui, 212; NASA, 212b). SLR tekniği, GNSS ve LEO yörüngelerinin doğrulaması veya kontrolü için
97 85 kullanılabilir (Beutler ve ark., 27). Bu tez çalışmasında ILRS nin temel veri formatı olan normal nokta verisi (Normal PoinT data) baz alınarak elde edilen yörüngelerin kontrolü yapılmıştır. NPT aynı zamanda hızlı-görünüm verisi (quicklook data) olarak isimlendirilir. Çünkü NPT verileri uydu geçişini yaptıktan kısa bir süre sonra üretilir ve hızlı bir biçimde(birkaç saat içerisinde) veri merkezlerine iletilir (ILRS, 212d). Bunun yanında SLR istasyonları genelde GPS sabit istasyonlarının yanına tesis edilir. Böylece SLR gözlemleri kolay bir biçimde GPS sistem zamanı ile eşleştirilebilir (Jäggi, 27). Bernese v5. programının GPSEST modülü yardımıyla yörünge kontrolü, SLR ye göre uzaklık hataları olarak hesaplanır. Bu hesaplama SLR istasyonu ile gözlem yapılan uydu arasındaki uzaklığın, istasyon koordinatları ve uydu yörüngesinden türetilen uzaklık ile karşılaştırılmasına dayanır (Beutler ve ark., 27). SLR tekniğiyle ilgili detaylı bilgi Seeber (23); Tapley ve ark. (24); Montenbruck ve ark. (25); ILRS (212d); NASA (212b) kaynaklarından edinilebilir. Ayrıca, SLR uzaklık ölçümlerinin düzeltmeleri için genellikle Marrini- Murray troposferik modeli kullanılır (Bae, 26; Beutler ve ark., 27). Detaylı bilgi için McCarthy ve Petit (24) e bakılabilir. 4.6 Duyarlı Yörünge Belirleme Stratejisi Bu bölümde DYB işlemlerinin Bernese v5. programıyla nasıl belirleneceği üzerinde durulacaktır. Kinematik yörünge yukarıda da bahsedildiği üzere SF ve IBDK kombinasyonu kullanılarak belirlenmektedir. Bernese programı ardışık epokların faz gözlemleri arasındaki farklarını oluşturarak bilinmeyen parametreleri ortadan kaldırmayı hedefleyen etkin bir yaklaşım kullanır (Svehla ve Rothacher, 22). Programda kinematik yörünge belirleme işlemi iteratif bir yaklaşımla üç adımda ele alınır (Bock, 23): İlk işlem adımı uyduya ait önsel bir konum bilgisi olmaksızın sadece LEO kod gözlemleri kullanılarak kinematik konumların kestirilmesidir. Kestirilen konumlar kod gözlemlerinin doğruluğuna (birkaç metre) yakındır. Bu konumlar indirgenmiş dinamik yörünge belirlemek için sözde-gözlemler (pseudo-observations) olarak kullanılır. Bu belirlenen yörünge, ikinci aşama için önsel yörünge olarak ele alınır.
98 86 İkinci işlem adımı yine sadece LEO kod gözlemlerinin kullanılmasıyla bir tarama işlemini içerir. Tarama işleminden sonra ikinci bir yörünge belirlenir ve bu yörünge son işlem adımına önsel bilgi olarak sokulur. Son işlem adımı faz ve kod ölçülerinin birlikte kullanılmasıdır. Faz bilinmeyenlerini elemine etmek için faz ölçümleri zaman farkı gözlemleri şeklinde oluşturulur. Böylece sadece konum farkları kestirilir. Bu konum farkları faz gözlemlerinin duyarlılığına (mm, cm) yakındır. Son olarak kinematik çözüm, konum ve konum farkları kullanılarak en küçük karelerle dengeleme işleminden türetilir. Yukarıda da söz edildiği üzere program modüllerinden biri olan GPSEST ile LEO uydularının kinematik, dinamik ve indirgenmiş dinamik yörünge hesaplamaları yapılabilir (Bock, 23; Jäggi, 27). Tüm hesaplamalar için genel bir akış şeması Şekil 4.6 da verilmiştir. Modüller ve LEO uydularının yörünge belirlemesi hakkında detaylı bilgi Beutler ve ark. (27) den elde edilebilir. RXOBV3 - Veri dönüşümü * RINEX gözlemleri * CODE final ürünleri * LEO ürünleri KINPRE - Önsel Yörüngeden hassas yörünge dosyası belirleme (LEO) Şekil 4.6. Bernese yörünge belirleme iş akış şeması
99 87 Şekil 4.6 incelendiğinde iteratif bir yaklaşım kullanıldığı açıkça görülmektedir. Genelde ikinci iterasyonda yörünge sonuçları tutarlı hale gelir. Ayrıca değerlendirmeye geçmeden önce Bernese ftp sitesinden programın kullandığı dosyaların güncel halleri edinilmelidir. Unutulmaması gereken bir başka detay ise LEO uyduları ile değerlendirmeye geçmeden önce program içerisinde bir takım değişiklikler yapılmalıdır. LEO uydularının çok hızlı yer değiştirmesinden dolayı bilinmeyen sayısı oldukça fazladır. Bu yüzden bir günlük verinin değerlendirilmesi için algoritmanın işleyebileceği şekilde parametre (boyut) değişikliğine gidilmesi gerekir (bkz. (Beutler ve ark., 27)).
100 88 5. SAYISAL UYGULAMA Bu bölümde öncelikle uydu yörünge belirleme işlemlerinde bozucu kuvvetlerin konuma olan etkisi ortaya konmuştur. Sonrasında duyarlı yörünge belirleme yöntemleri CHAMP ve GRACE uyduları üzerinde uygulanmış; sonuçlar diğer enstitüler tarafından üretilen yörünge sonuçları ile karşılaştırılmıştır. Bu işleme ilave olarak SLR verileri yardımıyla her uydu için yörünge kontrolleri gerçekleştirilmiştir. Öte yandan GOCE uydusunun yörünge belirleme işlemleri, CHAMP ve GRACE için kullanılan Bernese yazılımından farklı olarak, XML-Parser programı kullanılarak tamamlanmıştır. Bu işlemle, kinematik ve indirgenmiş dinamik yörünge model sonuçları elde edilmiş ve SLR kontrolü yapılmıştır. 5.1 SP3/TLE verileriyle dinamik yörünge belirleme LEO uydularının yörüngelerinin belirlenmesi kapsamında MATLAB ortamında bir yazılım (DINORB) geliştirilmiştir. Yazılım TLE (Two Line Elements) veri analizi, SGP (Simplified General Perturbations) modelleri kullanılarak çoklu uydu kestirimi ve dinamik yörünge modelini barındırmaktadır. Yörünge bilgileri farklı formatlar ve çeşitli doğruluk seviyelerinde bazı kurumlar tarafından yayımlanmaktadır. Bu formatlardan birisi de TLE formatıdır. NASA Goddard Space Flight Center (GSFC), Space-Track (The Source for Space Surveillance Data), GFZ Potsdam Prediction Center ve CelesTrack gibi kuruluşlar bu formatı yayımlarlar. Bu ürün dosyaları GPS, SLR ve yörünge verilerinden türetilir ve günde iki kez güncellenerek yayımlanır. Hoots ve Roehrich (198) e göre TLE verilerinde uygun kestirimler elde etmek için SGP, SGP4, SDP4, SGP8 ve SDP8 modellerinden yörünge yüksekliğine göre uygun olanının veya birleşik modellerin kullanılması gerektiği açıklanmıştır. Yazılımın TLE analizi kısmında uydulara ait bir TLE verisinin yayılım modelleri ile değerlendirilip konum ve hızları elde edilmektedir. Kullanılan yayılım modeli SGP4/SDP4 kombine modelidir. Ayrıca bu bölümde ECI, ECEF, coğrafi koordinat sistemleri arasında dönüşümler ve Google-Earth gösterimleri, rapor dosyaları bulunmaktadır. TLE verisi hakkında daha detaylı bilgi Hoots ve Roehrich (198); Kelso (1998); Baranov (29); Miura (29); Levit ve Marshall (211) kaynaklarında bulunabilir. Tez kapsamında bu veri
101 89 türü ile yapılan uygulamalara değinilmemiştir. Tezde söz edilen dinamik güç modeline ilişkin kuvvetlerin ortaya konması amacıyla geliştirilen dinamik yörünge belirleme modülünün giriş ve çizim paneli Şekil 5.1 de verilmiştir. Şekil 5.1 de görüldüğü üzere ilk panel giriş paneli olup uyduya ait başlangıç konum ve hızları, zaman bilgisi, güç modeli ve bozucu etkileri içerir. İkinci panel ise sonuçların hesaplandığı ve gösterildiği paneldir. Burada konum ve hızlar hem ECI hem de RAC sisteminde gösterilir. Ayrıca farklı gravite alanları ve aynı gravite alanına ait farklı derece, sıra karşılaştırılması yapılabilir. DINORB yazılımına ilişkin akış diyagramı Şekil 5.2 de verilmiştir. Şekil 5.1. Dinamik yörünge belirleme için giriş ve çizim paneli Yer gravite alanı (4.21) Başlangıç Yörünge Bilgisi (SP3/TLE) Atmosferik sürüklenme (4.26) Ay ve Güneş'in çekim etkileri (4.22) Yörünge Kestirim Sonuçları Radyasyon basıncı (4.27) Kontrol (SP3) Farklar (ECI ve RAC) Gravite Alan Karşılaştırması Raporlama ve Grafik Gösterim Şekil 5.2. DINORB yazılımı akış diyagramı
102 9 Uygulama için CHAMP uydusuna ait bir değerlendirme yapılmıştır. Değerlendirmede CHAMP uydusuna etki eden bozucu kuvvetlerin etkileri ayrı ayrı ortaya konmuştur. Uygulamada sayısal integrasyon yöntemi olarak Runge-Kutta yöntemi ve bağıl hata değeri olarak 1e-15 seçilmiştir. Sayısal analiz çözümü ile 6 saatlik CHAMP yörünge çözüm sonuçları metre seviyelerinde elde edilmiştir. Ayrıca bozucu kuvvetlerin etkilerinin ayrı ayrı değerlendirmesi sonucunda en büyük etkinin gravite alanından kaynaklandığı görülmüştür. Yazılımda birden fazla gravite alan seçeneği mevcuttur. İstenilen gravite alanı, derece ve sıra tanımlaması yapılabilir. Yazılımda şu anda gravite alan modellerinden EIGEN-GL4C, WGS84, EGM96, WGS84-EGM96, JGM-2 ve JGM-3 modelleri kullanılabilmektedir. Ayrıca dinamik güç modeli için yer gravite alanı, atmosferik sürüklenme, güneş radyasyon basıncı ve üçüncü cisimlerin etkisi incelenebilmektedir. Bu etkilerin ayrı ayrı konum ve hız bileşeni üzerine olan etkisini ortaya koymak için sıfır derece terimi (zero degree term) ifadesi tanımlanmıştır. Bu ifade, kullanılan gravite alanının derece ve sırasının sıfır olarak alınması ve herhangi bir bozucu kuvvetin uydu hareket denklemine etki etmemesi anlamına gelir. Dinamik yörünge belirlemede bozucu kuvvetlerin etkileri Bu bilgiler ışığında bozucu kuvvetlerin etkileri ayrı ayrı ortaya konulmuş ve uydu konum, hızına maksimum etki miktarları hesaplanmıştır. Çizelge 5.1 de 6 saatlik integrasyon sonucunda bozucu kuvvetlerin uydu konum ve hız bileşenlerine olan en büyük etki değerleri gösterilmiştir. Çizelge 5.1. Bozucu kuvvetlerin etkileri Bozucu etki Konum Farkı (km) Hız Farkı (km/sn) Şekil No Güneş in etkisi Ay ın etkisi Güneş radyasyon basıncı Atmosferik sürüklenme Gravite alanı (7x7)
103 91 Şekil 5.3. Güneş in etkisi Şekil 5.4. Ay ın etkisi
104 92 Şekil 5.5. Güneş radyasyon basıncı etkisi Şekil 5.6. Atmosferik sürüklenme etkisi
105 93 Şekil 5.7. Gravite alan etkisi (EIGENGL4C-7x7) Bu etkiler hesaplandıktan sonra gerçek yörünge ile kestirilen yörünge arasındaki farklar iki ayrı sistemde ortaya konmuştur (Şekil 5.8 ve 5.9). Gerçek yörünge dosyası için NGS nin CHAMP e ait SP3 yörünge yayını baz alınmıştır. Kestirilen yörünge ise yukarıda hesaplanan etkilerle ile birlikte sayısal integrasyon çözümü olarak bulunan yörüngeyi temsil etmektedir. Şekil 5.8. ECI sisteminde gerçek ve kestirilen konumlara ait farklar
106 Radial Along Cross 25 difference (m) epochs (interval is 6 seconds) Şekil 5.9. RAC sisteminde gerçek ve kestirilen konumlara ait farklar Şekillerden görüldüğü üzere integrasyon zamanı arttıkça dinamik modelin kalitesi düşmektedir. Fakat uydunun yaklaşık iki devri için kestirim sonuçları birkaç metre civarında elde edilmiştir. Buradan uydunun tam bir devri için dinamik model sonuçlarının iyi olduğu söylenebilir. Bu durumu daha net görebilmek için uydu konumlarının farklı kestirim sürelerine ilişkin RMS değerleri hesap edilmiştir(çizelge 5.2). Çizelge 5.2. Farklı kestirim sürelerine ilişkin RMS değerleri Süre (dk) RMS x (m) RMS y (m) RMS z (m) Ayrıca yazılımda farklı gravite alanlarının kullanılmasıyla elde edilebilecek doğruluk gösterimi yapılmıştır (Şekil 5.1). Böylece kullanılabilecek gravite alanları hakkında hızlı bir fikir edinilmesi amaçlanmıştır. Benzer şekilde aynı gravite alanı için farklı derece ve sıra seçiminin etkisi Şekil 5.11 de gösterilmiştir. Bu iki şekilden CHAMP uydusu için EIGEN-GL4C ve 7x7 derece ve sıra seçiminin uygun olduğu görülmüştür.
107 95 Şekil 5.1. Gravite alanlarının karşılaştırılması (7x7) Gravity model is EIGENGL4C 2 12x12 24x24 7x7 15 magnitude (m) epochs (interval is 6 seconds) Şekil Gravite alanı derece ve sıra karşılaştırılması (EIGENGL4C) 5.2 CHAMP Uydusu için DYB İşlemleri CHAMP uydusu, bilindiği üzere gravite alanı belirleme amaçlı olarak gönderilen ilk uydu sıfatını taşımaktadır. Yörünge yüksekliği yaklaşık 454 km ve yörünge periyodu 96 dakika civarında olan bir LEO uydusudur (bkz. Bölüm 2). LEO uydularının yörüngelerinin hesaplanması için GPS uydularına ait saat bilgisini de içeren duyarlı yörünge dosyaları (EPH/SP3 uzantılı-15 dakika aralıklı) ve bunlardan türetilen yüksek duyarlıklı saat dosyaları (CLK uzantılı-3 sn aralıklı), yer dönüklük parametreleri (ERP uzantılı) ve LEO uydularına ait gözlem dosyaları gereklidir (bkz. Bölüm 3). CHAMP uydusuna ait gözlem dosyası GFZ ye bağlı ISDC veri merkezinden kullanıcılara ücretsiz olarak sunulmaktadır. Uydu gözlem dosyası RINEX formatında olup örneklem aralığı 1 sn dir.
UYDU JEODEZISI: ÖLÇME YÖNTEM VE TEKNIKLERI
 UYDU JEODEZISI: ÖLÇME YÖNTEM VE TEKNIKLERI Gözlem noktasına baglı yöntemler: Yerden uyduya Uydudan yer noktasına Uydudan uyduya Ölçünün cinsine baglı yöntemler: Dogrultu ölçmeleri (geometrik yöntem) Çift
UYDU JEODEZISI: ÖLÇME YÖNTEM VE TEKNIKLERI Gözlem noktasına baglı yöntemler: Yerden uyduya Uydudan yer noktasına Uydudan uyduya Ölçünün cinsine baglı yöntemler: Dogrultu ölçmeleri (geometrik yöntem) Çift
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ (Ölçüler Yöntemleri) Prof. Dr. Mualla YALÇINKAYA
 JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ (Ölçüler Yöntemleri) Prof. Dr. Mualla YALÇINKAYA ÖLÇÜ TEKNİKLERİ I- Uydu ve Uzay Teknikleri VLBI SLR GPS DORIS INSAR Gravite Uydu Sistemleri (Uydu ve Uzay Teknikleri)
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ (Ölçüler Yöntemleri) Prof. Dr. Mualla YALÇINKAYA ÖLÇÜ TEKNİKLERİ I- Uydu ve Uzay Teknikleri VLBI SLR GPS DORIS INSAR Gravite Uydu Sistemleri (Uydu ve Uzay Teknikleri)
GNSS Teknikleri ve Uygulamaları
 GNSS Teknikleri ve Uygulamaları Yrd. Doç. Dr. Sefa YALVAÇ Gümüşhane, 2017 Gümüşhane Üniversitesi, 2017 Versiyon: 2017.0 Bölüm-1 Tarihçe Tarih boyunca insanlar, Neredeyim? Nereye gidiyorum? sorularına cevap
GNSS Teknikleri ve Uygulamaları Yrd. Doç. Dr. Sefa YALVAÇ Gümüşhane, 2017 Gümüşhane Üniversitesi, 2017 Versiyon: 2017.0 Bölüm-1 Tarihçe Tarih boyunca insanlar, Neredeyim? Nereye gidiyorum? sorularına cevap
Uydu Jeodezisi. Lisans Ders Notları. Yrd. Doç. Dr. Aydın ÜSTÜN. Konya, 2010. Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi
 Uydu Jeodezisi Lisans Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Harita Mühendisliği Bölümü Konya, 2010 A. Üstün (Selçuk Üniversitesi) Uydu Jeodezisi (v.02.11.10)
Uydu Jeodezisi Lisans Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Harita Mühendisliği Bölümü Konya, 2010 A. Üstün (Selçuk Üniversitesi) Uydu Jeodezisi (v.02.11.10)
JEODEZİK ÖLÇMELER DERSİ. Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE
 JEODEZİK ÖLÇMELER DERSİ Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM 1. Hafta Ders Notları REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM Referans (Koordinat)
JEODEZİK ÖLÇMELER DERSİ Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM 1. Hafta Ders Notları REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM Referans (Koordinat)
JEOİD ve JEOİD BELİRLEME
 JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
HARİTA DAİRESİ BAŞKANLIĞI. İSTANBUL TKBM HİZMET İÇİ EĞİTİM Temel Jeodezi ve GNSS
 HİZMET İÇİ EĞİTİM MART 2015 İSTANBUL TAPU VE KADASTRO II.BÖLGE MÜDÜRLÜĞÜ SUNUM PLANI 1- Jeodezi 2- Koordinat sistemleri 3- GNSS 3 JEODEZİ Jeodezi; Yeryuvarının şekil, boyut, ve gravite alanı ile zamana
HİZMET İÇİ EĞİTİM MART 2015 İSTANBUL TAPU VE KADASTRO II.BÖLGE MÜDÜRLÜĞÜ SUNUM PLANI 1- Jeodezi 2- Koordinat sistemleri 3- GNSS 3 JEODEZİ Jeodezi; Yeryuvarının şekil, boyut, ve gravite alanı ile zamana
JEODEZİ. Şekil1: Yerin şekli YERİN ŞEKLİ JEOİD
 JEODEZİ Jeodezi, üç boyutlu ve zaman değişkenli uzayda, çekim alanı ile birlikte, yeryuvarının ve öteki gök cisimlerinin ölçülmesi ve haritaya aktarılması ile uğraşan bilim dalıdır. Şekil1: Yerin şekli
JEODEZİ Jeodezi, üç boyutlu ve zaman değişkenli uzayda, çekim alanı ile birlikte, yeryuvarının ve öteki gök cisimlerinin ölçülmesi ve haritaya aktarılması ile uğraşan bilim dalıdır. Şekil1: Yerin şekli
EKVATORAL KOORDİNAT SİSTEMİ
 EKVATORAL KOORDİNAT SİSTEMİ Dünya nın yüzeyi üzerindeki bir noktayı belirlemek için enlem ve boylam sistemini kullanıyoruz. Gök küresi üzerinde de Dünya nın kutuplarına ve ekvatoruna dayandırılan ekvatoral
EKVATORAL KOORDİNAT SİSTEMİ Dünya nın yüzeyi üzerindeki bir noktayı belirlemek için enlem ve boylam sistemini kullanıyoruz. Gök küresi üzerinde de Dünya nın kutuplarına ve ekvatoruna dayandırılan ekvatoral
Sistemin Bileşenleri
 International Terrestrial Reference System (ITRS) International Terrestrial Reference Frame (ITRF) Sistemin Bileşenleri International Terrestrial Reference System International Terrestrial Reference Frame
International Terrestrial Reference System (ITRS) International Terrestrial Reference Frame (ITRF) Sistemin Bileşenleri International Terrestrial Reference System International Terrestrial Reference Frame
Gravite alanı belirlemede modern yaklaşımlar
 Gravite alanı belirlemede modern yaklaşımlar Lisansüstü Ders Notları Aydın ÜSTÜN Selçuk Üniversitesi Harita Mühendisliği austun@selcuk.edu.tr Konya, 2016 A. Üstün (Selçuk Üniversitesi) Gravite alanı belirleme
Gravite alanı belirlemede modern yaklaşımlar Lisansüstü Ders Notları Aydın ÜSTÜN Selçuk Üniversitesi Harita Mühendisliği austun@selcuk.edu.tr Konya, 2016 A. Üstün (Selçuk Üniversitesi) Gravite alanı belirleme
Dünyanın dönmesi: Yer sabit -> gök sistemleri arasındaki dönüşüm r gök = Qr yer-sabit Neden dünyanın dönmesi ile ilgileniyoruz?
 Dünyanın Dönmesi Dünyanın dönmesi: Yer sabit -> gök sistemleri arasındaki dönüşüm r gök = Qr yer-sabit Neden dünyanın dönmesi ile ilgileniyoruz? yer sistemi ve gök sistemini ilişkilendirmek istiyoruz quasarlar
Dünyanın Dönmesi Dünyanın dönmesi: Yer sabit -> gök sistemleri arasındaki dönüşüm r gök = Qr yer-sabit Neden dünyanın dönmesi ile ilgileniyoruz? yer sistemi ve gök sistemini ilişkilendirmek istiyoruz quasarlar
ACCURACY OF GPS PRECISE POINT POSITIONING (PPP)
 i by Simge TEKİÇ B.S., Geodesy and Photogrammetry Engineering Yıldız Technical University, 2006 Submitted to the Kandilli Observatory and Earthquake Research Institute in partial fulfillment of the requirements
i by Simge TEKİÇ B.S., Geodesy and Photogrammetry Engineering Yıldız Technical University, 2006 Submitted to the Kandilli Observatory and Earthquake Research Institute in partial fulfillment of the requirements
EKVATORAL KOORDİNAT SİSTEMİ_devam. Serap Ak
 EKVATORAL KOORDİNAT SİSTEMİ_devam http://star-www.st-and.ac.uk/~fv/webnotes/chapter5.htm http://star-www.st-and.ac.uk/~fv/webnotes/chapter4.htm Gök küresinde bulunan önemli yıldızların ekvatoral koordinatları
EKVATORAL KOORDİNAT SİSTEMİ_devam http://star-www.st-and.ac.uk/~fv/webnotes/chapter5.htm http://star-www.st-and.ac.uk/~fv/webnotes/chapter4.htm Gök küresinde bulunan önemli yıldızların ekvatoral koordinatları
Astronomik Zaman Sistemleri
 Astronomik Zaman Sistemleri Astronomik Zaman Sistemleri İki türlüdür Dünyanın kendi etrafında dönüşüne bağlı olarak tanımlanan zamanlar Atom saatleri ile (yani atomik salınımlarınfrekansı) ile yürütülen
Astronomik Zaman Sistemleri Astronomik Zaman Sistemleri İki türlüdür Dünyanın kendi etrafında dönüşüne bağlı olarak tanımlanan zamanlar Atom saatleri ile (yani atomik salınımlarınfrekansı) ile yürütülen
MADDESEL NOKTANIN EĞRİSEL HAREKETİ
 Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
GNSS Teknikleri. Lisans Ders Notları. Aydın ÜSTÜN. Kocaeli Üniversitesi Harita Mühendisliği.
 GNSS Teknikleri Lisans Ders Notları Aydın ÜSTÜN Kocaeli Üniversitesi Harita Mühendisliği aydin.ustun@kocaeli.edu.tr Kocaeli, 2016 A. Üstün (Kocaeli Üniversitesi) GNSS teknikleri (v.11/10/16) 1/18 İçerik
GNSS Teknikleri Lisans Ders Notları Aydın ÜSTÜN Kocaeli Üniversitesi Harita Mühendisliği aydin.ustun@kocaeli.edu.tr Kocaeli, 2016 A. Üstün (Kocaeli Üniversitesi) GNSS teknikleri (v.11/10/16) 1/18 İçerik
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Bağıl Konum Belirleme. GPS ile Konum Belirleme
 Mutlak Konum Belirleme Bağıl Konum Belirleme GPS ile Konum Belirleme büroda değerlendirme (post-prosessing) gerçek zamanlı (real-time) statik hızlı statik kinematik DGPS (kod) gerçek zamanlı kinematik
Mutlak Konum Belirleme Bağıl Konum Belirleme GPS ile Konum Belirleme büroda değerlendirme (post-prosessing) gerçek zamanlı (real-time) statik hızlı statik kinematik DGPS (kod) gerçek zamanlı kinematik
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
TEKNOLOJİK ARAŞTIRMALAR
 www.teknolojikarastirmalar.com ISSN:1305-631X Yapı Teknolojileri Elektronik Dergisi 2005 (2) 47-52 TEKNOLOJİK ARAŞTIRMALAR Teknik Not Global Konum Belirlemede Hata Kaynakları Saffet ERDOĞAN, Mevlüt GÜLLÜ,
www.teknolojikarastirmalar.com ISSN:1305-631X Yapı Teknolojileri Elektronik Dergisi 2005 (2) 47-52 TEKNOLOJİK ARAŞTIRMALAR Teknik Not Global Konum Belirlemede Hata Kaynakları Saffet ERDOĞAN, Mevlüt GÜLLÜ,
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
GNSS Teknikleri ve Uygulamaları
 GNSS Teknikleri ve Uygulamaları Yrd. Doç. Dr. Sefa YALVAÇ Gümüşhane, 2017 Gümüşhane Üniversitesi, 2017 Versiyon: 2017.0 Bölüm-1 Tarihçe Tarih boyunca insanlar, Neredeyim? Nereye gidiyorum? sorularına cevap
GNSS Teknikleri ve Uygulamaları Yrd. Doç. Dr. Sefa YALVAÇ Gümüşhane, 2017 Gümüşhane Üniversitesi, 2017 Versiyon: 2017.0 Bölüm-1 Tarihçe Tarih boyunca insanlar, Neredeyim? Nereye gidiyorum? sorularına cevap
Harita Projeksiyonları ve Koordinat Sistemleri. Doç. Dr. Senem KOZAMAN
 Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Jeodezide Koordinat Sistemleri Ders Kodu:
 Jeodezide Koordinat Sistemleri Ders Kodu: 0010070029 (4. Yarıyıl) Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 06.09.2013 1 1 Giriş Bu bölümde; koordinat
Jeodezide Koordinat Sistemleri Ders Kodu: 0010070029 (4. Yarıyıl) Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 06.09.2013 1 1 Giriş Bu bölümde; koordinat
Newton un ikinci yasası: Bir cisim ivmesi cisim üzerine etki eden toplam kuvvet ile doğru orantılı cismin kütlesi ile ters orantılıdır.
 Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
UAK Ulusal Astronomi Kongresi Erzurum 5-9 Eylül TÜRKSAT Gözlemevinde Gerçekleştirilen GEO Kuşak Uydu Gözlem Faaliyetleri
 UAK-2016 20. Ulusal Astronomi Kongresi Erzurum 5-9 Eylül 2016 TÜRKSAT Gözlemevinde Gerçekleştirilen GEO Kuşak Uydu Gözlem Faaliyetleri SUNUM İÇERİĞİ Türksat Gözlemevi Uzay Trafiği Türksat Uyduları GEO
UAK-2016 20. Ulusal Astronomi Kongresi Erzurum 5-9 Eylül 2016 TÜRKSAT Gözlemevinde Gerçekleştirilen GEO Kuşak Uydu Gözlem Faaliyetleri SUNUM İÇERİĞİ Türksat Gözlemevi Uzay Trafiği Türksat Uyduları GEO
TUSAGA-AKTİF CORS İSTASYONLARININ YER DEĞİŞİKLİĞİNİN AĞ BAZLI RTK ÖLÇÜMLERİNE ETKİSİ. Sermet Öğütcü, İbrahim Kalaycı Necmettin Erbakan Üniversitesi
 TUSAGA-AKTİF CORS İSTASYONLARININ YER DEĞİŞİKLİĞİNİN AĞ BAZLI RTK ÖLÇÜMLERİNE ETKİSİ Sermet Öğütcü, İbrahim Kalaycı Necmettin Erbakan Üniversitesi ÇALIŞMA BÖLGESİ ÖLÇÜMLER Konya Aksaray-Cihanbeyli-Yunak
TUSAGA-AKTİF CORS İSTASYONLARININ YER DEĞİŞİKLİĞİNİN AĞ BAZLI RTK ÖLÇÜMLERİNE ETKİSİ Sermet Öğütcü, İbrahim Kalaycı Necmettin Erbakan Üniversitesi ÇALIŞMA BÖLGESİ ÖLÇÜMLER Konya Aksaray-Cihanbeyli-Yunak
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
GÜNEY YARIM KÜRESİ İÇİN ŞEKİL
 GÜNEY YARIM KÜRESİ İÇİN ŞEKİL Bu şekilde, gözlemcinin zeniti bundan önceki şekillerdeki gibi yerleştirilir. Bu halde gök ufku şekildeki gibi olur. Güney yarım kürede Q güney kutbu ufkun üzerindedir. O
GÜNEY YARIM KÜRESİ İÇİN ŞEKİL Bu şekilde, gözlemcinin zeniti bundan önceki şekillerdeki gibi yerleştirilir. Bu halde gök ufku şekildeki gibi olur. Güney yarım kürede Q güney kutbu ufkun üzerindedir. O
LANDSAT 7 UYDUSU İÇİN YÖRÜNGE ANALİZİ
 LANDSAT 7 UYDUSU İÇİN YÖRÜNGE ANALİZİ Hüseyin Yaşar DEU, Dokuz Eylül Üniversitesi, Fen Bilimleri Enstitüsü, Geographic Information System, Tınaztepe 35370 İzmir, huseyinyasar87@gmail.com ÖZET Çalışma,
LANDSAT 7 UYDUSU İÇİN YÖRÜNGE ANALİZİ Hüseyin Yaşar DEU, Dokuz Eylül Üniversitesi, Fen Bilimleri Enstitüsü, Geographic Information System, Tınaztepe 35370 İzmir, huseyinyasar87@gmail.com ÖZET Çalışma,
AKDENİZ ÜNİVERSİTESİ. Anten Parametrelerinin Temelleri. Samet YALÇIN
 AKDENİZ ÜNİVERSİTESİ Anten Parametrelerinin Temelleri Samet YALÇIN Anten Parametrelerinin Temelleri GİRİŞ: Bir antenin parametrelerini tanımlayabilmek için anten parametreleri gereklidir. Anten performansından
AKDENİZ ÜNİVERSİTESİ Anten Parametrelerinin Temelleri Samet YALÇIN Anten Parametrelerinin Temelleri GİRİŞ: Bir antenin parametrelerini tanımlayabilmek için anten parametreleri gereklidir. Anten performansından
Yıldızların uzaklıkları ve uzay hareketleri Zeki Aslan
 Yıldızların uzaklıkları ve uzay hareketleri Zeki Aslan Çıplak gözle ya da teleskopla yıldızlara ve diğer gök cisimlerine bakarak onların gerçek parlaklıklarını ve gerçek büyüklüklerini algılayamayız. Nesnenin
Yıldızların uzaklıkları ve uzay hareketleri Zeki Aslan Çıplak gözle ya da teleskopla yıldızlara ve diğer gök cisimlerine bakarak onların gerçek parlaklıklarını ve gerçek büyüklüklerini algılayamayız. Nesnenin
İyonosfer TEİ Hesabında Uydu Alıcı Bağıl Geometrisine Uygun Yeni Bir Ağırlık Fonksiyonu Wgeo
 TMMOB Harita ve Kadastro Mühendisleri Odası, 15. Türkiye Harita Bilimsel ve Teknik Kurultayı, 25 28 Mart 2015, Ankara. İyonosfer TEİ Hesabında Uydu Alıcı Bağıl Geometrisine Uygun Yeni Bir Ağırlık Fonksiyonu
TMMOB Harita ve Kadastro Mühendisleri Odası, 15. Türkiye Harita Bilimsel ve Teknik Kurultayı, 25 28 Mart 2015, Ankara. İyonosfer TEİ Hesabında Uydu Alıcı Bağıl Geometrisine Uygun Yeni Bir Ağırlık Fonksiyonu
JEODEZİK AĞLARIN OPTİMİZASYONU
 JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
Uydu Yörüngelerine Giriş
 Uydu Yörüngelerine Giriş Niçin Uydular Dolanıyor? Merkezcil kuvvet ile çekim kuvveti t ye bağlı değişim göstermezse yörünge dairesel olur. Eğer hız biraz fazla veya az ise, yani t ye bağlı değişiyorsa
Uydu Yörüngelerine Giriş Niçin Uydular Dolanıyor? Merkezcil kuvvet ile çekim kuvveti t ye bağlı değişim göstermezse yörünge dairesel olur. Eğer hız biraz fazla veya az ise, yani t ye bağlı değişiyorsa
COMPARING THE PERFORMANCE OF KINEMATIC PPP AND POST PROCESS KINEMATICS METHODS IN RURAL AND URBAN AREAS
 KİNEMATİK PPP VE POST PROCESS KİNEMATİK YÖNTEMLERİNİN KIRSAL VE MESKUN ALANLARDAKİ PERFORMANSLARININ KARŞILAŞTIRILMASI A. CEYLAN 1, C.Ö. YİGİT 2, S. ALÇAY 1, B. N. ÖZDEMİR 1 1 Selçuk Üniversitesi, Mühendsilik
KİNEMATİK PPP VE POST PROCESS KİNEMATİK YÖNTEMLERİNİN KIRSAL VE MESKUN ALANLARDAKİ PERFORMANSLARININ KARŞILAŞTIRILMASI A. CEYLAN 1, C.Ö. YİGİT 2, S. ALÇAY 1, B. N. ÖZDEMİR 1 1 Selçuk Üniversitesi, Mühendsilik
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
BÖLÜM I GİRİŞ (1.1) y(t) veya y(x) T veya λ. a t veya x. Şekil 1.1 Dalga. a genlik, T peryod (veya λ dalga boyu)
 BÖLÜM I GİRİŞ 1.1 Sinyal Bir sistemin durum ve davranış bilgilerini taşıyan, bir veya daha fazla değişken ile tanımlanan bir fonksiyon olup veri işlemde dalga olarak adlandırılır. Bir dalga, genliği, dalga
BÖLÜM I GİRİŞ 1.1 Sinyal Bir sistemin durum ve davranış bilgilerini taşıyan, bir veya daha fazla değişken ile tanımlanan bir fonksiyon olup veri işlemde dalga olarak adlandırılır. Bir dalga, genliği, dalga
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
GLOBAL KONUM BELÝRLEME SÝSTEMÝ (GPS)
 PAMUKKALE ÜNÝVERSÝTESÝ MÜHENDÝSLÝK YIL FAKÜLTESÝ PAMUKKALE UNIVERSITY ENGINEERING CÝLT COLLEGE MÜHENDÝSLÝK BÝLÝMLERÝ SAYI DERGÝSÝ JOURNAL OF ENGINEERING SAYFA SCIENCES : 1996 : 2 : 2 : 103-108 GLOBAL KONUM
PAMUKKALE ÜNÝVERSÝTESÝ MÜHENDÝSLÝK YIL FAKÜLTESÝ PAMUKKALE UNIVERSITY ENGINEERING CÝLT COLLEGE MÜHENDÝSLÝK BÝLÝMLERÝ SAYI DERGÝSÝ JOURNAL OF ENGINEERING SAYFA SCIENCES : 1996 : 2 : 2 : 103-108 GLOBAL KONUM
GPS ÖLÇÜMLERİNİN DEĞERLENDİRİLMESİNDE FARKLI FAZ KOMBİNASYONLARININ KULLANILMASI
 GPS ÖLÇÜMLERİNİN DEĞERLENDİRİLMESİNDE FARKLI FAZ KOMBİNASYONLARININ KULLANILMASI H. Kemaldere 1, H. Kutoğlu 2, Ç. Mekik 3 1 Zonguldak Karaelmas Üniversitesi, Jeodezi ve Fotogrametri Müh.Bölümü, Jeodezi
GPS ÖLÇÜMLERİNİN DEĞERLENDİRİLMESİNDE FARKLI FAZ KOMBİNASYONLARININ KULLANILMASI H. Kemaldere 1, H. Kutoğlu 2, Ç. Mekik 3 1 Zonguldak Karaelmas Üniversitesi, Jeodezi ve Fotogrametri Müh.Bölümü, Jeodezi
Fizik Dr. Murat Aydemir
 Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
1. GİRİŞ 2. GNSS SİSTEMLERİ
 1. GİRİŞ İnsanoğlu daha kaliteli ve güvenli bir yaşam amacıyla, bulunduğu bölgeleri terk edip daha uygun yaşam alanları bulmak için geçmişten günümüze sürekli bir arayış içerisinde olmuştur. Bunun için
1. GİRİŞ İnsanoğlu daha kaliteli ve güvenli bir yaşam amacıyla, bulunduğu bölgeleri terk edip daha uygun yaşam alanları bulmak için geçmişten günümüze sürekli bir arayış içerisinde olmuştur. Bunun için
TMMOB Harita ve Kadastro Mühendisleri Odası Konya Şubesi Uydu Teknikleri ve Kullanımı Hakkında Meslek Eğitimi Semineri
 TMMOB Harita ve Kadastro Mühendisleri Odası Konya Şubesi Uydu Teknikleri ve Kullanımı Hakkında Meslek Eğitimi Semineri Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi e-posta: austun@selcuk.edu.tr Ocak,
TMMOB Harita ve Kadastro Mühendisleri Odası Konya Şubesi Uydu Teknikleri ve Kullanımı Hakkında Meslek Eğitimi Semineri Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi e-posta: austun@selcuk.edu.tr Ocak,
Hareket Kanunları Uygulamaları
 Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
Fiz Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi
 Fiz 1011 - Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi Açısal Yerdeğiştirme, Hız ve İvme Dönme Kinematiği: Sabit Açısal İvmeli Dönme Hareketi Açısal ve Doğrusal Nicelikler Dönme Enerjisi Eylemsizlik
Fiz 1011 - Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi Açısal Yerdeğiştirme, Hız ve İvme Dönme Kinematiği: Sabit Açısal İvmeli Dönme Hareketi Açısal ve Doğrusal Nicelikler Dönme Enerjisi Eylemsizlik
Bölüm 3: Vektörler. Kavrama Soruları. Konu İçeriği. Sunuş. 3-1 Koordinat Sistemleri
 ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Jeodezide Yaklaşım Yöntemleri: Enterpolasyon ve Kollokasyon
 Jeodezide Yöntemleri: ve Lisansüstü Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Fen Bilimleri Enstitüsü e-posta: austun@selcuk.edu.tr Konya, 2007 A. Üstün yöntemleri 1 / 28 Bir soruyu ya
Jeodezide Yöntemleri: ve Lisansüstü Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Fen Bilimleri Enstitüsü e-posta: austun@selcuk.edu.tr Konya, 2007 A. Üstün yöntemleri 1 / 28 Bir soruyu ya
DİNAMİK. Ders_9. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 DİNAMİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ: ÖTELENME&DÖNME Bugünün
DİNAMİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ: ÖTELENME&DÖNME Bugünün
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 13 Parçacık Kinetiği: Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 13 Parçacık
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 13 Parçacık Kinetiği: Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 13 Parçacık
A UNIFIED APPROACH IN GPS ACCURACY DETERMINATION STUDIES
 A UNIFIED APPROACH IN GPS ACCURACY DETERMINATION STUDIES by Didem Öztürk B.S., Geodesy and Photogrammetry Department Yildiz Technical University, 2005 Submitted to the Kandilli Observatory and Earthquake
A UNIFIED APPROACH IN GPS ACCURACY DETERMINATION STUDIES by Didem Öztürk B.S., Geodesy and Photogrammetry Department Yildiz Technical University, 2005 Submitted to the Kandilli Observatory and Earthquake
GPS İN GENEL ESASLARI
 GPS 1. Tarihçe GPS İN GENEL ESASLARI Ölçme Bilgisi insanoğlunun varolduğu tarihten günümüze dek herkesin dikkatini çekmiştir. İnsan ilk önce yeryüzünde bulunduğu yeri bilmek ister. Ayrıca şahıslar sahip
GPS 1. Tarihçe GPS İN GENEL ESASLARI Ölçme Bilgisi insanoğlunun varolduğu tarihten günümüze dek herkesin dikkatini çekmiştir. İnsan ilk önce yeryüzünde bulunduğu yeri bilmek ister. Ayrıca şahıslar sahip
MEKANİZMA TEKNİĞİ (3. Hafta)
 MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
Cismin Ağırlığı Düzlemsel Alanda Ağırlık Merkezi - İntegrasyon Yöntemi Örnekler Düzlemsel Eğride Ağırlık Merkezi - İntegrasyon Yöntemi
 4. 4. Cismin ğırlığı Düzlemsel landa ğırlık erkezi - İntegrasyon Yöntemi Düzlemsel Eğride ğırlık erkezi - İntegrasyon Yöntemi 4.3 Bileşik Plak ve Teller 4.4 Pappus Guldinus Teoremleri 4.5 Üç Boyutlu Cisimlerde
4. 4. Cismin ğırlığı Düzlemsel landa ğırlık erkezi - İntegrasyon Yöntemi Düzlemsel Eğride ğırlık erkezi - İntegrasyon Yöntemi 4.3 Bileşik Plak ve Teller 4.4 Pappus Guldinus Teoremleri 4.5 Üç Boyutlu Cisimlerde
Toplam
 Gerçek basittir ama basit görülmez. Blaise Pascal Ad Soyad: Okul: 1 2 3 4 5 6 7 8 9 10 Toplam /6 /7 /12 /10 /11 /8 /10 /12 /10 /14 /100 SINAV KURALLARI 1) Sınav toplam 5 sayfadan oluşmaktadır, lütfen sınava
Gerçek basittir ama basit görülmez. Blaise Pascal Ad Soyad: Okul: 1 2 3 4 5 6 7 8 9 10 Toplam /6 /7 /12 /10 /11 /8 /10 /12 /10 /14 /100 SINAV KURALLARI 1) Sınav toplam 5 sayfadan oluşmaktadır, lütfen sınava
T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA
 T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA ÇİFT STANDART DAİRELİ KONFORM LAMBERT PROJEKSİYONUNDA TÜRKİYE HARİTASININ YAPILMASI Hrt. Tğm. Soner ÖZDEMİR
T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA ÇİFT STANDART DAİRELİ KONFORM LAMBERT PROJEKSİYONUNDA TÜRKİYE HARİTASININ YAPILMASI Hrt. Tğm. Soner ÖZDEMİR
INVESTIGATION OF ELEVATION CHANGE WITH DIFFERENT GEODETIC MEASUREMENT METHODS
 FARKLI JEODEZİK ÖLÇME YÖNTEMLERİ İLE YÜKSEKLİK DEĞİŞİMLERİNİN İNCELENMESİ B. GELİN 1, S.O. DÜNDAR 1, S. ÇETİN 2, U. DOĞAN 2 1 Yıldız Teknik Üniversitesi, İnşaat Fakültesi, Harita Mühendisliği, İstanbul
FARKLI JEODEZİK ÖLÇME YÖNTEMLERİ İLE YÜKSEKLİK DEĞİŞİMLERİNİN İNCELENMESİ B. GELİN 1, S.O. DÜNDAR 1, S. ÇETİN 2, U. DOĞAN 2 1 Yıldız Teknik Üniversitesi, İnşaat Fakültesi, Harita Mühendisliği, İstanbul
Veri toplama- Yersel Yöntemler Donanım
 Veri toplama- Yersel Yöntemler Donanım Data Doç. Dr. Saffet ERDOĞAN 1 Veri toplama -Yersel Yöntemler Optik kamera ve lazer tarayıcılı ölçme robotu Kameradan gerçek zamanlı veri Doç. Dr. Saffet ERDOĞAN
Veri toplama- Yersel Yöntemler Donanım Data Doç. Dr. Saffet ERDOĞAN 1 Veri toplama -Yersel Yöntemler Optik kamera ve lazer tarayıcılı ölçme robotu Kameradan gerçek zamanlı veri Doç. Dr. Saffet ERDOĞAN
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
GPS/INS Destekli Havai Nirengi
 GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ
 KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
1. HAFTA. Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler.
 1. HAFTA Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler. Statikte üç temel büyüklük vardır. Uzay: Fiziksel olayların meydana geldiği geometrik bir bölgedir. İncelenen problemin
1. HAFTA Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler. Statikte üç temel büyüklük vardır. Uzay: Fiziksel olayların meydana geldiği geometrik bir bölgedir. İncelenen problemin
olmak üzere 4 ayrı kütükte toplanan günlük GPS ölçüleri, baz vektörlerinin hesabı için bilgisayara aktarılmıştır (Ersoy.97).
 1-) GPS Ölçülerinin Yapılması Ölçülerin yapılacağı tarihlerde kısa bir süre gözlem yapılarak uydu efemerisi güncelleştirilmiştir. Bunun sonunda ölçü yapılacak bölgenin yaklaşık koordinatlarına göre, bir
1-) GPS Ölçülerinin Yapılması Ölçülerin yapılacağı tarihlerde kısa bir süre gözlem yapılarak uydu efemerisi güncelleştirilmiştir. Bunun sonunda ölçü yapılacak bölgenin yaklaşık koordinatlarına göre, bir
Fizik 101-Fizik I 2013-2014. Dönme Hareketinin Dinamiği
 -Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
-Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
DİNAMİK - 1. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 1 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü http://acikders.ankara.edu.tr/course/view.php?id=190 1. HAFTA Kapsam:
DİNAMİK - 1 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü http://acikders.ankara.edu.tr/course/view.php?id=190 1. HAFTA Kapsam:
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
Bölüm-4. İki Boyutta Hareket
 Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Ulusal Metroloji Enstitüsü GENEL METROLOJİ
 Ulusal Metroloji Enstitüsü GENEL METROLOJİ METROLOJİNİN TANIMI Kelime olarak metreden türetilmiş olup anlamı ÖLÇME BİLİMİ dir. Metrolojinin Görevi : Bütün ölçme sistemlerinin temeli olan birimleri (SI
Ulusal Metroloji Enstitüsü GENEL METROLOJİ METROLOJİNİN TANIMI Kelime olarak metreden türetilmiş olup anlamı ÖLÇME BİLİMİ dir. Metrolojinin Görevi : Bütün ölçme sistemlerinin temeli olan birimleri (SI
Küresel Konumlama Sistemi Yrd. Doç. Dr. Okan Yıldız Yrd. Doç. Dr. Mustafa Dihkan Öğr.Gör.Dr. Deniztan Ulutaş
 Küresel Konumlama Sistemi Yrd. Doç. Dr. Okan Yıldız Yrd. Doç. Dr. Mustafa Dihkan Öğr.Gör.Dr. Deniztan Ulutaş Ölçme Bilgisi Ders Notları 2015-2016 Bahar Yarıyılı Golabal Positioning System(GPS) Nedir? Küresel
Küresel Konumlama Sistemi Yrd. Doç. Dr. Okan Yıldız Yrd. Doç. Dr. Mustafa Dihkan Öğr.Gör.Dr. Deniztan Ulutaş Ölçme Bilgisi Ders Notları 2015-2016 Bahar Yarıyılı Golabal Positioning System(GPS) Nedir? Küresel
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
UYDU GÖRÜNTÜLERİ VE SAYISAL UZAKTAN ALGILAMA
 UYDU GÖRÜNTÜLERİ VE SAYISAL UZAKTAN ALGILAMA Son yıllarda teknolojinin gelişmesi ile birlikte; geniş alanlarda, kısa zaman aralıklarında ucuz ve hızlı sonuç alınabilen uzaktan algılama tekniğinin, yenilenebilir
UYDU GÖRÜNTÜLERİ VE SAYISAL UZAKTAN ALGILAMA Son yıllarda teknolojinin gelişmesi ile birlikte; geniş alanlarda, kısa zaman aralıklarında ucuz ve hızlı sonuç alınabilen uzaktan algılama tekniğinin, yenilenebilir
r r s r i (1) = [x(t s ) x(t i )]î + [y(t s ) y(t i )]ĵ. (2) r s
![r r s r i (1) = [x(t s ) x(t i )]î + [y(t s ) y(t i )]ĵ. (2) r s r r s r i (1) = [x(t s ) x(t i )]î + [y(t s ) y(t i )]ĵ. (2) r s](/thumbs/55/37178256.jpg) Bölüm 4: İki-Boyutta Hareket(Özet) Bir-boyutta harekeçin geliştirilen tüm kavramlar iki-boyutta harekeçin genelleştirilebilir. Bunun için hareketli cismin(parçacığın) yer değiştirme vektörü xy-düzleminde
Bölüm 4: İki-Boyutta Hareket(Özet) Bir-boyutta harekeçin geliştirilen tüm kavramlar iki-boyutta harekeçin genelleştirilebilir. Bunun için hareketli cismin(parçacığın) yer değiştirme vektörü xy-düzleminde
MANYETIZMA. Manyetik Alan ve Manyetik Alan Kaynakları
 MANYETIZMA Manyetik Alan ve Manyetik Alan Kaynakları MAGNETİZMA Mıknatıs ve Özellikleri Magnetit adı verilen Fe 3 O 4 (demir oksit) bileşiği doğal bir mıknatıstır ve ilk olarak Manisa yakınlarında bulunduğu
MANYETIZMA Manyetik Alan ve Manyetik Alan Kaynakları MAGNETİZMA Mıknatıs ve Özellikleri Magnetit adı verilen Fe 3 O 4 (demir oksit) bileşiği doğal bir mıknatıstır ve ilk olarak Manisa yakınlarında bulunduğu
KONUM BELİRLEME YÖNTEMLERİ
 KONUM BELİRLEME YÖNTEMLERİ SUNUM ÖZETİ GPS Nedir? DGPS ve RTK Kavramları VRS Nedir? VRS Nasıl Çalışır? VRS de Modellenmesi Gereken Hata Kaynakları Sonuç ve Öneriler ANTALYA AKHİSAR MİHALIÇÇIK EŞME YUNAK
KONUM BELİRLEME YÖNTEMLERİ SUNUM ÖZETİ GPS Nedir? DGPS ve RTK Kavramları VRS Nedir? VRS Nasıl Çalışır? VRS de Modellenmesi Gereken Hata Kaynakları Sonuç ve Öneriler ANTALYA AKHİSAR MİHALIÇÇIK EŞME YUNAK
Bölüm 2. Bir boyutta hareket
 Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
7. BÖLÜM İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI .= 1 1 + + Genel: Vektörler bölümünde vektörel iç çarpım;
 İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
TUSAGA-AKTİF istasyonları koordinat ve koordinat değişimlerinin yılları GNSS verilerinden yararla belirlenmesi ve uygulamada kullanılması
 TÜRKİYE ULUSAL JEODEZİ KOMİSYONU 2017 YILI BİLİMSEL TOPLANTISI SABİT GNSS İSTASYONLARI UYGULAMALARI TUSAGA-AKTİF istasyonları koordinat ve koordinat değişimlerinin 2009-2017 yılları GNSS verilerinden yararla
TÜRKİYE ULUSAL JEODEZİ KOMİSYONU 2017 YILI BİLİMSEL TOPLANTISI SABİT GNSS İSTASYONLARI UYGULAMALARI TUSAGA-AKTİF istasyonları koordinat ve koordinat değişimlerinin 2009-2017 yılları GNSS verilerinden yararla
G( q ) yer çekimi matrisi;
 RPR (DÖNEL PRİZATİK DÖNEL) EKLE YAPISINA SAHİP BİR ROBOTUN DİNAİK DENKLELERİNİN VEKTÖR-ATRİS FORDA TÜRETİLESİ Aytaç ALTAN Osmancık Ömer Derindere eslek Yüksekokulu Hitit Üniversitesi aytacaltan@hitit.edu.tr
RPR (DÖNEL PRİZATİK DÖNEL) EKLE YAPISINA SAHİP BİR ROBOTUN DİNAİK DENKLELERİNİN VEKTÖR-ATRİS FORDA TÜRETİLESİ Aytaç ALTAN Osmancık Ömer Derindere eslek Yüksekokulu Hitit Üniversitesi aytacaltan@hitit.edu.tr
HAREKET HAREKET KUVVET İLİŞKİSİ
 HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
MEVCUT GPS/NİVELMAN VERİ KÜMESİNİN JEOİT MODELLEME AÇISINDAN DEĞERLENDİRİLMESİ
 MEVCUT GPS/NİVELMAN VERİ KÜMESİNİN JEOİT MODELLEME AÇISINDAN DEĞERLENDİRİLMESİ Mustafa İNAM, Mehmet SİMAV, Ali TÜRKEZER, Serdar AKYOL, Ahmet DİRENÇ, A.İhsan KURT, Mustafa KURT Harita Genel Komutanlığı,
MEVCUT GPS/NİVELMAN VERİ KÜMESİNİN JEOİT MODELLEME AÇISINDAN DEĞERLENDİRİLMESİ Mustafa İNAM, Mehmet SİMAV, Ali TÜRKEZER, Serdar AKYOL, Ahmet DİRENÇ, A.İhsan KURT, Mustafa KURT Harita Genel Komutanlığı,
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
GPS ile Hassas Tarım Uygulamaları
 GPS ile Hassas Tarım Uygulamaları Hassas tarım değişken oranlar ilkesiyle gerekeni, gerektiği yere, gerektiği zaman, gerektiği kadar kullanımı temel almış olan bir teknoloji olduğu için, konumsal bilgi
GPS ile Hassas Tarım Uygulamaları Hassas tarım değişken oranlar ilkesiyle gerekeni, gerektiği yere, gerektiği zaman, gerektiği kadar kullanımı temel almış olan bir teknoloji olduğu için, konumsal bilgi
TİTREŞİM VE DALGALAR BÖLÜM PERİYODİK HAREKET
 TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK. Bölüm 1 Temel Kavramlar ve İlkeler
 MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK Bölüm 1 Temel Kavramlar ve İlkeler Mekanik Mekanik Rijit-Cisim Mekaniği Şekil değiştiren Cismin Mekaniği Statik Dinamik Dengedeki Cisimler Hareketsiz veya durgun
MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK Bölüm 1 Temel Kavramlar ve İlkeler Mekanik Mekanik Rijit-Cisim Mekaniği Şekil değiştiren Cismin Mekaniği Statik Dinamik Dengedeki Cisimler Hareketsiz veya durgun
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ
 HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Konuları_Ders# 5 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ JEODEZİ Yeryuvarının şekil,
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Konuları_Ders# 5 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ JEODEZİ Yeryuvarının şekil,
Fotogrametride işlem adımları
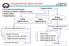 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
V = g. t Y = ½ gt 2 V = 2gh. Serbest Düşme NOT:
 Havada serbest bırakılan cisimlerin aşağı doğru düşmesi etrafımızda her zaman gördüğümüz bir olaydır. Bu düşme hareketleri, cisimleri yerin merkezine doğru çeken bir kuvvetin varlığını gösterir. Daha önceki
Havada serbest bırakılan cisimlerin aşağı doğru düşmesi etrafımızda her zaman gördüğümüz bir olaydır. Bu düşme hareketleri, cisimleri yerin merkezine doğru çeken bir kuvvetin varlığını gösterir. Daha önceki
T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.
![T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir. T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.](/thumbs/55/35591809.jpg) * = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
* = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
ORM 7420 USING SATELLITE IMAGES IN FOREST RESOURCE PLANNING
 ORM 7420 USING SATELLITE IMAGES IN FOREST RESOURCE PLANNING Asst. Prof. Dr. Uzay KARAHALİL Week IV NEDEN UYDU GÖRÜNTÜLERİ KULLANIRIZ? Sayısaldır (Dijital), - taramaya gerek yoktur Hızlıdır Uçuş planı,
ORM 7420 USING SATELLITE IMAGES IN FOREST RESOURCE PLANNING Asst. Prof. Dr. Uzay KARAHALİL Week IV NEDEN UYDU GÖRÜNTÜLERİ KULLANIRIZ? Sayısaldır (Dijital), - taramaya gerek yoktur Hızlıdır Uçuş planı,
