YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
|
|
|
- Nesrin Ateş
- 7 yıl önce
- İzleme sayısı:
Transkript
1 YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
2 Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını denge denklemleri yardımıyla hesaplayabiliyorsak sistem izostatiktir.
3 Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler :
4 Yapı Sistemleri: Hiperstatik (Statikçe Belirsiz) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonları denge denklemleri yardımıyla hesaplanamıyorsa sistem hiperstatiktir.
5 Yapı Sistemleri: Hiperstatik Sistemlerin Çözümü için : * Denge Denklemleri * Geometrik uygunluk şartları * Bünye Denklemleri (Gerilmeler ve Deformasyonlar arasındaki ilişkiler)
6 Hiperstatik Sistemlerde Kesit tesiri oluşturan etkiler * Dış yükler * Mesnet çökmesi * Sıcaklık değişimi
7 Hiperstatik Sistemlerde Çözüm Yöntemleri Kuvvet Metodu Deplasman Metodu Deplasman Metodları Açı Metodu Cross (Moment Dağıtma) Metodu Rijitlik Matrisi Metodu
8 Hiperstatik Sistemler : Dolu gövdeli sistemlerin hiperstatiklik derecesi iki gruba ayrılır. ) Dıştan hiperstatiklik : Yapıda hesaplanamayan mesnet reaksiyonu sayısına eşittir. Mesnet reaksiyon sayısı (r) ise r-3 (dıştan hiperstatiklik derecesi)
9 t/m 8 t 5 t/m I I 0 t I I I m I I 5 m 5 m m 8 m 8 m m
10 ) İçten Hiperstatiklik : Yapıda hesaplanamayan iç kuvvet sayısı ile ilglidir. Dolu gövdeli sistemlerde n = 3*m r - 3j denklemiyle bulunur. n: Hiperstatiklik derecesi m: Eleman Sayısı r : Mesnet reaksiyonları sayısı j : Düğüm noktası sayısı
11 Düğüm noktası sayısı (j): 6 Mesnet reaksiyonu sayısı (r) : 3 Eleman sayısı (m): 6 Hiperstatiklik derecesi n : 3*mr-3j n : 3*6 3 3*6 = 3 0 hiperstatik Sistem dıştan izostatik ancak içten hiperstatiktir. Yani sistemin tüm mesnet reaksiyonları hesaplanabilir ancak tüm çubuk kuvvetleri bulunamaz.
12 Düğüm noktası sayısı (j) : 9 Mesnet reaksiyonu sayısı (r) : 6 Eleman sayısı (m) : 0 Hiperstatiklik derecesi n : 3*mr-3j n : 3*0 6 3*9 = 9 0 hiperstatik Sistem 9 0 hiperstatiktir. Mesnet reaksiyonları incelendiğinde sistemin Dıştan 3 0 hiperstatik olduğu görülür. Yani sistem İçten 6 0 hiperstatiktir
13 Mafsal olması durumunda Eğer mafsal eleman üzerinde ise hiperstatiklik derecesi azaltılır. Eğer mafsal düğümde ise düğümde birleşen eleman sayısının eksiği kadar hiperstatiklik derecesi azaltılır. Düğümde 3 eleman birleşiyor 3-= derece azaltılır.
14 KUVVET METODU Düzlem Hiperstatik sistemlerin sabit yükler,sıcaklık değişimi ve mesnet çökmesi gibi dış etkilerlerden dolayı oluşan kesit tesirleri ve yer değiştirmelerini bulmaya yarayan virtuel iş ilkesine dayalı çözüm yöntemidir. Kuvvet metodu ile çözüm yapılırken yapılacak ilk iş izostatik esas sistemin seçilmesidir. İzostatik esas sistem, hiperstatik sistemde hiperstatiklik derecesi kadar bilinmeyenin belirlenmesi ile elde edilir. Hiperstatik sistemde hangi bilinmeyenlerin hesaplanacağı belirlenerek sistem izostatik hale getirilir.
15 İzostatik Esas Sistem: Hiperstatik sistem izostatik hale getirilir. Bunu yaparken ya sisteme mafsal yerleştirilir yada mesnetlerdeki serbestlikler arttırılır. İzostatik esas sitem seçilirken hangi sistemi daha kolay çözebileceğimizi düşünüyorsak o sistemi seçebiliriz. Bir hiperstatik sistemin pek çok izostatik esas sistemi vardır. Mafsal eklenmesi durumunda mafsalın her iki yanına bilinmeyen olarak moment yazılır. Mesnetlenme durumunun değiştirilmesi durumunda ise hangi yönde serbestlik arttırılırsa o yönde yönde bilinmeyen kuvvet veya moment yazılır.
16 . Dereceden hiperstatik sistem İzostatik Esas Sistem İzostatik esas sistem belirlenirken mesnetlenme durumu izostatik hale getirilir bu arada serbest bırakılan her mesnet reaksiyonu için bir bilinmeyen yazılır veya sisteme mafsal yerleştirilerek mafsalın olduğu yerde bilinmeyen olarak moment yazılır.
17 İzostatik esas sistem belirlenirken aynı zamanda hesap edilecek bilinmeyenlerde seçilmiş olmaktadır. Bu yüzden izostatik esas sistem belirlenirken hesaplarda kolaylık sağlayacak sistemlerin seçilmesine çalışılır. Yani izostatik esas sistem ve bilinmeyenlerin birim yüklemeleri için yapılacak hesapların daha kolay yapılabileceği sistemler izostatik sistem olarak seçilmeye çalışılır.
18 Mafsal eklenmesi durumunda mafsalın her iki yanına bilinmeyen olarak moment yazılır.
19 Mesnetlenme durumunun değiştirilmesi durumunda ise hangi yönde serbestlik arttırılırsa o yönde yönde bilinmeyen kuvvet veya moment yazılır.. Dereceden hiperstatik sistem İzostatik esas sistem
20 . Dereceden hiperstatik sistem için izostatik esas sistemler
21 Kuvvet Yöntemine göre Hiperstatik sistemdeki etkiler, İzostatik esas sistemdeki etkiler ile,,, n bilinmeyen kuvvetlerin oluşturduğu etkilerin uygun şekilde birleştirilmesiyle bulunur.,,, n bilinmeyenlerinin bulunması hiperstatik sistemdeki etkilerin bulunması için şarttır. Bilinmeyen sayısı sistemin hiperstatiklik derecesi kadardır.
22 Kuvvet Yöntemine göre Hiperstatik sistemdeki etkiler hesaplanırken, hiperstatiklik derecesi belirlenip izostatik esas sistem seçildikten sonra sistem uygunluk denklemi yazılır. n nn n n n nt nw n n n t w n n t w n n t w = = = = M
23 Uygunluk denklemi hiperstatiklik derecesi kadar yazılır. Sistem dereceden hiperstatik ise denklem tanedir 0 t w = Sistem. dereceden hiperstatik ise denklem tane olacaktır 0 0 t w t w = = Sistem 3. dereceden hiperstatik ise denklem 3 tane olacaktır t w t w t w = = =
24 Sistemde sıcaklı değişimi ve mesnet çökmesi yok ise sadece dış yük etkisi var ise denklem şu hale gelir: 0 t w = Sistem. dereceden hiperstatik ise denklem tane olacaktır 0 0 t w t w = = Sistem 3. dereceden hiperstatik ise denklem 3 tane olacaktır t w t w t w = = =
25 Uygunluk denkleminde görülen deplasman ifadelerinin altındaki ilk indis yeri, ikinci indis ise sebebi göstermektedir. M i iw it i0 i i in i yönündeki deplasman i yönünde mesnet çökmesinden dolayı oluşan deplasman değeri i yönünde sıcaklık değişiminden dolayı oluşan deplasman değeri i yönünde dış yükten oluşan deplasman değeri i yönünde nolu birim yüklemeden dolayı oluşan deplasman değeri i yönünde nolu birim yüklemeden dolayı oluşan deplasman değeri i yönünde n nolu birim yüklemeden dolayı oluşan deplasman değeri.
26 P P. dereceden hiperstatik sistem İzostatik esas sistem Kuvvet metodu ile çözüm yapılırken hiperstatiklik derecesi belirlenip izostatik esas sistem belirlendikten sonra uygunluk denklemleri yazılır. Bundan sonra uygunluk denklemindeki değerleri bulmak sırasıyla yüklemeler yapılır.
27 Sistem. dereceden hiperstatik ise denklem tane olacaktır = = 0 0 P P 0 0
28 P 0 Yüklemesi P İzostatik esas sisteme dış yük yüklenerek sistemde oluşan M 0 N 0 T 0 değişim diyagramları çizilir. 0 Yüklemesi İzostatik esas sistemde sadece dış yük etkisinde M, N, T kesit tesirleri diyagramları çizilir. M 0 : İzostatik esas sistemde dış etkilerden dolayı oluşan moment N 0 : İzostatik esas sistemde dış etkilerden dolayı oluşan normal kuvvet T o : İzostatik esas sistemde dış etkilerden dolayı oluşan kesme kuvveti.
29 Birim Yüklemeler İzostatik esas sistemde, sırasıyla seçilen her bir bilinmeyen için birim yüklemeler yapılır. =, =, 3 =,., n = Bu durumda her bir birim yükleme için sistem kesit tesirleri (M, N, T) çizilir. Bu kesit tesirleri hesaplanırken sistemde dış yük yoktur.
30 Yüklemesi İzostatik esas sistemde sadece nolu bilinmeyen yönünde birim yükleme yapılması durumu. Bu durumda izostatik esas sistemde oluşacak M : İzostatik esas sistemde nolu birim yüklemeden etkilerden dolayı oluşan moment N : İzostatik esas sistemde nolu birim yüklemeden dolayı oluşan normal kuvvet T : İzostatik esas sistemde nolu birim yüklemeden dolayı oluşan kesme kuvveti.
31 İzostatik esas sistem Yüklemesi İzostatik esas sistemde sadece nolu bilinmeyen yönünde birim yükleme yapılması durumu. Bu durumda izostatik esas sistemde oluşacak M : İzostatik esas sistemde nolu birim yüklemeden etkilerden dolayı oluşan moment N : İzostatik esas sistemde nolu birim yüklemeden dolayı oluşan normal kuvvet T : İzostatik esas sistemde nolu birim yüklemeden dolayı oluşan kesme kuvveti.
32 Uygunluk denklemindeki deplasman ifadelerinin bulunması için mukavemette görülen virtuel iş teoremi kullanılır. Dolu gövdeli ij sistemler için bu ifade şu şekildedir: ds ds = M im j NiN j TT i EI EF j ds GF Bu denklemde görülen EI= Eğilme Rijitliği EF= Uzama Rijitliği GF = Kayma Rijitliği, ifadeleridir.
33 Deplasman ifadelerinin simetri özelliği vardır. ij = ji Mesela deplasmanı ile deplasmanı birbirine eşittir ve şu denklemle bulunur: = ds ds = M M N N TT EI EF ds GF Bu deplasmanların bulunması sırasında genellikle N ve T kesme ifadeleri ihmal edilir. Moment ifadeleri de matematiksel olarak yazılır ve uzunluk boyunca integral alınır.
34 Deplasman ifadeleri hesaplandıktan sonra aşağıdaki uygunluk denkleminde yerine konarak denklem takımı çözülür ve bilinmeyenler olarak seçilen ve reaksiyon kuvvetleri bulunur. = = 0 0
35 P P Bundan sonra hesaplanan değerleri kullanılarak hiperstatik sistemde oluşacak kesit tesirleri bulunabilir. Bunun için hesaplanan değerleri dış yükler ile sisteme etki ettirilir. Yada süperpozisyon denklemleri yazılarak daha önce çizilen M,N,T diyagramları kullanılarak hiperstatik sistemin kesit tesirleri hesaplanır. Sistemde herhangi bir noktadaki kesit tesirlerini hesaplamak için M=M 0 M M M 3 3..M n n T = T 0 T T..T n n N = N 0 N N...N n n Süperpozisyon denklemleri kullanılabilir. Bu denklemler yardımıyla sistemde istenilen noktadaki kesit tesirleri hesaplanabilir.
36 0 kn m m Hiperstatik sistem (. dereceden) 0 kn İzostatik esas sistem 0 kn İzostatik esas sistem 0 kn İzostatik esas sistem
37 A 0 kn m B m 0 kn C Hiperstatik sistem (. dereceden) İzostatik esas sistem. Dereceden hiperstatik olduğu için uygunluk denklemi = 0
38 0 kn m m 0 Yüklemesi 40 kn.m 0 kn 0 kn ΣF y = 0 A y =0 ΣM A = 0 M A = 0* = 40 kn.m 40 m M 0 Diyagramı
39 Yüklemesi 4 m = 4 kn.m kn = ΣF y = 0 A y = ΣM A = 0 M A = *4 = 4 kn.m m m M Diyagramı 4
40 40 = 0 m M 0 Diyagramı m m M Diyagramı 4 0 ds M M ihmal EI = 0 EI 0 = ( x).( 0x) dx 0 EI 0 = ds M M ihmal EI = EI 4 = x).( x) 0 EI = 64 \ 3 = ( dx.333
41 i=40 = 0 m m 0 m M 0 Diyagramı ds M M ihmal EI = 0 EI 0 = Li ( k k 6 ) k =4 EI 0 = **( 40)*( *4) = k = M Diyagramı
42 = 0 m m k =4 k = M Diyagramı ds M M ihmal EI = EI = Li k = *4*4*4 = 64 / 3 =
43 = 0 = 0 = =6.5 0 kn 0 kn m m =6.5
44 0 kn A B C = T M
45 i=40 A A C m B M 0 Diyagramı 4 M A = M 0A M A * = (-40) 4*(6.5) = - 5 M B = M 0B M B * = (0) *(6.5) = 3.5 M C = M 0C M C * = (0) *(0) = 0 m B m M Diyagramı C 5 A - B 3.5 C
46 0 kn m m Hiperstatik sistem (. dereceden) Aynı sistemi çözmek için izostatik esas sistemi farklı seçelim. 0 kn İzostatik esas sistem
47 0 kn İzostatik esas sistem 0 kn 0 kn 0 kn M 0 0 kn.m
48 0 kn İzostatik esas sistem kn.m 4 m 0.5 kn 0.5 kn kn.m M
49 = 0 kn.m kn.m M 0 Diyagramı M Diyagramı 0 ds M M ihmal EI = 0 EI 0 = Li k Li (k k 3 6 ) EI 0 = **(0)*( 0.5) **(0)*(*( 0.5) ( )) = 0 3 6
50 kn.m = 0 M Diyagramı = ds MM = Li k = 4.( ).( ) =.333 EI 3 3 EI =.333
51 = 0 = 0 = =5 0 kn m m =5 0 kn
52 =5 0 kn T M
53 t/m Hiperstatik sistem (. dereceden) 3 m ( I ) 4 m (I) 3 m ( I ) = = m 4 m (I) 3 m İzostatik esas sistem ( I ) ( I )
54 t/m 4 m (I) 3 m 3 m 0 ( I ) ( I ) 6 6 tm 6 ( - ) ( o ) 8 t ( - ) M 0
55 4 m 4 ( - ) 0 3 m ( - ) M 4 tm =t t 3 ( ) 3 4 m 3 m ( ) M ( ) = 0 0
56 6 = = ( - ) ( o ) 4 ( - ) ( - ) M 0 ( - ) M 3 ( ) 3 ( ) ( ) M
57 6 6 ( - ) ( o ) 4 ( - ) ( - ) M 0 ( - ) M 0 = M M 0 ds EI EI 0 = *( Li k) 4 Li k EI 0 = *( *4*( 4)*( 6)) 3* 4* 6 4 EI 0 = 4
58 6 6 ( o ) ( - ) 3 ( ) 3 ( - ) M 0 ( ) M ( ) 0 EI = M M 0 ds EI *( *4* 6*3) ( *3* 3 EI = *( Li k) ( 3 0 = EI 0 = 04 0 Li k 6*3) )
59 4 ( - ) 3 ( ) 3 ( ) ( - ) ( ) M M = = M M ds EI EI = *( Li k) ( Li k ) EI = = EI EI *( *4*3* 4) ( *3*3* = 30 4)
60 4 ( - ) = ( - ) M M ds EI M EI = *( Li k) ( Li k) 3 EI = *( *4* 4* 4) (3* 4* 4) 3 EI =
61 3 ( ) 3 3 ( ) 3 ( ) ( ) ( ) ( ) M M = M M ds EI EI = ( Li k) *( Li k) ( 3 3 Li k ) EI = ( *3*3*3) *(4*3*3) 3 EI = 36 ( 3 *3*3*3)
62 = = 0 0 EI = 4 0 EI = EI 0 = 04 = = EI EI EI = = = = 0 = 0 = = 0.5
63 t/m t/m 4 m (I) 4 m (I) 3 m ( I ) 3 m ( I ) 3 m ( I ) 3 m ( I ) =0.5 = 4.079
64 t/m m ( I ) 4 m (I) 3 m ( I ) =0.5 ( - ) N ( - ) = () ( - ) T ( - ) ( - ) ( - ). - - M.53 ( - )
65 4 m 3 m İzostatik esas sistem t/m t/m 0 Yüklemesi 4 m m m m 0 4
66 t/m 4 m m M 0 0 4
67 4 m 4 m 3 m 3 m = = 4 m = 3 m I M
68 4 m 3 m = 4 m = = m M
69 = = M 0 I M 0 = M M 0 ds EI EI = *( 3 0 Li k ) EI *( *4*4*( 3 0 = EI0 =.667 ))
70 4 M M 0 0 = M M 0 ds EI EI = *( 3 0 Li k ) EI 0 = *( 3 *4*4*) EI 0 = 5.333
71 - I M = M M ds EI EI = *( Li k) ( Li k) 3 EI EI = *( *** 4) 3 = (**3)
72 M = M M ds EI EI = ( Li k) *( Li k) ( 3 3 Li k ) EI = ( *3**) *(4**) 3 EI = 4 ( 3 *3**)
73 - I M M = = M M ds EI EI = *( Li k) ( Li k ) EI = *( *4* *) ( *3* * ) = = EI EI.5
74 = = 0 0 EI0 =.667 EI = EI 0 = = = EI EI EI = 4.5 = = = 0 = 0 = 0.36 =.53
75 4 m = m = ( - ) ( - ) 0.36 M
76 ÖRNEK N/m 3 m 3 m Yandaki hiperstatik sistemin moment ve kesme kuvveti değişim grafiklerini çiziniz.. Dereceden hiperstatik = 0 İzostatik esas sistem
77 ÖRNEK 0 Yüklemesi N/m 3 m 3 m 3 N 3 N M 0 Moment diyagramı M 0 =.5
78 ÖRNEK Yüklemesi 3 m 3 m = N M Moment diyagramı 3 N.m
79 ÖRNEK M 0 =.5 M 0 Moment diyagramı 3 N.m M Moment diyagramı = 0 0 = = M M 0 M M ds EI ds EI EI = ( Li k) = *3*3* = EI = ( Li k) ( Li k) = *3*3*3 *3*3*3 =
80 ÖRNEK = 0 = =0 = N/m 3 m 3 m = 0.375
81 ÖRNEK N/m.65 3 m 3 m 3.75 = T M
Hiperstatik sistemlerin çözümünde, yer değiştirmelerin küçük olduğu ve gerilme - şekil değiştirme bağıntılarının lineer olduğu kabul edilmektedir.
 1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
Yapı Sistemlerinde Elverişsiz Yüklemeler:
 Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
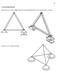 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
9 m 3 m. 10 kn/m. 5 m m. 3 m P=50 kn. 10 kn/m. P=50 kn. 20 kn/m. 10 kn/m. 1 8 m 2 m 3 m 3 m. 10 kn/m. 5 m. (Şekil-1b) (Şekil-1a) 20 kn /m
 NOT: u çalışma öyü, dersin uygulama kısmında sürenin yetersiz kalabileceği düşünülerek konuları daha iyi kavrayabilmeniz amacıyla hazırlanmıştır. Konu anlatımlarından sonra ilgili soruları ele alarak değerlendirmeniz
NOT: u çalışma öyü, dersin uygulama kısmında sürenin yetersiz kalabileceği düşünülerek konuları daha iyi kavrayabilmeniz amacıyla hazırlanmıştır. Konu anlatımlarından sonra ilgili soruları ele alarak değerlendirmeniz
Mukavemet-I. Yrd.Doç.Dr. Akın Ataş
 Mukavemet-I Yrd.Doç.Dr. Akın Ataş Bölüm 5 Eğilmede Kirişlerin Analizi ve Tasarımı Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mukavemet-I Yrd.Doç.Dr. Akın Ataş Bölüm 5 Eğilmede Kirişlerin Analizi ve Tasarımı Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
MUKAVEMET Öğr. Gör. Fatih KURTULUŞ
 www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
28. Sürekli kiriş örnek çözümleri
 28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
AÇI YÖNTEMİ Slope-deflection Method
 SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
29. Düzlem çerçeve örnek çözümleri
 9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (3. Hafta)
 TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
MOMENT DAĞITMA HARDY CROSS YÖNTEMİ
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSİĞİ BÖÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II MOMENT DAĞITMA HARDY CROSS YÖNTEMİ Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSİĞİ BÖÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II MOMENT DAĞITMA HARDY CROSS YÖNTEMİ Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele
 EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele alınmıştı. Bu bölümde ise, eksenel yüklü elemanların şekil
EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele alınmıştı. Bu bölümde ise, eksenel yüklü elemanların şekil
KAYMA GERİLMESİ (ENİNE KESME)
 KAYMA GERİLMESİ (ENİNE KESME) Demir yolu traversleri çok büyük kesme yüklerini taşıyan kiriş olarak davranır. Bu durumda, eğer traversler ahşap malzemedense kesme kuvvetinin en büyük olduğu uçlarından
KAYMA GERİLMESİ (ENİNE KESME) Demir yolu traversleri çok büyük kesme yüklerini taşıyan kiriş olarak davranır. Bu durumda, eğer traversler ahşap malzemedense kesme kuvvetinin en büyük olduğu uçlarından
SEM2015 programı kullanımı
 SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Çözebileceği sistemler: Düzlem/uzay kafes: Evet Düzlem/uzay çerçeve:
SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Çözebileceği sistemler: Düzlem/uzay kafes: Evet Düzlem/uzay çerçeve:
Açı Yöntemi. 1 ql 8. Açı yöntemi olarak adlandırılan denklemlerin oluşturulmasında aşağıda gösterilen işaret kabulü yapılmaktadır.
 çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
YAPI STATİĞİ Prof. Dr. P. Marti
 İlk yayın, 9 Temmuz 05 www.guven-kutay.ch YPI STTİĞİ Prof. Dr. P. arti Hiperstatik Sistemler -0- u dosyayı _00_Yapı Statiğine Giriş ve Özet dosyasıyla beraber incelerseniz daha iyi anlarsınız. Çevirenler:.
İlk yayın, 9 Temmuz 05 www.guven-kutay.ch YPI STTİĞİ Prof. Dr. P. arti Hiperstatik Sistemler -0- u dosyayı _00_Yapı Statiğine Giriş ve Özet dosyasıyla beraber incelerseniz daha iyi anlarsınız. Çevirenler:.
7. Kafes sistem sayısal örnekleri
 7. Kafes sistem sayısal örnekleri 7. Düzlem kafes sistem sayısal örneği Şekil 7. deki kafes sistem elastisite modülü.. 5 N/mm olan çelik borulardan imal edilmiştir. a noktasındaki kuvvetlerinden oluşan:
7. Kafes sistem sayısal örnekleri 7. Düzlem kafes sistem sayısal örneği Şekil 7. deki kafes sistem elastisite modülü.. 5 N/mm olan çelik borulardan imal edilmiştir. a noktasındaki kuvvetlerinden oluşan:
Yararlanılabilecek Bazı Kaynaklar
 2 Abdulkadir Cüneyt AYDIN Yararlanılabilecek Bazı Kaynaklar 1. Yapı Statiği II Adnan ÇAKIROĞLU ve Enver ÇETMELİ 2. Yapı Statiği II İbrahim EKİZ 3. Yapı Statiği-Hiperstatik Sistemler Konuralp GİRGİN, M.
2 Abdulkadir Cüneyt AYDIN Yararlanılabilecek Bazı Kaynaklar 1. Yapı Statiği II Adnan ÇAKIROĞLU ve Enver ÇETMELİ 2. Yapı Statiği II İbrahim EKİZ 3. Yapı Statiği-Hiperstatik Sistemler Konuralp GİRGİN, M.
Burulma (Torsion) Amaçlar
 (Torsion) Amaçlar Bu bölümde şaftlara etkiyen burulma kuvvetlerinin etkisi incelenecek. Analiz dairesel kesitli şaftlar için yapılacak. Eleman en kesitinde oluşan gerilme dağılımı ve elemanda oluşan burulma
(Torsion) Amaçlar Bu bölümde şaftlara etkiyen burulma kuvvetlerinin etkisi incelenecek. Analiz dairesel kesitli şaftlar için yapılacak. Eleman en kesitinde oluşan gerilme dağılımı ve elemanda oluşan burulma
İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER
 İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER Yapı Elemanları İnşaat Mühendisliği ile ilgili yapı sistemleri üç ayrı tipteki yapı elemanlarının birleşiminden oluşur. 1)Çubuk Elemanlar: İki boyutu üçüncü boyutuna
İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER Yapı Elemanları İnşaat Mühendisliği ile ilgili yapı sistemleri üç ayrı tipteki yapı elemanlarının birleşiminden oluşur. 1)Çubuk Elemanlar: İki boyutu üçüncü boyutuna
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Kesit Tesirleri Tekil Kuvvetler
 Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
İNM 208 DERS TANITIM
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II İNM 208 DERS TANITIM Y.Doç.Dr. Mustafa KUTANİS DR.MUSTAFA KUTANİS SLIDE 1 ADRES INM 208 YAPI STATİĞİ
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II İNM 208 DERS TANITIM Y.Doç.Dr. Mustafa KUTANİS DR.MUSTAFA KUTANİS SLIDE 1 ADRES INM 208 YAPI STATİĞİ
25. SEM2015 programı ve kullanımı
 25. SEM2015 programı ve kullanımı Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
25. SEM2015 programı ve kullanımı Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
MECHANICS OF MATERIALS
 T E CHAPTER 2 Eksenel MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Yükleme Fatih Alibeyoğlu Eksenel Yükleme Bir önceki bölümde, uygulanan yükler neticesinde ortaya çıkan
T E CHAPTER 2 Eksenel MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Yükleme Fatih Alibeyoğlu Eksenel Yükleme Bir önceki bölümde, uygulanan yükler neticesinde ortaya çıkan
İzostatik Sistemlerin Hareketli Yüklere Göre Hesabı
 İzostatik Sistemlerin Hareketli Yüklere Göre Hesabı Hareketli Yük Çeşitleri: a) I. tip hareketli yük: Sistemin tümünü veya bir bölümünü kaplayan, boyu değişken düzgün yayılı hareketli yüklerdir (insan,
İzostatik Sistemlerin Hareketli Yüklere Göre Hesabı Hareketli Yük Çeşitleri: a) I. tip hareketli yük: Sistemin tümünü veya bir bölümünü kaplayan, boyu değişken düzgün yayılı hareketli yüklerdir (insan,
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
 5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
Kirişlerde Kesme (Transverse Shear)
 Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
Mukavemet-II. Yrd.Doç.Dr. Akın Ataş
 Mukavemet-II Yrd.Doç.Dr. Akın Ataş Bölüm 9 Kirişlerin Yer Değiştirmesi Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok. 9.1 Giriş
Mukavemet-II Yrd.Doç.Dr. Akın Ataş Bölüm 9 Kirişlerin Yer Değiştirmesi Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok. 9.1 Giriş
25. SEM2015 programı kullanımı
 25. SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
25. SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
STATIK VE MUKAVEMET. 6.Düzlem ve Uzay kafes Sistemler. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 6.Düzlem ve Uzay kafes Sistemler Doç. Dr. NURHAYAT DEĞİRMENCİ Birbirlerine bağlı birden fazla parçadan yapılmış sistemlerin dengesi için dıs kuvvetlere ilaveten iç kuvvetler de düşünülmelidir.
STATIK VE MUKAVEMET 6.Düzlem ve Uzay kafes Sistemler Doç. Dr. NURHAYAT DEĞİRMENCİ Birbirlerine bağlı birden fazla parçadan yapılmış sistemlerin dengesi için dıs kuvvetlere ilaveten iç kuvvetler de düşünülmelidir.
Doç. Dr. Bilge DORAN
 Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
İÇ KUVVETLER. Amaçlar: Bir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi
 İÇ KUVVETLER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
İÇ KUVVETLER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 303 YAPI STATIĞI II. Genel Kavramlar
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 303 YAPI STATIĞI II Genel Kavramlar Yapı mühendisliğinin amacı Yapı Tasarım Süreci Yapı statiğinde yapılan kabuller
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 303 YAPI STATIĞI II Genel Kavramlar Yapı mühendisliğinin amacı Yapı Tasarım Süreci Yapı statiğinde yapılan kabuller
Kirişlerde İç Kuvvetler
 Kirişlerde İç Kuvvetler B noktasındaki iç kuvvetlerin bulunması B noktasındaki iç kuvvetler sol ve sağ parça İki boyutlu problemlerde eleman kesitinde üç farklı iç kuvvet oluşur! 2D 3D Pozitif normal/eksenel
Kirişlerde İç Kuvvetler B noktasındaki iç kuvvetlerin bulunması B noktasındaki iç kuvvetler sol ve sağ parça İki boyutlu problemlerde eleman kesitinde üç farklı iç kuvvet oluşur! 2D 3D Pozitif normal/eksenel
SONLU ELEMANLAR YÖNTEMİ
 SONLU ELEMANLAR YÖNTEMİ Kurs Kapsamı SONLU ELEMANLAR KAVRAMI SONLU ELEMANLAR FORMULASYONU UYGULAMALARI Sonlu Elemanlar Çözümleri Rijitlik Metodu Esneklik Metodu Karışık Kullanımlar Rijitlik Metodu Kullanılarak
SONLU ELEMANLAR YÖNTEMİ Kurs Kapsamı SONLU ELEMANLAR KAVRAMI SONLU ELEMANLAR FORMULASYONU UYGULAMALARI Sonlu Elemanlar Çözümleri Rijitlik Metodu Esneklik Metodu Karışık Kullanımlar Rijitlik Metodu Kullanılarak
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım)
 İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
EĞİLME. Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır.
 EĞİLME Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır. EĞİLME Mühendislikte en önemli yapı ve makine elemanları mil ve kirişlerdir. Bu bölümde, mil ve kirişlerde
EĞİLME Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır. EĞİLME Mühendislikte en önemli yapı ve makine elemanları mil ve kirişlerdir. Bu bölümde, mil ve kirişlerde
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
BURSA TEKNİK ÜNİVERSİTESİ DOĞA BİLİMLERİ, MİMARLIK VE MÜHENDİSLİK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ 3 NOKTA EĞME DENEYİ FÖYÜ
 BURSA TEKNİK ÜNİVERSİTESİ DOĞA BİLİMLERİ, MİMARLIK VE MÜHENDİSLİK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ 3 NOKTA EĞME DENEYİ FÖYÜ BURSA - 2016 1. GİRİŞ Eğilme deneyi malzemenin mukavemeti hakkında tasarım
BURSA TEKNİK ÜNİVERSİTESİ DOĞA BİLİMLERİ, MİMARLIK VE MÜHENDİSLİK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ 3 NOKTA EĞME DENEYİ FÖYÜ BURSA - 2016 1. GİRİŞ Eğilme deneyi malzemenin mukavemeti hakkında tasarım
Proje Genel Bilgileri
 Proje Genel Bilgileri Çatı Kaplaması : Betonarme Döşeme Deprem Bölgesi : 1 Yerel Zemin Sınıfı : Z2 Çerçeve Aralığı : 5,0 m Çerçeve Sayısı : 7 aks Malzeme : BS25, BÇIII Temel Taban Kotu : 1,0 m Zemin Emniyet
Proje Genel Bilgileri Çatı Kaplaması : Betonarme Döşeme Deprem Bölgesi : 1 Yerel Zemin Sınıfı : Z2 Çerçeve Aralığı : 5,0 m Çerçeve Sayısı : 7 aks Malzeme : BS25, BÇIII Temel Taban Kotu : 1,0 m Zemin Emniyet
İÇ KUVVETLER. Amaçlar: Bir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi
 İÇ KUVVELER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
İÇ KUVVELER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor
 3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
CS MÜHENDİSLİK PROJE YAZILIM HİZMETLERİ www.csproje.com. EUROCODE-2'ye GÖRE MOMENT YENİDEN DAĞILIM
 Moment CS MÜHENİSLİK PROJE YAZILIM HİZMETLERİ EUROCOE-2'ye GÖRE MOMENT YENİEN AĞILIM Bir yapıdaki kuvvetleri hesaplamak için elastik kuvvetler kullanılır. Yapının taşıma gücüne yakın elastik davranmadığı
Moment CS MÜHENİSLİK PROJE YAZILIM HİZMETLERİ EUROCOE-2'ye GÖRE MOMENT YENİEN AĞILIM Bir yapıdaki kuvvetleri hesaplamak için elastik kuvvetler kullanılır. Yapının taşıma gücüne yakın elastik davranmadığı
Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir.
 BASINÇ ÇUBUKLARI Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir. Basınç çubukları, sadece eksenel basınç kuvvetine maruz kalırlar. Bu çubuklar üzerinde Eğilme ve
BASINÇ ÇUBUKLARI Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir. Basınç çubukları, sadece eksenel basınç kuvvetine maruz kalırlar. Bu çubuklar üzerinde Eğilme ve
KESİT TESİR DİYAGRAMLARI YAPI STATİĞİ 1
 KESİT TESİR DİYAGRAMLARI YAPI STATİĞİ 1 GİRİŞ Sabit yu klerden meydana gelen kesit tesiri fonksiyonlarından elde edilen grafiklere Kesit Tesir Diyagramları denir. Du zlem c ubuk sistemlerde M, N, T (V)
KESİT TESİR DİYAGRAMLARI YAPI STATİĞİ 1 GİRİŞ Sabit yu klerden meydana gelen kesit tesiri fonksiyonlarından elde edilen grafiklere Kesit Tesir Diyagramları denir. Du zlem c ubuk sistemlerde M, N, T (V)
Elastisite Teorisi Düzlem Problemleri için Sonuç 1
 Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
Eksenel Yükleme Amaçlar
 Eksenel Yükleme Amaçlar Geçtiğimiz bölümlerde eksenel yüklü elemanlarda oluşan normal gerilme ve normal şekil değiştirme konularını gördük, Bu bölümde ise deformasyonların bulunması ile ilgili bir metot
Eksenel Yükleme Amaçlar Geçtiğimiz bölümlerde eksenel yüklü elemanlarda oluşan normal gerilme ve normal şekil değiştirme konularını gördük, Bu bölümde ise deformasyonların bulunması ile ilgili bir metot
KOCAELİ ÜNİVERSİTESİ Mühendislik Fakültesi Makina Mühendisliği Bölümü Mukavemet II Final Sınavı (2A)
 KOCELİ ÜNİVERSİTESİ ühendislik ültesi ina ühendisliği ölümü ukavemet II inal Sınavı () dı Soyadı : 5 Haziran 01 Sınıfı : No : SORU 1: Şekilde sistemde boru anahtarına 00 N luk b ir kuvvet etki etmektedir.
KOCELİ ÜNİVERSİTESİ ühendislik ültesi ina ühendisliği ölümü ukavemet II inal Sınavı () dı Soyadı : 5 Haziran 01 Sınıfı : No : SORU 1: Şekilde sistemde boru anahtarına 00 N luk b ir kuvvet etki etmektedir.
KONU 3. STATİK DENGE
 KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
Mukavemet-II. Yrd.Doç.Dr. Akın Ataş
 Mukavemet-II Yrd.Doç.Dr. Akın Ataş Bölüm 11 Enerji Yöntemleri Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok. 11.1 Giriş Önceki bölümlerde
Mukavemet-II Yrd.Doç.Dr. Akın Ataş Bölüm 11 Enerji Yöntemleri Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok. 11.1 Giriş Önceki bölümlerde
Gerilme. Bölüm Hedefleri. Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı
 Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
YAPI STATİĞİ 2 DERSİ IM 302 GENEL TANITIM. Doç. Dr. Deniz GÜNEY.
 YAPI STATİĞİ 2 DERSİ IM 302 GENEL TANITIM Doç. Dr. Deniz GÜNEY www.yarbis.yildiz.edu.tr/deguney 1 1. Hiperstatik Sistemlerde Tanımlar. Hiperstatiklik Derecesinin Belirlenmesi. Kuvvet Yönteminin Prensibi
YAPI STATİĞİ 2 DERSİ IM 302 GENEL TANITIM Doç. Dr. Deniz GÜNEY www.yarbis.yildiz.edu.tr/deguney 1 1. Hiperstatik Sistemlerde Tanımlar. Hiperstatiklik Derecesinin Belirlenmesi. Kuvvet Yönteminin Prensibi
36. Basit kuvvet metodu
 36. Basit kuvvet metodu Basit kuvvet metodu hakkında çok kısa bilgi verilecektir. Basit kuvvet metodunda hiperstatik bilinmeyenlerinin hesaplanmasına, dolayısıyla buna ait denklem sisteminin kurulmasına
36. Basit kuvvet metodu Basit kuvvet metodu hakkında çok kısa bilgi verilecektir. Basit kuvvet metodunda hiperstatik bilinmeyenlerinin hesaplanmasına, dolayısıyla buna ait denklem sisteminin kurulmasına
Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar. 7.3 Yatayda Yayılı Yük Aktaran Kablolar
 7.1 7.2 Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar 7.3 Yatayda Yayılı Yük Aktaran Kablolar 7.4 Örnekler Kendi Ağırlığını Taşıyan Kablolar (Zincir Eğrisi)
7.1 7.2 Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar 7.3 Yatayda Yayılı Yük Aktaran Kablolar 7.4 Örnekler Kendi Ağırlığını Taşıyan Kablolar (Zincir Eğrisi)
KİRİŞLERDE VE İNCE CİDARLI ELEMANLARDA KAYMA GERİLMELERİ
 KİRİŞLERDE VE İNCE CİDARLI ELEMANLARDA KAYMA GERİLMELERİ x Göz önüne alınan bir kesitteki Normal ve Kayma gerilmelerinin dağılımı statik denge denklemlerini sağlamalıdır: F F F x y z = = = σ da = 0 x τ
KİRİŞLERDE VE İNCE CİDARLI ELEMANLARDA KAYMA GERİLMELERİ x Göz önüne alınan bir kesitteki Normal ve Kayma gerilmelerinin dağılımı statik denge denklemlerini sağlamalıdır: F F F x y z = = = σ da = 0 x τ
BAŞKENT ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MAK 402 MAKİNA MÜHENDİSLİĞİ LABORATUVARI DENEY - 3 ÜÇ NOKTALI EĞİLME DENEYİ
 BAŞKENT ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MAK 402 MAKİNA MÜHENDİSLİĞİ LABORATUVARI DENEY - 3 ÜÇ NOKTALI EĞİLME DENEYİ GİRİŞ Yapılan herhangi bir mekanik tasarımda kullanılacak malzemelerin belirlenmesi
BAŞKENT ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MAK 402 MAKİNA MÜHENDİSLİĞİ LABORATUVARI DENEY - 3 ÜÇ NOKTALI EĞİLME DENEYİ GİRİŞ Yapılan herhangi bir mekanik tasarımda kullanılacak malzemelerin belirlenmesi
Çerçeve ve Makineler
 Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
23. Sistem denge denklemlerinin direkt kurulması
 . Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
. Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
KirişlerdeİçKuvvetler Normal Kuvvet, KesmeKuvveti vemoment Diyagramları
 KirişlerdeİçKuvvetler Normal Kuvvet, KesmeKuvveti vemoment Diyagramları Kesme ve Moment Diyagramlarının Oluşturulması için Grafiksel Yöntem (Alan Yöntemi) Kiriş için işaret kabulleri (hatırlatma): Pozitif
KirişlerdeİçKuvvetler Normal Kuvvet, KesmeKuvveti vemoment Diyagramları Kesme ve Moment Diyagramlarının Oluşturulması için Grafiksel Yöntem (Alan Yöntemi) Kiriş için işaret kabulleri (hatırlatma): Pozitif
İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz
 Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
ELEKTRONİK VE HABERLEŞME MÜHENDİSLİĞİ ÖLÇME VE DEVRE LABORATUVARI DENEY 2
 ELEKTRONİK VE HABERLEŞME MÜHENDİSLİĞİ ÖLÇME VE DEVRE LABORATUVARI DENEY 2 2.1. ÇEVRE AKIMLAR YÖNTEMİ Elektrik devrelerinin çözümünde kullanılan en basit ve en kolay yöntemlerden biri çevre akımları yöntemidir.
ELEKTRONİK VE HABERLEŞME MÜHENDİSLİĞİ ÖLÇME VE DEVRE LABORATUVARI DENEY 2 2.1. ÇEVRE AKIMLAR YÖNTEMİ Elektrik devrelerinin çözümünde kullanılan en basit ve en kolay yöntemlerden biri çevre akımları yöntemidir.
Kafes Sistemler. Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir.
 Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Tablo 1 Deney esnasında kullanacağımız numunelere ait elastisite modülleri tablosu
 BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
GERİLME Cismin kesilmiş alanı üzerinde O
 GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
MUKAVEMET I ÇÖZÜMLÜ ÖRNEKLER
 MUKAEMET I ÇÖZÜMÜ ÖRNEKER ders notu Yard. Doç. Dr. Erdem DAMCI Şubat 15 Mukavemet I - Çözümlü Örnekler / 7 Örnek 1. Üzerinde yalnızca yayılı yük bulunan ve açıklığı olan bir basit kirişe ait eğilme momenti
MUKAEMET I ÇÖZÜMÜ ÖRNEKER ders notu Yard. Doç. Dr. Erdem DAMCI Şubat 15 Mukavemet I - Çözümlü Örnekler / 7 Örnek 1. Üzerinde yalnızca yayılı yük bulunan ve açıklığı olan bir basit kirişe ait eğilme momenti
34. Dörtgen plak örnek çözümleri
 34. Dörtgen plak örnek çözümleri Örnek 34.1: Teorik çözümü Timoshenko 1 tarafından verilen dört tarafından ankastre ve merkezinde P=100 kn tekil yükü olan kare plağın(şekil 34.1) çözümü 4 farklı model
34. Dörtgen plak örnek çözümleri Örnek 34.1: Teorik çözümü Timoshenko 1 tarafından verilen dört tarafından ankastre ve merkezinde P=100 kn tekil yükü olan kare plağın(şekil 34.1) çözümü 4 farklı model
STATIK MUKAVEMET. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
p 2 p Üçgen levha eleman, düzlem şekil değiştirme durumu
 Üçgen levha eleman düzlem şekil değiştirme durumu Üçgen levha eleman düzlem şekil değiştirme durumu İstinat duvarı basınçlı uzun boru tünel ağırlık barajı gibi yapılar düzlem levha gibi davranırlar Uzun
Üçgen levha eleman düzlem şekil değiştirme durumu Üçgen levha eleman düzlem şekil değiştirme durumu İstinat duvarı basınçlı uzun boru tünel ağırlık barajı gibi yapılar düzlem levha gibi davranırlar Uzun
Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri
 Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri belirlenmesi 1. katta döşemelerin çözümü ve çizimi Döşeme
Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri belirlenmesi 1. katta döşemelerin çözümü ve çizimi Döşeme
Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta ( ):
 Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
Kafes Sistemler. Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir.
 KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN
 Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ
 T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ 3 NOKTA EĞME DENEY FÖYÜ ÖĞRETİM ÜYESİ YRD.DOÇ.DR.ÖMER KADİR
T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ 3 NOKTA EĞME DENEY FÖYÜ ÖĞRETİM ÜYESİ YRD.DOÇ.DR.ÖMER KADİR
KOÜ. Mühendislik Fakültesi Makine Mühendisliği Bölümü (1. ve 2.Öğretim / B Şubesi) MMK208 Mukavemet II Dersi - 1. Çalışma Soruları 23 Şubat 2019
 SORU-1) Aynı anda hem basit eğilme hem de burulma etkisi altında bulunan yarıçapı R veya çapı D = 2R olan dairesel kesitli millerde, oluşan (meydana gelen) en büyük normal gerilmenin ( ), eğilme momenti
SORU-1) Aynı anda hem basit eğilme hem de burulma etkisi altında bulunan yarıçapı R veya çapı D = 2R olan dairesel kesitli millerde, oluşan (meydana gelen) en büyük normal gerilmenin ( ), eğilme momenti
q = 48 kn/m q = 54 kn/m 4 m 5 m 3 m 3 m
 Soru 1) (50 Puan) şağıda verilen sistemin üzerine etkiyen yükler ve konumları şekil üzerinde belirtilmiştir. una ek olarak mesneti cm aşağı yönlü oturmuştur. Tüm kolon ve kirişlerin atalet momenti, elastik
Soru 1) (50 Puan) şağıda verilen sistemin üzerine etkiyen yükler ve konumları şekil üzerinde belirtilmiştir. una ek olarak mesneti cm aşağı yönlü oturmuştur. Tüm kolon ve kirişlerin atalet momenti, elastik
KİRİŞLERDE PLASTİK MAFSALIN PLASTİKLEŞME BÖLGESİNİ VEREN BİLGİSAYAR YAZILIMI
 IM 566 LİMİT ANALİZ DÖNEM PROJESİ KİRİŞLERDE PLASTİK MAFSALIN PLASTİKLEŞME BÖLGESİNİ VEREN BİLGİSAYAR YAZILIMI HAZIRLAYAN Bahadır Alyavuz DERS SORUMLUSU Prof. Dr. Sinan Altın GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ
IM 566 LİMİT ANALİZ DÖNEM PROJESİ KİRİŞLERDE PLASTİK MAFSALIN PLASTİKLEŞME BÖLGESİNİ VEREN BİLGİSAYAR YAZILIMI HAZIRLAYAN Bahadır Alyavuz DERS SORUMLUSU Prof. Dr. Sinan Altın GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ
İNŞ 320- Betonarme 2 Ders Notları / Prof Dr. Cengiz DÜNDAR Arş. Gör. Duygu BAŞLI
 a) Denge Burulması: Yapı sistemi veya elemanında dengeyi sağlayabilmek için burulma momentine gereksinme varsa, burulma denge burulmasıdır. Sözü edilen gereksinme, elastik aşamada değil taşıma gücü aşamasındaki
a) Denge Burulması: Yapı sistemi veya elemanında dengeyi sağlayabilmek için burulma momentine gereksinme varsa, burulma denge burulmasıdır. Sözü edilen gereksinme, elastik aşamada değil taşıma gücü aşamasındaki
Yararlanılabilecek Bazı Kaynaklar
 2 Yararlanılabilecek Bazı Kaynaklar 1. Yapı Statiği I-II Adnan ÇAKIROĞLU ve Enver ÇETMELİ 2. Çözümlü Örneklerle Yapı Statiği Hüsnü CAN 3. Taşıyıcı Sistemler ve Yapı Statiği İsmail İlhan SUNGUR 4. Yapı
2 Yararlanılabilecek Bazı Kaynaklar 1. Yapı Statiği I-II Adnan ÇAKIROĞLU ve Enver ÇETMELİ 2. Çözümlü Örneklerle Yapı Statiği Hüsnü CAN 3. Taşıyıcı Sistemler ve Yapı Statiği İsmail İlhan SUNGUR 4. Yapı
R 1Y kn R 1X R 1Z R 4Y R 3Y 4 R 4X R 3Z R 3X R 4Z. -90 kn. 80 kn 80 kn R 1Y =10 R 1X =-10 R 4Y =10 R 1Z =0 R 3Y =70 4 R 3X =-70 R 4X =0
 27. Uzay kafes örnek çözümleri Örnek 27.: Şekil 27. de verilen uzay kafes sistem çelik borulardan imal edilecektir. a noktasındaki dış yüklerden oluşan eleman kuvvetleri, reaksiyonlar, gerilmeler ve düğüm
27. Uzay kafes örnek çözümleri Örnek 27.: Şekil 27. de verilen uzay kafes sistem çelik borulardan imal edilecektir. a noktasındaki dış yüklerden oluşan eleman kuvvetleri, reaksiyonlar, gerilmeler ve düğüm
ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR PROGRAMI
 DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 3 Sayı: 3 sh. 33-50 Ekim 2001 ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR
DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 3 Sayı: 3 sh. 33-50 Ekim 2001 ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR
 ÇALIŞMA SORULARI 1) Yukarıdaki şekilde AB ve BC silindirik çubukları B noktasında birbirleriyle birleştirilmişlerdir, AB çubuğunun çapı 30 mm ve BC çubuğunun çapı ise 50 mm dir. Sisteme A ucunda 60 kn
ÇALIŞMA SORULARI 1) Yukarıdaki şekilde AB ve BC silindirik çubukları B noktasında birbirleriyle birleştirilmişlerdir, AB çubuğunun çapı 30 mm ve BC çubuğunun çapı ise 50 mm dir. Sisteme A ucunda 60 kn
TORNA TEZGAHINDA KESME KUVVETLERİ ANALİZİ
 İMALAT DALI MAKİNE LABORATUVARI II DERSİ TORNA TEZGAHINDA KESME KUVVETLERİ ANALİZİ DENEY RAPORU HAZIRLAYAN Osman OLUK 1030112411 1.Ö. 1.Grup DENEYİN AMACI Torna tezgahı ile işlemede, iş parçasına istenilen
İMALAT DALI MAKİNE LABORATUVARI II DERSİ TORNA TEZGAHINDA KESME KUVVETLERİ ANALİZİ DENEY RAPORU HAZIRLAYAN Osman OLUK 1030112411 1.Ö. 1.Grup DENEYİN AMACI Torna tezgahı ile işlemede, iş parçasına istenilen
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Çatı katında tüm çevrede 1m saçak olduğu kabul edilebilir.
 Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri belirlenmesi 1. katta döşemelerin çözümü ve çizimi Döşeme
Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri belirlenmesi 1. katta döşemelerin çözümü ve çizimi Döşeme
KOCAELİ ÜNİVERSİTESİ Mühendislik Fakültesi Makina Mühendisliği Bölümü Mukavemet I Final Sınavı
 KOCEİ ÜNİVERSİTESİ Mühendislik akültesi Makina Mühendisliği ölümü Mukavemet I inal Sınavı dı Soadı : 9 Ocak 0 Sınıfı : h No : SORU : Şekildeki ucundan ankastre, ucundan serbest olan kirişinin uzunluğu
KOCEİ ÜNİVERSİTESİ Mühendislik akültesi Makina Mühendisliği ölümü Mukavemet I inal Sınavı dı Soadı : 9 Ocak 0 Sınıfı : h No : SORU : Şekildeki ucundan ankastre, ucundan serbest olan kirişinin uzunluğu
TC. SAKARYA ÜNİVERSİTESİ, MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering YAPI STATİĞİ 1 KAFES SİSTEMLER 1 KAFES KÖPRÜLER
 TC. SAKARYA ÜNİVERSİTESİ, MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering YAPI STATİĞİ 1 KAFES SİSTEMLER 1 DR. MUSTAFA KUTANİS SLIDE 1 KAFES KÖPRÜLER DR. MUSTAFA KUTANİS SAÜ İNŞ.MÜH. BÖLÜMÜ
TC. SAKARYA ÜNİVERSİTESİ, MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering YAPI STATİĞİ 1 KAFES SİSTEMLER 1 DR. MUSTAFA KUTANİS SLIDE 1 KAFES KÖPRÜLER DR. MUSTAFA KUTANİS SAÜ İNŞ.MÜH. BÖLÜMÜ
