NÜMER IK ANAL IZ. Nuri ÖZALP. SAYISAL TÜREV ve INTEGRAL. Bilimsel Hesaplama Matemati¼gi
|
|
|
- Ufuk Kaya
- 7 yıl önce
- İzleme sayısı:
Transkript
1 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP SAYISAL TÜREV ve INTEGRAL Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 1 / 23
2 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev ve Richardson D şkestirimi Bir f fonksiyonunun de¼gerleri x 0, x 1,..., x n noktalar nda verilsin. Bu bilgi ile f 0 (c) türevi ya da R b a f (x)dx integrali tahmin edilebilir mi? Yan t s n rl bir evettir? Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 2 / 23
3 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev ve Richardson D şkestirimi Bir f fonksiyonunun de¼gerleri x 0, x 1,..., x n noktalar nda verilsin. Bu bilgi ile f 0 (c) türevi ya da R b a f (x)dx integrali tahmin edilebilir mi? Yan t s n rl bir evettir? f nin ba¼g l olarak daha küçük bir fonksiyon ailesine ait oldu¼guna dair bir bilgiye sahip olmad ¼g m z sürece, tek baş na f (x 0 ), f (x 1 ),..., f (x n ) de¼gerlerinden f hakk nda çok fazla bilgi elde etmek imkans zd r. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 2 / 23
4 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev ve Richardson D şkestirimi Bir f fonksiyonunun de¼gerleri x 0, x 1,..., x n noktalar nda verilsin. Bu bilgi ile f 0 (c) türevi ya da R b a f (x)dx integrali tahmin edilebilir mi? Yan t s n rl bir evettir? f nin ba¼g l olarak daha küçük bir fonksiyon ailesine ait oldu¼guna dair bir bilgiye sahip olmad ¼g m z sürece, tek baş na f (x 0 ), f (x 1 ),..., f (x n ) de¼gerlerinden f hakk nda çok fazla bilgi elde etmek imkans zd r. Örne¼gin, e¼ger f nin tüm reel de¼gerli sürekli fonksiyonlar ailesinde olmas na izin verilirse, bu durumda f (x i ) de¼gerinin bilinmesi neredeyese kullan şs zd r. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 2 / 23
5 1 Say sal Türev ve Richardson D şkestirimi Şekil alt noktada ayn de¼gerleri alan üç sürekli fonksiyonu göstermektedir. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 3 / 23
6 1 Say sal Türev ve Richardson D şkestirimi E¼ger f nin en fazla n. dereceden bir polinom oldu¼gunu biliyorsak, Kesim 6.1 (s. 308) deki interpolasyon teorisinden, f nin n + 1 noktadaki de¼gerleri f yi kesin olarak belirler. Bu durumda, f yi kesin olarak geri elde ederiz ve buradan f 0 (c) ve R b f (x)dx i tam bir güvenle hesaplayabiliriz. Bununla a beraber, gerçekçi durumlar n ço¼gunda eldeki bilgi f yi tam olarak belirlemeye yetmez, ve e¼ger içerilen hatalarla ilgili baz s n rlar da verilmemişse, f nin türevinin veya integralinin herhangi bir say sal tahminine şüphe ile yaklaş lmal d r. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 4 / 23
7 Say sal Türev 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Bu durumlar f 0 (x) in limit tan m ndan do¼grudan ortaya ç kan bir say sal türev formülünü inceleyerek başlayal m: f 0 (x) 1 [f (x + h) f (x)] (1) h Bir lineer fonksiyon, f (x) = ax + b için (1) yaklaş m formülü kesindir; yani, s f rdan farkl herhangi bir h de¼geri için f 0 (x) in do¼gru de¼gerini verir. Formül başka durumlarda da kesin olabilir, fakat bu sadece şans eseridir. O halde, şimdi say sal türev için verilen bu formüle ait hatay de¼gerlendirmeye çal şal m. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 5 / 23
8 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Başlang ç noktam z Taylor Teoremi nin aşa¼g daki formudur: f (x + h) = f (x) + hf 0 (x) + h2 2 f 00 (ξ) (2) Burada ξ, x ile x + h aras ndaki aç k aral kta bir noktad r. (2) eşitli¼ginin geçerli olmas için, f ve f 0 nün x ve x + h aras ndaki kapal aral kta sürekli olmalar ve f 00 nün de karş l k gelen aç k aral kta var olmas gereklidir. (2) eşitli¼ginin yeniden düzenlenmesi verir. f 0 (x) = 1 h [f (x + h) f (x)] h 2 f 00 (ξ) (3) = 1 [f (x + h) f (x)] + O(h) h Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 6 / 23
9 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Örnek E¼ger f (x) = cos x türevini x = π/4 te h = 0.01 ile hesaplamak için Formül (1) kullan l rsa, yan t ne olur ve duyarl l ¼g nedir? Çözüm Bir hesap makinesi kullanarak f 0 (x) 1 1 h [f (x + h) f (x)] = 0.01 [ ] = buluruz. (3) den: h 2 f 00 (ξ) = jcos ξj 0.005π/4 < ξ < π/4 + h gerçe¼gini ve böylece jcos ξj < eşitsizli¼gini kullanarak daha güçlü bir s n r elde edebiliriz. Bu bize s n r n verir. Gerçek hata ise sin π = dur. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 7 / 23
10 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev (3) eşitli¼gindeki (h/2)f 00 (ξ) terimi kesme hatas olarak adland r l r. Bu, ortaya ç kan hatad r, çünkü türevlemenin belli bir aşamas nda, bir Taylor serisi kesilmektedir. Buradaki durumda, (1) yaklaş m formülü f (x + h) = f (x) + hf 0 (x) + h2 2 f 00 (x) + h3 3! f 000 (x) + serisi kesilerek aşa¼g daki gibi elde edilmiştir: f (x + h) f (x) + hf 0 (x) Kesme hatas ve yuvarlama hatas (1) formülünün ve di¼ger benzerlerinin kullan m nda eşit önemde rol oynarlar. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 8 / 23
11 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Eşitlik (3) gözden geçirildi¼ginde, f 0 (x) i duyarl hesaplamak için, h ad m uzunlu¼gunun küçük olmak zorunda oldu¼gu görülür. Bu nedenle, şimdi h n n bir de¼gerler dizisiyle s f ra do¼gru yaklaşt ¼g ve karş l k gelen f 0 (x) e yaklaş mlar n hesapland ¼g bir deneme yapal m. f (x) = tan 1 x seçelim ve x = p 2 noktas n kullanal m. Sonuç p 2 de 1/3 olup, f 0 (x) = (x 2 + 1) 1 olmal d r. Bu amaca yönelik algoritma aşa¼g dad r: f (x) := tan p 1 x girdi s 2; h 1; M 26 F 1 f (s) k = 0 dan M ye döngü F 2 f (s + h) d F 2 F 1 r d/h ç kt k, h, F 2, F 1, d, r h h/2 döngü sonu Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 9 / 23
12 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev 32-bitlik bir bilgisayardan al nan baz ç kt lar aşa¼g da gösterilmiştir: k h F 2 F 1 d r Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 10 / 23
13 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Her bir sat rda F 2 F 1 in fark olarak d hesaplanmakta ve d/h oran olarak da r hesaplanmaktad r. Ç karma sadeleşmesi nedeniyle, sonunda d = 0 ve r = 0 oluncaya kadar, d gittikçe daha az say da anlaml rakama sahip olur. r nin en iyi de¼geri k = 12 iken elde edilir, ve e¼ger dört desimal noktaya yuvarlan rsa, dört do¼gru rakama sahiptir. k n n bu de¼gerinde, d nin dört duyarl rakama sahip oldu¼guna dikkat edelim. k artt kça, d deki duyarl rakamlar n say s azal r, ve r nin d den daha fazla duyarl rakama sahip olamayaca¼g na kuşku yoktur. Böylece, h küçük iken, yuvarlama hatas daha duyarl de¼gerler elde etmemize engel olur. d de daha fazla duyarl l ¼ga sahip olmak için F 1 ve F 2 de daha fazla duyarl l k gereklidir ve bu da temel hesaplarda yüksek duyarl l k gerektirir. Çoklu duyarl l k kullanabiliriz veya hesaplar m z daha büyük kelime uzunluklu makinelerde yapabiliriz. Yan tlar n daha kötüleşti¼gi ad m, kullan lan özel makinedeki kelime uzunlu¼guna (veya daha net olarak, birim yuvarlama hatas na) ba¼gl olacakt r. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 11 / 23
14 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Hata O(h) oldu¼gundan dolay, (3) formülü çok güçlü say lmaz. Daha üstün bir formül f 0 (x) 1 [f (x + h) f (x h)] (4) 2h d r. Bu, Taylor Teoreminin iki ifadesi kullan larak bulunur: f (x + h) = f (x) + hf 0 (x) + h2 2 f 00 (x) + h3 3! f 000 (ξ 1 ) (5) f (x h) = f (x) hf 0 (x) + h2 2 f 00 h (x) 3! f 000 (ξ 2 ) (6) Bu eşitliklerin birini di¼gerinden ç kar p, yeniden düzenlersek f 0 (x) = 1 2h [f (x + h) f (x h)] h 2 f 000 (ξ 12 1 ) + f 000 (ξ 2 ) (7) = 1 2h [f (x + h) f (x h)] h 2 6 f 000 (ξ) (8) elde ederiz. Bu sonuç daha tatminkard r, çünkü hatada h 2 terimini içerir. Fakat, hatan n f 000 terimini içerdi¼gine dikkat edelim. Bu hata terimi, e¼ger f 000 mevcut ise uygulanabilirdir. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 12 / 23
15 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Ikinci türev için önemli bir formül (5) ve (6) eşitliklerine bir terim daha ekleyip, altalta toplayarak elde edilir. Düzenleme yap ld ktan sonra biraz önceki yöntem uygulan rsa, ξ 2 (x h, x + h) olmak üzere f 00 (x) = 1 h 2 [f (x + h) 2f (x) + f (x h)] h 2 12 f (4) (ξ) (9) bulunur. Bu formül ikinci basamaktan diferensiyel denklemlerin nümerik çözümlerinde s kl kla kullan l r. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 13 / 23
16 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Örnek f (x) = tan 1 x ve x = p 2 olmak üzere f 0 (x) e yaklaşmak için bir bilgisayar kullan n z. (8) eşitli¼gini 0 a yaklaşan h ad m uzunlu¼gu ile kullan n z. Do¼gru de¼gerin 1/3 oldu¼gunu hat rlay n z. k h F 2 F 1 d r Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 14 / 23
17 1 Say sal Türev ve Richardson D şkestirimi Say sal Türev Ç karma sadeleşmesi nedeniyle, h s f ra yaklaş rken tekrar gözle görülür bir bozulma oldu¼gunu görürüz. Ç kt bu olguyu k = 12 de göstermeye başlar. F 1 ve F 2 nin de¼gerleri birbirlerine oldukça yak nd r ve bunlar n fark olan d çok ciddi rakam duyarl l ¼g kay b na maruz kal r. Sonunda, h! 0 + iken F 1 ve F 2 nin de¼gerleri makinede ayn olacakt r ve bir 0 de¼geri türev olarak hesaplanacakt r. Burada, k = 26 da bu durum oluşur. Bu davran ş farkl kelime uzunluklu bilgisayarlarda farkl k de¼gerlerinde görülecektir. Fonksiyonlar n, sadece deneysel olarak bilinen, say sal diferensiyellenmesi riskli bir yöntemdir, çünkü verideki hatalar süreç s ras nda gittikçe büyüyecektir. Bu durum, örne¼gin (8) eşitli¼ginden çok kolay görülmektedir. E¼ger f (x h) ordinatlar duyars zken, x h örneklem noktalar duyarl şekilde belirlenmekteyse, bu durumda ordinatlardaki hata 1/(2h) ile çarp lacakt r. h küçük olaca¼g ndan dolay, hatalar n etkisi büyük olacakt r. (Bu oluşum nümerik integralde görülmez.) Bu nedenle, deneysel verilerin say sal türevinden kaç n lmal d r veya çok dikkatli şekilde ele al nmal d r. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 15 / 23
18 1 Say sal Türev ve Richardson D şkestirimi Richardson D şkestirimi Richardson d şkesitirimi Şimdi, Richardson d şkesitirimi (ekstrapolasyonu) olarak bilinen bir yordam n baz say sal formüllerden daha duyarl sonuçlar üretmek için nas kullan labilece¼gini belirtece¼giz. Daha yüksek terimlere genişletilmiş şekilde, (5) ve (6) formüllerini göz önüne alal m. f (x) in f (x + h) = f (x h) = k=0 k=0 1 k! hk f (k) (x) (10) 1 k! ( 1)k h k f (k) (x) (11) Taylor serileri ile temsil edildi¼gini varsayal m. E¼ger ikinci eşitlik birincisinden ç kar l rsa, bu durumda k n n çift de¼gerli tüm terimleri yok olacakt r ve geriye f (x + h) f (x h) = 2hf 0 (x) + 2 3! h3 f 000 (x) + 2 5! h5 f (5) (x) + kalacakt r. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 16 / 23
19 1 Say sal Türev ve Richardson D şkestirimi Richardson D şkestirimi Bunun yeniden düzenlenmesi ile de f 0 (x) = 1 [f (x + h) f (x h)] 2h 1 3! h2 f 000 (x) + 1 5! h4 f (5) (x) + 1 7! h6 f (7) (x) + bulunur. L, f 0 (x) i göstermek üzere, bu eşitlik L = ϕ(h) + a 2 h 2 + a 4 h 4 + a 6 h 6 + (12) formuna sahiptir. Son denklemi h yerine h/2 alarak yeniden yazal m: L = ϕ(h/2) + a 2 h 2 /4 + a 4 h 4 /16 + a 6 h 6 /64 + (13) Hata serisindeki lider terim a 2 h 2, (12) denklemini (13) denkleminin 4 kat ndan ç kararak, aşa¼g daki gibi yok edilebilir: Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 17 / 23
20 1 Say sal Türev ve Richardson D şkestirimi Richardson D şkestirimi Böylece, L = ϕ(h) + a 2 h 2 + a 4 h 4 + a 6 h 6 + 4L = 4ϕ(h/2) + a 2 h 2 + a 4 h 4 /4 + a 6 h 6 /16 + 3L = 4ϕ(h/2) ϕ(h) 3a 4 h 4 /4 15a 6 h 6 /16 L = 4 3 ϕ(h/2) 1 3 ϕ(h) a 4h 4 /4 5a 6 h 6 /16 (14) elde ederiz. (14) eşitli¼gi Richardson d şkestirimindeki ilk ad m meydana getirmektedir. Bu, ϕ(h) ve ϕ(h/2) nin basit bir bileşiminin O(h 4 ) duyarl l kla L ye bir kestirim sa¼glad ¼g n göstermektedir. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 18 / 23
21 1 Say sal Türev ve Richardson D şkestirimi Richardson D şkestirimi (14) eşitli¼ginde ψ(h) = 4 3 ϕ(h/2) 1 3 ϕ(h) diyelim. Bu durumda, olup, böylece L = ψ(h) + b 4 h 4 + b 6 h 6 + L = ψ(h/2) + b 4 h 4 /16 + b 6 h 6 /64 + L = 16L = buluruz. Buradan da elde ederiz. ψ(h) + b 4 h 4 + b 6 h 6 + ψ(h/2) + b 4 h 4 /16 + b 6 h 6 / L = 16ψ(h/2) ψ(h) 3b 6 h 6 /4 L = ψ(h/2) 1 15 ψ(h) b 6h 6 /20 (15) Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 19 / 23
22 1 Say sal Türev ve Richardson D şkestirimi Richardson D şkestirimi Tekrar, (15) eşitli¼ginde θ(h) = ψ(h/2) 1 15 ψ(h) ve böylece L = θ(h) + c 6 h 6 + c 8 h 8 + alarak ayn işlemi tekrarlayabiliriz. Böylece, yukar dakine benzer şekilde buluruz. L = θ(h/2) 1 63 θ(h) 3c 8h 8 /252 Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 20 / 23
23 1 Say sal Türev ve Richardson D şkestirimi Richardson D şkestirimi Asl na bak l rsa, artan duyarl l kta formüller elde etmek için herhangi say da ad m uygulanabilir. Şimdi Richardson d şkestirim algoritmas nda M ad ma izin veren tam algoritmay verelim: 1. Uygun bir h (örne¼gin h = 1) seçiniz ve M + 1 tane de¼gerini hesaplay n z. D(n, 0) = ϕ(h/2 n ) (0 n M) 2. k = 1, 2,..., M ve n = k, k + 1,..., M için D(n, k) = 4k 4 k 1 D(n, k 1) 1 4 k D(n 1, k 1) (16) 1 formülünden di¼ger de¼gerleri hesaplay n z. Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 21 / 23
24 1 Say sal Türev ve Richardson D şkestirimi Richardson D şkestirimi D(0, 0) = ϕ(h), D(1, 0) = ϕ(h/2) ve D(1, 1) = ψ(h) oldu¼guna dikkat edelim. D(n, 1) nicelikleri, (14) eşitli¼ginde h n n ardarda h/2 ile de¼giştirilmesine karş l k gelir. Benzer şekilde, D(n, 2) ler (15) eşitli¼gine karş l k gelir ve böyle devam eder. Hipotezimizden ve hesaplamalar m zdan oldu¼gu aç kt r. D(n, 0) = L + O(h 2 ) D(n, 1) = L + O(h 4 ) D(n, 2) = L + O(h 6 ) D(n, 3) = L + O(h 8 ) D(n, k 1) = L + O(h 2k ) (h! 0) Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 22 / 23
25 1 Say sal Türev ve Richardson D şkestirimi Richardson D şkestirimi D(n, 0) ve D(n, k) için verilen formüller bir üçgensel matris oluşturmam za izin verir: D(0, 0) D(1, 0) D(1, 1) D(2, 0) D(2, 1) D(2, 2) D(M, 0) D(M, 1) D(M, 2)... D(M, M) Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 23 / 23
NÜMER IK ANAL IZ. Nuri ÖZALP FONKS IYONLARA YAKLAŞIM. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
NÜMER IK ANAL IZ. Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 1 Denklemlerin Köklerini Bulma Giriş Denklemlerin Köklerini Bulma
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 1 Denklemlerin Köklerini Bulma Giriş Denklemlerin Köklerini Bulma
NÜMER IK ANAL IZ. Nuri ÖZALP. Sabit Nokta ve Fonksiyonel Yineleme. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ. Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 2012
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 27 Çok farkl durumlara uygulanabilen genel bir yöntemdir. Reel de¼gişkenli,
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 27 Çok farkl durumlara uygulanabilen genel bir yöntemdir. Reel de¼gişkenli,
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ. Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 2012
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6! L INEER S ISTEMLER IN ÇÖZÜMÜ / . Pivotlama ve
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6! L INEER S ISTEMLER IN ÇÖZÜMÜ / . Pivotlama ve
fonksiyonu, her x 6= 1 reel say s için tan ml d r. (x 1)(x+1) = = x + 1 yaz labilir. Bu da; f (x) = L
 Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
(z z 0 ) n. n=1. Z f (z) dz = 2ib 1
 0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
NÜMER IK ANAL IZ. Nuri ÖZALP. Lineer Programlama. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Lineer Programlama Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 7 7! Lineer Programlama 1 / 32 Simpleks Algoritmas Standart teknikler anlam
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Lineer Programlama Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 7 7! Lineer Programlama 1 / 32 Simpleks Algoritmas Standart teknikler anlam
2010 oldu¼gundan x 2 = 2010 ve
 ) 444400 say s ndaki rakamlar n yerleri de¼giştirilerek 7 basamakl kaç farkl say yaz labilir? Çözüm : Bu rakamlar n bütün farkl 7 li dizilişlerinin say s 7! olacakt r. Bu dizilişlerin 4!! soldan ilk rakam
) 444400 say s ndaki rakamlar n yerleri de¼giştirilerek 7 basamakl kaç farkl say yaz labilir? Çözüm : Bu rakamlar n bütün farkl 7 li dizilişlerinin say s 7! olacakt r. Bu dizilişlerin 4!! soldan ilk rakam
ÜN TE II L M T. Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler
 ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
Bir H Hilbert uzay üzerinde herhangi bir kompakt simetrik T operatörü için,
 Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
1998 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
1) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir?
 ) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
SAYISAL ÇÖZÜMLEME. Yrd.Doç.Dr.Esra Tunç Görmüş. 1.Hafta
 SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
Do ufl Üniversitesi Matematik Kulübü Matematik Bireysel Yar flmas 2004 Soru ve Yan tlar
 o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2004 Soru ve Yan tlar Soru. S f rdan farkl bir a say s için sonsuz ondal klarla oluflan ifadesinin de eri nedir? ise, Soru 2. 0 < < 0 olmak
o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2004 Soru ve Yan tlar Soru. S f rdan farkl bir a say s için sonsuz ondal klarla oluflan ifadesinin de eri nedir? ise, Soru 2. 0 < < 0 olmak
ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ
 Giriş ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ Sayısal Analiz Nedir? Mühendislikte ve bilimde, herhangi bir süreci tanımlayan karmaşık denklemlerin
Giriş ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ Sayısal Analiz Nedir? Mühendislikte ve bilimde, herhangi bir süreci tanımlayan karmaşık denklemlerin
8 LAURENT SER I GÖSTER IMLER I
 8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
SORULAR. 1. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim. 1 n sin. lim. q 1 x 1+x
 SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
Iki Boyutlu Sabit Katsay l Lineer Homogen Diferensiyel Denklem Sistemleri (Euler Metodu)
 Iki Boyulu Sabi Kasay l Lineer Homogen Diferensiyel Denklem Sisemleri (Euler Meodu) Bu bölümde sabi kasay l, lineer, homogen 8 >< d = a 1x + b 1 y >: dy d = a 2x + b 2 y sisemi ele al nmakad r. Burada
Iki Boyulu Sabi Kasay l Lineer Homogen Diferensiyel Denklem Sisemleri (Euler Meodu) Bu bölümde sabi kasay l, lineer, homogen 8 >< d = a 1x + b 1 y >: dy d = a 2x + b 2 y sisemi ele al nmakad r. Burada
Analiz III Ara S nav Sorular 24 Kas m 2010
 Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
Istatistik ( IKT 253) Normal Da¼g l m Çal şma Metni
 TO-ETÜ, Iktisat ölümü Istatistik ( IKT 253) Normal Da¼g l m Çal şma Metni Ortalamas 0, standart sapmas 1 olan normal da¼g l ma standart normal da¼g l m denir ve bu da¼g l m n de¼gerleri z ile gösterilir.
TO-ETÜ, Iktisat ölümü Istatistik ( IKT 253) Normal Da¼g l m Çal şma Metni Ortalamas 0, standart sapmas 1 olan normal da¼g l ma standart normal da¼g l m denir ve bu da¼g l m n de¼gerleri z ile gösterilir.
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
AKDEN IZ ÜN IVERS ITES I 21. ULUSAL ANTALYA MATEMAT IK OL IMP IYATI SORULARI
 KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
BÖLÜM 7 BİLGİSAYAR UYGULAMALARI - 1
 1 BÖLÜM 7 BİLGİSAYAR UYGULAMALARI - 1 Belli bir özelliğe yönelik yapılandırılmış gözlemlerle elde edilen ölçme sonuçları üzerinde bir çok istatistiksel işlem yapılabilmektedir. Bu işlemlerin bir kısmı
1 BÖLÜM 7 BİLGİSAYAR UYGULAMALARI - 1 Belli bir özelliğe yönelik yapılandırılmış gözlemlerle elde edilen ölçme sonuçları üzerinde bir çok istatistiksel işlem yapılabilmektedir. Bu işlemlerin bir kısmı
Ard fl k Say lar n Toplam
 Ard fl k Say lar n Toplam B u yaz da say sözcü ünü, 1, 2, 3, 4, 5 gibi, pozitif tamsay lar için kullanaca z. Konumuz ard fl k say lar n toplam. 7 ve 8 gibi, ya da 7, 8 ve 9 gibi ardarda gelen say lara
Ard fl k Say lar n Toplam B u yaz da say sözcü ünü, 1, 2, 3, 4, 5 gibi, pozitif tamsay lar için kullanaca z. Konumuz ard fl k say lar n toplam. 7 ve 8 gibi, ya da 7, 8 ve 9 gibi ardarda gelen say lara
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü
 Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 10 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 8 Aralık 1999 Saat: 09.54 Problem 10.1 (a) Bir F kuvveti ile çekiyoruz (her iki ip ile). O
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 10 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 8 Aralık 1999 Saat: 09.54 Problem 10.1 (a) Bir F kuvveti ile çekiyoruz (her iki ip ile). O
Saymak San ld Kadar Kolay De ildir
 Saymak San ld Kadar Kolay De ildir B ir matematikçinin bir zamanlar dedi i gibi, saymas n bilenler ve bilmeyenler olmak üzere üç tür insan vard r Bakal m siz hangi türdensiniz? Örne in bir odada bulunan
Saymak San ld Kadar Kolay De ildir B ir matematikçinin bir zamanlar dedi i gibi, saymas n bilenler ve bilmeyenler olmak üzere üç tür insan vard r Bakal m siz hangi türdensiniz? Örne in bir odada bulunan
Belirsiz Integraller. 1.1 Ilkel Fonksiyon ve Belirsiz Integral. 1.1.1 Temel Tan mlar ve Sonuc. lar
 Ic. indekiler Belirsiz Integraller 3. Ilkel Fonksiyon ve Belirsiz Integral................ 3.. Temel Tan mlar ve Sonuc.lar............... 3. Temel Integral Alma Yöntemleri................ 0.. De giṣken
Ic. indekiler Belirsiz Integraller 3. Ilkel Fonksiyon ve Belirsiz Integral................ 3.. Temel Tan mlar ve Sonuc.lar............... 3. Temel Integral Alma Yöntemleri................ 0.. De giṣken
DENKLEMLER CAUCHY-EULER DENKLEMİ. a n x n dn y dx n + a n 1x n 1 dn 1 y
 SABİT KATSAYILI DENKLEMLERE DÖNÜŞTÜREBİLEN DENKLEMLER Bu bölümde sabit katsayılı diferansiyel denklemlere dönüşebilen değişken katsayılı diferansiyel denklemlerden Cauchy Euler ve Legendre difarensiyel
SABİT KATSAYILI DENKLEMLERE DÖNÜŞTÜREBİLEN DENKLEMLER Bu bölümde sabit katsayılı diferansiyel denklemlere dönüşebilen değişken katsayılı diferansiyel denklemlerden Cauchy Euler ve Legendre difarensiyel
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
PROBLEM SET I ARALIK 2009
 PROBLEM SET I - 5 09 ARALIK 009 Soru 1 (Besanko ve Braeutigam (00), sayfa 405): Aşa¼g da tam rekabet piyasas nda faaliyet gösteren bir rman n k sa dönem toplam maliyet fonksiyonu verilmiştir: Piyasa denge
PROBLEM SET I - 5 09 ARALIK 009 Soru 1 (Besanko ve Braeutigam (00), sayfa 405): Aşa¼g da tam rekabet piyasas nda faaliyet gösteren bir rman n k sa dönem toplam maliyet fonksiyonu verilmiştir: Piyasa denge
3. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 3. HAFTA SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi TAYLOR TEOREMİ Eğer f C n [a,b] ve f n+1 [a,b] de mevcut ise, x
3. HAFTA SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi TAYLOR TEOREMİ Eğer f C n [a,b] ve f n+1 [a,b] de mevcut ise, x
Deneysel Verilerin Değerlendirilmesi
 Deneysel Verilerin Değerlendirilmesi Ölçme-Birimler-Anlamlı Rakamlar Ölçme: Bir nesnenin bazı özelliklerini (kütle, uzunluk vs..) standart olarak belirlenmiş birimlere göre belirlenmesi işlemidir (ölçüm,
Deneysel Verilerin Değerlendirilmesi Ölçme-Birimler-Anlamlı Rakamlar Ölçme: Bir nesnenin bazı özelliklerini (kütle, uzunluk vs..) standart olarak belirlenmiş birimlere göre belirlenmesi işlemidir (ölçüm,
256 = 2 8 = = = 2. Bu kez de iflik bir yan t bulduk. Bir yerde bir yanl fl yapt k, ama nerde? kinci hesab m z yanl fl.
 Bölünebilme B ir tamsay n n üçe ya da dokuza tam olarak bölünüp bölünmedi ini anlamak için çok bilinen bir yöntem vard r: Say - y oluflturan rakamlar toplan r. E er bu toplam üçe (dokuza) bölünüyorsa,
Bölünebilme B ir tamsay n n üçe ya da dokuza tam olarak bölünüp bölünmedi ini anlamak için çok bilinen bir yöntem vard r: Say - y oluflturan rakamlar toplan r. E er bu toplam üçe (dokuza) bölünüyorsa,
Do ufl Üniversitesi Matematik Kulübü Matematik Bireysel Yar flmas 2005 Soru ve Yan tlar
 Matematik ünyas, 2005 Yaz o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2005 Soru ve Yan tlar 1. Maliyeti üzerinden yüzde 25 kârla sat lan bir mal n sat fl fiyat ndan yüzde onluk bir
Matematik ünyas, 2005 Yaz o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2005 Soru ve Yan tlar 1. Maliyeti üzerinden yüzde 25 kârla sat lan bir mal n sat fl fiyat ndan yüzde onluk bir
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
6 Devirli Kodlar. 6.1 Temel Tan mlar
 6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
HOMOGEN OLMAYAN DENKLEMLER
 n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
7 TAYLOR SER I GÖSTER IMLER I
 7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ "A" OLARAK CEVAP KÂĞIDINA İŞARETLEMEYİ UNUTMAYINIZ. SAYISAL BÖLÜM SAYISAL-2 TESTİ
 ALES İlkbahar 007 SAY DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ "A" OLARAK CEVAP KÂĞIDINA İŞARETLEMEYİ UNUTMAYINIZ. SAYISAL BÖLÜM SAYISAL- TESTİ Sınavın bu testinden alacağınız standart puan, Sayısal Ağırlıklı
ALES İlkbahar 007 SAY DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ "A" OLARAK CEVAP KÂĞIDINA İŞARETLEMEYİ UNUTMAYINIZ. SAYISAL BÖLÜM SAYISAL- TESTİ Sınavın bu testinden alacağınız standart puan, Sayısal Ağırlıklı
MIT Açık Ders Malzemeleri Kompleks Değişkenli Fonksiyonlar 2008 Güz
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
mat 103. Çal şma Sorular 1
 mat 0. Çal şma Sorular. FONKS IYONLA. Aşa¼g daki kurallarla verilen fonksiyonlar n gra klerini çiziniz. (a) f() 4 jj (b) f() jj (c) f() 4 jj (ç) f() j j (d) f() j j (e) f() j j (f) f() j j. Aşa¼g daki
mat 0. Çal şma Sorular. FONKS IYONLA. Aşa¼g daki kurallarla verilen fonksiyonlar n gra klerini çiziniz. (a) f() 4 jj (b) f() jj (c) f() 4 jj (ç) f() j j (d) f() j j (e) f() j j (f) f() j j. Aşa¼g daki
TEMEL KAVRAMLAR MATEMAT K. 6. a ve b birer do al say r. a 2 b 2 = 19 oldu una göre, a + 2b toplam kaçt r? (YANIT: 28)
 TEMEL KAVRAMLAR 6. a ve b birer do al say r. a b = 19 oldu una göre, a + b toplam (YANIT: 8) 1. ( 4) ( 1) 6 1 i leminin sonucu (YANIT: ). ( 6) ( 3) ( 4) ( 17) ( 5) :( 11) leminin sonucu (YANIT: 38) 7.
TEMEL KAVRAMLAR 6. a ve b birer do al say r. a b = 19 oldu una göre, a + b toplam (YANIT: 8) 1. ( 4) ( 1) 6 1 i leminin sonucu (YANIT: ). ( 6) ( 3) ( 4) ( 17) ( 5) :( 11) leminin sonucu (YANIT: 38) 7.
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Bir özvektörün sıfırdan farklı herhangi bri sabitle çarpımı yine bir özvektördür.
 ÖZDEĞER VE ÖZVEKTÖRLER A n n tipinde bir matris olsun. AX = λx (1.1) olmak üzere n 1 tipinde bileşenleri sıfırdan farklı bir X matrisi için λ sayıları için bu denklemi sağlayan bileşenleri sıfırdan farklı
ÖZDEĞER VE ÖZVEKTÖRLER A n n tipinde bir matris olsun. AX = λx (1.1) olmak üzere n 1 tipinde bileşenleri sıfırdan farklı bir X matrisi için λ sayıları için bu denklemi sağlayan bileşenleri sıfırdan farklı
Do ufl Üniversitesi Matematik Kulübü Matematik Yar flmas 2003 Bireysel Yar flma Soru ve Çözümleri
 o ufl Üniversitesi Matematik Kulübü Matematik Yar flmas 2003 ireysel Yar flma Soru ve Çözümleri olamayaca ndan (çünkü bir kareköke eflit), y = 1/2 bulunur. olay s yla = y 2 = 1/4. 2a + 4b = 6a 3b oldu
o ufl Üniversitesi Matematik Kulübü Matematik Yar flmas 2003 ireysel Yar flma Soru ve Çözümleri olamayaca ndan (çünkü bir kareköke eflit), y = 1/2 bulunur. olay s yla = y 2 = 1/4. 2a + 4b = 6a 3b oldu
Çözümlü Yüksek Matematik Problemleri. Doç. Dr. Erhan Pişkin
 Çözümlü Yüksek Matematik Problemleri Doç. Dr. Erhan Pişkin Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ ISBN 978-605-38-45-5 Kitap içeriğinin tüm sorumluluğu yazarına aittir. 06, Pegem Akademi
Çözümlü Yüksek Matematik Problemleri Doç. Dr. Erhan Pişkin Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ ISBN 978-605-38-45-5 Kitap içeriğinin tüm sorumluluğu yazarına aittir. 06, Pegem Akademi
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
1.3. Normal Uzaylar. Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak. baz temel özellikleri incelenecektir.
 1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
Türev Uygulamaları. 9.1 Ortalama Değer teoremi
 1 2 Bölüm 9 Türev Uygulamaları 9.1 Ortalama Değer teoremi Türevin çok farklı uygulamaları vardır. Bunlar arasında çok önemli olan bazılarını ele alacağız. Ortalama Değer Teoremi ni daha önce görmüştük.
1 2 Bölüm 9 Türev Uygulamaları 9.1 Ortalama Değer teoremi Türevin çok farklı uygulamaları vardır. Bunlar arasında çok önemli olan bazılarını ele alacağız. Ortalama Değer Teoremi ni daha önce görmüştük.
VOB-DOLAR/ONS ALTIN. VOB-DOLAR/ONS ALTIN VADEL filem SÖZLEfiMES
 VOB-DOLAR/ONS ALTIN VOB-DOLAR/ONS ALTIN VADEL filem SÖZLEfiMES Copyright Vadeli fllem ve Opsiyon Borsas A.fi. Aral k 2010 VOB-DOLAR/ONS ALTIN VADEL filem SÖZLEfiMES V A D E L fi L E M V E O P S Y O
VOB-DOLAR/ONS ALTIN VOB-DOLAR/ONS ALTIN VADEL filem SÖZLEfiMES Copyright Vadeli fllem ve Opsiyon Borsas A.fi. Aral k 2010 VOB-DOLAR/ONS ALTIN VADEL filem SÖZLEfiMES V A D E L fi L E M V E O P S Y O
Ad ve Soyad : Numaras : Analiz III Aras nav Sorular
 Analiz III Aras nav Sorular 30. 11. 2006 1. (a) A = fx 2 R : x 2 4x 5 < 0g ise sup A =? (b) A R boş olmayan ve üstten s n rl bir küme olsun. > 0 ise sup(a) = sup A oldu¼gunu gösteriniz. 2. A = f(x; y)
Analiz III Aras nav Sorular 30. 11. 2006 1. (a) A = fx 2 R : x 2 4x 5 < 0g ise sup A =? (b) A R boş olmayan ve üstten s n rl bir küme olsun. > 0 ise sup(a) = sup A oldu¼gunu gösteriniz. 2. A = f(x; y)
20. ULUSAL ANTALYA MATEMAT IK OL IMP IYATI SORULARI A A A A A A A
 KDEN IZ ÜN IVERS ITES I 20. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 3 May s 2015 - Pazar
KDEN IZ ÜN IVERS ITES I 20. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 3 May s 2015 - Pazar
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
11. SINIF KONU ANLATIMLI. 2. ÜNİTE: KUVVET ve HAREKET 3. Konu TORK, AÇISAL MOMENTUM ve DENGE ETKİNLİK ve TEST ÇÖZÜMLERİ
 11. SINIF ONU ANAIMI 2. ÜNİE: UVVE ve HAREE 3. onu OR, AÇISA MOMENUM ve DENGE EİNİ ve ES ÇÖZÜMERİ 2 2. Ünite 3. onu ork, Aç sal Momentum ve Denge A n n Yan tlar 1. Çubuk dengede oldu una göre noktas na
11. SINIF ONU ANAIMI 2. ÜNİE: UVVE ve HAREE 3. onu OR, AÇISA MOMENUM ve DENGE EİNİ ve ES ÇÖZÜMERİ 2 2. Ünite 3. onu ork, Aç sal Momentum ve Denge A n n Yan tlar 1. Çubuk dengede oldu una göre noktas na
HATA VE HATA KAYNAKLARI...
 İÇİNDEKİLER 1. GİRİŞ... 1 1.1 Giriş... 1 1.2 Sayısal Analizin İlgi Alanı... 2 1.3 Mühendislik Problemlerinin Çözümü ve Sayısal Analiz... 2 1.4 Sayısal Analizde Bilgisayarın Önemi... 7 1.5 Sayısal Çözümün
İÇİNDEKİLER 1. GİRİŞ... 1 1.1 Giriş... 1 1.2 Sayısal Analizin İlgi Alanı... 2 1.3 Mühendislik Problemlerinin Çözümü ve Sayısal Analiz... 2 1.4 Sayısal Analizde Bilgisayarın Önemi... 7 1.5 Sayısal Çözümün
B02.8 Bölüm Değerlendirmeleri ve Özet
 B02.8 Bölüm Değerlendirmeleri ve Özet 57 Yrd. Doç. Dr. Yakup EMÜL, Bilgisayar Programlama Ders Notları (B02) Şimdiye kadar C programlama dilinin, verileri ekrana yazdırma, kullanıcıdan verileri alma, işlemler
B02.8 Bölüm Değerlendirmeleri ve Özet 57 Yrd. Doç. Dr. Yakup EMÜL, Bilgisayar Programlama Ders Notları (B02) Şimdiye kadar C programlama dilinin, verileri ekrana yazdırma, kullanıcıdan verileri alma, işlemler
Elemanter fonksiyonlarla yaklaşım ve hata
 Elemanter fonksiyonlarla yaklaşım ve hata Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi Matematik Bölümü Kasım, 2018 e 5 Kasım, 2018 1 / 48 Elemanter fonksiyonlarla yaklaşım ve hata
Elemanter fonksiyonlarla yaklaşım ve hata Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi Matematik Bölümü Kasım, 2018 e 5 Kasım, 2018 1 / 48 Elemanter fonksiyonlarla yaklaşım ve hata
LYS MATEMATİK DENEME - 1
 LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Bu yaz girifle gereksinmiyor. Do rudan, kan tlayaca m z
 Yoksulun fians Bu yaz girifle gereksinmiyor. Do rudan, kan tlayaca m z sonuca geçelim: Teorem. Yoksulun zengine karfl flans yoktur. Bu çok bilinen teorem i kan tlayabilmek için her fleyden önce önermeyi
Yoksulun fians Bu yaz girifle gereksinmiyor. Do rudan, kan tlayaca m z sonuca geçelim: Teorem. Yoksulun zengine karfl flans yoktur. Bu çok bilinen teorem i kan tlayabilmek için her fleyden önce önermeyi
SDÜ Matematik Bölümü Analiz-IV Final S nav
 Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
1/3 Nerde ya da Kaos a Girifl
 1/3 Nerde ya da Kaos a Girifl K aos, matemati in oldukça yeni kuramlar ndan biridir. Kaos, kargafla anlam na gelen Yunanca kökenli bir sözcüktür. Kaos kuram n biraz aç klamaya çal flay m. fiöyle kuvvetlice
1/3 Nerde ya da Kaos a Girifl K aos, matemati in oldukça yeni kuramlar ndan biridir. Kaos, kargafla anlam na gelen Yunanca kökenli bir sözcüktür. Kaos kuram n biraz aç klamaya çal flay m. fiöyle kuvvetlice
BİR SAYININ ÖZÜ VE DÖRT İŞLEM
 ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon
 Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon Levent ÖZBEK Fikri ÖZTÜRK Ankara Üniversitesi Fen Fakültesi İstatistik Bölümü Sistem Modelleme ve Simülasyon Laboratuvarı 61 Tandoğan/Ankara
Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon Levent ÖZBEK Fikri ÖZTÜRK Ankara Üniversitesi Fen Fakültesi İstatistik Bölümü Sistem Modelleme ve Simülasyon Laboratuvarı 61 Tandoğan/Ankara
Olas l k Hesaplar (II)
 Olas l k Hesaplar (II) B ir önceki yaz daki örneklerde olay say s sonluydu. Örne in, iki zarla 21 olay vard. fiimdi olay say m z sonsuz yapaca z. Kolay bir soruyla bafllayal m: [0, 1] aral nda rastgele
Olas l k Hesaplar (II) B ir önceki yaz daki örneklerde olay say s sonluydu. Örne in, iki zarla 21 olay vard. fiimdi olay say m z sonsuz yapaca z. Kolay bir soruyla bafllayal m: [0, 1] aral nda rastgele
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Bir odada sonsuz say da insan n bulundu unu varsayal m. Bu
 Ramsey Teoremi Bir odada sonsuz say da insan n bulundu unu varsayal m. Bu odada bulunan herhangi iki kifli birbirlerini ya tan rlar ya da tan mazlar. Buras belli. Yan t belli olmayan soru flu: Bu odadan,
Ramsey Teoremi Bir odada sonsuz say da insan n bulundu unu varsayal m. Bu odada bulunan herhangi iki kifli birbirlerini ya tan rlar ya da tan mazlar. Buras belli. Yan t belli olmayan soru flu: Bu odadan,
1999 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1999 ULUSL NTLY MTMT IK L IMP IYTI IR IN I ŞM SRULRI Lise 1- S nav Sorular 1. f1; ; 3; :::; 1999g kümesinin, eleman say s tek say olan kaç tane alt kümesi vard r? ) 1999 ) 1998 ) 1998-1 ) 999 ) hiçbiri.
1999 ULUSL NTLY MTMT IK L IMP IYTI IR IN I ŞM SRULRI Lise 1- S nav Sorular 1. f1; ; 3; :::; 1999g kümesinin, eleman say s tek say olan kaç tane alt kümesi vard r? ) 1999 ) 1998 ) 1998-1 ) 999 ) hiçbiri.
Öncelikle Markamıza göstermiş olduğunuz ilgiden dolayı teşekkür ederiz.
 Sayın Prefix İş Ortağımız, Öncelikle Markamıza göstermiş olduğunuz ilgiden dolayı teşekkür ederiz. İşletmenize daha fazla kazanç sağlayabilmek, daha kaliteli ve daha süratli hizmet verebilmek için, mevcut
Sayın Prefix İş Ortağımız, Öncelikle Markamıza göstermiş olduğunuz ilgiden dolayı teşekkür ederiz. İşletmenize daha fazla kazanç sağlayabilmek, daha kaliteli ve daha süratli hizmet verebilmek için, mevcut
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I
 DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984.
 Çankırı Karatekin Üniversitesi Matematik Bölümü 2015 Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984. (Adi ) Bir ya da daha fazla bağımsız değişkenden oluşan bağımlı değişken ve türevlerini
Çankırı Karatekin Üniversitesi Matematik Bölümü 2015 Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984. (Adi ) Bir ya da daha fazla bağımsız değişkenden oluşan bağımlı değişken ve türevlerini
Y l Sonu S nav Önerilen Çözümleri. C t = :85Y t 1 I t = 6(Y t 1 Y t 2 ) G t = 100
 Ankara Üniversitesi, Siyasal Bilgiler Fakültesi Iktisat Bölümü 013-014 Bahar Dönemi Matematiksel Iktisat Prof.Dr. Hasan Şahin Y l Sonu S nav Önerilen Çözümleri 1. ve. sorular 30 puan 4. soru 40 puan de¼gerindedir.
Ankara Üniversitesi, Siyasal Bilgiler Fakültesi Iktisat Bölümü 013-014 Bahar Dönemi Matematiksel Iktisat Prof.Dr. Hasan Şahin Y l Sonu S nav Önerilen Çözümleri 1. ve. sorular 30 puan 4. soru 40 puan de¼gerindedir.
TAR H MATEMAT K PROBLEMLER - I. Ahmet A A H y l A + (A H) Hasan H. A H y l. Kavram Dersaneleri 56
 TAR H MATEMAT K PROBLEMLER - I ÖRNEK 1: Bir lisenin son s n f ö rencileri her grupta eflit say da ö renci olmak üzere 10 gruba ayr l yor. Bu ö renciler 7 gruba ayr lsayd her gruptaki ö renci say s 6 fazla
TAR H MATEMAT K PROBLEMLER - I ÖRNEK 1: Bir lisenin son s n f ö rencileri her grupta eflit say da ö renci olmak üzere 10 gruba ayr l yor. Bu ö renciler 7 gruba ayr lsayd her gruptaki ö renci say s 6 fazla
BURSA DAKİ ENBÜYÜK 250 FİRMAYA FİNANSAL ANALİZ AÇISINDAN BAKIŞ (2005) Prof.Dr.İbrahim Lazol
 BURSA DAKİ ENBÜYÜK 250 FİRMAYA FİNANSAL ANALİZ AÇISINDAN BAKIŞ (2005) Prof.Dr.İbrahim Lazol 1. Giriş Bu yazıda, Bursa daki (ciro açısından) en büyük 250 firmanın finansal profilini ortaya koymak amacındayız.
BURSA DAKİ ENBÜYÜK 250 FİRMAYA FİNANSAL ANALİZ AÇISINDAN BAKIŞ (2005) Prof.Dr.İbrahim Lazol 1. Giriş Bu yazıda, Bursa daki (ciro açısından) en büyük 250 firmanın finansal profilini ortaya koymak amacındayız.
1.BÖLÜM SORU SORU. (x 1) (x 3) = A + B. x 3 ise, d(p(x)) ve d(q(x)) polinomlar n derecelerini göstermek. A. B çarp m kaçt r?
 1.BÖLÜM MATEMAT K Derginin bu say s nda Polinomlar konusunda çözümlü sorular yer almaktad r. Bu konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü
1.BÖLÜM MATEMAT K Derginin bu say s nda Polinomlar konusunda çözümlü sorular yer almaktad r. Bu konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü
TAR H MATEMAT K PROBLEMLER - III. Kavram Dersaneleri 78. ÖRNEK 1: % 24 'ü olan say kaçt r? ÖRNEK 2:
 TAR H MATEMAT K PROBLEMLER - III ÖRNEK 1: % 24 'ü 86424 olan say kaçt r? A) 360 B) 354196 C) 320120 D) 36 E) 360 (ÖSS - 1999) ÖRNEK 2: Bir miktar pastan n 3 ini lknur, geriye kalan n da Buse yemifltir.
TAR H MATEMAT K PROBLEMLER - III ÖRNEK 1: % 24 'ü 86424 olan say kaçt r? A) 360 B) 354196 C) 320120 D) 36 E) 360 (ÖSS - 1999) ÖRNEK 2: Bir miktar pastan n 3 ini lknur, geriye kalan n da Buse yemifltir.
M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009
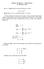 M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009 Soru 1: Aşa¼g daki gibi bir üretim fonksiyonu verilsin: = L 1=3 K 2=3 Eme¼gin yat w = ve sermayenin yat r = 1 olsun. a- Firma kadar ç kt üretmek istemektedir.
M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009 Soru 1: Aşa¼g daki gibi bir üretim fonksiyonu verilsin: = L 1=3 K 2=3 Eme¼gin yat w = ve sermayenin yat r = 1 olsun. a- Firma kadar ç kt üretmek istemektedir.
PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ KAZANIM NO KAZANIMLAR
 2013-2014 PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 12 32173 Üslü İfadeler 2 13 42016 Rasyonel ifade kavramını örneklerle açıklar ve
2013-2014 PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 12 32173 Üslü İfadeler 2 13 42016 Rasyonel ifade kavramını örneklerle açıklar ve
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK (10+10 p.) 2. (15 p.) 3. (7+8 p.) 4. (15+10 p.) 5. (15+10 p.) TOPLAM
 TOBB-ETÜ, MATEMATİK BÖLÜMÜ, GÜZ DÖNEMİ 2014-2015 MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK 2014 Adı Soyadı: No: İMZA: 1. 10+10 p.) 2. 15 p.) 3. 7+8 p.) 4. 15+10 p.) 5. 15+10 p.) TOPLAM 1. a) NOT: Tam
TOBB-ETÜ, MATEMATİK BÖLÜMÜ, GÜZ DÖNEMİ 2014-2015 MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK 2014 Adı Soyadı: No: İMZA: 1. 10+10 p.) 2. 15 p.) 3. 7+8 p.) 4. 15+10 p.) 5. 15+10 p.) TOPLAM 1. a) NOT: Tam
Bu bölümde birkaç yak nsak dizi örne i daha görece iz.
 19B. Yak sak Gerçel Dizi Örekleri Bu bölümde birkaç yak sak dizi öre i daha görece iz. Verdi imiz örekleri her biri hem kedi bafl a hem de kulla la yötem aç s da öemlidir. Örek 19B.1. lim 1/ = 1. Ka t:
19B. Yak sak Gerçel Dizi Örekleri Bu bölümde birkaç yak sak dizi öre i daha görece iz. Verdi imiz örekleri her biri hem kedi bafl a hem de kulla la yötem aç s da öemlidir. Örek 19B.1. lim 1/ = 1. Ka t:
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Đlkbahar / Sayısal II / 22 Nisan 2007. Matematik Soruları ve Çözümleri
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Đlkbahar / Sayısal II / Nisan 007 Matematik Soruları ve Çözümleri 1. 3,15 sayısının aşağıdaki sayılardan hangisiyle çarpımının sonucu bir tam
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Đlkbahar / Sayısal II / Nisan 007 Matematik Soruları ve Çözümleri 1. 3,15 sayısının aşağıdaki sayılardan hangisiyle çarpımının sonucu bir tam
5. Salih Zeki Matematik Araştırma Projeleri Yarışması PROJENİN ADI DİZİ DİZİ ÜRETEÇ PROJEYİ HAZIRLAYAN ESRA DAĞ ELİF BETÜL ACAR
 5. Salih Zeki Matematik Araştırma Projeleri Yarışması PROJENİN ADI DİZİ DİZİ ÜRETEÇ PROJEYİ HAZIRLAYAN ESRA DAĞ ELİF BETÜL ACAR ÖZEL BÜYÜKÇEKMECE ÇINAR KOLEJİ 19 Mayıs Mah. Bülent Ecevit Cad. Tüyap Yokuşu
5. Salih Zeki Matematik Araştırma Projeleri Yarışması PROJENİN ADI DİZİ DİZİ ÜRETEÇ PROJEYİ HAZIRLAYAN ESRA DAĞ ELİF BETÜL ACAR ÖZEL BÜYÜKÇEKMECE ÇINAR KOLEJİ 19 Mayıs Mah. Bülent Ecevit Cad. Tüyap Yokuşu
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ.
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ Neslihan ÇAVUNT MATEMATİK ANABİLİM DALI ANKARA 202 Her hakkı saklıdır
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ Neslihan ÇAVUNT MATEMATİK ANABİLİM DALI ANKARA 202 Her hakkı saklıdır
17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A
 AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
Okut. Yüksel YURTAY. İletişim : (264) Sayısal Analiz. Giriş.
 Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Baki Karl ¼ga. Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü Ankara/Türkiye
 H IPERBOL IK VE KÜRESEL ÜÇGENLERIN KENAR UZUNLUKLARINA BA ¼GLI ALAN FORMÜLLER I Baki Karl ¼ga karliaga@gazi.edu.tr Murat Savaş msavas@gazi.edu.tr Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü
H IPERBOL IK VE KÜRESEL ÜÇGENLERIN KENAR UZUNLUKLARINA BA ¼GLI ALAN FORMÜLLER I Baki Karl ¼ga karliaga@gazi.edu.tr Murat Savaş msavas@gazi.edu.tr Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü
İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ
 İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ Deneyde dolu alan tarama dönüşümünün nasıl yapıldığı anlatılacaktır. Dolu alan tarama
İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ Deneyde dolu alan tarama dönüşümünün nasıl yapıldığı anlatılacaktır. Dolu alan tarama
ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI
 ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI 1 Rassal Değişken Bir deney ya da gözlemin şansa bağlı sonucu bir değişkenin aldığı değer olarak düşünülürse, olasılık ve istatistikte böyle bir
ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI 1 Rassal Değişken Bir deney ya da gözlemin şansa bağlı sonucu bir değişkenin aldığı değer olarak düşünülürse, olasılık ve istatistikte böyle bir
ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER
 ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER Şekil-1: BREADBOARD Yukarıda, deneylerde kullandığımız breadboard un şekli görünmektedir. Bu board üzerinde harflerle isimlendirilen satırlar ve numaralarla
ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER Şekil-1: BREADBOARD Yukarıda, deneylerde kullandığımız breadboard un şekli görünmektedir. Bu board üzerinde harflerle isimlendirilen satırlar ve numaralarla
Do al say lar kümesi, yani {0, 1, 2, 3, 4,... } kümesi, toplama
 Ç karma ve Kare Alma Alt nda Kapal Kümeler Do al say lar kümesi, yani {0, 1, 2, 3, 4,... } kümesi, toplama ve çarpma ifllemleri alt nda kapal d r; bir baflka deyiflle, iki do al say y toplarsak ya da çarparsak
Ç karma ve Kare Alma Alt nda Kapal Kümeler Do al say lar kümesi, yani {0, 1, 2, 3, 4,... } kümesi, toplama ve çarpma ifllemleri alt nda kapal d r; bir baflka deyiflle, iki do al say y toplarsak ya da çarparsak
MATEMAT IK-I (SORULAR)
 Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
POL NOMLAR. Polinomlar
 POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
Temel Bilgisayar Programlama
 BÖLÜM 9: Fonksiyonlara dizi aktarma Fonksiyonlara dizi aktarmak değişken aktarmaya benzer. Örnek olarak verilen öğrenci notlarını ekrana yazan bir program kodlayalım. Fonksiyon prototipi yazılırken, dizinin
BÖLÜM 9: Fonksiyonlara dizi aktarma Fonksiyonlara dizi aktarmak değişken aktarmaya benzer. Örnek olarak verilen öğrenci notlarını ekrana yazan bir program kodlayalım. Fonksiyon prototipi yazılırken, dizinin
