MATEMATİK EĞİTİMİNDE ÖĞRENME GÜÇLÜKLERİ
|
|
|
- Canan Aykaç
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Mustafa Kemal Üniversitesi Sosyal Bilimler Enstitüsü Dergisi Mustafa Kemal University Journal of Social Sciences Institute Yıl/Year: 2008 Cilt/Volume: 5 Sayı/Issue: 9 MATEMATİK EĞİTİMİNDE ÖĞRENME GÜÇLÜKLERİ Yrd. Doç. Dr. Enver Tatar Kahramanmaraş Sütçü İmam Üniversitesi Prof. Dr. Ramazan Dikici Atatürk Üniversitesi Özet Bu çalışmada öğrenme güçlüğü ile ilgili literatür taraması yapılmıştır. Yapılan literatür taramasında, bu kavramı sosyolojik ve psikolojik faktörlerden ziyade bilişsel faktörler açısından ele alan yayınlar dikkate alınmıştır. Çalışmada ilgili literatür sırasıyla; öğrenme güçlüğü kavramının eğitimdeki ve özelliklede matematik eğitimindeki önemi nedir, matematikte hangi konularda ne tür güçlükler vardır ve bu güçlükleri gidermenin yolları nelerdir gibi sorulara cevap arama çerçevesinde incelenmiştir. Yapılan incelemenin sonucunda öğrenme güçlüklerini gidermeye yönelik çalışmaların, güçlükleri belirleme türündeki çalışmalara nazaran yok denecek kadar az olduğu görülmüştür. Anahtar Kelimeler: Öğrenme güçlükleri, matematik eğitimi, literatür taraması LEARNING DIFFICULTIES IN MATHEMATICS EDUCATION Abstract In this study, literature review about learning difficulties was carried out. In the conducted literature survey, publications have been taken into account, which study this concept in terms of cognitive factors rather than sociological and psychological factors. In the study, it is focus on the answers of these questions, respectively: What is the importance of the learning difficulties in education and in mathematics education especially? What kinds of difficulties are there in any given topic in mathematics? What are the ways to overcome these difficulties? As a result of the conducted examination, it has been observed that there are scarcely any studies oriented to overcome the learning difficulties compared to the studies oriented to determine these difficulties. Keywords: Learning Difficulties, Mathematics Education, Literature Review
2 Enver Tatar & Ramazan Dikici GİRİŞ Herhangi bir konuda öğrencilerin karşılaştıkları güçlükleri bilmek, öğrenme üzerine yapılan çalışmalar için önemli bir ilk adımdır. Böyle bir bilginin sonraki çalışmalarla sentezlenmesi ve bağlantı kurulması; gelecek müfredatların düzenlenmesinde ve öğretim modelinin oluşturulmasında önemli bir temel sayılacaktır (Rasmussen, 1998). Çağdaş eğitim anlayışı, öğretmenleri, öğrenmeyi maksimum düzeyde gerçekleştirecek öğretim yaklaşımlarını seçme ve uygulama zorunluluğu ve sorumluluğu ile karşı karşıya bırakmıştır (Yılmaz, 2001). Hangi branşta olursa olsun bütün öğreticiler için anlattığı konu ile ilgili öğrencilerin ne tür öğrenme güçlüklerine sahip olduğunu bilmesi, bu öğretim yaklaşımlarını seçmede fayda sağlayacaktır. Öğrenme sürecinde ve katıldığı etkinliklerde öğrencinin bir takım öğrenme güçlükleri ve başarısız olduğu durumlar olacaktır. Bunların belirlenmesi ve giderilmesi, öğrenme sürecinde öğrenciye yardımcı olunması ve rehberlik edilmesi, öğretmenin görevlerindendir (Ersoy ve Ardahan, 2003). Bu çalışmada öğrenme güçlüğü ile ilgili literatür taraması yapılmıştır. Yapılan literatür taramasında, bu kavramı sosyolojik ve psikolojik faktörlerden ziyade bilişsel faktörler açısından ele alan yayınlar dikkate alınmıştır. MATEMATİK EĞİTİMİNDE ÖĞRENME GÜÇLÜKLERİ Matematik eğitiminin amacı bütün öğrencilerin öğrenmeyi en üst düzeyde gerçekleştirmesidir. Fakat birkaçının bunu gerçekleştirmesine karşın büyük çoğunluğun matematikte zorluk yaşaması yaşamın bir gerçeği olarak görülür (Tall ve Razali, 1993: 209). Yaşanan bu güçlüklerin bir an önce tespit edilip giderilmesi gerekir (Duval, 2002: 14). Çünkü ön-şart oluş ilişkilerinin güçlü olduğu, matematikte bir konuda öğrenme güçlüğü yaşayan bir öğrencinin daha sonraki konularda başarılı olması zordur. Yetkin (2003), matematikte kavramayı geliştirmenin önemli fakat güç bir hedef olduğunu ifade ederek; öğrencilerin matematikteki öğrenme güçlüklerini ve bu güçlüklerin kaynağını bilmenin, onları gidermek için öğretim yöntemi dizayn etmenin, bu hedefe ulaşmada önemli bir adım olduğunu belirtmiştir. 184
3 Matematik Eğitiminde Öğrenme Güçlükleri Öğrenme Güçlüklerinin Belirlenmesi Matematiğin farklı konularındaki öğrenme güçlüklerini ortaya çıkarmak üzere birçok çalışma yapılmıştır. Bu bölümde incelenen ilgili literatür yayınlanma tarihine göre aktarılacaktır. Tall (1993: 17), matematikte öğrenme güçlüklerini araştırmak için uygulanan değişik çalışmaların var olduğunu ve tespit edilen bu güçlüklerden bazılarını genel olarak; (1) temel kavramların yetersiz bir şekilde kavranması, (2) sözel problemleri matematiksel olarak formülize etmedeki yetersizlik ve (3) cebirsel, geometrik ve trigonometrik becerilerdeki eksiklik şeklinde sınıflamıştır. Tall ve Razali (1993: 209, 219) dört işlem, çarpanlara ayırma, denklem çözme, mutlak değer, fonksiyon ve logaritma gibi çeşitli konulardan soruların yer aldığı çoktan seçmeli bir tespit testi kullandıkları çalışmada; öğrenme güçlüklerinin, öğrencilerin kavramları kullanma ve işlemleri koordine etmede yoğunlaştığını belirtmişlerdir. Keza, işlemsel olarak algılayanların karşılaştıkları güçlüklerin kavramsal olarak algılayanların karşılaştıkları güçlüklerden daha çok olduğunu ifade etmişlerdir. Üniversite öğrencilerinin matematiksel ispatları yapmayı öğrenmede yaşadıkları güçlükleri incelemek amacıyla yaptığı çalışmada Moore (1994: 249), araştırma verilerini; öğrenciler ile eğitim oturumları, öğretim elemanı ve öğrenciler ile mülakatlar ve sınıf gözlemleri aracılığı ile toplamıştır. Verilerin tümevarımcı analizi, yani kodlamaya dayalı içerik analizi sonucunda, öğrencilerin güçlüklerinin; (1) kavramı anlama, (2) matematiksel dil ve notasyon, (3) ispata başlama şeklinde üç ana kaynağı olduğunu ortaya çıkarmıştır. Ayrıca öğrencilerin matematiği ve ispatı algılama şekillerinin, ispat yapmalarını etkilediği de belirtilmiştir. Öğrencilerin kavramı anlamadaki güçlükleri, kavramın tanımı, kavramın zihindeki görüntüsü ve kavramın kullanımını içeren kavram-anlama şeması açısından ele alınmıştır. Güçlüklerin diğer ana kaynakları bu şema ile ilişkili olarak incelenmiştir. Zaslavsky ve Peled (1996: 67, 68, 77) in yaptıkları çalışmanın amacı, ikili işlemin değişme ve birleşme özellikleri ile ilgili matematik öğretmenlerinin ve aday öğretmenlerin karşılaştıkları güçlükleri belirlemek ve bu güçlüklerin olası kaynaklarını ortaya çıkarmaktır. Çalışmada katılımcılardan karşıt örnekler (birleşmeli olup da değişmeli olmayan bir ikili işlem, vb.) oluşturmaları istenmiştir. Elde edilen cevaplar; doğruluk, verimlilik (doğruluk ve niteliğe bakılmaksızın oluşturulan örnek sayısı), matematiksel içerik ve öne çıkan güçlükler olmak üzere dört kategoriye göre analiz edilmiştir. Analiz sonucunda her iki grubun da doğru bir örnek üretmedeki başarısızlığı ve sınırlı bir içerik kullanması ile zayıf bir kavrayışa sahip olduğu belirtilmiştir. 185
4 Enver Tatar & Ramazan Dikici Değişmeli olup da birleşmeli olmayan bir ikili işlemin olmayacağı yanlış inanışına sahip olanların yüzdesinin yüksek olduğu bulunmuştur. Ayrıca öğretmenlerin, doğruluk ve verimlilik kategorilerinde, aday öğretmenlerden daha iyi olduğu ortaya çıkarılmıştır. Lise ve üniversite öğrencilerinin matematiksel tümevarım ispat tekniğini öğrenirken karşılaştıkları güçlüklerin ne olduğunu ortaya çıkarmak amacıyla yaptığı çalışmada Baker (1996: 5, 6, 15), araştırmasını iki kısımdan oluşturmuştur. Birinci kısım, matematiksel tümevarımın anlatıldığı yaklaşık iki haftalık bir öğretimden sonra tamamlanmıştır. Öğrencilere, temel matematik, ispat ve matematiksel tümevarım, ispat-yazma ve ispat-analiz ile ilgili sorulardan oluşan bir test uygulanmıştır. Çalışmanın ikinci kısmında ise, öğrencilerin teste vermiş oldukları yazılı cevapları açıklığa kavuşturmak ve ayrıntılarına girmek amacıyla bireysel mülakatlar yapılmıştır. Sonuç olarak, çalışmaya katılan lise ve üniversite öğrencilerinin ispat teknikleri ile ilgili hem kavramsal hem de işlemsel olarak önemli güçlüklere sahip oldukları tespit edilmiştir. Bu güçlüklerde öğrencilerin matematik bilgisinin eksikliğinin önemli bir rol oynadığı kanısına varılmıştır. Çoğu öğrencinin matematiksel tümevarımın kavramsal yönünden daha çok işlemsel yönüne odaklandığı belirlenmiştir. Doğrulamada, çoğu öğrenci için örneklerin önemli bir role sahip olduğu bulunmuştur. Türkiye de cebir öğretiminin durumunu ve niteliğini kalın çizgilerle belirlemek, öğrencilerin cebir konularını öğrenmede karşılaştıkları birtakım güçlükleri ve kavram yanılgılarını belirlemek amacıyla yaptıkları çalışmada Ersoy ve Erbaş (1998: 175, 179), 7. ve 8. sınıf matematik öğretim programındaki cebir konuları göz önünde bulundurularak hazırlanmış iki farklı cebir testi kullanmışlardır. Öğrencilerden testlerdeki soruları çözerken izledikleri basamakları da ayrılan boş yerlere yazmaları istenmiştir. Çalışmanın sonunda, öğrencilerin, özellikle de ekonomik yönden az gelişmiş yörede oturan öğrencilerin cebir konularını öğrenmede çok sayıda güçlüklerinin olduğu saptanmıştır. Farklı sınıf seviyelerinde bile öğrenci başarıları hemen hemen aynı çıkmıştır. Ayrıca, güçlüklerin belirlenmesi için öğrencilerle bire bir görüşmeler yapılmasının, bunların da kaydedilmesinin tanıya yönelik çalışmalar için etkili olabileceği ileri sürülmüştür. Rasmussen (1998), diferansiyel denklemlerdeki öğrencilerin güçlüklerini ve kavrayışlarını, nitel ve nicel analiz yöntemleri ile incelemiştir. Veriler öğrencilerle yapılan yarı-yapılandırılmış mülakatlarla, sınavlar ve bilgisayar ödevleri ile toplanmıştır. Öğrencilerden problemleri çözerken sesli düşünmeleri istenmiştir. Çalışmada, diferansiyel denklemlerde öğrencilerin güçlüklerini anlama ve sınıflandırmada bir metot olarak kullanmak amacıyla; (1) fonksiyon konusundaki güçlükler, (2) uygun olmayan genelleştirme (aşı- 186
5 Matematik Eğitiminde Öğrenme Güçlükleri rı genelleştirme) eğilimi, (3) standart olmayan veya sezgisel kavramlardan kaynaklanan karışıklık ve (4) grafikleri yorumlayamama şeklinde dört kategori geliştirilmiştir. Benzer bir çalışmada Artigue vd. (1990: 262) ise öğrencilerin diferansiyel ile ilgili kavrayışlarını ve öğrenme güçlüklerini araştırmıştır. Öğrencilerin genellikle diferansiyel ve integral işlemlerini, neden gerekli olduğu ve nerelerde kullanıldığı hakkında tam bir düşünceye sahip olmaksızın uyguladıklarını ortaya çıkarmışlardır. Soyut cebirde herhangi bir teoremin ispatının nasıl oluşturulduğunun öğrenilmesindeki güçlükleri ortaya çıkarmak amacıyla yaptığı çalışmasında Weber (2001: 101, 107, 115), araştırmaya katılan her bir öğrenciden 7 tane grup homomorfizması ile ilgili teoremi, düşündüklerini sesli bir şekilde ifade ederek ispatlamalarını istemiştir. Bu ispat denemelerinin her birini; doğru (katılımcı geçerli bir ispat oluşturmuş), bilgiye başvurmadaki başarısızlık (katılımcı gerekli bilgiye sahip fakat ispatı oluşturmada bunu uygulayamıyor), yetersiz bilgi (katılımcı teoremin ispatını oluşturmak için gerekli olan bilgiye sahip değil) ve mantıksal hata (katılımcı geçerli bir ispat yaptığına inanıyor fakat yapılan ispat geçersiz) şeklinde kodlamıştır. Weber çalışmasının sonunda, grup homomorfizmasında bir ispatı oluşturan kavrayışa ve bilgiye sahip olmanın ispatın yapılabilmesi için yeterli olmadığını ortaya çıkarmıştır. Özellikle çalışmadaki üniversite öğrencilerinin çoğu kez bir ifadeyi ispatlamak için gerekli olan bilginin farkında oldukları fakat ispat yapmada güçlükler yaşadıkları belirtilmektedir. Yusof ve Rahman (2001), katlı integral kavramıyla ilgili olarak öğrencilerin karşılaştıkları güçlükleri araştırarak bunları; (1) bölge ve yüzeylerin görselleştirilmesi, (2) grafiklerin yorumu, (3) algoritmik hatalar ve (4) cebirsel işlem hataları olmak üzere dört ana kategoride gruplandırmıştır. Öğrencilerin fonksiyon kavramını öğrenmedeki güçlüklerini araştırmak amacıyla yaptığı çalışmasında Zachariades vd. (2002), her bir soruda verilen gösterimlerin bir fonksiyona ait olup olmadığını sorgulayan açık uçlu sorulardan oluşan bir test kullanmıştır. Bu testin birinci bölümünde simgesel biçimde verilen bağıntılar, ikinci bölümünde ise bağıntı grafikleri vardır. Simgesel ve grafiksel biçimdeki sorulardan oluşan bu iki bölümde, öğrencilerin yaşadıkları güçlükler arasında istatistiksel olarak anlamlı bir farkın olduğu belirlenmiştir. Öğrencilerin simgesel olarak verilen ifadelerde, grafiksel gösterimleriyle verilenlerden daha kolay bir şekilde fonksiyonu tanıdıkları tespit edilmiştir. Bağıntı ve fonksiyon konusundaki öğrenme güçlüğü ile öğrencinin matematiğe yönelik tutumu, matematik benlik duygusu ve kullanılan öğretim metotları arasında bir ilişkinin olup olmadığını araştırmak amacıyla yaptık- 187
6 Enver Tatar & Ramazan Dikici ları çalışmada Dikici ve İşleyen (2004: 105, 115), verileri kendileri tarafından geliştirilen anketlerle toplamışlardır. Elde edilen verilerin analizinde varyans analizi, korelasyon analizi ve aritmetik ortalama kullanılmıştır. Sonuç olarak bağıntı ve fonksiyon konusundaki öğrenme güçlüğü ile öğrencinin matematiğe yönelik tutumu, matematik benlik duygusu ve kullanılan öğretim metotları arasında anlamlı bir ilişki bulunmuştur. Durmuş (2004a: 125, 127), ortaöğretim matematik derslerinde zor olarak algılanan konuları belirlemek ve bu zorlukların arkasında yatan nedenleri ortaya çıkarmak amacıyla yaptığı çalışmada ortaöğretim matematik müfredatındaki tüm konuların, likert tipi bir anketle zorluk indeksini tespit etmiştir. Öğrencilerle yaptığı görüşmeler sonunda zorluk sebebi olarak motivasyon eksikliği ve kavramların soyutluluğu gibi iki önemli noktanın ortaya çıktığını belirtmiştir. Durmuş (2004b), benzer bir çalışmayı ilköğretim matematik konuları içinde uygulayarak çalışmasında, ilköğretim matematik konularından zor olarak algılanan konuların ilköğretimin son yıllarında yer aldığını ve bunun nedeninin de bu yıllardaki konuların, önceki yıllara göre daha çok soyut içerikli olmasından kaynaklandığını belirtmiştir. Ersoy ve Erbaş (2005), çalışmalarında uluslararası öğrenci başarısını belirlemeye yönelik Kassel projesi çerçevesinde geliştirilen, 2000 yılı başına kadar 15 ülkede uygulanan bir araştırmanın Türkiye de pilot uygulamasını rapor etmektedirler. Kassel projesinin amacının, araştırmaya katılan ülkelerde genelde ilköğretim matematik eğitimi programının tümünde, özelde programın bir parçası olarak cebir öğretiminde öğrencilerin akademik başarısına dayalı olarak gelişimini izlemek ve sonuçları karşılaştırmak, başarıya etki eden öğrenme güçlükleri başta olmak üzere ortak yanlışlar ve kavram yanılgılarını, öğrenme etkinliklerinin özelliklerini incelemek olduğu belirtilmiştir. Çalışmanın sonunda öğrencilerin Kassel projesi cebir testindeki işlem ağırlıklı sorularda başarı oranlarının daha yüksek olduğu, eşitlikler (denklemler) ve problemler ile ilgili sorulardaki başarının düşük olduğu, öğrencilerin çok sayıda ve değişik türlerde yanlış yaptıkları ifade edilmiştir. Gözlemlenen bu durumun, öğrencilerin cebir konularını öğrenmede bir takım öğrenme güçlüklerinin olduğunun belirgin işaretleri olup özellikle eşitlik ve değişken kavramlarında birtakım kavram yanılgılarının olabileceğinden; ayrıca, tanıya yönelik uygun ölçme araçları geliştirilerek derinlemesine inceleme yapılması gerekliliğinden bahsedilmiştir. Barnett (2006), çalışmasında öğrencilerin ne anladığını belirlemenin bir yolunun doğru-yanlış tipi sorular sormak olduğunu vurgulamıştır. Verilen ifadenin doğru ya da yanlıştır cevabına ilaveten neden doğru ya da yanlış olduğunun da sorgulanması gerektiğini söyleyerek bu sorulardaki amacın öğrencileri yanıltmaktan ziyade kavramların önemli özelliklerine dikkatlerin 188
7 Matematik Eğitiminde Öğrenme Güçlükleri 2 çekilmesini sağlamak olduğunu belirtmiştir. Her a reel sayısı için a = a ifadesi doğru mu yoksa yanlış mıdır? Neden?, Büküm noktası aynı zamanda bir ekstremum noktadır ifadesi doğrumu yoksa yanlış mıdır? Neden? biçimindeki sorulara verilen yazılı açıklamaların, doğru/yanlış tipi ya da yalnızca cevap seçeneğinin belirtildiği çoktan seçmeli soru tiplerine verilen cevaplara nazaran öğrencilerin yanılgılarını ve öğrenme güçlüklerini belirlemede son derece önemli olduğunu ifade etmiştir. Barnett ayrıca doğru bir cevap için yapılan yetersiz bir açıklamanın yanlış bir cevap için yapılan iyi bir açıklamadan daha az güvenilir olacağını da vurgulamıştır. Öğrenme Güçlüklerinin Giderilmesi Bu bölümde öğrenme güçlüklerinin giderilmesi ile ilgili yayınlara yer verilecektir. Bu tür çalışmalar güçlüklerin belirlenmesi türündeki çalışmalara nazaran oldukça az olduğu gözlenmiştir. Woerner (1980: i), çalışmasında lise öğrencilerinin kesirleri toplarken yaptıkları hataları tespit edip giderme işleminde bilgisayar teknolojisinin kullanımını araştırmıştır. Çalışma, kesirlerde toplama işleminde yapılan hatalar için bilgisayar tabanlı tespit sistemi geliştirme ve bu sistemin etkinliğini değerlendirmeyi içermektedir. Kesirleri toplama işleminde öğrencilerin karşılaştıkları güçlükleri analiz etmek için BASIC programlama dilinin kullanıldığı bir bilgisayar programı yazılmıştır. Öğrencilerin cevaplarını değerlendiren bu bilgisayar programı, hataları özel kategorilere ayırmıştır. Çalışmanın sonuçları, bilgisayarın tespit amaçlı kullanılabilirliğini desteklemektedir. Ayrıca Woerner bu çalışmada, bilgisayarın lise öğrencilerinin kesirlerde toplama işlemindeki öğrenme güçlüklerini belirleyip bu güçlükleri gidermek için etkili bir şekilde kullanılabileceği sonucuna varmıştır. Harel (1989: 139, 140, 147), çalışmasında öğrencilerin lineer cebirdeki temel kavramlarla ilgili sahip oldukları öğrenme güçlüklerinin nedenleri ve onları gidermek için nasıl bir program dizayn edilmesi gerektiği üzerinde durmuştur. Bu güçlüklerin nedenlerinden birincisinin kavramların soyut yapılar olduğu, ikincisinin uygulama alanlarının öğrenciler için alışılmışın dışında olduğu ve üçüncüsünün de çoğu öğrencinin henüz ispat ve aksiyomatik metotları bilmeyişi olarak ifade etmiştir. Ayrıca Harel, öğrenme güçlüklerini gidermede görselleştirmenin öneminden bahsederek, lineer cebirdeki temel kavramların geometriksel olarak gösterilmediği, yani görselleştirme yapılmadığında öğrencilerin bu kavramları öğrenmede güçlükler yaşayacaklarını ifade etmiştir. Lise matematik öğretmenleri ile işbirliği içinde yürüttükleri matematiksel öğrenme güçlüklerinin giderilmesi isimli çalışmalarını Yusof vd. (1999: 189
8 Enver Tatar & Ramazan Dikici 376, 377, 378), (1) öğrenme güçlüklerinin incelenmesi, (2) kavram gelişimi, (3) alternatif stratejiler ve (4) sınıf içi uygulama şeklinde dört safhada gerçekleştirmişlerdir. Yine aynı çalışmada, lise öğretmenleri ile yaptıkları işbirliği sonucunda bazı öğretmenlerin belli konuların (logaritma, fonksiyonlar, eşitsizlikler, olasılık, matris ve eğri altındaki alan) öğretiminde güçlük yaşadıklarını ortaya çıkarmışlardır. Çalışmada, birlikte çalıştıkları lise öğretmenlerine alternatif öğretim (materyal kullanımı, vb) ve problem çözme stratejileri gibi tavsiyelerde bulunduklarını ifade etmişlerdir. Bu durumda öğrencilerin öğrenme güçlüklerinde gözle görülür bir oranda azalma olduğu tespit edilmiştir. Öğretim elemanı olarak girdiği lineer cebir derslerindeki kişisel deneyimlerinden yola çıkarak hazırladığı çalışmanın ilk aşamasında Haddad (1999: iii, 6, 20, 187), lineer cebir öğrenmede öğrencilerin güçlüklerini; lineer cebirin doğası, lineer cebirin öğretimi ve öğrencilerin lineer cebirin nasıl öğrendiği şeklinde üç farklı perspektiften ele almıştır. Öğrencilerin lineer cebirde öğrenme güçlüğü yaşamalarının temel nedenleri, dersin soyut olmasına karşın öğrencilerin yeterince soyut düşünmemeleri, lineer cebirin aksiyomatik bir karakterde olması ve öğrencilerin yetersiz bir matematik temeline sahip olmaları şeklinde sıralanmıştır. İkinci aşamada ise lineer cebirin öğrenimi ve öğretimindeki güçlükleri göz önünde bulundurup buna göre bir matematiksel yazılımı (Cabri) kullanmıştır. Bu yazılım ile lineer cebirin belli konularını sunmada alternatif bir yolu test etmek için bir araştırma projesi uygulamıştır. Elde edilen bulgular farklı açılardan yorumlanmıştır. SONUÇ VE ÖNERİLER Yapılan inceleme sonucunda matematikte öğrenme güçlüklerini belirleme çalışmalarında genelde veri toplama aracı olarak; Çoktan seçmeli sorulardan oluşan testler, Açık uçlu sorulardan oluşan testler, Öğretmenlerle yapılan mülakatlar, Öğrencilerle yapılan mülakatlar, Sınıf gözlemleri ve Bilgisayar programları kullanılmıştır. Araştırma deseni olarak da daha çok durum çalışması deseni nin kullanıldığı tespit edilmiştir. 190
9 Matematik Eğitiminde Öğrenme Güçlükleri Araştırmada genel olarak matematikteki öğrenme güçlüklerinin; (1) uygulanan matematik öğretimindeki eksiklik, (2) konuların soyutluluğu (soyut oluşuna karşın öğrencilerin yeterince soyut düşünememeleri), (3) sözel ifadeleri yorumlayamama ve (4) öğrencilerin hazır bulunuşluk düzeylerindeki yetersizlik şeklinde dört temel kaynağı olduğu ortaya çıkmaktadır. Güçlükleri giderme çalışmalarının, güçlükleri belirleme çalışmalarından oldukça az olduğu gözlenmiştir. Bu çalışmalarda da güçlükleri gidermeye yönelik olarak; (1) bilgisayar programları, (2) görselleştirme, (3) uygun materyal kullanımı ve (4) öğrenme güçlükleri doğrultusunda öğretimi yeniden tasarlamanın kullanıldığı tespit edilmiştir. Bu sonuçlara göre, eğitimciler ve eğitim alanında çalışma yapan araştırmacılar için faydalı olacağı düşünülen öneriler aşağıda sunulmaktadır. Hem matematikte hem de diğer alanlarda öğrencilerin sıklıkla yaşadıkları öğrenme güçlükleri tespit edilip bunları gidermeye yönelik yöntemler geliştirilerek; etkinlikleri üzerine çalışmalar yapılabilir. Öğretmenler, konu bazında yapılmış bu tip araştırmaları takip etmeli ve anlatacağı konu ile ilgili öğrencilerinin ne tür güçlüklerle karşılaşabileceklerinden haberdar olmalıdırlar. Ayrıca, matematik öğretmenleri yukarıda belirtilen temel hususlara dikkat ederek anlatacakları dersi şekillendirmelidirler. Yani; kavramsal bilgi ile işlemsel bilginin dengelendiği bir matematik öğretimi gerçekleştirmeli, anlatılacak kavramın soyutluluğunu azaltacak materyallerden yararlanılmalı ve öğrencilerin hazır bulunuşluk düzeyine dikkat edilmeli, gerekirse bu düzey anlatılacak konuya adapte edilmelidir. KAYNAKLAR Artigue, M., Menigaux, J. and Viennot, L. (1990) Some aspects of students' conceptions and difficulties about differentials. European Journal Physics, 11, Baker, J. D. (1996) Students difficulties with proof by mathematical induction, The Annual Meeting of American Educational Research Association, New York. Barnett, J.H. (2006) True or False? Explain!. University of Southern Colorado. İndirilme tarihi: , es49/101.html#1 Dikici, R. ve İşleyen, T. (2004) Bağıntı ve fonksiyon konusundaki öğrenme güçlüklerinin bazı değişkenler açısından incelenmesi. Kastamonu Eğitim Dergisi, 12(1),
10 Enver Tatar & Ramazan Dikici Durmuş, S. (2004a) Matematikte öğrenme güçlüklerinin saptanması üzerine bir çalışma. Kastamonu Eğitim Dergisi, 12(1), Durmuş, S. (2004b) İlköğretim matematiğinde öğrenme zorluklarının saptanması ve zorlukların gerisinde yatan nedenler üzerine bir çalışma. VI. Ulusal Fen Bilimleri ve Matematik Eğitimi Kongresi, Marmara Üniversitesi, İstanbul. İndirilme tarihi: , www:web: nan/files/ ozetler.pdf Duval, R. (2002) The cognitive analysis of problems of comprehension in the learning of mathematics. Mediterranean Journal for Research in Mathematics Education, 1(2), Ersoy, Y. ve Erbaş, K. (1998) İlköğretim okullarında cebir öğretimi: öğrenmede güçlükler ve öğrenci başarıları. Cumhuriyetin 75. yılında İlköğretim I. Ulusal Sempozyumu, Başkent Öğretmen Evi, Ankara. Ersoy, Y. ve Ardahan, H. (2003) İlköğretim okullarında kesirlerin öğretimi-ii: Tanıya yönelik etkinlikler düzenleme. İndirilme tarihi: , Ersoy, Y. ve Erbaş, A.K. (2005) Kassel projesi cebir testinde bir grup Türk öğrencinin genel başarısı ve öğrenme güçlükleri. İlköğretim-Online, 4(1), İndirilme tarihi: , Harel, G. (1989) Learning and teaching linear algebra: difficulties and an alternative approach to visualizing concepts and processes. Focus on Learning Problems in Mathematics, 11(2), Haddad, M. (1999) Difficulties in the learning and teaching of linear algebra a personal experience. Unpublished Master Dissertation, Concordia University, Montreal, Quebec, Canada. Moore, R. C. (1994) Making the transition to formal proof. Educational Studies in Mathematics, 27, Rasmussen, C. L. (1998) Reform in Differential Equations: A Case Study of Students Understandings and Difficulties. The Annual Meeting of American Educational Research Association, San Diego, CA. İndirilme tarihi: , 0/15/8e/cb.pdf Tall, D. (1993) Students difficulties in calculus, Proceedings of Working Group 3 on Students Difficulties in Calculus. ICME-7, Quebec, Canada, Tall, D. O. and Razali, M. R. (1993) Diagnosing students difficulties in learning mathematics. International Journal of Mathematical Education in Science and Technology, 24(2), Weber, K. (2001) Student difficulty in constructing proofs: the need for strategic knowledge. Educational Studies in Mathematics, 48, Woerner, K. L. W. (1980) Computer based diagnosis and remediation of computational errors with fractions. Unpublished Doctoral Dissertation, The University of Texas, Austin. 192
11 Matematik Eğitiminde Öğrenme Güçlükleri Yetkin, E. (2003) Student Difficulties in Learning Elementary Mathematics. ERIC Clearinghouse for Science, Mathematics and Environmental Education, Columbus, OH., ED İndirilme tarihi: , www:web: eric.ed.gov. Yılmaz, A. (2001) İşbirliğine dayalı öğrenme, etkili ancak ihmal edilen ya da yanlış kullanılan bir metot. Milli Eğitim, 150. İndirilme tarihi: , Yusof, Y. M., Rahman, R. A., Razali, M. R., Abu, M. S., Bakar, M. N. and Tiong, O. C. (1999) Overcoming mathematical learning difficulties: a case study of collaborative research. Proceeding 8th Southeast Asian Conference, , Manila, Phillippine Yusof, Y. M. and Rahman, R. A. (2001) Students' difficulties with multiple integration: a preliminary study. 3rd Southern Hemisphere Symposium, South Africa. Zachariades, T., Christou, C., and Papageorgiou, E. (2002) The difficulties and reasoning of undergraduate mathematics students in the identification of functions. Proceedings in the 10th ICME Conference, Crete, Greece. Zaslavsky, O. and Peled, I. (1996) Inhibiting factors in generating examples by mathematics teachers and student teachers: the case of binary operation. Journal for Research in Mathematics Education, 27,
ORTAÖĞRETİM MATEMATİĞİNDE ÖĞRENME GÜÇLÜKLERİNİN SAPTANMASINA YÖNELİK BİR ÇALIŞMA
 Ekim 2008 Cilt:16 No:2 Kastamonu Eğitim Dergisi 507-516 ORTAÖĞRETİM MATEMATİĞİNDE ÖĞRENME GÜÇLÜKLERİNİN SAPTANMASINA YÖNELİK BİR ÇALIŞMA Enver TATAR Ağrı İbrahim Çeçen Üniversitesi, Ağrı Eğitim Fakültesi,
Ekim 2008 Cilt:16 No:2 Kastamonu Eğitim Dergisi 507-516 ORTAÖĞRETİM MATEMATİĞİNDE ÖĞRENME GÜÇLÜKLERİNİN SAPTANMASINA YÖNELİK BİR ÇALIŞMA Enver TATAR Ağrı İbrahim Çeçen Üniversitesi, Ağrı Eğitim Fakültesi,
ĐLKÖĞRETĐM ANABĐLĐM DALI MATEMATĐK EĞĐTĐMĐ BĐLĐM DALI YÜKSEK LĐSANS PROGRAMI 2013-2014 EĞĐTĐM ÖĞRETĐM PLANI GÜZ YARIYILI DERSLERĐ
 ĐLKÖĞRETĐM ANABĐLĐM DALI MATEMATĐK EĞĐTĐMĐ BĐLĐM DALI YÜKSEK LĐSANS PROGRAMI 2013-2014 EĞĐTĐM ÖĞRETĐM PLANI GÜZ YARIYILI DERSLERĐ Kodu Adı T U AKTS Ders Türü ĐME 500* Seminer 0 2 6 Zorunlu ĐME 501 Eğitimde
ĐLKÖĞRETĐM ANABĐLĐM DALI MATEMATĐK EĞĐTĐMĐ BĐLĐM DALI YÜKSEK LĐSANS PROGRAMI 2013-2014 EĞĐTĐM ÖĞRETĐM PLANI GÜZ YARIYILI DERSLERĐ Kodu Adı T U AKTS Ders Türü ĐME 500* Seminer 0 2 6 Zorunlu ĐME 501 Eğitimde
ONBĠRĠNCĠ SINIF MATEMATĠK ÖĞRETĠM PROGRAMINDA ZORLUK ÇEKĠLEN KONULAR VE OLASI NEDENLERĠ
 ONBĠRĠNCĠ SINIF MATEMATĠK ÖĞRETĠM PROGRAMINDA ZORLUK ÇEKĠLEN KONULAR VE OLASI NEDENLERĠ KürĢat YENĠLMEZ 1 Emre EV ÇĠMEN 1 Doç. Dr., EskiĢehir Osmangazi Üniversitesi, Eğitim Fakültesi, Ġlköğretim Bölümü,
ONBĠRĠNCĠ SINIF MATEMATĠK ÖĞRETĠM PROGRAMINDA ZORLUK ÇEKĠLEN KONULAR VE OLASI NEDENLERĠ KürĢat YENĠLMEZ 1 Emre EV ÇĠMEN 1 Doç. Dr., EskiĢehir Osmangazi Üniversitesi, Eğitim Fakültesi, Ġlköğretim Bölümü,
EĞİTİM FAKÜLTESİ Ortaöğretim Fen ve Ortaöğretim Fen ve ENSTİTÜSÜ
 ÖZGEÇMİŞ VE ESERLER LİSTESİ Adı Soyadı : SAFİYE ASLAN Doğum Tarihi : 15/05/1979 E-posta : safiyeaslan@gmail.com 1. EĞİTİM DURUMU Unvan Bölüm/Anabilim Dalı Fakülte / Y.Okul Üniversite Yıllar Lisans Kimya
ÖZGEÇMİŞ VE ESERLER LİSTESİ Adı Soyadı : SAFİYE ASLAN Doğum Tarihi : 15/05/1979 E-posta : safiyeaslan@gmail.com 1. EĞİTİM DURUMU Unvan Bölüm/Anabilim Dalı Fakülte / Y.Okul Üniversite Yıllar Lisans Kimya
ÖZGEÇMİŞ VE ESERLER LİSTESİ - 1. Derece Bölüm/Program Üniversite Yıl Lisans Ortaöğretim Matematik Öğretmenliği
 ÖZGEÇMİŞ Adı Soyadı: Burçin GÖKKURT Doğum Tarihi: 01.06.1984 Öğrenim Durumu: Doktora ÖZGEÇMİŞ VE ESERLER LİSTESİ - 1 Derece Bölüm/Program Üniversite Yıl Lisans Ortaöğretim Öğretmenliği Karadeniz Teknik
ÖZGEÇMİŞ Adı Soyadı: Burçin GÖKKURT Doğum Tarihi: 01.06.1984 Öğrenim Durumu: Doktora ÖZGEÇMİŞ VE ESERLER LİSTESİ - 1 Derece Bölüm/Program Üniversite Yıl Lisans Ortaöğretim Öğretmenliği Karadeniz Teknik
EĞİTİM FAKÜLTESİ Ortaöğretim Fen ve Ortaöğretim Fen ve ENSTİTÜSÜ
 ÖZGEÇMİŞ VE ESERLER LİSTESİ Adı Soyadı E-posta : SAFİYE ASLAN : safiyeaslan@gmail.com 1. EĞİTİM DURUMU Unvan Bölüm/Anabilim Dalı Fakülte / Y.Okul Üniversite Yıllar Lisans Kimya Öğretmenliği/ EĞİTİM FAKÜLTESİ
ÖZGEÇMİŞ VE ESERLER LİSTESİ Adı Soyadı E-posta : SAFİYE ASLAN : safiyeaslan@gmail.com 1. EĞİTİM DURUMU Unvan Bölüm/Anabilim Dalı Fakülte / Y.Okul Üniversite Yıllar Lisans Kimya Öğretmenliği/ EĞİTİM FAKÜLTESİ
ÖZGEÇMİŞ. Derece Alan Üniversite Yıl. Y. Lisans Matematik Eğitimi University of Warwick 2010 Y. Lisans Matematik Eğitimi University of Cambridge 2012
 ÖZGEÇMİŞ 1. Adı Soyadı: Gülay BOZKURT İletişim Bilgileri: Adres: Eskişehir Osmangazi Üniversitesi Eğitim Fakültesi Oda No: 403 Odunpazarı/Eskişehir Telefon: 0(222) 2293123 1676 email: gbozkurt@ogu.edu.tr
ÖZGEÇMİŞ 1. Adı Soyadı: Gülay BOZKURT İletişim Bilgileri: Adres: Eskişehir Osmangazi Üniversitesi Eğitim Fakültesi Oda No: 403 Odunpazarı/Eskişehir Telefon: 0(222) 2293123 1676 email: gbozkurt@ogu.edu.tr
ÖZGEÇMĠġ VE ESERLER LĠSTESĠ
 ÖZGEÇMĠġ VE ESERLER LĠSTESĠ ÖZGEÇMĠġ Adı Soyadı : Melihan ÜNLÜ Doğum Tarihi (gg/aa/yy): Adres : Aksaray Üniversitesi, Eğitim Fakültesi, İlköğretim Bölümü Telefon : 03822882263 E-posta : melihanunlu@yahoo.com
ÖZGEÇMĠġ VE ESERLER LĠSTESĠ ÖZGEÇMĠġ Adı Soyadı : Melihan ÜNLÜ Doğum Tarihi (gg/aa/yy): Adres : Aksaray Üniversitesi, Eğitim Fakültesi, İlköğretim Bölümü Telefon : 03822882263 E-posta : melihanunlu@yahoo.com
Ders Adı Kodu Yarıyılı T+U Saati Ulusal Kredisi AKTS. Temel Matematik 1 TEM
 DERS BİLGİLERİ Ders Adı Kodu Yarıyılı T+U Saati Ulusal Kredisi AKTS Temel Matematik 1 TEM425 7 3+0 3 4 Ön Koşul Dersleri Dersin Dili Dersin Seviyesi Dersin Türü Türkçe Lisans Yüz Yüze / Zorunlu Dersin
DERS BİLGİLERİ Ders Adı Kodu Yarıyılı T+U Saati Ulusal Kredisi AKTS Temel Matematik 1 TEM425 7 3+0 3 4 Ön Koşul Dersleri Dersin Dili Dersin Seviyesi Dersin Türü Türkçe Lisans Yüz Yüze / Zorunlu Dersin
MATEMATİK BİLİM GRUBU III KURS PROGRAMI
 MATEMATİK BİLİM GRUBU III KURS PROGRAMI 1.Kurumun Adı 2.Kurumun adresi 3.Kurucunun Adı 4.Programın Adı : OĞUZHAN ÖZKAYA ÖZEL ÖĞRETİM KURSU : Onur Mahallesi Leylak Sok.No:9 Balçova-İzmir : Oğuzhan Özkaya
MATEMATİK BİLİM GRUBU III KURS PROGRAMI 1.Kurumun Adı 2.Kurumun adresi 3.Kurucunun Adı 4.Programın Adı : OĞUZHAN ÖZKAYA ÖZEL ÖĞRETİM KURSU : Onur Mahallesi Leylak Sok.No:9 Balçova-İzmir : Oğuzhan Özkaya
MATEMATİK VE FEN BİLİMLERİ EĞTİMİ ANABİLİM DALI MATEMATİK EĞİTİMİ BİLİM DALI TEZLİ YÜKSEK LİSANS PROGRAMI
 I.YARIYIL MATEMATİK VE FEN BİLİMLERİ EĞTİMİ ANABİLİM DALI MATEMATİK EĞİTİMİ BİLİM DALI TEZLİ YÜKSEK LİSANS PROGRAMI 3715055832012 Z Uzmanlık Alan Dersi 3715055702017 Z Bilimsel Araştırma Yöntemleri ve
I.YARIYIL MATEMATİK VE FEN BİLİMLERİ EĞTİMİ ANABİLİM DALI MATEMATİK EĞİTİMİ BİLİM DALI TEZLİ YÜKSEK LİSANS PROGRAMI 3715055832012 Z Uzmanlık Alan Dersi 3715055702017 Z Bilimsel Araştırma Yöntemleri ve
CEBİRDEKİ KAVRAMLARA YÖNELİK ÖĞRENME GÜÇLÜKLERİ ÜZERİNE BİR ÇALIŞMA
 Eylül 2011 Cilt:19 No:3 Kastamonu Eğitim Dergisi 939-952 Özet CEBİRDEKİ KAVRAMLARA YÖNELİK ÖĞRENME GÜÇLÜKLERİ ÜZERİNE BİR ÇALIŞMA Tuğrul KAR, Alper ÇİLTAŞ, Ahmet IŞIK Atatürk Üniversitesi, Kazım Karabekir
Eylül 2011 Cilt:19 No:3 Kastamonu Eğitim Dergisi 939-952 Özet CEBİRDEKİ KAVRAMLARA YÖNELİK ÖĞRENME GÜÇLÜKLERİ ÜZERİNE BİR ÇALIŞMA Tuğrul KAR, Alper ÇİLTAŞ, Ahmet IŞIK Atatürk Üniversitesi, Kazım Karabekir
Zirve Üniversitesi Eğitim Fakültesi Sınıf Öğretmenliği ABD Ders Ġçerikleri
 Zirve Üniversitesi Eğitim Fakültesi Sınıf Öğretmenliği ABD Ders Ġçerikleri 5.DÖNEM 6.DÖNEM DERSLER T U K ECTS DERSLER T U K ECTS SNF 301 FEN VE TEK. ÖĞR. 4 0 4 6 SNF 304 TÜRKÇE ÖĞRETIMI 4 0 4 6 SNF 303
Zirve Üniversitesi Eğitim Fakültesi Sınıf Öğretmenliği ABD Ders Ġçerikleri 5.DÖNEM 6.DÖNEM DERSLER T U K ECTS DERSLER T U K ECTS SNF 301 FEN VE TEK. ÖĞR. 4 0 4 6 SNF 304 TÜRKÇE ÖĞRETIMI 4 0 4 6 SNF 303
Eğitim Fakültesi, Kimya Öğretmenliği Programı, Yüzüncü Yıl Üniversitesi. 1999-2004 Eğitim Fakültesi, Kimya Öğretmenliği Lisansla
 Ünvanı : Yrd. Doç. Dr. Adı Soyadı : Nail İLHAN Doğum Yeri ve Tarihi : Osmaniye- 1981 Bölüm: İlköğretim Bölümü E-Posta: naililhan @ gmail.com naililhan @ kilis.edu.tr Website: http://atauni.academia.edu/naililhan
Ünvanı : Yrd. Doç. Dr. Adı Soyadı : Nail İLHAN Doğum Yeri ve Tarihi : Osmaniye- 1981 Bölüm: İlköğretim Bölümü E-Posta: naililhan @ gmail.com naililhan @ kilis.edu.tr Website: http://atauni.academia.edu/naililhan
Genel Matematik (MATH 103) Ders Detayları
 Genel Matematik (MATH 103) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Genel Matematik MATH 103 Güz 3 2 0 4 6 Ön Koşul Ders(ler)i - Dersin Dili Dersin
Genel Matematik (MATH 103) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Genel Matematik MATH 103 Güz 3 2 0 4 6 Ön Koşul Ders(ler)i - Dersin Dili Dersin
EPİSTEMOLOJİK İNANÇLAR ÜZERİNE BİR DERLEME
 EPİSTEMOLOJİK İNANÇLAR ÜZERİNE BİR DERLEME Fatih KALECİ 1, Ersen YAZICI 2 1 Konya Necmettin Erbakan Üniversitesi, Eğitim Bilimleri Enstitüsü, Matematik Eğitimi 2 Adnan Menderes Üniversitesi, Eğitim Fakültesi,
EPİSTEMOLOJİK İNANÇLAR ÜZERİNE BİR DERLEME Fatih KALECİ 1, Ersen YAZICI 2 1 Konya Necmettin Erbakan Üniversitesi, Eğitim Bilimleri Enstitüsü, Matematik Eğitimi 2 Adnan Menderes Üniversitesi, Eğitim Fakültesi,
Genel Matematik (MATH 103) Ders Detayları
 Genel Matematik (MATH 103) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Genel Matematik MATH 103 Güz 3 2 0 4 6 Ön Koşul Ders(ler)i - Dersin Dili Dersin
Genel Matematik (MATH 103) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Genel Matematik MATH 103 Güz 3 2 0 4 6 Ön Koşul Ders(ler)i - Dersin Dili Dersin
ÖZEL ÖĞRETİM KURSU MATEMATİK-III ÇERÇEVE PROGRAMI. : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA
 ÖZEL ÖĞRETİM KURSU MATEMATİK-III ÇERÇEVE PROGRAMI 1.KURUMUN ADI 2.KURUMUN ADRESİ 3.KURUCUNUN ADI :Tercih Özel Öğretim Kursu : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA : ARTI ÖZEL EĞİTİM ÖĞRETİM
ÖZEL ÖĞRETİM KURSU MATEMATİK-III ÇERÇEVE PROGRAMI 1.KURUMUN ADI 2.KURUMUN ADRESİ 3.KURUCUNUN ADI :Tercih Özel Öğretim Kursu : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA : ARTI ÖZEL EĞİTİM ÖĞRETİM
Doç.Dr. EYLEM YILDIZ FEYZİOĞLU
 Doç.Dr. EYLEM YILDIZ FEYZİOĞLU Eğitim Fakültesi Matematik Ve Fen Bilimleri Eğitimi Bölümü Fen Bilgisi Eğitimi Anabilim Dalı Eğitim Bilgileri Eğitim Fakültesi Matematik Ve Fen Bilimleri 1994-1999 Lisans
Doç.Dr. EYLEM YILDIZ FEYZİOĞLU Eğitim Fakültesi Matematik Ve Fen Bilimleri Eğitimi Bölümü Fen Bilgisi Eğitimi Anabilim Dalı Eğitim Bilgileri Eğitim Fakültesi Matematik Ve Fen Bilimleri 1994-1999 Lisans
KAMU PERSONELÝ SEÇME SINAVI PUANLARI ÝLE LÝSANS DÝPLOMA NOTU ARASINDAKÝ ÝLÝÞKÝLERÝN ÇEÞÝTLÝ DEÐÝÞKENLERE GÖRE ÝNCELENMESÝ *
 Abant Ýzzet Baysal Üniversitesi Eðitim Fakültesi Dergisi Cilt: 8, Sayý: 1, Yýl: 8, Haziran 2008 KAMU PERSONELÝ SEÇME SINAVI PUANLARI ÝLE LÝSANS DÝPLOMA NOTU ARASINDAKÝ ÝLÝÞKÝLERÝN ÇEÞÝTLÝ DEÐÝÞKENLERE
Abant Ýzzet Baysal Üniversitesi Eðitim Fakültesi Dergisi Cilt: 8, Sayý: 1, Yýl: 8, Haziran 2008 KAMU PERSONELÝ SEÇME SINAVI PUANLARI ÝLE LÝSANS DÝPLOMA NOTU ARASINDAKÝ ÝLÝÞKÝLERÝN ÇEÞÝTLÝ DEÐÝÞKENLERE
KÖKLÜ SAYILARIN BÜYÜKLÜĞÜNE KARAR VEREMEME VE SAYI DOĞRUSUNA YERLEŞTİREMEME
 KÖKLÜ SAYILARIN BÜYÜKLÜĞÜNE KARAR VEREMEME VE SAYI DOĞRUSUNA YERLEŞTİREMEME Arş. Gör. Zeki Aksu Artvin Çoruh Üniversitesi Eğitim Fakültesi zekiaksu25@artvin.edu.tr Solmaz Damla Gedik Atatürk Üniversitesi
KÖKLÜ SAYILARIN BÜYÜKLÜĞÜNE KARAR VEREMEME VE SAYI DOĞRUSUNA YERLEŞTİREMEME Arş. Gör. Zeki Aksu Artvin Çoruh Üniversitesi Eğitim Fakültesi zekiaksu25@artvin.edu.tr Solmaz Damla Gedik Atatürk Üniversitesi
Türkiye de Biyoloji Eğitimi. Türkiye de Biyoloji Eğitimi İÇERİK
 24.3.215 TÜRKİYE DE BİYOLOJİ EĞİTİMİ ALANINDA YAPILAN ARAŞTIRMALARA YÖNELİK BİR İÇERİK ANALİZİ ÇALIŞMASI İÇERİK Biyoloji Eğitimi ŞEYDA GÜL Atatürk Üniversitesi K.K. Eğitim Fak. Biyoloji Eği t i m i MUSTAFA
24.3.215 TÜRKİYE DE BİYOLOJİ EĞİTİMİ ALANINDA YAPILAN ARAŞTIRMALARA YÖNELİK BİR İÇERİK ANALİZİ ÇALIŞMASI İÇERİK Biyoloji Eğitimi ŞEYDA GÜL Atatürk Üniversitesi K.K. Eğitim Fak. Biyoloji Eği t i m i MUSTAFA
İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ PROGRAMI
 Program Tanımları İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ PROGRAMI Kuruluş: İlköğretim Matematik Öğretmenliği Programı 2013 yılından itibaren öğrenci almaya başlamıştır ve henüz mezun vermemiştir. Amaç: İlköğretim
Program Tanımları İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ PROGRAMI Kuruluş: İlköğretim Matematik Öğretmenliği Programı 2013 yılından itibaren öğrenci almaya başlamıştır ve henüz mezun vermemiştir. Amaç: İlköğretim
FEN BİLGİSİ ÖĞRETMENLERİNİN YENİ FEN BİLGİSİ PROGRAMINA YÖNELİK DÜŞÜNCELERİ
 FEN BİLGİSİ ÖĞRETMENLERİNİN YENİ FEN BİLGİSİ PROGRAMINA YÖNELİK DÜŞÜNCELERİ Ayşe SAVRAN 1, Jale ÇAKIROĞLU 2, Özlem ÖZKAN 2 1 Pamukkale Üniversitesi, Eğitim Fakültesi, İlköğretim Bölümü, Fen Bil. ABD, DENİZLİ
FEN BİLGİSİ ÖĞRETMENLERİNİN YENİ FEN BİLGİSİ PROGRAMINA YÖNELİK DÜŞÜNCELERİ Ayşe SAVRAN 1, Jale ÇAKIROĞLU 2, Özlem ÖZKAN 2 1 Pamukkale Üniversitesi, Eğitim Fakültesi, İlköğretim Bölümü, Fen Bil. ABD, DENİZLİ
Öğrenim Durumu: Derece Bölüm/Program/Alan Üniversite Bitirme Yılı Lisans Fizik / Fen Edebiyat / Fizik Dicle Üniversitesi 2004
 ÖZGEÇMİŞ ve ESERLER LİSTESİ Genel Bilgiler: Adı Soyadı : Cihat DEMİR Doğum Yeri ve Tarihi : Diyarbakır - 14 Haziran 1982 Yazışma Adresi : Dicle Üniversitesi Ziya Gökalp Eğitim Fakültesi İlköğretim Bölümü
ÖZGEÇMİŞ ve ESERLER LİSTESİ Genel Bilgiler: Adı Soyadı : Cihat DEMİR Doğum Yeri ve Tarihi : Diyarbakır - 14 Haziran 1982 Yazışma Adresi : Dicle Üniversitesi Ziya Gökalp Eğitim Fakültesi İlköğretim Bölümü
Öğrenim Kazanımları Bu programı başarı ile tamamlayan öğrenci;
 Image not found http://bologna.konya.edu.tr/panel/images/pdflogo.png Ders Adı : ANALİZ I Ders No : 0310250035 : 4 Pratik : 2 Kredi : 5 ECTS : 8 Ders Bilgileri Ders Türü Öğretim Dili Öğretim Tipi Zorunlu
Image not found http://bologna.konya.edu.tr/panel/images/pdflogo.png Ders Adı : ANALİZ I Ders No : 0310250035 : 4 Pratik : 2 Kredi : 5 ECTS : 8 Ders Bilgileri Ders Türü Öğretim Dili Öğretim Tipi Zorunlu
TAM SAYILARLA ĠLGĠLĠ ĠġLEMLERDE ĠLKÖĞRETĠM DÜZEYĠNDE YAPILAN HATALAR VE KARġILAġILAN ZORLUKLAR
 1648 TAM SAYILARLA ĠLGĠLĠ ĠġLEMLERDE ĠLKÖĞRETĠM DÜZEYĠNDE YAPILAN HATALAR VE KARġILAġILAN ZORLUKLAR Özet. Tevfik AVCU, Eskişehir Osmangazi Üniversitesi, Eğitim Bilimleri Enstitüsü, tavcu@ogu.edu.tr Burcu
1648 TAM SAYILARLA ĠLGĠLĠ ĠġLEMLERDE ĠLKÖĞRETĠM DÜZEYĠNDE YAPILAN HATALAR VE KARġILAġILAN ZORLUKLAR Özet. Tevfik AVCU, Eskişehir Osmangazi Üniversitesi, Eğitim Bilimleri Enstitüsü, tavcu@ogu.edu.tr Burcu
Available online at
 Available online at www.sciencedirect.com Procedia - Social and Behavioral Sciences 55 ( 2012 ) 1079 1088 *English Instructor, Abant Izzet Baysal University, Golkoy Campus, 14100, Bolu, Turkey (karakis_o@ibu.edu.tr)
Available online at www.sciencedirect.com Procedia - Social and Behavioral Sciences 55 ( 2012 ) 1079 1088 *English Instructor, Abant Izzet Baysal University, Golkoy Campus, 14100, Bolu, Turkey (karakis_o@ibu.edu.tr)
MODÜLER ARİTMETİK KAVRAMI İLE İLGİLİ ÖĞRENME GÜÇLÜKLERİNİN BELİRLENMESİ *
 MODÜLER ARİTMETİK KAVRAMI İLE İLGİLİ ÖĞRENME GÜÇLÜKLERİNİN BELİRLENMESİ * Onur COŞKUN ** Gürsel GÜLER *** Ramazan DİKİCİ **** ÖZET Bu araştırmanın amacı 9. sınıf öğrencilerinin modüler aritmetik ve özellikleri
MODÜLER ARİTMETİK KAVRAMI İLE İLGİLİ ÖĞRENME GÜÇLÜKLERİNİN BELİRLENMESİ * Onur COŞKUN ** Gürsel GÜLER *** Ramazan DİKİCİ **** ÖZET Bu araştırmanın amacı 9. sınıf öğrencilerinin modüler aritmetik ve özellikleri
Sınıf Öğretmenliği Anabilim Dalı Yüksek Lisans Ders İçerikleri
 Sınıf Öğretmenliği Anabilim Dalı Yüksek Lisans Ders İçerikleri Okuma-Yazma Öğretimi Teori ve Uygulamaları ESN721 1 3 + 0 7 Okuma yazmaya hazıroluşluk, okuma yazma öğretiminde temel yaklaşımlar, diğer ülke
Sınıf Öğretmenliği Anabilim Dalı Yüksek Lisans Ders İçerikleri Okuma-Yazma Öğretimi Teori ve Uygulamaları ESN721 1 3 + 0 7 Okuma yazmaya hazıroluşluk, okuma yazma öğretiminde temel yaklaşımlar, diğer ülke
ÖZGEÇMİŞ VE ESERLER LİSTESİ - 1. Derece Bölüm/Program Üniversite Yıl Lisans Ortaöğretim Matematik Öğretmenliği
 ÖZGEÇMİŞ Adı Soyadı: Burçin GÖKKURT Doğum Tarihi: 01.06.1984 Öğrenim Durumu: Doktora ÖZGEÇMİŞ VE ESERLER LİSTESİ - 1 Derece Bölüm/Program Üniversite Yıl Lisans Ortaöğretim Matematik Öğretmenliği Karadeniz
ÖZGEÇMİŞ Adı Soyadı: Burçin GÖKKURT Doğum Tarihi: 01.06.1984 Öğrenim Durumu: Doktora ÖZGEÇMİŞ VE ESERLER LİSTESİ - 1 Derece Bölüm/Program Üniversite Yıl Lisans Ortaöğretim Matematik Öğretmenliği Karadeniz
Matematiksel Analiz (MATH101T) Ders Detayları
 Matematiksel Analiz (MATH101T) Ders Detayları Ders Adı Matematiksel Analiz Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati MATH101T Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Dersin Dili
Matematiksel Analiz (MATH101T) Ders Detayları Ders Adı Matematiksel Analiz Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati MATH101T Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Dersin Dili
Matematik Eğitimi ABD. Mesleki Deneyim: Indiana University, School of Education, Curriculum and
 Adı soyadı Belma Türker Biber Lisans Y. Lisans Ankara Üniversitesi, Fen Fakültesi, Matematik Bölümü. Ankara Üniversitesi, Fen Bilimleri Enstitüsü, Matematik ABD. Hacettepe Üniversitesi, Eğitim Bilimleri
Adı soyadı Belma Türker Biber Lisans Y. Lisans Ankara Üniversitesi, Fen Fakültesi, Matematik Bölümü. Ankara Üniversitesi, Fen Bilimleri Enstitüsü, Matematik ABD. Hacettepe Üniversitesi, Eğitim Bilimleri
ÖZGEÇMİŞ VE ESERLER LİSTESİ
 ÖZGEÇMİŞ VE ESERLER LİSTESİ ÖZGEÇMİŞ Adı Soyadı: Hüseyin KÜÇÜKÖZER Doğum Tarihi: 23 Ekim 1971 Öğrenim Durumu: Derece Bölüm/Program Üniversite Yıl Lisans OFMAE / Fizik Eğitimi Balıkesir Üniversitesi 1995
ÖZGEÇMİŞ VE ESERLER LİSTESİ ÖZGEÇMİŞ Adı Soyadı: Hüseyin KÜÇÜKÖZER Doğum Tarihi: 23 Ekim 1971 Öğrenim Durumu: Derece Bölüm/Program Üniversite Yıl Lisans OFMAE / Fizik Eğitimi Balıkesir Üniversitesi 1995
Adi Diferansiyel Denklemler Teorisine Giriş (MATH360) Ders Detayları
 Adi Diferansiyel Denklemler Teorisine Giriş (MATH360) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati Adi Diferansiyel Denklemler Teorisine Giriş MATH360
Adi Diferansiyel Denklemler Teorisine Giriş (MATH360) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati Adi Diferansiyel Denklemler Teorisine Giriş MATH360
ÖĞRETMEN ADAYLARININ PROBLEM ÇÖZME BECERİLERİ
 ÖĞRETMEN ADAYLARININ PROBLEM ÇÖZME BECERİLERİ Doç. Dr. Deniz Beste Çevik Balıkesir Üniversitesi Necatibey Eğitim Fakültesi Güzel Sanatlar Eğitimi Bölümü Müzik Eğitimi Anabilim Dalı beste@balikesir.edu.tr
ÖĞRETMEN ADAYLARININ PROBLEM ÇÖZME BECERİLERİ Doç. Dr. Deniz Beste Çevik Balıkesir Üniversitesi Necatibey Eğitim Fakültesi Güzel Sanatlar Eğitimi Bölümü Müzik Eğitimi Anabilim Dalı beste@balikesir.edu.tr
MATEMATİK BÖLÜMÜ BÖLÜM KODU:3201
 BÖLÜM KODU:01 011-01 01.Yarıyıl Dersleri 0.Yarıyıl Dersleri MTK 101 Analiz I Analysis I 4 1 5 6 MTK 10 Analiz II Analysis II 4 1 5 6 MTK 11 Lineer Cebir I Linear Algebra I 1 4 MTK 1 Lineer Cebir II Linear
BÖLÜM KODU:01 011-01 01.Yarıyıl Dersleri 0.Yarıyıl Dersleri MTK 101 Analiz I Analysis I 4 1 5 6 MTK 10 Analiz II Analysis II 4 1 5 6 MTK 11 Lineer Cebir I Linear Algebra I 1 4 MTK 1 Lineer Cebir II Linear
1. GİRİŞ Yapısalcı (constructivism) yaklaşım, bilginin öğrenme sürecinde öğrenciler tarafından yeniden yapılandırılmasıdır. Biz bilginin yapısını
 uygulanmıştır. Ayrıca her iki gruptan 6 şar öğrenci ile görüşme yapılmıştır. Elde edilen veriler istatistiksel yöntemlerle değerlendirilerek deneme ve kontrol grupları arasında anlamlı farklar olup olmadığı
uygulanmıştır. Ayrıca her iki gruptan 6 şar öğrenci ile görüşme yapılmıştır. Elde edilen veriler istatistiksel yöntemlerle değerlendirilerek deneme ve kontrol grupları arasında anlamlı farklar olup olmadığı
BEZCİ-BİRCAN, FİLİZ EĞİTİM DURUMU:
 BEZCİ-BİRCAN, FİLİZ E-mail: filizbezci@gmail.com Tel: 0376 218 95 50-7513 Adres: Uluyazı Kampüsü Çankırı Karatekin Üniversitesi Edebiyat Fakültesi Oda No:227 EĞİTİM DURUMU: 2013 Devam Yüksek Lisans (Tez
BEZCİ-BİRCAN, FİLİZ E-mail: filizbezci@gmail.com Tel: 0376 218 95 50-7513 Adres: Uluyazı Kampüsü Çankırı Karatekin Üniversitesi Edebiyat Fakültesi Oda No:227 EĞİTİM DURUMU: 2013 Devam Yüksek Lisans (Tez
Uygulamalı Matematik (MATH 463) Ders Detayları
 Uygulamalı Matematik (MATH 463) Ders Detayları Ders Adı Uygulamalı Matematik Ders Kodu MATH 463 Dönemi Ders Uygulama Saati Saati Laboratuar Saati Kredi AKTS Güz 4 0 0 4 8 Ön Koşul Ders(ler)i Math 262 Adi
Uygulamalı Matematik (MATH 463) Ders Detayları Ders Adı Uygulamalı Matematik Ders Kodu MATH 463 Dönemi Ders Uygulama Saati Saati Laboratuar Saati Kredi AKTS Güz 4 0 0 4 8 Ön Koşul Ders(ler)i Math 262 Adi
Matematik Başarısında Dünya Ülkeleri İçerisinde Türkiye nin Konumu: TIMSS * Verileri
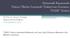 Matematik Başarısında Dünya Ülkeleri İçerisinde Türkiye nin Konumu: TIMSS * Verileri Yrd. Doç. Dr. Nuray Ç. Dedeoğlu İlköğretim Matematik Eğitimi ndedeoglu@sakarya.edu.tr *TIMSS-Trends in International
Matematik Başarısında Dünya Ülkeleri İçerisinde Türkiye nin Konumu: TIMSS * Verileri Yrd. Doç. Dr. Nuray Ç. Dedeoğlu İlköğretim Matematik Eğitimi ndedeoglu@sakarya.edu.tr *TIMSS-Trends in International
MATEMATİĞİN DOĞASI, YAPISI VE İŞLEVİ
 İÇİNDEKİLER Önsöz.III Bölüm I: MATEMATİĞİN DOĞASI, YAPISI VE İŞLEVİ 11 1.1. Matematiğin Tanımına Çeşitli Yaklaşımlar 12 1.2.Matematik Öğrenmenin Amaçları 13 1.3.Matematik ile Diğer Öğrenme Alanlarının
İÇİNDEKİLER Önsöz.III Bölüm I: MATEMATİĞİN DOĞASI, YAPISI VE İŞLEVİ 11 1.1. Matematiğin Tanımına Çeşitli Yaklaşımlar 12 1.2.Matematik Öğrenmenin Amaçları 13 1.3.Matematik ile Diğer Öğrenme Alanlarının
ÖZEL EGE LİSESİ EGE BÖLGESİ OKULLAR ARASI MATEMATİK YARIŞMASI 1.AŞAMA KONU KAPSAMI
 ÖZEL EGE LİSESİ EGE BÖLGESİ OKULLAR ARASI MATEMATİK YARIŞMASI 1.AŞAMA KONU KAPSAMI 6. SINIF 5. SINIF TÜM KONULARI 1.ÜNİTE: Geometrik Şekiller 1) Verileri Düzenleme, Çokgenler ve Süsleme 2) Dörtgenler 3)
ÖZEL EGE LİSESİ EGE BÖLGESİ OKULLAR ARASI MATEMATİK YARIŞMASI 1.AŞAMA KONU KAPSAMI 6. SINIF 5. SINIF TÜM KONULARI 1.ÜNİTE: Geometrik Şekiller 1) Verileri Düzenleme, Çokgenler ve Süsleme 2) Dörtgenler 3)
ÖZGEÇMİŞ VE ESERLER LİSTESİ
 ÖZGEÇMİŞ VE ESERLER LİSTESİ Adı Soyadı: Doç. Dr. Cavide DEMİRCİ Öğrenim Durumu: Derece Bölüm/Program Üniversite Yıl Lisans Eğitim Fakültesi Almanca Biyoloji Hacettepe Üniversitesi 1993 Öğretmenliği Y.
ÖZGEÇMİŞ VE ESERLER LİSTESİ Adı Soyadı: Doç. Dr. Cavide DEMİRCİ Öğrenim Durumu: Derece Bölüm/Program Üniversite Yıl Lisans Eğitim Fakültesi Almanca Biyoloji Hacettepe Üniversitesi 1993 Öğretmenliği Y.
İşletme ve Ekonomi Öğrencileri için Matematik (MATH102T) Ders Detayları
 İşletme ve Ekonomi Öğrencileri için Matematik (MATH102T) Ders Detayları Ders Adı İşletme ve Ekonomi Öğrencileri için Matematik Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati MATH102T
İşletme ve Ekonomi Öğrencileri için Matematik (MATH102T) Ders Detayları Ders Adı İşletme ve Ekonomi Öğrencileri için Matematik Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati MATH102T
ÖĞRETMEN ADAYLARININ MESLEK BİLGİSİ DERSLERİ ÜZERİNE BAKIŞ AÇILARI
 ÖĞRETMEN ADAYLARININ MESLEK BİLGİSİ DERSLERİ ÜZERİNE BAKIŞ AÇILARI Çiğdem ŞAHİN TAŞKIN* Güney HACIÖMEROĞLU** *Yrd. Doç. Dr., Çanakkale Onsekiz Mart Üniversitesi, Eğitim Fakültesi, İlköğretim Bölümü **
ÖĞRETMEN ADAYLARININ MESLEK BİLGİSİ DERSLERİ ÜZERİNE BAKIŞ AÇILARI Çiğdem ŞAHİN TAŞKIN* Güney HACIÖMEROĞLU** *Yrd. Doç. Dr., Çanakkale Onsekiz Mart Üniversitesi, Eğitim Fakültesi, İlköğretim Bölümü **
ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ ÖZEL EĞİTİM ANABİLİM DALI
 ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ ÖZEL EĞİTİM ANABİLİM DALI EĞİTİMDE BÜTÜNLEŞTİRME UYGULAMALARI TEZSİZ II. ÖĞRETİM YÜKSEK LİSANS PROGRAMINA İLİŞKİN BİLGİLER Özel gereksinimli
ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ ÖZEL EĞİTİM ANABİLİM DALI EĞİTİMDE BÜTÜNLEŞTİRME UYGULAMALARI TEZSİZ II. ÖĞRETİM YÜKSEK LİSANS PROGRAMINA İLİŞKİN BİLGİLER Özel gereksinimli
Yrd. Doç. Dr. Celal Deha DOĞAN. Ankara Üniversitesi Eğitim Bilimleri Enstitüsü Ölçme ve Değerlendirme Bilim Dalı- Doktora
 Yrd. Doç. Dr. Celal Deha DOĞAN Öğrenim Durumu Ankara Üniversitesi Eğitim Bilimleri Enstitüsü Ölçme ve Değerlendirme Bilim Dalı- Doktora- 2005-2011 Ankara Üniversitesi Eğitim Bilimleri Enstitüsü Ölçme ve
Yrd. Doç. Dr. Celal Deha DOĞAN Öğrenim Durumu Ankara Üniversitesi Eğitim Bilimleri Enstitüsü Ölçme ve Değerlendirme Bilim Dalı- Doktora- 2005-2011 Ankara Üniversitesi Eğitim Bilimleri Enstitüsü Ölçme ve
ERRORS OF PROSPECTIVE MIDDLE SCHOOL MATHEMATICS TEACHERS IN PROBLEMS USİNG ELEMENTARY ROW OPERATIONS IN LINEAR ALGEBRA COURSE
 Article History Received / Geliş Accepted / Kabul Available Online / Yayınlanma 24.02.2017 14.03.2017 25.03.2017 ERRORS OF PROSPECTIVE MIDDLE SCHOOL MATHEMATICS TEACHERS IN PROBLEMS USİNG ELEMENTARY ROW
Article History Received / Geliş Accepted / Kabul Available Online / Yayınlanma 24.02.2017 14.03.2017 25.03.2017 ERRORS OF PROSPECTIVE MIDDLE SCHOOL MATHEMATICS TEACHERS IN PROBLEMS USİNG ELEMENTARY ROW
ÖZEL ÖĞRETİM KURSU MATEMATİK-I ÇERÇEVE PROGRAMI. :Kesikkapı Mah. Atatürk Cad.No.79 Fethiye /MUĞLA
 ÖZEL ÖĞRETİM KURSU MATEMATİK-I ÇERÇEVE PROGRAMI 1.KURUMUN ADI 2.KURUMUN ADRESİ 3.KURUCUNUN ADI :Tercih Özel Öğretim Kursu :Kesikkapı Mah. Atatürk Cad.No.79 Fethiye /MUĞLA : ARTI ÖZEL EĞİTİM ÖĞRETİM Danışmanlık
ÖZEL ÖĞRETİM KURSU MATEMATİK-I ÇERÇEVE PROGRAMI 1.KURUMUN ADI 2.KURUMUN ADRESİ 3.KURUCUNUN ADI :Tercih Özel Öğretim Kursu :Kesikkapı Mah. Atatürk Cad.No.79 Fethiye /MUĞLA : ARTI ÖZEL EĞİTİM ÖĞRETİM Danışmanlık
ÖZEL ÖĞRETİM KURSU MATEMATİK-IV ÇERÇEVE PROGRAMI. 2. KURUMUN ADRESİ : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA
 ÖZEL ÖĞRETİM KURSU MATEMATİK-IV ÇERÇEVE PROGRAMI 1. KURUMUN ADI : Tercih Özel Öğretim Kursu 2. KURUMUN ADRESİ : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA 3. KURUCUNUN ADI : ARTI ÖZEL EĞİTİM ÖĞRETİM
ÖZEL ÖĞRETİM KURSU MATEMATİK-IV ÇERÇEVE PROGRAMI 1. KURUMUN ADI : Tercih Özel Öğretim Kursu 2. KURUMUN ADRESİ : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA 3. KURUCUNUN ADI : ARTI ÖZEL EĞİTİM ÖĞRETİM
Murat ALTUN Tel: +90 (224) 294 21 57 e-mail: maltun@uludag.edu.tr
 Murat ALTUN Tel: +90 (224) 294 21 57 e-mail: maltun@uludag.edu.tr Adı Soyadı : Murat Altun Doğum Yeri ve Tarihi : Şavşat 26.03.1952 EĞİTİM Doktora, Hacettepe Üniversitesi Sosyal Bilimler Enstitüsü (1995)
Murat ALTUN Tel: +90 (224) 294 21 57 e-mail: maltun@uludag.edu.tr Adı Soyadı : Murat Altun Doğum Yeri ve Tarihi : Şavşat 26.03.1952 EĞİTİM Doktora, Hacettepe Üniversitesi Sosyal Bilimler Enstitüsü (1995)
Aygil TAKIR ÖZGEÇMİŞ
 Aygil TAKIR ÖZGEÇMİŞ Adı-Soyadı: Aygil TAKIR Doğum Tarihi: 07.10.1978 Doğum Yeri: Magosa-KKTC Medeni Durumu: Evli Uyruğu: TC-KKTC KİŞİSEL BİLGİLER EĞİTİM 2005-2011, Doktora, Orta Doğu Teknik Üniversitesi,
Aygil TAKIR ÖZGEÇMİŞ Adı-Soyadı: Aygil TAKIR Doğum Tarihi: 07.10.1978 Doğum Yeri: Magosa-KKTC Medeni Durumu: Evli Uyruğu: TC-KKTC KİŞİSEL BİLGİLER EĞİTİM 2005-2011, Doktora, Orta Doğu Teknik Üniversitesi,
Gönül GÜNEŞ Osman BİRGİN Ramazan GÜRBÜZ. Derya ÇELİK Serhat AYDIN Duygu TAŞKIN Kadir GÜRSOY. Gökay AÇIKYILDIZ Zeynep Medine ÖZMEN Mustafa GÜLER
 İlköğretim Matematik Öğretmeni Adaylarına Üniversitelerde Sunulan Öğrenme Fırsatlarının Öğretmen Adaylarının Görüşleri Bağlamında İncelenmesi: Türkiye Örneği Derya ÇELİK Serhat AYDIN Duygu TAŞKIN Kadir
İlköğretim Matematik Öğretmeni Adaylarına Üniversitelerde Sunulan Öğrenme Fırsatlarının Öğretmen Adaylarının Görüşleri Bağlamında İncelenmesi: Türkiye Örneği Derya ÇELİK Serhat AYDIN Duygu TAŞKIN Kadir
ÖZGEÇMİŞ VE ESERLER LİSTESİ
 ÖZGEÇMİŞ VE ESERLER LİSTESİ ÖZGEÇMİŞ Adı Soyadı Adres : Melihan ÜNLÜ : Aksaray Üniversitesi, Eğitim Fakültesi, Matematik ve Fen Bilimleri Bölümü Telefon : 03822883375 E-posta : melihanunlu@yahoo.com 1.
ÖZGEÇMİŞ VE ESERLER LİSTESİ ÖZGEÇMİŞ Adı Soyadı Adres : Melihan ÜNLÜ : Aksaray Üniversitesi, Eğitim Fakültesi, Matematik ve Fen Bilimleri Bölümü Telefon : 03822883375 E-posta : melihanunlu@yahoo.com 1.
Doç.Dr. HİLAL AKTAMIŞ
 Doç.Dr. HİLAL AKTAMIŞ Eğitim Fakültesi Matematik Ve Eğitim Bilgileri 1994-1998 Lisans-Yandal Buca Eğitim Fakültesi Matematik Ve Fen Dokuz Eylül ÜniversitesiBilimleri Eğitimi Bölümü Fizik Öğretmenliği Pr.
Doç.Dr. HİLAL AKTAMIŞ Eğitim Fakültesi Matematik Ve Eğitim Bilgileri 1994-1998 Lisans-Yandal Buca Eğitim Fakültesi Matematik Ve Fen Dokuz Eylül ÜniversitesiBilimleri Eğitimi Bölümü Fizik Öğretmenliği Pr.
BİYOLOJİ ÖĞRETMENLERİNİN LABORATUVAR DERSİNE YÖNELİK TUTUMLARININ FARKLI DEĞİŞKENLER AÇISINDAN İNCELENMESİ
 BİYOLOJİ ÖĞRETMENLERİNİN LABORATUVAR DERSİNE YÖNELİK TUTUMLARININ FARKLI DEĞİŞKENLER AÇISINDAN İNCELENMESİ Gülay EKİCİ Gazi Üniversitesi, Teknik Eğitim Fakültesi, Eğitim Bilimleri Bölümü, ANKARA Özet Bu
BİYOLOJİ ÖĞRETMENLERİNİN LABORATUVAR DERSİNE YÖNELİK TUTUMLARININ FARKLI DEĞİŞKENLER AÇISINDAN İNCELENMESİ Gülay EKİCİ Gazi Üniversitesi, Teknik Eğitim Fakültesi, Eğitim Bilimleri Bölümü, ANKARA Özet Bu
Dersi Alan Dersi Veren Dersin Optik Kod Dersin Adı Saat Öğr. Grubu Öğretim Üyesi Yeri
 T. C. E. Ü. FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ 2015-2016 Öğretim Yılı Güz Dönemi Haftalık Ders Programı İkinci Öğretim A. Fakülte İçinde "BÖLÜMÜMÜZ" Öğrencilerine Verdiğimiz Dersler I. YARIYIL 1104001062003
T. C. E. Ü. FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ 2015-2016 Öğretim Yılı Güz Dönemi Haftalık Ders Programı İkinci Öğretim A. Fakülte İçinde "BÖLÜMÜMÜZ" Öğrencilerine Verdiğimiz Dersler I. YARIYIL 1104001062003
ORTAÖĞRETİM MATEMATİK ÖĞRETMENİ ÖZEL ALAN YETERLİKLERİ MİLLİ EĞİTİM BAKANLIĞI ÖĞRETMEN YETİŞTİRME VE EĞİTİMİ GENEL MÜDÜRLÜĞÜ ORTA ÖĞRETİM PROJESİ
 MİLLİ EĞİTİM BAKANLIĞI ÖĞRETMEN YETİŞTİRME VE EĞİTİMİ GENEL MÜDÜRLÜĞÜ ORTA ÖĞRETİM PROJESİ MATEMATİK ÖĞRETMENİ ÖZEL ALAN İ Doç.Dr. Cengiz ALACACI Yrd. Doç. Dr. Ayhan Kürşat ERBAŞ Yrd. Doç.Dr. Bülent ÇETİNKAYA
MİLLİ EĞİTİM BAKANLIĞI ÖĞRETMEN YETİŞTİRME VE EĞİTİMİ GENEL MÜDÜRLÜĞÜ ORTA ÖĞRETİM PROJESİ MATEMATİK ÖĞRETMENİ ÖZEL ALAN İ Doç.Dr. Cengiz ALACACI Yrd. Doç. Dr. Ayhan Kürşat ERBAŞ Yrd. Doç.Dr. Bülent ÇETİNKAYA
KAHRAMANMARAŞ SÜTÇÜ İMAM ÜNİVERSİTESİ EĞİTİM ÖĞRETİM YILI FEN-EDEBİYAT FAKÜLTESİ MATEMATİK BÖLÜMÜ BİRİNCİ VE İKİNCİ ÖĞRETİM DERSLERİ
 I. YARIYIL Adı Teori Uygulama KSU MT101 Analiz I 6 4 2 5 7 MT107 Soyut Matematik I 4 4 0 4 5 MT109 Analitik Geometri I 4 4 0 4 5 FZ173 Fizik I 4 4 0 4 4 OZ101 Türk Dili I 2 2 0 2 2 OZ121 Ingilizce I 2
I. YARIYIL Adı Teori Uygulama KSU MT101 Analiz I 6 4 2 5 7 MT107 Soyut Matematik I 4 4 0 4 5 MT109 Analitik Geometri I 4 4 0 4 5 FZ173 Fizik I 4 4 0 4 4 OZ101 Türk Dili I 2 2 0 2 2 OZ121 Ingilizce I 2
Ortaokul Sınıflar Matematik Dersi Öğretim Programı*: Kazandırılması Öngörülen Temel Beceriler
 Ortaokul 5.- 8. Sınıflar Matematik Dersi Öğretim Programı*: Kazandırılması Öngörülen Temel Beceriler Yrd. Doç. Dr. Nuray Ç. Dedeoğlu İlköğretim Matematik Eğitimi * MEB (2013). Ortaokul matematik dersi
Ortaokul 5.- 8. Sınıflar Matematik Dersi Öğretim Programı*: Kazandırılması Öngörülen Temel Beceriler Yrd. Doç. Dr. Nuray Ç. Dedeoğlu İlköğretim Matematik Eğitimi * MEB (2013). Ortaokul matematik dersi
Ortaöğretim Matematik Müfredatında Zor Olarak Algılanan Konular ve Bunların Nedenleri 1
 Gaziantep Üniversitesi Sosyal Bilimler Dergisi (http://sbe.gantep.edu.tr) 2011 10(4):1311-1323 ISSN: 1303-0094 Ortaöğretim Matematik Müfredatında Zor Olarak Algılanan Konular ve Bunların Nedenleri 1 Subjects
Gaziantep Üniversitesi Sosyal Bilimler Dergisi (http://sbe.gantep.edu.tr) 2011 10(4):1311-1323 ISSN: 1303-0094 Ortaöğretim Matematik Müfredatında Zor Olarak Algılanan Konular ve Bunların Nedenleri 1 Subjects
Muhammet Demirbilek, PhD
 Muhammet Demirbilek, PhD İlk olarak 1995 yılında Bernie Dodge ve Tom March tarafından San Diego State Üniversitesi nde Eğitim Teknolojileri Bölümü nde geliştirilmiştir. Bernie DODGE Webquest Öğrencilerin
Muhammet Demirbilek, PhD İlk olarak 1995 yılında Bernie Dodge ve Tom March tarafından San Diego State Üniversitesi nde Eğitim Teknolojileri Bölümü nde geliştirilmiştir. Bernie DODGE Webquest Öğrencilerin
Matematiksel Analiz III (MATH 235) Ders Detayları
 Matematiksel Analiz III (MATH 235) Ders Detayları Ders Adı Matematiksel Analiz III Ders Kodu MATH 235 Dönemi Ders Uygulama Saati Saati Laboratuar Kredi AKTS Saati Güz 4 2 0 5 8 Ön Koşul Ders(ler)i Math
Matematiksel Analiz III (MATH 235) Ders Detayları Ders Adı Matematiksel Analiz III Ders Kodu MATH 235 Dönemi Ders Uygulama Saati Saati Laboratuar Kredi AKTS Saati Güz 4 2 0 5 8 Ön Koşul Ders(ler)i Math
KIMYA BÖLÜMÜ ÖĞRENCİLERİNİN ENDÜSTRİYEL KİMYAYA YÖNELİK TUTUMLARI VE ÖZYETERLİLİK İNANÇLARI ARASINDAKİ İLİŞKİ; CELAL BAYAR ÜNİVERSİTESİ ÖRNEĞİ
 KIMYA BÖLÜMÜ ÖĞRENCİLERİNİN ENDÜSTRİYEL KİMYAYA YÖNELİK TUTUMLARI VE ÖZYETERLİLİK İNANÇLARI ARASINDAKİ İLİŞKİ; CELAL BAYAR ÜNİVERSİTESİ ÖRNEĞİ Öğr. Gör. Gülbin KIYICI Arş.Gör.Dr. Nurcan KAHRAMAN Prof.
KIMYA BÖLÜMÜ ÖĞRENCİLERİNİN ENDÜSTRİYEL KİMYAYA YÖNELİK TUTUMLARI VE ÖZYETERLİLİK İNANÇLARI ARASINDAKİ İLİŞKİ; CELAL BAYAR ÜNİVERSİTESİ ÖRNEĞİ Öğr. Gör. Gülbin KIYICI Arş.Gör.Dr. Nurcan KAHRAMAN Prof.
Matris Analizi (MATH333) Ders Detayları
 Matris Analizi (MATH333) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Matris Analizi MATH333 Her İkisi 3 0 0 3 6 Ön Koşul Ders(ler)i Math 231 Linear Algebra
Matris Analizi (MATH333) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Matris Analizi MATH333 Her İkisi 3 0 0 3 6 Ön Koşul Ders(ler)i Math 231 Linear Algebra
1. Matematik analiz ve diferansiyel denklemlerle ilgili temel kavramları öğrenecektir.
 BÖLÜM EKONOMETRİ Amaç:Türev ve integralin uygulamaları ile diferansiyel denklemlerin çözüm tekniklerini öğretmek bu dersin başlıca amacıdır. Çok sayıda örnek problem çözümleriyle bu teknikler öğrenciye
BÖLÜM EKONOMETRİ Amaç:Türev ve integralin uygulamaları ile diferansiyel denklemlerin çözüm tekniklerini öğretmek bu dersin başlıca amacıdır. Çok sayıda örnek problem çözümleriyle bu teknikler öğrenciye
DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS BİLİMSEL ARAŞTIRMA YÖNTEMLERİ GK- 373 V Ön Koşul. Yok
 DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS BİLİMSEL ARAŞTIRMA YÖNTEMLERİ GK- 373 V. 2+0 2 4 Ön Koşul Yok Dersin Dili Dersin Seviyesi Dersin Türü Dersi Veren Öğretim Elemanı Dersin Yardımcıları
DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS BİLİMSEL ARAŞTIRMA YÖNTEMLERİ GK- 373 V. 2+0 2 4 Ön Koşul Yok Dersin Dili Dersin Seviyesi Dersin Türü Dersi Veren Öğretim Elemanı Dersin Yardımcıları
GAZİ ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ/BİYOLOJİ EĞİTİMİ (DR)
 YAKUP DOĞAN YARDIMCI DOÇENT E-Posta Adresi yakupdogan06@gmail.com Telefon (İş) Telefon (Cep) Faks Adres 3488142662-1713 3488142663 KİLİS 7 ARALIK ÜNİVERSİTESİ/MUALLİM RIFAT EĞİTİM FAKÜLTESİ Mehmet Sanlı
YAKUP DOĞAN YARDIMCI DOÇENT E-Posta Adresi yakupdogan06@gmail.com Telefon (İş) Telefon (Cep) Faks Adres 3488142662-1713 3488142663 KİLİS 7 ARALIK ÜNİVERSİTESİ/MUALLİM RIFAT EĞİTİM FAKÜLTESİ Mehmet Sanlı
Adi Diferansiyel Denklemler (MATH 262) Ders Detayları
 Adi Diferansiyel Denklemler (MATH 262) Ders Detayları Ders Adı Adi Diferansiyel Denklemler Ders Kodu MATH 262 Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Bahar 4 0 0 4 6 Ön Koşul Ders(ler)i
Adi Diferansiyel Denklemler (MATH 262) Ders Detayları Ders Adı Adi Diferansiyel Denklemler Ders Kodu MATH 262 Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Bahar 4 0 0 4 6 Ön Koşul Ders(ler)i
Yrd.Doç.Dr. AYŞE ELİTOK KESİCİ
 Yrd.Doç.Dr. AYŞE ELİTOK KESİCİ Eğitim Fakültesi Eğitim Bilimleri Bölümü Eğitim Programları Ve Öğretim Anabilim Dalı Eğitim Bilgileri 1991-1996 Lisans Dokuz Eylül Üniversitesi Buca Eğitim Fakültesi Eğitim
Yrd.Doç.Dr. AYŞE ELİTOK KESİCİ Eğitim Fakültesi Eğitim Bilimleri Bölümü Eğitim Programları Ve Öğretim Anabilim Dalı Eğitim Bilgileri 1991-1996 Lisans Dokuz Eylül Üniversitesi Buca Eğitim Fakültesi Eğitim
Arş. Gör. Dr. Mücahit KÖSE
 Arş. Gör. Dr. Mücahit KÖSE Dumlupınar Üniversitesi Eğitim Fakültesi İlköğretim Bölümü Evliya Çelebi Yerleşkesi (3100) KÜTAHYA Doğum Yeri ve Yılı: Isparta/Yalvaç Cep Telefonu: Telefon:765031-58 E-posta:
Arş. Gör. Dr. Mücahit KÖSE Dumlupınar Üniversitesi Eğitim Fakültesi İlköğretim Bölümü Evliya Çelebi Yerleşkesi (3100) KÜTAHYA Doğum Yeri ve Yılı: Isparta/Yalvaç Cep Telefonu: Telefon:765031-58 E-posta:
ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ
 ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ Güven SAĞDIÇ Dokuz Eylül Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik
ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ Güven SAĞDIÇ Dokuz Eylül Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik
YÜKSEKÖĞRETİM KURULU YARDIMCI DOÇENT 17.12.2014
 AYHAN KARAMAN ÖZGEÇMİŞ YÜKSEKÖĞRETİM KURULU YARDIMCI DOÇENT 17.12.2014 Adres : Sinop Üniversitesi Eğitim Fakültesi İlköğretim Bölümü 57000 SİNOP Telefon : 3682715526-2079 E-posta : akaraman@sinop.edu.tr
AYHAN KARAMAN ÖZGEÇMİŞ YÜKSEKÖĞRETİM KURULU YARDIMCI DOÇENT 17.12.2014 Adres : Sinop Üniversitesi Eğitim Fakültesi İlköğretim Bölümü 57000 SİNOP Telefon : 3682715526-2079 E-posta : akaraman@sinop.edu.tr
ĠLKÖĞRETĠM II. KADEME MATEMATĠK ÖĞRETĠM PROGRAMININ OLASILIK VE ĠSTATĠSTĠK ALT ÖĞRENME ALANININ ĠSTATĠSTĠK BOYUTUNUN ĠNCELENMESĠ
 ĠLKÖĞRETĠM II. KADEME MATEMATĠK ÖĞRETĠM PROGRAMININ OLASILIK VE ĠSTATĠSTĠK ALT ÖĞRENME ALANININ ĠSTATĠSTĠK BOYUTUNUN ĠNCELENMESĠ Yunus KAYNAR 1 Erdoğan HALAT 2 1 Akdoğan ilköğretim okulu, Kızılcahamam
ĠLKÖĞRETĠM II. KADEME MATEMATĠK ÖĞRETĠM PROGRAMININ OLASILIK VE ĠSTATĠSTĠK ALT ÖĞRENME ALANININ ĠSTATĠSTĠK BOYUTUNUN ĠNCELENMESĠ Yunus KAYNAR 1 Erdoğan HALAT 2 1 Akdoğan ilköğretim okulu, Kızılcahamam
İÇİNDEKİLER BÖLÜM III: HAYAT BİLGİSİ VE SOSYAL BİLGİLER
 Önsöz İÇİNDEKİLER BÖLÜM I: HAYAT BİLGİSİ VE SOSYAL BİLGİLER ÖĞRETİMİNİN TANIMI, ÖNEMİ VE ÖZELLİKLERİ 11 Giriş 12 Hayat ve Sosyal Bilgilerin Tanımı 13 Sosyal Bilimler ile Sosyal Bilgiler Farkı 13 Demokratik
Önsöz İÇİNDEKİLER BÖLÜM I: HAYAT BİLGİSİ VE SOSYAL BİLGİLER ÖĞRETİMİNİN TANIMI, ÖNEMİ VE ÖZELLİKLERİ 11 Giriş 12 Hayat ve Sosyal Bilgilerin Tanımı 13 Sosyal Bilimler ile Sosyal Bilgiler Farkı 13 Demokratik
International Journal of Progressive Education, 6(2), 27-47.
 ÖZGEÇMİŞ VE ESERLER LİSTESİ ÖZGEÇMİŞ Adı Soyadı: AYŞE AYPAY Doğum Tarihi: 24 02 1969 Öğrenim Durumu: Doktora Derece Bölüm/Program Üniversite Yıl Lisans Psikoloji Bölümü Ankara Üniversitesi 1989 Y. Lisans
ÖZGEÇMİŞ VE ESERLER LİSTESİ ÖZGEÇMİŞ Adı Soyadı: AYŞE AYPAY Doğum Tarihi: 24 02 1969 Öğrenim Durumu: Doktora Derece Bölüm/Program Üniversite Yıl Lisans Psikoloji Bölümü Ankara Üniversitesi 1989 Y. Lisans
KİMYA ÖĞRETMEN ADAYLARININ ÖĞRENME VE ÖĞRETME ANLAYIŞLARI İLE ÖĞRENME STİLLERİNİN YAPILANDIRMACILIK FELSEFESİ İLE OLAN UYUMU
 KİMYA ÖĞRETMEN ADAYLARININ ÖĞRENME VE ÖĞRETME ANLAYIŞLARI İLE ÖĞRENME STİLLERİNİN YAPILANDIRMACILIK FELSEFESİ İLE OLAN UYUMU Filiz KABAPINAR OYA AĞLARCI M.Ü. Atatürk Eğitim Fakültesi OFMA Eğitimi Böl.
KİMYA ÖĞRETMEN ADAYLARININ ÖĞRENME VE ÖĞRETME ANLAYIŞLARI İLE ÖĞRENME STİLLERİNİN YAPILANDIRMACILIK FELSEFESİ İLE OLAN UYUMU Filiz KABAPINAR OYA AĞLARCI M.Ü. Atatürk Eğitim Fakültesi OFMA Eğitimi Böl.
Mustafa SÖZBİLİR Şeyda GÜL Fatih YAZICI Aydın KIZILASLAN Betül OKCU S. Levent ZORLUOĞLU. efe.atauni.edu.tr
 Mustafa SÖZBİLİR Şeyda GÜL Fatih YAZICI Aydın KIZILASLAN Betül OKCU S. Levent ZORLUOĞLU efe.atauni.edu.tr Bu çalışma TÜBİTAK tarafından 114K725 nolu proje kapsamında desteklenmektedir. Araştırmaya gönüllü
Mustafa SÖZBİLİR Şeyda GÜL Fatih YAZICI Aydın KIZILASLAN Betül OKCU S. Levent ZORLUOĞLU efe.atauni.edu.tr Bu çalışma TÜBİTAK tarafından 114K725 nolu proje kapsamında desteklenmektedir. Araştırmaya gönüllü
Orhan KAYA KPSS ÖLÇME VE DEĞERLENDİRME PROGRAM GELİŞTİRME
 T A K K İ D ÖSYM nin Vazgeçemedigi Orhan KAYA KPSS ÖLÇME VE DEĞERLENDİRME PROGRAM GELİŞTİRME Soru Tipleri Güzel ülkemin güzel insanı... Eser Adı Dikkat Çıkabilir Ölçme ve Değerlendirme & Program Geliştirme
T A K K İ D ÖSYM nin Vazgeçemedigi Orhan KAYA KPSS ÖLÇME VE DEĞERLENDİRME PROGRAM GELİŞTİRME Soru Tipleri Güzel ülkemin güzel insanı... Eser Adı Dikkat Çıkabilir Ölçme ve Değerlendirme & Program Geliştirme
Matematik II (MATH 102) Ders Detayları
 Matematik II (MATH 102) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Matematik II MATH 102 Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Math 101 Matematiksel Analiz
Matematik II (MATH 102) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Matematik II MATH 102 Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Math 101 Matematiksel Analiz
Eğitim Fakülteleri ve İlköğretim Öğretmenleri için Matematik Öğretimi
 Dicle Üniversitesi Ziya Gökalp Eğitim Fakültesi Dergisi, 19 (2012) 269-273 269 KİTAP İNCELEMESİ Eğitim Fakülteleri ve İlköğretim Öğretmenleri için Matematik Öğretimi Prof. Dr. Murat ALTUN Dilek SEZGİN
Dicle Üniversitesi Ziya Gökalp Eğitim Fakültesi Dergisi, 19 (2012) 269-273 269 KİTAP İNCELEMESİ Eğitim Fakülteleri ve İlköğretim Öğretmenleri için Matematik Öğretimi Prof. Dr. Murat ALTUN Dilek SEZGİN
Matematiksel Analiz (MATH101) Ders Detayları
 Matematiksel Analiz (MATH101) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati Matematiksel Analiz MATH101 Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Yok Dersin Dili
Matematiksel Analiz (MATH101) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati Matematiksel Analiz MATH101 Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Yok Dersin Dili
Kısmi Diferansiyel Denklemler (MATH378) Ders Detayları
 Kısmi Diferansiyel Denklemler (MATH378) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati Kısmi Diferansiyel Denklemler MATH378 Bahar 3 0 0 3 6 Ön Koşul Ders(ler)i
Kısmi Diferansiyel Denklemler (MATH378) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Kredi AKTS Saati Kısmi Diferansiyel Denklemler MATH378 Bahar 3 0 0 3 6 Ön Koşul Ders(ler)i
ÖZGEÇMĐŞ. Derece Bölüm/Program Üniversite Yıl Lisans
 ÖZGEÇMĐŞ Adı Soyadı: Yeşim Özek Kaloti Doğum Tarihi: 1969 Öğrenim Durumu: Derece Bölüm/Program Üniversite Yıl Lisans Đngilizce DĐCLE ÜNĐVERSĐTESĐ 1988-1992 Öğretmenliği Y. Lisans TESOL University of Stirling
ÖZGEÇMĐŞ Adı Soyadı: Yeşim Özek Kaloti Doğum Tarihi: 1969 Öğrenim Durumu: Derece Bölüm/Program Üniversite Yıl Lisans Đngilizce DĐCLE ÜNĐVERSĐTESĐ 1988-1992 Öğretmenliği Y. Lisans TESOL University of Stirling
FEN VE TEKNOLOJİ ÖĞRETMENLERİNİN KİŞİLERARASI ÖZYETERLİK İNANÇLARININ BAZI DEĞİŞKENLER AÇISINDAN İNCELENMESİ
 FEN VE TEKNOLOJİ ÖĞRETMENLERİNİN KİŞİLERARASI ÖZYETERLİK İNANÇLARININ BAZI DEĞİŞKENLER AÇISINDAN İNCELENMESİ AN INVESTIGATION OF SCIENCE TEACHERS INTERPERSONAL SELF-EFFICACY BELIEFS IN TERMS OF SOME VARIABLES
FEN VE TEKNOLOJİ ÖĞRETMENLERİNİN KİŞİLERARASI ÖZYETERLİK İNANÇLARININ BAZI DEĞİŞKENLER AÇISINDAN İNCELENMESİ AN INVESTIGATION OF SCIENCE TEACHERS INTERPERSONAL SELF-EFFICACY BELIEFS IN TERMS OF SOME VARIABLES
Topoloji (MATH372) Ders Detayları
 Topoloji (MATH372) Ders Detayları Ders AdıDers Kodu Dönemi Ders Uygulama Saati Saati Laboratuar Saati Kredi AKTS Topoloji MATH372 Bahar 3 0 0 3 6 Ön Koşul Ders(ler)i MATH 251 Dersin Dili Dersin Türü Dersin
Topoloji (MATH372) Ders Detayları Ders AdıDers Kodu Dönemi Ders Uygulama Saati Saati Laboratuar Saati Kredi AKTS Topoloji MATH372 Bahar 3 0 0 3 6 Ön Koşul Ders(ler)i MATH 251 Dersin Dili Dersin Türü Dersin
Matematik II (MATH 102) Ders Detayları
 Matematik II (MATH 102) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Matematik II MATH 102 Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Math 101 Matematiksel Analiz
Matematik II (MATH 102) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Matematik II MATH 102 Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Math 101 Matematiksel Analiz
T. C. E. Ü. FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ. 2015-2016 Öğretim Yılı Güz Dönemi Haftalık Ders Programı
 T. C. E. Ü. FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ 2015-2016 Öğretim Yılı Güz Dönemi Haftalık Ders Programı A. Fakülte İçinde "BÖLÜMÜMÜZ" Öğrencilerine Verdiğimiz Dersler I. YARIYIL 405001072003 Soyut Matematik
T. C. E. Ü. FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ 2015-2016 Öğretim Yılı Güz Dönemi Haftalık Ders Programı A. Fakülte İçinde "BÖLÜMÜMÜZ" Öğrencilerine Verdiğimiz Dersler I. YARIYIL 405001072003 Soyut Matematik
Diferansiyel Denklemler (MATH 276) Ders Detayları
 Diferansiyel Denklemler (MATH 276) Ders Detayları Ders Adı Diferansiyel Denklemler Ders Kodu MATH 276 Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Bahar 4 0 0 4 6 Ön Koşul Ders(ler)i Math
Diferansiyel Denklemler (MATH 276) Ders Detayları Ders Adı Diferansiyel Denklemler Ders Kodu MATH 276 Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Bahar 4 0 0 4 6 Ön Koşul Ders(ler)i Math
Proje Tabanlı Öğrenme Yaklaşımını Temel Alan Çalışmaların Değerlendirilmesi: Türkiye Örneği
 8. Ulusal Eğitim Yönetimi Kongresi Proje Tabanlı Öğrenme Yaklaşımını Temel Alan Çalışmaların Değerlendirilmesi: Türkiye Örneği H. Coşkun ÇELİK a,samet GÜNDÜZ b (a) Siirt Üniversitesi, Eğitim Fakültesi,
8. Ulusal Eğitim Yönetimi Kongresi Proje Tabanlı Öğrenme Yaklaşımını Temel Alan Çalışmaların Değerlendirilmesi: Türkiye Örneği H. Coşkun ÇELİK a,samet GÜNDÜZ b (a) Siirt Üniversitesi, Eğitim Fakültesi,
Temel Mantık ve Cebir (MATH 111) Ders Detayları
 Temel Mantık ve Cebir (MATH 111) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Temel Mantık ve Cebir MATH 111 Güz 3 0 0 3 6.5 Ön Koşul Ders(ler)i Yok Dersin
Temel Mantık ve Cebir (MATH 111) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Temel Mantık ve Cebir MATH 111 Güz 3 0 0 3 6.5 Ön Koşul Ders(ler)i Yok Dersin
ÖZGEÇMİŞ. BSc - Matematik ve Bilgisayar Öğretmenliği, Doğu Akdeniz Üniversitesi, Gazimağusa, 2000
 ÖZGEÇMİŞ Kişisel Bilgiler: Adı-Soyadı : Begüm Çubukçuoğlu Devran Doğum Tarihi : 29.09.1978 E-mail adresi : begum1978@yahoo.com Eğitim: Ed.D - Eğitim Doktorası, Sheffield Universitesi, İngiltere, 2012 MA
ÖZGEÇMİŞ Kişisel Bilgiler: Adı-Soyadı : Begüm Çubukçuoğlu Devran Doğum Tarihi : 29.09.1978 E-mail adresi : begum1978@yahoo.com Eğitim: Ed.D - Eğitim Doktorası, Sheffield Universitesi, İngiltere, 2012 MA
Araştırma Metodları ve İletişim Becerileri (MMR 501) Ders Detayları
 Araştırma Metodları ve İletişim Becerileri (MMR 501) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Araştırma Metodları ve İletişim Becerileri MMR 501 Her
Araştırma Metodları ve İletişim Becerileri (MMR 501) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Araştırma Metodları ve İletişim Becerileri MMR 501 Her
FEN ÖĞRETİMİNDE LABORATUVAR YAKLAŞIMLARI. Burak Kağan Temiz (burak@gazi.edu.tr)
 FEN ÖĞRETİMİNDE LABORATUVAR YAKLAŞIMLARI 1800 lerden günümüze Bilgi Bilginin Elde Ediliş Yöntemleri Demonstrasyon Bireysel Yapılan Deneyler Öğretmen Merkezli Öğrenci Merkezli Doğrulama (ispat) Keşfetme
FEN ÖĞRETİMİNDE LABORATUVAR YAKLAŞIMLARI 1800 lerden günümüze Bilgi Bilginin Elde Ediliş Yöntemleri Demonstrasyon Bireysel Yapılan Deneyler Öğretmen Merkezli Öğrenci Merkezli Doğrulama (ispat) Keşfetme
EK - 4A ÖZGEÇMİŞ. 1. Adı Soyadı : Burak Yasin YILMAZ İletişim Bilgileri Adres
 EK - 4A ÖZGEÇMİŞ 1. Adı Soyadı : Burak Yasin YILMAZ İletişim Bilgileri Adres : Eskişehir Osmangazi Üniversitesi Eğitim Fakültesi Eğitim Bilimleri Bölümü Eğitim Programları ve Öğretim ABD Meşelik Yerleşkesi
EK - 4A ÖZGEÇMİŞ 1. Adı Soyadı : Burak Yasin YILMAZ İletişim Bilgileri Adres : Eskişehir Osmangazi Üniversitesi Eğitim Fakültesi Eğitim Bilimleri Bölümü Eğitim Programları ve Öğretim ABD Meşelik Yerleşkesi
Güz Dönemi Fizik Bölümü Titreşim ve Dalgalar Dersi Çıktılarının Gerçekleşme Derecesi
 2014-2015 Güz Dönemi Fizik Bölümü Titreşim ve Dalgalar Dersi Çıktılarının Gerçekleşme Derecesi 1 Orta 2 3 4 5 Bu ders ile ilgili temel kavramları, yasaları ve bunlar arasındaki %8 %0 %8 %67 %17 ilişkileri
2014-2015 Güz Dönemi Fizik Bölümü Titreşim ve Dalgalar Dersi Çıktılarının Gerçekleşme Derecesi 1 Orta 2 3 4 5 Bu ders ile ilgili temel kavramları, yasaları ve bunlar arasındaki %8 %0 %8 %67 %17 ilişkileri
DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ
 DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati (T+U+L) Kredi AKTS DİFERANSİYEL DENKLEMLER FEB-211 2/ 1.YY 3+0+0 3 3 Dersin Dili Dersin Seviyesi
DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati (T+U+L) Kredi AKTS DİFERANSİYEL DENKLEMLER FEB-211 2/ 1.YY 3+0+0 3 3 Dersin Dili Dersin Seviyesi
T.C. MALTEPE ÜNİVERSİTESİ FEN-EDEBİYAT FAKÜLTESİ MATEMATİK LİSANS PROGRAMI. 2013-14 Güz Yarıyılı. 1 yıl 1. yarıyıl Lisans Zorunlu
 AKTS Kredisi 5 T.C. MALTEPE ÜNİVERSİTESİ FEN-EDEBİYAT FAKÜLTESİ MATEMATİK LİSANS PROGRAMI Dersin adı: 2013-14 Güz Yarıyılı Genel Matematik I Dersin Kodu emat 151 1 yıl 1. yarıyıl Lisans Zorunlu 3 s/hafta
AKTS Kredisi 5 T.C. MALTEPE ÜNİVERSİTESİ FEN-EDEBİYAT FAKÜLTESİ MATEMATİK LİSANS PROGRAMI Dersin adı: 2013-14 Güz Yarıyılı Genel Matematik I Dersin Kodu emat 151 1 yıl 1. yarıyıl Lisans Zorunlu 3 s/hafta
