Konikler ÜNİTE. Amaçlar. İçindekiler. Yazar Doç.Dr. Hüseyin AZCAN
|
|
|
- Adem Özer
- 7 yıl önce
- İzleme sayısı:
Transkript
1 Konikler Yazar Doç.Dr. Hüsein AZCAN ÜNİTE 7 Amaçlar Bu ünitei çalıştıktan sonra; lise ıllarından da tanıdığınız çember, elips, parabol ve hiperbol gibi konik kesitleri olarak adlandırılan geometrik nesneleri akından tanıacak ve bunların kefi bir dik koordinat sisteminde denklemlerini elde edebileceksiniz. İçindekiler Giriş 17 Çember 17 Elips 13 Parabol 140 Hiperbol 148 Özet 154 Değerlendirme Soruları 154
2 Çalışma Önerileri Bu ünitei çalışmadan önce; konik kesitleri hakkındaki lise notlarınıza göz gezdiriniz. düzlemin eşmetrel dönüşümlerini (dönme ve öteleme ünitelerini) tekrar ediniz. ANADOLU ÜNİ VERSİ TESİ
3 KONİ KLER Giriş Konikler (a da koni kesitleri) en önemli geometrik nesnelerdendir. Analitik geometrinin ortaa çıkışıla özellikle koni kesitlerinin incelenmesi çok kolalaşmıştır. Bu inceleeceğimiz nesnelere neden koni kesitleri denildiğini daha sonraki bölümlere bırakarak, bu nesneleri alnız geometrik er tanımlarını kullanarak inceleelim. Bir koni kesiti denildiğinde şu nesneler anlaşılır: Çember, elips, parabol ve hiperbol. Hatta bir sonraki bölümde göreceğimiz gibi çember de özel bir elips olarak algılanırsa temel olarak üç çeşit koni kesitinden bahsedebiliriz. Her ne kadar özel bir elips olsa da biz çember ile koni kesitlerini incelemee başlaalım.. Çember Düzlemde verilen bir noktaa eşit uzaklıktaki noktaların geometrik erine bir çember denir. Bu verilen noktaa çemberin merkezi ve alınan eşit uzaklığa da çemberin arıçapı denir. Bu tanımdan sonra çemberi verilen bir koordinat sisteminde analitik olarak ifade edelim. Ötelenmiş ve dönmüş koordinat sistemlerini de göz önüne alacağımızdan, merkezi (0, 0) başlangıç noktası almamızda bir sakınca oktur. (, ) R 0 Eğer bir (, ) R noktası (0, 0) merkezli R arıçaplı çembere ait bir nokta ise tanıma göre bunun başlangıç noktasına olan uzaklığı R saısına eşit olacaktır. O halde d (0, 0), (, ) = + = R ani çember üzerinde bulunan (, ) noktası + = R koşulunu sağlamalıdır. AÇIKÖĞ RETİ M FAKÜLTESİ
4 18 KONİ KLER Tersine (0, 0) başlangıç noktasına uzaklığı R olan bütün noktalar tanımdan dolaı çember üzerindedir. O halde bir çember, merkezi ve arıçapı ile tek türlü belirgin olarak ifade edilebilir. İlk olarak düzlemin bir dönmesi altında çember denkleminin değişmediğini görelim. Düzleme bir R θ dönmesi verildiğinde koordinat değişimi = ' cosθ - ' sinθ = ' sinθ + ' cosθ idi. Şimdi bu değerleri + = R denkleminde erine koarsak (' cosθ - ' sinθ) + (' sinθ + ' cosθ) = R ' cos θ - '' sinθcosθ + ' sin θ + ' sin θ + '' sinθcosθ + ' cos θ = R ' + ' = R elde edilir. Görüldüğü gibi çemberin denklemi R θ dönmesinden hiç etkilenmedi. Bunun nedeni çemberin başlangıç noktasından geçen her doğrua göre simetrik olmasındandır. Şimdi düzlemin T (a, b) ötelemesi altında çember denkleminin nasıl değiştiğini görelim. Bildiğimiz gibi T (a, b) dönüşümü T (a, b) (, ) = (-a, -b) ani = ' + a, = ' + b olarak tanımlanmıştı. Bu koordinat değişimi + = R çember denkleminde erine konulursa: ( - a) + ( - b) = R ' + ' = R + - a - b + a + b - R = 0 şeklini alır. Bu son elde edilen denklemi sıfırdan farklı bir A saısı ile çarparsak A + A + aa + ba + A (a + b - R ) = 0 (7.1) (a, b) R merkezli R arıçaplı en genel çember denklemini elde etmiş oluruz. O halde çember denkleminde. teriminin katsaısı sıfır, ve terimlerinin katsaıları eşittir. ANADOLU ÜNİ VERSİ TESİ
5 KONİ KLER 19 Bu durumda doğal olarak bu koşulları sağlaan her denklem bir çemberi midir sorusu sorulabilir. A + A + B + C + D = 0 denklemini göz önüne alalım. Bütün katsaıları A ile bölerek + + B A + C A + D A = 0 denklemini elde ederiz. Eğer bu denklem (a, b) merkezli R arıçaplı bir çemberin denklemi ise bunu (7.1) denklemi ile karşılaştırarak -a = B A, -b = C A a = -B A, b = -C A -B merkez koordinatları olarak elde edilir. Şimdi arıçapı belirleelim. Yarıçaptaki en önemli kısıt, arıçapın pozitif bir gerçel saı olmasıdır. Yine son A, -C A denklemimizi (7.1) denklemi ile karşılaştırarak D A = -B + -C - R A A elde edilir. Buradan R = B + C - 4AD 4 A olur 4 A > 0 ve R > 0 olduğundan B + C - 4 AD > 0 olmalıdır. Bu durumda arıçap R = B + C - 4AD 4 A = 1 A B + C - 4AD dır. Birkaç örnekle bu anlattıklarımızı pekiştirelim. Örnek (-1, ) merkezli 3 arıçaplı çemberin denklemini azınız. Çözüm Bu çemberin denklemi ( - (-1)) + ( - ) = 9 AÇIKÖĞ RETİ M FAKÜLTESİ
6 130 KONİ KLER = 0 olarak elde edilir. Örnek = 0 denklemile verilen eğrinin bir çember olup olmadığını inceleiniz. Çözüm Denklemde bütün katsaılar ile oranlanarak = 0 olur (Eğer formülleri anımsaamazsanız karee tamamlama öntemini izleebilirsiniz). + 3 = = = = Bu ifadeleri denklemde erlerine koarsak: = = 3 = 0 elde edilir. O halde denklem - 3 merkezli ve arıçaplı bir çember, 1 3 gösterir. Çemberin çok önemli bir başka analitik ifadesini de aşağıdaki şekilde elde edebiliriz. Bu parametrik form ardımıla geometrinin bir cebir probleminin çözümünde nasıl çok güzel bir şekilde kullanıldığını görelim. ANADOLU ÜNİ VERSİ TESİ
7 KONİ KLER 131 = m + 1 = m + 1 doğrusu + = 1 birim çemberini iki noktada keser. Bu noktalardan bir tanesi (0, 1) dir. Diğerini ise hesaplaalım. = m = 1 + (m + 1) = 1 + m + m + 1 = 1 (m + 1) + m = 0 = 0 a da = - m m + 1 elde edilir. = - m m + 1 = m + 1 = m - m m e karşılık gelen değeri elde edilir. -m = + m + 1 m + 1 = 1 - m 1 + m Bu durumda çember ile doğrunun kesiştiği diğer nokta -m m + 1, 1 - m dir. 1 + m Yani çember üzerindeki kefi bir (, ) noktasının koordinatları = - m 1 + m, = 1 - m 1 + m şeklindedir. Bu parametrizasonun bir sonucu olarak + = z şeklindeki Pisagor üçlülerini belirleebiliriz. Yani,, z tamsaılar olmak üzere AÇIKÖĞ RETİ M FAKÜLTESİ
8 13 KONİ KLER + = z denklemini çözebiliriz. Yukarıdaki birim çemberin parametrizasonunda m doğrunun eğimini bir rasonel saı alırsak ve 1 0, bu durumda m = k l, k, l Z (tam saılar kümesi) = - k l 1 + k l = - k l. l k + l = - kl k + l = 1 - k l 1 + k l = l -k. l = l - k l k + l l + k olurlar. Bu (, ) sıralı ikilisi birim çembere ait bir nokta olduğundan birim çemberin denklemi olan = 0 denklemini sağlar. Denklemde ve i erine koarsak: - kl k + l + l - k l + k + 1 = 0 (kl) + (l - k ) = (l + k ) olur Yani + = z denklemini bazı çözümlerinin k, l tamsaılar olmak üzere = kl, = l - k, z = l + k olur. Yine birim çemberi inceleerek bütün çözümlerin bunlardan ibaret olduğunu da siz gösteriniz. Örneğin k = 107 ve l = 53 için = kl = = 1134 = l - k = = z = l + k = = 1458 olur. Yalnızca çok pratik bir Pisagor saıları üreteci elde edilmekle kalınmaıp, bütün Pisagor saılarını veren bir öntem geliştirilmiş oldu. 3. Elips Elips çemberin biraz deforme olmuş formu olan bir geometrik nesnedir. Tanımı şu şekilde apılabilir. ANADOLU ÜNİ VERSİ TESİ
9 KONİ KLER 133 Düzlemde verilen F 1 = (a 1, b 1 ) ve F = (a, b ) noktalarına uzaklıkları toplamı verilen sabit bir a saısına eşit olan noktaların geometrik erine bir elips denir. Bu verilen (a 1, b 1 ) ve (a, b ) noktalarına elipsin odakları denir. Başlangıç olarak odakları c > 0 olmak üzere F 1 = (c, 0) ve F = (-c, 0) noktalarında olan ve odaklara uzaklıkları toplamı a a eşit olan noktaların geometrik erinin analitik ifadesini elde edelim: X = (, ) F = (-c, 0) F 1 = (c, 0) (, ) R noktası adı geçen elipse ait bir nokta olsun. Bu durumda tanım gereğince + c c + = a - c + = a - + c + - c + = 4a - 4a + c c + 0 = 4a - 4a + c + + 4c a + c = a + c + c + a 4 + a c + c = a + a c + a c + a c - a - a = a c - a 4 c - a - a = a c - a F 1 X F üçgeninde iki kenar toplamı üçüncü kenardan büük olduğundan a > c a > c dir. Bu durumda a - c > 0. Eğer b = a - c denilirse b + a = a b a + b = 1 AÇIKÖĞ RETİ M FAKÜLTESİ
10 134 KONİ KLER elde edilir. Açıkça görüldüğü gibi eğer (, ) noktası elips üzerinde ise (-, ) noktasıda elips üzerindedir. O halde elips eksenine göre simetriktir. Diğer andan (, ) elipse çift ise (, -) ve (-, -) noktaları da elipse ait olduğundan elips hem eksenine hem de başlangıç noktasına göre simetriktir. Denklemden görüleceği gibi elips eksenini (a, 0) ve (-a, 0) noktalarında - eksenini de (0, b) ve (0, -b) noktalarında keser ve b < a olduğundan eksenine elipsin büük ekseni ve - eksenine de elipsin küçük ekseni denir. Elipsin eksenleri kestiği (a, 0) (-a, 0), (0, b), (0, -b) noktalarına da elipsin köşeleri denir. Son olarak e = c (0, 1) saısına a da elipsin dış merkezliği denir. Eğer e = 0 ise c = 0 olur ve özel bir elips olan çember elde edilir. Yukarıda elde ettiğimiz elips ile devam edecek olursak, denklemleri = a e ve = - a e denklemleri ile verilen özel iki doğru vardır. 0 < e < 1 olduğundan a > a ve - a dır. Dolaısıla Şekil 7.1 de görüldüğü gibi elipsin her iki e e < -a anında er alırlar. = - a e = a e (0, b) (-a, 0) (a, 0) - a e, 0 F = (-c, 0) F 1 = (c, 0) a e, 0 Şekil 7.1: Odakları F 1 = (c, 0) ve F = (-c, 0) Noktaları Olan Merkezil Elips Bu doğrulara elipsin doğrultmanları denir. Bu doğrultmanların elips için özel iki doğru olduklarını görmek için F 1 = (c, 0) odağını, = a doğrultmanını e ve elips üzerinde bir X = (, ) noktası alalım. Bu X noktasını F 1 odağına olan uzaklığı: d, F 1 = - c + = - c + c + b - b a a + b = 1 olduğundan = 1 - b a - c + c + b ANADOLU ÜNİ VERSİ TESİ 1 - b a = a - b a = c a olduğundan = e
11 KONİ KLER 135 = e - ea + a = a - e olur. (a - e > 0 olduğundan Diğer andan X = (, ) noktasının a - = 1 (a - e) dir. e e O halde = a e doğrusuna olan uzaklığı ise (, ) noktasının (c, 0) odağına uzaklığı (, ) noktasının = a e doğrultmanına uzaklığı uzaklığı = e (7.) ve benzer öntemle aşağıda verilen eşitlik de elde edilebilir., noktasının -c, 0 odağına uzaklığı, noktasının = - a e doğrultmanına uzaklığı = e (7.3) Aslında bu elde edilen son iki denklemin her biri elipsin tanımı olarak alınabilir. Bunu şu şekilde görebiliriz. Bir (, ) R noktası (7.) denklemini sağlasın ani: - c + - a e = e olsun. Bu durumda - c + = e - a e - c + c + = e - ae + a 1 - e + = a - c (c = a. e olduğundan c = ae dir) a > c olduğundan b = a - c, e = c a azarsak b + a = a b a + b = 1 elde edilir. Bu durumda elipsin tanımı olarak düzlemde (7.1) a da (7.) özelliğini sağlaan noktaların kümesi olarak alınabilir. Son olarak her iki simetri ekseninin ara kesiti olan noktaa çemberden esinlenerek elipsin merkezi denilebilir. Bizim ukarıda kuruluşunu verdiğimiz elipsin merkezi (0, 0) başlangıç noktasıdır. Şimdi elipsin denkleminin düzlemin dönme ve ötelemesi altında nasıl değiştiğini görelim. Öncelikle T (α, β) (, ) = ( - α, - β) AÇIKÖĞ RETİ M FAKÜLTESİ
12 136 KONİ KLER ötelemesi altında elipsin denkleminin değişimini inceleelim. = ' - α, = ' - β koordinat değişimi a + b = 1 denklemine ugulanır sa: ' - α a + ' - β = 1 b ' + ' a b - α a ' - β ' + α b a + β b = 1 1 a ' + 1 ' - α b a ' - β ' + α b a elde edilir. + β b - 1 = 0 (7.4) Şimdi bu durumun tersine bakalım. Yani A + B + C + D + E = 0 denklemile verilen eğrinin ne zaman (7.4) tipinde bir elips denklemi olacağını inceleelim. (7.4) denkleminde ' ve ' nin katsaıları 1 anı işarete sahiptirler, o a ve 1 b halde a A > 0 ve B > 0 a da A < 0 ve B < 0 olmalıdır. A > 0 ve B > 0 olarak alırsak karee tamamlama ile A + B + C + D + E = 0 A + C + B + D A B A + C + B + D A B - C 4A - D 4B + E = 0 = C 4A + D 4B - E olur. Bu durumda bu denklem merkezi C 4A + D 4B - E > 0 - C A, - C B olmalıdır. Eğer A > B ise kolaca görülebilir ki noktasında ve eksen uzunlukları a = C + C 4A 4AB - E A olan bir elipstir. ve b = C 4AB + D 4B - E B A < B durumunu da benzer şekilde siz inceleiniz. ANADOLU ÜNİ VERSİ TESİ
13 KONİ KLER 137 Örnek = 0 denklemi ile verilen eğrinin bir elipsin olduğunu gösteriniz. Bu elipsin merkezini, odaklarını ve doğrultmanlarını belirleiniz. Çözüm = 0 4 ( - ) = 0 4 ( ) + ( + ) = 0 ( + ) + 4 ( + 1) - 4 = = 1 elde edilir. O halde merkez (-, 1) noktası ve a = 4, b = 1 olduğundan c = a - b = 3 olur. Bu durumda e = a c = 3 ve doğrultmanları + = ± 4 3 = ' = (-, ) (-4, 1) (-, 1) (0, 1) (-- 3, 1) (-+ 3, 1) (-, 0) ' olur. Düzlemin R θ dönmesi altında elipsin denkleminin hangi formu aldığını da görebiliriz. = ' cosθ - ' sinθ = ' sinθ + ' cosθ koordinat değişimi altında, a + b = 1 denklemi ' cosθ - ' sinθ a + ' sinθ + ' cosθ = 1 a AÇIKÖĞ RETİ M FAKÜLTESİ
14 138 KONİ KLER cos θ a + sin θ b ' + sin θ a + cos θ b ' + - sin θ a + sin θ b ' ' = 1 b cos θ + a sin θ ' + b sin θ + a cos θ ' + sin θ a - b ' ' = a b ifadesi elde edilir. Görüldüğü gibi bu ifadede ' nin ve ' nin katsaılarının her ikiside anı işarettedir. Son olarak düzlemin bu ötelemesi ve dönmesi altında doğrultman ve odaklarına da anı hareket ugulanır. Şimdi örnekleri inceleelim. Örnek Köşeleri (0, 0), (4, 4), (1, 3), (3, 1) noktaları olan elipsin denklemini azınız, doğrultmanlarını ve dış merkezliğini hesaplaınız. Çözüm Düzlemde bu noktaları işaretlersek (1, 3). (4, 4) (3, 1) (0, 0) Şekilden görüldüğü gibi elipsin büük ekseni (0, 0) noktasını (4, 4) noktasına birleştiren doğru üzerindedir. Bu noktalar arasındaki uzaklık a idi. O halde a = = 4 a = olur Benzer şekilde küçük eksen uzunluğu b = = b = olur Öte andan c = a - b olduğu anımsanırsa: c = 8 - = 6 olur O halde bu koşulları sağlaan merkezil elips ANADOLU ÜNİ VERSİ TESİ
15 KONİ KLER 139 '' (0, ) (-, 0) (- 6, 0) ( 6, 0) (, 0) '' (0, - ) denklemi " + " 8 doğrultmanları = 1 dir. Bu elipsin dış merkezliği e = a c = 6 = 3 ve " = a doğrularıdır. Şimdi düzlem e = 3/ = 4 3 ve " = π kadar dönme verip ve (, ) ötelemesi aparsak elde edilen merkezil elipsin görüntüsü istenen 4 elipstir. Aşağıdaki şekilde belirtildiği gibi " ' " π 4 O' ' O Önce "O'" koordinat sisteminde denklemi " 8 + " = 1 olan elipsi 'O' koordinat sistemindeki denklemini azalım: " = 1 ' + ', " = 1 - ' + ' θ = π 4 olduğunda 1 ' + ' + 8 ' + ' + ' ' ' + ' = 1 + ' - ' ' + ' 4 = 1 5' + 5' - 6' ' = 16 elde edilir. AÇIKÖĞ RETİ M FAKÜLTESİ
16 140 KONİ KLER O' noktasının O sistemindeki koordinatları (,) olduğundan ' = -, ' = - kullanılarak 5 ( - ) + 5 ( - ) - 6 ( - )( - ) = = 0 denklemi elde edilir. Doğrulmanları içinde anı işlem apılırsa " = 4 3 ve " = ' + ' = 4 3 ve 1 ' + ' = -4 3 olur. Nihaet O sisteminde = 4 3 ve = = 0 ve = 0 doğrultman doğruları elde edilir. 4. Parabol Çember ve elipsten sonra diğer bir önemli konik paraboldür. Parabol de diğer konikler gibi aşağıdaki şekilde tanımlanabilir. Düzlemde bir F = (a, b) noktasına ve bir l doğrusuna anı uzaklıkta olan noktaların geometrik erine bir parabol denir. Eğer X parabole ait bir nokta ise d(x, l) = d(x, F) d(x, l) d(x, F) = 1 olur. Burada adı geçen l doğrusuna parabolün doğrultmanı ve F = (a, b) noktasına parabolün odağı denir. Şimdi ilk olarak a > 0 olmak üzere odağı F = (a, 0) noktası ve doğrultmanı = -a doğrusu olan parabolün analitik ifadesini elde edelim. ANADOLU ÜNİ VERSİ TESİ
17 KONİ KLER a = (, ) ( - a) + F = (a, 0) = -a d (, ), l = + a d (, ), F = ( - a) + değerlerini tanıma göre eşitleerek parabolün analitik ifadesini elde edebiliriz. + a = ( - a) + + a + a = - a + a + 4a = O halde odağı F = (a, 0) ve doğrultmanı = -a doğrusu olan parabolün denklemi = 4a elde edilir. Düzlemin ötelemesi ve dönmesi altında diklik ve uzaklıklar korunacağından ekseninin görüntüsü doğrultmanın görüntüsüne dik kalmaa devam eder. Bu nedenle doğrultmana dik olan doğrua (bizim denklemini elde ettiğimiz parabol için eksenine) parabolün asal ekseni denir. Parabol asal eksenini bir noktada keser (bizim denklemini elde ettiğimiz parabolde (0, 0) noktası) bu noktaa parabolün köşesi denir. Açık olarak göründüğü gibi parabol asal ekseni olan eksenine göre simetriktir. Yani (, ) parabole ait bir nokta ise bunun eksenine göre simetriği olan (, -) noktası da parabole aittir. Bu bilgilerle parabolün şekli kabaca (, ) (0, 0) F = (a, 0) Şekil 7. AÇIKÖĞ RETİ M FAKÜLTESİ
18 14 KONİ KLER olarak çizilir. Şimdi bu elde ettiğimiz parabole öteleme ve dönme dönüşümlerini ugulaarak kefi doğrultman ve kefi odağa sahip olan parabol denklemlerini elde edip bunların özelliklerini belirleelim. İlk olarak düzlemin T (α, β) öteleme dönüşümü altında incelemee başlaalım. T (α, β) : R R, T (α, β) (, ) = ( + α, + β) öteleme dönüşümü verilsin. ' 0' = (α, β) ' 'O'' koordinat sisteminde odağı F' = (a, 0) noktası ve doğrultmanı = -a doğrusu parabölün denklemi ' = 4a' dür. Şimdi buradan orjinal koordinat sistemine geçersek ' = - a, ' = - β değişken değişimile ( - α) = 4a ( - β) - α + α = 4a - 4aβ - α + 4a + α + 4aβ = 0 elde edilir. Görüldüğü ötelenmiş bir parabol denklemi terimi içermez. Şimdi benzer olarak düzlemin R θ dönmesi altında parabol denkleminin ne hal aldığını görelim. Düzlemin R θ (, ) = ( cosθ + sinθ, - sinθ + cosθ) ANADOLU ÜNİ VERSİ TESİ
19 KONİ KLER 143 ' ' θ 0 = 0' 'O'' koordinat sisteminde odağı bu koordinat sisteminde (a, 0) ve doğrultmanı ine 'O'' koordinat sisteminde = - a doğrusu alan parabolün denklemi ' = a' dür. Bu parabölün O orjinal koordinat sistemindeki denklemi ' = cosθ + cosθ ' = cosθ + cosθ koordinat dönüşümü kullanılarak ( cosθ + sinθ) = 4a (- sinθ + cosθ) cos θ + sinθ cosθ + sin θ = -4a sinθ + 4a cosθ cos θ + sin θ + sin θ + 4a sinθ - 4a cosθ = 0 şeklini alır. Bu durumda kefi bir parabolün denklemi dönme öteleme ile kolaca azılabilir. Örnek Doğrultmanı = 0 doğrusu ve odağı F = (0, 0) noktası olan parabolün denklemini azınız. Çözüm Öncelikle doğrultman ve odağı düzlemde geometrik olarak gösterelim. AÇIKÖĞ RETİ M FAKÜLTESİ
20 144 KONİ KLER (0, 1) asal eksen ' (0, 0) 5, 1 5 1, 0 ' Asal eksen, odaktan geçip doğrultman dik olacağı için eğimi m = 1/ ve denklemi = 1 Doğrultman ile asal eksenin kesim noktası dir. = = 0 denklem sisteminin çözümünden, = 5, 1 5 bulunur. O halde doğrultmanın odağa olan uzaklığı a = = 1 5 olur Yani a = 1 5 elde edilir. Devamla parabolün köşesini 1 5, 1 noktası olarak hesaplaabiliriz. Bu bilgilerle önce a = ve odağı 1 5, 0 doğrultmanı = - 1 olan parabolün denklemi 5 = = 5 olur. = , 0 ANADOLU ÜNİ VERSİ TESİ
21 KONİ KLER 145 Şimdi bir R θ dönmesi ugulaarak parabolün asal eksenini = doğrusu apalım. Yalnız bu dönmei ugularken önede dikkat ederek dönme açısını hesaplaalım θ 5 dik üçgeninde sinθ = 1/5 1/ 5 = 5 ve cosθ = /5 5 1/ 5 = 5 5 dönme açısı θ erine θ + π olmalıdır. olur. Yön nedenile sin θ + π = - sinθ = - 5 5, cos θ + π = - cosθ = dir. Bu durumda = 5 parabolüne R π + θ, = , dönmesi ugulanarak: = = = - olur. Bu parabolün grafiği Bu parabolün doğrultmanı ise görüntü ise = - 5 doğrusunun görüntüsü olacaktır. Bu AÇIKÖĞ RETİ M FAKÜLTESİ
22 146 KONİ KLER = = = 1 noktası- olur. Şimdi son olarak başlangıç noktası parabolün köşesi na öteelim. 1 5, , koordinat değişimi ugulanırsa parabolün denklemi = = - olur. Doğrultmanın denklemi ise anı koordinat dönüşümüle = = = 0 elde edilir Bir başka örnek olarak F = (4, 3) (3, ) Şekilde görüldüğü gibi köşesi (3, ) noktası ve odağı F = (4, 3) noktası olan parabolün denklemini azalım. ANADOLU ÜNİ VERSİ TESİ
23 KONİ KLER 147 Çözüm Parabolün ekseni (3, ) ve (4, 3) noktaları tarafından belirlenen doğrudur. Bu doğrunun denklemi = 0 dır. Diğer andan parabolün parametresi a = d 3,, 4, 3 = = dir. Bu durumda doğrultmanı = - doğrusu odağı (, 0) noktası olan parabolün denklemi = 4 olup grafiği 7.3'deki gibi çizilir., 0 = - Şekil 7.3 Bu parabole dönme ve öteleme ugulanarak sorudaki parabol elde edilir. Önce dönme açısını odak ve köşe ardımıla hesaplanabilir. (4, 3) 1 θ (3, ) 1 Şekilden θ = π 4 hesaplanır. Hatta sin θ = cosθ = 1 dir. O halde R π 4 dönmesi R π 4, = 1 + 1, = 1 +, - + AÇIKÖĞ RETİ M FAKÜLTESİ
24 148 KONİ KLER koordinat değişimi = 4 denklemine ugulanırsa 1 + = = olur. Son olarak düzlem (3, ) köşesine ötelenirse T (3, ) (, ) = ( - 3, - ) koordinat değişimi ile = = elde edilir. 5. Hiberbol Önceki kısımlarda dış merkezliğin e = 0, 0 < e < 1 ve e = 1 olması durumlarını inceledik. Bu durumlarda elde edilen koni kesitleri sırasıla çember, elips ve parabol idi. Şimdi kalan tek durum olan e > 1 durumunu inceleeceğiz. e > 1 ve c > 0 olmak üzere, elipsteki kuruluşa paralel olarak, (c, 0) noktasını bir odak ve = c e = c/e = e a a = e e c olarak tanımlandı bir doğrultman doğrusu olsunlar. e > 1 olduğundan a < a < c dir. Bu girişten sonra hiperbolü tanımlaalım. e Düzlemde odağa uzaklığının doğrultmana uzaklığına oranı "e" olan noktaların geometrik erine bir hiperbol denir. - a e (, ) - c + (C, 0) = a e Şekil 7.4 ANADOLU ÜNİ VERSİ TESİ
25 KONİ KLER 149 Şekil 7.4 de de belirtilen uzunlukları kullanarak tanım gereğince - c + - a e = e azılabilir. Bu eşitliği basitleştirirsek: - c + = e - a e = e - a ( -c) + = (e - a) - c + c + = e - ae + a (1 - e ) + = a - c (ae = c olduğundan) c > a olduğundan b = c - a olarak tanımlanırsa b = a c a - 1 = a e e = - b a Bu tanımlamalar kullanılarak: olur olur. - b + = - b a a - b = 1 (7.5) Benzer şekilde (- c, 0) noktasını odak ve = - a doğrusunu doğrultman olarak alsadık ine anı hiperbolü elde edecektik. (Bunu hesaplaarak görmee çalı- e şınız.) (7.5) denklemine akından bakılırsa elips gibi hiperbol de -eksenine, eksenine ve başlangıç noktasına göre simetriktir. Yine elipsteki gibi başlangıç noktasına hiperbolün merkezi denir. Yine (7.5) denkleminden -eksenini (a, 0) ve (- a, 0) noktalarından keser. Bu iki noktaa hiperbolün köşeleri denir. Diğer andan hiper bol -eksenini kesmez. Çünkü (7.5) denklemin de = 0 alınırsa ki bu imkansızdır. - b = 1 olur Hiperbolün tanımı da elips için verdiğimiz orjinal tanıma benzer olarak da apabiliriz. Eğer (c, 0) ve (- c, 0) noktalarını odaklar olarak alırsak. Bu durumda düzlemde bu iki noktaa uzaklıkları farkının mutlak değeri sabit olan (bu sabiti a alalım) noktalarını geometrik erine bir hiperbol denir. AÇIKÖĞ RETİ M FAKÜLTESİ
26 150 KONİ KLER X = (, ) d 1 d - c, 0 = F c, 0 = F 1 X F 1 F üçgeninde iki kenar farkı d 1 - d üçüncü kenar c dan daha küçüktür. Yani d 1 - d = a < c a < c olur. Şimdi bu uzaklıkları hesaplaarak hiperbolün analitik ifadesini bu olla elde edelim. d 1 - d = a + c c + = a olur. Bu son eşitliğin her iki tarafının karesi alınırsa (bu saede mutlak değerden de kurtuluruz). + c c c + = 4a + + c - a = + c + - c c 4 + 4a c + c - 4 a - 4 a - 4c a = c 4 - c + + c 4a c - 4 a - 4 a - 4c a = 0 c - a - a = a c - a c > a olduğundan b = c - a olarak tanımlanırsa a - b = 1 elde edilir. Yine anı denklemi elde ettik. İşlemi tam apmış olmak için diğer önde ispatı siz apınız. Yakından bakılacak olursa hiperbolle akından ilgili olan iki tane doğru vardır. Eğer birinci dördüncü (, ) noktalarını göz önüne alırsak ( (, ) birinci dördünde olduğundan 0, 0 dir). Buradan = b a - a < b a dir. Şimdi eterince büük 'ler için birinci dördündeki hiperbole ait (, ) noktalarının = b doğrusuna olan düşe uzaklık a ANADOLU ÜNİ VERSİ TESİ
27 KONİ KLER 151 b a - = b a - b a - a = b a - - a = b a = b a + - a - - a + - a a + - a < ab olur. Yani a b - < ab dir. Diğer andan = a b ile kesişmez. Çünkü doğrusu a - b = 1 hiperbolü - b a = 1 a b olur ki bu da bir çelişki verir. Yukarıda ise eterince büük ' ler için hiperbol üzerindeki (, ) noktası da = a - a = 1 0 = 1 a b doğrusun eterince akındır. Bu nedenle = doğrusuna hiperbolün asimptotu denir. Simetriden dolaı = - doğrusu da hiperbolün diğer asimptotudur. Şimdi bazı saısal a b a b örnekler apalım. Örnek Odakları (± 3, 0) noktalarında ve asimptotları = ± 1 olan hiperbolün 5 denklemi nedir? Çözüm = = 1 5 (-3, 0) (3, 0) AÇIKÖĞ RETİ M FAKÜLTESİ
28 15 KONİ KLER 1 5 = a b a = 5b olmalıdır. Diğer andan b = c - a b = 9 - a olur. Buradan b = 9-5b 4b = 9, b = 6 3 ve a = olur. O halde hiperbolün denklemi: = = 1 olur Bu hiperbolün dış merkezliği e = c a = olur. O halde doğrultma doğruları = ± 10 6 / 3 3 / 10 6 = ± = ± doğrularıdır. Şimdi düzlemin ötelemesi altında hiperbol denkleminin nasıl değiştiğini görelim: T (α, β) (, ) = ( - α, - β) ötelemesi altında hiperbolüne taşınır. a - = 1 hiperbolü de b - α a - - β = 1 b Bu durumda odaklar T α, β (± c, 0) = (± c - α, β) noktalarına, doğrultmanları T α, β ± a e, 0 = ± a e - α, β olur. Yani eni doğrultmanlar = ± a e - α olur. Son olarak asimptotlar T α, β, ± b a = - α, ± b a - β olur. Yani eni asimptotlar - - β = ± b a - α olur. Şimdi ötelenmiş hiperbolün denklemini açık olarak azarsak: - α a - - β = 1 b 1 a - 1 b - α a + β + α b a - β b - 1 = 0 b - a - αb + βa + b - α β - a b = 0 olur. Şimdi şu örneği inceleelim: ANADOLU ÜNİ VERSİ TESİ
29 KONİ KLER 153 Örnek = 0 hiperbolünün köşelerini, odaklarını, dış merkezliğini, doğrultmanlarını ve asimptotlarını bulunuz. Çözüm Karee tamamlaarak = 0 3( - ) - ( + 4) - 11 = 0 3[( - 1) -1] - [( + ) - 4] - 11 = 0 3( -1) - ( + ) = = 1 elde edilir. O halde a = a = ve b = 3 b = 3 olur. c = b + a = 5 c = 5 ve e = c a = 5 bulunur. Hiperbolün merkezi (1, -) olduğundan odakla 1 ± 5, - noktaları, doğrultmanlar - 1 = ± 5 ve asimptotlar ise + = ± 3-1 olarak elde edilir. Şimdi düzlemin bir R θ dönmesi altında hiperbol denklemin nasıl değiştiğini görelim. R θ (, ) = ( cosθ - sinθ, sinθ + cosθ) dönmesi altında a - = 1 hiperbolünün görüntü b ' cosθ - ' sinθ a - ' sinθ + ' cosθ = 1 şeklini alır. b Odaklar, doğrultmanlar ve asimptotlarında R θ altındaki görüntüleri eni odakları, doğrultmanları ve asimptotları verir. Son olarak asimptotları biribirlerine dik olan bir hiperbola bir ikiz kenar hiperbol denir. AÇIKÖĞ RETİ M FAKÜLTESİ
30 154 KONİ KLER Örnek (3, 5) = F 1 F = (1, 3) (, ) Şekilde verilen hiperbolün denklemini bulunuz. Özet Bu ünitede belki de analitik geometrinin gelişmesindeki en önemli motivason olan konik kesitlerini tanımladık ve sınıflandırdık. Dönme ve öteleme dönüşümleri kullanarak kefi bir koordinat sisteminde bir elipsin, bir parabolün a da bir hiperbolün analitik denkleminin ifadesinin nasıl elde edilebileceğini gördük. Değerlendirme Soruları (1,3) (3,4) (3,) (5,3) 1.,., 3. ve 4. soruları ukarıdaki şekle göre cevaplaınız. 1. Elipsin denklemi aşağıdakilerden hangisidir? A = 0 B = 0 C = 0 D = 0 E = 0 ANADOLU ÜNİ VERSİ TESİ
31 KONİ KLER 155. Elipsin doğrultmanlarının bir tanesinin denklemi nedir? A. 3 B. 3 C. 1 D. 1 E Elipsin dış merkezliği nedir? A. 3 B. 3 C. 1 D. 1 E Elipsin odaklarından birisi nedir? A , 3 B. - 3, 3 C. 3, 4-3 D. 3, + 3 E. 5-3, 3 AÇIKÖĞ RETİ M FAKÜLTESİ
32 156 KONİ KLER (,) + = 1 5., 6. ve 7. soruları ukarıdaki şekle göre cevaplaınız. 5. Parabolün asal ekseni aşağıdaki doğrulardan hangisidir? A. = B. = + 1 C. = + D. = - E. - = Parabolün parametresi aşağıdakilerden hangisidir? A. 3 B. 3 C. 3 D. 3 E. 7. Parabolün odağı aşağıdaki noktalardan hangisidir? A. 4, 4 B. 5, 5 C. 5, 5 D. 9, 9 E. 7, 7 ANADOLU ÜNİ VERSİ TESİ
33 KONİ KLER = 0 çemberinin arı çapı nedir? A. 1 B. C. 3 D. 4 E A. 13, 0 = 1 hiperbolünün odaklarından birinin koordinatlarını bulunuz. B. 0, 13 C. 0, 5 D. 5, 0 E. 5, A. 13 B C. 5 D. 5 E. 5 = 1 hiperbolünün dış merkezliği nedir? Değerlendirme Sorularının Yanıtları 1. A. C 3. B 4. B 5. A 6. D 7. E 8. B 9. B 10. B AÇIKÖĞ RETİ M FAKÜLTESİ
MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI
 MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI SORU 1. Köşeleri (1,4) (3,0) (7,2) noktaları olan ABC üçgeninin bir ikizkenar dik üçgen (İpucu:, ve vektörlerinden yararlanın) SORU 2. Bir ABC üçgeninin
MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI SORU 1. Köşeleri (1,4) (3,0) (7,2) noktaları olan ABC üçgeninin bir ikizkenar dik üçgen (İpucu:, ve vektörlerinden yararlanın) SORU 2. Bir ABC üçgeninin
PARABOL. Merkezil parabol. 2px. 2py F 0, 2 F,0. Şekil I. Şekil II. p Odağı F 2. Odağı F 0, Doğrultmanı x. Doğrultmanı y
 ARABL Tanım: Düzlemde verilen sabit bir noktası ile bir d doğrusuna uzaklıkları eşit olan noktaların geometrik erine arabol denir. Sabit noktaa arabolün odağı; doğrua ise doğrultmanı denir. Merkezil arabol
ARABL Tanım: Düzlemde verilen sabit bir noktası ile bir d doğrusuna uzaklıkları eşit olan noktaların geometrik erine arabol denir. Sabit noktaa arabolün odağı; doğrua ise doğrultmanı denir. Merkezil arabol
ÜN TE I. KON KLER N ANAL T K NCELENMES
 ÜN TE I. KON KLER N ANAL T K NCELENMES 1. G R fi. EL PS I. Tan mlar II. Elipsin eksenleri ve özel noktalar a. Asal eksen b. Yedek eksen c. Merkezil elips d. Elipsin köfleleri e. Elipsin odak noktalar f.
ÜN TE I. KON KLER N ANAL T K NCELENMES 1. G R fi. EL PS I. Tan mlar II. Elipsin eksenleri ve özel noktalar a. Asal eksen b. Yedek eksen c. Merkezil elips d. Elipsin köfleleri e. Elipsin odak noktalar f.
= e DIŞ MERKEZLİK HAZİNE-1 HAZİNE-2
 HAZİNE-1 HAZİNE-2 Bir eksen üzerinde verilen noktadan geçen ve eksen ile belirli açı yaparak dönen doğrunun oluşturduğu yüzeye konik yüzey denir. Konik yüzeyin değişik düzlemler ile arakesit kümeleri çember,
HAZİNE-1 HAZİNE-2 Bir eksen üzerinde verilen noktadan geçen ve eksen ile belirli açı yaparak dönen doğrunun oluşturduğu yüzeye konik yüzey denir. Konik yüzeyin değişik düzlemler ile arakesit kümeleri çember,
Taşkın, Çetin, Abdullayeva
 BÖLÜM Taşkın, Çetin, Abdullaeva FONKSİYONLAR.. FONKSİYON KAVRAMI Tanım : A ve B boş olmaan iki küme a A ve b B olmak üzere ( ab, ) sıralı eleman çiftine sıralı ikili denir. ( ab, ) sıralı ikilisinde a
BÖLÜM Taşkın, Çetin, Abdullaeva FONKSİYONLAR.. FONKSİYON KAVRAMI Tanım : A ve B boş olmaan iki küme a A ve b B olmak üzere ( ab, ) sıralı eleman çiftine sıralı ikili denir. ( ab, ) sıralı ikilisinde a
a 2 = b 2 +c 2 a 2 +b 2 =c 2
 1.1. ELİPS 1.2. HİPERBOL 1.3. ORTAK özellikler =-a 2 /c =a 2 /c K =-a 2 /c B(b,0) K =a 2 /c Asal Eksen Uzunluğu: AA =2a Yedek Eksen Uzunluğu: BB =2b p A'(-a,0) F'(-c,0) p p Odak Uzaklığı: FF =2c Dış Merkezlik:
1.1. ELİPS 1.2. HİPERBOL 1.3. ORTAK özellikler =-a 2 /c =a 2 /c K =-a 2 /c B(b,0) K =a 2 /c Asal Eksen Uzunluğu: AA =2a Yedek Eksen Uzunluğu: BB =2b p A'(-a,0) F'(-c,0) p p Odak Uzaklığı: FF =2c Dış Merkezlik:
- 2-1 0 1 2 + 4a a 0 a 4a
 İKİNCİ DERECEDEN FNKSİYNLARIN GRAFİKLERİ a,b,c,z R ve a 0 olmak üzere, F : R R f() = a + b + c şeklinde tanımlanan fonksionlara ikinci dereceden bir değişkenli fonksionlar denir. Bu tür fonksionların grafikleri
İKİNCİ DERECEDEN FNKSİYNLARIN GRAFİKLERİ a,b,c,z R ve a 0 olmak üzere, F : R R f() = a + b + c şeklinde tanımlanan fonksionlara ikinci dereceden bir değişkenli fonksionlar denir. Bu tür fonksionların grafikleri
Cebirsel Fonksiyonlar
 Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
İÇİNDEKİLER UZAY AKSİYOMLARI... 001-006... 01-03 UZAYDA DOGRU VE DÜZLEMLER... 007-010... 04-05 DİK İZDÜŞÜM... 011-014... 06-07
 UZY GEMETRİ İÇİNDEKİLER Safa No Test No UZY KSİYMLRI... 001-00... 01-0 UZYD DGRU VE DÜZLEMLER... 007-010... 0-05 DİK İZDÜŞÜM... 011-01... 0-07 PRİZMLR... 015-0... 08-1 KÜP... 05-00... 1-15 SİLİNDİR...
UZY GEMETRİ İÇİNDEKİLER Safa No Test No UZY KSİYMLRI... 001-00... 01-0 UZYD DGRU VE DÜZLEMLER... 007-010... 0-05 DİK İZDÜŞÜM... 011-01... 0-07 PRİZMLR... 015-0... 08-1 KÜP... 05-00... 1-15 SİLİNDİR...
Üç Boyutlu Uzayda Bazı Yüzeyler ve Koordinat Sistemleri
 Üç Boyutlu Uzayda Bazı Yüzeyler ve Koordinat Sistemleri Yazar Doç.Dr. Hüseyin AZCAN ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; Küresel Koordinatlar Silindirik Koordinatları Dönel Yüzeylerin Elde Edilmesi
Üç Boyutlu Uzayda Bazı Yüzeyler ve Koordinat Sistemleri Yazar Doç.Dr. Hüseyin AZCAN ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; Küresel Koordinatlar Silindirik Koordinatları Dönel Yüzeylerin Elde Edilmesi
TÜRKİYE GENELİ DENEME SINAVI LYS - 1 MATEMATİK
 TÜRKİY GNLİ SINVI LYS - 1 7 MYIS 017 LYS 1 - TSTİ 1. u testte 80 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için arılan kısmına işaretleiniz. + k+ n 15 + 10 1. : = + 6 16 + 8 0 + 8 olduğuna
TÜRKİY GNLİ SINVI LYS - 1 7 MYIS 017 LYS 1 - TSTİ 1. u testte 80 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için arılan kısmına işaretleiniz. + k+ n 15 + 10 1. : = + 6 16 + 8 0 + 8 olduğuna
NOKTANIN ANALİTİK İNCELEMESİ NOKTANIN ANALİTİK İNCELEMESİ
 NKTANIN ANALİTİK İNCELEMESİ NKTANIN ANALİTİK İNCELEMESİ Başlangıç noktasında birbirine dik olan iki saı doğrusunun oluşturduğu sisteme "Dik Koordinat Sistemi" denir. Dik Koordinat Sisteminin belirttiği
NKTANIN ANALİTİK İNCELEMESİ NKTANIN ANALİTİK İNCELEMESİ Başlangıç noktasında birbirine dik olan iki saı doğrusunun oluşturduğu sisteme "Dik Koordinat Sistemi" denir. Dik Koordinat Sisteminin belirttiği
PARABOL. çözüm. kavrama sorusu. çözüm. kavrama sorusu
 PARABL Bu bölümde birinci dereceden fonksion =f()=a+b ve ikinci dereceden fonksion =f()=a +b+c grafiklerini üzesel olarak inceleeceğiz. f()=a +b+c ikinci dereceden bir bilinmeenli polinom fonksionun grafiği
PARABL Bu bölümde birinci dereceden fonksion =f()=a+b ve ikinci dereceden fonksion =f()=a +b+c grafiklerini üzesel olarak inceleeceğiz. f()=a +b+c ikinci dereceden bir bilinmeenli polinom fonksionun grafiği
( ) ( ) ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. Cevap D. Cevap C. noktası y ekseni üzerinde ise, a + 4 = 0 A 0, 5 = 1+
 ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. a+ = b 4. a = b 0+ a b a b = b a+ b = 0. A ( a + 4, a) noktası y ekseni üzerinde ise, ( + ) a + 4 = 0 A 0, 5 a = 4 B b, b 0 noktası x ekseni
ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. a+ = b 4. a = b 0+ a b a b = b a+ b = 0. A ( a + 4, a) noktası y ekseni üzerinde ise, ( + ) a + 4 = 0 A 0, 5 a = 4 B b, b 0 noktası x ekseni
Kuadratik Yüzeyler Uzayda İkinci Dereceden Yüzeyler
 İÇİNDEKİLER Kuadratik Yüeler Uada İkinci Dereceden Yüeler 1 0.1. Elipsoid 2 0.2. Hiperboloid 4 0.2.1. Tek Kanatlı Hiperboloid 4 0.2.2. Çift Kanatlı Hiperboloid 4 0.3. Paraboloid 5 0.3.1. Eliptik Paraboloid
İÇİNDEKİLER Kuadratik Yüeler Uada İkinci Dereceden Yüeler 1 0.1. Elipsoid 2 0.2. Hiperboloid 4 0.2.1. Tek Kanatlı Hiperboloid 4 0.2.2. Çift Kanatlı Hiperboloid 4 0.3. Paraboloid 5 0.3.1. Eliptik Paraboloid
2.2 Bazıözel fonksiyonlar
 . Bazıözel fonksionlar Kuvvet fonksionu, polinomlar ve rasonel fonksionlar, mutlak değer ve tam değer fonksionları, pratik grafik çizimleri. 1-) Lineer fonksionlar: m ve n sabit saılar olmak üzere f()
. Bazıözel fonksionlar Kuvvet fonksionu, polinomlar ve rasonel fonksionlar, mutlak değer ve tam değer fonksionları, pratik grafik çizimleri. 1-) Lineer fonksionlar: m ve n sabit saılar olmak üzere f()
H. Turgay Kaptanoğlu. Ç. Dışmerkezlilik ve Doğrultmanlar Dışmerkezlilik kavramı, inceledimiz dört
 KONİNİN KESİTLERİ (II) H. Turgay Kaptanoğlu Ç. Dışmerkezlilik ve Doğrultmanlar Dışmerkezlilik kavramı, inceledimiz dört eğriyi aynı bakış açısı etrafında toplamamızı sağlayacak. Dışmerkezlilik hakkında
KONİNİN KESİTLERİ (II) H. Turgay Kaptanoğlu Ç. Dışmerkezlilik ve Doğrultmanlar Dışmerkezlilik kavramı, inceledimiz dört eğriyi aynı bakış açısı etrafında toplamamızı sağlayacak. Dışmerkezlilik hakkında
BÖLÜM 24 TÜREV VE UYGULAMALARI TÜREV VE UYGULAMALARI TÜREV VE UYGULAMALARI
 TÜREV VE UYGULAMALARI TÜREV VE UYGULAMALARI YILLAR 966 967 968 969 97 97 97 975 976 977 978 980 98 98 98 98 985 986 987 988 989 990 99 99 99 99 995 996 997 998 006 007 ÖSS / ÖSS-I ÖYS / ÖSS-II 5 6 6 5
TÜREV VE UYGULAMALARI TÜREV VE UYGULAMALARI YILLAR 966 967 968 969 97 97 97 975 976 977 978 980 98 98 98 98 985 986 987 988 989 990 99 99 99 99 995 996 997 998 006 007 ÖSS / ÖSS-I ÖYS / ÖSS-II 5 6 6 5
İÇİNDEKİLER. Ön Söz...2. Noktanın Analitik İncelenmesi...3. Doğrunun Analitiği Analitik Düzlemde Simetri...25
 İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
KUTUPSAL KOORDİNATLAR
 KUTUPSAL KOORDİNATLAR Geometride, bir noktanın konumunu belirtmek için değişik yöntemler uygulanır. Örnek olarak çok kullanılan Kartezyen (Dik ) Koordinat sistemini anımsatarak çalışmamıza başlayalım.
KUTUPSAL KOORDİNATLAR Geometride, bir noktanın konumunu belirtmek için değişik yöntemler uygulanır. Örnek olarak çok kullanılan Kartezyen (Dik ) Koordinat sistemini anımsatarak çalışmamıza başlayalım.
2. Dereceden Denklem ve Eşitsizlikler x 2 2x + 2m + 1 = 0 denkleminin kökleri x 1 ve x 2 dir. 4x 1 + 5x 2 = 7 ise m aşağıdakilerden hangisidir?
 MC www.matematikclub.com, 006 Cebir Notları Gökhan DEMĐR, gdemir3@ahoo.com.tr. Dereceden Denklem ve Eşitsizlikler- TEST I A) 1 B) C) 3 D) 4 E) 5 1. 1/ = 0 denkleminin köklerinin toplamı aşağıdakilerden
MC www.matematikclub.com, 006 Cebir Notları Gökhan DEMĐR, gdemir3@ahoo.com.tr. Dereceden Denklem ve Eşitsizlikler- TEST I A) 1 B) C) 3 D) 4 E) 5 1. 1/ = 0 denkleminin köklerinin toplamı aşağıdakilerden
1 (c) herhangi iki kompleks sayı olmak üzere
 KOMPLEKS FONKSİYONLAR TEORİSİ UYGULAMA SORULARI- Problem. Aşağıdaki (a) ve (b) de olmak üere (a) olduklarını gösterini. (b) (c) Imi Re Çöüm (a) i olsun. i i (b) i olsun. i i i i i i i i i i Im i Re i (c)
KOMPLEKS FONKSİYONLAR TEORİSİ UYGULAMA SORULARI- Problem. Aşağıdaki (a) ve (b) de olmak üere (a) olduklarını gösterini. (b) (c) Imi Re Çöüm (a) i olsun. i i (b) i olsun. i i i i i i i i i i Im i Re i (c)
2014 LYS MATEMATİK. x lü terimin 1, 3. 3 ab olduğuna göre, ifadesinin değeri kaçtır? 2b a ifade- sinin değeri kaçtır? olduğuna göre, x.
 4 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. ifadesinin değeri kaçtır? 5. P() polinomunda katsaısı kaçtır? 4 lü terimin 4 log log çarpımının değeri kaçtır? 6. 4 olduğuna göre,.
4 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. ifadesinin değeri kaçtır? 5. P() polinomunda katsaısı kaçtır? 4 lü terimin 4 log log çarpımının değeri kaçtır? 6. 4 olduğuna göre,.
4. y=-2 doğrusundan 5 birim uzaklıkta. 5. O(0,0) başlangıç noktasından 3 birim. 6. A(1,2) ve B(5,8) noktalarından eşit. 7. x=-2 doğrusundan ve A(2,0)
 GEOMETRİK YER HAZİNE-1 Analitik düzlemde, verilen bir ortak özelliği sağlayan P(x,y) noktalarının apsis ve ordinatı arasındaki bağıntıya Geometrik yer denklemi denir. Geometrik yer üzerindeki noktalar
GEOMETRİK YER HAZİNE-1 Analitik düzlemde, verilen bir ortak özelliği sağlayan P(x,y) noktalarının apsis ve ordinatı arasındaki bağıntıya Geometrik yer denklemi denir. Geometrik yer üzerindeki noktalar
LİSE ÖĞRENCİLERİNE OKULLARDA YARDIMCI VE ÜNİVERSİTE SINAVLARINA. (YGS ve LYS na) HAZIRLIK İÇİN. Örnek çözümlü. Deneme sınavlı GEOMETRİ-2.
 LİSE ÖĞRENCİLERİNE OKULLARDA YARDIMCI VE ÜNİVERSİTE SINAVLARINA (YGS ve LYS na) HAZIRLIK İÇİN Konu anlatımlı Örnek çözümlü Test çözümlü Test sorulu Deneme sınavlı GEOMETRİ-2 Hazırlayan Erol GEDİKLİ Matematik
LİSE ÖĞRENCİLERİNE OKULLARDA YARDIMCI VE ÜNİVERSİTE SINAVLARINA (YGS ve LYS na) HAZIRLIK İÇİN Konu anlatımlı Örnek çözümlü Test çözümlü Test sorulu Deneme sınavlı GEOMETRİ-2 Hazırlayan Erol GEDİKLİ Matematik
6 II. DERECEDEN FONKSÝYONLAR 2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK. y f(x) f(x)
 6 II. DERECEDEN FNKSÝYNLR (Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MTEMTÝK 1. f(). f() 6 8 T Yukarıda grafiği verilen = f() parabolünün denklemi nedir?( = 6) Yukarıda grafiği verilen
6 II. DERECEDEN FNKSÝYNLR (Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MTEMTÝK 1. f(). f() 6 8 T Yukarıda grafiği verilen = f() parabolünün denklemi nedir?( = 6) Yukarıda grafiği verilen
1-A. Adı Soyadı. Okulu. Sınıfı LYS-1 MATEMATİK TESTİ. Bu Testte; Toplam 50 Adet soru bulunmaktadır. Cevaplama Süresi 75 dakikadır.
 -A Adı Soadı kulu Sınıfı LYS- MATEMATİK TESTİ Bu Testte; Toplam Adet soru bulunmaktadır. Cevaplama Süresi 7 dakikadır. Süre bitiminde Matematik Testi sınav kitapçığınızı gözetmeninize verip Geometri Testi
-A Adı Soadı kulu Sınıfı LYS- MATEMATİK TESTİ Bu Testte; Toplam Adet soru bulunmaktadır. Cevaplama Süresi 7 dakikadır. Süre bitiminde Matematik Testi sınav kitapçığınızı gözetmeninize verip Geometri Testi
1996 ÖYS. 2 nin 2 fazlası kız. 1. Bir sınıftaki örencilerin 5. örencidir. Sınıfta 22 erkek öğrenci olduğuna göre, kız öğrencilerin sayısı kaçtır?
 996 ÖYS. Bir sınıftaki örencilerin nin fazlası kız örencidir. Sınıfta erkek öğrenci olduğuna göre, kız öğrencilerin saısı kaçtır? 8 C) 6 D) E) 6. Saatteki hızı V olan bir hareketti A ve B arasındaki olu
996 ÖYS. Bir sınıftaki örencilerin nin fazlası kız örencidir. Sınıfta erkek öğrenci olduğuna göre, kız öğrencilerin saısı kaçtır? 8 C) 6 D) E) 6. Saatteki hızı V olan bir hareketti A ve B arasındaki olu
ÖZEL TANIMLI FONKSİYONLAR
 ÖZEL TANIMLI FONKSİYONLAR Fonksionlar ve Özel Tanımlı Fonksionlar Özel tanımlı fonksionlar konusu fonksionların alt bir dalıdır. Bu konuu daha ii anlaabilmemiz için fonksionlar ile ilgili bilgilerimizi
ÖZEL TANIMLI FONKSİYONLAR Fonksionlar ve Özel Tanımlı Fonksionlar Özel tanımlı fonksionlar konusu fonksionların alt bir dalıdır. Bu konuu daha ii anlaabilmemiz için fonksionlar ile ilgili bilgilerimizi
7. f(x) = 2sinx cos2x fonksiyonunun. π x 3 2 A) y = 9. f(x) = 1 2 x2 3x + 4 eğrisinin hangi noktadaki teğetinin D) ( 10 3, 4 9 ) E) ( 2 3, 56
 , 006 MC Cebir Notları Gökhan DEMĐR, gdemir@ahoo.com.tr Türev TEST I 7. f() = sin cos fonksionunun. f()= sin( + )cos( ) için f'() nin eşiti nedir? A) B) C) 0 D) E) için erel minimum değeri nedir? A) B)
, 006 MC Cebir Notları Gökhan DEMĐR, gdemir@ahoo.com.tr Türev TEST I 7. f() = sin cos fonksionunun. f()= sin( + )cos( ) için f'() nin eşiti nedir? A) B) C) 0 D) E) için erel minimum değeri nedir? A) B)
Doğrusal Fonksiyonlar, Karesel Fonksiyonlar, Polinomlar ve Rasyonel Fonksiyonlar, Fonksiyon Çizimleri
 Doğrusal Fonksionlar, Karesel Fonksionlar, Polinomlar ve Rasonel Fonksionlar, Fonksion Çizimleri Bir Fonksionun Koordinat Kesişimleri(Intercepts). Bir fonksionun grafiğinin koordinat eksenlerini kestiği
Doğrusal Fonksionlar, Karesel Fonksionlar, Polinomlar ve Rasonel Fonksionlar, Fonksion Çizimleri Bir Fonksionun Koordinat Kesişimleri(Intercepts). Bir fonksionun grafiğinin koordinat eksenlerini kestiği
ÜNİTE. MATEMATİK-1 Prof.Dr.Murat ÖZDEMİR İÇİNDEKİLER HEDEFLER GRAFİK ÇİZİMİ. Simetri ve Asimtot Bir Fonksiyonun Grafiği
 HEDEFLER İÇİNDEKİLER GRAFİK ÇİZİMİ Simetri ve Asimtot Bir Fonksionun Grafiği MATEMATİK-1 Prof.Dr.Murat ÖZDEMİR Bu ünitei çalıştıktan sonra; Fonksionun simetrik olup olmadığını belirleebilecek, Fonksionun
HEDEFLER İÇİNDEKİLER GRAFİK ÇİZİMİ Simetri ve Asimtot Bir Fonksionun Grafiği MATEMATİK-1 Prof.Dr.Murat ÖZDEMİR Bu ünitei çalıştıktan sonra; Fonksionun simetrik olup olmadığını belirleebilecek, Fonksionun
İKİNCİ DERECEDEN FONKSİYONLAR VE GRAFİKLERİ
 İKİNCİ DERECEDEN FONKSİYONLAR VE GRAFİKLERİ TANIM: a, b, c R ve a olmak üzere, f : R R, = f ( ) = a + b + c fonksionuna, ikinci dereceden bir bilinmeenli fonksion denir. { } (, ) : = f ( ) R kümesinin
İKİNCİ DERECEDEN FONKSİYONLAR VE GRAFİKLERİ TANIM: a, b, c R ve a olmak üzere, f : R R, = f ( ) = a + b + c fonksionuna, ikinci dereceden bir bilinmeenli fonksion denir. { } (, ) : = f ( ) R kümesinin
ETKİNLİK ÇÖZÜMLERİ ADIM m(ëa) + m(b) = m(ëa) = ise 2.m(ëA ) = =
 ETKİNLİK ÇÖZÜMLERİ DIM 0. m(ë) 0 0 7 ise.m(ë ) 80 60 8 0.m(ë) m(ë) 8 0 8 7 99 7 66 60. m(ë) m() 8 60 08 dir. 08 R 80 08. R 80 radandır. 99 8 6. 60 06 9 8 60 0 79 8 6 79 8 6 7. irim çemberin üzerindeki
ETKİNLİK ÇÖZÜMLERİ DIM 0. m(ë) 0 0 7 ise.m(ë ) 80 60 8 0.m(ë) m(ë) 8 0 8 7 99 7 66 60. m(ë) m() 8 60 08 dir. 08 R 80 08. R 80 radandır. 99 8 6. 60 06 9 8 60 0 79 8 6 79 8 6 7. irim çemberin üzerindeki
[ AN ] doğrusu açıortay olduğundan;
![[ AN ] doğrusu açıortay olduğundan; [ AN ] doğrusu açıortay olduğundan;](/thumbs/69/60247548.jpg) . Bir havuzu bir musluk 6 saatte, başka bir musluk 8 saatte dolduruyor. Bu iki musluk kapalı iken, havuzun altında bulunan üçüncü bir musluk, dolu havuzu saatte boşaltabiliyor. Üç musluk birden açılırsa,boş
. Bir havuzu bir musluk 6 saatte, başka bir musluk 8 saatte dolduruyor. Bu iki musluk kapalı iken, havuzun altında bulunan üçüncü bir musluk, dolu havuzu saatte boşaltabiliyor. Üç musluk birden açılırsa,boş
FONKSİYONLAR ÜNİTE 3. ÜNİTE 3. ÜNİTE 3. ÜNİTE 3. ÜNİT
 FONKSİYONLAR ÜNİTE. ÜNİTE. ÜNİTE. ÜNİTE. ÜNİT. Kazanım : Gerçek saılar üzerinde tanımlanmış fonksion kavramını açıklar. Tanım kümesi, değer kümesi, görüntü kümesi kavramlarını açıklar.. Kazanım : Fonksionların
FONKSİYONLAR ÜNİTE. ÜNİTE. ÜNİTE. ÜNİTE. ÜNİT. Kazanım : Gerçek saılar üzerinde tanımlanmış fonksion kavramını açıklar. Tanım kümesi, değer kümesi, görüntü kümesi kavramlarını açıklar.. Kazanım : Fonksionların
Gerilme Dönüşümü. Bölüm Hedefleri
 Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
25. f: R { 4} R 28. ( ) 3 2 ( ) 26. a ve b reel sayılar olmak üzere, 27. ( ) eğrisinin dönüm noktasının ordinatı 10 olduğuna göre, m kaçtır?
 . f: R { 4} R, > ise ( ) 4 f =, ise 6 8. ( ) f = 6 + m + 4 eğrisinin dönüm noktasının ordinatı olduğuna göre, m kaçtır? ) 7 ) 8 ) 9 ) E) fonksiyonu aşağıdaki değerlerinin hangisinde süreksizdir? ) ) )
. f: R { 4} R, > ise ( ) 4 f =, ise 6 8. ( ) f = 6 + m + 4 eğrisinin dönüm noktasının ordinatı olduğuna göre, m kaçtır? ) 7 ) 8 ) 9 ) E) fonksiyonu aşağıdaki değerlerinin hangisinde süreksizdir? ) ) )
Trigonometrik Fonksiyonlar
 Trigonometrik Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 6 Amaçlar Bu üniteyi çalıştıktan sonra; açı kavramını hatırlayacak, açıların derece ölçümünü radyan ölçümüne ve tersine çevirebilecek, trigonometrik
Trigonometrik Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 6 Amaçlar Bu üniteyi çalıştıktan sonra; açı kavramını hatırlayacak, açıların derece ölçümünü radyan ölçümüne ve tersine çevirebilecek, trigonometrik
11 SINIF MATEMATİK. Fonksiyonlarda Uygulamalar Denklemler ve Eşitsizlik Sistemleri
 SINIF MATEMATİK Fonksionlarda Ugulamalar Denklemler ve Eşitsizlik Sistemleri Fonksionlarla İlgili Ugulamalar İkinci Dereceden Fonksionlar ve Grafikleri Fonksionların Dönüşümleri Denklem ve Eşitsizlik Sistemleri
SINIF MATEMATİK Fonksionlarda Ugulamalar Denklemler ve Eşitsizlik Sistemleri Fonksionlarla İlgili Ugulamalar İkinci Dereceden Fonksionlar ve Grafikleri Fonksionların Dönüşümleri Denklem ve Eşitsizlik Sistemleri
Chapter 1 İçindekiler
 Chapter 1 İçindekiler Kendinizi Test Edin iii 10 Birinci Mertebeden Diferansiel Denklemler 565 10.1 Arılabilir Denklemler 566 10. Lineer Denklemler 571 10.3 Matematiksel Modeller 576 10.4 Çözümü Olmaan
Chapter 1 İçindekiler Kendinizi Test Edin iii 10 Birinci Mertebeden Diferansiel Denklemler 565 10.1 Arılabilir Denklemler 566 10. Lineer Denklemler 571 10.3 Matematiksel Modeller 576 10.4 Çözümü Olmaan
BÖLÜM 4 4- TÜREV KAVRAMI 4- TÜREV KAVRAMI. Tanım y = fonksiyonunda x değişkeni x. artımını alırken y de. kadar artsın. = x.
 - TÜREV KAVRAMI - TÜREV KAVRAMI 7 iadesinin türevini alınız. Çözüm lim lim 7 7 lim 7 7 lim lim onksionunun türevini alınız. Tanım onksionunda değişkeni artımını alırken de kadar artsın. oranının giderken
- TÜREV KAVRAMI - TÜREV KAVRAMI 7 iadesinin türevini alınız. Çözüm lim lim 7 7 lim 7 7 lim lim onksionunun türevini alınız. Tanım onksionunda değişkeni artımını alırken de kadar artsın. oranının giderken
LYS Matemat k Deneme Sınavı
 LYS Matematk Deneme Sınavı. Üç basamaklı doğal saılardan kaç tanesi, 8 ve ile tam bölünür? 8 9. ile in geometrik ortası z dir. ( z). ( z ). z aşağıdakilerden hangisidir?. 9 ifadesinin cinsinden değeri
LYS Matematk Deneme Sınavı. Üç basamaklı doğal saılardan kaç tanesi, 8 ve ile tam bölünür? 8 9. ile in geometrik ortası z dir. ( z). ( z ). z aşağıdakilerden hangisidir?. 9 ifadesinin cinsinden değeri
ÜNİTE. MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI İÇİNDEKİLER HEDEFLER DOĞRULAR VE PARABOLLER
 HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
ÖRNEK : x. y = 1 biçiminde verilen fonksiyonun grafiğini. çiziniz. Çizim : x. y = 1 olması ancak x =1ve y =1 yada x =-1ve. x =1ve x =-1ve ÖRNEK :
 MC www.matematikclub.com, 6 Cebir Notları Gökhan DEMĐR, gdemir@ahoo.com.tr Özel Tanımlı Fonksionlar. Tam değer fonksionu: Tanım: Tamsaı ise kendisi, tamsaı değilse kendinden önce gelen ilk tamsaı (kendinden
MC www.matematikclub.com, 6 Cebir Notları Gökhan DEMĐR, gdemir@ahoo.com.tr Özel Tanımlı Fonksionlar. Tam değer fonksionu: Tanım: Tamsaı ise kendisi, tamsaı değilse kendinden önce gelen ilk tamsaı (kendinden
12. SINIF. Fonksiyonlar - 1 TEST. 1. kx + 6 fonksiyonu sabit fonksiyon olduğuna göre aşağıdakilerden hangisidir? k. = 1 olduğuna göre k. kaçtır?
 . SINIF M Fonksionlar. f ( + a ) + vef( ) 7 olduğuna göre a kaçtır? E) TEST. f ( ) k + 6 fonksionu sabit fonksion olduğuna f ( ) göre aşağıdakilerden k E). f( ) 6 k ve f ( ) olduğuna göre k kaçtır? E)
. SINIF M Fonksionlar. f ( + a ) + vef( ) 7 olduğuna göre a kaçtır? E) TEST. f ( ) k + 6 fonksionu sabit fonksion olduğuna f ( ) göre aşağıdakilerden k E). f( ) 6 k ve f ( ) olduğuna göre k kaçtır? E)
MATEMATİK MATEMATİK-GEOMETRİ SINAVI LİSANS YERLEŞTİRME SINAVI-1 TESTİ SORU KİTAPÇIĞI 08
 LİSNS YRLŞTİRM SINVI- MTMTİK-GMTRİ SINVI MTMTİK TSTİ SRU KİTPÇIĞI 08 U SRU KİTPÇIĞI LYS- MTMTİK TSTİ SRULRINI İÇRMKTİR. . u testte 0 soru vardýr. MTMTİK TSTİ. evaplarýnýzý, cevap kâðýdýnın Matematik Testi
LİSNS YRLŞTİRM SINVI- MTMTİK-GMTRİ SINVI MTMTİK TSTİ SRU KİTPÇIĞI 08 U SRU KİTPÇIĞI LYS- MTMTİK TSTİ SRULRINI İÇRMKTİR. . u testte 0 soru vardýr. MTMTİK TSTİ. evaplarýnýzý, cevap kâðýdýnın Matematik Testi
Üç Boyutlu Uzayda Koordinat sistemi
 Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Parametrik doğru denklemleri 1
 Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
PROJE ADI: Bir Koniğin Üzerindeki Veya Dışındaki Bir Noktadan Çizilen Teğetlerin Denklemlerini Matrisler Yardımıyla Bulma
 PROJE ADI: Bir Koniğin Üzerindeki Veya Dışındaki Bir oktadan Çizilen Teğetlerin Denklemlerini Matrisler Yardımıyla Bulma PROJEİ AMACI: Bu projede herhangi bir koniğin üzerindeki veya dışındaki bir noktadan
PROJE ADI: Bir Koniğin Üzerindeki Veya Dışındaki Bir oktadan Çizilen Teğetlerin Denklemlerini Matrisler Yardımıyla Bulma PROJEİ AMACI: Bu projede herhangi bir koniğin üzerindeki veya dışındaki bir noktadan
11. SINIF GEOMETRİ KONU ÖZETİ
 2012 11. SINIF GEOMETRİ KONU ÖZETİ TOLGA YAVAN Matematik Öğretmeni 1. ÜNİTE: DÖRTGENLER DÖRTGEN VE TEMEL ELEMANLARI Herhangi üçü doğrusal olmayan A, B, C ve D noktaları verilsin. [AB], [BC], [CD] ve [DA]
2012 11. SINIF GEOMETRİ KONU ÖZETİ TOLGA YAVAN Matematik Öğretmeni 1. ÜNİTE: DÖRTGENLER DÖRTGEN VE TEMEL ELEMANLARI Herhangi üçü doğrusal olmayan A, B, C ve D noktaları verilsin. [AB], [BC], [CD] ve [DA]
{ } ( ) ( ) 3. β = (x,y) : y - x = 1, x,y R bağıntısı Aşağıdaki sayılardan hangisi asal alabilir?
 . Aşağıdaki saılardan hangisi asal alabilir? A) 5!+7! B) 7 - ) 54 D) A seçeneği: 5!+7! 5! ( + 6.7 ) 5!.4 7 - E ) 57 5!.4 saısı 5! ile bölünür.o halde asal değildir. B seçeneği: 7-8- 7 7 kendisi hariç hiçbir
. Aşağıdaki saılardan hangisi asal alabilir? A) 5!+7! B) 7 - ) 54 D) A seçeneği: 5!+7! 5! ( + 6.7 ) 5!.4 7 - E ) 57 5!.4 saısı 5! ile bölünür.o halde asal değildir. B seçeneği: 7-8- 7 7 kendisi hariç hiçbir
Analitik Geometri Özeti
 Analitik Geometri Özeti David Pierce 3 Nisan 2015, 10:49 Matematik Bölümü Mimar Sinan Güzel Sanatlar Üniversitesi İstanbul dpierce@msgsu.edu.tr http://mat.msgsu.edu.tr/~dpierce/ İçindekiler 1 Denklik bağıntıları
Analitik Geometri Özeti David Pierce 3 Nisan 2015, 10:49 Matematik Bölümü Mimar Sinan Güzel Sanatlar Üniversitesi İstanbul dpierce@msgsu.edu.tr http://mat.msgsu.edu.tr/~dpierce/ İçindekiler 1 Denklik bağıntıları
9. BÖLÜM. Özel Tanımlı Fonksiyonlar ÇİFT VE TEK FONKSİYONLAR: ÖRNEK ÖRNEK ÇÖZÜM ÇÖZÜM. M A T E M A T İ K
 M A T E M A T İ K www.akademitemellisesi.com ÇİFT VE TEK FONKSİYONLAR: f:ar (A R) fonksionu için, 9. BÖLÜM ) Her A için f( ) = f() ise f e çift fonksion denir. olduğundan ne tek nede çifttir. MUTL AK DEĞER
M A T E M A T İ K www.akademitemellisesi.com ÇİFT VE TEK FONKSİYONLAR: f:ar (A R) fonksionu için, 9. BÖLÜM ) Her A için f( ) = f() ise f e çift fonksion denir. olduğundan ne tek nede çifttir. MUTL AK DEĞER
Vektörler. Skaler büyüklükler. Vektörlerin 2 ve 3 boyutta gösterimi. Vektörel büyüklükler. 1. Şekil I de A vektörü gösterilmiştir.
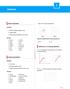 1 Vektörler Skaler büüklükler 1. de A vektörü gösterilmiştir. Özellikler: Sadece büüklüğü (şiddeti) vardır. Negatif olabilir. Skaler fiziksel büüklüklerin birimi vardır. Örnekler: Zaman Kütle Hacim Özkütle
1 Vektörler Skaler büüklükler 1. de A vektörü gösterilmiştir. Özellikler: Sadece büüklüğü (şiddeti) vardır. Negatif olabilir. Skaler fiziksel büüklüklerin birimi vardır. Örnekler: Zaman Kütle Hacim Özkütle
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
MECHANICS OF MATERIALS
 00 The McGraw-Hill Companies, Inc. All rights reserved. T E CHAPTER 7 Gerilme MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Dönüşümleri Fatih Alibeoğlu 00 The McGraw-Hill
00 The McGraw-Hill Companies, Inc. All rights reserved. T E CHAPTER 7 Gerilme MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Dönüşümleri Fatih Alibeoğlu 00 The McGraw-Hill
1998 ÖYS. 1. Üç basamaklı bir x doğal sayısının 7. iki basamaklı bir y doğal sayısına eşittir. Buna göre, y doğal sayısı en az kaç olabilir?
 99 ÖYS. Üç basamaklı bir doğal saısının 7 katı, iki basamaklı bir doğal saısına eşittir. Buna göre, doğal saısı en az kaç olabilir? A) B) C) 6. Bugünkü aşları 6 ve ile orantılı olan iki kardeşin 6 ıl sonraki
99 ÖYS. Üç basamaklı bir doğal saısının 7 katı, iki basamaklı bir doğal saısına eşittir. Buna göre, doğal saısı en az kaç olabilir? A) B) C) 6. Bugünkü aşları 6 ve ile orantılı olan iki kardeşin 6 ıl sonraki
Fonksiyonlar ve Grafikleri
 Fonksionlar ve Grafikleri Isınma Hareketleri Aşağıda verilenleri inceleiniz. A f f(a) 7 f: Çocukları annelerine götürüor. Fonksion olma şartı: Her çocuğun annesi olmalı ve bir tane olmalı. ( çocuk annenin
Fonksionlar ve Grafikleri Isınma Hareketleri Aşağıda verilenleri inceleiniz. A f f(a) 7 f: Çocukları annelerine götürüor. Fonksion olma şartı: Her çocuğun annesi olmalı ve bir tane olmalı. ( çocuk annenin
DERSİN ADI: MATEMATİK II MAT II (12) KUTUPSAL KOORDİNATLAR VE UYGULAMALARI 1. KUTUPSAL KOORDİNATLAR 2. EĞRİ ÇİZİMLERİ
 DERSİN ADI: MATEMATİK II MAT II (1) ÜNİTE: KUTUPSAL KOORDİNATLAR VE UYGULAMALARI 1. KUTUPSAL KOORDİNATLAR. EĞRİ ÇİZİMLERİ GEREKLİ ÖN BİLGİLER 1. Trigonometrik fonksiyonlar. İntegral formülleri KONU ANLATIMI
DERSİN ADI: MATEMATİK II MAT II (1) ÜNİTE: KUTUPSAL KOORDİNATLAR VE UYGULAMALARI 1. KUTUPSAL KOORDİNATLAR. EĞRİ ÇİZİMLERİ GEREKLİ ÖN BİLGİLER 1. Trigonometrik fonksiyonlar. İntegral formülleri KONU ANLATIMI
1. BÖLÜM Polinomlar BÖLÜM II. Dereceden Denklemler BÖLÜM II. Dereceden Eşitsizlikler BÖLÜM Parabol
 ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
1977 ÜSS. 2 y ifadesi aşağıdakilerden hangisine eşittir? 1 x. 2 y. 1 y. 1 y. 1 x. 2 x. 2 x. 1 x. 1 y. 1 x. 1 y. 1 x. 1 y 2 C) 4 E)
 77 ÜSS. ifadesi aşağıdakilerden hangisine eşittir?. C) 4 E). Şekilde a+b+c+d açılarının toplamı kaç dik açıdır? (açılar pozitif önlüdür.) 4 C) 6 7 E) 8 Verilen şekilde açıların ölçüleri verilmiştir. En
77 ÜSS. ifadesi aşağıdakilerden hangisine eşittir?. C) 4 E). Şekilde a+b+c+d açılarının toplamı kaç dik açıdır? (açılar pozitif önlüdür.) 4 C) 6 7 E) 8 Verilen şekilde açıların ölçüleri verilmiştir. En
Lys x 2 + y 2 = (6k) 2. (x 2k) 2 + y 2 = (2k 5) 2 olduğuna göre x 2 y 2 =? Cevap: 14k 2
 1. 1 =? Lys 1 7. x + y = (6k) (x k) + y = (k 5) olduğuna göre x y =?. 6 a.b = ise a + 1 b. b 1 a =? 1k 8. x ve y birbirinden farklı pozitif gerçel sayılar olmak üzere, x y y x. x.y = (x y) ise x y =?.
1. 1 =? Lys 1 7. x + y = (6k) (x k) + y = (k 5) olduğuna göre x y =?. 6 a.b = ise a + 1 b. b 1 a =? 1k 8. x ve y birbirinden farklı pozitif gerçel sayılar olmak üzere, x y y x. x.y = (x y) ise x y =?.
Basým Yeri: Ceren Matbaacılık AŞ. Basým Tarihi: Haziran / ISBN Numarası: Sertifika No: 33674
 kapak safası İÇİNDEKİLER. ÜNİTE FNKSİYNLARDA İŞLEMLER VE UYGULAMALARI Fonksionların Simetrileri ve Cebirsel Özellikleri... 4 Tek ve Çift Fonksionlar... 4 Fonksionlarda İşlemler... 6 Konu Testleri -...
kapak safası İÇİNDEKİLER. ÜNİTE FNKSİYNLARDA İŞLEMLER VE UYGULAMALARI Fonksionların Simetrileri ve Cebirsel Özellikleri... 4 Tek ve Çift Fonksionlar... 4 Fonksionlarda İşlemler... 6 Konu Testleri -...
EŞİTSİZLİK SİSTEMLERİ Test -1
 EŞİTSİZLİK SİSTEMLERİ Test -1 1. 9 5. 69 A) (, ] B) (, ) C) (, ) D) [, ] E) [, ) A) B) {} C) {, } D) R E) R {}. 5 6. 1 A) (, 5) B) [, 5] C) (, 5) D) (5, ) E) (, ) A) (, 1] B) (, ) C) [1, ) D) (, ] [1,
EŞİTSİZLİK SİSTEMLERİ Test -1 1. 9 5. 69 A) (, ] B) (, ) C) (, ) D) [, ] E) [, ) A) B) {} C) {, } D) R E) R {}. 5 6. 1 A) (, 5) B) [, 5] C) (, 5) D) (5, ) E) (, ) A) (, 1] B) (, ) C) [1, ) D) (, ] [1,
Aralıklar, Eşitsizlikler, Mutlak Değer
 ARALIKLAR Gerçel sayıların, aralık olarak adlandırılan bazı kümeleri kalkülüste sık sık kullanılır ve geometrik olarak doğru parçalarına karşılık gelir. Örneğin, a < b ise, a dan b ye açık aralık, a ile
ARALIKLAR Gerçel sayıların, aralık olarak adlandırılan bazı kümeleri kalkülüste sık sık kullanılır ve geometrik olarak doğru parçalarına karşılık gelir. Örneğin, a < b ise, a dan b ye açık aralık, a ile
Noktanın y = a Doğrusuna Göre Simetriği Noktanın y = x ve y = x (I. ve II. açıortay) Doğrularına Göre Simetriği Noktanın Doğruya Göre
 İÇİNDEKİLER Dik Koordinat Sistemi... Dik Koordinat Sisteminde Bölgeler... İki Nokta Arası Uzaklık... rta Nokta... İki Doğru Parçasını Belli randa Bölen Noktanın Koordinatları... Analitik Düzlemde Paralelkenar...
İÇİNDEKİLER Dik Koordinat Sistemi... Dik Koordinat Sisteminde Bölgeler... İki Nokta Arası Uzaklık... rta Nokta... İki Doğru Parçasını Belli randa Bölen Noktanın Koordinatları... Analitik Düzlemde Paralelkenar...
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ
 DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için arılan
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için arılan
H. Turgay Kaptanoğlu. Bu yazüda çember, elips, parabol ve hiperbolden. çemberin denklemi olan
 KONİNİN KESİTLERİ (I) H. Turgay Kaptanoğlu Bu yazüda çember, elips, parabol ve hiperbolden söz edeceğiz. Bu düzlem eğrilerinin denklemlerini elde ettikten sonra birkaç değişik konuyu açacağüz. Bunlar,
KONİNİN KESİTLERİ (I) H. Turgay Kaptanoğlu Bu yazüda çember, elips, parabol ve hiperbolden söz edeceğiz. Bu düzlem eğrilerinin denklemlerini elde ettikten sonra birkaç değişik konuyu açacağüz. Bunlar,
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
İÇİNDEKİLER. Tekrar Zamanı TÜREVİN GEOMETRİK YORUMU ÇÖZÜMLÜ TEST 1... 52 ÇÖZÜMLÜ TEST 2... 54 MAKS. - MİN. PROBLEMLERİ. Uygulama Zamanı 1...
 İÇİNDEKİLER TÜREVİN GEOMETRİK YORUMU Teğet ve Normal Doğruların Eğimi... Teğet Doğrusunun Eğim Açısı... Teğet ve Normal Denklemleri... Eğrinin Teğetine Paralel ve Dik Doğrular... Grafikte Teğet I... 5
İÇİNDEKİLER TÜREVİN GEOMETRİK YORUMU Teğet ve Normal Doğruların Eğimi... Teğet Doğrusunun Eğim Açısı... Teğet ve Normal Denklemleri... Eğrinin Teğetine Paralel ve Dik Doğrular... Grafikte Teğet I... 5
[ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1
![[ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1 [ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1](/thumbs/96/127250868.jpg) ..3 Ters Trigonometrik Fonksionlar Önceki kesimde belirtilen bütün trigonometrik fonksionlar perodik olduklarından görüntü kümesindeki her değeri sonsuz noktada alırlar. Bölece trigonometrik fonksionlar
..3 Ters Trigonometrik Fonksionlar Önceki kesimde belirtilen bütün trigonometrik fonksionlar perodik olduklarından görüntü kümesindeki her değeri sonsuz noktada alırlar. Bölece trigonometrik fonksionlar
DOĞRUNUN ANALİTİK İNCELEMESİ
 Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
Fonksiyonlar ve Grafikleri
 Fonksionlar ve Grafikleri Isınma Hareketleri Aşağıda verilenleri inceleiniz. A f f(a) 7 çocuk baan f: Çocukları annelerine götürüor. Fonksion olma şartı: Her çocuğun annesi olmalı ve bir tane olmalı. (
Fonksionlar ve Grafikleri Isınma Hareketleri Aşağıda verilenleri inceleiniz. A f f(a) 7 çocuk baan f: Çocukları annelerine götürüor. Fonksion olma şartı: Her çocuğun annesi olmalı ve bir tane olmalı. (
1998 ÖYS. orantılı olacaktır. Bu iki kardeşten büyük olanın bugünkü yaşı kaçtır? 1. Üç basamaklı bir x doğal sayısının 7
 998 ÖYS. Üç basamaklı bir doğal sayısının 7 katı, iki basamaklı bir y doğal sayısına eşittir. Buna göre, y doğal sayısı en az kaç olabilir? orantılı olacaktır. Bu iki kardeşten büyük olanın bugünkü yaşı
998 ÖYS. Üç basamaklı bir doğal sayısının 7 katı, iki basamaklı bir y doğal sayısına eşittir. Buna göre, y doğal sayısı en az kaç olabilir? orantılı olacaktır. Bu iki kardeşten büyük olanın bugünkü yaşı
Cebir Notları. Karmaşık sayılar TEST I. Gökhan DEMĐR, 2006
 MC Karmaşık saılar www.matematikclub.cm, 006 Cebir Ntları Gökhan DEMĐR, gdemir@ah.cm.tr TEST I. i 897 + i 975 + i 997 i 995 tplamının snucu i B) i C) i D) i E) 5i 8. Z = i nin kutupsal biçimi (cs0 + isin0)
MC Karmaşık saılar www.matematikclub.cm, 006 Cebir Ntları Gökhan DEMĐR, gdemir@ah.cm.tr TEST I. i 897 + i 975 + i 997 i 995 tplamının snucu i B) i C) i D) i E) 5i 8. Z = i nin kutupsal biçimi (cs0 + isin0)
A A A A A A A A A A A
 LYS 1 GMTRİ TSTİ 1. u testte sırasıyla Geometri (1 ) nalitik Geometri (3 30) ile ilgili 30 soru vardır.. evaplarınızı, cevap kâğıdının Geometri Testi için ayrılan kısmına işaretleyiniz. 1. bir üçgen =
LYS 1 GMTRİ TSTİ 1. u testte sırasıyla Geometri (1 ) nalitik Geometri (3 30) ile ilgili 30 soru vardır.. evaplarınızı, cevap kâğıdının Geometri Testi için ayrılan kısmına işaretleyiniz. 1. bir üçgen =
Ders 7: Konikler - Tanım
 Ders 7: Konikler - Tanım Şimdie kadar nokta ve doğrular ve bunların ilişkilerini konuştuk. Bu derste eni bir kümeden söz edeceğiz: kuadrikler ve düzlemdeki özel adı konikler. İzdüşümsel doğrular, doğrusal
Ders 7: Konikler - Tanım Şimdie kadar nokta ve doğrular ve bunların ilişkilerini konuştuk. Bu derste eni bir kümeden söz edeceğiz: kuadrikler ve düzlemdeki özel adı konikler. İzdüşümsel doğrular, doğrusal
İç-Çarpım Uzayları ÜNİTE. Amaçlar. İçindekiler. Yazar Öğr. Grv. Dr. Nevin ORHUN
 İç-Çarpım Uzayları Yazar Öğr. Grv. Dr. Nevin ORHUN ÜNİTE Amaçlar Bu üniteyi çalıştıktan sonra; R n, P n (R), M nxn vektör uzaylarında iç çarpım kavramını tanıyacak ve özelliklerini görmüş olacaksınız.
İç-Çarpım Uzayları Yazar Öğr. Grv. Dr. Nevin ORHUN ÜNİTE Amaçlar Bu üniteyi çalıştıktan sonra; R n, P n (R), M nxn vektör uzaylarında iç çarpım kavramını tanıyacak ve özelliklerini görmüş olacaksınız.
2 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var ise bulunuz.
 ANALİZ 1.) a) sgn. sgn( 1) = 1 denkleminin çözüm kümesini b) f ( ) 3 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var
ANALİZ 1.) a) sgn. sgn( 1) = 1 denkleminin çözüm kümesini b) f ( ) 3 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var
çemberi ile O Çemberlerin birbirine göre durumlarını inceleyelim. İlk durumda alalım. olduğu takdirde O2K1
 . merkezli R yarıçaplı Ç çemberi ile merkezli R yarıçaplı ve noktasından geçen Ç çemberi veriliyor. Ç üzerinde, T Ç K T Ç, ve K K T K olacak şekilde bir T noktası alınıyor. Buna göre, uzunluklarından birinin
. merkezli R yarıçaplı Ç çemberi ile merkezli R yarıçaplı ve noktasından geçen Ç çemberi veriliyor. Ç üzerinde, T Ç K T Ç, ve K K T K olacak şekilde bir T noktası alınıyor. Buna göre, uzunluklarından birinin
z z Genel yükleme durumunda, bir Q noktasını üç boyutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni
 GERİLME VE ŞEKİL DEĞİŞTİRME DÖNÜŞÜM BAĞINTILARI Q z Genel ükleme durumunda, bir Q noktasını üç boutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni gösterilebilir: σ, σ, σ z, τ, τ z, τ z.
GERİLME VE ŞEKİL DEĞİŞTİRME DÖNÜŞÜM BAĞINTILARI Q z Genel ükleme durumunda, bir Q noktasını üç boutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni gösterilebilir: σ, σ, σ z, τ, τ z, τ z.
12-B. Polinomlar - 1 TEST. olduğuna göre P(x - 2, y + 4) polinomunun katsayılar toplamı kaçtır? olduğuna göre A B kaçtır? A) 78 B) 73 C) 62 D 58 E) 33
 -B TEST Polinomlar -. Py _, i= y- y + 5y- olduğuna göre P( -, y + ) polinomunun katsayılar toplamı. - 6 = A - 5 + - + B - olduğuna göre A B 78 B) 7 6 D 58 E) B) D) - E) -. -a- b = _ + -5i_ -ci eşitliğine
-B TEST Polinomlar -. Py _, i= y- y + 5y- olduğuna göre P( -, y + ) polinomunun katsayılar toplamı. - 6 = A - 5 + - + B - olduğuna göre A B 78 B) 7 6 D 58 E) B) D) - E) -. -a- b = _ + -5i_ -ci eşitliğine
ÖSYM. 1. Bu testte 40 soru vardır. 2. Cevaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz AYT/Matematik
 MATEMATİK TESTİ 1. Bu testte 40 soru vardır. 2. Cevaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz. 1. 2. a bir gerçel sayı olmak üzere, karmaşık sayılarda eşitliği veriliyor.
MATEMATİK TESTİ 1. Bu testte 40 soru vardır. 2. Cevaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz. 1. 2. a bir gerçel sayı olmak üzere, karmaşık sayılarda eşitliği veriliyor.
11. SINIF. No Konular Kazanım Sayısı GEOMETRİ TRİGONOMETRİ Yönlü Açılar Trigonometrik Fonksiyonlar
 11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
7 2 işleminin sonucu kaçtır? A) 7 B) 6 C) 5 D) 4 E) 3. Not : a buluruz. Doğru Cevap : E şıkkı
 ) 3 4 5 3 0 A) B) 6 C) 5 D) 4 E) 3 0 Not : a 0 3 4 5 3 4 5 3 3 3.3.3... ÜSLÜ SAYILAR QUİZİ VE CEVAPLARI 6 4 4 3 buluruz. Doğru Cevap : E şıkkı 0 ) n bir doğal saı olmak üzere, ( ) ( ) n ( ) n n n A) 4
) 3 4 5 3 0 A) B) 6 C) 5 D) 4 E) 3 0 Not : a 0 3 4 5 3 4 5 3 3 3.3.3... ÜSLÜ SAYILAR QUİZİ VE CEVAPLARI 6 4 4 3 buluruz. Doğru Cevap : E şıkkı 0 ) n bir doğal saı olmak üzere, ( ) ( ) n ( ) n n n A) 4
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ
 DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için arılan
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için arılan
diferansiyel hale getiren) bir integrasyon çarpanı olur? belirleyiniz, bu çarpanı kullanarak denklemin çözümünü bulunuz.
 Diferansiel Denklemler I /8 Çalışma Soruları 9.0.04 A. Aşağıda istenilenleri elde ediniz!. ( e +. d + ( e + k. d 0 denkleminin tam diferansiel denklem olabilmesi için ugun k saısını belirleiniz. Bu k saısı
Diferansiel Denklemler I /8 Çalışma Soruları 9.0.04 A. Aşağıda istenilenleri elde ediniz!. ( e +. d + ( e + k. d 0 denkleminin tam diferansiel denklem olabilmesi için ugun k saısını belirleiniz. Bu k saısı
LYS Matemat k Deneme Sınavı
 LYS Matematk Deneme Sınavı. abba dört basamaklı, ab iki basamaklı doğal saıları için, abba ab. a b eşitliğini sağlaan kaç farklı (a, b) doğal saı ikilisi vardır? 7 olduğuna göre, a b toplamı kaçtır? 9.,,
LYS Matematk Deneme Sınavı. abba dört basamaklı, ab iki basamaklı doğal saıları için, abba ab. a b eşitliğini sağlaan kaç farklı (a, b) doğal saı ikilisi vardır? 7 olduğuna göre, a b toplamı kaçtır? 9.,,
12. SINIF. Uzayda Vektörler-1 TEST. 1. Uzaydaki doğru parçaları için aşağıdaki önermelerden hangisi yanlıştır?
 1. SINIF Uada Vektörler-1 1. Uadaki doğru parçaları için aşağıdaki önermelerden hangisi anlıştır? Akırı doğru parçaları farklı dülemlerdedir. Akırı doğru parçaları farklı doğrultudadır. İki doğru parçasının
1. SINIF Uada Vektörler-1 1. Uadaki doğru parçaları için aşağıdaki önermelerden hangisi anlıştır? Akırı doğru parçaları farklı dülemlerdedir. Akırı doğru parçaları farklı doğrultudadır. İki doğru parçasının
NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl
![NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl](/thumbs/70/62427826.jpg) NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm lan Örnek 0 nalitik düzlemde ( 0 c h b h a h c b ( 0 ( 0 a a h b h a b c h lan( = = = c Yukarıdaki verilenlere göre lan( kaç birimkaredir? 6 8 9 E c b Taban:
NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm lan Örnek 0 nalitik düzlemde ( 0 c h b h a h c b ( 0 ( 0 a a h b h a b c h lan( = = = c Yukarıdaki verilenlere göre lan( kaç birimkaredir? 6 8 9 E c b Taban:
DERS 2. Fonksiyonlar
 DERS Fonksionlar.1. Fonksion Kavramı. Her bilim dalının önemli bir işlevi, çeşitli nesneler vea büüklükler arasında eşlemeler kurmaktır. Böle bir eşleme kurulması tahmin ürütme olanağı verir. Örneğin,
DERS Fonksionlar.1. Fonksion Kavramı. Her bilim dalının önemli bir işlevi, çeşitli nesneler vea büüklükler arasında eşlemeler kurmaktır. Böle bir eşleme kurulması tahmin ürütme olanağı verir. Örneğin,
4. y=-2 doğrusundan 5 birim uzaklıkta. 5. O(0,0) başlangıç noktasından 3 birim. 6. A(1,2) ve B(5,8) noktalarından eşit. 7. x=-2 doğrusundan ve A(2,0)
 GEOMETRİK YER HAZİNE-1 Analitik düzlemde, verilen bir ortak özelliği sağlayan P(x,y) noktalarının apsis ve ordinatı arasındaki bağıntıya Geometrik yer denklemi denir. 4. y=-2 doğrusundan 5 birim uzaklıkta
GEOMETRİK YER HAZİNE-1 Analitik düzlemde, verilen bir ortak özelliği sağlayan P(x,y) noktalarının apsis ve ordinatı arasındaki bağıntıya Geometrik yer denklemi denir. 4. y=-2 doğrusundan 5 birim uzaklıkta
MATEMATİK TESTİ LYS YE DOĞRU. 1. Bu testte Matematik ile ilgili 50 soru vardır.
 MTMTİK TSTİ LYS-. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a, b, c birer reel sayı
MTMTİK TSTİ LYS-. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a, b, c birer reel sayı
Matematikte karşılaştığınız güçlükler için endişe etmeyin. Emin olun benim karşılaştıklarım sizinkilerden daha büyüktür.
 - 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
- 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
Mustafa YAĞCI, Parabol ile Eğrilerin Kesişimi
 www.mustafaagci.com.tr, 11 Ceir Notları Mustafa YAĞCI, agcimustafa@ahoo.com Paraol ile Eğrilerin Kesişimi P araol İle Doğrunun Birirlerine Göre Durumları. Aslında sadece paraol ve doğru çifti için değil,
www.mustafaagci.com.tr, 11 Ceir Notları Mustafa YAĞCI, agcimustafa@ahoo.com Paraol ile Eğrilerin Kesişimi P araol İle Doğrunun Birirlerine Göre Durumları. Aslında sadece paraol ve doğru çifti için değil,
Öğrenci Seçme Sınavı (Öss) / 18 Haziran Matematik II Soruları ve Çözümleri. = 1 olur.
 Öğrenci Seçme Sınavı (Öss) / 8 Haziran 6 Matematik II Soruları ve Çözümleri x, x. f(x) x ise fonksiyonu için,, x olduğuna göre, a b kaçtır? lim + x f ( x) a ve lim x f ( x) b A) B) C) D) E) Çözüm x x için
Öğrenci Seçme Sınavı (Öss) / 8 Haziran 6 Matematik II Soruları ve Çözümleri x, x. f(x) x ise fonksiyonu için,, x olduğuna göre, a b kaçtır? lim + x f ( x) a ve lim x f ( x) b A) B) C) D) E) Çözüm x x için
BİRİM ŞEKİLDEĞİŞTİRME DÖNÜŞÜMÜ
 BİRİM ŞEKİLDEĞİŞTİRME DÖNÜŞÜMÜ DÜZLEM-BİRİM ŞEKİLDEĞİŞTİRME 3D durumda, bir noktadaki birim şekil değiştirme durumu 3 normal birim şekildeğiştirme bileşeni,, z, ve 3 kesme birim şekildeğiştirme bileşeninden,
BİRİM ŞEKİLDEĞİŞTİRME DÖNÜŞÜMÜ DÜZLEM-BİRİM ŞEKİLDEĞİŞTİRME 3D durumda, bir noktadaki birim şekil değiştirme durumu 3 normal birim şekildeğiştirme bileşeni,, z, ve 3 kesme birim şekildeğiştirme bileşeninden,
Örnek...1 : Örnek...5 : n bir pozitif tamsayı ise i 4 n + 2 +i 8 n + 1 2 +i 2 0 n + 6 =?
 KARMAŞIK SAYILAR Karmaşık saılar x 2 + 1 = 0 biçimindeki denklemlerin çözümünü apabilmek için tanım lanm ıştır. Örnek...2 : Toplamları 6 ve çarpımları 34 olan iki saı bulunuz. a ve b birer reel saı ve
KARMAŞIK SAYILAR Karmaşık saılar x 2 + 1 = 0 biçimindeki denklemlerin çözümünü apabilmek için tanım lanm ıştır. Örnek...2 : Toplamları 6 ve çarpımları 34 olan iki saı bulunuz. a ve b birer reel saı ve
Mustafa YAĞCI, yagcimustafa@yahoo.com Parabol Denkleminin Yazılması
 www.mustafaagci.com.tr, 11 Cebir Notları Mustafa YAĞCI, agcimustafa@ahoo.com Parabol Denkleminin Yazılması B ir doğru kaç noktasıla bellidi? İki, değil mi Çünkü tek bir noktadan geçen istediğimiz kadar
www.mustafaagci.com.tr, 11 Cebir Notları Mustafa YAĞCI, agcimustafa@ahoo.com Parabol Denkleminin Yazılması B ir doğru kaç noktasıla bellidi? İki, değil mi Çünkü tek bir noktadan geçen istediğimiz kadar
