Lojik Fonksiyonların Yalınlaştırılması (İndirgenmesi)
|
|
|
- Serkan Gönül
- 7 yıl önce
- İzleme sayısı:
Transkript
1 Lojik Fonksiyonların Yalınlaştırılması (İndirgenmesi) ir lojik fonksiyonun birçok cebirsel ifadesi vardır. (kz. kanonik açılımlar ve yalınlaştırılmış ifadeleri) Yalınlaştırmada amaç, belli bir maliyet kriterine göre bu cebirsel ifadeler içinden en uygun olanını seçmektir. Maliyet kriteri uygulamaya göre değişebilir. Örneğin tasarım aşamasında istenen özellikler şunlar olabilir: İfadenin az sayıda çarpım (ya da toplam) içermesi, her çarpımda az sayıda değişken olması, devrenin aynı tip bağlaçlar (örneğin TVE) ile gerçeklenebilmesi, elde var olan bağlaçların kullanılabilmesi gibi. Yalınlaştırmanın amaçları: evrenin boyutlarını küçültmek Enerji tüketimini azaltmak (pil, soğutma problemi) Gecikmeyi azaltmak (hızı arttırmak) (kz. 3.20: Yayılma gecikmesi) Maliyeti azaltmak ers Notlarının reative ommons lisansı Feza UZLU ya aittir. Lisans: Feza UZLU 4. sal Çarpım (Temel İçeren) Prime Implicant : Hatırlatma: ir fonksiyonun. kanonik açılımını oluşturan çarpımlar (minterimler) bu fonksiyon tarafından örtülürler (içerilirler).. kanonik açılımda yer alan bazı çarpımları birleştirerek daha az değişken içeren ve birden fazla "doğru" noktaya karşı gelen yeni çarpımlar elde edilebilir. aha fazla basitleştirilemeyen ve fonksiyonun mümkün olan en fazla sayıda doğru noktasını örten çarpımlar asal çarpımdır. Örnek: F Yalınlaştırma İle İlgili Tanımlar F(,, )= Σm(,3,5,6,7) :. kanonik açılım = '' + ' + ' + ' + u çarpımlar, asal çarpım (temel içeren) değildir, çünkü onlardan daha az değişkene sahip olan bölenleri de bu fonksiyonun içinde yer almaktadır. u durum basitleştirme sonucu görülmüştü ve fonksiyon için aşağıdaki ifade elde edilmişti. F= + Kanonik açılımdaki çarpımlar sadece adet doğru nokta örterken çarpımı 2 adet, ise 4 adet nokta örtmektedir Feza UZLU 4.2
2 Örnek (devamı): F(,, )= Σm(,3,5,6,7) :. kanonik açılım = '' + ' + ' + ' + F= + sal çarpım (temel içeren) kendi bölenleri fonksiyonda yer almayan (daha fazla sadeleştirilemeyen) ve mümkün olan en fazla sayıda doğru noktayı örten çarpımlardır. Örneğin yukarıdaki örnekte ' bir asal çarpım değildir, çünkü onun böleni olan de fonksiyon tarafından örtülmektedir. ise bir asal çarpımdır, çünkü onun bölenleri ve fonksiyon tarafından örtülmez (daha fazla üretiyorlar, fonksiyonun ifadesinde yer alamazlar). Lojik fonksiyonları yalınlaştırma işlemi:. Tüm asal çarpımlar kümesinin bulunması 2. Fonksiyonun tüm "doğru" noktalarını örtecek şekilde, asal çarpımlardan en uygun olanların seçilmesi Feza UZLU 4.3 sal Çarpımların ulunması: Çarpım terimlerini birleştirerek daha az değişkene sahip ve daha çok doğru noktayı örten çarpımlar elde etmek için oole cebri kullanılabilir. u işlemi özellikle büyük fonksiyonlar için elle kağıt üstünde yapmak zor olur. u işlemler bilgisayar programları ile yapılır. Fonksiyonun cebirsel ifadesini kullanmadan daha pratik olarak uygulanabilecek bir yöntem: oğruluk tablosunda "" üreten kombinezonlar incelenir, Sadece bir değişkenin değer değiştirdiği, bir veya daha fazla değişkenin (girişin) sabit kaldığı kombinezonlar birleştirilir, eğeri sabit kalan değişkenler çarpımda kalır, değişenler çarpımdan çıkarılır. Örnek: ebirsel olarak birleştirme: F = ''+' = ('+)' = ' F sabit. Her ikisinde de =0. değişkeni yeni çarpımda yer alacak. nın değeri değişiyor. yeni çarpımda olmayacak. =0 olduğu için yeni çarpım: ' Feza UZLU 4.4
3 Yapılan işlemin oole küpünde gösterilmesi: F Yapılan işlemin Karnaugh diyagramında gösterilmesi: F oyutu 0 olan iki nokta birleştirilerek boyutu olan bir çizgi elde edildi. u çizgi =0'ı yani nin tümleyenini temsil etmektedir. u tür gruplamaları Karnaugh diyagramları ile yapmak daha kolaydır. itişiklilik özelliğinden yararlanılarak komşu noktalar gruplanabilir. Yukarıda gruplamanın yapıldığı sütunda =0 (sabit), ise değişkendir. u sütun nin tümleyenini temsil etmektedir Feza UZLU 4.5 ynı anda birden fazla değişken sabit kalıyorsa gruplama sonucu bu değişkenlerin çarpımı oluşur Örnek: F =, = ve sabit. ise değişiyor. u gruplama sonucu çarpımı oluşur. ebirsel: ' + = ('+) = =, = ve sabit. ise değişiyor. u gruplama sonucu çarpımı oluşur. ebirsel: ' + = ('+) = F Feza UZLU 4.6
4 Gruplamalarda 2'den daha fazla nokta da birleştirilebilir. Örnek: F(,,) = Σ(4,5,6,7) = ve sabit. ve ise değişiyor. Küpün bu yüzü yı temsil ediyor. ebirsel: '' + ' + ' + = '+ = Karnaugh diyagramı ile: F = ve sabit. ve ise değişiyor Feza UZLU 4.7 sal Çarpımların Karnaugh iyagramları İle ulunması: Karnaugh diyagramlarındaki bitişiklilik ve çevrimlilik özelliği nedeniyle komşu gözler arasındaki geçişlerde sadece değişken (giriş) değer değiştirir, diğerleri sabit kalır. Girişlerin sabit kaldığı komşu gözlerdeki "doğru" noktaları 2'li, 4'lü, 8'li gruplarda toplamak mümkündür. şağıda 3 ve 4 değişkenli Karnaugh diyagramları için girişlerin sabit kaldıkları alanlar gösterilmiştir Lisans: ynı diyagram, değişkenler farklı şekillerde yerleştirilerek de yandaki gibi oluşturulabilir Feza UZLU 4.8
5 Örnek: şağıda verilen fonksiyonun asal çarpımlarının bulunması F(,,,) = Σ (0,2,5,8,9,0,,2,3,4,5) F sal Çarpımlar:, '', ' sal çarpımlar bulunurken fonksiyonun "doğru" noktaları mümkün olan en büyük gruplara yerleştirilirler. ir grupta yer alan iki nokta tekrar birleştirilerek daha küçük bir grup oluşturulmaz. Örneğin ayrı ayrı 4 'lü gruplarda bulunan iki nokta birleştirilerek 2'li yeni bir grup oluşturmaya gerek yoktur. Yeni bir 4 lü grup oluşturulabilir. ncak noktalardan biri daha büyük bir gruba ait değilse (yukarıdaki 00 gibi) o nokta gruptaki başka bir nokta ile kümelenebilir Feza UZLU 4.9 Tüm sal Çarpımlar Kümesinin ulunması: Lojik devre tasarımında yalınlaştırma işlemi o fonksiyonun bütün asal çarpımlarının bulunmasıyla başlar. ütün asal çarpımların oluşturduğu kümeye tüm asal çarpımlar kümesi (tüm temel içeren tabanı) denir. İndirgemenin 2. aşamasında fonksiyonun bütün doğru noktalarını örtecek şekilde, tüm asal çarpımlar kümesinden en uygun asal çarpımlar seçilir. Fonksiyonun bütün doğru noktalarını örten asal çarpımların oluşturduğu kümeye yeterli küme denir. Yeterli kümeden bir asal çarpım kaldırılırsa fonksiyonun tüm doğru noktaları örtülmemiş olur. una göre bir fonksiyonu yalınlaştırma işlemi en uygun (ucuz) yeterli kümeyi (minimal covering sum) bulmak demektir Örnek: şağıdaki fonksiyonun tüm asal çarpımlar kümesini bulunuz. sal Çarpımlar: ', ', ', ', ', ' Feza UZLU 4.0
6 ynı fonksiyonun bir çok yeterli kümesi olabilir F(,,)= ' + ' + ' F(,,)= ' + ' + ' + ' F(,,)= ' + ' + ' Yeterli küme bir asal çarpım kaldırıldığında tüm doğru noktalar kapsanmamış olur. F(,,)= ' + ' + ' + ' aşlıca Nokta ve Gerekli sal çarpım (Essential Prime Implicant): azı fonksiyonlarda bazı doğru noktalar sadece bir asal çarpım tarafından örtülürler. u noktalara başlıca nokta denir. u noktaları örten asal çarpımlara da gerekli asal çarpım (essential prime implicant) denir. Gerekli asal çarpımlar fonksiyonun yeterli kümesinde mutlaka yer alırlar. Çünkü başlıca noktaların başka asal çarpımlar tarafından örtülmesi mümkün değildir. Örnek: F Tüm sal Çarpımlar Kümesi: ', ', ', ','', ' aşlıca Noktalar Gerekli çarpımlar 000 ' 000 '' 000 ' 0 ' 0 ' uradaki gerekli asal çarpımlar fonksiyonun tüm doğru noktalarını örtmektedir. u özel bir durumdur. F= ' + '' + ' + ' + ' Feza UZLU 4.2
7 Örnek: ir fonksiyonun tüm asal çarpımlar kümesinin, başlıca noktalarının ve gerekli çarpımların bulunması. F Tüm sal Çarpımlar Kümesi:,, ',, '', ' 0 0 aşlıca Noktalar Gerekli çarpımlar 0000 '' Feza UZLU 4.3 Lisans: Yalınlaştırma: Uygun sal Çarpımların Seçilmesi Hatırlatma: Yalınlaştırma işlemi 2 aşamadan oluşmaktadır:. Tüm asal çarpımlar kümesinin (Tüm temel içerenlerin) bulunması 2. Fonksiyonun tüm "doğru" noktalarını örtecek şekilde, asal çarpımlardan en uygun (ucuz) olanların seçilmesi. En uygun asal çarpımların (yeterli kümenin) seçilmesinde kullanılan yöntemlerden biri seçenekler tablosu yöntemidir. Seçenekler Tablosu: Fonksiyonun asal çarpımları bulunduktan sonra bu çarpımlara isimler verilir. Örneğin,,,.. gibi. Verilen bir maliyet kriterine göre her asal çarpımın maliyeti hesaplanır. Seçenekler tablosu bir matris şeklinde hazırlanır. Tablonun satırlarında, fonksiyonun asal çarpımlarının isimleri yer alır. Sütunlarda ise o fonksiyonun doğru noktalarının numaraları bulunur. En son sütuna asal çarpımların maliyetleri yazılır. ir asal çarpım bir noktayı örtüyorsa matrisin ilgili gözüne X konur Feza UZLU 4.4
8 Örnek: Verilen fonksiyonun tüm asal çarpımlar kümesini bulunuz ve seçenekler tablosunu oluşturunuz. f(x, x 2, x 3, x 4 )=Σm(2, 4, 6, 8, 9, 0, 2, 3, 5) Maliyet hesabında her değişken 2 birim, her tümleme işlemi birim maliyete sahip olacaktır. f x 3 x 4 x x 2 00 x x 0 x 2 x 4 Tüm sal Çarpımlar Kümesi: x x 3 ' x 2 x 3 ' x 4 ' x 'x 2 x 4 ' x x 2 x 4 x 'x 3 x 4 ' x 2 ' x 3 x 4 ' x x 2 ' x 4 ' Semboller: E F G Maliyetler: Örttüğü Noktalar:8,9,2,3 4,2 4, 6 3, 5 2, 6 2, 0 8, Feza UZLU 4.5 x x 3 ' Tüm sal Çarpımlar Kümesi: x 2 x 3 ' x 4 ' x 'x 2 x 4 ' x x 2 x 4 x 'x 3 x 4 ' x 2 ' x 3 x 4 ' x x 2 ' x 4 ' Semboller: E F G Maliyetler: Örttüğü Noktalar:8,9,2,3 4,2 4, 6 3, 5 2, 6 2, 0 8, 0 E F G Fonksiyonun "doğru" noktaları Maliyet X X X X 5 X X X X 6 X X X Feza UZLU 4.6
9 Seçenekler Tablosunun İndirgenmesi. aşlıca noktalar belirlenir. ir sütunda sadece bir tane X varsa o sütundaki nokta başlıca noktadır. aşlıca noktayı örten asal çarpım (gerekli asal çarpım) mutlaka fonksiyonun ifadesinde yer alacağından seçilir. u asal çarpıma ait satır ve onun örttüğü noktalara ait sütunlar tablodan kaldırılır. 2. Tabloda j. satırın X olan her gözünde i. satırda da X varsa i. satır, j. satırı örtüyor denir. Yani j. satırın örttüğü bütün noktaları i. satır da örtüyordur. Eğer i. satır j. satırı örtüyorsa ve i. satırdaki maliyet j. satırdaki maliyetten küçükse veya ona eşitse j. satır (örtülen satır) tablodan kaldırılır. 3. ir sütun başka bir sütunu örtüyorsa örten sütun (daha fazla X'e sahip olan) tablodan silinir. i j i j k X X 4 X 5 X X X X X u kurallar peş peşe uygulanarak fonksiyonun doğru noktaları toplam maliyet en az olacak şekilde örtülmeye çalışılır Feza UZLU 4.7 Örnek: şağıda verilen fonksiyona ait seçenekler tablosunun indirgenmesi. f(x, x 2, x 3, x 4 )=Σm(2, 4, 6, 8, 9, 0, 2, 3, 5) x x 3 ' x 2 x 3 ' x 4 ' x 'x 2 x 4 ' x x 2 x 4 x 'x 3 x 4 ' x 2 ' x 3 x 4 ' x x 2 ' x 4 ' E F G Fonksiyonun "doğru" noktaları Maliyet X X X X 5 X X X X 6 X X X. dım: u tabloda 9 ve 5 başlıca noktalardır. ve gerekli çarpımlar oldukları için onlara ait satır ve örttükleri sütunlar tablodan kaldırılır. u çarpımlar daha sonra sonucu oluştururken kullanılmak üzere işaretlenir Feza UZLU 4.8
10 Maliyet x 8 x x 8 E x x 8 F x x 8 G x 8 2. dım: u tabloda, 'yi örter. Maliyetleri aynı olduğu için örtülen satır () tablodan silinir. enzer şekilde F, G'yi örter ve maliyetleri aynıdır. u nedenle G satırı tablodan silinir. u çarpımlar sonuç ifadede yer almayacaktır Maliyet x x 8 E x x 8 F x x 8 3. dım: u tabloda 4 ve 0 başlıca noktalardır. u nedenle ve F çarpımlarını almak gerekir. u iki asal çarpım seçildiğinde tüm noktalar örtülmüş olur Feza UZLU 4.9 Lisans: Sonuç: İşaretlenmiş olan asal çarpımlar fonksiyonun en ucuz ifadesini oluştururlar. Seçilen asal çarpımlar: F Toplam Maliyet= = 27 f(x, x 2, x 3, x 4 ) = x x 3 ' + x x 2 x 4 + x 'x 2 x 4 ' + x 2 ' x 3 x 4 ' Karnaugh diyagramı ile hangi asal çarpımların seçildiğini görebiliriz. f x 3 x 4 x x 2 00 x x 0 x 4 x 2 u seçimde tüm ler örtülmeli ve bir fazlalık olmamalı. Seçilmiş olan asal çarpımlar bir yeterli küme oluşturmalı. Yani çarpımlardan biri kaldırıldığında tüm noktalar örtülememeli. x x 3 ' x 'x 2 x 4 ' x x 2 x 4 x 2 ' x 3 x 4 ' Feza UZLU 4.20
11 Tümüyle Tanımlanmamış Fonksiyonların Yalınlaştırılması Hatırlatma:Tümüyle tanımlanmamış fonksiyonlarda, bazı giriş kombinezonları için fonksiyonun alacağı değer belirsizdir (önemli değildir). Çünkü bu giriş kombinezonları ilgili devrede fiziksel olarak oluşamazlar ya da tasarımcı tarafından yasaklanmışlardır. Örnek: sayıları arttıran devre I I2 I4 I8 u girişler için devrenin (fonksiyonun) çıkışlarının alacağı değer belirsizdir. elirsiz değerleri göstermek için X yerine Φ sembolü de kullanılır. O O2 O4 O8 I8 I4 I2 I O8 O4 O2 O X X X X 0 X X X X 0 0 X X X X 0 X X X X 0 X X X X X X X X Feza UZLU 4.2 elirsiz eğerlerin (Φ) Seçilmesi: Yalınlaştırma işleminde, belirsiz değerler (Φ) en ucuz ifadeyi elde edecek şekilde gerektiğinde lojik 0, gerektiğinde lojik olarak seçilebilirler. Tüm asal çarpımlar kümesi bulunurken daha basit çarpımlar elde etmek için (Karnaugh diyagramında daha büyük gruplamalar yapabilmek için) Φ = olarak seçilir. Seçenekler tablosunda kapsanması gereken noktalar yazılırken Φ = 0 olarak seçilir. Çünkü bu noktaların çarpımlar tarafından örtülmesine gerek yoktur. Örnek: şağıda verilen tümüyle tanımlanmamış fonksiyonu en düşük maliyetle tasarlayınız. f(x, x 2, x 3, x 4 )=Σ m (2, 4, 8, 9, 3, 5 ) + Σ Φ (6,0,2) Not: f(x, x 2, x 3, x 4 )= (2, 4, 8, 9, 3, 5 ) + Φ (6,0,2) şeklinde de yazılabilir. Maliyet hesabında her değişken 2 birim, her tümleme işlemi birim maliyete sahip olacaktır Feza UZLU 4.22
12 f x 3 x 4 x x x 0 x Φ Φ Φ x 4 x 2 sal çarpımlar bulunurken Φ ler olarak seçilir. Tüm sal Çarpımlar Kümesi: x x 3 ' x 2 x 3 ' x 4 ' x 'x 2 x 4 ' x x 2 x 4 x 'x 3 x 4 ' x 2 ' x 3 x 4 ' x x 2 ' x 4 ' Semboller: E F G Maliyetler: Örttüğü Noktalar: 8,9, , Feza UZLU 4.23 x x 3 ' Tüm sal Çarpımlar Kümesi: x 2 x 3 ' x 4 ' x 'x 2 x 4 ' x x 2 x 4 x 'x 3 x 4 ' x 2 ' x 3 x 4 ' x x 2 ' x 4 ' Semboller: E F G Maliyetler: Örttüğü Noktalar: 8,9, , Fonksiyonun "doğru" noktaları E F G Maliyet X X X 5 X X 6 Tablo oluşturulurken Φ ler 0 olarak seçilir. u noktaların örtülmesine gerek olmadığından Φ ler seçenekler tablosunda yer almazlar Feza UZLU 4.24
13 Fonksiyonun "doğru" noktaları E F G Maliyet X X X 5 X X 6.dım: u tabloda 9 ve 5 başlıca noktalardır. ve gerekli çarpımlar oldukları için onlara ait satır ve örttükleri sütunlar tablodan kaldırılır. u çarpımlar daha sonra sonucu oluştururken kullanılmak üzere işaretlenir Feza UZLU 4.25 Lisans: Maliyet x 8 x 8 E x 8 F x 8 2. dım: ve aynı noktaları örtmektedir ve maliyetleri eşittir. u nedenle bu iki çarpım arasında bir seçim yapmak mümkün değildir. Verilen maliyet kriterine göre herhangi biri seçilebilir. ynı durum E ve F çarpımları için de geçerlidir. una göre fonksiyon aşağıdaki ifadelerden herhangi biri kullanılarak gerçeklenebilir: f= E = x x 3 ' + x x 2 x 4 + x 2 x 3 ' x 4 ' + x 'x 3 x 4 ' f= F = x x 3 ' + x x 2 x 4 + x 2 x 3 ' x 4 ' + x 2 ' x 3 x 4 ' f= E = x x 3 ' + x x 2 x 4 + x 'x 2 x 4 ' + x 'x 3 x 4 ' f= F = x x 3 ' + x x 2 x 4 + x 'x 2 x 4 ' + x 2 ' x 3 x 4 ' Tüm tasarımların maliyeti eşittir (27) Feza UZLU 4.26
14 Genel Fonksiyonların Yalınlaştırılması Hatırlatma: Genel fonksiyonların birden fazla çıkışı vardır. x x 2 x 3 y y Φ Φ Φ Φ 0 x y x 2 f x 3 y = f (x,x 2,x 3 ) y 2 = f 2 (x,x 2,x 3 ) y 2 Genel fonksiyonlar yalınlaştırılırken her çıkışa ait fonksiyon için ayrı ayrı tüm asal çarpımlar kümesi bulunur ve bunların içinden seçim yapılır. urada dikkat edilmesi gereken nokta her iki çıkış için ortak çarpımların kullanılmaya çalışılmasıdır. Genel fonksiyonlar yalınlaştırılması bu dersin kapsamı dışında tutulmuştur Feza UZLU 4.27 Tüm sal Çarpımlar Kümesinin Tablo Yöntemiyle (Quine-Mcluskey) ulunması Karnaugh diyagramları görsel özellikleri nedeniyle az değişkenli fonksiyonlarla ilgili çalışmalarda kolaylık sağlarlar. ncak değişken sayısı 5 ve daha fazla olduğunda Karnaugh diyagramlarını çizmek ve bitişiklilik özelliğini kullanmak zorlaşır. Tablo yöntemi (Quine-Mcluskey) ise sistematik bazı işlemlerin peş peşe tekrarlanmasından oluşmaktadır. u işlemleri elle yapmak fazla zaman alabilir, ancak söz konusu işlemleri bilgisayar programı ile gerçekleştirmek kolaydır. Tablo (Quine-Mcluskey) Yöntemi: Hatırlanacağı gibi, asal çarpımları bulmak için değeri üreten ve bitişik olan giriş kombinezonları (minterimler) gruplanmaya çalışılıyordu. Sadece bir değişkenin değiştiği (bitişik) olan kombinezonlar aynı gruba alınıyordu. (kz. 4.4 teki şekil) Tablo yönteminde değeri olan her kombinezon (minterim) diğer minterimler ile karşılaştırılır. Eğer iki kombinezon arasında sadece bir giriş (değişken) farklıysa o iki kombinezon gruplanır. Farklı olan değişken silinerek yeni terim elde edilir. u durum hiç gruplama yapılamayana kadar devam eder. Hiç bir gruba girmeyen terimler asal çarpımlardır Feza UZLU 4.28
15 Yöntem: Willard Van Orman Quine ( ), Felsefe, lojik Edward J. Mcluskey(929-) Elektrik müh.. dım: Tüm asal çarpımlar kümesinin bulunması oğruluk tablosunda üreten giriş kombinezonlarını belirleyin. Karşılaştırma kolaylığı sağlamak için içindeki 'lerin sayısına göre kombinezonları kümeleyin. Örneğin; 0 giriş kombinezonunda üç adet vardır. Komşu kümlerdeki kombinezonları karşılaştırın. Tek girişin farklı olduğu kombinezonları gruplayıp yeni kombinezonlar oluşturun. Yeni kombinezonlarda değeri değişen giriş yer almayacaktır. ir gruba girmiş olan kombinezonları işaretleyin. Yeni oluşan kombinezonlar üzerinde de aynı gruplama işlemlerini yeni gruplar oluşmayıncaya kadar sürdürün. Hiç bir gruba girmemiş olan kombinezonlar (işaretsizler) tüm asal çarpımlar kümesini oluştururlar. 2. dım: En ucuz yeterli kümenin (minimal covering sum) bulunması Tüm asal çarpımlar kümesi bulunduktan sonra yalınlaştırma işlemi için yine seçenekler tablosu kullanılarak en ucuz yeterli küme bulunur Feza UZLU 4.29 Örnek: şağıda verilen fonksiyonun tüm asal çarpımlar kümesini Quine-Mcluskey yöntemiyle bulunuz. f(x, x 2, x 3, x 4 )= Σ m (0,, 2, 8, 0,, 4, 5 ) K.No x x 2 x 3 x K.No x x 2 x 3 x 4 0, , , , , , 0-0,4-0,5-4,5 - K.No x x 2 x 3 x 4 0,2,8, ,8,2, ,,4, ,4,,5 - - ynı olanları yazmaya gerek yok Tüm asal çarpımlar kümesi (İşaretsiz olanlar): x ' x 2 ' x 3 ', x 2 ' x 4 ', x x 3 En ucuz çözümü elde etmek için bu aşamadan sonra seçenekler tablosu oluşturulur ve en ucuz yeterli küme bulunur Feza UZLU 4.30
Lojik Fonksiyonların Yalınlaştırılması (İndirgenmesi) F(A, B, C)= Σm(1,3,5,6,7) : 1. kanonik açılım = A'B'C + A'BC + AB'C + ABC' + ABC A B C F F= AB+C
 Lojik Fonksiyonların Yalınlaştırılması (İndirgenmesi) ir lojik fonksiyonun birçok cebirsel ifadesi vardır. (kz. kanonik açılımlar ve yalınlaştırılmış ifadeleri) Yalınlaştırmada amaç, belli bir maliyet
Lojik Fonksiyonların Yalınlaştırılması (İndirgenmesi) ir lojik fonksiyonun birçok cebirsel ifadesi vardır. (kz. kanonik açılımlar ve yalınlaştırılmış ifadeleri) Yalınlaştırmada amaç, belli bir maliyet
BOOLE CEBRİ. BOOLE cebri. B={0,1} kümesi üzerinde tanımlı İkili işlemler: VEYA, VE { +,. } Birli işlem: tümleme { } AKSİYOMLAR
 OOLE ERİ 54 YILINDA GEORGE OOLE, LOJİĞİ SİSTEMATİK OLARARAK ELE ALIP OOLE ERİNİ GELİŞTİRDİ. 93 DE.E. SHANNON ANAHTARLAMA ERİNİ GELİŞTİREREK OOLE ERİNİN ELEKTRİKLİ ANAHTARLAMA DEVRELERİNİN ÖZELLİKLERİNİ
OOLE ERİ 54 YILINDA GEORGE OOLE, LOJİĞİ SİSTEMATİK OLARARAK ELE ALIP OOLE ERİNİ GELİŞTİRDİ. 93 DE.E. SHANNON ANAHTARLAMA ERİNİ GELİŞTİREREK OOLE ERİNİN ELEKTRİKLİ ANAHTARLAMA DEVRELERİNİN ÖZELLİKLERİNİ
SAYISAL DEVRELER. Analog - Sayısal (Dijital) İşaretler:
 SYISL DEVRELER Yrd.Doç.Dr. Feza UZLU İstanbul Teknik Üniversitesi ilgisayar Mühendisliği ölümü www.buzluca.info/sayisal. nalog - Sayısal (Dijital) İşaretler: Gerçek dünyada karşılaştığımız bir çok fiziksel
SYISL DEVRELER Yrd.Doç.Dr. Feza UZLU İstanbul Teknik Üniversitesi ilgisayar Mühendisliği ölümü www.buzluca.info/sayisal. nalog - Sayısal (Dijital) İşaretler: Gerçek dünyada karşılaştığımız bir çok fiziksel
Boole Cebiri ve Temel Geçitler
 oole ebiri ve Temel Geçitler İL 2 Geçit düzeyinde yalınlaştırma (Gate-Level Minimization) Hacettepe Üniversitesi ilgisayar Müh. ölümü oole cebiri (oolean algebra ) oole işlevleri (oolean functions) Temel
oole ebiri ve Temel Geçitler İL 2 Geçit düzeyinde yalınlaştırma (Gate-Level Minimization) Hacettepe Üniversitesi ilgisayar Müh. ölümü oole cebiri (oolean algebra ) oole işlevleri (oolean functions) Temel
Boole Cebri. (Boolean Algebra)
 Boole Cebri (Boolean Algebra) 3 temel işlem bulunmaktadır: Boole Cebri İşlemleri İşlem: VE (AND) VEYA (OR) TÜMLEME (NOT) İfadesi: xy, x y x + y x Doğruluk tablosu: x y xy 0 0 0 x y x+y 0 0 0 x x 0 1 0
Boole Cebri (Boolean Algebra) 3 temel işlem bulunmaktadır: Boole Cebri İşlemleri İşlem: VE (AND) VEYA (OR) TÜMLEME (NOT) İfadesi: xy, x y x + y x Doğruluk tablosu: x y xy 0 0 0 x y x+y 0 0 0 x x 0 1 0
Ders Notlarının Creative Commons lisansı Feza BUZLUCA ya aittir. Lisans: http://creativecommons.org/licenses/by-nc-nd/3.0/
 Eşzamanlı (Senkron) Ardışıl Devrelerin Tasarlanması (Design) Bir ardışıl devrenin tasarlanması, çözülecek olan problemin sözle anlatımıyla (senaryo) başlar. Bundan sonra aşağıda açıklanan aşamalardan geçilerek
Eşzamanlı (Senkron) Ardışıl Devrelerin Tasarlanması (Design) Bir ardışıl devrenin tasarlanması, çözülecek olan problemin sözle anlatımıyla (senaryo) başlar. Bundan sonra aşağıda açıklanan aşamalardan geçilerek
BİL 201 Geçit düzeyinde yalınlaştırma (Gate-Level Minimization) Hacettepe Üniversitesi Bilgisayar Müh. Bölümü
 BİL 2 Geçit düzeyinde yalınlaştırma (Gate-Level Minimization) Hacettepe Üniversitesi Bilgisayar Müh. Bölümü Boole Cebiri ve Temel Geçitler Boole cebiri (Boolean algebra ) Boole işlevleri (Boolean functions)
BİL 2 Geçit düzeyinde yalınlaştırma (Gate-Level Minimization) Hacettepe Üniversitesi Bilgisayar Müh. Bölümü Boole Cebiri ve Temel Geçitler Boole cebiri (Boolean algebra ) Boole işlevleri (Boolean functions)
DERS NOTLARI. Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi
 DERS NOTLARI Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi DERS-5 14.03.2016 Karnaugh Haritaları Çarpımlar toplamı yada toplamlar çarpımı formundaki lojikifadelerin sadeleştirilmesine
DERS NOTLARI Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi DERS-5 14.03.2016 Karnaugh Haritaları Çarpımlar toplamı yada toplamlar çarpımı formundaki lojikifadelerin sadeleştirilmesine
(I) şimdiki. durum (S) belleği. saat. girşi
 ers Notlarının Creative Commons lisansı Feza BUZLUCA ya aittir. Lisans: http://creativecommons.org/licenses/by-nc-nd/3.0/ Eşzamanlı (Senkron) Ardışıl evreler (Synchronous Sequential Circuits) Ardışıl (sequential)
ers Notlarının Creative Commons lisansı Feza BUZLUCA ya aittir. Lisans: http://creativecommons.org/licenses/by-nc-nd/3.0/ Eşzamanlı (Senkron) Ardışıl evreler (Synchronous Sequential Circuits) Ardışıl (sequential)
Deney 2: Lojik Devre Analizi
 eney : Lojik evre nalizi Genel ilgiler: u deneyde, SSI (Small Scale Integration: Küçük Ölçekte Tümleştirme, - kapı) devreler kullanılarak, lojik kapıların, oole fonksiyonlarının, oole ebri aksiyom ve teoremlerinin
eney : Lojik evre nalizi Genel ilgiler: u deneyde, SSI (Small Scale Integration: Küçük Ölçekte Tümleştirme, - kapı) devreler kullanılarak, lojik kapıların, oole fonksiyonlarının, oole ebri aksiyom ve teoremlerinin
T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ
 T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR 1 3. HAFTA Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR Karnaugh Haritaları Karnaugh
T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR 1 3. HAFTA Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR Karnaugh Haritaları Karnaugh
LOJİK İFADENİN VE-DEĞİL VEYA VEYA-DEĞİL LOJİK DİYAGRAMLARINA DÖNÜŞTÜRÜLMESİ
 LOJİK İFADENİN VE-DEĞİL VEYA VEYA-DEĞİL LOJİK DİYAGRAMLARINA DÖNÜŞTÜRÜLMESİ Sayısal tasarımcılar tasarladıkları devrelerde çoğu zaman VE-Değil yada VEYA-Değil kapılarını, VE yada VEYA kapılarından daha
LOJİK İFADENİN VE-DEĞİL VEYA VEYA-DEĞİL LOJİK DİYAGRAMLARINA DÖNÜŞTÜRÜLMESİ Sayısal tasarımcılar tasarladıkları devrelerde çoğu zaman VE-Değil yada VEYA-Değil kapılarını, VE yada VEYA kapılarından daha
MİNTERİM VE MAXİTERİM
 MİNTERİM VE MAXİTERİM İkili bir değişken Boolean ifadesi olarak değişkenin kendisi (A) veya değişkenin değili ( A ) şeklinde gösterilebilir. VE kapısına uygulanan A ve B değişkenlerinin iki şekilde Boolean
MİNTERİM VE MAXİTERİM İkili bir değişken Boolean ifadesi olarak değişkenin kendisi (A) veya değişkenin değili ( A ) şeklinde gösterilebilir. VE kapısına uygulanan A ve B değişkenlerinin iki şekilde Boolean
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
BÖLÜM - 5 KARNOUGH HARITALARI
 ÖLÜM - 5 KRNOUGH HRITLRI KRNOUGH HRITLRI oolean fonksiyonlarını teoremler,kurallar ve özdeşlikler yardımı ile indirgeyebileceğimizi bir önceki bölümde gördük. ncak yapılan bu sadeleştirme işleminde birbirini
ÖLÜM - 5 KRNOUGH HRITLRI KRNOUGH HRITLRI oolean fonksiyonlarını teoremler,kurallar ve özdeşlikler yardımı ile indirgeyebileceğimizi bir önceki bölümde gördük. ncak yapılan bu sadeleştirme işleminde birbirini
Boole Cebri. Muhammet Baykara
 Boole Cebri Boolean Cebri, Mantıksal Bağlaçlar, Lojik Kapılar ve Çalışma Mantıkları, Doğruluk Tabloları, Boole Cebri Teoremleri, Lojik İfadelerin Sadeleştirilmeleri Muhammet Baykara mbaykara@firat.edu.tr
Boole Cebri Boolean Cebri, Mantıksal Bağlaçlar, Lojik Kapılar ve Çalışma Mantıkları, Doğruluk Tabloları, Boole Cebri Teoremleri, Lojik İfadelerin Sadeleştirilmeleri Muhammet Baykara mbaykara@firat.edu.tr
Deney 1: Lojik Kapıların Lojik Gerilim Seviyeleri
 eney : Lojik Kapıların Lojik Gerilim Seviyeleri eneyin macı: Lojik kapıların giriş ve çıkış lojik gerilim seviyelerinin ölçülmesi Genel ilgiler: ir giriş ve bir çıkışlı en basit lojik kapı olan EĞİL (NOT)
eney : Lojik Kapıların Lojik Gerilim Seviyeleri eneyin macı: Lojik kapıların giriş ve çıkış lojik gerilim seviyelerinin ölçülmesi Genel ilgiler: ir giriş ve bir çıkışlı en basit lojik kapı olan EĞİL (NOT)
Fatih University- Faculty of Engineering- Electric and Electronic Dept.
 Dijital Devre Tasarımı EEE122 A Ref. Morris MANO & Michael D. CILETTI DIGITAL DESIGN 4 th edition Fatih University- Faculty of Engineering- Electric and Electronic Dept. Chapter 3 Boole Fonksiyon Sadeleştirmesi
Dijital Devre Tasarımı EEE122 A Ref. Morris MANO & Michael D. CILETTI DIGITAL DESIGN 4 th edition Fatih University- Faculty of Engineering- Electric and Electronic Dept. Chapter 3 Boole Fonksiyon Sadeleştirmesi
Fatih University- Faculty of Engineering- Electric and Electronic Dept.
 Dijital Devre Tasarımı EEE122 A Ref. Morris MANO & Michael D. CILETTI DIGITAL DESIGN 4 th edition Fatih University- Faculty of Engineering- Electric and Electronic Dept. 2. BÖLÜM Boole Cebri ve Mantık
Dijital Devre Tasarımı EEE122 A Ref. Morris MANO & Michael D. CILETTI DIGITAL DESIGN 4 th edition Fatih University- Faculty of Engineering- Electric and Electronic Dept. 2. BÖLÜM Boole Cebri ve Mantık
T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ
 T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR 1 5. HAFTA BİLEŞİK MANTIK DEVRELERİ (COMBINATIONAL LOGIC) Veri Seçiciler (Multiplexer)
T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR 1 5. HAFTA BİLEŞİK MANTIK DEVRELERİ (COMBINATIONAL LOGIC) Veri Seçiciler (Multiplexer)
TAMSAYILAR. 9www.unkapani.com.tr. Z = {.., -3, -2, -1, 0, 1, 2, 3, } kümesinin her bir elemanına. a, b, c birer tamsayı olmak üzere, Burada,
 TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
DERS NOTLARI. Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi
 DERS NOTLARI Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi DERS-4 07.03.2016 Standart Formlar (CanonicalForms) Lojik ifadeler, çarpımlar toplamı ya da toplamlar çarpımı formunda ifade
DERS NOTLARI Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi DERS-4 07.03.2016 Standart Formlar (CanonicalForms) Lojik ifadeler, çarpımlar toplamı ya da toplamlar çarpımı formunda ifade
Bulanık Küme Kavramı BULANIK KÜME. Sonlu ve Sonsuz Bulanık Kümeler. Sonlu ve Sonsuz Bulanık Kümeler
 ULNIK KÜME ulanık Küme Kavramı Elemanları x olan bir X evrensel (universal küme düșünelim. u elemanların ÌX alt kümesine aitliği, yani bu altkümelerin elemanı olup olmadığı X in {0,1} de olan karakteristik
ULNIK KÜME ulanık Küme Kavramı Elemanları x olan bir X evrensel (universal küme düșünelim. u elemanların ÌX alt kümesine aitliği, yani bu altkümelerin elemanı olup olmadığı X in {0,1} de olan karakteristik
SAYISAL ELEKTRONİK. Ege Üniversitesi Ege MYO Mekatronik Programı
 SYISL ELEKTRONİK Ege Üniversitesi Ege MYO Mekatronik Programı ÖLÜM 4 OOLEN RİTMETİĞİ VE DEMORGN TEOREMLERİ OOLEN TOPLM oolean toplama VEY işlemine eşittir. Toplamanın kuralı: 0+0=0 0+= +0= += oolean aritmetiğinde
SYISL ELEKTRONİK Ege Üniversitesi Ege MYO Mekatronik Programı ÖLÜM 4 OOLEN RİTMETİĞİ VE DEMORGN TEOREMLERİ OOLEN TOPLM oolean toplama VEY işlemine eşittir. Toplamanın kuralı: 0+0=0 0+= +0= += oolean aritmetiğinde
Atatürk Anadolu. Temel Kavramlar Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
8.SINIF CEBirsel ifadeler
 KAZANIM : 8.2.1.1. Basit cebirsel ifadeleri anlar ve farklı biçimlerde yazar. Hatırlatma 2 + 4y - 5 ifadesi bir cebirsel ifadedir ve değişkenler ve y dir. Cebirsel İfade: İçinde bir veya birden fazla bilinmeyen
KAZANIM : 8.2.1.1. Basit cebirsel ifadeleri anlar ve farklı biçimlerde yazar. Hatırlatma 2 + 4y - 5 ifadesi bir cebirsel ifadedir ve değişkenler ve y dir. Cebirsel İfade: İçinde bir veya birden fazla bilinmeyen
BÖLÜM 6. Karnaugh (Karno) Haritaları. (Karnaugh Maps) Amaçlar. Başlıklar
 Karnaugh (Karno) Haritaları ÖLÜM 6 (Karnaugh Maps) maçlar Lojik eşitliklerin sadeleştirilmesinde kullanılan Karnaugh Haritası yönteminin tanıtılması İki-üç-dört değişkenli Karnaugh Haritalarının hücrelerin
Karnaugh (Karno) Haritaları ÖLÜM 6 (Karnaugh Maps) maçlar Lojik eşitliklerin sadeleştirilmesinde kullanılan Karnaugh Haritası yönteminin tanıtılması İki-üç-dört değişkenli Karnaugh Haritalarının hücrelerin
Birden Çok Tabloda Sorgulama (Join)
 Birden Çok Tabloda Sorgulama (Join) Join(Birleştirici), iki ya da daha fazla tabloyu aynı anda sorgulayarak bir sonuç tablosu (result table) oluşturmaya yarar. Örneğin: İki tabloyu birleştirici ile birleştirerek
Birden Çok Tabloda Sorgulama (Join) Join(Birleştirici), iki ya da daha fazla tabloyu aynı anda sorgulayarak bir sonuç tablosu (result table) oluşturmaya yarar. Örneğin: İki tabloyu birleştirici ile birleştirerek
Rakam : Sayıları yazmaya yarayan sembollere rakam denir.
 A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
BLM 221 MANTIK DEVRELERİ
 6. HAFTA BLM 221 MANTIK DEVRELERİ Prof Dr Mehmet AKBABA mehmetakbaba@karabuk.edu.tr Temel Kavramlar KARNO HARITALARI İki ve Üç değişkenli Karno Haritaları Dört değişkenli Karno Haritaları Beş değişkenli
6. HAFTA BLM 221 MANTIK DEVRELERİ Prof Dr Mehmet AKBABA mehmetakbaba@karabuk.edu.tr Temel Kavramlar KARNO HARITALARI İki ve Üç değişkenli Karno Haritaları Dört değişkenli Karno Haritaları Beş değişkenli
Lineer Cebir. Doç. Dr. Niyazi ŞAHİN TOBB. İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler
 Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
ÜNİTE 1: TEMEL KAVRAMLAR
 MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
Excel de Pivot Tablolar Tasarım ve Kullanımı
 FARUK ÇUBUKÇU EXCEL AKADEMİ Excel de Pivot Tablolar Tasarım ve Kullanımı Pivot tablolar; satışlar, siparişler gibi verileri gruplamayı, alt toplamlarını almayı ve filtreleme işlemleri yapmayı sağlayan
FARUK ÇUBUKÇU EXCEL AKADEMİ Excel de Pivot Tablolar Tasarım ve Kullanımı Pivot tablolar; satışlar, siparişler gibi verileri gruplamayı, alt toplamlarını almayı ve filtreleme işlemleri yapmayı sağlayan
EXCEL 2007 ELEKTRONİK ÇİZELGE
 EXCEL 2007 ELEKTRONİK ÇİZELGE Excel, Microsoft Office paketinde yer alan ve iş hayatında en sık kullanılan programlardandır. Bir hesap tablosu programıdır. Excel, her türlü veriyi (özellikle sayısal verileri)
EXCEL 2007 ELEKTRONİK ÇİZELGE Excel, Microsoft Office paketinde yer alan ve iş hayatında en sık kullanılan programlardandır. Bir hesap tablosu programıdır. Excel, her türlü veriyi (özellikle sayısal verileri)
BSE 207 Mantık Devreleri Lojik Kapılar ve Lojik Devreler (Logic Gates And Logic Circuits)
 SE 207 Mantık Devreleri Lojik Kapılar ve Lojik Devreler (Logic Gates nd Logic Circuits) Sakarya Üniversitesi Lojik Kapılar - maçlar Lojik kapıları ve lojik devreleri tanıtmak Temel işlemler olarak VE,
SE 207 Mantık Devreleri Lojik Kapılar ve Lojik Devreler (Logic Gates nd Logic Circuits) Sakarya Üniversitesi Lojik Kapılar - maçlar Lojik kapıları ve lojik devreleri tanıtmak Temel işlemler olarak VE,
1 Vektör Uzayları 2. Lineer Cebir. David Pierce. Matematik Bölümü, MSGSÜ mat.msgsu.edu.tr/~dpierce/
 Vektör Uzayları Lineer Cebir David Pierce 5 Mayıs 2017 Matematik Bölümü, MSGSÜ dpierce@msgsu.edu.tr mat.msgsu.edu.tr/~dpierce/ Bu notlarda, alıştırma olarak her teorem, sonuç, ve örnek kanıtlanabilir;
Vektör Uzayları Lineer Cebir David Pierce 5 Mayıs 2017 Matematik Bölümü, MSGSÜ dpierce@msgsu.edu.tr mat.msgsu.edu.tr/~dpierce/ Bu notlarda, alıştırma olarak her teorem, sonuç, ve örnek kanıtlanabilir;
BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES)
 BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES) Lagrange ve Neville yöntemlerinin bazı olumsuz yanları vardır: İşlem sayısı çok fazladır (bazı başka yöntemlere kıyasla) Data setinde bir nokta ilavesi veya çıkartılması
BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES) Lagrange ve Neville yöntemlerinin bazı olumsuz yanları vardır: İşlem sayısı çok fazladır (bazı başka yöntemlere kıyasla) Data setinde bir nokta ilavesi veya çıkartılması
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
FONKSİYONLARIN TABLO ŞEKLİNDE HESAPLANMASI
 FONKSİYONLARIN TABLO ŞEKLİNDE HESAPLANMASI Bu kısımda bir fonksiyon değerlerinin tablo şeklinde hesaplanması incelenecektir. İncelenecek fonksiyon y=f(x) şeklinde bir değişenli veya z=f(x,y) şeklinde iki
FONKSİYONLARIN TABLO ŞEKLİNDE HESAPLANMASI Bu kısımda bir fonksiyon değerlerinin tablo şeklinde hesaplanması incelenecektir. İncelenecek fonksiyon y=f(x) şeklinde bir değişenli veya z=f(x,y) şeklinde iki
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1
 ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
( ) (, ) Kombinasyon. Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir.
 Kombinasyon Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir. n elemanın tüm r li kombinasyonlarının sayısı; (, ) C n r ( ) r n P n, r n!
Kombinasyon Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir. n elemanın tüm r li kombinasyonlarının sayısı; (, ) C n r ( ) r n P n, r n!
DOĞRULUK TABLOLARI (TRUTH TABLE)
 LOJİK KAPILAR DOĞRULUK TABLOLARI (TRUTH TABLE) Doğruluk tabloları sayısal devrelerin tasarımında ve analizinde kullanılan en basit ve faydalı yöntemdir. Doğruluk tablosu giriş değişkenlerini alabileceği
LOJİK KAPILAR DOĞRULUK TABLOLARI (TRUTH TABLE) Doğruluk tabloları sayısal devrelerin tasarımında ve analizinde kullanılan en basit ve faydalı yöntemdir. Doğruluk tablosu giriş değişkenlerini alabileceği
Bu tanım aralığı pozitif tam sayılar olan f(n) fonksiyonunun değişim aralığı n= 1, 2, 3,, n,
 DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
Her bir kapının girişine sinyal verilmesi zamanı ile çıkışın alınması zamanı arasında çok kısa da olsa fark bulunmaktadır -> kapı gecikmesi
 Kapılardaki gecikme Her bir kapının girişine sinyal verilmesi zamanı ile çıkışın alınması zamanı arasında çok kısa da olsa fark bulunmaktadır -> kapı gecikmesi Kapılardaki gecikme miktarının hesaplanması
Kapılardaki gecikme Her bir kapının girişine sinyal verilmesi zamanı ile çıkışın alınması zamanı arasında çok kısa da olsa fark bulunmaktadır -> kapı gecikmesi Kapılardaki gecikme miktarının hesaplanması
KABA KÜME TEORİSİ (Rough Set Theory) Dr. Sedat TELÇEKEN
 KABA KÜME TEORİSİ (Rough Set Theory) Dr. Sedat TELÇEKEN Giriş Bilgi teknolojisindeki gelişmeler ve verilerin dijital ortamda saklanmaya başlanması ile yeryüzündeki bilgi miktarı her 20 ayda iki katına
KABA KÜME TEORİSİ (Rough Set Theory) Dr. Sedat TELÇEKEN Giriş Bilgi teknolojisindeki gelişmeler ve verilerin dijital ortamda saklanmaya başlanması ile yeryüzündeki bilgi miktarı her 20 ayda iki katına
Minterm'e Karşı Maxterm Çözümü
 Minterm'e Karşı Maxterm Çözümü Şimdiye kadar mantık sadeleştirme problemlerine Çarpımlar-ın-Toplamı (SOP) çözümlerini bulduk. Her bir SOP çözümü için aynı zamanda Toplamlar-ın-Çarpımı (POS) çözümü de vardır,
Minterm'e Karşı Maxterm Çözümü Şimdiye kadar mantık sadeleştirme problemlerine Çarpımlar-ın-Toplamı (SOP) çözümlerini bulduk. Her bir SOP çözümü için aynı zamanda Toplamlar-ın-Çarpımı (POS) çözümü de vardır,
Buna göre, eşitliği yazılabilir. sayılara rasyonel sayılar denir ve Q ile gösterilir. , -, 2 2 = 1. sayıdır. 2, 3, 5 birer irrasyonel sayıdır.
 TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
DENEY 3a- Yarım Toplayıcı ve Tam Toplayıcı Devresi
 DENEY 3a- Yarım Toplayıcı ve Tam Toplayıcı Devresi DENEYİN AMACI 1. Aritmetik birimdeki yarım ve tam toplayıcıların karakteristiklerini anlamak. GENEL BİLGİLER Toplama devreleri, Yarım Toplayıcı (YT) ve
DENEY 3a- Yarım Toplayıcı ve Tam Toplayıcı Devresi DENEYİN AMACI 1. Aritmetik birimdeki yarım ve tam toplayıcıların karakteristiklerini anlamak. GENEL BİLGİLER Toplama devreleri, Yarım Toplayıcı (YT) ve
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
10.Konu Tam sayıların inşası
 10.Konu Tam sayıların inşası 1. Tam sayılar kümesi 2. Tam sayılar kümesinde toplama ve çarpma 3. Pozitif ve negatif tam sayılar 4. Tam sayılar kümesinde çıkarma 5. Tam sayılar kümesinde sıralama 6. Bir
10.Konu Tam sayıların inşası 1. Tam sayılar kümesi 2. Tam sayılar kümesinde toplama ve çarpma 3. Pozitif ve negatif tam sayılar 4. Tam sayılar kümesinde çıkarma 5. Tam sayılar kümesinde sıralama 6. Bir
ÜNİTE. MATEMATİK-1 Doç.Dr.Erdal KARADUMAN İÇİNDEKİLER HEDEFLER ÖZDEŞLİKLER, DENKLEMLER VE EŞİTSİZLİKLER
 HEDEFLER İÇİNDEKİLER ÖZDEŞLİKLER, DENKLEMLER VE EŞİTSİZLİKLER Özdeşlikler Birinci Dereceden Bir Bilinmeyenli Denklemler İkinci Dereceden Bir Bilinmeyenli Denklemler Yüksek Dereceden Denklemler Eşitsizlikler
HEDEFLER İÇİNDEKİLER ÖZDEŞLİKLER, DENKLEMLER VE EŞİTSİZLİKLER Özdeşlikler Birinci Dereceden Bir Bilinmeyenli Denklemler İkinci Dereceden Bir Bilinmeyenli Denklemler Yüksek Dereceden Denklemler Eşitsizlikler
Ders 9: Bézout teoremi
 Ders 9: Bézout teoremi Konikler doğrularla en fazla iki noktada kesişir. Şimdi iki koniğin kaç noktada kesiştiğini saptayalım. Bunu, çok kolay gözlemlerle başlayıp temel ve ünlü Bézout teoremini kanıtlayarak
Ders 9: Bézout teoremi Konikler doğrularla en fazla iki noktada kesişir. Şimdi iki koniğin kaç noktada kesiştiğini saptayalım. Bunu, çok kolay gözlemlerle başlayıp temel ve ünlü Bézout teoremini kanıtlayarak
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
 YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
Projenin Adı: Matrisler ile Diskriminant Analizi Yaparak Sayı Tanımlama. Giriş ve Projenin Amacı:
 Projenin Adı: Matrisler ile Diskriminant Analizi Yaparak Sayı Tanımlama Giriş ve Projenin Amacı: Bu projenin amacı; matrisler ile diskriminant analizi yaparak, bir düzlem üzerine el ile yazılan bir sayının
Projenin Adı: Matrisler ile Diskriminant Analizi Yaparak Sayı Tanımlama Giriş ve Projenin Amacı: Bu projenin amacı; matrisler ile diskriminant analizi yaparak, bir düzlem üzerine el ile yazılan bir sayının
ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOULU
 ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOULU BMT109 SAYISAL ELEKTRONİK Öğr.Gör.Uğur YEDEKÇİOğLU Boolean İfadesinden Sayısal Devrelerin Çizilmesi Örnek : D = B+AC ifadesini lojik kapıları kullanarak çiziniz.
ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOULU BMT109 SAYISAL ELEKTRONİK Öğr.Gör.Uğur YEDEKÇİOğLU Boolean İfadesinden Sayısal Devrelerin Çizilmesi Örnek : D = B+AC ifadesini lojik kapıları kullanarak çiziniz.
VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN
 VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Kümeleme İşlemleri Kümeleme Tanımı Kümeleme Uygulamaları Kümeleme Yöntemleri Kümeleme (Clustering) Kümeleme birbirine
VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Kümeleme İşlemleri Kümeleme Tanımı Kümeleme Uygulamaları Kümeleme Yöntemleri Kümeleme (Clustering) Kümeleme birbirine
Algoritmalar ve Programlama. Algoritma
 Algoritmalar ve Programlama Algoritma Algoritma Bir sorunu / problemi çözmek veya belirli bir amaca ulaşmak için gerekli olan sıralı mantıksal adımların tümüne algoritma denir. Algoritma bir sorunun çözümü
Algoritmalar ve Programlama Algoritma Algoritma Bir sorunu / problemi çözmek veya belirli bir amaca ulaşmak için gerekli olan sıralı mantıksal adımların tümüne algoritma denir. Algoritma bir sorunun çözümü
(m+2) +5<0. 7/m+3 + EŞİTSİZLİKLER A. TANIM
 EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ
 T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ Yrd. Doç. Dr. Mustafa H.B. UÇAR 1 2. HAFTA Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR Entegre Yapıları Lojik Kapılar Lojik
T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ Yrd. Doç. Dr. Mustafa H.B. UÇAR 1 2. HAFTA Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR Entegre Yapıları Lojik Kapılar Lojik
Elektra Raporlama Sistemi Sunumu
 Elektra Raporlama Sistemi Sunumu Raporlama Araçları Açıklamaları: 1-Seçilen nesneyi raporlar. 2-Yeni boş bir rapor eklemeyi sağlar. 3-Seçilen raporları düzenlemeyi sağlar. 4-Seçilen raporu siler. 5-Seçilen
Elektra Raporlama Sistemi Sunumu Raporlama Araçları Açıklamaları: 1-Seçilen nesneyi raporlar. 2-Yeni boş bir rapor eklemeyi sağlar. 3-Seçilen raporları düzenlemeyi sağlar. 4-Seçilen raporu siler. 5-Seçilen
Tez Danışmanı : Prof. Dr. Ahmet DERVİŞOĞLU
 İSTANBUL TEKNİK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ KISMEN BELİRLİ ARDIŞIL MAKİNELERDE DURUM İNDİRGEME YÖNTEMLERİNİN KARŞILAŞTIRILMASI VE BİLGİSAYAR PROGRAMI GELİŞTİRİLMESİ YÜKSEK LİSANS TEZİ Müh. Murat
İSTANBUL TEKNİK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ KISMEN BELİRLİ ARDIŞIL MAKİNELERDE DURUM İNDİRGEME YÖNTEMLERİNİN KARŞILAŞTIRILMASI VE BİLGİSAYAR PROGRAMI GELİŞTİRİLMESİ YÜKSEK LİSANS TEZİ Müh. Murat
DOĞRUSAL OLMAYAN PROGRAMLAMA -I-
 DOĞRUSAL OLMAYAN PROGRAMLAMA -I- Dışbükeylik / İçbükeylik Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST38 Yöneylem Araştırması Dersi 0-0 Öğretim Yılı Doğrusal olmayan
DOĞRUSAL OLMAYAN PROGRAMLAMA -I- Dışbükeylik / İçbükeylik Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST38 Yöneylem Araştırması Dersi 0-0 Öğretim Yılı Doğrusal olmayan
Ekle sekmesindeki Tablolar grubundaki Tablo seçeneği ile tablo oluşturulur.
 4. EKLE SEKMESİ Ekle sekmesi Excel de tablo, grafik, köprü ve resim eklendiği sekmedir. 4.1. Tablolar Ekle sekmesindeki Tablolar grubundaki Tablo seçeneği ile tablo oluşturulur. Tablo oluşturulmak istenen
4. EKLE SEKMESİ Ekle sekmesi Excel de tablo, grafik, köprü ve resim eklendiği sekmedir. 4.1. Tablolar Ekle sekmesindeki Tablolar grubundaki Tablo seçeneği ile tablo oluşturulur. Tablo oluşturulmak istenen
İÇİNDEKİLER BASİT EŞİTSİZLİKLER. HARFLİ İFADELER Harfli İfadeler ve Elemanları Eşitsizlik Sembolleri ve İşaretin Eşitsizlik İfadesi...
 İÇİNDEKİLER HARFLİ İFADELER Harfli İfadeler ve Elemanları... 1 Benzer Terim... Harfli İfadenin Terimlerini Toplayıp Çıkarma... Harfli İfadelerin Terimlerini Çarpma... Harfli İfadelerde Parantez Açma...
İÇİNDEKİLER HARFLİ İFADELER Harfli İfadeler ve Elemanları... 1 Benzer Terim... Harfli İfadenin Terimlerini Toplayıp Çıkarma... Harfli İfadelerin Terimlerini Çarpma... Harfli İfadelerde Parantez Açma...
Excel de çalışma alanı satır ve sütunlardan oluşur. Satırları rakamlar, sütunları ise harfler temsil eder. Excel çalışma sayfası üzerinde toplam
 Microsoft Excel Microsoft Office paket programı ile bizlere sunulan Excel programı bir hesap tablosu programıdır. her türlü veriyi tablolar yada listeler halinde tutmak ve bu veriler üzerinde hesaplamalar
Microsoft Excel Microsoft Office paket programı ile bizlere sunulan Excel programı bir hesap tablosu programıdır. her türlü veriyi tablolar yada listeler halinde tutmak ve bu veriler üzerinde hesaplamalar
Bölüm 3 Toplama ve Çıkarma Devreleri
 Bölüm 3 Toplama ve Çıkarma Devreleri DENEY 3- Yarım ve Tam Toplayıcı Devreler DENEYİN AMACI. Aritmetik birimdeki yarım ve tam toplayıcıların karakteristiklerini anlamak. 2. Temel kapılar ve IC kullanarak
Bölüm 3 Toplama ve Çıkarma Devreleri DENEY 3- Yarım ve Tam Toplayıcı Devreler DENEYİN AMACI. Aritmetik birimdeki yarım ve tam toplayıcıların karakteristiklerini anlamak. 2. Temel kapılar ve IC kullanarak
Algoritma ve Programlamaya Giriş
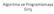 Algoritma ve Programlamaya Giriş Algoritma Bir sorunu çözebilmek için gerekli olan sıralı ve mantıksal adımların tümüne Algoritma denir. Doğal dil ile yazılabilir. Fazlaca formal değildir. Bir algoritmada
Algoritma ve Programlamaya Giriş Algoritma Bir sorunu çözebilmek için gerekli olan sıralı ve mantıksal adımların tümüne Algoritma denir. Doğal dil ile yazılabilir. Fazlaca formal değildir. Bir algoritmada
6. SINIF ÖF RETH M PROGRAMI
 6. SINIF ÖF RETH M PROGRAMI Öğrenme Alanları ve Alt Öğrenme Alanları 6.1. Sayılar ve İşlemler 6.1.1. Doğal Sayılarla İşlemler 6.1.2. Çarpanlar ve Katlar 6.1.3. Tam Sayılar 6.1.4. Kesirlerle İşlemler 6.1.5.
6. SINIF ÖF RETH M PROGRAMI Öğrenme Alanları ve Alt Öğrenme Alanları 6.1. Sayılar ve İşlemler 6.1.1. Doğal Sayılarla İşlemler 6.1.2. Çarpanlar ve Katlar 6.1.3. Tam Sayılar 6.1.4. Kesirlerle İşlemler 6.1.5.
13 Aralık 2007. Đlgili Versiyon/lar : ETA:SQL, ETA:V.8-SQL. Đlgili Modül/ler : Raporlar. Kullanıcı Tanımlı Raporlar Bölümünden Yapabildiklerimiz
 13 Aralık 2007 Đlgili Versiyon/lar : ETA:SQL, ETA:V.8-SQL Đlgili Modül/ler : Raporlar KULLANICI TANIMLI RAPORLAR Kullanıcı Tanımlı Raporlar Bölümünden Yapabildiklerimiz Kendi isteklerinize özel rapor tasarımları
13 Aralık 2007 Đlgili Versiyon/lar : ETA:SQL, ETA:V.8-SQL Đlgili Modül/ler : Raporlar KULLANICI TANIMLI RAPORLAR Kullanıcı Tanımlı Raporlar Bölümünden Yapabildiklerimiz Kendi isteklerinize özel rapor tasarımları
Mustafa Sezer PEHLİVAN. Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü
 * Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
* Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
.:: BÖLÜM I ::. MATRİS ve DETERMİNANT
 SAKARYA ÜNİVERSİTESİ İŞLETME FAKÜLTESİ İŞLETME BÖLÜMÜ.:: BÖLÜM I ::. MATRİS ve DETERMİNANT Halil İbrahim CEBECİ BÖLÜM I 1. Matris Cebirine Giriş MATRİS VE DETERMİNANT Sayıların, değişkenlerin veya parametrelerin
SAKARYA ÜNİVERSİTESİ İŞLETME FAKÜLTESİ İŞLETME BÖLÜMÜ.:: BÖLÜM I ::. MATRİS ve DETERMİNANT Halil İbrahim CEBECİ BÖLÜM I 1. Matris Cebirine Giriş MATRİS VE DETERMİNANT Sayıların, değişkenlerin veya parametrelerin
biçimindeki ifadelere iki değişkenli polinomlar denir. Bu polinomda aynı terimdeki değişkenlerin üsleri toplamından en büyük olanına polinomun dereces
 TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU ÖDEV: Aşağıda verilen 100 öğrenciye ait gözlem değerlerinin aritmetik ortalama, standart sapma, ortanca ve tepe değerini bulunuz. (sınıf aralığını 5 alınız) 155 160 164 165 168
Prof.Dr.İhsan HALİFEOĞLU ÖDEV: Aşağıda verilen 100 öğrenciye ait gözlem değerlerinin aritmetik ortalama, standart sapma, ortanca ve tepe değerini bulunuz. (sınıf aralığını 5 alınız) 155 160 164 165 168
HOMOGEN OLMAYAN DENKLEMLER
 n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
Fonksiyonlarda limiti öğrenirken değişkenlerin limitini ve sağdan-soldan limit kavramlarını öğreneceksiniz.
 8.2. Fonksiyonlarda Limit Fonksiyonlarda limiti öğrenirken değişkenlerin limitini ve sağdan-soldan limit kavramlarını öğreneceksiniz. 8.2.1. Değişkenin Limiti Sonsuz sayıda değer alabilen bir x değişkeninin
8.2. Fonksiyonlarda Limit Fonksiyonlarda limiti öğrenirken değişkenlerin limitini ve sağdan-soldan limit kavramlarını öğreneceksiniz. 8.2.1. Değişkenin Limiti Sonsuz sayıda değer alabilen bir x değişkeninin
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Sihirbaz Kullanarak Sorgu Oluştur : Sihirbaz sorguyu hazırlayan kişiye sorular sorar ve yanıtlarına göre sorgu oluşturur.
 BÖLÜM17 3. SORGULAR Access Veritabanında sorgu; tablolara yazılan bilgilerin hepsinin veya istenilen (belirlenen) şarta uyanlarının bulunmasıdır. Örneğin Tıp Fakültesinde okuyan öğrenciler gibi. Sorguları
BÖLÜM17 3. SORGULAR Access Veritabanında sorgu; tablolara yazılan bilgilerin hepsinin veya istenilen (belirlenen) şarta uyanlarının bulunmasıdır. Örneğin Tıp Fakültesinde okuyan öğrenciler gibi. Sorguları
Bölüm 6 Multiplexer ve Demultiplexer
 Bölüm 6 Multiplexer ve Demultiplexer DENEY 6- Multiplexer Devreleri DENEYİN AMACI. Multiplexer ın çalışma prensiplerini anlamak. 2. Lojik kapıları ve TTL tümdevre kullanarak multiplexer gerçekleştirmek.
Bölüm 6 Multiplexer ve Demultiplexer DENEY 6- Multiplexer Devreleri DENEYİN AMACI. Multiplexer ın çalışma prensiplerini anlamak. 2. Lojik kapıları ve TTL tümdevre kullanarak multiplexer gerçekleştirmek.
EBOB - EKOK EBOB VE EKOK UN BULUNMASI. 2. Yol: En Büyük Ortak Bölen (Ebob) En Küçük Ortak Kat (Ekok) www.unkapani.com.tr. 1. Yol:
 EBOB - EKOK En Büyük Ortak Bölen (Ebob) İki veya daha fazla pozitif tamsayıyı aynı anda bölen pozitif tamsayıların en büyüğüne bu sayıların en büyük ortak böleni denir ve kısaca Ebob ile gösterilir. Örneğin,
EBOB - EKOK En Büyük Ortak Bölen (Ebob) İki veya daha fazla pozitif tamsayıyı aynı anda bölen pozitif tamsayıların en büyüğüne bu sayıların en büyük ortak böleni denir ve kısaca Ebob ile gösterilir. Örneğin,
Microsoft Office Excel 2007
 2014 Microsoft Office Excel 2007 Öğr. Gör. Serkan KORKMAZ Harran Üniversitesi Birecik Meslek Yüksekokulu İçindekiler MİCROSOFT OFFİCE EXCEL 2007... 4 EXCEL ORTAMINDA ÇALIŞMAK... 4 EXCEL ÇALIŞMA SAYFASI...
2014 Microsoft Office Excel 2007 Öğr. Gör. Serkan KORKMAZ Harran Üniversitesi Birecik Meslek Yüksekokulu İçindekiler MİCROSOFT OFFİCE EXCEL 2007... 4 EXCEL ORTAMINDA ÇALIŞMAK... 4 EXCEL ÇALIŞMA SAYFASI...
SAYILAR DOĞAL VE TAM SAYILAR
 1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
Bu sekme ile genel olarak biçimlendirme ile ilgili ayarlamaların yapıldığı sekmedir.
 3. GİRİŞ SEKMESİ Bu sekme ile genel olarak biçimlendirme ile ilgili ayarlamaların yapıldığı sekmedir. 3.1. Excel 2010 da Kesme, Kopyalama, Yapıştırma ve Biçim Boyacısı Giriş sekmesinin ilk grubu olan Pano
3. GİRİŞ SEKMESİ Bu sekme ile genel olarak biçimlendirme ile ilgili ayarlamaların yapıldığı sekmedir. 3.1. Excel 2010 da Kesme, Kopyalama, Yapıştırma ve Biçim Boyacısı Giriş sekmesinin ilk grubu olan Pano
Ders İçerik Bilgisi. Karmaşık Sistemlerin Tek Bir Transfer Fonksiyonuna İndirgenmesi
 Dr. Hakan TERZİOĞLU Ders İçerik Bilgisi Karmaşık Sistemlerin Tek Bir Transfer Fonksiyonuna İndirgenmesi 1. Blok Diyagramları İle (GeçenHafta) 2. İşaret Akış Diyagramları İle (Bu Hafta) Sadeleştirme yoluyla
Dr. Hakan TERZİOĞLU Ders İçerik Bilgisi Karmaşık Sistemlerin Tek Bir Transfer Fonksiyonuna İndirgenmesi 1. Blok Diyagramları İle (GeçenHafta) 2. İşaret Akış Diyagramları İle (Bu Hafta) Sadeleştirme yoluyla
AKIŞ ŞEMASI AKIŞ ŞEMASI AKIŞ ŞEMASI ŞEKİLLERİ GİRİŞ
 GİRİŞ AKIŞ ŞEMASI Bir önceki ünitede algoritma, bilgisayarda herhangi bir işlem gerçekleştirmeden ya da program yazmaya başlamadan önce gerçekleştirilmesi düşünülen işlemlerin belirli bir mantık ve plan
GİRİŞ AKIŞ ŞEMASI Bir önceki ünitede algoritma, bilgisayarda herhangi bir işlem gerçekleştirmeden ya da program yazmaya başlamadan önce gerçekleştirilmesi düşünülen işlemlerin belirli bir mantık ve plan
1. Ünite - ÜTT. 1. Ünite. Aşağıdaki karşılaştırmalardan hangisi yanlıştır? Aşağıdakilerden hangisi 256 sayısına eşit değildir? 1 57 < < 3 4
 . Ünite - ÜTT. Ünite. şağıdakilerden hangisi 6 sayısına eşit değildir?. şağıdaki karşılaştırmalardan hangisi yanlıştır? < 6 < 3 = 6 3 > 3. ir postacı, her gün tane eve birer adet fatura bırakmaktadır.
. Ünite - ÜTT. Ünite. şağıdakilerden hangisi 6 sayısına eşit değildir?. şağıdaki karşılaştırmalardan hangisi yanlıştır? < 6 < 3 = 6 3 > 3. ir postacı, her gün tane eve birer adet fatura bırakmaktadır.
1. BÖLÜM Mantık BÖLÜM Sayılar BÖLÜM Rasyonel Sayılar BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler
 ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
6. Ali her gün cebinde kalan parasının (2009) a, b ve c farklı pozitif tamsayılar, 9. x, y, z pozitif gerçek sayılar,
 1. 9 2 x 2 ifadesinin açılımında sabit x terim kaç olur? A) 672 B) 84 C) 1 D) -84.E) -672 6. Ali her gün cebinde kalan parasının %20 sini harcamaktadır. Pazartesi sabahı haftalığını alan Ali ni Salı günü
1. 9 2 x 2 ifadesinin açılımında sabit x terim kaç olur? A) 672 B) 84 C) 1 D) -84.E) -672 6. Ali her gün cebinde kalan parasının %20 sini harcamaktadır. Pazartesi sabahı haftalığını alan Ali ni Salı günü
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
Veritabanı. SQL (Structured Query Language)
 Veritabanı SQL (Structured Query Language) SQL (Structured Query Language) SQL, ilişkisel veritabanlarındaki bilgileri sorgulamak için kullanılan dildir. SQL, bütün kullanıcıların ve uygulamaların veritabanına
Veritabanı SQL (Structured Query Language) SQL (Structured Query Language) SQL, ilişkisel veritabanlarındaki bilgileri sorgulamak için kullanılan dildir. SQL, bütün kullanıcıların ve uygulamaların veritabanına
(Boolean Algebra and Logic Simplification) Amaçlar Lojik sistemlerin temeli olarak Booleron Matematiğini tanıtmak
 Boolean Kuralları ve Lojik İfadelerin Sadeleştirilmesi BÖLÜM 4 (Boolean lgebra and Logic Simplification) maçlar Lojik sistemlerin temeli olarak Booleron Matematiğini tanıtmak Başlıklar Booleron Kurallarını
Boolean Kuralları ve Lojik İfadelerin Sadeleştirilmesi BÖLÜM 4 (Boolean lgebra and Logic Simplification) maçlar Lojik sistemlerin temeli olarak Booleron Matematiğini tanıtmak Başlıklar Booleron Kurallarını
10. SINIF MATEMATİK FONKSİYONLARDA İŞLEMLER-2
 . SINIF MTEMTİK FONKSİYONLRD İŞLEMLER- ÇKEY NDOLU LİSESİ MTEMTİK ÖLÜMÜ . ÜNİTE.. FONKSİYONLRD DÖRT İŞLEM Neler öğreneceksiniz? Fonksiyonlarda dört işlem yani toplama çıkarma, çarpma ve bölmeyi öğreneceksiniz.
. SINIF MTEMTİK FONKSİYONLRD İŞLEMLER- ÇKEY NDOLU LİSESİ MTEMTİK ÖLÜMÜ . ÜNİTE.. FONKSİYONLRD DÖRT İŞLEM Neler öğreneceksiniz? Fonksiyonlarda dört işlem yani toplama çıkarma, çarpma ve bölmeyi öğreneceksiniz.
BMT 101 Algoritma ve Programlama I 3. Hafta. Yük. Müh. Köksal GÜNDOĞDU 1
 BMT 101 Algoritma ve Programlama I 3. Hafta Yük. Müh. Köksal GÜNDOĞDU 1 Akış Diyagramları ve Sözde Kodlar Yük. Müh. Köksal GÜNDOĞDU 2 Sözde Kodlar (pseudo-code) Yük. Müh. Köksal GÜNDOĞDU 3 Sözde Kod Sözde
BMT 101 Algoritma ve Programlama I 3. Hafta Yük. Müh. Köksal GÜNDOĞDU 1 Akış Diyagramları ve Sözde Kodlar Yük. Müh. Köksal GÜNDOĞDU 2 Sözde Kodlar (pseudo-code) Yük. Müh. Köksal GÜNDOĞDU 3 Sözde Kod Sözde
Mühendislikte Veri Tabanları Dersi Uygulamaları (MS-Access)
 Mühendislikte Veri Tabanları Dersi Uygulamaları (MS-Access) İstanbul Teknik Üniversitesi, İnşaat Fakültesi, Geomatik Mühendisliği Bölümü Prof. Dr. Nebiye MUSAOĞLU Doç. Dr. Elif SERTEL Y. Doç. Dr. Şinasi
Mühendislikte Veri Tabanları Dersi Uygulamaları (MS-Access) İstanbul Teknik Üniversitesi, İnşaat Fakültesi, Geomatik Mühendisliği Bölümü Prof. Dr. Nebiye MUSAOĞLU Doç. Dr. Elif SERTEL Y. Doç. Dr. Şinasi
25. Aşağıdaki çıkarma işlemlerini doğrudan çıkarma yöntemi ile yapınız.
 BÖLÜM. Büyüklüklerin genel özellikleri nelerdir? 2. Analog büyüklük, analog işaret, analog sistem ve analog gösterge terimlerini açıklayınız. 3. Analog sisteme etrafınızdaki veya günlük hayatta kullandığınız
BÖLÜM. Büyüklüklerin genel özellikleri nelerdir? 2. Analog büyüklük, analog işaret, analog sistem ve analog gösterge terimlerini açıklayınız. 3. Analog sisteme etrafınızdaki veya günlük hayatta kullandığınız
ELK2016 SAYISAL TASARIM DERSİ LABORATUVARI DENEY NO: 2
 ELK2016 SAYISAL TASARIM DERSİ LABORATUVARI DENEY NO: 2 DENEYİN ADI: LOJİK FONKSİYONLARIN SADECE TEK TİP KAPILARLA (SADECE NAND (VEDEĞİL), SADECE NOR (VEYADEĞİL)) GERÇEKLENMESİ VE ARİTMETİK İŞLEM DEVRELERİ
ELK2016 SAYISAL TASARIM DERSİ LABORATUVARI DENEY NO: 2 DENEYİN ADI: LOJİK FONKSİYONLARIN SADECE TEK TİP KAPILARLA (SADECE NAND (VEDEĞİL), SADECE NOR (VEYADEĞİL)) GERÇEKLENMESİ VE ARİTMETİK İŞLEM DEVRELERİ
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
İnternet Programcılığı Öğr. Gör. Serkan AKSU PHP de Dizi-Değişkenler, Nesneler. Dizi Oluşturma. Tek Boyutlu Diziler
 PHP de Dizi-Değişkenler, Nesneler Dizilerle ilgili örneklere geçmeden önce aşağıdaki tabloyu inceleyelim. Tabloda dizi kavramının mantığı açıklanmaktadır. Tablonun tamamını bir dizi olarak düşünün ve bu
PHP de Dizi-Değişkenler, Nesneler Dizilerle ilgili örneklere geçmeden önce aşağıdaki tabloyu inceleyelim. Tabloda dizi kavramının mantığı açıklanmaktadır. Tablonun tamamını bir dizi olarak düşünün ve bu
ELEKTRONİK ÇİZELGE. Hücreleri Biçimlendirme. Formülleri Kullanma. Verileri Sıralama. Grafik Oluşturma 1) HÜCRELERİ BİÇİMLENDİRME
 Hücreleri Biçimlendirme ELEKTRONİK ÇİZELGE Formülleri Kullanma Verileri Sıralama Grafik Oluşturma 1) HÜCRELERİ BİÇİMLENDİRME Elektronik Çizelge de sayıları; bin ayracı, yüzde oranı, tarih/saat ve para
Hücreleri Biçimlendirme ELEKTRONİK ÇİZELGE Formülleri Kullanma Verileri Sıralama Grafik Oluşturma 1) HÜCRELERİ BİÇİMLENDİRME Elektronik Çizelge de sayıları; bin ayracı, yüzde oranı, tarih/saat ve para
