Yapı Çerçevelerinin Göçme Yükünün Belirlenmesinde Yeni Bir Hesaplama Tekniği
|
|
|
- Levent Öcal
- 7 yıl önce
- İzleme sayısı:
Transkript
1 BAÜ FBE Dergisi Cilt:12, Sayı:1, 19-3 Temmuz 21 Yapı Çerçevelerinin Göçme Yükünün Belirlenmesinde Yeni Bir Hesaplama Tekniği Perihan (Karakulak) EFE Balıkesir Üniversitesi, ühendislik imarlık Fakültesi, İnşaat ühendisliği Bölümü, Balıkesir. Özet Yapı çerçevelerinin göçme yüklerinin belirlenmesi konusunda değişik hesap metotları mevcuttur. Ancak mevcut hesap yöntemleri ile hesap yapılırken, özellikle hiperstatiklik derecesi yüksek olan karmaşık sistemlerin göçme yüklerinin belirlemesi konusunda sıkıntılar yaşanabilmektedir. Bu çalışmada, değişik yüklemelere maruz yapı çerçevelerinin göçme yükü parametresini belirleyen yeni bir hesaplama tekniği takdim edilmiştir. Bu hesap tekniğine ait denklem takımının çözümünde indo ineer Optimizasyon Bilgisayar Programı kullanılmıştır. Bu hesap metoduyla herhangi bir yapı çerçevesinin göçme yükü parametresi kısa sürede belirlenmekte ve çözüm sonucunda, yapıda mafsalların hangi kesitlerde oluştuğu görülebilmektedir. Anahtar kelimeler: Göçme, göçme yükü, göçme yükü parametresi. A New Calculation Technique in Determinine Collapse oad of Frame Structures Abstract Several methods are available in determing collapse load in frame structures. However, While determing collapse load in structures with available calculation techniques especially with a high degree undeterminated complicated systems can be experienced difficulties. In this study, a new calculation technique that determine collapse load parameter of frame structures subjected to different load has been presented. indo ineer Optimization of Computer Programs was used to solve the batch of the equations concerning calculation technique.. By means of this calculation method, collapse load parameter of any frame structure are determined in a short time and after determination, it can be seen which cross-section does the joints Keywords: Collapse, collapse load, parameter of collapse load. pefe@balikesir.edu.tr, Tel: (266)
2 Perihan (Karakulak) EFE 1. Giriş Bir yapının göçmesi, gerçek anlamda göçüp yerle bir olması anlamında değildir. Göçme herhangi bir yapının hiperstatiklik derecesi kadar mafsalla donatıldıktan sonra sonsuz küçük bir deplasman ile ilave bir mafsalın oluşması sonucunda yapının labil duruma geçerek taşıma gücünü yitirmesidir. Göçme denildiğinde yapının hangi yük altında taşıma gücünü yitireceği anlaşılmalıdır. Şayet bu yük veya yük çarpanı belirlenebiliyorsa yapının göçmeye karşı güvenliği de belirlenmiş olur [1]. Herhangi bir yapının göçme yükünün belirlenmesinde Virtüel İş etodu, ekanizmaların Süperpozisyonu, Eşitsizlikler etodu, Yük-Değiştirme etodu, oment-dağıtımı etodu, Ardışık Yaklaşım etodu v.b. gibi metodlar mevcuttur. Ancak özellikle çok katlı ve çok açıklıklı karmaşık yapıların göçme yükleri belirlenirken, Ardışık Yaklaşım etodu dışındaki diğer metodlarla yapılan hesaplar yetersiz kalabilmekte veya mevcut yöntemlerle yapılan hesapların çok karmaşık ve yorucu olması nedeniyle de çoğu zaman kesin sonuca gidilememektedir [2, 3, 4]. Bu düşünce ile çalışmada; herhangi bir yapıya ait göçme yükünü kesin ve kısa sürede hesaplayabilme imkanı sağlayan yeni bir hesaplama tekniği verilmiştir. Ayrıca 4 nolu literatürde birkaç yöntemin süperpozisyonu ile göçme yükü parametresi belirlenen, yatay ve düşey tekil yüklerle yüklü dört katlı ve üç açıklıklı bir yapı çerçevesi gözönüne alınarak; çalışmamızda verilen hesap tekniği ile bu çerçeveye ait göçme yükü parametresi belirlenmiş ve sonuçlar karşılaştırılmıştır. 2. Çalışmada önerilen hesap tekniği Çalışmada verilen hesap tekniği, Göçme incelemesinde göz önüne alınan ana prensip ve teoremlerin yanı sıra [2, 4, 5], Kiriş ve Kolon teoremi olmak üzere iki özel teorem üzerine kurulmaktadır [1]. Bu teoremler; a) Kiriş Teoremi: Herhangi bir hiperstatik yapı sisteminde, göz önüne alınan bir kirişin herhangi bir kesitinde, moment diyagramı kapama çizgisi ile moment diyagramı çizgisi arasındaki ordinat, aynı yük ile yüklü ve aynı açıklıklı basit kirişin o kesitinde oluşan moment değerine eşittir. b) Kolon Teoremi: Eşit kat yükseklikli herhangi bir hiperstatik yapı sisteminde, en üst kattan başlayarak herhangi bir kata kadar yatay kuvvetlerden dolayı oluşan momentler o katın kolon uçlarına dağılırlar. Çalışmada verilen hesap tekniği ile herhangi bir yapı sisteminin göçme yükü parametresi belirlenmeye çalışılırken, izlenecek yol aşağıda kısaca maddeler halinde verilmektedir. Yapıya etki eden yükler, en küçük yük birim alınarak tek bir parametreye bağlı olarak ifade edilirler. Yapının seçilen en küçük açıklık veya yüksekliği birim alınarak, bütün açıklık ve yükseklikler bu birime bağlı olacak şekilde tek bir parametreye bağlı olarak ifade edilirler. 2
3 Yapı Çerçevelerinin Göçme Yükünün Belirlenmesinde Yeni Bir Hesaplama Tekniği Sistemdeki kritik kesitler (En büyük moment değerlerini alabilecek kesitler) belirlenir ve bu kesitlerde yükler altında oluşan momentler; kritik kesitlerin numaraları ile adlandırılırlar. Kiriş ve kolon teoremleri göz önüne alınarak her bir kat kirişi ve kat kolonlarına ait denge denklemleri ile düğüm noktalarına ait denge denklemleri yazılır. Denge denklemleri yazılırken, düğüm noktalarında saat ibresi tersi yönündeki momentler, açıklıklarda ise altta çekme yapan momentler pozitif kabul edilir. Her bir kritik kesit için kısıtlayıcı denklemler yazılır. Denge denklemleri ve kısıtlayıcı denklemlerin bütün elemanları kesit taşıma momentine bölünerek boyutsuz hale getirilirler. Boyutsuz hale getirilen denklemler i / =m i olacak şekilde yeni bir notasyonla gösterilirler. Ayrıca moment denge denklemlerinde kuvvet ve mesafeye bağlı olarak ifade edilen moment ifadeleri ile bölündükten sonra elde edilen yeni parametre (göçme yükü parametresi) F/ =f kabul edilerek denklem takımına yerleştirilir. Son olarak denge denklemlerinde m i =X i -K i dönüşümü yapılır. Buradaki K i katsayısı her m i değeri için ait olduğu elemanın moment taşıma kapasitesi katsayısıdır. Kısıtlayıcı denklemler de kesit taşıma momentine bölünerek boyutsuz hale getirilirler. Boyutsuz hale getirilen kısıtlayıcı denklemlerin denklem sistemine katılabilmesi için tek taraflı olmaları gereklidir. Bunun içinde bir takım matematiksel operasyonlarla denklemler tek taraflı hale getirilirler. Boyutsuz hale getirilen ve lineer denklem takımına dönüştürülen denklemler bir lineer programlama programı ile çözülerek, o yapıya ait göçme yükü parametresi F/ =f belirlenir Önerilen hesap tekniği ile herhangi bir yapı çerçevesinin göçme yükü parametresinin belirlenmesi Bu bölümde yatay ve düşey tekil yüklere maruz 4 nolu literatürde birkaç yöntemin süperpozisyonu ile göçme yükü parametresi belirlenen, dört katlı ve üç açıklıklı bir yapı çerçevesinin; çalışmamızda önerilen hesap tekniği ile göçme yükü parametresi belirlenmiş ve sonuçlar karşılaştırılmıştır. Çerçeveye etki eden yatay ve düşey yükler ile çerçevenin boyutları ve her bir elemanın kesit taşıma momentleri Şekil 1 de gösterilmektedir. Göçme yükü parametresi belirlenecek olan bu çerçevenin kritik kesitleri ve bu kesitlerde oluşacak olan momentler, kritik kesitlerin numaraları ile adlandırılarak Şekil 2 de gösterilmektedir. Çalışmada verilen hesap tekniği ile çözüm yapılırken, çerçeveye ait denge denklemleri kritik kesitler göz önüne alınarak yazılmıştır. Göz önüne alınan çerçevede kiriş ve kolon teoremlerine göre her bir kat kirişi ve kat kolonları için yazılan moment denge denklemlerinin yanısıra düğüm noktaları için yazılan moment denge denklemleri ve her bir kritik kesit için yazılan kısıtlayıcı denklemler aşağıda verilmektedir. 21
4 Perihan (Karakulak) EFE 2F F F F F F F 2F 2F 2F 2F 2F 2F 2F F 3F 3F 3F 3F 3F 2 2F F F 5F 5F 5F 5F 5F /3 /3 /3 /3 /3 /3 /3 /3 /3 Şekil 1. Göçme yükü parametresi belirlenecek olan yapı çerçevesi. Düğüm noktalarına ait moment denge denklemleri; = = = = = = = = (2.1) = = = = = = = = Kat kolonlarına ait moment denge denklemleri; F= F= (2.2) F= F= 22
5 Yapı Çerçevelerinin Göçme Yükünün Belirlenmesinde Yeni Bir Hesaplama Tekniği Şekil 2. Kritik kesitler ve bu kesitlerde oluşan momentler. 1.kat kirişlerine ait moment denge denklemleri; F= F= F= (2.3) F= F= F= 2.kat kirişlerine ait moment denge denklemleri; F= F= F= (2.4) F= F= F= 3. kat kirişlerine ait moment denge denklemleri; i: Kiriş uç momentleri i: Kiriş açıklık momentleri i: Kolon uç momentleri F= F= F= (2.5) F= F= F= 23
6 Perihan (Karakulak) EFE 4. kat kirişlerine ait moment denge denklemleri; F= F= F= (2.6) F= F= F= Ayrıca her bir kritik kesit için yazılan kısıtlayıcı denklemler aşağıda verilmektedir (2.7) Göçme yükü belirlenecek olan çerçeve göz önüne alınarak, yazılan moment denge denklemleri ve kısıtlayıcı denklemlerde i/ =m i dönüşümü yapılarak denklemler boyutsuz hale getirildikten sonra, mi=x i -K i ve F/ =f=x 81 dönüşümleri yapılarak X değişkenine bağlı olarak ifade edilirler [6]. Birinci kat kirişlerine ait moment denge denklemlerinden biri ve bir kısıtlayıcı denklem üzerinde bu dönüşümlerin nasıl yapıldığı gösterilirse; Birinci kat kirişlerine ait moment denge denklemlerinden ilki göz önüne alınırsa; F= F = m + m + 3m 5f (2.8) = ( X 4) + ( X 4) + 3( X 4) 5X = -2X 4 +X 24 +3X 57-5X 81 =8 İlk kritik kesit için yazılan kısıtlayıcı denklem göz önüne alınırsa; 24
7 Yapı Çerçevelerinin Göçme Yükünün Belirlenmesinde Yeni Bir Hesaplama Tekniği m m (2.9) m m X X 1 8 ( ) 8 Boyutsuz hale getirilen ve X değişkenine bağlı olarak ifade edilen tüm denge denklemleri ve kısıtlayıcı denklemler aşağıda toplu olarak verilmektedir. Düğüm noktalarına ait boyutsuz denge denklemleri; X 2 +X 3 +X 4 =11 X 5 +X 6 +X 7 =8 X 8 +X 9 +X 1 =5 X 11 +X 12 =2 X 13 +X 14 +X 15 =3 X 16 +X 17 +X 18 +X 19 =7 X 2 +X 21 +X 22 +X 23 =11 X 24 +X 25 +X 26 +X 27 =15 (2.1) X 29 +X 3 +X 31 =3 X 32 +X 33 +X 34 +X 35 =7 X 36 +X 37 +X 38 +X 39 =11 X 4 +X 41 +X 42 +X 43 =15 X 45 +X 46 =2 X 47 +X 48 +X 49 =5 X 5 +X 51 +X 52 =8 X 53 +X 54 +X 55 =11 Kat kolonlarına ait boyutsuz denge denklemleri; -X 1 -X 2 -X 27 -X 28 -X 43 -X 44 -X 55 -X 56-8X 81 =32 -X 3 -X 5 -X 23 -X 25 -X 39 -X 41 -X 52 -X 54-6X 81 =24 (2.11) -X 6 -X 8 -X 19 -X 21 -X 35 -X 37 -X 49 -X 51-4X 81 =16 -X 9 -X 11 -X 15 -X 17 -X 31 -X 33 -X 46 -X 48-2X 81 =8 25
8 Perihan (Karakulak) EFE 1.kat kirişlerine ait boyutsuz denge denklemleri; -2X 4 +X 24 +3X 57-5X 81 =8 -X 4 +2X 24 +3X 58-5X 81 =16-2X 26 +X 4 +3X 59-5X 81 =8 (2.12) -X 26 +2X 4 +3X 6-5X 81 =16-2X 42 +X 53 +3X 61-5X 81 =8 -X 42 +2X 53 +3X 62-5X 81 =16 2.kat kirişlerine ait boyutsuz denge denklemleri; -2X 7 +X 2 +3X 63-3X 81 =6 -X 7 +2X 2 +3X 64-3X 81 =12-2X 22 +X 36 +3X 65-3X 81 =6 (2.13) -X 22 +2X 36 +3X 66-3X 81 =12-2X 38 +X 5 +3X 67-3X 81 =6 -X 38 +2X 5 +3X 68-3X 81 =12 3.kat kirişlerine ait boyutsuz denge denklemleri; -2X 1 +X 16 +3X 69-2X 81 =4 -X 1 +2X 16 +3X 7-2X 81 =8-2X 18 +X 32 +3X 71-2X 81 =4 (2.14) -X 18 +2X 32 +3X 72-2X 81 =8-2X 34 +X 47 +3X 73-2X 81 =4 -X 34 +2X 47 +3X 74-2X 81 =8 4.kat kirişlerine ait boyutsuz denge denklemleri; -2X 12 +X 13 +3X 75 -X 81 =2 -X 12 +2X 13 +3X 76 -X 81 =4-2X 14 +X 29 +3X 77 -X 81 =2 (2.15) -X 14 +2X 29 +3X 78 -X 81 =4-2X 3 +X 45 +3X 79 -X 81 =2 -X 3 +2X 45 +3X 8 -X 81 =4 kısıtlayıcı denklemler; X 1 8 X 2 8 X 3 6 X 4 8 X 5 6 (2.16) X 79 2 X
9 Yapı Çerçevelerinin Göçme Yükünün Belirlenmesinde Yeni Bir Hesaplama Tekniği Boyutsuz hale getirilen ve X değişkenine bağlı olarak ifade edilen 44 adet denge denklemi ile 8 adet kısıtlayıcı denklemden oluşan denklem takımı bir lineer programlama programı ile çözülerek X i değerleri ve göçme yükü parametresi f=f/ değeri elde edilir [7]. Yapılan çözümlerin sonucunda çerçeveye ait göçme yükü parametresi; X 81 =f=f/ = (2.17) olarak elde edilmiştir. Denklem takımının çözümünden elde edilen X i değerleri ve bu değerlere bağlı olarak hesaplanan m i boyutsuz moment değerleri aşağıda verilmektedir. X 1 =. m 1 =X 1 K 1 =.-4.= -4. X 2 = m 2 = X 3 =. m 3 =-3.* X 4 = m 4 = X 5 = m 5 = X 6 = m 6 = X 7 = m 7 = X 8 = m 8 = X 9 = m 9 = X 1 = m 1 = X 11 = m 11 = X 12 = m 12 = X 13 =2. m 13 =1.* X 14 =1. m 14 =. X 15 =. m 15 =-1.* X 16 =4. m 16 =2.* X 17 =. m 17 =-1.* X 18 =3. m 18 =1. X 19 =. m 19 =-2.* X 2 =6. m 2 =3.* X 21 =. m 21 =-2.* X 22 = m 22 = X 23 = m 23 = X 24 =8. m 24 =4.* X 25 = m 25 = X 26 = m 26 = X 27 =. m 27 =-4.* X 28 =. m 28 =-4.* X 29 =2. m 29 =1.* X 3 =1. m 3 =. X 31 =. m 31 =-1.* X 32 =4. m 32 =2.* X 33 =. m 33 =-1.* X 34 =3. m 34 =1. X 35 =. m 35 =-2.* X 36 =6. m 36 =3.* X 37 =. m 37 =-2.* Kesit taşıma momenti değerine ulaşılan kesitler ve bu kesitlerdeki boyutsuz moment değerleri 27
10 Perihan (Karakulak) EFE X 38 = m 38 = X 39 = m 39 = X 4 =8. m 4 =4.* X 41 = m 41 = X 42 = m 42 = X 43 =. m 43 =-4.* X 44 =. m 44 =-4.* X 45 =2. m 45 =1.* X 46 =. m 46 =-1.* X 47 =4. m 47 =2.* X 48 =1. m 48 =. X 49 =. m 49 =-2.* X 5 =6. m 5 =3.* X 51 =2. m 51 =. X 52 =. m 52 =-3.* X 53 =8. m 53 =4.* X 54 = m 54 = X 55 = m 55 = X 56 =. m 56 =-4.* X 57 =8. m 57 =4.* X 58 = m 58 = X 59 =8. m 59 =4.* X 6 = m 6 = X 61 =8. m 61 =4.* X 62 = m 62 = X 63 =6. m 63 =3.* X 64 = m 64 = X 65 =6. m 65 =3.* X 66 = m 66 = X 67 =6. m 67 =3.* X 68 = m 68 = X 69 =4. m 69 =2.* X 7 = m 7 = X 71 = m 71 = X 72 = m 72 = X 73 = m 73 = X 74 = m 74 = X 75 =2. m 75 =1.* X 76 = m 76 = X 77 = m 77 = X 78 = m 78 = X 79 = m 79 = X 8 = m 8 = Göçme yükü parametresi ifadesindeki F ve değerleri sırasıyla göz önüne alınan çerçeveye etki eden en küçük birim yük ile çerçeveye ait en küçük birim boyutu, değeri ise en küçük kesit taşıma momentini göstermektedir. Göçme yükü belirlenecek çerçeveye ait P, ve ifadelerinin değerleri göçme yükü parametresi ifadesindeki yerlerine konulduğu takdirde o çerçeveye ait göçme yükünün gerçek sayısal değeri hesaplanmış olur. 28
11 Yapı Çerçevelerinin Göçme Yükünün Belirlenmesinde Yeni Bir Hesaplama Tekniği Denklem takımının çözümünden elde edilen X i değerlerine bağlı olarak hesaplanan mi boyutsuz moment değerleri kesit taşıma momenti ile çarpıldığı zaman ( i =m i. ) o kesitteki gerçek moment değeri elde edilmiş olur. Kesit taşıma moment değerine ulaşan moment değerlerinin bulunduğu kesitlere mafsallar yerleştirildiği taktirde yapı çerçevesinin göçme modu elde edilmiş olur. Yapılan hesaplama sonucunda çerçevede oluşan mafsallar ve mafsalların oluştuğu kesitler Şekil 3 de gösterilmektedir. Çalışmamızda verilen hesap yöntemi ile yapılan çözümlerin sonucunda göz önüne alınan çerçeveye ait göçme yükü parametresi f=f/ = olarak hesaplanırken, aynı çerçeve için 4 nolu literatürde bu değer f=f/ =2.866 olarak hesaplanmıştır. Sonuçlara bakıldığında; çalışmamızda verilen hesap yöntemi ile elde edilen göçme yükü parametresi değerinin 4 nolu literatürde verilen değer ile aynı olduğu görülmektedir. Şekil 3. Çerçevede mafsalların oluştuğu kesitler 3. Sonuç ve Öneriler Bu çalışmada Alt ve Üst Sınır Teoremlerini iki özel teorem ( Kiriş ve Kolon Teoremi) ile pekiştiren bir çözüm tekniği kullanılarak, tekil yüklerin etkisi altındaki dört katlı ve üç açıklıklı bir yapı çerçevesinin göçme yükü paremetresi belirlenmiş ve 4 nolu literatürde aynı çerçeve için farklı bir hesaplama tekniği ile hesaplanan göçme yükü parametresi ile karşılaştırılmıştır. 29
12 Perihan (Karakulak) EFE Çalışmada sunulan hesap tekniği ile herhangi yapı çerçevesinin göçme yükü parametresi belirlenirken, problem hiçbir hiperstatik bilinmeyene bağlı kalınmadan yazılan denge denklemleri ile kritik nokta sayısı kadar yazılan kısıtlayıcı denklemden oluşan denklem takımını içeren bir optimizasyon problemi haline getirilerek çözüm yapılmıştır. Bu hesaplama tekniği ile herhangi bir çerçeve yapının göçme yükü parametresi kısa sürede belirlenmekte ve çözüm sonucunda mafsalların hangi kesitlerde oluştuğu görülebilmektedir. Ayrıca hesap sonucunda elde edilen göçme yükü parametresi f=f/ değerinin mevcut yükler ile yapı göçmesi arasındaki güvenliği belirlemekte de yeterli olduğu düşünülmektedir. Kaynaklar [1] Oğuz, S., Çelik ve Betonarme Yapıların Göçme Yükü Teorisi, Balıkesir, Ocak, (21). [2] Oğuz, S., Yapıların Plastik Analizine Giriş Kurs Notları, TOB İnşaat ühendisleri Odası Ankara Şubesi, Ankara, Şubat, (1983). [3] Neal, B.G., The Plastic ethods of Structural Analysis, Third Edition, John Wiley&Sons, New York, (1977). [4] Hodge, P.G., Yapıların Plastik Analizi, Çeviri: Şuhubi, E.-Cinemre, V., Arı Kitabevi atbaası, (1967). [5] Horne,.R. and orris,.j., Plastic Design of ow-rise Frames, Granada Publishing imited, Great Britain, (1981). [6] Efe (Karakulak), P., Prefabrike Konut Yapılarında Göçme Yükü Hesabı, Doktora Tezi, Balıkesir Üniversitesi, Fen Bilimleri Enstitüsü, Balıkesir, (25). [7] INDO (inear Interactive Discrete Optimizer) ineer optimizasyon Bilgisayar Programı, Release 6.1 (12 ay 3), INDO Systems, Inc., Chicago. 3
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
 YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
AÇI YÖNTEMİ Slope-deflection Method
 SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
Hiperstatik sistemlerin çözümünde, yer değiştirmelerin küçük olduğu ve gerilme - şekil değiştirme bağıntılarının lineer olduğu kabul edilmektedir.
 1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
BETONARME-II (KOLONLAR)
 BETONARME-II (KOLONLAR) ONUR ONAT Kolonların Kesme Güvenliği ve Kesme Donatısının Belirlenmesi Kesme güvenliği aşağıdaki adımlar yoluyla yapılır; Elverişsiz yükleme şartlarından elde edilen en büyük kesme
BETONARME-II (KOLONLAR) ONUR ONAT Kolonların Kesme Güvenliği ve Kesme Donatısının Belirlenmesi Kesme güvenliği aşağıdaki adımlar yoluyla yapılır; Elverişsiz yükleme şartlarından elde edilen en büyük kesme
KİRİŞLERDE PLASTİK MAFSALIN PLASTİKLEŞME BÖLGESİNİ VEREN BİLGİSAYAR YAZILIMI
 IM 566 LİMİT ANALİZ DÖNEM PROJESİ KİRİŞLERDE PLASTİK MAFSALIN PLASTİKLEŞME BÖLGESİNİ VEREN BİLGİSAYAR YAZILIMI HAZIRLAYAN Bahadır Alyavuz DERS SORUMLUSU Prof. Dr. Sinan Altın GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ
IM 566 LİMİT ANALİZ DÖNEM PROJESİ KİRİŞLERDE PLASTİK MAFSALIN PLASTİKLEŞME BÖLGESİNİ VEREN BİLGİSAYAR YAZILIMI HAZIRLAYAN Bahadır Alyavuz DERS SORUMLUSU Prof. Dr. Sinan Altın GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ
Yapı Sistemlerinde Elverişsiz Yüklemeler:
 Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir.
 BASINÇ ÇUBUKLARI Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir. Basınç çubukları, sadece eksenel basınç kuvvetine maruz kalırlar. Bu çubuklar üzerinde Eğilme ve
BASINÇ ÇUBUKLARI Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir. Basınç çubukları, sadece eksenel basınç kuvvetine maruz kalırlar. Bu çubuklar üzerinde Eğilme ve
Proje Genel Bilgileri
 Proje Genel Bilgileri Çatı Kaplaması : Betonarme Döşeme Deprem Bölgesi : 1 Yerel Zemin Sınıfı : Z2 Çerçeve Aralığı : 5,0 m Çerçeve Sayısı : 7 aks Malzeme : BS25, BÇIII Temel Taban Kotu : 1,0 m Zemin Emniyet
Proje Genel Bilgileri Çatı Kaplaması : Betonarme Döşeme Deprem Bölgesi : 1 Yerel Zemin Sınıfı : Z2 Çerçeve Aralığı : 5,0 m Çerçeve Sayısı : 7 aks Malzeme : BS25, BÇIII Temel Taban Kotu : 1,0 m Zemin Emniyet
DEPREM HESABI. Doç. Dr. Mustafa ZORBOZAN
 BETONARME YAPI TASARIMI DEPREM HESABI Doç. Dr. Mustafa ZORBOZAN Mart 2009 GENEL BİLGİ 18 Mart 2007 ve 18 Mart 2008 tarihleri arasında ülkemizde kaydedilen deprem etkinlikleri Kaynak: http://www.koeri.boun.edu.tr/sismo/map/tr/oneyear.html
BETONARME YAPI TASARIMI DEPREM HESABI Doç. Dr. Mustafa ZORBOZAN Mart 2009 GENEL BİLGİ 18 Mart 2007 ve 18 Mart 2008 tarihleri arasında ülkemizde kaydedilen deprem etkinlikleri Kaynak: http://www.koeri.boun.edu.tr/sismo/map/tr/oneyear.html
KISA KOLON TEŞKİLİNİN YAPI HASARLARINA ETKİSİ. Burak YÖN*, Erkut SAYIN
 Erciyes Üniversitesi Fen Bilimleri Enstitüsü Dergisi 24 (1-2) 241-259 (2008) http://fbe.erciyes.edu.tr/ ISSN 1012-2354 KISA KOLON TEŞKİLİNİN YAPI HASARLARINA ETKİSİ Burak YÖN*, Erkut SAYIN Fırat Üniversitesi,
Erciyes Üniversitesi Fen Bilimleri Enstitüsü Dergisi 24 (1-2) 241-259 (2008) http://fbe.erciyes.edu.tr/ ISSN 1012-2354 KISA KOLON TEŞKİLİNİN YAPI HASARLARINA ETKİSİ Burak YÖN*, Erkut SAYIN Fırat Üniversitesi,
İNM 208 DERS TANITIM
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II İNM 208 DERS TANITIM Y.Doç.Dr. Mustafa KUTANİS DR.MUSTAFA KUTANİS SLIDE 1 ADRES INM 208 YAPI STATİĞİ
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II İNM 208 DERS TANITIM Y.Doç.Dr. Mustafa KUTANİS DR.MUSTAFA KUTANİS SLIDE 1 ADRES INM 208 YAPI STATİĞİ
Doç. Dr. Bilge DORAN
 Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
29. Düzlem çerçeve örnek çözümleri
 9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
Üç Boyutlu Çerçeve Yapıların Statik Analizi için Geliştirilen Bir Bilgisayar Programı: YapAn05
 Akademik Bilişim 10 - XII. Akademik Bilişim Konferansı Bildirileri Üç Boyutlu Çerçeve Yapıların Statik Analizi için Geliştirilen Bir Bilgisayar Programı: YapAn05 Dumlupınar Üniversitesi, İnşaat Mühendisliği
Akademik Bilişim 10 - XII. Akademik Bilişim Konferansı Bildirileri Üç Boyutlu Çerçeve Yapıların Statik Analizi için Geliştirilen Bir Bilgisayar Programı: YapAn05 Dumlupınar Üniversitesi, İnşaat Mühendisliği
Dairesel Temellerde Taban Gerilmelerinin ve Kesit Zorlarının Hesabı
 Prof. Dr. Günay Özmen İTÜ İnşaat Fakültesi (Emekli), İstanbul gunozmen@yahoo.com Dairesel Temellerde Taban Gerilmelerinin ve Kesit Zorlarının Hesabı 1. Giriş Zemin taşıma gücü yeter derecede yüksek ya
Prof. Dr. Günay Özmen İTÜ İnşaat Fakültesi (Emekli), İstanbul gunozmen@yahoo.com Dairesel Temellerde Taban Gerilmelerinin ve Kesit Zorlarının Hesabı 1. Giriş Zemin taşıma gücü yeter derecede yüksek ya
idecad Çelik 8 idecad Çelik Kullanarak AISC ve Yeni Türk Çelik Yönetmeliği ile Kren Tasarımı Hazırlayan: Nurgül Kaya
 idecad Çelik 8 idecad Çelik Kullanarak AISC 360-10 ve Yeni Türk Çelik Yönetmeliği ile Kren Tasarımı Hazırlayan: Nurgül Kaya www.idecad.com.tr Konu başlıkları III. I. Kren Menüsü II. Analiz AISC 360-10
idecad Çelik 8 idecad Çelik Kullanarak AISC 360-10 ve Yeni Türk Çelik Yönetmeliği ile Kren Tasarımı Hazırlayan: Nurgül Kaya www.idecad.com.tr Konu başlıkları III. I. Kren Menüsü II. Analiz AISC 360-10
Açı Yöntemi. 1 ql 8. Açı yöntemi olarak adlandırılan denklemlerin oluşturulmasında aşağıda gösterilen işaret kabulü yapılmaktadır.
 çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
DOĞRUSAL OLMAYAN ANALİZ İÇİN KULLANILAN TİCARİ PROGRAMLARIN ÇERÇEVE SİSTEMLER İÇİN KARŞILAŞTIRILMASI
 DOĞRUSAL OLMAYAN ANALİZ İÇİN KULLANILAN TİCARİ PROGRAMLARIN ÇERÇEVE SİSTEMLER İÇİN KARŞILAŞTIRILMASI YÜKSEK LİSANS TEZİ İbrahim GENCER İnşaat Mühendisliği Anabilim Dalı Yapı Mühendisliği Programı Tez Danışmanı:
DOĞRUSAL OLMAYAN ANALİZ İÇİN KULLANILAN TİCARİ PROGRAMLARIN ÇERÇEVE SİSTEMLER İÇİN KARŞILAŞTIRILMASI YÜKSEK LİSANS TEZİ İbrahim GENCER İnşaat Mühendisliği Anabilim Dalı Yapı Mühendisliği Programı Tez Danışmanı:
Tablo 1 Deney esnasında kullanacağımız numunelere ait elastisite modülleri tablosu
 BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
BETONARME BİNALARIN FARKLI HESAP YÖNTEMLERİNE GÖRE PERFORMANS SINIRLARININ İNCELENMESİ ÜZERİNE BİR DEĞERLENDİRME
 BETONARME BİNALARIN FARKLI HESAP YÖNTEMLERİNE GÖRE PERFORMANS SINIRLARININ İNCELENMESİ ÜZERİNE BİR DEĞERLENDİRME Mehmet Sefa Orak 1 ve Zekai Celep 2 1 Araştırma Görevlisi, İnşaat Müh. Bölümü, İstanbul
BETONARME BİNALARIN FARKLI HESAP YÖNTEMLERİNE GÖRE PERFORMANS SINIRLARININ İNCELENMESİ ÜZERİNE BİR DEĞERLENDİRME Mehmet Sefa Orak 1 ve Zekai Celep 2 1 Araştırma Görevlisi, İnşaat Müh. Bölümü, İstanbul
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
MEVCUT BİNALARDA DEPREM PERFORMANSLARININ AYRINTILI İNCELEME YÖNTEMLERİ İLE DEĞERLENDİRİLMESİ
 . Uluslararası Deprem Mühendisliği ve Sismoloji Konferansı - Ekim 7 ANADOLU ÜNİVERSİTESİ ESKİŞEHİR MEVCUT BİNALARDA DEPREM PERFORMANSLARININ AYRINTILI İNCELEME YÖNTEMLERİ İLE DEĞERLENDİRİLMESİ Ç. ÇIRAK,
. Uluslararası Deprem Mühendisliği ve Sismoloji Konferansı - Ekim 7 ANADOLU ÜNİVERSİTESİ ESKİŞEHİR MEVCUT BİNALARDA DEPREM PERFORMANSLARININ AYRINTILI İNCELEME YÖNTEMLERİ İLE DEĞERLENDİRİLMESİ Ç. ÇIRAK,
Eksenel Yükleme Amaçlar
 Eksenel Yükleme Amaçlar Geçtiğimiz bölümlerde eksenel yüklü elemanlarda oluşan normal gerilme ve normal şekil değiştirme konularını gördük, Bu bölümde ise deformasyonların bulunması ile ilgili bir metot
Eksenel Yükleme Amaçlar Geçtiğimiz bölümlerde eksenel yüklü elemanlarda oluşan normal gerilme ve normal şekil değiştirme konularını gördük, Bu bölümde ise deformasyonların bulunması ile ilgili bir metot
Mukavemet-I. Yrd.Doç.Dr. Akın Ataş
 Mukavemet-I Yrd.Doç.Dr. Akın Ataş Bölüm 5 Eğilmede Kirişlerin Analizi ve Tasarımı Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mukavemet-I Yrd.Doç.Dr. Akın Ataş Bölüm 5 Eğilmede Kirişlerin Analizi ve Tasarımı Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
CS MÜHENDİSLİK PROJE YAZILIM HİZMETLERİ www.csproje.com. EUROCODE-2'ye GÖRE MOMENT YENİDEN DAĞILIM
 Moment CS MÜHENİSLİK PROJE YAZILIM HİZMETLERİ EUROCOE-2'ye GÖRE MOMENT YENİEN AĞILIM Bir yapıdaki kuvvetleri hesaplamak için elastik kuvvetler kullanılır. Yapının taşıma gücüne yakın elastik davranmadığı
Moment CS MÜHENİSLİK PROJE YAZILIM HİZMETLERİ EUROCOE-2'ye GÖRE MOMENT YENİEN AĞILIM Bir yapıdaki kuvvetleri hesaplamak için elastik kuvvetler kullanılır. Yapının taşıma gücüne yakın elastik davranmadığı
28. Sürekli kiriş örnek çözümleri
 28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
Düzlem Çerçeve Yapıların Elverişsiz Yük Dağılımına Göre Analizi
 Düzlem Çerçeve Yapıların Elverişsiz Yük Dağılımına Göre Analizi Mahmud Sami Döven, Mustafa Halûk Saraçoğlu, Burak Kaymak, Mehmet Tevfik Bayer Dumlupınar Üniversitesi, İnşaat Mühendisliği Bölümü, Kütahya
Düzlem Çerçeve Yapıların Elverişsiz Yük Dağılımına Göre Analizi Mahmud Sami Döven, Mustafa Halûk Saraçoğlu, Burak Kaymak, Mehmet Tevfik Bayer Dumlupınar Üniversitesi, İnşaat Mühendisliği Bölümü, Kütahya
İNŞ 320- Betonarme 2 Ders Notları / Prof Dr. Cengiz DÜNDAR Arş. Gör. Duygu BAŞLI
 a) Denge Burulması: Yapı sistemi veya elemanında dengeyi sağlayabilmek için burulma momentine gereksinme varsa, burulma denge burulmasıdır. Sözü edilen gereksinme, elastik aşamada değil taşıma gücü aşamasındaki
a) Denge Burulması: Yapı sistemi veya elemanında dengeyi sağlayabilmek için burulma momentine gereksinme varsa, burulma denge burulmasıdır. Sözü edilen gereksinme, elastik aşamada değil taşıma gücü aşamasındaki
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
YAPILARDA BURULMA DÜZENSİZLİĞİ
 YAPILARDA BURULMA DÜZENSİZLİĞİ M. Sami DÖNDÜREN a Adnan KARADUMAN a M. Tolga ÇÖĞÜRCÜ a Mustafa ALTIN b a Selçuk Üniversitesi Mühendislik Mimarlık Fakültesi İnşaat Mühendisliği Bölümü Konya b Selçuk Üniversitesi
YAPILARDA BURULMA DÜZENSİZLİĞİ M. Sami DÖNDÜREN a Adnan KARADUMAN a M. Tolga ÇÖĞÜRCÜ a Mustafa ALTIN b a Selçuk Üniversitesi Mühendislik Mimarlık Fakültesi İnşaat Mühendisliği Bölümü Konya b Selçuk Üniversitesi
K VE DİRSEK TİPİ EĞİK ELEMANLARLA RİJİTLEŞTİRİLMİŞ DEPREM ETKİSİNDEKİ YAPILARIN LİNEER DAVRANIŞLARININ KARŞILAŞTIRMALI OLARAK İNCELENMESİ
 K VE DİRSEK TİPİ EĞİK ELEMANLARLA RİJİTLEŞTİRİLMİŞ DEPREM ETKİSİNDEKİ YAPILARIN LİNEER DAVRANIŞLARININ KARŞILAŞTIRMALI OLARAK İNCELENMESİ Özlem ÇAVDAR 1, Yusuf AYVAZ 2 ozlem_cavdar@hotmail.com, ayvaz@ktu.edu.tr
K VE DİRSEK TİPİ EĞİK ELEMANLARLA RİJİTLEŞTİRİLMİŞ DEPREM ETKİSİNDEKİ YAPILARIN LİNEER DAVRANIŞLARININ KARŞILAŞTIRMALI OLARAK İNCELENMESİ Özlem ÇAVDAR 1, Yusuf AYVAZ 2 ozlem_cavdar@hotmail.com, ayvaz@ktu.edu.tr
Çelik Yapılar - INS /2016
 Çelik Yapılar - INS4033 2015/2016 DERS III Yapısal Analiz Kusurlar Lineer Olmayan Malzeme Davranışı Malzeme Koşulları ve Emniyet Gerilmeleri Arttırılmış Deprem Etkileri Fatih SÖYLEMEZ Yük. İnş. Müh. İçerik
Çelik Yapılar - INS4033 2015/2016 DERS III Yapısal Analiz Kusurlar Lineer Olmayan Malzeme Davranışı Malzeme Koşulları ve Emniyet Gerilmeleri Arttırılmış Deprem Etkileri Fatih SÖYLEMEZ Yük. İnş. Müh. İçerik
MUTO YÖNTEMİ. Çerçeve Sistemlerin Yatay Yüklere Göre Çözümlenmesi. 2. Katta V 2 = F 2 1. Katta V 1 = F 1 + F 2 1/31
 Çerçeve Sistemlerin Yatay Yüklere Göre Çözümlenmesi MUTO Yöntemi (D katsayıları yöntemi) Hesap adımları: 1) Taşıyıcı sistem her kat kolonlarından kesilerek üste kalan yatay kuvvetlerin toplamlarından her
Çerçeve Sistemlerin Yatay Yüklere Göre Çözümlenmesi MUTO Yöntemi (D katsayıları yöntemi) Hesap adımları: 1) Taşıyıcı sistem her kat kolonlarından kesilerek üste kalan yatay kuvvetlerin toplamlarından her
Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı. Doç.Dr. Bilge Doran
 Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı Dersin Adı : Yapı Mühendisliğinde Bilgisayar Uygulamaları Koordinatörü : Doç.Dr.Bilge DORAN Öğretim Üyeleri/Elemanları: Dr. Sema NOYAN ALACALI,
Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı Dersin Adı : Yapı Mühendisliğinde Bilgisayar Uygulamaları Koordinatörü : Doç.Dr.Bilge DORAN Öğretim Üyeleri/Elemanları: Dr. Sema NOYAN ALACALI,
Güçlendirme Alternatiflerinin Doğrusal Olmayan Analitik Yöntemlerle İrdelenmesi
 YDGA2005 - Yığma Yapıların Deprem Güvenliğinin Arttırılması Çalıştayı, 17 Şubat 2005, Orta Doğu Teknik Üniversitesi, Ankara. Güçlendirme Alternatiflerinin Doğrusal Olmayan Analitik Yöntemlerle İrdelenmesi
YDGA2005 - Yığma Yapıların Deprem Güvenliğinin Arttırılması Çalıştayı, 17 Şubat 2005, Orta Doğu Teknik Üniversitesi, Ankara. Güçlendirme Alternatiflerinin Doğrusal Olmayan Analitik Yöntemlerle İrdelenmesi
36. Basit kuvvet metodu
 36. Basit kuvvet metodu Basit kuvvet metodu hakkında çok kısa bilgi verilecektir. Basit kuvvet metodunda hiperstatik bilinmeyenlerinin hesaplanmasına, dolayısıyla buna ait denklem sisteminin kurulmasına
36. Basit kuvvet metodu Basit kuvvet metodu hakkında çok kısa bilgi verilecektir. Basit kuvvet metodunda hiperstatik bilinmeyenlerinin hesaplanmasına, dolayısıyla buna ait denklem sisteminin kurulmasına
34. Dörtgen plak örnek çözümleri
 34. Dörtgen plak örnek çözümleri Örnek 34.1: Teorik çözümü Timoshenko 1 tarafından verilen dört tarafından ankastre ve merkezinde P=100 kn tekil yükü olan kare plağın(şekil 34.1) çözümü 4 farklı model
34. Dörtgen plak örnek çözümleri Örnek 34.1: Teorik çözümü Timoshenko 1 tarafından verilen dört tarafından ankastre ve merkezinde P=100 kn tekil yükü olan kare plağın(şekil 34.1) çözümü 4 farklı model
BALIKESİR ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ BAÜ MÜH.MİM. FAK. İNŞAAT MÜH. BL. ÇELİK KAFES SİSTEM TASARIMI DERS NOTLARI
 BALIKESİR ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ ÇELİK KAFES SİSTEM TASARIMI DERS NOTLARI Yrd.Doç.Dr. Kaan TÜRKER 1.HAFTA (2016) 1 DERS PLANI KONULAR 1. Çelik Çatı Sisteminin Geometrik
BALIKESİR ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ ÇELİK KAFES SİSTEM TASARIMI DERS NOTLARI Yrd.Doç.Dr. Kaan TÜRKER 1.HAFTA (2016) 1 DERS PLANI KONULAR 1. Çelik Çatı Sisteminin Geometrik
GENEL KESİTLİ KOLON ELEMANLARIN TAŞIMA GÜCÜ (Ara donatılı dikdörtgen kesitler)
 GENEL KESİTLİ KOLON ELEMANLARIN TAŞIMA GÜCÜ (Ara donatılı dikdörtgen kesitler) BOYUTLANDIRMA VE DONATI HESABI Örnek Kolon boyutları ne olmalıdır. Çözüm Kolon taşıma gücü abaklarının kullanımı Soruda verilenler
GENEL KESİTLİ KOLON ELEMANLARIN TAŞIMA GÜCÜ (Ara donatılı dikdörtgen kesitler) BOYUTLANDIRMA VE DONATI HESABI Örnek Kolon boyutları ne olmalıdır. Çözüm Kolon taşıma gücü abaklarının kullanımı Soruda verilenler
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
YAPI SİSTEMLERİNİN DOĞRUSAL OLMAYAN ÇÖZÜMLEMESİ İÇİN BİR BİLGİSAYAR PROGRAMI
 PAMUKKALE ÜNİVERSİTESİ MÜHENDİ SLİK FAKÜLTESİ PAMUKKALE UNIVERSITY ENGINEERING COLLEGE MÜHENDİSLİK BİLİMLERİ DERGİSİ JOURNAL OF ENGINEERING SCIENCES YIL CİLT SAYI SAYFA : 2003 : 9 : 2 : 215-222 YAPI SİSTEMLERİNİN
PAMUKKALE ÜNİVERSİTESİ MÜHENDİ SLİK FAKÜLTESİ PAMUKKALE UNIVERSITY ENGINEERING COLLEGE MÜHENDİSLİK BİLİMLERİ DERGİSİ JOURNAL OF ENGINEERING SCIENCES YIL CİLT SAYI SAYFA : 2003 : 9 : 2 : 215-222 YAPI SİSTEMLERİNİN
Perdeli-Çerçeveli Taşıyıcı Sistemli Binalarda Taşıyıcı Sistem Seçiminin Yapı Davranışı Üzerindeki Etkisinin İncelenmesi
 Perdeli-Çerçeveli Taşıyıcı Sistemli Binalarda Taşıyıcı Sistem Seçiminin Yapı Davranışı Üzerindeki Etkisinin İncelenmesi 1 Hüseyin KASAP, * 1 Necati MERT, 2 Ezgi SEVİM, 2 Begüm ŞEBER 1 Yardımcı Doçent,
Perdeli-Çerçeveli Taşıyıcı Sistemli Binalarda Taşıyıcı Sistem Seçiminin Yapı Davranışı Üzerindeki Etkisinin İncelenmesi 1 Hüseyin KASAP, * 1 Necati MERT, 2 Ezgi SEVİM, 2 Begüm ŞEBER 1 Yardımcı Doçent,
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (3. Hafta)
 TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
ÖZHENDEKCİ BASINÇ ÇUBUKLARI
 BASINÇ ÇUBUKLARI Kesit zoru olarak yalnızca eksenel doğrultuda basınca maruz kalan elemanlara basınç çubukları denir. Bu tip çubuklara örnek olarak pandül kolonları, kafes sistemlerin basınca çalışan dikme
BASINÇ ÇUBUKLARI Kesit zoru olarak yalnızca eksenel doğrultuda basınca maruz kalan elemanlara basınç çubukları denir. Bu tip çubuklara örnek olarak pandül kolonları, kafes sistemlerin basınca çalışan dikme
Erdal İRTEM-Kaan TÜRKER- Umut HASGÜL BALIKESİR ÜNİVERSİTESİ MÜH. MİM. FAKÜLTESİ İNŞAAT MÜH. BL.
 Erdal İRTEM-Kaan TÜRKER- Umut HASGÜL BALIKESİR ÜNİVERSİTESİ MÜH. MİM. FAKÜLTESİ İNŞAAT MÜH. BL. BALIKESİR ÜNİVERSİTESİ MÜH. MİM. FAKÜLTESİ İNŞAAT MÜH. BL. ÇAĞIŞ 10145, BALIKESİR 266 612 11 94 266 612 11
Erdal İRTEM-Kaan TÜRKER- Umut HASGÜL BALIKESİR ÜNİVERSİTESİ MÜH. MİM. FAKÜLTESİ İNŞAAT MÜH. BL. BALIKESİR ÜNİVERSİTESİ MÜH. MİM. FAKÜLTESİ İNŞAAT MÜH. BL. ÇAĞIŞ 10145, BALIKESİR 266 612 11 94 266 612 11
KAYMA GERİLMESİ (ENİNE KESME)
 KAYMA GERİLMESİ (ENİNE KESME) Demir yolu traversleri çok büyük kesme yüklerini taşıyan kiriş olarak davranır. Bu durumda, eğer traversler ahşap malzemedense kesme kuvvetinin en büyük olduğu uçlarından
KAYMA GERİLMESİ (ENİNE KESME) Demir yolu traversleri çok büyük kesme yüklerini taşıyan kiriş olarak davranır. Bu durumda, eğer traversler ahşap malzemedense kesme kuvvetinin en büyük olduğu uçlarından
YAPI STATİĞİ MESNETLER
 YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
BETONARME YAPI TASARIMI DERSİ Kolon betonarme hesabı Güçlü kolon-zayıf kiriş prensibi Kolon-kiriş birleşim bölgelerinin kesme güvenliği M.S.
 BETONARME YAPI TASARIMI DERSİ Kolon betonarme hesabı Güçlü kolon-zayıf kiriş prensibi Kolon-kiriş birleşim bölgelerinin kesme güvenliği M.S.KIRÇIL y N cp ex ey x ex= x doğrultusundaki dışmerkezlik ey=
BETONARME YAPI TASARIMI DERSİ Kolon betonarme hesabı Güçlü kolon-zayıf kiriş prensibi Kolon-kiriş birleşim bölgelerinin kesme güvenliği M.S.KIRÇIL y N cp ex ey x ex= x doğrultusundaki dışmerkezlik ey=
10 - BETONARME TEMELLER ( TS 500)
 TS 500 / Şubat 2000 Temel derinliği konusundan hiç bahsedilmemektedir. EKİM 2012 10 - BETONARME TEMELLER ( TS 500) 10.0 - KULLANILAN SİMGELER Öğr.Verildi b d l V cr V d Duvar altı temeli genişliği Temellerde,
TS 500 / Şubat 2000 Temel derinliği konusundan hiç bahsedilmemektedir. EKİM 2012 10 - BETONARME TEMELLER ( TS 500) 10.0 - KULLANILAN SİMGELER Öğr.Verildi b d l V cr V d Duvar altı temeli genişliği Temellerde,
Kafes Sistemler. Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir.
 KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN
 Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
SONLU FARKLAR GENEL DENKLEMLER
 SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım)
 İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
Prof. Dr. Cengiz DÜNDAR
 Prof. Dr. Cengiz DÜNDAR BASİT EĞİLME ETKİSİNDEKİ ELEMANLARIN TAŞIMA GÜCÜ Çekme çubuklarının temel işlevi, çekme gerilmelerini karşılamaktır. Moment kolunu arttırarak donatının daha etkili çalışmasını sağlamak
Prof. Dr. Cengiz DÜNDAR BASİT EĞİLME ETKİSİNDEKİ ELEMANLARIN TAŞIMA GÜCÜ Çekme çubuklarının temel işlevi, çekme gerilmelerini karşılamaktır. Moment kolunu arttırarak donatının daha etkili çalışmasını sağlamak
MOMENT YENİDEN DAĞILIM
 MOMENT YENİDEN DAĞILIM Yeniden Dağılım (Uyum) : Çerçeve kirişleri ile sürekli kiriş ve döşemelerde betonarme bir yapının lineer elastik davrandığı kabulüne dayalı bir statik çözüm sonucunda elde edilecek
MOMENT YENİDEN DAĞILIM Yeniden Dağılım (Uyum) : Çerçeve kirişleri ile sürekli kiriş ve döşemelerde betonarme bir yapının lineer elastik davrandığı kabulüne dayalı bir statik çözüm sonucunda elde edilecek
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
YAPILARIN ÜST RİJİT KAT OLUŞTURULARAK GÜÇLENDİRİLMESİ
 YAPILARIN ÜST RİJİT KAT OLUŞTURULARAK GÜÇLENDİRİLMESİ Hasan KAPLAN 1, Yavuz Selim TAMA 1, Salih YILMAZ 1 hkaplan@pamukkale.edu.tr, ystama@pamukkale.edu.tr, syilmaz@pamukkale.edu.tr, ÖZ: Çok katlı ların
YAPILARIN ÜST RİJİT KAT OLUŞTURULARAK GÜÇLENDİRİLMESİ Hasan KAPLAN 1, Yavuz Selim TAMA 1, Salih YILMAZ 1 hkaplan@pamukkale.edu.tr, ystama@pamukkale.edu.tr, syilmaz@pamukkale.edu.tr, ÖZ: Çok katlı ların
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
RİSKLİ BİNALARIN DEĞERLENDİRİLMESİ ÜZERİNE BİR İNCELEME
 RİSKLİ BİNALARIN DEĞERLENDİRİLMESİ ÜZERİNE BİR İNCELEME ÖZET: H. Tekeli 1, H. Dilmaç 2, K.T. Erkan 3, F. Demir 4, ve M. Şan 5 1 Yardımcı Doçent Doktor, İnşaat Müh. Bölümü, Süleyman Demirel Üniversitesi,
RİSKLİ BİNALARIN DEĞERLENDİRİLMESİ ÜZERİNE BİR İNCELEME ÖZET: H. Tekeli 1, H. Dilmaç 2, K.T. Erkan 3, F. Demir 4, ve M. Şan 5 1 Yardımcı Doçent Doktor, İnşaat Müh. Bölümü, Süleyman Demirel Üniversitesi,
EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele
 EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele alınmıştı. Bu bölümde ise, eksenel yüklü elemanların şekil
EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele alınmıştı. Bu bölümde ise, eksenel yüklü elemanların şekil
R 1Y kn R 1X R 1Z R 4Y R 3Y 4 R 4X R 3Z R 3X R 4Z. -90 kn. 80 kn 80 kn R 1Y =10 R 1X =-10 R 4Y =10 R 1Z =0 R 3Y =70 4 R 3X =-70 R 4X =0
 27. Uzay kafes örnek çözümleri Örnek 27.: Şekil 27. de verilen uzay kafes sistem çelik borulardan imal edilecektir. a noktasındaki dış yüklerden oluşan eleman kuvvetleri, reaksiyonlar, gerilmeler ve düğüm
27. Uzay kafes örnek çözümleri Örnek 27.: Şekil 27. de verilen uzay kafes sistem çelik borulardan imal edilecektir. a noktasındaki dış yüklerden oluşan eleman kuvvetleri, reaksiyonlar, gerilmeler ve düğüm
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
Kesit Tesirleri Tekil Kuvvetler
 Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
DERS BİLGİ FORMU. Dersin Adı / Course Name. Ders. Laboratuvar Local Credit. (saat/hafta) / (hour/week)
 DERS BİLGİ FORMU Dersin Adı / Course Name Kodu/Code Normal Yarıyılı / Regular Semester Yapı Statiği II / Structural Analysis II 0423512 BAHAR / SPRING Yerel Kredisi / AKTS Kredisi / Ders Uygulama Laboratuvar
DERS BİLGİ FORMU Dersin Adı / Course Name Kodu/Code Normal Yarıyılı / Regular Semester Yapı Statiği II / Structural Analysis II 0423512 BAHAR / SPRING Yerel Kredisi / AKTS Kredisi / Ders Uygulama Laboratuvar
Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri
 Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri belirlenmesi 1. katta döşemelerin çözümü ve çizimi Döşeme
Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri belirlenmesi 1. katta döşemelerin çözümü ve çizimi Döşeme
BETONARME-II ONUR ONAT HAFTA-1 VE HAFTA-II
 BETONARME-II ONUR ONAT HAFTA-1 VE HAFTA-II GENEL BİLGİLER Yapısal sistemler düşey yüklerin haricinde aşağıda sayılan yatay yüklerin etkisine maruz kalmaktadırlar. 1. Deprem 2. Rüzgar 3. Toprak itkisi 4.
BETONARME-II ONUR ONAT HAFTA-1 VE HAFTA-II GENEL BİLGİLER Yapısal sistemler düşey yüklerin haricinde aşağıda sayılan yatay yüklerin etkisine maruz kalmaktadırlar. 1. Deprem 2. Rüzgar 3. Toprak itkisi 4.
ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR PROGRAMI
 DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 3 Sayı: 3 sh. 33-50 Ekim 2001 ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR
DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 3 Sayı: 3 sh. 33-50 Ekim 2001 ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR
Kirişlerde Kesme (Transverse Shear)
 Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ
 T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ 3 NOKTA EĞME DENEY FÖYÜ ÖĞRETİM ÜYESİ YRD.DOÇ.DR.ÖMER KADİR
T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ 3 NOKTA EĞME DENEY FÖYÜ ÖĞRETİM ÜYESİ YRD.DOÇ.DR.ÖMER KADİR
BETONARME KESİT DAVRANIŞINDA EKSENEL YÜK, MALZEME MODELİ VE SARGI DONATISI ORANININ ETKİSİ
 Beşinci Ulusal Deprem Mühendisliği Konferansı, 26-30 Mayıs 2003, İstanbul Fifth National Conference on Earthquake Engineering, 26-30 May 2003, Istanbul, Turkey Bildiri No: AT-124 BETONARME KESİT DAVRANIŞINDA
Beşinci Ulusal Deprem Mühendisliği Konferansı, 26-30 Mayıs 2003, İstanbul Fifth National Conference on Earthquake Engineering, 26-30 May 2003, Istanbul, Turkey Bildiri No: AT-124 BETONARME KESİT DAVRANIŞINDA
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
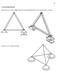 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
SONLU ELEMANLAR YÖNTEMI ile (SAP2000 UYGULAMASI) 3D Frame Analysis. Reza SHIRZAD REZAEI
 SONLU ELEMANLAR YÖNTEMI ile (SAP2000 UYGULAMASI) 3D Frame Analysis Reza SHIRZAD REZAEI SONLU ELEMANLAR YÖNTEMİ Sonlu Elemanlar (SE)Yöntemi, çesitli mühendislik problemlerine kabul edilebilir bir yaklasımla
SONLU ELEMANLAR YÖNTEMI ile (SAP2000 UYGULAMASI) 3D Frame Analysis Reza SHIRZAD REZAEI SONLU ELEMANLAR YÖNTEMİ Sonlu Elemanlar (SE)Yöntemi, çesitli mühendislik problemlerine kabul edilebilir bir yaklasımla
Yapıların Yatay Yük Etkisi Altında Depreme Karşı Hesabı
 ECAS2002 Uluslararası Yapı ve Deprem Mühendisliği Sempozyumu, 14 Ekim 2002, Ortadoğu Teknik Üniversitesi, Ankara, Türkiye Yapıların Yatay Yük Etkisi Altında Depreme Karşı Hesabı S. Oğuz Balıkesir Üniversitesi,
ECAS2002 Uluslararası Yapı ve Deprem Mühendisliği Sempozyumu, 14 Ekim 2002, Ortadoğu Teknik Üniversitesi, Ankara, Türkiye Yapıların Yatay Yük Etkisi Altında Depreme Karşı Hesabı S. Oğuz Balıkesir Üniversitesi,
Üç Boyutlu Çerçeve Yapıların Statik Analizi için Geliştirilen Bir Bilgisayar Programı: YapAn05
 Üç Boyutlu Çerçeve Yapıların Statik Analizi için Geliştirilen Bir Bilgisayar Programı: YapAn05 Mahmud Sami Döven, Burak Kaymak, Mehmet Tevfik Bayer Dumlupınar Üniversitesi, İnşaat Mühendisliği Bölümü,
Üç Boyutlu Çerçeve Yapıların Statik Analizi için Geliştirilen Bir Bilgisayar Programı: YapAn05 Mahmud Sami Döven, Burak Kaymak, Mehmet Tevfik Bayer Dumlupınar Üniversitesi, İnşaat Mühendisliği Bölümü,
R d N 1 N 2 N 3 N 4 /2 /2
 . SÜREKLİ TEELLER. Giriş Kolon yüklerinin büyük ve iki kolonun birbirine yakın olmasından dolayı yapılacak tekil temellerin çakışması halinde veya arsa sınırındaki kolon için eksantrik yüklü tekil temel
. SÜREKLİ TEELLER. Giriş Kolon yüklerinin büyük ve iki kolonun birbirine yakın olmasından dolayı yapılacak tekil temellerin çakışması halinde veya arsa sınırındaki kolon için eksantrik yüklü tekil temel
9 m 3 m. 10 kn/m. 5 m m. 3 m P=50 kn. 10 kn/m. P=50 kn. 20 kn/m. 10 kn/m. 1 8 m 2 m 3 m 3 m. 10 kn/m. 5 m. (Şekil-1b) (Şekil-1a) 20 kn /m
 NOT: u çalışma öyü, dersin uygulama kısmında sürenin yetersiz kalabileceği düşünülerek konuları daha iyi kavrayabilmeniz amacıyla hazırlanmıştır. Konu anlatımlarından sonra ilgili soruları ele alarak değerlendirmeniz
NOT: u çalışma öyü, dersin uygulama kısmında sürenin yetersiz kalabileceği düşünülerek konuları daha iyi kavrayabilmeniz amacıyla hazırlanmıştır. Konu anlatımlarından sonra ilgili soruları ele alarak değerlendirmeniz
Yeşilköy Anadolu Lisesi
 Yeşilköy Anadolu Lisesi TANIM (KONUYA GİRİŞ) a, b, c gerçel sayı ve a ¹ 0 olmak üzere, ax 2 + bx + c = 0 biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir. Bu açık önermeyi
Yeşilköy Anadolu Lisesi TANIM (KONUYA GİRİŞ) a, b, c gerçel sayı ve a ¹ 0 olmak üzere, ax 2 + bx + c = 0 biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir. Bu açık önermeyi
SAP 2000 İLE BETONARME HESAPLAMA. Hazırlayan: Dr. Onur TUNABOYU Eskişehir Teknik Üniversitesi Müh. Fak. İnşaat Müh. Bölümü
 SAP 2000 İLE BETONARME HESAPLAMA Hazırlayan: Dr. Onur TUNABOYU Eskişehir Teknik Üniversitesi Müh. Fak. İnşaat Müh. Bölümü SİSTEMİN MODELLENMESİ 1- Birim seçilir. 2- File New Model Grid Only IZGARA (GRID)
SAP 2000 İLE BETONARME HESAPLAMA Hazırlayan: Dr. Onur TUNABOYU Eskişehir Teknik Üniversitesi Müh. Fak. İnşaat Müh. Bölümü SİSTEMİN MODELLENMESİ 1- Birim seçilir. 2- File New Model Grid Only IZGARA (GRID)
Çatı katında tüm çevrede 1m saçak olduğu kabul edilebilir.
 Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri belirlenmesi 1. katta döşemelerin çözümü ve çizimi Döşeme
Proje ile ilgili açıklamalar: Döşeme türleri belirlenir. Döşeme kalınlıkları belirlenir. Çatı döşemesi ve 1. kat normal döşemesinde döşeme yükleri belirlenmesi 1. katta döşemelerin çözümü ve çizimi Döşeme
İZMİR İLİ BUCA İLÇESİ 8071 ADA 7 PARSEL RİSKLİ BİNA İNCELEME RAPORU
 İZMİR İLİ BUCA İLÇESİ 8071 ADA 7 PARSEL RİSKLİ BİNA İNCELEME RAPORU AĞUSTOS 2013 1.GENEL BİLGİLER 1.1 Amaç ve Kapsam Bu çalışma, İzmir ili, Buca ilçesi Adatepe Mahallesi 15/1 Sokak No:13 adresinde bulunan,
İZMİR İLİ BUCA İLÇESİ 8071 ADA 7 PARSEL RİSKLİ BİNA İNCELEME RAPORU AĞUSTOS 2013 1.GENEL BİLGİLER 1.1 Amaç ve Kapsam Bu çalışma, İzmir ili, Buca ilçesi Adatepe Mahallesi 15/1 Sokak No:13 adresinde bulunan,
DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 8 Sayı: 1 s. 101-108 Ocak 2006
 DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 8 Sayı: s. -8 Ocak 6 BETONARME BİNALARIN DEPREM DAVRANIŞINDA DOLGU DUVAR ETKİSİNİN İNCELENMESİ (EFFECT OF INFILL WALLS IN EARTHQUAKE BEHAVIOR
DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 8 Sayı: s. -8 Ocak 6 BETONARME BİNALARIN DEPREM DAVRANIŞINDA DOLGU DUVAR ETKİSİNİN İNCELENMESİ (EFFECT OF INFILL WALLS IN EARTHQUAKE BEHAVIOR
Ç E R Ç E V E L E R. L y2. L y1
 ADİL ALTUDAL Mart 2011 Ç E R Ç E V E L E R Betonarme yapıların özelliklerinden bir tanesi de monolitik olmasıdır. Bu özellik sayesinde, kirişlerin birleştiği kolonlarla birleşme noktaları olan düğüm noktalarının
ADİL ALTUDAL Mart 2011 Ç E R Ç E V E L E R Betonarme yapıların özelliklerinden bir tanesi de monolitik olmasıdır. Bu özellik sayesinde, kirişlerin birleştiği kolonlarla birleşme noktaları olan düğüm noktalarının
DEPREM TASARIMINDA ÖTELENMENİN VE ENERJİ TÜKETİMİNİN KONTROLÜ
 DEPREM TASARIMINDA ÖTELENMENİN VE ENERJİ TÜKETİMİNİN KONTROLÜ Hamide TEKELİ Danışman Prof. Dr. Ergin ATIMTAY II. Danışman Y. Doç. Dr. Mustafa TÜRKMEN DOKTORA TEZİ İNŞAAT MÜHENDİSLİĞİ ANABİLİM DALI ISPARTA
DEPREM TASARIMINDA ÖTELENMENİN VE ENERJİ TÜKETİMİNİN KONTROLÜ Hamide TEKELİ Danışman Prof. Dr. Ergin ATIMTAY II. Danışman Y. Doç. Dr. Mustafa TÜRKMEN DOKTORA TEZİ İNŞAAT MÜHENDİSLİĞİ ANABİLİM DALI ISPARTA
İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER
 İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER Yapı Elemanları İnşaat Mühendisliği ile ilgili yapı sistemleri üç ayrı tipteki yapı elemanlarının birleşiminden oluşur. 1)Çubuk Elemanlar: İki boyutu üçüncü boyutuna
İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER Yapı Elemanları İnşaat Mühendisliği ile ilgili yapı sistemleri üç ayrı tipteki yapı elemanlarının birleşiminden oluşur. 1)Çubuk Elemanlar: İki boyutu üçüncü boyutuna
Yapı Elemanlarının Davranışı
 SÜNEKLİK KAVRAMI Yapı Elemanlarının Davranışı Yrd. Doç. Dr. Barış ÖZKUL Eğrilik; kesitteki şekil değişimini simgeleyen geometrik bir parametredir. d 2 d d y 1 2 dx dx r r z z TE Z z d x Eğrilik, birim
SÜNEKLİK KAVRAMI Yapı Elemanlarının Davranışı Yrd. Doç. Dr. Barış ÖZKUL Eğrilik; kesitteki şekil değişimini simgeleyen geometrik bir parametredir. d 2 d d y 1 2 dx dx r r z z TE Z z d x Eğrilik, birim
SEM2015 programı kullanımı
 SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Çözebileceği sistemler: Düzlem/uzay kafes: Evet Düzlem/uzay çerçeve:
SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Çözebileceği sistemler: Düzlem/uzay kafes: Evet Düzlem/uzay çerçeve:
Deprem Etkisindeki Bina Türü Çelik Yapıların Kapasite Eğrisinin Belirlenmesi İçin Bir Bilgisayar Programı (İMEP-3D)
 Deprem Etkisindeki Bina Türü Çelik Yapıların Kapasite Eğrisinin Belirlenmesi İçin Bir Bilgisayar Programı (İMEP-3D Erdal İrtem* Özet Bu çalışmada, deprem etkisindeki bina türü yapıların kapasite eğrisinin
Deprem Etkisindeki Bina Türü Çelik Yapıların Kapasite Eğrisinin Belirlenmesi İçin Bir Bilgisayar Programı (İMEP-3D Erdal İrtem* Özet Bu çalışmada, deprem etkisindeki bina türü yapıların kapasite eğrisinin
BASINÇ ÇUBUKLARI. Yapısal çelik elemanlarının, eğilme momenti olmaksızın sadece eksenel basınç kuvveti altında olduğu durumlar vardır.
 BASINÇ ÇUBUKLARI BASINÇ ÇUBUKLARI Yapısal çelik elemanlarının, eğilme momenti olmaksızın sadece eksenel basınç kuvveti altında olduğu durumlar vardır. Kafes sistemlerdeki basınç elemanları, yapılardaki
BASINÇ ÇUBUKLARI BASINÇ ÇUBUKLARI Yapısal çelik elemanlarının, eğilme momenti olmaksızın sadece eksenel basınç kuvveti altında olduğu durumlar vardır. Kafes sistemlerdeki basınç elemanları, yapılardaki
Mukavemet. Betonarme Yapılar. İç Kuvvet Diyagramları. Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği
 Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği KİRİŞ MESNETLENME TİPLERİ VE YÜKLER KİRİŞ MESNETLENME TİPLERİ VE YÜKLER (a) Basit kiriş (b) Sürekli kiriş (c) Konsol
Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği KİRİŞ MESNETLENME TİPLERİ VE YÜKLER KİRİŞ MESNETLENME TİPLERİ VE YÜKLER (a) Basit kiriş (b) Sürekli kiriş (c) Konsol
YARI RİJİT BİRLEŞİMLİ ÇELİK ÇERÇEVELERİN ANALİZİ
 YARI RİJİT BİRLEŞİMLİ ÇELİK ÇERÇEVELERİN ANALİZİ ARAŞ. GÖR. ÖZGÜR BOZDAĞ İş Adresi: D.E.Ü. Müh. Fak. İnş.Böl. Kaynaklar Yerleşkesi Tınaztepe-Buca / İZMİR İş Tel-Fax: 0 232 4531191-1073 Ev Adresi: Yeşillik
YARI RİJİT BİRLEŞİMLİ ÇELİK ÇERÇEVELERİN ANALİZİ ARAŞ. GÖR. ÖZGÜR BOZDAĞ İş Adresi: D.E.Ü. Müh. Fak. İnş.Böl. Kaynaklar Yerleşkesi Tınaztepe-Buca / İZMİR İş Tel-Fax: 0 232 4531191-1073 Ev Adresi: Yeşillik
YAPI STATİĞİ Prof. Dr. P. Marti
 İlk yayın, 9 Temmuz 05 www.guven-kutay.ch YPI STTİĞİ Prof. Dr. P. arti Hiperstatik Sistemler -0- u dosyayı _00_Yapı Statiğine Giriş ve Özet dosyasıyla beraber incelerseniz daha iyi anlarsınız. Çevirenler:.
İlk yayın, 9 Temmuz 05 www.guven-kutay.ch YPI STTİĞİ Prof. Dr. P. arti Hiperstatik Sistemler -0- u dosyayı _00_Yapı Statiğine Giriş ve Özet dosyasıyla beraber incelerseniz daha iyi anlarsınız. Çevirenler:.
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
GERİLME Cismin kesilmiş alanı üzerinde O
 GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
BETONARME YAPI TASARIMI -KOLON ÖN BOYUTLANDIRILMASI-
 BETONARME YAPI TASARIMI -KOLON ÖN BOYUTLANDIRILMASI- Yrd. Doç. Dr. Güray ARSLAN Arş. Gör. Cem AYDEMİR 28 GENEL BİLGİ Betonun Gerilme-Deformasyon Özellikleri Betonun basınç altındaki davranışını belirleyen
BETONARME YAPI TASARIMI -KOLON ÖN BOYUTLANDIRILMASI- Yrd. Doç. Dr. Güray ARSLAN Arş. Gör. Cem AYDEMİR 28 GENEL BİLGİ Betonun Gerilme-Deformasyon Özellikleri Betonun basınç altındaki davranışını belirleyen
DEPREME DAVRANIŞI DEĞERLENDİRME İÇİN DOĞRUSAL OLMAYAN ANALİZ. NEJAT BAYÜLKE 19 OCAK 2017 İMO ANKARA ŞUBESİ
 DEPREME DAVRANIŞI DEĞERLENDİRME İÇİN DOĞRUSAL OLMAYAN ANALİZ NEJAT BAYÜLKE nbayulke@artiproje.net 19 OCAK 2017 İMO ANKARA ŞUBESİ Deprem davranışını Belirleme Değişik şiddette depremde nasıl davranacak?
DEPREME DAVRANIŞI DEĞERLENDİRME İÇİN DOĞRUSAL OLMAYAN ANALİZ NEJAT BAYÜLKE nbayulke@artiproje.net 19 OCAK 2017 İMO ANKARA ŞUBESİ Deprem davranışını Belirleme Değişik şiddette depremde nasıl davranacak?
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
EĞRİSEL YAPI ELEMANLARININ ETKİN SAYISAL ANALİZİ ÜZERİNE BİR ARAŞTIRMA 1. A Study on An EfficientNumerical Analysis of TheCurvedStructuralElements
 EĞRİSEL YAPI ELEMANLARININ ETKİN SAYISAL ANALİZİ ÜZERİNE BİR ARAŞTIRMA 1 A Study on An EfficientNumerical Analysis of TheCurvedStructuralElements Timuçin Alp ASLAN İnşaat Mühendisliği Anabilim Dalı Beytullah
EĞRİSEL YAPI ELEMANLARININ ETKİN SAYISAL ANALİZİ ÜZERİNE BİR ARAŞTIRMA 1 A Study on An EfficientNumerical Analysis of TheCurvedStructuralElements Timuçin Alp ASLAN İnşaat Mühendisliği Anabilim Dalı Beytullah
MAK4061 BİLGİSAYAR DESTEKLİ TASARIM
 MAK4061 BİLGİSAYAR DESTEKLİ TASARIM (Shell Mesh, Bearing Load,, Elastic Support, Tasarım Senaryosunda Link Value Kullanımı, Remote Load, Restraint/Reference Geometry) Shell Mesh ve Analiz: Kalınlığı az
MAK4061 BİLGİSAYAR DESTEKLİ TASARIM (Shell Mesh, Bearing Load,, Elastic Support, Tasarım Senaryosunda Link Value Kullanımı, Remote Load, Restraint/Reference Geometry) Shell Mesh ve Analiz: Kalınlığı az
