ÖRNEK 3712 nin esas ölçüsünü bulunuz. ÇÖZÜM esas ölçüsü 112 olur. ÖRNEK ÇÖZÜM cos 1, 1 sin 1
|
|
|
- İbrahi̇m Sezen
- 6 yıl önce
- İzleme sayısı:
Transkript
1 MTEMTİK TRİGONOMETRİ - I irim Çember II III sin I IV 0 nin esas ölçüsünü bulunuz olduğundan, esas ölçüsü olur I ölge (0 < < II ölge ( ) < < ) III ölge ( < < IV ölge ( ) < < ) sin tan cot gradın esas ölçüsünü bulunuz olduğundan, esas ölçüsü 00 olur çı Ölçü irimleri erece: Çemberin 0 da ini gören merkez açıya denir Grad: Çemberin 00 de ini gören merkez açıya G denir Radyan: Çemberin yarıçap uzunluğundaki yayı gören merkez açıya rad denir Trigonometrik Fonksiyonlar Sin - os sin (0,) P(, sin) sin (, 0) (, 0) * 0 G 00 R (0, ) * ı 0 ı ıı 0 Esas Ölçü 0 < 0 ve k Z, + k 0 ise nın Esas ölçüsü 0 < 00 G ve k Z, + k 00 G ise, nın Esas Ölçüsü G 0 < ve k Z, + k ise nın Esas ölçüsü Rad, sin sin0 0 sin 90 sin 0 0 sin 0 os0 os sin Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı w w w a k a d e m i v i z y o n c o m t r
2 T R İ G O N O M E T R İ - l Tan - ot sin cot tan ( ) P tan cot (y ) tan 0 0 cot 0 (Tanımsız) tan cot tan90 (Tanımsız) cot 90 0 sin tan, cot sin Sekant Kosekant (sec ec) sec ec, sin sec90 Tanımsız, ec 0 Tanımsız sec 0 Tanımsız, ec 0 Tanımsız tan 0 0 cot 0 (Tanımsız) ec sin sec P tan 0 (Tanımsız) cot < < iken, sin < tan < < cot < < 90 iken, < cot < sin < tan açısı 0 ile 90 arasında artarken, sin ve tan artar, ve cot azalır sin sin 0 0 sin sin 0 0 sin 90 0 tan 0 cot 90 0 tan 0 cot 0 tan cot tan 0 cot 0 tan 90 cot 0 Tanımsız Trigonometrik Fonksiyonlarda Özdeşlikler 0 < < olmak üzere, ( ) ( + ) [ bölge] [ bölge] sin ( ) sin ( ) tan ( ) tan cot ( ) cot, sin ( + ) sin, ( + ), tan ( + ) tan, cot ( + ) cot ik Üçgende ar çıların Trigonometrik Oranları Hipotenis (c) Komşu dik kenar (b) Karşı a sin Hipotenüs c tan sec Karşı Komşu sin tan cot a cot b c b 90 iken, sec ec olur ec Karşı dik kenar (a) Komşu Hipotenüs Komşu Karşı b a c sin a b c ( ) ( + ) ( ) ( ) [ bölge], ( + ) () (çının kendisi bölge) sin ( ) sin ( ) tan ( ) tan cot ( ) cot ( θ) ( θ) [ bölge] [ bölge] sin ( ), sin ( ) ( ) sin, ( ) sin tan ( ) cot, tan ( ) cot cot ( ) tan, cot ( ) tan Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı w w w a k a d e m i v i z y o n c o m t r
3 M T E M T İ K θ θ [ bölge] [ bölge] sin ( ), sin( ) ( ) sin, ( ) sin tan ( ) cot, tan( ) cot cot ( ) tan, cot( ) tan şağıdaki trigonometrik değerleri hesaplayınız a sin c e tan g cot a sin ( ) ( ) b sin ( 0) d ( 0) f tan ( 0) h cot ( 0) sin ( ) sin b sin ( 0) sin 0 c ( ) ( + d ( 0) 0 e tan ( ) tan ( f tan ( 0) tan (0) ) ) tan g cot ( ) cot ( ) cot h cot ( 0) cot ( 0) cot 0 sin + cot 0 + işleminin sonucunu bulunuz sin + cot ( cot 0) f( ) sin ( sin ( ) ( )) + sin + sin + sin ( ) ( ( )) cot 00tan 0 sin 00 işleminin sonucunu bulunuz cot 00 cot 0 tan 0 tan 0 sin 00 sin 0 cot 00 tan 0 sin 00 ( ) ( ) ( ) Trigonometrik Oranlardan iri Verildiğinde iğerinin ulunması (, ) ve sin olduğuna göre,, tan, cot değerlerini bulunuz (, ) sin bölge tan f() sin ( ) + sin ( ) f( ) değerini bulunuz olduğuna göre, cot w w w a k a d e m i t e m e l l i s e s i c o m Ö z e l c a r K a l i t e e ğ e r M i l a t T e m e l L i s e s i
4 T R İ G O N O M E T R İ - l (, ) ve olduğuna göre, değerini bulunuz,,, tan < < ve tan olduğuna göre, cot tan ifadesinin sayısal değerini bulunuz F E F FE E ve olduğuna göre, tan( E değerini bulunuz F E y sin < < ( bölge) tan tan, tan tan 0 00 olsun olur tan tan( y) tany Şekil eş kareden oluşmaktadır cot çarpımı kaçtır? sin 0 + sin + sin + + sin 0 toplamını bulunuz + 90 iken sin ve sin + kurallarından yararlanılarak, sin 0+sin + +sin ( ) tane Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı olsun olur cot Toplam ve Fark Formülleri sin(a b) sinab sinba sin(a b) sinab sinba w w w a k a d e m i v i z y o n c o m t r
5 M T E M T İ K sin0 ve sin değerlerini bulunuz sin 0 sin (0 + ) sin 0 + sin 0 sin sin ( 0) sin 0 sin 0 ( a b) ab sinasinb ( a b) ab sinasinb ve değerlerini bulunuz ( + 0) 0 sin sin 0 (0 ) [veya ( 0)] 0 + sin 0 sin tan a tan b tan(a b) tan atanb tan a tan b tan(a b) tan atan b kare, E E olduğuna göre, tan değerini bulunuz y tan tany tan tan( y) tantany tan in sayısal değerini bulunuz E tan tan0 tan ( 0) tantan0 cotacotb cot( a b) cota cotb cotacotb cot( a b) cota cotb E ir üçgeninde açısının tanjantı, açısının cot 0 olduğuna göre, cot değerini bulunuz tanjantı olduğuna göre, açısının tanjantını bulunuz tan ( + tan (0 tan tan tan tan tan ( + tantan tan olduğuna göre, tan, cot cot ( 0) cotcot0 cot cot0 w w w a k a d e m i t e m e l l i s e s i c o m Ö z e l c a r K a l i t e e ğ e r M i l a t T e m e l L i s e s i
6 T R İ G O N O M E T R İ - l şağıdaki ifadelerin sayısal değerlerini bulunuz a cot0cot0 cot0 cot0 b (0 + a) ( a) sin(0 + a) sin( a) c d sin + 0 sin sin 0 cot0cot0 a cot( 0 0) cot0 cot0 cot 0 b (0 + a) ( a) sin (0 + a) sin( a) c [(0 + a) + ( a)] d sin + sin 0 + sin 0 sin (0 ) 0 sin 0 ( sin sin ) 0 0 ( ) 0 ( ) 0 9 t olduğuna göre, sin değerini bulunuz sin sin tan tan tan cot cot cot şağıdaki ifadeleri hesaplayınız a sin 0 sin b 0 c d e sin a sin 0 b sin 0 sin 0 sin0 0 c ( ) sin0 0, sin 0 ( 0) sin sin ( 9) 9 t sin ( 9) sin 9 sin 9 t t t t t ( t ) t Yarım çı Formülleri t d 0 e sin sin sin Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı w w w a k a d e m i v i z y o n c o m t r
7 M T E M T İ K y olduğuna göre, ile y arasındaki ilişki nedir? y y y ( ) y y + (0, ) ve sin olduğuna göre, değerini bulunuz sin sin olduğuna göre, sin değerini bulunuz a b a b sina sinb sin a b a b sina sinb sin a b a b a b a b a b a b sin sin sin(a b) tana tanb ab sin(a b) tana tanb ab sin(a b) cota cotb sinasinb sin(b a) cota cotb sinasinb farkını bulunuz sin sin 0 sin ( ) sin + toplamını bulunuz sin + sin + sin sin + sin sin sin 0 sin una göre, sin a sin a sin a a a tan a tana tana tan a sin sin () sin sin 9 önüşüm Formülleri a siny + y olduğuna göre, y oranını bulunuz siny sin sin y sin y y y y sin y w w w a k a d e m i t e m e l l i s e s i c o m Ö z e l c a r K a l i t e e ğ e r M i l a t T e m e l L i s e s i
8 T R İ G O N O M E T R İ - l sin y sin y sin siny y y sin sin oranını bulunuz sin 0 Ters önüşüm Formülleri sina sinb cot - [(a+ b) - (a- b)] a b [(a+ b) (a- b)] sina b [sin(a+ b) sin(a- b)] çarpımını bulunuz [ ] [0 + ] sin çarpımını bulunuz sin sin [sin 0 + sin 0] [ ] Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı sin 0 sin 0 sin 0 sin 0 çarpımını bulunuz sin 0sin 0 sin 0 sin 0 sin 0 [ sin 0 [ sin 0 [ [ [ ( 0 0)] ( sin )] ] sin 0 (sin 0 + sin( 0)] + (sin 0 sin 0 + sin )] + sin [0 + sin ] sin 0 sin 0 sin 0 çarpımını bulunuz çarpımını bulunuz ( ) ( ) [ + ] [sin + sin ] olmak üzere, ( )( ) [ sin ] [ ) ( ] [ ] [0] 0 w w w a k a d e m i v i z y o n c o m t r
9 M T E M T İ K Ç Ö Z Ü M L Ü T E S T 0 lik yayın esas ölçüsü kaçtır? sin 00, 0, tan 9 nin işaretleri sırası ile aşağıdakilerden hangisidir?, +,,, +,, +, +, +,, + 0 lik yayın esas ölçüsü aşağıdakilerden hangisidir? < < ve olduğuna göre, kaçtır? tan cot ifadesinin değeri ıı lik açı kaç derece kaç dakika kaç saniyedir? ı ıı ı ıı ı ıı ı ıı ıı 0 < < ve olduğuna göre, kaçtır? olduğuna göre, kaçtır? tan 9 [, ) olmak üzere, olduğuna göre, sec kaçtır? a tan b tan 0 c tan 0 a, b ve c nin sayısal değerlerinin büyükten küçüğe sıralanışı aşağıdakilerden hangisidir? c > a > b a > c > b c > b > a a > b > c b > a > c 0 + y 90 ve sin y olduğuna göre, + y toplamı kaçtır? w w w a k a d e m i t e m e l l i s e s i c o m 9 Ö z e l c a r K a l i t e e ğ e r M i l a t T e m e l L i s e s i
10 T R İ G O N O M E T R İ - l sin olduğuna göre, sin nedir? sin00 ifadesinin eşiti kaçtır? 0 0 ifadesinin sonucu kaçtır? sin ifadesinin sonucu kaçtır? sin sin işleminin sonucu kaçtır? sin toplamı kaçtır? olmak üzere, sin ( )sin( ) ifadesinin değeri kaçtır? 9 sin çarpımı kaçtır? sin ifadesinin eşiti kaçtır? 0 sin ifadesinin değeri kaçtır? Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı 0 w w w a k a d e m i v i z y o n c o m t r
11 M T E M T İ K olduğundan esas ölçü 0 evap dır Ç Ö Z Ü M L E R olduğundan esas ölçü 0 olur evap dir tan < < ( bölge), cot ( tan cot 0 < <, ( bölge) ) (, ) evap dir,, ıı 0 ıı 0 ıı 9 ı 0 ı 0 ı ıı ı ıı ı ıı evap dir tan 0 0 evap dir 90 ve sin olur evap dir a tan tan b tan 0 tan 0 c tan 0 tan 0 Tanjant fonksiyonunun değeri (0 den 90 ye doğru) açı büyüdükçe artar tan < tan 0 < tan 0, buradan da a > b > c evap dir 9 [,, sec ] ( bölge) evap dir sin 00 (III bölge) 0 (II bölge) tan 9 (III bölge) + evap E dir 0 + y 90 sin y ise y + 90, y + + y 90 y + denklem sistemi çözülürse, ve y 9 olur + y evap dir w w w a k a d e m i t e m e l l i s e s i c o m Ö z e l c a r K a l i t e e ğ e r M i l a t T e m e l L i s e s i
12 T R İ G O N O M E T R İ - l sin, sin sin () sin sin (sin a sina sin a) evap dir sin0 sin evap dir (a b sin 0 sin a b sin 0 sin 0 sin a b sin ) 0 evap dir sin (sin )(sin + ) (sin )() ( ) ( ) 0 evap dır sin sin sin ( sin ) (sin sin ) (sina sin b sin a b sin 0 sin 0 0 a b ) evap dir sin () (sin) sin sin (sin ) sin +, + sin 0 +, sin sin0 evap dir sin ( ) sin ( ) [ ( ) ( )] [ ( sin )] 9 sin sin sin evap E dir evap dir sin sin sin0 evap dir 0 sin 0 ( 0 sin ) ( 0) + evap dir Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı w w w a k a d e m i v i z y o n c o m t r
13 M T E M T İ K K O N U T E K R R T E S T İ 0 kaç radyandır? eşkenar üçgen, olduğuna göre, tan kaçtır? 00 grad kaç derecedir? ikizkenar üçgeninde, br 0 br H radyanlık yayın esas ölçüsü kaç radyandır? [] [H] olduğuna göre, kaçtır? 0 radyanlık yayın esas ölçüsü kaç radyandır? karesinde, E E olduğuna göre, tan kaçtır? 9 9 E bir dikdörtgen, E > E br 0 br m( m(e olduğuna göre, E uzunluğu kaç br dir? 0 9 E 9 toplamı kaçtır? w w w a k a d e m i t e m e l l i s e s i c o m Ö z e l c a r K a l i t e e ğ e r M i l a t T e m e l L i s e s i
14 T R İ G O N O M E T R İ - l 0 toplamının yarısı aşağıdakilerden hangisidir? sec ec < < olmak üzere, sin tan tan ifadesi aşağıdakilerden hangisine eşittir? + tan tan + tan I sin( ) II ( ) III tan ( ) cot IV cot ( ) cot Yukarıdaki ifadelerden kaç tanesi doğrudur? Hiçbiri şağıdakilerden hangisi sin ( a) ifadesine özdeş değildir? a ( + a) ( a) sin ( a) sin( + a) T sin ( ) ( ) sin( ) olduğuna göre, T aşağıdakilerden hangisine eşittir? 9 ( ) olduğuna göre, tancot çarpımı kaçtır? sin( ) + ( + ) + ( + ) ifadesi aşağıdakilerden hangisine eşittir? ( ) ifadesi aşağıdakilerden hangisine eşit değildir? sin( + ) sin ( ) sin( ) ( ) 9 0 aşağıdakilerden hangisine eşittir? sin sin 0 < < ve 0 olduğuna göre, kaçtır? ifadesinin eşiti aşağıdakilerden han- 0 sin ( ) gisidir? Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı w w w a k a d e m i v i z y o n c o m t r
15 M T E M T İ K K O N U T E K R R T E S T İ sin ifadesinin eşiti kaçtır? 0 nin değeri aşağıdakilerden hangisidir? tan nin değeri kaçtır? sin ifadesinin eşiti kaçtır? 0 < < ve olduğuna göre, kaçtır? Şekilde verilen dörtgenine göre, kaçtır? 0 olduğuna göre, kaçtır? ikizkenar dik üçgeninde br m( 90 m ( olduğuna göre, tan nın değeri kaçtır? 9 aşağıdakilerden hangisine eşit değildir? sin ( ) sin ( ) ( ) sin sin w w w a k a d e m i t e m e l l i s e s i c o m Ö z e l c a r K a l i t e e ğ e r M i l a t T e m e l L i s e s i
16 T R İ G O N O M E T R İ - l 0 0 < < olduğuna göre, ifadesi aşağıdakilerden hangisidir? olduğuna göre, ifadesinin en sade hali nedir? sin + olduğuna göre, kaçtır? kesrinin en sade hali nedir? sin tan cot tan ifadesinin aşağıdakilerden hangisine sin0 sin0 sin eşittir? üçgeninde, m( 90 olduğuna göre, kaçtır? (a b) (a b) ifadesinin en sade sinb şekli aşağıdakilerden hangisidir? sina sina a sina a tan + tan toplamı kaçtır? 9 sin0sin0 ifadesinin değeri aşağıdakilerden hangisidir? 0 + sin toplamının sonucu aşağıdakilerden hangisidir? sin0 ifadesinin değeri kaçtır? Ü n i v e r s i t e y e H a z ı r l ı k M a t e m a t i k e r g i s i / S a y ı w w w a k a d e m i v i z y o n c o m t r
TRİGONOMETRİ Test -1
TRİGONOMETRİ Test -. y. y K O O. nalitik düzlemde verilen O merkezli birim çemberde hangi noktanın koordinatları (0, ) dir? (O noktası orijindir.) O y [OK] açıortay olmak üzere, nalitik düzlemde verilen
Cebir Notları. Trigonometri TEST I. 37π 'ün esas ölçüsü kaçtır? Gökhan DEMĐR,
, 00 M ebir Notları Gökhan EMĐR, gdemir@yahoo.com.tr Trigonometri. TEST I π 'ün esas ölçüsü kaçtır? ) p ) p ) p ) π p. tanθ = ) ) olduğuna göre, sinθ değeri kaçtır? ) ). 0 'nin esas ölçüsü kaçtır?. θ
TEST 1. ABCD bir dörtgen AF = FB DE = EC AD = BC D E C. ABC bir üçgen. m(abc) = 20. m(bcd) = 10. m(acd) = 50. m(afe) = 80.
11 ÖLÜM SİZİN İÇİN SÇTİLR LRİMİZ 1 80 0 bir dörtgen = = = m() = 80 m() = 0 Verilenlere göre, açısının ölçüsü kaç derecedir? 0 10 0 bir üçgen m() = 0 m() = 10 m() = 0 Yukarıda verilenlere göre, oranı kaçtır?
ÜNİVERSİTEYE HAZIRLIK 11. ve 12. SINIF OKULA YARDIMCI KONU ANLATIMLI SORU BANKASI MATEMATİK TRİGONOMETRİ
ÜNİVERSİTEYE HAZIRLIK. ve. SINIF OKULA YARDIMCI KONU ANLATIMLI SORU BANKASI TRİGONOMETRİ ÜNİVERSİTEYE HAZIRLIK. ve. SINIF OKULA YARDIMCI KONU ANLATIMLI SORU BANKASI ISBN 97 60 7 6 4 Genel Yayın Koordinatörü
TOPLAM VE FARK YAYLAR. PA + = olup, OP = 1 alınacak olursa, OP P
TOPLM VE FRK YYLR a, b R için; Sin( a + b) Sina. sb +. sa Sin( a b) Sina. sb. sa s ( a + b) sa. sb Sina. s ( a b) sa. sb + Sina. İspat: a) Sin( a b) P + lup, OP alınacak lursa, OP P Sin( a + b) P bulunur.
Trigonometrik Fonksiyonlar
Trigonometrik Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 6 Amaçlar Bu üniteyi çalıştıktan sonra; açı kavramını hatırlayacak, açıların derece ölçümünü radyan ölçümüne ve tersine çevirebilecek, trigonometrik
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
ÜÇGENLER ÜNİTE 4. ÜNİTE 4. ÜNİTE 4. ÜNİTE 4. ÜNİT
ÜÇGNLR ÜNİT. ÜNİT. ÜNİT. ÜNİT. ÜNİT ÜÇGNLRİN ŞLİĞİ Üçgende çılar. azanım : ir üçgenin iç açılarının ölçüleri toplamının 80, dış açılarının ölçüleri toplamının 0 olduğunu gösterir. İki Üçgenin şliği. azanım
POLİNOMLAR I MATEMATİK LYS / 2012 A1. 1. Aşağıdakilerden kaç tanesi polinomdur? 6. ( ) ( ) 3 ( ) 2. 2. ( ) n 7 8. ( ) 3 2 3. ( ) 2 4.
POLİNOMLAR I MATEMATİK. Aşağıdakilerden kaç tanesi polinomdur? I. ( ) P = + II. ( ) P = + III. ( ) + + P = + 6. ( ) ( ) ( ) P = a b a + b sabit polinom olduğuna göre ( ) ( ) ( ) P a +P b +P 0 toplamı kaçtır?
9. ÜNİTE ÜÇGENLER, ÇOKGENLER VE MESLEKÎ UYGULAMALARI
9. ÜNİTE ÜÇGENLER, ÇOKGENLER VE MESLEKÎ UYGULAMALARI KONULAR DİK ÜÇGENLERDE METRİK BAĞINTILAR 1. Pythagoras (Pisagor) Bağıntısı. Euclides (öklit) Bağıntısı 3. Pisagor ve öklit Bağıntıları ile İlgili Problemler
CEVAP ANAHTARI 1-B 2-C 3-C 4-C 5-B 6-E 7-D 8-E 9-C 10-E 11-E 12-A 13-A 1-A 2-D 3-C 4-D 5-D 6-B 7-D 8-B 9-D 10-E 11-D 12-C
1. BÖLÜM: AÇISAL KAVRAMLAR VE DOĞRUDA AÇILAR 1-B 2-C 3-C 4-C 5-B 6-E 7-D 8-E 9-C 10-E 11-E 12-A 13-A 1-E 2-A 3-E 4-C 5-C 6-C 7-D 8-D 9-D 10-E 11-B 12-C 2. BÖLÜM: ÜÇGENDE AÇILAR 1-A 2-D 3-C 4-D 5-D 6-B
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe olan mesafeyi bulmak istiyoruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu sorunun üstesinden gelmek için
ÖZEL EGE LİSESİ EGE BÖLGESİ 14. OKULLAR ARASI MATEMATİK YARIŞMASI 8. SINIF ELEME SINAVI TEST SORULARI
EGE ÖLGESİ 4. OKULLR RSI MTEMTİK YRIŞMSI 8. SINIF ELEME SINVI TEST SORULRI. n bir tamsayı olmak üzere, n n 0 ( 4.( ) +.( ) + 7 + 8 ) işleminin sonucu kaçtır? ) 0 ) 5 ) 6 ). ir kitapçıda rastgele seçilen
LYS Y OĞRU MTMTİK TSTİ LYS-. u testte Matematik ile ilgili soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a ve b asal
ÖĞRENCİNİN ADI SOYADI: NUMARASI: SINIFI: KONU: Trigonometrik Fonksiyonlar tanx. 1 cos x sinx ifadesi, aşağıdakilerden hangisine eşittir?
ÖĞRENİNİN I SOYI: NUMRSI: ersin dı KONU: Trignmetrik Fnksiynlar ersin Knusu. cs x sinx ifadesi, aşağıdakilerden. cs x ct x sin x sec x + sec x ) cs x csec x + csec x ) cs x. ct x cs ec x ct x. sec x csec
25. f: R { 4} R 28. ( ) 3 2 ( ) 26. a ve b reel sayılar olmak üzere, 27. ( ) eğrisinin dönüm noktasının ordinatı 10 olduğuna göre, m kaçtır?
. f: R { 4} R, > ise ( ) 4 f =, ise 6 8. ( ) f = 6 + m + 4 eğrisinin dönüm noktasının ordinatı olduğuna göre, m kaçtır? ) 7 ) 8 ) 9 ) E) fonksiyonu aşağıdaki değerlerinin hangisinde süreksizdir? ) ) )
8. SINIF PİSAGOR BAĞINTISI
06. SINIF PİSGOR ĞINTISI a c (hipotenüs) 5 b 6 a 2 +b 2 =c 2 Pisagor bağıntısını kullanabilmek için dik üçgen olması gerekir. ÖR: şağıda verilmeyen kenarları bulunuz. 6 2 Pisagor bağıntısı kullanırken
Örnek...1 : Birim çember kullanarak aşağıdaki ifadeleri hesapla yın ız. Örnek...2 : sin 2 12+cos sin 67+cos 34. sin41 işleminin sonucu kaçtır?
RİGNMERİ İR AÇININ KSİNÜS VE SİNÜS DEĞERLERİ Merk ezi orijin ve arıçapı birim olan çem bere birim çem ber denir. Standart pozisonda (Köşesi orijinde, başlangıç kenarı ve Kosinüs Sinüs önü pozitif ön olan
. K. AÇI I ve UZUNLUK 5. C. e k s TR e m. m(cab)= 5x, m(acd)= 3x, m(abe)= 2x. O merkezli çemberde m(bac)= 75º . O ? F 75º
Geometri Çözmek ir yrıcal calıkt ktır ÇI I ve UZUNLUK 1? m()=, m()=, m()= 7º merkezli çemberde m()= 7º Verilenlere göre açısının ölçüsü kaç derecedir? ) 10 ) 1 ) 10 ) 1 ) 17 Verilenlere göre açısının ölçüsü
8. ÜNİTE TRİGONOMETRİK FONKSİYONLAR
8. ÜNİTE TRİGONOMETRİK FONKSİYONLAR KONULAR 1. TRİGONOMETRİ 2. Açı 3. Yönlü Açı 4. Yönlü Yaylar 5. Birim Çember 6. Açı Ölçü Birimleri 7. Derece 8. Radyan 9. Grad 10. Esas Ölçü 11. TRİGONOMETRİK FONKSİYONLAR
LYS Y ĞRU MTMTİK TSTİ. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.., y reel sayılar
1986 ÖYS. 1. Aşağıdaki ABC üçgeninde. BD kaç cm dir? C) 3 A) 11 B) 10 C) 3 D) 8 E) 7 E) 2
8 ÖYS. Aşağıdaki ABC üçgeninde. BD kaç cm dir? 8 7. Aşağıdaki şekilde ABCD bir yamuk ve AECD bir paralel kenardır.. Aşağıdaki şekilde EAB ve FBC eşkenar üçgendir. AECD nin alanı 8 cm Buna göre CEB üçgeninin
TEST. Dik Üçgen ve Pisagor Bağıntısı. 4. Dik Kenarlar Hipotenüs. 5. Aşağıdaki dik üçgenlerden hangisinin çevre uzunluğu en fazladır?
ik Üçgen ve Pisagor ağıntısı. Sınıf atematik Soru ankası TEST 1.. ik enarlar Hipotenüs m m cm 1 cm cm 60 cm y cm 100 cm z cm 1, cm 1,3 cm ir el fenerinden çıkan ışık m yol alarak yukarıdaki m uzunluğundaki
SINIF TEST. Üslü Sayılar A) 4 B) 5 C) 6 D) 7 A) - 5 B) - 4 C) 5 D) 7. sayısı aşağıdakilerden hangisine eşittir?
8. SINIF. Üslü Sayılar - = T olduğuna göre T kaçtır? A) - B) - C) D) 7 TEST.. 0 - işleminin sonucu kaç basamaklı bir sayıdır? A) B) C) 6 D) 7. n =- 7 için n ifadesinin değeri kaçtır? A) - 8 B) - C) 8 D)
MC TEST-I Aşağıdaki eşitliklerin doğru olduğunu gösteriniz π 2π
MC TEST-I Aşağıdaki eşitliklerin doğru olduğunu gösteriniz π π 1) 4 sin.sin +.sin + = sin ) π π 4 cos.cos +.cos + = cos www.matematikclub.com, 006 Cebir Notları Gökhan DEMĐR, gdemir@yahoo.com.tr TRĐGONOMETRĐ
4. 8. A. D 2. ABC üçgeninin alanı kaç birim karedir? ABC üçgeninin alanı kaç birim karedir? A) 16 B) 18 C) 20 D) 24 E) 32 120º 135º
ğlence başlıyor yor 1 º 0º üçgeninin alanı kaç birim karedir? ) ) 9 LN SI 1 LN SI 1 )1 ) üçgeninin alanı kaç birim karedir? üçgeninin alanı kaç birim karedir? ) ) ) ) ) ) üçgen, = birim, = birim, m() =
LYS YE DOĞRU MATEMATİK TESTİ
MTMTİK TSTİ LYS-. u testte Matematik ile ilgili 50 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 75 dakikadır.. a, b ve c birer rakam
örnektir örnektir Geometri TYT Yeni müfredata tam uygun MİKRO KONU TARAMA TEST AYRINTILARI VE ÖRNEKLERİ (1-10. Testler)
TYT Geometri MİKRO KONU TRM TST YRINTILRI V ÖRNKLRİ (-0. Testler) Yeni müfredata tam uygun eğerli öğretmenimiz, branşınızla ilgili TYT konu tarama testlerimizden bazı örnekleri incelemeniz için size sunuyoruz.
7. ÜNİTE DOĞRUDA VE ÜÇGENDE AÇILAR
7. ÜNİTE DOĞRUDA VE ÜÇGENDE AÇILAR KONULAR 1. DOĞRUDA AÇILAR 2. Açı 3. Açının Düzlemde Ayırdığı Bölgeler 4. Açı Ölçü Birimleri 5. Ölçülerine Göre Açılar 6. Açıortay 7. Tümler Açı 8. Bütünler Açı 9. Ters
TÜRKİYE GENELİ DENEME SINAVI LYS - 1 MATEMATİK
TÜRKİY GNLİ SINVI LYS - 1 7 MYIS 017 LYS 1 - TSTİ 1. u testte 80 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için arılan kısmına işaretleiniz. + k+ n 15 + 10 1. : = + 6 16 + 8 0 + 8 olduğuna
MATEMATİK TESTİ LYS YE DOĞRU. 1. Bu testte Matematik ile ilgili 50 soru vardır.
MTMTİK TSTİ LYS-. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a, b, c birer reel sayı
Sayfa No. Test No İÇİNDEKİLER TRİGONOMETRİ
TRİGONOMETRİ İÇİNDEKİLER Sayfa No Test No YÖNLÜ AÇI VE YÖNLÜ YAY KAVRAMI -AÇI ÖLÇÜ BİRİMLERİ...00-00.... BİRİM ÇEMBER...00-00.... BİR AÇININ ESAS ÖLÇÜSÜ...00-00.... BİR AÇININ TRİGONOMETRİK ORANLARININ
DERS: MATEMATİK I MAT101(04)
DERS: MATEMATİK I MAT0(0) ÜNİTE: FONKSİYONLAR KONU:. TRİGONOMETRİK FONKSİYONLAR Öncelikle açı ölçü birimlerine göz atalım: Bilindiği gibi bir tam açının ölçüsü 0 derecedir. Diğer bir açı ölçü birimi de
1986 ÖYS. 3 b. 2 b C) a= 1. Aşağıdaki ABC üçgeninde. BD kaç cm dir? C) 3 D) 8 E)
ÖYS. Aşağıdaki ABC üçgeninde. BD kaç cm dir? 0. Aşağıdaki şekilde ABCD bir yamuk ve AECD bir paralel kenardır.. Aşağıdaki şekilde EAB ve FBC eşkenar üçgendir. AECD nin alanı cm Buna göre CEB üçgeninin
TEST. Düzgün Çokgenler. 4. Bir iç açısı 140 olan düzgün çokgenin iç açılar 5. A B. 2. Bir dış açısı Çevresi. toplamı kaç derecedir?
üzgün Çokgenler 7. Sınıf Matematik Soru ankası S 49 1. 4. ir iç açısı 140 olan düzgün çokgenin iç açılar toplamı kaç derecedir? ) 70 ) 900 ) 1080 ) 160 Şekilde verilen düzgün çokgenine göre, I., köşesine
2011 YGS MATEMATİK Soruları
0 YGS MTEMTİK Soruları. + + ) 8 ) 0 ) 6 ) E). a = 6 b = ( a)b olduğuna göre, ifadesinin değeri kaçtır? ) ) 6 ) 9 ) 8 E). (.0 ) ) 0, ) 0, ) 0, ) E) 6. x = y = 8 z = 6 olduğuna göre, aşağıdaki sıralamalardan
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe olan mesafeyi bulmak istiyoruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu sorunun üstesinden gelmek için
9SINIF MATEMATİK. Üçgenler Veri
9SINIF MTEMTİ Üçgenler Veri 4 YYIN RİNTÖRÜ ğuz GÜMÜŞ EİTÖR Hazal ÖZNR - Uğurcan YIN İZGİ Muhammed RTŞ SYF TSRIM - P F. Özgür FZ Eğer bir gün sözlerim bilim ile ters düşerse, bilimi seçin... M. emal tatürk
YARDIRMALI MATEMATİK TÜREV FASİKÜLÜ
YRIRMLI MTEMTİK TÜREV FSİKÜLÜ Maksimum-Minimum Problemleri MESUT ERİYES MKSİMUM - MİNİMUM PROLEMLERİ Maksimum ve minimum problemlerini çözmek için şu kurallar ugulanır; 1) Maksimum a da minimum olması
1981 ÖSS olduğuna göre, aşağıdakilerden c hangisi kesinlikle doğrudur? A) a>0 B) c<0 C) a+c=0 D) a 0 E) c>0 A) 12 B) 2 9 C) 10 D) 5 E) 11
98 ÖSS. >0 olmak koşulu ile 2+, 3+, 4+ sayıları bir dik üçgenin kenar uzunluklarını göstermektedir. Bu üçgenin hipotenüs uzunluğu kaç birimdir? A) 2 B) 2 9 C) 0 D) 5 E) 2a c 6. 0 olduğuna göre, aşağıdakilerden
TÜBİTAK TÜRKİYE BİLİMSEL VE TEKNİK ARAŞTIRMA KURUMU BİLİM ADAMI YETİŞTİRME GRUBU ULUSA L İLKÖĞRETİM MA TEMATİK OLİMPİYADI DENEME SINAVI.
Bu sınav iki bölümden oluşmaktadır. TÜBİTAK TÜRKİYE BİLİMSEL VE TEKNİK ARAŞTIRMA KURUMU BİLİM ADAMI YETİŞTİRME GRUBU ULUSA L İLKÖĞRETİM MA TEMATİK OLİMPİYADI DENEME SINAVI Birinci Bölüm DENEME-6 * Çoktan
TEST. Çemberde Açılar. 1. Yandaki. 4. Yandaki saat şekildeki. 2. Yandaki O merkezli. 5. Yandaki O merkezli. 6. Yandaki. O merkezli çemberde %
Çemberde çılar 7. Sınıf Matematik Soru ankası 58. Yandaki merkezli s ( ) = 50c 4. Yandaki saat şekildeki gibi 04.00 ı gösterdiğinde akrep ile yelkovan arasında oluşan x açısı kaç derecedir? ' olduğuna
5. ÜNİTE AÇILAR, ÜÇGENLER VE MESLEKİ UYGULAMALARI
5. ÜNİTE ÇILR, ÜÇGENLER VE MESLEKİ UYGULMLRI açılar KONULR 1. çı, çı Türleri ve Mesleki Uygulamaları 2. Tümler ve ütünler çılar ÜÇGENLER 1. Üçgene it Temel ilgiler 2. Üçgen Türleri 3. Üçgenin Yardımcı
6. ABCD dikdörtgeninde
Çokgenler ve örtgenler Test uharrem Şahin. enar sayısı ile köşegen sayısı toplamı olan düzgün çokgenin bir dış açısı kaç derecedir? ) ) 0 ) ) 0 ). Şekilde dikdörtgeninin içindeki P noktasının üç köşeye
AÇILAR / TEST-1. B, C, E doğrusal = 50 E C. A, B, L doğrusal = 100 = 30 = 40 C 60 D
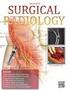ÇIR / TST-1 P = [P] m( P ) = //,, doğrusal m( ) = 30 // m( ) m( ) = = 30 d3 // d3 // d4 m( ) = Verilenlere göre, + + ) 250 ) 260 ) 270 ) 280 ) 300 Verilenlere göre, m( ) ) 25 ) 30 ) 35 ) 40 ) 50 10 Verilenlere
7. f(x) = 2sinx cos2x fonksiyonunun. π x 3 2 A) y = 9. f(x) = 1 2 x2 3x + 4 eğrisinin hangi noktadaki teğetinin D) ( 10 3, 4 9 ) E) ( 2 3, 56
, 006 MC Cebir Notları Gökhan DEMĐR, gdemir@ahoo.com.tr Türev TEST I 7. f() = sin cos fonksionunun. f()= sin( + )cos( ) için f'() nin eşiti nedir? A) B) C) 0 D) E) için erel minimum değeri nedir? A) B)
KARMAŞIK SAYILAR Test -1
KARMAŞIK SAYILAR Test -. i olmak üere, i olduğuna göre, Re() kaçtır? B) C) 0 D) E). i olmak üere, 00 0 06 i i i işleminin sonucu aşağıdakilerden hangisine i B) i C) i + D) E) i. i olmak üere, i olduğuna
9. SINIF Geometri TEMEL GEOMETRİK KAVRAMLAR
TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
Aralıklar, Eşitsizlikler, Mutlak Değer
ARALIKLAR Gerçel sayıların, aralık olarak adlandırılan bazı kümeleri kalkülüste sık sık kullanılır ve geometrik olarak doğru parçalarına karşılık gelir. Örneğin, a < b ise, a dan b ye açık aralık, a ile
[ AN ] doğrusu açıortay olduğundan;
![[ AN ] doğrusu açıortay olduğundan;](/thumbs/69/60247548.jpg "[ AN ] doğrusu açıortay olduğundan;")
. Bir havuzu bir musluk 6 saatte, başka bir musluk 8 saatte dolduruyor. Bu iki musluk kapalı iken, havuzun altında bulunan üçüncü bir musluk, dolu havuzu saatte boşaltabiliyor. Üç musluk birden açılırsa,boş
12-B. Polinomlar - 1 TEST. olduğuna göre P(x - 2, y + 4) polinomunun katsayılar toplamı kaçtır? olduğuna göre A B kaçtır? A) 78 B) 73 C) 62 D 58 E) 33
-B TEST Polinomlar -. Py _, i= y- y + 5y- olduğuna göre P( -, y + ) polinomunun katsayılar toplamı. - 6 = A - 5 + - + B - olduğuna göre A B 78 B) 7 6 D 58 E) B) D) - E) -. -a- b = _ + -5i_ -ci eşitliğine
Öğrenci Seçme Sınavı (Öss) / 19 Nisan Matematik Soruları ve Çözümleri
Öğrenci Seçme Sınavı (Öss) / 9 Nisan 99 Matematik Soruları ve Çözümleri. Üç basamaklı bir sayının iki basamaklı bir sayıyla çarpımı en az kaç basamaklı bir sayı olur? A) B) C) D) 6 E) 7 Çözüm I. Yol basamaklı
A A A A A A A A A A A
LYS 1 GOMTRİ TSTİ 1. u testte sırasıyla Geometri (1 ) nalitik Geometri (3 30) ile ilgili 30 soru vardır.. evaplarınızı, cevap kâğıdının Geometri Testi için ayrılan kısmına işaretleyiniz. 1. [ [ [ [] []
Öğrenci Seçme Sınavı (Öss) / 18 Haziran Matematik II Soruları ve Çözümleri. ise fonksiyonu için, = b olduğuna göre, a b kaçtır? = 1 olur.
Öğrenci Seçme Sınavı (Öss) 8 Haziran 6 Matematik II Soruları ve Çözümleri. f (x) + x lim f ( x) a x x ve, x ise fonksiyonu için,, x lim f ( x) b olduğuna göre, a b kaçtır? x A) B) C) D) E) Çözüm x x için,
ç Ğ İ Ş İ Ş Ç Ç Ğ Ü ç Ş Ş Ç Ğ Ü İ ç ç Ğ İ Ğ Ö Ö Ğ Ü Ş İ ç Ğ » İ «İ Ç Ğ Ş Ö İ Ü İ Ş Ş» Ğ Ğ Ğ İ İ « İ Ş İç Ö»» Ğ Ş İ İ ç Ğ ç « Ü ğ ğ ğ ğ ğ Ü ğ ğ ğ ğ ğ ç ğ ç ğ Ş ç ğ ğ ç ç ç İ İ ğ ğ ğ ğ ğ ğ ç ğ ğ ç ç ğ ğ
11. SINIF. No Konular Kazanım Sayısı GEOMETRİ TRİGONOMETRİ Yönlü Açılar Trigonometrik Fonksiyonlar
11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
π a) = cosa Öğrenci Seçme Sınavı (Öss) / 17 Haziran 2007 Matematik II Soruları ve Çözümleri
Öğrenci Seçme Sınavı (Öss) 7 Haziran 7 Matematik II Soruları ve Çözümleri. Karmaşık sayılar kümesi üzerinde * işlemi, Z * Z Z + Z + Z Z biçiminde tanımlanıyor. Buna göre, ( i) * ( + i) işleminin sonucu
BÖLÜM I MATEMATİK NEDİR? 13 1.1. Matematik Nedir? 14
İÇİNDEKİLER Önsöz. V BÖLÜM I MATEMATİK NEDİR? 13 1.1. Matematik Nedir? 14 BÖLÜM II KÜMELER 17 2.1.Küme Tanımı ve Özellikleri 18 2.2 Kümelerin Gösterimi 19 2.2.1 Venn Şeması Yöntemi 19 2.2.2 Liste Yöntemi
EVVET ARKADAŞLAR HOŞGELDİNİZ BU DERSİMİZDE ÜÇGENLER VE ÖZELLİKLERİNE GÖZ ATACAĞIZ.
DERS : GEOMETRİ KONU : ÜÇGEN EVVET ARKADAŞLAR HOŞGELDİNİZ BU DERSİMİZDE ÜÇGENLER VE ÖZELLİKLERİNE GÖZ ATACAĞIZ. AMAN SIKILMAYIN NOT BİRAZ UZUN DA :-) Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının
DİK ÜÇGEN. şekilde, m(a) = 90. [BC] kenarı hipotenüs. [AB] ve [AC] kenarları. dik kenarlardır. P İSAGOR BAĞINTISI
![DİK ÜÇGEN. şekilde, m(a) = 90. [BC] kenarı hipotenüs. [AB] ve [AC] kenarları. dik kenarlardır. P İSAGOR BAĞINTISI](/thumbs/65/52464044.jpg "DİK ÜÇGEN. şekilde, m(a) = 90. [BC] kenarı hipotenüs. [AB] ve [AC] kenarları. dik kenarlardır. P İSAGOR BAĞINTISI")
DİK ÜÇGEN Bir açısının ölçüsü 90 olan üçgene dik üçgen denir. Dik üçgende 90 nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir. Hipotenüs üçgenin daima en uzun kenarıdır. şekilde,
8. SINIF MATEMATİK. Asal Çarpanlar Test sayısının kaç tane asal çarpanı vardır?
8. SINIF MTEMTİ sal Çarpanlar Test. 84 sayısının kaç tane asal çarpanı vardır? ) 2 ) 3 ) 4 ) 5 5. İki basamaklı 9m sayısı asal sayıdır. una göre m yerine kaç farklı rakam yazılabilir? ) ) 2 ) 3 ) 4 2.
EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
TRİGONOMETRİK FONKSİYONLARIN GRAFİKLERİ
TRİGONOMETRİK FONKSİYONLARIN GRAFİKLERİ A. PERİYODİK FONKSİYONLAR A, düna ve güneşin hareketleri, a ve güneş tutulmaları her 7 ılda bir Halle kuruklu ıldızının dünamızı ziareti periodik olarak medana gelen
5. 5a. b a + 4 b = 3 3a + 2 2b. Cevap C. 6. x = 3, y = 7, z = 9 olduğundan x + z < y ve. Cevap C
eneme - / Mat MTEMTİK ENEMESİ..= 0 0..=0 =..=0 =..= = 8. =, = = y. 7, = +. 7 y + = + 00 y + + = + y + = + =, y = alınr ı. ^ - h. ^ + h. ^ + h= - ^ h. ^ + h= = = = bulunur. evap. a a $ = = a = $ 7b b =
6. loga log3a log5a log4a. 7. x,y R olmak üzere;
log. 5 5 0 olduğuna göre, değeri kaçtır? A) 5 B) 0 C) 6 8 E) 6. loga loga log5a loga eşitliğini sağlaan a değeri kaçtır? 5 A) 5 5 B) 5 5 C) 5 E) 5. loga logb logc ifadesinin eşiti aşağıdakilerden a c A)
ÜÇGENDE AÇILAR. Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir.
![ÜÇGENDE AÇILAR. Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir.](/thumbs/51/27890487.jpg "ÜÇGENDE AÇILAR. Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir.")
ÜÇGENDE AÇILAR Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir. Burada; A, B, C noktaları üçgenin köşeleri, [AB], [AC], [BC] doğru parçaları
Üçgende Açı ABC bir ikizkenar. A üçgen 30
1. 4. bir ikizkenar üçgen 0 = m () = 0 m () = 70 70 Kıble : Müslümanların namaz kılarken yönelmeleri gereken, Mekke kentinde bulunan Kabe'yi gösteren yön. arklı iki ülkede bulunan ve noktalarındaki iki
BİRLİKTE ÇÖZELİM. ayırdığı parçalardan birinin uzunluğuna. Şekildeki ABC dik üçgeninde [AB] ^ [BC], G noktası ağırlık merkezi,
![BİRLİKTE ÇÖZELİM. ayırdığı parçalardan birinin uzunluğuna. Şekildeki ABC dik üçgeninde [AB] ^ [BC], G noktası ağırlık merkezi,](/thumbs/88/116416355.jpg "BİRLİKTE ÇÖZELİM. ayırdığı parçalardan birinin uzunluğuna. Şekildeki ABC dik üçgeninde [AB] ^ [BC], G noktası ağırlık merkezi,")
. SINI TTİ İRİT ÇÖZİ 1. P Yandaki, PRS ve üçgenlerinin sırasıyla [], [RS] ve [] ye ait kenarortaylarını çiziniz. R S 2. r O O merkezli, r yarıçaplı çemberde çapı gören açısının ölçüsü 90 dir. [O], hem
MAKSİMUM-MİNİMUM PROBLEMLERİ
1 MAKSİMUM-MİNİMUM PROBLEMLERİ En büyük veya en küçük olması istenen değer (uzunluk, alan, hacim, vb.) tek değişkene bağlı bir fonksiyon olacak şekilde düzenlenir. Bu fonksiyonun türevinden ekstremum noktasının
4. Şekil 1'deki ABCD karesi şeklindeki karton E ve F orta
airede lan - 1. sım çevre uzunluğu 0 birim olan kare biçimindeki kağıdın üzerine, merkezleri bu kağıdın köşelerinde yer alan ve birbirine teğet olan dört çeyrek daireyi şekildeki gibi belirliyor. Sonra
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI GEOMETRİ TESTİ
İKKT! SRU KİTPÇIĞINIZIN TÜRÜNÜ LRK VP KÂĞIINIZ İŞRTLMYİ UNUTMYINIZ. MTMTİK SINVI GMTRİ TSTİ 1. u testte 30 soru vardır. 2. evaplarınızı, cevap kâğıdının Geometri Testi için ayrılan kısmına işaretleyiniz.
TEST: 1. Şekilde verilenlere göre x kaç derecedir? Şekilde verilenlere göre x kaç derecedir? A) 100 B) 110 C) 120 D) 130 E) 140
TEST: 1 1. 4. A) 20 B) 30 C) 40 D) 50 E) 60 A) 100 B) 110 C) 120 D) 130 E) 140 2. 5. A) 100 B) 110 C) 120 D) 130 E) 140 A) 96 B) 112 C) 121 D) 128 E) 134 3. 6. A) 40 B) 50 C) 60 D) 70 E) 80 A) 40 B) 50
MEB Ölçme, Değerlendirme ve Sınav Hizmetleri Genel Müdürlüğü MATEMATİK TESTİ ,4 işleminin sonucu kaçtır?
Ölçme, eğerlendirme ve Sınav Hizmetleri Genel Müdürlüğü MTEMTİ TESTİ. 2 5 20 + 25 işleminin sonucu kaçtır? ) 5 ) 6 5 ) 2 5 ) 27 5. 5 5, işleminin sonucu kaçtır? 9 ) ) 8 ) 6 ) 5 2. 2 Şekilde, verilen modeller
Matematikte karşılaştığınız güçlükler için endişe etmeyin. Emin olun benim karşılaştıklarım sizinkilerden daha büyüktür.
- 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
2000 ÖSS Soruları 2,3 0, ,1 işleminin sonucu kaçtır? 13 E) 11 A) 2 B) 3 C) 4 D) 5 E) 6 O O 2. 3
. 2, 0,2 2, + 0, işleminin sonucu 5. Rakamları birbirinden farklı olan üç basamaklı KM sayısı ve 5 ile kalansız bölünebiliyor. una göre, K kaç farklı değer alabilir? 2 ) 4 ) ) 2 ) ) ) 2 ) ) 4 ) 5 ) 6 2.
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
12.SINIF A VE B GRUBU MATEMATİK-GEOMETRİ DERSİ KURS KONULARI VE TESTLERİ
.SINIF A VE B GRUBU MATEMATİK-GEOMETRİ DERSİ KURS KONULARI VE TESTLERİ A-TEST SAYILAR- TEMEL KAVRAMLAR A-TEST SAYILAR- POLİNOMLAR B-TEST POLİNOMLAR- PARALEL DOĞRULARDA VE ÜÇGENDE AÇILAR A- B TEST PARALEL
8. SINIF. Soru 1. Soru 2. Soru 3. = 4 ve a+c = 39 eşitlikleri veriliyor. Bu verilenlere göre a kaçtır? Soru 4
8. SINIF Soru 1 0,2012 sayısı aşağıdaki aralıkların hangisinde yer alır? A ) (0, 1 10 ) B ) ( 1 10, 1 5 ) C ) (1 5, 1 4 ) D ) ( 1 4, 1 3 ) E ) ( 1 3, 1 2 ) Soru 2 8+ 7 = 8,070 eşitliği verildiğine göre
Öğrenci Seçme Sınavı (Öss) / 18 Nisan Matematik Soruları ve Çözümleri
Öğrenci Seçme Sınavı (Öss) / 8 Nisan 99 Matematik Soruları ve Çözümleri. Bir sayının inin fazlası, aynı sayıya eşittir. Bu sayı kaçtır? A) B) 0 C) D) 0 E) Çözüm Sayı olsun.. + +. Bir sınıftaki toplam öğrenci
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ 1. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için
1990 ÖYS. 1. si 13 olan si kaçtır? A) 91 B) 84 C) 72 D) 60 E) 52 A) 65 B) 63 C) 56 D) 54 E) 45
990 ÖYS. si olan si kaçtır? A) 9 B) 8 C) D) 60 E) 5. Ağırlıkça %0 si şeker olan 0 kg lık un-şeker karışımına 8 kg daha un eklendiğine göre, yeni şeker (kg) karışımın oranı kaçtır? un (kg) A) B) C) D) E)
İLKÖĞRETİM MTEMTİK ÖĞRETMENLERİ ZÜMRESİ WWW.GRETMENFRUMU.M YKLŞN SINV KRKUYU SEVİNE ÖNÜŞTÜREN GRUP UNUTMYIN SİZLER İÇİN İZ HERŞEYE HZIRIZ! Sadece MTEMTİK Öğretmenlerine Özel Grubumuz www.facebook.com/groups/ilkmatzum
SBS MATEMATİK DENEME SINAVI
SS MTEMTİK DENEME SINVI 8. SINIF SS MTEMTİK DENEME SINVI. 4.. Güneş ile yut gezegeni arasındaki uzaklık 80000000 km dir. una göre bu uzaklığın bilimsel gösterimi aşağıdakilerden hangisidir? ),8.0 9 km
NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl
![NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl](/thumbs/70/62427826.jpg "NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl")
NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm lan Örnek 0 nalitik düzlemde ( 0 c h b h a h c b ( 0 ( 0 a a h b h a b c h lan( = = = c Yukarıdaki verilenlere göre lan( kaç birimkaredir? 6 8 9 E c b Taban:
ÜÇGEN VE KENARLARI ARASINDA BAĞINTILAR
ÜÇGEN VE KENARLARI ARASINDA BAĞINTILAR 1. Bir üçgende ölçüsü büyük olan açının karşısındaki kenar uzunluğu, ölçüsü küçük olan açının karşısındaki kenar uzunluğundan daha büyüktür. ABC üçgeninde m(a) >
LYS GENEL KATILIMLI TÜRKİYE GENELİ ONLİNE DENEME SINAVI
LYS GNL KTILIMLI TÜRKİY GNLİ NLİN NM SINVI GMTRİ (M-TM) 1. u testte Geometri ile ilgili 30 soru vardır.. evaplarınızı, cevap kâğıdının Geometri Testi için arılan kısmına işaretleiniz. 3. u test için süreniz
Öğrenci Seçme Sınavı (Öss) / 18 Haziran Matematik II Soruları ve Çözümleri. = 1 olur.
Öğrenci Seçme Sınavı (Öss) / 8 Haziran 6 Matematik II Soruları ve Çözümleri x, x. f(x) x ise fonksiyonu için,, x olduğuna göre, a b kaçtır? lim + x f ( x) a ve lim x f ( x) b A) B) C) D) E) Çözüm x x için
FRAKTAL KONU ÖZETİ VE ETKİNLİKLERİ * 2,4,6,8,10...
FRAKTAL KONU ÖZETİ VE ETKİNLİKLERİ ÖRÜNTÜLER Belirli bir kurala göre devam eden şekil veya sayı dizilimleridir. *,4,6,8,10... Yukarıdaki dizilim ikişer ikişer artarak devam eden bir örüntüdür. 1.adım.adım
1999 ÖSS-II. 6. Üç basamaklı 4AB sayısı, iki basamaklı BA sayısının 13 katından 7 fazladır. Buna göre, BA sayısı kaçtır? işleminin sonucu. kaçtır?
999 ÖSS-II. 0, 0, kaçtır? 0, 0, 0,4 0,44 işleminin sonuu A) B), C) D) E) 6. Üç asamaklı 4AB sayısı, iki asamaklı BA sayısının katından 7 fazladır. Buna göre, BA sayısı kaçtır? A) 9 B) 5 C) 7 D) 9 E). a,,
Ö.S.S MATEMATĐK II SORULARI ve ÇÖZÜMLERĐ
Ö.S.S. 7 MATEMATĐK II SORULARI ve ÇÖZÜMLERĐ. Karmaşık sayılar kümesi üzerinde * işlemi, Z * Z Z + Z + Z Z biçiminde tanımlanıyor. Buna göre, ( i) * (+i) işleminin sonucu nedir? A) + 8i B) - 8i C) 8 + i
Öğr. Grv. Halil İbrahim SOLAK
27.09.2018 Bu ders sizin düşünmenizi ister. Bu ders sizin hesaplamanızı ister. Bu ders sizin problemi tespit etmenizi ister. Bu ders sizin problemi çözmenizi ister. Bu ders sizin alternatif çözüm üretmenizi
MATEMATÝK GEOMETRÝ DENEMELERÝ
NM 1 MTMTÝK OMTRÝ NMLRÝ 1. o o = 75 ve y = 5 olduğuna göre,. 3 + 8 = 0 sin( y)cos( + y) + sin( + y)cos( y) sin( y)sin( + y) cos( + y)cos( y) denkleminin kaç tane farklı reel kökü vardır? ifadesinin eşiti
ÖZEL SERVERGAZİ LİSELERİ
S R İ M Y ÖZL SRVRGZİ LİSLRİ VI. İ L K Ö Ğ R T İ M OKU L L R I R S I MT M Tİ K YRIŞMSI ÇIKLMLR u sınav çoktan seçmeli 5 ve klasik sorudan oluşmaktadır. Sınav süresi 50 dakikadır. Tavsiye edilen süre (5*=05
SERĠMYA 2011 - IX. ULUSAL ĠLKÖĞRETĠM MATEMATĠK OLĠMPĠYATI. 9. Ulusal. serimya. İLKÖĞRETİM 7. Ve 8. SINIFLAR ARASI MATEMATİK YARIŞMASI.
Sayfa1 9. Ulusal serimya İLKÖĞRETİM 7. Ve 8. SINIFLAR ARASI MATEMATİK YARIŞMASI 2011 Sayfa2 1. Bir ABCD konveks dörtgeninde AD 10 cm ise AB CB? m( Dˆ ) 90, ( ˆ) 150 0 0 m C ve m Aˆ m Bˆ ( ) ( ) olarak
EĞİTİM ÖĞRETİM YILI. FEN LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
AOB : [OA başlangıç kenarı, [OB bitim kenarı ( Negatif yön: Saat ibresinin dönme yönü) BOA : [OB başlangıç kenarı, [OA bitim kenarı
TRİGONOMETRİ Trigonometri, üçgenin kenar uzunlukları ve açıları arasındaki ilişkileri inceler. Öncelikle konumuzun en önemli öğesi olan açı kavramını ve özelliklerini gözden geçirelim. AÇI: Başlangıç noktaları
Küre Küre Üzerinde Hesap. Ders Sorumlusu Prof. Dr. Mualla YALÇINKAYA 2018
Küre Küre Üzerinde Hesap Ders Sorumlusu Prof. Dr. Mualla YALÇINKAYA 2018 Küre ve Küre ile İlgili Tanımlar Küre: «Merkez» adı verilen bir noktaya eşit uzaklıktaki noktaların bir araya getirilmesiyle, ya
TEMEL MATEMATİK TESTİ
TEMEL MTEMTİK TESTİ 1. u testte 0 soru vardır.. evaplarınızı, cevap kâğıdının Temel Matematik Testi için ayrılan kısmına işaretleyiniz. 010 YGS / MT 1. 0, 0,0 0,. + 1 ) 1 7 0 ) 1 + 1 1.. ( a+ 1) ( a )
arşılıklı kenar uzunlukları ve açılarının ölçüleri birbirine eşit olan çokgenlere eş çokgenler denir şlik sembolü dir m () m () 3 cm m () m () m(g) m(h) m() m() 4 2 cm GH H 3 cm G 4 2 cm GH H G Yukarıdaki
SERİMYA II. MATEMATİK YARIŞMASI I. AŞAMA SORULARI
SERİMYA - 4 II. MATEMATİK YARIŞMASI I. AŞAMA SORULARI. 4? 4 4. A B denkleminde A ve B birbirinden farklı pozitif tam sayılar olduğuna göre, A + B toplamı kaçtır? işleminin sonucu kaçtır? A) 6 B) 8 C) D)