ÜSTEL DAĞILIM. üstel dağılımın parametresidir. Birikimli üstel dağılım fonksiyonu da, olarak bulunur. olduğu açık olarak görülmektedir.
|
|
|
- Eser Halefoğlu
- 8 yıl önce
- İzleme sayısı:
Transkript
1 ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım dnir. icin digr durumlarda üsl dağılımın paramrsidir. Biriimli üsl dağılım onsiyonu da P X PX d olara bulunur. X X olduğu açı olara görülmdir. için için için 78 5 = = Örn : X Pr olan üsl dağılım sahip bir sadüi olsun. 5 X Pr X v PrX /X Çözüm : X in biriimli olasılı onsiyonunu bulalım. 5 /5 /5 d olasılılarını bulunuz. dir. Şu hald aranılan olasılılar;
2 Pr X 8 /5 Ya da aynı olasılı 5 Pr /5 d 5 /5. /5. dn d bulunabilir. Pr X / Pr Pr /5. /5. / olara bulunur. 67 Üsl Dağılımın Arimi Oralaması X μ d d şiir. T paramry sahip üsl dağılımın arimi oralaması b paramrnin rsin Üsl Dağılımın Varyansı a. Arimi Oralama Kavramı il; d d u v d dv olara l alındığında d d
3 olduğundan X X VX bulunur. b. Momn Çıaran onsiyon M M" X. M' X v X V bulunur. Üsl Dağılımın Momn Çıaran onsiyonu d M d lim Burada momn çıaran onsiyonun mvcu olabilmsi için lim dolayısıyla da < olması grir. Böylc M bulunur.
4 Örn : X rassal dğişni blirli bir müzi sinin ömrünü yıl olara gösrsin v aşağıdai gibi bir olasılı onsiyonuna sahip olsun. 6 /6 digr durumlarda a. Bu müzi sinin n az 6 yıl dayanma olasılığını bulunuz. b. Bu müzi sinin yıl dayandığı bilindiğin gör n az dayanma olasılığını bulunuz. c. Oralama dayanma sürsini bulunuz. Çözüm : a. P X 6 6 /6 d /6 67 b. PrX 6/ c. X 6 yıl 6 Pr X 6 v X Pr X Pr X 6 Pr X Örn : X mara vidoların oralama ullanım sürsinin yalaşı olara 5 yıl olan bir üsl dağılımla msil dcği bilindiğin gör bu vido cihazlarından bir an saın alan bir müşrinin cihazını 5 yıl ullanabilm olasılığını bulunuz. Çözüm : X=5 Üsl dağılımın blnn dğr anımından X dan olara bulunur. 5 olasılı yoğunlu onsiyonu is;
5 5 dir. 5 Pr d = - = Örn : İsanbul Aaür Havalimanında hr daiada oralama olara uçağın indiği bilinmdir. a. İniş gçn uçalar arasındai sürnin dağılım onsiyonunu bulunuz. b. daia içind hiç uçağın inmmsi c. Birbirini izlyr iniş gçn ii uça arasındai zamanın n azla 5 daia olması d. İi uça arasında gçn sürnin 5 daia vya daha azla olması olasılılarını bulunuz. Çözüm : a. Zaman birimi daia olara l alınırsa havalimanına daiada oralama olara P / = uça inmdir. O zaman in dağılımı.!... olur. daiada oralama uçağın iniş yapması bilindiğindn daiada oralama sayıda uça [] aralığında havalimanına incir. O zaman olasılı yoğunlu onsiyonu olur. b. PX= = 8! 5 P d vya c. T P T 5
6 = d. P T 5 5 GAMA DAĞILIMI Tanım : = - = 6 ld dilir. d şlind anımlanan onsiyona Gamma onsiyonu dnir. Yuarıdai ingral ısmi ingrasyon modu uygulanırsa d dv v u olma üzr; bulunur. d d pozii am sayı is;... ld dilir. Burada; d dir. Böylc;! olara bulunur. Gamma onsiyonunun şu özllilr sahipir : i. ii. 6
7 7 iii.! n n iv. v. n n n n vi. s du u u s s Tanım : X > için bir sürli rassal dğişn olsun. ğr X in olasılı onsiyonu aşağıdai gibi anımlanmış is X bir Gamma olasılı onsiyonu na sahipir. digr durumlarda icin X/ Gamma olasılı onsiyonu > v > olma üzr paramry sahipir. Biriimli Gamma Dağılım onsiyonu is şöyldir: d. X P d / Y = / olara anımlanırsa dy = d olur..dy y y y y y - dy y y - -! - -y! y
8 Örn : = - / şlind anımlanan in bir olasılı yoğunlu onsiyonu gösriniz Çözüm : > v > v > olduğunda > olur. ; d olmalıdır. - / d y diylim = y olur. d = dy y - y dy O hald ; bir olasılı yoğunlu onsiyonudur. y - y y - dy y dy Gamma Dağılımının Arimi Oralaması X / - d. / d 8
9 = v / d dv dönüşümü yapıldığında - -/ /. d d = y v d = dy dönüşümü il y X - y.dy y dy. bulunur. Gamma Dağılımının Varyansı X - / d / d u v / d dv dönüşümü yapılırsa y / y d dy y y y -!! bulunur. VX X X 9
10 VX olara ld dilir. Momn Çıaran onsiyonu is; M. - d - / d y / dönüşümü yapılırsa -. y y y dy dy bulunur. y - y olur. - dy d Şimdi d M aracılığıyla X v VX i bulalım - X M' - -. " -- X M VX X X = bulunur. Örn : X sadüi dğişni aşağıdai biçimd gamma dağılım gösriyorsa; X in = = v = = için - / icin
11 a. Pr{ } b. Pr{ > } olasılılarını bulunuz. Çözüm : a. = = için gamma onsiyonu Şu hald / / olur. / / Pr d / Şu hald isnn olasılı Pr{ } Pr{ } b. = = için Pr bulunur. / / olur / d / d v / d dv dönüşümü il d= du / v 8 / 8 / d
12 bulunur d / / / Buradan; bulunur..8 P 8 r.886}.585 { } 6 { } { 8 bulunur P r 8. } { ÖRNK : Aşağıdai gamma onsiyonunun onsiyonunu bulunuz. dağağıl b dğğrlri V a için dğğrl v / ÇÖZÜM: onsiyonu gamma için dğğrl v bulunur. V d d bulunur. d { d { d d olur. / ] [ } } b- için o { { d P r } } } {
13 Kİ-KAR DAĞILIMI Tanım: gamma dağılmış bir rassal dğişn in > v amsayı olma üzr =/ v =/ is özl olara Ki-Kar dağılmış rassal dğişn dnir. Ki-Kar dağılmış bir rassal dğişn is bunun yoğunlu onsiyonu gamma dağılımında =/ v =/ için yada ş şal olur. Gamma dağılımının özl bir durumu olan Ki-ar dağılımının il gösriln v pozii amsayı dğr alabiln paramrsi vardır. Dağılımın bu paramrsin srbsli drcsi K dnir. X paramrsi olan Ki-ar dağılmış bir rassal dğişn in şlind yazılır v srbsli drcsi olan Ki-ar dağılmış bir rassal dğişn olara ounur. ÖRNK : 5 İKN P.6 P>. P.5< 5.9 olasılılarıyla 8 in P = 95 şiliğini grçlyn dğrini bulunuz. ÇÖZÜM : P.6 = P>. = - P. = = 8 P.5< 5.9 = 99 5 = 9 olara bulunur. 8 in P = 95 şiliğini sağlayan dğri; = 7 dir. in Arimi Oralama v Varyansı v olduğldgörülür. 8 in Momn Çıaran onsiyonu
14 M M yada olur. Örn : X rassal dğişninin olasılı yoğunlu onsiyonu ; 6 / şlind is; v M yi bulunuz Çözüm : şiliğindn = 6 olup / 8 v! / dir. / 6 /. olduğundan X ~ X 6 dır. Böylc / = = 6 = = v M is Örn : X rassal dğişninin dir. X 5 olduğu bilindiğin gör bunun olasılı yoğunlu onsiyonunu yazıp arimi oralama varyans v momn çıaran onsiyonunu bulunuz. / 5/ Çözüm : = 5 in özlliğiyl 5.. olduğundan X in yoğunlu onsiyonu Π digr durumlarda olara bulunur. = 5 olduğuna gör X in arimi oralama v varyansı; = 5 = olup momn çıaran onsiyonu; M 5 z>/ şlinddir.
Makine Öğrenmesi 4. hafta
 ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
Tanım : Bir rassal deney yapıldığında bir deneyin sonucu sadece iki sonuç içeriyorsa bu deneye Bernoulli deneyi denir.
 BRNOULLİ DAĞILIMI Broulli dağılımı bir rassal dy yaıldığıda yalızca iyi öü olumlu-olumsuz başarılı-başarısız gibi sadc ii souç ld dildiğid ullaılır. Taım : Bir rassal dy yaıldığıda bir dyi soucu sadc ii
BRNOULLİ DAĞILIMI Broulli dağılımı bir rassal dy yaıldığıda yalızca iyi öü olumlu-olumsuz başarılı-başarısız gibi sadc ii souç ld dildiğid ullaılır. Taım : Bir rassal dy yaıldığıda bir dyi soucu sadc ii
GABOR TABANLI AYRIK EVRİMSEL DÖNÜŞÜM KULLANILARAK GÖRÜNTÜ DAMGALAMA
 GABOR TABANL AYRK EVRİSEL DÖNÜŞÜ KULLANLARAK GÖRÜNTÜ DAGALAA ahmu ÖZTÜRK (), Aydın AKAN (),, Yalçın ÇEKİÇ () Elri-Elroni ühndisliği Bölümü () İsanbul Ünivrsisi, Avılar, 343, İsanbul mahmuoz@isanbul.du.r,
GABOR TABANL AYRK EVRİSEL DÖNÜŞÜ KULLANLARAK GÖRÜNTÜ DAGALAA ahmu ÖZTÜRK (), Aydın AKAN (),, Yalçın ÇEKİÇ () Elri-Elroni ühndisliği Bölümü () İsanbul Ünivrsisi, Avılar, 343, İsanbul mahmuoz@isanbul.du.r,
Üstel Dağılım SÜREKLİ ŞANS DEĞİŞKENLERİNİN OLASILIK YOĞUNLUK FONKSİYONLARI
 ..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
e sayısı. x için e. x x e tabanında üstel fonksiyona doğal üstel fonksiyon (natural exponential function) denir. (0,0)
 DERS 4 Üstl v Logaritik Fonksionlar 4.. Üstl Fonksionlar(Eponntial Functions). > 0, olak üzr f ( ) = dnkli il tanılanan fonksiona taanında üstl fonksion (ponntial function with as ) dnir. Üstl fonksionun
DERS 4 Üstl v Logaritik Fonksionlar 4.. Üstl Fonksionlar(Eponntial Functions). > 0, olak üzr f ( ) = dnkli il tanılanan fonksiona taanında üstl fonksion (ponntial function with as ) dnir. Üstl fonksionun
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 2007 SORULARI
 DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
BÖLÜM 7. Sürekli hal hatalarının değerlendirilmesinde kullanılan test dalga şekilleri: Dalga Şekli Giriş Fiziksel karşılığı. Sabit Konum.
 9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
Lisans Yerleştirme Sınavı 1 (Lys 1) / 18 Haziran Matematik Soruları ve Çözümleri
 Lisans Yrlşirm Sınavı (Lys ) 8 Haziran Mamaik Soruları v Çözümlri. (,5) işlminin sonucu kaçır?, A) 5 B) C) 5 D) E) Çözüm (,5), 5 ( ) ( ) 5 ( ) ( ).( ) 5 ( ) 5 5 6 . < < olduğuna gör, aşağıdakilrdn hangisi
Lisans Yrlşirm Sınavı (Lys ) 8 Haziran Mamaik Soruları v Çözümlri. (,5) işlminin sonucu kaçır?, A) 5 B) C) 5 D) E) Çözüm (,5), 5 ( ) ( ) 5 ( ) ( ).( ) 5 ( ) 5 5 6 . < < olduğuna gör, aşağıdakilrdn hangisi
RASGELE SÜREÇLER. Bir X rasgele değişkenin, a ve b arasında tekdüze dağılımlı olabilmesi için olasılık yoğunluk fonksiyonu aşağıdaki gibi olmalıdır.
 RASGELE SÜREÇLER Eğer bir büyülüğün her t anında alacağı değeri te bir şeilde belirleyen matematisel bir ifade verilebilirse bu büyülüğün deterministi bir büyülü olduğu söylenebilir. Haberleşmeden habere
RASGELE SÜREÇLER Eğer bir büyülüğün her t anında alacağı değeri te bir şeilde belirleyen matematisel bir ifade verilebilirse bu büyülüğün deterministi bir büyülü olduğu söylenebilir. Haberleşmeden habere
DERS 9. Grafik Çizimi, Maksimum-Minimum Problemleri. 9.1. Grafik çiziminde izlenecek adımlar. y = f(x) in grafiğini çizmek için
 DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
DERS 9. Grafik Çizimi, Maksimum Minimum Problemleri
 DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
Dr. Mehmet AKSARAYLI
 Dr. Mehmet AKSARAYLI Şans Değişeni: Bir dağılışı olan ve bu dağılışın yaısına uygun freansta oluşum gösteren değişendir. Şans Değişenleri KESİKLİ RASSAL DEĞİŞKENLER ve OLASILIK DAĞILIMLARI Kesili Şans
Dr. Mehmet AKSARAYLI Şans Değişeni: Bir dağılışı olan ve bu dağılışın yaısına uygun freansta oluşum gösteren değişendir. Şans Değişenleri KESİKLİ RASSAL DEĞİŞKENLER ve OLASILIK DAĞILIMLARI Kesili Şans
Sınav süresi 80 dakika. 1. (a) 20 puan 2 dy. Solution: 2 dy. y = 2t denklemi lineer diferansiyel denklemdir. Denklemin integrasyon çarpanını bulalım.
 May 7, 7 3:-4:3 MATH6 Final Exam / MAT6 Final Sınavı Pag of 7 Your Nam / İsim Soyisim Your Signaur / İmza Sudn ID # / Öğrnci Numarası Profssor s Nam / Öğrim Üysi Kopya çkn vya kopya çkm girişimind bulunan
May 7, 7 3:-4:3 MATH6 Final Exam / MAT6 Final Sınavı Pag of 7 Your Nam / İsim Soyisim Your Signaur / İmza Sudn ID # / Öğrnci Numarası Profssor s Nam / Öğrim Üysi Kopya çkn vya kopya çkm girişimind bulunan
İ.T.Ü. Makina Fakültesi Mekanik Ana Bilim Dalı Bölüm 7. Seviye Düzlemi
 İTÜ Makina Fakültsi Ağırlığın Potansiyl Enrjisi W=, δh kadar yukarıya doğru yr dğiştirsin, Virtül iş, δu = Wδh= δh NOT: Eğr cisi aşağıya doğru δh yr dğişii yapıyorsa v +h aşağıya doğru is δu = Wδh= δh
İTÜ Makina Fakültsi Ağırlığın Potansiyl Enrjisi W=, δh kadar yukarıya doğru yr dğiştirsin, Virtül iş, δu = Wδh= δh NOT: Eğr cisi aşağıya doğru δh yr dğişii yapıyorsa v +h aşağıya doğru is δu = Wδh= δh
Anaparaya Dönüş (Kapitalizasyon) Oranı
 Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
5. Ders. Dağılımlardan Rasgele Sayı Üretilmesi Ters Dönüşüm Yöntemi
 5. Drs Dağılımlarda Rasgl Sayı Ürtilmsi Trs Döüşüm Yötmi sürkli bir rasgl dğişk v bu rasgl dğişki dağılım foksiyou olsu. Dağılımı dstk kümsi üzrid dağılım foksiyou arta v bir-bir bir foksiyo olmaktadır.
5. Drs Dağılımlarda Rasgl Sayı Ürtilmsi Trs Döüşüm Yötmi sürkli bir rasgl dğişk v bu rasgl dğişki dağılım foksiyou olsu. Dağılımı dstk kümsi üzrid dağılım foksiyou arta v bir-bir bir foksiyo olmaktadır.
Bölüm V Darbe Kod Modülasyonu
 - Güz Bölüm V Dare Kod Modülasyonu emel Bilgiler Bi nerjisi Gürülü Gücü İlinisel lıcı Uygun Süzgeçli lıcı Bi Haa Olasılığı Semoller rası Girişim DKM ve Ha Kodlama DC veya Bilgisayardan sayısal daa k Semol
- Güz Bölüm V Dare Kod Modülasyonu emel Bilgiler Bi nerjisi Gürülü Gücü İlinisel lıcı Uygun Süzgeçli lıcı Bi Haa Olasılığı Semoller rası Girişim DKM ve Ha Kodlama DC veya Bilgisayardan sayısal daa k Semol
FIRAT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EMÜ-419 OTOMATİK KONTROL LABORATUARI DENEY 5
 FIRT ÜNİVERSİTESİ MÜHENDİSLİK FKÜLTESİ ELEKTRİKELEKTRONİK MÜHENDİSLİĞİ ÖLÜMÜ EMÜ419 OTOMTİK KONTROL LORTURI DENEY 5 PID KONTROLÖR KRKTERİSTİKLERİNİN İNELENMESİ VE NLOG OLRK POZİSYON KONTROL SİSTEMLERİNDE
FIRT ÜNİVERSİTESİ MÜHENDİSLİK FKÜLTESİ ELEKTRİKELEKTRONİK MÜHENDİSLİĞİ ÖLÜMÜ EMÜ419 OTOMTİK KONTROL LORTURI DENEY 5 PID KONTROLÖR KRKTERİSTİKLERİNİN İNELENMESİ VE NLOG OLRK POZİSYON KONTROL SİSTEMLERİNDE
DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİK KONTROL I Dr. Uğur HASIRCI
 DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
Bir Kompleks Sayının n inci Kökü.
 Prof.Dr.Hüsy ÇAKALLI Br Komplks Sayıı c Kökü. hrhag br sab doğal sayı olmak ür, br komplks sayıı c kökü, c kuvv bu sayıya ş ola komplks sayıdır. ( r(cos s olsu v (cos s dylm. Bu akdrd ( [ (cos s] dr v
Prof.Dr.Hüsy ÇAKALLI Br Komplks Sayıı c Kökü. hrhag br sab doğal sayı olmak ür, br komplks sayıı c kökü, c kuvv bu sayıya ş ola komplks sayıdır. ( r(cos s olsu v (cos s dylm. Bu akdrd ( [ (cos s] dr v
ANADOLU ÜNİVERSİTESİ BEKLENEN DEĞER. X beklenen değeri B[X] ile gösterilir. B[X] = İST 213 OLASILIK DERSİ BEKLENEN DEĞER VE MOMENTLER
![ANADOLU ÜNİVERSİTESİ BEKLENEN DEĞER. X beklenen değeri B[X] ile gösterilir. B[X] = İST 213 OLASILIK DERSİ BEKLENEN DEĞER VE MOMENTLER ANADOLU ÜNİVERSİTESİ BEKLENEN DEĞER. X beklenen değeri B[X] ile gösterilir. B[X] = İST 213 OLASILIK DERSİ BEKLENEN DEĞER VE MOMENTLER](/thumbs/63/49372208.jpg) ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ BEKLENEN DEĞER VE MOMENTLER DOÇ. DR. NİHAL ERGİNEL 2015 X beklenen değeri B[X] ile gösterilir. B[X] = BEKLENEN DEĞER Belli bir malzeme taşınan kolilerin ağırlıkları
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ BEKLENEN DEĞER VE MOMENTLER DOÇ. DR. NİHAL ERGİNEL 2015 X beklenen değeri B[X] ile gösterilir. B[X] = BEKLENEN DEĞER Belli bir malzeme taşınan kolilerin ağırlıkları
KESİKLİ DÜZGÜN DAĞILIM
 KESİKLİ DÜZGÜN DAĞILIM Eğer X kesikli rassal değişkeninin alabileceği değerler (,,..., ) eşit olasılığa sahip ise, kesikli düzgün dağılım söz konusudur. p(x) =, X=,,..., şeklinde gösterilir. Bir kutuda
KESİKLİ DÜZGÜN DAĞILIM Eğer X kesikli rassal değişkeninin alabileceği değerler (,,..., ) eşit olasılığa sahip ise, kesikli düzgün dağılım söz konusudur. p(x) =, X=,,..., şeklinde gösterilir. Bir kutuda
DRC ile tam bölünebilmesi için bir tane 2 yi ayırıyoruz. 3 ile ) x 2 2x < (
 nm - / YT / MT MTMTİK NMSİ. il tam bölünbilmsi için bir tan i aırıoruz. il bölünmmsi için bütün lri atıoruz... 7 saısının pozitif tam böln saısı ( + ). ( + ). ( + ) bulunur. vap. 0 + + 0 + ) < ( 0 + +
nm - / YT / MT MTMTİK NMSİ. il tam bölünbilmsi için bir tan i aırıoruz. il bölünmmsi için bütün lri atıoruz... 7 saısının pozitif tam böln saısı ( + ). ( + ). ( + ) bulunur. vap. 0 + + 0 + ) < ( 0 + +
OLASILIK ve ÝSTATÝSTÝK ( Genel Tekrar Testi-1) KPSS MATEMATÝK. Bir anahtarlıktaki 5 anahtardan 2 si kapıyı açmak - tadır.
 OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
kirişli döşeme Dört tarafından kirişlere oturan döşemeler Kenarlarının bazıları boşta olan döşemeler Boşluklu döşemeler Düzensiz geometrili döşemeler
 Kirişli döşmlr Dört tarafından irişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşlulu döşmlr Düznsiz gomtrili döşmlr bir tarafı irişli üç tarafı boşta döşm (Konsol döşm) Đi tarafı irişli ii
Kirişli döşmlr Dört tarafından irişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşlulu döşmlr Düznsiz gomtrili döşmlr bir tarafı irişli üç tarafı boşta döşm (Konsol döşm) Đi tarafı irişli ii
SÜREKLİ DÜZGÜN DAĞILIM
 SÜREKLİ DÜZGÜN DAĞILIM X rassal değişkenin olasılık yoğunluk fonksiyonu; şeklinde ise x e düzgün dağılmış rassal değişken, f(x) e sürekli düzgün dağılım denir. a 0 olduğuna göre, f(x) >0 olur.
SÜREKLİ DÜZGÜN DAĞILIM X rassal değişkenin olasılık yoğunluk fonksiyonu; şeklinde ise x e düzgün dağılmış rassal değişken, f(x) e sürekli düzgün dağılım denir. a 0 olduğuna göre, f(x) >0 olur.
ISI GERİ KAZANIMI (Çapraz Akış) DENEY FÖYÜ
 ISI GERİ KAZANIMI (Çapraz Akış) DENEY FÖYÜ (Dny Yürüücüsü: Arş. Gör. Doğan ERDEMİR) Dnyin Amacı v Dny Hakkında Gnl Bilgilr Dnyin amacı sı gri kazanımı (çapraz akış) sismlrind;. Sıcaklık dğişimlrinin ölçümü
ISI GERİ KAZANIMI (Çapraz Akış) DENEY FÖYÜ (Dny Yürüücüsü: Arş. Gör. Doğan ERDEMİR) Dnyin Amacı v Dny Hakkında Gnl Bilgilr Dnyin amacı sı gri kazanımı (çapraz akış) sismlrind;. Sıcaklık dğişimlrinin ölçümü
4) Seyrek rastlanılan bir hastalık için belli bir zaman araalığında bu hastalığa yakalananların sayısının gözlenmesi,
 POĐSSON DAĞILIMI Poisson Dağılımı sürekli oramlarda (zaman, alan, hacim, ) kesikli sonuçlar veren ve aşağıda a),b),c) şıklarında belirilen özelliklere sahip deneylerin modellenmesinde kullanılan bir dağılım
POĐSSON DAĞILIMI Poisson Dağılımı sürekli oramlarda (zaman, alan, hacim, ) kesikli sonuçlar veren ve aşağıda a),b),c) şıklarında belirilen özelliklere sahip deneylerin modellenmesinde kullanılan bir dağılım
RİSK ANALİZİ VE AKTÜERYAL MODELLEME
 SORU 1: Bir hasar sıklığı dağılımının rassal değişken olan ortalaması (0,8) aralığında tekdüze dağılmaktadır. Hasar sıklığı dağılımının Poisson karma dağılıma uyduğu bilindiğine göre 1 ya da daha fazla
SORU 1: Bir hasar sıklığı dağılımının rassal değişken olan ortalaması (0,8) aralığında tekdüze dağılmaktadır. Hasar sıklığı dağılımının Poisson karma dağılıma uyduğu bilindiğine göre 1 ya da daha fazla
Kollektif Risk Modellemesinde Panjér Yöntemi
 Douz Eylül Üniversitesi İtisadi ve İdari Bilimler Faültesi Dergisi, Cilt:6, Sayı:, Yıl:, ss.39-49. olletif Ris Modellemesinde anér Yöntemi ervin BAYAN İRVEN Güçan YAAR Özet Hayat dışı sigortalarda, olletif
Douz Eylül Üniversitesi İtisadi ve İdari Bilimler Faültesi Dergisi, Cilt:6, Sayı:, Yıl:, ss.39-49. olletif Ris Modellemesinde anér Yöntemi ervin BAYAN İRVEN Güçan YAAR Özet Hayat dışı sigortalarda, olletif
WEIBULL DAĞILIMI WEIBULL DAĞILIMI ANADOLU ÜNİVERSİTESİ
 ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ SÜREKLİ DAĞILIMLAR-2 DOÇ. DR. NİHAL ERGİNEL 2015 WEIBULL DAĞILIMI Weibull dağılımı, pek çok farklı sistemlerin bozulana kadar geçen süreleri ile ilgilenir. Dağılımın
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ SÜREKLİ DAĞILIMLAR-2 DOÇ. DR. NİHAL ERGİNEL 2015 WEIBULL DAĞILIMI Weibull dağılımı, pek çok farklı sistemlerin bozulana kadar geçen süreleri ile ilgilenir. Dağılımın
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI. Yrd. Doç. Dr. Emre ATILGAN
 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
denklemini x=0 adi nokta civarında çözünüz.
 dklmii = adi okta ivarıda çözüüz. Rküra bağıtıı DİFERANSİYEL DENKLEMLER UFUK ÖZERMAN y +y +( /6y= ( dklmi içi = oktaıı düzgü tkil okta olduğuu götri, İdi dklmii köklrii bulu v çözü. P( = = = = tkil okta
dklmii = adi okta ivarıda çözüüz. Rküra bağıtıı DİFERANSİYEL DENKLEMLER UFUK ÖZERMAN y +y +( /6y= ( dklmi içi = oktaıı düzgü tkil okta olduğuu götri, İdi dklmii köklrii bulu v çözü. P( = = = = tkil okta
Atomlardan Kuarklara. Test 1
 4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
LOGARİTMA. Örnek: çizelim. Çözüm: f (x) a biçiminde tanımlanan fonksiyona üstel. aşağıda verilmiştir.
 LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
Bilgi Tabanı (Uzman) Karar Verme Kontrol Kural Tabanı. Bulanık. veya. Süreç. Şekil 1 Bulanık Denetleyici Blok Şeması
 Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
Hafta 8: Ayrık-zaman Fourier Dönüşümü
 Hafta 8: Ayrı-zama ourir Döüşümü El Alıaca Aa Koular Ayrı-zama ourir döüşümü Ayrı-zama priyodi işartlr içi ourir döüşümü Ayrı-zama ourir döüşümüü özllilri Doğrusal, sabit atsayılı far dlmlriyl taımlaa
Hafta 8: Ayrı-zama ourir Döüşümü El Alıaca Aa Koular Ayrı-zama ourir döüşümü Ayrı-zama priyodi işartlr içi ourir döüşümü Ayrı-zama ourir döüşümüü özllilri Doğrusal, sabit atsayılı far dlmlriyl taımlaa
İyon Kaynakları ve Uygulamaları
 İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu rcpoglu@tak.gov.tr HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu rcpoglu@tak.gov.tr HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
Sönümlü Serbest Titreşim
 .5.. Söülü Srbs Tirşi Sosza kadar dva d sabi glikli irşilrl grçk hayaa karşılaşılaakadır. Bilidiği gibi, sis irşi harki başladıka bir sür sora hark yavaş yavaş zayıflar. olayısıyla hark dklii aşağıdaki
.5.. Söülü Srbs Tirşi Sosza kadar dva d sabi glikli irşilrl grçk hayaa karşılaşılaakadır. Bilidiği gibi, sis irşi harki başladıka bir sür sora hark yavaş yavaş zayıflar. olayısıyla hark dklii aşağıdaki
ANADOLU ÜNİVERSİTESİ. ENM 317 Prof. Dr. Nihal ERGİNEL
 ANADOLU ÜNİVERSİTESİ ENM 317 Prof. Dr. Nihal ERGİNEL 2 ÖRNEKLEME Anakütleden n birimlik örnek alınması ve anakütle parametrelerinin örnekten tahmin edilmesidir. 3 ÖRNEKLEME ALMANIN NEDENLERİ Anakütleye
ANADOLU ÜNİVERSİTESİ ENM 317 Prof. Dr. Nihal ERGİNEL 2 ÖRNEKLEME Anakütleden n birimlik örnek alınması ve anakütle parametrelerinin örnekten tahmin edilmesidir. 3 ÖRNEKLEME ALMANIN NEDENLERİ Anakütleye
( ) ( ) Be. β - -bozunumu : +β - + ν + Q - Atomik kütleler cinsinden : (1) β + - bozunumu : nötral atom negatif iyon leptonlar
 6.. BETA BOZUUU Çkirdğin pozitif vya ngatif lktron yayması vya atomdan bir lktron yakalaması yolu il atom numarası ± 1 kadar dğişir. β - -bozunumu : ( B 4 4 ( B 4 nötral atom Atomik kütllr insindn : (
6.. BETA BOZUUU Çkirdğin pozitif vya ngatif lktron yayması vya atomdan bir lktron yakalaması yolu il atom numarası ± 1 kadar dğişir. β - -bozunumu : ( B 4 4 ( B 4 nötral atom Atomik kütllr insindn : (
1.58 arasındaki her bir değeri alabileceği için sürekli bir
 7.SUNUM Hatırlanacağı gibi, kesikli rassal değişkenler sonlu (örneğin; 0, 1, 2,...,10) veya sayılabilir sonsuzlukta (örneğin; 0, 1, 2,...) değerler alabilmektedir. Fakat birçok uygulamada, rassal değişkenin
7.SUNUM Hatırlanacağı gibi, kesikli rassal değişkenler sonlu (örneğin; 0, 1, 2,...,10) veya sayılabilir sonsuzlukta (örneğin; 0, 1, 2,...) değerler alabilmektedir. Fakat birçok uygulamada, rassal değişkenin
İÇİNDEKİLER. Ön Söz Saymanın Temel Kuralları Permütasyon (Sıralama) Kombinasyon (Gruplama) Binom Açılımı...
 İÇİNDEKİLER Ön Söz... Saymanın Temel Kuralları... Permütasyon (Sıralama)... 8 Kombinasyon (Gruplama)... 6 Binom Açılımı... Olasılık... 9 İstatistik... 8... Dağılımlar... 5 Genel Tarama Sınavı... 6 RASTGELE
İÇİNDEKİLER Ön Söz... Saymanın Temel Kuralları... Permütasyon (Sıralama)... 8 Kombinasyon (Gruplama)... 6 Binom Açılımı... Olasılık... 9 İstatistik... 8... Dağılımlar... 5 Genel Tarama Sınavı... 6 RASTGELE
= + ise bu durumda sinüzoidal frekansı. genlikli ve. biçimindeki bir taşıyıcı sinyalin fazının modüle edildiği düşünülsün.
 4.2. çı Modülasyonu Yüse reanslı bir işaret ile bilgi taşıa, işaretin genliğinin, reansının veya azının bir esaj işareti ile odüle edilesi ile gerçeleştirilebilir. Bu üç arlı odülasyon yöntei sırasıyla,
4.2. çı Modülasyonu Yüse reanslı bir işaret ile bilgi taşıa, işaretin genliğinin, reansının veya azının bir esaj işareti ile odüle edilesi ile gerçeleştirilebilir. Bu üç arlı odülasyon yöntei sırasıyla,
19.11.2013 EME 3105 SİSTEM SİMÜLASYONU. Sürekli Dağılımlar (2) Sürekli Rassal Değişkenlerin Modellemesinde Kullanılan Dağılımlar.
 9..03 EME 305 SİSTEM SİMÜLASYONU Simulasyonda İstatistiksel Modeller-II Ders 5 Sürekli Rassal Değişkenlerin Modellemesinde Kullanılan Dağılımlar Sürekli Düzgün (Uniform) Dağılım Normal Dağılım Üstel (Exponential)
9..03 EME 305 SİSTEM SİMÜLASYONU Simulasyonda İstatistiksel Modeller-II Ders 5 Sürekli Rassal Değişkenlerin Modellemesinde Kullanılan Dağılımlar Sürekli Düzgün (Uniform) Dağılım Normal Dağılım Üstel (Exponential)
DESTEK DOKÜMANI. Mali tablo tanımları menüsüne Muhasebe/Mali tablo tanımları altından ulaşılmaktadır.
 Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
Simülasyonda İstatiksel Modeller
 Simülasyonda İstatiksel Modeller Amaç Model-geliştirici dünyaya deterministik değil olasıksal olarak bakar. İstatiksel modeller değişimleri iyi tanımlayabilir. İlgilenilen olayın örneklenmesi ile uygun
Simülasyonda İstatiksel Modeller Amaç Model-geliştirici dünyaya deterministik değil olasıksal olarak bakar. İstatiksel modeller değişimleri iyi tanımlayabilir. İlgilenilen olayın örneklenmesi ile uygun
- BANT TAŞIYICILAR -
 - BANT TAŞIYICILAR - - YAPISAL ÖZELLİKLER Bir bant taşıyıcının nl örünümü aşağıdaki şkild vrilmiştir. Bant taşıyıcıya ismini vrn bant (4) hm taşınacak malzmyi için alan bir kap örvi örn, hm d harkt için
- BANT TAŞIYICILAR - - YAPISAL ÖZELLİKLER Bir bant taşıyıcının nl örünümü aşağıdaki şkild vrilmiştir. Bant taşıyıcıya ismini vrn bant (4) hm taşınacak malzmyi için alan bir kap örvi örn, hm d harkt için
Bu malzemelere atıfta bulunmak veya kullanım şartlarını öğrenmek için http://ocw.mit.edu/terms sitesini ziyaret ediniz
 MIT OpnoursWar http://ocw.mt.du 5.6 Thrmodnamk v Kntk Bahar 8 Bu malzmlr atıfta bulunmak vya kullanım şartlarını öğrnmk çn http://ocw.mt.du/trms stsn zyart dnz MODEL SİSTEMLER Molkülr gçş, dönm v rşm çn
MIT OpnoursWar http://ocw.mt.du 5.6 Thrmodnamk v Kntk Bahar 8 Bu malzmlr atıfta bulunmak vya kullanım şartlarını öğrnmk çn http://ocw.mt.du/trms stsn zyart dnz MODEL SİSTEMLER Molkülr gçş, dönm v rşm çn
MENKUL KIYMET DEĞERLEMESİ
 MENKUL KIYMET EĞERLEMESİ.. Hiss Sdii Tk ömlik Gtirisii Hsaplaması Bir mkul kıymti gtirisi, bkl akit akımlarıı, şimdiki piyasa fiyatıa şitly iskoto oraıdır. Mkul kıymti özlliği gör bu akit akımları faiz
MENKUL KIYMET EĞERLEMESİ.. Hiss Sdii Tk ömlik Gtirisii Hsaplaması Bir mkul kıymti gtirisi, bkl akit akımlarıı, şimdiki piyasa fiyatıa şitly iskoto oraıdır. Mkul kıymti özlliği gör bu akit akımları faiz
EME Sistem Simülasyonu. Giriş. Olasılık Dağılımı. Rassal Degiskenler
 EME 3105 1 Giriş Sistem Simülasyonu Önümüzdeki hafta simulasyon girdilerinin modellenmesinde kullanılan kesikli ve sürekli Simulasyonda İstatistiksel Modeller-I Ders 4 dağılımlar hatırlatılacaktır. Rassal
EME 3105 1 Giriş Sistem Simülasyonu Önümüzdeki hafta simulasyon girdilerinin modellenmesinde kullanılan kesikli ve sürekli Simulasyonda İstatistiksel Modeller-I Ders 4 dağılımlar hatırlatılacaktır. Rassal
Tablo (2): Atıştırma Sayısı ve Günlük Sınav Sayısı Atıştırma Sınav Sayısı (X) 0 0.07 0.09 0.06 0.01
 Ortak Varyans ve İstatistiksel Bağımsızlık Bir rassal değişken çifti istatistiksel olarak bağımsız ise aralarındaki ortak varyansın değeri 0 dır. Ancak ortak varyans değerinin 0 olması, iki rassal değişkenin
Ortak Varyans ve İstatistiksel Bağımsızlık Bir rassal değişken çifti istatistiksel olarak bağımsız ise aralarındaki ortak varyansın değeri 0 dır. Ancak ortak varyans değerinin 0 olması, iki rassal değişkenin
DERS 7. Türev Hesabı ve Bazı Uygulamalar II
 DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
SİGORTA MATEMATİĞİ SINAV SORULARI WEB. Belirli yaşlar için hesaplanan kommütasyon tablosu aşağıda verilmiştir.
 SORU 1 SİGORTA MATEMATİĞİ SINAV SORULARI WEB Şimdiki yaşı 56 olan Ahmet, Bireysel Emeklilik Sistemi (BES) ile biriktirmiş olduğu 250.000 TL yi yaşam süresi boyunca sabit ödemeli dönem başı yıllık maaş
SORU 1 SİGORTA MATEMATİĞİ SINAV SORULARI WEB Şimdiki yaşı 56 olan Ahmet, Bireysel Emeklilik Sistemi (BES) ile biriktirmiş olduğu 250.000 TL yi yaşam süresi boyunca sabit ödemeli dönem başı yıllık maaş
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ YARIŞAN BAĞIMLI RİSKLERLE SAĞKALIM ANALİZİNDE ARCHIMEDEAN KAPULA YAKLAŞIMI.
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ YARIŞAN BAĞIMLI RİSKLERLE SAĞKALIM ANALİZİNDE ARCHIMEDEAN KAPULA YAKLAŞIMI Çiğdem TOPÇU İSTATİSTİK ANABİLİM DALI ANKARA 203 Her Haı Salıdır ÖZET
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ YARIŞAN BAĞIMLI RİSKLERLE SAĞKALIM ANALİZİNDE ARCHIMEDEAN KAPULA YAKLAŞIMI Çiğdem TOPÇU İSTATİSTİK ANABİLİM DALI ANKARA 203 Her Haı Salıdır ÖZET
ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR
 ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR 1- İlaçla tedavi edilen 7 hastanın ortalama iyileşme süresi 22.6 gün ve standart sapması.360 gündür. Ameliyatla tedavi edilen 9 hasta için
ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR 1- İlaçla tedavi edilen 7 hastanın ortalama iyileşme süresi 22.6 gün ve standart sapması.360 gündür. Ameliyatla tedavi edilen 9 hasta için
YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS-YGS
 MTEMTĐK ĐM YILLR 00 003 00 005 006 007 008 009 00 0 ÖSS-YGS - - - HREKET PROLEMLERĐ Hız msaa verildiğinden süre de saa olmalıdır lınan yol : x Hız: Zaman : ir araç x yolunu hızıyla sürede alır Yol Hız
MTEMTĐK ĐM YILLR 00 003 00 005 006 007 008 009 00 0 ÖSS-YGS - - - HREKET PROLEMLERĐ Hız msaa verildiğinden süre de saa olmalıdır lınan yol : x Hız: Zaman : ir araç x yolunu hızıyla sürede alır Yol Hız
Yoksulun Kazanabildiği Bir Oyun Ali Nesin
 Yosulun Kazanabildiği Bir Oyun Ali Nesin B u yazıda yosulu azandıracağız. Küçü bir olasılıla da olsa, yosul azanabilece. Oyunu açılamadan önce, Sonlu Oyunlar adlı yazımızdai oyunu anımsayalım: İi oyuncu
Yosulun Kazanabildiği Bir Oyun Ali Nesin B u yazıda yosulu azandıracağız. Küçü bir olasılıla da olsa, yosul azanabilece. Oyunu açılamadan önce, Sonlu Oyunlar adlı yazımızdai oyunu anımsayalım: İi oyuncu
BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ
 BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ - Nair Stos dnlmlri - Nair Stos dnlmlrinin tam çözümlri - Daimi, ii-botl, laminr sınır tabaa dnlmlri - Daimi, ii-botl, laminr sınır
BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ - Nair Stos dnlmlri - Nair Stos dnlmlrinin tam çözümlri - Daimi, ii-botl, laminr sınır tabaa dnlmlri - Daimi, ii-botl, laminr sınır
UYGULAMALI DİFERANSİYEL DENKLEMLER
 UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
BİYOİSTATİSTİK Bazı Olasılık Dağılışları Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Bazı Olasılık Dağılışları Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Uygulamalı bilim
BİYOİSTATİSTİK Bazı Olasılık Dağılışları Dr. Öğr. Üyesi Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Uygulamalı bilim
LYS Matemat k Deneme Sınavı
 LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
UFUK ÖZERMAN- 2012-2013 Page 1
 - GÜZ P,Q,R fokiolrı poliom olmk üzr d d P Q R d d v P d d Q d P d R P p q dklmi içi P şrıı ğl = okı di ok dir, çözümlri di okıı civrıd şklid rrız. =+-+- +... = = okı; p=q/ P, q= R/ P fokiolrı okıd liik
- GÜZ P,Q,R fokiolrı poliom olmk üzr d d P Q R d d v P d d Q d P d R P p q dklmi içi P şrıı ğl = okı di ok dir, çözümlri di okıı civrıd şklid rrız. =+-+- +... = = okı; p=q/ P, q= R/ P fokiolrı okıd liik
Simülasyonda İstatiksel Modeller. Banks, Carson, Nelson & Nicol Discrete-Event System Simulation
 Simülasyonda İstatiksel Modeller Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Amaç Model-geliştirici dünyaya deterministik değil olasıksal olarak bakar. İstatiksel modeller değişimleri
Simülasyonda İstatiksel Modeller Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Amaç Model-geliştirici dünyaya deterministik değil olasıksal olarak bakar. İstatiksel modeller değişimleri
Yatrm getirileri bir gecikmeli hareketli ortalama modeline uyduunda performans kriterine dayal optimal amortisman süresinin belirlenmesi
 www.isaisikcilr.org saisikçilr Drgisi (9) 7-8 saisikçilr Drgisi Yarm girilri bir gcikmli harkli oralama modlin uyduunda prformans kririn dayal opimal amorisman sürsinin blirlnmsi Yasmin Gnçürk Hacp Ünivrsisi
www.isaisikcilr.org saisikçilr Drgisi (9) 7-8 saisikçilr Drgisi Yarm girilri bir gcikmli harkli oralama modlin uyduunda prformans kririn dayal opimal amorisman sürsinin blirlnmsi Yasmin Gnçürk Hacp Ünivrsisi
metal (bakır) metaloid (silikon) metal olmayan (cam) iletken yar ı iletken yalıtkan
 1 YARI İLETKENLER Enstrümantal Analiz ir yarı iltkn, iltknliği bir iltkn il bir yalıtkan arasında olan kristal bir malzmdir. Çok çşitli yarıiltkn malzm vardır, silikon v grmanyum, mtalimsi bilşiklr (silikon
1 YARI İLETKENLER Enstrümantal Analiz ir yarı iltkn, iltknliği bir iltkn il bir yalıtkan arasında olan kristal bir malzmdir. Çok çşitli yarıiltkn malzm vardır, silikon v grmanyum, mtalimsi bilşiklr (silikon
İstatistik I Ders Notları
 İstatistik I Ders Notları Sürekli Rassal Değişkenler Hüseyin Taştan Kasım 2, 26 İçindekiler Sürekli Rassal Değişkenlerin Özellikleri 2 2 Olasılık Yoğunluk Fonksiyonu 2 Birikimli Olasılık Fonksiyonu 6 4
İstatistik I Ders Notları Sürekli Rassal Değişkenler Hüseyin Taştan Kasım 2, 26 İçindekiler Sürekli Rassal Değişkenlerin Özellikleri 2 2 Olasılık Yoğunluk Fonksiyonu 2 Birikimli Olasılık Fonksiyonu 6 4
GAZİ ÜNİVERSİTESİ, İ.İ.B.F, İSTATİSTİK VE OLASILIĞA GİRİŞ I, UYGULAMA SORULARI. Prof. Dr. Nezir KÖSE
 GAZİ ÜNİVERSİTESİ, İ.İ.B.F, İSTATİSTİK VE OLASILIĞA GİRİŞ I, UYGULAMA SORULARI Prof. Dr. Nezir KÖSE 30.12.2013 S-1) Ankara ilinde satın alınan televizyonların %40 ı A-firması tarafından üretilmektedir.
GAZİ ÜNİVERSİTESİ, İ.İ.B.F, İSTATİSTİK VE OLASILIĞA GİRİŞ I, UYGULAMA SORULARI Prof. Dr. Nezir KÖSE 30.12.2013 S-1) Ankara ilinde satın alınan televizyonların %40 ı A-firması tarafından üretilmektedir.
MATEMATİK (LİSE) ÖĞRETMENLİĞİ
 KAMU PERSONEL SEÇME SINAVI MATEMATİK (LİSE) ÖĞRETMENLİĞİ TÜRKİYE GENELİ ÇÖZÜMLER 9 MATEMATİK (LİSE) ÖĞRETMENLİĞİ. A 6. D. C 7. B. C 8. C. B 9. C 5. C. D 6. D. C 7. B. A 8. D. E 9. C. B. A 5. A. B 6. A.
KAMU PERSONEL SEÇME SINAVI MATEMATİK (LİSE) ÖĞRETMENLİĞİ TÜRKİYE GENELİ ÇÖZÜMLER 9 MATEMATİK (LİSE) ÖĞRETMENLİĞİ. A 6. D. C 7. B. C 8. C. B 9. C 5. C. D 6. D. C 7. B. A 8. D. E 9. C. B. A 5. A. B 6. A.
EME 3117 SISTEM SIMÜLASYONU. Üçgensel Dağılım. Sürekli Düzgün Dağılım. Sürekli Rassal Değişkenlerin Modellemesinde Kullanılan Dağılımlar
 0..07 EME 37 SISTEM SIMÜLASYONU Simulasyonda İstatistiksel Modeller-II Ders 5 Sürekli Rassal Değişkenlerin Modellemesinde Kullanılan Dağılımlar Sürekli Düzgün (Uniform) Dağılım Normal Dağılım Üstel (Exponential)
0..07 EME 37 SISTEM SIMÜLASYONU Simulasyonda İstatistiksel Modeller-II Ders 5 Sürekli Rassal Değişkenlerin Modellemesinde Kullanılan Dağılımlar Sürekli Düzgün (Uniform) Dağılım Normal Dağılım Üstel (Exponential)
SİSTEM DİNAMİĞİ VE KONTROL
 ABANT İZZET BAYSA ÜNİVERSİTESİ MÜHENDİSİK MİMARIK FAKÜTESİ MAKİNE MÜHENDİSİĞİ BÖÜMÜ SİSTEM DİNAMİĞİ VE KONTRO. aplac Dönüşümli Yd. Doç. D. Tuan ŞİŞMAN - BOU . APACE DÖNÜŞÜMERİ.. Giiş Doğual dianiyl dnklmlin
ABANT İZZET BAYSA ÜNİVERSİTESİ MÜHENDİSİK MİMARIK FAKÜTESİ MAKİNE MÜHENDİSİĞİ BÖÜMÜ SİSTEM DİNAMİĞİ VE KONTRO. aplac Dönüşümli Yd. Doç. D. Tuan ŞİŞMAN - BOU . APACE DÖNÜŞÜMERİ.. Giiş Doğual dianiyl dnklmlin
ANADOLU ÜNİVERSİTESİ ÖRNEK: GEOMETRİK DAĞILIM
 ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ KESİKLİ DAĞILIMLAR-2 DOÇ. DR. NİHAL ERGİNEL 2015 GEOMETRİK DAĞILIM Bir Bernoulli deneyi ilk olumlu sonuç elde edilmesine kadar tekrarlansın. X: ilk olumlu sonucun
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ KESİKLİ DAĞILIMLAR-2 DOÇ. DR. NİHAL ERGİNEL 2015 GEOMETRİK DAĞILIM Bir Bernoulli deneyi ilk olumlu sonuç elde edilmesine kadar tekrarlansın. X: ilk olumlu sonucun
Stokastik Süreçler. Bir stokastik Süreç ya da rastgele süreç şöyle tanımlanabilir.
 Stoasti Süreçler Bir stoasti Süreç ya da rastgele süreç şöyle tanımlanabilir. Zamanla değişen bir rastgele değişendir. Rastgele değişenin alacağı değer zamanla değişmetedir. Deney çıtılarına atanan rastgele
Stoasti Süreçler Bir stoasti Süreç ya da rastgele süreç şöyle tanımlanabilir. Zamanla değişen bir rastgele değişendir. Rastgele değişenin alacağı değer zamanla değişmetedir. Deney çıtılarına atanan rastgele
{ } { } Ters Dönüşüm Yöntemi
 KESĐKLĐ DAĞILIMLARDAN RASGELE SAYI ÜRETME Trs Dönüşüm Yöntmi F dağılım fonksiyonuna sahip bir X rasgl dğişknin dağılımından sayı ürtmk için n çok kullanılan yöntmlrdn biri, F dağılım fonksiyonunun gnllştirilmiş
KESĐKLĐ DAĞILIMLARDAN RASGELE SAYI ÜRETME Trs Dönüşüm Yöntmi F dağılım fonksiyonuna sahip bir X rasgl dğişknin dağılımından sayı ürtmk için n çok kullanılan yöntmlrdn biri, F dağılım fonksiyonunun gnllştirilmiş
TG 12 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞREMENLİK ALAN İLGİSİ ESİ İLKÖĞREİM MAEMAİK ÖĞREMENLİĞİ G ÖA İLKÖĞREİM MAEMAİK u tstlrin hr hakkı saklıdır. Hangi amaçla olursa olsun, tstlrin tamamının va bir kısmının İhtiaç
KAMU PERSONEL SEÇME SINAVI ÖĞREMENLİK ALAN İLGİSİ ESİ İLKÖĞREİM MAEMAİK ÖĞREMENLİĞİ G ÖA İLKÖĞREİM MAEMAİK u tstlrin hr hakkı saklıdır. Hangi amaçla olursa olsun, tstlrin tamamının va bir kısmının İhtiaç
SÜREKLİ ŞANS DEĞİŞKENLERİ. Üstel Dağılım Normal Dağılım
 SÜREKLİ ŞANS DEĞİŞKENLERİ Üstel Dağılım Normal Dağılım 1 Üstel Dağılım Meydana gelen iki olay arasındaki geçen süre veya bir başka ifadeyle ilgilenilen olayın ilk defa ortaya çıkması için geçen sürenin
SÜREKLİ ŞANS DEĞİŞKENLERİ Üstel Dağılım Normal Dağılım 1 Üstel Dağılım Meydana gelen iki olay arasındaki geçen süre veya bir başka ifadeyle ilgilenilen olayın ilk defa ortaya çıkması için geçen sürenin
IE 303T Sistem Benzetimi DERS 4 : O L A S I L I K T E K R A R
 IE 303T Sistem Benzetimi DERS 4 : O L A S I L I K T E K R A R Geçen Ders Envanter yonetımı: Gazetecı problemı Rastsal Rakamlar Üret Talebi hesapla Geliri hesapla Toplam maliyeti hesapla Günlük ve aylık
IE 303T Sistem Benzetimi DERS 4 : O L A S I L I K T E K R A R Geçen Ders Envanter yonetımı: Gazetecı problemı Rastsal Rakamlar Üret Talebi hesapla Geliri hesapla Toplam maliyeti hesapla Günlük ve aylık
ÜSLÜ İFADELER VE ÜSTEL FONKSİYONLAR LOGARİTMA FONKSİYONU, ÜSTEL, LOGARİTMİK DENKLEM VE EŞİTSİZLİKLER
 BÖÜ ÜÜ İFD V Ü FOİO Üslü İfdlrd İşlmlr...7 Üslü Dnklmlr... Üstl Fonksiyon...7 ygulm stlri...5 BÖÜ OGİ FOİO, Ü, OGİİ D V ŞİİZİ ogritm Fonksiyonu...7 ogritm Fonksiyonunun Özlliklri...9 bn Dğiştirm...55 Üstl
BÖÜ ÜÜ İFD V Ü FOİO Üslü İfdlrd İşlmlr...7 Üslü Dnklmlr... Üstl Fonksiyon...7 ygulm stlri...5 BÖÜ OGİ FOİO, Ü, OGİİ D V ŞİİZİ ogritm Fonksiyonu...7 ogritm Fonksiyonunun Özlliklri...9 bn Dğiştirm...55 Üstl
YÖNEYLEM ARAŞTIRMASI-II Hafta 14
 9.0.07 YÖNEYLEM ARAŞTIRMASI-II Hafta ERT ANALİZİ Olasılıksal roje Değerlendirme ve Gözden Geçirme Tekniği ERT (robabilistic Evaluation and Review Technique) Eğer projenin faaliyetlerinin tamamlanma süresi
9.0.07 YÖNEYLEM ARAŞTIRMASI-II Hafta ERT ANALİZİ Olasılıksal roje Değerlendirme ve Gözden Geçirme Tekniği ERT (robabilistic Evaluation and Review Technique) Eğer projenin faaliyetlerinin tamamlanma süresi
Negatif Binom Dağılımı
 Ngatif Binom Dağılımı Brnoulli dnyinin tüm varsayımları ngatif binom dağılımı içind gçrlidir. Binom dağılımında n dnmd adt başarı olasılığı l ğ il ilgilnilirkn, ili ngatif binom dağılımındağ d is şans
Ngatif Binom Dağılımı Brnoulli dnyinin tüm varsayımları ngatif binom dağılımı içind gçrlidir. Binom dağılımında n dnmd adt başarı olasılığı l ğ il ilgilnilirkn, ili ngatif binom dağılımındağ d is şans
Kirişli döşemeler (plaklar)
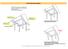 Kirişli döşmlr (plaklar) Dört tarafından kirişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşluklu döşmlr Düznsiz gomtrili döşmlr Üç tarafı kirişli bir tarafı boşta döşm Bir tarafı kirişli
Kirişli döşmlr (plaklar) Dört tarafından kirişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşluklu döşmlr Düznsiz gomtrili döşmlr Üç tarafı kirişli bir tarafı boşta döşm Bir tarafı kirişli
Dr. Mehmet AKSARAYLI
 Dr. Mehmet AKSARAYLI Şans Değişkeni: Bir dağılışı olan ve bu dağılışın yapısına uygun frekansta oluşum gösteren değişkendir. Şans Değişkenleri KESİKLİ RASSAL DEĞİŞKENLER ve OLASILIK DAĞILIMLARI Kesikli
Dr. Mehmet AKSARAYLI Şans Değişkeni: Bir dağılışı olan ve bu dağılışın yapısına uygun frekansta oluşum gösteren değişkendir. Şans Değişkenleri KESİKLİ RASSAL DEĞİŞKENLER ve OLASILIK DAĞILIMLARI Kesikli
TEK BOYUTLU RASSAL DEĞİŞKENLER
 TEK BOYUTLU RASSAL DEĞİŞKENLER Rassal değişken: S örnek uzayının her bir basit olayını yalnız bir gerçel değere dönüştüren fonksiyonuna rassal (tesadüfi) değişken denir. İki para birlikte atıldığında üste
TEK BOYUTLU RASSAL DEĞİŞKENLER Rassal değişken: S örnek uzayının her bir basit olayını yalnız bir gerçel değere dönüştüren fonksiyonuna rassal (tesadüfi) değişken denir. İki para birlikte atıldığında üste
ELM207 Analog Elektronik
 ELM7 Alog Elkroik Giriş Bir Fourir srisi priyodik bir ) oksiyouu, kosiüs v siüslri sosuz oplmı biçimid bir çılımdır. ) cos b si ) Bşk dyişl, hrhgi bir priyodik oksiyo sbi bir dğr, kosiüs v siüs oksiyolrıı
ELM7 Alog Elkroik Giriş Bir Fourir srisi priyodik bir ) oksiyouu, kosiüs v siüslri sosuz oplmı biçimid bir çılımdır. ) cos b si ) Bşk dyişl, hrhgi bir priyodik oksiyo sbi bir dğr, kosiüs v siüs oksiyolrıı
Kesikli Şans Değişkenleri İçin; Olasılık Dağılımları Beklenen Değer ve Varyans Olasılık Hesaplamaları
 Kesikli Şans Değişkenleri İçin; Olasılık Dağılımları Beklenen Değer ve Varyans Olasılık Hesaplamaları 1 Şans Değişkeni: Bir dağılışı olan ve bu dağılışın yapısına uygun frekansta oluşum gösteren değişkendir.
Kesikli Şans Değişkenleri İçin; Olasılık Dağılımları Beklenen Değer ve Varyans Olasılık Hesaplamaları 1 Şans Değişkeni: Bir dağılışı olan ve bu dağılışın yapısına uygun frekansta oluşum gösteren değişkendir.
z Hertz dipolü, çok küçük ve ince olduğu için üzerindeki akım sabit kabul edilir. jkr d R l / 2 l / 2 jkr z jkr z jkr z
 İnc Antnl Çaplaı boylaına gö küçük olan antnl inc antnl dni Alanlaın hsabında antnlin sonsu inc kabul dilmsi kolaylık sağla Ancak antn mpdansı bulunmak istndiğind kalınlığın iş katılması gki Ht Dipolü
İnc Antnl Çaplaı boylaına gö küçük olan antnl inc antnl dni Alanlaın hsabında antnlin sonsu inc kabul dilmsi kolaylık sağla Ancak antn mpdansı bulunmak istndiğind kalınlığın iş katılması gki Ht Dipolü
Diferensiyel Denklemler I Uygulama Notları
 2004 Diferensiyel Denklemler I Uygulama Notları Mustafa Özdemir İçindekiler Temel Bilgiler...................................................................... 2 Tam Diferensiyel Denklemler........................................................4
2004 Diferensiyel Denklemler I Uygulama Notları Mustafa Özdemir İçindekiler Temel Bilgiler...................................................................... 2 Tam Diferensiyel Denklemler........................................................4
IKTI 102 25 Mayıs, 2010 Gazi Üniversitesi-İktisat Bölümü
 DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
3 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI
 ÖNSÖZ İÇİNDEKİLER III Bölüm 1 İSTATİSTİK ve SAYISAL BİLGİ 11 1.1 İstatistik ve Önemi 12 1.2 İstatistikte Temel Kavramlar 14 1.3 İstatistiğin Amacı 15 1.4 Veri Türleri 15 1.5 Veri Ölçüm Düzeyleri 16 1.6
ÖNSÖZ İÇİNDEKİLER III Bölüm 1 İSTATİSTİK ve SAYISAL BİLGİ 11 1.1 İstatistik ve Önemi 12 1.2 İstatistikte Temel Kavramlar 14 1.3 İstatistiğin Amacı 15 1.4 Veri Türleri 15 1.5 Veri Ölçüm Düzeyleri 16 1.6
TANITIM ve KULLANIM KILAVUZU. Modeller UBA4234-R. Versiyon : KK_UBA_V3.0210
 SAT-IF / CATV Ultra Gniş Bantlı Dağıtım Yükslticilri (UBA-Srisi) TANITIM v KULLANIM KILAVUZU Modllr UBA4234-R Vrsiyon : KK_UBA_V3.0210 1.Gnl Tanıtım UBA Srisi Dağıtım Yükslticilri, uydu (950-2150MHz) v
SAT-IF / CATV Ultra Gniş Bantlı Dağıtım Yükslticilri (UBA-Srisi) TANITIM v KULLANIM KILAVUZU Modllr UBA4234-R Vrsiyon : KK_UBA_V3.0210 1.Gnl Tanıtım UBA Srisi Dağıtım Yükslticilri, uydu (950-2150MHz) v
İNTEGRAL KONU ANLATIMI ÖRNEKLER
 İNTEGRL KONU NLTIMI ÖRNEKLER Ġtgrl lmk, türi ril ir oksio lmk tır d,, d oksio olrk rildiğii =F i istdiğii rslım d içi i cid idsi: d = + dir, hrhgi ir sit df d koģl sğl = F oksio i gör itgrli dir d F içimid
İNTEGRL KONU NLTIMI ÖRNEKLER Ġtgrl lmk, türi ril ir oksio lmk tır d,, d oksio olrk rildiğii =F i istdiğii rslım d içi i cid idsi: d = + dir, hrhgi ir sit df d koģl sğl = F oksio i gör itgrli dir d F içimid
B OSC2 VOD PIC16F84 MİKRODENETLEYİCİSİ KULLANILARAK CİHAZLARIN TELEFON İLE KONTROLÜNE BİR UYGULAMA. Rabman YAKAR, Etem KÖKLÜKAYA.
 SAU Fn Bilimlri Enstitüsü Drgisi PIC16F84 Mikrodntlcisi Kullanılarak Ciaziarın Tlfon D Kontrolün Bir Uygulama PIC16F84 MİKRODENETLEYİCİSİ KULLANILARAK CİHAZLARIN TELEFON İLE KONTROLÜNE BİR UYGULAMA Rabman
SAU Fn Bilimlri Enstitüsü Drgisi PIC16F84 Mikrodntlcisi Kullanılarak Ciaziarın Tlfon D Kontrolün Bir Uygulama PIC16F84 MİKRODENETLEYİCİSİ KULLANILARAK CİHAZLARIN TELEFON İLE KONTROLÜNE BİR UYGULAMA Rabman
π βk F -F 0.4 0.3 0.2 0.1 0 0.01 0.02 0.03 0.04 kayma 1 2 F + F 1 2 Döndüren kasnak Döndürülen kasnak
 TİMAK-Taarım İmalat Analiz Kongri 6-8 Nian 006 - BALIKESİ KAYIŞ KASNAK MEKANİZMALAINDA KAYMA OLAYINI ETKİLEYEN AKTÖLEİN ANALİZİ M. Ndim GEGE Maina Mühndiliği Bölümü Mühndili aülti -Balıir/Türi Özt Kaış
TİMAK-Taarım İmalat Analiz Kongri 6-8 Nian 006 - BALIKESİ KAYIŞ KASNAK MEKANİZMALAINDA KAYMA OLAYINI ETKİLEYEN AKTÖLEİN ANALİZİ M. Ndim GEGE Maina Mühndiliği Bölümü Mühndili aülti -Balıir/Türi Özt Kaış
k adet olay ortaya çıkar. Başka bir deyişle k adet olay mevcuttur:
 Gama Dağılışıı Poisso Sürci il ilişisi: Bazı rmlara W şas ğişi a ola oraa çııcaa aar gç ölçği aımlar. ğr sabi olara abl ils W ağılım fosio G P W P W W zlğa a ola oraa çııorsa W rm içi fazla a ola oraa
Gama Dağılışıı Poisso Sürci il ilişisi: Bazı rmlara W şas ğişi a ola oraa çııcaa aar gç ölçği aımlar. ğr sabi olara abl ils W ağılım fosio G P W P W W zlğa a ola oraa çııorsa W rm içi fazla a ola oraa
4.3. Türev ile İlgili Teoremler
 4.. Türev ile İlgili Teoremler Bu kesimde ortalama değer teoremini vereceğiz. Ortalama değer teoremini ispatlarken kullanılacak olan Fermat teoremini ve diğer bazı teoremleri ispat edeceğiz. 4...Teorem
4.. Türev ile İlgili Teoremler Bu kesimde ortalama değer teoremini vereceğiz. Ortalama değer teoremini ispatlarken kullanılacak olan Fermat teoremini ve diğer bazı teoremleri ispat edeceğiz. 4...Teorem
Rassal Değişken. Yrd. Doç. Dr. Tijen ÖVER ÖZÇELİK
 Rassal Değişken Yrd. Doç. Dr. Tijen ÖVER ÖZÇELİK tover@sakarya.edu.tr S örnek uzayı içindeki her bir basit olayı yalnız bir gerçel (reel) değere dönüştüren fonksiyona rassal değişken adı verilir. O halde
Rassal Değişken Yrd. Doç. Dr. Tijen ÖVER ÖZÇELİK tover@sakarya.edu.tr S örnek uzayı içindeki her bir basit olayı yalnız bir gerçel (reel) değere dönüştüren fonksiyona rassal değişken adı verilir. O halde
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ ORTAÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG 9 ÖABT ORTAÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ ORTAÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG 9 ÖABT ORTAÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
BÖLÜM 4 LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ
 BÖLÜM LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ GİRİŞ Dnklm sismlrin linr cbir drsindn şin olmlısınız Anck bu ür dnklmlrd hrhngi bir difrnsiyl büyüklük vy ürv bulunmz Bşk bir dyişl cbirsl dnklm sismi, y (
BÖLÜM LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ GİRİŞ Dnklm sismlrin linr cbir drsindn şin olmlısınız Anck bu ür dnklmlrd hrhngi bir difrnsiyl büyüklük vy ürv bulunmz Bşk bir dyişl cbirsl dnklm sismi, y (
Girdi Analizi. 0 Veri toplama 0 Girdi sürecini temsil eden olasılık dağılımı belirleme. 0 Histogram 0 Q-Q grafikleri
 Girdi Analizi 0 Gerçek hayattaki benzetim modeli uygulamalarında, girdi verisinin hangi dağılımdan geldiğini belirlemek oldukça zor ve zaman harcayıcıdır. 0 Yanlış girdi analizi, elde edilen sonuçların
Girdi Analizi 0 Gerçek hayattaki benzetim modeli uygulamalarında, girdi verisinin hangi dağılımdan geldiğini belirlemek oldukça zor ve zaman harcayıcıdır. 0 Yanlış girdi analizi, elde edilen sonuçların
Z = S n E(S n ) V ar(sn ) = S n nµ. S nn. n 1/2 n σ
 YTÜ-İktisat İstatistik II Merkezi Limit Teoremi 1 MERKEZİ LİMİT TEOREMİ CENTRAL LIMIT THEOREM X 1,X 2,...,X n herbirinin ortalaması µ ve varyansı σ 2 olan ve aynı dağılıma uyan n tane bağımsız r.d. olsun.
YTÜ-İktisat İstatistik II Merkezi Limit Teoremi 1 MERKEZİ LİMİT TEOREMİ CENTRAL LIMIT THEOREM X 1,X 2,...,X n herbirinin ortalaması µ ve varyansı σ 2 olan ve aynı dağılıma uyan n tane bağımsız r.d. olsun.
