Otonom Gezgin Robotların Bağlantılı Grup Halinde Gezinimi

Transkript

1 TOK'7 Bildiriler Kitab stanbul, -7 Elül 27 Otonom Gezgin Robotların Bağlantılı Grup Halinde Gezinimi Ahmet Cezairli 1, Feza Kerestecioğlu 2 1 Elektrik-Elektronik Mühendisliği Bölümü Boğaziçi Üniversitesi, Bebek, İstanbul ahmet.cezairli@boun.edu.tr 2 Elektronik Mühendisliği Bölümü Kadir Has Üniversitesi, Cibali, İstanbul kerestec@khas.edu.tr Özetçe Bu çalışmada hareketli otonom robot gruplarının gezinimi konu edilmiştir. Çizge kuramından alınan tanımlar robot gruplarını betimlemede kullanılmıştır. Bir erel idare stratejisi önerilmiş ve bu strateji grup içindeki her robot tarafından ugulandığında genel sonucun tüm grubun bir noktadan başka bir noktaa bağlantılılık özelliğini kabetmeden hareket edebildiği gösterilmiştir. Bu sonuç, robotlar arasında herhangi bir haberleşme gerektirmeden, alnızca sınırlı-mesafeli konum algılaıcıları kullanılarak elde edilmiştir. 1. Giriş Bazı işlerin tek bir robot tarafından apılması mümkün olmaabilir, vea mümkün olsa bile verimli olmaabilir. Bu gibi durumlarda, tek bir robot erine bir robot grubunun böle işleri başarabileceği düşünülür. Gerçekten de, doğadaki bir takım canlı türlerinde buna benzer kolektif çalışmanın apıldığı örnekler görmek mümkündür. Balık ve kuş sürüleri, arı ve karınca kolonileri kolektif davranışın sergilendiği örneklerin başında gelmektedir [1][2][3]. Literatürde otonom robotların işbirliğine daalı birçok çalışma bulunmaktadır. Kolektif çalışma apan canlı türlerini modelleen ilk çalışmalardan birisi 1987 ılında kuş sürüleri hakkında apılmıştır [4]. Bu çalışmada, büük grup davranışlarının aslında her grup üesince ugulanan basit hareket ilkeleri sonucu oluştuğu öne sürülmüştür. Bu fikrin arık-zaman için önemli bir ugulaması 199 te apılmıştır []. Sonraki ıllarda kolektif hareket kavramı önemli bir gelişim göstermiştir. Robot gruplarının dizilim oluşturması [6][7][8] ve grup davranışını sağlamak için potansiel fonksion ve apa kuvvetlerden ararlanılmasına daalı çalışmalar mevcuttur [3][9][1]. Bazı öntemler grup içindeki robotlar arasında sınırlı ölçüde haberleşmee daalıdır [11][12]. Bu kavramların gelişimi ve geçmiş çalışmaların özeti ile ilgili daha geniş bilgi [13] ve onun içinde belirtilen kanaklarda bulunabilir. Bu makalede, çizge kuramını kullanarak, otonom robotların bağlantılı gruplar halinde gezinimini sağlaan bir öntem geliştirilmektedir. Önce robot gruplarının bağlantılılığı tanımlanmış ve sonra erel bir idare stratejisi geliştirilmiştir. Bu erel idare stratejisi grubun bağlantılılığını garanti etmektedir. Robotların haberleşme eteneğine sahip olmadığı ve konum algılaıcılarının da sınırlı mesafei algılaabildiği varsaılmıştır. Gezgin robotlar ile doğadaki kümeleşen havan grupları arasında benzerlik kurduğumuz düşünüldüğünde, bu varsaımlar çalışmamızı daha gerçekçi kılmaktadır. Literatürde çizge kuramını kullanan başka çalışmalar da mevcuttur [14][1][16][17], ancak bildiğimiz kadarıla, haberleşmesiz robot gruplarının bağlantılılığını garanti eden bir öntem mevcut değildir. [1] ve [16] da konum ve hız bilgisinden oluşan durum vektörünün ölçülebildiği ve tüm robotların birbirini algılaabildiği varsaılmıştır. Bu kanaklardaki çalışmalar ve [18] deki çalışma tüm hareket bounca grup bağlantılılığını da kendi öntemlerinin başarısı için arıca bir ön koşul olarak kabul etmektedir. Burada anlatılan makalede ise alnızca sınırlı uzaklıktan konum ölçümü apılabildiği varsaılarak değişken topolojie sahip bir robot grubunun bağlantılı hareketi için gerekli hareket mekanizması geliştirilmiştir. Bu makale şu şekilde düzenlenmiştir: Bölüm 2 de temel çizge kuramına daalı problem tanımı verilmektedir. Bölüm 3 te, robotların otonom hareketleri için bir erel idare stratejisi önermekteiz. Bu stratejinin hesaplama malieti Bölüm 4 te incelenmiş ve hesaplama ükünü azaltmak için bir öntem sunulmuştur. Önerilen öntemin çeşitli robot grupları için sınanması Bölüm te, sonuçlar ve tartışma ise Bölüm 6 da bulunmaktadır. 2. Problem Tanımı Bu çalışmadaki robotların fiziksel özellikler bakımından özdeş oldukları varsaılmıştır. Robotlar arasında haberleşme bulunmamaktadır. R ile gösterilmekte olan her bir robot tüm önlerde hareket edebilmektedir ve sınırlı-mesafeli konum algılaıcılarıla donatılmıştır. Konum algılaıcıları, algılama uzaklığı içindeki diğer robotları üksek doğrulukla algılaabilmektedir. Bu konum algılama işlevi, algılaan robot ile onun algılama alanı içindeki her robot arasında bir bağlantı oluşturur. Algılama eteneğinin tüm önlerde ve sürekli olduğunu varsamaktaız. Diğer robotları algılamak, o robotları tanımak anlamında olmaıp, alnızca onların konumlarını 236

2 Ahmet Cezairli, Feza Kerestecio lu belirleebilmei kasdetmektedir. Robotlar herhangi bir kimlik taşımadıkları gibi, bir robot kendi kimliğini (vea numarasını) dahi bilmemektedir. Bu tür robotlardan iki a da daha fazlası, bu çalışmada bahsedilen bir robot grubunu oluşturur. Çalışmanın devamında, böle bir grubun gezinimini inceleeceğiz. Aşağıdaki tanımlar çizge kuramından uarlanmış olup, bu konuda detalı bilgi [19] ve [2] içinde bulunabilir. Tanım 1 Bir grup G, bağlantılarla birleştirilebilen N adet otonom gezgin robottan oluşan bir kümedir {R i, i = 1,...,N}. Tanım 2 Grup G içindeki her bir robottan diğer tüm robotlara bağlantılarla oluşturulmuş bir ol çizilebiliorsa grup G bağlantılıdır. Aralarında bu tür bir ol oluşturulamaan en az bir robot çifti içeren grup ise bağlantısız bir gruptur. Robotlardaki konum algılaıcıları, d ma ile gösterilen uzaklıktan küçük bölge içindeki tüm önlerde kesintisiz ve doğru konum bilgisi sağlamaktadır. Algılama uzaklığının sınırlı olduğunu varsadığımızdan ve grup içindeki robot saısı çok fazla olabileceğinden, her robot diğer tüm robotları algılaamaabilir. Bu düşünce ile, alt-grupları şöle tanımlamaktaız: Tanım 3 Bir alt-grup S i, robot R i tarafından algılanan robotlar grubudur. Grup içinde N tane robot bulunduğuna göre, tanım gereği, her robot için bir tane olmak üzere N tane alt-grup vardır. S i, merkezinde R i bulunan küresel bir şekle sahiptir. Şekil 1 üç robottan oluşan bir grubu göstermektedir. Şekilde, R 2 S 1 ve R 1 S 2 olduğu görülebilir. Bu durum, C 12 ve C 21 bağlantılarını oluşturur. R 2 ve R 3 arasındaki bağlantılar da benzer biçimde oluşturulur. R 2 robotu hem R 1 hem de R 3 robotlarının konum bilgilerini ölçebilmekte iken, R 1 ve R 3 robotları, aralarındaki uzaklık d ma tan büük olduğu için birbirlerini algılaamamaktadır. Robot grubunun bir başlangıç konumundan bir hedef konuma doğru hareket etmesi gerekmektedir. Grup üelerinden alnızca bir tanesinin hedef konumu bildiğini varsamaktaız. Hedefin konum bilgisine sahip bu robotu grup lideri olarak adlandıracağız ve R L ile göstereceğiz. Lider, gruptaki diğer robotlarla tümüle eşit fiziksel özelliklere ve eteneklere sahiptir. Liderle diğer robotlar arasındaki tek fark, hedefin bulunduğu ön bilgisinin lidere verilmiş olması ve liderin kendi hareketini belirlerken bu bilgii kullanmasıdır. Bununla birlikte, bu çalışmada liderlik gizlidir. Gruptaki hiç bir robot lideri farklı bir üe gibi tanımaz. Diğer bir deişle, R L robotu R j tarafından algılanabiliorsa, ani R L S j, R j onu alnızca komşularından birisi gibi görür ve R L nin liderliği R j nin erel idare stratejisinde bir farklılık aratmaz. Makalenin bundan sonraki kısmında N robotluk bir grubu, bir R L ve N 1 adet takipçi robot R j, j = 1,...,N 1, olarak düşüneceğiz. İzleen bölümde bu tanımları kullanarak ve bir robot kümesinin bağlantılı bir grup olarak harekete başladığını varsaarak, hareketin her anında Tanım 2 e göre grup bağlantılılığının korunacağını garanti eden ve etkili bir grup gezinimi sağlaan bir dağıtılmış idare öntemi geliştireceğiz. Şekil 1: Üç robottan oluşan bir grup ve alt-gruplar. 3. Otonom Hareket Robotların otonom hareketini iki durumda inceleeceğiz. Birinci durumda tüm robotlar eşzamanlı saatlere sahiptir. Her robot alnızca kendisine arılmış zaman diliminde hareket edebilir. Bölece robotların hareketleri sıralı bir şekilde olur. Her bir zaman diliminde alnızca tek bir robot hareket edebilir. Eğer bir robotun erel idare stratejisi o robotun belli bir zaman diliminde sabit kalmasını gerektirirse, o zaman bu robota arılmış zaman diliminde herhangi bir hareket gerçekleşmez. İkinci durumda ise robotlar arasında bir senkronizasona gerek oktur. Her bir robot düzenli aralıklarla komşu robotların, ani algılaabildiği tüm robotların, konumlarını belirler ve erel idare stratejisini ugular. Robotların eşzamanlı hareketi mümkündür. Her iki durumda, herhangi bir t anında t + t ile bir sonraki örnekleme zamanını göstereceğiz. Burada t > bir robotun kendi algılama sınırları içinde kalan diğer robotların konumlarını algıladığı küçük bir zaman dilimidir. Bir t anında R i robotunun konumunu X i(t), i =1,...,N, ile belirleteğiz. Tüm robotlar otonom hareket ettiği için her bir robot için erel hareket kuralları oluşturacağız. Bu çalışmada, Renolds tarafından apılan ön çalışmadan [4] esinlenerek bir erel idare stratejisi önermekteiz. Her t anında, lider R L verilen hedef konuma doğru giderken, her takipçi robot R j, j =1,...,N 1, kendi alt-grubundaki robotların konumlarını algılaarak kendisine erel bir hedef konum belirler. R j orijinde olmak üzere bunu R j nin erel koordinatlarında tanımlamak daha ugundur. Yerel koordinatlardaki konum vektörünü (t) ile gösterelim. Kullanacağımız notasonda vektöründeki altsimge hangi robotun koordinat çerçevesinin kullanıldığını belirtirken, üstsimge hangi robotun konumu olduğunu belirtecektir. Örneğin, R k robotunun konumunu R j nin koordinat çerçevesinde j k ile göstereceğiz. Tanım gereği, Rj nin kendi koordinat çerçevesindeki erel konum vektörü j j sıfıra eşittir. Alt-grup S i, i =1,...,N,içindeki robotlar için, i k(t) def = X k (t) X i(t), k =1,...,M (1) Burada M alt-grup S i içindeki robotların saısını göstermektedir. Şimdi aşağıdaki erel idare stratejisini tanımlaabiliriz. Yerel İdare Stratejisi: Her örnekleme zamanı t anında, gruptaki her robot t + t zamanı için bir hedef konum hesaplar ve bu konuma doğru hareket eder. Öle ki, 237

3 Otonom Gezgin Robotlar n Ba lant l Grup Halinde Gezinimi 1. her takipçi R j, j = 1...,N 1, için hedef konum j j (t+ t), Sj içindeki robotların konumlarından hesaplanan bir maliet fonksionu (J( j j (t + t))) minimize eder, 2. R L için hareket önü daima grubun verilen hedefi önündedir, ve hem R L hem de her R j için hareket şu kısıta tabidir: i i(t+ t) K(d ma ma i k(t) ),K { 1, 1} (2) k 2 Burada i =1,...,N ve i k(t) (1) te tanımlandığı gibidir. Tüm robotlar sıralı hareket ettiğinde K =1,tüm robotlar eş zamanlı hareket etme özelliğine sahip olduğunda ise K = 1 alınır. 2 i k(t) ve i i(t + t), R i nin t anındaki koordinat çerçevesinde azılmış konum vektörleridir. R i nin hedeflediği konum i i(t + t) (2) te bir üst sınır tarafından kısıtlanmıştır. Bu üst sınır grubun bağlantılılığını garanti etmek için kullanılmaktadır. Yerel idare stratejisinin ugulanması için çeşitli maliet fonksionları kullanılabilir. Örneğin her takipçi robot R j için J( j j (t + t)) = ma j j (t + t) k j k (t) şeklinde bir maliet fonksionu kullanıldığında her robot algıladığı en uzak robota olan uzaklığını azaltacak şekilde hareket eder. Bir başka olası aklaşım ise, her robotun algıladığı tüm robotlara istenilen bir sabit uzaklık kadar akında olmaa çalışması olabilir. Bu istenilen sabit uzaklığı d (d d ma) ile gösterelim. Bu durumda her takipçi robot R j, j = 1,...,N 1, için kullanılan maliet fonksionu şöledir: J( j j (t + t)) = M k=1 ( j j (t + t) j k (t) d ) 2. (3) Grubun bağlantılılık özelliğini korumaı amaçlaarak aşağıdaki iki teoremi vereceğiz. Teorem 1 N otonom gezgin robottan oluşan ve t =anında Tanım 2 e göre bağlantılı olan bir G grubunu düşünelim. Eğer bu gruptaki robotlar ukarıda verilen Yerel İdare Stratejisi ne göre sıralı olarak hareket ederlerse, grup G t > için bağlantılılığını korur. Kanıt Sıralı hareket nedenıle (2) içinde K = 1 dir. göre, Buradan, Buna i i(t + t) +ma i k(t) d ma, i (4) k i i(t + t) + i k(t) d ma, i, k () Üçgen eşitsizliğini kullanarak, i i(t + t) i k(t) d ma, i, k (6) S i içindeki robotlar [t, t + t] periodunda hareket etmediği için, i i(t + t) i k(t + t) d ma, i, k (7) Denklem (7) nin sol tarafı, R i nin t anındaki koordinat ekseninde, R k S i robotlarının t + t anında R i robotuna olan uzaklıklarını gösterir. (7) den t+ t anı için R k S i olduğunu elde ederiz. Bu bütün robotlar R i, i =1,...,N, ve onların altgrupları S i,için geçerli olduğundan, t anında bağlantılı olan bir grup t+ t anında da bağlantılı kalacaktır. Bölece, Yerel İdare Stratejisi altında bağlantılılık tüm t>bounca korunur. Teorem 2 N otonom gezgin robottan oluşan ve t =anında Tanım 2 e göre bağlantılı olan bir G grubunu düşünelim. Eğer bu gruptaki robotların ukarıda verilen Yerel İdare Stratejisi ne göre eşzamanlı olarak hareket etmelerine izin verilmişse, grup G t> için bağlantılılığını korur. Kanıt Robotlar eşzamanlı hareket edebildiği için (2) i K = 1 2 ile kullanacağız. R a ve R b t anında birbirlerini algılaabilen iki robot olsun, ani, R a S b ve R b S a. M a ve M b ise S a ve S b içindeki robotların saısı olsun. Bölece (2) i kullanarak, ve 2 a a(t+ t) +ma a k(t) d ma,k=1,...,m a (8) k 2 b b(t + t) +ma b l (t) d ma,l=1,...,m b (9) l azabiliriz. ma k a k(t) a b (t), ma l b l (t) b a(t),ve a b (t) = b a(t) olduğundan, (8) ve (9) dan a a(t + t) + b b(t + t) + a b (t) d ma (1) Üçgen eşitsizliğini kullanarak, a a(t + t) ( a b (t)+ b b(t + t)) d ma (11) Burada a b (t)+ b b(t + t) terimi R b nin t + t anındaki konum vektörüdür ve R a nın t anındaki koordinat çerçevesinde ifade edilmiştir. Bu nedenle, (11) R a ve R b robotları arasındaki uzeklığın d ma tan daha fazla olamaacağını gösterir. Teorem 1 in ispatındakilere benzer argümanlarla, eğer grup t = anında bağlantılı ise, tüm t>için debağlantılı kalır sonucunu elde ederiz. Her iki hareket önteminde de (sıralı vea eşzamanlı), her alt-grup S i başlangıçta S i içinde bulunan robotları içermee devam edecektir. Bölece S i içindeki robotların saısı asla azalmaacak, hatta eni robotlar R i nin algılama bölgesine girip S i nin elemanı oldukça bu saı artabilecektir. Yerel İdare Stratejisi içindeki (2) ile verilen hareket kısıtı özel bir durumda tüm robotların hareketsiz kalmasına neden olabilir. Bu patolojik başlangıç durumları tüm robotların birbirinden d ma kadar uzakta bulunduğu durumlardır. Bu halde (2) nin sağ tarafı tüm robotlar için sıfır olacağından grup hareketsiz kalacak ancak Teorem 1 ve Teorem 2 grubun bağlantılılığı ile ilgili olduğu için bu patolojik durumlarda da geçerliliğini koruacaktır. 4. Hesaplamaa İlişkin Notlar Bu çalışmadaki robotların oldukça basit ve özellikle hesaplama etenekleri bakımından sınırlı cihazlar oldukları varsaılmıştır. Amacımız, böle basit robotlara bile ugulanabilen ve tatmin 238

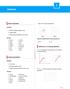
4 Ahmet Cezairli, Feza Kerestecio lu edici grup gezinimi sağlaan bir dağıtık denetim mekanizması geliştirmektir. Bu bölümde, önceki bölümde önerilen Yerel İdare Stratejisi nin minimizason koşulunu inceleeceğiz ve hesaplama ükünü ciddi şekilde azaltarak bu stratejii geliştireceğiz. Denklem (3) te verilen maliet fonksionunun minimum noktaları, her örnekleme anında her bir takipçi robotun ulaşmak istediği konumlardır. S j içindeki robotların saısı arttıkça (3) ün minimizasonu daha fazla hesaplama gücü gerektirir. Bir alt-grup S j de alnızca tek bir robot bulunduğunda, bu robot R m olsun, minimizasonun çözümü R 2 de bir çember ve R 3 te bir küredir. Bu durumda J i minimize eden sonsuz saıda nokta vardır, ancak robot R j bunlardan kendısıne en akın olanı seçer. Bu da R j nin R j ile R m i birleştiren doğru üzerinde hareket etmesine neden olur. Eğer R j ile R m arasındaki uzaklık d dan büükse hareketin önü R m e doğru, aksi takdirde ters öndedir. Kolaca tahmin edileceği gibi, eğer R j oaniçin zaten en ii konumda bulunuorsa hareketsiz kalır. Bir S j içinde alnızca iki robot varsa, bunlar R m ve R n olsun, en ii konumu gösteren noktaların saısı duruma göre farklılık gösterir. Eğer R m ve R n arasındaki uzaklık 2 d dan büük a da buna eşitse, çözüm kümesi R 2 ve R 3 te tek bir noktadan oluşur bu nokta R m ile R n i birleştiren doğru parçasının merkezidir. Aksi takdirde, R 2 de R m ile R n i birleştiren doğrunun her iki anında simetrik olarak bulunan iki tane en ii nokta vardır. Bu durumda R j kendisine akın olan noktaı erel hedef olarak seçer. R 3 te ise, en ii noktaların saısı sonsuzdur ve bunlar merkezi R m ile R n i birleştiren doğru parçasının merkezi olan bir çember oluştururlar. Bu doğru parçası çözüm noktalarının oluşturduğu çemberin normalidir. Bu durumda R j ine bu çember üzerinde kendisine en akın noktaı hedef olarak seçer. Görüldüğü gibi, alnızca bir vea iki robot algılandığında hesaplama işlevi koladır. Ancak üç a da daha fazla robot S j içinde olduğunda (3) te tanımlanan J nin minimizasonu doğrusal olmaan eşitlik sisteminin çözümünü gerektirir. Minimum ve maksimum noktalarda J M ( ) 2 = j j (t + t) j k (t) d = (12) j j j k=1 j Denklem (12) deki sistemin çözümü tek olmaabilir. Bu sistemi çözdükten sonra çözüm noktalarının minimum, maksimum vea eer noktalarından hangisi olduğu sınanmalıdır. Çözümün erel vea genel minimum olması için maliet fonksionunun Hessian matrisi pozitif-tanımlı olmalıdır. Eğer birden fazla minimum nokta varsa, global minimum(lar) (3) te verilen maliet fonksionunun bu noktalarda değerlendirilmesile bulunur. Şunu belirtmek gerekir ki, her takipçi robot R j için her t anında en ii noktalar hesaplanmaktadır. En ii noktaların konumu, S j içindeki robotların konumuna bağlıdır. S j içindeki robotlar da otonom biçimde hareket ettiğinden, hesaplanan en ii noktaların konumu her an değişecektir. Çok büük bir olasılıkla R j henüz belirlediği en ii noktaa ulaşamadan bu noktanın konumu değişecek ve R j eni bir nokta hesaplaacaktır. Bir bakıma çözüm aslında alnızca en ii noktaların önünü vermektedir. Bu gerçek bize erel idare stratesisindeki hesaplama ükünü azaltma şansı verir. Maliet fonksionunun minimum noktalarını çözmek erine, her bir takipçi robot R j maliet fonksionunun R j nin pozisonunda değerlendirilen negatif gradanı önünde hareket eder. Diğer bir ifadele, j j (t + t) =j j (t) γ J(j j (t + t)) j j (t + t) j j (t+ t)=j j (t) (13) Burada γ>bir pozitif kazanç ve j j Rj nin erel koordinatlardaki konum vektörüdür. (3) den J( j j (t + t)) j j (t + t) =2 M ) ( jj (t + t) jk (t) d k=1 j j (t + t) j k (t) j j (t + t).(14) j k (t) azabiliriz. j j (t) =olduğundan, (13) ve (14) ten M j j (t + t) =2γ ) j ( jk (t) d k (t). (1) (t) k=1 j k elde ederiz. Denklem (1) hareketin önünü göstermesi bakımından anlamlıdır ve bu öndeki hareket (2) deki eşitsizliği sağladığı takdirde ugulanır. Görüldüğü gibi, (1) in ugulanması (12) deki sistemi çözmekten çok daha koladır. Takip eden bölümde önerdiğimiz öntemi (1) te elde ettiğimiz gradan hesaplaması ile ugulaarak performansını sınaacağız.. Benzetim Sonuçları Önceki bölümlerde anlatılan teorem ve teorik sonuçları bilgisaar benzetimleri ile sınaacağız. Benzetimler MATLAB de gerçekleştirilmiştir ve çalışma uzaı R 2 deki -düzleminin bir parçasıdır. Konum algılama mesafesi (d ma) 8 birim ve istenen uzaklık (d ) birimdir. Benzetim senarosu şöledir: Bir robot grubu Yerel İdare Stratejisi altında gezinime başlar. Yerel idare (1) in γ =.1 ile kullanımı sonucu gerçekleşir. Lider Şekil 2 de görülen gezinge üzerinde ilerlerken, da lideri izlerler t=3 s. t= t=1 s. t=6 s Şekil 2: Liderin gezingesi. 239

5 Otonom Gezgin Robotlar n Ba lant l Grup Halinde Gezinimi İlk benzetim çalışmasında bir lider ve sekiz takipçi olmak üzere dokuz robot vardır. Bu grup sıralı hareket öntemi uguladığında elde edilen sonuç Şekil 3 te görülmektedir. Robotlar hedef konuma ulaştıklarında grubun bağlantılılığı artmıştır. Başlangıçta ve liderin t = 6 s. deki keskin dönüşü sırasında bazı ın en ii uzaklığı korumak için hafifçe geri doğru hareket ettiği göze çarpmaktadır. Anı grubun eşzamanlı hareketi Şekil 4 te verilmiştir. Grubun bağlantılılığı bu durumda da artarak korunmaktadır. Önerdiğimiz öntemin büük gruplar için de etkinliğini göstermek için benzetimlerin ikinci bölümü 17 robottan oluşan bir grup ile apılmıştır. Konum algılama sınırı (d ma) veistenen uzaklık (d ) sırasıla 12 ve 6 birim olarak alınmıştır. Robotların gezinimi Şekil de görülmektedir. Bu benzetimde robot saısı fazla olduğu için, gezinimi iki kısımda inceleeceğiz. Şekil a benzetimin ilk altı sanielik kısmını gösterir. Robotlar başlangıçta oldukça dağınık bir durumda olmalarına rağmen, önerilen öntem gezinim başlar başlamaz robotların bir araa toplanmasını sağlamaktadır. Bununla birlikte liderin gruptan biraz daha uzak durduğu göze çarpmaktadır. Algılama sınırı üksek olduğunda algılanan robotların saısı da fazladır. Eğer lider ve grubun diğer üeleri sanal bir düzlemin arı taraflarında ise, liderin hemen arkasındaki takipçi robot kendi alt-grubundaki çok saıda robottan öle etkilenmektedir ki, maliet fonksionunun negatif gradanının önü lidere doğru değil grubun diğer elemanlarına doğru çıkmaktadır. Bu nedenle lider hareketini kendisini izleen gruba göre aarlar. Eğer grup liderin arkasında kalırsa lider bağlantılılığı korumak için grubun kendine aklaşmasını bekler. Şekil b grubun hedef konuma ulaştığı andaki durumu göstermektedir. Şekillerde karmaşıklığa ol açmamak için ın izlediği ollar çizilmemiş, alnızca liderin izlediği ol belirtilmiştir BASLANGIÇ KONUMLARI SON KONUMLAR Şekil 4: 9 robotun gezinimi (eşamanlı hareket). Burada, balık ve kuş sürüleri gibi bazı canlı gruplarından esinlenerek, gezinim bounca grup bağlantılılığını koruacak bir erel idare stratejisi önerdik. Önerilen bu öntemde her robot algıladığı robotlara olan uzaklığını istenen belirli bir düzede tutmaa çalışmaktadır. Grubun bağlantılılığını garanti etmek için robotların hareketleri sabit sınırlarla kısıtlandırılmıştır. Benzetim sonuçları öntemimizin başarısını doğrulamaktadır. Hem sıralı, hem de eşzamanlı hareket durumları için gruplar tüm gezinim bounca bağlantılılık özelliklerini korumaktadırlar. Benzetimlerdeki örnekleme aralığı oldukça küçük olduğundan, sıralı ve eşzamanlı hareket öntemlerinin birbirine çok akın sonuçlar verdiği anlaşılmıştır Robotlar arasında istenen ideal uzaklık d ın d ma ile olan ilişkisi de belirtilmee değerdir. d ma d olduğunda, her alt-gruptaki algılanan robot saısı çok artmakta ve bu durum ın liderden çok gruba önelme eğilimini arttırmaktadır. Önerdiğimiz erel idare stratejisi. d ma d.9 d ma olduğunda en ii sonuçları vermektedir. 1 2 BASLANGIÇ KONUMLARI SON KONUMLAR Şekil 3: 9 robotun gezinimi (sıralı hareket). 6. Sonuçlar Bu makalede gezgin robot gruplarının bağlantılılığı incelenmiştir. Robotlar arasında merkezi bir denetim mekanizması a da haberleşme eteneği bulunmadığında, robotların otonom hareketleri grubun bağlantılılığını bozabilir. Bu çalışma gezgin robotların bağlantılı grup halinde gezinimine olanak veren basit ve güvenli bir öntem sağlamaktadır. Robotlar arasında haberleşme a da hierarşi bulunmadığı için eni robotlar gruba kolaca eklenebilir. Anı şekilde, grup bağlantılılığını bozmadığı sürece bazı robotların gruptan arılması da herhangi bir sorun aratmaz. Bu saede modellenen robot grubu değişken topolojie sahiptir ve doğadaki geniş canlı sürülerinin modellenmesinde oldukça başarılıdır. Bu konuda bundan sonraki çalışmalar erel idare stratejisindeki kısıtların gevşetilmesi ve robotların gezinimi sırasında engel oluşturan nesnelerin varlığının düşünülmesi olabilir. Bu öntem arıca hedef konumda bir dizilim oluşturma öntemleri ile de birleştirilebilir. 7. Teşekkür Yazarlar, bu makalei inceleip düzeltme ve orumlarını bildirerek katkıda bulunan anonim hakemlere teşekkür ederler. 24

6 Ahmet Cezairli, Feza Kerestecio lu (a) (b) Şekil : 17 robotun gezinimi (eşzamanlı hareket). 8. Kanakça [1] A. Okubo, Dnamical aspects of animal grouping: Swarms, schools, flocks, and herds, Advanced Biophsics, vol. 22, pp. 1-94, [2] K. Warburton ve J. Lazarus, Tendenc-distance models of social cohesion in animal groups, J. Theoretical Biolog, vol. 1, pp , [3] V. Gazi ve K. M. Passino, Stabilit analsis of swarms, IEEE Trans. Automatic Control, vol. 48, pp , 23. [4] C. Renolds, Flocks, birds, and schools: A distributed behavioral model, Computer Graphics, vol. 21, pp. 2-34, [] T. Vicsek, A. Czirok, E. Ben-Jacob, I. Cohen ve O. Shochet, Novel tpe of phase transition in a sstem of self-driven particles, Phs. Rev. Letters, vol. 7, pp , 199. [6] T. Balch ve R. C. Arkin, Behavior-based formation control for multirobot teams, IEEE Trans. Robotics and Automation, vol. 14, pp , [7] H. Yamaguchi, A cooperative hunting behavior b mobile-robot troops, Int. J. Robotics Research, vol. 18, pp , [8] M. Egerstedt ve X. Hu, Formation constrained multiagent control, IEEE Trans. Robotics and Automation, vol. 17, pp , 21. [9] J. H. Reif ve H. Wang, Social potential fields: A distributed behavioral control for autonomous robots, Robotics and Autonomous Sstems, vol. 27, pp , [1] N. E. Leonard ve E. Fiorelli, Virtual leaders, artificial potentials and coordinated control of groups, in Proc. Conf. Decision and Control, Orlando, FL, Dec. 21, pp [11] D. J. Stilwell ve B. E. Bishop, Platoons of underwater vehicles, IEEE Control Sstems Magazine, vol. 2, pp. 4-2, 2. [12] A. V. Savkin, The problem of coordination and consensus achievement in groups of autonomous mobile robots with limited communication, Nonlinear Analsis, vol. 6, pp , 26. [13] L. Baındır ve E. Şahin, A review of studies in swarm robotics, TÜBİTAK Turkish J. Electrical Eng. & Computer Sciences, vol. 1, pp , 27. [14] J. P. Desai, J. Ostrowski ve V. Kumar, Modeling and control of formations of nonholonomic mobile robots, IEEE Trans. Robotics and Automation, vol. 17, pp. 9-98, 21. [1] H. G. Tanner, A. Jadbabaie ve G. J. Pappas, Stable flocking of mobile agents, Part I: Fied Topolog, in Proc. Conf. Decision and Control, Maui, Hawaii USA, Dec. 23, pp [16] H. G. Tanner, A. Jadbabaie ve G. J. Pappas, Stable flocking of mobile agents, Part II: Dnamic Topolog, in Proc. Conf. Decision and Control, Maui, Hawaii USA, Dec. 23, pp [17] Z. Lin, M. Broucke ve B. Francis, Local control strategies for groups of mobile autonomous agents, IEEE Trans. Automatic Control, vol. 49, pp , 24. [18] A. Jadbabaie, J. Lin ve A. S. Morse, Coordination of groups of mobile autonomous agents using nearest neighbor rules, IEEE Trans. Automatic Control, vol. 48, pp , 23 [19] W. Maeda, Graph Theor, New-York: John Wile & Sons, [2] W. Koca ve D. L. Kreher, Graphs, Algorithms and Optimization, Boca Raton: Chapman & Hall/CRC Press,