Dergimiz sayfalarmm, meslektaşlarımıza ve mesleğimize Mgi duyanlara açık bulunduğunu zevkle ifade ederken hepimize hayırlı olmasını dileriz.
|
|
|
- Ömer Remzi
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Bir cemiyet hayatına kıyasla 10 yıl gibi kısa bir mazisi olan Türk Mühendis ve Mimar Odaları Birliğimiz ve ihtisas Odamız* 7303 sayılı kanım ffle muaddel 6235 sayılı kamunla kendilerine verilen, mesleğin gelişmesiyle ilgili faaliyetlerde olduğu kadar «Ammenin ve memleketin menfaatlerinin sağlanmasında, yardım tabiî, ziraî ve sanayi istihsalimin artırılmasında, memleketin san'at ve teknik kalkınmasında lüzumlu gördüğü bilumum teşebbüs ve faaliyetlerde bulunmak» görevini' de imkânları nisbetinde gerçekleştirmeye çalışmış ve çalışmaktadır. Bu cümleden olarak, mesleğimize ve meslektaşlarımıza Mzraet arraısn ile, Odamızın kuruluşundan beri, Yönetim Kurullarında görev alan arkadaşlarımız her nebadar Odanm gayesine uygun bir dergi yayımlamak için bir çok etüt İ ve çalışmalar yapmışlar isede gerek mali gücümüzün yetersizliğinden ve gerekse üye sayimian azlığımdan dolayı, Odanın gayeleri içine de giren peryodîk bir derginin yayınlanması bu güne kadar mümkün olamamıştı» Bununla beraber Odamız, kendi çalışma sahası içine giren konularda zaman zaman bazı serler yayımlamış bulunmaktadır ydmda «Haritacının El..Kitabı II Dengeleme (Muvazene) adlı eserden sonra bilhassa plânlı kalkm-. ma devresine girdiğimiz 1962 yılında yayımlanan «Türkiye Kadastrosu Hakkında Rapor», 1963 de yayımlanan «Harita, Tapu, Kadastro Sektörü ve T.B.M.M. Üyelerinin Gözü ile Kadastro Davamız» adlî eserler bu konuda çalışmak isteyenlere ışık tutmuş, Birinci Beş Yıllık Kalkınma Plânmda Harita, Tapu, Kadastro ve İmar Plânlan Sektörünün mühim yer işgal etmesinde son imsî oldukça faydalı olmuştur. Peryodilc olarak (şimdilik 4 ayda bir) yaynaliyaşağımız «HABlTA E KADASTRO MÜHENDİSLİĞİ» adlî dergimiz Odamızın yayın organı olacak Jeodezi, Astronomi, Fotogrametri, Topografya, Harita, Kadastro, imar Plânları v.b. gibi mesleğimizle ilgili konularda dünyada ve yurdumuzdaki ilmî ve meslekî gelişmeler, kongreler yer alacak, mühendise olduğu kadar tekniker, teknisyen ve haritacılıkla ilgili her seviyede teknik elemana Mtap edecek nitelikte yazılar ve problemleri kapsayacaktır. Oia olarak, meslepmiz ve meslekdaşlarmaizla ilgili kanun, tüzük, ve mevzuat hakkındaki görüşlerimizi de kamu oyuna açıklamak özere dergimizde yayınlayacağız. Kâr gayesi gütmeyen dergimizin yaşaması, üyelerimizin aidat ve yazı hususunda gösterecekleri ilgiye bağüi bulunmaktadır. Dergimizde yayımlanan her çeşit yazıya telif ve tercüme hakkı ödenecektir. Odamızın miitevazi bütçesinden ödenecek bu para meslekî ve ilmî bir yazmm belm tam değeri olamiyacak, fakat yazarlarımızın emek ve zarurî masraflarımın bir kısmını karşılamış olacaktır. Dergimiz sayfalarmm, meslektaşlarımıza ve mesleğimize Mgi duyanlara açık bulunduğunu zevkle ifade ederken hepimize hayırlı olmasını dileriz. YÖNETİM KURULU 8
2 Avrupa Niiengisinin ikinci SFEROtD YE KABULLER Yazan : Çeviren : GnL RAMFORD Müh. Mahmut ŞATIR (*) Uluslararası Jeodezi Birliği 9 Ekim 1S62 günü kuruluşunun 100. yıldönümünü kutlamak toere Batı Almanya'nın Münih şehrinde toplanmıştır. Dünya çapındaki ta toplantıya Münih- Yüksele Teknik Okulunun davetlisi olarak katılan Sayın Hocamız Macit Erbudak'm yurda döfl.ttşlerinde? çeşitli makamlara bu arada odamizada göndermek nezaketinde bulunduklari mektubundan ve buna ek rapordan, bu toplantıda Türkiye'yi eok yakından ilgilendiren koraların tartışıldığını öğrenmiştik. Okurlarımıza, toplantı sırasındaki konuşma ve tartışmalar hakkında derinliğine bilgiler veremîyeeeğiz, ancak yukarda sözü edilen ve İngiliz Bilgimi BOMFORD tarafından hazirlanmiş bulanan, raporun Türkge çevirisini, aşağıda sunmakla yetineceğiz;. Konunun önemi ve aktaalitesi bugünde devam etmektedir. Okurlarımıza faydalı olacağına inandığımız rapor özet olarak, Avrupa nirengi şebekesinin dengelemesine temel teşkil edecek, bütün dünyayı bâpsiyan Bir hesap yüzeyinden söz etmektedir.' Boyutları bilgin Mrs. Fisher tarafmdan hesaplanmış olan bu Spheroid Törkiye^îiîn yüzeyi ile en iyi durumda çakişabilmeyi sağlamaktadır. apîlımiş olan teklife göre dengelemeye Avrupa'nın güneyinden başlanacak ve memleketimizin batısında bulunan bir İLaplaee noktasına dayanacakfar. Eğer Türkiye birlikte dengelemeye kamacak olursa,, bü defa yurdumuzun doğusunda bulunan ikinci bir İLapiaee noktasının öncelikle ele alınması zornnlnğn ortaya konulmaktadır Kabilleri; Avrupa nirengisinin birinci dengelenmesinde (1950) Sferoid ve kabuller aşağıdaki gibi idi: a = m ^ f 1/297 0 I* Milletlerarası Sferoid (*) Çeviren Harita ye Kadastro Mühendisi olup Tapu ve Kadastro Gn. Md. A. K. Fotograrnetri Dairesi Reis Muavini'dir. 4
3 g 0 = +3" 36 Güney Ti 7j o = + 1" 78 (Batı) i Potsdamda N 0 =0m J Herhangi bir nirenginin hesabedildiği irca Sferoidinin, geoide en fazla çakışması hiç esas alınmamakla beraber geoid ile sferoid arasında fazla açılmalar arzu edilmez Potsdam kabullerinin geoid ile sferoid arasındaki mümkün en iyi çakışmayı vermediği çok önce bilinmekle beraber, ayrılmaları Avrupada 30 m yi geçmez (AIG Travaux cilt 20, fasikül 5, şekil 3, 1958). Fakat Avrupa kabulleri Sibirya'ya, Güney Asya'ya ve Afrika'ya uzatılınca, ayrılma namüsait olarak büyür; Sibirya'da 110 m, Seylan'da 220 m ve Güney Afrika'da 180 m (Cilt 20, Şekil 3 ve Bull. Geod. 56, Sayfa ). Avrupa'ya tatbik edilecek sferoid ve kabullerin Asya ve Afrika'da da kabule şayan olması çok arzu edilir, fakat Asya ve Afrika kısımlarında 1/ kadar gayrı tabiî bir mikyas değişmesini zorluyan sferoidle geoid arasındaki değişme, mevzii olarak kabule şayan olmıyacaktır. Bu sebeple 1963 de Avrupa için yeni kabuller üzerinde duracağız. 2. Sferoidin. basıklığı: Sun'i peykler 1/298.2 ile 1/298.3 arasında bir basıklık verir ve umumiyetle bunun doğru olduğuna inanılır. Son zamanlarda 1/297.0 dan daha küçük bir değer vermek temayülünde olan geoidal ölçülerde bir dereceye kadar tatbik edilmiştir. Meselâ Krassovsky (1948) 1/298.3, ve Oxford (1959) 1/ değerlerini veriyor (Bull. Geod. 56 Sayfa 183) Helmert.(1901), Krossovsky (1948) ve Fischer (1961) tarafından kullanılmış olması ve AİG Komisyonu tarafından Güney Asya'nın halihazır dengelemesinde kabul edilmiş olduğu için, kolaylık olsun diye 1/298.3 değeri, diğer buna yakın değerlere tercihan tavsiye edilir. S. Sferoidin eksenleri; Geoidal ölçülere dayanan son araştırmalar hep internasyonal elipsoidden küçük eksenler veriyor. Meselâ : Eksen (metre) Kabul edilen basıldık Jeffreys (1948)... 6,378,099 1/297.1 Krassovsky (1948) /298.3 Hough (1950) /297.0 (sabit tutulmuş) Oxford (1959) / Fischer (1961) /298.3 (sabit tutulmuş) Üçgenlerin esas kenarları, küçük eksenin tâyininin büyük eksene nisbetle oldukça kuvvetli olacak yerlere yerleştirilmiştir. 1/298.3 gibi küçük bir basıklık kabulü, 1/297.Ö ile elde edilecekten birkaç desimetre daha küçük bir büyük eksen verir. Fischer'in bu değeri en yenidir, en büyük sahayı kaplar ve en muhtemel basıklığa dayanır (Bull. Geod ) Eksen için 6,378,155 değeri tavsiye edilir. 6,378,166 gibi diğer değerleri şüphesiz aynı şekilde ihtimal dahilindedir. Fakat farkın tesiri yoktur ve 6,378,155 Güney Asya'nın dengelemesi için kabul edilmiştir. 4. Başlangıç ve bilinenler s Bull. Geod. 61, Sayfa 261 de Şekil 8, Bayan Fischer'in 1/298.3 ve rakkamlanna göre ve ncu sayfalarda tarif edildiği gibi cihetlondirilmiş
4 olarak geoid münhanilerini gösterir. Şekil 10 (Sayfa 263) gravimetrik olarak cihetlendirilmiş olarak hemen hemen aynı ve geoid münhanilerine çok benzer sferoidi gösteriyor. Mevcut bilgiler ve bu cihetlendirmeler esasına göre Avrupa ve Avrupa - Asya - Afrika için bilinenleri teşkil ediyor. Şekil 8, Güney Asya için kabul edildi. Şekil 8 den Bayan Fischer'in «Dünya Bilinenleri» Avrupa için kabul edilmesi tavsiye edilir. Bayan Fischer kendi «Dünya Bilinenleri» ni (f == 1/298.3, a = 6,378,155), 1950 «Avrupa Bilinenleri» ile kendi bilinenleri arasındaki fark için (D. B - A. B.) aşağıdaki formüllerle tarif ediyor. (Henüz neşredilmemiş de arz edilmiştir). 3g" = 3.40 sin<. cos^ 1-35 sin,<. sin \ + 3,61 cos < sin 2< Srç" == 3.40 sinx C S X N _ _ cos «. cos \ 112 sin ^ 94 sin 2 ^ 42 cos <. sin \ "'. metre. Bu dönüştürme formülünü kullanarak aşağıdakileri elde ederiz.. % KaUanpur Haravii dağı Since bayın «n * C4İÎ8TO ; Hindistan Doğa Türkiye Batı TiMdy rmbawa ' & ı.-_mlu<mi-uı.u-i T_İU_J. nuıııınotıırn ıııırınrrr-.tiııı "ir n-tı..ıııı ı.j L_U_I-I.IUI mı... Iİ~_..J~JIJ -ı-ıum.,-». ııııı ıı ııı... 1 II.LI.III «..i...,...,...,.....» nırr-ın r nn-mn ınn T, Geodetik Enlem (A. B.) 24 07' 17" '?? 41 27'?? 52 22' 51",45, - Geodetik Enlem (D. B.) 24 07' 12".7O ' 49",18 ' ' (A. B.) 6, 44 3,90 5,15 + 3, 36 g (D. B.) 1, 73 0,20-1,88 + 5, 63 Geodetik Boylam (A. B.) 77 39' 11", '?? 26 28'?? 13 03' 5&".U Geodetik Boylam (D. B.) 77 39'14",88 13 Ö3'57".84 rç (A. B.) + 5,49 3,18 + 3,33 + 1» 78 H (D.' B.) + 2,46 + 1J6 + 3,02 + 2, 33 N (A. B.) metre N (D. B.) metre > Not: A. B = Avrupa bilinenleri (1950) D. B = Bayan Pischer'in sferoidi (Dünya bilinenleri) e = Boylamda sapma Yİ Enlemde sapma N = Elipsoid üzerinde geoidin yüksekliği. Türkiye için geodetik ^ ve \ halen mevcut değildir. Değerler tahkik edilmelidir. Elipsoidin cihetlendirilmesi ya bu yerlerin herhangi birinde ^ \ ve N veya, ^ ve N ile ya da başka daha uygun bir yerde temin edilebilir. Eğer küçük bir karışıklığa sebep olmasaydı, bilhassa yeni dengeleme Potsdam ile Türkiye arasındaki nirengiye küçük değişiklikler ithal etmeseydi, Avrupa bilinenlerinin tâyininde Potsdam rakkamlarını kabul etmek tabiî olurdu. Şu halde, Potsdam için verilen rakkamlar kabul edilirse, yeni «Avrupa Bilinenleri» ile son Güney Asya dengelemesi arasında küçük kapanma hataları olacaktır. Kapanma îıatası büyük olmıyacak, muhtemelen A ve^'da 0",3 (10 m) den az olacak, fakat böyle kapanma hataları çok müşkülât ve karışıklığa sebep olabilir. Türkiye yeni dengelemeye ithal edilecekse Haravildağı, edilmiyecekse Since bayırı gibi Avrupanm güney doğusu Türkiye'de bir mebde alınırsa Avrupa'nın yeni dengelemesi için' fotr.mügktilâtın Önüne geçilebilir. Avrupa'nın dengeleme neticesi, Potsdam değerleri kabul edildiği haldeki kadar hassas ve uygun olur ve GÜ- 6
5 ney Asya ile kapanma hatasının önüne geçilmiş olur. Netice olarak, dengeleme bitince, sferoidin cihetlendirilmesini, (istenirse) geodezik koordinatlarla (veya sapmalarla) ve Fotsdamda bulunan N ile tarif etmek mümkün olacak. 5. Milas»: Avrupa'nın yeni dengelemesi için kabul edilecek sferoidin : f = 1/298.3 a = 6,378,155 m ile tarif edilebileceğini ve, cihetiendirilmesinin, Türkiye nirengisinin Avrupa nirengisi ile yeniden dengelemeye girip girmiyeceğine göre Haravildağı veya Since bayırında, 4 üncü paragrafta verilen rakkamlarla tarif edilebileceği tavsiye edilmiştir., AIG, sferoidi ve bilinenleri kullanmak için karar verirse, Avrupa Geoid : Etüt Gurubu, baz doğrularının elipsoid seviyesine indirgenmesi için, Avrupa'-'*,nm geoid grafiklerini meydana getirmeye muktedir olacak. 1"
6 Koordinatı Belli iki Köi Noktaya Bağlı Bii Poligonun incelenmesi (Poîygonzüge Vuit Beidereeitigem Koordinaten Ölme Richtungsanschluss) *' ' Yazan: Y. Mtth. Macit EBBUDAK ; t LT.T.O. Öğretim Üyesi 1947 yılında îzmir Tapu ve Kadastro Müdürlüklerini Y. Mühendis Burhanettin Tansuğ ile birlikte teftişimiz sırasında, fen amirlerinden Niyazi Erkan, önümüze şöyle bir problem koymuştu :. İzmir'in işlek bir caddesinde mülkiyet sınırlarında meydana gelen değişikliklerin Kadastro Paftasına işlenmesi için, eski poligon noktaları aranmış, ancak caddenin iki ucuna yakın Pi ve Pk gibi iki nokta ele geçirilebilmişti. Üstelik bu noktalardan hiç bir sabit nokta görünmüyordu. Açıklık bağlantısı da olmadığından ne açı ne de koordinat dengelemesi yapılabilecekti. Bu durum karşısında açılara verilecek P ağırlığı ne olmalıydı? Bu problemin çözümü için n noktalı ve eşkenarlı gergin bir poligon alalım. Bu takdirde : olur. (1) eşitliğinin diferansiyeli alınırsa : d y a =s.^cos ai d a İ (2) bulunur. x ekseni, poligona parelel alındığından : <*y n =s.%d ai (2) yazılır. Ayrıca : 8
7 a i = ao+pı + P 2 + ~... +Pı 180. i (4) olduğundan û ai = ^dj3 ; (5) olur. (5) ve (3) de yerine konursa : dy a =s.[(n-l) djsj + dı-2) d/ &p B -ı 1 (6) elde edilir - Pn + 1 dyn+1 Öte yandan, Poligonun orta noktasının sapma miktarı, (6) n-fl 2 2 da n yerine koymak suretiyle bulunur : 2 dyn+l = i- [(»"D <tfı + ( n -3) cl/ d^^ ] (7) 2 S Açı ve kenarlardaki ölçü hatalarından dolayı, hesap neticesinde Pn yerine Pn + 1 Pn' elde edilir. Fakat Pn', Pn noktasına kaydırılacak olursa, orta nokdyn 2 tası kadar yer değiştirerek hakiki yerine : ~ ^^İl ^\jl~ İ5L 2 2 t 2 Pn + 1 kadar yaklaşmış olur. d farkı, açı hatalarından dolayı noktasının artık 2 sapma miktarıdır.... 2d/3 n. 2 d/3 n. ) (8) olur. (8) den de : m* d = m 2 (-i-) s jî2 + 2^ (Ş)«+ (Ş)«+ (Ş)* ^ +-ilj(0) bulunur n3 = n (n + 1} (2n + X) olduğundan, 6 (n2 2n+3)(n 1).., ' ive neticede S = (n-ı) s olmak üzere, m»a - m 2 (3^(n 2-2n+3)(n-l) m«hl*(5îz^±ş_ ^ç 8 - : lt_(lo) elde edilir, n yeter derecede büyükse m*d = S* (11) olur. Dayalı poligonlardajjı 2 A = -S olduğundan, m*^ =- ^~ (12) '" ' p ", -. ' ' 4'- eşitliği kurulmuş olur. Bu şu demektir : Açıklık bağlantısı yoksa, açılar düzeltilemiyeceğinden,.doğruluk derecesini bir tutabilmek.için, açıların iki tam silsileyle ölçülmesi gerekir. 9
8 Bu proplem 1951 tarihli ZfV (Alman ölçü dergisi) nde Lösch ve 1960 tarihli AVN (Alman ölçü haberleri) nde Kuntz tarafından ele alınmıştır. Kuntz, aynı sonunca başka bir yoldan varmıştır. örnek: Açıklığı bilinemediğinden Pi Pı Kenarına 00 lik geçici bir değer verilmiş olsun. '.' Pi ve Pk noktalarının Koordinatı bellîidir. x p 2 3 açılarıyla s t s 2 s 3 s 4 kenarları.ölçülmüştür., - * (Pi Pİ)* == 90, geçici açıklık yardımiyle (Pi Pk)* açıklığı hesaplanarak, (Pi Pk) ile karşılaştırılırsa (Pi Pı) hakikiaçıklık bulunmuş ve $P lf P 2, P 3 noktg,larıda böylece şehir poligon şebekesine bağlanmış olurlar. ', 198, tg (Pi Pk)* == - '» 1,336367' «tg 53 iy 30* 507,77 ~"*~~*~ d ««(Pi Pk) * m ı Pk) W M s 39' 20" (Pi Pi)- > ' ap* : * 6S ' 20' '.40*. 10 (.
9
10 Dünyanın Sekli ve Yüksekliklei Hakkında, Yazan : Dr. Müh. Ahmet AKSOY Bir noktanın yüksekliği veya kotu denilince aklımıza akûl istikametinde o noktanın deniz yüzeyine olan mesafesini düşünür, bu suretle şakul doğrui- ;. tuşunun deniz yüzeyinin kıt'alar altındaki uzantısına dik olduğunu kabul edefiz. Nitekim kotu bilinen bir noktadan diğer bir noktaya geometrik nivelmanla kot taşırken yaptığımız malûm işlemler bu kabulümüzün bir neticesidir. Ya- ^ni Nivo düzeciyle elde ettiğimiz şakul istikametine dik düzlemin deniz yüzeyinin uzantısı yüzeye teğet olduğunu kabul etmiş oluyoruz. Fark çok olmamakla beraber bunun böyle olmadığım aşağıda izaha çalışacağız. Fakat bu husustaki açıklamamıza geçmeden önce bir şeye daha işaret edelim; yukarıdaki ifadelerimizle dünya şeklini yükseklik bakımından kıt'alar altında da uzannuş olarak tasavvur ettiğimiz deniz yüzeyi olarak kabul ettik ki biz bu yüzeye «Geoid» diyoruz. Halbuki biz memleket ölçüsünde mesafeleri bir döner elipsoid yüzeyine iz düşürür ve bütün üçgen hesaplarını da yine bu elipsoid üzerine intikal ettirilmiş değerlerle yaparız. Yani kısaca noktalar durumları bakımından elipsoid yüzeyine göre, yükleklikleri bakımından da Geoid yüzeyine göre mütalâa edilir. O halde haritalarımızda yer yüzünü temsil eden iki ayrı yüzey mevcuttur. Bu iki yüzeyin bir birine benzerliğinin incelenmesi çok ilgi çekici olmakla beraber kafi bir açıklama bu gün için ilim dünyasında henüz yapılamamakta, bazı açıklamalar da hipotezlere bağlı kalmaktadır. Fakat yükseklikten söz konusu eçtığımız için biz sadece geoid yüzeyini tarif etmeye çalışacağız. Bunun için de dünyanın herhangi küçük bir kütlesine tesir eden kuvvetleri incelememiz gerekir. Dünyanın küçük bir kütlesine, bu kütlenin toplam olarak dünyamıza elektronik, manyetik, mekanik v.s. olmak üzere çeşitli kuvvetler tesir etmektedir. Bu kuvvetlerden bizi ilgilendireni mekanik kuvvetlerdir. Mekanik kuvvetleri de yine ikiye ayıracağız 1 Kütle çekim kuvveti, 2 Dünyanın kendi ekseni etrafında dönmesinden doğan merkezkaç kuvveti. Atmosferin kütlesi ile dünya dışındaki kütlelerin (Ay, Güneş ve Peykler) tesirlerini problemimizde nazarı itibare almıyacağız. 1 Kütle Çekim Kuvveti : N e w t o n Kanununa göre, kütleleri m x m 2 ve aralarındaki uzaklık e olan iki cisim biri birini K A kuvveti ile çekiyorlarsa, f = (66,68 x 10" 9 ) [cm» g~ı san?] : (1) dir. burada f = «Gravitasyon sabitesi» dir. 12
11 $Ş7. e 2 W 'ur. Bu kanuna göre dünyanın dışında bir P x noktasında bulunan bir m : kütlesiyle, dünyanın bir dm kütlesi arasındaki çekimi dk = c olacaktır, nij = 1 dersek ' ---- = d k = =- f rnı ' ' e 3 çekim kuvveti ivmesi olacaktır. Bu ivmeyi vektör olarak ifade eder, birim vektörü de r 0 la gösterirsek : dk = db = f. P noktasındaki birim kütleyi çekme kuvvetini arıyorsak, her bir dm kitlesinin çekme kuvvetini bulup bunları toplamamız icab eder, yani Kuvveti : b "" L J («,"?" r# (3) integralini (E) bütün Yer yuvarlağı için almamız gerekir. Bir uzay dik koordinatlar sistemi (X, Y, Z) kabul edersek e2=(x'-x) 2 + (y' - y) - + ( z ' - z) 2 olacağından db çekim kuvvetinin X, Y, Z ekldb (x ) senlerindeki iz düşümleri : i! db x " x bağıntısından, ve aynı e şekilde db< x )l= X ' ' X db ^... x' - x f dm_ r ûm f t e h 2. db (v) h f^(/ _ y) db< s > =f.^ş(z / - z) < 5 > bulunur 2 M e r k e z K a ç Bir eksen etrafında dönen bir cismin kütlesi m, eksene olan uzaklığı r ve açısal hızı w ise merkez kaç Kuvvet I ki = r. w 2, m. Problemimizde daha evvel aldığımız P noktasındaki birim kütlenin merkezkaç kuvvetini düşünürsek, k] = r. w 2. (6) olur. P noktası yeryüzüne yakın bir nokta olduğu için dünyanın dönme hareketine katılır. Daha evvel aldığımız koordinat sistemini öyle seçim olalımki Z ekseni dünyanın dönme ekseni ile çakışmış olsun. O takdirde 15
12 r = v x2 + y 2 ve ı k ı = v^-fy 8^2 (7) olur. Veya vektör olarak göstermek istersek ve dönme eksenine dik birim vektörü n ile gösterirsek k = r. w 2, n (8) olacaktır. Merkezkaç kuvvetinin X Y Z eksenleri üzerindeki izdüşümleri ise k( x ) = x. w2 k<y) = y. w2 (9) k< z ) =. O Olduğu kolayca bulunabilir. t Dünya kendi ekseni etrafındaki dönmesini 24 saatta (Yıldız zamanı) ta-' marnladığına göre, açısal hız :,» 2. w = h (Yıldız zamanı) dır. 1 yıldız günü = 0, ortalama güneş günü = ortalama zaman saniyesi olduğuna göre : t' ' 9. * ' w = = [san i]dir (8) ze göre k] = r. w 2 idi. _$> ' Kutup noktasında r = 0 dır, k 90 ] = 0 (yani = 90 Coğrafi enleminde) Ekvatorda ise ( 0 ü ) r 0 = a = 6378 Km alırsak : lk o [ = 6378 (7, )2 = [Cm. San 2 ] lk o j = 392 gal = m gal (miligal) bulunuyor. Yerçekimi İvmesi (Gravite) s Bir P. noktasındaki birim kütleye iki kuvvetin tesir ettiğini (kütle çekim kuvveti ve merkezkaç kuvvet) gördük. Bu kuvvetlerin bileşkesi, yani vaktöri- >yel toplam bize yerçekimi ivmesi g yi verir. Yani : "g = f +' k (10) dm ~» f veya g = f _» ^ _» J (E) r o + r W2 n (11) c 3 g nin X Y Z bileşenleri ise (5) ve (9) za göre :, dm. ' g<*) *=f I (x' - -x) + W2. x J CE) e»
13 14
14 f dm (y' - y) +w2. y (E) es r dm g (z ) =f (z' - z). olacaktır. J(E) 63 ve nihayet gravite dediğimiz g buradan _»-_> g(x) + g(y) + g(z) (i3) olur. _> i. j ve k X, Y, Z istikametindeki birim vaktörleri ise ( i n= ' j = k = 1) g = g(x) i -j--g(y). j + g( z ). k (14).olur. r Gravite'hin Potensîyeli W " ' Öyle bir fonksiyon bulalım ki, bu fonksiyonun x, y, z te göre kısmi türevi bize yerçekimi ivmesinin x y z bileşenlerini versin yani Bu fonksiyona W dersek (*) SW ç dm = g (*) = f (x' - x) + x w2 (15) gx J es İ W /- dm = g(v) = f (y' - y) +yw2 olsun gy Jw e3 W r dm - - = gfe) = f (z' - z) Z. J e» isbat edilebilirki bu fonksiyon, rdm x 2 + y 2 W = f w 2 (16) fonksiyonudur. J e 2 e = V( x ' " x ) 2 + (y' - y) 2 + ( z/ - z) 2 konular da W fonksiyonunun kısmi türevleri alınırsa (15) eşitliği bulunur. İşte W ye gravite kuvvetinin potensiyeli denilir. O halde (14) eşitliğine göre : g _j_ j _j_ k olacaktır (17) Sx Sy oz > Aynı P noktasında bir dr vektörü alalım. Aynı koordinat sisteminde : >»» dr = dx. i -j- dy. j -j- dz. k olacaktır. Burada d x, dy, dz, dr. Sikalar değerinin X, Y, -Z deki izdüşümleridir. (*) Bu yazı içinde geçen 8 harfi parsiyel türev işareti yerine.kullanılmıştır..16
15 ' * '.. > dr vektörüne «kaydırma vektörü» denilir. şimdi g. dr teşkil edelim. g- dr = i dx. i -f i dy. j i. dz. k 8* gy 8z 8W._^ > ow_^ > SW» > j. dx. i + - j dy j -{ j dz k sy ây sy _j_ k, dk. i k. dy. j H k. dz. k 8 Z 8z 8 z 1; a, b gibi iki vektörün sikalar çarpım a. b = a., b. cos a i, A bu iki vektörün mutlak değerleri ile aralarındaki açının Cosinüsünü çarpmak demektir. Birim vektörlerinde ' ' o halde i. i == ji lt cos a = 1 a = 0 olduğu için k. k = ==1 4 j k = \i\. \k.\. cos, a = 0 a = 90» olduğu için. Buna göre :.^^ 8W 8 W S W g. dr = dx dy -f dz olacaktır. (18) 8^ 8y 8 Z eşitliğin sağ tarafı dikkat edilirse W fonksiyonunun toplam veya tam diferensiyelidir. (dw) o halde g. dr = dw (19) yazabiliriz. dr >» dw = g. den f _> -^ f.2 -^ _> p_» -» w ı- 2 ' g. dr = g (-dr) = g dr olur. ıj ıj 2J W ı>9 =. g dr, Ç, = g. dr ise Wl a 'V^! = 0 veya (/> g. dr = 0 elde edilir (19 a) Veya (rotasyon not g = 0 denilir. Burada çıkarttığımız eşitliğin pratik teki manasını ilerdeki, bahislerden saha iyi anhyacağız. g yerçekimi ivmesi P noktasındaki bir kitleye tesir eden kuvvetlerin bileşkesi idi. O halde bir kitleyi bırakırsak bu bileşke istikametinde düşecek, veya bir kitleyi serbest ararsak ipimiz yine bu bileşkenin doğrultusunu gösterecek- 16
16 tir. O halde bu doğrultu akul istikametinden başka bir şey değildir, d r doğrultumuzu şakul doğrultusunda ve fakat ters yönde, yani zenit istikametinde alır ve dr = dh dersek, dw = g. dh olur. g ile dh arasındaki açı 180 olduğu için, sikalar çarpım; dw = g. dh = \g\. dh}. cos 180 d W = g. dh (20) olacaktır. Nivo Yüzeyleri : «Afiıipotensiyel yüzeyler» T a r i f : bir nivo yüzeyi, W potensiyel değerleri aynı olan noktaların geometrik yeridir. Yani bir nivo yüzeyi için W = sabittir. W sabit olunca dw = O olacaktır. (18) de d W = g dr idi dr vektörünü bu defa nivo yüzeyitıin üzerinde alalım ve dr 0 ile gösterelim, g ile dr o arasındaki açı da aa ise; '" ' dw = g. dr 0 = g [drf Cos ao 0 olacaktır. g ve dr 0 dan her ikisi de sıfırdan farklı değerlerdir. O halde Gos ao = 0 ve neticede ao = 90 dir.. Bu u demektir ; Nivo yüzeyleri her noktada şakul istikametine diktirler. Şimdi bir birine komşu iki nivo yüzeyini ele alalım : Bu iki nivo yüzeyi arasındaki potensiyel farkı dw olsun Bu iki komşu yüzeyin dw potensiyel farkı sabit olacağından (çünki her iki yüzeyin potensiyeli de sabittir). dw = g. dh = sabit olacaktır. Halbuki g değeri bir ; nivo yüzeyinin her noktasında aynı değildir, değişir (Bu yapılan ölçülerle tesbit edilmiştir.) dw dw sabit olduğundan g = eşitliğine göre bir nivo ytizeyinse g dedh gerinin arttığı yerlerde dh değeri azalacaktır, yani iki komşu nivo yüzeyi bir birine yaklaşacaktır. Netice : Nivo yüzeyleri birbirlerine paralel değildirler. 17
17 Şakul eğrileri nivo yüzeylerine diktirler. Yukarda her nivo yüzeyinde her noktada şakul istikametlerinin nivo yüzeyine dik olduğunu çıkartmıştık. Diğer taraftan nivo yüzeyleri (ki cc i sayıda nivo yüzeyi vardır), biribirlerine paralel değildirler. O halde bir nivo yüzeyine dik olan şakul doğrultusu, diğerine dik değildir. Birbirlerine çok yakın nivo yüzeylerine ait şakul doğrularını birbirleri ile birleştirirsek bir eğri meydana gelir. Bu eğriye «Şakul Eğrisi» denir. G e o i d : Sonsuz sayıdaki nivo yüzeylerinden bir tanesini seçerek bunun W potensiyelini Wo ile gösterelim. Şimdi Wo değerini öyle seçelim ki, buna ait nivo yüzeyi okyanuslar yüzeyi ile çakışsın. îşte bu nivo yüzeyine «Geoid» denilir. Mamafih geoid tam olarak okyanus yüzeyi ile, hava basıncının, su sıcaklığının ve tuz miktarı her yerde aynı olmamasından ve akıntılardan dolayı, tam olarak çakışmaz. Okyanus yüzeyinin kıt'aların altına da uzandığını düşünürsek, yeryüzünün şekli olarak kabul ettiğimiz Geoidi tahayyül edebiliriz. Geoidin okyanuslar ötesindeki uzantısının nasıl bir gidiş izliyeceği hakkında bir bilgiye sahip olamadığımızdan, Geoid'i kapalı bir fonksiyon olarak ifade edebilmemiz mümkün değildir. Ancak bazı hipotezler yapmak suretiyle münferit geoid noktaları hakkında malumat sahibi olmak veya geoidi nokta nokta tayin etmek için çalışmalar yapılmaktadır. Şimdi iki nivo yüzeyi alalım. Bunlardan birisi geoid diğeri de Topoğrafik yüzey üzerindeki bir P noktasından geçen nivo yüzeyi olsun P den geçen nivo yüzeyi geoide paralel olmayacağından P deki şakul istikameti geoide dik değildir. Geoid yüzeyi ile P noktası arasındaki şakul eğrisinin yay uzun liığuna P noktasının «Orfhometrih: Yüksekliği» denilir. Isbat edilebilir ki iki yüzeyin şakul istikameti arasındaki açı (Şakul eğrisinin 1 ve 2 noktalarındaki teğetleri arasındaki açı ki buna şakul istikametinin istikamet değişmesi de diyebiliriz)
18 Buradan şakul eğrisinin asal normali istikametindeki birim vektörüdür. Mamafih teorik olan bu entegrali alabilmek için yerin içi için kabul edilebilecek g x ve gy değerleri bulmak gerekir ki yine bazı hipotezler yapmayı icab ettirir. Burada gx ve gy, Z ekseni şakul istikametinde alınan koordinat sisteminde g nin X ve Y eksenindeki bileşenleri Nivo S f e r o i d i : W Potensiyeli için bulduğumuz eşitliği (16) tekrar yazalım. J dm x 2 + j2 e W2 Bu eşitliğin sağ tarafındaki birinci terim, kütle çekiminden, ikinci terim ise merkezkaç kuvvetinden gelmektedir. İlk terimi V ile gösterelim, yanı f dm V == f ~e~ olsun. Bu entegrali alabilmek için bazı yardımcı işlemler yapmak 5 J._ zorundayız. (E) xx' + yy' + zz' O halde Cos m = rr' olacaktır. (21) eşitliğinde r 2 parantezine alırsak r'2 r'.. r' e 2 = r2 (1 -\ cos^) olur == P dersek r2 r r Şekil «o» dünyanın merkezi ^ r ve r' arasındaki açı olmak üzere e2 _ r 2 _j_ r '2 2rr? Cos ^ (21) yazabiliriz. e2 = (x' - X)2 + (y' - y)2 + ( 2 /. Z )2 idi = X'2 -f- y'2 _J_ Z /2 _J_ X 2 -f y2 + Z2 (2xx' + 2yy' + 2 zz') r l_ = (1 + p 2 2p cos ^ 2 olur. Bu ifadeyi p değişken olmak üzere e ' / f (o) f" (o) f (p)=f (o) p -J p2 _j_... Maclaurin Serisine açarsak 1! 2! cos2 ^-1 5 eos^-s cos ^ = (1 + p. cos^ + p _j_ p j_.., ) (22) er '2 2 '19
19 elde edebiliriz. Bu sürenin yakınsak olabilmesi için p <" 1 yani -- <" 1 \ r ^ olmalıdır. Bu demektirki şekilde P noktası her zaman dünyanın dışında alınmalıdır. f dm 1 eşitliğinde, yerine (22 deki eşidini koyarsak e e r -' r ' V = dm 1 + cos^ + ( Acos2^ 2_) +... (23) r J ( E) r r a elde ederiz. Entegrali parçalara ayırıp herbir parçaya, V o -f V x V 3 -f-... dersek V= V 0 + V ı + fei -+V, +... olur. V o = ( dm r J(E). f Vj = r' cos^dm rs j f ç 3 1 V 2 = r'z ( cos 2 j, ) dm 't ' r» J 2 2 f j- 5 3 V 3 = r'3 ( cos 3^ cos^ ) dm dir. r 4 J 2 2 r ' 2 r' * - Şimdi her entegrali ayrı ayrı inceleyelim. f V o = r J r dm de yerin toplam kütlesine M dersek f V o = M olarak ifade edilebilir. (24) r îr xx' + yy' + zz' Vj == r' cos ^. dm entegralinde cos ^ = koyalım f r xx' + yy r + zz' Bu takdirde V ı = dm r 2 J r elde edilir. W ' = x x'dm + y y'dm + z z'dm rs _ J(E) J (E) J (E) _ Devamı gelecek sayıda
20 Havai Nirengide Kolon Dengelemesi Yazan : Y. Müh. A. Fahrettin AYDIN O.D.T.Ü. Yard. Profesör Orta Doğa Teknik Üniversitesi Mühendislik Fakültesi Yard. Profesörü A. Fahrettin Aydın, «HAVAt NÎRENGt» Konusunda hazırlamış olduğu bu eserinin yayınlanması müsaadesini, Odamıza vermiş bulunmaktadır. Odamız bu eseri kısım kısım yayinliyarak tamamliyacaktir* Bu şekilde' kurîanrara havai nirengi konusunda tam bir kitap elde etmiş olacaklardır», önsöz Bu kitap daha ziyade Fotogrametri ilminin teorisinde ve pratiğinde bilgisi olanlar için hazırlanmışf<ır. Birinci kısımda, havai nirenginin tatbikatında meydana gelecek sabit ve değişebilen hatalar, tesir sahaları, yayüma prensipleri hakkında şekiller ve matematiki formüllerle izahat verilmiştir. ikinci kısım, Kolon dengelemesinin çeşitli çözüm metodkm ve bugün en çok kullanılan ZarzycM grafik metodu, grafik ve nümerik dengelemenin karşılaştırılması, kolon nirengisinin hassasiyeti, grafik çözümün Gauss.un en küçük kareler (Lemst 8qıtare Adjustment) metoduna göre analizi grafiklerle izah edilmiştir. Üçüncü kısımda, Blok dengelemesine ait olup, bilhassa Avrupada kullanılan Gauss en küçük kareler metodunu mekanik olarak tatbik eden Jerie nin Analog hesaplama metodudur. Bu metodîa bir blokun planimetrik ve yükseklik dengelemesi, hassasiyeti tafsilattı olarak izah. edilmiştir. Umumi olarak bu eserde bugün Avrupa ve Amerikada tatbik edilmekte olan en yeni metodlar hakkında lüzumlu bilgi verilmiştir Benesi%âm itibaren teorik ve pratik foiogram&tri çahşmaîan- 21.
21 mın tecrübesine dayanarak bu eseri hazırladım. Havai Nirenginin hatalarının teorisinde ve tatbikatında çok faydalı olacağını ümit ederim. Kısım kısım basılması istenilen bu yazıda kitabın ikinci kısmını teşkil eden Havai Nirengide Kolon dengelemesi başa alınmıştır', hatalar teorisi ile Blok dengelemesi bunu takip edecektir. KOLON DENGELEMESİ 1. Giriş 2. Dengelemenin Sınıflanması 3. Zarzycki Grafik Metodu 4. Kısa kolonlar için Nümerik înterpolasyon Metodu 5. En küçük kareler Metodu (Least Square) dengeleme. 6. Ackerman (ITC) a göre umumî en küçük kareler metodu. I. GÎRÎŞ : Stereoskopik fotogrametri aletlerinde bir modelin kıymetlen- dirilmesi için önceden yapılan karşılıklı ve kati (absülüt) cihetlendirmede ara-, iride en az 2 noktanın x ye y koordinatları ile 3 noktanın yüksekliklerinin bi linmesi lazımdır. Geniş ölçüde arazi projelerinin yapılmasında bu noktalar önemli sayıda çoğalır. Arazi üzerinde bu noktaların klasik ölçme metodları ile koordinat ve yüksekliklerinin bulunması çok zaman kayıbı ile fazla para sar fiyatına sebep olur. * Havai nirenginin faydası çok sayıda olan bu noktaları en ekonomik şekilde en az arazi çalışması yaparak, fotogrametri aletleri kullanarak koordinatlarını temin etmektir. Havai nirengi başlıca iki kısma ayrılır. I. Yatay (Planimetrik,ışınsal) Ha-, vai Nirengi : Bu kısımda yatay kıymetlendirme (Radial plotter - Wild, Zeiss) fotogrametri aletleri yardımı ile noktaların yalnız koordinat değerleri (x, y) okunur^ yükseklikler okunmaz; ve transformasyon formülleri yardımı ile bu alet okumaları arazi koordinatlarına çevrilir. II. Uzay Havai Nirengi: Bu kısımda noktaların x, y, ve z koordinatları tayin edilir. Uzay havai nirengide iki kısma ayrılır: a. Analog metod b. Analitik metod.. - Amafog Metod s Birinci sınıf universal stereo kıymetlendirme aletleri (Wild - A7, Zeiss Stereoplanigraph C8, Santoni IV) kullanılmak suretile noktaların alet koordinatları (x, y, z) okunur. Transformasyon formülleri yardımı ile alette okunan bu değerler arazi değerlerine çevrilir. Bu usulde koordinat değerlerinin dengelenmesi grafik metodla yapılır. Bu metodlar hakkında ilerde lüzumlu açiklama yapılacaktır. Analitik Metod s Stereokomparator (Zeiss, Wild, Nistri,,,...) aletleri yardımı ile noktaların x, y, alet koordinatları okunur, ve analitik fotogrametri formülleri yardımı ile hasırlanan program Elektronik (IJB.M 1650, 1620 veya diğer marka) hesap makinelerinde değerlendirilir. Ve istenilen noktaların arazi koordinatları <x, y, z) tayin edilir. Bu usule digital havai nirengide denir. 8*
T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.
![T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir. T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.](/thumbs/55/35591809.jpg) * = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
* = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
TOPOĞRAFYA. Ölçme Bilgisinin Konusu
 TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
NÎRENÇİ NOKTALARININ ARANMASI
 NÎRENÇİ NOKTALARININ ARANMASI Yazan ; -.. İsmail Hakkı GÜNEŞ 1, '. ' ' (Ankara) Haritaları yapılmış meskun ve meskun olmayan alanlarda bulunamıyan ve taşları kaybolan nirengilerin yeraltındaki sigorta
NÎRENÇİ NOKTALARININ ARANMASI Yazan ; -.. İsmail Hakkı GÜNEŞ 1, '. ' ' (Ankara) Haritaları yapılmış meskun ve meskun olmayan alanlarda bulunamıyan ve taşları kaybolan nirengilerin yeraltındaki sigorta
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN
 Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN Topografya (Surveying) Nedir? Topografya geleneksel olarak, Dünya yüzeyinin üzerindeki, üstündeki veya altındaki noktalarının rölatif konumlarını belirleyen
Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN Topografya (Surveying) Nedir? Topografya geleneksel olarak, Dünya yüzeyinin üzerindeki, üstündeki veya altındaki noktalarının rölatif konumlarını belirleyen
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ
 ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
02.04.2012. Düşey mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi
 Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
İnşaat Mühendisliğine Giriş İNŞ-101. Yrd.Doç.Dr. Özgür Lütfi Ertuğrul
 İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
YÜKSEKLİK ÖLÇÜMÜ. Ölçme Bilgisi Ders Notları
 YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
DİK KOORDİNAT SİSTEMİ VE
 Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
İÇİNDEKİLER BİRİNCİ BÖLÜM... 1 Genel Hükümler... 1 Amaç... 1 Kapsam... 1 Dayanak... 1 Tanımı... 1 İKİNCİ BÖLÜM...
 İÇİNDEKİLER BİRİNCİ BÖLÜM... 1 Genel Hükümler... 1 Amaç... 1 Kapsam... 1 Dayanak... 1 Tanımı... 1 İKİNCİ BÖLÜM... 2 Fen Adamlarının Gruplandırılması... 2 ÜÇÜNCÜ BÖLÜM... 4 Fen Adamlarının Yetki ve... 4
İÇİNDEKİLER BİRİNCİ BÖLÜM... 1 Genel Hükümler... 1 Amaç... 1 Kapsam... 1 Dayanak... 1 Tanımı... 1 İKİNCİ BÖLÜM... 2 Fen Adamlarının Gruplandırılması... 2 ÜÇÜNCÜ BÖLÜM... 4 Fen Adamlarının Yetki ve... 4
Uygulamada Gauss-Kruger Projeksiyonu
 JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
TEMEL HARİTACILIK BİLGİLERİ. Erkan GÜLER Haziran 2018
 TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
Ölçme Bilgisi ve Kadastro Anabilim Dalı
 ÖLÇME BİLGİSİ Ölçme Bilgisi ve Kadastro Anabilim Dalı Ders Kodu:264 Yrd.Doç.Dr. Muhittin İNAN Anabilim Dalımız "İstanbul Yüksek Orman Mektebi" nin 1934 yılında Ankara Yüksek Ziraat Enstitüsüne bir fakülte
ÖLÇME BİLGİSİ Ölçme Bilgisi ve Kadastro Anabilim Dalı Ders Kodu:264 Yrd.Doç.Dr. Muhittin İNAN Anabilim Dalımız "İstanbul Yüksek Orman Mektebi" nin 1934 yılında Ankara Yüksek Ziraat Enstitüsüne bir fakülte
PAFTA BÖLÜMLENDİRİLMESİ
 PAFTA BÖLÜMLENDİRİLMESİ Türkiye kadastrosunda yukarıda değinilen ada sistemi pafta bölümleme ve adlandırma sistemi dışında çeşitli pafta bölümleme ve adlandırma sistemleri kullanılmıştır ve Yapım Yönetmeliği
PAFTA BÖLÜMLENDİRİLMESİ Türkiye kadastrosunda yukarıda değinilen ada sistemi pafta bölümleme ve adlandırma sistemi dışında çeşitli pafta bölümleme ve adlandırma sistemleri kullanılmıştır ve Yapım Yönetmeliği
YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ
 YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ Yrd.Doc.Dr. Hüseyin İNCE ÖZET Yol projelerinde yatay kurpta enkesitler arasında yapılacak kübaj hesabında, kurbun eğrilik durumu
YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ Yrd.Doc.Dr. Hüseyin İNCE ÖZET Yol projelerinde yatay kurpta enkesitler arasında yapılacak kübaj hesabında, kurbun eğrilik durumu
ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ. Doç. Dr. Alper Serdar ANLI. 8. Hafta
 ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ Doç. Dr. Alper Serdar ANLI 8. Hafta DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ Noktaların yükseklikleri düşey ölçmelerle belirlenir.
ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ Doç. Dr. Alper Serdar ANLI 8. Hafta DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ Noktaların yükseklikleri düşey ölçmelerle belirlenir.
Fotogrametride işlem adımları
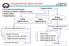 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
T.C YÜKSEKOVA BELEDİYE BAŞKANLIĞI EMLAK VE İSTİMLAK MÜDÜRLÜĞÜ KURULUŞ GÖREV VE ÇALIŞMA ESASLARI YÖNETMELİĞİ BİRİNCİ BÖLÜM
 T.C YÜKSEKOVA BELEDİYE BAŞKANLIĞI EMLAK VE İSTİMLAK MÜDÜRLÜĞÜ KURULUŞ GÖREV VE ÇALIŞMA ESASLARI YÖNETMELİĞİ BİRİNCİ BÖLÜM AMAÇ, KAPSAM, DAYANAK ve TANIMLAR Amaç MADDE 1- Bu Yönetmeliğin amacı, Yüksekova
T.C YÜKSEKOVA BELEDİYE BAŞKANLIĞI EMLAK VE İSTİMLAK MÜDÜRLÜĞÜ KURULUŞ GÖREV VE ÇALIŞMA ESASLARI YÖNETMELİĞİ BİRİNCİ BÖLÜM AMAÇ, KAPSAM, DAYANAK ve TANIMLAR Amaç MADDE 1- Bu Yönetmeliğin amacı, Yüksekova
ÖLÇME BİLGİSİ. PDF created with FinePrint pdffactory trial version http://www.fineprint.com. Tanım
 ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
Harita Projeksiyonları ve Koordinat Sistemleri. Doç. Dr. Senem KOZAMAN
 Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Kaman Meslek Yüksekokulu Harita ve Kadastro Programı Öğr. Gör. Emre İNCE
 Kaman Meslek Yüksekokulu Harita ve Kadastro Programı Öğr. Gör. Emre İNCE İmar Terimleri Parsel Cephesi: Parselin üzerinde bulunduğu yoldaki cephesini ifade eder. Parselin üzerinde bulunduğu yoldaki cephesidir.
Kaman Meslek Yüksekokulu Harita ve Kadastro Programı Öğr. Gör. Emre İNCE İmar Terimleri Parsel Cephesi: Parselin üzerinde bulunduğu yoldaki cephesini ifade eder. Parselin üzerinde bulunduğu yoldaki cephesidir.
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü
 Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 7 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 7 Kasım 1999 Saat: 21.50 Problem 7.1 (Ohanian, sayfa 271, problem 55) Bu problem boyunca roket
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 7 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 7 Kasım 1999 Saat: 21.50 Problem 7.1 (Ohanian, sayfa 271, problem 55) Bu problem boyunca roket
1. Hafta Uygulama Soruları
 . Hafta Uygulama Soruları ) x ekseni, x = doğrusu, y = x ve y = x + eğrileri arasında kalan alan nedir? ) y = x 3 ve y = 4 x 3 parabolleri arasında kalan alan nedir? 3) y = x, x y = 4 eğrileri arasında
. Hafta Uygulama Soruları ) x ekseni, x = doğrusu, y = x ve y = x + eğrileri arasında kalan alan nedir? ) y = x 3 ve y = 4 x 3 parabolleri arasında kalan alan nedir? 3) y = x, x y = 4 eğrileri arasında
11.1 11.2. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti. 11.3 Örnek Eylemsizlik Momenti. 11.4 Eylemsizlik Yarıçapı
 11.1 11. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti 11.3 Örnek Eylemsizlik Momenti 11.4 Eylemsizlik Yarıçapı 11.5 Eksen Takımının Değiştirilmesi 11.6 Asal Eylemsizlik Momentleri
11.1 11. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti 11.3 Örnek Eylemsizlik Momenti 11.4 Eylemsizlik Yarıçapı 11.5 Eksen Takımının Değiştirilmesi 11.6 Asal Eylemsizlik Momentleri
2 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var ise bulunuz.
 ANALİZ 1.) a) sgn. sgn( 1) = 1 denkleminin çözüm kümesini b) f ( ) 3 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var
ANALİZ 1.) a) sgn. sgn( 1) = 1 denkleminin çözüm kümesini b) f ( ) 3 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI
 BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
Cebirsel Fonksiyonlar
 Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları
 JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Dünya nın şekli. Küre?
 Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
JEOİD ve JEOİD BELİRLEME
 JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Hakan AKÇIN* SUNU Ali ihsan ŞEKERTEKİN
 AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
Bölüm 3: Vektörler. Kavrama Soruları. Konu İçeriği. Sunuş. 3-1 Koordinat Sistemleri
 ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN
 YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN Yrd. Doç. Dr. Ayhan CEYLAN Yrd. Doç. Dr. İsmail ŞANLIOĞLU 9.3. Nivelman Ağları ve Nivelman Röper Noktası Haritası yapılacak olan arazi üzerinde veya projenin
YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN Yrd. Doç. Dr. Ayhan CEYLAN Yrd. Doç. Dr. İsmail ŞANLIOĞLU 9.3. Nivelman Ağları ve Nivelman Röper Noktası Haritası yapılacak olan arazi üzerinde veya projenin
Diferensiyel denklemler sürekli sistemlerin hareketlerinin ifade edilmesinde kullanılan denklemlerdir.
 .. Diferensiyel Denklemler y f (x) de F ( x, y, y, y,...) 0 veya y f ( x, y, y,...) x ve y değişkenlerinin kendileri ve türevlerini içinde bulunduran denklemlerdir. (Türevler; "Bağımlı değişkenin değişiminin
.. Diferensiyel Denklemler y f (x) de F ( x, y, y, y,...) 0 veya y f ( x, y, y,...) x ve y değişkenlerinin kendileri ve türevlerini içinde bulunduran denklemlerdir. (Türevler; "Bağımlı değişkenin değişiminin
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları
 TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
İÇİNDEKİLER. Çizelgelerin ele alınışı. Uygulamalı Örnekler. Birim metre dikiş başına standart-elektrod miktarının hesabı için çizelgeler
 ELEKTROD SARFİYAT ÇİZELGELERİ İÇİNDEKİLER Kısım A Genel bilgiler Kısım B Çizelgelerin ele alınışı Kısım C Uygulamalı Örnekler Kısım D Birim metre dikiş başına standart-elektrod miktarının hesabı için çizelgeler
ELEKTROD SARFİYAT ÇİZELGELERİ İÇİNDEKİLER Kısım A Genel bilgiler Kısım B Çizelgelerin ele alınışı Kısım C Uygulamalı Örnekler Kısım D Birim metre dikiş başına standart-elektrod miktarının hesabı için çizelgeler
PDF created with FinePrint pdffactory trial version Düşey mesafelerin (Yüksekliklerin) Ölçülmesi
 Düşey mesafelerin (Yüksekliklerin) Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen deniz
Düşey mesafelerin (Yüksekliklerin) Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen deniz
Fizik 101: Ders 21 Gündem
 Fizik 101: Ders 21 Gündem Yer çekimi nedeninden dolayı tork Rotasyon (özet) Statik Bayırda bir araba Statik denge denklemleri Örnekler Asılı tahterevalli Asılı lamba Merdiven Ders 21, Soru 1 Rotasyon Kütleleri
Fizik 101: Ders 21 Gündem Yer çekimi nedeninden dolayı tork Rotasyon (özet) Statik Bayırda bir araba Statik denge denklemleri Örnekler Asılı tahterevalli Asılı lamba Merdiven Ders 21, Soru 1 Rotasyon Kütleleri
KESİTLERİN ÇIKARILMASI
 KESİTLERİN ÇIKARILMASI Karayolu, demiryolu, kanal, yüksek gerilim hattı gibi inşaat işlerinde projelerin hazırlanması, toprak hacminin bulunması amacı ile boyuna ve enine kesitlere ihtiyaç vardır. Boyuna
KESİTLERİN ÇIKARILMASI Karayolu, demiryolu, kanal, yüksek gerilim hattı gibi inşaat işlerinde projelerin hazırlanması, toprak hacminin bulunması amacı ile boyuna ve enine kesitlere ihtiyaç vardır. Boyuna
JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur.
 JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur. Prof. Dr. Gündüz Horasan Deprem dalgalarını incelerken, yeryuvarının esnek, homojen
JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur. Prof. Dr. Gündüz Horasan Deprem dalgalarını incelerken, yeryuvarının esnek, homojen
HAREKET HAREKET KUVVET İLİŞKİSİ
 HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
TORK VE DENGE. İçindekiler TORK VE DENGE 01 TORK VE DENGE 02 TORK VE DENGE 03 TORK VE DENGE 04. Torkun Tanımı ve Yönü
 İçindekiler TORK VE DENGE TORK VE DENGE 01 Torkun Tanımı ve Yönü Torka Sebep Olan ve Olmayan Kuvvetler Tork Bulurken İzlenen Yöntemler Çubuğa Uygulanan Kuvvet Dik Değilse 1) Kuvveti bileşenlerine ayırma
İçindekiler TORK VE DENGE TORK VE DENGE 01 Torkun Tanımı ve Yönü Torka Sebep Olan ve Olmayan Kuvvetler Tork Bulurken İzlenen Yöntemler Çubuğa Uygulanan Kuvvet Dik Değilse 1) Kuvveti bileşenlerine ayırma
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
i/leşlerimizle İlgili l\nrıimmn tanıtıyoruz r-^-r-^ ÖL : O J İLLER BANKASI HARİTA DAtEESl REİSLİC!
 i/leşlerimizle İlgili l\nrıimmn tanıtıyoruz r-^-r-^ ÖL : O J İLLER BANKASI HARİTA DAtEESl REİSLİC! s KISA TARİHÇESİ : İlhan Kaya DUMAN Ankara 1933 yılında «Belediyeler Bankası» adıyla kurulan İLLER BANKASI
i/leşlerimizle İlgili l\nrıimmn tanıtıyoruz r-^-r-^ ÖL : O J İLLER BANKASI HARİTA DAtEESl REİSLİC! s KISA TARİHÇESİ : İlhan Kaya DUMAN Ankara 1933 yılında «Belediyeler Bankası» adıyla kurulan İLLER BANKASI
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ
 HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Kavramları_Ders#4 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ Çevre Düzeni Planı: Ülke ve
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Kavramları_Ders#4 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ Çevre Düzeni Planı: Ülke ve
ÜNİTE. MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI İÇİNDEKİLER HEDEFLER DOĞRULAR VE PARABOLLER
 HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
Alan Hesapları. Şekil 14. Üç kenarı belli üçgen alanı
 lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
TOPOĞRAFİK HARİTALAR VE KESİTLER
 TOPOĞRAFİK HARİTALAR VE KESİTLER Prof.Dr. Murat UTKUCU Yrd.Doç.Dr. ŞefikRAMAZANOĞLU TOPOĞRAFİK HARİTALAR VE Haritalar KESİTLER Yeryüzü şekillerini belirli bir yöntem ve ölçek dahilinde plan konumunda gösteren
TOPOĞRAFİK HARİTALAR VE KESİTLER Prof.Dr. Murat UTKUCU Yrd.Doç.Dr. ŞefikRAMAZANOĞLU TOPOĞRAFİK HARİTALAR VE Haritalar KESİTLER Yeryüzü şekillerini belirli bir yöntem ve ölçek dahilinde plan konumunda gösteren
MADDE 3 (1) Bu Yönetmelik, 23/6/1965 tarihli ve 634 sayılı Kat Mülkiyeti Kanununun 68 inci maddesine dayanılarak hazırlanmıştır.
 Resmi Gazete Tarihi: 16.08.2008 Resmi Gazete Sayısı: 26969 TOPLU YAPILARDA KAT MÜLKİYETİ VE KAT İRTİFAKI TESİSİNE DAİR YÖNETMELİK BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak ve Tanımlar Amaç MADDE 1 (1) Bu Yönetmeliğin
Resmi Gazete Tarihi: 16.08.2008 Resmi Gazete Sayısı: 26969 TOPLU YAPILARDA KAT MÜLKİYETİ VE KAT İRTİFAKI TESİSİNE DAİR YÖNETMELİK BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak ve Tanımlar Amaç MADDE 1 (1) Bu Yönetmeliğin
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI
 ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
HARİTA BİLGİSİ ETKİNLİK
 HARİTA Dünya nın tamamının veya bir bölümünün kuş bakışı, küçültülerek bir düzleme aktarılmasıdır. kuşbakışı PLAN... Bir çizimin harita olabilmesi için... KROKİ... PROJEKSİYONLAR: Dünya nın şeklinin geoit
HARİTA Dünya nın tamamının veya bir bölümünün kuş bakışı, küçültülerek bir düzleme aktarılmasıdır. kuşbakışı PLAN... Bir çizimin harita olabilmesi için... KROKİ... PROJEKSİYONLAR: Dünya nın şeklinin geoit
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ
 Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
Ölçme Bilgisi. Dr. Hasan ÖZ. SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr
 Ölçme Bilgisi Dr. Hasan ÖZ SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr 1 Ölçme Bilgisi; yeryüzünün küçük ya da büyük parçalarının şekil ve büyüklüklerinin ölçülmesi ve elde
Ölçme Bilgisi Dr. Hasan ÖZ SDÜ Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü www.hasanoz.com.tr 1 Ölçme Bilgisi; yeryüzünün küçük ya da büyük parçalarının şekil ve büyüklüklerinin ölçülmesi ve elde
STATİK KUVVET ANALİZİ (2.HAFTA)
 STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
2013 YILI SAYISAL HALİHAZIR HARİTA BİRİM FİYATLARI
 İLLER BANKASI ANONİM ŞİRKETİ İHALE DAİRESİ BAŞKANLIĞI 2013 YILI SAYISAL HALİHAZIR HARİTA BİRİM FİYATLARI İLLER BANKASI ANONİM ŞİRKETİ ANKARA - 2013 AÇIKLAMALAR : 1- Bu birim fiyatların kullanıldığı hesaplardaki
İLLER BANKASI ANONİM ŞİRKETİ İHALE DAİRESİ BAŞKANLIĞI 2013 YILI SAYISAL HALİHAZIR HARİTA BİRİM FİYATLARI İLLER BANKASI ANONİM ŞİRKETİ ANKARA - 2013 AÇIKLAMALAR : 1- Bu birim fiyatların kullanıldığı hesaplardaki
R.G.) MAR KANUNUNUN (2.11.1985/18916 38. MADDES
 Bayındırlık ve İskan Bakanlığından: (2.11.1985/18916 sayılı Mükerrer R.G.) İMAR KANUNUNUN 38. MADDESİNDE SAYILAN MÜHENDİSLER, MİMARLAR VE ŞEHİR PLANCILARI DIŞINDA KALAN FEN ADAMLARININ YETKİ, GÖREV VE
Bayındırlık ve İskan Bakanlığından: (2.11.1985/18916 sayılı Mükerrer R.G.) İMAR KANUNUNUN 38. MADDESİNDE SAYILAN MÜHENDİSLER, MİMARLAR VE ŞEHİR PLANCILARI DIŞINDA KALAN FEN ADAMLARININ YETKİ, GÖREV VE
ULAŞIM YOLLARINA AİT TANIMLAR
 ULAŞIM YOLLARINA AİT TANIMLAR Geçki: Karayolu, demiryolu gibi ulaştıma yapılarının, yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgisinin harita ya da arazideki izdüşümüdür. Topografik
ULAŞIM YOLLARINA AİT TANIMLAR Geçki: Karayolu, demiryolu gibi ulaştıma yapılarının, yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgisinin harita ya da arazideki izdüşümüdür. Topografik
 Geometrik nivelmanda önemli hata kaynakları Nivelmanda oluşabilecek model hataları iki bölümde incelenebilir. Bunlar: Aletsel (Nivo ve Mira) Hatalar Çevresel Koşullardan Kaynaklanan Hatalar 1. Aletsel
Geometrik nivelmanda önemli hata kaynakları Nivelmanda oluşabilecek model hataları iki bölümde incelenebilir. Bunlar: Aletsel (Nivo ve Mira) Hatalar Çevresel Koşullardan Kaynaklanan Hatalar 1. Aletsel
Firmamız mühendislik hizmet sektöründe kurulduğu 1998 yılından bugüne 16 yılı aşkın sürede faaliyette bulunmaktadır.
 Firmamız mühendislik hizmet sektöründe kurulduğu 1998 yılından bugüne 16 yılı aşkın sürede faaliyette bulunmaktadır. Tüm altyapı çalışmalarının ilk adımı olan harita mühendislik hizmetlerinin ülke kalkınmasındaki
Firmamız mühendislik hizmet sektöründe kurulduğu 1998 yılından bugüne 16 yılı aşkın sürede faaliyette bulunmaktadır. Tüm altyapı çalışmalarının ilk adımı olan harita mühendislik hizmetlerinin ülke kalkınmasındaki
***Yapılan bir çizimin harita özelliğini gösterebilmesi için çizimin belirli bir ölçek dahilinde yapılması gerekir.
 HARİTA BİLGİSİ Harita Kuşbakışı görünümün Ölçekli Düzleme aktarılmasıdır. ***Yapılan bir çizimin harita özelliğini gösterebilmesi için çizimin belirli bir ölçek dahilinde yapılması gerekir. Kroki Kuşbakışı
HARİTA BİLGİSİ Harita Kuşbakışı görünümün Ölçekli Düzleme aktarılmasıdır. ***Yapılan bir çizimin harita özelliğini gösterebilmesi için çizimin belirli bir ölçek dahilinde yapılması gerekir. Kroki Kuşbakışı
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
Fizik Dr. Murat Aydemir
 Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON
 JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
STATİĞİN TEMEL PRENSİPLERİ
 1.1. Temel Kavramlar ve Tanımlar Mühendislik mekaniği: Kuvvet etkisi altındaki cisimlerin denge veya hareket koşullarını inceleyen bilim dalı Genel olarak mühendislik mekaniği Sert (rijit) katı cisimlerin
1.1. Temel Kavramlar ve Tanımlar Mühendislik mekaniği: Kuvvet etkisi altındaki cisimlerin denge veya hareket koşullarını inceleyen bilim dalı Genel olarak mühendislik mekaniği Sert (rijit) katı cisimlerin
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU. Yrd. Doç. Dr. Hüseyin KEMALDERE
 JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
TOPOĞRAFYA Takeometri
 TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1: [2]
![Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1: [2] Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1: [2]](/thumbs/56/37903003.jpg) Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1:4.500.000 [2] 2 25 Şekil 2.23: Orta Akdeniz (İtalya, Adriyatik Denizi, Kuzey Afrika Kıyıları). Ölçek ~ 1:4.500.000 [2] 2 26 Şekil 2.24:
Şekil 2.22: Doğu Akdeniz, Ege Denizi, Balkan Yarımadası. Ölçek ~ 1:4.500.000 [2] 2 25 Şekil 2.23: Orta Akdeniz (İtalya, Adriyatik Denizi, Kuzey Afrika Kıyıları). Ölçek ~ 1:4.500.000 [2] 2 26 Şekil 2.24:
ÝÇÝNDEKÝLER. 5 Baþvuru ve Ýzlenen Yöntem. 7 Talebe Baðlý Olarak Kadastro Müdürlüklerince Yapýlan Ýþlemler. 19 Birleþtirme (Tevhit) Ýþlemleri
 ÝÇÝNDEKÝLER Sayfa No Konu 3 Tarihçe 5 Baþvuru ve Ýzlenen Yöntem 7 Talebe Baðlý Olarak Kadastro Müdürlüklerince Yapýlan Ýþlemler 7 Plan Örneði 9 Yer Gösterme 11 Aplikasyon 13 Cins Deðiþikliði 16 Ýrtifak
ÝÇÝNDEKÝLER Sayfa No Konu 3 Tarihçe 5 Baþvuru ve Ýzlenen Yöntem 7 Talebe Baðlý Olarak Kadastro Müdürlüklerince Yapýlan Ýþlemler 7 Plan Örneði 9 Yer Gösterme 11 Aplikasyon 13 Cins Deðiþikliði 16 Ýrtifak
Nazım imar planı nedir?
 INSAAT-IMAR-RUHSAT İmar planı nedir? Nüfusu 10.000 i aşan belediyeler ile nüfusu daha az olduğu halde il merkezi olan veya gelecekte imar işleri bakımından plana gereksinimi bulunduğu Bayındırlık ve İskan
INSAAT-IMAR-RUHSAT İmar planı nedir? Nüfusu 10.000 i aşan belediyeler ile nüfusu daha az olduğu halde il merkezi olan veya gelecekte imar işleri bakımından plana gereksinimi bulunduğu Bayındırlık ve İskan
1. HAFTA. Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler.
 1. HAFTA Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler. Statikte üç temel büyüklük vardır. Uzay: Fiziksel olayların meydana geldiği geometrik bir bölgedir. İncelenen problemin
1. HAFTA Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler. Statikte üç temel büyüklük vardır. Uzay: Fiziksel olayların meydana geldiği geometrik bir bölgedir. İncelenen problemin
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
EKVATORAL KOORDİNAT SİSTEMİ_devam. Serap Ak
 EKVATORAL KOORDİNAT SİSTEMİ_devam http://star-www.st-and.ac.uk/~fv/webnotes/chapter5.htm http://star-www.st-and.ac.uk/~fv/webnotes/chapter4.htm Gök küresinde bulunan önemli yıldızların ekvatoral koordinatları
EKVATORAL KOORDİNAT SİSTEMİ_devam http://star-www.st-and.ac.uk/~fv/webnotes/chapter5.htm http://star-www.st-and.ac.uk/~fv/webnotes/chapter4.htm Gök küresinde bulunan önemli yıldızların ekvatoral koordinatları
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
T.C. İZMİR BÜYÜKŞEHİR BELEDİYE BAŞKANLIĞI
 T.C. İZMİR BÜYÜKŞEHİR BELEDİYE BAŞKANLIĞI PARK VE BAHÇELER DAİRESİ BAŞKANLIĞI YEŞİL ALANLAR PLANLAMA PROJE ŞUBE MÜDÜRLÜĞÜ ÇALIŞMA USUL VE ESASLARI HAKKINDA YÖNERGE BİRİNCİ BÖLÜM Genel Hükümler Amaç ve
T.C. İZMİR BÜYÜKŞEHİR BELEDİYE BAŞKANLIĞI PARK VE BAHÇELER DAİRESİ BAŞKANLIĞI YEŞİL ALANLAR PLANLAMA PROJE ŞUBE MÜDÜRLÜĞÜ ÇALIŞMA USUL VE ESASLARI HAKKINDA YÖNERGE BİRİNCİ BÖLÜM Genel Hükümler Amaç ve
DÜZLEMDE GERİLME DÖNÜŞÜMLERİ
 3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
TÜREVİN GEOMETRİK YORUMU
 TÜREVİN GEOMETRİK YORUMU f :R R, =f ( fonksionuna düzlemde A karşılık gelen f( +h eğri anda ki =f( P gibi olsun. f( Eğrinin P(,f( noktasındaki teğetlerini +h araştıralım. Bunun için P(,f( noktasının sağıda
TÜREVİN GEOMETRİK YORUMU f :R R, =f ( fonksionuna düzlemde A karşılık gelen f( +h eğri anda ki =f( P gibi olsun. f( Eğrinin P(,f( noktasındaki teğetlerini +h araştıralım. Bunun için P(,f( noktasının sağıda
İmar ve Şehircilik Müdürlüğünün görev, yetki ve sorumlulukları;
 İmar ve Şehircilik Müdürlüğünün görev, yetki ve sorumlulukları; a) Belediye ve varsa mücavir alan sınırları içerisindeki tüm yapılaşmaların plan, fen, sağlık ve çevre şartlarına uygun teşekkülünü sağlamak,
İmar ve Şehircilik Müdürlüğünün görev, yetki ve sorumlulukları; a) Belediye ve varsa mücavir alan sınırları içerisindeki tüm yapılaşmaların plan, fen, sağlık ve çevre şartlarına uygun teşekkülünü sağlamak,
BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak ve Tanımlar
 BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak ve Tanımlar Amaç MADDE 1 (1) Bu Yönetmeliğin amacı, Antalya Büyükşehir Belediyesi İmar ve Şehircilik Dairesi Başkanlığı Harita ve İstimlak Şube Müdürlüğü Gelir Tarifelerinin
BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak ve Tanımlar Amaç MADDE 1 (1) Bu Yönetmeliğin amacı, Antalya Büyükşehir Belediyesi İmar ve Şehircilik Dairesi Başkanlığı Harita ve İstimlak Şube Müdürlüğü Gelir Tarifelerinin
deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır.
 deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır. 7) Fotogrametrik modellerden harita üretim amacına yönelik olarak derlenen veriler, mikrobilgisayarların
deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır. 7) Fotogrametrik modellerden harita üretim amacına yönelik olarak derlenen veriler, mikrobilgisayarların
Düzlemde Dönüşümler: Öteleme, Dönme ve Simetri. Not 1: Buradaki A noktasına dönme merkezi denir.
 Düzlemde Dönüşümler: Öteleme, Dönme ve Simetri Düzlemin noktalarını, düzlemin noktalarına eşleyen bire bir ve örten bir fonksiyona düzlemin bir dönüşümü denir. Öteleme: a =(a 1,a ) ve u =(u 1,u ) olmak
Düzlemde Dönüşümler: Öteleme, Dönme ve Simetri Düzlemin noktalarını, düzlemin noktalarına eşleyen bire bir ve örten bir fonksiyona düzlemin bir dönüşümü denir. Öteleme: a =(a 1,a ) ve u =(u 1,u ) olmak
Harita Nedir? Haritaların Sınıflandırılması. Haritayı Oluşturan Unsurlar
 Harita Nedir? Yeryüzünün tamamının veya bir kısmının kuşbakışı görünüşünün belli bir ölçek dahilinde düzleme aktarılmasıyla oluşan çizimlere denir. Haritacılık bilimine kartografya denir. Bir çizimin harita
Harita Nedir? Yeryüzünün tamamının veya bir kısmının kuşbakışı görünüşünün belli bir ölçek dahilinde düzleme aktarılmasıyla oluşan çizimlere denir. Haritacılık bilimine kartografya denir. Bir çizimin harita
Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur.
 Üç Boyutlu Geometri Nokta (Point,Vertex) Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur. Kartezyen Koordinat Sistemi Uzayda bir noktayı tanımlamak
Üç Boyutlu Geometri Nokta (Point,Vertex) Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur. Kartezyen Koordinat Sistemi Uzayda bir noktayı tanımlamak
MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK. Bölüm 1 Temel Kavramlar ve İlkeler
 MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK Bölüm 1 Temel Kavramlar ve İlkeler Mekanik Mekanik Rijit-Cisim Mekaniği Şekil değiştiren Cismin Mekaniği Statik Dinamik Dengedeki Cisimler Hareketsiz veya durgun
MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK Bölüm 1 Temel Kavramlar ve İlkeler Mekanik Mekanik Rijit-Cisim Mekaniği Şekil değiştiren Cismin Mekaniği Statik Dinamik Dengedeki Cisimler Hareketsiz veya durgun
