JEODEZİ. Prof. Dr. Sebahattin BEKTAŞ
|
|
|
- Serhat Bagci
- 6 yıl önce
- İzleme sayısı:
Transkript
1 JEODEZİ Prof. Dr. Sebahattin BEKTAŞ SAMSUN 00
2 ii İÇİNDEKİLE.GİİŞ.. Temel Bilgiler ve Tanımlar..... Jeodezinin Ödevleri Dünanın Şekli ve Büüklüğü. 3.4 Potansiel Teorisi Gravite... ELİPS ve ELİPSOİD GEOMETİSİ. 8. Düna Elipsoidinin Boutlarının Belirlenmesi... Elipsoidal Coğrafi Koordinatlar. 6.3 Elipsoidde Enlem Çeşitleri: 9.4 Elipsoid Üzerinde Bazı Büüklüklerin Hesabı 3 3. YÜZEYLE VE EĞİLE Uza Eğrileri I. Dereceden Temel Büüklükler E, F, G Eğrilik.. 47 L M, N 3.4 II. Dereceden Temel Büüklükler, Normal Kesit Ve Eğik Kesit Jeodezik Eğri Jeodezik Eğrilik Clairaut Denklemi Elipsoid Yüzeinde Ugulamalar Elipsoid Yerine Kürenin Kullanılması KÜEDE JEODEZİK HESAPLAMALA Küre Geometrisi Küre Üzerinde Bazı Büüklüklerin Hesabı Küre Yüzeinde Özel Eğriler Küre Yüzeinde Üçgen Hesabı Küresel Trigonometri Teoremleri Küresel Üçgenlerin Çözümleri Küresel Koordinat Sistemleri Coğrafi Koordinatlar Kartezen (Global Dik) Koordinat Sistemi Küresel Jeodezik Dik Koordinat Sistemleri Soldner Sisteminde Temel Ödev Çözümleri Küre Yüzeinde Jeodezik Kutupsal Koordinatlar Soldner Koordinatlarıla Coğrafi Koordinatlar Arasında Dönüşümler Küre Yüzeinde Kestirme Hesapları Önden Kestirme Geriden Kestirme 4.9 Kürede Jeodezik Hesaplamaların Düzlem Esaslara Göre (İndirgemele) Yapılması Küre Yüzeinde İndirgeme Formüllerile Kestirme Hesapları 9 4. Kürede Önden Kestirme Kürede Geriden Kestirme. 4.3 Küre Yüzeinde Poligon Hesabı. 4
3 iii 5. HAİTA POJEKSİYONLAI Projeksionların Sınıflandırılması Kürenin Düzleme Ordinat Koruan Projeksionu Kürenin Düzleme Gauss-Krüger Projeksionu Küresel Coğrafi Koordinatlardan Gauss-Krüger Koordinatlarının Hesabı Ordinat Koruan ve Gauss-Krüger Projeksionun Karşılaştırılması NİENGİ(YATAY KONTOL) NOKTALAI Nirengi Ağlarının Konum,Ölçek ve Yönünün Belirlenmesi ELİPSOİDDE JEODEZİK HESAPLAMALA Dönel Elipsoidin Yerleştirilmesi ve Yöneltilmesi Elipsoid Yüzeine İzdüşümler ÖLÇÜLEİN ELİPSOİD YÜZEYİNE İNDİGENMESİ Yata Doğrultuların Elipsoid Yüzeine İndirgenmesi Uzunlukların Elipsoid Yüzeine İndirgenmesi Elipsoidde Üçgen Hesabı Elipsoidal Koordinat Sistemleri Elipsoidal Jeodezik Dik Koordinat Sistemi Elipsoidal Coğrafi Koordinatlarla Temel Ödev Hesapları Elipsoid Yüzeinde Jeodezik Dik Koordinatlarla Temel Ödev Çözümleri Küresel Hesaplamalarla Elipsoidde Temel Ödev Çözümleri ELİPSOİDİN DÜZLEME GAUSS-KÜGE POJEKSİYONU Gauss-Krüger Projeksionunda Yaklaşma Açısı Coğrafi Koordinatlardan Gauss-Krüger Koordinatlarının Eldesi Harita Paftalarının Bölümlemesi ve Pafta Köşe Noktalarının Koordinatlarının Bulunması Gauss-Krüger Koordinatlarından Coğrafi Koordinatların Bulunması Gauss-Krüger Projeksion Yüzeinde Hesaplamalar Ölçülerin Gauss-Krüger Projeksion Yüzeine İndirgenmesi UTM Projeksionu Değiştirilmiş UTM Projeksionu Gauss-Krüger Projeksionunda Komşu Dilimler Arasında Koordinat Dönüşümü ÜÇ BOYUTLU JEODEZİ ve GPS Üç Boutlu Jeodezi Global ve Yerel Dik Koordinat Sistemi ve Aralarında Dönüşümler. 0.. Udu Jeodezisi Sistemleri GPS Küresel Konumlama Sistemi GPS Koordinatlarından Ülke Koordinatlarına Dönüşüm GPS Yüksekliklerinden Ortometrik Yüksekliklerin Eldesi... KAYNAKLA. 5
4 Temel Tanımlar. GİİŞ.. TEMEL BİLGİLE ve TANIMLA JEODEZİNİN TANIMI VE TAİHÇESİ: İlk çağlardan günümüze kadar, bir andan insanoğlunun üzerinde aşadığı dünanın şekil ve büüklüğünü öğrenme merakı, diğer andan savunma, ulaşım, baındırlık ve kadastral hizmetlerin ürütülmesi için gerek duulan harita apımı ve ugulaması çabaları jeodezi biliminin doğma ve gelişmesine neden olmuştur. Jeodezinin ugarlık tarihinin ilk mesleklerinden olduğu tartışma götürmemektedir. M.Ö. 400 ıllarında Mısır da Nil nehri çevresinde aşaan insanların, Nil nehrinin taşması sonucu ekilen arazilerinin zarar görmesi ve arazi sınırlarının eniden belirlenmesi çalışmalarından (mülkiet kadastrosu) ilk jeodezik faaliet olarak bahsedilmektedir. Anı dönemde ilk düna haritası Babilliler tarafından bir tablet üzerine çizilmiştir. Bu tarihten günümüze kadar jeodezi bilimi bilimsel ve teknolojik gelişmelere bağlı olarak pek çok gelişme geçirmiştir. Bugün jeodezi udu tekniklerini ve bilgi sistemlerini agın olarak kullanan bir noktaa gelmiştir. Jeodezi kelimesi köken olarak; jeo: er, dezi: ölçmek, bölmek anlamına gelen iki kelimenin birleşmesinden ortaa çıkmıştır. Ancak buradaki -dezi son ekininin Jeodezi kelimesi dışında hemen hemen hiç kullanılmaması Jeodezinin kamuou tarafından anlaşılmasını olabildiğince güçlendirmiş ve uzun ıllar jeodezi kelimesinin ülkemizde eterince anlaşılamamasına neden olmuştur. Jeodezi basit tanım olarak er ölçüsü anlamına gelmektedir. Jeodezinin daha genel tanımı için, eruvarının tamamının a da bir parçasının zamana bağlı olarak şeklini, büüklüğünü ve çekim alanını belirlemei amaç edinmiş bir bilim dalıdır diebiliriz. Bu tanımlamadan jeodezinin iki temel görevinin olduğu ortaa çıkmaktadır. Bunlardan birincisi kapsam olarak matematik jeodezie giren eruvarının şekli ve büüklüğünü belirlemek, pratik anlamda eruvarının tamamının a da belli bir parçasının bir ölçek dahilinde
5 Matematik Jeodezi S.Bektaş küçültülüp bir altlık üzerinde gösterilmesidir. Diğeri ise fiziksel jeodezie giren erçekimi-gravite vektörünün büüklüğünü ve önünü (çekül doğrultusunu) belirlemektir. Jeodezinin bu iki temel görev alanının sınırlarını kesin olarak birbirinden aırmak mümkün değildir. Örneğin tüm jeodezik ölçümlerde çekül doğrultusunun referans alınması fiziksel jeodezii matematik jeodezinin içine sokmaktadır. Fiziksel erüzünün tamamının vea bir parçasının şeklinin ve büüklüğünün belirlenmesi a da diğer bir deişle haritasının çıkarılması için erüzünde eter sıklıkta ve doğrulukta noktaların konumlarının (üç boutlu koordinatlarının) belirlenmesi gerekir. Bu konum belirleme işlemi düna için seçilecek bir üç boutlu dik koordinat sistemi üzerinde gerçekleştirilebilir. Buna üç boutlu jeodezi (3D) dioruz. Konum belirleme probleminin diğer bir çözümü de klasik parçalı aklaşımdır. Klasik parçalı aklaşımda (D+D), ata konum ve düşe konum arı arı belirlenir. Önce erüzündeki noktalar seçilen bir referans üzeine (elipsoid, küre, teğet düzlem) izdüşürülür ve apılan doğrultu ve uzaklık ölçülerinden ararlanarak noktaların bu referans üzei üzerindeki ata konumları (D) belirlenir. Noktaların düşe konumları (D) için söz konusu izdüşüm noktaları ile asıl noktalar arasındaki uzaklıklar arıca belirlenir. Pratik gereksinimler için klasik parçalı aklaşım öntemleri günümüzde de geçerliliklerini korumaktadırlar. Bu kitabın kapsamı genel olarak (D) jeodezi tekniklerini içermektedir. Jeodezii oluşturan alt bilim dalları: ) Matematiksel Jeodezi: Yapılan uzunluk, doğrultu (açı) ve ükseklik farkı ölçmelerinden ararlanarak, dünanın belirli bir kısmının şeklini belirlemek için apılan işlemlerin tümü matematiksel jeodezii oluşturur. ) Fiziksel Jeodezi: Yerçekimi (g) ivmesi ölçmelerinden ararlanarak dünanın şeklini belirlemei amaç edinmiş bir bilim dalıdır. Çekim alanlarının belirlenmesi fiziksel jeodezinin konusudur. 3) Udu Jeodezisi: Udularla apılan uzaklık ölçmesi, faz farkı ölçmeleri ve fotoğrafik gözlemler sonucu noktaların konumlarının belirlenmesile ilgilenir. 4) Jeodezik Astronomi: Yerüzü noktalarının enlem ve bolamlarını, bazı kenarların semtlerinin ıldız rasatlarıla belirlenmesini konu edinir.
6 Temel Tanımlar. JEODEZİNİN ÖDEVLEİ: Jeodezinin ödevlerini iki grupta toplaabiliriz[]. I.grupta jeodezinin katkısıla ve diğer disiplinlerle ortak ürütülen faalietler olarak; - Toplu halde aşama ilkesine önelik Toplumsal faalietler (Savunma,kadastro,imar ugulaması,arazi toplulaştırması) - Doğaı tanımaa önelik Bilimsel faalietler (Dünanın şekli, büüklüğü ve gravite alanının belirlenmesi,er dinamiği problemleri gibi) - Doğaı eniden düzenlemee önelik Teknolojik faalietler (Yol,baraj,içme suu,enerji iletimi,kanalizason,sulama ve kurutma faalietleri gibi) II.grupta alnızca jeodezik faalietler olarak; -Temel ağların(nirengi,nivelman,gravite) kurulması ve aşatılması -Temel haritaların apımı ve güncelleştirilmesi -Jeodezik veri tabanı CBS(coğrafi bilgi sistemi) oluşturma ve sürdürme saılabilir..3 DÜNYANIN ŞEKLİ ve BÜYÜKLÜĞÜ İlk çağlardan beri insanların üzerinde aşadıkları doğaı tanıma meraklarından dolaı dünanın şekli ve büüklüğü konusu ilgisini çekmiştir. İnsanların doğaı tanıma merakları bilimsel faalietlerin odak noktasını oluşturmuştur. Gerçekten de bugün pek çok bilim dalı, doğaı, doğadaki olaların neden ve sonuçlarını araştırmakta ve bunları kurallara bağlamaa çalışmaktadır. Gerek bilimsel amaçlara, gerekse pratik amaçlara önelik olsun jeodezik çalışmaların değerlendirilebilmesi için erüzünün gerçek şekline bir model kabul etmek ve bu modelin tanımını apmak gerekir. Yerüzünün modeli olarak, erin atmosfer ile arakesitini almak mümkün değildir. Her ne kadar düna denizleri (okanuslar) düzenli bir şekil gösteriorsa da çeşitli engebeleri olan kara parçalarında böle bir düzen oktur. Yerüzünün modeli olarak alınacak üzein erin fiziksel apısına ugun olması, matematik olarak ifade edilebilmesi ve ölçü işlemleri ile bağlantısının kola olması gibi özellikler beklenir[4],[6], [0]. 3
7 Matematik Jeodezi S.Bektaş İlk çağlardan günümüze kadar dünanın şekli hakkındaki varsaımlar değişik aşamalar geçirmiştir. Yeruvarının şekli olarak tarihsel süreç içinde sırala düzlem,küre,elipsoid ve jeoid şekilleri alınmıştır [5]. M.Ö.400 ıllarında Babillilere göre dünanın şekli etrafı denizlerle çevrili bir daire,disk (düzlem) olarak kabul edilmiştir. Bu tarihlerde Hecetaeus (M.Ö ) apmış olduğu ilk harita Şekil- de görülmektedir. Şekil Hecetaeus un düna haritası M.Ö.600 ıllarında Pisagor kardeşlerce, düzenli üzeler arasında en ugunun küre olması düşüncesi ile erin şeklinin küre biçiminde olduğu ileri sürülmüştür. Aristoteles (M.Ö.384-3) de apmış olduğu gözlemlerle dünanın şeklinin küre olması gerektiğini ileri sürdü. Aristoteles; belirli bir önde gidildiğinde ufkun sürekli değişmesi, açık denizden karaa aklaşan bir geminin önce bacasının sonra güvertesinin görünmesi ve a tutulmasında dünanın a üstündeki gölgesinin daire aı biçiminde olması gibi nedenlere daalı olarak erin şeklinin küre olduğunu ispatlamaa çalışmıştır. Dünanın şekli olarak alınan kürenin arıçapını ölçülere daalı olarak belirleen ilk bilgin Erastosthenes tir (M.Ö.50). Erastosthenes den sonra da daha bir çok bilim adamı dünanın şekli olarak kabul edilen kürenin arıçapını belirlemek için çalışmalar apmıştır. 4
8 Temel Tanımlar Yata İskenderie Asuan H S 7. 0 Şekil. Şekil. Erastosthenes, Bugün Mısır da bulunan Asuan da güneş ışınlarının ere tam dik geldiği anda ertesi ıl anı anda İskenderie de güneş ışınlarının ere düşele 7. 0 açı aparak geldiğini ölçerek belirlemiştir. Yerin küre olduğu varsaımından hareketle bu açının İskenderie ile Asuan kentini erin merkezinde gören açı olduğu ortaa çıkar (şekil. ). İki şehir arasındaki uzaklık o zamanki uzunluk ölçü birimi stada ( Stada = 85m) biriminden 5000 stada olduğu belirlenmiştir. Bu durumda eruvarının arıçapı, merkez açı = a / arıçap eşitliğinden a= S/ ms m ma=? ds d da=? Diferansiel da= (/).ds (/ ).S.d Hata aılma kuralı ma = (/).ms (/ ).S.m (arıçap) = 5000 stada / (7. 0 / 0 ) = stada = 736km. 5
9 Matematik Jeodezi S.Bektaş 0 = 80 0 / = (derecei radana çevirme katsaısı) olarak belirlemiştir. Yunanlı astronom ve coğrafacı Batlamus un (Ptolemius) (87-5) azdığı 3 ciltlik Almagest ölümünden sonrada çok uzun süre astronomlara el kitabı oldu. 87 de Arapçaa.üzılda latincee çevrildi. Bugünkü anlamda eski çağ dünasının ilk haritasını (şekil- 4) aptı. Şekil 4 Yerin arıçapı değişik bir şekilde de Biruni ( ) tarafından belirlenmiştir. Biruni, deniz kıısında (H) üksekliği belli olan bir tepede deniz ufkuna apılabilen bir gözlemle ata ile ufuk arasındaki ölçülebilen düşe açının () eruvarı merkezindeki açıa eşit olacağından hareketle eruvarı arıçapının (şekil-.) den cos = H = H cos cos 6
10 Temel Tanımlar biçiminde hesaplanabileceğini göstermiştir. Biruni bu işlemi Hint okanusu kıısında, denizden üksekliği H = 65 arşın olan Zira-El-Sevda dağında aparak açısını 33' olarak ölçmüş ve arıçapı 3333 Arap mili ( km) ve derecelik meriden aı uzunluğunu 58. Arap mili (8. km) ve erin çevresini 456 km olarak hesaplamıştır. Ancak teorik daanağı tam olan bu öntem pratikte düşe açılar üzerindeki refraksion (ışın kırılması) etkisinin tam olarak giderilememesi üzünden hatalı sonuçlar vermektedir. Yeruvarının büüklüğü karşılıklı düşe açı ölçümlerinden de ararlanarak belirlenebilir(şekil-3). = Z + Z = a / arıçap = S / den eruvarının arıçapı = o S / eşitliğinden bulunur. Şekil 3 Bu önteme göre birbirini gören ve olabildiğince birbirinden uzak iki nokta arasında karşılıklı düşe açı ölçümleri (Z, Z ) ve noktalar arası a uzunluğu (S) den aralanarak bu S uzunluğuna karşılık gelen merkez açı bulunabilir. Ancak bu öntemde de düşe açılar üzerindeki refraksion etkisi nedenile sağlıklı sonuçlar alınamamaktadır. Örnek: Dünanın arıçapının aklaşık olarak belirlenmesine önelik olarak birbirinden 30km uzaklıktaki iki tepeden birbirine karşılıklı olarak düşe açı gözlemi apılmış ve Z = ve Z = değerleri ölçülmüştür. Söz konusu ölçümlerden ararlanarak dünanın arıçapının belirleiniz. Bu öntemle arıçap belirlemenin ne gibi sakıncaları olacağını irdeleiniz. 7
11 Matematik Jeodezi S.Bektaş Örnek:Deniz kıısında üksekliği H olan bir tepeden deniz ufkuna bakılıor ve düşe açı değeri Z=00.5 g olarak ölçülüor. Buna göre H üksekliğini bulunuz. Örnek:Yeruvarının arıçapının belirlenmesine önelik olarak; H=580m üksekliğindeki bir tepeden deniz ufkuna olan düşe açı, Z=00,86 g olarak ölçülmüştür. Yeruvarının arıçapını belirleiniz. Örnek: Deniz kıısında üksekliği H olan bir tepeden deniz ufkuna bakılıor ve düşe açı değeri Z=00.35 g olarak ölçülüor. Buna göre H üksekliğini bulunuz. Cevap: α = 0.35 g H = H=96,68m 8
12 Temel Tanımlar Örnek: Deniz kıısında bou 70cm olan birisinin görebileceği ufuk mesafesini hesaplaın. Haag Leiden Willemstadt Leidenden geçen meriden A (A)Alkmaar Amsterdam Haarlem Utrecht Gouda Dortrecht (B)Bergen op Zoom B Breda Şekil-4 Snellius un triangülason ağı O dönemlerde eruvarı büüklüğünün belirlenmesinde dar boğazın uzunluk ölçüsünde olduğu görülmektedir ıllarındaki ölçme aletleri düşünüldüğünde, kilometrelerce uzunluğun belirli bir incelikte ölçülmesi oldukça zor, hatta olanaksız olacağı tahmin edilebilir. Bu dar boğaz triangülason ile ortadan kaldırılmıştır. Bu öntemle, birbirine göre çok uzakta olan iki nokta arasındaki uzaklık, araa kurulacak zincir üçgenler ardımıla dolalı olarak bulunabilmektedir. 65 de Snellius tarafından Hollanda da kurulan bu triangülasonun (şekil-4) açıları arıçapı.5 aaklık kuadrant denilen çerek daire aı biçimindeki açı ölçü aleti ile ölçmüştür. Açı ölçmelerinde ' ( derece dakikası) direkt ve ' da tahmin şeklinde okunmaktadı. Bu üçgen zincirinin bir kenarı Haag-Leiden arası baz olarak rute bulunmuştur ( rute = 3,767m). Zincirin en kuze ve 9
13 Matematik Jeodezi S.Bektaş en güneindeki Alkmaar ve Bergen op Zoom da apılan astronomik gözlemlerle bu noktaların enlemleri hesaplanmıştır. Bu enlem değerleri, A = ve B = olup, bu iki nokta arasındaki enlem farkı = 0 30 dir. Triangülason ardımıla bu aa ait meriden uzunluğu rute, buradan eruvarının çevresi 38640km olarak bulunmuştur. Benzer öntemle ıllarında Picard, Malvoisine ile Amiens arasına (Paris merideni) 3 üçgenlik bir zincir döşeerek derecelik meriden bounu.km. buna göre eruvarının çevresi km ve eruvarının arıçapını da 637.9km olarak bulmuştur. 7.üzılın ortalarına kadar erin şekli küre şeklinde sanılıorken, iki Hollandalı fizikçi Hugens ve hemen sonra Newton, erin kendi ekseni etrafında dönmesinin, şeklini etkileeceği, bölece bu şeklin kutuplarda basık bir küre ani, dönel elipsoid olması gerektiğini ileri sürmüşlerdir. Fransız Bilimleri Akademisi fizikçilerin bu iddialarını ispatlamak için farklı enlemlerde meriden a bolarının ölçümüne karar verdi. Cassini ailesi tarafından gerçekleştirilen a bou ölçümlerinden beklenenin tam tersine derecelik a bounun kutuplara doğru azaldığı ortaa çıkmıştı bu ölçümlere göre düna kutuplardan değil de ekvatordan basık oluordu. Kısa sürede bu çelişkinin apılan bir hesap hatasından kanaklandığı anlaşılmıştı. Akademi tarafından eniden Lapona ve Peru a gönderilen iki ekibin aptığı meriden aı ölçmeleri sonucu dünanın şeklinin kutuplarda basık bir elipsoid olduğu eniden kanıtlanmıştır. 8.üzıl ortalarında elipsoid üzerinde apılan hesapların ölçü inceliğinin ötesinde bazı çelişkiler göstermesi sonucu, eruvarının şekli olarak elipsoidin de eterli bir tanım olamaacağı anlaşılmıştır. Bu konuda diğer önemli bir kanıt da çekül sapmalarıdır. Bilindiği gibi çekül sapması bir noktada elipsoid normali ile çekül doğrultusu (jeoid normali) arasındaki açıdır. Yapılan jeodezik ve astronomik ölçüler elipsoid normallerinin çekül doğrultusunda olmadığını göstermiştir. Bu amaçla 873 ılında Listing tarafından erüzüne en ugun şekil olarak Jeoid tanımlanmıştır. JEOİD: üzgar, dalga, gel-git, ısı değişimi, akıntılar gibi dış bozucu etkilerden arınmış olarak düşünülen ortalama okanus üzeinden ve bunun karalar içinde de devam ettiği varsaılmasıla oluşan kapalı bir denge üzeidir. 0
14 Temel Tanımlar Bir eşpotansielli üze (nivo üzei) olan jeoidin şeklini erin çekim kuvveti belirler. Çekim kuvvetinin doğrultusunu her noktada bir çekülle belirleme olanağı vardır. Jeoid her noktasında çekül doğrultusula dik açı apar. Yerin kitle dağılımı düzensiz olduğu için buna bağlı olan çekül doğrultuları da düzensizdir ve bunun sonucu olarak çekül doğrultularına dik jeoid üzei basit geometrik bir üze olmakla beraber şekil önünden genel olarak bir dönel elipsoid üzeinden çok farklı olmaan bir üzedir. Helmert bir jeoid üzei ile onun erine alınacak bir elipsoid üzei arasında en çok 00 m. ükseklik farkı olabileceğini sölemiştir. Düna için kabul edilen referans elipsoidi ile jeoid arasında her noktada değişen ükseklik farkı vardır. Eksi ve artı olabilen bu farklara jeoid üksekliği (jeoid ondülasonu) denir ve N j ile gösterilir. Çeşitli iç ve dış kuvvetlerin etkisile jeoidin ondülasonlu bir apısı vardır. Son ıllarda apılan udu gözlemlerinden, Hint Okanusunda deniz düzeinin ortalama deniz düzeinden aklaşık 00m daha alçak olduğu tespit edilmiştir. Bu çöküntüde olan bir gemi erin merkezine 00m daha akındır. Geminin çöküntüü terk edebilmesi için 00m ükseklikli bir dağa tırmanması kadar ek bir güç harcaması gerektiği akla gelebilir. Ancak deniz üzeinin eş potansielli üze (nivo üzei) oluşu nedenile gemi hiçbir ek güç harcamadan bu çöküntüü terk eder. eferans elipsoidi ile jeoidin uumu seçilen ortak bir noktada (genellikle çalışma bölgesinin ortalarında) elipsoid jeoide teğet hale getirilir. Bölece elipsoid normali ile anı noktadaki çekül doğrultusu da çakışır (N j =0 ve =0 ). Yerüzünün bu ortak noktası dışındaki diğer bütün noktalarda elipsoid jeoidle çakışmaz ani N j jeoid üksekliği ve çekül sapması değerleri sıfırdan farklı olur. Eş potansielli üzein her noktasında potansiel sabittir. Dengede bulunan durgun su üzei bir eş potansielli üzedir. Dünada sonsuz saıda eş potansielli üze düşünülebilir (şekil 5). Örneğin deniz seviesinden üksekteki bir krater gölünün su üzei de eş potansielli bir üzedir. Eş potansielli üzeler her noktasında çekül doğrultusula dik açı apar. Eş potansielli üze olan jeoidin şeklini erin çekim kuvveti belirler.
15 Matematik Jeodezi S.Bektaş Çekim kuvvetinin (gravitenin) doğrultusunu her noktada bir çekülle belirlemek mümkündür. Yerüzünün büük kısmının % 73 ünün okanuslarla kaplı oluşu ve doğada gözle görülebilmesi eş potansielli üzelerden jeoidin erüzünün şekli olarak alınmasını daha da anlamlı kılmaktadır. Eş potansielli üzeler birbirini kesmez, sürekli ve uvarlaktırlar (köşesizdirler). Eş potansielli üzeler er kitlelerinin homojen oğunlukta olmaması nedenile birbirlerine paralel değildirler. Çekül doğrultusu... Şekil-5: Eşpotansielli Yüzelerin Gösterimi... Jeoid Eş potansielli üzeler (Nivo üzei) Tüm eş potansielli üzeleri normal olarak(dikine) kesen eğriler tam doğru olmaıp, hafifçe eğridirler. Bunlara çekül eğrileri denir. Herhangi bir noktadaki gravite vektörü bu noktadaki çekül eğrisine teğettir. Yerüzüne en ugun şekil, matematiksel ve fiziksel kavramlarla tanımlanabilen jeoid dir. Yani jeoid geometrik bir üze değil fiziksel bir denge üzeidir..4 POTANSİYEL TEOİSİ Çekim ve Potansiel: Newton çekim asasına göre bütün cisimler birbirlerini kütlelerinin büüklüğüle doğru orantılı aralarındaki uzaklığın karesile ters orantılı olacak şekilde çekerler. Newton çekim asasına göre kütleleri m ve m aralarındaki uzaklık l olan iki cisim G kuvvetile birbirlerini çekerler, m m G = - k l m l m
16 Temel Tanımlar Bu G kuvveti cisimleri birleştiren doğru bouncadır. k a newton çekim sabiti denir ve değeri k = 66.7 x 0-9 cm 3 g - sn - dir. Her ne kadar m ve m kütleleri birbirini tam bir simetri ile çekerlerse de geleneksel olarak bunlardan birine çeken, diğerine de çekilen kütle adı verilir. Kolalık sağlaması amacıla burada çekilene birim kütle çekene de alnızca m denecektir. m l G = - k formülü m kütlesinin kendisinden l kadar uzaklığındaki bir birim kütle üzerine uguladığı kuvveti vermektedir. Çekim potansieli adı verilen skaler fonksion V = m k l olur. Çekim kuvveti G nin bileşenleri G = (x,, z) = grad V şeklinde azılır. Bölece kuvvet vektörü skaler fonksion V nin gradient vektörü olur. Eğer m, m,..., m n gibi nokta kütlelerinden oluşan bir sistem söz konusu ise, bu sistemin potansieli her bir nokta kütlesinin katıldığı bir toplam olan V = m k l m + k l m n k = l n n k i ile verilir. Hacim elemanı dv, kütle elemanı da dm olmak üzere oğunluğun = dm dv şeklinde tanımlandığı bir v hacmi içinde nokta kütlelerinin kesiksiz bir dağılımı olduğu düşünülürse toplam potansiel V = k V dm k l V dv l şeklinde integralle ifade edilir. Buradaki l, kütle elemanı dm = dv ile çekilen nokta arasındaki uzaklıktır. m l i i.5 GAVİTE Yerüzünde duran bir cisme etki eden kuvvet, Newton çekim asasına göre oluşan bir çekim kuvveti ve eruvarının kendi ekseni etrafında dönmesile oluşan merkezkaç kuvvetin bileşkesidir. Bu iki kuvvetin bileşkesi o noktadaki 3
17 Matematik Jeodezi S.Bektaş gravite vektörünü verir. Bilindiği gibi gravite vektörü o noktadaki eğrisinin teğetidir (Şekil-6). çekül Merkezkaç kuvvet : Bir birim kütle üzerindeki merkezkaç kuvvet f, eruvarının kendi ekseni etrafında dönüşünün açısal hızı w ile kütlenin dönme eksenine olan dik uzaklığı r = olmak üzere x Z r G g Çekül Eğrisi f f = w r Şekil-6 Gravite Vektörü X,Y şeklinde tanımlanır. Merkezkaç kuvvet anı zamanda F = türetilebilir. F F F f gradf (,, ) x z w r şeklinde bir potansielden de Çekim kuvveti ile merkezkaç kuvvetin bileşkesi olan toplam kuvvete gravite denir. Gravitenin W potansieli, çekim kuvvetinin V potansieli ile merkezkaç kuvvetin F potansielinin toplamına eşittir ; ani, W = W(x,,z) = V + F = k dv w r l V olup integral tüm eruvarını kapsamaktadır. Yukarıdaki ifadee bakıldığında merkezkaç potansielin basit bir analitik fonksion olmasına karşılık V çekim potansieli, üzerinde işlemler apılması en güç olan parçaı oluşturur. Merkezkaç kuvvet olan F = w r ifadesinin türevi F F F F x z w eşitliğini verir. Bu eşitlik V için verilen V = -4 k poisson denklemi ile birlikte ele alınırsa W gravite potansieli için W = -4 k + w olan genelleştirilmiş poisson denklemi elde edilir. W nin gradient vektörü, g W W W gradw (,, ) x z olup 4
18 Temel Tanımlar g x = W x, g = W, g z = W z dir. Bileşenlerile gravite vektörü adını alır. Bu bir birim kütlee etki eden toplam (çekim+merkezkaç) kuvvettir. Bir vektör olarak büüklüğü ve doğrultusu vardır. g büüklüğüne gravite denir. Boutu bir ivmenin fiziksel boutu olup gal ile ölçülür ( gal = cm/s ). g nin saısal değeri aklaşık olarak ekvatorda 978 gal, kutuplarda 983 gal dir. Eşpotansielli üzein her noktasında potansiel sabittir. Dengede bulunan durgun su üzeinin her noktasında çekül doğrultusu dik açı apar. Bu eşpotansielli üzein üzerinde bir cisim hareket ettirilirse hiçbir iş apılmaz. da g* dl olur. g dl İş = kuvvet x ol ilişkisinde vektör gösterimile er çekimi kuvveti g olmak üzere diferansiel anlamda apılan iş, olduğu için bu iki vektörün skaler çarpımı, da g dl cos olur. = 90 olduğu için da = 0 olur. Buna karşılık bir kitle çekül doğrultusundan kaldırılırsa çekül doğrultusundaki ol dh olmak üzere apılan iş, da g* dh g dh cos ve = 0 o ile da = g *dh olur. Herhangi bir su üzeinde H = 0 alınırsa, bu üzein bir noktasından başlamak üzere çekül doğrultusunda bir birim kitle sonsuz üksekliğe kaldırılırsa burada A = gdh = - W işi apılmış olur. Burada W, o su üzeinin o potansieli adını alır. O halde bir su üzeinin potansieli bir birim kitlenin sonsuz ükseklikten su üzeinin bir noktasına indirilmesinde kabedilen iştir. Burada dw = - g dh = - da dır. Bir birim kitle dengedeki bir su üzeinde taşınırsa hiçbir iş apılmaacağından potansielde değişmez. Dengedeki bir su üzei eşpotansielli bir üzedir ve böle sonsuz saıda üze düşünülebilir. Bunlardan bir tanesi de jeoiddir. Eşpotansielli üzeler birbirini kesmez, sürekli ve uvarlaktırlar(köşesizdirler). Tüm eşpotansielli üzeleri normal olarak(dikine) kesen eğriler tam doğru olmaıp, hafifçe eğridirler. Bunlara çekül eğrileri denir. Herhangi bir noktadaki gravite vektörü bu noktadaki çekül eğrisine teğettir. 5
19 Matematik Jeodezi S.Bektaş İki eşpotansielli üzein herhangi iki noktası arasındaki potansiel farkı sabittir (Şekil-7). O halde birbirine çok akın böle iki üzein iki noktasındaki çekül doğrultusunda potansiel farkı w = w' w = -g H = -g H olur. P' P' w' sabit H H g g P P Şekil-7 w sabit P ve P noktalarındaki erçekimi ivmeleri erin coğrafi enlemine ve noktalardaki kitle oğunluklarına bağlı olarak değişir. Yani g g olur. O halde ukardaki eşitliğin sağlanabilmesi için H H olmalıdır. Buradan eşpotansielli üzelerin birbirine paralel olmadıkları sonucu ortaa çıkar. Bir nivo üzeinin bir noktasından çekül doğrultusunda jeoide olan uzaklığına o noktanın ortometrik üksekliği (H) denir. Herhangi iki noktanın potansiellerinin eşitliği ortometrik üksekliklerinin eşitliğini gerektirmez. Düzlem Küre Elipsoid Şekil-8: Düzlem, Küre ve Elipsoid Yüzelerinde Yüze Normallerinin Gösterimi Yukarıdaki şekillerde dünanın erine hesap üzei olarak alınacak çeşitli üzelerde üze normallerinin nasıl olduğu gösterilmektedir. Matematiksel jeodezide, jeoide en ugun ve çok akın olan dönel elipsoidle çalışılır. 6
20 Temel Tanımlar karalar denizler b a Fiziksel erüzü Jeoid Elipsoid Küre X Y Doğruluk Düzlem Küre Elipsoid Jeoid Kolalık Teğet Düzlem Şekil-9 Düna için alınabilecek referans üzeleri Bu nedenle jeodezik ugulamalarda ölçme ve hesaplamalara kolalık sağlaan geometrik üzeler kullanılır(şekil-9). Söz konusu geometrik üzeler sırasıla; dönel elipsoid, küre ve düzlemdir. Çok büük alanların ölçülmesinde dönel elipsoid referans (daanak) üzei olarak kullanılır. Daha küçük alanların ölçülmesinde küre ve düzlem (eruvarına teğet) referans üzei olarak kullanılır. Genelde jeodezik çalışma bölgesi alan olarak, 500 km den küçük ise plan ve deta çalışmaları için eruvarının şekli düzlem alınmakta (ükseklik boutu için küresellik dikkate alınmalıdır), km aralığında alanlar için arıçapı g = MN şeklinde hesaplanacak küre, 5000 km den daha büük alanlar için eruvarının şekli dönel elipsoid olarak alınır. Yukarıdaki gösterimden de (şekil-7) anlaşılacağı gibi, jeodezik çalışmalarda hesaplama kolalığı aranınca doğruluktan ödün verilmesi, doğruluk istenince de hesaplamaların zorlaştığı ortaa çıkmaktadır. Günümüzde gelişen bilgisaar 7
21 Matematik Jeodezi S.Bektaş teknolojisi saesinde hesaplama zorluğu büük ölçüde ortadan kalkmıştır. En karmaşık hesaplamalar bilgisaarlar aracılığıla çok hızlı ve doğru bir şekilde apılabilmektedir. Jeoid Normali (Çekül doğrultusu) Elipsoid Normali Fiziksel erüzü N.. Jeoid Elipsoid : çekül sapması g: erçekimi ivmesi N: jeoid üksekliği g Şekil-0 Fiziksel erüzünde Elipsoid ve Jeoidin bir arada gösterimi Jeodezik hesaplamalarda hangi referans üzei kullanılacaksa o üzee ait jeodezik bağıntılarla (geometri ve trigonometri kurallarıla) hesaplama apılır. Yeruvarı için söz konusu olabilecek referans üzelerinden elipsoid daha genel bir üze olduğundan elipsoid üzerindeki jeodezik bağıntılardan diğer üzeler (küre ve düzlem) için gerekli jeodezik bağıntılar rahatlıkla elde edilebilir. Zira elipsoidin arı eksen uzunlukları birbirine eşit alındığında elipsoid küree dönüşür. Anı şekilde düzlemi de arıçapı sonsuz olan bir küre olarak düşünebiliriz. Yeruvarı üzerinde bir noktada apılan jeodezik ölçmelerde (uzunluk, açı) esas olan o noktadaki düşei tanımlaan çekül doğrultusudur (jeoid normali). Osa elipsoid üzerindeki jeodezik hesaplamalarda elipsoid normalleri esas alınır. Bu nedenle elipsoid üzerindeki jeodezik hesaplamalarda bu farklılıklar dikkate alınır. Şekil-0 dan da görülebileceği gibi düna için kabul edilen referans elipsoidi ile jeoid arasında her noktada değişen ükseklik farkı vardır. Eksi ve artı değer alabilen bu farklara jeoid üksekliği (jeoid ondülasonu) denir ve N ile gösterilir. Helmert bir jeoid üzei ile onun erine alınacak bir elipsoid üzei arasında en çok 00m ükseklik farkı olacağını sölemiştir. Özet olarak eruvarının şekli olarak seçilecek referans üzeini çalışmadan istenen doğruluk ve çalışma bölgesinin büüklüğü belirler. Bu bağlamda; -Büük ölçekli haritaların apımında, Kent haritalarında ve mühendislik ölçmelerinde eruvarının şekli Düzlem alınır. Pratik jeodezik çalışmaların çok 8
22 Temel Tanımlar büük kısmında eruvarı için düzlem model esas alınır. Şüphesiz düzlem model harita bilgilerinin zemine işlenmesinde de (aplikasonda) büük kolalık sağlar. -Küçük ölçekli haritaların apımında, coğrafada ve orta doğruluktaki jeodezik hesaplamalar için eruvarının şekli Küre alınır. -Çok büük alanları (ülke, kıta çapında) kapsaan ve üksek doğruluk isteen jeodezik çalışmalar için eruvarının şekli Elipsoid alınır. -Düşe konumun (üksekliklerin) duarlı olarak belirlenmesinde eruvarının şekli olarak Jeoid modeli esas alınır. Ancak matematiksel olarak jeoidin tanımının güçlüğü nedenile gözlemler jeoid üzeine indirgenememekte ve dolaısıla jeodezik hesaplamalar jeoid üzerinde apılamamaktadır. Bu nedenlerle jeoid sınırlı ugulamalar dışında eruvarı için model olarak kabul edilmez. Yeruvarı için en ugun geometrik model olan elipsoid modelinin kullanılması genellikle jeodezi bilim dalına özgü bir durum olup diğer disiplinler küre modelini basitliği nedenile tercih ederler. Yerin şekline en ugun geometrik üze olan dönel elipsoidin, küreden farkı-ani basıklığı çok küçüktür (aklaşık /97) bu basıklık çıplak gözle fark edilemez. Dünadaki deniz seviesinden en büük ükseltinin Everest tepesi (8848m) ve dünanın arıçapının aklaşık 6370km olduğu düşünülürse Everest tepesinin dünanın arıçapına oranı /70 olur. Yani 70 birim arıçapında bir küre üzerinde Everest tepesinin üksekliği birim olur. Bu nedenlerle ugun konumda ve arıçaptaki bir kürenin eruvarının şekli olarak kabul edilmesi çoğu jeodezik çalışmalar için bile eterli olmaktadır. 9
23 Matematik Jeodezi S.Bektaş. ELİPS ve ELİPSOİD GEOMETİSİ z a b a F F E F b x x a b z Elips denklemi Şekil- Elips Elips: Tanım olarak F ve F gibi iki odak noktasına uzaklıkları sabit olan noktaların geometrik eri olarak tanımlanır. Bir elips, büük ve küçük arı eksen uzaklıkları olan a ve b ile tanımlanır. Bir elipsin basıklığı Şeklinde hesaplanır f a b a Elipsin doğrusal dış merkezliği E, odak noktasının elipsin merkezine olan uzaklığıdır. Dolaısıla ; E = a b E ile.eksentrisite (dış merkezlik) e ve.eksentrisite e e = E / a e = E / b olarak ifade edilir. Elips geometrik şekillerden çemberin genel durumudur. Diğer bir deişle elipsin özel bir durumu çemberdir. Elipsin arı eksenlerinin birbirine eşit olması (a = b) durumunda elips bir çembere dönüşür ve çemberin arıçapı ( = a = b) elipsin arı eksen uzunluğu olur. 8
24 Elips ve Elipsoid Geometrisi Elipsoid ve Dönel Elipsoid: Elipsoid deimi aslında merkezi üç boutlu bir dik koordinat sisteminin (XYZ) orjininde, X ekseni önünde arı eksen uzunluğu a, Y ekseni önünde arı eksen uzunluğu c ve Z ekseni önünde arı eksen uzunluğu b olan ve denklemi aşağıdaki gibi olan kapalı düzgün bir şekildir (şekil-). Z x a c z b Genel Elipsoid Denklemi a b c Y X Şekil- Elipsoid Jeodezide kullanılan dönel elipsoid,bir elipsin düşe Z ekseni (küçük arı ekseni) etrafında 80 o döndürülmesile elde edildiğinden X ve Y eksenleri bounca arı eksen uzunlukları birbirine (a = c) eşit olur (şekil-4). Bundan böle elipsoid kavramı dönel elipsoid erine kullanılacaktır. Elipsoid üç boutlu geometrik kapalı şekillerden kürenin genel bir halidir. Diğer bir deişle küre elipsoidin özel bir halidir( a = b = c = ). a Z b X Enlem D. Ekvator D. G a b L Z P a B Elipsoid normali Y Şekil-3 Elips X Bolam D. Şekil-4 Dönel Elipsoid x a z b Dönel elipsoidin denklemi 9
25 Matematik Jeodezi S.Bektaş 0 Elipsoid Parametreleri: Dönel elipsoid, meriden elipsinin verilmesile tanımlanır. Meriden elipsi de a büük arı eksen, b küçük arı eksen değerlerinin verilmesile belirlenir. Yarı eksen uzunluklarının her ikisinin verilmesile elipsin (elipsoidin) büüklüğü ve şekli belirli olur. Aşağıdaki parametreler elipsin sadece şeklini belirler. Bunlar; Elipsoidin basıklığı (f a da ), birinci eksentrisite (e ) ve ikinci eksentrisite (e' ) dir. Buradan bir elipsin büüklüğünün belirlenebilmesi için en az bir arı eksen uzunluğunun, elipsin şeklinin belirlenebilmesi için basıklık vea eksentrisitelerden herhangi birinin bilinmesinin a da hesaplanabilmesinin eterli olduğu ortaa çıkar. Elips geometrisinden kanaklanan nedenlerden dolaı elips ve elipsoid ile ilgili çoğu hesaplamalar kapalı formüllerle apılamaz ugun saısal teknikler kullanmak suretile eteri doğruluk veren aklaşık hesaplama öntemlerine başvurulur. Bu öntemlerden biride serie açma öntemidir. Basıklık ve eksentrisite değerlerinin den küçük sıfıra oldukça akın saısal değerler olmaları itibarile bunlara daanan seri açılımları hemen akınsar,serilerin ilk birkaç terimile etinilmesi halinde bile amaçlanan doğruluk elde edilir. Eksentrisiteler ve arı eksenler arasındaki diğer ilişkiler aşağıdaki gibidir ; c : kutup noktasındaki meriden eğrilik arıçapı ; b b a e ; a b a e ; a b a α f - e e e e e a e b e b e a e a b a c e e e e a b
26 Elips ve Elipsoid Geometrisi. DÜNYA ELİPSOİDİNİN BOYUTLAININ BELİLENMESİ Düna elipsoidinin büüklüğü ve basıklığının belirleme öntemleri iki ana grupta toplanabilir. Bunlar geometrik öntem ve dinamik öntemdir. Geometrik öntemde er üzerinde apılan a bou ölçümlerinden ve astronomik gözlemlerden ararlanılır. Dinamik öntem ise sarkaç vea gravimetri aletleri ardımıla apılan er çekimi ölçülerine daanır. Karalarda olduğu kadar denizlerde ve havada da gravite ölçüleri apılabildiğinden dinamik öntem daha pratik ve daha doğru sonuçlar verir. Ancak dinamik öntemle alnız elipsoidin basıklık değeri bulunabilir. a) GEOMETİK YÖNTEM Düna elipsoidinin (dönel elipsoidin) büüklüğünün ve şeklinin belirlenebilmesi için meriden elipsinin (elipsoidin dönme ekseninden geçen bir düzlemle arakesiti) belirlenmesi eterlidir. Bir elipsin belirlenmesi büük ve küçük arı eksenlerinin (a,b) bilinmesi a da bir arı eksenle elipsin şeklini veren basıklık ( f ) a da eksentirisitenin (e vea e ) bilinmesile mümkündür. Dünaı temsil edecek bir elipsoid için bu ölçüleri direkt olarak apmak mümkün değildir. Pratikte bu bout belirleme işlemi için anı meriden elipsi üzerinde iki a bou S ve S ölçülür ve bu aların uçlarındaki elips normalleri arasındaki açılar B ve B bilinirse S ve S küçük elips aları, aklaşık daire aları olarak alınırsa, meriden önünde eğrilik arıçapları M ve M S S M = M = B B eşitliklerinden hesaplanabilir(şekil-5). Diğer taraftan meriden elipsininin eksentrisitesi e = (a -b ) / a olmak üzere S a( e ) ( e sin B ) M = 3 / a( e ) ( e sin B ) M = 3 / a b M B B B M S B Şekil-5
27 Matematik Jeodezi S.Bektaş Yukarıdaki M,,M denklemlerinden e e = M ( M ) M ( M 3 sin ) 3 B sin B şeklinde çekilir ve daha sonra örneğin bulunan e değeri örneğin M denkleminde erine konarak a değeri ve istenirse b = eşitliğinden de b değeri hesaplanır. Yukarıdaki şekildeki B ve B enlemleri ilgili aların orta noktalarının elipsoidal enlemleridir. B ve B enlemleri astronomik gözlemlerle belirlenir. a e Görüldüğü gibi meriden elipsinin boutlarını belirlemek için bir çift a ölçüsü eterlidir. Eğer erin şekli gerçekten bir dönel elipsoid olsadı, arı arı a çiftlerinden hesaplanacak a, b değerleri ölçülerin doğruluk derecelerile orantılı farklılıklar gösterecektir. Osa erin değişik kesimlerinde apılan a ölçüleri çiftlerinden elde edilen a, b değerlerinde ölçü hatalarıla açıklanamaacak büüklükte farklar çıkmıştır. Buradan erin gerçek şeklinin elipsoid olmadığı ortaa çıkmıştır ve bunu ilk defa ünlü jeodezi bilgini Helmert ileri sürmüştür. Bu konuda diğer bir önemli kanıtda çekül sapmalarıdır. Bilindiği gibi çekül sapması bir er noktasında elipsoid normali ile çekül doğrultusu (jeoid normali) arasındaki açıdır. Yapılan jeodezik ve astronomik ölçüler elipsoid normallerinin çekül doğrultusunda olmadığını göstermiştir. Yerin gerçek şeklinin (jeoidin) tam bir dönel elipsoid olmaışı bilim adamlarını eni araışlara itmiş bu nedenle üç eksenli elipsoid ( üç eksenli bir elipsoid tartışmasız olarak dünaa dönel elipsoidden daha ii uum sağlar)ve hatta meriden kesiti elipsten biraz farklı dönel şekiller denenmiş ancak pratiğe arar sağlaacak bir sonuca ulaşılamamış ve sonuç olarak dönel elipsoidin jeoide en ugun düzgün geometrik şekil olduğu bir kez daha ortaa çıkmıştır. Örnek: Düna elipsoidinin boutlarının belirlenmesine önelik olarak iki farklı enlemde a bou ölçümleri apılmış ve ölçü değerleri aşağıda verilmiştir. Elipsoidin boutlarını (a,b), basıklığını (f) ve eksentrisite (e,e ) değerlerini bulunuz. Enlem(B) o lik a bou (S) B =30 o S = m B =45 o S = 8.60m
28 Elips ve Elipsoid Geometrisi Çözüm: Önce B ve B enlemlerindeki meriden önündeki ana eğrilik arıçaplarını M ve M i bulalım B =B = 0 M = S B I.eksentrisite değeri e e = M ( M ) M ( M 3 sin ) 3 büük arıeksen a a( e ) ( e sin B ) = m M = B sin M = 3 / a = M ( e sin ( e B ) ) 3 / B = den çekilirse küçük arıeksen b b = a e = m Geometrik basıklık f f = = m a = / = b a II.eksentrisite değeri e e = (a -b ) / b = S B = m Soru: Meriden a bou ölçümlerinden elipsoidin büüklüğü ve şeklinin belirlenmesine önelik olarak 3 0 enleminde meriden doğrultusunda 0 lik a bou km 36 0 enleminde meriden doğrultusunda 0 lik a bou 4km olarak ölçülmüştür. Söz konusu elipsoidin apılan ölçülere göre a,b değerlerini bulunuz. Cevap: B =3 0 M =635983,56m B =36 0 M =6477,305m 3
29 Matematik Jeodezi S.Bektaş Örnek: Meriden a bou ölçümlerinden elipsoidin büüklüğü ve şeklinin belirlenmesine önelik olarak 3 0 enleminde meriden doğrultusunda 0 lik a bou km 36 0 enleminde meriden doğrultusunda 0 lik a bou km olarak ölçülmüştür. Söz konusu elipsoidin apılan ölçülere göre a,b değerlerini bulunuz. Örnek: B=30 0 enleminde 0 lik meriden aı 0 km, B=45 0 enleminde 0 lik meriden aı 5 km olarak ölçülmüştür. Söz konusu ölçülere daanarak elipsoidin basıklığını hesaplaınız enleminde 0 lik meriden aı 0 km ise; 4
30 Elips ve Elipsoid Geometrisi Örnek: B=30 0 enleminde 0 lik meriden aı 0 km, B=45 0 enleminde 0 lik meriden aı 5km olarak ölçülmüştür. Söz konusu ölçülere daanarak elipsoidin parametrelerini (a,b,f) belirleiniz. B=30 0 enleminde 0 lik meriden aı 0 km ise 0 lik a=0km olur. Örnek: B=30 0 enleminde 0 lik meriden aı 0km, B=45 0 enleminde 0 lik meriden aı km olarak ölçülmüştür. Söz konusu ölçülere daanarak elipsoidin eksen uzunluklarını ve basıklığını belirleiniz. 5
31 Matematik Jeodezi S.Bektaş b) DİNAMİK YÖNTEM 60 de Galile basit sarkacı inceleerek modern mekaniğin temelini oluşturan T = l g ilişkisini buldu. Yani l uzunluğunda bir sarkacın T salınım süresi gözlenerek herhangi bir erin g erçekimi g = T l hesaplanabilecektir. Yerçekimi ivmesi birimi cm/s olup Galile isminin anısına Gal denmiştir ( gal = cm/s ). Yerüzü üzerindeki her nokta iki kuvvetin etkisi altındadır. Bunlardan birisi merkezkaç kuvveti, diğeri ise erin çekim kuvvetidir. Bu iki kuvvetin bileşkesi o noktadaki gravite değeridir. Merkezkaç kuvveti, kutuplarda sıfır olup en büük değerini aldığı ekvatorda bile erçekiminin 0,0035 i kadardır. Bu değer aklaşık 0,0339 m/s dir. Merkezkaç kuvveti olmasa bile kutupların, erin merkezine aklaşık km daha akın olması dolaısı ile erçekimi ekvatordakinden daha büüktür. Bu iki kuvvetin bileşkesi olan gravite de dolaısı ile ekvatordan kutuplara doğru artmaktadır. 6
32 Elips ve Elipsoid Geometrisi Clairaut, coğrafi enlemlerle gravite arasındaki ilişkii g = g o ( + sin - sin ) formülü ile verilmiştir. Burada; g : herhangi bir enlemindeki gravite g o : ekvatordaki gravite g 90 g 0 : dinamik basıklık = g g 90 : kutuptaki gravite : sabit bir saı 0 : geometrik basıklık = a b a Geometrik basıklıkla dinamik basıklık arasındaki ilişkii 743 ılında Clairaut + = 5 w g a 0 olarak verilmiştir. Burada ; w : erin açısal hızı, a : büük arı eksen uzunluğu, w a değeri ekvatordaki merkezkaç kuvvetidir. Yerüzü üzerinde çeşitli enlemlerde ölçülen gravite değerlerinden ukarıda verilen formüller ardımı ile geometrik basıklık = 5 w g a 0 - şeklinde hesaplanabilir. Bölece eruvarı boutlarının saptanmasında jeodezik ve astronomik ölçülerin anında fiziksel ölçülerin de birlikte düşünülmesi ilkesinin gereği ortaa çıkmıştır. Başlangıçta avaş bir ilerleme gösteren ve alnız sarkaçta kalan gravite ölçülerinde teorik çalışmaların derinleştirilmesi, aletlerin geliştirilmesi ile prezison ükseltilebilmiştir. Pratikte genellikle gravite farklarını ölçmek daha koladır. Bunun için gravitesi belli olan bir noktada bir sarkacın salınım süresi gözlenip, eni noktalarda da anı gözlem apılarak salınım süresi farklarından gravite farkları hesaplanmıştır. Bu değerlerin birbirleri ile karşılaştırılabilmesi için hepsinin belli bir noktaa bağlanmış olması gerekir. Bu nokta Avrupa da Potsdam daki jeodezi enstitüsündedir. Bu noktanın mutlak 7
33 Matematik Jeodezi S.Bektaş gravite değeri Helmert önetiminde on ıllık ölçülerden hesaplanmıştır. Yani Paris teki uluslararası metre, uzunluk ölçülerinde ne anlama geliorsa, Potsdam daki gravite değeri de gravite ölçüleri için anı anlamı taşımaktadır. Sarkaçların anısıra başka ilkelere göre çalışan gravimetre aletleri apılmıştır. Bu aletlerle 0,0 miligal inceliğinde gravite değerleri elde etmek mümkün olup arazi çalışmalarında kolalık sağlaacak şekilde küçük ve hafif apılmışlardır. eferans Elipsoidi eferans elipsoidi iki aklaşım vardır. Bunlardan biri eruvarının tamamını temsil eden ortalama er elipsoidi diğeri ise erel elipsoid dir. Ortalama er (jeosentrik) elipsoidinin merkezi dünanın ağırlık merkezi ile çakışır. Ünlü jeodezi bilgini Helmert böle bir ortalama er elipoidi ile jeoid arasındaki farkların ± 00m den fazla olamaacığını ileri sürmüştür. Şekil- Jeosentrik elipsoid ve erel elipsoid Günümüze kadar düna için pek çok ortalama er elipsoidi tanımlanmıştır. Teknolojideki ilerlemee paralel olarak gelişen jeodezik ölçüm ve değerlendirme teknikleri saesinde düna için daha gerçekçi elipsoid parametreleri saptanmıştır. Tarihsel süreç içinde tanımlanan elipsoidlere örnek olarak: Delambre (80), Air (830),Bessel Elipsoidi 84, Haford Elipsoidi 90, Krassowsk Elipsoidi 940, GS80 Elipsoidi, WGS84 Elipsoidi saılabilir. Bunlardan en çok kullanılan Haford Elipsoidi (International- Uluslararası Elipsoid) dir. Ülkemizde de temel jeodezik çalışmalarda bu elipsoid kullanılmıştır. Son ıllarda GPS ugulamalarının agınlaşması nedenile ülkemizde de WGS84 elipsoidi kullanılmaa başlamıştır. Aşağıda her iki elipsoide ait parametreler tabloda verilmiştir. 8
34 Elips ve Elipsoid Geometrisi Parametreler Haford Elipsoidi WGS84 Elipsoidi Büük arıeksen a m m Küçük arıeksen b m m Kutup noktası meriden m m eğrilik arıçapı c Basıklık f, / 97 = / = I.eksentrisite e II.eksentrisite e Ülkelerarası a da kıtalararası büük çaplı jeodezik faalietlerde hep ortalama er elipsoidleri kullanılır. Klasik jeodezik faalietlerde ise Türkie de olduğu gibi her ülke jeodezik datumunu (ED50) kendi erel elipsoidinde tanımlamıştır.. Elipsoidal Coğrafi Koordinatlar Elipsoidal coğrafi koordinatlar (B,L,h) ve Elipsoidal üç boutlu dik koordinatlar (X,Y,Z), elipsoidin merkezine erleştirilmiş, Z ekseni dönme eksenile çakışan bir (XYZ) üç boutlu dik koordinat sisteminde tanımlanabilir (Şekil-6). Bu sisteme Jeosentrik (er merkezli) dik koordinat sistemi a da Global dik koordinat sistemi de denir. Elipsoidin XY düzlemini içeren düzleme ekvator düzlemi, Z dönme eksenini içeren düzlemlere de meriden düzlemleri denir. P noktasındaki meriden düzleminin, XZ düzlemi( Greenwich ten geçen başlangıç meriden düzlemi) ile aptığı L açısına elipsoidal (coğrafi) bolam denir. Bolamlar X ekseninin pozitif önünden itibaren doğua doğru 0 ile +80 arasında, X ekseninin pozitif önünden itibaren batıa doğru 0 ile -80 arasında değerler alır. Elipsoidin bir P noktasındaki üze normalinin ekvator düzlemi ile aptığı B açısına elipsoidal (coğrafi) enlem denir. Elipsoidal enlem ekvatordan kuzee doğru 0 ile +90 arasında, ekvatordan günee doğru 0 ile -90 arasında değerler alır. Bu şekilde tanımlanan enlem ve bolam, elipsoid üzerinde coğrafi koordinat sistemi oluşturur. Elipsoidal coğrafi koordinatlar ile fiziksel erüzünde noktaların üksekliklerini tanımlamak için de (h) elipsoidal üksekliğinden ararlanılır. Bir noktanın elipsoidal üksekliği, ilgili noktadan referans elipsoidine indirilen dikin uzunluğudur. 9
35 Matematik Jeodezi S.Bektaş Elipsoidal coğrafi koordinatlardan elipsoidal üç boutlu dik koordinatlara geçiş; Z (B, L, h) (X, Y, Z) Greenwich başl. merideni X L=0 G O L Yp (-e )N e N B h P Zp Xp Yer noktası B=0 Y Şekil-6 (X,Y,Z) Global dik koordinat sistemi ile (B,L,h) Elipsoidal coğrafi koordinat sistemi Elipsoidal coğrafi koordinatlar verildiğinde Kartezen koordinatların hesabı, (B, L, h) (X, Y, Z) X = (N+h) cos B cos L Y = (N+h) cos B sin L Z = [(-e )N+h] sin B a N e sin B a e eşitlikleri ile gerçekleştirilir. Burada; N meridene dik doğrultudaki normal kesit eğrilik arıçapı, e ise elipsoidin I.eksentrisitesidir. Örnek: Elipsoidal coğrafi koordinatları B=39 o, L=40 o ve h=00m olarak verilen noktanın Kartezen koordinatlarını hesaplaınız (Haford elipsoidine göre). a Çözüm: N = m e sin B X = (N+h) cos B cos L= m Y = (N+h) cos B sin L= m Z = [(-e )N+h] sin B= m olarak bulunur. a b 30
36 Elips ve Elipsoid Geometrisi Kartezen koordinatlar verildiğinde elipsoidal coğrafi koordinatların hesabı, (X, Y, Z) (B, L, h) Elisoidal bolam L, L = arctan ( Y / X ) X 0 L = 80 o + arctan ( Y / X ) X < 0 ve Y 0 L = -80 o + arctan ( Y / X ) X < 0 ve Y < 0 şeklinde hesaplanır. Elipsoidal enlem B direkt vea iteratif olarak hesaplanabilir i) B nin direkt hesabı, P X Y a Z (( f ) e ) arctan r P ve 3 Z( f ) e a.sin B arctan 3 ( f )( P e a.cos ) ii) B nin iteratif hesabı (Bektaş,S.,99) r P Z f ( a b) / a Z B arctan (i=0,,, ) i P e Ni cos Bi ) B o başlangıç değeri için B o = arctan (Z / P) değeri alınabileceği gibi her durumda sıfır olarak da alınabilir. Elipsoidal ükseklik h, h = -N + Y / (sin L cos B) şeklinde hesaplanır. Örnek: Kartezen koordinatları X= m, Y= m ve Z= m. olarak verilen noktanın elipsoidal coğrafi koordinatlarını hesaplaınız (Haford elipsoidine göre). Y Çözüm : L arctan = 40 o X i) B nin direkt hesabı, 3
37 Matematik Jeodezi S.Bektaş P X Y = m r P Z = m a Z (( f ) e ) arctan r = o =38 o P 3 Z( f ) e a.sin B arctan 3 = 39 o ( f )( P e a.cos ) B nin iteratif hesabı, B o başlangıç değeri için B o = arctan (Z / P) = arctan ( ) değerile iterasona başlanırsa Z B arctan (i=0,,, ) i P e Ni cos Bi ) B o = o B = o B = o B 3 = 39 o B o = 0 değerile iterasona başlanırsa B = o B = o B 3 = o B 4 = 39 o Elipsoidal ükseklik h, h = -N + Y / (sin L cos B) = 00m Soru: Global dik koordinatları XQ= m YQ= m ZQ= m olan bir Q noktasının Haford Elipsoidine göre coğrafi koordinatlarını bulunuz. Q noktasında jeoid üksekliği +35m olduğuna göre bu noktanın (H) ortometrik üksekliğini bulunuz. Cevap: P=49785,96m r = ,849m 3
38 Elips ve Elipsoid Geometrisi f =0, Q=39, B= = h=,894m H=h-N= -.06 Soru: Elipsoid üzerinde bulunan bir P noktasının kartezen koordinatları X=43857m Y= m olarak verilior. Söz konusu noktanın elipsoidal coğrafi koordinatlarını (B,L) i derece dakika ve sanie olarak bulunuz. Cevap: Soru:Elipsoid üzerindeki bir P noktasının, global dik koordinatları; X= ,53m Y= ,55m Z=33990,49m olarak verilior. P noktasının, elipsoidal coğrafi koordinatlarını (B,L) bulunuz. Cevap: B=3 0,467= ,6 L=39, 0 = Elipsoid üzerindeki bir P noktasının global dik koordinatları; X= m Y= m Z= m olarak verilior. P noktasının, elipsoidal coğrafi koordinatlarını (B,L) bulunuz. 33
39 Matematik Jeodezi S.Bektaş B=36 0 G= m GB=G+50000= m B0=0 B=38,73839 B=38,54836 B3=38, B4=38, BC= ,35 S=50000m Cevap: X=38004,3585m b=63569,946m Y=390,095m L=39, Z= ,566m L= k=4978,96 DENETİM: X=N.cosB B=39,576778= ,46.3 Elipsoidde Enlem Çeşitleri: Elipsoid üzerinde coğrafi enlemin anında, çeşitli amaçlarla başka enlemler de tanımlanmıştır. Bunlar; coğrafi enlem (B), indirgenmiş enlem (), jeosentrik enlem () ve izometrik enlem (q) dür (şekil-7). a b P' P Şekil-7 :Bir P elipsoid noktasının farklı enlemleri anda gösterilmektedir. B a 34
40 Elips ve Elipsoid Geometrisi ) Coğrafi Enlem (B): Elipsoidin bir P noktasındaki üze normalinin ekvator düzlemi ile aptığı açıdır. ) İndirgenmiş Enlem (): P elipsoid noktası, dönme eksenine paralel bir doğru ile, elipsoid ile anı merkezli ve a arıçaplı bir küre üzerine izdüşürülürse P noktası elde edilir. P noktasını merkeze birleştiren doğrunun ekvator düzlemi ile aptığı açıdır. 3) Jeosentrik Enlem (): P elipsoid noktasını ile elipsoidin merkezini birleştiren doğrunun ekvator düzlemi ile aptığı açıdır. Jeosentrik enleme merkezi enlem de denir. 4) İzometrik Enlem (q) : Elipsoid üzerinde, coğrafi bolamın diferansiel artımı dl e eşit metrik diferansiel artımı olan enleme izometrik enlem denir. Coğrafi enleme ve izometrik enleme göre herhangibir elipsoid eğrisinin a elemanı ds = M db + N cos B dl (coğrafi koordinatlara göre) ds = N cos B (dq +dl ) (izometrik enleme göre) şeklinde ifade edilir. O halde coğrafi koordinatlar sistemi izometrik değildir. Yani q izometrik enlemi ile L coğrafi bolamı elipsoid üzerinde F = 0 ve E = G = N cos B olan ortogonal bir parametre ağı medana getirirler. Bunun gerçekleşmesi için izometrik enlem B M q = db N cos B 0 integralinden hesaplanmalıdır. Bu dört enlem arasındaki bağıntılar aşağıda verilmiştir: 35
41 Matematik Jeodezi S.Bektaş b arc tan( tan B) arctan( e a a arc tan( tan ) arctan( b e b arc tan( tan B) arctan(( e ) tan B)) a b arc tan( tan ) arctan( e tan ) a a B arc tan( tan ) arctan( tan ) b e a B arc tan( b tan ) arctan( e tan B) tan ) tan ) İzometrik enlemle coğrafi enlem arasındaki ilişki aşağıdaki gibidir. q = arc tanh (sin B) e arc tanh (e sin B) e=sqr(e )= a b /a B i+ = arc sin { tanh [ q + e arc tanh (e sin B i )] } ( i = 0,,,...) İteratif hesaplama için coğrafi enlemin aklaşık değeri B 0 = arc sin ( tanh q) alınabilir. q izometrik enleminden B coğrafi enlemini direkt olarak iterasonsuz biçimde aşağıdaki gibi seri açınımından hesaplanabilir. = arc sin ( tanh q ) B = + C sin + C 4 sin 4 + C 6 sin 6 + C 8 sin Bu serideki C katsaıları ; C = o C 4 = o C 6 = o C 8 = o Bilgi : Hiperbolik fonksionların açık eşitlikleri aşağıda verilmiştir. (e = ) x x x x x e e e e sinh x e e sinh x = cosh x = tanh x = x cosh x e e hiperbolik fonksionlarda argüman (x) her zaman birimsiz, radan olmalıdır. x = x Örnek: Coğrafi enlemi B=39 olan elipsoid noktasının indirgenmiş, jeosentrik ve izometrik enlemini bulunuz (Haford elipsodine göre). 36
42 Elips ve Elipsoid Geometrisi e = = arctan - e o tan B o arctan e tan B q = arc tanh (sin B) e arc tanh (e sin B) q = o {arc tanh (sin B) e arc tanh (e sin B)} q = o ( ) q = 4 o Örnek: İndirgenmiş enlemi = 38 o , jeosentrik enlemi =38 o ve izometrik enlemi q = 4 o olan elipsoid noktasının B coğrafi enlemini bulunuz(haford elipsodine göre). B arctan a b a B arctan b tan arctan tan 39 e tan tan arctan 39 e i) B coğrafi enlemin direkt hesabı q = 4 o = arc sin ( tanh q ) = o B = + C sin + C 4 sin 4 + C 6 sin 6 + C 8 sin B = o sin o sin o sin o sin 8 B = 39 o olarak bulunur. o o ii) B coğrafi enleminin iteratif hesabı B i+ = arc sin { tanh [ q + e arc tanh (e sin B i )] } ( i = 0,,,...) B enlemi için ilk aklaşık değer her durumda B o = q olarak alınabilir ve bu değerle iterasona başlanırsa B o = 4 o B = o B = o B 3 = o B 4 = o İstenen enlem değeri B = 39 olarak bulunur. - Coğrafi enlemi B= olan noktanın izometrik enlemini derece dakika sanie cinsinden hesaplaınız. 37
43 Matematik Jeodezi S.Bektaş - Coğrafi enlemi B=4 0 olan noktanın izometrik enlemini bulunuz. 3- İzometrik enlemi q=39 0 olan noktanın coğrafi enlemini bulunuz. 4- Coğrafi enlemi B=39 0 olan noktanın izometrik enlemini derece cinsinden hesaplaınız. - Coğrafi enlemi B=39 0 olan noktanın izometrik enlemini derece cinsinden hesaplaınız. - Coğrafi enlemi B= olan noktanın izometrik enlemini derece dakika sanie cinsinden hesaplaınız. 3- Coğrafi enlemi B=4 0 olan noktanın izometrik enlemini bulunuz. 4- İzometrik enlemi q=39 0 olan noktanın coğrafi enlemini bulunuz. 38
44 Elips ve Elipsoid Geometrisi.4 ELİPSOİD ÜZEİNDE BAZI BÜYÜKLÜKLEİN HESABI Elipsoidde Meriden Yaı Uzunluğu Hesabı: Meriden elipsinin a elemanı dg = M db dir. Bu ifadenin integrali alınırsa, ekvatordan B enlemine kadar olan G meriden aı elde edilir[0]. G = A' B + B' sinb + C' sin4b + D' sin6b +... olur. Buradaki katsaılar; db M dg Şekil-8 B G ekvator A = c e e e e B c e e e e C c e e e D c e e Uluslararası Haford Elipsoidi için bu değerler; A' = m/ B' = m C' = 6.976m D' = -0.03m dir. Başka elipsoidler kullanılması durumunda katsaılar ukarıda verilen eşitliklerde ilgili elipsoid parametreleri kullanılarak eniden hesaplanır. Örnek-: Ekvatorla B=39 enlemi arasındaki meriden aı uzunluğunun hesabı G = A' B + B' sinb + C' sin4b+ D' sin6b = m Meriden Yaı Uzunluğundan Enlemin Belirlenmesi: 39
45 Matematik Jeodezi S.Bektaş Meriden a uzunluğunu hesaplamaa araan G = A' B + B' sinb + C' sin4b + D' sin6b +... serisinden B enleminin B i+ = {G (B' sinb i + C' sin4b i + D' sin6b i )}/ A' ( i = 0,,,..) şeklinde çekilerek iteratif olarak hesaplanabilir. Örnek-: Bir meriden elipsi üzerinde ekvatordan uzaklığı G = m kadar olan noktanın B enlemini bulunuz. Çözüm: B enlemi için ilk aklaşık değer her durumda B o = 0 alınabilir ve bu değerle iterasona başlanırsa B = G / A' = o B = o B 3 = o B 4 = o B 5 = o = İstenen enlem değeri B = olarak bulunur. Elipsoidde Kısa Meriden Yalarının Hesabı B ve B enlemleri arasında kalacak kısa G meriden aları örneğin pafta kenarlarının hesabında olduğu gibi aşağıdaki şekilde hesaplanır. B B B m olmak üzere B m ortalama enlemile hesaplanacak aşağıdaki değerlerle B B, m V B t = tanbm, e cos B, V, M c / 3 B M G M 4 8V şeklinde hesaplanır. t 4 t B 3 Örnek-3: B =38 ve B =39 enlemleri arasında kalan meriden aı uzunluğunu bulunuz. Çözüm-: G AB G AB Bsin B Bsin B Csin 4B Csin 4B Dsin6B 40 Dsin6B
46 Elips ve Elipsoid Geometrisi G = G - G = G = m olarak bulunur. Burada G ekvatordan B enlemine kadar meriden a uzunluğu, G ekvatordan B enlemine kadar meriden a uzunluğu G, B ve B enlemleri arasındaki meriden aıdır. Çözüm-: İkinci çözüm, kısa meriden alarının hesabından; B m B B B m = 38.5 B = B -B = t = tan B m = e V M cos c V 3 B m B t 4 t 009. m B M G M V olarak bulunur. - formülü, ekvatordan bir B enlemine kadar olan meriden a uzunluğunu vermektedir. Buradaki katsaılar; 3 Ekvatordan itibaren meriden a uzunluğu G= m olan noktanın B enlemini hesaplaınız. 5- Ekvatordan B enlemine kadar olan meriden a uzunluğu formülü olarak verilmektedir. Bu formülden ararlanarak G meriden a uzunluğu G= m olan noktanın B enlemini hesaplaınız. 4
47 Matematik Jeodezi S.Bektaş B = m C =6.976m D =-0.03m Elipsoidde Paralel Daire Yaı Uzunluğu Hesabı: Elipsoidin bir B enlemli paralel dairesi üzerinde L bolam farkına karşılık gelecek S=AB a uzunluğu küre üzerinde olduğu gibi hesaplanır (Şekil-9). dl S B Burada B = N cosb olup, B paralel dairesinin arıçapını vermektedir. - Elipsoid üzerinde B=30 0 enlem dairesi üzerinde 0 lik enlem aını hesaplaınız. Soru: Elipsoid üzerindeki 45 0 paralel dairesinde 0 lik paralel daire aının uzunluğunu bulunuz. Cevap: - Elipsoid üzerinde 45 0 paralel dairesinde 0 lik paralel daire aının uzunluğunu bulunuz. 5- Haford elipsoidinde B enleminde 0 lik paralel daire aı uzunluğu 08km olarak ölçülmüştür. B enlemini bulunuz. B
48 Elips ve Elipsoid Geometrisi Ya da doğrudan sinb ( ( B B / a) / a) e Formülünden B enlemi hesaplanır. - Elipsoid üzerinde B=30 0 enlem dairesi üzerinde 0 lik enlem aını hesaplaınız. Elipsoidde Alan Hesabı: Elipsoidde B ile B+dB paralel daireleri ve L ile L+dL meridenleri ile sınırlanmış diferansiel ABCD dörtgeninin df alanı, L D A df B M L+dL dl C dl NcosB N db N 43 B B+dB B
49 Matematik Jeodezi S.Bektaş Şekil-9 Elipsoidde Alan Hesabı Şekil-9 dan, AD = M db, AB = N cosb dl olur. df = AD x AB = M N cosb db dl Bu diferansielin 0 ile arasında integrali alınırsa elipsoid kuşağının alanı dz = M N cosb db şeklinde bulunur. M ve N ana eğrilik arıçaplarının değerleri erine konursa, cos B cos B dz b db b W db 4 e sin B olur. Bu ifadenin B ve B enlemleri arasındaki integralinin z b B B e cos B sin db B İntegralin Binom serisi ardımıla çözümü, z 4b B B B B B Bm olmak üzere 3 ( Asin B cos Bm Bsin B cos3bm Csin 7 9 Dsin B cos7bm Esin B cos9b...) B cos5b Bölece B ve B enlemli paralel daireleri arasındaki z elipsoid kuşağının alanı hesaplanır. İstenen F grid alanı 5 m F = z L 360 o eşitliğinden bulunur. 44
50 Elips ve Elipsoid Geometrisi İntegralde geçen katsaıların seri açılımları ile Haford elipsoidi için saısal değerleri aşağıda verilmiştir. A e B e 6 C e 80 3 e e e e e e * e 6 e *0 3 D e e *0 E e *0 Örneğin B =0 ve B =90 değerleri alınırsa elipsoidin arı alanı ve bunun da iki katının alınmasıla elipsoidin tamamının alanı bulunur F e 4b e e e e e Bu formül ile Haford Elipsoidinin alanı, F e = km olarak elde edilir. Örnek-4 : Alt kenarının enlemi B = o olan /5000 lik paftanın tüm kenar uzunluklarını ve alanını hesaplaınız. B = o B = L = 7' 30'' = 0.5 o Paftanın alt kenarının hesabı (B = o ) 7'30'' 7'30'' /5000 pafta B+B 7'30'' N alt = c V a = m e sin B 7'30'' B=40.86 o 45
51 Matematik Jeodezi S.Bektaş r B = N alt cosb = m. (B enlem dairesinin arıçapı) S alt = r B L / = m. (Paftanın alt kenarı ) Benzer şekilde paftanın üst kenarı için (B = o ) N üst = m S üst = m. (Paftanın üst kenarı ) Paftanın sağ ve sol kenarları birbirine eşit olup B alt = o ile B üst = o enlem daireleri arasındaki G meriden a uzunluğu formülünden S sağ ve sol = m. olarak bulunur. Pafta alan hesabı için önce B alt ile B üst enlem daireleri arasındaki z kuşak alanı hesaplanır. B B m = alt B üst o B = L = 7' 30'' = 0.5 o z 4b z = 4b ( E E E ) z = km olarak kuşak alanı bulunur. pafta alanı ise, F = z ( Asin B cos Bm 7 Dsin B cos7b L 360 o Bsin 3 Esin 9 = km olur. m B cos3b m B cos9b...) 5 Csin B cos5b m Örnek-5: Türkienin coğrafi sınırlarını kapsaan; B =36, B =4 enlemli paralel daireleri ile L =6, L =45 bolamlı meridenlerin sınırladığı elipsoid gridinin alanını bulunuz. B m = 39, B = 6 L = 9 değerlerile z kuşak alanı formülünden z = km olarak bulunur. İstenen grid alanı L F z km
52 Elips ve Elipsoid Geometrisi Soru: 7 30 x 7 30 boutundaki /5000 lik bir paftanın alt tabanı 36 derece paralelidir. Söz konusu paftanın arazide kapladığı alanı bulunuz. Elipsoid üzerinde kuşak alan formülü: Cevap: Z= ,755m F= m - Şekilde enlem ve bolam dairelerile sınırlı B=36 0 Sü Sa B=37 0 taralı gridin bütün kenar uzunluklarını metre cinsinden bulunuz. L=39 0 L=40 0 Ekvator - Şekilde enlem ve bolam dairelerile sınırlı taralı gridin bütün kenar uzunluklarını metre B=37 cinsin den bulunuz. B=36 0 Sü 0 Sa L=39 0 Ekvator 47
53 Matematik Jeodezi S.Bektaş L= Haford elipsoidinde B enleminde 0 lik paralel daire aı uzunluğu 08km olarak ölçülmüştür. B enlemini bulunuz. B
54 Elips ve Elipsoid Geometrisi Soru: Elipsoid üzerinde, coğrafi koordinatları B=36 0 ve L=36 0 olan bir A noktasından kuzee doğru meriden doğrultusunda 50km gidilerek B noktasına varılıor. B noktasından da paralel daire bounca 50km batıa gidilerek C noktasına varılıor. B ve C noktalarının coğrafi koordinatlarını derece dakika ve sanie olarak bulunuz. Uluslar arası Haford Elipsoidi için bu değerler; (i=0,,,..) Cevap: GA = G36 = m GB = GA+50km= m GB BB= ,35 = B L B C Soru: Elipsoid üzerinde, enlemi B=36 0 olan bir A noktasından günee doğru meriden doğrultusunda 50km gidilerek B notasına varılıor. B noktasından da paralel daire bounca 50km batıa gidilerek C noktasına varılıor. B ve C noktalarının Coğrafi koordinatlarını derece dakika ve sanie olarak bulunuz. Uluslar arası Haford Elipsoidi için bu değerler; (i=0,,,..) Cevap: G36= km GB= G36-50km= km BB= =
55 Matematik Jeodezi S.Bektaş m Soru: formülü, ekvatordan bir B enlemine kadar olan meriden a uzunluğunu vermektedir. Buradaki katsaılar; Ekvatordan itibaren meriden a uzunluğu G= m olan noktanın B enlemini hesaplaınız. Cevap: B= B= B3= B= = Soru: Elipsoid üzerinde enlemi B=36 0 ve B=38 0 olan iki nokta arasındaki meriden a uzunluğunu cm inceliğinde hesaplaınız. Uluslar arası Haford Elipsoidi için bu değerler; Cevap: G= m G= m - Enlemi 36 0 olan bir A noktasından kuzee doğru meriden doğrultusunda 50 km gidilerek B noktasına varılıor. B noktasının enlem değerini hesaplaınız. 50
56 Elips ve Elipsoid Geometrisi Uluslar arası Haford Elipsoidi için bu değerler; 5
57 Yüzeler ve Eğriler 3. YÜZEYLE VE EĞİLE Eğer bir C uza eğrisi söz konusu ise eğrinin üzerindeki noktaların koordinatları tek bir eğri parametresi adı verilen bir değişkenin (t) fonksionu olan üç koordinat x(t), (t), z(t) ile tanımlanır. C uza eğrisi er vektörü x(t), ile genel olarak x(t) = x(t) i + (t) j + z(t) k ifade edilebilir. Eğrinin (t) parametresi erine a uzunluğu s kullanılabilir. Bu durumda er vektörü, x(s) = x(s) i + (s) j + z(s) k olur. 39
58 Matematik Jeodezi S.Bektaş Eğer bir üze söz konusu ise üze üzerindeki noktaların koordinatları (u,v gibi) iki parametree bağlı olarak X = X(u,v), Y=Y(u,v), Z=Z(u,v) olarak ifade edilebilir. Üç boutlu (x,,z) uza dik koordinat sisteminde bir üze kapalı, açık ve parametrik olmak üzere üç farklı biçimde gösterilebilir. ) f(x,,z) = 0 (Kapalı) ) z = f(x,) (Açık) u ve v şeklinde iki üze parametresi ile üzein herhangi bir noktasının (x,,z) üç boutlu dik koordinatları ; 3) x = x(u,v) = (u,v) z = z(u,v) Parametrik şeklindede gösterilebilir. Bu gösterim tarzına Gauss parametrik gösterimi de denir. Herhangi bir üze erine dönel elipsoid alınırsa üze parametresi olarak B coğrafi enlemi ve L coğrafi bolamı seçersek x = x(b,l) = N cosb cos L = (B,L) = N cosb sin L z = z(b,l) = N (-e ) sin B elipsoidin parametrik denklemi elde edilir. Benzer şekilde kürenin coğrafi enlemi ve coğrafi bolamı cinsinden parametrik denklemini elde etmek için, kürenin elipsoidin özel hali olduğu dikkate alınarak, elipsoid için verilen eşitliklerde B erine, L erine, N eğrilik arıçapı erine küre arıçapı ve eksentirisite erine e =0 alınarak; x = x(,) = cos cos = (,) = cos sin z = z(,) = sin kürenin parametrik denklemleri kurulur. 40
59 Yüzeler ve Eğriler Z N n r v U=U o (V parametre eğrisi) P o (u o,v o ) u,v parametre eğrileri X i k O j j r = xi +j +zk zk xi Y ru v=vo (u parametre eğrisi) Burada; OP o = r = x i + j + z k : arıçap vektörüdür (er vektörü); r er vektörünün skaler değeri (normu); r = x z dir. Burada (x,,z) P noktasının dik koordinatlarını, (i,j,k) ise x,,z doğrultularındaki birim vektörlerdir. Yani, i=j=k=, i.j = i.k = j.k = 0, i.i = j.j = k.k = Yüzein bir P o noktasındaki parametre eğrileri bounca üze teğetlerini elde etmek için r er vektörünün P o noktasında türevleri alınır. u eğrisinin u = u o noktasındaki teğeti r u r x ru = ( )o = ( ). i +( u u u z ). j +( ).k = x u. i +u.j +zu. k u v eğrisinin v = v o noktasındaki teğeti r v r x z r v = ( )o = ( ). i +( ). j +( ).k = x v. i +v. j +zv. k v v v v şeklinde olur. 4
60 Matematik Jeodezi S.Bektaş r u ve r v vektörlerinin vektörel çarpımı bu noktadaki üze normalini verir. P o noktasındaki üze normali ; N= ru x rv dir. 3. UZAY EĞİLEİ Eğer koordinatlar bir t parametresine bağlı ise t nin değişmesi ile üze üzerinde bir eğri medana gelir. x = x(t), = (t), z = z(t) Oskülatör düzlem h Normal düzlem b Teğet düzlem t=h=b= Z P P P r t Uza eğrisi t : Teğet vektör h : Asal normal vektör b : Binormal vektör X O Y Burada eğrinin er vektörü r = x(t)i + (t)j + z(t) k dir. Herhangi bir uza eğrisinin P teğet noktası için aşağıdaki düzlem ve vektör tanımlamaları apılabilir. Uza eğrisi üzerinde birbirine çok akın P, P ve P noktalarından geçen düzleme oskülatör düzlem,eğrinin P noktasındaki teğetini içeren oskülatör düzleme dik düzleme teğet düzlem denir. Teğet ve oskülatör düzlemlere dik olan ve P den geçen düzleme normal düzlem denir. Normal düzlemle teğet düzlemin ara kesiti binormal vektörü (b),normal düzlem ile oskülatör düzlemin arakesiti asal normal vektörü (h), (t) ise eğrinin oskülatör düzlem üzerindeki teğet vektörüdür. 4
61 Yüzeler ve Eğriler t, b ve h vektörlerine ek üçlü adı verilir. r(s) = x(s). i +(s).j +z(s).k (s, a uzunluğunu parametre olarak alırsak) t teğet vektörü r er vektörünün türevine eşittir. t = r' = dr ( s) ds = dx(s) ds i + d(s) ds j + dz(s) ds k Asal normal birim vektörü ise teğet vektörün birim vektörüne eşittir. h = t' t' r" r" d x d d z i j k ds ds ds d x d d z ds ds ds b = t x h = r' x r" r" 3. I. DEECEDEN TEMEL BÜYÜKLÜKLE E, F, G Koordinatları q, q, q 3,... q n olan n boutlu bir koordinat sisteminde en genel a elemanı formülü; ds = n i n j h ij dq i dq j biçimindedir. i j iken h ij = 0 ise q i = değişken ile q j = değişken çizgileri birbirini dik açıla keser. i = j iken h ii = h jj = ise q i ve q j değişken koordinat çizgileri doğrusaldır. Herhangi bir üze üzerinde birbirine çok akın iki nokta arasındaki a uzunluğu için ; dik koordinatlar türünden ; ds² = dx² + d² + dz² eşitliği azılabilir. 43
62 Matematik Jeodezi S.Bektaş Koordinatları u, v üze parametreleri cinsinden azar, x = x(u,v), = (u,v), z = z(u,v) ve gerekli türevleri alırsak dx²= (xu du +xv dv )² xu = d²= (u du +v dv )² u = dz²= (zu du +v dv )² zu = x u u z u, xv =, v =, zv = x v v z v ds²= dx²+ d²+ dz² ds²= (xu du +xv dv )²+(u du +v dv )²+(zu du +v dv )² ds²=(xu ²+ u ²+ zu ²)du²+ (xu xv + u v + zu zv )du dv+ (xv ²+ v ²+ zv ² )dv² E F G I = ds² = E du² + F du dv + G dv² I. temel form E, F, G büüklükleri I. derece temel büüklükler olup, erüzündeki bir nokta için sabit olup ancak üze değişirse değişirler. E = ru ² (E, ru nun modülünün karesine eşittir.) G = rv ² ( G, rv nin " " " ) F = ru rv Buradan, ru = (F, ru ve rv vektörlerinin skaler çarpımına eşittir.) E ve rv = G olur. Parametre Eğrileri Arasındaki Açı u ve v parametre eğrileri arasındaki açısı bu eğrilerin kesim noktasındaki çizilen ve anı zamanda üzee de teğet olan teğet vektörler arasındaki açıdır. Söz konusu açısı teğet vektörler r u ve r v nin skaler çarpımından aşağıdaki şekilde bulunur. ru v = sabit T P rs rv ds u = sabit 44
63 Yüzeler ve Eğriler ru rv = ru rv cosθ ( ru ve rv vektörlerinin skaler çarpımı) cos = = u v ise θ = 90 ve cos θ = 0 olur ve dolaısıla F = 0 dır. sin θ = r u r r u v r v F EG EG F cos EG W * EG W* = EG F ( I. temel formun diskriminant formülü) T Açısının Değerini Veren Formüller: Herhangi bir parametre eğrisi örneğin ukarıdaki şekilde u ( v = sabit) eğrisile bir üze eğrisi arasındaki T açısı da ine teğet vektörlerin skaler çarpımından bulunur. s parametreli üze eğrisinin teğet vektörü r s = vektördür. dr ds birim ru r s = ru r s cos T ru rs cos T = r r u s ru = E r s = olacağından cos T = r u r s E olur. Diğer andan r er vektörü r = r {u(s),v(s)} şeklinde a uzunluğunun fonksionu olarak azarsak r s nin değeri, dr ds = r s = r u du ds + r v dv ds dv ds = r u du ds + r v dv ds olur. Buradan ru r s çarpımını teşkil edersek, du ru r s = r u r u + ru r v ds du dv ru r s = E + F olur. Bu değeri açı eşitliğinde erine koarsak ds ds Edu Fdv EG F dv EG F cos T = sin T = tan T = dv Eds Eds Edu Fdv eşitlikleri çıkar. Parametre eğrileri ortogonal ise F = 0 olacağından açı değerleri, Edu ds cos T = = ( u) G ds sin T = = ( v) G dv ds tan T = = ( v) ds ds dsdv ds E du ds( u) olur. 45
64 Matematik Jeodezi S.Bektaş Yüze Normali Yüzein bir noktasındaki normal vektörü, bu noktadaki üzein teğet düzlemine diktir. Öte andan bir üze noktasındaki teğet düzlem içindeki herhangi iki vektöre dik olan vektör teğet düzlemine de diktir. O halde böle bir vektör o noktada üze normalidir. Bir üze noktasındaki parametre eğrilerinin teğet vektörleri üzee de o noktada teğettir, ani o noktadaki teğet düzlem içindedir. Bu durumda bir noktasında parametre eğrilerinin teğet vektörlerine dik olan vektör o noktadaki üze normalidir. İki vektörün vektörel çarpımı bu vektörlere dik bir vektör oluşturur. O halde bir üze noktasındaki üze normali, bu noktada parametre eğrilerinin teğet vektörlerinin vektörel çarpımı ile oluşan bir vektördür. Bölece üze normali N= ru x rv ( x işareti vektörel çarpımı göstermektedir) olur ve normal vektörü doğrultusundaki birim vektör bu vektörü skaler değerine bölmekle elde edilir birim vektöre n denilirse ; n = N N = ru xrv r xr u v = r u xr v ( ru xrv ) diğer taraftan r ) = r u x r V =r u r V sin ( u xrv ( u xrv r ) = E G - F = W * elde edilir. Bölece normal doğrultusundaki birim vektör r u v n = olur. * W xr Yüze Alan Elemanı Diferansiel anlamda alan elemanı olarak parametre eğrilerini ds (u) ve ds (v) diferansiel a elemanlarının oluşturduğu paralel kenarın alanı, df = ds (u) ds (v) sin P u eğrisi ds(u) ds(v) P v eğrisi 46
65 Yüzeler ve Eğriler sin θ = ds (u) = * EG F W değeri erine konursa EG EG E df = EG F du ve ds (v) = dv du dv = W* du dv W* = r u x r v olduğu dikkate alınırsa alan elemanı df = r u x r v du dv olur. G 3.3 EĞİLİK Düzlemde bir = f (x) eğrisinin eğriliği, ( ' = 3 / '' ) şeklinde hesaplanır. Burada eğriliği, eğrilik arıçapını, d ' dx ve d '' dx türevleri göstermektedir. Eğrinin bir P o (x o, o ) noktasındaki eğriliği, eğrilik formülünde P o noktasının koordinatları erine azılmak suretile '' o = hesaplanır. Geometrik olarak eğrinin bir noktasındaki 3 / ( o ' ) eğriliği, teğet noktada eğrie diferansiel anlamda uan çemberin arıçapının tersidir. Öle ki teğet noktada bu çemberin eğimi ve eğriliği = f (x) eğrisinin eğimi ve eğriliğine eşittir. Soru: Düzlemde denklemi olan eğrinin noktasındaki eğriliğini ve eğrilik arıçapını hesaplaınız. Cevap: Soru: Düzlemde denklemi olan eğrinin noktasındaki eğriliğini ve eğrilik arıçapını hesaplaınız. Cevap: 47
66 Matematik Jeodezi S.Bektaş - Düzlemde denklemi olan eğrinin x 0= noktasındaki eğriliğini ve eğrilik arıçapını hesaplaınız. YÜZEY EĞİSİNDE EĞİLİK Bir üze eğrisinin teğet vektörü t ile gösterilir ve eğrii veren parametre a uzunluğu olarak alınırsa dr( s) rs r' t ve t = ds du dv r rv ds ds dr r' ru u' rv v' ds (t = t = t = u a da başka bir gösterimle olur. t = ) t = olur. Eşitliğin her iki tarafının türevi alınırsa, t 0 t = t' = dt, t t ' 0 olur. ds dr r' olduğuna göre ds dt d t r' ' ds ds r' r'' = t t = 0 elde edilir. İki vektörün skaler çarpımının sıfır olması için bu iki vektörün birbirlerine dik a da vektörlerden birinin sıfır olması gerekmektedir. O halde t ve t' vektörlerinin birbirlerine dik oldukları ortaa çıkmaktadır. Eğrinin bir noktasındaki teğete dik olan t' özel vektörüne asal normal a da eğrilik vektörü denir. Asal normal vektörü birim vektör değildir. Bu vektör doğrultusundaki birim vektör h ile gösterilirse, skaler bir saı olmak üzere 48
67 Yüzeler ve Eğriler t' = r'' = h azılabilir. Bu eşitlikte, s e bağlı bir fonksiondur ve uza eğrisinin eğriliği adını alır. Eğrilik anı zamanda bir eğrinin küçük bir alanda bir doğrudan sapmasını gösterir. Eğriliğin geometrik orumunu apmak için eğri üzerinde birbirine diferansiel anlamda akın iki nokta alınır. Bu noktadaki teğetler t ve t + dt ve aralarındaki açı d olmak üzere dt ds h t t = ve t h = 0 olduğundan d ds = / eğrilik ve ds eğrilik arıçapıdır. d t d ds d t+dt 3.4 II. DEECEDEN TEMEL BÜYÜKLÜKLE L, M, N Bir üze eğrisinin teğeti, o noktada üzee de teğet olduğu için üze normaline diktir. O halde, n t = 0 (skaler çarpım) n x t = (vektörel çarpım) olur. birinci eşitliğin s e göre türevi alınırsa, dn ds t + n dt ds = 0 ve t = r' = dr olmak üzere, ds dn dr d r ds + n ds ds = 0 elde edilir. 49
68 Matematik Jeodezi S.Bektaş n= n(u,v) olmak üzere n, u ve v parametrelerine bağlı olduğu için dn ds = ve anı şekilde, dr ds = n u r u du ds du ds + + n v r v dv ds dv ds bu değerleri dn ds ( n u du ds + dr ds n v + n dv )( ds d r ds r u = 0 eşitliğinde erine koarsak du ds r + v dv ) + n ds d r ds = 0 ukarıdaki eşitliğin son terimindeki ikinci türev erine nu r u du ds + (nu r v + n v r u ) n r du u u u v v n h = ( n r ds dudv ds + n v r v dv ds n r ) dudv n r dv u v v d r ds + n h = 0 eşitliğin padası I.temel form olup paına da II. temel form dersek, II. Temel Form = nuru du ( nurv nvru ) dudv nvrv dv II. Temel Form = L du M dudv N dv = h azarsak olur. Burada ikinci derece temel büüklükler olan ; L aşağıdaki gibi determinantlardan da hesaplanabilir. xu u zu ru rv ruu L = -n u r u = n r uu = = x z W * * W x v uu v uu z v uu, M ve N nin değerleri M = -/ (n u r v + n v r u ) = n r uv = ru rv ruv = W * W * x x x u v uv u v uv z z z u v uv N = -n v r v = n r vv = ru rv rvv = W * W * x x x u v vv u v vv z z z u v vv Ldu n h = Mdudv Ndv ds 50
69 Yüzeler ve Eğriler n h = II. Temel Form I. Temel Form I = ds² = E du² + F du dv + G dv² I. temel form II. Temel Form = L du M dudv N dv burada, üze eğrisinin bir noktasındaki eğriliği h : üzein asal normalindeki birim vektör n : o noktadaki üze normalinin birim vektörüdür. 3.5 NOMAL KESİT VE EĞİK KESİT Yüzein bir noktasındaki normalinden sonsuz düzlem geçer. Bu düzlemlerin üze ile arakesitlerine normal kesit denir. h n Normal Düzlem t Teğet Düzlem Yüze Normal Kesit Burada; N hem üzein normalidir,hem de normal kesitin asal normalidir. n ve h çakışınca = 0 ve cos 0 = dir. Buradan normal eğrilik, n h ve n h = NO = = II I NO şeklinde II. temel formun I.temel forma oranlanmasıla elde edilir. 5
70 Matematik Jeodezi S.Bektaş Eğik Düzlem Normal Düzlem heğik h n t Teğet Düzlem Normal Kesit Eğik Kesit Yüze Yüze normalini içermeen düzlemlerin üze ile arakesitlerine eğik kesit denir. Aşağıdaki şekilde bir üze üzerinde normal kesit ile eğik kesit bir arada gösterilmektedir. Eğik düzlemle normal düzlem arasındaki açı ise n h = n h cos = cos = II I n ve h birim vektörler olduğu için çarpımları bire eşit olur. cos = r cos = NO NO : Normal kesitin eğrilik arıçapı r : eğik kesitin eğrilik arıçapı r = NO cos Eğik kesitle normal kesitin eğrilik arıçapları arasındaki bağıntı (Meusnier teoremi) Yüze Eğriliği Bir üzein herhangi bir noktasındaki eğrilik söz konusu olduğunda; o noktadan üze normalini içeren sonsuz saıda düzlem geçer bu düzlemlerle üzein ara kesitleri ine sonsuz saıda normal kesit eğrileri (NKE) oluşturur. Birer düzlem eğri olan NKE lerin eğrilikleri bulundukları düzlemin doğrultusuna göre farklı değerler alırlar. Ancak bunların içinde öle iki NKE vardır ki bunların birinde eğrilik en küçük diğerinde eğrilik en büüktür. Bunlara ananormal kesit eğrileri, eğriliklerine de ana eğrilik denir ve eğrilik arıçapları min ve max ile gösterilirse üze eğriliği için aşağıdaki tanımlamalar apılabilir. 5
71 Yüzeler ve Eğriler ) Gauss Eğrilik Ölçütü (K) : Bir üze noktasındaki eğrilik ölçütü K, Gauss a göre min ve max anaeğrilik arıçapı olmak üzere; K = min max olur. )Ortalama Eğrilik (H) : Bir üze noktasındaki iki ana eğriliğin ortalamasıdır. H = ( ) min max 3.6 JEODEZİK EĞİ Jeodezik eğri; Jeodezik eğriliği sıfır olan bir üze eğrisidir. Jeodezik eğrinin belli bir bölgede tanımlanması gerekir. Jeodezik eğrinin ana normalleri her noktada üze normalleri ile çakışır. İki nokta arasındaki en kısa ol jeodezik eğridir(jeodezik eğrinin küre üzerindeki karşılığı büük daire aı ve düzlem üzerindeki karşılığı da iki noktaı birleştiren doğrudur). Bu tanımın anında; Jeodezik eğri, her noktasında jeodezik eğriliği sıfır olan üze eğrisi olarak da tanımlanır. Jeodezik Eğrinin Özellikleri: -Jeodezik eğrinin jeodezik eğriliği sıfıra eşittir. -Her noktasında asal normal ile üze normali çakışır. 3-Düzlem üzerindeki doğrunun, küre üzerindeki karşılığı büük daire aı, elipsoid üzerindeki karşılığı jeodezik eğridir. Dolaısıla bir üze üzerindeki iki nokta arasında en kısa ol jeodezik eğridir. Ancak bu ifadenin tersi her zaman doğru değildir. Yani iki noktaı birleştiren her jeodezik eğri en kısa ol değildir. Bunun için jeodezik eğrinin sınırlı bir bölgede tanımlanması gerekir. 4-Yüze üzerindeki bir noktadan verilen bir teğet doğrultuda alnız bir jeodezik eğri vardır. Elipsoid üzerinde, meriden aları, ekvator aları birer jeodezik eğridir.ancak paralel daire aları birer jeodezik eğri değildirler. Çünkü paralel daire üzerindeki bir noktada üze normali ile asal normal Yüze Normali δ=b Asal Normal Paralel Daire Yaı 53
72 Matematik Jeodezi S.Bektaş çakışmaz aralarında B enlemi kadar açı farkı olur. Jeodezik eğriliği gösteren j erine sıfır konursa jeodezik eğrinin diferansiel denklemi elde edilir. da j = - - ds EG d E cos A dv da = d E d G ( cos A sin A ) ds EG dv du d G sin A EG du = 0 Küre üzeinde jeodezik eğrinin diferansiel denklemleri; d cos A cos A ds E d sin A sin A ds G cos da tansin A ds Bu eşitliklerin oranlanmasından, da tantan d da sin d şeklindedir. denklemleri elde edilir. Elipsoid üzeinde jeodezik eğrinin diferansiel denklemleri; db cos A ds M dl sin A ds N cos B da tan Bsin A ds N şeklindedir. Bu eşitliklerin oranlanmasından, da M t tan B tan A tan A db N V da sin B denklemleri elde edilir. dl 54
73 Yüzeler ve Eğriler 3.7 JEODEZİK EĞİLİK Bir üze eğrisinin bir noktasında, sonsuz küçük bir kesiminin o noktada üzee teğet düzleme dik izdüşümünün eğriliğine jeodezik eğrilik denir. jeodezik eğriliğin diferansiel denklemi değişik ollardan bulunabilir. Örneğin üze eğrisine, bir noktasında teğet ve o noktada üze teğet düzlemine dik bir silindir geçirilirse, silindirin üze teğet düzlemi ile diferansiel anlamda arakesiti olan eğrinin eğriliği, üze eğrisinin jeodezik eğriliğidir. r r (u, v) n P t b h r j r r (s) şekilde; r j : üze eğrisinin jeodezik eğrilik arıçapı r : üze eğrisinin eğrilik arıçapı h : üze eğrisinin asal normal birim vektörü b : üze eğrisinin binormal birim vektörü n : üze normali birim vektörüdür. 55
74 Matematik Jeodezi S.Bektaş Jeodezik eğrilik şu şekilde de tanımlanabilir: üze üzerinde bulunan bir eğrinin jeodezik eğriliği birbirine diferansiel anlamda (çok akın) P ve P gibi iki noktada eğrie çizilen teğetler P J ve P J jeodezik eğrileri arasındaki d açısı ve ds aı ardımıla tanımlanır. Eğrilik formülü, j = d ds dır. Teğet Eğik kesitle normal kesit eğrilik arıçapları arasındaki ilişkii veren Meusnier formülünden J P ds d P Teğet J ü r. cos azılabilir. üze normaline dik olan izdüşüm eğrisi asal normali ile üze eğrisi asal normali (b ile n vektörü) arasındaki açı + = 90 o = 90 o - ine Meusnier formülünden r = cos(90 o - ) = sin olur. Yüze eğrisinin binormal birim vektörü b, asal normal birim vektörü h a dik olduğundan, iki vektörün skaler çarpımından aralarındaki açı, cos = b n elde edilir. Yüze eğrisi ile bunun anı zamanda normal kesit eğrisi olan izdüşüm eğrisinin eğrilik arıçapları arasında Meusnier formülünden, r r. cos eşitliği azılabilir. Buradan jeodezik eğrilik, j j cos rj r olur. üze eğrisinin eğriliği, r olmak üzere j = cos j = b n elde edilir. 00- r 56
75 Yüzeler ve Eğriler Diğer taraftan er vektörünün ikinci türevi, d r ds r vektörel çarpılırsa, h eşitliği t = r' ile soldan t x h = b r' x r'' = (t x h) = b elde edilir ve bu vektör eşitliğinin de n ile skaler çarpımından j = b n = ( r' x r'' )n bulunur ve n erine değeri azılırsa, jeodezik eğrilik rr j u r r v ( r x r ). n ( r x r ).( r u x r v ) W * W * r r u r r v ukarıdaki gibi olur. Burada; r ruu rvv r ruu(u) rvv(v) ruvuv ruu rvv u ve v parametrelerin dik ve v = sabit (u parametre eğrisi) ile ds üze eğrisinin aptığı açı T olmak üzere jeodezik eğrilik dt G E j ( sin T cost) ds EG u v olur. u ve v parametrelerinin ortogonal oldukları dikkate alınarak bu parametre eğrilerin jeodezik eğrilikleri u parametre eğrisi (v = sabit, T = 0) ju EG E v v parametre eğrisi (u = sabit, T = 90 o ) jv EG G u 57
76 Matematik Jeodezi S.Bektaş ju ve jv parametre eğrilerinin jeodezik eğriliklerinden ararlanarak bir üze eğrisinin jeodezik eğriliği j = ju cos T + jv sin T + T s olur. u, v parametreleri erine coğrafi koordinatlar kullanıldığında küre ve elipsoid üzerinde değişik üze eğrilerinin eğrilikleri aşağıda tablo halinde verilmiştir. Küre Elipsoid Coğrafi koord. (enlem,, B, L bolam) Ya uzunluğu ds d cos. d ds M db N I. derece temel, F 0, G.cos E M, F 0, G büüklükler (E,F,G) u = enlem parametre j = 0 ( sabit) jb = 0 eğrisinin jeodezik eğriliği r j= r jb = ve eğrilik arıçapı v = bolam parametre eğrisinin jeodezik eğriliği ve eğrilik arıçapı u = enlem parametre eğrisile A açısı apan üze eğrisinin jeodezik eğriliği u = enlem parametre eğrisile A açısı apan jeodezik eğrinin diferansiel denklemi j = 0 cos B. dl E N.cos B j j tan r j = cot tan. sin A da ds j = jl r jl = tan B N N tan B tan B. sin A N da da tan.sin A tan B.sin A ds ds N da ds 3.8 CLAİAUT DENKLEMİ Dönel elipsoidde enleme bağlı olarak herhangi bir paralel dairenin arıçapı, r B N cos B dir. Burada N meridene dik doğrultudaki eğrilik arıçapıdır. N c V e c cos B 58
77 Yüzeler ve Eğriler r B nin B e göre türevi alınırsa, drb N sin B M sin B db V B +B max A A =45 o B dr B M sin B db N cos B dl rb dl tan A MdB MdB dr sin Br cot A dl olur. B da sinb erine dl dr r cot A da B B B konursa B o=0 A o -B max A o' dr r B B dr r B ln r ln r r B B B B cot A da cos A da sin A ln sina ln k ln k sina r B k sina a da k r B sina eşitliği elde edilir. Yani dönel elipsoid de jeodezik eğrinin bir noktasında, meridenle aptığı açının sinüsü ile o noktadaki paralel daire arıçapının çarpımı, jeodezik eğrinin her noktasında sabittir. Örneğin ekvatorda meridenle A açısı apan bir jeodezik eğri kuzee doğru gittikçe paralel daire arıçapı küçüleceğinden eğrinin meridenle apacağı A açısı giderek büüecektir. A açısının kuzede alacağı en büük değer A = 90 o olacaktır. Günede de A açısının en büük değeri A =70 o olacaktır. Bu noktalarda jeodezik eğri dönüş aparak kuzeden günee ve güneden kuzee zıt işaretli iki paralel daire arasında sinüzoidal bir üze eğrisi çizer. o Örnek: Elipsoid üzerinde enlemi B 30 olan bir noktadan geçen ve meridenle o A 45 açı apan bir jeodezik eğrinin;b =35 o enlemi ile ekvatorda meridenle aptığı açıları bulunuz.söz konusu jeodezik eğrinin güne ve kuze arı kürelerde dönüş aptığı noktaların B max enlemlerini bulunuz. Çözüm: o o a) B 30 ve A 45 için k sabiti o o o a 3 k r30 sin 45 N 30 cos30 sin 45 o e sin m 59
78 Matematik Jeodezi S.Bektaş B =35 o enleminde meridenle aptığı açı, k r30 sin 45 k r35 sin A sina r r o o A A =80-A = o =3 o B = 0 o enleminde(ekvator) meridenle aptığı açı, r o = a olur. k sin A0 a o o A o o A ' ' b) jeodezik eğrinin dönüş aptığı B max enlemi ise olacağından k = r Bmax sin 90 o c ise k = r Bmax = e' cos B A 90 cos B max = c o k e' k o N N max cos30 cos35 cos B = Bmax = 5 o olarak bulunur. Soru: Elipsoid üzerindeki Normal kesit eğrisinin eğriliği o o max şeklinde verildiğine göre 39 derece enleminde 40 derece azimutundaki doğrultunun eğrilik arıçapını hesaplaınız. Cevap: - Clairaut denklemi olarak verildiğine göre a- Ekvatorda meridenle A=30 0 azimut apan bir jeodezik eğrinin B=45 0 enleminde meridenle apacağı azimutu, b- a şıkkındaki jeodezik eğrinin, kuze arı kürede dönüş aptığı noktanın enlemini bulunuz. B=45 0 enleminde 60
79 Yüzeler ve Eğriler Soru: Clairaut denklemi, olarak verildiğine göre, a) Ekvatorda meridenle A=30 0 azimut apan bir jeodezik eğrinin B=45 0 enleminde meridenle apacağı azimutu, b) a şıkkındaki jeodezik eğrinin, kuze arı kürede dönüş aptığı noktanın enlemini bulunuz. Cevap: a) B=0 b) Cevap: B=36 0 G= m GB=G+50000= m B0=0 B=38,73839 B=38,54836 B3=38, B4=38, BC= ,35 S=50000m Cevap: X=38004,3585m b=63569,946m 6
80 Matematik Jeodezi S.Bektaş Y=390,095m L=39, Z= ,566m L= k=4978,96 B=39,576778= ,46 DENETİM: X=N.cosB.cosL Y= N.cosB.sinL - Haford Elipsoidinin tamamı erine bir küre kullanılmak istenior. Kürenin hacminin elipsoidin hacmine eşit olacağı ilkesinden hareket ederek söz konusu kürenin arıçapını belirleiniz. - Elipsoid üzerindeki normal kesit eğrisinin eğriliği şeklinde verildiğine göre 39 0 enleminde 40 0 azimutundaki doğrultunun eğrilik arıçapını hesaplaınız. 3- Elipsoid üzerindeki bir P noktasının global dik koordinatları; X= m Y= m Z= m olarak verilior. P noktasının, elipsoidal coğrafi koordinatlarını (B,L) bulunuz. 6
81 Yüzeler ve Eğriler 4- Enlemi B=39 0 olan nokta için Gauss küresi arıçapını hesaplaınız. 5- Ekvatordan B enlemine kadar olan meriden a uzunluğu formülü olarak verilmektedir. Bu formülden ararlanarak G meriden a uzunluğu G= m olan noktanın B enlemini hesaplaınız. B = m C =6.976m D =-0.03m 6- Elipsoid üzerindeki normal kesit eğrisinin eğriliği şeklinde verildiğine göre 39 0 enleminde 40 0 azimutundaki doğrultunun eğrilik arıçapını hesaplaınız. M= N= A= m 63
82 Matematik Jeodezi S.Bektaş 3.9 ELİPSOİD YÜZEYİNDE UYGULAMALA P deki normal düzlem NKE P P K P deki normal düzlem NKE Jeodezik Eğri Ekvator K Elipsoid üzerinde herhangi iki noktanın anı meriden a da anı paralel daire üstünde olmaları özel durumu dışında genelde iki noktadaki üze normalleri akırı doğrular olduğu için (anı düzlemde olmadıkları için normaller kesişmez ), bu iki noktaı birleştiren iki arı normal kesit eğrisi vardır. Bu üzden elipsoid üzerinde normal kesit eğrileri, iki noktaı birleştiren tek anlamlı bir bağlantı eğrisi olarak kullanılmaz. Elipsoid üzerinde bu iki noktaı tek anlamlı olarak jeodezik eğri birleştirir. NK ab B Jeodezik Eğri NK ba NK bc Normal Kesit Eğrisi NK cb A NK ac C : Normal Kesit Eğrisinden Jeodezik Eğrie Geçiş Düzeltmesi NK ca Elipsoid üzerinde A, B ve C gibi üç nokta normal kesit eğrileri ile birbirlerile birleştirildiğinde tek anlamlı bir üçgen oluşmaz, ancak noktalar jeodezik eğrilerle birleştirildiğinde tek anlamlı bir üçgen oluşur ve buna jeodezik üçgen denir. Jeodezik çalışmalarda hep bu jeodezik üçgenler kullanılır. 60
83 Elipsoid Yüzeinde Ugulamalar Elipsoidde I. Derece Temel Büüklükler: Elipsoid üzeinde Gauss parametreleri u ve v erine elipsoidde kullandığımız B, L jeodezik enlem ve bolamını ani u = B ve v = L alırsak, r er vektörü; r = x(b,l)i + (B,L)j + z(b,l)k olur. I. derece büüklükler; olur. E = r u = r B F = r u r v = r B r L G = r v = r L r nin B e göre kısmi türevi r nin L e göre kısmi türevi Elipsoid üzerindeki bir P noktasının uza dik koordinatları (x,, z) Z x = = z = a cos B cos L c cos B cos L W V a cos Bsin L c cos Bsin L W V a( e )sin B csin B W V ( e' ) X a b O L Y r B P Z X a Y merkezi arıçap r, r = x tan = r = W V r B a W z b tan B a cos B cos e e sin cos a W cos B ( e ) eşitliğinden olarak bulunur. B B r x z i j k B B B B sin B 6
84 Matematik Jeodezi S.Bektaş B e göre kısmi türevleri alırsak x c dv cos L sin B c.cos B.cos L B V V db dv e cos Bsin B e cos B tan B db V V x c c cos Lsin B cos B cos L tan B 3 B V V c M 3 V uza dik koordinatlara göre türevler x M coslsin B B Msin Lsin B B z M cos B B olur. Buradan r B i tekrar azarsak e cos B r B M cos Lsin B i sin Bsin L j cos B k olur. Benzer şekilde r L i hesaplamak için r L r x z i j k L L L L L e göre kısmi türevleri alırsak x N cos Bsin L L L r N cos B sin L i cos L j L N cos Bcos L z L 0 E = r B F = r B r L G= r L E, F ve G erine ukarıdaki değerleri azılırsa, elipsoidde I. derece temel büüklükler; E M cos Lsin B M sin Lsin B M cos B E M G N F 0 (u ve v dik oldukları için) cos B 6
85 Elipsoid Yüzeinde Ugulamalar Elipsoidde I. temel form I ds sin A cos A tan A M db dl G ds db E ds GdL EdB N N cos B db M ds N cos cos dl ds BdL MdB BdL E db=mdb L=sabit A 90 o GdL ds N cos BdL B =sabit üze normal birim vektörü r u v n = idi. * W xr Elipsoid üzeinde normal birim vektörünü hesaplamak için elipsoid parametrelerini erine azarsak, W * = E G - F değeri elipsoid üzeinde W * = M N cos B olur. n rb xrl MN cos B MN cos B i x B x L j B L k z B z L n cos B cos L i cos Bsin L j sin olur. B k 63
86 Matematik Jeodezi S.Bektaş ELİPSOİDDE MEİDYEN YÖNÜNDEKİ EĞİLİK YAIÇAPI (M) Meriden önündeki eğrilik arıçapı M ile gösterilmektedir. Meridenin eğriliği sabit değildir. Çünkü geometrisi elipstir. Meridenin herhangi bir noktasındaki eğriliği hesaplanabilir. Yandaki şekilden enlem değerine bağlı olarak M eğrilik arıçapı aşağıdaki gibi bulunabilir. z M db ds /4Meriden Elipsi db = M = ( ds M ds db den M = ) arıca ds db ds = dz + d a uzunluğu dik koordinatlara göre azılır. M = ( ) + ( ) d d = ( ) dz d +( ) d d M = ( d db d db ) { ( dz db d dz ) ( d db ve db ) } z ve dik koordinatlarını indirgenmiş enlemi cinsinden azarsak, z = b sin = a cos olur. Bu ifadelerin a göre türevleri dz d = b cos = -a sin d d db tan = e tan B eşitliğinin türevi alınırsa db d cos d e db e cos cos cos B B ve W = cos cos B den W = - e sin B ve V = + e cos B kısaltmalarıla 64
87 Elipsoid Yüzeinde Ugulamalar d db W e olur. bunlar erine konursa; ( e W M = 4 ) (a sin + b cos ) burada b erine b = a (-e ) değeri alınırsa M = M = M = ( e 4 W ) a ( e ) 4 W a ( e ) 4 W a ( e M = 6 W (a sin + a (-e )cos ) ) (-e cos ) ( e sin B e W { ( sin Kutup noktasındaki eğrilik arıçapı c = a / b Meriden önünde eğrilik arıçapını veren eşitlik aşağıdaki gibi elde edilir. c V a( e W ) a( e ) ( e sin B) M = / B) } ELİPSOİDDE MEİDYENE DİK YÖNDEKİ EĞİLİK YAIÇAPI (N) Meridene dik öndeki eğrilik arıçapı N ile gösterilmektedir. r = N cos z r P B koordinatı ile B elipsoidal enlemi arasındaki ilişki = a cos B W r erine, N erine N ve erine B değeri kullanılırsa = N cos B bulunur. Buradan meridene dik öndeki eğrilik arıçapı, B N B z /4Meriden Elipsi a ( e sin B) c a N = = = V W / 65
88 Matematik Jeodezi S.Bektaş olarak bulunur. Elipsoidde II. Derece Temel Büüklükler: Elipsoidde II. Derece temel büüklükler olan aşağıdaki gibi hesaplanabilir. L, M ve N nin değerleri L n. r M B B n N -n L. r L B r L n L r B ukarıdaki eşitliklerde n B, r B, n L ve r L erine aşağıdaki değerleri azılırsa n n. r r n cos B cos Li cos Bsin Lj sin Bk B L B L sin B cos Li sin Bsin Lj cos Bk cos Bsin Li cos B cos Lj M cos Lsin Bi M sin Bsin Lj M cos Bk N cos B(sin L i - cosl buradan elipsoid üzeinde II. Derece temel büüklükler, L L M M 0 j) sin B cos L i sin B sin L j cos B k. M cos Lsin B i M sin Bsin L j M cos B k N N cos B olarak bulunur. II. Temel Form = L du M dudv N dv olduğuna göre Elipsoidde II. Temel form: olur. II. Temel Form = M db + N cos B dl 66
89 Elipsoid Yüzeinde Ugulamalar Elipsoid Yüzeinde Bir Doğrultudaki Eğrilik Elipsoidde eğrilik tanım gereği II. Temel formun I. temel forma bölünmesile elde edilir. Elipsoidin normal eğriliği K NO aşağıdaki gibi hesaplanır. II MdB N cos BdL KNO I M db N cos BdL NO NO M M db M db N cos BdL N M N db cos N BdL cos BdL NO NO M M N cos BdL MdB tan A N N MdB N cos BdL tan A Elipsoidin herhangi bir noktasında A azimutundaki doğrultunun normal eğrilik ve eğrilik arıçapı aşağıdaki gibi elde edilir. K NO NO NO M sin cos A sin A M N MN A N cos A EULE FOMÜLÜ elipsoidde eğriliğin maximum ve minimum olduğu doğrultuları bulmak için ukarıdaki eşitliğin türevi alınır ve sıfıra eşitlenir. A NO N ( V sin A( V ) cos A sin A) 0 burada eşitliğin paı; N sin A(V -) = 0 olmalıdır. N ve V sıfır olamaacağı için sin A = 0 olmalıdır. Buradan ; A = 0 o A = 0 o = min = M A =80 o A = 90 o = max = N - Elipsoid üzerindeki normal kesit eğrisinin eğriliği şeklinde verildiğine göre 39 0 enleminde 40 0 azimutundaki doğrultunun eğrilik arıçapını hesaplaınız. 67
90 Matematik Jeodezi S.Bektaş Elipsoidde Eğrilik Yarıçapları ve Eğrilik Ölçütleri : Yukarıda tanımlanan elipsoidin ana eğrilik arıçaplarından biri, dönel bir üze olarak elipsoidde meriden eğrisidir. Bu öndeki anaeğrilik maximum dolaısıla meriden eğrilik arıçapı M minimumdur. Meridene dik öndeki ananormal kesit eğrisinin eğriliği minimum,eğrilik arıçapı N maximumdur. Buna enine eğrilik arıçapı da denir. Elipsoid üzei için başlıca eğrilik ölçütleri; ) Minimum Normal Eğrilik : K min = max N ) Maximum Normal Eğrilik : K max = min M 3)Gauss Eğrilik Ölçütü (K) : K = min max MN olur. 4)Ortalama Eğrilik (H) : min = M N MN max H = ( ) Gauss Eğrilik Yarıçapı (g): Gauss eğrilik arıçapı her iki ana eğrilik arıçapının geometrik ortalamasıdır. g arıçaplı bu küre, söz konusu noktadan elipsoidle anı Gauss eğrilik ölçüsüne sahip ve anı zamanda elipsoidin konform tasviri olan Gauss küresidir. 68
91 Elipsoid Yüzeinde Ugulamalar g K min max MN Elipsoidin ana eğrilik arıçapları olan M ve N değerleri arasında M g N eşitsizliği vardır. Eşitlik hali elipsoidde alnız kutup noktalarında geçerlidir. Kutup noktalarında M = g = N = c olur. (c : kutup noktası eğrilik arıçapıdır.) Gauss küresi, elipsoidal enlemi B olan bir elipsoid noktasında elipsoide üzesel teğettir. Buna karşılık M arıçaplı küre elipsoide meriden aı bounca, N arıçaplı küre ise elipsoide B enlemli paralel daire bounca çizgisel teğet olur. Gauss eğrilik arıçapı bir dönel elipsoid noktasında tüm normal eğrilik arıçaplarının ortalamasıdır. g MN Gauss eğrilik arıçapının jeodezide önemi büüktür. Jeodezik çalışma apılan bölgenin 50km. arıçaplı bir daireden büük olmaması durumunda elipsoid üzeinde hesap apmak erine elipsoide o noktada teğet g arıçaplı Gauss küresinin kullanılmasıla teorik olarak farklı sonuçlar elde edilmesine karşın pratikte bu farklar anlamsız saılacak düzededir. Hesaplamalarda elipsoid erine kürenin kullanılması büük kolalık sağlar. Örnek : Elipsoidal koordinatları B= 3 o ve L= 39 o 00 olarak verilen bir P noktasında ; a) Meriden önündeki eğrilik arıçapını (M) b) Meridene dik öndeki eğrilik arıçapını (N) c) Gauss küresi arıçapını ( g ), Soldner küresi arıçapını ( S ) d) Meridenle A= 45 o azimut açısı apan doğrultudaki normal kesit eğrisinin eğrilik arıçapını, e) P noktasındaki elipsoid normalile = 7 o açı apan doğrultudaki eğik kesitin eğrilik arıçapını ve eğriliğini, anı doğrultudaki jeodezik eğrinin eğriliğini, f) Söz konusu P noktasından diferansiel anlamda uzak (db = ve dl = 3 ) olan Q noktası arasındaki PQ jeodezik eğri uzunluğunu, g) P noktasının üç boutlu dik koordinatlarını hesaplaınız. Çözüm: B= 3 o = 3 o.467 L= 39 o 00 = 39 o c = m e = V = (+ e cos B) / =
92 Matematik Jeodezi S.Bektaş a) Meriden önündeki eğrilik arıçapı M= c / V 3 = m b) Meridene dik öndeki eğrilik arıçapı N = c /V = m c)gauss küresi arıçapı g = c / V = MN = m Soldner küresi arıçapı S = N = m d)meridenle A= 45 o azimut açısı apan doğrultudaki normal kesit eğrisinin eğrilik arıçapı A = M sin MN A N cos Eğrilik, K A = / A =.57x0-7 A = m e)p noktasındaki elipsoid normalile = 7 o açı apan doğrultudaki eğik kesitin eğrilik arıçapı r = A cos Meusnier teoremi r = m eğik kesit eğrilik arıçapı K = / r =.76E-7 eğik kesitin eğriliği Anı doğrultudaki jeodezik eğrinin eğriliği K g, K g = K A tan = K sin = 8 x0-8 f)söz konusu P noktasından diferansiel anlamda uzak (db = ve dl = 3 ) olan Q noktası arasındaki PQ jeodezik eğri uzunluğu Çözüm için I.Temel Form eşitliğinden ararlanabiliriz. I = ds = M db + N cos BdL db = ve dl = 3 B= 3 o = 3 o.467 M = N = m ds = M db + N cos BdL = m PQ= ds = m g)p noktasının üç boutlu dik koordinatları 70
93 Elipsoid Yüzeinde Ugulamalar X = N cosb cosl = m Y = N cosb sinl = m Z = N(-e ) sinb = m olur. Kontrol amacıla Z değeri için, daha önce bulunan X ve Y değerleri elipsoid denkleminde erine konursa Z = [(-e )(a -X -Y )] / = m olur. Soru: Elipsoid üzerindeki Normal kesit eğrisinin eğriliği şeklinde verildiğine göre 39 derece enleminde 40 derece azimutundaki doğrultunun eğrilik arıçapını hesaplaınız. Cevap: - Elipsoid üzerindeki normal kesit eğrisinin eğriliği şeklinde verildiğine göre 39 0 enleminde 40 0 azimutundaki doğrultunun eğrilik arıçapını hesaplaınız. M= N= A= m 3.0 ELİPSOİD YEİNE KÜENİN KULLANILMASI Daha önceki bölümlerde sölendiği gibi jeodezik çalışmalarda hesap üzei olarak elipsoid erine kürenin kullanılmasıla doğruluktan bir miktar ödün vermekle beraber hesaplamalarda büük kolalık sağlanır. Jeodezik çalışma apılan bölgenin büüklüğüne ve istenen doğruluk derecesine göre elipsoidin tamamı erine bir küre alınabileceği gibi biraz daha fazla doğruluk için elipsoidin küçük parçaları erine de bir küre hesap üzei olarak alınabilir. Örneğin çok küçük ölçekli haritaların (atlaslar gibi) apımında ve özellikle kartografik çalışmalar için elipsoidin tamamı erine kürenin kullanılması son 7
94 Matematik Jeodezi S.Bektaş derece eterli olur. Burada seçilecek kürenin elipsoide göre konumu ve arıçapı önemlidir. Bu konuda iki farklı aklaşım vardır. Birinci aklaşımda; elipsoidin merkezi ile kürenin merkezi çakıştırılır ve düna elipsoidinin tamamı erine bir küre kullanılır. Ancak bu şekilde elipsoidinin tamamı erine bir kürenin alınmasında duarlık düşük olur ve bu nedenle de bu aklaşım jeodezik amaçlı çalışmalar için ugun olmaz. İkinci aklaşımda; sınırlı bir bölgede (arıçapı 50km den küçük) apılacak jeodezik çalışmalar için sadece o bölgede elipsoide en ii uan küre alınır. Doğaldır ki bu durumda küre ile elipsoidin merkezlerinin çakışması düşünülmez. Ölçü bölgesinin ortasında her iki üzein en az bir ortak noktasının olması, eğriliklerin eşit olması ve bu noktadaki üze normallerinin çakışması eterlidir. Jeodezik ugulamalarda sınırlı çalışma bölgelerinde genellikle Gauss küreleri kullanılmaktadır. b a o I g P o Şekil-.a Şekil-.b Yukarıdaki şekil-.a da elipsoidin tamamı erine kürenin alınması gösterilmektedir. Bu durumda elipsoid ile kürenin merkezi çakışmakla beraber, küre bazı enlemlerde elipsoide çok akın (hatta teğet) olduğu halde bazı enlemlerde de elipsoidden büük ölçüde uzaklaşır. Şekil-.b de ise g arıçaplı Gauss küresi çalışma bölgesinin ortalarındaki bir P o noktasında elipsoide teğet duruma getirilmektedir. a) ELİPSOİDİN TAMAMI YEİNE KÜENİN KULLANILMASI Elipsoidin merkezi ile kürenin merkezinin çakışması ön koşulula elipsoid erine alınacak kürenin arıçapının belirlenmesi farklı kabullere göre apılabilir. 7
95 Elipsoid Yüzeinde Ugulamalar Aşağıda dört farklı kabule göre elipsoidin tamamı erine kullanılabilecek küre arıçapının nasıl hesaplanacağı ve uluslararası Haford elipsoidi parametrelerine göre arıçapının saısal değerleri verilmiştir. ) Yarıçapı elipsoid arıçaplarının ortalaması olan küre; Kürenin arıçapı a b 3 ) Hacmi elipsoidin hacmine eşit olan küre; Bir dönel elipsoidin hacmi 3 Kürenin hacmi V π Buradan 4 3 πa 3 4 b π 3 k 4 3 V m e 4 πa 3 3 a b ) Alanı elipsoidin alanına eşit olan küre; 4 6 Dönel elipsoidin alanı F 4π b ( e e e...) Kürenin alanı F 4π e k Alanların eşitliğinden; a( e e e...) m b 3 5 m ) Elipsoidle arasındaki mesafelerin karelerinin toplamı minimum olan küre; küre b d elipsoid σ a e sin γ e b cos γ a Elipsoidle eşmerkezli ve arıçaplı küre arasındaki mesafeler Yukarıdaki koşul, π/ γ0 d i π/ ( - σ γ0 i ) min Buradan hesaplanacak arıçapı, a( e 4 7 e e ) m d i σ i olur. 73
96 Matematik Jeodezi S.Bektaş 3- Haford Elipsoidinin tamamı erine bir küre kullanılmak istenior. Kürenin hacminin elipsoidin hacmine eşit olacağı ilkesinden hareket ederek söz konusu kürenin arıçapını belirleiniz. b) ELİPSOİDİN KÜÇÜK PAÇALAI YEİNE KÜENİN KULLANILMASI Elipsoidin tamamı erine alınacak küre bazı enlemlerde elipsoide çok akın (hatta teğet) olduğu halde bazı enlemlerde de elipsoidden büük ölçüde uzaklaşır. Jeodezik ugulamalarda elipsoidin küçük parçaları erine Soldner ve Gauss küreleri olarak adlandırılan küreler kullanılmaktadır. ) Soldner Küresi Çalışma bölgesinin ortasındaki bir P o noktasındaki anaeğrilik arıçapı N o kürenin arıçapı olarak alınır. Bu durumda küre, başlangıç noktasından geçen paralel daire bounca elipsoide teğet olacaktır. Bu paralel daire dışında hiçbir noktada soldner küresi elipsoidi kesmez, teğet olmaz ve elipsoidi tamamen içine alır. s = N o N o B o P o B o ) Gauss Küresi 74
97 Elipsoid Yüzeinde Ugulamalar Gauss küresi, ölçü bölgesinin ortasındaki bir P o noktasında elipsoidle ortak bir noktaa sahiptir ve bu P o noktasında her iki üzein normalleri çakışır. Gauss küresinin arıçapı, M değeri alınır. 0 0N 0 M o ve N o elipsoidin P o noktasındaki ana eğrilik arıçaplarıdır. Elipsoid P o Elipsoid P o Gauss Küresi M o N o Gauss Küresi Meriden düzleminde Meridene dik ana normal kesit düzleminde Şekilden de görüldüğü gibi Gauss küresi bir önde elipsoidin dışında ve buna dik önde elipsoidin içinde kalmaktadır. Burada iki üzein birbirine. Dereceden teğet olması söz konusudur. Bu teğet P o noktası civarında iki üze soldner küresine göre birbiri ile daha ii uum gösterir. Eğrilik ölçütlerine bakıldığında, Elipsoid için ; Ke M on o K s s N 0 K g M N Soldner küresi için ; Gauss Küresi için ; g 0 0 olduğu görülür. Yukarıdan Gauss küresi ile elipsoidin anı eğrilikleri olduğu ortaa çıkmaktadır. Yerüzünün belli bir bölgesinde apılacak jeodezik hesaplamalarda elipsoid erine o bölge için hesaplanacak Gauss küresi kullanılır. Gauss küresi ile elipsoid çalışma bölgesinin ortalarındaki bir P o noktasında birbirine üzesel teğettir. Gauss küresi ile elipsoid teğet noktada anı eğriliğe sahip olup çalışma 75
98 Matematik Jeodezi S.Bektaş bölgesinde elipsoid üzei ile çok ii uum sağlar. Çalışma apılacak bölgenin 50 km arıçaplı bir daireden büük olmaması halinde çalışma bölgesinin ortalarındaki bir noktanın coğrafi enlemile hesaplanacak Gauss küresi hesap üzei olarak alınabilir. Elipsoid erine Gauss küresinin alınması nedenile hesaplamalarda ortaa çıkacak farklar (<cm) pratik olarak ihmal edilecek düzededir. Gauss küresinin arıçapı çalışma bölgesinin ortalarındaki bir P o noktasının B o coğrafi enleminden aşağıdaki gibi hesaplanır. [],[4] g = MN = c e' cos Yukarıdaki parametreler Haford elipsoidi için; Kutup noktası eğrilik arıçapı c = a / b = m Haford elipsoidinin II.eksentrisitesi e = Örneğin B= 39 o için Gauss küresinin arıçapı g = m. olur. B o Ülkemiz Enlemlerinde Kullanılacak Gauss Kürelerinin Yarıçapları B N(m) M(m) MN (m) 36 o o o
99 Matematik Jeodezi S.Bektaş 4. KÜEDE JEODEZİK HESAPLAMALA Dünanın şekline en ugun geometrik üzein bir dönel elipsoid olduğunu bilioruz. Jeodezik hesaplamaların dönel elipsoid erine küre üzerinde apılması bir miktar doğruluk kabına neden olmakla beraber hesaplamalarda büük kolalık sağlar. Elipsoid geometrisinden kanaklanan zorluklar nedenile elipsoid üzerinde jeodezik hesaplamaların apılması oldukça zahmetlidir. Ancak, jeodezide küre elipsoid erine de kullanılabilmektedir. Sınırlı büüklükteki çalışma bölgelerinde Gauss küresi üzerindeki hesaplamalarla elipsoid üzeindeki sonuçların elde edilebilmesi küre üzerindeki jeodezik hesaplamaları daha önemli kılmaktadır. Ölçülerin Küre Yüzeine İndirgenmesi H S ( ) S' H S' ( ) S S S H Şekil-3 Küre üzeinde jeodezik hesaplamalar için ölçülerin (ata doğrultu, ata uzunluk gibi) küre üzeinde verilmesi gerekir. Gerçekte ölçüler fiziksel erüzünde apıldığı için ölçülerin küre üzeine indirgenmesi gerekmektedir. Fiziksel erüzünde ölçülen doğrultulardan hesaplanan açılar, çekül sapmaları göz ardı edilirse küre üzeindemiş gibi alınabilir. Nirengi noktaları arasında ölçülen uzunlukların küre üzeine indirgenmesi için ölçümün apıldığı bölgenin referans üzeinden (küreden a da deniz seviesinden) H üksekliğinin bilinmesi gerekir. H üksekliğinde erel atada ölçülen S uzaklığının küre üzeindeki S karşılığı ukarıdaki gibi olur. Soru: Denizden 500m ükseklikli bir noktada erel atada m olarak ölçülen bir nirengi kenarının deniz seviesindeki karşılığını bulunuz (=6370km). Cevap: 76
100 Kürede Jeodezik Hesaplamalar Soru: Denizden 500m ükseklikli bir noktada erel atada ölçülen bir kenarın deniz seviesine indirgenmiş değeri m dir. kenarın indirgenmemiş ölçülen değerini bulunuz (=6370km). Cevap: S =S(+H/)= KÜE GEOMETİSİ Küre, uzada bir sabit (O) noktasından sabit uzaklıktaki noktaların geometrik eri olarak tanımlanır. Merkezi orijinde olan bir kürenin üçboutlu dik koordinat sisteminde denklemi, X + Y + Z = dir. Küre üzeinin bütün normalleri kürenin merkezinde kesişir. Küre üzeinin her noktasında eğrilik sabit olup küre arıçapının tersine eşittir ( K= / ). Küre üzei üzerinde iki noktaı tek anlamlı olarak birleştiren ve anı zamanda en kısa uzaklık büük daire aıdır (ortodrom eğrisi). KÜESEL TİGONOMETİ Küre üzerinde hesaplamalar küresel trigonometrinin konusudur. Küresel Trigonometriden küre üzeinde trigonometri diğer bir deişle küre üzeinde üçgen hesabı anlaşılır. Bilindiği üzere küre üzeinin bütün normalleri kürenin merkezinde kesişir. Küre üzeinin her noktasında her doğrultuda eğrilik sabittir. Küre üzei üzerinde iki noktaı tek anlamlı olarak birleştiren ve anı zamanda en kısa uzaklık büük daire aıdır (ortodrom eğrisi). Bu nedenle küre üzeindeki jeodezik amaçlı hesaplamalarda noktalar hep büük daire aları ile birleştirilir. arıçaplı bir kürenin herhangi bir düzlemle arakesiti her zaman bir dairedir. Bu arakesit dairenin arıçapı D için 0 D eşitsizliği vardır. Büük Daire: Kürenin merkezinden geçen bir düzlemle ara kesitidir. Ekvator dairesi, meriden dairesi gibi. Büük dairenin arıçapı kürenin arıçapına eşittir. Büük daire, küre üzerindeki iki noktaı birleştiren en kısa eğrii de içerir. Küçük Daire: Kürenin merkezinden geçmeen bir düzlemle ara kesitidir. Örneğin enlem daireleri birer küçük dairedirler. 77
101 Matematik Jeodezi S.Bektaş Şekil P Q Küresel Uzaklık: Küre üzerinde iki noktaı birleştiren büük daire aının kısa olan parçasıdır. Yandaki şekil- de gösterilen P ve Q noktalarını birleştiren büük daire aının kısa parçası küresel uzaklık olarak adlandırılır. PQ = Büük daire aı Küresel Açı: Küre üzerindeki iki büük daire aı arasındaki açıklığa küresel açı denir. Bu açı her iki büük daire düzlemleri arasındaki ölçek açı ile ölçülür. 4.. KÜE ÜZEİNDE BAZI BÜYÜKLÜKLEİN HESABI a) Küre üzerinde meriden aı hesabı Küre üzerinde meriden aı hesabı, meriden dairesinin geometrisi arıçaplı bir çember olduğu için merkez açıı gören a eşitliğinden bulunur. Örneğin derecelik meriden aı (b) kürenin her erinde birbirine eşit olup, b = dan hesaplanır. arıçapı erine 6370km değeri alınırsa derecelik meriden aı uzunluğu.77 km olur. b) Küre üzerinde paralel daire aı hesabı Küre üzerinde paralel daire aı hesabı apmak için önce paralel dairenin arıçapı bulunur. enlemli paralel dairenin arıçapı = cos den bulunur. Paralel dairenin arıçapı bulunduktan sonra ine merkez açıı gören a eşitliğinden paralel daire aı hesaplanır. Örneğin 39 o enlemindeki derecelik paralel daire aı (s) =39 o = 6370km = cos = m (39 o enlem dairesinin arıçapı) derecelik paralel daire aı 78
102 Kürede Jeodezik Hesaplamalar s = = m olur. Paralel daire aları ekvatordan kutuplara doğru gidildikçe kısalır. - Kürede 39 0 paralel dairesi üzerindeki iki nokta arasındaki bolam farkı 3 derecedir. Söz konusu iki nokta arasındaki paralel daire a uzaklığı ile küresel uzaklığı bulunuz. Hangisinin kısa olduğunu belirtiniz. 3 0 paralel daire aı Küresel Uzaklık c) Küre Üzerinde Alan Hesabı Bilindiği gibi arıçaplı bir kürenin tamamının alanı; F = 4 eşitliğinden hesaplanabilmektedir [8]. Küre üzerinde ve paralel daireleri ile, meriden dairelerinin sınırladığı gridin (F) alanı (şekil-) hesaplanmak istenirse, önce üksekliği h olan, paralel dairelerin sınırladığı küre kuşağının s alanı aşağıdaki biçimde bulunur, h F s π h h (sin sin ) h sin cos s 4π sin cos Şekil İstenen F grid alanı s kuşak alanından aşağıdaki gibi hesaplanır; 79
103 Matematik Jeodezi S.Bektaş Δλ λ λ o Δλ/ρ F s π Δλ F o ρ o sin cos 4.3 Küre Üzerinde Özel Eğriler ) Ortodrom Eğrisi: Küre üzerinde coğrafi koordinatlarıla bilinen P (, ) ve P (, ) noktalarını birleştiren büük daire aıdır. Büük daire söz konusu iki nokta ile kürenin merkezinden geçen bir düzlemin kürele arakesitidir. Bu daire üzerindeki P ve P noktalarını birleştiren alardan kısa olanı büük daire aıdır. P 90 o - K s 90 o - P Δλ λ λ Kenar-kosinüs teoreminden s ortodrom eğrisinin uzunluğu hesaplanır. coss sin sin cos cos cosδ ekvator ) Loksodrom Eğrisi: Coğrafi koordinatlarıla bilinen P ( ve P ( noktalarını birleştiren eğri meriden doğrultularıla hep sabit bir açısı apıorsa bu eğrie loksodrom eğrisi denir. Eğri üzerinde her noktanın kuzele aptığı açı değişmediği için eğrie sabit pusula açısı altında gidilen ol denir. Loksodrom eğrisi özellikle deniz trafiğinde önemlidir. Gemiler olculuklarını sabit kuze açısı altında ve loksodrom eğrisi üzerinde aparlar. P K Pi i i P PPoP diferansiel üçgeninin PP kenarı ds PPo kenarı d kadardır. Üçgenin P noktasındaki açısı (90-) dır. Kürenin arıçapı olduğuna göre daçısının uzunluk cinsinden değeri, d P P o ρ PPo paralel daire aı parçasının uzunluğu da, dλ PP o 80 cos ρ dλ λ - λ
104 Kürede Jeodezik Hesaplamalar PP o P diferansiel üçgeni, dik bir düzlem üçgen kabul edilebilir. Buna göre; o PPo cot(90 α) tanα PP K dλ cos ρ dλ cos tanα d d ρ o d dλ tanα cos diferansiel bağıntısı elde edilir. Bu son bağıntının integrali alınırsa, d dλ tanα cos o λ tanα [lntan(45 ) c] olur. PP loksodrom eğrisi üzerinde P ve P noktaları için son eşitlik azılırsa belirsizlik giderilmiş olur. o λ tanα [lntan(45 ) c] o λ tanα [lntan(45 ) c] o o λ λ tanα [lntan(45 ) - lntan(45 )] λ λ tanα o o lntan(45 ) - lntan(45 ) Bu bağıntıla loksodrom eğrisinin kuze açısı hesaplanır. Eğri için özel durumlar; a) = ise tan = ve = 90 o ani loksodrom eğrisi P P den geçen paralel daire aıdır. b) = ise = 0 ani loksodrom eğrisi P P den geçen meridendir. Loksodrom eğrisinin uzunluğu ds, d P d P Po 8
105 Matematik Jeodezi S.Bektaş PPo ds cosα d ds cosα ρ bu diferansiel bağıntıdan P ve P sınırları içinde integrali alınırsa d ds cosα ρ s cosα ρ olur. 4.4 KÜE YÜZEYİNDE ÜÇGEN HESABI Dünanın şekli olarak elipsoid erine küre alınması, bir miktar doğruluk kabına sebep olmakla beraber hesaplamalarda büük kolalık sağlar. Küre üzerinde jeodezik hesaplamaların nasıl apılacağı küresel trigonometrinin konusudur. Ancak jeodezik çalışmalarda kullanılan üçgenler birer küçük küresel üçgen (kenar uzunlukları maksimum 50 km) oldukları göz önünde bulundurulursa bu tür üçgenlerin çözümü için eteri doğruluk verebilecek iki aklaşık öntem geliştirilmiştir. Bunlar; Legendre ve Additament (ekleme) öntemleridir. Ekses (Küresel Artık) Bilindiği gibi bir üçgenin iç açılarının toplamı e ani 80 o e eşit olması kuralı düzlem trigonometri için geçerlidir. Küresel üçgenlerde iç açıların toplamı her zaman 80 o den büüktür. Bir küresel üçgenin iç açıları toplamının 80 o den fazla olacağı ilk bakışta görülebilir. Şöle ki kürenin meriden daireleri (kutuplardan geçen büük daireler) ekvatoru dik olarak keserler. İki meridenle ekvatorun teşkil ettiği bir ekvator-kutup küresel ABC üçgeninde iç açılarının toplamı den meridenler arasındaki kadar fazladır. Bunun gibi her küresel üçgende iç açıların toplamı ani 80 o den, üçgenin büüklüğüne göre az vea çok farklı olur. Bu farka küresel ekses denir ve ile gösterilir. Küresel üçgenin F ukarıdaki gibidir. = F F. alanı eksesile doğru orantılıdır. Aralarındaki ilişki 8
106 Kürede Jeodezik Hesaplamalar Örneğin; kenarları km olan eşkenar bir üçgen eksesi kenarları 0 km olan eşkenar bir üçgen eksesi kenarları 50 km olan eşkenar bir üçgen eksesi ε ε 0. ε 5.48 dir. Jeodezide karşılaşılan üçgenlerin kenarları 50 km i geçmeeceğine göre ekses hiçbir zaman 5, 6 i geçmez. Diğer taraftan olduğundan küresel üçgenin alanı erine düzlem üçgenin alanı alınabilir. ε 0 Teorik olarak bir küresel üçgende eksesten alan hesabı ve alandan ekses hesabı apmak mümkündür. Ancak pratikte ölçülen açılar kullanılarak apılacak ekses hesabı ölçü hataları nedenile doğru sonuç vermez. Bu şekilde ölçülen açılardan hesaplanacak ekses değerinden küresel üçgenin alanı bulunurken ekses değerinin gibi çok büük bir saı ile çarpılıor olması eksesteki hataı çok büüterek alan değerine ansıtmaktadır. Bu nedenle ekses değerinin alandan hesaplanması a da ölçülen açılar erine küresel üçgenin kenarlarından bulunması ugun olacaktır. Bunun için küresel trigonometrideki L Huilier ve Serret formülleri kullanılabilir. u u a u b u c a b c tan tan tan tan tan u 4 Ekses, kenarları küresel üçgenin kenarlarına eşit bir düzlem üçgenin alanı () türünden hesaplanmak istenirse,kenarları a, b ve c olan düzlem üçgenin alanı = u( u a)( u b)( u c) ; düzlem üçgenin alanı Anı kenar uzunluklarına sahip olan düzlem üçgenin alanından küresel üçgenin alanı ve eksesi hesaplanmak istenirse aşağıdaki formüller kullanılabilir. a b c F ( ) ; 4 a b c ( ) olur KÜESEL TİGONOMETİ TEOEMLEİ - Sinüs Teoremi A sin a sin sin b sin sin c m sin 83 B c a b C
107 Matematik Jeodezi S.Bektaş - Kenar Kosinüs Teoremi cos a cos b cos c + sin b sin c cos (*) 3- Açı Kosinüs Teoremi Şekil 4 cos cos cos sin sin cos a (*) 4- Neper Formülleri () (*) tan b c tan a cos cos tan b c tan a sin sin Neper Formülleri () (*) tan cot b c cos b c cos tan cot b c sin b c sin Not : (*) lı eşitlikler küresel üçgenin diğer elemanları için de dönerli olarak azılabilir. Örneğin cos a cos b cos c + sin b sin c cos şeklinde verilen Kenar Kosinüs Teoremi şu şekilde orumlanmalıdır ; bir kenarın (a) kosinüsü = diğer iki kenarın (b,c) kosinüsleri çarpımı + diğer iki kenarın (b,c) sinüsleri ve başlangıçtaki kenarın (a) karşısındaki açının () kosinüsü çarpımına eşittir. Söz konusu teoremi diğer kenarlar için de ukarıdaki orumlaa sadık kalarak aşağıdaki gibi azabiliriz. cos b cos a cos c + sin a sin c cos cos c cos b cos a + sin b sin a cos 5- Kotanjant Teoremi (Dört Parça Teoremi ) 84
108 Kürede Jeodezik Hesaplamalar C b IV A Dört parça teoremi gereği aşağıdaki eşitlik her zaman sağlanır. cos III cos II sin III cot I sin II cot IV cos a cos sin a cot c sin cot 6- L Huilier ve Serret Eşitliği a III Şekil 5 II c I B Dört parça teoreminin genel azılışı şu şekildedir: Küresel üçgenin her hangi bir kenarından başlamak koşulula üçgenin elemanları sırala (saat ibresi vea tersi önde) I den IV e kadar numaralandırılır. Örneğin şekil-5 deki küresel üçgen için numaralandırmaa c kenarından başlar ve saat ibresi önünde hareket edersek numaralama ci II aiii IV şeklinde olur. Bu eşitlik küresel üçgenin eksesini kenarlar cinsinden vermektedir. tan 4 u u a u b u c tan tan tan tan u a b c 4.6 KÜESEL ÜÇGENLEİN ÇÖZÜMLEİ Bir küresel üçgenin çözülebilmesi için üçü kenar, üçü de açı olmak üzere toplam altı elemanından herhangi üçünün verilmesi eterlidir. Düzlem trigonometriden farklı olarak üç açısı bilinen küresel üçgenler de çözülebilmektedir. Zira kürenin arıçapının sabit olmasıla küresel üçgenin üç iç açısı üçgeni belirlemektedir. Küresel üçgenin verilen elemanlarına ugun küresel trigonometri teoremleri kullanılarak üçgen çözümleri gerçekleştirilir [4],[7],[9]. Soru: Kürede ve A=39 0, S=39km olarak verilior. II. noktanın coğrafi kordinatlarını ve A derece dakika ve sanie olarak bulunuz. Cevap: 85
109 Matematik Jeodezi S.Bektaş Soru 4 0 enlem dairesi üzerindeki P ve Q noktaları arasındaki enlem dairesi a uzunluğu 5km dir. P noktasının bolamı 39 o dir. Q noktasının bolamını bulunuz (=6370km). Cevap: Soru: Küre üzerinde, enlem ve bolamı 39 0 olan bir noktadan enlem dairesi bounca 00km doğua sonra da bu noktadan meriden bounca 00km kuzee gidilerek P noktasına ukaşılıor. P noktasının coğrafi koordinatlarını derece dakika ve sanie olarak bulunuz (=6370km). Cevap: 86
110 Kürede Jeodezik Hesaplamalar Soru: Kürede 39 0 paralel dairesi üzerindeki iki nokta arasındaki bolam farkı 3 derecedir. Söz konusu iki nokta arasındaki paralel daire a uzaklığı ile küresel uzaklığı bulunuz hangisinin kısa olduğunu belirtiniz (=6370km) Cevap: (Paralel daire aı uzunluğu) (3 0 lik paralel daire aı) 39 0 paralel dairesi üzerinde bolam farkı 3 0 olan ikinokta arasındaki büük daire aı uzaklığı Soru: Kürede ve noktaları arasında II. Temel ödev çözümü aparak küresel s(m), A, A, değerlerini derece dakika ve sanie olarak bulunuz. Cevap: - Kürede enlemi (ϕ=39 0 λ=39 0 ) olan bir A noktasından kuzee doğru meriden doğrultusunda 50km gidilerek B noktasına, doğua doğru paralel daire üzerinde 50km gidilerek C noktasına varılıor. B ve C noktalarının enlem ve bolam değerlerini hesaplaınız. 87
111 Matematik Jeodezi S.Bektaş enlem dairesi üzerindeki P ve Q noktaları P Q ϕ=4 0 arasındaki enlem dairesi aı uzunluğu 5 km dir. Q noktasının λ=0 bolamını bulunuz. (=6370 km) λp= Legendre Teoremi İle Küresel Üçgenlerin Yaklaşık Çözümü Küçük küresel üçgenlerin aşağıda belirtilen şekilde eterli aklaşıkta çözülmeleri mümkündür. Legendre önteminde küresel üçgenin açıları eksesin üçte biri kadar küçültülürse, küçük küresel üçgenler eşit kenarlı düzlem üçgenler gibi çözülebilir[4],[9]. B c a A C b Şekil 6.a Küresel Üçgen c A * C b Şekil 6.b Yardımcı Düzlem Üçgen B a Yardımcı düzlem üçgenin açıları küresel üçgenin açılarından aşağıdaki gibi hesaplanır. * ε * ε * ε α α, β β, γ γ Küresel trigonometrideki sinüs teoremi erine aşağıdaki düzlem sinüs teoremi kullanılabilir. sina sinα sinb sinβ sinc sinγ sinα a sinα a * ε 3 b sinβ b sinβ * c sinγ ε 3 * c sin γ ε 3 88
112 Kürede Jeodezik Hesaplamalar Örnek-3: Bir ABC küresel üçgenin aşağıdaki üç elemanı verilior. Küresel üçgeni Legendre öntemine göre çözünüz. (= m) Verilenler: c m, 47 o , β 8 o İstenenler: açısı, a ve b kenarlarının Legendre öntemile çözümü Çözüm: Önce küresel üçgenin alanından eksesi hesaplanır. ε F ρ c ε 4.47 sin sinβ ρ sin(α β) ε F m γ 80 γ 49 o o ε (α β) Yardımcı düzlem üçgenin iç açıları; * ε o α α * ε o β β * ε o γ γ Düzlem sinüs teoreminden istenen a ve c kenarı; c a sinγ c b sinγ * * sinα sinβ * * m m olarak bulunur. 89
113 Matematik Jeodezi S.Bektaş Soru: Bir ABC küresel üçgeninin elemanları; a=60km, =50 0, =75 0, olarak verilior. Küresel üçgeni Legandre öntemine göre çözerek diğer elemanlarını bulunuz. Cevap: - Bir ABC küresel üçgeninin elemanları; c=56 km, α=4 0, β=34 0 olarak verilior. Küresel üçgenin diğer elemanlarını Legendre öntemine göre hesaplaınız Additament (Ekleme) Yöntemi İle Küresel Üçgen Çözümü 90
114 Kürede Jeodezik Hesaplamalar Bu öntemde küçük küresel üçgenlerin çözümü için kullanılan aklaşık öntemlerden biridir. Soldner tarafından bulunduğu için Soldner Additament öntemi olarak da adlandırılmaktadır. Bu öntemde küresel üçgenin (s) kenarları 3 s 6 kadar küçültülerek elde edilen kenarlarla küresel üçgenin açıları kullanılarak düzlem trigonometri formüllerile çözüm apılır. Bu öntemde açıları küresel üçgenin açılarına kenarları ukarıdaki kurala göre kısaltılmış ardımcı düzlem üçgen kullanılarak çözüm apılır. A A b b C a B C a B Şekil 7.a Küresel Üçgen Şekil 7.b Yardımcı Düzlem Üçgen Kısaltılmış kenarlar 3 a a 6 3 b b b 6 a Örnek: Bir ABC küresel üçgeninin aşağıdaki üç elemanı verilior. Küresel üçgeni Additament öntemine göre çözünüz. (= m) Verilenler: c m α 47 β 8 o o İstenenler: açısı, a ve b kenarlarının Additament öntemile çözümü F sinα sinβ ρ ε ρ c 4.47 sin(α β) F m o o γ 80 ε (α β) Verilen c küresel kenarından c düzlem kenarı; 9
115 Matematik Jeodezi S.Bektaş 3 c c olarak bulunur. 6 c a ve b düzlem kenarları; c a sinα a m sinγ c b sinβ b m sinγ a ve b küresel kenarlar; 3 a a a m 6 3 b b b m 6 Osa problemin gerçek çözümü (küresel trigonometri teoremlerinden); Açı-kosinüs teoreminden açısı için cosγ sinα sinβ cosc - cosα cosβ azılabilir. Buradan açısı c m c 0 o γ olarak bulunur. o o " İstenen a ve b kenarları küresel sinüs teoreminden a kenarı; sinc sina sinα sinγ b kenarı; sinc sinb sinβ sinγ a m b m olarak bulunur. Görüldüğü gibi gerek Legendre gerekse Additament öntemleri gerçek çözüme oldukça ii aklaşmaktadır. Soru: Bir ABC küresel üçgeninin elemanları; a=40km, =50 0, c=56km, olarak verilior. Küresel üçgeni Additament öntemine göre çözerek diğer elemanlarını bulunuz. (=6370km) Cevap: 9
116 Kürede Jeodezik Hesaplamalar Düzlem tanjant formülünden ararlanılarak; = = =50 = DENETİM: - Bir ABC küresel üçgeninin aşağıdaki üç elemanı verilior. c= m α= β= = m ABC küresel üçgenini Additament öntemine göre çözünüz. - Kenarları 30km, 40km, 50km olan bir küresel üçgeni Additament öntemile çözünüz. 93
117 Matematik Jeodezi S.Bektaş 94
118 Küresel Koordinat Sistemleri KÜESEL KOODİNAT SİSTEMLEİ Küresel koordinat sistemleri küre üzeindeki noktaların konumlarını belirlemee ve noktalar arasında çeşitli hesaplamaları (doğrultu,uzaklık gibi) apmaa olanak sağlar. Küresel koordinat sistemlerini üç grup halinde inceleebiliriz [4],[7]. a) Küresel coğrafi koordinatlar () b) Kartezen (global) dik koordinatlar (X,Y,Z) c) Küresel jeodezik dik (x, ) ve jeodezik kutupsal koordinatlar (S, COĞAFİ KOODİNATLA Düna üzerindeki noktaların konumlarını belirlemek amacıla bütün dünaı saran bir koordinat ağı tasarlanmıştır (şekil-7). Coğrafi koordinat ağı denilen bu sistem paralel ve meridenlerden oluşur. Dünaı kuze ve güne arım küreler olarak ikie aıran ekvator düzlemine paralel düzlemlerin erküre ile arakesitleri paralel daireleri oluşturur. Başlangıç meriden dairesi (Greenwich) =0 o K P P den geçen üze normali P den geçen paralel daire : sabit Ekvator düzlemi = 0 o P den geçen meriden dairesi : sabit G Şekil 7 Coğrafi koordinatlar Ekvatorun kuzeinde kalan paralellere kuze paraleli, güneinde kalan dairelere güne paraleli denir. Paralel daireler kuzede ve günede 90 ar tane olmak üzere 80 tanedirler. Ekvatoru dik olarak kesen, kutuplardan ve erin merkezinden geçen düzlemlerin erküre ile arakesitleri de meriden dairelerini oluşturur. Londra da Greenwich gözlemevinde bulunan bir gök dürbününün ekseninden geçtiği varsaılan meriden, başlangıç meridenidir. Başlangıç merideninin doğusunda bulunanlara doğu merideni, batısında kalanlara batı merideni 89
119 Matematik Jeodezi S.Bektaş denir. Meridenler 80 tanesi doğu ve 80 tanesi batıda olmak üzere 360 tanedir. Küre üzerindeki bir P noktasının enlemi o noktadaki üze normalinin ekvator düzlemi ile aptığı açıdır. Başka bir deişle noktanın ekvatora meriden bounca olan uzaklığını er merkezinde gören açıa o noktanın enlemi denir ve ile gösterilir. Bir noktadan geçen meriden düzlemi ile başlangıç meriden düzlemi arasında kalan açıa da o noktanın bolamı denir. aralıkla geçen meridenler arasında zaman farkı 4 dakikadır. Bolamlar ile gösterilir. bolamı; Greenwich ten doğua doğru pozitif ve batıa doğru negatif olmak üzere 0 ile 80 arasında değişir. enlemi ise ekvatordan kuze kutbuna doğru (+), güne kutbuna doğru (-) olmak üzere 0 ile 90 arasında değişir. Coğrafi Koordinatlarla Temel Ödevlerin Çözümü Coğrafi koordinatlarla temel ödev çözümlerinde kenarların doğrultu değerleri için azimut açısı (A) kullanılır. Azimut açısı, bir kenarın o noktadaki meriden doğrultusu ile saat ibresi önünde aptığı açıdır. Açıklık açısı() verilirse o noktadaki meriden konvergensinden ( ararlanılarak azimut açısına çevrilir (A =. Küre üzeinde açıklık açısı ve meriden konvergensi için soldner koordinat sistemine bakınız[4],[7],[0]. Coğrafi Koordinatlarla I. Temel Ödev: Verilenler: P (, s, A İstenenler: P (, A s σ arcsin(sin cosσ cos sinσ cosa sina Δ λ arctan( cotσ cos sin cosa λ A λ uzunluk olarak verilen kenarın açısal karşılığı Δλ sina arctan( cosσ cosa tan ) sinσ ) ) π P 90 o - A K s 90 o - ekvator Şekil 8 P A Örnek-: 90
120 Küresel Koordinat Sistemleri Verilenler: İstenenler: 0 8 s = m A = 4 o = m Çözüm: s σ arcsin(sin cosσ cos sinσ cosa ) sina Δ λ arctan( cotσ cos sin cosa ) λ A λ Δλ arctan( cosσ sina ) π cosa tan sinσ = o 36, ' = 30 A = 3 o olarak bulunur. Coğrafi Koordinatlarla II. Temel Ödev: Verilenler: P (P ( İstenenler: s, A, A σ arccos(sin sin cos cos cosδ) A A sinδ λ arctan tan cos sin cosδ sinδ λ arctan π cosδ sin cos tan Örnek-: Verilenler: İstenenler: 0 8 s, 36, ' = m Çözüm için ukarıdaki eşitlikleri kullanırsak, s = m A = 4 o A = 3 o olarak bulunur. 9
121 Matematik Jeodezi S.Bektaş Uarı : Küre üzeinde ikinci temel ödev hesaplamalarında azimut açısı bulunurken tıpkı düzlem trigonometride olduğu gibi koordinat farklarına göre bölge irdelemesinin apılması gerekir. - ve noktaları arasında II. Temel Ödev çözümü aparak küresel s(m), A, A değerlerini bulunuz KATEZYEN (GLOBAL) KOODİNAT SİSTEMİ Z P P noktasından geçen normal O YP ZP XP Y Ekvator düzlemi X Grw.Başlangıç Merideni P noktasından geçen meriden Şekil 9 Kartezen koordinat sisteminde de küre üzeindeki noktaların konumunu belirlemek mümkündür. Yakın geçmişe kadar fazla rağbet görmeen bu koordinat sistemi udu jeodezisi (GPS gibi) çalışmalarının agınlaşmasıla nispeten güncellik kazanmıştır. Bu sistemde kürenin merkezine erleştirilmiş bir XYZ üç boutlu dik koordinat sisteminde noktaların konumları tanımlanabilmektedir. Kartezen koordinat sisteminin orijini kürenin merkezinde, Z ekseni kürenin dönme ekseninden geçip, X ve Y eksenleri ekvator düzlemlerinde olup arıca X ekseninin başlangıç (Greenwich) merideni 9
122 Küresel Koordinat Sistemleri düzleminden geçtiği varsaılır. Küre üzei üzerindeki bütün noktalar X + Y + Z = küre denklemini sağlar [4],[7]. Kartezen ve Coğrafi Koordinatlar Arasında Dönüşümler Küresel coğrafi koordinatlar verildiğinde global dik koordinatlar ukarıdaki şekil-9 dan aşağıdaki gibi elde edilebilir. P(,λ) P(X p,yp, Zp ) X cos cosλ Y Z P P P cos sinλ sin Global dik koordinatlar verildiğinde ise küresel coğrafi koordinatlar eldesi aşağıdaki gibi olur. P(X p,y, Z p p tan ) P(,λ) X p Y X Z p p p Y Z p p a da Zp sin = arctan ( Y P / X P ) X P 0 = 80 o + arctan (Y P / X P ) X P < 0 ve Y P 0 = -80 o + arctan (Y P / X P ) X P < 0 ve Y P < 0 Örnek-3 : Aşağıda küre üzeindeki dört noktanın coğrafi koordinatlarıla beraber Global dik koordinatları listelenmiştir. (= m.) Nokta X Y Z 39 o o o o o o o o KÜESEL JEODEZİK DİK KOODİNAT SİSTEMLEİ Küresel jeodezik dik koordinat sistemleri kendi içinde aşağıdaki gibi ) Soldner (Merideni esas alan dik) koordinat sistemi ) Ekvatoru esas alan dik koordinat sistemi 93
123 Matematik Jeodezi S.Bektaş 3) Büük dairei esas alan dik koordinat sistemi olmak üzere üçe arılmaktadır. Meriden ve ekvator sistemleri büük daire sisteminin özel halleridir. Küresel jeodezik dik koordinat sistemlerinde referans alınan dairee ilgili noktadan indirilen dik (büük daire aı biçiminde), noktanın jeodezik dik koordinatlarını belirler (şekil-0). Ekvator sistemindeki jeodezik koordinatlar coğrafi koordinatların metrik karşılıklarıdır. Küresel jeodezik dik koordinat sistemlerinden hangisinin tercih edileceğini genellikle çalışma apılan bölgenin konumu belirler. Bu şekilde tercih apılırsa küçük koordinatlarla çalışma imkanı doğar. Arıca projeksion apılması söz konusu ise deformasonların aşırı olmaması için çalışma bölgesinin sınırlı tutulması diğer bir deişle referans daireden fazla uzaklaşmamak gerekir. Çalışma bölgesinin büüklüğü buna imkan vermiorsa birden fazla koordinat sistemi oluşturulur. Örneğin Soldner sistemi kullanılıorsa çalışma bölgesinin büüklüğüne göre farklı meriden sistemleri seçilir. Bu nedenlerle, ekvator sistemini ekvator bounca uzanan ülkelerde, meriden sistemini bir meriden bounca uzanan ülkelerde, büük daire sistemi ise genel hal olduğu için her bölgede ve özellikle coğrafi koordinatlara göre diagonal biçimde uzanan bölgelerde tercih etmek ugun olur. Söz konusu büük dairenin tek anlamlı olarak belirlenebilmesi için ekvatoru kestiği noktanın bolamı ile bu noktadaki meridenle aptığı açının (azimutun) bilinmesi a da hesaplanabilmesi gerekir. Şekil-0 da bir P noktasının koordinatları çeşitli jeodezik dik koordinat sitemlerinde gösterilmektedir. Coğrafi koordinatlar P(,) P o noktası başlangıçlı Soldner koordinatları P(Xs,Ys) P o noktası başlangıçlı Ekvator Sistemi koordinatları P(Xe,Ye) B noktası başlangıçlı Büük Daire Sistemi koordinatları P(Xb,Yb) Başlangıç Merideni Po S XS YS Ye Xe E P Xb C Yb B Ekvator Xs=P os Ys=PS Xe=PE= ( Ye= PoE=( Xb=PC Yb=BC Büük Daire P noktasından geçen meriden Şekil 0 Küresel Jeodezik Dik Koordinatlar 94
124 Küresel Koordinat Sistemleri Küre üzeinde jeodezik hesaplamalar farklı koordinat sistemlerinde (örneğin coğrafi koordinatlarla) apılabilmekle beraber jeodezide kürenin elipsoid erine kullanıldığı düşünülürse küresel jeodezik dik koordinatlarla çalışmak ugun düşer. Zira coğrafi koordinatların tanımına esas olan üze normalleri küre ve elipsoidde çakışmadıklarından dolaı coğrafi koordinatlarla hesaplamalarda elipsoid erine küre kullanılması doğru sonuçlar vermez. Coğrafi koordinatların kullanılması durumunda küre ile elipsoidin eğriliklerinin farklı oluşu koordinat hesaplarını doğrudan etkiler. Örneğin küre üzerinde eğrilik her noktada ve her doğrultuda sabittir. Osa elipsoid üzerinde eğrilik enleme bağlı olarak her noktada ve her doğrultuda değişmektedir. Bu nedenle küre üzerinde jeodezik amaçlı hesaplamalar için eğriliğe direkt bağlı olmaan küresel jeodezik dik koordinatlarla çalışmak ugun düşer. Küresel jeodezik dik koordinatlardan Soldner koordinat sistemi jeodezi ugulamalarında agın olarak kullanılmaktadır. Coğrafi koordinatlarla jeodezik hesaplamalarda duarlık sorunu da bir dar boğaz oluşturmaktadır. Coğrafi koordinatlardaki lik değişme er küre üzerinde aklaşık 30m e tekabül etmektedir. Bu durumda bir noktanın coğrafi koordinatlarından cm konum doğruluğu elde edebilmek için ekvatora akın bölgelerde bile enlem ve bolamın incelikte hesaplanması gereği vardır. Bu incelik küçük elektronik (cep) hesap makinelerile sağlanamaz. İstenen incelik ancak çift duarlıklı (double precision) saılarla çalışma olanağı sağlaan bilgisaarlarda gerçekleştirilebilir. Arıca coğrafi koordinatların açı birimli oluşu pratikte kullanımlarını engellemektedir. Jeodezik dik koordinatların pratikte daha anlaşılır metrik sistemde oluşu nedenile jeodezik dik koordinatların kullanımı eğlenmektedir[4]. Şimdi de küre üzerinde jeodezik hesaplamaların apıldığı Soldner koordinat sistemini arıntılarıla görelim. Soldner (Merideni Esas Alan ) Jeodezik Dik Koordinat Sistemi Bu sistem, adından da anlaşılacağı gibi merideni esas almaktadır. Sistemi tanımlaan meriden ana meriden olarak adlandırılır ve çalışma bölgesinin akınlarındaki bir meriden ana meriden olarak alınır [7],[0]. 95
125 sabit Matematik Jeodezi S.Bektaş K ekvator F Po F x x S P x sabit P O K Meriden Başlangıç Meridenine paralel ( sabit) A: Azimut : Semt (açıklık açısı) : meriden konvergensi A P Başlangıç (Ana)Merideni P A Şekil.a Şekil.b Bu sistemde x ekseni seçilen ana meridendir (şekil-.a). Meriden sisteminde küre üzerindeki bir P noktasının koordinatları şöle tanımlanmaktadır. P noktasından başlangıç meridenine indirilen dikin uzaklığı F P anı zamanda P noktasının değeridir ( = F P ). Dik aağı noktası F in ana (başlangıç) meriden üzerindeki başlangıç noktası P o a olan uzaklığı da x koordinatını verir (x = P o F ). P o başlangıç noktası ekvator üzerinde de alınabilir. Küre üzerindeki hesaplamalarda kullanılan kenarların ( şekil-.a daki; s,,x,,x değerleri) birer büük daire aı olmaları zorunluluğu vardır. Şekil.a daki O noktası başlangıç meriden dairesinin kutubu olmaktadır. Dolaısıla her zaman OF = OF = OP o = / dir. Soldner koordinat sisteminde kenarların açıklık açılarının referans doğrultusu o noktada başlangıç meridenine çizilen paralel =sabit dairesidir (şekil-.b). Soldner sistemi başlangıç merideni ile belirlidir. Her meriden sistemi arı bir koordinat sistemi oluşturur. Başlangıç merideninin solunda kalan noktaların ordinatları negatiftir. Anı şekilde başlangıç noktasının aşağısındaki noktaların apsisleri de negatif değerler alır. Jeodezik kutupsal koordinatlara örnek olarak şekil-.a daki P noktasını verebiliriz. P noktasının kutupsal koordinatları,p noktasına daalı olarak P deki meriden doğrultusu a da P deki başlangıç meridenine çizilen paralel başlangıç doğrultusu olmak üzere (S, A) a da (S,) ile tanımlanır. 96
126 Küresel Koordinat Sistemleri SOLDNE SİSTEMİNDE TEMEL ÖDEV ÇÖZÜMLEİ I. Temel Ödev : Jeodezik dik koordinatlarla temel ödev çözümlerinde açıklık açısı () kullanılır. Azimut açısı verilirse o noktadaki meriden konvergensinden ararlanarak açıklık açısına ( çevrilir [7],[0]. Verilenler: P (,x ), s, İstenenler: P (,x ), Çözüm: P P O küresel üçgeninde kosinüs ve kotanjant teoremleri ugulanırsa; F / (x-x)/ F arcsincos / s P sin sin s s - / Şekil- P / (x-x)/ cos sinα O x x arctan cot s cos cosα sin sinα cos α arctan Örnek-3: s sinα cosα tan sin s Verilenler; x = m = m 97
127 Matematik Jeodezi S.Bektaş = 4 o s = m (= m) İstenenler :, x, Çözüm : Yukarıdaki, x, formülleri kullanılırsa = m x = m = 3 o olarak bulunur. II. Temel Ödev: Verilenler: P (,x ), P (, x ) İstenenler: s,, Şekil-5 deki P P O küresel üçgeninde kenar kosinüs ve sinüs teoremleri ugulanırsa; s arccossin sin cos cos Δx sin α arccos cos s sin Δx sin α arccos cos π s sin Δx x x Δx cos Örnek-4: Verilenler: Nokta x (= m) İstenenler: s,, Çözüm : Yukarıdaki s,, formülleri kullanılırsa 98
128 Küresel Koordinat Sistemleri s = m = 4 o = 3 o olarak bulunur Soldner Sisteminde Temel Ödevlerin Serilerle Çözümü Jeodezik temel ödev çözümlerinde kullanılan kenarlar her zaman 50 km den ve ordinat değerleri de 00km den küçük olduğundan karşılıkları olan açı değerleri de çok küçük olacağından bunların trigonometrik fonksionları erine seri açılımlarının aşağıdaki gibi ilk iki terimlerinin alınması eterli olur. sin x x - 3 x 6 cos x - Daha önce temel ödev çözümleri için bulunan eşitliklerde bu düzenlemeler apılarak temel ödev çözümleri gerçekleştirilebilir [4],[0],[8]. Serilerle I. Temel Ödev Çözümü x Verilenler : P (x, ), s, İstenenler : P (x, ), Soldner koordinatlarıla I. temel ödev çözüm eşitliklerinde seri açılımları kullanılırsa u v. u = + s sin - v = s sin 6 u. u. v x = x + s cos + u = s cos 6 = - x x olur. Yukarıdaki eşitliklerde küresel düzeltmeler olarak aşağıdaki kısaltmaları kullanırsak = - u v 3 x = v 3 u 99
129 Matematik Jeodezi S.Bektaş = - u v P noktasının koordinatları ve karşı semt,,x ve küresel düzeltmelerile, olur. = + v + x = x + u + x = + Küre üzeindeki I.temel ödev eşitliklerinin düzlem eşitliklere benzerliği açıkça görülmektedir. Düzlemi arıçapı sonsuz olan bir küre düşünürsek diğer bir deişle = alırsak ukarıdaki eşitlikler (küresel düzeltmeler sıfır olacağından) düzlem eşitliklere döner. = 90 o vea 70 o olması a da kenarın ordinat dairesi üstünde olması halinde tüm küresel düzeltmeler sıfır olur. Kenar (s) ve ordinat ( ) değerlerinin 4km nin altında kalması halinde küresel düzeltmeler,x ve çok küçük (<mm) olacaklarından düzlem hesap apmak eterli olur. Örnek-5: Verilenler; x = m = m = 4 o s = m (= m) İstenenler :, x, Çözüm: v = s sin = m u = s cos = = - u v 3 x = v 3 u = - u v = m x = -0.84m = = + v + = m x = x + u + x = m = + =
130 Küresel Koordinat Sistemleri Serilerle II. Temel Ödev Çözümü Verilenler : P (x, ), P (x, ) İstenenler : s,, Çözüm için Soldner koordinatlarıla II. temel ödev çözüm eşitliklerinde seri açılımları kullanılırsa v = u x = x x = - x 3 x = x 3 tan = v u x x x s = sin x x x cos x x = - x = + = - x Örnek-6: Verilenler: Nokta x (= m) İstenenler: s,, Çözüm: Yukarıdaki eşitliklerden x değerleri hesaplanır. = x = x x 0
131 Matematik Jeodezi S.Bektaş = - = - tan = x x v u x 3 x x = m x = x = 4 o = + = 3 o s = sin x x x cos s = m 3 - Soldner koordinatları; ( = , x = ) ve ( =0, x = ) olan iki nokta arasında II. Temel Ödev hesabını apınız Küre üzeinde jeodezik kutupsal koordinatlar Düzlemde olduğu gibi küre üzeinde de bir noktanın konumu hem dik hem de kutupsal koordinatlarla gösterilebilmektedir. ) Küresel jeodezik kutupsal koordinat sistemi 0
132 Küresel Koordinat Sistemleri ) Küresel jeodezik dik koordinat sistemi u P q Bir P o başlangıç noktasına göre küre üzerindeki bir P noktası (u,v) kutupsal olarak (p,q) ile dik koordinat olarak tanımlanabilmektedir. v Po p p Küresel Jeodezik Dik ve Kutupsal Koordinatların Birbirine Dönüştürülmesi Dik koordinatlardan kutupsal koordinatlara dönüşüm (p,q) (u,v) p q u arccos cos cos q tan v arctan arccos cot p sin u tan p Kutupsal koordinatlardan dik koordinatlara dönüşüm (u,v) (p,q) u q arcsinsin sinv p arctan tan u cosv arcsin tan q cotv EKVATOU ESAS ALAN DİK KOODİNAT SİSTEMİ K Greenwich merideni P0 p P x p ekvator x p p ρ λ ρ 03
133 Matematik Jeodezi S.Bektaş Ekvator sistemi, coğrafi koordinat sisteminin metrik karşılığının kullanıldığı bir jeodezik dik koordinat sistemidir. Bu sistemde bir P noktasının x değeri, ilgili P noktasından ekvatora meriden bounca olan uzaklığıdır. P nokrasından ekvatora indirilen dikin aağının ekvator üzerinde P o başlangıç noktasına olan uzaklığı da değeri olur. Ekvator Sisteminde I. Temel Ödev: Ekvator sistemindeki temel ödev hesaplamaları, anı coğrafi koordinatlarda olduğu gibi apılabilir. Verilenler: P (, x ), s, A İstenenler: P (, x ), A x A x s x arcsinsin cos cos sin arctan cot arctan cosa s sina x x cos sin cosa sina s cos sin Ekvator Sisteminde II. Temel Ödev: Verilenler: P (,x ), P (, x ) İstenenler: s, A, A s s cosa π x tan 04
134 Küresel Koordinat Sistemleri x x x x Δ s arccossin sin cos cos cos A A Δ sin arctan x x x Δ tan cos sin cos Δ sin arctan π Δ x x x cos sin cos tan Örnek: Verilenler İstenenler x = m x,, A = m x = m s = m = m A = 6 o A = 96 o = m MEİDYEN YAKINSAMASI (KONVEGENSİ) Meriden sisteminde doğrultuları belirlemek için söz konusu noktadan başlangıç meridenine çizilen paralelin kuze kanadı başlangıç doğrultusu olarak alınırken coğrafi koordinat sisteminde o noktadan geçen meridenin kuze kanadı başlangıç doğrultusu olarak alınır. Dolaısıla bulunacak semt () ile azimut (A) arasında bir () meriden akınsaması farkı olacaktır.( = A - ) Başlangıç merideni x/) Po F x K P A ekvator Başlangıç meridenine paralel P of = x, FP = FK = / ( o + x / ) KPF dik üçgeninde Neper kuralından; 05
135 Matematik Jeodezi S.Bektaş sin tanγ cot o x x sin sin o cos nin x ve den hesabı x cos o cotδ λ tan nın x ve den hesabı tanγ sin / cotδ λ sin tanδ λ Örnek : P o ( başlangıçlı meriden sisteminde P ( noktasındaki meriden konvergensini bulunuz. Çözüm : tan = sin tan olarak bulunur. HEHANGİ Bİ BÜYÜK DAİEYİ ESAS ALAN DİK KOODİNAT SİSTEMİ Bu sistem, meriden ve ekvator sisteminin genel halidir. Diğer bir deişle büük daire sisteminin özel halleri meriden ve ekvator dik koordinat sistemleridir. Bu sistem özellikle bir meriden a da paralel daire sistemine umaan çalışma bölgeleri için ararlı olabilmektedir. Bir büük dairenin küre üzerinde belirli olabilmesi için a üzerindeki iki noktanın koordinatlarının bilinmesi a da ekvatoru kestiği noktanın bolamı ile o noktada meridenle aptığı açının (bilinmesi eterlidir. =0 Po K ekvator 90-p P x p Po noktasının o bolamı ve Po noktasındaki azimutu büük dairei belirler. Başlangıç alınan büük daire aı Büük daire sistemindeki temel ödevler, anen ekvator sisteminde olduğu gibi apılabilir. K 06
136 Küresel Koordinat Sistemleri P x BD A s P x x ekvator Q Herhangi bir büük daire sisteminde koordinatları verilen bir P noktasının coğrafi koordinatlarının hesaplanması A 90 0 K P x B Büük Daire Verilenler:A ve açısı, P(,x) İstenenler: P() Ekv. ABP küresel dik üçgeninde; x cosap cos cos sin cotθ x tan θ θ θ tanθ x tan sin AKP küresel üçgeninde, kotanjant teoreminden cotap cotδ λ p λ A Δλ sinθ AKP küresel üçgeninde sinüs teoreminden 07
137 Matematik Jeodezi S.Bektaş sinθ sinap cos p sinδ Örnek: Bir büük daire sisteminde ( A = 0 o ve = 30 o ) P noktasının koordinatları, = m x = m = m olarak verilior. P noktasının coğrafi koordinatlarını bulunuz., x koordinatlarının açısal karşılıkları o o x o ρ ρ o cosap cos cosx AP tanθ θ θ θ tanx sin θ tanδ sinθ tanap Δλ sinθ sinap cos p p sinδ o o o o 0 0 o o o λ p Soldner Koordinatlarıla Coğrafi Koordinatlar Arasında Dönüşümler = 0 o F o K /- X/ Po /- /- P(X,Y) Y/ (, ) P o ( o, o ) başlangıçlı bir Soldner koordinat sisteminde koordinatları Y, X olan bir noktanın coğrafi koordinatlarının eldesi a da bu işlemin tersi aşağıdaki gibi gerçekleştirilir. Çözüm şekil-4 deki KFP küresel dik üçgeninden apılır [6]. o Şekil-4 ekvator a) Jeodezik Dik Koordinatlardan Coğrafi Koordinatların Eldesi 08
138 Küresel Koordinat Sistemleri Bu dönüşüm probleminde P noktasının P o ( o, o ) başlangıçlı jeodezik dik koordinat sistemindeki (Y, X) koordinatlarından (, ) coğrafi koordinatları istenmektedir. P noktasından ana meridene inilen dikin F aak noktasının enlemi, X o ve Neper kuralından Y cos cot( ) cot olur. Buradan, Y tan arctan cos o Yine anı üçgende KP kenarı için Neper ugulaması, Y cos( ) sin( )sin Y ve buradan, arcsin(cos sin ) meriden konvergensi, Y arctan(sin tan ) arctan(sin.tan ) Dönüşüm formülleri özet olarak aşağıdaki gibi olur ; X o Y tan arctan( o ) cos Y arcsin(cos.sin ) Y arctan(sin.tan ) b)coğrafi Koordinatlardan Jeodezik Dik Koordinatların Eldesi 09
139 Matematik Jeodezi S.Bektaş Bu dönüşüm probleminde coğrafi koordinatları verilen P(, ) noktasının P o ( o, o ) başlangıçlı jeodezik dik koordinat sistemindeki (Y, X) koordinatları istenmektedir. o KFP küresel dik üçgende neper kuralı ugulanırsa, cos cot.cot( ) arctan(tan / cos ) X.( ) o X.arctan(tan / cos ). o ve Y. arcsin(sin.cos ) olarak bulunur. Özet olarak ugulama formülleri aşağıdaki gibi olur, o arctan(tan / cos) X ( o ) Y arcsin(sin.cos) Y arctan(sin.tan ) arctan(sin.tan ) Örnek : P o ( o = 39 o, o = 35 o ) başlangıçlı Soldner jeodezik dik koordinat sisteminde koordinatları, Y = m X = m olarak verilen P noktasının coğrafi koordinatlarını bulunuz ( = m). ψ λ λ o o X arctan ( o ρ ψ Y tan ρ cosψ o ) λ Y o arcsin( cos ρ. sinψ) Y arctan ( sin ρ. tanψ) 90. Örnek : Coğrafi koordinatlardan jeodezik dik koordinatların eldesi Verilenler: Bir P noktasının coğrafi koordinatları 0
140 Küresel Koordinat Sistemleri = 39 o = 35 o şeklinde verilmektedir ( = m). İstenenler: P o ( o = 39 o, o = 35 o ) başlangıçlı jeodezik dik koordinat sisteminde P noktasının Y, X koordinatları, o 0.5 o arctan(tan / cos) o X ( o ) X m Y arcsin(sin.cos) Y m arctan(sin.tan ) KÜE YÜZEYİNDE KESTİME HESAPLAI Tıpkı düzlemde olduğu gibi Küre üzeinde de, kestirme hesapları apmak mümkündür. Aşağıda Küresel Jeodezik dik koordinatlardan en çok kullanılan meriden sisteminde (Soldner koordinatlarıla) Önden ve geriden kestirmenin nasıl apılacağı bütün işlem adımlarıla gösterilmiştir ÖNDEN (İLEİDEN KESTİME) Verilenler: A(x a, a ), B(x b, b ), İstenilenler: P(x,),, Önden kestirme probleminin düzlemdeki çözümünde olduğu gibi kürede çözümünde de kestirilecek noktadaki açısının ölçülme zorunluluğu oktur. açısının ölçülmesi aranan koordinatların doğruluk derecesini arttırır ve arıca açı ölçmelerinde kontrolü sağlar. A P B Çözüm:
141 Matematik Jeodezi S.Bektaş Önce jeodezik dik koordinatlardan temel ödev çözümlerinden ararlanarak (AB), (BA) açıklık açıları ile AB kenarı hesaplanır. u = x b -x a, v = b - a u a u v u u v AB, b xab 6 6 olmak üzere b a ab tan (AB) = x x AB = b a b sin( AB) a ab = x x ab b x a cos(ab) x ab eşitlikleri ile (AB) açıklık açısıla AB kenarı kontrollü olarak bulunur. (BA) açıklık acısı için ab ( )( x x a b b a (BA) = (AB) + şeklinde hesaplanır. ab ) Eksesi hesaplaabilmek ABP üçgeninin üç açısı da ölçülmüş olsa bile eksesi ε = o şeklinde ölçülen açılardan hesaplamak ölçü hataları nedenile pratikte doğru sonuç vermez. Bu nedenle eksesin küresel ABP üçgeninin alanından hesaplanması hatta ABP üçgenini düzlem üçgen şeklinde düşünülerek ine alanından aşağıdaki gibi hesaplanması çoğu kez eteri doğruluğu verir. AB sin sin F F = ve Alandan ekses hesabı, ε = sin( ) şeklinde ABP üçgeninin eksesi hesaplanır. Ölçülen üçgen açılarının düzeltilmesi için iki durum söz konusudur: a) açısının da ölçülmüş olması, ölçülen açılar,, ve w da üçgen kapanması olmak üzere + + = ε + w eşitliği azılabileceğinden, düzeltilmiş açılar,, olmak üzere w w w ' ' ' 3, 3, şeklinde bulunur. b) açısı ölçülmemişse, bu durumda üçgen kapanmasını belirlemek mümkün değildir. Ekses ukarıdaki gibi hesaplanır. açısı aşağıdaki gibi hesaplanır. = 80 + ε ( + ) 3
142 Küresel Koordinat Sistemleri ve düzeltilmiş açılar,, olmak üzere w w ', ', 3 3 şeklinde bulunur. w ' 3 Üçgen kenarlarının hesaplanması düzeltilmiş açılardan ararlanarak Legendre öntemine göre hesaplanabilir. AP = AB ' sin ' sin, BP = AB ' sin ' sin eşitliklerinden AP ve BP kenarları hesaplanır. P noktasının koordinatlarının hesaplanması: (AP) = (AB)-( - w / 3), (BP) = (BA)+( - w / 3) açıklık acıları ile u A AP. cos( AP) v A AP. sin( AP) u B BP. cos( BP) v B BP. sin( BP) hesaplanır ve küresellik düzeltmelerinin hesabı için gerekli p değeri için aklaşık değer P A va şeklinde hesaplanır. Küresellik düzeltmeleri u A A u AvA ub B ubvb AP,, BP 6 6 u A P u Av A ub P ubvb xap,, xbp 6 6 ukarıdaki gibi hesaplanır ve P noktasının aranan koordinatları aşağıdaki gibi hem A noktasından hem de B noktasından kontrollü olarak hesaplanır. P A v A AP, P B vb BP xp x A u A xap, xp xb u B xbp 4.8.-GEİDEN KESTİME Verilenler: A( A,x A ), M( M,x M ), B( B,x B ), acıları İstenilenler: P(, x ) P P İşlem adımları: A M B - AM, MA,MA, BM, MB büüklükleri hesaplanır ( xm x A) A ( xm x A) ( M A) AM 6 ( xm x A) M ( xm xa) ( M A) xam 6 olmak üzere α β P 3
143 Matematik Jeodezi S.Bektaş tan( AM ) x ile (AM) bulunur. AM M M ( M ( AM ) x A A A )(x M YAM XAM x A ) (MA)= AM ile (MA) hesaplanır. MA kenarı, x x M A AM M A xam MA sin( AM ) cos( AM ) kontrollü olarak hesaplanır. (BM), (MB) ve MB kenarı da benzer biçimde hesaplanır. - = (MA) (MB) ile açısı hesaplanır. 3- AMP ve BMP üçgenlerinde ekses, üçgenlerin düzlem alanlarından ararlanarak F A F B B A eşitlikleri ile hesaplanır. Eğer üçgen eksesleri, nin hesapla bulunması isteniorsa () ve () aklaşık değerleri bulunur. Bunun için () + () ve() - () değerleri aşağıdaki gibi bulunur. ( ) ( ) 0 ( ) 80 ( ) ( ) 0 ( ) ( ) arctan{cot(45 ( )) tan } ; A B MBsin sin( ) cot( ) MA sin sin( ) ukarıdaki iki denklem taraf tarafa bir toplanıp bir de çıkarılırsa () ve () değerleri bulunur. MA sin( ( ))sin( ) MB sin( ( ))sin( ) A ; ; B sin sin 4- açıların Legendre öntemine göre indirgenmesi ve ( ), ( ) ardımcı açılarının hesaplanması ' A ' B ' B A, 3 3 olmak üzere AMP ve MBP üçgeninde S ortak kenarı da sinüs teoreminden ' ' AM sin sin ' tan ' ' BM sin sin denilerek hesaplanır. Bölece ' ' ' ' ' ' ' ' ' ' ( ) ve tan tan cot( ) eşitlikleri ile ' ' ve çıkarılmalarıla ' ' 3 değerleri bulunur. Bu değerlerin taraf tarafa toplanıp ve 4 4
144 Küresel Koordinat Sistemleri ' ' ' ' ' ' ve ' ' ' ve elde edilir. 5- AP, BP, (AP) ve (BP) değerlerinin hesabı AP ' sin( ) sin ' ' ' AM, BP BM ' ' ' ' sin( ) sin ' A ' B ( AP) ( AM ) ( ), ( BP) ( BM) ( ) P noktasının koordinatları APsin( AP) BPsin( BP) x P P A A AP B AP x APcos( AP) x BPcos( BP) şeklinde bulunur. xap B x AP ' 5
145 Matematik Jeodezi S.Bektaş 4.9 KÜEDE JEODEZİK HESAPLAMALAIN DÜZLEM ESASLAA GÖE (İNDİGEMEYLE) YAPILMASI Küre üzeindeki Soldner koordinatları hiçbir değişiklik apılmaksızın düzlem koordinatlar olarak ele alınırsa küre üzeinin düzleme ordinat koruan projeksionu (Cassini-Soldner Projeksionu) apılmış olur. Bu durumda küre üzerindeki P ve P noktalarının düzlemdeki karşılıkları P ve P olur(şekil-6). Sözkonusu iki nokta arasında hesaplanacak semt,kenar değerleri her iki üzede farklı olacaktır. x x x P S P r x x x x s t P P r t Şekil-6 Küre Yüzei Projeksion Yüzei (Düzlem) = ve x = x x koordinat farkları olmak üzere, Düzlemde; tan t = x x sin t cost s = x t = t Kürede; Serilerle temel ödev eşitliklerinden (Bölüm ) tan = x x x x sin cos = + S = x x Yukarıdaki eşitliklerde geçen, x, küresellik düzeltmeleri olup aşağıdaki formüllerden hesaplanırlar. 4
146 Kürede İndirgemelerle Jeodezik Hesaplamalar = - = - x x 3 x = x 3 Küre ve düzlemde hesaplanan semt ve kenar değerleri arasındaki farklar hesaplanabilir[4],[7],[6]. t = - t : semt indirgemesi s = S s : kenar indirgemesi s s S s cos t 6 t t x( ) sint cost 6 6 Öte andan semt farkları erine doğrultu farklarının alınabileceği gerçeğinden hareketle doğrultu indiregemesinin semt indirgemesine eşit olacağı ortaa çıkar. r =t =r r Yukarıdaki indirgeme eşitliklerine bakıldığında indirgeme miktarlarının doğrultua bağlı olduğu buradan Ordinat koruan projeksionun konform (açı koruan) bir projeksion olmadığı ortaa çıkar. Başlangıç meridenine akın bölgelerde bu indirgeme farkları dikkate alınmaacak kadar küçük olmakla beraber başlangıç merideninden uzaklaşıldıkça bu farkların dikkate alınması gereği ortaa çıkar. İndirgeme miktarlarının büüklüğü ilgili kenarın doğrultusuna ve meridenden uzaklaşmaa bağlıdır. x =0 olması a da kenarın ordinat ekseni önünde (=90 o a da 70 o ) olması halinde tüm indirgemeler sıfır olur. Ordinat koruan projeksionun adı da buradan gelmektedir. Arıca tüm indirgeme eşitliklerinde geçen /6 terimi nedenile s ve t düzlem değerleri erine S, küresel değerlerinin indirgeme eşitliklerinde kullanılması sorun aratmaz. İndirgeme formüllerinde geçen noktalardan herhangi birinin sözgelimi P noktasının Soldner koordinatları (x, ) şaet bilinmiorsa, bu noktaa koordinatları bilinen bir noktadan (örneğin P den) düzlem esaslara göre I.temel ödevden aşağıdaki gibi koordinat taşınabilir. x x x x S cos s cost S sin ssin t t = (P P )=tan - (/x) 5
147 Matematik Jeodezi S.Bektaş Şüphesiz bu şekilde P noktasının hesaplanan koordinatları aklaşık olup sadece indirgeme işlemi için kullanılabilir. değerler O halde küre üzeinde verilen :semt (r:doğrultu),s:kenar ölçü değerleri düzleme t = - t r =r - t s=s - s şeklinde indirgenerek elde edilecek düzlem değerlerle düzlem esaslara göre hesaplamalar ürütülürse bulunacak koordinatlar anı zamanda küre üzeindeki Soldner koordinatları olacaktır. Bölece düzlem hesapla küresel koordinatlar bulunmaktadır. Bu şekilde küre üzeindeki temel ödev hesapları,kestirme hesapları,poligon hesapları apılabilir. Ancak bu şekildeki hesaplamalar sınırlı büüklükteki çalışma bölgeleri için ürütülebilir. Özet olarak küre üzeindeki hesaplamaları düzlem esaslara göre apmak istersek, apılması gereken sadece küre üzeindeki semt,doğrultu ve uzunluk (,r ve S) ölçülerinin ordinat koruan projeksion kuralına göre indirgenerek düzlem karşılıklarının (t,r ve s) bulunması ve bu değerlerle düzlem hesap apılmasıdır Küre Yüzeinde Temel Ödev Çözümlerinin İndirgemelerle Yapılması Küre üzerindeki temel ödev çözümleri, eğer ölçüler ordinat koruan projeksion kuralına göre indirgenirse düzlem esaslara göre temel ödev çözümleri apılabilir. Bölece hesaplamalarda büük kolalık sağlanır. I. Temel Ödevin İndirgeme Formüllerile Çözümü Verilenler : P (x, ), S, İstenenler : P (x, ), İndirgeme formüllerinde ikinci noktanın koordinatları da gerektiği için öncelikle bu amaç için ikinci noktanın aklaşık koordinatları hesaplanmalıdır. + S sin x x + S cos İndirgenmiş açıklık açısı ve kenar değeri 6
148 Kürede İndirgemelerle Jeodezik Hesaplamalar s s S s cos t 6 t t x( ) 6 6 sint cost ukarıdaki indirgeme formüllerinden, t = - t t = t s = S - s şeklinde elde edilir. İstenen ikinci noktanın kesin koordinatları düzlem I. Temel ödev çözümüne göre, = + s sin t x = x + s cos t karşı açıklık açısı de t indirgemesi hesaplanarak = t + t olur. Bu öntemle temel ödev çözümünde, indirgeme değerleri ikinci noktanın aklaşık koordinatları kullanılarak hesaplandığı için doğruluğu artırmak amacıla kesin koordinat değerleri kullanılarak indirgeme değerleri eniden hesaplanmalı şaet anlamlı bir fark varsa bu eni indirgeme değerlerile hesaplama tekrarlanmalıdır. İndirgeme önteminin kullanıldığı tüm jeodezik hesaplamalarda bu durum söz konusudur. Örnek-7: Verilenler; x = m = m = 4 o S = m (= m) İstenenler :, x, Çözüm: İkinci noktanın aklaşık koordinatları + S sin = m x x + S cos = m İndirgenmiş açıklık açısı ve kenar değeri ukarıdaki indirgeme formüllerinden, s s S s cos t 6 t t x( ) sint cost 6 6 t = , t = ve s = m 7
149 Matematik Jeodezi S.Bektaş t = t =4 o t = t = 3 o s = S - s = m şeklinde elde edilir. İstenen ikinci noktanın kesin koordinatları düzlem I. Temel ödev çözümüne göre, = + s sin t = m x = x + s cos t = m karşı açıklık açısı de = t + t = 3 o olarak hesaplanır. - Soldner sisteminde I. Temel ödev formülleri aşağıda verildiğine göre Y =3000m X =435654m ve iki nokta arasındaki küresel uzunluk s =65000m ve α =4 0 olarak verilior.. noktanın soldner koordinatlarını ve α bulunuz. II. Temel Ödevin İndirgeme Formüllerile Çözümü Verilenler : P (x, ), P (x, ) İstenenler : S,, Çözüm: Önce projeksion düzlemindeki açıklık açısı ve uzunluk değerleri noktaların verilen koordinatlarından ararlanılarak hesaplanır. = ve x = x x tan t = x x sin t cost s = x t = t indirgeme formüllerinden ararlanarak küresel değerler, s s S s cos t 6 t t x( ) 6 6 = t + t = t + t S = s + s sint cost 8
150 Kürede İndirgemelerle Jeodezik Hesaplamalar şeklinde elde edilir. II.temel ödev çözümünde noktaların koordinatları verildiği için iterasona gerek oktur. Örnek-8: Verilenler: Nokta x (= m) İstenenler : S,, Çözüm: Önce projeksion düzlemindeki açıklık açısı ve uzunluk değerleri noktaların verilen koordinatlarından ararlanılarak hesaplanır. = = x = x x = t = arc tan x = o =4 o , t = t = o = 3 o ve s = x = m İndirgeme formüllerinden ararlanarak küresel değerler, t = , t = ve s = m = t + t = 4 o = t + t = 3 o S = s + s = m şeklinde elde edilir. Soru: Soldner koordinatları; Y=765.00m Y= m X= m X= m Olan iki nokta arasında II. temel ödev parak istenenleri bulunuz. Cevap: (=6370km) 9
151 Matematik Jeodezi S.Bektaş - Soldner koordinatları Y =765.00m Y = m X = m X = m olan iki nokta arasında II. Temel Ödev çözümü aparak istenenleri bulunuz. (=6370km) 3- Soldner koordinatları aşağıdaki gibi verilen iki nokta arasında II. Temel Ödev çözümü aparak S, α ve α değerlerini bulunuz. = m x = m = m x = m = m ***** ***** 0
152 Kürede İndirgemelerle Jeodezik Hesaplamalar 4.0. Küre Yüzeinde İndirgeme Formüllerile Kestirme Hesapları Küre üzeinde kestirme hesapları için geliştirilmiş özel öntemler olup bunlar literatürde mevcuttur [],[4],[0]. Ancak burada kestirme hesapları hesap kolalığı nedenile indirgemeler suretile düzlem esaslara göre apılacaktır. Bu amaçla apılan tüm ölçüler indirgeme formüllerile düzlem değerlere dönüştürülür. Şaet ölçülen açılar verilmişse bunlar doğrultulara çevrilir[7]. s s S s cos t 6 t t x( ) 6 6 Şeklinde verilen indirgeme formüllerinde, sin t = s sint cost cos t = değerleri kullanılarak indirgeme formülleri aşağıdaki gibi daha sade bir biçime sokulabilir. P ve P noktaları arasında küresel uzunluk S, küre üzeinde ölçülen doğrultu r ise bu değerlerin düzlem karşılıkları s ve r aşağıdaki gibi bulunur. = x s S 6 S x r' r 6 ve x = x x olmak üzere x s x Ölçüler indirgeme eşitliklerile düzleme indirgendikten sonra tamamen düzlem trigonometri esaslarına göre bütün jeodezik hesaplamalar (temel ödev, kestirme, poligon hesapları gibi) düzlemdemiş gibi apılır ve soldner sisteminde koordinatları bilinen noktalara daalı olarak diğer noktaların kesin koordinatları hesaplanır. İndirgeme işlemlerinde aklaşık koordinatlar kullanılmışsa düzlem hesap sonucunda bulunan kesin koordinatlarla indirgeme büüklükleri eniden hesaplanır. Eğer eni hesaplanan indirgeme değerleri ile ilk hesaplanan indirgeme değerleri arasında anlamlı bir fark varsa bu eni değerlerle hesaplama tekrarlanır ani iterason apılır.
153 Matematik Jeodezi S.Bektaş 4. KÜEDE ÖNDEN KESTİME X P Verilenler: A(x a, a ), B(x b, b ),, İstenilenler: P(x,) Y rap Çözüm: Küre üzeinde ölçüldüğü varsaılan açılar (ata doğrultular) düzleme indirgenir. Ölçülen açılar doğrultu farkları şeklinde düşünülürse aralarındaki ilişki, = r ab - r ap = r bp - r ba şeklinde olur. Bu dört r ik doğrultusu aşağıdaki şekilde indirgenir r' x r 6 x ve elde edilen r ik doğrultularıla düzlemdeki ve açıları bulunur ve bu değerlerle düzlem önden kestirme hesabı apılarak sonuca ulaşılır. Bu indirgeme işlemlerinde kestirilecek noktanın koordinatlarının aklaşık da olsa bilinmesi gerekmektedir. Bu nedenle kestirilecek noktanın aklaşık koordinatları problemin bütün verilenlerile düzlemde kabul edilip çözülmesile elde edilir. Örnek-: Soldner sisteminde koordinatları verilen ve 3 noktalarından kestirilecek noktasına olan doğrultu ölçüleri verilmiştir. noktasının soldner koordinatlarını bulunuz (şekil-8). A rab Şekil-7 rba rbp B Nokta Y X (A) (B) Şekil-8 r X Y DN BN rik (Ölç.Doğrultu) o r3 r3 r3 3
154 Kürede İndirgemelerle Jeodezik Hesaplamalar İstenilenler: ()P(x,) koordinatları P () noktasının aklaşık koordinatlarını düzlem önden kestirme hesabıla bulabilmek için öncelikle ölçülen doğrultu farklarından ve taban açıları hesaplanırsa aşağıdaki değerler elde edilir. = o ve = o Taban açılarıla önden kestirme eşitliklerinden kestirilecek noktanın aklaşık koordinatları, ( b a )cot ( xb xa ) p a = m cot cot ( xb xa )cot ( b a ) x p xa = m cot cot olarak bulunur. Not: Bu eşitlikler şekil-7 e göredir ve kestirilecek olan nokta AB doğrusunun solunda kalmaktadır. Yani kestirilecek noktadan bakıldığında sağdaki nokta A ve bu noktada ki taban açısı, soldaki nokta B ve bu noktadaki taban açısı dır. AB doğrusunun sağında kalan P noktası için ukarıdaki eşitliklerdeki ve açılarının eksi işaretli alınması gerekir. Ölçülen doğrultular indirgenerek düzlem değerlere dönüştürüldüğünde DN BN rik(ölç.doğr.) İndirgeme r ik(indirg.doğr.) o o değerleri elde edilir. Bu indirgenmiş doğrultularla düzlem taban açıları = r 3 r = r 3 r 3 = o ve = o olur ve bu açılarla eniden düzlem önden kestirme apılırsa, P () noktasının kesin koordinatları p a ( b a )cot' ( xb xa ) = m cot' cot ' 3
155 Matematik Jeodezi S.Bektaş ( xb xa )cot' ( b a ) x p xa = m cot' cot ' olarak bulunur. İndirgeme değerlerini kontrol amacıla ukarıda bulunan koordinatlarla doğrultu indirgeme değerleri eniden hesaplanmış ancak anı değerler tekrar elde edildiğinden iterasona gerek kalmamıştır. 4. KÜEDE GEİDEN KESTİME Verilenler: A( A,x A ), B( B,x B ), C( C,x C ), açıları İstenilenler: P( ), x P P A X B C Çözüm: Küre üzerinde ölçüler (doğrultular) düzleme indirgenir. Ölçülen açılar doğrultu farkları şeklinde düşünülürse aralarındaki ilişki, 0 rpa rpb P rpc + Y = r pb - r pa şeklinde olur. = r pc - r pb Şekil-9 Bu üç r ik doğrultusu aşağıdaki şekilde indirgenir x r' r 6 x ve elde edilen r ik doğrultularıla düzlemdeki ve açıları bulunur ve düzlem geriden kestirme hesabı apılarak sonuca ulaşılır. Bu indirgeme işlemlerinde kestirilecek noktanın koordinatlarının aklaşık da olsa bilinmesi gerekmektedir. 4
156 Kürede İndirgemelerle Jeodezik Hesaplamalar Örnek-: Kestirilecek noktasından soldner sisteminde koordinatları verilen, 3 ve 4 noktalarına olan doğrultu ölçüleri verilmiştir. noktasının soldner koordinatlarını bulunuz (şekil-0). Nokta Y X (C) (B) (A) (P) 4(A) 3(B) DN BN rik (Ölç.Doğrultu) o İstenilenler: (P) noktasının (x,) değerleri (C) Şekil-0 Çözüm: Öncelikle ölçülen doğrultu farklarından ve taban açıları hesaplanırsa aşağıdaki değerler elde edilir. = o ve = o Kestirilecek noktasının aklaşık koordinatları Delambre önteminden tan t b = ( Ya Yb)cot ( Yc Yb)cot ( Xc Xa) ( Xa Xb)cot ( Xc Xb)cot ( Yc Ya) t b = o Buradan kestirilecek noktasının aklaşık koordinatları; X = Yc Ya Xa tan( t tan( t b b ) Xc tan( t ) tan( t b ) b ) = m Y = Ya + (X -Xa) tan(t b - ) = -.m olarak bulunur. 5
157 Matematik Jeodezi S.Bektaş Ölçülen doğrultular indirgeme formüllerile düzlem değerlere dönüştürüldüğünde DN BN rik(ölç.doğr.) İndirgeme r ik(indirg.doğr.) o o doğrultu değerleri elde edilir. Bu indirgenmiş doğrultularla düzlem taban açılar = r 3 r 4 = r r 3 = o ve = o olur ve bu açılarla eniden düzlem geriden kestirme apılırsa, tan t b = ( Ya Yb)cot' ( Yc Yb)cot ' ( Xc Xa) ( Xa Xb)cot' ( Xc Xb)cot ' ( Yc Ya) t b = o Buradan kestirilecek noktasının kesin koordinatları; X = Yc Ya Xatan( tb ') Xctan( t tan( t ') tan( t ') b b b ') = m Y = Y a + (X -X a ) tan(t b - ) = m olarak bulunur. İndirgeme değerlerini kontrol amacıla ukarıda bulunan koordinatlarla doğrultu indirgeme değerleri eniden hesaplanmış ancak anı değerler tekrar elde edildiğinden iterasona gerek kalmamıştır. 4.3 KÜE YÜZEYİNDE POLİGON HESABI Çok uzun kenarlı poligonların hesabının düzlemde apılması doğru olmaz poligon hesabının küre üzeinde apılması gerekir. İndirgeme formüllerile küre üzerinde poligon hesabı apmak mümkündür. Bunun için ölçülen poligon açıları (doğrultular) ve kenarlar (deniz seviesindeki) indirgeme eşitlikleri ardımıla düzlem değerlere dönüştürülür. Ölçülerin indirgenmesi aşamasında poligon noktalarının aklaşık da olsa koordinatlarının bilinmesi gerekir. Bunun için düzlem esaslara göre apılacak bir poligon hesabı ile poligon noktalarının aklaşık koordinatları bulunur. İndirgeme işlemleri tamamlandıktan sonra 6
158 Kürede İndirgemelerle Jeodezik Hesaplamalar indirgenmiş ölçülerle apılacak ikinci bir poligon hesabı ile poligon noktalarının soldner koordinatları bulunur[7]. Örnek-3: Küre üzeinde uzun kenarlı poligon hesabı S 0 S 3 0 S Şekil- Uzun Kenarlı Poligon Geçkisi Şekil- deki uzun kenarlı poligon geçkisinde,,3 ve 4 nolu nirengi noktalarının soldner sisteminde koordinatları, şekilde gösterilen kırık açıları ve deniz seviesine indirgenmiş ata kenar uzunlukları verilmiştir. Poligon hesabını aparak 0 ve 0 nolu poligon noktalarının soldner sisteminde koordinatlarını bulunuz. Nokta Y X Poligon açı ve kenar ölçüleri = g S = m = g S = m 3 = g S 3 = m 4 =.3667 g (= m) Çözüm: Öncelikle indirgeme işlemlerinin apılabilmesi için eni poligon noktalarının aklaşık koordinatlarına ihtiaç vardır. Bu amaçla düzlem poligon hesabıla noktaların aklaşık koordinatları hesaplanır. Ölçülen poligon açıları doğrultulara çevrilir. Poligon hesabıla bulunan noktaların aklaşık koordinatları kullanılarak tüm doğrultularla ölçülen ata kenarların aşağıdaki indirgeme eşitliklerine göre indirgemeleri apılarak düzlem değerler hesaplanır. 7
159 Matematik Jeodezi S.Bektaş NNo Kırılma Açıları f = -33 cc Açıklık Açıları t Kenar S =s.sint x=s.cost Y X = x= s= 3338m Poligonların Yaklaşık Koordinatlarının Hesabı f= 5.98m fx= 0.765m = x s S 6 S x r' r 6 ve x = x x olmak üzere Doğrultuların (açıların) İndirgenmesi x DN BN Ölç.Doğ dr=r -r İndg.Doğr. İndg.Açı r(g) (cc) r (g) (g)
160 Kürede İndirgemelerle Jeodezik Hesaplamalar Kenarların İndirgenmesi DN BN Ölç.Kenar ds=s-s İndg. kenar S(m) (cm) s(m) İndirgenmiş açı ve kenar uzunluklarıla apılacak eni bir düzlem poligon hesabıla poligon noktalarının kesin soldner koordinatları bulunur. NNo Kırılma Açıları f = -3 cc Açıklık Açıları t Kenar s s= 3349 =s.sint x=s.cost Y X = Kesin Poligon Hesabı x= f= 0.0m fx= m HESAP BÖLGESİNİN SINILILIĞI Soldner koordinat sisteminde verilen jeodezik hesaplama eşitliklerinden başlangıçta Bölüm de(safa 96) verilen temel ödev eşitlikleri (kapalı formüller) geneldir. Yani her kenar uzunluğu ve her ordinat değeri için geçerlidir. Osa serilerle ve indirgemeli hesaplamalar için çıkarılan eşitliklerde ordinat ve kenar uzunlukları değerlerinin her durumda Y max <00km ve S max <50km olacakları varsaımından hareket edilmiştir. 9
161 Matematik Jeodezi S.Bektaş Pratik olarak, S+Y >50km olması halinde serilerle vea indirgemeli hesaplamalar tavsie edilmez. Aşağıdaki tablo bu konuda fikir verecektir. Hata Serili ve İndirgemeli formüllerde aşılmaması gereken Y ve S için sınır değerler (km) <mm Y:60 S : <cm Y:40 S : Bu nedenle başlangıç merideninden çok uzaklaşılması vea çok uzun kenarların kullanılması halinde bu eşitlikler tam doğru sonuçlar vermez. Öte andan bu sınır değerler de jeodezi ugulamaları için genel de her zaman eterli olur. Zira soldner sisteminde başlangıç merideni çalışma bölgesinin ortalarında seçilir. Buna rağmen bu sınır değerler aşılıorsa ikinci bir meriden sistemi seçilir ve gerekiorsa dilimler (meriden sistemleri) arası koordinat dönüşümü apılır. Farklı dilimler arasında koordinat dönüşümü apmak için önce bir sistemdeki soldner koordinatlarından küresel coğrafi koordinatlar hesaplanır sonra da hesaplanan bu coğrafi koordinatlardan ikinci sistemdeki soldner koordinatlarına geçiş apılır (Bkz. Bölüm 4.7.5). SOLDNE SİSTEMİNDE KOMŞU DİLİMLE AASINDA KOODİNAT DÖNÜŞÜMÜ Soldner sisteminde serilerle ve indirgemeli formüllerin kullanılması durumunda dilim genişliklerinin sınırlı tutulması gerektiğini bilioruz. Arıca küre üzeinin düzleme projeksion söz konusu olduğunda dilim orta merideninden (D.O.M) uzaklaşmalar deformasonları aşırı büütür. Bu nedenle dilim genişliklerinin sınırlı tutulur. Hesap bölgesi birden fazla dilimi kapsıorsa komşu dilimler arasında koordinat dönüşümü gerekebilir[4]. Sol Dilimin D.O.M o p Xp Yp P X p Y p p Sol (Batı) Dilim Sağ (Doğu) Dilim Şekil- Sağ Dilimin D.O.M o 30
162 Kürede İndirgemelerle Jeodezik Hesaplamalar Örneğin şekil- de bir P noktasının o sisteminde Y p,x p soldner koordinatları verilmekte ve anı noktanın komşu o sisteminde Y p,x p soldner koordinatları istenmektedir. Çözüm için verilen soldner koordinatlarından önce noktanın coğrafi koordinatları sonra da coğrafi koordinatlardan ikinci sistemdeki soldner koordinatları hesaplanmaktadır. (X p,y p ) o ( p p ) (X p,y p ) o Örnek-4: 33 0 meriden sisteminde soldner koordinatları; Y= m X = m olarak verilen noktanın 36 0 meriden sistemindeki soldner koordinatlarını bulunuz. (= m) Çözüm: Bölüm de verilen eşitlikler kullanılır. Önce noktanın verilen soldner koordinatlarından coğrafi koordinatlar bulunur. o =33 o için ( =X / ) = o +arc tan[tan(y/) / cos )]= o = 35 o = arc sin[cos(y/) * sin )] = o = 43 o Bu coğrafi koordinatlardan o =36 o için soldner koordinatları hesaplanır. =- o = o = arc tan[tan()/cos()]= o Noktanın o =36 o meriden sistemindeki soldner koordinatları X=(/)= m Y= (/) arc sin[cos() sin()]= m şeklinde bulunur. 3
163 Matematik Jeodezi S.Bektaş - Kürede 33 0 meriden sisteminde Soldner koordinatları Y= -5000m. ve X=37365 m. olan bir P noktasının coğrafi koordinatlarını ve P noktasındaki meriden akınsamasını bulunuz. λ Δ P σ Y ϕp X Soru: Kürede 33 0 meriden isteminde Soldner koordinatları Y=-5000m ve X=37365m olan bir P noktasının coğrafi koordinatlarını ve P noktasındaki meriden akınsamasını bulunuz. Cevap: Soru:Küre üzeindeki A noktasının Soldner ( ) sisteminde koordinatları Y=-55000m ve X=437365m dir. A noktasının ekvator sistemindeki koordinatlarını bulunuz. (6370km) Cevap: A noktasının Coğrafi koordinatları 3
164 Kürede İndirgemelerle Jeodezik Hesaplamalar Cevap: 33
165 Matematik Jeodezi S.Bektaş 5. HAİTA POJEKSİYONLAI Harita Projeksionunun Tanımı: Yeruvarının topoğrafik üzeindeki doğal ve apa her türlü özellik ve tesislerin bir haritaa aktarılabilmesi için erüzü bilgileri önce eruvarı için kabul edilmiş bulunan elipsoid vea küre gibi referans üzeine indirgenir. Daha sonra bu bilgiler bir harita düzlemine taşınır. eferans üzei olarak alınacak küre vea elipsoid gibi eğri üzeler doğrudan doğrua düzleme açılamazlar. Bu nedenle referans üzeine indirgenmiş erüzü bilgileri matematiksel vea geometrik kurallar ugulanarak a doğrudan doğrua a da düzleme açılabilen silindir ve koni gibi ara üzelere aktarılırlar. Bu işleme Harita Projeksionu denir. Harita projeksionunda ararlanılan düzlem a da düzleme dönüşebilen koni ve silindir gibi ardımcı üzelere projeksion üzei adı verilir [4],[6],[8]. Doğaldır ki jeodezik çalışmalar için referans üzeinin düzlem alınması durumunda projeksion işlemine gerek duulmaz. Fiziksel erüzündeki harita apımına konu olan bilgiler arasında uzunluk, alan ve şekil (açı) bakımından daima bir ilişki vardır. Bu bilgiler projeksion üzeine aktarıldığında aralarında bulunan ilişkilerin esas üzedeki gibi kalması beklenemez ve ilişkilerde bazı değişmeler ve bozulmalar olur. Projeksionda ortaa çıkan kaçınılmaz değişme ve bozulmalara deformason denir. Projeksion öntemlerinde deformasonların hesaplanabilme olanağı vardır. Küre ve elipsoid gibi üzelerin düzleme projeksionları söz konusu olduğunda orijinal üze üzerindeki şekil düzleme geçirilirken mutlaka şekil, uzunluk, açı a da alan cinsinden değişikliğe uğrar. Yukarıda saılan üç özelliğin bir arada korunduğu bir projeksion türü mevcut değildir. 5.. Projeksionların Sınıflandırılması Değişik türleri bulunan ve farklı özellikler taşıan harita projeksionları,kullanılan projeksion üzelerine ve projeksionun özelliklerine bağlı olarak iki ana gruba arılarak sınıflandırılır. Her grup içinde er alan değişik projeksion türlerinden söz edilebilir. Harita projeksionları, projeksionun oluşumunda kullanılan üzelerin cinsine göre düzlem,silindirik ve konik projeksionlar olmak üzere üçe arılır. Bu projeksionlardan konik projeksionlar en genel durumdur. Zira koninin tepe açısı sıfır alındığında koni silindire,tepe açısı 80 derece alınması durumunda koni düzleme dönüşür. 30
166 Harita Projeksionları Harita projeksionları,projeksionun özelliğine göre; açı koruan (konform), alan koruan,belirli doğrultularda uzunluk koruan olarak üçe arılır. Projeksion üzelerinin referans üzeile ortak noktalarına göre teğet üzeli,kesen üzeli ve çok üzeli olmak üzerede sınıflandırma apılabilir. Aşağıda çeşitli projeksionların sınıflandırılması çizelge üzerinde gösterilmektedir. Şekil- Çeşitli Projeksion Türleri 3
167 Matematik Jeodezi S.Bektaş Harita projeksion öntemleri geliştirilirken orijinal üze üzerindeki uzunluk, alan ve şekil (açı) ilişkilerinden bir tanesinin korunması istenir. Bu durumda karşımıza üç değişik harita projeksionu çıkar. ) Uzunluk Koruan Projeksionlar Uzunluk koruan projeksionlara örnek olarak silindirik transversal bir projeksion olan Ordinat Koruan Projeksion (Cassini-Soldner Projeksionu) verilebilir. Bu projeksionda Y ekseni bounca uzunluk korunur (Bölüm 7.). ) Açı Koruan (Konform) Projeksionlar Bu projeksion türünde, uzunluk deformasonu doğrultua bağlı olmaksızın her önde eşit olduğundan şekillerde bozulma olmaz, açılar korunur. Gauss-Kruger Projeksionu ile Lambert (Konik) Projeksionu açı koruan projeksionlardır. 3) Alan Koruan Projeksionlar Alan koruan projeksionda orijinal üzedeki alan ile projeksion üzeindeki alan arasında bir fark oktur. Bu tür projeksiona örnek olarak Bonne Projeksionu verilebilir. BÖHYY ve şu an ürürlükte olan BÖHHBÜY ata kontrol (nirengi) noktalarının koordinatlarının üç derecelik Gauss-Krüger Projeksion üzeinde hesaplanması gerektiğini belirtmektedir (madde-7). Bu nedenle harita projeksionlarından alnızca Gauss-Krüger Projeksionu hakkında özet bilgi verilecektir. 5. Kürenin Düzleme Ordinat Koruan (Cassini-Soldner Projeksionu) Projeksionu Herhangi bir projeksion kuralı komaksızın küresel meriden dik koordinatları (Soldner dik koordinatları) düzlem koordinatlar gibi işleme tabi tutulursa, kürenin düzleme ordinat koruan projeksionu elde edilir. Bu projeksionda düzlem ve küresel dik koordinatlar arasındaki ilişki; x = X =Y şeklindedir. 3
168 Harita Projeksionları X X Y Y T S P T x x s T t P t T X P x P Küre Yüzei Projeksion Yüzei Ancak, bu şekilde projeksion düzlemi koordinatları ile hesaplanan uzunluk ve doğrultular, karşılıkları olan uzunluk ve doğrultulardan farklı olur. Başlangıç meridenine akın bölgelerde bu farklar dikkate alınmaacak kadar küçük olmakla beraber başlangıç merideninde uzaklaşıldıkça bu farkların dikkate alınması gereği ortaa çıkar. Ordinat Koruan Projeksionda Uzunluk İndirgemesi: Uzunluk indirgemesi P P büük daire aının S uzunluğu ile P P doğrusunun s uzunluğu arasındaki farktır. Uzunluk indirgemesi s S s şeklinde ifade edilmiştir. s s S s cos t 6 Yukarıdaki formüldeki t erine T ve s erine S kullanılması, sonucu büük ölçüde değiştirmez. T / için s 0 olur. Bu da projeksionun ordinat koruduğunun bir göstergesidir. T = 0 için de s max olur. Bu durumda da = olur. Ordinat koruan projeksion konform (açı koruan) bir projeksion değildir. Ordinat Koruan Projeksionda Doğrultu İndirgemesi: T t cos 6 6 T t x x sint cost 6 6 x x sint t 33
169 Matematik Jeodezi S.Bektaş Bu formüllerde T ve t farklarının çok küçük olduğu gerekçesi ile t erine T de kullanılabilir. Ordinat Koruan Projeksionda Alan İndirgemesi: Küre üzerinde apsis ve ordinat daireleri ile sınırlandırılmış bir şekil projeksion düzlemine bir dikdörtgen olarak geçer. Küre üzeindeki F alanı ile projeksion üzeindeki f alanı arasındaki fark aşağıdaki gibidir. F Ortalama bir f f 6 m değeri için alan farkı F m f f olur. Ordinat Koruan Projeksionda Jeodezik Temel Ödevlerin Çözümü: l. Jeodezik Temel Ödev Verilenler: P (X,Y ), T, S İstenenler: P (X, Y ), T İşlem Adımları: ) Projeksion koordinatları hesaplanır. x = X = Y ) İndirgeme formüllerinde kullanılmak üzere x, için aklaşık değer hesaplanır. x x S cost S sin T 3) s ve t için indirgemeler ve düzlem değerler hesaplanır. S s S cos t 6 t T x x 6 6 sint cost 34
170 Harita Projeksionları 4) Problem düzlemde çözülür. x = x + s cost = + s sint t = t 5) T için t değerinden fadalanarak indirgeme formülü ile değeri hesaplanır. T 6 6 x x sint t t cos 6)Projeksion kuralına göre küresel değerlere geçilir. X = x Y = 4. işlem adımında bulunan kesin koordinatlar (x, ) kullanılarak 3. adımdaki düzeltme değerleri eniden hesaplanır ve değişiklik olup olmadığına bakılır. Eğer değişiklik miktarı önemli ise 4. Adımdaki koordinat hesabı eniden apılmalıdır. Örnek: Verilenler: P (X,Y ), T, S X = m S= m T Y = m = m İstenenler: P (X, Y ), T x = X = m = Y = m x x + S cost m + S sint 7.4 m S s S 6 t T 6 cos t 6 x x sint cost s = S +.64 m = m t T
171 Matematik Jeodezi S.Bektaş x = x + s cost = m = + s sint = m Kontrol için bulunan bu x ve değerleri ile s ve t değerleri eniden hesaplanır. t T s = S +.64m = m Anı indirgeme büüklükleri elde edildiği için iterasona gerek oktur. Karşıt semt; t T T t cos 6 6 t t ll. Jeodezik Temel Ödev x x sint t Verilenler: P (X,Y ), P (X, Y ) İstenenler: S, T, T Bu problemde l.jeodezik temel problemde olduğu gibi iteratif işlem gerekmez. İşlem Adımları: ) Projeksion koordinatları hesaplanır. x = X = Y x = X = Y ) Düzlemde. temel problem çözümü apılır. x = x - x = - t arctan s x t x t 36
172 Harita Projeksionları 37 3) İndirgemelerle küresel S, T ve T değerlerine geçilir. Örnek: Verilenler: P (X,Y ), P (X, Y ) X = m X = m Y = m Y = m = m İstenenler: S, T, T x = X = m x = X = m = Y = m = Y = m x = x - x = m = - = m t x S arctan t x t m t x s t t cos sin 6 6 cos 6 t t x t T t s s S cos sin 6 6 t t x t T cos sin 6 6 cos 6 t t x t T t s s S cos sin 6 6 t t x t T
173 Matematik Jeodezi S.Bektaş S = s m = m T T t t Not: Projeksion düzlemindeki jeodezik hesaplamalar için daha pratik ol tüm ölçüler(doğrultu ve kenarlar) önce projeksion düzlemine indirgenir. Gerekli bütün jeodezik hesaplar(kestirme, poligon hesapları) düzlemde apılır. Gerekiorsa sonunda düzlemden küree geçilir. 5.3 Kürenin Düzleme Gauss Krüger (Konform) Projeksionu 93 ılından beri ülkemizde de kullanılmakta olan Gauss-Kruger Projeksionu silindirik, transversal, açı koruan(konform) bir projeksiondur. İzdüşüm üzei olan silindir, küree başlangıç olarak seçilen meriden bounca teğettir. Bu meridene başlangıç merideni denir. Ülkemiz genelindeki çalışmalar için belirlenmiş başlangıç meridenleri vardır. Bunlar 7,30,33,36,39,4, 45 meridenleridir. K dx L x PN dxcos K M d ds L Xg L dxg M dxg dg ds L K g K P0 Ekvator dxg=dx PS P0 Yg Küre Gauss-Kruger Projeksion GKP de seçilen başlangıç merideninin Gauss-Kruger projeksionu düzlemindeki karşılığı X g ekseni olarak alınır. Bu durumda başlangıç merideninde uzunluk deformasonu oktur. Gauss-Kruger projeksionunda x g değerleri ekvatordan başlar. Bu üzden jeodezik dik koordinat sisteminin başlangıç noktasının ekvator üzerinde olduğu düşünülmelidir. 38
174 Harita Projeksionları P 0 başlangıç noktasının Gauss-Kruger projeksion düzlemindeki karşılığı olarak seçilen Başlangıç merideninde uzunluk korunduğundan P 0 noktasından X ekseninin karşılığı olacak herhangi bir x g ekseni alınır. P K P K 0 P L L P alınarak K,L noktalarının karşılıkları bulunur. K, L noktalarının karşılıklarını bulmak için noktalarından çıkılan dikler üzerinde g ve g +d g değerleri kadar alınır. Bu değerler projeksion formüllerinden hesaplanır. K, L K, L GKP konform açı koruan bir projeksiondur. Şekildeki küre üzeindeki diferansiel KLM üçgeni ile projeksion düzlemindeki karşılığı K L M üçgeninin benzer olmalıdır.bu benzerliğin olabilmesi için, ds dg dxg ds d dx.cosy olmalıdır. X ler eşit olduğu için dx g = dx azılabilir. Bu durumda; d g m ( m : ölçek,diferansiel büüme oranı) d cos Y Buradan dx g = dx d g = d / cos Y çıkar. Bu eşitliklerin her iki tarafının integrali alınırsa, x X g g 3 Y Y 6 5 Y 4 4 a da g Y arctan hsin bölelikle jeodezik dik (Soldner) koordinatlarıla Gauss-Kruger koordinatları arasındaki ilişki çıkarılmış olur Jeodezik Dik (Soldner) Koordinatlardan Gauss-Kruger Koordinatlarının Bulunması Verilenler: X,Y İstenenler: x g, g 39
175 Matematik Jeodezi S.Bektaş x g X g Y 3 Y 6 5 Y 4 4 a da g Y arctan hsin Örnek: Başlangıç noktası ekvatordan olan bir jeodezik dik koordinat sisteminde koordinatları X = 48367m ve Y = 5378m olan noktanın Gauss-Kruger projeksion koordinatlarını bulunuz. ( = m) x g = X = 48367m g = = m 5.3. Gauss- Kruger Koordinatlarından Jeodezik Dik (Soldner) Koordinatlarının Bulunması Verilenler: xg, g İstenenler: X, Y X x g 3 5 g g Y g g Y arcsin (tanh ) a da Örnek: Gauss-Kruger koordinatları xg = m ve g = m olan noktanın jeodezik dik koordinatlarını hesaplaınız. X = xg = m Y g 6 3 g 5 g 4 4 Y = m m m Y = m = 5378 m 5.4 KÜESEL COĞAFİ KOODİNATLADAN GAUSS- KÜGE KOODİNATLAININ HESABI Bir P noktasının () küresel coğrafi koordinatları bilinmektedir. Bu noktanın 0 bolam başlangıcına göre Gauss- Krüger (x, ) koordinatları istenmektedir. Bolam farkı olarak, 40
176 Harita Projeksionları λ Δλ λ P λ 0 0=0 F F X π F Y K = π P(x, ) (, ) ekvator Küresel meriden sistemi dik koordinatları cinsinden projeksion eşitliği, x X ve X x Y Y arctanh (sin ) arcsin (tanh ) Küre üzerinde meriden sistemi dik koordinatları, coğrafi koordinatlar cinsinden, tan X arctan ( ) cosλ Y arcsin (sinλ cos) şeklindedir. Bu değerler x ve li eşitliklerde erine konulursa, olur. tan x arctan( ) cosλ arctanh (sinλ cos) Gauss- Krüger Koordinatlardan Küresel Coğrafi Koordinatların Hesabı Küresel coğrafi koordinatlar küresel meriden dik koordinatları cinsinden, 4
177 Matematik Jeodezi S.Bektaş X Y arcsin(sin cos ) Y tan λ arctan( ) X cos Gauss- Krüger koordinatları cinsinden, Örnek : x sin arcsin( ) cosh sinh λ arctan( ) x cos Verilenler: Küresel coğrafi koordinatları = 38 o 4.6 = 3 o 0 9. olarak verilior. İstenenler: o = 30 o sistemindeki (x, ) Gauss- Krüger koordinatları = m λ Δλ λ λ 0 o 0 9. tan x arctan( ) m cosλ arctanh (sinλ cos) m Örnek : Verilenler: Bir noktanın o = 30 o sisteminde Gauss- Krüger koordinatları x = m = m olarak verilior = m İstenenler: () küresel coğrafi koordinatlar 4
178 Harita Projeksionları x sin o arcsin( ) cosh sinh λ arctan( o ) 0 9. x cos Gauss -Kruger Projeksionunda Uzunluk Deformasonu Gauss-Kruger projeksionunda her önde uzunluk deformasonu eşit olduğundan (açı koruan) olma özelliği nedenile ölçek; Y m g m 4 5Y 4 4 g olur. Projeksion üzündeki kenar her zaman erüzündeki karşılığından büüktür. δ δ s s s S s ( 6 m S s S ) Gauss- Kruger Projeksionunda (Açıklık Açısı) Doğrultu İndirgemesi Yerüzündeki açıklık açısıla projeksion düzlemindeki karşılığı arasındaki farka açıklık açısı redüksionu denir ve δ t T t şeklinde gösterilir. δ δ ρ ρ T t (x x)( ) (x x)( ) 4 ρ ρ T t (x x )( ) (x x )( ) 4 Bu formüller daha kısa olacak şekilde aşağıdaki gibi tek terimde azılabilir. 43
179 Matematik Jeodezi S.Bektaş δ δ ρ T t x( ) 6 ρ T t x( ) 6 x üzerinde hesap apılan kenarlar kısa ise redüksion bağıntıları daha basit biçime dönüştürülebilir. ve erine bunların ortalama değeri, alınırsa m T t T t ρ ρ m x m x x x Gauss -Kruger Projeksionunda Alan edüksionu Küre üzeindeki F alanı ile projeksion üzeindeki f alanı arasındaki fark aşağıdaki gibidir. F f F f f f m 3 Gauss -Kruger Projeksionunda Jeodezik Temel Ödevlerin Çözümü I. Jeodezik Temel Ödevin Çözümü Verilenler: P (X, Y ), T ve S İstenenler: P (X, Y ), T Ordinat koruan projeksionda olduğu gibi Gauss-Kruger projeksionda I. Jeodezik temel ödevlerin çözümü için bir iteratif işlem söz konusudur. İşlem adımları; ) Projeksion koordinatları hesaplanır. 44
180 Harita Projeksionları x X 3 5 Y Y Y Y *arctanh(sin ) ) İndirgeme formülleri için x, nin aklaşık değerleri hesaplanır. x x S.cosT S.sinT 3) s ve t için indirgemeleri ve düzlem değerleri hesaplanır. S s S ( ) 6 ρ t T Δx( ) 6 4) Problem düzlemde çözülür x x s.cost s.sint Bu adımdan sonra x, değerleri ile 3. adıma dönülerek uzunluk ve doğrultu indirgemeleri formülleri ile s ve t değerleri eniden hesaplanır. Eğer değişme oksa 5. adıma geçilir. 5) T için t değerinden ararlanarak indirgeme formüllerile değeri hesaplanır. t T t t π ρ 6 Δx( ) 6) Projeksion kurallarına göre küresel değerlere geçilir. X Y Örnek: Verilenler: x arcsin(tanh ) X = m Y = m S = m T = 3 o
181 Matematik Jeodezi S.Bektaş İstenenler: X, Y ve T x x X m Y * arctanh(sin ) m x ScosT m SsinT m S s S ( ) 6 s S m ρ t T Δx( ) 6 t T.74 t x o x scost m scost m Bu adımdan sonra son bulunan x, değerleri kullanılarak indirgeme eşitlikleri ile s ve t değerleri eniden hesaplanır. s S m m o t T ani değerler değişmemiştir. O halde x ve için apılan düzlem hesap sonucu bulunan değerler kesin değerlerdir. Son olarak karşı noktadaki semt hesaplanır. t T T t π ρ t Δx( 6 o o ) t 8.7 istenirse projeksion kuralına göre küresel koordinatlar hesaplanır. X Y x m arcsin(tanh ) m Gauss- Kruger Projeksionda II. Jeodezik Temel Ödevin Çözümü Verilenler: P (X, Y ), P (X, Y ) İstenenler: S, T ve T 46
182 Harita Projeksionları Bu problemlerin çözümünde I. Jeodezik temel ödevinde olduğu gibi iteratif işleme gereksinim duulmaz. Öncelikle projeksion koordinatları hesaplanır. Problem düzlemde çözülür ve elde edilen düzlem hesap sonuçlarından indirgemelerle küresel karşılıklarına geçilir. İşlem adımları aşağıda açıklanmıştır. ) Projeksion koordinatları hesaplanır. x x X X Y arctanh (sin ) Y arctanh (sin ) ) Düzlemde II. temel problem çözümü apılır. Δx x t t Örnek: Verilenler: x Δ arctan ( ) Δx t π Δ s Δx Δ 3) İndirgemelerle küresel S, T ve T değerlerine geçilir. s S s ( ) 6 ρ T t Δx( ) 6 ρ T t Δx( ) 6 X Y m m m X Y m m İstenenler: S, T ve T 47
183 Matematik Jeodezi S.Bektaş x x t t s X m Y arctan h (sin ) m X m Y arctan h (sin ) m Δx x Δ o arctan( ) Δx t Δx x Δ Δ m o π s S s ( ) 6 S s 3.653m m ρ o T t Δx( ) t ρ o T t Δx( ) t Ordinat Koruan ve Gauss- Krüger Projeksionların Karşılaştırılması Küresel dik koordinatlardan hareket edildiğinde ordinat koruan projeksion büük kolalık sağlar. Çünkü küresel dik koordinatlarla projeksion koordinatları anı saısal değerlere eşittir. Bu kolalık sebebile ordinat koruan projeksion geçen üzılda geniş kullanım alanı bulmuştur. İndirgemeler açısından karşılaştırıldığında durum şöledir [6]: Uzunluk İndirgemesi s Ordinat koruan projeksionda; S s ( )cos t 6 s Gauss- Krüger projeksionunda; S s ( ) 6 Görüldüğü gibi her iki formülün apısı da anı fakat Gauss- Krüger projeksionunda cos t çarpanı oktur. Bu demektir ki Gauss- Krüger projeksionundaki uzunluk indirgemesi her zaman için ordinat koruan projeksionundakinin maksimumudur. Buna karşılık Gauss- Krüger 48
184 Harita Projeksionları projeksionunda uzunluk indirgemesi doğrultudan bağımsız olduğu için daha basit şekilde hesaplanır. km lik bir küresel kenar Gauss- Krüger projeksionunda, = 90 km için 0 cm = 5 km için 0 cm = 00 km için 50 cm uzamış olur. Alan İndirgemesi f Ordinat koruan projeksionda; F f ( ) 6 f Gauss- Krüger projeksionunda; F f ( ) 3 Formüllerden görüldüğü gibi ordinat koruan projeksiondaki alan indirgemesi Gauss- Krüger projeksionundakinin arısı kadardır. Ancak her iki projeksionda da bu indirgeme büüklükleri kabul edilen hata sınırlarının altında kalır. Bu sebepten dolaı sadece çok büük alanların hesabında bu indirgemeler dikkate alınır. Doğrultu İndirgemesi Ordinat koruan projeksionda; ρ ρ T t Δx ( ) ( ) sint cost 6 6 Gauss- Krüger projeksionunda; ρ T t Δx ( ) 6 görüldüğü gibi ordinat koruan projeksionda büük değer ikinci terimdedir. Gauss- Krüger projeksionunda bu terim oktur. O halde Gauss- Krüger projeksionunda doğrultu indirgemesi özellikle kısa kenarlarda daha küçük olmaktadır. 49
185 Matematik Jeodezi S.Bektaş Kürede I. jeodezik temel problemlerin hem ordinat koruan hem de Gauss- Krüger projeksionla çözümünde küresel sonuçlar ani P noktasının küresel dik koordinatları ve T semti her iki öntemde anı olup, X = m Y = m T = 4 o değerleri bulunmuştur. Fakat hesap adımları içinde ara değerleri her iki projeksion türündeki düzlem s,, t ve t değerleri farklıdır. Çünkü bu düzlem değerlerin karşılıkları ile ilişkilerini sağlaan indirgeme formülleri farklıdır. Değerler aşağıdaki tabloda verilmiştir. Ordinat koruan projeksion Gauss- Krüger projeksion s m m t 3 o o m m x Her ikisinde de anıdır ( x = X ) 50
186 Elipsoide Jeodezik Hesaplamalar 6. NİENGİ (YATAY KONTOL) NOKTALAI Jeodezinin en önemli uğraşlarından biri, fiziksel erüzünde eterli sıklıkta üç boutlu koordinatları bilinen daanak (nirengi) noktaları üretmektir. Tüm jeodezik çalışmalarda bu daanak noktalarından ararlanılır. Söz konusu daanak noktalarının tümünün bir kerede ve anı doğrulukta üretilmesini beklemek ekonomik olmadığı gibi teknik olarak da fazla bir arar getirmez. Bu nedenle daanak noktaları aşama sıralı (hierarşik) bir apıda üretilir[4]. Bilindiği üzere ülkemizde bu daanak noktaları ; dır. I. Derece Nirengi Noktaları (30-50km kenar uzunluklu) II.Derece Nirengi Noktaları (aklaşık 0km kenar uzunluklu) III. Derece Nirengi Noktaları (5-0km kenar uzunluklu) IV. Derece Tamamlama Nirengi Noktaları (-5km kenar uzunluklu) ve Dizi Nirengi Noktaları ( m kenar uzunluklu) Hierarşik apı gereği, önce üst derece nirengi ağ noktaları tesis edilir, gerekli jeodezik ölçümler apılarak ağ noktalarının belirli bir sistemde koordinatları dengelemeli olarak belirlenir. Bir alt derece ağın noktaları, üst derece ağ noktalarını sıklaştıracak şekilde tesis edilir ve koordinatlarının hesabında kendinden daha önce hesaplanmış üst seviedeki noktaların koordinatlarından (hatasız oldukları kabul edilerek) ararlanılır. Üst derece ağ noktalarının daha duarlı olmaları doğaldır. Bunun için üst derece ağ noktaları için apılan ölçülerin daha duarlı olması gerekir. Teknik önetmelikler hangi ağ seviesinde ölçülerin ne kadar duarlıkta apılması gerektiğini ve hesaplama standartlarını belirlerler. Ülkemizde; ukarıda sözü edilen nirengi noktalarından I.derece, II.derece ve kısmen III.derece nirengi noktalarının dengelenmesi tamamlanmış olup alım için sıklaştırma amacıla atılan üçüncü derece ve dördüncü derece nirengi noktalarının koordinatları daha üst seviedeki nirengilerden ararlanarak hesaplanmaktadır. Nirengi ağları, ülke ölçmeleri dışında lokal harita gereksinimleri,büük mühendislik apılarındaki olası deformasonları ve depremlerin önceden kestirilmesine önelik olarak er kabuğu hareketlerinin izlenmesi amacıla bağımsız olarak da tesis edilirler. Bir bölgede nirengi ağının oluşturulması için; önce istikşaf (noktaların erlerinin seçimi) apılır. Sonra inşaat (noktaların zemin ve zemin üstü işaretlerinin apımı) işleri tamamlanır. İstikşaf işlemi için bölgenin daha önce apılmış küçük ölçekli bir haritası varsa kurulacak nirengi ağının biçimine ve eni nirengi noktalarının neree atılacağına bu harita üzerinde karar verilir. Büroda apılan bu çalışmaa ön seçim denir []. Ön 5
187 Matematik Jeodezi S.Bektaş seçimle belirlenen geçici ağ biçimi ve nokta erleri, daha sonra arazideki koşullara ugunluğu (örneğin noktaların birbirini görüp görmediği) bizzat mahallinde kontrol edilir ve gerekli düzeltmeler apılır. Nokta erlerinin seçiminde aşağıdaki hususlar gözetilir: -Nirengi noktalarının oluşturacağı şekil (ağ) çalışma alanını kaplamalı ve bir miktar da dışına taşmalıdır. -Birbirine akın noktalar arasında görüş olanağı olmalıdır. -Noktaların olabildiğince eşkenar üçgen oluşturmalarına özen gösterilmeli ve hiçbir zaman 36 graddan küçük açılı üçgen bulunmamalıdır. -Üçgen kenarları bölgesel koşulların elverdiği ölçüde uzun ve birbirine olurunca eşit seçilmelidir. -Noktalar sağlam zeminlerde seçilmeli, zemin ve zemin üstü işaretleri erleştirilerek röperlenmelidir. -Yerleşme bölgeleri ve ağaçlık alanlar gibi görüş olanaklarının az ve güç olduğu bölgelerde görüş olanağı üksek minare, kule,anten tesisleri, bina üstleri nirengi noktası olarak seçilmelidir. -Bölgede önceden tesis edilmiş nirengi noktalarından ugun konumda olanlardan ararlanılmalıdır. -Hierarşik sırada önce ana daha sonra ara nirengi noktalarının seçimi apılmalıdır. Nirengi noktalarının tesisinden sonra ağda gerekli açı ve uzunluk ölçüleri apılır, ağda en az koordinatı bilinen iki nokta oksa ağın önlendirilebilmesi için semt ölçüsü de apılır. Bütün bu işlemlerin nasıl apılacağı teknik önetmelikte belirlenmiştir. Örnek nirengi kanavası şekli EK:0 da verilmiştir. Bir bölgede nirengi ağı tesis edilirken çalışma bölgesinin büüklüğü hesap üzeini belirler. Genişliği a da uzunluğu 0km i geçmeen erel ağlarda hesap üzei düzlemdir. Bu tip ağlarda hesaplama apılırken erin şekli düzlem alınmakta ve tüm ölçülerin düzlemde apıldıkları varsaılmaktadır. Boutları 0 km den daha büük a da ülke ağına daanmaları zorunlu olan büük bölgesel ağlarda hesap üzei elipsoid olup ağ noktalarının Gauss-Krüger projeksion üzeindeki düzlem dik koordinatları hesaplanır. Doğaldır ki bu tip ağlarda önce ölçüleri elipsoid üzeine ardından da projeksion üzeine indirgeip hesaplamaa başlanmalıdır. Ölçülerin Gauss-Krüger projeksion düzlemine nasıl indirgeneceği Harita Projeksionları (Bölüm 9) konusunda gösterilmiştir. BÖHYY, Dördüncü derece nirengi olarak adlandırılan Ara nirengi, Tamamlaıcı nirengi ve Dizi nirengiler hakkında; 5
188 Elipsoide Jeodezik Hesaplamalar Ara Nirengi: Daha üst derece nirengilerden nokta dengelemesi ile hesaplanan ve kendinden başka nirengilere çıkış veren nirengi noktalarıdır (Madde 36). Tamamlaıcı Nirengi: Başka bir nirengie çıkış vermeen ve çıkış aldığı noktalardan uzaklıkları 3km den kısa olan noktalardır. Tamamlaıcı noktalar karşılıklı gözlem apılabilen, ufka ugun şekilde dağılmış en az dört noktadan koordinatları hesaplanır (Madde 38,39,40,4,4,43). Dizi Nirengi: Çıkış veren nirengiler arasında tesis edilecek poligon hesabı ile belirlenen noktalardır, eteri kadar çıkış sağlanamaan ormanlık ve benzeri erlerde tamamlaıcı nirengi erine dizi nirengi tesis edilebileceği, dizi nirengi güzergahlarının olabildiğince gergin,kenar uzunluklarının 800m ile 500m arasında toplam güzergah uzunluğu 7km den kısa ve güzergahtaki nirengi saısı 7 den az olmalıdır (Madde 44,45). Dizi nirengilerin koordinat hesapları daalı poligon hesabındaki esaslara göre apılır. Dizi nirengilerde; Açı kapanma hatası: F = 60 cc + 0 cc Enine hata (metre): F Q = S km Bouna hata (metre): n F L = n (n: açı ölçümü apılan nokta saısı) formüllerinin verdiği değerden daha büük olamaz. Dördüncü derece nirengilerde ata açılar cc i doğrudan ölçen aletlerle ara nirengilerde 6 silsile, tamamlaıcı ve dizi nirengilerde 4 silsile olarak apılır. Gözlemler cc inceliğinde apılır ve silsile ortalamaları cc e kadar hesaplanır. Silsileler ortalamasındaki bir doğrultunun karesel ortalama hatası ara nirengilerde 7 cc i tamamlaıcı nirengilerde 0 cc i geçemez. Ara nirengi nokta dengelemesinde nokta konum hatası 5cm den büük olamaz demektedir (Madde 5,5,53,54,55,56,57). 53
189 Matematik Jeodezi S.Bektaş 6. NİENGİ AĞLAININ KONUM, ÖLÇEK ve YÖNÜNÜN BELİLENMESİ Bir nirengi ağındaki noktaların koordinatlarının hesaplanabilmesi için alnız ata doğrultu ve uzunluk ölçüleri eterli değildir. Ağın datum parametreleri dediğimiz konumu ölçeği ve önünün de belirli olması gerekir. Genelde nirengi ağlarında apılan klasik ölçüler (ata doğrultu ve kenar ölçüleri GPS ölçüleri hariç) bu datum parametrelerinin tamamını belirlemez. Diğer bir deişle apılan ölçüler nirengi ağının bir koordinat sisteminde tanımı için gerekli bilgilerin tamamını içermez. Bu datum parametreleri; nirengi ağlarında dört tanedir ( koordinat eksenleri önünde öteleme, ölçek ve dönüklükten ibarettir). Bir nirengi ağında koordinatı bilinen (sabit) iki nokta olması halinde ağın konumu,önü ve ölçeği kendiliğinden belirlenmiş olur. Ağın Ölçeğinin Belirlenmesi: Ağda apılan doğrultu ölçüleri ağın büüklüğü hakkında hiçbir bilgi vermez. Bu nedenle nirengi ağının en az bir kenarı ölçülmüş olmalıdır. Bu ölçülen kenara baz adı verilir. Ağın diğer kenarları bu bazdan ararlanarak hesaplanır. Nirengi ağının konum doğruluğunu ükseltmek için bütün üçgen açıları ve ağda ugun şekilde dağılmış olabildiğince fazla saıda kenarın ölçülmesi gerekir. Ağın Yönünün Belirlenmesi: Ağda apılan doğrultu ve kenar ölçüleri ağın önü hakkında hiçbir bilgi vermez. Bu nedenle nirengi ağında en az bir kenarın semtinin (kuzele aptığı açının) bilinmesi gerekir. Bu semt belirleme işlemi genellikle ağda koordinatları bilinen noktalardan aralanarak bulunur. Ağda koordinatları bilinen en az iki nokta oksa semt belirleme işlemi güneşe a da ıldızlara apılan astronomik gözlemlerle ağdaki bir kenarın semti belirlenir. Bu da apılamıorsa ağdaki bir kenarın kuzele aptığı açı bir pusula ile belirlenir. Semt Belirleme Nirengi ağlarının önlendirme işlemi kuze önünden itibaren apılır. Çeşitli kuze doğrultuları bulunduğundan doğruların bunlarla oluşturduğu semt açıları da çeşitli adlar alır. Üç çeşit semt açısı vardır. Bunlar; - Coğrafi (Astronomik) semt açısı, - Jeodezik semt açısı, 3- Manetik semt açısı dır. 54
190 Elipsoide Jeodezik Hesaplamalar K Meriden X Başlangıç Meridenine paralel A: Azimut : Semt (açıklık açısı) : meriden konvergensi A P MK CK X A P P P Coğrafi semt (Azimut) ; AManetik semt; = A + + Coğrafi semt açısı, Her hangi bir noktanın coğrafi (astronomik) kuzei (CK), o nokta ile er küresinin kutup noktalarından geçen bolam dairesinin kuze önüdür. Buna göre anı bolam dairesi üzerindeki bütün noktaların kuze önü anıdır. Bir doğrunun bir ucundaki semt açısı, doğrunun o ucundan geçen bolam dairesi ile doğrunun saat ibresi önünde oluşturduğu açıdır ve Azimut açısı (A) adını alır. Astronomik semt taininde,genellikle coğrafi kutup noktasına çok akın olan kutup ıldızının a da her hangi bir ıldızın vea güneşin,bulunduğumuz noktanın meriden dairesinden geçiş anındaki önü ile tespit edilir. KUTUP YILDIZI KUTUP NOKTASI 5 birim birim KÜÇÜK AYI BÜYÜK AYI Kutup ıldızı kuze kutbuna en akın olan,oldukça parlak,küçük Aı ıldız grubunun kuruğundaki son (üçüncü) ıldızdır. Kutup ıldızı, Büük Aı ıldız grubunun kepçesinin altındaki iki ıldızı birleştiren doğrunun aklaşık olarak uzantısında ve bu iki ıldız arasındaki uzaklığın beş katı kadar uzaklıktadır[],[4]. 55
191 Matematik Jeodezi S.Bektaş Jeodezik semt açısı, Dünamız küree benzediği için,bolam daireleri birbirine paralel olmaıp kutuplara doğru birbirlerine aklaşırlar. Bu nedenle değişik bolam daireleri üzerinde bulunan noktaları birleştiren doğruların iki ucundaki kuze önleri birbirine paralel değildir. Her hangi bir bolam dairesini X ekseni olarak kabul eden bir dik koordinat sisteminde (örneğin soldner koordinat sistemi), başlangıç bolamından (orta meridenden) doğua ve batıa doğru uzaklaşıldıkça coğrafi kuze ile karelaj-grid kuzei (paftanın ukarı önü) arasında bir açı oluşur. Bu açı meriden akınsaması(meriden konvergensi) açısıdır ve ile gösterilir. Bir P P doğrusunun jeodezik semt açısı a da kısaca semt açısı = (P P ) ile gösterilir. Düzlem jeodezide X ekseni meridenle çakışık olarak düşünüldüğü için meriden akınsaması sıfırdır dolaısıla azimut açısı semt açısına eşit olur. Manetik semt açısı, Bir doğrunun manetik kuze ile oluşturduğu açıdır. Manetik kuze doğrultusu (MK) pusula ile belirlenir. Manetik semt açısı ile gösterilir. Manetik kuze genellikle astronomik kuze ile çakışmaz, aralarında pusula sapması (manetik deklinason) denilen ve ile gösterilen açı oluşur. Pusula sapması açısı değişik erlerde değişik ön gösterebilir. Arıca pusula sapması günlük ve senelik değişimler gösterir. Senelik değişme ortalama olarak 6-7 dakika civarındadır. Ağın Konumunun Belirlenmesi: Nirengi ağının konumunun belirli olabilmesi için ağda en az bir noktanın koordinatının bilinmiş olması gerekir. Eğer bu koşul sağlanamıorsa ağdaki bir noktanın koordinatları kefi olarak alınır örneğin Y =50 000m, X =50 000m gibi. Bu kefi koordinat belirleme işleminde ağdaki tüm noktaların koordinatlarının pozitif olabilmesine dikkat edilir. Ağdaki bir noktanın ukarıdaki gibi koordinatlarının kefi olarak belirlenmesi durumunda anı zamanda kefi bir koordinat sistemi tanımlanmış olmaktadır. Bu nedenle böle nirengi ağlarında hesaplanacak nokta koordinatları da erel (lokal) koordinatlar olacaktır. Söz konusu bu nirengi ağ noktalarının başka bir nirengi ağına örneğin ülke nirengi ağına bağlanmaları söz konusu olduğunda bir koordinat dönüşümü apılarak erel koordinatlar ülke koordinatlarına dönüştürülür. 56
192 Elipsoide Jeodezik Hesaplamalar 7. ELİPSOİDDE JEODEZİK HESAPLAMALA Ülke ölçmeleri söz konusu olduğunda seçilecek referans üzei dönel elipsoiddir. Nirengi noktalarının ata koordinatları (B,L vea Y,X) elipsoid üzerinde hesaplanırken, noktaların düşe konumu için elipsoid referans üzei olarak alınmaz, noktaların jeoidden itibaren çekül doğrultusu bounca (H) ortometrik ükseklikleri hesaplanır. Elipsoid üzerinde jeodezik hesaplamalar apılırken noktaları en kısa oldan tek anlamlı olarak birleştiren jeodezik eğri kenarlar esas alınır. Elipsoid üzerinde jeodezik hesaplamaların apılabilmesi için fiziksel erüzünde apılan gözlemlerin elipsoid üzeine indirgenmeleri gerekir. Söz konusu ölçümlerin elipsoid üzeine nasıl indirgeneceği Yata Kontrol Ağları bölümünde (Bölüm 0 ) anlatılmıştır. 7.. Dönel Elipsoidin Yerleştirilmesi ve Yöneltilmesi Ülke nirengi ağları için hesap üzei olarak dönel elipsoid seçilir. Böle bir dönel elipsoidin boutları, a dünanın gerçek şekli olarak tanımlanan jeoidin tüm üzeine en ugun varsaılan bir elipsoidin boutları, a da nirengi ağının bulunduğu ülkedeki jeoid kesimine en ugun bir elipsoidin boutlarıdır. Bu ikinci özellikteki elipsoidin boutlarını bulmak ve jeoide göre konumunu belirlemek daha güç olduğu ve pratik gereksinmeler için fazla arar sağlamadığı için genellikle birinci özelliği taşıan elipsoid hesap üzei olarak alınır. Bu nedenle ülkemizde de uluslararası Haford elipsoidi kullanılmaktadır[],[8]. Hesap üzei olarak alınan ukarıdaki elipsoidin jeoide göre konumunu belirlemek için, ülkenin ortalarına düşen bir nirengi noktasında, jeoid normali (çekül doğrultusu) ile elipsoid normali çakıştırılır. Çakıştırma işlemi bu noktada (ülkemizde Meşedağı noktası) astronomik gözlemlerle belirlenen astronomik enlem ve bolamın (, ) nın elipsoidal enlem ve bolam (B,L) e eşit alınması ile sağlanır. Bunun anında başlangıç noktasından başka bir nirengi noktasına giden kenarın astronomik gözlemlerle bulunan A astronomik azimutu (kenarın kuze doğrultusu ile saat ibresi önünde aptığı açı), elipsoid üzünde düşünülecek bu kenar için elipsoidal azimutu olarak alınır. Bölece nirengi ağı önlendirilmiş olur. Özet olarak, başlangıç noktasında astronomik enlem ve bolamın elipsoidal enlem ve bolam alınması (B =, L = ) ve bu noktadaki jeoid üksekliği de sıfır (N j = 0) alınmak suretile referans elipsoidi jeoide teğet hale getirilir ve bu noktada çekül sapması sıfır olur. eferans elipsoidinin dönme ekseninin eruvarının dönme eksenine paralelliği ine başlangıç noktasından bir diğer nirengi noktasına giden kenarın astronomik 57
193 Matematik Jeodezi S.Bektaş azimutu elipsoidal azimut ( = A) alınarak nirengi ağı önlendirilmiş olur. Başlangıç noktasında çekül sapması bileşenleri ve jeoid üksekliği sıfır olur. ( = = = N =0 ) 7.. Elipsoid Yüzeine İzdüşümler Fiziksel erüzü üzerindeki bir P noktası doğal koordinatlar olarak da adlandırılan erin gravite alanıla ilgili astronomik enlem (), bolam () ve ortometrik üksekliğinin (H) verilmesile tanımlanabilir[]. (,,H) doğal koordinatlarından (B,L,h) elipsoidal coğrafi koordinatlarının eldesi için, B = - L = - sec B h = H + N eşitlikleri kullanılır. Burada; = -B : Çekül sapmasının kuze-güne bileşeni = ( - L) cos B : Çekül sapmasının doğu-batı bileşeni = + : Çekül sapmasıdır. Fiziksel erüzündeki P noktasının elipsoid üzerindeki karşılığını bulmak diğer bir deişle elipsoid üzüne indirgemek iki farklı şekilde mümkündür. Bunlar Helmert izdüşümü ve Pizetti izdüşümü dür. a) Helmert İzdüşümü : Bu öntemde fiziksel erüzündeki P noktası elipsoid normali ardımıla elipsoid üzerinde Q noktasına indirgenir (şekil-). b) Pizetti İzdüşümü : Bu öntemde ise P noktası önce çekül eğrisi bounca jeoid üzerinde P o noktasına daha sonra jeoid üzerinden elipsoid üzerindeki Q o noktasına indirgenir (şekil-). 58
194 Elipsoide Jeodezik Hesaplamalar Bu öntemlerden Helmert önteminde P arazi noktası h elipsoidal üksekliğile doğrudan elipsoid üzerindeki Q noktasına, Pizetti önteminde ise P arazi noktası önce H ortometrik üksekliğile jeoid üzerinde P o noktasına sonra da N jeoid üksekliğile elipsoid üzerindeki Q o noktasına izdüşürülmektedir. Şekil- de görüldüğü gibi her iki öntemde elipsoid üzerinde Q ve Q o gibi iki farklı nokta elde edilmekle beraber bu iki nokta arasındaki fark QQ o H h pratikte ihmal edilebilecek düzededir. P H h Q g Po N Qo Çekül doğrultusu (jeoid normali) Elipsoid normali Fiziksel Yerüzü Jeoid Elipsoid Şekil- Elipsoid üzeine izdüşümler : Çekül sapması P Q = h : Elipsoidal ükseklik PPo = H : Ortometrik ükseklik PoQo = N : Jeoid üksekliği Helmert ve Pizetti öntemile elde edilen elipsoidal koordinatların birbirile ilişkisi aşağıdaki gibidir. B Helmert = B pizetti + L Helmert = L pizetti + H H sec B Bu öntemlerden Helmert izdüşüm öntemi basitliği ve global kartezen dik koordinatlar (X,Y,Z) ile elipsoidal koordinatlar (B,L,h ) arasında direkt dönüşüme izin vermesi nedenile jeodezide daha çok kullanılmaktadır. 8. ÖLÇÜLEİN ELİPSOİD YÜZEYİNE İNDİGENMESİ Elipsoid üzeinde hesap apabilmek için ölçülerin elipsoid üzeinde verilmesi gerekir. Osa ölçmeler fiziksel erüzünde apılmaktadır. Bu nedenle ölçülerin elipsoid üzeine (deniz seviesine) indirgenmesi gerekir [4]. Elipsoid üzei ile deniz seviesi teorik olarak farklı olmakla beraber pratik jeodezi ugulamaları için bu fark rahatlıkla göz ardı edilir. 59
195 Matematik Jeodezi S.Bektaş 8.. Yata Doğrultuların Elipsoid Yüzüne İndirgenmesi Fiziksel erüzünde P i ve P k gibi iki nokta arasında gözlenen r' ik ata doğrultusunun bu noktaları elipsoid üzünde temsil eden Q i ve Q k noktalarını birleştiren jeodezik eğri kenarın ata doğrultusu r ik a indirgenmesi gerekir. Bu işlem üç aşamada gerçekleştirilir. İlk aşamada gözlenen r' ik doğrultusuna çekül sapması indirgemesi sonra hedef noktası üksekliği indirgemesi ve normal kesit eğrisinden jeodezik eğrie geçiş indirgemesi apılır. Çekül Sapması Nedenile Ugulanacak İndirgeme Bir P i durak (istason) noktasından P k hedef noktasına apılan r' ik ata doğrultu gözleminde çekül doğrultuları (jeoid normalleri) esas alındığından jeoid normal kesit eğrisinin doğrultusu elde edilir. Osa istenen elipsoid üzünde bu noktaları birleştiren jeodezik eğri kenarın doğrultusudur. Çekül sapması bilindiği gibi bir noktadaki elipsoid normali ile çekül doğrultusu arasındaki açısıdır. Elipsoidin fiziksel erüzünde bulunmadığı ve farklı elipsoidlerin kullanılabileceği gözönüne alınırsa çekül sapmalarının mutlak anlamda olmadığı ortaa çıkar. Bu nedenle çekül sapmalarına bağıl çekül sapmaları da denir. Bir noktadaki çekül doğrultusu astronomik gözlemlerle belirlenir. Elipsoid normali ise jeodezik ölçüler ardımıla belirlenir. Merkezi P noktasında olan bir küre ardımıla çekül sapmasının açıklanması andaki şekilde görünmektedir. Şekilde; Greenwich (-L)cosB P L -L B n çekül doğrultusu normali n elipsoid normali, : P noktasının astronomik enlem ve bolamı B, L : P noktasının elipsoidal (coğrafi) enlem ve bolamı = : P noktasındaki çekül sapması 60
196 Elipsoide Jeodezik Hesaplamalar = - B : çekül sapmasının güne-kuze doğrultusundaki bileşeni = ( - L)cosB : çekül sapmasının doğu-batı doğrultusundaki bileşenini göstermektedir. Bir P i noktasındaki çekül sapmasının açıklık açısındaki bir doğrultudaki bileşeni = i cos + i sin şeklinde hesaplanır. Bir noktada bağıl çekül sapması, a da bunun güne-kuze doğrultusundaki bileşeni ile doğu-batı doğrultusundaki bileşeni biliniorsa, i durulan nokta, k bakılan nokta indisi olmak üzere ölçülen doğrultu açısına çekül sapması nedenile getirilecek düzeltme (r ik ) ç = i tan B i + ( i sin ik - i cos ik ) hk hi S eşitliği ile verilmiştir. Burada h, ilgili noktaların denizden üksekliği, S iki nokta arasındaki uzaklık, ik doğrultunun azimutu, B i ise P i noktasının elipsoidal enlemidir. Bu indirgeme eşitliğine bakıldığında birinci terimin bir durak noktasından bakılan bütün hedef noktaları için anı olduğu için etkisizdir. İkinci teriminde hedef doğrultusunun ataa akın olması durumunda sıfıra anaştığı görülmektedir. ik Hedef Noktası Yükseltisi Nedenile Ugulanacak İndirgeme P i noktasından P k noktasına apılan ata doğrultu gözlemine çekül sapması indirgemesi apılarak elipsoidden h k üksekliğindeki P k noktasına ait elipsoid üzerindeki normal kesit eğrisinin doğrultusu elde edilir. Osa istenen P i ve P k noktalarını elipsoid üzerinde temsil eden Q i ve Q k noktalarını birleştiren normal kesit eğrisinin doğrultusudur. P i durak noktasının elipsoid üzerindeki izdüşümü olan Q i noktası anı elipsoid normali üzerinde oldukları için durak noktasının Pi Qi hk Qk Pk 6
197 Matematik Jeodezi S.Bektaş üksekliği sorun aratmaz. Ancak P k hedef noktasının elipsoid üzerindeki izdüşümü Q k anı elipsoid normalinde (durak noktasına göre) bulunmadığı için andaki şekilde görüldüğü gibi bu iki doğrultu arasındaki açısı kadar farkın hesaplanıp ölçülen doğrultua eklenmesi gerekir. Bu düzeltme; (r ik ) h = e h a eşitliği ile verilmiştir. k sin ik cosb i Normal Kesit Eğrisinden Jeodezik Eğrie Geçiş İndirgemesi Buraa kadar apılan düzeltmelerle elipsoid üzünde bir noktadan diğer noktaa giden normal kesit eğrilerinin ata doğrultusu bulunmuş olur. Ancak noktaların anı meridende a da anı paralel daire üstünde olmamaları halinde durulan noktadaki elipsoid normali ile bakılan noktadaki elipsoid normali anı düzlem içinde olmadıkları için, durulan noktadan bakılan noktaa giden normal kesit eğrisi alnız durulan noktada normal kesit eğrisi özelliğini taşır. Bu durumda elipsoid üzerindeki Q i ve Q k gibi iki nokta NKE ik ve NKE ki, gibi iki arı normal kesit eğrisi ile birleşir. Bu durumda örneğin üç nokta elipsoid üzünde normal kesit eğrilerile birleştirildiğinde tek anlamlı bir üçgen şekli oluşturmaz. Bu nedenle normal kesit eğrileri erine, iki noktaı elipsoid üzerinde tek anlamlı olarak birleştiren tek bir üze eğrisi vardır. Bu özellikte alınacak üze eğrilerinin en ugunu, noktalar arasındaki jeodezik eğri dir. NKEik Jeodezik eğri Qi j Qk NKEki Normal Kesit Eğrisi j: Normal Kesit Eğrisinden Jeodezik Eğrie Geçiş Düzeltmesi Bir noktada (örneğin şekilde Q i noktasında) normal kesit doğrultusu ile jeodezik eğri arasındaki doğrultu farkı e s a (r ik ) j = sin ik cosb i 6
198 Elipsoide Jeodezik Hesaplamalar eşitliği ile verilmiştir. Ancak kenar uzunluklarının 00km. i geçmediği hallerde indirgeme değeri, ihmal edilebilecek bir değer olan 0.0'' nin altında kalır. Özet olarak fiziksel erüzünde ölçülen r' ik ata doğrultusunu elipsoid üzeine indirgemek için getirilecek toplam düzeltme r ik = r' ik + (r ik ) ç + (r ik ) h + (r ik ) j olur. Fiziksel erüzünde P i ve P k gibi iki nokta arasında gözlenen r' ik ata doğrultusunun bu noktaları elipsoid üzünde temsil eden Q i ve Q k noktalarını birleştiren jeodezik eğri kenarın ata doğrultusu r ik a indirgenmesi gerekir. Bu işlem üç aşamada gerçekleştirilir: İlk aşamada gözlenen r' ik doğrultusuna çekül sapması indirgemesi sonra hedef noktası üksekliği indirgemesi ve normal kesit eğrisinden jeodezik eğrie geçiş indirgemesi apılır. Ancak kenar uzunluklarının 00km. i geçmediği hallerde tüm bu indirgeme değerleri 0.0'' den az olur, ulaşılabilen ölçü duarlığının çok altında kalınması nedenile bu indirgemeler I.derece nirengi ağları dışında apılmaz, ani fiziksel erüzünde apılan ata doğrultu gözlemlerinin doğrudan elipsoid üzeinde apıldıkları varsaılır. 8.. Uzunlukların Elipsoid Yüzüne (Deniz Seviesine) İndirgenmesi Elektronik uzaklık ölçerler (EUÖ) ile ölçülen kenarları elipsoid üzeine indirgeebilmek için meteorolojik ve geometrik düzeltmenin getirilmesi zorunludur. Söz konusu indirgeme işlemleri bir çizelge üzerinde gerçekleştirilir (EK:5). EUÖ den kanaklanacak düzenli alet hataları arıca ele alınacaktır. a) Meteorolojik Düzeltme EUÖ ile ölçülen bir kenar değeri, arazide söz konusu iki noktaı birleştiren eğri olun uzunluğuna (D ) eşittir(şekil-). EUÖ nün ölçüm sonucunda verdiği uzunluk değeri referans atmosfer (ön görülen meteorolojik veriler) için geçerlidir. Osa arazide ölçümün apıldığı anlardaki meteorolojik veriler farklı olur. Meteorolojik verilerdeki (hava basıncı, ıslak ve kuru sıcaklıklar,havanın nemi gibi) değişimler ölçülen uzunlukları etkiler. Bu nedenle EUÖ ile ölçülen kenarlara K hız düzeltmesi ile K ışın olu eğriliği düzeltilmesi getirilir. Burada; D' K = D (n-n o ) K = -k 4 n o : eferans atmosfere karşılık kırılma indisi (alet içi) n : Ölçme anındaki kenar bounca kırılma indisi k : efraksion katsaısıdır. Elektro-optik uzaklık ölçerler için 0.3 ve mikrodalga uzaklık ölçerler için 0.5 dir. 3 63
199 Matematik Jeodezi S.Bektaş Ölçme anındaki kenar bounca kırılma indisi, ugulamada söz konusu kenarın uç noktalarında ölçülen meteorolojik verilerin ortalamasından ararlanılarak aşağıdaki gibi hesaplanır. NG=( E = 0 7.5t' t ' ) : Grup kırılma indisi e =E (t-t ) P n = N G. P t e t Burada; : ölçmede kullanılan dalga bou t : kenarın uç noktalarındaki ortalama ıslak sıcaklık ( o C) t : kenarın uç noktalarındaki ortalama kuru sıcaklık ( o C) P : kenarın uç noktalarındaki ortalama hava basıncıdır (mmhg) 5 Bu durumda hesaplanacak K hız düzeltmesi ve K ışın olu eğriliği düzeltmelerile meteorolojik düzeltme getirilmiş eğik uzunluk; D = D + K 0 + K + K K 0 : sıfır noktası eki hatası olur. 5 km i geçmeen uzunluklarda K ışın olu eğriliği düzeltmesi mm den az olması nedenile ihmal edilir. b) Geometrik Düzeltme Fiziksel erüzünde P i ve P k gibi iki nokta arasında gözlenen D eğik uzunluğundan bu noktaları elipsoid üzünde temsil eden Q i ve Q k noktalarını birleştiren jeodezik eğri kenarın S uzunluğunun elde edilmesi gerekir. Fiziksel erüzünde ükseklikleri farklı P i ve P k gibi iki nokta arasında ölçülen ve meteorolojik düzeltmesi apılan eğik uzaklık önce jeoidelipsoid üzüne (deniz üzeine) indirgenir(şekil-). 64
200 Elipsoide Jeodezik Hesaplamalar Pi Zik Hi Qi D D Yerüzü S lo l Hk Qk Pk h Elipsoid r r = D/ r D / r ( k = / r ) = / = k D / r : ışın olu eğrilik arıçapı : refraksion etkisi O Şekil- O EUÖ lerle apılan ve meteorolojik düzeltme getirilmiş eğik uzunluk (D) ölçülerinden aşağıdaki gibi elipsoid üzeindeki (S) kenarlar indirgenerek hesaplanır. Bu indirgeme iki farklı şekilde apılabilir. l 0 D ( H k H i ) H i H k ( )( ) S = arc sin ( l0 a da elipsoid üzeine indirgeme BÖHYY de belirtildiği gibi a da S = biçiminde apılır. Burada; DH ( cos( )) D ) DH HD : Durulan nok.denizden üksekliği HB : Bakılan nok. denizden üksekliği IE : EUÖ aletinin üksekliği TP : Yansıtıcı (reflektör) üksekliği D : Ölçülen eğik kenar (meteorolojik düzeltme getirilmiş) l : Pi deki erel ataa indirgenmiş uzunluk lo : Elipsoidin kiriş uzunluğu S : Deniz üzeindeki kenar : Kenar doğrultusundaki elipsoid normal kesit eğrisi arıçapı a da ülkemiz için aklaşık olarak m alınabilir. Hi = HD + IE Hk = HB + TP DH = HK - Hİ 65
201 Matematik Jeodezi S.Bektaş = D H i Bu indirgeme ile bulunan deniz seviesindeki S kenarının elipsoid üzüne de indirgenmesi gerekir. Ancak bu indirgeme değerinin büüklüğü pratikte rahatlıkla göz ardı edilebilir miktardadır. Bu nedenle ölçülen kenarların elipsoid üzündeki değeri erine jeoid üzündeki (deniz seviesindeki) değeri alınır. Kenar uzunlukları 0km i geçmeen ağlarda ölçülen (D) eğik uzaklığı ve P i deki refraksion indirgemesi getirilmiş düşe açı (Z=Z+) ölçüsüle, l = D sin( Z - ) cos ( /) : P i deki erel ataa indirgenmiş uzunluk elde edildikten sonra S = l H i şeklinde deniz üzeine indirgenmiş uzunluk hesaplanır. Bu biçimde hesaplanan S uzaklığı elipsoid üzeindeki jeodezik eğrinin uzunluğu olarak alınabilir. Özet olarak fiziksel erüzünde iki nokta arasında ölçülen eğik kenarın elipsoid üzerindeki karşılığı olan jeodezik eğri uzunluğunu elde etmek için ölçülen eğik kenarın alnızca deniz düzeine indirgenmesi eterlidir diebiliriz. Düşe açılar ardımıla indirgeme EUÖ ler ile apılan ve meteorolojik düzeltme getirilmiş eğik uzunluk ölçüleri aşağıdaki şekilde düşe açı ölçülerile de elipsoid üzeine indirgenebilir. P i ve P k noktaları arasındaki eğik uzunluk D, P i noktasında ölçülen düşe açı Z olmak üzere H i üksekliğindeki ata uzunluk, önce noktalar arasındaki ükseklik farkı küresellik ve refraksion etkileri de göz önüne alınarak aşağıdaki formülle bulunur. h= H B -H D =D cosz (D km sinz ) + a i Noktalar arası ata uzunluk, S' D h bağıntısı ile elde edilir. P i noktasındaki erel atadaki S uzunluğundan deniz seviesindeki (elipsoid üzeindeki) S uzunluğu 66
202 Elipsoide Jeodezik Hesaplamalar S = S ( H i eşitliğinden bulunur. ) Örnek: Elektronik uzaklık ölçerle bir kenarın 5 kez ölçülmesi sonucunda ortalaması D = m olarak bulunmuştur. Aşağıda gerekli bilgiler verildiğine göre söz konusu kenarın deniz seviesindeki karşılığını tüm indirgemeleri aparak bulunuz. Verilenler: D = m n o : H DN =40.5m H BN = m N G : I E :.54m T P =.55m t = o C t =3 o C = m P =755mmHg K o =0.005m Çözüm: a) Meteorolojik düzeltmelerin getirilmesi E = 0 7.5t' t ' = e =E (t-t ) P = n = N G. P t e t 5 = D' K = D (n-n o )= m K = -k = mm 4 Meteorolojik düzeltme getirilmiş eğik uzunluk, D = D + K 0 + K + K = m b)geometrik düzeltmenin getirilmesi Hi = HDN + IE = 4.69m Hk = HBN + TP= m DH = HK - Hİ = 37.6m = D H i 3 = radan 67
203 Matematik Jeodezi S.Bektaş Deniz seviesindeki uzunluk, S = DH ( cos( )) DH = m D olarak bulunur. Geometrik düzeltmenin getirilmesi değişik olarak aşağıdaki formülden de apılabilir. D = m H i = 4.69m H k = m l 0 D ( H k H i ) =736.03m H i H k ( )( ) S = arc sin ( l0 ) = m Ölçülere apılan tüm bu indirgemelerle fiziksel erüzündeki nirengi ağı erine, elipsoid üstünde, kenarları jeodezik eğri olan üçgenlerden oluşan bir ağ elde edilmiş olur. Başucu Kuze N 6 Q 6 N h Q (B,L ) Z N 5 S D N 7 Q 7 Elipsoid h N Q (B,L ) N 4 N 3 Fiziksel Yerüzü h3 Q 3 (B 3,L 3) Q 5 Q 4 Şekil- Elipsoid üzeinde konum belirleme işlemi için, fiziksel erüzünde oluşturulan nirengi ağında apılan ölçümler elipsoid üzeine indirgenerek elipsoid üstünde, kenarları jeodezik eğri olan üçgenlerden oluşturulan bir ağın çözümü suretile elde edilir. Elipsoid üzerindeki bu ağ jeodezik üçgenlerden oluşur 68
204 Elipsoide Jeodezik Hesaplamalar (şekil-). Böle bir ağda ağın hesaplanması için gerekenden fazla ölçü olduğundan ağ noktalarının istenen elipsoidal koordinatları dengeleme hesabıla bulunur. Ağ noktalarının projeksion üzeindeki koordinatları istenirse, ölçüler elipsoid üzeinden bu defa projeksion üzeine indirgenir ve ine dengelemeli olarak ağ noktalarının koordinatları bulunur Elipsoidde Üçgen Hesabı Elipsoid üzeindeki jeodezik üçgenler ardımcı bir düzlem üçgen aracılığıla çözülebilmektedir. 87 ılında Gauss herhangi bir üze üzerindeki jeodezik üçgeni ardımcı düzlem üçgen kullanarak çözmüştür(şeki.a,.b). Çözüm için seçilecek ardımcı düzlem üçgenin kenarları jeodezik üçgenin kenarlarının anısıdır. Açıları ise aşağıdaki gibi hesaplanır. c B a c B a A b C A * b C Şekil-.a Jeodezik Üçgen Şekil-.b Yardımcı Düzlem Üçgen Jeodezik üçgen erine alınan ardımcı düzlem üçgenin açıları K a Kb K c a 7b 7 K K a Kb K c 7a b 7 K * K a Kb K c 7a 7b c K * c * c şeklinde hesaplanır.abc Jeodezik üçgeninin eksesi (iç açılarının toplamının 80 o den farkı) K a Kb K c a b c K dır Bu eşitliklerde; kenarları a, b, c olan düzlem üçgenin alanını K a, K b, K c jeodezik üçgenin köşelerindeki Gauss eğrilik ölçüsüdür. K ise üçgen için ortalama vea aklaşık eğrilik ölçüsünü belirtmektedir. Buradaki eğrilik ölçüsü eğrilik arıçapının karesi olarak alınmalıdır. 69
205 Matematik Jeodezi S.Bektaş Jeodezik üçgenin (F) alanı, ardımcı düzlem üçgenin alanı () cinsinden Ka Kb F ( a b c ) (a 0 0 şeklinde hesaplanabilmektedir. b c Kc ) (a 0 b c ) 8.4. ELİPSOİDAL KOODİNAT SİSTEMLEİ Elipsoidal koordinat sistemleri diğer koordinat sistemlerinde olduğu gibi elipsoid üzeinde konum belirlemee ve noktalar arasında çeşitli hesaplamalar apmaa arar. Başlıca elipsoidal koordinat sistemleri ; a) Elipsoidal Coğrafi Koordinatlar (B,L,h) b) Kartezen Dik (Global) Koordinatlar (X,Y,Z) c) Jeodezik Dik Koordinatlar (x,) d) Kutupsal Koordinatlar (S,A a da S,) dır. Bu sistemlerinden Elipsoidal Coğrafi Koordinat sistemi ve Kartezen Dik Koordinat sistemi ve aralarındaki dönüşümler daha önce Bölüm. de gösterilmişti. Bu koordinat sistemlerinden en kullanışlı olanı jeodezik dik koordinatlardır Elipsoidal jeodezik dik koordinat sistemi Z Grw F H x x p GB Po p B:sabit O l B A P(B;L) Başlangıç Meridenine paralel paralel S B=0 A = + A : Azimut açısı : Semt açısı : Meriden akınsaması Lo:Başlangıç Merideni X Şekil-5 Elipsoidal jeodezik dik koordinatlar 70
206 Elipsoide Jeodezik Hesaplamalar Bu sistem küre üzerindeki meriden (soldner) sisteminin elipsoide uarlanmış halidir. Elipsoidal jeodezik dik koordinat sisteminde ugun bir meriden x ekseni olarak alınır ve genellikle bu meridenin ekvatoru kestiği P o noktası başlangıç noktası olarak alınır (şekil-5). Elipsoid üzerinde konumu belirlenmek istenen bir P noktasından başlangıç meridenine (x eksenine) indirilen dik jeodezik eğrisinin uzunluğu P noktasının değeridir ( p =PF). Dik aağı F noktası ile başlangıç noktası P o arasındaki meriden aının uzunluğu da P noktasının x değeri (x p =P o F) olur. Benzer olarak şekil-5 de olduğu gibi noktasının da kutupsal koordinatları P noktası başlangıç noktası, P den geçen meriden a da P noktasında başlangıç meridenine çizilen paralel başlangıç doğrultusu olmak üzere S jeodezik eğri uzunluğu ve A azimutula a da semtile belirlenir. Coğrafi Koordinatlardan Jeodezik Dik Koordinatların Eldesi Verilenler: P noktasının elipsoidal coğrafi koordinatları P(B, L) İstenenler: L o meriden sistemindeki jeodezik dik koordinatlar P(x,) ve meriden akınsaması (konvergensi) açısı Çözüm: Önce B enlemine karşılık gelen G B =P o H meriden a uzunluğu hesaplanır. G B = A' B + B' sinb + C' sin4b + D' sin6b l = L L 0 l bolam farkını göstermek üzere P noktasının jeodezik dik koordinatları L o meridenine göre aşağıdaki gibi hesaplanır. N x = sin B cosb N + 4 sin B cos3 B5 t x = G B + x ( x = HF ) N N cos B 6 3 sin Bcos B sin Bcos 3 B = 5 3 = sin B + sin Bcos B... 3 N 0 t = tan B F, = e cos B F, V =+, N = c / V t 7
207 Matematik Jeodezi S.Bektaş Örnek - : Verilenler: P noktasının coğrafi koordinatları, B= 39 o 00 36, L = 39 o İstenenler : L o =39 o meridenindeki jeodezik dik koordinatlar P(x,) ve meriden akınsaması (konvergensi) açısı Çözüm: Önce B enlemine karşılık gelen G B meriden a uzunluğu hesaplanır. B= 39 o için G B = A' B + B' sinb + C' sin4b + D' sin6b = m olur. Buradaki katsaılar (Haford elipsoidi için); A' = m/ B' = m C' = 6.976m ve ukarıdaki formüller kullanılırsa, N x = sin B cosb x = G B + x ( x = HF ) D' = -0.03m N sin B cos B x = 8.954m bulunur. Bu değere G B değeri eklenirse x = G B + x = m N N cos B 6 5 t sin Bcos B sin Bcos 3 B = 5 = m 3 = sin B + sin Bcos B... 3 olarak bulunur. = o = N 0 Örnek -a : Verilenler: P3 noktasının coğrafi koordinatları, B 3 = 39 o 30 8 L 3 = 39 o t 7
208 Elipsoide Jeodezik Hesaplamalar İstenenler : L o =39 o meridenindeki jeodezik dik koordinatlar P(x,) ve meriden akınsaması (konvergensi) açısı G B = A' B + B' sinb + C' sin4b + D' sin6b = m x = m bulunur. Bu değere G B değeri eklenirse x = G B + x = m = m = o = olarak bulunur. Jeodezik Dik Koordinatlardan Coğrafi Koordinatların Eldesi Verilenler: L o merideninde jeodezik dik koordinatlar P(x, ) İstenenler: Coğrafi koordinatlar P(B,L) ve meriden akınsaması (konvergensi) açısı Z Grw F H x x p GB Po p B:sabit O l B A P(B;L) Başlangıç Meridenine paralel paralel S B=0 X Lo:Başlangıç Merideni Çözüm: Öncelikle x değerine karşılık gelen B F enlemi hesaplanır(şekil-5). Ekvatordan F aak noktasına kadar olan a uzunluğu P noktasının x değeridir. Bu B F enleminden P noktasının B enlemi (anı zamanda H noktasının enlemi) ve diğer istenenler aşağıdaki eşitliklerden hesaplanır. Elipsoidde ekvatordan bir B enlemine kadar olan meriden a uzunluğu G = A' B + B' sinb + C' sin4b + D' sin6b 73
209 Matematik Jeodezi S.Bektaş eşitliği ile hesaplanmaktadır. Ekvatordan itibaren G=x meriden a uzunluğuna karşılık gelecek B enlemi ukarıdaki eşitlikten çekilir ve B i+ = { G- B sinb i - C sin4b i - D sin6b i } / A (i=0,,,..) iteratif olarak hesaplanır. Bu şekilde bulunan B F enlemi istenirse aşağıdaki seriden direkt olarak da hesaplanabilir. B F = + B''sin + C''sin4 + D''sin serisi elde edilir. Buradaki katsaılar (haford elipsoidi için); = G / A A' = m/ C'' = B'' = D'' = B F enlemi elde edildikten sonra P noktasının istenen coğrafi koordinatları ve meriden akınsaması aşağıdaki formüllerden elde edilir. Formüllerdeki F alt indisi bütün hesaplamaların B F enlemile apılacağını göstermektedir. V t V t 4 B = B F - ( ) ( ) ( 3t 9 t )... F 4 F F N 4N t 3 t ( 3t ) 5 L = L o + ( ) F ( ) ( )... 3 F 5 F N cos B 3N cos B 5N cos B t t 3 = ( ) F t( )... 3 F N 6N t = tan B F, = e cos B F, V =+, N = c / V Örnek - : L o =39 o meriden sisteminde, bir P noktasının jeodezik dik koordinatları x= m, = m olarak verilior. İstenenler : Coğrafi koordinatlar P(B,L) ve meriden akınsaması (konvergensi) açısı Çözüm: G = x için hesaplanacak B F enlemi, B F = + B''sin + C''sin4 + D''sin6 +...= o ve ukarıdaki formüllerden, B = 39.0 o = 39 o L = o = 39 o
210 Elipsoide Jeodezik Hesaplamalar = o = olarak elde edilir. Burada jeodezik hesaplamaların coğrafi koordinatlarla ve jeodezik dik koordinatlarla apılması ispata girilmeksizin verilecektir [4],[8] Elipsoidde Coğrafi Koordinatlarla Temel Ödev Hesapları Literatürde elipsoid üzeinde temel ödev hesapları için çok saıda öntem olup bunların başlıcalarından Legendre Serisi öntemi, Gauss Ortalama Enlem öntemi, Schreiber öntemi ve Vincent öntemi saılabilir. Bu öntemlerden Schreiber öntemile I. Temel ödev ve Gauss ortalama enlem öntemile de II. Temel ödev çözümleri ele alınacaktır. Daha geniş bilgi için kanaklar kısmındaki eserlere başvurulması tavsie edilir. Elipsoidde hesaplama zorlukları nedenile hesaplamaların bilgisaar ortamında apılması tavsie edilir. İnternet ortamında bu amaçla hazırlanmış ugulama programlarından (applet) ararlanılabilir. Coğrafi Koordinatlarla I. Temel Ödevin Schreiber öntemile Çözümü Verilenler: Pi(Bi,Li) ve Aik, Sik İstenenler : P k (B k,l k ) ve A ki Z L=0 o Grw Li F Aik Lk Sik Aki P k P i Bi Bk B=0 o X Şekil-4 75
211 Matematik Jeodezi S.Bektaş 76 Bu problemde bir P i noktasının enlem ve bolam değerleri ile P k noktasına olan A ik azimut açısı ve S ik jeodezik eğri kenar uzunluğu verilir. P k noktasının coğrafi koordinatları ile A ki azimutu istenir. Problemin Schreiber öntemile çözümde önce P k noktasından P i noktasından geçen meriden üzerine indirilen dikin aak noktası F nin enlemi B F hesaplanır. u = S cos A ik, v = S sin A ik B F = B i +... ) 5 ( 3 3 u N t t u N t N M v u M i i i i i i i i i i i i Bölece P k noktasının elipsoidal koordinatları B k, L k ve A ki azimutu, = v u v / (6M i N i ), z = / N F B k = B F + )]} 0sin (3 cos [ ) ( { F F F F F F B t e t B e z z t V L k = L i +... ) 3 ( 5 3 cos 4 4 F F F F t z t z t B z A ki = A ik + )] sin (3 cos [ ) ( 6 F F F F F i F B t e t B e z t z z B B olarak ifade edilebilir. t F = tan B F, V F = + F = + e cos B F, N F = c / V F ve M = c / V 3 F Örnek-3: Verilenler: B = 39 o 30 8 L =39 o 00 00
212 Elipsoide Jeodezik Hesaplamalar 77 S = m A = 4 o İstenenler : B, L, A Çözüm: Önce ukarıdaki B F eşitliğinden B F enlem değeri hesaplanır. u = S cos A ik = , v = S sin A ik = M = m N= m B F = B i +... ) 5 ( 3 3 u N t t u N t N M v u M i i i i i i i i i i i i B F = o = v u v / (6M i N i ) = z = / N F = ukarıdaki formül takımından, B = B F + )]} 0sin (3 cos [ ) ( { F F F F F F B t e t B e z z t V B =39.0 o = 39 o L = L +... ) 3 ( 5 3 cos 4 4 F F F F t z t z t B z L = 39.5 o = 39 o A = A + )] sin (3 cos [ ) ( 6 F F F F F i F B t e t B e z t z z B B A = o = 3 o olarak bulunur. Coğrafi Koordinatlarla II. Temel Ödevin Gauss Ortalama Enlem Yöntemile Çözümü Verilenler: P i (B i,l i ) ve P k (B k,l k ) İstenenler : S ik, A ik ve A ki
213 Matematik Jeodezi S.Bektaş İkinci temel ödevin elipsoid üzeinde çözümü için, b = B k B i, l = L k - L i, B = (B k + B i ) / hesaplanır A =A ki - A ik A = (A ki + A ik )/ kabulleri apılarak ve B ortalama enlemile aşağıda geçen gerekli katsaılar bulunur. u = S ik cos A ik = Mb l cos 4 l cos ( t) B 4 8 V b Nl cos B l sin B 9 t v = S ik sin A ik = V A = l sin B l cos 3 8 B 4 V ukarıdaki v değeri u değerine bölünürse, tan A v u A ortalama azimut değeri ve istenen azimutlar 4 b b A ik = A - A / ve A ki = A + A / S ik kenarı da, u v S ik cos A sin A şeklinde kontrollü olarak bulunur. Örnek-4: İki noktanın elipsoidal coğrafi koordinatları aşağıda verilmektedir. Verilenler: B = 39 o 30 8 L =39 o B = 39 o L = 39 o İstenenler : S, A, A Çözüm: b = B k B i = o, l = L k - L i = 0.5 o, B = (B k + B i ) / = o 78
214 Elipsoide Jeodezik Hesaplamalar N = m M = m u = S cos A = m v = S sin A = m A = o = 0 o A = o = 4 o A = A - A / = o = 4 o A = A + A / = o = 3 o S u cos A v sin A = m olarak bulunur. Örnek-4a: İki noktanın elipsoidal coğrafi koordinatları aşağıda verilmektedir. Verilenler: B = 39 o L =39 o B 3 = 39 o 30 8 L 3 = 39 o İstenenler : S 3, A 3, A 3 Çözüm: b = B k B i = o, l = L k - L i = 0.5 o, B = (B k + B i ) / = o N = m M = m u = S 3 cos A 3 = m v = S 3 sin A 3 = m A = o = 0 o A = o = o A 3 = A - A / = o = o A 3 = A + A / = o = 0 o S u v = m olarak bulunur. cos A sin A 8.6. Elipsoid Yüzeinde Jeodezik Dik Koordinatlarla Temel Ödevlerin Çözümü 79
215 Matematik Jeodezi S.Bektaş Literatürde, elipsoid üzeinde jeodezik dik koordinatlarla hesap apmaa araan çok saıda öntem vardır. Bu öntemlerden nispeten en sadeleri ispata girilmeksizin verilecektir [4],[8]. I.Temel Ödev Çözümü Verilenler: x,, S, İstenenler : x,, Çözüm:. noktanın istenen, x jeodezik dik koordinatları ve elipsoidal semti jeodezik eğrinin seri açılımından aşağıdaki şekilde elde edilebilir. u = S cos, v = S sin olmak üzere = + v + x = x + u + x = + Yukarıdaki üç formülün son terimleri düzlem I.temel ödev eşitliklerinden farkı oluşturmaktadırlar. Esasında bu formül takımı Küre üzeinde soldner sisteminde serilerle temel ödev formülleridir. Formüllerin son terimleri,x ve küresel düzeltmelerdir. Burada bu küresel düzeltmeler biraz daha zenginleştirilerek elipsoidal düzeltmeler haline getirilmişlerdir. 3 u v t u u = 3v u v t u u x = 5 4u v u v t u u = ) ( 3v) 4 ( Küre ve elipsoid arasındaki farkı altı çizili olan parametreler oluşturmaktadır. Yukarıdaki eşitliklerde; u = S cos, v = S sin, = M.N e cos B t = tanb dir. 80
216 Elipsoide Jeodezik Hesaplamalar Örnek-5: Verilenler: x = m = 0.000m S = m = 4 o İstenenler :, x, Çözüm: Önce G=x değerine karşılık gelen enlem değeri için Gauss küresinin arıçapı hesaplanır. G=x = m B = o = m u = S cos = v = S sin = m u v t u u 6 = 3v u v t u u x = 5 4u v u v t u u = ( ) ( 3v) x = m = m = 6.08 bulunur.. noktanın istenen, x jeodezik dik koordinatları ve elipsoidal semti, x = x + u + x = m = + v + = m = + = o = 3 o olarak bulunur. 4 II. Temel Ödev Çözümü Verilenler: x,, x, İstenenler : S,, Çözüm: Önce G = x değerine karşılık gelen enlem değeri için Gauss küresinin arıçapı hesaplanır. I.temel ödevdeki,x ve elipsoidal düzeltmeler 8
217 Matematik Jeodezi S.Bektaş 8 u = x -x v = - = v u u t v u x = v u u u t v u = ) 3 ( 3 ) ( 4 3 v u u t v u alınarak hesaplanır. = arc tan ( x u v )= arc tan ( x x x ) = + S= ) ( cos sin x x x x x x Örnek-6: Verilenler: x = m = 0.000m x = m = m İstenenler : S,, Çözüm: Önce G=x değerine karşılık gelen enlem değeri için Gauss küresinin arıçapı hesaplanır. G=x = m B = o = m u = x -x = v = - =
218 Elipsoide Jeodezik Hesaplamalar 83 = v u u t v u x = v u u u t v u = ) 3 ( 3 ) ( 4 3 v u u t v u Yukarıdaki formüllerden x = m = m = 6.08 bulunur. = arc tan ( x u v )= arc tan ( x x x ) = 4 o = + = 3 o S= ) ( cos sin x x x x x x S = m olarak bulunur. Yukarıda hesaplanan semti ile anı noktada daha önceden hesaplanan A azimutu arasındaki fark tanım gereği noktasındaki meriden akınsamasını verecektir. Söz konusu meriden akınsamasının bu şekilde hesaplanan değeri daha önceden bulunan değere eşit çıkmıştır. A = 3 o (örnek-3 ve 4 ) = 3 o = ( ) (örnek- ve )
219 Matematik Jeodezi S.Bektaş 84 Örnek-6a: Verilenler: x = m = m x = m = m İstenenler : S,, Çözüm: Önce G=x değerine karşılık gelen enlem değeri için Gauss küresinin arıçapı hesaplanır. G=x = m B = o = m u = x -x = v = - = = v u u t v u x = v u u u t v u = ) 3 ( 3 ) ( 4 3 v u u t v u Yukarıdaki formüllerden x =.706m = -.887m = bulunur. = arc tan ( x u v )= arc tan ( x x x ) = o = + = 0 o.73
220 Elipsoide Jeodezik Hesaplamalar sin S = m x x x cos S= ) ( x x x olarak bulunur. NOT: Çalışma bölgesi sınırlı ise elipsoid üzeinde jeodezik dik koordinatlarla apılan temel ödev çözümlerine Gauss küresi ile küre üzeinde jeodezik dik koordinatlarla apılacak temel ödev hesaplamaları (Bölüm / / 4.9) ile de ulaşmak mümkündür. Bunun için küresel hesaplama eşitliklerinde geçen arıçapı erine g Gauss küresi arıçapının alınması eterlidir KÜESEL HESAPLAMALALA ELİPSOİDDE TEMEL ÖDEV ÇÖZÜMLEİ Örnek-7: Örnek-5 de elipsoid üzeinde jeodezik dik koordinatlarla apılan I. Temel ödev çözümün küre üzeinde apılması Verilenler: x = m = 0.000m S = m = 4 o İstenenler :, x, Çözüm: Önce G=x değerine karşılık gelen enlem değeri için Gauss küresinin arıçapı hesaplanır. G=x = m B = o = m Küre üzeinde Soldner koordinatlarıla I. Temel ödev çözümü ukarıda hesaplanan Gauss küresi arıçapıla formüller kullanılarak (Bölüm / / 4.9), 85
221 Matematik Jeodezi S.Bektaş x arcsincos x s arctan cot sin sin s s cos sinα cosα cos sin sinα m m α cos arctan s sinα tan sin cosα Örnek-8: s 3 o 4' " Örnek-6 da elipsoid üzeinde jeodezik dik koordinatlarla apılan II. Temel ödev çözümün küre üzeinde apılması Verilenler: x = m = 0.000m x = m = m İstenenler : S,, Çözüm: Önce x m =(x +x )/ değerine karşılık gelen enlem değeri için Gauss küresinin arıçapı hesaplanır. x m = m B = o = m Küre üzeinde Soldner koordinatlarıla II. Temel ödev çözümü ukarıda hesaplanan Gauss küresi arıçapıla formüller kullanılarak (Bölüm / / 4.9), Δx x x =
222 Elipsoide Jeodezik Hesaplamalar α α s arccossin sin cos cos Δx sin o arccos cos =4 4' 55.78" s sin Δx sin o arccos cos π = 3 s sin 4' " Δx cos = m 87
223 Elipsoid Yüzeinde Jeodezik Hesaplamalar 9. ELİPSOİDİN DÜZLEME GAUSS KÜGE POJEKSİYONU 93 ılından beri ülkemizde de kullanılmakta olan Gauss-Kruger Projeksionu (GKP) silindirik, transversal (atık eksenli), açı koruan (konform) bir projeksiondur. Bu üzden Gauss-Krüger projeksionuna Transversal Merkator projeksionu (TM) dendiği de olur. İzdüşüm üzei olan silindir, elipsoide başlangıç olarak seçilen meriden bounca teğettir. Ülkemiz genelindeki çalışmalar için belirlenmiş başlangıç meridenleri vardır [4],[8]. Bunlar; 7 0,30 0,33 0,36 0,39 0,4 0,45 0 meridenleridir. Yerel çalışmalar için seçilmiş herhangi bir jeodezik dik koordinat sistemi varsa, bu sistemin başlangıç noktasından geçen meriden de başlangıç merideni olarak alınabilir. Buna göre; a) Seçilen başlangıç merideninin Gauss-Kruger projeksionu düzlemindeki karşılığı X g ekseni olarak alınır. b) Bu durumda başlangıç merideninde uzunluk deformasonu oktur. Başlangıç merideni ile ekvatorun kesiştiği nokta sistemin başlangıç noktasıdır. 9.. Gauss-Krüger Projeksionunda Yaklaşma Açısı Kürede olduğu gibi elipsoidde de bir noktadaki aklaşma açısı o noktadaki meriden doğrultusula X ekseni ( Y= sabit) arasındaki açısıdır. Benzer durum Gauss-Krüger projeksion düzleminde meriden doğrultusula Xg ekseni (Yg = sabit) arasındaki C açısının varlığıdır. C açısına Gauss aklaşma açısı denir ve elipsoidal semt ile azimut arasında geçiş apmaa olanak sağlar [6],[8]. Grw x p F L o L p Başlangıç Meridenine paralel (Y=sabit) P A S P L =sbt Y =sbt C g=sbt P t A T s P L o:başlangıç Merideni Şekil-.a Elipsoid Şekil-.b GKP Düzlemi 87
224 Matematik Jeodezi S.Bektaş Elipsoidde; A : PP nin elipsoidal azimutu : P deki aklaşma (konvergens) açısı = A - : PP nin elipsoidal semt (açıklık) açısı S: PP Jeodezik eğri uzunluğu Projeksion Düzleminde; T = A - C : P P nin Gauss açıklık açısı t = T - : P P nin Projeksion düzlemindeki açıklık açısı : Projeksion düzleminde P deki doğrultu redüksionu C : P deki Gauss aklaşma (konvergens) açısı s: P P uzunluğu (projeksion düzleminde) : PP Jeodezik eğri uzunluğunun projeksion düzlemindeki karşılığı( s) C ve açıları teorik olarak farklı olmakla beraber aralarındaki fark pratikte rahatlıkla göz ardı edilebilmektedir [6]. Örneğin C ve açıları aralarındaki fark B= 40 o ve l = o için C - = dir. C = t N g C= sin Bl + ( t - 3 t ) 3 ) 3 3 sin Bcos B (+3 ( N g (x, koordinatlarından hesabı) 3 sin Bl sin B cos B( ) l +... ) l (elipsoidal koordinatlarından) 9.. Elipsoidal Coğrafi Koordinatlardan Gauss-Krüger Koordinatlarının Bulunması Şekil-3 L=0 o x L o F B F =sbt P B K L l B =sbt G Ekvator P(B,l ) G Elipsoidal coğrafi koordinatlardan Gauss-Krüger koordinatlarının bulunması problemile jeodezi ugulamalarında sıklıkla karşılaşılır (şekil-3). Örneğin pafta köşe koordinatlarının hesabı probleminde olduğu gibi [4],[8]. 88
225 Elipsoid Yüzeinde Jeodezik Hesaplamalar Verilenler: P(B,L) noktasının coğrafi koordinatları, İstenenler: L o başlangıç meridenli sistemde P(x g, g ) Gauss-Krüger koordinatları ve C meriden konvergensi açısı Çözüm : l = L - L o bolam farkı ve G : ekvatordan itibaren B enlemine kadar olan meriden a uzunluğu x g, g Gauss-Krüger koordinatları ve C meriden konvergensi açısı olmak üzere t = tan B, = e cos B, V = + ve N = c / V hesaplanır. Önce B enlemine kadar olan G meriden a uzunluğu G = A' B + B' sinb + C' sin4b + D' sin6b şeklinde hesaplanır. G değeri ukarıdaki gibi hesaplandıktan sonra Gauss-Krüger koordinatları coğrafi koordinatlara bağlı olarak, N x g = G + sin B cos Bl (5 t ) cos Bl 4 g = N cos Bl ( 6 t )cos Bl (5 0 8t t 4 58 t )cos 4 Bl 4 eşitliklerinden hesaplanabilir. Gauss aklaşma açısı derece cinsinden C = sin B l o { x0-4 (+3 )cos B l o } şeklinde hesaplanır. 89
226 Matematik Jeodezi S.Bektaş Örnek-: Elipsoidal coğrafi koordinatları B = 39 o ve L = 39 o olarak verilen noktanın L o = 39 o başlangıçlı sistemdeki x g, g Gauss-Krüger koordinatlarını ve C meriden akınsamasını bulunuz. Çözüm : olmak üzere l = L - L o = 30 bolam farkı ve B = 39 o enlemi için G değeri G = A' B + B' sinb + C' sin4b + D' sin6b = m t = tan B= = e cos B= , V = + = N = c / V= N x g =G+ sin B cos Bl (5 t ) cos Bl 4 = m g = N cos Bl ( 6 t )cos Bl (5 0 8t t 4 58 t )cos 4 Bl 4 g = m C=sinBl o { x0-4 (+3 )cos Bl o }= o = olarak bulunur. 90
227 Elipsoid Yüzeinde Jeodezik Hesaplamalar 9.3. Harita Paftalarının Bölümlemesi ve Pafta Köşe Koordinatlarının Bulunması Nato üesi ülkelerin kullandığı Universal Transverse Mercator (UTM) projeksionu açı koruan, silindirik, transversal bir projeksiondur.bu sistemde düna 80 kuze ve güne enlemleri arası 8 lik paralellerle bölünmüştür. Güneden başlanarak her bölgee bir harf verilmiştir. Arıca düna 6 lik bolamlarla 60 dilime bölünmüştür [9],[8]. Dilimler 80 bolamından başlaarak saat ibresinin tersi önünde den başlaarak numaralanmıştır. Türkie 35,36,37 ve 38. dilimler içindedir. Dilim orta meridenlerinin bolamları 7,33,39,45 dir. Örneğin 35. dilim orta merideninin bolamı 7 dir. 6 6 Q P N 6 o M L K 8 o 0 o 8 lik enlemler ve 6 lik bolamlarla sınırlanmış bölgee GİD BÖLGESİ denir. Örneğin andaki şekilde taralı alan 33 P Grid Bölgesidir K L Grid Bölgesi 33 P a d 30' b c : Düna Paftası 30' 5' 4 3 : ' 7 '30' 30' : VAN 7 '30' : VAN K48 : VAN K48-b : VAN K48-b3 9
228 Matematik Jeodezi S.Bektaş 5' : VAN K48-b 5 5' a d 3' b 07 3' c : VAN K48-b-07 '30'' B C 5 3 '30' 4 3 A 4 : VAN K48-b-07-d D Ülkemizde pafta isimlendirilmesi şöle olmaktadır. / lik paftalar o x o 30 boutundadır. Pafta içindeki en büük şehrin adıla anılır (VAN). / lik paftalar 30 x30 boutundadır. / lik paftaların 6 a bölünmesile elde edilir. Adlandırma şöle apılır: ülkemizde 44 o enleminden 36 o enlemine kadar 30 aralıklarla A dan başlaarak P e kadar harf verilir. 4 o bolamından 48 o bolamına kadar den başlaarak 59 a kadar numara verilir. / lik pafta bu gridlerden hangisine girior ise o ismi alır (VAN K48). / lik paftalar / lik paftaların 4 parçaa bölünmesile elde edilir. Parçalara sol üst köşeden başlaarak saat ibresi önünde a, b, c, d harfleri verilir. / lik paftalar 5 x5 boutundadır ve pafta isimlendirmesi (VAN K48- b) şeklinde apılır. / lik paftalar / lik paftaların 4 parçaa bölünmesile elde edilir. Parçalara sol üst köşeden başlaarak saat ibresi önünde,,3,4 numaraları verilir. / lik paftalar 7 30 x7 30 boutundadır ve pafta isimlendirmesi (VAN K48 b-3) şeklinde apılır. / lik paftalar / lik paftaların 5 parçaa bölünmesile elde edilir. Parçalara sol üst köşeden başlaarak 0,0,03,...,4,5 numaraları verilir. / lik paftalar 3 x3 boutundadır ve pafta isimlendirmesi (VAN K48-b-07) şeklinde apılır. / lik paftalar /0 000 lik paftaların 4 parçaa bölünmesile elde edilir. Parçalara sol üst köşeden başlaarak saat ibresi önünde a,b,c,d harfleri verilir. / lik paftalar 30 x 30 boutundadır ve pafta isimlendirmesi (VAN K48- b-07-d) şeklinde apılır. Ülkemizde /5000 lik paftaların köşe noktalarının koordinatları 3 derecelik Değiştirilmiş UTM sisteminde hesaplanır. Bilindiği gibi bu sistemdeki koordinatlar Gauss-Kruger koordinatlarından sadece Y değerine m eklenerek bulunur. Söz konusu Gauss-Kruger koordinatları da coğrafi koordinatlardan hesaplanır. /5000 den daha büük ölçekli haritalar kenar 9
229 Elipsoid Yüzeinde Jeodezik Hesaplamalar uzunluklarının arısı vea köşelerin Gauss-Kruger koordinatlarının ortalaması alınarak oluşturulur. Tüm bu paftaların boutları 70x90 cm dir. B b b a e d c 5 d : 000 K48-b-07-d- c a x A B C D b II I V III 4 3 e c IV : 000 K48-b-07-d--b a b c d e I II III IV V II V III : 500 K48-b-07-d--b- / 000 lik paftalar /5 000 lik paftaların pafta kenarlarının iki eşit parçaa arılması suretile 4 parçaa bölünmesile elde edilir. Parçalara sol üst köşeden başlaarak saat ibresi önünde,,3,4 numaraları verilir. Pafta isimlendirmesi (VAN K48-b-07-d-) şeklinde apılır. / 000 lik paftalar / 000 lik paftaların pafta kenarlarının iki eşit parçaa arılması suretile 4 parçaa bölünmesile elde edilir. Parçalara sol üst köşeden başlaarak saat ibresi önünde a,b,c,d harfleri verilir. Pafta isimlendirmesi (VAN K48-b-07-d--b) şeklinde apılır. / 500 lik paftalar / 000 lik paftaların pafta kenarlarının iki eşit parçaa arılması suretile 4 parçaa bölünmesile elde edilir. Parçalara sol üst köşeden başlaarak saat ibresi önünde,,3,4 numaraları verilir. Pafta isimlendirmesi (VAN K48-b-07-d--b-) şeklinde apılır. 93
230 Matematik Jeodezi S.Bektaş 9.4. Gauss-Krüger Koordinatlarından Elipsoidal Coğrafi Koordinatların Bulunması Bu problemde; bir L o sisteminde P(x g, g ) Gauss-Krüger koordinatları verilen noktanın P(B,L) elipsoidal coğrafi koordinatları ve C meriden akınsaması açısının bulunması amaçlanır. Çözüm : Önce F aak noktasının B F enlemi G = x g meriden aını gören enlem değeri olarak hesaplanır. = G / A B F = + B''sin + C''sin4 + D''sin Buradaki katsaılar; A = m/ o C = o B = o D = o Noktanın elipsoidal coğrafi koordinatları; F aak noktasının B F enlemi ukarıdaki gibi hesaplandıktan sonra istenen B,L ve C değerleri aşağıdaki gibi elde edilir. g g B = B F - tan BF ( ) F (5 6 F 3t F 6 Ft F )( ) N F N F g g 4 g 4 L=L 0 + ( ) ( F t F )( ) (5 8t F 4t F )( ) cos B N F 6 N F 0 N F t t( t ) 3 C = g - ( g ) N 3 N NOT: B F enleminin hesabı, diğer katsaıların hesabında kullanıldığı için çok önemlidir. Bu nedenle eteri doğrulukta en az duarlıkta hesaplanmalıdır. 94
231 Elipsoid Yüzeinde Jeodezik Hesaplamalar Örnek-: Gauss-Krüger koordinatları L o =30 o sisteminde x g = m g = m olarak verilen noktanın (B, L) elipsoidal coğrafi koordinatlarını bulunuz. ve C meriden akınsaması açısının bulunması amaçlanır. Çözüm : Önce B F aak noktasının enlemi G = x g meriden aını gören enlem değeri olarak hesaplanır. = G / A B F = + B''sin + C''sin4 + D''sin6 = o B F aak noktasının enlemi ukarıdaki gibi hesaplandıktan sonra, t = tan B F = , = e cos B F = E-3 V F = + = N F = c / V= değerleri hesaplanır, ve aşağıdaki eşitliklerden diğer istenenler bulunur. g B = B F - tan BF ( ) F (5 6 F 3t N F B = o = 40 o g F 6 Ft F )( N F ) g g L=L o + ( ) ( F t F )( ) (5 8t cos B N F 6 N F 0 L = o = 9 o F 4t 4 F )( N g F 4 ) C = t N g ( t - t ) 3 ) 3 ( N g = o = olarak bulunur. Not: Coğrafi koordinatlar ile Gauss-Kruger (UTM) koordinatları arasında dönüşüm hesaplarının elle apılması orucu olabilir. Bu nedenle hesaplamaların 95
232 Matematik Jeodezi S.Bektaş bilgisaar ortamında apılması ugun olur. Bu amaçla internet ortamında kullanıma sunulan hazır programlardan da ararlanılabilir GAUSS-KÜGE POJEKSİYON YÜZEYİNDE HESAPLAMALA Gauss-Kruger projeksionu (GKP) üzeinde jeodezik hesaplamaların apılabilmesi için gerekli matematik bağıntılar literatürde mevcuttur. Ancak burada ölçülerin (doğrultu, uzunluk) GKP üzeine indirgenmesi suretile jeodezik hesaplamaların nasıl apılacağı gösterilecektir. Eğer ölçüleri projeksion üzeine indirgersek jeodezik hesaplamalar çok kolalaşır. Projeksion üzei de bir düzlem olduğuna göre apılacak tüm jeodezik hesaplamalar düzlem esaslara göre gerçekleştirilir. Doğaldır ki hesaplamalarda kullanılacak sabit (daanak) noktalarının koordinatlarının projeksion düzlemindeki değerler olması gerekir [4],[6]. GKP de indirgemeli hesaplamalar Bölüm 7. de anlatılan küre üzeinde soldner koordinatlarıla apılan indirgemeli hesaplara benzer tek fark indirgeme eşitliklerinin değişik olmasıdır ÖLÇÜLEİN GAUSS-KÜGE POJEKSİYON YÜZEYİNE İNDİGENMESİ Fiziksel erüzünde apılan gözlemlerin referans üzei olarak seçilen elipsoid üzeine indirgedikten sonra projeksion üzeindeki hesaplamalar için ölçülerin projeksion üzeine de indirgenmeleri gerekir. Gauss-Kruger projeksion koordinatları ile apılacak uzunluk, açıklık açısı ve alan hesapları sonucunda bulunacak değerler projeksion üzei değerleri olacaktır. Şüphesiz bu değerler orijinal üze (küre a da elipsoid) üzerindeki değerlerden farklı olacaktır. Uzunluk, açı ve alandaki değişimler aşağıdaki indirgeme (redüksion) eşitliklerinden hesaplanabilir. İndirgeme eşitliklerindeki arıçapı olarak çalışma bölgesindeki Gauss küresi arıçapı g alınmalıdır [4]. T s t P r' t r P S S : Elipsoidal uzunluk T : Elipsoidal semt r : Ölçülen doğrultu s : GKP üzeindeki uzunluk t : GKP üzeindeki semt r : GKP üzeindeki doğrultu t : Doğrultu indirgemesi (redüksionu) Şekil-4 GKP de İndirgemeler 96
233 Elipsoid Yüzeinde Jeodezik Hesaplamalar Gauss Kruger Projeksionunda Uzunluk indirgemesi Gauss-Kruger projeksion üzeindeki kenar her zaman elipsoid üzeindeki karşılığından büüktür. Projeksion üzeindeki kenarı s, elipsoid üzerindeki kenarı S ile gösterirsek indirgeme (redüksion) miktarı s δs s S ( ) 6 olur. Kısa kenarlar söz konusu ise ve koordinatları erine bunların ortalaması m değeri kullanılırsa indirgeme eşitliği aşağıdaki gibi daha sade bir görünüm alır. δ s m s S s m Pratikte ve fazla doğruluk gerektirmeen işlemlerde, örneğin poligon hesaplarında kenarların deniz düzeine indirgenmesi ile projeksion indirgemesi aşağıdaki gibi toplu olarak apılabilir. Burada; H m H H s S H ' : Ort.ükseklik S : P noktasındaki erel atada ölçülen kenar s : deniz seviesine ve GKP üzeine indirgenmiş kenar dır. Gauss-Kruger Projeksionunda (Açıklık Açısı) Doğrultu İndirgemesi Elipsoid üzeindeki açıklık açısını (doğrultuu) T= ile projeksion üzeindeki açıklık açısını(doğrultuu) t ile gösterirsek δt T t r r' r : ölçülen doğrultu (elipsoid üzeindeki) r : projeksion düzlemindeki doğrultu şeklinde hesaplanacak farka açıklık açısı (doğrultu) redüksionu denir. Aşağı eşitliklerden indirgeme değerleri hesaplanır. ρ δ t T t (x x)( ) 6 üzerinde hesap apılan kenarlar kısa ise redüksion bağıntıları daha basit biçime dönüştürülebilir. ve erine bunların ortalama m değeri alınırsa, 97
234 Matematik Jeodezi S.Bektaş ρ T t m (x x) Gauss Kruger Projeksionunda Alan edüksionu Elipsoid üzeindeki F alanı ile projeksion üzeindeki f alanı arasındaki fark aşağıdaki gibidir. F f f 3 m F f f Örnek-3: Şekil-5 de P noktasından P, P 3 ve P 4 noktalarına olan ata doğrultular ve elipsoid üzeindeki kenar ölçüleri verilmiştir. Söz konusu ölçüleri Gauss-Krüger projeksion üzeine indirgeiniz. (= m) D.N B.N Yat. Doğrultu Kenar P P g m P P N.N Xg Yg P P P P P P 3 P Şekil-5 P 4 Çözüm: Noktaların Gauss-Krüger projeksion üzeindeki koordinatları da verildiğine göre projeksion üzeindeki değerler indirgeme eşitliklerinden ararlanarak aşağıdaki çizelgede olduğu gibi hesaplanır. D.N B.N Ölçülen Yata doğrultu rik Elipsoid Yüzündeki Kenar Sik İndirg. dtik [cc] İndirg. dsik [cm] GKP deki doğrultu rik =rik - dtik GKP deki kenar sik=sik+dsik P P g m g m P P
235 Elipsoid Yüzeinde Jeodezik Hesaplamalar Örnek-4: GKP Yüzeinde Önden Kestirme Gauss-Krüger Projeksion sisteminde koordinatları verilen ve 3 noktalarından kestirilecek noktasına olan doğrultu ölçüleri verilmiştir. noktasının GKP koordinatlarını önden kestirmele bulunuz (= m). Nokta Yg Xg (A) (B) (P) DN BN r ik (Ölç.Doğrultu) g (A) (B) İstenilenler: (P) noktasının (Yg,Xg) koordinatları Çözüm: GKP üzeinde önden kestirme apabilmek için verilen doğrultu ölçülerinin GKP üzeine indirgenmesi gerekir. İndirgeme işlemini apabilmek için de noktasının aklaşık koordinatlarına ihtiaç vardır. Bu aklaşık koordinatları düzlem önden kestirme hesabıla bulabilmek için öncelikle ölçülen doğrultu farklarından ve taban açıları hesaplanırsa aşağıdaki değerler elde edilir. = g ve = g Taban açılarıla önden kestirme eşitliklerinden kestirilecek noktanın aklaşık GKP koordinatları, ( b a )cot ( xb xa ) p a = m cot cot ( xb xa )cot ( b a ) x p xa = m cot cot olarak bulunur(*). (*) Bu eşitlikler ukarıdaki şekle göredir ve kestirilecek olan P noktası AB doğrusunun solunda kalmaktadır. Eğer P noktası sağda kalıor ise ukarıdaki eşitliklerdeki ve açılarının eksi işaretli alınması gerekir. 99
236 Matematik Jeodezi S.Bektaş Ölçülen doğrultuların GKP düzlemine indirgenmesi DN BN r ik (Ölç.Doğr.) İndirgeme r ik (İndirg.Doğr.) T dt=t-t t g cc g değerleri elde edilir. Bu indirgenmiş doğrultularla düzlem taban açıları = g ve =4.764 g olur. Şaet problemde ölçülen doğrultular erine taban açıları ve verilmiş olsadı. Bu açılar, doğrultu farkları ilgili açı değerlerini verecek şekilde doğrultulara dönüştürülür. İndirgenmiş açılarla eniden düzlem önden kestirme apılırsa, P () noktasının kesin GKP koordinatları ( b a )cot' ( xb xa ) p a = 0.037m cot' cot ' ( xb xa )cot' ( b a ) x p xa = m cot' cot ' olarak bulunur. İndirgeme değerlerini kontrol amacıla ukarıda bulunan koordinatlarla doğrultu indirgeme değerleri eniden hesaplanmış ancak anı değerler tekrar elde edildiğinden iterasona gerek kalmamıştır UTM POJEKSİYONU Universal Transvers Mercator (UTM) kelimelerinin baş harflerinden oluşan UTM projeksionu Gauss-Krüger projeksionundan başka bir şe değildir. Ancak koordinatları Gauss-Krüger koordinatlarından türetilen SAĞA ve YUKAI değerler olarak ifade edilir. İkinci düna savaşından sonra bütün düna ülkeleri için ortak bir harita projeksionunun geliştirilmesi düşüncesi ortaa atılmış, ugulanacak projeksionda şu noktaların bulunması istenmiştir [4],[6],[8]. 00
237 Elipsoid Yüzeinde Jeodezik Hesaplamalar a) Doğrultu deformasonlarının az olması için konformluk, b) Olabildiğince az saıda projeksion üzeinin kullanılması ve üzeler arasında dönüşümlerin mümkün olması, c) Ölçek deformasonunun belirtilecek sınırlar arasında kalması, d) Dik koordinat sisteminde beraberliğin sağlanması, e) Meriden akınsamasının 5 dereceden küçük olması. Yukarıdaki koşullara en ii uum sağlaabilecek projeksion türünün GKP olduğu saptanmış ancak bu projeksionda bazı değişiklikler apılmış ve sonuçta UTM projeksionu ortaa çıkmıştır. D.O.M (Dilim Orta Merideni) 6 o dilim Ekvator 3 o dilim D.N (Dilim Numarası) Şekil-6 Ülkemizde kullanılan 6 o ve 3 o dilimler UTM sisteminde düna 6 0 lik dilimlere bölünmüştür. UTM de 80 0 merideninden başlamak üzere düna 6 0 bolam aralıklı 60 dilime arılmıştır. Dilimler den başlamak üzere doğua doğru artan sırada olmak üzere ile 60 arasında numaralandırılmıştır. Her bir dilim bir projeksion sistemini belirler. Silindir, dilimin orta merideni bounca dünaa teğet alınır. Bölece bir dilimin 3 0 sağı ve 3 0 solu anı bir dilim içinde er alır. Ülkemiz 35, 36, 37 ve 38 nolu dilimler içinde kalmaktadır (şekil-6). Dilim orta merideni (L 0 ) ile Dilim Numarası (DN) arasındaki ilişki; L 0 83 DN L 0 = (DN)* şeklindedir. 6 0
238 Matematik Jeodezi S.Bektaş L bolamlı bir noktanın hangi 6 0 lik vea 3 0 lik dilime girdiği aşağıdaki şekilde bulunur. 6 0 lik dilimde, dilim numarası DN= INT(L/6) lik dilimde, dilim orta merideni L o = 6 x INT(L/6) lik dilimde, dilim orta merideni L o = 3 x INT[(L+.5 0 )/3] Burada; INT(.): tam değer fonksionunu gösterir. Örneğin INT(3.)=3 ve INT(3.8)=3 dir. UTM projeksionunda, bir dilimde ekvatordan 80 0 kuzei ve 80 0 günei arasında kalan kısmın projeksionu apılır paralelleri ile kutup noktaları arasında kalan bölgelerin haritaları, deformasonlar aşırı olacağından UTM projeksion sisteminde apılmaz. Bu bölgelerin haritaları Universal Polar Stereografik (UPS) denilen açı koruan normal konumlu düzlem projeksion sistemine göre apılır. UTM projeksionunda 6 0 genişliğinde dilimlerin kullanılması deformasonları artıracaktır. Bilindiği üzere GKP da diferansiel ölçek ani büüme oranı; m dir Görüldüğü gibi ölçek, değerinin (başlangıç merideninden olan uzaklık) karesi ile orantılı olarak artmaktadır. Dilim orta merideninde ölçek m = olur ve 3 0 lik dilim sisteminde dilimin en sağında a da en solunda olacak büüme oranı,5 0 = 66,766 km m =, lik dilim kullanıldığında dilimin en sağında a da en solunda olacak büüme oranı 3 0 = 333,53 km m =,0037 olmaktadır. Gauss-Krüger projeksionunda, dilim orta merideninden uzaklaşıldıkça artan, bu düzensiz büüme UTM projeksionunda ugun şekilde dağıtılmaa çalışılmıştır. Bu amaçla dilim orta merideni ile dilim sınırı arasındaki uzaklığın aklaşık ortasına gelen kısımda ölçek faktörü m 0 = olması istenmiştir. Yani dilim eksenindeki ölçek faktörü bu defa m 0 olacaktır. O halde herhangi bir Y uzaklığındaki m ölçek faktörü Y m m 0 0
239 Elipsoid Yüzeinde Jeodezik Hesaplamalar bağıntısı ile hesaplanabilecektir. 6 0 lik dilim genişliğinde dilim ekseninin sınır noktaa olan uzaklığı ekvatordaki 340 km kabul edilirse bu uzaklığın arısı 70 km olur. Y = 70 km için m = olacağından dilim ekseni için m 0 ölçek faktörü Y m 0 m. 0,9996 olarak bulunur. UTM projeksionunda uzaklıkların anormal büümesini önlemek amacıla hesaplanan X g ve Y g değerleri m 0 ölçek faktörü ile küçültülerek kullanılır. Dilim ekseninin solunda kalan noktaların Y g değerlerinin (ordinatlarının) eksi değerden kurtulması için Y g değeri m 0 ile küçültüldükten sonra m eklenir. X g değerleri kuze arı kürede pozitif olduğu için herhangi bir değer eklenmesine gerek oktur. Ancak güne arı küre için m 0 ile küçültülen X g değerine m eklenir. Pozitif apılan ordinatlara hangi dilimde olduğunu göstermek üzere o dilimin numarası tanıtıcı olarak baş tarafına eklenir. Bölece elde edilen koordinat değerlerine SAĞA ve YUKAI isimleri verilir. SAĞA ve YUKAI koordinatları UTM projeksionunun dik koordinat sistemindeki değerleridir. Bu değerlerle hesaplama apılmaz sadece çizim apılır. Noktalar arasında uzunluk, alan, doğrultu gibi büüklüklerin hesaplanması gerektiğinde SAĞA ve YUKAI değerlerden geri giderek söz konusu noktaların Y g ve X g ile tanımlanan GKP koordinatlarının bulunup bu değerlerle hesapların apılması gerekir. GKP koordinatlarından hesaplanacak değerler de şüphesiz projeksion üzeindeki değerler olacaktır. Küre vea elipsoid üzeindeki değerler istenirse redüksion değerlerinden hesaplanması oluna gidilir[4],[7],[3]. Gauss-Krüger koordinatları bilinen bir noktada UTM koordinatları aşağıdaki gibi hesaplanır. SAĞA = (DN) ( m 0.Y g ) (m 0 = 0,9996) YUKAI = m 0.X g (kuze arı küre için) YUKAI = m 0.X g (güne arı küre için) m.000 UTM GKP Dilim Orta Merideni Y (km)
240 Matematik Jeodezi S.Bektaş Şekil-7 UTM ve GKP projeksionunda ölçek faktörünün değişimi Şekil-8 UTM ve GKP projeksionunda ölçek faktörünün değişimi 04
241 Elipsoid Yüzeinde Jeodezik Hesaplamalar Türkie de ülke nirengi ağına daalı /5000 ölçekli temel haritalar 6 0 dilim genişlikli Gauss-Krüger sistemine göre üretilmiştir. /5000 ölçekli Standart Topografik (ST) ve Standart Topografik Kadastral (STK) haritalar 3 0 lik dilim genişlikli Gauss-Krüger sisteminde üretilmektedir DEĞİŞTİİLMİŞ UTM POJEKSİYONU /5000 ve daha büük ölçekli haritaların apılmasında dilim genişliği 3 0 olan değiştirilmiş UTM projeksionu kullanılmaktadır. Bu projeksionda m 0 =.0000 alınır. SAĞA ve YUKAI değerlerin hesabı UTM projeksionunda olduğu gibi hesaplanır. Ancak SAĞA değerin önünde bulunan dilim numarası bu projeksionda kullanılmaz. Değiştirilmiş UTM projeksionunda bir noktanın sağa ve ukarı değerleri aşağıdaki gibi hesaplanır [8]. SAĞA = Y g YUKAI = X g Görüldüğü gibi, Değiştirilmiş UTM projeksionu, Gauss-Krüger projeksionundan başka bir şe değildir. Aradaki fark, koordinatların sağa ve ukarı olarak adlandırılması ve Y g değerlerine m eklenmesidir. Örnek-: UTM koordinatları aşağıdaki şekilde verilen noktanın Gauss-Krüger koordinatlarını ve anı D.O.M daki değiştirilmiş UTM koordinatlarını bulunuz. SAĞA = m YUKAI = m Çözüm: Verilen SAĞA değerinden dilim numarasının DN = 36 olduğu görülmektedir. Noktanın Gauss-Krüger koordinatları; (m 0 = ) SAĞA = (DN) ( m 0.Y g ) YUKAI = m 0.X g Y g = (SAĞA ) / m 0 = m X g = YUKAI / m 0 = m 05
242 Matematik Jeodezi S.Bektaş Dilim orta merideni; L 0 = (DN)* = lik değiştirilmiş UTM koordinatları (m 0 =.0000 ) SAĞA = m 0.Y g = m YUKAI = m 0.X g = m Örnek- : Dilim orta merideni L 0 = 7 0 sisteminde Değiştirilmiş UTM koordinatları SAĞA = m YUKAI = m olarak verilen noktanın anı dilimdeki UTM koordinatlarını bulunuz. Çözüm: DN = (L ) / 6 0 = 35 X g = YUKAI / m 0 = m (m 0 =.0000) Y g = (SAĞA ) / m 0 = m UTM koordinatlarının hesabı (m 0 = ) SAĞA = (DN) ( m 0.Y g ) = YUKAI = m 0.X g = GAUSS-KÜGE POJEKSİYONUNDA KOMŞU DİLİMLE AASINDA KOODİNAT DÖNÜŞÜMÜ Jeodezik hesaplamaların apılacağı bölge birden fazla dilimi kapsıorsa bütün noktaların anı bolam başlangıcına göre ifade edilmesi (dönüştürülmesi) gerekir. Dönüştürme işlemi, anı genişlikli dilimler arasında olabileceği gibi farklı dilim genişlikli sistemler arasında da olabilir. Bu dönüştürme işlemini dolalı ve direkt olarak iki şekilde apmak mümkündür. Burada basitliği nedenile alnızca dolalı dönüşüm ele alınacaktır. L L 0 L Xg Yg P 06 Y g X g
243 Elipsoid Yüzeinde Jeodezik Hesaplamalar Şekil-8 Dolalı Dönüşüm: Bir noktanın bir (L) dilimindeki X g,y g Gauss-Krüger koordinatları verilmişken bu dilime komşu vea komşu olmaan diğer bir (L ) dilimindeki X g,y g koordinatlarını bulmak için (şekil-8) bu öntemde noktanın bir dilimde verilen Gauss-Krüger koordinatlarından önce elipsoidal coğrafi koordinatlara geçiş ve daha sonra da bu koordinatlardan ikinci dilimdeki Gauss-Krüger koordinatlarına geçiş apılır [4]. (X g,y g ) L (B,L) (X g,y g ) L Örnek-: 33 0 diliminde Gauss-Krüger koordinatları; g = m ve x g = m olarak verilen noktanın 30 0 dilimindeki Gauss-Krüger koordinatlarının dolalı öntemle bulunması. Çözüm: Önce noktanın verilen Gauss-Krüger koordinatlarından aşağıdaki eşitliklerden coğrafi koordinatlar bulunur ( Bölüm 9..). F aak noktasının B F enlemi G = x g meriden aını gören enlem değeri olarak hesaplanır. = G / A üzere B = B F - B F = + B''sin + C''sin4 + D''sin6 = o t = tan B F = , = e cos B F = E-3, V = + = , N = c / V= olmak F g g tan BF ( ) (5 6 F 3t F 6 FtF )( N F N F ) 07
244 Matematik Jeodezi S.Bektaş B = 44 08' 7.999" L = L o + ( cos B N g F ) ( 6 F t F )( N g F ) 0 (5 8t F 4t 4 F )( N g F ) 4 L = 30 56' 9.654" Meriden akınsaması ise ilgili eşitlikten C = o olarak bulunur. Hesaplanan coğrafi koordinatlardan bu defa ( Bölüm 9..) deki eşitliklerden Gauss-Krüger koordinatları (L o =30 o ) sisteminde, l = L - L o = 56' 9.654" = bolam farkı B = 44 08' 7.999" enlemile hesaplanan terimler, t = tan B = , = e cos B = E-3, V = + = , N = c / V= G = A' B + B' sinb + C' sin4b + D' sin6b = m olmak üzere Gauss-Krüger koordinatları, N x g = G + sin B cos Bl (5 t ) cos Bl 4 = m g = N cos Bl ( 6 t )cos Bl (5 0 8t t 4 58 t )cos 4 Bl 4 g = 75.03m meriden akınsaması ise ilgili eşitlikten C = o olarak bulunur. Örnek-: UTM koordinatları; SAĞA= m YUKAI= m olarak verilen noktanın 30 0 dilimindeki değiştirilmiş UTM koordinatlarını bulunuz. Çözüm: Noktanın verilen UTM koordinatlarından dilim numarasının 35 olduğu ve dilim orta merideninin 7 0 merideni olduğu anlaşılmaktadır. Bu nedenle önce noktanın 7 0 meridenindeki Gauss-Kruger koordinatlarını bulmak ve daha sonra bu koordinatları 30 0 meridenine dönüştürmek gerekir. Noktanın 7 0 meridenindeki Gauss-Kruger koordinatları; 08
245 Elipsoid Yüzeinde Jeodezik Hesaplamalar DN=35 DOM=7 0 Y g = (SAĞA ) / m 0 Y g = ( ) / = m X g = YUKAI / m 0 X g = / = m olarak bulunur. Dolaısıla noktanın 7 0 meridenindeki değiştirilmiş UTM koordinatları; SAĞA= m YUKAI= m olur. Noktanın 7 0 meridenindeki Gauss-Krüger koordinatlarından 30 0 meridenindeki Gauss-Krüger koordinatları dolalı dönüşüm eşitliklerinden ; Önce noktanın coğrafi koordinatları; B=39 4' " L=9 06' " C= 0' 6.896" olarak bulunur. Noktanın 30 derece meridenindeki Gauss-Krüger koordinatları; Y g = m X g = m olur. Noktanın 30 0 dilimindeki değiştirilmiş UTM koordinatları; SAĞA = Y g = m YUKAI = X g = m 09
246 Üç Boutlu Jeodezi ve GPS 0. ÜÇ BOYUTLU JEODEZİ ve GPS Jeodezinin temel görevi olan noktaların üç boutlu uzada konumlarının belirlenmesi akın geçmişe kadar parçalı klasik öntemle (iki boutlu jeodezi) gerçekleştirilmektedi. Klasik parçalı aklaşımda konum belirleme problemi iki aşamada ata kontrol ve düşe kontrol olarak arı arı ele alınmaktadı. İlk önce seçilen bir referans üzei üzerinde; örneğin seçilecek üze düzlemse, düzlem dik koordinatlar, seçilecek üze küre ise soldner dik koordinatları a da küresel coğrafi koordinatlar, seçilecek üze elipsoid ise elipsoidal coğrafi koordinatlar a da elipsoidal soldner dik koordinatları hesaplanır (Yata Kontrol). Noktaların düşe konumunu belirleebilmek için de söz konusu noktaların referans üzeine olan düşe uzaklıkları arıca belirlenir (Düşe Kontrol). Ülke ölçmeleri söz konusu olduğunda ata konum için seçilecek referans üzei dönel elipsoiddir. Nirengi noktalarının ata konum koordinatları (B,L vea Y,X) elipsoid üzerinde hesaplanırken, noktaların düşe konumu için elipsoid referans üzei olarak alınmaz, noktaların jeoidden itibaren çekül doğrultusu bounca (H) ortometrik ükseklikleri hesaplanır. Pratik gereksinmeler için klasik parçalı jeodezik öntemler günümüzde de geçerliliklerini korumaktadır. Konum bilgileri birbirinden bağımsız iki arı şekilde çözülmee çalışılsa da bağımsızlığı tam olarak sağlamak mümkün değildir. Üç boutlu bir uzada gözlenen jeodezik verilerin stokastik anlamda birbirlerinden bağımsız oldukları sölenemez. Arıca gözlemlerin indirgenmesi aşamasında ata konum belirlenirken düşe konum bilgilerine, düşe konum belirlenirken de ata konum bilgilerine gereksinim duulur. Günümüzde çağdaş bilimsel çalışmaların öncülüğünde noktaların konumlarının belirlenmesi, Üç Boutlu Jeodezi aklaşımıla bir kerede noktaların üç boutlu uza dik koordinatlarını belirlemee öneliktir. Üç boutlu jeodezi düşüncesi eni olmamakla beraber güncel bir konudur. İlk kez 868 de Villarceau ve 878 de Bruns tarafından ortaa atılmıştır. Önceleri ölçmelerin eteri incelikte apılamaması, kenar ölçmelerinin güçlükle apılması, refraksion problemi ve hesaplama güçlükleri nedenile üç boutlu jeodezi uzun zaman ugulama alanı bulamamıştır. Günümüzde ölçme alet ve tekniklerinin gelişmesi, elektronik uzaklık ölçerler, apa er uduları, bilgisaarlar, istatistik öntemler ile sağlanan geniş hesaplama olanakları, geometrik verilerin anında fiziksel ölçülerinde (gravite, potansiel farkı gibi) göz önüne alınmasını gerektirmiş ve hesaplara eni boutlar getirmiştir. Bu değişim ve gelişmelerin sonucunda parçalı klasik 09
247 Matematik Jeodezi S.Bektaş aklaşım erini üç boutlu (3D) bütüncül (integrated) jeodezie, hatta zamana bağlı olarak eruvarındaki tektonik hareketler sonucu konum bilgilerinin değişmesi nedenile zaman boutunun da dikkate alınmasıla dört boutlu (4D) aklaşımlara bırakmıştır [3]. 0.. ÜÇ BOYUTLU JEODEZİ İki boutlu jeodezinin ukarıda saılan mahzurları nedenile 3D jeodezide noktaların üç boutlu uza dik koordinatları bir kerede hesaplanır. 3D jeodezide iki boutlu jeodezik ağlarda apılan ve noktaların göreli konumları hakkında bilgi veren ölçülerin tamamı (ata doğrultu,düşe açı, eğik uzunluk,nivelmanla bulunan geometrik ükseklik farkı ölçüleri,gravite farkı ölçüleri) kullanılabilir. Bunlara ek olarak noktaların mutlak konumlarını belirlemee araan ölçüler (astronomik enlem, bolam ve azimut, apa udu gözlemlerinden-gps vea inersial ölçü sistemlerinden elde edilen koordinatlar) de kullanılabilir. Üç boutlu jeodezik ağlarda kullanılan ölçü çeşitleri bu kadar farklı olmasına rağmen ugulamada ata doğrultu, eğik uzunluk ve düşe açı ölçüleri ön plana çıkar. 3D jeodezide doğal olarak üç boutlu koordinat sistemleri kullanılır. Bu sistemlerden üç boutlu erel dik koordinat (toposentrik) sistemi xz ile global, er merkezli dik koordinat (geosentrik) sistemi XYZ agın olarak kullanılır. Global dik koordinat sistemi ile elipsoidal coğrafi koordinat sistemini daha önce görmüştük. Greenwich başl. merideni X L=0 G Z O L Yp x po B h P Zp Xp z d B=0 Şekil-: (X,Y,Z) Global dik koordinat sistemi, (B,L,h) Elipsoidal coğrafi koordinat sistemi ve (x,,z) Yerel üç boutlu dik koordinat sistemi N t Q Y x (kuze) t P z (başucu) d Q z x (doğu) Şekil-: (t,,d) Yerel kutupsal koordinatlar ile (x,,z) Yerel üç boutlu dik koordinatlar 0
248 Üç Boutlu Jeodezi ve GPS Bilindiği gibi üç boutlu erel dik koordinat sistemi (x,,z) çalışma alanı çok büük olmaan bölgelerde kullanılabilir. Sistemin başlangıç noktası genelde çalışma bölgesinin ortalarında seçilir. Bu sistemde; z ekseni başlangıç noktasından geçen çekül eğrisinin teğeti (a da aklaşık elipsoid normali) ile çakışır. x ekseninin önü astronomik kuze olarak adlandırılır. ekseni bir sol el sistemi oluşturacak şekilde doğua önelmiştir (şekil-). XYZ global dik koordinat sistemi ise bir sağ el sistemidir(şekil-). Kutupsal koordinatlar ile erel dik koordinatlar arasında dönüşümler, x, ve z iki nokta arasındaki erel dik koordinat farklarını göstermek üzere söz konusu noktalar arasındaki kutupsal değerlerden (ölçümlerden) koordinat farkları ve koordinat farklarından kutupsal elemanlar aşağıdaki eşitliklerden elde edilir. x = d sin cos t d = (x + + z ) / : eğik uzunluk = d sin sin t t = arc tan ( / x) : semt (ata doğrultu) z = d cos = arc cos (z / d ) : düşe açı Global koordinatlardan kutupsal elemanların hesabı, X,Y ve Z iki nokta arasındaki global dik koordinat farklarını göstermek üzere söz konusu noktalar arasında kutupsal değerler (eğik kenar,semt,düşe açı) aşağıdaki eşitliklerden elde edilir. d = X Y Z t = arc tan = x z X sin Y cos X sin cos Y sin sin Z cos = arc tan ( / x) =arc cos X cos cos Y cossin Z sin X Y Z = arc cos (z / d ) Yukarıdaki formüllerde geçen, değerleri durulan noktanın astronomik enlem ve bolam değerleridir. Pratikte, erine elipsoidal B,L değerleri kullanılır. Bu B,L değerleri de durulan noktanın global dik koordinatlarından her zaman hesaplanabilir.
249 Matematik Jeodezi S.Bektaş 0... Global ve Yerel Dik Koordinat Sistemi Arasında Dönüşümler XYZ global dik koordinat sistemi ile xz üç boutlu erel dik koordinat sistemleri arasında dönüşüm her zaman apılabilir. İki üç boutlu dik koordinat sistemi arasında benzerlik dönüşümü apabilmek için 7 datum parametresi gereklidir. Bu parametreler; koordinat eksenleri önünde 3 öteleme,3 dönüklük ve ölçek faktörüdür[8]. Her iki sistem arasında ölçek faktörü farklılığı olmadığı düşünülürse dönüşüm parametreleri saısı 6 olur. Bu 6 parametre; P orijin noktasının global dik koordinatları (X P,Y P,Z P ) a da elipsoidal coğrafi koordinatları (B P,L P,h P ) ve orijin noktasındaki çekül doğrultusunu belirleen astronomik enlem ve bolamın ( P, P ) bilinmesile belirlenmiş olur. Zira orijin noktasındaki çekül doğrultusunun belirlenmesi xz sisteminin eksen önlerini (kuze,doğu,başucu) belirli kılar. Çekül sapmasının varlığı astronomik koordinatlar ( P, P ) ile elipsoidal coğrafi koordinatları (B P,L P ) farklı kılar bu değerler arasındaki ilişkiler Bölüm 7. de verilmiştir. Pratik ugulamalarda, P başlangıç noktasındaki çekül sapması göz ardı edilir ve astronomik enlem ve bolam değerleri erine elipsoidal coğrafi koordinatlar kullanılır ani çekül doğrultusunun elipsoid normalile çakıştığı varsaılır. Aşağıdaki dönüşüm eşitlikleri de bu varsaıma göre çıkarılacaktır. Bu durumda P orijin noktasındaki enlem ve bolam değeri noktanın global dik koordinatlarından hesaplanabilir. Özet olarak çekül sapmalarının göz ardı edilmesi halinde XYZ sistemi ile xz sistemi arasında koordinat dönüşümü apabilmek için sadece xz sisteminin başlangıç noktasının global dik koordinatları (X P,Y P,Z P ) a da elipsoidal coğrafi koordinatlarının (B P,L P,h P ) bilinmesi eterli olur. (B,L,h) elipsoidal coğrafi koordinat sisteminde h elipsoidal üksekliği xz erel dik koordinat sisteminde üçüncü boutu z olarak alınmaktadır. P ve Q noktalarının xz erel dik, XYZ global dik ve BLh elipsoidal coğrafi koordinatları arasında dönüşümler aşağıdaki eşitliklerden gerçekleştirilir. x = x z Q Q Q x z P P P X = X Y Z Q Q Q X Y P Z P P koordinat fark vektörlerini göstermek üzere, P = sin BP cos L sin LP cos BP cos LP P sin B cos B P P cos L sin L P sin L P P cos B 0 sin B P P
250 Üç Boutlu Jeodezi ve GPS P ortogonal dönüşüm matrisinden ararlanarak ( T = - ) Global dik koordinat farklarından erel dik koordinat farkları x =. X eşitliğinden Yerel dik koordinat farklarından global dik koordinat farkları X = T. x eşitliklerinden elde edilir. Örnek-: WGS84 sisteminde elipsoidal coğrafi koordinatları, B = 39 o 30 8 L = 39 o h = 00m. olan P noktası başlangıçlı erel üç boutlu dik koordinat sisteminde P noktasının erel dik koordinatları, x p = 0.000m p = 0.000m z p = m olarak verilmektedir. Söz konusu P noktasından bir Q noktasına apılan kutupsal ölçümler sonucunda, d= m =89 o t =84 o değerleri elde edilmiştir( açısına refraksion indirgemesi apılmış). a) P noktasının global dik koordinatlarını bulunuz b) Q noktasının P noktası orijinli erel üç boutlu dik koordinat sistemindeki koordinatlarını bulunuz. c) Q noktasının global dik koordinatlarını bulunuz d) Q noktasının elipsoidal coğrafi koordinatlarını bulunuz. e) P ve Q noktalarının global dik koordinatlarından ararlanarak iki nokta arasında eğik kenarın,düşe açının ve semt açısının değerini hesaplaınız. Çözüm: a) P noktasının global dik koordinatları, N X = (N+h) cos B cos L= m Y = (N+h) cos B sin L= m Z = [(-e )N+h] sin B= m a e e sin B a b a eşitlikleri ile gerçekleştirilir. Burada; N meridene dik doğrultudaki normal kesit eğrilik arıçapı, a elipsoidin büük arı eksen uzunluğu, e ise elipsoidin I. eksentrisitesidir. Söz konusu parametreler için WGS84 elipsoidi değerleri alınmıştır. 3
251 Matematik Jeodezi S.Bektaş b) Q noktasının erel üç boutlu koordinatları x = d sin cos t = m x Q = x p +x = m = d sin sin t = m Q = p + = m z = d cos = m z Q = z p +z = m c) Q noktasının global dik koordinatları, Q noktasının hesaplanan erel dik koordinatlarından aralanarak, x = x z Q Q Q x z P P P x = z B = 39 o 30 8 ve L = 39 o değerlerile oluşturulacak dönüşüm matrisi P = sin BP cos L sin LP cos BP cos LP P sin B cos B P P cos L sin L P sin L P P cos B 0 sin B P P = Yerel dik koordinat farklarından Global dik koordinat farkları X = T x çarpımından hesaplanır. Q noktasının global dik koordinatları X = X Y Z X Y Z Q Q Q Q Q Q X Y P Z Y Z P P X P P P X = Y Z X Y Z d) Q noktasının elipsoidal coğrafi koordinatları Q noktasının hesaplanan global dik koordinatlarından ararlanarak aşağıdaki gibi hesaplanır. Y L arctan LQ = 39 o 0 00 X P X Y r P Z f ( a b) / a 4
252 Üç Boutlu Jeodezi ve GPS a Z (( f ) e ) arctan r P 3 Z( f ) e a.sin B arctan 3 BQ = 39 o 3 00 ( f )( p e a.cos ) h = -N + Y / (sin L cos B) hq =00.000m Q noktasının hesaplanan elipsoidal üksekliği hq ile daha önce hesaplanan zq değeri arasında n= hq - zq =6.59m fark vardır. Bu fark küresellikten kanaklanmakta olup aşağıdaki gibi hesaplanabilir. n d ( A : A azimutundaki WGS84 elipsoidinin eğrilik arıçapı) A B = 39 o 30 8 enlemi ve A t = o için A = m olur. Bu eğrilik arıçapı ve d = m mesafesile hesaplanacak n değeri d n A = 6.6m olur. e) P ve Q noktalarının global dik koordinatlarından ararlanarak iki nokta arasındaki eğik kenarın,düşe açının ve semt açısının hesaplanması. X P = m Y P = m Z P = m X Q = m Y Q = m Z Q = m Noktalar arasındaki koordinat farkları, X = Y = Z = P noktasının coğrafi koordinatları B= 39 o 30 8, L = 39 o d PQ = X Y Z t PQ = arc tan PQ =arc cos eşitliklerinden X sin L Y cos L X sin B cos L Y sin Lsin B Z cos B X cos B cos L Y cos Bsin L Z sin B X Y Z 5
253 Matematik Jeodezi S.Bektaş d PQ = m t PQ = o = 84 o PQ = o = 89 o olarak hesaplanır. 0.. UYDU JEODEZİSİ SİSTEMLEİ Günümüz jeodezi ugulamalarında, artık noktaların üç boutlu koordinatları bir kerede üksek doğrulukta ve gaet hızlı bir biçimde udu jeodezisi tekniklerile direkt olarak belirlenebilmektedir. Navigason, konum belirleme ve bilimsel amaçlı çalışmalar için udu jeodezisinden ararlanma çabaları giderek artmaktadır. Tüm bu çalışmalar için uzada oluşturulmuş udu sistemlerinden ararlanılmaktadır. Başlıca udu sistemleri olarak; GPS, GLONASS, DOIS,PAE,TOPEX/POSEIDON,GALİLEO saılabilir. Bu sistemler dışında özellikle bilimsel amaçlı çalışmalarda kullanılan SL ve VLBI sistemleri de mevcuttur[5]. Ancak burada udu sistemlerinden sadece pratikte en çok kullanılan GPS sistemi özet olarak ele alınacaktır. 0.. GPS - KÜESEL KONUMLAMA SİSTEMİ Klasik jeodezik öntemlere 960 lı ıllardan sonra udu jeodezisi öntemi eklenmiştir. Önceleri salt askeri amaçlarla geliştirilmiş bu öntem daha sonraları sivil amaçlar için kullanılmaa başlanmıştır. GPS (Global Positioning Sstem- Küresel Konumlama Sistemi) adı verilen bu sistem erden aklaşık 000km üksekte ekvator düzlemile aklaşık 55 o açı apan 6 farklı örünge düzleminde her örüngede 4 udu olmak üzere düna etrafında sürekli dolanan ve kodlandırılmış rado sinalleri aan 4 udula Temmuz 993 de tamamlanmıştır (şekil-3). S S3 S d d3 S4 d d4 GPS alıcısı P Şekil 3 GPS uduları ve örüngeleri Şekil 4 Mutlak konum belirleme 6
254 Üç Boutlu Jeodezi ve GPS Bu udulardan 3 tanesi edek olacak şekilde tanımlanmıştır. Bölece dünanın her erinde, günün her saatinde, her türlü hava koşullarında en az 5 o eğim açısı altında 4 ile 8 udu anı anda gözlenecek şekilde tesis edilmiştir[]. Bu sistemle dünadaki herhangi bir noktanın global (er merkezli) XYZ koordinatları ölçülebilmektedir. Sistemin temeli uzunluklarla uza geriden kestirmee daanmaktadır[7]. Bilindiği gibi uza geriden kestirme önteminde bir P noktasının üç boutlu konumunu belirleebilmek için koordinatları bilinen üç sabit noktaa olan uzaklıkların ölçülmesi eterlidir (Bölüm 3.9). Bölece merkezleri sabit noktalar (udular) ve arıçapları ölçülen uzunluklar olan üç kürenin kesişimi koordinatları istenen P noktasıdır (şekil-4). Gerçi bu üç kürenin kesişimi çift nokta olmakla beraber gerçek çözüm bir dördüncü noktaa (udua) olan uzaklıkla belirlenebilir. GPS önteminde bilinen noktalar udular olup herhangi bir anda udunun koordinatlarının hesaplanabileceği udu örünge değerleri, udu tarafından modüle edilmiş rado sinalleri ile aınlanmaktadır ve her an kullanıcının ararlanmasına hazırdır. Koordinatları aranan gözlem noktası ile udu arasındaki uzaklık için, ududan sinal çıkış ve alıcıa giriş zamanının üksek doğrulukla belirlenmesi gerekmektedir. Ududa bulunan bir saatin sinal üzerinde üreteceği zaman işaretleri ile sinal aımının zaman noktaları belirlenebilmekte, geliş zamanı ise alıcıda bulunan bir saatle saptanmaktadır. Ududaki ve alıcıdaki her iki saat tam olarak senkronize edilemeeceğinden, geometrik uzaklığı bu iki saat verileri ile istenilen doğrulukta belirlemek mümkün değildir. Yüksek doğruluklu udu saatinin hatasız ve tüm udu saatlerinin senkron çalıştıklarının kabul edilebilir olmasına karşılık, alıcı saat hatasını bir bilinmeen olarak işleme sokmak gerekir. Bu durumda uzasal konum belirleme için, konumu belirlenmek istenen noktanın üç koordinatına ek olarak, alıcıdaki saat hatası da 4. bilinmeen olarak belirlenmek durumundadır ve bu bilinmeen değişik udulardan anı anda belirlenen uzaklıkların sıfır noktası eki gibi düşünülebilir. Bu üzden ölçü değerleri pseudo (=akıştırma) uzaklıklar olarak tanımlanır. Bu dört bilinmeeni belirlemek için dört pseudo uzaklığa gerek vardır. O halde bir gözlem erinde anı anda dört udu gözlenebilmelidir. Mevcut GPS sistemide bu olanağı vermektedir. A: Sabit nokta B: Koordinatı belirlenecek nokta S S3 S db da3 db db3 S4 da da da4 db4 A bab Şekil-5 İki GPS alıcısı ile ölatif Konum Belirleme B B = A+b AB A =[X A Y A Z A] T B =[X B Y B Z B] T b AB= X Y Z B B B X Y A Z A A 7
255 Matematik Jeodezi S.Bektaş Jeodezik amaçlarla GPS alıcıları ile faz ölçülerine daalı olarak er noktasıudu arasındaki uzaklıklardan, GPS koordinat sistemi olan WGS84 sisteminde gözlem noktasının üç boutlu (X,Y,Z) koordinatları hesaplanır. Gözlem öntemleri; Tek nokta belirlemesi ve ölatif nokta belirleme olmak üzere sınıflandırılabilir. Tek nokta belirlemesinde (mutlak konum belirleme) tek bir alıcı ile her bir noktanın arı arı belirlenmesi söz konusudur. Bu öntemde (örneğin refraksion, udu örünge hatası gibi) çok saıda hatanın etkisi ile günümüzde ancak 0m. gibi düşük bir doğruluk elde edilebilmektedir. Birden fazla alıcı ile eş zamanda anı udular gözleniorsa, rölatif nokta belirlemesi apılabilir. Bu belirlemeden iki nokta arasında koordinat farkları ve bunlardan da baz vektörü vea baz doğrusu elde edilir(şekil-5). Bu değerlerden nokta koordinatlarının belirlenmesi için, alım noktalarından en az birisinin referans noktası olarak koordinatlarının verilmesi gereklidir. ölatif nokta belirlemenin doğruluğu, tek nokta belirlemesine oranla çok üksektir. Çünkü iki noktanın gözlem verilerinin kombinasonu ile çeşitli hata etkileri ok edilebilmektedir. Aşağıdaki tablo bu öntem hakkında bir fikir verecektir. Yöntem Doğruluk Özellikler Statik 0.mm ppm Uzun gözlem süresi(saat), sınırsız baz uzunluğu Kısa zamanlı statik 5mm ppm Kısa gözlem süresi(dak.), baz uzuluğu<0km, tercihen frekanslı alıcı,ii udu geometrisi gerekli Kinematik 3mm 0 ppm Kısa gözlem süresi(san.),başlangıç değerlerinin belirlenmesinden sonra 4 ududan sürekli sinal alımı gerekli Pseudo kinematik 5mm ppm Kısa gözlem süresi(dak.), alıma ara vermek önemsiz Tablo- ölatif nokta belirleme öntemlerinin özellikleri ve ulaşılan doğruluklar Günümüzde profesonel (jeodezik amaçlı) GPS alıcıları anısıra geliştirilen cep telefonu büüklüğünde El GPS alıcılarıla bile 3m duarlığında konum belirlenebilmektedir. El GPS alıcılarının fiatlarının son derece ekonomik oluşları saesinde hassas jeodezi ugulamaları dışında büük kullanım alanı bulmuşlardır. Ülkemizde, mevcut ülke nirengi ağının (ED-50) bölgesel bozulmalar sonucu pratik gereksinimleri karşılaamaz duruma düşmesi nedenile GPS teknolojisine daalı eni bir temel jeodezik ağ kurulması düşünülmüş ve TUTGA-99 olarak 8
256 Üç Boutlu Jeodezi ve GPS adlandırılan bu ağın ölçme ve değerlendirme çalışmaları ılları arasında tamamlanmıştır. TUTGA-99 ağı, ülke üzeini kapsaan 5-70km sıklıkta 600 noktadan oluşmuştur. Ağ noktalarının ITF (Uluslar arası Yersel eferans Sisteminde ) birkaç cm doğruluğunda üç boutlu koordinatları (X,Y,Z) bu koordinatların zamana bağlı değişimleri (hızları;vx,v,vz) ve ortometrik ükseklikleri (H) ile jeoid ükseklikleri (N) belirlenmiştir[5] GPS KOODİNATLAINDAN ÜLKE KOODİNATLAINA DÖNÜŞÜM ABD ordusunda 980 ılından sonra oğun olarak kullanılmaa başlanan GPS in daandığı WGS84 datumunun, 990 lı ılların başından itibaren NATO içerisindeki ortak harekatlarda ve harita üretimlerinde kullanım zorunluluğu doğmuştur. Diğer taraftan, günümüzde sivil (kalkınma) amaçlı harita üretimlerinde de GPS alıcıları ile WGS84 sisteminde konum belirleme ve harita üretimi eğilimi iice artmıştır. Bu gelişmeler doğrultusunda,ülkemizde askeri ve sivil amaçlarla 00 ılına kadar Avrupa Datumu-950 (European Datum-950: ED50) sisteminde üretilen /5.000,/ ve / ölçekli topoğrafik haritaların 00 ılından itibaren WGS84 sisteminde üretimine geçilmiştir. 00 ılına kadar ülkemizde üretilen haritaların ED50 datumunda, 00 ılından sonra üretilecek haritaların WGS84 datumunda olması ve GPS alıcıları vea diğer öntemlerle WGS84 sisteminde belirlenen koordinatların ED50 datumunda üretilmiş olan haritalar ile uuşumunun sağlanması için dönüşüm zorunluluğu doğmuştur [0], [9]. ED50 datumunda; referans elipsoidi olarak Uluslararası (Haford) 94 elipsoidi (a= m; b= m; f=/97) kullanılmıştır. WGS84 datumunda kullanılan referans elipsoidinin parametreleri ise (a= m ; b= m; f=/ ) dir. WGS84 koordinat sistemi anı zamanda er gravite alanına ait fiziksel özellikleri de bünesinde toplaan bir sistemdir. Bu nedenle ED50 sistemine göre üstündür. 005 ılında ürürlüğe giren BÖHHBÜY Madde-0 da Bu Yönetmelik kapsamında hesaplanacak koordinatlar, en son güncellenmiş TUTGA a bağlı, GS80 elipsoidi ve Transversal Mercator (TM) izdüşümünde üç derecelik dilim esasına göre belirlenir. demektedir. Yani hesaplamalarda GS80 elipsoidinin kullanılacağı sölenmektedir. GS80 elipsoidinin parametreleri(a= m ; f=/98.570) dir. GPS alıcılarının ürettiği ham koordinatlar WGS84 sistemindeki (XYZ) kartezen koordinatlarıdır. Osa ülke koordinatları ED50 sistemindedir. Bu 9
257 Matematik Jeodezi S.Bektaş 0 nedenle GPS koordinatlarından ülke koordinatlarına geçiş bir dizi dönüşüm gerektirir. Genelde GPS alıcıları kendi üzerlerindeki azılımlarla ve ölçü anında kullanılan sabit nokta koordinatlarından ararlanarak bu dönüşümü kendiliğinden apabilmektedir. GPS koordinatlarından ülke koordinatlarına geçiş için gerekli dönüşüm adımları aşağıda saılmıştır : i-) Önce (XYZ) WGS84 koordinatlardan üç boutlu bir koordinat dönüşümü ile (XYZ) ED50 koordinatları elde edilir. Bilindiği üzere iki üç boutlu koordinat sistemi arasında dönüşüm apabilmek için 7 adet dönüşüm (datum) parametresinin bilinmesi gerekir. Söz konusu 7 adet datum parametresi 3 öteleme (t X,t Y, t Z ) 3 dönüklük(ε X,ε Y,ε Z ) ve ölçek (k) her iki koordinat sisteminde de en az noktanın (XYZ) koordinatları ve diğer bir noktanın alnız bir koordinatı biliniorsa cebrik olarak belirlenir. Üç a da daha fazla saıda noktanın her iki sistemde koordinatları biliniorsa dönüşüm parametreleri dengelemeli olarak belirlenir [8]. WGS84 sistemile ED50 sistemi arasında öteleme farkı olduğu, dönüklüklerin son derece küçük olduğu bilinmektedir. Her iki koordinat sistemi arasındaki dönüklükler küçük ise özel durum olarak aşağıdaki dönüşüm eşitliği kullanılabilir WGS X Y X Z Y Z Z Y X ED Z Y X k k k t t t Z Y X () HGK tarafından apılan bir çalışma ile WGS84 sistemi ile ED50 sistemi arasındaki dönüşüm parametreleri aşağıda gösterilmiştir. WGS84 den ED50 e dönüşüm parametreleri aklaşık olarak aşağıdaki gibi belirlenmiştir. t X = m t Y = 0.35 m t Z = m k = ppm ε X = " ε Y = " ε Z = " ED-50 den WGS-84 e dönüşüm apılması istenirse Z Y X ED X Y X Z Y Z WGS t t t Z Y X k k k Z Y X () ukarıdaki ters dönüşüm eşitliği kullanılır.
258 Üç Boutlu Jeodezi ve GPS ii-) ED50 sistemindeki (XYZ) kartezen koordinatlarından elipsoidal coğrafi koordinatlar (BLh) hesaplanır. iii-) (BLh) den Gauss-Krüger koordinatları ve son olarak da ülke koordinatları (SAĞA,YUKAI) hesaplanır. (XYZ) WGS84 (XYZ) ED50 (BLh) ED50 ( g,x g ) (SAĞA,YUKAI) Ancak ED50 sistemi ile WGS84 sistemi arasında ukarıda anlatıldığı gibi geometrik dönüşüm apmak eterli olmamakta fiziksel etkileri de göz önüne almak gerekmektedir. Diğer bir deişle iki sistem arasında tüm ülke çapında dönüşümü sağlaacak dönüşüm parametreleri bulunamaz. Zira ülke temel nirengi ağının ölçülerinin apıldığı 934 ile 99 ılları arasında ülkemizde çok saıda deprem olmuş ve bu depremler sırasında ata ve düşe konumda 3m e varan konum değişiklikleri olmuş bu nedenle ülke temel nirengi ağında bölgesel ve erel nitelikli bozulmalar olmuştur. Harita Genel Komutanlığı, ED50 sistemi ile WGS84 sistemi arasında datum farklılığının belirlenmesi amacıla ; değişik zamanlarda apılan periodik GPS ölçüleri ardımıla erkabuğu hareketlerinin hızını modellemiş ve datum dönüşümü için 3 x3 sıklığında grid dönüşüm dosası hazırlaıp Nisan 00 tarihi itibarile kullanıma sunmuştur [0]. Örnek-: WGS84 sisteminde kartezen koordinatları (X= Y= Z= ) WGS84 olarak verilen P noktasının, ukarıda verilen dönüşüm parametrelerini kullanarak ED50 sistemindeki kartezen koordinatlarını ve UTM koordinatlarını bulunuz. Çözüm : Noktanın ED50 sisteminde koordinatları X Y Z ED50 t t t X Y Z k Z Y Z k X Y X X. Y k Z WGS 84 dönüşüm eşitliği kullanılırsa; (X= Y= Z= ) ED50 olarak noktanın, ED50 sisteminde koordinatları bulunur. Noktanın UTM koordinatlarını bulmak için önce noktanın ED50 sisteminde elipsoidal coğrafi koordinatları
259 Matematik Jeodezi S.Bektaş (B = 4 o L = 36 o h = 8.874m.) ED50 olarak bulunur. Noktanın UTM koordinatları için önce, noktanın Gauss-Krüger koordinatları; Yg = m Xg = m ( L o = 36 o ) Yg = m Xg = m ( L o = 39 o ) 6 0 lik UTM koordinatları (m 0 = ) DN= INT(L/6)+3 = 37 (D.O.M = 39 o ) SAĞA = (DN)( m 0.Y g ) = m YUKAI = m 0.X g = m 3 0 lik Değiştirilmiş UTM koordinatları (m 0 =.0000 ) (D.O.M = 36 o ) SAĞA = m 0.Y g = m YUKAI = m 0.X g = m Örnek-3: Örnek- deki P noktasının WGS84 sisteminde coğrafi koordinatları (B= 4 o L = 36 o 5.79 h = 7m) WGS84 dır. P noktasının, ED50 sistemindeki coğrafi koordinatlarını bulunuz. Çözüm : Bu problem için Örnek- deki hesaplamalara ugun olarak (BLh) WGS84 (XYZ) WGS84 (XYZ) ED50 (BLh) ED50 sırasında işlem apılırsa; P noktasının ED50 sistemindeki coğrafi koordinatları (B = 4 o L = 36 o h = 8.874m.) ED50 olur GPS YÜKSEKLİKLEİNDEN OTOMETİK YÜKSEKLİKLEİN ELDESİ GPS koordinatlarından elde edilen h ükseklikleri elipsoidal ükseklikler olup pratikte kullanılan H ortometrik üksekliklerinden (deniz seviesinden itibaren ) farklıdır. Bu nedenle her iki ükseklik sistemi arasında geçişin apılabilmesi için o bölgedeki jeoid üksekliklerinin (N) bilinmesi gerekir. Bir P i noktasının üksekliği için h i = H i + N i dönüşüm eşitliği kullanılır.
260 Üç Boutlu Jeodezi ve GPS Geniş çalışma bölgelerinde jeoid ükseklikleri değişim gösterecektir. Ugulamada bu nedenle çalışma bölgesinde jeoid ükseklikleri bilinen noktalardan ararlanarak bir nevi enterpolasonla bölgedeki diğer noktaların jeoid üksekliklerinin bulunması oluna gidilir. Enterpolason işlemi grafik a da saısal olarak apılır. Grafik enterpolason olarak jeoid ükseklikleri bilinen noktalardan ararlanarak eş jeoid ükseklik eğrileri çizilir ve daha sonra jeoid üksekliği belirlenmesi istenen noktalar için çizim üzerinde enterpolason apılır. Saısal olarak jeoid ükseklik belirleme işlemi için bölgedeki jeoid ükseklikleri bilinen noktalardan ararlanarak arazinin saısal jeoid ükseklik modeli oluşturulur ve enterpolason işlemi bu saısal model üzerinden gerçekleştirilir. Saısal jeoid ükseklik modeli belirleme işlemi tüm çalışma bölgesini kapsaacak şekilde apılabileceği gibi çalışma bölgesi parçalara arılarak da apılabilir [5]. Saısal enterpolason öntemleri olarak genelde Multiquadric enterpolason öntemi a da düşük dereceden bir üze fonksionu, örneğin 3.dereceden N(x,)= a x 3 + a 3 + a 3 x + a 4 x + a 5 x + a 6 + a 7 şeklinde bir üze fonksionu kullanılabilir. Dengelemeli olarak belirlenen üze parametreleri ( ukarıdaki üze fonksionunun katsaıları) aracılığıla çalışma bölgesindeki herhangi bir noktanın x, koordinatlarından noktanın jeoid üksekliği hesaplanır. Pratikte, jeoid üksekliklerinin sınırlı bir çalışma bölgesinde değişmediği varsaılır. Dolaısıla elipsoidal ükseklik farkları ortometrik ükseklik farkları olarak değerlendirilir. hij = hj - hi Hj - Hi (Nj Ni) 3
261 Matematik Jeodezi S.Bektaş 4
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
PROF.DR. MURAT DEMİR AYDIN. ***Bu ders notları bir sonraki slaytta verilen kaynak kitaplardan alıntılar yapılarak hazırlanmıştır.
 PO.D. MUAT DEMİ AYDIN ***Bu ders notları bir sonraki slatta verilen kanak kitaplardan alıntılar apılarak hazırlanmıştır. Mühendisler için Vektör Mekaniği: STATİK.P. Beer, E.. Johnston Çeviri Editörü: Ömer
PO.D. MUAT DEMİ AYDIN ***Bu ders notları bir sonraki slatta verilen kanak kitaplardan alıntılar apılarak hazırlanmıştır. Mühendisler için Vektör Mekaniği: STATİK.P. Beer, E.. Johnston Çeviri Editörü: Ömer
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları. KUVVET SİSTEMLERİ - İki Boutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları. KUVVET SİSTEMLERİ - İki Boutlu
VEKTÖRLER KT YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
JEOİD ve JEOİD BELİRLEME
 JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
TOPOĞRAFYA. Ölçme Bilgisinin Konusu
 TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
Vektörler. Skaler büyüklükler. Vektörlerin 2 ve 3 boyutta gösterimi. Vektörel büyüklükler. 1. Şekil I de A vektörü gösterilmiştir.
 1 Vektörler Skaler büüklükler 1. de A vektörü gösterilmiştir. Özellikler: Sadece büüklüğü (şiddeti) vardır. Negatif olabilir. Skaler fiziksel büüklüklerin birimi vardır. Örnekler: Zaman Kütle Hacim Özkütle
1 Vektörler Skaler büüklükler 1. de A vektörü gösterilmiştir. Özellikler: Sadece büüklüğü (şiddeti) vardır. Negatif olabilir. Skaler fiziksel büüklüklerin birimi vardır. Örnekler: Zaman Kütle Hacim Özkütle
Harita Projeksiyonları ve Koordinat Sistemleri. Doç. Dr. Senem KOZAMAN
 Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
AVRASYA ÜNİVERSİTESİ
 Ders Tanıtım Formu Dersin Adı Öğretim Dili MATEMATİK JEODEZİ Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x) Uzaktan Öğretim(
Ders Tanıtım Formu Dersin Adı Öğretim Dili MATEMATİK JEODEZİ Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x) Uzaktan Öğretim(
2. İKİ BOYUTLU MATEMATİKSEL MODELLER
 . İKİ BOYULU MAEMAİKSEL MODELLER.. Genel Bilgiler Şimdi konform dönüşüm teknikleri ile çözülebilen kararlı durum ısı akışı elektrostatik ve ideal sıvı akışı ile ilgili problemleri göz önüne alacağız. Konform
. İKİ BOYULU MAEMAİKSEL MODELLER.. Genel Bilgiler Şimdi konform dönüşüm teknikleri ile çözülebilen kararlı durum ısı akışı elektrostatik ve ideal sıvı akışı ile ilgili problemleri göz önüne alacağız. Konform
Harita Projeksiyonları
 Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Chapter 1 İçindekiler
 Chapter 1 İçindekiler Kendinizi Test Edin iii 10 Birinci Mertebeden Diferansiel Denklemler 565 10.1 Arılabilir Denklemler 566 10. Lineer Denklemler 571 10.3 Matematiksel Modeller 576 10.4 Çözümü Olmaan
Chapter 1 İçindekiler Kendinizi Test Edin iii 10 Birinci Mertebeden Diferansiel Denklemler 565 10.1 Arılabilir Denklemler 566 10. Lineer Denklemler 571 10.3 Matematiksel Modeller 576 10.4 Çözümü Olmaan
Fizik 101: Ders 3 Ajanda
 Anlamlı Saılar Fizik 101: Ders 3 Ajanda Tekrar: Vektörler, 2 ve 3D düzgün doğrusal hareket Rölatif hareket ve gözlem çerçeveleri Düzgün dairesel hareket Vektörler (tekrar) Vektör (Türkçe) ; Vektör (Almanca)
Anlamlı Saılar Fizik 101: Ders 3 Ajanda Tekrar: Vektörler, 2 ve 3D düzgün doğrusal hareket Rölatif hareket ve gözlem çerçeveleri Düzgün dairesel hareket Vektörler (tekrar) Vektör (Türkçe) ; Vektör (Almanca)
Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları
 JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
İÇİNDEKİLER UZAY AKSİYOMLARI... 001-006... 01-03 UZAYDA DOGRU VE DÜZLEMLER... 007-010... 04-05 DİK İZDÜŞÜM... 011-014... 06-07
 UZY GEMETRİ İÇİNDEKİLER Safa No Test No UZY KSİYMLRI... 001-00... 01-0 UZYD DGRU VE DÜZLEMLER... 007-010... 0-05 DİK İZDÜŞÜM... 011-01... 0-07 PRİZMLR... 015-0... 08-1 KÜP... 05-00... 1-15 SİLİNDİR...
UZY GEMETRİ İÇİNDEKİLER Safa No Test No UZY KSİYMLRI... 001-00... 01-0 UZYD DGRU VE DÜZLEMLER... 007-010... 0-05 DİK İZDÜŞÜM... 011-01... 0-07 PRİZMLR... 015-0... 08-1 KÜP... 05-00... 1-15 SİLİNDİR...
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Quartic Authalic Projeksiyonu ve Bir Bilgisayar Programı: Pseudo
 Harita Teknolojileri Elektronik Dergisi Cilt: 1, No:, 009 (10-19) Electronic Journal of Map Technologies Vol: 1, No:, 009 (10-19) TEKNOLOJİK ARAŞTIRMALAR www.teknolojikarastirmalar.com e-issn:1309-3983
Harita Teknolojileri Elektronik Dergisi Cilt: 1, No:, 009 (10-19) Electronic Journal of Map Technologies Vol: 1, No:, 009 (10-19) TEKNOLOJİK ARAŞTIRMALAR www.teknolojikarastirmalar.com e-issn:1309-3983
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU. Yrd. Doç. Dr. Hüseyin KEMALDERE
 JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
UYGULAMALI DİFERANSİYEL DENKLEMLER
 UYGULAMALI DİFERANSİYEL DENKLEMLER GİRİŞ Birçok mühendislik, fizik ve sosal kökenli problemler matematik terimleri ile ifade edildiği zaman bu problemler, bilinmeen fonksionun bir vea daha üksek mertebeden
UYGULAMALI DİFERANSİYEL DENKLEMLER GİRİŞ Birçok mühendislik, fizik ve sosal kökenli problemler matematik terimleri ile ifade edildiği zaman bu problemler, bilinmeen fonksionun bir vea daha üksek mertebeden
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
Küre Küre Üzerinde Hesap. Ders Sorumlusu Prof. Dr. Mualla YALÇINKAYA 2018
 Küre Küre Üzerinde Hesap Ders Sorumlusu Prof. Dr. Mualla YALÇINKAYA 2018 Küre ve Küre ile İlgili Tanımlar Küre: «Merkez» adı verilen bir noktaya eşit uzaklıktaki noktaların bir araya getirilmesiyle, ya
Küre Küre Üzerinde Hesap Ders Sorumlusu Prof. Dr. Mualla YALÇINKAYA 2018 Küre ve Küre ile İlgili Tanımlar Küre: «Merkez» adı verilen bir noktaya eşit uzaklıktaki noktaların bir araya getirilmesiyle, ya
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
2.2 Bazıözel fonksiyonlar
 . Bazıözel fonksionlar Kuvvet fonksionu, polinomlar ve rasonel fonksionlar, mutlak değer ve tam değer fonksionları, pratik grafik çizimleri. 1-) Lineer fonksionlar: m ve n sabit saılar olmak üzere f()
. Bazıözel fonksionlar Kuvvet fonksionu, polinomlar ve rasonel fonksionlar, mutlak değer ve tam değer fonksionları, pratik grafik çizimleri. 1-) Lineer fonksionlar: m ve n sabit saılar olmak üzere f()
JEODEZİK ÖLÇMELER DERSİ. Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE
 JEODEZİK ÖLÇMELER DERSİ Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM 1. Hafta Ders Notları REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM Referans (Koordinat)
JEODEZİK ÖLÇMELER DERSİ Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM 1. Hafta Ders Notları REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM Referans (Koordinat)
Taşkın, Çetin, Abdullayeva
 BÖLÜM Taşkın, Çetin, Abdullaeva FONKSİYONLAR.. FONKSİYON KAVRAMI Tanım : A ve B boş olmaan iki küme a A ve b B olmak üzere ( ab, ) sıralı eleman çiftine sıralı ikili denir. ( ab, ) sıralı ikilisinde a
BÖLÜM Taşkın, Çetin, Abdullaeva FONKSİYONLAR.. FONKSİYON KAVRAMI Tanım : A ve B boş olmaan iki küme a A ve b B olmak üzere ( ab, ) sıralı eleman çiftine sıralı ikili denir. ( ab, ) sıralı ikilisinde a
z z Genel yükleme durumunda, bir Q noktasını üç boyutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni
 GERİLME VE ŞEKİL DEĞİŞTİRME DÖNÜŞÜM BAĞINTILARI Q z Genel ükleme durumunda, bir Q noktasını üç boutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni gösterilebilir: σ, σ, σ z, τ, τ z, τ z.
GERİLME VE ŞEKİL DEĞİŞTİRME DÖNÜŞÜM BAĞINTILARI Q z Genel ükleme durumunda, bir Q noktasını üç boutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni gösterilebilir: σ, σ, σ z, τ, τ z, τ z.
NÜMERİK ANALİZ. Sayısal Yöntemlerin Konusu. Sayısal Yöntemler Neden Kullanılır?!! Denklem Çözümleri
 Saısal Yöntemler Neden Kullanılır?!! NÜMERİK ANALİZ Saısal Yöntemlere Giriş Yrd. Doç. Dr. Hatice ÇITAKOĞLU 2016 Günümüzde ortaa konan problemlerin bazılarının analitik çözümleri apılamamaktadır. Analitik
Saısal Yöntemler Neden Kullanılır?!! NÜMERİK ANALİZ Saısal Yöntemlere Giriş Yrd. Doç. Dr. Hatice ÇITAKOĞLU 2016 Günümüzde ortaa konan problemlerin bazılarının analitik çözümleri apılamamaktadır. Analitik
Bilginin Görselleştirilmesi
 Bilginin Görselleştirilmesi Bundan önceki konularımızda serbest halde azılmış metinlerde gerek duduğumuz bilginin varlığının işlenmee, karşılaştırmaa ve değerlendirmee atkın olmadığını, bu nedenle bilginin
Bilginin Görselleştirilmesi Bundan önceki konularımızda serbest halde azılmış metinlerde gerek duduğumuz bilginin varlığının işlenmee, karşılaştırmaa ve değerlendirmee atkın olmadığını, bu nedenle bilginin
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
HARİTA PROJEKSİYONLARI
 1 HARİTA PROJEKSİYONLARI Haritacılık mesleğinin faaliyetlerinden birisi, yeryüzünün bütününün ya da bir parçasının haritasını yapmaktır. Harita denilen şey ise, basit anlamıyla, kapsadığı alandaki çeşitli
1 HARİTA PROJEKSİYONLARI Haritacılık mesleğinin faaliyetlerinden birisi, yeryüzünün bütününün ya da bir parçasının haritasını yapmaktır. Harita denilen şey ise, basit anlamıyla, kapsadığı alandaki çeşitli
EĞİM, BİR DOĞRUNUN DENKLEMİ VE EĞİMİ ARASINDAKİ İLİŞKİ
 Özgür EKER EĞİM, BİR DOĞRUNUN DENKLEMİ VE EĞİMİ ARASINDAKİ İLİŞKİ Eğim: ETKİNLİK : Bir bisiklet arışındaki iki farklı parkur aşağıdaki gibidir. I. parkurda KL 00 metre ve II. parkurda AB 00 metre olduğuna
Özgür EKER EĞİM, BİR DOĞRUNUN DENKLEMİ VE EĞİMİ ARASINDAKİ İLİŞKİ Eğim: ETKİNLİK : Bir bisiklet arışındaki iki farklı parkur aşağıdaki gibidir. I. parkurda KL 00 metre ve II. parkurda AB 00 metre olduğuna
Bölümün İçeriği ve Amacı:
 ölümün İçeriği ve macı: Koordinat Sistemleri Vektör ve Skaler Nicelikleri Vektörlerin azı Özellikleri ir Vektörün ileşenleri ve irim Vektörler ölüm 3: Vektörler Vektör kavramının fizikteki önemi ve gerekliliğini
ölümün İçeriği ve macı: Koordinat Sistemleri Vektör ve Skaler Nicelikleri Vektörlerin azı Özellikleri ir Vektörün ileşenleri ve irim Vektörler ölüm 3: Vektörler Vektör kavramının fizikteki önemi ve gerekliliğini
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.
![T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir. T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.](/thumbs/55/35591809.jpg) * = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
* = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
TÜRKİYE GENELİ DENEME SINAVI LYS - 1 MATEMATİK
 TÜRKİY GNLİ SINVI LYS - 1 7 MYIS 017 LYS 1 - TSTİ 1. u testte 80 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için arılan kısmına işaretleiniz. + k+ n 15 + 10 1. : = + 6 16 + 8 0 + 8 olduğuna
TÜRKİY GNLİ SINVI LYS - 1 7 MYIS 017 LYS 1 - TSTİ 1. u testte 80 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için arılan kısmına işaretleiniz. + k+ n 15 + 10 1. : = + 6 16 + 8 0 + 8 olduğuna
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON
 JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
Gerilme Dönüşümü. Bölüm Hedefleri
 Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
HAREKET HAREKET KUVVET İLİŞKİSİ
 HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
Uygulamada Gauss-Kruger Projeksiyonu
 JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI
 ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
LYS GENEL KATILIMLI TÜRKİYE GENELİ ONLİNE DENEME SINAVI
 LYS GNL KTILIMLI TÜRKİY GNLİ NLİN NM SINVI GMTRİ (M-TM) 1. u testte Geometri ile ilgili 30 soru vardır.. evaplarınızı, cevap kâğıdının Geometri Testi için arılan kısmına işaretleiniz. 3. u test için süreniz
LYS GNL KTILIMLI TÜRKİY GNLİ NLİN NM SINVI GMTRİ (M-TM) 1. u testte Geometri ile ilgili 30 soru vardır.. evaplarınızı, cevap kâğıdının Geometri Testi için arılan kısmına işaretleiniz. 3. u test için süreniz
ÖLÇME BİLGİSİ. PDF created with FinePrint pdffactory trial version http://www.fineprint.com. Tanım
 ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
- 2-1 0 1 2 + 4a a 0 a 4a
 İKİNCİ DERECEDEN FNKSİYNLARIN GRAFİKLERİ a,b,c,z R ve a 0 olmak üzere, F : R R f() = a + b + c şeklinde tanımlanan fonksionlara ikinci dereceden bir değişkenli fonksionlar denir. Bu tür fonksionların grafikleri
İKİNCİ DERECEDEN FNKSİYNLARIN GRAFİKLERİ a,b,c,z R ve a 0 olmak üzere, F : R R f() = a + b + c şeklinde tanımlanan fonksionlara ikinci dereceden bir değişkenli fonksionlar denir. Bu tür fonksionların grafikleri
BÖLÜM 2 AKIŞKANLARIN STATİĞİ (HİDROSTATİK)
 BÖLÜM AKIŞKANLARIN STATİĞİ (HİDROSTATİK) Hidrostatik duran akışkanlar ile üniform olarak hareket eden ( akışkanın hızının her erde anı olduğu ) akışkanların durumunu inceler. 1 BİR NOKTADAKİ BASINÇ Hidrostatik
BÖLÜM AKIŞKANLARIN STATİĞİ (HİDROSTATİK) Hidrostatik duran akışkanlar ile üniform olarak hareket eden ( akışkanın hızının her erde anı olduğu ) akışkanların durumunu inceler. 1 BİR NOKTADAKİ BASINÇ Hidrostatik
MESLEKİ HESAPLAMALAR
 MESLEKİ HESAPLAMALAR Jeodezi: Yer yuvarı şekil, boyut ve granite alanı ile zamana bağlı değişmelerin üç boyutlu bir koordinat sisteminde tanımlanmasını amaçlayan bir bilim dalıdır. Jeodezinin Bilimsel
MESLEKİ HESAPLAMALAR Jeodezi: Yer yuvarı şekil, boyut ve granite alanı ile zamana bağlı değişmelerin üç boyutlu bir koordinat sisteminde tanımlanmasını amaçlayan bir bilim dalıdır. Jeodezinin Bilimsel
31.10.2014. CEV 361 CBS ve UA. Koordinat ve Projeksiyon Sistemleri. Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli
 CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714 km
CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714 km
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ
 DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için arılan
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için arılan
BİRİM ŞEKİLDEĞİŞTİRME DÖNÜŞÜMÜ
 BİRİM ŞEKİLDEĞİŞTİRME DÖNÜŞÜMÜ DÜZLEM-BİRİM ŞEKİLDEĞİŞTİRME 3D durumda, bir noktadaki birim şekil değiştirme durumu 3 normal birim şekildeğiştirme bileşeni,, z, ve 3 kesme birim şekildeğiştirme bileşeninden,
BİRİM ŞEKİLDEĞİŞTİRME DÖNÜŞÜMÜ DÜZLEM-BİRİM ŞEKİLDEĞİŞTİRME 3D durumda, bir noktadaki birim şekil değiştirme durumu 3 normal birim şekildeğiştirme bileşeni,, z, ve 3 kesme birim şekildeğiştirme bileşeninden,
MECHANICS OF MATERIALS
 00 The McGraw-Hill Companies, Inc. All rights reserved. T E CHAPTER 7 Gerilme MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Dönüşümleri Fatih Alibeoğlu 00 The McGraw-Hill
00 The McGraw-Hill Companies, Inc. All rights reserved. T E CHAPTER 7 Gerilme MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Dönüşümleri Fatih Alibeoğlu 00 The McGraw-Hill
BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI
 36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
TÜREVİN GEOMETRİK YORUMU
 TÜREVİN GEOMETRİK YORUMU f :R R, =f ( fonksionuna düzlemde A karşılık gelen f( +h eğri anda ki =f( P gibi olsun. f( Eğrinin P(,f( noktasındaki teğetlerini +h araştıralım. Bunun için P(,f( noktasının sağıda
TÜREVİN GEOMETRİK YORUMU f :R R, =f ( fonksionuna düzlemde A karşılık gelen f( +h eğri anda ki =f( P gibi olsun. f( Eğrinin P(,f( noktasındaki teğetlerini +h araştıralım. Bunun için P(,f( noktasının sağıda
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir.
 STATIK VE MUKAVEMET 4. Ağırlık Merkezi AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük bir alana etki eden birbirlerine
STATIK VE MUKAVEMET 4. Ağırlık Merkezi AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük bir alana etki eden birbirlerine
CEV 361 CBS ve UA. Koordinat ve Projeksiyon Sistemleri. Yrd. Doç. Dr. Özgür ZEYDAN Yerin Şekli
 CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Yrd. Doç. Dr. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714
CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Yrd. Doç. Dr. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
12. SINIF. Fonksiyonlar - 1 TEST. 1. kx + 6 fonksiyonu sabit fonksiyon olduğuna göre aşağıdakilerden hangisidir? k. = 1 olduğuna göre k. kaçtır?
 . SINIF M Fonksionlar. f ( + a ) + vef( ) 7 olduğuna göre a kaçtır? E) TEST. f ( ) k + 6 fonksionu sabit fonksion olduğuna f ( ) göre aşağıdakilerden k E). f( ) 6 k ve f ( ) olduğuna göre k kaçtır? E)
. SINIF M Fonksionlar. f ( + a ) + vef( ) 7 olduğuna göre a kaçtır? E) TEST. f ( ) k + 6 fonksionu sabit fonksion olduğuna f ( ) göre aşağıdakilerden k E). f( ) 6 k ve f ( ) olduğuna göre k kaçtır? E)
BÖLÜM 3: MATEMATİKSEL KARTOGRAFYA - TANIMLAR
 BÖLÜM 3: MATEMATİKEL KARTOGRAFYA - TANIMLAR Türkay Gökgöz (www.yildiz.edu.tr/~gokgoz) 3 İÇİNDEKİLER 3. Bir Haritanın Matematiksel Çatısı... 3-3 3.. Ölçek. 3-3 3... Kesir ölçek 3-3 3... Grafik ölçek.. 3-4
BÖLÜM 3: MATEMATİKEL KARTOGRAFYA - TANIMLAR Türkay Gökgöz (www.yildiz.edu.tr/~gokgoz) 3 İÇİNDEKİLER 3. Bir Haritanın Matematiksel Çatısı... 3-3 3.. Ölçek. 3-3 3... Kesir ölçek 3-3 3... Grafik ölçek.. 3-4
1998 ÖYS. 1. Üç basamaklı bir x doğal sayısının 7. iki basamaklı bir y doğal sayısına eşittir. Buna göre, y doğal sayısı en az kaç olabilir?
 99 ÖYS. Üç basamaklı bir doğal saısının 7 katı, iki basamaklı bir doğal saısına eşittir. Buna göre, doğal saısı en az kaç olabilir? A) B) C) 6. Bugünkü aşları 6 ve ile orantılı olan iki kardeşin 6 ıl sonraki
99 ÖYS. Üç basamaklı bir doğal saısının 7 katı, iki basamaklı bir doğal saısına eşittir. Buna göre, doğal saısı en az kaç olabilir? A) B) C) 6. Bugünkü aşları 6 ve ile orantılı olan iki kardeşin 6 ıl sonraki
MATEMATİK MATEMATİK-GEOMETRİ SINAVI LİSANS YERLEŞTİRME SINAVI-1 TESTİ SORU KİTAPÇIĞI 08
 LİSNS YRLŞTİRM SINVI- MTMTİK-GMTRİ SINVI MTMTİK TSTİ SRU KİTPÇIĞI 08 U SRU KİTPÇIĞI LYS- MTMTİK TSTİ SRULRINI İÇRMKTİR. . u testte 0 soru vardýr. MTMTİK TSTİ. evaplarýnýzý, cevap kâðýdýnın Matematik Testi
LİSNS YRLŞTİRM SINVI- MTMTİK-GMTRİ SINVI MTMTİK TSTİ SRU KİTPÇIĞI 08 U SRU KİTPÇIĞI LYS- MTMTİK TSTİ SRULRINI İÇRMKTİR. . u testte 0 soru vardýr. MTMTİK TSTİ. evaplarýnýzý, cevap kâðýdýnın Matematik Testi
Düzlem Elektromanyetik Dalgalar
 Düzlem Elektromanetik Dalgalar Düzgün Düzlem Dalga: E nin, (benzer şekilde H nin) aılma önüne dik sonsuz düzlemlerde, anı öne, anı genliğe ve anı faza sahip olduğu özel bir Maxwell denklemleri çözümüdür.
Düzlem Elektromanetik Dalgalar Düzgün Düzlem Dalga: E nin, (benzer şekilde H nin) aılma önüne dik sonsuz düzlemlerde, anı öne, anı genliğe ve anı faza sahip olduğu özel bir Maxwell denklemleri çözümüdür.
9. SINIF Geometri TEMEL GEOMETRİK KAVRAMLAR
 TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
1- AYNALI STEREOSKOP UYGULAMASI. X (Uçuş Doğrultusu) H1 H1. 1. resim (sol) 2. resim (sağ) KARTON ÜZERİNDEKİ İŞLEMLER D 1 D 2
 - YNLI STEREOSKO UYGULMSI KRTON ÜZERİNDEKİ İŞLEMLER D D 70 cm 6 cm X (Uçuş Doğrultusu) 00 cm Yukardaki bilgiler karton üzerine çizilir. Kartonun sağ alt köşesine çalışan kişilerin no-adı soadı, resim numaraları,
- YNLI STEREOSKO UYGULMSI KRTON ÜZERİNDEKİ İŞLEMLER D D 70 cm 6 cm X (Uçuş Doğrultusu) 00 cm Yukardaki bilgiler karton üzerine çizilir. Kartonun sağ alt köşesine çalışan kişilerin no-adı soadı, resim numaraları,
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
Saf Eğilme (Pure Bending)
 Saf Eğilme (Pure Bending) Bu bölümde, doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki deformasonları incelenecek. Burada çıkarılacak formüller, en kesiti an az bir eksene göre simetrik
Saf Eğilme (Pure Bending) Bu bölümde, doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki deformasonları incelenecek. Burada çıkarılacak formüller, en kesiti an az bir eksene göre simetrik
KOÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) Bölümleri MÜH 110 Statik Dersi - 1. Çalışma Soruları 03 Mart 2017
 KÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) ölümleri SRU-1) Mühendislik apılarında kullanılan elemanlar için KSN (Tarafsız eksen) kavramını tanımlaınız ve bir kroki şekil çizerek
KÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) ölümleri SRU-1) Mühendislik apılarında kullanılan elemanlar için KSN (Tarafsız eksen) kavramını tanımlaınız ve bir kroki şekil çizerek
Hakan AKÇIN* SUNU Ali ihsan ŞEKERTEKİN
 AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl
![NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl](/thumbs/70/62427826.jpg) NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm lan Örnek 0 nalitik düzlemde ( 0 c h b h a h c b ( 0 ( 0 a a h b h a b c h lan( = = = c Yukarıdaki verilenlere göre lan( kaç birimkaredir? 6 8 9 E c b Taban:
NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm lan Örnek 0 nalitik düzlemde ( 0 c h b h a h c b ( 0 ( 0 a a h b h a b c h lan( = = = c Yukarıdaki verilenlere göre lan( kaç birimkaredir? 6 8 9 E c b Taban:
DERS 2. Fonksiyonlar
 DERS Fonksionlar.1. Fonksion Kavramı. Her bilim dalının önemli bir işlevi, çeşitli nesneler vea büüklükler arasında eşlemeler kurmaktır. Böle bir eşleme kurulması tahmin ürütme olanağı verir. Örneğin,
DERS Fonksionlar.1. Fonksion Kavramı. Her bilim dalının önemli bir işlevi, çeşitli nesneler vea büüklükler arasında eşlemeler kurmaktır. Böle bir eşleme kurulması tahmin ürütme olanağı verir. Örneğin,
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER. Yatay bir düzlem yüzeye gelen hidrostatik kuvvetin büyüklüğünü ve etkime noktasını bulmak istiyoruz.
 BTMIŞ YÜZEYLERE ELEN HİDROSTTİK KUVVETLER DÜZLEM YÜZEYLER Yata Yüeler Sıvı üei Yata bir dülem üee gelen idrostatik kuvvetin büüklüğünü ve etkime noktasını bulmak istioru. d d Kuvvetin Büüklüğü :Şekil deki
BTMIŞ YÜZEYLERE ELEN HİDROSTTİK KUVVETLER DÜZLEM YÜZEYLER Yata Yüeler Sıvı üei Yata bir dülem üee gelen idrostatik kuvvetin büüklüğünü ve etkime noktasını bulmak istioru. d d Kuvvetin Büüklüğü :Şekil deki
1996 ÖYS. 2 nin 2 fazlası kız. 1. Bir sınıftaki örencilerin 5. örencidir. Sınıfta 22 erkek öğrenci olduğuna göre, kız öğrencilerin sayısı kaçtır?
 996 ÖYS. Bir sınıftaki örencilerin nin fazlası kız örencidir. Sınıfta erkek öğrenci olduğuna göre, kız öğrencilerin saısı kaçtır? 8 C) 6 D) E) 6. Saatteki hızı V olan bir hareketti A ve B arasındaki olu
996 ÖYS. Bir sınıftaki örencilerin nin fazlası kız örencidir. Sınıfta erkek öğrenci olduğuna göre, kız öğrencilerin saısı kaçtır? 8 C) 6 D) E) 6. Saatteki hızı V olan bir hareketti A ve B arasındaki olu
BÖLÜM 24 TÜREV VE UYGULAMALARI TÜREV VE UYGULAMALARI TÜREV VE UYGULAMALARI
 TÜREV VE UYGULAMALARI TÜREV VE UYGULAMALARI YILLAR 966 967 968 969 97 97 97 975 976 977 978 980 98 98 98 98 985 986 987 988 989 990 99 99 99 99 995 996 997 998 006 007 ÖSS / ÖSS-I ÖYS / ÖSS-II 5 6 6 5
TÜREV VE UYGULAMALARI TÜREV VE UYGULAMALARI YILLAR 966 967 968 969 97 97 97 975 976 977 978 980 98 98 98 98 985 986 987 988 989 990 99 99 99 99 995 996 997 998 006 007 ÖSS / ÖSS-I ÖYS / ÖSS-II 5 6 6 5
MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI
 MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI SORU 1. Köşeleri (1,4) (3,0) (7,2) noktaları olan ABC üçgeninin bir ikizkenar dik üçgen (İpucu:, ve vektörlerinden yararlanın) SORU 2. Bir ABC üçgeninin
MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI SORU 1. Köşeleri (1,4) (3,0) (7,2) noktaları olan ABC üçgeninin bir ikizkenar dik üçgen (İpucu:, ve vektörlerinden yararlanın) SORU 2. Bir ABC üçgeninin
6 II. DERECEDEN FONKSÝYONLAR 2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK. y f(x) f(x)
 6 II. DERECEDEN FNKSÝYNLR (Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MTEMTÝK 1. f(). f() 6 8 T Yukarıda grafiği verilen = f() parabolünün denklemi nedir?( = 6) Yukarıda grafiği verilen
6 II. DERECEDEN FNKSÝYNLR (Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MTEMTÝK 1. f(). f() 6 8 T Yukarıda grafiği verilen = f() parabolünün denklemi nedir?( = 6) Yukarıda grafiği verilen
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (2. Hafta)
 AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Konikler ÜNİTE. Amaçlar. İçindekiler. Yazar Doç.Dr. Hüseyin AZCAN
 Konikler Yazar Doç.Dr. Hüsein AZCAN ÜNİTE 7 Amaçlar Bu ünitei çalıştıktan sonra; lise ıllarından da tanıdığınız çember, elips, parabol ve hiperbol gibi konik kesitleri olarak adlandırılan geometrik nesneleri
Konikler Yazar Doç.Dr. Hüsein AZCAN ÜNİTE 7 Amaçlar Bu ünitei çalıştıktan sonra; lise ıllarından da tanıdığınız çember, elips, parabol ve hiperbol gibi konik kesitleri olarak adlandırılan geometrik nesneleri
HARİTA. Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir.
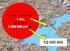 HARİTA BİLGİSİ HARİTA Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir. ÇEŞİTLİ ÖLÇEKLİ HARİTALARIN NUMARALANMA SİSTEMİ
HARİTA BİLGİSİ HARİTA Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir. ÇEŞİTLİ ÖLÇEKLİ HARİTALARIN NUMARALANMA SİSTEMİ
Alan Hesapları. Şekil 14. Üç kenarı belli üçgen alanı
 lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
KUVVET SORULAR. Şekil-II 1.) 3.)
 UET SRULAR 1.) 3.) X Y Z X, Y ve Z noktasal cisimlerine ata düzlemde etki eden kuvvetler şekildeki gibidir. Bu cisimlere etkien net kuvvetlerin büüklükleri F X, F ve F z dir. Noktasal parçacığı sürtünmesiz
UET SRULAR 1.) 3.) X Y Z X, Y ve Z noktasal cisimlerine ata düzlemde etki eden kuvvetler şekildeki gibidir. Bu cisimlere etkien net kuvvetlerin büüklükleri F X, F ve F z dir. Noktasal parçacığı sürtünmesiz
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki outlu Kuvvet
Statik Ders Notları Sınav Soru ve Çözümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki outlu Kuvvet
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Kuadratik Yüzeyler Uzayda İkinci Dereceden Yüzeyler
 İÇİNDEKİLER Kuadratik Yüeler Uada İkinci Dereceden Yüeler 1 0.1. Elipsoid 2 0.2. Hiperboloid 4 0.2.1. Tek Kanatlı Hiperboloid 4 0.2.2. Çift Kanatlı Hiperboloid 4 0.3. Paraboloid 5 0.3.1. Eliptik Paraboloid
İÇİNDEKİLER Kuadratik Yüeler Uada İkinci Dereceden Yüeler 1 0.1. Elipsoid 2 0.2. Hiperboloid 4 0.2.1. Tek Kanatlı Hiperboloid 4 0.2.2. Çift Kanatlı Hiperboloid 4 0.3. Paraboloid 5 0.3.1. Eliptik Paraboloid
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik ers Notları Sınav Soru ve Çözümleri ĞHN MÜHENİSİK MEKNİĞİ STTİK MÜHENİSİK MEKNİĞİ STTİK İÇİNEKİER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMERİ - İki Boutlu Kuvvet Sistemleri
Statik ers Notları Sınav Soru ve Çözümleri ĞHN MÜHENİSİK MEKNİĞİ STTİK MÜHENİSİK MEKNİĞİ STTİK İÇİNEKİER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMERİ - İki Boutlu Kuvvet Sistemleri
AKIŞKANLAR MEKANİĞİ 1. YILİÇİ SINAVI ( )
 1 3 4 5 6 T AKIŞKANLAR MEKANİĞİ 1. YILİÇİ SINAVI (13.11.008) Ad-Soad: No: Grup: 1) a) İdeal ve gerçek akışkan nedir? Hız dağılımlarını çiziniz. Pratikte ideal akışkan var mıdır? Açıklaınız. İdeal Akışkan;
1 3 4 5 6 T AKIŞKANLAR MEKANİĞİ 1. YILİÇİ SINAVI (13.11.008) Ad-Soad: No: Grup: 1) a) İdeal ve gerçek akışkan nedir? Hız dağılımlarını çiziniz. Pratikte ideal akışkan var mıdır? Açıklaınız. İdeal Akışkan;
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
ANALİZ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI
 ÖABT ANALİZ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI Yasin ŞAHİN ÖABT ANALİZ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI Her hakkı saklıdır. Bu kitabın tamamı a da bir kısmı, azarın izni olmaksızın, elektronik, mekanik,
ÖABT ANALİZ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI Yasin ŞAHİN ÖABT ANALİZ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI Her hakkı saklıdır. Bu kitabın tamamı a da bir kısmı, azarın izni olmaksızın, elektronik, mekanik,
STATİK VE MUKAVEMET AĞIRLIK MERKEZİ. Öğr.Gör. Gültekin BÜYÜKŞENGÜR. Çevre Mühendisliği
 STATİK VE MUKAVEMET AĞIRLIK MERKEZİ Öğr.Gör. Gültekin BÜYÜKŞENGÜR Çevre Mühendisliği STATİK Ağırlık Merkezi Örnek Sorular 2 Değişmeyen madde miktarına kütle denir. Diğer bir anlamda cismin hacmini dolduran
STATİK VE MUKAVEMET AĞIRLIK MERKEZİ Öğr.Gör. Gültekin BÜYÜKŞENGÜR Çevre Mühendisliği STATİK Ağırlık Merkezi Örnek Sorular 2 Değişmeyen madde miktarına kütle denir. Diğer bir anlamda cismin hacmini dolduran
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
PARABOL. çözüm. kavrama sorusu. çözüm. kavrama sorusu
 PARABL Bu bölümde birinci dereceden fonksion =f()=a+b ve ikinci dereceden fonksion =f()=a +b+c grafiklerini üzesel olarak inceleeceğiz. f()=a +b+c ikinci dereceden bir bilinmeenli polinom fonksionun grafiği
PARABL Bu bölümde birinci dereceden fonksion =f()=a+b ve ikinci dereceden fonksion =f()=a +b+c grafiklerini üzesel olarak inceleeceğiz. f()=a +b+c ikinci dereceden bir bilinmeenli polinom fonksionun grafiği
Fotogrametride işlem adımları
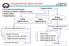 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
ÜNİTE. MATEMATİK-1 Prof.Dr.Murat ÖZDEMİR İÇİNDEKİLER HEDEFLER GRAFİK ÇİZİMİ. Simetri ve Asimtot Bir Fonksiyonun Grafiği
 HEDEFLER İÇİNDEKİLER GRAFİK ÇİZİMİ Simetri ve Asimtot Bir Fonksionun Grafiği MATEMATİK-1 Prof.Dr.Murat ÖZDEMİR Bu ünitei çalıştıktan sonra; Fonksionun simetrik olup olmadığını belirleebilecek, Fonksionun
HEDEFLER İÇİNDEKİLER GRAFİK ÇİZİMİ Simetri ve Asimtot Bir Fonksionun Grafiği MATEMATİK-1 Prof.Dr.Murat ÖZDEMİR Bu ünitei çalıştıktan sonra; Fonksionun simetrik olup olmadığını belirleebilecek, Fonksionun
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
NOKTANIN ANALİTİK İNCELEMESİ NOKTANIN ANALİTİK İNCELEMESİ
 NKTANIN ANALİTİK İNCELEMESİ NKTANIN ANALİTİK İNCELEMESİ Başlangıç noktasında birbirine dik olan iki saı doğrusunun oluşturduğu sisteme "Dik Koordinat Sistemi" denir. Dik Koordinat Sisteminin belirttiği
NKTANIN ANALİTİK İNCELEMESİ NKTANIN ANALİTİK İNCELEMESİ Başlangıç noktasında birbirine dik olan iki saı doğrusunun oluşturduğu sisteme "Dik Koordinat Sistemi" denir. Dik Koordinat Sisteminin belirttiği
BÖLÜM V BİRİNCİ MERTEBEDEN DİFERANSİYEL DENKLEMLERİN UYGULAMALARI
 96 BÖLÜM V BİRİNCİ MERTEBEDEN DİFERANSİYEL DENKLEMLERİN UYGULAMALARI Bu bölümde birinci mertebeden diferansiel denklemlerin geometrik ve fiziksel ugulamalarına er verilmiştir. Diferansiel denklemler, geometrik
96 BÖLÜM V BİRİNCİ MERTEBEDEN DİFERANSİYEL DENKLEMLERİN UYGULAMALARI Bu bölümde birinci mertebeden diferansiel denklemlerin geometrik ve fiziksel ugulamalarına er verilmiştir. Diferansiel denklemler, geometrik
