ODAKLANAN KÜBİK, ODAKLANAN KUİNTİK ORTAMDA PT-SİMETRİSİNE SAHİP KAFESLER ÜZERİNDE NLS DENKLEMİNİN TEMEL SOLİTON ÇÖZÜMLERİ
|
|
|
- Bercu Özel
- 6 yıl önce
- İzleme sayısı:
Transkript
1 XIX. ULUSAL MEKANİK KONGRESİ Ağustos 2015, Karadeniz Teknik Üniversitesi, Trabzon ODAKLANAN KÜBİK, ODAKLANAN KUİNTİK ORTAMDA PT-SİMETRİSİNE SAHİP KAFESLER ÜZERİNDE NLS DENKLEMİNİN TEMEL SOLİTON ÇÖZÜMLERİ İzzet Göksel 1, Nalan Antar 2 ve İlkay Bakırtaş 3 1,2,3 İTÜ Matematik Mühendisliği Bölümü, İstanbul ABSTRACT In this work, the existence and stability properties of two-dimensional optical solitons in cubic-quintic nonlinear Schrödinger (CQNLS) equation with several defective PT-symmetric potentials are studied. The numerical existence of fundamental solitons on these PTsymmetric lattices is shown for various potential depths and defects in self-focusing cubic, self-focusing quintic media. ÖZET Bu çalışmada, parite-zaman (PT) simetrisine sahip birtakım bozuk kafesler üzerinde kübikkuintik, doğrusal olmayan Schrödinger (CQNLS) denkleminin iki boyutlu optik solitonlarının varlıkları ve kararlılıkları incelenmiştir. PT simetrisine sahip bu kafesler üzerinde temel solitonların sayısal varlığı; odaklanan kübik, odaklanan kuintik ortamda farklı potansiyel derinlikleri ve kusurlar için gösterilmiştir. 508 GİRİŞ Hem kübik hem kuintik terim içeren doğrusal olmayan Schrödinger (CQNLS) denklemi, birçok fiziksel durumu betimler ve özellikle de optikte karşımıza çıkar [1]. Doğrusal olmayan optikte, CQNLS denklemi bir elektromanyetik dalganın ışık kırıcı maddelerde yayılımını betimler. Kübik-kuintik doğrusalsızlık, madde içindeki bir öz rezonans yüzündendir ve güçlü iki-foton emilimini beraberinde getirir [2]. Bu çalışmada, parite-zaman (PT) simetrisine sahip birtakım kafesler üzerinde optik solitonların varlığı ve kararlılığı incelenecektir. Kullanılan fiziksel modeli ifade eden eşitlik; 2+1 boyutlu, odaklanan kübik, odaklanan kuintik ortamda, doğrusal olmayan, dış potansiyelli Schrödinger denklemidir: iu u u u u u u V u (1) 2 4 z xx yy PT 0. Burada u( x, y, z ) karmaşık değerli fonksiyonu, xy -düzleminde olup z ekseni boyunca yayılan alanın yavaşça değişen genliğine; uxx uyy kırınıma; VPT ( xy, ) PT simetrisine sahip dış potansiyele karşı gelmektedir. ve sırasıyla kübik ve kuintik doğrusalsızlık katsayılarıdır ve bunların pozitif olması odaklanmaya, negatif olması ise odaktan sapmaya
2 karşı gelmektedir. Çalışmada odaklanan kübik, odaklanan kuintik ortam ele alındığından, olarak seçilmiştir. 1 (1) denkleminin çözümü spektral yöntemlerle bulunacaktır [3]. İncelenecek potansiyeller, PT * simetrisinin gerek koşulu olan VPT ( x, y) VPT ( x, y) eşitliğini [4] sağlamakta olup aşağıdaki yapıdadır: V 2 0 i ( x, y) VPT ( x, y) 2cos( x) 2cos( y) e iw0 sin(2 x) sin(2 y). (2) 25 Burada ve etmektedir ve V 0 W 0 sırasıyla potansiyelin gerçel ve sanal kısımlarının derinliklerini temsil y y ( xy, ) arctan arctan x x (3) ile ifade edilen faz fonksiyonu, artı veya eksi işaretine göre kafes yapısında pozitif veya negatif bir kusur meydana getirmektedir [5]. katsayısının 0 olarak alınması potansiyelde kusur olmadığı duruma, 1 olarak alınması kusur olduğu duruma karşı gelmektedir. Çalışmada incelenen potansiyellerin gerçel ve sanal kısımlarına ait üstten görünüşleri ve köşegen kesitleri aşağıdaki şekillerde verilmiştir. Şekil 1'de kusur içermeyen potansiyel, Şekil 2'de pozitif kusur içeren potansiyel, Şekil 3'te negatif kusur içeren potansiyel resmedilmiştir. ( xy, ) Şekil 1: (Soldan sağa) V0 1 ; W0 0,1 ; 0 değerleri için (2) potansiyelinin gerçel kısmının üstten görünüşü, gerçel kısmının köşegen kesiti, sanal kısmının üstten görünüşü ve sanal kısmının köşegen kesiti. XIX. Ulusal Mekanik Kongresi 509
3 Şekil 2: (Soldan sağa) (3) denklemindeki işaret ' ' olmak üzere V0 1 ; W0 0,1 ; 1 değerleri için (2) potansiyelinin gerçel kısmının üstten görünüşü, gerçel kısmının köşegen kesiti, sanal kısmının üstten görünüşü ve sanal kısmının köşegen kesiti. Şekil 3: (Soldan sağa) (3) denklemindeki işaret ' ' olmak üzere V0 1 ; W0 0,1 ; 1 değerleri için (2) potansiyelinin gerçel kısmının üstten görünüşü, gerçel kısmının köşegen kesiti, sanal kısmının üstten görünüşü ve sanal kısmının köşegen kesiti. Bu çalışmada, PT simetrisine sahip kafesler üzerinde temel solitonların sayısal varlığı farklı potansiyel derinlikleri ve kusurlar için gösterilecektir. Sonrasında, elde edilen solitonların kararlılıkları incelenecek ve kafes yapısındaki kusurların bunlara olan etkisi tartışılacaktır. YÖNTEM CQNLS denkleminin sayısal çözümünde, tayfi yeniden normalleştirme [3] olarak bilinen yöntemden yararlanılmıştır. Temelde bir Fourier yinelemesi olan bu yöntemde, sonuçlar i z u( x, y, z) f ( x, y) e çözüm önerisi ve f ( x, y) w( x, y), dönüşümünde sonra Fourier uzayına geçilerek başlangıç koşulu f x olarak alınan 2 2 0(, y) exp( x y ) n n n n n 2 2 kx ky 2 ( w w ) ( w w ) ( VPT wn ) wˆ, n (4) 6 özyinelemesiyle 10 mertebesinde yakınsaklık sağlanmasıyla elde edilmiştir. Çalışmada, 1 olarak alınmıştır. Doğrusal kararlılık incelemesi, çözümlere ufak bir tedirgeme (pertürbasyon) eklenip elde edilen doğrusal tayfın özdeğerlerine bakılarak gerçekleştirilmiştir. 0 1 olmak üzere, 510 XIX. Ulusal Mekanik Kongresi
4 u( x, y, z) f ( x, y) e g( x, y) e h ( x, y) e e * iz z * z iz (5) tedirgenmiş çözümün doğrusal tayfı, L f f f olmak üzere 2 3 * xx yy PT L1 2 f 3 f V ve L1 L2 g g i * * L2 L 1 h h (6) denklem sistemiyle ifade edilmektedir. (5) denkleminden görüleceği üzere, çözümün patlamaması için özdeğerlerinin gerçel kısımlarının sıfır olması gerekmektedir. Doğrusal olmayan kararlılık incelemesi, çözümlerin doğrudan benzetimle ilerletilmesi sırasında şekil, konum ve genliklerinin korunup korunmamasına bakılarak gerçekleştirilmiştir. Bu amaçla, çözümler zaman basamaklı Fourier (split-step Fourier) yöntemiyle boyunca ilerletilmiş ve her adımda bahsedilen özelliklerinin değişip değişmediği incelenmiştir. z TEMEL SOLİTON ÇÖZÜMLER VE KARARLILIK İNCELEMESİ Odaklanan kübik, odaklanan kuintik ortamda temel solitonlar değişik potansiyel derinlikleri için elde edilmiştir. Temsili olarak, V0 1 ; W0 0,1 derinlikleri için elde edilen solitonlar Şekil 4'te kusur içermeyen potansiyel, Şekil 5'te pozitif kusur içeren potansiyel ve Şekil 6'da negatif kusur içeren potansiyel için resmedilmiştir. Şekil 4: 1 ; 1 ; =0 ; 1 ; V0 1 ; W0 0,1 değerleri için elde edilen solitonun gerçel ve sanal kısımlarının görüntüleri. Şekil 5: (3) denklemindeki işaret ' ' olmak üzere, 1 ; 1 ; =1 ; 1 ; V0 1 ; W0 0,1 değerleri için elde edilen solitonun gerçel ve sanal kısımlarının görüntüleri. XIX. Ulusal Mekanik Kongresi 511
5 Şekil 6: (3) denklemindeki işaret ' ' olmak üzere, 1 ; 1 ; =1 ; 1 ; V0 1 ; W0 0,1 değerleri için elde edilen solitonun gerçel ve sanal kısımlarının görüntüleri. Farklı kusurların ve potansiyelin gerçel kısmının derinliğinin solitonların varlık ve kararlılıkları üzerindeki etkilerini incelemek için, sanal kısmın derinliği sabit tutularak farklı V 0 değerleri ve kusurlar için çözümler elde edilmiş ve sonuçlar Şekil 7'de gösterilmiştir. W 0 Şekil 7: Farklı kusurlar ve 1 ; 1 ; 1 ; W0 0,1 değerleri için elde edilen solitonların varlıkları ve doğrusal olmayan anlamda kararlılıkları. Her ne kadar pozitif kusur, solitonların elde edildiği yarık genişliğini daraltsa da kusur olmadığı durumdaki bazı kararsız çözümleri kararlı hale getirmesi bakımından olumlu bir etkide bulunmuştur. Şekil 8'deki pozitif kusur ve V0 2,3 için elde edilen solitonun doğrudan benzetimi incelendiğinde; bu solitonun, şekil, konum ve genliği korunduğundan doğrusal olmayan anlamda kararlı olduğu görülmektedir. Ancak Şekil 9'daki negatif kusur ve V0 2,3 için elde 512 XIX. Ulusal Mekanik Kongresi
6 edilen solitonun doğrudan benzetimi incelendiğinde; bu çözümün, soliton şeklini koruyamadığından doğrusal olmayan anlamda kararsız olduğu görülmektedir. Şekil 8: Pozitif kusur ve 1 ; 1 ; 1, V0 2,3 ; W0 0,1 değerleri için elde edilen solitonun z boyunca ilerletilmesi sırasında üstten görünüşü ve genliğinin değişim grafiği. Şekil 9: Negatif kusur ve 1 ; 1 ; 1, V0 2,3 ; W0 0,1 değerleri için elde edilen solitonun boyunca ilerletilmesi sırasında üstten görünüşü. z Şekil 10'daki V0 1 için elde edilen solitonların doğrusal tayfları incelendiğinde; tayflarındaki saf sanal olmayan özdeğerlerden dolayı, bu solitonların doğrusal anlamda kararsız oldukları görülmektedir. Benzer şekilde, elde edilen tüm solitonların doğrusal anlamda kararsız oldukları gözlemlenmiştir. Şekil 10: Farklı kusurlar ve 1 ; 1 ; 1 ; V0 1 ; W0 0,1 değerleri için elde edilen solitonların doğrusal tayfların özdeğerleri. XIX. Ulusal Mekanik Kongresi 513
7 SONUÇ Bu çalışmada, PT simetrisine sahip çeşitli bozuk kafesler üzerinde temel solitonların sayısal varlığı; odaklanan kübik, odaklanan kuintik ortamda farklı potansiyel derinlikleri ve kusurlar için gösterilmiş ve bu soliton çözümlerin kararlılıkları hem doğrusal hem doğrusal olmayan anlamda incelenmiştir. PT-simetrisine sahip bu kafeslerde pozitif veya negatif bir kusur yarık genişliğini azaltmaktadır. Odaklanan kübik, odaklanan kuintik ortamda; negatif kusur elde edilen solitonları doğrusal olmayan anlamda kararsızlaştırmaktadır. Öte yandan, elde edilen tüm solitonlar doğrusal anlamda kararsızdır. KAYNAKLAR [1] C. T. Zhou, X. T. He, Third- and fifth-order optical nonlinearities in a new stilbazolium derivative, Journal of the Optical Society of America B. 19 (2002) [2] G. Boudebsa, S. Cherukulappuratha, H. Leblonda, J. Trolesb, F. Smektalab, F. Sancheza, Experimental and theoretical study of higher-order nonlinearities in chalcogenide glasses, Optics Communications. 219 (2003) [3] M. J. Ablowitz, Z. H. Musslimani, Spectral renormalization method for computing selflocalized solutions to nonlinear systems, Optic Letters. 30 (2005) [4] C. M. Bender, S. Boettcher, Real spectra in non-hermitian Hamiltonians having PT Symmetry, Physical Review Letters. 80 (1998) [5] M. J. Ablowitz, B. Ilan, E. Schonbrun, R. Piestun, Solitons in two-dimensional lattices possessing defects, dislocations, and quasicrystal structures, Physical Review E. 74 (2006) (R). 514 XIX. Ulusal Mekanik Kongresi
SAYISAL KARARLILIK. Zaman Uzayı Sonlu Farklar Yöntemi
 Dr. Serkan Aksoy SAYISAL KARARLILIK Sayısal çözümlerin kararlı olması zorunludur. Buna göre ZUSF çözümleri de uzay ve zamanda ayrıklaştırma kapsamında kararlı olması için kararlılık koşullarını sağlaması
Dr. Serkan Aksoy SAYISAL KARARLILIK Sayısal çözümlerin kararlı olması zorunludur. Buna göre ZUSF çözümleri de uzay ve zamanda ayrıklaştırma kapsamında kararlı olması için kararlılık koşullarını sağlaması
8.04 Kuantum Fiziği Ders X. Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler.
 Schrödinger denklemi Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler. Köşeli parantez içindeki terim, dalga fonksiyonuna etki eden bir işlemci olup, Hamilton
Schrödinger denklemi Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler. Köşeli parantez içindeki terim, dalga fonksiyonuna etki eden bir işlemci olup, Hamilton
Zaman Uzayı Sonlu Farklar Yöntemi
 Dr. Serkan Aksoy SAYISAL KARARLILIK Sayısal çözümlerin kararlı olması zorunludur. Buna göre ZUSF çözümleri de uzay ve zamanda ayrıklaştırma kapsamında kararlı olması için kararlılık koşullarını sağlaması
Dr. Serkan Aksoy SAYISAL KARARLILIK Sayısal çözümlerin kararlı olması zorunludur. Buna göre ZUSF çözümleri de uzay ve zamanda ayrıklaştırma kapsamında kararlı olması için kararlılık koşullarını sağlaması
Bölüm 1: Lagrange Kuramı... 1
 İÇİNDEKİLER Bölüm 1: Lagrange Kuramı... 1 1.1. Giriş... 1 1.2. Genelleştirilmiş Koordinatlar... 2 1.3. Koordinat Dönüşüm Denklemleri... 3 1.4. Mekanik Dizgelerin Bağ Koşulları... 4 1.5. Mekanik Dizgelerin
İÇİNDEKİLER Bölüm 1: Lagrange Kuramı... 1 1.1. Giriş... 1 1.2. Genelleştirilmiş Koordinatlar... 2 1.3. Koordinat Dönüşüm Denklemleri... 3 1.4. Mekanik Dizgelerin Bağ Koşulları... 4 1.5. Mekanik Dizgelerin
HESAPLAMALI AKIŞKANLAR MEKANİĞİ ÇALIŞMALARI İÇİN SIKIŞTIRILABİLİR FOURIER TAYFI YÖNTEMİ
 XIX. ULUSAL MEKANİK KONGRESİ 4-8 Ağustos 015, Karadeniz Teknik Üniversitesi, Trabzon HESAPLAMALI AKIŞKANLAR MEKANİĞİ ÇALIŞMALARI İÇİN SIKIŞTIRILABİLİR FOURIER TAYFI YÖNTEMİ Cihan BAYINDIR 1 1 Işık Üniversitesi,
XIX. ULUSAL MEKANİK KONGRESİ 4-8 Ağustos 015, Karadeniz Teknik Üniversitesi, Trabzon HESAPLAMALI AKIŞKANLAR MEKANİĞİ ÇALIŞMALARI İÇİN SIKIŞTIRILABİLİR FOURIER TAYFI YÖNTEMİ Cihan BAYINDIR 1 1 Işık Üniversitesi,
H a t ı r l a t m a : Şimdiye dek bilmeniz gerekenler: 1. Maxwell denklemleri, elektromanyetik dalgalar ve ışık
 H a t ı r l a t m a : Şimdiye dek bilmeniz gerekenler: 1. Maxwell denklemleri, elektromanyetik dalgalar ve ışık 2. Ahenk ve ahenk fonksiyonu, kontrast, görünebilirlik 3. Girişim 4. Kırınım 5. Lazer, çalışma
H a t ı r l a t m a : Şimdiye dek bilmeniz gerekenler: 1. Maxwell denklemleri, elektromanyetik dalgalar ve ışık 2. Ahenk ve ahenk fonksiyonu, kontrast, görünebilirlik 3. Girişim 4. Kırınım 5. Lazer, çalışma
ZAMAN SERİLERİNDE REGRESYON ANALİZİ
 ZAMAN SERİLERİNDE REGRESYON ANALİZİ 1 1. GİRİŞ Trent, serinin genelinde yukarıya ya da aşağıya doğru olan hareketlere denmektedir. Bu hareket bazen düz bir doğru şeklinde olmaktadır. Bu tür harekete sahip
ZAMAN SERİLERİNDE REGRESYON ANALİZİ 1 1. GİRİŞ Trent, serinin genelinde yukarıya ya da aşağıya doğru olan hareketlere denmektedir. Bu hareket bazen düz bir doğru şeklinde olmaktadır. Bu tür harekete sahip
KUADRATİK FORM. Tanım: Kuadratik Form. Bir q(x 1,x 2,,x n ) fonksiyonu
 KUADRATİK FORMLAR KUADRATİK FORM Tanım: Kuadratik Form Bir q(x,x,,x n ) fonksiyonu q x : n şeklinde tanımlı ve x i x j bileşenlerinin doğrusal kombinasyonu olan bir fonksiyon ise bir kuadratik formdur.
KUADRATİK FORMLAR KUADRATİK FORM Tanım: Kuadratik Form Bir q(x,x,,x n ) fonksiyonu q x : n şeklinde tanımlı ve x i x j bileşenlerinin doğrusal kombinasyonu olan bir fonksiyon ise bir kuadratik formdur.
İşaret ve Sistemler. Ders 2: Spektral Analize Giriş
 İşaret ve Sistemler Ders 2: Spektral Analize Giriş Spektral Analiz A 1.Cos (2 f 1 t+ 1 ) ile belirtilen işaret: f 1 Hz frekansında, A 1 genliğinde ve fazı da Cos(2 f 1 t) ye göre 1 olan parametrelere sahiptir.
İşaret ve Sistemler Ders 2: Spektral Analize Giriş Spektral Analiz A 1.Cos (2 f 1 t+ 1 ) ile belirtilen işaret: f 1 Hz frekansında, A 1 genliğinde ve fazı da Cos(2 f 1 t) ye göre 1 olan parametrelere sahiptir.
8.04 Kuantum Fiziği DersXIX
 Bu takdirde yani, 1 = a ˆ 0 de bir enerji özdurumudur, ancak 0 için enerjisi 1hω yerine 3 hω dir. 2 2 Benzer şekilde, 2 = a ˆ 1 inde bir enerji özdurumu olduğunu fakat enerjisinin 5 hω, vs. 2 söyleyebiliriz.
Bu takdirde yani, 1 = a ˆ 0 de bir enerji özdurumudur, ancak 0 için enerjisi 1hω yerine 3 hω dir. 2 2 Benzer şekilde, 2 = a ˆ 1 inde bir enerji özdurumu olduğunu fakat enerjisinin 5 hω, vs. 2 söyleyebiliriz.
LİNEER OLMAYAN OLUŞUM DENKLEMLERİNİN ÜSTEL RASYONEL FONKSİYON METODUYLA ÇÖZÜMÜ. Geliş Tarihi: 05.08.2014 Kabul Tarihi: 09.06.2015
 LİNEER OLMAYAN OLUŞUM DENKLEMLERİNİN ÜSTEL RASYONEL FONKSİYON METODUYLA ÇÖZÜMÜ Melike KAPLAN 1, Arzu AKBULUT 2, Mehmet Naci ÖZER 3 1 Eskişehir Osmangazi Üniversitesi, Fen-Edebiyat Fakültesi, Matematik-Bilgisayar
LİNEER OLMAYAN OLUŞUM DENKLEMLERİNİN ÜSTEL RASYONEL FONKSİYON METODUYLA ÇÖZÜMÜ Melike KAPLAN 1, Arzu AKBULUT 2, Mehmet Naci ÖZER 3 1 Eskişehir Osmangazi Üniversitesi, Fen-Edebiyat Fakültesi, Matematik-Bilgisayar
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MASSACHUSETTS TEKNOLOJİ ENSTİTÜSÜ Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 2 Salı, Mart 14, :00-12:30
 Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 2 Salı, Mart 14, 2006 11:00-12:30 SOYADI ADI Öğrenci No. Talimat: 1. TÜM ÇABANIZI GÖSTERİN. Tüm cevaplar sınav kitapçığında gösterilmelidir? 2. Bu kapalı bir sınavdır.
Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 2 Salı, Mart 14, 2006 11:00-12:30 SOYADI ADI Öğrenci No. Talimat: 1. TÜM ÇABANIZI GÖSTERİN. Tüm cevaplar sınav kitapçığında gösterilmelidir? 2. Bu kapalı bir sınavdır.
A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili
 A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili Momentum işlemcisinin konum temsili Konum işlemcisinin momentum temsili
A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili Momentum işlemcisinin konum temsili Konum işlemcisinin momentum temsili
DEVRE VE SİSTEM ANALİZİ ÇALIŞMA SORULARI
 DEVRE VE SİSTEM ANALİZİ 01.1.015 ÇALIŞMA SORULARI 1. Aşağıda verilen devrede anahtar uzun süre konumunda kalmış ve t=0 anında a) v 5 ( geriliminin tam çözümünü diferansiyel denklemlerden faydalanarak bulunuz.
DEVRE VE SİSTEM ANALİZİ 01.1.015 ÇALIŞMA SORULARI 1. Aşağıda verilen devrede anahtar uzun süre konumunda kalmış ve t=0 anında a) v 5 ( geriliminin tam çözümünü diferansiyel denklemlerden faydalanarak bulunuz.
Matematikte karşılaştığınız güçlükler için endişe etmeyin. Emin olun benim karşılaştıklarım sizinkilerden daha büyüktür.
 - 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
- 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
Otomatik Kontrol. Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri
 Otomatik Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri H a z ı r l aya n : D r. N u r d a n B i l g i n Kapalı Çevrim Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri Bir önceki
Otomatik Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri H a z ı r l aya n : D r. N u r d a n B i l g i n Kapalı Çevrim Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri Bir önceki
 LYS Y OĞRU MTMTİK TSTİ LYS-. u testte Matematik ile ilgili soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a ve b asal
LYS Y OĞRU MTMTİK TSTİ LYS-. u testte Matematik ile ilgili soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a ve b asal
Ortak Akıl MATEMATİK DENEME SINAVI
 Ortak Akıl LYS MATEMATİK DENEME SINAVI 0505- Ortak Akıl Adem ÇİL Ali Can GÜLLÜ Ayhan YANAĞLIBAŞ Barbaros GÜR Barış DEMİR Celal İŞBİLİR Deniz KARADAĞ Engin POLAT Erhan ERDOĞAN Ersin KESEN Fatih TÜRKMEN
Ortak Akıl LYS MATEMATİK DENEME SINAVI 0505- Ortak Akıl Adem ÇİL Ali Can GÜLLÜ Ayhan YANAĞLIBAŞ Barbaros GÜR Barış DEMİR Celal İŞBİLİR Deniz KARADAĞ Engin POLAT Erhan ERDOĞAN Ersin KESEN Fatih TÜRKMEN
Hanta-virüs Modelinden Elde Edilen Lojistik Diferansiyel Denklem. Logistic Differential Equations Obtained from Hanta-virus Model
 SDU Journal of Science (E-Journal), 2016, 11 (1): 82-91 Hanta-virüs Modelinden Elde Edilen Lojistik Diferansiyel Denklem Zarife Gökçen Karadem 1,*, Mevlüde Yakıt Ongun 2 1 Süleyman Demirel Üniversitesi,
SDU Journal of Science (E-Journal), 2016, 11 (1): 82-91 Hanta-virüs Modelinden Elde Edilen Lojistik Diferansiyel Denklem Zarife Gökçen Karadem 1,*, Mevlüde Yakıt Ongun 2 1 Süleyman Demirel Üniversitesi,
2012 LYS MATEMATİK SORU VE ÇÖZÜMLERİ Niyazi Kurtoğlu
 .SORU 8 sayı tabanında verilen (5) 8 sayısının sayı tabanında yazılışı nedir?.soru 6 3 3 3 3 4 6 8? 3.SORU 3 ise 5? 5 4.SORU 4 5 olduğuna göre, ( )? 5.SORU (y z) z(y ) y z yz bulunuz. ifadesinin en sade
.SORU 8 sayı tabanında verilen (5) 8 sayısının sayı tabanında yazılışı nedir?.soru 6 3 3 3 3 4 6 8? 3.SORU 3 ise 5? 5 4.SORU 4 5 olduğuna göre, ( )? 5.SORU (y z) z(y ) y z yz bulunuz. ifadesinin en sade
FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ YAZ OKULU DERS İÇERİGİ. Bölümü Dersin Kodu ve Adı T P K AKTS
 Bir Dönemde Okutulan Ders Saati MAT101 Genel I (Mühendislik Fakültesi Bütün Bölümler, Fen Fakültesi Kimya ve Astronomi Bölümleri) 1 Kümeler, reel sayılar, bir denklem veya eşitsizliğin grafiği 2 Fonksiyonlar,
Bir Dönemde Okutulan Ders Saati MAT101 Genel I (Mühendislik Fakültesi Bütün Bölümler, Fen Fakültesi Kimya ve Astronomi Bölümleri) 1 Kümeler, reel sayılar, bir denklem veya eşitsizliğin grafiği 2 Fonksiyonlar,
8.04 Kuantum Fiziği Ders XII
 Enerji ölçümünden sonra Sonucu E i olan enerji ölçümünden sonra parçacık enerji özdurumu u i de olacak ve daha sonraki ardışık tüm enerji ölçümleri E i enerjisini verecektir. Ölçüm yapılmadan önce enerji
Enerji ölçümünden sonra Sonucu E i olan enerji ölçümünden sonra parçacık enerji özdurumu u i de olacak ve daha sonraki ardışık tüm enerji ölçümleri E i enerjisini verecektir. Ölçüm yapılmadan önce enerji
ÜÇ BOYUTLU SINIR TABAKA AKIŞLARININ KARARLILIK ÖZELLİKLERİNİN DOĞRUSAL KARARLILIK TEORİSİ YAKLAŞIMI İLE BELİRLENMESİ
 V. ULUSAL HAVACILIK VE UZAY KONFERANSI 8-10 Eylül 2014, Erciyes Üniversitesi, Kayseri ÜÇ BOYUTLU SINIR TABAKA AKIŞLARININ KARARLILIK ÖZELLİKLERİNİN DOĞRUSAL KARARLILIK TEORİSİ YAKLAŞIMI İLE BELİRLENMESİ
V. ULUSAL HAVACILIK VE UZAY KONFERANSI 8-10 Eylül 2014, Erciyes Üniversitesi, Kayseri ÜÇ BOYUTLU SINIR TABAKA AKIŞLARININ KARARLILIK ÖZELLİKLERİNİN DOĞRUSAL KARARLILIK TEORİSİ YAKLAŞIMI İLE BELİRLENMESİ
Potansiyel Engeli: Tünelleme
 Potansiyel Engeli: Tünelleme Şekil I: Bir potansiyel engelinde tünelleme E
Potansiyel Engeli: Tünelleme Şekil I: Bir potansiyel engelinde tünelleme E
HOMOGEN OLMAYAN DENKLEMLER
 n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
İŞARET ve SİSTEMLER (SIGNALS and SYSTEMS) Dr. Akif AKGÜL oda no: 303 (T4 / EEM)
 İşaret ve Sistemler İŞARET ve SİSTEMLER (SIGNALS and SYSTEMS) Dr. Akif AKGÜL aakgul@sakarya.edu.tr oda no: 303 (T4 / EEM) Kaynaklar: 1. Signals and Systems, Oppenheim. (Türkçe versiyonu: Akademi Yayıncılık)
İşaret ve Sistemler İŞARET ve SİSTEMLER (SIGNALS and SYSTEMS) Dr. Akif AKGÜL aakgul@sakarya.edu.tr oda no: 303 (T4 / EEM) Kaynaklar: 1. Signals and Systems, Oppenheim. (Türkçe versiyonu: Akademi Yayıncılık)
FİZİK 4. Ders 10: Bir Boyutlu Schrödinger Denklemi
 FİZİK 4 Ders 10: Bir Boyutlu Schrödinger Denklemi Bir Boyutlu Schrödinger Denklemi Beklenen Değer Kuyu İçindeki Parçacık Zamandan Bağımsız Schrödinger Denklemi Kare Kuyu Tünel Olayı Basit Harmonik Salınıcı
FİZİK 4 Ders 10: Bir Boyutlu Schrödinger Denklemi Bir Boyutlu Schrödinger Denklemi Beklenen Değer Kuyu İçindeki Parçacık Zamandan Bağımsız Schrödinger Denklemi Kare Kuyu Tünel Olayı Basit Harmonik Salınıcı
NONLİNEER HİPERELASTİK BİR PLAKTA DÜZLEM İÇİ SİMETRİK DALGALARIN MODÜLASYONU. İTÜ Fen-Edebiyat Fakültesi, Matematik Bölümü, İSTANBUL
 NONLİNEER HİPERELASTİK BİR PLAKTA DÜZLEM İÇİ SİMETRİK DALGALARIN MODÜLASYONU Ali Demirci Mevlüt Teymür İTÜ Fen-Edebiyat Fakültesi, Matematik Bölümü, İSTANBUL 1. GİRİŞ Daha önceleri akışkanlar mekaniği,
NONLİNEER HİPERELASTİK BİR PLAKTA DÜZLEM İÇİ SİMETRİK DALGALARIN MODÜLASYONU Ali Demirci Mevlüt Teymür İTÜ Fen-Edebiyat Fakültesi, Matematik Bölümü, İSTANBUL 1. GİRİŞ Daha önceleri akışkanlar mekaniği,
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme
 Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
SAYISAL İŞARET İŞLEME LABORATUARI LAB 5: SONSUZ DÜRTÜ YANITLI (IIR) FİLTRELER
 SAYISAL İŞARET İŞLEME LABORATUARI LAB 5: SONSUZ DÜRTÜ YANITLI (IIR) FİLTRELER Bu bölümde aşağıdaki başlıklar ele alınacaktır. Sonsuz dürtü yanıtlı filtre yapıları: Direkt Şekil-1, Direkt Şekil-II, Kaskad
SAYISAL İŞARET İŞLEME LABORATUARI LAB 5: SONSUZ DÜRTÜ YANITLI (IIR) FİLTRELER Bu bölümde aşağıdaki başlıklar ele alınacaktır. Sonsuz dürtü yanıtlı filtre yapıları: Direkt Şekil-1, Direkt Şekil-II, Kaskad
Bölüm 3. Tek Serbestlik Dereceli Sistemlerin Zorlanmamış Titreşimi
 Bölüm 3 Tek Serbestlik Dereceli Sistemlerin Zorlanmamış Titreşimi Sönümsüz Titreşim: Tek serbestlik dereceli örnek sistem: Kütle-Yay (Yatay konum) Bir önceki bölümde anlatılan yöntemlerden herhangi biri
Bölüm 3 Tek Serbestlik Dereceli Sistemlerin Zorlanmamış Titreşimi Sönümsüz Titreşim: Tek serbestlik dereceli örnek sistem: Kütle-Yay (Yatay konum) Bir önceki bölümde anlatılan yöntemlerden herhangi biri
Ahenk (Koherans, uyum)
 Girişim Girişim Ahenk (Koherans, uyum Ahenk (Koherans, uyum Ahenk (Koherans, uyum http://en.wikipedia.org/wiki/coherence_(physics#ntroduction Ahenk (Koherans, uyum Girişim İki ve/veya daha fazla dalganın
Girişim Girişim Ahenk (Koherans, uyum Ahenk (Koherans, uyum Ahenk (Koherans, uyum http://en.wikipedia.org/wiki/coherence_(physics#ntroduction Ahenk (Koherans, uyum Girişim İki ve/veya daha fazla dalganın
Fizik 101: Ders 23 Gündem
 Fizik 101: Ders 3 Gündem Basit Harmonik Hereket Yatay yay ve kütle Sinus ve cosinus lerin anlamı Düşey yay ve kütle Enerji yaklaşımı Basit sarkaç Çubuk sarkaç Basit Harmonik Hareket (BHH) Ucunda bir kütle
Fizik 101: Ders 3 Gündem Basit Harmonik Hereket Yatay yay ve kütle Sinus ve cosinus lerin anlamı Düşey yay ve kütle Enerji yaklaşımı Basit sarkaç Çubuk sarkaç Basit Harmonik Hareket (BHH) Ucunda bir kütle
Prof. Dr. Abdullah YILDIZ KİŞİSEL BİLGİLER: Adı Soyadı : Abdullah Yıldız Doğum Yeri : Kayseri/Yahyalı Doğum Tarihi:8.1.1951 ÖĞRENİM DURUMU :
 Prof. Dr. Abdullah YILDIZ KİŞİSEL BİLGİLER: Adı Soyadı : Abdullah Yıldız Doğum Yeri : Kayseri/Yahyalı Doğum Tarihi:8.1.1951 ÖĞRENİM DURUMU : 1972 Lisans, Ankara Üniversitesi Fen Fakültesi 1982 Yüksek Lisans,
Prof. Dr. Abdullah YILDIZ KİŞİSEL BİLGİLER: Adı Soyadı : Abdullah Yıldız Doğum Yeri : Kayseri/Yahyalı Doğum Tarihi:8.1.1951 ÖĞRENİM DURUMU : 1972 Lisans, Ankara Üniversitesi Fen Fakültesi 1982 Yüksek Lisans,
1986 ÖYS. 3 b. 2 b C) a= 1. Aşağıdaki ABC üçgeninde. BD kaç cm dir? C) 3 D) 8 E)
 ÖYS. Aşağıdaki ABC üçgeninde. BD kaç cm dir? 0. Aşağıdaki şekilde ABCD bir yamuk ve AECD bir paralel kenardır.. Aşağıdaki şekilde EAB ve FBC eşkenar üçgendir. AECD nin alanı cm Buna göre CEB üçgeninin
ÖYS. Aşağıdaki ABC üçgeninde. BD kaç cm dir? 0. Aşağıdaki şekilde ABCD bir yamuk ve AECD bir paralel kenardır.. Aşağıdaki şekilde EAB ve FBC eşkenar üçgendir. AECD nin alanı cm Buna göre CEB üçgeninin
Plazma İletiminin Optimal Kontrolü Üzerine
 Plazma İletiminin Optimal Kontrolü Üzerine 1 Yalçın Yılmaz, 2 İsmail Küçük ve 3 Faruk Uygul *1 Faculty of Arts and Sciences, Dept. of Mathematics, Sakaya University, Sakarya, Turkey 2 Faculty of Chemical
Plazma İletiminin Optimal Kontrolü Üzerine 1 Yalçın Yılmaz, 2 İsmail Küçük ve 3 Faruk Uygul *1 Faculty of Arts and Sciences, Dept. of Mathematics, Sakaya University, Sakarya, Turkey 2 Faculty of Chemical
ÖZGEÇMİŞ Doç. Dr. NİLÜFER TOPSAKAL
 ÖZGEÇMİŞ Doç. Dr. NİLÜFER TOPSAKAL TC Kimlik No / Pasaport No: Doğum Yılı: 1978 Yazışma Adresi : Telefon : 346-2191010/1531 e-posta : Fen Fakültesi Matematik Bölümü 58140 Sivas/ ntopsakal@cumhuriyet.edu.tr
ÖZGEÇMİŞ Doç. Dr. NİLÜFER TOPSAKAL TC Kimlik No / Pasaport No: Doğum Yılı: 1978 Yazışma Adresi : Telefon : 346-2191010/1531 e-posta : Fen Fakültesi Matematik Bölümü 58140 Sivas/ ntopsakal@cumhuriyet.edu.tr
FİZ217 TİTREŞİMLER VE DALGALAR DERSİNİN 2. ARA SINAV SORU CEVAPLARI
 1) Gerilmiş bir ipte enine titreşimler denklemi ile tanımlıdır. Değişkenlerine ayırma yöntemiyle çözüm yapıldığında için [ ] [ ] ifadesi verilmiştir. 1.a) İpin enine titreşimlerinin n.ci modunu tanımlayan
1) Gerilmiş bir ipte enine titreşimler denklemi ile tanımlıdır. Değişkenlerine ayırma yöntemiyle çözüm yapıldığında için [ ] [ ] ifadesi verilmiştir. 1.a) İpin enine titreşimlerinin n.ci modunu tanımlayan
HAFTA 8: FOURIER SERİLERİ ÖZELLİKLERİ. İçindekiler
 HAFA 8: FOURIER SERİLERİ ÖZELLİKLERİ İçindekiler 4.4. Fourier serisinin özellikleri... 2 4.4.1 Doğrusallık özelliği (Linearity property)... 2 4.4.2 Zamanda tersine çevirme özelliği (ime Reversal Property)...
HAFA 8: FOURIER SERİLERİ ÖZELLİKLERİ İçindekiler 4.4. Fourier serisinin özellikleri... 2 4.4.1 Doğrusallık özelliği (Linearity property)... 2 4.4.2 Zamanda tersine çevirme özelliği (ime Reversal Property)...
Prof.Dr.F.Nejat EKMEKCİ, Prof. Dr. Yusuf YAYLI, BAHAR
 MAT 114 LİNEER CEBİR ( İSTATİSTİK, ASTRONOMİ ve UZAY BİLİMLERİ) Hafta 8: İç Çarpım Prof.Dr.F.Nejat EKMEKCİ, Prof. Dr. Yusuf YAYLI, Doç.Dr.İsmail GÖK 2017-2018 BAHAR İç Çarpım Tanım 23: V bir reel vektör
MAT 114 LİNEER CEBİR ( İSTATİSTİK, ASTRONOMİ ve UZAY BİLİMLERİ) Hafta 8: İç Çarpım Prof.Dr.F.Nejat EKMEKCİ, Prof. Dr. Yusuf YAYLI, Doç.Dr.İsmail GÖK 2017-2018 BAHAR İç Çarpım Tanım 23: V bir reel vektör
İÇİNDEKİLER KISIM 1: BİRİNCİ MERTEBE ADİ DİFERENSİYEL DENKLEMLER
 İÇİNDEKİLER KISIM 1: BİRİNCİ MERTEBE ADİ DİFERENSİYEL DENKLEMLER 1.1. Fiziksel Kanunlar ve Diferensiyel Denklemler Arasındaki İlişki... 1 1.2. Diferensiyel Denklemlerin Sınıflandırılması ve Terminoloji...
İÇİNDEKİLER KISIM 1: BİRİNCİ MERTEBE ADİ DİFERENSİYEL DENKLEMLER 1.1. Fiziksel Kanunlar ve Diferensiyel Denklemler Arasındaki İlişki... 1 1.2. Diferensiyel Denklemlerin Sınıflandırılması ve Terminoloji...
Matematik I: Analiz und Lineer Cebir I Sömestr Ders Saati D 2 U 2 L 1 AKTS 6 Lisans/ Yüksek Lisans Lisans Dersin Kodu MAT 106 Sömestr 2
 Dersin Adı Matematik I: Analiz und Lineer Cebir I Sömestr Ders Saati D 2 U 2 L 1 AKTS 6 Lisans/ Yüksek Lisans Lisans Dersin Kodu MAT 106 Sömestr 2 Dersin Dili Almanca Dersi Veren(ler) Yrd. Doç. Dr. Adnan
Dersin Adı Matematik I: Analiz und Lineer Cebir I Sömestr Ders Saati D 2 U 2 L 1 AKTS 6 Lisans/ Yüksek Lisans Lisans Dersin Kodu MAT 106 Sömestr 2 Dersin Dili Almanca Dersi Veren(ler) Yrd. Doç. Dr. Adnan
S4 u(x, y) = ln ( sin y. S5 u(x, y) = 2α 2 sec(α(x 4α 2 t)) fonksiyonunun
 Kısmi Türevli Denklemler Problem Seti-I S1 u = u(x, y ve a, b, c R olmak uzere, ξ = ax + by ve η = bx ay degisken degistirmesi yaparak n cozunuz. au x + bu y + cy = 0 S2 Aşa gidaki denklemleri Adi Diferensiyel
Kısmi Türevli Denklemler Problem Seti-I S1 u = u(x, y ve a, b, c R olmak uzere, ξ = ax + by ve η = bx ay degisken degistirmesi yaparak n cozunuz. au x + bu y + cy = 0 S2 Aşa gidaki denklemleri Adi Diferensiyel
Diferensiyel denklemler sürekli sistemlerin hareketlerinin ifade edilmesinde kullanılan denklemlerdir.
 .. Diferensiyel Denklemler y f (x) de F ( x, y, y, y,...) 0 veya y f ( x, y, y,...) x ve y değişkenlerinin kendileri ve türevlerini içinde bulunduran denklemlerdir. (Türevler; "Bağımlı değişkenin değişiminin
.. Diferensiyel Denklemler y f (x) de F ( x, y, y, y,...) 0 veya y f ( x, y, y,...) x ve y değişkenlerinin kendileri ve türevlerini içinde bulunduran denklemlerdir. (Türevler; "Bağımlı değişkenin değişiminin
Prof. Dr. Hüseyin Şirin Hüseyin 17 Temmuz 1951 tarihinde Azerbaycan da dünyaya geldi yılında Bakü Devlet Üniversitesi, Matematik Bölümü nde Lisa
 Prof. Dr. Prof. Dr. Hüseyin Şirin Hüseyin 17 Temmuz 1951 tarihinde Azerbaycan da dünyaya geldi. 1973 yılında Bakü Devlet Üniversitesi, Matematik Bölümü nde Lisans eğitimini tamamladı. 1977 yılında Moskova
Prof. Dr. Prof. Dr. Hüseyin Şirin Hüseyin 17 Temmuz 1951 tarihinde Azerbaycan da dünyaya geldi. 1973 yılında Bakü Devlet Üniversitesi, Matematik Bölümü nde Lisans eğitimini tamamladı. 1977 yılında Moskova
STURM-LIOUVILLE OPERATÖRÜNÜN SAYISAL ÖZDEĞERLERİ NUMERICAL EIGENVALUES OF STURM-LIOUVILLE OPERATORS
 Niğde Üniversitesi Mühendislik Bilimleri Dergisi, Cilt 2, Sayı 2, (2013), 43-49 STURM-LIOUVILLE OPERATÖRÜNÜN SAYISAL ÖZDEĞERLERİ Güldem YILDIZ 1*, Bülent YILMAZ 2 Matematik Bölümü, Fen Edebiyat Fakültesi,
Niğde Üniversitesi Mühendislik Bilimleri Dergisi, Cilt 2, Sayı 2, (2013), 43-49 STURM-LIOUVILLE OPERATÖRÜNÜN SAYISAL ÖZDEĞERLERİ Güldem YILDIZ 1*, Bülent YILMAZ 2 Matematik Bölümü, Fen Edebiyat Fakültesi,
tayf kara cisim ışınımına
 13. ÇİZGİ OLUŞUMU Yıldızın iç kısımlarından atmosfere doğru akan ışınım, dalga boyunun yaklaşık olarak sürekli bir fonksiyonudur. Çünkü iç bölgede sıcaklık gradyenti (eğimi) küçüktür ve madde ile ışınım
13. ÇİZGİ OLUŞUMU Yıldızın iç kısımlarından atmosfere doğru akan ışınım, dalga boyunun yaklaşık olarak sürekli bir fonksiyonudur. Çünkü iç bölgede sıcaklık gradyenti (eğimi) küçüktür ve madde ile ışınım
ÖZGEÇMİŞ. 1. Adı Soyadı: Bahaddin SİNSOYSAL 2. Doğum Tarihi: Ünvanı: Doç. Dr. 4. Öğrenim Durumu:
 1. Adı Soyadı: Bahaddin SİNSOYSAL 2. Doğum Tarihi: 02.0.1969. Ünvanı: Doç. Dr.. Öğrenim Durumu: ÖZGEÇMİŞ Derece Alan Üniversite Yıl Lisans Matematik Karadeniz Teknik Üniversitesi 1991 Y. Lisans Matematik
1. Adı Soyadı: Bahaddin SİNSOYSAL 2. Doğum Tarihi: 02.0.1969. Ünvanı: Doç. Dr.. Öğrenim Durumu: ÖZGEÇMİŞ Derece Alan Üniversite Yıl Lisans Matematik Karadeniz Teknik Üniversitesi 1991 Y. Lisans Matematik
Sistem Dinamiği. Bölüm 2- Dinamik Cevap ve Laplace Dönüşümü. Doç.Dr. Erhan AKDOĞAN
 Sistem Dinamiği - Dinamik Cevap ve Laplace Dönüşümü Doç. Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Soru MATLAB Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası
Sistem Dinamiği - Dinamik Cevap ve Laplace Dönüşümü Doç. Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Soru MATLAB Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası
Yrd. Doç. Dr.Yiğit Aksoy
 Yrd. Doç. Dr.Yiğit Aksoy ÖĞRENİM DURUMU Derece Üniversite Bölüm / Program Lisans Celal Bayar Üniversitesi Makine Mühendisliği 00 Y. Lisans Celal Bayar Üniversitesi Makine Mühendisliği 00 Doktora Celal
Yrd. Doç. Dr.Yiğit Aksoy ÖĞRENİM DURUMU Derece Üniversite Bölüm / Program Lisans Celal Bayar Üniversitesi Makine Mühendisliği 00 Y. Lisans Celal Bayar Üniversitesi Makine Mühendisliği 00 Doktora Celal
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ
 DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ 1. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için
DİKKAT! SORU KİTAPÇIĞINIZIN TÜRÜNÜ A OLARAK CEVAP KÂĞIDINIZA İŞARETLEMEYİ UNUTMAYINIZ. MATEMATİK SINAVI MATEMATİK TESTİ 1. Bu testte 50 soru vardır.. Cevaplarınızı, cevap kâğıdının Matematik Testi için
LYS Matemat k Deneme Sınavı
 LYS Matematk Deneme Sınavı. Üç basamaklı doğal saılardan kaç tanesi, 8 ve ile tam bölünür? 8 9. ile in geometrik ortası z dir. ( z). ( z ). z aşağıdakilerden hangisidir?. 9 ifadesinin cinsinden değeri
LYS Matematk Deneme Sınavı. Üç basamaklı doğal saılardan kaç tanesi, 8 ve ile tam bölünür? 8 9. ile in geometrik ortası z dir. ( z). ( z ). z aşağıdakilerden hangisidir?. 9 ifadesinin cinsinden değeri
Standart ve Standart Olmayan Theta Metotlarının Bazı Uygulamaları ve Sonuçları
 SDU Journal of Science (E-Journal), 2016, 11 (2): 109-120 Standart ve Standart Olmayan Theta Metotlarının Bazı Uygulamaları ve Sonuçları Fatih ER* 1 Mevlüde YAKIT ONGUN 2 1 Süleyman Demirel Üniversitesi,
SDU Journal of Science (E-Journal), 2016, 11 (2): 109-120 Standart ve Standart Olmayan Theta Metotlarının Bazı Uygulamaları ve Sonuçları Fatih ER* 1 Mevlüde YAKIT ONGUN 2 1 Süleyman Demirel Üniversitesi,
Fotonik Kristallerin Fiziği ve Uygulamaları
 Fotonik Kristallerin Fiziği ve Uygulamaları Ekmel Özbay, İrfan Bulu, Hümeyra Çağlayan, Koray Aydın, Kaan Güven Bilkent Üniversitesi, Fizik Bölümü Bilkent, 06800 Ankara ozbay@fen.bilkent.edu.tr, irfan@fen.bilkent.edu.tr,
Fotonik Kristallerin Fiziği ve Uygulamaları Ekmel Özbay, İrfan Bulu, Hümeyra Çağlayan, Koray Aydın, Kaan Güven Bilkent Üniversitesi, Fizik Bölümü Bilkent, 06800 Ankara ozbay@fen.bilkent.edu.tr, irfan@fen.bilkent.edu.tr,
LYS MATEMATİK DENEME - 1
 LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
1. BÖLÜM Polinomlar BÖLÜM II. Dereceden Denklemler BÖLÜM II. Dereceden Eşitsizlikler BÖLÜM Parabol
 ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
ANALİTİK GEOMETRİ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI
 ÖABT ANALİTİK GEOMETRİ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI Yasin ŞAHİN ÖABT ANALİTİK GEOMETRİ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI Her hakkı saklıdır. Bu kitabın tamamı ya da bir kısmı, yazarın izni olmaksızın,
ÖABT ANALİTİK GEOMETRİ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI Yasin ŞAHİN ÖABT ANALİTİK GEOMETRİ KONU ANLATIMLI ÇÖZÜMLÜ SORU BANKASI Her hakkı saklıdır. Bu kitabın tamamı ya da bir kısmı, yazarın izni olmaksızın,
DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİK KONTROL I Dr. Uğur HASIRCI
 KARARLILIK Kontrol sistemlerinin tasarımında üç temel kriter göz önünde bulundurulur: Geçici Durum Cevabı Kararlılık Kalıcı Durum Hatası Bu üç temel spesifikasyon arasında en önemlisi kararlılıktır. Eğer
KARARLILIK Kontrol sistemlerinin tasarımında üç temel kriter göz önünde bulundurulur: Geçici Durum Cevabı Kararlılık Kalıcı Durum Hatası Bu üç temel spesifikasyon arasında en önemlisi kararlılıktır. Eğer
Şekil-1. Doğru ve Alternatif Akım dalga şekilleri
 2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
Lys x 2 + y 2 = (6k) 2. (x 2k) 2 + y 2 = (2k 5) 2 olduğuna göre x 2 y 2 =? Cevap: 14k 2
 1. 1 =? Lys 1 7. x + y = (6k) (x k) + y = (k 5) olduğuna göre x y =?. 6 a.b = ise a + 1 b. b 1 a =? 1k 8. x ve y birbirinden farklı pozitif gerçel sayılar olmak üzere, x y y x. x.y = (x y) ise x y =?.
1. 1 =? Lys 1 7. x + y = (6k) (x k) + y = (k 5) olduğuna göre x y =?. 6 a.b = ise a + 1 b. b 1 a =? 1k 8. x ve y birbirinden farklı pozitif gerçel sayılar olmak üzere, x y y x. x.y = (x y) ise x y =?.
Enerji Sistemleri Mühendisliği Bölümü
 YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
Temel Matematik Testi - 5
 Test kodunu sitemizde kullanarak sonucunuzu öğrenebilir, soruların video çözümlerini izleyebilirsiniz. Test Kodu: 005. u testte 40 soru vardır.. Tavsiye edilen süre 40 dakikadır. Temel Matematik Testi
Test kodunu sitemizde kullanarak sonucunuzu öğrenebilir, soruların video çözümlerini izleyebilirsiniz. Test Kodu: 005. u testte 40 soru vardır.. Tavsiye edilen süre 40 dakikadır. Temel Matematik Testi
EĞİTİM - ÖĞRETİM YILI 10. SINIF MATEMATİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ
 EKİM 07-08 EĞİTİM - ÖĞRETİM YILI 0. SINIF MATEMATİK DERSİ 0... Olayların gerçekleşme sayısını toplama ve çarpma prensiplerini kullanarak hesaplar. 0... Sınırsız sayıda tekrarlayan nesnelerin dizilişlerini
EKİM 07-08 EĞİTİM - ÖĞRETİM YILI 0. SINIF MATEMATİK DERSİ 0... Olayların gerçekleşme sayısını toplama ve çarpma prensiplerini kullanarak hesaplar. 0... Sınırsız sayıda tekrarlayan nesnelerin dizilişlerini
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 1- GİRİŞ Doç. Dr. Ali Rıza YILDIZ 1 Mühendislikte, herhangi bir fiziksel sistemin matematiksel modellenmesi sonucu elde edilen karmaşık veya analitik çözülemeyen denklemlerin
MAK 210 SAYISAL ANALİZ BÖLÜM 1- GİRİŞ Doç. Dr. Ali Rıza YILDIZ 1 Mühendislikte, herhangi bir fiziksel sistemin matematiksel modellenmesi sonucu elde edilen karmaşık veya analitik çözülemeyen denklemlerin
Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir.
 1 DENKLEMLER: Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir. Bir denklemde eşitliği sağlayan(doğrulayan) değerlere; verilen denklemin kökleri veya
1 DENKLEMLER: Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir. Bir denklemde eşitliği sağlayan(doğrulayan) değerlere; verilen denklemin kökleri veya
MIT 8.02, Bahar 2002 Ödev # 11 Çözümler
 Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 11 Çözümler 15 Mayıs 2002 Problem 11.1 Tek yarıkta kırınım. (Giancoli 36-9.) (a) Bir tek yarığın genişliğini iki katına çıkarırsanız, elektrik
Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 11 Çözümler 15 Mayıs 2002 Problem 11.1 Tek yarıkta kırınım. (Giancoli 36-9.) (a) Bir tek yarığın genişliğini iki katına çıkarırsanız, elektrik
TEMEL MEKANİK 5. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
Otomatik Kontrol. Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri. Hazırlayan: Dr. Nurdan Bilgin
 Otomatik Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri Hazırlayan: Dr. Nurdan Bilgin Kapalı Çevrim Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri Tüm uygulamalar için aşağıdaki
Otomatik Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri Hazırlayan: Dr. Nurdan Bilgin Kapalı Çevrim Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri Tüm uygulamalar için aşağıdaki
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
Denklem (3.1) deki ikinci dereceden diferensiyel denklemin çözüm fonksiyonun + ve, gibi iki tane keyfi sabit vardır. Bu keyfi
 3. ÖZDEĞERLER VE ÖZVEKTÖRLER Özdeğerler ( karakteristik değerler) ve özvektörleri (karakteristik özvektörler), fiziksel bir sistemin sahi olabileceği özel değerlerde nasıl davrandıklarını belirlemek için
3. ÖZDEĞERLER VE ÖZVEKTÖRLER Özdeğerler ( karakteristik değerler) ve özvektörleri (karakteristik özvektörler), fiziksel bir sistemin sahi olabileceği özel değerlerde nasıl davrandıklarını belirlemek için
ANALİTİK GEOMETRİ ÇÖZÜMLÜ SORU BANKASI
 ÖABT ANALİTİK GEOMETRİ ÇÖZÜMLÜ SORU BANKASI Yasin ŞAHİN ÖABT ANALİTİK GEOMETRİ ÇÖZÜMLÜ SORU BANKASI Her hakkı saklıdır. Bu kitabın tamamı ya da bir kısmı, yazarın izni olmaksızın, elektronik, mekanik,
ÖABT ANALİTİK GEOMETRİ ÇÖZÜMLÜ SORU BANKASI Yasin ŞAHİN ÖABT ANALİTİK GEOMETRİ ÇÖZÜMLÜ SORU BANKASI Her hakkı saklıdır. Bu kitabın tamamı ya da bir kısmı, yazarın izni olmaksızın, elektronik, mekanik,
DEÜ MÜHENDİSLİK FAKÜLTESİ MÜHENDİSLİK BİLİMLERİ DERGİSİ Cilt: 13 Sayı: 3 sh Ekim 2011 KESİRLİ FOURIER DÖNÜŞÜMÜNÜN SİMETRİ ÖZELLİKLERİ
 DEÜ MÜHENDİSLİK FAKÜLTESİ MÜHENDİSLİK BİLİMLERİ DERGİSİ Cilt: 1 Sayı: sh. 5-61 Ekim 011 KESİRLİ FOURIER DÖNÜŞÜMÜNÜN SİMETRİ ÖZELLİKLERİ (SYMMETRY PROPERTIES OF THE FRACTIONAL FOURIER TRANSFORM) Olcay AKAY
DEÜ MÜHENDİSLİK FAKÜLTESİ MÜHENDİSLİK BİLİMLERİ DERGİSİ Cilt: 1 Sayı: sh. 5-61 Ekim 011 KESİRLİ FOURIER DÖNÜŞÜMÜNÜN SİMETRİ ÖZELLİKLERİ (SYMMETRY PROPERTIES OF THE FRACTIONAL FOURIER TRANSFORM) Olcay AKAY
7.2 Fonksiyon ve Fonksiyon Tanımları (I) Fonksiyon ve Fonksiyon Tanımları (II)
 7.2 Fonksiyon ve Fonksiyon Tanımları (I) Tanım kümesindeki her elemanın değer kümesinde bir ve yalnız bir görüntüsü varsa, tanım kümesinden değer kümesine olan bağıntıya fonksiyon denir. Fonksiyonu f ile
7.2 Fonksiyon ve Fonksiyon Tanımları (I) Tanım kümesindeki her elemanın değer kümesinde bir ve yalnız bir görüntüsü varsa, tanım kümesinden değer kümesine olan bağıntıya fonksiyon denir. Fonksiyonu f ile
İşaret ve Sistemler. Ders 1: Giriş
 İşaret ve Sistemler Ders 1: Giriş Ders 1 Genel Bakış Haberleşme sistemlerinde temel kavramlar İşaretin tanımı ve çeşitleri Spektral Analiz Fazörlerin frekans düzleminde gösterilmesi. Periyodik işaretlerin
İşaret ve Sistemler Ders 1: Giriş Ders 1 Genel Bakış Haberleşme sistemlerinde temel kavramlar İşaretin tanımı ve çeşitleri Spektral Analiz Fazörlerin frekans düzleminde gösterilmesi. Periyodik işaretlerin
Soru 1: Şekil-1 de görülen düzlem gerilme hali için: b) elemanın saat yönünde 30 0 döndürülmesi ile elde edilen yeni durum için elemana tesir
 Soru 1: Şekil-1 de görülen düzlem gerilme hali için: a) elemanın saat yönünde 30 0 döndürülmesi ile elde edilen yeni durum için elemana tesir eden gerilme bileşenlerini, gerilme dönüşüm denklemlerini kullanarak
Soru 1: Şekil-1 de görülen düzlem gerilme hali için: a) elemanın saat yönünde 30 0 döndürülmesi ile elde edilen yeni durum için elemana tesir eden gerilme bileşenlerini, gerilme dönüşüm denklemlerini kullanarak
( ) ( ) ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. Cevap D. Cevap C. noktası y ekseni üzerinde ise, a + 4 = 0 A 0, 5 = 1+
 ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. a+ = b 4. a = b 0+ a b a b = b a+ b = 0. A ( a + 4, a) noktası y ekseni üzerinde ise, ( + ) a + 4 = 0 A 0, 5 a = 4 B b, b 0 noktası x ekseni
ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. a+ = b 4. a = b 0+ a b a b = b a+ b = 0. A ( a + 4, a) noktası y ekseni üzerinde ise, ( + ) a + 4 = 0 A 0, 5 a = 4 B b, b 0 noktası x ekseni
H(s) B(s) V (s) Yer Kök Eğrileri. Şekil13. V s R s = K H s. B s =1için. 1 K H s
 Yer Kök Eğrileri R(s) K H(s) V (s) V s R s = K H s 1 K H s B s =1için B(s) Şekil13 Kapalı çevrim sistemin kutupları 1+KH(s)=0 özyapısal denkleminden elde edilir. b s H s = a s a s K b s =0 a s K b s =0
Yer Kök Eğrileri R(s) K H(s) V (s) V s R s = K H s 1 K H s B s =1için B(s) Şekil13 Kapalı çevrim sistemin kutupları 1+KH(s)=0 özyapısal denkleminden elde edilir. b s H s = a s a s K b s =0 a s K b s =0
1986 ÖYS. 1. Aşağıdaki ABC üçgeninde. BD kaç cm dir? C) 3 A) 11 B) 10 C) 3 D) 8 E) 7 E) 2
 8 ÖYS. Aşağıdaki ABC üçgeninde. BD kaç cm dir? 8 7. Aşağıdaki şekilde ABCD bir yamuk ve AECD bir paralel kenardır.. Aşağıdaki şekilde EAB ve FBC eşkenar üçgendir. AECD nin alanı 8 cm Buna göre CEB üçgeninin
8 ÖYS. Aşağıdaki ABC üçgeninde. BD kaç cm dir? 8 7. Aşağıdaki şekilde ABCD bir yamuk ve AECD bir paralel kenardır.. Aşağıdaki şekilde EAB ve FBC eşkenar üçgendir. AECD nin alanı 8 cm Buna göre CEB üçgeninin
Toplam İkinci harmonik. Temel Üçüncü harmonik. Şekil 1. Temel, ikinci ve üçüncü harmoniğin toplamı
 FOURIER SERİLERİ Bu bölümde Fourier serilerinden bahsedeceğim. Önce harmoniklerle (katsıklıklarla) ilişkili sinüsoidin tanımından başlıyacağım ve serilerin trigonometrik açılımlarını kullanarak katsayıları
FOURIER SERİLERİ Bu bölümde Fourier serilerinden bahsedeceğim. Önce harmoniklerle (katsıklıklarla) ilişkili sinüsoidin tanımından başlıyacağım ve serilerin trigonometrik açılımlarını kullanarak katsayıları
HATA VE HATA KAYNAKLARI...
 İÇİNDEKİLER 1. GİRİŞ... 1 1.1 Giriş... 1 1.2 Sayısal Analizin İlgi Alanı... 2 1.3 Mühendislik Problemlerinin Çözümü ve Sayısal Analiz... 2 1.4 Sayısal Analizde Bilgisayarın Önemi... 7 1.5 Sayısal Çözümün
İÇİNDEKİLER 1. GİRİŞ... 1 1.1 Giriş... 1 1.2 Sayısal Analizin İlgi Alanı... 2 1.3 Mühendislik Problemlerinin Çözümü ve Sayısal Analiz... 2 1.4 Sayısal Analizde Bilgisayarın Önemi... 7 1.5 Sayısal Çözümün
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
MUKAVEMET I ÇÖZÜMLÜ ÖRNEKLER
 MUKAEMET I ÇÖZÜMÜ ÖRNEKER ders notu Yard. Doç. Dr. Erdem DAMCI Şubat 15 Mukavemet I - Çözümlü Örnekler / 7 Örnek 1. Üzerinde yalnızca yayılı yük bulunan ve açıklığı olan bir basit kirişe ait eğilme momenti
MUKAEMET I ÇÖZÜMÜ ÖRNEKER ders notu Yard. Doç. Dr. Erdem DAMCI Şubat 15 Mukavemet I - Çözümlü Örnekler / 7 Örnek 1. Üzerinde yalnızca yayılı yük bulunan ve açıklığı olan bir basit kirişe ait eğilme momenti
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
BÖLÜM 16 KUANTUM : AYRILABİLEN SİSTEMLER
 BÖLÜM 16 KUANTUM : AYRILABİLEN SİSTEMLER Farklı eksenlere karşılık gelen operatörler, komut verilerek birbiriyle komute olabilir. Ayrıca, bir değişken için olan operatör, başka bir operatörün fonksiyonu
BÖLÜM 16 KUANTUM : AYRILABİLEN SİSTEMLER Farklı eksenlere karşılık gelen operatörler, komut verilerek birbiriyle komute olabilir. Ayrıca, bir değişken için olan operatör, başka bir operatörün fonksiyonu
Tek Boyutlu Potansiyeller: Potansiyel eşiği
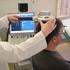 Tek Boyutlu Potansiyeller: Potansiyel eşiği Şekil I: V 0 yüksekliğindeki potansiyel eşiği. Parçacık soldan gelmekte olup, enerjisi E dir. Zamandan bağımsız bir durumu analiz ediyoruz ki burada iyi belirlenmiş
Tek Boyutlu Potansiyeller: Potansiyel eşiği Şekil I: V 0 yüksekliğindeki potansiyel eşiği. Parçacık soldan gelmekte olup, enerjisi E dir. Zamandan bağımsız bir durumu analiz ediyoruz ki burada iyi belirlenmiş
25. KARARLILIK KAPALI ÇEVRİM SİSTEMLERİNİN KARARLILIK İNCELENMESİ
 25. KARARLILIK KAPALI ÇEVRİM SİSTEMLERİNİN KARARLILIK İNCELENMESİ a-) Routh Hurwitz Kararlılık Ölçütü b-) Kök Yer Eğrileri Yöntemi c-) Nyquist Yöntemi d-) Bode Yöntemi 1 2 3 4 a) Routh Hurwitz Kararlılık
25. KARARLILIK KAPALI ÇEVRİM SİSTEMLERİNİN KARARLILIK İNCELENMESİ a-) Routh Hurwitz Kararlılık Ölçütü b-) Kök Yer Eğrileri Yöntemi c-) Nyquist Yöntemi d-) Bode Yöntemi 1 2 3 4 a) Routh Hurwitz Kararlılık
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH
 OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
ELASTİK DALGA YAYINIMI
 18.0.016 ELASTİK DALGA YAYINIMI Prof.Dr. Eşref YALÇINKAYA (016-1. DERS 1 Zaman ve Yer Ders saati : 10:0 13:00 Ara : 11:15 11:30 Ders yeri : D-331 1 18.0.016 Sizden beklenen Derse devamın sağlanması çok
18.0.016 ELASTİK DALGA YAYINIMI Prof.Dr. Eşref YALÇINKAYA (016-1. DERS 1 Zaman ve Yer Ders saati : 10:0 13:00 Ara : 11:15 11:30 Ders yeri : D-331 1 18.0.016 Sizden beklenen Derse devamın sağlanması çok
HARMONİK DENKLEM. Burada göz önüne alınacak problem Dirichlet problemidir; yani fonksiyonun sınırda kendisinin verilmesi halidir. 2 2 (15.
 HARMONİK DENKLEM Harmonik denklemin sağ tarafının sıfır olması haline Laplace, sağ tarafının sıfır olmaması haline de Possion denklemi adı verilir. Possion ve Laplace denklemi, kısaca harmonik denklem
HARMONİK DENKLEM Harmonik denklemin sağ tarafının sıfır olması haline Laplace, sağ tarafının sıfır olmaması haline de Possion denklemi adı verilir. Possion ve Laplace denklemi, kısaca harmonik denklem
Akışkan Kinematiği 1
 Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
3. TAHMİN En Küçük Kareler (EKK) Yöntemi 1
 3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
FZM 220. Malzeme Bilimine Giriş
 FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Bölüm 2. İşaretler ve Doğrusal Sistemler
 Bölüm 2 İşaretler ve Doğrusal Sistemler 2.1 TEMEL KAVRAMLAR 2.1.1 İşaret Üzerinde Temel İşlemler 2.1.2.İşaretlerin Sınıflandırılması 2.1.3 Bazı Önemli İşaretler ve Özellikleri 2.1.4. Sistemlerin Sınıflandırılması
Bölüm 2 İşaretler ve Doğrusal Sistemler 2.1 TEMEL KAVRAMLAR 2.1.1 İşaret Üzerinde Temel İşlemler 2.1.2.İşaretlerin Sınıflandırılması 2.1.3 Bazı Önemli İşaretler ve Özellikleri 2.1.4. Sistemlerin Sınıflandırılması
Şekil 1. DEÜ Test Asansörü kuyusu.
 DOKUZ EYLÜL ÜNĐVERSĐTESĐ TEST ASANSÖRÜ KUYUSUNUN DEPREM YÜKLERĐ ETKĐSĐ ALTINDAKĐ DĐNAMĐK DAVRANIŞININ ĐNCELENMESĐ Zeki Kıral ve Binnur Gören Kıral Dokuz Eylül Üniversitesi, Mühendislik Fakültesi, Makine
DOKUZ EYLÜL ÜNĐVERSĐTESĐ TEST ASANSÖRÜ KUYUSUNUN DEPREM YÜKLERĐ ETKĐSĐ ALTINDAKĐ DĐNAMĐK DAVRANIŞININ ĐNCELENMESĐ Zeki Kıral ve Binnur Gören Kıral Dokuz Eylül Üniversitesi, Mühendislik Fakültesi, Makine
ATATÜRK ANADOLU LİSESİ MATEMATİK. Karmaşık Sayılar Üzerine Kısa Çalışmalar
 ATATÜRK ANADOLU LİSESİ MATEMATİK Karmaşık Sayılar Üerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 KARMAŞIK SAYILAR. Karmaşık Sayılar Kavramı Denklemlerin, baı kümelerde çöümleri bulunmamaktadır. x 5 0 denkleminin
ATATÜRK ANADOLU LİSESİ MATEMATİK Karmaşık Sayılar Üerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 KARMAŞIK SAYILAR. Karmaşık Sayılar Kavramı Denklemlerin, baı kümelerde çöümleri bulunmamaktadır. x 5 0 denkleminin
