ANALYSİS OF THE EFFECTS OF DİFFERENT SLACK BUS SELECTİON ON THE OPTİMAL POWER FLOW
|
|
|
- Ömer Saylan
- 6 yıl önce
- İzleme sayısı:
Transkript
1 FARKLI SALINIM BARASI SEÇİMLERİNİN OPTİMAL GÜÇ AKIŞI ÜZERİNDEKİ ETKİLERİNİN İNCELENMESİ Serdar ÖZYÖN Celal YAŞAR ÖZET Günümüzde enerjiye olan ihtiyacın artmasına bağlı olarak enerji sistemlerinin büyümesi, işletilmelerini daha karmaşık hale getirmektedir. Büyük boyutlu enerji sistemlerinin optimal işletilmesi, optimal planlamayı gerektirmektedir. Bu sistemlerin verimsiz bir şekilde planlanması ve işletilmesi hem büyük elektriksel kayıplara hem de büyük maddi kayıplara neden olmaktadır. Bu nedenle bu tip problemleri içeren optimal yük akışı problemi son zamanlarda çok çalışılan problem olarak öne çıkmaktadır. Genel bir kural olarak optimal yük akışı problemlerinde salınım barası, generatör baraları veya daha fazla sayıda hattın bir araya geldiği baralar arasından seçilmektedir. Bu seçim tamamen tecrübeye dayalı olup bazı durumlarda yakınsamayı büyük ölçüde etkilemektedir. Yapılan çalışmada farklı salınım barası seçimlerinin generatör baralarındaki optimal güç değerleri, hat kayıpları ve üretim maliyetleri üzerine etkileri incelenmiştir. Optimal yük akışı probleminin çözümü için sezgisel algoritmalardan biri olan Diferansiyel Gelişim Algoritması (DGA), Newton-Raphson yöntemi ile birlikte kullanılmıştır. Örnek uygulama olarak IEEE 30 baralı generatörlü sistem seçilmiştir. Farklı farklı seçilen salınım baraları için, generatörlerin optimal güç üretimleri, iletim hattı kayıpları, üretim maliyetleri hesaplanmış ve elde edilen sonuçlar tartışılmıştır. Anahtar Kelimeler: Optimal güç akışı, Salınım barası seçimi, Diferansiyel gelişim algoritması. ANALYSİS OF THE EFFECTS OF DİFFERENT SLACK BUS SELECTİON ON THE OPTİMAL POWER FLOW ABSTRACT Today the growth of energy systems due to the increase in the need of energy makes it more complicated to operate them. The optimum operation of the big-size energy systems requires optimum planning. The inefficient planning and operation of these systems cause both big electrical losses and big economical losses. Therefore, optimal load flow problem including this type of problems comes into prominence as the most studied problem recently. As a general rule, the slack bus is selected from among generator buses or buses in which greater number of lines come together. This selection depending totally on experience affects the convergence highly in some cases. In this study, the effects of the selection of different slack bus on the optimum power values in generator buses, line losses and the generation costs have been analyzed. The optimal load flow of the energy system has been done by using Differential Evolution algorithm, which is one of the meta-heuristic algorithms, together with Newton-Raphson method. The IEEE system with 30 buses and generators has been selected as the sample system. For differently selected slack buses, optimum power generation of the generators, transmission line losses, generation costs have been calculated and the obtained results have been discussed. Keywords: Optimal load flow, The selection of slack bus, Differential evolution algorithm. Giriş Fosil kaynaklı yakıtlar elektrik enerjisi üretimi için kullanılan en önemli kaynaklardır. Bu kaynakların giderek azalması, enerji üretiminin mümkün olan minimum maliyetlerle yapılmasını önemli bir problem haline getirmiştir. Optimal yük akışı problemi bütün eşitlik ve eşitsizlik kısıtları altında sistemin amaç fonksiyonu olan enerji üretim maliyetinin optimal değerini bulma problemidir. Bu optimizasyon probleminin çözümü araştırılırken problemin değişkenleri durum ve kontrol değişkenleri şeklinde tanımlanır. Durum değişkenleri olarak salınım barasının aktif çıkış gücü, yük baralarının gerilim genlik değerleri ve generatör baralarının reaktif çıkış güçleri alınmaktadır. Kontrol değişkenleri olarak ise, salınım barası hariç diğer generatör baralarının aktif çıkış güçleri, generatör baralarının gerilim genlik değerleri, transformatör kademe değerleri ve şönt kapasite değerleri alınmaktadır [Ayan ve Kılıç 0, Cabadag vd. 0]. Optimal yük akışı problemleri sayısal ve sezgisel metotlar olmak üzere iki farklı yapıdaki metotlarla çözülmektedir. Sayısal metotlar başlangıç noktasına bağlı olarak yerel minimuma takılma problemi yaşarken, sezgisel metotlar genel minimumu veya genel minimuma yakın optimum çözümleri daha kolay elde edebilmektedir [Özyön 009]. Arş. Gör., Dumlupınar Üniversitesi, serdar.ozyon@dpu.edu.tr Doç. Dr., Dumlupınar Üniversitesi, celal.yasar@dpu.edu.tr 0
2 Genel bir kural olarak optimal yük akışı problemlerinde salınım barası, generatör baraları veya daha fazla sayıda hattın bir araya geldiği baralar arasından seçilmektedir. Bu seçim tamamen tecrübeye dayalı olup bazı durumlarda yakınsamayı büyük ölçüde etkilemektedir [Ayan ve Kılıç 0, Cabadag vd. 0]. Literatürde çeşitli optimal güç akışı problemlerine birçok farklı algoritmayla çözümler aranmıştır. Bunlardan bazıları genetik algoritma (GA) [Osman vd. 00], diferansiyel gelişim algoritması (DGA) [Abou vd. 00, Özyön vd. 0], parçacık sürüsü optimizasyonu (PSO) [Abido, 00], harmoni arama algoritması (HAA) [Özyön vd. 0] ve yapay arı koloni optimizasyon algoritması (YAKOA) [Xuanhu vd. 0, Dinh vd. 03] olarak belirtilebilir. Çalışılan örnek sistemlerde genel olarak, sistemdeki birinci bara salınım barası olarak seçilerek çözümler elde edilmiştir. Literatürde farklı salınım barası seçimlerinin güç sistemlerinin gerilim kararlılığı ve sistem bileşenleri üzerindeki etkileri gibi olayları incelemek üzere farklı çalışmalar yapılmıştır [Abacı vd. 00, 00, 007]. Bu çalışmada ekonomik güç dağıtımı probleminin amaç fonksiyonu olan yakıt maliyetinin optimizasyonundan çok, sistemde yer alan generatör baralarından hangisinin salınım barası olarak belirlenmesi daha uygun olur sorusuna cevap aranmıştır. Farklı salınım barası seçimlerinin termik sistemin toplam yakıt maliyeti, generatör baralarındaki güç üretimleri ve iletim hattı kayıpları üzerine etkileri incelenmiştir. Örnek olarak IEEE 30 baralı generatörlü sistem belirlenmiştir. Sistemdeki iletim hattı kayıplarının belirlenmesi için Newton-Raphson (NR) yöntemi ile güç akışı yapılmış ve yakıt maliyeti minimizasyonu için Diferansiyel Gelişim algoritması (DGA) kullanılmıştır. Altı farklı generatör barası, sırayla salınım barası olarak belirlenmiş ve sistem çözülmüştür. Elde edilen sonuçlar değerlendirilmiştir. Problemin Formülasyonu Çalışmada sadece termik üretim birimlerinden oluşan bir sistem seçilmiştir. Termik üretim birimlerin giriş-çıkış eğrisi saat başına harcanan paranın aktif çıkış gücüne göre değişimi şeklinde tanımlanmıştır. Şekil de termik üretim birimlerinin ait giriş-çıkış eğrisi verilmiştir [Özyön 009]. F T (R/h) P min P max P (MW) Şekil. Termik üretim birimlerine ait giriş-çıkış eğrisi Sistemdeki üretim birimlerinin termik maliyetleri, birimlerin çıkış gücü cinsinden. derece fonksiyon olarak denklem () de verildiği gibi alınmıştır. F ( P ) a b. P c. P ( R / h) () n GT, n n n GT, n n GT, n Denklemde ( GT, n) olarak alınmaktadır. Termik maliyet ( ), birimin saat başına aktif güç üretiminin, sanal bir para birimi ( R ) olarak yakıt maliyetini ifade etmektedir. Kayıplı sistemdeki güç denge eşitlik kısıtı denklem () de gösterilmiştir. P nin birimi MW PGT, n Pyük Pkayıp 0, n NT () n NT Denklemdeki N T termik üretim birimleri kümesini göstermektedir. Termik üretim birimlerinin aktif güç üretim sınırlarını veren eşitsizlik kısıtı denklem (3) de verilmiştir. min max PGT, n PGT, n PGT, n, n NT (3) F n n. DGA ile minimize edilecek olan amaç fonksiyonu, elektrik güç sisteminin toplam yakıt maliyet fonksiyonu ( TYMF ) denklem () de verilmiştir. 09
3 TYMF F ( P ), ( R / h) () n NT n GT, n Diferansiyel Gelişim Algoritması (Dga) Ve Probleme Uygulanması DGA, 99 yılında geliştirilen işleyişi genetik algoritmaya dayanan popülasyon temelli sezgisel bir optimizasyon tekniğidir. Sürekli parametreli problemlerin çözümünde oldukça etkilidir. Algoritma popülasyona dayalı çalışmayıp, tek tek kromozomlar operatörlere tabi tutularak yeni bir birey elde edilir. Bu işlem sırasında mutasyon ve çaprazlama operatörleri kullanılır. Yeni bireyin uygunluğu eskisinden daha iyi ise yeni birey, aksi takdirde eski birey bir sonraki popülasyona aktarılır [Abou vd. 00, Özyön vd. 0]. DGA da kullanılan parametreler; popülasyon büyüklüğü NP, değişken sayısı (gen sayısı) D, nesil (jenerasyon) (,,3,.,gmax) g, çaprazlama oranı CR ve ölçekleme faktörü F şeklinde gösterilir. DGA nın işlem basamakları kodlama, mutasyon, çaprazlama ve seçim olarak belirtilebilir. DGA da yeni kromozomların üretilmesi için mevcut kromozom dışında üç adet kromozom daha gereklidir. Bu nedenle popülasyon büyüklüğü üçten büyük olmalıdır (NP>3). NP adet D boyutlu kromozomdan meydana gelen başlangıç popülasyonunun üretimi denklem () kullanılarak bulunur [Abou vd. 00, Özyön vd. 0]. x x rand x x () ( l) ( u) ( l) j, i, g 0 j j[0,].( j j ) Denklemde xj,i,g, g neslindeki i kromozomunun j parametresini, ( l) ( u) ( xj, xj ) değişkenlere ait alt ve üst değerleri göstermektedir. Mutasyon, kromozomun genleri üzerinde rastgele değişiklikler yapmaktır. DGA da mutasyona tabi tutulmak için kromozom dışında ve birbirlerinden farklı olan üç kromozom seçilir. İlk ikisinin farkı alınır ve F ile çarpılır. F genellikle 0~ arasında değişen bir değer alınmaktadır. Ağırlıklandırılmış fark kromozomu ile üçüncü kromozom toplanır. n x F.( x x ) () j, i, g j, r3, g j, r, g j, r, g Denklemde n j, i, g mutasyon ve çaprazlaştırmaya tabi tutulmuş ara kromozom, x j, r, g, x j, r, g kromozom üretilmesinde kullanılacak rastgele seçilmiş kromozomları r NP, ve x j, r 3, g,,3,,3,,, r r r 3 i göstermektedir. Mutasyon sonucunda elde edilen fark kromozomu ve xi,g kromozomu kullanılarak yeni kromozom ( uig, ) üretilir. Deneme kromozomu için genler CR olasılıkla fark kromozomundan, (-CR) olasılıkla mevcut kromozomdan seçilir. j j koşulu, en az bir tane genin üretilen yeni kromozomdan alınmasını rand garanti etmek için kullanılmaktadır. Rastgele seçilen n j, i, g den seçilir [Abou vd. 00, Özyön vd. 0]. x j, u, g x j, n, g eğer rand[0,] CR veya j j x j,, i g aksi durumda j j noktasındaki gen CR değerine bakılmaksızın rand Mutasyon ve çaprazlama operatörleri kullanılarak hedef kromozomla birlikte üç farklı kromozom kullanılarak yeni bir kromozom (deneme kromozu) elde edilmiştir. Yeni nesile ( g g ) aktarılacak olan kromozom uygunluk değerine bakılarak belirlenir. Hedef kromozun uygunluk değeri zaten bilinmektedir. Problemin amaç fonksiyonu değeri uygunluk fonksiyonu olarak hesaplanır. Kromozomlardan uygunluğu yüksek olan kromozom yeni nesile aktarılır. Döngü (g=gmax) olana kadar devam eder, gmax olduğunda mevcut en iyi birey çözüm olarak alınır. x ig, x u, g eğer f ( xu, g ) f ( xi, g ) x ig, diğer durumlarda Algoritmada amaç sürekli daha iyi uygunluk değerine sahip kromozomlar elde etmek ve optimum değeri yakalamak ya da yaklaşmaktır. Bu döngü g g olana kadar devam ettirilir. Algoritmanın max durdurulması belirlenen maksimum iterasyon sayısına bağlıdır. Çalışmada iterasyon sayısı 00 olarak alınmıştır. Genel olarak yukarıda anlatılan adımlardan oluşan DGA nın ekonomik güç dağıtım problemlerine uygulanması Şekil de verilen akış diyagramında özetlenmiştir. rand yeni (7) () 0
4 DGA Parametrelerini gir Salınım Barasını Belirle. Rastgele birey oluştur. (Salınım barası hariç) NR ile Yük akışı yap. Kayıpları ve Salınım Barası Değerlerini Hesapla. Bireyi Popülasyona Kat. Birey sayısı = Birey sayısı+ Hayır Popülasyondaki birey sayısı tamamlandı mı? Evet İlk popülasyonu oluştur Bireylerin toplam yakıt maliyetlerini hesapla. Evet Durma Kriteri sağlanıyor mu? Hayır Popülasyondaki en iyi çözümü yazdır. Bireyleri seç. DUR Çaprazlama ve Mutasyon İşlemleriyle yeni bireyi oluştur. Popülasyondaki Bireylerin toplam yakıt maliyetlerini hesapla. NR ile Yük akışı yap. Kayıpları ve Salınım Barası Değerlerini Hesapla. Bireyi Popülasyona Kat. Birey sayısı = Birey sayısı+ Popülasyon sayısı = Popülasyon sayısı+ Evet Popülasyondaki birey sayısı tamamlandı mı? Hayır Şekil. DGA nın probleme uygulanmasının akış diyagramı Akış diyagramında verilen adımlar, örnek sistemde yer alan üretim birimlerinden, sırasıyla seçilen her farklı salınım barası için ayrı ayrı uygulanmıştır. Çözüm metodu, başlangıç parametreleri belirlendikten sonra, denklem (9) a göre rastgele oluşturulan bireylerle doldurulan popülasyonla ilk iterasyona başlar. P P U(0,) ( P P ) (9) min max min GT, n GT, n GT, n GT, n Denklemde U (0,) sıfırla bir arasında düzgün dağılmış rastgele sayıdır. Daha sonraki adımlar, belirlenen maksimum iterasyon sayısı bitinceye kadar devam eder. Maksimum iterasyon sayısı tamamlandıktan sonra popülasyondaki en iyi toplam yakıt maliyetine sahip birey problemin çözümü olarak alınır. Örnek Sistemin Çözümü Farklı salınım barası seçimlerinin optimal güç akışı üzerine etkilerinin incelenmesi için Şekil 3 te tek hat diyagramı verilen IEEE 30 baralı generatörlü güç sistemi seçilmiştir. Test sisteminde adet iletim hattı ve adet yük barası bulunmaktadır [Xuanhu vd. 0]. Sistemdeki transformatörlerin kademe ayarları olarak alınmıştır. Çalışmada kullanılan baz değerler Sbaz=00 MVA, Vbaz=30 kv ve Zbaz=9 Ohm dur. Bu sistem literatürde bütün çalışmalarda. baraya bağlı G generatörü salınım barası olarak seçilmiştir. Bu çalışmada örnek sistem DGA ile iletim hattı kayıpları dikkate alınarak çözülmüştür. Salınım barasının aktif ve reaktif güç üretim değerleri ve iletim hattı kayıpları Newton Raphson metoduyla yük akışı yapılarak bulunmuştur. Sistemde generatör bulunduğundan her defasında farklı bir üretim biriminin bağlı olduğu bara salınım barası olarak belirlenerek farklı çözüm yapılmıştır.
5 Şekil 3. IEEE 30 bara generatörlü örnek sistemin tek hat diyagramı Örnek sistemdeki termik üretim birimlerinin yakıt maliyeti fonksiyonlarına ait katsayılar ve aktif güç üretim limitleri Tablo de, İletim hatlarının nominal eşdeğer devrelerine ait pu seri empedans ve paralel admitans değerleri Tablo de, yük baralarındaki aktif ve reaktif yük değerleri Tablo 3 de ve sistemdeki üretim birimlerine ait başlangıç reaktif güç üretim değerleri Tablo te verilmiştir [Özyön 009]. Tablo. Örnek sistemdeki termik üretim birimlerinin yakıt maliyeti fonksiyonlarına ait katsayılar ve aktif güç üretim limitleri Katsayılar ve Üretim birimlerinin bağlı olduğu bara no, (n) Üretim Limitleri G G G G G G3 a b c P, (pu) 0,0 0,0 0,0 0,0 0,0 0,0 min GT n max P GT, n (pu),,,,,, Tablo. İletim hatlarının nominal eşdeğer devrelerine ait pu seri empedans ve paralel admitans değerleri Baradan Baradan R (pu) X (pu) B (pu) baraya baraya R (pu) X (pu) B (pu) - 0,09 0,07 0,0-3 0,0000 0, ,0 0, 0,00-0,3 0,9 0-0,070 0,737 0,03-0,0 0,30 0-0,07 0,93 0,0-0,09 0,97 0-0,0 0,73 0,07-0,0 0, ,03 0,0379 0,00-0,070 0, 0-0,09 0,0 0, ,000 0, , 0-7 0,0 0, ,00 0,0 0,00-9 0,039 0,9 0
6 -7 0,07 0,00 0, ,030 0,00 0-0,00 0,00 0,09-0,0 0, ,0000 0,00 0-0,0 0, ,0000 0, ,30 0, ,09 0,099 0,03-0, 0,39 0-0,03 0,000 0,0-0, 0, ,0000 0, ,093 0, ,0000 0, ,9 0, ,03 0, ,30 0, ,093 0, ,0000 0, ,03 0, ,399 0, ,077 0,99 0 Tablo 3. Örnek sistemde aktif ve reaktif yük değerleri Bara Bara P (pu) Q (pu) no no P (pu) Q (pu) 0,7 0,7 7 0,090 0,0 3 0,0 0,0 0,03 0,009 0,07 0,0 9 0,09 0,03 0,9 0,90 0 0,0 0, , 0,09 0,7 0, 0,300 0, ,03 0,0 0 0,0 0,00 0,07 0,07 0, 0,07 0,03 0,03 0,03 0,0 9 0,0 0,009 0,0 0,0 30 0,0 0,09 0,0 0,0 TOPLAM,3, Tablo. Sistemdeki üretim birimlerine ait başlangıç reaktif güç üretim değerleri Üretim birimlerini no, (n) Q bas GT, n (pu) G G G G G G3 0,00 0,00 0,00 0,00 0,00 0,00 Örnek sistemin Tablo 3 teki yük talebi için DGA ile farklı salınım barası için çözümleri yapılmıştır. Yapılan çözümlerde sırasıyla G, G, G, G, G ve G3 generatörlerinin bağlı olduğu baralar salınım barası olarak alınmıştır. DGA nın problemi çözüm aşamasında, nolu baranın salınım barası seçilmesi durumunda, toplam yakıt maliyetinin iterasyon sayısına göre değişimi Şekil de, toplam iletim hattı kaybının iterasyon sayısına göre değişimi Şekil te ve üretim birimlerinin aktif güç çıkışlarının iterasyon sayısına göre değişimleri Şekil da verilmiştir. 3
7 Şekil. Toplam yakıt maliyetinin iterasyon sayısına göre değişimi Şekil. Aktif güç üretimlerinin iterasyon sayısına göre değişimleri Şekil. Toplam iletim hattı kaybının iterasyon sayısına göre değişimleri
8 Şekil ten toplam yakıt maliyetinin 30. iterasyondan sonra minimum maliyet değerini ( R/h) yakaladığı görülmektedir. Şekil te verilen generatör çıkış güçlerinin 30. iterasyona göre çok fazla değişim gösterdiği fakat daha sonra belli bir aralıkta oynadığı 70. iterasyondan itibaren ise bütün üretim birimlerinin optimum değerlerini yakaladıkları söylenebilir. Şekil dan görüldüğü gibi iletim hatlarındaki güç kaybının değişimi ise yaklaşık. iterasyondan sonra sabitlenmiş ve 0.0 pu değerine oturmuştur. Salınım barası olarak diğer üretim birimlerinin bağlı olduğu baralar alındığında bu değişimlerin benzer şekillerde değiştiği gözlenmiştir. Farklı salınım barası seçimlerine göre yapılan çözümlerde elde edilen üretim birimlerinin çıkış güçleri, toplam yakıt maliyeti, iletim hattı kayıp miktarları ve çözüm süreleri Tablo te, salınım barasına ait reaktif güç üretim değerleri ve sistemdeki bütün (30 bara) baralara ait gerilim aralıkları ise Tablo da verilmiştir. Seçilen Salınım Barası 3 Tablo. Farklı salınım barası seçimlerine göre üretim birimlerinin çıkış güçleri, toplam yakıt maliyeti ve iletim hattı kayıp miktarları Üretim birimlerinin çıkış güçleri, (pu) Çözüm TYMF Pkayıp Süresi PGT, PGT, PGT, PGT, PGT, PGT,3 (R/h) (pu) (sn) 0, 0, 0,77 0,33 0,9 0,0 0,3070 0,90 3 0,97 0, ,99 0, ,990 0,0 0,337 0, ,07 9 0, ,9 0,930 0,9937,07,000,0 3 0,0 0,0 0,70 0,79 0,0 7 0, 7 0,3 0,373 0,37 0 0,3377 0,390 0,370 0, ,3,77 0,7 9 0, ,73 7 0,0,3903 0,0397,3 0,00,3703 0,03,70 0,07,993 0,000,309 Tablo. Salınım baralarının reaktif güç çözüm değerleri ve Sistemdeki tüm baraların gerilim aralıkları Seçilen salınım bara no, (n) Q çözüm GT n min n, (pu) 3 0,30 0,777 0,7 0, 7 7 0,39 0,70 V (pu) 0,93 0,93 0,9 0,9 0,9 0,93 V (pu),0,0,0,0,0,0 max n Tablo incelendiğinde bütün generatör baraları salınım barası olarak seçildiğinde bütün çözümlerde yakınsama sağlanmıştır. Ayrıca optimal güç akışı probleminde farklı salınım barası seçimlerinin generatörler tarafından üretilen aktif güç üretimlerini etkilediğinden dolayı, bu seçimin iletim hattı kayıpları ve toplam yakıt maliyeti üzerinde etkili olduğu görülmüştür. Seçilen örnek sitemde sırasıyla seçilen salınım baralarından 3. barada hem minimum iletim hattı kaybı hem de minimum toplam yakıt maliyeti elde edilmiştir. Algoritmanın çözüm süresine bakıldığında ise ortalama, sn de çözüme ulaşılmaktadır. Tablo da seçilen salınım baraları tarafından üretilen reaktif güçlerin sistem kısıtlarını sağlamış olmasının yanında, sistemdeki bütün bara gerilimlerinin 0,9-,0 pu aralığında olduğu gözlenmiştir. Salınım barası seçimi yapılırken bu değerin yanısıra daha fazla hattın bir araya geldiği baralar tercihi önemlidir. Bu nedenle bu sistemde bütün şartları sağlaması açısından sırasıyla,, ve nolu baraların salınım barası olarak seçilmesi daha uygundur. En düşük kayıp ve maliyeti sağlamasına rağmen. ve 3. baralar sisteme sadece bir hat üzerinden bir diğer baraya bağlı olmaları nedeniyle salınım barası olarak seçilmesi uygun olmadığı söylenebilir. Sonuçlar Çalışmada farklı salınım barası seçimlerinin generatörlerin aktif güç üretimleri, iletim hattı kayıpları ve sistemin toplam yakıt maliyeti üzerinde etkileri incelenmiştir. Örnek sistem üzerinde farklı salınım baraları için NR ile yük akışı, DGA ile yakıt maliyeti minimizasyonu yapılarak iletim hatlarındaki kayıplar, reaktif güç üretimleri ve bara gerilimleri bulunmuştur. Çalışmada bütün çözümlerde güç akışında yakınsamalar
9 sağlanmıştır. Farklı salınım barası seçiminin optimal güç akışını etkilediği bulunan değerlerden gözlemlenmiştir. Çalışmada bütün çözümlerde tüm baraların gerilim genlikleri kabul edilebilir sınırlar arasında kalmıştır. Sonraki çalışmalarda sistemdeki hat taşıma kapasiteleri, yasak işletim bölgeleri yada valf noktası etkileri gibi kısıtlarda probleme katılarak konu daha detaylı olarak incelenebilir. Referanslar Abacı K., Yalçın M.A., Uyaroğlu Y. (007), Farklı Salınım Barası Seçiminde Kademe Değiştirici Transformatörlerin Gerilim Kararlılığına Etkisi, II. Enerji Verimliliği ve Kalitesi Sempozyumu (EVK007), Sayfa 9-300, Kocaeli. Abacı, K., Yalçın M.A., Uyaroğlu Y. (00), Seri Kompanzasyonda Farklı Salınım Barası Seçiminin Sürekli Hal Gerilim Kararlılığına Etkileri, I. Enerji Verimliliği ve Kalitesi Sempozyumu (EVK00), Sayfa -, Kocaeli. Abacı, K., Yalçın, M.A., Uyaroğlu, Y. (00), Güç Sistemlerinde Farklı Salınım Barası Seçiminin Gerilim Kararlılığı Açısından İncelenmesi, Elektrik-Elektronik-Bilgisayar Mühendisliği Sempozyumu (ELECO00), Sayfa 79-3, Bursa. Abido, M.A., (00), Optimal power flow using particle swarm optimization, International Journal of Electrical Power & Energy Systems,, 3-7. Abou A.A., Abido M.A., Spea S.R., Differential evolution algorithm for emission constrained economic power dispatch problem, Electric Power Systems Research 0, s.-9, 00. Ayan, K., Kılıç, U. (0), Optimal Güç Akışı Probleminin Çözümü için GA, MA ve YAK Algoritmalarının Karşılaştırılması, th International Advanced Technologies Symposium (IATS ), - May 0, Electrical & Electronics Technologies Papers, Vol., pp.3-, Elazığ, TURKEY. Cabadağ, R.I., Türkay, B.E., Tunç, A. (0), Optimal Güç Akışı Çözümlerinde Lineer Programlama ve İç nokta Algoritması Yöntemlerinin Karşılaştırmalı Analizi, II. Elektrik Tesisat Ulusal Kongresi, -7 Kasım 0, İzmir, (Erişim tarihi :07.0.0). Dinh, L.L., Ngoc, D.V., Vasant, P. (03), Artificial Bee Colony Algorithm for Solving Optimal Power Flow Problem, The ScientificWorld Journal, 03, -9. Osman, M.S., Abo-Sinna, M.A., Mousa, A.A. (00), A solution to the optimal power flow using genetic algorithm, Applied Mathematics and Computation,, Özyön, S. (009), Genetik algoritmanın bazı çevresel ekonomik güç dağıtım problemlerine uygulanması, Yüksek Lisans Tezi, Dumlupınar Üniversitesi, 3 s. (yayımlanmamış). Özyön, S., Yaşar, C., Temurtaş, H. (0), Diferansiyel gelişim algoritmasının valf nokta etkili konveks olmayan ekonomik güç dağıtım problemlerine uygulanması, th International Advanced Technologies Symposium (IATS ), - May 0, Electrical & Electronics Technologies Papers, Vol., pp.-, Elazığ, TURKEY. Özyön, S., Yaşar, C., Temurtaş, H. (0), Harmoni arama algoritmasının çevresel ekonomik güç dağıtım problemlerine uygulanması, Çukurova Üniversitesi, Mühendislik-Mimarlık Fakültesi Dergisi, Cilt., Sayı., pp.-7. Xuanhu, H., Wang, W., Jiuchun, J., Lijie, X. (0), An Improved Artificial Bee Colony Algorithm and Its Application to Multi-Objective Optimal Power Flow, Energies,, -37.
OPTİMUM GÜÇ AKIŞININ YAPAY ARI KOLONİSİ İLE SAĞLANMASI
 OPTİMUM GÜÇ AKIŞININ YAPAY ARI KOLONİSİ İLE SAĞLANMASI A. Doğan 1 M. Alçı 2 Erciyes Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik Mühendisliği Bölümü 1 ahmetdogan@erciyes.edu.tr 2 malci@erciyes.edu.tr
OPTİMUM GÜÇ AKIŞININ YAPAY ARI KOLONİSİ İLE SAĞLANMASI A. Doğan 1 M. Alçı 2 Erciyes Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik Mühendisliği Bölümü 1 ahmetdogan@erciyes.edu.tr 2 malci@erciyes.edu.tr
Diferansiyel Gelişim Algoritmasının Yasak İşletim Bölgeli Ekonomik Güç Dağıtım Problemine Uygulanması
 61 Diferansiyel Gelişim Algoritmasının Yasak İşletim Bölgeli Ekonomik Güç Dağıtım Problemine Uygulanması Serdar ÖZYÖN 1, Celal YAŞAR 2, Hasan TEMURTAŞ 3, Gıyasettin ÖZCAN 4 1,2 Dumlupınar Üniversitesi,
61 Diferansiyel Gelişim Algoritmasının Yasak İşletim Bölgeli Ekonomik Güç Dağıtım Problemine Uygulanması Serdar ÖZYÖN 1, Celal YAŞAR 2, Hasan TEMURTAŞ 3, Gıyasettin ÖZCAN 4 1,2 Dumlupınar Üniversitesi,
VALF NOKTA ETKİLİ KONVEKS OLMAYAN EKONOMİK GÜÇ DAĞITIM PROBLEMLERİNİN HARMONİ ARAMA ALGORİTMASIYLA ÇÖZÜMÜ
 VALF NOKTA ETKİLİ KONVEKS OLMAYAN EKONOMİK GÜÇ DAĞITIM PROBLEMLERİNİN HARMONİ ARAMA ALGORİTMASIYLA ÇÖZÜMÜ Serdar ÖZYÖN 1,*, Celal YAŞAR 2, Hasan TEMURTAŞ 3 1 Dumlupınar Üniversitesi, Mühendislik Fakültesi,
VALF NOKTA ETKİLİ KONVEKS OLMAYAN EKONOMİK GÜÇ DAĞITIM PROBLEMLERİNİN HARMONİ ARAMA ALGORİTMASIYLA ÇÖZÜMÜ Serdar ÖZYÖN 1,*, Celal YAŞAR 2, Hasan TEMURTAŞ 3 1 Dumlupınar Üniversitesi, Mühendislik Fakültesi,
HAM ENERJİ KAYNAĞI KISITLI TERMİK BİRİM İÇEREN SİSTEMLERDE ÇEVRESEL EKONOMİK GÜÇ DAĞITIMI PROBLEMİNİN ÇÖZÜMÜ
 Eskişehir Osmangazi Üniversitesi Mühendislik Mimarlık Fakültesi Dergisi Cilt:XXIV, Sayı:, 2011 Journal of Engineering and Architecture Faculty of Eskişehir Osmangazi University, Vol: XXIV, No:1, 2011 Makalenin
Eskişehir Osmangazi Üniversitesi Mühendislik Mimarlık Fakültesi Dergisi Cilt:XXIV, Sayı:, 2011 Journal of Engineering and Architecture Faculty of Eskişehir Osmangazi University, Vol: XXIV, No:1, 2011 Makalenin
Deniz ERSOY Elektrik Yük. Müh.
 Deniz ERSOY Elektrik Yük. Müh. AMACIMIZ Yenilenebilir enerji kaynaklarının tesis edilmesi ve enerji üretimi pek çok araştırmaya konu olmuştur. Fosil yakıtların giderek artan maliyeti ve giderek tükeniyor
Deniz ERSOY Elektrik Yük. Müh. AMACIMIZ Yenilenebilir enerji kaynaklarının tesis edilmesi ve enerji üretimi pek çok araştırmaya konu olmuştur. Fosil yakıtların giderek artan maliyeti ve giderek tükeniyor
SEZGİSEL ALGORİTMA KULLANILARAK RÜZGÂR ÇİFTLİKLERİNİN GÜÇ SİSTEMİNE ETKİSİNİN İNCELENMESİ. Öğr. Gör. Mehmet Fatih Tefek Doç. Dr.
 SEZGİSEL ALGORİTMA KULLANILARAK RÜZGÂR ÇİFTLİKLERİNİN GÜÇ SİSTEMİNE ETKİSİNİN İNCELENMESİ Öğr. Gör. Mehmet Fatih Tefek Doç. Dr. Harun Uğuz * Rüzgâr kaynaklı enerji üretimi, yenilenebilir enerji kaynakları
SEZGİSEL ALGORİTMA KULLANILARAK RÜZGÂR ÇİFTLİKLERİNİN GÜÇ SİSTEMİNE ETKİSİNİN İNCELENMESİ Öğr. Gör. Mehmet Fatih Tefek Doç. Dr. Harun Uğuz * Rüzgâr kaynaklı enerji üretimi, yenilenebilir enerji kaynakları
Problemlerine Geliştirilmiş Parçacık
 Çankaya University Journal of Science and Engineering Volume 9 (2012), No. 2, 89 106 Yasak İşletim Bölgeli Ekonomik Güç Dağıtım Problemlerine Geliştirilmiş Parçacık Sürü Optimizasyonu Yaklaşımı Serdar
Çankaya University Journal of Science and Engineering Volume 9 (2012), No. 2, 89 106 Yasak İşletim Bölgeli Ekonomik Güç Dağıtım Problemlerine Geliştirilmiş Parçacık Sürü Optimizasyonu Yaklaşımı Serdar
EREĞLİ ELEKTRİK DAĞITIM ŞEBEKESİNDE GENETİK ALGORİTMA VE NEWTON RAPHSON YÖNTEMLERİYLE REAKTİF GÜÇ OPTİMİZASYONUNUN GERÇEKLEŞTİRİLMESİ
 EREĞLİ ELEKTRİK DAĞITIM ŞEBEKESİNDE GENETİK ALGORİTMA VE NEWTON RAPHSON YÖNTEMLERİYLE REAKTİF GÜÇ OPTİMİZASYONUNUN GERÇEKLEŞTİRİLMESİ 1 Hamza YAPICI 2 Nurettin ÇETİNKAYA 1 Ereğli Kemal Akman Meslek Yüksek
EREĞLİ ELEKTRİK DAĞITIM ŞEBEKESİNDE GENETİK ALGORİTMA VE NEWTON RAPHSON YÖNTEMLERİYLE REAKTİF GÜÇ OPTİMİZASYONUNUN GERÇEKLEŞTİRİLMESİ 1 Hamza YAPICI 2 Nurettin ÇETİNKAYA 1 Ereğli Kemal Akman Meslek Yüksek
YZM 5257 YAPAY ZEKA VE UZMAN SİSTEMLER DERS#6: GENETİK ALGORİTMALAR
 YZM 5257 YAPAY ZEKA VE UZMAN SİSTEMLER DERS#6: GENETİK ALGORİTMALAR Sınıflandırma Yöntemleri: Karar Ağaçları (Decision Trees) Örnek Tabanlı Yöntemler (Instance Based Methods): k en yakın komşu (k nearest
YZM 5257 YAPAY ZEKA VE UZMAN SİSTEMLER DERS#6: GENETİK ALGORİTMALAR Sınıflandırma Yöntemleri: Karar Ağaçları (Decision Trees) Örnek Tabanlı Yöntemler (Instance Based Methods): k en yakın komşu (k nearest
Genetik Algoritmalar. Bölüm 1. Optimizasyon. Yrd. Doç. Dr. Adem Tuncer E-posta:
 Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: adem.tuncer@yalova.edu.tr Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: adem.tuncer@yalova.edu.tr Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
DENGESİZ GÜÇ AKIŞI ANALİZLERİ İÇİN SABİT HIZLI ASENKRON GENERATÖRLÜ RÜZGAR TÜRBİNİ MODELİ BÖLÜM 1: GENERATÖR MODELİ BÖLÜM 2: YÜK AKIŞI UYGULAMALARI
 DENGESİZ GÜÇ AKIŞI ANALİZLERİ İÇİN SABİT HIZLI ASENKRON GENERATÖRLÜ RÜZGAR TÜRBİNİ MODELİ BÖLÜM 1: GENERATÖR MODELİ BÖLÜM 2: YÜK AKIŞI UYGULAMALARI Ahmet KÖKSOY Gebze Teknik Üniversitesi Elektronik Mühendisliği
DENGESİZ GÜÇ AKIŞI ANALİZLERİ İÇİN SABİT HIZLI ASENKRON GENERATÖRLÜ RÜZGAR TÜRBİNİ MODELİ BÖLÜM 1: GENERATÖR MODELİ BÖLÜM 2: YÜK AKIŞI UYGULAMALARI Ahmet KÖKSOY Gebze Teknik Üniversitesi Elektronik Mühendisliği
PARÇACIK SÜRÜ OPTİMİZASYONU BMÜ-579 METASEZGİSEL YÖNTEMLER YRD. DOÇ. DR. İLHAN AYDIN
 PARÇACIK SÜRÜ OPTİMİZASYONU BMÜ-579 METASEZGİSEL YÖNTEMLER YRD. DOÇ. DR. İLHAN AYDIN 1995 yılında Dr.Eberhart ve Dr.Kennedy tarafından geliştirilmiş popülasyon temelli sezgisel bir optimizasyon tekniğidir.
PARÇACIK SÜRÜ OPTİMİZASYONU BMÜ-579 METASEZGİSEL YÖNTEMLER YRD. DOÇ. DR. İLHAN AYDIN 1995 yılında Dr.Eberhart ve Dr.Kennedy tarafından geliştirilmiş popülasyon temelli sezgisel bir optimizasyon tekniğidir.
METASEZGİSEL YÖNTEMLER
 METASEZGİSEL YÖNTEMLER Ara sınav - 30% Ödev (Haftalık) - 20% Final (Proje Sunumu) - 50% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn: Zaman çizelgeleme, en kısa yol bulunması,
METASEZGİSEL YÖNTEMLER Ara sınav - 30% Ödev (Haftalık) - 20% Final (Proje Sunumu) - 50% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn: Zaman çizelgeleme, en kısa yol bulunması,
GÜÇ SİSTEMLERİ KONFERANSI Kasım 2018 Ankara
 Yenilenebilir Enerji Sistemleri Entegrasyonunun Sezgisel Optimizasyon estekli inamik Stokastik ile Analizi Analysis of enewable Energy Systems Integration with Heuristic Optimization Supported ynamic Stochastic
Yenilenebilir Enerji Sistemleri Entegrasyonunun Sezgisel Optimizasyon estekli inamik Stokastik ile Analizi Analysis of enewable Energy Systems Integration with Heuristic Optimization Supported ynamic Stochastic
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Genetik Algoritma (Genetic Algorithm) Doç.Dr. M. Ali Akcayol Genetik Algoritma 1970 li yıllarda John Holland tarafından geliştirilmiştir. 1989 yılında David E. Goldberg Genetik
Zeki Optimizasyon Teknikleri Genetik Algoritma (Genetic Algorithm) Doç.Dr. M. Ali Akcayol Genetik Algoritma 1970 li yıllarda John Holland tarafından geliştirilmiştir. 1989 yılında David E. Goldberg Genetik
Fonksiyon Optimizasyonunda Genetik Algoritmalar
 01-12-06 Ümit Akıncı Fonksiyon Optimizasyonunda Genetik Algoritmalar 1 Fonksiyon Optimizasyonu Fonksiyon optimizasyonu fizikte karşımıza sık çıkan bir problemdir. Örneğin incelenen sistemin kararlı durumu
01-12-06 Ümit Akıncı Fonksiyon Optimizasyonunda Genetik Algoritmalar 1 Fonksiyon Optimizasyonu Fonksiyon optimizasyonu fizikte karşımıza sık çıkan bir problemdir. Örneğin incelenen sistemin kararlı durumu
SEZGİSEL YÖNTEMLER KULLANARAK OPTİMAL GÜÇ AKIŞI PROBLEMİ ÇÖZÜMÜ YÜKSEK LİSANS TEZİ. Rengin İdil CABADAĞ. Enerji Bilim ve Teknoloji Anabilim Dalı
 İSTANBUL TEKNİK ÜNİVERSİTESİ ENERJİ ENSTİTÜSÜ SEZGİSEL YÖNTEMLER KULLANARAK OPTİMAL GÜÇ AKIŞI PROBLEMİ ÇÖZÜMÜ YÜKSEK LİSANS TEZİ Rengin İdil CABADAĞ Enerji Bilim ve Teknoloji Anabilim Dalı Enerji Bilim
İSTANBUL TEKNİK ÜNİVERSİTESİ ENERJİ ENSTİTÜSÜ SEZGİSEL YÖNTEMLER KULLANARAK OPTİMAL GÜÇ AKIŞI PROBLEMİ ÇÖZÜMÜ YÜKSEK LİSANS TEZİ Rengin İdil CABADAĞ Enerji Bilim ve Teknoloji Anabilim Dalı Enerji Bilim
Minumum Kayıplar İçin Güç Şebekelerinde Statcom Yerinin ve Değerinin Yer çekimsel Arama Algoritması Kullanılarak Belirlenmesi
 Minumum Kayıplar İçin Güç Şebekelerinde Statcom Yerinin ve Değerinin Yer çekimsel Arama Algoritması Kullanılarak Belirlenmesi *1 Yalçın Alcan, 2 Ali Öztürk, 3 Hasan Dirik, 4 Memnun Demir *1 Elektrik ve
Minumum Kayıplar İçin Güç Şebekelerinde Statcom Yerinin ve Değerinin Yer çekimsel Arama Algoritması Kullanılarak Belirlenmesi *1 Yalçın Alcan, 2 Ali Öztürk, 3 Hasan Dirik, 4 Memnun Demir *1 Elektrik ve
GENETİK ALGORİTMALAR. Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ
 GENETİK ALGORİTMALAR Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ GENETİK ALGORİTMALAR Genetik algoritmalar, Darwin in doğal seçim ve evrim teorisi ilkelerine dayanan bir arama ve optimizasyon yöntemidir.
GENETİK ALGORİTMALAR Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ GENETİK ALGORİTMALAR Genetik algoritmalar, Darwin in doğal seçim ve evrim teorisi ilkelerine dayanan bir arama ve optimizasyon yöntemidir.
Ev Tipi Yenilenebilir Hibrit Sistem İçin Mikro-Genetik Algoritma ile Optimal Yük Planlaması
 Ev Tipi Yenilenebilir Hibrit Sistem İçin Mikro-Genetik Algoritma ile Optimal Yük Planlaması Özay CAN, Nedim TUTKUN Düzce Üniversitesi Elektrik/Elektronik Mühendisliği Kapsam Giriş Hibrit Sistem ve Güç
Ev Tipi Yenilenebilir Hibrit Sistem İçin Mikro-Genetik Algoritma ile Optimal Yük Planlaması Özay CAN, Nedim TUTKUN Düzce Üniversitesi Elektrik/Elektronik Mühendisliği Kapsam Giriş Hibrit Sistem ve Güç
KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI
 KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI Hatice YANIKOĞLU a, Ezgi ÖZKARA a, Mehmet YÜCEER a* İnönü Üniversitesi Mühendislik Fakültesi Kimya Mühendisliği
KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI Hatice YANIKOĞLU a, Ezgi ÖZKARA a, Mehmet YÜCEER a* İnönü Üniversitesi Mühendislik Fakültesi Kimya Mühendisliği
OPTİMAL GÜÇ AKIŞI ÇÖZÜMLERİNDE LİNEER PROGRAMLAMA ve İÇ NOKTA ALGORİTMASI YÖNTEMLERİNİN KARŞILAŞTIRMALI ANALİZİ
 OPTİMAL GÜÇ AKIŞI ÇÖZÜMLERİNDE LİNEER PROGRAMLAMA ve İÇ NOKTA ALGORİTMASI YÖNTEMLERİNİN KARŞILAŞTIRMALI ANALİZİ Rengin İdil CABADAĞ, Belgin Emre TÜRKAY, Abdullah TUNÇ İstanbul Teknik Üniversitesi, Elektrik-Elektronik
OPTİMAL GÜÇ AKIŞI ÇÖZÜMLERİNDE LİNEER PROGRAMLAMA ve İÇ NOKTA ALGORİTMASI YÖNTEMLERİNİN KARŞILAŞTIRMALI ANALİZİ Rengin İdil CABADAĞ, Belgin Emre TÜRKAY, Abdullah TUNÇ İstanbul Teknik Üniversitesi, Elektrik-Elektronik
Başlangıç Temel Programının Bilinmemesi Durumu
 aşlangıç Temel Programının ilinmemesi Durumu İlgili kısıtlarda şartlar ( ) ise bunlara gevşek (slack) değişkenler eklenerek eşitliklere dönüştürülmektedir. Ancak sınırlayıcı şartlar ( ) veya ( = ) olduğu
aşlangıç Temel Programının ilinmemesi Durumu İlgili kısıtlarda şartlar ( ) ise bunlara gevşek (slack) değişkenler eklenerek eşitliklere dönüştürülmektedir. Ancak sınırlayıcı şartlar ( ) veya ( = ) olduğu
KAOTİK ATEŞBÖCEĞİ OPTİMİZASYON ALGORİTMASI KULLANILARAK TERMİK GÜÇ SANTRALLERİ ETKİSİNDEKİ EKONOMİK YÜK DAĞITIM PROBLEMLERİNİN ÇÖZÜMÜ
 KAOTİK ATEŞBÖCEĞİ OPTİMİZASYON ALGORİTMASI KULLANILARAK TERMİK GÜÇ SANTRALLERİ ETKİSİNDEKİ EKONOMİK YÜK DAĞITIM PROBLEMLERİNİN ÇÖZÜMÜ Nihat PAMUK TEİAŞ 5. İletim Tesis ve İşletme Grup Müdürlüğü, Test Grup
KAOTİK ATEŞBÖCEĞİ OPTİMİZASYON ALGORİTMASI KULLANILARAK TERMİK GÜÇ SANTRALLERİ ETKİSİNDEKİ EKONOMİK YÜK DAĞITIM PROBLEMLERİNİN ÇÖZÜMÜ Nihat PAMUK TEİAŞ 5. İletim Tesis ve İşletme Grup Müdürlüğü, Test Grup
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
Serdar BİROĞUL YÜKSEK LİSANS TEZİ (ELEKTRİK EĞİTİMİ) GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ANKARA
 i GENETİK ALGORİTMA YAKLAŞIMIYLA ATÖLYE ÇİZELGELEME Serdar BİROĞUL YÜKSEK LİSANS TEZİ (ELEKTRİK EĞİTİMİ) GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ OCAK 2005 ANKARA ii Serdar BİROĞUL tarafından hazırlanan
i GENETİK ALGORİTMA YAKLAŞIMIYLA ATÖLYE ÇİZELGELEME Serdar BİROĞUL YÜKSEK LİSANS TEZİ (ELEKTRİK EĞİTİMİ) GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ OCAK 2005 ANKARA ii Serdar BİROĞUL tarafından hazırlanan
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
GÜÇ SİSTEM GERİLİM KARARLILIĞINDA YÜK MODELLEMELERİNİN ÖNEMİ
 GÜÇ SİSTEM GERİLİM KARARLILIĞINDA YÜK MODELLEMELERİNİN ÖNEMİ Mustafa BAYSAL Mehmet UZUNOĞLU Celal KOCATEPE Elektrik Mühendisliği Bölümü Elektrik-Elektronik Fakültesi Yıldız Teknik Üniversitesi, 34349,
GÜÇ SİSTEM GERİLİM KARARLILIĞINDA YÜK MODELLEMELERİNİN ÖNEMİ Mustafa BAYSAL Mehmet UZUNOĞLU Celal KOCATEPE Elektrik Mühendisliği Bölümü Elektrik-Elektronik Fakültesi Yıldız Teknik Üniversitesi, 34349,
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ELEKTRİK DAĞITIM HATLARINDA GÜÇ OPTİMİZASYONUNUN GERÇEKLEŞTİRİLMESİ VE BİR ELEKTRİK DAĞITIM BÖLGESİNE UYGULANMASI Hamza YAPICI YÜKSEK LİSANS TEZİ Elektrik
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ELEKTRİK DAĞITIM HATLARINDA GÜÇ OPTİMİZASYONUNUN GERÇEKLEŞTİRİLMESİ VE BİR ELEKTRİK DAĞITIM BÖLGESİNE UYGULANMASI Hamza YAPICI YÜKSEK LİSANS TEZİ Elektrik
Kaotik Tabanlı Diferansiyel (Farksal) Gelişim Algoritması
 Kaotik Tabanlı Diferansiyel (Farksal) Gelişim Algoritması 1 Mehmet Eser * 1 Uğur Yüzgeç 1 Bilecik Şeyh Edebali Üniversitesi, Bilgisayar Mühendisliği Bölümü, 111, Gülümbe, Bilecik 1. Giriş Abstract Differential
Kaotik Tabanlı Diferansiyel (Farksal) Gelişim Algoritması 1 Mehmet Eser * 1 Uğur Yüzgeç 1 Bilecik Şeyh Edebali Üniversitesi, Bilgisayar Mühendisliği Bölümü, 111, Gülümbe, Bilecik 1. Giriş Abstract Differential
GÜNEŞ ENERJİSİ VE RÜZGÂR ENERJİSİ DÂHİL OLAN HİBRİT GÜÇ SİSTEMİNDE FARKLI ALGORİTMALAR İLE EKONOMİK YÜK DAĞITIMININ İNCELENMESİ
 3. İzmir Rüzgâr Sempozyumu // 8-10 Ekim 2015 // İzmir 29 GÜNEŞ ENERJİSİ VE RÜZGÂR ENERJİSİ DÂHİL OLAN HİBRİT GÜÇ SİSTEMİNDE FARKLI ALGORİTMALAR İLE EKONOMİK YÜK DAĞITIMININ İNCELENMESİ Gül Kurt 1, Deniz
3. İzmir Rüzgâr Sempozyumu // 8-10 Ekim 2015 // İzmir 29 GÜNEŞ ENERJİSİ VE RÜZGÂR ENERJİSİ DÂHİL OLAN HİBRİT GÜÇ SİSTEMİNDE FARKLI ALGORİTMALAR İLE EKONOMİK YÜK DAĞITIMININ İNCELENMESİ Gül Kurt 1, Deniz
Ahmet Aydın a, Mustafa Şeker b,arif Memmedov c
 MAKALE HAKKINDA Geliş : Kasım 2016 Kabul: Mart 2017 BİNGÖL ORTA GERİLİM ŞEBEKESİNİN TEKNİK KAYIPLARIN ANALİZİ İÇİN DİGSLİENT POWER FACTORY YAZILIMI İLE BİLGİSAYAR DESTEKLİ ŞEBEKE MODELİ COMPUTER ADDED
MAKALE HAKKINDA Geliş : Kasım 2016 Kabul: Mart 2017 BİNGÖL ORTA GERİLİM ŞEBEKESİNİN TEKNİK KAYIPLARIN ANALİZİ İÇİN DİGSLİENT POWER FACTORY YAZILIMI İLE BİLGİSAYAR DESTEKLİ ŞEBEKE MODELİ COMPUTER ADDED
Sigma 2006/3 Araştırma Makalesi / Research Article A SOLUTION PROPOSAL FOR INTERVAL SOLID TRANSPORTATION PROBLEM
 Journal of Engineering and Natural Sciences Mühendislik ve Fen Bilimleri Dergisi Sigma 6/ Araştırma Makalesi / Research Article A SOLUTION PROPOSAL FOR INTERVAL SOLID TRANSPORTATION PROBLEM Fügen TORUNBALCI
Journal of Engineering and Natural Sciences Mühendislik ve Fen Bilimleri Dergisi Sigma 6/ Araştırma Makalesi / Research Article A SOLUTION PROPOSAL FOR INTERVAL SOLID TRANSPORTATION PROBLEM Fügen TORUNBALCI
GENETEK. Güç Sistemlerinde Kısa Devre Analizi Eğitimi. Güç, Enerji, Elektrik Sistemleri Özel Eğitim ve Danışmanlık San. Tic. Ltd. Şti.
 GENETEK Güç, Enerji, Elektrik Sistemleri Özel Eğitim ve Danışmanlık San. Tic. Ltd. Şti. Güç Sistemlerinde Kısa Devre Analizi Eğitimi Yeniköy Merkez Mh. KOÜ Teknopark No:83 C-13, 41275, Başiskele/KOCAELİ
GENETEK Güç, Enerji, Elektrik Sistemleri Özel Eğitim ve Danışmanlık San. Tic. Ltd. Şti. Güç Sistemlerinde Kısa Devre Analizi Eğitimi Yeniköy Merkez Mh. KOÜ Teknopark No:83 C-13, 41275, Başiskele/KOCAELİ
Journal of the Faculty of Engineering and Architecture of Gazi University 33:2 (2018)
 Journal of the Faculty of Engineering and Architecture of Gazi University 33: (08) 54-556 A new approach in the solution of the environmental economic power dispatch problems with piecewise quadratic fuel
Journal of the Faculty of Engineering and Architecture of Gazi University 33: (08) 54-556 A new approach in the solution of the environmental economic power dispatch problems with piecewise quadratic fuel
Yapay Zeka Yöntemlerinin Otomotiv Sektöründe Ürün Tasarımı Çalışmalarında Kullanılması
 Yapay Zeka Yöntemlerinin Otomotiv Sektöründe Ürün Tasarımı Çalışmalarında Kullanılması Doç. Dr. Ali Rıza YILDIZ 04.11.2014 Doç. Dr. Ali Rıza YILDIZ - "Hibrid Evrimsel Yöntemler İle Taşıt Elemanlarının
Yapay Zeka Yöntemlerinin Otomotiv Sektöründe Ürün Tasarımı Çalışmalarında Kullanılması Doç. Dr. Ali Rıza YILDIZ 04.11.2014 Doç. Dr. Ali Rıza YILDIZ - "Hibrid Evrimsel Yöntemler İle Taşıt Elemanlarının
GENETİK ALGORİTMA İLE RÜZGAR TÜRBİNİ KANAT SAYISI SEÇİMİ
 VI. Ulusal Temiz Enerji Sempozyumu UTES 2006 25 27 Mayıs 2006, Isparta Sf.756 764 GENETİK ALGORİTMA İLE RÜZGAR TÜRBİNİ KANAT SAYISI SEÇİMİ Nida Nurbay ve Ali Çınar Kocaeli Üniversitesi Tek. Eğt. Fak. Makine
VI. Ulusal Temiz Enerji Sempozyumu UTES 2006 25 27 Mayıs 2006, Isparta Sf.756 764 GENETİK ALGORİTMA İLE RÜZGAR TÜRBİNİ KANAT SAYISI SEÇİMİ Nida Nurbay ve Ali Çınar Kocaeli Üniversitesi Tek. Eğt. Fak. Makine
Eğitim ve Öğretim Araştırmaları Dergisi Journal of Research in Education and Teaching Mayıs 2017 Cilt: 6 Sayı: 2 Makale No: 33 ISSN:
 KISA VE ORTA ENERJİ İLETİM HATLARININ SAYISAL ANALİZİ İÇİN BİR ARAYÜZ TASARIMI Öğr. Gör. Hakan Aydogan Uşak Üniversitesi, Uşak hakan.aydogan@usak.edu.tr Öğr. Gör. Mehmet Feyzi Özsoy Uşak Üniversitesi,
KISA VE ORTA ENERJİ İLETİM HATLARININ SAYISAL ANALİZİ İÇİN BİR ARAYÜZ TASARIMI Öğr. Gör. Hakan Aydogan Uşak Üniversitesi, Uşak hakan.aydogan@usak.edu.tr Öğr. Gör. Mehmet Feyzi Özsoy Uşak Üniversitesi,
PROCEEDING BOOK. DAĞITIM SİSTEMİNE YEREL ELEKTRİK SANTRALLERİNİN YERLEŞTİRİLMESİ ALLOCATION of DISTRIBUTED GENERATORS in DISTRIBUTION SYSTEM
 DAĞITIM SİSTEMİNE YEREL ELEKTRİK SANTRALLERİNİN YERLEŞTİRİLMESİ ALLOCATION of DISTRIBUTED GENERATORS in DISTRIBUTION SYSTEM Ayşe Aybike Şeker 1, Mehmet Hakan Hocaoğlu 2 1. Elektronik Mühendisliği Bölümü
DAĞITIM SİSTEMİNE YEREL ELEKTRİK SANTRALLERİNİN YERLEŞTİRİLMESİ ALLOCATION of DISTRIBUTED GENERATORS in DISTRIBUTION SYSTEM Ayşe Aybike Şeker 1, Mehmet Hakan Hocaoğlu 2 1. Elektronik Mühendisliği Bölümü
Plazma İletiminin Optimal Kontrolü Üzerine
 Plazma İletiminin Optimal Kontrolü Üzerine 1 Yalçın Yılmaz, 2 İsmail Küçük ve 3 Faruk Uygul *1 Faculty of Arts and Sciences, Dept. of Mathematics, Sakaya University, Sakarya, Turkey 2 Faculty of Chemical
Plazma İletiminin Optimal Kontrolü Üzerine 1 Yalçın Yılmaz, 2 İsmail Küçük ve 3 Faruk Uygul *1 Faculty of Arts and Sciences, Dept. of Mathematics, Sakaya University, Sakarya, Turkey 2 Faculty of Chemical
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
DİFERANSİYEL GELİŞİM ALGORİTMASI
 İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi Yıl: 5 Sayı: 9 Bahar 2006/1 s.85-99 DİFERANSİYEL GELİŞİM ALGORİTMASI Timur KESKİNTÜRK ÖZET Doğrusal olmayan problemlerin çözümüne yönelik olarak geliştirilmiş
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi Yıl: 5 Sayı: 9 Bahar 2006/1 s.85-99 DİFERANSİYEL GELİŞİM ALGORİTMASI Timur KESKİNTÜRK ÖZET Doğrusal olmayan problemlerin çözümüne yönelik olarak geliştirilmiş
Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım. Mehmet Ali Aytekin Tahir Emre Kalaycı
 Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım Mehmet Ali Aytekin Tahir Emre Kalaycı Gündem Gezgin Satıcı Problemi GSP'yi Çözen Algoritmalar Genetik Algoritmalar
Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım Mehmet Ali Aytekin Tahir Emre Kalaycı Gündem Gezgin Satıcı Problemi GSP'yi Çözen Algoritmalar Genetik Algoritmalar
GENETİK ALGORİTMALAR BÜŞRA GÜRACAR
 GENETİK ALGORİTMALAR BÜŞRA GÜRACAR 201420404036 İÇERİK Genetik Algoritmanın, Amacı Kullanım Alanları Kavramları Uygulama Adımları Parametreler Genetik Algoritma Kodlama Türleri Genetik Algoritma Genetik
GENETİK ALGORİTMALAR BÜŞRA GÜRACAR 201420404036 İÇERİK Genetik Algoritmanın, Amacı Kullanım Alanları Kavramları Uygulama Adımları Parametreler Genetik Algoritma Kodlama Türleri Genetik Algoritma Genetik
FARKSAL GELİŞİM ALGORİTMASI İLE KARMA YEM MALİYET OPTİMİZASYONU THE COST OPTIMIZATION OF MIXED FEED WITH DIFFERENTIAL EVOLUTION ALGORITHM
 FARKSAL GELİŞİM ALGORİTMASI İLE KARMA YEM MALİYET OPTİMİZASYONU *Yaşar YAŞAR 1 Burhanettin DURMUŞ 2 1 yasaartr@gmail.com 2 Dumlupınar Üniversites Mühendislik Fakültes Elektrik-Elektronik Mühendisliği Bölümü
FARKSAL GELİŞİM ALGORİTMASI İLE KARMA YEM MALİYET OPTİMİZASYONU *Yaşar YAŞAR 1 Burhanettin DURMUŞ 2 1 yasaartr@gmail.com 2 Dumlupınar Üniversites Mühendislik Fakültes Elektrik-Elektronik Mühendisliği Bölümü
Kahramanmaras Sutcu Imam University Journal of Engineering Sciences
 KSU Mühendislik Bilimleri Dergisi, 20(2), 2017 97 KSU Journal of Engineering Sciences, 20(2), 2017 Kahramanmaras Sutcu Imam University Journal of Engineering Sciences Yerel Elektrik Santrallerin Dağıtım
KSU Mühendislik Bilimleri Dergisi, 20(2), 2017 97 KSU Journal of Engineering Sciences, 20(2), 2017 Kahramanmaras Sutcu Imam University Journal of Engineering Sciences Yerel Elektrik Santrallerin Dağıtım
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA
 GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA Nedim TUTKUN Düzce Üniversitesi Elektrik Elektronik Mühendisliği Bölümü nedimtutkun@duzce.edu.tr Düzce Üniversitesi Elektrik&Elektronik Mühendisliği
GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA Nedim TUTKUN Düzce Üniversitesi Elektrik Elektronik Mühendisliği Bölümü nedimtutkun@duzce.edu.tr Düzce Üniversitesi Elektrik&Elektronik Mühendisliği
BBO Algoritmasının Optimizasyon Başarımının İncelenmesi Optimization Performance Investigation of BBO Algorithm
 BBO Algoritmasının Optimizasyon Başarımının İncelenmesi Optimization Performance Investigation of BBO Algorithm Tufan İNAÇ 1, Cihan KARAKUZU 2 1 Bilgisayar Mühendisliği Anabilim Dalı Bilecik Şeyh Edebali
BBO Algoritmasının Optimizasyon Başarımının İncelenmesi Optimization Performance Investigation of BBO Algorithm Tufan İNAÇ 1, Cihan KARAKUZU 2 1 Bilgisayar Mühendisliği Anabilim Dalı Bilecik Şeyh Edebali
ÖZGEÇMİŞ 2003 MÜHENDİSLİĞİ İSTANBUL ÜNİVERSİTESİ ÜNİVERSİTESİ
 ÖZGEÇMİŞ 1. Adı Soyadı: İPEK EKER 2. Doğum Tarihi: 31.01.1980 3. Ünvanı: ÖĞRETİM GÖREVLİSİ 4. Öğrenim Durumu: Derece Alan Üniversite Yıl Lisans ENDÜSTRİ İSTANBUL KÜLTÜR 2003 MÜHENDİSLİĞİ ÜNİVERSİTESİ Y.Lisans
ÖZGEÇMİŞ 1. Adı Soyadı: İPEK EKER 2. Doğum Tarihi: 31.01.1980 3. Ünvanı: ÖĞRETİM GÖREVLİSİ 4. Öğrenim Durumu: Derece Alan Üniversite Yıl Lisans ENDÜSTRİ İSTANBUL KÜLTÜR 2003 MÜHENDİSLİĞİ ÜNİVERSİTESİ Y.Lisans
OPTİMİZASYON TEKNİKLERİ. Kısıtsız Optimizasyon
 OPTİMİZASYON TEKNİKLERİ Kısıtsız Optimizasyon Giriş Klasik optimizasyon yöntemleri minimum veya maksimum değerlerini bulmak için türev gerektiren ve gerektirmeyen teknikler olarak bilinirler. Bu yöntemler
OPTİMİZASYON TEKNİKLERİ Kısıtsız Optimizasyon Giriş Klasik optimizasyon yöntemleri minimum veya maksimum değerlerini bulmak için türev gerektiren ve gerektirmeyen teknikler olarak bilinirler. Bu yöntemler
Bulanık Mantık Tabanlı Uçak Modeli Tespiti
 Bulanık Mantık Tabanlı Uçak Modeli Tespiti Hüseyin Fidan, Vildan Çınarlı, Muhammed Uysal, Kadriye Filiz Balbal, Ali Özdemir 1, Ayşegül Alaybeyoğlu 2 1 Celal Bayar Üniversitesi, Matematik Bölümü, Manisa
Bulanık Mantık Tabanlı Uçak Modeli Tespiti Hüseyin Fidan, Vildan Çınarlı, Muhammed Uysal, Kadriye Filiz Balbal, Ali Özdemir 1, Ayşegül Alaybeyoğlu 2 1 Celal Bayar Üniversitesi, Matematik Bölümü, Manisa
Simpleks Yönteminde Kullanılan İlave Değişkenler (Eşitliğin yönüne göre):
 DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
Tek Değişkenli Optimizasyon OPTİMİZASYON. Gradient Tabanlı Yöntemler. Bisection (İkiye Bölme) Yöntemi
 OPTİMİZASYON Gerçek hayatta, çok değişkenli optimizasyon problemleri karmaşıktır ve nadir olarak problem tek değişkenli olur. Bununla birlikte, tek değişkenli optimizasyon algoritmaları çok değişkenli
OPTİMİZASYON Gerçek hayatta, çok değişkenli optimizasyon problemleri karmaşıktır ve nadir olarak problem tek değişkenli olur. Bununla birlikte, tek değişkenli optimizasyon algoritmaları çok değişkenli
GENETİK ALGORİTMA ÖZNUR CENGİZ HİLAL KOCA
 GENETİK ALGORİTMA ÖZNUR CENGİZ 201410306014 HİLAL KOCA 150306024 GENETİK ALGORİTMA Genetik Algoritma yaklaşımının ortaya çıkışı 1970 lerin başında olmuştur. 1975 te John Holland ın makine öğrenmesi üzerine
GENETİK ALGORİTMA ÖZNUR CENGİZ 201410306014 HİLAL KOCA 150306024 GENETİK ALGORİTMA Genetik Algoritma yaklaşımının ortaya çıkışı 1970 lerin başında olmuştur. 1975 te John Holland ın makine öğrenmesi üzerine
EMM4131 Popülasyon Temelli Algoritmalar (Population-based Algorithms)
 2017-2018 Güz Yarıyılı EMM4131 Popülasyon Temelli Algoritmalar (Population-based Algorithms) 4 Genetik Algoritma Örnek Uygulamalar (Sırt Çantası Problemi, Sınav Programı Çizelgeleme) Yrd. Doç. Dr. İbrahim
2017-2018 Güz Yarıyılı EMM4131 Popülasyon Temelli Algoritmalar (Population-based Algorithms) 4 Genetik Algoritma Örnek Uygulamalar (Sırt Çantası Problemi, Sınav Programı Çizelgeleme) Yrd. Doç. Dr. İbrahim
EĞİTİM AMACIYLA KULLANILMAK ÜZERE MATLAB GUI DE GELİŞTİRİLEN YÜK AKIŞI PROGRAMI
 EĞİTİM AMACIYLA KULLANILMAK ÜZERE MATLAB GUI DE GELİŞTİRİLEN YÜK AKIŞI PROGRAMI Alper MUTLU 1 Tankut YALÇINÖZ 2 1,2 Niğde Üniversitesi Mühendislik Mimarlık Fakültesi Elektrik Elektronik Mühendisliği Niğde,
EĞİTİM AMACIYLA KULLANILMAK ÜZERE MATLAB GUI DE GELİŞTİRİLEN YÜK AKIŞI PROGRAMI Alper MUTLU 1 Tankut YALÇINÖZ 2 1,2 Niğde Üniversitesi Mühendislik Mimarlık Fakültesi Elektrik Elektronik Mühendisliği Niğde,
Self Organising Migrating Algorithm
 OPTİMİZASYON TEKNİKLERİ Self Organising Migrating Algorithm Kendini Organize Eden Göç/Geçiş Algoritması MELİH HİLMİ ULUDAĞ Fırat Üniversitesi Teknoloji Fakültesi Yazılım Mühendisliği Bölümü İletişim: www.melihhilmiuludag.com
OPTİMİZASYON TEKNİKLERİ Self Organising Migrating Algorithm Kendini Organize Eden Göç/Geçiş Algoritması MELİH HİLMİ ULUDAĞ Fırat Üniversitesi Teknoloji Fakültesi Yazılım Mühendisliği Bölümü İletişim: www.melihhilmiuludag.com
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik (Eşitlik Kısıtlı Türevli Yöntem) Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik (Eşitlik Kısıtlı Türevli Yöntem) Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde
Üstel Öğrenme ve Genel Bozulma Etkili Akış Tipi Çizelgeleme Problemi: Maksimum Tamamlanma Zamanı Minimizasyonu
 Üstel Öğrenme ve Genel Bozulma Etkili Akış Tipi Çizelgeleme Problemi: Maksimum Tamamlanma Zamanı Minimizasyonu Tamer Eren Kırıkkale Üniversitesi, Mühendislik Fakültesi, Endüstri Mühendisliği Bölümü, 71451,
Üstel Öğrenme ve Genel Bozulma Etkili Akış Tipi Çizelgeleme Problemi: Maksimum Tamamlanma Zamanı Minimizasyonu Tamer Eren Kırıkkale Üniversitesi, Mühendislik Fakültesi, Endüstri Mühendisliği Bölümü, 71451,
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 1- GİRİŞ Doç. Dr. Ali Rıza YILDIZ 1 Mühendislikte, herhangi bir fiziksel sistemin matematiksel modellenmesi sonucu elde edilen karmaşık veya analitik çözülemeyen denklemlerin
MAK 210 SAYISAL ANALİZ BÖLÜM 1- GİRİŞ Doç. Dr. Ali Rıza YILDIZ 1 Mühendislikte, herhangi bir fiziksel sistemin matematiksel modellenmesi sonucu elde edilen karmaşık veya analitik çözülemeyen denklemlerin
ELEKTRİK ENERJİ DAĞITIM SİSTEMİNDE EKONOMİK AKTİF GÜÇ DAĞITIMININ GENETİK ALGORİTMA İLE BELİRLENMESİ
 Eskişehir Osmangazi Üniversitesi Mühendislik Mimarlık Fakültesi Dergisi Cilt:XXII, Sayı:3, 009 Journal of Engineering and Architecture Faculty of Eskişehir Osmangazi University, Vol: XXII, No:3, 009 Makalenin
Eskişehir Osmangazi Üniversitesi Mühendislik Mimarlık Fakültesi Dergisi Cilt:XXII, Sayı:3, 009 Journal of Engineering and Architecture Faculty of Eskişehir Osmangazi University, Vol: XXII, No:3, 009 Makalenin
ÜRETĠCĠLERDEN REAKTĠF GÜÇ DESTEĞĠ SAĞLANMASI ve GERĠLĠM KONTROLU
 ÜRETĠCĠLERDEN REAKTĠF GÜÇ DESTEĞĠ SAĞLANMASI ve GERĠLĠM KONTROLU BÖLGESEL YÜKTEVZĠ MERKEZLERĠ ve ELEKTRĠK ÜRETĠCĠLERĠ ni BĠLGĠLENDĠRME TOPLANTISI 13-14.12.2010 Milli Yüktevzi Merkezi, Ankara Oğuz YILMAZ
ÜRETĠCĠLERDEN REAKTĠF GÜÇ DESTEĞĠ SAĞLANMASI ve GERĠLĠM KONTROLU BÖLGESEL YÜKTEVZĠ MERKEZLERĠ ve ELEKTRĠK ÜRETĠCĠLERĠ ni BĠLGĠLENDĠRME TOPLANTISI 13-14.12.2010 Milli Yüktevzi Merkezi, Ankara Oğuz YILMAZ
Kısıtsız Optimizasyon OPTİMİZASYON Kısıtsız Optimizasyon
 OPTİMİZASYON Bu bölümde çok değişkenli kısıtsız optimizasyon problemlerinin çözüm yöntemleri incelenecektir. Bu bölümde anlatılacak yöntemler, kısıtlı optimizasyon problemlerini de çözebilmektedir. Bunun
OPTİMİZASYON Bu bölümde çok değişkenli kısıtsız optimizasyon problemlerinin çözüm yöntemleri incelenecektir. Bu bölümde anlatılacak yöntemler, kısıtlı optimizasyon problemlerini de çözebilmektedir. Bunun
Genetik Algoritmalar (GA) Genetik Algoritmalar Đçerik Nesin Matematik Köyü E rim Ç lı l ş ı ta t yı Nisan, 2012 Mustafa Suphi Erden
 Genetik Algoritmalar Nesin Matematik Köyü Evrim Çalıştayı 20-23 Nisan, 202 Genetik Algoritmalar (GA Đçerik Biyolojiden esinlenme GA nın özellikleri GA nın unsurları uygulama Algoritma Şema teoremi Mustafa
Genetik Algoritmalar Nesin Matematik Köyü Evrim Çalıştayı 20-23 Nisan, 202 Genetik Algoritmalar (GA Đçerik Biyolojiden esinlenme GA nın özellikleri GA nın unsurları uygulama Algoritma Şema teoremi Mustafa
DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY)
 DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY) 1 DOĞRUSAL PROGRAMLAMADA İKİLİK (DUALİTE-DUALITY) Doğrusal programlama modelleri olarak adlandırılır. Aynı modelin değişik bir düzende oluşturulmasıyla Dual (İkilik)
DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY) 1 DOĞRUSAL PROGRAMLAMADA İKİLİK (DUALİTE-DUALITY) Doğrusal programlama modelleri olarak adlandırılır. Aynı modelin değişik bir düzende oluşturulmasıyla Dual (İkilik)
Rössler Tabanlı Kaotik Farksal Gelişim Algoritması
 Bilecik Şeyh Edebali Üniversitesi Fen Bilimleri Dergisi, Cilt:1, Sayı:, 1 ISSN: 1-33 (http://edergi.bilecik.edu.tr/index.php/fbd) Araştırma Makalesi/Research Article Rössler Tabanlı Kaotik Farksal Gelişim
Bilecik Şeyh Edebali Üniversitesi Fen Bilimleri Dergisi, Cilt:1, Sayı:, 1 ISSN: 1-33 (http://edergi.bilecik.edu.tr/index.php/fbd) Araştırma Makalesi/Research Article Rössler Tabanlı Kaotik Farksal Gelişim
Yöneylem Araştırması II
 Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Geriye Yayılım ve Levenberg Marquardt Algoritmalarının YSA Eğitimlerindeki Başarımlarının Dinamik Sistemler Üzerindeki Başarımı. Mehmet Ali Çavuşlu
 Geriye Yayılım ve Levenberg Marquardt Algoritmalarının YSA Eğitimlerindeki Başarımlarının Dinamik Sistemler Üzerindeki Başarımı Mehmet Ali Çavuşlu Özet Yapay sinir ağlarının eğitiminde genellikle geriye
Geriye Yayılım ve Levenberg Marquardt Algoritmalarının YSA Eğitimlerindeki Başarımlarının Dinamik Sistemler Üzerindeki Başarımı Mehmet Ali Çavuşlu Özet Yapay sinir ağlarının eğitiminde genellikle geriye
Facts cihazlarının gerilim kararlılığına etkisinin incelenmesi. Effects of facts devices voltage stability
 SAÜ. Fen Bil. Der. 7. Cilt, 2. Sayı, s. 6-66, 23 SAU J. Sci. Vol 7, No 2, p. 6-66, 23 Facts cihazlarının gerilim kararlılığına etkisinin incelenmesi Talha Enes Gümüş *, Mehmet Ali Yalçın * Sakarya Üniversitesi,
SAÜ. Fen Bil. Der. 7. Cilt, 2. Sayı, s. 6-66, 23 SAU J. Sci. Vol 7, No 2, p. 6-66, 23 Facts cihazlarının gerilim kararlılığına etkisinin incelenmesi Talha Enes Gümüş *, Mehmet Ali Yalçın * Sakarya Üniversitesi,
METASEZGİSEL YÖNTEMLER. Genetik Algoritmalar
 METASEZGİSEL YÖNTEMLER Genetik Algoritmalar 1970 li yıllarda John Holland tarafından geliştirilmiştir. 1989 yılında David E. Goldberg Genetik Genetik Algoritma Algoritma Uygulamaları üzerine klasik eser
METASEZGİSEL YÖNTEMLER Genetik Algoritmalar 1970 li yıllarda John Holland tarafından geliştirilmiştir. 1989 yılında David E. Goldberg Genetik Genetik Algoritma Algoritma Uygulamaları üzerine klasik eser
Yrd. Doç. Dr. A. Burak İNNER
 Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
4.4. Gerilim Kararlılığının Temel Geçici Hal Durumu
 49 4.4. Gerilim Kararlılığının Temel Geçici Hal Durumu Đletim sistemine bağlı bir asenkron motorun şekil (4.3.b) ' deki P-V eğrileriyle, iletim sisteminin P-V eğrilerini biraraya getirerek, sürekli hal
49 4.4. Gerilim Kararlılığının Temel Geçici Hal Durumu Đletim sistemine bağlı bir asenkron motorun şekil (4.3.b) ' deki P-V eğrileriyle, iletim sisteminin P-V eğrilerini biraraya getirerek, sürekli hal
Yenilenebilir Kaynakları İçeren Güç Sistemlerinin PowerWorld Programı ile Analizi
 Yenilenebilir Kaynakları İçeren Güç Sistemlerinin PowerWorld Programı ile Analizi Yasin İçel 1, Burhan Baran 2, Asım Kaygusuz 2, Ömer Bektaş 3 1 Meslek Yüksekokulu, Elektrik ve Enerji Bölümü Adıyaman Üniversitesi,
Yenilenebilir Kaynakları İçeren Güç Sistemlerinin PowerWorld Programı ile Analizi Yasin İçel 1, Burhan Baran 2, Asım Kaygusuz 2, Ömer Bektaş 3 1 Meslek Yüksekokulu, Elektrik ve Enerji Bölümü Adıyaman Üniversitesi,
KONTROLSÜZ SINIFLANDIRMADA DİFERANSİYEL GELİŞİM ALGORİTMASININ KULLANIMI
 KONTROLSÜZ SINIFLANDIRMADA DİFERANSİYEL GELİŞİM ALGORİTMASININ KULLANIMI Ü.H. Atasever 1, C. Özkan 1, F. Sunar 2 1 Erciyes Üniversitesi Mühendislik Fakültesi, Harita Mühendisliği Bölümü, Uzaktan Algılama
KONTROLSÜZ SINIFLANDIRMADA DİFERANSİYEL GELİŞİM ALGORİTMASININ KULLANIMI Ü.H. Atasever 1, C. Özkan 1, F. Sunar 2 1 Erciyes Üniversitesi Mühendislik Fakültesi, Harita Mühendisliği Bölümü, Uzaktan Algılama
ALTERNATİF AKIMIN TEMEL ESASLARI
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIMIN TEMEL ESASLARI Dr. Öğr. Üyesi Ahmet ÇİFCİ Elektrik enerjisi, alternatif akım ve doğru akım olarak
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIMIN TEMEL ESASLARI Dr. Öğr. Üyesi Ahmet ÇİFCİ Elektrik enerjisi, alternatif akım ve doğru akım olarak
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
GÜÇ SİSTEM ANALİZLERİNİN ENERJİ VERİMLİLİĞE ETKİLERİ
 EVK 2015 GÜÇ SİSTEM ANALİZLERİNİN ENERJİ VERİMLİLİĞE ETKİLERİ Turhan Türker Siemens A.Ş. Answers for energy management. Nedir? Güç sistemlerinin normal işletme koşullarında veya arızalarda nasıl çalışacağını
EVK 2015 GÜÇ SİSTEM ANALİZLERİNİN ENERJİ VERİMLİLİĞE ETKİLERİ Turhan Türker Siemens A.Ş. Answers for energy management. Nedir? Güç sistemlerinin normal işletme koşullarında veya arızalarda nasıl çalışacağını
MATLAB KULLANARAK BARA ADMİNTANS MATRİSİNİN OLUŞUMU
 Tarih: Deney-5 MATLAB KULLANARAK BARA ADMİNTANS MATRİSİNİN OLUŞUMU Amaç: Verilen güç sistem şebekesi için bara admintans matrisinin belirlenmesi Cihaz: MATLAB 7.7 Teori: Y BARA matrisinin oluşumu Bara
Tarih: Deney-5 MATLAB KULLANARAK BARA ADMİNTANS MATRİSİNİN OLUŞUMU Amaç: Verilen güç sistem şebekesi için bara admintans matrisinin belirlenmesi Cihaz: MATLAB 7.7 Teori: Y BARA matrisinin oluşumu Bara
Yerçekimsel Arama Algoritması ile PID Denetleç Parametrelerinin Tespiti PID Controller Parameters' Optimization Using Gravitational Search Algorithm
 Yerçekimsel Arama Algoritması ile PID Denetleç Parametrelerinin Tespiti PID Controller Parameters' Optimization Using Gravitational Search Algorithm Nesibe Yalçın 1, Semih Çakır 2, Metin Kesler 1, Nihan
Yerçekimsel Arama Algoritması ile PID Denetleç Parametrelerinin Tespiti PID Controller Parameters' Optimization Using Gravitational Search Algorithm Nesibe Yalçın 1, Semih Çakır 2, Metin Kesler 1, Nihan
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU
 ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x)
ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x)
FAZ KAYDIRICI TRANSFORMATÖRLERİN STATİK GERİLİM KARARLILIĞI ÜZERİNDEKİ ETKİLERİNİN İNCELENMESİ
 İleri Teknoloji Bilimleri Dergisi Cilt 2, Sayı 3, 43-52, 203 Journal of Advanced Technology Sciences Vol 2, No 3, 43-52, 203 FAZ KAYDIRICI TRANSFORMATÖRLERİN STATİK GERİLİM KARARLILIĞI ÜZERİNDEKİ ETKİLERİNİN
İleri Teknoloji Bilimleri Dergisi Cilt 2, Sayı 3, 43-52, 203 Journal of Advanced Technology Sciences Vol 2, No 3, 43-52, 203 FAZ KAYDIRICI TRANSFORMATÖRLERİN STATİK GERİLİM KARARLILIĞI ÜZERİNDEKİ ETKİLERİNİN
Programlama Dilleri 1. Ders 3: Rastgele sayı üretimi ve uygulamaları
 Ders 3: Rastgele sayı üretimi ve uygulamaları Ders 3 Genel Bakış Giriş Rastgele Sayı Rastgele Sayı Üreteci rand Fonksiyonunun İşlevi srand Fonksiyonunun İşlevi Monte Carlo Yöntemi Uygulama 1: Yazı-Tura
Ders 3: Rastgele sayı üretimi ve uygulamaları Ders 3 Genel Bakış Giriş Rastgele Sayı Rastgele Sayı Üreteci rand Fonksiyonunun İşlevi srand Fonksiyonunun İşlevi Monte Carlo Yöntemi Uygulama 1: Yazı-Tura
MANİSA CELAL BAYAR ÜNİVERSİTESİ MURADİYE YERLEŞKESİ İÇİN PSS SINCAL TABANLI GÜÇ AKIŞ ANALİZİ
 MANİSA CELAL BAYAR ÜNİVERSİTESİ MURADİYE YERLEŞKESİ İÇİN PSS SINCAL TABANLI GÜÇ AKIŞ ANALİZİ Sezai TAŞKIN, Tuğba KANYILMAZ, Sinem YENİÇERİ Manisa Celal Bayar Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik
MANİSA CELAL BAYAR ÜNİVERSİTESİ MURADİYE YERLEŞKESİ İÇİN PSS SINCAL TABANLI GÜÇ AKIŞ ANALİZİ Sezai TAŞKIN, Tuğba KANYILMAZ, Sinem YENİÇERİ Manisa Celal Bayar Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik
QUANTILE REGRESYON * Quantile Regression
 QUANTILE REGRESYON * Quantile Regression Fikriye KURTOĞLU İstatistik Anabilim Dalı Olcay ARSLAN İstatistik Anabilim Dalı ÖZET Bu çalışmada, Lineer Regresyon analizinde kullanılan en küçük kareler yöntemine
QUANTILE REGRESYON * Quantile Regression Fikriye KURTOĞLU İstatistik Anabilim Dalı Olcay ARSLAN İstatistik Anabilim Dalı ÖZET Bu çalışmada, Lineer Regresyon analizinde kullanılan en küçük kareler yöntemine
Ders İçerik Bilgisi. Dr. Hakan TERZİOĞLU Dr. Hakan TERZİOĞLU 1
 Dr. Hakan TERZİOĞLU Ders İçerik Bilgisi PID Parametrelerinin Elde Edilmesi A. Salınım (Titreşim) Yöntemi B. Cevap Eğrisi Yöntemi Karşılaştırıcı ve Denetleyicilerin Opamplarla Yapılması 1. Karşılaştırıcı
Dr. Hakan TERZİOĞLU Ders İçerik Bilgisi PID Parametrelerinin Elde Edilmesi A. Salınım (Titreşim) Yöntemi B. Cevap Eğrisi Yöntemi Karşılaştırıcı ve Denetleyicilerin Opamplarla Yapılması 1. Karşılaştırıcı
GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA
 GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA Nedim TUTKUN Düzce Üniversitesi Elektrik Elektronik Mühendisliği Bölümü nedimtutkun@duzce.edu.tr Düzce Üniversitesi Elektrik&Elektronik Mühendisliği
GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA Nedim TUTKUN Düzce Üniversitesi Elektrik Elektronik Mühendisliği Bölümü nedimtutkun@duzce.edu.tr Düzce Üniversitesi Elektrik&Elektronik Mühendisliği
DENGESİZ GÜÇ AKIŞI ANALİZLERİ İÇİN SABİT HIZLI ASENKRON GENERATÖRLÜ RÜZGAR TÜRBİNİ MODELİ BÖLÜM 1: GENERATÖR MODELİ
 DENGESİZ GÜÇ AKIŞI ANALİZLERİ İÇİN SABİT HIZLI ASENKRON GENERATÖRLÜ RÜZGAR TÜRBİNİ MODELİ BÖLÜM 1: GENERATÖR MODELİ Ahmet KÖKSOY 1 Onur ÖZTÜRK 1 1 Gebze Teknik Üniversitesi Elektronik Müh. Böl. 41400 Gebze
DENGESİZ GÜÇ AKIŞI ANALİZLERİ İÇİN SABİT HIZLI ASENKRON GENERATÖRLÜ RÜZGAR TÜRBİNİ MODELİ BÖLÜM 1: GENERATÖR MODELİ Ahmet KÖKSOY 1 Onur ÖZTÜRK 1 1 Gebze Teknik Üniversitesi Elektronik Müh. Böl. 41400 Gebze
EV TİPİ YENİLENEBİLİR HİBRİT SİSTEM İÇİN MİKRO-GENETİK ALGORİTMA İLE OPTİMAL YÜK PLANLAMASI
 EV TİPİ YENİLENEBİLİR HİBRİT SİSTEM İÇİN MİKRO-GENETİK ALGORİTMA İLE OPTİMAL YÜK PLANLAMASI Özay CAN Düzce Üniversitesi Elektrik Elektronik Müh. ozaycan28@hotmail.com Nedim TUTKUN Düzce Üniversitesi Elektrik
EV TİPİ YENİLENEBİLİR HİBRİT SİSTEM İÇİN MİKRO-GENETİK ALGORİTMA İLE OPTİMAL YÜK PLANLAMASI Özay CAN Düzce Üniversitesi Elektrik Elektronik Müh. ozaycan28@hotmail.com Nedim TUTKUN Düzce Üniversitesi Elektrik
SICAKLIK VE ENTALP KONTROLLÜ SERBEST SO UTMA UYGULAMALARININ KAR ILA TIRILMASI
 Türk Tesisat Mühendisleri Derne i / Turkish Society of HVAC & Sanitary Engineers 8. Uluslararası Yapıda Tesisat Teknolojisi Sempozyumu / 8. International HVAC +R Technology Symposium 12-14 Mayıs 2008,
Türk Tesisat Mühendisleri Derne i / Turkish Society of HVAC & Sanitary Engineers 8. Uluslararası Yapıda Tesisat Teknolojisi Sempozyumu / 8. International HVAC +R Technology Symposium 12-14 Mayıs 2008,
Evrimsel Algoritmalar Kullanarak Daha Düşük Dereceden Sistem Modeli Tasarımı Design of Lower Order System Model Using Evolutionary Algorithms
 2016 Published in 4th International Symposium on Innovative Technologies in Engineering and Science 3-5 November 2016 (ISITES2016 Alanya/Antalya - Turkey) Evrimsel Algoritmalar Kullanarak Daha Düşük Dereceden
2016 Published in 4th International Symposium on Innovative Technologies in Engineering and Science 3-5 November 2016 (ISITES2016 Alanya/Antalya - Turkey) Evrimsel Algoritmalar Kullanarak Daha Düşük Dereceden
V cn V ca. V bc. V bn. V ab. -V bn. V an HATIRLATMALAR. Faz-Faz ve Faz-Nötr Gerilimleri. Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri
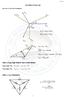 HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V aa = V cc = V bb V aa = V bb = V cc V bn V bc V ab 30 -V bn V aa = V aa V bb V aa = V aa cos(30) 30 V an V aa = V aa cos(30) =
HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V aa = V cc = V bb V aa = V bb = V cc V bn V bc V ab 30 -V bn V aa = V aa V bb V aa = V aa cos(30) 30 V an V aa = V aa cos(30) =
FARKLI PANEL TİPLERİ İÇİN EŞDEĞER DEVRE MODELİNİN PARAMETRE DEĞERLERİNİN BULUNMASI
 FARKLI PANEL TİPLERİ İÇİN EŞDEĞER DEVRE MODELİNİN PARAMETRE DEĞERLERİNİN BULUNMASI Erdem ELİBOL Melih AKTAŞ Nedim TUTKUN Özet Bu çalışmada fotovoltaik güneş panellerinin matematiksel eşdeğer devrelerinden
FARKLI PANEL TİPLERİ İÇİN EŞDEĞER DEVRE MODELİNİN PARAMETRE DEĞERLERİNİN BULUNMASI Erdem ELİBOL Melih AKTAŞ Nedim TUTKUN Özet Bu çalışmada fotovoltaik güneş panellerinin matematiksel eşdeğer devrelerinden
AST416 Astronomide Sayısal Çözümleme - II. 6. Monte Carlo
 AST416 Astronomide Sayısal Çözümleme - II 6. Monte Carlo Bu derste neler öğreneceksiniz? Monte Carlo Yöntemleri Markov Zinciri (Markov Chain) Rastgele Yürüyüş (Random Walk) Markov Chain Monte Carlo, MCMC
AST416 Astronomide Sayısal Çözümleme - II 6. Monte Carlo Bu derste neler öğreneceksiniz? Monte Carlo Yöntemleri Markov Zinciri (Markov Chain) Rastgele Yürüyüş (Random Walk) Markov Chain Monte Carlo, MCMC
Ö Z G E Ç M İ Ş. 1. Adı Soyadı: Mustafa GÖÇKEN. 2. Doğum Tarihi: 12 Haziran 1976. 3. Unvanı: Yrd. Doç. Dr. 4. Öğrenim Durumu: Ph.D.
 Ö Z G E Ç M İ Ş 1. Adı Soyadı: Mustafa GÖÇKEN 2. Doğum Tarihi: 12 Haziran 1976 3. Unvanı: Yrd. Doç. Dr. 4. Öğrenim Durumu: Ph.D. Derece Alan Üniversite Yıl Lisans Endüstri Mühendisliği Çukurova Üniversitesi
Ö Z G E Ç M İ Ş 1. Adı Soyadı: Mustafa GÖÇKEN 2. Doğum Tarihi: 12 Haziran 1976 3. Unvanı: Yrd. Doç. Dr. 4. Öğrenim Durumu: Ph.D. Derece Alan Üniversite Yıl Lisans Endüstri Mühendisliği Çukurova Üniversitesi
TEK BÖLGELİ GÜÇ SİSTEMLERİNDE BULANIK MANTIK İLE YÜK FREKANS KONTRÜLÜ
 TEKNOLOJİ, Yıl 5, (2002), Sayı 3-4, 73-77 TEKNOLOJİ TEK BÖLGELİ GÜÇ SİSTEMLERİNDE BULANIK MANTIK İLE YÜK FREKANS KONTRÜLÜ Ertuğrul ÇAM İlhan KOCAARSLAN Kırıkkale Üniversitesi, Mühendislik Fakültesi, Elektrik-Elektronik
TEKNOLOJİ, Yıl 5, (2002), Sayı 3-4, 73-77 TEKNOLOJİ TEK BÖLGELİ GÜÇ SİSTEMLERİNDE BULANIK MANTIK İLE YÜK FREKANS KONTRÜLÜ Ertuğrul ÇAM İlhan KOCAARSLAN Kırıkkale Üniversitesi, Mühendislik Fakültesi, Elektrik-Elektronik
Modelleme bir sanattan çok bir Bilim olarak tanımlanabilir. Bir model kurucu için en önemli karar model seçiminde ilişkileri belirlemektir.
 MODELLEME MODELLEME Matematik modelleme yaklaşımı sistemlerin daha iyi anlaşılması, analiz edilmesi ve tasarımının etkin ve ekonomik bir yoludur. Modelleme karmaşık parametrelerin belirlenmesi için iyi
MODELLEME MODELLEME Matematik modelleme yaklaşımı sistemlerin daha iyi anlaşılması, analiz edilmesi ve tasarımının etkin ve ekonomik bir yoludur. Modelleme karmaşık parametrelerin belirlenmesi için iyi
