ÜN TE II MPULS VE MOMENTUM
|
|
|
- Meryem Gürsel
- 6 yıl önce
- İzleme sayısı:
Transkript
1 ÜN TE II MPULS VE MOMENTUM 1. mpuls ( tme) 2. Momentum (Lineer Momentum) 3- ki Cismin Çarp flmas nda Momentum De iflmeleri a) Hareketli Bir Cisimle Duran Bir Cismin Merkezî Çarp flmas b) Hareketli Bir Cisimle Duran Cismin Merkezî Çarp flma Sonunda Kenetlenerek Hareket Etmesi c) Hareketli Bir Cisimle Duran Bir Cismin Merkezî Olmayan Çarp flmas 4. Momentumun Korunumu 5. Roketler ÖZET Ö REND KLER M Z PEK fit REL M DE ERLEND RME SORULARI Ünite II ile lgili Problemler Ünite II ile lgili Test Sorular
2 BU BÖLÜMÜN AMAÇLARI Bu bölümü çal flt n zda ; Momentum ve itme kavramlar n ö renecek, Cisimlerin çarp flma sonucu kenetlenmesiyle oluflan sistemin hareketini kavrayacak, Momentumun korunumu yasas n bilecek, Roketlerin çal flma prensiplerini ö reneceksiniz. NASIL ÇALIfiMALIYIZ? Bu bölümü çal flmaya bafllamadan önce vektörel büyüklüklerin toplanmas n, ivmenin tan m ile Newton un II. ve III. Hareket Kanunu nu yeniden çal flman z yararl olacakt r. 34
3 1- MPULS ( TME) Newton un II. Hareket Kanunu (dinami in temel prensibi) olarak ifade etti imiz F = m a ba nt s ndaki ivme (a) yerine efliti olan Δv/Δt yaz l rsa, F = m a ba nt s ndaki ivme (a) yerine efliti olan Δv/Δt yaz l rsa, F = m Δv Δt F. Δt = mδv elde edilir. Bu ba nt ya göre, m kütleli bir cisme Δt süreyle F kuvvetinin uygulanmas na (FΔt çarp m na ) impuls (itme) denir. Kuvvet vektörel büyüklüktür. Dolay s ile itmede vektörel büyüklük olup kuvvet ile ayn yönlüdür. Bir cisme birden fazla kuvvet etki ediyorsa toplam itme, itmelerin cebirsel toplam na eflittir. Toplam itme = F. Δt = F 1 Δt 1 + F 2 Δt F n Δt n dir. Toplama ifllemi yap l rken bir yöndeki kuvvetlerin iflareti pozitif (+) z t yönlü kuvvetlerin iflareti negatif (- ) al n r. Nicelik Kuvvet Zaman de iflimi tme ( mpuls) Sembol F Δt F.Δt Birim N s N.s Tablo 2.1 : Birim tablosu Grafik 2.1 deki kuvvet - zaman grafiklerinin alt ndaki alan toplam itmeye eflittir. Toplam itme = F. Δt Toplam itme = F 1 Δt 1 - F 2 Δt 2 Toplam itme = F. Δt (a) (b) (c) Grafik 2.1 : Kuvvet-zaman grafikleri 35
4 2- MOMENTUM (Lineer Momentum) Bu kitapta bir do ru boyunca hareket eden cisimlerin momentumu (Lineer momentum) incelenecektir. Aç sal momentumla kar flt r lmamal d r. Bir cismin kütlesiyle h z n n çarp m na o cismin momentumu veya hareket miktar denir. Momentum, P = mv 'dir. H z vektörel bir büyüklüktür. Dolay s yla momentumda vektörel bir büyüklük olup, h z vektörü ile ayn yöndedir. Nicelik Kütle H z Momentum Sembol m v P Birim kg m/s kg.m /s Tablo 2.2 : Birim tablosu Grafik 2.2 deki momentum - zaman grafi inde do runun e imi cisme etkiyen kuvveti (net kuvvet) verir. E im = tan α = ΔP Δt ΔP = F. Δt = F Momentum de iflimi itmeye eflittir. Grafik 2.2 : Momentum-zaman grafi i ÖRNEK 1 18 km/h h zla hareket eden 1200 kg kütleli bir kamyonla eflit momentuma sahip olabilmesi için, 800 kg kütleli bir otomobilin h z kaç m/s olmal d r? v kam = 18 km/h = m 3600 s = 5 m/s 36
5 Kamyon ve otomobilin momentumlar eflit olaca ndan. P kam = P oto m kam. v kam = m oto. v oto v oto = m kam. v m kam = 1200 oto v oto = 7,5 m/s 3- K C SM N ÇARPIfiMASINDA MOMENTUM DE fimeler Duran ki Cismin Etkileflmesi S k flt r lm fl bir yay n etkisindeki eflit kütleli iki deney arabas (fiekil 2.1.a), serbest b rak ld nda z t yönde hareket ettikleri, Δt kadar sonra yer de ifltirmelerinin eflit oldu u görülür (fiekil 2.1.b). a Etkileflmeden önce P 1 =0 P 2 = 0 b Etkileflmeden sonra P 1 = mv 1 P 2 = mv 2 fiekil 2.1 : Momentum de iflimleri Δx 1 = -Δ x 2 eflitli inde de erler d yerine yaz l rsa, v 1 Δt = - v 2 Δt'den, 1 2 v 1 = -v 2 bulunur. Eflitli in her iki taraf m ile çarp l rsa, mv 1 = -mv 2 P 1 = -P 2 olur. - iflaretinin yönü belirtti ini hat rlay n z. 37
6 Hareketli ki Cismin Çarp flmas fiekil 2.2 deki hareketli cisimlerin çarp flmas nda, bir cismin kazand momentum, di erinin kaybetti i momentuma eflittir. Yani hareketli iki cismin momentum de iflimleri büyüklükçe eflit ve z t yönlüdür. ΔP 1 = -ΔP 2 fiekil 2.2 : Hareketli iki cismin çarp flmas a) Hareketli Bir Cisimle Duran Bir Cismin Merkezî Çarp flmas I. m 1 = m 2 ise Cisimlerin kütleleri eflit oldu undan merkezî çarp flma sonras duran cisim, çarpan cismin h z kadar h z kazan r ve bu h zla hareket eder (fiekil 2.3). Bileflke momentumun çarp flmadan sonra yönü, do rultusu ve büyüklü ü de iflmez. P 1 m 1 = m 2 = m P 2 Çarp flmadan önce Çarp flmadan sonra fiekil 2.3 : Eflit kütleli hareketli bir cisimle duran bir cismin merkezî çarp flmas II. m 1 > m 2 ise fiekil 2.4 te m 1 > m 2 oldu unda merkezî çarp flma sonras m 2 kütlesinin h z n n, m 1 kütlesinin ilk h z yönünde oldu u görülmektedir. P m 1 > m 2 P 1 P 2 38 Çarp flmadan önce Çarp flmadan sonra fiekil 2.4 : Kütleleri farkl hareketli bir cisimle duran bir cismin merkezî çarp flmas
7 III. m 1 < m 2 ise fiekil 2.5 te m 1 < m 2 oldu unda merkezî çarp flma sonras m 1 ve m 2 kütleli cisimlerin h zlar n n z t yönlü oldu u görülmektedir. Momentumum ve enerjinin korundu u çarp flmalara esnek çarp flma denir. P 1 P 1 P 2 m 1 < m 2 Çarp flmadan önce Çarp flmadan sonra fiekil 2.5: Kütleleri farkl hareketli bir cisimle duran bir cismin merkezî çarp flmas b) Hareketli Bir Cisimle Duran Cismin Merkezî Çarp flma Sonunda Kenetlenerek Hareket Etmesi fiekil 2.6 da çarp flma sonras, cisimler kenetlenerek hareket ettiklerinden h zlar ortakt r. Ortak h z n yönü v 1 h z ile ayn yönlü olup ayn do rultuludur. Momentumun korundu u, ancak enerjinin korunmad böyle çarp flmalara esnek olmayan çarp flma denir. P 1 m 1 < m 2 P Çarp flmadan önce Çarp flmadan sonra fiekil 2.6 : Hareketli bir cisimle duran bir cismin merkezî çarp flma sonunda kenetlenerek hareket etmesi 39
8 c) Hareketli Bir Cisimle Duran Bir Cismin Merkezî Olmayan Çarp flmas m 1 < m 2 fiekil 2.7 : Hareketli bir cisimle duran bir cismin merkezî olmayan çarp flmas fiekil 2.8 : Momentum vektörlerinin gösterilmesi fiekil fiekil 5.7' 2.7 de de m m 1 < m 2 oldu unda merkezî olmayan çarp flma sonras P 1 ve 1 < m 2 old olmayan çarp flma sonras P 1 ve P r n n bileflkesi fiekil fiekil 2.8 de 5.8'de görüldü ü görüldü ü gibi gibi bulunarak bulunarak çarp flma çarp flma öncesi öncesi P 22 momentumlar n n bileflkesi fiekil 5.8'de gö P 1 momentumu bulunur. H z n do rultusu, tan α = P 1 P 1 den bulunur. 4- MOMENTUMUN KORUNUMU Kesim 2.3 te iki cismin çarp flmas nda ΔP 1 = -ΔP 2 ya da, ΔP 1 + ΔP 2 = 0 sonucu elde edilmiflti. Bu ba nt dan, sistemdeki toplam momentum de ifliminin s f r, ya da toplam momentum de ifliminin sabit oldu u söylenebilir. Buna Momentumun Korunumu Kanunu denir ve iki cismin Çarp flmadan önceki toplam momentumlar, çarp flmadan sonraki toplam momentumlar na eflittir. fleklinde ifade edilir. Kanun, P 1 + P 2 = P 1 + P 2 veya 40 m 1 v 1 + m 2 v 2 = m 1 v 1 + m 2 v 2 olarak yaz l r. Bu ba nt esnek ve esnek olmayan çarp flmalar n her ikisi için de geçerlidir.
9 5- ROKETLER Bir oyuncak balonu fliflirip, anîden serbest b rakt m zda balon gaz n ç k fl yönüne z t yönde hareket eder. Roketler için de durum benzerdir. Rokette yanma sonucu oluflan gaz, büyük bir ç k fl h z yla at l r. Roketin ileri hareketi d flar büyük bir h zla at lan gaz n tepki kuvvetiyle sa lan r. Momentum aç klan rken kütle sürekli sabit düflünülmüfltü, oysa roketlerin ateflleme sisteminin çal flmas ndan yak tlar n n bitimine kadar kütleleri azal rken h z sürekli artar. Momentumun korunumundan roketin vektörel h z ndaki de iflim, m Δv = Δm v gaz Δv = Δm m vgaz olur. Ba nt daki; m: Roketin gaz at ld ktan sonraki kütlesi, Δm: D flar at lan gaz n kütlesi, v gaz : D flar at lan gaz n h z, Δv : Roketin h z ndaki de iflimidir. ÖRNEK 2 Bir roketin toplam kütlesi 1500 kg d r. Roketten 2000 m/s h zla 300 kg l k yak t at ld nda roket kaç m/s lik h z kazan r? m toplam = 1500 kg v gaz = 2000 m/s Δm = 300 kg Δv =? m toplam = m roket + Δm m roket = m roket = 1200 kg Δv = Δm m rok v gaz Δv = Δv = 500 m/s 41
10 ÖZET Bir cismin momentumu, kütlesiyle h z n n çarp m olarak tan mlan r. P = mv Bir kuvvetle, bu kuvvetin bir cisim üzerine etkime süresinin çarp m na impuls (itme) denir. tme; cismin momentum de iflimine eflittir. F. Δt = ΔP F. Δt = mv 2 - mv 1 Bir çarp flmada cisimlerin momentumlar ndaki de iflimin toplam s f r olur. Dolay s yla bu sistemdeki cisimlerin momentumlar n n toplam sabit kal r. Ya da herhangi bir çarp flma olay nda, sistemin çarp flmadan önceki momentumu, çarp flmadan sonraki momentumuna eflit olur. Buna momentumun korunumu kanunu denir. P 1 + P P n = P 1 + P P n = SAB T m 1 v 1 + m 2 v m n vn = m 1 v 1 + m 2 v m n v n = SAB T Çarp flmalar iki çeflittir. Esnek çarp flmalarda hem momentum, hem kinetik enerji korunur. Esnek olmayan çarp flmalarda ise momentum korunur, ancak kinetik enerji korunmaz. Roketlerin hareketi Newton un III. Hareket Kanunu na (Etki-Tepki Prensibi) dayan r. 42
11 Ö REND KLER M Z PEK fit REL M 1-4 saniye süreyle 10 N luk kuvvet uyguland nda, h z nda 8 m/s lik art fl gözlenen cismin kütlesi kaç kg d r? Δt = 4 s F = 10 N Δv = 8 m/s m =? F. Δt = m Δv = m. 8 m = 40 8 m = 5 kg 2-4 kg kütleli bir tüfe in atefllenmesiyle 20 g l k bir mermi 800 m/s h zla tüfe i terkediyor. Tüfe in geri tepme h z kaç m/s dir? m t = 4 kg m m = 0,02 kg v m = 800 m/s v t = 0 v m = 0 v t =? Momentumun korunumu kanununa göre m t v t + m m v m = m t v t + m m v m ,02. 0 = 4 v t + 0, v t = -16 v t = v t = - 4 m/s 3- Durmakta olan 2 kg kütleli bir cisme Grafik 2.3 teki gibi zamanla de iflen bir kuvvet etki ediyor. Cismin 15 s deki h z de ifliminin büyüklü ü kaç m/s dir? Grafik 2.3 Kuvvet (F) -zaman (t) grafi inin alt ndaki alan itmeyi verir. (0-5) s aras (bölge üçgendir.) Alan = = 50 2 = 25 N. s (5-15) s aras (bölge dikdörtgendir.) Alan = = 100 N. s Toplam alan = tme = F. Δt = 125 N. s tme momentum de iflimine eflittir. F. Δt = m Δv 125 = 2. Δv Δv = Δv = 62,5 m/s 43
12 4- Kütlesi 20 g olan bir mermi, sürtünmesiz bir ortamda durmakta olan 880 g kütleli bir tahta blo a saplan yor (fiekil 2.9). Çarp flmadan sonra mermi ve tahta blo un h z 4 m/s oldu una göre merminin çarp flmadan önceki h z kaç m/s dir? fiekil 2.9 Çarp flma sonras cisimler birbirine kenetlenerek ortak h zla hareket eder. Esnek olmayan çarp flmada momentum eflitli i, m m = 0,02 kg m t = 0,88 kg v ort = 4 m/s v m =? m m v m + m t v t = (m m + m t )v ort ' dan 0,02. v m + 0,88. 0 = (0,02 + 0,88) 4 0,02 v m = 0,9. 4 v m = 3,6 0,02 v m = 180 m/s olur. 5- fiekil 2.10 daki eflit kütleli, biri hareketsiz iki bilyeden m 1 k ü t l e s i n i n çarp flmadan önceki h z v 1 = 6 m/s, çarp flmadan sonraki h z v 1 = 0 d r. m 2 kütlesinin çarp flmadan sonraki h z kaç m/s dir? m 1 = m 2 fiekil 2.10 m 1 v 1 + m 2 v 2 = m 1 v 1 + m 2 v 2 m 1 = m 2 oldu undan mv 1 + mv 2 = mv 1 + mv 2 den m. 6 + m. 0 = m. 0 + mv m = mv 2 v 2 = 6 m/s bulunur.
13 6- fiekil 2.11 deki m 1 = 0,4 kg'l k çelik bir bilye v 1 = 6m/s h zla, durmakta olan m 2 = 0,2 kg kütleli cam cam bilyeye bilyeye merkezî merkezî olarak olarak çarp yor. çarp yor. Çarp flmadan Çarp flmadan sonra sonra m 1 m kütlesinin h z v 1 = 4 m/s oldu una göre, m 2 kütlesinin v 2 h z kaç m/s'dir? fiekil 2.11 m 1 v 1 + m 2 v 2 = m 1 v 1 + m 2 v 2 den 0, ,2. 0 = 0, , 2 v 2 2,4 = 1,6 + 0,2 v 2 0,8 = 0,2 v 2 v 2 = 0,8 0,2 v 2 = 4 m/s olur. 7- fiekil 2.12 deki m 1 = 0,2 kg'l k cam bilye v 1 = 6 m/s h zla, durmakta olan m 2 = 0,4 kg'l k lik çelik bir bir bilyeye bilyeye merkezî merkezî olarak olarak çarp yor. çarp yor. Çarp flmadan Çarp flmadan sonra sonra m 2 kütlesinin h z v 2 = 4 m/s oldu una göre, m 1 kütlesinin v 1 h z kaç m/s'dir? fiekil 2.12 m 1 v 1 + m 2 v 2 = m 1 v 1 + m 2 v 2 den 0, ,4. 0 = 0, 2 v ,2 + 0 = 0,2 v 1 + 1,6 1,2-1,6 = 0,2 v 1-0,4 = 0,2 v 1 v 1 = - 0,4 0,2 v 1 = -2 m/s olur. 45
14 8- fiekil 2.13 teki m 1 = 0,2 kg kütleli ve v 1 = 6 m/s h zl cam bir bilye, duran m 2 = 0,4 kg kütleli cam macunundan yap lm fl bir bilyeye merkezi olarak çarp yor. Çarp flmadan sonra birlikte hareket eden sistemin ortak h z kaç m/s dir? fiekil 2.13 m 1 v 1 + m 2 v 2 = (m 1 + m 2 ) v ort dan 0, ,4. 0 = (0,2 + 0,4) v ort 1,2 = 0,6 v ort v ort = 1,2 0,6 v ort = 2 m/s bulunur Kütlesi Kütlesi m 0,2 kg olan cam bilye v 1 = 8 m/s h zla, durmakta olan m 2 = 0,4 kg 1 = 0,2 kg o v 1 = 8 m/s h zla, durmakta olan m 2 = 0,4 kg kütleli çelik bir bilyeyle fiekil 2.14 teki i gibi merkezî olmayan çarp flma yap yor. kütleli çelik bir bilyeyle fiekil 5.14'teki gibi merkezî olmayan çarp flma yap yor. m kütlesi ilk hareket do 0 lik aç yaparak v = 4 m/s h zla hareketini 1 kütlesi ilk hareket do rultusu ile 90 lik aç yaparak v 1 = 4 m/s h zla hareketini sürdürüyor. m 2 kütlesinin çarp flmadan sonraki h z v 2 kaç m/s'dir? 46 fiekil 2.14
15 P 2 2 = P P 1 P 2 = P P 1 P 2 = (m 1 v 1 ) 2 + (m 1 v 1 ) 2 P 2 = (0,2. 8) 2 + (0,2. 4) 2 P 2 = 1, ,8 2 P 2 = 2,56 + 0,64 P 2 = 3,2 P 2 = m 2 v 2 m 2 v 2 = 3,2 0,4 v 2 = 3,2 v 2 = 1,78 0,4 v 2 = 4,47 m/s olur. fiekil m/s h zla ilerlemekte olan 60 kg kütleli bir kay k üzerinde durmakta olan 40 kg kütleli bir çocuk nehire göre 3 m/s h zla ve ters yönde atlarsa, kay n h z kaç m/s olur? fiekil 2.16 m ç +m k v ort = m ç v 1 + m k v = v = v = 60 v = 60 v 2 v 2 = v 2 = 8 m/s 47
16 . DE ERLEND RME SORULARI a) BÖLÜM LE LG L PROBLEMLER 1-0,05 kg l k bir tenis topu 30 m/s h zla çarpt raket taraf ndan 40 m/s h zla geri itiliyor. Topun raketle etkileflme süresi 0,02 saniye oldu una göre, raketin topa uygulad ortalama kuvvet kaç N dur? kg kütleli bir minibüs 20 m/s h zla, durmakta olan 900 kg kütleli bir otomobile çarp yor. Çarp flmadan sonra birlikte sürüklenen araçlar n ortak h z kaç m/s dir? 3-80 m yükseklikten serbest b rak lan 20 kg kütleli bir cisim yere çarpt nda yerin cisme karfl uygulad ortalama direnç kuvveti N dur. Yere çarpan cismin h z n n s f r olmas için kaç saniye süreyle yerle etkileflmelidir? (g = 10 m/s 2 al nacak) 4-6 m/s h zla ilerlemekte olan 60 kg kütleli bir araba üzerinde durmakta olan 40 kg kütleli bir çocuk yere göre araban n iki kat bir h zla ve ters yönde atlarsa araban n h z kaç m/s olur? 5- fiekil 2.16 daki 2000 kg kütleli kamyon 1m/s h zla hareket etmektedir. fiekil 2.16: Problem 2.5 Kamyonu durdurmak için 500 N luk sabit bir fren kuvveti uygulan yor. Kamyonun; a. Durma süresi kaç s dir? b. Bu süredeki yer de ifltirmesi (durma uzakl ) kaç m dir? 48
17 b) BÖLÜM LE LG L TEST SORULARI 1-20 N luk bir kuvvetin etkisiyle 4 kg kütleli bir cismin h z 10 m/s den 20 m/s ye yükseliyor. Kuvvetin cisim ile etkileflme süresi kaç saniyedir? A) 2 B) 2,5 C) 4 D) 8,75 2- Bir cisme etki eden net kuvvetin, zamana göre de iflimi grafikteki gibi oldu una göre 15 s sonunda toplam itme kaç N.s olur? A) -75 B) -25 C) 25 D) km/h h zla giden 5 tonluk bir kamyonetin momentumu kaç kg m/s dir? A) 360 B) C) D)
18 4- Durmakta olan bir cisim iç patlama sonucu iki parçaya bölünüyor. Parçalardan 2 kg kütleli olan 10 m/s h zla do u yönünde, di eri ise z t yönde 5 m/s h zla ilerliyor. Bu cismin patlamadan önceki kütlesi kaç kg d r? A) 3 B) 4 C) 5 D) 6 5- m 1 ve m 2 kütleli iki cisim flekildeki gibi v 1 = 3 m/s ve v 2 = 6 m/s lik h zlarla esnek olmayan merkezî çarp flma yap yor. Çarp flma sonras cisimlerin ortak h zlar kaç m/s dir? A) -5 B) -3 C) 3 D) 5 50
19 6- t = 0 an nda durmakta olan cisme etkiyen kuvvetin zamanla de iflim grafi ine göre, ayn cismin momentum-zaman grafi i afla dakilerden hangisidir? A) B) C) D) 7- Sürtünmesiz düzlemde m 1 = 2 kg kütleli cisim v 1 = 30 m/s h zla durmakta olan m 2 = 4 kg kütleli cisme merkezî çarparak kenetleniyor. Kenetlenen bu cisimler daha sonra 6 kg kütleli durmakta olan bir baflka cisimle merkezî çarp flarak kenetleniyor. kinci çarp flman n sonunda, kenetlenen cisimlerin ortak h z kaç m/s olur? A) 3 B) 4 C) 5 D) 6 51
20 8-60 kg kütleli bir avc 4 kg l k tüfekle at fl yap yor. Kütlesi 0,04 kg olan merminin tüfekten ç k fl h z 640 m/s dir. Avc tüfe i omuzuna çok s k bast rd na göre tüfe in geri tepme h z kaç m/s dir? A) 0,4 B) 1 C) 10 D) 25,6 9- Durmakta olan 10 kg kütleli bir cisme, s ras yla do uya do ru 5 saniye süreyle 12 N luk, kuzeye do ru 4 saniye süreyle 20 N luk baflka bir kuvvet uygulan yor. Cismin son h z n n büyüklü ü kaç m/s dir? A) 6 B) 8 C) 10 D) Durmakta olan flekildeki m 2 = 6,4 kg kütleli cisme, h z v 1 = 100 m/s, kütlesi m 1 = 1,6 kg olan cisim yatayla 60 lik aç yapacak flekilde gelerek saplan yor. Sistemin son h z kaç m/s dir? (Cos 60 = 0,5) A) 4 B) 5 C) 8 D) 10 52
F Z K 3 ÜN TE II HAREKET
 ÜN TE II HAREKET 1. Bir Do ru Üzerinde Konum ve Yer De ifltirme 2. Düzgün Hareket 3. Ortalama H z ve Anî H z 4. Ortalama vme ve Anî vme 5. Sabit vmeli Hareket ÖZET Ö REND KLER M Z PEK fit REL M DE ERLEND
ÜN TE II HAREKET 1. Bir Do ru Üzerinde Konum ve Yer De ifltirme 2. Düzgün Hareket 3. Ortalama H z ve Anî H z 4. Ortalama vme ve Anî vme 5. Sabit vmeli Hareket ÖZET Ö REND KLER M Z PEK fit REL M DE ERLEND
11. SINIF KONU ANLATIMLI. 2. ÜNİTE: KUVVET ve HAREKET 4. KONU AĞIRLIK MERKEZİ - KÜTLE MERKEZİ ETKİNLİK ÇÖZÜMLERİ
 11. SINIF KNU ANLATIMLI 2. ÜNİTE: KUVVET ve HAREKET 4. KNU AĞIRLIK MERKEZİ - KÜTLE MERKEZİ ETKİNLİK ÇÖZÜMLERİ 2 2. Ünite 4. Konu 3. A rl k Merkezi - Kütle Merkezi A nn Çözümleri su 1. BM fiekil I fiekil
11. SINIF KNU ANLATIMLI 2. ÜNİTE: KUVVET ve HAREKET 4. KNU AĞIRLIK MERKEZİ - KÜTLE MERKEZİ ETKİNLİK ÇÖZÜMLERİ 2 2. Ünite 4. Konu 3. A rl k Merkezi - Kütle Merkezi A nn Çözümleri su 1. BM fiekil I fiekil
11. SINIF KONU ANLATIMLI. 1. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM ETKİNLİK VE TEST ÇÖZÜMLERİ
 . SINIF KONU ANLATIMLI. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM ETKİNLİK VE TEST ÇÖZÜMLERİ 7 İtme ve Çizgisel Momentum. Ünite 7. Konu (İtme ve Çizgisel Momentum) A nın Çözümleri. Eğik
. SINIF KONU ANLATIMLI. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM ETKİNLİK VE TEST ÇÖZÜMLERİ 7 İtme ve Çizgisel Momentum. Ünite 7. Konu (İtme ve Çizgisel Momentum) A nın Çözümleri. Eğik
BU ÜN TEN N AMAÇLARI
 ÜN TE III YÜKLÜ PARÇACIKLARIN ELEKTR K ALANDA HAREKET 1. Elektron 2. Proton 3. Yüklü Parçac klara Etki Eden Kuvvet 4. Yüklü Parçac klar n vme ve H zlar 5. Yüklü Parçac klar n Yörüngeleri 6. Kütlenin H
ÜN TE III YÜKLÜ PARÇACIKLARIN ELEKTR K ALANDA HAREKET 1. Elektron 2. Proton 3. Yüklü Parçac klara Etki Eden Kuvvet 4. Yüklü Parçac klar n vme ve H zlar 5. Yüklü Parçac klar n Yörüngeleri 6. Kütlenin H
Bölüm 9: Doğrusal momentum ve çarpışmalar
 Bölüm 9: Doğrusal momentum ve çarpışmalar v hızıyla hareket eden m kütleli bir parçacığın doğrusal momentumu kütle ve hızın çarpımına eşittir; p = mv Momentum vektörel bir niceliktir, yönü hız vektörü
Bölüm 9: Doğrusal momentum ve çarpışmalar v hızıyla hareket eden m kütleli bir parçacığın doğrusal momentumu kütle ve hızın çarpımına eşittir; p = mv Momentum vektörel bir niceliktir, yönü hız vektörü
Fizik 203. Ders 5 İş-Enerji- Momentum Ali Övgün. Ofis: AS242 Fen ve Edebiyat Fakültesi Tel:
 Fizik 203 Ders 5 İş-Enerji- Momentum Ali Övgün Ofis: AS242 Fen ve Edebiyat Fakültesi Tel: 0392-630-1379 ali.ovgun@emu.edu.tr www.aovgun.com İşinTanımı Güç KinetikEnerji NetKuvvetiçinİş-EnerjiTeoremi EnerjininKorunumuYasası
Fizik 203 Ders 5 İş-Enerji- Momentum Ali Övgün Ofis: AS242 Fen ve Edebiyat Fakültesi Tel: 0392-630-1379 ali.ovgun@emu.edu.tr www.aovgun.com İşinTanımı Güç KinetikEnerji NetKuvvetiçinİş-EnerjiTeoremi EnerjininKorunumuYasası
11. SINIF KONU ANLATIMLI. 2. ÜNİTE: KUVVET ve HAREKET 7. Konu İŞ ve ENERJİ ETKİNLİK ve TEST ÇÖZÜMLERİ
 . SINIF KONU NLTIMLI. ÜNİTE: KUVVET ve HREKET 7. Konu İŞ ve ENERJİ ETKİNLİK ve TEST ÇÖZÜMLERİ .. Ünite 7. Konu ( fl ve Enerji) n n Çözümleri E K W s m./4v f s. /4x m.v f s.x f s mv x Cismin K noktas nda
. SINIF KONU NLTIMLI. ÜNİTE: KUVVET ve HREKET 7. Konu İŞ ve ENERJİ ETKİNLİK ve TEST ÇÖZÜMLERİ .. Ünite 7. Konu ( fl ve Enerji) n n Çözümleri E K W s m./4v f s. /4x m.v f s.x f s mv x Cismin K noktas nda
DİNAMİK 01 Giriş ve Temel Prensipler
 DİNAMİK 01 Giriş ve Temel Prensipler Dinamik, kuvvet ile hareket arasındaki ilişkiyi inceler. Kuvvet Hareketsiz bir cismi harekete ettiren ve ya hareketini değiştiren etkiye kuvvet denir. Dinamiğin, Newton
DİNAMİK 01 Giriş ve Temel Prensipler Dinamik, kuvvet ile hareket arasındaki ilişkiyi inceler. Kuvvet Hareketsiz bir cismi harekete ettiren ve ya hareketini değiştiren etkiye kuvvet denir. Dinamiğin, Newton
F Z K BASINÇ. Kavram Dersaneleri 42
 F Z BASINÇ ÖRNE : ÇÖZÜ : Özdefl iki tu lan n I, II, III konumlar ndayken yere uygulad klar toplam bas nç kuvvetleri, iki tu lan n a rl klar toplamlar na eflittir. Bu nedenle F = F = F olur. yer I II III
F Z BASINÇ ÖRNE : ÇÖZÜ : Özdefl iki tu lan n I, II, III konumlar ndayken yere uygulad klar toplam bas nç kuvvetleri, iki tu lan n a rl klar toplamlar na eflittir. Bu nedenle F = F = F olur. yer I II III
GAZLAR ÖRNEK 16: ÖRNEK 17: X (g) Y (g) Z (g)
 ÖRNEK 16: ÖRNEK 17: X (g) Y (g) Z (g) Sürtünmesiz piston H (g) He Yukar daki üç özdefl elastik balon ayn koflullarda bulunmaktad r. Balonlar n hacimleri eflit oldu una göre;. Gazlar n özkütleleri. Gazlar
ÖRNEK 16: ÖRNEK 17: X (g) Y (g) Z (g) Sürtünmesiz piston H (g) He Yukar daki üç özdefl elastik balon ayn koflullarda bulunmaktad r. Balonlar n hacimleri eflit oldu una göre;. Gazlar n özkütleleri. Gazlar
2. ÜN TE KUVVET VE HAREKET 1. HIZ NED R? NASIL HESAPLANIR? 2. KUVVET NASIL ÖLÇÜLÜR? NASIL GÖSTER L R? 3. B RDEN FAZLA KUVVET N ETK S
 . ÜN TE. KUVVET VE HAREKET 1. HIZ NED R? NASIL HESAPLANIR?. KUVVET NASIL ÖLÇÜLÜR? NASIL GÖSTER L R? 3. B RDEN FAZLA KUVVET N ETK S 4. TÜM VARLIKLARI HER ZAMAN ETK LEYEN KUVVET Bir cismin bulundu u noktaya
. ÜN TE. KUVVET VE HAREKET 1. HIZ NED R? NASIL HESAPLANIR?. KUVVET NASIL ÖLÇÜLÜR? NASIL GÖSTER L R? 3. B RDEN FAZLA KUVVET N ETK S 4. TÜM VARLIKLARI HER ZAMAN ETK LEYEN KUVVET Bir cismin bulundu u noktaya
TEST Levhan n a rl G olsun. G a rl n n O F 1 TORK (KUVVET MOMENT ) - DENGE
 R (UVVE MME ) - DEE ES -... evhalar dengede oldu una göre, desteklerin oldu u noktalara göre moment al n rsa,...... oldu u görülür. CEVA B d d d d. ucuna göre moment cambaz den ye giderken momenti azald
R (UVVE MME ) - DEE ES -... evhalar dengede oldu una göre, desteklerin oldu u noktalara göre moment al n rsa,...... oldu u görülür. CEVA B d d d d. ucuna göre moment cambaz den ye giderken momenti azald
11. SINIF KONU ANLATIMLI. 2. ÜNİTE: KUVVET ve HAREKET 3. Konu TORK, AÇISAL MOMENTUM ve DENGE ETKİNLİK ve TEST ÇÖZÜMLERİ
 11. SINIF ONU ANAIMI 2. ÜNİE: UVVE ve HAREE 3. onu OR, AÇISA MOMENUM ve DENGE EİNİ ve ES ÇÖZÜMERİ 2 2. Ünite 3. onu ork, Aç sal Momentum ve Denge A n n Yan tlar 1. Çubuk dengede oldu una göre noktas na
11. SINIF ONU ANAIMI 2. ÜNİE: UVVE ve HAREE 3. onu OR, AÇISA MOMENUM ve DENGE EİNİ ve ES ÇÖZÜMERİ 2 2. Ünite 3. onu ork, Aç sal Momentum ve Denge A n n Yan tlar 1. Çubuk dengede oldu una göre noktas na
F Z K A IRLIK MERKEZ ÖRNEK 1 : ÇÖZÜM 1: Bir cisim serbestçe dönebilece i bir noktadan as l rsa, düfley do rultu daima a rl k merkezinden
 F Z A IRI EREZ ÖRNE 1 : I m II 2m ütleleri m, 2m olan eflit bölmeli, düzgün ve türdefl I ve II levhalar flekildeki gibi birbirine tutturularak noktas ndan bir iple as l yor. Bu levhalar afla dakilerden
F Z A IRI EREZ ÖRNE 1 : I m II 2m ütleleri m, 2m olan eflit bölmeli, düzgün ve türdefl I ve II levhalar flekildeki gibi birbirine tutturularak noktas ndan bir iple as l yor. Bu levhalar afla dakilerden
Q8.1. A. 20 kg m/s sağa B. 20 kg m/s sola C. 4.0 kg m/s sağa D. 4.0 kg m/s sola
 Q8.1 Kütlesi 0.40 kg olan bir top sola doğru 30 m/s hızla çarpıyor ve 20 m/s hızla geri dönüyor. Bu çarpışma boyunca toplam itme nedir ve hangi yöndedir? A. 20 kg m/s sağa B. 20 kg m/s sola C. 4.0 kg m/s
Q8.1 Kütlesi 0.40 kg olan bir top sola doğru 30 m/s hızla çarpıyor ve 20 m/s hızla geri dönüyor. Bu çarpışma boyunca toplam itme nedir ve hangi yöndedir? A. 20 kg m/s sağa B. 20 kg m/s sola C. 4.0 kg m/s
ÜN TE I NEWTON UN HAREKET KANUNLARI
 ÜN TE I 1. Newton un I. Hareket Kanunu ve Uygulamalar 2. Newton un II. Hareket Kanunu ve Uygulamalar a) Sabit Bir Kuvvet Etkisinde H z De iflmeleri b) vmenin, Kuvvetin Büyüklü üne Ba l l 3. Newton un III.
ÜN TE I 1. Newton un I. Hareket Kanunu ve Uygulamalar 2. Newton un II. Hareket Kanunu ve Uygulamalar a) Sabit Bir Kuvvet Etkisinde H z De iflmeleri b) vmenin, Kuvvetin Büyüklü üne Ba l l 3. Newton un III.
İÇİNDEKİLER
 İÇİNDEKİLER 27.10.2016 DİNAMİK 01 Giriş ve Temel Prensipler Dinamiğin Prensipleri (Newton Kanunları) 1) Eylemsizlik Prensibi (Dengelenmiş Kuvvetler) 2) Temel Prensip (Dengelenmemiş Kuvvetler) 3) Etki-Tepki
İÇİNDEKİLER 27.10.2016 DİNAMİK 01 Giriş ve Temel Prensipler Dinamiğin Prensipleri (Newton Kanunları) 1) Eylemsizlik Prensibi (Dengelenmiş Kuvvetler) 2) Temel Prensip (Dengelenmemiş Kuvvetler) 3) Etki-Tepki
4. Sistem dengede oldu una. hareketli piston. P o. esnek CEVAP E. balon ESEN YAYINLARI P X. 6atm 5L. .g 200 = 8 (20 + V D. Buna göre; 25 = 20 + V D
 AZ BASINCI ES - 1 1. Balona etki eden toplam bas nç; aç k ava bas nc - na, yüksekli ine ve un a rl na ba l - d r. Bu büyüklükler kald rma kuvvetini etkiledi inden, gerilme kuvvetini de etkiler. areketli
AZ BASINCI ES - 1 1. Balona etki eden toplam bas nç; aç k ava bas nc - na, yüksekli ine ve un a rl na ba l - d r. Bu büyüklükler kald rma kuvvetini etkiledi inden, gerilme kuvvetini de etkiler. areketli
Doğrusal Momentum ve Çarpışmalar Doğrusal Momentum ve Korunumu
 Fiz 1011 - Ders 9 Doğrusal Momentum ve Çarpışmalar Doğrusal Momentum ve Korunumu İmplus (itme) ve Momentum Çarpışmalar Kütle Merkezi Roket Hareketi http://kisi.deu.edu.tr/mehmet.tarakci/ Momentum Newton
Fiz 1011 - Ders 9 Doğrusal Momentum ve Çarpışmalar Doğrusal Momentum ve Korunumu İmplus (itme) ve Momentum Çarpışmalar Kütle Merkezi Roket Hareketi http://kisi.deu.edu.tr/mehmet.tarakci/ Momentum Newton
DİNAMİK Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi. Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
11. SINIF SORU BANKASI. 1. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM TEST ÇÖZÜMLERİ
 . SINIF SORU BANKASI. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM TEST ÇÖZÜMLERİ 7 İtme e Çizgisel Momentum Test in Çözümleri. Patlamadan önceki momentum +x yönünde; P 5 4 0 kg.m/s. Cismin
. SINIF SORU BANKASI. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM TEST ÇÖZÜMLERİ 7 İtme e Çizgisel Momentum Test in Çözümleri. Patlamadan önceki momentum +x yönünde; P 5 4 0 kg.m/s. Cismin
FIZ Uygulama Vektörler
 Vektörler Problem 1 - Serway 61/75 Bir dikdörtgenler prizmasının boyutları şekildeki gibi a=10,0 cm, b=20,0 cm ve c=15,0 cm dir. a) Yüz köşegen vektörü R 1 nedir? b) Cisim köşegen vektörü R 2 nedir? c)
Vektörler Problem 1 - Serway 61/75 Bir dikdörtgenler prizmasının boyutları şekildeki gibi a=10,0 cm, b=20,0 cm ve c=15,0 cm dir. a) Yüz köşegen vektörü R 1 nedir? b) Cisim köşegen vektörü R 2 nedir? c)
KKKKK VERİLER. Yer çekimi ivmesi : g=10 m/s 2. Metrik Ön Takılar sin 45 = cos 45 = 0,7
 VERİLER Yer çekimi ivmesi : g=10 m/s Metrik Ön Takılar sin = cos = 0, Numara Ön Takı Simge sin = cos = 0,6 sin = cos = 0,8 10 9 giga G tan = 0, 10 6 mega M sin 0 = cos 60 = -cos 10 = 0, 10 kilo k sin 60
VERİLER Yer çekimi ivmesi : g=10 m/s Metrik Ön Takılar sin = cos = 0, Numara Ön Takı Simge sin = cos = 0,6 sin = cos = 0,8 10 9 giga G tan = 0, 10 6 mega M sin 0 = cos 60 = -cos 10 = 0, 10 kilo k sin 60
K MYA GAZLAR. ÖRNEK 2: Kapal bir cam kapta eflit mol say s nda SO ve NO gaz kar fl m vard r. Bu kar fl mda, sabit s - cakl kta,
 K MYA GAZLAR ÖRNEK 1 : deal davran fltaki X H ve YO gazlar ndan oluflan bir kar fl m, 4,8 mol H ve 1,8 mol O atomu 4 8 içermektedir. Bu kar fl m n, 0 C ve 1 atm deki yo unlu u,0 g/l oldu una göre, kütlesi
K MYA GAZLAR ÖRNEK 1 : deal davran fltaki X H ve YO gazlar ndan oluflan bir kar fl m, 4,8 mol H ve 1,8 mol O atomu 4 8 içermektedir. Bu kar fl m n, 0 C ve 1 atm deki yo unlu u,0 g/l oldu una göre, kütlesi
GEOMETR 7 ÜN TE III S L ND R
 ÜN TE III S L ND R 1. S L ND R K YÜZEY VE TANIMLAR 2. S L ND R a. Tan m b. Silindirin Özelikleri 3. DA RESEL S L ND R N ALANI a. Dik Dairesel Silindirin Alan I. Dik Dairesel Silindirin Yanal Alan II. Dik
ÜN TE III S L ND R 1. S L ND R K YÜZEY VE TANIMLAR 2. S L ND R a. Tan m b. Silindirin Özelikleri 3. DA RESEL S L ND R N ALANI a. Dik Dairesel Silindirin Alan I. Dik Dairesel Silindirin Yanal Alan II. Dik
Fiz 1011 I. Vize UYGULAMA
 Fiz 1011 I. Vize UYGULAMA Bölüm 1. Fizik ve Ölçme 1. Aşağıdaki ölçme sonuçlarını 3 anlamlı rakamla gösteriniz. (a) 145,61 (b) 23457 (c) 2,4558 (d) 0,023001 (e) 0,12453 2. Farklı hasaslıkta aletler kullanılarak
Fiz 1011 I. Vize UYGULAMA Bölüm 1. Fizik ve Ölçme 1. Aşağıdaki ölçme sonuçlarını 3 anlamlı rakamla gösteriniz. (a) 145,61 (b) 23457 (c) 2,4558 (d) 0,023001 (e) 0,12453 2. Farklı hasaslıkta aletler kullanılarak
6 MADDE VE ÖZELL KLER
 6 MADDE VE ÖZELL KLER TERMOD NAM K MODEL SORU 1 DEK SORULARIN ÇÖZÜMLER MODEL SORU 2 DEK SORULARIN ÇÖZÜMLER 1. Birbirine temasdaki iki cisimden s cakl büyük olan s verir, küçük olan s al r. ki cisim bir
6 MADDE VE ÖZELL KLER TERMOD NAM K MODEL SORU 1 DEK SORULARIN ÇÖZÜMLER MODEL SORU 2 DEK SORULARIN ÇÖZÜMLER 1. Birbirine temasdaki iki cisimden s cakl büyük olan s verir, küçük olan s al r. ki cisim bir
2. POTANSİYEL VE KİNETİK ENERJİ 2.1. CİSİMLERİN POTANSİYEL ENERJİSİ. Konumundan dolayı bir cismin sahip olduğu enerjiye Potansiyel Enerji denir.
 BÖLÜM POTANSİYEL VE KİNETİK ENERJİ. POTANSİYEL VE KİNETİK ENERJİ.1. CİSİMLERİN POTANSİYEL ENERJİSİ Konumundan dolayı bir cismin sahip olduğu enerjiye Potansiyel Enerji denir. Mesela Şekil.1 de görülen
BÖLÜM POTANSİYEL VE KİNETİK ENERJİ. POTANSİYEL VE KİNETİK ENERJİ.1. CİSİMLERİN POTANSİYEL ENERJİSİ Konumundan dolayı bir cismin sahip olduğu enerjiye Potansiyel Enerji denir. Mesela Şekil.1 de görülen
FİZİKÇİ. 2. Kütlesi 1000 kg olan bir araba 20 m/sn hızla gidiyor ve 10 m bir uçurumdan aşağı düşüyor.
 1. Aşağıdakilerden hangisi Frekans ı tanımlamaktadır? a) Birim zamandaki titreşim sayısıdır ve boyutu sn -1 b) Birim zamandaki hızlanmadır c) Bir saniyedeki tekrarlanmadır d) Hızın zamana oranıdır 6. İki
1. Aşağıdakilerden hangisi Frekans ı tanımlamaktadır? a) Birim zamandaki titreşim sayısıdır ve boyutu sn -1 b) Birim zamandaki hızlanmadır c) Bir saniyedeki tekrarlanmadır d) Hızın zamana oranıdır 6. İki
F Z K TEST A) X X = X Y = X Z B) X X > X Y > X Z C) X X > X Z > X Y D) X X > X Y = X Z E) X Y = X Z > X X D KKAT! H z. 2t Zaman. A s v s. A s v s.
 F Z TEST D AT! + Bu testte 30 soru vard r. + Bu test için ayr lan cevaplama süresi 45 dakikad r. + Cevaplar n z, cevap ka d n n Fizik Testi için ayr lan k sma iflaretleyiniz.. 3. H z v Y 0 t t Zaman A
F Z TEST D AT! + Bu testte 30 soru vard r. + Bu test için ayr lan cevaplama süresi 45 dakikad r. + Cevaplar n z, cevap ka d n n Fizik Testi için ayr lan k sma iflaretleyiniz.. 3. H z v Y 0 t t Zaman A
ÜN TE II L M T. Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler
 ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
(ÖSS ) ÇÖZÜM 2:
 MTEMT K PROLEMLER - II ÖRNEK : ve kentlerinden saatteki h zlar s ras yla V ve V olan (V > V ) iki araç, birbirlerine do ru 2 2 ayn anda hareket ederlerse saat sonra karfl lafl yorlar. u araçlar ayn kentlerden
MTEMT K PROLEMLER - II ÖRNEK : ve kentlerinden saatteki h zlar s ras yla V ve V olan (V > V ) iki araç, birbirlerine do ru 2 2 ayn anda hareket ederlerse saat sonra karfl lafl yorlar. u araçlar ayn kentlerden
GEOMETR 7 ÜN TE V KÜRE
 ÜN TE V KÜRE 1. KÜRE a. Tan m b. Bir Kürenin Belirli Olmas c. Bir Küre ile Bir Düzlemin Ara Kesiti 2. KÜREN N ALANI 3. KÜREN N HACM 4. KÜREDE ÖZEL PARÇALAR a. Küre Kufla I. Tan m II. Küre Kufla n n Alan
ÜN TE V KÜRE 1. KÜRE a. Tan m b. Bir Kürenin Belirli Olmas c. Bir Küre ile Bir Düzlemin Ara Kesiti 2. KÜREN N ALANI 3. KÜREN N HACM 4. KÜREDE ÖZEL PARÇALAR a. Küre Kufla I. Tan m II. Küre Kufla n n Alan
DİNAMİK TEKNOLOJİNİN BİLİMSEL İLKELERİ
 7 TEKNOLOJİNİN BİLİMSEL İLKELERİ Adem ÇALIŞKAN Hareket veya hareketteki değişmelerin sebeplerini araştırarak kuvvetle hareket arasındaki ilişkiyi inceleyen mekaniğin bölümüne dinamik denir. Hareket, bir
7 TEKNOLOJİNİN BİLİMSEL İLKELERİ Adem ÇALIŞKAN Hareket veya hareketteki değişmelerin sebeplerini araştırarak kuvvetle hareket arasındaki ilişkiyi inceleyen mekaniğin bölümüne dinamik denir. Hareket, bir
F Z K ELEKTROSTAT K ÖRNEK 2: ÖRNEK 1 :
 F Z EETROSTAT ÖRNE 1 : ÖRNE : Q 0 X M Z yal tkan yal tkan fiekildeki yal tkan sapl özdefl ve iletken,, M kürelerinin elektrik yükleri s ras yla, Q ve 0 (s f r) d r. M küresi ye dokundurulup ayr ld ktan
F Z EETROSTAT ÖRNE 1 : ÖRNE : Q 0 X M Z yal tkan yal tkan fiekildeki yal tkan sapl özdefl ve iletken,, M kürelerinin elektrik yükleri s ras yla, Q ve 0 (s f r) d r. M küresi ye dokundurulup ayr ld ktan
FİZİK 109 ÖRNEK SORULAR (3) 52) M=5 kg kütleli bir cisim A noktasından serbest bırakılıyor. Cismin B ve C noktalarındaki süratini hesaplayınız.
 FİZİK 109 ÖRNEK SORULAR (3) 51) SI birim sisteminde momentumun birimi nedir? 52) M=5 kg kütleli bir cisim A noktasından serbest bırakılıyor. Cismin B ve C noktalarındaki süratini 53) Şekildeki kayakçının
FİZİK 109 ÖRNEK SORULAR (3) 51) SI birim sisteminde momentumun birimi nedir? 52) M=5 kg kütleli bir cisim A noktasından serbest bırakılıyor. Cismin B ve C noktalarındaki süratini 53) Şekildeki kayakçının
MEKATRONİĞİN TEMELLERİ HAREKET
 MEKATRONİĞİN TEMELLERİ HAREKET Bir Doğru Boyunca Hareket Konum ve Yer-değiştirme Ortalama Hız Ortalama Sürat Anlık Hız Ortalama ve Anlık İvme Bir Doğru Boyunca Hareket Kinematik, cisimlerin hareketini
MEKATRONİĞİN TEMELLERİ HAREKET Bir Doğru Boyunca Hareket Konum ve Yer-değiştirme Ortalama Hız Ortalama Sürat Anlık Hız Ortalama ve Anlık İvme Bir Doğru Boyunca Hareket Kinematik, cisimlerin hareketini
Dinamik. Fatih ALİBEYOĞLU -8-
 1 Dinamik Fatih ALİBEYOĞLU -8- Giriş 2 Önceki bölümlerde F=m.a nın maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini kullandık. Hız değişimlerinin yapılan
1 Dinamik Fatih ALİBEYOĞLU -8- Giriş 2 Önceki bölümlerde F=m.a nın maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini kullandık. Hız değişimlerinin yapılan
İş, Güç ve Enerji. Fiz Ders 7. Sabit Bir Kuvvetin Yaptığı İş. Değişen Bir Kuvvetin Yaptığı İş. Güç. İş-Kinetik Enerji Teoremi
 Fiz 1011 - Ders 7 İş, Güç ve Enerji Sabit Bir Kuvvetin Yaptığı İş Değişen Bir Kuvvetin Yaptığı İş Güç İş-Kinetik Enerji Teoremi http://kisi.deu.edu.tr/mehmet.tarakci/ Günlük yaşamda iş kavramı bir çok
Fiz 1011 - Ders 7 İş, Güç ve Enerji Sabit Bir Kuvvetin Yaptığı İş Değişen Bir Kuvvetin Yaptığı İş Güç İş-Kinetik Enerji Teoremi http://kisi.deu.edu.tr/mehmet.tarakci/ Günlük yaşamda iş kavramı bir çok
50 ELEKTR K VE ELEKTRON K
 50 EETR E EETRO ODSTÖRER ODE SORU DE SORURI ÇÖZÜER. ε. ba nt - s na göre, ε azal nan konan- satörün s as azal r. I. yarg o ruur. + onansatör üretece ba l iken, levhalar aras naki potansiyel fark e iflmez.
50 EETR E EETRO ODSTÖRER ODE SORU DE SORURI ÇÖZÜER. ε. ba nt - s na göre, ε azal nan konan- satörün s as azal r. I. yarg o ruur. + onansatör üretece ba l iken, levhalar aras naki potansiyel fark e iflmez.
Fizik 101-Fizik I 2013-2014. Dönme Hareketinin Dinamiği
 -Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
-Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
Kinetik Problemleri için Çözüm yöntemleri i.) Newton un 2. yasası F = m a. ii.) İş-Enerji Yöntemi. iii.) İmpuls-momentum yöntemi
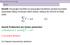 Giriş Kinetik: Parçacığın hareketi ve parçacığın hareketini yaratan kuvvetler arasındaki ilişkiyi inceleyen bilim dalıdır. Kabaca bir formül ile ifade edilir. F = m a 1 Kinetik Problemleri için Çözüm yöntemleri
Giriş Kinetik: Parçacığın hareketi ve parçacığın hareketini yaratan kuvvetler arasındaki ilişkiyi inceleyen bilim dalıdır. Kabaca bir formül ile ifade edilir. F = m a 1 Kinetik Problemleri için Çözüm yöntemleri
Bir cisme etki eden kuvvetlerin bileşkesi sıfır ise, cisim ya durur, ya da bir doğru boyunca sabit hızla hareketine devam eder.
 DİNAMİK Hareket veya hareketteki değişmelerin sebeplerini araştırarak kuvvetle hareket arasındaki ilişkiyi inceleyen mekaniğin bölümüne dinamik denir. Dinamiğin üç temel prensibi vardır. 1. Eylemsizlik
DİNAMİK Hareket veya hareketteki değişmelerin sebeplerini araştırarak kuvvetle hareket arasındaki ilişkiyi inceleyen mekaniğin bölümüne dinamik denir. Dinamiğin üç temel prensibi vardır. 1. Eylemsizlik
CO RAFYA. DÜNYA NIN fiekl N N VE HAREKETLER N N SONUÇLARI ÖRNEK 1 :
 CO RAFYA DÜNYA NIN fiekl N N VE HAREKETLER N N SONUÇLARI ÖRNEK 1 : K rk nc paralel üzerindeki bir noktan n hangi yar mkürede yer ald afla dakilerin hangisine bak larak saptanamaz? A) Gece-gündüz süresinin
CO RAFYA DÜNYA NIN fiekl N N VE HAREKETLER N N SONUÇLARI ÖRNEK 1 : K rk nc paralel üzerindeki bir noktan n hangi yar mkürede yer ald afla dakilerin hangisine bak larak saptanamaz? A) Gece-gündüz süresinin
6. Tabloya bakt m za canl lardan K s 1 CEVAP B. 7. Titreflim hareketi yapan herfley bir ses kayna d r ve. II. ve III. yarg lar do rudur.
 SES DALGALARI 1. Kesik koni biçiminde k vr lm fl bir mukavvan n dar k sm kula a tutuldu unda sesin daha iyi duyulmas sesin mukavvan n yüzeyinde çarp p yans mas n n bir sonucudur. Di erleri sesin iletimi
SES DALGALARI 1. Kesik koni biçiminde k vr lm fl bir mukavvan n dar k sm kula a tutuldu unda sesin daha iyi duyulmas sesin mukavvan n yüzeyinde çarp p yans mas n n bir sonucudur. Di erleri sesin iletimi
: Bir d do rusu üzerinde; A, B, C ve D noktalar alal m. d. n n uzunlu u denir ve. d d1 d2 F G. E, F d G, H d ve ise. d // d 1 2
 VI. ÖLÜM ÜZLEME VEKTÖRLER YÖNLÜ RU PRÇSI Tan m : üzlemde ve noktalar verilsin. [] n n dan e do ru önlendirildi ini düflünelim. öle do ru parçalar na, önlü do ru parçalar denir. önlü do ru parças, ile gösterilir.
VI. ÖLÜM ÜZLEME VEKTÖRLER YÖNLÜ RU PRÇSI Tan m : üzlemde ve noktalar verilsin. [] n n dan e do ru önlendirildi ini düflünelim. öle do ru parçalar na, önlü do ru parçalar denir. önlü do ru parças, ile gösterilir.
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
ÜN TE III. YÜZDELER VE MESLEKÎ UYGULAMALARI
 ÜN TE III. YÜZDELER VE MESLEKÎ UYGULAMALARI BU ÜN TEDE NELER Ö RENECE Z? A-YÜZDELER VE MESLEKÎ UYGULAMALARI B-YÜZDE HESAPLARI VE MESLEKÎ UYGULAMALARI C-FA Z HESAPLARI VE MESLEKÎ UYGULAMALARI D-YÜZDE VE
ÜN TE III. YÜZDELER VE MESLEKÎ UYGULAMALARI BU ÜN TEDE NELER Ö RENECE Z? A-YÜZDELER VE MESLEKÎ UYGULAMALARI B-YÜZDE HESAPLARI VE MESLEKÎ UYGULAMALARI C-FA Z HESAPLARI VE MESLEKÎ UYGULAMALARI D-YÜZDE VE
Newton un ikinci yasası: Bir cisim ivmesi cisim üzerine etki eden toplam kuvvet ile doğru orantılı cismin kütlesi ile ters orantılıdır.
 Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
4. İKİ BOYUTLU UZAYDA ÇARPIŞMA
 4. İKİ BOYUTLU UZAYDA ÇARPIŞMA AMAÇ. İki cismin çarpışması olayında momentumun korunumu ilkesinin incelenmesi,. Çarpışmada mekanik enerjinin korunumu ilkesinin incelenmesi, 3.Ölçü sonuçlarından yararlanarak
4. İKİ BOYUTLU UZAYDA ÇARPIŞMA AMAÇ. İki cismin çarpışması olayında momentumun korunumu ilkesinin incelenmesi,. Çarpışmada mekanik enerjinin korunumu ilkesinin incelenmesi, 3.Ölçü sonuçlarından yararlanarak
4.DENEY: ĠKĠ BOYUTLU UZAYDA ÇARPIġMA
 4.DENEY: ĠKĠ BOYUTLU UZAYDA ÇARPIġMA AMAÇ 1. Ġki cismin çarpıģması olayında momentumun korunumu ilkesinin incelenmesi, 2. ÇarpıĢmada mekanik enerjinin korunumu ilkesinin incelenmesi, 3. Ölçü sonuçlarından
4.DENEY: ĠKĠ BOYUTLU UZAYDA ÇARPIġMA AMAÇ 1. Ġki cismin çarpıģması olayında momentumun korunumu ilkesinin incelenmesi, 2. ÇarpıĢmada mekanik enerjinin korunumu ilkesinin incelenmesi, 3. Ölçü sonuçlarından
Fizik 1 Laboratuvarı. Deney 5: Momentumun Korunumu ALANYA ALAADDİN KEYKUBAT ÜNİVERSİTESİ RAFET KAYIŞ MÜHENDİSLİK FAKÜLTESİ
 Deney 5: ALANYA ALAADDİN KEYKUBAT ÜNİVERSİTESİ RAFET KAYIŞ MÜHENDİSLİK FAKÜLTESİ 1. DENEYİN AMACI Doğrusal hareket halindeki iki cismin yapmış olduğu farklı çarpışma türleri için momentum ve kinetik enerjinin
Deney 5: ALANYA ALAADDİN KEYKUBAT ÜNİVERSİTESİ RAFET KAYIŞ MÜHENDİSLİK FAKÜLTESİ 1. DENEYİN AMACI Doğrusal hareket halindeki iki cismin yapmış olduğu farklı çarpışma türleri için momentum ve kinetik enerjinin
Video 01. Bir kuvvet, etkidiği cismin yerini değiştirebiliyorsa iş yapılıyor denir. İşin oluşabilmesi için kuvvet gerek şarttır.
 Video 01 01.İŞ GÜÇ ENERJİ A) İŞİN TANIMI Bir kuvvet, etkidiği cismin yerini değiştirebiliyorsa iş yapılıyor denir. İşin oluşabilmesi için kuvvet gerek şarttır. Bir başka deyişle kuvvetin X yolu boyunca
Video 01 01.İŞ GÜÇ ENERJİ A) İŞİN TANIMI Bir kuvvet, etkidiği cismin yerini değiştirebiliyorsa iş yapılıyor denir. İşin oluşabilmesi için kuvvet gerek şarttır. Bir başka deyişle kuvvetin X yolu boyunca
Çözüm: K ve M çünkü, Cisim sabit alabilmesi için kuvvetin sıfır olması gerekir
 KUVVET SORULARI (I)- L nin kütlesi K nın kütlesinden büyüktür. Çünkü hareket yönü aşağıya doğrudur. (II)- Sürtünme olup olmadığı kesin değildir. (III)- L nin ağırlığı, ipte oluşan T gerilme kuvvetinden
KUVVET SORULARI (I)- L nin kütlesi K nın kütlesinden büyüktür. Çünkü hareket yönü aşağıya doğrudur. (II)- Sürtünme olup olmadığı kesin değildir. (III)- L nin ağırlığı, ipte oluşan T gerilme kuvvetinden
TEST Dalga homojen ortamda sabit h zla yay l r. 3. I. Yol: 6. Yay lma h z yaln zca ortamdaki YAY DALGALARI
 A DAGAARI TEST - 1 1. g y i. kal n ince x y g i ince kal n y al n yaydan ince yaya ve ince yaydan kal n yaya geçiflte iletilen ve yans yan atmalar flekildeki gibidir. al n yaydan ince yaya geçiflte atman
A DAGAARI TEST - 1 1. g y i. kal n ince x y g i ince kal n y al n yaydan ince yaya ve ince yaydan kal n yaya geçiflte iletilen ve yans yan atmalar flekildeki gibidir. al n yaydan ince yaya geçiflte atman
Doğrusal Momentum ve Çarpışmalar
 Doğrusal Momentum ve Çarpışmalar 1. Kütlesi m 1 = 0.5 kg olan bir blok Şekil 1 de görüldüğü gibi, eğri yüzeyli m 2 = 3 kg kütleli bir cismin tepesinden sürtünmesiz olarak kayıyor ve sürtünmesiz yatay zemine
Doğrusal Momentum ve Çarpışmalar 1. Kütlesi m 1 = 0.5 kg olan bir blok Şekil 1 de görüldüğü gibi, eğri yüzeyli m 2 = 3 kg kütleli bir cismin tepesinden sürtünmesiz olarak kayıyor ve sürtünmesiz yatay zemine
1. STATİĞE GİRİŞ 1.1 TANIMLAR MEKANİK RİJİT CİSİMLER MEKANİĞİ ŞEKİL DEĞİŞTİREN CİSİMLER AKIŞKANLAR MEKANİĞİ DİNAMİK STATİK
 STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
GEOMETR 7 ÜN TE II P RAM T
 ÜN TE II P RAM T 1. P RAM TLER N TANIMI. DÜZGÜN P RAM T a. Tan m b. Düzgün Piramidin Özelikleri. P RAM D N ALANI a. Düzgün Olmayan Piramidin Alan b. Düzgün Piramidin Alan 4. P RAM D N HACM 5. DÜZGÜN DÖRTYÜZLÜ
ÜN TE II P RAM T 1. P RAM TLER N TANIMI. DÜZGÜN P RAM T a. Tan m b. Düzgün Piramidin Özelikleri. P RAM D N ALANI a. Düzgün Olmayan Piramidin Alan b. Düzgün Piramidin Alan 4. P RAM D N HACM 5. DÜZGÜN DÖRTYÜZLÜ
VEKTÖR SORULARI SORU 1 : ÇÖZÜM : A şıkkında bileşke kuvvet 3N - 2N = 1N dir. B şıkkında 3N - 1N = 2N dir. C şıkkında 3N + 2N = 5N dir.
 VEKTÖR SORULARI SORU 1 : ÇÖZÜM : A şıkkında bileşke kuvvet 3N - 2N = 1N dir. B şıkkında 3N - 1N = 2N dir. C şıkkında 3N + 2N = 5N dir. D şıkkında 3N - 1N = 2N dir. E şıkkında kök 10 dur. 3 ün karesi artı
VEKTÖR SORULARI SORU 1 : ÇÖZÜM : A şıkkında bileşke kuvvet 3N - 2N = 1N dir. B şıkkında 3N - 1N = 2N dir. C şıkkında 3N + 2N = 5N dir. D şıkkında 3N - 1N = 2N dir. E şıkkında kök 10 dur. 3 ün karesi artı
Fizik 101: Ders 9 Ajanda
 Fizik 101: Ders 9 Ajanda İş & Enerji Müzakere Tanımlar Sabit bir kuvvetin yaptığı iş İş/kinetik enerji theoremi Çoklu sabit kuvvetin yaptığı iş Yorum İş & Enerji Fiziğin en önemli kavramlarından biri Mekaniğe
Fizik 101: Ders 9 Ajanda İş & Enerji Müzakere Tanımlar Sabit bir kuvvetin yaptığı iş İş/kinetik enerji theoremi Çoklu sabit kuvvetin yaptığı iş Yorum İş & Enerji Fiziğin en önemli kavramlarından biri Mekaniğe
SU DALGALARI. 6. I ve II engelleri aras ndaki aç 60 dir. I. KL do rusal dalga I ve II engellerinde flekildeki gibi yans r.
 SU DAGAAR MDE SRU DE SRUARN ÇÖZÜMER 4 70 70 40 40 70 do rusal dalga ve engellerinde flekildeki gibi yans r do rusal dalgan n k sm engelinden, k sm ise engelinden flekildeki gibi yans r do rusal dalga ve
SU DAGAAR MDE SRU DE SRUARN ÇÖZÜMER 4 70 70 40 40 70 do rusal dalga ve engellerinde flekildeki gibi yans r do rusal dalgan n k sm engelinden, k sm ise engelinden flekildeki gibi yans r do rusal dalga ve
KKKKK. Adı Soyadı : Numarası : Bölümü : İmzası : FİZİK I
 Adı Soyadı : Numarası : Bölümü : İmzası : FİZİK I 1. Sınav süresi 10 dakikadır.. Bu sınavda eşit puanlı 0 adet soru vardır.. Elinizdeki soru kitapçığı K türü soru kitapçığıdır.. Yanıtlarınızı Yanıt Kağıdı
Adı Soyadı : Numarası : Bölümü : İmzası : FİZİK I 1. Sınav süresi 10 dakikadır.. Bu sınavda eşit puanlı 0 adet soru vardır.. Elinizdeki soru kitapçığı K türü soru kitapçığıdır.. Yanıtlarınızı Yanıt Kağıdı
İtme Momentum Açısal Momentum. Futbol da Şut
 İtme Momentum Açısal Momentum Futbol da Şut SBA 206 Spor Biyomekaniği 22 Nisan 2010 Arif Mithat Amca 1 Kütle Çekim Kuvveti Kütle Ağırlık Moment Denge Ağırlık/Kütle Merkezi İnsanda Vücut Kütle/Ağırlık Merkezinin
İtme Momentum Açısal Momentum Futbol da Şut SBA 206 Spor Biyomekaniği 22 Nisan 2010 Arif Mithat Amca 1 Kütle Çekim Kuvveti Kütle Ağırlık Moment Denge Ağırlık/Kütle Merkezi İnsanda Vücut Kütle/Ağırlık Merkezinin
TAR H MATEMAT K PROBLEMLER - III. Kavram Dersaneleri 78. ÖRNEK 1: % 24 'ü olan say kaçt r? ÖRNEK 2:
 TAR H MATEMAT K PROBLEMLER - III ÖRNEK 1: % 24 'ü 86424 olan say kaçt r? A) 360 B) 354196 C) 320120 D) 36 E) 360 (ÖSS - 1999) ÖRNEK 2: Bir miktar pastan n 3 ini lknur, geriye kalan n da Buse yemifltir.
TAR H MATEMAT K PROBLEMLER - III ÖRNEK 1: % 24 'ü 86424 olan say kaçt r? A) 360 B) 354196 C) 320120 D) 36 E) 360 (ÖSS - 1999) ÖRNEK 2: Bir miktar pastan n 3 ini lknur, geriye kalan n da Buse yemifltir.
6. Kütlesi 600 g ve öz ısısı c=0,3 cal/g.c olan cismin sıcaklığı 45 C den 75 C ye çıkarmak için gerekli ısı nedir?
 ADI: SOYADI: No: Sınıfı: A) Grubu Tarih.../.../... ALDIĞI NOT:... ( ) a) Termometreler genleşme ilkesine göre çalışır. ( ) b) Isı ve sıcaklık eş anlamlı kavramlardır. ( ) c) Fahrenheit ve Celsius termometrelerinin
ADI: SOYADI: No: Sınıfı: A) Grubu Tarih.../.../... ALDIĞI NOT:... ( ) a) Termometreler genleşme ilkesine göre çalışır. ( ) b) Isı ve sıcaklık eş anlamlı kavramlardır. ( ) c) Fahrenheit ve Celsius termometrelerinin
ÜN TE III L NEER CEB R
 ÜN TE III L NEER CEB R MATR SLER Matrisin ki matrisin eflitli i Toplama ifllemi ve özellikleri Matrislerde skalarla çarpma ifllemi ve özellikleri Matrislerde çarpma ifllemi Çarpma ifllemine göre birim
ÜN TE III L NEER CEB R MATR SLER Matrisin ki matrisin eflitli i Toplama ifllemi ve özellikleri Matrislerde skalarla çarpma ifllemi ve özellikleri Matrislerde çarpma ifllemi Çarpma ifllemine göre birim
Fizik 101-Fizik I 2013-2014
 Fizik 101-Fizik I 2013-2014 Doğrusal Momentum ve Çarpışmalar Nurdan Demirci Sankır Ofis: 325, Tel:4331 1 Doğrusal Momentum ve Korunumu v hızı ile hareket eden m kütleli bir parçacığın doğrusal momentumu
Fizik 101-Fizik I 2013-2014 Doğrusal Momentum ve Çarpışmalar Nurdan Demirci Sankır Ofis: 325, Tel:4331 1 Doğrusal Momentum ve Korunumu v hızı ile hareket eden m kütleli bir parçacığın doğrusal momentumu
İtme Momentum Açısal Momentum. Futbol da Şut (LAB 7) V = 8 m/s. m = 75 kg. P = 75x8 = 600 kg.m/s. Çarpışma öncesindeki toplam momentum
 İtme Momentum Momentum Futbol da Şut (LAB 7) Doğrusal Momentum Doğru boyunca hareket eden bir cismin hareket miktarının (taşıdığı hareketin) ölçüsüdür Momentum bir cismin çarpma gücüdür Momentum un miktarı
İtme Momentum Momentum Futbol da Şut (LAB 7) Doğrusal Momentum Doğru boyunca hareket eden bir cismin hareket miktarının (taşıdığı hareketin) ölçüsüdür Momentum bir cismin çarpma gücüdür Momentum un miktarı
K MYA K MYASAL TEPK MELER VE HESAPLAMALARI ÖRNEK 1 :
 K MYA K MYASAL TEPK MELER VE ESAPLAMALARI ÖRNEK 1 : ÖRNEK : X ile Y tepkimeye girdi inde yaln z X Y oluflturmaktad r. Tepkimenin bafllang c nda 0, mol X ve 0, mol Y al nm flt r. Bu tepkimede X ve Y ten
K MYA K MYASAL TEPK MELER VE ESAPLAMALARI ÖRNEK 1 : ÖRNEK : X ile Y tepkimeye girdi inde yaln z X Y oluflturmaktad r. Tepkimenin bafllang c nda 0, mol X ve 0, mol Y al nm flt r. Bu tepkimede X ve Y ten
Aç ve Aç Ölçüsü. Üçgen, Kare ve Dikdörtgen. Geometrik Cisimler. Simetri. Örüntü ve Süslemeler
 MTEMT K ç ve ç Ölçüsü Üçgen, Kare ve ikdörtgen Geometrik Cisimler Simetri Örüntü ve Süslemeler Temel Kaynak 4 ç ve ç Ölçüsü ÇI VE ÇI ÖLÇÜSÜ ç lar n dland r lmas C Resimde aç oluflturulan yerlerin baz lar
MTEMT K ç ve ç Ölçüsü Üçgen, Kare ve ikdörtgen Geometrik Cisimler Simetri Örüntü ve Süslemeler Temel Kaynak 4 ç ve ç Ölçüsü ÇI VE ÇI ÖLÇÜSÜ ç lar n dland r lmas C Resimde aç oluflturulan yerlerin baz lar
Kuvvet. Kuvvet. Newton un 1.hareket yasası Fizik 1, Raymond A. Serway; Robert J. Beichner Editör: Kemal Çolakoğlu, Palme Yayınevi
 Kuvvet izik 1, Raymond A. Serway; Robert J. Beichner Editör: Kemal Çolakoğlu, Palme Yayınevi 2 Kuvvet Kuvvet ivmelenme kazandırır. Kuvvet vektörel bir niceliktir. Kuvvetler çift halinde bulunur. Kuvvet
Kuvvet izik 1, Raymond A. Serway; Robert J. Beichner Editör: Kemal Çolakoğlu, Palme Yayınevi 2 Kuvvet Kuvvet ivmelenme kazandırır. Kuvvet vektörel bir niceliktir. Kuvvetler çift halinde bulunur. Kuvvet
1. BÖLÜM FİZİĞİN DOĞASI - VEKTÖRLER DENGE - MOMENT - AĞIRLIK MERKEZİ
 1. BÖLÜM FİZİĞİN DĞASI - VEKÖRLER DENGE - MMEN - AĞIRLIK MERKEZİ FİZİĞİN DĞASI - VEKÖRLER - DENGE - MMEN - AĞIRLIK MERKEZİ SRULAR 1. I. ork (x) II. Güç (P) III. Açısal momentum (L) Yukarıdakilerden hangisi
1. BÖLÜM FİZİĞİN DĞASI - VEKÖRLER DENGE - MMEN - AĞIRLIK MERKEZİ FİZİĞİN DĞASI - VEKÖRLER - DENGE - MMEN - AĞIRLIK MERKEZİ SRULAR 1. I. ork (x) II. Güç (P) III. Açısal momentum (L) Yukarıdakilerden hangisi
F Z K OPT K. Kavram Dersaneleri 6. Çözüm: ÖRNEK 1 : Karanl k bir ortamda, küresel bir X fl k kayna n n önüne flekil I deki gibi Y topu konulmufltur.
 F Z OT ÖRNE 1 : fiekil I L M aranl k bir ortamda, küresel bir fl k kayna n n önüne flekil I deki gibi topu konulmufltur fiekil II Ifl kl bölge fiekil III ayna a, L, M noktalar n n birinden bak ld nda,
F Z OT ÖRNE 1 : fiekil I L M aranl k bir ortamda, küresel bir fl k kayna n n önüne flekil I deki gibi topu konulmufltur fiekil II Ifl kl bölge fiekil III ayna a, L, M noktalar n n birinden bak ld nda,
Bağıl hız ve bağıl ivme..
 Bağıl hız ve bağıl ivme.. Bağıl hareket, farklı referans sistemlerindeki farklı gözlemciler tarafından hareketlerin nasıl gözlemlendiğini ifade eder. Aynı hızla giden iki otomobilden birisinde bulunan
Bağıl hız ve bağıl ivme.. Bağıl hareket, farklı referans sistemlerindeki farklı gözlemciler tarafından hareketlerin nasıl gözlemlendiğini ifade eder. Aynı hızla giden iki otomobilden birisinde bulunan
VERİLER. Yer çekimi ivmesi : g=10 m/s 2
 VERİER Yer çekimi ivmesi : g=10 m/s Metrik Ön Takılar sin 4 = cos 4 = 0,7 Rakam Ön Takı Simge sin 7 = cos = 0,6 sin = cos 7 = 0,8 10 9 giga G tan 7 = 0,7 10 6 mega M sin 0 = cos 60 = -cos 10 = 0, 10 kilo
VERİER Yer çekimi ivmesi : g=10 m/s Metrik Ön Takılar sin 4 = cos 4 = 0,7 Rakam Ön Takı Simge sin 7 = cos = 0,6 sin = cos 7 = 0,8 10 9 giga G tan 7 = 0,7 10 6 mega M sin 0 = cos 60 = -cos 10 = 0, 10 kilo
YGS Soru Bankas MATEMAT K Temel Kavramlar
 9. 7 = 3.3.3, 07 = 3.3.3 007 = 3.3.3, 0007 = 3.3.3,... Yukar daki örüntüye göre, afla daki say lar n hangisi 81'in kat d r? A) 00 007 B) 0 000 007 C) 000 000 007 D) 00 000 000 007 13. Ard fl k 5 pozitif
9. 7 = 3.3.3, 07 = 3.3.3 007 = 3.3.3, 0007 = 3.3.3,... Yukar daki örüntüye göre, afla daki say lar n hangisi 81'in kat d r? A) 00 007 B) 0 000 007 C) 000 000 007 D) 00 000 000 007 13. Ard fl k 5 pozitif
Elektrik ve Manyetizma
 9 Elektrik ve anyetizma ODE SOU DE SOUI ÇÖÜE. letkenin kesitinden geçen yük miktar, q n.e 5.0 9.,6.0-9 8 C olur. Bu durumda oluflan ak m, I q 8 ` t 8 olur.. S kesitinden saniyede geçen yük miktar, ( )
9 Elektrik ve anyetizma ODE SOU DE SOUI ÇÖÜE. letkenin kesitinden geçen yük miktar, q n.e 5.0 9.,6.0-9 8 C olur. Bu durumda oluflan ak m, I q 8 ` t 8 olur.. S kesitinden saniyede geçen yük miktar, ( )
Hareket Kanunları. Newton un Hareket Kanunları. Fiz 1011 Ders 5. Eylemsizlik - Newton un I. Yasası. Temel - Newton un II. Yasası
 Fiz 1011 Ders 5 Hareket Kanunları Newton un Hareket Kanunları Eylemsizlik - Newton un I. Yasası Temel - Newton un II. Yasası Etki-Tepki - Newton un III. Yasası http://kisi.deu.edu.tr/mehmet.tarakci/ DİNAMİK
Fiz 1011 Ders 5 Hareket Kanunları Newton un Hareket Kanunları Eylemsizlik - Newton un I. Yasası Temel - Newton un II. Yasası Etki-Tepki - Newton un III. Yasası http://kisi.deu.edu.tr/mehmet.tarakci/ DİNAMİK
KUVVET VE HAREKET ÜN TE: 2
 ÜN TE: KUVVET VE HAREKET SARMAL YAYLARI TANIYALIM 6. s n fta kuvvet ölçen araçlar olan dinamometrelerin içinde çelikten yap lm fl yaylar oldu unu ö renmifltiniz. Bu çelik yaylar, esneklik özellikleri ile
ÜN TE: KUVVET VE HAREKET SARMAL YAYLARI TANIYALIM 6. s n fta kuvvet ölçen araçlar olan dinamometrelerin içinde çelikten yap lm fl yaylar oldu unu ö renmifltiniz. Bu çelik yaylar, esneklik özellikleri ile
Doç.Dr. Cesim ATAŞ MEKANİK ŞEKİL DEĞİŞTİREN CİSİMLER MEKANİĞİ DİNAMİK
 STATİK (Ders Notları) Kaynak: Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige, Wiley Yardımcı Kaynak: Mühendislik Mekaniği: Statik, R.C Hibbeler & S.C. Fan, Literatür
STATİK (Ders Notları) Kaynak: Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige, Wiley Yardımcı Kaynak: Mühendislik Mekaniği: Statik, R.C Hibbeler & S.C. Fan, Literatür
3. kg = kütle birimi, m = uzunluk birimi, s = zaman birimi olduğuna göre gücün birimi nedir?
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ MÜHENDİSLİK FİZİĞİ DERSİ ÇALIŞMA SORULARI 1. Yarıçapı 20 cm olan içi boş küre kaç litre su alır? (П=3 alınız) 2. A = 570 ± 1 ve B = 570 ± 10 olarak verilen iki ölçüm sonucunu
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ MÜHENDİSLİK FİZİĞİ DERSİ ÇALIŞMA SORULARI 1. Yarıçapı 20 cm olan içi boş küre kaç litre su alır? (П=3 alınız) 2. A = 570 ± 1 ve B = 570 ± 10 olarak verilen iki ölçüm sonucunu
Dinamik ÜNİTE. Amaçlar. İçindekiler. Öneriler. Bu üniteyi çalıştıktan sonra,
 ÜNİTE 4 Dinamik Bu üniteyi çalıştıktan sonra, Amaçlar Newton'un hareket kanunlarını, serbest düşmeyi, eğik atışı, merkezkaç kuvvetini, momentum kavramlarını öğreneceksiniz. İçindekiler Giriş Birinci Hareket
ÜNİTE 4 Dinamik Bu üniteyi çalıştıktan sonra, Amaçlar Newton'un hareket kanunlarını, serbest düşmeyi, eğik atışı, merkezkaç kuvvetini, momentum kavramlarını öğreneceksiniz. İçindekiler Giriş Birinci Hareket
İTME VE MOMENTUM. 1. P i
 7 BÖÜM İTME E MOMENTUM AIŞTIRMAAR ÇÖZÜMER İTME E MOMENTUM P i 0/s kg P s 0/s kg x +x düzle a Du va rın cis e u gu la dı ğı it e, o en tu de ği şi i ne eşit tir P i i 0 0 kg/s P s s ( 0 0 kg/s it e P P
7 BÖÜM İTME E MOMENTUM AIŞTIRMAAR ÇÖZÜMER İTME E MOMENTUM P i 0/s kg P s 0/s kg x +x düzle a Du va rın cis e u gu la dı ğı it e, o en tu de ği şi i ne eşit tir P i i 0 0 kg/s P s s ( 0 0 kg/s it e P P
Hareket ÜNİTE. Amaçlar. İçindekiler. Öneriler. Bu üniteyi çalıştıktan sonra,
 ÜNİTE 3 Hareket Bu üniteyi çalıştıktan sonra, Amaçlar hareket kavramını, hareketi doğuran kuvvetleri, hız kavramını, ivme kavramını, enerji kavramını, hareket ile enerji arasındaki ilişkiyi öğreneceksiniz.
ÜNİTE 3 Hareket Bu üniteyi çalıştıktan sonra, Amaçlar hareket kavramını, hareketi doğuran kuvvetleri, hız kavramını, ivme kavramını, enerji kavramını, hareket ile enerji arasındaki ilişkiyi öğreneceksiniz.
GÜZ YARIYILI FİZİK 1 DERSİ
 2015-2016 GÜZ YARIYILI FİZİK 1 DERSİ 1 Bölüm 6 Momentum, İtme ve Çarpışma 2 İçerik Çizgisel Momentum İtme (İmpuls) Çizgisel Momentumun korunumu Esnek ve esnek olmayan çarpışmalar İki ve üç boyutta momentumun
2015-2016 GÜZ YARIYILI FİZİK 1 DERSİ 1 Bölüm 6 Momentum, İtme ve Çarpışma 2 İçerik Çizgisel Momentum İtme (İmpuls) Çizgisel Momentumun korunumu Esnek ve esnek olmayan çarpışmalar İki ve üç boyutta momentumun
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
MATEMAT K TEST. 3. a ve b reel say lar olmak üzere, 3 a = 4 ve 3 2a b 3 = 8 oldu una göre,
 MTMT K TST KKT! + u testte 80 soru vard r. + u test için ar lan cevaplama süresi 5 dakikad r. + evaplar n z, cevap ka d n n Matematik Testi için ar lan k sma iflaretleiniz.. a, b, c pozitif reel sa lard
MTMT K TST KKT! + u testte 80 soru vard r. + u test için ar lan cevaplama süresi 5 dakikad r. + evaplar n z, cevap ka d n n Matematik Testi için ar lan k sma iflaretleiniz.. a, b, c pozitif reel sa lard
GEOMETR 7 ÜN TE I PR ZMALAR
 ÜN TE I PR ZMALAR 1. PR ZMAT K YÜZEY VE TANIMLAR 2. PR ZMA a. Tan m b. Prizman n Özelikleri 3. D K PR ZMA a. Tan m b. Dik Prizman n Özelikleri 4. E K PR ZMA a. Tan m b. E ik Prizman n Özelikleri 5. DÜZGÜN
ÜN TE I PR ZMALAR 1. PR ZMAT K YÜZEY VE TANIMLAR 2. PR ZMA a. Tan m b. Prizman n Özelikleri 3. D K PR ZMA a. Tan m b. Dik Prizman n Özelikleri 4. E K PR ZMA a. Tan m b. E ik Prizman n Özelikleri 5. DÜZGÜN
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
Kütlesi 10 kg olan bir taş yerden 5 m yüksekte duruyor. Bu taşın sahip olduğu potansiyel enerji kaç Joule dür? (g=10n/s2)
 Soru 1 Kütlesi 10 kg olan bir taş yerden 5 m yüksekte duruyor. Bu taşın sahip olduğu potansiyel enerji kaç Joule dür? (g=10n/s2) Soru 2 Kütlesi 20 kg olan bir cisim 10 m/s hızla hareket ederken kinetik
Soru 1 Kütlesi 10 kg olan bir taş yerden 5 m yüksekte duruyor. Bu taşın sahip olduğu potansiyel enerji kaç Joule dür? (g=10n/s2) Soru 2 Kütlesi 20 kg olan bir cisim 10 m/s hızla hareket ederken kinetik
İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ÖLÇME VE BİRİM SİSTEMLERİ
 İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ÖLÇME VE BİRİM SİSTEMLERİ 1.1. FİZİKTE ÖLÇME VE BİRİMLERİN ÖNEMİ... 2 1.2. BİRİMLER VE BİRİM SİSTEMLERİ... 2 1.3. TEMEL BİRİMLERİN TANIMLARI... 3 1.3.1. Uzunluğun
İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ÖLÇME VE BİRİM SİSTEMLERİ 1.1. FİZİKTE ÖLÇME VE BİRİMLERİN ÖNEMİ... 2 1.2. BİRİMLER VE BİRİM SİSTEMLERİ... 2 1.3. TEMEL BİRİMLERİN TANIMLARI... 3 1.3.1. Uzunluğun
BÖLÜM 03. Doğrusal Hareket Alt yüzeyi yere paralel olarak yerleştirilmiş, camdan yapılmış
 Doğrusal Hareket - 3 BÖÜ 03 Test 03 1. Alt yüzeyi yere paralel olarak yerleştirilmiş, camdan yapılmış küp yere dik paralel ışık ile aydınlatılmaktadır. üpün noktasında bulunan karınca şekildeki - - - N
Doğrusal Hareket - 3 BÖÜ 03 Test 03 1. Alt yüzeyi yere paralel olarak yerleştirilmiş, camdan yapılmış küp yere dik paralel ışık ile aydınlatılmaktadır. üpün noktasında bulunan karınca şekildeki - - - N
İŞ Bir F kuvveti uygulandığı cismin yer değiştirmesini sağlıyor ise bu kuvvet cisim üzerine iş yapıyor demektir. İş W sembolü ile gösterilir.
 İŞ Bir F kuvveti uygulandığı cismin yer değiştirmesini sağlıyor ise bu kuvvet cisim üzerine iş yapıyor demektir. İş W sembolü ile gösterilir. W = F. Δr =!F! Δr cosθ Yola paralel bir F! kuvveti cismin yatay
İŞ Bir F kuvveti uygulandığı cismin yer değiştirmesini sağlıyor ise bu kuvvet cisim üzerine iş yapıyor demektir. İş W sembolü ile gösterilir. W = F. Δr =!F! Δr cosθ Yola paralel bir F! kuvveti cismin yatay
TORK VE DENGE 01 Torkun Tanımı ve Yönü
 TORK VE DENGE 01 Torkun Tanımı ve Yönü Kuvvetin döndürme etkisine tork ya da moment denir. Bir kuvvetin bir noktaya göre torku; kuvvet ile dönme noktasının kuvvete dik uzaklığının çarpımına eşittir. Moment
TORK VE DENGE 01 Torkun Tanımı ve Yönü Kuvvetin döndürme etkisine tork ya da moment denir. Bir kuvvetin bir noktaya göre torku; kuvvet ile dönme noktasının kuvvete dik uzaklığının çarpımına eşittir. Moment
Bölüm 6 AKIŞ SİSTEMLERİNİN MOMENTUM ANALİZİ
 Akışkanlar Mekaniği Bölüm 6 AKIŞ SİSTEMLERİNİN MOMENTUM ANALİZİ Doç. Dr. İ. Gökhan AKSOY Denizanasının (Aurelia aurita) düzenli yüzme hareketi. Denizanası gövdesini kasıp akışkanı ittikten sonra süzülerek
Akışkanlar Mekaniği Bölüm 6 AKIŞ SİSTEMLERİNİN MOMENTUM ANALİZİ Doç. Dr. İ. Gökhan AKSOY Denizanasının (Aurelia aurita) düzenli yüzme hareketi. Denizanası gövdesini kasıp akışkanı ittikten sonra süzülerek
Potansiyel Enerji. Fiz Ders 8. Kütle - Çekim Potansiyel Enerjisi. Esneklik Potansiyel Enerjisi. Mekanik Enerjinin Korunumu
 Fiz 1011 - Ders 8 Potansiyel Enerji Kütle - Çekim Potansiyel Enerjisi Esneklik Potansiyel Enerjisi Mekanik Enerjinin Korunumu Korunumlu ve Korunumsuz Kuvvetler Enerji Diyagramları, Sistemlerin Dengesi
Fiz 1011 - Ders 8 Potansiyel Enerji Kütle - Çekim Potansiyel Enerjisi Esneklik Potansiyel Enerjisi Mekanik Enerjinin Korunumu Korunumlu ve Korunumsuz Kuvvetler Enerji Diyagramları, Sistemlerin Dengesi
ÜN TE III ORGAN K K MYA HAKKINDA GENEL B LG LER
 ÜN TE III ORGAN K K MYA HAKKINDA GENEL B LG LER 3.1. ORGAN K K MYANIN TAR HÇES VE KONUSU 3.2. ORGAN K MADDELERDE C, H, O ve N ARANMASI a. Organik Maddelerde C ve H Aranmas b. Organik Maddelerde N Aranmas
ÜN TE III ORGAN K K MYA HAKKINDA GENEL B LG LER 3.1. ORGAN K K MYANIN TAR HÇES VE KONUSU 3.2. ORGAN K MADDELERDE C, H, O ve N ARANMASI a. Organik Maddelerde C ve H Aranmas b. Organik Maddelerde N Aranmas
Do ufl Üniversitesi Matematik Kulübü Matematik Bireysel Yar flmas 2004 Soru ve Yan tlar
 o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2004 Soru ve Yan tlar Soru. S f rdan farkl bir a say s için sonsuz ondal klarla oluflan ifadesinin de eri nedir? ise, Soru 2. 0 < < 0 olmak
o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2004 Soru ve Yan tlar Soru. S f rdan farkl bir a say s için sonsuz ondal klarla oluflan ifadesinin de eri nedir? ise, Soru 2. 0 < < 0 olmak
İş-Kinetik Enerji, Potansiyel Enerji, Enerji Korunumu
 İş-Kinetik Enerji, Potansiyel Enerji, Enerji Korunumu 1. Kütlesi 7 kg olan motorsuz oyuncak bir araba, sürtünmesiz yatay bir düzlem üzerinde 4 m/s ilk hız ile gitmektedir. Araba daha sonra ilk hızı ile
İş-Kinetik Enerji, Potansiyel Enerji, Enerji Korunumu 1. Kütlesi 7 kg olan motorsuz oyuncak bir araba, sürtünmesiz yatay bir düzlem üzerinde 4 m/s ilk hız ile gitmektedir. Araba daha sonra ilk hızı ile
