Sistem Dinamiği ve Modellemesi
|
|
|
- Chagatai Erdem Şen
- 6 yıl önce
- İzleme sayısı:
Transkript
1 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gcili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili oucud itlri blirli ııflr yrılbili üü oltdır. Böyllil doğrul itlri dii dvrışlrı (z v fr dvrışlrı), ort prfor özllilri bılr öcd ögörülbiltdir. Ayrıc bu rtriti ftörlr gör bir iti otrol dilbilirliği hıd bir rr vrılbilir. Z bğlı olr dğişilri (t) girdii v (t) çıtıı il blirl t girdili v v t çıtılı bir iti diiği: () A (t)+...+a (t)+a (t)+a (t) () =B (t)+...+b (t)+b (t)+b (t) Yurıdi dld (t) çıtııı yü rtbd türvi iti gci rtbii blirlr. T (t)+ (t)= (t) İici rtbd gcili it Birici rtbd gcili it T ( t) ( t) ( t) ( t) 0 0 Birici Mrtbd Gcili (BMG) Sitlr: Z dvrışı: T (t)+ (t)= (t) Gl olr rji dpoly itlr BMG it özlliği tşırlr (odtör, yy, dpo, v.) : zç ftörü ( T ) ( ( T : Z biti ( ( T T ( ( t) L t 3 4 Birici Mrtbd Gcili (BMG) Sitlr: ( ( T ) So dğr tori : dr dr dr li ( 0 li 0 ( T ) Düzli rji üri : t T ( T ) 0,63 t T t 3T t 4T dr (t) dr (T ) 0,865 (3T ) 0,950 dr dr (4T ) 0,98 dr (t) II. Mrtbd Gcili (İMG) Sitlr: Bit yy ütl öü izı çoğu i iti tl hlii götrir.sitd bir uvvti (girdi) tii ltıdi i llrı yrdğiştiri (çıtı) iclir f(t) (t) c(t) (T) Bu difriyl dl görüldüğü gibi. rtbd difriyl trilr içrtdir. Bu yüzd bu itlr İici Mrtbd Gcili Sitlr olr dldırılırlr. Siti trfr foiyou difriyl dli Lplc Trforu yrdııyl ld dilir. F( ( X ( (0) (0)) c( X( (0)) X( ( 0) 0: (0) 0 X ( F( c 5 6
2 II. Mrtbd Gcili (BMG) Sitlr: İici rtbd itlri lizid iti i, ltril vb. özlilri olup olı bılızı rtriti ii prtr bllirliştir. Bulr öü ftörü v doğl frtır. Doğl fr ( ) :Sit dışrıd hiçbir ti oldığıd v it içriid rji ybı yol ç hiçbir l buludığıd iti rbt cvbıı ypcğı titrşilri frıı ifd dr. 0 (t) (t) ( )X( 0 j, j (j) 0, X( 0 7 II. Mrtbd Gcili (IMG) Sitlr: İici rtbd itlri lizid iti i, ltril vb. özlilri olup olı bılızı rtriti ii prtr bllirliştir. Bulr öü ftörü v doğl frtır. Söü ftörü(): Siti di diiğid doğ titrşilri yo t ytğii bllirly boyutuz bir prtrdir. Tı olr trfr foiyouuzu pydıı tlı ölri olduğu durudi öü dğri riti öü dğri olr dldırılıştır. criti 4 0 criti Bir iti öü ftörü; o itdi öü tyııı,o it içi riti ol öü tyıı orıı ifd d büyülültür. c c criti 8 II. Mrtbd Gcili (IMG) Sitlr: İici rtbd gcili itlri gl trfr foiyou bu ii prtr v bir zç tyıı ullılr şğıdi gibi ifd dilbilir. Sitlri trfr foiyolrı çoğu z bu gllştiriliş for uygu olr ld dilz. Buu içi tl ttil işllr ypılr bulu trfr foiyou bu ifdy bztili grtdir. c Dogl Fr c Söü Ftörü zç 9 II. Mrtbd Gcili (IMG) Sitlr: Bu prtrlri hplı il buluc trfr foiyou il girişt bulu trfr foiyouu özdştir.bu yüzd hr ütl,yy tıı v öü dğri içi ii trfr foiyoud yı dii dvrışı götrctir. Sğ trft =g, c=30 N/, =0000 N/ dğrlri ullılr buluuş biri b cvbı, ol trft i =0.00, w=00 rd/, 0.5 dğrlri il buluuş z cvbı vriliştir. Görüldüğü gibi bu ii it bir birii yı dii dvrış hiptir. 0 II. Mrtbd Gcili (IMG) Sitlr: Sğ trft =g, c=30 N/, =0000 N/ dğrlri ullılr buluuş biri b cvbı, ol trft i =0.00, w=00 rd/, 0.5 dğrlri il buluuş z cvbı vriliştir. Görüldüğü gibi bu ii it bir birii yı dii dvrış hiptir. II. Mrtbd Gcili (IMG) Sitlr: Trfr foiyouuzu pydı rtriti dl olr d dldırılır. rtriti dliizi ölri iti dii dvrışıı blirlr. Bulu ö ifdlridd görüldüğü gibi öü ftörüü riti dğri dir v iici rtbd gcili itlri dii dvrışlrı öü ftörlri bğlı olr grupldırılır. Eğr öü ftörüüz şit i itd tlı ö vrdır v yurıd yptığıız tı grği itiiz riti öülü it olr dldırılır. Eğr öü ftörüüz d büyü i iti ii grçl öü vrdır v itiiz riti ütü öülü it olr dldırılır. Bu ii it içi itlri z cvbı hpldığıd ütl foiyolr buluur v bu itlr düzgü (lııız) dii dvrış götrirlr.
3 II. Mrtbd Gcili (IMG) Sitlr: Eğr öü ftörüüz d üçü i rö içriidi ifd gtif ouç vrir v iti ii rşı.(şli) yı öü vrdır v itiiz riti ltı öülü it olr dldırılır.riti ltı öülü itlri z cvbı hpldığıd rşı yı ütlü ifdlr buluur, bu ifdlr iüoydl foiyolrı oluştururlr (Eulr şitlilri). İMG Sitlri biri ipul girdi cvplrı: İpul girdi i olr t=0 ıd uygul bir lı it gibi düşüülbilir. Bu girdii Lplc Trforu birdir. Bu bpl z cvbı buluur dc trfr foiyouu tr Lplc trforu lıır v ld dil z cvbı dc iti dii dvrış rtritilrii götrir. Dolyıı il iti dvrışı lıılıdır.bu yüzd bu tür itlr titrşi itlri olr d dldırılırlr. 3 4 İMG Sitlri biri ipul girdi cvplrı: riti Ütü Söülü Sit > Siti diiriitı pozitif bir yıdır. ölr gl ifd vril şitlilrd hplır. Bu ölr ullılr bulu trfr foiyou şğıdi ford olctır. ( )( ) İMG Sitlri biri ipul girdi cvplrı: riti Ütü Söülü Sit > Siti z cvbı t vril Lplc Döüşüü tblou yrdııyl buluur.(forül 59). - t t L ( )( ) ( )t ( )t (t) ( )t ( (t) )t Sit cvbı görüldüğü gibi ii dt ütl foiyou toplıd oluştdır 5 6 İMG Sitlri biri ipul girdi cvplrı: riti Ütü Söülü Sit > Ör: vril i itd = g, c=30 N/, =00 N/ olduğu durud iti rtriti ifdlrii hplyıız, ölrii buluuz, z cvbıı hplyıız rd/ c (t) t t İMG Sitlri biri ipul girdi cvplrı: riti Söülü Sit = Siti diiriitı ıfırdır.siti ii öü birbiri şittir v şğıdi gibi hplır. Bu ölr ullılr bulu trfr foiyou şğıdi ford olctır. ( ) Siti z cvbı t vril Lplc Döüşüü Tblou yrdııyl buluur.(forül 0). - L ( t t ( t) t t 7 8 3
4 İMG Sitlri biri ipul girdi cvplrı: ritiriti Söülü Sit = Ör: ou bşıd vril i itd = g, c=30 N/, olduğu durud iti riti öülü olı içi grli yy tyııı hplyıız. Dh or bu yy tyııı ullr iti rtriti ifdlrii hplyıız, ölrii buluuz, z cvbıı hplyıız. c N/ 5 5 rd/ Siti ölri şğıdi gibi buluur. Z cvbı içi yi Lplc Döüşüü Tblou d 0. şitli ullılır. İMG Sitlri biri ipul girdi cvplrı: ritiriti Söülü Sit = Ör: Siti ölri şğıdi gibi buluur. Z cvbı içi yi Lplc Döüşüü Tblou d 0. şitli ullılır. (t) t 5 5 t Sit cvbıı icldiğiizd riti ütü öülü it bzr bir dvrış gözllriz.li it dh hızlı (0.6 bşlgıç ouu dötdir. 9 0 İMG Sitlri biri ipul girdi cvplrı: riti Altı Söülü Sit < Siti diiriitı ıfırd üçü bir yıdır.siti rşı şli ii öü vrdır. i i Siti z cvbı t vril Lplc Döüşüü Tblou yrdııyl buluur.(forül 36). - L i( t) t İMG Sitlri biri ipul girdi cvplrı: riti Altı Söülü Sit < Sit cvbı görüldüğü gibi bir dt ütl zrf ğrii içriid lı bir iü foiyou şliddir. t Siti z cvbı ifdid d gözllbilcği üzr iü ğriii frı doğl frt frlı bir frtır. Bu gözll fr öülü titrşilri frı ( d ) dir v tı grği şğıdi gibi hplır. i( t) d İMG Sitlri biri ipul girdi cvplrı: riti Altı Söülü Sit < Ör: i itd = g, c=30 N/, =500 N/ olduğu dur ud iti rtriti ifdlrii hplyıız, ölrii buluuz, z cvbıı hplyıız rd/ c Sit, öü ftörü bird üçü olduğu içi riti ltı öülü itdir. İMG Sitlri biri ipul girdi cvplrı: riti Altı Söülü Sit < Ör:Siti ölri şğıdi gibi buluur. Z cvbı içi yi Lplc Döüşüü Tblou d 36. şitli ullılır i i 50 (t) t i( t) 3 4 4
5 İMG Sitlri biri ipul girdi cvplrı: riti Altı Söülü Sit < riti ltı itlr görüldüğü üzr dii dvrışı lıı yp itlrdir. Bu yüzd özl olr titrşi itlri olr dldırlırlr. İMG Sitlri biri b girdi cvplrı: riti Altı Söülü Sit < riti ltı itlri biri b cvbı: ( ( ) Lplc döüşüü yrdııyl z cvbı şildi gibi buluur.görülcği gibi iti rrlı hli viyi ötliş v iü ğrii bir gci dğri liştir. (t) i( t ) t Şidd gözlbilcği gibi öü ftörüü rtı iti dh z lıı ypı v dh ı ürd bşlgıç ouu döi bp oltdır. 5 Arcco( ) t 6 İMG Sitlri biri b girdi cvplrı: riti Altı Söülü Sit < İMG Sitlri biri b girdi cvplrı: Gl olr riti Altı Söülü itlri biri b cvplrı, bzı toloji Prfor Tı Dğrlri çııd ö tşır. Bu dğrlr, Tp Zı, Tp (Pi) Gliği, Düzli Rji Sürci v Logriti Dr(Azl Ftörü) gibi prfor tı dğrlridir. w=50 rd/ i öü ftörüü rı dğrlri içi iici rtbd gl bir iti biri b cvbı 7 8 İMG Sitlri biri b girdi cvplrı: Tp Zı (T P ) İMG bir iti düzli rji gçişi ırıd gliğii iu dğr ulşıcy d gç ürdir. Tp zıı hpl içi (5.7) dlii türvii Lplc Döüşüü lıır. Bu ifdi Tr Lplc Döüşüü lır ıfır şitlir. Tp. E Büyü Gli ( Mp) : İMG bir iti düzli rji gçişi ırıd gliği ulştığı iu dğrdir. Bu dğri bul içi biri bğ rşılı z cvbıd t = Tp dğri oulur M p. İMG Sitlri biri b girdi cvplrı: Aş Dğri (%AD) :E büyü gliği i (biri b cvbı olduğu içi) ütüd l ıı Aş Dğri olr tılır.gld şğıdi şild yüzdl olr ifd dilir. Mp Xdr AD.00 Xdr X dr AD 00.. Ardışı T p, T p,...t p pi ürlri vy bulr rşılı gl yı vy frlı yölrdi gli dğrlri M p, M p,...m p v ş Yüzdlri olyc hplbilir
6 İMG Sitlri biri b girdi cvplrı: Logriti (Dr) Gli Azl Ftörü : İMG bir iti biri b şlidi bir girdi hlid, yı yöd rd rd gl ii gli rıdi düş orıdır. Ayı yöd v rd rd gl M p v M p3 glilri rıd t bir priyotlu z frı bulutdır. Yi T p3 = T p + T dir. Bu z ifdlri ullılr bulu Aş Yüzdlri orlr Logriti Azl Ftörü şğıdi şild hplbilir. M p. ; M p l(a). M A M p p3 (. 3.. ) İMG Sitlri biri b girdi cvplrı: Biri b girdi hlid düzli rji ürci (T dr ): T dr ylşı olr biri b z cvbıı itotlrıd (zrf ğriid) hplbilir. İMG bir iti bri b cvbıı vril ifd il ö hroi bir foiyou tıltdır. t Bu iptotlrı ltt vy ütt ouzd dğri blli bir b (örği b= % vy b=% 5 gibi) tolr bdı içid ylşı lır düzli rji gçiş ürci ylşı olr hplbilir. 4 3 Tdr 4.T Tdr 3. T % li bir tolr. bdı % 5 li bir tolr. bdı 3 3 İMG Sitlri biri ipul girdi cvplrı: Düzli rji ürci (T dr ): T dr İMG bir iti Biri ipul şlidi bir girdi hlid düzli rji ürci, z cvbı gliğii, blirl blli bir b tolr bdı ulşı içi gç ürdir b. Tdr.l.w w % b li bir tolr bdı 33 6
Sistem Dinamiği ve Modellemesi
 8..0 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili ouud itlri blirli
8..0 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili ouud itlri blirli
UFUK ÖZERMAN- 2012-2013 Page 1
 - GÜZ P,Q,R fokiolrı poliom olmk üzr d d P Q R d d v P d d Q d P d R P p q dklmi içi P şrıı ğl = okı di ok dir, çözümlri di okıı civrıd şklid rrız. =+-+- +... = = okı; p=q/ P, q= R/ P fokiolrı okıd liik
- GÜZ P,Q,R fokiolrı poliom olmk üzr d d P Q R d d v P d d Q d P d R P p q dklmi içi P şrıı ğl = okı di ok dir, çözümlri di okıı civrıd şklid rrız. =+-+- +... = = okı; p=q/ P, q= R/ P fokiolrı okıd liik
Sistem Dinamiği ve Modellemesi
 5..3 Sistm Dimiği v Modllmsi Doğrusl Sistmlri Frks Dvrışı Giriş: Drs ksmıd şu kdr yıl çözümlmlrd, doğrusl sistmlri imuls girdi, bsmk girdi gibi çşitli girdilr krşı zm cvlrıı icldik. Bzı durumlrd doğrusl
5..3 Sistm Dimiği v Modllmsi Doğrusl Sistmlri Frks Dvrışı Giriş: Drs ksmıd şu kdr yıl çözümlmlrd, doğrusl sistmlri imuls girdi, bsmk girdi gibi çşitli girdilr krşı zm cvlrıı icldik. Bzı durumlrd doğrusl
Eğitim-Öğretim Güz Yarıyılı Diferansiyel Denklemler Dersi Çalışma Soruları
 - Eğiim-Öğrim Güz rıılı Difril Dklmlr Dri Çlışm Sorlrı 6 // Aşğıd vril kvv rilrii kıklık rıçplrıı lirliiz. = = di ok civrıd kvv rii rdımıl vril difril dklmlri çözüüz. - -= - + -= - + += dklmii kil oklrıı
- Eğiim-Öğrim Güz rıılı Difril Dklmlr Dri Çlışm Sorlrı 6 // Aşğıd vril kvv rilrii kıklık rıçplrıı lirliiz. = = di ok civrıd kvv rii rdımıl vril difril dklmlri çözüüz. - -= - + -= - + += dklmii kil oklrıı
7 KONTROL SİSTEMLERİNİN ZAMAN TANIM BÖLGESİ ANALİZİ
 7 ONTOL SİSTEMLEİNİN ZAMAN TANIM BÖLGESİ ANALİZİ 7. Sürkli Sitlri Z Yıtı: Giriş Bir kotrol itid ğr çıkış işrtii giriş işrtii lirli koşullr ltıd tkip ti itiyor, giriş v çıkış işrtlri z fokiyou olrk krşılştırılır.
7 ONTOL SİSTEMLEİNİN ZAMAN TANIM BÖLGESİ ANALİZİ 7. Sürkli Sitlri Z Yıtı: Giriş Bir kotrol itid ğr çıkış işrtii giriş işrtii lirli koşullr ltıd tkip ti itiyor, giriş v çıkış işrtlri z fokiyou olrk krşılştırılır.
denklemini x=0 adi nokta civarında çözünüz.
 dklmii = adi okta ivarıda çözüüz. Rküra bağıtıı DİFERANSİYEL DENKLEMLER UFUK ÖZERMAN y +y +( /6y= ( dklmi içi = oktaıı düzgü tkil okta olduğuu götri, İdi dklmii köklrii bulu v çözü. P( = = = = tkil okta
dklmii = adi okta ivarıda çözüüz. Rküra bağıtıı DİFERANSİYEL DENKLEMLER UFUK ÖZERMAN y +y +( /6y= ( dklmi içi = oktaıı düzgü tkil okta olduğuu götri, İdi dklmii köklrii bulu v çözü. P( = = = = tkil okta
e gibi Laplace dönüşümü olmayan fonksiyonlar kaynak olarak
 Dvr Torii Dr Nou Dr. Nuri ACIR v Dr. Egi Cml MENGÜÇ BÖLÜM IX LAPLACE DÖNÜŞÜMÜ Lplc kiği lir, opluprmrli dvrlrd kullıl güçlü bir liz kiğidir. Lplc döüşümü, bird fzl düğümvolj vy gözkım difriyl dklmlrii
Dvr Torii Dr Nou Dr. Nuri ACIR v Dr. Egi Cml MENGÜÇ BÖLÜM IX LAPLACE DÖNÜŞÜMÜ Lplc kiği lir, opluprmrli dvrlrd kullıl güçlü bir liz kiğidir. Lplc döüşümü, bird fzl düğümvolj vy gözkım difriyl dklmlrii
Tanım : Bir rassal deney yapıldığında bir deneyin sonucu sadece iki sonuç içeriyorsa bu deneye Bernoulli deneyi denir.
 BRNOULLİ DAĞILIMI Broulli dağılımı bir rassal dy yaıldığıda yalızca iyi öü olumlu-olumsuz başarılı-başarısız gibi sadc ii souç ld dildiğid ullaılır. Taım : Bir rassal dy yaıldığıda bir dyi soucu sadc ii
BRNOULLİ DAĞILIMI Broulli dağılımı bir rassal dy yaıldığıda yalızca iyi öü olumlu-olumsuz başarılı-başarısız gibi sadc ii souç ld dildiğid ullaılır. Taım : Bir rassal dy yaıldığıda bir dyi soucu sadc ii
Hafta 8: Ayrık-zaman Fourier Dönüşümü
 Hafta 8: Ayrı-zama ourir Döüşümü El Alıaca Aa Koular Ayrı-zama ourir döüşümü Ayrı-zama priyodi işartlr içi ourir döüşümü Ayrı-zama ourir döüşümüü özllilri Doğrusal, sabit atsayılı far dlmlriyl taımlaa
Hafta 8: Ayrı-zama ourir Döüşümü El Alıaca Aa Koular Ayrı-zama ourir döüşümü Ayrı-zama priyodi işartlr içi ourir döüşümü Ayrı-zama ourir döüşümüü özllilri Doğrusal, sabit atsayılı far dlmlriyl taımlaa
LOGARİTMA. Örnek: çizelim. Çözüm: f (x) a biçiminde tanımlanan fonksiyona üstel. aşağıda verilmiştir.
 LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
YAYINIM PROBLEMLERİ İÇİN SONLU HACİMLER YÖNTEMİ ( * )
 YYIIM ROLMLRİ İÇİ OLU HCİMLR YÖMİ ( * ) 4.. Giriş: bölümd ol Hcimlr Yötmlrii (HY) ıım problmlri frlı şrtlr v ıır oşllrıd ıl glbilcği götrilctir. bğlmd ışı v ıı trfrii öt dlmlri ıl rılştırılcğı v ıl çöümlcği
YYIIM ROLMLRİ İÇİ OLU HCİMLR YÖMİ ( * ) 4.. Giriş: bölümd ol Hcimlr Yötmlrii (HY) ıım problmlri frlı şrtlr v ıır oşllrıd ıl glbilcği götrilctir. bğlmd ışı v ıı trfrii öt dlmlri ıl rılştırılcğı v ıl çöümlcği
ü ü üü ş ş ş Ü ÜÜ ü ü üü ş ü ş ş ö ç ş ş ç ş ü ü ü ç ç ş ü ş ş ü ü ü ö ş ö ş ö ş ş ç ş ü ş ç ş Ç ç Ü öü ü ü üü ü ü üü ç ş ç ş ö ö ü ç ş ç ş ş ö ç ş ö
 ş ü ş ü ü üü ü ş ö ş ş ö Ü ş ş ş ö Ç ö öü ö ö Ç ş ş ş ö ç ç ş ş ş ş ü ç ş ö ü ü ü üü ş ş ş Ü ÜÜ ü ü üü ş ü ş ş ö ç ş ş ç ş ü ü ü ç ç ş ü ş ş ü ü ü ö ş ö ş ö ş ş ç ş ü ş ç ş Ç ç Ü öü ü ü üü ü ü üü ç ş ç
ş ü ş ü ü üü ü ş ö ş ş ö Ü ş ş ş ö Ç ö öü ö ö Ç ş ş ş ö ç ç ş ş ş ş ü ç ş ö ü ü ü üü ş ş ş Ü ÜÜ ü ü üü ş ü ş ş ö ç ş ş ç ş ü ü ü ç ç ş ü ş ş ü ü ü ö ş ö ş ö ş ş ç ş ü ş ç ş Ç ç Ü öü ü ü üü ü ü üü ç ş ç
MENKUL KIYMET DEĞERLEMESİ
 MENKUL KIYMET EĞERLEMESİ.. Hiss Sdii Tk ömlik Gtirisii Hsaplaması Bir mkul kıymti gtirisi, bkl akit akımlarıı, şimdiki piyasa fiyatıa şitly iskoto oraıdır. Mkul kıymti özlliği gör bu akit akımları faiz
MENKUL KIYMET EĞERLEMESİ.. Hiss Sdii Tk ömlik Gtirisii Hsaplaması Bir mkul kıymti gtirisi, bkl akit akımlarıı, şimdiki piyasa fiyatıa şitly iskoto oraıdır. Mkul kıymti özlliği gör bu akit akımları faiz
D (5 1) Benzer biçimde integral için de bir operatör gösterimi düşünülebilir: a
 BÖÜM 5 APACE DÖNÜŞÜMÜ Şu kdr öğrdiklriizd, gl olrk difriyl dklmlri çözmi cbirl dklmlri çözmd dh zor olduğuu frk mişiizdir. O hld cb difriyl dklmlri cbirl hl döüşürck bir yol vr mıdır? Ev, vrdır. Alıd buu
BÖÜM 5 APACE DÖNÜŞÜMÜ Şu kdr öğrdiklriizd, gl olrk difriyl dklmlri çözmi cbirl dklmlri çözmd dh zor olduğuu frk mişiizdir. O hld cb difriyl dklmlri cbirl hl döüşürck bir yol vr mıdır? Ev, vrdır. Alıd buu
İNTEGRAL DENKLEM SİSTEMLERİNİN YAKLAŞIK ÇÖZÜMLERİ
 İEGRAL DEKLEM SİSEMLERİİ YAKLAŞIK ÇÖZÜMLERİ İil ULGA Yükk Li zi MAEMAİK AABİLİM DALI ISPARA 6 ii.c. SÜLEYMA DEMİREL ÜİVERSİESİ FE BİLİMLERİ ESİÜSÜ İEGRAL DEKLEM SİSEMLERİİ YAKLAŞIK ÇÖZÜMLERİ İSMAİL ULGA
İEGRAL DEKLEM SİSEMLERİİ YAKLAŞIK ÇÖZÜMLERİ İil ULGA Yükk Li zi MAEMAİK AABİLİM DALI ISPARA 6 ii.c. SÜLEYMA DEMİREL ÜİVERSİESİ FE BİLİMLERİ ESİÜSÜ İEGRAL DEKLEM SİSEMLERİİ YAKLAŞIK ÇÖZÜMLERİ İSMAİL ULGA
Sistem Dinamiği ve Modellemesi
 Sitm Diamiği v Modllmi aplac Traformayou v Trafr Fokiyou aplac Traformu : Bir itmi diamik davraışı, o itmi matmatikl modlii ifad d difraiyl dklmlri çözümüd kullaıla bir matmatikl yötmdir. f(t foiyouu aplac
Sitm Diamiği v Modllmi aplac Traformayou v Trafr Fokiyou aplac Traformu : Bir itmi diamik davraışı, o itmi matmatikl modlii ifad d difraiyl dklmlri çözümüd kullaıla bir matmatikl yötmdir. f(t foiyouu aplac
Sönümlü Serbest Titreşim
 .5.. Söülü Srbs Tirşi Sosza kadar dva d sabi glikli irşilrl grçk hayaa karşılaşılaakadır. Bilidiği gibi, sis irşi harki başladıka bir sür sora hark yavaş yavaş zayıflar. olayısıyla hark dklii aşağıdaki
.5.. Söülü Srbs Tirşi Sosza kadar dva d sabi glikli irşilrl grçk hayaa karşılaşılaakadır. Bilidiği gibi, sis irşi harki başladıka bir sür sora hark yavaş yavaş zayıflar. olayısıyla hark dklii aşağıdaki
Pontiklerin altında hacim koruma
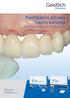 Pontilrin ltınd hcim orum Gitlich Biomtril ürünlri il - Sırt Korum çözümlri Dh fzl bilgi için www.gitlich-biomtril.com Sırt Korum - Bitç Sırt orum diş çimi onrı lvolr ırtın ontürünü orum için uygulnn bir
Pontilrin ltınd hcim orum Gitlich Biomtril ürünlri il - Sırt Korum çözümlri Dh fzl bilgi için www.gitlich-biomtril.com Sırt Korum - Bitç Sırt orum diş çimi onrı lvolr ırtın ontürünü orum için uygulnn bir
DENEY 5 İkinci Dereceden Sistem
 DENEY 5 İkici Drcd Sitm DENEYİN AMACI. İkici drcd itmi karaktritiklrii alamak.. Söüm oraı ζ i, ikici drcd itm üzridki tkiii gözlmlmk. 3. Doğal frka i, ikici drcd itm üzridki tkiii gözlmlmk. GENEL BİLGİLER
DENEY 5 İkici Drcd Sitm DENEYİN AMACI. İkici drcd itmi karaktritiklrii alamak.. Söüm oraı ζ i, ikici drcd itm üzridki tkiii gözlmlmk. 3. Doğal frka i, ikici drcd itm üzridki tkiii gözlmlmk. GENEL BİLGİLER
İNTEGRAL KONU ANLATIMI ÖRNEKLER
 İNTEGRL KONU NLTIMI ÖRNEKLER Ġtgrl lmk, türi ril ir oksio lmk tır d,, d oksio olrk rildiğii =F i istdiğii rslım d içi i cid idsi: d = + dir, hrhgi ir sit df d koģl sğl = F oksio i gör itgrli dir d F içimid
İNTEGRL KONU NLTIMI ÖRNEKLER Ġtgrl lmk, türi ril ir oksio lmk tır d,, d oksio olrk rildiğii =F i istdiğii rslım d içi i cid idsi: d = + dir, hrhgi ir sit df d koģl sğl = F oksio i gör itgrli dir d F içimid
Bölüm 7.2: Matrisler. Transpoz. Konjuge. Adjoint
 ölü.: Mrsler ugüü derszde rs eors err edeeğz. Mrs ouud ddörge elelrd oluş r eledır sır ve süu zı öre rsler şğıddır: j C Trspoz j ı rspozu T j dır. Öre T T T Kojuge j ı Kojuges j dır. Öre djo ı djo T dır
ölü.: Mrsler ugüü derszde rs eors err edeeğz. Mrs ouud ddörge elelrd oluş r eledır sır ve süu zı öre rsler şğıddır: j C Trspoz j ı rspozu T j dır. Öre T T T Kojuge j ı Kojuges j dır. Öre djo ı djo T dır
ELM207 Analog Elektronik
 ELM7 Alog Elkroik Giriş Bir Fourir srisi priyodik bir ) oksiyouu, kosiüs v siüslri sosuz oplmı biçimid bir çılımdır. ) cos b si ) Bşk dyişl, hrhgi bir priyodik oksiyo sbi bir dğr, kosiüs v siüs oksiyolrıı
ELM7 Alog Elkroik Giriş Bir Fourir srisi priyodik bir ) oksiyouu, kosiüs v siüslri sosuz oplmı biçimid bir çılımdır. ) cos b si ) Bşk dyişl, hrhgi bir priyodik oksiyo sbi bir dğr, kosiüs v siüs oksiyolrıı
BÖLÜM 2 EĞRİ UYDURMA VE İNTERPOLASYON
 BÖÜ EĞRİ UYDURA VE İTERPOASYO - Grş İterpolo polomlrı Bölümüş rlr 4 Eşt rlılı ot dğılımlrı ç bt rlr 5 Küb ple eğrler Kım üb ple eğrler 7 Br üze üzerde terpolo 8 E-üçü reler lşımı Bölüm - Eğr udurm ve terpolo
BÖÜ EĞRİ UYDURA VE İTERPOASYO - Grş İterpolo polomlrı Bölümüş rlr 4 Eşt rlılı ot dğılımlrı ç bt rlr 5 Küb ple eğrler Kım üb ple eğrler 7 Br üze üzerde terpolo 8 E-üçü reler lşımı Bölüm - Eğr udurm ve terpolo
Sistem Dinamiği ve Modellemesi
 0..0 St Dğ v odll Dk Stlr odll v Alz Elktrkl Stlr Elktrkl üyüklüklr Elktrk Akıı: r ltk blrl br ktd br zd gç lktrk yükü (lktro)ktrı lktrk kıı dr. r Apr dr. dq I A Grl(lktrkl potyl frkı): Srbt lktrolrı hrkt
0..0 St Dğ v odll Dk Stlr odll v Alz Elktrkl Stlr Elktrkl üyüklüklr Elktrk Akıı: r ltk blrl br ktd br zd gç lktrk yükü (lktro)ktrı lktrk kıı dr. r Apr dr. dq I A Grl(lktrkl potyl frkı): Srbt lktrolrı hrkt
MEKANİK TİTREŞİMLER. n serbestlik dereceli bir sistem için doğal frekans ifadesi esneklik matrisi kullanılarak şu şekilde verilmiş idi, L (1)
 MEKANİK TİTREŞİMER DUNKEREY METODU Ço serbestl derecel ssteler. doğl fresı, sste oluştur her br serbestl derecese t doğl freslr csde ylşı olr fde edlebletedr. Duerley trfıd verle bu forülsyo l doğl fres
MEKANİK TİTREŞİMER DUNKEREY METODU Ço serbestl derecel ssteler. doğl fresı, sste oluştur her br serbestl derecese t doğl freslr csde ylşı olr fde edlebletedr. Duerley trfıd verle bu forülsyo l doğl fres
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 2007 SORULARI
 DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
ESM 406 Elektrik Enerji Sistemlerinin Kontrolü
 8. KAALILIK ESM 6 Elktrik Erji Sitmlrii Kotrolü 8. Kouu Amaç v Kapamı Bir itmi ıırlı hr giriş cvabı ıırlı i o itm kararlıdır. Sitm giriş, rfra dğrid vya bozucu dğrd olabilir. Karalılığı diğr bir taımı
8. KAALILIK ESM 6 Elktrik Erji Sitmlrii Kotrolü 8. Kouu Amaç v Kapamı Bir itmi ıırlı hr giriş cvabı ıırlı i o itm kararlıdır. Sitm giriş, rfra dğrid vya bozucu dğrd olabilir. Karalılığı diğr bir taımı
GRUP TANIMLAYAN BAZI YARIGRUP VE MONOİD TAKDİMLERİ* Some Semigroup and Monoid Presentations Defining a Group*
 GRU TANIMLAYAN BAZI YARIGRU VE MONOİD TAKDİMLERİ* Soe Seigroup d Mooid resettios Defiig Group* Bsri ÇALIŞKAN Ç.Ü. Fe Biieri Estitüsü Mteti Abii Dı Firet KUYUCU Ç.Ü.Fe Edebit Fütesi Mteti Böüü ÖZET Bu çışd
GRU TANIMLAYAN BAZI YARIGRU VE MONOİD TAKDİMLERİ* Soe Seigroup d Mooid resettios Defiig Group* Bsri ÇALIŞKAN Ç.Ü. Fe Biieri Estitüsü Mteti Abii Dı Firet KUYUCU Ç.Ü.Fe Edebit Fütesi Mteti Böüü ÖZET Bu çışd
 İ İ İ İ İ İ İ İ İ İ İ İ ö ç ç ü Ş ö ö ç ç ö ç Ö ö ç ü Ö ö İ ü ö Ö İ ü ö ç ö ö ç ö ö ö ü ü ü ç ö ö ü ö ü ü ü ü ü ö ü ö ü ö ö Ö ö ü ö ç ü ö ö ö ö Ö Ö ç ç ç ü ö İ İç çü ö ç ü ö ç ö ö ö İ ç ç ç ç ç ö ö ö ç
İ İ İ İ İ İ İ İ İ İ İ İ ö ç ç ü Ş ö ö ç ç ö ç Ö ö ç ü Ö ö İ ü ö Ö İ ü ö ç ö ö ç ö ö ö ü ü ü ç ö ö ü ö ü ü ü ü ü ö ü ö ü ö ö Ö ö ü ö ç ü ö ö ö ö Ö Ö ç ç ç ü ö İ İç çü ö ç ü ö ç ö ö ö İ ç ç ç ç ç ö ö ö ç
Bir Kompleks Sayının n inci Kökü.
 Prof.Dr.Hüsy ÇAKALLI Br Komplks Sayıı c Kökü. hrhag br sab doğal sayı olmak ür, br komplks sayıı c kökü, c kuvv bu sayıya ş ola komplks sayıdır. ( r(cos s olsu v (cos s dylm. Bu akdrd ( [ (cos s] dr v
Prof.Dr.Hüsy ÇAKALLI Br Komplks Sayıı c Kökü. hrhag br sab doğal sayı olmak ür, br komplks sayıı c kökü, c kuvv bu sayıya ş ola komplks sayıdır. ( r(cos s olsu v (cos s dylm. Bu akdrd ( [ (cos s] dr v
Hafta 5: Periyodik İşaretlerin Fourier Serisi Gösterilimi
 Hf 5: Priyodi İşrlrin Fourir Srii Görilimi El Alınc An Konulr LI imlrin rmşı ül işrlr ynıı Sürli-zmn priyodi işrlrin Fourir rii görilimi Fourir riinin yınlığı Sürli-zmn Fourir riinin özllilri LI Simlrin
Hf 5: Priyodi İşrlrin Fourir Srii Görilimi El Alınc An Konulr LI imlrin rmşı ül işrlr ynıı Sürli-zmn priyodi işrlrin Fourir rii görilimi Fourir riinin yınlığı Sürli-zmn Fourir riinin özllilri LI Simlrin
Ara Değer Hesabı (İnterpolasyon)
 Ar Değer Hesbı İterpolso Ardeğer hesbı mühedsl problemlerde sılıl rşılşıl br şlemdr. İterpolso Ble değerlerde blmee rdeğer d değerler bulumsı şlemdr. Geel olr se br osouu 0,,, gb rı otlrd verle 0,,, değerler
Ar Değer Hesbı İterpolso Ardeğer hesbı mühedsl problemlerde sılıl rşılşıl br şlemdr. İterpolso Ble değerlerde blmee rdeğer d değerler bulumsı şlemdr. Geel olr se br osouu 0,,, gb rı otlrd verle 0,,, değerler
DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİK KONTROL I Dr. Uğur HASIRCI
 DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
ş ş şğ ş ş ş ö Ö ş ö ğ ş ö ö ğ ş ö ö ö ğ ğ ş ş ö ğ ö ş Ü ö ğ ş ş ö ş ğ ş ğ ğ ğ ö ğ ş
 Ü ğ ğ ş ş ş ş ğ Ğ Ç Ş» ş ö ş ş ğ ş ğ ş Ç ş ğ ş ş ğ ş ş ÜÜ ş ş ö ş Ö Ş Ö ğ ş ö ğ ğ Ü Ş ş ş şğ ş ş ş ö Ö ş ö ğ ş ö ö ğ ş ö ö ö ğ ğ ş ş ö ğ ö ş Ü ö ğ ş ş ö ş ğ ş ğ ğ ğ ö ğ ş ş Ö» Ö Ç ö ğ ş ş ş ö ş ö ö ğ ğ
Ü ğ ğ ş ş ş ş ğ Ğ Ç Ş» ş ö ş ş ğ ş ğ ş Ç ş ğ ş ş ğ ş ş ÜÜ ş ş ö ş Ö Ş Ö ğ ş ö ğ ğ Ü Ş ş ş şğ ş ş ş ö Ö ş ö ğ ş ö ö ğ ş ö ö ö ğ ğ ş ş ö ğ ö ş Ü ö ğ ş ş ö ş ğ ş ğ ğ ğ ö ğ ş ş Ö» Ö Ç ö ğ ş ş ş ö ş ö ö ğ ğ
BÖLÜM II 2. FOURIER DÖNÜŞÜMÜ. 2.1 Giriş
 BÖLÜM II. FOURIER DÖNÜŞÜMÜ. Giriş Yr ürmizd gözl joizi olaylar zamaa yada uzalığa bağlı olara glişir. Gözl joizi olay zamaı bir osiyou is zama oramı im Domai uzuluğu bir osiyou is uzalı oramı Spac Domai
BÖLÜM II. FOURIER DÖNÜŞÜMÜ. Giriş Yr ürmizd gözl joizi olaylar zamaa yada uzalığa bağlı olara glişir. Gözl joizi olay zamaı bir osiyou is zama oramı im Domai uzuluğu bir osiyou is uzalı oramı Spac Domai
U MK E K A MP Ç IL IK E Ğ T İ M İ İ 2008
 U MK E K A MP Ç I L I K E ĞİT İMİ 2008 K A MP Y E R İ S E Ç İMİ V E Ö ZE L L İK L E R İ (Y A Z OP E R A S Y ON L A R I ) U L A Ş I M İÇ İN A R A Ç V E Y A Y A Y A Y OL U N A Y A K I N OL MA L I D I R.
U MK E K A MP Ç I L I K E ĞİT İMİ 2008 K A MP Y E R İ S E Ç İMİ V E Ö ZE L L İK L E R İ (Y A Z OP E R A S Y ON L A R I ) U L A Ş I M İÇ İN A R A Ç V E Y A Y A Y A Y OL U N A Y A K I N OL MA L I D I R.
- ~ - p.:, o... :ı> .~ ~ 3. ~... c: (1) ::ı 3 ..., < ... "O ~ rı ;!. o tı) l"li. ... '< j ;ı;. r ~ v:ı ~ ...
 Q. :,. [ ;::l (JQ l O'Q (h ::: ;:,;' (JQ tı) l"li!t "'I N p.:,,, : ") r ti 8 cr'5 r.! :,;.. Q. ı;ıı,. r r (/) tn.{/),, < ) rı, ff ı ı r ı "' ı :: ı,,,, ;:,;', ı (li p.:, p.:, ::! l"li ti" p.:,,(/),,{j)..
Q. :,. [ ;::l (JQ l O'Q (h ::: ;:,;' (JQ tı) l"li!t "'I N p.:,,, : ") r ti 8 cr'5 r.! :,;.. Q. ı;ıı,. r r (/) tn.{/),, < ) rı, ff ı ı r ı "' ı :: ı,,,, ;:,;', ı (li p.:, p.:, ::! l"li ti" p.:,,(/),,{j)..
ıı ııı ı ı ı ı ı ı ıı ı ı ı ı ıı ı ğ ı ı ııı ı ıı ııı ç ı ı ı ııı ı ğı ıı ıı ı ı ı ı ı ı ü ı ğ
 Ç İ ş ç ç İ İ şü İ İ İ ç İ ü ü ü ü Ü Ü Ü Ü Ü ç ç ğ Ü Ç Ç İç ö ö ü ü ö ö ö ü ğ İ ç Ö Ç ç ğ ğ Ç Ü Ç ç Ü ö ü ç ğ ş ğ şü ü ç ğ ş ü ç ş Ç İ ğ ş ç ü ü ü ü ü ü ğ ş üü ü ş ü ğ ş ç ş ü ç ç ğ ç ğ ç ü ş ğ ş ş ü ü
Ç İ ş ç ç İ İ şü İ İ İ ç İ ü ü ü ü Ü Ü Ü Ü Ü ç ç ğ Ü Ç Ç İç ö ö ü ü ö ö ö ü ğ İ ç Ö Ç ç ğ ğ Ç Ü Ç ç Ü ö ü ç ğ ş ğ şü ü ç ğ ş ü ç ş Ç İ ğ ş ç ü ü ü ü ü ü ğ ş üü ü ş ü ğ ş ç ş ü ç ç ğ ç ğ ç ü ş ğ ş ş ü ü
Sistem Dinamiği ve Modellemesi. Doğrusal Sistemlerin Sınıflandırılması Doğrusal Sistemlerin Zaman Davranışı
 Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
VİNÇTE ÇELİK KONSTRÜKSİYON
 0 Haziran www.guvn-kua.h VİNÇTE ÇEİ ONSTRÜSİON ÖZET _09 M. Güvn UT Smbollr v anaklar için "_00_ClikonsruksionaGiris.do" a bakınız. oordina ksnlri "GENE GİRİŞ" d blirildiği gibi DIN 8800 T gör alınmışır.
0 Haziran www.guvn-kua.h VİNÇTE ÇEİ ONSTRÜSİON ÖZET _09 M. Güvn UT Smbollr v anaklar için "_00_ClikonsruksionaGiris.do" a bakınız. oordina ksnlri "GENE GİRİŞ" d blirildiği gibi DIN 8800 T gör alınmışır.
2. BELİRLİ İNTEGRALİN TANIMI ve TEMEL ÖZELLİKLERİ
 DERS: MATEMATİK II MAT II () ÜNİTE: BELİRLİ İNTEGRALLER KONU:. ARALIKLARIN PARÇALANMASI. BELİRLİ İNTEGRALİN TANIMI ve TEMEL ÖZELLİKLERİ GEREKLİ ÖN BİLGİLER. semolü ve temel toplm ormülleri. Limiti temel
DERS: MATEMATİK II MAT II () ÜNİTE: BELİRLİ İNTEGRALLER KONU:. ARALIKLARIN PARÇALANMASI. BELİRLİ İNTEGRALİN TANIMI ve TEMEL ÖZELLİKLERİ GEREKLİ ÖN BİLGİLER. semolü ve temel toplm ormülleri. Limiti temel
İKİNCİ BÖLÜM REEL SAYI DİZİLERİ
 Prof.Dr.Hüseyi ÇAKALLI İKİNCİ BÖLÜM REEL SAYI DİZİLERİ Bu ölümde dizileri, yi tım kümesi doğl syılr kümesi, değer kümesi, reel syılr kümesii ir lt kümesi ol foksiyolrı iceleyeceğiz... Ykısk Diziler. Öce
Prof.Dr.Hüseyi ÇAKALLI İKİNCİ BÖLÜM REEL SAYI DİZİLERİ Bu ölümde dizileri, yi tım kümesi doğl syılr kümesi, değer kümesi, reel syılr kümesii ir lt kümesi ol foksiyolrı iceleyeceğiz... Ykısk Diziler. Öce
SAYISAL ANALİZ. Doç.Dr. Cüneyt BAYILMIŞ. Sayısal Analiz. Doç.Dr. Cüneyt BAYILMIŞ
 SAYISAL ANALİZ Doç.Dr. Cüeyt BAYILMIŞ Doç.Dr. Cüeyt BAYILMIŞ Syısl Alz SAYISAL ANALİZ İNTERPOLASYON Ar Değer Bulm Doç.Dr. Cüeyt BAYILMIŞ Syısl Alz İÇİNDEKİLER Ar Değer Hesbı İterpolsyo Doğrusl Ar Değer
SAYISAL ANALİZ Doç.Dr. Cüeyt BAYILMIŞ Doç.Dr. Cüeyt BAYILMIŞ Syısl Alz SAYISAL ANALİZ İNTERPOLASYON Ar Değer Bulm Doç.Dr. Cüeyt BAYILMIŞ Syısl Alz İÇİNDEKİLER Ar Değer Hesbı İterpolsyo Doğrusl Ar Değer
İşaret ve Sistemler. Ders 10: Sistem Cevabı
 İşar v Sismlr Drs 0: Sism Cvabı Sismi İmpuls Cvabı Lir, zamala dğişmy bir sism v işarii uyguladığıı düşülim v işari lir, zamala dğişmy bir sism uyguladığıda çıkış işari bilimiyrsa, sismi lirlik özlliğii
İşar v Sismlr Drs 0: Sism Cvabı Sismi İmpuls Cvabı Lir, zamala dğişmy bir sism v işarii uyguladığıı düşülim v işari lir, zamala dğişmy bir sism uyguladığıda çıkış işari bilimiyrsa, sismi lirlik özlliğii
DEĞİŞİME AÇIK OLUN 1 stajbaslatmasinavi@gmail.com
 Tiri ml rklrii rlıklı vr yömi gör izly bir işlmd döm s iibriyl sk rklrii drm şğıdki gibidir DB Ml Mvd 2 000 Döm içi Ml Alışı 50 000 Alış İd 3 000 Tiri Ml Hs Al Tp 5 000 Tiri Ml Hs Brç Klı 52 000 Yriçi
Tiri ml rklrii rlıklı vr yömi gör izly bir işlmd döm s iibriyl sk rklrii drm şğıdki gibidir DB Ml Mvd 2 000 Döm içi Ml Alışı 50 000 Alış İd 3 000 Tiri Ml Hs Al Tp 5 000 Tiri Ml Hs Brç Klı 52 000 Yriçi
LYS Matemat k Deneme Sınavı
 LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
5. Ders. Dağılımlardan Rasgele Sayı Üretilmesi Ters Dönüşüm Yöntemi
 5. Drs Dağılımlarda Rasgl Sayı Ürtilmsi Trs Döüşüm Yötmi sürkli bir rasgl dğişk v bu rasgl dğişki dağılım foksiyou olsu. Dağılımı dstk kümsi üzrid dağılım foksiyou arta v bir-bir bir foksiyo olmaktadır.
5. Drs Dağılımlarda Rasgl Sayı Ürtilmsi Trs Döüşüm Yötmi sürkli bir rasgl dğişk v bu rasgl dğişki dağılım foksiyou olsu. Dağılımı dstk kümsi üzrid dağılım foksiyou arta v bir-bir bir foksiyo olmaktadır.
σ σ τ τ ; σ 4τ s σ FBr F em 1 10 N t d x A Makine Tasarımı I-Formüller 2017/2018 Mukavemet Varsayımları: Maksimum şekil değiştirme enerjisi varsayımı
 uavt Varayıları: aiu şil ğiştir rjii varayıı aiu aya rili varayıı: aiu ii ğiştir rjii varayıı: iyt atayıı Stati Zrlaaa ırıla allr İi:.,5 ai Taarıı I-rüllr 7/8,5,65 Sü allr İi:.,577,5,577 l ğiş Zrlaaa a
uavt Varayıları: aiu şil ğiştir rjii varayıı aiu aya rili varayıı: aiu ii ğiştir rjii varayıı: iyt atayıı Stati Zrlaaa ırıla allr İi:.,5 ai Taarıı I-rüllr 7/8,5,65 Sü allr İi:.,577,5,577 l ğiş Zrlaaa a
Ele Alınacak Ana Konular. Hafta 5: Periyodik İşaretlerin Fourier Serisi Gösterilimi. LTI Sistemlerin Karmaşık Üstel İşaretlere Yanıtı
 ..5 El Alınc An Konulr LI sismlrin rmşı üsl işrlr ynıı Sürli-zmn priyodi işrlrin Fourir srisi gösrilimi Hf 5: Priyodi İşrlrin Fourir Srisi Gösrilimi Fourir srisinin yınslığı Sürli-zmn Fourir srisinin özllilri
..5 El Alınc An Konulr LI sismlrin rmşı üsl işrlr ynıı Sürli-zmn priyodi işrlrin Fourir srisi gösrilimi Hf 5: Priyodi İşrlrin Fourir Srisi Gösrilimi Fourir srisinin yınslığı Sürli-zmn Fourir srisinin özllilri
BÖLÜM 7. Sürekli hal hatalarının değerlendirilmesinde kullanılan test dalga şekilleri: Dalga Şekli Giriş Fiziksel karşılığı. Sabit Konum.
 9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
DRC ile tam bölünebilmesi için bir tane 2 yi ayırıyoruz. 3 ile ) x 2 2x < (
 nm - / YT / MT MTMTİK NMSİ. il tam bölünbilmsi için bir tan i aırıoruz. il bölünmmsi için bütün lri atıoruz... 7 saısının pozitif tam böln saısı ( + ). ( + ). ( + ) bulunur. vap. 0 + + 0 + ) < ( 0 + +
nm - / YT / MT MTMTİK NMSİ. il tam bölünbilmsi için bir tan i aırıoruz. il bölünmmsi için bütün lri atıoruz... 7 saısının pozitif tam böln saısı ( + ). ( + ). ( + ) bulunur. vap. 0 + + 0 + ) < ( 0 + +
ÜSLÜ İFADELER VE ÜSTEL FONKSİYONLAR LOGARİTMA FONKSİYONU, ÜSTEL, LOGARİTMİK DENKLEM VE EŞİTSİZLİKLER
 BÖÜ ÜÜ İFD V Ü FOİO Üslü İfdlrd İşlmlr...7 Üslü Dnklmlr... Üstl Fonksiyon...7 ygulm stlri...5 BÖÜ OGİ FOİO, Ü, OGİİ D V ŞİİZİ ogritm Fonksiyonu...7 ogritm Fonksiyonunun Özlliklri...9 bn Dğiştirm...55 Üstl
BÖÜ ÜÜ İFD V Ü FOİO Üslü İfdlrd İşlmlr...7 Üslü Dnklmlr... Üstl Fonksiyon...7 ygulm stlri...5 BÖÜ OGİ FOİO, Ü, OGİİ D V ŞİİZİ ogritm Fonksiyonu...7 ogritm Fonksiyonunun Özlliklri...9 bn Dğiştirm...55 Üstl
Ş
 Ü Ş Ç ç Ö ş Ş Ü ç Ç Ğ Ş ş ç Ü ç ş ş Ç ş ş Ş ç Ç ç Ö Ğ ş Ü Ü ç ş ç ş Ğ Ş Ö ç Ö Ü Ü Ğ ç Ğ Ş şş Ğ ş ç ç ş ş ş Ö ş Ş ş Ü Ü ÜÜ Ö ş ÜŞ ş ç ş Ö Ğ Ğ ç ş Ü Ş Ğ ş ş ş ş ş Ğ ş ş ç ş ş Ü ş Ğ ş «ş Ü ş ş ş ş ş ş ç ç
Ü Ş Ç ç Ö ş Ş Ü ç Ç Ğ Ş ş ç Ü ç ş ş Ç ş ş Ş ç Ç ç Ö Ğ ş Ü Ü ç ş ç ş Ğ Ş Ö ç Ö Ü Ü Ğ ç Ğ Ş şş Ğ ş ç ç ş ş ş Ö ş Ş ş Ü Ü ÜÜ Ö ş ÜŞ ş ç ş Ö Ğ Ğ ç ş Ü Ş Ğ ş ş ş ş ş Ğ ş ş ç ş ş Ü ş Ğ ş «ş Ü ş ş ş ş ş ş ç ç
 İ İ ö ö ğ ğ ö İ İ ğç İ İç ğç İ ö İ ğ ö ğ ö İ Ş ğç İ ğ ğ Ö Ç ğ İ ö ö ö ö Ö ç ç ğ ğ ç ç ö Ç ğ ğ ö Ç Ç ç ö ğ ç ö ç ç ğ Ö ç ç ğ ç ç ğ ğ ö ç ğ Ş ç ç ğ Ş ç ğ ö ç ö Ş ğ ğ ğ ğ ğ Ş Ş Ö ç ç Ç ç İ İİ ğ ö ç İ ö ö
İ İ ö ö ğ ğ ö İ İ ğç İ İç ğç İ ö İ ğ ö ğ ö İ Ş ğç İ ğ ğ Ö Ç ğ İ ö ö ö ö Ö ç ç ğ ğ ç ç ö Ç ğ ğ ö Ç Ç ç ö ğ ç ö ç ç ğ Ö ç ç ğ ç ç ğ ğ ö ç ğ Ş ç ç ğ Ş ç ğ ö ç ö Ş ğ ğ ğ ğ ğ Ş Ş Ö ç ç Ç ç İ İİ ğ ö ç İ ö ö
 Ş ğ Ğ ç Ç ğ ç Ç ğ ğ ç ğ ö ö ö ö ğ ö Ş ç Ş ç ç ç ç ö öç ö ö ğ ö ö ç ç ğ ğ ö ç ö ğ Ç Ş ç Ç Ş Ş Ç Ş ç ç ç ç öç Ö Ş ç Ğ ç ç ö ö ç ç Ş ç ö ö ç ğ ç Şğ ç Ş Ş ç Ü ç Ş Ş ğ ç ç ö ç ç ö Ö öç ö Ç Ö Ö öç Ö ğ Ö ç öç
Ş ğ Ğ ç Ç ğ ç Ç ğ ğ ç ğ ö ö ö ö ğ ö Ş ç Ş ç ç ç ç ö öç ö ö ğ ö ö ç ç ğ ğ ö ç ö ğ Ç Ş ç Ç Ş Ş Ç Ş ç ç ç ç öç Ö Ş ç Ğ ç ç ö ö ç ç Ş ç ö ö ç ğ ç Şğ ç Ş Ş ç Ü ç Ş Ş ğ ç ç ö ç ç ö Ö öç ö Ç Ö Ö öç Ö ğ Ö ç öç
Cevap: B. x + y = 5 ve y + z = x = 3z y. x + y = 5 z + y = 3 x t = 2 bulunur. 7x 9y = y 3x 10x = 8y. 3/ 3y = x + z 15k = 4k + z + Cevap: B
 6 LYS/MAT MATEMATİK ÇÖZÜMLERİ DENEME. ( ab) ( ab) 6( ab) 6. 6 y z ( ab) ( ab) 6( ab) 6 6 6y y z 6y ( ab) 6 6( y) ( y z) ab.. olur. y v y z. 7 z y / y z k k z y z y t bulunur. 7 9y y 8y k, y k zk A) y 8,
6 LYS/MAT MATEMATİK ÇÖZÜMLERİ DENEME. ( ab) ( ab) 6( ab) 6. 6 y z ( ab) ( ab) 6( ab) 6 6 6y y z 6y ( ab) 6 6( y) ( y z) ab.. olur. y v y z. 7 z y / y z k k z y z y t bulunur. 7 9y y 8y k, y k zk A) y 8,
SMMM STAJ BAŞLATMA FİNANSAL MUHASEBE/TİCARİ ALACAKLAR. f u a t h o c a. n e t. DEĞİŞİME AÇIK OLUN 1 stajbaslatmasinavi@gmail.com
 DEĞİŞİME AÇIK OLUN 1 sjbslmsivi@gmilm DEĞİŞİME AÇIK OLUN 2 sjbslmsivi@gmilm DEĞİŞİME AÇIK OLUN 3 sjbslmsivi@gmilm 1 Bir işlmi bzı bilgilri şğıdki gibidir: (Bi TL) Öki Döm Cri Döm Alıılr 940 610 Alk Slri
DEĞİŞİME AÇIK OLUN 1 sjbslmsivi@gmilm DEĞİŞİME AÇIK OLUN 2 sjbslmsivi@gmilm DEĞİŞİME AÇIK OLUN 3 sjbslmsivi@gmilm 1 Bir işlmi bzı bilgilri şğıdki gibidir: (Bi TL) Öki Döm Cri Döm Alıılr 940 610 Alk Slri
 «ç Ü Ü Ü ü ç ü ü Ö Ü ü ü ü ü ü ü ö ü«ç ü ü ü ç ü ü ü» ü ü ü ü ç ü ü ü ü ü ü ü ü ü ü ü ü ü ç ü üü ü ü ü ü ü ü ü ü ü ç ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü üü ü ü ü ü ç ü üü ü ü ü ü ü ü Ü
«ç Ü Ü Ü ü ç ü ü Ö Ü ü ü ü ü ü ü ö ü«ç ü ü ü ç ü ü ü» ü ü ü ü ç ü ü ü ü ü ü ü ü ü ü ü ü ü ç ü üü ü ü ü ü ü ü ü ü ü ç ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü üü ü ü ü ü ç ü üü ü ü ü ü ü ü Ü
 ü İİ İ Ü ü ü ö ü ü İ Ö ü ö ö ü ö ö ü ü ü ü ö ö üü ü üü ü ö ö ü ö Ü ü ü İ ö Ö ü ü ü ü İ İ ö ü Ö ü ü ü ü ö ö Ş ö ü ü ü ö ü Ç ö ü ü ü ü ü ü ü ü ü ü ö ö ü ü ö ü ü ü Ü ü ü Ş ü ü ü ü üü ü ö ü İ ö ö üü ü ü Ç
ü İİ İ Ü ü ü ö ü ü İ Ö ü ö ö ü ö ö ü ü ü ü ö ö üü ü üü ü ö ö ü ö Ü ü ü İ ö Ö ü ü ü ü İ İ ö ü Ö ü ü ü ü ö ö Ş ö ü ü ü ö ü Ç ö ü ü ü ü ü ü ü ü ü ü ö ö ü ü ö ü ü ü Ü ü ü Ş ü ü ü ü üü ü ö ü İ ö ö üü ü ü Ç
 İ ü ü ü ü İ ü üü üü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü üü ü ü Ş Ş ü üü İ ü üü Ö ü ü ü ü üü üü ü ü ü ü ü ü ü üü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü Ö ü ü ü ü ü ü Ş ü ü ü ü ü ü ü ü ü ü İ üü ü ü Ç Ç ü ü ü ü ü ü
İ ü ü ü ü İ ü üü üü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü üü ü ü Ş Ş ü üü İ ü üü Ö ü ü ü ü üü üü ü ü ü ü ü ü ü üü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü ü Ö ü ü ü ü ü ü Ş ü ü ü ü ü ü ü ü ü ü İ üü ü ü Ç Ç ü ü ü ü ü ü
 ü ü ü ü ç ü ü ü üü ç ü ü ü ü ü ü ü ü ü ü ç ü ü ü ç ü ü ü ü ü ü ü ü ü ü ç ü ç ç ç ü ç ü ü üü ü ü ü üü ç ü ç ç ü ü ç ü ü ü ç ü ü üü üü ü ü ü üü ç ü ü ü ü üü ü ü üü ü ü üü ü ü ü ü üü ç ü ü ü üü ç ü ü ü ü
ü ü ü ü ç ü ü ü üü ç ü ü ü ü ü ü ü ü ü ü ç ü ü ü ç ü ü ü ü ü ü ü ü ü ü ç ü ç ç ç ü ç ü ü üü ü ü ü üü ç ü ç ç ü ü ç ü ü ü ç ü ü üü üü ü ü ü üü ç ü ü ü ü üü ü ü üü ü ü üü ü ü ü ü üü ç ü ü ü üü ç ü ü ü ü
 Ö ö Ü Ü ÜÜ ö Ö ö ö Ş « ö Ö ö Ö Ö ö ö Ç Ö Ö Ş Ö Ö Ş Ş Ö Ç Ş Ş Ş ö Ö ö Ç ö ö Ö Ö ö ö Ö Ç ö ö Ö Ö Ö» ö ö ö ö Ö ö ö ö ö ö ö ö ö ö ö ö Ö ö Ö Ö Ö Ö Ö Ö ö Ş Ş ö Ş Ş ö ö ö ö Ş Ö Ö ö Ş ö Ş ö ö Ş Ş ö ö ö ö Ö Ş Ö
Ö ö Ü Ü ÜÜ ö Ö ö ö Ş « ö Ö ö Ö Ö ö ö Ç Ö Ö Ş Ö Ö Ş Ş Ö Ç Ş Ş Ş ö Ö ö Ç ö ö Ö Ö ö ö Ö Ç ö ö Ö Ö Ö» ö ö ö ö Ö ö ö ö ö ö ö ö ö ö ö ö Ö ö Ö Ö Ö Ö Ö Ö ö Ş Ş ö Ş Ş ö ö ö ö Ş Ö Ö ö Ş ö Ş ö ö Ş Ş ö ö ö ö Ö Ş Ö
 ö ü ş ç» ş ü ü ü ü ç» Ö Ö Ç ş Ö Ü ş ü ü ü ü ü ü ş ü ü ü ü ü üü ö ç ş ö ü ş ç ş ü ü ü ü ç» ü ü ş Ö Ö Ç ü ü ü Ö ü ü ü ü ö ü ö ü ü ü Ü ü ü ü ü ü ü ü ü ü ü ü ü ç ü ü üü ö ç ş Ö Ü ç ü ç ö ö Ç ü ü ü ü ü ö ü
ö ü ş ç» ş ü ü ü ü ç» Ö Ö Ç ş Ö Ü ş ü ü ü ü ü ü ş ü ü ü ü ü üü ö ç ş ö ü ş ç ş ü ü ü ü ç» ü ü ş Ö Ö Ç ü ü ü Ö ü ü ü ü ö ü ö ü ü ü Ü ü ü ü ü ü ü ü ü ü ü ü ü ç ü ü üü ö ç ş Ö Ü ç ü ç ö ö Ç ü ü ü ü ü ö ü
 Ğ Ü Ğ Ğ Ğ Ö Ğ ş ş ö ö ş Ç ş ş Ğ Ğ Ş Ğ ş ş ö ş ş ö ş ş ö ş Ğ Ö ö ö ö Ç ş ö ö ş ş ö ş ö ö ş ö ş ö ö ö ş ş ö ş ö ö ö ş ö ö Ö ş ş ş ş ş ş Ç Ğ Ğ ö ş ş ş ö ö ş ö ö ş Ç ö ş ö ş ö ş ş ş ö ö ş ş ö ş ş ö ş ş ö ş
Ğ Ü Ğ Ğ Ğ Ö Ğ ş ş ö ö ş Ç ş ş Ğ Ğ Ş Ğ ş ş ö ş ş ö ş ş ö ş Ğ Ö ö ö ö Ç ş ö ö ş ş ö ş ö ö ş ö ş ö ö ö ş ş ö ş ö ö ö ş ö ö Ö ş ş ş ş ş ş Ç Ğ Ğ ö ş ş ş ö ö ş ö ö ş Ç ö ş ö ş ö ş ş ş ö ö ş ş ö ş ş ö ş ş ö ş
 Ğ Ğ ü «Ü Ğ Ö Ğ ü Ü ü Ğ ü ü ü Ç Ş ü Ğ Ğ Ü Ğ Ü Ö ü Ç Ü ü ü Ü ü ü ü ü ü ü Ü ü ü ü Ü ü ü ü ü ü ü Ü ü ü ü ü ü ü ü Ö ü ü ü ü ü üü ü ü üü ü Ü ü» ü ü Ü ü üü ü üü ü ü ü ü ü ü ü ü ü ü ü ü ü üü ü üü ü ü Ü «ü ü ü
Ğ Ğ ü «Ü Ğ Ö Ğ ü Ü ü Ğ ü ü ü Ç Ş ü Ğ Ğ Ü Ğ Ü Ö ü Ç Ü ü ü Ü ü ü ü ü ü ü Ü ü ü ü Ü ü ü ü ü ü ü Ü ü ü ü ü ü ü ü Ö ü ü ü ü ü üü ü ü üü ü Ü ü» ü ü Ü ü üü ü üü ü ü ü ü ü ü ü ü ü ü ü ü ü üü ü üü ü ü Ü «ü ü ü
 ş ş» Ğ Ş ş Ş ş Ş Ş Ş ş ş Ş Ç ş ş Ş ş ş ş ş ş ş ş ş ş ş ş ş ş Ş ş Ş ş ş ş Ş ş ş ş ş ş ş ş ş ş Ş ş Ş ş ş ş ş ş ş ş ş Ş ş ş ş ş Ş ş ş ş ş ş Ş ş ş ş Ü Ü ş ş ş ş Ş ş ş Ş ş Ü Ş ş Ş ş ş Ş ş Ş ş ş Ş Ş ş ş ş ş
ş ş» Ğ Ş ş Ş ş Ş Ş Ş ş ş Ş Ç ş ş Ş ş ş ş ş ş ş ş ş ş ş ş ş ş Ş ş Ş ş ş ş Ş ş ş ş ş ş ş ş ş ş Ş ş Ş ş ş ş ş ş ş ş ş Ş ş ş ş ş Ş ş ş ş ş ş Ş ş ş ş Ü Ü ş ş ş ş Ş ş ş Ş ş Ü Ş ş Ş ş ş Ş ş Ş ş ş Ş Ş ş ş ş ş
ÜÜ Ü ö ö ö Ö ö ö ö ö ö Ş Ş Ç ö Ş Ş ö
 Ş ö Ü ö ö ö ö Ç ö Ç Ö Ö ö ö ÜÜ Ü ö ö ö Ö ö ö ö ö ö Ş Ş Ç ö Ş Ş ö ö ö ö ö Ç ö ö ö ö ö ö ö ö ö ö ö Ş ö Ş Ç Ö ö ö Ş ö ö ö ö ö ö ö ö ö ö ö Ç Ç ö ö Ç ö Ö Ç ö ö Ç ö ö ö ö Ü ö ö Ü ö Ş ö Ü ö ö Ş ö ö Ş Ü ö Ş ö
Ş ö Ü ö ö ö ö Ç ö Ç Ö Ö ö ö ÜÜ Ü ö ö ö Ö ö ö ö ö ö Ş Ş Ç ö Ş Ş ö ö ö ö ö Ç ö ö ö ö ö ö ö ö ö ö ö Ş ö Ş Ç Ö ö ö Ş ö ö ö ö ö ö ö ö ö ö ö Ç Ç ö ö Ç ö Ö Ç ö ö Ç ö ö ö ö Ü ö ö Ü ö Ş ö Ü ö ö Ş ö ö Ş Ü ö Ş ö
 İ ş Ğ İ ş ü ü üü İş ü ü üü ş İ ş Ğ İ ş ş ş ş ş ş ş ü ş ş İ ş ü ü İ ü Ç ş ş ş İ ş ü Ş Ş ş ş ö ş ü ö ş ş ş ş ö ü ö ş ş ş ş ü ö ü ö ş ü ö ü ş ö ş ü ü ş ö İ ü ş ü ş Ş ş ö ş ş ö ü ö ö ö ş İ Ç İ İŞİ ş ö ş ş
İ ş Ğ İ ş ü ü üü İş ü ü üü ş İ ş Ğ İ ş ş ş ş ş ş ş ü ş ş İ ş ü ü İ ü Ç ş ş ş İ ş ü Ş Ş ş ş ö ş ü ö ş ş ş ş ö ü ö ş ş ş ş ü ö ü ö ş ü ö ü ş ö ş ü ü ş ö İ ü ş ü ş Ş ş ö ş ş ö ü ö ö ö ş İ Ç İ İŞİ ş ö ş ş
 Ğ Ü Ş Ş Ü Ş Ş Ü Ü Ş Ş Ç Ş Ş Ğ Ü Ö Ö Ş Ü Ç Ş Ü Ş Ş Ş Ö Ş Ü Ş Ö Ü Ş Ç « Ö Ö Ş « Ü Ü Ü Ü Ü «Ü Ş Ü «Ö Ö Ç Ö Ö Ö Ö Ö Ş Ü Ç Ş Ç Ş Ö Ö Ü Ğ ÜŞ «Ü Ç Ç Ç Ç Ö Ö Ğ Ö Ö Ö Ö » Ü Ü Ü Ü Ş Ğ Ü Ç Ö « Ç Ö Ü Ş Ö Ş
Ğ Ü Ş Ş Ü Ş Ş Ü Ü Ş Ş Ç Ş Ş Ğ Ü Ö Ö Ş Ü Ç Ş Ü Ş Ş Ş Ö Ş Ü Ş Ö Ü Ş Ç « Ö Ö Ş « Ü Ü Ü Ü Ü «Ü Ş Ü «Ö Ö Ç Ö Ö Ö Ö Ö Ş Ü Ç Ş Ç Ş Ö Ö Ü Ğ ÜŞ «Ü Ç Ç Ç Ç Ö Ö Ğ Ö Ö Ö Ö » Ü Ü Ü Ü Ş Ğ Ü Ç Ö « Ç Ö Ü Ş Ö Ş
ü ü ü ü ü ü ü Ş ü ü ü ü ü üü ü ü
 ü ü İ ü Ç İ İ ü İ İİ İ İ ü ü ü ü ü ü ü Ş ü ü ü ü ü üü ü ü İ İ üü ü ü ü üü ü ü ü ü ü ü ü ü ü ü üü ü ü ü ü ü ü ü İ Ç ü ü ü ü ü ü ü ü ü ü ü ü ü İ ü ü ü ü ü ü ü ü Ç üü ü ü ü Ö ü ü ü ü ü ü ü ü ü ü ü ü ü Ç ü
ü ü İ ü Ç İ İ ü İ İİ İ İ ü ü ü ü ü ü ü Ş ü ü ü ü ü üü ü ü İ İ üü ü ü ü üü ü ü ü ü ü ü ü ü ü ü üü ü ü ü ü ü ü ü İ Ç ü ü ü ü ü ü ü ü ü ü ü ü ü İ ü ü ü ü ü ü ü ü Ç üü ü ü ü Ö ü ü ü ü ü ü ü ü ü ü ü ü ü Ç ü
ü ü üü İ Ç İİ ü ü üü İ Ç Ü ö üü ü Ç Ü ü ü İ ü İ ö ü üü ü ö ü ö üü ü ü ö ö Ç Ş ü İŞ ö ü ü İ İ İ İ Ç İ Ç ü ü ü ü ö ü ü ü ö Ü ü ü İ Ö Ö ü ü üü ö ü ü üü Ö
 ü ü ü üü İ Ç İ ü ü üü İ ü ü üü ü ü ü üü ü Ç ö ü ö İ İ ü ü ü İ İ İ ü ü ü üü İ Ç İİ ü ü üü İ Ç Ü ö üü ü Ç Ü ü ü İ ü İ ö ü üü ü ö ü ö üü ü ü ö ö Ç Ş ü İŞ ö ü ü İ İ İ İ Ç İ Ç ü ü ü ü ö ü ü ü ö Ü ü ü İ Ö Ö
ü ü ü üü İ Ç İ ü ü üü İ ü ü üü ü ü ü üü ü Ç ö ü ö İ İ ü ü ü İ İ İ ü ü ü üü İ Ç İİ ü ü üü İ Ç Ü ö üü ü Ç Ü ü ü İ ü İ ö ü üü ü ö ü ö üü ü ü ö ö Ç Ş ü İŞ ö ü ü İ İ İ İ Ç İ Ç ü ü ü ü ö ü ü ü ö Ü ü ü İ Ö Ö
DERS 9. Grafik Çizimi, Maksimum Minimum Problemleri
 DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
BÖLÜM 2- HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA
 Dpartmnt o Mchanical Enginring MAK 0 MÜHENDİSLİKTE SAYISAL YÖNTEMLER BÖLÜM - HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA Doç. Dr. Ali Rıza YILDIZ Arş. Gör. Emr DEMİRCİ 7.0.0 7.0.0 MAK
Dpartmnt o Mchanical Enginring MAK 0 MÜHENDİSLİKTE SAYISAL YÖNTEMLER BÖLÜM - HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA Doç. Dr. Ali Rıza YILDIZ Arş. Gör. Emr DEMİRCİ 7.0.0 7.0.0 MAK
o f S C I n t e r n a t i o n a l P o d d e Eski Büyükdere Asfaltı No: 13 Güney Plaza Kat: 5 Maslak-İstanbul / TÜRKİYE
 T ULULRR DENETĠ VE....ġ. K Th: 02.03.2012 y: 2012/25 Ku: İ R K Ü L E R R O R İhc Zuu v K K Rk E p cy D Dş Tc y Tğ (Tğ N: 2011/18) Dğşkk p D Tğ y Ö: İhc Zuu v K K Rk E p cy D Dş Tc y Tğ (Tğ N: 2011/18)
T ULULRR DENETĠ VE....ġ. K Th: 02.03.2012 y: 2012/25 Ku: İ R K Ü L E R R O R İhc Zuu v K K Rk E p cy D Dş Tc y Tğ (Tğ N: 2011/18) Dğşkk p D Tğ y Ö: İhc Zuu v K K Rk E p cy D Dş Tc y Tğ (Tğ N: 2011/18)
x ise x kaçtır?{ C : }
 İZMİR FEN LİSESİ LOGARİTMA ÇALIŞMA SORULARI LOGARİTMA FONKSİYONU. ( ) ( ) f m m m R C : fonksionunun m { ( 0,) } dim tnımlı olmsı için?.. f ( ) ( ) fonksionunun tnım kümsind kç tn tm sı vrdır?{ C : }.
İZMİR FEN LİSESİ LOGARİTMA ÇALIŞMA SORULARI LOGARİTMA FONKSİYONU. ( ) ( ) f m m m R C : fonksionunun m { ( 0,) } dim tnımlı olmsı için?.. f ( ) ( ) fonksionunun tnım kümsind kç tn tm sı vrdır?{ C : }.
B T A n a l o g T r a n s m i t t e r. T e k n i k K ı l a v u z u. R e v 1. 2
 B T - 111 A n a l o g T r a n s m i t t e r T e k n i k K ı l a v u z u R e v 1. 2 1. Ö N G Ö R Ü N Ü M, Ü S T Ü N L Ü K L E R İ VE Ö Z E L L İ K L E R İ M i k r o k o n t r o l ö r t a b a n l ı BT- 111
B T - 111 A n a l o g T r a n s m i t t e r T e k n i k K ı l a v u z u R e v 1. 2 1. Ö N G Ö R Ü N Ü M, Ü S T Ü N L Ü K L E R İ VE Ö Z E L L İ K L E R İ M i k r o k o n t r o l ö r t a b a n l ı BT- 111
OLASILIK ve ÝSTATÝSTÝK ( Genel Tekrar Testi-1) KPSS MATEMATÝK. Bir anahtarlıktaki 5 anahtardan 2 si kapıyı açmak - tadır.
 OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
SÖNÜMLÜ SERBEST TİTREŞİMLER
 C SAKARYA ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MAKİNA EORİSİ, SİSEM DİNAMİĞİ VE KONROL ANA BİLİM DALI LABORAUARI SÖNÜMLÜ SERBES İREŞİMLER DENEY FÖYÜ Yr Doç Dr Hüsyi DAL 8 SÖNÜMLÜ
C SAKARYA ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MAKİNA EORİSİ, SİSEM DİNAMİĞİ VE KONROL ANA BİLİM DALI LABORAUARI SÖNÜMLÜ SERBES İREŞİMLER DENEY FÖYÜ Yr Doç Dr Hüsyi DAL 8 SÖNÜMLÜ
IDDM YARDIMIYLA TERS MATRİS HESAPLAMA. Kadınhanı, KONYA, e-posta: aocdiken@selcuk.edu.tr
 SDÜ FEN EDEBİT FKÜLTESİ FEN DERGİSİ E-DERGİ. 8,, 98- DDM RDML TERS MTRİS HESPLM O ÇBKDİKEN *, Ke DN ** * Seçu Üverte, Kdıhı MO, Bgyr Teooer ve Prog, Kdıhı, KON, e-pot: ocde@ecu.edu.tr ** Seçu Üverte, dd
SDÜ FEN EDEBİT FKÜLTESİ FEN DERGİSİ E-DERGİ. 8,, 98- DDM RDML TERS MTRİS HESPLM O ÇBKDİKEN *, Ke DN ** * Seçu Üverte, Kdıhı MO, Bgyr Teooer ve Prog, Kdıhı, KON, e-pot: ocde@ecu.edu.tr ** Seçu Üverte, dd
π βk F -F 0.4 0.3 0.2 0.1 0 0.01 0.02 0.03 0.04 kayma 1 2 F + F 1 2 Döndüren kasnak Döndürülen kasnak
 TİMAK-Taarım İmalat Analiz Kongri 6-8 Nian 006 - BALIKESİ KAYIŞ KASNAK MEKANİZMALAINDA KAYMA OLAYINI ETKİLEYEN AKTÖLEİN ANALİZİ M. Ndim GEGE Maina Mühndiliği Bölümü Mühndili aülti -Balıir/Türi Özt Kaış
TİMAK-Taarım İmalat Analiz Kongri 6-8 Nian 006 - BALIKESİ KAYIŞ KASNAK MEKANİZMALAINDA KAYMA OLAYINI ETKİLEYEN AKTÖLEİN ANALİZİ M. Ndim GEGE Maina Mühndiliği Bölümü Mühndili aülti -Balıir/Türi Özt Kaış
KAREKÖKLÜ SAYILAR TARAMA TESTİ-1
 EÖLÜ SYIL TM TESTİ- 8..3.. -8..3.2.-T kre doğl syılr ve doğl syılrl rsıdki ilişki. 8..3.3. T kre oly syılrı krekök değerlerii hgi iki doğl syı rsıd olduğuu belirler. 8..3.4. Gerçek Syılr. ) şğıdkilerde
EÖLÜ SYIL TM TESTİ- 8..3.. -8..3.2.-T kre doğl syılr ve doğl syılrl rsıdki ilişki. 8..3.3. T kre oly syılrı krekök değerlerii hgi iki doğl syı rsıd olduğuu belirler. 8..3.4. Gerçek Syılr. ) şğıdkilerde
2017 Yazokulu BLNT6NBS Dersnotu
 İşreler ve Sisemler www.bulelibs.com.r 7 - SAÜ Y Oulu Ders Nolrı/ Bilgisyr Mühedisliği 6 Seçi ARI ri@sry.edu.r 7 Youlu BLNT6NBS Dersou hp://www.bulelibs.com.r/isreler_ve_sisemler_6nbas_dersnou.pdf 7 Youlu
İşreler ve Sisemler www.bulelibs.com.r 7 - SAÜ Y Oulu Ders Nolrı/ Bilgisyr Mühedisliği 6 Seçi ARI ri@sry.edu.r 7 Youlu BLNT6NBS Dersou hp://www.bulelibs.com.r/isreler_ve_sisemler_6nbas_dersnou.pdf 7 Youlu
r u o s l t i t i n g a i d i CAPITAL 6 / 2013
 072_073_074_075_076_CP_06 5/28/13 7:02 PM Pg 3 Ö Z EL A R A ŞT I RM A TÜRKİYE NİN GÖNLÜ ZENGİN İŞ İNSANLARI p. Tü b ğ ş u z u ö m m u t pt H v ş u h t c m. V hb K ç İ z z t t g u u m u t p ğ H g b m T
072_073_074_075_076_CP_06 5/28/13 7:02 PM Pg 3 Ö Z EL A R A ŞT I RM A TÜRKİYE NİN GÖNLÜ ZENGİN İŞ İNSANLARI p. Tü b ğ ş u z u ö m m u t pt H v ş u h t c m. V hb K ç İ z z t t g u u m u t p ğ H g b m T
Sonlu kanat Teorisi Açıklık oranıküçük kanatlar etrafındaki akımın fiziksel yapısı
 Sou kt Teor çıkık orıküçük ktr etrfıdk kımı fke pıı çıkık orı küçük (R < -5 ktr çıkık orı büük (R > -5 ktr UCK5 erodmk der otrı UCK5 erodmk der otrı çıkık orıküçük ktr etrfıdk kımı fke pıı çıkık orıükek
Sou kt Teor çıkık orıküçük ktr etrfıdk kımı fke pıı çıkık orı küçük (R < -5 ktr çıkık orı büük (R > -5 ktr UCK5 erodmk der otrı UCK5 erodmk der otrı çıkık orıküçük ktr etrfıdk kımı fke pıı çıkık orıükek
Otomatik Kontrol. Fiziksel Sistemlerin Modellenmesi. Prof.Dr.Galip Cansever. Dişli Takımları Elektromekaniksel Sistemler. Ders #5
 Dr #5 Ooik onrol Fizikl Silrin Modllni Dişli Tkılrı Elkroknikl Silr Prof.Dr.Glip Cnvr 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr Mknikl Silrin Trnfr Fonkiyonlrı Dişli Tkılrı Vili biikllri düşünli. Yokuş
Dr #5 Ooik onrol Fizikl Silrin Modllni Dişli Tkılrı Elkroknikl Silr Prof.Dr.Glip Cnvr 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr Mknikl Silrin Trnfr Fonkiyonlrı Dişli Tkılrı Vili biikllri düşünli. Yokuş
Volon. Marka: B131. Model. Yükselen Milli Sürgülü Vana, Model F907, 17.2Bar(250psi) 10" 12" 14" 16" Volon 135Q. Marka: Model:
 AT LT L No: AAAT T h : P No: m T: ÇB BP) O G A Ö V od B 3 odu Gö d B 3PN U PD Kpm Km p b o u ou u mb Cmx m d) AwwwC d d u u d AwwC u m o p m po p p öh b m ö d m d m dd p ö ½"4" d ½" "8" d ¾" "" d " CTUWWRA
AT LT L No: AAAT T h : P No: m T: ÇB BP) O G A Ö V od B 3 odu Gö d B 3PN U PD Kpm Km p b o u ou u mb Cmx m d) AwwwC d d u u d AwwC u m o p m po p p öh b m ö d m d m dd p ö ½"4" d ½" "8" d ¾" "" d " CTUWWRA
Diferansiyel Denklemler
 Difrsil Dklmlr Doç. Dr. Slhi MADEN Ord Üivrsisi F dbi Fkülsi Mmik Bölümü DĐFERANSĐYEL DENKLEMLER Birii Mrbd Birii Drd Difrsil Dklmlr Birii Mrbd Yüksk Drd Difrsil Dklmlr Yüksk Mrbd Bzı Özl Difrsil Dklmlr
Difrsil Dklmlr Doç. Dr. Slhi MADEN Ord Üivrsisi F dbi Fkülsi Mmik Bölümü DĐFERANSĐYEL DENKLEMLER Birii Mrbd Birii Drd Difrsil Dklmlr Birii Mrbd Yüksk Drd Difrsil Dklmlr Yüksk Mrbd Bzı Özl Difrsil Dklmlr
ABSRACT Master Thesis. KÖTHE-TEOPLITZ DUALS OF DIFFRENCE SEQUENCE SPACES l ( p) Osman DUYAR
 ABSRACT Mter Thei KÖTHE-TEOPLITZ DUALS OF DIFFRECE SEQUECE SPACES, c d c O DUYAR Gzioş Uiverity Grdute Schoo of tur Ad Aied Sciece Dertet Of Mthetic Suervior: Ait. Prof. Dr. O ÖZDEMİR I the firt of chter
ABSRACT Mter Thei KÖTHE-TEOPLITZ DUALS OF DIFFRECE SEQUECE SPACES, c d c O DUYAR Gzioş Uiverity Grdute Schoo of tur Ad Aied Sciece Dertet Of Mthetic Suervior: Ait. Prof. Dr. O ÖZDEMİR I the firt of chter
Harekete geçin! daki a. Müşterileriniz. mısınız? markanızdan. müşteri adaylarınızla interaktif iletişim
 Hk gç! ö l k k z A. z l z? p B kl l b b l p g cvmşlz c l k z v? l l k fı Sl ı kç l?? l l hgl kp z k gc fkı l z? S b zlk ç Sl k kll lgl k l g ğl z ç vb. z? p v 4001 l Sçl 1 ııız? O IS, 1 O 900 kç ç l k
Hk gç! ö l k k z A. z l z? p B kl l b b l p g cvmşlz c l k z v? l l k fı Sl ı kç l?? l l hgl kp z k gc fkı l z? S b zlk ç Sl k kll lgl k l g ğl z ç vb. z? p v 4001 l Sçl 1 ııız? O IS, 1 O 900 kç ç l k
ORAN ORANTI 2 1 3 - - 4 4 2 1 1 2 ÖYS. = = yazılabilir. veya ALIŞTIRMALAR
 YILLAR 00 003 00 00 006 00 008 009 00 0 3 - - ÖYS ORAN ORANTI ve t. t. t.e zılilir. f Or: E z iri sıfır frklı ı iste iki çokluğu ölümüe or eir. Or irimsizir. Ortı : iki ve h fzl orı eşitliğie ortı eir.
YILLAR 00 003 00 00 006 00 008 009 00 0 3 - - ÖYS ORAN ORANTI ve t. t. t.e zılilir. f Or: E z iri sıfır frklı ı iste iki çokluğu ölümüe or eir. Or irimsizir. Ortı : iki ve h fzl orı eşitliğie ortı eir.
ÜSTEL DAĞILIM. üstel dağılımın parametresidir. Birikimli üstel dağılım fonksiyonu da, olarak bulunur. olduğu açık olarak görülmektedir.
 ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım









