KROMATOGRAFİYE GİRİŞ. Ref. e_makaleleri, Enstrümantal Analiz
|
|
|
- Canan Koçoğlu
- 9 yıl önce
- İzleme sayısı:
Transkript
1 1 KROMATOGRAFİYE GİRİŞ Ref. e_makaleleri, Enstrümantal Analiz Bir analitte bulunan engelleyici maddeler fiziksel veya kimyasal yöntemlerle ayrılabilir; bunlar çok bilinen distilasyon, kristalizasyon, çözgen ekstraksiyonu ve kimyasal veya elektrolitik çöktürmedir. Bilimin her dalına uygulanabilen bir ayırma yöntemi de " kromatografik " ayırmadır. Kromatografi, 20. yüzyılın başlarında Rus botanikcisi Mikhail Tswett tarafından bulundu. Tswett, Klorofil ve ksantofiller gibi çeşitli pigmentleri içeren bir çözeltiyi, toz halinde kalsiyum karbonatla doldurulmuş bir cam kolondan geçirerek birbirinden ayırmayı başardı. Ayrılan maddeler kolonda renkli bölgeler halinde gruplar oluşturdu; Bu nedenle ayırma yöntemine, renkli fotoğraf anlamına gelen kromatografi (chromatography ) adını verdi. Kromatografi uygulamaları ve yeni yöntemler geliştirilmesi son 50 yılda büyük aşamalar gösterdi. Bu alandaki çalışmaları ile A.J.P. Martin ve R.L.M. Synge 1952 yılında Nobel ödülünü kazandılar. Kromatografi, kompleks karışımlardaki çeşitli maddeleri birbirinden ayırmaya ve tanımlamaya olanak veren ve bilim adamlarının çalışmalarını kolaylaştıran bir seri ayırma yöntemleri tekniğidir. Tüm kromatografik uygulamalarda bir "sabit faz" ve bir "hareketli faz" bulunur. Bir karışımdaki maddeler hareketli faz ile sürüklenerek sabit faz üzerinden taşınır; Örnekteki maddelerin göç etme hızlarının farklı olması, her bir maddenin sabit faz üzerinde gruplaşarak ilerlemesine yol açar, böylece karışım içindeki maddeler birbirinden ayrılırlar.
2 2 Kromatografik Metotların Sınıflandırılması A. Ayırma Mekanizmasına Göre Sınıflandırma 1. Adsorbsiyon Kromatografi 2. Dağılma (Partition) Kromatografi 3. İyon-değiştirme kromatografi (veya iyon kromatografi) 4. Jel geçirgenlik veya Jel süzme (Moleküler-Exclusion veya Size-Exclusion) Kromatografi) 5. Zone Elektroforez 6. Afinite (veya Bioafinite) Kromatografi 7. Chiral Kromatografi B. Hareketrli Faza Göre Sınıflandırma 1. Sıvı Kromatografisi (LC) 2. Gaz Kromatografisi (GC) C. Uygulanan Tekniğe Göre Sınıflandırma 1. Kolon Kromatografi 2. Düzlem Kromatografi (İnce Tabaka Kromatografi, TLC; Kağıt Kromatografi, PC) D. Kullanım Amacına Göre Sınıflandırma 1. Analitik Kromatografi (Kalitatif Kromatografi; Kantitatif Kromatografi) 2. Preparatif Uygulamalar (Karışımlardan Saf madde Elde Etme)
3 3 Sabit Faz Tipleri Kromatografide, ayrılacak maddeler hareketli fazda çözünebilmeli ve sabit faz ile de bazı etkileşimlerde bulunabilmelidirler; Örneğin, sabit fazda çözünme, adsorblanma veya kimyasal reaksiyona girme gibi. Ayırma işlemi süresince maddeler iki faz arasında dağıtılırlar. Bazı uygulamalarda sabit faz, ince bir cam veya metal çubuk içine doldurulmuş toz halinde katı bir maddedir. Gaz veya sıvı haldeki hareketli faz basınç altında (veya kendi ağırlığı ile) katı içinden geçirilir. Bu yönteme " kolon kromatografisi" denir. Bir de "düzlemsel kromatografisi" vardır; bunda sabit faz poröz bir kağıt veya bir cam levha üzerine yayılmış ince toz halinde katı bir maddedir. Düzlem kromatografisinde hareketli faz kapiler etkisi veya kendi ağırlığı ile sabit faz üzerinde ilerler. Sabit faz, hareketli fazla karışmayan ve akıcı olmayan bir sıvı da olabilir. Bu durumda sabit sıvı fazı bir yerde tutabilmek için çeşitli yöntemler uygulanır. Örneğin, toz halindeki bir katının üzerine bir sabit faz sıvısından ince bir tabaka kaplanır ve kaplanmış katı madde bir cam veya metal tüpe doldurulur; hareketli faz bu tüpten geçirilir. Burada katı maddenin ayırma işleminde herhangi bir rolü yoktur, sadece faz sıvısını tutma (adsorblayarak) görevi yapar. Başka bir yöntemde sabit sıvı faz bir kapiler tüpün cidarlarına kaplanarak tutulur, gaz hareketli faz bu tüpten geçirilir. Bir diğer yöntemde ise sabit sıvı fazı tutmak için kağıt lifleri veya üzerinde çok ince öğütülmüş katı tanecikler bulunan bir cam levha kullanılır. Tablo-1'de, sabit ve hareketli fazların yapılarına göre uygulanan çeşitli kromatografik yöntemler verilmiştir. Bu kısımda dağılma (partisyon) ve gaz-sıvı kromatografisi anlatılacaktır. Gerekli değişiklikler yapılarak bu kavramlar diğer yöntemlere de uygulanabilir.
4 4 Tablo-1: Kromatografik Ayırmaların Sınıflandırılması Adı Hareketli faz tipi Sabit faz tipi Gaz-sıvı Gaz Sıvı Sabit fazı tutma yöntemi Bir tüp içindeki poröz katı üzerinde veya kapiler bir tüpün iç cidarı üzerinde adsorblanır Gaz-katı Gaz Katı Bir kolon (tüp) içinde tutulur Dağıtma Sıvı Sıvı Bir kolon (tüp) içindeki poröz bir katı üzerinde adsorblanır Adsorbsiyon Sıvı Katı Bir kolon (tüp) içinde tutulur Kağıt Sıvı Sıvı İnce tabaka Sıvı Sıvı-katı Jel Sıvı Sıvı İyon değiştirme Sıvı Katı Kalın bir kağıdın gözenekleri içinde tutulur Bir cam levhadaki ince toz halindeki katı üzerinde tutulur Polimerik bir katının lifleri arasında tutulur Bir kolondaki (tüp) iyon değiştirici reçine üzerinde tutulur Doğrusal Kromatografi Tüm kromatografik ayırmalar hareketli ve sabit fazlar arasında dağılan maddelerin değişik yayılma (hareket) özelliklerine dayanır. "Dağıtma katsayısı, K" denilen ve sıcaklığa bağımlı bir sabit ile kantitatif bir denklem verilebilir. C S K = (1) C M Burada C S maddenin sabit fazdaki analitik konsantrasyonu, C M ayni maddenin hareketli fazdaki konsantrasyonudur. İdeal halde, geniş bir madde konsantrasyonu aralığında dağılma kat sayısı sabittir; yani C S, C M ile doğru orantılıdır. Çok sık olmasa da C S ile C M arasında doğrusal olmayan bir ilişkiyle karşılaşılabilir. Şekil-1'de bazı tipik dağılma eğrileri verilmiştir. Şekilde görülen C eğrisi ideal bir hali gösterir. Bu eğri ayrışma (disosiyasyon) veya birleşme (asosiyasyon) reaksiyonları bulunmayan ve birbiriyle karışmayan iki sıvı arasındaki dağılma dengesine yaklaşır.
5 5 A B C D C S C M Şekil-1: Tipik dağılma eğrileri; C S, maddenin sabit fazdaki konsantrasyonu, C M, aynı maddenin hareketli fazdaki konsantrasyonu B ve D eğrileri böyle bir dengenin bulunduğu hale daha çok benzerlik gösterirler. Örneğin, eğer sabit faz su hareketli faz da benzen ise, zayıf bir organik asit içeren bir madde için B de görülen şekilde bir eğri elde edilir. Burada benzen içinde sadece disosiye olmayan asit çözünürken, sulu çözeltide bir miktar disosiye olmayan asit ile onun konjuge bazı da bulunur; asit ve konjuge baz asındaki oran konsantrasyona bağımlı değildir. Bu nedenle düşük konsantrasyonlarda, toplam asitin az bir miktarının iki solvent arasında dağılması yeterlidir ve dağılma katsayısı büyüktür. Diğer taraftan, eğer hareketli faz benzen değil de su ise D'deki gibi bir eğri elde edilir. Buharın hareketli fazı olduğu buhar-sıvı dengelerinde de eğriler B şeklindedir. A eğrisi tipik bir "adsorbsiyon izotermi" dir ve bir katı yüzey üzerinde adsorblanan madde miktarının, katının temasta olduğu çözeltideki madde konsantrasyonu ile olan ilişkisini gösterir. Madde konsantrasyonu arttıkça katı yüzeyde adsorbsiyon da artar ve bu durum yüzeyin adsorblama kapasitesi doluncaya kadar devam eder; sonra madde konsantrasyonundan bağımsız hale gelir. Bu tip eğriler k ve n sabit olmak üzere, C S = k C M n eşitliğiyle tanımlanır.
6 6 Fraksiyonlama proseslerinde uygulanabilir bir denklem elde edebilmek için yaklaşık bir K sabiti kullanılır. Şekil-1'deki dört eğrinin de düşük konsantrasyonlar aralığında doğrusal olması, sınırlı bir bölgede yaklaşık K değerinin kullanılmasının önemli hatalara neden olmayacağını gösterir. Geniş konsantrasyon aralıklarında ise yukarıdaki denklem, madde konsantrasyonunun K da yapacağı değişiklikler dikkate alınarak değiştirilir. Bir kromatografik kolondaki konsantrasyon, çoğunlukla düşüktür. K 'nın sabit olduğu bu koşullarda alınan kromatograflara "doğrusal kromatografi" denir. Bu bölümde, bu tip kromatograflar ele alınacaktır. Doğrusal Sıyırma Kromatografisi Sıyırma (elusyon) kromatografide, bir miktar örnek önce hareketli fazda (solvent) çözülür ve hazırlanan çözelti kolona verilir (Şekil-2) ; kolonda, örneğin içerdiği maddeler kendi kendine iki faz (hareketli ve sabit) arasında dağılır. Çözelti injeksiyonundan sonra kolona bir miktar saf halde hareketli faz (sıyırıcı) verilir. Sıyırıcı olarak çalışan bu kısım, çözeltiyi kolonun alt kısımlarına doğru iter: böylece hareketli faz (içinde hala sabit faza geçecek kısımlar vardır) ile aşağı kısımlardaki taze sabit faz arasında daha ileri derecelerde dağılma sağlanır. Ayni anda taze hareketli faz ile üst kısımlardaki sabit faz (içinde hareketli faza geçecek kısımlar vardır) arasında da yeniden dağılma olur. Sürekli olarak taze çözgen ilave edilerek örnekdeki moleküller, hareketli ve sabit fazlar arasındaki geçişlerle kolonun altına kadar taşınır. Maddedeki moleküller sadece hareketli faz eşliğinde ilerleyebildiklerinden, bir maddenin ortalama göçme (ilerleme) hızı, onun hareketli fazda kalma süresine bağlıdır. Bu süre, maddelerin dağılma oranlarından anlaşılabilir; sabit fazdaki madde konsantrasyonu yüksekse süre kısa, hareketli fazdaki konsantrasyon yüksekse süre uzundur. En ideal hal, hızlar arasındaki farkların, bir karışımdaki maddeleri kolon uzunluğu boyunca ayrı bantlar halinde ayırabildiği durumdur. (Şekil-2 ve 3). Kolondan yeteri kadar hareketli faz geçirilerek bölgeler halinde toplanmış maddeler kolondan sıra ile çıkarılır ve kendilerini tanımlayan bandlar halinde kaydedilir. Başka bir yöntemde, her maddenin toplandığı kolon dolgu maddesi bölgesi ölçülerek hesapla sonuca gidilir. Kolona verilen örneğin taze çözgen ilavesiyle yıkanması işlemine "sıyırma" veya "elüsyon" denir. Kolonun sonunda örnekteki madde konsantrasyonlarını algılayan bir detektör bulunması halinde alınan sinyaller zamanın fonksiyonu olarak simetrik eğriler verir (Şekil-2 nin alt kısmındaki eğriler). Böyle bir grafiğe "kromotogram" denir ve kalitatif/kantitatif analizlerde kullanılır. Piklerin konumları maddenin cinsini, alanları ise konsantrasyonlarını tanımlar.
7 7 Sıyırma (Elüsyon) Kromatografisi Teorileri Şekil-3'de, bir kromatografik kolonda A ve B maddeleri karışımı bir örneğin, sıyırma işleminin kısa ve uzun olması halinde verdiği konsantrasyon profili görülmektedir. Maddelerden A'nın ayrılma katsayısı B'ninkinden daha büyüktür; bu nedenle göç işlemi sırasında A geride kalır. Kolonun buyu uzadıkça iki pik arasındaki u- zaklık artar. Ayni zamanda iki bandda da genişleme olur; bu durum kolonun ayırma verimini düşürür. Ancak göç mesafesi uzadıkça görülen bu band genişlemesi, ayni koşullarda bandların birbirinden ayrılma etkinliğine göre daha zayıftır. Böylece Şekil-3 de ikinci kısımdaki gibi iyi bir ayırım elde edebilmek için yeteri kadar uzun bir kolona gereksinim vardır. örnek çözücü A + B dolgulu kolon B A B A A B t 0 t 1 t 2 t 3 t 4 B dedektör Chapter%2026%20Chromatographic%20Separation.ppt#9 Sinyal A B Zaman, t Şekil-2: İki maddeli bir karışımın ayırma kromatografisi yöntemiyle ayrılmasını gösteren şematik diyagram
8 8 t 1 Konsantrasyon t 2 Göç edilen mesafe, L Şekil-3: A ve B maddeleri kolondan aşağı ilerlerken iki ayrı noktada alınan konsantrasyon profilleri İyi bir kromatografik ayırmada, (a) maddelerin göç etme hızı, ve (b) madde piklerinin genişlemeye başladığı bölgenin (uzaklık) tanımlanması önemlidir. Kromatografinin orijinal teorisi "tepsi teorisi" dir ve göç hızını kantitatif anlamda tarif eder. Ancak bu teori piklerin bölgesel genişlemelerine yol açan çok sayıdaki değişkeni açıklayamaz. Bu nedenle tepsi teorisinin yerini, bu değişkenleri de tanımlayan "kinetik" veya "hız teorisi" almıştır. Kinetik teoride kullanılan iki terim vardır: "teorik tepsi sayısı" ve "teorik tepsinin eşdeğer yüksekliği, TTEY" (veya teorik tepsinin yükseklik eşdeğeri). Bu iki terimi açıklayabilmek için tepsi teorisine kısaca değinmek gerekir. Kromatografi tepsi teorisini Martin ve Synge geliştirmiştir. Buna göre bir kromatografik kolonun ayrı ayrı, fakat birbirine bitişik dar, yatay bir seri tabakalardan (teorik tepsi denen) o- luştuğu varsayılır. Her tepside maddenin hareketli ve sabit fazlar arasında dengeye ulaştığı kabul edilir. Madde ve çözücünün hareketi, bir tepsiden diğerine kademeler halinde geçiş şeklindedir. Kromatografik bir kolonun bir ayırma sistemi olarak verimi, denge sayısının artmasıyla yükselir, yani teorik tepsi sayısı arttıkça kolonun verimi de artar. Buna göre yukarıda belirtilen birinci terim "teorik tepsilerin sayısı, N" kolon veriminin bir ölçüsüdür. İkinci terim "eşdeğer tepsi yüksekliği, H" da bu kavrama yardımcı bir parametredir. Bu iki parametre arasında, N = L / H (2)
9 9 bağıntısı bulunur; L kolon dolgusunun yüksekliğini gösterir. Kolon verimi yükseldikçe H düşer, H 'ın küçülmesi kolonun belirli bir uzunluğundaki denge sayısının büyümesine yol açar. Kısaca, H küçük, N büyük olduğunda kolon verimliliği artar. H ve N hız teorisinde verim parametreleridir ve denklem (2) uygulanabilir. Ancak bir kolonda fiziksel anlamda tepsi bulunamaz, tepsi ve tepsi yüksekliği terimleri kolon verimi için kullanılan birer değer birimleridir. KROMATOGRAFİK HIZ TEORİSİ Kromatografik hız teorisi, bir bandın genişliğini etkileyen değişkeleri ve bu bandın kolondan çıkma zamanını tanımlayabilen başarılı bir teoridir. Bölge (Zone) Şekilleri Tipik bir kromatogram (Şekil-2 ve 3) Gaussian eğrilerine benzer. Bir Gaussian eğrisi,normal bir hata eğrisidir ve tekrarlanan ölçüm değerlerinin ortalama değerden sapma miktarlarına göre grafiğe alınmasıyla elde edilir. Böyle bir eğri, herhangi bir ölçümdeki hatanın, çok sayıda küçük, tayin edilemeyen ve rasgele hataların (pozitif veya negatif) bir toplamı olduğu kabul edilerek çizilir. Bu hataların çoğu birbirini giderir ve bir ortalama değer bulunur. Veriler, ortalama değere göre simetrik dağılım gösterirler. Bir kromatogramın Gaussian şeklindeki eğrisi de, kromatografik banddaki veya bölgedeki sayısız madde taneciklerinin rasgele hareketlerinin birbirine eklenmesiyle oluşur. Tek bir madde taneciğinin davranışı incelenirse, tanecik göç etme sırasında sabit ve hareketli fazlar arasında binlerce defa gidip gelir. Fazlardan birinde, bir geçişteki kalma süresi düzensizdir ve çevresinden tesadüfen aldığı termal enerji yeterli düzeye ulaştığında diğer faza geçer. Böylece bir fazda kalma süresi bazan çok kısa bazan da çok uzun olabilir. Tanecik sadece hareketli fazda kalış süresince kolonda ilerleyebilir. Buna göre, kolondaki ilerlemesi de düzensizdir. Fazlarda kalış süresinin kararlı olmayışı her taneciğin hareketli faza geçişindeki ortalama hızın da değişik olmasına yol açar. Bazı tanecikler hareketli fazda tesadüfen daha uzun süre kalırlar. Bazılarının da, tersine sabit fazda kalış süreleri ortalamadan daha uzun olur. Bu rasgele bireysel olayların sonucunda hız, ortalama değer etrafında simetrik bir dağılım gösterir.
10 10 Kolonun alt bölgelerine inildikçe alınan kromatografi eğrisinin genişliği artar; çünkü taneciklerin bir fazda kalma zamanı dolayısıyla göç etme süresi uzar. Buna göre bölgesel band genişlemesi kolondaki kalma süresi ile bağıntılıdır ve hareketli fazın akış hızıyla ters orantılıdır. Hareketi fazın akış hızı sıvı ve gaz kromatografisinde oldukça fraklıdır. Tipik bir örnek Şekil-4 de görülmektedir. GC de H değerleri daha yüksektir, ancak verim de yüksektir. Ölçüm sayısı, y Gaussian Eğrisi (x i - ) 2 / 2 2 e y = Ortalamadan sapma, (x i - ) Şekil-4: Hareketli fazın akış hızı; (a) sıvı kromatografisi, (b) gaz kromatografisi (H: tepsi yükseklikleri, u: akış hızı)
11 11 Bölge Genişlemesinde Standart Sapma Bir Gaussian eğrisinin genişliği standart sapma ( ) denilen tek bir parametreye bağlıdır. Eğrinin altındaki alanın yaklaşık %96'sı, eğri maksimumunun, ±2 standart sapma değeri içindedir. Buna göre,bir kromatogramdan çıkarılan standart sapma, bölgesel genişlemenin kantitatif bir ölçüsüdür. Bir kromatografik pikin standart sapması, zaman birimi ile veya kolon uzunluğu boyunca olan mesafe ile tarif edilir. Buna göre Şekil-3'deki bölge profillerinden çıkarılan bir standart sapmanın birimi uzunluk (cm cinsinden) olacaktır. Şekil-5 'deki kromatogramda görüldüğü gibi bir kromatogramın apsisinin saniye veya dakika gibi zaman birimleri cinsinden ifadesi daha çok uygulanan bir yöntemdir. Hangi birimin kullanıldığı tanınan sembollerle belirtilir; uzunluk birimi için sembolü, zaman birimi için de sembolü kullanılır. veya 'nun bir kromatogramdaki ifadesi, Şekil-5'de gösterilmiştir. Eğrinin iki tarafından çizilen teğetler apsis eksenine doğru uzatılırsa birer üçgen elde edilir. Uzantıların ekseni kestiği nokta, maksimumdan eksene inilen dikin, ekseni kestiği noktadan yaklaşık olarak ±2 kadardır; ve tabii W = 4 'dir. Dedektör sinyali 0 W 0 Zaman, dakika Şekil-5: Bir kromatografik pikten standart sapma nun tayini; W = 4, t R : kolon dolgusu içinde maddenin alıkonma zamanı, t M : kolonda tutulmayan kısmın çıkma zamanı (t M, kolondan geçen hareketli faz molekülünün çıkma zamanı)
12 12 Bölge Genişlemesinden H ve N in Hesaplanması Kromatografik bir bölgenin genişlemesi birim uzunluktaki kolon için standard sapmanın karesi(değişiklik) olarak aşağıdaki eşitlikle verilir. 2 H = (3) L Burada H cm cinsinden tepsi yüksekliğini gösterir ve verimi ifade eder, L kolonun uzunluğunu (cm) gösterir; nin birimi H ve L ile olan bağıntısı nedeniyle uzunluk birimidir (cm). Denklem(3), (2) ile bileştirilip yeniden düzenlenirse bir kolonunun ayırma özelliklerini tanımlayan diğer bir ifade elde edilir. L 2 N = (4) 2 N, L uzunluğundaki bir kolondaki tepsi sayısını verir; yani, tepsi sayısının artması ve tepsi yüksekliğin azalması kolon veriminin yükselmesini sağlar. N ve H ın Deneysel Olarak Değerlendirilmesi Şekil-5'de görüldüğü gibi deneylerde elde edilen kromatogramların çoğunda apsis ekseni zamanı gösterir. Tabii bu tip eğrilerden çıkarılan standart sapmanın birimi de uzunluk (cm) değil zaman (saniye, dakika) birimi olacaktır. Şekil-5 deki t R alıkonma zamanıdır ve örneğin injeksiyonundan, kromatografik kolonun sonundan çıkışına kadar geçen zamanı gösterir. Madde taneciklerinin kat ettikleri yol boyunca olan ortalama hareket hızları L/t R 'dir. Buna göre standart sapmanın uzunluk ve zaman birimleri arasındaki ilişki, = (5) L/t R ifadesi ile verilebilir. Burada zaman birimli standart sapmayı gösterir. Daha önce de değinildiği gibi Şekil-5 'deki gibi bir Gaussian eğrisi için W = 4 dur. Bu eşitliğin denklem (5) de yerine konmasıyla aşağıdaki bağıntı elde edilir. L W = 4 t R Bu ifade denklem (3) de yerine konursa, L W 2 H = (6) 2 16t R
13 13 denklemi bulunur. N 'yi elde edebilmek için denklem(2) 'deki H yerine yukardaki H ifadesi yazılır ve denklem yeniden düzenlenir. Buna göre, t R N = 16 ( ) 2 (7) W denklemi çıkarılır. Bu ifade kullanılarak iki zaman ölçmesi olan t R ve W den N hesaplanabilir, H 'ın bulunması için kolon uzunluğunun da bilinmesi gerekir. Band Genişlemesinin Kaynakları Kromatografik pikler kinetik olarak kontrol edilen üç işlem nedeniyle genişler; bunlar: (1) girdap difüzyonu, (2) boylamasına difüzyon ve (3) dengesiz kütle transferidir. Bu etkilerin büyüklüklerini akış hızı, dolgu maddesinin tanecik büyüklüğü, difüzyon hızları ve sabit fazın kalınlığı gibi kontrol edilebilen değişkenler belirler. Bu üç işlemi de kapsayacak şekilde kromatografik kolonların verimini hesaplamada kullanılabilecek çeşitli denklemler geliştirilmiştir. Bunlardan ilk bulunanı ve en basit olanı "van Deemter" denklemidir ve gaz-sıvı kromatografisi için çıkarılmıştır; denklem, akış hızı u ile tepsi yüksekliği H arasında yaklaşık bir ilişki verir; burada A girdap difüzyonu ile, B boylamasına difüzyon ile ve C dengesiz kütle transferi ile ilgili terimlerdir. B H = A + + C u (8) u Girdap Difüzyonu Bir molekülün dolgulu bir kolondan geçerken karşılaştığı patikaların sayısı artıkça girdap difüzyonu etkisiyle bölge genişlemesi meydana gelir. Şekil-6'da görüldüğü gibi bu patikaların uzunlukları farklıdır; bunun sonucu olarak ayni maddeye ait moleküllerin kolonda alıkonma süreleri de farklı olur. Böylece tüm moleküllerin kolonun sonuna ulaşmaları bir zaman aralığında gerçekleşir ve çıkan band da geniş bir şekil alır. Denklem(8) deki A miktarı girdap difüzyonun etkisini gösterir ve sabit fazın tanecik büyüklüğü, geometrisi ve kolondaki sıkışıklığı ile ilişkilidir. Birinci yaklaştırma olarak A 'nın akış hızına bağlı olmadığı varsayılır ve aşağıdaki ifade yazılabilir A = 2 d R
14 14 Burada d R ortalama tanecik capı, sıkışıklık faktörüdür. nın değerlerini, sabit fazın tanecik büyüklüğü aralığı ve doldurulma şekli belirler. akış yönü A 1 2 (2) numaralı molekülün kat ettiği yol (1) numaralı olana kıyasla daha uzundur; bu durumda (2) molekülü kolon sonuna (1) molekülünden daha sonra ulaşır B Şekil-6: Kromatografik sıyırma işlemi sırasında aynı maddeye ait iki molekülün izlediği patika yollar Örneğin, mesh aralığındaki tanecikler için ~ 1 dolayında, meshlik tanecikler için ise 8 dolayındadır. Bir kolon doldurulurken küçük ve küresel, dar aralıklı boyutlarda dolgu maddesinin kullanılarak girdap difüzyonu nedeniyle oluşan band genişlemesi en düşük düzeye indirilebilir. Kolondaki dolgu maddesinin aralarında açık kanallar bulunmamalıdır. Özenle doldurulan bir kolonda girdap difüzyonu çok düşük seviyelerdedir. Boylamasına Difüzyon Boylamasına difüzyon bir bandın yoğun merkez kısmındaki moleküllerin, bandın iki tarafındaki daha seyreltik bölgelere doğru göç etme eğilimlerinden kaynaklanır. Hareketli ve sabit fazların her ikisinde de oluşabilen bu tip difüzyonun yarattığı band genişlemesi oldukça fazladır. Boylamasına difuzyon hareketli fazın gaz olduğu bir ortamda çok önem kazanır, çünkü gaz fazındaki difüzyon hızlarının büyüklüğü sıvılara göre birkaç derece fazladır. Difüzyon miktarı zamanla artar; akış hızı azaldıkça band genişlemesi de artar.
15 15 Denklem(8)'deki ikinci terim (boylamasına difüzyon terimi) akış hızıyla ters orantılıdır. B bir sabittir ve D M ile, B = 2 D M denklemiyle belirtilen bir ilişkidedir. Burada, D M hareketli fazda bulunan maddenin difüzyon katsayısı, blokaj faktörüdür ve sabit fazdaki taneciklerin, serbest moleküler difüzyonu engellemelerinin bir ölçüsüdür; dolgu maddesinin tipine göre değeri aralığında değişebilir. Boylamasına difüzyonun neden olduğu band genişlemesi sıcaklığı düşürmek (böylece D M de düşer) ve akış hızını artırmakla azaltılabilir. Dengesiz Kütle Transferi Kromatografik bandların genişlemesine yol açan bir diğer neden de hareketli faz akışının çok hızlı olması ve fazlar arasında gerçek bir dengenin kurulamamasıdır. Örneğin, hareketli fazın taze sabit fazla karşılaştığı band bölgesinin ön tarafında henüz denge konumuna ulaşılmamıştır. Bu durumda madde, kolonun gerçek dengeye gelindiği halde bulunması gereken kısmından daha ileride bir yerde bulunur. Benzer şekilde, bölgenin sonunda, sabit fazdaki maddeler taze hareketli fazla karşılaşırlar. Yine, madde taneciklerinin fazlar arasındaki geçişi hemen gerçekleşemez ve denge konumuna gelinmesi için yeterli zaman olmadığından bölgenin uzantısı yayılır. Dengesiz kütle transferinin etkisi akış hızı düşürülerek küçültülebilir (Denklem-8), çünkü dengeye ulaşılabilmesi için daha fazla zamana gereksinim vardır. Ayrıca, hareketli fazın aktığı kanalların dar olması halinde madde moleküllerinin sabit faza difüzlenmeleri daha kolay olacağından denge konumuna daha çabuk ulaşılır. Ayni nedenle, sabit bir faz üzerine akmayan sıvıların kaplandığı hallerde sıvı tabakaların mümkün olduğu kadar ince olması gerekir. Denklem(8)deki son terim hareketli fazın bir gaz olduğu durumda, yüksek akış hızlarında çok önemlidir. C değeri iki terimden oluşur. Birincisi sabit fazdaki kütle transferi ile, diğeri hareketli fazdaki hızla ilişkilidir. Bu iki terimin C ye bağlılığı aşağıdaki denklemle verilir. 2 2 q R (1 - R) d f w d R C = + D S D M
16 16 d f, filmin veya çapı d R olan sabit faz taneciklerinin kalınlığını gösterir. R miktarı alıkonma oranıdır ve t M /t R ye eşittir (Şekil-5). D S ve D M terimleri maddenin sabit ve hareketli fazlardaki difüzyon katsayılarıdır. q ve w; dolgu maddesinin yapısı ve konfigrasyonuna bağlı sabitlerdir. W, 1.3 civarında bir değerdir. Katı bir destek üzerinde bulunan düzgün bir sıvı filmi için q = 0.5 'dir. C'iyi etkileyen en önemli değişken d f dir. Çok ince sıvı faz tabakaları kullanılarak kolon verimi önemli derecede artırılabilir. Yüksek sıcaklıklarda ve düşük solvent viskozitelerinde dengeye daha çabuk ulaşılabilir. Bant Genişlemesi Yapan Proseslerin Net Sonuçları Şekil 7(a)'da van Deemter denklemindeki üç terimin eğrileri çizilmiştir (Kesikli çizgi); eğriler H değerinin hareketli faz hızı ile değişimini göstermektedir. Bu üç terimin net sonucu ise kesiksiz eğri ile verilmiştir. Görüldüğü gibi optimum verim kesiksiz eğrinin minimumunda elde edilir. Bu tip deneysel eğrilerden herhangi bir kolon için A, B, C değerleri bulunabilir. Bu gibi veriler bir dolgu maddesinin daha verimli koşullarda kullanılmasına yardımcı olur. van Deemter denklemi tepsi yüksekliğinin bulunmasında kullanılan ilk yaklaştırma yöntemidir. Kolon verimi etkileyen değişkenleri tanımlamada bundan daha hassas bazı yöntemler de geliştirilmiştir. Tepsi yüksekliğii H, mm net etki C u A B / u (a) Hareketli faz hızı, u, cm/s (b) Doğrusal hız, cm/s Şekil-7: (a) (H = A + B/u + C u) denklemin deki değişkenlerin tepsi yüksekliğine etkisi, (b) Van Deemter eşitliği; akış hızının kolon verimi ile ilişkisi
17 17 KOLONLARDAKİ AYIRMA Bir kromatografik kolonun verimi, içerdiği teorik tepsi sayısı ile belirlenir. Burada herhangi bir ayırma işleminde, bir kolondaki tepsilerin sayısı ile gerekli zaman arasındaki ilişki anlatılacaktır. Maddenin Göç Etme Hızı Şekil-5 de verilmiş olan kromatogramda zaman eksenindeki sıfır, örneğin kolona injekte edildiği ve sıyırma işleminin başladığı anı gösterir. t M de çıkan pik, kolon dolgu maddesi tarafından tutulmayan maddeye (çoğunlukla hava) aittir; bu maddenin hareket hızı, hareketli fazdaki örnek moleküllerinin ortalama hızı ile aynidir. Alıkonma zamanı t R (örnek pikine aittir), maddenin kolonun sonundaki detektöre ulaşması için gerekli zamanı gösterir. Maddenin ortalama göç etme hızı v aşağıdaki denklemle verilir. L v = (9) t R Benzer şekilde moleküllerin hareketli fazdaki ortalama hızı u da, L u = (10) t M denklemiyle verilir. Maddenin göç etme hızı ayni zamanda hareketli fazın hızına göre de tarif edilebilir, buna göre, v = u (maddenin hareketli fazda bulunduğu zamanın kesri) Bu kesir herhangi bir anda maddenin hareketli fazda bulunan mol sayısına (ortalama), kolondaki toplam mol sayısına bölünmesiyle bulunur. Yani, hareketli fazdaki mol sayısı v = u ( ) toplam mol sayısı veya, C M V M 1 v = u ( ) = u ( ) C M V M + C S V S 1 + C S V S / C M V M
18 18 Burada C M ve C S, hareketli ve sabit fazlardaki madde konsantrasyonları, V M ve V S iki fazın kolondaki toplam hacimleridir. Denklem(1) deki eşitlik yukarıdaki ifade ile birleştirilerek aşağıdaki eşitlikler bulunur. veya, 1 v = u ( ) 1+K V S / V M 1 v = u ( ) (11) 1 + k k kapasite faktörüdür ve maddenin dağıtma katsayısı ile ilişkilidir. K V S k = (12) V M Denklem (9), (10) ve (11)'den t R çıkarılır. K V S t R = t M (1 + k ) = (1 + ) (13) V M Buna göre bir maddenin alıkonma zamanı t R, maddenin dağıtma katsayısı ve fazların hacimleri arasındaki oran ile artar. Denklem(13) yeniden düzenlenerek, deneysel parametreler olan t R ve t M den, bir maddenin kapasite faktörü k 'nün hesaplanabileceği bir denklem bulunur. t R - t M k = (14) t M Kolon Resolusyonu (Ayırma Gücü) Kromatografideki en önemli konu bir kolonun iki maddeyi birbirinden ayırabilme özelliğidir. Bir kolonun kantitatif anlamdaki ayırma gücü, "rezolusyon" terimi ile tarif edilir ve R S ile gösterilir. 2 Z 2 [(t R ) S -(t R ) A ] R S = = (15) W A + W B W A + W B
19 19 W A ve W B piklerin taban genişlikleridir ve birimleri zamandır. Z maddelerin detektöre ulaşma zamanları arasındaki farkı gösterir (Şekil-8). İki pikin genişlikleri W ile gösterilirse denklem(15) aşağıdaki şekilde basitleşir. Z R S = W Birbirine yakın çıkan piklerde W X ve W Y de birbirine yakın değerlerde olurlar; bu durumda tek bir değerin ölçülmesi yeterlidir. Şekil-8 'de iki maddenin bulunduğu bir karışımın üç ayrı rezolusyonda alınan kromatogramları görülmektedir. R S = 1.5 da A ve B maddeleri birbirlerinden tam olarak ayrılmışlardır. R S = 0.75 'de ise ayırma yapılamamıştır. R S = 1.0 değerindeki uygulamada A maddesinde % 4 kadar B maddesi ve B de de % 4 kadar A maddesi kalmıştır; rezolusyonun 1.5 olduğu durumda bu karışma % 0.3 kadardır. Aynı kolon dolgu maddesi ile rezolusyonun yükseltilmesi için kolon boyu uzatılır; dolayısıyla teorik tepsi sayısı artırılmış olur. R S ile Kolon Özellikleri Arasındaki İlişki Bir kromatografik kolonun bazı özellikleri ile R S arasında çeşitli ilişkiler bulunabilir. Aşağıdaki örnekte bu ilişkilerin nasıl çıkarılabileceği gösterilmiştir. ÖRNEK R S ile (t R ) A ve (t R ) B arasında bir ilişki çıkarılması; son iki terim Şekil-8'deki kromatogramdan ölçülen alıkonma zamanlarıdır. Daha önce de belirtildiği gibi, W = W B W A alınabilir. Bu durumda denklem(15) aşağıdaki gibi yazılır. (t R) B - (t R) A R S = W B Denklem(7), W Y yi (t R ) X ve N cinsinden vermektedir. Buna göre (t R ) B - (t R ) A N R S = x (t R ) B 4
20 20 Dedektör sinyali 0 Zaman, dakika Şekil-8: Üç ayrı ayırma gücü için kromatogramlar; RS = 2 Z / (WA + WB)
21 21 Denklem (13)'deki t R nin yukardaki ifade ile birleştirilmesiyle, R S değeri X ve Y nin kapasite faktörleri ile tanımlanmış olur. ( k B - k A ) N R S = x (1 + k B ) 4 k B / k A terimine "seçicilik faktörü" denir ve ile gösterilir k B = (16) k A k B /k A terimi yerine konularak R S denklemi yeniden düzenlenir ve k A denklemden çıkarılır. N - 1 k B R S = ( ) ( ) (17) k B En uygun rezolusyonu bulmak için gerekli teorik tepsi sayısı hesaplanmalıdır. Bunun için de denklem(17) yeniden düzenlenerek elde edilen aşağıdaki eşitlik kullanılır. 1 + k B N = 16 RS 2 ( ) 2 ( ) 2 (18) -1 k B Seçicilik Faktörünün ( ) Özellikleri Denklem(17) ve (18)in uygulamalarına geçmeden seçicilik faktörü nın özelliklerini bilmek yararlı olacaktır. Bu değer Şekil-8 de görüldüğü gibi bir kromatogramdan doğru olarak bulunabilir. değeri denklem(14) ün denklem(17) de yerine konmasıyla ve sonra da denklem(12) nin denklem(16) da yerine konmasıyla iki farklı şekilde ifade edilebilir. (t R ) B - t M = (19) (t R ) A - t M K B = (20) K A Rezolusyon ve Ayırma Zamanı Denklem(17) ve (18)'de, önemli bir performans özelliği olan, tam bir ayırma için gerekli olan zaman yoktur. Bu önemli değişkenin de rezolusyon ile ilişkisini sağ-
22 22 lamak için denklem (19) dan, önce daha yavaş hareket eden maddenin(b) hızı bulunur 1 v B = (t R ) B Sonra bu bağıntı denklem(11) ve (12) ile birleştirilerek (t R ) B çıkarılır NH (1+ k B ) (t R) B = u Burada (t R ) B, hareketli fazın hızı u olduğunda B nin çıkması için gerekli zamanı gösterir. Bu eşitlik denklem(18) ile birleştirilerek (t R ) B için rezolusyon (R S ) ile ilişkili aşağıdaki denklem elde edilir. 16 RS 2 H (1+ k B) 3 (t ) = ( ) 2 R B (21) u -1 (k B ) 2 Kolon Performansının Optimizasyonu Denklem(17) ve (21), kolon kromatografisinde çok önemlidir; uygun rezolusyon derecesini sağlayacak koşulların seçiminde bu iki denklemden yararlanılır. Denklemler üçer kısımdan oluşmuşlardır. Birinci terimler kolonun N veya H cinsinden verimini tanımlar. İkinci terimlerde katsayısı vardır ve secicilik terimidir; bu terim örnekteki iki maddenin sadece özelliklerine bağlıdır. Denklemlerdeki üçüncü terimler kapasite terimleridir, k B faktörünü içerirler ve hem maddenin ve hem de kolonun özelliklerine bağlıdır. Kolon Verimi Denklem(17)'de görüldüğü gibi rezolusyon, kolondaki tepsi sayılarının kare kökü ile orantılıdır. iyi bir ayırma yapabilmek için tepsi sayısı artırılabilir. Bu durumda H değerinin küçültülüp kolon boyunun da uzatılmasıyla ayırma işlemi için gerekli zamanın uzamaması sağlanabilir. Daha önce anlatılan hız teorisinde (2. kısım) verimin en yüksek, H ın ise en düşük olmasını sağlayan değişkenler tanımlanmıştır.
23 23 Kapasite Faktöründeki Değişme Bir maddenin kapasite faktörü k B, hareketli veya sabit fazların bileşimlerinin değiştirilmesiyle farklı değerler alır. Hareketli fazın bileşiminin değiştirilmesi kolaydır ve bir ayırma işleminin optimize edilmesinde çoğunlukla uygulanan bir yöntemdir. Denklem(12)'ye göre k B değeri, sabit fazın hareketli faza oranının değiştirilmesiyle de artırılabilir veya azaltılabilir. Sabit fazı oluşturan malzemenin tanecik boyutlarının küçültülmesi de k B değerini artırır, çünkü yüzey alanı artar ve dolayısıyla V S büyür. k B nin artması rezolusyonu (R S ) artırır, fakat pikin çıkma zamanını ([tr] B )uzatır. Bu iki etkiyi daha iyi anlayabilmek için, Denklem(17) ve (21) aşağıdaki şekilde yazılabilir. k B (1+ k B ) 2 R S = Q 1+ k B ve, (t R ) B = Q (k B ) 2 Burada, denklem(17) ve (21)'deki ilk ikişer terim Q ve Q harfleri ile gösterilmiştir. R S /Q ve (t R ) B / Q değerleri k B nin fonksiyonu olarak grafiğe alındığında, Şekil- 9'daki gibi iki eğri elde edilir; Q ve Q nun sabit kaldığı varsayılmıştır. k B değerinin 10'dan daha büyük olması istenmez, çünkü bu değerin üstünde, şekilde de görüldüğü gibi rezolusyondaki artışın çok az olmasına karşın ayırma zamanındaki u- zama fazladır. Maddenin ayrıldığı en kısa zaman süresi k B 'nin 2-3 arasında olduğu bölgedir. k nin optimum değeri; çoğunlukla 2-5 arasındadır. rezolusyon R S (t R ) Y / Q veya R S / Q çıkma zamanı (t R ) Y Kapasite faktörü, k X Şekil-9: Kapasite faktörü k y nin çıkma zamanı (t R ) y ye etkisi, k nün değişiminde Q ve Q nün sabit olduğu kabul edilmiştir
24 24 Seçicilik Faktöründeki Değişme Denklem(17) 'ye göre, seçicilik faktörü büyüdükçe rezolusyon da artar. Bu parametrenin 2 'den büyük olması halinde en kısa zamanda iyi bir ayırma yapılabilir. Diğer taraftan, nın 1 'e yaklaşması durumunda çok uzun bir kolon kullanılmazsa rezolusyon kaybolur. Denklem(21)'de görüldüğü gibi 1 'e yakın değerlerinde ayırma zamanı anormal derecede uzar. Örneğin, 'nın 1.1 değerine karşılık 1.01 olması durumunda ayni rezolusyon için gerekli zaman 84 kat daha fazla olur. ÖRNEK 30.0 cm 'lik bir kolonda A ve B maddelerin alıkonma süreleri sırasıyla ve dakikadır. Tutulmayan kısımlar kolondan 1.30 dakikada çıkmaktadır. Pik genişlikleri 1.11 ve 1.21 mm olduğuna göre aşağıdaki ; (a) kolon rezolusyonunu, (b) kolondaki ortalama tepsi sayısını, (c) tepsi yüksekliğini, (d) rezolusyonun 1.5 olması için gerekli kolon uzunluğunu, ve (e) uzun kolonda B maddesinin çıkması için gerekli zamanı hesaplayınız. (a) Kolon rezolusyonu (R S ) denklem (15)'den hesaplanır 2 Z 2 [(t R ) B - (t R ) A ] R S = = W A + W B W A + W B 2 ( ) R S = = (b) Ortalama tepsi sayısı denklem(7)'den bulunur. t R N = 16 ( ) 2 N = 16 ( ) 2 = 3493 W N = 16 ( ) 2 = N ort = ( )/2 = 3445 = 3.44 x 10 3 (c) Tepsi yüksekliğinde, denklem(3) ve (4)'den çıkarılan H = L/N eşitliği kullanılır. 2 L 2 H = N = L 2 L 2 L 2 L = H = H = N NL N
25 25 30 H = = x 10-3 = 8.71 x 10-3 cm 3445 (d) N ve L nin artması ile k ve değişmez. Denklem(18) N 1 ve N 2 cinsinden yazılır ve iki denklem birbirin bölünerek N 1 /N 2 bulunur. 1+ k B N = 16 RS 2 ( ) 2 ( ) 2-1 k B 1 + k B N = 16 (R ) 2 ( ) 2 ( ) 2 1 S 1-1 k B 1 + k B N 2 = 16 (R S) 2 2 ( ) 2 ( ) 2-1 k B N (R ) 2 1 S 1 = N 2 (R S ) 2 2 Burada (1) ve (2) orijinal ve daha uzun kolonları gösterir. N 1, (R S ) 1 ve (R S ) 2 'nin değerleri yerlerine konularak N 2 hesaplanır (1.06) 2 = N 2 (1.5) N 2 = 3445 x = 6.90 x L = N 2 H = 6.90 x 10 3 x 8.71 x 10 3 L = 60.1 cm (e) Denklem(21) den (t R ) 1 /(t R ) 2 eşitliği bulunur. 16 RS 2 H (1 + k B ) 2 (t R) B = ( ) 2 u - 1 (k B ) 2 2 (t R ) 1 (R S ) (1.06) 2 = = = 2 (t R ) 2 (R S ) 2 (t R ) 2 (1.5) 2 (t R ) 2 = 35.3 dakika Kromatografide kullanılan terimler, miktarlar ve bunların birbirleri ile olan ilişkileri çok ve oldukça karmaşıktır. Tablo-2'de bazı tanımların özeti verilmiştir.
26 26 Tablo-2: Önemli Kromatografik Değerler ve İlişkilerin Özeti Deneyle Bulunan Değerler Adı Sembolü Nereden Bulunduğu Alıkonma zamanı, hareketli faz t M Kromatogramdan (Şekil-8) Alıkonma zamanı, A ve B nin (t R ) A, (t R ) B Kromatogramdan (Şekil-8) Pik genişlikleri, A ve B nin W A, W B Kromatogramdan (Şekil-8) Kolon dolgu maddesinin uzunluğu L Doğrudan ölçme Akış hızı F Doğrudan ölçme Sabit fazın hacmi V S Dogu hazırlama verisi Maddenin sabit ve hareketli fazlardaki konsantrasyonları C M, C S Analiz ve hazırlama verileri Hesaplanan Değerler Adı Hesaplama Değerleri Diğer Özelliklerle İlişkileri Hareketli fazın hızı u = L / t M Hareket fazın hacmi V M = t M F Kapasite t R - t M K V S k = k = faktörü Dağıtma katsayısı Seçicilik faktörü Rezolusyon Tepsi sayısı Alıkonma zamanı t M k V M K = V S V M C S K = (t R) Y - t M k Y K Y = = = (t R ) X - t M k X K X 2 [(t R) Y (t R) X] N - 1 k' R S = R Y S = ( ) W X + W Y k' Y t R L 1 + k N = 16 ( ) 2 Y N = = 16 RS 2 ( ) 2 ( ) 2 W H 1 k Y 16 RS 2 H 2 (1 + k Y) 3 (t R) Y = u ( 1) 2 (k Y ) 2 C M
27 27 Kromatografi, benzer özellikteki maddelerin birbirinden ayrılmasında uygulanan yöntemler arasında birinci sırayı alır. Ayrıca, ayrılan maddelerin kalitatif tanımlanmasında ve kantitatif tayininde de kullanılır. Bu bölümde tam bir analizin yapılmasında kullanılan genel kromatografik kavramlar açıklanacaktır. Kalitatif Analiz Bir kromatogram, örnekteki her bir madde hakkında çok az bilgi verir; bunlar maddenin alıkonma zamanı veya bir sıyırma periyodu süresince maddenin sabit fazdaki konumunu gösteren bilgilerdir. İlave bilgiler elde edilebilmesi için hareketli ve sabit fazlar değiştirilip çeşitli sıyırma sıcaklıkları uygulanabilir. Yine de bir madde için kromatografide alınan veriler, IR, NMR veya kütre spektrumunda alınanlara göre oldukça azdır. Spektral apsislerdeki veriler (,, veya m/e) kromatografik apsiste alınana (t R ) kıyasla daha hassastır. Bu gerçekler kromatografinin kalitatif analizlerde başarısız bir yöntem olduğunu göstermez. İsimleri bilinen ve çoğunlukla birarada bulunan bazı madde karışımlarının tanımlanması yapılabilir. Örneğin, bir protein hidroliz örneğinde 30 veya daha çok sayıdaki amino asidin varlığı veya yokluğu, ince bir kromatografik levhada açığa çıkan görüntülerin şiddetine göre saptanabilir. Yine de teşhisin kesin olması için ayrılan maddelerin spektral veya kimyasal tanımına gerek vardır. Karmaşık yapılı bir örneğin spektroskopik yöntemlerle tanımlanması için önceden kromatografik bir ayırmaya gereksinim vardır. Yani kalitatif spektroskopik analizlerde analizin geleceği kromatografiye bağlıdır. Kantitatif Analizler Kromatografi süratli, basit, ve çok iyi bir ayırma yöntemi olması nedeniyle son 30 yılda büyük bir alana yayılmıştır. Bunda kromatografinin kantitatif analizlerde çok kullanılması en önemli etken olmuştur. Kantitatif kromatografide analit pikinin yüksekliği veya alanı bir veya daha çok sayıdaki standartla kıyaslanır. Çalışma koşulları kontrol edilebiliyorsa bu iki parametre de konsantrasyonla doğrusal olarak değişir.
28 28 Pik Yüksekliğine Göre Analiz Bir kromatografik pikin yüksekliğini ölçmek için pikin iki yanındaki taban çizgileri düz bir doğru ile birleştirilir ve pik tepesinden bu doğruya bir dik inilir; dikin uzunluğu, pik yüksekliğidir. Yükseklik çok hassas olarak ölçülebilir. Kolon koşullarını etkileyen değişkenler, örnek ve standartların kromatogramlarının alındığı süre boyunca sabit tutulmalıdır. Çok iyi kontrol edilmesi gereken değişkenler kolon sıcaklığı, sıyırıcının akış hızı ve örneğin injeksiyon hızıdır. Ayrıca kolonun aşırı yüklenmemesine de dikkat edilmesi gerekir. Örnek injeksiyon hızı bir kromatogramda ilk çıkan pikler için önemlidir ve % 5-10 'a kadar ulaşan relatif hatalara yol açar. Pik Alanlarına Göre Analiz Yukarıdaki paragrafta belirtilen değişkenler pik alanında genişleme etkisi yapmazlar. Bu bakımdan alana göre yapılan analizler yüksekliğe göre yapılanlara kıyasla daha yeterlidir. Diğer yönden pik yüksekliklerin ölçülmesi daha kolaydır ve dar piklerde bu yöntemle daha doğru sonuçlar alınır. Modern kromatografi cihazlarında bilya ve disk veya elektronik bilgisayarlar vardır. Bunlarda pik alanları hassas olarak ölçülebilir. Bu tip sistemlerin olmaması durumunda hesaplamalar el ile yapılır. Uygun genişlikteki simetrik piklerde alan basit bir yöntemle hesaplanır; pikin yüksekliği, yüksekliğin tam ortasından çizilen yatay doğrunun uzunluğu (o noktadaki pik genişliği) ile çarpılır. Pik alanı pikin bir planimetre ile taranmasıyla da bulunabilir. Bir başka yöntem de pikin kesilerek tartılması ve tartımın, ayni kaydedici kağıdın alanı bilinen bir parçasının ağırlığı ile kıyaslanmasıdır. McNair ve Bonelli, 10 örnek üzerinde bu yöntemlerin hassasiyetlerini inceleyen bir çalışma yapmışlardır. Çalışma sonuçlarına göre aşağıdaki standart sapmalar belirlenmiştir. Standartlarla Yapılan Kalibrasyon Kantitatif kromatografik analizde en çok uygulanan yöntem örnekteki maddelerin bileşimine yakın bileşimlerdeki bir seri standart çözelti ile çalışılmasıdır. Standartların kromatogramları alınarak pik yüksekliklerinin veya alanlarının, madde konsantrasyonlarına göre " kalibrasyon grafiği" çizilir; grafik orijinden geçen bir doğru şeklindedir. Örneğin analizi bu grafiğe göre yapılır. Yüksek hassasiyet alınabilmesi için standart çözeltilerin ve kalibrasyon grafiğinin sık sık kontrol edilmesi gerekir.
29 29 Analizdeki en önemli hata kaynağı, injekte edilen standart ve analit örnek hacminin tam sabit olamayışıdır; ayrıca injeksiyon hızı da hataya neden olan bir faktördür. Örnek miktarı çoğunlukla 1 mikrolitre gibi çok az miktarlardır ve her defasında ayni hacimde madde verebilmek için bir mikro şırınga kullanılarak relatif hata % birkaç seviyesine kadar düşürülebilir. Bu hata gaz-sıvı kromatografisinde daha da büyüktür; örnek sıcak bir uçtan injekte edildiğinde, şırınga ucundaki buharlaşma kolona verilen madde hacminde büyük farklılıklar olmasına yol açar. Örnek hacmindeki hatalar, Şekil-10'da görülen bir "döner gaz örnek valfi ile verilen miktarın % 1-2'sine kadar düşürülebilir. (a)'daki örnek yuvası örnekle doldurulur; valfin 45 0 döndürülmesiyle yuvadaki örnekten belirli bir miktarı hareketli faz akımı içine verilir. sürükleyici girişi sürükleyici kolona sürükleyici girişi sürükleyici ve örnek C kolona A C B B A örnek girişi örnek çıkışı örnek girişi örnek çıkışı (a) (b) Şekil-10: Döner bir örnek valfi; (a) örnek yuvası ABC nin doldurulduğu valf konumu, (b) örneğin kolona verilmesi İç Standart Yöntemi Kantitatif kromatografide en hassas sonuçlar örnek injeksiyonundan kaynaklanan hataların bulunmadığı iç standart yöntemi ile elde edilir. Bu yöntemde örnek ve standartlara çok hassas tartılmış bir iç standart maddesi ilave edilir; analit pik alanının (veya yüksekliğinin) iç standart pik alanına (veya yüksekliğine) oranı analitik parametre olarak kullanılır. Yöntemin başarılı olabilmesi için iç standart pikinin ötnekdeki diğer maddelerin piklerinden uzakta (R S > 1.25), analit pikinin
30 30 yakınında olması gerekir. Uygun bir iç standart kullanıldığında relatif hata %0.5-1 civarındadır. (Ref. Kalibrasyon) Alan Normalizasyonu Yöntemi Örnek injeksiyonundaki düzensizliğin yaratığı hata alan normalizasyonu ile de giderilebilir. Bu yöntemde örnekteki tüm maddelerin kolondan çıkması gerekir. Kromatogramdaki tüm piklerin alanları hesaplanır ve her madde için bilinen detektör algılama faktörü ile çarpılarak düzeltilir. Analitin konsantrasyonu, analit pikine ait alanın toplam pik alanlarına bölünmesiyle hesaplanır. Aşağıda bu yöntemdeki hesaplamalara bir örnek verilmiştir. (Ref. Kalibrasyon) ÖRNEK Aşağıdaki veriler butil-alkoller karışımı bir örneğin kromatogramından alınmıştır (detektör hassasiyeti düzeltme faktörleri bilinen miktarlarda saf alkoller kullanılarak ayrı deneylerde saptanmıştır). 2 Dedektör algılama Alkol Pik alanı, cm faktörü Düzeltilmiş alanlar, cm 2 n-bütil i-bütil s-bütil t-bütil toplam: n-bütil alkol, % = x 100/8.943 = 18.5 i-bütil alkol, % = x 100/8.943 = 45.1 s-bütil alkol, % = x 100/8.943 = 23.8 t-bütil alkol, % = x 100/8.943 = 12.6 toplam, %: 100
31 31 Bilgisayarlı Kromatografi Modern kromatografi cihazlarında kolon sıcaklığı, sıyırıcı akış hızı, örnek injeksiyon zamanı ve örnek sıcaklığı gibi parametreler " mikroprosesör" lerle kontrol edilir. Bunlarda kişiler tarafından yapılan hiç bir kontrol yoktur veya çok azdır. Cihazlar çok karmaşık fakat son derece otomatiktir. Örnekler (bir kaç düzine olabilir) dönen bir sistem içine konur. Her analizden sonra kolon otomatik olarak başlangıç noktası gelir, döner örnek tablası da yeni bir örneği kolonun önüne getirecek şekilde döner, örnek otomatik olarak çekilir ve kolona injekte edilir, ktomatogramı alınır ve bir bilgisayar hafızasına yerleştirilir. Veriler kromatogram ve tablo şeklinde alınır; tabloda alıkonma zamanları, relatif pik alanları ve bazılarında her pikin hangi bileşiğe ait olduğu da kaydedilir. GC kanal hesaplama integratörü kaydedici modülü GC REC. digital analog ROM RMM RAM KASET çalışma yöntem pik alanlar adlar ve programı deposu ve RT ler faktörler ÖN CPU PANEL aritmetik kaydedici TTY işlemler bağlantısı bağlantısı kanal modülü kaydedici hesaplama integratörü TTY Şekil-11: Bir kromatografi hesaplama integratörü Yararlanılan Kaynaklar Principles of Instrumental Analysis, D.A.Skoog, D.M. West, II. Ed. 1981
BİLECİK ÜNİVERSİTESİ FEN EDEBİYAT FAKÜLTESİ KİMYA BÖLÜMÜ KROMATOGRAFİYE GRİŞ. Sedat TURE
 1 BİLECİK ÜNİVERSİTESİ FEN EDEBİYAT FAKÜLTESİ KİMYA BÖLÜMÜ KROMATOGRAFİYE GRİŞ Sedat TURE 2013-2014 2 Kromatografik Metotların Sınıflandırılması A. Ayırma Mekanizmasına Göre Sınıflandırma 1. Adsorbsiyon
1 BİLECİK ÜNİVERSİTESİ FEN EDEBİYAT FAKÜLTESİ KİMYA BÖLÜMÜ KROMATOGRAFİYE GRİŞ Sedat TURE 2013-2014 2 Kromatografik Metotların Sınıflandırılması A. Ayırma Mekanizmasına Göre Sınıflandırma 1. Adsorbsiyon
YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ (YPSK) HIGH-PERFORMANCE LIQUID CHROMATOGRAPHY (HPLC)
 YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ (YPSK) HIGH-PERFORMANCE LIQUID CHROMATOGRAPHY (HPLC) 1 Kromatografi nedir? Kromatografi, karışımlardaki çeşitli maddeleri birbirinden ayırmaya ve böylece kalitatif
YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ (YPSK) HIGH-PERFORMANCE LIQUID CHROMATOGRAPHY (HPLC) 1 Kromatografi nedir? Kromatografi, karışımlardaki çeşitli maddeleri birbirinden ayırmaya ve böylece kalitatif
KROMATOGRAFİ. Bir parça kağıt şeridin aşağı hizasından 1 cm kadar yukarısına bir damla siyah mürekkep damlatınız.
 KROMATOGRAFİ Kromatografi, bir karışımda bulunan maddelerin, biri sabit diğeri hareketli faz olmak üzere birbirleriyle karışmayan iki fazlı bir sistemde ayrılması ve saflaştırılması yöntemidir. KROMATOGRAFİ
KROMATOGRAFİ Kromatografi, bir karışımda bulunan maddelerin, biri sabit diğeri hareketli faz olmak üzere birbirleriyle karışmayan iki fazlı bir sistemde ayrılması ve saflaştırılması yöntemidir. KROMATOGRAFİ
Sıvılardan ekstraksiyon:
 Sıvılardan ekstraksiyon: Sıvı haldeki bir karışımdan bir maddenin, bu maddenin içinde bulunduğu çözücü ile karışmayan ve bu maddeyi çözen bir başka çözücü ile çalkalanarak ilgili maddenin ikinci çözücüye
Sıvılardan ekstraksiyon: Sıvı haldeki bir karışımdan bir maddenin, bu maddenin içinde bulunduğu çözücü ile karışmayan ve bu maddeyi çözen bir başka çözücü ile çalkalanarak ilgili maddenin ikinci çözücüye
YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ (YPSK) HIGH-PERFORMANCE LIQUID CHROMATOGRAPHY (HPLC)
 YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ (YPSK) HIGH-PERFORMANCE LIQUID CHROMATOGRAPHY (HPLC) 1 Ayırma teknikleri Bir analiz sürecinde karşılaşılan numuneler büyük çoğunlukla farklı maddelerin karışımı
YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ (YPSK) HIGH-PERFORMANCE LIQUID CHROMATOGRAPHY (HPLC) 1 Ayırma teknikleri Bir analiz sürecinde karşılaşılan numuneler büyük çoğunlukla farklı maddelerin karışımı
BİYOTEKNOLOJİDE KULLANILAN YÖNTEMLER. Araş. Gör. Dr. Öğünç MERAL
 BİYOTEKNOLOJİDE KULLANILAN YÖNTEMLER Araş. Gör. Dr. Öğünç MERAL Kromatografi, katı veya sıvı bir durağan fazın yüzeyine veya içine uygulanmış bir karışımdaki moleküllerin, sıvı veya gaz halindeki bir hareketli
BİYOTEKNOLOJİDE KULLANILAN YÖNTEMLER Araş. Gör. Dr. Öğünç MERAL Kromatografi, katı veya sıvı bir durağan fazın yüzeyine veya içine uygulanmış bir karışımdaki moleküllerin, sıvı veya gaz halindeki bir hareketli
ALETLİ ANALİZ YÖNTEMLERİ
 ALETLİ ANALİZ YÖNTEMLERİ Yüksek Performanslı Sıvı Kromatografisi (HPLC) Yrd. Doç. Dr. Gökçe MEREY SIVI KROMATOGRAFİSİ Hareketli fazın sıvı olduğu bu kromatografi türünde sabit faz bir dolgu maddesi üzerine
ALETLİ ANALİZ YÖNTEMLERİ Yüksek Performanslı Sıvı Kromatografisi (HPLC) Yrd. Doç. Dr. Gökçe MEREY SIVI KROMATOGRAFİSİ Hareketli fazın sıvı olduğu bu kromatografi türünde sabit faz bir dolgu maddesi üzerine
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
AKTİVİTE KATSAYILARI Enstrümantal Analiz
 1 AKTİVİTE KATSAYILARI Enstrümantal Analiz Bir taneciğin, aktivitesi, a M ile molar konsantrasyonu [M] arasındaki bağıntı, a M = f M [M] (1) ifadesiyle verilir. f M aktivite katsayısıdır ve birimsizdir.
1 AKTİVİTE KATSAYILARI Enstrümantal Analiz Bir taneciğin, aktivitesi, a M ile molar konsantrasyonu [M] arasındaki bağıntı, a M = f M [M] (1) ifadesiyle verilir. f M aktivite katsayısıdır ve birimsizdir.
KESİKLİ İŞLETİLEN PİLOT ÖLÇEKLİ DOLGULU DAMITMA KOLONUNDA ÜST ÜRÜN SICAKLIĞININ SET NOKTASI DEĞİŞİMİNDE GERİ BESLEMELİ KONTROLU
 KESİKLİ İŞLETİLEN PİLOT ÖLÇEKLİ DOLGULU DAMITMA KOLONUNDA ÜST ÜRÜN SICAKLIĞININ SET NOKTASI DEĞİŞİMİNDE GERİ BESLEMELİ KONTROLU B. HACIBEKİROĞLU, Y. GÖKÇE, S. ERTUNÇ, B. AKAY Ankara Üniversitesi, Mühendislik
KESİKLİ İŞLETİLEN PİLOT ÖLÇEKLİ DOLGULU DAMITMA KOLONUNDA ÜST ÜRÜN SICAKLIĞININ SET NOKTASI DEĞİŞİMİNDE GERİ BESLEMELİ KONTROLU B. HACIBEKİROĞLU, Y. GÖKÇE, S. ERTUNÇ, B. AKAY Ankara Üniversitesi, Mühendislik
KİMYASAL DENGE. AMAÇ Bu deneyin amacı öğrencilerin reaksiyon denge sabitini,k, deneysel olarak bulmalarıdır.
 KİMYASAL DENGE AMAÇ Bu deneyin amacı öğrencilerin reaksiyon denge sabitini,k, deneysel olarak bulmalarıdır. TEORİ Bir kimyasal tepkimenin yönü bazı reaksiyonlar için tek bazıları için ise çift yönlüdür.
KİMYASAL DENGE AMAÇ Bu deneyin amacı öğrencilerin reaksiyon denge sabitini,k, deneysel olarak bulmalarıdır. TEORİ Bir kimyasal tepkimenin yönü bazı reaksiyonlar için tek bazıları için ise çift yönlüdür.
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ ORGANİK KİMYA LABORATUVARI DENEY 8 : YÜZEY GERİLİMİNİN BELİRLENMESİ
 ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ ORGANİK KİMYA LABORATUVARI DENEY 8 : YÜZEY GERİLİMİNİN BELİRLENMESİ DENEYİN AMACI Gazlarda söz konusu olmayan yüzey gerilimi sıvı
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ ORGANİK KİMYA LABORATUVARI DENEY 8 : YÜZEY GERİLİMİNİN BELİRLENMESİ DENEYİN AMACI Gazlarda söz konusu olmayan yüzey gerilimi sıvı
5. BORU HATLARI VE BORU BOYUTLARI
 h 1 h f h 2 1 5. BORU HATLARI VE BORU BOYUTLARI (Ref. e_makaleleri) Sıvılar Bernoulli teoremine göre, bir akışkanın bir borudan akabilmesi için, aşağıdaki şekilde şematik olarak gösterildiği gibi, 1 noktasındaki
h 1 h f h 2 1 5. BORU HATLARI VE BORU BOYUTLARI (Ref. e_makaleleri) Sıvılar Bernoulli teoremine göre, bir akışkanın bir borudan akabilmesi için, aşağıdaki şekilde şematik olarak gösterildiği gibi, 1 noktasındaki
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Bölüm 3 SAF MADDENİN ÖZELLİKLERİ
 Bölüm 3 SAF MADDENİN ÖZELLİKLERİ 1 Amaçlar Amaçlar Saf madde kavramının tanıtılması Faz değişimi işleminin fizik ilkelerinin incelenmesi Saf maddenin P-v-T yüzeylerinin ve P-v, T-v ve P-T özelik diyagramlarının
Bölüm 3 SAF MADDENİN ÖZELLİKLERİ 1 Amaçlar Amaçlar Saf madde kavramının tanıtılması Faz değişimi işleminin fizik ilkelerinin incelenmesi Saf maddenin P-v-T yüzeylerinin ve P-v, T-v ve P-T özelik diyagramlarının
İnstagram:kimyaci_glcn_hoca GAZLAR-1.
 GAZLAR-1 Gazların Genel Özellikleri Maddenin en düzensiz hâlidir. Maddedeki molekül ve atomlar birbirinden uzaktır ve çok hızlı hareket eder. Tanecikleri arasında çekim kuvvetleri, katı ve sıvılarınkine
GAZLAR-1 Gazların Genel Özellikleri Maddenin en düzensiz hâlidir. Maddedeki molekül ve atomlar birbirinden uzaktır ve çok hızlı hareket eder. Tanecikleri arasında çekim kuvvetleri, katı ve sıvılarınkine
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM
 YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
Ölçme Bilgisi DERS 9-10. Hacim Hesapları. Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ )
 Ölçme Bilgisi DERS 9-10 Hacim Hesapları Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Büyük inşaatlarda, yol ve kanal çalışmalarında kazılacak toprak miktarının hesaplanması, maden işletmelerinde
Ölçme Bilgisi DERS 9-10 Hacim Hesapları Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Büyük inşaatlarda, yol ve kanal çalışmalarında kazılacak toprak miktarının hesaplanması, maden işletmelerinde
3. AKIŞKANLARDA FAZ DEĞİŞİKLİĞİ OLMADAN ISI TRANSFERİ
 1 3. AKIŞKANLARDA FAZ DEĞİŞİKLİĞİ OLMADAN ISI TRANSFERİ (Ref. e_makaleleri) Isı değiştiricilerin büyük bir kısmında ısı transferi, akışkanlarda faz değişikliği olmadan gerçekleşir. Örneğin, sıcak bir petrol
1 3. AKIŞKANLARDA FAZ DEĞİŞİKLİĞİ OLMADAN ISI TRANSFERİ (Ref. e_makaleleri) Isı değiştiricilerin büyük bir kısmında ısı transferi, akışkanlarda faz değişikliği olmadan gerçekleşir. Örneğin, sıcak bir petrol
EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ
 EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ Giriş Isı değiştiricileri (eşanjör) değişik tiplerde olup farklı sıcaklıktaki iki akışkan arasında ısı alışverişini temin ederler. Isı değiştiricileri başlıca yüzeyli
EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ Giriş Isı değiştiricileri (eşanjör) değişik tiplerde olup farklı sıcaklıktaki iki akışkan arasında ısı alışverişini temin ederler. Isı değiştiricileri başlıca yüzeyli
Gaz hali genel olarak molekül ve atomların birbirinden uzak olduğu ve çok hızlı hareket ettiği bir haldir.
 GAZLAR Maddeler tabiatta katı, sıvı ve gaz olmak üzere üç halde bulunurlar. Gaz hali genel olarak molekül ve atomların birbirinden uzak olduğu ve çok hızlı hareket ettiği bir haldir. Gaz molekülleri birbirine
GAZLAR Maddeler tabiatta katı, sıvı ve gaz olmak üzere üç halde bulunurlar. Gaz hali genel olarak molekül ve atomların birbirinden uzak olduğu ve çok hızlı hareket ettiği bir haldir. Gaz molekülleri birbirine
2 Hata Hesabı. Hata Nedir? Mutlak Hata. Bağıl Hata
 Hata Hesabı Hata Nedir? Herhangi bir fiziksel büyüklüğün ölçülen değeri ile gerçek değeri arasındaki farka hata denir. Ölçülen bir fiziksel büyüklüğün sayısal değeri, yapılan deneysel hatalardan dolayı
Hata Hesabı Hata Nedir? Herhangi bir fiziksel büyüklüğün ölçülen değeri ile gerçek değeri arasındaki farka hata denir. Ölçülen bir fiziksel büyüklüğün sayısal değeri, yapılan deneysel hatalardan dolayı
HPLC/YPSK HIGH PERFORMANCE LIQUID CHROMATOGRAPHY YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ
 HPLC/YPSK HIGH PERFORMANCE LIQUID CHROMATOGRAPHY YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ Kromatografi: Kimyasal bir karışımı oluşturan farklı yapıdaki maddelerin birbiriyle karışmayan biri hareketli, diğeri
HPLC/YPSK HIGH PERFORMANCE LIQUID CHROMATOGRAPHY YÜKSEK PERFORMANSLI SIVI KROMATOGRAFİSİ Kromatografi: Kimyasal bir karışımı oluşturan farklı yapıdaki maddelerin birbiriyle karışmayan biri hareketli, diğeri
Isı Kütle Transferi. Zorlanmış Dış Taşınım
 Isı Kütle Transferi Zorlanmış Dış Taşınım 1 İç ve dış akışı ayır etmek, AMAÇLAR Sürtünme direncini, basınç direncini, ortalama direnc değerlendirmesini ve dış akışta taşınım katsayısını, hesaplayabilmek
Isı Kütle Transferi Zorlanmış Dış Taşınım 1 İç ve dış akışı ayır etmek, AMAÇLAR Sürtünme direncini, basınç direncini, ortalama direnc değerlendirmesini ve dış akışta taşınım katsayısını, hesaplayabilmek
KROMOTOGRAFİK YÖNTEMLER
 KROMOTOGRAFİK YÖNTEMLER A. METODUN ÖZETİ Kromatografi, bir karışımda bulunan maddelerin, biri sabit diğeri hareketli faz olmak üzere birbirleriyle karışmayan iki fazlı bir sistemde ayrılması ve saflaştırılması
KROMOTOGRAFİK YÖNTEMLER A. METODUN ÖZETİ Kromatografi, bir karışımda bulunan maddelerin, biri sabit diğeri hareketli faz olmak üzere birbirleriyle karışmayan iki fazlı bir sistemde ayrılması ve saflaştırılması
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUARI
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI SINIR TABAKA DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEYİ YAPTIRAN ÖĞRETİM ELEMAN
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI SINIR TABAKA DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEYİ YAPTIRAN ÖĞRETİM ELEMAN
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
Bölüm 7 ENTROPİ. Bölüm 7: Entropi
 Bölüm 7 ENTROPİ 1 Amaçlar Termodinamiğin ikinci kanununu hal değişimlerine uygulamak. İkinci yasa verimini ölçmek için entropi olarak adlandırılan özelliği tanımlamak. Entropinin artış ilkesinin ne olduğunu
Bölüm 7 ENTROPİ 1 Amaçlar Termodinamiğin ikinci kanununu hal değişimlerine uygulamak. İkinci yasa verimini ölçmek için entropi olarak adlandırılan özelliği tanımlamak. Entropinin artış ilkesinin ne olduğunu
KİNETİK GAZ KURAMI. Doç. Dr. Faruk GÖKMEŞE Kimya Bölümü Hitit Üniversitesi Fen Edebiyat Fakültesi 1
 Kinetik Gaz Kuramından Gazların Isınma Isılarının Bulunması Sabit hacimdeki ısınma ısısı (C v ): Sabit hacimde bulunan bir mol gazın sıcaklığını 1K değiştirmek için gerekli ısı alışverişi. Sabit basınçtaki
Kinetik Gaz Kuramından Gazların Isınma Isılarının Bulunması Sabit hacimdeki ısınma ısısı (C v ): Sabit hacimde bulunan bir mol gazın sıcaklığını 1K değiştirmek için gerekli ısı alışverişi. Sabit basınçtaki
MAKRO-MEZO-MİKRO. Deney Yöntemleri. MİKRO Deneyler Zeta Potansiyel Partikül Boyutu. MEZO Deneyler Reolojik Ölçümler Reometre (dinamik) Roww Hücresi
 Kolloidler Bir maddenin kendisi için çözücü olmayan bir ortamda 10-5 -10-7 cm boyutlarında dağılmasıyla oluşan çözeltiye kolloidal çözelti denir. Çimento, su, agrega ve bu sistemin dispersiyonuna etki
Kolloidler Bir maddenin kendisi için çözücü olmayan bir ortamda 10-5 -10-7 cm boyutlarında dağılmasıyla oluşan çözeltiye kolloidal çözelti denir. Çimento, su, agrega ve bu sistemin dispersiyonuna etki
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ONDOKUZ MAYIS ÜNİVERSİTESİ KİMYA MÜHENDİSLİĞİ
 ONDOKUZ MAYIS ÜNİVERSİTESİ KİMYA MÜHENDİSLİĞİ 2013 - S A M S U N DAMITMA (DİSTİLASYON) Distilasyon, bir sıvının ısıtılması ve buharlaştırılmasından oluşmaktadır ve buhar bir distilat ürünü oluşturmak için
ONDOKUZ MAYIS ÜNİVERSİTESİ KİMYA MÜHENDİSLİĞİ 2013 - S A M S U N DAMITMA (DİSTİLASYON) Distilasyon, bir sıvının ısıtılması ve buharlaştırılmasından oluşmaktadır ve buhar bir distilat ürünü oluşturmak için
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Gazların Özellikler Barometre Basıncı Basit Gaz Yasaları
 İÇERİK Gazların Özellikler Barometre Basıncı Basit Gaz Yasaları Boyle Yasası Charles Yasası Avogadro Yasası Gaz Davranışları ve Standart Koşullar İdeal ve Genel Gaz Denklemleri Gaz Karışımları Gaz Yasalarına
İÇERİK Gazların Özellikler Barometre Basıncı Basit Gaz Yasaları Boyle Yasası Charles Yasası Avogadro Yasası Gaz Davranışları ve Standart Koşullar İdeal ve Genel Gaz Denklemleri Gaz Karışımları Gaz Yasalarına
ÇÖZELTİLERİN KOLİGATİF ÖZELLİKLERİ
 ÇÖZELTİLERİN KOLİGATİF ÖZELLİKLERİ Çözeltilerin sadece derişimine bağlı olarak değişen özelliklerine koligatif özellikler denir. Buhar basıncı düşmesi, Kaynama noktası yükselmesi, Donma noktası azalması
ÇÖZELTİLERİN KOLİGATİF ÖZELLİKLERİ Çözeltilerin sadece derişimine bağlı olarak değişen özelliklerine koligatif özellikler denir. Buhar basıncı düşmesi, Kaynama noktası yükselmesi, Donma noktası azalması
METEOROLOJİ. IV. HAFTA: Hava basıncı
 METEOROLOJİ IV. HAFTA: Hava basıncı HAVA BASINCI Tüm cisimlerin olduğu gibi havanın da bir ağırlığı vardır. Bunu ilk ortaya atan Aristo, deneyleriyle ilk ispatlayan Galileo olmuştur. Havanın sahip olduğu
METEOROLOJİ IV. HAFTA: Hava basıncı HAVA BASINCI Tüm cisimlerin olduğu gibi havanın da bir ağırlığı vardır. Bunu ilk ortaya atan Aristo, deneyleriyle ilk ispatlayan Galileo olmuştur. Havanın sahip olduğu
Hidrograf. Hiyetograf. Havza. Hidrograf. Havza Çıkışı. Debi (m³/s) Zaman (saat)
 Hidrograf Analizi Hidrograf Hiyetograf Havza Debi (m³/s) Havza Çıkışı Hidrograf Zaman (saat) Hidrograf Q Hiyetograf Hidrograf t Hidrograf Gecikme zamanı Q Pik Debi Yükselme Eğrisi (kabarma) A B C Alçalma
Hidrograf Analizi Hidrograf Hiyetograf Havza Debi (m³/s) Havza Çıkışı Hidrograf Zaman (saat) Hidrograf Q Hiyetograf Hidrograf t Hidrograf Gecikme zamanı Q Pik Debi Yükselme Eğrisi (kabarma) A B C Alçalma
Toprakta Kireç Tayini
 Toprakta Kireç Tayini Toprakta kireç tayininde genellikle kalsimetre düzeneği kullanılır ve % kireç miktarı CaCO 3 cinsinden ifade edilir. Elde edilen veriler doğrultusunda toprakların kireç içeriğine
Toprakta Kireç Tayini Toprakta kireç tayininde genellikle kalsimetre düzeneği kullanılır ve % kireç miktarı CaCO 3 cinsinden ifade edilir. Elde edilen veriler doğrultusunda toprakların kireç içeriğine
HPLC. Yüksek Performanslı Sıvı Kromatografisi
 HPLC Yüksek Performanslı Sıvı Kromatografisi HPLC Nedir? HPLC nin Kısımları: Hareketli Faz Rezervuarı Pompa Sistemi Numune enjeksiyon Sistemi Kolon Dedektör HPLC Çeşitleri HPLC Uygulamaları HPLC Yüksek
HPLC Yüksek Performanslı Sıvı Kromatografisi HPLC Nedir? HPLC nin Kısımları: Hareketli Faz Rezervuarı Pompa Sistemi Numune enjeksiyon Sistemi Kolon Dedektör HPLC Çeşitleri HPLC Uygulamaları HPLC Yüksek
BÖLÜM I GİRİŞ (1.1) y(t) veya y(x) T veya λ. a t veya x. Şekil 1.1 Dalga. a genlik, T peryod (veya λ dalga boyu)
 BÖLÜM I GİRİŞ 1.1 Sinyal Bir sistemin durum ve davranış bilgilerini taşıyan, bir veya daha fazla değişken ile tanımlanan bir fonksiyon olup veri işlemde dalga olarak adlandırılır. Bir dalga, genliği, dalga
BÖLÜM I GİRİŞ 1.1 Sinyal Bir sistemin durum ve davranış bilgilerini taşıyan, bir veya daha fazla değişken ile tanımlanan bir fonksiyon olup veri işlemde dalga olarak adlandırılır. Bir dalga, genliği, dalga
ÖĞRENME ALANI : FİZİKSEL OLAYLAR ÜNİTE 2 : KUVVET VE HAREKET
 ÖĞRENME ALANI : FİZİKSEL OLAYLAR ÜNİTE 2 : KUVVET VE HAREKET A BASINÇ VE BASINÇ BİRİMLERİ (5 SAAT) Madde ve Özellikleri 2 Kütle 3 Eylemsizlik 4 Tanecikli Yapı 5 Hacim 6 Öz Kütle (Yoğunluk) 7 Ağırlık 8
ÖĞRENME ALANI : FİZİKSEL OLAYLAR ÜNİTE 2 : KUVVET VE HAREKET A BASINÇ VE BASINÇ BİRİMLERİ (5 SAAT) Madde ve Özellikleri 2 Kütle 3 Eylemsizlik 4 Tanecikli Yapı 5 Hacim 6 Öz Kütle (Yoğunluk) 7 Ağırlık 8
1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları
 1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları Sol üstte yüzey seftleştirme işlemi uygulanmış bir çelik
1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları Sol üstte yüzey seftleştirme işlemi uygulanmış bir çelik
SIVILAR YÜZEY GERİLİMİ. Bir sıvı içindeki molekül diğer moleküller tarafından sarılmıştır. Her yöne eşit kuvvetle çekilir.daha düşük enerjilidir.
 SIVILAR YÜZEY GERİLİMİ Bir sıvı içindeki molekül diğer moleküller tarafından sarılmıştır. Her yöne eşit kuvvetle çekilir.daha düşük enerjilidir. Yüzeydeki molekül için durum farklıdır Her yönde çekilmediklerinden
SIVILAR YÜZEY GERİLİMİ Bir sıvı içindeki molekül diğer moleküller tarafından sarılmıştır. Her yöne eşit kuvvetle çekilir.daha düşük enerjilidir. Yüzeydeki molekül için durum farklıdır Her yönde çekilmediklerinden
DENEY 0. Bölüm 1 - Ölçme ve Hata Hesabı
 DENEY 0 Bölüm 1 - Ölçme ve Hata Hesabı Amaç: Ölçüm metodu ve cihazına bağlı hata ve belirsizlikleri anlamak, fiziksel bir niceliği ölçüp hata ve belirsizlikleri tespit etmek, nedenlerini açıklamak. Genel
DENEY 0 Bölüm 1 - Ölçme ve Hata Hesabı Amaç: Ölçüm metodu ve cihazına bağlı hata ve belirsizlikleri anlamak, fiziksel bir niceliği ölçüp hata ve belirsizlikleri tespit etmek, nedenlerini açıklamak. Genel
FİZİKOKİMYA I ARASINAV SORU VE CEVAPLARI 2013-14 GÜZ YARIYILI
 Soru 1: Aşağıdaki ifadeleri tanımlayınız. a) Sistem b)adyabatik sistem c) Kapalı sistem c) Bileşen analizi Cevap 1: a) Sistem: Üzerinde araştırma yapmak üzere sınırladığımız bir evren parçasına verilen
Soru 1: Aşağıdaki ifadeleri tanımlayınız. a) Sistem b)adyabatik sistem c) Kapalı sistem c) Bileşen analizi Cevap 1: a) Sistem: Üzerinde araştırma yapmak üzere sınırladığımız bir evren parçasına verilen
Vakum Teknolojisi * Prof. Dr. Ergun GÜLTEKİN. İstanbul Üniversitesi Fen Fakültesi
 Vakum Teknolojisi * Prof. Dr. Ergun GÜLTEKİN İstanbul Üniversitesi Fen Fakültesi Giriş Bilimsel amaçla veya teknolojide gerekli alanlarda kullanılmak üzere, kapalı bir hacim içindeki gaz moleküllerinin
Vakum Teknolojisi * Prof. Dr. Ergun GÜLTEKİN İstanbul Üniversitesi Fen Fakültesi Giriş Bilimsel amaçla veya teknolojide gerekli alanlarda kullanılmak üzere, kapalı bir hacim içindeki gaz moleküllerinin
MOTORLAR-5 HAFTA GERÇEK MOTOR ÇEVRİMİ
 MOTORLAR-5 HAFTA GERÇEK MOTOR ÇEVRİMİ Yrd.Doç.Dr. Alp Tekin ERGENÇ GERÇEK MOTOR ÇEVRİMİ Gerçek motor çevrimi standart hava (teorik) çevriminden farklı olarak emme, sıkıştırma,tutuşma ve yanma, genişleme
MOTORLAR-5 HAFTA GERÇEK MOTOR ÇEVRİMİ Yrd.Doç.Dr. Alp Tekin ERGENÇ GERÇEK MOTOR ÇEVRİMİ Gerçek motor çevrimi standart hava (teorik) çevriminden farklı olarak emme, sıkıştırma,tutuşma ve yanma, genişleme
Fiziksel özellikleri her yerde aynı olan (homojen) karışımlara çözelti denir. Bir çözeltiyi oluşturan her bir maddeye çözeltinin bileşenleri denir.
 GENEL KİMYA 1 LABORATUARI ÇALIŞMA NOTLARI DENEY: 8 ÇÖZELTİLER Dr. Bahadır KESKİN, 2011 @ YTÜ Fiziksel özellikleri her yerde aynı olan (homojen) karışımlara çözelti denir. Bir çözeltiyi oluşturan her bir
GENEL KİMYA 1 LABORATUARI ÇALIŞMA NOTLARI DENEY: 8 ÇÖZELTİLER Dr. Bahadır KESKİN, 2011 @ YTÜ Fiziksel özellikleri her yerde aynı olan (homojen) karışımlara çözelti denir. Bir çözeltiyi oluşturan her bir
Bölüm 2. Bir boyutta hareket
 Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
ONDOKUZ MAYIS ÜNİVERSİTESİ KİMYA MÜH. BÖLÜMÜ KML I LAB. ÜÇLÜ NOKTA SAPTANMASI DENEY FÖYÜ
 AMAÇ ONDOKUZ MAYIS ÜNİVERSİTESİ KİMYA MÜH. BÖLÜMÜ KML I LAB. ÜÇLÜ NOKTA SAPTANMASI DENEY FÖYÜ Çalışmanın amacı üç bileşenli sistemlerin incelenmesi ve bu sistemler için sıvı-sıvı faz diyagramlarının oluşturulmasıdır.
AMAÇ ONDOKUZ MAYIS ÜNİVERSİTESİ KİMYA MÜH. BÖLÜMÜ KML I LAB. ÜÇLÜ NOKTA SAPTANMASI DENEY FÖYÜ Çalışmanın amacı üç bileşenli sistemlerin incelenmesi ve bu sistemler için sıvı-sıvı faz diyagramlarının oluşturulmasıdır.
ÖĞRENME ALANI: Kuvvet ve Hareket 2.ÜNİTE: Kaldırma Kuvveti ve Basınç. Kaldırma Kuvveti
 ÖĞRENME ALANI: Kuvvet ve Hareket 2.ÜNİTE: Kaldırma Kuvveti ve Basınç Kaldırma Kuvveti - Dünya, üzerinde bulunan bütün cisimlere kendi merkezine doğru çekim kuvveti uygular. Bu kuvvete yer çekimi kuvveti
ÖĞRENME ALANI: Kuvvet ve Hareket 2.ÜNİTE: Kaldırma Kuvveti ve Basınç Kaldırma Kuvveti - Dünya, üzerinde bulunan bütün cisimlere kendi merkezine doğru çekim kuvveti uygular. Bu kuvvete yer çekimi kuvveti
KANTİTATİF ANALİTİK KİMYA PRATİKLERİ
 KANTİTATİF ANALİTİK KİMYA PRATİKLERİ Kantitatif analiz yöntemleri, maddenin miktar tayinlerine dayalı analiz yöntemleridir. Günümüzde miktar tayinine yönelik birçok yöntem bilinmektedir. Pratik çalışmalarda
KANTİTATİF ANALİTİK KİMYA PRATİKLERİ Kantitatif analiz yöntemleri, maddenin miktar tayinlerine dayalı analiz yöntemleridir. Günümüzde miktar tayinine yönelik birçok yöntem bilinmektedir. Pratik çalışmalarda
Mühendislikte İstatistik Yöntemler
 .0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
.0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ DOYMA BASINCI DENEY FÖYÜ 3
 BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ DOYMA BASINCI DENEY FÖYÜ 3 Hazırlayan: Arş. Gör. Gülcan ÖZEL 1. Deney Adı: Doyma çizgisi kavramı 2. Deney Amacı:
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ DOYMA BASINCI DENEY FÖYÜ 3 Hazırlayan: Arş. Gör. Gülcan ÖZEL 1. Deney Adı: Doyma çizgisi kavramı 2. Deney Amacı:
Aeresol. Süspansiyon. Heterojen Emülsiyon. Karışım. Kolloidal. Çözelti < 10-9 m Süspansiyon > 10-6 m Kolloid 10-9 m m
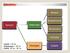 Aeresol Süspansiyon Karışım Heterojen Emülsiyon Kolloidal Çözelti < 10-9 m Süspansiyon > 10-6 m Kolloid 10-9 m - 10-6 m Homojen Çözelti Dağılan Faz Dağılma Fazı Kolloid Tipi katı katı,sıvı,gaz sol katı
Aeresol Süspansiyon Karışım Heterojen Emülsiyon Kolloidal Çözelti < 10-9 m Süspansiyon > 10-6 m Kolloid 10-9 m - 10-6 m Homojen Çözelti Dağılan Faz Dağılma Fazı Kolloid Tipi katı katı,sıvı,gaz sol katı
RADYASYON ÖLÇÜM YÖNTEMLERİ
 RADYASYON ÖLÇÜM YÖNTEMLERİ Prof. Dr. Doğan BOR ORANTILI SAYAÇLAR DERS 2 GAZ DOLDURULMUŞ DEDEKTÖRLERİN FARKLI ÇALIŞMA BÖLGELERİ N 2 = 10 000 N 1 = 100 İyonizasyon Bölgesi İyonizasyon akımı primer iyon çiftlerinin
RADYASYON ÖLÇÜM YÖNTEMLERİ Prof. Dr. Doğan BOR ORANTILI SAYAÇLAR DERS 2 GAZ DOLDURULMUŞ DEDEKTÖRLERİN FARKLI ÇALIŞMA BÖLGELERİ N 2 = 10 000 N 1 = 100 İyonizasyon Bölgesi İyonizasyon akımı primer iyon çiftlerinin
Gazların sıcaklık,basınç ve enerji gibi makro özelliklerini molekül kütlesi, hızı ve sayısı gibi mikroskopik özelliklerine bağlar.
 KİNETİK GAZ KURAMI Gazların sıcaklık,basınç ve enerji gibi makro özelliklerini molekül kütlesi, hızı ve sayısı gibi mikroskopik özelliklerine bağlar. Varsayımları * Gazlar bulundukları kaba göre ve aralarındaki
KİNETİK GAZ KURAMI Gazların sıcaklık,basınç ve enerji gibi makro özelliklerini molekül kütlesi, hızı ve sayısı gibi mikroskopik özelliklerine bağlar. Varsayımları * Gazlar bulundukları kaba göre ve aralarındaki
DENEY 3. MADDENİN ÜÇ HALİ: NİTEL VE NİCEL GÖZLEMLER Sıcaklık ilişkileri
 DENEY 3 MADDENİN ÜÇ HALİ: NİTEL VE NİCEL GÖZLEMLER Sıcaklık ilişkileri AMAÇ: Maddelerin üç halinin nitel ve nicel gözlemlerle incelenerek maddenin sıcaklık ile davranımını incelemek. TEORİ Hal değişimi,
DENEY 3 MADDENİN ÜÇ HALİ: NİTEL VE NİCEL GÖZLEMLER Sıcaklık ilişkileri AMAÇ: Maddelerin üç halinin nitel ve nicel gözlemlerle incelenerek maddenin sıcaklık ile davranımını incelemek. TEORİ Hal değişimi,
ATOM HAREKETLERİ ve ATOMSAL YAYINIM
 ATOM HAREKETLERİ ve ATOMSAL YAYINIM 1. Giriş Malzemelerde üretim ve uygulama sırasında görülen katılaşma, çökelme, yeniden kristalleşme, tane büyümesi gibi olaylar ile kaynak, lehim, sementasyon gibi işlemler
ATOM HAREKETLERİ ve ATOMSAL YAYINIM 1. Giriş Malzemelerde üretim ve uygulama sırasında görülen katılaşma, çökelme, yeniden kristalleşme, tane büyümesi gibi olaylar ile kaynak, lehim, sementasyon gibi işlemler
Analitik Kimya. (Metalurji ve Malzeme Mühendisliği)
 Analitik Kimya (Metalurji ve Malzeme Mühendisliği) 1. Analitik Kimya Maddenin bileşenlerinin belirlenmesi (teşhisi), bileşenlerinin ayrılması veya bileşenlerinin bağıl miktarlarının tayiniyle ilgilenir.
Analitik Kimya (Metalurji ve Malzeme Mühendisliği) 1. Analitik Kimya Maddenin bileşenlerinin belirlenmesi (teşhisi), bileşenlerinin ayrılması veya bileşenlerinin bağıl miktarlarının tayiniyle ilgilenir.
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
KROMATOGRAFIK AYIRMA İŞLEMLERI
 KROMATOGRAFIK AYIRMA İŞLEMLERI Kromatografinin Temeli Analizlenecek bir örnek karışımında bulunan bileşenlerin birbirinden ayrılması esasına dayanır. Kalitatif (nitel) ve kantitatif (nicel) analizler yapılabilir.
KROMATOGRAFIK AYIRMA İŞLEMLERI Kromatografinin Temeli Analizlenecek bir örnek karışımında bulunan bileşenlerin birbirinden ayrılması esasına dayanır. Kalitatif (nitel) ve kantitatif (nicel) analizler yapılabilir.
OPTİK ÇEVİRME DAĞILIMI VE DAİRESEL DİKROİZM
 1 OPTİK ÇEVİRME DAĞILIMI VE DAİRESEL DİKROİZM Ref. e_makaleleri, Enstrümantal Analiz Optik çevirme dağılımı ve dairesel dikroizm, her ikisi de, dairesel polarize ışının optikce aktif taneciklerle etkileşimine
1 OPTİK ÇEVİRME DAĞILIMI VE DAİRESEL DİKROİZM Ref. e_makaleleri, Enstrümantal Analiz Optik çevirme dağılımı ve dairesel dikroizm, her ikisi de, dairesel polarize ışının optikce aktif taneciklerle etkileşimine
02.04.2012. Düşey mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi
 Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
Korelasyon katsayısı (r)
 Korelasyon katsayısı (r) Açıklanabilen varyasyonun, açıklanamayan varyasyona oranı, korelasyon katsayısı olarak tanımlanır. N Σ xy Σx Σy r = [[N Σ x 2 (Σx) 2 ] [N Σy 2 (Σy) 2 ]] 1/2 1 Eğer doğrusal eğri,
Korelasyon katsayısı (r) Açıklanabilen varyasyonun, açıklanamayan varyasyona oranı, korelasyon katsayısı olarak tanımlanır. N Σ xy Σx Σy r = [[N Σ x 2 (Σx) 2 ] [N Σy 2 (Σy) 2 ]] 1/2 1 Eğer doğrusal eğri,
Termal Genleşme İdeal Gazlar Isı Termodinamiğin 1. Yasası Entropi ve Termodinamiğin 2. Yasası
 Termal Genleşme İdeal Gazlar Isı Termodinamiğin 1. Yasası Entropi ve Termodinamiğin 2. Yasası Sıcaklık, bir gaz molekülünün kütle merkezi hareketinin ortalama kinetic enerjisinin bir ölçüsüdür. Sıcaklık,
Termal Genleşme İdeal Gazlar Isı Termodinamiğin 1. Yasası Entropi ve Termodinamiğin 2. Yasası Sıcaklık, bir gaz molekülünün kütle merkezi hareketinin ortalama kinetic enerjisinin bir ölçüsüdür. Sıcaklık,
OPTİK Işık Nedir? Işık Kaynakları Işık Nasıl Yayılır? Tam Gölge - Yarı Gölge güneş tutulması
 OPTİK Işık Nedir? Işığı yaptığı davranışlarla tanırız. Işık saydam ortamlarda yayılır. Işık foton denilen taneciklerden oluşur. Fotonların belirli bir dalga boyu vardır. Bazı fiziksel olaylarda tanecik,
OPTİK Işık Nedir? Işığı yaptığı davranışlarla tanırız. Işık saydam ortamlarda yayılır. Işık foton denilen taneciklerden oluşur. Fotonların belirli bir dalga boyu vardır. Bazı fiziksel olaylarda tanecik,
Enerji iş yapabilme kapasitesidir. Kimyacı işi bir süreçten kaynaklanan enerji deyişimi olarak tanımlar.
 Kinetik ve Potansiyel Enerji Enerji iş yapabilme kapasitesidir. Kimyacı işi bir süreçten kaynaklanan enerji deyişimi olarak tanımlar. Işıma veya Güneş Enerjisi Isı Enerjisi Kimyasal Enerji Nükleer Enerji
Kinetik ve Potansiyel Enerji Enerji iş yapabilme kapasitesidir. Kimyacı işi bir süreçten kaynaklanan enerji deyişimi olarak tanımlar. Işıma veya Güneş Enerjisi Isı Enerjisi Kimyasal Enerji Nükleer Enerji
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
İSTATİSTİKSEL PROSES KONTROLÜ
 İSTATİSTİKSEL PROSES KONTROLÜ ZTM 433 KALİTE KONTROL VE STANDARDİZASYON PROF: DR: AHMET ÇOLAK İstatistiksel işlem kontrolü (İPK), işlemle çeşitli istatistiksel metotların ve analiz sapmalarının kullanımını
İSTATİSTİKSEL PROSES KONTROLÜ ZTM 433 KALİTE KONTROL VE STANDARDİZASYON PROF: DR: AHMET ÇOLAK İstatistiksel işlem kontrolü (İPK), işlemle çeşitli istatistiksel metotların ve analiz sapmalarının kullanımını
BÖLÜM 1: TEMEL KAVRAMLAR
 Sistem ve Hal Değişkenleri Üzerinde araştırma yapmak üzere sınırladığımız bir evren parçasına sistem, bu sistemi çevreleyen yere is ortam adı verilir. İzole sistem; Madde ve her türden enerji akışına karşı
Sistem ve Hal Değişkenleri Üzerinde araştırma yapmak üzere sınırladığımız bir evren parçasına sistem, bu sistemi çevreleyen yere is ortam adı verilir. İzole sistem; Madde ve her türden enerji akışına karşı
KİNETİK GAZ KURAMI. Doç. Dr. Faruk GÖKMEŞE Kimya Bölümü Hitit Üniversitesi Fen Edebiyat Fakültesi 1
 Kinetik Gaz Kuramının Varsayımları Boyle, Gay-Lussac ve Avagadro deneyleri tüm ideal gazların aynı davrandığını göstermektedir ve bunları açıklamak üzere kinetik gaz kuramı ortaya atılmıştır. 1. Gazlar
Kinetik Gaz Kuramının Varsayımları Boyle, Gay-Lussac ve Avagadro deneyleri tüm ideal gazların aynı davrandığını göstermektedir ve bunları açıklamak üzere kinetik gaz kuramı ortaya atılmıştır. 1. Gazlar
Termodinamik Termodinamik Süreçlerde İŞ ve ISI
 Termodinamik Süreçlerde İŞ ve ISI Termodinamik Hareketli bir pistonla bağlantılı bir silindirik kap içindeki gazı inceleyelim (Şekil e bakınız). Denge halinde iken, hacmi V olan gaz, silindir çeperlerine
Termodinamik Süreçlerde İŞ ve ISI Termodinamik Hareketli bir pistonla bağlantılı bir silindirik kap içindeki gazı inceleyelim (Şekil e bakınız). Denge halinde iken, hacmi V olan gaz, silindir çeperlerine
Kimyasal analiz : bir örnekteki bileşenleri v bileşenlerin konsantrasyonların bulmak için yapılan işlemi genel adıdır.
 Analitik Kimya Kimyanın, maddelerin hangi bileşenlerden ve bileşenlerin hangi oranlarda (bağıl miktarlarda) olduğunu inceleyen dalı Analitik Kimya olarak isimlendirilir. bir ürünün istenen kalitede olup
Analitik Kimya Kimyanın, maddelerin hangi bileşenlerden ve bileşenlerin hangi oranlarda (bağıl miktarlarda) olduğunu inceleyen dalı Analitik Kimya olarak isimlendirilir. bir ürünün istenen kalitede olup
BÖLÜM 1: TEMEL KAVRAMLAR
 BÖLÜM 1: TEMEL KAVRAMLAR Hal Değişkenleri Arasındaki Denklemler Aralarında sıfıra eşitlenebilen en az bir veya daha fazla denklem kurulabilen değişkenler birbirine bağımlıdır. Bu denklemlerden bilinen
BÖLÜM 1: TEMEL KAVRAMLAR Hal Değişkenleri Arasındaki Denklemler Aralarında sıfıra eşitlenebilen en az bir veya daha fazla denklem kurulabilen değişkenler birbirine bağımlıdır. Bu denklemlerden bilinen
GAZLAR GAZ KARIŞIMLARI
 DALTON KISMİ BASINÇLAR YASASI Aynı Kaplarda Gazların Karıştırılması Birbiri ile tepkimeye girmeyen gaz karışımlarının davranışı genellikle ilgi çekicidir. Böyle bir karışımdaki bir bileşenin basıncı, aynı
DALTON KISMİ BASINÇLAR YASASI Aynı Kaplarda Gazların Karıştırılması Birbiri ile tepkimeye girmeyen gaz karışımlarının davranışı genellikle ilgi çekicidir. Böyle bir karışımdaki bir bileşenin basıncı, aynı
( PİRUVİK ASİT + SU + ALKOL ) ÜÇLÜ SIVI-SIVI SİSTEMLERİNİN DAĞILIM DENGESİNİN İNCELENMESİ
 TOA17 ( PİRUVİK ASİT + SU + ALKOL ) ÜÇLÜ SIVI-SIVI SİSTEMLERİNİN DAĞILIM DENGESİNİN İNCELENMESİ B. Başlıoğlu, A. Şenol İstanbul Üniversitesi, Mühendislik Fakültesi, Kimya Mühendisliği Bölümü, 34320, Avcılar
TOA17 ( PİRUVİK ASİT + SU + ALKOL ) ÜÇLÜ SIVI-SIVI SİSTEMLERİNİN DAĞILIM DENGESİNİN İNCELENMESİ B. Başlıoğlu, A. Şenol İstanbul Üniversitesi, Mühendislik Fakültesi, Kimya Mühendisliği Bölümü, 34320, Avcılar
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ
 BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ MÜKEMMEL GAZ DENEY FÖYÜ 1.Deneyin Adı: Mükemmel bir gazın genişlemesi
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ MÜKEMMEL GAZ DENEY FÖYÜ 1.Deneyin Adı: Mükemmel bir gazın genişlemesi
1. HAFTA Giriş ve Temel Kavramlar
 1. HAFTA Giriş ve Temel Kavramlar TERMODİNAMİK VE ISI TRANSFERİ Isı: Sıcaklık farkının bir sonucu olarak bir sistemden diğerine transfer edilebilen bir enerji türüdür. Termodinamik: Bir sistem bir denge
1. HAFTA Giriş ve Temel Kavramlar TERMODİNAMİK VE ISI TRANSFERİ Isı: Sıcaklık farkının bir sonucu olarak bir sistemden diğerine transfer edilebilen bir enerji türüdür. Termodinamik: Bir sistem bir denge
Şekil 7.1 Bir tankta sıvı birikimi
 6 7. DİFERENSİYEL DENKLEMLERİN SAYISAL ÇÖZÜMLERİ Diferensiyel denklemlerin sayısal integrasyonunda kullanılabilecek bir çok yöntem vardır. Tecrübeler dördüncü mertebe (Runge-Kutta) yönteminin hemen hemen
6 7. DİFERENSİYEL DENKLEMLERİN SAYISAL ÇÖZÜMLERİ Diferensiyel denklemlerin sayısal integrasyonunda kullanılabilecek bir çok yöntem vardır. Tecrübeler dördüncü mertebe (Runge-Kutta) yönteminin hemen hemen
Bölüm 4 KAPALI SİSTEMLERİN ENERJİ ANALİZİ. Bölüm 4: Kapalı Sistemlerin Enerji Analizi
 Bölüm 4 KAPALI SİSTEMLERİN ENERJİ ANALİZİ 1 Amaçlar Özellikle otomobil motoru ve kompresör gibi pistonlu makinelerde yaygın olarak karşılaşılan hareketli sınır işi veya PdV işi olmak üzere değişik iş biçimlerinin
Bölüm 4 KAPALI SİSTEMLERİN ENERJİ ANALİZİ 1 Amaçlar Özellikle otomobil motoru ve kompresör gibi pistonlu makinelerde yaygın olarak karşılaşılan hareketli sınır işi veya PdV işi olmak üzere değişik iş biçimlerinin
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
ISI VE SICAKLIK. 1 cal = 4,18 j
 ISI VE SICAKLIK ISI Isı ve sıcaklık farklı şeylerdir. Bir maddeyi oluşturan bütün taneciklerin sahip olduğu kinetik enerjilerin toplamına ISI denir. Isı bir enerji türüdür. Isı birimleri joule ( j ) ve
ISI VE SICAKLIK ISI Isı ve sıcaklık farklı şeylerdir. Bir maddeyi oluşturan bütün taneciklerin sahip olduğu kinetik enerjilerin toplamına ISI denir. Isı bir enerji türüdür. Isı birimleri joule ( j ) ve
KİMYASAL ANALİZ KALİTATİF ANALİZ (NİTEL) (NİCEL) KANTİTATİF ANALİZ
 KİMYASAL ANALİZ KALİTATİF ANALİZ (NİTEL) KANTİTATİF ANALİZ (NİCEL) KANTİTATİF ANALİZ Bir numunedeki element veya bileşiğin bağıl miktarını belirlemek için yapılan analizlere denir. 1 ANALİTİK ANALİTİK
KİMYASAL ANALİZ KALİTATİF ANALİZ (NİTEL) KANTİTATİF ANALİZ (NİCEL) KANTİTATİF ANALİZ Bir numunedeki element veya bileşiğin bağıl miktarını belirlemek için yapılan analizlere denir. 1 ANALİTİK ANALİTİK
İletkenlik, maddenin elektrik akımını iletebilmesinin ölçüsüdür.
 İletkenlik, maddenin elektrik akımını iletebilmesinin ölçüsüdür. C= 1/R dir. Yani direncin tersidir. Birimi S.m -1 dir. (Siemens birimi Alman bilim insanı ve mucit Werner von Siemens e ithafen verilmiştir)
İletkenlik, maddenin elektrik akımını iletebilmesinin ölçüsüdür. C= 1/R dir. Yani direncin tersidir. Birimi S.m -1 dir. (Siemens birimi Alman bilim insanı ve mucit Werner von Siemens e ithafen verilmiştir)
Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta ( ):
 Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ
 BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METOTLAR II DOĞRUSAL ISI İLETİMİ DENEYİ 1.Deneyin Adı: Doğrusal ısı iletimi deneyi..
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METOTLAR II DOĞRUSAL ISI İLETİMİ DENEYİ 1.Deneyin Adı: Doğrusal ısı iletimi deneyi..
VİSKOZİTE SIVILARIN VİSKOZİTESİ
 VİSKOZİTE Katı, sıvı veya gaz halinde bütün cisimler, kitlelerinin bir bölümünün birbirine göre şekil ya da göreceli yer değiştirmelerine karşı bir mukavemet arz ederler. Bu mukavemet değişik türlerde
VİSKOZİTE Katı, sıvı veya gaz halinde bütün cisimler, kitlelerinin bir bölümünün birbirine göre şekil ya da göreceli yer değiştirmelerine karşı bir mukavemet arz ederler. Bu mukavemet değişik türlerde
Fizik 203. Ders 6 Kütle Çekimi-Isı, Sıcaklık ve Termodinamiğe Giriş Ali Övgün
 Fizik 203 Ders 6 Kütle Çekimi-Isı, Sıcaklık ve Termodinamiğe Giriş Ali Övgün Ofis: AS242 Fen ve Edebiyat Fakültesi Tel: 0392-630-1379 ali.ovgun@emu.edu.tr www.aovgun.com Kepler Yasaları Güneş sistemindeki
Fizik 203 Ders 6 Kütle Çekimi-Isı, Sıcaklık ve Termodinamiğe Giriş Ali Övgün Ofis: AS242 Fen ve Edebiyat Fakültesi Tel: 0392-630-1379 ali.ovgun@emu.edu.tr www.aovgun.com Kepler Yasaları Güneş sistemindeki
2. AKIŞKANLARDAN ISI AKIŞI İLKELERİ
 1 2. AKIŞKANLARDAN ISI AKIŞI İLKELERİ (Ref. e_makaleleri) Kimya mühendisliğinde çok sık karşılaşılan bir işlem, katı bir malzeme içinden geçen sıcak bir akışkan yoluyla, daha soğuk bir akışkana ısı transferidir.
1 2. AKIŞKANLARDAN ISI AKIŞI İLKELERİ (Ref. e_makaleleri) Kimya mühendisliğinde çok sık karşılaşılan bir işlem, katı bir malzeme içinden geçen sıcak bir akışkan yoluyla, daha soğuk bir akışkana ısı transferidir.
KMB0404 Kimya Mühendisliği Laboratuvarı III GAZ ABSORSPSİYONU. Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1
 GAZ ABSORSPSİYONU Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Kuru kolon boyunca havanın basınç değişimi ile kolon içinde aşağı yönde akan suya absorbe olan CO2 miktarını tespit
GAZ ABSORSPSİYONU Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Kuru kolon boyunca havanın basınç değişimi ile kolon içinde aşağı yönde akan suya absorbe olan CO2 miktarını tespit
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
DİŞLİ ÇARKLAR I: GİRİŞ
 DİŞLİ ÇARKLAR I: GİRİŞ Prof. Dr. İrfan KAYMAZ Mühendislik Fakültesi Makine Mühendisliği Bölümü Giriş Dişli Çarklar Bu bölüm sonunda öğreneceğiniz konular: Güç ve Hareket İletim Elemanları Basit Dişli Dizileri
DİŞLİ ÇARKLAR I: GİRİŞ Prof. Dr. İrfan KAYMAZ Mühendislik Fakültesi Makine Mühendisliği Bölümü Giriş Dişli Çarklar Bu bölüm sonunda öğreneceğiniz konular: Güç ve Hareket İletim Elemanları Basit Dişli Dizileri
SÜLEYMAN DEMİREL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMM 302 KİMYA MÜHENDİSLİĞİ LABORATUVARI-I ÖĞÜTME ELEME DENEYİ
 SÜLEYMAN DEMİREL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMM 302 KİMYA MÜHENDİSLİĞİ LABORATUVARI-I ÖĞÜTME ELEME DENEYİ ISPARTA, 2014 ÖĞÜTME ELEME DENEYİ DENEYİN AMACI: Kolemanit mineralinin
SÜLEYMAN DEMİREL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMM 302 KİMYA MÜHENDİSLİĞİ LABORATUVARI-I ÖĞÜTME ELEME DENEYİ ISPARTA, 2014 ÖĞÜTME ELEME DENEYİ DENEYİN AMACI: Kolemanit mineralinin
5. AKIM İÇİNDEKİ CİSİMLERDEN AKIŞ. (Ref. e_makaleleri)
 1 5. AKIM İÇİNDEKİ CİSİMLERDEN AKIŞ (Ref. e_makaleleri) (Ref. e_makaleleri)bir akışkanın, içinde bulunan katı cisim üzerinde akım yönünde meydana getirdiği kuvvete "engelleme = drag" denir. Cismin duvarı
1 5. AKIM İÇİNDEKİ CİSİMLERDEN AKIŞ (Ref. e_makaleleri) (Ref. e_makaleleri)bir akışkanın, içinde bulunan katı cisim üzerinde akım yönünde meydana getirdiği kuvvete "engelleme = drag" denir. Cismin duvarı
TAŞINIMIN FİZİKSEL MEKANİZMASI
 BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
KAYMA GERİLMESİ (ENİNE KESME)
 KAYMA GERİLMESİ (ENİNE KESME) Demir yolu traversleri çok büyük kesme yüklerini taşıyan kiriş olarak davranır. Bu durumda, eğer traversler ahşap malzemedense kesme kuvvetinin en büyük olduğu uçlarından
KAYMA GERİLMESİ (ENİNE KESME) Demir yolu traversleri çok büyük kesme yüklerini taşıyan kiriş olarak davranır. Bu durumda, eğer traversler ahşap malzemedense kesme kuvvetinin en büyük olduğu uçlarından
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
Zeminlerin Sıkışması ve Konsolidasyon
 Zeminlerin Sıkışması ve Konsolidasyon 2 Yüklenen bir zeminin sıkışmasının aşağıdaki nedenlerden dolayı meydana geleceği düşünülür: Zemin danelerinin sıkışması Zemin boşluklarındaki hava ve /veya suyun
Zeminlerin Sıkışması ve Konsolidasyon 2 Yüklenen bir zeminin sıkışmasının aşağıdaki nedenlerden dolayı meydana geleceği düşünülür: Zemin danelerinin sıkışması Zemin boşluklarındaki hava ve /veya suyun
DENEYSELVERİLERİN GRAFİĞE AKTARILMASI
 DENEYSELVERİLERİN GRAFİĞE AKTARILMASI 1 Değişken (variable): Miktarı, yani sayısal bir değeri ifade etmektedir. Cebirsel eşitliklerde değişkenler, Latin alfabesinin başlangıç ve son harfleri ile ifade
DENEYSELVERİLERİN GRAFİĞE AKTARILMASI 1 Değişken (variable): Miktarı, yani sayısal bir değeri ifade etmektedir. Cebirsel eşitliklerde değişkenler, Latin alfabesinin başlangıç ve son harfleri ile ifade
