The Mathematics-Oriented Epistemological Belief Scale (MOEBS): Validity and Reliability Study
|
|
|
- Yonca Zarakolu
- 10 yıl önce
- İzleme sayısı:
Transkript
1 Kuramsal Eğitimbilim Drgisi, 6(3), , Tmmuz 2013 Journal of Thortical Educational Scinc, 6(3), , July 2013 [Onlin]: DOI numbr: Th Mathmatics-Orintd Epistmological Blif Scal (MOEBS): Validity and Rliability Study Mustafa İLHAN Bayram ÇETİN Rcivd: 30 Novmbr 2012 Accptd: 09 May 2013 ABSTRACT:Th prsnt study aims to dvlop a valid and rliabl instrumnt to masur high school studnts' mathmatics-orintd pistmological blifs. Th participants wr 406 high school studnts studying in Batman and Diyarbakır infall of 2012 who wr considrd undr two sparat study groups. Exprt rviw was don to chck contnt and fac validity. Th xploratory factor analysis (EFA) and confirmatory factor analysis (CFA) wr prformd in ordr to chck construct validity. As a rsult of th EFA, a 27-itmthr-factor structur mrgd, xplaining 40.57%of varianc. Th mrging factors wr calld as a blif of that larning dpnds on ffort (BLDE), a blif of that larning dpnds on talnt (BLDT), and a blif of that thr is only on truth (BTOOT). Th findings indicatd all 27 itms and a thr-factor structur rlatd to th MOEBS hav satisfactory indics of goodnss of fit.as a rsult of rliability analysis, it was dtrmind that intrnal consistncy and tst-rtst cofficints wr accptabl.th findings of th itm analyss showd that all of th itms wr discriminatory. In light of ths findings, it can b argud that th scal is rliabl and valid and can b usd to masur high school studnts mathmatics-orintd pistmological blifs. Kywords: mathmatics-orintd pistmological blif, th mathmatics-orintd pistmological blif scal, rliability, validity. Extndd Abstract Purpos and Significanc:A rviw of thlitratur rvald that an instrumnt to masur mathmatics-orintd pistmological blifs has bn lacking inturkish cultur.mathmatics-orintd pistmological blifs ar significant in mathmatics ducation sinc dtrmining mathmatics-orintd pistmological blifs may guid dcisions on how to support studnts, how to organiz larning nvironmnts, and how to dvlop mathmatics curricula.thrfor, it is of grat significanc to dvlopa Turkish instrumnt to dtrmin studnts pistmological blifsrgarding mathmatics.in this rspct, th prsnt study aims to dvlop a valid and rliabl instrumnt to masur mathmatics-orintd pistmological blifs. Mthod:Th participants wr 406 high school studnts studying in Batman and Diyarbakır in fall of 2012 who wr considrd undr two sparat study groups.th first group comprisd 315 studnts, 182 of whom wr fmal (57.80%) and 133 wr mal (42.20%), who wr studying in fiv diffrnt high schools in Batman, Turky. Data obtaind from this group of studnts wr analyzd to chck construct validity, concurrnt validity,calculat intrnal consistncy cofficints and to do itm analysis. Th scond group comprisd 91 studnts, 39 of whom wr fmal (38.46%) and 52 of Rs. Assist., Dicl Univrsity, Diyarbakir, Turky, [email protected] Assoc.Prof. Dr., Gaziantp Univrsity, Gaziantp, Turky, [email protected] Copyright 2013 by AKU ISSN:
2 360 Mustafa İLHAN & Bayram ÇETİN whom wr mal (57.14%), who wr studying in Silvan Anatolian Tachr High School, Diyarbakır, Turky. Data obtaind from this group wr analyzd to chck tstrtst rliability. Th MOEBS was dvlopd upon th BLDE, BLDT and BTOOT subscals dvlopd by Schommr (1990) and adaptd into Turkish by Dryakulu and Büyüköztürk (2002, 2005).11 itms undr th BLDE, 10 itms undr th BLDT, and 14 itms undr th BTOOTformd an itm pool of 35 itms. Exprt rviw was don to chck contnt and fac validity. Th xploratory factor analysis (EFA) and confirmatory factor analysis (CFA) wr prformd in ordr to chck construct validity. In trms of concurrnt validity, th corrlation btwn studnts' scors obtaind from th MOEBSand mathmatics achivmnt scors was calculatd.studnts prvious yar GPA scors of mathmatics wr considrd as mathmatics achivmnt scors. Considring th fact that th BLDEscors indicat wll-dvlopd pistmological blifsand high scors from th BLDT and th BTOOT indicat undrdvlopd pistmological blifs, it was hypothsizd that a positiv rlationship will b btwn th BLDE and mathmatics achivmnt, and a ngativ rlationship will bbtwn th BLDT and th BTOOTand mathmatics achivmnt. Thrliability cofficints wr calculatd by mans of intrnal consistncy and tst-rtst mthod.in ordr to dtrminitms discriminatory and prdictiv powr, scors of both top and bottom 27% of groups wr compard and corrctd itm-total corrlations wr prformd. Rsults: According to th first EFA rsults, a thr-factor structur xplaining 37.90% of total varianc mrgd. Sinc th factor loads of itm 21 and 23 wr blow.30and itm 22 was not thorticallysupportd by its factor, ths itms wr xcludd from th instrumnt.aftr rmoving ths thr itms, EFA was prformd again and also, a thr-factor structur xplaining 40.57% of total varianc mrgd.taking contnt and thortical background into account, th first factor was calld as th BLDE, th scond factor th BLDT, and th third factor th BTOOT. Th BLDE comprisd 10 itms and xplaind 16.27% of total varianc. Th factor loads of th itms in th BLDE varid btwn.54 and.76. Th BLDT comprisd 10 itms and xplaind 14.12% oftotal varianc. Th factor loads of th itms in th BLDT varid btwn.42 and.70. Th BTOOT comprisdsvn itms and xplaind 10.19% of total varianc. Th factor loads of th itms in th BTOOT varid btwn.42 and.74. In ordr to undrstand whthr all 27 itms and a thr-factor structur provid satisfactory indics of goodnss of fit and to show furthr vidnc for construct validity, CFA was prformd. Th findings obtaind from CFA showd that th scal has satisfactory indics of goodnss of fit. According to th rsults of concurrnt validity,thr is a positiv rlationship btwn th BLDE and mathmatics achivmnt [n=315, r=.48, p<.001], and a ngativ rlationship btwn th BLDT, th BTOOT, and mathmatics achivmnt [n=315, r=-.25 p<.001, r=-.26, p<.001 rspctivly].ths findings provd that th MOEBS has concurrnt validity.th rliability of th MOEBS was chckd by mans of intrnal consistncy and tst-rtst rliability.th intrnal consistncy cofficints wr found to b.84 for th BLDE,.81 for th BLDT, and.71 for th BTOOT. In ordr to chck tst-
3 Matmatik Odaklı Epistmolojik İnanç Ölçği 361 rtst rliability, th scal was administrd to 100 studnts twic in a two-wk intrval.in ordr to dmonstrat consistncy btwn th first and th scond administration, th corrlation btwn scors obtaind from both two practics was calculatd. Tst-rtst cofficints wr found to b.96 for th BLDE,.95 for th BLDT and.95 for th BTOOT. Givn that scals with a rliability cofficint of.70 and highr ar rgardd as rliabl, it can b argud that th calculatd rliability cofficints wr high.in ordr to idntifydiscriminatory and prdictiv powr of th itms, corrctditmtotal corrlations wrcalculatd and both top and bottom 27% of groups wr compard. Parson Product Momnt Corrlation was usd to dtrmin corrctd-itm total corrlation. To compar both top and bottom 27% of groups, indpndnt-sampls ttst was prformd. In itm analysis, it was found out that itm-total corrlations varid btwn.27 and.66 and diffrncs btwn both top and bottom 27% of groups wr significant for all itms. Discussion and Conclusions:In this rsarch, th findings from statistical analyss of psychomtric charactristics of th MOEBS rvald that th scal can b usd as a valid and rliabl instrumnt to masur studnts pistmological blifs rlatd to mathmatics. As a rsult of th prsnt study which aims to contribut to th Turkish litratur with th MOEBS, it can b argud that an instrumnt which has satisfactory psychomtric charactristicsto masur studnts blifs on mathmatical knowldg and mathmaticslarning has bn dvlopd. In addition, du to th fact that th prsnt study was carrid out with mrly high school studnts, it might b implid that th MOEBS is an instrumnt whos validity has bn chckd only with high school studnts. In this rspct, futur studis should chck rliability and validity of th scal with diffrnt sampls.
4 362 Mustafa İLHAN & Bayram ÇETİN Matmatik Odaklı Epistmolojik İnanç Ölçği (MOEİÖ): Gçrlik v Güvnirlik Çalışması Mustafa İLHAN Bayram ÇETİN Makal Göndrm Tarihi: 30 Kasım 2012 Makal Kabul Tarihi: 09 Mayıs 2013 ÖZET:Bu araştırmada ortaöğrtim öğrncilrinin matmatik odaklı pistmolojik inançlarını ölçmy olanak tanıyacak gçrli v güvnilir bir ölçm aracının gliştirilmsi amaçlanmaktadır. Araştırma, ğitimöğrtim yılı güz yarıyılında Batman v Diyarbakır illrind toplam 406 ortaöğrtim öğrncisindn oluşan iki ayrı çalışma grubu üzrind yürütülmüştür. Araştırmada, ölçğin kapsam v görünüş gçrliği için uzman görüşün başvurulmuş, yapı gçrliği için Açımlayıcı Faktör Analizi (AFA) v Doğrulayıcı Faktör Analizi (DFA) uygulanmıştır. AFA sonucunda, toplam varyansın %40.57 sini açıklayan, 27 madd v üç faktördn oluşan bir yapı ld dilmiştir. Ortaya çıkan faktörlr,öğrnmnin Çabaya Bağlı Olduğuna İnanç (ÖÇBOİ), Öğrnmnin Ytnğ Bağlı Olduğuna İnanç (ÖYBOİ) v Tk Bir Doğrunun Var Olduğuna İnanç (TBDVOİ) olarak adlandırılmıştır. DFA dan ld diln bulgular, MOEİÖ y ilişkin 27 madd v üç faktörlü yapının ytrli uyum indkslrin sahip olduğunu göstrmiştir. ÖÇBOİ, ÖYBOİ v TBDVOİ alt ölçklrinin güvnirliği iç tutarlık v tst-tkrar tst yöntmlriyl inclnmiş v hsaplanan güvnirlik katsayılarının kabul dilbilir sınırlar içrisind yr aldığı blirlnmiştir. Madd analizindn ld diln bulgular, ölçkt yr alan maddlrin tamamının ayırt dici olduğunu göstrmiştir. Bu bulgulara dayanarak, ölçğin ortaöğrtim öğrncilrinin matmatik odaklı pistmolojik inançlarını ölçmk amacıyla kullanılabilck gçrli v güvnilir bir ölçm aracı olduğu söylnbilir. Anahtar Sözcüklr: matmatik odaklı pistmolojik inanç, matmatik odaklı pistmolojik inanç ölçği, gçrlik, güvnirlik. Giriş İnançlar, biryin tcrüblri aracılığıyla şkillnn (Nspor, 1987; Pajars, 1992) tutum, davranış (Fischbin & Ajzn, 1975; Hazır-Bıkmaz, 2002; Mansour, 2009; Olson, Ros, & Zanna, 1996; Pintrich & Schunk, 2002), motivasyon (Dwck & Lggtt, 1988) v zihinsl sürçlrini tkilyn (Schommr, 1998), yaşamda karşılaştığı hr türlü olay, olgu, kişi ya da nsnyi nasıl algıladığını, anlamlandırdığını, ona karşı nasıl davrandığını blirlyn (Dryakulu, 2006; Fishbin & Ajzn, 1975; Pajars, 1992) v biry tarafından kuşku duyulmaksızın doğru olduğu varsayılan (Dryakulu, 2006; Koballa & Crowly, 1985; Krows, 1999) içsl kabullr ya da önrmlr olarak tanımlanmaktadır (Dryakulu, 2004; Olivr & Koballa, 1992; Richardson, 2003). İnançların birylrin düşünc v davranışları üzrind sahip olduğu bu güçlü blirlyici tki, ğitimcilrin öz ytrlik inancı, zkâya yönlik inanç, öğrnmy yönlik inanç gibi birçok farklı inancı öğrnm v öğrtm sürçlri açısından dikkat almalarını zorunlu kılmaktadır (Dryakulu, 2006). Öğrnm-öğrtm sürcind dikkat alınması grkn inançlardan biri d pistmolojik inançlardır (Schommr, Crous, & Rhods, 1992, Tsai, 2000). Epistmolojik inançlar, bilginin doğası v nasıl ld dildiği il ilgili inançlar olup(bndixn, Dunkl,& Schraw, 1994; Hofr & Pintrich, 1997, Prry, 1981; Schommr, 1994) öğrncilrin akadmik prformanslarını (Hofr, 2000; Rukavina & Danman, 1996; Ryan, 1984, Schraw, Bndixn, & Dunkl, 2002), öğrnm Araş. Gör., Dicl Ünivrsitsi, [email protected] Doç. Dr., Gaziantp Ünivrsitsi, [email protected]
5 Matmatik Odaklı Epistmolojik İnanç Ölçği 363 yaklaşımlarını (Cano, 2005; Phan, 2008),motivasyonlarını (Buhl & Alxandr, 2005) biliş v bilişüstü stratjilrini (Paulsn & Fldman, 1999) v problm çözm bcrilrini (Aksan & Sözr, 2007; Bndixn & Schraw, 2001) tkilmktdir. Epistmolojik inançlar, ilk olarak Prry (1970) tarafından inclnmiştir. Prry (1970),ünivrsitd öğrnim görn rkk öğrncilrin pistmolojik inançlarını boylamsal olarak incldiği araştırma sonucunda, pistmolojik inançların dört tml inanç çrçvsind ilrldiğini rapor tmiştir. Prry (1970) tarafından ortaya konulan bu rapor, pistmolojik inançların glişimin ilişkin ilri sürüln ilk modl olma özlliği taşımaktadır. Bu modl gör, pistmolojik inançlar; ikicilik (dualism), çoğulculuk (multiplism), görclilik (rlativism) v bağlılık (commitmnt) olmak üzr glişimsl bir syir izlyn dört düzydn oluşmaktadır. Bu düzylrdn ilki, bilginin doğru/yanlış şklind mutlak grçklrdn oluştuğu v uzmanlar tarafından birylr aktarılabildiği inancını yansıtan ikiciliktir. İkiciliktn sonra, kişisl görüşlrin v mutlak doğruların birlşimindn mydana gln çoğulculuk düzyi yr almaktadır. Çoğulculuk, birtakım mutlak doğruların olduğunu, bununla birlikt bazı şylrin ksin olarak bilinmycği inancını yansıtmaktadır. Prry(1970) in modlin gör, pistmolojik inançların glişimin ilişkin üçüncü düzy, birylrin bilgiyi birysl olarak yapılandırdığı inancını yansıtan görcliliktir. Görcliliğin tmlind, doğruların birylrin kişisl tcrüblri v yorumları il ilişkili olduğu, bu ndnl mutlak doğruların bulunmadığı v asla olmayacağı anlayışı yatmaktadır. Prry (1970) tarafından ön sürüln modlin son düzyini bağlılık oluşturmaktadır. Bağlılık düzyind, görcli düşünm dvam tmkl brabr, bazı inançlar diğrlrindn daha dğrli görülmkt v bu inançlara snk bir biçimd inanılmaktadır. Prry nin çalışmasının yalnızca ünivrsitd öğrnim görn rkk katılımcılar il sınırlı tutulması, Blnky, Clinchy, Goldbrgr v Tarul (1986) tarafından bir sınırlılık olarak yorumlanmıştır. Blnky v diğrlri (1986), bu sınırlılığın aşılabilmsi için grçklştirdiklri çalışmada, akadmik gçmişi olan v olmayan bayan katılımcılardan oluşan 135 kişilik bir gruba ahlâki, bilişsl v kimlik glişimini yansıtan açık uçlu sorular yönltmişlrdir. Eld diln vrilrin analizi sonucunda, pistmolojik inançların glişimin ilişkin Prry (1970) tarafından önriln modl bnzr bir sınıflama yapılmıştır. Bu sınıflamaya gör, pistmolojik inançlar; sssizlik (silnc), kabul diln bilgi (rcivd bilgi), öznl bilgi (subjctiv), işlmsl bilgi (procdural) v yapılandırılmış bilgi (constructd) olmak üzr bş düzyli bir yapıya sahiptir. Sssizlik düzyind birylr sssiz v pasif bir duruş srgilr. Kabul diln bilgi düzyi, Prry (1970) tarafından ön sürüln ikiciliğ bnzmktdir. Birylr bu düzyd, bilginin ksin v mutlak olduğuna inanır v bilgiyi uzman otoritsindn alan bir konumdadırlar. Öznl bilgi düzyi, Prry(1970) in modlindki çoğulculuğa karşılık glmktdir. Birylr bu düzyd, bilgiy ilişkin kişisl v öznl bir bakış açısına sahiptirlr. İşlmsl bilgi düzyi, Prry (1970) tarafından görclilik olarak ifad diln düzy karşılık glmktdir. Birylr bu düzyd, bilgiy ilişkin bağımsız, nsnl v lştirl bir bakış açısına sahiptirlr. Yapılandırılmış bilgi düzyi is, Prry (1970) tarafından bağlılık
6 364 Mustafa İLHAN & Bayram ÇETİN olarak ifad diln düzy bnzmktdir. Bu düzyd birylr, bilginin yapılandırıldığı v bu yapılandırma sürcind biryin aktif bir rol aldığı inancına sahiptilr. Prry (1970) v Blnky v diğrlri (1986) tarafından pistmolojik inançlara ilişkin ilri sürüln düzylr bnzr bir diğr sınıflama, Baxtr Magolda (1992) tarafından yapılmıştır. Baxtr Magolda, 51 i bayan v 50 si rkk olmak üzr toplam101 ünivrsit öğrncisi il bş yıl sürn boylamsal bir çalışma grçklştirmiştir. Çalışma kapsamında, hr yıl öğrncilrl, pistmolojik inançlarını yansıtan kısa cvaplı v açık uçlu sorulardan oluşan görüşmlr yapılmıştır. Çalışmada sonucunda, pistmolojik inançlar; ksinlik (absolut), gçiş (transitional), bağımsız (indpndnt) v bağlamsal (commitmnt) olarak adlandırılan dört boyut il açıklanmıştır. Bilginin ksinliğin inananlar, tüm bilgilrin mutlak olduğu, uzmanların tüm doğruları bildiği, biryin görvinin uzmanlar tarafından aktarılan bilgilri zbrlmk olduğu şklind bir anlayışa sahiptirlr. Bilginin gçişliğin inananlar, uzmanların hr şyi bilmdiklrini, bilginin blirsizliğini v ksin olmadığını anlamaya başlarlar. Bilginin bağımsızlığına inananlar, bilginin büyük bir bölümünün ksin olmayan içriklrdn oluştuğu v uzmanların bilginin tk kaynağı olmadığı şklind bir anlayışa sahiptirlr. Bağlamsal bilgiy inanlar, bilginin doğasında ksinlik olmadığı anlayışına sahip olmakla birlikt, l alındığı içriğ bağlı olarak bazı bilgilrin diğrlrindn daha dğrli olabilcğini düşünürlr. Prry (1970), Blnky v diğrlri (1986) v Baxtr Mogalda (1994) tarafından ön sürüln modllrd, pistmolojik inançlar, bilginin doğası il ilgili inançlar olarak l alınmıştır. Schommr (1990), pistmolojik inançları bilginin doğası il ilgili inançlarla sınırlayan bu modllrin, öğrnmnin doğası hakkındaki inançları açıklamada ytrsiz kaldığını ifad tmiştir. Bu ytrsizliğin gidrilbilmsi için, Schommr (1990) pistmolojik inançları, bilginin doğası v öğrnmnin doğası hakkındaki inançlardan oluşan bir inanç sistmi olarak kavramsallaştırmıştır. Bilginin doğası il ilgili inançlar bilginin yapısı, bilginin ksinliği, bilginin kaynağı boyutlarından mydana glirkn; öğrnmnin doğası il ilgili inançlar öğrnm ytnği v öğrnm hızı boyutlarından oluşmaktadır. Bilginin yapısı il ilgili glişmmiş pistmolojik inançlara sahip birylr bilginin basit olduğunu düşünürkn, bilginin yapısı il ilgili glişmiş pistmolojik inançlara sahip birylr bilginin karmaşık bir yapıya sahip olduğuna inanırlar. Bilginin ksinliği il ilgili glişmmiş pistmolojik inançlara sahip birylr, bilginin mutlak olduğunu düşünürkn; bilginin ksinliği il ilgili glişmiş pistmolojik inançlara sahip birylr bilginin dğişbilir bir yapıya sahip olduğuna inanırlar. Bilginin kaynağı il ilgili glişmmiş pistmolojik inançlara sahip birylr, bilginin uzmanlar tarafından aktarıldığını düşünürkn; bilginin kaynağı il ilgili glişmiş pistmolojik inanca sahip birylr bilginin biry tarafından yapılandırıldığına inanırlar. Öğrnm ytnği il ilgili glişmmiş pistmolojik inanca sahip birylr öğrnm ytnğinin doğuştan gln dğiştirilmz bir özllik olduğuna inanırkn; öğrnm ytnği il ilgili glişmiş pistmolojik inanca sahip birylr öğrnm ytnğinin gliştirilbilir bir özllik olduğuna inanırlar. Öğrnm hızı il ilgili glişmmiş pistmolojik inanca sahip birylr, öğrnmnin hmn mydana gldiği v hmn grçklşmyn öğrnmlrin
7 Matmatik Odaklı Epistmolojik İnanç Ölçği 365 bir daha grçklşmycği inancına sahipkn; öğrnm ytnği il ilgili glişmiş pistmolojik inanca sahip birylr öğrnmnin yavaş yavaş grçklştiğini düşünürlr. Schommr (1990), pistmolojik inançlar il ilgili blirldiği kavramsal çrçvy dayanarak pistmolojik inançları ölçmy olanak tanıyacak bir ölçk gliştirmiştir. Gliştirdiği ölçğin gçrliğini inclmk üzr uyguladığı faktör analizi sonucunda, bş boyutlu torik yapıdan farklı olarak 63 madd v dört faktördn mydana gln bir yapı ld tmiştir. Schommr(1994) gör, pistmolojik inançlar az ya da çok birbirindn bağımsızdır v pistmolojik inançlara ilişkin farklı boyutlar ş zamanlı olarak glişmybilir. Örnğin, bir biry bilginin yapısı il ilgili glişmiş pistmolojik inançlara sahip ikn, bilginin ksinliği il ilgili glişmmiş pistmolojik inançlara sahip olabilir. Bir başka dyişl, bilginin karmaşık v iç iç gçmiş olduğuna inanan bir biry aynı zamanda bilginin asla dğişmycğin d inanabilir. Dolayısıyla biryin pistmolojik inançlarının anlaşılabilmsi için pistmolojik inanç ölçğinin farklı boyutlarından alınan puanların ayrı ayrı dğrlndirilmsi grkmktdir. Schommr (1990) tarafından gliştiriln pistmolojik inanç ölçği daha sonra birçok araştırmacı tarafından kullanılmış v ölçğin gçrliği farklı örnklmlr üzrind tst dilmiştir (Jhng, Johnson, & Andrson, 1993; Schraw, Bndixn, & Dunkl, 2002; Wood & Kardash, 2002). Epistmolojik inanç ölçğinin Türk kültürün uyarlaması is, Dryakulu v Büyüköztürk (2002, 2005) tarafından yapılmıştır. Uyarlama çalışmasından diln bulgular, pistmolojik inanç ölçğinin Türkç formunun Öğrnmnin Çabaya Bağlı Olduğuna İnanç (ÖÇBOİ), Öğrnmnin Ytnğ Bağlı Olduğuna İnanç (ÖYBOİ) v Tk Bir Doğrunun Var Olduğuna İnanç (TBDVOİ) şklind üç boyutlu bir yapıya sahip olduğunu göstrmiştir. Epistmolojik inançların şkillnmsind kültürl özlliklr önmli tkiy sahip olduğundan (Buhl & Alxandr, 2006; Chan & Elliot, 2004; Schommr, 2004) Türk kültüründpistmolojik inançlar il ilgili yapılan birçok araştırmada (Başçiftçi-Gülç, Akdoğan, &Koç, 2011; Dmirci, Türl, &Özmn, 2010; Ern, 2006; Hacıömroğlu, 2011; Özşkr, Canpolat, &Yıldız, 2011; Yılmaz, 2007) pistmolojik inanç ölçğinin Türkçy uyarlanması sonucu ortaya çıkan ÖÇBOİ, ÖYBOİ v TBDVOİ boyutları tml alınmıştır. Epistmolojik inançların boyutlarıyla birlikt, araştırmacıların pistmolojik inançlara ilişkin farklı görüşlr sahip olduğu bir diğr konu pistmolojik inançların gnl mi yoksa alan odaklı mı olduğuyla ilgilidir (Buhl & Alxandr, 2002; Eynd, Cort,& Vrschaffl, 2006; Gill, Ashton,& Algina, 2004; Hammr, 1994; Limon, 2006; Stockon, 2010). Örnğin, Schommr v Walkr (1995) pistmolojik inançların bir alana özgü olmasından ziyad, farklı alanlara gnllnbilcğini ifad drkn; Ruddick (1996), Caldrhad (1996), Hofr v Pintrich (1997), Mori (1997) v Buhl v Alxandr (2004) pistmolojik inançların alana özgü olduğunu savunmuştur. Bu durum, pistmolojik inançların gnl mi yoksa alan odaklı mı l alınmasının daha doğru olacağını ortaya koymak üzr grup içi v gruplar arası dsnd çşitli araştırmaların yapılmasına ndn olmuştur (Muis, Bndixn,& Harl, 2006). Epistmolojik inançlarla ilgili olarak grup içi dsnd grçklştiriln araştırmalarda, öğrncilrin gnl v alan odaklı pistmolojik inançları arasında anlamlı farklılıkların
8 366 Mustafa İLHAN & Bayram ÇETİN bulunduğu blirlnmiştir (Brs, 1988; Buhl, Alxandr,& Murphy, 2002; Hofr, 2000; Mori, 1999; Roth & Roychoudhury, 1994; Schonfld, 1989). Bnzr şkild, pistmolojik inançlar il ilgili gruplar arası dsnd grçklştiriln çalışmalar, farklı alanlarda öğrnim görn öğrncilrin gnl pistmolojik inançları arasında anlamlı farklılıklar bulunduğunu göstrmiştir (Aypay, 2011; Can &Arabacıoğlu, 2009; Dryakulu &Büyüköztürk, 2005; Enman & Lupart, 2000; Ern, 2006;Jhng, Johnson, & Andrson, 1993; Kurt, 2009; Paulsn& Wlls, 1997; Strobl, Crnusca, & Jonassn, 2004). Söz konusu araştırmalardan ld diln bulgular, gnl pistmolojik inançların yanı sıra alan odaklı pistmolojik inançların da dikkat alınması grktiği yönündki inançları güçlndirmiştir. Buna bağlı olarak, farklı alanlara yönlik pistmolojik inançları blirlmk amacıyla kullanılabilck alan odaklı pistmolojik inanç ölçklrinin gliştirilmsi ihtiyacı doğmuştur. Bu ihtiyaç, dğişik alanlara yönlikçşitli alan odaklı pistmolojik inanç ölçklrinin gliştirilmsin kaynaklık tmiştir.hofr (2000) tarafından yapılan araştırmada, psikoloji v fn bilimlri alanlarına, Buhl, Alxandr v Murphy (2002) tarafından yapılan araştırmada matmatik v tarih alanlarına, Schommr, Dull v Barkr (2003) tarafından yapılan araştırmada matmatik, sosyal bilimlr v iş alanlarına, Ern (2006) tarafından yapılan araştırmada fizik, kimya, kamu yöntimi, iktisat, özl ğitim v Türkç ğitimi alanlarına, Walkr- Whlr (2007) v Tang (2010) tarafından yapılan araştırmalarda matmatik alanına yönlik pistmolojik inanç ölçklri gliştirilmiştir. Litratürdki, alan odaklı pistmolojik inanç ölçklri inclndiğind, fn bilimlri v sosyal bilimlr alanlarına yönlik hm farklı kültürlrd (Buhl, Alxandr, & Murphy, 2002; Hofr, 2000; Schommr-Aikins, Dull,& Barkr, 2003) hm d Türk kültüründ (Ern, 2006) çşitli ölçm araçlarının bulunduğu görülmktdir. Diğr taraftan, farklı kültürlrd matmatik alanına yönlik pistmolojik inançları blirlmk amacıyla çok sayıda ölçk (Buhl, Alxandr, & Murphy,2002; Schommr, Dull,& Barkr, 2003; Tang, 2010; Walkr-Whlr, 2007) bulunmasına rağmn, Türk kültüründ öğrncilrin matmatik odaklı pistmolojik inançları blirlmk amacıyla kullanılabilck bir ölçm aracına rastlanmamıştır. Oysa matmatik odaklı pistmolojik inançlar matmatik öğrniminin önmli bir bilşni olup (Ertkin, Dilmaç, Yazıcı, &Pkr, 2010), matmatik odaklı pistmolojik inançların blirlnmsi; öğrnm sürcind öğrncilri dstklmk için nlr yapılması, öğrnm ortamlarının nasıl düznlnmsi v matmatik öğrtim programları hazırlanırkn nlr dikkat dilmsi grktiğin rhbrlik dbilir (Abdalaziz & Akmar, 2012). Bu bağlamda, öğrncilrin matmatik alanına yönlik pistmolojik inançlarını blirlmk amacıyla kullanılabilck bir ölçğin Türk kültürün kazandırılması önm arz tmktdir. Matmatik odaklı pistmolojik inanç ölçğinin Türk kültürün kazandırılabilmsi için, alanyazındaki gnl v alan odaklı pistmolojik inanç ölçklrindn harktl matmatik odaklı pistmolojik inanç ölçğinin gliştirilmsi vya farklı kültürlrd gliştiriln matmatik odaklı pistmolojik inanç ölçklrindn hrhangi birinin Türkçy uyarlanması şklind iki farklı yol takip dilbilir. Bununla birlikt, pistmolojik inançların kültürl faktörlrin tkisiyl şkillndiği (Buhl &Alxandr, 2006; Chan & Elliot, 2004; Schommr, 2004) göz önün alındığında, farklı kültürd
9 Matmatik Odaklı Epistmolojik İnanç Ölçği 367 gliştiriln matmatik odaklı pistmolojik inanç ölçklrindn hrhangi birini Türkçy uyarlamak yrin gnl v alan odaklı pistmolojik inanç ölçklrindn yola çıkarak bir ölçk gliştirmnin daha doğru bir trcih olacağı düşünülmüştür. Bu kapsamda araştırmada, öğrncilrin matmatik odaklı pistmolojik inançlarını ölçmy olanak tanıyacak gçrli v güvnilirbir ölçm aracının gliştirilmsi amaçlanmaktadır. Yöntm Araştırma Grubu Araştırma, ğitim-öğrtim yılı güz yarıyılındaortaöğrtim öğrncilrindn oluşan iki farklı çalışma grubu üzrind yürütülmüştür. Birinci çalışma grubu, Batman il mrkzindki bş farklı lisdn 236 sı (%56.32) kız v 183 ü (%43.68) rkk olmak üzr toplam 419 öğrncidn oluşmaktadır. Ancak, çok sayıda cvapsız maddnin bulunması, bir madd için birdn fazla sçnğin işartlnmiş olmasıvya ölçm aracında yr alan olumlu-olumsuz tüm maddlr aynı cvabın vrilmiş olmasından dolayı maddlrin okunmadan ölçm aracının doldurulduğu izlnimini uyandıran vrilr, vri stinin dışında tutulmuştur. Bu ndnl, toplamda 104 (54 kız v 50 rkk) öğrnciy ait vri, istatistiksl analizlr grçklştirilmdn önc vri stindn çıkarılmıştır. Böyllikl birinci çalışma grubunda, 182 si kız (%57.80) v 133 ü rkk olmak üzr (%42.20) toplam 315 öğrnciy ait vri kalmıştır. Bu öğrncilrin 122 si (%38.70) fn lissind, 154 ü (% 48.90) mslk lissind v 39 u (% 12.40) gnl lisd öğrnim görmktdir. Ayrıca, öğrncilrin 166 sı (%52.70) 9. sınıfa, 38 i (%12.10) 10. sınıfa, 76 sı (%24.10) 11. sınıfa v 35 i (% 11.10) 12. sınıfa dvam tmktdir. Ölçğin yapı gçrliği, uyum gçrliği, iç tutarlık güvnirliği v madd analizlri bu gruptan ld diln vrilr üzrind grçklştirilmiştir. İkinci çalışma grubu is, Diyarbakır ili Silvan ilçsi Anadolu Öğrtmn Lissi nd öğrnim görn 47 si (%44.34) kız v 59 si rkk (%55.66) olmak üzr toplam 106 öğrncidn oluşmaktadır.bu gruptaki öğrncilrin 56 sı (%52.83) 9.sınıfa v 50 si (%47.17) 10.sınıfa dvam dn öğrncilrdir. Ölçğin tst-tkrar tst güvnirliği bu gruptan ld diln vrilr üzrindn hsaplanmıştır.tst-tkrar tst güvnirliğin yönlik istatistiksl analizlr grçklştirilmdn önc, tst-tkrar tst güvnirliği için iki hafta ara il grçklştiriln iki uygulamadan hrhangi birin katılmayan 15(8 kız v 7 rkk) öğrnciy ait vrilr, vri stindn çıkarılmıştır. Bu işlmin ardından, tst-tkrar tst güvnirliğin yönlik grçklştiriln hr iki uygulamada da yr alan 91 öğrnciy ait vri üzrindn ölçğin tst-tkrar tst güvnirlik katsayısı hsaplanmıştır. İşlm Matmatik Odaklı Epistmolojik İnanç Ölçği (MOEİÖ) nün gliştirilmsi sürcind, Cronbach (1984), Crockr v Algina (1986) v DVllis (2003) tarafından önriln adımlar takip dilmiştir. Buna gör, ölçk gliştirm sürcind izlnn basamaklar aşağıda öztlnmiştir.
10 368 Mustafa İLHAN & Bayram ÇETİN Ölçktn alınan puanlar il ölçülck özllik/özlliklrin blirlnmsi.moeiö il öğrncilrin matmatiksl bilginin v matmatik öğrnmnin doğasına ilişkin inançlarının ölçülmsi amaçlanmaktadır. Ölçülck yapıyı tmsil dn davranışların tanımlanması.moeiö gliştirilirkn Schommr (1990) tarafından gliştirilip Dryakulu v Büyüköztürk (2002, 2005) tarafından Türkçy uyarlanan gnl pistmolojik inanç ölçğindki ÖÇBOİ, ÖYBOİ v TBDVOİ boyutları tml alınmıştır. ÖÇBOİ il matmatik öğrnm ytnğinin birysl tcrüblr il n ölçüd gliştirilbilcğin ilişkin inançların ölçülmsi amaçlanmaktadır.öyboi boyutu il matmatik öğrnm ytnğinin doğuştan gln, dğişmz bir özllik olduğuna ilişkin inançların ölçülmsi hdflnmktdir.tbdvoi boyutuyla is, matmatiksl bilginin ksinliği v dğişmzliğin ilişkin inançların ölçülmsi amaçlanmaktadır. Ölçkt yr alacak maddlrin yazılması.moeiö d yr alacak maddlrin yazımında, gnl pistmolojik inanç ölçklri (Dryakulu&Büyüköztürk, 2002, 2005; Schommr, 1990) il alan odaklı pistmolojik inanç ölçklrindn (Abdalaziz & Akmar, 2012; Buhl, Alxandr,& Murphy, 2002; Ern, 2006; Hofr, 2000; Stinr, 2007; Stockton, 2010; Walkr-Whlr, 2007)yararlanılmış;matmatik öğrtmnlrinin, matmatik ğitimi v ğitimi bilimlri uzmanlarının görüşlrin başvurulmuştur.madd havuzu, ölçk gliştirm sürcind tml alınan ÖÇBOİ, ÖYBOİ v TBDVOİ boyutlarından yola çıkılarak oluşturulmuştur. ÖÇBOİ boyutunu yansıtan 11 madd, ÖYBOİ boyutunu yansıtan 10 madd v TBDVOİ boyutunu yansıtan 14 madd yazılarak toplamda 35 madddn oluşan bir madd havuzu ld dilmiştir.ölçkt yr alan ifadlr için Ksinlikl Katılıyorum (5), Katılıyorum (4), Kararsızım (3), Katılmıyorum (2) v Ksinlikl Katılmıyorum (1) şklind bşli Likrt tipi bir drclndirm kullanılmıştır. Taslak ölçm aracında yr alan maddlr için uzman görüşü alınması v ölçğin ynidn gözdn gçirilmsi.moeiö nin kapsam v görünüş gçrliğini sağlamak için birölçm dğrlndirm uzmanı, üçğitim programları v öğrtim uzmanı v ikimatmatik ğitimi uzmanı olmak üzr toplam altıuzmandan görüş alınmıştır.bir konu il ilgili kapsamın blirlnmsi, bir yargılamayı grktirdiğindn uzmanlar il ölçm aracını gliştirn kişilrin ortak tanımlarının olması grklidir (Tavşancıl, 2010).Özllikl, birdn fazla alt ölçktn oluşan çok boyutlu ölçm araçlarında ölçülmk istnn yapının farklı boyutlarını blirlmk amacıyla yazılan maddlrin, yr almaları bklnn boyut il ilgili olup olmadığının uzmanlartarafından dğrlndirilmsi grkir (DVllis, 2003). Bu grkliliğ bağlı olarak, uzmanlardan, ölçği, ölçk maddlrinin hazırlanması sürcind araştırmacılar tarafından tml alınan ÖÇBOİ, ÖYBOİ v TBDVOİ boyutları ışığında dğrlndirmlri istnmiştir. Uzmanlardan gln görüşlr sonucunda, ÖÇBOİ boyutuna yönlik olarak hazırlanan 11 madddn biriv TBDVOİ boyutuna yönlik olarak hazırlanan 14 madddn dördü ölçktn çıkarılmıştır. Bu işlmin ardından, ölçkt ÖÇBOİ boyutunu yansıtan 10 madd, ÖYBOİ boyutunu yansıtan 10 madd v TBDVOİ boyutunu yansıtan 10 madd olmak
11 Matmatik Odaklı Epistmolojik İnanç Ölçği 369 üzr toplam 30 madd kalmıştır. Uzmanların ölçktn çıkarılmasını önrdiği bşmaddnin ölçtüğü özlliği blirlmy yönlik farklı maddlr ölçkt yr aldığından, söz konusu maddlrin ölçm aracından çıkarılması ölçğin kapsam gçrliğin zarar vrmmiştir. Ayrıca, uzmanlardan alınan görüşlr doğrultusunda, hazırlanan bazı maddlrin ifad diliş şkillrind dğişikliğ gidilmiştir. Örnğin, uzmanlardan ikisi, TBDVOİ yi yansıtan Matmatik alanındaki konular tartışmaya açık dğildir maddsind yr alan konular ifadsi yrin doğrular ifadsinin kullanılmasının daha uygun olacağını blirtmişlrdir. Bunun üzrin, bu madd Matmatik alanındaki doğrular tartışmaya açık dğildir şklind ynidn ifad dilmiştir. Uzman görüşlrindn yola çıkılarak, ölçk maddlrind grkli dğişikliklr yapıldıktan sonra, ölçm aracının dil açısından anlaşılabilirliğini sağlamak amacıyla, üçtürk Dili uzmanından görüş alınmıştır. Uzmanların yazım kuralları v noktalama işartlrinin kullanımı il ilgili görüşlri doğrultusundaölçk maddlri gözdn gçirilmiştir. Uygulama öncsind küçük bir grup üzrind ön uygulama yapılması.moeiö d yr alan maddlrin anlaşılırlığı v ölçğin uygulama sürsi hakkında gri bildirim almak için, 13 lis öğrncisi (altıkız v ydirkk) üzrind ön uygulama yapılmıştır. MOEİÖ yü cvaplandıran öğrncilrl uygulamanın ardından görüşmlr grçklştirilmiştir.görüşmlrdöğrncilrin ölçkt yr alan maddlrin anlaşılırlığına ilişkin fikirlri alınmıştır. Öğrncilr ayrıca, ölçğin amacını, ölçktki madd sayısını v ölçğin nasıl doldurulması grktiğini blirtmk üzr ölçğin başında sunulan yönrg hakkındaki düşünclri sorulmuştur. Yapılan görüşmlr, ölçk için hazırlanan yönrgd v ölçk maddlrind hrhangi bir dğişikliğ ihtiyaç duyulmadığını göstrmiştir.ölçğin yaklaşık uygulama sürsi olarak, ön uygulamanın grçklştirildiği 13 kişilik grupta, ölçği n kısa sürd dolduran öğrnci il n uzun sürd dolduran öğrncinin harcadıkları sürlrin ortalaması blirlnmiştir.bu sürçlrdn sonra ölçk gniş bir çalışma grubu üzrind uygulamaya hazır hâl glmiştir. Ölçğin tmsil özlliği yüksk gniş bir örnklm uygulanması v ölçğin psikomtrik özlliklrini blirlmy yönlik analizlrin grçklştirilmsi.uygulamalar, ölçğin psikomtrik özlliklrini ortaya koymak için ytrli katılımcıdan oluşan bir araştırma grubu üzrind grçklştirilmiştir.ölçk, sınıf ortamında öğrncilr uygulanmıştır. Uygulama sırasında, araştırmacının sınıfta bulunmasına özn göstrilmiştir. Uygulamaya başlamadan önc, öğrncilr araştırmanın amacı hakkında bilgilndirilmiştir. Öğrncilr, ld diln vrilrin yalnızca araştırmanın amacı için kullanılacağı, başka hrhangi bir kurum ya da kişiyl paylaşılmayacağı blirtilmiştir. Yin uygulamadan önc, öğrncilr araştırmaya katılımın zorunlu olmadığı hatırlatılarak araştırma grubunun yalnızca gönüllü katılımcılardan oluşması sağlanmıştır. Öğrncilr, ölçği nasıl doldurmaları grktiği anlatılmış, maddlrin doğru ya da yanlışcvaplarınınolmadığı, vriln ifady dayalı olarak kndilri için uygun olan sçnği işartlmlri istnmiştir. Öğrncilr,
12 370 Mustafa İLHAN & Bayram ÇETİN birbirlrini tkilmmlri konusunda uyarılmıştır. Ayrıca, ölçği içtnlikl yanıtlamalarının gçrli v güvnilir sonuçlar ld dilbilmsi için son drc önmli olduğu araştırmacı tarafından katılımcılara ifad dilmiştir.uygulama sürsinc araştırmacının sınıf ortamında bulunması, ölçğin uygulanması sırasında karşılaşılan problmlr doğrudan müdahal tm imkânı tanımıştır. Örnğin, ölçkt uyarı olarak blirtilmsin v uygulamadan önc hatırlatılmasına rağmn, ölçğin arka sayfasını doldurmayı unutan öğrncilr grkli hatırlatmalar yapılabilmiştir.vri toplama sürcinin ardından ölçğin psikomtrik özlliklrini blirlmy yönlik istatistiksl analizlr grçklştirilmiştir. Ölçğin nasıl puanlanacağına v nasıl yorumlanacağına ilişkin bir yönrgnin hazırlanması.moeiö nün alt boyutlarından alınabilck puanların hangi aralıkta dğişbilcği blirtilmiştir. Ayrıca, ölçğin alt boyutlarından alınan yüksk v düşük puanların nasıl yorumlanması grktiği açıklanmıştır. Gçrlik, güvnirlik v madd analizin yönlik olarak grçklştiriln istatistiksl analizlr.moeiöaraştırma grubuna uygulandıktan sonra, ölçğin psikomtrik özlliklrini ortaya koymak için istatistiksl analizlr grçklştirilmiştir. İlk olarak ölçğin yapı gçrliği inclnmiş, bu amaçla Açımlayıcı Faktör Analizi (AFA) v Doğrulayıcı Faktör Analizi (DFA) uygulanmıştır. MOEİÖ nün uyum gçrliği kapsamında, MOEİÖ nün alt boyutları il öğrncilrin matmatik başarıları (bir öncki yıla ait karn notları) arasındaki korlasyon hsaplanmıştır. MOEİÖ nün güvnirliği, iç tutarlık v tst-tkrar tst yöntmlriyl inclnmiştir. MOEİÖ d yr alan maddlrin ayırt dicilik düzylrini saptamak amacıyla düzltilmiş madd toplam korlasyonu hsaplanmış v %27 lik alt-üst grup karşılaştırmalarına yr vrilmiştir. Araştırmanın vrilri SPSS 20.0 v LISREL 8.54 pakt programları kullanılarak analiz dilmiştir. Bulgular Yapı Gçrliği Bu çalışmada, MOEİÖ nün yapı gçrliği kapsamında AFA v DFA uygulanmıştır. Açımlayıcı faktör analizi (AFA).AFA grçklştirilmdn önc vri stinin faktör analizin uygun olup olmadığının inclnmsi grkir. Örnklm büyüklüğü, bu inclmd ilk sırada yr almaktadır (Akbulut, 2010). Faktör analizi çalışmalarında yr alması grkn katılımcı sayısı konusunda farklı araştırmacılar tarafından dğişik önrilr gtirilmiştir. Cattll (1978), faktör analizi çalışmalarında, ölçktki madd sayısının üçil altıkatı kadar katılımcının çalışma grubuna dâhil dilmsini önrmkt v faktör analizi için 200 katılımcıyı kabul dilbilir, 500 katılımcıyı is oldukça iyi bir sayı olarak ifad tmktdir. Hair, Andrson, Tatham v Grablowsky (1979), faktör analizi için, ölçkt yr alan madd sayısının 20 katı kadar katılımcının çalışma grubuna dâhil dilmsini önrmktdir. Gorsuch (1983) faktör analizi çalışmalarında ölçkt yr
13 Matmatik Odaklı Epistmolojik İnanç Ölçği 371 alan hr madd için çalışma grubunda n az bşkatılımcının bulunması önrmkt, bununla birlikt katılımcı sayısının 100 dn az olmaması grktiğini blirtmktdir (Cramr. 2003). Crowly v L (1992) faktör analizi için 100 katılımcıyı ytrsiz, 200 ü ortalama, 300 ü iyi, 500 ü çok iyi v 1000 katılımcıyı mükmml olarak nitlndirmktdir(akbulut, 2010).Frguson v Cox (1993) faktör analizi çalışmalarında ölçüt olarak alınması grkn katılımcı sayısının n az 100 olduğunu blirtmktdir. Klin (1994) is, faktör analizind güvnilir sonuçlar ld tmk için 200 kişilik örnklmin gnllikl ytrli olacağını, faktör yapısının açık v az sayıda olduğu durumlarda bu rakamın 100 kadar indirilbilcğini, ancak büyük örnklmlrl çalışmanın daha uygun olacağını vurgulamaktadır. Faktör analizi için uygun örnklm büyüklüğü tahminind farklı yaklaşımlar dikkat alındığında, litratürd yr vriln ölçütlrdn n az ikisini karşılayacak bir büyüklüğ ulaşılması önrilmktdir (Çokluk, Şkrcioğlu, &Büyüköztürk. 2012). Bu ölçütlr gör, araştırmadaki katılımcı sayısının faktör analizi için ytrli olduğu söylnbilir. Vrilrin faktör analizin uygun olup olmadığını blirlmk amacıyla yapılacak bir diğr işlm Kaisr-Mayr-Olkin (KMO) v Barltt tstlrinin grçklştirilmsidir. KMO, sıfır il birarasında dğişn dğrlr alabilmktdir. Kaisr (1974) gör0.5 in üzrindki KMO dğrlri kabul dilbilir dğrlrdir (Fild, 2009). Bununla birlikt, 0.5 il 0.7 arasındaki KMO dğrlrinin orta, 0.7 il 0.8 arasındaki dğrlrin iyi, 0.8 il 0.9 arasındaki dğrlrin çok iyi v 0.9 un üzrindki dğrlrin is mükmml olduğu kabul dilmktdir (Hutchson & Sofroniou, 1999). Bu araştırmada, KMO dğri.811 bulunmuş v Barltt tstinin istatistiksl olarak anlamlı olduğu (χ 2 = , sd=435) blirlnmiştir. Bu sonuca gör, vrilrin faktör analizin uygun olduğu söylnbilir. Bu tspitin ardından AFA da tml bilşnlr yöntmi v dik (varimax) döndürm sonucunda, toplam varyansın %37.90 ını açıklayan üç faktörlü bir yapı ld dilmiştir. Gnl pistmolojik inanç ölçklrind, ölçk boyutlarının birbirindn bağımsız olması (Dryakulu &Büyüköztürk, 2002, 2005; Schommr, 1990), MOEİÖ d d ölçk faktörlri arasında bir ilişki olmayacağını düşündürmüştür. Ölçk faktörlrinin birbirlriyl ilişkili olmayacağına yönlik bu öngörü ndniyl AFA da dik döndürm tkniği kullanılmıştır. AFA sonucunda ld diln bulgular Tablo 1 d sunulmuştur.
14 372 Mustafa İLHAN & Bayram ÇETİN Tablo 1 MOEİÖ AFA İlk Analiz Sonuçları Madd No Faktör 1 Faktör 2 Faktör 3 MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ MOEİÖ AFA nın ilk sonuçlarına gör, 21. v 23. maddlr faktör yükü.30 dan düşük olduğu için (Büyüköztürk, 2010; Costllo & Osborn, 2005; Martin & Nwll, 2004; Pallant, 2005; Schrishim & Eisnbach, 1995), 22. madd is yr aldığı faktörl kuramsal olarak dstklnmdiği için ölçm aracından çıkarılmıştır. Bu üç maddnin çıkarılmasından sonra, AFA tkrarlanmış v toplam varyansın %40.57 sini açıklayan üç faktörlü bir yapı ld dilmiştir. Faktörlrd toplanan maddlrin içriklri v kuramsal yapı dikkat alınarak birinci faktör ÖÇBOİ, ikinci faktör ÖYBOİ v üçüncü faktör TBDVOİ olarak adlandırılmıştır. ÖÇBOİ alt ölçği 10 madddn oluşmakta v toplam varyansın %16.27 sini açıklamaktadır. Bu alt ölçkt yr alan maddlrin faktör yüklri.54 il.76 arasında dğişmktdir. ÖYBOİ alt ölçği 10 madddn oluşmakta v toplam varyansın %14.12 sini açıklamaktadır. Bu alt ölçkt yr alan maddlrin faktörü yüklri.42 il.70 arasında sıralanmaktadır. TBDVOİ alt ölçği ydi madddn oluşmakta v toplam varyansın %10.19 unu açıklamaktadır. Bu alt ölçkt yr alan maddlrin faktör yüklri.42 il.74 dğişmktdir. MOEİÖ nün açıkladığı varyans oranı v faktör yüklrin ilişkin bulgular is Tablo 2 d göstrilmiştir.
15 Matmatik Odaklı Epistmolojik İnanç Ölçği 373 Tablo 2 MOEİÖ Çıkarılan Maddlrin Ardından Tkrarlanan AFA Sonuçları Faktör Madd No Maddlr Faktör Yükü ÖÇBOİ ÖYBOİ TBDVOİ MOEİÖ1 Bir öğrncinin matmatiği n kadar iyi öğrnbilcği n kadar çaba harcadığına bağlıdır..755 MOEİÖ2 N kadar ytnkli olursanız olun, çaba harcamadan matmatik alanında başarılı olamazsınız..656 MOEİÖ3 Yalnızca çok çaba sarf dn kişilr iyi bir matmatikçi olabilirlr..653 MOEİÖ4 İnsanların matmatik başarılarındaki farklılık ortaya koydukları çabanın farklı olmasından kaynaklanmaktadır..634 MOEİÖ5 Grçktn çaba harcarsa hr biry matmatik öğrnbilir.636 MOEİÖ6 Matmatik alanındaki zor konuları yalnızca çok çaba sarf dn birylr öğrnbilir..598 MOEİÖ7 Matmatik alanındaki bir konuyu hmn anlamayan bir öğrnci anlamak için çaba sarf tmyi sürdürmlidir..567 MOEİÖ8 Matmatik alanında çaba sarf tmdn bilgi sahibi olunamayacağını bilmk matmatik alanında başarılı olabilmnin ilk adımıdır..565 MOEİÖ9 Matmatik alanındaki n başarılı insanlar n fazla çaba harcayan insanlardır..700 MOEİÖ10 Doğru çalışma bcrilrini öğrnmk biryin matmatik ytnğini gliştirbilir..540 Açıkladığı Varyans % MOEİÖ11 İnsanlar yni şylr öğrnbilirlr ancak sahip oldukları matmatik ytnğini dğiştirmzlr.502 MOEİÖ12 Matmatik alanında başarılı olan insanlar doğuştan matmatik ytnğiyl dünyaya glmiş olan kişilrdir.613 MOEİÖ13 İnsanların çoğu rkn yaşlardan itibarn matmatik alanında başarılı olup olamayacaklarını bilirlr.552 MOEİÖ14 Bir matmatik problmini birkaç dakika içind çözmyn bir öğrnci n kadar çaba harcarsa harcasın muhtmln problmi çözmycktir.636 MOEİÖ15 Yalnızca matmatik alanında ytnkli olan kişilr iyi bir matmatikçi olabilirlr.662 MOEİÖ16 İnsanların matmatik başarılarındaki farklılık matmatik ytnklrinin farklı olmasından kaynaklanmaktadır.419 MOEİÖ17 Matmatik alanındaki zor konuları, yalnızca matmatik alanında ytnkli olan insanlar öğrnbilir.698 MOEİÖ18 Matmatik ytnği olmayan bir öğrncinin matmatik öğrnmk için çaba harcaması vakit kaybıdır.620 MOEİÖ19 N kadar çaba harcarsanız harcayın matmatik alanındaki başarınızı bu alandaki ytnklriniz blirlr.634 MOEİÖ20 Matmatik alanında ytnkli olmayan bir öğrncinin bu alandaki başarılı olabilmk için yapacak çok şyi yoktur.622 Açıkladığı Varyans % MOEİÖ24 Matmatik alanında kuram (tori) halin glmiş bir bilginin yanlış olması mümkün dğildir.701 MOEİÖ25 Matmatik alanındaki konular tartışmaya açık dğildir.558 MOEİÖ26 Matmatik alanındaki hr konu hakkında yalnızca tk bir doğru vardır.576 MOEİÖ27 Matmatik alanındaki doğrular dğişmzdir.735 MOEİÖ28 Matmatik alanında, bugün doğru olduğu düşünüln bir bilginin ilrlyn zamanlarda yanlış olduğu anlaşılabilir.557 MOEİÖ29 Matmatik alanındaki hrhangi bir konu farklı bakış açılarıyla l alınsa da o konuya ilişkin ancak tk bir doğru olabilir.424 MOEİÖ30 Matmatik alanında hakkında n fazla bilgiy sahip olunun konuların bil doğrulukları sorgulanabilir.463 Açıkladığı Varyans % Açıklanan Toplam Varyans %
16 374 Mustafa İLHAN & Bayram ÇETİN Doğrulayıcı faktör analizi (DFA).AFA sonucunda ld diln 27 madd v üç faktördn oluşan yapının ytrli uyum indkslri vrip vrmdiğini blirlmk v MOEİÖ nün yapı gçrliğin ilişkin k kanıt ld tmk için DFA uygulanmıştır. DFA da sınanan modlin ytrliğini ortaya koymak üzr pk çok uyum indksi kullanılmaktadır. Bu çalışmada DFA için Ki-Kar Uyum Tsti (Chi-Squar Goodnss), karşılaştırmalı uyum indksi (Comparativ Fit Indx, CFI), normlaştırılmamış uyum indksi (Non-Normd Fit Indx, NNFI), fazlalık uyum indksi (Incrmntal Fit Indx, IFI),tahmin hatalarının ortalamasının karkökü (Root Man Squar Error of Approximation, RMSEA) v standartlaştırılmış hata karlri ortalamasının karkökü (Standardizd Root Man Squar Rsidual, SRMR) uyum indkslri inclnmiştir. CFI, NNFI v IFI indkslri için.90 dğri kabul dilbilir uyuma v.95 dğri mükmml uyuma işart tmktdir (Bntlr, 1980; Bntlr & Bontt, 1980; Marsh, Hau, Artlt, Baumrt,& Pschar, 2006). RMSEA için.08dğri kabul dilbilir uyum v.05 dğri mükmml uyum ölçütü olarak alınmaktadır (Brown & Cudck, 1993; Byrn & Campbll, 1999). SRMR için is.05 dğri mükmml uyumu v.10 dğri kabul dilbilir uyumu ifad tmktdir (Hu & Bntlr, 1999; Klin, 2011). Yapılan DFA da, ld diln modlin uyum indkslri inclnmiş v minimum χ 2 dğrinin (χ 2 =772.69, N=315, p=.00) anlamlı olduğu görülmüştür.uyum indksi dğrlri is, CFI=.90, NNFI=.90, IFI=.90, RMSEA=.066 v SRMR=.089 olarak bulunmuştur.sınanan modlin ytrliğini ortaya koymak amacıyla inclnn uyum indkslrin ilişkin kabul dilbilir v mükmml uyum dğrlri il DFA dan ld diln uyum indksi dğrlri v bu doğrultuda ortaya çıkan sonuçlar Tablo 3 t göstrilmiştir. Tablo 3 Araştırmada İnclnn Uyum İndkslrin İlişkin Mükmml v Kabul dilbilir Uyum Dğrlri il DFA dan Eld Ediln Uyum İndksi Dğrlri Uyum Mükmml Kabul Edilbilir DFA İndkslri Uyum Ölçütü Uyum Ölçütü Sonuçları Sonuç X 2 /sd 0 X 2 /sd 2 2 X 2 /sd Kabul dilbilir uyum CFI.95 CFI CFI Kabul dilbilir uyum NNFI.95 NNFI NNFI Kabul dilbilir uyum IFI.95 IFI IFI Kabul dilbilir uyum RMSEA.00 RMSEA RMSEA Kabul dilbilir uyum SRMR.00 SRMR SRMR Kabul dilbilir uyum Tablo 4 dki uyum indkslrin ilişkin mükmml v kabul dilbilir uyum ölçütlri, DFA dan ld diln üç faktörlü modlin uyumlu olduğunu göstrmktdir. Üç boyutlu modl ilişkin faktör yüklri Şkil 1 d görülmktdir.şkil 1 d görülbilcği gibi, ÖÇBOİ alt boyutu için faktör yüklri.44 il.72 arasında, ÖYBOİ alt boyutu için.29 il.67 arasında v TBDVOİ alt boyutu için faktör yüklri is.26 il.79 arasında dğişmktdir.
17 Matmatik Odaklı Epistmolojik İnanç Ölçği 375 Şkil 1. MOEİÖ y İlişkin Path Diyagramı, Faktör Yüklri v Hata Varyansları MOEİÖ 1 MOEİÖ 2 MOEİÖ 3 MOEİÖ MOEİÖ 5 MOEİÖ ÖÇBOİ MOEİÖ 7 MOEİÖ 8 MOEİÖ 9 MOEİÖ 10 MOEİÖ 11 MOEİÖ 12 MOEİÖ 13 MOEİÖ MOEİÖ MOEİÖ TBDVOİ MOEİÖ 26 MOEİÖ MOEİÖ 28 MOEİÖ 29 MOEİÖ MOEİÖ 15 MOEİÖ ÖYBOİ.53 MOEİÖ MOEİÖ 18 MOEİÖ MOEİÖ 20 Uyum gçrliği.epistmolojik inançlara ilişkin litratür inclndiğind, matmatiğ yönlik glişmiş pistmolojik inançlara sahip olan öğrncilrin, glişmmiş pistmolojik inançlara sahip olan öğrncilr gör, akadmik başarılarının daha yüksk olduğu görülmktdir (Tang, 2010). Bu noktadan harktl, MOEİÖ nün uyum gçrliği kapsamında, öğrncilrin ölçğin alt boyutlarından aldıkları puanlar il matmatik başarıları arasındaki korlasyon hsaplanmıştır. Öğrncilrin bir öncki yıla ait karnlrindki matmatik drsi notları, matmatik başarı puanı olarak alınmıştır. ÖÇBOİ alt boyutundan alınan puanların glişmiş pistmolojik inançlara işart ttiği, ÖYBOİ v TBDVOİ alt boyutlarındanalınan yüksk puanların is glişmmiş pistmolojik inançlara işart ttiği göz önünd bulundurularak, ÖÇBOİ alt boyutu il matmatik başarısı arasında pozitif; ÖYBOİ v TBDVOİ alt boyutları il matmatik
18 376 Mustafa İLHAN & Bayram ÇETİN başarısı arasında ngatif bir ilişkinin bulunduğu hipotzi tst dilmiştir. Korlasyon analizi sonucunda, ÖÇBOİ il matmatik başarısı arasında pozitif yönd [n=315, r=.48, p<.001], ÖYBOİ v TBDVOİ il matmatik başarısı arasında ngatif yönd [n=315 v sırasıyla r=-.25 p<.001, r=-.26, p<.001] anlamlı ilişkilrin bulunduğu saptanmıştır. Bu bulgular, MOEİÖ nün uyum gçrliğinin sağlandığına dair bir kanıt olarak dğrlndirilmiştir. Güvnirlik.MOEİÖ nün güvnirliği, iç tutarlık v tst-tkrar tst güvnirlik yöntmlri il hsaplanmıştır. İç tutarlık katsayıları, ÖÇBOİ alt ölçği için.84, ÖYBOİ alt ölçği için.81 v TBDVOİ alt ölçği için.71 olarak bulunmuştur. Ölçğin tst-tkrar tst güvnirliğini blirlmk için 91 öğrnci üzrind iki hafta ara il iki uygulama yapılmıştır. Birinci v ikinci uygulama arasındaki tutarlığı ortaya koymak amacıyla, iki uygulamadan ld diln puanlar arasındaki korlasyonkatsayıları hsaplanmıştır. Tsttkrar tst güvnirlik katsayıları, ÖÇBOİ alt ölçği için.96, ÖYBOİ alt ölçği için.95 v TBDVOİ alt ölçği için.95 olarak hsaplanmıştır. Güvnirlik katsayısı.70 v üzrind olan ölçklrin güvnilir kabul dildiği (Domino & Domino, 2006; Frankl, Walln,& Hyun, 2012; Lch, Barltt,& Morgan, 2005; Pallant, 2005; Tzbaşaran, 1997; Şkr &Gnçdoğan, 2006; Urbina, 2004) göz önün alındığında, hsaplanan güvnirlik katsayılarının ytrli olduğu söylnbilir. Güvnirlik analizin yönlik sonuçlar Tablo 4 t sunulmuştur. Tablo 4 MOEİÖ nün İç Tutarlılık v Tst-Tkrar Tst Yöntmlriyl Hsaplanan Güvnirlik Katsayıları Alt Ölçklr İç Tutarlık (Cronbach Alpha) Tst-Tkrar Tst ÖÇBOİ ÖYBOİ TBDVOİ Madd analizi.moeiö d yr alan maddlrin ayırt dicilik düzylrini blirlmk v toplam puanı yordama gücünü saptamak amacıyla düzltilmiş madd toplam korlasyonu hsaplanmış v %27 lik alt-üst grup karşılaştırmalarına yr vrilmiştir. Düzltilmiş madd toplam korlasyonun hsaplanmasında Parson Momntlr Çarpımı Korlasyonu kullanılmıştır.%27 likalt-üst grup karşılaştırmalarında is ilişkisiz örnklmlrt tstindn yararlanılmıştır. Madd analizi sonucunda ld diln bulgular Tablo 5 t sunulmuştur.
19 Matmatik Odaklı Epistmolojik İnanç Ölçği 377 Tablo 5 MOEİÖ Madd Analizi Sonuçları Alt Boyut ÖÇBOİ N=315 Cronbach alpha=.84 ÖYBOİ N=315 Cronbach alpha=.81 TBDVOİ N=315 Cronbach alpha=.71 Madd Çıkarıldığında Düzltilmiş Madd No Ölçk Ortalaması Ölçk Varyansı Ölçk Alfası Madd Toplam Korlasyonu t MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * MOEİÖ * sd=169 *p<.001 sd=172 *p<.001 sd=208 *p<.001 Tablo 5 tki bulgular inclndiğind, %27 lik alt v üst grupların madd puanlarındaki farklara ilişkin t dğrlrlrinin ÖÇBOİ alt ölçği için 8.32 il arasında (sd=169, p<.001), ÖYBOİ alt ölçği için 5.86 il arasında (sd=172, p<.001), TBDVOİ alt ölçği için is 6.46 il (sd=208, p<.001) arasında dğiştiği görülmktdir.tablo 6 ya gör ayrıca, madd toplam korlasyonuna ilişkin sonuçlar, ÖÇBOİ alt ölçği için.41 il.66 arasında, ÖYBOİ alt ölçği için.28 il.59 arasında, TBDVOİ alt ölçği için is.27 il.62 arasında sıralanmaktadır. Madd toplam korlasyonu yorumlanırkn dğri.30 v üzrind olan maddlr,ölçülck özlliği ayırt tm açısından ytrli kabul dilmktdir (Büyüköztürk, 2010; Erkuş, 2012; Fild, 2009). ÖYBOİ alt ölçğind yr alan 16. madd il TBDVOİ alt ölçğind yr alan 30.
20 378 Mustafa İLHAN & Bayram ÇETİN madd dışındaki maddlrin tamamı bu ölçütü sağlar nitliktdir. Bununla birlikt, %27 lik alt-üst grup karşılaştırmaları sonucu ld diln t dğrlrinin düzltilmiş madd toplam korlasyonu.30 un altında olan 16 v 30. maddlr için d anlamlı olduğu görülmktdir. Alt v üst grup arasındaki farklara ilişkin t dğrlrinin anlamlı olması maddnin ayırt diciliği için bir kanıt olarak dğrlndirilmktdir (Erkuş, 2012).Bu bulgulardan harktl, ölçkt yr alan maddlrin tamamının ayırt dici olduğu söylnbilir. MOEİÖ nün puanlarının dğrlndirilmsi.moeiö d 27madd bulunmaktadır.ölçkt Ksinlikl Katılıyorum(5) dan Ksinlikl Katılmıyorum(1) a dğişn5 li Likrt tipi bir drclndirm kullanılmıştır. Ölçk, ÖÇBOİ, ÖYBOİ v TBDVOİ olmak üzr üç boyutla bir yapıya sahiptir. ÖÇBOİ alt boyutunda, 10 madd bulunduğundan bu boyuttan alınabilck n yüksk puan 50, n düşük puan is 10 dur. Bu alt boyutta yr alan maddlrin tamamı olumlu olup trstn puanlanan madd bulunmamaktadır. Aynı şkild, ÖYBOİ alt boyutunda 10 madd yr aldığından bu boyuttan alınabilck n yüksk puan 50, n düşük puan is 10 dur. Bu boyuttaki maddlrin tamamı öğrnmnin ytnğ bağlı olduğunu dstklyn olumlu maddlrdir.dolayısıyla ÖYBOİ boyutunda da trstn puanlanan madd bulunmamaktadır.tbdvoi boyutunda is ydimadd yr almaktadır. Bu boyuttan alınabilck n yüksk puan 35, n düşük puan is ydidir. Bu boyuttaki maddlrin bşi olumludur (tk bir doğrunun var olduğunu dstklyn). Kalan ikimadd is olumsuz (tk bir doğrunun olduğunu dstklmyn) olup trstn puanlanmıştır.moeiö nün alt boyutlarından alınan puanların yükslmsi, öğrncilrin ilgili boyuta ait inançlarının yüksk düzyd olduğu anlamına glmktdir. MOEİÖ nün ÖÇBOİ alt ölçğindn alınan yüksk puanlar matmatik alanına yönlik glişmiş/olgunlaşmış pistmolojik inançlara işart drkn; ÖYBOİ v TBDVOİ alt ölçklrindn alınan yüksk puanlar matmatik alanına yönlik glişmmiş/olgunlaşmamış pistmolojik inançlara işart tmktdir. Sonuç v Tartışma Bu araştırmada, öğrncilrin matmatik alanına yönlik pistmolojik inançlarınıölçmy olanak tanıyacak gçrli v güvnilir bir ölçm aracının gliştirilmsi amaçlanmıştır. MOEİÖ gliştirilirkn, Schommr (1990) tarafından gliştirip Dryakulu v Büyüköztürk (2002, 2005) tarafından Türkçy uyarlanan gnl pistmolojik inanç ölçğindki ÖÇBOİ,ÖYBOİ v TBDVOİ boyutları dikkat alınmıştır. ÖÇBOİ yi yansıtan 10 madd, ÖYBOİ yi yansıtan 11 madd v TBDVOİ yi yansıtan 14 madd olmak üzr toplam 35 madddn oluşan bir madd havuzu oluşturulmuştur. Ölçğin kapsam v görünüş gçrliğini sağlamak için uzman görüşü alınmıştır. Uzman görüşlri doğrultusunda, biriöçboi yi, dördütbdvoi yi yansıtan toplam bş madd ölçktn çıkarılmıştır. Bu işlmin ardından, ölçkt ÖÇBOİ boyutunu yansıtan 10 madd, ÖYBOİ boyutunu yansıtan 10 madd v TBDVOİ boyutunu yansıtan 10 madd olmak üzr toplam 30 madd kalmıştır. 30 madd, Ksinlikl
21 Matmatik Odaklı Epistmolojik İnanç Ölçği 379 Katılıyorum(5) dan Ksinlikl Katılmıyorum(1) a dğişn5 li Likrt tipi bir drclndirm il araştırma grubundaki öğrncilr uygulanmıştır. MOEİÖ nün yapı gçrliği için AFA v DFA uygulanmıştır. AFA sonucunda üç madd ölçktn çıkarılmış, kalan 27 maddnin toplam varyansın %40.57 sini açıklayan üç faktörlü bir yapıya sahip olduğu blirlnmiştir.faktörlrd toplanan maddlrin içriklri v kuramsal çrçvdikkat alınarak birinci faktör ÖÇBOİ, ikinci faktör ÖYBOİ v üçüncü faktör TBDVOİ olarak adlandırılmıştır. AFA dan ld diln üç faktörlü yapının ytrli uyum indksi vrip vrmdiğini blirlmk v MOEİÖ nün yapı gçrliğin ilişkin k kanıt ld tmk için DFA uygulanmıştır. DFA dan ld diln bulgular, MOEİÖ y ilişkin üç faktörlü yapıya ait uyum indkslrinin ytrli olduğunu göstrmiştir. AFA da açıklanan varyans oranı için %30 v üzrindki dğrlrin ölçüt olarak alındığı (Bayram, 2009; Büyüköztürk, 2010), ölçkt yr alan maddlr ait faktör yüklrinin.30 alt sınırının(büyüköztürk, 2010; Costllo & Osborn, 2005; Fostr, 2002; Pallant, 2005; Schrishim & Eisnbach, 1995)üzrind olduğu v DFA dan ld diln uyum indkslrinin kabul dilbilir sınırlar içrisind yr aldığı düşünüldüğünd MOEİÖ nün yapı gçrliğinin sağlandığı söylnbilir. MOEİÖ nün uyum gçrliği için, öğrncilrin ölçğin alt boyutlarından aldıkları puanlar il matmatik başarıları arasındaki korlasyon hsaplanmıştır. Öğrncilrin bir öncki yıla ait karnlrindki matmatik drsi notları, matmatik başarı puanı olarak alınmıştır.korlasyon analizindn ld diln bulgular, öğrncilrin matmatik alanına yönlikpistmolojik inançları il matmatik başarıları arasındaki ilişkinin pistmolojik inançlara ilişkin litratür il uyumlu olduğunu göstrmiştir. MOEİÖ nün güvnirliği, iç tutarlık v tst-tkrar tst yöntmlriyl inclnmiştir. Hsaplanan iç tutarlık katsayıları ÖÇBOİ alt ölçği için.84, ÖYBOİ alt ölçği için.81 v TBDVOİ alt ölçği için.71 şklinddir. Tst-tkrar tst güvnirlik katsayıları is, ÖÇBOİ alt ölçği için.96, ÖYBOİ alt ölçği için.95 v TBDVOİ alt ölçği için.95 olarak bulunmuştur. Güvnirlik katsayısı.70 v üzrind olan ölçklrin güvnilir kabul dildiği (Anastasi, 1982; Muijs, 2004; Nunnaly & Brnstin, 1994; Sipahi, Yurtkoru,& Çinko, 2010; Stangor, 2010) göz önün alındığında, hsaplanan iç tutarlık v tst-tkrar tst güvnirlik katsayıları ölçğin güvnirliğin yönlik bir kanıt olarak dğrlndirilbilir. İnançların uzun sürd şkillnn v dğişim dirnç göstrn yapılar olması (Nspor, 1987), MOEİÖ nün tst-tkrar tst güvnirliğin yönlik birinci v ikinci uygulama arasındaki korlasyonun oldukça yüksk olmasının ndni olabilir. MOEİÖ d yr alan maddlrin toplam puanı yordama gücünü blirlmk v ayırt dicilik düzylrini saptamak amacıyla madd analizi yapılmıştır. Madd analizi kapsamında, düzltilmiş madd toplam korlasyonu inclnmiş v %27 lik alt-süt grup karşılaştırmalarına yr vrilmiştir. Analiz sonucunda, düzltilmiş madd toplam korlasyonlarının ÖÇBOİ alt ölçği için.41 il.66 arasında, ÖYBOİ alt ölçği için.28 il.59 arasında, TBDVOİ alt ölçği için is.27 il.62 arasında sıralandığı v %27 lik alt v üst grup arasındaki farklara ilişkin t dğrlrin ölçkt yr alan tüm maddlr için anlamlı olduğu blirlnmiştir. Bu bulgular, MOEİÖ d yr alan maddlrin tamamının ayırt dici olduğuna işart tmktdir.
22 380 Mustafa İLHAN & Bayram ÇETİN Araştırmada, MOEİÖ nün psikomtrik özlliklrini inclmk amacıyla grçklştiriln istatistiksl analizlrdn ld diln bulgular, ölçğin öğrncilrin matmatik alanına yönlik pistmolojik inançlarını blirlmd gçrli v güvnilir bir araç olarak kullanılabilcğini ortaya koymaktadır. Sonuç olarak, Türk kültürün, öğrncilrin matmatik odaklı pistmolojik inançlarını ölçmk amacıyla kullanılabilck bir ölçk kazandırmayı amaçlayan bu çalışma il öğrncilrin matmatiksl bilginin v matmatik öğrnmnin doğasına yönlik inançlarını ölçmd kullanılabilck ytrli psikomtrik özlliklr sahip bir ölçm aracına ulaşıldığı söylnbilir. Önrilr Alanyazın inclndiğind, Türk kültüründ fizik, kimya, kamu yöntimi, iktisat, özl ğitim v Türkç ğitimi gibi farklı alanlara yönlik pistmolojik inanç ölçklrinin bulunduğu görülmktdir. Ancak, ulusal litratürd öğrncilrin matmatik odaklı pistmolojik inançlarını blirlmk amacıyla kullanılabilck bir ölçğ rastlanmamıştır. MOEİÖ nün gliştirilmsinin amaçlandığı bu çalışmanın litratürdki bu boşluğu dolduracağına inanılmakta v dolayısıyla önmli olduğu düşünülmktdir. Bununla birlikt, bu ölçk gliştirm çalışmasının yalnızca ortaöğrtim öğrncilrindn oluşan bir çalışma grubu üzrind yürütülmüş olması, MOEİÖ nün sadc ortaöğrtim öğrncilrind gçrliği kanıtlanmış bir ölçm aracı olduğu anlamına glbilir. Bu bağlamda, ölçğin gçrliği v güvnirliği için farklı örnklmlr üzrind yapılacak çalışmalar önm arz tmktdir. Bu araştırmada, MOEİÖ nün uyum gçrliği kapsamında, öğrncilrin MOEİÖ d yr alan alt ölçklrdn aldıkları puanlar il matmatik başarıları arasındaki ilişki inclnmiştir. Epistmolojik inançlara ilişkin alanyazın inclndiğind, pistmolojik inançların; drs çalışma stratjilri (Dryakulu, 2004), öğrnm yaklaşımları (Cano, 2005; Hofr & Pintrich, 1997; Rodríguz & Cano, 2006; Schommr, Crous, & Rhods, 1992), yansıtıcı düşünm (Phan, 2006), problm çözm bcrisi (Aksan &Sözr, 2007), yaşam boyu öğrnm ğilimi (Bath & Simth, 2002) v dğr trcihlri (Başçiftçi, Gülç, Akdoğan, &Koç, 2011) gibi çok sayıda dğişkn il ilişkili olduğu görülmktdir. Bu noktadan harktl, matmatik odaklı pistmolojik inançların söz konusu dğişknlr il nasıl bir ilişki içrisind olduğunu blirlmy yönlik araştırmaların yürütülmsiönrilbilir. MOEİÖ nün kullanılacağı araştırmaların yürütülmsi, ölçğin ölçm gücün katkı sağlayacak olması açısından oldukça önmlidir. Litratür inclndiğind, pistmolojik inançların gnl mi, alan odaklı mı yoksa hm gnl hm d alan odaklı mı olduğunu blirlmk amacıyla yapılan araştırmaların gnllikl farklı kültürlrd grçklştirildiği, Türk kültüründ is gnl v alan odaklı pistmolojik inançlar arasındaki ilişkiyi inclmy yönlik sınırlı sayıda araştırma (Ern, 2006) olduğugörülmktdir.epistmolojik inançların şkillnmsind kültürlfaktörlrin tkili bir rol oynadığı (Buhl & Alxandr, 2006; Chan & Elliot, 2004; Schommr, 2004) göz önün alındığında, gnl v pistmolojik inançlar arasındaki ilişkinin d kültürl özlliklrdn tkilncği düşünülbilir. Dolayısıyla,
23 Matmatik Odaklı Epistmolojik İnanç Ölçği 381 Türk kültüründ gnl v alan odaklı pistmolojik inançlar arasındaki ilişkiyi blirlmy yönlik araştırmalar, pistmolojik inançlara ilişkin gnl alan odaklı tartışmalarına ışık tutabilir. Bu bağlamda, araştırma kapsamında gliştiriln MOEİÖ kullanılaraköğrncilrin gnl v matmatik odaklı pistmolojik inançları arasındaki ilişkilrin inclncği araştırmalarla, gnl v alan odaklı pistmolojik inançlar il ilgili litratür katkı sağlanabilir. Kaynakça Abdalaziz, N.,& Akmar, S.N. (2012). Epistmology blifs about mathmatical problm solving among Malaysian studnts.oida Intrnational Journal of Sustainabl Dvlopmnt,5(1), Aksan, N.,& Sözr, M.A. (2007). Ünivrsit öğrncilrinin pistmolojik inançları il problm çözm bcrilri arasındaki ilişkilr. Ahi Evran Ünivrsitsi Eğitim Fakültsi Drgisi,8(1), Anastasi, A. (1982). Psychological tsting.nw York: MacMillan PublishingCo. Inc. Aypay, A. (2011). Epistmolojik inançlar ölçğinin Türkiy uyarlaması v öğrtmn adaylarının pistmolojik inançlarının inclnmsi.eskişhir Osmangazi Ünivrsitsi Sosyal Bilimlr Drgisi, 12(1), Başçiftçi, F., Gülç, N., Akdoğan, T.,& Koç, Z. (2011, Nisan). Öğrtmn adaylarının dğr trcihlri il pistmolojik inançlarının inclnmsi.2. Uluslararası Eğitimd Yni Yönlimlr v Uygulamaları Smpozyumunda sunulmuş sözlü bildiri, Antalya, Türkiy. Bath, D.M.,& Smith, C.D. (2009).Th rlationship btwn pistmological blifs and th propnsity for liflong larning.studis in Continuing Education,31(2), Baxtr-Magolda, M. (1992) Knowing and rasoning in collg: Gndr-rlatd pattrns in studnts intllctual dvlopmnt.san Francisco: Jossy-Bass. Bayram, N. (2009). Sosyal bilimlrd SPSS il vri analizi. Bursa: Ezgi Kitabvi. Brs, S. E. (1988). Epistmological assumptions and collg taching: Intractions in th collg classrooms. Journal of Rsarch and Dvlopmnt,21(4), Blnky, M., Clinchy, B.M., Goldbrgr, N.R.,& Tarul, J.M. (1986).Womn's ways of knowing. Nw York: Basic Books. Bndixn, L.D., & Schraw, G. (2001).Why do pistmological blifs affct ill-dfind problm solving?papr prsntd at th Annual Mting of th Amrican Educational Rsarch Association, Sattl, WA. Bntlr, P.M. (1980). Multivariat analysis with latnt variabls: Causal modling. Annual Rviw of Psychology, 31, Bntlr, P.M.,& Bontt, D.G. (1980).Significanc tsts and goodnss of fit in th analysis of covarianc structurs.psychological Bulltin,88,
24 382 Mustafa İLHAN & Bayram ÇETİN Brown, M., & Cudck, R. (1993). Altrnativ ways of assssing modl fit. InK. Bolln & J. Long(Eds.), Tstingstructural quation modls(pp ). London: Sag Publications. Buhl, M.M.,& Alxandr, P.A.(2006).Examining th dual natur of pistmological blifs.intrnational Journal of Educational Rsarch, 45, Buhl, M.M., Alxandr, P.A., & Murphy, P.K.(2002). Blifs about schoold knowldg: Domain spcific or domain gnral? Contmporary Educational Psychology,27, Büyüköztürk, Ş. (2010). Sosyal bilimlr için vri analizi l kitabı.ankara: Pgm Akadmi Yayınları. Caldrhad, J. (1996). Tachrs: Blifs and knowldg. In D. Brlinr & R. Calf (Eds.), Handbook of ducational psychology(pp ). Nw York: Macmillan Library Rfrnc. Can, B.,& Arabacıoğlu, S. (2009). Th obsrvation of th tachr candidats pistmological blifs according to som variabls.procdia Social and Bhavioral Scincs, 1(1), Cano, F. (2005). Epistmological blifs and approachs to larning: Thir chang through scondary school and thir influnc on acadmic prformanc. British Journal of Educational Psychology,75, Cattll, R.B. (1978). Th scintific us of factor analysis in bhavioral and lif scincs. Nw York: Plnum. Chan, K.,& Elliot, R.G. (2004). Epistmological blifs across culturs: Critiqu and analysis of blifs structur studis. Educational Psychology,24(2), Colby, G.T. (2007). Studnts pistmological blifs of mathmatics whn taught using traditional vrsus rform curricula in rural Main high schools (Unpublishd mastr s thsis). Univrsity of Main, Main. Costllo, A.B.,& Osborn, J.W. (2005). Bst practics in xploratory factor analysis: Four rcommndations for gtting th most from your analysis. Practical Assssmnt Rsarch & Evaluation, 10(7), 1-9. Cramr, D. (2003).Advancd quantitativ data analysis. Philadlphia, PA: McGrawHill. Çokluk, Ö., Şkrcioğlu, G.,& Büyüköztürk, Ş. (2012). Sosyal bilimlr için çok dğişknli istatistik: SPSS v LISREL uygulamaları. Ankara: Pgm Akadmi Yayıncılık. Crockr, L.,& Algina, J. (1986).Introduction to classical and modrn tst thory. Fort Worth, TX: Holt, Rinhart and Winston Inc. Cronbach, L.J. (1984). Essntials of psychological tsting. Nw York: Harpr Row. Dmirli, C., Türl, Y.K., & Özmn, B. (2010, Nisan). Bilişim tknolojilri öğrtmn adaylarının pistmolojik inançlarının inclnmsi.uluslararası Eğitim
25 Matmatik Odaklı Epistmolojik İnanç Ölçği 383 Tknolojilri Smpozyumunda sunulmuş sözlü bildiri, Boğaziçi Ünivrsitsi, İstanbul, Türkiy. Dryakulu, D. (2004). Ünivrsit öğrncilrinin öğrnm v drs çalışma stratjilri il pistmolojik inançları arasındaki ilişki. Kuram v Uygulamada Eğitim Yöntimi,38, Dryakulu, D. (2006). Epistmolojik inançlar. Y. Kuzgun &D. Dryakulu(Ed.) içind, Eğitimd birysl farklılıklar(ss ). Ankara: Nobl Yayın Dağıtım. Dryakulu, D.,& Büyüköztürk, Ş. (2002). Epistmolojik inanç ölçğinin gçrlik v güvnirlik çalışması. Eğitim Araştırmaları Drgisi,2(8), Dryakulu, D.,& Büyüköztürk, Ş. (2005). Epistmolojik inanç ölçğinin faktör yapısının ynidn inclnmsi: Cinsiyt v öğrnim görüln program türün gör pistmolojik inançların karşılaştırılması. Eğitim Araştırmaları Drgisi,18, DVllis, R. F. (2003). Scal dvlopmnt: Thory and applications. Nwbury Park: Sag Publications. Domino, G.,& Domino, M.L. (2006).Psychological tsting: An introduction. Cambridg: Cambridg Univrsity Prss. Dwck, C.,& Lggtt, E. (1988).A social-cognitiv approach to motivation and prsonality.psychological Rviw,95, Enman, M.,& Lupart, J. (2000). Talntd fmal studnts' rsistanc to scinc: an xploratory study of post-scondary achivmnt motivation, prsistnc, and pistmological charactristics. High Ability Studis,11(2), Ern, A. (2006). Ünivrsit öğrncilrinin gnl v alan-odaklı pistmolojik inançlarının inclnmsi (Yayımlanmamış doktora tzi). Abant İzzt Baysal Ünivrsitsi, Bolu. Erkuş, A. (2012). Psikolojid ölçm v ölçk gliştirm. Ankara: Pgm Akadmi Yayınları. Ertkin, E., Dilmaç, B., Dlic A., & Aydın, E. (2009). Tachrtrains pistmologicalblifs: Effcts of gndr, institution, anddisciplin (mathmatics / socialscincs). Nw Educational Rviw,18(2), Ertkin, E., Dilmaç, B., Yazıcı, E.,& Pkr, M. (2010). Th rlationship btwn pistmological blifs and taching anxity in mathmatics.educational Rsarch and Rviw, 5(10), Eynd, P.O., D Cort, E.,& Vrschaffl, L. (2006). Epistmic dimnsions of studnts mathmatics-rlatd blif systms. Intrnational Journal of Educational Rsarch,45, Frguson, E.,& Cox, T. (1993). Exploratory factor analysis: A usrs guid. Intrnational Journal of Slction and Assssmnt, 1(2), Fostr, J. (2002). Data analysis using SPSS for Windows (v8-10). London: Sag Publications.
26 384 Mustafa İLHAN & Bayram ÇETİN Frankl, J.R., Walln, N.E.,& Hyun, H.H. (2012).How to dsign and valuat rsarch in ducation. Nw York: McGraw Hill. Fild, A. (2009). Discovring statistics using SPSS. London: SAGE Publications Ltd. Fishbin, M.,& Ajzn, I. (1975). Blif, attitud, intntion and bhavior: An introduction to thory and rsarch. Rading, MA: Addison-Wsly Publishing. Gill, M.G., Ashton, P.T.,& Algina, J. (2004).Changing prsrvic tachrs pistmological blifs about taching and larning in mathmatics: An intrvntion study.contmporary Educational Psychology, 29, Gorsuch, R.L. (1983). Factor analysis. Hillsdal, NJ: Lawrnc Erlbaum. Hacıömroğlu, G. (2011). Sınıf öğrtmni adaylarının matmatiksl problm çözmy ilişkin inançlarını yordamada pistmolojik inançlarının inclnmsi. Buca Eğitim Fakültsi Drgisi,30, Hair, J.F., Andrson, R.E., Tatham, R.L.,& Grablowsky, B.J. (1979). Multivariat data analysis. Tulsa, OK: Pip Books. Hammr, D. (1994). Epistmological blifs in introductory physics.cognition and Instruction,12(2), Hofr, B. (2000) Dimnsionality and diffrncs in prsonal pistmology.contmporary Educational Psychology,25, Hofr, B.,& Pintrich, P.R. (1997).Th dvlopmnt of pistmological thoris: Blifs about knowldg and knowing and thir rlation to larning. Rviw of Educational Rsarch,67(1), Hu, L.T., & Bntlr, P.M. (1999). Cutoff critria for fit indxs in covarianc structural analysis: Convntional critria vrsus nw altrnativs. Structural Equation Modling,6, Hutchson, G.,& Sofroniou, N. (1999).Th multivariat social scintist. London: Sag. Hazır-Bıkmaz, F. (2002). Fn Öğrtimind öz ytrlilik inancı. Eğitim Bilimlri v Uygulama, 1(2), Jhng, J.C.J., Johnson, S.D., & Andrson, R.C. (1993). Schooling and studnts pistmological blifs about larning.contmporary Educational Psychology,18(1), Klin, R.B. (1994). An asy guid to factor analysis.nw York: Routldg. Klin, R.B. (2011). Principls and practic of structural quation modling. Nw York: Th Guilford Prss. Koballa, T.R., & Crowly, F.E. (1985).Th influnc of attitud on scinc taching and larning.school Scinc and Mathmatics,85(3), Krows, A.J.(1999). Prsrvic tachrs blif systms and attituds toward mathmatics in th contxt of a progrssiv lmntary tachr prparation
27 Matmatik Odaklı Epistmolojik İnanç Ölçği 385 program (Unpublishd doctoral dissrtation).th Univrsity of Oklohama, Oklohoma. Kurt, F. (2009). Cinsiytin, sınıf sviysinin v ğitim gördüklri alanların, öğrncilrin pistmolojik inançları üzrindki tkisi (Yayımlanmamış yüksk lisans tzi). Ortadoğu Tknik Ünivrsitsi, Ankara, Türkiy. Lch, N.L.,Barltt, K.C.,& Morgan, G.A. (2005). SPSS for intrmdiat statistics: Us and intrprtation. Mahwah, NJ: Lawrnc Erlbaum Associats. Limon, M. (2006).Th domain gnrality spcificity of pistmological blifs: A thortical problm, a mthodological problm or both? Intrnational Journal of Educational Rsarch, 45, Mansour, N. (2009). Scinc tachrs blifs and practics: Issus, implications and rsarch agnda. Intrnational Journal of Environmntal & Scinc Education,4(1), Marsh, H.W., Hau, K.T., Artlt, C., Baumrt, J.,& Pschar, J.L.(2006). OECD s brif slf-rport masur of ducational psychology s most usful affctiv constructs: Cross-
28 386 Mustafa İLHAN & Bayram ÇETİN Pajars, F. (1992). Tachrs blifs and ducational rsarch: Claning up a mssy construct. Rviw of Educational Rsarch, 62(3), Pallant, J. (2005). SPSS survival manual: A stp by stp guid to data analysis using SPSS for Wındows. Australia: Australian Copyright. Paulsn, M. B., & Fldman, K. A. (1999).Epistmological blifs and slf-rgulatd larning.journal of Staff, Program, and Organizational Dvlopmnt,16, Paulsn, M.B., & Wlls, C.T.(1998).Domain diffrncs in th pistmological blifs of collg studnts.rsarch in Highr Education,39(4), Phan, H.P.(2006). Examination of studnt larning approachs, rflctiv thinking and pistmological blifs: A latnt variabls approach. Elctronic Journal of Rsarch Educational Psychology, 4(3), Phan, H.P. (2008). Prdicting chang in pistmological blifs, rflctiv thinking and larning styls: A longitudinal study. British Journal of Educational Psychology, 78, Pintrich, P.R.,& Schunk, D.H.(2002).Motivation in ducation: Thory, rsarch and applications. Uppr Saddl Rivr, NJ: Mrrill Prntic Hall. Richardson, V. (2003).Pr-Srvic tachrs blifs. In J. Raths & A. C. McAninch (Eds.),Tachr blifs and classroom prformanc: Th impact of tachr ducation (pp. 1-22). Grnwich, CT: Information Ag Publishing. Rodríguz, L.,& Cano, F. (2006): Th pistmological blifs, larning approachs and study orchstrations of univrsity studnts. Studis in Highr Education,31(5), Roth, W.M., & Roychoudhury, A. (1994).Physics studnts pistmologis and viws about knowing and larning.journal of Rsarch in Scinc Taching,31(1), Ruddick, S. (1996) Rason s fminity: A cas for connctd knowing.in N. Goldbrgr, J. Tarul, B. Clinchy,&M. Blnky(Eds.), Knowldg, diffrnc and powr (pp ).Nw York: Basic Books. Rukavina, I., & Danman, M. (1996).Intgration and its ffcts in acquiring knowldg about compting scintific thoris from txt.journal of Educational Psychology,88, Ryan, M.P.(1984). Monitoring txt comprhnsion: Individual diffrncs in pistmological standards.journal of Educational Psychology,76, Schonfld, A.H. (1989). Exploration of studnts mathmatical blifs and bhavior.journal for Rsarch in Mathmatics Education,20, Schommr, M. (1990).Effcts of blifs about th natur of knowldg on comprhnsion.journal of Educational Psychology,82(3), Schommr, M.A.(1998). Th influnc of ag and ducation on pistmological blifs.british Journal of Educational Psychology,68(4),
29 Matmatik Odaklı Epistmolojik İnanç Ölçği 387 Schommr, M. (2004).Explaining th pistmological blif systm: Introducing th mbddd systmic modl and coordinatd rsarch approach.educational Psychologist,39(1), Schommr, M., Crous, A., & Rhods, N. (1992). Epistmological blifs and mathmatical txt comprhnsion: Bliving it is simpl dos not mak it so. Journal of Educational Psychology,84, Schommr, M.A., Dull, O. K.,& Barkr, S. (2003). Epistmological blifs across domains using Biglan s classification of acadmic disciplins.rsarch in Highr Education,44(3), Schommr, M.A., & Walkr, K. (1995).Ar pistmological blifs similar across domains? Journal of Educational Psychology, 87(3), Schraw, G., Bndixn, L.D., & Dunkl, M.E.(2002). Dvlopmnt and validation of th pistmic blif invntory (EBI). In B.K. Hofr & P.R. Pintrich (Eds.), Prsonal pistmology: Th psychology of blifs about knowldg and knowing (pp ). Mahwah, NJ: Lawrnc Erlbaum. Schrishim, C.A., & Eisnbach, R.J.(1995). An xploratory and confirmatory factor analytic invstigation of itm wording ffcts on obtaind factor structurs of survy qustionnair masurs. Journal of Managmnt,21(6), Stinr,L.A.(2007).Th ffct of prsonal and pistmological blifs on prformanc in a collg dvlopmntal mathmatics class (Unpublishd doctoral dissrtation).kansas Stat Univrsity, Kansas. Sipahi, B., Yurtkoru, S., & Çinko, M. (2010). Sosyal bilimlrd SPSS l vri analizi. İstanbul: Bta Basım Yayım Dağıtım. Stangor, C. (2010). Rsarch mthods for th bhavioral scincs. Wadsworth. Stockton, J.C. (2010). A study of th rlationships btwn pistmological blifs and slf-rgulatd larning among advancd placmnt calculus studnts in th contxt of mathmatical problm solving (Unpublishd doctoral dissrtation).knnsaw Stat Univrsity, Knnsaw, GA. Strobl, J., Crnusca, D.,& Jonassn, D.H.(2011).Diffrntmajors diffrnt pistmological blifs?acadmic Exchang Quartrly,12, Şkr, H.,& Gnçdoğan, B. (2006). Psikolojid v ğitimd ölçm aracı gliştirm. Ankara: Nobl Yayın Dağıtım. Tang, J. (2007). Exploratory and confirmatory factor analysis of pistmic blifs qustionnair about mathmatics for Chins junior middl school studnts.journal of Mathmatics Education,3(2), Tavşancıl, E. (2009). Tutumların ölçülmsi v SPSS il vri analizi. Ankara: Nobl Yayın Dağıtım. Tzbaşaran, A. (1997). Likrt tipi ölçk hazırlama kılavuzu. Ankara: Türk Psikologlar Drnği.
30 388 Mustafa İLHAN & Bayram ÇETİN Tsai, C.C.(2000). Th ffcts of STS-orintd instruction on fmal tnth gradrs' cognitiv structur outcoms and th rol of studnt scintific pistmological blifs. Intrnational Journal of Scinc Education,22(10), Urbina, S. (2004).Essntials of psychological tsting. NJ: John Wily & Sons. Inc. Walkr-Whlr, D.L.(2007).Th dvlopmnt and construct validation of th pistmological blifs survy for mathmatics (Unpublishd doctoral dissrtation). Oklahoma Stat Univrsity, Oklahoma. Wood, P.K., & Kardash, C.A.(2002).Critical lmnts in th dsign and analysis of studis of pistmology. In B.K. Hofr & Paul R. Pintrich (Eds.), Prsonal pistmology: Th psychology of blifs about knowldg and knowing (pp ). Mahwah, NJ: Erlbaum. Yılmaz, Ö. (2007). Öğrncilrin pistmolojik v matmatik problmi çözümlrin yönlik inançlarının problm çözm sürcin tkisinin araştırılması (Yayımlanmamış yüksk lisans tzi). Marmara Ünivrsitsi, İstanbul.
VOLEYBOLCULARIN FARKLI MAÇ PERFORMANSLARI İÇİN TEKRARLANAN ÖLÇÜMLER YÖNTEMİNİN KULLANILMASI
 96 OLEBOLCULAIN FAKLI MAÇ PEFOMANSLAI İÇİN TEKALANAN ÖLÇÜMLE ÖNTEMİNİN KULLANILMASI ÖET Gürol IHLIOĞLU Süha KAACA Farklı yr, zaman v matryallr üzrind tkrarlanan dnylr il bir vya birdn fazla faktörün tkisi
96 OLEBOLCULAIN FAKLI MAÇ PEFOMANSLAI İÇİN TEKALANAN ÖLÇÜMLE ÖNTEMİNİN KULLANILMASI ÖET Gürol IHLIOĞLU Süha KAACA Farklı yr, zaman v matryallr üzrind tkrarlanan dnylr il bir vya birdn fazla faktörün tkisi
GİRİŞİMCİ WEB SAYFALARININ DEĞERLENDİRİLMESİNDE BULANIK BİLİŞSEL HARİTALAMA YÖNTEMİNİN KULLANIMI
 EKEV AKADEİ DERGİSİ Yıl: 14 Sayı: 44 (Yaz 2010) 335 GİRİŞİCİ WEB SAYFALARININ DEĞERLENDİRİLESİNDE BULANIK BİLİŞSEL HARİTALAA YÖNTEİNİN KULLANII. Dursun KAYA (*) A. Samt HAŞILOĞLU (**) Slçuk Burak HAŞILOĞLU
EKEV AKADEİ DERGİSİ Yıl: 14 Sayı: 44 (Yaz 2010) 335 GİRİŞİCİ WEB SAYFALARININ DEĞERLENDİRİLESİNDE BULANIK BİLİŞSEL HARİTALAA YÖNTEİNİN KULLANII. Dursun KAYA (*) A. Samt HAŞILOĞLU (**) Slçuk Burak HAŞILOĞLU
Anaparaya Dönüş (Kapitalizasyon) Oranı
 Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
IKTI 102 25 Mayıs, 2010 Gazi Üniversitesi-İktisat Bölümü
 DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
Hizmet Kalitesinin Servqual Metodu İle Ölçümü ve Sonuçların Yapısal Eşitlik Modelleri İle Analizi: Öğretmen Evi Uygulaması
 19 Hizmt Kalitsinin Srvqual Mtodu İl Ölçümü v Sonuçların Yapısal Eşitlik Modllri İl Analizi: Öğrtmn Evi Uygulaması Sülyman Ersöz, Mhmt Pınarbaşı, A.Kürşad TÜRKER, Mustafa YÜZÜKIRMIZI Endüstri Mühndisliği
19 Hizmt Kalitsinin Srvqual Mtodu İl Ölçümü v Sonuçların Yapısal Eşitlik Modllri İl Analizi: Öğrtmn Evi Uygulaması Sülyman Ersöz, Mhmt Pınarbaşı, A.Kürşad TÜRKER, Mustafa YÜZÜKIRMIZI Endüstri Mühndisliği
Geleneksel Devlet Anlayışından e-devlete: Türkiye ve Irak e- devlet Algısı Karşılaştırması
 BİLİŞİM TEKNOLOJİLERİ DERGİSİ, CİLT: 7, SAYI: 3, EYLÜL 214 21 Glnksl Dvlt Anlayışından -dvlt: Türkiy v Irak - dvlt Algısı Karşılaştırması Wadullah Majd FADHIL 1, Alptkin SÖKMEN 2, Emr Burak EKMEKÇİOĞLU
BİLİŞİM TEKNOLOJİLERİ DERGİSİ, CİLT: 7, SAYI: 3, EYLÜL 214 21 Glnksl Dvlt Anlayışından -dvlt: Türkiy v Irak - dvlt Algısı Karşılaştırması Wadullah Majd FADHIL 1, Alptkin SÖKMEN 2, Emr Burak EKMEKÇİOĞLU
TANITIM ve KULLANIM KILAVUZU. Modeller UBA4234-R. Versiyon : KK_UBA_V3.0210
 SAT-IF / CATV Ultra Gniş Bantlı Dağıtım Yükslticilri (UBA-Srisi) TANITIM v KULLANIM KILAVUZU Modllr UBA4234-R Vrsiyon : KK_UBA_V3.0210 1.Gnl Tanıtım UBA Srisi Dağıtım Yükslticilri, uydu (950-2150MHz) v
SAT-IF / CATV Ultra Gniş Bantlı Dağıtım Yükslticilri (UBA-Srisi) TANITIM v KULLANIM KILAVUZU Modllr UBA4234-R Vrsiyon : KK_UBA_V3.0210 1.Gnl Tanıtım UBA Srisi Dağıtım Yükslticilri, uydu (950-2150MHz) v
DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİK KONTROL I Dr. Uğur HASIRCI
 DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ
 ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ Srkan SUNU - Srhan KÜÇÜKA Dokuz Eylül Ünivrsitsi Makina Mühndisliği Bölümü -posta: [email protected] Özt: Bu çalışmada, komprsör,
ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ Srkan SUNU - Srhan KÜÇÜKA Dokuz Eylül Ünivrsitsi Makina Mühndisliği Bölümü -posta: [email protected] Özt: Bu çalışmada, komprsör,
AISI 316L ÇELİĞİNİN İŞLENMESİNDE TAKIM RADYÜSÜ VE KESME PARAMETRELERİNİN TAGUCHİ YÖNTEMİYLE OPTİMİZASYONU
 Gazi Üniv. Müh. Mim. Fak. Dr. Journal of th Faculty of Enginring and Architctur of Gazi Univrsity Cilt 28, No 3, 437-444, 2013 Vol 28, No 3, 437-444, 2013 AISI 316L ÇELİĞİNİN İŞLENMESİNDE TAKIM RADYÜSÜ
Gazi Üniv. Müh. Mim. Fak. Dr. Journal of th Faculty of Enginring and Architctur of Gazi Univrsity Cilt 28, No 3, 437-444, 2013 Vol 28, No 3, 437-444, 2013 AISI 316L ÇELİĞİNİN İŞLENMESİNDE TAKIM RADYÜSÜ
 HR.Ü.Z.F.Drgisi, 2008, 12(4):65-71 J.Agric.Fac.HR.U., 2008, 12(4):65-71 SÜNE MÜCADELESİNDE ÇİFTÇİ DAVRANIŞLARI: ADIYAMAN- DİYARBAKIR-MARDİN-ŞANLIURFA ÖRNEĞİ Mhmt DUMAN Clalttin GÖZÜAÇIK Vdat KARACA Çtin
HR.Ü.Z.F.Drgisi, 2008, 12(4):65-71 J.Agric.Fac.HR.U., 2008, 12(4):65-71 SÜNE MÜCADELESİNDE ÇİFTÇİ DAVRANIŞLARI: ADIYAMAN- DİYARBAKIR-MARDİN-ŞANLIURFA ÖRNEĞİ Mhmt DUMAN Clalttin GÖZÜAÇIK Vdat KARACA Çtin
DERS 9. Grafik Çizimi, Maksimum Minimum Problemleri
 DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
Asenkron Makinanın Alan Yönlendirme Kontrolünde FPGA Kullanımı ALAN İ., AKIN Ö.
 Asnkron Makinanın Alan Yönlndirm Kontrolünd FPGA Kullanımı ALAN İ., AKIN Ö. ABSTRACT In this study, th fasibility of usag of fild programmabl gat arrays (FPGA) in th fild orintd control (FOC) of induction
Asnkron Makinanın Alan Yönlndirm Kontrolünd FPGA Kullanımı ALAN İ., AKIN Ö. ABSTRACT In this study, th fasibility of usag of fild programmabl gat arrays (FPGA) in th fild orintd control (FOC) of induction
Çocuklara Yabancı Dil Öğretiminin Duyuşsal Hedefleri Ölçeği
 Çocuklara Yabancı Dil Öğretiminin Duyuşsal Hedefleri Ölçeği Şad, S. N., & Gürbüztürk, O. (2015). The affective objectives in early foreign language teaching: A scale development study. International Journal
Çocuklara Yabancı Dil Öğretiminin Duyuşsal Hedefleri Ölçeği Şad, S. N., & Gürbüztürk, O. (2015). The affective objectives in early foreign language teaching: A scale development study. International Journal
TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ
 TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ Cünyt DUMRUL * ÖZ Bu çalışma ticarî dışa açıklık, bklnn döviz kuru, bklnn nflasyon oranı v Türkiy il
TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ Cünyt DUMRUL * ÖZ Bu çalışma ticarî dışa açıklık, bklnn döviz kuru, bklnn nflasyon oranı v Türkiy il
Kamuoyuna, Emek Taşınmaz Değerleme ve Danışmanlık A.Ş. İstanbul, 5 Ocak 2015
 Emk Taşınmaz Dğrlm v Danışmanlık A.Ş. İstanbul, 5 Ocak 2015 Kamuoyuna, Ektki rapor Bankacılık Düznlm v Dntlm Kurumu tarafından 1 Kasım 2006 tarih v 26333 sayılı Rsmi Gazt d yayımlanan Bankalara Dğrlm Hizmti
Emk Taşınmaz Dğrlm v Danışmanlık A.Ş. İstanbul, 5 Ocak 2015 Kamuoyuna, Ektki rapor Bankacılık Düznlm v Dntlm Kurumu tarafından 1 Kasım 2006 tarih v 26333 sayılı Rsmi Gazt d yayımlanan Bankalara Dğrlm Hizmti
ALTI TEKERLEKLİ TAŞITIN DİNAMİK ANALİZİ
 Altı krlkli aşıtın Dinamik Analizi HAVACILIK VE UZAY EKNOLOJİLERİ DERGİSİ EMMUZ 5 CİL SAYI (1-14) ALI EKERLEKLİ AŞIIN DİNAMİK ANALİZİ Cihan DEMİR Yıldız knik Ünivrsitsi, Makin Fakültsi, Makin Mühndisliği
Altı krlkli aşıtın Dinamik Analizi HAVACILIK VE UZAY EKNOLOJİLERİ DERGİSİ EMMUZ 5 CİL SAYI (1-14) ALI EKERLEKLİ AŞIIN DİNAMİK ANALİZİ Cihan DEMİR Yıldız knik Ünivrsitsi, Makin Fakültsi, Makin Mühndisliği
YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ ÖZET
 YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ LEVENT YILMAZ Istanbul Tknik Ünivrsitsi, İnşaat Fakültsi, Hidrolik v Su Yapıları Kürsüsü, 8626, Maslak, Istanbul. ÖZET
YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ LEVENT YILMAZ Istanbul Tknik Ünivrsitsi, İnşaat Fakültsi, Hidrolik v Su Yapıları Kürsüsü, 8626, Maslak, Istanbul. ÖZET
YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ
 . Ulusal Tasarım İmalat v Analiz Kongrsi 11-1 Kasım 010- Balıksir YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ Aydın DEMİRCAN*, M. Ndim
. Ulusal Tasarım İmalat v Analiz Kongrsi 11-1 Kasım 010- Balıksir YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ Aydın DEMİRCAN*, M. Ndim
DERS 9. Grafik Çizimi, Maksimum-Minimum Problemleri. 9.1. Grafik çiziminde izlenecek adımlar. y = f(x) in grafiğini çizmek için
 DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Denetleyici ile Doğru Akım Motorunun Hız Denetim Performansının İncelenmesi
 Ahmt GANİ/APJES II-I (24) 6-23 Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Dntlyici il Doğru Akım Motorunun Hız Dntim Prformansının İnclnmsi * Ahmt Gani, 2 Hasan Rıza Özçalık, 3 Hakan Açıkgöz,
Ahmt GANİ/APJES II-I (24) 6-23 Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Dntlyici il Doğru Akım Motorunun Hız Dntim Prformansının İnclnmsi * Ahmt Gani, 2 Hasan Rıza Özçalık, 3 Hakan Açıkgöz,
Günlük Bülten. 27 Aralık 2012. Merkez Bankası Baş Ekonomisti Hakan Kara 2012 yılının %6 civarında enflasyonla tamamlanacağını düşündüklerini söyledi
 27 Aralık 2012 Prşmb Günlük Bültn İMKB vrilri İMKB 100 77,991.1 Piyasa Dğri-TÜM ($m) 304,387.4 Halka Açık Piyasa Dğri-TÜM ($m) 87,677.3 Günlük İşlm Hami-TÜM ($m) 1,243.42 Yurtdışı piyasalar Borsalar Kapanış
27 Aralık 2012 Prşmb Günlük Bültn İMKB vrilri İMKB 100 77,991.1 Piyasa Dğri-TÜM ($m) 304,387.4 Halka Açık Piyasa Dğri-TÜM ($m) 87,677.3 Günlük İşlm Hami-TÜM ($m) 1,243.42 Yurtdışı piyasalar Borsalar Kapanış
ETİL ASETAT ÜRETİMİNİN YAPILDIĞI TEPKİMELİ DAMITMA KOLONUNUN AYIRIMLI ( DECOUPLING ) PID KONTROLÜ
 Onuncu Ulual Kimya Mühndiliği Kongri, 3-6 Eylül 2012, Koç Ünivriti, İtanbul ETİL ASETAT ÜRETİMİNİN YAPILDIĞI TEPKİMELİ DAMITMA KOLONUNUN AYIRIMLI ( DECOUPLING ) PID KONTROLÜ Abdulwahab GIWA, Sülyman KARACAN
Onuncu Ulual Kimya Mühndiliği Kongri, 3-6 Eylül 2012, Koç Ünivriti, İtanbul ETİL ASETAT ÜRETİMİNİN YAPILDIĞI TEPKİMELİ DAMITMA KOLONUNUN AYIRIMLI ( DECOUPLING ) PID KONTROLÜ Abdulwahab GIWA, Sülyman KARACAN
Kayıplı Dielektrik Cisimlerin Mikrodalga ile Isıtılması ve Uç Etkileri
 Kayıplı Dilktrik Cisimlrin Mikrodalga il Isıtılması v Uç Etkilri Orhan Orhan* Sdf Knt** E. Fuad Knt*** *Univrsity of Padrborn, Hinz ixdorf Institut, Fürstnall, 3302 Padrborn, Almanya [email protected] **Istanbul
Kayıplı Dilktrik Cisimlrin Mikrodalga il Isıtılması v Uç Etkilri Orhan Orhan* Sdf Knt** E. Fuad Knt*** *Univrsity of Padrborn, Hinz ixdorf Institut, Fürstnall, 3302 Padrborn, Almanya [email protected] **Istanbul
Ruppert Hız Mekanizmalarında Optimum Dişli Çark Boyutlandırılması İçin Yapay Sinir Ağları Kullanımı
 Makin Tknolojilri Elktronik Drgisi Cilt: 6, No: 2, 2009 (-8) Elctronic Journal of Machin Tchnologis Vol: 6, No: 2, 2009 (-8) TEKNOLOJİK ARAŞTIRMALAR www.tknolojikarastirmalar.com -ISSN:304-44 Makal (Articl)
Makin Tknolojilri Elktronik Drgisi Cilt: 6, No: 2, 2009 (-8) Elctronic Journal of Machin Tchnologis Vol: 6, No: 2, 2009 (-8) TEKNOLOJİK ARAŞTIRMALAR www.tknolojikarastirmalar.com -ISSN:304-44 Makal (Articl)
Birleştirilmiş E-Öğrenme Tasarımı Modeli ve Hızlı Öğretim Tasarımı Stratejileri
 Özt Birlştirilmiş E-Öğrnm Tasarımı Modli v Hızlı Öğrtim Tasarımı Stratjilri Doç.Dr. İsmail İpk & Yrd. Doç. Dr. Ömr Faruk Sözcü Fatih Ünivrsitsi Bilgisayar v Öğrtim Tknolojilri Eğitimi Bölümü 34500 Büyükçkmc-İstanbul
Özt Birlştirilmiş E-Öğrnm Tasarımı Modli v Hızlı Öğrtim Tasarımı Stratjilri Doç.Dr. İsmail İpk & Yrd. Doç. Dr. Ömr Faruk Sözcü Fatih Ünivrsitsi Bilgisayar v Öğrtim Tknolojilri Eğitimi Bölümü 34500 Büyükçkmc-İstanbul
Çelik. Her şey hesapladığınız gibi!
 Çlik Hr şy hsapladığınız gibi! idyapi Bilgisayar Dstkli Tasarım Mühndislik Danışmanlık Taahhüt A.Ş. Piyalpaşa Bulvarı Famas Plaza B-Blok No: 10 Kat: 5 Okmydanı Şişli 34384 İstanbul Tl : (0212) 220 55 00
Çlik Hr şy hsapladığınız gibi! idyapi Bilgisayar Dstkli Tasarım Mühndislik Danışmanlık Taahhüt A.Ş. Piyalpaşa Bulvarı Famas Plaza B-Blok No: 10 Kat: 5 Okmydanı Şişli 34384 İstanbul Tl : (0212) 220 55 00
Çay Atıklarından Aktif Karbon Üretimi ve Adsorpsiyon Proseslerinde Kullanımı
 ÖZET Çay Atıklarından Aktif Karbon Ürtimi v Adsorpsiyon Prosslrind Kullanımı Mrym OZMAK a, Işıl Gürtn b, Emin YAĞMUR b, Zki AKTAŞ b a DSİ Gn.Md. TAKK Dairsi Başkanlığı, Ankara, 61 b Ankara Ünivrsitsi Mühndislik
ÖZET Çay Atıklarından Aktif Karbon Ürtimi v Adsorpsiyon Prosslrind Kullanımı Mrym OZMAK a, Işıl Gürtn b, Emin YAĞMUR b, Zki AKTAŞ b a DSİ Gn.Md. TAKK Dairsi Başkanlığı, Ankara, 61 b Ankara Ünivrsitsi Mühndislik
Makine Öğrenmesi 4. hafta
 ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
Bilgi Tabanı (Uzman) Karar Verme Kontrol Kural Tabanı. Bulanık. veya. Süreç. Şekil 1 Bulanık Denetleyici Blok Şeması
 Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
- BANT TAŞIYICILAR -
 - BANT TAŞIYICILAR - - YAPISAL ÖZELLİKLER Bir bant taşıyıcının nl örünümü aşağıdaki şkild vrilmiştir. Bant taşıyıcıya ismini vrn bant (4) hm taşınacak malzmyi için alan bir kap örvi örn, hm d harkt için
- BANT TAŞIYICILAR - - YAPISAL ÖZELLİKLER Bir bant taşıyıcının nl örünümü aşağıdaki şkild vrilmiştir. Bant taşıyıcıya ismini vrn bant (4) hm taşınacak malzmyi için alan bir kap örvi örn, hm d harkt için
LOGARİTMA. Örnek: çizelim. Çözüm: f (x) a biçiminde tanımlanan fonksiyona üstel. aşağıda verilmiştir.
 LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
Eğitimde şimdilik son hamle olmak üzere Bilim Merkezi ni Bayrampaşalı genç araştırmacıların hizmetine sunmuş bulunduğumuzu da burada ifade edelim.
 Dğrli Bayrampaşalılar, Atila AYDINER İçind bulunduğumuz v Bilgi Çağı olarak tanımlanan bu dönmd, büyük dvltlrin v büyük özl sktör yapılanmalarının n önmli gidr kalmini bilgi v tknoloji harcamaları oluşturuyor.
Dğrli Bayrampaşalılar, Atila AYDINER İçind bulunduğumuz v Bilgi Çağı olarak tanımlanan bu dönmd, büyük dvltlrin v büyük özl sktör yapılanmalarının n önmli gidr kalmini bilgi v tknoloji harcamaları oluşturuyor.
SIVILAŞMAYA KARŞI GÜVENLİK KATSAYISININ YAPAY SİNİR AĞLARI İLE TAHMİN EDİLMESİ: DENİZLİ-GÜMÜŞLER ÖRNEĞİ
 S.Ü. Müh.-Mim. Fak. Drg., c.3, s.-, 007 J. Fac.Eng.Arch. Slcuk Univ., v.3, n.-, 007 SIVILAŞMAYA KARŞI GÜVENLİK KATSAYISININ YAPAY SİNİR AĞLARI İLE TAHMİN EDİLMESİ: DENİZLİ-GÜMÜŞLER ÖRNEĞİ Gulmustafa ŞEN,
S.Ü. Müh.-Mim. Fak. Drg., c.3, s.-, 007 J. Fac.Eng.Arch. Slcuk Univ., v.3, n.-, 007 SIVILAŞMAYA KARŞI GÜVENLİK KATSAYISININ YAPAY SİNİR AĞLARI İLE TAHMİN EDİLMESİ: DENİZLİ-GÜMÜŞLER ÖRNEĞİ Gulmustafa ŞEN,
Günlük Bülten. 27 Şubat 2013. TCMB, Şubat ayı PPK toplantısı özetini yayınladı
 27 Şuat 2013 Çarşama Günlük Bültn İMKB vrilri İMKB 100 77,514.3 Piyasa Dğri-TÜM ($m) 302,886.2 Halka Açık Piyasa Dğri-TÜM ($m) 86,403.0 Günlük İşlm Hacmi-TÜM ($m) 1,629.94 Yurtdışı piyasalar Borsalar Kapanış
27 Şuat 2013 Çarşama Günlük Bültn İMKB vrilri İMKB 100 77,514.3 Piyasa Dğri-TÜM ($m) 302,886.2 Halka Açık Piyasa Dğri-TÜM ($m) 86,403.0 Günlük İşlm Hacmi-TÜM ($m) 1,629.94 Yurtdışı piyasalar Borsalar Kapanış
Bağımsızlığının 20. Yılında Azerbaycan
 Bağımsızlığının 20. Yılında Azrbaycan Dr. Ali ASKER* 1980 lrin ortalarından itibarn Sovytlr Birliğind uygulanan ynidn yapılanma v saydamlık politikalarının amacı (n azından sözd), dmokratiklşm yoluyla
Bağımsızlığının 20. Yılında Azrbaycan Dr. Ali ASKER* 1980 lrin ortalarından itibarn Sovytlr Birliğind uygulanan ynidn yapılanma v saydamlık politikalarının amacı (n azından sözd), dmokratiklşm yoluyla
KANUN TOHUMCULUK KANUNU. Kanun No. 5553 Kabul Tarihi : 31/10/2006 BİRİNCİ BÖLÜM. Amaç, Kapsam ve Tanımlar
 8 Kasım 2006 ÇARŞAMBA Rsmî Gazt Sayı : 26340 KANUN TOHUMCULUK KANUNU Kanun No. 5553 Kabul Tarihi : 31/10/2006 Amaç BİRİNCİ BÖLÜM Amaç, Kapsam v Tanımlar MADDE 1 Bu Kanunun amacı; bitkisl ürtimd vrim v
8 Kasım 2006 ÇARŞAMBA Rsmî Gazt Sayı : 26340 KANUN TOHUMCULUK KANUNU Kanun No. 5553 Kabul Tarihi : 31/10/2006 Amaç BİRİNCİ BÖLÜM Amaç, Kapsam v Tanımlar MADDE 1 Bu Kanunun amacı; bitkisl ürtimd vrim v
Yuvarlakada Kavşakların Kapasiteleri Üzerine Bir Tartışma *
 İMO Tknik Drgi, 21 4935-4958, Yazı 323 Yuvarlakada Kavşakların Kapasitlri Üzrin Bir Tartışma * Srhan TANYEL* Nadir YAYLA** ÖZ Çalışmada, İzmir d bulunan dört kavşağa ait gözlmlrdn yararlanılarak, çok şritli
İMO Tknik Drgi, 21 4935-4958, Yazı 323 Yuvarlakada Kavşakların Kapasitlri Üzrin Bir Tartışma * Srhan TANYEL* Nadir YAYLA** ÖZ Çalışmada, İzmir d bulunan dört kavşağa ait gözlmlrdn yararlanılarak, çok şritli
Atomlardan Kuarklara. Test 1
 4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
İyon Kaynakları ve Uygulamaları
 İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu [email protected] HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu [email protected] HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
GERİ ÖDEME TALEP FORMU T.C. LONDRA BÜYÜKELÇİLİĞİ EĞİTİM MÜŞAVİRLİĞİNE, Sort Kod : Hesap No : İmzası E-posta : Telefon Nu :
 T.C. LONDRA BÜYÜKELÇİLİĞİ EĞİTİM MÜŞAVİRLİĞİ GERİ ÖDEME TALEP FORMU B-1 T.C. LONDRA BÜYÜKELÇİLİĞİ EĞİTİM MÜŞAVİRLİĞİNE, 1416 Sayılı Kanuna gör MEB (... Ünivrsitsi) adına rsmi burslu statüd öğrnim görmk
T.C. LONDRA BÜYÜKELÇİLİĞİ EĞİTİM MÜŞAVİRLİĞİ GERİ ÖDEME TALEP FORMU B-1 T.C. LONDRA BÜYÜKELÇİLİĞİ EĞİTİM MÜŞAVİRLİĞİNE, 1416 Sayılı Kanuna gör MEB (... Ünivrsitsi) adına rsmi burslu statüd öğrnim görmk
SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU
 SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU A. ÖZER, D.ÖZER Fırat Ünivrsitsi, Mühndislik Fakültsi, Kimya Mühndisliği Bölümü. 23279-ELAZIĞ ÖZET Bu çalışmada, sülfürik
SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU A. ÖZER, D.ÖZER Fırat Ünivrsitsi, Mühndislik Fakültsi, Kimya Mühndisliği Bölümü. 23279-ELAZIĞ ÖZET Bu çalışmada, sülfürik
DESTEK DOKÜMANI. Mali tablo tanımları menüsüne Muhasebe/Mali tablo tanımları altından ulaşılmaktadır.
 Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
BULANIK MANTIK KONTROLLÜ TERMOELEKTRİK BEYİN SOĞUTUCUSU
 BULANIK MANIK KONROLLÜ ERMOELEKRİK BEYİN SOĞUUCUSU A.Hakan YAVUZ 1, Raşit AHISKA 2,Mahmut HEKİM 3 1Niksar Mslk Yükskokulu,Gaziosmanpaşa Ünivrsitsi Niksar,okat 2knik Eğitim Fakültsi,Elktronik Bilgisayar
BULANIK MANIK KONROLLÜ ERMOELEKRİK BEYİN SOĞUUCUSU A.Hakan YAVUZ 1, Raşit AHISKA 2,Mahmut HEKİM 3 1Niksar Mslk Yükskokulu,Gaziosmanpaşa Ünivrsitsi Niksar,okat 2knik Eğitim Fakültsi,Elktronik Bilgisayar
Siirt Üniversitesi Eğitim Fakültesi. Halil Coşkun ÇELİK
 Siirt Üniversitesi Eğitim Fakültesi Halil Coşkun ÇELİK 15 Mayıs 2008 Hemen hemen her bilim alanındaki gelişmeler, yapılmış sistematik araştırmaların katkılarına bağlıdır. Bu yüzden genel olarak araştırma,
Siirt Üniversitesi Eğitim Fakültesi Halil Coşkun ÇELİK 15 Mayıs 2008 Hemen hemen her bilim alanındaki gelişmeler, yapılmış sistematik araştırmaların katkılarına bağlıdır. Bu yüzden genel olarak araştırma,
OLASILIK ve ÝSTATÝSTÝK ( Genel Tekrar Testi-1) KPSS MATEMATÝK. Bir anahtarlıktaki 5 anahtardan 2 si kapıyı açmak - tadır.
 OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
BÖLÜM 7. Sürekli hal hatalarının değerlendirilmesinde kullanılan test dalga şekilleri: Dalga Şekli Giriş Fiziksel karşılığı. Sabit Konum.
 9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
TAKIM LİDERİNİN ÇALIŞANLARIN MOTİVASYONU ÜZERİNDEKİ ETKİSİ: ÇAĞRI MERKEZİ İNCELEMESİ. Araş. Gör. Gündüz AKSU
 TAKIM LİDERİNİN ÇALIŞANLARIN MOTİVASYONU ÜZERİNDEKİ ETKİSİ: ÇAĞRI MERKEZİ İNCELEMESİ Araş. Gör. Gündüz AKSU ÖZ İltişim, nformayon, ulaşım v tknoloji gibi alanlarda kürllşn dünyada artık ürtimin yrl olmaktan
TAKIM LİDERİNİN ÇALIŞANLARIN MOTİVASYONU ÜZERİNDEKİ ETKİSİ: ÇAĞRI MERKEZİ İNCELEMESİ Araş. Gör. Gündüz AKSU ÖZ İltişim, nformayon, ulaşım v tknoloji gibi alanlarda kürllşn dünyada artık ürtimin yrl olmaktan
BÖLÜM II A. YE Đ BETO ARME BĐ ALARI TASARIM ÖR EKLERĐ ÖR EK 2
 BÖLÜ II A. YE Đ BETO ARE BĐ ALARI TASARI ÖR EKLERĐ ÖR EK SÜ EKLĐK DÜZEYĐ YÜKSEK 6 KATLI BETO ARE PERDELĐ / ÇERÇEELĐ BĐ A SĐSTEĐ Đ EŞDEĞER DEPRE YÜKÜ YÖ TEĐ ĐLE A ALĐZĐ E TASARII.1. GENEL BĐNA BĐLGĐLERĐ...II./..
BÖLÜ II A. YE Đ BETO ARE BĐ ALARI TASARI ÖR EKLERĐ ÖR EK SÜ EKLĐK DÜZEYĐ YÜKSEK 6 KATLI BETO ARE PERDELĐ / ÇERÇEELĐ BĐ A SĐSTEĐ Đ EŞDEĞER DEPRE YÜKÜ YÖ TEĐ ĐLE A ALĐZĐ E TASARII.1. GENEL BĐNA BĐLGĐLERĐ...II./..
DERS 7. Türev Hesabı ve Bazı Uygulamalar II
 DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
LYS Matemat k Deneme Sınavı
 LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
Üstel Dağılım SÜREKLİ ŞANS DEĞİŞKENLERİNİN OLASILIK YOĞUNLUK FONKSİYONLARI
 ..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
Tüm Öğretmenlerimizin Öğretmenler Günü Kutlu Olsun...
 HABER BÜLTENİ KASIM 2012 YIL 1 SAYI 9 www.iszu.du.tr Tm Öğrtmnlrimizin Öğrtmnlr Gn Kutlu Olsun... Öğrtmnliğin Gzlliklri Paylaşıldı Kitap Fuarında Yazarlarla Buluştuk Çocuklara Muhtşm Göstri 01 İSZÜ HABER
HABER BÜLTENİ KASIM 2012 YIL 1 SAYI 9 www.iszu.du.tr Tm Öğrtmnlrimizin Öğrtmnlr Gn Kutlu Olsun... Öğrtmnliğin Gzlliklri Paylaşıldı Kitap Fuarında Yazarlarla Buluştuk Çocuklara Muhtşm Göstri 01 İSZÜ HABER
metal (bakır) metaloid (silikon) metal olmayan (cam) iletken yar ı iletken yalıtkan
 1 YARI İLETKENLER Enstrümantal Analiz ir yarı iltkn, iltknliği bir iltkn il bir yalıtkan arasında olan kristal bir malzmdir. Çok çşitli yarıiltkn malzm vardır, silikon v grmanyum, mtalimsi bilşiklr (silikon
1 YARI İLETKENLER Enstrümantal Analiz ir yarı iltkn, iltknliği bir iltkn il bir yalıtkan arasında olan kristal bir malzmdir. Çok çşitli yarıiltkn malzm vardır, silikon v grmanyum, mtalimsi bilşiklr (silikon
Tekirdağ&Ziraat&Fakültesi&Dergisi&
 ISSN:130*7050 NamıkKmalÜnivrsitsi TkirdağZiraatFakültsiDrgisi Jurnal(f(Tkirdag(Agricultural(Faculty( ( ( ( ( ( ( An(Intrnatinal(Jurnal(f(all(Subjcts(f(Agricultur( Cilt(/(Vlum:(1Sayı(/(Numbr:((((((Yıl(/(Yar:(015
ISSN:130*7050 NamıkKmalÜnivrsitsi TkirdağZiraatFakültsiDrgisi Jurnal(f(Tkirdag(Agricultural(Faculty( ( ( ( ( ( ( An(Intrnatinal(Jurnal(f(all(Subjcts(f(Agricultur( Cilt(/(Vlum:(1Sayı(/(Numbr:((((((Yıl(/(Yar:(015
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 2007 SORULARI
 DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
Kirişli döşemeler (plaklar)
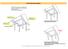 Kirişli döşmlr (plaklar) Dört tarafından kirişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşluklu döşmlr Düznsiz gomtrili döşmlr Üç tarafı kirişli bir tarafı boşta döşm Bir tarafı kirişli
Kirişli döşmlr (plaklar) Dört tarafından kirişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşluklu döşmlr Düznsiz gomtrili döşmlr Üç tarafı kirişli bir tarafı boşta döşm Bir tarafı kirişli
SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU
 SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU Vyis SELEN, Ali YARAŞ 2, Cansu YILMAZ 3, M. Şaban TANYILDIZI 4, Dursun ÖZER 5 Fırat Ünivrsitsi Mühndislik Fakültsi Kimya
SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU Vyis SELEN, Ali YARAŞ 2, Cansu YILMAZ 3, M. Şaban TANYILDIZI 4, Dursun ÖZER 5 Fırat Ünivrsitsi Mühndislik Fakültsi Kimya
Örtü Torba Yöntemi ile Örneklenen Sürütme Ağlarında Seçicilik Parametrelerinin Hesaplanması Üzerine Bir Bilgisayar Programı (L50 Sürüm: 1.0.
 Su Ürünlri Drgisi Cilt No: 15 Sayı:3-4 305-314 İzmir-Bornova 1998 Örtü Tora Yöntmi il Örnklnn Sürütm Ağlarında Sçicilik Paramtrlrinin Hsaplanması Üzrin Bir Bilgisayar Programı (L50 Sürüm: 1.0.0) Akın T.
Su Ürünlri Drgisi Cilt No: 15 Sayı:3-4 305-314 İzmir-Bornova 1998 Örtü Tora Yöntmi il Örnklnn Sürütm Ağlarında Sçicilik Paramtrlrinin Hsaplanması Üzrin Bir Bilgisayar Programı (L50 Sürüm: 1.0.0) Akın T.
GEBAM BÜLTENİ. Hacettepe Üniversitesi GERİATRİK BİLİMLER Araştırma ve Uygulama Merkezi. Geriatri ve Gerontoloji Kursu
 2007 www.gbam.hacttp.du.tr GEBAM BÜLTENİ Hacttp Ünivrsitsi GERİATRİK BİLİMLER Araştırma v Uygulama Mrkzi Griatri v Grontoloji Kursu Ülkmizd hr yıl Mart ayında çşitli tkinliklrin grçklştiği Ulusal Yaşlılar
2007 www.gbam.hacttp.du.tr GEBAM BÜLTENİ Hacttp Ünivrsitsi GERİATRİK BİLİMLER Araştırma v Uygulama Mrkzi Griatri v Grontoloji Kursu Ülkmizd hr yıl Mart ayında çşitli tkinliklrin grçklştiği Ulusal Yaşlılar
aktüel NEÜ Avrupa Komisyonundan üniversitemize AKTS ETİKETİ Ödülü verildi Rektörümüz Prof. Dr. Filiz Kılıç'tan Nevşehir basın mensuplarına teşekkür
 Kitapsvrlrin ilgisini çkbilck kitap önrilri Satranç oyununa bu kz farklı bir açıdan bakalım... SAYFA 3'TE SAYFA 7'DE SAYFA 8'DE Erasmus Dğişim Programı il Polonya da ğitim görn öğrncimizdn mktup var aktül
Kitapsvrlrin ilgisini çkbilck kitap önrilri Satranç oyununa bu kz farklı bir açıdan bakalım... SAYFA 3'TE SAYFA 7'DE SAYFA 8'DE Erasmus Dğişim Programı il Polonya da ğitim görn öğrncimizdn mktup var aktül
BİLEŞENLER. Demiryolu Araçları için yüksek hızlı DC devre kesiciler Tip UR6, UR10 ve UR15
 İLŞNLR miryolu raçları için yüksk hızlı dvr ksicilr Tip R, R v R Gnl bilgi R, R v R; doğal soğutmalı, açmasız, tk kutuplu, çift yönlü, lktromanytik üflmli, lktrik kontrol dvrlrin v doğrudan aşırı akım
İLŞNLR miryolu raçları için yüksk hızlı dvr ksicilr Tip R, R v R Gnl bilgi R, R v R; doğal soğutmalı, açmasız, tk kutuplu, çift yönlü, lktromanytik üflmli, lktrik kontrol dvrlrin v doğrudan aşırı akım
Matris Konverterden Beslenen Lineer Asenkron Motor Modeli ve Matlab/Simulink ile Benzetimi
 6 th Intrnational Advancd Tchnologis Symposium (IATS ), 6-8 May, Elazığ, Turky Matris Konvrtrdn Bslnn inr Asnkron Motor Modli v Matlab/Simulink il Bnztimi M. Ş. Üny, H. Altun Univrsity of Şırnak, Şırnak/Turky,
6 th Intrnational Advancd Tchnologis Symposium (IATS ), 6-8 May, Elazığ, Turky Matris Konvrtrdn Bslnn inr Asnkron Motor Modli v Matlab/Simulink il Bnztimi M. Ş. Üny, H. Altun Univrsity of Şırnak, Şırnak/Turky,
Pamukkale Üniversitesi Mühendislik Bilimleri Dergisi. Pamukkale University Journal of Engineering Sciences
 Pamukkal Ünivrsitsi Mühndislik Bilimlri Drgisi, Cilt 19, Sayı 6, 013, Sayfalar 66-74 Pamukkal Ünivrsitsi Mühndislik Bilimlri Drgisi Pamukkal Univrsity Journal of Enginring Scincs DIŞ MERKEZ ÇAPRAZLI BİR
Pamukkal Ünivrsitsi Mühndislik Bilimlri Drgisi, Cilt 19, Sayı 6, 013, Sayfalar 66-74 Pamukkal Ünivrsitsi Mühndislik Bilimlri Drgisi Pamukkal Univrsity Journal of Enginring Scincs DIŞ MERKEZ ÇAPRAZLI BİR
NOKTASAL KAYNAKLI TOPRAK KİRLİLİĞİNİN KONTROLÜ YÖNETMELİĞİ. BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak ve Tanımlar
 NOKTASAL KAYNAKLI TOPRAK KİRLİLİĞİNİN KONTROLÜ YÖNETMELİĞİ Amaç BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak v Tanımlar MADDE 1 Bu Yöntmliğin amacı; alıcı ortam olarak toprağın kirliliktn korunması, noktasal kaynaklı
NOKTASAL KAYNAKLI TOPRAK KİRLİLİĞİNİN KONTROLÜ YÖNETMELİĞİ Amaç BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak v Tanımlar MADDE 1 Bu Yöntmliğin amacı; alıcı ortam olarak toprağın kirliliktn korunması, noktasal kaynaklı
KULLANMA TALİMATI. EXCİPİAL LİPO %4 Emülsiyon Cilt üzerine uygulanır.
 KULLANMA TALİMATI EXCİPİAL LİPO %4 Emülsiyon Cilt üzrin uygulanır. Etkiıı madd: Hr 1 g mülsiyonda 40 rng Ür (Karbamid) içrir. Yardımcı ıııaddlr: Sodyum laktat, Laktik asit, Triklozan, Orta zincirli triglisritlr,
KULLANMA TALİMATI EXCİPİAL LİPO %4 Emülsiyon Cilt üzrin uygulanır. Etkiıı madd: Hr 1 g mülsiyonda 40 rng Ür (Karbamid) içrir. Yardımcı ıııaddlr: Sodyum laktat, Laktik asit, Triklozan, Orta zincirli triglisritlr,
MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ
 Onuncu Ulusal Kimya Mühndisliği Kongrsi, 3-6 Eylül 1, Koç Ünivrsitsi, İstanbul MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ İlkr KIPÇAK, Turgut Giray ISIYEL Eskişhir Osmangazi
Onuncu Ulusal Kimya Mühndisliği Kongrsi, 3-6 Eylül 1, Koç Ünivrsitsi, İstanbul MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ İlkr KIPÇAK, Turgut Giray ISIYEL Eskişhir Osmangazi
DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. 4 ADET PARSEL
 DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. İZMİR MENEMEN - SÜZBEYLİ 4 ADET PARSEL Bu taşınmaz dğrlm raporu, Ekiz Kimya Sanayi v Ticart A.Ş. nin istmi üzrin hazırlanmıştır. İlgilisi v hazırlanış
DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. İZMİR MENEMEN - SÜZBEYLİ 4 ADET PARSEL Bu taşınmaz dğrlm raporu, Ekiz Kimya Sanayi v Ticart A.Ş. nin istmi üzrin hazırlanmıştır. İlgilisi v hazırlanış
TG 13 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN İLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖAT İLKÖĞRETİM MATEMATİK u tstlrin hr hakkı saklıdır. Hangi amaçla olursa olsun, tstlrin tamamının va bir kısmının
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN İLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖAT İLKÖĞRETİM MATEMATİK u tstlrin hr hakkı saklıdır. Hangi amaçla olursa olsun, tstlrin tamamının va bir kısmının
MENKUL KIYMET DEĞERLEMESİ
 MENKUL KIYMET EĞERLEMESİ.. Hiss Sdii Tk ömlik Gtirisii Hsaplaması Bir mkul kıymti gtirisi, bkl akit akımlarıı, şimdiki piyasa fiyatıa şitly iskoto oraıdır. Mkul kıymti özlliği gör bu akit akımları faiz
MENKUL KIYMET EĞERLEMESİ.. Hiss Sdii Tk ömlik Gtirisii Hsaplaması Bir mkul kıymti gtirisi, bkl akit akımlarıı, şimdiki piyasa fiyatıa şitly iskoto oraıdır. Mkul kıymti özlliği gör bu akit akımları faiz
PNOZ Emniyet Röleleri
 PNOZ Emniyt Röllri Emniyt Röllri PNOZ X, PNOZsigma v PNOZlog, Modülr mniyt röllri PNOZmulti v PNOZpowr Hr talp için uygun mniyt çözümü. İş Faaliytlri Excllnt Componnts Snsör tknolojisi Emniyt şaltrlri
PNOZ Emniyt Röllri Emniyt Röllri PNOZ X, PNOZsigma v PNOZlog, Modülr mniyt röllri PNOZmulti v PNOZpowr Hr talp için uygun mniyt çözümü. İş Faaliytlri Excllnt Componnts Snsör tknolojisi Emniyt şaltrlri
Dönüşüm Simülatörü Tasarımı The Design of Transform Simulator
 7 Publishd in 5th Intrnational Symposium on Innovativ Tchnologis in Enginring and Scinc 9-3 Sptmbr 7 (ISITES7 Baku - Azrbaijan) Dönüşüm Simülatörü Tasarımı Th Dsign of Transform Simulator * Fahri Vatansvr
7 Publishd in 5th Intrnational Symposium on Innovativ Tchnologis in Enginring and Scinc 9-3 Sptmbr 7 (ISITES7 Baku - Azrbaijan) Dönüşüm Simülatörü Tasarımı Th Dsign of Transform Simulator * Fahri Vatansvr
TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK (1)
 Rsmi Gazt Tarii: 08.06.2010 Rsmi Gazt Sayısı: 27605 TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK (1) BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak v Tanımlar Amaç MADDE 1
Rsmi Gazt Tarii: 08.06.2010 Rsmi Gazt Sayısı: 27605 TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK (1) BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak v Tanımlar Amaç MADDE 1
TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK (1)
 Rsmi Gazt Tarii: 08.06.2010 Rsmi Gazt Sayısı: 27605 TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK (1) BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak v Tanımlar Amaç MADDE 1
Rsmi Gazt Tarii: 08.06.2010 Rsmi Gazt Sayısı: 27605 TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK (1) BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak v Tanımlar Amaç MADDE 1
ÖĞRETMEN ADAYLARININ PROBLEM ÇÖZME BECERİLERİ
 ÖĞRETMEN ADAYLARININ PROBLEM ÇÖZME BECERİLERİ Doç. Dr. Deniz Beste Çevik Balıkesir Üniversitesi Necatibey Eğitim Fakültesi Güzel Sanatlar Eğitimi Bölümü Müzik Eğitimi Anabilim Dalı [email protected]
ÖĞRETMEN ADAYLARININ PROBLEM ÇÖZME BECERİLERİ Doç. Dr. Deniz Beste Çevik Balıkesir Üniversitesi Necatibey Eğitim Fakültesi Güzel Sanatlar Eğitimi Bölümü Müzik Eğitimi Anabilim Dalı [email protected]
Sosyal Bilgiler Odaklı Akademik Risk Alma Ölçeğinin (SOARAÖ) Geliştirilmesi: Geçerlik ve Güvenirlik Çalışması
 Sosyal Bilgiler Odaklı Akademik Risk Alma Ölçeğinin (SOARAÖ) Geliştirilmesi: Geçerlik ve Güvenirlik Çalışması Arş Gör Melehat GEZER* Dicle Üniversitesi, Ziya Gökalp Eğitim Fakültesi, Sur / Diyarbakır /
Sosyal Bilgiler Odaklı Akademik Risk Alma Ölçeğinin (SOARAÖ) Geliştirilmesi: Geçerlik ve Güvenirlik Çalışması Arş Gör Melehat GEZER* Dicle Üniversitesi, Ziya Gökalp Eğitim Fakültesi, Sur / Diyarbakır /
bir süzgeç tasarım programı
 bir süzgç tasarım programı turhan çiftçi başı özay hüsyin söndürm işlvinin vriln koşullara uymasını sağlayan bir k(s) = karaktristik işlvin bulunmasını grktirmktdir. Kullanılan yaklaştırma işlvinin sçimind
bir süzgç tasarım programı turhan çiftçi başı özay hüsyin söndürm işlvinin vriln koşullara uymasını sağlayan bir k(s) = karaktristik işlvin bulunmasını grktirmktdir. Kullanılan yaklaştırma işlvinin sçimind
Enerji Dönüşüm Temelleri. Bölüm 3 Bir Fazlı Transformatörler
 Enrji Dönüşüm Tmllri Bölüm 3 Bir Fazlı Transformatörlr Birfazlı Transformatorlar GİRİŞ Transformatörlrin grçk özllik v davranışlarını daha kolay anlamak için ilk aşamada idal transformatör üzrind durulacaktır.
Enrji Dönüşüm Tmllri Bölüm 3 Bir Fazlı Transformatörlr Birfazlı Transformatorlar GİRİŞ Transformatörlrin grçk özllik v davranışlarını daha kolay anlamak için ilk aşamada idal transformatör üzrind durulacaktır.
08 Haziran 2010 Resmî Gazete Sayı : 27605 YÖNETMELİK TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK
 08 Haziran 2010 Rsmî Gazt Sayı : 27605 YÖNETMELİK Çvr v Orman Bakanlığından: TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK Amaç BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak
08 Haziran 2010 Rsmî Gazt Sayı : 27605 YÖNETMELİK Çvr v Orman Bakanlığından: TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK Amaç BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak
BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR
 BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR sabit-oğnlkl, sabit-özllikli, harici, türbülanslı sınır tabaka akımları ZB 386 Sınır Tabaka Drs notları - M. TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr
BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR sabit-oğnlkl, sabit-özllikli, harici, türbülanslı sınır tabaka akımları ZB 386 Sınır Tabaka Drs notları - M. TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr
Eğitim ve Bilim. Cilt 39 (2014) Sayı Sınıf Değerlendirme Atmosferi Ölçeği nin (SDAÖ) Geliştirilmesi: Geçerlik ve Güvenirlik Çalışması
 Eğitim ve Bilim Cilt 39 (2014) Sayı 176 31-50 Sınıf Değerlendirme Atmosferi Ölçeği nin (SDAÖ) Geliştirilmesi: Geçerlik ve Güvenirlik Çalışması Mustafa İlhan 1, Bayram Çetin 2 Öz Bu araştırmada öğrencilerin
Eğitim ve Bilim Cilt 39 (2014) Sayı 176 31-50 Sınıf Değerlendirme Atmosferi Ölçeği nin (SDAÖ) Geliştirilmesi: Geçerlik ve Güvenirlik Çalışması Mustafa İlhan 1, Bayram Çetin 2 Öz Bu araştırmada öğrencilerin
Yüksek Öğrenim Enstitüleri İçin Marka Kimliği Ölçeğinin Türkçeye Uyarlanması: Güvenirlik ve Geçerlilik Çalışması
 Geliş Tarihi : 01 Kasım 2017 Finans Ekonomi ve Sosyal Araştırmalar Dergisi Kabul Tarihi : 08 Kasım 2017 Yıl : 2017 Cilt : 2 Sayı :3 Dijital Baskı Tarihi : 23 Kasım 2017 ISSN : 2602-2486 Makale DOI : 10.29106/fesa.348306
Geliş Tarihi : 01 Kasım 2017 Finans Ekonomi ve Sosyal Araştırmalar Dergisi Kabul Tarihi : 08 Kasım 2017 Yıl : 2017 Cilt : 2 Sayı :3 Dijital Baskı Tarihi : 23 Kasım 2017 ISSN : 2602-2486 Makale DOI : 10.29106/fesa.348306
NEM ALMALI SOĞUTMA SİSTEMLERİ
 NEM ALMALI SOĞUTMA SİSTEMLERİ Alpr YILMAZ, Hüsamttin BULUT Çukurova Ünivrsitsi, Makina Mühndisliği Bölümü, 01330-ADANA ÖZET Son yıllarda iklimlndirm tknolojisind hızlı glişmlr yaşanmaktadır. Ozon tabakasına
NEM ALMALI SOĞUTMA SİSTEMLERİ Alpr YILMAZ, Hüsamttin BULUT Çukurova Ünivrsitsi, Makina Mühndisliği Bölümü, 01330-ADANA ÖZET Son yıllarda iklimlndirm tknolojisind hızlı glişmlr yaşanmaktadır. Ozon tabakasına
Bazik Mavi-16 Boyarmaddesinin Kil Üzerine Adsorpsiyonu &
 Avrupa Bilim v Tknoloji Drgisi Cilt. 1, No. 2, S. 29-38, Haziran 214 Tlif hakkı EJOSAT a aittir Araştırma Makalsi www.josat.com ISSN:2148-2683 Europan Journal of Scinc and Tchnology Vol. 1, No. 2, pp.
Avrupa Bilim v Tknoloji Drgisi Cilt. 1, No. 2, S. 29-38, Haziran 214 Tlif hakkı EJOSAT a aittir Araştırma Makalsi www.josat.com ISSN:2148-2683 Europan Journal of Scinc and Tchnology Vol. 1, No. 2, pp.
Hücre bölünmesi sırasında önce... sonra... bölünmesi gerçekleşir.
 2.Mitoz Hücr Bölünmsi Hücr bölünmsi tüm canlılarda görüln bir olaydır. Hücr bölünmsi büyüm, glişm, yaraların iyilşmsi, ürm hücrlrinin oluşması v tk hücrli canlıların çoğalması olaylarında tkilidir. Bir
2.Mitoz Hücr Bölünmsi Hücr bölünmsi tüm canlılarda görüln bir olaydır. Hücr bölünmsi büyüm, glişm, yaraların iyilşmsi, ürm hücrlrinin oluşması v tk hücrli canlıların çoğalması olaylarında tkilidir. Bir
Veteriner Farmakoloji ve Toksikoloji Derneği Bülteni
 r in r t V r Farmakoloji v Toksikoloji D r n ð i Vtrinr Farmakoloji v Toksikoloji Drnği Bültni Vtrinr Farmakoloji v Toksikoloji Drnği Yayın Organı Yıl: 2011 Sayı: 4 ISSN: 1309-4769 www.vtfarmatoks.org.tr
r in r t V r Farmakoloji v Toksikoloji D r n ð i Vtrinr Farmakoloji v Toksikoloji Drnği Bültni Vtrinr Farmakoloji v Toksikoloji Drnği Yayın Organı Yıl: 2011 Sayı: 4 ISSN: 1309-4769 www.vtfarmatoks.org.tr
Malzeme Güvenliği Bilgi Formu (EC) No. 1907/2006 (REACH) Düzenlemesi ile uyumludur Hazırlandığı tarih: 02/03/09 Revize edildiği tarih: 12/11/12
 BÖLÜM 1. MADDENİN/KARIŞIMIN VE FİRMANIN/İŞLETMENİN TANIMI 1.1 Ürün kimliği: EB25SS Ticari isim: Ekstra Güçlü Pisuar Kapakları 1.2 Maddnin vya karışımın blirtiln ilgili kullanımları v blirtiln kullanımlara
BÖLÜM 1. MADDENİN/KARIŞIMIN VE FİRMANIN/İŞLETMENİN TANIMI 1.1 Ürün kimliği: EB25SS Ticari isim: Ekstra Güçlü Pisuar Kapakları 1.2 Maddnin vya karışımın blirtiln ilgili kullanımları v blirtiln kullanımlara
SINIF ÖĞRETMENLİĞİ ALAN SINAVI ÖLÇEĞİNİN GELİŞTİRİLMESİ : GEÇERLİK VE GÜVENİRLİK ÇALIŞMASI
 SINIF ÖĞRETMENLİĞİ ALAN SINAVI ÖLÇEĞİNİN GELİŞTİRİLMESİ : GEÇERLİK VE GÜVENİRLİK ÇALIŞMASI Çavuş ŞAHİN Serdar ARCAGÖK Çanakkale Onsekiz Mart Üniversitesi Eğitim Fakültesi ÖZET Bu çalışmanın amacı sınıf
SINIF ÖĞRETMENLİĞİ ALAN SINAVI ÖLÇEĞİNİN GELİŞTİRİLMESİ : GEÇERLİK VE GÜVENİRLİK ÇALIŞMASI Çavuş ŞAHİN Serdar ARCAGÖK Çanakkale Onsekiz Mart Üniversitesi Eğitim Fakültesi ÖZET Bu çalışmanın amacı sınıf
KULLANMA TALİMATI. Başlıkları yer almaktadır. 1. KESTİNE nedir ve ne için kullanılır?
 KULLANMA TALİMATI KESTİNE 10 mg film tablt Ağızdan alınır. Etkin madd: 10 mg bastin. Yardımcı maddlr: Mikrokristaliz slüloz (E-460i), prjlatiniz mısır nişastası, laktoz monohidrat, kroskarmlloz sodyum
KULLANMA TALİMATI KESTİNE 10 mg film tablt Ağızdan alınır. Etkin madd: 10 mg bastin. Yardımcı maddlr: Mikrokristaliz slüloz (E-460i), prjlatiniz mısır nişastası, laktoz monohidrat, kroskarmlloz sodyum
Günlük Bülten. 05 Mart 2013. Şubat ayında TÜFE %0.30 arttı, ÜFE %0.13 azaldı. Şubat ayında elektrik tüketimi %6 düşüş gösterdi
 XU 100 U SD /TR Y (S ağ taraf) 05 Mart 2013 Salı Günlük Bültn İMKB vrilri İMKB 100 80,612.2 Piyasa Dğri-TÜM ($m) 315,101.9 Halka Açık Piyasa Dğri-TÜM ($m) 89,968.2 Günlük İşlm Hacmi-TÜM ($m) 1,595.93 Şuat
XU 100 U SD /TR Y (S ağ taraf) 05 Mart 2013 Salı Günlük Bültn İMKB vrilri İMKB 100 80,612.2 Piyasa Dğri-TÜM ($m) 315,101.9 Halka Açık Piyasa Dğri-TÜM ($m) 89,968.2 Günlük İşlm Hacmi-TÜM ($m) 1,595.93 Şuat
ÖZEL KONU ANLATIMI SENCAR Başarının sırrı, bilginin ışığı
 GENİŞLETİLMİŞ GERÇEL SAYILARDA LİMİT R = Q I küsin Rl Sayılar Küsi dniliyor. Rl Sayılar Küsid; = Tanısız v = olduğunu biliyorduk. -- R = R { -, + } gnişltiliş grçl sayılar küsind: li = -, - = -, li = +
GENİŞLETİLMİŞ GERÇEL SAYILARDA LİMİT R = Q I küsin Rl Sayılar Küsi dniliyor. Rl Sayılar Küsid; = Tanısız v = olduğunu biliyorduk. -- R = R { -, + } gnişltiliş grçl sayılar küsind: li = -, - = -, li = +
B OSC2 VOD PIC16F84 MİKRODENETLEYİCİSİ KULLANILARAK CİHAZLARIN TELEFON İLE KONTROLÜNE BİR UYGULAMA. Rabman YAKAR, Etem KÖKLÜKAYA.
 SAU Fn Bilimlri Enstitüsü Drgisi PIC16F84 Mikrodntlcisi Kullanılarak Ciaziarın Tlfon D Kontrolün Bir Uygulama PIC16F84 MİKRODENETLEYİCİSİ KULLANILARAK CİHAZLARIN TELEFON İLE KONTROLÜNE BİR UYGULAMA Rabman
SAU Fn Bilimlri Enstitüsü Drgisi PIC16F84 Mikrodntlcisi Kullanılarak Ciaziarın Tlfon D Kontrolün Bir Uygulama PIC16F84 MİKRODENETLEYİCİSİ KULLANILARAK CİHAZLARIN TELEFON İLE KONTROLÜNE BİR UYGULAMA Rabman
Günlük Bülten. 06 Mart 2013. Merkez Bankası, Şubat Ayı Fiyat Gelişmelerini açıkladı. Yurtiçi otomotiv satışları Şubat ta geçen yıla göre %17 arttı
 XU 100 US D/TRY (Sağ taraf) 06 Mart 2013 Çarşama Günlük Bültn İMKB vrilri İMKB 100 81,051.2 Piyasa Dğri-TÜM ($m) 318,088.0 Halka Açık Piyasa Dğri-TÜM ($m) 90,822.1 Günlük İşlm Hacmi-TÜM ($m) 1,695.51 Yurtdışı
XU 100 US D/TRY (Sağ taraf) 06 Mart 2013 Çarşama Günlük Bültn İMKB vrilri İMKB 100 81,051.2 Piyasa Dğri-TÜM ($m) 318,088.0 Halka Açık Piyasa Dğri-TÜM ($m) 90,822.1 Günlük İşlm Hacmi-TÜM ($m) 1,695.51 Yurtdışı
Zaman Serileri Analizi ve Trafik Kazası Verilerine Uygulanması
 Araşırma Makalsi / Rsarch Aricl Iğdır Üni. Fn Bilimlri Ens. Dr. / Iğdır Univ. J. Ins. Sci. & Tch. 3(4): 43-5, 03 Zaman Srilri Analizi v Trafik Kazası Vrilrin Uygulanması Iğdır Ünivrsisi Fn Bilimlri Ensiüsü
Araşırma Makalsi / Rsarch Aricl Iğdır Üni. Fn Bilimlri Ens. Dr. / Iğdır Univ. J. Ins. Sci. & Tch. 3(4): 43-5, 03 Zaman Srilri Analizi v Trafik Kazası Vrilrin Uygulanması Iğdır Ünivrsisi Fn Bilimlri Ensiüsü
