BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR

Transkript

1 BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR sabit-oğnlkl, sabit-özllikli, harici, türbülanslı sınır tabaka akımları ZB 386 Sınır Tabaka Drs notları - M. TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr Türbülanslıakımlar zamana bağlı üç-botldr. Zamana bağlılığın rkansı ölçği çşitli büüklük mrtblrind dağılır. B ndnlrl türbülanslıakımın bütün arıntılarıla analizi, düz lha üzrindki gibi basit bir akım olsa bil çok hacimli bir problmdir. Türbülanslıharktin ölçği çşitli büüklük mrtblrind dağılım göstrdiğin gör saısal bir hsaplama için, hücr gnişliklrinin gn sçimi önmlidir. Hücr büüklüğüharktin önmli bir kısmının ölçğindn büük is sonçlar çok kaba olr. B bakımdan gnl olarak türbülanslıbir sınır tabakanın bir istasonnda 3 4 ağnoktası toplam 6 7 ağnoktasına grksinim dlmaktadır. Pratiktki bir türbülanslıakımın bütün arıntılarıiçin günümüzd gnl bir analiz öntmi gliştirmk hnüz mümkün olmamıştır. Kompl bir simülasonn hsaplama maliti R 3 il dğişmktdir. Dolaısıla çok büük miktarda bilgisaar sürlri harcansa bil günümüz imkanlarıla ancak çok düşük R saısındaki akımlar inclnbilir. ZB 386 Sınır Tabaka Drs notları - M.

2 TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr Gnl dğrlndirm karamsar olmakla birlikt tasarım için türbülanslıakım analizindn bklnn bilgi sınırlıolp, laminrhald oldğ gibi sınır tabaka analizindn bklnn bilgi önclikl C üz sürtünm katsaısı, daha sonra da, θgibi sınır tabaka kalınlıklarıdır. Tasarımda çoğ hald arıntılı hız sıcaklık proili gibi bilgilrin kllanımı daha kısıtlıdır. Arıca türbülanslıakım için örnğin C in n anlama gldiğini düşünmkt arar ardır. Örnk olarak sabit hızdaki bir gmi için sürtünm dirncinintahminiproblmi göz önün alınırsa, bnn için üz üzrindki hrhangi bir noktada üz grilmsinin çalkantıdğrlrinin bilinmsi grkmz. Daha ziad b gmii çkmk için grkli pran ktinin bilinmsin ihtiaçardır. Bnn için d C in zaman ortalamasının bilinmsi trlidir. Bna gör türbülanslıakımın analizind ihtiaçdaha ziad sadc zaman-ortalamasıaortalama dğrlrin blnmasıolarak gözükmktdir. B gibi büüklüklr daimi a zamana bağlı, iki-botl a üç-botl olabilir. ZB 386 Sınır Tabaka Drs notları - M. 3 TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr Tasarımcıaçısından trli gözükn, sadc ortalama büüklüklrin tahminini amaçlaan bir türbülans analizinin günümüz analitik saısal imkanlarıiçrisind kalacağıgörülbilir. Ancak b gün kadar türbülanslıakımların günilir tkin tahmini olnda sadc sınırlıbir başarıld dilbilmiştir. Pratiktki bazıdrmlarda akımın arıntılıçalkantıkaraktristiğininbilinmsi önmlidir. Bna bir örnk akıt-akıcı karışımı şklindki akımın ttşma anması olaıdır. Al içrisind kimasal nrjinin ısı nrjisin dönüşüm hızıanlık lokal sıcaklıklara hali non-linr bir biçimd bağlıdır. Bna gör hrhangi bir noktadaki daimi ısı ürtimini tahmin tmk için sadc T, nin bilinmsi trli olmaz, T,,z,t nin hsaplanması sonçların zaman ortalamasının alınmasıgrkir. Ortalama akım analizin girmdn önc mct ampirik bilgilrin bir kısmınıgözdn gçirmkt arar blnmaktadır. Zira b bilgilr analitik gliştirmlrin tabanınıolştracaktır. Anlık çalkantıharktinin bütün arıntılarınıdikkat almadan ortalama akımın inclnbilmsi için daha ziad dnsl ri tabanına ağırlık rmk grkcktir. Bölc ampirik bilgilr harkt dnklmlri çrçsind kllanılarakarı-ampirikbir analiz gliştirilcktir ZB 386 Sınır Tabaka Drs notları - M. 4

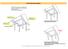
3 Ortalama akımla ilgili ampirik bilgilr. Bir düz lhaüzrind laminr türbülanslıhallrd ölçüln botsz hız proillri, arasında önmli bir arklılık ardır. Türbülanslı hald şkild göstriln botsz ortalama hız proili darısıırdan daha büük bir hızda ksior gibi gözükmktdir. Aslında hız dar akınında aaşbir dğişm göstrirkn çok kısa bir aralıkta anidn sııra gitmktdir. B hız proili iki arklı tabakaa sahip, -.5 /. aralığında üksk iskozitli - /.5 aralığında daha düşük iskozitli.8.6 / Laminr.4. Türbülanslı / bir akışkanın r aldığılaminrbir sınır tabakaa bnztilbilir. B iki tabakanın birlştiği üzd kama grilmlri şit olacağından µ araksit µ araksit B drmda hız gradantınınaraksiti gçrkn µ /µ gibi bir oranla ani bir dğişim göstrmsi grkir. B hss türbülanslısınır tabaka modllmsindki n önmli ikirlrdn birinin sasıdır ZB 386 Sınır Tabaka Drs notları - M. 5 Ortalama akımla ilgili ampirik bilgilr Düz lha üzrindki laminr türbülanslı sınır tabakalar arasında önmli bir ark daha ardır. Şöl ki: Laminrsınır tabakada akışkan cinsi, Rnoldssaısı, pürüzlülüks n olrsa olsn botsz hız proillri anıdır.. Bna karşılık türbülanslı sınır tabakada Rnolds saısı/a pürüzlülüktki dğişimc idğiştirir. B da botsz hız proilinin şklini tkilr. Hız proillrinin b tabiatısınır tabakaların analizind doğrdan önm kazanmaktadır. Farklıkoşllarda olşan hız proillrinin şklini tanımlamak üzr H/θ -şkil paramtrsindn ararlanmak istnbilir. Bir düz lhaüzrindki laminrsınır tabakaiçin Hbüüklüğüdaima.6dır. Klbano Dihl düz dar Hama düz dar.8 Hama 8 hücrli lk / Hama hücrli lk.6.4 Artan C / ZB 386 Sınır Tabaka Drs notları - M. 6 3

4 Ortalama akımla ilgili ampirik bilgilr Ancak türbülanslısınır tabakada HbüüklüğününC bağlıolacağıtahmin dilbilir. Bna gör blli birdp/dbasınçdağılımına sahip hrhangi bir cisimüzrindki türbülanslısınır tabakada olşacak hız proillrinin şklini H paramtrsi il blirlmk mümkün dğildir. Mct ampirik bilgilrin olabiln n kısa biçimd snm kllanımı açısından güçlü kapsamlı korlason dğişknlri gliştirilmsi çok önmlidir. Problm karmaşık olp çok miktarda da ri blnmaktadır. B üzdn mct rilri n basit biçimd dikkat almak adalı olacaktır. Düz lha üzrindki basit türbülanslısınır tabaka halind bil korlason için / /dğişknlrini almanın trli olmaacağı açıktır. Varılacak sonca bir çok araştırmacının katkısı olmakla birlikt n açık n kapsamlı katkı Clasr956 taraından apılmıştır. ZB 386 Sınır Tabaka Drs notları - M. 7 Ortalama akımla ilgili ampirik bilgilr Şkil d r alan hız proillrinin hrhangi bir ölçk aktörü il çarpılarak tk bir ğri dönüştürülmsi bklnmz. Bnnla birlikt, sınır tabaka içrisind knar hızına nazaran mdana gln - hız kaıpları dikkat alınırsa, şkl gör C dğri büüdükçdaha büük hız kabı olşmaktadır. Daha büük bir C, sınır tabaka içindki akışkana daha büük bir aaşlatıcı kt tkimsi dolaısıla hızda momntmda daha büük bir kaıpolmasıanlamına glmktdir.. Klbano Dihl düz dar Hama düz dar.8 Hama 8 hücrli lk / Hama hücrli lk.6.4 Artan C / Bna gör knar hızıla botszlaştırılmışhız kaıplarının üz sürtünm katsaısıla orantılıoldğ sölnbilir C ZB 386 Sınır Tabaka Drs notları - M. 8 4

5 Ortalama akımla ilgili ampirik bilgilr B iki büüklüğün oranıla tanımlanan bir dğişknl bütün ğrilrin korlason sağlanabilir: Sağtarataki iadnin padasıhız botnda bir büüklüktür τ w / sürtünm hızı / C /. τw ½ρ / τ / ρ w Bölc düz lha üzrindki sınır tabakada hız proillrinin ordinatı / için korlason dğişkni C / Diğr ksn için / oranının kllanılmasıtrli olacaktır. Bölc: kaıp kann Türbülanslısınır tabaka hız proillri için koordinatların b şkildki sçiminin n dnli başarılıoldğ şkildn görülmktdir. / ZB 386 Sınır Tabaka Drs notları - M. Klbano Dihl Schltz-Grnow Hama J.H.. pürüzlü dar Ortalama akımla ilgili ampirik bilgilr Ancak b korlasonn gnl başarısı / nın küçük dğrlrind ani dara akın bölgd görülmmktdir. B bölgd hız çabk bir biçimd dğişmktolp çşitli hallr arasındaki arklılıkb şkild snlan bir graiktn kola anlaşılamaz. B graikt, sınır tabakanın üst kısımlarındaki lokal ortalama hızların sınır tabaka knar hızına gör büüklüklrinin, -, önmli oldğ görülürkn lokal ortalama hızların dar üzrindki sıır hız dğrin kıasla drmdoğrdan dikkat alınmamıştır. Osa dara akın n alt tabakada b karşılaştırma önmli olacaktır. Dar bölgsind hızlar için ölçklici büüklük olarak in sürtünm hızının alınmasıgn gözükmktdir /.4. Klbano Dihl Schltz-Grnow Hama J.H.. pürüzlü dar ZB 386 Sınır Tabaka Drs notları - M. 5

6 Ortalama akımla ilgili ampirik bilgilr Sınır tabakanın üst bölgsindki korlasonlarda konm şklind bir oranla tmsil dilmiştir. Darın tkisinin baskın oldğ alt bölgd is sınır tabaka kalınlığınınönminin daha azoldğ kabl dilbilir. B alt bölg sınır tabakanın toplam kalınlığının sadc küçük bir kısmını % tşkil tmkt olp ciarında olşan dğişikliklrin tkisi alt bölgd çok az hissdilir. B drmda büüklüğünün dara akın bölgd bir başka biçimd botszlaştırılmasıdaha gn olacaktır. ν B korlason büüklüğüsürtünm hızıcinsindn azılmışbir tür lokal Rnolds saısıdır B dğişknlr kllanılarak ν a dar kann ZB 386 Sınır Tabaka Drs notları - M. dar kann Ortalama akımla ilgili ampirik bilgilr, ν 4 3 / Laminr alt tabaka / /ν / 5.6 log / ν 4.9 Ldwig Tillmann Klbano Dihl Frman Schltz-Grnow Lar - pip /ν ZB 386 Sınır Tabaka Drs notları - M. 6

7 Ortalama akımla ilgili ampirik bilgilr B noktada blirtilmlidir ki, büüklüğü hız proillrinin anlaşılmasında bölsin kilit bir rol onadığı için τ w dar grilmsinindoğr tspitiönm kazanmaktadır. Yüz grilmsi ilk kz 95 liıllarda başarılıüz grilmsi balanslarının gliştirilmsil ölçülbilir hal glmiştir Dhawan, 953. B tip bir cihaz üzin ilgilniln kısmında üzl tmas tmn küçük bir parça şklind olp, bölc üzin b küçük alanındaki grilm kti doğrdan ölçülür. Daha öncki araştırmacılar τ w itspit tmk için hız proilinin üz üzrindki ğimini kllanmaıdnmişlr, ancak proilin dar akınındaki şkli ndnil doğr sonçlara laşamamışlardır Tkrar dar bölgsin dönülck olrsa, düzgün katıbir üzin çok akınındaki hız çalkantıları, tam dar üzrind w olması ndnil ktli biçimd sönümlnir. Bna gör türbülanslısınır tabakanın dar akın çok inc bir kısmındaki akım laminrapıdadır. B bölg litratürd laminr alt tabaka olarak adlandırılır. ZB 386 Sınır Tabaka Drs notları - M. 3 Ortalama akımla ilgili ampirik bilgilr dar bölgsindki akımıtanımlaan bir lokal Rnoldssaısıoldğna gör b Rnoldssaısının, hakim akımın laminr oldğn blirln, bir alt sınır dğri olmalıdır. B alt sınırla blirlnck bir ükskliğinin altında kalan sınır tabaka bölgsi laminralt tabakaolacaktır Dar üzrind τ oldğndan laminralt bölgd τ τ w oldğ arsaılabilir. τ µ τ w olmak üzr τ intgr dilrk µ w τnintipik dğişimi il botszlaştırılarak τ µ τ µ τ / ρ µ ρ w w w / ν a dar kann dğişknlri cinsindn τ tot τ w ZB 386 Sınır Tabaka Drs notları - M. 4 7

8 4 Ortalama akımla ilgili ampirik bilgilr 3 / Laminr alt tabaka / /ν / 5.6 log / ν 4.9 Ldwig Tillmann Klbano Dihl Frman Schltz-Grnow Lar - pip Ykarıdaki şkildn dnsl rilrin /ν bağıntısını 5 7 dğrlrin kadar izldiği görülmktdir B görüntülaminrbir alt tabakanın arlığınıdoğrlamaktadır. Tabakanın kalınlığı nın% indn daha küçüktür. Sınır tabakanın kalınlığıkabaca O5 mrtbsind olp 5-7büüklüğüd nın/i ciarındadır. ZB 386 Sınır Tabaka Drs notları - M. 5 Ortalama akımla ilgili ampirik bilgilr Bölc biri alt tabakaadiğri d dıştabakaaait olmak üzr başarılıiki korlason kann ortaa konlmştr. ; g ν Fizik grği b iki bölg arasındaki gçişani olamaz. Aksin arada ortak bir birlşm bölgsi r almalıdır b bölgd hr iki bölgdki bağıntılar gçrli olmalıdır. B bağıntılar nidn düznlnrk g ν ; Vrilmişbir sınır tabaka hız proili için ; ν büüklüklri birr sabit olp il dğişmz. Bna gör, g onksion içindki ν sabitçarpanıonksionn dışında toplam şklindki bir sabitl anıtki sahip olmalıdır. Böl bir özllik sadc bir logaritma onksionnda ardır. Çünküçarpımın logaritmasıiki logaritmanın toplamışklind azılabilir. ZB 386 Sınır Tabaka Drs notları - M. 6 8

9 Ortalama akımla ilgili ampirik bilgilr Bna gör, dar bölgsindki dış bölgdki hız proillri için logaritmik bağıntılar tanımlanarak: Düz lhaa ait rilrl daha önc snlan, dar kannna ait graik logaritmik ölçkt tkrar çizilmişolp şkild görülmktdir g ν A log B A log C ν Clasr956 b şkild çiziln rii dikkat alarak logaritmik bağıntılardaki sabitlr için A5.6, B-.5 C4.9 dğrlrini önrmiştir Frman Klbano Dihl Schltz-Grnow Hama - JH pürüzlü dar Hama pürüzlü dar - Moor çok pürüzlü dar / ZB 386 Sınır Tabaka Drs notları - M. 7 Ortalama akımla ilgili ampirik bilgilr Bazı araştırmacılar anı ri için Clasr inkindn çok az arklı başka sabit dğrlri ld tmiştir. Başka araştırmacılar bağıntıları tabii logaritma il azarak A sabitin Kln/Aşklind bağlıolan bir başka Ksabiti kllanmışlardır. ln C K ν A5.6için K.4 Cols956 sınır tabakanın dış bölgsindki hız proillrini tanımlamak için iz kann karamını ortaa komştr. Cols, hızlarda logaritmik kanna gör görüln sapmaların, daki maksimm sapma il normaliz dildiği takdird sadc / nın onksion oldğn dikkat almıştır. B normalizdilmişsapmaları, bir W/ iz onksionil blirtrk W Wolmak üzr korlason grçklştirmiştir. / ln C K ν W / ln C K ν Cols iz onksion ZB 386 Sınır Tabaka Drs notları - M. 8 9

10 Ortalama akımla ilgili ampirik bilgilr Cols956 Wonksionn W sin π W Đz onksion şklind önrmiştir. Sonçolarak iz kann birlşm bölgsini üst bölgi birlikt tanımlaacak biçimd ln K ν Π C W K Log Logaritmik kann Brada Π-KB/ bir iz paramtrsi olp, B-.5, için Π.5 dircols.55 dğrini tasi tmiştir. ZB 386 Sınır Tabaka Drs notları - M. 9 Ortalama akımla ilgili ampirik bilgilr Sonçolarak türbülanslısınır tabakanın tamamıdört bölgdn olşmşgibi düşünülbilir. Koaszn 967 gör hr bir bölgnin kndi znlk hız skalasıardır. -En alttaki laminralt-tabakanın znlk skalası ν/, hız skalasıis dır. -İçbölgnin znlk hız skalalarısırasıla dır. -Dışbölgnin znlk skalası, hız skalasıis dir. -Corrsin Kistlr 955 süpr-tabaka adında dördüncübir tabaka daha tanımlamıştır. Süpr tabaka sınır tabakanın dışknarındaki iskoz tabaka il iskoz olmaan dışakım arasında r alan inc kırımlı bir gçiş bölgsidir. B bölgd hız skalasıolarak katılım hızı alınabilir. B, dışakımdan sınır tabaka içrisin birim zamanda girn akım dbisi il orantılıbir hızdır. Anızamanda türbülans ara-üzünün türbülanslıolmaan dışakıma nazaran ilrlm hızınıiad dr. Koaszn967 katılım hızını V d d şklind tanımlaıp süpr-tabaka için ν V şklind bir znlk skalası olştrmştr ZB 386 Sınır Tabaka Drs notları - M.

11 Ortalama akımla ilgili ampirik bilgilr Alt dış bölglr için azılan logaritmik bağıntılardan limin dilrk A log B A log ν C C B A log R C B C şklind bir üz sürtünm kann blnabilir A log C ν B bağıntıaklaşık biçimd azılaraka ampirik rilr ğri drlarakbaşka, daha basit açık ormüllr d türtilmiştir. En basit birisi Blasis n, Schltz-Grnow94 taraından da doğrlanan bağıntısıdır C.456 R / 4 aklaşık R 7 dğrin kadar gçrli Çoğ kims taraından kllanılan bir başka bağıntı C R C log Schonhrr93 Lznlğnda bir düz lha üzrind türbülanslısınır tabaka halind sürtünm dirnci katsaısı, C D, için b iki araştırmacı ş bağıntıları ld tmiştir:.47 C D 4.3 log R.64 LCD log R.47 C L D ZB 386 Sınır Tabaka Drs notları - M. Sçilmiş ampirik türbülans bilgilri Öncki kısımda apılan analizin amacı hr n kadar ortalama akımın gnl özlliğinin anlaşılması olarak ortaa konlmşolsa da türbülanslıakımın çalkantılıdoğasının anlaşılmasıda sastır. Şkild bir düz lhaüzrindki türbülanslı sınır tabakada üç doğrltdaki türbülans şiddti dağılımlarır almaktadır. Akım doğrltsnda türbülans şiddtinin n büük oldğ, anal öndki türbülans şiddtinin d dik öndkindn daha büük oldğ görülmktdir: > w > ² Klbano, w / / Bnn ndni akımın anal doğrltlarda salınım srbstisi olmasına karşın darın dirkt kısıtlaıcıtkisi ndnil anı srbstinin dik doğrltda olmaışıdır. ZB 386 Sınır Tabaka Drs notları - M.

12 Sçilmiş ampirik türbülans bilgilri Pürüzlübir düz lha üzrindki akım için Corrsin Kistlr 954taraından ld diln türbülans şiddti proillri d şkil d r almaktadır. Bradaki pürüzlülük brştrlmş kağıt biçimind olp iki-botl aklaşık sinüzoidaldir. Pürüz ükskliği. cmolp b üksklik akımıtamamn pürüzlürjim sokmak için trlidir. Blnan türbülans şiddtidüzlri düzgün dar halindkindn çok daha azladır. Fakat üçbilşnin birbirin gör sıralamasıanıdır. ² R 6.7 ν.55 w / ZB 386 Sınır Tabaka Drs notları - M. 3 Sçilmiş ampirik türbülans bilgilri Türbülanslıbir sınır tabakanın dış knarı zamana bağlı, düzgün olmaan bir sınırla karaktriz dilir. Bn anlamak için ortalama konmna bir sıcak-tl anmomtrsi rlştirilirs anmomtrnin aralıklı olarak türbülanslı akım iskoz olmaan akım ölçtüğü görülür. B drm aralıklılık intrmittnc adıriln arasında dğişn bir Ω büüklüğü il ansıtılır. Ωbüüklüğüakımın n kadar sür il türbülanslıoldğn oransal olarak blirtmktdir.. Bazı ölçm sonçları şkild snlmştr. Sınır tabakanın dışına aklaşıldıkça aralıklılığın dğrindn hali küçük kaldığıgörülmktdir..8 Ω.6.4. Corrsin Kistlr Klbano / ZB 386 Sınır Tabaka Drs notları - M. 4

13 Sçilmiş ampirik türbülans bilgilri Sınır tabaka içind akışkanın -doğrltsndaki momntmnn türbülans taraından dik doğrltda taşındığıbilinn bir hsstr. B ola bolamasına dik doğrltdaki çalkantıhızlarının B büüklük akışkanın oğnlğ il çarpılırsa grilm botn alır ρ şklindki korlason il ilişkilidir. Türbülanslıkama grilmsi Rnolds grilmsi ÖlçülmüşRnoldsgrilmlrinin sürtünm hızıla normaliz dilmiş biçimdki bir graiği şkild snlmştr. B büüklük dar akınında n büük dğrini almakta olp darın daha akınındaki inc laminralt-tabakanın içrisind anidn sııra düşmktdir. K: Türbülans kintik nrjisi Κ K R / ZB 386 Sınır Tabaka Drs notları - M Sçilmiş ampirik türbülans bilgilri Laminralt bölgdki dğişim şkild gnişltilmişolarak görülmktdir...8 τlam τ τw K: Türbülans kintik nrjisi üç çalkantıhız bilşninin birim kütl başına kintik nrjisi olp.6.4 R K K w w şklind tanımlanmaktadır / ν / Akımın n kadar türbülanslıoldğn tari tmk için hrhangi bir büüklük kllanılmasıgrkirs, n mantıklısçim türbülans kintik nrjisi olacaktır. ZB 386 Sınır Tabaka Drs notları - M. 6 3

14 Sçilmiş ampirik türbülans bilgilri Türbülans çalkantılar gniş bir zaman ölçği aralığında olşr. Bn göstrmk üzr bolamasına türbülans çalkantılarının spktraölçümlrinin bazılarıdalga nmarasının k onksion olarak şkild snlmştr. Brada rkans k π ortalama hız E k - - E k büüklüğüd k k dk bandındaki bolamasına türbülans nrjisinin miktarı olp dk Bna gör E k -3-4 R ν Dalga saısının büük dğrlrind arkdilirbir harkt görülmktdir. Katıdar büük ölçkli harktlri nglldiği için dara aklaştıkça daha büük ölçkli girdapçıklar dd içrisindki nrji azalmaktadır -5-6 / k cm - ZB 386 Sınır Tabaka Drs notları - M. 7 Sçilmiş ampirik türbülans bilgilri Hrhangi bir türbülanslı kamalı akımda türbülans nrjisinin ürtimi, taşınımı, aınımı dissipasonsöz konsdr Dissipasonbaşlıca laminriskozitnin daha küçük dilrüzrindki tkisindn kanaklanır. B büüklüğü ölçmk zordr. Fakat bazı sonçlar şkild göstrilmiştir. Akımın tam türbülanslı bölglrind dağılımı görmk için b gibi sonçlarıaralıklılığın tkisin bağlamak alışılaglmiştir. ε o---o-- dissipason /Ω dissipason / ZB 386 Sınır Tabaka Drs notları - M. 8 4

15 Sçilmiş ampirik türbülans bilgilri Ykarıdaki blirtiln bütün prosslrin dağılımışkild snldğ gibi bir türbülanslıkintik nrji dngsi biçimind göstrilbilir. Dışknar akınlarıhariçbütünsl dng ana katkılar ürtim dissipasondan kanaklanmaktadır. B ikisi hmn hmn birbirini dnglmktdir kazanç kaıp Taşınım Yaınım Ürtim dissipason ν / ZB 386 Sınır Tabaka Drs notları - M. 9 Sçilmiş ampirik türbülans bilgilri Gçirgn üzlr üzrindki akımların türbülans büüklüklril ilgili bilgi, ortalama akımla ilgili olanlardaki gibi katı üzdkilr kıasla daha zaıtır. Daha önc ortalama akımın tartışıldığı altı üz üzrind üçü katı üçü gçirgn ksnl normal doğrltlardaki türbülans şiddtlri Rnoldsgrilmlrin ait bir kısım ri izln şkillrd snlmştr. 8 6 ² 4 Düzgün katı üz Pürüzlü katı üz Göznkli, sintrlnmiş üz Göznkli, dlikli Ti tabakası Göznkli, ızgaralı üz Izgaralı, arkası katı üz / ZB 386 Sınır Tabaka Drs notları - M. 3 5

16 Sçilmiş ampirik türbülans bilgilri Gçirgn üzlr üzrindki akımların türbülans büüklüklril ilgili bilgi, ortalama akımla ilgili olanlardaki gibi katı üzdkilr kıasla daha zaıtır Düzgün katı üz Pürüzlü katı üz Göznkli, sintrlnmiş mtal Göznkli, dlikli Ti tabakası Göznkli, ızgaralı üz Izgaralı, arkası katı üz ² / ZB 386 Sınır Tabaka Drs notları - M. 3 Sçilmiş ampirik türbülans bilgilri Türbülansın çalkantıdoğasınıansıtan çşitli büüklüklr ilişkin ölçüm sonçlarına ilatn b büüklüklrl ilgili prosslrin iziksl bir tasiri d adalıdır. Türbülans şiddtlri gibi b büüklüklr d zaman üzrind ortalamalardır. Türbülanslı akımın grçk iziğini anlamak için arık, zamana bağlı türbülans olalarının daranışını bilm ihtiaçardır. Bradaki kısa anlatım ana hatlarıla Klin Robinson99 taraından apılan inclm daanmaktadır. Münrit diikri grçktn açık özllikl ardımcıdğildir. Zira türbülanslıakımda anızamanda anırd çok çşitli botlarda dilrmcttr. B bakımdan akışkan kümlri girdap çizgilri düşünmk daha adalıdır. Bir türbülanslıakım içrisind bir akışkan kümsinin bir konmdan diğrin harkt ttiği sölnbilir. B noson Rnolds grilmsini tanımlamak için kllanılacaktır. Türbülanslıakım kabaca girdap çizgilrinin süprpozisonolarak dikkat alınabilir. ZB 386 Sınır Tabaka Drs notları - M. 3 6

17 Sçilmiş ampirik türbülans bilgilri Türbülanslı akım kabaca girdap çizgilrinin süprpozison olarak dikkat alınabilir. Bna gör dçapında, Lznlğnda açısal hızı ωolan bir girdap çizgisi göz önün alınırsa, bnn kütlsi ρld il, kintik nrjisi ρld 4 ω il, açısal momntm da ρld 4 ω il orantılıdır. B girdap lmanı, kütlsi açısal momntm sabit kalmak kadıla sündürülürski b düşük aınım için ii bir aklaşımdır, L arttıkça çap azalacak açısal hız artacak b da kintik nrjii arttıracaktır. Bölc lmanı zatmak için çları üzrind apılan iş lmanın kintik nrjisind artış aratmaktadır. B drm daha önc blirtiln nrji kaskadınıntasirini sağlar. Enrji büük ölçkli harktlrdn bnlar içindki küçük ölçkli harktlr doğr, küçük ölçkli harktlrdki girdap çizgilrinin büük ölçkli harktlrl sündürülmsisonc, akmaktadır. ZB 386 Sınır Tabaka Drs notları - M. 33 Sçilmiş ampirik türbülans bilgilri Ortalama harktin iki-botl oldğ türbülanslıbir akımda girdap çizgilri daha ziad akımla çaprazdır. Sündürm d b doğrltda olacağından türbülans üç-botl olacaktır. Ortalama girdaplılığın çoğ, ortalama hız proilinin şklin gör dar ciarında oğnlaşmıştır Şkil 7.. B hss girdap sünmsinin bir başka soncn ortaa koar: girdap lmanlarının dar ciarında rastgl ükslmsini ani çalkantılar patlama brsting dışbölg sıçramalar izlr...8 /.6.4. Klbano Dihl düz dar Hama düz dar Hama 8 hücrli lk Hama hücrli lk Artan C / ZB 386 Sınır Tabaka Drs notları - M. 34 7

18 8 ZB 386 Sınır Tabaka Drs notları - M. 35 Sabit özllikli akışkanın daimi olmaan, sıkıştırılamaz akımı için Nair-Stoksdnklmlri ν ρ ν ρ ν ρ z w w w z p z w w w w t w z p z w t z p z w t z w B dnklmlr çıkartılırkn rastgl çalkantılıbir harkt hariçttlmamıştır. Türbülans olaıüç-botl, çok gnişbir aralıktaki ölçk rkanslara sahip çalkantılar içrn biçimd zamana rastgl bağlı, büük bir hsaplama problmi aratmakta olp, dnklmlr karıdaki şklil b hsaplamalarıkolalaştırmamaktadır. ZB 386 Sınır Tabaka Drs notları - M. 36 Bna gör akıma ait hr bir büüklük,,,,,,,, t z z t z şklind bir ortalama büüklük il bir çalkantı kısmına arılıp Türbülanslı sınır tabaka konsna başlarkn tasarım analiz amacı için ksritl sadc zamanortalamalıakımla ilgilndiği blirtilmişti. dnklmlrd rlştirilir. Sonra hr bir trimin zaman üzrind ortalamasıalınabilir. Ortalama alma il ilgili bazı krallar g G g F F ds ds s F s G F g F F G F g şklindki iki onksion için ortalama kralları gçrlidir Bradaki üst çizgi r aldığıbüüklüğün ortalamasının alındığınıblirtmktdir.

19 9 ZB 386 Sınır Tabaka Drs notları - M. 37 Brada sadc -B, türbülanslısınır tabakalarla ilgilnilmktdir. Sürklilik dnklmi için ortalama Zaman ortalamasıla p t ν ρ V V V, V Arıca Görüldüğügibi ortalama akım için sürklilik dnklmi laminrakımdakil anıdır. Anlık çalkantılar da anı biçimd bir sürklilik dnklmini sağlamaktadır. ZB 386 Sınır Tabaka Drs notları - M. 38 Momntm dnklmi için ortalama Ortalama çalkantı büüklüklri cinsindn iadlr kllanılarak p t ν ρ Taşınım trimlrin sürklilik dnklmi klnrk Momntm dnklmindki non-linr trimlrin inclnmsi sırasında dikkatli olnmalıdır 443 V V V Hr bir trimin zaman ortalamaları alınarak V V V V V

20 ZB 386 Sınır Tabaka Drs notları - M. 39 Momntm dnklmi için ortalama İlk iki tür açılarak sürklilik dnklmi kllanılarak Momntm dnklmindki diğr trimlrin ortalamalarıda kolalıkla alınır V V V V V 443 P p P p t t t Görüldüğü gibi iskoz trimd önmli bir dğişiklik oktr ZB 386 Sınır Tabaka Drs notları - M. 4 Momntm dnklmi için ortalama Sonç olarak daimi akımdaki türbülanslı sınır tabaka dnklmlri Eld diln bütün ortalama dğrlr momntm dnklmind rlştirilrk P V t ν ρ Şat ortalama akım daimi is ilk trim ortadan kalkacaktır t Arıca dnlrl doğrlanmıştır ki << P V V ρ ρ ν ρ Dardan trinc zakta laminr kama grilmsi trimi türbülansla momntm transport trimi anında küçük kabl dilrk ihmal dilbilir.

21 Momntm dnklmi için ortalama Şüphsizdir ki momntm dnklmind momntm transport trimi ihmal dilmz. Aksi hald dnklm tamamıla laminr akım halindkin dönr. Blirtiln b trim dnklmd türbülanslıakımın çalkantılıdoğasının tkisini ansıtan tk trimdir. Hrhangi bir sınır tabaka problmind oldğ gibi V P ρ, V ν ρ ρ dnklmlril iad diln türbülanslıakım problmind d iskoz olmaan bir dışakım taraından sınır tabaka üzrin tki dn P basınç dağılımının bilindiği kabl dilmktdir. Bna gör b iki dnklmin iki bilinmn için V çözülmsi bklnmktdir. Bnnla birlikt momntm dnklminin sağtarataki n son trim momntm transport trimi ila bir bilinmnolarak r almaktadır. ZB 386 Sınır Tabaka Drs notları - M. 4 Rnolds grilmsi Momntm dnklminin sağ taraında r alan ρ ρ trimi momntm transri trimi olp, laminr akımdaki basit Nwtonin kama il anı rolü onamaktadır. B bakımdan ρ türbülanslıkama grilmsia Rnolds grilmsi olarak adlandırılmaktadır. B türbülanslı kama triminin laminr iskoz trimdn glmdiği, akat iskoz olmaan taşınımsal trimlrdn gldiği blirtilmlidir. Türbülanslısınır tabaka dnklmlril çalışırkn dnklm sistminin çözülbilirhal glmsi için Rnolds grilmsini içrn trimin d diğr bağımsız a bağımlı dğişknlr cinsindn iad dilmsi grklidir. Diğr dğişknlrin hpsi d ortalama dğrlr olarak dikkat alındığından böl bir bağıntıortalama akım modliolarak nitlndirilir. ZB 386 Sınır Tabaka Drs notları - M. 4

22 Kapama closr problmi Blirtiln zorlğ nmnin kola bir ol oktr. Kon, bölümün sonnda daha karmaşık ormülasonlara aracak, akat hp dnklmlrdn daha azla bilinmn olacaktır. B azladan bilinmnlr hp ρ gibi türbülans büüklüklri olacak, sistmi matmatiksl olarak kapatmakiçin hp azladan, gnllikl arı-ampirikbağıntılara grk olacaktır. B drm türbülanslıakımların kapatmaclosrproblmi olarak anılır. Aslında ortalama akım çalkantıbüüklüklrini blirtrk a harkt dnklmlrini kllanarak, a da brada apıldığıgibi zaman üzrind ortalama alarak grçktn önmli hiçbir ş apılmadığıüzrind düşünülürs b şaşırtıcıdrma nasıl glindiğini karamak daha kola olr. B noktaa kadar, matmatiksl ormülasonn gliştirilmsind türbülanslı akımların grçk doğası hakkında hiçbir ş sölnmmiştir. Formülasonntamamlanmasından önc b kon üzrind drlmalıdır. ZB 386 Sınır Tabaka Drs notları - M. 43 Kama grilmsi modli Türbülanslı kama modli gliştirm konsnda ilrlmdn önc çalkantılarla momntm transri olgsnn iziksl bir izahınıhatırlatmakta arar ardır. Şkild göstrildiği gibi sınır tabakanın sisind blnan bir akışkan kümsi daha alt sidki bir konmna r dğiştirdiği takdird ski konmndaki ortalama hızınıkorma ğilimindolacaktır. B hız akışkan kümsinin ni konmnda ortalama hızına gör poziti işartli bir çalkantı hızı kadar artmış gözükcktir. B drmda konmndan düzlmin taşınan anlık kütl akımı ρ olp b kütl ni konmdaki çalkantı hızı il ρ kadar bir momntm artışı aratacaktır. < < Şat akışkan kümsi alt tabakadan daha üst bir tabakaa r dğiştirirs bnn trsi olacaktır. ZB 386 Sınır Tabaka Drs notları - M. 44

23 Kama grilmsi modli Şat zaman üzrind bir ortalama alınırsa hız çalkantılarıasıtasılabolamasına momntmdadik doğrltda olşan momntm transri olarak ld dilir. ρ Ortalama akım türbülans transport ormülasonları Bir ortalama akım türbülans analizi gliştirmk için öncki inclmlr çrçsind _ şklind bir bağıntı blmaa çalışılmalıdır., ;, V, P a, µ ρ τ ρ, T B bağıntının ampirik bilgilr daanmasıgrktiği açıktır. Bağıntının sağtaraında türbülans büüklüklrinin r almadığı blirtilmlidir. B noktada modllm çabalarının amacınıaçıkça blirtmk için sınır tabaka alt bölgsini örnk olarak dikkat almak adalıolacaktır. ZB 386 Sınır Tabaka Drs notları - M. 45 Ortalama akım türbülans transport ormülasonları Biçimsl olarak _, ;, V, P a, µ ρ τ ρ, T il blirtiln blnacak bağıntısınır tabaka dnklmlrind kllanıldığında şkildki ri arasından gçn dol çizgi ld dilcktir. 4 3 / Laminr alt tabaka / /ν / 5.6 log /ν 4.9 Ldwig Tillmann Klbano Dihl Frman Schltz-Grnow Lar - pip /ν B tiptn bir analiz arı-ampirik olarak nitlndirilir. Ampirik bir aklaşım basitç ri drlmş ğrilri kllanacaktır. ZB 386 Sınır Tabaka Drs notları - M. 46 3

24 Ortalama akım türbülans transport ormülasonları Blirtiln amaç birbiril ilişkili iki ormülasonla başarılmıştır. İlki Bossinsq877 taraından, laminrakıma bnztm olla ortaa konmştr τ T _ ρ µ T diiskozitsi ormülason Bradaki µ T diiskozitsinin sadc akışkanın dğil akımın drmna bağlıolacağıbklnmlidir. Yani diiskozitsi laminriskozit gibi alnızca akışkanın trmoizikslbir özlliği dğildir. İkinci ormülasonprandtl95 taraından önrilmiştir τ T _ ρ ρl m karışım znlğ ormülason Karışım znlğ bir tkilşim msasi olarak, molküllr arasıortalama srbst örüng bnztilbilir. Sadc, molküllr arasında dğil d türbülans kümlri arasında tanımlanmaktadır. ZB 386 Sınır Tabaka Drs notları - M. 47 Ortalama akım türbülans transport ormülasonları Akışkan kümlrinin harkt msasi olarak dğil d şkidgöstrildiği gibi l m alınırsa: Şat akışkan üsttabakadan alttabakaa r dğiştiriorsa, < dir l m şklind bir boznt hızı tanımlanabilir. l m Şat akışkan kümsi aşağıdan karıa çıkıorsa b da > olp, boznt hızıda l m l m l m şklinddir. l m > < Sürklilik grği, ~ olp, b son iki bağıntı doğrdan karışım znlğ bağıntısınırir. Yalnız b bağıntıda τ T ninişartini doğr rbilmk için rin azmak daha doğr olr. ZB 386 Sınır Tabaka Drs notları - M. 48 4

25 Ortalama akım türbülans transport ormülasonları Karışım znlğ ormülasonndakil m için d bağımsız dğişkn a paramtrlrina da ortalama bağımlıdğişknlrinonksion olan ila bir bağıntıa ihtiaçardır. B bağıntıda diiskozitsi gibi, akışkanın dğilakımın drmnnbir onksion olacaktır. B aşamada τ T _ ρ µ T τ T _ ρ ρl m ormülasonlarılailgili bazı gözlmlr gn olacaktır İlkin, di iskozitsi karışım znlğ ormülasonları, transport prossini tmsiln ilgili bağımlı dğişknin gradantını/ içrmlri ndnil gradan transport ormülasonları olarak anılır. Bna gör laminrmomntm ısıl nrjitransportiçin azılan τ µ, T q k bağıntılarıda gradanttransport ormülasonlarıolmaktadır. Türbülanslıkamalıakımlar için b gibi ormülasonlarınözl bir zaaitiardır ZB 386 Sınır Tabaka Drs notları - M. 49 Ortalama akım türbülans transport ormülasonları B zaiti şkildki gibi bir hız proili halind kolaca görmk mümkündür. B tip proillr, örnğin, dardaki bir arıktan türbülanslıakıma tğtsl doğrltda üksk hızla akışkan njksion halind ld dilir. ortalama hız proili bir maksimma sahip olp / olan bir nokta mcttr. B noktada hr iki ormülasonda τ T _ ρ rir Formülasonlarınb zaılıklarınıgidrmnin basit bir ol oktr. Bnnla birlikt çoğ sınır tabaka akımında b şkildki maksimm a minimmlar blnmamaktadır. Bir iz bölgsind oldğ gibi simtrik bir hız proili için simtri düzlmind / olp in anı drm görülmktdir. ZB 386 Sınır Tabaka Drs notları - M. 5 5

26 Ortalama akım türbülans transport ormülasonları İki ormülasonlailgili ikinci gnl gözlm d b ikisinin sasn şdğr olmasıdır. τ T τ T ρ _ ρ _ ρl µ m T ormüllrin bakılarak µ T ρ l m azılabilir. Dolaısıla µ T için bir bağıntıbiliniorsa b son bağıntıdan l m için mütkabil bağıntıblnabilir. Ediiskozitsi karışım znlğ için özl modllr ilrid çıkartılacaktır. Bndan önc, türbülanslısınır tabakaların analizi için intgralöntmlr göz atılacaktır. ZB 386 Sınır Tabaka Drs notları - M. 5 Ortalama akım intgral öntmlri Türbülanslıakımların analizi için d laminrakımlardaki intgralöntmlrinin bnzri öntmlr mcttr. Bnlar türbülanslıanalizd kabaca, laminrhaldki gibi diransil ormülasonlaradaanan bağıntıları kllanırlar. Yöntmlrin glanmasıgnllikl basit olp mühndislik çalışmalarıiçin gn sonçlar rmktdir. Brada öntmlrdn ikisi kısaca izah dilcktir. Bnlardan daha ski olan Prandtlöntmi sadc çok basit problmlr için gndr. Daha ni olanıis Moss969 taraından ortaa konmşolp daha gnl akımlar için kllanılabilmktdir. Hr iki hald d grkli türbülanslı kama modllmsinin analiz nasıl girdiği dikkati çkmktdir. ZB 386 Sınır Tabaka Drs notları - M. 5 6

27 Prandtl öntmi İntgralöntmin türbülanslıakımda ilk glamasıprandtl97 taraında düz-lha problmi için apılmıştır. dθ d d w d θ C VonKarman momntm-intgraldnklmi B dnklm, türbülanslı daimi bir ortalama akım için, bütün bağımlı dğişknlr ortalama büüklüklr şklind dğrlndirilmk srtil kllanılabilir. Gçirgn olmaan bir düz-lha üzrindki akım için d θ d C Momntm kalınlığı θ d bradaki ortalama hız proilidir Çözüm için, laminr hald oldğ gibi, kabl dilmiş bir hız proilin ihtiaç ardır ZB 386 Sınır Tabaka Drs notları - M. 53 Prandtl öntmi Düz lha üzrindki türbülanslıakım için ortalama hız proili kabaca / n 6 7 R için n 7 B hız proili il ötlm momntm kalınlıkları 8, θ 7 7 B hız proilinin izln aşamada dar kamasını hsaplamak için kllanılması bklnmktdir. Ancak dar kama grilmsi tanımıiçrisind / w türi r almakta olp, hız proili için riln üssl bağıntıa gör / n / n / n / n n / n n / n / n n n7 için dar üzrind 7 ZB 386 Sınır Tabaka Drs notları - M. 54 7

28 Prandtl öntmi Bna gör türbülanslı akım hsabında kama için ila bir bilgi grk dlacaktır. Prandtlöntmind, önclikli bağımlıdğişkn olp, sadc dar üzrindki C kamasının cinsindn C R şklind bilinmsin ihtiaçardır. Laminr analiz için dar kaması arklı biçimd l alınmış olmakla birlikt anı rolü onamıştır. Prandtl97 grkn C için C. 456 R bağıntısınıkllanmıştır. / 4 Bölc d θ d C dθ C.456 d R / d d.456 ν / 4 Düznlnrk / 4 ν d.345 / 4 olmak üzr aralığında intgr dilrk d 5 / 4 ν / 4 / 4 ZB 386 Sınır Tabaka Drs notları - M. 55 Prandtl öntmi / 5 ν / 5 ν.375 Laminr sınır tabaka için Blasis çözümü B iki bağıntıa gör: 4 / 5 laminr hald türbülanslı hald / 5 ~ R /.375 / 5 R 5. / R.5 / 5. 8 ~ R ~ ~ B sonç türbülanslı sınır tabakanın laminr sınır tabakaa kıasla daha çabk şkild kalınlaştığını göstrmktdir. ZB 386 Sınır Tabaka Drs notları - M. 56 8

29 9 ZB 386 Sınır Tabaka Drs notları - M. 57 Prandtl öntmi Prandtl öntmindn ld diln sonç nisptn kabadır. Zira: -Türbülanslıbir sınır tabaka için n ii bir dğişkn grplamasıüzrin otrmaanbir hız proili kllanmaktadır. -Yöntm gçişi lhanın başlangıcındaki laminrakım bölgsini tamamıla ihmal tmktdir. B öntml daha azlasını apmak mümkün dğildir. Örnğin, basınçgradantıiçrn problmlr çözülmk istnsdi dp/dtürinin gnl hallri için C R,dP/d şklind bilgi ihtiaçolacaktı. Ama, şat b azla bilgi mct olsadı, zatn b analiz d ihtiaç olmaacaktı ZB 386 Sınır Tabaka Drs notları - M. 58 Moss öntmi Moss öntmi 969 momntm dnklminin daha gnl bir halini kllanmaktadır: Brada /büüklüğü-.arasında hrhangi bir dğr alabilir. /.için b dnklm alışılagln momntm intgraldnklmin dönüşür. d d R d R d d d R d d w µ τ τ / / / / / /nınbaşka dğrlri için, arı, ila dnklmlr ld dilir. Daha sonra < olmak üzr d:: botlarındaki bir kontrol hacmin kütl momntmn kornm ilklri glanacaktır ki daha önc H olmak üzr d:h: botlarındaki bir kontrol hacmi kllanılmıştı. Sonçlar arasındaki n büük arklılık, daha öncki inclmlrd Hda kama sıır olp dnklmlrd gözükmüor ikn bradaki inclmlrd d kamanın gözükmsidir. d d d R d d d R d d w ν µ τ

30 Moss öntmi Moss /. /.3kllanarak iki dnklm ld tmiştir. İkinci dğr kabaca tabaka bonca momntm kabının iki bölünmsin karşılık glmktdir. Grkn hız proili için Mossiz kannnn aklaşık bir biçimini kllanmıştır.w/ büüklüğünün tanımıla birlikt C büüklüğünü kllanarak / ln K / ln K ln K ν / ν / ν C W C Π C W K dnklmini dnklmini nidn azmış iz onksionn sonçta 3 W 3 şklind aklaşık biçimini ld tmiş C / Π C ln W K İadsin rişmiştir K ZB 386 Sınır Tabaka Drs notları - M. 59 Moss öntmi Moss, laminralt tabaka için bir başka polinomkllanmış, üksk Rnoldssaısındaki akımlarda intgralöntm için b inc tabaka içrisind proilin sçiminin önmli olmadığınıblirtmiştir. B sçim intgrallrindğrini önmli ölçüd tkilmmktdir. / n Türbülanslı kama modli rin böl birlşik bir hız proili almak daha doğrdr τ T _ ρ Moss in kllandığımomntm dnklmind sadc τ / büüklüğügçtiğindnb intgral öntmi için türbülanslıkamanın bir tk / / noktasında modllnmsitrlidir. B hss öntmin ktli taraıdır. Zira türbülans modllmsi sadc grçkt problmin çıktısıolan üz sürtünmsini basitç almak rin çok daha tml bir sid apılmıştır. µ T di-iskozitsi modli Moss, Cols96 taraından riln bir kısım ri ğri drarak ld ttiği µ T µ ρ θ şklind tamamil ampirik bir di-iskozitsi modli kllanmıştır. / 5.5 R ZB 386 Sınır Tabaka Drs notları - M. 6 3

31 Moss öntmi Bütün bnlarla birlikt sistm momntm dnklminin /. /.3 d C / Π ln K K C W hız proilil birlikt dğrlndirilmsi sonc ld diln iki adi diransil dnklmdn olşmaktadır. Dnklm sistminin iki bilinmni olp bnlar R il iad diln C dir. B iki dnklm adidiransil dnklm çözümünd kllanılan hrhangi bir saısal öntml çözülbilir. Moss969, öntmini bazıdnsl hallr için glamış, mct intgralöntmlrindn hrhangi biri kadar gn sonçlar ld tmiştir. Gnl olarak m C gibi bütünsl büüklüklr için n ii diransil öntmlrl ld dilnlr kadar iidir. ZB 386 Sınır Tabaka Drs notları - M. 6 Moss öntmi Çşitli hsap öntmlrinin prormansınıortaa koabilmk için, gidrk artan karmaşıklıkta üçadt trs-basınç-gradantlı akım örnk olarak sçilmiştir. El alınan öntmlrin hpsi düz lha halind sıır basınçgradantı ii prormans srgilmktdir. Olml basınç gradantı halind prormans biraz daha iddiasızdır. Sözüdiln üçörnk hald Clasr in956 daha önc blirtiln dng qiliblim hali, Schbar Klbano n95 klasik dni, 3 Nwman ın95 kanat proili l alınmıştır. B üçakımla ilgili bilgilr d anlamsız hsaplamalara ol açmaacak ri il karşılaştırmaa imkan rck biçimd trinc ii bir şkild dokümant dilmiştir. B akımlar 968 d Stanord da grçklştiriln AFOSR-IFP konransında sınır tabaka hsaplama öntmlri için tst hali olarak sçilmişn karmaşık akımlardan üçüdür Klin arkadaşları, 969. ZB 386 Sınır Tabaka Drs notları - M. 6 3

32 Moss öntmi Moss in969 hsaplama sonçları θ C büüklüklri için b üçhald ld diln rilrl karşılaştırılmıştır. Moss öntmi Schbar- Klbano Rθ C Yüz sürtünmsi Momntm kalınlığı. C Moss öntmi Nwman 4 4 Rθ Schbar-Klbanoil Nwmanhallrind arılmaa kadar m ii ikn, Clasr indng hali için mn zaı oldğ görülmktdir Yüz sürtünmsi Momntm kalınlığı.3 Moss öntmi Clasr 4 C. Rθ 4. Yüz sürtünmsi Momntm kalınlığı ZB 386 Sınır Tabaka Drs notları - M. 63 Moss öntmi Çşitli öntm modllrin prormansınıgöstrmk için, 98 d Stanord da grçklştiriln bir başka konranstaki bazı hallr daha l alınmıştır Klin arkadaşları, 98. Saml Jobrt974 taraından düşük-hızda trs-basınçgradantlıhald grçklştiriln dn sonçlarıla Mossöntmi sonçlarıkarşılaştırılmışolp m gnl olarak ii gözükmktdir..4 C.. Vri Analiz.. 3. m ZB 386 Sınır Tabaka Drs notları - M. 64 3

33 Moss öntmi Brada inclnn Moss intgral öntmi laminr akım için daha inc izah diln Thwaits-Walz intgral öntmil birlikt kllanılabilir. Kompl akımıçözck bir öntm ld tmk için gçişsl bölgd d D Nararshima99 taraından önriln aralıklılık dağılımı alınabilir. Bradaki tml ikir γ aralıklılık aktörüolmak üzr gçişsl bölgd ötlm kalınlıklarıiçin şklind bir dağılım almaktır. γ γ lam trb ZB 386 Sınır Tabaka Drs notları - M. 65 Örnk problm 5m znlğndaki bir düz lha m/s hızdaki akıma marz olp düz lhanın bitimindn itibarn r alan rampa 5- m/s şklind dğişn bir dışakım aratmaktadır. Akışkanın iskozitsini ν -5 m²/s alarak b üz bonca 7. m msasin kadar türbülanslısınır tabakanın glişimini incliniz. Sınır tabaka arılır mı, blirliniz. Akımın ilk kısmı düz lha üzrind basınç gradantsız olp b bölgd basit bir intgral çözümüglanarak 5 d, θ C büüklüklri hsaplanabilir. Hsaplanan b dğrlr üzin kalan rampa kısmındaki hsaplar için başlangıçdğrlri olarak kllanılacaktır. Lhanın düz kısmındaki hsaplar için Prandtl öntmi glanırsa R ν.375 m / s 5 m 5. ν. m / s /5 R 6 5. R 6 R ZB 386 Sınır Tabaka Drs notları - M

34 Örnk problm R ν R. R C.456 R / 4 C C.665 dθ C d dθ d ν R ν ν.5.8 ν R ν.375. R ν.375 ν dθ d.8 ν θ.8 dθ 375 ν..5. d. ZB 386 Sınır Tabaka Drs notları - M. 67 Örnk problm θ ν.8 ν.8 ν ν θ.8 ν.8.8 R R θ R R R θ R θ Bna gör rampa başlangıcında C.665 R θ 837.5dğrlri ld dilmktdir. Hsaplamalar 7 mnoktasına rişinc kadar. maralıklarla adımda grçklştirilmiştir. Hsaplamalar Schtztaraından riln bir FORTRAN programıvbasic dilin arlanarak grçklştirilmiş olp ld diln sonçlar aşağıdaki tabloda r almaktadır. ZB 386 Sınır Tabaka Drs notları - M

35 Örnk problm X C θ R H Görüldüğü gibi sınır tabaka kalınlığı gidrk artmaktadır. Nisptn ktli saılabilck b trs basınçgradantıaltında sınır tabaka 7mmsasin kadar arılmamaktadır C>. Ancak sınır tabaka kalınlığınrds iki katlanmakta sürtünm katsaısıda %4 azalmaktadır. ZB 386 Sınır Tabaka Drs notları - M. 69 Had öntmi Had intgral öntmi, momntm sürklilik intgral dnklmlrinin ş zamanlı olarak intgrason sasına daanır. dθ C θ d VonKarman momntm intgraldnklmi H d d Sürklilik intgralkatılım dnklmi d d E C E E d d E B iki dnklmd toplam 5 bilinmn θ, E, C, C E, H blnmakta olp çözüm için ila ampirik bağıntılar aşağıdaki gibi rilmiştir Costi C.46 R C E.68 θ.36 H H H H Ldwig-Tillman bağıntısı Brada H E θ θ Rθ ν ZB 386 Sınır Tabaka Drs notları - M. 7 35

36 Had öntmi B iki adi diransil dnklmin çözümührhangi standart bir öntml örnğin Rng-Ktta öntmi grçklştirilbilir. Daha basit bir çözüm ol is. drcdn Talor açılımına daanan Elr öntmidir θ i dθ θi i d i E i E i d E i d i Çözüm için başlangıçdğrlri tr dki laminrsınır tabaka çözümlrindn alınacaktır. ZB 386 Sınır Tabaka Drs notları - M. 7 Had öntmi Akış şması θ, H, H tr d E θ H C C E / H.678 H 3 / R θ dθ d i de d C θ C E E H d d d d i i Et Haır H H H 3.3 θ θ i E E E i.7 i H i dθ i d i / θ E i d d i Türbülanslı arılma ZB 386 Sınır Tabaka Drs notları - M. 7 36

37 Örnk problm Daha önc Mossöntmi il inclnn Lharampa üzrindki türbülanslısınır tabakaıhadöntmi il incliniz. Hatılatma: XI5m, XL7m, m/s, 5- m/s, ν -5 m²/s Lhanın düz kısmında Prandtl öntmi il apılan hsaplama sonçları: R ν / 5 R θ..8 ν Arıca E H E θ ZB 386 Sınır Tabaka Drs notları - M