GÜÇ SİSTEMLERİ ANALİZİ
|
|
|
- Turgay Polat
- 9 yıl önce
- İzleme sayısı:
Transkript
1 T.C. ANADOLU ÜNİVERSİTESİ YAYINI NO: 735 AÇIKÖĞRETİM FAKÜLTESİ YAYINI NO: 696 GÜÇ SİSTEMLERİ ANALİZİ Yazar Yrd.Doç.Dr. Şener AĞALAR (Ünite - 6) Editör Yrd.Doç.Dr. Şener AĞALAR ANADOLU ÜNİVERSİTESİ i
2 Bu kitabın basım, yayım ve satış hakları Anadolu Üniversitesine aittir. Uzaktan Öğretim tekniğine uygun olarak hazırlanan bu kitabın bütün hakları saklıdır. İlgili kuruluştan izin almadan kitabın tümü ya da bölümleri mekanik, elektronik, fotokopi, manyetik kayıt veya başka şekillerde çoğaltılamaz, basılamaz ve dağıtılamaz. Copyright 0 by Anadolu University All rights reserved No part of this book may be reproduced or stored in a retrieval system, or transmitted in any form or by any means mechanical, electronic, photocopy, magnetic tape or otherwise, without permission in writing from the University. UZAKTAN ÖĞRETİM TASARIM BİRİMİ Genel Koordinatör Doç.Dr. Müjgan Bozkaya Genel Koordinatör Yardımcısı Doç.Dr. Hasan Çalışkan Öğretim Tasarımcıları Yrd.Doç.Dr. Seçil Banar Öğr.Gör.Dr. Mediha Tezcan Grafik Tasarım Yönetmenleri Prof. Tevfik Fikret Uçar Öğr.Gör. Cemalettin Yıldız Öğr.Gör. Nilgün Salur Kitap Koordinasyon Birimi Uzm. Nermin Özgür Kapak Düzeni Prof. Tevfik Fikret Uçar Öğr.Gör. Cemalettin Yıldız Dizgi Açıköğretim Fakültesi Dizgi Ekibi Güç Sistemleri Analizi ISBN Baskı Bu kitap ANADOLU ÜNİVERSİTESİ Web-Ofset Tesislerinde adet basılmıştır. ESKİŞEHİR, Mart 04 ii
3 İçindekiler Önsöz... iv. Güç Sistemlerine Genel Bakış ve Temel Kavramlar... Simetrik Bileşenler Güç Transformatörleri İletim Hatlarına Ait Donanımlar Yatışkın - Durum İletim Hat Modelleri Güç Akışı 50 iii
4 Önsöz Endüstriyel ve ticari faaliyetlerin gerçekleştirilebilmesi için gerekli önemli girdilerin başında elektrik enerjisi gelmektedir. Elektrik enerjisi insanoğlu tarafından sürekli olarak kullanılan, kullanım öncesinde kalitesi güvence altına alınamayan bir uygarlık aracıdır. İçinde bulunduğumuz bu çağda, teknolojik gelişmelere paralel olarak enerji tüketimi de gittikçe artan bir ivme kazanmaktadır. Günümüzde, ülkelerin refah seviyeleri ve gelişmişlik düzeyleri, kişi başına düşen elektrik enerjisi tüketimi ile ölçülmektedir. Dünya nüfusundaki hızlı artışa paralel olarak geleneksel enerji kaynaklarındaki hızlı tükenme toplumları bir yandan mevcut enerji potansiyelini daha etkin bir şekilde kullanmaya iterken diğer yandan da yeni enerji kaynakları bulmaya yönlendirmektedir. Ayrıca geleneksel enerji kaynaklarının Dünya üzerindeki homojen olmayan dağılımı ve son yıllarda gelişen çevre bilinci; su, güneş ve rüzgar gibi yenilenebilir enerji kaynaklarındandaha fazla yararlanmayı ve bu yönde yeni teknolojiler geliştirmeyi gerekli kılmaktadır. Üretilen elektrik enerjisinin tüketicilere kaliteli, sürekli,güvenli ve ucuz olarak sunulması, o bölgenin gelişmesinde, işletmelerin verimli ve emniyetli çalışması açısından önemli bir faktördür. Bu sebeple güç sistemleri oluşturulurken iyi bir planlamanın yanında, iyi bir mühendislik çalışması da yapılarak uygun şebeke elemanları seçilmeli, koruma elemanları belirlenmelidir. Güç sistemleri normal çalışma koşulları yanında, bir arıza esnasında meydana gelebilecek önemli değişikliklere dayanabilmeli ve sistemler kendini koruyabilmelidir. Bu nedenle güç sistemlerinde olası arızalar dikkate alınarak hesaplar yapılmalı, bu arızalara uygun malzemeler seçilmelidir. Elinizdeki kitap; elektrik enerjisi üretiminde, iletiminde ve dağıtımında kullanılan güç sistemlerini, bu sistemler içindeki elemanları ve üretim yöntemlerini tanımak ve bu yöntemlerin altında yatan fiziksel gerçekleri kavramak açısından sizlere yeni ufuklar açacaktır. Öğrencilerimize başarılar dilerim. Editör Yrd.Doç.Dr. Şener AĞALAR iv
5
6 Amaçlarımız Bu üniteyi tamamladıktan sonra; Alternatif akımın ve gerilimin temel ilkelerini tanımlayabilecek, Fazör gösterimini ve alternatif akımın (AC) dalga biçimini matematiksel olarak ifade edebilecek, Direnç, endüktör ve kondansatörde AC akım ile gerilim arasındaki faz ilişkisini fazör gösterimleri ile açıklayabilecek, Şebeke eşitliklerini matematiksel olarak ifade edebilecek, Güç kavramını tanımlayabilecek, Dengeli üç-faz devreler üzerindeki temel hesaplamaları yapabilecek, bilgi ve becerilere sahip olabilirsiniz. Anahtar Kavramlar Fazör Güç Anlık Güç Kapasitif Güç Reaktif Güç Faz Farkı Kompanzasyon Tek-Faz Devreler Üç-Faz Dengeli Devreler Üçgen-Yıldız Dönüşümleri İçindekiler Giriş Güç Sistemlerinde Kullanılan Temel Kavramlar Devre Eşitlikleri Dengeli Üç-Fazlı Devreler Dengeli Üç-Fazlı Sistemlerdeki Güç Hesabı Dengeli Üç-Fazlı Sistemlerin Tek-Fazlı Sistemlere Göre Avantajları
7 Güç Sistemlerine Genel Bakış ve Temel Kavramlar GİRİŞ Direkt olarak ölçülemeyen bir nicelik olan enerji, doğada çeşitli biçimlerde bulunur. Bu enerji sürekli olarak bu biçimler arasında dönüşüm halindedir. Elektrik enerjisinin hareket, ısı, ışık, vs. gibi diğer enerji türlerine dönüştürülmesi, uzak mesafelere taşınması, dağıtılması ve kullanılması önemlidir. Elektrik enerjisi, basit bir elektrik devresinde olduğu gibi enerji santralinde başlayıp son kullanıcı olan biz tüketicilere kadar uzanan ve tekrar enerji santraline dönen kapalı bir devrede taşınır. Elektrik enerjisinin ekonomik olarak çok uzaklara iletilmesi ancak yüksek gerilimler yardımıyla olmaktadır. Transformatörler yardımıyla alternatif gerilimlerin büyüklükleri çok az bir kayıpla değiştirilebildiğinden, elektrik enerjisinin enerji iletim ve dağıtım şebekelerinde uzak mesafelere iletimi yüksek gerilimli alternatif akımlarla yapılmaktadır. Alternatif akım periyodik olarak yönü ve şiddeti sürekli değişen bir elektrik akımıdır. Alternatif akımda; akım ve gerilim daha çok sinüssel biçimde zamanla değişir. Şu an evlerimizde kullandığımız elektriğin karakteristiği sinüssel dalga şeklindedir. Ülkemizde, Doğalgaz santralleri başta olmak üzere; Hidroelektrik santraller, termik santraller, az da olsa rüzgar türbünleri ve güneş panelleri alternatif akımın üretildiği başlıca tesislerdir. Bu bölümde elektrik enerjisi ile ilgili temel kavramlara giriş yapılacak ve bu kavramların bağlı olduğu niceliklere ve hesaplamalara değinilecektir. İlk olarak fazör kavramı anlatıldıktan sonra anlık güç kavramı ve bu gücün farklı yük koşullarındaki hesaplamalarına değinilecektir. Literatürde kullanılan farklı güç kavramları ifade edilerek güç üçgeni çıkarılacaktır. Tek-fazlı devrelerin ardından üç-fazlı devrelere geçiş yapılacak, denge konumu açıklandıktan sonra dengeli üç-fazlı devrelere ait çeşitli bağlantı şekilleri incelenecektir. Bu bağlantı şekilleri arasındaki ilişkiler belirtildikten sonra ise üç-fazlı devrelerde güç hesaplamaları için gerekli olan matematiksel eşitlikler anlatılacak ve son olarak ise dengeli üç-fazlı sistemler ile tek-fazlı sistemler arasındaki farklar açıklanacaktır. GÜÇ SİSTEMLERİNDE KULLANILAN TEMEL KAVRAMLAR Bu kısımda; güç sistemlerinde ve bu kitabın geri kalan bölümünde karşınıza çıkacak temel kavramlara değinilecektir. Öncelikle; hesaplamaların çoğunda karşılaşacağınız en temel kavramlardan biri olan fazör kavramından başlayacak olursak; Fazör Elektrik terminolojisinde kullanılan iki temel kavram vardır; bunlardan birincisi gerilim veya diğer adıyla voltajdır. Birimi Volt tur ve V simgesiyle gösterilir. Diğer ikinci kavram ise akım olarak adlandırılır. Birimi Amper dir ve A simgesiyle gösterilir. Sabit frekanslı sinüssel (Sinüs dalgası biçiminde) akım ya da gerilim (voltaj) iki farklı karakteristik özelliğe sahiptir; bu özellikler gerilimin maksimum (tepe) değeri ve faz açısıdır. V maksimum değerinde ve cos( ω t) faz açısına göre δ faz farkına sahip bir gerilimin anlık değeri: mak vt () = Vmak cos( ωt+ δ) şeklinde ifade edilir. Sinüssel bir gerilimin etkin (rms) değeri: (.) 3
8 V mak V= (.) jφ Euler eşitliğine göre sinüssel büyüklükler, e = cosφ + jsinφ şeklinde fazör olarak gösterilirler. Yukarıdaki (.) eşitliğinde verilen anlık gerilim için, j( ωt+ δ) jδ jωt vt ( ) = Re[V make ] = Re[ (V e ) e ] (.3) olur. Buradaki gösterimde j = ve Re ise gerilimin gerçek kısmı anlamındadır. Herhangi bir gerilimin rms değeri üç farklı şekilde gösterilebilir. Bunlar; üstel, kutupsal (polar) ve kartezyen gösterimdir. j V = Ve δ = V δ = Vcos( δ) + jvsinδ Üstel Kutupsal Kartezyen Fazörler, her üç gösterime de kolaylıkla çevrilebilmektedir. Kutupsal gösterimden kartezyen gösterime dönüştürme Şekil. deki fazör diyagramında gösterilmektedir. Euler eşitliği de üstel gösterimden kartezyen gösterime geçişte kullanılabilir. Bir örnek olarak; (.4) vt ( ) = 69,7cos( ωt+ 60 ) V (.5) anlık geriliminin maksimum değeri V koordinatlarda rms fazör gösterimi ise mak = 69,7 V, faz açısı ise cos( ω t) ye göre δ = 60 dir. Kutupsal V = 0 60 V (.6) Akım da aynı şekilde ifade edilecek olursa; it ( ) = 00cos( ωt+ 45 ) A (.7) şeklinde gösterilir. (.7) eşitliğindeki akımın maksimum değeri Imak I = 00 = 70,7 A, faz açısı 45 ve fazör gösterimi ise; = 00 A, rms değeri I = = e = + j j45 70, , A (.8) olarak ifade edilir. Elektrik devrelerinde kullanılan direnç, endüktör (bobin) ve kapasitör (kondansatör) için gerilim ve akım fazörleri arasındaki ilişki Şekil. de gösterilmektedir. Bu elemanlar, pasif elemanlar olarak adlandırılmaktadır. Şekilde R, L, C değerlerinin sabit olduğu ve sinüssel denge durumunda uyartıldığı kabul edilmektedir. Kitapta küçük harflerle gösterilen vt () ve it () gibi değerler anlık değerleri belirtirken, büyük harflerle gösterilen V ve I gibi değerler rms değerleri, büyük ve italik harflerle gösterilen V ve I gibi değerler ise rms fazör değerleri belirtmektedir. Yine kitapta belirtilen herhangi bir akım ya da gerilim değeri, aksi belirtilmediği sürece rms değeri olarak kabul edilecektir. 4
9 Sanal Eksen Gerçek Eksen Şekil.: Fazör Diyagramı Şekil.: Sinüssel Denge Durumunda R, L, ve C Elemanlarındaki Gerilim ve Akım Arasındaki İlişki Tek-Faz Alternatif Akım (AC) Devrelerinde Anlık Güç Güç terimi; zamana göre enerji değişim oranı olarak ifade edilmektedir. Gücün birimi Watt tır ve bu birim aynı zamanda joule/saniye ye eşittir. Bir elektrik yükünün çektiği anlık güç, bu yükün üzerine düşen anlık gerilim değerinin bu yük üzerinden geçen anlık akımın değeri ile çarpımıdır. Yük üzerindeki gerilim değerinin, (.9) eşitliğindeki gibi olduğu varsayılırsa: vt () = Vmak cos( ωt+ δ) V (.9) yük tarafından çekilen güç; saf rezistif, saf kapasitif, saf endüktif ve bunların genel birleşiminden oluşan genel RLC devreler için ayrı ayrı incelenebilir. Sonraki ünitelerde güç kavramıyla bağlantılı olarak aktif güç, reaktif güç ve güç faktörü açıklanacak, ayrıca; aktif ve reaktif güç arasındaki fiziksel bağlantı detaylı olarak verilecektir. 5
10 Saf Rezistif Yük Saf rezistif yüklerde, yükten geçen akım ile yük üzerindeki gerilim ile aynı fazdadır; diğer bir deyişle aralarındaki faz açısı sıfır derecedir. I = V /R olur ve direnç üzerinden geçen akım; i () t = I cos( ωt+ δ) A R Rmak (.0) şeklinde gösterilir. Direnç üzerinden geçen maksimum akım, I Rmak =Vmak Rşeklindedir ve direnç tarafından çekilen anlık güç; R () = () R () = VmakIRmak cos( ω + δ) p t v t i t t = V mak I + cos + Rmak { ( ωt δ) } { ( ωt δ) } = VIR + cos + W (.) (.) de gösterildiği gibi direncin çektiği gücün ortalama değeri V P=VI= R R =IR R W R (.) olur ve ayrıca çift frekanslı terim ise VI cos ( ωt + δ) Saf Endüktif Yük Saf endüktif yükte; akım gerilimden 90 geridedir, I=V( X) R L şeklinde gösterilir. j olur ve akım L i () t = I cos( ωt+ δ 90) A L Lmak (.3) şeklinde ifade edilir. Burada I Lmak =V mak X L ve XL = ωldeğeri bobinin endüktif reaktans değeridir. Endüktör tarafından çekilen anlık güç ise; p () t = v() t i () t = V I cos( ωt+ δ)cos( ωt+ δ 90) L L mak Lmak = V mak I Lmak cos ( ) 90 ωt + δ = VIL sin ( ωt + δ) W (.4) şeklinde ifade edilir. (.4) eşitliğinden de görüleceği gibi endüktör tarafından çekilen anlık güç, ortalama değeri sıfır olan çift frekanslı bir sinüssel terimdir. Saf Kapasitif Yük Saf kapasitif yük düşünüldüğünde, akım gerilimden 90 ilerdedir, I V ( jx ) C =, ve C i () t = I cos( ωt+ δ + 90) A C Cmak (.5) olur ve burada Cmak mak C XC = ωc şeklinde ifade edilir. X kapasitif reaktans olarak C adlandırılır. Kondansatör tarafından çekilen anlık güç ise; I =V X ve ( ) 6
11 p () t = v() t i () t = V I cos( ωt+ δ)cos( ωt+ δ + 90) C C mak Cmak = V mak I Cmak cos ( ) 90 ωt + δ + = VIC sin ( ωt + δ) W (.6) formülü ile hesaplanır. Kondansatör tarafından çekilen anlık güç, tıpkı endüktörde olduğu gibi, ortalama değeri sıfır olan çift frekanslı bir sinüssel terimdir. Genel RLC Yük R, L ve C elemanlarından oluşan genel bir devrede, denge durumundaki bir sinüssel gerilim kaynağından çekilen akım; it () = I cos( ωt+ β) A mak (.7) Yük tarafından çekilen toplam güç ise; cos A cos B= cos ( A - B ) +cos(a+b) eşitliğinden faydalanılarak. pt () = vtit ()() = V I cos( ωt+ δ)cos( ωt+ β) mak mak = V mak I mak { cos ( δ β) + cos ( ) ( ) } ωt + δ δ β = VI cos( δ β) + VI cos( δ β) cos ( ωt+ δ) +VIsin ( δ β) sin ( ωt+ δ) { } ( ) ( ) ( ) ( ) pt ( ) = VI cos δ β + cos ωt+ δ +VIsin δ β sin ωt+ δ Icos ( δ β) = I ve R Isin ( δ β) IX = şeklinde gösterilirse; { ( ω δ) } X ( ω δ) pt () = VIR + cos t+ +VI sin t+ (.8) p () t p () t R X eşitliğiyle ifade edilir. (.8) eşitliğinden görüldüğü üzere, yük tarafından çekilen anlık güç iki bileşenden oluşmaktadır. Bu bileşenlerden biri; yükteki direnç (rezistif) elemanının çektiği güç p () t, R diğeri ise reaktif elemanlar (endüktif ya da kapasitif) tarafından çekilen güç p () X t dir. Çekilen gücün p () R t kısmı (.) eşitliği ile aynıdır. IR = Icos( δ β) akım bileşeni; yük akımının gerilimle aynı fazda olan kısmıdır. ( δ β) faz açısı; gerilimle akım arasındaki açıyı göstermektedir. Gücü oluşturan ikinci bileşen p () t ise (.4) veya (.6) eşitlikleri ile benzerdir. X IX = Isin( δ β) akım bileşeni ise yük akımının gerilimle 90 faz farkı oluşturan kısmıdır. Gerçek Güç (.8) eşitliği gösteriyor ki rezistif yük tarafından çekilen güç, p () R t, çift frekanslı bir sinüs olmakla birlikte ortalama değeri P dir ve R ( δ β) P= VI = VIcos W (.9) olarak hesaplanır. Gerçek güç birimi olarak Watt (W) kullanılır. Gerçek güç aynı zamanda aktif güç ya da ortalama güç olarak da adlandırılmaktadır. 7
12 Güç Faktörü Eşitlik (.9) daki cos ( δ β) ( δ β) terimi güç faktörü olarak ifade edilmektedir. Gerilim ile akım arasındaki açısı güç faktörü açısı olarak adlandırılır. Doğru akım (DC) devreleri için yük tarafından çekilen güç; DC yük gerilimi ile DC yük akımının çarpımından oluşur, ancak alternatif akım devrelerinde yük tarafından çekilen ortalama güç (.9) eşitliğinde görüldüğü gibi; yük üzerindeki gerilimin rms değeri, cos δ β nın çarpımından oluşur. Endüktif yükler için yükten geçen akımın rms değeri ve güç faktörü ( ) akım gerilimden geridedir, yani β değeri δ dan küçüktür, bu yüzden güç faktörü geride denir. Kapasitif yüklerde ise, akım gerilimden ilerdedir, yani β değeri δ dan büyüktür, bu yüzden güç faktörü ilerde denir. Genel olarak güç faktörü pozitiftir. Eğer δ β, 90 den büyükse, akım için alınan referans yön değiştirilerek; cos( δ β) Reaktif Güç değerinin pozitif olması sağlanır. Yükün reaktif bileşenleri tarafından çekilen ve (.8) eşitliğinde p () X t ile gösterilen reaktif güç, sıfır ortalama değerinde ve çift frekanslı bir sinüstür. p () X t nin genliği Q ise; X ( δ β) Q= VI = VIsin VAR (.0) Q, reaktif güç olarak adlandırılır. Gerçek güçle aynı birimleri içermelerine rağmen reaktif güç birimi olarak Volt Amper Reaktif (VAR) kullanılır. Örnek. 0 Ω'luk bir dirençle XL = ωl= 3,77 Ω değerindeki endüktif reaktans paralel bağlıdır. vt ( ) = 4,4cos( ωt) V değerindeki bir gerilim kaynağı, birbirine paralel bağlı bu iki yüke enerji sağlamaktadır. Direnç ve bobin tarafından çekilen anlık gücü hesaplayınız. Ayrıca yük tarafından çekilen aktif ve reaktif gücü, güç faktörünü hesaplayınız. Çözüm: 4,4 Devre ve fazör diagramı Şekil.3 (a) da görülmektedir. Gerilim; V = 0 = 00 0 V V 00 Direnç üzerinden geçen akım; I R = = 0 = 0 0 A R 0 V 00 Bobin üzerinden geçen akım; I = L 0 6,53 90 A jx = j3,77 = Toplam yük akımı ise; I = IR + IL = 0 j6,53 = 8,35 69,34 A L şeklinde hesaplanır. Direnç tarafından çekilen anlık güç (.) denklemine göre; p ( t) = (00)(0)[ + cos( ωt)] R = 000[ + cos( ωt)] W Bobin tarafından çekilen anlık güç, (.4) denklemine göre; p ( ) (00)(6,53)sin( ) L t = ωt = 653sin( ωt) W 8
13 Yük tarafından çekilen gerçek güç, (.9) eşitliğine göre; P=VIcos( δ β) = (00)(8,53)cos(0 + 69,34 ) = 000 W (Not: P aynı zamanda VI = V R ye eşittir.) R Yük tarafından çekilen reaktif güç, (.0) denklemine göre; Q=VIsin( δ β) = (00)(8,35) sin(0 + 69,34 ) = 653 VAR (Not: Q aynı zamanda VI = V L X ye eşittir.) L ve son olarak güç faktörü de; gf = cos( δ β) = cos(69,34 ) = 0,358 geride olarak hesaplanır. Voltaj, akım ve güç için dalga şekilleri Şekil.3 (b) de verilmiştir. Görüldüğü gibi RL paralel yükü için aktif güç (000 W) sadece direnç tarafından çekilmektedir, reaktif güç (653 VAR) ise sadece bobin tarafından çekilmektedir. Direnç akımı i () R t, devre voltajıyla aynı fazdayken, bobin akımı i () L t ise devre voltajından 90 geridedir. Güç faktörü RL yükü için gecikmelidir. 9
14 Sanal eksen Gerçek eksen (a) Devre ve fazör diyagramı (b) Dalga Şekilleri Şekil.3: Örnek. için Devre ve Fazör Diyagramı Dikkat edilmelidir ki; eşitlik (.8) de verilen p () t ve p () R X t sadece paralel RX yükü için geçerlidir. Genel bir RLC devresi için, rezistif ve reaktif elemanlar üzerine düşen gerilim, devre gerilimiyle aynı fazda olmayabilir ve p () t ve R p () X t ye ek olarak faz kaymaları olabilir. Ancak P ve Q için (.9) ve (.0) eşitlikleri tüm RLC devreleri için geçerlidir. Aktif ve Reaktif Gücün Fiziksel Anlamı Aktif (P) gücün fiziksel anlamı kolaylıkla anlaşılabilir. Bir yük tarafından t zaman aralığında çekilen toplam enerji, sinüssel gerilimin bir periyodunu içeren, P t Watt-saniye (Ws) dir. Toplamda n periyotluk zaman diliminde rezistif eleman tarafından çekilen toplam enerji P(nT) Ws dir. Kilowatt-saat metre cihazı, belirli bir ( t t) zaman aralığında şebekeden çekilen enerjiyi ölçmek için tasarlanmıştır. Ancak reaktif (Q) gücün fiziksel anlamı bu kadar kolay anlaşılamaz. Q ; yükteki reaktif eleman tarafından çekilen anlık gücün maksimum değerini ifade eder. Eşitlik (.8) ile verilen px () t anlık reaktif güç ise, zamanla pozitif ve negatif olarak yön değiştirebilen ve yükteki reaktif eleman tarafından alınan veya sağlanan gücü ifade eder. Q nun değeri (.0) deki ( δ β) nin işaretine bağlı olarak pozitif veya negatif olarak değişebilir. Reaktif güç Q, güç sisteminin çalışmasını en iyi şekilde ifade eder (daha sonraki ünitelerde bu durum ele alınacaktır ). Bu uygulamaya örnek olarak; dağıtım sistemlerinde paralel kondansatör kullanılarak aşırı yüklenme durumlarında voltajın genliğinin arttırılması sağlanmaktadır. 0
15 Kompleks Güç Alternatif akım devrelerinde sinüssel denge durumundaki aktif ve reaktif güç; kompleks güç yardımıyla hesaplanır. Bir devre elemanının uçları arasındaki gerilimin V = V δ V, elemanlar üzerinden geçen devre akımının ise I = I β Aolduğu varsayılırsa; Kompleks güç, gerilim ile akımın kompleks eşleniğinin çarpımından oluşur: [ ][ ] * * S VI j = = V δ I β = VI δ β = VI cos( δ β) + VIsin( δ β) (.) burada ( δ β) açısı, gerilim ile akım arasındaki faz açısıdır. Eşitlik (.) ile (.9) ve (.0) eşitlikleri karşılaştırılırsa, kompleks güç S şu şekilde yazılabilir; S= P+ jq (.) Kompleks gücün büyüklüğü, ( S=VI ) görünür güç olarak adlandırılır. Her ne kadar görünür güç S ; P ve Q ile aynı birime sahip olsa da; S nin birimi volt-amper dir ve kısaca VA ile gösterilir. Gerçek güç (P), görünür gücün (S=VI) güç faktörü ( gf = cos( δ β) ) ile çarpımından oluşur. Bir devre elemanının şebekeden güç çektiğini ya da şebekeye güç sağladığına karar verebilmek için gerekli olan açıklama Şekil.4 de yapılmıştır. Burada yük gösterimi ve kaynak gösterimi şeklinde iki temel gösterim mevcuttur. Şekil.4 (a) da kare şeklinde kutucukla gösterilen devre elemanı, yük gösteriminde ise akım devre elemanının pozitif ucundan girmektedir. Devre elemanı tarafından çekilen kompleks güç, eşitlik (.) deki gibi hesaplanır. Bu eşitlikteki ( δ β) değerine bağlı olarak P değeri, pozitif ya da negatif olabilmektedir. Eğer P pozitif ise devre elemanı şebekeden gerçek güç çekiyor demektir. Ancak P negatif ise; devre elemanı negatif gerçek güç çekiyor demektir. Negatif gerçek güç çekmek kavramı da aslında bu devre elemanının devreye pozitif gerçek güç sağladığı anlamındadır. Benzer şekilde Q değeri pozitif ise, Şekil.4(a) daki devre elemanı pozitif reaktif güç çekiyor demektir. Eğer Q negatif ise devre elemanı negatif reaktif güç çekiyordur; yani devreye pozitif reaktif güç sağlıyor demektir. Şekil.4 (b) de jeneratör durumu gösterilmektedir ki burada; akım devre elemanının pozitif ucundan çıkmaktadır ve kompleks güç eşitlik (.) e göre hesaplanmaktadır. P nin pozitif (negatif) olduğu durumda devre elemanı; devrenin geri kalanına pozitif (negatif) gerçek güç sağlar. Benzer şekilde Q değeri pozitif (negatif) iken devre elemanı; devrenin geri kalanına pozitif (negatif) reaktif güç sağlar. I a) Yük Durumu: Akım devre elemanının pozitif ucundan girmektedir. Eğer P pozitif ise pozitif gerçek güç çekilir. Eğer Q pozitif ise pozitif reaktif güç çekilir. Eğer P ( Q ) negatif ise; devreye pozitif gerçek (reaktif) güç sağlanır. I b) Jeneratör Durumu: Akım devre elemanının pozitif ucundan çıkar. Eğer P pozitif ise gerçek güç sağlanır. Eğer Q pozitif ise; devreye reaktif güç sağlanır. Eğer P ( Q ) negatif ise; pozitif gerçek (reaktif) güç çekilir. Şekil.4: Yük ve Jeneratör Durumu
16 Örnek.: V = V değerindeki tek-fazlı bir gerilim kaynağı, devreye I = 0 0 A şiddetinde akım sağlamaktadır. Akım, kaynağın pozitif ucundan çıkmaktadır. Kaynağın aktif ve reaktif gücünü hesaplayıp bu güçleri şebekeden çektiğini ya da şebekeye sağladığını gösteriniz. Çözüm: Akım, kaynağın pozitif ucundan çıktığı için jeneratör durumu düşünülerek sağlanan kompleks güç (.) denklemine göre hesaplanırsa, * [ ][ 0 0 ] ( ) [ S] [ S] =+ 866 VAR S = VI = S = = j866 P = Re = 500 W Q=Im * değerleri bulunur. Burada Re gerçek kısım, Im sanal kısım anlamındadır. Gerilim kaynağı 500 W aktif güç çekmektedir ve şebekeye 866 VAR reaktif güç sağlamaktadır. Elektrik makinalarıyla ilgilenenler görecektir ki; aslında bu ifade, basit bir senkron motora ait bir denklemdir. Senkron motor normal çalışma koşullarında şebekeden aktif güç çeker ve şebekeye reaktif güç sağlar. Şekil. deki RLC elemanı için yük durumu kullanılmıştır. Bu yüzden bu elemanların çektikleri güçler aşağıdaki gibi hesaplanabilir. Yük voltajının V = V δ V olduğu varsayılırsa; (.) eşitliğinden V V SR = VIR = δ δ = R R * Direnç için: [ V ] S VI V V L = L = δ=+ jx j L X * Bobin için: [ V δ] * Kondansatör için: [ V δ] S VI V V C = C = δ= jx j C X Kompleks güç ifadelerinden aşağıdaki çıkarımlar yapılabilir; L C (.3) (.4) (.5) Direnç; PR = V R W gerçek güç ve sıfır reaktif güç QR = 0 VAR çeker, Bobin; sıfır aktif güç PL = 0 W ve pozitif QL = V X L VAR reaktif güç çeker Kondansatör ise; sıfır aktif güç P = 0 W C ve negatif QC = -V X C VAR reaktif güç çeker ya da diğer bir ifadeyle; kondansatör, şebekeye pozitif reaktif güç Q C = +V X C VAR sağlar. RLC elemanlarından oluşan genel bir yük durumunda, kompleks güç S (.) denklemi kullanılarak da hesaplanabilir. Pasif devre elemanı tarafından çekilen gerçek güç P=Re(S) pozitiftir. Yük tarafından çekilen reaktif güç Q=Im(S) pozitif ya da negatif olabilir. Yük endüktif olduğu zaman; akım voltajdan geridedir; yani β, δ dan daha küçüktür. Bu yüzden de çekilen reaktif güç (.) eşitliğine göre pozitiftir. Yük kapasitif olduğu zaman; akım voltajdan ilerdedir; yani β, δ dan daha büyüktür. Bu yüzden de çekilen reaktif güç negatiftir ya da diğer bir ifadeyle kondansatör, şebekeye pozitif reaktif güç sağlar.
17 Şekil.5: Güç Üçgeni Kompleks güç Şekil.5 teki güç üçgeni ile özetlenebilir. Görüldüğü gibi görünen güç S, aktif güç P ve reaktif güç Q ; güç üçgeninin birer kenarını oluşturur. Güç faktörü de şekilde görülmektedir. Güç üçgeninden aşağıdaki eşitlikler çıkarılabilir. S= P + Q ( δ β) = tan ( Q P) Q= Ptan( δ β) (.6) (.7) (.8) P P gf = cos( δ β) = = S P + Q (.9) Örnek.3: Tek-fazlı bir güç kaynağı, kendisine bağlı yüke 0,8 gecikmeli bir güç faktörü ile 00 kw güç sağlamaktadır. Güç faktörünü 0,95 gecikmeli şekilde yeniden düzenlemek için güç kaynağına bağlanacak bir adet kondansatörün sağlayacağı reaktif gücü hesaplayınız. Ayrıca yük ile güç kaynağı için güç üçgenini çiziniz. Gerilim değerinin değişmediğini kabul ediniz ve kaynak ile yük arasındaki iletim hattının direncini ihmal ediniz. Çözüm: Şekil.6 da devre çizimi ve güç üçgeni görülmektedir. Kaynak tarafından sağlanan ve direnç tarafından çekilen toplam aktif güç P= PS = P, kondansatörün sadece reaktif güç R Q sağlamasından C dolayı; kondansatörün paralel bağlanmasından sonra gerçek güç değişmeyecektir. Yük için güç faktörü açısı, çekilen reaktif güç ve görünür güç aşağıdaki gibidir. θ = δ β L = = L ( ) cos (0,8) 36,87 Q = P tanθ = 00 tan(36,87 ) = 75 kvar L L S L P = = 5 kva cosθ L Kondansatörün paralel bağlanmasından sonra; güç faktörü açısı, kaynak tarafından sağlanan reaktif güç ve görünür güç; θ = δ β = = S ( S) cos (0, 95) 8,9 3
18 Q = P tanθ = 00tan(8,9 ) = 3,87 kvar S S P 00 S S = = = 05,3 kva cosθ 0, 95 S Kondansatörün sağladığı güç; QC = QL QS = 75 3,87 = 4,3 kvar P S Kaynak Q S P R Q L Q C Yük Kondansatör S L = 5 kva Q C = 4,3 kvar Q L = 75 kvar Q S = 3,87 kvar P = P S = P R = 00 kw Şekil.6: Örnek.3 için Devre Gösterimi ve Güç Üçgeni Kondansatörün endüktif yüke paralel olarak bağlanmasına güç faktörü düzeltmesi denilir. Kondansatörün etkisi; kaynak tarafından yüke sağlanan gücün güç faktörünü arttırmaktır. Bunun yanında kaynağın görünür gücünde de düşüş meydana gelir. Şekil.6 da görüldüğü gibi kondansatörün bağlı olmadığı durumdaki görünür güç; kondansatörün bağlanmasıyla azalarak 5 kva dan 05,3 kva ya düşmüştür. Benzer şekilde kaynak akımı da azalır. Kaynakla yük arasındaki iletim hattının empedansı da göz önüne alındığında; kaynak akımının azalması iletim hattındaki kayıpların azalmasını ve hat üzerinde meydana gelen gerilim düşümünün azalmasını sağlayacaktır. Sonuç olarak; güç faktörü düzeltmesi işlemi verimliliği ve gerilim regülasyonunu iyileştirmektedir. DEVRE EŞİTLİKLERİ Sinüssel denge durumundaki devreler için Kirchhoff un gerilimler kanunu (KGK) ve akımlar kanunu (KAK), fazör gösterimi için de uygulanabilir. Bu yüzden; hem kapalı bir devrede bir düğüm noktasına gelen fazör akımlarının toplamı, hem de kapalı bir döngü üzerindeki gerilimlerin toplamı sıfırdır. Kirchhoff yasalarına dayanan devre analizi tekniklerinden; düğüm noktası analizi, döngü analizi, süperpozisyon yöntemi, kaynak dönüşümü yöntemi ve Thevenin teoremi gibi yöntemlerden 4
19 faydalanılabilir. Devre çözümlerine sistematik bir bakış getiren ve düğüm noktası analizine dayalı çeşitli bilgisayar çözümlemeleri geliştirilmiştir. Şekil.7 deki devrede, voltaj kaynakları E, S E ve S E S3 fazörleri ile gösterilmekte ve devrenin sinüssel denge durumunda olduğu varsayılarak düğüm noktası analizi yapılmaktadır. Düğüm noktası eşitlikleri aşağıda belirtilen üç aşamada yazılabilir; Adım : ( N + ) düğüm noktasından oluşan bir devrede herhangi bir düğüm noktası referans alınarak diğer tüm gerilimler bu noktaya göre yazılır. Şekil.7 deki devrede toplam 4 adet düğüm noktası bulunmaktadır, yani ( N + ) = 4 ya da N = 3, referans seçilen noktaya göre V, 0 V ve 0 V voltajları yazılır. 30 Adım : Bir direnç üzerinden seri bağlı tüm gerilim kaynakları, dirence paralel bağlı akım kaynaklarına dönüştürülür. Ayrıca empedans değerlerinin yerine admitans değerleri yazılır. Her bir akım kaynağı; gerilim kaynağı empedans değerine bölünerek bulunur. Şekil.8 deki eşdeğer devrede I, I ve I 3 akımları ile tüm empedans değerlerinin admitansa dönüştürülmüş hali görülmektedir. 3 E S E S + E S Şekil.7: Düğüm Noktası Analizi İçin Devre Şeması Adım 3: Aşağıda görüldüğü gibi düğüm noktası eşitlik matrisi yazılır: (.30) Matris notasyonu kullanılarak eşitlik (.30), aşağıdaki gibi ifade edilir; YV = I (.3) 5
20 Burada Y ; N N elemanlı bara admitans matrisini, V ; N adet bara voltajının sutun vektörünü, I ; N adet akım kaynağının sütun vektörünü ifade etmektedir. Bara admitans matrisindeki her bir Y kn elemanının bulunması aşağıda izah edildiği gibidir; Köşegen üzerinde: ( ) Y = k. baraya gelen tüm admitansların toplamı k=,,3...,n kk (.3) Köşegen haricinde: Y = ( k ve n baraları arasındaki tüm admitansların toplamı)( k n) kn (.33) Köşegen üzerindeki admitans elemanı Y kk, k barasının öz-admitans değeridir. Köşegen dışındaki admitanslar ise ilgili k ve n baraları arasındaki karşılıklı-admitanslardır. Ykn = Y olduğundan Y nk admitans matrisi simetriktir. Şekil.8 deki devre için (.30) eşitliği yazılırsa: ( 3 0) ( 3) 0 ( 3) ( 3 ) ( ) 0 ( ) ( 4) j j j V0 I j j j + j j j j V = I 0 j j j j j V 30 I V0 I j 3 V = I V 30 I 3 (.34) eşitliği bulunur. Bu şekilde düğüm noktası eşitliklerinin yazılmasının avantajı, bilgisayarlar yardımı ile hem Y admitans matrisi oluşturulabilirken hem de istenilen V bara gerilimi, (.3) eşitliği çözülerek bulunabilir. Referans baraya göre devre tanımlandıktan sonra devredeki Ykn admitansları eşitlik (.3) ya da (.33) yardımıyla bulunur ve bara bağlantıları sadece bilgisayar hesaplaması için gerekli olan giriş değerleridir. Bara admitans matrisi Y oluşturulduktan sonra bilinen akım kaynaklarının I değerleri ile bilgisayar yardımıyla her bir düğüm noktası için V voltaj değerleri hesaplanabilir. 3 + I V I I 0 3 V V 30 - Şekil.8: Şekil.7 Devresinin Eşdeğer Hali; Voltaj Kaynaklarının Akım Kaynağına, Empedansların Admitansa Çevrilmiş Hali 6
21 Bu kitapta kullanılan çift harfli alt indisli notasyon ile gösterilen voltaj değeri, ikinci harf referans noktasına göre birinci harfteki voltajı gösterir. Örneğin; Şekil.8 deki V 0 voltajı rakamı ile gösterilen düğüm noktasının 0 rakamlı düğüm noktasına göre voltajını ifade eder. Benzer şekilde, I ab gösterimi de akımın a dan b ye doğru gittiğini göstermektedir. Bu yüzden çift harf notasyonunun kullanıldığı yerlerde voltaj için (+ -) akım için ise ( ) referans gösterimine gerek yoktur. Şekil.8 de V 0, V ve V 0 30 voltajları için polarite gösterimine gerek olmamasına rağmen anlaşılabilirlik açısından şekilde bu gösterime yer verilmiştir. Ancak I, I ve I 3 akımlarında tek harf notasyonu olduğundan; akımların yönünü belirten ( ) sembolünün kullanımı gereklidir. Kitap boyunca matris ve vektör gösterimi koyu italik harflerle (V,Y, vb.) yapılacaktır. DENGELİ ÜÇ-FAZLI DEVRELER Bu bölümde; Y bağlantıları, faz ile nötr (faz-nötr) arasındaki gerilim, faz ile faz (faz-faz) arasındaki gerilim, hat akımları, Δ bağlı yükler, Δ Y dönüşümü ve üç-fazlı devre için faz-nötr eşdeğer devre çıkarımı gösterilecektir. c I c C E an a I a A Z Y Z Y E cn n N I n E bn Z Y b I b B Şekil.9: Yıldız Bağlı Yükün Kaynak Tarafından Beslenmesine Ait Devre Şekli Dengeli Yıldız ( Y ) Bağlantısı Şekil.9 daki devrede kaynağın terminal uçları a, b, ve c ile gösterilirken; faz-nötr arası gerilimleri E, an E ve E ile gösterilmiştir. Tüm kaynakların gerilimleri, birbirleri ile eşit genliğe sahipse ve aralarında bn cn 0 şer derece faz farkı var ise kaynaklar denge halindedir. Dengeli faz-nötr gerilimlerine örnek olarak; E E E an bn cn = 0 0 = 0 0 = V = = 0 40 (.35) 7
22 E cn E an E bn Şekil.0: E Referansına Göre Pozitif Sıralı Dengeli Gerilimlerin Fazör Gösterimi an gerilimleri örnek olarak verilebilir. Tüm gerilimlerin genliği 0 V ve E gerilimi ise referans fazördür. an Şekildeki faz sıralaması pozitif faz sıralaması veya abc sıralaması olarak adlandırılır. Saatin dönüş yönündedir. Pozitif faz sıralamasında E gerilimi E geriliminden 0 ilerdedir. E nin E an geriliminden 0 geride olduğu sıralama ise negatif faz sıralaması veya acb sıralaması olarak adlandırılır. Saatin dönüş yönüne ters yöndedir. Eşitlik (.35) deki gerilimler E, E den 0 ilerde olduğundan pozitif faz sıralamasındadırlar. İlgili fazör diyagramı Şekil.0 da gösterilmektedir. Dengeli Faz-Faz Arası Gerilimler İki faz arasında kalan E, ab E ve bc E gerilimleri faz-faz gerilimi olarak adlandırılır. Şekil.9 daki ca devre için a, b ve c noktalarında KGK ya göre eşitlik yazılırsa; bn an bn an bn Eab = Ean Ebn (.36) (.35) eşitliğindeki faz-nötr gerilimleri için, E E ab ab j 3 = = j = 3( 0) = 3( 0 30 ) V (.37) Benzer şekilde E ve bc E faz-faz arası gerilimleri, ca Ebc = Ebn Ecn = = V ( ) Eca = Ecn Ean = = V ( ) (.38) (.39) (.37) - (.39) denklemlerindeki gerilimler eşit genliğe ve aralarında 0 faz farkına sahip oldukları için kendi aralarında dengeli olarak adlandırılırlar. Faz-faz gerilimleri ile faz-nötr gerilimleri karşılaştırıldığında aşağıdaki sonuçlara ulaşılır; Dengeli üç-faz Y bağlı bir gerilim kaynağında faz-faz arası gerilimler, faz-nötr arası gerilimlerin 3 katı kadardır ve onlardan 30 ilerdedir. Yani; 8
23 E E E ab bc ca = 3E + 30 an = 3E + 30 bn = 3E + 30 cn (.40) şeklinde ifade edilir. Bu önemli sonuç Şekil. de özetlenmiştir. Şekil. (a) da herbir fazör orjin (merkez) noktasından başlayarak çizilmiştir. Şekil. (b) de ise faz-faz arası gerilimler; kendilerine ait bara isimleri a, b ve c harfleri ile adlandırılarak üçgenin kenarları oluşturulurken, faz-nötr gerilimleri ise; a, b, ve c bara isimlerini, n ise nötr hattını ifade edecek şekilde üçgenin kenarlarına dik şekilde başlayıp üçgen merkezinde bitecek şekilde çizilmişlerdir. Şekil. (b) de saat yönündeki abc sıralamasından da anlaşılacağı gibi pozitif sıralama mevcuttur. Çizimlerde E gerilimi referans alınmış an olsa da çizimlerin uygun şekilde döndürülmesiyle diğer gerilimler de referans olarak alınabilir. Şekil. de görüldüğü gibi; üçgen üzerindeki faz-faz arası gerilimlerin vektörel toplamı dengeli olsun olmasın, daima sıfırdır. Faz-nötr arasındaki gerilimlerin vektörel toplamları ise dengeli sistemlerde sıfıra eşittir. E ca E cn Eab b E ab E bn E an a E an E cn E bc E bn E ca c E bc a) Fazör Diyagramı b) Gerilim Üçgeni Şekil.: Üç-Fazlı Dengeli Y Bağlı Bir Sistemde Pozitif Sıralı Faz-Faz Gerilimleri ile Faz-Nötr Gerilimleri Dengeli Faz Akımları Şekil.9 daki iletim hatlarının empedansı ihmal edildiğinden, n ve N baraları aynı gerilim değerine sahiptirler, E nn = 0. Her bir faz için KGK eşitlikleri yazılarak faz akımları incelendiğinde; I = E Z a an Y I = E Z b bn Y I = E Z c cn Y (.4) şeklinde ifade edilir. Örneğin her bir Y bağlı empedans değeri Z = 30 Ω için akımlar; Y I I I a b c 0 0 = = 5 30 A = = 5 50 A = = 5 90 A 30 (.4) 9
24 bulunur. Görüldüğü gibi faz akımları da eşit büyüklüğe ve 0 faz farkına sahip olduğundan dengededirler. Nötr akımı I n, Şekil.9 daki N barası için KAK eşitlikleri yazılarak çıkartılabilir. In = Ia + Ib + Ic A (.43) Eşitlik (.4) deki faz akımları kullanılarak; In = j 3 j In = j5= 0 A (.44) nötr akımı bulunur. Faz akımlarına ait fazör diagramı Şekil. de görülmektedir. Bu akımlar eşkenar bir I üçgen üzerinde olduğundan; akımların vektörel toplamına eşit olan n nötr akımının değeri sıfırdır. Genel olarak herhangi bir üç-fazlı dengeli sistemde fazör büyüklükleri kapalı bir üçgen üzerinde olduğundan; bu büyüklüklerin toplamı sıfırdır. Bu yüzden dengeli sistemde nötr akımının değeri; ister nötr hattı kısadevre ( 0 Ω ) olsun, ister açık-devre ( Ω) olsun, denge durumu korunduğu müddetçe sıfırdır. Eğer denge durumu yoksa yani gerilim kaynaklarından, hat empedanslarından ya da yük empedanslarından herhangi biri denge durumunu bozuyorsa n ve N baraları arasında nötr akımı akar. I b I c I a Dengeli Üçgen (Delta) ( Δ ) Yük Şekil.: Dengeli Üç-fazlı Sistemlerde Faz Akımları Şekil.3 de yıldız (Y ) bağlı bir gerilim kaynağı ile üçgen Δ (ya da delta) bağlı dengeli bir yük beslenmektedir. Dengeli bir üçgen bağlantıda, Şekil.3 de görüldüğü gibi eşit empedanslı Z Δ yükleri üçgen şeklinde A, B ve C baralarına bağlanmıştır. Δ bağlantıda nötr hattı bulunmaz. Şekil.3 deki devrede iletim hattının empedansı ihmal edilirse; gerilim kaynağındaki faz-faz arası gerilim değeri yükteki faz-faz arası gerilim değerine eşittir. 0
25 c I c Ean a I a C I CA Z Δ A E cn n Z Δ Z Δ I BC I AB E bn B b I b Yük üzerindeki akımlar ise; Şekil.3: Yıldız Bağlı Kaynak İle Üçgen Bağlı Yük Devre Diyagramı I = E Z AB BC CA ab I = E Z bc I = E Z ca Δ Δ Δ A A A (.45) şeklinde ifade edilir. Örnek olarak; eğer faz-faz arası gerilimler, eşitlik (.37) - (.39) ile verilen değerlerde ve Z Δ = 5 30 Ω ise Δ yük akımları; I I I AB BC CA 0 30 = 3 = 3, A = 3 = 3, A = 3 = 3, A 5 30 (.46) şeklinde bulunur. Üçgen bağlı yük için KAK denklemleri yazılarak faz akımları da ayrı ayrı bulunabilir. AB BC CA CA AB BC ( ) ( ) ( ) I = I I = 3, , = 3 3, a I = I I = 3, , = 3 3, b I = I I = 3, , = 3 3, c (.47) Görüldüğü gibi hem eşitlik (.46) da verilen Δ yük akımları hem de (.47) de verilen faz akımları dengededir. Bu yüzden denge durumundaki Δ bağlı yüklerde yük akımları toplamı ( IAB + IBC + ICA ) sıfırdır. Faz akımları toplamı ( I + I + I ) ise nötr hattı olmadığından sistem dengeli olsun veya olmasın a b c daima sıfırdır. Eşitlik (.46) ve (.47) karşılaştırıldığında; Pozitif sıralı kaynak tarafından beslenen denge durumundaki Δ bağlı yük için faz akımları yük akımlarının 3 katıdır ve 30 gecikmelidirler. Yani;
26 I I I a b c = 3I 30 AB = 3I 30 BC = 3I 30 CA (.48) Bu sonuçlar Şekil.4 te özetlenmektedir. Şekil.4: Dengeli Δ Bağlı Yük durumunda Faz Akımları ve Yük Akımlarının Fazör Diyagramı Dengeli Yükler için Üçgen-Yıldız ( Δ Y ) Dönüşümü Şekil.5 te dengeli yük durumundaki üçgen yıldız dönüşümü görülmektedir. Şekildeki yüklere dengeli bir gerilim kaynağı bağlanırsa, her iki yük de A, B ve C baralarında aynı değerde ifade edilecektir. Δ bağlantıdaki hat akımı yıldız bağlantıdaki hat akımı ile aynıdır. Δ bağlantı için; I A = = 3E 30 Z Δ AB 3IAB 30 A (.49) Yıldız bağlı yük için; I E AN A = = ZY E AB 30 A 3Z Y (.50) Eşitlik (.49) ile (.50) karşılaştırıldığında I A nın hem Δ bağlı yük; hem de Y bağlı yük konumunda aynı olabilmesi için Z 3 Δ Z Y = Ω (.5) olmalıdır, ayrıca diğer I B ve I C hat akımları da Z 3 Y = Z Δ Ω olması durumunda eşit olacaktır. Bu yüzden üçgen bağlı dengeli bir yükü, eşdeğer yıldız bağlantısına çevirmek için üçgen bağlı yük 3 e bölünür. Δ bağlantı ile eşdeğer yıldız bağlantıdaki yüklerin açıları ise eşittir. Benzer şekilde dengeli bir Y bağlantı her bir empedans değeri 3 ile çarpılarak eşdeğer Δ bağlantısına çevrilebilir. ( ZΔ = 3 ZY Ω) Denge durumundaki üç-fazlı devrelerle çalışırken tek-fazın incelenmesi yeterlidir. Δ bağlı yükler Y eşdeğerine çevrilerek, kaynak ve yük nötr noktaları nötr hattı ile birleştirilebilir. Bu şekilde elde edilen tek-fazlı devre çözümlerde kullanılabilir. Geriye kalan iki faza ait akım ve gerilimler; incelenen tek-fazlı devreyle eşit büyüklükte ve ± 0 faz farkına sahiptirler. Kitap boyunca işlenen tüm üç-fazlı konularda aksi belirtilmedikçe verilen tüm gerilim değerleri, iki faz (faz-faz) arasındaki gerilim değerleridir. Endüstriyel kullanımda da bu standart kullanılır.
27 A + I A + A I A C Z Δ C E AB Z Δ Z Δ E AB Z Y Z Y N - - B a) Dengeli Δ Bağlı Yük B b) Dengeli Y Bağlı Eşdeğer Yük Şekil.5: Dengeli Yükler İçin Δ Y Dönüşümü DENGELİ ÜÇ-FAZLI SİSTEMLERDEKİ GÜÇ HESABI Bu bölümde, dengeli üç-fazlı motor ve jeneratörler ile dengeli Y veya Δ bağlı yüklere değinilecek; ayrıca bu yüklere ait anlık güç ile kompleks güç kavramlarına değinilecektir. Anlık Güç: Dengeli Üç-Fazlı Jeneratörler Şekil.6 da Y bağlı bir jeneratör; üç adet gerilim kaynağı, her biri jeneratör empedansına eşit empedansı ve nötr hattı ile gösterilmiştir. Jeneratörün dengeli durumda çalıştığı varsayıldığında jeneratör terminal voltajının anlık değeri; Za an LN ( ω δ) v ( t) = V cos t+ V (.5) Jeneratör tarafından sağlanan a fazına ait akımın anlık değeri ise; a L ( ωt β) i ( t) = I cos + A (.53) V faz-nötr arası voltajın rms değerini, I LN L ise faz akımının rms değerini belirtmektedir. Jeneratörün a fazı tarafından sağlanan anlık güç pa () t ; pa() t = van() t ia() t = V I cos( ωt+ δ)cos( ωt+ β) LN L = VLNIL cos( δ β) + VLNIL cos( ωt + δ + β) W (.54) Denge durumunda çalışma koşulları varsayıldığında; b ve c fazlarının akım ve voltaj değerleri a fazı ile aynı büyüklükte fakat ± 0 faz farklı olacaktır. Bu yüzden b fazı için anlık güç; 3
28 p ( t) = V I cos( ωt+ δ 0 ) cos( ωt+ β 0 ) b LN L = V I cos( δ β) + V I cos(ωt + δ + β 40 ) W LN L LN L (.55) Aynı şekilde c fazı için anlık güç; p ( t) = V I cos( ωt+ δ + 0 ) cos( ωt+ β + 0 ) c LN L = V I cos( δ β) + V I cos(ωt + δ + β + 40 ) W LN L LN L (.56) c + a - - n - + b Şekil.6: Y Bağlı Jeneratör Jeneratörün toplam üç fazı tarafından sağlanan toplam anlık güç p () t, herbir faz için sağlanan anlık 3 güç değerlerinin toplamına eşittir. (.54) - (.56) eşitlikleri yardımı ile; φ p () t = p () t + p () t + p () t 3φ a b c = 3V I cos( δ β) + V I [ cos( ωt + δ + β) LN L LN L + cos(ωt + δ + β 40 ) + cos(ωt + δ + β + 40 )] W (.57) bulunur. Köşeli parantez içerisindeki üç farklı kosinüs terimi, dengeli fazör seti olarak ifade edildiğinde; bu üç terimin toplamının sıfır olduğu görülür. Bu yüzden δ, β ve t nin herhangi bir değeri için eşitlik (.57) aşağıdaki gibi sadeleştirilebilir; p3 φ() t = P3 φ = 3VLNILcos( δ β) W (.58) Eşitlik (.58) faz-nötr gerilimi yerine faz-faz arası gerilim değeri durumu için yeniden düzenlenirse; V kullanılarak dengeli çalışma LL VLN = VLL 3 ve P3 φ = 3VLLIL cos( δ β) W (.59) 4
29 (.59) denklemi incelendiğinde şu sonuca varılır; Üç-fazlı jeneratörün denge durumunda çalışmasında; jeneratör tarafından sağlanan toplam anlık güç zamandan bağımsızdır ve sabittir p () t = P. 3φ 3φ Anlık Güç: Dengeli Üç-fazlı Motor ve Yük Empedansı Üç-fazlı motorlar tarafından denge durumunda çekilen anlık güç sabittir. Şekil.6, akım yönleri değiştirilerek üç-fazlı motor gösteriminde kullanılabilir. Jeneratörün sağladığı güç hesabında kullanılan (.5) - (.59) eşitlikleri motor tarafından çekilen güç hesabında da kullanılabilir. Bu eşitlikler aynı zamanda üç-fazlı sistemlerde dengeli empedans yükleri tarafından çekilen anlık güç değeri için de geçerlidir. Kompleks Güç: Dengeli Üç-Fazlı Jeneratörler Eşitlik (.5) ve (.53) deki voltaj ve akımın fazör gösterimi; Van Ia = V δ V L LN = I β A (.60) (.6) burada I a, jeneratörün pozitif a terminalinden çıkan akımdır. Jeneratörün a güç S a ; fazının sağladığı kompleks S = V I = V I * a an a LN L LN L ( δ β) ( δ β) jv I sin( δ β) = V I cos + LN L (.6) Denge durumundaki jeneratörde b ve c fazı tarafından sağlanan kompleks güç; S a ile aynıdır. Bu yüzden jeneratör tarafından sağlanan toplam kompleks güç S3 φ ; S = S + S + S = 3S 3φ a b c a =3V I LN L ( δ β) ( δ β) j ( δ β) = 3V I cos + 3V I sin LN L LN L (.63) Toplam aktif ve reaktif güç cinsinden ise; S = P + jq 3φ 3φ 3φ (.64) şeklinde ifade edilir. Burada; ( S ) ( ) P3 φ = Re 3φ = 3VLNILcos δ β ve LL L ( δ β) = 3V I cos W ( S ) ( ) Q3 φ = Im 3φ = 3VLNILsin δ β LL L ( δ β) = 3V I sin VAR olarak hesaplanır. Ayrıca toplam görünür güç ise; S = S = 3V I = 3V I VA 3φ 3φ LN L LL L 5 (.65) (.66) (.67)
30 Kompleks Güç: Dengeli Üç-Fazlı Motorlar Üç-fazlı jeneratörler tarafından sağlanan kompleks, aktif, reaktif ve görünür güç ifadeleri aynı zamanda üç-fazlı motorlar tarafından çekilen kompleks, aktif, reaktif ve görünür güç değerleri için de geçerlidir. Kompleks Güç: Dengeli Y Yükler ve Dengeli Δ Yükler (.64) - (.67) eşitlikleri Y veya Δ bağlı empedanslar için de geçerlidir. Denge durumundaki Y bağlı yük için; a fazına bağlı empedans uçlarındaki gerilim değeri ile bu fazdaki akım, (.60) ve (.6) eşitlikleri ile ifade edilebilir. Daha sonra (.63) - (.67) eşitlikleri Y bağlı dengeli yük tarafından çekilen güç için de geçerlidir. Dengeli Δ bağlı yük için a ve b aşağıdaki gibi ifade edilebilir; fazları arasındaki faz-faz arası gerilim değeri ile faz akımı Vab Iab = V δ V LL = I β A Δ (.68) (.69) V, faz-faz arası rms gerilimi, I LL Δ ise rms yük akımını göstermektedir. a b fazları Burada; arasındaki empedans yükü tarafından çekilen kompleks güç S ; ab * ab ab ab LL Δ ( ) S = V I = V I δ β (.70) Δ bağlı yük tarafından çekilen toplam kompleks güç ise; S = S + S + S = 3S 3φ ab bc ca ab =3V I LL Δ LL Δ ( δ β) ( δ β) j3v I sin ( δ β) = 3V I cos + LL Δ (.7) Eşitlik (.70) ; toplam aktif ve reaktif güç cinsinden yeniden yazılırsa; S = P + jq 3φ 3φ 3φ ( S ) Δ ( ) P3 φ = Re 3φ = 3VLLI cos δ β LL L ( δ β) = 3V I cos W ( S ) Δ ( ) Q3 φ = Im 3φ = 3VLLI sin δ β LL L ( δ β) = 3V I sin VAR Burada Δ yük akımı, I Δ, eşitlik (.73) ve (.74) te hat akımı cinsinden yazılmıştır Toplam görünür güç ise; S = S = 3V I = 3V I VA 3φ 3φ LL Δ LL L I L (.7) (.73) (.74) = 3I. Δ (.75) Görüldüğü gibi Δ bağlı yük için çıkarılan (.7) - (.75) eşitlikleri; (.64) - (.67) eşitlikleri ile aynıdır. 6
31 Örnek.4: 400 kw, 0,8 gecikmeli güç faktörüyle çalışan asenkron motor ile, 50 kva, 0,9 ileri güç faktörü ile çalışan senkron motor paralel bağlı şekilde 460 V luk dengeli üç-fazlı kaynaktan beslenmektedir. Kaynak ile yük arasındaki iletim hattının empedansı ihmal edilmektedir. a. Her bir motor için ayrı güç üçgeni ile toplam yük için güç üçgenini çiziniz. b. Toplam yük için güç faktörünü bulunuz. c. Kaynak tarafından sağlanan faz akımının büyüklüğünü bulunuz d. Üçgen bağlı bir kapasitör grubu yüke paralel bağlanıyor. Güç faktörünü yapmak için gerekli olan kapasitör reaktans değerini bulunuz e. Kapasitör grubu eklendikten sonra kaynak tarafından sağlanan faz akımını hesaplayınız Çözüm: Asenkron motor için, P=400 kw ve; S = P gf = = 500 kva ( ) ( ) Q= S P = = 300 kvar çekilen Senkron motor için S=50 kva ve ( gf ) ( ) ( ) ( ) P = S = 50 0, 9 = 35 kw Q= S P = = 65,4 kvar sağlanan Toplam motor yükü için; P = = 535 kw ve Q = ,4 = 34,6 kvar çekilen ( ) ( ) S= P + Q = ,6 = 584, kva Her iki motor için ve toplam motor yükü için güç üçgenleri Şekil.7 de görülmektedir. S=500 kva P=400 kw Q=300 kvar P=35 kw S=50 kva Q=65,4 kvar S=584, kva P=535 kw Q=34,6 kvar Asenkron Motor Senkron Motor Toplam Motor Yükü Şekil.7: Örnek.4 için Güç Üçgenleri Toplam motor yükü durumundaki güç faktörü gf =P S = , = 0,96 geride Kaynak tarafından sağlanan faz akımı I= S ( 3V) burada S toplam motor yük için görünür güç iken, V faz-faz arası yük gerilimidir. Bu örnek için; 7
32 I = 584, ( 3 460) = 0, 08 ka = 8, A ( bir faz için ). Güç faktörünün olabilmesi için kondansatör grubu tarafından sağlanan toplam reaktif gücün, motorlar tarafından çekilen toplam reaktif güce eşit olması gerekir. Bu yüzden Q = 34,6 kvar Üçgen bağlı kondansatör grubu için, Qc = 3V X Δ dır. Burada; V kapasitörler üzerindeki faz-faz arası gerilim, X Δ ise kapasitif reaktansdır. Bu yüzden üçgen bağlı her bir kondansatörün kapasitif reaktansı, ( ) X = 3V Q = Δ ,6 0 =,3 Ω 3 c olarak hesaplanır. Kondansatör grubunun bağlanmasından sonra güç faktörünün olmasıyla kaynak tarafından sağlanan görünür güç S, aktif güç P ile aynı olur. Çekilen faz akımı da; c I = S ( 3V) = P ( 3V) = 535 ( 3 460) = 0, 0743 ka=74,3 A ( her bir faz için) Bu örnekte; kaynak voltajı 460 V un faz-faz mı yoksa faz-nötr arasında mı olduğu ya da rms mi yoksa maksimum değer mi olduğu verilmemiştir. Bu yüzden, genelde olduğu gibi kaynak voltajı, rms ve faz-faz arası olarak kabul edildi. Her iki motorun oluşturduğu toplam yük, kaynaktan 535 kw aktif güç çekmektedir. Gecikmeli güç faktörü ile çalışan asenkron motor 300 kvar reaktif güç çekerken, ileri güç faktörü ile çalışan senkron motor 65.4 kvar reaktif güç sağlamaktadır. Çekilen faz akımı da kondansatör gurubunun bağlanmasıyla 8, A den 74,3 A e indirilmiştir. Bu yüzden iletim hatları ve kablolarda açığa çıkan IR kayıpları da azalmıştır. DENGELİ ÜÇ-FAZLI SİSTEMLERİN TEK-FAZLI SİSTEMLERE GÖRE AVANTAJLARI Şekil.8 de ayrı ayrı üç farklı tek-fazlı sistem görülmektedir. Her bir tek-fazlı sistemde birbirinin aynısı olarak yer alan elemanlar; bir gerilim kaynağı ile gösterilen ve Za empedansına sahip jeneratör, gidiş ve dönüş için Z L empedansına sahip iki farklı iletim hattı, Z ile gösterilen yük empedansıdır. Üç ayrı tekfazlı sistem şekilde yıldız bağlantısını anımsatacak şekilde belirtilerek üç-fazlı sistemin avantajı Y gösterilmeye çalışılmıştır. Her bir tek-faz için gidiş ve dönüş olmak üzere yük akımını veya daha fazlasını taşıyabilecek iki farklı iletken gerekmektedir. Ancak, eğer Şekil.8 deki kaynak ve yükün nötr noktaları birleştirilerek üç-fazlı bir sistem oluşturulduğunda ve kaynak gerilimleri birbiriyle aynı büyüklükte fakat 0 faz farklı olarak seçildiğinde; nötr akımı sıfırlanır [bakınız (.44)] ve bu şekilde de üç farklı nötr hattına gerek kalmaz. 8
33 Z L Z L N n Z Z Y L n n 3 N Z Y Z L N 3 Z Y Şekil.8: Üç Adet Tek-Fazlı Sistem Bu yüzden üç-fazlı dengeli sistemler, tek-fazlı sistem ile iletilen gücün aynısını iletirken, tek-fazlı sistem için gereken iletken miktarının yarısına gerek duyarlar. Ayrıca üç-fazlı sistemlerde IR kayıpları ve iletim hattındaki gerilim düşümü; tek-fazlı sisteme göre yarı yarıyadır. Bu yüzden üç-fazlı sistemin ayrık tek-fazlı sistemlere göre avantajlarından biri enerji iletim ve dağıtım maliyeti olarak daha düşük olması ve daha iyi voltaj düzenlemesine sahip olmasıdır. Bazı üç-fazlı sistemlerde nötr hattı yoktur örneğin Δ bağlantıda veya 3 iletkenli Y bağlantıda nötr hattı bulunmaz. Ancak çoğu üç-fazlı sistem 4 iletkenli Y bağlantıdan oluşur ve topraklanmış nötr hattı bulunur. Nötr hattı, şimşek sonucu oluşan aşırı gerilimlerin sönümlenmesinde kullanılır ve asimetrik yüklenmeler sonucunda oluşan dengesiz akımların taşınmasını sağlar. Nötr hatları normal çalışma durumlarında neredeyse sıfır akım taşıdığı için genelde faz hatlarına göre daha küçük kesitlidirler. Bu yüzden nötr hattının maliyeti faz hatlarına göre daha düşüktür. Nötr hattı olsun veya olmasın üç-fazlı sistemlerin yapım ve işletme maliyeti ayrı ayrı tek-fazlı sistemlere göre daha düşüktür. Üç-fazlı sistemlerin bir diğer avantajı da, üç-fazlı dengeli jeneratörler tarafından sağlanan güç denge durumunda hemen hemen sabittir. Üç-fazlı sistemlerdeki jeneratör (şaft üzerindeki uyartım sargısı ve 0 faz farkı ile yerleştirilmiş stator sargılarından oluşan jeneratör) elektrik gücünü mekanik güçten elde ettiği için hemen hemen sabit bir mekanik güce ihtiyaç duyar. Diğer bir yandan, denge konumunda tek-fazlı jeneratör tarafından sağlanan anlık güç, eşitlik (.54) te verilen pa () t üç-fazlı sistemdeki jeneratörlerden birinin sağladığı anlık güce eşittir. Bu eşitlikte de görüleceği gibi pa () t ; biri sabit diğeri ise çift frekanslı bir sinüsoid olmak üzere, iki bileşenden oluşmaktadır. Bu yüzden tek-fazlı jeneratörün hem mekanik giriş gücü hem de mekanik şaft torku çift frekanslı sinüssel bileşenden ötürü şaft üzerinde titreşimlere ve gürültüye neden olur. Bu titreşimler ve gürültü ise mekanik sistemlerde kısa zamanda aşınma ve bozulmalara neden olur. Bu yüzden 5 kva ve üzeri jeneratörler ve motorlar; titreşim ve gürültüyü önlemek için üç-fazlı olarak imal edilirler. 9
34 Özet Yönü ve şiddeti zamanla periyodik olarak değişen akımlar alternatif akımlar olarak tanımlanırlar. Alternatif akımda, akım ve gerilim daha çok sinüssel biçimde zamanla değişir. Sinüssel AC kaynağının polaritesi (kutupları) periyodik aralıklarla sinüssel dalga biçiminin pozitif veya negatif kısmına bağlı olarak değişir. Kaynağın polaritesine bağlı olarak alternatif akımın yönü de periyodik olarak değişmektedir. Bir alternatif dalga biçimi anlık değer, tepe değeri, periyot, frekans gibi kavramlar ile tanımlanmaktadır. Sinüs dalgası; direnç, endüktör ve kondansatör elemanlarının tepkisinden etkilenmeyen şekle sahip bir dalga biçimidir. Eğer bir direnç, endüktör veya kondansatör üzerindeki gerilim sinüssel ise oluşan akım da sinüssel karakteristiğe sahiptir. Dönen bir vektörden geliştirilen bir sinüs dalgasının fiziksel temsili akım veya gerilim için kullanılabilir. Bir alternatif akımın etkin değeri; aynı dirençte, aynı zamanda ve eşit miktarda ısı açığa çıkaran doğru akımın değerine eşittir. Bir AC devresinde etkin akım ve etkin gerilim değerleri; sırası ile akım ve gerilimin maksimum değerlerinin 0,707 katlarına eşittirler. Kullandığımız AC ampermetre ve voltmetreleriyle ölçülen değerler alternatif akımın etkin değerleridir. Akım ve gerilim arasındaki faz ilişkisini ifade etmek için fazör diyagramı olarak adlandırılan grafiksel ifadeler kullanılır. Bu ifadelerde, akım ve gerilim fazör denilen dönen vektörlerle temsil edilir. Fazör saatin dönüş yönünün tersi yönünde döner. Fazör diyagramı kullanılarak direnç, endüktör veya kondansatör devresi için akım ve gerilim arasındaki faz ilişkisi; ilgili fazörler kullanılarak belirlenir. Bir direnç devresinde akım ve gerilim fazörleri aynı doğru boyunca olduğundan akım ve voltaj aynı fazdadırlar ve aralarında faz farkı yoktur. Bir endüktörde, voltaj akımın 90 ilerisindedir. Bir kondansatörde ise voltaj akımın 90 gerisindedir. AC devrelerde herhangi bir andaki gerilimle akımın çarpımı ani güç olarak tanımlanır. Gücün her an farklı değerler aldığı bu durumlarda genelde ortalama güç temel alınır ve aktif güç olarak adlandırılır. 30
35 Kendimizi Sınayalım. vt ( ) = 0cos(34,6t + 60 ) V şeklinde verilen gerilim değerinin etkin değeri nedir? a. 34,6 3 V b. 34,6 V c. 0 V d. 0 V e V. Saf endüktif yük durumunda; akımın konumu gerilime göre nasıldır? a. Akım, gerilimden 90 ileridedir. b. Akım, gerilimden 90 ileridedir. c. Akım, gerilimden 90 geridedir. d. Akım, gerilimden 90 geridedir e. Akım, gerilim ile aynı fazdadır. 3. vt ( ) = 0cos(34,6t + 60 ) V şeklinde verilen gerilim değerinin frekansı nedir? a. 0 V b. 34,6 Hz c. 50 Hz d. 60 Hz e Pozitif-sıralı, dengeli üç-faz Y bağlı bir gerilim kaynağında E faz-faz arası gerilimi ile ab E faz-nötr arası geriliminin arasındaki ilişki an nasıldır? E = 3E 30 a. ab an E = 3E + 30 b. an ab E = 3E + 30 c. ab an E d. ab an = 3E Üç-fazlı jeneratörün denge konumunda çalışması durumunda; jeneratörün sağladığı anlık güç ile zaman arasında nasıl bir ilişki vardır? a. Zamana bağlı değildir. b. Zaman ile doğru orantılıdır. c. Zamanın karesi ile doğru orantılır. d. Zaman ile ters orantılıdır. e. Zamanın karesi ile ters orantılıdır. 6. Güç üçgeni düşünüldüğünde; 80 kw aktif güce ve 00 kva kompleks güce sahip bir yükün reaktif güç değeri ne olur? a. 80 VAR b. 0 VAR c. 80 Hz d. 60 VAR e. 8 VAR. 7. Üç-fazlı dengeli sistemler, üç adet tek-fazlı sistem ile aynı değerde güç iletmek için tek fazlı sisteme göre ne kadar iletkene ihtiyaç duyarlar? a. Tek-fazlı sistemin katı iletken b. Tek-fazlı sistemin 4 katı iletken c. Tek-fazlı sistem ile aynı sayıda iletken d. Tek-fazlı sistemin katı iletken e. Tek-fazlı sistemin katı iletken 8. Türkiyede evlerde kullanılan elektriğin karakteristiği ne şekildedir? a. Karesel b. Dairesel c. Sinüssel d. Üçgensel e. Kutupsal 9. Bara admitans matrisi üzerindeki köşegen üzerindeki elemanlar neyi ifade ederler? e. ab an E = 3E 30 a. Karşılıklı-empedans değerlerini b. Karşılıklı-admitans değerlerini c. Öz-empedans değerlerini d. Öz-kapasitans değerlerini e. Öz-admitans değerlerini 3
36 0. Üç-fazlı dengeli sistemler, üç adet tek-fazlı system ile aynı değerde güç iletirken oluşan I R kayıpları tek-fazlı sisteme göre nasıldır? a. / kat b. / kat c. kat d. kat e. 4 kat Kendimizi Sınayalım Yanıt Anahtarı. d Yanıtınız yanlış ise Güç Sistemlerinde Kullanılan Temel Kavramlar başlıklı konuyu yeniden gözden geçiriniz.. c Yanıtınız yanlış ise Güç Sistemlerinde Kullanılan Temel Kavramlar başlıklı konuyu yeniden gözden geçiriniz. 3. c Yanıtınız yanlış ise Güç Sistemlerinde Kullanılan Temel Kavramlar başlıklı konuyu yeniden gözden geçiriniz. 4. c Yanıtınız yanlış ise Dengeli Üç-Fazlı Devreler başlıklı konuyu yeniden gözden geçiriniz. 5. a Yanıtınız yanlış ise Dengeli Üç-Fazlı Sistemlerdeki Güç Hesabı başlıklı konuyu yeniden gözden geçiriniz. 6. d Yanıtınız yanlış ise Dengeli Üç-Fazlı Sistemlerdeki Güç Hesabı başlıklı konuyu yeniden gözden geçiriniz. 7. d Yanıtınız yanlış ise Dengeli Üç-Fazlı Sistemlerin Tek-Fazlı Sistemlere göre Avantajları başlıklı konuyu yeniden gözden geçiriniz. 8. c Yanıtınız yanlış ise Giriş başlıklı konuyu yeniden gözden geçiriniz. 9. e Yanıtınız yanlış ise Devre Eşitlikleri başlıklı konuyu yeniden gözden geçiriniz. 0. b Yanıtınız yanlış ise Dengeli Üç-Fazlı Sistemlerin Tek-Fazlı Sistemlere göre Avantajları başlıklı konuyu yeniden gözden geçiriniz. Yararlanılan Kaynaklar Fitzgerald, A. E., Higginbotham, D. E. & Grabel, A. (000). Fundamental Electric Engineering. (Çev. Ed. Kıymaç, K.) Temel Elektrik Mühendisliği Cilt. (3. Baskı). Ankara: Bilim Center. Demir, S. (0). Elektrik Enerjisi Üretimi ve Dağıtımı, Anadolu Üniversitesi Yayınları. Arifoğlu, U. (000). Alternatif Akım Devreleri: cilt, İstanbul: Alfa Basım Yayım Dağıtım Ltd. Şti. Boylestad, R. L. (990). Introductory Circuit Analysis (6th ed.), New York: Macmillan Publishing Company. Glover, D.J., and Sarma, M.S. (989). Power system analysis and design, PWS-Kent Publishing Com., Boston. Saadat, H. (004). Power System Analysis. McGraw-Hill Inc
37
38 Amaçlarımız Bu üniteyi tamamladıktan sonra; Üç-fazlı sistemlerle ilgili olan simetrik bileşenleri yorumlayabilecek, Simetrik bileşenler yardımıyla sıralı bileşen devreleri tanımlayabilecek, Dengeli ve dengesiz sistemleri kıyaslayıp aralarındaki farkları ayırt edebilecek, Şebekede kullanılan çeşitli sabit ve dönen elemanların eşdeğer sıralı devrelerini oluşturabilecek, Üç-fazlı sistemlerdeki iletilen gücü hesaplayabilecek, bilgi ve becerilere sahip olabilirsiniz. Anahtar Kavramlar Simetrik Bileşenler Dönüşüm Matrisi Sıralı Devreler Empedans Matrisi Y Bağlantı Δ Bağlantı Faz Kayması Birim Sıralı Devre Transformatör Senkron Jeneratör İçindekiler Giriş Simetrik Bileşenlerin Tanımı Empedans Yüklerin Sıralı Devreleri Seri Empedanslar İçin Sıralı Devreler Üç-Fazlı İletim Hatlarının Sıralı Devreleri Dönen Makinelere Ait Sıralı Devreler Üç-Fazlı ve İki-Sargılı Transformatörlerin Birim Sıralı Modelleri Üç-Fazlı ve Üç-Sargılı Transformatörlerin Birim Sıralı Modelleri Sıralı Devrelerde Güç Hesabı 34
39 Simetrik Bileşenler GİRİŞ Bu bölümde, güç sistemlerindeki hesaplamalarda sıkça kullanılan simetrik bileşenler yönteminden detaylıca bahsedilecektir. İlk olarak C. L. Fortescue tarafından açıklanan Simetrik bileşenler metodu dengesiz sistemlerle ilgilidir. Bu teoreme göre n fazörlü dengesiz bir sistem, dengeli fazörlerden oluşan n adet ayrık sistemle çözülebilir ve bunun ispatı Fortescue tarafından yapılmıştır. n fazörlü dizinin bileşenlerinin herbirinin genlikleri ve dizinin fazörleri arasındaki faz açıları birbirine eşittir. Normalde dengeli olan üç-fazlı bir sistemde dengesiz hata durumları, her fazda dengesiz akım ve buna bağlı olarak da dengesiz gerilimlerin oluşmasını sağlar. Akım ve gerilim değerleri sabit empedanslarla ilişkiliyse, sistem lineer sistem olarak adlandırılır. Sistemin Simetrik bileşenleri makinalarla, transformatörlerle, iletim hatlarıyla ve yük oluşumlarıyla ilgilidir. Üç-fazlı bir sistemin çözümlenebilmesi için üç tane eşdeğer devresinin bulunması gerekir. Simetrik bileşenlerle analiz, simetrik olmayan hataların ve üç faz hatalarının çözümlenip ayrıştırılmasında önemli bir yere sahiptir. Bu konular ilerleyen ünitelerde detaylıca işlenecektir. Üç-fazlı sistemlerde, sitemin analizinin yapılıp matematiksel hesaplamaların düzgün bir biçimde yapılabilmesi için şebeke elemanlarına ait eşdeğer devrelerin sıralı bileşen devrelerinin oluşturulması gereklidir. Bu sayede pozitif-sıralı, negatif-sıralı ve sıfır-sıralı eşdeğer devreleri ayrı ayrı bulunup analiz edilebilir. Bu devreleri birbirinden ayrı ayrı analiz edebilme özelliği, hesapmalarda büyük kolaylık sağlar. Bu ünitede öncelikle empedans yüklere ait sıralı devreler çıkarıldıktan sonra kapsam daha da genişletilerek, seri bağlı empedanslar için sıralı devreler ve üç-fazlı iletim hatlarına ait sıralı devreler incelenecektir. Ardından motor ve jeneratör gibi dönen makinelerin sıralı devrelerine geçilecektir. Şebekenin önemli elemanlarından olan üç-fazlı transformatörlerin sıralı eşdeğer devreleri ile ilgili örnekler yapıldıktan sonra incelenen tüm sıralı devrelerdeki güç hesabına geçilecektir. SİMETRİK BİLEŞENLERİN TANIMI Üç-fazlı sistemlerdeki herbir faza ait gerilimler V a, V b ve V c şeklinde isimlendirilir. Fortescue ye göre; bu faz gerilimlerinin aşağıdaki üç grup sıralı (ardışık) bileşene ayrılarak çözümlemesi yapılabilir. Şekil.(a) da görüldüğü gibi sıfır-sıralı bileşenler, eşit büyüklükte ve aralarında 0 faz kaymasına sahip üç ayrı fazörden meydana gelmektedirler. Şekil.(b) da görüldüğü gibi pozitif-sıralı bileşenler eşit büyüklükte, aralarında ± 0 faz kaymasına sahip ve açısal olarak pozitif yönde sıralanmış üç ayrı fazörden meydana gelmektedirler. Açısal olarak pozitif yön, saat yönünü ifade eder Şekil.(c) da görüldüğü gibi negatif-sıralı bileşenler eşit büyüklükte, aralarında ± 0 faz kaymasına sahip ve açısal olarak negatif yönde sıralanmış üç ayrı fazörden meydana gelmektedirler. Açısal olarak negatif yön, saat yönünün tersini ifade eder Biz bu kitapta sadece a fazına ait gerilimin sıfır, pozitif ve negatif sıralı bileşenleri üzerinde duracağız ki; bu fazörler yazılış sırasına göre V, V a0 a ve V şeklinde ifade edilirler. Gösterimi daha a sade ve anlaşılır hale getirmek için alt indis olan a kaldırılıp bu sıralı bileşenler V 0, V ve V şeklinde 35
40 gösterilecektir. Üç-fazlı nicelikler ve bunların sıralı bileşenleri ile olan ilişkisini daha iyi anlayabilmek için aşağıdaki dönüşüm denklemi yararlı olacaktır. Va V0 V b a a V = V c a a V (.) (a) Sıfır-sıralı bileşenler (b) Pozitif-sıralı bileşenler (c) Negatif-sıralı bileşenler a fazı b fazı c fazı Şekil.: Faz Gerilimlerinin Sıralı Bileşenler Cinsinden Gösterimi Bu denklemde; büyüklüğü ve faz açısı 0 olan a fazörü aşağıdaki şekillerde ifade edilir. 3 a= 0 = + j (.) (.) deki matris gösterimi, aşağıda gösterildiği gibi 3 farklı denkleme ayrıştırılabilir. V = V + V + V (.3) a b 0 V = V + a V + av (.4) c 0 V = V + av + a V (.5) 0 (.) deki denklemde; a birim büyüklüğe ve 0 faz açısına sahip kompleks bir sayıdır ve aynı zamanda bir fazördür. Herhangi başka bir fazör, a ile çarpıldığında; bu fazör saat yönünün tersi istikametinde 0 döner. Aynı şekilde, herhangi bir fazör a ile çarpıldığında ise; bu fazör saat yönünün tersi istikametinde 40 döner. Aşağıdaki ifadeler, a fazörünü içeren genel özdeşlikleri listelemektedir. 4 3 a = a= 0 a = 40 a = 0 + a+ a = 0 a= 3 30 a = 3 30 a a= 3 70 ja= 0 + a= a = 60 + a = a= 60 a+ a = = 80 36
41 Kompleks bir sayı olan a, yine kompleks sayı olan j = = 90 ile benzerdir. Dolayısıyla j ile a arasındaki tek fark açı değerleridir. j nin açısı 90 iken a nın açısı ise 0 dir. (.) deki denklem, vektör ve matris gösterimi kullanılarak daha basitleştirilmiş bir şekilde yeniden yazılabilir. Niceliklere ve fazörlere ait V ve V vektörleri ile A matrisi aşağıdaki şekilde tanımlanabilir. p s Va V p = V b (.6) V c V0 V s = V (.7) V A = a a (.8) a a V p faz gerilimlerinin sütun vektörüdür, V s sıralı gerilimlerin sütun vektörüdür ve 3 3 lük A matrisi ise dönüşüm matrisi olarak adlandırılır. Bu tanımlamaları kullanarak (.) deki denklem şu hale gelir. V = AV (.9) p s A matrisinin tersi = a a 3 a a A (.0) (.0) denkleminde hesaplanmıştır ve bu denklem, ispat edilerek doğrulanabilir. Ayrıca AA çarpımının birim matrise ( U ) eşit olduğu A ile (.9) denkleminin soldan çarpımı şu şekilde olur; Vs = A V (.) p (.6), (.7) ve (.0) kullanılarak (.) deki denklem, aşağıdaki gibi ifade edilebilir. V0 Va V a a V = b 3 V a a V c (.) (.) denklemindeki matris gösterimi, üç ayrı denklem olarak ayrıştırılırsa; V0 = ( Va + Vb + Vc) (.3) 3 V = V + av + a V (.4) ( ) 3 a b c V = ( Va + a Vb + avc) (.5) 3 37
42 denklemleri elde edilir. (.3) denklemi gösterir ki dengeli üç-fazlı sistemde sıfır-sıralı gerilim yoktur çünkü üç dengeli fazörün toplamı (vektörel olarak) sıfırdır. Dengede olmayan üç-fazlı sistemde, hat-nötr gerilimleri sıfır-sıralı bileşene sahip olabilir. Oysa ki, hat-hat arası gerilimler hiçbir zaman sıfır-sıralı bileşene sahip olamazlar, çünkü KGK ya göre bu gerilimlerin toplamları her zaman sıfırdır. Aşağıda görüldüğü gibi simetrik bileşen dönüşümü; gerilimlere uygulanabildiği gibi aynı zamanda akımlara da uygulanabilir: I = AI (.6) p s I p, faz akımlarının sütun vektörü olmak üzere; Ia I p = I b (.7) I c I s, sıralı akımların sütun vektörü olmak üzere; I0 I s = I (.8) I Ayrıca; Is = A I (.9) p elde edilir. (.6) ve (.9) denklemleri, aşağıdaki gibi ayrı ayrı denklemler halinde yazılabilir. Faz akımları; I = I + I + I (.0) a b 0 I = I + a I + ai (.) c 0 I = I + ai + a I (.) 0 ve sıralı akımlar; I = I + I + I (.3) 0 ( ) 3 a b c I = I + ai + a I (.4) ( ) 3 a b c I = I + a I + ai (.5) ( ) 3 a b c şeklinde gösterilir. Üç-fazlı Y bağlı bir sistemde; I n nötr akımı, hat akımlarının fazör olarak vektörel toplamına eşittir. In = Ia + Ib + I (.6) c (.6) ve (.3) kıyaslanırsa; In = 3I (.7) 0 38
43 eşitliği elde edilir. Nötr akımı, sıfır-sıralı akımın üç katına eşittir. Dengeli Y bağlı sistemde; hat akımları sıfır-sıralı bileşene sahip değildir çünkü nötr akım sıfırdır. Ayrıca; nötr yolu olmayan herhangi bir üç fazlı sistemde, örneğin üçgen bağlı sistem veya topraklanmamış üç-kablolu Y bağlı sistem gibi, hat akımları sıfır-sıralı bileşene sahip değildir. Aşağıdaki üç farklı örnek, simetrik bileşenler konusunun daha iyi anlaşılmasına yardımcı olacaktır. Örnek. abc sıralaması ile verilen aşağıdaki dengeli hat-nötr gerilimlerinin sıralı bileşenlerini hesaplayınız. V p Van 77 0 = V bn 77 0 = V V cn Çözüm: (.3) - (.5) aralığındaki denklemler kullanarak V0 = ( ) = 0 3 V = ( 0 0 ) 77 ( 0 40 ) 77 0 V = = Van V = ( ) + 77 ( ) = ( ) = Buradan çıkarılacak sonuç; abc sıralı (pozitif-sıralı) dengeli üç-fazlı sistemler, sıfır-sıralı veya negatifsıralı bileşenlere sahip değillerdir. Bu örnek için V pozitif-sıralı gerilimi V an ye eşittir. Sıfır-sıralı ve negatif-sıralı gerilimlerin her ikisinin de değeri sıfıra eşittir. Örnek. Y bağlı bir yük acb sıralaması ile aşağıda verilen dengeli akımlara sahiptir. Sıralı akımları hesaplayınız. I p Ia 0 0 = I b 0 0 = A I c 0 0 Çözüm: (.3) - (.5) aralığındaki denklemler kullanılarak I0 = ( ) = 0 3 I = ( 0 0 ) 0 ( 0 40 ) ( ) = + + = 3 I = ( ) + 0 ( ) = 0 0 A = Ia 3 Buradan çıkarılacak sonuç; acb sıralı (negatif-sıralı) dengeli üç-fazlı sistemler, sıfır-sıralı veya pozitifsıralı bileşenlere sahip değillerdir. Bu örnek için I negatif-sıralı akımı I a ya eşittir. Sıfır-sıralı ve pozitif-sıralı akımların her ikisinin de değeri sıfıra eşittir. Örnek.3 Y bağlı bir yükü besleyen üç-fazlı bir hattın fazlarından biri ( b fazı) devreden koparak faz açıkdevre haline gelmiştir. Yük üzerindeki nötr noktası topraklanmıştır ve dengesiz hat akımları aşağıdaki değerlerle verilmiştir. Sıralı akımları ve nötr akımını hesaplayınız. 39
44 I p Ia 0 0 = I b 0 = A I c 0 0 Çözüm: Bahsedilen devre, Şekil. de görülmektedir. (.3) - (.5) aralığındaki denklemler kullanılarak sıralı akımlar aşağıdaki şekilde bulunur. I0 = ( ) = 3,33 60 A 3 I = ( 0 40 ) 6,67 0 A = I = ( ) = 3,33 60 A 3 Nötr akımı ise (.6) denklemi kullanılarak aşağıdaki işlemle hesaplanır. In = = 0 60 A = 3I 0 a c b Şekil.: Örnek.3 için Kullanılacak Devre EMPEDANS YÜKLERİN SIRALI DEVRELERİ Şekil.3, dengeli ve Y bağlı yük empedansını göstermektedir. Herbir fazın empedansı, Z Y olarak belirlenmiştir ve Z n nötr empedansı ise yükün nötr noktası ile toprak arasına bağlanmıştır. Şekil.3 te hat-toprak arası gerilim V ag ile belirtilmiştir. Bundan sonraki gösterimlerde toprak bağlantısı için g indisi kullanılacaktır. ( ) ( ) V = Z I + Z I = Z I + Z I + I + I = Z + Z I + Z I + Z I (.8) ag Y a n n Y a n a b c Y n a n b n c Benzer denklemler V ve bg V hat-toprak gerilimleri için de yazılabilir. cg ( ) V = Z I + Z + Z I + Z I (.9) bg n a Y n b n c ( ) V = Z I + Z I + Z + Z I (.30) cg n a n b Y n c (.8) - (.30) aralığındaki denklemler, aşağıdaki denklemde olduğu gibi matris şeklinde ifade edilebilir. 40
45 ( ) V ag ZY + Zn Zn Zn Ia Vbg Zn ( ZY Zn ) Z n I = + b V cg Zn Zn ( ZY + Zn ) I c (.3) Şekil.3: Dengeli Y Bağlı Empedans Yükü (.3) denklemi daha anlaşılır biçimde şu şekilde yazılabilir. Vp = ZpI (.3) p V p hat-toprak arası gerilimleri ( veya faz gerilimleri) içeren sütun vektörü, I p hat akımlarını içeren (veya faz akımları) sütun vektörü ve Z ise (.3) de ifade edilen p 3 3 lük faz empedans matrisi olarak adlandırılır. (.9) ve (.6) denklemleri, sıralı gerilim ve sıralı akımlar arasındaki ilişkiyi belirlemek amacıyla (.3) denklemi içinde kullanılabilir. AVs = Z pai (.33) s (.33) denkleminde eşitliğin her iki tarafı, sol taraftan, ( ) s p s A ile çarpılırsa; V = A Z A I (.34) veya Vs = ZsI (.35) s ki; Zs = A ZpA (.36) bulunur. (.36) da tanımlanan Z s empedans matrisi sıralı empedans matrisi olarak adlandırılır. (.8), (.0) ve (.3) denklemlerinde verilen A, A ve Z p tanımlarını kullanarak Y bağlı dengeli yük için, Z s sıralı empedans matrisi şu şekilde hesaplanır. 4
46 ( + ) ZY Zn Zn Zn Z s = a a Zn ( ZY Zn) Z n a a 3 + (.37) a a Zn Zn ( ZY + Zn) a a (.37) de belirtilen matris çarpımlarını yaparak ve ( a a ) ( ) ( ) ( ) + + = 0 özdeşliğini kullanarak ( ) ZY + 3Zn ZY ZY ZY + 3Zn Z s = a a ZY Zn a ZY azy 0 ZY = (.38) 3 a a ZY + Zn azy a ZY 0 0 ZY denklemi bulunur. (.38) eşitliği yorumlanacak olursa; Şekil.3 teki Y bağlı dengeli yük için sıralı empedans matrisi olan Z s, köşegen tipindedir ( köşegen üzerinde elemanları olan ve diğer elemanları sıfır olan matris). Z s köşegen matris olduğu için (.35) denklemi üç ayrık denklem biçiminde ifade edilebilir. (.35) eşitliği içinde (.7), (.8) ve (.38) denklemleri kullanılarak; ( + ) V0 ZY 3Zn 0 0 I0 V = 0 Z 0 I Y V 0 0 Z Y I (.39) bulunur. (.39), üç ayrı denklem olarak yeniden yazılırsa; ( 3 ) V = Z + Z I = Z I (.40) 0 Y n V = Z I = Z I (.4) Y V = Z I = Z I (.4) Y bağıntıları elde edilir. (.40) eşitliğinden anlaşılacağı üzere; V 0 sıfır-sıralı gerilimi, sadece I 0 sıfır-sıralı akım değeri ile Z0 = ZY + 3Z sıfır-sıralı empedans n değerine bağlıdır. V pozitif-sıralı gerilimi, sadece I pozitif-sıralı akım değeri ile Z = Z Y pozitif-sıralı empedans değerine bağlıdır. V negatif-sıralı gerilimi ise sadece I negatif-sıralı akım değeri ile Z = Z Y negatif-sıralı empedans değerine bağlıdır. (.40) - (.4) aralığındaki denklemler, Şekil.4 te gösterilen üç ayrı sıralı devre ile temsil edilir. Bu devreler; sıfır-sıralı, pozitif-sıralı ve negatif- sıralı devreler olarak adlandırılır. Görüldüğü gibi herbir sıralı devre kendine özgü ve ve diğer iki devreden ayrık durumdadır. Bu sıralı devrelerin ayrıklığı, Z matrisinin dengeli ve Y bağlı yük için köşegen tipte olmasının sonucudur. Bu ayrıklık, simetrik bileşen analizinin faydasını ve avantajını ortaya koyar. Dikkat edilmesi gerekir ki; Şekil.4 te görüldüğü gibi nötr empedans, pozitif- ve negatif-sıralı devrelerde görülmez. Bu şu gerçeği açıklar; pozitif- ve negatif-sıralı akımlar, nötr empedans üzerinden akmaz. Ayrıca, nötr empedans 3 ile çarpılır ve sıfır-sıralı devresinde yer alır. In = 3I olduğu için, 3Z 0 n empedansı üzerindeki I0 ( 3 Z n ) gerilimi, Şekil.3 te gösterilen n gerilim düşümüdür. Şekil.3 te gösterilen Y yükünün nötr noktasının dönüş yolu olmadığında, Z nötr empedansı üzerindeki IZ n Z n nötr empedansı s n 4 sonsuz değerde olur ve Şekil.4 te sıfır-sıralı devresindeki 3Z n terimi açık-devre olur. Nötr noktası açık
47 devre olunca, bu devreden sıfır-sıralı akım da akmaz. Eğer Y yükünün nötr noktası sıfır-ohm luk bir iletken ile topraklandığında, nötr empedans değeri sıfır olur ve sıfır-sıralı devresindeki 3Z n terimi kısadevre olur. Düzgün topraklanmış nötr koşullarında; yüke uygulanan dengesiz gerilimlerin sebep olduğu sıfır-sıralı gerilimin varlığı sonucunda, I 0 sıfır-sıralı akımı oluşabilir Sıfır-sıralı devre Pozitif-sıralı devre Negatif-sıralı devre Şekil.4: Dengeli Y Bağlı Empedans Yüke ait sıralı devreler Şekil.5, dengeli Δ (delta) yük ve onun eşdeğeri olan dengeli Y yükünü temsil etmektedir. Δ yük nötr bağlantıya sahip olmadığı için Şekil.5 teki eşdeğer olan Y yükü açık-devre nötr noktasına sahiptir. Dengeli konumdaki Δ yüküne karşılık gelen eşdeğer Y yükünün sıralı devreleri Şekil.5 te gösterilmektedir. Görüldüğü gibi eşdeğer Y Z empedansı olan ZY = Δ, herbir sıralı devrede 3 gösterilmektedir. Ayrıca, açık-devre nötr noktasına karşılık gelen Z = eşitliğinden dolayı sıfır-sıralı devre açık-devre bağlantısına sahiptir. Δ yüke eşdeğer Y yükünde sıfır-sıralı akım oluşmaz. n Şekil.5: Dengeli Δ Bağlı Empedans Yükün eşdeğer Y devresine ait sıralı devreler Şekil.5 teki sıralı devreler, bağlantı uçlarından görülen dengeli Δ yükünü temsil etmektedir; fakat sıralı devreler iç yük karakteristiğini temsil etmez. Şekil.5 te gösterilen I 0, I ve I akımları, Δ yükünü besleyen hat akımlarının sıralı bileşenleridir. ( Δ içerisindeki yük akımlarını temsil etmezler) (.48) deki hat akımlarıyla bağlantılı olan Δ yük akımları, Şekil.5 de gösterilmemiştir. ZY Örnek.4 Dengeli Y yükü ile dengeli Δ bağlı kapasitör yükü ile paralel bağlanmıştır. Y yükü herbir fazda = 3+ j4 Ω empedansa sahiptir ve nötr noktası X Ω değerinde endüktif reaktans ile n = 43
48 topraklanmıştır. Kapasitör bankası ise herbir fazda X 30 ait sıralı devreleri çiziniz ve sıralı yük empedanslarını hesaplayınız. c = Ω luk kapasitif reaktansa sahiptir. Bu yüke Çözüm: Şekil.6 da sıralı devreler gösterilmektedir. Görüldüğü gibi sıfır-sıralı devresindeki Y yükünün empedansı, nötr empedansının üç katı ile seridir. Ayrıca, sıfır- sıralı devresindeki Δ yük kısmı açık-devredir, çünkü Δ yükünden sıfır-sıralı akımı akmaz. Pozitif ve negatif-sıralı devrelerde Δ yük empedansı 3 e bölünür ve Y yük empedansı ile paralel bağlanır. Eşdeğer sıralı empedanslar şu şekildedir; 0 ( ) Z = Z + 3Z = 3 + j4 + 3 j = 3 + j0 Ω Y n ( 3+ j4 j30 )( 3 ) ( 5 53,3 )( 0 90 ) Z Z = Z / / Δ Y = =7,454 6,57 3 = Ω 3+ j4 j( 30 ) 6, , 43 3 Z = Z = 7,454 6,57 Ω Sıfır-sıralı devre Pozitif-sıralı devre Negatif-sıralı devre Şekil.6: Örnek.4 e Ait Sıralı Devreler Şekil.7, genel üç-fazlı lineer empedans yükünü göstermektedir. Bu yük, dengeli Δ, dengeli Y veya dengesiz empedans yükünü temsil edebilir. Bu yük için, hat-toprak gerilimleri ve hat akımları arasındaki genel bağıntı şu şekilde yazılmaktadır: V ag Zaa Zab Zac Ia V bg Zab Zbb Z bc I = b V cg Zac Zbc Z cc I c (.43) 44
49 veya, Vp = ZpI (.44) p Vp hat-nötr (ya da faz) gerilim vektörüdür, I p hat (ya da faz) akımları vektörüdür ve Z ise 3x3 lük p faz empedans matrisidir. Burada, yükün dönmediği (hareketsel açıdan) ve çift yönlü devreye karşılık gelen Z nin simetrik matris olduğu kabul edilmiştir. p Şekil.7: Genel Üç-fazlı Empedans Yük Gösterimi (Doğrusal, Çift Taraflı Şebeke ve Dönmeyen Elemanlar için) (.44), (.3) ile aynı forma sahip olduğu için; Şekil.6 daki genel üç-fazlı yük için sıralı gerilimler ve akımlar arasındaki bağıntı, (.35) ve (.36) ile aynıdır ve şu şekilde yeniden yazılabilir: Vs = ZsI (.45) s Zs = A ZpA (.46) (.46) da verilen sıralı empedans matrisi matristir ve aşağıdaki gibi tanımlanmıştır: Z s, dokuz adet sıralı empedans değeri ile birlikte 3x3 lük Z0 Z0 Z0 Z s = Z0 Z Z (.47) Z0 Z Z Bu matristeki Z 0, Z ve Z köşegen empedansları; sıfır-, pozitif- ve negatif-sıralı devrelerin öz empedanslarıdır. Köşegen dışı empedanslar sıralı devreler arasındaki karşılıklı empedanslardır. Z, A, Z ve A tanımlarını kullanarak, (.46) denklemi aşağıdaki şekle dönüştürülebilir: s p Z Z Z Z Z Z aa ab ac Z0 Z Z a a Zab Zbb Z bc a a = 3 Z0 Z Z a a Zac Zbc Z cc a a (.48) 45
50 (.48) de belirtilen çarpma işlemlerini yaparak ve ( a a ) ayrık denklemler elde edilir: Köşegen sıralı empedanslar: + + = 0 özdeşliğini kullanarak, aşağıdaki Z0 = ( Zaa + Zbb + Zcc + Zab + Zac + Zbc ) (.49) 3 Z = Z = ( Zaa + Zbb + Zcc Zab Zac Zbc ) (.50) 3 Köşegen dışı sıralı empedanslar: Z0 = Z0 = ( Zaa + a Zbb + azcc azab a Zac Zbc ) (.5) 3 Z0 = Z0 = ( Zaa + azbb + a Zcc a Zab azac Zbc ) (.5) 3 Z ( = Zaa + a Zbb + azcc + azab + a Zac + Zbc ) (.53) 3 Z ( = Zaa + azbb + azcc+ azab + azac + Zbc ) (.54) 3 Simetrik yük, sıralı empedans matrisi köşegen olan yük olarak tanımlanmaktadır; yani, (.5)-(.54) aralığındaki bütün karşılıklı empedanslar sıfırdır. Bu karşılıklı empedansları sıfıra eşitledikten sonra bu eşitliklerin çözümü yapılmak istenirse; simetrik yük için aşağıdaki iki bağıntıyı kullanmak gerekir; Zaa = Zbb = Z (.55) cc Zab = Zac = Z (.56) bc sonrasında Z0 = Z0 = Z0 = Z0 = Z = Z = 0 (.57) Z = Z + Z (.58) 0 aa ab Z = Z = Zaa Z (.59) ab Sıfır-sıralı devre Pozitif-sıralı devre Negatif-sıralı devre Şekil.8: Üç-fazlı Simetrik Yüke Ait Sıralı Devreler (Doğrusal, Çift Taraflı Şebeke ve Dönmeyen Elemanlar için) Simetrik yük için olması gereken şartlar şu şekildedir ki; köşegen faz empedansları eşittir ve aynı şekilde köşegen dışı faz empedansları da eşittir. Bu durumlar, (.55) ve (.56) ile birlikte bütün karşılıklı 46
51 sıralı empedansların sıfır olduğunu göstermek için kullanılan (.5) - (.54) denklemlerindeki ( a a ) + + = 0eşitliği kullanılarak doğrulanabilir. Şuna dikkat edilmelidir ki; (.59) da gösterildiği gibi pozitif- ve negatif-sıralı empedanslar simetrik yük için eşittir ve aynı şekilde (.50) de gösterilen simetrik olmayan yük için de eşittir. Transformatör ve iletim hatları gibi dönmeyen elemanları temsil eden lineer ve simetrik empedanslar için, bu tanım her zaman doğrudur. Öte yandan, jeneratörler ve motorlar gibi dönen elemanların pozitif- ve negatif-sıralı empedansları genellikle eşit değildir. Ayrıca; Z 0 sıfır-sıralı empedansı, Zab = Zac = Z karşılıklı faz empedansları sıfıra eşit olduğu sürece, simetrik yükün pozitifbc ve negatif-sıralı empedanslarına eşit değildir. Simetrik empedans yükünün sıralı devreleri Şekil.8 de gösterilmektedir. simetrik yük için köşegen olduğundan dolayı sıralı devreler ayrıktır. SERİ EMPEDANSLAR İÇİN SIRALI DEVRELER Z s sıralı empedans matrisi, Şekil.9 da abc ve abc ile ifade edilen iki adet üç-fazlı bara, seri empedanslar ile bağlanmıştır. Her bir fazın öz empedansları Zaa, Zbb ve Z ile ifade edilmektedir. Genel olarak; seri bağlı devreler, fazlar cc arasında karşılıklı empedanslara sahip olabilir. Seri faz empedansları üzerindeki gerilim düşümleri şu şekilde verilir: Van Va n Vaa Zaa Zab Zac Ia V V = V = Z Z Z I bn b n bb ab bb bc b Vcn V c n V cc Zac Zbc Z cc I c (.60) (.60) denklemi hem öz empedansları hem de karşılıklı empedansları içermektedir. Çift yönlü devreyi temsil eden empedans matrisi simetrik olarak kabul edilir Şekil.9: Üç-fazlı Seri Empedanslar (Doğrusal, Çift Yönlü Devre, Dönmeyen Elemanlar) Ayrıca bu empedansların dönmeyen elemanlara ait olduğu kabul edilmektedir. İletim hatları ve transformatörlerin seri empedansları bu tipteki empedanslara örnek olarak verilebilir. (.60) denklemi aşağıdaki forma sahiptir: V V = Z I (.6) p p p p 47
52 V p, abc barasındaki hat-nötr gerilimlerinin vektörüdür; V, p gerilimlerinin vektörüdür; I p, hat akımlarının vektörüdür ve abc barasındaki hat-nötr Z ise seri devre için 3x3 lük faz empedans p matrisidir. (.6) denklemi, yüke ait faz empedanslarını sıralı devrelere dönüştürmek için kullanılabilir; V V = Z I (.6) s s s s Zs = A ZpA (.63) Simetrik seri empedanslar için, köşegendir. Z s sıralı empedans matrisi aşağıdaki iki şart sağlandığında Z = Z = Z aa bb cc Z = Z = Z ab ac bc (.64) (.60) denklemindeki Z faz empedans matrisi, eşit öz empedanslara ve eşit karşılıklı empedanslara p sahip ise (.63) denklemi aşağıdaki şekle dönüşür: Z0 0 0 Z s = 0 Z 0 (.65) 0 0 Z olur ki; Z = Z + Z (.66) 0 aa ab Z = Z = Zaa Z (.67) ab ve (.6) üç ayrık denklem haline gelir, aşağıdaki şekilde yazılır; V V = Z I (.68) V V = Z I (.69) V V = Z I (.70) (.68) - (.70) aralığındaki denklemler, Şekil.0 da gösterilen üç ayrık sıralı devre tarafından temsil edilmektedir. Şekle bakıldığında; simetrik seri empedanslar için pozitif-sıralı akımların sadece pozitifsıralı gerilim düşümüne sebep olduğu gözlenir. Benzer şekilde; negatif-sıralı akımlar sadece negatif-sıralı gerilim düşümü üretir ve sıfır-sıralı akımlar da yine sadece sıfır-sıralı gerilim düşümü üretir. Bununla birlikte, seri empedanslar simetrik değilse, Z s matrisi köşegen değildir, sıralı devreler ayrık değildir ve herhangi bir sıralı devre üzerindeki gerilim düşümü tüm sıralı akımlara bağlıdır. 48
53 Sıfır-sıralı devre Pozitif-sıralı devre Negatif-sıralı devre Şekil.0: Üç-fazlı Simetrik Seri Empedansların Sıralı Devreleri (Doğrusal, Çift Yönlü Devre, Dönmeyen Elemanlar) ÜÇ-FAZLI İLETİM HATLARININ SIRALI DEVRELERİ Üç-fazlı iletim hatlarının sıralı devrelerini elde etmek için aşağıdaki denklemden yola çıkılabilir ZS = A ZPA (.7) Z S, elemanları aşağıda gösterilen 3x3 lük seri sıralı empedans matrisidir Z0 Z0 Z0 Z S = Z0 Z Z Ω/m (.7) Z0 Z Z Genellikle Z S köşegen değildir. Bununla birlikte, eğer hat tamamen devrik hale getirilirse; Zˆ ˆ Z ˆ ˆ S = A ZPA = 0 Z 0 (.73) 0 0 Zˆ olur. Hattın devrik hale getirilmesi işlemi ilerleyen ünitelerde detaylıca anlatılacaktır. (.66) ve (.67) den; Z ˆ = Z ˆ + Z ˆ (.74) 0 aaeş abeş Zˆ = Zˆ = Zˆ Zˆ (.75) aaeş abeş Tamamen devrik hale getirilmiş üç-fazlı iletim hattının seri sıralı empedans devreleri Şekil. de gösterilmektedir. 49
54 Sıfır-sıralı devre Pozitif-sıralı devre Negatif-sıralı devre Şekil.: Tamamen Devrik Yapılmış Üç-fazlı Hattın Seri Sıralı Empedans Devreleri Üç-fazlı iletim hatları şönt admitanslar cinsinden ifade edilirse, sıralı devreler aşağıdaki şekilde bulunabilir. YS = A YPA (.76) ve ( π f ) Y = G + j C (.77) S S S C0 C0 C0 C S = C0 C C F/m (.78) C0 C C Genellikle C S köşegen değildir. Bununla birlikte, tamamen devrik yapılmış hat için; ˆ yˆ 0 0 C 0 0 Yˆ A Yˆ A ˆ (.79) 0 0 S = P = 0 y 0 ( ) 0 ˆ = j π f C yˆ ˆ 0 0 C 0 C ˆ = C ˆ + C ˆ F/m (.80) aa ab C ˆ = C ˆ = C ˆ C ˆ F/m (.8) aa ab C negatif olduğu için sıfır-sıralı kapasitans Ĉ ˆab 0 genellikle pozitif- veya negatif-sıralı kapasitanstan değer olarak daha küçüktür. Tamamen devrik hale getirilmiş üç-fazlı hattın faz ve sıralı kapasitans devreleri Şekil. de gösterilmektedir. 50
55 Şekil.: Tamamen Transpoze Edilmiş Üç-fazlı Hattın Kapasitelerinin Devre Gösterimleri DÖNEN MAKİNELERE AİT SIRALI DEVRELER Şekil.3 te Z n nötr empedans üzerinden topraklanmış Y bağlı senkron jeneratör gösterilmektedir. Jeneratörün iç gerilimleri Ea, Eb ve E olarak ve jeneratöre ait hat akımları da c Ia, Ib ve I olarak c belirlenmiştir. Jeneratörün sıralı devreleri Şekil.4 te gösterilmektedir. Üç-fazlı senkron jeneratör sadece pozitif-sıralı bileşen ile Ea, Eb ve E dengeli iç faz gerilimlerini üretmek için dizayn edildiğinden, c kaynak gerilimi E sadece pozitif-sıralı devreye dahil edilmektedir. Jeneratör terminallerindeki hat- g toprak gerilimlerinin sıralı bileşenleri, Şekil.4 de V0, V ve V olarak gösterilmektedir. Jeneratör nötr empedansındaki gerilim düşümü ZI dir ve n n ( 3Z n ) I 0 şeklinde de yazılabilir. Çünkü (.7) den şu çıkarım yapılabilir; nötr akımı sıfır-sıralı akımının üç katıdır. Bu gerilim düşümü sadece sıfır-sıralı akımına bağlı olduğu için; 3Z n empedansı, Şekil.4 teki sıfır-sıralı devresinde jeneratöre ait Z sıfır-sıralı empedansı ile seri olarak gösterilmiştir. g 0 Dönen makinelerin sıralı empedansları genellikle eşit değildir. Sıralı makine empedanslarının detaylı analizi makine teorisi ile ilgili kaynaklardan araştırılabilir. Bu kitapta; konu, detaya inilmeden yüzeysel olarak anlatılmıştır. Kararlı durumda; senkron jeneratöre ait stator dengeli üç-fazlı pozitif-sıralı akımlara sahip olduğunda, bu pozitif-sıralı akımlar tarafından üretilen net mmk, rotor ile aynı yönde ve rotor hızı ile senkron bir şekilde döner. Bu şartlarda, manyetik akının büyük bir kısmı rotor içine dağılır ve Z pozitif-sıralı g empedansı yüksek değere sahip olur. Kararlı durumda, pozitif-sıralı jeneratör empedansı senkron empedans olarak adlandırılır. Senkron jeneratöre ait stator, dengeli üç-fazlı negatif-sıralı akımlara sahip olduğunda; bu akımlar tarafından üretilen net mmk, rotorun dönüş yönüne ters yönde ve senkron hızda döner. Net mmk rotor referansına göre kararlı değildir fakat senkron hızın iki katı hızda döner. Bu koşul altında; rotor üzerine dağılan manyetik akıyı önleyen rotor sargılarında akımlar endüklenir. Böyle olunca da, Z negatif-sıralı g empedans, pozitif-sıralı senkron empedanstan daha küçüktür. Senkron jeneratör sadece sıfır-sıralı akımlarına (eşit büyüklük ve faza sahip olan hat ya da faz akımları) sahip ise; bu akımlar tarafından üretilen net mmk teorik olarak sıfır olur. Jeneratöre ait Z g 0 sıfır-sıralı empedansı, en küçük sıralı empedanstır ve değeri, kaçak akıya ve harmonik akıya bağlıdır. 5
56 Şekil.3:Y Bağlı Senkron Jeneratör Devresi Şekil.4: Y Bağlı Senkron Jeneratörün Sıralı Devreleri Üç-fazlı senkron motorların ve üç-fazlı endüksiyon (asenkron) motorların sıralı devreleri Şekil.5 te gösterilmektedir. Senkron motorlar, senkron jeneratörler ile aynı sıralı devrelere sahiptir. Aralarındaki tek fark; senkron motorların sıralı akımlarının akış yönünün, sıralı devrelerin dışına doğru değil, devrelerin içine doğru olmasıdır. Ayrıca, endüksiyon motorları ile senkron motorların sıralı devreleri benzerdir. Aralarındaki tek fark; E pozitif sıralı gerilim kaynağı, endüksiyon motorunun pozitif-sıralı devresinde m bulunmamaktadır. Bunun sebebi ise; Endüksiyon motorları rotor devrelerinde manyetik akı oluşturacak DC kaynağa sahip değillerdir ve bu nedenle E in değeri sıfırdır (ya da kısa-devre). m Şekil.4 ve.5 te gösterilen sıralı devreler, dönen makineler için sadeleştirilmiş devrelerdir. Bu devrelerde; çıkık kutuplar, akısal doyma etkileri ve süreksizlik etkileri gibi durumlar ihmal edilmiştir. Bu ihmal durumuna rağmen, basitleştirilmiş bu devreler güç sistemlerinin analizi için çoğu durumda yeterince doğru sonuçlar vermektedirler. 5
57 Sıfır-sıralı devre Pozitif-sıralı devre (a) Senkron Motor Negatif-sıralı devre Sıfır-sıralı devre Pozitif-sıralı devre Negatif-sıralı devre (b) Endüksiyon (Asenkron) Motor Şekil.5: Üç-fazlı Motorların Sıralı Devreleri Örnek.5 Dengeli, pozitif-sıralı ve Y bağlı üç-fazlı jeneratör, a ve b fazları arasında E ab = Volacak şekilde Δ bağlı üç-faz yüke uygulanıyor. Δ bağlantıdaki her bir kolun empedans değeri Z Δ = Ω ve jeneratör ile yük arasına bağlanan hattın faz başına empedansı ise Z L = 85 Ω olarak verilmiştir. Bu devre için sıralı devreleri çiziniz ve hat akımının sıralı bileşenlerini hesaplayınız. Jeneratörün Zn = j0 Ω nötr empedansı üzerinden topraklandığını ve bu jeneratöre ait sıralı empedansların sırasıyla Zg 0 = j Ω, Z = j Ω ve Z = j3 Ω şeklinde olduğunu kabul edelim. g 5 g Çözüm: Sıralı devreler Şekil.6 da gösterilmiştir. Bunlar; Şekil.5,.0 ve.4 te verilen dengeli Δ yükü, seri hat empedansları ve senkron jeneratör yardımıyla birbirine bağlanan sıralı devreler oluşturulmuştur. Şekil.6 da açık bir şekilde görülmektedir ki; sıfır- ve negatif-sıralı devrelerinde hiç kaynak olmadığı için, I 0 = I = 0 ifadesi yazılabilmektedir. Ayrıca; V pozitif-sıralı jeneratör terminal gerilimi, jeneratöre ait hat-nötr arası terminal gerilimine eşittir. (.0) denkleminde, I 0 = I = 0 olduğundan; I akımı I a hat akımına eşittir. Bu nedenle, şekilde gösterilen pozitif-sıralı devreden aşağıdaki değer elde edilir: I V = 5,83 73,78 A = = ZL + Z Δ 3 I a 53
58 Aşağıdaki diğer örnek, dengesiz sistemlerin analizi için simetrik bileşenler kullanmanın avantajını göstermektedir. Sıfır-sıralı devre Pozitif-sıralı devre Negatif-sıralı devre Örnek.6 Şekil.6: Örnek.5 te Kullanılan Sıralı Devreler Aşağıdaki dengesiz gerilimlere sahip Y bağlı gerilim kaynağı, Örnek.5 teki Δ yük ile aradaki hatta uygulanmaktadır. Gerilim kaynağına ait nötr noktası topraklanmıştır. Simetrik bileşenler metodunu kullanarak Ia, Ib ve I kaynak akımlarını hesaplayınız. c V ag 77 0 V bg 60 0 = V V cg 95 5 Çözüm: Kaynak gerilimlerinin sıralı bileşenleri (.3)-(.5) denklemleri kullanılarak aşağıdaki şekilde hesaplanır. V0 = ( ) = 7,445 + j 4,065 = 5,9 6, V 3 V = ( ( ) + 95 ( )) = ( ) 3 3 = 76,96 j8,5703 = 77,, 77 V V = 7, 407 j5, 4944 = 9, 8 6,59 V = ( + ( + ) + ( + )) = ( + + ) Bu sıralı gerilimler Şekil.7 de gösterilen hat ve yükün sıralı devrelerine uygulanmaktadır. 54
59 Şekil.7: Örnek.6 da Kullanılan Sıralı Devreler Bu şeklin sıralı devreleri ayrıktır ve kaynak akımlarının sıralı bileşenleri aşağıdaki şekilde kolayca hesaplanabilir: I I 0 = 0 A = = = 5,8 45,55 A = = = Z L V 77,, 77 I 0, 73 43, 78 ZL + ZΔ 3 V 9, 8 6,59 0,859 7,8 A 0, 73 43, 78 + ZΔ 3 (.0) - (.) denklemleri kullanılarak, kaynak akımları aşağıdaki şekilde hesaplanır. I I I a b c ( ) j ( ( ) ( )) ( ( ) ( )) = 0 + 5,8 45, ,859 7,8 = 7, 3 8, 3 = 5,5 46, 76 A = 0 + 5,8 45, ,859 7,8 + 0 = 4, 67 j7, 35 = 5, 7 96, 34 A = 0 + 5,8 45, ,859 7, = 7, 44+ j5, 56 = 6, 6 73, 77 A ÜÇ-FAZLI VE İKİ SARGILI TRANSFORMATÖRLERİN BİRİM SIRALI MODELLERİ Şekil.8(a), Z N ve Z n nötr empedansları üzerinden topraklanmış ideal Y Y transformatörünün şematik gösterimidir. Şekil.8(b-d) ise bu ideal transformatörün birim sıralı devrelerini göstermektedir. Dengeli pozitif- veya negatif-sıralı akımlar transformatöre uygulandığında, nötr akımlar sıfır olur ve nötr empedanslar üzerinde gerilim düşümü olmaz. Bu nedenle, ideal Y Y transformatörünün birim pozitif- ve negatif-sıralı devreleri, Şekil.8(c) ve (d), Şekil 3.9(b) deki tek-faz ideal transformatörün birim devresi ile aynıdır. 55
60 Şekil.8: İdeal Y Y Transformatör Sıfır-sıralı akımları eşit büyüklük ve eşit faz açılarına sahiptir. IA0 = IB0 = I birim sıralı akımları C0 ideal Y Y transformatörünün yüksek-gerilim sargılarına uygulandığında; Z üzerinden akan N IN = 3I0 nötr akımı, ( 3Z N ) I 0 kadarlık gerilim düşümüne sebep olur. Ayrıca, I 0 birim sıfır-sıralı akımı herbir alçak-gerilim sargısı üzerinden de akar ve bu yüzden In = 3I akımı, Z 0 n nötr empedansı üzerinden akar 3Z n ve ( ) 0 I değerinde gerilim düşümüne sebep olur. 3Z N ve 3Z n empedanslarını içeren birim sıfır-sıralı devresi Şekil.8(b) de gösterilmektedir. Dikkat edilmelidir ki, eğer ideal transformatörün her iki nötr noktasından herhangi biri topraklanmazsa, yüksek- ve alçak-gerilim sargılarının hiçbirinden sıfır-sıralı akımı akmaz. Örneğin; eğer yüksek-gerilim sargısının nötr noktası açık-devre ise, IN = 3I = 0 olur ve bu durum, alçak-gerilim 0 tarafında I 0 = 0 olmasına sebep olur. Bu durum, Şekil.8(b) deki sıfır-sıralı devresinde Z in açık- N devre ( Z N = Ω) yapılmasıyla gösterilebilir. Pratik Y Y transformatörünün birim sıralı devreleri Şekil.9(a) da gösterilmektedir. Bu devreler aşağıda açıklandığı gibi ideal transformatörün sıralı devrelerine dış empedansların eklenmesiyle elde edilir. Yüksek-gerilim sargılarının kaçak empedansları, Şekil.9 daki fazlar arasında kuplaj olmayan ( Z = 0 ) seri empedanslar gibi, seri empedanslardır. Eğer ab, ve c fazlarının sargıları eşit ab Z = R + jx kaçak empedanslarına sahiplerse; seri empedanslar Şekil.0 da gösterildiği gibi sıralı H H H devreler ile simetrik olarak adlandırılır ( ZH0 = ZH = ZH = Z ). Benzer şekilde, alçak-gerilim H sargılarının kaçak empedansları da ZX0 = ZX = ZX = Z empedansları ile simetriktir. Bu seri kaçak X empedanslar Şekil.9(a) nın birim sıralı devrelerinde gösterilmiştir. Uyarma akımını temsil eden pratik Y Y transformatörünün paralel (şönt) kolları, Şekil.3 teki Y yükü ile eşdeğerdir. Şekil.3 teki her bir faz, mıknatıslanma endüktansı ile çekirdek kaybı direncini paralel olarak gösterir. Her bir faz için bunların aynı olduğu varsayılırsa Y bağlı yük simetrik olur ve sıralı devreleri de Şekil.4 te gösterilmiştir. Bu paralel kollar ayrıca Şekil.9(a) da gösterilmiştir. Dikkat edilmelidir ki 3Z n ve 3Z N empedansları sıfır-sıralı devresine dahil edilmiştir. 56
61 Şekil.9(a) da gösterilen pratik Y Y transformatörünün birim pozitif- ve negatif-sıralı transformatör empedansları özdeştir ki; bu durum tüm dönmeyen makinalar için her zaman doğrudur. Bununla birlikte, birim sıfır-sıralı devresi, Z ve Z nötr empedanslarına bağlıdır. N n Şekil.9(b) de gösterilen Y Δ transformatörünün birim sıralı devreleri aşağıdaki özelliklere sahiptir: Birim empedanslar sargı bağlantı tiplerine bağlı değildir. Yani; Y Y, Y Δ, Δ Y veya Δ Δ bağlı transformatörlerin birim empedansları aynıdır. Sadece baz gerilimleri sargı bağlantı tiplerine bağlıdır. Birim pozitif- ve negatif-sıralı devreler, faz kaymasını içermektedir. Amerikan standartlarına göre, Y Δ transformatörünün yüksek-gerilim tarafındaki pozitif-sıralı gerilim ve akımları, alçak-gerilim tarafındaki aynı niceliklere karşılık gelen değerlerin açısal olarak 30 ilerisindedirler. Negatif sıralama için yüksek-gerilim nicelikleri, 30 geridedir. Sıfır-sıralı akımları, sadece nötr bağlantısı olan Y bağlı sargılar üzerinden akabilir ve ayrıca Δ bağlantısında sıfır-sıralı akımları var ise; bu akımlar bağlantı içinde kalır. Bu bağlantıda sıfırsıralı akımlar, Δ sargısına girmez ve Δ sargısını terk etmez. Şekil.9(b) deki Y Δ bağlı transformatörün pozitif- ve negatif-sıralı devrelerindeki faz kaymaları, Şekil 3.4 deki faz kaydırıcı transformatör ile temsil edilmektedir. Ayrıca, Şekil.9(b) deki sıfır-sıralı devre Y bağlı tarafta sıfır-sıralı akımının akmasını sağlar fakat Δ bağlı tarafta ise sıfır-sıralı akım giriş ve çıkışı olmaz. Şekil.9(c) de gösterilen Δ Δ bağlı transformatörün birim sıralı devreleri aşağıdaki özelliklere sahiptir: Birbirine özdeş olan pozitif- ve negatif-sıralı devreler, Y Y transformatörlerinde olduğu gibi aynıdır. Sargıların noktalandığı ve bu sayede faz kaymasının olmadığı kabul edilmektedir. Ayrıca, birim empedanslar sargı bağlantı tiplerine bağlı değildir; fakat baz gerilimleri bağlıdır. Sıfır-sıralı akımlar, Δ sargısına girmez ve Δ sargısını terk etmez. Sadece delta bağlantının içinde, dönecek şekilde akarlar. 57
62 Tek hat Diyagramı Şematik Birim Sıfırsıralı Devre Birim Pozitifsıralı Devre Birim Negatif-sıralı Devre Örnek.7: Şekil.9: Y Y, Δ Y ve Δ Δ Bağlı Transformatörlerin Birim Sıralı Devreleri Nötr noktası topraklanmış 75-kVA, 480 V Δ / 08 V Y transformatörü, Örnek.5 teki kaynak ve hat arasına bağlanmıştır. Transformatör kaçak reaktansı Xeş = 0, birimdir. Sargı dirençleri ve uyarma akımı ihmal edilmiştir. Baz değerler olarak transformatör anma değerlerini kullanarak; birim sıralı devreleri çiziniz ve a fazının kaynak akımı olan I a yı hesaplayınız. Çözüm: 75 Baz değerler olarak; S = baz φ 5 kva 3 =, VbazHLN = = 77, V, VbazXLN = = 0, V ve 3 3 ( 0) ZbazX = = 0,577 Ω alınır. Asıl kaynak gerilimlerinin sıralı bileşenleri Şekil.7 de verilmiştir Birim sistemde, bu gerilimler; 58
63 5,9 6, V0 = = 0, , br 77, 77,, 77 V = =,0,77 br 77, 9, 8 6,59 V = = 0, ,59 br 77, olarak hesaplanır. Transformatörün alçak-gerilim tarafındaki birim hat ve birim yük empedansları şu şekilde bulunur:, 0 85 ZL0 = ZL = ZL = =, br 0,577 ZΔ 0 40 Zyük = Zyük = = =, br 3 0,577 0,577 ( ) Birim sıralı devreler Şekil.0 de gösterilmektedir. Birim hat ve yük empedanslarının; faz kaydırıcı transformatörün yüksek-gerilim tarafına yönlendirilirken, (3.6) da görüldüğü gibi değişmediklerine dikkat edilmelidir. Bu nedenle, Şekil.0 den, kaynak akımlarının sıralı bileşenleri aşağıdaki şekilde hesaplanabilir; I0 = 0 V,0,77 I = = = 0, , 77 br jxeş + ZL + Zyük j0,+, ,33 40 V 0, ,59 I = = = 0, ,59 br jx + Z + Z 8, eş L yük a fazının kaynak akımı olan I a, öncelikle birim değerler ve (.0) kullanılarak hesaplanır ve ardından baz değerle çarpılarak aşağıdaki şekilde amper cinsinden gerçek değeri bulunur: Ia = I0 + I+ I = 0 + 0, , , ,59 = 0, ,9 br I bazh = = 90, A I = 0, ,9 br 90, A = 4, ,9 A a ( )( ) Birim Sıfır-sıralı Birim Pozitif-sıralı devre Birim Negatif-sıralı devre Şekil.0: Örnek.7 ye Ait Birim Sıralı Devreler 59
64 ÜÇ-FAZLI VE ÜÇ-SARGILI TRANSFORMATÖRLERİN BİRİM SIRALI MODELLERİ Birbirine özdeş üç adet tek-fazlı üç-sargılı transformatör, üç-fazlı transformatör bankası elde etmek için birbirlerine bağlanabilir. Şekil., üç-fazlı üç-sargılı transformatörün genel birim sıralı devrelerini göstermektedir. Tek-fazlı transformatör sargıları için yapılan, ve 3 şeklindeki etiketlemenin yerine; H, M ve X harfleri sırasıyla yüksek-,orta- ve alçak-gerilim sargılarını etiketlemek için kullanılır. Genel bir kabul olarak; H, M ve X terminalleri için sadece tek bir S değeri dikkate alınır ve baz V bazh, V bazm ve V bazx baz gerilim değerleri de transformatörün anma hat-hat arası gerilimleriyle orantılı olarak seçilir. Genel bir sıfır-sıralı devre için, Şekil.(a) da gösterildiği gibi, H-H terminalleri arasındaki bağlantı, yüksek-gerilim sargılarının bağlantı tiplerine bağlıdır, aşağıda görüldüğü gibi; Tamamen topraklanmış Y --- H ile H arası kısa-devre Z üzerinden topraklanmış Y --- H ile H arasına N 3Z N direnci bağlanmış Topraklanmamış Y --- H ile H arası açık-devre Δ --- H terminali referans baraya kısa-devre yapılmış Birim Sıfır-sıralı Birim Pozitif- veya Negatif sıralı devre Şekil.: Üç-fazlı Üç Sargılı Transformatörlere Ait Birim Sıralı Devreler X-X ve M-M terminalleri benzer tarzda bağlanmıştır. Birim negatif-sıralı devrelerin empedansları, birim pozitif-sıralı devrelerininkiyle aynıdır. Bu durum, sadece bu dönmeyen elemanlar için her zaman doğrudur. Şekil.(b) de gösterilmeyen faz kaydırıcı transformatörler, Δ ve Y sargıları arasındaki faz kaymasını modellemek için devreye dahil edilebilir. Örnek.8: Örnek 3.5 te anlatılan birbirine özdeş üç transformatör, 3,8 kv luk jeneratörden çıkan 900 MVA lik üç-faz gücü, 345 kv luk iletim ve 34,5 kv luk dağıtım hatlarını beslemek için üç-fazlı transformatör bankası olarak bağlanmıştır. Transformatör sargıları aşağıdaki gibi bağlanmıştır: 3,8 kv sargıları (X): Δ, jeneratöre 9,9 kv sargıları (M): Z = j0, Ω üzerinden topraklanmış Y, 34,5 kv luk hatta n 99, kv sargıları (H): tamamen topraklanmış Y, 345 kv luk hatta Yüksek- ve orta-gerilim Y sargılarının pozitif-sıralı gerilim ve akımları, düşük-gerilim Δ sargılarının benzer niceliklerinden 30 ileridedir. S baz = 900 MVA ve V bazx = 3,8 kv değerlerini kullanarak bu örneğe ait birim sıralı devreleri çiziniz. 60
65 Çözüm: Birim sıralı devreleri Şekil. de gösterilmektedir. V bazx = 3,8 kv, X terminalinin hathat arası anma gerilimi olduğu için; M terminalinin hat-hat arası anma gerilimi VbazM ( ) = 3 9,9 =34,5 kv olur. Orta-gerilim terminalinin baz empedansı şu şekildedir: ( 34,5) ZbazM = =,35 Ω 900 Bu nedenle, birim nötr empedansı da; j0, Zn = = j0,0756 br birim,35 hesaplanır. 3Z = j0,68 empedansı birim sıfır-sıralı devresinde M-M terminalleri arasına n bağlanmıştır. Yüksek-gerilim sargılarının nötr noktası topraklandığı için, sıfır-sıralı devresinde H-H terminalleri arası kısa-devre yapılmıştır. Ayrıca, faz kaydırıcı transformatörler pozitif- ve negatif-sıralı devrelere dahil edilebilir. Birim Sıfır-sıralı Birim Pozitif-sıralı devre Birim Negatif-sıralı devre Şekil.: Örnek.8 e Ait Birim Sıralı Devreler SIRALI DEVRELERDE GÜÇ HESABI Üç-fazlı şebekeye iletilen güç, şebekenin sıralı devrelerine iletilen güç değerinden hesaplanabilir. S p yi Şekil.7 deki üç fazlı yüke iletilen toplam kompleks güç olarak düşünürsek; bu güç değeri aşağıdaki şekilde hesaplanabilir; S = V I + V I + V I (.8) * * * p ag a bg b cg c (.8) denklemi ayrıca Şekil (.3) teki üç-fazlı jeneratör tarafından iletilen toplam kompleks güç hesabı veya herhangi bir üç-fazlı baraya iletilmiş kompleks güç hesabı için de geçerlidir. (.8) denklemi matris formatında yeniden düzenlenirse; I S V V V I * a * T * p = ag bg cg b= p p * Ic VI (.83) şeklinde gösterilir. Burada T, matrisin tranzpoze ya da diğer bir deyişle devrik olmasını simgelemektedir ve * simgesi ise kompleks eşlenik olarak temsil edilmektedir. Kompleks eşlenik terimini açıklamak gerekirse; örneğin x= y δ fazörünün kompleks eşleniği * x = y δ olur. Fazörün büyüklüğü değişmez, sadece açı değeri eksi işaret alır. Şimdi, (.9) ve (.6) denklemleri kullanılarak; 6
66 ( ) ( ) T * T T * * p s s s s S = AV AI = V A A I (.84) hesaplanır. (.8) de verilen A matrisi yardımıyla (.84) deki köşeli parantez içindeki ifade bulunabilir ( a ve a birbirlerinin eşleniğidir.) T * = = = = a a a a a a a a T * AA a a a a a a a a U (.85) (.85) denklemi, (.84) denklemi içinde kullanılırsa aşağıdaki ifade elde edilir: * I 0 T * * Sp = 3VI s s = 3[ V0 V V] I (.86) * I * * * ( 0 0 ) S = 3 V I + VI + V I = 3S (.87) p Bu sayede, üç-fazlı devreye iletilen s S p toplam kompleks gücü, sıralı devrelere iletilen S s toplam kompleks gücünün üç katına eşittir. Üç faktörü (.85) denkleminden gelmektedir. U matrisine birim matris adı verilir ve matris çarpımlarında etkisiz eleman olarak görev yapar. S p Örnek.9: Örnek.6 daki üç-fazlı kaynak tarafından iletilen = 3S olduğunu ispatlayınız. s Çözüm: (.8) denklemi kullanılarak; S p S p ve S s güç değerlerini ayrı ayrı hesaplayınız ve ( 77 0 )( 5,5 46,76 ) ( 60 0 )( 5,7 96,34 ) ( 95 5 )( 6, 6 73,77 ) = + + = , , ,3 = j4870 = ,78 VA Sıralı devrelerdeki güç ise aşağıdaki gibi bulunur; * * * Ss = V0I0+ VI + VI = + + = + = + = , 78 VA 0 ( 77,, 77 )( 5,8 45,55 ) ( 9, 8 6,59 )( 0,859 7,8 ) ( , 78 ) ( 7,99 43, 78 ) 57 j4958 ( ) 3S = ,78 = ,78 = S ifadesi ispatlanır. s p 6
67 Özet İlk olarak C.L. Fortescue tarafından açıklanan Simetrik bileşenler metodu dengesiz sistemlerle ilgilidir. Bu teoreme göre n fazörlü dengesiz bir sistem, dengeli fazörlerden oluşan n adet ayrık sistemle çözülebilir ve bunun ispatı Fortescue tarafından yapılmıştır. n fazörlü dizinin bileşenlerinin herbirinin genlikleri ve dizinin fazörleri arasındaki faz açıları birbirine eşittir. Üç-fazlı sistemde gerilim veya akım değerleri üç farklı sıralı devreden oluşurlar ve bunlara sırasıyla sıfır-sıralı, pozitif-sıralı ve negatif sıralı bileşen adı verilir. a fazına ait gerilimin sıfır-, pozitif- ve negative-sıralı bileşenleri yazılış sırasına göre V a0, V a ve V a şeklinde ifade edilirler. Gösterimi daha sade ve anlaşılır hale getirmek için alt indis olan a kaldırılıp bu sıralı bileşenler V 0, V ve V şeklinde gösterilir. Dengeli üç-fazlı sistemde sıfır-sıralı gerilim yoktur çünkü üç dengeli fazörün toplamı (vektörel olarak) sıfırdır. Dengede olmayan üçfazlı sistemde, hat-nötr gerilimleri sıfır-sıralı bileşene sahip olabilir. Oysa ki, hat-hat arası gerilimler hiçbir zaman sıfır-sıralı bileşene sahip olamazlar, çünkü KGK ya göre bu gerilimlerin toplamları her zaman sıfırdır. Nötr akımı, sıfırsıralı akımın üç katına eşittir. Dengeli Y bağlı sistemde; hat akımları sıfır-sıralı bileşene sahip değildir çünkü nötr akım sıfırdır. Ayrıca; nötr yolu olmayan herhangi bir üç fazlı sistemde, örneğin üçgen bağlı sistem veya topraklanmamış üç-kablolu Y bağlı sistem gibi, hat akımları sıfırsıralı bileşene sahip değildir. Akım ve gerilim niceliklerinde olduğu gibi empedans yüklerin de kendilerine özgü sıralı devreleri vardır ve bu sıralı devreler matematiksel hesaplamalarda model olarak kullanılırlar. Herbir empedans yük; seri, Y veya Δ bağlantılar için farklı sıralı devreler oluştururlar. Bunlara ek olarak; iletim hatların, dönen makinelerin (senkron, asenkron, DC makineler), transformatörlerin ve üç-fazlı sistemlerde kullanılan diğer elemanların da kendilerine ait üçer adet sıralı devreleri mevcuttur. Üç-fazlı şebekeye iletilen güç, şebekenin sıralı devrelerine ayrı ayrı iletilen güç değerlerinin toplamından hesaplanabilir. 63
68 Kendimizi Sınayalım. V şeklinde gösterilen fazör aşağıdakilerden c hangisini ifade etmektedir? a. a fazına ait pozitif-sıralı bileşeni b. c fazına ait negatif-sıralı bileşeni c. b fazına ait negatif-sıralı bileşeni d. c fazına ait pozitif-sıralı bileşeni e. c fazına ait sıfır-sıralı bileşeni. Üç-fazlı dengeli sistemlerde, hesaplamalarda kullanılan a fazörü aşağıdakilerden hangisidir? a. a = 0 b. a = 90 c. a = 3 45 d. a = 0 e. a = 0 3. Dengeli Y bağlı empedans yüke ait sıfırsıralı empedans değeri aşağıdakilerden hangisidir? a. Z0 = Z + 3Z b. Z0 = 3Z Y + Z n Z = Z Y c. 0 Y Z = Z d. 0 n n e. Z0 = ZY + Zn 4. Dengeli Δ bağlı empedans yüke ait sıfırsıralı akımı aşağıdakilerden hangisidir? a. I0 = I = I I = 3I b. 0 I = I c. 0 d. I 0 = e. I 0 = 0 5. Üç-fazlı sistemde Y Δ bağlı transformatörde hangi sıralı devreler faz kayması içerirler? a. Pozitif- ve negatif-sıralı devreler. b. Sıfır- ve Pozitif-sıralı devreler. c. Sıfır- ve negatif-sıralı devreler d. Pozitif-,negatif- ve sıfır-sıralı devrelerin hepsi. e. Pozitif-,negatif- ve sıfır-sıralı devrelerin hiçbiri Herhangi bir d fazörü d = f g şeklinde ifade ediliyorsa; bu fazörün kompleks eşlenik * değeri ( d ) ne olur? a. b. c. d. * d = f g * d f g = ( + 90 ) * d = f g * d = f g e. d = f g 7. Dengeli Y bağlı bir yük; Z Y ve Z n empedanslarına sahip ise; bu yüke ait sıralı empedans matrisi ( Z ) nasıl gösterilir? a. b. c. d. e. ( Z + Z ) Y 3 n 0 0 Z s = 0 3ZY Z Y ( Z + Z ) Y 3 n 0 0 Z s = 0 ZY Z Y ( Z + Z ) 0 0 Y n Z s = 0 Zn Z n ( Z + Z ) s Y 3 n 0 0 Z s = 0 ( ZY + 3Zn) Y 3 ZY 0 0 Z s = 0 Zn Z n ( Z + Z ) 8. Üç-fazlı şebekelerde seri empedanslar simetrik değillerse, aşağıdakilerden hangisi doğrudur? a. Z s matrisi köşegendir. b. Z s matrisi köşegen değildir. c. Y s matrisi köşegendir. d. Y s matrisi köşegen değildir. e. Y s matrisi üst-üçgensel matristir. n
69 9. Kararlı durumda; senkron jeneratöre ait stator, dengeli üç fazlı pozitif-sıralı akımlara sahip olduğunda, akımlar tarafından üretilen net mmk nasıl bir etki gösterir? a. Rotorun dönüş yönüne ters şekilde döner b. Rotor ile aynı yönde döner c. Rotor hızının ½ katı kadar hızda döner d. Rotor hızının katı kadar hızda döner e. Rotor hızının katı kadar hızda döner 0. Kararlı durumda; senkron jeneratöre ait pozitif-sıralı jeneratör empedansına ne ad verilir? a. Şönt empedans b. Karakteristik empedans c. Jeneratör empedans d. Asenkron empedans e. Senkron empedans Kendimizi Sınayalım Yanıt Anahtarı. b Yanıtınız yanlış ise Simetrik Bileşenlerin Tanımı başlıklı konuyu yeniden gözden geçiriniz.. d Yanıtınız yanlış ise Simetrik Bileşenlerin Tanımı başlıklı konuyu yeniden gözden geçiriniz. 3. a Yanıtınız yanlış ise Empedans Yüklerin Sıralı Devreleri başlıklı konuyu yeniden gözden geçiriniz. 4. e Yanıtınız yanlış ise Empedans Yüklerin Sıralı Devreleri başlıklı konuyu yeniden gözden geçiriniz. 5. a Yanıtınız yanlış ise Üç-Fazlı ve İki-Sargılı Transformatörlerin Birim Sıralı Modelleri başlıklı konuyu yeniden gözden geçiriniz. 6. d Yanıtınız yanlış ise Üç-Fazlı ve Üç-Sargılı Transformatörlerin Birim Sıralı Modelleri başlıklı konuyu yeniden gözden geçiriniz. 7. b Yanıtınız yanlış ise Empedans Yüklerin Sıralı Devreleri başlıklı konuyu yeniden gözden geçiriniz. 8. b Yanıtınız yanlış ise Seri Empedanslar İçin Sıralı Devreler başlıklı konuyu yeniden gözden geçiriniz. 9. b Yanıtınız yanlış ise Dönen Makinelere Ait Sıralı Devreler başlıklı konuyu yeniden gözden geçiriniz. 0. e Yanıtınız yanlış ise Dönen Makinelere Ait Sıralı Devreler başlıklı konuyu yeniden gözden geçiriniz. 65 Yararlanılan Kaynaklar Althusser, L. (000). Machlavell and Us. London: Verso. Grainger, J.J. (994). Power System Analysis. McGraw-Hill Inc. Saadat, H. (004). Power System Analysis. McGraw-Hill Inc. Arifoğlu, U. (00). Güç Sistemlerinin Bilgisayar Destekli Analizi. İstanbul: Alfa Basım Yayım Dağıtım Ltd. Şti. Odoğlu, H. (006). Transformatör Deneyleri. İstanbul: Bileşim Yayınlan. Tosun,. (007). Enerji İletimi ve Dağıtımı. İstanbul: Birsen Yayınevi. Glover, D.J., and Sarma, M.S. (989). Power system analysis and design, PWS-Kent Publishing Com., Boston. Saner Y. (000). Güç Dağıtımı (Eneıji Dağıtımı) Dağıtım Transformatörleri, İstanbul. Peterson, N.M. and Meyer, W.S. (97). Automatic adjustment of transformer and phase shifter taps in Newton power flow, IEEE Trans, vol. PAS- 90, pp , Jan./Feb
70 3 Amaçlarımız Bu üniteyi tamamladıktan sonra; Transformatörlerin temel ilkelerini ve çalışma prensiplerini açıklayabilecek, Transformatörlerin eşdeğer devrelerini matematiksel olarak ifade edebilecek, Birim sistemi kullanarak şebekeye ait parametreleri hesaplayabilecek, Güç sistemlerinde transformatörlerle ilgili hesaplamaları yapabilecek, Transformatörlere çeşitli testler uygulayarak transformatörün parametrelerini çıkarabilecek, bilgi ve becerilere sahip olabilirsiniz. Anahtar Kavramlar Transformatör Manyetik Alan Sargı Baz Değer Birim Sistem Açık-Devre Testi Kısa-Devre Testi Eşdeğer Devre Üç-Faz Bağlantı Şekilleri Oto-Transformatör İçindekiler Giriş İdeal Transformatör Tek-Faz Pratik Transformatör Eşdeğer Devresi Birim Sistem Dengeli Üç-Fazlı ve Çift-Sargılı Transformatörün Birim Eşdeğer Devresi Üç-Sargılı Transformatörler Oto-Transformatörler 66
71 Güç Transformatörleri GİRİŞ Elektrik enerjisinin en önemli özelliklerinden biri de üretildiği santrallerden çok uzaktaki bölgelere kolayca taşınabilir olmasıdır. Bu taşıma işleminin verimli bir şekilde yapılabilmesi için gerilimin efektif değerinin yeteri kadar büyük olması gerekir. Bilindiği gibi elektrik enerjisi, iki farklı tipte olmak üzere; doğru akım (DC) ya da alternatif akım (AC) olarak üretilir. Doğru akımla üretimde, yüksek gerilimli enerji iletimi son zamanlarda büyük önem kazanmıştır fakat şu an için istenilen seviyelere gelememiştir. Teknoloji her geçen gün ilerlediğinden dolayı, enerji sistemlerinde doğru akım kullanımı ilerleyen zamanlarda üst seviyelere çıkacaktır. Buna karşılık; alternatif akım tipindeki elektrik enerjisinin gerilimi, iletimde kullanılmak için, transformatörler vasıtasıyla alçaltılıp yükseltildiğinden günümüzde elektrik enerjisinin alternatif akım ile iletilip kullanılması daha fazla yaygındır. Transformatör, ideal olarak kabul edildiğinde (üzerinde oluşan kayıplar ihmal edildiğinde) alternatif akımın gücünü ve frekansını değiştirmeden gerilim değerini istenilen seviyelere yükseltmeye veya alçaltmaya yarayan bir çeşit elektrik makinesidir. Elektrik enerjisinin alternatif akımla taşınmasında transformatörün önemli rolü vardır ve enerji sistemlerinin yapı taşlarından biridir. Santrallerde jeneratörler yardımı ile üretilen elektrik enerjisinin gerilimi çok yüksek değildir. Jeneratör çıkış gerilimleri 0,4-3,3-6,3-0,6-3,0-4,7-5,8 ve 35 kv mertebelerindedir. Bu gerilimler; enerjinin çok uzak bölgelere taşınabilmesini sağlayacak kadar yüksek olmadığından gerilimin yükseltilmesi ancak transformatör ile gerçekleştirilir. Gerilim yükseltme ve alçaltma işlemi için temelde iki farklı transformatör tipi vardır. Bunlar; Alçaltıcı Transformatörler: Birincil (primer) sargısına uygulanan gerilim değerini ikincil (sekonder) sargısından daha düşük bir değer olarak elde ettiğimiz transformatörlere alçaltıcı tip transformatörler adı verilir. Yükseltici Transformatörler: Birincil sargısına uygulanan gerilim değerini ikincil sargısından daha yüksek bir değer olarak elde ettiğimiz transformatörlere yükseltici tip transformatörler adı verilir. Transformatörler çeşitli özellikleri dikkate alınarak sınıflandırılır:. Manyetik nüvenin yapılış şekline göre: a. Çekirdek tipi b. Mantel tipi c. Dağıtılmış nüve tipi. Faz sayısına göre: a. Birincil ve ikincil sargıda aynı sayıda faza sahip olanlar b. Birincil ve ikincil sargıda farklı sayıda faza sahip olanlar 67
72 3. Soğutma şekline göre: a. Kuru transformatörler b. Yağlı transformatörler 4. Kuruluş yerlerine göre a. İç mekanlarda kullanılan tip b. Açık havada kullanılan tip 5. Sargı tiplerine göre a. Silindirik sargı b. Dilimli sargı 6. Çalışma prensibine göre a. Sabit akımlı b. Sabit gerilimli 7. Sargı durumlarına göre a. Yalıtılmış sargılı b. Oto-transformatörler 8. Soğutucu cinsine göre a. Hava ile soğutulan b. Yağ ile soğutulan c. Su ile soğutulan 9. Kullanılış amaçlarına göre a. Güç transformatörleri b. Ölçü transformatörleri c. Çeşitli aygıt ve makinalarda kullanılan diğer transformatörler Kitabın bu bölümünde, güç sistemlerinde kullanılan transformatörleri kavrayabilmek için öncelikle ideal transformatör kavramı anlatılacak, ideal transformatörün matematiksel eşitlikleri çıkarıldıktan sonra eşdeğer devre şeması elde edilecektir. Daha sonra ise birim sistem üzerinde durulacak ve tek-fazlı transformatörden üç-fazlı transformatöre geçilecektir. Son olarak ise; oto-transformatörlerden kısaca bahsedilecektir. 68
73 İDEAL TRANSFORMATÖR İki sargısı manyetik bir çekirdeğe sarılmış olan çift sargılı tek-fazlı transformatör Şekil 3. de gösterilmiştir. Transformatörün sinüssel uyartımda ve kararlı durumda çalıştığı kabul edilmektedir. E Şekilde; sargılar üstündeki fazör gerilimleri ve E, N adet sargısı olan birincil sargıya ait I fazör akımı ve N adet sargıya sahip olan ikincil sargıdan çıkan I fazör akımı ile gösterilmektedir. Ayrıca çekirdekte oluşan Φc fazör akısı ve Hc fazör manyetik alan yoğunluğu ile gösterilmektedir. Çekirdeğin kesit alanı A c l, ortalama manyetik alan uzunluğu c olarak ifade edilmektedir. ve sabit kabul edilen manyetik geçirgenliği μc Manyetik geçirgenlik l Kesit Ortalama manyetik alan uzunluğu Birincil (Primer) sargı sarım İkincil (Sekonder) sargı sarım Şekil 3.: Tek-faz İki Sargılı Temel Transformatör İdeal bir transformatör için aşağıdakiler kabul edilir:. Sargıların direnci sıfırdır ve bu yüzden sargılardaki IR kayıplarının değeri sıfır olur.. Çekirdek geçirgenliği μ c sonsuzdur; bu da sıfır çekirdek relüktansına (manyetik direnç) karşılık gelmektedir. 3. Kaçak akı yok olarak kabul edilir; tüm akı, çekirdek ve sargılarda sınırlandırılmıştır. 4. Çekirdek kaybı yok. Çift sargılı transformatörün şematik gösterimi Şekil 3. de gösterilmektedir. İdeal transformatöre ait matematiksel eşitlikleri oluşturmak için yukarıdaki varsayımlarla birlikte Amper ve Faraday yasaları kullanılabilir. Amper yasası ; kapalı bir yol boyunca bütünleşmiş manyetik alan yoğunluğu vektörüne teğet bir bileşenin, bu yol ile kapalı net akıma eşit olduğunu belirtir. H dl I teğet = kapalı (3.) Eğer Şekil 3. de gösterilen çekirdeğin merkez hattı kapalı yol olarak seçilirse ve yol boyunca sabitse, (3.) denklemi H teğet olduğu c olur. Hl = NI NI cc 69 (3.)
74 I Bobinin her döngüsü için bir kere olmak üzere; N akımı kere, I akımı N kere çevrelenmiştir. I Ayrıca, sağ-el kuralına göre; I akımı saat yönünde oluşuyorsa, akımı saat yönünün tersi yönündedir. Bu nedenle, (3.) de ilişkili net akım NI NI μ olarak ifade edilir. Sabit c çekirdek geçirgenliği için, B çekirdek içindeki c manyetik akı yoğunluğu, B ve = μ H c c c Wb/m Φ çekirdek akısı, c (3.3) Φ c = BcA c Wb bulunur. (3.3) ve (3.4) eşitlikleri kullanılırsa (3.4) lb c c l c NI NI = = Φc μc μcac (3.5) denklemi elde edilir. R c çekirdek relüktansı (manyetik direnç) ise; R c lc = μ A c c olarak tanımlanır. Bu işlemin ardından (3.5) denklemi NI NI = Φ R c c şeklinde yazılır. (3.6) (3.7) Şekil 3.: Tek-faz Çift-sargılı Transformatörün Şematik Gösterimi Manyeto-motor kuvvet olan mmk = NI NI eşitliği R c ile Φ çarpımına eşit olması sebebiyle; c (3.7) eşitliği manyetik devreler için Ohm yasası olarak adlandırılabilir. Manyetik bir devrede akı oluşumunu engelleyen R c relüktansı, elektrik devresindeki direnç elemanıyla benzerdir. İdeal transformatör için (3.6) daki gelir ve (3.7) denklemi, μ c sonsuz kabul edilmektedir ki; bu kabul R c nin sıfır olduğu anlamına 70
75 NI = NI (3.8) şekline dönüşür. Pratik olarak, güç transformatörünün sargıları ve çekirdekleri muhafaza içinde tutulmaktadır ve sargı yönleri görünür değildir. Sargı bilgisini ifade etmenin bir yolu, her sargının akım giren ucuna bir nokta yerleştirmektir. Bu işlem, aynı yönde hareket eden bir mmk oluşturur. Nokta gösterimi Şekil 3. de gösterilmektedir. Noktalar, kutup işaretleri olarak adlandırılırlar. (3.8) denklemi, noktalı uca giren I ve noktalı uçtan çıkan I akımları için yazılmıştır. N I = I N olduğundan dolayı I ve I akımları aynı fazdadır. I için ters yön seçilirse, her iki akım da kendi noktalı uçlarından girerler ve I in fazı I ye göre 80 kayar ve aralarında 80 faz farkı oluşur. Faraday yasası na göre; N - sarımlı bir sargı üzerinde endüklenen et () voltajının, sargıdaki zamanla değişen φ() t akısı ile arasındaki ilişki; () t dφ et () = N dt (3.9) şeklindedir. Sabit ω frekanslı sinüssel kararlı durumda, et () ile φ () t nin E ve Φ fazörleriyle ifade edilmesiyle (3.9) denklemi aşağıdaki şekilde ifade edilir. ( ) E= N jω Φ (3.0) İdeal transformatörde oluşan akının, her iki sargıda da çekirdek içinde sınırlı olduğu varsayılır. Faraday yasası na göre Şekil 3. in sargılarında endüklenen gerilimler; ( ) E = N jω Φ c ( ) E = N jω Φ c olur. (3.) ve (3.) oranlanırsa; E E veya E N N = N E = N denklemleri ortaya çıkar. (3.) (3.) (3.3) (3.4) Şekil 3. de gösterilen noktalar, + kutupları noktalanmış uçlar olan aynı fazdaki E ve E voltajlarını göstermektedir. Şekil 3. deki seçilen gerilimlerden birinin kutbu ters ise; E gerilimi E gerilimine göre 80 faz farkına sahiptir. a t sarım oranı aşağıdaki gibi tanımlanır; a t N = N 7 (3.5)
76 a t, (3.8) ve (3.4) te kullanılırsa; ideal tek-faz çift sargılı bir transformatör için aşağıdaki temel eşitlikler bulunur. N E = E = at E N (3.6) N I I = I = N at (3.7) Kompleks güç ve empedansa bağlı eşitlikler (3.6) ve (3.7) denklemlerinden elde edilebilir. Şekil 3. de birincil sargıya giren kompleks güç; S = E I olarak gösterilir. (3.6) ve (3.7) kullanılarak (3.8) * * I * S = EI = ( at E) = EI = S at (3.9) S elde edilir. (3.9) da görüldüğü gibi, birincil sargıya giren kompleks gücü, ikincil sargıdan çıkan S kompleks gücüne eşittir. Bu yüzden; ideal transformatörde gerçek ve reaktif güç kaybı olmadığı varsayılır. Şekil 3. de ideal bir transformatörün ikincil sargısına Z empedansı bağlanırsa, Z E = I elde edilir. Bu empedans birincil sargıdan ölçüldüğü takdirde; (3.0) E ae t N Z = = = at Z = Z I I at N (3.) Z olur. Bu yüzden ikincil sargıya bağlanan empedansı birincil sargıya gore; Z nin sarım oranının karesinin a çarpımı ile ifade edilir. t Örnek 3. Çift sargılı, tek-fazlı bir transformatör 60 Hz frekans değerinde 0 kva, 480/0 V anma değerleri ile Z verilmiştir. Birincil sargıya bağlanan kaynak, transformatördeki ikincil sargıya bağlanan empedans yüküne enerji sağlamaktadır. Yük üzerine düşen gerilim 8 V olduğunda; yük, 0,8 geride güç faktörüyle 5 kva güç çekmektedir. Transformatörün ideal olduğunu varsayarak aşağıdaki değerleri hesaplayın. a. 480 V (birincil) sargı üzerindeki gerilim. b. Yük empedansı. c. 480 V sargıya göre yük empedansı. d. 480 V sargıya sağlanan gerçek ve reaktif güç. 7
77 Çözüm: a. Şekil 3.3 te gösterilen devrede, 480V birincil sargıyı ve 0V ikincil sargıyı ifade etmektedir. Referans olarak yük gerilimi E seçilirse, E = 8 0 V (3.3) ten sarım oranı, ( ) a N E 480 anma t = = = = 4 olarak bulunur ve birinci sargıdaki gerilim N Eanma 0 E = ae t = = 47 0 V şeklinde hesaplanır. b. Yük tarafından çekilen S kompleks gücü S = E I = 8I = 5000 cos (0,8) = ,87 VA * * I Denklem çözülürse; yük akımı I = 7, 36,87 A Z, yük empedansı Z E 8 0 = = = 0,983 36,87 Ω I 7, 36,87 c. 480V sargıya göre yük empedansı, (3.) eşitliğinden bulunur. ( ) ( ) Z = = = Ω at Z 4 0,983 36,87 4,85 36,87 d. (3.9) eşitliğinden ise gerçek ve reaktif güç değerleri hesaplanır. S = S = ,87 = j9000 VA Böylece, 480V sargıya sağlanan gerçek ve reaktif güç aşağıdaki şekilde hesaplanır ( S ) ( S ) P = Re = 000 W = kw Q = Im = 9000 VAR = 9 kvar Şekil 3.3: Örnek 3. e Ait Devre Şekil 3.4 tek-fazlı ve faz kaydırıcı transformatörün şematik gösterimidir. Fiziksel olarak kompleks sayı değerinde bir sarım oranı elde etmek mümkün olmadığından bu transformatör gerçek bir transformatörün idealleştirmesi değildir. Bu gösterim; daha sonra üç-fazlı transformatörün faz kaymasının matematiksel olarak ifade edilmesinde kullanılacaktır. Şekil 3.4 te gösterildiği gibi, faz kaydırıcı transformatör için tanımlanan kompleks sarım oranı a t ; 73
78 a t jφ e = = e jφ (3.) Burada φ, faz kayma açısı olarak adlandırılır. Transformatördeki bağıntılar aşağıdaki şekle dönüşür. E = a E = e E j φ t I I = = e I jφ * at (3.3) (3.4) E in faz açısı, E nin faz açısından φ açısı kadar ileridedir. Benzer şekilde; I akımı I den φ açısı kadar ileridedir ve büyüklükleri aynıdır. E = E ve I = I Bu iki ilişkiden, aşağıdaki eşitlikler elde edilir: * * I * = = ( t ) * = = at S EI ae E I S E ae Z a Z Z t = = = t = I I * at (3.5) (3.6) Bu nedenle ideal faz kaydırıcı transformatörde bir sargıdan diğerine geçerken empedans sabittir. Ayrıca S = S olduğundan bu transformatörde gerçek ve reaktif güç kaybı olmadığı varsayılır. Faz kaydırıcı transformatörde kullanılan (3.3) ve (3.4) denklemleri, (3.4) teki eşlenik dışında fiziksel olarak ideal transformatör için kullanılan (3.6) ve (3.7) denklemleriyle aynıdır. Faz kaydırıcı transformatörde S = S eşitliğinin sağlanması için (3.5) te gösterilen kompleks eşlenik gereklidir. Kompleks eşlenik kavramı. ünitede açıklanmıştır. Şekil 3.4: Tek-fazlı, Faz Kaydırıcı Transformatörün Gösterimi 74
79 TEK-FAZ PRATİK TRANSFORMATÖR EŞDEĞER DEVRESİ Şekil 3.5 te ideal transformatörden farklı olarak pratik tek-faz çift-sargılı transformatörün eşdeğer devresi gösterilmektedir. Pratik transformatörün ideal transformatörden farkları aşağıda açıklanmıştır. Pratik transformatörde; a. Sargılarda direnç vardır. b. μ c çekirdek geçirgenliği sonludur. c. Manyetik akı tamamen çekirdek ile sınırlı değildir. d. Çekirdek üzerinde gerçek ve reaktif güç kayıpları vardır. Şekil 3.5: Pratik Tek-faz Çift-sargılı Transformatörün Eşdeğer Devresi Birincil sargıdaki seri bağlı R direnci; bu sargıdaki IR kayıplarını ifade etmek içindir. Aynı şekilde; bu sargının kaçak reaktans olarak adlandırılan X içermesi de kaçak akıyı temsil eder. Bu kaçak akı sadece birincil sargıya bağlı akının bileşenidir, ikincil sargı ile ilişkisi yoktur; bu akı, I ile doğru orantılı olan ve I e göre 90 ileride olan ( X ) I j değerinde gerilim düşümüne yol açar ve kaçak reaktansa bağlı olarak IX değerinde reaktif güç kaybı da oluşturur. İkincil sargı için de benzer şekilde; ikincil sargıya seri olarak bağlanan R direnci ve X kaçak reaktansı bulunmaktadır. (3.7) denklemi μ c sonlu çekirdek geçirgenliği için, toplam mmk nın sıfır olmadığını göstermektedir. Denklem (3.7), N ile bölünürse ve (3.) eşitliği kullanılırsa aşağıdaki denklem elde edilir.. N R R c c E R c I I = Φ c = = j E N N N jωn jωn (3.7) (3.7) nin sağ tarafındaki terim, Im manyetik akım olarak tanımlanır. I m E akımının in 90 R c B m = mhos ωn gerisinde olduğu belirgindir ve suseptans değeri olan paralel bir endüktörle gösterilebilir. Suseptans birimi Siemens (S) yada mhos olarak gösterilir. Ancak gerçekte, çekirdek kaybı akımı olarak adlandırılan I c akımını taşıyan ve iletkenliği G c mhos olan paralel bağlı bir direnç vardır. Ic ile E aynı fazdadır. Çekirdek kaybı akımı da dahil edildiğinde (3.7) eşitliği, 75
80 N I I = Ic + Im = ( Gc jbm) E N (3.8) olur. ( G jb ) c admitansını paralel kol olarak içeren Şekil 3.5 teki eşdeğer devre, KAK denklemi m (3.8) i sağlamaktadır. İkincil sargı açık-devre olduğunda ( I = 0) ve V sinüssel gerilimi birincil sargıya uygulandığında, (3.8) denklemi I akımının iki bileşeni olduğunu gösterir: Bunlar; I c çekirdek kaybı akımı ve I mıknatıslanma akımıdır. m I c yle bağlantılı olarak gerçek güç kaybı I c G c = E G W olur. Bu gerçek güç; çekirdekteki histerezis ve girdap (eddy) akımı kayıplarını açıklar. Histerezis kaybı çekirdekteki çevrimsel akı değişiminin ısı olarak yayılımı sonucunda oluşur. Histerezis kayıpları; çekirdek malzemesi olarak özel yüksek dereceli çelik alaşımlar kullanılarak azaltılabilir. Girdap akımı kaybının nedeni ise manyetik çekirdekteki akıya dik olarak endüklenen akımdır. Çelik alaşımlı ve ince tabakalı levhaların kullanılmasıyla girdap akımı kayıpları azaltılabilir. I m ile bağlantılı olarak reaktif güç kaybı I m B m = E B VARolur. Reaktif güç için çekirdeğin mıknatıslanması gerekmektedir. ( I + I ) m akımlarının fazör toplamları, I e uyarma akımı olarak adlandırılır. Şekil 3.6, pratik tek-faz çift-sargılı bir transformatör için 3 farklı eşdeğer devreyi göstermektedir. Şekil 3.6(a) daki ikincil sarının direnci R ve kaçak reaktansı X, birincil sargı referans alınarak (3.) denklemi ile gösterilmiştir. Şekil 3.6 (b) de paralel kolun yok edilmesi; uyarma akımının ihmal edildiği anlamına gelir. Uyarma akımı genellikle anma akımının %5 inden az olduğu için güç sistemlerinde bunu ihmal etmek, transformatör verimi ya da uyarma akımının özel bir önemi olmadıkça, problem yaratmaz. Anma değeri 500 kva dan daha büyük güç transformatörleri için, kaçak reaktansa göre küçük olan sargı dirençleri Şekil 3.6(c) de gösterildiği gibi ihmal edilebilir. Sinüssel kararlı durumda çalışan pratik bir transformatör, harici empedans ve admitanslı ideal bir transformatöre Şekil 3.6 da gösterildiği gibi eşittir. Aşağıdaki örnekte gösterildiği gibi harici kol elemanları kısa-devre ve açık-devre testleri ile bulunabilir. c c m 76
81 (a) Birincil sargıya göre referans alınmış ve (b) Uyarma akımının ihmal edilmesi (c) Uyarma akımı ve sargı kaybının ihmal edilmesi Şekil 3.6: Pratik Tek-faz Çift-sargılı Transformatörün Eşdeğer Devresi Örnek 3. Çift sargılı tek-fazlı bir transformatörün anma değerleri 60 Hz de 0 kva, 480/0 V olarak verilmiştir. Kısa-devre testinde; 0 V sargısı (ikincil sargı) kısa-devre yapılarak anma frekansındaki anma akımı 480 V sargısına (birincil sargı) uygulandığında V = 35 V, P = 300 W değerleri elde edilmiştir. Açık-devre testinde ise; birincil sargı açık-devre yapılarak anma gerilimi ikincil sargıya uygulandığında I = A, P = 00 W değerleri ölçülmüştür. a. Kısa-devre testinden, birincil sargıya göre eşdeğer seri empedansı Zeş = Reş+ jx i belirleyin. eş (Paralel admitans ihmal edilecek) b. Açık-devre testinden, birincil sargıya göre paralel admitansı Ym = Gc jb i belirleyin. (Seri m empedans ihmal edilecek) Çözüm: a. Şekil 3.7(a) da kısa-devre testi için gösterilen eşdeğer devrede paralel admitans kolu ihmal edilmiştir. Birincil sargı için anma akımı 77
82 I S 0000 Z, R ve X belirlenir: anma anma = = = 4,667 A olur ve sonrasında eş eş eş Vanma 480 P 300 V 35 R = = = 0,78 Ω ve Zeş = = = 0,84 Ω I 4, 667 eş Ianma 4, 667 eş eş eş ( ) X = Z R = 0,8 Ω ve Zeş = R eş+ jxeş = 0,78 + j0,8 = 0,84 78,3 Ω olur. anma (a) Kısa-devre testi (paralel admitans ihmal edilecek) (b) Açık-devre testi (seri empedans ihmal edilecek) edilmesi Şekil 3.7: Örnek 3. nin Devresi b. Seri empedansın ihmal edildiği açık-devre testi için; verilen eşdeğer devre Şekil 3.7(b) de gösterilmektedir. (3.6) dan, N 480 V = E = a E = V = ( 0) = 480 V olur. Y m, G c ve B aşağıdaki gibi belirlenir: m 0 t anma N N 0 P 00 ( ) ( )( ) G = c 0, S V = 480 = N I 480 Y m = = = 0,0065 S V 480 ( ) ( ) ( ) Bm = Ym Gc = 0, , = 0, 0069 S Y = G jb = 0, j0, 0069 = 0, , 0 S m c m şeklinde bulunur. 78
83 Eşdeğer seri empedans genellikle kısa-devre testindeki anma akım değerinde belirlenir, paralel admitans ise açık-devre testindeki anma gerilim değerinde belirlenir. Anma değerlerinde çalışan transformatördeki ufak değişiklikler için empedans ve admitans değerleri sabit kabul edilir. BİRİM SİSTEM Güç sistemlerinde kullanılan voltaj, akım, güç ve empedans gibi nicelikler genellikle birim sistem ile ya da bu niceliklerin baz değerlerinin yüzdesiyle ifade edilirler. Baz değer; aynı zamanda taban değer yada referans değer olarak da adlandırılır. Örneğin, baz gerilimi 0 kv olarak belirtilmişse ve uygulanan gerilim 8 kv ise bu gerilim değeri; birim sistemde, (8/0)=0,9 birim ya da %90 olarak ifade edilir. Güç sistemlerindeki matematiksel hesaplamalar gerçek niceliklerden ziyade birim niceliklerle yapılır. Birim sistemin bir avantajı; uygun baz nicelikleri seçilerek transformatör eşdeğer devresindeki matematiksel işlemler basitleştirilebilir. Birim sistemde ifade edilen voltaj, akım, harici empedans ve admitans değerleri; transformatörün bir sargısından diğer sargısına yönlendirildiğinde değişmediğinden ideal transformatör sargıları görmezden gelinebilir. Bu yüzden birim sistem kullanımı; yüzlerce transformatörü içeren orta büyüklükteki güç sistemlerinde büyük bir avantaj sağlayabilir. Birim sistem; transformatörün bir sargısından diğerine yönlendirirken ciddi hesaplama hataları yapılmasına izin vermez. Birim sistemin diğer bir avantajı da; cihazların anma değerleri baz değer olarak kullanıldığında, benzer tip elektrikli cihazların birim empedansları birbirine yakın dar bir sayısal aralık içinde olur. Bu yüzden, birim empedans verilerinde hata var ise bu hatalar, bilgi sahibi birisi tarafından birim miktarlarıyla hızla kontrol edilebilir. Buna ek olarak, üreticiler genellikle etiket değerlerini; transformatör ve makinelerin empedanslarının birim değerleri ya da yüzdeleriyle belirtirler. Birim değerler aşağıdaki gibi hesaplanabilir; birim değer gerçek değer = baz değer (3.9) Burada gerçek değer, sayının gerçek birimdeki değeridir. Baz değer ise gerçek değer ile aynı birime sahiptir, bu yüzden birim değer boyutsuzdur. Ayrıca, baz değer her zaman gerçek bir sayıdır. Bu nedenle birim değerin faz açısıyla gerçek değerin faz açısı aynıdır. Güç sistemlerinde bir noktada iki bağımsız baz değeri rasgele seçilebilir. Genellikle baz gerilimi V ve baz kompleks gücü bazln Sbaz φ ; tek-faz devreler ya da üç-faz devrelerin tek fazı için seçilir. Birim sistemde elektrik kanunlarının geçerli olabilmesi için diğer baz değerleri için aşağıdaki ilişkiler kullanılmalıdır. P = Q = S I bazφ bazφ bazφ baz bazln (3.30) Sbaz φ = (3.3) V V V bazln bazln baz = baz = baz = = (3.3) baz baz Z R X I S φ Ybaz = Gbaz = Bbaz = (3.33) Z baz yukarıdaki (3.30) - (3.33) denklemlerinde üç-fazlı devreler için kullanılan; LN ve ϕ indisleri hatnötr arası ve faz-başına veya tek-faz terimlerini ifade etmektedir. Ayrıca bu eşitlikler, indisler ihmal edildiğinde, tek-fazlı devreler için de geçerlidir. 79
84 Hesaplamalarda baz değerler için aşağıdaki iki kural kabul edilir:. Sbaz φ değeri, ilgili güç sisteminin tamamında aynıdır.. Transformatörün herhangi bir tarafındaki baz gerilim oranı, transformatörün anma gerilim oranlarıyla aynı seçilir. Bu iki kural uygulandığında, transformatörün bir tarafından diğer tarafına yönlendirme yapılırken kullanılan birim empedans değeri değişmeden kalır. Örnek 3.3 Tek-faz çift sargılı bir transformatörün anma değerleri 0 kva, 480/0 V ve 60 Hz olarak verilmiştir. İkincil sargıya göre yönlendirilen transformatörün eşdeğer kaçak empedans değeri Zeş = 0,055 78,3 Ω dur. Transformatör anma değerlerini baz değer olarak kullanarak, birincil sargıya göre ve ikincil sargıya göre birim kaçak empedansını hesaplayın. Çözüm: Transformatör baz değerleri Sbaz = 0 kva, Vbaz = 480 V ve Vbaz = 0 V olacak şekilde seçilir. (3.3) yi kullanarak, transformatörün 0 V tarafındaki baz empedansı: ( 0) Vbaz Zbaz = = = 0,7 Ω olur ve sonra, (3.9) u kullanarak, ikincil sargıya göre birim kaçak Sbaz 0000 Zeş 0, ,3 empedansı: Zeş br = = = 0, ,3 birim olarak hesaplanır. Z nin birincil eş Z 0,7 baz N 480 Zeş = t Zeş = Zeş = 0,055 78,3 = 0,84 78,3 Ω N 0 sargıya göre değeri: a ( ) Transformatörün 480 V tarafındaki baz empedansı: baz ( 480) olur. Vbaz Zbaz = = =,5 Ω dur ve birincil S 0000 Zeş 0,84 78,3 sargıya göre birim kaçak reaktans: Zeş br = = = 0, ,3 birim = Zeş br şeklinde Z,5 baz bulunur. Sonuç olarak; transformatörün ikincil sargısından birincil sargısına yönlendirilirken birim empedans değişmeden sabit kalır. Bu yoruma aşağıdaki denklemle ulaşılabilir: V V 480 V V 0 baz anma = = = baz anma 4 Şekil 3.8 de tek-faz çift-sargılı bir transformatörün üç farklı birim devresi gösterilmektedir. Şekil 3.8(a) da gösterilen ideal transformatör aşağıdaki eşitliklerden çıkarılan E br = E ve br I br = I br eşitlikleri birim ilişkilerini doğrular. İlk olarak (3.6) eşitliği V ile bölünürse: baz E br E N E = = V N V baz baz (3.34) Sonra, V V V N = = V N baz anma baz anma eşitliklerinden E N E E = = = E br br N N V baz Vbaz N (3.35) 80
85 Benzer şekilde, (3.7) denklemi I ile bölünürse: baz I br I N I = = I N I baz baz (3.36) sonra, S S N baz baz Ibaz = = = Ibaz Vbaz N N V N baz kullanılarak; I N I I = = = I br br N N I baz Ibaz N (3.37) Bu yüzden, Şekil 3. deki ideal transformatör sargısı Şekil 3.8(a) daki birim devreden farklılık gösterir. Şekil 3.8(b) birim kaçak empedans içermektedir ve devreyi tam olarak ifade etmek için Şekil 3.8(c) de birim paralel admitans kol eklenmiştir. (a) İdeal transformatör (b) Uyarma akımının ihmal edilmesi (c) Tam gösterim Şekil 3.8: Tek-faz Çift-sargılı Transformatörün Birim Eşdeğer Devresi Transformatör gibi sadece bir bileşen düşünülürse, bu bileşenin etiket değerleri genellikle baz değer olarak seçilir. Sistemde birden fazla bileşen varsa, sistem baz değerleri, herhangi bir cihazın etiket değerinden farklı olabilir. O zaman; cihazın etiket değerindeki birim empedansını sistemin baz değerine dönüştürmek gerekir. Birim empedansı eski değerden yeni değere dönüştürmek için, 8
86 Z Z Z Z gerçek br.eski baz.eski br.yeni = = Zbaz.yeni Zbaz.yeni (3.38) ya da (3.3) den Z baz.eski baz.yeni br.yeni = Zbr.eski Vbaz.yeni Sbaz.eski V S (3.39) denklemleri kullanılır. DENGELİ ÜÇ-FAZLI, ÇİFT-SARGILI TRANSFORMATÖRÜN BİRİM EŞDEĞER DEVRESİ Şekil 3.9(a) Z ve Z N n nötr empedansları üzerinden topraklanan ideal bir Y Y transformatörünün gösterimidir. Şekil 3.9(b) de ise dengeli üç-faz durumunda çalışan bu ideal transformatörün eşdeğer birim devresi gösterilmiştir. Bu metnin kalanında aksi belirtilmedikçe birim nicelikler kullanılacakır. Ayrıca br indisi birim niceliği ifade etmektedir ve çoğu durumda belirtilmeyecektir. (a) Şematik gösterim (b) Dengedeki üç-fazlı çalışma için birim eşdeğer devre Şekil 3.9: İdeal Y Y Transformatörü Geleneksel olarak, baz değerlerini seçebilmek için aşağıdaki iki kural uygulanır:. H ve X terminallerinin ikisi için de ortak bir S seçilir. baz V V baz gerilimlerin oranı VanmaHLL faz-faz arası anma gerilimlerinin oranına eşit seçilir. bazx VanmaXLL 8. bazh
87 Dengeli üç-faz akımlar transformatöre uygulandığı zaman, nötr akımları sıfır olur ve nötr empedansları üzerinde gerilim düşümü veya potansiyel farkı oluşmaz. Bu nedenle, Y Y ideal transformatörünün birim eşdeğer devresi, Şekil 3.9(b), ideal tek-faz transformatörün birim eşdeğer devresiyle aynıdır. Şekil 3.8(a). Pratik bir Y Y transformatörün birim eşdeğer devresi Şekil 3.0(a) da gösterilmektedir. Bu şebeke, Şekil 3.8(c) de olduğu gibi eşdeğer devreye harici empedanslar eklenerek elde edilebilir. Pratik bir Y Δ transformatörün faz kaymasını da içeren birim eşdeğer devresi Şekil 3.0(b) de gösterilmektedir. Amerikan standardına göre, Y Δ transformatörün yüksek-gerilim tarafındaki pozitifsıralı gerilim ve akımlar, alçak-gerilim tarafındaki niceliklere göre 30 ileridedir. Şekil 3.0(b) nin eşdeğer devresindeki faz kayması, Şekil 3.4 teki faz-kaydırıcı transformatörde gösterilmiştir. Şekil 3.0(c) de gösterilen Δ Δ transformatörünün birim eşdeğer devresi Y Y transformatörün birim eşdeğer devresiyle aynıdır. Bu nedenle sargılar arasında faz kayması olmadığı kabul edilir. Ayrıca birim empedanslar sargı bağlantı şekillerinden etkilenmezler fakat baz gerilimler etkilenir. Tek-faz diyagramı Birim eşdeğer devre (a) (b) (c) Şekil 3.0: Dengedeki Üç-fazlı Çalışmada Pratik Y Örnek 3.4 Y, Y Δ ve Δ Δ Transformatörlerin Birim Eşdeğer Devreleri Üç adet tek-faz çift sargılı transformatör, her biri 400 MVA, 3,8/99, kv anma değerlerine sahip, Xeş = 0, birim kaçak empedansıyla üç-fazlı transformatör bankası oluşturacak şekilde bağlanmıştır. Sargı dirençleri ve uyarma akımı ihmal edilmiştir. Yüksek-gerilim sargıları Y bağlanmıştır. Yüksekgerilim tarafındaki dengeli pozitif-sıralı durumda çalışan üç-fazlı bir yük, V AN = 99, 0 kv ile 0,9 geride güç faktörüyle 000 MVA güç çekmektedir. Alçak-gerilim sargıları (a) Y, (b) Δ olarak bağlandığında bu sargılardaki VAN gerilimini bulunuz. Çözüm: Birim eşdeğer devre Şekil 3. de gösterilmiştir. Transformatör bankası değerleri baz değer olarak kullanılırsa, S = baz3φ 00 MVA, VbazHLL = 345 kv ve IbazH = 00 =,008 ka elde ( 345 3) edilir. O zaman, birim yük gerilimi ve yük akımı: 83
88 V AN ( ) =, 0 0 birim ve IA = cos 0,9 = 0,8333 5,84 birim,008 olarak bulunur. a. Y Y transformatörü için, Şekil 3.(a), Ia = IA = 0,8333 5,84 birim V = V + jx I ( ) an AN eş A ( j )( ) =, ,0 0,8333 5,84 =, 0 + 0, ,6 =, j0, 075 =, 039 4,39 =, 039 4,39 birim Y bağlı sargıların alçak-gerilim tarafı için ( ) VbazXLN = 3,8 kvolduğundan V =,039 3,8 = 4,34 kv ve V = 4,34 4,39 kv şeklinde bulunur. an an (a) bağlı alçak-gerilim sargıları (b) bağlı alçak-gerilim sargıları b. Δ Y transformatörü için, Şekil 3.(b), j30 Ean e VAN j30 Ia e IA Şekil 3.: Örnek 3.4 için Birim Devreler = = 30 birim = = 0,8333 5,84 30 = 0, ,84 birim ( ) ( Xeq ), 0 30 ( 0,0)( 0, ,84 ) Van = Ean + j Ia = + j V =, 039 5,86 birim an Δ bağlı sargıların alçak-gerilim tarafı için V ( ) bazxln 3,8 = = 7,967 kv olduğundan 3 V =,039 7,967 = 8,78 kv ve V = 8,78 5,86 kv an ÜÇ-SARGILI TRANSFORMATÖRLER an Şekil 3.(a) tek-faz üç-sargılı temel bir transformatörü göstermektedir. Çift-sargılı bir transformatör için (3.8) ve (3.4) ideal transformatör eşitlikleri, üç-sargılı ideal bir transformatörün denklemlerini elde etmek için kullanılabilir. Gerçek birimlerinde bu eşitlikler aşağıdaki gibi ifade edilir. NI = NI + NI (3.40)
89 E E E N N N 3 = = (3.4) 3 Burada I akımı, noktalı olan terminale girmekte, I ve I 3 akımları ise noktalı terminalden çıkmaktadırlar. E, E ve E noktalı uçlarında kendi ait + kutupları vardır. Birim sistemde (3.40) ve 3 (3.4) yardımıyla I = I + I (3.4) br br 3br E = E = E (3.43) br br 3br Burada her üç sargı için ortak bir S baz ve sargıların anma değerleriyle doğru orantılı olarak baz gerilimleri seçilir. Bu iki ilişki Şekil 3.(b) de gösterilen birim eşdeğer devresi tarafından sağlanır. Ayrıca Şekil 3.(c) de gösterilen pratik üç-sargılı transformatör devresi harici olarak bağlanan seri empedans ve paralel admitansı da içermektedir. Paralel admitans kolu; manyetik endüktör ile paralel çekirdek kayıp direncinin birleşimi, açık-devre testiyle hesaplanır. Ayrıca; bir sargı açık-devre yapılırsa üç-sargılı transformatör, iki-sargılı bir transformatör olarak davranır. Birim kaçak empedansını belirlemede aşağıda açıklanan standart kısa-devre testi kullanılabilir: Z br =. Sargının kısa-devre ve 3. sargının açık-devre yapılmasıyla;.sargıdan ölçülen birim kaçak empedansı Z 3br =3. Sargının kısa-devre ve. sargının açık-devre yapılmasıyla;.sargıdan ölçülen birim kaçak empedansı Z 3br = 3. Sargının kısa-devre ve. sargının açık-devre yapılmasıyla;.sargıdan ölçülen birim kaçak empedansı Şekil 3.: Tek-faz Üç Sargılı Transformatör 85
90 Şekil 3.(c) den.sargının kısa-devre ve 3.sargının açık-devre yapılmasıyla.sargıdan ölçülen kaçak birim empedans değeri; (paralel admitans ihmal edilecek) Z = Z + Z (3.44) br br br Benzer şekilde, ve Z = Z + Z (3.45) 3br br 3br Z = Z + Z (3.46) 3br br 3br (3.44) - (3.46) denklemleri çözülürse, Z br = ( Zbr + Z3br Z3br ) (3.47) Zbr = ( Zbr + Z3 br Z3 br ) (3.48) Z3 br = ( Z3 br + Z3 br Zbr ) (3.49) bulunur. (3.47) - (3.49) eşitlikleri, sargıdaki kısa-devre testleriyle belirlenen Z br, Z 3 br ve Z 3 birim br kaçak empedanslarından, üç-sargılı transformatör eşdeğer devresinin Z br, Z br ve Z 3 birim seri br empedanslarını hesaplamak için kullanılabilir. Üç-sargılı bir transformatördeki her sargının kva değerleri birbirinden farklı olabilir. Sargılardaki kısa-devre testiyle belirlenen kaçak empedanslar, sargının anma değerlerine bağlı olarak birim sistemde verilirse, öncelikle (3.47) - (3.49) eşitliklerinde kullanılmadan önce ortak bir S birim değerine dönüşümleri yapılmalıdır. Örnek 3.5 Tek-faz üç-sargılı bir transformatörün anma değerleri:.sargı: 300 MVA, 3,8 kv.sargı: 300 MVA, 99, kv 3.sargı: 50 MVA, 9,9 kv Kısa-devre testine göre kaçak reaktanslar: X = 0,0 birim (300-MVA ve 3,8 kv baz değerlerinde) X 3 = 0,6 birim (50-MVA ve 3,8 kv baz değerlerinde) X 3 = 0,4 birim (50-MVA ve 99, kv baz değerlerinde) Sargı dirençleri ve uyarma akımı ihmal edilmiştir. 300 MVA ve.terminal için 3,8 kv değerleri baz olarak kullanıldığında; birim eşdeğer devrenin empedansı ne olur? Çözüm: Sbaz = 300 MVA her üç sargı için de aynıdır. Ayrıca.terminal için belirlenen baz gerilimi Vbaz = 3,8 kv tur.. ve 3.terminallerin baz gerilim değerleri; bu sargıların anma değerleri olan Vbaz = 99, kv ve V baz3 = 9,9 kv tur. Verilen bilgilere göre; devre için belirlenen aynı baz değerlerini kullanarak.terminalden X = 0,0 birim ölçülmüştür. Ancak 50 MVA baz değerindeki X 3 = 0,6 ve X 3 = 0,4 birim değerleri öncelikle 300 MVA baz değerine çevrilmelidir. baz 86
91 ( ) 300 X3 0,6 0, 96 birim ve X3 ( 0,4) 300 = = = = 0,84 birim bulunur. (3.47)-(3.49) eşitliklerinden, 3 ( ) ( ) ( ) X = 0,0 + 0, 96 0,84 = 0, birim X = 0,0 + 0,84 0, 96 = 0,0 birim X = 0,84 + 0, 96 0,0 = 0,85 birim değerleri elde edilir. Üç-sargılı bu transformatörün birim eşdeğer devresi Şekil 3.3 te gösterilmiştir. X nin negatif olduğunu unutmayın. Bu durum; X, X ve X 3 ün kaçak reaktans olmadığı gerçeğini; ancak onun yerine kaçak reaktanstan türetilen eşdeğer reaktans olduklarını açıklar. Kaçak reaktanslar her zaman pozitif değerdedirler. Üç eşdeğer reaktansın bağlandığı nokta transformatörde fiziksel olarak herhangi bir yere karşılık gelmemektedir. Şekil 3.3: Örnek 3.5 Bağlantı Şeması OTO-TRANSFORMATÖRLER Tek-faz çift sargılı bir transformatör Şekil 3.4(a) da iki ayrı sargısıyla, aynı transformatör Şekil 3.4(b) de ise iki sargısı seri bağlanmış olarak gösterilmiştir. Şekil 3.4(b) deki bağlantı şekline ototransformatör denir. Şekil 3.4(a) daki bildiğimiz genel tek-faz transformatörde; çift sargı ortak çekirdek akısı üzerinden manyetik olarak birleştirilmiştir. Oto-transformatörde ise, Şekil 3.4(b), sargılar hem elektriksel hem de manyetik olarak birleştirilmiştir. Oto-transformatörlerin birim kaçak empedansları bilinen genel transformatörlerden daha küçüktür; Bunun sonucunda hem daha küçük seri-gerilim düşümü oluşur (avantaj) hem de daha yüksek kısa-devre akımları (dezavantaj) oluşur. Oto-transformatörlerin ayrıca daha düşük birim kayıpları (daha yüksek verim), daha düşük uyarma akımları ve sarım oranı çok büyük değilse daha az maliyetleri vardır. Sargıların elektriksel bağlantıları; kısa süreli aşırı gerilimlerin oto-transformatörden kolayca geçmelerine izin verir. 87
92 Şekil 3.4: İdeal Tek-faz Transformatörler Örnek 3.6 Örnek 3.3 te kullanılan tek-fazlı çift-sargılı 0 kva, 480/0 V anma değerlerine sahip transformatör Şekil 3.4(b) deki gibi oto-transformatör olarak bağlanmıştır. Birincil sargı 0 V luk sargıdır. Bu ototransformatör için, aşağıda istenen değerleri bulun. a. Alçak- ve yüksek-gerilim uçlarındaki E X ve E H gerilim değerleri, b. Anma kva değeri c. Birim kaçak empedansı Çözüm: a. 0 V sargısı alçak-gerilim terminaline bağlı olduğundan E X = 0 V. E X = E = 0 V olur. Alçak-gerilim terminaline bağlandığı zaman, kaçak empedans üzerindeki gerilim düşümü ihmal edilerek 480 V sargısı üzerinde E = 480 V gerilim endüklenir. Böylece, E H = E + E = = 600 V olur. b. Normal çift-sargılı 0 kva anma değerli transformatörde, 480 V sargısının anma akımı I = I H = 0.000/480 = 4,667 A dir. Oto-transformatörde ise 480 V sargısı aynı akımı taşıyabilir. Böylece anma kva değerleri S H = E H I H = (600)(4,667) = 5 kva olur. I H = I = 4,667 A değerine ulaştığında 0 V sargısında I = 480/0(4,667) =66,7 A akımı endüklenir. Böylece I X = I + I = 08,3 A (uyarma akımının ihmaliyle) ve S X = E X I X = (0)(08,3) = 5 kva olur (yüksek-gerilim terminali için hesaplanan değerin aynısı). c. Örnek 3.3 e göre kaçak empedans normal çift-sargılı bir transformatör için 0,079 78,3 Ω dur. Çekirdek ve sargılar, normal transformatör ve oto-transformatör için aynı olduğundan (sadece harici sargı bağlantıları farklı), ohm cinsinden kaçak empedans değeri her ikisi için de aynıdır. Ancak, baz empedansları farklıdır. Yüksek-gerilim terminali için (3.3) yi kullanırsak; 88
93 ( 480) ZbazHeski = =, 5 Ω normal transformatör olarak ( 600) ZbazHyeni = = 4,4 Ω oto-transformatör olarak Böylece, (3.38) i kullanırsak,,5 Zbr.yeni = ( 0, ,3 ) = 0, ,3 birim 4,4 Bu örnekteki oto-transformatör için 5 kva, 0/600 V anma değerlerine karşılık normal transformatör için 0 kva, 0/480 V anma değerleri oluşur. Aynı maliyet için düşünülürse; ototransformatör, daha yüksek kva ve gerilim oranına sahiptir. Ayrıca oto-transformatörün birim kaçak empedansı daha küçüktür. Ancak kva ve gerilim oranındaki artışa paralel olarak her iki sargıda da daha fazla elektriksel izolasyona ihtiyaç duyulur. 89
94 Özet Elektrik enerjisinin en önemli özelliklerinden biri de üretildiği santrallerden çok uzaktaki bölgelere kolayca taşınabilir olmasıdır. Bu taşıma işleminin verimli bir şekilde yapılabilmesi için gerilimin efektif değerinin yeteri kadar büyük olması gerekir. Alternatif akım tipindeki elektrik enerjisinin gerilimi, iletimde kullanılmak için, transformatörler vasıtasıyla alçaltılıp yükseltildiğinden günümüzde elektrik enerjisinin alternatif akım ile iletilip kullanılması daha fazla yaygındır. Transformatör, ideal olarak kabul edildiğinde (üzerinde oluşan kayıplar ihmal edildiğinde) alternatif akımın gücünü ve frekansını değiştirmeden gerilim değerini istenilen seviyelere yükseltmeye veya alçaltmaya yarayan bir çeşit elektrik makinesidir. Transformatörün elektrik enerjisinin alternatif akımda taşınmasında önemli rolü vardır ve enerji sistemlerinin yapı taşlarından biridir. Gerilim yükseltme ve alçaltma işlemi için temelde iki farklı transformatör tipi vardır. Bunlar; Alçaltıcı transformatörler; Birincil (primer) sargısına uygulanan gerilim değerini ikincil (sekonder) sargısından daha düşük bir değer olarak elde ettiğimiz transformatörlere alçaltıcı tip transformatörler adı verilir. Yükseltici transformatörler; Birincil sargısına uygulanan gerilim değerini ikincil sargısından daha yüksek bir değer olarak elde ettiğimiz transformatörlere yükseltici tip transformatörler adı verilir. Transformatörler çeşitli özellikleri dikkate alınarak sınıflandırılır. Ayrıca eşdeğer devre oluştururken ve hesaplamaları basitleştirmek için bazı kabuller altında, gerçek (pratik) transformatörler ideal kabul edilir. İdeal bir transformatör için aşağıdakiler geçerlidir: Pratik transformatörün ideal transformatörden farkları aşağıda açıklanmıştır. Pratiktransformatörde; Sargılarda direnç vardır. μ c çekirdek geçirgenliği sonludur. Manyetik akı tamamen çekirdek ile sınırlı değildir. Çekirdek üzerinde gerçek ve reaktif güç kayıpları vardır. Eşdeğer devre elemanları bulunurken transformatörlere iki farklı test uygulanır. Bunlar; kısa-devre ve açık-devre testleridir. Güç sistemlerinde kullanılan gerilim, akım, güç ve empedans gibi nicelikler genellikle birim sistem ile ya da bu niceliklerin baz değerlerinin yüzdesiyle ifade edilirler. Birim sistemin bir avantajı; uygun baz nicelikleri seçilerek transformatör eşdeğer devresindeki matematiksel işlemler basitleştirilebilir. Transformatör tek-fazlı olmalarının yanında üç-fazlı olarak da üretilirler. Üç-fazlı sistemlerde bu tip transformatörlerin ciddi faydası vardır. Ayrıca Oto-transformatörde ise, sargılar hem elektriksel hem de manyetik olarak birleştirilmiştir. Oto-transformatörlerin birim kaçak empedansları bilinen genel transformatörlerden daha küçüktür; Bunun sonucunda hem daha küçük seri-gerilim düşümü oluşur (avantaj) hem de daha yüksek kısa-devre akımları (dezavantaj) oluşur. Sargılardaki direnç sıfır; bu yüzden sargılardaki IR kayıpları sıfır. Çekirdek geçirgenliği μ c sonsuzdur; bu da sıfır çekirdek relüktansına (manyetik direnç) karşılık gelmektedir. Kaçak akı yok olarak kabul edilir; tüm akı, çekirdek ve sargılarda sınırlandırılmıştır. Çekirdek kaybı yok. 90
95 Kendimizi Sınayalım. İdeal transformatör ile Pratik transformatörün farkı aşağıdakilerden hangisidir? a. Pratik transformatör üzerinde oluşan kayıplar ihmal edilir. b. İdeal transformatör üzerinde oluşan kayıplar ihmal edilir. c. Pratik ve ideal transformatör arasında herhangi bir fark yoktur. d. İdeal transformatörde giriş gücü, çıkış gücünden daha fazladır. e. Pratik transformatörde çıkış gücü, giriş gücünden daha fazladır.. İdeal transformatör için aşağıdakilerden hangisi yanlıştır? a. Çekirdek geçirgenliği μ c sonsuzdur; bu da sıfır çekirdek relüktansına (manyetik direnç) karşılık gelmektedir. b. Kaçak akı yok olarak kabul edilir; tüm akı, çekirdek ve sargılarda sınırlandırılmıştır. c. Sargılardaki direnç sonsuzdur; bu yüzden sargılardaki IR kayıpları sıfır olur. d. Çekirdek kaybı sıfırdır. e. Giriş ve çıkış güçleri birbirine eşittir. 3. Manyeto-motor kuvvet olan mmk = NI NI eşitliği R c ile Φ çarpımına c eşit olması sebebiyle; elektrik devrelerindeki..nın manyetik devrelere uyarlanmış şeklidir. Boşluk kısma aşağıdakilerden hangisi gelmelidir? a. Faraday yasası b. Maxwell yasası c. Kelvin yasası d. Ohm yasası e. Transformatör yasası 4. Çift sargılı tek-fazlı bir transformatör, 60 Hz, 0 kva ve 500/00 V anma değerleri ile veriliyorsa bu transformatörün ( a t ) sarım oranı nedir? a. 0, V b. 0, c. 60 Ω d. 60 Hz e Transformatör üzerindeki histerezis kayıplarını azaltmak için aşağıdaki iyileştirmelerden hangisi yapılabilir? a. Sargılarda daha büyük kesitli tel kullanılabilir. b. Yüksek dereceli çelik alaşımlı çekirdekler kullanılabilir. c. Sargılarda daha küçük kesitli tel kullanılabilir. d. Sargılar metal yerine ahşap plakalara sarılabilir. e. Düşük dereceli alüminyum alaşımlı çekirdekler kullanılabilir. 6. Kısa-devre ve açık-devre testlerinin belirli şartlar altında yapılmaları gereklidir. Aşağıdakilerden hangisinde bu şartlar doğru olarak verilmiştir? a. Kısa-devre testi anma akımında, açık-devre testi ise anma geriliminde b. Kısa-devre testi anma geriliminde, açık-devre testi ise anma akımında c. Kısa-devre testi anma akımında, açık-devre testi ise anma akımında d. Kısa-devre testi anma geriliminde, açık-devre testi ise anma geriliminde e. Kısa-devre testi anma direncinde, açık-devre testi ise anma direncinde kva, 380 V ve 50 Hz değerlerindeki üçfazlı Y bağlı transformatörün kol akımına ait baz değeri nedir? a. ka b. ka c. 0,5 ka d. ka e. ka 8. Alçaltıcı tipteki transformatörün görevi aşağıdakilerden hangisidir? a. Giriş gerilimini düşürmek b. Giriş frekansını düşürmek c. Giriş akımını düşürmek d. Çıkış frekansını düşürmek e. Çıkış akımını düşürmek 9
96 9. Aşağıdakilerden hangisi, transformatörlerde manyetik nüvenin yapılış şekline göre yapılan sınıflandırmalardan biridir? a. Kuru tip b. Silindirik sargılı tip c. Sabit akımlı tip d. Mantel tip e. Yağlı tip 0. Manyetik devredeki relüktans elemanının elektrik devresindeki eşdeğeri nedir? a. Kapasitans b. Endüktans c. Direnç d. Frekans e. Akım Kendimizi Sınayalım Yanıt Anahtarı. b Yanıtınız yanlış ise Giriş başlıklı konuyu yeniden gözden geçiriniz.. c Yanıtınız yanlış ise İdeal Transformatör başlıklı konuyu yeniden gözden geçiriniz. 3. d Yanıtınız yanlış ise İdeal Transformatör başlıklı konuyu yeniden gözden geçiriniz. 4. e Yanıtınız yanlış ise İdeal Transformatör başlıklı konuyu yeniden gözden geçiriniz. 5. b Yanıtınız yanlış ise Tek-Faz Pratik Transformatör Eşdeğer Devresi başlıklı konuyu yeniden gözden geçiriniz. 6. a Yanıtınız yanlış ise Tek-Faz Pratik Transformatör Eşdeğer Devresi başlıklı konuyu yeniden gözden geçiriniz. 7. b Yanıtınız yanlış ise Birim Sistem başlıklı konuyu yeniden gözden geçiriniz. 8. a Yanıtınız yanlış ise Giriş başlıklı konuyu yeniden gözden geçiriniz. 9. d Yanıtınız yanlış ise Giriş başlıklı konuyu yeniden gözden geçiriniz. 0. c Yanıtınız yanlış ise İdeal Transformatör başlıklı konuyu yeniden gözden geçiriniz. Yararlanılan Kaynaklar Bayram M. (99). Elektrik Tesisleri ile İlgili Sorular ve Çözümler, İTÜ Elektrik Elektronik Fakültesi Elektrik Mühendisliği Anabilim Dalı. Çakır, H. (989), Enerji İletimi Elektrik Hesapları, Birsen Yayınları. Saner Y. (000). Güç Dağıtımı (Eneıji Dağıtımı) Dağıtım Transformatörleri, İstanbul. Prof. Dr. Şerifoğlu N. (003) Elektrik Enerji Sistemleri cilt, Papatya yayıncılık. Distribution Transformer Handbook, ABB Glover, D.J., and Sarma, M.S. (989). Power system analysis and design, PWS-Kent Publishing Com., Boston. Kundur, P. (994). Power system stability and control, McGraw-Hill, Inc. Dalfes, M. (993). Elektroteknik. (7. Baskı). İstanbul: Seç Yayın Dağıtım. Odoğlu, H. (006). Transformatör Deneyleri. İstanbul: Bileşim Yayınları. 9
97 93
98 4 Amaçlarımız Bu üniteyi tamamladıktan sonra; Enerji sistemlerin kullanılan en temel elemanları tanımlayabilecek, Elektrik şebekelerini sınıflandırabilecek, Farklı amaçlara göre; elektrik hatlarına ait elemanları karşılaştırabilecek, Şebekelerde kullanılan donanımların iç yapılarını, çalışma prensiplerini ve kullanım yerlerini aktarabilecek, bilgi ve becerilere sahip olabilirsiniz. Anahtar Kavramlar Şebeke Direk Gerilim Seviyeleri Enterkonnekte Parafudr Kablo İzolatör Mesnet Ayırıcı Sf 6 Gazı Kreozot Zincir Santrifüj Vibre İçindekiler Giriş Elektrik Şebekeleri Direkler Kablolar İzolatörler Parafudrlar Ayırıcılar Kesiciler 94
99 İletim Hatlarına Ait Donanımlar GİRİŞ Elektrik enerjisi ilk üretildiği zamanlarda doğru akım (DC) formatında üretilmiştir. Jeneratörlerin verebildiği alçak-gerilimle üretilen bu enerjinin, üretildiği santralin civarında kullanılma zorunluluğu vardı. Çünkü alçak-gerilimde üretilen elektrik enerjisinin uzak yerlere taşınmasında çok büyük kayıplar oluşacağından iletim ve taşımada büyük zorluklarla karşılaşılmıştı. Zamanla alternatif gerilimin büyük bir hızla gelişmesi, çeşitli tipteki güç transformatörlerinin geliştirilmesi, elektrik enerjisinin verimli ve ekonomik şekilde, az kayıplı olarak; üretilen yerden tüketileceği yere kadar iletilmesini sağlamıştır. Alternatif akım (AC) taşıyan ilk iletim hatları tek-fazlı olup, genellikle aydınlatma amaçlı kullanılmıştır. Bu tarihlerde elektrik enerjisinin sıkça kullanıldığı elektrik motorları yeterince geliştirilmemişti. Üstün özellikli üç-fazlı elektrik motorlarının geliştirilmesi ile tek-fazlı sistemden üç-fazlı sisteme geçiş daha hızlı bir şekilde sağlanmıştır. İlk olarak Amerika'da 886 yılında Great Barrington kentinde 500 V'luk gerilim 600 m uzağa taşınmıştır. Aynı yılda İtalya'nın Cerchi kentinde 0 kv'luk bir gerilim 000 V ile 7 km uzağa taşınmıştır. Almanya'da 89 yılında ise 50 kv'luk bir gerilim, 70 km uzak mesafeye iletilmiştir. 936 yılında Amerika'da Hoover Barajı ile Los Angeles kenti arasındaki iletim hattı 87 kv olarak yapıldı. 95 yılında İsveç'te hidroelektrik santralinden, Güney İsveç'teki tüketim merkezlerine 380 kv'luk taşıma hattı yapılmıştır. Türkiye'de ise ilk defa 90 yılında Tarsus'ta değirmen miline bağlı bir jeneratörde kw'lık güç üretilmiş ve Tarsus'a elektrik verilmiştir. Türkiye'de elektrik enerjisinin yaygın kullanımı 93 yılında İstanbul Silahtarağa Santrali'nin devreye girmesi ile başlamıştır. Silahtarağa- Yedikule arasında 5 kv'luk enerji hattı kurulmuştur. Daha sonra 99'da Trabzon'da 6 kv, 940 yılında da 33 kv ile İvriz-Ereğli arasında enerji taşıma hatları devreye girmiştir. Türkiye'de enterkonnekte sisteme geçiş 945 yılından sonra başlamıştır. 948 yılında devreye giren Çatalağzı Santrali'nde ilk defa yüksek-gerilim taşıma hattı kurulmuş ve elektrik enerjisi 66 kv olarak Ereğli-Çatalağzı arasında taşınmıştır. Günümüzde elektrik enerjisi genel olarak üç-fazlı sistemle taşınmaktadır. Elektrik enerjisi Avrupa'da 400 kv, Rusya'da 500 kv, Kanada'da 700 kv'luk iletim hatları ile taşınmaktadır. Bu ünitede güç sistemlerinde kullanılan ve enerji akışına yardımcı olarak; elektriğin üretim aşamasından biz tüketicilere kadar iletilmesini sağlayan destek elemanları genel olarak incelenecektir. Bu elemanların çeşitlerine, çalışma prensiplerine, kullanım alanlarına, avantaj ve dezavantajlarına değinilecektir. Güç sistemlerinde enerji naklinde kullanılan temel elemanlar; şebekeler, şebekeleri oluşturan direkler, direkleri birbirine bağlayan kablolar, izolatörler, parafudrlar, ayırıcılar ve kesiciler olarak sınıflandırılabilir. ELEKTRİK ŞEBEKELERİ Elektrik enerjisinin üretilip sonrasında tüketicilere dağıtıldığı santraller genellikle tüketicilerin bulunduğu alanlara uzak yerlerde inşa edilir. Bu yüzden; santraller tarafından üretilen elektrik enerjisinin üretildiği santralden tüketicilerin bulunduğu alanlara iletilmesi gerekmektedir. Günlük hayatta pek çok kullanım alanı bulunan elektrik enerjisinin iletim ve dağıtımının ekonomik bir şekilde yapılabilmesi, enerji alanında en önemli konulardan biridir. Elektrik enerjisinin üretiminden tüketicilere ulaşıncaya kadar gerekli olan tesisleri; üretim, iletim ve dağıtım olmak üzere üç kısımda incelemek mümkündür. Elektrik 95
100 enerjisinin üretildiği yer elektrik santralleridir. Elektrik enerjisinin, üretilen yerden alınıp tüketim bölgelerine ulaştırılması için gerekli olan sistemlere iletim şebekesi denilir. Elektrik enerjisinin bir tüketim bölgesi içerisinde alçaltıcı trafo merkezinden alınıp, tüketicilere ulaştırılması için gerekli olan sistemlere ise dağıtım şebekesi denir. Bu sistemler, genellikle orta-gerilim şebekesi (-35 kv) ile trafo merkezleri ve alçak-gerilim şebekesinden meydana gelir. Enerji sistemlerindeki gerilim sınıfları aşağıdaki şekilde dört grup altında toplanır;. Alçak-gerilim şebekesi (AG): (0-) kv arası gerilimler. Orta-gerilim şebekesi (OG): (-35) kv arası gerilimler, 3. Yüksek-gerilim Sınıfı (YG): (35-54) kv arası gerilimler 4. Çok-yüksek-gerilim şebekesi (ÇYG): 54 kv'tan daha büyük gerilimler Alçak-gerilim şebekeleri (AG) 000 volt a kadar olan gerilim değerlerine karşılık gelen şebekelerdir. AG şebekeleri üzerinde gerilim düşümü fazla olacağından bu tipteki şebekeleri, enerji iletiminden ziyade enerji dağıtımında kullanmak verimliliği arttırır. Türkiye de kullanılan AG şebekelerinin faz-faz arası gerilimi 380 V, faz-nötr arası gerilimi ise 0 V tur. OG şebekeleri, şebeke gerilim değeri olarak kv ile 35 kv arası olan şebekelerdir. OG şebekeleri, AG şebekeleri ile YG şebekeleri arasında kalır ve bu iki farklı şebekeyi birbirine bağlar. YG şebekeleri ile iletilen gerilim değerlerini alıcıların doğrudan kullanmaları uygun olmadığı için OG şebekeler, sadece YG şebekeleri ile iletilen enerjiyi tüketicilere ulaştırmak için kullanılır. Bu tür gerilim şebekeleri küçük şehirlerin ve kasabaların birbirine bağlanmasında kullanılır. Türkiye de kullanılan OG şebekeleri standart olarak 34,5 kv tur. Üçüncü şebeke tipi olan YG şebekeler, gerilim değeri olarak 35 kv-54 kv arasında olan şebekelerdir. YG şebekelerinde, aynı OG şebekelerinde olduğu gibi enerji dağıtımı yapılmaz. Bu tür gerilim şebekeleri sadece enerji iletiminde kullanılır. Yüksek-gerilim şebekelerinin görevi; üretilen elektrik enerjisini üretim yerinden alarak şehirlerarası veya bölgeler arası iletip OG hatlara ulaştırmaktır. İletimde YG kullanmanın birinci ve en önemli sebebi; iletimde oluşacak kayıpları en aza indirmektir. İletilen gücün teorik olarak akım ile gerilimin çarpımı olduğu ve iletim boyunca değerinin sabit kaldığı varsayılırsa; gerilim yükseltildiğinde akım da ters orantılı olarak azalır. P=I R formülünden görüldüğü gibi iletim hattındaki güç kaybı akımın karesi ile doğru orantılı olduğundan, akımın azaltılması ile bu kayıplar en az düzeye indirilir. Diğer bir sebep ise; yüksek akımın taşınması (iletkenlerin akım taşıma kapasitelerinden dolayı) teknik olarak çok zordur, çok büyük kesitli kablolara ihtiyaç vardır. Bu sebeple, akım azaltılarak iletken kesiti küçültülmüş olur. Türkiye de kullanılan YG değerleri genellikle 66 kv ve 54 kv tur. Son olarak, çok-yüksek-gerilim şebekeleri (ÇYG) ise şebeke gerilim değeri olarak 54 kv un üstündeki şebekelerdir. Enerji ihtiyacının artması ve bazı bölgelerdeki enerji miktarının; o bölgenin enerji ihtiyacını karşılayamaması durumunda, enerji üretimi fazla olan bölgeden enerji üretimi az olan uzak bölgeye enerji iletimi yaparken ÇYG şebekeleri kullanılır. ÇYG şebekeleri santraller arası ve şehirlerarası bağlantılarda kullanılır. Türkiye de kullanılan ÇYG şebekelerinin gerilim değeri genellikle 380 kv tur. İhtiyaca Uygun Dağıtım Şebekesinin Belirlenme Esasları Bir dağıtım şebekesi; havai hat ve yeraltı kabloları olmak üzere iki farklı şekilde kurulabilir. Dağıtım sisteminde aynı değerdeki gücün havai hat veya yeraltı kablosu ile dağıtılması arasında ekonomik bir karşılaştırma ve analiz yapıldığında; havai hat şebekesinin maliyetinin yeraltı kablo şebekesinin maliyetine göre daha ucuz olduğu, başka bir deyişle kablo şebekesinin maliyetinin, havai hat şebekesinin mâliyetinden 0-5 kat daha fazla olduğu bilinmektedir. Bunun nedeni yeraltı kablosunun üretim şekli, kullanılan özel malzemeler ve kablonun yeraltına döşenmesindeki ek masraflardır. Yeraltı kablosu ile oluşturulan şebekelerde başlıca önemli işletme zorlukları şunlardır; Kablolardaki termal ısınma. Yeraltındaki arızalı kısmın bulunması ve onarılması esnasında karşılaşılan güçlükler. Yalıtkan malzeme kayıpları. Yeraltı kablosunun üretim maliyetinin yüksek olması. Kablonun yeraltına döşenmesi esnasındaki ek masraflar. 96
101 Bunun yanı sıra özellikle büyük ve kalabalık yerleşim bölgelerinde yeraltı kablo şebekeleri estetik ve güvenlik açısından havai hatlara göre daha uygundur. Havai hatların sakıncaları ise; baskı ve gergi aparatları ile izolatörlerden dolayı ortaya çıkan ek maliyet, sürekli olarak çevresel etkilere maruz kalma şeklinde sıralanabilir. Arıza yerinin daha kolay bulunabilmesi ve havai hattın daha kolay onarılabilmesi ise havai hatların önemli avantajlarındandır. Türkiye'de Kullanılan Dağıtım Sistemi Gerilimleri Türkiye'de dağıtım sisteminde kullanılabilecek standart gerilimler, TS-83 numaralı Türk Standartlarında belgesinde belirlenmiştir. Bu standartlara göre; V (000 V dahil) arası alçak-gerilimler; tekfazlı elektrik şebekeleri 0 ve 0 V, üç-fazlı elektrik şebekeleri 0/90 V ve 0/380 V olan şebekelerdir. Normal şartlarda bir dağıtım hattındaki gerilimin değeri için izin verilen sınır değerler, anma geriliminden en fazla ± %0 kadar değişim gösterebilir. Şartların uygunluğu halinde hatlardaki gerilim değişiminin ±%5 olarak alınması en uygunudur. Yine TS-83'e göre doğru akım şebekelerinde kullanılabilecek standart gerilimler 600 V, 00 V, ve 400 V değerleridir. Doğru akım şebekelerinde en büyük gerilim, anma geriliminin en fazla ± % 0'si kadar, en küçük gerilim ise anma geriliminin en fazla ± % 33'ü kadar değişim göstermelidir. Ülkemizde, anma gerilim değeri 30 kv olan standart alternatif gerilim dışında bu gerilim sınıfına dahil olarak 30-3, , ,5 kv'luk gerilimler de kullanılmaktadır. Bu durum ise şebekeler arasında uyum sorunu oluşturmakta ve buna bağlı olarak malzeme değişimlerini zorlaştırmaktadır. Bu nedenle şebeke içerisinde en uygun gerilim kademesinin seçilmesi ve yeni yapılacak tesislerde sadece bu gerilim kademesinin standart olarak kabul edilmesi uygun olacaktır. Ülkemizde, bahsedilen bu gerilim serisinde en çok 34,5 kv ve daha sonrada 3,5 kv gerilimler kullanılmıştır. Fakat orta-gerilim şebekelerinde 34,5 kv'luk gerilim kullanıldığında 3,5 kv'a göre aktif ve reaktif güç kayıpları ile gerilim düşümü % 7 azalırken, taşınan güçte % 9,5 oranında bir artış meydana gelir. Bu nedenle Türkiye'deki orta-gerilim şebekelerinde en çok kullanılan gerilim kademesi 34,5 kv'tur. Enerji iletiminde ve dağıtımında, enerjinin uygun ve ekonomik bir şekilde dağıtımı açısından şebeke çeşitlerinden verimli olanı seçilmelidir. Bu seçim esnasında enerjinin üretildiği santralle enerjiyi kullanacak olan tüketiciler arasındaki mesafe ve dağıtım şeklinin uygunluğu da göz önünde bulundurulmalıdır. Yapılarına göre şebeke çeşitleri üç ana grupta toplanır. Bunlar;. Kapalı (ring ve gözlü) şebeke: Bu şebekeler kapalı olarak tasarlanır ve oluşturulur. Ring şebeke ve gözlü şebeke olmak üzere iki kısımda incelenir. a. Ring (Halka) şebeke: Birbirine paralel olarak bağlanan birden fazla besleme transformatörünün kullanıldığı kapalı şebeke tipine ring şebeke adı verilir. Ring şebekelere halka, bukle...vb. isimler de verilmektedir. Ring şebeke tipinde besleme birden fazla transformatör ile yapıldığı için şebekenin herhangi bir noktasında oluşabilecek bir arıza durumunda şebekenin tamamı etkilenmez. Arızalı bölge haricindeki abonelerin enerji ihtiyacı kesintisiz olarak sağlanabilir. Sadece arızalı bölgenin aboneleri enerjisiz kalır. Ring şebekelerde, kapalı tip ve birden fazla besleme transformatörü kullanıldığından şebekenin iletken kesiti her yerde aynı olur; bundan dolayı daha fazla iletken kullanılır ve maliyet artar. Bu şebekelerde işletme sürekliliği ve güvencesi de üst seviyededir. OG şebekelerinin birçoğu ring şebeke türünde düzenlenir. Ayrıca köy, kasaba dağıtım şebekelerinde, endüstri işletmeleri ile benzeri işletmelerde, fabrika, motel, park, kamplar vb. yerlerin iç aydınlatmalarında ring şebeke kullanılır. b. Ağ (Gözlü) şebeke: Beslemenin bir veya birden fazla yerden yapıldığı ve alıcıları gözlere ayırarak bir ağ şeklinde besleyen şebekelere ağ şebeke adı verilir. Şebekenin herhangi bir noktasında arıza olması durumunda sadece arızalı hatta bağlı aboneler enerjisiz kalır, diğerleri bu durumdan etkilenmezler. Arızalı hat koruma elemanlarıyla devreden çıkarılarak diğer aboneleri etkilemeden sorun giderilebilir. Bu şebekelerde iletim baraları en az iki koldan enerji almaktadır. Bu nedenle besleme sürekli şekilde yapılabilmektedir. Düğüm noktalarından beslenen baralar ve bu baralardan enerji alan abonelerde enerjinin kesilmesi çok düşük bir ihtimal dahilindedir. Düğüm noktalarından ayrıldıkça kısa-devre akımı küçülür. Bu şebekelerin kuruluşu ve bakımı zordur fakat bu sistemde gerilim düşümü oldukça küçük değerlerde olduğundan gerilim açısından verimlidir. Şebekenin gözlere 97
102 ayrılıp ağ şeklinde örülmesi şebekenin maliyetini arttırır. Bir ağ şebekede kolların iletken kesitleri aynı olmalıdır. Eğer bu durum sağlanamıyorsa kesitler birbirine yakın olmalıdır. Kesitler aynı ise bu durum hesaplamalarda kolaylık sağlar. İşlemlerde dirençler yerine uzunluklar alınabilir. Ağ şebekelerde bütün besleme noktalarının şebekede akım dağılımı yapıldıktan sonra gerilim düşümünün maksimum olduğu noktalar belirlenir ve bütün ana kollar için aynı kesit seçilerek gerilim düşümü hesaplanır. Bulunan gerilim düşümlerinden en büyüğü, nominal gerilimin % 5'inden daha büyük olmamalıdır. Eğer hesaplamalar sonucunda bulunan gerilim düşümü, nominal gerilimin % 5'inden daha büyük ise tüm sistemin ana kollarındaki iletken kesitlerinde bir üst standart kesit seçilir. En büyük gerilim düşümünün meydana geldiği nokta için gerilim düşümü tekrar kontrol edilir. Bu defa hattaki gerilim düşümü % 5 veya % 5'in altına düşmüş ise seçilen iletken kesiti uygun demektir. Gerilim düşümünün % 5'in çok altına düşmesi de uygun değildir. Böyle olunca kesit gereğinden fazla seçilmiş demektir. Kesit küçültülerek gerilim düşümünün % 5'e yakın bir değer çıkması sağlanır.. Açık (dalbudak, radyal) şebeke: Beslemenin genellikle tek kaynaktan yapıldığı ve genelde nüfusun yoğun olmadığı köy, kasaba, şehir, sanayi merkezleri ve yerleşim birimlerinde kullanılan şebeke çeşitlerine açık (dalbudak, radyal) şebekeler denir. Bu tür şebekelerde tek besleme olduğundan dolayı dağıtım transformatöründen son tüketiciye kadar hat üzerinde kademeli olarak gerilim düşümü olur. Bu şebekelerin maliyetini düşürmek için dağıtım transformatörüne yakın olan hatlar kalın kesitli iletkenlerle donatılır ve tüketiciye kadar olan hat boyunca iletken kesiti giderek azaltılır. Dağıtım transformatörüne yakın olan hatlara ana hat denir. Ana hattan ayrılan ve tüketiciye kadar olan hatlara ise branşman denir. Branşmanların kesitleri, ana hatta göre küçüktür. Gerilim düşümünden minimum oranda etkilenmek için transformatör, beslenecek yerleşim merkezinin orta kısmına konur. Şebeke için en büyük hat kesiti bulunurken, şebekenin en uç noktalarındaki kolların gerilim düşümleri birbiriyle kıyaslanıp, en büyük gerilim düşümünün meydana geldiği hat parçası ile ana kolun gerilim düşümü dikkate alınarak en büyük kesit hesabı yapılır. Bu şebekeler havai hat şeklinde olabileceği gibi yeraltı kablosu ile de düzenlenebilir. Hatların geçeceği yerler; sokak ve caddelerdir. Bunlar dağıtım projelerinde belirtilir. Dalbudak şebekelerin avantajları ve dezavantajları kısaca şöyle sıralanabilir. Avantajları: Arıza noktalarının bulunması kolaydır. Kuruluşu, işletmesi ve bakımı hem ucuz hem de kolaydır. Trafodan uzaklaştıkça iletken kesiti düşer ve kurulum maliyeti düşer. Kısa-devre gücü düşük olduğundan az sayıda kesici kullanmak yeterlidir. Dezavantajları: Gerilim dengesizliği vardır ve trafodan uzaklaştıkça gerilim düşer. Hat üzerindeki arıza noktasından sonraki aboneler enerjisiz kalır. İşletme maliyeti düşüktür. Hatlardaki işletme verimi düşüktür. 3. Enterkonnekte şebeke: Kesintisiz bir enerji sağlamak ve mevcut enerji ihtiyacını karşılamak için, elektrik santrallerini ve bütün şebekeleri birbirine bağlayan sistemlere enterkonnekte sistem denir. Bu tür sistemlerde santral farkı gözetilmeksizin bütün santraller (HES, Termik, Doğalgaz, vb.) sisteme dahil edilir. Ayrıca santrallerin büyüklüğü veya küçüklüğü sisteme dahil olması için engel teşkil etmez. Bu sayede ülke genelinde bütün şebekeler birbirine bağlanmış olur. Bu bağlama şekli ile ülkeler arası bağlantılar da kurularak enerji alışverişi sağlanır. Enterkonnekte sistemde, arıza meydana geldiğinde sadece arızalı olan kısım enerjisiz kalır. Bu arıza, enterkonnekte sisteme bir zarar vermediğinden alıcılar arasında enerji alışverişi devam eder. Enterkonnekte şebekelerin avantajları; verimleri yüksektir, sistemde kesintisiz enerji vardır ve Bundan dolayı alıcılar enerjisiz kalmaz, santraller ekonomik olarak çalışır, yedek generatör sayısı azdır. Enterkonnekte şebekelerin dezavantajları ise sistemin kısa-devre akımı çok fazladır, sistemin kısa-devre akımından alıcılar etkilenebilir, sistemin kararlılığını sağlamak zordur. 98
103 DİREKLER Elektrik enerjisinin üretildiği santrallerden tüketim merkezlerine ve abonelere havai hatlar yardımıyla iletilmesini sağlayan, toprakla iletken arasında yalıtkanlık oluşturan ve hat boyunca uygun aralık ve yükseklikte yerleştirilen şebeke donanımına direk adı verilir. Direk ve konsollar, enerji taşıyan kabloları, izolatörler yardımıyla yerden ve birbirinden belirli uzaklıklarda tutarak yalıtımı sağlayan ve bunların kısadevre yapmalarını engelleyen elemanlardır. İmal edildikleri malzemelere göre direkler üç ana grupta toplanırlar. Bunlar;. Demir direkler: Temel yapı elemanı demir olan bu direkler, enerji iletim ve dağıtımında en yaygın kullanılan direk çeşididir. Gerilim değerine göre L, U, veya I demirinden yapılırlar. 3/0 AWG iletkenli galvaniz gövde ve galvaniz civatalı demir direkli projeler; tek devreli, iki devreli, dört devreli ve altı devreli olarak düzenlenir. Rutubetten, havadan ve sanayi bölgelerindeki atık gazlardan etkilenmemeleri için dış yapıları koruyucu izolasyon malzemeleri ile kaplanır. Bu direkler, demir profilden imal edildikten sonra üretilen bu kısımlar kaynak ve civatalarla birbirlerine sabitlenir. İletim hattında kullanılacak direkler bölgelere göre, taşıdığı iletken türü ve iletken sayısına göre tepe kuvvetleri hesaplanarak değişik yapıda ve büyüklükte tasarlanır ve üretilirler. Bu şekilde tasarlanan demir direklere demir konstrüksiyon direkler denir. Her demir direk için direk boyları, tepe ve dip genişlikleri detaylı statik hesaplamalar yapıldıktan sonra belirlenir. Direklerin dikileceği bölgelerde her zaman düz bir zemin bulunamaz; böyle durumlarda farklı boyutlarda ve değişik ayaklı direkler tasarlanarak ihtiyaca uygun direk üretilir. Bu direklerin avantaj ve dezavantajları şu şekilde sıralanabilir; Avantajları: Sağlamdır. Onarımları kolaydır Ömürleri uzundur. Tepe kuvvetleri büyüktür. Parçalara ayrılabildiği için taşınması ve montajı kolaydır. Dezavantajları: Bakımları pahalıdır Maliyeti yüksektir. Yalıtımı zordur. Havanın nem etkisine karşı korumak gerekir. Demir direklerin temeline genellikle beton dökülür, başka malzemeler kullanılmaz. Dikileceği toprağın seviyesi üzerinde, direği de içerisine alacak şekilde 0-0 cm kalınlığında yağmurluk betonu atılır. Demir direklerin bakım ve yalıtımları ağaç ve beton direklere nazaran masraflı olup, ağaç ve beton direklere oranla maliyetleri daha fazladır. Bunun yanı sıra, demir direkler küçük parçalara ayrıştırılabildiği için lojistik olarak taşınmaları kolaydır. İletken sayısı ve kesite göre direkte takviyeler yapılabilir. Demir direklerin, ağaç ve beton direklere oranla baskı ve çekme kuvvetlerine karşı mukavemetleri daha azdır.. Ağaç direkler: Bu direkler, geniş yapraklı kestane ve meşe ağacının veya iğne yapraklı ağaçlardan olan ladin, ardıç, çam veya köknar ağaçlarının özel işlemlerden geçirilmesi ile üretilirler. Fakat bu ağaçlardan meşe, ardıç ve kestane, nadir bulunduğundan ve özelliklerinin ihtiyacı karşılayacak şekilde olmamasından dolayı fazla tercih edilmezler. Ağaca zarar veren canlılar mantar ve böceklerdir. Ayrıca ağaç direklerin dikildiği bölgedeki hava şartları, rutubet ve su direğin kullanım ömrünü azaltır. Direk imalatında kullanılacak ağaçlar belli işlemlerden geçirildikten sonra kimyasal ve mekanik mukavemetleri arttırılarak enerji taşıma işleminde kullanılabilirler. Ağaç direkler hazırlanırken tornalama işleminden sonra ilaç havuzuna 99
104 daldırılarak hava şartlarına, zararlı böcek ve mantarlara karşı dayanıklı hale getirilir. Direklerin ilaç daldırma işleminde kullanılan başlıca maddeler; kreozot ve suda eritilerek kullanılan kimyasal ilaçlardır. Kreozot, kömür katranının C sıcaklıkta kaynatılıp damıtılmasıyla elde edilir. Daldırma işleminde kullanılan kimyasal ilaçlar ise bakır-krom-bor veya bakır-kromarsenik tuzlarından oluşan ve suda eriyen karışımlardır. Ayrıca bazı daldırma yöntemlerinde fluorid-dinitrofenol-arsenik karışımı da kullanılabilir. Ağaç direklerde daldırma işlemi; ağaç hücreleri arasındaki hava, vakum ile boşaltılıp belirli bir basınç altında bu hücreler özel ilaç maddesi ile doldurulur. Daldırmada kreozot kullanılmışsa, bu işlem 80 C'de yapılmalıdır. Ağaç direklerin temeli, toprakla sıkıştırılmış taş dolgu ile yapılır. Bu işlemde beton dolgu kullanılmaz. Eğer beton kullanılırsa; temel dolgu yüzeyinin en üst kısmında direkle temas noktası (ankastre noktası), zamanla ağaç direği kesmeye başlar ve direğin kırılmasına sebep olur. Bunun yanı sıra rutubet ve direğe zarar verebilecek zararlıları önlemek için bakım yapmak amacıyla ağaç direğin temeli belli bir seviyeye kadar kazılarak toprakla direğin temas noktaları enjeksiyon yardımıyla ilaçlanır. Direk temelinin beton dolgu olarak yapılması bu imkanı da ortadan kaldırır. Ağaç direkler sadece taşıyıcı (T) ve köşe taşıyıcı (KT) direk olarak kullanılırlar. Bu direklerin içleri dolu olduğundan baskı ve çekme kuvvetlerine karşı oldukça dayanıklıdırlar. Ağaç direkler, 30 kv'a kadar enerji iletiminde kullanılabilir. Bu direkler gerektiği taktirde çift ağaç direk (Ç) (ikiz direk) olarak kullanılabilir. Ağaç direklerde demir veya galvanizli traversler kullanılır ve üzerine kar ve yağmur suları birikmemesi için direk tepesi açılı olarak kesilir. Standart boyları 8-8,5-9- 9,5-0-0,5--,5-3-3,5 metredir. Ağaç direkler için mekanik dayanıklılık ve tepe kuvveti sınırlı olduğundan, direkler arası mesafenin kısa tutulması gerekir. Bu direklerin avantaj ve dezavantajları şu şekilde sıralanabilir; Avantajları: Esnektir, her yöndeki kuvvetlere karşı aynı direnci gösterir. Kaçak akımlara karşı daha güvenlidir. Boya masrafı yoktur. Ucuzdur. Hafif olduklarından dolayı taşımaları ve dikilmeleri kolaydır. Tekrar tekrar farklı yerlerde kullanılabilme özelliğine sahiptir. Tırmanması kolaydır. Dezavantajları: Yıldırım düşmesi halinde yanabilir. Yüksek-gerilimlerde kullanılmaz. Tepe kuvvetleri düşüktür. Ömürleri kısadır. Esnek olduklarından fleş (sarkma) değişebilir. 3. Betonarme direkler: Çimento, kum, su ve diğer katkı maddelerinin eklenmesiyle hazırlanan beton ile yüksek dayanımlı çelik tel ve çelik çubukların birarada kullanılmasıyla elde edilen direklerdir. Beton direklerde demir direklere oranla %50 demir tasarrufu sağlanır ve bu sebeple daha ucuzdurlar. Mekanik dayanımları oldukça fazladır. Bakım ihtiyaçları en alt seviyelerdedir. Bataklık gibi çok nemli yerlerde, sahil kesimlerinde, sanayi bölgelerinde zararlı buhar ve gazlardan çok az etkilendikleri için tercih edilirler. Her çeşit gerilim kademesinde kullanılmakla beraber ülkemizde alçak-gerilim, orta-gerilim ve yüksek-gerilimler için betonarme direkler yapılmaktadır. İmal edilen direk uzunlukları ise; 8-8,5-9-9,3-9,5-0-0,5--,5--,5-3- 3, metredir. Beton direkler konik ve silindirik şekilde imal edilirler. Beton direkler üzerinde direk etiketi mevcuttur. Etikete direk tipi ve direk boyu yazılır. Bu direklerin avantajları ve dezavantajları aşağıdaki şekilde sıralanabilir; 00
105 Avantajları: Kimyasal etkilerden etkilenmez. Demir direklere oranla maliyetleri daha düşüktür. Hava şartlarından etkilenmez. Ucuz temel işçiliği gerektirir. Bakıma ihtiyaç göstermez. Değişik amaçlara göre dizayn edilebilir. (aydınlatma, taşıma... gibi) Tepe kuvvetleri büyüktür. Ömürleri uzundur. Dezavantajları: Taşınmaları, montajı ve dikilmeleri zordur. Ağır ve kırılgandır. Beton direkler; santrifüj (SBA) ve vibre (VBA) olmak üzere iki tipte imal edilirler. Santrifüj direklerin içi boş, vibre direklerin içi doludur. Genellikle hat başı, hat sonu ve köşe direği olarak çift vibre veya çift santrifüj direkler tercih edilir. Beton direkler üzerinde bulunması gereken aparatlar; topraklama somunu, tepe izolatör somunu, tırmanma somunu, sigorta, sac ve sac kapağıdır. a. Santrifüj betonarme (SBA) direkler: Santrifüj direklerin imalat aşamasında parçalar kalıp içerisine yerleştirilir. Özel olarak üretilen beton karışımı ve demir, kalıba dökülür ve kalıp, santrifüj tezgâhında yüksek devirde döndürülür. Oluşan merkezkaç kuvveti etkisiyle beton, kalıp kenarlarına çevresel olarak yapışarak kalıbın ortası boşalır ve çok sıkı bir yapı oluşur. Direkler beklemeye alındıktan sonra, erken mukavemet kazanmaları için buhar kürüne yatırılırlar. Betonun mukavemeti, kum ve çakılın yapısına, çimentonun kalitesine, buharlaşma sıcaklığına ve süresine bağlıdır. Santrifüj direkler konik yapıdadır. Tepe kuvvetlerine göre çapları değişmektedir. Tepe kuvveti büyük olan direklerde demir oranı daha azdır. Orta-gerilim (OG) enerji taşıma sisteminde 50 kg'dan 3500 kg'a kadar değişen tepe kuvvetine sahip çeşitli tip ve boyutlarda santrifüj betonarme direkler (SBA) kullanılmaktadır. Direklerin tepe çapları mm arasında değişir ve direkler yukarıdan aşağıya doğru her m'de 5-8 mm genişler. Boyları 9-5 m arasında değişir ve kullanım ömürleri yıl arasındadır. SBA betonarme direklerin tepe kuvveti 3500 kg'dan daha fazla olması halinde, direk, beton muflar yardımıyla çiftlenir. Çiftleme işlemi aynı boy ve aynı tipteki iki direkle yapılır. Muflar arası mesafe ise en fazla 3 m olmalıdır. Muf montaj işlemi direk dikilirken mahallinde yapılır. Toplam direk boyu (H), temel derinliği (t), traversler arası uzaklık (D) ve n=travers adedi- olmak üzere muf sayısı aşağıdaki bağıntı ile bulunur; ( ) H nd+ t Muf sayısı = 3 Örnek 4. Temel derinliği m, boyu m, traversleri arası mesafe,5 m olan 3 traversli bir beton direk için kullanılacak muf adedini bulunuz. Çözüm: H= m, D=l,5 m, Travers adedi=3, n=, t= m olduğuna göre muf sayısı; ( ) (, 5 ) H nd+ t + Muf sayısı = = = 4,66 5 adet 3 3 (4.) 0
106 b. Vibre betonarme (VBA) direkler: Vibre betonarme direkler ise kare, dikdörtgen veya daire kesitli olabilirler. Zeminden yukarıya doğru daralan bir yapıya sahiptirler. Direğin her iki yüzünde boşluklar bırakılarak hem daha hafif olması sağlanır hem de mukavemeti arttırılır. Vibre direkler tek vibre ve çift vibre olmak üzere başlıca iki şekilde imal edilirler. Orta- ve alçak-gerilimlerde kullanılırlar. Bu direkler ülkemizde çok yaygın kullanım alanına sahip değildir. Kuvvetli akım elektrik tesisatının bakım, işletme ve tesisine dair yönetmeliğin 93. maddesinde belirtildiği gibi direkler, kullanılım yerlerine göre yedi farklı şekilde sınıflandırılır. Bunlar;. Dağıtım (Ayırım (A)-Branşman (B)) direkleri: Ana hattın kollara ayrıldığı yerlerde kullanılan direklerdir. Üzerlerinde dağıtım için gerekli bağlama donanımları, kesiciler ve ayırıcılar bulunabilir.. Durdurucu direkler (D): Hava hattını belli bir yerde sabitlemek için kullanılan direklerdir. Görevleri; hem hat iletkenlerini taşımak hem de durdurucu bağ ile bunları tespit etmek olan doğrusal güzergâhtaki iletkenlerin gergin durması ve sarkmaması için kullanılan direklere durdurucu direkler denir. Enerji nakil hatlarında genellikle 7 adet taşıyıcı direkten sonra adet durdurucu direk kullanılır. Direkler aracılığıyla taşınan hat iletkenlerinin hat boyunca belli aralıklarla sabit ve sağlam noktalara bağlanması gerekir. İki durdurucu direk arasında tel kopması, direk devrilmesi gibi hallerde diğer kısımlar etkilenmez. İletim hatlarında güzergah boyunca belli aralıklarda normal taşıyıcı direklerden daha sağlam yapıda durdurucu direkler kullanılır ve iletkenler izolatörlere durdurucu bağ ile bağlanır. 3. Köşe durdurucu direkler (KD): Havai enerji nakil hatlarında iletkenleri taşımak amacıyla köşe noktalarda kullanılırlar. Hattın köşede durdurulma işlemi, doğrusal hat üzerindeki durdurucu direklerde yapılan durdurma işlemi ile tamamen aynıdır. Doğrusal yönde giden hattın yön değiştirip büyük sapma gösterdiği yerlerde kullanıldığı ve iletkenlerin izolatörlere durdurucu bağ ile bağlandığı direklerdir. 4. Taşıyıcı direkler (T): Düz bir havai hat boyunca sadece iletkenleri taşımak amacıyla kullanılan direklerdir. Bu direkler, hattın aynı doğrultuda olan kısımlarında iletkenleri taşımaya ve birer sabitleme noktası olarak hattı zeminden belirli bir uzaklıkta tutmaya yararlar. Kablolar, izolatörlere taşıyıcı bağ ile bağlanırlar. Taşıyıcı direklerde, direğin her iki yanındaki çekme kuvvetleri, hemen hemen birbirlerine eşit olduklarından direkler hat iletkenlerinin çekme kuvvetlerine maruz kalmazlar ve bu direklere sadece hat istikametine dik yöndeki rüzgar kuvveti etki eder. Rüzgar kuvvetinin buradaki etkisi, direkler arasına çekilmiş olan hat iletkenlerine ve direklerin rüzgara karşı duran yüzeyine olan etkidir. Taşıyıcı direklerde iletkenler, mesnet izolatörlerine bağ teli ile kayar şekilde bağlandıkları gibi, zincir izolatörlere bağsız olarak doğrudan da bağlanabilirler. 5. Köşe taşıyıcı direkler (KT): Havai enerji iletim hattının yön değiştirmesini gerektiren köşe noktalarda kullanılan taşıyıcı direklerdir. Köşe direklerinin tipleri, tepe kuvvetlerine bağlı olarak değişir. Genel olarak (A) veya kafes tipli direkler kullanılır. İletkenler izolatörlere taşıyıcı bağ ile bağlanırlar. 6. Nihayet (Son) direkler (N): Havai hattın başlangıç veya bitiş noktalarında kullanılan direk çeşididir. Nihayet direklerine bağlı iletkenlerin germe kuvveti sadece tek bir yönde etki eder. Bu direkler hat başlangıcı ve hat sonunda kullanıldıkları için üzerlerine etki eden tek yönlü çekme kuvvetine dayanıklı olmaları gerekir. Nihayet direklerinde iletkenler, mesnet izolatörlere durducu bağ ile, gergi zincir izolatörlere ise doğrudan bağlanırlar. 7. Geçit direkler (G): Havai hat boyunca yer alan karayolu, demiryolu, su yolu gibi yerleri geçmek amacıyla kullanılan özel yapıya sahip olan direklerdir. OG hatlarındaki direklere, yatay ve düşey olmak üzere başlıca iki kuvvet etkisinin olduğu kabul edilir. Bu kuvvetleri aşağıdaki şekilde gösterilebilir;. Yatay kuvvetler Rüzgâr Kuvveti İletken Çekme (Germe) Kuvveti İletkene Etki Eden Ek Rüzgar Yükü 0
107 . Düşey kuvvetler İletkene Etki Eden Ek-Buz Yükü İletken Ağırlığı İzolatör Ağırlığı Direğin Kendi Ağırlığı Montör Ağırlığı KABLOLAR Kablo, elektrik enerjisini iletmeye yarayan ve farklı iki elektrik noktasını elektriksel bakımdan birbirine bağlayan, dış çevresi elektrik akımına karşı yalıtılmış, bir ya da birden çok damarı bulunan iletim elemanıdır. Elektrik enerjisinin iletimi ve dağıtımında kullanılan hatları, havai hatlar ve yeraltı hatları olmak üzere iki kısımda incelemek mümkündür. Herhangi bir gerilim düzeyinde kablo seçimi yaparken aşağıdaki şartların önemle dikkate alınması gerekir: Taşınacak gerilim ve akımın cinsi ve değeri Kablonun geçeceği ortamın en düşük ve en yüksek ısı değerleri Kablonun maliyeti Belirlenen amortisman ömrü Nötr iletkeninin toprağa döşenme şekli Belirlenen gerilim düşümü değeri Yol verme akım değerleri Enerji alınacak yer ve beslenecek yerin yapısı, şekli Yüke ait güç faktörü Kısa-devre akımlarının değerleri ve süreleri Türk Standartlarına göre kablolar, işletme şartları ve kullanılış amacına göre altı farklı gruba ayrılır;. B-kabloları (TS-96): bu gruptaki kablolar, dış kısmı termoplastikten üretilmiş ve hareketli tesislerde kullanılan ağır işletme koşullarına uygun olarak imal edilen kablolardır. Yeraltı uygulamalarında bu kablolar kullanılmazlar. Kablo üzerinden geçen işletme gerilimi, kablo anma geriliminden en fazla %5 kadar daha fazla olabilir ve üç-fazlı alternatif akım şebekelerinde faz-faz arası gerilim, kablo anma geriliminin,5 katını aşmamalıdır. Simetrik gerilim dağılımlı tek-fazlı AC tesisleri ve DC tesislerinde işletme gerilimi, kablo anma geriliminin,5 katından daha büyük olamaz.. F-kabloları (TS-936): F-Kabloları, normal ve hafif işletme koşullarına uygun, hareketli tesislerde kullanma imkanı sağlayan kablolardır. Tıpkı B-kablolarda olduğu gibi bu kablolar da yeraltına, sıva içine ve altına döşenmezler. F-kabloları üzerinden en fazla kablo anma geriliminin %5'i kadar fazla gerilim iletilebilir. Bu kablo çeşidinde damar iletkenleri bakır telden üretilir. Yalıtkan lastik kılıflı F-kablolarında kimyasal etkiyi önlemek için lastiğin iletken ile teması, özel bir yalıtkan madde tabakası kaplanarak tamamen önlenmelidir. 3. Alvinal kablolar: Alüminyum, diğer malzemelerle karşılaştırıldığında; daha ucuz olması, doğada bol miktarda bulunması, daha kolay elde edilmesi, ucuzluğunun yanı sıra hafif oluşu gibi birçok üstünlüğünden dolayı, iletim hatlarında en çok tercih edilen malzemelerin başında gelmektedir. Bu üstünlüklerinden dolayı, özellikle son yirmi yıldır pek çok ülkede alçak- ve orta-gerilim enerji iletiminde güç kablosu olarak kullanımında büyük artışlar olmuştur. Güç iletimi amacıyla alvinal alüminyum iletkenli yeraltı kabloları geliştirilmiştir. Damar sayısı ve kullanım amacına göre alvinal kablolar başlıca; Alvinal-D, Alvinal-K ve Alvinal-Z olmak üzere 3 ayrı çeşit olarak üretilirler. 03
108 Y-Kablolarında kullanılan ortak kılıf, preslenmiş dolgu maddesinden veya uygun dolgu maddesinden yapılmış şeritlerle bir ya da birkaç sargı biçiminde olabilir. Ortak kılıfın bakır siper görevi gördüğü kablolarda, dolgu maddesinin yarı-iletken niteliğinde olması gerekir. Ancak, kullanılan dolgu maddesi, yalıtkan kılıfa olumsuz etki yapacak ve nem çekici özellikte olmamalıdır. Zırh, çok damarlı kablolarda dış kılıfın altında bulunur ve eğer siper veya konsantrik iletkenin hemen üstüne konulması halinde, zırh ile siper arasına herhangi bir iç koruyucu kılıf yerleştirilmez. Zırh üzerinde bulunan ve zırhı kavrayan, galvanizli çelik şeritten yapılmış ve helis biçiminde, bir veya ikili çapraz sarılmış tutucu bir sargı mevcuttur. Çapı 5 mm ve daha küçük olan kablolarda zırh, galvanizli yuvarlak çelik tellerden yapılır ve bu tellerin çapı en az 0,6 mm'dir. Çapı 5 mm'den daha büyük kablolarda ise zırh, galvanizli yuvarlak çelik tel ya da yassı çelik tellerden imal edilir ve yuvarlak tel ile yassı tellerin kalınlıkları en az 0,8 mm'dir. Ayrıca, zırh için kullanılan teller düzgün, pürüzsüz olmalı ve zırhta kopuk ve dışarı fırlamış teller olmamalıdır. En dış koruyucu kılıfı bulunmayan kablolarda zırh, düz bitümlü, yüksek erime noktalı bitümlü, veya alev boğan bitümlü lak ile korunmalıdır. 04 a. Alvinal-D kablosu: Dört damarlı, düşük kesitli nötr iletkenli ve plastik yalıtkanlı kablolar olup, sabit tesislerde ve ağır işletme koşullarına dayanıklı şekilde imal edilmişlerdir. Kesiti 6 mm olan alvinal-d kabloları daire kesitli-som, 5 mm olanları daire kesitli, diğerleri ise daire dilimi (sektör) kesitlidir. İletkenler sıkıştırılarak şekillendirilmiş, düzgün yüzeyli, çok telli örgülü şekilde imal edilirler. Bu kabloların dış kılıfı siyah PVC plastikten üretilmiştir ve üzerlerine, fazları belirtmek için,, 3, nötrü belirtmek için ise 0 rakamı basılmıştır. Alvinal-D alüminyum iletkenli kablolar; bina içi ve dışında, şalt ve endüstri tesislerinde, kablo kanallarında, güç merkezlerinde, yerel enerji dağıtımında, kablo yalıtımına zarar verebilecek dış etkenlere karşı önlemler almak şartıyla, ağır işletme şartlarında ve değişik toprak ortamlarında (killi, sulu, nemli, kuru, kayalık, kumlu,... vs.) kullanılır. b. Alvinal-K Kablosu: Üç damarlı, nötrü konsantrik bakır iletkenden imal edilmiş, plastik yalıtkanlı, sabit ve ağır işletme şartlarında çalışmaya elverişli olan alüminyum iletkenli yeraltı kablolarıdır. Alvinal-K kablolarının kesiti 6 mm olanları daire kesitli-som, 5 mm olanlar daire kesitli, diğerleri ise sıkıştırılarak şekil verilmiş, düzgün yüzeyli, çok telli, burularak sarılmış şekilde imal edilirler. Damarlar üzerinde fazlar,, 3 şeklinde numaralandırılmıştır. Bakırdan imal edilen konsantrik nötr iletkeni ise tavlama işlemine tabi tutulmuştur. Alvinal-K kabloları genellikle toprak içerisine serilir. Bakırdan imal edilmiş olan konsantrik nötr iletkeni, kablonun elektrik ve mekanik bakımdan mukavemetini artırır. Bu kablolar; sokak aydınlatması, endüstri, şalt, yerel enerji taşıma durumunda, ayrıca değişik toprak ortamlarında (killi, sulu, nemli, kuru, kayalık, kumlu,... vs.), ağır hizmet şartlarında kullanılmaya elverişlidir. c. Alvinal-Z kablosu: Çelik zırh geçirilmiş, nötr iletkeni düşük kesitli olarak imal edilen, dört damarlı, ağır işletme şartlarına dayanıklı, sabit tesislerde kullanılan, plastik yalıtkanlı ve alüminyum iletkenli enerji kablolarıdır.,6 mm kesitli alvinal-z kabloları daire kesitlisom, 5 mm olanları daire kesitli, diğerleri ise daire dilimi (sektör) kesitli olup, iletkenler sıkıştırılarak şekillendirilmiş, düzgün yüzeyli, çok telli ve örgülü olarak sarılmıştır. Kablonun dış kılıfı siyah PVC plastikten yapılmış, damar üzerlerine, fazları belirtmek için,, 3, nötrü belirtmek için ise 0 rakamı basılmıştır. Alvinal-Z kabloları; yerel enerji taşımasında, kablo kanallarında, şalt ve endüstri tesislerinde, mekanik zorlamaların fazla olduğu yerlerde, ağır işletme şartlarında, nehir ve deniz içi ortamlarında, değişik toprak ortamlarında (killi, sulu, nemli, kuru, kayalık, kumlu,... vs.), ağır hizmet şartlarında kullanılmaya elverişlidir. 4. Y-Kabloları (TS-): Y-Kabloları, sabit tesislerde ve ağır işletme şartlarında kullanılan dayanıklı kablolardır. Bu kablolar, enerji kabloları ile sinyal ve kumanda kabloları olmak üzere başlıca iki gruba ayrılır. Y-Kabloları bakır ve alüminyum iletkenli olarak üretilirler. Yalıtkan olarak ise, lastik yalıtkanlı ve termoplastik yalıtkanlı olmak üzere iki çeşittir. Çok telli daire biçimli alüminyum ve bakır iletkenli Y- Kabloları 5,8 kv'a kadar olan gerilimlerde kullanılır ve bu gerilimde kullanılacak olan termoplastik kablolarda, damar iletkeninin ve yalıtkan kılıfın üzerinde birer yarı-iletken kılıf bulunur. Damar sayısı dörtten fazla olan enerji kabloları sadece 0,6 kv gerilimler için imal edilirler. Çok damarlı kablolarda, kablonun her üç-faz damarı için, faz damarı ile burulmuş düşük kesitli iletken yerleştirilmiş olabilir.
109 Korozyona karşı kabloyu koruyan madde; koyu, boşluksuz olmalı, kuruyup çatlayan özellikte olmamalıdır. Korozyona karşı ek bir koruyucu tabaka eklenmek istendiğinde, zırh üzerine ve en dış kılıfın hemen altına emdirilmiş kağıtla iki kat sargı sarılır. Sıcağa karşı kablonun dayanımını artırmak için en dış koruyucu kılıfın içerisine erime noktası yüksek bir madde katılır. Aleve karşı kablo dayanımını artırmak için ise, en dış kılıfın içerisine alev boğucu madde katılır. Sıcağa ve aleve dayanıklı koruyucu tabaka üzerine gerekli durumlarda, yukarıda bahsedilen korozyona karşı ek tabaka da getirilebilir. kv'a kadar olan alçak-gerilim kablolarının koruyucu dış kılıfı siyah, kv'tan yukarı olan yüksek-gerilim kablolarının koruyucu dış kılıfı ise kırmızı renktedir. 5. N-kabloları (TS-833): N-Kabloları, sabit olan elektrik tesislerinde, normal ve hafif işletme şartlarında kullanılan kablolardır. Eşit gerilim dağılımlı (simetrik) üç-fazlı elektrik tesislerinde, tek-fazlı elektrik tesislerinde ve doğru akım tesislerinde işletme gerilimi, anma geriliminin,5 katından daha büyük olmamalıdır. Topraklanmış bir fazlı alternatif akım ve doğru akım tesislerindeki işletme gerilimi, kullanılacak N tipi kablo anma geriliminin 0,66 katından daha büyük olmamalıdır. Kullanılan N tipi kablonun dış kılıfı lastik ile yalıtılmış ve bu lastik kılıf iletken ile devamlı temas halinde ise karşılıklı kimyasal etkileşmeyi önlemek için iletkenler kalaylanmalı ve lastik yalıtkan kılıfın iletken ile teması, boyalı bir film tabakası veya buna eşdeğer başka bir tabaka ile tümüyle önlenmelidir. Çok telli N tipi kablolarda iletkenler burularak sarılmış olmalı ve tel anma çapları birbirine eşit olmalıdır. Burularak sarılmış olan bu iletkenlerin üzerleri düzgün olmalı, keskin köşeler ve dışarı çıkmış telleri bulunmamalıdır. 6. Alpek kablolar: Alpek kablolar, askı telli, plastik yalıtkanlı alüminyum kablolardır. Enerji iletim tesislerinde kullanılan kablolar, teknik ve ekonomik nedenlerle sürekli gelişim ve değişim içindedir. Daha önceleri enerji iletim tesislerinde sıkça kullanılan bakır, günümüzde yerini alüminyuma bırakmaktadır. Alpek kabloların teknik ve ekonomik bakımdan çıplak kablolar ile yeraltı kablolarının arasında yer almaktadır. Bu kablolardaki plastik yalıtkanlı (PE) alüminyum faz iletkenleri, çıplak nötr iletkeninin etrafına bükülerek sarılırlar. Faz iletkenleri, hava şartlarına dayanıklı, sıfır derecenin altındaki ısılarda esnekliğini muhafaza eden siyah polietilen (PE) ile yalıtılmıştır. Çıplak nötr askı teli, tüm yükü ve gerilmeleri taşır. Askı teli, alüminyum alaşımından sıkıştırılarak düzgün yüzeyli olarak imal edilir ve kesiti, standart faz iletken kesitinin bir kademe üstünde seçilir. Enerji iletiminde kullanılan alüminyum alaşımlı askı telinin kopma gerilmesi en az 30 kg/mm olması gerekir. Faz isimleri, iletim boyunca kablo yalıtkanı üzerindeki kabartmalarla belirlenir. İki kabartma birinci fazı, üç kabartma ikinci fazı ve dört kabartma ise üçüncü fazı belirtir. Ancak, sokak aydınlatmalarında faz yalıtkanı üzerinde kabartma yoktur. Tesis masrafının az olması, çıplak iletkenlerde olduğu gibi tabiat etkisi ile oluşan aşırı salınım olayının neden olduğu enerji kesintilerinin olmayışı, telefon hatları ve yüksek-gerilim enerji hatları ile beraber aynı direkte güvenli şekilde kullanılması, hatların yalıtılmasından dolayı daha güvenli oluşu ve şebeke geliştirilmesine imkan sağlamasından dolayı alpek kablolar daha yaygın bir kullanım alanı bulmuştur. Alpek kablolar, inşaat halinde veya yeniden inşa edilen yerleşim bölgelerinin alçak-gerilim tesislerinde, 750 Volt'a kadar olan hava hatlarında, bina kenarları veya geçici tesislerde, sokak ve yol aydınlatmalarında, ağaç, demir ve beton direkli şehir ve köylerin alçak-gerilim elektrik tesislerinde, çıplak veya yalıtkanlı bakır kablolarla çıplak alüminyum hatların yerine, yeraltı kablosunun kullanılmadığı durumlarda, çıplak iletkenli hatlardan sokak branşman hatlarına geçişlerde, ev, apartman ve endüstri branşman hatlarında, ağaçların ve doğal örtünün korunmasının gerekli olduğu alanlarda, alçak-gerilim kablosu bulunmayan bir trafo merkezinden diğer transformatöre çıkış yapılması durumlarında kullanılır. Çelik Özlü Alüminyum İletkenler Orta-gerilim enerji nakil hatlarında, mekanik zorlamaların fazla olması nedeniyle çelik özlü alüminyum iletkenler (St-Al) kullanılmaktadır. Genellikle Kanada Standartlarına uygun olarak üretilen bu tip iletkenlerle ilgili TS-490 Türk Standardı aynı esaslara dayanmaktadır. Enerji hatlarında kullanılan alüminyum iletkenler çelik damarlarla donatılarak mekanik mukavemetleri artırılır. Akım taşıma 05
110 kapasiteleri aynı olan alüminyum ve bakır iletkenlerin kopma yükleri yaklaşık olarak aynıdır. Bir alüminyum iletkenin kopma gerilmesi 8 kg/mm iken, çelik özlü alüminyum iletkenin (St-Al) kopma gerilmesi 30 kg/mm dir. Bu ise St-Al iletkeninin, normal Al iletkenine göre,66 kat daha dayanıklı olduğu anlamına gelmektedir. Bunun yanı sıra St-Al iletkenin bakır iletkene oranla,5-,6 kat daha hafif olması, özellikle engebeli arazide nakliye ve montajda büyük ekonomi sağlamaktadır. Bu gün ülkemizde orta-gerilim enerji hatlarında, 3 AWG, /0 AWG, 3/0 AWG, 66,8 MCM ve 477 MCM çelik özlü alüminyum iletkenler kullanılmaktadır. Kullanılan iletken sembollerinin anlamları ise şöyledir; AWG (American Wire Gauge): Bu adlandırmada AWG nin ön kısmı 0000, 000, 00, 0,,, 3, 40'a kadar numaralandırılmıştır. Fakat kısaltma amacıyla 0000=4/0, 000=3/0, 00=/0, 0=/0 şeklinde ifade edilir. Her bir numara belli bir çap, dolayısıyla da bir kesite karşılık gelir. Örneğin; 3 AWG=3 AWG (Swallow) 0 AWG=l/0 AWG (Raven) 000 AWG=3/0 AWG (Pigeon) MCM: Daha büyük kesitli St-Al çelik özlü alüminyum iletken kesitler, CM (Circular Mile) olarak adlandırılan bir birimle ifade edilir. Burada CM, çapı 0,00 inch olan daire yüzey kesitine eşittir. O halde; CM=506,7x0-6 mm dir. CM değerin 000 katı ise MCM'ye eşit olup, MCM=506,7x0-3 mm =0,5067 mm olur. St-Al iletkenler; iletkenin direkteki askı noktalarında meydana gelen titreşimler nedeniyle zarar görmesini önlemek, hat üzerinde gerekli esnekliği (fleksibilite) sağlamak, iletkenin yorulmasını ve kopmasını engellemek için spiral şekilde örgülü olarak sarılırlar. Swallow, raven ve pigeon iletkenler; en iç kısımda adet çelik tel üzerine, değişik kesitlerde bir kat alüminyum iletken sarılarak imal edilmişlerdir. 66,8 MCM ve 477 MCM iletkenlerde ise;. katta,. katta 6 olmak üzere toplam 7 adet St iletken ile, 3. katta 0 ve 4. katta 6 olmak üzere çeşitli kesitlerde toplam 6 adet Al iletken burularak örgü şeklinde sarılmıştır. Nötr İletkeni Alçak-gerilim şebekelerini besleyen transformatörlerin alçak-gerilim kısmındaki yıldız noktası direkt olarak mutlaka topraklanmalıdır. Aksi taktirde, herhangi bir fazda, faz-nötr veya faz-toprak arasında kısadevre meydana gelirse, diğer sağlam olan fazlardaki gerilimler, nötr iletkeninin gerilimine göre daha fazla olur. Bu durumda hem gerilim dalgalanması meydana gelir hem de tüketiciler zarar görebilir. Transformatörün yıldız noktasından çıkan topraklanmış nötr iletkeni, şebekede sıfır iletkeni olarak kullanılabilir. Sıfırlama, nötr iletkeni aracılığıyla yapılan topraklamadır. Tüketicileri tehlikeli temas geriliminden korumak için alıcıların metal kısımları bu nötr veya sıfır iletkenine bağlanır. Bir cihazın metal olan gövdesi nötr iletkenine bağlanarak topraklanmışsa sıfırlama yapılmış demektir. Cihazlarının metal kısımları topraklanmış olan bir şebekede herhangi bir arıza nedeni ile faz iletkeni metal kısımlara temas ediyorsa, faz-toprak arası kısa-devre meydana gelir. Bu durumda devrede bulunan aşırı akıma karşı koruma cihazları (sigorta, otomatik şalter...vs.) akımı keserek gövdenin sürekli gerilim altında kalmasını önler. Herhangi bir şebekede nötr iletkeninin sıfırlama iletkeni olarak kullanılmasına izin veriliyorsa, transformatörün yıldız noktası dışında nötr iletkeni, şebekenin birçok noktasında topraklanmalıdır. İç tesisatta çıplak olarak çekilen nötr iletkeni, duvarların gerilim altında kalmasına neden olur. Bu da insan sağlığı açısından oldukça tehlikeli bir durumdur. Sıfırlama yapılan şebekelerde, nötr iletkeni yalnız transformatörün yıldız noktasında topraklanır ve bu iletken herhangi bir nedenle kopacak olursa diğer parçası izolatör üzerinde kalabilir. Bu durumda izolatör üzerinde kalan iletkene herhangi bir nedenle enerji verildiğinde nötr iletkeni ve buna bağlı olan cihazların metal gövdeleri ölüm tehlikesi yaratır. Bu tehlikeyi önlemek için nötr iletkeni şebekenin bütün son noktalarında topraklanmalıdır. Böylelikle nötr iletkeni ilk ve son noktalar arasında hangi noktada koparsa kopsun; her iki parça da topraklanmış olduğundan herhangi bir tehlike söz konusu olmaz. Çoğu zaman hattın son noktasında demir veya beton direğin kendisi topraklanmakta, izolatöre bağlı olan nötr iletkeninin topraklaması ise yapılmamaktadır. Eğer nötr iletkeni izolatör üzerinden çekilmişse direk ile birlikte nötr iletkeni de topraklanmalı ve bu duruma dikkat edilmelidir. Bazen ana dağıtım hattından tüketici binasına gelen hattaki nötr iletkeninin 06
111 kopması halinde aynı tehlike söz konusudur. Bu sakıncayı önlemek için ana giriş veya dağıtım tablosunda şebekenin nötr iletkeni topraklanmalıdır. Netice itibariyle, sıfırlama yapılmasına müsaade edilen bir şebekede nötr iletkeni, tüm ilk ve son direklerde, önemli ayrım direklerinde, uzun hatlarda ve arada birkaç direkte topraklanmalıdır. Şayet sıfırlamaya izin verilmiyorsa, bu durumda nötr iletkeninin gerilim altında bulunan bir iletken olduğu unutulmamalıdır. İZOLATÖRLER Havai enerji nakil hatlarında kullanılan iletkenlerin direklere bağlantısını sağlayan, iletkenleri taşımaya yarayan, taşıdığı iletkenlerin direklere, toprağa ve diğer iletkenlere karşı yalıtımını sağlayan cihazlara izolatör denir. Havai hatlarda işletmenin güvenliği ve sürekliliği önemli ölçüde hattın yalıtımına bağlıdır. İzolatörlerin, yapıları yüksek derecedeki sıcaklıklara dayanıklı olmalı ve elektriksel direnç değerleri de çok büyük olmalıdır. Ayrıca; mekanik sağlamlıkları iyi olmalı, kir tutmamalı, üzerlerindeki kirleri yağmur sularıyla rahatça uzaklaştırabilmelidirler. Yapıldıkları malzeme çeşidine göre üç çeşit izolatör vardır;. Porselen izolatörler: Genelde % 50 kaolin, % 5 kuvars ve % 5 feldspat silikat gibi kimyasal malzemeler karıştırılarak ve yüksek ısılarda fırınlanarak elde edilirler. Ani ısı farklarından çok az etkilenirler ve cama göre daha dayanıklıdırlar. Üzerinde daha az kaçak akım meydana gelir. Malzemeye şekil verilip kurutulduktan sonra yalıtkanlık dayanımlarını arttırmak için üzeri püskürtme veya daldırma yöntemlerinden birisi kullanılarak beyaz veya kahverengi sır tabakası ile sırlanır. Sırlama işlemi ile izolatör yüzeylerinin pürüzsüz ve kaygan olması sağlanır. Böylece, izolatörün kir ve yağmur suyu tutması, ortamdaki nemi emmesi engellenmiş olur ve dolayısıyla kirlenmeye bağlı kaçak akımlar oluşmaz. Sır maddesi; Kaolin, mermer, feldspat ve renk verici maddenin 400 C de karıştırılmasıyla elde edilir. Sır tabakası ani ısı farklarından etkilenmemeli, atmosferdeki asidik ve alkali etkilere karşı dayanıklı olmalıdır; çünkü, sır çatladığı takdirde izolatör yalıtkanlıktan uzaklaşarak kaçak akımları iletmeye başlar. Elektrik enerjisinin, izolatördeki çatlaklardan ani ve kesintili olarak sıçraması kıvılcım şeklinde meydana gelir. İzolatörün yalıtkanlığı yetersiz ise izolatör içinden izolatör sabitleme demirine doğru bir akım meydana gelir. Bu durumda, izolatörde elektriksel delinme olayı gerçekleşir.. Cam izolatörler: Cam malzeme, porselene göre daha ucuz olmasına rağmen porselene göre daha az tercih edilir. Bunun sebeplerini sıralamak gerekirse; sodyum silikat ile kalsiyum silikat karışımından elde edilen cam izolatörler; üzerlerinde oluşan nemi tutarlar ve bu sebeple; hava tozları, yüzeylerinde yoğunlaşıp kir meydana getirirler. Bu kirler ise elektriksel atlamalara ve kaçak akımlara neden olur. Bir diğer dezavantajı da camın cinsine göre ortam sıcaklığı yalıtkanlığı etkileyebilir. Bu etkiyi en alt seviyeye çekmek için preks türü camlar kullanılır. Cam izolatörler yumuşama noktasına kadar ısıtılıp sonra aniden soğutulur. İzolatörün iç kısmı yumuşak olarak kalırken önce dış kısmı, daha sonra da iç kısmı katılaşmaya başlar. Camın mukavemeti 5-6 kat artırılmış olur, bu artışa parallel olarak elektriksel delinme zorlaşır ve böylece cam izolatör; deşarj akımlarının neden olduğu termik değişimlere karşı daha dayanıklı hale gelir. Cam iyi tavlandığı taktirde yüksek bir özdirence ve elektriksel mukavemete sahip olabilir. Şeffaf olması nedeniyle camdaki çatlaklar kolaylıkla görülebilir. Çatlak olan cam izolatör etrafa dağıldığı için arıza tespiti porselene göre daha kolay olur. Yüzeysel boşalma gerilimini büyütmek için katı yalıtkan maddenin yüzeyine uygun sayıda ve biçimde çıkıntılar eklenir. Uygun koşullarda, 5 kv'a kadar cam izolatörler kullanılabilir. 3. Epoksi reçineli izolatörler: Epoksi reçine kullanılarak üretilen izolatör çeşididir. Porselen ve cama göre uygulama alanları çok azdır, gerekli olmadıkça tercih edilmezler. Enerji iletim hatlarında kullanılacak izolatörler; işletme gerilimine, hat güzergahına, kullanım açısına, iletken kesitine, iletken cinsine ve yüzey kirlenmesine göre seçilmelidir. İletim gerilimi, kullanılacak olan izolatörün ebatlarını belirler. Gerilim değeri arttıkça izolatör boyutu büyümektedir. Enerji hattının izleyeceği güzergah boyunca hava şartlarının ve çevresel etkilerin izolatörü ne derecede etkileyeceği iyi tespit edilmelidir. İletimde kullanılacak kesite göre izolatör kopma kuvveti seçilmelidir. İzolatörün yalıtkanlık yeteneğini, nem ile birlikte izolatörün yüzeyinde oluşan kirlenme etkiler. Deniz kıyılarında tuzlu su, sanayi alanlarında çeşitli tuzlar, demir tozları, kum taneleri ve tarım alanlarında havada uçuşan gübre tozları nemli ortamda izolatör yüzeyine yapışarak iletkenliğe neden olabilir. 07
112 Kullanım amaçlarına göre izolatörler, üç farklı gruba ayrılırlar;. Mesnet izolatörler: Enerji hatlarının ve baraların, kesinlikle temas edilmemesi gereken elektriksel kısımlarından yalıtımını sağlayan izolatörlerdir. Tek parçalı olarak imal edilen mesnet (fincan) tipi izolatörler 33 kv'a kadar emniyetle kullanılabilirler. Daha büyük gerilimlerde tek parçalı büyük izolatörler kullanmak gerekir. Bu izolatörleri tek parçalı olarak üretmek zor olduğundan dolayı çok parçalı olarak yapılırlar. Bu parçalar daha sonra beyaz çimento ile birbirlerine yapıştırılarak 80 kv'a kadar gerilimlerde kullanılabilirler. Ancak daha büyük gerilimlerde zincir tipi izolatör kullanmak hem ekonomik hem de daha emniyetlidir. Mesnet izolatör kullanılan hatların direk boyları daha kısadır. Direk boyunun kısalması hattın birim maliyetini azaltır. Bunun yanında arızalanan bir mesnet izolatörünü değiştirmek zordur. Mesnet izolatörlerde iletken, izolatörün üst veya yan yuvasına yerleştirilir ve özel bir klemensle izolatörün boynuna sabitlenir. İzolatör ise direğe, çubuk veya deveboynu şeklindeki bir izolatör demiri ile tutturulur. Yağmurda bütün izolatör yüzeylerinin ıslanmaması için bu izolatörlerin etekleri aşağı doğru yönlendirilmiş şekilde imal edilir. Porselenin havaya göre dielektrik katsayısı 4-6 kat daha fazladır. Dolayısıyla elektriksel zorlamanın büyük bir kısmı havaya isabet eder. Bu nedenle ceketler arasındaki hava aralığı oldukça büyük tutulur. Eğer bu mesafe kısa tutulursa büyük atlamalar oluşur. Bu da hem ark atlama mesafesinin, hem de kaçak yolun küçülmesine neden olur. Kaçak direnç ise mesafe ile doğru, kesit ile ters orantılıdır. Bu nedenle belli aralığa varıldıktan sonra ceket çapının arttırılması kaçak direnci önemli ölçüde arttırmaz. Kaçak direnci artırmanın yolu; izolatörün boyunu artırmak veya kesitini azaltmaktan ziyade ceket sayısını arttırmakla mümkündür.. Zincir izolatörler: Aynı tip malzemelerden yapılmış izolatörlerin birbirine eklenmesi sonucu oluşan izolatörlere zincir izolatörler denir. Mesnet izolatörleri 80 kv'a kadar olan gerilimler için imal edilirler. Zincir izolatörler ise zincirdeki eleman sayısı arttırılarak daha büyük OG ve YG gerilimlerde kullanılabilir. Zincir izolatörlerin tercih nedenlerini şöyle sıralayabiliriz; Hat geriliminin arttığı durumlarda zincirdeki eleman sayısı arttırılarak kullanılabilir. Mesnet izolatörlere göre daha hafiftir. Zincir izolatörler daha ekonomiktir. Mukavemetleri ve mekanik dayanımları fazladır. Zincir izolatörler kafes tipi demir direklerde kullanıldıklarında; iletkene yıldırım düşme ihtimali azdır. Şöyle ki; bu tip izolatörlerde iletken, her taşıma noktasında toprakla irtibatlı konsolun altında ve zincir sonunda asılı halde bulunur. Bu da bir nevi paratoner görevi yapar. (K) ve (VK) olmak üzere iki çeşit zincir izolatör vardır. (K) tipi zincir izolatörlerde porselen veya cam eteğin üzerine dökme demir kep geçirilmiş, göbeğine ise alttan başlı demir yerleştirilmiştir. Bu tip izolatörlerde elemanlar arası bağlantıyı sağlayan çelik çubuğun, eleman içindeki yuvasına montaj şekli önemlidir. Bu montaj şekliyle kuvvet, porselendeki çekme yerine baskı kuvvetine çevrilmiştir. Tespit yerindeki çelik çubuklar ile porselen arasındaki boşluğun kurşun veya çimento ile doldurulması gerekir. (VK) tipi zincir izolatörlerde ise (K) tipinden farklı olarak, porselenin baskı yerine çekme kuvvetine maruz kalmasıdır. (VK) tipi elemanlarla kurulu bir zincir tip izolatörün eleman sayısı, (K) tipi elemanlarla kurulu zincir tip izolatörün eleman sayısına göre daha azdır. Ancak; gerek (K) tipi zincir izolatörde, gerekse (VK) tipi zincir izolatörde zincir uzunluğu hemen hemen aynıdır. 3. Geçit izolatörler: Kesicilerde, kondansatörlerde, transformatörlerde ve diğer işletme araçlarının gerilim bağlantısında kullanılırlar. Geçit izolatörlerinin orta kısmında bir flanş bulunur. Bu flanş yardımıyla izolatör, cihaza veya duvara sabitlenir. Gerilim büyüklüğüne göre boyutları değişim gösterir. Geçit izolatörlerde yüzeysel boşalmaları önlemek için izolatör yüzeyi çıkıntılı yapılır. Yüksek-gerilimlerde porselenden başka ilave sıvı veya katı yalıtkan maddeler de kullanılabilir. Örneğin; 400 kv'luk bir transformatörün geçit izolatörlerinin boyu yaklaşık 6 m, çapı m ve ağırlığı ise 4,5 ton civarındadır. Geçit izolatörlerinin iç izolasyonunda hava, yağ veya kağıt kullanılır. 08
113 PARAFUDRLAR Parafudrlar, enerji nakil hatlarını, jeneratör ve transformatörlerin yalıtkanlarını yıldırımın zararlı etkilerine karşı korumak amacıyla kullanılan koruyucu devre elemanlarıdır. Enerji iletim hatlarında meydana gelen aşırı gerilimler genellikle aşağıdaki nedenlerden dolayı ortaya çıkar; İletim hatlarındaki arızalar sonucunda. Yıldırımın hatta düşmesi sonucunda. Geçici olaylar sonucunda. İletim hattındaki açma-kapama işlemlerinde. Atmosfer şartlarından dolayı ortaya çıkan yüksek-gerilimler, genelde yıldırımın hat üzerine düşmesi sonucunda ortaya çıkar. Yıldırım, hat ile toprak arasında meydana gelen bir yük boşalmasıdır. Bu yük boşalması, toprağın yüküne ve bulutta biriken yük durumuna göre, topraktan buluta veya buluttan toprağa doğru olabilir. Hat üzerine düşen yıldırım milyonlarca voltluk gerilim meydana getirebilir. Bu gerilim dalgası; hattın her iki yönünde ilerleyip hat üzarinde bulunan yalıtkanlar üzerinden atlayarak birçok alet ve makinayı kullanılamaz hale getirir. Işık hızına yakın bir hızla hareket eden yıldırım, etkisini düştüğü noktadan uzaklaştıkça hızla kaybeder. Özellikle parafudrlar, trafoların giriş ve çıkışları ile baralarda sıkça kullanılır. Parafudrlar normal şartlarda toprağa karşı akım geçirmezler. Fakat hat üzerine yıldırım düşmesi sonucunda aşırı değerlere yükselen akım, parafudr üzerinden toprağa akar. Parafudr, yıldırımın ani etkisini kaybetmesiyle normal çalışma koşullarına döner. Normal çalışmada ise parafudr, açık-devre durumunda olan bir elemandır ve bu anda toprağa herhangi bir yük boşalması meydana gelmez. AYIRICILAR Güç sistemlerinde, OG ve YG iletim hatlarında devre yüksüz halde iken açma-kapama işlemi için kullanılan ve tasarım bakımından en basit tipteki ayırma elemanına ayırıcı veya diğer adıyla seksiyoner adı verilir. İletim aşamasında, bölümleri birbirinden ayırarak şebeke üzerindeki bakım ve control işlemlerinin güvenli bir şekilde yapılmasını sağlar. Ayrıca; çoklu ana baraya sahip şebekelerin açmakapama işlemine hazırlanması ve birbirlerine bağlanmasında önemli rol oynar. Ayırıcılarda dikkat edilmesi gereken en önemli nokta; devredeki açma-kapama işleminin yüksüz olarak yapılması zorunludur, yük altında ayırıcı üzerinden akım geçerken açma-kapama işlemi kesinlikle yapılmamalıdır. Yüklü durumdayken bu işlem gerçekleştirilirse; ayırıcı ve ayırıcıya müdahale eden operatör zarar görebilir. Bu nedenle şebeke üzerinde sırasıyla; önce kesici açılmalı, kesici açıldıktan sonra da ayırıcı açılmalıdır. Genel olarak; ayırıcılar yedi farklı bileşenden oluşurlar. Bunlar;. Hareketli kontaklar: Açma-kapama işleminde hareket aksamıyla beraber hareket eden kontaklardır. Ayırıcı üzerindeki hareketli kontakların sayısı üç adettir. Kapama işlemi sırasında sabit kontaklarla birleşerek devreyi kapatırlar. Eğer kontaklar birbirlerine düzgünce birleşmiyorlarsa elektriksel ve mekanik etkilere karşı dayanıksız olurlar. Temassızlık sonucu kontaklarda ark ve ısınma oluşur ve sonuç olarak; ayırıcı kısa sürede arızalanır. Hareketli kontaklar elektrolitik bakırdan üretilerek üzerleri gümüş kaplanır.. Kilit: Bıçaklı ayırıcılarda hat ayırıcısı ile toprak bıçağı arasında bulunan ve her iki aksamın senkronize biçimde açılıp kapanmasını engelleyen elektriksel veya mekanik cihazlardır. Kilit düzeneği sadece hat ayırıcılarında kullanılır. 3. Mesnet izolatörleri: Ayırıcı üzerindeki gerilim altında bulunan kısımlardan ve topraktan yalıtılmış, üzerine sabit kontak ve hareketli kontakların monte edildiği yalıtkan kısımdır. Mesnet izolatörlerin sayısı altı adet olup, harici tip ayırıcılar 0-5 mm/kv kaçak mesafeli olarak porselen malzemeden yapılır. Dahili tip izolatörler ise porselen veya epoksi adı verilen reçineden imal edilir. 4. Şase: Açma-kapama düzeneğinin ve izolatörlerin sabitlendiği köşebent veya profilden imal edilen metal parçadır. Şaseler genellikle daldırma galvanizli veya elektrostatik toz boyalı olarak üretilir. 09
114 5. Mekanik Düzen: Açma-kapama işleminde hareketli kontakları hareket ettiren kısımdır. Boyutları, ayırıcının çeşidine göre değişir. Hareket için kullanılan tahrik milleri 30 mm çapında galvanizli çelik malzemeden yapılır ve pirinç döküm yataklarda hareket eder. Dönme hareketinin daha kolay olması için bazı ayırıcı modellerinde pirinç yataklar gresörlükle donatılmıştır. Gresör, yağlama işlemi yapan bir elemandır. 6. Sabit Kontaklar: Açma-kapama esnasında sabit kalan hareketsiz parçalardır. Üç-fazlı sistem için ayırıcı üzerindeki sabit kontakların sayısı, her faz için bir tane olmak üzere toplamda üç adettir. Bu kontaklar anma ve kısa-devre akımlarına uygun olarak bakır malzemeden üretilirler. 7. Yaylar: Yük ayırıcılarında ve özel tip ayırıcılarda kullanılırlar. Elektrolitik bobinden üretilerek açma-kapama işleminin hızlı şekilde gerçeklemesini sağlarlar. Ayırıcı Çeşitleri ve Özellikleri; Monte edildikleri yere göre ayırıcılar iki çeşittir;. Dahili Tip Ayırıcı: Dahili tip ayırıcılar bina içlerinde, duvar veya sac hücreler üzerine monte edilir ve ayırıcının mekanik kumanda kolu hücre dışında bırakılır. Gerilim altındaki hücre içi kısımlar tel kafesle emniyet altına alınır. Bu ayırıcılar açık alanlarda kullanılmazlar.. Harici Tip Ayırıcı: Harici ayırıcılar direk üzerinde veya açık hava şebekelerde kullanılır. Dahili tip ayırıcıların açık havada kullanılamayacağı hesaba katılarak açık hava şartlarına göre üretilirler. Kumanda mekanizması, kullanıcı operatörün rahatça açıp kapatabileceği şekilde tasarlanır. Yapı özelliklerine göre ayırıcılar, dokuz farklı gruba ayrılırlar;. Tek döner izolatörlü ayırıcı: Bu ayırıcılar yüksek ve çok yüksek gerilimli trafo merkezlerinde 60, 54, 00, 380 ve 800 kv gerilim değerlerinde kullanılırlar. Bu tarz ayırıcıların izolatörlerinden birisi kendi etrafında dönebilecek şekilde tasarlanmıştır. Döner izolatörün üzerinde çıkıntılı bir kontak bulunur. Ayırıcıya ait hareketli kontağın kendi ekseni etrafında 90 dönmesi sonucu bu çıkıntılı kontak, sabit izolatör üzerinde bulunan girintili kontak ile birbirine yapışır ve ayırıcı kapanmış olur.. Çift döner izolatörlü ayırıcı: Her iki kontağı da kendi ekseni etrafında 90 dönebilecek şekilde dizayn edilmiştir. Bu kontaklar kendi etraflarında döndürülerek devreyi kapama işlemi rahatça gerçekleştirilir. Bu tip ayırıcılar genellikle zorlu hava şartlarının hakim olduğu yerlerde tercih edilir. 3. Toprak ayırıcı: Dahili veya harici olarak imal edilen bu ayırıcılar, hattın girişine veya çıkışına konulan ve hattın enerjisi kesildiğinde toprak bıçağını kapatarak hat üzerinde biriken yükü toprağa aktaran ayırıcılardır. Böylece hattın enerjisi kesildikten sonra topraklama ayırıcısı kapatılarak hat üzerinde emniyetli çalışma ortamı sağlanmış olur. Topraklayıcılar ve kısa-devre topraklayıcıları, enerjisi kesilen bölümlerin topraklanmasında ve kısa-devre topraklamasında kullanılırlar. Topraklayıcılar, kısa-devre darbe akımları kv'ta 5 ka'e ve 36 kv'ta 80 ka'e kadar olan ayırıcılara doğrudan monte edilebilirler. 4. Dahili tip bıçaklı ayırıcı: Bu ayırıcıların hareketli kontakları bıçağa benzediği için bu şekilde adlandırılırlar. Bu tip ayırıcılar bina içerisindeki hücrelere yerleştirilerek kumanda kolu emniyetli mesafede hücre dışına çıkarılır. Dahili tip bıçaklı ayırıcıların çalışma gerilimleri 0, 5, 30 ve 45 kv olup, akımları ise 400, 630, 50, 600 A'dir. Basit bir dahili tip bıçaklı ayırıcı; mesnet izolatörü, şase, kollu hareket mekanizmaları, sabit ve hareketli kontaklardan meydana gelir. Ayırıcı kontakları standart olarak nikel veya isteğe bağlı olarak gümüş kaplamalı olup, profillendirilmiş bakır malzemden imal edilir. Örneğin; 50 ve 600 A anma akımına sahip dahili tip bıçaklı ayırıcıların bıçakları ile sabit kontakları gümüş kaplamalı olarak yapılır. 5. Harici tip bıçaklı ayırıcı: Harici tip bıçaklı ayırıcılar, bina dışındaki direk üzeri veya açık hava şebekeleri gibi yerlerde kullanılırlar. Bu yüzden harici tip bıçaklı ayırıcılar havanın ısı, nem veya rüzgar gibi olumsuz şartları göz önüne alınıp, buna uygun olarak imal edilmelidirler. Bu tip ayırıcılardaki kumanda kolu, güvenli mesafede ayakta durarak açma-kapama yapan bir kişinin bu işi rahatça yapabilmesine imkan verecek özellikte olmalıdır. Enerji hattının bağlandığı ayırıcılarda, hattın enerjisi kesildikten sonra hat üzerinde biriken elektrik yükünü toprağa aktarmak için bıçaklı ayırıcıya bir de topraklama ayırıcısı ilave edilir ve her ikisi arasına bir kilit tertibatı konulur. Böylece asıl ayırıcı açılmadan topraklama ayırıcısı kapanmaz. 0
115 6. Sigortalı ayırıcı: Aşırı darbe akımlarında; kontaklarına seri olarak bağlı sigortası devreye giren, bağlı olduğu hat üzerindeki arızaları şebekenin diğer kısımlarına hissettirmeyen ve devreyi açan ayırıcı çeşididir. Bir kez devreye girip devreyi açan sigortaya tekrar tel sarılmaz, atmış halde bulunan sigorta yeni ve orjinali ile değiştirilir. Sigortalı ayırıcılar; köy sapmalarında, küçük güçlü müşteri sapmalarında, 400 kva'e kadar olan direk tipi trafoların girişlerinde, OG modüler hücrelerinde, gerilim, ölçü ve servis transformatörlerinin girişlerinde kullanılırlar. 7. Çabuk açma-kapamalı (Otomatik) yük ayırıcı: Biri açma diğeri kapama olmak üzere iki adet yayı vardır. Açma işlemi operatör müdahalesi ile olabildiği gibi bir röle veya sigortanın etkisi ile olabilir. Kapama işlemi ise sadece operatörün müdahalesiyle mümkündür. 8. Alttan sigorta ilaveli yük ayırıcı: Sigortalar mekanik çarpmalı, pimli cihazlar olup, herhangi bir arıza veya kısa-devre durumunda Newton'luk bir çarpma kuvvetine sahiptir. Herhangi bir nedenle sigorta atması sonucu sigortanın pimi, açma mekanizmasını uyararak şalterin otomatik olarak açılmasını sağlar. Bu tür ayırıcılar, herhangi bir nedenle sigortalardan birisinin atmasından sonra ani olarak devreyi açarak tesisin tek veya iki faza kalmasını önler. Şaltere bir açma magneti ilave edilerek, trafodaki termometre veya Bucholz rölesinden gelebilecek bir etki ile otomatik olarak açma yapmak mümkündür. 9. Tek salt yaylı yük ayırıcı: Tek salt yayı vardır. Kontaklarının pozisyonu gözle görülebilen, normal yüklü devreleri açıp kapatan, kesiciden tasarruf etmek amacıyla kullanılan ayırıcılardır. Yük ayırıcılarının kullanıldığı bir yerde ayrıca kesici kullanmak, masrafı gereksiz yere 3-5 kat artırır. Tek bara sistemlerinde tek güç ayırıcısının bulunduğu yerlerde bu ayırıcıların devresine seri olarak bağlı bir YG sigortası bulunur. Yük ayırıcıları, OG şalt tesislerinde ayırıcılar ve kesiciler arasındaki büyük boşluğu doldurmak amacıyla geliştirilen cihazlardır. Bu ayırıcılar genellikle dikey olarak monte edilir. Ayırıcı, yatay olarak monte edilecekse kesme gücünün %0 azalacağı unutulmamalıdır. Toplam açma süreleri 0, saniyedir. Kapama işlemi sırasında önce ana bıçak kontaklar, daha sonra yardımcı çabuk açma kontakları kapanır. Açma işleminde ise önce ana bıçak kontaklar, hemen sonra, çok kısa bir süreliğine yükü üzerine alan çabuk açma kontak çubukları devreden çıkar. Çabuk açma kontak çubuklarının ucuna, yüksek ısıya dayanıklı özel sert metal parça eklenmiştir. Açma işlemi sırasında bu metal parça ile ayırıcının sabit kontağı arasında meydana gelen ark, ark söndürme hücrelerinde söndürülür. Ark söndürme süresi yaklaşık olarak 0-45 milisaniyedir. Ark hücreleri kuru sistemlerdir. Söndürme hücrelerinde arkı söndürmek için herhangi bir akışkan veya tazyikli hava kullanılmadığı için bu hücrelerin tozunu almaktan başka bir bakım gerekmez. Otomatik açma-kapama yapamaz. Sadece operatörün isteği ile açma-kapama yapabilir. Otomatik açmanın istenmediği yerlerde, yük altındaki açma-kapamalarda, yük manevralarında ve ring şebekelerde büyük emniyet ve kararlılıkla kullanılabilir. Bir şalt tesisindeki ani kısa-devre akımlarına karşı koruma ana kesiciler yardımıyla yapılır. Fakat tesis özelliğine göre yük ayırıcılarının bulunduğu yerlerde de ani kısa-devre akımlarına karşı koruma istenirse şalterin alt ya da üstüne sigorta ilave edilebilir. Görevlerine göre ayırıcılar altı gruba ayrılır;. Bara ayırıcı: Enerji iletim hatlarında kesici ile bara arasına bağlanan ve kesicinin açık olduğu durumlarda açma-kapama işlemi yapabilen ayırıcılardır.. Bara bölümleyici ayırıcı: Gerilim değerleri eşit olan baraların birleştirilmesi veya birbirlerinden ayrılması amacıyla kullanılan ayırıcılardır. 3. Topraklama ayırıcı: Arıza sonucu enerjisiz kalan iletim hattı üzerinde artık yükler kalabilir. Enerji iletim hatlarında hat üzerinde biriken artık kapasitif elektrik yükünü toprağa aktarmak için kullanılan özel tip ayırıcılardır. Birlikte kullanıldığı kesici açıldıktan sonra toprak ayırıcısı kapatılarak toprağa yük boşalması gerçekleştirilir. İletim hattında enerji varken toprak ayırıcısının kapanmasını engellemek amacıyla farklı şekillerde kilit mekanizmaları geliştirilmiştir. Bu mekanizmalar sayesinde, kesici ve ayırıcı kapalı durumdayken topraklama ayırıcısının kapanması engellenmiş olur. Hat veya direk üzerinde kullanılan topraklama ayırıcıları açıldığında hattın enerjisiz olan çıkış uçları topraklanır. OG modüler hücre sistemlerinde kullanılan ayırıcılarda kilitleme sistemleri sayesinde, diğer ayırıcılar devredeyken topraklama ayırıcısı kapatılamaz. 4. Hat ayırıcı: İletim hattının giriş ve çıkışlarında, kendisiyle birlikte kullanılan kesici ile hat arasına bağlanırlar. Bu ayırıcılar, birlikte kullanıldığı kesici açık iken açma-kapama yapabilirler.
116 5. By-pass ayırıcı: Kesiciye paralel bağlanan ve kesici kapalı iken açılıp kapatılabilen ayırıcılardır. Ayrıca, kesici arızalı veya bakımda olduğu zaman kesici gibi kullanılarak baraya enerji vermeye yarayan bir yük ayırıcısıdır. 6. Transfer ayırıcı: Tek baralı sistemde transformatör ve hatlar; kesici ve ayırıcılar üzerinden aynı baraya bağlıdır. Tek baralı sistemde arıza olduğunda veya bakım anında sistemin enerjisi kesileceğinden sistem komple enerjisiz kalır. Çift bara sisteminde iki adet bara mevcuttur. Bu baralardan; bara giriş kısmının ve hat kesicilerinin ayırıcılar üzerinden bağlı olduğu baraya ana bara denir. Hat ve transformatörlerin bir ayırıcı ile bağlı olduğu baraya ise transfer bara denir. Normal işletme şartlarında ana bara enerjilidir. Transfer bara ise enerjisizdir. Ana bara ile transfer bara arasındaki ayırıcıya transfer ayırıcı denir. Bu sayede sistemde bir arıza meydana geldiğinde veya bakım yapılacağı zaman transfer bara ve transfer ayırıcılar yardımıyla şebekenin enerjisiz kalması önlenir. Bu ayırıcılar, çıkış beslemesine ait (fider) kesici ve ayırıcılarda bakım veya arıza olduğu durumlarda enerjinin sürekliliğini sağlamak amacıyla transfer bara üzerinden fiderin beslemesini sağlarlar. Kumanda şekillerine göre ise ayırıcılar dört bölümde incelenebilir;. Elektrik motoru ile kumandalı ayırıcı: Ayırıcıda açma-kapama işlemini yapan düzeneğin hareketi, bir DC veya AC motor yardımıyla gerçekleştirilir. Bu tip ayırıcılarda motorun dönme hareketi, özel bir dişli yardımıyla çıkış miline transfer edilir. Motor bir yönde döndüğünde ayırıcı kapanır, diğer yönde döndüğünde ise ayırıcı açılır. Motor, motor dişli sistemi ve yardımcı kontak sistemi, ısıtıcılı ve kapalı şekildeki bir kutu içerisine alınarak dış etkilere karşı korunmuştur.. Mekanik kumandalı ayırıcı: Açma-kapama işlemi, 30 mm çapında ve 3 m boyundaki galvanizli çelik malzemeden yapılmış, elle kumanda edilen bir cihaz yardımıyla gerçekleştirilir. Bazı mekanik kumandalı ayırıcılarda ise bu cihaz dişli hareketinin iletilmesi ile çalışır. 3. Elle kumandalı ayırıcı: Emniyet mesafesi yeterli olan bazı ayırıcı türlerinde açma-kapama işlemini gerçekleştiren mekanik kol, ıstanka adı verilen ucu kancalı, fiber malzemeden yapılan, uzun sopa şeklindeki alet yardımı ile manuel olarak el ile kumanda edilir. 4. Basınçlı hava ile kumandalı ayırıcı: Açma-kapama işlemini gerçekleştiren mekanik düzenek, hava basıncıyla çalışan pnömatik bir sistemle kontrol edilir. Pnömatik sistemin düz çalışmasıyla ayırıcı kapanır, ters çalışmasıyla ise ayırıcı açılır. Ayırıcılarda Açma-Kapama İşlem Sırası İletim hattı üzerinden bir akım geçiyorsa ya da başka bir deyişle devre yüklü iken ayırıcılarla açmakapama işlemi yapılmaz. Kesici ve ayırıcılarla yapılan işlemlere manevra adı verilir. Ayırıcılarda açmakapama işlemi aşağıdaki sıraya göre yapılmalıdır.. İlk olarak kesici açılarak hat enerjisi kesilir.. Kesicinin giriş ve çıkışındaki ayırıcılar açılır. 3. Devrede kesici yoksa, önce hat alıcılarının yükü devreden çıkarılır, sonra ayırıcı açılır. 4. Kapama işleminde ise bu işlemlerin tersi yapılır ve önce ayırıcılar kapatılır. 5. Daha sonra kesici kapatılarak hatta enerji verilir. Ayırıcı Montajında Dikkat Edilmesi Gerekenler Ayırıcı girişine bağlanan iletken ve bara değerleri, ayırıcıdan sonra kullanılan iletken ve bara değerlerinden daha küçük olmamalıdır. Ayırıcıların bağlantı noktaları bakırdan imal edilmiştir. Havai hat tarafından gelen iletken alüminyum olduğu için bu tarafta alüminyum/bakır klemensler kullanılır. Havai hat iletkeni klemensin alüminyum kısmına, ayırıcı bağlantı noktasındaki iletken ise klemensin bakır kısmına sıkıca bağlanır. Bara ve kablo iletkenleri ayırıcıya, bağlantı yerinde itme, çekme veya döndürme kuvveti oluşturmayacak şekilde bağlanmalıdır. Ayrıca daire kesitli iletken kullanılmışsa, iletkenin ayırıcı bağlantı noktasında mutlaka özel klemens kullanılmalıdır. İletken bağlanmadan önce klemensin altını şalterin bağlantı noktalarına monte etmek gerekir.
117 Ayırıcı Montajında İşlem Sırası Harici Sistemlerde: Havai hat tarafından gelen hattın iletkenlerinin boyu, ayırıcının sabit kontağına denk gelecek şekilde uygun uzunlukta kesilir. Kesme işlemi yapılırken bölgenin kar, rüzgar, yağmur gibi iklim şartları göz önünde bulundurulmalıdır. Ayırıcının sabit kontağına havai hat tarafından gelen iletkenler alüminyum/bakır klemens ile bağlanır. Ayırıcının hareketli kontak tarafında bakır bağlantı noktalı sigorta altlığı bulunur. Sigorta altlığı bağlantı noktaları bakır olduğu için, bu nokta ile trafo arasında bakır iletken ölçülerek kesildikten sonra klemenslere sıkıca tutturulur. Topraklama bağlantı noktası topraklama şeridi ile birleştirilir. Dahili Sistemlerde: Dahili sistemlerdeki ayırıcı bağlantısı baralarla yapıldığı için ayırıcı yerine sabitlendikten sonra itinayla bükümleri yapıldıktan sonra kontaklarına baralar bağlanır. Herbir faz için, ana bara ile ayırıcı bağlantı noktalarının ölçüsü alınır. Alınan ölçülere göre kesilen baralar uygun şekilde büküldükten sonra üzerine bağlantı delikleri açılır. Herbir faza ait bara, ait olduğu ana baraya sırasıyla bağlanır. Kumanda sisteminin bağlantısı yapılır. KESİCİLER Kesiciler konusunu incelemeden önce bu konunun daha iyi anlaşılabilmesi için öncelikle ark kavramının irdelenmesi lazımdır. Kesicilerin varlığının sebebi olan ark, elektrik tesislerinde açma-kapama olayı esnasında kontaklar arasında meydana gelen elektrik atlamasına denir. OG ve YG de yük akımı kesilirken yüksek değerde ark oluşur. Kesici, arkın, kısa-devre akımının ve yük akımının şebekeye olan zararlı etkilerini yok edecek şekilde tasarlanıp geliştirilen koruma elemanıdır. Devrede meydana gelen ark, çok kısa sürede söndürülmezse hem kontaklar arasında elektrik akışı devam eder hem de kesici görevini tam olarak yapamaz. Arkı söndürücü özelliğinden dolayı kesiciler, şebekede kullanılan diğer sistem elemanlarını korurken aynı zamanda insanların can güvenliğini de sağlar. Ark söndürme işleminde en çok kullanılan yöntem; kesici içerisindeki ark yolunun uzatılmasıdır. Ark, uzatılarak inceltilir. Böylece arkın direnci artırılmış olur. Direnci artan arkın akımı düşer, sıcaklığı azalır ve enerjisi, iyonizasyonun devam etmesinde yetersiz kalır. Ayrıca, açma işleminin ardından tekrar ark oluşmaması için kontaklar birbirlerinden yeteri kadar uzaklaşmış olmalıdır. OG de anma gerilimleri kv'dan 36 kv'a kadar, YG de ise 5 kv'dan 765 kv'a kadar olan kesiciler üretilmektedir. Kesicilerin en önemli görevi; kısa-devre sırasında devreyi açmaktır. Hattaki yük akımı kesilirken önce kesici, sonra ayırıcı açılır. Kesiciler, kendilerinden önce gelen devre elemanlarını arızalı yerden ayırarak bu elemanların şebekeye yaptıkları zorlamanın önüne geçer. İdeal bir kesici; açma sırasında meydana gelen arkı çok hızlı şekilde söndürebilen, süratli ve ardarda açma-kapama yapabilen, kontakları nominal akım altında ısınmayan, kısa-devre akımlarını bir süre taşıyabilecek özellikte olmalıdır. Alternatif akımın özelliği gereği kesici, bir tam periyotta sinüssel akımın sıfırdan geçtiği zaman noktasında devreyi açabilirse; kontakları arasında herhangi bir ısınma meydana gelmez. Bu ise, hem kesicinin hem de devrede kullanılan elemanların ömürlerinin uzaması ve fazla yıpranmaması anlamına gelir. Kesicilerde akım oluşması ve açma olayı, devredeki akımın doğru veya alternatif akım olmasına göre değişiklik gösterir. Doğru akımda meydana gelen ark, alternatif akımda meydana gelen arktan daha zor kesilir. Çünkü alternatif akım her bir yarım periyotta sıfır değerini aldığı için oluşan ark da her yarım periyotta sıfır değerini alır. Fakat doğru akımda, akım değeri hiç bir zaman sıfır olmadığından dolayı oluşacak arkın değeri de sıfır olmaz. Kesiciler iki temel kısımdan oluşurlar. Bunlar; 3
118 Sabit ve Hareketli Kontaklar: Kontaklar yağlı ve parçalı dilimli olarak yapılmış olup, biri hareketli diğeri ise sabittir. Kesicinin akım taşıyan kısmıdır. Ark söndürme hücresi: Kontakların birbirinden ayrıldığı bölümdür. Ayrılma işlemi esnasında arkın meydana geldiği ve yine bu arkın söndürüldüğü ortam ark söndürme hücresidir. Kesicinin tipine göre boyutları. Ark söndürme hücrelerinde arkın boyu ark seperatörleri yardımıyla parçalara ayrılarak söndürme işlemi hızlandırılır. Kesicilerde, devreyi açma işlemi sırasında oluşan arkın etrafında bir yağ dalgası oluşur. Meydana gelen bu yağ dalgası, arkın daha kısa sürede sönmesini sağlar. Genel olarak kesiciler, çalışma mekanizmalarına göre dört ana gruba ayrılır;. Elektromanyetik bobinli mekanizma: Kesicinin hareketli kontağı, mil çubuk ve demir çekirdekli bobinler tarafından hareket ettirilir. Demir çekirdekli bobin enerjilendiği zaman mil çubuk, bobindeki manyetik alan tarafından oluşturulan kuvvete bağlı olarak aşağı-yukarı hareket eder ve açma-kapama işlemi gerçekleştirilir.. Elle kurmalı yaylı mekanizma: Kesici kontaklarının kol gücüyle manuel olarak açılıp kapatıldığı düzenektir. Ancak, kesicilerde açma-kapama işlemi süratli yapılması gerektiğinden, ilaveten bu işlemi hızlandırması için yay kullanılır. Kilitleme düzeneği mevcuttur ve bu düzenek kapama sırasında yay aracılığıyla kurulur. Elle kumanda edilen bu sistemin kullanım alanı geniş değildir. Bu sistem daha çok küçük güçlü ve gerilimli kesicilerde kullanılır. 3. Basınçlı havalı mekanizma: Bu mekanizmalarda kesici kontaklarının açılıp kapanmasını sağlayan etki, kompresörden elde edilen hava kuvvetinden elde edilir. Bu mekanizma çeşidi genelde büyük güçlerin kumandasında kullanılır. Ancak, gürültülü çalışması ve kompresör için ayrı bir düzeneğin gereksinimi bu mekanizma için bir dezavantajdır. 4. Motorla sürülen yaylı mekanizma: Açma-kapama işleminin, 75 W gibi küçük güçlü, DC veya AC akımla çalışan motorlarla gerçekleştirildiği düzeneklerdir. Büyük güçlerin kumandasında kullanılır. Kumanda devresinde kontaktör ve limit anahtarı gibi elemanlar kullanılarak motorun dönüş yönü değiştirilir. Motor bir yönde dönerken kesici kontağını kapatır, ters yönde dönerken ise kontağı açar. Motor devreyi açarken aynı zamanda mekanizmadaki yayı da kurar. Sistemde enerji devamlılığı istenildiğinden kurulan yay, herhangi bir müdahaleye gerek kalmadan otomatik olarak kontakları tekrar kapatır. Genel olarak kesiciler ark söndürme ortamına göre altı farklı gruba ayrılır;. Tam yağlı kesiciler: Tüm açma-kapama ve ark söndürme işlemleri yağ içindedir. Tam yağlı kesiciler fazla miktarda yağ içerirler. Bu da yangın riskini arttırdığı için günümüzde pek kullanım alanları yoktur. Kesicinin devreyi açması esnasında kontaklar birbirinden ayrılır ayrılmaz ark oluşur. Bu sırada yağ, ark sıcaklığının etkisiyle gaz haline dönüşerek arkın etrafını bir gaz balonu şeklinde sarar. Kesme işleminde meydana gelen bu gaz ağırlıklı olarak hidrojen gazıdır ve ortamdan dışarı atılmalıdır. Atılmadığı takdirde basınç yükselir ve çevreye büyük zararlar verebilir. Belli bir basınca sahip olan gaz, yağı iterek seviyesini yükseltir. Kontaklar arasındaki mesafe arttıkça gaz balonu daha da büyüyerek yağ kazanının en üst kısmında bulunan havanın tamamının hava çıkış deliğinden dışarı çıkmasına neden olur. Belirli kontak açıklığında ve hızında bu basınç artışı ark sönünceye kadar devam eder. Bu sırada gaz balonu tarafından itilen yağ ise üst kapağa dayanır. Üst kapakta, çıkan havanın hacmi kadar gaz oluşur. Kesici içerisindeki havanın hacmi ne kadar büyükse; basınç o kadar küçük olur. Böylece kesici içerisindeki hava miktarı ayarlanarak basınç belirli sınırlar içinde tutulabilir. Burada yağ, hem söndürme maddesi olarak hem de kutuplar arasında ve kutuplarla topraklanmış kısımlar arasında yalıtım maddesi olarak görev yapar. Bu tür kesiciler, basit bir yapıya sahip olmaları, gaz patlama etkisinin olması, ekonomik olmayışları, kaçak güvenilirliğinin az olması, tekrar kapama işlemini yavaş yapmaları, ebatlarının çok büyük oluşu ve teknolojilerinin çok geri olması sebebiyle tercih edilmezler.. Az yağlı kesiciler: Az yağlı kesicilerin herbir fazı, izolatör ve hava aralığıyla birbirinden ayrıldıklarından ve herbirinin yağ hücresi bağımsız olduğundan daha az yağa ihtiyaç duyarlar. Bu gruptaki kesiciler; tam yağlı kesicilerin geliştirilmiş şekli olup burada kullanılan yağın görevi izolasyonu sağlamak değil, açma-kapama esnasında oluşan arkı söndürmektir. Ark kesme hücreleri fiber elemanlı sabit ark söndürme alanları ile donatılmış ve ark söndürme hücreleri 4
119 belirli bir basınca dayanabilecek şekilde boyutlandırılmıştır. Hareketli kontak, düşey olarak silindir plaka şeklindeki ark söndürme elemanlarının ortasında hareket eder. Ancak kontağın hareketi, kesici tipine göre alt kraterden veya üst kafadan başlayacak biçimde farklılık gösterebilir. Bu kesicilerdeki kesme işlemi de tam yağlı kesicilerde olduğu gibi yağ dolu kesme hücresinde gerçekleşir. Fakat az yağlı kesicilerdeki yağ miktarı tam yağlı kesicilerdeki yağ miktarından çok daha az olduğu için kullanılan yağ daha çabuk kirlenir (kontaminasyon) ve özelliğini kaybeder. Bu nedenle az yağlı kesicilerin bakımı ve yağ değişimi daha sık yapılmalıdır. Yağ içinde kapalı halde bulunan kontağın açılması sonucu meydana gelen ark, etrafında bulunan yağı buharlaştırarak büyük bir kısmını gaz haline getirir. Meydana gelen gaz ve buhar tanecikleri ark etrafında, içerisinde farklı sıcaklık seviyeleri bulunan bir küre meydana getirir. Kürenin en iç bölgesindeki ark çekirdeği en sıcak bölge olup, sıcaklığı yaklaşık C'dir. Bu bölgenin dışını gaz zarfı oluşturur. Daha sonra sırasıyla dışa doğru buhar bölgesi, buhar kabuğu bölgesi ve yağ bölgesiyle sona erer. Yağın buharlaşması sırasında meydana gelen gaz-buhar karışımı, yağın yüzeyine doğru çıkarken beraberinde arkı da hücre içindeki plakalar yardımıyla sürükler. Buhar ve gaz karışımı arkın etrafında girdap şeklinde dönerek çapını küçültür. Hem oluşan girdap etkisi, hem de ark yolunun uzamasıyla sönme işlemi daha kolay gerçekleştirilir. 3. SF 6 gazlı kesiciler: Kimyasal açılımı Kükürt Hegza Florür olan SF 6 gazının, delinme dayanımı havanınkinin -3 katıdır ve ark söndürme karakteristiği çok iyidir. Moleküler ağırlığı 46 dır. Oksijen molekülünün 3, Azot molekülünün 8 ağırlığa sahip olduğu düşünülürse hava yanında çok ağır bir gaz olduğu saptanır. Bu da; SF 6 nın sızıntılarda birikme özelliğine sahip bir gaz olduğunu gösterir. Normal şartlar altında renksiz, kokusuz, tatsız, zehirsiz, yanmaz bir gazdır. Ama kesicilerde beraberinde kullanıldığı karışımlarla ve ark esnasındaki ayrışmalar sonucu zehirleyici özelliği ortaya çıkabilir. SF 6 gazının termik ve elektronegatif özellikleri ideal bir ark kesme ortamı oluşmasını sağlar. Yüksek termik kapasitesi, ark esnasında oluşan ısıyı hızlıca uzaklaştırır. Hızlı rejenerasyon özelliği de kontaklar arasındaki dielektrik dayanımının hızla tekrar kullanılmasını sağlar. Bu kesiciler, kutup kısmı, açma-kapama mekanizması ve elektrik donanımı olmak üzere üç ana bölümden oluşur. Açma işlemi sırasında oluşan ark üzerine, kesme hücresinde bulunan ve piston vasıtasıyla sıkıştırılmış olan sabit basınçtaki SF 6 gazının üflenmesi sonucu arkın koparılması prensibine göre çalışır. Kesme hücresindeki SF 6 gazının basıncı,5 bar civarındadır ve bu gazın yalıtım özelliğinden dolayı kontaklar arası açılma mesafesi oldukça küçüktür. Kesicinin devreyi açması sırasında oluşan arkın üzerine basınçlı gaz üflenerek önce ark soğutulur sonra kontaklar arası ortam iletkenliğini kaybederek yalıtkan duruma geçer. SF 6 gazı, açma sıcaklığında kesme hücresine kükürt ve flor iyonları ile elektronlar gönderir. Bu sırada aşırı elektronegatif olan flor iyonları ortamda bulunan elektronları yakalayarak, bir elektrik akışı olan ark akımını sınırlar. SF 6 gazının ısıyı çabuk dağıtma özelliğinden dolayı hücre ortam sıcaklığı hızla düşer, ark soğur ve söner. Ark bölgesindeki sıcaklık C arasındadır. Bu sıcaklıkta SF 6 gazı ayrışarak ortama kükürt ve florür iyonları ve elektronlar verir. Bu sırada sıcaklık hızla düşer ve elektronegatif olan florür iyonları, ortamdaki elektronları yakalayarak akımı sınırlarlar. Aniden 000 C ye düşen sıcaklıkta, kükürt florür iyonları tekrar SF 6 gazına dönüşerek yalıtkan hale geçerler. Kesici tüm ömrü boyunca elektriksel özelliğini korur. Kesici içerisindeki ortam gaz olduğundan kesme sırasında basınç en fazla bir bar artarak,5 bara ulaşır. Bu kesicilerin bakımının daha zor olması, ilgili personelin daha iyi eğitilme gerekliliği ve bakım için özel cihazların gerekliliği bu kesicilerin olumsuz yanıdır. Gerilim dayanımları, basınçlı havalı kesicilere göre daha iyidir. SF 6 gazlı kesiciler, yalıtım sınıflarına göre, hava yalıtımlı ve gaz yalıtımlı olmak üzere ikiye ayrılır. Hava yalıtımlı kesiciler 7,5 ile 40 kv arası, gaz yalıtımlı kesiciler ise 36 ile 500 kv arasındaki gerilimlerde kullanılmaktadır. 4. Manyetik itmeli kesiciler: Bu gruptaki kesicilerde, açma işleminde oluşan arka ait doğal manyetik alan, demir gövde vasıtasıyla şiddetlendirilir ve ark; oluşan manyetik alan yardımıyla tek bir yöne doğru itilir. Bu itmenin etkisiyle iletken yapıya sahip olan ark, metal levhalara yaklaşır ve burada ısı konveksiyonu ve türbülansla beraber soğutulur. Böylece manyetik kuvvet ile metal levhalar arasında arkın boyu uzatılır, ısısı düşürülür ve sonuç olarak ark söndürülmüş olur. Manyetik itme bobinleri devredeki hat akımının değerine göre devreye alınır veya devreden çıkartılır. Üstünlükleri arasında; bakıma az ihtiyaç göstermeleri, peşpeşe çok sayıda açmakapama yapabilmeleri ve basit yapıda olmaları gösterilebilir. Olumsuz yanları ise; YG de kullanıma uygun olmamaları, yangın riski yaratmaları, doğru akımdaki kesme işleminde verimli çalışmamaları gösterilebilir. 5
120 5. Vakumlu kesiciler: Vakumlu kesiciler 7,5- kv arasındaki gerilim kademelerinde kullanılırlar. Bu kesicilerde akımın kesilmesi daha anidir ve bu özellik; kapasitif akımların kesilmesinde olumlu, küçük endüktif akımların kesilmesinde ise olumsuz etki oluşturur. Kutup kısımlarında hava bulunmadığı için kontakların oksitlenmesi söz konusu değildir. Kesme hücresi ise yüksek vakumlu silindir şeklindeki seramik gövdeli bir kap ile hareketli ve sabit kontaklardan oluşur. Kabın içerisinde 06 ile 07 torr basıncında vakum bulunur ve arkı söndürücü başka bir madde kullanılmaz. Sabit kontak; sabit kontak kolu ile kesici hücresi içine yerleştirilmiştir. Hareketli kontak kolu ise, üzerinde hareketli kontağı barındırır ve metal bir körük vasıtasıyla hücre içinde hareket eder. Ayrıca hareketli kontak devamlı hareket halinde olduğu için paslanmaya karşı çelik malzeme ile kaplanır. Bu kesicilerde % 5-%70 krom içeren krom-bakır kontakların yanı sıra tungsten-bakır ve bizmut-bakır kontak başları da kullanılmaktadır. Kullanılan kontaklar, termal iletkenliği yüksek, erimeye karşı dayanıklı, korozyon seviyesi düşük, yüzeyleri pürüzsüz, uzun ömürlü, kesme yeteneği ve mekanik mukavemeti yüksek malzemeden yapılır. 0 kv'un üstündeki akımlarda kullanılan vakumlu kesici kontakları, özel biçimler verilerek üretilir. Kontaklar açılırken ark akımı, alternatif akımın özelliğinden dolayı akım sıfır noktasına kadar akışını sürdürür. Akımın sıfır noktasında ark söner ve maden buharı kontaklar üzerinde yoğunlaşır. Ark odası dışında yüksek vakum bölgesi olduğundan maden buharı hızla bu bölgeye akar ve ortam hızlı bir şekilde yalıtkan hale gelir. Böylece ark tamamen söndürülmüş olur. Vakumlu kesicilerin tasarımında hareketli parça sayısı az olduğundan mekanizma oldukça küçük bir enerjiyle çalışır. Sonuç olarak; ark söndürme ortamı ve işletme mekanizmasına ait üstün özellikleriyle, bakım gerektirmeyen, oldukça çeşitli anahtarlama fonksiyonları olan bu kesiciler, ilgili gerilim aralığında tercih edilirler. 6. Basınçlı hava üflemeli kesiciler: Bu tip kesiciler, basınçlı havanın ark üzerine gönderilip arkın söndürülmesi ilkesi ile çalışırlar. Üzerine gönderilen basınçlı hava sonucunda deiyonizasyonun ile hızla soğuyan ark, açma anından itibaren yaklaşık bir periyot sonra, akımın sıfır noktasından geçtiği anda söndürülmüş olur. Kesicinin tipine göre radyal, aksiyal ya da nadiren de olsa doğrudan açık hava üflenerek çalışan çeşitleri vardır. Basınçlı hava üflemeli kesicilerde basınçlı hava iletimi için kompresör, hava depolamak için hava tankı, hava dağıtımı için boru tesisatı kullanıldığı için fiyatları oldukça pahalıdır. Bu tip kesicilerin üzerinde ayrıca, homojen gerilim dağılımını sağlamak için kondansatör elemanları ve açma-kapama işlemi sırasında anormal gerilim yükselmelerini engellemek için açma-kapama dirençleri vardır. Çok hızlı açma yapabilirler. 6
121 Özet Elektrik enerjisinin üretilip sonrasında tüketicilere dağıtıldığı santraller genellikle tüketicilerin bulunduğu alanlara uzak yerlerde inşa edilir. Bu yüzden; santraller tarafından üretilen elektrik enerjisinin üretildiği santralden tüketicilerin bulunduğu alanlara iletilmesi gerekmektedir. Enerji sistemlerindeki gerilim sınıfları AG, OG, YG ve ÇYG olmak üzere dört farklı grupta toplanabilir. Bir dağıtım şebekesi; havai hat ve yeraltı kabloları olmak üzere iki farklı şekilde kurulabilir. Dağıtım sisteminde aynı değerdeki gücün havai hat veya yeraltı kablosu ile dağıtılması arasında ekonomik bir karşılaştırma ve analiz yapıldığında; havai hat şebekesinin maliyetinin yeraltı kablo şebekesinin maliyetine göre daha ucuz olduğu, başka bir deyişle kablo şebekesinin maliyetinin, havai hat şebekesinin mâliyetinden çok daha fazla olduğu bilinmektedir. Türkiye'de dağıtım sisteminde kullanılabilecek standart gerilimler, TS-83 numaralı Türk Standartlarında belgesinde belirlenmiştir. Bu standartlara göre; V (000 V dahil) arası alçak-gerilimler; tek-fazlı elektrik şebekeleri 0 ve 0 V, üç-fazlı elektrik şebekeleri 0/90 V ve 0/380 V olan şebekelerdir. Şebekeler yapılarına göre 3 farklı şekilde gruplandırılar. Bunlar; Kapalı şebekeler, açık şekeler ve enterkonnekte şebekelerdir. Elektrik enerjisinin üretildiği santrallerden tüketim merkezlerine ve abonelere havai hatlar yardımıyla iletilmesini sağlayan, toprakla iletken arasında yalıtkanlık oluşturan ve hat boyunca uygun aralık ve yükseklikte yerleştirilen şebeke donanımına direk adı verilir. Direk ve konsollar, enerji taşıyan kabloları, izolatörler yardımıyla yerden ve birbirinden belirli uzaklıklarda tutarak yalıtımı sağlayan ve bunların kısa-devre yapmalarını engelleyen elemanlardır. İmal edildikleri malzemelere göre direkler; demir, ağaç ve betonarme olarak üç ana grupta toplanırlar. Kablo, elektrik enerjisini iletmeye yarayan ve farklı iki elektrik noktasını elektriksel bakımdan birbirine bağlayan, dış çevresi elektrik akımına karşı yalıtılmış, bir ya da birden çok damarı bulunan iletim elemanıdır. Elektrik enerjisinin iletimi ve dağıtımında kullanılan hatları, havai hatlar ve yeraltı hatları olmak üzere iki kısımda incelemek mümkündür. Herhangi bir gerilim düzeyinde kablo seçimi yaparken belirli şartlara uyulmalıdır. Havai enerji nakil hatlarında kullanılan iletkenlerin direklere bağlantısını sağlayan, iletkenleri taşımaya yarayan, taşıdığı iletkenlerin direklere, toprağa ve diğer iletkenlere karşı yalıtımını sağlayan cihazlara izolatör denir. Havai hatlarda işletmenin güvenliği ve sürekliliği önemli ölçüde hattın yalıtımına bağlıdır. İmal edildikleri malzemelere göre izolatörler; porselen, cam ve epoksi reçineli olarak üç ana grupta toplanırlar. Güç sistemlerinde, OG ve YG iletim hatlarında devre yüksüz halde iken açma-kapama işlemi için kullanılan ve tasarım bakımından en basit tipteki ayırma elemanına ayırıcı adı verilir. İletim aşamasında, bölümleri birbirinden ayırarak şebeke üzerindeki bakım ve control işlemlerinin güvenli bir şekilde yapılmasını sağlar. Ayrıca; çoklu ana baraya sahip şebekelerin açma-kapama işlemine hazırlanması ve birbirlerine bağlanmasında önemli rol oynar. Monte edildiklere yere göre dahili ve harici ayırıcılar olarak gruplandırılırlar. Kesici, arkın, kısa-devre akımının ve yük akımının şebekeye olan zararlı etkilerini yok edecek şekilde tasarlanıp geliştirilen koruma elemanıdır. Devrede meydana gelen ark, çok kısa sürede söndürülmezse hem kontaklar arasında elektrik akışı devam eder hem de kesici görevini tam olarak yapamaz. Arkı söndürücü özelliğinden dolayı kesiciler, şebekede kullanılan diğer sistem elemanlarını korurken aynı zamanda insanların can güvenliğini de sağlar. 7
122 Kendimizi Sınayalım. Elektrik enerjisinin, üretildiği bölgeden alınıp tüketim bölgelerine ulaştırılması için gerekli olan sistemlere. adı verilir. Boşluk olan kısma gelmesi gereken en uygun tanım aşağıdakilerden hangisidir? a. Üretim şebekesi b. Tüketim şebekesi c. İletim şebekesi d. Transformatör şebekesi e. Santral şebekesi. Aşağıdakilerden hangisi kullanım yerlerine göre sınıflandırılan direk tiplerinden biri değildir? a. Durdurucu direkler b. Köşe durdurucu direkler c. Geçit direkler d. Nihayet direkler e. Seksiyoner direkler 3. Kesintisiz bir enerji sağlamak ve mevcut enerji ihtiyacını karşılamak için, elektrik santrallerini ve bütün şebekeleri birbirine bağlayan sistemlere. denir. Boşluk olan kısma gelmesi gereken en uygun tanım aşağıdakilerden hangisidir? a. Dalbudak şebeke b. Ring şebeke c. Dağıtım şebekesi d. Enterkonnekte sistem e. Branşman 4. Havai enerji nakil hatlarında kullanılan iletkenlerin direklere bağlantısını sağlayan, iletkenleri taşımaya yarayan, taşıdığı iletkenlerin direklere, toprağa ve diğer iletkenlere karşı yalıtımını sağlayan cihazlara.. denir. Boşluk olan kısma gelmesi gereken en uygun tanım aşağıdakilerden hangisidir? a. Kesici b. İzolatör c. Ayırıcı d. Mesnet e. Kreozot 5. Aşağıdaki olaylardan hangisi iletimde aşırı gerilimlere sebep olmaz? a. Geçici olaylar b. Yıldırımın hat üzerine düşmesi c. İletim hattındaki açma-kapama işlemleri d. Yüksek Güçteki motorların çalıştırılması e. İletim hatlarındaki arızalar 6. Porselen izolatörlerin içeriğini genel olarak aşağıdaki karışımlardan hangisi en iyi biçimde ifade eder? a. %5 kaolin, %5 feldspat ve %50 kuvars b. %5 kaolin, %50 feldspat ve %5 kuvars c. %50 kaolin, %5 feldspat ve %5 kuvars d. %30 kaolin, %30 feldspat ve %40 kuvars e. %30 kaolin, %40 feldspat ve %30 kuvars 7. Enerji iletiminde Yüksek-gerilim (YG) kullanılmasının en önemli sebebi aşağıdakilerden hangisidir? a. YG hatlarının kurulum ve işletme maliyeti azdır. b. YG de oluşacak elektriksel kayıplar diğer AG ve OG ye göre daha azdır. c. YG de iletilen akım değeri, AG ve OG ye göre daha fazladır. d. YG de gerilim seviyesi, AG ve OG ye göre daha düşüktür. e. AG ve OG hatların giriş ve çıkış güçleri arasındaki fark YG ye göre daha düşüktür. 8. Ağaç direkler, kullanım yerlerine göre hangi şekilde kullanılırlar? a. Dağıtım direği olarak b. Nihayet direk olarak c. Taşıyıcı ve köşe taşıyıcı direk olarak d. Köşe durdurucu ve ayırıcı direk olarak e. Geçit ve nihayet direk olarak 8
123 9. Ayırıcılar görevlerine göre çeşitli sınıflara ayrılırlar. Aşağıdakilerden hangisi bu sınıflandırmalardan biri değildir? a. Bara ayırıcı b. Topraklama ayırıcı c. Sigortalı ayırıcı d. Hat ayırıcı e. By-pass ayırıcı 0. Ayırıcılarda açma-kapama işlemi sırasında ilk olarak hangi işlem yapılır? a. Kesici açılır b. Kesici kapatılır c. Ayırıcı açılır d. Ayırıcı kapatılır e. Yük devreden çıkarılır Kendimizi Sınayalım Yanıt Anahtarı. c Yanıtınız yanlış ise Elektrik Şebekeleri başlıklı konuyu yeniden gözden geçiriniz.. e Yanıtınız yanlış ise Direkler başlıklı konuyu yeniden gözden geçiriniz. 3. d Yanıtınız yanlış ise Elektrik Şebekeleri başlıklı konuyu yeniden gözden geçiriniz. 4. b Yanıtınız yanlış ise İzolatörler başlıklı konuyu yeniden gözden geçiriniz. 5. d Yanıtınız yanlış ise Parafudrlar başlıklı konuyu yeniden gözden geçiriniz. 6. c Yanıtınız yanlış ise İzolatörler başlıklı konuyu yeniden gözden geçiriniz. 7. b Yanıtınız yanlış ise Elektrik Şebekeleri başlıklı konuyu yeniden gözden geçiriniz. 8. c Yanıtınız yanlış ise Direkler başlıklı konuyu yeniden gözden geçiriniz. 9. c Yanıtınız yanlış ise Ayırıcılar başlıklı konuyu yeniden gözden geçiriniz. 0. a Yanıtınız yanlış ise Ayırıcılar başlıklı konuyu yeniden gözden geçiriniz. Yararlanılan Kaynaklar Tosun,. (007). Enerji İletimi ve Dağıtımı. İstanbul: Birsen Yayınevi. Üstünel, M., Altın M., Kızılgedik, M. (00). Endüstriyel Elektrik. Mesleki ve Teknik Öğretim Okulları İçin Ders Kitabı, Ankara: MEB Dalfes, M. (993). Elektroteknik. (7. Baskı). İstanbul: Seç Yayın Dağıtım. Fitzgerald, A. E., Higginbotham, D. E. & Grabel, A. (000). Fundamental Electric Engineering. (Çev. Ed. Kıymaç, K.) Temel Elektrik Mühendisliği Cilt. (3. Baskı). Ankara: Bilim Center. Turgut, E., Selçuk, K. (0). Elektrik Enerjisi Üretimi ve Dağıtımı, Detay Yayınları. Glover, D.J., and Sarma, M.S. (989). Power system analysis and design, PWS-Kent Publishing Com., Boston. Prof. Dr. Şerifoğlu N. (003) Elektrik Enerji Sistemleri cilt, Papatya yayıncılık. Garzon, Ruben D. (997). High Voltage Circuit Breakers: Design and Applications, Marcel Dekker
124 5 Amaçlarımız Bu üniteyi tamamladıktan sonra; Çeşitli uzunluktaki hat modelleri arasındaki farkları ayırt edebilecek, Kayıplı ve kayıpsız hatları kıyaslayıp, bu hatlara ait çeşitli parametreleri hesaplayabilecek, İletim hatlarına ait çeşitli kavram ve tanımları yorumlayabilecek, Yüklenmeye bağlı durumlarda, hatlara ait gerilim profillerini tanımlayabilecek, Enerji hatlarındaki maksimum güç akışını ifade edebilecek, bilgi ve becerilere sahip olabilirsiniz. Anahtar Kavramlar Hat Modelleri Gönderici-Uç Alıcı-Uç Dalga Empedansı Regülasyon Yayılım Sabiti Karakteristik Empedans ABCD Parametreleri Dalga Boyu Maksimum Güç Akışı Yüklenme İçindekiler Giriş Kısa ve Orta Uzunluktaki Hat Benzetimleri İletim Hatlarına Ait Diferansiyel Denklemler Eşdeğer π Devresi Kayıpsız İletim Hatları Maksimum Güç Akışı 0
125 Yatışkın-Durum İletim Hat Modelleri GİRİŞ Elektrik enerjisinin üretilip sonrasında tüketicilere dağıtıldığı santraller genellikle tüketicilerin bulunduğu alanlara uzak yerlerde inşa edilir. Bu yüzden; santraller tarafından üretilen elektrik enerjisinin üretildiği santralden tüketicilerin bulunduğu alanlara iletilmesi gerekmektedir. Günlük hayatta pek çok kullanım alanı bulunan elektrik enerjisinin iletim ve dağıtımının ekonomik bir şekilde yapılabilmesi, enerji alanında en önemli konulardan biridir. Elektrik enerjisinin üretiminden tüketicilere ulaşıncaya kadar gerekli olan tesisleri; üretim, iletim ve dağıtım olmak üzere üç kısımda incelemek mümkündür. Elektrik enerjisinin üretildiği yer elektrik santralleridir. Elektrik enerjisinin, üretilen yerden alınıp tüketim bölgelerine ulaştırılması için gerekli olan sistemlere iletim şebekesi denilir. Elektrik enerjisinin bir tüketim bölgesi içerisinde alçaltıcı trafo merkezinden alınıp, tüketicilere ulaştırılması için gerekli olan sistemlere ise dağıtım şebekesi denir. Bu sistemler, genellikle orta-gerilim şebekesi (-35 kv) ile trafo merkezleri ve alçak-gerilim şebekesinden meydana gelir. Enerjinin iletilebilmesi için gerekli olan elemanların en başında iletim hatları gelmektedir. Genelde havai iletim hatları tercih edilmektedir. Enerji iletim hatları yatışkın-durum ve anlık durum olmak üzere iki farklı şekilde incelenip analiz edilmektedirler. İletim hatlarının anlık durum incelemesi ve modellenmesi oldukça zordur ve çok fazla matematiksel teorem ve işlem gerektirir. İletim hatları genel olarak anlık durumdan ziyade yatışkın-durum dediğimiz sürekli hal durumlarında incelenip modellenmektedir. Bu ünitede yatışkın durumdaki tek-fazlı ve üç-fazlı enerji iletim hatları incelenecektir. Enerji iletim hatları iki kapılı devreler ile modellenecek ve bu modeller çeşitli karakteristik parametrelerle ifade edilecektir. Hatların uzunluklarına bağlı olarak; parametrelerin etkileri değiştiği için hatlar belli uzunluk sınırları içinde kısa, orta ve uzun hatlar olmak üzere üç ana gruba ayrılırlar. Bu ünitede herbir iletim hattı çeşidi ayrı ayrı analiz edilip, parametreleri elde edilecek ve hat modelleri ortaya çıkarılacaktır. KISA VE ORTA UZUNLUKTAKİ HAT BENZETİMLERİ Bu bölümde, ABCD parametreleri olarak gösterilen kısa ve orta uzunluktaki iletim hatlarından bahsedeceğiz. İletim hattı, Şekil 5. de gösterildiği gibi iki kapılı şebeke olarak tanımlanabilir. Şeklin sol tarafındaki ilk kapı gönderici-uç ve sağ taraftaki ikinci kapı ise alıcı-uç olarak adlandırılır. Gösterimde, S indisi gönderici-uç tarafını, R indisi ise alıcı-uç tarafını simgelemektedir. V S ve I S, sırasıyla gönderici-uç tarafındaki gerilim ve akım değerlerini, V R ve I R ise alıcı-uç tarafındaki gerilim ve akımın fazör değerlerini ifade etmektedir. Bu iki kapı arasındaki ilişki aşağıdaki şekilde ifade edilebilir. VS = AVR + BI (5.) R IS = CVR + DI (5.) R veya matris formatı olarak aşağıdaki şekilde yazılabilir. V A B V = S R I C D S I R (5.3)
126 Burada A, B, C ve D parametreleri iletim hattındaki R, L, C ve G sabitlerine bağlıdır. A, B, C ve D parametreleri genellikle kompleks (karmaşık) sayılardır. A ve D boyutsuz veya birimsizdir. B sabiti Ω (ohm) birimine ve C sabiti de S (siemens) birimine sahiptir. Devre teorisi bizlere gösteriyor ki, A, B, C ve D parametreleri doğrusal, pasif ve iki yönlü iki-kapılı şebekelere aşağıdaki genel ilişki içerisinde uygulanabilir. AD BC = (5.4) 80 km den kısa havai hatlar kısa iletim hattı olarak adlandırılır, Şekil 5. deki devre bu tipteki bir hattı göstermektedir. Bu hat tipi sadece seri direnç ve reaktans içerir, şönt admitans ihmal edilir. Bu devre, tekfazlı veya denge koşullarında çalışan transpoz edilmiş üç-fazlı havai hatlara uygulanabilir. İki kapılı şebeke Şekil 5.: İki-kapılı Şebeke Gösterimi Üç-fazlı hatlarda, Z seri empedans değeri, V S ve VR pozitif sıralı hat-nötr arasındaki gerilim değeri, I S ve I R ise hatlardaki pozitif-sıralı akım değerleri olur. Toplam seri empedans ile birim uzunluk başına düşen seri empedans arasındaki farkı anlamak ve bu iki nicelik arasındaki ilişkiyi karıştırmamak için aşağıdaki gösterim kullanılır. z= R+ jωl Ω /m, birim uzunluktaki seri empedans y= G+ jωc S/m, birim uzunluktaki şönt admitans Z = zl Ω, toplam seri empedans Y = yl S, toplam şönt admitans l m, hat uzunluğu
127 Şekil 5.: Kısa İletim Hattı Tekrar hatırlayacak olursak, G olarak isimlendirilen şönt iletkenliği genellikle havadan gerçekleştirilen enerji iletimlerinde ihmal edilir. Şekil 5. deki kısa iletim hattında A, B, C ve D parametreleri KGK ve KAK eşitlikleri yazılarak kolayca elde edilebilir. VS = VR + ZI (5.5) R I S = I (5.6) R veya matris formatı şeklinde yazılırsa aşağıdaki ifade bulunur. V S Z VR I = 0 S I R (5.7) (5.3) ve (5.7) yi karşılaştırırsak, A, B, C ve D parametreleri; A= D= br (5.8) B = Z Ω (5.9) C = 0 S (5.0) Uzunluğu 80 km ile 50 km arasında değişen orta uzunluktaki hatlarda, toplam şönt kapasitans değeri genel olarak hattın her iki ucuna yarı yarıya dağıtılır. Şekil 5.3 te gösterilen ve nominal π devresi olarak adlandırılan devrede A, B, C ve Dparametrelerini bulabilmek için, şekil 5.3 teki seri kısımdaki akım değeri VY R I R + şeklinde alınır ve daha sonra KGK denklemi yazılır. VY R YZ VS = VR + Z IR + = + VR + ZIR (5.) Aynı zamanda KAK denklemi, gönderici-uç tarafında yazılırsa; I S VY R VY S = IR + + elde edilir. (5.) denklemi (5.) denklemi içinde kullanılacak olursa; (5.) 3
128 VY R YZ Y YZ YZ IS = IR + + VR ZIR Y VR IR + + = (5.3) gönderici-uç akımı hesaplanır. (5.) ve (5.3) ün matris formatında yazımı; VS YZ VR + Z = YZ YZ Y + + I 4 S IR (5.4) (5.4) ve (5.3) karşılaştırıldığında aşağıdaki ifadeler elde edilir. YZ A= D= + br (5.5) B = Z Ω (5.6) YZ C = Y + S 4 (5.7) Şekil 5.3: Orta İletim Hattı Nominal π devresi Dikkat edilmelidir ki; hem kısa hem de orta uzunluktaki hatlar için, AD BC = ilişkisi sağlanır. Ayrıca, aynı hat olduğu sürece herhangi bir uçtan bakıldığında A= D olur. Şekil 5.4 kısa hat gösterimi olan seri empedans ve orta uzunluktaki hat gösterimi olan π devrelerini içeren çeşitli devrelerin A, B, C ve D parametrelerini vermektedir. Orta uzunluktaki hat gösterimi Şekil 5.4 de gösterilen T devresinin seri empedans değerini hattın her iki ucuna dağıtarak oluşturulabilir. Seri bağlı şebekelerin genel A, B, C ve D parametreleri, herbir şebekenin bireysel A, B, C ve D matrislerinin çarpımı yapılarak hesaplanabilir. A, B, C ve D parametreleri; hattaki yüklenme ile birlikte hat voltajındaki değişikliklerin ifade edilmesi için kullanılır. Yüklenme terimi uçlara bağlanan yükün elektriksel olarak artması veya azalması durumudur. Gerilim regülasyonu; gönderici-uçtaki voltajın sabit tutulması durumunda alıcı-uç tarafında bulunan yükün, yüksüz durumdan tam-yük durumuna geçerken yine alıcı-uç tarafında gerçekleşen voltaj değişimidir. Gerilim regülasyonu, genellikle tam-yük voltaj yüzdesi olarak aşağıdaki şekilde belirtilir; VRNL VRFL %VR = 00 V RFL 4 (5.8)
129 Şekil 5.4: Genel Şebeke Çeşitlerine ait ABCD Parametreleri Belirtilen VR değeri yüzde olarak voltaj regülasyon değeridir. V yüksüz durumdaki alıcı-uç RNL tarafının gerilim büyüklüğüdür, V tam-yük durumundaki alıcı-uç tarafındaki gerilim büyüklüğüdür. RFL Kısa hatlar için voltaj regülasyonundaki yüke ait güç faktörü etkisi Şekil 5.5 te fazör diyagramı olarak gösterilmiştir. Fazör diyagramları (5.5) denkleminin geride ve ileride güç faktöründeki grafiksel gösterimidir. Yüksüz durumda, (5.5) denkleminden kısa hatlar için I RNL = 0 ve V S = V RNL hesaplanır. Şekilde gösterildiği gibi; yüksek (kötü) voltaj regülasyonu, geride güç faktöründe V RNL değerinin V RFL değerini büyük ölçüde aştığı kısımda gerçekleşir. Küçük veya eksi değerdeki negatif voltaj regülasyonları ise ileride güç faktörü durumlarında gerçekleşir. Genel olarak; yüksüz gerilimin değeri, I RNL = 0 olduğu anda ki değerdir. 5
130 V RNL VS = A olur ve bu değer, (5.8) denklemindeki voltaj regülasyonunu belirlemek için kullanılır. (5.9) Geride güç faktörü İleride güç faktörü Şekil 5.5: Kısa İletim Hattına ait Fazör Diyagramlar Pratik olarak; iletim hattı elektriksel açıdan nominal değerden daha fazla yüklendiğinde iletim hat geriliminin değeri düşer, aksine daha az yüklendiğinde ise gerilim değeri yükselir. Çok yüksek gerilim (ÇYG) hatlarında anma geriliminin ± 5% değerine karşılık, yaklaşık olarak %0 luk bir voltaj regülasyonu ortaya çıkar. Alçak-gerilim hatlarında, trafolara ait gerilim düşümleri de hesaba katıldığında %0 luk bir voltaj regülasyonu iyiye yakın çalışma koşulları olarak kabul edilebilir. Voltaj regülasyonunun yanında; ek olarak hattın elektriksel olarak yüklenebilirliği de verimli işletme koşullarında çok önemli bir faktördür. Hattın yüklenebilirlik durumu için üç temel sınırlandırma aşağıda sıralanmıştır;. Termal limit. Voltaj-düşüm limiti 3. Yatışkın-durum kararlılık limiti İletken malzemenin maksimum sıcaklığı onun termal limitini belirler. İletkenin sıcaklığı; direkler arasındaki iletkenin gerginliğini, bükülümünü ve de gerilme direncindeki kaybı etkiler. Eğer ki sıcaklık çok yüksek ise önceden belirlenmiş şartlar karşılanmayacak ve iletkenin elastik esneme limiti aşıldığından dolayı malzeme soğutulduğunda tekrar eski orjinal formuna dönemeyecektir. İletkenin sıcaklığı aşağıdaki 5 temel faktöre bağlıdır; a. iletken üzerinden geçen akımın büyüklüğüne b. iletken üzerinden geçen akımın geçiş zamanına c. Ortam sıcaklığına d. Rüzgar hızına e. İletken yüzeyindeki şartlara. Kısa iletim hatlarının (80 km den kısa havai hatlar) yüklenebilirliği; genellikle iletkenin termal limiti veya devre kesiciler gibi hat terminaline bağlı araçların anma değerlerine bağlıdır. Uzunlukları 300 km ye kadar olan orta uzunluktaki hatlar için hat yüklenebilirliği; çoğu kez gerilim-düşüm limiti ile belirlenir. Bazı durumlarda çok şiddetli gerilim-düşümleri tolere edilebilecek olmasına rağmen, aşırı bir şekilde 6
131 V /V 0,95 R S yüklenen hat üzerinde güvenli çalışma şartlarının sağlandığı kabul edilir. Uzunluğu 300 km üzerinde olan uzun hatlarda ise yatışkın-durum kararlılığı bir limit faktörü olmaya başlar. Örnek 5. Üç-fazlı, 60 Hz, tamamen transpoz edilmiş 345 kv, 00 km lik hat aşağıdaki pozitif-sıralı hat sabitlerine sahiptir. z = 0,03 + j0,35 Ω / km 6 y= j4, 0 S / km Alıcı-uç tarafındaki tam-yük, 0,99 ileride güç faktöründe ve %95 anma gerilim değerinde 700 MW aktif güç çekmektedir. Orta uzunluktaki hat olarak düşünülen bu hat için, aşağıdakileri hesaplayınız. a. Nominal π devresinin parametreleri b. V S Gönderici-uç voltajı, I S Gönderici-uç akımı ve P S Gönderici-uç gerçek gücü. c. Voltaj regülasyon yüzdesi d. Tam-yük halinde iletim hattının verimliliği Çözüm: a. Toplam seri empedans ve şönt admitans değerleri; ( )( ) ( )( ) Z = zl = 0,03 + j0,35 00 = 6,4 + j70 = 70,9 84,78 Ω 6 4 Y = yl = j4, 0 00 = 8, S (5.5) - (5.7) denklemlerinden; ( )( ) A= D= + 8, , 9 84, 78 = 0, j0, 0069 = 0,9706 0,59 br B = Z = 70,9 84,78 Ω 4 ( )( ) C = + = 4 4 8, , , 78 8, , 08 S b. Alıcı-uç voltajı ve akım değerleri; 37,8 VR = ( 0, 95)( 345) = 37,8 kv LL VR = 0 = 89, 0 kv cos 0, 99 I = =, 46 8, ka R ( 3)( 0, )( 0, 99) (5.) ve (5.) den gönderici-uç tarafına ait gerilim, akım ve gerçek güç değerleri ise; S ( 0,9706 0,59 )( 89, 0 ) ( 70, 9 84,78 )(, 46 8, ) 99, 6 6,4 kvln V = + = V = 99,6 3 = 345,8 kv.00 br S LL LN I S 4 ( 8, , 08 )( 89, 0 ) ( 0,9706 0,59 )(, 46 8, ) = + =,96 + j0,33 =, 4 5,5 ka P = ( 3)( 345,8)(, 4) cos( 6,4 5, 5 S ) = 730, 5 MW 7
132 c. Yüksüz durumdaki alıcı-uç tarafının gerilimi (5.9) denkleminden bulunur; V 345,8 V = S 356,3 kv A = RNL 0, 9706 = LL ve (5.8) den; 356,3 37,8 %VR = 00 = 8,7% 37,8 d. Tam-yükteki hat kayıpları PS PR = 730,5 700 = 30,5 MW ve hattın tam-yükteki iletim verimliliği PR 700 % verim = η = 00 = 00 = 95,8% P 730,5 S İLETİM HATLARINA AİT DİFERANSİYEL DENKLEMLER R, L ve C olarak adlandırılan hat sabitlerinin birim uzunluk başına düşen değerleri Ω /m, H/m ve F/molarak ifade edilir. Toplu halde, tek bir yerde değildirler fakat hat uzunluğu boyunca eşit orantılı bir şekilde dağıldıkları varsayılır. İletim hat sabitlerinin bu şekildeki doğal dağılımlarını hesaplamak için hattın Δ x uzunluğundaki bir parçasını gösteren Şekil 5.6 daki devreyi inceleyebiliriz. Şekil 5.6: İletim hattının Δ x boyutundaki kısmı x noktasının uzunluk olarak değeri, hattın sağ tarafından yani alıcı-uç tarafından itibaren birim I x simgeleri sırasıyla hattın x noktasındaki gerilim ve akım uzunluk cinsinden ölçülür. V( x) ve ( ) değerlerini gösterirler. Benzer şekilde V( x+ Δ x) ve I( x+ Δ x) değerleri de hattın ( x x) + Δ noktasındaki gerilim ve akım değerlerini göstermektedir. Devre sabitleri aşağıdaki şekilde hesaplanır. z= R+ jωl Ω /m (5.0) y= G + jωc S/ m (5.) İşlem kolaylığı açısından, G sabiti genelde havai hatlar için ihmal edilir. Devre için KGK denklemi yazıldığında gerilim, aşağıdaki şekilde ifade edilir; V( x+ Δ x) = V( x) + ( zδx) I( x) V (5.) 8
133 ve (5.) denklemi yeniden düzenlenirse; ( + Δ ) ( ) V x x V x = zi ( x) Δ x (5.3) Δ x sıfıra yaklaşacak şekilde limiti alındığında, ( ) dv x dx ( ) = zi x (5.4) elde edilir. Benzer şekilde; devre için KAK denklemi yazıldığında ise; I( x+ Δ x) = I( x) + ( yδ x) V( x+ Δx) A (5.5) ve (5.5) yeniden düzenlendiğinde; ( + Δ ) ( ) I x x I x = yv ( x) Δ x (5.6) Δ x sıfıra yaklaşacak şekilde limiti alındığında, ( ) di x dx ( ) = yv x (5.7) denklemine ulaşılır. (5.4) ve (5.7) denklemleri, birinci dereceden iki bilinmeyenli ( V( x) ve I( x )) ve homojen diferansiyel denklemlerdir. (5.4) denkleminin türevini alarak ve de (5.7) denklemini aşağıdaki gibi kullanarak I( x ) bilinmeyenini ortadan kaldırabiliriz. dv x dx veya ( ) di( x) ( ) ( ) = z = zyv x dx dv x zyv ( x) = 0 dx (5.8) (5.9) denklemleri elde edilir. (5.9) denklemi tek bilinmeyenli ( V( x )) doğrusal, ikinci dereceden homojen bir denklemdir. Bu denklemin çözümü aşağıdaki şekilde bulunur. γx γx ( ) = + V V x Ae Ae (5.30) γ = zy m (5.3) Burada; A ve A değerleri integrasyon sabitleri olarak, γ ise yayılım sabiti olarak adlandırılır. (5.30) ve (5.3) denklemleri (5.9) denkleminin içine konulursa diferansiyel denklemin çözümü ispatlanabilir. Çözüm hakkında detaylı bilgi için diferansiyel denklemlerle ilgili kitapları inceleyebilirsiniz. Sonrasında (5.30) denklemi (5.4) içinde kullanılırsa; 9
134 ( ) dv x dx ( ) γx γx Ae γae zi x = γ = (5.3) ve I( x) bilinmeyeni için çözüldüğünde; Ae γx Ae ( ) = I x z / γ γx (5.33) (5.3) i kullanarak z/ γ = z/ zy = z/ y eşitliği elde edilir ve (5.33) denklemi aşağıdaki şekle dönüşür. Ae γx Ae Z ( ) = I x Z c z = Ω y c γx (5.34) (5.35) Z c, birimi Ω olan karakteristik empedans olarak isimlendirilir. A ve A integrasyon sabitleri sınır koşullarından belirlenir. x = 0 olduğu anda, tam olarak alıcı-uç noktası üzerinde, alıcı-uç gerilim ve akım değerleri; VR IR = V = I ( 0) ( 0) olarak gösterilir ve ayrıca x = 0 (5.36) (5.37) noktasında (5.30) ve (5.34) denklemleri aşağıdaki biçimde ifade edilir. V = A + A (5.38) I R A A R = (5.39) Zc A ve A integrasyon sabitleri çözüldüğünde; VR + ZcIR A = (5.40) VR ZcIR A = (5.4) ve bu sabitler, (5.30) ve (5.34) denklemlerinde yerine koyulduğunda; VR + ZcIR γx VR ZcIR V( x) = e + e VR + ZcI R γx VR ZcI R I( x) = e e Zc Zc γx γx (5.4) (5.43) (5.4) ve (5.43) yeniden düzenlecek olursa; 30
135 γx x x x e e ( ) γ γ γ + e e V x = V + Z I R c R γx x x x e e ( ) γ γ γ e + e I x = VR + I Zc R (5.44) (5.45) Yukarıdaki denklemlere dikkatli bakıldığında parantez içindeki ifadelerin hiperbolik fonksiyonlar olan cosh ve sinh ifadeleri olduğu anlaşılır. Bu fonksiyonlardan yola çıkarak;; ( ) cosh( γ ) sinh ( γ ) V x = x V + Z x I (5.46) R c R I( x) = sinh ( γx) VR + cosh ( γx) I (5.47) R Z c eşitlikleri bulunur. (5.46) ve (5.47) denklemleri, dağıtım hattının ABCD parametrelerini vermektedir. Matris formatında gösterim ise; ( ) ( ) ( ) Bx ( ) ( ) D( x) V x Ax VR = I x C x I R (5.48) şeklindedir. Bu denklemdeki parametreler, aşağıda ifade edilmiştir. ( ) ( ) ( γ ) Ax= Dx= cosh x br (5.49) ( ) sinh ( γ ) B x = Z x Ω (5.50) c C( x) = sinh ( γ x) S (5.5) Z c (5.48) denklemi bizlere, hattın herhangi bir x noktasındaki gerilim ve akımın değerini alıcı-uç noktasındaki gerilim ve akım cinsinden verir. Hattın toplam uzunluğu l ise; x = l olduğu anda V gönderici-uç noktasındaki gerilim ve akım değerleri () l = VS I() l = IS olur. Hattın en sol tarafındaki gönderici-uçta tarafındaki değerler matris formatında aşağıdaki gibi gösterilir. V A B S VR I = C D I S R (5.5) Bu denklemdeki parametreler, aşağıda ifade edilmiştir. ( γ ) A= D= cosh l br (5.53) ( γ ) B= Z sinh l Ω (5.54) c C = sinh ( γ l) S (5.55) Z c (5.53) - (5.55) denklemleri dağıtım hattının ABCD parametrelerini vermektedir. Bu denklemlerde karşımıza çıkan γ yayılım sabiti, gerçek kısmı α ve sanal kısmı ise β olan kompleks bir sayıdır ve aşağıdaki şekilde ifade edilir. 3
136 γ = α + jβ m (5.56) γ l niceliği boyutsuzdur ve γl ( αl+ jβl) αl jβl αl e = e = e e = e βl (5.57) şeklinde gösterilir. (5.57) i kullanarak cosh ve sinh hiperbolik fonksiyonları aşağıdaki gibi hesaplanır; cosh sinh γl γl e + e = = + (5.58) αl αl ( γl) ( e βl e βl) γl γl e e = = (5.59) αl αl ( γl) ( e βl e βl) Ayrıca bu gösterime alternatif olarak aşağıdaki özdeşlikler de çözüm için kullanılabilir. ( αl jβl) ( αl) ( βl) j ( αl) ( βl) cosh + = cosh cos + sinh sin (5.60) ( αl jβl) ( αl) ( βl) j ( αl) ( βl) sinh + = sinh cos + cosh sin (5.6) Unutmayınız ki, (5.58) - (5.6) denklemlerindeki boyutsuz nicelik olan radyan cinsindendir. Hesaplamalarda bu açı değeri radyan olarak alınmalıdır. β l derece cinsinden değil (5.53) - (5.55) arasında verilen ABCD parametreleri, uzunluğu herhangi bir değerde olan hat için geçerli olan kesin parametrelerdir. Hatasız hesaplamalar yapmak için, bu denklemler 50 km den uzun olan havai hatlar için kullanılmalıdır. Bölüm 5. de elde edilen ABCD parametreleri, kısa ve orta uzunluktaki hatlar için kullanılan ve el hesaplamalarında sonucu bulmayı kolaylaştıran yaklaşık parametre değerleridir. Tablo 5.; bizlere kısa, orta, uzun ve kayıpsız (Bölüm 5.5 te anlatılacak) hatların ABCD parametrelerini özetler; Tablo 5.: İletim Hatlarına Ait ABCD Parametreleri Parametre A=D B C Birimler br S Kısa hat Z 0 Orta hat (nominal devresi) YZ YZ + Z Y + 4 Uzun hat (eşdeğer devresi) ( γ l) = + Z sinh ( γ l) = Z cosh YZ c YZ Zc sinh l = Y + 4 ( ) ( γ ) Kayıpsız hat (R=G=0) cos ( β l) jz sin ( βl) c j sin ( βl) Z c 3
137 Örnek 5. Üç-fazlı, 765 kv, 60 Hz, 300 km uzunluğundaki hat aşağıdaki pozitif-sıralı empedans ve admitans değerlerine sahiptir. z = 0,065 + j0,3306 = 0,33 87,4 Ω / km y= j 6 4,674 0 S / km Pozitif-sıralı uygulamayı temel alarak, hattın kesin ABCD parametrelerini hesaplayınız. Kesin B parametresi ile nominal π devresine ait B parametresini karşılaştırınız. Çözüm: (5.3) ve (5.35) ten yola çıkarak Zc 0, 33 87,4 4, = = 7,08 0,86 = 66,,43 Ω ( 0,33 87,4 )( 4, ) ( 300), ,4 ( 300) γ l = = = 0,373 88,57 = 0,0093+ j0,373 br değerleri elde edilir. (5.57) den γ l 0,0093 j0,373 e = e e = = + j,0094 0,373 radyan 0,94 0,3678 l 0,0093 j0,373 e γ = e e = = j 0,9907 0,373 radyan 0,96 0,36 hesaplanır ve sonra (5.58) ve (5.59) dan ( γ l) ( γ l) ( 0, 94 + j0, 3678) + ( 0, 96 j0, 36) cosh = = 0, 933+ j0, 0034 = 0, 933 0, 09 ( 0, 94 + j0, 3678) ( 0, 96 j0, 36) sinh = = 0, j0, 3644 = 0, , 63 elde edilir. Son olarak ise (5.53) - (5.55) denklemlerinden ( γ ) A= D= cosh l = 0,933 0,09 br B = ( 66,,43 )( 0, ,63 ) = 97 87, Ω 0, ,63 C = = 66,, 43 3, ,06 S hattın kesin ABCD parametreleri bulunur. (5.6) denkleminden de nominal π devresine ait B parametresi şu şekilde bulunur. ( )( ) B = nominal Z = 0,33 π 87,4 300 = 99,3 87,4 Ω Görüldüğü gibi nominal π devresine ait B parametresi, kesin B parametresinden yaklaşık % daha büyüktür. 33
138 EŞDEĞER π DEVRESİ Güç sistemlerinin analiz ve tasarımında kullanılan pek çok program, iletim hattı ve trafo gibi şebeke elemanlarının devre gösterimlerini ve şemalarını kullanırlar. Bu yüzden iletim hattının terminal karakteristiklerinin ve özelliklerinin gösteriminde ABCD parametrelerini kullanmak yerine eşdeğer devrelerini kullanmak daha uygundur. Şekil 5.7 de gösterilen devre, eşdeğer π devresi olarak isimlendirilir. Yapısal olarak Şekil 5.3 teki nominal π devresine benzemektedir. İki devre arasındaki tek fark; eşdeğer π devresinde Z ve Y parametreleri yerine Z ve Y parametreleri kullanılmıştır. Buradaki amacımız; Z ve Y parametrelerini bulmaktır. (5.53) - (5.55) denklemlerinden yola çıkarak, dağıtılmış hattın ABCD parametrelerinin eşdeğer π devresinin parametreleriyle aynı olduğu gözlenir. Şekil 5.7: İletim Hattına ait Eşdeğer π Devresi YZ A= D= + br (5.6) B= Z Ω (5.63) YZ C = Y + S 4 (5.64) Burada, (5.5) - (5.7) de yer alan Z ve Y simgeleri, (5.6) - (5.64) denklemlerinde Z ve Y ile yer değiştirmiştir. (5.63) denklemini (5.54) denklemine eşitlediğimizde; z Z = Zc sinh l = l y ( γ ) sinh ( γ ) (5.65) elde edilir. Yukarıdaki denklemi, nominal π devresinin Z = zl empedansı cinsinden yeniden yazacak olursak; ( γl) sinh ( γl) z sinh Z = zl = zl = ZF Ω y zl zyl (5.66) 34
139 sinh F = γl ( γl) br (5.67) olarak hesaplanır. Aynı şekilde, (5.6) denklemi (5.53) denklemine eşitlenirse; ( γ l) Y cosh = Z (5.68) ifadesi bulunur. (5.65) ifadesi ile hale gelir. ( γ ) ( γ l) γ l cosh l tanh = sinh özdeşliği kullanılırsa; (5.68) ifadesi aşağıdaki ( ) ( γ ) ( ) ( ) Y cosh γl tanh γl/ tanh γl/ = = = Zcsinh l Zc z y (5.69) Yukarıdaki denklemi, nominal π devresinin Y = yl admitansı cinsinden yeniden yazılacak olursa; Y yl tanh ( γl/ ) yl tanh ( γl/ ) Y = = = F S z yl zyl/ y (5.70) ( γl ) tanh / F = γl / br (5.7) ifadeleri elde edilir. (5.67) ve (5.7) denklemlerindeki F ve F parametreleri düzeltme faktörleri olarak isimlendirilir. Görevleri; nominal π devresindeki Z ve Y parametrelerini, eşdeğer π devresindeki Z ve Y parametrelerine dönüştürmektir. Örnek 5.3 Örnek 5. deki uzun hattın nominal π ve eşdeğer π devrelerini karşılaştırınız. Çözüm: Nominal π devresi için; ( )( ) Z = zl = 0,330 87,4 300 = 99,3 87,4 Ω 6 Y yl j4, = = ( ) = , S (5.67) ve (5.7) den düzeltme faktörleri bulunur. 0, ,63 F = = 0,9769 0,06 br 0,373 88,57 35
140 ( γ ) ( γ ) l/ ( l/) sinh( l) tanh l/ cosh l 0,933 j0,0034 F = γ = γ γ = + 0,373 88,57 ( 0, ,63 ) 0, j0,0034 0, ,7 = = =,0 0,03 br 0,068 77, 0,068 77, Sonra, (5.66) ve (5.70) den eşdeğer π devresi için aşağıdaki değerler hesaplanır. ( )( ) ( )( ) Z = 99,3 87,4 0,9769 0,06 = 97 87, Ω Y = = = + j ,0 0 90,0 0,03 7, ,97 S 3,7 0 7,095 0 S Nominal ve eşdeğer π devrelerinin değerleri karşılaştırıldığında; Z nin Z den % daha küçük ve Y / nin de Y / den % daha büyük olduğu anlaşılır. Bu hat için devre değerleri neredeyse aynı olsa da, uzun hatları kapsayan hassas ve hatasız hesaplamalar için eşdeğer π devresi kullanılmalıdır. KAYIPSIZ İLETİM HATLARI Bu bölümde, kayıpsız olarak nitelendirilen iletim hatları için; dalga empedansı, ABCD parametreleri, dalga boyu, eşdeğer π devresi, dalga empedans yüklenmesi, gerilim profilleri ve denge durumundaki kararlılık limiti kavramları anlatılacaktır. Hat kayıpları ihmal edildiğinde, hat parametrelerinin ayrı ayrı hesabı için daha basit ve sade ifadeler elde edilir. Böylece, kayıpsız hatlar için bu konunun başında bahsi geçen kavramlar daha kolayca anlaşılır. Güç transferi yapılan iletim ve dağıtım hatları genellikle düşük kayıplar olacak şekilde dizayn edilir. Fiziksel olarak da böyle olması gayet normaldir. Bu kısımda anlatılacak olan denklemler ve geliştirilen tanımlamalar; sadece hızlı ve doğruya yakın el hesaplamaları yapmak ve şebeke hakkında kabaca fikir edinmek için kullanılabilir. Hatasız ve daha hassas hesaplamalar için yapılacak analizlerin ve tasarımların kayıplı hat modellerine göre ve bilgisayar programları yardımıyla yapılması önerilir. Dalga Empedansi Kayıpsız kabul edilen bir hat için, R = G = 0 ve z= jωl Ω / m (5.7) y= jωc S / m (5.73) (5.3) ve (5.35) denklemlerinden karakteristik empedans ve yayılım sabiti aşağıdaki gibi bulunur. Z c z jωl L = = = Ω (5.74) y jωc C ( L)( C) LC m γ = zy = jω jω = jω = jβ (5.75) β = ω LC m (5.76) Z = L/C karakteristik empedans, kayıpsız hatlar için aynı zamanda dalga empedansı olarak c tanımlanır. Saf rezistiftir ve değer olarak gerçek (reel) sayıdır. γ yayılım katsayısının değeri ise sanal sayıdır. ( jβ ) 36
141 ABCD Parametreleri (5.49) - (5.5) denklemlerinden ABCD parametreleri; jβx jβx e + e Ax ( ) = Dx ( ) = cosh( γx) = cosh( jβx) = = cos ( βx) br (5.77) jβx jβx e e sinh( γx) = sinh( jβx) == = jsin ( βx) br (5.78) L B( x) = Zcsinh ( γx) = jzcsin( βx) = j sin ( βx) Ω (5.79) C ( ) C x ( γx) jsin( βx) sinh = = Zc L S (5.80) C A( x ) ve D( x ) reel, B( x ) ve C( x) paramatreleri Tablo 5. de karşılaştırılmıştır. sanal sayılardır. Kayıpsız ve kayıplı hatlara ait ABCD Eşdeğer π Devresi Eşdeğer π devresi için (5.65) kullanılırsa; ( β ) Z = jz sin l = jx Ω (5.8) c veya (5.66) ve (5.67) eşitliklerinden; sin( βl) Z = ( jωll) = jx Ω βl (5.8) elde edilir. Ayrıca, (5.70)ve (5.7) den ( ) ( ) ( ) ( ) tan ( βl / ) ωc ( ) ( ) ( ) Y Y tanh jβl/ Y sinh jβl/ jωcl jsin βl/ = = = jβl/ jβl/ cosh jβl/ jβl/ cos βl/ jωcl j l = = S βl / (5.83) eşitlikleri bulunur. Z ve Y nin her ikiside sanal sayıdır. Ayrıca; β l nin π radyandan küçük değeri için, Z saf endüktif ve Y de saf kapasitiftir. Bu yüzden kayıpsız hatlar için Şekil 5.8 de gösterilen eşdeğer π devresinin kendisi de kayıpsızdır. Dalga Boyu Dalga boyu; gerilim veya akımın fazını, π radyan veya 360 periyodunda değiştirmesi için gerekli olan uzaklık olarak tanımlanır. λ simgesiyle gösterilir. Kayıpsız hatlar için, (5.48) eşitliğini kullanarak; ( ) ( ) ( ) cos( β ) sin ( β ) Vx= AxV+ BxI = xv+ jz xi (5.84) R R R c R ( β x) jsin I( x) = C( x) VR + D( x) IR = VR + cos( β x) IR (5.85) Z c 37
142 değerleri bulunabilir. (5.84) ve (5.85) ten yola çıkılarak; x π / β = olduğunda, V( x ) ve I( x ) niceliklerinin fazlarını π radyan değerinde değiştirdiği kolayca anlaşılabilir. Dalga boyu, λ olarak ifade edildiğinde (5.76) denklemi kullanılırsa; π π λ = β = ω LC = f LC veya m (5.86) f λ = LC (5.87) değerlerine ulaşılır. / LC terimi; kayıpsız hat boyunca gerilim ve akım dalgalarının yayılım hızını 8 gösterir. Havai hatlar için değeri, ( / LC) 3 0 m/s alınır ve örneğin f = 60 Hz frekansındaki enerji iletimi için dalga boyu, (5.87) denkleminden aşağıdaki gibi hesaplanır λ = m Şekil 5.8: Kayıpsız Hat için Kullanılan Eşdeğer π Devresi ( βl < π) Dalga Empedans Yüklenmesi (SIL) Dalga empedans yüklenmesi, kısa adıyla (SIL) terimi, kayıpsız hat aracılığıyla dalga empedansına eşit değerdeki bir yük direncine iletilen güç değeridir. Burada dalga empedansı Zc = L/ C ye eşittir. Şekil 5.9, yukarıda açıklanan olayı özetleyen bir devre şemasını göstermektedir. Bu şemadaki kayıpsız hat hem tek-fazlı hem de dengeli üç-fazlı bir hattın faz-nötr hattı olarak gösterilebilir. SIL durumunda (5.84) denkleminden yola çıkılarak; 38
143 V R V( x) = cos( βxv ) R + jzcsin( βxi ) R = cos( βxv ) R + jzcsin( βx) = ( cos βx+ jsin βxv ) R Zc (5.88) jβ x = e VR V V( x) = V R V (5.89) sonuçlarına ulaşılır. SIL durumunda gerilim profili yataydır. Bu demek oluyor ki; SIL koşullarında gerilimin büyüklüğü, kayıpsız hat üzerindeki herhangi bir x noktasında sabittir. (5.85) denkleminden ( β ) jsin x VR VR jβ x VR I( x) = VR + ( cos βx) = ( cos βx+ jsin βx) = ( e ) A (5.90) Z Z Z Z c c c c akım denklemi bulunur. Ayrıca (5.88) ve (5.90) eşitlikleri kullanılarak; hat üzerindeki herhangibir x noktasına iletilen kompleks güç değeri de; * jβ x V * jβ x e V R R S( x) = P( x) + jq( x) = V( x) I ( x) = ( e VR ) = Z Z ile hesaplanır. c c (5.9) Şekil 5.9: Kendine ait Dalga Empedansı ile sonlandırılan Kayıpsız Hat modeli Sonuç olarak; SIL durumunda, kayıpsız hat üzerindeki gerçek güç akışı gönderici-uç tarafından alıcıuç tarafına kadar sabit değerde kalır. Reaktif güç akışı ise yoktur, yani değeri sıfırdır. Hattın anma gerilim değerinde iletilen gerçek güç veya diğer adıyla SIL, (5.9) den V SIL = Z anma c (5.9) Buradaki anma gerilim değeri hat-nötr arası gerilim olursa; tek faz iletilen güç değeri, eğer ki hat-hat arası gerilim değeri olursa; üç-faz iletilen toplam güç değeri hesaplanmış olur. 39
144 Gerilim Profilleri Pratikte, güç hatları kendilerine ait dalga empedanslarıyla sonlandırılmazlar. Bunun yerine, yükler hafif yüklenme koşullarında SIL değerinden çok az bir şekilde saparlar. Ağır yüklenme koşullarında ise hat uzunlugu ve hat kompanzasyonuna bağlı olarak SIL değerinin katları biçiminde sapmalar olur. Eğer hat, dalga empedansı ile sonlandırılmamışsa buna bağlı olarak gerilim profile de düzgün olmaz. Şekil 5.0 çeyrek dalga boyuna kadar hat uzunlukları için sabit V S gerilimindeki gerilim profillerini göstermektedir. Bu şekil üzerinde aşağıda açıklanan dört farklı yüklenme durumu gösterilmiştir.. (Yüksüz durum) IRNL = 0 ve (5.84) denkleminden; ( x) = ( β x) V cos V NL RNL (5.93) eşitliği bulunur. Yüksüz durumdaki gerilim değeri; gönderici-uç tarafından alıcı-uç tarafına doğru giderken ( x azalırken) artar. (SIL durumu) (5.89) den SIL durumundaki gerilim profili yatayda düzgündür. 3. (Kısa-devre durumu) Yükteki kısa devre için, VRSC = 0 ve (5.84) denklemi aşağıdaki eşitliği sağlar. ( x) = ( Z β x) V sin I SC c RSC Voltaj değeri, gönderici-uç tarafında V ( sinβl)( Z I ) VRSC = 0 değerine kadar düşer. S (5.94) = değerinden alıcı-uç tarafındaki 4. (Tam-yük durumu) tam-yük akımının özelliğine bağlı olarak tam-yükteki gerilim profili, grafiksel olarak kısa-devre gerilim profilinin üst kısmında kalır. c RSC Yüksüz durum SIL Tam-yük Kısa-devre Gönderici-uç Alıcı-uç Şekil 5.0: Kayıpsız Hat için Geçerli Olan Voltaj Profilleri 40
145 Yatışkın-Durum Kararlılık Limiti Şekil 5.8 deki eşdeğer π devresi kayıpsız hat tarafından sağlanan gerçek güç değerine ait bir denklem oluşturmak için kullanılabilir. Hattın her iki ucundaki V S ve V R gerilim değerlerinin büyüklüklerinin sabit tutulduğunu varsayalım. δ, gönderici-uçtaki gerilimin alıcı-uçtaki gerilime göre faz açısı olsun. KGK dan alıcı-uç tarafındaki I R akımı; I V V V e jδ S R Y S VR jωc l = V = V Z jx (5.95) R R R ve alıcı-uç tarafına iletilen kompleks güç değeri ise; S jδ * jδ * VSe V R jωc l VSe V R jωcl R = VRIR = VR + VR = VR + VR jx jx j δ + δ j jω l = + X VVcos R S VVsin R S VR C V R (5.96) olacak şekilde ifade edilir. İletilen gerçek güç ise; VV R S P = PS = PR = Re( SR) = sin δ W X (5.97) Hat kayıpsız olduğu için P S = P olur. (5.97) denklemi Şekil 5. de çizilmiştir. Sabit V S ve V R değerleri için sağlanan gerçek güç arttıkça, δ faz açısı da 0 den durumda hattın sağlayabileceği maksimum güç; R 0 90 ye artar. δ = 90 olduğu VV S R P mak = W X (5.98) denklemi ile hesaplanır. P değeri kayıpsız hattın teorik olarak Yatışkın-durum kararlılık limiti olarak ifade edilir. Bu mak limit değeri aşıldığı durumlarda; gönderici-uçlara bağlı senkron makineler ve alıcı-uçlara bağlı olanlarla aralarındaki senkronizasyonu kaybederler ve kararlı durumdan çıkarak kararsız duruma geçerler. Böyle bir durum istenmeyen tehlikeli sonuçlara yol açabilir. 4
146 Gerçek güç (P) Şekil 5.: Voltaj Açısına Bağlı Olarak Kayıpsız Hat Tarafından İletilen Gerçek Güç Yatışkın-durum kararlılık limitini SIL cinsinden açıklamak mümkündür. (5.8) denklemi (5.97) denklemi içinde kullanılırsa; VV S Rsinδ VV S R sinδ P = = Z sin l c βl Z π c sin λ (5.99) V S ve V R değerleri, anma hat geriliminin birim değerleri cinsinden gösterilirse; V V V S R anma sinδ sinδ P = = VS.br VR.br ( SIL ) W V anma Vanma Z c πl πl sin sin λ λ (5.00) ve δ = 90 için, yatışkın-durum kararlılık limitinin teorik olarak değeri; ( ) V V SIL πl sin λ (5.0) S.br R.br P mak = W (5.98) - (5.0) aralığındaki denklemler yatışkın-durum kararlılık limitini etkileyen iki önemli faktör olduğunu gösterir. İlk olarak, (5.98) den, yatışkın-durum kararlılık limiti hat voltajının karesiyle doğru orantılı olarak artmaktadır. Örneğin; voltajın iki katına çıkması maksimum güç akışını da dört kat arttırır. İkinci olarak, yatışkın-durum kararlılık limiti hat uzunluğu ile birlikte azalır. Denklem (5.0), Şekil 5. de VS.br = VR.br =, λ = 5000 km ve hat uzunluğu da 00 km ye çıkabilecek şekliyle çizilmiştir. Şekilde gösterildiği gibi; teorik yatışkın-durum kararlılık limiti, 00 km lik hat için 4(SIL) değerinden 400 km lik hat için (SIL) değerine düşer. Örnek 5.4 Hat kayıpları ihmal edildiğinde, örnek 5. deki 300 km lik hat için teorik yatışkın-durum kararlılık limitini hesaplayınız. Dalga empedansını 66, Ω, dalga boyunu 5000 km ve V = V = 765 kv alınız. S R 4
147 Çözüm: (5.9) den ( 765 ) SIL = = 99 MW 66, (5.0) den l = 300 km ve λ = 5000 ()()( 99) ( )( ) km değerleri yardımıyla, Pmak = =, = 5974 MW π 300 sin 5000 hesaplanır. Alternatif olarak şekil 5. den 300 km lik hat için teorik yatışkın-durum kararlılık limiti ( ) ( )( ), 7 SIL =, 7 99 = 5980 MW. Şekil yardımıyla, yukarıdaki sonuca yakın bir sonuç bulunur. Termal limit Yatışkın-durum kararlılık limiti Pratik hat yüklenebilirliği Hat uzunluğu (km) Şekil 5.: İletim Hattına Ait Yüklenme Eğrileri MAKSİMUM GÜÇ AKIŞI Kayıpsız hatlar için yukarıdaki bölümde incelenen maksimum güç akışı; bu bölümde ABCD parametreleri açısından kayıplı hatlar için incelenecektir. Aşağıdaki gösterimler kullanılacaktır. ( ) A A= cosh γl = A θ ; B= Z = Z θ ; V = V δ; V = V 0 Z S S R R (5.5) denklemini, alıcı-uç tarafındaki akım için çözülürse; I R jδ jθa VS AVR VSe AVRe = = jθz B Ze (5.0) bulunur ve alıcı-uç tarafına sağlanan kompleks güç ise; 43
148 j( δ θz ) j( θa θz ) Se Re R S j( θ δ) R j( θ θ ) * V AV V V AV Z SR = PR + jqr = VRIR = VR = e e Z Z Z Z A (5.03) olarak ifade edilir. Alıcı-uç tarafına sağlanan gerçek ve reaktif güç ise dolayısıyla aşağıdaki gibi hesaplanır; VV AV PR = Re R = cos Z cos Z Z Z R S R ( S ) ( θ δ) ( θ θ ) VV AV QR = Im R = sin Z sin Z Z Z R S R ( S ) ( θ δ) ( θ θ ) A A (5.04) (5.05) o o Kayıpsız hatlar için θ A = 0, B= Z = jx, Z = X ve θz = 90 olarak alınır ve (5.04) denklemi aşağıdaki duruma dönüşür. VV R S AV VV P cos( 90 ) R R S R = δ cos( 90 ) = sinδ X X X (5.06) Yukarıdaki denklem, (5.97) ye benzer bir denklemdir. Teorik anlamda iletilen maksimum gerçek güç veya yatışkın-durum kararlılık limiti, (5.04) denklemi içinde δ = θ olduğu durumda gerçekleşir. P VV AV ( θ θ ) Z Z (5.07) R S R Rmak = cos Z A Yukarıdaki denklemdeki ikinci terim; Z, X den büyük olduğunda, kayıpsız hatlar için verilen değerden daha az bir değere düşürür. Örnek 5.5 Z P R değerini (5.98) de mak Örnek 5. deki sağlanabilecek teorik maksimum güç değerini MW ve SIL birimi cinsinden bulunuz. V = V = 765 kv alınız S R Çözüm: Örnek 5. den; A= 0,933 br; θ = 0,09 ; B= Z = 97 Ω ; θ = 87, ; Z = 66, Ω A Z c (5.07) den V = V = 765 kv değerleriyle S R ( 765) ( 0,933)( 765) ( ) PR mak = cos 87, 0, 09 = = 5738 MW (5.9) den ( 765) SIL = = 99 MW 66, 5738 PR mak = =,6 br 99 değerleri hesaplanır. Bu değer, kayıpların ihmal edildiği örnek 5.4 den %4 daha azdır. 44
149 İletim Hatlarında Reaktif Güç Kompanzasyon Teknikleri Endüktör ve kapasitör devre elemanları, orta ve uzun hatlarda, hat gerilimlerini nominal değere yakın tutmak ve hattın yüklenebilirliğini artırmak için kullanılırlar. Şönt endüktanslar yüksek gerilim hattı boyunca seçilen noktalarda herbir faz ile toprak arasına bağlanırlar. Bu elemanlar bağlandıkları kısımda reaktif gücü emerler ve hafif yük koşullarında meydana gelebilecek aşırı gerilimleri azaltıcı etki yaparlar. Bunlar; aynı zamanda açma-kapama olaylarında ve yıldırım düşmesi sonucu hatlarda meydana gelen geçici aşırı gerilimlerin genliklerini de azaltırlar. Ancak, şönt endüktör tam-yük durumunda devreden ayrılamaz ise iletim hattının yüklenebilirliğini de azaltır. Şönt reaktörlere ilaveten şönt kapasitörler de reaktif güç vermek için kullanılırlar. Kapasitörler, ağır yük koşullarında iletim geriliminin genliğini artırırlar. Şönt kompanzasyonun bir diğer türü de statik VAR sistemleri olarak adlandırılan tristör anahtarlamalı sistemlerdir. Bu sistemler üç ana grup altında toplanabilir; a. tristör anahtarlamalı kapasitörler, b. tristör anahtarlamalı endüktörler, c. paralel kapasiteli tristör anahtarlamalı endüktörler. Son grup; besleme sistemine hem kapasitif hem de endüktif güç verebilme özelliğinden dolayı pratikte ilk iki gruba göre daha çok tercih edilir. Bunlar hafif yük koşullarında şebekeden reaktif güç emerler, ağır yük koşullarında ise şebekeye reaktif güç verirler. Bu denetim mekanizması, tristörlerin yükün güç katsayısına bağlı olarak tetiklenmesi ile yapılır. Tristör anahtarlamalı endüktörler, gerilim dalgalanmalarını en alt seviyeye indirir ve hattın yüklenebilirliğini arttırırlar. Statik VAR sistemlerinin en büyük üstünlüğü; ani yük değişimlerine çok hızlı cevap verebilmeleridir. Bu özellikleri sebebiyle bu sistemler, özellikle ark fırınlarının olumsuz reaktif güç etkisini kontrol etmek için kullanılırlar. En önemli problemleri ise harmonik adı verilen şebekeye zararlı parazitleri üretmeleridir. Senkron kondenserler (miline mekanik yük bağlı olmadan çalışan senkron motorlar) statik VAR sistemleri kadar hızlı çalışmasalar da reaktif güç miktarını kontrol etmek için kullanılan dönen elektrik makinalarıdır. Bunlarda uyarma alanı değiştirilerek, reaktif güç denetimi yapılabilir. Üç faz için ayrı ayrı denetim imkanı olmaması, senkron kondenserlerin bir diğer olumsuz yönüdür. Seri kapasitörler bazen uzun hatlarda hattın yüklenebilirliğini arttırmak için kullanılırlar. Kapasitör bankaları belirlenen yerlerde her bir faza ayrı ayrı seri olarak bağlanırlar. Bunlar hattın reaktansına seri olarak bağlandıklarından, hat üzerindeki gerilim düşümünü azaltır ve yatışkın-durum kararlılık limitini artırırlar. Seri kapasitör bankalarının kısa devre akımlarına karşı korunmaları gerekir. Bunun için otomatik koruma ekipmanları kullanılır ve bu ekipmanlar sistemde bir kısa devre olması halinde kapasitör bankalarını kısa devre durumuna getirirler. Otomatik koruma ekipmanları, normal çalışma şartlarına dönüldüğünde ise kapasitör bankalarını tekrar hatta seri bağlı duruma getirirler. Seri kompanzasyonun bir dezavantajı da düşük frekanslı gerilim dalgalanmalarına sebep olmasıdır. Bu etkiye senkronaltı rezonans adı verilir. Bu etki türbin-jeneratör milinde zarar meydana getirir. Ancak, yeni inşa edilecek hattın maliyetinden çok daha az oranda harcama yapılarak iletim hattına seri olarak bağlanan seri kompanzasyon tesisi ile hattın yüklenebilirliği arttırılabilir. Nominal Gerilim ve Reaktif Güç Ayarı Motor, lamba, ısıtıcı gibi cihazların en verimli çalıştığı gerilim nominal gerilim değeridir. Gerilim değişimlerinin genliği belirli bir değeri aştığı zaman, genellikle kullanıcılarda ya bir arıza meydana gelir ya da verimsiz bir çalışma ortamı oluşur. Eğer gerilim; nominal değerde çok yüksek ise motorun demir kayıpları artar ve ısınır, lambanın ise ömrü kısalır. Eğer gerilim; nominal değerden çok düşükse, lamba daha az aydınlatır, motor momenti dönme eylemi için yetersiz kalır, asenkron makinanın rotoru kayar ve ısınma tehlikesi ortaya çıkar. O halde dağıtım şebekesinin belirli bir noktasındaki gerilimin genliğini nominal değerine yakın ve mümkün olduğu kadar sabit bir değerde tutmak gerekir. Bu amaca ulaşmak için her merkezde gerilim ayarı yapmak ekonomik değildir. Yalnızca güç ileten iletim şebekelerinde büyük gerilim değişimleri kabul edilebilir; çünkü, bu durumdan son kullanıcı olan bizlere ait cihazların 45
150 etkilenme imkanı yoktur. Gerilim nominal değerinin %±5 civarında değişse bile, büyük güçteki jeneratör ve transformatörler güçlerinin tamamını vermeye devam edebilecek özelliktedirler. Özellikle tam yüklenmedikleri durumlarda gerilim değişimlerinden daha az etkilenirler. Sonuç olarak; çok yüksek gerilim değerlerinde transformatörlerin doyması, çok alçak gerilimlerde ise kayıpların aşırı artması, iletim şebekesinin kararlılık ve senkronizmasının kaybı problemlerini ortaya çıkarır. Ayrıca iletim şebekesindeki gerilim genlik değişimlerinin, bu değişimler dağıtım şebekesine kısmen ulaştığında, iletim şebekesi tarafından beslenen dağıtım şebekelerinde kurulmuş ayar düzenlerinin sınırlarını aşmaması gerekir. Bu ve buna benzer sebeplerden dolayı şebekenin belirli bir noktasındaki gerilim değişiminin, ortalama bir değerin en fazla %±0 una eşit genlikte bir aralıkta tutulmasına özen gösterilir. Bir dağıtım şebekesi ile bir iletim şebekesi gerilimlerinin ayar problemi farklı biçimde ele alınır. Dağıtım şebekesinde gerilim mümkün olduğu kadar sabit tutulmaya çalışılır. İletim şebekesinde ise yukarıda sayılan problemlerden dolayı yüksek toleranslı ve geniş aralıklı gerilim kontrolü yapılabilir. 46
151 Özet Elektrik enerjisinin üretilip sonrasında tüketicilere dağıtıldığı santraller genellikle tüketicilerin bulunduğu alanlara uzak yerlerde inşa edilir. Günlük hayatta pek çok kullanım alanı bulunan elektrik enerjisinin iletim ve dağıtımının ekonomik bir şekilde yapılabilmesi, enerji alanında en önemli konulardan biridir. Elektrik enerjisinin üretildiği yer elektrik santralleridir. Elektrik enerjisinin, üretilen yerden alınıp tüketim bölgelerine ulaştırılması için gerekli olan sistemlere iletim şebekesi denilir. verimsiz bir çalışma ortamı oluşur. Bir dağıtım şebekesi ile bir iletim şebekesi gerilimlerinin ayar problemi farklı biçimde ele alınır. Dağıtım şebekesinde gerilim mümkün olduğu kadar sabit tutulmaya çalışılır. İletim şebekesinde ise yüksek toleranslı ve geniş aralıklı gerilim kontrolü yapılabilir. Enerjinin iletilebilmesi için gerekli olan elemanların en başında iletim hatları gelmektedir. Genelde havai iletim hatları tercih edilmektedir. Enerji iletim hatları yatışkın-durum ve anlık durum olmak üzere iki farklı şekilde incelenip analiz edilmektedirler. İletim hatlarının anlık durum incelemesi ve modellenmesi oldukça zordur ve çok fazla matematiksel teorem ve işlem gerektirir. İletim hatları genel olarak anlık durumdan ziyade yatışkın-durum dediğimiz sürekli hal durumlarında incelenip modellenmektedir. Enerji iletim hatları iki kapılı devreler ile modellenir ve bu modeller çeşitli karakteristik parametrelerle ifade edilirler. Hatların uzunluklarına bağlı olarak; parametrelerin etkileri değiştiği için hatlar belli uzunluk sınırları içinde kısa, orta ve uzun hatlar olmak üzere üç ana gruba ayrılırlar. Kısa hat, orta hat ve uzun hat çeşitleri için ayrı ayrı hat modelleri bulunmakta ve herbir hattın karakteristik parametreleri uzunluğa göre değişmektedir. Ayrıca hatlar, kendi için kayıplı ve kayıpsız hatlar olmak üzere ikiye ayrılmaktadır. Hatları kayıpsız ve ideal olarak kabul etmek; matematiksel işlemlerde ciddi kolaylık ve hızlar sağlamaktadır. Iletim hattının veriminin yüksek olması ve üzerinden maksimum elektriksel gücü geçirmesi önemlidir. Maksimum güç transferi çeşitli koşullar altında sağlanmaktadır. Endüktör ve kapasitör devre elemanları, orta ve uzun hatlarda, hat gerilimlerini nominal değere yakın tutmak ve hattın yüklenebilirliğini artırmak için kullanılırlar. Senkron kondenserler (miline mekanik yük bağlı olmadan çalışan senkron motorlar) statik VAR sistemleri kadar hızlı çalışmasalar da reaktif güç miktarını kontrol etmek için kullanılan dönen elektrik makinalarıdır. Motor, lamba, ısıtıcı gibi cihazların en verimli çalıştığı gerilim nominal gerilim değeridir. Gerilim değişimlerinin genliği belirli bir değeri aştığı zaman, genellikle kullanıcılarda ya bir arıza meydana gelir ya da 47
152 Kendimizi Sınayalım. Bir iletim hattının gönderici-uç tarafında bulunan I akımının; ABCD,,, parametreleri S ve alıcı-uç tarafındaki V R ve I R nicelikleri cinsinden ifadesi aşğıdakilerden hangisidir? a. IS = AVR + BIR b. IS = AVR + CIR c. IS = BVR + AIR d. IS = CVR + DIR e. IS = DVR + CIR. ABCD,,, parametreleri ile ilgili aşağıdaki ifadelerden hangisi yanlıştır? a. B parametresinin birimi Ω dur. b. A parametresinin birimi Ω dur. c. D parametresinin birimsizdir. d. A parametresinin birimsizdir. e. C parametresinin birimi S dir. 3. z = 3 Ω / m ve y= 7 S/ m değerlerine sahip bir iletim hattının yayılım sabitinin ( γ ) değeri aşağıdakilerden hangisi olur? a. b. c. d. e. - 3 m m - 9 m m - 8 m 4. z = 3 Ω / m ve y= 7 S/ m değerlerine sahip bir iletim hattının karakteristik empedansının Z değeri aşağıdakilerden hangisi olur? ( ) c a. 3 Ω b. 3 3 Ω c. 3 Ω d. 3 3 Ω 5. Eşdeğer π devresindeki F ve F düzeltme sabitlerinin birimleri aşağıdakilerden hangisidir? a. Her ikisi de birimsizdirler b. F c. F Ω ve F H ve F d. F S ve F e. F V ve F S Hz Ω A 6. Eşdeğer π devresindeki F ve F düzeltme sabitlerinin görevleri aşağıdakilerden hangisidir? a. Güç faktörünü düzeltmek b. Gerilim düşümünü düzeltmek c. Kısa hatları uzun hatlara dönüştürmek d. Verimi Yükseltmek e. Nominal π devresindeki parametreleri eşdeğer π devresindeki parametrelere dönüştürmek Hz, 0 kv anma değerlerine sahip kayıpsız iletim hattının karakteristik empedans değeri 484 Ω ise dalga empedans yüklenmesinin değeri ne olur? a. 0 MW b. 00 MW c. 50 MW d. 40 MW e. 5 MW 8. Kayıpsız iletim hattında, hangi δ (gönderici-uçtaki gerilimin alıcı-uçtaki gerilime göre faz açısı) değeri için iletilen gerçek güç maksimum olur? a. 0 b. 80 c. 90 d. 45 e. 35 e. 9 Ω 48
153 9. Kısa iletim hatlarında aşağıdakilerden hangisi ihmal edilir? a. Seri direnç b. Seri kapasitans c. Seri endüktans d. Şönt admitans e. Şönt direnç 0. İletim hattı nominal değerden daha fazla yüklendiğinde, iletim hattında aşağıdakilerden hangisi gözlenir? a. İletim hat akımı düşer b. İletim hat akımı yükselir c. İletim hat gerilimi düşer d. İletim hat gerilimi yükselir e. İletim hat gücü yükselir Kendimizi Sınayalım Yanıt Anahtarı. d Yanıtınız yanlış ise Kısa ve Orta Uzunluktaki Hat Benzetimleri başlıklı konuyu yeniden gözden geçiriniz.. b Yanıtınız yanlış ise Kısa ve Orta Uzunluktaki Hat Benzetimleri başlıklı konuyu yeniden gözden geçiriniz. 3. c Yanıtınız yanlış ise İletim Hatlarına Ait Diferansiyel Denklemler başlıklı konuyu yeniden gözden geçiriniz. 4. c Yanıtınız yanlış ise İletim Hatlarına Ait Diferansiyel Denklemler başlıklı konuyu yeniden gözden geçiriniz. 5. a Yanıtınız yanlış ise Eşdeğer π Devresi başlıklı konuyu yeniden gözden geçiriniz. 6. e Yanıtınız yanlış ise Eşdeğer π Devresi başlıklı konuyu yeniden gözden geçiriniz. 7. b Yanıtınız yanlış ise Kayıpsız İletim Hatları başlıklı konuyu yeniden gözden geçiriniz. 8. c Yanıtınız yanlış ise Maksimum Güç Akışı başlıklı konuyu yeniden gözden geçiriniz. 9. d Yanıtınız yanlış ise Kısa ve Orta Uzunluktaki Hat Benzetimleri başlıklı konuyu yeniden gözden geçiriniz 0. c Yanıtınız yanlış ise Kısa ve Orta Uzunluktaki Hat Benzetimleri başlıklı konuyu yeniden gözden geçiriniz Yararlanılan Kaynaklar Palo A. (005). EPRI AC Transmission Line Reference Book 00 kv and Above, Electric Power Research Institute (EPRI). Hayt., W. H. (006), Engineering Circuit Analysis, 7th ed. NewYork: McGraw-Hill. Güney İ. (994). Çözümlü Enerji İletim Hatları Problemleri, Marmara Üniversitesi Yayınları. Peşint M. A. (996). Elektrik Santralleri Enerji İletimi ve Dağıtımı. Güney,. (00). Çözümlü Enerji İletim Hatları Problemleri, İstanbul, Marmara Üniversitesi Yayınları. Prof. Dr. Şerifoğlu N. (003) Elektrik Enerji Sistemleri cilt, Papatya yayıncılık. Glover, D.J., and Sarma, M.S. (989). Power system analysis and design, PWS-Kent Publishing Com., Boston. Fitzgerald, A. E., Higginbotham, D. E. & Grabel, A. (000). Fundamental Electric Engineering. (Çev. Ed. Kıymaç, K.) Temel Elektrik Mühendisliği Cilt. (3. Baskı). Ankara: Bilim Center. Arifoğlu, U. (00). Güç Sistemlerinin Bilgisayar Destekli Analizi. İstanbul: Alfa Basım Yayım Dağıtım Ltd. Şti. Grainger, J.J. (994). Power System Analysis. McGraw-Hill Inc. Saadat, H. (004). Power System Analysis. McGraw-Hill Inc
154 6 Amaçlarımız Bu üniteyi tamamladıktan sonra; Lineer cebir denklemlerini Gauss elemesi ve geri-çıkarım ile hesaplayabilecek, Jacobi ve Gauss-Seidel tekrarlı çözüm yöntemlerini karşılaştırabilecek, Güç akışı problemlerini tanımlayıp çözebilecek, Güç akışı kontrolünü yorumlayabilecek, bilgi ve becerilere sahip olabilirsiniz. Anahtar Kavramlar Geri-Çıkarım Gauss-Elemesi Lineer Denklem Jacobi Yöntemi Gauss-Seidel Yöntemi Newton-Raphson Yöntemi Güç Akışı Jacobian Matrisi Salınım Barası Admitans Matrisi İçindekiler Giriş Lineer Cebir Denklemlerinde Doğrudan Çözümler: Gauss Elemesi Yöntemi Lineer Cebir Denklemleri İçin Tekrarlı Çözümler: Jacobi ve Gauss-Seidel Yöntemleri Lineer Olmayan Cebir Denklemleri İçin Tekrarlı Çözümler: Newton-Raphson Yöntemi Güç Akışı Problemi Gauss-Seidel Yöntemi ile Güç Akışı Çözümü Newton-Raphson Yöntemi ile Güç Akışı Çözümü Hızlı Ayrışık Güç Akışı Güç Akışı Kontrolü 50
155 Güç Akışı GİRİŞ Üç-fazlı, dengeli ve yatışkın-durum koşulları altında enerji sistemlerinde hesaplanan güç akışı, aşağıdaki durumlarda geçerliliğini korur. Jeneratörlerin, şebekeye bağlı tüm yük taleplerini ve iletim hatlarındaki toplam güç kaybını karşıladıkları kabul edilir. Bütün baralara ait gerilim genliklerinin, nominal gerilim sınırları içerisinde olduğu varsayılır. Jeneratörlerin, kendilerine ait güç sınırlarını aşmadıkları kabul edilir. Transformatör ve iletim hatlarının, aşırı yüklenmedikleri varsayılır. Güç akışını hesaplamak için kullanılan algoritma yada program sona erdiğinde, şebekedeki baralara ait gerilim genlikleri, gerilim açıları, baralardan ve iletim hatlarından akan aktif ve reaktif güçler ve toplam güç kaybı hesaplanmış olur. Hesaplama için kullanılan verilerdeki şebekeye ait yük değerleri empedans yerine aktif veya reaktif güç olarak verildiğinden; ayrıca, güç üreten jeneratörler gerilim yada akım kaynağı olarak değil de güç kaynağı olarak gösterildiğinden, bilinen devre denklemleri ile güç akışı hesaplaması yapılamaz. Aktif ve reaktif güç terimleri kullanıldığı için bu denklemler lineer olmayan denklemlerdir. Bu ünitede güç akışı hesaplarında kullanılan iki farklı yöntem incelenecektir. Bunlar; Gauss Seidel ve Newton-Raphson yöntemleridir. Ayrıca son olarak; hızlı ayrışık güç akışına değinilecek ve güç akışındaki kontrol mekanizmaları detaylıca anlatılacaktır. LİNEER CEBİR DENKLEMLERİNDE DOĞRUDAN ÇÖZÜMLER: GAUSS ELEMESİ YÖNTEMİ Lineer denklem kümeleri aşağıdaki gibi; veya Ax = y matris formatında ifade edilebilir. Burada x ve y; N boyutlu vektörler ve A ise N N lik kare matristir. x, y ve A nın elemanları gerçek yada kompleks sayı olabilir. A ve y nin bilinen verileri ışığında x bilinmeyen vektörünün çözümü yapılır. A matrisinin determinantının sıfır olmadığı farzedilirse (6.) denklemi için sadece bir çözüm vardır. (6.) (6.) 5
156 A matrisi; sıfırdan farklı köşegen elemanlarla üst-üçgensel matris formatında olduğu zaman, x in çözümü kolayca elde edilebilir. (6.3) te en alt satırdaki son denklem sadece x N i içerdiğinden; kolayca hesaplanır. (6.3) x N in değeri aşağıdaki denklemden y x N = A N NN (6.4) x N hesaplandıktan sonra, son denklemin bir üst tarafındaki denklem de aşağıdaki gibi basitçe çözülebilir. x N y = A N N, N N A N, N x (6.5) Genel olarak; hesaplanan xn, xn,..., x değerleri ile aşağıdaki k ıncı denklem çözülebilir. k+ N yk Aknxn xk = n= k+ A k = N, N,, kk (6.6) Çözüm için kullanılan (6.3) teki bu yönteme geri-çıkarım adı verilir. Eğer ki A matrisi üst-üçgensel değilse, (6.) denklemi üst-üçgensel matris ile eşdeğer bir denkleme dönüştürülebilir. Gauss elemesi adı verilen bu dönüşüm aşağıda (N-) basamakta belirtilmiştir. Birinci basamakta; x i kalan denklemden ayırmak için (6.) deki birinci denklem kullanılır. Birinci denklem, A A ile çarpılır ve n inci n n=,3,..., N. Birinci basamak tamamlandıktan sonra; denklemden çıkarılır ( ) (6.7) denklemi, aşağıdaki denklem formuna dönüşür. (6.7) 5
157 Üst simge olarak gösterilen (), Gauss elemesi işleminin birinci basamağını ifade etmektedir. İkinci basamakta ise x yi denklemden ayırmak için (6.8) deki ikinci denklem kullanılır. İkinci denklem, () () A A n= 3,4,..., N. İkinci basamaktan sonra; n ile çarpılır ve n inci denklemden çıkarılır ( ) (6.8) k ıncı basamakta çözüm yapılacaksa; öncelikle ( k ) ( k ) A x= y ile başlanır. Daha önceden ( k ) ( k ) üçgenselleştirilen denklemin, ilk k denklemi değiştirilmeden çıkarılır ve k ıncı denklem A A ile çarpılır ve n inci denklemden çıkarılır ( n= k+, k+,..., N). ( N ) üst-üçgensel matrise sahip olan ( N ) ( N ) A x= y eşdeğer denkleme ulaşılır. Örnek 6.: Aşağıdaki denklemi, geri-çıkarım ve Gauss elemesini kullanarak çözünüz. nk inci basamaktan sonra, kk (6.9) ( N ) A 0 5 x 6 = 9 x 3 Çözüm: N = olduğundan; bu denklemde ( N ) = adet Gauss eleme basamağı vardır. İlk denklem A A = 0 ile çarpılıp ikinci denklemden çıkarılırsa; 0 5 x x 6 () = veya ( 5 ) ( 6) 0 8 x =.8 denklemi elde edilir. A üstüçgensel olur ve denklem x 0 0 () () A x= y formuna benzer. Bu aşamadan sonra; geri-çıkarım kullanılırsa, k = için (6.6) denklemi, () y () A,8 x = = = 0,5 ve k = için 8 () () y Ax () A ( )( ) 6 5 0, 5 x = = = 0, 4875 değerlerini verir. 0 53
158 Örnek 6.: Aşağıdaki denklemi, üçgenselleştirmek için Gauss eleme yöntemini kullanınız. 3 x x = x 3 9 Çözüm: N = 3 olduğundan; bu denklemde ( N ) = adet Gauss eleme basamağı vardır. İlk denklem A A = 4 = ile çarpılıp ikinci denklemden çıkarılırsa ve ilk denklem A3 A = 0 = 5 ile çarpılıp üçüncü denklemden çıkarılırsa; 3 x x = 7 5 ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) x veya 3 x x = x 3 6 elde edilir. () () A x= y. İkinci basamakta, ikinci denklem denklemden çıkarılırsa; veya 54 () () A3 A = 3= 0,5ile çarpılıp üçüncü 3 x x = ( 0, 5)( 6) x 3 6 ( 0, 5)( 7) 3 x x = ,5 x 3, 75 üçgenselleştirilmiş matris denklemi elde edilir. Bu aşamadan sonra x vektörü geri-çıkarım ile kolayca bulunabilir. Gauss elemesi ve geri-çıkarım için bilgisayar tarzı matematik işlemcilerin A için N hafıza adresine, ( k ) y için N hafıza adresine gereksinimi vardır. A ve y nin muhafazası için bir gereksinim yok ise A, ( k ) A nın adresinde ve aynı şekilde y, y nin adresinde depolanabilir. Tekrarlanan döngüler, aritmetik ifadeler ve çalışma alanları için ek hafıza gereklidir. Bilgisayar zaman gereksinimleri; Gauss elemesi ve geri-çıkarımlar için gerekli olan aritmetik uygulamaların belirlenmesiyle hesaplanabilir. 3 3 Gauss elemesi; ( N N) 3 çarpım, ( N)( N ) bölme ve ( N N) 3 çıkarma işlemi gerektirir. Geri-çıkarım ise; ( N)( N ) çarpım, ( N ) bölme ve ( N)( N ) çıkarma işlemi gerektirir. Bu yüzden; (6.) denkleminin Gauss elemesi ve geri-çıkarım yöntemleriyle çözülebilmesi için gerekli olan N 3 çıkarma işlemiyle doğru orantılıdır. yaklaşık zaman ( N ) çarpma ve ( ) Güç akışı problemlerinin birçok baradan oluşan güç sistemleri içinde, onbinlerce çözüm içermesinden dolayı, Gauss eleme yöntemi tek başına iyi bir çözüm sunamamaktadır. Ancak seyrek matris olarak bilinen ve sadece sıfırdan farklı birkaç elemanı bulunan matrisler, bilgisayar depolama ve zaman gereksinimlerini düşürmek amacıyla kullanılabilir. Genel olarak bütün büyük güç sistemleri seyrek matrisleri kullanabilecek şekilde modellenmektedir.
159 LİNEER CEBİR DENKLEMLERİ İÇİN TEKRARLI ÇÖZÜMLER: JACOBI VE GAUSS-SEIDEL YÖNTEMLERİ (6.) denklemine ait genel tekrarlı çözümler aşağıdaki gibi ilerlemektedir. İlk olarak tahmini bir x( 0) başlangıç değeri seçilir ve ardından aşağıdaki denklem kullanılır. ( ) ( ) x i+ = g x i i= 0,,, (6.0) Burada x () i, i inci tahmin ve g ise tekrarlı yöntemi belirten fonksiyonların N boyutlu vektörüdür. Aşağıdaki bitirme, durma şartı sağlanana kadar tekrarlı prosedüre devam edilir. k ( + ) k( ) x () i x i x i k xk () i, x () i < ε k =,,..., N (6.) nin k ıncı elemanıdır ve ε ise tolerans derecesi olarak adlandırılır. Çözüme ulaşmak için aşağıdaki soruların cevaplarına ihtiyaç vardır. Tekrarlama prosedürü tek bir çözüme yakınsayacak mı? Yakınsama oranı nedir? (kaç tane tekrarlama gerekli?) Sayısal bilgisayar kullanıldığında; depolama ve zaman gereksinimleri ne olacak? Bu soruların cevabı bizlere; Jacobi ve Gauss-Seidel adındaki iki farklı çözüm yöntemini işaret eder. Jacobi yönteminin diğer adı Gauss yöntemidir. Jacobi (Gauss) yöntemi aşağıdaki denklem gibi, (6.) in k ıncı denklemi düşünülerek çıkarılmıştır. y = A x + A x + + A x + + A x (6.) k k k kk k kn N x k yı çözmek için aşağıdaki denklem kullanılır; x = y x + + x + x + + x A ( A A, A, + + A ) k k k k k k k k k kn N kk k N = k Akn n Akn n A y x x kk n= n= k+ Jacobi yöntemi (6.3) ün sol tarafındaki yeni ( ) tekrarlanan i değerlerinde, x () i nin eski değerlerini kullanır. k (6.3) x i+ değerleri üretmek için (6.3) ün sağında k N xk( i+ ) = k Akn n() Akn n(),,, A y x i x i k = N kk n= n= k+ (6.4) te verilen Jacobi yöntemi ayrıca aşağıdaki matris formunda da yazılabilir. (6.4) ( i+ ) = ( i) + x Mx D y (6.5) M= D ( D A ) (6.6) ve D matrisi aşağıdaki şekilde ifade edilir. 55
160 Jacobi yönteminde D matrisi, A matrisinin köşegen elemanlarını içerir. Örnek 6.3: Jacobi yöntemini kullanarak Örnek 6. i çözün. Başlangıç koşulları için; x ( ) x ( ) 4 başlayın ve (6.) de ε = 0 şartı sağlanıncaya kadar çözüme devam edin. Çözüm: N = ile (6.4) den k = x ( i+ ) = y A x () i = 6 5x () i A 0 k = x ( i+ ) = y A x () i = 3 x () i A 9 Alternative olarak, matris formunda (6.5)-(6.7) denklemlerini kullanarak; D = 0 9 = M = 0 = x () i 0 6 x ( i+ ) 0 0 = = x ( i ) x () i Üst taraftaki iki formül birbirine özdeştir. x ( ) x ( ) (6.7) 0 = 0 = 0 ile 0 = 0 = 0ile çözüme başlanıldığında yakınsama kriteri aşağıda gösterildiği gibi 0. tekrarlamada elde edilmiştir. Ara basamakların gösterimi yapılmamıştır. x () = 0, 6 x () = 0,33333 x () = 0, x () = 0, x (3) = 0,5 x (3) = 0, 3704 x (4) = 0,4848 x (4) = 0, x (5) = 0,48889 x (5) = 0,634 x (6) = 0,48683 x (6) = 0,469 ( ) x ( ) x ( ) x (7) = 0,48766 x (7) = 0,55 x (8) = 0, x (8) = 0, 496 x 0 9 0, , = = 6, 0 < ε 9 0, x (9) = 0,4875 x (9) = 0,50 x (0) = 0, x (0) = 0, 5 56
161 x ( ) x ( ) x ( ) 0 9 0, 5 0, 50 = = 8,9 0 < ε 9 0, 50 5 Gauss-Seidel Yöntemi de aşağıda verilmiştir. k N xk i k kn n kn n A y x i x i kk n= n= k+ ( + ) = A ( + ) A ( ) (6.8) (6.8) ve (6.4) denklemleri karşılaştırıldığında; Gauss-Seidel yöntemindeki tekrarlama sırasında sağ x i, n k x i+ üretmesi tarafta kullanılan yeni değerlerin ( + ) <, sol tarafta kullanılan yeni değerleri ( ) n dışında her iki yöntem de birbirine benzerdir. Diğer bir ifadeyle, Gauss-Seidel yönteminin yukardaki Gauss yönteminden tek farkı; aynı tekrar içinde elde edilen herhangi bir değişken değerinin, bir sonraki değişkenle ilgili denklemde, diğer tekrarı beklemeden yerine konmasıdır. Bu durum, yakınsama tekrar sayısını Gauss yöntemine göre azaltmaktadır. (6.8) deki Gauss-Seidel yöntemi ayrıca (6.5) ve (6.6) denklemlerinin matris formatlarında yazılabilir. k (6.9) Gauss-Seidel için (6.9) daki D, A matrisinin alt-üçgensel kısmı olmasına karşın; Jacobi yöntemi için (6.7) deki D, A matrisinin köşegen parçasıdır. Örnek 6.4: Gauss-Seidel yöntemini kullanarak Örnek 6.3 ü çözün. Başlangıç koşulları için; x ( ) x ( ) 4 başlayın ve (6.) de ε = 0 şartı sağlanıncaya kadar çözüme devam edin. Çözüm: k = x ( i+ ) = y A x () i = 6 5x () i A 0 k = x ( i+ ) = y A x ( i+ ) = 3 x ( i+ ) A 9 x ( i+ ) ve ( ) x i+ için bu denklem kullanılırsa; x i x i 9 0 ( + ) = () Alternatif olarak, matris formatında (6.9), (6.5) ve (6.6) denklemleri kullanılırsa; 0 = 0 = 0 ile D = 9 =
162 M = 0 0 = x( i+ ) 0 x() i = + x ( i ) 0 + x () i x () = 0, 6 x () = 0, x () = 0,5 x () = 0, x (3) = 0, x (3) = 0, 469 x (4) = 0,48765 x (4) = 0,497 x (5) = 0, 4875 x (5) = 0, 5 x (6) = 0, 4875 x (6) = 0, 5 Üst taraftaki iki formül birbirine özdeştir. x ( ) x ( ) 0 = 0 = 0ile çözüme başlanıldığında yakınsama kriteri 6. tekrarlamada elde edilmektedir. Oysa Jacobi de bu yakınsama 0. basamakta gerçekleşmişti. Yukarıdaki örnekte olduğu gibi Gauss-Seidel yönteminin yakınsama hızı bazı A matrisleri için Jacobi ye göre daha hızlı iken, diğer bazı A matrisleri için Jacobi yönteminin yakınsama hızı Gauss- Seidel e göre daha hızlı olabilmektedir. Bazı durumlarda ise bir yöntem sonuca yakınsarken diğeri çözümden uzaklaşabilmektedir. LİNEER OLMAYAN CEBİRSEL DENKLEMLER İÇİN TEKRARLI ÇÖZÜMLER: NEWTON-RAPHSON YÖNTEMİ Lineer olmayan denklemlerin kümesi matris formunda aşağıda verilmiştir; (6.0) Burada y ve x terimleri N vektörü ve f( x ) de fonksiyonların N vektörüdür. Değerleri bilinen y ve f( x ) e göre; bizden x in çözümü istenmektedir. Bölüm 6.3 te açıklanan tekrarlı yöntemler, lineer olmayan denklemler için aşağıdaki şekilde genişletilebilir. (6.0) denklemi farklı şekilde yazılacak olursa; 0= y f( x ) (6.) ve yukarıdaki denklemin her iki tarafına da Dx ilave edilirse denklem aşağıdaki şekilde ifade edilebilir. Burada D matrisi, N N boyutlarında tersi alınabilen kare matristir. ( ) Dx = Dx + y f x (6.) Denklemin her iki tarafı da sol taraftan D matrisi ile çarpılırsa; ( ) x = x + D y f x (6.3) (6.3) ün sağ tarafında bulunan eski () için kullanılır. ( i+ ) = ( i) + ( ( i) ) x i değerleri, sol taraftaki yeni x( ) i + değerlerini üretmek x x D y f x (6.4) 58
163 Lineer denklemler için, f( x)= Ax eşitliği sağlanır ve (6.4) denklemi aşağıdaki denkleme indirgenir. ( i ) () i () i ( ) () i x + = x + D y Ax = D D A x + D y (6.5) Yukarıdaki gösterim; (6.5) teki Jacobi ve Gauss-Seidel yöntemleriyle özdeştir. Lineer olmayan denklemler için (6.4) teki D matrisinin belirtilmesi gerekir. D matrisinin belirtilmesi için kullanılan yönteme Newton-Raphson yöntemi adı verilir. Bu yöntemin temeli; f( x) fonksiyonunu x0 noktası etrafında Taylor serisine açmaktır. df y = f x + x x ( ) ( ) 0 0 d x x= x0 (6.6) daki yüksek dereceli terimleri ihmal edip, denklem x için çözülürse; (6.6) df x= x0 + ( 0) d y f x x x= x0 (6.7) Newton-Raphson yöntemi; (6.7) de x 0 ı eski x() i değeriyle değiştirirken, aynı zamanda x i de yeni x( i +) değeriyle değiştirir. Sonuç olarak; ( i+ ) = () i + () i ( () i ) x x J y f x (6.8) (6.9) (6.9) da elemanları kısmi türevli olarak gösterilen N N lik J matrisi Jacobian matrisi olarak adlandırılır. (6.4) deki D nin yerini, (6.8) deki J () i nin alması haricinde, Newton Raphson metodu, genişletilmiş Gauss-Seidel yöntemi ile benzerdir. Örnek 6.5: f ( x) = y skaler fonksiyonunu 9 a. Newton-Raphson yöntemi ile f x = x y =, ( ) b. Genişletilmiş Gauss-Seidel yöntemi ile ( D = 3 ve Çözüm: ( ) x f x x ve ( 0) = için çözünüz. ε 4 = 0 şartına göre) = ile (6.9) kullanılırsa; J() i = ( x ) = x = x () () () i d x x i x= x i dx = 59
164 ve J() i matrisi (6.8) denklemi içinde kullanılırsa; ( ) ( ) ( ) x 0 = ile tekrarlı Newton-Raphson çözümü yapılırsa; xi () () xi+ = xi+ 9 x i elde edilir. x () = 5, x () = 3,4, x (3) = 3,0353, x (4) = 3,00009 ve x (5) = 3 değerleri elde edilir. D = 3 ile (6.4) kullanılırsa tekrarlı Gauss-Seidel çözümü aşağıdaki gibi bulunur; x () = 3,66667, x () =,859, x (3) = 3,5935, x (4) =,8908, x (5) = 3,5445 ve x (6) =,35945 ε = 0 Örnek 6.6: Newton-Raphson yöntemini kullanarak ve aşağıdaki x( 0) değerinden başlayarak denklemi çözünüz. 4 x+ x 5 4 ( 0) xx = = 50 x 9 Çözüm: ( ) f = x + x ve f = xx ile (6.9) u kullanarak; Elde edilir ve J () i (6.8) içinde kullanılırsa; matrisleri bulunur. Bu matrisin elemanları, iki ayrı denklem şeklinde yazılırsa; ( ) x ( i) ( ) ( ) () 5 () () 50 () () x() i x() i x() i 5 x() i x() i 50 x() i x() i x () i x () i x i x i x i x i x i x i+ = + + x i+ = x i + eşitlikleri elde edilir. Tekrarlı Newton-Raphson çözümü yapılırsa; x () = 5,, x () = 9,8 x () = 4,993, x () = 0, 0087 x (3) = 4,99998 ve x (3) = 0, 0000 x (4) = 5 x (4) = 0 değerleri hesaplanır. (6.8) denklemi J matrisinin tersi olan J matrisini içermektedir. (6.8) denklemi aşağıdaki gibi yeniden yazılabilir. J matrisini hesaplamak yerine 60
165 () i Δ () i = Δ () i J x y (6.30) () i ( i ) () i Δ x = x + x (6.3) () i () i Δ y = y f x (6.3) Çözüm için; bundan sonraki herbir tekrarda aşağıdaki dört basamak tamamlanır.. basamak: Δy () i yi (6.3) den hesapla. basamak: J () i yi (6.9) dan hesapla 3. basamak: Gauss elemesi ve geri-çıkarım kullanarak Δx() i için (6.30) u çöz 4. basamak: (6.3) den x ( i +) i hesapla Örnek 6.7: Örnek 6.6 nın ilk tekrarlı çözümünde yukarıda bahsedilen dört farklı basamağı kullanın. Çözüm:. basamak: Δ y( 0) = y f x( 0) = = 50 ( 4)( 9 ) 4. basamak: J ( 0) 3. basamak: Δy ( 0) ve J( 0) = = x( 0) x( 0) 9 4 ( ) ( ) Δx = Δx 0 4 kullanıldığında (6.30) denklemi aşağıdaki şekle dönüşür. Gauss elemesi kullanılarak; birinci denklem ikinci denklemden aşağıdaki sonuca ulaşılır. ( ) ( ) Δx 0 = 0 5 Δx 0 4 Yukarıdaki denklem geri-çıkarım ile çözüldüğünde; aşağıdaki değerler bulunur. 4 Δ x ( 0) = = 0,8 5 Δ x 0 = 0,8=, ( ) 4. basamak: x() x( 0) x ( 0) 4, 5, = +Δ = 9 + = 0,8 9,8 J / J = 9/= 9defa çıkarılarak Güç akışı çalışmalarından elde edilen tecrübeler gösteriyor ki; Gauss-Seidel ve Jacobi yöntemlerinin çözümden ıraksadığı pek çok durumda Newton-Raphson yöntemi çözüme yakınsamaktadır. Buna ilaveten Newton-Raphson yönteminde yakınsama için gerekli olan tekrarlama sayısı N boyutundan bağımsızdır. Ancak; Jacobi ve Gauss-Seidel için durum farklıdır ve boyut büyüdükçe tekrarlama sayısı da artar. Newton-Raphson ile çözülen güç akışı problemlerinin çoğu 0 tekrarlamadan daha az sayılarda çözüme yakınsar. 6
166 GÜÇ AKIŞI PROBLEMİ Güç akışı problemi; dengeli 3-fazlı ve yatışkın durumdaki güç sistemlerinde, herbir bara üzerindeki gerilim büyüklüğünün ve faz açısının hesaplanmasıdır. Bu hesaplamanın sonucunda; iletim hattı ve trafolar gibi şebeke elemanlarındaki aktif ve reaktif güç akışları bulunur ve elemanlar üzerindeki güç kayıpları hesaplanır. Güç akışı probleminin başlangıç noktası; güç sistemlerinde, bilgisayar çözümleri için gerekli olan giriş verilerinin alınabildiği tek-hat diyagramıdır. Giriş verileri temel olarak; bara, iletim hattı ve transformatör verilerinden oluşur. Şekil 6. de gösterildiği gibi herbir k barası, dört farklı değişken ile ilişkilendirilir. Bu değişkenler; V k gerilim genliği, δ k faz açısı, P k net gerçek güç ve Q k reaktif güç olarak ifade edilir. Herbir barada, bu değişkenlerden iki tanesi giriş verisi olarak kabul edilir ve diğer bilinmeyen veriler güç akışı yardımıyla hesaplanır. Hesaplamalarda ve gösterimde kolaylık olması açısından; Şekil 6. deki k barasına iletilen güç, jeneratör ve yük terimleri olarak iki kısma ayrılmıştır ve aşağıdaki denklemlerle ifade edilmiştir. P = P P k Gk Lk Q = Q Q k Gk Lk (6.33) Herbir k barası aşağıdaki üç farklı bara tipinden birine göre sınıflandırılır.. Salınım barası: sistemde sadece bir adet salınım barası bulunur ve genellikle hesaplamalarda sayısı ile numaralandırılır. Salınım barası aynı zamanda referans barasıdır ve üzerindeki V δ giriş verisi,0 0 br olarak alınır. Güç akışı sonunda, P ve Q değerleri hesaplanır.. Yük ( PQ) barası: P k ve Q k değerleri giriş verileridir. Sistemdeki çoğu bara genellikle bu bara tipindedir. Güç akışı sonunda, V k ve δ k değerleri hesaplanır. 3. Gerilim kontrollü ( PV) bara: P k ve V k değerleri giriş verileridir. Sistemdeki jeneratörlerin, anahtarlamalı şönt kapasitörlerin ve statik VAR sistemlerin bağlı olduğu baralar, gerilim kontrollü bara sınıfına girerler. Güç akışı sonunda, Q k ve δ k değerleri hesaplanır. Ayrıca dikkat edilmesi gereken diğer bir nokta; eğer k barası üretim olmayan bir yük barası ise Pk = P L olur ve bu durum, k barasına sağlanan gerçek gücün negatif olduğu anlamına gelir. Aynı k şekilde; eğer yük, endüktif ise Q = Q olur. k Lk Önceki ünitede, Şekil 5.7 de gösterildiği gibi iletim hatları eşdeğer π devresi ile gösterilir. Benzer şekilde çeşitli tipteki transformatörlerin de kendilerine ait eşdeğer devreleri vardır. Herbir iletim hattının giriş verisi; birim eşdeğer π devresindeki Z seri empedansı, Y şönt admitansı, hattın bağlandığı her iki barayı ve hattın maksimum çalışma gücünü içerir. Benzer şekilde herbir transformatörün giriş verisi; Z birim sarım empedansı, Y birim uyartım admitansı, sargıların bağlı olduğu baraları ve maksimum çalışma gücünü içerir. 6
167 Jeneratör Yük Şekil 6.: Genel Amaçlı Bara Gösterimi Bara admitans matrisi ( Y bara ) hat ve transformatörlerin giriş verilerine bakılarak oluşturulur. Daha önce birinci ünitede (.3) ve (.33) denklemlerinde ifade edildiği gibi; bara admitans matrisinin elemanları aşağıdaki şekilde hesaplanır. ( ) Köşegen üzerinde: Y = k. baraya gelen tüm admitansların toplamı k=,,3...,n kk Köşegen haricinde: Y = ( k ve n baraları arasındaki tüm admitansların toplamı)( k n) kn (6.34) Bara admitans matrisi kullanılarak, enerji şebekeleri için düğüm denklemleri aşağıdaki şekilde yazılabilir; I = Y V (6.35) bara Yukarıdaki denklemde I herbir baraya gelen akımları ifade eden N vektörüdür ve V ise bara gerilimlerinin gösterildiği N vektörüdür. k barası için (6.35) teki k ıncı denklem I N = Y V (6.36) k kn n n= ile gösterilir. k barasına iletilen kompleks güç ise aşağıdaki gibidir. S = P + jq = V I (6.37) k k k k k Gauss-Seidel yöntemi ile güç akışı çözümü (6.36) ve (6.37) denklemleri kullanılarak aşağıdaki gibi bulunabilir. N Pk + jqk = Vk YknVn k =,,, N (6.38) n= Ayrıca, aşağıdaki iki gösterim j V = V e δn (6.39) n n jθ Y = Y e kn = G + jb k, n=,,, N (6.40) kn kn kn kn 63
168 (6.38) denkleminde kullanıldığında; k k k kn n n= N j( ) k n kn P + jq = V Y V e δ δ θ (6.4) denklemine dönüşür. (6.4) denkleminin gerçek ve sanal kısımları ayrı ayrı kullanılırsa, güç denklemleri aşağıdaki şekilde yazılabilir. N P = V Y V cos ( δ δ θ ) (6.4) k k kn n k n kn n= N ( δ δ θ ) k N (6.43) Q = V Y V sin =,,, k k kn n k n kn n= veya Y kn kutupsal koordinatlar cinsinden ifade edildiğinde; (6.4) ve (6.43) denklemleri aşağıdaki şekle dönüşür. N P = V G cos + B sin V ( δ δ ) ( δ δ ) (6.44) K K n kn k n kn k n n= N V ( δ δ ) ( δ δ ) k N (6.45) Q = V G sin B cos =,,, K K n kn k n kn k n n= Yukarıdaki denklemler; lineer olmayan güç akışı problemlerine Newton-Raphson yaklaşımıyla çözüm getirirler. GAUSS-SEIDEL YÖNTEMİ İLE GÜÇ AKIŞI ÇÖZÜMÜ I = YbaraV düğüm denklemleri, bölüm 6.3 de Gauss-Seidel kullanılarak çözülen y=ax denklemine benzer lineer denklemler kümesidir. Güç akışındaki bara verileri; yük baraları için P k ve Q k yı veya gerilim kontrollü baralar için P k ve V k yı içerdiğinden, düğüm denklemleri lineer denklem tipine tam olarak uymaz. Akım kaynağı vektörü I, bilinmeyendir ve denklemleri lineer değildir. Her bir yük barası için I k değerleri, (6.37) denkleminden hesaplanabilir. I k Pk j Qk = (6.46) V k (6.8) denklemindeki Gauss-Seidel yöntemi yukarıda verilen I k ile düğüm denklemlerine uygulandığında; k N Pk j Q k Vk( i+ ) = YknVn i+ YknVn i Ykk Vk () i n= n= k+ ( ) ( ) (6.47) elde edilir. Çözüm esnasında, herbir tekrarlamada yük baraları için (6.47) denklemi iki kere uygulanır. İlk seferde, denklemin sağ tarafında V () i kullanılır, ikinci uygulamada ise V () i yerini V ( i+ ) e bırakır. k Gerilim kontrollü baralarda Q k bilinmemektedir, fakat (6.43) denkleminden hesaplandığında; N Q = V Y V sin δ δ θ (6.48) () i () i () i () i k k kn n k n kn n= Q = Q + Q ve Gk k Lk bulunur. k k 64
169 Eğer QG k nin hesaplanan değeri kendi sınır değerlerini aşmıyorsa; o zaman Q k, (6.47) denkleminde Vk ( i+ ) = V k( i+ ) δk( i+ ) değerini bulmak için kullanılır. Bu işlemin ardından; V( k i + ) genliği V k olarak değişir. Bu değer gerilim kontrollü baranın giriş verisidir. Son olarak (6.47) denklemi ile gerilim kontrollü baraların δ ( i + ) açısı hesaplanır. k Eğer QG k nin hesaplanan değeri kendi sınır değerlerini aşıyorsa; o zaman ilgili bara gerilim kontrollü bara tipinden çıkarak yük barasına dönüşür ve Q k sınır değerine eşitlenir. G numaralı barayı temsil eden salınım barası için V ve δ giriş verileridir. Bu bara için tekrarlamalı işlem gerekli değildir. (6.4) ve (6.43) denklemlerinden P ve Q değerleri hesaplanır. NEWTON-RAPHSON YÖNTEMİ İLE GÜÇ AKIŞI ÇÖZÜMÜ (6.4) ve (6.43) denklemleri, bölüm 6.4 te Newton-Raphson yöntemi kullanılarak çözülen y=f( x ) denklemine benzer lineer olmayan denklemlerdir. Güç akışı çözümü için gerekli olan x, y ve f vektörleri aşağıdaki gibi tanımlanır; (6.49) Bu denklemde kullanılan V, P ve Q terimleri birim değer ve δ açısı ise radyan cinsinden gösterilir. Salınım barasına ait olan V ve δ değişkenlerinin değerleri bilindiği için bu değişkenler (6.49) denkleminden çıkarılmıştır. (6.4) ve (6.43) denklemleri k =,3,..., N için aşağıdaki şekle dönüşürler. N y = P = P = V Y V cos ( ) ( δ δ θ ) x (6.50) k k k k kn n k n kn n= N y = Q = Q = V Y V sin ( ) ( δ δ θ ) x (6.5) k+ N k k k kn n k n kn n= (6.9) denkleminin Jacobian matrisi aşağıdaki formda olur. 65
170 (6.5) Bu matris, dört farklı blok olarak ayrılmıştır. Herbir bloktaki kısmi türevler (6.50) ve (6.5) denklemlerinden yola çıkılarak hesaplanmış ve aşağıda verilmiştir. Pk n k Jkn = = Vk YknVn sin δk δn θkn δ J J3 J4 n ( ) Pk = = V Y cos V ( δ δ θ ) kn k kn k n kn n Qk = = V Y V cos δ Qk = = V Y sin V ( δ δ θ ) kn k kn n k n kn n ( δ δ θ ) kn k kn k n kn n P n= k J = = V Y V sin δ δ θ N k kk k kn n k n kn δ k n= n k ( ) P J V Y cos Y V cos N k kk = = k kk θkk + kn n δk δn θkn Vk n= Q J3 V Y V cos J4 N k kk = = k kn n k n kn δ k n= n k kk Qk = = Vk Y V k ( δ δ θ ) N ( ) ( ) sinθ + Y V sin δ δ θ kk kk kn n k n kn n= (6.53) (6.54) 66
171 Bu aşamadan sonra bölüm 6.4 te açıklanan Newton-Raphson yönteminin basamakları; i inci () δ i tekrarlama için x() i = ifadesi kullanılarak oluşturulur. V() i. basamak: (6.50) ve (6.5) denklemlerini aşağıdaki ifadeyi hesaplamak için kullan. () i () i () i () i ΔP P P () i x Δ y = = ΔQ Q Q x. basamak: (6.53) ve (6.54) denklemlerini Jacobian matrisini hesaplamak için kullan. 3. basamak: Gauss elemesi ve geri-çıkarım kullanarak aşağıdaki ifadeyi çöz. () () () () () () () () J i J i Δδ i ΔP i = 3 i 4 i J J ΔV i ΔQ i 4. basamak: Aşağıdaki ifadeyi hesapla. ( 0) x ( i ) ( ) ( ) () () () () δ i+ δ i Δδ i + = = + V i+ V i ΔV i 67 (6.55) (6.56) (6.57) x, ilk başlangıç değeriyle başladıktan sonra tekrarlama prosedürü; sonuca yakınsama sağlanıncaya kadar devam eder veya tanımlanan maksimum tekrarlama değeri aşılınca son bulur. Yakınsama kriteri genelde Δx () i den çok Δy () i ye bağlıdır. Elektrik şebekesinde herbir gerilim kontrollü bara için V k gerilim genliği önceden bilinmektedir ve bu yüzden Q k ( x ) fonksiyonuna ihtiyaç yoktur. Bu yüzden gerilim kontrollü baralar için V k x vektöründen, Q k ise y vektöründen hariç tutulur, çıkarılır. Jacobian matrisinde ise; V k nın kısmi türevlerine karşılık gelen sütunlar ve Q k ( x ) in kısmi türevlerine karşılık gelen satırlar hariç tutulur. Çözüme ulaşmak için yapılan herbir tekrar işleminde; herbir gerilim kontrollü baraya ait olan V( ) k i + değeri V k ya reset edilip eşitlenir. Herbir tekrarlamanın sonunda, Q k ( ) gerilim konrollü bara için Q = Q ( ) + Q Gk k Lk niceliğin sınır değerlerini aşıyorsa; bara tipi yük barası olarak değiştirilir ve x değeri (6.5) den hesaplanır ve ardından herbir x değerleri bulunur. Eğer hesaplanan Q Gk değeri, bu QG k değeri sınır değerine eşitlenir. Bu aşamadan sonra, güç akışı ile V k için yeni bir değer hesaplanır. Gauss-Seidel ve Newton-Raphson yöntemleri karşılaştırıldığında; güç akışı problemlerinden elde edilen tecrübeler gösteriyor ki, Jacobi ve Gauss-Seidel yöntemlerinin çözüme ıraksadığı birçok durumda Newton-Raphson yöntemi çözüne yakınsamaktadır. Ayrıca; Newton-Raphson yönteminde yakınsama için gerekli olan tekrarlama sayısı N bara sayısından bağımsız iken, Jacobi ve Gauss-Seidel yöntemlerinde bu sayısı N kadar artmaktadır. Jacobi ve Gauss-Seidel yöntemlerinin bilgisayarda kullanılan hafıza ve düşük hesap yetenekleri bakımından avantajı olmasına rağmen, günümüz teknolojisi ile Newton-Raphson yöntemi diğer Jacobi ve Gauss-Seidel e göre daha çok tercih edilir ve bu yöntemle güvenilir hesaplamalar yapılır. HIZLI AYRIŞIK GÜÇ AKIŞI Çok fazla baraya ve iletim hattına sahip olan büyük boyutlu enerji şebekelerinin izlenmesi ve kontrolü amacıyla ana bilgisayarda sık sık güç akışı programı çalıştırılıp güç akışı hesabı yapılır. Yöntem olarak Newton-Raphson seçilmişse, sistemin büyümesi Jacobian matrisini de oldukça büyütür. Böylece, bilgisayarın hafıza gereksinimi artar ve yöntemin sonuca yakınsama zamanı uzar. Hızlı ayrışık güç akışı yöntemleri bu olumsuzlukları azaltmak için geliştirilmiştir. Güç akışı yönteminde kullanılan Jacobian matrisi içinde, Q δ ve P-Varasındaki zayıf ilişki sebebiyle, hızlı ayrışık güç akışı yönteminde J ve J 3 alt matrisleri ihmal edilir. Böylece yöntem hem hızlanır hem de bilgisayarın bellek gereksinimi azalır. Yöntemin daha da hızlandırılması için
172 Vk Vn br kabul edilerek δk δ alınabilir. Son kabuller uygulandıktan sonra J ve J 4 sabit matris n özelliği kazanır. Bu durumda Newton-Raphson yönteminde her tekrarlamada Jacobian matrisinin tekrar tekrar hesaplanması gerekmez ve böylece yöntemin yakınsama hızı artar. Bu yaklaşım, ihmallerin olmadığı önceki yaklaşıma göre yaklaşık sonuçlar üretirler ama zamanın önemli olduğu durumlarda ufak hatalara göz yumulabilir. GÜÇ AKIŞI KONTROLÜ Enerji sistemlerinde güç akışını ve iletilen enerjinin kontrolünü sağlayan çeşitli şebeke elemanları mevcuttur. Güç akışı genel olarak aşağıdaki üç şekilde kontrol edilir;. Jeneratörlerin uyartım kısımlarının kontrolü. Şönt kapasitör, şönt reaktör ve statik VAR sistemlerin anahtarlanması 3. Regüleli ve kademe değiştiricili transformatörlerin kontrolü Dengeli yatışkın-durum şartlarında çalışan jeneratöre ait basit Thevenin eşdeğer modeli Şekil 6. de gösterilmektedir. V t jeneratöre ait terminal gerilimini, E g uyartım gerilimini, δ güç açısını ve X g ise pozitif-sıralı senkron reaktansı ifade etmektedir. Şekilden de anlaşılacağı üzere, jeneratöre ait akım değeri ve jeneratör tarafından şebekeye sağlanan kompleks güç değeri aşagıdaki iki denklemde ifade edilmiştir; j Ege δ Vt I = (6.58) j X g ( δ δ) jδ E V VE cos sin V * ge t t g j + j t S = P+ jq= VI t = Vt = j X g Xg Şebekeye sağlanan gerçek ve reaktif güç değerleri ise; (6.59) VE t g P= ReS = sinδ (6.60) X g Vt Q= ImS = ( Egcosδ Vt) (6.6) X g olarak bulunur. (6.60) denkleminden anlaşılacağı üzere δ güç açısı arttıkça gerçek güç değeri de artmaktadır. Şebeke işlemi olarak düşünüldüğünde; uyartım gerilimi sabit tutularak jeneratörün giriş gücü türbün vasıtasıyla yükseltilirse, jeneratöre ait rotorun dönüş hızı artar. Rotor hızının artmasına paralel olarak δ güç açısının değeri artar ve bu artış da jeneratörün çıkışındaki P gerçek gücünü arttırır. Ayrıca, (6.6) denklemine göre Q reaktif güç çıkışında da azalma meydana gelir. δ güç açısının 5 den düşük olduğu durumlarda; P deki artış, Q daki azalıştan çok daha fazladır. Güç akışı açısından düşünüldüğünde; türbün gücünün artışı, jeneratörün bağlı olduğu sabit gerilim barasında P artışına sebep olur. Güç akışı, Q daki küçük değişiklikle beraber δ güç açısındaki artışı hesaplar. (6.6) denklemi bize E g uyartım geriliminin artmasıyla Q reaktif güç çıkışının da artacağını gösterir. Şebeke işlemi olarak düşünüldüğünde; türbün gücü sabit tutularak jeneratörün uyartım gerilimi yükseltildiğinde, rotor akımı artar. Rotor akımındaki artışa bağlı olarak E g uyartım gerilimi de artar ve bu artış jeneratöre ait Q reaktif güç çıkışının artmasına sebep olur. (6.60) denklemindeki P gücünü sabit tutabilmek için E g artışının δ güç açısında küçük değişimler meydana getirdiği görülmektedir. Güç akışı açısından düşünüldüğünde; jeneratörün uyartım gerilimindeki artış, jeneratörün bağlı olduğu sabitgerilim barasındaki gerilimin genliğini arttırır. Güç akışı, jeneratör tarafından sağlanan Q reaktif güç çıkışındaki artışı δ güç açısındaki küçük değişime göre hesaplar. 68
173 Şekil 6.3 te güç sistemindeki baraya şönt kapasitör bankası eklenmesinin etkileri gösterilmektedir. Buradaki sistem Thevenin eşdeğer devresiyle modellenmiştir. AN anahtarı kapatılmadan önce kapasitörün bağlanacağı baranın gerilimi E Th değerine eşittir. AN anahtarı kapatıldığında kapasitör üzerindeki I akımı, yük barası gerilimi olan C V t den 90 ileridedir. Şekil 6.3 te görüldüğü gibi V t fazörü, E fazöründen genlik olarak oldukça büyüktür. Güç akışı açısından bakıldığında, yük barasına Th bir kapasitör ilave edilmesi sisteme negatif yük ilavesi gibi yansır. Bu demek oluyor ki; kapasitör negatif değerde bir yük tüketicisidir. Böyle durumda güç akışı, küçük değerdeki δ değişimlerinde oluşan bara gerilim genliğinin artış miktarını hesaplar. Aynı şekilde sisteme şönt endüktör bağlandığında sistem üzerinde oluşan etki, yük barasına pozitif değerde bir yük bağlandığındaki oluşan etkiyle aynıdır. Böyle durumda güç akışı, küçük değerdeki δ değişimlerinde oluşan bara gerilim genliğindeki azalmayı hesaplar. Kademe ayarlı transformatörlerin kademe ayar değerleri değiştirilerek, bağlandıkları baraların gerilimine etki edilebilir. Bu kontrol mekanizması, hatlardan akan reaktif güç değerini değiştirir. Yük Şekil 6.: Jeneratöre ait Thevenin Eşdeğer Devre Şekil 6.3: Güç Sistem Barasına Şönt Kapasitör Eklenmesi 69
174 Özet Dengeli, üç-fazlı ve yatışkın-durum koşulları altında enerji sistemlerinde hesaplanan güç akışı hesaplamalarında; Jeneratörlerin, şebekeye bağlı tüm yük taleplerini ve iletim hatlarındaki toplam güç kaybını karşıladıkları kabul edilir. Bütün baralara ait gerilim genliklerinin, nominal gerilim sınırları içerisinde olduğu varsayılır. Jeneratörlerin, kendilerine ait güç sınırlarını aşmadıkları kabul edilir. Transformatör ve iletim hatlarının, aşırı yüklenmedikleri varsayılır. Güç akışını hesaplamak için kullanılan algoritma yada program sona erdiğinde, şebekedeki baralara ait gerilim genlikleri, gerilim açıları, baralardan ve iletim hatlarından akan aktif ve reaktif güçler ve toplam güç kaybı hesaplanmış olur. Gauss elemesi ve geri-çıkarım için bilgisayar tarzı matematik işlemcilerin A için N hafıza adresine, y için N hafıza adresine gereksinimi vardır. A ve y nin muhafazası için bir gereksinim yok ise A aynı şekilde ( k ), A nın adresinde ve ( k ) y, y nin adresinde depolanabilir. Tekrarlanan döngüler, aritmetik ifadeler ve çalışma alanları için ek hafıza gereklidir. Bilgisayar zaman gereksinimleri; Gauss elemesi ve geri-çıkarımlar için gerekli olan aritmetik uygulamaların belirlenmesiyle hesaplanabilir. Gauss-Seidel ve Newton-Raphson yöntemleri karşılaştırıldığında; güç akışı problemlerinden elde edilen tecrübeler gösteriyor ki, Jacobi ve Gauss-Seidel yöntemlerinin çözüme ıraksadığı birçok durumda Newton-Raphson yöntemi çözüne yakınsamaktadır. Ayrıca; Newton- Raphson yönteminde yakınsama için gerekli olan tekrarlama sayısı N bara sayısından bağımsız iken, Jacobi ve Gauss-Seidel yöntemlerinde bu sayısı N kadar artmaktadır. Jacobi ve Gauss- Seidel yöntemlerinin bilgisayarda kullanılan hafıza ve düşük hesap yetenekleri bakımından avantajı olmasına rağmen, günümüz teknolojisi ile Newton-Raphson yönteminde diğer Jacobi ve Gauss-Seidel e göre daha tercih edilir ve güvenilir hesaplamalar yapılmaktadır. 70
175 Kendimizi Sınayalım. Aşağıdakilerden hangisi, güç akışı programının hesapladığı sonuçlardan biri değildir? a. Bara gerilim genliği b. Bara gerilim frekansı c. Bara gerilim açısı d. Baradan akan aktif güç e. Baradan akan reaktif güç. Ax = y lineer denklem sisteminde A matrisi N N boyutunda, üst üçgensel tipte kare matris ise bu denklem sistemini çözmek için A matirisinin en alt satırından başlayarak en üst satıra doğru tüm bilinmeyenleri çözme yöntemine ne ad verilir? a. Jacobi b. Gauss c. Geri-çıkarım d. Gauss-Seidel e. Newton-Raphson 3. N bilinmeyenli denklem sistemini çözerken Gauss elemesi kullanılıyorsa, bu yöntem kaç adet çarpım işlemi gerektirir? ( N N) a. 3 ( N N) b. 3 ( N N ) c. 3 ( N N) d. 3 ( N N) e bilinmeyenli denklem sistemini çözerken geri çıkarım işlemi kullanılıyorsa, bu yöntem kaç adet çıkarma işlemi gerektirir? a. 3 b. 4 c. 6 d. e Güç akışı yöntemleriyle ilgili olarak aşağıdaki ifadelerden hangisi doğrudur? a. Jacobi yönteminde N boyutu büyüdükçe tekrarlama sayısı azalır. b. Gauss-Seidel yönteminde N boyutu büyüdükçe tekrarlama sayısı azalır. c. Jacobi yönteminde tekrarlama sayısı N den bağımsızdır. d. Gauss-Seidel yönteminde tekrarlama sayısı N den bağımsızdır. e. Newton-Raphson yönteminde tekrarlama sayısı N den bağımsızdır. 6. Güç akışı hesabında, şebekede sadece bir adet bulunan, genellikle hesaplamalarda sayısı ile numaralandırılan ve aynı zamanda referans barası olarak da adlandırılan bara tipi aşağıdakilerden hangisidir? a. Akım barası b. Gerilim barası c. Salınım barası d. Kapasitör barası e. Endüktör barası 7. Güç akışında, yük barası olarak adlandırılan bara ile ilgili olarak aşağıdakilerden hangisi doğrudur? a. b. δ c. k P k ve Q k değerleri giriş verileridir. Güç akışı sonunda, V k δ ve k değerleri hesaplanır. P k ve V k değerleri giriş verileridir. Güç akışı sonunda, Q δ k ve k değerleri hesaplanır. ve V k değerleri giriş verileridir. Güç akışı sonunda, Q k ve P k değerleri hesaplanır. δ d. k ve Q k değerleri giriş verileridir. Güç akışı e. sonunda, V k ve P k değerleri hesaplanır. P k δ ve k değerleri giriş verileridir. Güç akışı sonunda, V k ve Q k değerleri hesaplanır. 7
176 8. N bilinmeyenli bir denklem için, Jacobian matrisinin boyutu aşağıdakilerden hangisidir? a. xn b. Nx c. (N-)x d. (N-)x(N-) e. NxN 9. Newton-Raphson yönteminde çözüm için yapılan herbir tekrar kaç basamaktan oluşur? a. b. 3 c. 4 d. 5 e Güç akışında aktif güç ile bara geriliminin giriş verisi olduğu ve reaktif güç ile faz açısının hesaplandığı bara tipi aşağıdakilerden hangisidir? a. Salınım barası b. Yük barası c. Akım barası d. Kapasitor kontrollü bara e. Gerilim kontrollü bara Kendimizi Sınayalım Yanıt Anahtarı. b Yanıtınız yanlış ise Güç Akışı başlıklı konuyu yeniden gözden geçiriniz.. c Yanıtınız yanlış ise Lineer Cebir Denklemlerinde Doğrudan Çözümler: Gauss Elemesi Yöntemi başlıklı konuyu yeniden gözden geçiriniz. 3. d Yanıtınız yanlış ise Lineer Cebir Denklemlerinde Doğrudan Çözümler: Gauss Elemesi Yöntemi başlıklı konuyu yeniden gözden geçiriniz. 4. c Yanıtınız yanlış ise Lineer Cebir Denklemlerinde Doğrudan Çözümler: Gauss Elemesi Yöntemi başlıklı konuyu yeniden gözden geçiriniz. 5. e Yanıtınız yanlış ise Lineer Olmayan Cebirsel Denklemler İçin Tekrarlı Çözümler: Newton-Raphson Yöntemi başlıklı konuyu yeniden gözden geçiriniz. 6. c Yanıtınız yanlış ise Güç Akışı Problemi başlıklı konuyu yeniden gözden geçiriniz. 7. a Yanıtınız yanlış ise Güç Akışı Problemi başlıklı konuyu yeniden gözden geçiriniz. 8. e Yanıtınız yanlış ise Lineer Olmayan Cebirsel Deklemler İçin Tekrarlı Çözümler: Newton-Raphson Yöntemi başlıklı konuyu yeniden gözden geçiriniz. 9. c Yanıtınız yanlış ise Lineer Olmayan Cebirsel Denklemler İçin Tekrarlı Çözümler: Newton-Raphson Yöntemi başlıklı konuyu yeniden gözden geçiriniz. 0. e Yanıtınız yanlış ise Güç Akışı Problemi başlıklı konuyu yeniden gözden geçiriniz. 7
177 Yararlanılan Kaynaklar Palo A. (005). EPRI AC Transmission Line Reference Book 00 kv and Above, Electric Power Research Institute (EPRI). Hayt., W. H. (006), Engineering Circuit Analysis, 7th ed. NewYork: McGraw-Hill. Güney İ. (994). Çözümlü Enerji İletim Hatları Problemleri, Marmara Üniversitesi Yayınları. Peşint M. A. (996). Elektrik Santralleri Enerji İletimi ve Dağıtımı. Güney,. (00). Çözümlü Enerji İletim Hatları Problemleri, İstanbul, Marmara Üniversitesi Yayınları. Prof. Dr. Şerifoğlu N. (003) Elektrik Enerji Sistemleri cilt, Papatya yayıncılık. Glover, D.J., and Sarma, M.S. (989). Power system analysis and design, PWS-Kent Publishing Com., Boston. Fitzgerald, A. E., Higginbotham, D. E. & Grabel, A. (000). Fundamental Electric Engineering. (Çev. Ed. Kıymaç, K.) Temel Elektrik Mühendisliği Cilt. (3. Baskı). Ankara: Bilim Center. Arifoğlu, U. (00). Güç Sistemlerinin Bilgisayar Destekli Analizi. İstanbul: Alfa Basım Yayım Dağıtım Ltd. Şti. Grainger, J.J. (994). Power System Analysis. McGraw-Hill Inc. Saadat, H. (004). Power System Analysis. McGraw-Hill Inc
AC Circuits Review Assoc.Prof.Dr.Bahtiyar DURSUN Department of Energy Systems Engineering
 ESM 14701 POWER QUALITY IN ENERGY SYSTEMS AND HARMONICS AC Circuits Review Assoc.Prof.Dr.Bahtiyar DURSUN Department of Energy Systems Engineering FAZÖR (PHASOR) Elektrik terminolojisinde kullanılan iki
ESM 14701 POWER QUALITY IN ENERGY SYSTEMS AND HARMONICS AC Circuits Review Assoc.Prof.Dr.Bahtiyar DURSUN Department of Energy Systems Engineering FAZÖR (PHASOR) Elektrik terminolojisinde kullanılan iki
BÖLÜM VI DENGELENMİŞ ÜÇ FAZLI DEVRELER (3 )
 BÖLÜM VI DENGELENMİŞ ÜÇ FAZLI DEVRELER (3 ) Elektriğin üretim, iletimi ve dağıtımı genelde 3 devrelerde gerçekleştirilir. Detaylı analizi güç sistem uzmanlarının konusu olmakla birlikte, dengelenmiş 3
BÖLÜM VI DENGELENMİŞ ÜÇ FAZLI DEVRELER (3 ) Elektriğin üretim, iletimi ve dağıtımı genelde 3 devrelerde gerçekleştirilir. Detaylı analizi güç sistem uzmanlarının konusu olmakla birlikte, dengelenmiş 3
BÖLÜM 3 ALTERNATİF AKIMDA SERİ DEVRELER
 BÖÜM 3 ATENATİF AKMDA SEİ DEVEE 3.1 - (DİENÇ - BOBİN SEİ BAĞANMAS 3. - (DİENÇ - KONDANSATÖÜN SEİ BAĞANMAS 3.3 -- (DİENÇ-BOBİN - KONDANSATÖ SEİ BAĞANMAS 3.4 -- SEİ DEVESİNDE GÜÇ 77 ATENATİF AKM DEVE ANAİİ
BÖÜM 3 ATENATİF AKMDA SEİ DEVEE 3.1 - (DİENÇ - BOBİN SEİ BAĞANMAS 3. - (DİENÇ - KONDANSATÖÜN SEİ BAĞANMAS 3.3 -- (DİENÇ-BOBİN - KONDANSATÖ SEİ BAĞANMAS 3.4 -- SEİ DEVESİNDE GÜÇ 77 ATENATİF AKM DEVE ANAİİ
ALTERNATİF AKIMDA ANİ VE ORTALAMA GÜÇ
 ALTERNATİF AKIMDA ANİ VE A akımda devreye uygulanan gerilim ve akım zamana bağlı olarak değişir. Elde edilen güç de zamana bağlı değişir. Güç her an akım ve gerilimin çarpımına (U*I) eşit değildir. ORTALAMA
ALTERNATİF AKIMDA ANİ VE A akımda devreye uygulanan gerilim ve akım zamana bağlı olarak değişir. Elde edilen güç de zamana bağlı değişir. Güç her an akım ve gerilimin çarpımına (U*I) eşit değildir. ORTALAMA
Nedim Tutkun, PhD, MIEEE Düzce Üniversitesi Elektrik-Elektronik Mühendisliği Bölümü Konuralp Düzce
 ELEKTRİK DEVRELERİ II ÖRNEK ARASINAV SORULARI Nedim Tutkun, PhD, MIEEE [email protected] Düzce Üniversitesi Elektrik-Elektronik Mühendisliği Bölümü 81620 Konuralp Düzce Soru-1) Şekildeki devrede
ELEKTRİK DEVRELERİ II ÖRNEK ARASINAV SORULARI Nedim Tutkun, PhD, MIEEE [email protected] Düzce Üniversitesi Elektrik-Elektronik Mühendisliği Bölümü 81620 Konuralp Düzce Soru-1) Şekildeki devrede
7. Sunum: Çok Fazlı Devreler. Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık
 7. Sunum: Çok Fazlı Devreler Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Üç Fazlı Devreler Üç fazlı devreler bünyesinde üç fazlı gerilim içeren devrelerdir.
7. Sunum: Çok Fazlı Devreler Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Üç Fazlı Devreler Üç fazlı devreler bünyesinde üç fazlı gerilim içeren devrelerdir.
Şekil-1. Doğru ve Alternatif Akım dalga şekilleri
 2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
ÇOK FAZLI DEVRELER EBE-212, Ö.F.BAY 1
 ÇOK FAL DERELER EBE-212, Ö.F.BAY 1 Üç Fazlı Devreler EBE-212, Ö.F.BAY 2 Eğer gerilim kaynaklarının genlikleri aynı ve aralarında 12 faz farkı var ise böyle bir kaynağa dengeli üç fazlı gerilim kaynağı
ÇOK FAL DERELER EBE-212, Ö.F.BAY 1 Üç Fazlı Devreler EBE-212, Ö.F.BAY 2 Eğer gerilim kaynaklarının genlikleri aynı ve aralarında 12 faz farkı var ise böyle bir kaynağa dengeli üç fazlı gerilim kaynağı
ENERJİ DAĞITIMI. Doç. Dr. Erdal IRMAK. 0 (312) Erdal Irmak. G.Ü. Teknoloji Fak. Elektrik Elektronik Müh.
 ENERJİ DAĞITIMI Doç. Dr. Erdal IRMAK G.Ü. Teknoloji Fak. Elektrik Elektronik Müh. http://websitem.gazi.edu.tr/erdal 0 (312) 202 85 52 Erdal Irmak Önceki dersten hatırlatmalar Üç Fazlı Alternatif Akımda
ENERJİ DAĞITIMI Doç. Dr. Erdal IRMAK G.Ü. Teknoloji Fak. Elektrik Elektronik Müh. http://websitem.gazi.edu.tr/erdal 0 (312) 202 85 52 Erdal Irmak Önceki dersten hatırlatmalar Üç Fazlı Alternatif Akımda
ALTERNATİF AKIMDA GÜÇ
 1 ALTERNATİF AKIMDA GÜÇ Elektrik gücü bir elektrik devresi ile transfer edilen yada dönüştürülen elektrik enerjisinin oranıdır. Gücün SI birimi Watt (W) tır. Doğru akım devrelerinde elektrik gücü Joule
1 ALTERNATİF AKIMDA GÜÇ Elektrik gücü bir elektrik devresi ile transfer edilen yada dönüştürülen elektrik enerjisinin oranıdır. Gücün SI birimi Watt (W) tır. Doğru akım devrelerinde elektrik gücü Joule
Üç Fazlı Sistemler ALIŞTIRMALAR
 Üç Fazlı istemler 477 11.10. ALŞMALA oru 11.1: Üç fazlı yıldız bağlı dengeli bir yükün faz-nötr gerilimi 150V dur. Yükün hat (=fazlar arası) gerilimini bulunuz. (Cevap : Hat 260V) oru 11.2: Üç fazlı üçgen
Üç Fazlı istemler 477 11.10. ALŞMALA oru 11.1: Üç fazlı yıldız bağlı dengeli bir yükün faz-nötr gerilimi 150V dur. Yükün hat (=fazlar arası) gerilimini bulunuz. (Cevap : Hat 260V) oru 11.2: Üç fazlı üçgen
4. Sunum: AC Kalıcı Durum Analizi. Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık
 4. Sunum: AC Kalıcı Durum Analizi Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Giriş Aşağıdaki şekillere ve ifadelere bakalım ve daha önceki derslerimizden
4. Sunum: AC Kalıcı Durum Analizi Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Giriş Aşağıdaki şekillere ve ifadelere bakalım ve daha önceki derslerimizden
A.Ü. GAMA MYO. Elektrik ve Enerji Bölümü ÖLÇME TEKNİĞİ 9. HAFTA
 A.Ü. GAMA MYO. Elektrik ve Enerji Bölümü ÖLÇME TEKNİĞİ 9. HAFTA İÇİNDEKİLER Güç Çeşitleri ve Ölçümü Güç Çeşitleri Görünür Güç ve Hesaplaması Aktif Güç Aktif güç tüketen tüketiciler GÜÇ ÇEŞİTLERİ VE ÖLÇÜMÜ
A.Ü. GAMA MYO. Elektrik ve Enerji Bölümü ÖLÇME TEKNİĞİ 9. HAFTA İÇİNDEKİLER Güç Çeşitleri ve Ölçümü Güç Çeşitleri Görünür Güç ve Hesaplaması Aktif Güç Aktif güç tüketen tüketiciler GÜÇ ÇEŞİTLERİ VE ÖLÇÜMÜ
Cihazın Bulunduğu Yer: Enerji Sistemleri Mühendisliği Bölümü B-Blok, Enerji Verimliliği Laboratuvarı
 Ölçüm Cihazının Adı: Enerji Analizörü Cihazın Bulunduğu Yer: Enerji Sistemleri Mühendisliği Bölümü B-Blok, Enerji Verimliliği Laboratuvarı 1) Ölçümün Amacı Amaç; şebeke ya da cihazların(motor barındıran
Ölçüm Cihazının Adı: Enerji Analizörü Cihazın Bulunduğu Yer: Enerji Sistemleri Mühendisliği Bölümü B-Blok, Enerji Verimliliği Laboratuvarı 1) Ölçümün Amacı Amaç; şebeke ya da cihazların(motor barındıran
GENETEK. Güç Sistemlerinde Kısa Devre Analizi Eğitimi. Güç, Enerji, Elektrik Sistemleri Özel Eğitim ve Danışmanlık San. Tic. Ltd. Şti.
 GENETEK Güç, Enerji, Elektrik Sistemleri Özel Eğitim ve Danışmanlık San. Tic. Ltd. Şti. Güç Sistemlerinde Kısa Devre Analizi Eğitimi Yeniköy Merkez Mh. KOÜ Teknopark No:83 C-13, 41275, Başiskele/KOCAELİ
GENETEK Güç, Enerji, Elektrik Sistemleri Özel Eğitim ve Danışmanlık San. Tic. Ltd. Şti. Güç Sistemlerinde Kısa Devre Analizi Eğitimi Yeniköy Merkez Mh. KOÜ Teknopark No:83 C-13, 41275, Başiskele/KOCAELİ
ALTERNATİF AKIMIN TEMEL ESASLARI
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIMIN TEMEL ESASLARI Dr. Öğr. Üyesi Ahmet ÇİFCİ Elektrik enerjisi, alternatif akım ve doğru akım olarak
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIMIN TEMEL ESASLARI Dr. Öğr. Üyesi Ahmet ÇİFCİ Elektrik enerjisi, alternatif akım ve doğru akım olarak
DENEY-4 RL DEVRE ANALİZİ. Alternatif akım altında seri RL devresinin analizi ve deneysel olarak incelenmesi.
 DENEY-4 RL DEVRE ANALİZİ 1. DENEYİN AMACI Alternatif akım altında seri RL devresinin analizi ve deneysel olarak incelenmesi. Kullanılan Alet ve Malzemeler: 1. Osiloskop 2. Sinyal jeneratörü 3. Çeşitli
DENEY-4 RL DEVRE ANALİZİ 1. DENEYİN AMACI Alternatif akım altında seri RL devresinin analizi ve deneysel olarak incelenmesi. Kullanılan Alet ve Malzemeler: 1. Osiloskop 2. Sinyal jeneratörü 3. Çeşitli
ALTERNATİF AKIMDA EMPEDANS SERİ DEVRELER
 1 ALTERNATİF AKMDA EMPEDANS SERİ DEVRELER ALTERNATİF AKMDA EMPEDANS Empedans, gerilim uygulandığında bir elektrik devresinin akımın geçişine karşı gösterdiği zorluğun ölçüsüdür. Empedans Z harfi ile gösterilir
1 ALTERNATİF AKMDA EMPEDANS SERİ DEVRELER ALTERNATİF AKMDA EMPEDANS Empedans, gerilim uygulandığında bir elektrik devresinin akımın geçişine karşı gösterdiği zorluğun ölçüsüdür. Empedans Z harfi ile gösterilir
F AKIM DEVRELER A. DEVRE ELEMANLARI VE TEMEL DEVRELER
 ALTERNATİF AKIM DEVRELERİ A. DEVRE ELEMANLARI VE TEMEL DEVRELER Alternatif akım devrelerinde akımın geçişine karşı üç çeşit direnç (zorluk) gösterilir. Devre elamanları dediğimiz bu dirençler: () R omik
ALTERNATİF AKIM DEVRELERİ A. DEVRE ELEMANLARI VE TEMEL DEVRELER Alternatif akım devrelerinde akımın geçişine karşı üç çeşit direnç (zorluk) gösterilir. Devre elamanları dediğimiz bu dirençler: () R omik
DENEY 5: ALTERNATİF AKIMDA FAZ FARKI (R, L VE C İÇİN)
 DENEY 5: ALTERNATİF AKIMDA FAZ FARKI (R, L VE C İÇİN) A. DENEYİN AMACI : Bu deneyin amacı, pasif elemanların (direnç, bobin ve sığaç) AC tepkilerini incelemek ve pasif elemanlar üzerindeki faz farkını
DENEY 5: ALTERNATİF AKIMDA FAZ FARKI (R, L VE C İÇİN) A. DENEYİN AMACI : Bu deneyin amacı, pasif elemanların (direnç, bobin ve sığaç) AC tepkilerini incelemek ve pasif elemanlar üzerindeki faz farkını
5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri
 Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
ALTERNATİF AKIMDA GÜÇ
 1 ALTERNATİF AKIMDA GÜÇ ALTERNATİF AKIMDA GÜÇ Joule Kanunu Elektrik gücü, bir elektrik devresi ile transfer edilen yada dönüştürülen elektrik enerjisinin oranıdır. Gücün SI birimi Watt (W) tır. Doğru akım
1 ALTERNATİF AKIMDA GÜÇ ALTERNATİF AKIMDA GÜÇ Joule Kanunu Elektrik gücü, bir elektrik devresi ile transfer edilen yada dönüştürülen elektrik enerjisinin oranıdır. Gücün SI birimi Watt (W) tır. Doğru akım
4. ÜNİTE ALTERNATİF AKIMDA GÜÇ
 4. ÜNİTE ALTERNATİF AKIMDA GÜÇ KONULAR 1. Ani Güç, Ortalama Güç 2. Dirençli Devrelerde Güç 3. Bobinli Devrelerde Güç 4. Kondansatörlü Devrelerde Güç 5. Güç Üçgeni 6. Güç Ölçme GİRİŞ Bir doğru akım devresinde
4. ÜNİTE ALTERNATİF AKIMDA GÜÇ KONULAR 1. Ani Güç, Ortalama Güç 2. Dirençli Devrelerde Güç 3. Bobinli Devrelerde Güç 4. Kondansatörlü Devrelerde Güç 5. Güç Üçgeni 6. Güç Ölçme GİRİŞ Bir doğru akım devresinde
ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ
 1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp en çok kullanılan etkin değere eşit alınır.
1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp en çok kullanılan etkin değere eşit alınır.
V cn V ca. V bc. V bn. V ab 30. -V bn. V an HATIRLATMALAR. Faz-Faz ve Faz-Nötr Gerilimleri. Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri
 HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V bn V bc V ab 30 -V bn cos30 30 V an cos30 3 3 30 Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri Üçgen Bağlı Yük: V LN =
HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V bn V bc V ab 30 -V bn cos30 30 V an cos30 3 3 30 Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri Üçgen Bağlı Yük: V LN =
ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU
 ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYĠN ADI : DENEY TARĠHĠ : DENEYĠ YAPANLAR : RAPORU HAZIRLAYANIN
ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYĠN ADI : DENEY TARĠHĠ : DENEYĠ YAPANLAR : RAPORU HAZIRLAYANIN
Dengeli Üç Fazlı Devreler
 BÖLÜM 11 Dengeli Üç Fazlı Devreler Kaynak:Nilsson, Riedel, «Elektrik Devreleri» Büyük miktarda elektrik gücün üretimi, iletimi, dağıtımı ve kullanımı üç fazlı devrelerle gerçekleşir. Ekonomik nedenlerden
BÖLÜM 11 Dengeli Üç Fazlı Devreler Kaynak:Nilsson, Riedel, «Elektrik Devreleri» Büyük miktarda elektrik gücün üretimi, iletimi, dağıtımı ve kullanımı üç fazlı devrelerle gerçekleşir. Ekonomik nedenlerden
3 FAZLI SİSTEMLER fazlı sistemler 1
 3 FAL SİSTEMLER Çok lı sistemler, gerilimlerinin arasında farkı bulunan iki veya daha la tek lı sistemin birleştirilmiş halidir ve bu işlem simetrik bir şekilde yapılır. Tek lı sistemlerde güç dalgalı
3 FAL SİSTEMLER Çok lı sistemler, gerilimlerinin arasında farkı bulunan iki veya daha la tek lı sistemin birleştirilmiş halidir ve bu işlem simetrik bir şekilde yapılır. Tek lı sistemlerde güç dalgalı
Konu: GÜÇ HESAPLARI:
 Konu: GÜÇ HESAPLARI: Aktif Güç hesaplamaları Reaktif Güç hesaplamaları Görünen(gerçek) Güç hesaplamaları 3 fazlı sistemler Faz farkları 3 fazlı sistemlerde güç GÜÇ BİRİMLERİ kva birimi bir elektrik güç
Konu: GÜÇ HESAPLARI: Aktif Güç hesaplamaları Reaktif Güç hesaplamaları Görünen(gerçek) Güç hesaplamaları 3 fazlı sistemler Faz farkları 3 fazlı sistemlerde güç GÜÇ BİRİMLERİ kva birimi bir elektrik güç
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ DENEY FÖYÜ DENEY ADI AC AKIM, GERİLİM VE GÜÇ DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEY SORUMLUSU DENEY GRUBU: DENEY TARİHİ : TESLİM
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ DENEY FÖYÜ DENEY ADI AC AKIM, GERİLİM VE GÜÇ DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEY SORUMLUSU DENEY GRUBU: DENEY TARİHİ : TESLİM
ELEKTRİK MAKİNELERİ (MEP 112) (ELP211) Yazar: Yrd. Doç. Dr. Mustafa Turan S1
 ELEKTRİK MAKİNELERİ (MEP 112) Yazar: Yrd. Doç. Dr. Mustafa Turan S1 SAKARYA ÜNİVERSİTESİ Adapazarı Meslek Yüksekokulu Bu ders içeriğinin basım, yayım ve satış hakları Sakarya Üniversitesi ne aittir. "Uzaktan
ELEKTRİK MAKİNELERİ (MEP 112) Yazar: Yrd. Doç. Dr. Mustafa Turan S1 SAKARYA ÜNİVERSİTESİ Adapazarı Meslek Yüksekokulu Bu ders içeriğinin basım, yayım ve satış hakları Sakarya Üniversitesi ne aittir. "Uzaktan
ADIYAMAN ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ DEVRE ANALİZİ LABORATUVARI-II DENEY RAPORU
 ADIYAMAN ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ DEVRE ANALİZİ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYİN ADI : DENEY TARİHİ : DENEYİ YAPANLAR : RAPORU HAZIRLAYANIN
ADIYAMAN ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ DEVRE ANALİZİ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYİN ADI : DENEY TARİHİ : DENEYİ YAPANLAR : RAPORU HAZIRLAYANIN
Enerji Sistemleri Mühendisliği Bölümü
 YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
ALTERNATİF AKIMDA EMPEDANS (PARALEL DEVRELER)
 1 ALTERNATİF AKMDA EMPEDANS (PARALEL DEVRELER) Paralel Devreler Direnç, bobin ve kondansatör birbirleri ile paralel bağlanarak üç farkı şekilde bulunabilirler. Direnç Bobin (R-L) Paralel Devresi Direnç
1 ALTERNATİF AKMDA EMPEDANS (PARALEL DEVRELER) Paralel Devreler Direnç, bobin ve kondansatör birbirleri ile paralel bağlanarak üç farkı şekilde bulunabilirler. Direnç Bobin (R-L) Paralel Devresi Direnç
V cn V ca. V bc. V bn. V ab. -V bn. V an HATIRLATMALAR. Faz-Faz ve Faz-Nötr Gerilimleri. Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri
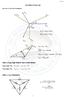 HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V aa = V cc = V bb V aa = V bb = V cc V bn V bc V ab 30 -V bn V aa = V aa V bb V aa = V aa cos(30) 30 V an V aa = V aa cos(30) =
HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V aa = V cc = V bb V aa = V bb = V cc V bn V bc V ab 30 -V bn V aa = V aa V bb V aa = V aa cos(30) 30 V an V aa = V aa cos(30) =
EET-202 DEVRE ANALİZİ-II DENEY FÖYÜ OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME
 OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME Deney No:1 Amaç: Osiloskop kullanarak AC gerilimin genlik periyot ve frekans değerlerinin ölçmesi Gerekli Ekipmanlar: AC Güç Kaynağı, Osiloskop, 2 tane 1k
OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME Deney No:1 Amaç: Osiloskop kullanarak AC gerilimin genlik periyot ve frekans değerlerinin ölçmesi Gerekli Ekipmanlar: AC Güç Kaynağı, Osiloskop, 2 tane 1k
ALTERNATİF AKIMDA EMPEDANS SERİ DEVRELER
 1 ALTERNATİF AKMDA EMPEDANS SERİ DEVRELER Empedans, gerilim uygulandığında bir elektrik devresinin akımın geçişine karşı gösterdiği zorluğun ölçüsüdür. Empedans Z harfi ile gösterilir ve birimi ohm(ω)
1 ALTERNATİF AKMDA EMPEDANS SERİ DEVRELER Empedans, gerilim uygulandığında bir elektrik devresinin akımın geçişine karşı gösterdiği zorluğun ölçüsüdür. Empedans Z harfi ile gösterilir ve birimi ohm(ω)
Uçlarındaki gerilim U volt ve içinden t saniye süresince Q coulomb luk elektrik yükü geçen bir alıcıda görülen iş:
 Etrafımızda oluşan değişmeleri iş, bu işi oluşturan yetenekleri de enerji olarak tanımlarız. Örneğin bir elektrik motorunun dönmesi ile bir iş yapılır ve bu işi yaparken de motor bir enerji kullanır. Mekanikte
Etrafımızda oluşan değişmeleri iş, bu işi oluşturan yetenekleri de enerji olarak tanımlarız. Örneğin bir elektrik motorunun dönmesi ile bir iş yapılır ve bu işi yaparken de motor bir enerji kullanır. Mekanikte
Alternatif Akım Devreleri
 Alternatif akım sürekli yönü ve şiddeti değişen bir akımdır. Alternatif akımda bazı devre elemanları (bobin, kapasitör, yarı iletken devre elemanları) doğruakım devrelerinde olduğundan farklı davranırlar.
Alternatif akım sürekli yönü ve şiddeti değişen bir akımdır. Alternatif akımda bazı devre elemanları (bobin, kapasitör, yarı iletken devre elemanları) doğruakım devrelerinde olduğundan farklı davranırlar.
Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi. Ders Notu-3 Doğru Akım Devreleri Hazırlayan: Yrd. Doç. Dr. Ahmet DUMLU
 Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi Ders Notu-3 Doğru Akım Devreleri Hazırlayan: Yrd. Doç. Dr. Ahmet DUMLU ELEKTROMOTOR KUVVETİ Kapalı bir devrede sabit bir akımın oluşturulabilmesi için
Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi Ders Notu-3 Doğru Akım Devreleri Hazırlayan: Yrd. Doç. Dr. Ahmet DUMLU ELEKTROMOTOR KUVVETİ Kapalı bir devrede sabit bir akımın oluşturulabilmesi için
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI ELEKTRİK İLETİM HATLARINDA GERİLİM DÜŞÜMÜ VE GÜÇ FAKTÖRÜ
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI ELEKTRİK İLETİM HATLARINDA GERİLİM DÜŞÜMÜ VE GÜÇ FAKTÖRÜ
ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ
 1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp
1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp
EEM 202 DENEY 8 RC DEVRELERİ-I SABİT BİR FREKANSTA RC DEVRELERİ
 Ad&oyad: DEELEİ- ABİT Bİ FEKANTA DEELEİ 8. Amaçlar abit Frekanslı seri devrelerinde empedans, akım ve güç bağıntıları abit Frekanslı paralel devrelerinde admitans, akım ve güç bağıntıları. 8.4 Devre Elemanları
Ad&oyad: DEELEİ- ABİT Bİ FEKANTA DEELEİ 8. Amaçlar abit Frekanslı seri devrelerinde empedans, akım ve güç bağıntıları abit Frekanslı paralel devrelerinde admitans, akım ve güç bağıntıları. 8.4 Devre Elemanları
COPYRIGHT ALL RIGHTS RESERVED
 IEC 60909 A GÖRE HESAPLAMA ESASLARI - 61 KISA-DEVRE AKIMLARININ HESAPLANMASI (14) TEPE KISA-DEVRE AKIMI ip (2) ÜÇ FAZ KISA-DEVRE / Gözlü şebekelerde kısa-devreler(1) H.Cenk BÜYÜKSARAÇ/ Elektrik-Elektronik
IEC 60909 A GÖRE HESAPLAMA ESASLARI - 61 KISA-DEVRE AKIMLARININ HESAPLANMASI (14) TEPE KISA-DEVRE AKIMI ip (2) ÜÇ FAZ KISA-DEVRE / Gözlü şebekelerde kısa-devreler(1) H.Cenk BÜYÜKSARAÇ/ Elektrik-Elektronik
EEM 202 DENEY 10. Tablo 10.1 Deney 10 da kullanılan devre elemanları ve malzeme listesi
 EEM 0 DENEY 0 SABİT FEKANSTA DEVEEİ 0. Amaçlar Sabit frekansta devrelerinin incelenmesi. Seri devresi Paralel devresi 0. Devre Elemanları Ve Kullanılan Malzemeler Bu deneyde kullanılan devre elemanları
EEM 0 DENEY 0 SABİT FEKANSTA DEVEEİ 0. Amaçlar Sabit frekansta devrelerinin incelenmesi. Seri devresi Paralel devresi 0. Devre Elemanları Ve Kullanılan Malzemeler Bu deneyde kullanılan devre elemanları
Gerilim beslemeli invertörler, akım beslemeli invertörler / 13. Hafta. Sekil-7.7 de endüktif yükte çalışan PWM invertör görülmektedir.
 1 fazlı Gerilim Kaynaklı PWM invertörler (Endüktif yükte); Sekil-7.7 de endüktif yükte çalışan PWM invertör görülmektedir. Şekil-7.7 den görüldüğü gibi yükün endüktif olması durumunda, yük üzerindeki enerjinin
1 fazlı Gerilim Kaynaklı PWM invertörler (Endüktif yükte); Sekil-7.7 de endüktif yükte çalışan PWM invertör görülmektedir. Şekil-7.7 den görüldüğü gibi yükün endüktif olması durumunda, yük üzerindeki enerjinin
ELEKTRİK DEVRELERİ-2 LABORATUVARI VI. DENEY FÖYÜ
 ELEKTİK DEELEİ-2 LABOATUAI I. DENEY FÖYÜ ALTENATİF AKIM DEESİNDE GÜÇ ÖLÇÜMÜ Amaç: Alternatif akım devresinde harcanan gücün analizi ve ölçülmesi. Gerekli Ekipmanlar: AA Güç Kaynağı, 1kΩ Direnç, 0.5H Bobin,
ELEKTİK DEELEİ-2 LABOATUAI I. DENEY FÖYÜ ALTENATİF AKIM DEESİNDE GÜÇ ÖLÇÜMÜ Amaç: Alternatif akım devresinde harcanan gücün analizi ve ölçülmesi. Gerekli Ekipmanlar: AA Güç Kaynağı, 1kΩ Direnç, 0.5H Bobin,
ELEKTRİK DEVRELERİ-2 LABORATUVARI IV. DENEY FÖYÜ
 EEKTİK DEEEİ-2 ABOATUAI I. DENEY FÖYÜ ATENATİF AKIM ATINDA DEE ANAİİ Amaç: Alternatif akım altında seri devresinin analizi ve deneysel olarak incelenmesi Gerekli Ekipmanlar: Güç Kaynağı, Ampermetre, oltmetre,
EEKTİK DEEEİ-2 ABOATUAI I. DENEY FÖYÜ ATENATİF AKIM ATINDA DEE ANAİİ Amaç: Alternatif akım altında seri devresinin analizi ve deneysel olarak incelenmesi Gerekli Ekipmanlar: Güç Kaynağı, Ampermetre, oltmetre,
BÖLÜM V SİNÜZOİDAL KARARLI DURUM GÜÇ HESAPLARI
 BÖÜM V SİNÜZOİDA KARARI DURUM GÜÇ HESAPARI Bir önceki bölümde, sinüzoidal kaynakla beslenen elektrik devrelerindeki kararlı durum voltajlarını ve akımlarını hesapladık. Bu bölümde ise amacımız, bir kararlı
BÖÜM V SİNÜZOİDA KARARI DURUM GÜÇ HESAPARI Bir önceki bölümde, sinüzoidal kaynakla beslenen elektrik devrelerindeki kararlı durum voltajlarını ve akımlarını hesapladık. Bu bölümde ise amacımız, bir kararlı
Elektrik Makinaları I
 Elektrik Makinaları I Açık Devre- Kısa Devre karakteristikleri Çıkık kutuplu makinalar, generatör ve motor çalışma, fazör diyagramları, güç ve döndürmemomenti a) Kısa Devre Deneyi Bağlantı şeması b) Açık
Elektrik Makinaları I Açık Devre- Kısa Devre karakteristikleri Çıkık kutuplu makinalar, generatör ve motor çalışma, fazör diyagramları, güç ve döndürmemomenti a) Kısa Devre Deneyi Bağlantı şeması b) Açık
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI ELEKTRİK İLETİM HATLARINDA GERİLİM DÜŞÜMÜ VE GÜÇ FAKTÖRÜ
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI ELEKTRİK İLETİM HATLARINDA GERİLİM DÜŞÜMÜ VE GÜÇ FAKTÖRÜ
ALTERNATİF AKIMDA ÜÇ FAZLI DEVRELER
 1 ÜÇ FAZLI DEVRELER ALTERNATİF AKIMDA ÜÇ FAZLI DEVRELER Alternatif Akımda Üç Fazlı Devreler Büyük değerlerdeki gücün üretimi, iletim ve dağıtımı üç fazlı sistemlerle gerçekleştirilir. Üç fazlı sistemin
1 ÜÇ FAZLI DEVRELER ALTERNATİF AKIMDA ÜÇ FAZLI DEVRELER Alternatif Akımda Üç Fazlı Devreler Büyük değerlerdeki gücün üretimi, iletim ve dağıtımı üç fazlı sistemlerle gerçekleştirilir. Üç fazlı sistemin
Doğru Akım Devreleri
 Doğru Akım Devreleri ELEKTROMOTOR KUVVETİ Kapalı bir devrede sabit bir akımın oluşturulabilmesi için elektromotor kuvvet (emk) adı verilen bir enerji kaynağına ihtiyaç duyulmaktadır. Şekilde devreye elektromotor
Doğru Akım Devreleri ELEKTROMOTOR KUVVETİ Kapalı bir devrede sabit bir akımın oluşturulabilmesi için elektromotor kuvvet (emk) adı verilen bir enerji kaynağına ihtiyaç duyulmaktadır. Şekilde devreye elektromotor
DENEY 2: ALTERNATİF AKIM DEVRELERİNDE KONDANSATÖR VE BOBİN DAVRANIŞININ İNCELENMESİ
 DENEY 2: ALTERNATİF AKIM DEVRELERİNDE KONDANSATÖR VE BOBİN DAVRANIŞININ İNCELENMESİ Deneyin Amacı *Alternatif akım devrelerinde sıklıkla kullanılan (alternatif işaret, frekans, faz farkı, fazör diyagramı,
DENEY 2: ALTERNATİF AKIM DEVRELERİNDE KONDANSATÖR VE BOBİN DAVRANIŞININ İNCELENMESİ Deneyin Amacı *Alternatif akım devrelerinde sıklıkla kullanılan (alternatif işaret, frekans, faz farkı, fazör diyagramı,
ELEKTRİK MAKİNELERİ (MEP 112) Yazar: Yrd. Doç. Dr. Mustafa Turan S1
 ELEKTRİK MAKİNELERİ (MEP 112) Yazar: Yrd. Doç. Dr. Mustafa Turan S1 SAKARYA ÜNİVERSİTESİ Adapazarı Meslek Yüksekokulu Bu ders içeriğinin basım, yayım ve satış hakları Sakarya Üniversitesi ne aittir. "Uzaktan
ELEKTRİK MAKİNELERİ (MEP 112) Yazar: Yrd. Doç. Dr. Mustafa Turan S1 SAKARYA ÜNİVERSİTESİ Adapazarı Meslek Yüksekokulu Bu ders içeriğinin basım, yayım ve satış hakları Sakarya Üniversitesi ne aittir. "Uzaktan
SENKRON MAKİNA DENEYLERİ
 DENEY-8 SENKRON MAKİNA DENEYLERİ Senkron Makinaların Genel Tanımı Senkron makina; stator sargılarında alternatif akım, rotor sargılarında ise doğru akım bulunan ve rotor hızı senkron devirle dönen veya
DENEY-8 SENKRON MAKİNA DENEYLERİ Senkron Makinaların Genel Tanımı Senkron makina; stator sargılarında alternatif akım, rotor sargılarında ise doğru akım bulunan ve rotor hızı senkron devirle dönen veya
Bölüm 3 AC Devreler. 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak.
 Bölüm 3 AC Devreler DENEY 3-1 AC RC Devresi DENEYİN AMACI 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak. GENEL BİLGİLER Saf
Bölüm 3 AC Devreler DENEY 3-1 AC RC Devresi DENEYİN AMACI 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak. GENEL BİLGİLER Saf
Alternatif Akım. Yrd. Doç. Dr. Aytaç Gören. Alternatif Akım
 Yrd. Doç. Dr. Aytaç Gören Paralel devre 2 İlk durum: 3 Ohm kanunu uygulandığında; 4 Ohm kanunu uygulandığında; 5 Paralel devrede empedans denklemi, 6 Kondansatör (Kapasitans) Alternatif gerilimin etkisi
Yrd. Doç. Dr. Aytaç Gören Paralel devre 2 İlk durum: 3 Ohm kanunu uygulandığında; 4 Ohm kanunu uygulandığında; 5 Paralel devrede empedans denklemi, 6 Kondansatör (Kapasitans) Alternatif gerilimin etkisi
T.C. ANADOLU ÜNİVERSİTESİ YAYINI NO: 3275 AÇIKÖĞRETİM FAKÜLTESİ YAYINI NO: 2138 HAVACILIK EMNİYETİ
 T.C. ANADOLU ÜNİVERSİTESİ YAYINI NO: 3275 AÇIKÖĞRETİM FAKÜLTESİ YAYINI NO: 2138 HAVACILIK EMNİYETİ Yazarlar Doç.Dr. Ender GEREDE (Ünite 1, 5, 7, 8) Yrd.Doç.Dr. Uğur TURHAN (Ünite 2) Dr. Eyüp Bayram ŞEKERLİ
T.C. ANADOLU ÜNİVERSİTESİ YAYINI NO: 3275 AÇIKÖĞRETİM FAKÜLTESİ YAYINI NO: 2138 HAVACILIK EMNİYETİ Yazarlar Doç.Dr. Ender GEREDE (Ünite 1, 5, 7, 8) Yrd.Doç.Dr. Uğur TURHAN (Ünite 2) Dr. Eyüp Bayram ŞEKERLİ
9. Ölçme (Ölçü) Transformatörleri. Bir magnetik devre üzerinde sarılı 2 sargıdan oluşan düzene transformatör denir.
 9. Ölçme (Ölçü) Transformatörleri Bir magnetik devre üzerinde sarılı 2 sargıdan oluşan düzene transformatör denir. Transformatörler, akım ve gerilim değerlerini frekansta değişiklik yapmadan ihtiyaca göre
9. Ölçme (Ölçü) Transformatörleri Bir magnetik devre üzerinde sarılı 2 sargıdan oluşan düzene transformatör denir. Transformatörler, akım ve gerilim değerlerini frekansta değişiklik yapmadan ihtiyaca göre
8. ALTERNATİF AKIM VE SERİ RLC DEVRESİ
 8. ATENATİF AKIM E SEİ DEESİ AMAÇA 1. Alternatif akım ve gerilim ölçmeyi öğrenmek. Direnç, kondansatör ve indüktans oluşan seri bir alternatif akım devresini analiz etmek AAÇA oltmetre, ampermetre, kondansatör
8. ATENATİF AKIM E SEİ DEESİ AMAÇA 1. Alternatif akım ve gerilim ölçmeyi öğrenmek. Direnç, kondansatör ve indüktans oluşan seri bir alternatif akım devresini analiz etmek AAÇA oltmetre, ampermetre, kondansatör
ELEKTRİK MAKİNELERİ (MEP 112) Yazar: Yrd. Doç. Dr. Mustafa Turan S1
 ELEKTRİK MAKİNELERİ (MEP 112) Yazar: Yrd. Doç. Dr. Mustafa Turan S1 SAKARYA ÜNİVERSİTESİ Adapazarı Meslek Yüksekokulu Bu ders içeriğinin basım, yayım ve satış hakları Sakarya Üniversitesi ne aittir. "Uzaktan
ELEKTRİK MAKİNELERİ (MEP 112) Yazar: Yrd. Doç. Dr. Mustafa Turan S1 SAKARYA ÜNİVERSİTESİ Adapazarı Meslek Yüksekokulu Bu ders içeriğinin basım, yayım ve satış hakları Sakarya Üniversitesi ne aittir. "Uzaktan
T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ TEMEL ELEKTRİK DEVRE LABORATUVARI TEMEL DEVRE TEOREMLERİNİN UYGULANMASI
 T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ TEMEL ELEKTRİK DEVRE LABORATUVARI TEMEL DEVRE TEOREMLERİNİN UYGULANMASI DENEY SORUMLUSU Arş. Gör. Şaban ULUS Şubat 2014 KAYSERİ
T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ TEMEL ELEKTRİK DEVRE LABORATUVARI TEMEL DEVRE TEOREMLERİNİN UYGULANMASI DENEY SORUMLUSU Arş. Gör. Şaban ULUS Şubat 2014 KAYSERİ
Bölüm 1. Elektriksel Büyüklükler ve Elektrik Devre Elemanları
 Bölüm Elektriksel Büyüklükler ve Elektrik Devre Elemanları. Temel Elektriksel Büyüklükler: Akım, Gerilim, Güç, Enerji. Güç Polaritesi.3 Akım ve Gerilim Kaynakları F.Ü. Teknoloji Fak. EEM M.G. .. Temel
Bölüm Elektriksel Büyüklükler ve Elektrik Devre Elemanları. Temel Elektriksel Büyüklükler: Akım, Gerilim, Güç, Enerji. Güç Polaritesi.3 Akım ve Gerilim Kaynakları F.Ü. Teknoloji Fak. EEM M.G. .. Temel
Ders 04. Elektronik Devre Tasarımı. Güç Elektroniği 1. Ders Notları Ege Üniversitesi Öğretim Üyesi Yrd.Doç.Dr. Mehmet Necdet YILDIZ a aittir.
 Elektronik Devre Tasarımı Ders 04 Ders Notları Ege Üniversitesi Öğretim Üyesi Yrd.Doç.Dr. Mehmet Necdet YILDIZ a aittir. www.ozersenyurt.net www.orbeetech.com / 1 AC-DC Dönüştürücüler AC-DC dönüştürücüler
Elektronik Devre Tasarımı Ders 04 Ders Notları Ege Üniversitesi Öğretim Üyesi Yrd.Doç.Dr. Mehmet Necdet YILDIZ a aittir. www.ozersenyurt.net www.orbeetech.com / 1 AC-DC Dönüştürücüler AC-DC dönüştürücüler
5. Sunum: Kalıcı Durum Güç Analizi. Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık
 5. Sunum: Kalıcı Durum Güç Analizi Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Giriş Bu bölümde AC devrelerde güç hesabı ele alınacakqr. Ayrıca güç
5. Sunum: Kalıcı Durum Güç Analizi Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Giriş Bu bölümde AC devrelerde güç hesabı ele alınacakqr. Ayrıca güç
ZENER DİYOTLAR. Hedefler
 ZENER DİYOTLAR Hedefler Bu üniteyi çalıştıktan sonra; Zener diyotları tanıyacak ve çalışma prensiplerini kavrayacaksınız. Örnek devreler üzerinde Zener diyotlu regülasyon devrelerini öğreneceksiniz. 2
ZENER DİYOTLAR Hedefler Bu üniteyi çalıştıktan sonra; Zener diyotları tanıyacak ve çalışma prensiplerini kavrayacaksınız. Örnek devreler üzerinde Zener diyotlu regülasyon devrelerini öğreneceksiniz. 2
TEK FAZLI VE ÜÇ FAZLI KONTROLSÜZ DOĞRULTUCULAR
 KARADENİZ TEKNİK ÜNİVERSİTESİ Mühendislik Fakültesi Elektrik-Elektronik Mühendisliği Bölümü Power Electronic Circuits (Güç Elektroniği Devreleri) TEK FAZLI VE ÜÇ FAZLI KONTROLSÜZ DOĞRULTUCULAR 1. DENEYİN
KARADENİZ TEKNİK ÜNİVERSİTESİ Mühendislik Fakültesi Elektrik-Elektronik Mühendisliği Bölümü Power Electronic Circuits (Güç Elektroniği Devreleri) TEK FAZLI VE ÜÇ FAZLI KONTROLSÜZ DOĞRULTUCULAR 1. DENEYİN
Yrd. Doç. Dr. Levent Çetin. Alternatif Gerilim. Alternatif Akımın Fazör Olarak İfadesi. Temel Devre Elemanlarının AG Etkisi Altındaki Davranışları
 Yrd. Doç. Dr. Levent Çetin İçerik Alternatif Gerilim Faz Kavramı ın Fazör Olarak İfadesi Direnç, Reaktans ve Empedans Kavramları Devresinde Güç 2 Alternatif Gerilim Alternatif gerilim, devre üzerindeki
Yrd. Doç. Dr. Levent Çetin İçerik Alternatif Gerilim Faz Kavramı ın Fazör Olarak İfadesi Direnç, Reaktans ve Empedans Kavramları Devresinde Güç 2 Alternatif Gerilim Alternatif gerilim, devre üzerindeki
14. SİNÜSOİDAL AKIMDA DİRENÇ, KAPASİTE, İNDÜKTANS VE ORTAK İNDÜKTANSIN ÖLÇÜLMESİ
 14. SİNÜSOİDAL AKIMDA DİRENÇ, KAPASİTE, İNDÜKTANS VE ORTAK İNDÜKTANSIN ÖLÇÜLMESİ Sinüsoidal Akımda Direncin Ölçülmesi Sinüsoidal akımda, direnç üzerindeki gerilim ve akım dalga şekilleri ve fazörleri aşağıdaki
14. SİNÜSOİDAL AKIMDA DİRENÇ, KAPASİTE, İNDÜKTANS VE ORTAK İNDÜKTANSIN ÖLÇÜLMESİ Sinüsoidal Akımda Direncin Ölçülmesi Sinüsoidal akımda, direnç üzerindeki gerilim ve akım dalga şekilleri ve fazörleri aşağıdaki
Per-unit değerlerin avantajları
 PER-UNİT DEĞERLER Per-unit değerlerin avantajları Elektriksel büyüklüklerin karşılaştırılmasında ve değerlendirilmesinde kolaylık sağlar. Trafoların per-unit eşdeğer empedansları primer ve sekonder taraf
PER-UNİT DEĞERLER Per-unit değerlerin avantajları Elektriksel büyüklüklerin karşılaştırılmasında ve değerlendirilmesinde kolaylık sağlar. Trafoların per-unit eşdeğer empedansları primer ve sekonder taraf
DAĞITIM ŞEBEKELERİNDE GERİLİM DÜŞÜMÜ HESABI Alternatif Akımda Enerji Dağıtımı Üç Fazlı Şebeke Bağlantıları Yıldız Bağlantı
 Alternatif Akımda Enerji Dağıtımı Üç Fazlı Şebeke Bağlantıları Yıldız Bağlantı Yıldız bağlantıda; Trafonun her faz sargı uçları kısa devre edilir. Kısa devre noktası yıldız noktası olup, bu hat nötr hattıdır.
Alternatif Akımda Enerji Dağıtımı Üç Fazlı Şebeke Bağlantıları Yıldız Bağlantı Yıldız bağlantıda; Trafonun her faz sargı uçları kısa devre edilir. Kısa devre noktası yıldız noktası olup, bu hat nötr hattıdır.
Problemler: Devre Analizi-II
 Problemler: Devre Analizi-II P.7.1 Grafiği verilen sinüsoidalin hem sinüs hem de kosinüs cinsinden ifadesini yazınız. v(t) 5 4 3 2 1 0-1 t(saniye) -2-3 -4-5 0 1 2 3 4 5 6 7 8 9 10 P.7.2 v1(t) 60Cos( 100
Problemler: Devre Analizi-II P.7.1 Grafiği verilen sinüsoidalin hem sinüs hem de kosinüs cinsinden ifadesini yazınız. v(t) 5 4 3 2 1 0-1 t(saniye) -2-3 -4-5 0 1 2 3 4 5 6 7 8 9 10 P.7.2 v1(t) 60Cos( 100
Düzenlenirse: 9I1 5I2 = 1 108I1 60I2 = 12 7I1 + 12I2 = 4 35I1 60I2 = I1 = 8 I 1
 ELEKTRİK-ELEKTRONİK DERSİ FİNAL/BÜTÜNLEME SORU ÖRNEKLERİ Şekiller üzerindeki renkli işaretlemeler soruya değil çözüme aittir: Maviler ilk aşamada asgari bağımsız denklem çözmek için yapılan tanımları,
ELEKTRİK-ELEKTRONİK DERSİ FİNAL/BÜTÜNLEME SORU ÖRNEKLERİ Şekiller üzerindeki renkli işaretlemeler soruya değil çözüme aittir: Maviler ilk aşamada asgari bağımsız denklem çözmek için yapılan tanımları,
EEM211 ELEKTRİK DEVRELERİ-I
 EEM211 ELEKTRİK DEVRELERİ-I Prof. Dr. Selçuk YILDIRIM Siirt Üniversitesi Elektrik-Elektronik Mühendisliği Kaynak (Ders Kitabı): Fundamentals of Electric Circuits Charles K. Alexander Matthew N.O. Sadiku
EEM211 ELEKTRİK DEVRELERİ-I Prof. Dr. Selçuk YILDIRIM Siirt Üniversitesi Elektrik-Elektronik Mühendisliği Kaynak (Ders Kitabı): Fundamentals of Electric Circuits Charles K. Alexander Matthew N.O. Sadiku
ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOKULU ELEKTRİK VE ENERJİ BÖLÜMÜ ALTERNATİF ENERJİ KAYNAKLARI TEKNOLOJİSİ
 ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOKULU ELEKTRİK VE ENERJİ BÖLÜMÜ ALTERNATİF ENERJİ KAYNAKLARI TEKNOLOJİSİ ELEKTRİK MAKİNALARI 4.HAFTA 1 İçindekiler Transformatörlerde Eşdeğer Devreler Transformatör
ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOKULU ELEKTRİK VE ENERJİ BÖLÜMÜ ALTERNATİF ENERJİ KAYNAKLARI TEKNOLOJİSİ ELEKTRİK MAKİNALARI 4.HAFTA 1 İçindekiler Transformatörlerde Eşdeğer Devreler Transformatör
DENEY 8- GÜÇ KATSAYISI KAVRAMI VE GÜÇ KATSAYISININ DÜZELTİLMESİ
 Devre nalizi DENEY 8 GÜÇ KTSYS KM E GÜÇ KTSYSNN DÜZELTİLMESİ 1.1. DENEYİN MÇL Güç katsayısı kavramını öğrenmek ve güç katsayısının düzeltilmesinin deneysel olarak inelenmesi Deneyde kullanılaak malzemeler:
Devre nalizi DENEY 8 GÜÇ KTSYS KM E GÜÇ KTSYSNN DÜZELTİLMESİ 1.1. DENEYİN MÇL Güç katsayısı kavramını öğrenmek ve güç katsayısının düzeltilmesinin deneysel olarak inelenmesi Deneyde kullanılaak malzemeler:
Enerji Sistemleri Mühendisliği
 Enerji Sistemleri Mühendisliği Temel Elektrik ve Elektronik AC Devre Analizi Karmaşık Sayılar Karmaşık sayılar dikdörtgen koordinat sisteminde aşağıdaki gibi gösterilebilir. Temel Elektrik ve Elektronik
Enerji Sistemleri Mühendisliği Temel Elektrik ve Elektronik AC Devre Analizi Karmaşık Sayılar Karmaşık sayılar dikdörtgen koordinat sisteminde aşağıdaki gibi gösterilebilir. Temel Elektrik ve Elektronik
ALTERNATİF AKIMIN TANIMI
 ALTERNATİF AKIM ALTERNATİF AKIMIN TANIMI Belirli üreteçler sürekli kutup değiştiren elektrik enerjisi üretirler. (Örnek: Döner elektromekanik jeneratörler) Voltajın zamana bağlı olarak sürekli yön değiştirmesi
ALTERNATİF AKIM ALTERNATİF AKIMIN TANIMI Belirli üreteçler sürekli kutup değiştiren elektrik enerjisi üretirler. (Örnek: Döner elektromekanik jeneratörler) Voltajın zamana bağlı olarak sürekli yön değiştirmesi
Alternatif Akım Devre Analizi
 Alternatif Akım Devre Analizi Öğr.Gör. Emre ÖZER Alternatif Akımın Tanımı Zamaniçerisindeyönüveşiddeti belli bir düzen içerisinde (periyodik) değişen akıma alternatif akımdenir. En bilinen alternatif akım
Alternatif Akım Devre Analizi Öğr.Gör. Emre ÖZER Alternatif Akımın Tanımı Zamaniçerisindeyönüveşiddeti belli bir düzen içerisinde (periyodik) değişen akıma alternatif akımdenir. En bilinen alternatif akım
ELEKTRİK ENERJİ SİSTEMLERİNDE OLUŞAN HARMONİKLERİN FİLTRELENMESİNİN BİLGİSAYAR DESTEKLİ MODELLENMESİ VE SİMÜLASYONU
 T.C. MARMARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ELEKTRİK ENERJİ SİSTEMLERİNDE OLUŞAN HARMONİKLERİN FİLTRELENMESİNİN BİLGİSAYAR DESTEKLİ MODELLENMESİ VE SİMÜLASYONU Mehmet SUCU (Teknik Öğretmen, BSc.)
T.C. MARMARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ELEKTRİK ENERJİ SİSTEMLERİNDE OLUŞAN HARMONİKLERİN FİLTRELENMESİNİN BİLGİSAYAR DESTEKLİ MODELLENMESİ VE SİMÜLASYONU Mehmet SUCU (Teknik Öğretmen, BSc.)
Temel Devre Elemanlarının Alternatif Gerilim Etkisi Altındaki Davranışları
 Temel Devre Elemanlarının Alternatif Gerilim Etkisi Altındaki Davranışları Direnç (R) Alternatif gerilimin etkisi altındaki direnç, Ohm kanunun bilinen ifadesini korur. Denklemlerden elde edilen sonuç
Temel Devre Elemanlarının Alternatif Gerilim Etkisi Altındaki Davranışları Direnç (R) Alternatif gerilimin etkisi altındaki direnç, Ohm kanunun bilinen ifadesini korur. Denklemlerden elde edilen sonuç
SERİ PARALEL DEVRELER
 1 SERİ PARALEL DEVRELER ALTERNATİF AKIMDA EMPEDANS Seri Paralel Devreler Çözüm Yöntemi: Seri ve paralel devrelerin bir arada bulunduğu devrelerdir. Devrelerin çözümünde Her kolun empedansı bulunur. Her
1 SERİ PARALEL DEVRELER ALTERNATİF AKIMDA EMPEDANS Seri Paralel Devreler Çözüm Yöntemi: Seri ve paralel devrelerin bir arada bulunduğu devrelerdir. Devrelerin çözümünde Her kolun empedansı bulunur. Her
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
 Enerjinin Taşınması Genel olarak güç, iletim hatlarında üç fazlı sistem ile havai hat iletkenleri tarafından taşınır. Gücün taşınmasında ACSR(Çelik özlü Alüminyum iletkenler) kullanılırken, dağıtım kısmında
Enerjinin Taşınması Genel olarak güç, iletim hatlarında üç fazlı sistem ile havai hat iletkenleri tarafından taşınır. Gücün taşınmasında ACSR(Çelik özlü Alüminyum iletkenler) kullanılırken, dağıtım kısmında
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI. Analiz. Cilt 2. Ünite 8-14
 ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
Yükseltici DA Kıyıcılar, Gerilim beslemeli invertörler / 12. Hafta
 E sınıfı DC kıyıcılar; E sınıfı DC kıyıcılar, çift yönlü (4 bölgeli) DC kıyıcılar olarak bilinmekte olup iki adet C veya iki adet D sınıfı DC kıyıcının birleşiminden oluşmuşlardır. Bu tür kıyıcılar, iki
E sınıfı DC kıyıcılar; E sınıfı DC kıyıcılar, çift yönlü (4 bölgeli) DC kıyıcılar olarak bilinmekte olup iki adet C veya iki adet D sınıfı DC kıyıcının birleşiminden oluşmuşlardır. Bu tür kıyıcılar, iki
Güç elektroniği elektrik mühendisliğinde enerji ve elektronik bilim dalları arasında bir bilim dalıdır.
 3. Bölüm Güç Elektroniğinde Temel Kavramlar ve Devre Türleri Doç. Dr. Ersan KABALC AEK-207 GÜNEŞ ENERJİSİ İLE ELEKTRİK ÜRETİMİ Güç Elektroniğine Giriş Güç elektroniği elektrik mühendisliğinde enerji ve
3. Bölüm Güç Elektroniğinde Temel Kavramlar ve Devre Türleri Doç. Dr. Ersan KABALC AEK-207 GÜNEŞ ENERJİSİ İLE ELEKTRİK ÜRETİMİ Güç Elektroniğine Giriş Güç elektroniği elektrik mühendisliğinde enerji ve
DENEY 1-1 AC Gerilim Ölçümü
 DENEY 1-1 AC Gerilim Ölçümü DENEYİN AMACI 1. AC gerilimlerin nasıl ölçüldüğünü öğrenmek. 2. AC voltmetrenin nasıl kullanıldığını öğrenmek. GENEL BİLGİLER AC voltmetre, ac gerilimleri ölçmek için kullanılan
DENEY 1-1 AC Gerilim Ölçümü DENEYİN AMACI 1. AC gerilimlerin nasıl ölçüldüğünü öğrenmek. 2. AC voltmetrenin nasıl kullanıldığını öğrenmek. GENEL BİLGİLER AC voltmetre, ac gerilimleri ölçmek için kullanılan
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
REAKTİF GÜÇ KOMPANZASYONU ve REZONANS HESAPLARI
 REAKTİF GÜÇ KOMPANZASYONU ve REZONANS HESAPLARI Alper Terciyanlı TÜBİTAK-BİLTEN [email protected] EMO Ankara Şube Reaktif Güç Kompanzasyonu Eğitimi 16.07.2005 1 Kapsam Genel Kavramlar Reaktif
REAKTİF GÜÇ KOMPANZASYONU ve REZONANS HESAPLARI Alper Terciyanlı TÜBİTAK-BİLTEN [email protected] EMO Ankara Şube Reaktif Güç Kompanzasyonu Eğitimi 16.07.2005 1 Kapsam Genel Kavramlar Reaktif
EET-202 DEVRE ANALİZİ-II DENEY FÖYÜ OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME
 OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME Deney No:1 Amaç: Osiloskop kullanarak AC gerilimin genlik periyot ve frekans değerlerinin ölçmesi Gerekli Ekipmanlar: AC Güç Kaynağı, Osiloskop, 2 tane 1k
OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME Deney No:1 Amaç: Osiloskop kullanarak AC gerilimin genlik periyot ve frekans değerlerinin ölçmesi Gerekli Ekipmanlar: AC Güç Kaynağı, Osiloskop, 2 tane 1k
10- KISA DEVRE ARIZA AKIMLARININ HESAPLANMASI TERĐMLER VE TANIMLAMALAR (IEC 60909)-2
 HESAPLANMASI TERĐMLER VE TANIMLAMALAR (IEC 60909)-2 EŞDEĞER GERĐLĐM KAYNAĞI, GERĐLĐM FAKTÖRÜ, c SENKRON BĐR MAKĐNENĐN SUBTRANSIENT GERĐLĐMĐ, E GENERATÖRDEN UZAK KISA-DEVRE GENERATÖRE YAKIN KISA-DEVRE KISA-DEVRE
HESAPLANMASI TERĐMLER VE TANIMLAMALAR (IEC 60909)-2 EŞDEĞER GERĐLĐM KAYNAĞI, GERĐLĐM FAKTÖRÜ, c SENKRON BĐR MAKĐNENĐN SUBTRANSIENT GERĐLĐMĐ, E GENERATÖRDEN UZAK KISA-DEVRE GENERATÖRE YAKIN KISA-DEVRE KISA-DEVRE
ALTERNATİF AKIM DEVRELERİNİN ÇÖZÜMLERİ
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIM DEVRELERİNİN ÇÖZÜMLERİ Dr. Öğr. Üyesi Ahmet ÇİFCİ KARMAŞIK SAYILAR 7.12.2018 2/28 Kutupsal Biçimde
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIM DEVRELERİNİN ÇÖZÜMLERİ Dr. Öğr. Üyesi Ahmet ÇİFCİ KARMAŞIK SAYILAR 7.12.2018 2/28 Kutupsal Biçimde
ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ
 Giresun Üniversitesi Mühendislik Fakültesi Elektrik Elektronik Mühendisliği Bölümü Bölüm Başkanı Bölümün tanıtılması Elektrik Elektronik Mühendisliğinin tanıtılması Mühendislik Etiği Birim Sistemleri Direnç,
Giresun Üniversitesi Mühendislik Fakültesi Elektrik Elektronik Mühendisliği Bölümü Bölüm Başkanı Bölümün tanıtılması Elektrik Elektronik Mühendisliğinin tanıtılması Mühendislik Etiği Birim Sistemleri Direnç,
AC/DC DÖNÜŞTÜRÜCÜLER (Doğrultucular)
 AC/DC DÖNÜŞTÜRÜCÜLER (Doğrultucular) AC-DC dönüştürücüler (doğrultucular), AC gerilimi DC gerilime dönüştüren güç elektroniği devreleridir. Güç elektroniğinin temel güç devrelerinden doğrultucuları 2 temel
AC/DC DÖNÜŞTÜRÜCÜLER (Doğrultucular) AC-DC dönüştürücüler (doğrultucular), AC gerilimi DC gerilime dönüştüren güç elektroniği devreleridir. Güç elektroniğinin temel güç devrelerinden doğrultucuları 2 temel
ELK273 Elektrik ve Elektronik Mühendisliğinin Temelleri Ders 8- AC Devreler. Yard.Doç.Dr. Ahmet Özkurt.
 ELK273 Elektrik ve Elektronik Mühendisliğinin Temelleri Ders 8- AC Devreler Yard.Doç.Dr. Ahmet Özkurt [email protected] http://ahmetozkurt.net İçerik AC ve DC Empedans RMS değeri Bobin ve kondansatörün
ELK273 Elektrik ve Elektronik Mühendisliğinin Temelleri Ders 8- AC Devreler Yard.Doç.Dr. Ahmet Özkurt [email protected] http://ahmetozkurt.net İçerik AC ve DC Empedans RMS değeri Bobin ve kondansatörün
Anahtarlama Modlu DA-AA Evirici
 Anahtarlama Modlu DA-AA Evirici Giriş Anahtarlama modlu eviricilerde temel kavramlar Bir fazlı eviriciler Üç fazlı eviriciler Ölü zamanın PWM eviricinin çıkış gerilimine etkisi Diğer evirici anahtarlama
Anahtarlama Modlu DA-AA Evirici Giriş Anahtarlama modlu eviricilerde temel kavramlar Bir fazlı eviriciler Üç fazlı eviriciler Ölü zamanın PWM eviricinin çıkış gerilimine etkisi Diğer evirici anahtarlama
EVK Enerji Verimliliği, Kalitesi Sempozyumu ve Sergisi Haziran 2015, Sakarya
 6. Enerji Verimliliği, Kalitesi Sempozyumu ve Sergisi 04-06 Haziran 2015, Sakarya KÜÇÜK RÜZGAR TÜRBİNLERİ İÇİN ŞEBEKE BAĞLANTILI 3-FAZLI 3-SEVİYELİ T-TİPİ DÖNÜŞTÜRÜCÜ DENETİMİ İbrahim Günesen [email protected]
6. Enerji Verimliliği, Kalitesi Sempozyumu ve Sergisi 04-06 Haziran 2015, Sakarya KÜÇÜK RÜZGAR TÜRBİNLERİ İÇİN ŞEBEKE BAĞLANTILI 3-FAZLI 3-SEVİYELİ T-TİPİ DÖNÜŞTÜRÜCÜ DENETİMİ İbrahim Günesen [email protected]
DENEY TARİHİ RAPOR TESLİM TARİHİ NOT
 DENEY 2 OHM-KIRCHOFF KANUNLARI VE BOBİN-DİRENÇ-KONDANSATÖR Malzeme Listesi: 1 adet 47Ω, 1 adet 100Ω, 1 adet 1,5KΩ ve 1 adet 6.8KΩ Dirençler 1 adet 100mH Bobin 1 adet 220nF Kondansatör Deneyde Kullanılacak
DENEY 2 OHM-KIRCHOFF KANUNLARI VE BOBİN-DİRENÇ-KONDANSATÖR Malzeme Listesi: 1 adet 47Ω, 1 adet 100Ω, 1 adet 1,5KΩ ve 1 adet 6.8KΩ Dirençler 1 adet 100mH Bobin 1 adet 220nF Kondansatör Deneyde Kullanılacak
Arttıran tip DC kıyıcı çalışması (rezistif yükte);
 NOT: Azaltan tip DC kıyıcı devresinde giriş gerilimi tamamen düzgün bir DC olmasına karsın yapılan anahtarlama sonucu oluşan çıkış gerilimi kare dalga formatındadır. Bu gerilimin düzgünleştirilmesi için
NOT: Azaltan tip DC kıyıcı devresinde giriş gerilimi tamamen düzgün bir DC olmasına karsın yapılan anahtarlama sonucu oluşan çıkış gerilimi kare dalga formatındadır. Bu gerilimin düzgünleştirilmesi için
