KM in Sorunları ve Başarısızlıkları
|
|
|
- Meryem Sarı
- 7 yıl önce
- İzleme sayısı:
Transkript
1 Klasik Mekanik (CM) makroskopik kuantum olaylarını betimlemede başarısızlığa uğramıştır. Mikroskopik özelliklerin makroskopik dünyaya taşınımına ait olaylar şunlardır: üstün akışkanlık Yeterince düşük sıcaklık derecelerinde helyum sürtünmesiz akabilir. üstün iletkenlik Akım kayıpsız olarak akar. ferromanyetizm Manyetik momentler/spinler kendiliğinden hizaya gelir. Bose-Einstein yoğuşumu Atomların üstün akıcılığı... Tüm bu problemler (ve daha birçoğu) fevkalade başarılı olan kuantum mekanik (KM) le çözülmüştür. KM in Sorunları ve Başarısızlıkları Bazı makroskopik kuantum davranışı (yüksek kritik sıcaklıkta üstün iletkenlik) için hiçbir model ortaya koyulamadı ve ancak KM içinde çözülebildi. KM genel görelilik ile uyuşmazlık halindedir. Bu sorun KM dışında belki de daha büyük bir kuramı ile çözülebilir. (sicim kuramı?) KM in matematiksel yapısındaki yorum karışıklıkları: - Ölçümün rölü - Olasılığa karşın belirlilik... İhtiyar biri zar atmaz. - Mikroskopik kuantum mekanikten makroskopik kuantum davranışa geçiş... (Schrödinger kedisi, ölü ve canlı ) - Dolaşıklık ve gizli-değişkenler... (Einstein-Podolsky-Rosen (EPR) paradoksu, Bell eşitsizlikleri) - Bohr (ve Born) Kopenhag yorumuna karşı çok-dünyalar-kuramı Kuantum Mekaniği Kuantum Mekaniği şimdiye kadar karşılaştığınız en acayip fizik kuramıdır. KM nin matematiksel yapısı çok iyi belirlenmiş olmasına karşın matematiksel sonuçların fiziksel yorumu aşikar paradokslara yol açmıştır ki bunlar gözlemlenirler ve ölçümlerdir. II-1
2 Bir nesneyi betimlemek için kullanılan matematiksel kavram, dalga fonksiyonu, nesnenin kendisiyle aynı değildir. Şekil I de görüldüğü gibi, boşlukta dağılan bir parçacık dalga paketi bizi KM nin olasılık yorumuna zorlamaktadır. Kopenhag Yorumu Dalga fonksiyonu parçacığın belli bir durum ve belli bir konumda bulunmasını sağlayan olasılık genliğidir (dalga fonksiyonunun karesinin büyüklüğü olasılık veya olasılık yoğunluğudur). Ölçümlerin sonuçlarına ait olasılıklar deterministik (belirlenlenimci) dir. Bunlar deterministik olarak gelişen dalga fonksiyonları ile belirlenebilir. Ancak, özel bir ölçümün sonucu genellikle öngörülemezdir. Biz Şekil I: Dalga Paketi deneyin beklenti değerlerini, varyansları, standart sapmaları öngörebiliriz fakat deneyin gerçekleşmesini öngöremeyiz. Schrödinger denk. (SE) bir dalga fonksiyonunun ψ deterministik gelişimini belirleyen bir kısmi diferansiyel denklemdir. ψ sistemi betimleyen tüm mevcut bilgileri içerir. Özel bir ölçümün (örneğin, bir parçacığın x ve x + Δx arasında bulunabilmesi) sonucuna ait olasılık ψ(x) 2 ile belirlenmiştir (Kopenhag Yorumu). Diğer Yorumlar Çoklu Dünyalar yorumu Bir ölçüm yaptığımız zaman, dünyamız birçok hale ayrılır ki bunlardan biri mümkün ölçüm sonucudur. Saçma? Bunun mümkün olmadığını kanıtlamak için bilinen bir yol yoktur. Gizli-Değişkenler kuramları Einstein tarafından savunulmuştur, Einstein-Podolsky-Rosen (EPR) paradoksu. Sistemin tam durumunu bilemediğimiz için gelişi güzellik ortaya çıkar. Dalga fonksiyonunda bulunmayan bazı bilgiler vardır ki bunlar prensipte mevcuttur. Bu durum klasik istatistik mekanikte karşılaşılan bir gelişi güzelliğe karşı gelir. Yıllar boyunca gizli-değişkenler kuramlarının metafizik olduğu sanılmıştır. Yani bunlar yanıltılamazlar veya standart Kopenhag yorumundan deneysel olarak ayırt edilemezler. Bununla beraber John Bell gizlideğişkenler kuramlarını, yani yerel gerçeklik kuramlarını standart KM den deneysel olarak ayırt edebilecek bir mümkünlüğü ortaya çıkarmıştır. Bell eşitsizlikleri Gizli-değişkenler kuramlarına tabi olan şartlı olasılıklardaki sınırlamalar standart KM ile ihlal edilmiştir. Şimdiye kadar yapılan deneyler gizli-değişken kuramlarıyla uyuşmazlık halinde olmasına karşın standart KM ile uyuşma halindedir. II-2
3 KM ne Ne Zaman İhtiyaç Duyarız? Hangi tarihi deneyler Klasik Mekanikte (CM) yeterince betimlenemez? Kronolojik bir yaklaşım yerine mantıksal bir yaklaşım sunacağız. CM ve E&M mikroskopik düzeyde genelde başarısızlığa uğrar, yani tek temel parçacıklarla uğraştığımızda (elekronlar, atomlar, fotonlar gibi tek kuantum parçacıkları) bu durum ortaya çıkar. Tek bir parçacığın / nesnenin klasik betimlemesi ne zaman bozulur? CM küçük bir d mesafesinde başarısızlığa uğrar. Yani, ölçümünüzün çözünürlüğü artan Δd hassasiyeti doğrultusunda parçacığın konumu ölçülürken artış gösterir. Bu mesafe ölçeği d, parçacığın momentumu p ye bağlıdır. Daha doğrusu yaptığınız Δp momentum ölçümündeki belirsizlik burada çok önem kazanır. CM in yetersiz olması Δd Δp (faz uzay alanı) niceliği ile belirlenir ki, kritik mesafe ölçeği Δd dir. Şekil II: Faz uzay alanı Birimler: [ Δd Δp] = m kg m s = J s Eğer Δd Δp» h ise, bu takdirde davranış klasiktir. II-3
4 8.04 Kuantum Fiziği Ders II h = 6, J s Plank sbt. Verilen bir ν frekansında aynı nicelik doğal bir enerji ölçeği E = hν verir. Eğer Δd Δp ~ h ise, bu takdirde KM gereklidir. Diğer Formulasyon [ d p] = [ r p] = [ l] (2-1) Eğer [ l]» h = CM (2-2) 2π [ l] ~ ise KM (2-3) = h 2π =1, J s (indirgenmiş Planck sbt.) (2-4) Verilen bir açısal frekans ω = 2πν da, doğal bir enerji ölçeği E = ω teşkil eder. Örnekler 1. Oda sıcaklığında bir kutudaki gaz: d = 1 cm m = 87 m p m p = kg p 2 2m = 1 2 k BT (1 Boyutta) (2-5) Δp ~ p 2 = mk B T = 2, kg m s (2-6) d ~ Δd =1cm (2-7) Δp Δd = 2, kg m2 s = 2, J s = h (2-8) CM yeterlidir. 2. Manyetik bir tuzaktaki lazerle soğutulmuş gaz Δp ~ mk B T = kg m s (2-9) hala klasiktir. Δp Δd = J s ~ 2000h (2-10) II-4
5 (a) T ~ 100µK li manyetik potansiyel (b) Atomun elektronu Şekil III: Manyetik potansiyel ve atom modeli 3. d ~ 1µm iken T ~ 1µK e kadar buharlaşma soğutulması Δp ~ kg m s (2-11) Δp Δd ~ 2h (2-12) atomlar bozon ise Bose-Einstein yoğuşumu atomlar fermiyon ise dejenere Fermi gazı KM betimleme gereklidir. 4. Atomun Elektronu l = pr = m = kg q = C r ~ 1A =10 10 m A s ε 0 = V m 2m q2 4πε 0 r ~ J s ~ (2-13) KM betimleme II-5
6 Klasik betimleme bu ölçekte niçin bozunur? Heisenberg belirsizliği parçacığın dalga boyu Bu soruna ışık tutmak üzere, Fermat ın en kısa zaman ilkesini inceleyelim. Fermat en kısa zaman ilkesi Şekil IV: Düz Doğru Yol Işık A dan B ye nasıl yol alır? Düz doğru boyunca Niçin? Nasıl Düz? Şekil V: Kırınım Işık nasıl yol alır? Şek. IV düz doğru boyunca Şek. V ara kesitte ışık Snell kuralına tabidir sinθ 1 sinθ 2 = n 2 n 1 II-6
7 Işık nasıl yol alır? Işık en kısa süreyi alacak şekilde bir yol takip eder. Cam içinde ışık c = c n 2 hızıyla hareket eder ki, doğru yol düz yola göre daha kısa zamanda vuku bulur. Ancak: Nasıl oluyorda ışık en kısa zamanlı yolu biliyor?. Bazı durumlarda ışık daha uzun süreli yolu takip etmektedir. Fermat ilkesinin geliştirilmiş hali Işık öyle bir yol takip eder ki, yakındaki yollar için yol alma zamanında birinci mertebeden hiçbir değişiklik olmaz. Okuma Feynman, Lectures on Physics I, Böl. 26. II-7
8.04 Kuantum Fiziği Ders IV. Kırınım olayı olarak Heisenberg belirsizlik ilkesi. ise, parçacığın dalga fonksiyonu,
 Geçen Derste Kırınım olayı olarak Heisenberg belirsizlik ilkesi ΔxΔp x 2 Fourier ayrışımı Bugün φ(k) yı nasıl hesaplarız ψ(x) ve φ(k) ın yorumu: olasılık genliği ve olasılık yoğunluğu ölçüm φ ( k)veyahut
Geçen Derste Kırınım olayı olarak Heisenberg belirsizlik ilkesi ΔxΔp x 2 Fourier ayrışımı Bugün φ(k) yı nasıl hesaplarız ψ(x) ve φ(k) ın yorumu: olasılık genliği ve olasılık yoğunluğu ölçüm φ ( k)veyahut
8.04 Kuantum Fiziği Ders X. Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler.
 Schrödinger denklemi Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler. Köşeli parantez içindeki terim, dalga fonksiyonuna etki eden bir işlemci olup, Hamilton
Schrödinger denklemi Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler. Köşeli parantez içindeki terim, dalga fonksiyonuna etki eden bir işlemci olup, Hamilton
Kuantum Mekaniğinin Varsayımları
 Kuantum Mekaniğinin Varsayımları Kuantum mekaniği 6 temel varsayım üzerine kurulmuştur. Kuantum mekaniksel problemler bu varsayımlar kullanılarak (teorik/kuramsal olarak) çözülmekte ve elde edilen sonuçlar
Kuantum Mekaniğinin Varsayımları Kuantum mekaniği 6 temel varsayım üzerine kurulmuştur. Kuantum mekaniksel problemler bu varsayımlar kullanılarak (teorik/kuramsal olarak) çözülmekte ve elde edilen sonuçlar
8.04 Kuantum Fiziği Ders V ( ) 2. = dk φ k
 Geçen Derste ψ( x) 2 ve φ( k) 2 sırasıyla konum ve momentum uzayındaki olasılık yoğunlukları Parseval teoremi: dxψ( x) 2 = dk φ k ( ) 2 Normalizasyon: 1 = dxψ( x) 2 = dk φ k ( ) 2 Ölçüm: x alet < x çözünürlüğü
Geçen Derste ψ( x) 2 ve φ( k) 2 sırasıyla konum ve momentum uzayındaki olasılık yoğunlukları Parseval teoremi: dxψ( x) 2 = dk φ k ( ) 2 Normalizasyon: 1 = dxψ( x) 2 = dk φ k ( ) 2 Ölçüm: x alet < x çözünürlüğü
MASSACHUSETTS TEKNOLOJİ ENSTİTÜSÜ Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 1 Salı, Mart 14, :00-12:30
 Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 1 Salı, Mart 14, 2006 11:00-12:30 SOYADI ADI Öğrenci No. Talimat: 1. TÜM ÇABANIZI GÖSTERİN. Tüm cevaplar sınav kitapçığında gösterilmelidir? 2. Bu kapalı bir sınavdır.
Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 1 Salı, Mart 14, 2006 11:00-12:30 SOYADI ADI Öğrenci No. Talimat: 1. TÜM ÇABANIZI GÖSTERİN. Tüm cevaplar sınav kitapçığında gösterilmelidir? 2. Bu kapalı bir sınavdır.
TOBB Ekonomi ve Teknoloji Üniversitesi. chem.libretexts.org
 9. Atomun Elektron Yapısı Elektromanyetik ışıma (EMI) Atom Spektrumları Bohr Atom Modeli Kuantum Kuramı - Dalga Mekaniği Kuantum Sayıları Elektron Orbitalleri Hidrojen Atomu Orbitalleri Elektron Spini
9. Atomun Elektron Yapısı Elektromanyetik ışıma (EMI) Atom Spektrumları Bohr Atom Modeli Kuantum Kuramı - Dalga Mekaniği Kuantum Sayıları Elektron Orbitalleri Hidrojen Atomu Orbitalleri Elektron Spini
Bölüm 1: Lagrange Kuramı... 1
 İÇİNDEKİLER Bölüm 1: Lagrange Kuramı... 1 1.1. Giriş... 1 1.2. Genelleştirilmiş Koordinatlar... 2 1.3. Koordinat Dönüşüm Denklemleri... 3 1.4. Mekanik Dizgelerin Bağ Koşulları... 4 1.5. Mekanik Dizgelerin
İÇİNDEKİLER Bölüm 1: Lagrange Kuramı... 1 1.1. Giriş... 1 1.2. Genelleştirilmiş Koordinatlar... 2 1.3. Koordinat Dönüşüm Denklemleri... 3 1.4. Mekanik Dizgelerin Bağ Koşulları... 4 1.5. Mekanik Dizgelerin
8.04 Kuantum Fiziği Ders VI
 Fotoelektrik Etki 1888 de gözlemlendi; izahı, Einstein 1905. Negatif yüklü metal bir levha ışıkla aydınlatıldığında yükünü yavaş yavaş kaybederken, pozitif bir yük geriye kalır. Şekil I: Fotoelektrik etki.
Fotoelektrik Etki 1888 de gözlemlendi; izahı, Einstein 1905. Negatif yüklü metal bir levha ışıkla aydınlatıldığında yükünü yavaş yavaş kaybederken, pozitif bir yük geriye kalır. Şekil I: Fotoelektrik etki.
A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili
 A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili Momentum işlemcisinin konum temsili Konum işlemcisinin momentum temsili
A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili Momentum işlemcisinin konum temsili Konum işlemcisinin momentum temsili
Tek Boyutlu Potansiyeller: Potansiyel eşiği
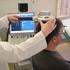 Tek Boyutlu Potansiyeller: Potansiyel eşiği Şekil I: V 0 yüksekliğindeki potansiyel eşiği. Parçacık soldan gelmekte olup, enerjisi E dir. Zamandan bağımsız bir durumu analiz ediyoruz ki burada iyi belirlenmiş
Tek Boyutlu Potansiyeller: Potansiyel eşiği Şekil I: V 0 yüksekliğindeki potansiyel eşiği. Parçacık soldan gelmekte olup, enerjisi E dir. Zamandan bağımsız bir durumu analiz ediyoruz ki burada iyi belirlenmiş
Kuantum Fiziği (PHYS 201) Ders Detayları
 Kuantum Fiziği (PHYS 201) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Kuantum Fiziği PHYS 201 Her İkisi 3 0 0 3 5 Ön Koşul Ders(ler)i PHYS 102, MATH 158
Kuantum Fiziği (PHYS 201) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Kuantum Fiziği PHYS 201 Her İkisi 3 0 0 3 5 Ön Koşul Ders(ler)i PHYS 102, MATH 158
Geçen Derste. ρ için sınır şartları serinin bir yerde sona ermesini gerektirir. 8.04 Kuantum Fiziği Ders XXIII
 Geçen Derste Verilen l kuantum sayılı açısal momentum Y lm (θ,φ) özdurumunun radyal denklemi 1B lu SD şeklinde etkin potansiyeli olacak şekilde yazılabilir, u(r) = rr(r) olarak tanımlayarak elde edilir.
Geçen Derste Verilen l kuantum sayılı açısal momentum Y lm (θ,φ) özdurumunun radyal denklemi 1B lu SD şeklinde etkin potansiyeli olacak şekilde yazılabilir, u(r) = rr(r) olarak tanımlayarak elde edilir.
1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ
 1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ Bohr Modelinin Yetersizlikleri Dalga-Tanecik İkiliği Dalga Mekaniği Kuantum Mekaniği -Orbital Kavramı Kuantum Sayıları Yörünge - Orbital Kavramları
1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ Bohr Modelinin Yetersizlikleri Dalga-Tanecik İkiliği Dalga Mekaniği Kuantum Mekaniği -Orbital Kavramı Kuantum Sayıları Yörünge - Orbital Kavramları
Newton un F = ma eşitliğini SD den türete bilir miyiz?
 burada yine kısmi integrasyon kullanıldı ve ± da Ψ ın yok olduğu kabul edildi. Sonuç olarak, p = p, yani p ˆ nin tüm beklenti değerleri gerçeldir. Bir özdeğer kendisine karşı gelen kararlı durumun beklenti
burada yine kısmi integrasyon kullanıldı ve ± da Ψ ın yok olduğu kabul edildi. Sonuç olarak, p = p, yani p ˆ nin tüm beklenti değerleri gerçeldir. Bir özdeğer kendisine karşı gelen kararlı durumun beklenti
8.04 Kuantum Fiziği Ders XII
 Enerji ölçümünden sonra Sonucu E i olan enerji ölçümünden sonra parçacık enerji özdurumu u i de olacak ve daha sonraki ardışık tüm enerji ölçümleri E i enerjisini verecektir. Ölçüm yapılmadan önce enerji
Enerji ölçümünden sonra Sonucu E i olan enerji ölçümünden sonra parçacık enerji özdurumu u i de olacak ve daha sonraki ardışık tüm enerji ölçümleri E i enerjisini verecektir. Ölçüm yapılmadan önce enerji
Özet: Açısal momentumun türetimi. Açısal momentum değiştirme bağıntıları. Artırıcı ve Eksiltici İşlemciler Kuantum Fiziği Ders XXI
 Özet: Açısal momentumun türetimi Açısal momentum değiştirme bağıntıları Levi- Civita simgesi Genel olarak, L x, L y, L z, nin eşzamanlı özdurumları yoktur L 2 ve bir bileşeni (L z ) nin eşzamanlı özdurumlarıdır.
Özet: Açısal momentumun türetimi Açısal momentum değiştirme bağıntıları Levi- Civita simgesi Genel olarak, L x, L y, L z, nin eşzamanlı özdurumları yoktur L 2 ve bir bileşeni (L z ) nin eşzamanlı özdurumlarıdır.
Parçacık Fiziği. Dr. Bora Akgün / Rice Üniversitesi CERN Türkiye Öğretmenleri Programı Temmuz 2015
 Parçacık Fiziği Dr. Bora Akgün / Rice Üniversitesi CERN Türkiye Öğretmenleri Programı Temmuz 2015 Parçacık Fiziğinin Standard Modeli fermion boson Dönü 2 Spin/Dönü Bir parçacık özelliğidir (kütle, yük
Parçacık Fiziği Dr. Bora Akgün / Rice Üniversitesi CERN Türkiye Öğretmenleri Programı Temmuz 2015 Parçacık Fiziğinin Standard Modeli fermion boson Dönü 2 Spin/Dönü Bir parçacık özelliğidir (kütle, yük
Kuantum Fiziği ÜNİTE. Amaçlar. İçindekiler. Yazarlar Doç. Dr. Mustafa ŞENYEL Yrd. Doç. Dr. A. Şenol AYBEK
 Kuantum Fiziği Yazarlar Doç. Dr. Mustafa ŞENYEL Yrd. Doç. Dr. A. Şenol AYBEK ÜNİTE 3 Amaçlar Bu üniteyi çalıştıktan sonra, çağdaş fiziğin temellerini oluşturan; Planck'ın kuantum varsayımlarını, Foton
Kuantum Fiziği Yazarlar Doç. Dr. Mustafa ŞENYEL Yrd. Doç. Dr. A. Şenol AYBEK ÜNİTE 3 Amaçlar Bu üniteyi çalıştıktan sonra, çağdaş fiziğin temellerini oluşturan; Planck'ın kuantum varsayımlarını, Foton
Bölüm 8: Atomun Elektron Yapısı
 Bölüm 8: Atomun Elektron Yapısı 1. Elektromanyetik Işıma: Elektrik ve manyetik alanın dalgalar şeklinde taşınmasıdır. Her dalganın frekansı ve dalga boyu vardır. Dalga boyu (ʎ) : İki dalga tepeciği arasındaki
Bölüm 8: Atomun Elektron Yapısı 1. Elektromanyetik Işıma: Elektrik ve manyetik alanın dalgalar şeklinde taşınmasıdır. Her dalganın frekansı ve dalga boyu vardır. Dalga boyu (ʎ) : İki dalga tepeciği arasındaki
FİZ304 İSTATİSTİK FİZİK. Klasik Yaklaşımda Kanonik Dağılım I. Prof.Dr. Orhan ÇAKIR Ankara Üniversitesi, Fizik Bölümü 2017
 FİZ304 İSTATİSTİK FİZİK Klasik Yaklaşımda Kanonik Dağılım I Prof.Dr. Orhan ÇAKIR Ankara Üniversitesi, Fizik Bölümü 2017 Klasik Yaklaşım Klasik kavramlarla yapılan bir istajsjk teorinin hangi koşullar alnnda
FİZ304 İSTATİSTİK FİZİK Klasik Yaklaşımda Kanonik Dağılım I Prof.Dr. Orhan ÇAKIR Ankara Üniversitesi, Fizik Bölümü 2017 Klasik Yaklaşım Klasik kavramlarla yapılan bir istajsjk teorinin hangi koşullar alnnda
BÖLÜM 12-15 HARMONİK OSİLATÖR
 BÖLÜM 12-15 HARMONİK OSİLATÖR Hemen hemen her sistem, dengeye yaklaşırken bir harmonik osilatör gibi davranabilir. Kuantum mekaniğinde sadece sayılı bir kaç problem kesin olarak çözülebilmektedir. Örnekler
BÖLÜM 12-15 HARMONİK OSİLATÖR Hemen hemen her sistem, dengeye yaklaşırken bir harmonik osilatör gibi davranabilir. Kuantum mekaniğinde sadece sayılı bir kaç problem kesin olarak çözülebilmektedir. Örnekler
8.04 Kuantum Fiziği DersXIX
 Bu takdirde yani, 1 = a ˆ 0 de bir enerji özdurumudur, ancak 0 için enerjisi 1hω yerine 3 hω dir. 2 2 Benzer şekilde, 2 = a ˆ 1 inde bir enerji özdurumu olduğunu fakat enerjisinin 5 hω, vs. 2 söyleyebiliriz.
Bu takdirde yani, 1 = a ˆ 0 de bir enerji özdurumudur, ancak 0 için enerjisi 1hω yerine 3 hω dir. 2 2 Benzer şekilde, 2 = a ˆ 1 inde bir enerji özdurumu olduğunu fakat enerjisinin 5 hω, vs. 2 söyleyebiliriz.
Modern Fizik (Fiz 206)
 Modern Fizik (Fiz 206) 3. Bölüm KUANTUM Mekaniği Bohr modelinin sınırları Düz bir dairenin çevresinde hareket eden elektronu tanımlar Saçılma deneyleri elektronların çekirdek etrafında, çekirdekten uzaklaştıkça
Modern Fizik (Fiz 206) 3. Bölüm KUANTUM Mekaniği Bohr modelinin sınırları Düz bir dairenin çevresinde hareket eden elektronu tanımlar Saçılma deneyleri elektronların çekirdek etrafında, çekirdekten uzaklaştıkça
Foton Kutuplanma durumlarının Dirac yazılımı
 Foton Kutuplanma durumlarının Dirac yazılımı Yatay Kutuplanmış bir foton h ve düşey kutuplanmış bir foton ise ν ile verilmiştir. Şekil I: Foton kutuplanma bazları h, ν ve +45, 45 in tanımı. ±45 boyunca
Foton Kutuplanma durumlarının Dirac yazılımı Yatay Kutuplanmış bir foton h ve düşey kutuplanmış bir foton ise ν ile verilmiştir. Şekil I: Foton kutuplanma bazları h, ν ve +45, 45 in tanımı. ±45 boyunca
Bugün için Okuma: Bölüm 1.5 (3. Baskıda 1.3), Bölüm 1.6 (3. Baskıda 1.4 )
 5.111 Ders Özeti #4 Bugün için Okuma: Bölüm 1.5 (3. Baskıda 1.3), Bölüm 1.6 (3. Baskıda 1.4 ) Ders #5 için Okuma: Bölüm 1.3 (3. Baskıda 1.6 ) Atomik Spektrumlar, Bölüm 1.7 de eģitlik 9b ye kadar (3. Baskıda
5.111 Ders Özeti #4 Bugün için Okuma: Bölüm 1.5 (3. Baskıda 1.3), Bölüm 1.6 (3. Baskıda 1.4 ) Ders #5 için Okuma: Bölüm 1.3 (3. Baskıda 1.6 ) Atomik Spektrumlar, Bölüm 1.7 de eģitlik 9b ye kadar (3. Baskıda
Kuantum Fiziğinin Gelişimi (Quantum Physics) 1900 den 1930 a
 Kuantum Fiziğinin Gelişimi (Quantum Physics) 1900 den 1930 a Kuantum Mekaniği Düşüncesinin Gelişimi Dalga Mekaniği Olarak da Adlandırılır Atom, Molekül ve Çekirdeği Açıklamada Oldukça Başarılıdır Kuantum
Kuantum Fiziğinin Gelişimi (Quantum Physics) 1900 den 1930 a Kuantum Mekaniği Düşüncesinin Gelişimi Dalga Mekaniği Olarak da Adlandırılır Atom, Molekül ve Çekirdeği Açıklamada Oldukça Başarılıdır Kuantum
İstatistiksel Mekanik I
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
Elektromanyetik Işıma Electromagnetic Radiation (EMR)
 Elektromanyetik Işıma Electromagnetic Radiation (EMR) Elektromanyetik ışıma (ışık) bir enerji şeklidir. Işık, Elektrik (E) ve manyetik (H) alan bileşenlerine sahiptir. Light is a wave, made up of oscillating
Elektromanyetik Işıma Electromagnetic Radiation (EMR) Elektromanyetik ışıma (ışık) bir enerji şeklidir. Işık, Elektrik (E) ve manyetik (H) alan bileşenlerine sahiptir. Light is a wave, made up of oscillating
MIT Açık Ders Malzemesi İstatistiksel Mekanik II: Alanların İstatistiksel Fiziği 2008 Bahar
 MIT Açık Ders Malzemesi http://ocw.mit.edu 8.334 İstatistiksel Mekanik II: Alanların İstatistiksel Fiziği 008 Bahar Bu malzemeye atıfta bulunmak ve Kullanım Şartlarımızla ilgili bilgi almak için http://ocw.mit.edu/terms
MIT Açık Ders Malzemesi http://ocw.mit.edu 8.334 İstatistiksel Mekanik II: Alanların İstatistiksel Fiziği 008 Bahar Bu malzemeye atıfta bulunmak ve Kullanım Şartlarımızla ilgili bilgi almak için http://ocw.mit.edu/terms
BÖLÜM 4 GİRİŞ MODERN ATOM TEORİSİ VE YENİ KUANTUM MEKANİĞİ
 BÖLÜM 4 MODERN ATOM TEORİSİ VE YENİ KUANTUM MEKANİĞİ GİRİŞ Ön Sıra, Soldan Sağa : I. Langmuir; M. Planck; M. Curie; H.A. Lorentz; A. Einstein; P. Langevin; C. Guye; C.T.R. Wilson; O.W. Richardson. Olmayanlar:
BÖLÜM 4 MODERN ATOM TEORİSİ VE YENİ KUANTUM MEKANİĞİ GİRİŞ Ön Sıra, Soldan Sağa : I. Langmuir; M. Planck; M. Curie; H.A. Lorentz; A. Einstein; P. Langevin; C. Guye; C.T.R. Wilson; O.W. Richardson. Olmayanlar:
FİZİK DE YENİ BİR ÇAĞ AÇAN BULUŞ : KUANTUM KURAMI (2)
 FİZİK DE YENİ BİR ÇAĞ AÇAN BULUŞ : KUANTUM KURAMI () MODERN KUANTUM KURAMI VE TEMEL İLKELERİ Prof. Dr. Süleyman BOZDEMİR, Ç.Ü. Fen-Ede. Fak. Fizik Böl. ADANA Yard. Doç. Dr. Sıtkı EKER, Ahi Evran Üniv.
FİZİK DE YENİ BİR ÇAĞ AÇAN BULUŞ : KUANTUM KURAMI () MODERN KUANTUM KURAMI VE TEMEL İLKELERİ Prof. Dr. Süleyman BOZDEMİR, Ç.Ü. Fen-Ede. Fak. Fizik Böl. ADANA Yard. Doç. Dr. Sıtkı EKER, Ahi Evran Üniv.
Franck-Hertz deneyi: atomlarla kuantumlanmış enerji düzeyleri (1913)
 Franck-Hertz deneyi: atomlarla kuantumlanmış enerji düzeyleri (1913) Franck-Hertz deneyi elektron-atom çarpışma tesir kesitinde rezonansları göstermiştir. Şekil I: Franck-Hertz gereci. Katottan neşredilen
Franck-Hertz deneyi: atomlarla kuantumlanmış enerji düzeyleri (1913) Franck-Hertz deneyi elektron-atom çarpışma tesir kesitinde rezonansları göstermiştir. Şekil I: Franck-Hertz gereci. Katottan neşredilen
ψ( x)e ikx dx, φ( k)e ikx dx ψ( x) = 1 2π θ açısında, dθ ince halka genişliğinin katı açısı: A. Fiziksel sabitler ve dönüşüm çarpanları
 A. Fiziksel sabitler ve dönüşüm çarpanları B. Seçilmiş bağıntılar Rutherford saçınımının diferansiyel kesiti: Compton kayması Bohr un hidrojenimsi atom modelinde izinli yörüngelerin yarıçapı: olup burada
A. Fiziksel sabitler ve dönüşüm çarpanları B. Seçilmiş bağıntılar Rutherford saçınımının diferansiyel kesiti: Compton kayması Bohr un hidrojenimsi atom modelinde izinli yörüngelerin yarıçapı: olup burada
Coulomb Kuvvet Kanunu H atomunda çekirdek ve elektron arasındaki F yi tanımlar.
 5.111 Ders Özeti #3 Bugün için okuma: Bölüm 1.2 (3. Baskıda 1.1 ), Bölüm 1.4 (3. Baskıda 1.2 ), 4. Baskıda s. 10-12 veya 3. Baskıda s. 5-7 ye odaklanın. Ders 4 için okuma: Bölüm 1.5 (3. Baskıda 1.3 ) Maddenin
5.111 Ders Özeti #3 Bugün için okuma: Bölüm 1.2 (3. Baskıda 1.1 ), Bölüm 1.4 (3. Baskıda 1.2 ), 4. Baskıda s. 10-12 veya 3. Baskıda s. 5-7 ye odaklanın. Ders 4 için okuma: Bölüm 1.5 (3. Baskıda 1.3 ) Maddenin
İÇİNDEKİLER 1: KRİSTALLERDE ATOMLAR...
 İÇİNDEKİLER Bölüm 1: KRİSTALLERDE ATOMLAR... 1 1.1 Katıhal... 1 1.1.1 Kristal Katılar... 1 1.1.2 Çoklu Kristal Katılar... 2 1.1.3 Kristal Olmayan (Amorf) Katılar... 2 1.2 Kristallerde Periyodiklik... 2
İÇİNDEKİLER Bölüm 1: KRİSTALLERDE ATOMLAR... 1 1.1 Katıhal... 1 1.1.1 Kristal Katılar... 1 1.1.2 Çoklu Kristal Katılar... 2 1.1.3 Kristal Olmayan (Amorf) Katılar... 2 1.2 Kristallerde Periyodiklik... 2
da. Elektronlar düşük E seviyesinden daha yüksek E seviyesine inerken enerji soğurur.
 5.111 Ders Özeti #6 Bugün için okuma: Bölüm 1.9 (3. Baskıda 1.8) Atomik Orbitaller. Ders #7 için okuma: Bölüm 1.10 (3. Baskıda 1.9) Elektron Spini, Bölüm 1.11 (3. Baskıda 1.10) Hidrojenin Elektronik Yapısı
5.111 Ders Özeti #6 Bugün için okuma: Bölüm 1.9 (3. Baskıda 1.8) Atomik Orbitaller. Ders #7 için okuma: Bölüm 1.10 (3. Baskıda 1.9) Elektron Spini, Bölüm 1.11 (3. Baskıda 1.10) Hidrojenin Elektronik Yapısı
BÖLÜM 1: Matematiğe Genel Bakış 1. BÖLÜM:2 Fizik ve Ölçme 13. BÖLÜM 3: Bir Boyutta Hareket 20. BÖLÜM 4: Düzlemde Hareket 35
 BÖLÜM 1: Matematiğe Genel Bakış 1 1.1. Semboller, Bilimsel Gösterimler ve Anlamlı Rakamlar 1.2. Cebir 1.3. Geometri ve Trigometri 1.4. Vektörler 1.5. Seriler ve Yaklaşıklıklar 1.6. Matematik BÖLÜM:2 Fizik
BÖLÜM 1: Matematiğe Genel Bakış 1 1.1. Semboller, Bilimsel Gösterimler ve Anlamlı Rakamlar 1.2. Cebir 1.3. Geometri ve Trigometri 1.4. Vektörler 1.5. Seriler ve Yaklaşıklıklar 1.6. Matematik BÖLÜM:2 Fizik
İÇİNDEKİLER -BÖLÜM / 1- -BÖLÜM / 2- -BÖLÜM / 3- GİRİŞ... 1 ÖZEL GÖRELİLİK KUANTUM FİZİĞİ ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ...
 İÇİNDEKİLER ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ... viii -BÖLÜM / 1- GİRİŞ... 1 -BÖLÜM / 2- ÖZEL GÖRELİLİK... 13 2.1. REFERANS SİSTEMLERİ VE GÖRELİLİK... 14 2.2. ÖZEL GÖRELİLİK TEORİSİ... 19 2.2.1. Zaman Ölçümü
İÇİNDEKİLER ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ... viii -BÖLÜM / 1- GİRİŞ... 1 -BÖLÜM / 2- ÖZEL GÖRELİLİK... 13 2.1. REFERANS SİSTEMLERİ VE GÖRELİLİK... 14 2.2. ÖZEL GÖRELİLİK TEORİSİ... 19 2.2.1. Zaman Ölçümü
Boşlukta Dalga Fonksiyonlarının Normalleştirilmesi
 Boşlukta Dalga Fonksiyonlarının Noralleştirilesi Konu tesilinde oentu özduruları, u p (x) ile belirlenir ve ile verilir. Ancak, boşlukta noralleştirilecek bir olasılık yoğunluğu gibi yorulanaaz zira (
Boşlukta Dalga Fonksiyonlarının Noralleştirilesi Konu tesilinde oentu özduruları, u p (x) ile belirlenir ve ile verilir. Ancak, boşlukta noralleştirilecek bir olasılık yoğunluğu gibi yorulanaaz zira (
SU Lise Yaz Okulu 2. Ders, biraz (baya) fizik. Dalgalar Elektromanyetik Dalgalar Kuantum mekaniği Tayf Karacisim ışıması
 SU Lise Yaz Okulu 2. Ders, biraz (baya) fizik Dalgalar Elektromanyetik Dalgalar Kuantum mekaniği Tayf Karacisim ışıması Dalga Nedir Enerji taşıyan bir değişimin bir yöne doğru taşınmasına dalga denir.
SU Lise Yaz Okulu 2. Ders, biraz (baya) fizik Dalgalar Elektromanyetik Dalgalar Kuantum mekaniği Tayf Karacisim ışıması Dalga Nedir Enerji taşıyan bir değişimin bir yöne doğru taşınmasına dalga denir.
Magnetic Materials. 7. Ders: Ferromanyetizma. Numan Akdoğan.
 Magnetic Materials 7. Ders: Ferromanyetizma Numan Akdoğan akdogan@gyte.edu.tr Gebze Institute of Technology Department of Physics Nanomagnetism and Spintronic Research Center (NASAM) Moleküler Alan Teorisinin
Magnetic Materials 7. Ders: Ferromanyetizma Numan Akdoğan akdogan@gyte.edu.tr Gebze Institute of Technology Department of Physics Nanomagnetism and Spintronic Research Center (NASAM) Moleküler Alan Teorisinin
Çift yarık: Foton saçılımı ve girişim deseninin matematiksel modeli
 Çift yarık: Foton saçılımı ve girişim deseninin matematiksel modeli Girişim olayına ait daha çok sezgi geliştirmek üzere; kuantum sistemi ve (klasik) gereç arasındaki eşilişkilerin kuantum mekaniğinin
Çift yarık: Foton saçılımı ve girişim deseninin matematiksel modeli Girişim olayına ait daha çok sezgi geliştirmek üzere; kuantum sistemi ve (klasik) gereç arasındaki eşilişkilerin kuantum mekaniğinin
FİZİK 4. Ders 10: Bir Boyutlu Schrödinger Denklemi
 FİZİK 4 Ders 10: Bir Boyutlu Schrödinger Denklemi Bir Boyutlu Schrödinger Denklemi Beklenen Değer Kuyu İçindeki Parçacık Zamandan Bağımsız Schrödinger Denklemi Kare Kuyu Tünel Olayı Basit Harmonik Salınıcı
FİZİK 4 Ders 10: Bir Boyutlu Schrödinger Denklemi Bir Boyutlu Schrödinger Denklemi Beklenen Değer Kuyu İçindeki Parçacık Zamandan Bağımsız Schrödinger Denklemi Kare Kuyu Tünel Olayı Basit Harmonik Salınıcı
Fen ve Mühendislik Bilimleri için Fizik
 Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
BÖLÜM 17 RİJİT ROTOR
 BÖLÜM 17 RİJİT ROTOR Birbirinden R sabit mesafede bulunan iki parçacığın dönmesini düşünelim. Bu iki parçacık, bir elektron ve proton (bu durumda bir hidrojen atomunu ele alıyoruz) veya iki çekirdek (bu
BÖLÜM 17 RİJİT ROTOR Birbirinden R sabit mesafede bulunan iki parçacığın dönmesini düşünelim. Bu iki parçacık, bir elektron ve proton (bu durumda bir hidrojen atomunu ele alıyoruz) veya iki çekirdek (bu
Theory Tajik (Tajikistan)
 Q3-1 Büyük Hadron Çarpıştırıcısı Bu probleme başlamadan önce ayrı bir zarfta verilen genel talimatları lütfen okuyunuz. Bu görevde, CERN de bulunan parçacık hızlandırıcısının LHC ( Büyük Hadron Çarpıştırıcısı)
Q3-1 Büyük Hadron Çarpıştırıcısı Bu probleme başlamadan önce ayrı bir zarfta verilen genel talimatları lütfen okuyunuz. Bu görevde, CERN de bulunan parçacık hızlandırıcısının LHC ( Büyük Hadron Çarpıştırıcısı)
Fen - Edebiyat Fakültesi Fizik Bölümü
 http://ogr.kocaeli.edu.tr/koubs/bologna/genel/listesi_prn.cfm?ed=0 1 / 5 22.05.2018 15:51 Fen - Edebiyat Fakültesi Fizik Bölümü Adı 2017/2018 Listesi 1. YARIYIL TLU Atatürk İlkeleri ve İnkılap 9905005
http://ogr.kocaeli.edu.tr/koubs/bologna/genel/listesi_prn.cfm?ed=0 1 / 5 22.05.2018 15:51 Fen - Edebiyat Fakültesi Fizik Bölümü Adı 2017/2018 Listesi 1. YARIYIL TLU Atatürk İlkeleri ve İnkılap 9905005
Fen ve Mühendislik Bilimleri için Fizik
 Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
BÖLÜM 25 HELYUM ATOMU
 BÖLÜM 25 HELYUM ATOMU Şimdi, Hidrojene benzer atomları daha detaylı inceleyelim. Bir sonraki en basit sistemi tartışmaya başlayalım: Helyum atomu. Bu durumda, R noktasında konumlanmış Z = 2 yükü bulunan
BÖLÜM 25 HELYUM ATOMU Şimdi, Hidrojene benzer atomları daha detaylı inceleyelim. Bir sonraki en basit sistemi tartışmaya başlayalım: Helyum atomu. Bu durumda, R noktasında konumlanmış Z = 2 yükü bulunan
İstatistiksel Mekanik I
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
Temel Parçacık Dinamikleri. Sunum İçeriği
 1 Sunum İçeriği 2 Genel Tekrar Leptonlar Örnek: elektron Fermionlar Kuarklar Örnek: u kuark Bozonlar Örnek: foton Kuarklar serbest halde görülmezler. Kuarklardan oluşan yapılar ise genel olarak şu şekilde
1 Sunum İçeriği 2 Genel Tekrar Leptonlar Örnek: elektron Fermionlar Kuarklar Örnek: u kuark Bozonlar Örnek: foton Kuarklar serbest halde görülmezler. Kuarklardan oluşan yapılar ise genel olarak şu şekilde
EĞİTİM-ÖĞRETİM YILI 12 SINIF FİZİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ
 EKİM 2017-2018 EĞİTİM-ÖĞRETİM YILI 12 SINIF FİZİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ Ay Hafta Ders Saati Konu Adı Kazanımlar Test No Test Adı Hareket Hareket 12.1.1.1. Düzgün
EKİM 2017-2018 EĞİTİM-ÖĞRETİM YILI 12 SINIF FİZİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ Ay Hafta Ders Saati Konu Adı Kazanımlar Test No Test Adı Hareket Hareket 12.1.1.1. Düzgün
ÇALIŞMA YAPRAĞI (KONU ANLATIMI)
 ÇALIŞMA YAPRAĞI (KONU ANLATIMI) ATOMUN YAPISI HAZIRLAYAN: ÇĐĞDEM ERDAL DERS: ÖĞRETĐM TEKNOLOJĐLERĐ VE MATERYAL GELĐŞTĐRME DERS SORUMLUSU: PROF.DR. ĐNCĐ MORGĐL ANKARA,2008 GĐRĐŞ Kimyayı ve bununla ilgili
ÇALIŞMA YAPRAĞI (KONU ANLATIMI) ATOMUN YAPISI HAZIRLAYAN: ÇĐĞDEM ERDAL DERS: ÖĞRETĐM TEKNOLOJĐLERĐ VE MATERYAL GELĐŞTĐRME DERS SORUMLUSU: PROF.DR. ĐNCĐ MORGĐL ANKARA,2008 GĐRĐŞ Kimyayı ve bununla ilgili
FİZ304 İSTATİSTİK FİZİK VE TERMODİNAMİK. Parçacık Sistemlerinin İstatistik Tanımlanması II
 FİZ304 İSTATİSTİK FİZİK VE TERMODİNAMİK Parçacık Sistemlerinin İstatistik Tanımlanması II Prof.Dr. Orhan ÇAKIR Ankara Üniversitesi, FizikBölümü 2017 Makroskopik Sistemde Girilebilir Durum Sayısı Dengedeki
FİZ304 İSTATİSTİK FİZİK VE TERMODİNAMİK Parçacık Sistemlerinin İstatistik Tanımlanması II Prof.Dr. Orhan ÇAKIR Ankara Üniversitesi, FizikBölümü 2017 Makroskopik Sistemde Girilebilir Durum Sayısı Dengedeki
Kadri Yakut 08.03.2012
 Kadri Yakut 08.03.2012 TEŞEKKÜR Lisans Kara Delikler Eser İş (2009-2010) Büyük Kütleli Kara Delikler Birses Debir (2010-2011) Astrofiziksel Kara Deliklerin Kütlelerinin Belirlenmesi Orhan Erece (2010-2011)
Kadri Yakut 08.03.2012 TEŞEKKÜR Lisans Kara Delikler Eser İş (2009-2010) Büyük Kütleli Kara Delikler Birses Debir (2010-2011) Astrofiziksel Kara Deliklerin Kütlelerinin Belirlenmesi Orhan Erece (2010-2011)
A B = A. = P q c A( X(t))
 Ders 19 Metindeki ilgili bölümler 2.6 Elektromanyetik bir alanda yüklü parçacık Şimdi, kuantum mekaniğinin son derece önemli başka bir örneğine geçiyoruz. Verilen bir elektromanyetik alanda hareket eden
Ders 19 Metindeki ilgili bölümler 2.6 Elektromanyetik bir alanda yüklü parçacık Şimdi, kuantum mekaniğinin son derece önemli başka bir örneğine geçiyoruz. Verilen bir elektromanyetik alanda hareket eden
MODERN FİZİĞİN DOĞUŞUNDA MOR ÖTESİ KRİZİNİN ROLÜ
 MODERN FİZİĞİN DOĞUŞUNDA MOR ÖTESİ KRİZİNİN ROLÜ Öğretmen Olcay NALBANTOĞLU Hazırlayanlar A.Cumhur ÖZCAN Mustafa GÖNENÇER Okan GİDİŞ Tolga TOLGAY İÇİNDEKİLER 1. Klasik Fiziğin Tanımı 2. Klasik Kuramın
MODERN FİZİĞİN DOĞUŞUNDA MOR ÖTESİ KRİZİNİN ROLÜ Öğretmen Olcay NALBANTOĞLU Hazırlayanlar A.Cumhur ÖZCAN Mustafa GÖNENÇER Okan GİDİŞ Tolga TOLGAY İÇİNDEKİLER 1. Klasik Fiziğin Tanımı 2. Klasik Kuramın
H(t) + O(ɛ 2 ) var. Yukarıda U(t + ɛ, t) için elde ettiğimiz sonucumuzu bu ifadede yerine koyunca her iki tarafı. = H(t)U(t, t 0 )
 Ders 12 Metindeki ilgili bölümler 2.1 Hamilton işlemcisi ve Schrödinger denklemi Şimdi, t den t + ɛ a zaman gelişimini düşünün. U(t + ɛ, t) = I + ɛ ( i ) H(t) + O(ɛ 2 ) elde ederiz. Her zamanki gibi, U
Ders 12 Metindeki ilgili bölümler 2.1 Hamilton işlemcisi ve Schrödinger denklemi Şimdi, t den t + ɛ a zaman gelişimini düşünün. U(t + ɛ, t) = I + ɛ ( i ) H(t) + O(ɛ 2 ) elde ederiz. Her zamanki gibi, U
Kısa İçindekiler. Fizik: İlkeler ve Pratik Cilt 1: 1-21 Bölümleri, Cilt 2: Bölümleri kapsar
 Kısa İçindekiler Fizik: İlkeler ve Pratik Cilt 1: 1-21 Bölümleri, Cilt 2: 22-34 Bölümleri kapsar Bölüm 1 Temeller 1 Bölüm 2 Bir Boyutta Hareket 28 Bölüm 3 İvme 53 Bölüm 4 Momentum 75 Bölüm 5 Enerji 101
Kısa İçindekiler Fizik: İlkeler ve Pratik Cilt 1: 1-21 Bölümleri, Cilt 2: 22-34 Bölümleri kapsar Bölüm 1 Temeller 1 Bölüm 2 Bir Boyutta Hareket 28 Bölüm 3 İvme 53 Bölüm 4 Momentum 75 Bölüm 5 Enerji 101
Çekirdek Modelleri. Alfa Bozunumu. Nükleer Fizikte Kullanışlı Birimler Çekirdeğin Yapısı ve Etkileşmeler. Çekirdeğin Sıvı Damlası Modeli
 NÜKLEER FİZİK Bu sunumun büyük bir bölümünü aşağıdaki siteden indirebilir veya fotokopiciden fotokopisini alabilirsiniz. http://s3.dosya.tc/server11/efgmzh/fotokopi.pdf.html Nükleer Fizikte Kullanışlı
NÜKLEER FİZİK Bu sunumun büyük bir bölümünü aşağıdaki siteden indirebilir veya fotokopiciden fotokopisini alabilirsiniz. http://s3.dosya.tc/server11/efgmzh/fotokopi.pdf.html Nükleer Fizikte Kullanışlı
UBT Foton Algılayıcıları Ara Sınav Cevap Anahtarı Tarih: 22 Nisan 2015 Süre: 90 dk. İsim:
 UBT 306 - Foton Algılayıcıları Ara Sınav Cevap Anahtarı Tarih: 22 Nisan 2015 Süre: 90 dk. İsim: 1. (a) (5) Radyoaktivite nedir, tanımlayınız? Bir radyoizotopun aktivitesi (A), izotopun birim zamandaki
UBT 306 - Foton Algılayıcıları Ara Sınav Cevap Anahtarı Tarih: 22 Nisan 2015 Süre: 90 dk. İsim: 1. (a) (5) Radyoaktivite nedir, tanımlayınız? Bir radyoizotopun aktivitesi (A), izotopun birim zamandaki
MASSACHUSETTS TEKNOLOJİ ENSTİTÜSÜ Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 2 Salı, Mart 14, :00-12:30
 Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 2 Salı, Mart 14, 2006 11:00-12:30 SOYADI ADI Öğrenci No. Talimat: 1. TÜM ÇABANIZI GÖSTERİN. Tüm cevaplar sınav kitapçığında gösterilmelidir? 2. Bu kapalı bir sınavdır.
Fizik Bölümü Fizik 8.04 Bahar 2006 SINAV 2 Salı, Mart 14, 2006 11:00-12:30 SOYADI ADI Öğrenci No. Talimat: 1. TÜM ÇABANIZI GÖSTERİN. Tüm cevaplar sınav kitapçığında gösterilmelidir? 2. Bu kapalı bir sınavdır.
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
ATOMUN KUANTUM MODELİ
 ATOMUN KUANTUM MODELİ 926 yıllarında Erwin Schrödinger Heisenberg den bağımsız olarak de Broglie nin hipotezinden ilham alarak tüm parçacıkların hareketinin hesaplanabileceği bir dalga mekaniği oluşturmuştur.
ATOMUN KUANTUM MODELİ 926 yıllarında Erwin Schrödinger Heisenberg den bağımsız olarak de Broglie nin hipotezinden ilham alarak tüm parçacıkların hareketinin hesaplanabileceği bir dalga mekaniği oluşturmuştur.
SU Lise Yaz Okulu. Evrenin Başlangıcı ve Enflasyon Teorisi
 SU Lise Yaz Okulu Evrenin Başlangıcı ve Enflasyon Teorisi Evrenin ilk zamanları Büyük patlamadan önce: Bilimsel olarak tar.şılamaz. Büyük patlama uzay ve zamanda bir tekilliğe karşılık gelir ve o noktada
SU Lise Yaz Okulu Evrenin Başlangıcı ve Enflasyon Teorisi Evrenin ilk zamanları Büyük patlamadan önce: Bilimsel olarak tar.şılamaz. Büyük patlama uzay ve zamanda bir tekilliğe karşılık gelir ve o noktada
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
Temel Sabitler ve Birimler
 Temel Sabitler ve Birimler Işığın boşluktaki hızı: c=299792458 m/s ~3x10 8 m/s Planck sabiti: h= 6.62606957(29)x10-34 Js İndirgenmiş Planck sabiti ħ = h/2π Temel elektrik yükü : e=1.60218x10-19 C İnce
Temel Sabitler ve Birimler Işığın boşluktaki hızı: c=299792458 m/s ~3x10 8 m/s Planck sabiti: h= 6.62606957(29)x10-34 Js İndirgenmiş Planck sabiti ħ = h/2π Temel elektrik yükü : e=1.60218x10-19 C İnce
Bohr Atom Modeli. ( I eylemsizlik momen ) Her iki tarafı mv ye bölelim.
 Bohr Atom Modeli Niels Hendrik Bohr, Rutherford un atom modelini temel alarak 1913 yılında bir atom modeli ileri sürdü. Bohr teorisini ortaya koyarak atomların çizgi spektrumlarının açıklanabilmesi için
Bohr Atom Modeli Niels Hendrik Bohr, Rutherford un atom modelini temel alarak 1913 yılında bir atom modeli ileri sürdü. Bohr teorisini ortaya koyarak atomların çizgi spektrumlarının açıklanabilmesi için
SCHRÖDİNGER: Elektronun yeri (yörüngesi ve orbitali) birer dalga fonksiyonu olan n, l, m l olarak ifade edilen kuantum sayıları ile belirlenir.
 . ATOMUN KUANTUM MODELİ SCHRÖDİNGER: Elektronun yeri (yörüngesi ve orbitali) birer dalga fonksiyonu olan n, l, m l olarak ifade edilen kuantum sayıları ile belirlenir. Orbital: Elektronların çekirdek etrafında
. ATOMUN KUANTUM MODELİ SCHRÖDİNGER: Elektronun yeri (yörüngesi ve orbitali) birer dalga fonksiyonu olan n, l, m l olarak ifade edilen kuantum sayıları ile belirlenir. Orbital: Elektronların çekirdek etrafında
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-1 Diferansiyel Formda Maxwell Denklemleri İntegral Formda Maxwell Denklemleri Fazörlerin Kullanımı Zamanda Harmonik Alanlar Malzeme Ortamı Dalga Denklemleri Michael Faraday,
Elektromanyetik Dalga Teorisi Ders-1 Diferansiyel Formda Maxwell Denklemleri İntegral Formda Maxwell Denklemleri Fazörlerin Kullanımı Zamanda Harmonik Alanlar Malzeme Ortamı Dalga Denklemleri Michael Faraday,
) 2, ω 2 = k ve ε m m
 Harmonik Salınıcı (HO) Harmonik salınıcı bir m kütlesine etki eden bir geri çağırıcı kuvvetin etkisiyle ortaya çıkar ki bu kuvvet başlangıç noktasından itibaren yerdeğiştirme ile orantılıdır. Bu problemin
Harmonik Salınıcı (HO) Harmonik salınıcı bir m kütlesine etki eden bir geri çağırıcı kuvvetin etkisiyle ortaya çıkar ki bu kuvvet başlangıç noktasından itibaren yerdeğiştirme ile orantılıdır. Bu problemin
RADYASYON ÖLÇÜM YÖNTEMLERİ DERS. Prof. Dr. Haluk YÜCEL RADYASYON DEDEKSİYON VERİMİ, ÖLÜ ZAMAN, PULS YIĞILMASI ÖZELLİKLERİ
 RADYASYON ÖLÇÜM YÖNTEMLERİ Prof. Dr. Haluk YÜCEL 101516 DERS RADYASYON DEDEKSİYON VERİMİ, ÖLÜ ZAMAN, PULS YIĞILMASI ÖZELLİKLERİ DEDEKTÖRLERİN TEMEL PERFORMANS ÖZELLİKLERİ -Enerji Ayırım Gücü -Uzaysal Ayırma
RADYASYON ÖLÇÜM YÖNTEMLERİ Prof. Dr. Haluk YÜCEL 101516 DERS RADYASYON DEDEKSİYON VERİMİ, ÖLÜ ZAMAN, PULS YIĞILMASI ÖZELLİKLERİ DEDEKTÖRLERİN TEMEL PERFORMANS ÖZELLİKLERİ -Enerji Ayırım Gücü -Uzaysal Ayırma
FİZİK 2 ELEKTRİK VE MANYETİZMA Elektrik yükü Elektrik alanlar Gauss Yasası Elektriksel potansiyel Kondansatör ve dielektrik Akım ve direnç Doğru akım
 FİZİK 2 ELEKTRİK VE MANYETİZMA Elektrik yükü Elektrik alanlar Gauss Yasası Elektriksel potansiyel Kondansatör ve dielektrik Akım ve direnç Doğru akım devreleri Manyetik alanlar Akım nedeniyle oluşan manyetik
FİZİK 2 ELEKTRİK VE MANYETİZMA Elektrik yükü Elektrik alanlar Gauss Yasası Elektriksel potansiyel Kondansatör ve dielektrik Akım ve direnç Doğru akım devreleri Manyetik alanlar Akım nedeniyle oluşan manyetik
DOKUZ EYLÜL ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MÜDÜRLÜĞÜ DERS/MODÜL/BLOK TANITIM FORMU. İstatistik Mekanik-II. Dersin Kodu: PHY 5118
 Dersi Veren Birim: Fen Bilimleri Enstitüsü Dersin Adı: İstatistik Mekanik-II Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Yüksek Lisans Dersin Kodu: PHY 8 Dersin Öğretim Dili: İngilizce Formun
Dersi Veren Birim: Fen Bilimleri Enstitüsü Dersin Adı: İstatistik Mekanik-II Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Yüksek Lisans Dersin Kodu: PHY 8 Dersin Öğretim Dili: İngilizce Formun
Bu durumu, konum bazında bileşenlerini, yani dalga fonksiyonunu, vererek tanımlıyoruz : ) 1. (ikx x2. (d)
 Ders 10 Metindeki ilgili bölümler 1.7 Gaussiyen durum Burada, 1-d de hareket eden bir parçacığın önemli Gaussiyen durumu örneğini düşünüyoruz. Ele alış biçimimiz kitaptaki ile neredeyse aynı ama bu örnek
Ders 10 Metindeki ilgili bölümler 1.7 Gaussiyen durum Burada, 1-d de hareket eden bir parçacığın önemli Gaussiyen durumu örneğini düşünüyoruz. Ele alış biçimimiz kitaptaki ile neredeyse aynı ama bu örnek
STANDART MODEL VE ÖTESİ. : Özge Biltekin
 STANDART MODEL VE ÖTESİ : Özge Biltekin Standart model, bilim tarihi boyunca keşfedilmiş parçacıkların birleşimidir. Uzay zamanda bir nokta en, boy, yükseklik ve zaman ile tanımlanır. Alanlar da uzay zamanda
STANDART MODEL VE ÖTESİ : Özge Biltekin Standart model, bilim tarihi boyunca keşfedilmiş parçacıkların birleşimidir. Uzay zamanda bir nokta en, boy, yükseklik ve zaman ile tanımlanır. Alanlar da uzay zamanda
MIT Açık Ders Malzemeleri Fizikokimya II 2008 Bahar
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
1.SINIF / 1.YARIYIL*
 PROGRAM ADI:MATEMATİK 1.SINIF / 1.YARIYIL* 1 FİZ 5 Mekanik I (Mechanics I) Z 4 2 6 5 8 2 FİZ 5 Mekanik I Laboratuvarı (Mechanics I Laboratuory) Z 0 4 4 2 4 3 MAT 1 Matematik I (Calculus I) Z 4 2 6 5 4
PROGRAM ADI:MATEMATİK 1.SINIF / 1.YARIYIL* 1 FİZ 5 Mekanik I (Mechanics I) Z 4 2 6 5 8 2 FİZ 5 Mekanik I Laboratuvarı (Mechanics I Laboratuory) Z 0 4 4 2 4 3 MAT 1 Matematik I (Calculus I) Z 4 2 6 5 4
SÜREKLĠ OLASILIK DAĞILIMLARI
 SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
İstatistiksel Mekanik I
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
Harici Fotoelektrik etki ve Planck sabiti deney seti
 Deneyin Temeli Harici Fotoelektrik etki ve Planck sabiti deney seti Fotoelektrik etki modern fiziğin gelişimindeki anahtar deneylerden birisidir. Filaman lambadan çıkan beyaz ışık ızgaralı spektrometre
Deneyin Temeli Harici Fotoelektrik etki ve Planck sabiti deney seti Fotoelektrik etki modern fiziğin gelişimindeki anahtar deneylerden birisidir. Filaman lambadan çıkan beyaz ışık ızgaralı spektrometre
İNSTAGRAM:kimyaci_glcn_hoca
 MODERN ATOM TEORİSİ ATOMUN KUANTUM MODELİ Bohr atom modeli 1 H, 2 He +, 3Li 2+ vb. gibi tek elektronlu atom ve iyonların çizgi spektrumlarını başarıyla açıklamıştır.ancak çok elektronlu atomların çizgi
MODERN ATOM TEORİSİ ATOMUN KUANTUM MODELİ Bohr atom modeli 1 H, 2 He +, 3Li 2+ vb. gibi tek elektronlu atom ve iyonların çizgi spektrumlarını başarıyla açıklamıştır.ancak çok elektronlu atomların çizgi
FİZ4001 KATIHAL FİZİĞİ-I
 FİZ4001 KATIHAL FİZİĞİ-I Bölüm 3. Örgü Titreşimleri: Termal, Akustik ve Optik Özellikler Dr. Aytaç Gürhan GÖKÇE Katıhal Fiziği - I Dr. Aytaç Gürhan GÖKÇE 1 Bir Boyutlu İki Atomlu Örgü Titreşimleri M 2
FİZ4001 KATIHAL FİZİĞİ-I Bölüm 3. Örgü Titreşimleri: Termal, Akustik ve Optik Özellikler Dr. Aytaç Gürhan GÖKÇE Katıhal Fiziği - I Dr. Aytaç Gürhan GÖKÇE 1 Bir Boyutlu İki Atomlu Örgü Titreşimleri M 2
Parçacıklar Telepati Yaparlar mı?
 Parçacıklar Telepati Yaparlar mı? Kuantum kuramına itiraz olarak öne sürülen bir düşünce deneyi uzun bir serüvenden sonra bu kuramın en güçlü kanıtlarından biri haline geldi. Bir Telepati Gösterisi Bir
Parçacıklar Telepati Yaparlar mı? Kuantum kuramına itiraz olarak öne sürülen bir düşünce deneyi uzun bir serüvenden sonra bu kuramın en güçlü kanıtlarından biri haline geldi. Bir Telepati Gösterisi Bir
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
Gerçek Hayat Düzeyinde Kuantum Mekaniği
 Gerçek Hayat Düzeyinde Kuantum Mekaniği Kuantum mekaniğini anlayamayanların en çok yakındığı şey, sağduyuya aykırı olmasıdır. Peki birçok insan bu konudan şikayetçiyken, gerçekte böyle midir? Evet, gerçekte
Gerçek Hayat Düzeyinde Kuantum Mekaniği Kuantum mekaniğini anlayamayanların en çok yakındığı şey, sağduyuya aykırı olmasıdır. Peki birçok insan bu konudan şikayetçiyken, gerçekte böyle midir? Evet, gerçekte
BİLİM FELSEFESİNİN KUANTUM EVRİMİ
 BİLİM FELSEFESİNİN KUANTUM EVRİMİ Prof. Dr.Sebahattin Tüzemen, Ph.D. Atatürk Üniversitesi, Fen-Edebiyat Fakültesi Fizik Bölümü 25240 Erzurum -GİRİŞ - -Eğitim -Araştırma Bilgi transferi Eğitim ve araştırmada
BİLİM FELSEFESİNİN KUANTUM EVRİMİ Prof. Dr.Sebahattin Tüzemen, Ph.D. Atatürk Üniversitesi, Fen-Edebiyat Fakültesi Fizik Bölümü 25240 Erzurum -GİRİŞ - -Eğitim -Araştırma Bilgi transferi Eğitim ve araştırmada
Mimar Sinan Güzel Sanatlar Üniversitesi, Fizik Bölümü Fizik I Dersi Final Sınavı
 Mimar Sinan Güzel Sanatlar Üniversitesi, Fizik Bölümü Fizik I Dersi Final Sınavı 17 Ocak 2013 Hazırlayan: Yamaç Pehlivan Başlama saati: 11:00 Bitiş Saati: 12:40 Toplam Süre: 100 Dakika Lütfen adınızı ve
Mimar Sinan Güzel Sanatlar Üniversitesi, Fizik Bölümü Fizik I Dersi Final Sınavı 17 Ocak 2013 Hazırlayan: Yamaç Pehlivan Başlama saati: 11:00 Bitiş Saati: 12:40 Toplam Süre: 100 Dakika Lütfen adınızı ve
LİNEER DALGA TEORİSİ. Page 1
 LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
AFYON KOCATEPE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ FİZİK ANABİLİM DALI BAŞKANLIĞI YÜKSEK LİSANS PROGRAMI
 YÜKSEK LİSANS PROGRAMI BİRİNCİ YIL BİRİNCİ YARIYIL FIZ-5501 UZMANLIK ALAN DERSİ Z 8 0 8 0 9 FIZ-5601 TEZ HAZIRLIK ÇALIŞMASI Z 0 1 1 0 1 20 1 21 12 30 İKİNCİ YARIYIL FIZ-5502 UZMANLIK ALAN DERSİ Z 8 0 8
YÜKSEK LİSANS PROGRAMI BİRİNCİ YIL BİRİNCİ YARIYIL FIZ-5501 UZMANLIK ALAN DERSİ Z 8 0 8 0 9 FIZ-5601 TEZ HAZIRLIK ÇALIŞMASI Z 0 1 1 0 1 20 1 21 12 30 İKİNCİ YARIYIL FIZ-5502 UZMANLIK ALAN DERSİ Z 8 0 8
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
Murat ŞENER Bursa Sınav Fen Lisesi
 Murat ŞENER Bursa Sınav Fen Lisesi Kütlenin kökeni Nötrino salınımı Madde-karşıt madde asimetrisi Karanlık madde ve karanlık enerjinin doğası gibi kuramsal olarak geliştirilmiş olayların açıklanmaya çalışılmasıdır.
Murat ŞENER Bursa Sınav Fen Lisesi Kütlenin kökeni Nötrino salınımı Madde-karşıt madde asimetrisi Karanlık madde ve karanlık enerjinin doğası gibi kuramsal olarak geliştirilmiş olayların açıklanmaya çalışılmasıdır.
fizik güncesi ALBERT EINSTEIN BİLİMİN DELİ DÂHİSİ Haftalık E-bülten MARMARİS KAMPÜSÜ
 fizik güncesi MARMARİS KAMPÜSÜ Haftalık E-bülten Sayı: 2 / 06.03.2015 Hazırlayanlar Rana Başak ŞİNİK Ceylin TETİK Azim paha biçilmezdir: "Çok zeki olduğumdan değil, sorunlarla uğraşmaktan vazgeçmediğimden
fizik güncesi MARMARİS KAMPÜSÜ Haftalık E-bülten Sayı: 2 / 06.03.2015 Hazırlayanlar Rana Başak ŞİNİK Ceylin TETİK Azim paha biçilmezdir: "Çok zeki olduğumdan değil, sorunlarla uğraşmaktan vazgeçmediğimden
KUANTUM FİZİĞİNDE BELİRSİZLİK İLKESİ: HİBRİT YAKLAŞIMLA ÖĞRETİMİN AKADEMİK BAŞARIYA ETKİSİ
 T.C. DOKUZ EYLÜL ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ ORTAÖĞRETİM FEN VE MATEMATİK ALANLAR EĞİTİMİ ANABİLİM DALI FİZİK ÖĞRETMENLİĞİ PROGRAMI YÜKSEK LİSANS TEZİ KUANTUM FİZİĞİNDE BELİRSİZLİK İLKESİ:
T.C. DOKUZ EYLÜL ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ ORTAÖĞRETİM FEN VE MATEMATİK ALANLAR EĞİTİMİ ANABİLİM DALI FİZİK ÖĞRETMENLİĞİ PROGRAMI YÜKSEK LİSANS TEZİ KUANTUM FİZİĞİNDE BELİRSİZLİK İLKESİ:
FİZ304 İSTATİSTİK FİZİK VE TERMODİNAMİK. Genel Termodinamik Etkileşme II. Prof.Dr. Orhan ÇAKIR Ankara Üniversitesi, FizikBölümü 2017
 FİZ304 İSTATİSTİK FİZİK VE TERMODİNAMİK Genel Termodinamik Etkileşme II Prof.Dr. Orhan ÇAKIR Ankara Üniversitesi, FizikBölümü 2017 Ista%s%k Termodinamiğin Temel Elemanları Termodinamiğin sı3rıncı yasası
FİZ304 İSTATİSTİK FİZİK VE TERMODİNAMİK Genel Termodinamik Etkileşme II Prof.Dr. Orhan ÇAKIR Ankara Üniversitesi, FizikBölümü 2017 Ista%s%k Termodinamiğin Temel Elemanları Termodinamiğin sı3rıncı yasası
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
GENEL KİMYA. Yrd.Doç.Dr. Tuba YETİM
 GENEL KİMYA ATOMUN ELEKTRON YAPISI Bohr atom modelinde elektronun bulunduğu yer için yörünge tanımlaması kullanılırken, kuantum mekaniğinde bunun yerine orbital tanımlaması kullanılır. Orbital, elektronun
GENEL KİMYA ATOMUN ELEKTRON YAPISI Bohr atom modelinde elektronun bulunduğu yer için yörünge tanımlaması kullanılırken, kuantum mekaniğinde bunun yerine orbital tanımlaması kullanılır. Orbital, elektronun
