BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR
|
|
|
- Savas Nalci
- 9 yıl önce
- İzleme sayısı:
Transkript
1 BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR 7.1- Giriş 7.- Mühndisliğin türbülans analizindki grksinimlri 7.3- Ortalama akımla ilgili ampirik bilgilr Düz lvha üzrindki akım 7.4- Sçilmiş ampirik türbülans bilgilri 7.5- Türbülanslı akımların analizindki mrkzi problm 7.6- Ortalama akım türbülanslı transport formülasyonları
2 1 BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR 7.1- Giriş B bölümd sınır tabakanın pratik bakımdan n önmli kısmı olan türbülanslı akımlarla ilgilnilcktir. Kon sabit-yoğnlkl, sabit-özllikli akımlarla sınırlandırılacak v sadc dvar üzrindki harici türbülanslı akımlar göz önün alınacaktır. 7.- Mühndisliğin türbülans analizindki grksinimlri Türbülanslı akımların mtlaka zamana bağlı v üç-boytl oldğ bilinmktdir. Ayrıca, zamana bağlılığın frkansının v harkt ölçğinin çşitli büyüklük mrtblrind dağıldığı blnmştr. B grçklr dikkat alınırsa bir türbülanslı akımın bütün ayrıntılarıyla analizinin, düz lvha üzrindki gibi basit bir akım olsa bil n kadar büyük bir problm oldğ anlaşılır. Bir örnk, konnn anlaşılması bakımından faydalı olacaktır. Şayt türbülanslı harktin ölçği çşitli büyüklük mrtblrind bir dağılım göstriyorsa sayısal bir hsaplama için ( x, y) hücr gnişliklrinin ygn sçimi bir sorn olacaktır. Nitkim, hücr büyüklüğü harktin önmli bir kısmının ölçğindn büyük is sonçların çok kaba olacağı açıktır. B bakımdan gnl olarak türbülanslı bir sınır tabakanın bir istasyonnda ağ noktası v toplam ağ noktasına grksinim dylmaktadır. Pratiktki bir türbülanslı akımın bütün ayrıntıları için günümüzd gnl bir analiz yöntmi gliştirmnin hnüz mümkün olmadığı söylnbilir. Kompl bir simülasyonn hsaplama maliyti R 3 il dğişmktdir. Dolayısıyla çok büyük miktarda bilgisayar sürlri harcansa bil günümüz imkanlarıyla ancak çok düşük R sayısındaki akımlar inclnbilir. Gnl dğrlndirm böyl ümitsiz olmakla birlikt tasarımcıların analitik araçlardan tamamıyla mahrm kaldığını söylmk doğr olmaz. Zira tasarım için türbülanslı akım analizindn bklnn bilgi sınırlıdır. Şayt laminr sınır tabaka için daha önc söylnn hsslar hatırlanırsa, sınır tabaka analizindn bklnn önclikli bilgi C f (x) yüzy sürtünm katsayısının, ayrılma noktası da dahil olmak üzr blnmasıdır. İkinci olarak δ(x), δ(x) v θ(x) gibi sınır tabaka kalınlıklarıyla ilgilnilir. Tasarım için çoğ hald ayrıntılı hız v sıcaklık profili gibi diğr büyüklüklrin kllanımı daha kısıtlıdır. B noktada daha ilriy gitmdn önc türbülanslı akım için örnğin C f (x) in n anlama gldiğini düşünmkt yarar vardır. Tipik bir mühndislik yglaması olarak sabit hızla ilrlyn bir gmi için sürtünm dirncinin tahmini problmi göz önün alınırsa, bnn için yüzy üzrindki hrhangi bir noktada yüzy grilmsinin çalkantı dğrlrinin bilinmsi grkmz. Daha ziyad b gmiyi çkmk için grkli prvan prformansının bilinmsin ihtiyaç vardır. Gminin hızı sabit kalmasa bil C f (x) in çalkantı dğrin ihtiyaç dylmaz. Tasarımcı açısından C f (x) in zamanla dğişimi sadc başlangıç koşllarının vya sınır koşllarının zamanla dğişmsiyl ilgilidir. (B noktada türbülanslı daimi-akım il zamana-bağlı türbülanslı akım kavramları arasındaki farkı dikkatli bir biçimd dğrlndirmk grklidir). Türbülanslı akımın analizind ihtiyaç daha ziyad sadc zaman-ortalaması vya ortalama dğrlrin blnması olarak gözükmktdir. B gibi büyüklüklr daimi vya zamana bağlı, iki-boytl vya üç-boytl olabilir. Bütün b hsslar çrçvsind sadc ortalama akımın [C f (x), δ(x) vb v blki d (x,y) gibi] tahminini amaçlayan bir türbülans analizinin tasarımcının sas amacına hizmt dcği gibi günümüz analitik v sayısal imkanları içrisind kalacağı görülbilir. Ancak b gün kadar türbülanslı akımların güvnilir v tkin tahmini yolnda sadc sınırlı bir başarı ld dilbildiği blirtilmlidir.
3 Pratikt bazı drmlar vardır ki akımın ayrıntılı çalkantı karaktristiğinin bilinmsi önmlidir. Bna bir örnk olarak yakıt-yakıcı karışımı şklindki akımın ttşma v yanması olayı göstrilbilir. Alv içrisind kimyasal nrjinin ısı nrjisin dönüşüm hızı anlık lokal sıcaklıklara hayli non-linr bir biçimd bağlıdır. Bna gör hrhangi bir noktadaki daimi ısı ürtimini tahmin tmk için sadc T(x,y) nin bilinmsi ytrli olmaz, T (x,y,z,t) nin hsaplanması v sonçların zaman ortalamasının alınması grkir. Bir büyüklüğün üssünün ortalaması il ortalamasının üssü aynı olmayıp gnllikl türbülans inclmlrind zaman ortalaması alınırkn hsaplama ( T ') şklind grçklştirilir Ortalama akım analizin girmdn önc mvct ampirik bilgilrin bir kısmını gözdn gçirmkt yarar blnmaktadır. Zira b bilgilr analitik gliştirmlrin tabanını olştracaktır. Anlık çalkantı harktinin bütün ayrıntılarını dikkat almadan ortalama akımın inclnbilmsi için daha ziyad dnysl vri tabanına ağırlık vrmk grkcktir. Böylc ampirik bilgilr harkt dnklmlri çrçvsind kllanılarak yarıampirik bir analiz gliştirilcktir Ortalama akımla ilgili ampirik bilgilr Düz lvha üzrindki akım Şayt bir düz lvha üzrind laminr v türbülanslı hallrd ölçüln hız profillri, msaflr sınır tabaka kalınlığıyla v hızlar da dış akım hızıyla boytszlaştırılarak karşılaştırılırsa iki profil arasında önmli bir farklılık oldğ tspit dilbilir Türbülanslı Şkil 7.1 d türbülanslı haldki ortalama hız profili dvarı sıfırdan daha büyük bir hızda ksiyor gibi gözükmktdir. Aslında hız dvar yakınında yavaş bir dğişm göstrirkn çok kısa bir aralıkta anidn sıfıra gitmktdir. /.4. Laminr B drm iki farklı tabakaya sahip,.5 y/δ 1. aralığında yüksk viskozitli bir akışkanın v y/δ.5 aralığında da daha düşük viskozitli akışkanın blndğ laminr bir sınır tabakaya bnztilbilir y / δ Şkil 7.1- Tipik laminr v türbülanslı sınır tabaka hız profillrinin karşılaştırması B iki tabakanın birlştiği yüzyd kayma grilmlri şit olacağından µ 1 y µ y (7.1) araksit araksit yazılabilir. B drmda hız gradyantının araksiti gçrkn µ /µ 1 gibi bir oranla ani bir dğişim göstrmsi grkir. İlrid görülcktir ki b hss türbülanslı sınır tabaka inclmlrindki n önmli fikirlrdn birinin sasıdır.
4 3 Düz lvha üzrindki laminr v türbülanslı sınır tabakalar arasında önmli bir fark daha vardır. Şöyl ki: 1..8 Laminr sınır tabakada akışkan cinsi, Rynolds sayısı, pürüzlülük vs n olrsa olsn boytsz hız profillri aynıdır. Bna karşılık türbülanslı sınır tabakada Rynolds sayısı v/vya pürüzlülüktki dğişim C f yi dğiştirir. B da boytsz hız profilinin şklini tkilr. Hız profillrinin Şkil 7. d göstriln b tabiatı sınır tabakaların analizind doğrdan önm kazanmaktadır..6 /.4. Artan C f Klbanoff v Dihl düz dvar Hama düz dvar Hama 8 hücrli lk Hama 1 hücrli lk Farklı koşllarda olşan hız profillrinin şklini tanımlamak üzr Hδ/θ - şkil paramtrsindn yararlanmak istnbilir. Bir düz lvha üzrindki laminr sınır tabaka için H büyüklüğü daima.6 dır y / δ Şkil 7.- Düzgün v pürüzlü düz lvhalar üzrind türbülanslı sınır tabaka hız profillri (Clasr, 1956, Th trblnt bondary layr, Adv Appl Mch 4, 1 51) Ancak b drm türbülanslı akım için gçrli dğildir. Nitkim Şkil 7. d snlan hız profillrindn düz lvha üzrindki türbülanslı sınır tabakada H büyüklüğünün C f y bağlı olacağı tahmin dilbilir. Bna gör blli bir dp/dx basınç dağılımına sahip hrhangi bir cisim üzrindki türbülanslı sınır tabakada olşacak hız profillrinin şklini H paramtrsi il blirlmk mümkün dğildir. Mvct ampirik bilgilrin olabiln n kısa biçimd snm v kllanımı açısından güçlü v kapsamlı korlasyon dğişknlri gliştirilmsi çok önmlidir. Problm karmaşık olp çok miktarda da vri blnmaktadır. B yüzdn mvct vrilri n basit biçimd dikkat almak faydalı olacaktır. Düz lvha üzrindki basit türbülanslı akım için bil korlasyon için / v y/δ dğişknlrini almanın ytrli olmayacağı açıktır. Varılacak sonca bir çok araştırmacının katkısı olmakla birlikt n açık v n kapsamlı katkı Clasr (1956) tarafından yapılmıştır. B yaklaşımın ana hatları aşağıda izlncktir. Şkil 7. d yr alan hız profillrinin hrhangi bir ölçk faktörü il çarpılarak tk bir ğriy dönüştürülmsi bklnmz. Bnnla birlikt sınır tabaka içrisind knar hızına nazaran mydana gln - hız kayıpları dikkat alınırsa, şkl gör C f dğri büyüdükç daha büyük hız kaybı olşmaktadır. Daha büyük bir C f, sınır tabaka içindki akışkana daha büyük bir yavaşlatıcı kvvt tkimsi v dolayısıyla hızda (v böylc momntmda) daha büyük bir kayıp olması anlamına glmktdir. Bna gör knar hızıyla boytszlaştırılmış hız kayıplarının 1 C f şklind yüzy sürtünm katsayısıyla orantılı oldğ söylnbilir. Bna gör b iki büyüklüğün oranıyla ld dilck bir dğişknl bütün ğrilrin korlasyonnn sağlanabilcği görülür:
5 4 / C f 1 / τ w ½ρ / τ / ρ w B ifadnin paydası hız boytnda bir büyüklük olp kısaca τw / (7.) şklind göstrilir v sürtünm hızı olarak adlandırılır. Böylc düz lvha üzrindki sınır tabakada hız profillrinin ordinatı için / 1 C / f şklind bir korlasyon dğişkni ld dilir. Diğr ksn için y/δ büyüklüğünün kornması ytrli olacaktır: y f δ kayıp kann Profillr için koordinatların b şkildki sçiminin n dnli başarılı oldğ Şkil 7.3 dn görülmktdir. y / δ Ancak b korlasyonn gnl başarısı y/δ nın küçük dğrlrind yani dvara yakın bölgd görülmmktdir. Daha önc d blirtildiği gibi b bölgd hız çabk bir biçimd dğişmkt olp çşitli hallrdki farklılık Şkil 7.3 dki gibi bir grafiktn kolay anlaşılamaz Klbanof v Dihl Schltz-Grnow Hama J.H.. pürüzlü dvar B korlasyon dğişknlrinin dvar yakınında gçrli olmayacağı fiziksl bir açıklamayla göstrbilir. - Şkil 7.3- Düzgün v pürüzlü düz lvhalar üzrindki türbülanslı sınır tabakaların dış bölglrind hız kayıpları Şöyl ki; sınır tabakanın üst kısımlarında lokal ortalama hızların sınır tabaka knar hızına gör büyüklüklrinin, (- ), önmli oldğ görülmüştü. B yaklaşımda lokal ortalama hızların dvar üzrindki sıfır hız dğrin kıyasla drm doğrdan dikkat alınmamıştır. Oysa dvara yakın n alt tabakada b karşılaştırma önmli olacaktır. Dvar bölgsind hızlar için ölçklyici büyüklük olarak yin sürtünm hızının alınması ygn gözükmktdir. Böylc + / şklind bir korlasyon dğişkni ld dilir.
6 5 Sınır tabakanın üst bölgsind y konm y/δ şklind bir oranla göstrilmişti. Dvarın baskın oldğ alt bölgd δ sınır tabaka kalınlığının önminin daha az oldğ izah dilbilir. B alt bölg sınır tabakanın toplam kalınlığının sadc küçük bir kısmını ( %1) tşkil tmkt olp yδ civarında olşacak dğişikliklrin tkisi alt bölgd çok az hissdilcktir. B drmda y büyüklüğünün dvara yakın bölgd bir başka biçimd boytszlaştırılması daha ygn olacaktır. Daha önc bir znlğn Rynolds sayısı kllanılarak nasıl boytsz hal gtirildiği görülmüştü. Mvct drmda da bnzri bir inclm il + y y (7.3) ν şklind tanımlanan bir tür R sayısına varmak mümkündür. B dğişknlr kllanılarak ld diln f y ν, + f ( y + ) şklindki ilişki litratürd dvar kann olarak anılmaktadır. Yapılan korlasyonlar sonc ld diln ğrilrin başarısı Şkil 7.4 d görülmktdir. 4 3 / + 1 Laminr alt tabaka / y /ν / 5.6 log(y /ν) Ldwig v Tillmann Klbanof v Dihl Frman Schltz-Grnow Lafr - pip y /ν y + Şkil 7.4- Düzgün katı yüzylr üzrindki türbülanslı sınır tabakalar için ünivrsal dvar kann (Clasr, 1956) Brada sadc düzgün katı dvarlara ait vrilrin yr aldığı blirtilmlidir. Pürüzlülüğün tkisi ilrid kısaca tartışılacaktır. Ayrıca logaritmik bir ölçk kllanılmasının mantığı v blirtiln ğrilrin kaynakları izlyn bölümd açıklanacaktır. B noktada blirtilmlidir ki, büyüklüğü hız profillrinin anlaşılmasında böyl kilit bir rol oynadığı için τ w dvar grilmsinin doğr tspiti önm kazanmaktadır. Yüzy grilmsi ilk kz 195 li yıllarda başarılı yüzy grilmsi balanslarının gliştirilmsiyl ölçülbilir hal glmiştir (Dhawan, 1953). B tip bir cihaz yüzyin ilgilniln kısmında yüzyl tmas tmyn küçük bir parça şklind olp, böylc yüzyin b küçük alanındaki grilm kvvti doğrdan ölçülür. Daha öncki araştırmacılar τ w yi tspit tmk için hız profilinin
7 6 yüzy üzrindki ğimini kllanmayı dnmişlr, ancak profilin dvar yakınındaki şkli ndniyl doğr sonçlara laşamamışlardır. Tkrar Şkil 7.4 dönülck olrsa, düzgün katı bir yüzy yakınındaki hız çalkantıları, tam dvar üzrind v w olması ndniyl kvvtli biçimd sönümlnir. Bna gör türbülanslı sınır tabakanın dahilind dvar yakınlarında çok küçük kalınlıkta bir laminr akım tabakası blnmaktadır. B bölg laminr alt tabaka olarak adlandırılır. Şayt y + y /ν b bölgdki akımı tanımlayan ygn bir Rynolds sayısı is öyl bir sınır dğri olacaktır ki bnn altında hakim akım laminr olsn. B hss vriln bir akım için y nin bir alt kritik dğri olacağı anlamına glir. Şayt böyl bir laminr alt tabaka varsa ksinlikl çok inc olacaktır. Yani b alt tabaka küçük bir y yükskliği dahilind kalacaktır. Dvar üzrind τ/ oldğndan b laminr alt bölgd τ τ w oldğ varsayılabilir. τ (y) nin tipik bir dğişimi Şkil 7.5 d göstrilmktdir. B kabll birlikt d δ τ µ F ( y ) y τ w (7.4) y yazılabilir. B bağıntı () olmak üzr intgr dilrk yτ w µ (7.5) v düznlnrk τ tot Şkil 7.5- Sınır tabakada kayma grilmsinin tipik dğişimi τ w yτw yτ y µ µ τ / ρ µ / ρ w w y ν (7.5a) vya dvar kann dğişknlri cinsindn + y + (7.5b) ld dilir. Şkil 7.4 dn görülbilir ki mvct vri (7.5b) bağıntısını y dğrlrin kadar izlmktdir. B görüntü laminr alt tabakanın varlığını doğrlamaktadır. Tabakanın kalınlığı δ nın %1 indn daha küçüktür. Şkil 7.4 i okrkn dikkatli olmak grkir. Şöyl ki, sınır tabakanın kalınlığı kabaca δ + O(5) mrtbsinddir. Şkil 7.4 sasn sınır tabakanın alt bölgsini inclmk için düznlnmiş bir grafik olp, b grafik üzrind δ nın büyüklüğünün aranması doğr olmaz. y büyüklüğü δ + nın 1/1 i mrtbsinddir. Böylc biri alt tabakaya diğri d dış tabakaya ait olmak üzr başarılı iki korlasyon kann ortaya konlmştr. Fizik grği b iki bölg arasındaki gçiş ani olamaz. Aksin arada ortak bir bölg olması bklnir. B ortak birlşm bölgsind hr iki bölgdki y f ; δ y g ν (7.6a)
8 7 bağıntıları gçrli olmalıdır. B iki bağıntı ynidn y f + δ ; y δ g δ ν (7.6b) şklind düznlnbilir. Birlşm bölgsind bütün y lr için b iki bağıntının aynı olması grkir. Bağımsız dğişkn olması ndniyl y büyüklüğü birlşm bölgsind kyfi olarak dğişbilir. Vrilmiş bir sınır tabaka hız profili için / v δ /ν büyüklüklri birr sabit olp y il dğişmz. Bna gör, g fonksiyonnn içindki sabit δ /ν çarpanı fonksiyonn dışında toplam şklindki bir sabitl aynı tkiy sahip olmalıdır. Böyl bir özllik sadc bir logaritma fonksiyonnda vardır. Çünkü çarpımın logaritması iki logaritmanın toplamı şklind yazılabilir. O hald birlşm bölgsind f v g fonksiyonları için logaritmik fonksiyonlar önrilrk (7.6a) bağıntıları aşağıdaki gibi yazılabilir: y A log + B δ (7.6) y A log + C (7.7) ν Halihazırda Şkil 7.4 d logaritmik ölçkl çizilmiş olan dvar kann il Şkil 7.3 dki hız kayıp kann logaritmik ölçkt tkrar çizilrk Şkil 7.6 daki gibi birlştirilbilir. Logaritma kannları vriyi izldiğindn v bölg küçük olmadığından (kabaca 3 y + 3 civarında) bir ara bölg oldğ açıktır Frman Klbanof v Dihl Schltz-Grnow Hama JH pürüzlü dvar Hama pürüzlü dvar Moor çok pürüzlü dvar y/δ Şkil 7.6- Düz lvha üzrindki türbülanslı sınır tabakalar için kayıp kannn logaritmik çizimi (Clasr, 1956)
9 8 B şkild çiziln vriyi dikkat alarak Clasr (1956) (7.6) v (7.7) logaritmik bağıntılarındaki sabitlr için A5.6, B-.5 v C4.9 dğrlrini önrmiştir. Başka araştırmacılar aynı vri için sabitlr çok az farklı dğrlr vrn farklı ğrilr ld tmiştir. Ancak brada Clasr in sabitlri kllanılacaktır. Yin bazı başka araştırmacılar da dnklmlri tabii logaritma il yazarak A sabitin Kln(1)/A şklind bağlı olan bir başka sabit kllanmışlardır. Böylc A5.6 v K.41 olmak üzr ld tmişlrdir. 1 y ln + C (7.7b) K ν Cols (1956) sınır tabakanın dış bölgsindki hız profillrini tanımlamak için iz kann kavramını ortaya koymştr. Hızlarda logaritmik kannn üzrind görüln sapmaların, yδ daki maksimm sapma il normaliz dildiği takdird sadc y/δ nın fonksiyon oldğ grçğini dikkat almıştır. B normaliz dilmiş sapmaları, bir W(y/δ) iz fonksiyon il blirtrk W() v W(1) olmak üzr korlasyon grçklştirmiştir. Cols n iz fonksiyon 1 / ln ( y / ν ) + C K 1 y W 1 δ / ln ( / ) C δ ν + K (7.8) şklind olp şmatik olarak Şkil 7.7 d göstrilmiştir. W İz fonksiyon Logaritmik kann Log y Şkil 7.7- Cols n iz fonksiyon Cols (1956) b W fonksiyonn y π y W sin δ δ (7.8a) şklind önrmiştir. Sonç olarak iz kann birlşm bölgsini v üst bölgyi birlikt tanımlayacak biçimd 1 y Π y ln + C+ W K ν K δ (7.9)
10 9 olarak düznlnbilir. Brada Π-KB/ bir iz paramtrsi olp, B-.5, için Π.51 dir (Cols.55 dğrini tavsiy tmiştir). Türbülanslı sınır tabakanın tamamı dört bölgdn olşmş gibi düşünülbilir. Kovaszny (1967) gör hr bir bölgnin kndi znlk v hız skalası vardır. - En alttaki laminr alt-tabakanın znlk skalası ν/, hız skalası is dır. - İç bölgnin znlk v hız skalaları sırasıyla y v dır. - Dış bölgnin znlk skalası δ, hız skalası is dir. - Corrsin v Kistlr (1955) süpr-tabaka adını vrdiklri dördüncü bir tabaka daha tanımlamışlardır. B tabaka sınır tabakanın dış knarında viskoz tabaka il viskoz olmayan dış akım arasında yr alan inc v kıvrımlı bir gçiş bölgsidir. B bölgdki hız skalası olarak katılım hızı alınabilir. Katılım hızı, dış akımdan sınır tabaka içrisin birim zamanda girn akım dbisi il orantılı bir hızdır. B hız aynı zamanda türbülans arayüzünün türbülanslı olmayan dış akıma nazaran ilrlm hızını ifad dr. Katılım hızı Kovaszny (1967) tarafından V d δ δ (7.1) dx ( ) şklind tanımlanmıştır. Kovaszny b bağıntıyı kllanarak süpr-tabaka için 1ν/V şklind bir karaktristik znlk skalası olştrmştr. v y büyüklüklri y A log + B δ (7.6) y A log + C (7.7) ν bağıntıları arasından limin dilrk δ log + ν A C B (7.11) v b bağıntı ynidn düznlnrk bir yüzy sürtünm kann C f Alog R δ + C B C f (7.1) şklind blnabilir. (7.1) bağıntısı yaklaşık biçimd yazılarak vya ampirik vrilr ğri ydrlarak başka, daha basit açık formüllr d türtilmiştir. En basit birisi Blasis a ait v Schltz-Grnow (194) tarafından doğrlanan ( ) / C. 456 R 14 (7.13) f δ
11 1 bağıntısıdır. B bağıntı konma bağlı Rynolds sayısının yaklaşık R x 1 7 dğrin kadar gçrlidir. Çoğ kims Schonhrr (193) in bağıntısını kllanmaktadır log( R xcf ) 17. C + (7.13) f L znlğndaki düz lvha üzrindki türbülanslı akımda toplam sürtünm dirnci katsayısı, C D, için b iki araştırmacı v C. 47 log ( R L ). 47 D 64. (7.13a) log( R L C D ) C (7.14a) D önrmişlrdir Sçilmiş ampirik türbülans bilgilri Ykarıdaki bölümlrd yapılan analizin amacı ortalama akımın gnl özlliğinin anlaşılması olarak ortaya konlmş olmakla birlikt türbülanslı akımın çalkantılı doğasının anlaşılması sastır. Kony izah amacıyla, 195 li yıllarda Amrikan lsal Standartlar Büros tarafından düz lvha üzrind ld diln zngin vridn yararlanılacaktır. B sçimin iki ana ndni vardır. Birincisi akımın basit olması, bna karşılık olayları tmsil tmsi, ikincisi d b akım için kompl ölçm sonçlarının mvct olmasıdır. Şkil 7.17 d sınır tabakada üç doğrltdaki türbülans şiddti profillri yr almaktadır..1.8 ()'² w.1.1 Şkildn ksnl türbülans şiddtinin n büyük oldğ, fakat yanal yöndki türbülans şiddtinin d diky yöndkindn daha büyük oldğ fark dilmktdir: '² w'² v'² > > Bnn ndni akımın yanal doğrltlarda salınım srbstisi olmasına karşın dvarın dirkt kısıtlayıcı tkisi ndniyl aynı srbstinin diky doğrltda olmayışıdır v y/δ y/δ Şkil Düz lvha üzrind türbülans şiddti profillri (Klbanoff, 1955)
12 11 Pürüzlü bir düz lvha üzrindki akım için Corrsin v Kistlr (1954) tarafından ld diln türbülans şiddti profillri Şkil 7.18 d yr almaktadır. B inclmdki pürüzlülük brştrlmş kağıt biçimind olp iki-boytl v yaklaşık sinüzoidaldir. Pürüz yükskliği. cm olp b yüksklik akımı tamamn pürüzlü rjim sokmak için ytrlidir. Blnan türbülans şiddti düzylri düzgün dvar halindkindn çok daha fazladır. Fakat üç bilşnin birbirin gör sıralaması aynıdır. ()'² δ R δ ν y/δ Şkil Tam pürüzlü düz lvha üzrind türbülans şiddti profillri (Corrsin v Kistlr, 1954) w v Türbülanslı bir sınır tabakanın dış knarı zamana bağlı, düzgün olmayan bir sınırla karaktriz dilir. Bn anlamak için yδ konmna bir sıcak-tl anmomtrsi yrlştirilirs anmomtrnin dğişimli olarak türbülanslı akım v viskoz olmayan akım ölçtüğü görülür. B drm aralıklılık (intrmittncy) adı vriln v 1 arasında dğişn bir Ω büyüklüğü il yansıtılır. Ω büyüklüğü akımın n kadar sür il türbülanslı oldğn oransal olarak blirtmktdir Ω.6.4. Corrsin v Kistlr Klbanof Bazı ölçm sonçları Şkil 7.19 da snlmştr. Sınır tabakanın dışına yaklaşıldıkça aralıklılığın 1 dğrindn hayli küçük kaldığı blirtilmlidir y/δ Şkil 7.19-Sınır tabaka içind aralıklılık dağılımı (Klbanoff, 1955, Corrsin v Kistlr, 1954) Sınır tabaka içind akışkanın x-doğrltsndaki momntmnn türbülans tarafından diky doğrltda taşındığı bilinn bir hsstr. B olay boylamasına v diky doğrltdaki çalkantı hızlarının ' v' şklindki korlasyon il ilişkilidir. Şayt b büyüklük akışkanın yoğnlğ il çarpılarak ρ 'v' şklind düznlnirs grilm boytn alır v türbülanslı kayma grilmsi vya Rynolds grilmsi olarak adlandırılır. B kavram izlyn bir bölümd daha dirkt bir biçimd çıkartılacaktır. Fakat şimdilik türbülans çalkantılarının sınır tabaka üzrindki başlıca tkisinin Rynolds grilmsi vasıtasıyla oldğnn gözlnmsi ytrlidir.
13 1 Rynolds grilmlrin ilişkin ölçm sonçlarının sürtünm hızıyla normaliz dilmiş biçimd bir grafiği Şkil 7. d snlmştr. B büyüklük dvar yakınında n büyük dğrini almakta olp dvarın daha yakınındaki inc laminr alt-tabakanın içrisind anidn sıfıra düşmktdir R δ Κ K - v v y/δ Şkil 7.- Düz lvha üzrindki türbülanslı sınır tabakada Rynolds grilmsi v türbülans klintik nrjisi profillri (Klbanoff, 1955) B laminr alt bölgdki dğişim Şkil 7.1 d gnişltilmiş olarak görülmktdir τ lam τ τ w Şkil 7. d ayrıca türbülanslı kintik nrji nin dğişimi göstrilmiştir. B, üç çalkantı hız bilşninin birim kütl başına kintik nrjisi olp '² + v'² + w'² K ' '² + v'² + w'² K (7.5).6 v.4. R δ y / ν y/δ Şkil 7.1- Sınır tabaka dvar bölgsind Rynold grilmsinin ayrıntılı dağılımı (Schbar, 1954) şklind tanımlanmaktadır. Akımın n kadar türbülanslı oldğn tarif tmk için hrhangi bir büyüklük kllanılması grkiyorsa, n mantıklı sçim türbülans kintik nrjisi olacaktır.
14 13 Türbülans çalkantılarının gniş bir zaman ölçği aralığında olştğ hssna açıklık gtirmk için boylamasına türbülans çalkantılarının spktra ölçümlrinin bazıları dalga sayısının (k 1 ) fonksiyon olarak Şkil 7. d snlmştr. Brada k 1 Dalga sayısı π frkans ortalama hız olp E 1 (k 1 ) büyüklüğü d k 1 k 1 +dk 1 bandındaki boylamasına türbülans nrjisinin miktarıdır. Böylc E 1 ( k 1 ) dk 1 ' (7.6) E ( k ) δ R δ ν y/δ olmaktadır. Bradaki ilk gözlm dalga sayısının büyük dğrlrind hissdilir bir harkt olmasıdır k1 (cm -1 ) Şkil 7.- Düz lvha üzrindki sınır tabakada ksnl türbülans şiddtinin spktrm (Klbanoff, 1955) İkinci bir hss, katı dvar büyük ölçkli harktlri nglldiğindn dvara yaklaştıkça daha büyük ölçkli dilr (girdapçıklar) içrisindki nrjinin azalmasıdır (y/δ.11 için küçük dalga sayısındaki vrilr bakınız). Büyük ölçkli dilrdn küçük ölçklilr doğr bir nrji akışı v sonnda viskozit il dissipasyon olşmaktadır. Büyük ölçkli harkt için grkli nrji dış akımdan çkilmktdir. Hrhangi bir türbülanslı kaymalı akımda türbülans nrjisinin ürtimi, taşınımı, yayınımı v dissipasyon söz konsdr dissipasyon /Ω dissipasyon Dissipasyon sasn laminr viskozitnin daha küçük dilr üzrindki aksiyonndan kaynaklanır. B büyüklüğü ölçmk zordr. Fakat bazı sonçlar Şkil 7.3 d göstrilmiştir. Akımın tam türbülanslı bölglrind dağılımı görmk için b gibi sonçları aralıklılığın tkisin bağlamak alışılaglmiştir. εδ y/δ Şkil 7.3- Düz lvha sınır tabakasında dissipasyon v türbülans kintik nrjisinin dağılımı (Klbanoff, 1955)
15 14 Ykarıdaki blirtiln bütün prosslrin dağılımı Şkil 7.4 d snldğ gibi bir türbülanslı kintik nrji dngsi biçimind göstrilbilir. Dış knar yakınları hariç bütünsl dngy ana katkılar ürtim v dissipasyondan kaynaklanmaktadır. B ikisi hmn hmn birbirini dnglmktdir. 1 kazanç kayıp 1 Taşınım Yayınım Ürtim dissipasyon δ ν y/δ Şkil 7.4- Düzgün yüzyli düz lvha üzrindki sınır tabakada türbülans nrji balansı (Klbanoff, 1955) Gçirgn yüzylr üzrindki akımların türbülans büyüklüklriyl ilgili bilgi, ortalama akımla ilgili olanlardaki gibi katı yüzydkilr kıyasla daha zayıftır. Daha önc ortalama akımın tartışıldığı altı yüzy üzrind (üçü katı üçü gçirgn) ksnl v normal doğrltlardaki türbülans şiddtlri v Rynolds grilmlrin ait bir kısım vri Şkil 7.5, 7.6 v 7.7 d snlmştr. Pürüzlü katı yüzylrin b üç büyüklüğü düzgün katı yüzylr kıyasla arttırdığı açıktır. Göznkliliğin farkdilir bir tkisi olp, b tki normal doğrltdaki türbülans şiddti v Rynolds grilmsi üzrind n büyüktür. Normal türbülans bilşni göznkli bir dvar tarafından düzgün bir dvar kadar sönümlnmmktdir ² 4 Düzgün katı yüzy Pürüzlü katı yüzy Göznkli, sintrlnmiş yüzy Göznkli, dlikli Ti tabakası Göznkli, ızgaralı yüzy Izgaralı, arkası katı yüzy y / δ Şkil 7.5- Çşitli katı v göznkli dvarlar üzrind ksnl doğrltdaki türbülans şiddti profillri (Kong v Schtz, 198) ² 4 Düzgün katı yüzy Pürüzlü katı yüzy Göznkli, sintrlnmiş mtal Göznkli, dlikli Ti tabakası Göznkli, ızgaralı yüzy Izgaralı, arkası katı yüzy y / δ Şkil 7.6- Çşitli katı v göznkli dvarlar üzrind normal doğrltdaki türbülans şiddti profillri (Kong v Schtz, 198)
16 Düzgün katı yüzy Pürüzlü katı yüzy Göznkli, sintrlnmiş mtal Göznkli, dlikli Ti tabakası Göznkli, ızgaralı yüzy Izgaralı, arkası katı yüzy v 1 3 ² y / δ Şkil 7.7- Çşitli katı v göznkli dvarlar üzrind Rynolds grilmlri (Kong v Schtz, 198) Türbülansın çalkantı doğasını yansıtan çşitli büyüklüklrin ölçüm sonçlarına ilavtn b büyüklüklrl ilgili prosslrin fiziksl bir tasviri d faydalıdır. Türbülans şiddtlri gibi b büyüklüklr d zaman üzrind ortalamalardır. Türbülanslı akımın grçk fiziğini anlamak için ayrık, zamana bağlı türbülans olaylarının davranışını bilmy ihtiyaç vardır. Bradaki kısa anlatım ana hatlarıyla Klin v Robinson (199) tarafından yapılan inclmy dayanmaktadır. Münfrit di fikri grçktn açık v özllikl yardımcı dğildir. Zira türbülanslı akımda aynı zamanda v aynı yrd çok çşitli boytlarda dilr mvcttr. Akışkan kümlri v girdap çizgilri düşünmk daha faydalıdır. Bir türbülanslı akım içrisind bir akışkan kümsinin bir konmdan diğrin harkt ttiği söylnbilir. B nosyon Rynolds grilmsini tanımlamak için kllanılacaktır. Türbülanslı akım kabaca girdap çizgilrinin süprpozisyon olarak dikkat alınabilir. Bna gör d çapında, L znlğnda v açısal hızı ω olan bir girdap çizgisi göz önün alınırsa, bnn kütlsi ρld il, kintik nrjisi ρld 4 ω il v açısal momntm da ρld 4 ω il orantılıdır. B girdap lmanı, kütlsi v açısal momntm sabit kalmak kaydıyla sündürülürs (ki b düşük yayınım için iyi bir yaklaşımdır), L arttıkça çap azalacak v açısal hız artacak b da kintik nrjiyi arttıracaktır. Böylc lmanı zatmak için çları üzrind yapılan iş lmanın kintik nrjisind artış yaratmaktadır. B drm daha önc blirtiln nrji kaskadının tasvirini sağlar. Enrji büyük ölçkli harktlrdn bnlar içindki küçük ölçkli harktlr doğr, küçük ölçkli harktlrdki girdap çizgilrinin büyük ölçkli harktlrl sündürülmsi sonc, akmaktadır. Ortalama harktin iki-boytl oldğ türbülanslı bir akımda girdap çizgilri daha ziyad akımla çaprazdır. Sündürm d b doğrltda olacağından türbülans üç-boytl olacaktır. Ortalama girdaplılığın çoğ, ortalama hız profilinin şklin gör dvar civarında yoğnlaşmıştır (Şkil 7.). B hss girdap sünmsinin bir başka soncn ortaya koyar: girdap lmanlarının dvar civarında rastgl yükslmsini ani çalkantılar v patlama (brsting) v dış bölgy sıçramalar izlr. B prosslr Klin v arkadaşları (1967) tarafından Şkil 7-8A da göstrildiği gibi tasvir dilmiştir. Daha yni çalışmalarda Şkil 7.8B d göstrildiği gibi, daha sık olşan çngl tipi yapılara işart dilmiştir. Brada sağ v sol çngllr rastgl gözükmktdir. Rao v arkadaşları (1971) ortalama patlama zamanı priyodn 5δ/ olarak blirlmiştir. Klin v arkadaşları (1967) bir patlamayla sıçrayan akışkanın akım doğrltsnda.8 civarında hıza sahip oldğn blmştr. Bna gör sıçrama prossi Rynolds grilmsinin bir kısmının sormlsdr. Sıçrayan bir akışkan kümsi, < v v > oldğndan ngatif işartli bir v korlasyon vrir. Kim v arkadaşları (1971) bütün
17 16 türbülans ürtiminin özllikl dvar yakınlarındaki patlama v sıçramanın sonc oldğn blirtmişlrdir. Dinamik bakımdan kararsız lokal kaymalı tabaka Baş İkincil akım Boyn Yükslmiş v sünmüş girdap lmanı y x İç taraf Bacak Dış taraf Küçük hızlı girdap z Ayak Akım a) Girdap sünmsi (Klin v arkadaşları, 1967) b) Çngl şkilli girdapsal yapı (Klin v Robinson, 199) Şkil 7.8- Türbülanslı sınır tabakanın dvar bölgsind girdapsal yapılar Dvar civarı zaman v konmda priyodik yapı srgilr. Akım doğrltsnda v açıklık doğrltsnda, znlğ δ mrtbsind v gnişliği 3ν/ mrtbsind düşükmomntml akışkan şritlri priyodik olarak olşr. B şritlrin üzrind y + 4 civarında yatay bir kayma tabakası olşr. B noktada lokal hız profili bir büküm göstrir. Sıçrayan (dış tabakaya itiln) akışkan ara bölgnin knarından (y + 4 civarında) aşağı tabakaya doğr kayan yüksk-momntml akışkanla yr dğiştirir. B kayma-sıçrama prossi d yin Rynolds grilmsinin önmli bir kısmını ürtir Türbülanslı akımların analizindki mrkzi problm Şayt sıkıştırılamaz akımda, daimi olmayan, laminr dnklmlrin türbülanslı harktin sas nsrlarını ihtiva ttiği kabl dils idi zamana bağlılığı içrn v w + + z (1.36) + + v + w +ν + + t z ρ z 1 p (1.37) + + v + w +ν + + t z ρ z v v v v 1 p v v v + + v + w +ν + + t z ρ z z w w w w 1 p w w w (1.38) (1.39) dnklmlrinin sabit-özllikli hald türbülanslı akım problminin çözümü için iş yarayacağı bklnirdi. B kabl n çlişkili n d çözüm için mldğ kadar yardımcı dğildir. Çlişkili dğildir, zira b dnklmlr çıkartılırkn rastgl çalkantılı bir harkt hariç ttlmamıştır.
18 17 Çok yardımcı dğildir, çünkü grçk bir kolaylaştırma gtirmmktdir. Yani haln üçboytl, fiziksl ölçklrd çok gniş bir aralıkta ölçğ v frkanslara sahip olan, zamana rastgl bağlı, büyük bir hsaplama problmi il karşı karşıya blnlmaktadır. Daha önc analizcinin ksriytl sadc zaman-ortalamalı akımla ilgilndiği blirtilmişti. B gnl amaç daimi olmayan dnklmlr dayanan bir formülasyona nasıl dönüştürülbilir sorsnn cvabı basitç zamana gör ortalama almaktan ibarttir. Akımın hrhangi bir büyüklüğü, örnğin düzlmsl, daimi (ortalama anlamında) akım halind (,,, ) (,, ) '(,,, ) xyzt xyz+ xyzt (1.67) şklind ortalama bir büyüklükl bir çalkantı kısmına ayrılarak ilgili dnklmlrd yrlştirilir. Sonra hr bir trimin zaman üzrindn ortalaması alınır. Brada dnklmlrin iki-boytl sınır tabaka biçimiyl ilgilnilcktir. Ayrıca ortalama alma il ilgili basit bazı krallar izlncktir. Şayt f v g iki çalkantı dğişkni, F v G d bnların ortalama dğrlri is f ' ; F F ; f + g F + G; f g F G f F ; f ds F ds s s (1.67) yazılabilir. Bradaki üst çizgi işarti üzrind yr aldığı büyüklüğün ortalamasının alındığını blirtmktdir. Daimi, sıkıştırılamaz, iki-boytl sürklilik dnklmindki hız bilşnlri ortalama v çalkantı dğrlrin ayrılarak ( ) ( V v ) v + ' + ' V ' v' (7.8) zaman ortalaması alınarak v ' v' V ' v' V ; + + s s s s s s s s V + (7.9) ld dilir. Görüldüğü gibi ortalama akım için sürklilik dnklmi laminr akımdakiyl aynıdır. Ayrıca b sonç (7.8) bağıntısında tkrar kllanılırsa ' v' + (7.3) oldğ, yani anlık çalkantıların aynı biçimd bir sürklilik dnklmini sağladığı görülür. İki-boytl, sıkıştırılamaz sınır tabakaya ait
19 18 t + + v 1 p ρ + ν momntm dnklmindki non-linr trimlrin inclnmsind dikkatli olnmalıdır. B çrçvd taşınım trimlrinin, sürklilik dnklmi d dikkat alınarak v v + v + v v ( ) ( v) + (7.31) şklind ynidn düznlnmsi faydalı olr. B drmda ortalama v çalkantı dğrlri kllanılarak ( ) ( v) ( ') ( ' )( V v' ) ( ' ' ) ( V V ' v ' ' v ') (7.3) hr bir trimin zaman ortalamaları alınarak ( ) ( V ) ( ' ) ( ' v' ) (7.3a) vya ilk iki trim açılarak V ( ' ) ( ' v' + + V + + ) v brada sürklilik dnklmi kllanılarak ( ' ) ( ' v' + V + + ) (7.3b) ld dilir. Momntm dnklmindki diğr trimlrin ortalamaları da kolaylıkla alınır: t ( + ' ) t t p ( P + p' ) P ( + ' ) (7.33) Görüldüğü gibi viskoz trimd önmli bir dğişiklik yoktr.
20 19 Eld diln bütün ortalama dğrlr momntm dnklmind yrlştirilrk ( ' ) ( ' v' ) t + + V P ρ + ν (7.34) blnr. Şayt ortalama akım daimi is ilk trim ortadan kalkacaktır. Ayrıca gnllikl ( ' ) ( ' v' << ) oldğ kabl dilir. B hss çoğ akım için dnyl doğrlanmıştır. B kabllr çrçvsind sonç olarak daimi akımdaki türbülanslı sınır tabaka dnklmlri V + (7.9) 1 P 1 ( ρ' v' + V + ν + ) ρ ρ (7.34a) şklind yazılabilir. Dvardan ytrinc zakta laminr kayma grilmsi trimi türbülansla momntm transport trimi yanında küçük kabl dilrk ihmal dilbilir. Şüphsiz ( ρ ' v' ) büyüklüğünü içrn trim ihmal dilmz. Aksi hald dnklm tamamıyla laminr akım halin döncktir. Blirtiln b trim dnklmd türbülanslı akımın çalkantılı doğasının tkisini yansıtan tk trimdir. Hrhangi bir sınır tabaka problmind oldğ gibi (7.9) v (7.34a) dnklmlriyl ifad diln problmd d viskoz olmayan bir dış akım tarafından sınır tabaka üzrin tki dn P(x) basınç dağılımının bilindiği kabl dilmktdir. Bna gör b iki dnklmin iki bilinmyn için ( v V) çözülmsi bklnmktdir. Bnnla birlikt momntm dnklmind sağ taraftaki n son trim ilav bir bilinmyn olarak yr almaktadır. B bir momntm transfri trimi olp, laminr akımdaki basit Nwtonin kayma il aynı rolü oynamaktadır. B bakımdan ( ρ' v' ) büyüklüğü türbülanslı kayma grilmsi vya daha önc d blirtildiği gibi Rynolds grilmsi olarak adlandırılmaktadır. B türbülanslı kayma triminin laminr viskoz trimdn glmdiği, fakat viskoz olmayan taşınımsal trimlrdn gldiği blirtilmlidir. (7.9) v (7.34a) dnklmlriyl çalışırkn dnklm sistminin kapalı (çözülbilir) hal glmsi için Rynolds grilmsini içrn trimin d diğr bağımsız vya bağımlı dğişknlr cinsindn ifad dilmsi grklidir. Diğr dğişknlrin hpsi d ortalama dğrlr olarak dikkat alındığından böyl bir bağıntı ortalama akım modli olarak nitlndirilir. B tip modllrin gliştirilmsi izlyn bölümlrd l alınacaktır. Blirtiln zorlğ ynmnin kolay bir yol yoktr. Kon, bölümün sonnda daha karmaşık formülasyonlara varacak, fakat hp dnklmlrdn daha fazla bilinmyn olacaktır. B fazladan bilinmyn(lr) hp ( ρ ' v' ) gibi türbülans büyüklüklri olacak, v sistmi matmatiksl olarak kapatmak için hp fazladan, gnllikl yarı-ampirik bağıntılara grk olacaktır. B drm türbülanslı akımların kapatma (closr) problmi olarak anılır. Aslında ortalama akım v çalkantı büyüklüklrini blirtrk, vya harkt dnklmlrini
21 kllanarak, ya da brada yapıldığı gibi zaman üzrind ortalama alarak grçktn önmli hiçbir şy yapılmadığı üzrind düşünülürs b şaşırtıcı drma nasıl glindiğini kavramak daha kolay olr. B noktaya kadar, matmatiksl formülasyonn gliştirilmsind türbülanslı akımların grçk doğası hakkında hiçbir şy söylnmmiştir. Formülasyonn tamamlanmasından önc b kon üzrind drlmalıdır. Türbülanslı kayma modli gliştirm konsnda ilrlmdn önc çalkantılarla momntm transfri olgsnn fiziksl bir izahını yapmakta yarar vardır. B amaçla Şkil 7.9 dikkat alınırsa, sınır tabakanın y + y sviysind blnan bir akışkan kümsi daha alt sviydki bir y konmna yr dğiştirdiği takdird ski konmndaki (y + y) ortalama hızını korma ğilimind olacaktır. B hız akışkan kümsinin yni konmnda (y ) ortalama hızına gör pozitif işartli bir çalkantı hızı kadar artmış gözükcktir. B drmda y + y konmndan yy düzlmin taşınan anlık kütl akımı ρv olp b kütl yni konmdaki çalkantı hızı il ρ v kadar bir momntm artışı yaratacaktır. y ( y + y ) y v < ( y ) y y < Şkil 7.9- Rynolds grilmsinin glişimi Şayt akışkan kümsi alt tabakadan daha üst bir tabakaya yr dğiştirirs bnn trsi olacaktır. Şayt zaman üzrind bir ortalama alınırsa hız çalkantıları vasıtasıyla boylamasına momntmda diky doğrltda olşan momntm transfri miktarı ( ρ' v' ) olarak ld dilir 7.6- Ortalama akım türbülans transport formülasyonları Bir ortalama akım türbülans analizi gliştirmk için ilk olarak Bölüm 7.5 dki inclmlr çrçvsind _ ( x, y ;, V, P vya, µ ρ) τ ρ ' v' f, (7.35) T şklind bir bağıntı blmaya çalışılmalıdır. Öyl ki (7.9) - (7.34a) dnklm sistmi kapalı hal glsin. B bağıntının ampirik bilgilr dayanması grktiği açıktır. B bakımdan tkrar Bölüm 7.3 dki ortalama akım bilgilrin baş vrlacaktır. B arada, (7.35) bağıntısının sağ tarafında türbülans büyüklüklrinin yr almadığı blirtilmlidir. B noktada modllm çabalarının amacını açıkça blirtmk için sınır tabaka alt bölgsini örnk olarak dikkat almak faydalı olacaktır. Biçimsl olarak (7.35) il blirtiln blnacak bağıntı (7.9) v (7.34a) harkt dnklmlrind kllanıldığında Şkil 7.4 dki vri arasından gçn dol çizgi ld dilcktir. B tiptn bir analiz yarı-ampirik olarak nitlndirilir. Ampirik bir yaklaşım basitç vriy ydrlmş ğrilri kllanacaktır. Blirtiln amaç birbiriyl ilişkili iki formülasyonla başarılmıştır. İlki Bossinsq (1877) tarafından, laminr akıma bnztm yolyla
22 1 τ T _ ρ ' v ' µ T (7.36) şklind ortaya konan di viskozitsi formülasyondr. Bradaki µ T di viskozitsinin sadc akışkanın dğil akımın drmna bağlı olacağı bklnmlidir. Yani di viskozitsi laminr viskozit gibi yalnızca akışkanın trmofiziksl bir özlliği dğildir. Prandtl (195) tarafından τ T _ ρ ' v ' ρlm (7.37) şklind önriln ikinci formülasyon karışım znlğ formülasyon olarak anılır. Bradaki l m büyüklüğü bir karışım znlğdr. Prandtl ın karışım znlğ kavramı Rynolds grilmsi için Bölüm 7.5 in sonnda yapılan fiziksl açıklamayı yakından izlmktdir. Karışım znlğ bir tkilşim msafsi olarak, molküllr arası ortalama srbst yörüngy bnztilbilir. Sadc, molküllr arasında dğil d türbülans kümlri arasında tanımlanmaktadır. Şayt Şkil 7.9 da akışkan kümlrinin harkt msafsi olarak y dğil d l m alınırsa, v (y )< olmak üzr ' ( y ) ( y + lm ) ( y ) lm (7.38) şklind bir boznt hızı tanımlanabilir. Şayt akışkan kümsi aşağıdan ykarıya çıkıyorsa b dfa v (y )< olmak üzr boznt hızı ' ( y ) ( y lm ) ( y ) l m (7.39) şklinddir. Sürklilik grği, v ~- olp, b son iki bağıntı doğrdan (7.37) bağıntısını vrir. B bağıntıdaki τ T nin işartini doğr vrbilmk için ( /) yrin yazmak daha doğr olr. l m için bağımsız dğişkn vya paramtrlrin ya da ortalama bağımlı dğişknlrin fonksiyon olan ilav bir bağıntıya ihtiyaç vardır. B bağıntı da di viskozitsi gibi, akışkanın dğil akımın drmnn bir fonksiyon olacaktır. B aşamada, (7.36) v (7.37) formülasyonlarıyla ilgili bazı gözlmlr ygn olacaktır: İlkin, di viskozitsi v karışım znlğ formülasyonları, transport prossini tmsiln ilgili bağımlı dğişknin gradyantını ( /) içrmlri ndniyl gradyan transport formülasyonları olarak anılır. Bna gör laminr momntm v ısıl nrji transport için yazdığımız τ µ v T q k bağıntıları da gradyant transport formülasyonları olmaktadır. Türbülanslı kaymalı akımlar için b gibi formülasyonların özl bir zaafiyti vardır
23 B zafiyti Şkil 7.3 daki gibi bir profil halind n kolay biçimd görmk mümkündür. B tip profillr, örnğin, dvar üzrindki bir yarıktan türbülanslı akıma tğtsl doğrltda yüksk hızla akışkan njksiyon halind ld dilir. y (x) ortalama hız profili bir maksimma sahip oldğndan / olan bir nokta olacaktır. B noktada hr iki formülasyon da (y) τ T _ ρ ' v' vrir. Formülasyonların b zayıflıklarını gidrmnin basit bir yol yoktr. Bnnla birlikt çoğ sınır tabaka akımlarında b şkild maksimm vya minimmlar blnmamaktadır. Simtrik bir profil için simtri düzlmind / olp yin aynı drm görülmktdir Şkil 7.4- Türbülanslı sınır tabakada bir maksimma sahip ( /) hız profili İki formülasyonla ilgili ikinci gnl gözlm d b ikisinin sasn şdğr olmasıdır. (7.36) v (7.37) dnklmlrin bakılarak açıkça µ T ρ l m y (7.4) yazılabilir. Dolayısıyla µ T için bir bağıntı biliniyorsa (7.4) bağıntısından l m için mütkabil bağıntı blnabilir. Edi viskozitsi v karışım znlğ için özl modllr Bölüm 7.8 d çıkartılacaktır. Bnnla birlikt, daha önc, türbülanslı sınır tabakaların analizi için intgral yöntmlr göz atılacaktır Ortalama akım intgral yöntmlri Türbülanslı akımların analizi için d laminr akımlardaki intgral yöntmlrinin bnzri yöntmlr mvcttr. Bnlar türbülanslı analizd kabaca, laminr haldki gibi difransiyl formülasyonlara dayanan bağıntıları kllanırlar. Yöntmlrin yglanması gnllikl basit olp mühndislik çalışmaları için ygn sonçlar vrmktdir. Brada yöntmlrdn ikisi kısaca izah dilcktir. Bnlardan daha ski olanı sadc çok basit problmlr için ygndr. Daha yni olanı is Moss (1969) tarafından ortaya konmş olp daha gnl akımlar için kllanılabilmktdir. Hr iki hald d grkli türbülanslı kayma modllmsinin analiz nasıl girdiği dikkati çkmktdir. Prandtl yöntmi İntgral yöntmin türbülanslı akımda ilk yglaması Prandtl (197) tarafında düz-lvha problmi için yapılmıştır. Daimi, laminr akımlar için daha önc dθ + dx 1 f d dx ( θ + δ ) v C w (.15) şklind çıkartılan momntm intgral dnklmi türbülanslı daimi bir ortalama akım için, bütün bağımlı dğişknlr ortalama büyüklüklr şklind dğrlndirilmk srtiyl kllanılabilir. Gçirgn olmayan bir düz-lvha üzrindki akım için b dnklm
24 3 d θ dx C f (.15a) şklini alır. θ momntm kalınlığı daha önc oldğ gibi δ θ 1 dy şklind tanımlanmakla birlikt, bradaki (y) ortalama hız profilidir. Çözüm için, laminr hald oldğ gibi, kabl dilmiş bir hız profilin ihtiyaç vardır. Düz lvha üzrindki türbülanslı akım için ortalama hız profili kabaca 1 / n y (7.41) δ şklind tmsil dilbilir. Brada R x için n 7 dir. Ancak, Bölüm dki inclmlr dikkat alınırsa, gnl hald b bağıntının doğr olmayacağı söylnbilir. Bna rağmn analizd b hız profili il ilrlnbilir. (7.41) hız profili kllanılarak n 7 için δ/δ 1/8 v θ/δ 7/7 ld dilir. İzlyn aşamada b hız profilinin dvar kaymasını hsaplamak için kllanılması bklnbilir. Ama dvar kayması ( /) w türvini içrmkt olp, b türv d (7.41) bağıntısına gör n 7 için dvar üzrind 6 7 y 7δ δ y şklind sonsza gitmktdir. Bnnla birlikt, türbülanslı akım içind kayma için ilav bir bilgiy grk dylacaktır. B yöntmd, δ önclikli bağımlı dğişkn olarak ortaya kondğndan, sadc dvar üzrindki C f kaymasının δ cinsindn C f (R δ ) şklind bilinmsin ihtiyaç vardır. Laminr analiz için dvar kayması farklı biçimd l alınmış olmakla birlikt δ aynı rolü oynamıştır. Prandtl (197) grkn C f (R δ ) için ( ) / C. 456 R 14 f (7.13) δ bağıntısını kllanmıştır. B bağıntıyla birlikt tspit diln θ/δ oranı da (.15a) bağıntısında kllanılarak dθ C f dx dδ / 4 ( R ) dx ( ) 1 / δ / ν 4 δ 7 7 dδ dx. 456 ν δ 1 / 4 (7.4) vya b bağıntı düznlnip intgr dilrk, δ () olmak üzr
25 4 ( x) δ x / 5 R x (7.43) ld dilir. B sonç düz lvha üzrindki laminr sınır tabaka için Blasis dnklmi kllanılarak ld diln ( x) δ x 5. 1/ R x Bağıntısıyla karşılaştırılırsa türbülanslı sınır tabakanın laminr sınır tabakaya kıyasla daha çabk bir şkild kalınlaşmakta oldğ göstrilbilir. Nitkim b iki bağıntıya gör: laminr hald δ /x ~ R x -1/ türbülanslı hald δ /x ~ R x -1/5 (δ ~ x 1/ ) (δ ~ x 4/5 ). B sonç nisptn kabadır. Bir kr türbülanslı bir sınır tabaka için n iyi bir dğişkn grplaması üzrin otrmayan bir hız profili kllanmaktadır. İkinci olarak, yöntm gçişi v lvhanın başlangıcındaki laminr akım bölgsini tamamıyla ihmal tmktdir. B yöntml daha fazlasını yapmak mümkün dğildir. Örnğin, basınç gradyantı içrn problmlr çözülmk istnsydi dp/dx türvinin gnl hallri için C f (R δ,dp/dx) şklind bilgiy ihtiyaç olacaktı. Ama, şayt b fazla bilgi mvct olsaydı, zatn b analiz d ihtiyaç olmayacaktı. Moss yöntmi Türbülanslı sınır tabakalar için ykarıda izah dilndn daha kabiliytli v yglanması daha basit bir intgral yöntmi Moss (1969) tarafından gliştirilmiştir. B yöntm (.15) momntm dnklminin ( / ) τ τ( y / δ) ( y / δ) Rδ d µ dx y1/ δ y1/ δ y1 δ d y 1 d y Rδ d R d dx δ δ dx δ w 1 1 (7.44) şklindki daha gnllştirilmiş bir halini kllanmaktadır. Brada y 1 /δ büyüklüğü il 1. arasında hrhangi bir dğr alabilir. y 1 /δ 1. için (7.44) dnklmi alışılagln momntm intgral dnklmin dönüşür. y 1 /δ nın başka dğrlri için, ayrı, ilav dnklmlr ld dilir. Daha sonra y 1 < δ olmak üzr dx : y 1 : 1 boytlarındaki bir kontrol hacmin kütl v momntmn kornm ilklri yglanacaktır (ki daha önc H δ olmak üzr dx : H : 1 boytlarındaki bir kontrol hacmi kllanılmıştı). Sonçlar arasındaki n büyük farklılık, daha öncki inclmlrd yh da kayma sıfır olp dnklmlrd gözükmüyor ikn bradaki inclmlrd y y 1 d kaymanın gözükmsidir. Moss y 1 /δ 1. v y 1 /δ.3 kllanarak iki dnklm ld tmiştir. İkinci dğr kabaca tabaka boynca momntm kaybının ikiy bölünmsin karşılık glmktdir. Grkn hız profili için Moss iz kannnn yaklaşık bir biçimini kllanmıştır. W(y/δ) büyüklüğünün tanımıyla birlikt
26 5 1 / ln ( y / ν ) + C K 1 y W 1 δ / ln ( / ) C δ ν + K (7.8) dnklmini v / / C büyüklüğünü kllanarak f 1 y Π y ln + C W K ν K δ (7.9) dnklmini ynidn yazmış v iz fonksiyonn 3 y y y W 3 (7.45) δ δ δ şklind yaklaşık biçimini ld tmiş, sonçta C f / y Π 1 + ln K δ K f C 1 y 1 W δ (7.46) İfadsin rişmiştir. Moss, laminr alt tabaka için bir başka polinom kllanmış, yüksk Rynolds sayısındaki akımlarda intgral yöntm için b inc tabaka içrisind profilin sçiminin önmli olmadığını blirtmiştir. B sçim intgrallrin dğrini önmli ölçüd tkilmmktdir. (7.41) dnklmind vrildiği gibi / f(y/δ) almak yrin böyl birlşik bir hız profili almak daha doğrdr Türbülanslı kayma modli olarak τ T _ ρ ' v ' µ T (7.36) di-viskozitsi modli alınmıştır. (7.44) dnklmind sadc τ(y 1 /δ) büyüklüğü gçtiğindn b intgral yöntmi için türbülanslı kaymanın bir tk y/δ y 1 /δ noktasında modllnmsi grklidir. B hss yöntmin kvvtli tarafıdır. Zira türbülans modllmsi sadc grçkt problmin çıktısı olan yüzy sürtünmsini basitç almak yrin çok daha tml bir sviyd yapılmıştır. Moss, Cols (196) tarafından vriln bir kısım vriy ğri ydrarak ld ttiği µ T ρ + µ θ y 1 / δ R δ (7.47) şklind tamamiyl ampirik bir di-viskozitsi modli kllanmıştır. Bütün bnlarla birlikt sistm (7.44) dnklminin y 1 /δ 1. v y 1 /δ.3 d (7.46) hız profiliyl birlikt dğrlndirilmsi sonc ld diln iki adi difransiyl dnklmdn olşmaktadır. Dnklm sistminin iki bilinmyni olp bnlar R δ il ifad diln δ (x) v C f dir. B iki dnklm adi-difransiyl dnklm çözümünd kllanılan hrhangi bir sayısal yöntml çözülbilir.
27 6 Moss (1969), yöntmini bazı dnysl hallr için yglamış, mvct intgral yöntmlrindn hrhangi biri kadar ygn sonçlar ld tmiştir. Gnl olarak ym (C f v δ(x) gibi bütünsl büyüklüklr için), n iyi difransiyl yöntmlrl ld dilnlr kadar iyidir. Çşitli hsap yöntmlrinin prformansını ortaya koyabilmk için, gidrk artan karmaşıklıkta üç adt trs-basınç-gradyantlı akım örnk olarak sçilmiştir. Yöntmlrin hpsi düz lvha halind (sıfır basınç gradyantı) iyi prformans srgilmktdir. Olml basınç gradyantı halind prformans biraz daha iddiasızdır. Sözü diln üç örnk hald (1) Calsr in (1956) daha önc blirtiln dng (qiliblim) hali, () Schbar v Klbanof n (195) klasik dnyi, (3) Nwman ın (1951) kanat profili l alınmıştır. B üç akımla ilgili bilgilr d anlamsız hsaplamalara yol açmayacak v vri il karşılaştırmaya imkan vrck biçimd ytrinc iyi bir şkild dokümant dilmiştir. B akımlar 1968 d Stanford da grçklştiriln AFOSR-IFP konfransında (Klin v arkadaşları, 1969) sınır tabaka hsaplama yöntmlri için tst hali olarak sçilmiş n karmaşık akımlardan üçüdür. Moss in (1969) hsaplamaları θ(x) v C f (x) büyüklüklri için b üç hald ld diln vri il Şkil d karşılaştırılmıştır. Schbar v Klbanof il Nwman hallrind ayrılmaya kadar ym iyi ikn, Clasr in dng hali için ymn zayıf oldğ görülmktdir. Şkil Moss yöntminin Clasr in (1956) vrilriyl karşılaştırması (Klin v arkadaşları, 1969) Şkil 7.3- Moss yöntminin Schbar v Klbanof n (195) vrilriyl karşılaştırması (Klin v arkadaşları, 1969) Şkil Moss yöntminin Nwman ın (1951) vrilriyl karşılaştırması (Klin v arkadaşları, 1969) Çşitli yöntm v modllrin prformansını göstrmk için, 1981 d Stanford da grçklştiriln bir başka konfranstaki (Klin v arkadaşları, 198) bazı hallr daha l
28 7 alınmıştır. Saml v Jobrt (1974) tarafından düşük-hızda trs-basınç gradyantlı hald grçklştiriln dny sonçlarıyla Moss yöntmi sonçları Şkil 7.34 d karşılaştırılmış olp ym gnl olarak iyi gözükmktdir..4 C f.. Vri Analiz x (m) Şkil Moss yöntminin trs basınç gradyantlı akım için Saml v Jobrt in (1974) vrilriyl karşılaştırması Brada inclnn intgral yöntmi laminr akım için daha inc izah diln Thwaits-Walz intgral yöntmiyl birlikt kllanılabilir. Kompl akımı çözck bir yöntm ld tmk için gçişsl bölgd d Dy v Nararshima (199) tarafından önriln aralıklılık dağılımı alınabilir. Bradaki tml fikir γ aralıklılık faktörü olmak üzr gçişsl bölgd ötlm kalınlıkları için ( 1 γ) δ +γδ lam şklind bir dağılım almaktır. trb Örnk 7.1- Türbülanslı sınır tabakada momntm intgral yöntminin yglanması 5m znlğndaki bir düz lvha 1. m/s hızdaki akıma marz olp düz lvhanın bitimindn itibarn yr alan rampa (x)15.-x m/s şklind dğişn bir dış akım yaratmaktadır. Akışkanın viskozitsini ν 1-5 m²/s alarak b yüzy boynca x 7. m msafsin kadar türbülanslı sınır tabakanın glişimini inclyiniz. Sınır tabaka ayrılır mı? Çözüm: Akımın ilk kısmı düz lvha üzrind v basınç gradyantsız olp b bölgd basit intgral çözümü yglanarak x5 d δ, θ v C f büyüklüklri hsaplanabilir. Hsaplanan b dğrlr yüzyin kalan rampa kısmındaki hsaplar için başlangıç dğrlri olarak kllanılacaktır. Bna gör rampa başlangıcında C f.665 v R θ dğrlri ld dilir. Hsaplamalar x.7 m noktasına rişincy kadar x.1 m aralıklarla 1 adımda grçklştirilmiştir. Hsaplamalar Schtz tarafından vriln bir program il grçklştirilmiş olp ld diln sonçlar aşağıdaki tabloda yr almaktadır.
29 8 X C f δ θ R δ H Görüldüğü gibi sınır tabaka kalınlığı gidrk artmaktadır. Nisptn kvvtli sayılabilck b trs basınç gradyantı altında sınır tabaka x7m d ayrılmamakta (C f > ), ancak sınır tabaka kalınlığı nrdys ikiy katlanmakta v sürtünm katsayısı da %4 azalmaktadır.
BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR
 BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR sabit-oğnlkl, sabit-özllikli, harici, türbülanslı sınır tabaka akımları ZB 386 Sınır Tabaka Drs notları - M. TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr
BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR sabit-oğnlkl, sabit-özllikli, harici, türbülanslı sınır tabaka akımları ZB 386 Sınır Tabaka Drs notları - M. TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr
BÖLÜM 5 SIKIŞTIRILABİLİR LAMİNER SINIR TABAKALAR
 BÖLÜM 5 SIKIŞIRILABİLİR LAMİNER SINIR ABAKALAR 5.1- Giriş 5.- Adabatik dar sıaklığı 5.3- Rfrans sıak öntmi 5.4-1 özl ali 5.5- Birdn farklı andtl saıları için grikazanım faktörü 5.6- Sıkıştırılabilm dönüşümlri:
BÖLÜM 5 SIKIŞIRILABİLİR LAMİNER SINIR ABAKALAR 5.1- Giriş 5.- Adabatik dar sıaklığı 5.3- Rfrans sıak öntmi 5.4-1 özl ali 5.5- Birdn farklı andtl saıları için grikazanım faktörü 5.6- Sıkıştırılabilm dönüşümlri:
VOLEYBOLCULARIN FARKLI MAÇ PERFORMANSLARI İÇİN TEKRARLANAN ÖLÇÜMLER YÖNTEMİNİN KULLANILMASI
 96 OLEBOLCULAIN FAKLI MAÇ PEFOMANSLAI İÇİN TEKALANAN ÖLÇÜMLE ÖNTEMİNİN KULLANILMASI ÖET Gürol IHLIOĞLU Süha KAACA Farklı yr, zaman v matryallr üzrind tkrarlanan dnylr il bir vya birdn fazla faktörün tkisi
96 OLEBOLCULAIN FAKLI MAÇ PEFOMANSLAI İÇİN TEKALANAN ÖLÇÜMLE ÖNTEMİNİN KULLANILMASI ÖET Gürol IHLIOĞLU Süha KAACA Farklı yr, zaman v matryallr üzrind tkrarlanan dnylr il bir vya birdn fazla faktörün tkisi
DERS 9. Grafik Çizimi, Maksimum Minimum Problemleri
 DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
İletkende seri olarak tel direnci ve magnetik alandan doğan reaktans ile şönt olarak elektrik alandan doğan toprak kapasitesi mevcuttur.
 9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ
 ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ MAK-LAB012 1. DENEY DÜZENEĞİNİN TANITILMASI Düznk sas olarak dikdörtgn ksitli bir kanaldan ibarttir. 1 hp gücündki lktrik motorunun çalıştırdığı bir vantilatör il kanal içind
ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ MAK-LAB012 1. DENEY DÜZENEĞİNİN TANITILMASI Düznk sas olarak dikdörtgn ksitli bir kanaldan ibarttir. 1 hp gücündki lktrik motorunun çalıştırdığı bir vantilatör il kanal içind
UYGULAMALI DİFERANSİYEL DENKLEMLER
 UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
Üstel Dağılım SÜREKLİ ŞANS DEĞİŞKENLERİNİN OLASILIK YOĞUNLUK FONKSİYONLARI
 ..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
İletkende seri olarak tel direnci ve magnetik alandan doğan reaktans ile şönt olarak elektrik alandan doğan toprak kapasitesi mevcuttur.
 9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
IŞINIM VE DOĞAL TAŞINIM DENEYİ
 IŞINIM VE DOĞAL TAŞINIM DENEYİ MAK-LAB005 1. DENEY DÜZENEĞİNİN TANITILMASI Dny düznği, şkild görüldüğü gibi çlik bir basınç kabının içind yatay olarak asılı duran silindirik bir lman ihtiva dr. Elman bakırdan
IŞINIM VE DOĞAL TAŞINIM DENEYİ MAK-LAB005 1. DENEY DÜZENEĞİNİN TANITILMASI Dny düznği, şkild görüldüğü gibi çlik bir basınç kabının içind yatay olarak asılı duran silindirik bir lman ihtiva dr. Elman bakırdan
IKTI 102 25 Mayıs, 2010 Gazi Üniversitesi-İktisat Bölümü
 DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
İyon Kaynakları ve Uygulamaları
 İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu [email protected] HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu [email protected] HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ
 BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ - Nair Stos dnlmlri - Nair Stos dnlmlrinin tam çözümlri - Daimi, ii-botl, laminr sınır tabaa dnlmlri - Daimi, ii-botl, laminr sınır
BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ - Nair Stos dnlmlri - Nair Stos dnlmlrinin tam çözümlri - Daimi, ii-botl, laminr sınır tabaa dnlmlri - Daimi, ii-botl, laminr sınır
Kayıplı Dielektrik Cisimlerin Mikrodalga ile Isıtılması ve Uç Etkileri
 Kayıplı Dilktrik Cisimlrin Mikrodalga il Isıtılması v Uç Etkilri Orhan Orhan* Sdf Knt** E. Fuad Knt*** *Univrsity of Padrborn, Hinz ixdorf Institut, Fürstnall, 3302 Padrborn, Almanya [email protected] **Istanbul
Kayıplı Dilktrik Cisimlrin Mikrodalga il Isıtılması v Uç Etkilri Orhan Orhan* Sdf Knt** E. Fuad Knt*** *Univrsity of Padrborn, Hinz ixdorf Institut, Fürstnall, 3302 Padrborn, Almanya [email protected] **Istanbul
Bilgi Tabanı (Uzman) Karar Verme Kontrol Kural Tabanı. Bulanık. veya. Süreç. Şekil 1 Bulanık Denetleyici Blok Şeması
 Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
{ } { } Ters Dönüşüm Yöntemi
 KESĐKLĐ DAĞILIMLARDAN RASGELE SAYI ÜRETME Trs Dönüşüm Yöntmi F dağılım fonksiyonuna sahip bir X rasgl dğişknin dağılımından sayı ürtmk için n çok kullanılan yöntmlrdn biri, F dağılım fonksiyonunun gnllştirilmiş
KESĐKLĐ DAĞILIMLARDAN RASGELE SAYI ÜRETME Trs Dönüşüm Yöntmi F dağılım fonksiyonuna sahip bir X rasgl dğişknin dağılımından sayı ürtmk için n çok kullanılan yöntmlrdn biri, F dağılım fonksiyonunun gnllştirilmiş
DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİK KONTROL I Dr. Uğur HASIRCI
 DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
BÖLÜM 7 BORULARDA GERÇEK AKIM
 BÖLÜM 7 BORULARA GERÇEK AKIM Enkesitin tamamen dol olarak aktığı akımlara basınçlı akım denir. Basınç altında sıvı nakleden kapalı akış yollarına bor adı verilmektedir. Borlar çeşitli enkesitlere sahip
BÖLÜM 7 BORULARA GERÇEK AKIM Enkesitin tamamen dol olarak aktığı akımlara basınçlı akım denir. Basınç altında sıvı nakleden kapalı akış yollarına bor adı verilmektedir. Borlar çeşitli enkesitlere sahip
ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ
 ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ Srkan SUNU - Srhan KÜÇÜKA Dokuz Eylül Ünivrsitsi Makina Mühndisliği Bölümü -posta: [email protected] Özt: Bu çalışmada, komprsör,
ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ Srkan SUNU - Srhan KÜÇÜKA Dokuz Eylül Ünivrsitsi Makina Mühndisliği Bölümü -posta: [email protected] Özt: Bu çalışmada, komprsör,
( ) ( ) Be. β - -bozunumu : +β - + ν + Q - Atomik kütleler cinsinden : (1) β + - bozunumu : nötral atom negatif iyon leptonlar
 6.. BETA BOZUUU Çkirdğin pozitif vya ngatif lktron yayması vya atomdan bir lktron yakalaması yolu il atom numarası ± 1 kadar dğişir. β - -bozunumu : ( B 4 4 ( B 4 nötral atom Atomik kütllr insindn : (
6.. BETA BOZUUU Çkirdğin pozitif vya ngatif lktron yayması vya atomdan bir lktron yakalaması yolu il atom numarası ± 1 kadar dğişir. β - -bozunumu : ( B 4 4 ( B 4 nötral atom Atomik kütllr insindn : (
Enerji Dönüşüm Temelleri. Bölüm 3 Bir Fazlı Transformatörler
 Enrji Dönüşüm Tmllri Bölüm 3 Bir Fazlı Transformatörlr Birfazlı Transformatorlar GİRİŞ Transformatörlrin grçk özllik v davranışlarını daha kolay anlamak için ilk aşamada idal transformatör üzrind durulacaktır.
Enrji Dönüşüm Tmllri Bölüm 3 Bir Fazlı Transformatörlr Birfazlı Transformatorlar GİRİŞ Transformatörlrin grçk özllik v davranışlarını daha kolay anlamak için ilk aşamada idal transformatör üzrind durulacaktır.
ELM202 ELEKTRONİK-II DERSİ LABORATUAR FÖYÜ
 T SKRY ÜNİERSİTESİ TEKNOLOJİ FKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ ELM202 ELEKTRONİK-II DERSİ LBORTUR FÖYÜ DENEYİ YPTIRN: DENEYİN DI: DENEY NO: DENEYİ YPNIN DI v SOYDI: SINIFI: OKUL NO: DENEY GRUP
T SKRY ÜNİERSİTESİ TEKNOLOJİ FKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ ELM202 ELEKTRONİK-II DERSİ LBORTUR FÖYÜ DENEYİ YPTIRN: DENEYİN DI: DENEY NO: DENEYİ YPNIN DI v SOYDI: SINIFI: OKUL NO: DENEY GRUP
Atomlardan Kuarklara. Test 1
 4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
DERS 9. Grafik Çizimi, Maksimum-Minimum Problemleri. 9.1. Grafik çiziminde izlenecek adımlar. y = f(x) in grafiğini çizmek için
 DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
metal (bakır) metaloid (silikon) metal olmayan (cam) iletken yar ı iletken yalıtkan
 1 YARI İLETKENLER Enstrümantal Analiz ir yarı iltkn, iltknliği bir iltkn il bir yalıtkan arasında olan kristal bir malzmdir. Çok çşitli yarıiltkn malzm vardır, silikon v grmanyum, mtalimsi bilşiklr (silikon
1 YARI İLETKENLER Enstrümantal Analiz ir yarı iltkn, iltknliği bir iltkn il bir yalıtkan arasında olan kristal bir malzmdir. Çok çşitli yarıiltkn malzm vardır, silikon v grmanyum, mtalimsi bilşiklr (silikon
BÖLÜM 6 GERÇEK AKIŞKANLARIN HAREKETİ
 BÖLÜM 6 GERÇEK AKIŞKANLARIN HAREKETİ Gerçek akışkanın davranışı viskoziteden dolayı meydana gelen ilave etkiler nedeniyle ideal akışkan akımlarına göre daha karmaşık yapıdadır. Gerçek akışkanlar hareket
BÖLÜM 6 GERÇEK AKIŞKANLARIN HAREKETİ Gerçek akışkanın davranışı viskoziteden dolayı meydana gelen ilave etkiler nedeniyle ideal akışkan akımlarına göre daha karmaşık yapıdadır. Gerçek akışkanlar hareket
Biyomedikal Mühendisliği Bölümü TBM 203 Diferansiyel Denklemler* Güz Yarıyılı
 Biomdikal Mühndiliği Bölümü TBM 0 Diranil Dnklmlr* 07-08 Güz Yarıılı Pro. Dr. Yn Emr ERDEMLİ [email protected] *B dr notları Yrd. Doç. Dr. Adnan SONDAŞ ın katkılarıla hazırlanmıştır. Diranil Dnklmlr Kanaklar
Biomdikal Mühndiliği Bölümü TBM 0 Diranil Dnklmlr* 07-08 Güz Yarıılı Pro. Dr. Yn Emr ERDEMLİ [email protected] *B dr notları Yrd. Doç. Dr. Adnan SONDAŞ ın katkılarıla hazırlanmıştır. Diranil Dnklmlr Kanaklar
TANITIM ve KULLANIM KILAVUZU. Modeller UBA4234-R. Versiyon : KK_UBA_V3.0210
 SAT-IF / CATV Ultra Gniş Bantlı Dağıtım Yükslticilri (UBA-Srisi) TANITIM v KULLANIM KILAVUZU Modllr UBA4234-R Vrsiyon : KK_UBA_V3.0210 1.Gnl Tanıtım UBA Srisi Dağıtım Yükslticilri, uydu (950-2150MHz) v
SAT-IF / CATV Ultra Gniş Bantlı Dağıtım Yükslticilri (UBA-Srisi) TANITIM v KULLANIM KILAVUZU Modllr UBA4234-R Vrsiyon : KK_UBA_V3.0210 1.Gnl Tanıtım UBA Srisi Dağıtım Yükslticilri, uydu (950-2150MHz) v
T.C. SELÇUK ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ
 T.C. SELÇUK ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU Bkir KARAGÜL YÜKSEK LĐSANS TEZĐ MAKĐNA ANABĐLĐM DALI KONYA 2010 ÖZET Yüksk Lisans Tzi GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU
T.C. SELÇUK ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU Bkir KARAGÜL YÜKSEK LĐSANS TEZĐ MAKĐNA ANABĐLĐM DALI KONYA 2010 ÖZET Yüksk Lisans Tzi GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU
Çelik. Her şey hesapladığınız gibi!
 Çlik Hr şy hsapladığınız gibi! idyapi Bilgisayar Dstkli Tasarım Mühndislik Danışmanlık Taahhüt A.Ş. Piyalpaşa Bulvarı Famas Plaza B-Blok No: 10 Kat: 5 Okmydanı Şişli 34384 İstanbul Tl : (0212) 220 55 00
Çlik Hr şy hsapladığınız gibi! idyapi Bilgisayar Dstkli Tasarım Mühndislik Danışmanlık Taahhüt A.Ş. Piyalpaşa Bulvarı Famas Plaza B-Blok No: 10 Kat: 5 Okmydanı Şişli 34384 İstanbul Tl : (0212) 220 55 00
DERS 7. Türev Hesabı ve Bazı Uygulamalar II
 DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ
 . Ulusal Tasarım İmalat v Analiz Kongrsi 11-1 Kasım 010- Balıksir YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ Aydın DEMİRCAN*, M. Ndim
. Ulusal Tasarım İmalat v Analiz Kongrsi 11-1 Kasım 010- Balıksir YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ Aydın DEMİRCAN*, M. Ndim
Çay Atıklarından Aktif Karbon Üretimi ve Adsorpsiyon Proseslerinde Kullanımı
 ÖZET Çay Atıklarından Aktif Karbon Ürtimi v Adsorpsiyon Prosslrind Kullanımı Mrym OZMAK a, Işıl Gürtn b, Emin YAĞMUR b, Zki AKTAŞ b a DSİ Gn.Md. TAKK Dairsi Başkanlığı, Ankara, 61 b Ankara Ünivrsitsi Mühndislik
ÖZET Çay Atıklarından Aktif Karbon Ürtimi v Adsorpsiyon Prosslrind Kullanımı Mrym OZMAK a, Işıl Gürtn b, Emin YAĞMUR b, Zki AKTAŞ b a DSİ Gn.Md. TAKK Dairsi Başkanlığı, Ankara, 61 b Ankara Ünivrsitsi Mühndislik
LYS Matemat k Deneme Sınavı
 LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
BÖLÜM II A. YE Đ BETO ARME BĐ ALARI TASARIM ÖR EKLERĐ ÖR EK 2
 BÖLÜ II A. YE Đ BETO ARE BĐ ALARI TASARI ÖR EKLERĐ ÖR EK SÜ EKLĐK DÜZEYĐ YÜKSEK 6 KATLI BETO ARE PERDELĐ / ÇERÇEELĐ BĐ A SĐSTEĐ Đ EŞDEĞER DEPRE YÜKÜ YÖ TEĐ ĐLE A ALĐZĐ E TASARII.1. GENEL BĐNA BĐLGĐLERĐ...II./..
BÖLÜ II A. YE Đ BETO ARE BĐ ALARI TASARI ÖR EKLERĐ ÖR EK SÜ EKLĐK DÜZEYĐ YÜKSEK 6 KATLI BETO ARE PERDELĐ / ÇERÇEELĐ BĐ A SĐSTEĐ Đ EŞDEĞER DEPRE YÜKÜ YÖ TEĐ ĐLE A ALĐZĐ E TASARII.1. GENEL BĐNA BĐLGĐLERĐ...II./..
- BANT TAŞIYICILAR -
 - BANT TAŞIYICILAR - - YAPISAL ÖZELLİKLER Bir bant taşıyıcının nl örünümü aşağıdaki şkild vrilmiştir. Bant taşıyıcıya ismini vrn bant (4) hm taşınacak malzmyi için alan bir kap örvi örn, hm d harkt için
- BANT TAŞIYICILAR - - YAPISAL ÖZELLİKLER Bir bant taşıyıcının nl örünümü aşağıdaki şkild vrilmiştir. Bant taşıyıcıya ismini vrn bant (4) hm taşınacak malzmyi için alan bir kap örvi örn, hm d harkt için
Mühendisler İçin DİFERANSİYEL DENKLEMLER
 Mühndislr İçin DİFERANSİYEL DENKLEMLER Doç. Dr. Tahsin Engin Prof. Dr. Yunus A. Çngl Sakara Ünivrsitsi Makina Mühndisliği Bölümü Elül 8 SAKARYA - - Mühndislr İçin Difransil Dnklmlr İÇİNDEKİLER BÖLÜM BİRİNCİ
Mühndislr İçin DİFERANSİYEL DENKLEMLER Doç. Dr. Tahsin Engin Prof. Dr. Yunus A. Çngl Sakara Ünivrsitsi Makina Mühndisliği Bölümü Elül 8 SAKARYA - - Mühndislr İçin Difransil Dnklmlr İÇİNDEKİLER BÖLÜM BİRİNCİ
Asenkron Makinanın Alan Yönlendirme Kontrolünde FPGA Kullanımı ALAN İ., AKIN Ö.
 Asnkron Makinanın Alan Yönlndirm Kontrolünd FPGA Kullanımı ALAN İ., AKIN Ö. ABSTRACT In this study, th fasibility of usag of fild programmabl gat arrays (FPGA) in th fild orintd control (FOC) of induction
Asnkron Makinanın Alan Yönlndirm Kontrolünd FPGA Kullanımı ALAN İ., AKIN Ö. ABSTRACT In this study, th fasibility of usag of fild programmabl gat arrays (FPGA) in th fild orintd control (FOC) of induction
TAŞINIMIN FİZİKSEL MEKANİZMASI
 BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 2007 SORULARI
 DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
BÖLÜM 2- HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA
 Dpartmnt o Mchanical Enginring MAK 0 MÜHENDİSLİKTE SAYISAL YÖNTEMLER BÖLÜM - HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA Doç. Dr. Ali Rıza YILDIZ Arş. Gör. Emr DEMİRCİ 7.0.0 7.0.0 MAK
Dpartmnt o Mchanical Enginring MAK 0 MÜHENDİSLİKTE SAYISAL YÖNTEMLER BÖLÜM - HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA Doç. Dr. Ali Rıza YILDIZ Arş. Gör. Emr DEMİRCİ 7.0.0 7.0.0 MAK
BÖLÜM 2 LAMİNER SINIR TABAKA İNTEGRAL DENKLEMLERİ VE ÇÖZÜMLERİ
 BÖLÜM LAMİNER SINIR ABAKA İNEGRAL DENKLEMLERİ VE ÇÖZÜMLERİ.1- Giriş.- İntgral momntm nklmi.- İntgral momntm nklminin çözümü..1- Pohlhasn öntmi..-haits-walz öntmi..-emmli v njksionl akımlar.4- İntgral nrji
BÖLÜM LAMİNER SINIR ABAKA İNEGRAL DENKLEMLERİ VE ÇÖZÜMLERİ.1- Giriş.- İntgral momntm nklmi.- İntgral momntm nklminin çözümü..1- Pohlhasn öntmi..-haits-walz öntmi..-emmli v njksionl akımlar.4- İntgral nrji
Anaparaya Dönüş (Kapitalizasyon) Oranı
 Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
İSTANBUL TEKNİK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 İSANBUL EKNİK ÜNİVERSİESİ FEN BİLİMLERİ ENSİÜSÜ SABİ KANAL DİKEY İNİŞ KALKŞ İNSANSZ HAVA ARAÇLAR BENZEİM VE KONROLÜ YÜKSEK LİSANS EZİ Uçak Müh Zafr ÖZNALBAN (511051027 zin Enstitüy Vrildiği arih: 2 mmuz
İSANBUL EKNİK ÜNİVERSİESİ FEN BİLİMLERİ ENSİÜSÜ SABİ KANAL DİKEY İNİŞ KALKŞ İNSANSZ HAVA ARAÇLAR BENZEİM VE KONROLÜ YÜKSEK LİSANS EZİ Uçak Müh Zafr ÖZNALBAN (511051027 zin Enstitüy Vrildiği arih: 2 mmuz
Özel Laboratuvar Deney Föyü
 Özel Laboratvar Deney Föyü Deney Adı: Mikrokanatlı borlarda türbülanslı akış Deney Amacı: Düşey konmdaki iç yüzeyi mikrokanatlı bordaki akış karakteristiklerinin belirlenmesi 1 Mikrokanatlı Bor ile İlgili
Özel Laboratvar Deney Föyü Deney Adı: Mikrokanatlı borlarda türbülanslı akış Deney Amacı: Düşey konmdaki iç yüzeyi mikrokanatlı bordaki akış karakteristiklerinin belirlenmesi 1 Mikrokanatlı Bor ile İlgili
BÖLÜM 7. Sürekli hal hatalarının değerlendirilmesinde kullanılan test dalga şekilleri: Dalga Şekli Giriş Fiziksel karşılığı. Sabit Konum.
 9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
Bağımsızlığının 20. Yılında Azerbaycan
 Bağımsızlığının 20. Yılında Azrbaycan Dr. Ali ASKER* 1980 lrin ortalarından itibarn Sovytlr Birliğind uygulanan ynidn yapılanma v saydamlık politikalarının amacı (n azından sözd), dmokratiklşm yoluyla
Bağımsızlığının 20. Yılında Azrbaycan Dr. Ali ASKER* 1980 lrin ortalarından itibarn Sovytlr Birliğind uygulanan ynidn yapılanma v saydamlık politikalarının amacı (n azından sözd), dmokratiklşm yoluyla
LOGARİTMA. Örnek: çizelim. Çözüm: f (x) a biçiminde tanımlanan fonksiyona üstel. aşağıda verilmiştir.
 LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
FONKSİYONEL DERECELENDİRİLMİŞ KONİK KESİTLİ MİKRO-KİRİŞLERİN SERBEST TİTREŞİM ANALİZİ
 FONKSİYONEL DERECELENDİRİLMİŞ KONİK KESİTLİ MİKRO-KİRİŞLERİN SERBEST TİTREŞİM ANALİZİ FREE VIBRATION ANALYSIS OF FUNCTIONALLY GRADED MICRO-BEAMS WITH TAPERED CROSS SECTION DUYGU İPCİ PROF. DR. BORA YILDIRIM
FONKSİYONEL DERECELENDİRİLMİŞ KONİK KESİTLİ MİKRO-KİRİŞLERİN SERBEST TİTREŞİM ANALİZİ FREE VIBRATION ANALYSIS OF FUNCTIONALLY GRADED MICRO-BEAMS WITH TAPERED CROSS SECTION DUYGU İPCİ PROF. DR. BORA YILDIRIM
Beta ( ) bozunumu Beta Bozunumu 1
 Bta () bozunumu 05.07.008 Bta Bozunumu 1 Bta bozunumu () 1918 yıllında Çkirdklrin ( - ) lktron yayınlanması bilinn bir olaydı. Fakat çkirdğin bir - yakalaması 1938 yıllında bulunmuştur. Boşalan - yrin
Bta () bozunumu 05.07.008 Bta Bozunumu 1 Bta bozunumu () 1918 yıllında Çkirdklrin ( - ) lktron yayınlanması bilinn bir olaydı. Fakat çkirdğin bir - yakalaması 1938 yıllında bulunmuştur. Boşalan - yrin
Kirişli döşemeler (plaklar)
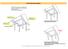 Kirişli döşmlr (plaklar) Dört tarafından kirişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşluklu döşmlr Düznsiz gomtrili döşmlr Üç tarafı kirişli bir tarafı boşta döşm Bir tarafı kirişli
Kirişli döşmlr (plaklar) Dört tarafından kirişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşluklu döşmlr Düznsiz gomtrili döşmlr Üç tarafı kirişli bir tarafı boşta döşm Bir tarafı kirişli
Yuvarlakada Kavşakların Kapasiteleri Üzerine Bir Tartışma *
 İMO Tknik Drgi, 21 4935-4958, Yazı 323 Yuvarlakada Kavşakların Kapasitlri Üzrin Bir Tartışma * Srhan TANYEL* Nadir YAYLA** ÖZ Çalışmada, İzmir d bulunan dört kavşağa ait gözlmlrdn yararlanılarak, çok şritli
İMO Tknik Drgi, 21 4935-4958, Yazı 323 Yuvarlakada Kavşakların Kapasitlri Üzrin Bir Tartışma * Srhan TANYEL* Nadir YAYLA** ÖZ Çalışmada, İzmir d bulunan dört kavşağa ait gözlmlrdn yararlanılarak, çok şritli
TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ
 TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ Cünyt DUMRUL * ÖZ Bu çalışma ticarî dışa açıklık, bklnn döviz kuru, bklnn nflasyon oranı v Türkiy il
TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ Cünyt DUMRUL * ÖZ Bu çalışma ticarî dışa açıklık, bklnn döviz kuru, bklnn nflasyon oranı v Türkiy il
TEST 12-1 KONU ELEKTRİK AKIMI. Çözümlerİ ÇÖZÜMLERİ
 OU 1 T Çözümlr TST 1-1 ÇÖÜ 5. 6 4 1. irncin boyuna bağlı olup olmadığını araştırdığı için ksitlri aynı, boyları farklı tllr kullanılmalıdır. Tllr aynı cins olmalı. u durumda v nolu tllr olmalıdır. 1. -
OU 1 T Çözümlr TST 1-1 ÇÖÜ 5. 6 4 1. irncin boyuna bağlı olup olmadığını araştırdığı için ksitlri aynı, boyları farklı tllr kullanılmalıdır. Tllr aynı cins olmalı. u durumda v nolu tllr olmalıdır. 1. -
Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Denetleyici ile Doğru Akım Motorunun Hız Denetim Performansının İncelenmesi
 Ahmt GANİ/APJES II-I (24) 6-23 Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Dntlyici il Doğru Akım Motorunun Hız Dntim Prformansının İnclnmsi * Ahmt Gani, 2 Hasan Rıza Özçalık, 3 Hakan Açıkgöz,
Ahmt GANİ/APJES II-I (24) 6-23 Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Dntlyici il Doğru Akım Motorunun Hız Dntim Prformansının İnclnmsi * Ahmt Gani, 2 Hasan Rıza Özçalık, 3 Hakan Açıkgöz,
y xy = x şeklinde bir özel çözümünü belirleyerek genel
 Difransil Dnklmlr I / 94 A Aşağıdaki difransil dnklmlrin çözümlrini bulunuz d d -( + ) 7 + n( ) +, () + n ( + ) 4 + - + 5 6 - ( - ) + 8 9 - - + + - ( -) d- ( + ) d + Not: Çözüm mtodu olarak: Tam difdnk
Difransil Dnklmlr I / 94 A Aşağıdaki difransil dnklmlrin çözümlrini bulunuz d d -( + ) 7 + n( ) +, () + n ( + ) 4 + - + 5 6 - ( - ) + 8 9 - - + + - ( -) d- ( + ) d + Not: Çözüm mtodu olarak: Tam difdnk
DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. 4 ADET PARSEL
 DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. İZMİR MENEMEN - SÜZBEYLİ 4 ADET PARSEL Bu taşınmaz dğrlm raporu, Ekiz Kimya Sanayi v Ticart A.Ş. nin istmi üzrin hazırlanmıştır. İlgilisi v hazırlanış
DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. İZMİR MENEMEN - SÜZBEYLİ 4 ADET PARSEL Bu taşınmaz dğrlm raporu, Ekiz Kimya Sanayi v Ticart A.Ş. nin istmi üzrin hazırlanmıştır. İlgilisi v hazırlanış
ÜNİFORM DAİRESEL KESİTLİ BORU AKIŞLARINDA KİNETİK ENERJİ VE MOMENTUM DÜZELTME FAKTÖRLERİNİN DEĞİŞİMİ
 P A M U K K A L E Ü N İ V E R S İ T E S İ M Ü H E N D İ S L İ K F A K Ü L T E S İ P A M U K K A L E U N I V E R S I T Y E N G I N E E R I N G C O L L E G E M Ü H E N D İ S L İ K B İ L İ M L E R İ D E R
P A M U K K A L E Ü N İ V E R S İ T E S İ M Ü H E N D İ S L İ K F A K Ü L T E S İ P A M U K K A L E U N I V E R S I T Y E N G I N E E R I N G C O L L E G E M Ü H E N D İ S L İ K B İ L İ M L E R İ D E R
İ.T.Ü. Makina Fakültesi Mekanik Ana Bilim Dalı Bölüm 7. Seviye Düzlemi
 İTÜ Makina Fakültsi Ağırlığın Potansiyl Enrjisi W=, δh kadar yukarıya doğru yr dğiştirsin, Virtül iş, δu = Wδh= δh NOT: Eğr cisi aşağıya doğru δh yr dğişii yapıyorsa v +h aşağıya doğru is δu = Wδh= δh
İTÜ Makina Fakültsi Ağırlığın Potansiyl Enrjisi W=, δh kadar yukarıya doğru yr dğiştirsin, Virtül iş, δu = Wδh= δh NOT: Eğr cisi aşağıya doğru δh yr dğişii yapıyorsa v +h aşağıya doğru is δu = Wδh= δh
KULLANMA TALİMATI. EXCİPİAL LİPO %4 Emülsiyon Cilt üzerine uygulanır.
 KULLANMA TALİMATI EXCİPİAL LİPO %4 Emülsiyon Cilt üzrin uygulanır. Etkiıı madd: Hr 1 g mülsiyonda 40 rng Ür (Karbamid) içrir. Yardımcı ıııaddlr: Sodyum laktat, Laktik asit, Triklozan, Orta zincirli triglisritlr,
KULLANMA TALİMATI EXCİPİAL LİPO %4 Emülsiyon Cilt üzrin uygulanır. Etkiıı madd: Hr 1 g mülsiyonda 40 rng Ür (Karbamid) içrir. Yardımcı ıııaddlr: Sodyum laktat, Laktik asit, Triklozan, Orta zincirli triglisritlr,
Ruppert Hız Mekanizmalarında Optimum Dişli Çark Boyutlandırılması İçin Yapay Sinir Ağları Kullanımı
 Makin Tknolojilri Elktronik Drgisi Cilt: 6, No: 2, 2009 (-8) Elctronic Journal of Machin Tchnologis Vol: 6, No: 2, 2009 (-8) TEKNOLOJİK ARAŞTIRMALAR www.tknolojikarastirmalar.com -ISSN:304-44 Makal (Articl)
Makin Tknolojilri Elktronik Drgisi Cilt: 6, No: 2, 2009 (-8) Elctronic Journal of Machin Tchnologis Vol: 6, No: 2, 2009 (-8) TEKNOLOJİK ARAŞTIRMALAR www.tknolojikarastirmalar.com -ISSN:304-44 Makal (Articl)
MATEMATİK (LİSE) ÖĞRETMENLİĞİ
 KAMU PERSONEL SEÇME SINAVI MATEMATİK (LİSE) ÖĞRETMENLİĞİ TÜRKİYE GENELİ ÇÖZÜMLER 9 MATEMATİK (LİSE) ÖĞRETMENLİĞİ. A 6. D. C 7. B. C 8. C. B 9. C 5. C. D 6. D. C 7. B. A 8. D. E 9. C. B. A 5. A. B 6. A.
KAMU PERSONEL SEÇME SINAVI MATEMATİK (LİSE) ÖĞRETMENLİĞİ TÜRKİYE GENELİ ÇÖZÜMLER 9 MATEMATİK (LİSE) ÖĞRETMENLİĞİ. A 6. D. C 7. B. C 8. C. B 9. C 5. C. D 6. D. C 7. B. A 8. D. E 9. C. B. A 5. A. B 6. A.
AISI 316L ÇELİĞİNİN İŞLENMESİNDE TAKIM RADYÜSÜ VE KESME PARAMETRELERİNİN TAGUCHİ YÖNTEMİYLE OPTİMİZASYONU
 Gazi Üniv. Müh. Mim. Fak. Dr. Journal of th Faculty of Enginring and Architctur of Gazi Univrsity Cilt 28, No 3, 437-444, 2013 Vol 28, No 3, 437-444, 2013 AISI 316L ÇELİĞİNİN İŞLENMESİNDE TAKIM RADYÜSÜ
Gazi Üniv. Müh. Mim. Fak. Dr. Journal of th Faculty of Enginring and Architctur of Gazi Univrsity Cilt 28, No 3, 437-444, 2013 Vol 28, No 3, 437-444, 2013 AISI 316L ÇELİĞİNİN İŞLENMESİNDE TAKIM RADYÜSÜ
ÇEV-220 Hidrolik. Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT
 ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Türbülanslı Akış Mühendislik uygulamalarında akışların çoğu türbülanslıdır ve bu yüzden türbülansın
ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Türbülanslı Akış Mühendislik uygulamalarında akışların çoğu türbülanslıdır ve bu yüzden türbülansın
DESTEK DOKÜMANI. Mali tablo tanımları menüsüne Muhasebe/Mali tablo tanımları altından ulaşılmaktadır.
 Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
SAĞLIK İLE BÜYÜME GİRİŞ ÖZET ABSTRACT. Yrd. Doç. Dr. İ. Hakan YETKİNER İzmir Ekonomi Üniversitesi
 SAĞLIK İLE BÜYÜME Yrd. Doç. Dr. İ. Hakan YETKİER İzmir Ekonomi Ünivrsitsi [email protected] ÖZET Bu çalışma sağlığın konomik büyüm üzrindki tkilrini inclmktdir. Emğin ürtim katılma tkinliğini blirlyn
SAĞLIK İLE BÜYÜME Yrd. Doç. Dr. İ. Hakan YETKİER İzmir Ekonomi Ünivrsitsi [email protected] ÖZET Bu çalışma sağlığın konomik büyüm üzrindki tkilrini inclmktdir. Emğin ürtim katılma tkinliğini blirlyn
BULANIK MANTIK KONTROLLÜ TERMOELEKTRİK BEYİN SOĞUTUCUSU
 BULANIK MANIK KONROLLÜ ERMOELEKRİK BEYİN SOĞUUCUSU A.Hakan YAVUZ 1, Raşit AHISKA 2,Mahmut HEKİM 3 1Niksar Mslk Yükskokulu,Gaziosmanpaşa Ünivrsitsi Niksar,okat 2knik Eğitim Fakültsi,Elktronik Bilgisayar
BULANIK MANIK KONROLLÜ ERMOELEKRİK BEYİN SOĞUUCUSU A.Hakan YAVUZ 1, Raşit AHISKA 2,Mahmut HEKİM 3 1Niksar Mslk Yükskokulu,Gaziosmanpaşa Ünivrsitsi Niksar,okat 2knik Eğitim Fakültsi,Elktronik Bilgisayar
Makine Öğrenmesi 4. hafta
 ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU
 SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU Vyis SELEN, Ali YARAŞ 2, Cansu YILMAZ 3, M. Şaban TANYILDIZI 4, Dursun ÖZER 5 Fırat Ünivrsitsi Mühndislik Fakültsi Kimya
SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU Vyis SELEN, Ali YARAŞ 2, Cansu YILMAZ 3, M. Şaban TANYILDIZI 4, Dursun ÖZER 5 Fırat Ünivrsitsi Mühndislik Fakültsi Kimya
YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ ÖZET
 YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ LEVENT YILMAZ Istanbul Tknik Ünivrsitsi, İnşaat Fakültsi, Hidrolik v Su Yapıları Kürsüsü, 8626, Maslak, Istanbul. ÖZET
YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ LEVENT YILMAZ Istanbul Tknik Ünivrsitsi, İnşaat Fakültsi, Hidrolik v Su Yapıları Kürsüsü, 8626, Maslak, Istanbul. ÖZET
Malzeme Güvenliği Bilgi Formu (EC) No. 1907/2006 (REACH) Düzenlemesi ile uyumludur Hazırlandığı tarih: 02/03/09 Revize edildiği tarih: 12/11/12
 BÖLÜM 1. MADDENİN/KARIŞIMIN VE FİRMANIN/İŞLETMENİN TANIMI 1.1 Ürün kimliği: EB25SS Ticari isim: Ekstra Güçlü Pisuar Kapakları 1.2 Maddnin vya karışımın blirtiln ilgili kullanımları v blirtiln kullanımlara
BÖLÜM 1. MADDENİN/KARIŞIMIN VE FİRMANIN/İŞLETMENİN TANIMI 1.1 Ürün kimliği: EB25SS Ticari isim: Ekstra Güçlü Pisuar Kapakları 1.2 Maddnin vya karışımın blirtiln ilgili kullanımları v blirtiln kullanımlara
Magnetic Materials. 4. Ders: Paramanyetizma-2. Numan Akdoğan.
 Mgntic Mtrils 4. Drs: Prmnytizm-2 Numn Akdoğn [email protected] Gbz Institut of Tchnology Dprtmnt of Physics Nnomgntism nd Spintronic Rsrch Cntr (NASAM) Kuntum mkniği klsik torinin özlliklrini dğiştirmdn,
Mgntic Mtrils 4. Drs: Prmnytizm-2 Numn Akdoğn [email protected] Gbz Institut of Tchnology Dprtmnt of Physics Nnomgntism nd Spintronic Rsrch Cntr (NASAM) Kuntum mkniği klsik torinin özlliklrini dğiştirmdn,
ALTI TEKERLEKLİ TAŞITIN DİNAMİK ANALİZİ
 Altı krlkli aşıtın Dinamik Analizi HAVACILIK VE UZAY EKNOLOJİLERİ DERGİSİ EMMUZ 5 CİL SAYI (1-14) ALI EKERLEKLİ AŞIIN DİNAMİK ANALİZİ Cihan DEMİR Yıldız knik Ünivrsitsi, Makin Fakültsi, Makin Mühndisliği
Altı krlkli aşıtın Dinamik Analizi HAVACILIK VE UZAY EKNOLOJİLERİ DERGİSİ EMMUZ 5 CİL SAYI (1-14) ALI EKERLEKLİ AŞIIN DİNAMİK ANALİZİ Cihan DEMİR Yıldız knik Ünivrsitsi, Makin Fakültsi, Makin Mühndisliği
5. SANTRİFÜJ POMPALARDA TEORİK ESASLAR
 5. SANTRİFÜJ POMPALARDA TEORİK ESASLAR 5.6. Santrifüj Pompalarda Karaktristik Eğrilr Santrifüj pompalar, pistonlu pompalardan farklı olarak sabit bir işltm hızında, pompa ölçülrind, proj dğrlrin v mm koşullarına
5. SANTRİFÜJ POMPALARDA TEORİK ESASLAR 5.6. Santrifüj Pompalarda Karaktristik Eğrilr Santrifüj pompalar, pistonlu pompalardan farklı olarak sabit bir işltm hızında, pompa ölçülrind, proj dğrlrin v mm koşullarına
Hücre bölünmesi sırasında önce... sonra... bölünmesi gerçekleşir.
 2.Mitoz Hücr Bölünmsi Hücr bölünmsi tüm canlılarda görüln bir olaydır. Hücr bölünmsi büyüm, glişm, yaraların iyilşmsi, ürm hücrlrinin oluşması v tk hücrli canlıların çoğalması olaylarında tkilidir. Bir
2.Mitoz Hücr Bölünmsi Hücr bölünmsi tüm canlılarda görüln bir olaydır. Hücr bölünmsi büyüm, glişm, yaraların iyilşmsi, ürm hücrlrinin oluşması v tk hücrli canlıların çoğalması olaylarında tkilidir. Bir
Cevap: B. x + y = 5 ve y + z = x = 3z y. x + y = 5 z + y = 3 x t = 2 bulunur. 7x 9y = y 3x 10x = 8y. 3/ 3y = x + z 15k = 4k + z + Cevap: B
 6 LYS/MAT MATEMATİK ÇÖZÜMLERİ DENEME. ( ab) ( ab) 6( ab) 6. 6 y z ( ab) ( ab) 6( ab) 6 6 6y y z 6y ( ab) 6 6( y) ( y z) ab.. olur. y v y z. 7 z y / y z k k z y z y t bulunur. 7 9y y 8y k, y k zk A) y 8,
6 LYS/MAT MATEMATİK ÇÖZÜMLERİ DENEME. ( ab) ( ab) 6( ab) 6. 6 y z ( ab) ( ab) 6( ab) 6 6 6y y z 6y ( ab) 6 6( y) ( y z) ab.. olur. y v y z. 7 z y / y z k k z y z y t bulunur. 7 9y y 8y k, y k zk A) y 8,
BÖLÜM 5 SANKİ-BİR-BOYUTLU AKIMLAR
 BÖLÜ 5 SNKİ-BİR-BOYULU KILR 5.- Giriş 5.- kımı yönn dnklmlr 5.3- Hugonio alan-hız bağınısı 5.4- Kalorik mükmml bir gazın dğişkn ksili kanalda izanroik akımı 5.5- Yakınsak-ıraksak lül içind izanroik akım
BÖLÜ 5 SNKİ-BİR-BOYULU KILR 5.- Giriş 5.- kımı yönn dnklmlr 5.3- Hugonio alan-hız bağınısı 5.4- Kalorik mükmml bir gazın dğişkn ksili kanalda izanroik akımı 5.5- Yakınsak-ıraksak lül içind izanroik akım
doldurulması sırasında yayınlanan karakteristik X-ışınlarını bulması
 BETA () BOZUNUMU Çkirdklrin lktron yayınlamaları yy ilk gözlnn radyoaktif olaylardan birisidir. Çkirdğin atom lktronlarından birisini yakalaması, 1938 d Amrikalı fizikci Luis Waltr Alvarz in çkirdk k tarafından
BETA () BOZUNUMU Çkirdklrin lktron yayınlamaları yy ilk gözlnn radyoaktif olaylardan birisidir. Çkirdğin atom lktronlarından birisini yakalaması, 1938 d Amrikalı fizikci Luis Waltr Alvarz in çkirdk k tarafından
IKTI Mayıs, 2012 Gazi Üniversitesi-İktisat Bölümü DERS NOTU 08
 DERS NOTU 08 TOPLAM ARZ EĞRİSİ (AS) VE DENGE ENFLASYON- İŞSİZLİK VE PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE
DERS NOTU 08 TOPLAM ARZ EĞRİSİ (AS) VE DENGE ENFLASYON- İŞSİZLİK VE PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE
Hizmet Kalitesinin Servqual Metodu İle Ölçümü ve Sonuçların Yapısal Eşitlik Modelleri İle Analizi: Öğretmen Evi Uygulaması
 19 Hizmt Kalitsinin Srvqual Mtodu İl Ölçümü v Sonuçların Yapısal Eşitlik Modllri İl Analizi: Öğrtmn Evi Uygulaması Sülyman Ersöz, Mhmt Pınarbaşı, A.Kürşad TÜRKER, Mustafa YÜZÜKIRMIZI Endüstri Mühndisliği
19 Hizmt Kalitsinin Srvqual Mtodu İl Ölçümü v Sonuçların Yapısal Eşitlik Modllri İl Analizi: Öğrtmn Evi Uygulaması Sülyman Ersöz, Mhmt Pınarbaşı, A.Kürşad TÜRKER, Mustafa YÜZÜKIRMIZI Endüstri Mühndisliği
KANUN TOHUMCULUK KANUNU. Kanun No. 5553 Kabul Tarihi : 31/10/2006 BİRİNCİ BÖLÜM. Amaç, Kapsam ve Tanımlar
 8 Kasım 2006 ÇARŞAMBA Rsmî Gazt Sayı : 26340 KANUN TOHUMCULUK KANUNU Kanun No. 5553 Kabul Tarihi : 31/10/2006 Amaç BİRİNCİ BÖLÜM Amaç, Kapsam v Tanımlar MADDE 1 Bu Kanunun amacı; bitkisl ürtimd vrim v
8 Kasım 2006 ÇARŞAMBA Rsmî Gazt Sayı : 26340 KANUN TOHUMCULUK KANUNU Kanun No. 5553 Kabul Tarihi : 31/10/2006 Amaç BİRİNCİ BÖLÜM Amaç, Kapsam v Tanımlar MADDE 1 Bu Kanunun amacı; bitkisl ürtimd vrim v
OLASILIK ve ÝSTATÝSTÝK ( Genel Tekrar Testi-1) KPSS MATEMATÝK. Bir anahtarlıktaki 5 anahtardan 2 si kapıyı açmak - tadır.
 OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
HİDROLİK. Yrd. Doç. Dr. Fatih TOSUNOĞLU
 HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
kirişli döşeme Dört tarafından kirişlere oturan döşemeler Kenarlarının bazıları boşta olan döşemeler Boşluklu döşemeler Düzensiz geometrili döşemeler
 Kirişli döşmlr Dört tarafından irişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşlulu döşmlr Düznsiz gomtrili döşmlr bir tarafı irişli üç tarafı boşta döşm (Konsol döşm) Đi tarafı irişli ii
Kirişli döşmlr Dört tarafından irişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşlulu döşmlr Düznsiz gomtrili döşmlr bir tarafı irişli üç tarafı boşta döşm (Konsol döşm) Đi tarafı irişli ii
MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ
 Onuncu Ulusal Kimya Mühndisliği Kongrsi, 3-6 Eylül 1, Koç Ünivrsitsi, İstanbul MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ İlkr KIPÇAK, Turgut Giray ISIYEL Eskişhir Osmangazi
Onuncu Ulusal Kimya Mühndisliği Kongrsi, 3-6 Eylül 1, Koç Ünivrsitsi, İstanbul MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ İlkr KIPÇAK, Turgut Giray ISIYEL Eskişhir Osmangazi
BİLEŞENLER. Demiryolu Araçları için yüksek hızlı DC devre kesiciler Tip UR6, UR10 ve UR15
 İLŞNLR miryolu raçları için yüksk hızlı dvr ksicilr Tip R, R v R Gnl bilgi R, R v R; doğal soğutmalı, açmasız, tk kutuplu, çift yönlü, lktromanytik üflmli, lktrik kontrol dvrlrin v doğrudan aşırı akım
İLŞNLR miryolu raçları için yüksk hızlı dvr ksicilr Tip R, R v R Gnl bilgi R, R v R; doğal soğutmalı, açmasız, tk kutuplu, çift yönlü, lktromanytik üflmli, lktrik kontrol dvrlrin v doğrudan aşırı akım
AÇIK KANAL AKIMLARINDA HIZ DAĞILIMININ ENTROPY YÖNTEMİ İLE İNCELENMESİ. Mehmet Ardıçlıoğlu. Ali İhsan Şentürk. Galip Seçkin
 AÇIK KANAL AKILARINDA HIZ DAĞILIININ ENTROPY YÖNTEİ İLE İNCELENESİ ehmet Ardıçlıoğl Yard. Doç. Dr., Erciyes Üniv. ühendislik Fak. İnşaat üh. Böl. Kayseri, Tel: 352 4378, Fax: 9 352 4375784 E-mail: [email protected]
AÇIK KANAL AKILARINDA HIZ DAĞILIININ ENTROPY YÖNTEİ İLE İNCELENESİ ehmet Ardıçlıoğl Yard. Doç. Dr., Erciyes Üniv. ühendislik Fak. İnşaat üh. Böl. Kayseri, Tel: 352 4378, Fax: 9 352 4375784 E-mail: [email protected]
Günlük Bülten. 27 Aralık 2012. Merkez Bankası Baş Ekonomisti Hakan Kara 2012 yılının %6 civarında enflasyonla tamamlanacağını düşündüklerini söyledi
 27 Aralık 2012 Prşmb Günlük Bültn İMKB vrilri İMKB 100 77,991.1 Piyasa Dğri-TÜM ($m) 304,387.4 Halka Açık Piyasa Dğri-TÜM ($m) 87,677.3 Günlük İşlm Hami-TÜM ($m) 1,243.42 Yurtdışı piyasalar Borsalar Kapanış
27 Aralık 2012 Prşmb Günlük Bültn İMKB vrilri İMKB 100 77,991.1 Piyasa Dğri-TÜM ($m) 304,387.4 Halka Açık Piyasa Dğri-TÜM ($m) 87,677.3 Günlük İşlm Hami-TÜM ($m) 1,243.42 Yurtdışı piyasalar Borsalar Kapanış
SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU
 SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU A. ÖZER, D.ÖZER Fırat Ünivrsitsi, Mühndislik Fakültsi, Kimya Mühndisliği Bölümü. 23279-ELAZIĞ ÖZET Bu çalışmada, sülfürik
SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU A. ÖZER, D.ÖZER Fırat Ünivrsitsi, Mühndislik Fakültsi, Kimya Mühndisliği Bölümü. 23279-ELAZIĞ ÖZET Bu çalışmada, sülfürik
GİRİŞİMCİ WEB SAYFALARININ DEĞERLENDİRİLMESİNDE BULANIK BİLİŞSEL HARİTALAMA YÖNTEMİNİN KULLANIMI
 EKEV AKADEİ DERGİSİ Yıl: 14 Sayı: 44 (Yaz 2010) 335 GİRİŞİCİ WEB SAYFALARININ DEĞERLENDİRİLESİNDE BULANIK BİLİŞSEL HARİTALAA YÖNTEİNİN KULLANII. Dursun KAYA (*) A. Samt HAŞILOĞLU (**) Slçuk Burak HAŞILOĞLU
EKEV AKADEİ DERGİSİ Yıl: 14 Sayı: 44 (Yaz 2010) 335 GİRİŞİCİ WEB SAYFALARININ DEĞERLENDİRİLESİNDE BULANIK BİLİŞSEL HARİTALAA YÖNTEİNİN KULLANII. Dursun KAYA (*) A. Samt HAŞILOĞLU (**) Slçuk Burak HAŞILOĞLU
300 = Ders notlarındaki ilgili çizelgeye göre; kömür için üst kaplama kalınlığı 4 mm, alt kaplama kalınlığı 2 mm olarak seçilmiştir.
 Soru-) Eğii, uzunluğu 50 olan dsandr y bant konvyör kurularak bununla saatt 300 ton tüvönan taş köürü taşınacaktır. Bant konvyörü boyutlandırınız. Kabullr: Bant hızı :,5 /s Köür yoğunluğu : 0,9 ton/ 3
Soru-) Eğii, uzunluğu 50 olan dsandr y bant konvyör kurularak bununla saatt 300 ton tüvönan taş köürü taşınacaktır. Bant konvyörü boyutlandırınız. Kabullr: Bant hızı :,5 /s Köür yoğunluğu : 0,9 ton/ 3
Eğitim-Öğretim Yılı Güz Dönemi Diferansiyel Denklemler Dersi Çalışma Soruları 1
 006-007 Eğitim-Öğrtim Yılı Güz Dönmi Difransil Dnklmlr Drsi Çalışma Soruları 1 1) d/dt +sint difransil dnklmini çözünüz. ) (4+t)d/dt + 6+t difransil dnklmini çözünüz. ) d/dt-7 difransil dnklmini (0)15
006-007 Eğitim-Öğrtim Yılı Güz Dönmi Difransil Dnklmlr Drsi Çalışma Soruları 1 1) d/dt +sint difransil dnklmini çözünüz. ) (4+t)d/dt + 6+t difransil dnklmini çözünüz. ) d/dt-7 difransil dnklmini (0)15
