Yrd. Doç. Dr. Levent Çetin. Alternatif Gerilim. Alternatif Akımın Fazör Olarak İfadesi. Temel Devre Elemanlarının AG Etkisi Altındaki Davranışları
|
|
|
- Can Dikmen
- 9 yıl önce
- İzleme sayısı:
Transkript
1 Yrd. Doç. Dr. Levent Çetin İçerik Alternatif Gerilim Faz Kavramı ın Fazör Olarak İfadesi Direnç, Reaktans ve Empedans Kavramları Devresinde Güç 2
2 Alternatif Gerilim Alternatif gerilim, devre üzerindeki akış yönü ve gerilim değeri zamana göre değişen gerilim çeşididir. Elde edilişinin, mekanik enerjiye çevrilmesinin kolay ve verimli olması, iletim esnasında daha az kayıp olması gibi ilk konuda sıralanan sebeplerden şebeke gerilimi alternatif gerilimdir. 3 Alternatif Gerilim 4
3 Alternatif Gerilim Şebekede kullanılan geriliminin değişimi bir sinüs fonksiyonu ile belirlenmiştir. V AG ( t ) = V max sin( 2π ft ) Bu denklem incelendiğinde alternatif gerilimin temel parametreleri olarak; a)f salınımı (frekans) b)v max en büyük gerilim değeri (genlik) göze çarpar. Frekans ya da salınım, dalgalı bir değişim olduğu durumda, gözlemlenen etkinin birim zaman içerisinde kaç kere kendini tekrar ettiğini gösteren büyüklüktür. Bu değer şebeke gerilim için Türkiye de 50 Hertzdir. (Frekans (salınım) birimi Hertz olsa da 1/s de kullanılmaktadır). Salınım değerinin tersi periyot olarak adlandırılır. Periyot kendi kendini tekrar eden sinyalerden bir tanesinin süresidir. Bu değer yine şebeke için 0.02 (1/50) saniyedir. Şebeke Gerilimi 5 Alternatif Gerilim 6
4 Alternatif Gerilim Alternatif gerilimin en büyük değeri veya genliği, sinüs sinyalinin yukarıda tanımlanmış periyot süresi içerisinde aldığı en büyük değeri belirtir. Bu değer şebeke için yaklaşık 311 Volt dur. Fakat bu genlik değeri anma değeri olarak çok yaygın kullanılmaz. Bunun yerine bu sinüs fonksiyonun etkin değeri (rms) kullanılır. Bu değer söz konusu alternatif gerilimin doğru gerilim eşdeğeri olarak görülebilir. Bir sinyalin etkin değeri aşağıdaki ifade ile bulunur. f RMS ( t) = 1 T T 0 f 2 ( t) dt V V = max RMS. 707 V 2 0 max Şebeke gerilimi için bu değer en büyük genliğin yaklaşık ile çapımı ile bulunur ve 220 Volt dur. 7 Faz Kavramı Zaman ile değişen iki fiziksel büyüklüğü ifade eden fonksiyonlar ile işlem yaparken dikkat edilmesi gereken noktalardan birisi sinyallerin senkron olup olmadığıdır. Elektriksel büyüklükler söz konusu olduğunda iki gerilim sinyali, iki akım sinyali ve ya bir gerilim sinyali ile bir akım sinyali arası ilişki iki türlü olabilir: Senkron ve ya faz farklı. İki sinyal eğer senkron ise aynı anda sıfır noktasından geçip aynı anda en büyük değerlerini alıyorlar demektir. 8
5 Faz Kavramı Faz kavramı ise senkronizasyonun olmadığı durumu ifade etmektedir. Buna göre iki sinyal bir birinden farklı zamanlarda sıfır noktasından geçip farkllı anlarda en büyük değerlerine ulaşmaktadır. İki sinyal arasındaki bu zamanlama farkına kayma denir. Bu durum sinüsoidal fonksiyonlarda faz ve ya faz kayması olarak adlandırılır ve derece ile ifade edilir. Faz ifadesi daha dar anlamda elektriksel büyülükler için, iki sinüs(oidal) sinyalin referans kabul edileni sıfır noktasına ulaştığı anda diğer sinyalin hangi açı değerinde olduğunu gösterir. Buna göre ve 0 derece faz farkına sahip sinyaller şekil üzerinde gösterilmiştir. 9 Faz Kavramı 10
6 ın Fazör Olarak İfadesi Buraya kadar anlatılanlardan görüleceği üzere devre üzerinde alternatif gerilim veya akımın net bir şekilde ifade edilebilmesi için üç büyüklüğün bilimesi gerekir. Bunlar frekans, genlik ve fazıdır. Frekans elektrik şebekesi üzerinde sabit bir değer olduğu için hangi ülkede olduğumuzu bilmemiz durumunda sabit bir değer olarak görülecektir. Böylelikle alternatif gerilim/akım fonksiyonlarının iki önemli fiziksel büyüklüğe bağlı ifadesi mümkün olur. Bu büyüklükleri net olarak ifade eden bir fiziksel matematiksel modelleme alternatif akım/gerilim büyüklüklerinin dönen vektörler (fazörler) ile gösterilmesidir. 11 ın Fazör Olarak İfadesi Şekilde görüldüğüüzere bir kartezyen koordinat eksenin orijini etrafında dönen bir vektörün dikey eksen üzerindeki izdüşümü sinüs fonksiyonunu verir. Bu gösterimde dönen vektörün uzunluğu (şiddeti) alternatif gerilimin genliğini ifade eder. Benzer şekilde vektörün herhangi bir anda yatay eksen ile yaptığı açıda faz değerini gösterir. Alternatif gerilimin frekansı ise bu dönen vektörün açısal hızını belirlemektedir. 12
7 ın Fazör Olarak İfadesi 13 ın Fazör Olarak İfadesi Alternatif gerilimin döner vektör şeklinde soyutlamasının matematiksel ifadesi karmaşık sayılardır. Bilindiği üzere karmaşık sayılar, reel ve sanal olmak üzere iki kısımdan oluşurlar ve karmaşık düzlemde gösterilirler. Genel gösterimleri kartezyen ifade ile aşağıda 1. denklemde verilmiştir. Lakin dönen vektör yani fazör şeklinde daha uygun olan gösterim de elektriksel devrelerin analizinde kullanılır denklem, 2 numaralı olandır. z a + bi = (1) z = r ϕ (2) 14
8 ın Fazör Olarak İfadesi z = a + bi z = r ϕ 1 b = tg ( ) a 2 2 ϕ r = a + b 15 ın Fazör Olarak İfadesi Karmaşık sayılarda dört işlem aşağıdaki şekilde yapılır. z + z = a + a ) + ( b b ) i 1 2 ( z z = a a ) + ( b b ) i 1 2 ( z 1 z2 = r1 r2 ϕ 1 + ϕ 2 z 1 z2 = r1 r2 ϕ1 ϕ2 Karmaşık sayıların aritmetiğinin alternatif gerilim/akım sinyallerine uygulanması ile ilgili temel uygulama, farklı faza sahip gerilim/akım kaynaklarının bir arada yarattığı etkinin incelenmesidir. Bu etkiyi çözümlemeden önce iki faz farklı sinyalin döner vektörler cinsinden bir birlerine durumunu anlamız gerekir. Bu ilişki basit olarak başlangıçnoktası aynı fakat yatay ile yaptıkları açı farklı vektörler şeklinde betimlenir. 16
9 ın Fazör Olarak İfadesi 17 ın Fazör Olarak İfadesi Birbirine bağlı gerilim/akım kaynaklarının bir arada yarattığı etki karmaşık sayılarda toplama ve çıkarma işlemleri ile belirlenir. 18
10 1 2 3 Direnç (R) Bobin (L) (Endüktans) Kapasitans (C) (Kondansatör) 19 Direnç (R) Alternatif gerilimin etkisi altındaki direnç, Ohm kanunun bilinen ifadesini korur. V V = V max sin( wt) R = Vmax I = sin( wt) I R Denklemlerden elde edilen sonuç gösterir ki bir direnç üzerine düşen gerilim ile akım arasında faz farkı yoktur. Sadece genlik Ohm kanuna uygun şekilde değişir. V = V P = V max max sin( wt )[V], I = I 2 I sin ( wt )[W] max max sin( wt )[A] 20
11 Bobin (L) (Endüktans) Alternatif gerilimin etkisi altındaki bobinler, dirençten farklı olarak akımın değişimine karşı bir direnç etkisi gösterirler. Üzerlerine düşen gerilim (bobinin iki ucu arasında ölçülen) Lenz Kanuna uygun olarak bulunur. di ( t ) Nµ A V ( t ) = L, L = dt l Bu ifadeyi alternatif akımı göz önüne alarak incelersek bir bobinin üzerinde düşen gerilim ile ilişkisini tahmin edebiliriz. 21 Bobin (L) (Endüktans) Alternatif gerilimin etkisi altındaki bobinler, dirençten farklı olarak akımın değişimine karşı bir direnç etkisi gösterirler. Üzerlerine düşen gerilim (bobinin iki ucu arasında ölçülen) Lenz Kanuna uygun olarak bulunur. di(t) V (t) = L dt Bu ifadeyi alternatif akımı göz önüne alarak incelersek bir bobinin üzerinde düşen gerilim ile ilişkisini tahmin edebiliriz. V(t) = V max sin(wt) I(t) = Imax cos( wt) (t) = I sin( wt 90) max 22
12 23 Bu sonuç bize gösterir ki bobinin üzerine düşen gerilim ile akım arasında 90 derece faz farkı vardır. Gerilim akımın 90 derece önündedir. Bu faz farkının doğal sonucu olarak elektriksel güç negatif/pozitif olmaktadır. Negatif güç ifadesi bobinin devreye güç aktardığını göstermektedir. Bobinlerin direnci zamana alternatif gerilimin frekansına bağlı olarak değişmektedir. Bunun için buna reaktans (Endüktif reaktans X L ) denmektedir. X L = wl X L = 2πfL 24
13 Reaktans ifadesi kullanılarak Ohm kanunu alternatif akım devrelerine kolayca uygulanabilir. Bu durumda sadece skaler sayılar yerine karmaşık sayılar ile hesap yapmak gerekecektir. XL = 2π = Ω V X = I I = Bu devreye 5 ohm luk bir direnç ekleyerek, direnç ve bobinin birlikte yarattığı karşı koyma etkisini hesaplayalım. V X 10 = = A Direnç değeri: R = jω Bobinin endüktif reaktansı X L = jω Bu iki etkinin bir arada ifadesine empedans denir. Z = R + XL = jω = Ω Genel anlamda alternatif gerilim devrelerinde direnç etkisinin karşılığı olarak kullanılır. Yukarıda da verildiği üzere Ohm kanununda direnç ifadesinin yerine kullanılır. 26
14 V Z = I Z = R + X = jω = Ω L 10 0Ω I = = A Ω 27 28
15 Paralel devre 29 İlk durum: 30
16 Ohm kanunu uygulandığında; 31 Ohm kanunu uygulandığında; 32
17 Paralel devrede empedans denklemi, 33 Kondansatör (Kapasitans) Alternatif gerilimin etkisi altındaki kondansatörler, üzerlerine düşen gerilimin değişmine bağlı tepki verirler, eğer kondansatör uçlarına, üzerinde mevcut olan gerilimden daha düşük bir gerilim uygulanırsa, kondansatör devreye akım sağlar, (deşarj olur), eğer kondansatör uçlarına, üzerinde mevcut olan gerilimden daha büyük bir gerilim uygulanırsa, kondansatör devreden akım çeker (Şarj olur). Bu bilgi ışığında kondansatörün akımı ve üzerindeki gerilim arasındaki ilşki aşağıdaki gibi verilir. dv( t) i( t) = C dt 34
18 35 Bu sonuç bize gösterir ki kondansatörün üzerine düşen gerilim ile akım arasında 90 derece faz farkı vardır. Akım gerilimin 90 derece önündedir. Bu faz farkının doğal sonucu olarak elektriksel güç negatif olmaktadır. Negatif güç ifadesi kondansatörün devreye güç aktardığını (deşarj olduğunu) göstermektedir. Kondansatörlerin direnci zamana alternatif gerilimin frekansına bağlı olarak değişmektedir. Kondansatörler gerlimdeki değişimler (frekans) arttıkça daha fazla akım geçirirler Bunun için buna kapasitans (kapasitiftif reaktans X c ) denmektedir. 1 X c = wc 1 X L = 2πfC 36
19 Yandaki devre yardımıyla kondansatörlerin alternatif gerilim etkisi altındaki davranışını matematiksel olarak inceleyelim. Kapasitif reaktans denklemi ve Ohm yasasının alternatif gerlime uygulamasından yararlanarak devreden akan akım bulunur. 37 Devre üzerinden akan alternatif akımın fazı, gerilimin 90 derece önünde olacaktır. Bu dikkate alınarak devredeki direnç etkisi bulunur. 38
20 Bu devreye 5 ohm luk bir direnç ekleyerek, direnç ve bobinin birlikte yarattığı karşı koyma etkisini hesaplayalım. Devredeki toplam karşı koyma etkisi; X c = j Ω R = j Ω Z = R + X = j Ω = c olarak bulunur. 39 Devreden geçen akım ise Ohm kanunun alternatif devreye uyarlanması ifadesinden bulunur. Burada kritik nokta gerilim kaynağının fazıdır. Bu tip devre analizlerinde bu değer hep 0 kabul edilir. Fark edildiği üzere seri kondansatör direnç devresinde akım, gerilimin derece önündedir. Sadece kondansatör kullanılan devrede bu değer 90 dereceydi. 40
21 Devre çözümü tablo yöntemi ile; Son tabloda direnç ve kondansatör hakkında bildiklerimizi gözden geçirelim. Direnç üzerine düşen akım ile gerilim aynı fazdadır fakat kondansatör üzerinde düşen gerilim akımın 90 derece önündedir. 41 Paralel direnç kondansatör devresi 42
22 43 44
23 Direnç, Reaktans ve Empedans Kavramları Bu noktaya kadar yapılan devre analizlerinde akıma karşı koyma etkisini 3 farklı şekilde adlandırdık. Direnç; ifadesi iletken içerisindeki elektron hareketinin karşılaştığı sürtünmeyi ifade eder. Sembolü R, birimi Ω Ohm dur. Direnç etkisi akım ile gerilim arasında bir faz farkı oluşturmaz. Reaktans; ifadesi elektronların ataletini (eylemsizliğini) belirtir. Bu etki gerilim ve akım değerlerinde değişim olduğunda, başka bir deyişle elektrik alan ve manyetik alan oluşumu söz konusu olduğunda ortaya çıkar. Kondansatör ve bobin bu etkinin en belirgin olduğu devre elemanlarıdır. Reaktans etkisi olduğunda akım ile gerilim arasında 90 derece faz farkı oluşur. Eğer söz konusu elaman bobin ise gerilim akımdan 90 derece ileri fazdadır, eğer kondansatör ise akım gerilimden 90 derece ileri fazdadır. 45 Direnç (R) Bobin (L) (Endüktans) Kapasitans (C) (Kondansatör) 46
24 Empedans ifadesi, bir elektrik devresinde akıma gösterilen zorluğun yani elektron hareketine karşı koyma etkisinin genel ifadesidir. Devredeki tüm elemanların direnç ve reaktans etkilerinin toplamını ifade eder. Empedans doğru akım devresindeki direnç etkisinin alternatif akım devresindeki tam karşılığıdır. Buna göre değiştirilmiş Ohm kanunu ifadesi aşağıda verildiği gibidir. Burada dikkat edilmesi gereken nokta tüm büyüklüklerin karmaşık sayı olduğudur. Z = Ohm kanunu gibi diğer devre analizi kanunları, Kirrchhoff gerilim ve akım yasaları, şebeke teoremleri de ifadeler karmaşık sayı olmak koşulu ile alternatif akım devrelerinde de aynen geçerlidir. Alternatif akım devrelerinde temel fark güç hesabında ortaya çıkmaktadır. Bu konu bir sonraki bölümde incelenecektir. V I 47 Seri RLC devreleri 48
25 49 50
26 Burada dikkat çeken durum kondansatör üzerine düşen gerilimin genliğinin devreye uygulanan gerilimin genliğinden yüksek olduğudur. Bunun sebebi kondansatör ve bobinin reaktanslarının birbirine ters etkisidir. Tüm devredeki empedans etkisi tek tek elemanların empedans etkilerinden daha küçük olmaktadır. Bu durum elemanların üzerine, bu gibi yüksek gerilimlerin düşmesine sebep olmaktadır. Fakat bu sonuç devredeki gerilimlerin toplamının, Kirchhoff un gerilim yasası gereği 0+0j olması durumunu değiştirmez. 51 Paralel RLC 52
27 53 54
28 Seri Paralel Karışık devreler 55 Fakat bu karmaşık devrede empedans hesabı kademe kademe yapılmalıdır. Önce C 2 ve L nin seri bağlı olduğu devre yolu ondan sonra bunlara paralel direnç ve en son da seri kondansatörün etkileri bir araya getirilmelidir. 56
29 57 58
30 59 Devresinde Güç Hesabı Yukarıda verilen devre analizlerinde alternatif akım devrelerinde akım ile gerilim arasında bir faz farkı olduğunu gördük. Bunun sebebinin karmaşık sayı ile ifade edilen empedans olduğu belirtildi. Alternatif akım devresinde güç hesabı yapılırken yine empedans ifadesi esas alınarak üç farklı tanım yapılır. Bunlar sırasıyla devredeki direnç etkisine istinaden bulunan gerçek (yada rezistif) güç: 60
31 Devresinde Güç Hesabı Devredeki reaktans etkisine istinaden bulunan reaktif (zahiri) güç: Bu etkinin bir arada ifadesi olan empedansa istinaden bulunan görünen güç: 61 Devresinde Güç Hesabı Verilen ifadelerde hep skaler hesaplamalar yapılmaktadır. Bulunan değerleri devredeki faz farkını ve direnç ile reaktans arasındaki 90 derecelik yön farkını hesaba katarak çizmeye çalıştığımızda bir dik üçgen elde deriz. Bu üçgene, güç üçgeni denir. Bu üçgende görüleceği üzere alternatif akım devresinde gücün bir kısmı kaybolmaktadır. Devre ancak gerçek güç ifadesi kadar işe yarar güç üretebilmektedir. Devredeki gerçek güç ile görünen güç arasındaki oran, güç faktörü (cosφ) olarak adlandırılmaktadır. Bu değer sadece direnç bulunan devrelerde birdir. Reaktans olan devrelerde 0 ila 1 arasında herhangi bir değer alabilir. 62
32 Devresinde Güç Hesabı Bu etkiyi incelemek için şekildeki devreyi ele alalım. Devrenin güç faktörü verile ifade yardımıyla bulunur. 63 Devresinde Güç Hesabı Bulunan değer bize şebekeden çekilen gücün yaklaşık % 70.5 inin işimize yaradığını söylemektedir. Bu doğal olarak istenmeyen bir şeydir. Bu yüzden devreler tasarlanırken güç faktörünün bire yakın olmasına dikkat edilir. Bunun için devredeki kapasitif reaktans ve endüktif reaktans değerlerinin yaklaşık aynı değerlerde olması sağlanmaya çalışılır. Eğer bu mümkün olmaz ise devreye dışarıdan kondansatör veya bobin eklenerek güç faktörü 1 e yaklaştırılır. Bu işleme kompanzasyon denir. Bir önceki aşamada hesapladığımız devreyi ele alalım Devrenin reaktansını bulalım. 64
33 Devresinde Güç Hesabı Devredeki reaktans, indüktiftir yani bobinden kaynaklanmaktadır. Bunu kompanze edebilmek için devreye bir kondansatör ekleyelim. Hesaplanan reaktansın aynısını ters yönde oluşturabilecek kondansatör değeri aşağıdaki hesap ile bulunur. 65 Devresinde Güç Hesabı Bulunan kondansatör değeri standart bir değer olmadığı için en yakın değer olan 22uF bir kondansatörü devreye paralel takıp sonucu inceleyelim. Yeni devrenin empedansı: 66
34 Devresinde Güç Hesabı Ve buna göre güç faktörü: Görüldüğü gibi devrede yapılan değişklik sonucu güç faktörü bire yakınlaştı. Buna paralel olarak devreden geçen toplam akım da düştü. Bu iki özellik tasarlanan sistemin hem verimlilik hem de ekonomik açıdan dah ugun hale geldiğini göstermektedir. 67
Alternatif Akım. Yrd. Doç. Dr. Aytaç Gören. Alternatif Akım
 Yrd. Doç. Dr. Aytaç Gören Paralel devre 2 İlk durum: 3 Ohm kanunu uygulandığında; 4 Ohm kanunu uygulandığında; 5 Paralel devrede empedans denklemi, 6 Kondansatör (Kapasitans) Alternatif gerilimin etkisi
Yrd. Doç. Dr. Aytaç Gören Paralel devre 2 İlk durum: 3 Ohm kanunu uygulandığında; 4 Ohm kanunu uygulandığında; 5 Paralel devrede empedans denklemi, 6 Kondansatör (Kapasitans) Alternatif gerilimin etkisi
Alternatif Akım. Alternatif Akım. Yrd. Doç. Dr. Aytaç Gören (MAK4075 Notları)
 09.10.2012 (MAK4075 Notları) Yrd. Doç. Dr. Aytaç Gören İçerik Alternatif Gerilim Faz Kavramı ın Fazör Olarak İfadesi Direnç, Reaktans ve Empedans Kavramları Devresinde Güç 2 Alternatif Gerilim Alternatif
09.10.2012 (MAK4075 Notları) Yrd. Doç. Dr. Aytaç Gören İçerik Alternatif Gerilim Faz Kavramı ın Fazör Olarak İfadesi Direnç, Reaktans ve Empedans Kavramları Devresinde Güç 2 Alternatif Gerilim Alternatif
Temel Devre Elemanlarının Alternatif Gerilim Etkisi Altındaki Davranışları
 Temel Devre Elemanlarının Alternatif Gerilim Etkisi Altındaki Davranışları Direnç (R) Alternatif gerilimin etkisi altındaki direnç, Ohm kanunun bilinen ifadesini korur. Denklemlerden elde edilen sonuç
Temel Devre Elemanlarının Alternatif Gerilim Etkisi Altındaki Davranışları Direnç (R) Alternatif gerilimin etkisi altındaki direnç, Ohm kanunun bilinen ifadesini korur. Denklemlerden elde edilen sonuç
Şekil-1. Doğru ve Alternatif Akım dalga şekilleri
 2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
Alternatif Akım; Zaman içerisinde yönü ve şiddeti belli bir düzen içerisinde değişen akıma alternatif akım denir.
 ALTERNATiF AKIM Alternatif Akım; Zaman içerisinde yönü ve şiddeti belli bir düzen içerisinde değişen akıma alternatif akım denir. Doğru akım ve alternatif akım devrelerinde akım yönleri şekilde görüldüğü
ALTERNATiF AKIM Alternatif Akım; Zaman içerisinde yönü ve şiddeti belli bir düzen içerisinde değişen akıma alternatif akım denir. Doğru akım ve alternatif akım devrelerinde akım yönleri şekilde görüldüğü
DENEY 2: ALTERNATİF AKIM DEVRELERİNDE KONDANSATÖR VE BOBİN DAVRANIŞININ İNCELENMESİ
 DENEY 2: ALTERNATİF AKIM DEVRELERİNDE KONDANSATÖR VE BOBİN DAVRANIŞININ İNCELENMESİ Deneyin Amacı *Alternatif akım devrelerinde sıklıkla kullanılan (alternatif işaret, frekans, faz farkı, fazör diyagramı,
DENEY 2: ALTERNATİF AKIM DEVRELERİNDE KONDANSATÖR VE BOBİN DAVRANIŞININ İNCELENMESİ Deneyin Amacı *Alternatif akım devrelerinde sıklıkla kullanılan (alternatif işaret, frekans, faz farkı, fazör diyagramı,
ALTERNATİF AKIMIN TEMEL ESASLARI
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIMIN TEMEL ESASLARI Dr. Öğr. Üyesi Ahmet ÇİFCİ Elektrik enerjisi, alternatif akım ve doğru akım olarak
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIMIN TEMEL ESASLARI Dr. Öğr. Üyesi Ahmet ÇİFCİ Elektrik enerjisi, alternatif akım ve doğru akım olarak
Alternatif Akım Devreleri
 Alternatif akım sürekli yönü ve şiddeti değişen bir akımdır. Alternatif akımda bazı devre elemanları (bobin, kapasitör, yarı iletken devre elemanları) doğruakım devrelerinde olduğundan farklı davranırlar.
Alternatif akım sürekli yönü ve şiddeti değişen bir akımdır. Alternatif akımda bazı devre elemanları (bobin, kapasitör, yarı iletken devre elemanları) doğruakım devrelerinde olduğundan farklı davranırlar.
BÖLÜM 3 ALTERNATİF AKIMDA SERİ DEVRELER
 BÖÜM 3 ATENATİF AKMDA SEİ DEVEE 3.1 - (DİENÇ - BOBİN SEİ BAĞANMAS 3. - (DİENÇ - KONDANSATÖÜN SEİ BAĞANMAS 3.3 -- (DİENÇ-BOBİN - KONDANSATÖ SEİ BAĞANMAS 3.4 -- SEİ DEVESİNDE GÜÇ 77 ATENATİF AKM DEVE ANAİİ
BÖÜM 3 ATENATİF AKMDA SEİ DEVEE 3.1 - (DİENÇ - BOBİN SEİ BAĞANMAS 3. - (DİENÇ - KONDANSATÖÜN SEİ BAĞANMAS 3.3 -- (DİENÇ-BOBİN - KONDANSATÖ SEİ BAĞANMAS 3.4 -- SEİ DEVESİNDE GÜÇ 77 ATENATİF AKM DEVE ANAİİ
DENEY 5: ALTERNATİF AKIMDA FAZ FARKI (R, L VE C İÇİN)
 DENEY 5: ALTERNATİF AKIMDA FAZ FARKI (R, L VE C İÇİN) A. DENEYİN AMACI : Bu deneyin amacı, pasif elemanların (direnç, bobin ve sığaç) AC tepkilerini incelemek ve pasif elemanlar üzerindeki faz farkını
DENEY 5: ALTERNATİF AKIMDA FAZ FARKI (R, L VE C İÇİN) A. DENEYİN AMACI : Bu deneyin amacı, pasif elemanların (direnç, bobin ve sığaç) AC tepkilerini incelemek ve pasif elemanlar üzerindeki faz farkını
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ DENEY FÖYÜ DENEY ADI AC AKIM, GERİLİM VE GÜÇ DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEY SORUMLUSU DENEY GRUBU: DENEY TARİHİ : TESLİM
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ DENEY FÖYÜ DENEY ADI AC AKIM, GERİLİM VE GÜÇ DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEY SORUMLUSU DENEY GRUBU: DENEY TARİHİ : TESLİM
ELK273 Elektrik ve Elektronik Mühendisliğinin Temelleri Ders 8- AC Devreler. Yard.Doç.Dr. Ahmet Özkurt.
 ELK273 Elektrik ve Elektronik Mühendisliğinin Temelleri Ders 8- AC Devreler Yard.Doç.Dr. Ahmet Özkurt Ahmet.ozkurt@deu.edu.tr http://ahmetozkurt.net İçerik AC ve DC Empedans RMS değeri Bobin ve kondansatörün
ELK273 Elektrik ve Elektronik Mühendisliğinin Temelleri Ders 8- AC Devreler Yard.Doç.Dr. Ahmet Özkurt Ahmet.ozkurt@deu.edu.tr http://ahmetozkurt.net İçerik AC ve DC Empedans RMS değeri Bobin ve kondansatörün
F AKIM DEVRELER A. DEVRE ELEMANLARI VE TEMEL DEVRELER
 ALTERNATİF AKIM DEVRELERİ A. DEVRE ELEMANLARI VE TEMEL DEVRELER Alternatif akım devrelerinde akımın geçişine karşı üç çeşit direnç (zorluk) gösterilir. Devre elamanları dediğimiz bu dirençler: () R omik
ALTERNATİF AKIM DEVRELERİ A. DEVRE ELEMANLARI VE TEMEL DEVRELER Alternatif akım devrelerinde akımın geçişine karşı üç çeşit direnç (zorluk) gösterilir. Devre elamanları dediğimiz bu dirençler: () R omik
DENEY-4 RL DEVRE ANALİZİ. Alternatif akım altında seri RL devresinin analizi ve deneysel olarak incelenmesi.
 DENEY-4 RL DEVRE ANALİZİ 1. DENEYİN AMACI Alternatif akım altında seri RL devresinin analizi ve deneysel olarak incelenmesi. Kullanılan Alet ve Malzemeler: 1. Osiloskop 2. Sinyal jeneratörü 3. Çeşitli
DENEY-4 RL DEVRE ANALİZİ 1. DENEYİN AMACI Alternatif akım altında seri RL devresinin analizi ve deneysel olarak incelenmesi. Kullanılan Alet ve Malzemeler: 1. Osiloskop 2. Sinyal jeneratörü 3. Çeşitli
AC Circuits Review Assoc.Prof.Dr.Bahtiyar DURSUN Department of Energy Systems Engineering
 ESM 14701 POWER QUALITY IN ENERGY SYSTEMS AND HARMONICS AC Circuits Review Assoc.Prof.Dr.Bahtiyar DURSUN Department of Energy Systems Engineering FAZÖR (PHASOR) Elektrik terminolojisinde kullanılan iki
ESM 14701 POWER QUALITY IN ENERGY SYSTEMS AND HARMONICS AC Circuits Review Assoc.Prof.Dr.Bahtiyar DURSUN Department of Energy Systems Engineering FAZÖR (PHASOR) Elektrik terminolojisinde kullanılan iki
3 FAZLI SİSTEMLER fazlı sistemler 1
 3 FAL SİSTEMLER Çok lı sistemler, gerilimlerinin arasında farkı bulunan iki veya daha la tek lı sistemin birleştirilmiş halidir ve bu işlem simetrik bir şekilde yapılır. Tek lı sistemlerde güç dalgalı
3 FAL SİSTEMLER Çok lı sistemler, gerilimlerinin arasında farkı bulunan iki veya daha la tek lı sistemin birleştirilmiş halidir ve bu işlem simetrik bir şekilde yapılır. Tek lı sistemlerde güç dalgalı
Problemler: Devre Analizi-II
 Problemler: Devre Analizi-II P.7.1 Grafiği verilen sinüsoidalin hem sinüs hem de kosinüs cinsinden ifadesini yazınız. v(t) 5 4 3 2 1 0-1 t(saniye) -2-3 -4-5 0 1 2 3 4 5 6 7 8 9 10 P.7.2 v1(t) 60Cos( 100
Problemler: Devre Analizi-II P.7.1 Grafiği verilen sinüsoidalin hem sinüs hem de kosinüs cinsinden ifadesini yazınız. v(t) 5 4 3 2 1 0-1 t(saniye) -2-3 -4-5 0 1 2 3 4 5 6 7 8 9 10 P.7.2 v1(t) 60Cos( 100
ALTERNATİF AKIMDA EMPEDANS SERİ DEVRELER
 1 ALTERNATİF AKMDA EMPEDANS SERİ DEVRELER ALTERNATİF AKMDA EMPEDANS Empedans, gerilim uygulandığında bir elektrik devresinin akımın geçişine karşı gösterdiği zorluğun ölçüsüdür. Empedans Z harfi ile gösterilir
1 ALTERNATİF AKMDA EMPEDANS SERİ DEVRELER ALTERNATİF AKMDA EMPEDANS Empedans, gerilim uygulandığında bir elektrik devresinin akımın geçişine karşı gösterdiği zorluğun ölçüsüdür. Empedans Z harfi ile gösterilir
Enerji Sistemleri Mühendisliği Bölümü
 YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
Sinüsoidal Gerilim ve Akım ALIŞTIRMALAR
 Sinüsoidal Gerilim ve Akım 65 2.7. ALŞTRMALAR Soru 2.1 : 4 kutuplu bir generatörde rotor (hareketli kısım) 3000 devir/dk ile döndüğüne göre, üretilen gerilimin frekansını bulunuz. (Cevap : f=100hz) Soru
Sinüsoidal Gerilim ve Akım 65 2.7. ALŞTRMALAR Soru 2.1 : 4 kutuplu bir generatörde rotor (hareketli kısım) 3000 devir/dk ile döndüğüne göre, üretilen gerilimin frekansını bulunuz. (Cevap : f=100hz) Soru
DENEY TARİHİ RAPOR TESLİM TARİHİ NOT
 DENEY 3 SERİ VE PARALEL RLC DEVRELERİ Malzeme Listesi: 1 adet 100mH, 1 adet 1.5 mh, 1 adet 100mH ve 1 adet 100 uh Bobin 1 adet 820nF, 1 adet 200 nf, 1 adet 100pF ve 1 adet 100 nf Kondansatör 1 adet 100
DENEY 3 SERİ VE PARALEL RLC DEVRELERİ Malzeme Listesi: 1 adet 100mH, 1 adet 1.5 mh, 1 adet 100mH ve 1 adet 100 uh Bobin 1 adet 820nF, 1 adet 200 nf, 1 adet 100pF ve 1 adet 100 nf Kondansatör 1 adet 100
Alternatif Akım Devre Analizi
 Alternatif Akım Devre Analizi Öğr.Gör. Emre ÖZER Alternatif Akımın Tanımı Zamaniçerisindeyönüveşiddeti belli bir düzen içerisinde (periyodik) değişen akıma alternatif akımdenir. En bilinen alternatif akım
Alternatif Akım Devre Analizi Öğr.Gör. Emre ÖZER Alternatif Akımın Tanımı Zamaniçerisindeyönüveşiddeti belli bir düzen içerisinde (periyodik) değişen akıma alternatif akımdenir. En bilinen alternatif akım
8. ALTERNATİF AKIM VE SERİ RLC DEVRESİ
 8. ATENATİF AKIM E SEİ DEESİ AMAÇA 1. Alternatif akım ve gerilim ölçmeyi öğrenmek. Direnç, kondansatör ve indüktans oluşan seri bir alternatif akım devresini analiz etmek AAÇA oltmetre, ampermetre, kondansatör
8. ATENATİF AKIM E SEİ DEESİ AMAÇA 1. Alternatif akım ve gerilim ölçmeyi öğrenmek. Direnç, kondansatör ve indüktans oluşan seri bir alternatif akım devresini analiz etmek AAÇA oltmetre, ampermetre, kondansatör
ALTERNATİF AKIMDA ANİ VE ORTALAMA GÜÇ
 ALTERNATİF AKIMDA ANİ VE A akımda devreye uygulanan gerilim ve akım zamana bağlı olarak değişir. Elde edilen güç de zamana bağlı değişir. Güç her an akım ve gerilimin çarpımına (U*I) eşit değildir. ORTALAMA
ALTERNATİF AKIMDA ANİ VE A akımda devreye uygulanan gerilim ve akım zamana bağlı olarak değişir. Elde edilen güç de zamana bağlı değişir. Güç her an akım ve gerilimin çarpımına (U*I) eşit değildir. ORTALAMA
EET-202 DEVRE ANALİZİ-II DENEY FÖYÜ OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME
 OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME Deney No:1 Amaç: Osiloskop kullanarak AC gerilimin genlik periyot ve frekans değerlerinin ölçmesi Gerekli Ekipmanlar: AC Güç Kaynağı, Osiloskop, 2 tane 1k
OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME Deney No:1 Amaç: Osiloskop kullanarak AC gerilimin genlik periyot ve frekans değerlerinin ölçmesi Gerekli Ekipmanlar: AC Güç Kaynağı, Osiloskop, 2 tane 1k
ALTERNATİF AKIMDA GÜÇ
 1 ALTERNATİF AKIMDA GÜÇ Elektrik gücü bir elektrik devresi ile transfer edilen yada dönüştürülen elektrik enerjisinin oranıdır. Gücün SI birimi Watt (W) tır. Doğru akım devrelerinde elektrik gücü Joule
1 ALTERNATİF AKIMDA GÜÇ Elektrik gücü bir elektrik devresi ile transfer edilen yada dönüştürülen elektrik enerjisinin oranıdır. Gücün SI birimi Watt (W) tır. Doğru akım devrelerinde elektrik gücü Joule
ALTERNATİF AKIMDA GÜÇ
 1 ALTERNATİF AKIMDA GÜÇ ALTERNATİF AKIMDA GÜÇ Joule Kanunu Elektrik gücü, bir elektrik devresi ile transfer edilen yada dönüştürülen elektrik enerjisinin oranıdır. Gücün SI birimi Watt (W) tır. Doğru akım
1 ALTERNATİF AKIMDA GÜÇ ALTERNATİF AKIMDA GÜÇ Joule Kanunu Elektrik gücü, bir elektrik devresi ile transfer edilen yada dönüştürülen elektrik enerjisinin oranıdır. Gücün SI birimi Watt (W) tır. Doğru akım
5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri
 Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
DENEY TARİHİ RAPOR TESLİM TARİHİ NOT
 DENEY 2 OHM-KIRCHOFF KANUNLARI VE BOBİN-DİRENÇ-KONDANSATÖR Malzeme Listesi: 1 adet 47Ω, 1 adet 100Ω, 1 adet 1,5KΩ ve 1 adet 6.8KΩ Dirençler 1 adet 100mH Bobin 1 adet 220nF Kondansatör Deneyde Kullanılacak
DENEY 2 OHM-KIRCHOFF KANUNLARI VE BOBİN-DİRENÇ-KONDANSATÖR Malzeme Listesi: 1 adet 47Ω, 1 adet 100Ω, 1 adet 1,5KΩ ve 1 adet 6.8KΩ Dirençler 1 adet 100mH Bobin 1 adet 220nF Kondansatör Deneyde Kullanılacak
4. Sunum: AC Kalıcı Durum Analizi. Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık
 4. Sunum: AC Kalıcı Durum Analizi Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Giriş Aşağıdaki şekillere ve ifadelere bakalım ve daha önceki derslerimizden
4. Sunum: AC Kalıcı Durum Analizi Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Giriş Aşağıdaki şekillere ve ifadelere bakalım ve daha önceki derslerimizden
Bölüm 3 AC Devreler. 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak.
 Bölüm 3 AC Devreler DENEY 3-1 AC RC Devresi DENEYİN AMACI 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak. GENEL BİLGİLER Saf
Bölüm 3 AC Devreler DENEY 3-1 AC RC Devresi DENEYİN AMACI 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak. GENEL BİLGİLER Saf
ALTERNATİF AKIMDA EMPEDANS SERİ DEVRELER
 1 ALTERNATİF AKMDA EMPEDANS SERİ DEVRELER Empedans, gerilim uygulandığında bir elektrik devresinin akımın geçişine karşı gösterdiği zorluğun ölçüsüdür. Empedans Z harfi ile gösterilir ve birimi ohm(ω)
1 ALTERNATİF AKMDA EMPEDANS SERİ DEVRELER Empedans, gerilim uygulandığında bir elektrik devresinin akımın geçişine karşı gösterdiği zorluğun ölçüsüdür. Empedans Z harfi ile gösterilir ve birimi ohm(ω)
ADIYAMAN ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ DEVRE ANALİZİ LABORATUVARI-II DENEY RAPORU
 ADIYAMAN ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ DEVRE ANALİZİ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYİN ADI : DENEY TARİHİ : DENEYİ YAPANLAR : RAPORU HAZIRLAYANIN
ADIYAMAN ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ DEVRE ANALİZİ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYİN ADI : DENEY TARİHİ : DENEYİ YAPANLAR : RAPORU HAZIRLAYANIN
ELEKTRİK DEVRELERİ-2 LABORATUVARI IV. DENEY FÖYÜ
 EEKTİK DEEEİ-2 ABOATUAI I. DENEY FÖYÜ ATENATİF AKIM ATINDA DEE ANAİİ Amaç: Alternatif akım altında seri devresinin analizi ve deneysel olarak incelenmesi Gerekli Ekipmanlar: Güç Kaynağı, Ampermetre, oltmetre,
EEKTİK DEEEİ-2 ABOATUAI I. DENEY FÖYÜ ATENATİF AKIM ATINDA DEE ANAİİ Amaç: Alternatif akım altında seri devresinin analizi ve deneysel olarak incelenmesi Gerekli Ekipmanlar: Güç Kaynağı, Ampermetre, oltmetre,
AC DEVRELERDE KONDANSATÖRLER
 A DEVRELERDE KONDANSATÖRLER 7.1 Amaçlar: Sabit frekansta çalışan kondansatörler Kondansatör voltaj ve akımı arasındaki faz farkının ölçülmesi Kondansatör voltaj ve akım şiddetleri arasındaki ilişkiler
A DEVRELERDE KONDANSATÖRLER 7.1 Amaçlar: Sabit frekansta çalışan kondansatörler Kondansatör voltaj ve akımı arasındaki faz farkının ölçülmesi Kondansatör voltaj ve akım şiddetleri arasındaki ilişkiler
Temel Kavramlar. Elektrik Nedir? Elektrik nedir? Elektrikler geldi, gitti, çarpıldım derken neyi kastederiz?
 Temel Kavramlar Elektrik Nedir? Elektrik nedir? Elektrikler geldi, gitti, çarpıldım derken neyi kastederiz? 1 Elektriksel Yük Elektrik yükü bu dış yörüngede dolanan elektron sayısının çekirdekteki proton
Temel Kavramlar Elektrik Nedir? Elektrik nedir? Elektrikler geldi, gitti, çarpıldım derken neyi kastederiz? 1 Elektriksel Yük Elektrik yükü bu dış yörüngede dolanan elektron sayısının çekirdekteki proton
SAKARYA ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK DEVRELER LABORATUARI
 SAKARYA ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK DEVRELER LABORATUARI DENEYİ YAPTIRAN: DENEYİN ADI: DENEY NO: DENEYİ YAPANIN ADI ve SOYADI: SINIFI: OKUL NO: DENEY GRUP NO:
SAKARYA ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK DEVRELER LABORATUARI DENEYİ YAPTIRAN: DENEYİN ADI: DENEY NO: DENEYİ YAPANIN ADI ve SOYADI: SINIFI: OKUL NO: DENEY GRUP NO:
Mekatronik Mühendisliği Lab1 (Elektrik-Elektronik) Seri ve Paralel RLC Devreleri
 YILDIZ TEKNİK ÜNİVERSİTESİ MAKİNA FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK LABORATUARI (LAB I) DENEY 3 Deney Adı: Seri ve Paralel RLC Devreleri Öğretim Üyesi: Yard. Doç. Dr. Erhan AKDOĞAN
YILDIZ TEKNİK ÜNİVERSİTESİ MAKİNA FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK LABORATUARI (LAB I) DENEY 3 Deney Adı: Seri ve Paralel RLC Devreleri Öğretim Üyesi: Yard. Doç. Dr. Erhan AKDOĞAN
AC (ALTERNATİF AKIM)
 AC (ALERNAİF AKIM) AC akı daii olarak pozitif ve negatif aksiu değerler arasında değişi gösterir. Pozitif ve negatif değerler arasındaki farka tepe-tepe değer, V p-p adı verilir. 9.03.013 1 AC (ALERNAİF
AC (ALERNAİF AKIM) AC akı daii olarak pozitif ve negatif aksiu değerler arasında değişi gösterir. Pozitif ve negatif değerler arasındaki farka tepe-tepe değer, V p-p adı verilir. 9.03.013 1 AC (ALERNAİF
Enerji Sistemleri Mühendisliği
 Enerji Sistemleri Mühendisliği Temel Elektrik ve Elektronik AC Devre Analizi Karmaşık Sayılar Karmaşık sayılar dikdörtgen koordinat sisteminde aşağıdaki gibi gösterilebilir. Temel Elektrik ve Elektronik
Enerji Sistemleri Mühendisliği Temel Elektrik ve Elektronik AC Devre Analizi Karmaşık Sayılar Karmaşık sayılar dikdörtgen koordinat sisteminde aşağıdaki gibi gösterilebilir. Temel Elektrik ve Elektronik
DENEY 4: SERİ VE PARALEL REZONANS DEVRELERİ
 Deneyin Amacı DENEY 4: SERİ VE PARALEL REZONANS DEVRELERİ Seri ve paralel RLC devrelerinde rezonans durumunun gözlenmesi, rezonans eğrisinin elde edilmesi ve devrenin karakteristik parametrelerinin ölçülmesi
Deneyin Amacı DENEY 4: SERİ VE PARALEL REZONANS DEVRELERİ Seri ve paralel RLC devrelerinde rezonans durumunun gözlenmesi, rezonans eğrisinin elde edilmesi ve devrenin karakteristik parametrelerinin ölçülmesi
ALTERNATİF AKIMDA EMPEDANS (PARALEL DEVRELER)
 1 ALTERNATİF AKMDA EMPEDANS (PARALEL DEVRELER) Paralel Devreler Direnç, bobin ve kondansatör birbirleri ile paralel bağlanarak üç farkı şekilde bulunabilirler. Direnç Bobin (R-L) Paralel Devresi Direnç
1 ALTERNATİF AKMDA EMPEDANS (PARALEL DEVRELER) Paralel Devreler Direnç, bobin ve kondansatör birbirleri ile paralel bağlanarak üç farkı şekilde bulunabilirler. Direnç Bobin (R-L) Paralel Devresi Direnç
KARADENİZ TEKNİK ÜNİVERSİTESİ Mühendislik Fakültesi Elektrik-Elektronik Mühendisliği Bölümü ELK222 TEMEL ELEKTRİK LABORATUARI-II
 ALTERNATİF AKIM KÖPRÜLERİ 1. Hazırlık Soruları Deneye gelmeden önce aşağıdaki soruları cevaplayınız ve deney öncesinde rapor halinde sununuz. Omik, kapasitif ve endüktif yük ne demektir? Açıklayınız. Omik
ALTERNATİF AKIM KÖPRÜLERİ 1. Hazırlık Soruları Deneye gelmeden önce aşağıdaki soruları cevaplayınız ve deney öncesinde rapor halinde sununuz. Omik, kapasitif ve endüktif yük ne demektir? Açıklayınız. Omik
ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU
 ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYĠN ADI : DENEY TARĠHĠ : DENEYĠ YAPANLAR : RAPORU HAZIRLAYANIN
ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYĠN ADI : DENEY TARĠHĠ : DENEYĠ YAPANLAR : RAPORU HAZIRLAYANIN
sbölüm I REZONANS DEVRELERİ
 sböüm I EZONANS DEVEEİ. GİİŞ ezonans, bobin ve kondansatör kullanılan A elektrik ve elektronik devrelerinde oluşan özel bir durumdur. Herhangi bir A devrede bobinin Endüktif eaktans ı ile kondansatörün
sböüm I EZONANS DEVEEİ. GİİŞ ezonans, bobin ve kondansatör kullanılan A elektrik ve elektronik devrelerinde oluşan özel bir durumdur. Herhangi bir A devrede bobinin Endüktif eaktans ı ile kondansatörün
DENEY 8. OPAMP UYGULAMALARI-II: Toplayıcı, Fark Alıcı, Türev Alıcı, İntegral Alıcı Devreler
 DENEY 8 OPAMP UYGULAMALARI-II: Toplayıcı, Fark Alıcı, Türev Alıcı, İntegral Alıcı Devreler 1. Amaç Bu deneyin amacı; Op-Amp kullanarak toplayıcı, fark alıcı, türev alıcı ve integral alıcı devrelerin incelenmesidir.
DENEY 8 OPAMP UYGULAMALARI-II: Toplayıcı, Fark Alıcı, Türev Alıcı, İntegral Alıcı Devreler 1. Amaç Bu deneyin amacı; Op-Amp kullanarak toplayıcı, fark alıcı, türev alıcı ve integral alıcı devrelerin incelenmesidir.
2- İşverenler işyerlerinde meydana gelen bir iş kazasını en geç kaç iş günü içerisinde ilgili bölge müdürlüğüne bildirmek zorundadır?
 1- Doğa ve çevreye fazla zarar vermeden devamlı ve kaliteli bir hizmet veya mal üretimi sırasında iş kazalarının meydana gelmemesi ve meslek hastalıklarının oluşmaması için alınan tedbirlerin ve yapılan
1- Doğa ve çevreye fazla zarar vermeden devamlı ve kaliteli bir hizmet veya mal üretimi sırasında iş kazalarının meydana gelmemesi ve meslek hastalıklarının oluşmaması için alınan tedbirlerin ve yapılan
DENEY FÖYÜ 7: Seri ve Paralel Rezonans Devreleri
 DENEY FÖYÜ 7: Seri ve Paralel Rezonans Devreleri Deneyin Amacı: Seri ve paralel rezonans devrelerini incelemek, devrelerin karakteristik parametrelerini hesaplamak ve ölçmek, rezonans eğrilerini çizmek.
DENEY FÖYÜ 7: Seri ve Paralel Rezonans Devreleri Deneyin Amacı: Seri ve paralel rezonans devrelerini incelemek, devrelerin karakteristik parametrelerini hesaplamak ve ölçmek, rezonans eğrilerini çizmek.
Aşağıdaki formülden bulunabilir. S16-Kesiti S1=0,20 mm²,uzunluğu L1=50 m,özdirenci φ=1,1 olan krom-nikel telin direnci kaç ohm dur? R1=?
 S1-5 kw lık bir elektrik cihazı 360 dakika süresince çalıştırılacaktır. Bu elektrik cihazının yaptığı işi hesaplayınız. ( 1 saat 60 dakikadır. ) A-30Kwh B-50 Kwh C-72Kwh D-80Kwh S2-400 miliwatt kaç Kilowatt
S1-5 kw lık bir elektrik cihazı 360 dakika süresince çalıştırılacaktır. Bu elektrik cihazının yaptığı işi hesaplayınız. ( 1 saat 60 dakikadır. ) A-30Kwh B-50 Kwh C-72Kwh D-80Kwh S2-400 miliwatt kaç Kilowatt
AC DEVRELERDE BOBİNLER
 AC DEVRELERDE BOBİNLER 4.1 Amaçlar Sabit Frekanslı AC Devrelerde Bobin Bobinin voltaj ve akımının ölçülmesi Voltaj ve akım arasındaki faz farkının bulunması Gücün hesaplanması Voltaj, akım ve güç eğrilerinin
AC DEVRELERDE BOBİNLER 4.1 Amaçlar Sabit Frekanslı AC Devrelerde Bobin Bobinin voltaj ve akımının ölçülmesi Voltaj ve akım arasındaki faz farkının bulunması Gücün hesaplanması Voltaj, akım ve güç eğrilerinin
ELEKTRİK DEVRELERİ-2 LABORATUVARI VI. DENEY FÖYÜ
 ELEKTİK DEELEİ-2 LABOATUAI I. DENEY FÖYÜ ALTENATİF AKIM DEESİNDE GÜÇ ÖLÇÜMÜ Amaç: Alternatif akım devresinde harcanan gücün analizi ve ölçülmesi. Gerekli Ekipmanlar: AA Güç Kaynağı, 1kΩ Direnç, 0.5H Bobin,
ELEKTİK DEELEİ-2 LABOATUAI I. DENEY FÖYÜ ALTENATİF AKIM DEESİNDE GÜÇ ÖLÇÜMÜ Amaç: Alternatif akım devresinde harcanan gücün analizi ve ölçülmesi. Gerekli Ekipmanlar: AA Güç Kaynağı, 1kΩ Direnç, 0.5H Bobin,
ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU
 ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYĠN ADI : DENEY TARĠHĠ : DENEYĠ YAPANLAR : RAPORU HAZIRLAYANIN
ADIYAMAN ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ ELEKTRĠK-ELEKTRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ DEVRE ANALĠZĠ LABORATUVARI-II DENEY RAPORU DENEY NO : DENEYĠN ADI : DENEY TARĠHĠ : DENEYĠ YAPANLAR : RAPORU HAZIRLAYANIN
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI ELEKTRİK İLETİM HATLARINDA GERİLİM DÜŞÜMÜ VE GÜÇ FAKTÖRÜ
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI ELEKTRİK İLETİM HATLARINDA GERİLİM DÜŞÜMÜ VE GÜÇ FAKTÖRÜ
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI ELEKTRİK İLETİM HATLARINDA GERİLİM DÜŞÜMÜ VE GÜÇ FAKTÖRÜ
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI ELEKTRİK İLETİM HATLARINDA GERİLİM DÜŞÜMÜ VE GÜÇ FAKTÖRÜ
DENEY 7 DALGALI GERİLİM ÖLÇÜMLERİ - OSİLOSKOP
 DENEY 7 DALGALI GERİLİM ÖLÇÜMLERİ - OSİLOSKOP Amaç: Bu deneyin amacı, öğrencilerin alternatif akım ve gerilim hakkında bilgi edinmesini sağlamaktır. Deney sonunda öğrencilerin, periyot, frekans, genlik,
DENEY 7 DALGALI GERİLİM ÖLÇÜMLERİ - OSİLOSKOP Amaç: Bu deneyin amacı, öğrencilerin alternatif akım ve gerilim hakkında bilgi edinmesini sağlamaktır. Deney sonunda öğrencilerin, periyot, frekans, genlik,
DENEY 1-1 AC Gerilim Ölçümü
 DENEY 1-1 AC Gerilim Ölçümü DENEYİN AMACI 1. AC gerilimlerin nasıl ölçüldüğünü öğrenmek. 2. AC voltmetrenin nasıl kullanıldığını öğrenmek. GENEL BİLGİLER AC voltmetre, ac gerilimleri ölçmek için kullanılan
DENEY 1-1 AC Gerilim Ölçümü DENEYİN AMACI 1. AC gerilimlerin nasıl ölçüldüğünü öğrenmek. 2. AC voltmetrenin nasıl kullanıldığını öğrenmek. GENEL BİLGİLER AC voltmetre, ac gerilimleri ölçmek için kullanılan
EET-202 DEVRE ANALİZİ-II DENEY FÖYÜ OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME
 OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME Deney No:1 Amaç: Osiloskop kullanarak AC gerilimin genlik periyot ve frekans değerlerinin ölçmesi Gerekli Ekipmanlar: AC Güç Kaynağı, Osiloskop, 2 tane 1k
OSİLOSKOP İLE PERİYOT, FREKANS VE GERİLİM ÖLÇME Deney No:1 Amaç: Osiloskop kullanarak AC gerilimin genlik periyot ve frekans değerlerinin ölçmesi Gerekli Ekipmanlar: AC Güç Kaynağı, Osiloskop, 2 tane 1k
Mekatronik Mühendisliği Lab1 (Elektrik-Elektronik) Ohm-Kirchoff Kanunları ve AC Bobin-Direnç-Kondansatör
 YILDIZ TEKNİK ÜNİVERSİTESİ MAKİNA FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK LABORATUARI (LAB I) DENEY 2 Deney Adı: Ohm-Kirchoff Kanunları ve Bobin-Direnç-Kondansatör Malzeme Listesi:
YILDIZ TEKNİK ÜNİVERSİTESİ MAKİNA FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK LABORATUARI (LAB I) DENEY 2 Deney Adı: Ohm-Kirchoff Kanunları ve Bobin-Direnç-Kondansatör Malzeme Listesi:
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ TEMEL ELEKTRİK DEVRE LABORATUVARI TEMEL DEVRE TEOREMLERİNİN UYGULANMASI
 T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ TEMEL ELEKTRİK DEVRE LABORATUVARI TEMEL DEVRE TEOREMLERİNİN UYGULANMASI DENEY SORUMLUSU Arş. Gör. Şaban ULUS Şubat 2014 KAYSERİ
T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ TEMEL ELEKTRİK DEVRE LABORATUVARI TEMEL DEVRE TEOREMLERİNİN UYGULANMASI DENEY SORUMLUSU Arş. Gör. Şaban ULUS Şubat 2014 KAYSERİ
DİRENÇ VE REAKTANS (OMİK DİRENÇ, BOBİN VE KONDANSATÖR)
 1 DİRENÇ VE REAKTANS (OMİK DİRENÇ, BOBİN VE KONDANSATÖR) Alternatif akım devrelerinde üç çeşit devre elemanı vardır. Bunlar; direnç, bobin ve kondansatördür. Sadece direnç bulunduran alternatif akım devreleri
1 DİRENÇ VE REAKTANS (OMİK DİRENÇ, BOBİN VE KONDANSATÖR) Alternatif akım devrelerinde üç çeşit devre elemanı vardır. Bunlar; direnç, bobin ve kondansatördür. Sadece direnç bulunduran alternatif akım devreleri
T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK SİSTEMLER LABORATUVARI 1 OPAMP DEVRELERİ-2
 T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK SİSTEMLER LABORATUVARI 1 OPAMP DEVRELERİ-2 DENEY SORUMLUSU Arş. Gör. Memduh SUVEREN MART 2015 KAYSERİ OPAMP DEVRELERİ
T.C. ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MEKATRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK SİSTEMLER LABORATUVARI 1 OPAMP DEVRELERİ-2 DENEY SORUMLUSU Arş. Gör. Memduh SUVEREN MART 2015 KAYSERİ OPAMP DEVRELERİ
DENEYDEN HAKKINDA TEORİK BİLGİ:
 DENEY NO : 1 DENEYİN ADI : SERİ RL-RC DEVRELERİ DENEYİN AMACI : Alternatif akım devrelerinde; seri bağlı direnç, bobin ve kondansatör davranışının incelenmesi DENEYDEN HAKKINDA TEORİK BİLGİ: Alternatif
DENEY NO : 1 DENEYİN ADI : SERİ RL-RC DEVRELERİ DENEYİN AMACI : Alternatif akım devrelerinde; seri bağlı direnç, bobin ve kondansatör davranışının incelenmesi DENEYDEN HAKKINDA TEORİK BİLGİ: Alternatif
Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi. Ders Notu-3 Doğru Akım Devreleri Hazırlayan: Yrd. Doç. Dr. Ahmet DUMLU
 Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi Ders Notu-3 Doğru Akım Devreleri Hazırlayan: Yrd. Doç. Dr. Ahmet DUMLU ELEKTROMOTOR KUVVETİ Kapalı bir devrede sabit bir akımın oluşturulabilmesi için
Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi Ders Notu-3 Doğru Akım Devreleri Hazırlayan: Yrd. Doç. Dr. Ahmet DUMLU ELEKTROMOTOR KUVVETİ Kapalı bir devrede sabit bir akımın oluşturulabilmesi için
Nedim Tutkun, PhD, MIEEE Düzce Üniversitesi Elektrik-Elektronik Mühendisliği Bölümü Konuralp Düzce
 ELEKTRİK DEVRELERİ II ÖRNEK ARASINAV SORULARI Nedim Tutkun, PhD, MIEEE nedimtutkun@duzce.edu.tr Düzce Üniversitesi Elektrik-Elektronik Mühendisliği Bölümü 81620 Konuralp Düzce Soru-1) Şekildeki devrede
ELEKTRİK DEVRELERİ II ÖRNEK ARASINAV SORULARI Nedim Tutkun, PhD, MIEEE nedimtutkun@duzce.edu.tr Düzce Üniversitesi Elektrik-Elektronik Mühendisliği Bölümü 81620 Konuralp Düzce Soru-1) Şekildeki devrede
SAKARYA ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK DEVRELER LABORATUARI
 SAKARYA ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK DEVRELER LABORATUARI DENEYİ YAPTIRAN: DENEYİN ADI: DENEY NO: DENEYİ YAPANIN ADI ve SOYADI: SINIFI: OKUL NO: DENEY GRUP NO:
SAKARYA ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRONİK DEVRELER LABORATUARI DENEYİ YAPTIRAN: DENEYİN ADI: DENEY NO: DENEYİ YAPANIN ADI ve SOYADI: SINIFI: OKUL NO: DENEY GRUP NO:
BÖLÜM IX DALGA MEYDANA GETİRME USULLERİ
 BÖLÜM IX DALGA MEYDANA GETİRME USULLERİ 9.1 DALGA MEYDANA GETİRME USÜLLERİNE GİRİŞ Dalga üreteçleri birkaç hertzden, birkaç gigahertze kadar sinyalleri meydana getirirler. Çıkışlarında sinüsoidal, kare,
BÖLÜM IX DALGA MEYDANA GETİRME USULLERİ 9.1 DALGA MEYDANA GETİRME USÜLLERİNE GİRİŞ Dalga üreteçleri birkaç hertzden, birkaç gigahertze kadar sinyalleri meydana getirirler. Çıkışlarında sinüsoidal, kare,
DİRENÇ VE REAKTANS (OMİK DİRENÇ, BOBİN VE KONDANSATÖR)
 1 DİRENÇ VE REAKTANS (OMİK DİRENÇ, BOBİN VE KONDANSATÖR) ALTERNATİFDA DİRENÇ VE REAKTANS Alternatif akım devrelerinde üç çeşit devre elemanı vardır. Omik Direnç, Bobin Kondansatör Sadece direnç bulunduran
1 DİRENÇ VE REAKTANS (OMİK DİRENÇ, BOBİN VE KONDANSATÖR) ALTERNATİFDA DİRENÇ VE REAKTANS Alternatif akım devrelerinde üç çeşit devre elemanı vardır. Omik Direnç, Bobin Kondansatör Sadece direnç bulunduran
ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOKULU ELEKTRİK VE ENERJİ BÖLÜMÜ ALTERNATİF ENERJİ KAYNAKLARI TEKNOLOJİSİ
 ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOKULU ELEKTRİK VE ENERJİ BÖLÜMÜ ALTERNATİF ENERJİ KAYNAKLARI TEKNOLOJİSİ ELEKTRİK MAKİNALARI 4.HAFTA 1 İçindekiler Transformatörlerde Eşdeğer Devreler Transformatör
ANKARA ÜNİVERSİTESİ GAMA MESLEK YÜKSEKOKULU ELEKTRİK VE ENERJİ BÖLÜMÜ ALTERNATİF ENERJİ KAYNAKLARI TEKNOLOJİSİ ELEKTRİK MAKİNALARI 4.HAFTA 1 İçindekiler Transformatörlerde Eşdeğer Devreler Transformatör
EEM 202 DENEY 8 RC DEVRELERİ-I SABİT BİR FREKANSTA RC DEVRELERİ
 Ad&oyad: DEELEİ- ABİT Bİ FEKANTA DEELEİ 8. Amaçlar abit Frekanslı seri devrelerinde empedans, akım ve güç bağıntıları abit Frekanslı paralel devrelerinde admitans, akım ve güç bağıntıları. 8.4 Devre Elemanları
Ad&oyad: DEELEİ- ABİT Bİ FEKANTA DEELEİ 8. Amaçlar abit Frekanslı seri devrelerinde empedans, akım ve güç bağıntıları abit Frekanslı paralel devrelerinde admitans, akım ve güç bağıntıları. 8.4 Devre Elemanları
DENEY 7 Pasif Elektronik Filtreler: Direnç-Kondansatör (RC) ve Direnç-Bobin (RL) Devreleri
 DENEY 7 Pasif Elektronik Filtreler: Direnç-Kondansatör (RC) ve Direnç-Bobin (RL) Devreleri 1. Amaç Bu deneyin amacı; alternatif akım devrelerinde, direnç-kondansatör birleşimi ile oluşturulan RC filtre
DENEY 7 Pasif Elektronik Filtreler: Direnç-Kondansatör (RC) ve Direnç-Bobin (RL) Devreleri 1. Amaç Bu deneyin amacı; alternatif akım devrelerinde, direnç-kondansatör birleşimi ile oluşturulan RC filtre
4. ÜNİTE ALTERNATİF AKIMDA GÜÇ
 4. ÜNİTE ALTERNATİF AKIMDA GÜÇ KONULAR 1. Ani Güç, Ortalama Güç 2. Dirençli Devrelerde Güç 3. Bobinli Devrelerde Güç 4. Kondansatörlü Devrelerde Güç 5. Güç Üçgeni 6. Güç Ölçme GİRİŞ Bir doğru akım devresinde
4. ÜNİTE ALTERNATİF AKIMDA GÜÇ KONULAR 1. Ani Güç, Ortalama Güç 2. Dirençli Devrelerde Güç 3. Bobinli Devrelerde Güç 4. Kondansatörlü Devrelerde Güç 5. Güç Üçgeni 6. Güç Ölçme GİRİŞ Bir doğru akım devresinde
EEM 202 DENEY 10. Tablo 10.1 Deney 10 da kullanılan devre elemanları ve malzeme listesi
 EEM 0 DENEY 0 SABİT FEKANSTA DEVEEİ 0. Amaçlar Sabit frekansta devrelerinin incelenmesi. Seri devresi Paralel devresi 0. Devre Elemanları Ve Kullanılan Malzemeler Bu deneyde kullanılan devre elemanları
EEM 0 DENEY 0 SABİT FEKANSTA DEVEEİ 0. Amaçlar Sabit frekansta devrelerinin incelenmesi. Seri devresi Paralel devresi 0. Devre Elemanları Ve Kullanılan Malzemeler Bu deneyde kullanılan devre elemanları
DERS BİLGİ FORMU. Haftalık Ders Saati. Okul Eğitimi Süresi
 DERS BİLGİ FORMU DERSİN ADI BÖLÜM PROGRAM DÖNEMİ DERSİN DİLİ DERS KATEGORİSİ ÖN ŞARTLAR SÜRE VE DAĞILIMI KREDİ DERSİN AMACI ÖĞRENME ÇIKTILARI VE YETERLİKLER DERSİN İÇERİĞİ VE DAĞILIMI (MODÜLLER VE HAFTALARA
DERS BİLGİ FORMU DERSİN ADI BÖLÜM PROGRAM DÖNEMİ DERSİN DİLİ DERS KATEGORİSİ ÖN ŞARTLAR SÜRE VE DAĞILIMI KREDİ DERSİN AMACI ÖĞRENME ÇIKTILARI VE YETERLİKLER DERSİN İÇERİĞİ VE DAĞILIMI (MODÜLLER VE HAFTALARA
HAFTA SAAT KAZANIM ÖĞRENME YÖNTEMLERİ ARAÇ-GEREÇLER KONU DEĞERLENDİRME
 75. YIL MESLEKİ VE TEKNİK ANADOLU LİSESİ ELEKTRİK ELEKTRONİK TEKNOLOJİSİ ALANI ELEKTRİK-ELEKTRONİK ESASLARI DERSİ 10. SINIF ÜNİTELENDİRİLMİŞ YILLIK DERS PLANI EYLÜL EYLÜL EKİM 1.(17-23) 2.(24-30) 3.(01-07)
75. YIL MESLEKİ VE TEKNİK ANADOLU LİSESİ ELEKTRİK ELEKTRONİK TEKNOLOJİSİ ALANI ELEKTRİK-ELEKTRONİK ESASLARI DERSİ 10. SINIF ÜNİTELENDİRİLMİŞ YILLIK DERS PLANI EYLÜL EYLÜL EKİM 1.(17-23) 2.(24-30) 3.(01-07)
Temel Elektronik Basic Electronic Düğüm Gerilimleri Yöntemi (Node-Voltage Method)
 Temel Elektronik Basic Electronic Düğüm Gerilimleri Yöntemi (Node-Voltage Method) Konular Düğüm Gerilimleri Yöntemi o Temel Kavramlar o Yönteme Giriş o Yöntemin Uygulanışı o Yöntemin Uygulanması o Örnekler
Temel Elektronik Basic Electronic Düğüm Gerilimleri Yöntemi (Node-Voltage Method) Konular Düğüm Gerilimleri Yöntemi o Temel Kavramlar o Yönteme Giriş o Yöntemin Uygulanışı o Yöntemin Uygulanması o Örnekler
Per-unit değerlerin avantajları
 PER-UNİT DEĞERLER Per-unit değerlerin avantajları Elektriksel büyüklüklerin karşılaştırılmasında ve değerlendirilmesinde kolaylık sağlar. Trafoların per-unit eşdeğer empedansları primer ve sekonder taraf
PER-UNİT DEĞERLER Per-unit değerlerin avantajları Elektriksel büyüklüklerin karşılaştırılmasında ve değerlendirilmesinde kolaylık sağlar. Trafoların per-unit eşdeğer empedansları primer ve sekonder taraf
BÖLÜM 2 DİYOTLU DOĞRULTUCULAR
 BÖLÜM 2 DİYOTLU DOĞRULTUCULAR A. DENEYİN AMACI: Tek faz ve 3 faz diyotlu doğrultucuların çalışmasını ve davranışlarını incelemek. Bu deneyde tek faz ve 3 faz olmak üzere tüm yarım ve tam dalga doğrultucuları,
BÖLÜM 2 DİYOTLU DOĞRULTUCULAR A. DENEYİN AMACI: Tek faz ve 3 faz diyotlu doğrultucuların çalışmasını ve davranışlarını incelemek. Bu deneyde tek faz ve 3 faz olmak üzere tüm yarım ve tam dalga doğrultucuları,
14. SİNÜSOİDAL AKIMDA DİRENÇ, KAPASİTE, İNDÜKTANS VE ORTAK İNDÜKTANSIN ÖLÇÜLMESİ
 14. SİNÜSOİDAL AKIMDA DİRENÇ, KAPASİTE, İNDÜKTANS VE ORTAK İNDÜKTANSIN ÖLÇÜLMESİ Sinüsoidal Akımda Direncin Ölçülmesi Sinüsoidal akımda, direnç üzerindeki gerilim ve akım dalga şekilleri ve fazörleri aşağıdaki
14. SİNÜSOİDAL AKIMDA DİRENÇ, KAPASİTE, İNDÜKTANS VE ORTAK İNDÜKTANSIN ÖLÇÜLMESİ Sinüsoidal Akımda Direncin Ölçülmesi Sinüsoidal akımda, direnç üzerindeki gerilim ve akım dalga şekilleri ve fazörleri aşağıdaki
EEM211 ELEKTRİK DEVRELERİ-I
 EEM211 ELEKTRİK DEVRELERİ-I Prof. Dr. Selçuk YILDIRIM Siirt Üniversitesi Elektrik-Elektronik Mühendisliği Kaynak (Ders Kitabı): Fundamentals of Electric Circuits Charles K. Alexander Matthew N.O. Sadiku
EEM211 ELEKTRİK DEVRELERİ-I Prof. Dr. Selçuk YILDIRIM Siirt Üniversitesi Elektrik-Elektronik Mühendisliği Kaynak (Ders Kitabı): Fundamentals of Electric Circuits Charles K. Alexander Matthew N.O. Sadiku
ALTERNATİF AKIMIN DENKLEMİ
 1 ALTERNATİF AKIMIN DENKLEMİ Ani ve Maksimum Değerler Alternatif akımın elde edilişi incelendiğinde iletkenin 90 ve 270 lik dönme hareketinin sonunda maksimum emk nın indüklendiği görülür. Alternatif akımın
1 ALTERNATİF AKIMIN DENKLEMİ Ani ve Maksimum Değerler Alternatif akımın elde edilişi incelendiğinde iletkenin 90 ve 270 lik dönme hareketinin sonunda maksimum emk nın indüklendiği görülür. Alternatif akımın
V cn V ca. V bc. V bn. V ab. -V bn. V an HATIRLATMALAR. Faz-Faz ve Faz-Nötr Gerilimleri. Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri
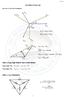 HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V aa = V cc = V bb V aa = V bb = V cc V bn V bc V ab 30 -V bn V aa = V aa V bb V aa = V aa cos(30) 30 V an V aa = V aa cos(30) =
HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V aa = V cc = V bb V aa = V bb = V cc V bn V bc V ab 30 -V bn V aa = V aa V bb V aa = V aa cos(30) 30 V an V aa = V aa cos(30) =
A.Ü. GAMA MYO. Elektrik ve Enerji Bölümü ÖLÇME TEKNİĞİ 9. HAFTA
 A.Ü. GAMA MYO. Elektrik ve Enerji Bölümü ÖLÇME TEKNİĞİ 9. HAFTA İÇİNDEKİLER Güç Çeşitleri ve Ölçümü Güç Çeşitleri Görünür Güç ve Hesaplaması Aktif Güç Aktif güç tüketen tüketiciler GÜÇ ÇEŞİTLERİ VE ÖLÇÜMÜ
A.Ü. GAMA MYO. Elektrik ve Enerji Bölümü ÖLÇME TEKNİĞİ 9. HAFTA İÇİNDEKİLER Güç Çeşitleri ve Ölçümü Güç Çeşitleri Görünür Güç ve Hesaplaması Aktif Güç Aktif güç tüketen tüketiciler GÜÇ ÇEŞİTLERİ VE ÖLÇÜMÜ
ELEKTRİK VE ELEKTRİK DEVRELERİ 2
 1 ELEKTİK VE ELEKTİK DEVELEİ ALTENATİF AKIM Enstrümantal Analiz, Doğru Akım Analitik sinyal transduserlerinden çıkan elektrik periyodik bir salınım gösterir. Bu salınımlar akım veya potansiyelin zamana
1 ELEKTİK VE ELEKTİK DEVELEİ ALTENATİF AKIM Enstrümantal Analiz, Doğru Akım Analitik sinyal transduserlerinden çıkan elektrik periyodik bir salınım gösterir. Bu salınımlar akım veya potansiyelin zamana
AET 113 DOĞRU AKIMI DEVRE ANALİZİ 1. HAFTA
 AET 113 DOĞRU AKIMI DEVRE ANALİZİ 1. HAFTA İçindekiler Temel Kavramlar Devre Elemanları Elektrik Devre Kaynakları GERİLİM (v) Pozitif ve negatif yük birbirinden ayrıldığı zaman enerji harcanır. Gerilim,
AET 113 DOĞRU AKIMI DEVRE ANALİZİ 1. HAFTA İçindekiler Temel Kavramlar Devre Elemanları Elektrik Devre Kaynakları GERİLİM (v) Pozitif ve negatif yük birbirinden ayrıldığı zaman enerji harcanır. Gerilim,
AA Motorlarında Yol Verme, Motor Seçimi Yrd. Doç. Dr. Aytaç Gören
 04.12.2011 AA Motorlarında Yol Verme, Motor Seçimi Yrd. Doç. Dr. Aytaç Gören İçerik AA Motorlarının Kumanda Teknikleri Kumanda Elemanları na Yol Verme Uygulama Soruları 25.11.2011 2 http://people.deu.edu.tr/aytac.goren
04.12.2011 AA Motorlarında Yol Verme, Motor Seçimi Yrd. Doç. Dr. Aytaç Gören İçerik AA Motorlarının Kumanda Teknikleri Kumanda Elemanları na Yol Verme Uygulama Soruları 25.11.2011 2 http://people.deu.edu.tr/aytac.goren
ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ
 1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp en çok kullanılan etkin değere eşit alınır.
1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp en çok kullanılan etkin değere eşit alınır.
Çukurova Üniversitesi Biyomedikal Mühendisliği
 Çukurova Üniversitesi Biyomedikal Mühendisliği BMM309 Elektronik-2 Laboratuarı Deney Föyü Deney#6 İşlemsel Kuvvetlendiriciler (OP-AMP) - 2 Doç. Dr. Mutlu AVCI Arş. Gör. Mustafa İSTANBULLU ADANA, 2015 DENEY
Çukurova Üniversitesi Biyomedikal Mühendisliği BMM309 Elektronik-2 Laboratuarı Deney Föyü Deney#6 İşlemsel Kuvvetlendiriciler (OP-AMP) - 2 Doç. Dr. Mutlu AVCI Arş. Gör. Mustafa İSTANBULLU ADANA, 2015 DENEY
Düzenlenirse: 9I1 5I2 = 1 108I1 60I2 = 12 7I1 + 12I2 = 4 35I1 60I2 = I1 = 8 I 1
 ELEKTRİK-ELEKTRONİK DERSİ FİNAL/BÜTÜNLEME SORU ÖRNEKLERİ Şekiller üzerindeki renkli işaretlemeler soruya değil çözüme aittir: Maviler ilk aşamada asgari bağımsız denklem çözmek için yapılan tanımları,
ELEKTRİK-ELEKTRONİK DERSİ FİNAL/BÜTÜNLEME SORU ÖRNEKLERİ Şekiller üzerindeki renkli işaretlemeler soruya değil çözüme aittir: Maviler ilk aşamada asgari bağımsız denklem çözmek için yapılan tanımları,
REZONANS DEVRELERİ. Seri rezonans devreleri bir bobinle bir kondansatörün seri bağlanmasından elde edilir. RL C Rc
 KTÜ, Elektrik Elektronik Müh. Böl. Temel Elektrik aboratuarı. Giriş EZONNS DEVEEİ Bir kondansatöre bir selften oluşan devrelere rezonans devresi denir. Bu devre tipinde selfin manyetik enerisi periyodik
KTÜ, Elektrik Elektronik Müh. Böl. Temel Elektrik aboratuarı. Giriş EZONNS DEVEEİ Bir kondansatöre bir selften oluşan devrelere rezonans devresi denir. Bu devre tipinde selfin manyetik enerisi periyodik
Bölüm 1. Elektriksel Büyüklükler ve Elektrik Devre Elemanları
 Bölüm Elektriksel Büyüklükler ve Elektrik Devre Elemanları. Temel Elektriksel Büyüklükler: Akım, Gerilim, Güç, Enerji. Güç Polaritesi.3 Akım ve Gerilim Kaynakları F.Ü. Teknoloji Fak. EEM M.G. .. Temel
Bölüm Elektriksel Büyüklükler ve Elektrik Devre Elemanları. Temel Elektriksel Büyüklükler: Akım, Gerilim, Güç, Enerji. Güç Polaritesi.3 Akım ve Gerilim Kaynakları F.Ü. Teknoloji Fak. EEM M.G. .. Temel
DENEY 3. Maksimum Güç Transferi
 ULUDAĞ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELN2024 Elektrik Devreleri Laboratuarı II 2013-2014 Bahar DENEY 3 Maksimum Güç Transferi Deneyi Yapanın Değerlendirme Adı
ULUDAĞ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELN2024 Elektrik Devreleri Laboratuarı II 2013-2014 Bahar DENEY 3 Maksimum Güç Transferi Deneyi Yapanın Değerlendirme Adı
Elektrik Devre Temelleri
 Elektrik Devre Temelleri 2. TEMEL KANUNLAR Doç. Dr. M. Kemal GÜLLÜ Elektronik ve Haberleşme Mühendisliği Kocaeli Üniversitesi Bu bölümde Ohm Kanunu Düğüm, dal, çevre 2.1. Giriş Kirchhoff Kanunları Paralel
Elektrik Devre Temelleri 2. TEMEL KANUNLAR Doç. Dr. M. Kemal GÜLLÜ Elektronik ve Haberleşme Mühendisliği Kocaeli Üniversitesi Bu bölümde Ohm Kanunu Düğüm, dal, çevre 2.1. Giriş Kirchhoff Kanunları Paralel
Cihazın Bulunduğu Yer: Enerji Sistemleri Mühendisliği Bölümü B-Blok, Enerji Verimliliği Laboratuvarı
 Ölçüm Cihazının Adı: Enerji Analizörü Cihazın Bulunduğu Yer: Enerji Sistemleri Mühendisliği Bölümü B-Blok, Enerji Verimliliği Laboratuvarı 1) Ölçümün Amacı Amaç; şebeke ya da cihazların(motor barındıran
Ölçüm Cihazının Adı: Enerji Analizörü Cihazın Bulunduğu Yer: Enerji Sistemleri Mühendisliği Bölümü B-Blok, Enerji Verimliliği Laboratuvarı 1) Ölçümün Amacı Amaç; şebeke ya da cihazların(motor barındıran
Elektrik. Alternatif Akım Motorlarının Kumanda Teknikleri Kumanda Elemanları
 Elektrik Alternatif Akım Motorlarının Kumanda Teknikleri Kumanda Elemanları 24.12.2013 Dr. Levent Çetin 2 24.12.2013 Dr. Levent Çetin 3 Buton/Anahtar / Limit Anahtarı Kalıcı butona basıldığında, buton
Elektrik Alternatif Akım Motorlarının Kumanda Teknikleri Kumanda Elemanları 24.12.2013 Dr. Levent Çetin 2 24.12.2013 Dr. Levent Çetin 3 Buton/Anahtar / Limit Anahtarı Kalıcı butona basıldığında, buton
V cn V ca. V bc. V bn. V ab 30. -V bn. V an HATIRLATMALAR. Faz-Faz ve Faz-Nötr Gerilimleri. Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri
 HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V bn V bc V ab 30 -V bn cos30 30 V an cos30 3 3 30 Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri Üçgen Bağlı Yük: V LN =
HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V bn V bc V ab 30 -V bn cos30 30 V an cos30 3 3 30 Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri Üçgen Bağlı Yük: V LN =
10. e volt ve akımıi(
 DEVRE ANALİZİ 1 1. Problemler 4t 1.1. Bir devre elemanından akan yükün zamana göre değişimi q(t ) 2 e Sin(10t ) olarak bilinmektedir. Elemandan geçen akımının değişimini bularak grafiğini çiziniz. 1.2.
DEVRE ANALİZİ 1 1. Problemler 4t 1.1. Bir devre elemanından akan yükün zamana göre değişimi q(t ) 2 e Sin(10t ) olarak bilinmektedir. Elemandan geçen akımının değişimini bularak grafiğini çiziniz. 1.2.
Şekil 1: Direnç-bobin seri devresi. gerilim düşümü ile akımdan 90 o ileri fazlı olan bobin uçlarındaki U L gerilim düşümüdür.
 1 TEME DEVEEİN KAMAŞIK SAYIAA ÇÖÜMÜ 1. Direnç Bbin Seri Devresi: (- Seri Devresi Direnç ve bbinin seri bağlı lduğu Şekil 1 deki devreyi alalım. Burada devre gerilimi birbirine dik lan iki bileşene ayrılabilir.
1 TEME DEVEEİN KAMAŞIK SAYIAA ÇÖÜMÜ 1. Direnç Bbin Seri Devresi: (- Seri Devresi Direnç ve bbinin seri bağlı lduğu Şekil 1 deki devreyi alalım. Burada devre gerilimi birbirine dik lan iki bileşene ayrılabilir.
DEVRE DEĞİŞKENLERİ Bir elektrik devresinde enerji ölçülebilen bir değer değildir fakat ölçülebilen akım ve gerilim değerlerinden hesaplanır.
 DEVRE DEĞİŞKENLERİ Bir elektrik devresinde enerji ölçülebilen bir değer değildir fakat ölçülebilen akım ve gerilim değerlerinden hesaplanır. Akımın yönü okla gösterilir. Gerilimin akım gibi gösterilen
DEVRE DEĞİŞKENLERİ Bir elektrik devresinde enerji ölçülebilen bir değer değildir fakat ölçülebilen akım ve gerilim değerlerinden hesaplanır. Akımın yönü okla gösterilir. Gerilimin akım gibi gösterilen
T.C. DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BMT103 ELEKTRİK DEVRE TEMELLERİ DERSİ LABORATUVARI DENEY NO: 7
 T.C. DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BMT103 ELEKTRİK DEVRE TEMELLERİ DERSİ LABORATUVARI DENEY NO: 7 KONDANSATÖRLER VE BOBİNLER Doç. Dr. İbrahim YÜCEDAĞ Arş. Gör. M.
T.C. DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BMT103 ELEKTRİK DEVRE TEMELLERİ DERSİ LABORATUVARI DENEY NO: 7 KONDANSATÖRLER VE BOBİNLER Doç. Dr. İbrahim YÜCEDAĞ Arş. Gör. M.
