2. SAYI SİSTEMLERİ VE KODLAR
|
|
|
- Yonca Gün
- 8 yıl önce
- İzleme sayısı:
Transkript
1 2. SAYI SİSTEMLERİ VE KODLAR 2.1. Sabit Noktalı Sayı Sistemleri Ondalık Sayı Sistemi Günlük yaşantımızda kullandığımız sayı sistemi ondalık (decimal) sayı sistemidir. Ayrıca 10 tabanlı sistem olarak da adlandırılır ve bu sistemde on tane sembol kullanılır. Semboller : 0,1,2,3,4,5,6,7,8,9 Ondalık sayı sisteminin genel biçimi ve terminolojisi aşağıda verilmiştir =234.56D En büyük Değerli (Most Significant Digit, MSD) Tam Kısım Kesir Kısmı Ondalık Nokta (Decimal Point, DP) En Küçük Değerli (Least Significant Digit, LSD) Değeri Ağırlığı = 2 x x x x x 10-2 Taban Değeri Bu açılım iki yöne genişletilirse; a basamak ağırlığı ve basamak değeri B a olmak üzere 10 tabanlı herhangi bir S sayısının genelleştirilmiş ifadesi aşağıdaki şekilde gösterilebilir İkili Sayı Sistemi B a a= S = 10 İkili (Binary) sayı sistemi, sayısal elektronik sistemlerinde yaygın olarak kullanılır. Günlük yaşantımızda kullandığımız ondalık sayı sisteminden iki yönlü dönüşüm yapılarak kullanılır. Bu sistemde, Boole cebrinde doğru ve yanlışı belirtmek üzere iki tane sembol kullanılır. Semboller : 0,1 İkili sayı sisteminin genel biçimi ve terminolojisi aşağıda verilmiştir. a En büyük Değerli Bit (Most Significant İkili Nokta (Binary Point, BP) Bit, MSB) En Küçük Değerli Bit (Least Significant Bit, LSB)
2 = B Değeri Ağırlığı = 1 x x x x x x 2-2 Taban Değeri Bu açılım iki yöne genişletilirse; a basamak ağırlığı ve basamak değeri B a olmak üzere 2 tabanlı herhangi bir S sayısının genelleştirilmiş ifadesi aşağıdaki şekilde gösterilebilir. B a a= S = 2 Bu ifadede taban değeri T olarak değişken alınırsa T tabanına göre genel durum aşağıdaki şekilde elde edilir. a S = a= B a T a Buradan hareket edilerek değişik tabandaki sayı sistemleri arasındaki dönüşüm için bir genel yöntem bulunabilir. Sayının tam ve kesirli kısmı ayrı gösterilse : S = St + n basamaklı sayının m basamaklı tam kısmı : St = T ( B0 + T ( B1 + T ( B2 +LT ( Bm) L))) şeklinde gösterilebilir. Bu ifade taban değerine bölünürse : St T = B0 + T ( B1 + T ( B2 +LT ( Bm) L)) K 0 kalandır ve sayının tam kısmının en düşük ağırlıklı basamağıdır. Bölme işlemine aynı şekilde devam edilirse B 1, B 2... B m-1 basamakları bulunarak sayının tamsayı kısmının dönüşümü işlemi tamamlanır. Sayının n-m basamaklı kesir kısmı aşağıdaki şekilde gösterilebilir. Sk = T ( B + T ( B 2 + T ( B 3 + LT ( B n+ m ) L))) Bu ifade taban değeriyle çarpılırsa aşağıdaki eşitlik elde edilir. Sk T = B 1 + T ( B 2 + T ( B 3 + LT ( B n+ m ) L)) B -1 tamsayıdır ve sayının kesirli kısmının en büyük ağırlıklı basamağıdır. Çarpma işlemine aynı şekilde devam edilirse B -2, B B -n+m basamakları bulunarak sayının kesirli kısmının dönüşüm işlemi tamamlanır. İki tabanlı sistemden on tabanlı sisteme dönüşüm için bir örnek aşağıda verilmiştir. Burada daha önce verilen kuvvet serisi şeklindeki açılım kullanılarak iki tabanlı sayının on tabanlı değeri elde edilmiştir = Sk
3 = (? ) 2 Birinci kısımda önce tamsayı kısmın dönüşümü yapılır. 13 = 6 + kalan = 3 + kalan = 1+ kalan = 0 + kalan 1 2 Buradan elde edilir. İkinci ve son kısımda ise kesirli kısmın dönüşümü yapılır x 2 = 0.5 tam kısmı x 2 = 1.0 tam kısmı 1 Sonuç olarak elde edilir = Sekizli Sayı Sistemi Sekizli (Octal) sayı sistemi, sayısal elektronik sistemlerinde ses ve müzik uygulamalarında yaygın olarak kullanılır. Müzikte kullanılan notalara (do re mi fa sol la si do) karşı gelmek üzere sekiz sembol kullanılır. Günlük yaşantımızda kullandığımız ondalık sayı sisteminden iki yönlü dönüşüm yapılarak kullanılır. Semboller 0,1,2,3,4,5,6,7 Sekizli sayı sisteminin genel biçimi ve terminolojisi aşağıda verilmiştir : En büyük Değerli (Most Significant Digit, MSD) Sekizli Nokta (Octal Point) En Küçük Değerli (Least Significant Digit, LSD) 8 tabanlı sayı sisteminin gösterimi ve sayıların kuvvet serisi şeklindeki açılımına bir örnek aşağıda verilmiştir =703.15O Değeri Ağırlığı = 7 x x x x x 8-2 Taban Değeri Sekiz tabanlı sistemden on tabanlı sisteme dönüşüm için bir örnek aşağıda verilmiştir. Burada daha önce verilen kuvvet serisi şeklindeki açılım kullanılarak sekiz tabanlı sayının on tabanlı değeri elde edilmiştir =
4 4 On tabanlı sistemden sekiz tabanlı sisteme dönüşüm için bir örnek aşağıda verilmiştir. Burada sayı sistemleri arasındaki dönüşüm için elde edilen yöntem sekiz tabanlı sisteme uyarlanarak sonuca gidilmiştir = (? ) 8 Birinci kısımda önce tamsayı kısmın dönüşümü yapılır. 451 = 56 + kalan = 7 + kalan = 0 + kalan 7 8 Buradan elde edilir. İkinci ve son kısımda ise kesirli kısmın dönüşümü yapılır x 8 = tam kısmı x 8 = 5.0 tam kısmı 5 Buradan elde edilir. Sonuç olarak elde edilir = Sekizli sistemden ikili sisteme dönüşüm için sekizli sayının her bir basamağının 3-bitlik ikili karşılığı (8=2 3 olduğu için bunu yapmaya hakkımız var) yazılarak elde edilmesi aşağıda verilmiştir = İkili sistemden sekizli sisteme dönüşüm için ikili sayı 3-bitlik gruplara ayrılır ve bunların ondalık karşılığı (8=2 3 olduğu için bunu yapmaya hakkımız var) yazılarak elde edilmesi aşağıda verilmiştir = Onaltılık Sayı Sistemi Onaltılık (Hexadecimal, Hex) sayı sistemi, sayısal elektronik sistemlerinde mikroişlemci temelli uygulamalarda yaygın olarak kullanılır. Günlük yaşantımızda kullandığımız ondalık sayı sisteminden iki yönlü dönüşüm yapılarak kullanılır. Bu sistemde, ondalık sayı sisteminde kullanılan sembollere ek olarak, dokuzdan büyük değerlere karşılık İngiliz alfabesinin ilk beş harfi ile birlikte on altı tane sembol kullanılır. Semboller 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Onaltılık sayı sisteminin genel biçimi ve terminolojisi aşağıda verilmiştir. En büyük Değerli (Most Significant Digit, MSD) 1 A 3. 1 F On altılı Nokta (Hexadecimal Point) En Küçük Değerli (Least Significant Digit, LSD)
5 5 On altı tabanlı sayı sisteminin gösterimi ve sayıların kuvvet serisi şeklindeki açılımına bir örnek aşağıda verilmiştir. 1A3.1F 16 =1A3.1FH Değeri Ağırlığı 1A3.1F 16 = 1 x x x x x 16-2 Taban Değeri Onaltılık sistemden ondalık sisteme dönüşüm için bir örnek aşağıda verilmiştir. Burada daha önce verilen kuvvet serisi şeklindeki açılım kullanılarak onaltılık sayının ondalık değeri elde edilmiştir. 1A3.1F 16 = On tabanlı sistemden iki tabanlı sisteme dönüşüm için bir örnek aşağıda verilmiştir. Burada sayı sistemleri arasındaki dönüşüm için elde edilen yöntem iki tabanlı sisteme uyarlanarak sonuca gidilmiştir = (? ) 16 Birinci kısımda önce tamsayı kısmın dönüşümü yapılır. 419 = 26 + kalan = 1 + kalan = 0 + kalan 1 16 Buradan 1 A 3 elde edilir. İkinci ve son kısımda ise kesirli kısmın dönüşümü yapılır x 16 = tam kısmı x 16 = 15.0 tam kısmı 15 Buradan 0. 1 F elde edilir. Sonuç olarak 1 A 3. 1 F elde edilir = 1A3.1F 16 Sekizli sistemden ikili sisteme dönüşüm için onaltılık sayının her basamağının 4-bitlik ikili karşılığı (16=2 4 olduğu için bunu yapmaya hakkımız var) yazılarak elde edilmesi aşağıda verilmiştir. 1A3.1F 16 = İkili sistemden onaltılık sisteme dönüşüm için ikili sayı 4-bitlik gruplara ayrılır ve bunların onaltılık karşılığı (16=2 4 olduğu için bunu yapmaya hakkımız var) yazılarak elde edilmesi aşağıda verilmiştir = B9.7 16
6 İkili Kodlanmış Ondalık Sayı Sistemi 6 İkili kodlanmış ondalık (Binary Coded Decimal, BCD) sayı sistemi, ikili sayıların ondalık karşılıklarının fiziksel dış dünyada gösterilmesini sağlamak üzere sayısal elektronik sistemlerinde yaygın olarak kullanılır. Günlük yaşantımızda kullandığımız ondalık sayı sisteminden iki yönlü dönüşüm yapılarak kullanılır. Bu sistemde, ikili sayı sisteminde olduğu gibi 2 tane sembol kullanılır. Semboller 0, 1 BCD sayı sisteminin genel biçimi ve terminolojisi aşağıda verilmiştir Ondalık sistemden BCD sisteme dönüşüm, her bir ondalık basamak ayrı ayrı 4-bit ikili sayıya dönüştürülerek yapılır = BCD BCD sistemden ikili sisteme dönüşüm için sayı önce ondalık nokta referans alınarak 4-bit gruplara ayrılır ve her bir 4-bit ikili sayı bağımsız olarak ondalık sayıya dönüştürülür. Sonra ondalık sayı ikili sayıya dönüştürülerek BCD sistemden ikili sisteme dönüşüm yapılır BCD = = İkili sistemden BCD sisteme dönüşüm yapmak için önce ikili sayı ondalık sayıya dönüştürülür. Sonra ondalık sistemden BCD sisteme dönüşüm için her bir ondalık basamak ayrı ayrı 4-bit ikili sayıya dönüştürülür = = BCD 2.2. İşaretli Sayılar Tablo 2-1 İkili sayıların (4-bit) işaretli gösterimi Ondalık Değer İşaretli 2 ye tümleyen İşaretli 1 e tümleyen İşaretli büyüklük
7 7 Buradaki gösterim şekilleri Şekil 2-1 ile karşılaştırıldığında en uygun ve verimli olan 2 ye tümleyen işaretli tamsayı gösterimidir ve matematiğe de en uygun olan şekildir =1111 0=0000-4= =0100-8= =0111 Şekil 2-1 İşaretli tamsayılar ile 2 ye tümleyen sayıların grafik gösterimi Pozitif İşaretli sayılardan negatif işaretli sayıların elde edilmesi : 1 e Tümleme İle Pozitif Sayıların Negatif 2 ye Tümleme İle Pozitif Sayıların Karşılığının Elde Edilmesi Negatif Karşılığının Elde Edilmesi ; önce sayının 1 e tümleyeni bulunur ; sonra 1 eklenir B 1011B İkili Sistemde On altılı Sistemde + 15 = e tümleme A 1 e tümleme FF 2A = D A = D B - 2AH D6H 2.3. Kayan Noktalı Sayı Sistemleri 32-bit ikili sayı ile işaretsiz olarak 0 ile 4,294,967,295 veya 2 ye tümleyen işaretli olarak - 2,147,483,648 ile 2,147,483,647 arasında ondalık sayıları gösterebiliriz. Daha büyük ve küçük değerli sayıları, ancak bilimsel gösterimden yararlanarak kayan noktalı (Floating Point) sayılar biçiminde gösterebiliriz. Aşağıda IEEE/ANSI 754 standardına uygun bir 32-bit kayan noktalı sayı biçimi gösterilmiştir. b31 b30 b23 b22 b0 İşaret Üst (127 eklenmiş) (1.) Kesir (sayının değeri) 1-bit 8-bit 23-bit (+ doğal halinden 1-bit)
8 8 Kayan Noktalı Sayıların (FPN, Floating Point Number) genel biçimi aşağıda verilmiştir. FPN )r = F x r E İki tabanı için kayan noktalı sayının genel biçimi aşağıda verilmiştir. S e A = ( ) f 2, S : işaret biti, e : üst kısmı, f : kesir kısmı eklenmiş şekildeki üst kısmının genel biçimi : m eb = e + 2, m : üst kısmın bit sayısı Kesir kısmının genel biçimi : n 1 ( k + 1) f = a( k) 2 k = 0 kesir kısmının sınırları 0.5 f < 1 olduğu için; n 1 k f = a( k) 2, a : kesir kısmı bit değerleri, n,k : bit numaraları k = 0 üst kısmın en küçük işaretsiz değeri 0 olacağından kesir kısmının sınırları 1 f < 2 şeklinde elde edilir. Üst kısmın ifadesi ise; = + m eb e 2 1 şeklinde olur. FPN 2 biçimindeki kayan noktalı sayıların sınır değerleri aşağıda verilmiştir. m = 8 için üst kısmın sınırları : -126 f 128 en küçük ve en büyük değer : eb = 1, e = -126, f = ( ) = 1.18 x eb = 255, e = 128, f = 7FFFFF ( ) = 3.4 x x 2 = 6.8 x Örnek 1 : = sayısı IEEE 32-bit normalize FPN 2 gösterimi: Önce sayının en büyük ağırlıklı biti dışında tamamı kesir haline getirilir = x 2 5 İşaret biti = 0 (pozitif) Üst (E xs ) = = = Kesir (F) = (MSB = 1 gösterilmez) b31 b30.b23 b22... b (1.) Bunun sonucunda IEEE normalize FPN FPN 2 = =42B72000h
9 Örnek 2 : için e = -3, f = Örnek 3 : 0.1 için e = -4, f = Dönüşümden elde edilen bu 32-bit kayan noktalı sonuç yeniden ondalık sayıya dönüştürülürse elde edilir. Örnek 4 : 1.0 için e = 0, f = Örnek 5 : 1.23x10 +3 için e = 10, f = Aritmetik İşlemler İkili sayılar ile dört işlem (toplama, çıkarma, çarpma ve bölme), özelliklede toplama ve çıkarma işlemleri sayısal elektronik sistemlerin programlanmasında sıkça kullanılan işlemlerdir Toplama / Çıkarma İşlemi İkili sayılar ile yapılan toplama işlemi, işleme giren sayıların karşılıklı bitleri bit bit toplanır ve oluşması halinde eldenin bir sonraki toplamaya eklenmesi şeklinde yapılır. Bu toplama işleminde işleme giren sayılar, 2 ye tümleyen işaretli değerler ise doğal olarak sayıların işareti dikkate alınarak doğru sonuç elde edilir. Çıkarma işlemi ise, toplama işlemine giren ikinci sayının işareti değiştirilerek gerçekleştirilir BH=43D, 78H=120D + 2B + 2B 2B - 2B D5-2B D (+) A3 (-) B3 (+) 1 4D (-) 1 5D Çarpma İşlemi İkili sayılarla çarpma işlemi, çarpan sayının çarpılan sayının bütün bitleri ile tek tek lojik VE işlemine sokulması ve çarpan sayının her bir biti için sola ötelenerek toplanması ile elde edilir. İkili Sistemde On altılı Sistemde 5 x 4 = x 26 = B x 0100B H x 1AH F B 270H
10 Bölme İşlemi Bölme işlemi, bölünen sayının bölen sayı ile karşılaştırılarak çıkarılması ve bu işleme bölünen sayının bölen sayıdan küçük olana kadar devam edilmesi şeklinde yapılır. İkili Sistemde On altılı Sistemde 50/5=10 9CH/06H B/ 0101B 9CH / 06H 101 (1) 6 (1) 001 3C 101 3C (A) 101 (01) (0) 1010B 1AH 2.5. Kodlar Sayısal Kodlar İkili sayıların sıralamasını değiştirmek veya bunlara fiziksel anlam yüklemek gibi özellikler katılmasıyla elde edilen sayı gruplarına, yapılan kodlama ile ilgili bir ad verilir. Tablo 2-2 Çok kullanılan bazı ikili kodlanmış ondalık kodlar Ondalık Sayı 2421 Kodu 3-Fazla Kodu parçalı LED (aktif 0 ) gfedcba a f g b e c d Şekil 2-2 Bir 7-parçalı göstergenin harfli kodlaması
11 11 Tablo 2-3 Çok kullanılan ikili kodlar Ondalık Sayı 4-bit İkili DCBA Gray DCBA (a) ikili kodlanmış disk (b) Gray kodlanmış disk Şekil 2-3 Mil açısı kodlayıcı diskler
12 Alfa Nümerik Kodlar Fiziksel dünyada bilgi iletişimde kullanılan semboller yalnız sayıları içermez. Bunlara ek olarak büyük ve küçük harfler, noktalama ve özel işaretler de kullanılır. Uluslararası, ulusal özelliklere göre değişen alfa nümerik kodlar kullanılır. Tablo 2-4 ASCII tablosu MSB Hex LSB 0 NUL DLE Boşluk P ` p 1 SOH DC1! 1 A Q a q 2 STX DC2 " 2 B R b r 3 ETX DC3 # 3 C S c s 4 EOT DC4 $ 4 D T d t 5 ENQ NAK % 5 E U e u 6 ACK SYN & 6 F V f v 7 BEL ETB ' 7 G W g w 8 BS CAN ( 8 H X h x 9 HT EM ) 9 I Y i y A LF SUB * : J Z j z B VT ESC + ; K [ k { C FF FS, < L \ l D CR GS = M ] m } E SO RS. > N ^ n ~ F SI US /? O _ o DEL Bunlardan en yaygın olanı Tablo 2-4 de verilen 128 sembolden oluşan ASCII ( AMERICAN STANDARD CODE for INFORMATION INTERCHANGE, Bilgi Değişimi için Standart Amerikan Kodu) alfa nümerik kodudur. Ör : A = 41H = 65 IBM uyumlu bilgisayarlarda EBCDIC (EXTENDED BCD INTERCHANGE CODE, Bilgi Değişimi için Genişletilmiş BCD Kodu) karakter kod tabloları kullanılır. Bu gelişmiş karakter kodu, ASCII koduna ek olarak fazladan 128 tane daha karakter kodu içerir ve bilginin yanında değişik uluslara göre özel karakterleri değişir. Tablo 2-5 Bir EBCDIC tablosu Ör : Ğ = D0H = 208
Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri. 2. Kayan Noktalı Sayı Sistemleri 2. SAYI SĐSTEMLERĐ VE KODLAR
 .1. Sabit Noktalı Sayı Sistemleri. SAYI SĐSTEMLERĐ VE KODLAR Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri. Kayan Noktalı Sayı Sistemleri.1.1. Sayı Sistemi Günlük yaşantımızda
.1. Sabit Noktalı Sayı Sistemleri. SAYI SĐSTEMLERĐ VE KODLAR Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri. Kayan Noktalı Sayı Sistemleri.1.1. Sayı Sistemi Günlük yaşantımızda
Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri. 2. Kayan Noktalı Sayı Sistemleri
 2. SAYI SİSTEMLERİ VE KODLAR Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri 2. Kayan Noktalı Sayı Sistemleri 2.1. Sabit Noktalı Sayı Sistemleri 2.1.1. Ondalık Sayı Sistemi Günlük
2. SAYI SİSTEMLERİ VE KODLAR Sayı sistemleri iki ana gruba ayrılır. 1. Sabit Noktalı Sayı Sistemleri 2. Kayan Noktalı Sayı Sistemleri 2.1. Sabit Noktalı Sayı Sistemleri 2.1.1. Ondalık Sayı Sistemi Günlük
1. Sabit Noktal Say Sistemleri
 2. SAYI SSTEMLER VE KODLAR Say sistemleri iki ana gruba ayrlr. 1. Sabit Noktal Say Sistemleri 2. Kayan Noktal Say Sistemleri 2.1. Sabit Noktal Say Sistemleri 2.1.1. Ondalk Say Sistemi Günlük yaantmzda
2. SAYI SSTEMLER VE KODLAR Say sistemleri iki ana gruba ayrlr. 1. Sabit Noktal Say Sistemleri 2. Kayan Noktal Say Sistemleri 2.1. Sabit Noktal Say Sistemleri 2.1.1. Ondalk Say Sistemi Günlük yaantmzda
SAYISAL ELEKTRONİK. Ege Ü. Ege MYO Mekatronik Programı
 SAYISAL ELEKTRONİK Ege Ü. Ege MYO Mekatronik Programı BÖLÜM 2 Sayı Sistemleri İkilik, Onaltılık ve İKO Sayılar İkilik Sayı Sistemi 3 Çoğu dijital sistemler 8, 16, 32, ve 64 bit gibi, 2 nin çift kuvvetleri
SAYISAL ELEKTRONİK Ege Ü. Ege MYO Mekatronik Programı BÖLÜM 2 Sayı Sistemleri İkilik, Onaltılık ve İKO Sayılar İkilik Sayı Sistemi 3 Çoğu dijital sistemler 8, 16, 32, ve 64 bit gibi, 2 nin çift kuvvetleri
3.3. İki Tabanlı Sayı Sisteminde Dört İşlem
 3.3. İki Tabanlı Sayı Sisteminde Dört İşlem A + B = 2 0 2 1 (Elde) A * B = Sonuç A B = 2 0 2 1 (Borç) A / B = Sonuç 0 + 0 = 0 0 0 * 0 = 0 0 0 = 0 0 0 / 0 = 0 0 + 1 = 1 0 0 * 1 = 0 0 1 = 1 1 0 / 1 = 0 1
3.3. İki Tabanlı Sayı Sisteminde Dört İşlem A + B = 2 0 2 1 (Elde) A * B = Sonuç A B = 2 0 2 1 (Borç) A / B = Sonuç 0 + 0 = 0 0 0 * 0 = 0 0 0 = 0 0 0 / 0 = 0 0 + 1 = 1 0 0 * 1 = 0 0 1 = 1 1 0 / 1 = 0 1
Barkod Referans Kılavuzu
 Barkod Referans Kılavuzu Sürüm 0 TUR 1 Giriş 1 Genel Bakış 1 1 Bu referans kılavuzunda, doğrudan Brother yazdırma aygıtına gönderilen kumanda komutlarını kullanan barkod yazdırma bilgileri sağlanmaktadır.
Barkod Referans Kılavuzu Sürüm 0 TUR 1 Giriş 1 Genel Bakış 1 1 Bu referans kılavuzunda, doğrudan Brother yazdırma aygıtına gönderilen kumanda komutlarını kullanan barkod yazdırma bilgileri sağlanmaktadır.
T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ
 T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR 1 MANTIK DEVRELERİ Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR Digital Electronics
T.C. KOCAELİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLİŞİM SİSTEMLERİ MÜHENDİSLİĞİ Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR 1 MANTIK DEVRELERİ Yrd. Doç. Dr. Mustafa Hikmet Bilgehan UÇAR Digital Electronics
C DERSĐ Programlamaya Giriş. Çağıltay, Selbes, Tokdemir, Turhan Bölüm 1 Genel Kavramlar 2
 Bölüm 1 Genel Kavramlar TOC Bilgisayarın Temel Birimleri Bilgi Saklama Bilgisayara İstediğimiz İşleri Nasıl Yaptırırız C Programlama Dili Nedir? C Programının Derlenmesi Bilgisayarın Temel Birimleri Bölüm
Bölüm 1 Genel Kavramlar TOC Bilgisayarın Temel Birimleri Bilgi Saklama Bilgisayara İstediğimiz İşleri Nasıl Yaptırırız C Programlama Dili Nedir? C Programının Derlenmesi Bilgisayarın Temel Birimleri Bölüm
2. Sayı Sistemleri. En küçük bellek birimi sadece 0 ve 1 değerlerini alabilen ikili sayı sisteminde bir basamağa denk gelen Bit tir.
 2. Sayı Sistemleri Bilgisayar elektronik bir cihaz olduğu için elektrik akımının geçirilmesi (1) yada geçirilmemesi (0) durumlarını işleyebilir. Bu nedenle ikili sayı sistemini temel alarak veri işler
2. Sayı Sistemleri Bilgisayar elektronik bir cihaz olduğu için elektrik akımının geçirilmesi (1) yada geçirilmemesi (0) durumlarını işleyebilir. Bu nedenle ikili sayı sistemini temel alarak veri işler
BLM1011 Bilgisayar Bilimlerine Giriş I
 BLM1011 Bilgisayar Bilimlerine Giriş I by Z. Cihan TAYŞİ İçerik Sayı sistemleri Binary, Octal, Decimal, Hexadecimal Operatörler Aritmetik operatörler Mantıksal (Logic) operatörler Bitwise operatörler Yıldız
BLM1011 Bilgisayar Bilimlerine Giriş I by Z. Cihan TAYŞİ İçerik Sayı sistemleri Binary, Octal, Decimal, Hexadecimal Operatörler Aritmetik operatörler Mantıksal (Logic) operatörler Bitwise operatörler Yıldız
Elektronik sistemlerde dört farklı sayı sistemi kullanılır. Bunlar;
 I. SAYI SİSTEMLERİ Elektronik sistemlerde dört farklı sayı sistemi kullanılır. Bunlar; i) İkili(Binary) Sayı Sistemi ii) Onlu(Decimal) Sayı Sistemi iii) Onaltılı(Heksadecimal) Sayı Sistemi iv) Sekizli(Oktal)
I. SAYI SİSTEMLERİ Elektronik sistemlerde dört farklı sayı sistemi kullanılır. Bunlar; i) İkili(Binary) Sayı Sistemi ii) Onlu(Decimal) Sayı Sistemi iii) Onaltılı(Heksadecimal) Sayı Sistemi iv) Sekizli(Oktal)
1. Bölüm Sayı Sistemleri
 1. Bölüm Sayı Sistemleri Algoritma ve Programlamaya Giriş Dr. Serkan DİŞLİTAŞ 1.1. Sayı Sistemleri Sayı sistemleri; saymak, ölçmek gibi genel anlamda büyüklüklerin ifade edilmesi amacıyla kullanılan sistemler
1. Bölüm Sayı Sistemleri Algoritma ve Programlamaya Giriş Dr. Serkan DİŞLİTAŞ 1.1. Sayı Sistemleri Sayı sistemleri; saymak, ölçmek gibi genel anlamda büyüklüklerin ifade edilmesi amacıyla kullanılan sistemler
BLM221 MANTIK DEVRELERİ
 2. HAFTA BLM221 MANTIK DEVRELERİ Prof. Dr. Mehmet Akbaba mehmetakbaba@karabük.edu.tr KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi Temel Kavramlar Tümleyen Aritmetiği r Tümleyeni
2. HAFTA BLM221 MANTIK DEVRELERİ Prof. Dr. Mehmet Akbaba mehmetakbaba@karabük.edu.tr KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi Temel Kavramlar Tümleyen Aritmetiği r Tümleyeni
2. Sayı Sistemleri. En küçük bellek birimi sadece 0 ve 1 değerlerini alabilen ikili sayı sisteminde bir basamağa denk gelen Bit tir.
 2. Sayı Sistemleri Bilgisayar elektronik bir cihaz olduğu için elektrik akımının geçirilmesi (1) yada geçirilmemesi (0) durumlarını işleyebilir. Bu nedenle ikili sayı sistemini temel alarak veri işler
2. Sayı Sistemleri Bilgisayar elektronik bir cihaz olduğu için elektrik akımının geçirilmesi (1) yada geçirilmemesi (0) durumlarını işleyebilir. Bu nedenle ikili sayı sistemini temel alarak veri işler
SAYI VE KODLAMA SİSTEMLERİ. Teknoloji Fakültesi/Bilgisayar Mühendisliği
 SAYI VE KODLAMA SİSTEMLERİ Teknoloji Fakültesi/Bilgisayar Mühendisliği Neler Var? Sayısal Kodlar BCD Kodu (Binary Coded Decimal Code) - 8421 Kodu Gray Kodu Artı 3 (Excess 3) Kodu 5 de 2 Kodu Eşitlik (Parity)
SAYI VE KODLAMA SİSTEMLERİ Teknoloji Fakültesi/Bilgisayar Mühendisliği Neler Var? Sayısal Kodlar BCD Kodu (Binary Coded Decimal Code) - 8421 Kodu Gray Kodu Artı 3 (Excess 3) Kodu 5 de 2 Kodu Eşitlik (Parity)
SAYISAL DEVRELER. İTÜ Bilgisayar Mühendisliği Bölümündeki donanım derslerinin bağlantıları
 SAYISAL DEVRELER Doç.Dr. Feza BUZLUCA İstanbul Teknik Üniversitesi Bilgisayar Mühendisliği Bölümü Sayısal Devreler Ders Notlarının Creative Commons lisansı Feza BUZLUCA ya aittir. Lisans: http://creativecommons.org/licenses/by-nc-nd/3.0/
SAYISAL DEVRELER Doç.Dr. Feza BUZLUCA İstanbul Teknik Üniversitesi Bilgisayar Mühendisliği Bölümü Sayısal Devreler Ders Notlarının Creative Commons lisansı Feza BUZLUCA ya aittir. Lisans: http://creativecommons.org/licenses/by-nc-nd/3.0/
SAYISAL ELEKTRONİK DERS NOTLARI:
 SAYISAL ELEKTRONİK DERS NOTLARI: SAYISAL (DİJİTAL) ELEKTRONİK Günümüz Elektroniği Analog ve Sayısal olmak üzere iki temel türde incelenebilir. Analog büyüklükler sonsuz sayıda değeri içermesine rağmen
SAYISAL ELEKTRONİK DERS NOTLARI: SAYISAL (DİJİTAL) ELEKTRONİK Günümüz Elektroniği Analog ve Sayısal olmak üzere iki temel türde incelenebilir. Analog büyüklükler sonsuz sayıda değeri içermesine rağmen
2. SAYI SİSTEMLERİ. M.İLKUÇAR - imuammer@yahoo.com
 Sayı Sistemleri İşlemci elektrik sinyalleri ile çalışır, bu elektrik sinyallerini 1/0 şeklinde yorumlayarak işlemcide olup bitenler anlaşılabilir hale getirilir. Böylece gerçek hayattaki bilgileri 1/0
Sayı Sistemleri İşlemci elektrik sinyalleri ile çalışır, bu elektrik sinyallerini 1/0 şeklinde yorumlayarak işlemcide olup bitenler anlaşılabilir hale getirilir. Böylece gerçek hayattaki bilgileri 1/0
2. SAYI SİSTEMLERİ 2. SAYI SİSTEMLERİ
 Decimal ( Onlu 0,,,3,4,5,6,7,8,9 On adet digit). D ile gösterilir. Binary ( İkili 0, iki adet digit ). B ile gösterilir. Oktal ( Sekizli 0,,,3,4,5,6,7 sekiz adet digit ). O ile gösterilir. Hexadecimal
Decimal ( Onlu 0,,,3,4,5,6,7,8,9 On adet digit). D ile gösterilir. Binary ( İkili 0, iki adet digit ). B ile gösterilir. Oktal ( Sekizli 0,,,3,4,5,6,7 sekiz adet digit ). O ile gösterilir. Hexadecimal
Elektroniğe Giriş 1.1
 İTÜ Bilgisayar Mühendisliği Bölümündeki donanım derslerinin bağlantıları Sayısal devreler bölümdeki diğer donanım dersinin temelini oluşturmaktadır. Elektroniğe Giriş SAYISAL DEVRELER Sayısal Elektronik
İTÜ Bilgisayar Mühendisliği Bölümündeki donanım derslerinin bağlantıları Sayısal devreler bölümdeki diğer donanım dersinin temelini oluşturmaktadır. Elektroniğe Giriş SAYISAL DEVRELER Sayısal Elektronik
Bilgisayar Mimarisi. Veri (DATA) Veri nedir? Veri bazı fiziksel niceliklerin ham ifadesidir. Bilgi verinin belli bir yapıdaki şeklidir.
 Bilgisayar Mimarisi Sayısallaştırma ve Sayı Sistemleri Yrd.Doç.Dr. Celal Murat KANDEMİR ESOGÜ Eğitim Fakültesi - BÖTE twitter.com/cmkandemir Veri nedir? Veri bazı fiziksel niceliklerin ham ifadesidir.
Bilgisayar Mimarisi Sayısallaştırma ve Sayı Sistemleri Yrd.Doç.Dr. Celal Murat KANDEMİR ESOGÜ Eğitim Fakültesi - BÖTE twitter.com/cmkandemir Veri nedir? Veri bazı fiziksel niceliklerin ham ifadesidir.
n. basamak... 4. basamak 3. basamak 2. basamak 1. basamak Üstel değer 10 n-1... 10 3 10 2 10 1 10 0 Ağırlık 10 n-1...
 KAYNAK : http://osmanemrekandemir.wordpress.com/ SAYI SISTEMLERI Decimal(Onlu) Sayı sistemi günlük hayatta kullandığım ız 0,1,2,3,4,5,6,7,8,9 rakamlarından oluşur. Decimal(Onlu) Sayı sisteminde her sayı
KAYNAK : http://osmanemrekandemir.wordpress.com/ SAYI SISTEMLERI Decimal(Onlu) Sayı sistemi günlük hayatta kullandığım ız 0,1,2,3,4,5,6,7,8,9 rakamlarından oluşur. Decimal(Onlu) Sayı sisteminde her sayı
DERS NOTLARI. Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi
 DERS NOTLARI Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi DERS-2 22.02.2016 Binary Numbers The Computer Number System İkili sayı Sistemi Bilgisayar Sayı Sistemi Sayı sistemleri nesneleri
DERS NOTLARI Yard. Doç. Dr. Namık AKÇAY İstanbul Üniversitesi Fen Fakültesi DERS-2 22.02.2016 Binary Numbers The Computer Number System İkili sayı Sistemi Bilgisayar Sayı Sistemi Sayı sistemleri nesneleri
SAYI SİSTEMLERİ. Sayı Sistemleri için Genel Tanım
 SAYI SİSTEMLERİ Algoritmalar ve Programlama dersi ile alakalı olarak temel düzeyde ve bazı pratik hesaplamalar dahilinde ikilik, onluk, sekizlik ve onaltılık sayı sistemleri üzerinde duracağız. Özellikle
SAYI SİSTEMLERİ Algoritmalar ve Programlama dersi ile alakalı olarak temel düzeyde ve bazı pratik hesaplamalar dahilinde ikilik, onluk, sekizlik ve onaltılık sayı sistemleri üzerinde duracağız. Özellikle
BLM221 MANTIK DEVRELERİ
 1. HAFTA BLM221 MANTIK DEVRELERİ Prof. Dr. Mehmet Akbaba mehmetakbaba@karabuk.edu.tr KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi Temel Kavramlar Sayı Sistemlerinin İncelenmesi
1. HAFTA BLM221 MANTIK DEVRELERİ Prof. Dr. Mehmet Akbaba mehmetakbaba@karabuk.edu.tr KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi Temel Kavramlar Sayı Sistemlerinin İncelenmesi
SAYI SİSTEMLERİ. 1. Sayı Sistemleri. Sayı Sistemlerinde Rakamlar
 SAYI SİSTEMLERİ 1. Sayı Sistemleri Sayı sistemleri; saymak, ölçmek gibi genel anlamda büyüklüklerin ifade edilmesi amacıyla kullanılan sistemler olarak tanımlanmaktadır. Temel olarak 4 sayı sistemi mevcuttur:
SAYI SİSTEMLERİ 1. Sayı Sistemleri Sayı sistemleri; saymak, ölçmek gibi genel anlamda büyüklüklerin ifade edilmesi amacıyla kullanılan sistemler olarak tanımlanmaktadır. Temel olarak 4 sayı sistemi mevcuttur:
Fatih University- Faculty of Engineering- Electric and Electronic Dept.
 SAYISAL DEVRE TASARIMI EEM122 Ref. Morris MANO & Michael D. CILETTI SAYISAL TASARIM 4. Baskı Fatih University- Faculty of Engineering- Electric and Electronic Dept. SAYISAL DEVRE NEDİR? Mühendisler, elektronik
SAYISAL DEVRE TASARIMI EEM122 Ref. Morris MANO & Michael D. CILETTI SAYISAL TASARIM 4. Baskı Fatih University- Faculty of Engineering- Electric and Electronic Dept. SAYISAL DEVRE NEDİR? Mühendisler, elektronik
Giriş MİKROİŞLEMCİ SİSTEMLERİ. Elektronik Öncesi Kuşak. Bilgisayar Tarihi. Elektronik Kuşak. Elektronik Kuşak. Bilgisayar teknolojisindeki gelişme
 Giriş MİKROİŞLEMCİ SİSTEMLERİ Bilgisayar teknolojisindeki gelişme Elektronik öncesi kuşak Elektronik kuşak Mikroişlemci kuşağı Yrd. Doç. Dr. Şule Gündüz Öğüdücü 1 Bilgisayar Tarihi Elektronik Öncesi Kuşak
Giriş MİKROİŞLEMCİ SİSTEMLERİ Bilgisayar teknolojisindeki gelişme Elektronik öncesi kuşak Elektronik kuşak Mikroişlemci kuşağı Yrd. Doç. Dr. Şule Gündüz Öğüdücü 1 Bilgisayar Tarihi Elektronik Öncesi Kuşak
Sayılar Teorisi SAYILAR TEORİSİ VE SAYILAR
 Sayılar Teorisi SAYILAR TEORİSİ VE SAYILAR Sayılar; insanların ilk çağlardan beri ihtiyaç duyduğu bir gereksinim olmuştur; sayılar teorisi de matematiğin en eski alanlarından birisidir. Sayılar teorisi,
Sayılar Teorisi SAYILAR TEORİSİ VE SAYILAR Sayılar; insanların ilk çağlardan beri ihtiyaç duyduğu bir gereksinim olmuştur; sayılar teorisi de matematiğin en eski alanlarından birisidir. Sayılar teorisi,
Algoritmalar ve Programlama. DERS - 2 Yrd. Doç. Dr. Ahmet SERBES
 Algoritmalar ve Programlama DERS - 2 Yrd. Doç. Dr. Ahmet SERBES Programlama Bilgisayara ne yapması gerektiğini, yani onunla konuşmamızı sağlayan dil. Tüm yazılımlar programlama dilleri ile yazılır. 1.
Algoritmalar ve Programlama DERS - 2 Yrd. Doç. Dr. Ahmet SERBES Programlama Bilgisayara ne yapması gerektiğini, yani onunla konuşmamızı sağlayan dil. Tüm yazılımlar programlama dilleri ile yazılır. 1.
Sayı Sistemleri. Onluk, İkilik, Sekizlik ve Onaltılık sistemler Dönüşümler Tümleyen aritmetiği
 Sayı Sistemleri Onluk, İkilik, Sekizlik ve Onaltılık sistemler Dönüşümler Tümleyen aritmetiği Giriş Bilgisayar ış ünyaan verileri sayılar aracılığı ile kabul eer. Günümüz teknolojisine bu işlem ikilik
Sayı Sistemleri Onluk, İkilik, Sekizlik ve Onaltılık sistemler Dönüşümler Tümleyen aritmetiği Giriş Bilgisayar ış ünyaan verileri sayılar aracılığı ile kabul eer. Günümüz teknolojisine bu işlem ikilik
OCTAL (SEKİZLİ) SAYI SİSTEMİ:
 5.HAFTA OCTAL (SEKİZLİ) SAYI SİSTEMİ: Sayısal Sistemler ikilik sayı sistemini kullansalar da bir tasarımcı için Binary (İkilik) sayılarla işlem yapmak zahmetli bir işlem olması nedeniyle ve hafızada daha
5.HAFTA OCTAL (SEKİZLİ) SAYI SİSTEMİ: Sayısal Sistemler ikilik sayı sistemini kullansalar da bir tasarımcı için Binary (İkilik) sayılarla işlem yapmak zahmetli bir işlem olması nedeniyle ve hafızada daha
BÖLÜM 1 GİRİŞ 1.1 SAYI SİSTEMLERİ Konumsal Sayı Sistemleri
 BÖLÜM 1 GİRİŞ 1.1 SAYI SİSTEMLERİ 1.1.1 Konumsal Sayı Sistemleri İkili sayı sistemi, sayısal bilgisayarlarda kullanılan en geleneksel ve kolay gerçeklenebilen bir sayı sistemidir. Bu gösterimde bir sayı
BÖLÜM 1 GİRİŞ 1.1 SAYI SİSTEMLERİ 1.1.1 Konumsal Sayı Sistemleri İkili sayı sistemi, sayısal bilgisayarlarda kullanılan en geleneksel ve kolay gerçeklenebilen bir sayı sistemidir. Bu gösterimde bir sayı
PROGRAMLANAB L R DENETLEY C LER. DERS 02 Sayı Sistemleri
 PROGRAMLANAB L R DENETLEY C LER DERS 02 Sayı Sistemleri i. SAYI S STEMLER Büyüklükleri ifade etmek amacıyla kullanılan sembollere sayı adı verilir. Sayı sistemleri tabanlarına göre isim alırlar. Günlük
PROGRAMLANAB L R DENETLEY C LER DERS 02 Sayı Sistemleri i. SAYI S STEMLER Büyüklükleri ifade etmek amacıyla kullanılan sembollere sayı adı verilir. Sayı sistemleri tabanlarına göre isim alırlar. Günlük
MANTIK DEVRELERİ HALL, 2002) (SAYISAL TASARIM, ÇEVİRİ, LITERATUR YAYINCILIK) DIGITAL DESIGN PRICIPLES & PRACTICES (3. EDITION, PRENTICE HALL, 2001)
 MANTIK DEVRELERİ DERSİN AMACI: SAYISAL LOJİK DEVRELERE İLİŞKİN KAPSAMLI BİLGİ SUNMAK. DERSİ ALAN ÖĞRENCİLER KOMBİNASYONEL DEVRE, ARDIŞIL DEVRE VE ALGORİTMİK DURUM MAKİNALARI TASARLAYACAK VE ÇÖZÜMLEMESİNİ
MANTIK DEVRELERİ DERSİN AMACI: SAYISAL LOJİK DEVRELERE İLİŞKİN KAPSAMLI BİLGİ SUNMAK. DERSİ ALAN ÖĞRENCİLER KOMBİNASYONEL DEVRE, ARDIŞIL DEVRE VE ALGORİTMİK DURUM MAKİNALARI TASARLAYACAK VE ÇÖZÜMLEMESİNİ
BÖLÜM 2 SAYI SĐSTEMLERĐ (NUMBER SYSTEMS)
 BÖLÜM 2 SAYI SĐSTEMLERĐ (NUMBER SYSTEMS) Giriş Sayma ve sayı kavramının yeryüzünde ilk olarak nerede ve ne zaman doğduğu bilinmemekle beraber, bazı buluntular Sümer lerin saymayı bildiklerini ve bugün
BÖLÜM 2 SAYI SĐSTEMLERĐ (NUMBER SYSTEMS) Giriş Sayma ve sayı kavramının yeryüzünde ilk olarak nerede ve ne zaman doğduğu bilinmemekle beraber, bazı buluntular Sümer lerin saymayı bildiklerini ve bugün
BİLGİSAYAR MİMARİSİ. İkili Kodlama ve Mantık Devreleri. Özer Çelik Matematik-Bilgisayar Bölümü
 BİLGİSAYAR MİMARİSİ İkili Kodlama ve Mantık Devreleri Özer Çelik Matematik-Bilgisayar Bölümü Kodlama Kodlama, iki küme elemanları arasında karşılıklığı kesin olarak belirtilen kurallar bütünüdür diye tanımlanabilir.
BİLGİSAYAR MİMARİSİ İkili Kodlama ve Mantık Devreleri Özer Çelik Matematik-Bilgisayar Bölümü Kodlama Kodlama, iki küme elemanları arasında karşılıklığı kesin olarak belirtilen kurallar bütünüdür diye tanımlanabilir.
Algoritma Geliştirme ve Veri Yapıları 3 Veri Yapıları. Mustafa Kemal Üniversitesi
 Algoritma Geliştirme ve Veri Yapıları 3 Veri Yapıları Veri yapısı, bilginin anlamlı sırada bellekte veya disk, çubuk bellek gibi saklama birimlerinde tutulması veya saklanması şeklini gösterir. Bilgisayar
Algoritma Geliştirme ve Veri Yapıları 3 Veri Yapıları Veri yapısı, bilginin anlamlı sırada bellekte veya disk, çubuk bellek gibi saklama birimlerinde tutulması veya saklanması şeklini gösterir. Bilgisayar
Yrd.Doç.Dr. Celal Murat KANDEMİR. Kodlama (Coding) : Bir nesneler kümesinin bir dizgi (bit dizisi) kümesi ile temsil edilmesidir.
 Bilgisayar Mimarisi İkilik Kodlama ve Mantık Devreleri Yrd.Doç.Dr. Celal Murat KANDEMİR ESOGÜ Eğitim Fakültesi - BÖTE twitter.com/cmkandemir Kodlama Kodlama (Coding) : Bir nesneler kümesinin bir dizgi
Bilgisayar Mimarisi İkilik Kodlama ve Mantık Devreleri Yrd.Doç.Dr. Celal Murat KANDEMİR ESOGÜ Eğitim Fakültesi - BÖTE twitter.com/cmkandemir Kodlama Kodlama (Coding) : Bir nesneler kümesinin bir dizgi
BÖL-1B. Fatih University- Faculty of Engineering- Electric and Electronic Dept.
 SAYISAL DEVRE TASARIMI EEM122 Ref. Morris MANO & Michael D. CILETTI SAYISAL TASARIM 4. Baskı BÖL-1B Fatih University- Faculty of Engineering- Electric and Electronic Dept. İŞARETLİ SAYILAR Bilgisayar gibi
SAYISAL DEVRE TASARIMI EEM122 Ref. Morris MANO & Michael D. CILETTI SAYISAL TASARIM 4. Baskı BÖL-1B Fatih University- Faculty of Engineering- Electric and Electronic Dept. İŞARETLİ SAYILAR Bilgisayar gibi
Floating Point (Kayan Noktalı Sayılar)
 Süleyman Demirel Üniversitesi / Mühendislik Fak. / Bilgisayar Mühendisliği Bölümü Floating Point (Kayan Noktalı Sayılar) BIL-304: Bilgisayar Mimarisi Dersi veren öğretim üyesi: Yrd. Doç. Dr. Fatih Gökçe
Süleyman Demirel Üniversitesi / Mühendislik Fak. / Bilgisayar Mühendisliği Bölümü Floating Point (Kayan Noktalı Sayılar) BIL-304: Bilgisayar Mimarisi Dersi veren öğretim üyesi: Yrd. Doç. Dr. Fatih Gökçe
Mikrobilgisayarda Aritmetik
 14 Mikrobilgisayarda Aritmetik SAYITLAMA DİZGELERİ Sayıları göstermek (temsil etmek) için tarih boyunca türlü simgeler kullanılmıştır. Konumuz bu tarihi gelişimi incelemek değildir. Kullanılan sayıtlama
14 Mikrobilgisayarda Aritmetik SAYITLAMA DİZGELERİ Sayıları göstermek (temsil etmek) için tarih boyunca türlü simgeler kullanılmıştır. Konumuz bu tarihi gelişimi incelemek değildir. Kullanılan sayıtlama
4.2. SAYISAL MANTIK SEVİYELERİ VE DALGA FORMLARI
 4. TEMEL DİJİTAL ELEKTRONİK 1 Yarı iletkenlerin ucuzlaması, üretim tekniklerinin hızlanması sonucu günlük yaşamda ve işyerlerinde kullanılan aygıtların büyük bir bölümü dijital elektronik devreli olarak
4. TEMEL DİJİTAL ELEKTRONİK 1 Yarı iletkenlerin ucuzlaması, üretim tekniklerinin hızlanması sonucu günlük yaşamda ve işyerlerinde kullanılan aygıtların büyük bir bölümü dijital elektronik devreli olarak
Kodlama ve Kodlar - (Coding and Codes) Sakarya Üniversitesi
 Kodlama ve Kodlar - (Coding and Codes) Sakarya Üniversitesi Kodlama ve Kodlar - İçerik Sayısal Kodlar BCD Kodu (Binary Coded Decimal Code) - 8421 Kodu Gray Kodu Artı 3 (Excess 3) Kodu 5 de 2 Kodu: Eşitlik
Kodlama ve Kodlar - (Coding and Codes) Sakarya Üniversitesi Kodlama ve Kodlar - İçerik Sayısal Kodlar BCD Kodu (Binary Coded Decimal Code) - 8421 Kodu Gray Kodu Artı 3 (Excess 3) Kodu 5 de 2 Kodu: Eşitlik
BARKOD OKUYUCU KULLANIM KILAVUZU
 ZEBEX Z-3071/WA RF BARKOD OKUYUCU KULLANIM KILAVUZU İ Ç İ N D E K İ L E R 3071 WA / RF in parçaları 2 3071 WA / RF in Görünümü 3 3071 WA / RF in Kurulumu 4 İlk rının Yapılması 5 Haberleşme ünitesinin kanal
ZEBEX Z-3071/WA RF BARKOD OKUYUCU KULLANIM KILAVUZU İ Ç İ N D E K İ L E R 3071 WA / RF in parçaları 2 3071 WA / RF in Görünümü 3 3071 WA / RF in Kurulumu 4 İlk rının Yapılması 5 Haberleşme ünitesinin kanal
SAYISAL ELEKTRONİK - I
 SYISL ELEKTRONİK - I SYISL ELEKTRONİK - I ÖLÜM u bölümde aşağıdki konu başlıkları incelenecektir. Temel elektronik kavramları Sayısal elektronik,nalog elektronik Sinyal,Sayısal eelktronik dalga formları
SYISL ELEKTRONİK - I SYISL ELEKTRONİK - I ÖLÜM u bölümde aşağıdki konu başlıkları incelenecektir. Temel elektronik kavramları Sayısal elektronik,nalog elektronik Sinyal,Sayısal eelktronik dalga formları
Bilgisayar Bilimlerine Giriş 1
 Bilgisayar Bilimlerine Giriş 1 Dokuz Eylül Üniversitesi Bilgisayar Bilimleri Bölümü DR. RESMİYE NASİBOĞLU E-POSTA: RESMİYE.NASİBOGLU@DEU.EDU.TR ARAŞ. GÖR BARIŞ TEKİN TEZEL E-POSTA: BARİS.TEZEL@DEU.EDU.TR
Bilgisayar Bilimlerine Giriş 1 Dokuz Eylül Üniversitesi Bilgisayar Bilimleri Bölümü DR. RESMİYE NASİBOĞLU E-POSTA: RESMİYE.NASİBOGLU@DEU.EDU.TR ARAŞ. GÖR BARIŞ TEKİN TEZEL E-POSTA: BARİS.TEZEL@DEU.EDU.TR
Sayıtlama Dizgeleri. (a n a n-1 a n1 a n0. b 1 b 2 b m )r. simgesi şu sayıyı temsil eder.
 1 Sayıtlama Dizgeleri Hint-Arap Sayıtlama Dizgesi Sayıları göstermek (temsil etmek) için tarih boyunca türlü simgeler kullanılmıştır. Sümerlerin, Mısırlıların, Romalıların ve diğer uygarlıkların kullandıkları
1 Sayıtlama Dizgeleri Hint-Arap Sayıtlama Dizgesi Sayıları göstermek (temsil etmek) için tarih boyunca türlü simgeler kullanılmıştır. Sümerlerin, Mısırlıların, Romalıların ve diğer uygarlıkların kullandıkları
Sayı Sistemleri. Mikroişlemciler ve Mikrobilgisayarlar
 Sayı Sistemleri 1 Desimal Sistem Günlük hayatımızda desimal sistemi kullanmaktayız Tabanı 10 dur Örn: 365 = 3.10 2 +6.10 1 +5.10 0 4827 = 4.10 3 +8.10 2 +2.10 1 +7.10 0 2 İkili Sayı Sistemi (Binary System)
Sayı Sistemleri 1 Desimal Sistem Günlük hayatımızda desimal sistemi kullanmaktayız Tabanı 10 dur Örn: 365 = 3.10 2 +6.10 1 +5.10 0 4827 = 4.10 3 +8.10 2 +2.10 1 +7.10 0 2 İkili Sayı Sistemi (Binary System)
Kare Kodlar: DataMatrix:
 7.HAFTA Aiken Kodu Aiken kodu 4 basamaklı olup basamak değerleri 2421 şeklinde ifade edilmektedir. Onlu sistemde 5 e kadar olan sayılar sağdaki bitler ile 5 ten sonraki rakamlar ise soldaki bitler ile
7.HAFTA Aiken Kodu Aiken kodu 4 basamaklı olup basamak değerleri 2421 şeklinde ifade edilmektedir. Onlu sistemde 5 e kadar olan sayılar sağdaki bitler ile 5 ten sonraki rakamlar ise soldaki bitler ile
BÖLÜM 3 - KODLAMA VE KODLAR - (CODING AND CODES)
 SAYISAL TASARIM-I 3.HAFTA BÖLÜM 3 - KODLAMA VE KODLAR - (CODING AND CODES) 1 İÇERİK: -Sayısal Kodlar -BCD Kodu (Binary Coded Decimal Code)-8421 Kodu -Gray Kodu -Artı 3 (Excess 3) Kodu -5 de 2 Kodu: -Eşitlik
SAYISAL TASARIM-I 3.HAFTA BÖLÜM 3 - KODLAMA VE KODLAR - (CODING AND CODES) 1 İÇERİK: -Sayısal Kodlar -BCD Kodu (Binary Coded Decimal Code)-8421 Kodu -Gray Kodu -Artı 3 (Excess 3) Kodu -5 de 2 Kodu: -Eşitlik
PROGRAMLAMA TEMELLERİ-ÜNİTE 2 SAYI SİSTEMLERİ, OPERATÖRLER VE İŞLEMLER
 PROGRAMLAMA TEMELLERİ-ÜNİTE 2 SAYI SİSTEMLERİ, OPERATÖRLER VE İŞLEMLER GİRİŞ İnsanoğlunun bilgiyi belirtmede kullandığı sembollerin bilgisayarda da ifade edilmesi gerekir. Bilgisayarın 0 ve 1 e karşılık
PROGRAMLAMA TEMELLERİ-ÜNİTE 2 SAYI SİSTEMLERİ, OPERATÖRLER VE İŞLEMLER GİRİŞ İnsanoğlunun bilgiyi belirtmede kullandığı sembollerin bilgisayarda da ifade edilmesi gerekir. Bilgisayarın 0 ve 1 e karşılık
Bilgisayarların Gelişimi
 Bilgisayarların Gelişimi Joseph Jacquard (1810) Bilgisayar tabanlı halı dokuma makinesi Delikli Kart (Punch Card) Algoritma ve Programlama 6 Bilgisayar Sistemi 1. Donanım fiziksel aygıtlardır. 2. Yazılım
Bilgisayarların Gelişimi Joseph Jacquard (1810) Bilgisayar tabanlı halı dokuma makinesi Delikli Kart (Punch Card) Algoritma ve Programlama 6 Bilgisayar Sistemi 1. Donanım fiziksel aygıtlardır. 2. Yazılım
Bir işaretli büyüklük sayısında en soldaki basamak bir işaret içerir. Diğer basamaklarda ise sayısal değerin büyüklüğü (mutlak değeri) gösterilir.
 İşaretli Tamsayı Gösterimi 1. İşaretli Büyüklük Bir işaretli büyüklük sayısında en soldaki basamak bir işaret içerir. Diğer basamaklarda ise sayısal değerin büyüklüğü (mutlak değeri) gösterilir. Örnek
İşaretli Tamsayı Gösterimi 1. İşaretli Büyüklük Bir işaretli büyüklük sayısında en soldaki basamak bir işaret içerir. Diğer basamaklarda ise sayısal değerin büyüklüğü (mutlak değeri) gösterilir. Örnek
Sayı sistemleri-hesaplamalar. Sakarya Üniversitesi
 Sayı sistemleri-hesaplamalar Sakarya Üniversitesi Sayı Sistemleri - Hesaplamalar Tüm sayı sistemlerinde sayılarda işaret kullanılabilir. Yani pozitif ve negatif sayılarla hesaplama yapılabilir. Bu gerçek
Sayı sistemleri-hesaplamalar Sakarya Üniversitesi Sayı Sistemleri - Hesaplamalar Tüm sayı sistemlerinde sayılarda işaret kullanılabilir. Yani pozitif ve negatif sayılarla hesaplama yapılabilir. Bu gerçek
KODLAMA SİSTEMLERİNİN TANIMI :
 KODLAMA SİSTEMLERİ KODLAMA SİSTEMLERİNİN TANIMI : Kodlama, iki küme elemanları arasında karşılıklı kesin olarak belirtilen kurallar bütünüdür diye tanımlanabilir. Diğer bir deyişle, görünebilen, okunabilen
KODLAMA SİSTEMLERİ KODLAMA SİSTEMLERİNİN TANIMI : Kodlama, iki küme elemanları arasında karşılıklı kesin olarak belirtilen kurallar bütünüdür diye tanımlanabilir. Diğer bir deyişle, görünebilen, okunabilen
BTP 207 İNTERNET PROGRAMCILIĞI I. Ders 8
 BTP 27 İNTERNET PROGRAMCILIĞI I Ders 8 Değişkenler 2 Tamsayı Değerler (Integer) Tamsayılar, tabanlı (decimal), 8 tabanlı (octal) veya 6 tabanlı (hexadecimal) olabilir. 8 tabanındaki sayıları belirtmek
BTP 27 İNTERNET PROGRAMCILIĞI I Ders 8 Değişkenler 2 Tamsayı Değerler (Integer) Tamsayılar, tabanlı (decimal), 8 tabanlı (octal) veya 6 tabanlı (hexadecimal) olabilir. 8 tabanındaki sayıları belirtmek
DİJİTAL ELEKTRONİK DERS NOTLARI
 DİJİTAL ELEKTRONİK DERS NOTLARI Analog sinyal Sonsuz sayıda ara değer alabilen, devamlılık arz eden büyüklük, analog büyüklük olarak tanımlanır. Dünyadaki çoğu büyüklük analogdur. Analog sinyal aslında
DİJİTAL ELEKTRONİK DERS NOTLARI Analog sinyal Sonsuz sayıda ara değer alabilen, devamlılık arz eden büyüklük, analog büyüklük olarak tanımlanır. Dünyadaki çoğu büyüklük analogdur. Analog sinyal aslında
ENDÜSTRİYEL OTOMASYON TEKNOLOJİLERI
 T.C. MİLLÎ EĞİTİM BAKANLIĞI ENDÜSTRİYEL OTOMASYON TEKNOLOJİLERI LOJİK DEVRELER 522EE63 ANKARA 2 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri
T.C. MİLLÎ EĞİTİM BAKANLIĞI ENDÜSTRİYEL OTOMASYON TEKNOLOJİLERI LOJİK DEVRELER 522EE63 ANKARA 2 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri
İleri Düzey Programlama Kılavuzu
 İleri Düzey Programlama Kılavuzu nbc Bu kılavuz Zebex çok yönlü lazer barkod okuyucuların programlanması için tasarlanmıştır. w w w. b i l k u r. c o m. t r 2 İ Ç İ NDEKİ LER Tanıtım 4 Okuyucu ayarlarını
İleri Düzey Programlama Kılavuzu nbc Bu kılavuz Zebex çok yönlü lazer barkod okuyucuların programlanması için tasarlanmıştır. w w w. b i l k u r. c o m. t r 2 İ Ç İ NDEKİ LER Tanıtım 4 Okuyucu ayarlarını
Konular MİKROİŞLEMCİ SİSTEMLERİ. Giriş. Bilgisayar Tarihi. Elektronik Kuşak. Elektronik Öncesi Kuşak
 Konular MİKROİŞLEMCİ SİSTEMLERİ Giriş: Bilgisayar Tarihi Mikroişlemci Temelli Sistemler Sayı Sistemleri Doç. Dr. Şule Gündüz Öğüdücü http://ninova.itu.edu.tr/tr/dersler/bilgisayar-bilisim-fakultesi/30/blg-212/
Konular MİKROİŞLEMCİ SİSTEMLERİ Giriş: Bilgisayar Tarihi Mikroişlemci Temelli Sistemler Sayı Sistemleri Doç. Dr. Şule Gündüz Öğüdücü http://ninova.itu.edu.tr/tr/dersler/bilgisayar-bilisim-fakultesi/30/blg-212/
1. ÜNİTE 2. ÜNİTE 3. ÜNİTE. Bölüm 1 : Üslü Sayılar... 8. Bölüm 2 : Doğal Sayılar... 18. Bölüm 3 : Doğal Sayı Problemleri... 30
 İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
Yrd. Doç. Dr. Caner ÖZCAN
 Yrd. Doç. Dr. Caner ÖZCAN İkilik Sayı Sistemi İkilik sayı sisteminde 0 lar ve 1 ler bulunur. Bilgisayar sistemleri yalnızca ikilik sayı sistemini kullanır. ( d 4 d 3 d 2 d 1 d 0 ) 2 = ( d 0. 2 0 ) + (
Yrd. Doç. Dr. Caner ÖZCAN İkilik Sayı Sistemi İkilik sayı sisteminde 0 lar ve 1 ler bulunur. Bilgisayar sistemleri yalnızca ikilik sayı sistemini kullanır. ( d 4 d 3 d 2 d 1 d 0 ) 2 = ( d 0. 2 0 ) + (
Integer Sınıfı. 9.1 Integer Sınıfına Uygulanan Başlıca Metotlar. Ruby de tamsayılar için kullanılan Fixnum ve Bignum sınıflarını üreten sınıftır.
 9 Integer Sınıfı Ruby de tamsayılar için kullanılan Fixnum ve Bignum sınıflarını üreten sınıftır. Integer Literal Tamsayı gösteren metinler, 1 0, 1, 123, 123456789012345678901234567890 biçiminde yalnızca
9 Integer Sınıfı Ruby de tamsayılar için kullanılan Fixnum ve Bignum sınıflarını üreten sınıftır. Integer Literal Tamsayı gösteren metinler, 1 0, 1, 123, 123456789012345678901234567890 biçiminde yalnızca
VHDL ile KODLAMA ve HATA BULMA TEKNİKLERİ
 KARADENİZ TEKNİK ÜNİVERSİTESİ Bilgisayar Mühendisliği Bölümü Sayısal Tasarım Laboratuarı VHDL ile KODLAMA ve HATA BULMA TEKNİKLERİ 1.Giriş Kodlama, elektronik dünyasında çok sık kullanılan, hatta vazgeçilmesi
KARADENİZ TEKNİK ÜNİVERSİTESİ Bilgisayar Mühendisliği Bölümü Sayısal Tasarım Laboratuarı VHDL ile KODLAMA ve HATA BULMA TEKNİKLERİ 1.Giriş Kodlama, elektronik dünyasında çok sık kullanılan, hatta vazgeçilmesi
C Dersi Bölüm 1. Bilgisayar Donanımı
 C Dersi Bölüm 1 M Bodur 1 Bilgisayar Donanımı Bilgisayarın yapısını ve çalışma prensiplerini bilmemiz Bir bilgisayar programından neler bekleyebileceğimizi anlamamızı sağlar. Bigisayar dört temel birimden
C Dersi Bölüm 1 M Bodur 1 Bilgisayar Donanımı Bilgisayarın yapısını ve çalışma prensiplerini bilmemiz Bir bilgisayar programından neler bekleyebileceğimizi anlamamızı sağlar. Bigisayar dört temel birimden
LASER LIGHT CAUTION DO NOT STARE INTO BEAM. 670nm LASER DIODE,1.0mW MAX OUTPUT IEC 825-1(1993)CLASS I,US 21 CFR 1040 CLASS IIa LASER PRODUCT
 LASER LIGHT CAUTION DO NOT STARE INTO BEAM 670nm LASER DIODE,1.0mW MAX OUTPUT IEC 825-1(1993)CLASS I,US 21 CFR 1040 CLASS IIa LASER PRODUCT PROGRAMLAMA KILAVUZU Z E B E X EL TİPİ BARKOD OKUYUCULAR ZBX00030301
LASER LIGHT CAUTION DO NOT STARE INTO BEAM 670nm LASER DIODE,1.0mW MAX OUTPUT IEC 825-1(1993)CLASS I,US 21 CFR 1040 CLASS IIa LASER PRODUCT PROGRAMLAMA KILAVUZU Z E B E X EL TİPİ BARKOD OKUYUCULAR ZBX00030301
TEMEL KAVRAMLAR Test -1
 TEMEL KAVRAMLAR Test -1 1. 6 ( ) 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 ( 3). ( 8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36:9 18 : 3 A) 1 B) 8 C) D) 4 E) 8 3. (4: 3 + 1):4 A) 3 B) 5
TEMEL KAVRAMLAR Test -1 1. 6 ( ) 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 ( 3). ( 8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36:9 18 : 3 A) 1 B) 8 C) D) 4 E) 8 3. (4: 3 + 1):4 A) 3 B) 5
Merkezi İşlem. Birimi
 VERİ: Kullanıcı veya bilgisayar tarafından sağlanırlar. Sayılar, harfler, sözcükler, ses sinyalleri ve komutlardır.. Veriler bilgisayarın giriş birimleri tarafından toplanırlar. Giriş İşlem Çıkış Önbellek
VERİ: Kullanıcı veya bilgisayar tarafından sağlanırlar. Sayılar, harfler, sözcükler, ses sinyalleri ve komutlardır.. Veriler bilgisayarın giriş birimleri tarafından toplanırlar. Giriş İşlem Çıkış Önbellek
SAYI SİSTEMLERİ ve BOOLE CEBİRİ 1+1=1 ÖĞR.GÖR. GÜNAY TEMÜR - TEKNOLOJİ F. / BİLGİSAYAR MÜH.
 SAYI SİSTEMLERİ ve BOOLE CEBİRİ 1+1=1 Ders Konusu 1854 yılında George Boole tarafından özellikle lojik devrelerde kullanılmak üzere ortaya konulmuş bir matematiksel sistemdir. İkilik Sayı Sistemi Çoğu
SAYI SİSTEMLERİ ve BOOLE CEBİRİ 1+1=1 Ders Konusu 1854 yılında George Boole tarafından özellikle lojik devrelerde kullanılmak üzere ortaya konulmuş bir matematiksel sistemdir. İkilik Sayı Sistemi Çoğu
ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR. (2 ) demek 2 tane 2 3 'ün çarpımı demektir. (2 ) = 2.2 = 2 eder.
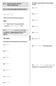 8.. ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR 8...A ÜSLÜ SAYILARIN KUVVETİNİ ALMA ) Aşağıda verilen eşitlikte bilinmeyen harfleri bulunuz. 6 a. 6 ( ) 8 b b) 7 Üslü bir sayının üssü alınırken, üsler çarpılır.
8.. ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR 8...A ÜSLÜ SAYILARIN KUVVETİNİ ALMA ) Aşağıda verilen eşitlikte bilinmeyen harfleri bulunuz. 6 a. 6 ( ) 8 b b) 7 Üslü bir sayının üssü alınırken, üsler çarpılır.
BÖLÜM 2 SAYI SĐSTEMLERĐ (NUMBER SYSTEMS)
 ÖLÜM ĐÇĐNDEKĐLER -sayı sistemleri 2-kodlama ve kodlar 3-boolean kuralları 4-lojik kapılar,lojik devreler 5-karnaugh haritaları 6-sayısal entereler 7-birleşik mantık devreleri 8-multi vibratörler ve flip-floplar
ÖLÜM ĐÇĐNDEKĐLER -sayı sistemleri 2-kodlama ve kodlar 3-boolean kuralları 4-lojik kapılar,lojik devreler 5-karnaugh haritaları 6-sayısal entereler 7-birleşik mantık devreleri 8-multi vibratörler ve flip-floplar
3. Bölüm Algoritmalar
 3. Bölüm Algoritmalar Algoritma ve Programlamaya Giriş Dr. Serkan DİŞLİTAŞ 3.1. Veri ve Bilgi Şekil 3.1 de bilgisayar sistemin temelini oluşturan veri işlem modeli görülmektedir. Hesaplama, saklama gibi
3. Bölüm Algoritmalar Algoritma ve Programlamaya Giriş Dr. Serkan DİŞLİTAŞ 3.1. Veri ve Bilgi Şekil 3.1 de bilgisayar sistemin temelini oluşturan veri işlem modeli görülmektedir. Hesaplama, saklama gibi
BĠLGĠSAYAR PROGRAMLAMA II C++ Programlamaya GiriĢ http://www.cplusplus.com/doc/tutorial/ Published by Juan Soulié
 BĠLGĠSAYAR PROGRAMLAMA II C++ Programlamaya GiriĢ http://www.cplusplus.com/doc/tutorial/ Published by Juan Soulié DERSİN WEB SİTESİ: http://nucleus.istanbul.edu.tr/~bilprog2/ DeğiĢkenler ve Data Türleri
BĠLGĠSAYAR PROGRAMLAMA II C++ Programlamaya GiriĢ http://www.cplusplus.com/doc/tutorial/ Published by Juan Soulié DERSİN WEB SİTESİ: http://nucleus.istanbul.edu.tr/~bilprog2/ DeğiĢkenler ve Data Türleri
25. Aşağıdaki çıkarma işlemlerini doğrudan çıkarma yöntemi ile yapınız.
 BÖLÜM. Büyüklüklerin genel özellikleri nelerdir? 2. Analog büyüklük, analog işaret, analog sistem ve analog gösterge terimlerini açıklayınız. 3. Analog sisteme etrafınızdaki veya günlük hayatta kullandığınız
BÖLÜM. Büyüklüklerin genel özellikleri nelerdir? 2. Analog büyüklük, analog işaret, analog sistem ve analog gösterge terimlerini açıklayınız. 3. Analog sisteme etrafınızdaki veya günlük hayatta kullandığınız
/ / _ \ ' ' / _` '_ \ / / / / _ (_) _ (_ / / / / _ \ / _ \ _ \, _ /_/ /_/ EK ================================================== Hazirlayan : Aras.
 5 10 15 20 25 30 35 40 45 50 55 60 65 70 / _ _ / _ \ ' ' / _` '_ \ / / / / _ (_) _ (_ / / / / _ \ / _ \ _ \,_ _ _ /_/ /_/ EK ================================================== Hazirlayan : Aras. Gor. Ozgur
5 10 15 20 25 30 35 40 45 50 55 60 65 70 / _ _ / _ \ ' ' / _` '_ \ / / / / _ (_) _ (_ / / / / _ \ / _ \ _ \,_ _ _ /_/ /_/ EK ================================================== Hazirlayan : Aras. Gor. Ozgur
Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi. Sayısal Elektronik
 Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi Sayısal Elektronik Günümüz Elektroniği Analog ve Sayısal olmak üzere iki temel türde incelenebilir. Analog büyüklükler sonsuz sayıda değeri içermesine
Makine Mühendisliği İçin Elektrik-Elektronik Bilgisi Sayısal Elektronik Günümüz Elektroniği Analog ve Sayısal olmak üzere iki temel türde incelenebilir. Analog büyüklükler sonsuz sayıda değeri içermesine
LOJİK DEVRELER DERS NOTLARI. Prof.Dr. Bekir ÇAKIR Yrd.Doç.Dr. Ersoy BEŞER Yrd.Doç.Dr. Esra KANDEMİR BEŞER
 LOJİK DEVRELER DERS NOTLARI Prof.Dr. Bekir ÇAKIR Yrd.Doç.Dr. Ersoy BEŞER Yrd.Doç.Dr. Esra KANDEMİR BEŞER 2015 Lojik Devreler Ders Notları B.ÇAKIR & E.BEŞER & E.KANDEMİR BEŞER 1 İÇİNDEKİLER 1. SAYI SİSTEMLERİ
LOJİK DEVRELER DERS NOTLARI Prof.Dr. Bekir ÇAKIR Yrd.Doç.Dr. Ersoy BEŞER Yrd.Doç.Dr. Esra KANDEMİR BEŞER 2015 Lojik Devreler Ders Notları B.ÇAKIR & E.BEŞER & E.KANDEMİR BEŞER 1 İÇİNDEKİLER 1. SAYI SİSTEMLERİ
Bilgi ve Bilgi Sistemleri. Bilgisayar Mühendisliğine Giriş 1
 Bilgi ve Bilgi Sistemleri Bilgisayar Mühendisliğine Giriş Sembol, Veri, Bilgi, Anlamlı Bilgi Anlamlı Bilgi (Knowledge) Bilgi, (Information) Veri(Data) Sembol (Symbol) Örnek: Semboller: 0,,2,.8,9,A,.,Y,Z,%,+,=,!
Bilgi ve Bilgi Sistemleri Bilgisayar Mühendisliğine Giriş Sembol, Veri, Bilgi, Anlamlı Bilgi Anlamlı Bilgi (Knowledge) Bilgi, (Information) Veri(Data) Sembol (Symbol) Örnek: Semboller: 0,,2,.8,9,A,.,Y,Z,%,+,=,!
Hatalar ve Bilgisayar Aritmetiği
 Hatalar ve Bilgisayar Aritmetiği Analitik yollardan çözemediğimiz birçok matematiksel problemi sayısal yöntemlerle bilgisayarlar aracılığı ile çözmeye çalışırız. Bu şekilde Sayısal yöntemler kullanarak
Hatalar ve Bilgisayar Aritmetiği Analitik yollardan çözemediğimiz birçok matematiksel problemi sayısal yöntemlerle bilgisayarlar aracılığı ile çözmeye çalışırız. Bu şekilde Sayısal yöntemler kullanarak
KODLAMA SİSTEMLERİ ve VERİLERİN BİLGİSAYARDA TEMSİLİ
 KODLAMA SİSTEMLERİ ve VERİLERİN BİLGİSAYARDA TEMSİLİ KODLAMA SİSTEMLERİNİN TANIMI : Kodlama, iki küme elemanları arasında karşılıklı kesin olarak belirtilen kurallar bütünüdür diye tanımlanabilir. Diğer
KODLAMA SİSTEMLERİ ve VERİLERİN BİLGİSAYARDA TEMSİLİ KODLAMA SİSTEMLERİNİN TANIMI : Kodlama, iki küme elemanları arasında karşılıklı kesin olarak belirtilen kurallar bütünüdür diye tanımlanabilir. Diğer
SAYISAL ELEKTRONĠK DERS NOTLARI: SAYISAL (DĠJĠTAL) ELEKTRONĠK
 SAYISAL ELEKTRONĠK DERS NOTLARI: SAYISAL (DĠJĠTAL) ELEKTRONĠK Günümüz Elektroniği Analog ve Sayısal olmak üzere iki temel türde incelenebilir. Analog büyüklükler sonsuz sayıda değeri içermesine rağmen
SAYISAL ELEKTRONĠK DERS NOTLARI: SAYISAL (DĠJĠTAL) ELEKTRONĠK Günümüz Elektroniği Analog ve Sayısal olmak üzere iki temel türde incelenebilir. Analog büyüklükler sonsuz sayıda değeri içermesine rağmen
BİL1001 Bilgisayar Bilimlerine Giriş 1
 DEÜ Bilgisayar Bilimleri Bölümü BİL1001 Bilgisayar Bilimlerine Giriş 1 Öğr. Gör. Dr. Alper VAHAPLAR 2017 Yaz Okulu BİL1001 Bilgisayar Bilimlerine Giriş 1 Ders İçeriği Bilgisayar Bilimlerine Giriş Sayı
DEÜ Bilgisayar Bilimleri Bölümü BİL1001 Bilgisayar Bilimlerine Giriş 1 Öğr. Gör. Dr. Alper VAHAPLAR 2017 Yaz Okulu BİL1001 Bilgisayar Bilimlerine Giriş 1 Ders İçeriği Bilgisayar Bilimlerine Giriş Sayı
1 ELEKTRONİK KAVRAMLAR
 İÇİNDEKİLER VII İÇİNDEKİLER 1 ELEKTRONİK KAVRAMLAR 1 Giriş 1 Atomun Yapısı, İletkenler ve Yarı İletkenler 2 Atomun Yapısı 2 İletkenler 3 Yarı İletkenler 5 Sayısal Değerler (I/O) 8 Dalga Şekilleri 9 Kare
İÇİNDEKİLER VII İÇİNDEKİLER 1 ELEKTRONİK KAVRAMLAR 1 Giriş 1 Atomun Yapısı, İletkenler ve Yarı İletkenler 2 Atomun Yapısı 2 İletkenler 3 Yarı İletkenler 5 Sayısal Değerler (I/O) 8 Dalga Şekilleri 9 Kare
İKİLİ SAYILAR VE ARİTMETİK İŞLEMLER
 İKİLİ SAYILAR VE ARİTMETİK İŞLEMLER DENEY 3 GİRİŞ Bu deneyde kurulacak devreler ile işaretsiz ve işaretli ikili sayılar üzerinde aritmetik işlemler yapılacak; işaret, elde, borç, taşma kavramları incelenecektir.
İKİLİ SAYILAR VE ARİTMETİK İŞLEMLER DENEY 3 GİRİŞ Bu deneyde kurulacak devreler ile işaretsiz ve işaretli ikili sayılar üzerinde aritmetik işlemler yapılacak; işaret, elde, borç, taşma kavramları incelenecektir.
BILGISAYAR ARITMETIGI
 1 BILGISAYAR ARITMETIGI Sayısal bilgisayarlarda hesaplama problemlerinin sonuçlandırılması için verileri işleyen aritmetik buyruklar vardır. Bu buyruklar aritmetik hesaplamaları yaparlar ve bilgisayar
1 BILGISAYAR ARITMETIGI Sayısal bilgisayarlarda hesaplama problemlerinin sonuçlandırılması için verileri işleyen aritmetik buyruklar vardır. Bu buyruklar aritmetik hesaplamaları yaparlar ve bilgisayar
Her veri tipine yetecek ve ancak o kadar anabellek alanı ayrılır. Programcı, ana bellekte ayrılacak adresin büyüklüğünü bilerek değişkenlerini
 1 Veri Tipleri Bazı diller veri tiplerini önceden ayırır, bazıları ayırmaz. Teknik olarak, veri tipini önceden belirleyen diller, anabelleğe yerleşecek verileri, orada kapsayacakları alanlara göre gruplara
1 Veri Tipleri Bazı diller veri tiplerini önceden ayırır, bazıları ayırmaz. Teknik olarak, veri tipini önceden belirleyen diller, anabelleğe yerleşecek verileri, orada kapsayacakları alanlara göre gruplara
CHAPTER 1 INTRODUCTION NUMBER SYSTEMS AND CONVERSION. Prof. Dr. Mehmet Akbaba CME 221 LOGİC CİRCUITS
 CHAPTER 1 INTRODUCTION NUMBER SYSTEMS AND CONVERSION Prof. Dr. Mehmet Akbaba CME 221 LOGİC CİRCUITS 1 Prof. M. Akbaba Digital Logic 10/12/2015 This Chapter includes: Digital Systems and Switching Circuits
CHAPTER 1 INTRODUCTION NUMBER SYSTEMS AND CONVERSION Prof. Dr. Mehmet Akbaba CME 221 LOGİC CİRCUITS 1 Prof. M. Akbaba Digital Logic 10/12/2015 This Chapter includes: Digital Systems and Switching Circuits
TAM SAYILAR. Tam Sayılarda Dört İşlem
 TAM SAYILAR Tam Sayılarda Dört İşlem Pozitif ve negatif tam sayılar konu anlatımı ve örnekler içermektedir. Tam sayılarda dört işlem ve bu konuyla ilgili örnek soru çözümleri bulunmaktadır. Grup_09 29.11.2011
TAM SAYILAR Tam Sayılarda Dört İşlem Pozitif ve negatif tam sayılar konu anlatımı ve örnekler içermektedir. Tam sayılarda dört işlem ve bu konuyla ilgili örnek soru çözümleri bulunmaktadır. Grup_09 29.11.2011
EGE ÜNİVERSİTESİ EGE MYO MEKATRONİK PROGRAMI
 EGE ÜNİVERSİTESİ EGE MYO MEKATRONİK PROGRAMI 23.02.2015 Yrd.Doç.Dr. Dilşad Engin PLC Ders Notları 2 PROGRAMLANABİLİR DENETLEYİCİLER NÜMERİK İŞLEME 23.02.2015 Yrd.Doç.Dr. Dilşad Engin PLC Ders Notları 3
EGE ÜNİVERSİTESİ EGE MYO MEKATRONİK PROGRAMI 23.02.2015 Yrd.Doç.Dr. Dilşad Engin PLC Ders Notları 2 PROGRAMLANABİLİR DENETLEYİCİLER NÜMERİK İŞLEME 23.02.2015 Yrd.Doç.Dr. Dilşad Engin PLC Ders Notları 3
Her bir kapının girişine sinyal verilmesi zamanı ile çıkışın alınması zamanı arasında çok kısa da olsa fark bulunmaktadır -> kapı gecikmesi
 Kapılardaki gecikme Her bir kapının girişine sinyal verilmesi zamanı ile çıkışın alınması zamanı arasında çok kısa da olsa fark bulunmaktadır -> kapı gecikmesi Kapılardaki gecikme miktarının hesaplanması
Kapılardaki gecikme Her bir kapının girişine sinyal verilmesi zamanı ile çıkışın alınması zamanı arasında çok kısa da olsa fark bulunmaktadır -> kapı gecikmesi Kapılardaki gecikme miktarının hesaplanması
Programlama Dilleri. C Dili. Programlama Dilleri-ders02/ 1
 Programlama Dilleri C Dili Programlama Dilleri-ders02/ 1 Değişkenler, Sabitler ve Operatörler Değişkenler (variables) bellekte bilginin saklandığı gözlere verilen simgesel isimlerdir. Sabitler (constants)
Programlama Dilleri C Dili Programlama Dilleri-ders02/ 1 Değişkenler, Sabitler ve Operatörler Değişkenler (variables) bellekte bilginin saklandığı gözlere verilen simgesel isimlerdir. Sabitler (constants)
Atatürk Anadolu. Temel Kavramlar Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
TEKNOLOJİ FAKÜLTESİ ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ EET-205 SAYISAL ELEKTRONİK - I LABORATUVARI
 TEKNOLOJİ FAKÜLTESİ ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ EET-205 SAYISAL ELEKTRONİK - I LABORATUVARI DENEY FÖYÜ 1 İÇİNDEKİLER Deney 1 SAYI SİSTEMLERİ... 2 Deney 2 LOJİK KAPILAR (VE/VEYA/DEĞİL)..... 7 Deney
TEKNOLOJİ FAKÜLTESİ ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ EET-205 SAYISAL ELEKTRONİK - I LABORATUVARI DENEY FÖYÜ 1 İÇİNDEKİLER Deney 1 SAYI SİSTEMLERİ... 2 Deney 2 LOJİK KAPILAR (VE/VEYA/DEĞİL)..... 7 Deney
7.Yazmaçlar (Registers), Sayıcılar (Counters)
 7.Yazmaçlar (Registers), Sayıcılar (Counters) 7..Yazmaçlar Paralel Yüklemeli Yazmaçlar Ötelemeli Yazmaçlar 7.2.Sayıcılar Đkili Asenkron Sayıcılar (Binary Ripple Counter) Đkili Kodlanmış Onlu Asenkron Sayıcı
7.Yazmaçlar (Registers), Sayıcılar (Counters) 7..Yazmaçlar Paralel Yüklemeli Yazmaçlar Ötelemeli Yazmaçlar 7.2.Sayıcılar Đkili Asenkron Sayıcılar (Binary Ripple Counter) Đkili Kodlanmış Onlu Asenkron Sayıcı
Uzaktan Eğitim Uygulama ve Araştırma Merkezi
 JAVA PROGRAMLAMA Öğr. Gör. Utku SOBUTAY İÇERİK 2 Java Veri Tipleri ve Özelilkleri Değişken Tanımlama Kuralları Değişken Veri Tipi Değiştirme (Type Casting) Örnek Kodlar Java Veri Tipleri ve Özelilkleri
JAVA PROGRAMLAMA Öğr. Gör. Utku SOBUTAY İÇERİK 2 Java Veri Tipleri ve Özelilkleri Değişken Tanımlama Kuralları Değişken Veri Tipi Değiştirme (Type Casting) Örnek Kodlar Java Veri Tipleri ve Özelilkleri
BM-311 Bilgisayar Mimarisi
 1 BM-311 Bilgisayar Mimarisi Hazırlayan: M.Ali Akcayol Gazi Üniversitesi Bilgisayar Mühendisliği Bölümü Konular Operand türleri Assembly dili 2 İşlemcinin yapacağı iş makine komutlarıyla belirlenir. İşlemcinin
1 BM-311 Bilgisayar Mimarisi Hazırlayan: M.Ali Akcayol Gazi Üniversitesi Bilgisayar Mühendisliği Bölümü Konular Operand türleri Assembly dili 2 İşlemcinin yapacağı iş makine komutlarıyla belirlenir. İşlemcinin
BLM-111 PROGRAMLAMA DİLLERİ I. Ders-8 Değişken Tipleri ve Temel Giriş/Çıkış İşlemleri
 BLM-111 PROGRAMLAMA DİLLERİ I Ders-8 Değişken Tipleri ve Temel Giriş/Çıkış İşlemleri Yrd. Doç. Dr. Ümit ATİLA umitatila@karabuk.edu.tr http://web.karabuk.edu.tr/umitatilla/ Temel Veri Tipleri C dilinde
BLM-111 PROGRAMLAMA DİLLERİ I Ders-8 Değişken Tipleri ve Temel Giriş/Çıkış İşlemleri Yrd. Doç. Dr. Ümit ATİLA umitatila@karabuk.edu.tr http://web.karabuk.edu.tr/umitatilla/ Temel Veri Tipleri C dilinde
BMT 101 Algoritma ve Programlama I 6. Hafta. Yük. Müh. Köksal Gündoğdu 1
 BMT 101 Algoritma ve Programlama I 6. Hafta Yük. Müh. Köksal Gündoğdu 1 C++ Veri Tipleri Yük. Müh. Köksal Gündoğdu 2 Veri Tipleri Tam sayı ve Ondalık sayı veri tipleri Veri Tipi Alt Sınıf Üst Sınıf Duyarlı
BMT 101 Algoritma ve Programlama I 6. Hafta Yük. Müh. Köksal Gündoğdu 1 C++ Veri Tipleri Yük. Müh. Köksal Gündoğdu 2 Veri Tipleri Tam sayı ve Ondalık sayı veri tipleri Veri Tipi Alt Sınıf Üst Sınıf Duyarlı
KODLAMA VE HATA BULMA TEKNİKLERİ
 Karadeniz Teknik Üniversitesi Mühendislik Fakültesi Bilgisayar Mühendisliği Bölümü Sayısal Tasarım Laboratuvarı KODLAMA VE HATA BULMA TEKNİKLERİ Kodlama eleketronik dünyasında çok sık kullanılan, hatta
Karadeniz Teknik Üniversitesi Mühendislik Fakültesi Bilgisayar Mühendisliği Bölümü Sayısal Tasarım Laboratuvarı KODLAMA VE HATA BULMA TEKNİKLERİ Kodlama eleketronik dünyasında çok sık kullanılan, hatta
