M BAKANLIĞI MEGEP (MESLEKÎ EĞİ
|
|
|
- Zeki Kinali
- 8 yıl önce
- İzleme sayısı:
Transkript
1 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİPROJESİ) PAZARLAMA VE PERAKENDE İSTATİSTİK ANKARA 2006
2 Milli Eğitim Bakanlığıtarafından geliştirilen modüller; Talim ve Terbiye Kurulu Başkanlığının tarih ve 269 sayılıkararıile onaylanan, Mesleki ve Teknik Eğitim Okul ve Kurumlarında kademeli olarak yaygınlaştırılan 42 alan ve 192 dala ait çerçeve öğretim programlarında amaçlanan mesleki yeterlikleri kazandırmaya yönelik geliştirilmişöğretim materyalleridir (Ders Notlarıdır). Modüller, bireylere mesleki yeterlik kazandırmak ve bireysel öğrenmeye rehberlik etmek amacıyla öğrenme materyali olarak hazırlanmış, denenmek ve geliştirilmek üzere Mesleki ve Teknik Eğitim Okul ve Kurumlarında uygulanmaya başlanmıştır. Modüller teknolojik gelişmelere paralel olarak, amaçlanan yeterliği kazandırmak koşulu ile eğitim öğretim sırasında geliştirilebilir ve yapılması önerilen değişiklikler Bakanlıkta ilgili birime bildirilir. Örgün ve yaygın eğitim kurumları, işletmeler ve kendi kendine mesleki yeterlik kazanmak isteyen bireyler modüllere internet üzerinden ulaşılabilirler. Basılmışmodüller, eğitim kurumlarında öğrencilere ücretsiz olarak dağıtılır. Modüller hiçbir şekilde ticari amaçla kullanılamaz ve ücret karşılığında satılamaz.
3 İÇİNDEKİLER AÇIKLAMALAR...iii GİRİŞ...1 ÖĞRENME FAALİYETİ İSTATİSTİK İstatistiğin Tanımıve Anlamı Tekil Anlamda İstatistik Çoğul Anlamda İstatistik Parametrenin Tahmini Sonucu İstatistik İstatistiğin Önemi İstatistiğin Diğer Bilimlerle İlişkisi İstatistik Bilgilerinin Toplanması Röleve, Birim (Ünite), İndis ve Önemleri...6 UYGULAMA FAALİYETİ...9 ÖLÇME VE DEĞERLENDİRME...10 ÖĞRENME FAALİYETİ TOPLANAN BİLGİLERİN DÜZENLENMESİ Röleve Sonuçlarının Ayrımı İstatistik Dizisi Basit Diziler YoğunlaştırılmışDiziler SınıflanmışKümülatif Frekans Dizileri UYGULAMA FAALİYETİ...21 ÖLÇME VE DEĞERLENDİRME...22 ÖĞRENME FAALİYETİ TOPLANAN BİLGİLERİN DEĞERLENDİRİLMESİ Grafikler Histogram Frekans Poligonu Kümülâtif Frekans Eğrisi Resim, Yıldız, Doğru ve Daire Şeklindeki Grafikler Ortalamalar Aritmetik Ortalama Aritmetik Ortalama Medyan (Ortanca) Mod İndeksler ve Hesaplanması Zaman İndeksi ve Türleri...43 UYGULAMA FAALİYETİ...44 ÖLÇME VE DEĞERLENDİRME...45 ÖĞRENME FAALİYETİ TOPLANAN BİLGİLERDEN SONUÇ ÇIKARMA Normal Bilgilerin Hazırlanmasıve Değerlendirilmesi Çan Eğrisi Standart Sapma ve Değişim Katsayısı...51 i
4 Standart Sapmanın Hesaplanması Değişim Katsayısı Korelâsyon ve Regresyon Korelâsyon Serpme Diyagram Regresyon Trent Hesaplanmasıve Ekonomik Olaylara Uygulanması Doğrusal Trend...62 UYGULAMA FAALİYETİ...64 ÖLÇME VE DEĞERLENDİRME...65 MODÜL DEĞERLENDİRME...68 CEVAP ANAHTARLARI...70 ÖNERİLEN KAYNAKLAR KAYNAKLAR ii
5 AÇIKLAMALAR KOD 460MI0011 ALAN Pazarlama ve Perakende DAL/MESLEK Alan Ortak MODÜLÜN ADI İstatistik MODÜLÜN TANIMI İstatistikî bilgilerin toplanması, düzenlenmesi, değerlendirilerek bu bilgilerden sonuç çıkarma işlemlerinin anlatıldığıöğrenme materyalidir. SÜRE 40/32 ÖN KOŞUL YETERLİK MODÜLÜN AMACI AÇIKLAMALAR İstatistik yöntemlerini uygulamak. Genel Amaç Ürünle ilgili yapılacak araştırmalara istatistik analiz yöntemlerini uygulayabileceksiniz. Amaçlar İşile ilgili istatistikî bilgileri toplayabileceksiniz. Toplanan istatistikî bilgileri düzenleyebileceksiniz. Toplanan istatistikî bilgileri değerlendirebileceksiniz. Toplanan istatistikî bilgilerin sonuçlarını uygulayabileceksiniz. EĞİTİM ÖĞRETİM ORTAMLARI VE DONANIMLARI Ortam: Sınıf ortamı, bilgisayar laboratuarı. Donanım: Hesap makinesi, bilgisayar, SPS programı, logaritma, ÖLÇME VE DEĞERLENDİRME Her öğrenme faaliyeti sonunda modülde verilen ölçme araçları ile ulaştığınız bilgi düzeyinizi kendiniz değerlendireceksiniz. Modül sonunda ise kazandığınız bilgi ve becerileri belirlemek amacıyla öğretmeniniz tarafından hazırlanacak bir ölçme aracıyla değerlendirileceksiniz. iii
6 iv
7 GİRİŞ Sevgili Öğrenci, GİRİŞ İstatistik de tüm diğer bilim dallarıgibi olaylarıkonu alır. Olay varsa istatistik vardır. Ancak her olay da istatistiğin konusu olmaz. İstatistik yığın olaylarla ilgilenir. Yığın olay, bir olaylar kümesinde tek bir olayın diğerlerini, bağlıolarak da ait olduğu kümeyi temsil edemeyen olaylardır. Eğer bir olaylar kümesinde tek bir olay, tüm olaylar kümesini temsil edebiliyorsa, bu tür olaylara tipik olay denir. Ancak istatistik tipik olaylarla ilgilenmez. Modül, mesleğinizin, şimdiki ve gelecekteki gelişiminin en önemli unsurlarından biridir. Sizin bu satırlarıokurken bile bu alanda yüzlerce değişme ve gelişme olmaktadır. Eğer söylediklerimizi ölçebilir veya rakamlandırabiliyorsanız söylediğiniz şeyler hakkında bir şeyler biliyorsunuz demektir. Bu modülü tamamladığınızda tercih ettiğiniz meslekle ilgili önemli bir aşama kaydedeceksiniz. Bu modülle; istatistikî analız yöntemlerinin işpiyasasındaki önemini ve piyasadaki verileri yorumlayarak bir sonuç çıkarmayıkavrayacaksınız. Kavradıklarınız, işhayatınızdaki verileri analiz noktasında sizi bir adım öne taşıyacak. Piyasa verilerini dikkatli bir şekilde analiz ederek yorumlayabileceksiniz.. 1
8 2
9 ÖĞRENME FAALİYETİ-1 AMAÇ ÖĞRENME FAALİYETİ- 1 Pazarlama alanında ürün ile ilgili yapılacak araştırmalarda istatistik analiz yöntemlerini kullanarak araştırılan ürün ile ilgili tahminlerde bulunup satacağımız ürünün piyasadaki durumuna ve gelecekte pazarlayacağımız ürünün durumu konusunda bilgilere ulaşabileceksiniz. ARAŞTIRMA Bu faaliyet öncesinde yapmanız gereken öncelikli araştırmalar şunlardır: Şirketlerin kullanmışolduklarıistatistikî analiz yöntemlerini araştırınız ve gazetelerdeki verileri yorumlayarak elde ettiğiniz sonuçlarısınıfta arkadaşlarınızla paylaşınız. 1. İSTATİSTİK 1.1. İstatistiğin Tanımıve Anlamı İstatistik çeşitli anlamlarda kullanılmıştır, istatistik sözcüğünün kökü hakkında çeşitli görüşler vardır. Bugün istatistik üç anlamda kullanılmaktadır Tekil Anlamda İstatistik Sayısal gerçeklerin toplanması, düzene konulması, analiz ve yorumunun yapılmasıile uğraşan bir metottur. İstatistik dilinde, sayısal gerçeklere ya da kısaca sayılara veri denir. İstatistikî işlemler için verilerin toplanması, toplanmışverilerden kolayca mantıklı sonuçlar çıkarabilmek için verileri belirli biçimlerde gruplanmasıdır Çoğul Anlamda İstatistik Sistemli bir şekilde toplanan sayısal gerçekleri ifade eder. Bu sayısal gerçeklere, (nüfus sayımı, tarım sayımı, bina sayımı) ya da anket (ücret anketi, fiyat anketi, işgücü anketi vb.) sonuçlarınıgösteren verilerdir. 3
10 Parametrenin Tahmini Sonucu İstatistik Parametre, istatistik teriminin en yeni anlamıdır. Yığın(Population): Gözlem alanında bulunan bireylerin tümüne denir. İstatistiki bireylerin iki özelliğe sahip olmasıgerekir; İstatistikî bireyleri sayılmaya, tartılmaya ve ölçülmeye elverişli olmalıdır. İstatistikî bireyler aynıtürden olmalıdır. Parametre: Yığındaki bireylerin tamamının sayılması, tartılması, ölçülmesi sonucunda bulunan sayılara dayanarak hesaplanan karakteristik değerlere denir. Örnekleme(Sampling): Bir yığından, belirli kurallara göre seçilen bireylerin oluşturduğu kümeye örnek; belirli kurallara göre seçme işine örnekleme denir. İstatistik: Örneklerin sayılmasısonucunda sağlanan sayılara dayanarak hesaplanan karakteristik değerlere denir. Yığın; gözlemin amacına göre küçülebilir, büyüyebilir, daralabilir ya da genişleyebilir. Sözgelimi, bir araştırmacıiçin lise öğrenceleri bir yığındır. Diğeri için İstanbul'da yüksek öğrenim yapıp da yurtta kalan öğrenciler bir yığındır. Bir başkasıiçin meslek liselerindeki erkek öğrenciler bir yığındır. Yığınıkarakterize eden; aritmetik ortalama, standart sapma, momentler, korelasyon kat sayısıvb. birer parametredir. Yığının ya da ana kitlenin sayılmasıçok masraflıve zaman alıcıbir iştir. Bundan dolayı, yığından belirli kurallara göre bazıörnekler alınır ve bu örneklerin, yığınıtemsil ettiği var sayılır. Örnekleri karakterize eden aritmetik ortalama, standart sapma, korelasyon kat sayısı, momentler gibi özet ölçüler birer istatistiktir. Araştırıcı, örnekten sağladığıbilgiler dayanarak yığın hakkında tahminlerde bulunur, ve yığınıkavramaya çalışır. İstatistikî tahmin: Örnek istatistiklerden yığının parametrelerini tahmin etme işlemine denir. Örnekleme metotlarının amacı, saptanan örnek istatistiklerden, yığının parametrelerini az masrafla ve gecikmeden tahmin etmektir. Tahminlerin doğruluğu ve güven sınırlarıtestlerle anlaşılır. Karakteristik ölçümlerin birer sembolle gösterilmesi geleneği vardır. Yığının parametrelerini örnek istatistiklerden ayırmak için farkısemboller kullanılır. Genellikle uygulamada, parametreler Grek harfleri ile istatistikler ise Latin harfleri ile gösterilir. Yığın ortalaması : μ Örneğin ortalaması : X Yığının standart sapması : σ Örneğin standart sapması : s Yığınların korelasyon kat sayısı : ρ Örneklerin korelasyon kat sayısı : r 4
11 İstatistiğin Önemi Verilerin toplanmasıyla devlet ile istatistik arasındaki sıkıilgi, ilk çağlardan beri devam etmektedir. Devletler, alacaklarıönlemlerin isabetini sağlamak ve uygulama sonuçlarınıdenetlemek için sağlık ve sürekli istatistikler toplama çabasındadır. Günlük gazetelere göz atıldığında, sayısal gerçeklerle sık sık karşılaşılmaktadır. İstatistik, insanları, genel kültürleri ve kişisel çıkarlarıyönündün yakından ilgilendirir. İstatistik, çevrede olup bitenleri kavrama ve bunlarıbaşkalarına anlatmada yardımcıdır. Lorda Kelvin in Eğer söylediklerinizi ölçebilir ve rakamlarla ifade edebilirseniz, onlar hakkında bir şeyler biliyorsunuz demektir, aksi halde bilgileriniz zayıf ve tatminkar değildi. Sözü bu nedenle çok önemlidir. İstatistikî çalışmalarda bir konuya dikkat etmek gerekir. Hiçbir istatistik metodu, kedin başına hatalara ya da yanlışsonuçlandırmalara karşıgaranti veremez. Bu nedenle, orijinal veriler sağlıklıolmalıdır. Metot, yerinde ve uzman kişilerce kullanılmalıdır. Sonuçlar da sadece istatistik metotlarından anlayanlarca değil; aynızamanda incelediği konuyu çok iyi bilen kişilerce yorumlanmalıdır. Öte yandan, her rakama kesin gözüyle bakmamak gerekir. Aynırakamıçeşitli sonuçlar çıkaracak şekilde ve abartarak yorumlayabiliriz. Rakamlar, iki yönü keskin bir kılıca benzer. İstenen yöne doğru çekilerek yorumlar yapılabilir. İstatistiğin eğitiminin amacı, sayıların hatalıve doğru yönlerini bilerek gerçeği ortaya seren kişiler yetiştirmektir İstatistiğin Diğer Bilimlerle İlişkisi Yaşamımız üzerindeki etkileri bakımından ekonomi ile istatistiğin ilişkisini özetlemekte yarar vardır. Ekonomik olaylar sayısal göstergelerle ölçülür. Sayısal göstergeler olmadan ekonomiden bahsedilemez. İstatistiklerden anlam çıkarmayıbilmeyen bir ekonomistin düşünülemez mümkün değildir. Yığın olaylarınıinceleyen ekonomi bilimi, verileri istatistikten alır. İstatistik, ekonomik teorilerin açkılanmasında yardımcıve bunların ispatında bir araçtır. Ücretler, fiyatlar, iç ve dışticaret, sınaî ve ziraî üretim, ulaştırma gibi ekonomik olaylarıincelerken elimizde istatistik bulunmazsa, ifadelerimiz yetersiz kalır. Ülkemizde enflasyon var mıdır? İthalat ile ihracat arasındaki fark olumlumudur olumsuz mudur? gibi soruların cevabını, istatistik biliminden faydalanmadan söylenemez. Bugün devlet, ekonomik devlet durumuna getirilmiştir. Gerçekten ekonomik devlet, alacağıekonomik önlemlerin isabetini sağlamak ve uygulama sonuçların denetlemek için sağlıklıve sürekli istatistikler derleyip onlarıuzman ekonomist istatistikçilere yorumlatır. 5
12 İstatistiğin amacısadece herhangi bir bilimde değil, tüm bilimlerce (fizik, biyoloji, tıp, ekonomi, eğitim vb.) kullanılabilir sayısal değerler vermektir. İstatistik faaliyetleri genel hatlarıyla iki ana grupta toplanır: Matematiksel istatistik Uygulamalıİstatistik Matematiksel istatistikçi, yeni teoriler geliştirerek bunu pratik problemlerle birleştirir. Uygulamalıistatistikçi ise diğer alanlarda (tıpta, mühendislikte, eczacılıkta, ekonomide, sosyolojide vb.) karşılaştığıproblemlerde uygun istatistik yöntemlerini seçmek ve bunlarıen iyi şekilde kullanmak zorundadır. Bunun için de bazen veri toplayarak bazen bir örnekleme çalışmasına katılarak bazen de istatistiksel kalite kontrolü yaparak problemlere çözüm getirir. İstatistik yöntemler, istatistiğin tanımında da verildiği gibi sayısal bilgileri toplama, düzenleme (tablo ve grafiklerle ilgililere sunma), analiz yapma ve yorumlama i şlemleriyle uğraşır. Bir istatistikçi hem matematiksel hem de uygulamalıistatistiği bilmek zorundadır. Anca böylece, kamu ve özel kesime, sanayiye, endüstriye, akademik kuruluşlara vb. yararlı olabilir İstatistik Bilgilerinin Toplanması Röleve, Birim (Ünite), İndis ve Önemleri Röleve Röleve sözcüğü Fransızcadaki röleve sözcüğü ile aynıanlamdadır. Türkçe karşılığı derleme demektir. Bilindiği gibi istatistiğin konusu, yığın olaylarıincelemek ve ayrıştırmaktır. Bunun için önce olayın kavranabilmesi amacıyla gözlem yaparak işe başlanır. Üzerinde çalışılacak konuya ilişkin eleman diğerlerinin ölçülmesi, tartılmasıya da sayılması gerekir. Bu evreye, bilgilerin toplanmasıanlamına gelen derleme ya da röleve denir Röleve Çeşitleri ve Uygulama Şekilleri Rölevelerin uygulama biçimleri iki türlüdür. Ani ve devamlıröleveler İstatistik olaylar, ömür süreleri itibarıyla ani ve devamlıolarak ikiye ayrılır. Devamlı olaylar, bir zaman süreci içinde herhangi bir anda gözlenebilen olaylardır. Buna karşıani olaylar, herhangi bir anda olup biten olaylardır. Örneğin; ölüm, doğum gibi. 6
13 Ömür süreleri bakımından farklıolan bu olaylar için ayrıayrıröleveler uygulama zorunluluğu vardır. Kural olarak ani olaylar için devamlıröleveler, devamlıolaylar için ise ani röleveler uygulanır. Genel ve kısmi röleveler İncelemek istenen yığının tamamının gözleme tabi tutulmasına genel röleve denir. Örneğin; bir ülkedeki bütün insanları, bisikletleri, evleri inceleme biçimlerine genel röleve denir. İncelenerek sadece bunların gözleme tabi tutulmasıişlemine kısmi röleve denir. Örneğin; bir ülkedeki bütün öğrencileri değil de bunların %10'unu seçip gözleme tabi tutma işine kısmi röleve denir Birim İstatistik olaylarının incelenmesinde önemli bir yeri olan birim, inceleme ve gözleme konu olarak alınan ortak olaylardan her biridir. Örneğin; öğrencilerle ile ilgili çalışmalarda birim, öğrencidir. Nüfus ile ilgili çalışmalarda birim insandır Birim Çeşitleri Maddi ve maddi olmayan birimler Araba, bina, insan vb. birimler maddi evlilik, boşanma, ölüm, sevgi gibi birimler maddi olmayan birimlerdir. Devamlıve ani birimler İnsan, bina, araba, bitki gibi birimler devamlıdır. Ölüm, doğum gibi birimlere ani birimlerdir. Bağımsız ve bağımlıbirimler Durumlarıitibarıyla bütünlük oluşturan birimlere bağımsız birim denir. Örnek; araba, ev, masa Bağımlıbirimler ise bütünlük oluşturmaz. Bu nedenle bu tür birimlere ayrık birim de denir. Örneğin; dakika, saniye Bunlar birleşince saat diliminde bir zamanıoluşturur. Gerçek ve varsayımsal birimler Fiilen var olan birimler (masa, sandalye, sıra) gerçek birimler, fiilen olmayan birimlere ise (hedefine atılan bir okun hedefi vurup vurmamasının gözlenmesi) varsayımsal birim denir. 7
14 İndis İstatistik olaylarıincelerken birim ne kadar önemli ise indis de o kadar önemlidir. İndis; hangi değerin, birimin hangi öğesine ilişkin olduğunu belirler. Örneğin; bir gruptaki öğrenciler üzerinde yapılan bir çalışmada birim, öğrencidir Hangi değerin hangi öğrenciye ilişkin olduğunun göstergesi ise indis ile belirlenir. İndis=7 ise bunun anlamı, 7. Öğrencinin sahip olduğu değer; indis=9 ise bunun anlamı, 9. Öğrencinin sahip olduğu değer demektir. 8
15 UYGULAMA UYGULAMA FAALİYETİ FAALİYETİ İstatistiğin tanımınıyapınız. İstatistiğin ekonomik açıdan önemini maddeler halinde sayınız. Röleveleri anlatınız. Röleve çeşitlerini sayınız. Birimi anlatınız. Birim çeşitlerini sayınız. İndisi anlatınız. İstatistiğin tanımınıyapmak için istatistiğin tanımıve anlamıkısmını okuyunuz. İstatistiğin diğer bölümlerler ilişkisi kısmınıokuyunuz. Röleveler kısmınıokuyunuz. Röleve çeşitleri kısmınıokuyunuz. Birim kısmınıokuyunuz. Birim çeşitleri kısmınıokuyunuz. İndis kısmınıokuyunuz. 9
16 ÖLÇME ÖLÇME VE VE DEĞERLENDİRME DEĞERLENDİRME OBJEKTİF TESTELER Bu faaliyet sonunda hangi bilgileri kazandığınızı, aşağıdaki sorularıcevaplayarak. belirleyiniz. 1. Sayısal gerçeklere verilen ad nedir? A) İstatistik B) Parametre C) Yığın D) Veri 2. Bir yığından belirli kurallara göre seçilen bireylerin oluşturduğu kümeye ne ad verilir? A) İstatistikî tahmin B) Örnekleme C) Veri D) Yığın 3. Ölü ve doğum gibi olaylar hangi röleve çeşidinin konusunu oluşturur? A) Devamlıröleveler B) Ani röleveler C) Külli röleveler D) Kısmi röleveler 4. Aşağıdakilerden hangisi maddi olmayan birimin konusunu oluşturur.?. A) Evlilik B) İnsan C) Ağaç D) Ev 5. Bir okulda yapılan araştırma sonucunda indis=22 bulunmasının anlamınedir? A) Hiçbir anlamıyoktur B) 22 öğrenci olduğunu gösterir C) 22. öğrencinin sahip olduğu değeri gösterir. D) Bir köy okulu olduğunu gösterir. Cevaplarınızımodülün sonundaki cevap anahtarıile karşılaştırınız. 10
17 Performans Değerlendirme Değerlendirme Kriterleri Evet Hayır Sayılabilen, ölçülebilen ve aynıtürden bireyleri bir araya getirerek bir yığın oluşturdunuz mu? Yığın içinden belirli kurlarla göre bireyler seçerek bir örnekleme oluşturdunuz mu? Çevrenizde meydana gelen olaylar içinde ani ve devamlı röleveleri tespit ettiniz mi? Değerlendirme Cevaplarınızımodülün sonundaki cevap anahtarıile karşılaştırınız. Doğru cevap sayınızıbelirleyerek kendinizi değerlendiriniz. Yanlışcevap verdiğiniz ya da cevap verirken tereddüt yaşadığınız sorularla ilgili konularıfaaliyete dönerek tekrar inceleyiniz. Tüm sorulara evet cevap verdiyseniz diğer faaliyete geçiniz. 11
18 ÖĞRENME FAALİYETİ-2 AMAÇ ÖĞRENME FAALİYETİ- 2 Pazarlama alanında ürün ile ilgili yapılacak araştırmalarda istatistik analiz yöntemlerini kullanarak araştırılan ürün ile ilgili tahminlerde bulunup satacağınız ürünün piyasadaki durumuna ve gelecekte pazarlayacağımız ürünün durumu konusunda bilgilere ulaşabileceksiniz. ARAŞTIRMA Bu faaliyet öncesinde yapmanız gereken öncelikli araştırmalar şunlardır: Şirketlerin kullanmışolduklarıistatistikî analiz yöntemlerini araştırın ve gazetelerde ki verileri yorumlayarak elde ettiğiniz sonuçlarısınıfta arkadaşlarınızla paylaşınız. 2. TOPLANAN BİLGİLERİN DÜZENLENMESİ 2.1. Röleve Sonuçlarının Ayrımı Toplanan verileri düzene koymada, tablo ve grafikler önemli rol oynar. Daha önceden toplanan ve karmaşık durumda bulunan verileri, tablo durumuna getirerek okuyucuya sunmak büyük kolaylıklar sağlar. Verileri tablo halinde sunmadan önce bazıkavramları öğrenmekte yarar vardır. İstatistikî gözlem: Yığın olaylarıoluşturan bireylerin ve bunların özelliklerinin tek tek kaydedilmesine istatistikî gözlem (röleve) denir. Veri: İstatistik gözlem sonucunda elde edilen sayılara denir. Seri: Verilerin oluşturduğu sayıkümesine denir. İlkel seri: Verilerin küçükten büyüğe ya da büyükten küçüğe doğru dizilmesi suretiyle elde edilen seriye denir. 12
19 2.2. İstatistik Dizisi Basit Diziler Bireylere ilişkin verilerin rasgele dizilmesi suretiyle elde edilen diziye basit dizi denir. Örnek: Bir ilköğretim okulundaki 40 öğrencinin kütleleri Tablo 1.1 ve 1.2'deki gibidir: Basit dizi(kg) İlkel seri Tablo 1.1: Basit dizi Tablo 1.2: İlkel seri 13
20 YoğunlaştırılmışDiziler Basit dizilerde gördüğümüz gibi birbirinin aynıolan sayılar defalarca yazılmıştır. Eğer izlediğimiz çok büyük bir grupsa bu kadar veriyi kolayca izleyemeyiz. Bundan dolayıseri hakkında sağlıklıbir düşünceye varamayız. Yoğunlaştırılmışdizilerde tekrar eden sayılar defalarca yazılmak yerine hangi sayının kaç defa tekrar ettiği sayının yanına yazılır. Böylece seriyi inceleme zamanıkısalır ve çalışmalar daha da kolaylaşır. Yoğunlaştırılmışdizi oluştururken yapmamız gereken benzer terimlerden sadece bir tanesi yazılarak yanına kaç kez tekrar ettiği yazılıp yeni bir seri oluşturmaktır. Böylece iki sütunlu bir dizi durumuna getirilir, birinci sütuna birim ya da indisler, ikincisine de kaç kez tekrar ettiği gösterilir ki bunlara birim sayısıya da frekans denir. Bu açıklamalara göre daha önce verilen 80 memurun kütlelerine ilişkin basit serinin, yoğunlaştırılmışdizi durumuna getirilmesi Tablo 1.3'te olduğu gibi yapılır. Kütle (kg) Kişi sayısı (Frekans) Tablo 1.3: 40 öğrencinin kütlelerine ilişkin yoğunlaştırılmışdizi (kg) 14
21 SınıflanmışKümülatif Frekans Dizileri Görüldüğü gibi ilkel serinin en küçük değeri ile en büyük değeri 23 kg ile 53 kg arasındadır. İstatistikî bilgilerin anlamının daha iyi kavranmasıiçin veriler tablo halinde düzene konulmasıgerekir. Frekans tablolarıgruplamalar sonucunda ortaya çıkar. Gruplama: Bireysel değerleri belirli sınırlar içine düşen bireyleri ortak sınıflarda toplama işlemidir. Sınıf Aralığı= En büyük değer-en küçük değer istenilen grup sayısı dır. Frekans tablosunu 7 gruplu yapacak olursak ilkel seride en büyük değer ile en küçük değer arasındaki fark (açıklık) Sınıf Aralığı= = 30 = 6 kg dır. 5 5 Bu sınıf aralığına göre i=6 ise frekans tablosu şöyle olur; (kg) (Frekans) (Yüzdeli frekanslar) Gruplar Memur Sayısı Nispi Frekanslar 23 29, , , , , Tablo 1.4: 40 öğrencinin kütlelerine ilişkin çokluk bölünümü Frekans tablosu (çokluk bölünümü): Gruplama sonucunda oluşan ve belirli bir özelliği temsil temsil eden birey sayısına denir. Frekans bir özelliğin olayda kaç kez tekrarlandığı gösterir. Frekans türleri: Frekanslarıiki ana grupta toplamak mümkündür. Mutlak frekanslar ve nispi (oransal) frekanslar. 15
22 Nispi frekanslar ise gözlem toplamına (40) oranlanarak bulunan frekanslardır. Tablo 1.4'ün incelenmesinde, nispi frekanslar % olarak gösterilmiştir. Bulunuşu ise şöyle açıklanabilir: Örneğin; 44 50,9 grubundaki 22,50 gerçekte %22,50 dir. Bu ise 6/80.100= % 7.50 şeklinde bulunur. Diğerlerinin bulunma yönteminde aynıdır. Değişken: Bireylerin ölçülebilen özelliklerine denir. Örneğin; öğrencilerin Mayıs ayındaki kilosu ile haziran ayındaki kilosu gibi. Değişkenleri iki ana başlıkta toplamak mümkündür. Sürekli değişken: Bir değişken belirle sınırlar arasında sonsuz değer alabiliyorsa, bu tür değişkenlere denir. Süreksiz değişken: Bir değişken belirli sınırlar arasında ancak belirli değerleri alabiliyorsa, bu tür değişkenlere denir. Sınıf aralığı: Frekans bölümlerinde, bir sınıfın alt ve üst sınırıarasında farka denir. Örneğin; Tablo 1.4 te, sınıfının aralığı(i)=44 51= 7 kg'dır. Bir sınıfın başladığıve bittiği değerlere sınıf sınırlarıdenir. Başladığıdeğere alt sınır bittiği değere ise üst sınır denir. Örneğin; Tablo 1.4'teki, 44 50,9 sınıfının alt sınırı44 kg, üst sınırıise 50,9 kg'dır. kg Gruplar Frekans Xi Sınıfın orta değeri 23 29, , , , , Tablo 1,5: 40 öğrencinin kütlelerine ilişkin çokluk bölünümü Sınıf aralığı(i) çok dar tutulursa tablo yığının yapısınıaksettiremez. Sınıf aralığı genişletilirse olaydaki düzen, kolayca kavranamaz. En uygun sınıf aralığınısaptamak için H.A. Sturges sınıf aralığıformülüne başvurmak gerekir. İ= Açıklık log N dır. Sonuç kesirli çıkarsa en yakın yuvarlak sayı, sınıf aralığıolarak alınır. Bu formül 40 öğrencinin kütlelerine uygulanırsa. 16
23 Açıklık= En büyük sınıf orta değeri - En küçük sınıf orta değeri Açıklık=54-26= 28kg bulunur Bu duruma göre 80 memurun kültelerine ilişkin çokluk bölünümü i=7 kg alarak şöyle belirlenir: İ= = log x (kg) Gruplar (Frekans) Nispi Frekanslar 23 26, , , , , , , , Tablo 1.6: 40 öğrencinin kütlelerine ilişkin çokluk bölünümü Açık sınıflar [(Open clases(opın klasis)]: Başlangıç ya da bitimi belirtilmeyen sınıflara denir. Böyle bir sınıf yapma gereği duyulmuşsa bu sınıfta yer alan bireylerin gerçek değerlerinin tablo altında not olarak yazılmasıgerekir. Belirsiz sınıflar: Başlangıcıve bitimi belli olman, bir başka ifadeyle, aldıklarıdeğerin ne olduğu belli olmayan bireylerin yer aldığısınıflardı. Hesap işlemlerini sağlıklı yapabilmek için açık sınıf ve belirsiz sınıflardan kaçınılmalıdır. 17
24 Sınav sonucu Öğrenci sayısı 20 ve daha az ve daha fazla 2 Bilinmeyen 4 Tablo 1.7: belirsiz sınıflar Burada iki açık sınıf bulunmaktadır: Birinci ve beşinci sınıflar. Bunun yanında bir de belirsiz sınıf (Son sınıf) bulunmaktadır. Diğerleri ise aralığıeşit olmayan sınıflardır. Böyle bir tablo, işlemlere pek elverişli değildir. Kümülâtif (Birikimli) çokluk bölünümü Kümülâtif çokluk bölünümlerine ya bir değerden a ya a belli bir değerden çok olayın sayısısöz konusu olduğu zaman başvurulur. Çok sık kullanılan kümülatif çokluk (frekans) ya den az ya da den fazla esasına göre iki ayrıbiçimdedir. den az; aldıklarıdeğer itibarıyla bireyleri, küçükten büyüğe doğru dizme işlemidir. den fazla; aldıklarıdeğer itibarıyla bireyleri, büyükten küçüğe doğru dizme işlemidir. 18
25 (Öğrenci (kg) sayısı) Gruplar (Frekans) Kilosu den az Öğrenci Sayısı 23 26, , , , , , , , (kg) (Öğrenci sayısı) Kilosu den fazla Öğrenci Sayısı Gruplar (Frekans) 23 26, , , , , , , , Tablo 1.8: Mutlak frekanslar üzerinde birikimli çokluk örnekleri 19
26 (kg) % (%) Gruplar (Frekans) Kilosu den Memur Sayısı Az 23 26, , , , , , , , (kg) % Gruplar (Frekans) Kilosu den fazla %Memur Sayısı 23 26, , , , , , , , Tablo 1.9: Nispi frekanslar üzerinden birikimli çokluk örnekleri 20
27 UYGULAMA UYGULAMA FAALİYETİ FAALİYETİ Tablo 1.2 deki ilkel seriyi oluşturunuz. Tablo 1.3 teki yoğunlaştırılmışdiziyi oluşturunuz. Tablo 1.4 teki frekans tablosunu oluşturunuz. Tablo 1,6 daki nispi frekanslarıbulunuz. İlkel seri oluşturulurken Tablo 1,1 deki basit seriden yola çıkınız. Yoğunlaştırılmışdiziyi çentikler yardımıyla oluşturacaksınız. İlkel seride tekrar eden her sayının yanına bir çentik atınız ve her sayıdan bir tane yazarak tekrar eden sayının karşısına kaç defa tekrar ettiğini yazınız. Tablo 1,4 teki frekans tablosu için sınıf aralığının tespit edilmesi lazım. Bunun için önce istenen grup sayısınıtespit edip en büyük değerden en küçük değeri çıkarıp istenen grup sayısına bölünüz. İstenilen grup sayısı5 dir. Nispi frekanslar gözlem toplamına (40 öğrenci) oranlanarak bulunmuştur. Frekans/40*100 şeklinde bulunur. 21
28 ÖLÇMEVE VE DEĞERLENDİRME Ölçme Soruları Bu faaliyet sonunda hangi bilgileri kazandığınızı, aşağıdaki sorularıcevaplayarak belirleyiniz. 1. Verilerin oluşturduğu sayıkümesine ne ad verilir? A) İstatistik B) Parametre C) Seri D) Veri 2. Tablo 1,4 te kaç memur 44 50,9 kg aralığındadır? A) 9 B) 33 C) 7 D) Bireylerin ölçülebilen özelliklerine ne ad verilir? A) DevamlıRöleveler B) Frekans C) Sayı D) Değişken 4. Enbüyükdeğer Enküçükdeğer İstenilenGrupSayıup A) İnsan sayısını B) Sınıf aralığını C) Kgramlarını. D) Özelliklerini =formülüyle neyi buluruz? 5. Bireylere ilişkin verilerin rastgele dizilmesi suretiyle elde edilen diziye nedir? A) Hiçbir anlamıyoktur. B) Yoğunlaştırılmışdizi C) Basit dizi D) İlkel seri Cevaplarınızıcevap anahtarıile karşılaştırınız. DEĞERLENDİRME Cevaplarınızımodülün sonundaki cevap anahtarıile karşılaştırınız. Doğru cevap sayınızıbelirleyerek kendinizi değerlendiriniz. Yanlışcevap verdiğiniz ya da cevap verirken tereddüt yaşadığınız sorularla ilgili konularıfaaliyete dönerek tekrar inceleyiniz. Tüm sorulara doğru cevap verdiyseniz diğer faaliyete geçiniz. 22
29 Performans Değerlendirme Değerlendirme Kriterleri Evet Hayır Tablo 1.1 deki basit diziyi oluşturarak ilkel seriyi düzenlediniz mi? Tablo 1.3 teki yoğunlaştırılmışdiziyi oluşturarak sınıf aralığınıtespit ettiniz mi? (istenilen grup sayısı5) Tablo 1.5 teki çokluk bölümünü oluşturarak sınıf orta değerlerini tespit ettiniz mi? Tablo 1.8 ve Tablo 1.9 daki den az den çok tablolarını oluşturdunuz mu? Değerlendirme Uyguladığınız performans testinde; Aşağıda belirtilen ölçütlere göre kendinizi değerlendiriniz. Eğer sonuca ulaştıysanız bir sonraki uygulama faaliyetine geçebilirsiniz. Sonuca ulaşamadıysanız uygulama faaliyetini yeniden gözden geçiriniz. Adımların aksayan bölümlerini öğretmeninizle konuşunuz. 23
30 ÖĞRENME FAALİYETİ-3 ÖĞRENME FAALİYETİ- 3 AMAÇ Bu faaliyet öncesinde yapmanız gereken öncelikli araştırmalar şunlardır: Şirketlerin kullanmışolduklarıistatistiki analiz yöntemlerini araştırın ve gazetelerde ki verileri yorumlayarak elde ettiğiniz sonuçlarısınıfta arkadaşlarınızla paylaşınız. ARAŞTIRMA Pazarlama alanında ürün ile ilgili yapılacak araştırmalarda istatistik analiz yöntemlerini kullanarak araştırılan ürün ile ilgili tahminlerde bulunup satacağımız ürünün piyasadaki durumuna ve gelecekte pazarlayacağımız ürünün durumu konusunda bilgilere ulaşabileceksiniz. 3. TOPLANAN BİLGİLERİN DEĞERLENDİRİLMESİ 3.1. Grafikler Sınıflandırılmışseriler, "Histogram" ya da frekans poligonu adıverilen grafiklerle gösterilir. Adıgeçen grafiklerin çizimi, aşağıda ayrıntılarıile ele alınmıştır Histogram Histogram: Alanıilgili sınıfın frekansına ve tabanıda ilgili sınıfın aralığına eşit, birbirine bitişik dikdörtgenlerden oluşan bir grafik gösterimdir. Bir histogram çizilmeden önce, sözü edilen dikdörtgenlerin uzunluklarının ayarlanmasıgerekir. Bunun için frekanslar sınıf aralığına bölünerek dikdörtgenlerin alanları ilgili sınıfların frekanslarına eşitlenir. Konuyla ilgili olarak aşağıdaki örneği dikkatlice gözden geçiriniz. Örnek: Sürekli bir x değişkenine ilişkin gözlem sonuçlarıaşağıdaki seriyle verilmiştir. 24
Mühendislikte İstatistik Yöntemler
 .0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
.0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin ortalamasını 5 yapabilmek için son sınavdan kaç alması gerekmektedir?
 İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
Merkezi Yığılma ve Dağılım Ölçüleri
 1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 2 x A fb C 229.5 n 40 20 100 221.5 3 Örnek:.
Prof.Dr.İhsan HALİFEOĞLU Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 2 x A fb C 229.5 n 40 20 100 221.5 3 Örnek:.
Merkezi Eğilim ve Dağılım Ölçüleri
 Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
TANIMLAYICI İSTATİSTİKLER
 TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
VERİ KÜMELERİNİ BETİMLEME
 BETİMLEYİCİ İSTATİSTİK VERİ KÜMELERİNİ BETİMLEME Bir amaç için derlenen verilerin tamamının olduğu, veri kümesindeki birimlerin sayısal değerlerinden faydalanarak açık ve net bir şekilde ilgilenilen özellik
BETİMLEYİCİ İSTATİSTİK VERİ KÜMELERİNİ BETİMLEME Bir amaç için derlenen verilerin tamamının olduğu, veri kümesindeki birimlerin sayısal değerlerinden faydalanarak açık ve net bir şekilde ilgilenilen özellik
İSTATİSTİK I KISA ÖZET KOLAYAOF
 DİKKATİNİZE: BURADA SADECE ÖZETİN İLK ÜNİTESİ SİZE ÖRNEK OLARAK GÖSTERİLMİŞTİR. ÖZETİN TAMAMININ KAÇ SAYFA OLDUĞUNU ÜNİTELERİ İÇİNDEKİLER BÖLÜMÜNDEN GÖREBİLİRSİNİZ. İSTATİSTİK I KISA ÖZET KOLAYAOF 2 Kolayaof.com
DİKKATİNİZE: BURADA SADECE ÖZETİN İLK ÜNİTESİ SİZE ÖRNEK OLARAK GÖSTERİLMİŞTİR. ÖZETİN TAMAMININ KAÇ SAYFA OLDUĞUNU ÜNİTELERİ İÇİNDEKİLER BÖLÜMÜNDEN GÖREBİLİRSİNİZ. İSTATİSTİK I KISA ÖZET KOLAYAOF 2 Kolayaof.com
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 3.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene
3.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ. Prof. Dr. Mualla YALÇINKAYA
 JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
Ders 8: Verilerin Düzenlenmesi ve Analizi
 Ders 8: Verilerin Düzenlenmesi ve Analizi Betimsel İstatistik Merkezsel Eğilim Ölçüleri Dağılım Ölçüleri Grafiksel Gösterimler Bir kitlenin tamamını, ya da kitleden alınan bir örneklemi özetlemekle (betimlemekle)
Ders 8: Verilerin Düzenlenmesi ve Analizi Betimsel İstatistik Merkezsel Eğilim Ölçüleri Dağılım Ölçüleri Grafiksel Gösterimler Bir kitlenin tamamını, ya da kitleden alınan bir örneklemi özetlemekle (betimlemekle)
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ KOMBİNEZON-JÜPON KALIBI
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ KOMBİNEZON-JÜPON KALIBI ANKARA 2008 Milli Eğitim Bakanlığı tarafından geliştirilen
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ KOMBİNEZON-JÜPON KALIBI ANKARA 2008 Milli Eğitim Bakanlığı tarafından geliştirilen
İÇİNDEKİLER ÖN SÖZ...
 İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
Kitle: Belirli bir özelliğe sahip bireylerin veya birimlerin tümünün oluşturduğu topluluğa kitle denir.
 BÖLÜM 1: FREKANS DAĞILIMLARI 1.1. Giriş İstatistik, rasgelelik içeren olaylar, süreçler, sistemler hakkında modeller kurmada, gözlemlere dayanarak bu modellerin geçerliliğini sınamada ve bu modellerden
BÖLÜM 1: FREKANS DAĞILIMLARI 1.1. Giriş İstatistik, rasgelelik içeren olaylar, süreçler, sistemler hakkında modeller kurmada, gözlemlere dayanarak bu modellerin geçerliliğini sınamada ve bu modellerden
Veri Analizi. Isınma Hareketleri. Test İstatistikleri. b) En çok tekrar eden: 7 (mod) c) Açıklık = En büyük En küçük = 10 1 = 9. d)
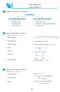 Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
TEMEL İSTATİSTİK BİLGİSİ. İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar
 TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
istatistik 4. Bir frekans dağılımına ilişkin birikimli seriler 1. Birimlerle ilgili aşağıdaki ifadelerden hangisi
 2010 S 4200- İstatistik sorulannın cevap l anmasında gerekli olabilecek t ablolar ve f ormüller bu kitapçığın sonunda verilmiştir. 1. Birimlerle ilgili aşağıdaki ifadelerden hangisi yanlıstır? ) Maddesel
2010 S 4200- İstatistik sorulannın cevap l anmasında gerekli olabilecek t ablolar ve f ormüller bu kitapçığın sonunda verilmiştir. 1. Birimlerle ilgili aşağıdaki ifadelerden hangisi yanlıstır? ) Maddesel
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ
 TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
Bölüm 3. Tanımlayıcı İstatistikler
 Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Temel İstatistik. Y.Doç.Dr. İbrahim Turan Mart Tanımlayıcı İstatistik. Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri
 Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Mühendislikte İstatistiksel Yöntemler
 Mühendislikte İstatistiksel Yöntemler BÖLÜM 2 AÇIKLAYICI (BETİMLEYİCİ) İSTATİSTİK Yrd. Doç. Dr. Fatih TOSUNOĞLU 1-Açıklayıcı (Betimleyici) İstatistik İnceleme sonucu elde edilen ham verilerin istatistiksel
Mühendislikte İstatistiksel Yöntemler BÖLÜM 2 AÇIKLAYICI (BETİMLEYİCİ) İSTATİSTİK Yrd. Doç. Dr. Fatih TOSUNOĞLU 1-Açıklayıcı (Betimleyici) İstatistik İnceleme sonucu elde edilen ham verilerin istatistiksel
GRAFİK YORUMLAMA. 1 ) Sütun Grafiği : Belirli bir zaman aralığında bazı veri grup-
 GRAFİK YORUMLAMA Verilerin veya karşılaştırılması yapılacak değişkenlerin çizgi, tablo, nokta veya şekillerle ifade edilmesine grafik adı verilir. Grafik türleri olarak; sütun, çizgi, daire, histogram,
GRAFİK YORUMLAMA Verilerin veya karşılaştırılması yapılacak değişkenlerin çizgi, tablo, nokta veya şekillerle ifade edilmesine grafik adı verilir. Grafik türleri olarak; sütun, çizgi, daire, histogram,
EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler VERİLERİN DÜZENLENMESİ VERİLERİN DÜZENLENMESİ
 09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI
 ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
İÇİNDEKİLER BÖLÜM 1 KAVRAMLAR VE YÖNTEMBİLİM
 İÇİNDEKİLER BÖLÜM 1 KAVRAMLAR VE YÖNTEMBİLİM I. İSTATİSTİK KAVRAMI ve TANIMI... 1 A. İSTATİSTİK KAVRAMI... 1 B. İSTATİSTİĞİN TANIMI... 2 C. İSTATİSTİĞİN TARİHÇESİ... 2 D. GÜNÜMÜZDE İSTATİSTİK VE ÖNEMİ...
İÇİNDEKİLER BÖLÜM 1 KAVRAMLAR VE YÖNTEMBİLİM I. İSTATİSTİK KAVRAMI ve TANIMI... 1 A. İSTATİSTİK KAVRAMI... 1 B. İSTATİSTİĞİN TANIMI... 2 C. İSTATİSTİĞİN TARİHÇESİ... 2 D. GÜNÜMÜZDE İSTATİSTİK VE ÖNEMİ...
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) TESİSAT TEKNOLOJİSİ VE İKLİMLENDİRME
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) TESİSAT TEKNOLOJİSİ VE İKLİMLENDİRME SOĞUK SU HAZIRLAMA (CHİLLER) GRUBU MONTAJI ANKARA 2008 Milli Eğitim
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) TESİSAT TEKNOLOJİSİ VE İKLİMLENDİRME SOĞUK SU HAZIRLAMA (CHİLLER) GRUBU MONTAJI ANKARA 2008 Milli Eğitim
ORTALAMA ÖLÇÜLERİ. Ünite 6. Öğr. Gör. Ali Onur CERRAH
 ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
Grafik üzerindeki bilgiler özetlenmiştir. Veriler arasındaki ilişkiler görünür haldedir.
 GRAFİK VE İSTATİSTİK Grafikler,verileri görsel hale getirerek,veriler üzerinde daha kolay işlem yapılmasına ve elde edilen sonuçları değerlendirerek üzerinde tahmin yapılmasına olanak sağlar. Grafik üzerindeki
GRAFİK VE İSTATİSTİK Grafikler,verileri görsel hale getirerek,veriler üzerinde daha kolay işlem yapılmasına ve elde edilen sonuçları değerlendirerek üzerinde tahmin yapılmasına olanak sağlar. Grafik üzerindeki
ÖLÇME VE DEĞERLENDİRME. Antrenörlük Eğitimi 4. Sınıf. Ölçme ve Değerlendirme - Yrd. Doç. Dr. Yetkin Utku KAMUK
 ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
PAZARLAMA VE PERAKENDE
 T.C. MİLLÎ EĞİTİM BAKANLIĞI PAZARLAMA VE PERAKENDE İSTATİSTİK 462I00001 Ankara, 2011 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri
T.C. MİLLÎ EĞİTİM BAKANLIĞI PAZARLAMA VE PERAKENDE İSTATİSTİK 462I00001 Ankara, 2011 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri
SÜREKLĠ OLASILIK DAĞILIMLARI
 SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ
 1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
İSTATİSTİK STATISTICS (2+0) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI
 İSTATİSTİK STATISTICS (+) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI KONU BAŞLIKLARI :. İSTATİSTİĞE GİRİŞ. VERİLERİN DÜZENLENMESİ. MERKEZİ EĞİLİM ÖLÇÜLERİ.
İSTATİSTİK STATISTICS (+) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI KONU BAŞLIKLARI :. İSTATİSTİĞE GİRİŞ. VERİLERİN DÜZENLENMESİ. MERKEZİ EĞİLİM ÖLÇÜLERİ.
8.Hafta. Değişkenlik Ölçüleri. Öğr.Gör.Muhsin ÇELİK. Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek,
 İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI. Ders 2 Merkezi Eğilim Ölçüleri
 ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri. Giriş Veri kümesi. Ortalamalar iki grupta incelenir. A. Duyarlı olan ortalama. B. Duyarlı olmayan ortalama
 GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri Yrd. Doç. Dr. Safa KARAMAN 1 2 Giriş Veri kümesi Verileri betimlemenin ve özetlemenin bir diğer yolu da verilerin bir
GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri Yrd. Doç. Dr. Safa KARAMAN 1 2 Giriş Veri kümesi Verileri betimlemenin ve özetlemenin bir diğer yolu da verilerin bir
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
VERİ SETİNE GENEL BAKIŞ
 VERİ SETİNE GENEL BAKIŞ Outlier : Veri setinde normal olmayan değerler olarak tanımlanır. Ders: Kantitatif Yöntemler 1 VERİ SETİNE GENEL BAKIŞ Veri setinden değerlendirme başlamadan çıkarılabilir. Yazım
VERİ SETİNE GENEL BAKIŞ Outlier : Veri setinde normal olmayan değerler olarak tanımlanır. Ders: Kantitatif Yöntemler 1 VERİ SETİNE GENEL BAKIŞ Veri setinden değerlendirme başlamadan çıkarılabilir. Yazım
BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ
 1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI Tanım
 2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
Copyright 2004 Pearson Education, Inc. Slide 1
 Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
T.C. MİLLÎ EĞİTİM BAKANLIĞI
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GEMİ YAPIMI BAŞ BLOK RESMİ ANKARA, 2009 Milli Eğitim Bakanlığı tarafından geliştirilen modüller; Talim ve
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GEMİ YAPIMI BAŞ BLOK RESMİ ANKARA, 2009 Milli Eğitim Bakanlığı tarafından geliştirilen modüller; Talim ve
YANLILIK. Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır.
 AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5
 Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
TEKSTİLDE KALİTE DERSİ. Reklamasyon durumlarını belirlemek. İstatistik hesaplamaları yapmak
 TEKSTİLDE KALİTE DERSİ Dersin Modülleri Kalite Güvence I Kalite Güvence II Kalite prosedörleri I Kalite prosedörleri II Reklamasyon İstatistik Kazandırılan Yeterlikler Kalite güvence sistemini hazırlamak
TEKSTİLDE KALİTE DERSİ Dersin Modülleri Kalite Güvence I Kalite Güvence II Kalite prosedörleri I Kalite prosedörleri II Reklamasyon İstatistik Kazandırılan Yeterlikler Kalite güvence sistemini hazırlamak
T.C. MİLLÎ EĞİTİM BAKANLIĞI
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ KADIN SPOR PANTOLON KALIBI ANKARA 2006 Milli Eğitim Bakanlığı tarafından geliştirilen
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ KADIN SPOR PANTOLON KALIBI ANKARA 2006 Milli Eğitim Bakanlığı tarafından geliştirilen
13. Olasılık Dağılımlar
 13. Olasılık Dağılımlar Mühendislik alanında karşılaşılan fiziksel yada fiziksel olmayan rasgele değişken büyüklüklerin olasılık dağılımları için model alınabilecek çok sayıda sürekli ve kesikli fonksiyon
13. Olasılık Dağılımlar Mühendislik alanında karşılaşılan fiziksel yada fiziksel olmayan rasgele değişken büyüklüklerin olasılık dağılımları için model alınabilecek çok sayıda sürekli ve kesikli fonksiyon
Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması
 Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması Projenin Amacı : YGS de başarılı olmak isteyen bir öğrencinin, istatistiksel yöntemler çerçevesinde, sınavda çıkan soru sayısını,
Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması Projenin Amacı : YGS de başarılı olmak isteyen bir öğrencinin, istatistiksel yöntemler çerçevesinde, sınavda çıkan soru sayısını,
MUHASEBE VE FİNANSMAN
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MUHASEBE VE FİNANSMAN MESLEKİ ARİTMETİK 344MV0068 Ankara, 2011 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri
T.C. MİLLÎ EĞİTİM BAKANLIĞI MUHASEBE VE FİNANSMAN MESLEKİ ARİTMETİK 344MV0068 Ankara, 2011 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) MATBAA TİFDRUK SİLİNDİR TEMİZLİĞİ
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) MATBAA TİFDRUK SİLİNDİR TEMİZLİĞİ ANKARA 2008 Milli Eğitim Bakanlığı tarafından geliştirilen modüller; Talim
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) MATBAA TİFDRUK SİLİNDİR TEMİZLİĞİ ANKARA 2008 Milli Eğitim Bakanlığı tarafından geliştirilen modüller; Talim
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri. BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014
 Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014)
 İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014) S-1) Bir otoyol üzerinde radarla hız kontrolü yapan, polis ekipler tarafından tespit edilen tane aracın hızları aşağıdaki tabloda
İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014) S-1) Bir otoyol üzerinde radarla hız kontrolü yapan, polis ekipler tarafından tespit edilen tane aracın hızları aşağıdaki tabloda
DERS BİLGİ FORMU. Zorunlu Ders X. Haftalık Ders Saati Okul Eğitimi Süresi
 DERSİN ADI BÖLÜM PROGRAM DÖNEMİ DERSİN DİLİ DERS KATEGORİSİ ÖN ŞARTLAR SÜRE VE DAĞILIMI KREDİ DERSİN AMACI ÖĞRENME ÇIKTILARI VE YETERLİKLER DERSİN İÇERİĞİ VE DAĞILIMI (MODÜLLER VE HAFTALARA GÖRE DAĞILIMI)
DERSİN ADI BÖLÜM PROGRAM DÖNEMİ DERSİN DİLİ DERS KATEGORİSİ ÖN ŞARTLAR SÜRE VE DAĞILIMI KREDİ DERSİN AMACI ÖĞRENME ÇIKTILARI VE YETERLİKLER DERSİN İÇERİĞİ VE DAĞILIMI (MODÜLLER VE HAFTALARA GÖRE DAĞILIMI)
ÖLÇME VE DEĞERLENDĠRME (3)
 ÖLÇME VE DEĞERLENDĠRME (3) ÖLÇME SONUÇLARI ÜZERĠNDE ĠSTATĠSTĠKSEL ĠġLEMLER VERĠLERĠN DÜZENLENMESĠ -Herhangi bir test uygulamasından önce verilerin düzenlenmesi için önce bütün puanların büyüklüklerine
ÖLÇME VE DEĞERLENDĠRME (3) ÖLÇME SONUÇLARI ÜZERĠNDE ĠSTATĠSTĠKSEL ĠġLEMLER VERĠLERĠN DÜZENLENMESĠ -Herhangi bir test uygulamasından önce verilerin düzenlenmesi için önce bütün puanların büyüklüklerine
KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR ANALİTİK OLMAYAN MERKEZİ. Aritmetik ortalama **Medyan(median)
 KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ 1 MERKEZİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR Bir örneklemde mevcut olan tüm veriler hesaba katılır. ANALİTİK OLMAYAN MERKEZİ EĞİLİM ÖLÇÜLERİ Bir örneklemdeki verilerin bir
KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ 1 MERKEZİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR Bir örneklemde mevcut olan tüm veriler hesaba katılır. ANALİTİK OLMAYAN MERKEZİ EĞİLİM ÖLÇÜLERİ Bir örneklemdeki verilerin bir
T.C. MİLLÎ EĞİTİM BAKANLIĞI
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) İNŞAAT TEKNOLOJİSİ CAM VE CAM ÇITASI ANKARA 2006 Milli Eğitim Bakanlığı tarafından geliştirilen modüller;
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) İNŞAAT TEKNOLOJİSİ CAM VE CAM ÇITASI ANKARA 2006 Milli Eğitim Bakanlığı tarafından geliştirilen modüller;
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI Tarih/Saat/Yer: 15.06.16/09:00-10:30/AS115-116-117 Instructor: Prof. Dr. Hüseyin
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI Tarih/Saat/Yer: 15.06.16/09:00-10:30/AS115-116-117 Instructor: Prof. Dr. Hüseyin
 A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
İSTATİSTİK MHN3120 Malzeme Mühendisliği
 İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :emre.yalamac@cbu.edu.tr YARDIMCI KAYNAKLAR Mühendiler
İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :emre.yalamac@cbu.edu.tr YARDIMCI KAYNAKLAR Mühendiler
T.C. MİLLÎ EĞİTİM BAKANLIĞI
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) SERAMİK VE CAM TEKNOLOJİSİ TIRNAKLI YAPRAK -2 ANKARA 2007 Milli Eğitim Bakanlığı tarafından geliştirilen
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKİ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) SERAMİK VE CAM TEKNOLOJİSİ TIRNAKLI YAPRAK -2 ANKARA 2007 Milli Eğitim Bakanlığı tarafından geliştirilen
T.C. MİLLİ EĞİTİM BAKANLIĞI
 T.C. MİLLİ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ TEMEL MESLEKİ HESAPLAMA ANKARA 2007 Milli Eğitim Bakanlığı tarafından geliştirilen
T.C. MİLLİ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ TEMEL MESLEKİ HESAPLAMA ANKARA 2007 Milli Eğitim Bakanlığı tarafından geliştirilen
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI Tarih/Saat/Yer: 24.06.16/11:00-12:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI Tarih/Saat/Yer: 24.06.16/11:00-12:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz
MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ)
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) DENİZ ARAÇLARI YAPIMI ENDAZE 2 ANKARA 2008 Milli Eğitim Bakanlığı tarafından geliştirilen modüller; Talim
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) DENİZ ARAÇLARI YAPIMI ENDAZE 2 ANKARA 2008 Milli Eğitim Bakanlığı tarafından geliştirilen modüller; Talim
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI Tarih/Saat/Yer: 20.06.16/15:00-16:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz Öğrenci
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI Tarih/Saat/Yer: 20.06.16/15:00-16:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz Öğrenci
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler
 Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
Verilerin Düzenlenmesi
 Verilerin Düzenlenmesi İstatistiksel verileri anlamlı hale getirmenin 5 ayrı yolu: 1. Sözel ifadelerle açıklama 2. Tablolar halinde düzenleme 3. Seriler halinde düzenleme 4. Grafiklerle gösterme 5. Bu
Verilerin Düzenlenmesi İstatistiksel verileri anlamlı hale getirmenin 5 ayrı yolu: 1. Sözel ifadelerle açıklama 2. Tablolar halinde düzenleme 3. Seriler halinde düzenleme 4. Grafiklerle gösterme 5. Bu
Örneklemden elde edilen parametreler üzerinden kitle parametreleri tahmin edilmek istenmektedir.
 ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
Mühendislikte İstatistiksel Yöntemler
 Mühendislikte İstatistiksel Yöntemler BÖLÜM 7 TAHMİNLER Yrd. Doç. Dr. Fatih TOSUNOĞLU 1 Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır.
Mühendislikte İstatistiksel Yöntemler BÖLÜM 7 TAHMİNLER Yrd. Doç. Dr. Fatih TOSUNOĞLU 1 Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır.
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU ÖDEV: Aşağıda verilen 100 öğrenciye ait gözlem değerlerinin aritmetik ortalama, standart sapma, ortanca ve tepe değerini bulunuz. (sınıf aralığını 5 alınız) 155 160 164 165 168
Prof.Dr.İhsan HALİFEOĞLU ÖDEV: Aşağıda verilen 100 öğrenciye ait gözlem değerlerinin aritmetik ortalama, standart sapma, ortanca ve tepe değerini bulunuz. (sınıf aralığını 5 alınız) 155 160 164 165 168
Yrd. Doç. Dr. Sedat Şen 9/27/2018 2
 2.SUNUM Belirli bir amaç için toplanmış verileri anlamlı haline getirmenin farklı yolları vardır. Verileri sözel ifadelerle açıklama Verileri tablolar halinde düzenleme Verileri grafiklerle gösterme Veriler
2.SUNUM Belirli bir amaç için toplanmış verileri anlamlı haline getirmenin farklı yolları vardır. Verileri sözel ifadelerle açıklama Verileri tablolar halinde düzenleme Verileri grafiklerle gösterme Veriler
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) KONAKLAMA VE SEYAHAT HİZMETLERI
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) KONAKLAMA VE SEYAHAT HİZMETLERI BİLGİSAYARDA DÖKÜMAN HAZIRLAMA ANKARA 2006 Milli Eğitim Bakanlığı tarafından
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) KONAKLAMA VE SEYAHAT HİZMETLERI BİLGİSAYARDA DÖKÜMAN HAZIRLAMA ANKARA 2006 Milli Eğitim Bakanlığı tarafından
rasgele değişkeninin olasılık yoğunluk fonksiyonu,
 3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
AVRASYA ÜNİVERSİTESİ
 Ders Tanıtım Formu Dersin Adı Öğretim Dili İSTATİSTİK Türkçe Dersin Verildiği Düzey Ön Lisans (X) Lisans ( ) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (X) Uzaktan Öğretim( ) Diğer
Ders Tanıtım Formu Dersin Adı Öğretim Dili İSTATİSTİK Türkçe Dersin Verildiği Düzey Ön Lisans (X) Lisans ( ) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (X) Uzaktan Öğretim( ) Diğer
ÖĞRENCİNİN ADI SOYADI:. NO:
 ÖĞRENCİNİN ADI SOYADI:. NO: İMZA: 2011-2012 ÖĞRETİM YILI TIP 1. SINIF TEMEL BİYOİSTATİSTİK DERSİ ARA SINAVI (04.11.2011) Biyoistatistik ve Tıp Bilişimi Anabilim Dalı Başarılar Temel Biyoistatistik dersi
ÖĞRENCİNİN ADI SOYADI:. NO: İMZA: 2011-2012 ÖĞRETİM YILI TIP 1. SINIF TEMEL BİYOİSTATİSTİK DERSİ ARA SINAVI (04.11.2011) Biyoistatistik ve Tıp Bilişimi Anabilim Dalı Başarılar Temel Biyoistatistik dersi
BÖLÜM 10 ÖRNEKLEME YÖNTEMLERİ
 İÇİNDEKİLER BÖLÜM 10 ÖRNEKLEME YÖNTEMLERİ I. ÖRNEKLEME... 1 II. ÖRNEKLEMENİN SAFHALARI... 2 III. ÖRNEK ALMA YÖNTEMLERİ 5 A. RASYONEL ÖRNEK ALMA... 5 B. TESADÜFİ ÖRNEK ALMA... 6 C. KADEMELİ ÖRNEK ALMA...
İÇİNDEKİLER BÖLÜM 10 ÖRNEKLEME YÖNTEMLERİ I. ÖRNEKLEME... 1 II. ÖRNEKLEMENİN SAFHALARI... 2 III. ÖRNEK ALMA YÖNTEMLERİ 5 A. RASYONEL ÖRNEK ALMA... 5 B. TESADÜFİ ÖRNEK ALMA... 6 C. KADEMELİ ÖRNEK ALMA...
Gruplanmış serilerde standart sapma hesabı
 Gruplanmış serilerde standart sapma hesabı Örnek: Verilen gruplanmış serinin standart sapmasını bulunuz? Sınıflar f i X X X m i f i. m i m i - (m i - ) f i.(m i - ) 0 den az 3 4 den az 7 4 6 dan az 4 6
Gruplanmış serilerde standart sapma hesabı Örnek: Verilen gruplanmış serinin standart sapmasını bulunuz? Sınıflar f i X X X m i f i. m i m i - (m i - ) f i.(m i - ) 0 den az 3 4 den az 7 4 6 dan az 4 6
İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği
 İSTATİSTİK E GİRİŞ TEMEL KAVRAMLAR İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği Elemanlarıl AMAÇ İstatistiğe
İSTATİSTİK E GİRİŞ TEMEL KAVRAMLAR İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği Elemanlarıl AMAÇ İstatistiğe
 009 BS 400- İstatistik sonılannın cevaplanmasında gerekli olabilecek tablolar ve formüller bu kitapçığın sonunda verilmiştir. 1. şağıdakilerden hangisi doğal birimdir? l TV alıcısı Bl Trafik kazası CL
009 BS 400- İstatistik sonılannın cevaplanmasında gerekli olabilecek tablolar ve formüller bu kitapçığın sonunda verilmiştir. 1. şağıdakilerden hangisi doğal birimdir? l TV alıcısı Bl Trafik kazası CL
T.C. MİLLÎ EĞİTİM BAKANLIĞI
 T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ ERKEK BERMUDA KALIBI ANKARA 2006 Milli Eğitim Bakanlığı tarafından geliştirilen
T.C. MİLLÎ EĞİTİM BAKANLIĞI MEGEP (MESLEKÎ EĞİTİM VE ÖĞRETİM SİSTEMİNİN GÜÇLENDİRİLMESİ PROJESİ) GİYİM ÜRETİM TEKNOLOJİSİ ERKEK BERMUDA KALIBI ANKARA 2006 Milli Eğitim Bakanlığı tarafından geliştirilen
BKİ farkı Standart Sapması (kg/m 2 ) A B BKİ farkı Ortalaması (kg/m 2 )
 4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
Oluşturulan evren listesinden örnekleme birimlerinin seçkisiz olarak çekilmesidir
 Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
Hatalar Bilgisi ve İstatistik Ders Kodu: Kredi: 3 / ECTS: 5
 Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
Temel Ġstatistik. Tanımlayıcı Ġstatistik. Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri. Y.Doç.Dr. Ġbrahim Turan Mart 2011
 Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
IİSTATIİSTIİK. Mustafa Sezer PEHLI VAN
 IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
istatistik El 10 1_ ve 2_ sorular a Ş3 gldakl bilgilere göre Al 4 Bl 6 cı 7 Dl 8 Al 5 B) 12 CL 27 D) 28 E) 35 2Q 10 BS 4200-A
 2Q 10 BS 4200- İstatistik sorulannın cevap l anmasında gerekli olabilecek tablolar ve f ormüller bu kita p ç ığın sonunda ver-ilmiştir. 1_ ve 2_ sorular a Ş3 gldakl bilgilere göre cevaplandırılacaktır
2Q 10 BS 4200- İstatistik sorulannın cevap l anmasında gerekli olabilecek tablolar ve f ormüller bu kita p ç ığın sonunda ver-ilmiştir. 1_ ve 2_ sorular a Ş3 gldakl bilgilere göre cevaplandırılacaktır
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
OLASILIK ve KURAMSAL DAĞILIMLAR
 OLASILIK ve KURAMSAL DAĞILIMLAR Kuramsal Dağılımlar İstatistiksel çözümlemelerde; değişkenlerimizin dağılma özellikleri, çözümleme yönteminin seçimi ve sonuçlarının yorumlanmasında önemlidir. Dağılma özelliklerine
OLASILIK ve KURAMSAL DAĞILIMLAR Kuramsal Dağılımlar İstatistiksel çözümlemelerde; değişkenlerimizin dağılma özellikleri, çözümleme yönteminin seçimi ve sonuçlarının yorumlanmasında önemlidir. Dağılma özelliklerine
VERİLERİN GRAFİKLER YARDIMIYLA SUNUMU. 3.2.1.Daire Grafikleri Yardımıyla Verilerin Sunumu. 3.2.2.Sütun(Çubuk) Grafikleri Yardımıyla Sunumu
 SAÜ 3. BÖLÜM VERİLERİN GRAFİKLER YARDIMIYLA SUNUMU PROF. DR. MUSTAFA AKAL İÇİNDEKİLER 3.2.Grafiksel Sunumlar 3.2.1.Daire Grafikleri Yardımıyla Verilerin Sunumu 3.2.2.Sütun(Çubuk) Grafikleri Yardımıyla
SAÜ 3. BÖLÜM VERİLERİN GRAFİKLER YARDIMIYLA SUNUMU PROF. DR. MUSTAFA AKAL İÇİNDEKİLER 3.2.Grafiksel Sunumlar 3.2.1.Daire Grafikleri Yardımıyla Verilerin Sunumu 3.2.2.Sütun(Çubuk) Grafikleri Yardımıyla
EL SANATLARI TEKNOLOJİSİ
 T.C. MİLLÎ EĞİTİM BAKANLIĞI EL SANATLARI TEKNOLOJİSİ KİLİM DOKUMA-2 Ankara, 2012 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri kazandırmaya
T.C. MİLLÎ EĞİTİM BAKANLIĞI EL SANATLARI TEKNOLOJİSİ KİLİM DOKUMA-2 Ankara, 2012 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri kazandırmaya
