Prof.Dr.İhsan HALİFEOĞLU
|
|
|
- Sanaz Avcı
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Prof.Dr.İhsan HALİFEOĞLU
2 FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç vardır. Bu ölçüler, verileri yalnızca özlü bir biçimde belirtmekle kalmaz karşılaştırmalara, genellemelere, yorumlamalara olanak sağlar. Araştırmalarda deneklerin kimi küçük, kimi orta kimi ise yüksek değerlerde olabilir. Bu değerlerin teker teker incelenmesi ya da en büyük ve en küçük değerleri belirtmek bir anlam taşımaz. 2
3 Örneğin, öğrencilerin istatistik dersi sınavında aldıkları puanların arasında değiştiğini söylemek anlamlı değildir. Öğrencilerin çoğu 95 civarında puan almış bir veya iki tanesi 45 puan almış olabilir ya da çoğunluğu 45 civarında iken bir veya iki tanesi 95 puan almış olabilir. Dağılımın tümünü temsil edecek bir ölçüye gereksinim vardır. 3
4 Frekans dağılımlarını tanımlayıcı ölçüler iki genel başlık altında toplanabilir: 1. Yer gösteren ölçüler a. Merkez ölçüleri: Ortalamalar b. Çeyrek ve yüzdelikler 2. Yaygınlık ölçüleri a. Standart sapma b. Varyans c. Varyasyon katsayısı d. Standat hata 4
5 MERKEZİ EĞİLİM ÖLÇÜLERİ (ORTALAMALAR) Ortalama, dağılımın orta noktasını gösteren ve incelenen deneklerin değerlerinin tek bir değerle temsil etmektedir. İncelenen bireylere ait değerler yüksek, düşük veya orta olabilir. Bu değerler tek başına bir anlam ifade etmezken, tümünü temsil eden bir değer daha anlamlı olmaktadır.ortalamalar, merkezi eğilim ölçüleri olarak da adlandırılır. Çünkü gözlem değerleri ortalama etrafında toplanma eğilimi gösterilirler. Merkezi eğilim ölçüleri, bir örnekteki bireyleri temsil eden tipik değerlerdir 5
6 Merkezi eğilim ölçüleri aşağıda sıralandığı gibi 5 gruba ayrılır: Eğer sadece "ortalama" denirse bunun ile kastedilen "aritmetik ortalama"dır. 1.Aritmetik Ortalama (Mean), 2.Ortanca değer (Medyan), 3.Tepe Değeri (Mod), 4.Geometrik Ortalama, 5.Harmonik Ortalama. 6
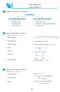
7 Aritmetik Ortalama (mean) Deneklerin aldığı değerlerin toplanıp denek sayısına bölümüyle elde edilen matematiksel bir değerdir. Aşağıdaki formülde görüldüğü gibi hesaplanır. Örneğin ilgilenilen değişkenin 1, 3, 5, 8, 9 değerlerini aldığı bilindiğinde bu değişkenin aritmetik ortalaması, terimlerin matematiksel toplamı olan 26 değerinin ( ) terim sayısı olan 5 e bölünmesiyle hesaplanır. Bu değişkenin aritmetik ortalaması 5,20 olacaktır. Bir seride yer alan gözlem birimleri x ile sembolize edilir, ayrıca bunların toplanacağını göstermek için sembolü kullanılır. 7
8 Bir seride aritmetik ortalama, seriyi oluşturan gözlem değerleri toplamı gözlem sayısına bölünerek hesaplanır. Eğer ana kütle aritmetik ortalaması hesaplanıyorsa aritmetik ortalama için μ sembolü kullanılırken aritmetik ortalama örneklem için hesaplanıyor ise kullanılır. x sembolü x x n 1 x2... xn i1 n n x i 8
9 A sınıfındaki 10 öğrencinin diploma notları; 65 54, 85, 72, 77, 58, 69, 62, 58 ve 60 oduğuna göre bu sınıfın ortalaması kaçtır? x x 1 x 2 Örnek: Bir şeker hastasının 15 günlük glukoz takibinde elde edilen glukoz x... xn i1 n n glukoz değeri nedir? Gün mg/dl şeker Gün n i değerleri aşağıda verilmektedir. Ortalama mg/dl şeker Gün mg/dl şeker Gün mg/dl şeker Gün mg/dl şeker x = 15 =
10 Bir dağılımda aşırı değerler varsa yapılacak işlemler şunlardır: 1. Kişilik farkına bağlı gerçek bir değer değilse ve olanak varsa ölçüm tekrarlanmalıdır. 2. Aşırı değerler değerlendirme dışı bırakılabilir. 3. Aşırı değerler alan bireylere diğer değerlere yakın bir değer atanabilir. Bunlar yapılamıyorsa aritmetik ortalama yerine başka bir ortalama ölçüsü, örneğin ortanca kullanılmalıdır. 10
11 Aşırı değerler katılarak ortalamanın hesaplanması sonuç gerçeği yansıtmayabilir veya yanlış yorumlamaya yol açar. Bir örnekle açıklanırsa; A hastalığına yakalanan kişilerin kanındaki bir maddenin artış gösterip göstermediğini incelemek için 10 hasta ve 10 sağlıklı kişide ölçüm yapılıyor ve aşağıdaki sonuçlar elde ediliyor. Aritmetrik ortalama Hasta Sağlam Hasta kişilerde aritmetrik ortalama 9.5, sağlıklı kişilerde ise 7.7 bulunmuştur. Her iki grupta değerler 7-9 arasında dağılım göstermektedir.ortalamanın daha düşük olması gerekirken hasta grubunda yüksek çıkmıştır. Bunu sebebi de ölçümlerden birinin uç değer (26) olmasıdır. 11
12 Şimdi bu aşırı değer yerine önerilen işlemleri uygulayalım: 1) Aşırı değer değerlendirme dışı bırakılıp örnek sayısı 9 alınırsa aritmetrik ortalama 7.67 olacaktır. Bu ortalama sağlam kişilerin ortalamasından (7.7) farksızdır. 2) Diğer değerlere yakın bir değer, örneğin 9 değerini tahmini olarak hasta değeri olarak kabul edersek ortalama 7.8 olacaktır. Bu ortalama da sağlam kişilerin ortalamasından (7.7) farksızdır. 3) Aritmetrik ortalama yerine ortancayı kullanırsak hasta kişilerde sadece 8, sağlam kişilerde ise 7.5 olacaktır. Bu iki değer de birbirine oldukça yakındır. 12
13 Sınıflandırılmış Verilerde Aritmetik Ortalama Veri sayısı çok olan araştırmalarda veya çalışmalarda aritmetik ortalamayı sınıflandırmadan hesaplamak, zor ve yorucudur. Ayrıca zaman alıcı ve hata yapma olasılığı fazladır.sınıflandırılmış verilerde aşağıdaki formül kullanılarak aritmetik ortalama hesaplanır. x A n fb C 13
14 Sınıflandırılmış verilerde aritmetik ortalama şu şekilde hesaplanır: 1. Sınıflar yazılır. 2. Sınıf değeri (SD) bulunur ve sınıfın karşısına yazılır. SD, sınıfın ortalamasıdır. Her sınıfın alt ve üst sınırları toplanarak ikiye bölünür. Çıkan sonuç SD yi oluşturur. 3. Her sınıfın frekansı karşısına yazılır. Frekans toplamı alınarak alt bölüme yazılır. 14
15 4. Çalışma birimi olarak adlandırılan b kolonu oluşturulur. Herhangi bir sınıfın (genellikle frekansı en büyük sınıfın karşısına) 0 değeri yazılır. Üste doğru eksi (-) olarak 1 den başlanarak ve birer artırılarak alta doğru artı (+) olarak 1 den başlanarak ve birer artırılarak çalışma birimleri yazılır 5. Frekansla çalışma biriminin çarpımları alınarak ve sınıfların karşısına yazılarak fb kolonu oluşturulur. Rakamların önündeki eksi ve artı işaretlerine dikkat ederek toplanır. Toplam fb (Σfb) bulunur, eksi veya artı olarak yazılır. 6. Değerler, formüle yerleştirilir ve aritmetik ortalama bulunur. 15
16 Sınıflandırılmış verilerde aritmetik ortalama aşağıdaki formül ile hesaplanır. x A n fb C Formülde: A: b kolonunda karşısına sıfır konulan sınıfın sınıf değeri (Genellikle frekansı yüksek olan sınıfın karşısına yazılır.) C: Sınıf aralığı Σfb: Frekansla çalışma biriminin çarpımlarının toplamı n: Denek sayısı 16
17 Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 17
18 x A fb C n
19 Örnek:. Aşağıda yaşların verilen 56 öğretmenin yaşlarının aritmetik ortalaması nedir? (Sınıf aralığını 5 olarak alınız) x A n fb C 19
20 Çözüm: Yaş Sınıf Değeri (SD) Frekans (f) b fb (SD) Toplam A = 42 C = 5 n = 56 Σfb = -42 Değerler formülde yerine yerleştirilir. x x fb A C n x
21 Ortanca (medyan): Ortanca, düzensiz verileri küçükten büyüğe veya büyükten küçüğe doğru sıraladıktan sonra, sıralamanın tam orta noktasındaki değer olarak tanımlanabilir. Ortanca dağılımdaki aşırı değerlerden etkilenmez. Dağılımda aşırı değerler varsa aritmetik ortalamanın yerine ortanca kullanılabilir. Ortancada, dağılımdaki değerlerin yarısı ortancaya eşit veya daha küçük, yarısı da ortancaya eşit veya daha büyüktür. Ortancanın hesaplanması, aritmetik ortalamada olduğu gibi sınıflandırılmamış ve sınıflandırılmış verilerde farklı şekilde yapılır. 21
22 Ortancanın tespiti: Dağılımdaki değerler büyükten küçüğe veya küçükten büyüğe doğru sıralandığında ortadaki değer ortancadır. Sınıflanmamış Verilerde Ortancanın Hesaplanması 1) Denek sayısı tek ise [(n+1)/2] ci değer, 2) Denek sayısı çift ise tam orta noktada bir değer olmadığından [n/2] ci değer ile [(n+2)/2] ci değer toplanıp 2 ye bölünerek ortanca tespit edilir. 22
23 Örnek: 15 çocuğun vücut ağırlıkarı aşağıda verilmiştir. Ortancayı bulunuz Önce değerleri küçükten büyüğe göre sıralayalım: n sayısı tek olduğundan [(15+1)/2]=8 ci değer 30.0 ortancadır. Örnek sayısının 14 olduğunu yani 39.9 değerin olmadığını düşündüğümüzde ise ortanca [14/2]=7 ci ve [(14+2)/2]=8 ci değerlein toplamımının yarısıdır. Yani ( )/2=29.7 dir. 23
24 Örnek: 7 öğrencinin ağırlıkları (kg) 55, 46, 75, 45, 50, 58, 53 olarak bulunmuştur. Ortancayı bulmak için; Önce değerler küçükten büyüğe doğru ya da tersi sıralanır. 45, 46, 50, 53, 55, 58, 75 n=7 olduğundan (7+1) / 2 = 4 Ortanca 4 ncü değer olan 53 tür. 24
25 Denek sayısı çift ise; n/2 nci sıradaki değer ile (n+2)/2 nci sıradaki değer toplanıp 2 ye bölünerek ortanca bulunur. Örnek: 8 öğrencinin ağırlıkları (kg): 55, 46, 60, 45, 50, 58, 53, 80 olduğuna göre ortanca kaçtır? Önce değerler küçükten büyüğe doğru ya da tersi sıralanır. 45, 46, 50, 53, 55, 58, 60, 80 n=8 (çift) olduğundan 8/2 = 4 ve (8 + 2)/2 = 5 4. ve 5. değerler, 53 ve 55 in ortalaması olan (53+55) /2 = 54 ortancadır. 25
26 Sınıflanmış Verilerde Ortancanın Hesaplanması Sınıflandırılmış verilerde ortancanın hesaplanmasında sırası ile şu işlemler yapılır: 1. Sınıflar yazılır. 2. Her sınıfın frekansı yazılır. 3. Yığılımlı frekans (yf) bulunur. Yığılımlı frekans her sınıfın frekansının önceki frekanslarla toplamıdır. 26
27 Sınıflandırılmış verilerde ortanca formülü: n yfi 2 Ortanca L x C f Formülde: L = Ortancanın içinde bulunduğu sınıfın sınıf ara değeridir. Bu değer; ortancanın içinde bulunduğu sınıfın alt sınırı ile bir üstündeki sınıfın üst sınırının toplanıp ikiye bölünmesi ile elde edilir. yfi = Ortancanın içinde bulunduğu sınıfın bir üstündeki sınıfın yığılımlı frekansı. f = Ortancanın içinde bulunduğu sınıfın frekansı. C = Sınıf aralığı. n = denek sayısı. 27
28 Örnek: Aşağıdaki sınıflandırılmış verilerde ortancanın hesaplanması: Formüle yerleştirilecek değerleri bulmak için önce ortancanın hangi sınıfın içinde olduğunu bulmak gerekir. Bunun için, (n/2) =100/2=50 bulunur. 50 yığılımlı frekans kolonunda 67 nin içinde bulunduğundan ortancanın içinde bulunduğu sınıf sınıfıdır. 28
29 L = (30+29)/2 = 29,5 n/ 2=50 yf = 37 C = 5 f = 30 Ortanca L n 2 yfi x C f Ortanca 29.5 x
30 Tepe değeri (Mod): Sınıflanmamış verilerde tepe değeri en çok görülen, yani en çok tekrarlayan değerdir. Aşağıdaki dağılımda tepe değeri 11.0 dır Bir dağılımda aynı sayıdan görülen değişik değerler varsa tepe değeri kullanılmamalıdır. Aşağıdaki dağılımda tepe değeri olabilecek 3 değer (24, 31 ve 54) vardır. Birbirinden farklı bu 3 değerin üçünü de tepe değeri olarak kullanmanın bir anlamı yoktur. Böyle bir durumda tepe değeri uygun bir ölçüt olmamaktadır
31 Örnek: Bir grubun matematik sınavından aldığı puanlar; 40, 40, 42, 42, 42, 43, 43, 43, 43, 45, 45, 50, 50, 55 ve 60 olsun. Bu dizide 43 en çok tekrarlanan değer olduğundan tepe değeri = 43 dür. Gözlem sonunda elde edilen ölçümlerin her birinin tekrar sayısı birbirine eşitse bu durumda tepe değeri olmaz. Örneğin; 45, 47, 55, 57, 60, 72, 77 ya da 45, 45, 50, 50, 56, 56, 58, 58, 60, 60, 75, 75 ve 80, 80 dizilerinde tepe değeri yoktur. Çünkü iki dizide de ölçümlerin hepsi eşit sayıda tekrarlanmıştır. 31
32 Ardışık iki ölçüm birbirine eşit sayıda ve öbür ölçümlerden daha çok tekrarlanmışsa, bu gibi durumlarda, tepe değeri ardışık iki ölçünün orta noktasıdır. Örnek: 50,50, 51, 51, 51, 52, 52, 52, 52, 53, 53, 53, 53, 54, 55, 55, 55 ve 56 şeklindeki bir dizide; Tepe değeri = 52,5 olur. Çünkü 52 ve 53 eşit sayıda ve öbür ölçümlerden daha çok tekrarlanmaktadır; bunların orta noktası da 52,5 dir. 32
33 Sınıflandırılmış verilerde tepe değeri en fazla frekansa sahip olan sınıfın değeridir. Ayrıca Sınıflandırılmış verilerde tepe değeri aşağıdaki formül kullanılarak da hesaplanır: d1 T.D. = L + C d 1+ d2 Bu formülde; TD = Tepe Değeri L= Frekansı en fazla olan sınıfın sınıf ara değeri d1 = Tepe sınıfı ile bir önceki sınıfın frekansları farkları d2 = Tepe sınıfı ile bir sonraki sınıfın frekansları farkları C= sınıf aralığı 33
34 Örnek: d1 T.D. = L + C d 1+ d2 Yukarıda frekansı en büyük değerin karşısındaki sınıf sınıfıdır. Bu sınıfın sınıf ara değeri ( ) / 2 = 14.5 dir. 34
35 Aritmetrik ortalama, ortanca ve tepe değeri ilişkileri: 1) Simetrik dağılımlarda aritmetrik ortalama, ortanca ve tepe değeri birbirine eşittir. 35
36 2) Sağa çarpık dağılımlarda küçük değerlerde bir yığılma olduğundan tepe değeri ortancadan, ortanca ise aritmetrik ortalamadan küçüktür. 36
37 3) Sola çarpık dağılımlarda büyük değerlerde yığılma olduğundan tepe değeri ortancadan ve ortanca da aritmetrik ortalamadan büyüktür. 37
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 2 x A fb C 229.5 n 40 20 100 221.5 3 Örnek:.
Prof.Dr.İhsan HALİFEOĞLU Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 2 x A fb C 229.5 n 40 20 100 221.5 3 Örnek:.
Merkezi Yığılma ve Dağılım Ölçüleri
 1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
Temel Ġstatistik. Tanımlayıcı Ġstatistik. Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri. Y.Doç.Dr. Ġbrahim Turan Mart 2011
 Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 3.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene
3.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene
MATE211 BİYOİSTATİSTİK
 MATE211 BİYOİSTATİSTİK ÇALIŞMA SORULARININ ÇÖZÜM VE CEVAPLARI Yapılan bir araştırmada, 136 erişkin kişinin kanlarındaki kolesterol düzeyleri gr/dl cinsinden aşağıda verilmiştir: 180 230 190 186 220 191
MATE211 BİYOİSTATİSTİK ÇALIŞMA SORULARININ ÇÖZÜM VE CEVAPLARI Yapılan bir araştırmada, 136 erişkin kişinin kanlarındaki kolesterol düzeyleri gr/dl cinsinden aşağıda verilmiştir: 180 230 190 186 220 191
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ. Prof. Dr. Mualla YALÇINKAYA
 JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
ORTALAMA ÖLÇÜLERİ. Ünite 6. Öğr. Gör. Ali Onur CERRAH
 ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
 A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ
 1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
Temel İstatistik. Y.Doç.Dr. İbrahim Turan Mart Tanımlayıcı İstatistik. Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri
 Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
ACİL SAĞLIK HİZMETLERİ
 T.C. MİLLÎ EĞİTİM BAKANLIĞI ACİL SAĞLIK HİZMETLERİ İSTATİSTİKSEL İŞLEMLER II 462I00008 Ankara, 2011 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan
T.C. MİLLÎ EĞİTİM BAKANLIĞI ACİL SAĞLIK HİZMETLERİ İSTATİSTİKSEL İŞLEMLER II 462I00008 Ankara, 2011 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan
Merkezi Eğilim ve Dağılım Ölçüleri
 Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri. Giriş Veri kümesi. Ortalamalar iki grupta incelenir. A. Duyarlı olan ortalama. B. Duyarlı olmayan ortalama
 GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri Yrd. Doç. Dr. Safa KARAMAN 1 2 Giriş Veri kümesi Verileri betimlemenin ve özetlemenin bir diğer yolu da verilerin bir
GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri Yrd. Doç. Dr. Safa KARAMAN 1 2 Giriş Veri kümesi Verileri betimlemenin ve özetlemenin bir diğer yolu da verilerin bir
EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler VERİLERİN DÜZENLENMESİ VERİLERİN DÜZENLENMESİ
 09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
YANLILIK. Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır.
 AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
Bölüm 3. Tanımlayıcı İstatistikler
 Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri. BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014
 Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ
 1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1
 EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1 5. BÖLÜM (9. KONU) TEST PUANLARI ÜZERİDE İSTATİSTİKİ İŞLEMLER MERKEZİ EĞİLİM/YIĞILIM ÖLÇÜLERİ ÇARPIKLIK VE YORUMU UĞUR YILMAZER 2 TEST İSTATİSTİKLERİ 1-
EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1 5. BÖLÜM (9. KONU) TEST PUANLARI ÜZERİDE İSTATİSTİKİ İŞLEMLER MERKEZİ EĞİLİM/YIĞILIM ÖLÇÜLERİ ÇARPIKLIK VE YORUMU UĞUR YILMAZER 2 TEST İSTATİSTİKLERİ 1-
TEMEL İSTATİSTİK BİLGİSİ. İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar
 TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
VERİ SETİNE GENEL BAKIŞ
 VERİ SETİNE GENEL BAKIŞ Outlier : Veri setinde normal olmayan değerler olarak tanımlanır. Ders: Kantitatif Yöntemler 1 VERİ SETİNE GENEL BAKIŞ Veri setinden değerlendirme başlamadan çıkarılabilir. Yazım
VERİ SETİNE GENEL BAKIŞ Outlier : Veri setinde normal olmayan değerler olarak tanımlanır. Ders: Kantitatif Yöntemler 1 VERİ SETİNE GENEL BAKIŞ Veri setinden değerlendirme başlamadan çıkarılabilir. Yazım
Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin ortalamasını 5 yapabilmek için son sınavdan kaç alması gerekmektedir?
 İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
8.Hafta. Değişkenlik Ölçüleri. Öğr.Gör.Muhsin ÇELİK. Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek,
 İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
Mühendislikte İstatistik Yöntemler
 .0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
.0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI
 ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ
 TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
ÖLÇME VE DEĞERLENDİRME. Antrenörlük Eğitimi 4. Sınıf. Ölçme ve Değerlendirme - Yrd. Doç. Dr. Yetkin Utku KAMUK
 ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
Konum ve Dağılım Ölçüleri. BBY606 Araştırma Yöntemleri Güleda Doğan
 Konum ve Dağılım Ölçüleri BBY606 Araştırma Yöntemleri Güleda Doğan Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl? Yakın, uzak? Sıklık dağılımlarının karşılaştırılması
Konum ve Dağılım Ölçüleri BBY606 Araştırma Yöntemleri Güleda Doğan Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl? Yakın, uzak? Sıklık dağılımlarının karşılaştırılması
Ölçme Sonuçları Üzerinde İstatistiksel İşlemler
 Ölçme Sonuçları Üzerinde İstatistiksel İşlemler Bir grup birey veya nesnenin belli bir özelliğe sahip olup olmadığı ya da belli bir özelliğe ne derece sahip olduğunu belirlemek amacı ile ölçme işlemi yapılır.
Ölçme Sonuçları Üzerinde İstatistiksel İşlemler Bir grup birey veya nesnenin belli bir özelliğe sahip olup olmadığı ya da belli bir özelliğe ne derece sahip olduğunu belirlemek amacı ile ölçme işlemi yapılır.
TANIMLAYICI İSTATİSTİKLER
 TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler
 Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI Tarih/Saat/Yer: 20.06.16/15:00-16:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz Öğrenci
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI Tarih/Saat/Yer: 20.06.16/15:00-16:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz Öğrenci
Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler
 Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik
Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK. Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005
 KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
Gruplanmış serilerde standart sapma hesabı
 Gruplanmış serilerde standart sapma hesabı Örnek: Verilen gruplanmış serinin standart sapmasını bulunuz? Sınıflar f i X X X m i f i. m i m i - (m i - ) f i.(m i - ) 0 den az 3 4 den az 7 4 6 dan az 4 6
Gruplanmış serilerde standart sapma hesabı Örnek: Verilen gruplanmış serinin standart sapmasını bulunuz? Sınıflar f i X X X m i f i. m i m i - (m i - ) f i.(m i - ) 0 den az 3 4 den az 7 4 6 dan az 4 6
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI Tarih/Saat/Yer: 15.06.16/09:00-10:30/AS115-116-117 Instructor: Prof. Dr. Hüseyin
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI Tarih/Saat/Yer: 15.06.16/09:00-10:30/AS115-116-117 Instructor: Prof. Dr. Hüseyin
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5
 Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II
 Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II İstatistik Nedir? İstatistik kelimesi farklı anlamlar taşımaktadır. Bunlar; Genel anlamda; üretim, tüketim, nüfus, sağlık, eğitim, tarım,
Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II İstatistik Nedir? İstatistik kelimesi farklı anlamlar taşımaktadır. Bunlar; Genel anlamda; üretim, tüketim, nüfus, sağlık, eğitim, tarım,
IİSTATIİSTIİK. Mustafa Sezer PEHLI VAN
 IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER
 NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER A) Normal Dağılım ile İlgili Sorular Sayfa /4 Hamileler ile ilgili bir araştırmada, bu grubun hemoglobin değerlerinin normal dağılım gösterdiği
NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER A) Normal Dağılım ile İlgili Sorular Sayfa /4 Hamileler ile ilgili bir araştırmada, bu grubun hemoglobin değerlerinin normal dağılım gösterdiği
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI. Ders 2 Merkezi Eğilim Ölçüleri
 ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
7. HAFTA. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
 7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 23.02.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 23.02.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
SÜREKLĠ OLASILIK DAĞILIMLARI
 SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
Unite 5. İstatistik. İstatistik nedir? İstatistik İki Gruba ayrılır. Öğr. Gör Ali Onur Cerrah. Verinin Ölçüm Biçimi (Veri Tipi)
 Unite 5. İstatistik Öğr. Gör Ali Onur Cerrah İstatistik nedir? Herhangi bir konuyu incelemek amacıyla; - çalışmanın planlanması, - verilerin toplanması, - değerlendirilmesi, - ve bir karara varılmasını
Unite 5. İstatistik Öğr. Gör Ali Onur Cerrah İstatistik nedir? Herhangi bir konuyu incelemek amacıyla; - çalışmanın planlanması, - verilerin toplanması, - değerlendirilmesi, - ve bir karara varılmasını
1. TANIMLAYICI İSTATİSTİK
 BİYOİSTATİSTİK Status: Devlet,durum İstatistik: Herhangi bir konuyu incelemek için gerekli verilerin toplanmasını, toplanan verilerin değerlendirilmesini ve değerlendirme sonucu karara varılmasını sağlayan
BİYOİSTATİSTİK Status: Devlet,durum İstatistik: Herhangi bir konuyu incelemek için gerekli verilerin toplanmasını, toplanan verilerin değerlendirilmesini ve değerlendirme sonucu karara varılmasını sağlayan
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI Tarih/Saat/Yer: 24.06.16/11:00-12:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI Tarih/Saat/Yer: 24.06.16/11:00-12:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz
7. HAFTA. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
 7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 14.04.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 14.04.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder.
 Yayılma Ölçütleri Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder. Bir başka ifade ile, bir veri setinin,
Yayılma Ölçütleri Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder. Bir başka ifade ile, bir veri setinin,
objektif değerlendirilmesini sağlayan bilim - veri arasındaki farkın olup olmadığını tespit
 İSTATİST STİK A. G E N E L B İ L G İ A. G E N E L B İ L G İ İstatistik, belli amacla tespit edilen verilerin objektif değerlendirilmesini sağlayan bilim dalıdır. Hedef - verilere anlam kazandırmak - veri
İSTATİST STİK A. G E N E L B İ L G İ A. G E N E L B İ L G İ İstatistik, belli amacla tespit edilen verilerin objektif değerlendirilmesini sağlayan bilim dalıdır. Hedef - verilere anlam kazandırmak - veri
Örneklemden elde edilen parametreler üzerinden kitle parametreleri tahmin edilmek istenmektedir.
 ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
İstatistik ve Olasılığa Giriş. İstatistik ve Olasılığa Giriş. Ders 3 Verileri Sayısal Ölçütlerle İfade Etme. Verileri Sayısal Ölçütlerle İfade Etme
 İstatistik ve Olasılığa Giriş Robert J. Beaver Barbara M. Beaver William Mendenhall Presentation designed and written by: Barbara M. Beaver İstatistik ve Olasılığa Giriş Ders 3 Verileri Sayısal Ölçütlerle
İstatistik ve Olasılığa Giriş Robert J. Beaver Barbara M. Beaver William Mendenhall Presentation designed and written by: Barbara M. Beaver İstatistik ve Olasılığa Giriş Ders 3 Verileri Sayısal Ölçütlerle
Ders 8: Verilerin Düzenlenmesi ve Analizi
 Ders 8: Verilerin Düzenlenmesi ve Analizi Betimsel İstatistik Merkezsel Eğilim Ölçüleri Dağılım Ölçüleri Grafiksel Gösterimler Bir kitlenin tamamını, ya da kitleden alınan bir örneklemi özetlemekle (betimlemekle)
Ders 8: Verilerin Düzenlenmesi ve Analizi Betimsel İstatistik Merkezsel Eğilim Ölçüleri Dağılım Ölçüleri Grafiksel Gösterimler Bir kitlenin tamamını, ya da kitleden alınan bir örneklemi özetlemekle (betimlemekle)
Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması
 Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması Projenin Amacı : YGS de başarılı olmak isteyen bir öğrencinin, istatistiksel yöntemler çerçevesinde, sınavda çıkan soru sayısını,
Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması Projenin Amacı : YGS de başarılı olmak isteyen bir öğrencinin, istatistiksel yöntemler çerçevesinde, sınavda çıkan soru sayısını,
İSTATİSTİK MHN3120 Malzeme Mühendisliği
 İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :[email protected] YARDIMCI KAYNAKLAR Mühendiler
İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :[email protected] YARDIMCI KAYNAKLAR Mühendiler
Copyright 2004 Pearson Education, Inc. Slide 1
 Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR ANALİTİK OLMAYAN MERKEZİ. Aritmetik ortalama **Medyan(median)
 KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ 1 MERKEZİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR Bir örneklemde mevcut olan tüm veriler hesaba katılır. ANALİTİK OLMAYAN MERKEZİ EĞİLİM ÖLÇÜLERİ Bir örneklemdeki verilerin bir
KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ 1 MERKEZİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR Bir örneklemde mevcut olan tüm veriler hesaba katılır. ANALİTİK OLMAYAN MERKEZİ EĞİLİM ÖLÇÜLERİ Bir örneklemdeki verilerin bir
VERİ KÜMELERİNİ BETİMLEME
 BETİMLEYİCİ İSTATİSTİK VERİ KÜMELERİNİ BETİMLEME Bir amaç için derlenen verilerin tamamının olduğu, veri kümesindeki birimlerin sayısal değerlerinden faydalanarak açık ve net bir şekilde ilgilenilen özellik
BETİMLEYİCİ İSTATİSTİK VERİ KÜMELERİNİ BETİMLEME Bir amaç için derlenen verilerin tamamının olduğu, veri kümesindeki birimlerin sayısal değerlerinden faydalanarak açık ve net bir şekilde ilgilenilen özellik
BÖLÜM 1 GİRİŞ: İSTATİSTİĞİN MÜHENDİSLİKTEKİ ÖNEMİ
 BÖLÜM..AMAÇ GİRİŞ: İSTATİSTİĞİ MÜHEDİSLİKTEKİ ÖEMİ Doğa bilimlerinde karşılaştığımız problemlerin birçoğunda olaydaki değişkenlerin değerleri bilindiğinde probleme kesin ve tek bir çözüm bulunabilir. Örneğin
BÖLÜM..AMAÇ GİRİŞ: İSTATİSTİĞİ MÜHEDİSLİKTEKİ ÖEMİ Doğa bilimlerinde karşılaştığımız problemlerin birçoğunda olaydaki değişkenlerin değerleri bilindiğinde probleme kesin ve tek bir çözüm bulunabilir. Örneğin
5. SUNUM. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
 5. SUNUM Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 08.09.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
5. SUNUM Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 08.09.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
Test İstatistikleri AHMET SALİH ŞİMŞEK
 Test İstatistikleri AHMET SALİH ŞİMŞEK İçindekiler Test İstatistikleri Merkezi Eğilim Tepe Değer (Mod) Ortanca (Medyan) Aritmetik Ortalama Merkezi Dağılım Dizi Genişliği (Ranj) Standart Sapma Varyans Çarpıklık
Test İstatistikleri AHMET SALİH ŞİMŞEK İçindekiler Test İstatistikleri Merkezi Eğilim Tepe Değer (Mod) Ortanca (Medyan) Aritmetik Ortalama Merkezi Dağılım Dizi Genişliği (Ranj) Standart Sapma Varyans Çarpıklık
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU ÖDEV: Aşağıda verilen 100 öğrenciye ait gözlem değerlerinin aritmetik ortalama, standart sapma, ortanca ve tepe değerini bulunuz. (sınıf aralığını 5 alınız) 155 160 164 165 168
Prof.Dr.İhsan HALİFEOĞLU ÖDEV: Aşağıda verilen 100 öğrenciye ait gözlem değerlerinin aritmetik ortalama, standart sapma, ortanca ve tepe değerini bulunuz. (sınıf aralığını 5 alınız) 155 160 164 165 168
Verilerin Düzenlenmesi
 Verilerin Düzenlenmesi İstatistiksel verileri anlamlı hale getirmenin 5 ayrı yolu: 1. Sözel ifadelerle açıklama 2. Tablolar halinde düzenleme 3. Seriler halinde düzenleme 4. Grafiklerle gösterme 5. Bu
Verilerin Düzenlenmesi İstatistiksel verileri anlamlı hale getirmenin 5 ayrı yolu: 1. Sözel ifadelerle açıklama 2. Tablolar halinde düzenleme 3. Seriler halinde düzenleme 4. Grafiklerle gösterme 5. Bu
ÖLÇME VE DEĞERLENDĠRME (3)
 ÖLÇME VE DEĞERLENDĠRME (3) ÖLÇME SONUÇLARI ÜZERĠNDE ĠSTATĠSTĠKSEL ĠġLEMLER VERĠLERĠN DÜZENLENMESĠ -Herhangi bir test uygulamasından önce verilerin düzenlenmesi için önce bütün puanların büyüklüklerine
ÖLÇME VE DEĞERLENDĠRME (3) ÖLÇME SONUÇLARI ÜZERĠNDE ĠSTATĠSTĠKSEL ĠġLEMLER VERĠLERĠN DÜZENLENMESĠ -Herhangi bir test uygulamasından önce verilerin düzenlenmesi için önce bütün puanların büyüklüklerine
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER ÖN SÖZ...
 İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir.
 Dr. Sedat Şen 1 Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir. Değer nedir? Bir veriyi (puanlar dizisini)
Dr. Sedat Şen 1 Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir. Değer nedir? Bir veriyi (puanlar dizisini)
ÖĞRENCİNİN ADI SOYADI:. NO:
 ÖĞRENCİNİN ADI SOYADI:. NO: İMZA: 2011-2012 ÖĞRETİM YILI TIP 1. SINIF TEMEL BİYOİSTATİSTİK DERSİ ARA SINAVI (04.11.2011) Biyoistatistik ve Tıp Bilişimi Anabilim Dalı Başarılar Temel Biyoistatistik dersi
ÖĞRENCİNİN ADI SOYADI:. NO: İMZA: 2011-2012 ÖĞRETİM YILI TIP 1. SINIF TEMEL BİYOİSTATİSTİK DERSİ ARA SINAVI (04.11.2011) Biyoistatistik ve Tıp Bilişimi Anabilim Dalı Başarılar Temel Biyoistatistik dersi
ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR
 ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR 1- İlaçla tedavi edilen 7 hastanın ortalama iyileşme süresi 22.6 gün ve standart sapması.360 gündür. Ameliyatla tedavi edilen 9 hasta için
ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR 1- İlaçla tedavi edilen 7 hastanın ortalama iyileşme süresi 22.6 gün ve standart sapması.360 gündür. Ameliyatla tedavi edilen 9 hasta için
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
Merkezi Eğilim Ölçüleri
 Merkezi Eğilim Ölçüleri 1) Parametrik merkezi eğilim ölçüleri Serinin bütün birimlerinden etkilenen merkezi eğilim ölçüleridir. 1) Aritmetik ortalama 2) Geometrik ortalama (G) 3) Harmonik ortalama (H)
Merkezi Eğilim Ölçüleri 1) Parametrik merkezi eğilim ölçüleri Serinin bütün birimlerinden etkilenen merkezi eğilim ölçüleridir. 1) Aritmetik ortalama 2) Geometrik ortalama (G) 3) Harmonik ortalama (H)
Yrd. Doç. Dr. Sedat Şen 9/27/2018 2
 2.SUNUM Belirli bir amaç için toplanmış verileri anlamlı haline getirmenin farklı yolları vardır. Verileri sözel ifadelerle açıklama Verileri tablolar halinde düzenleme Verileri grafiklerle gösterme Veriler
2.SUNUM Belirli bir amaç için toplanmış verileri anlamlı haline getirmenin farklı yolları vardır. Verileri sözel ifadelerle açıklama Verileri tablolar halinde düzenleme Verileri grafiklerle gösterme Veriler
BÖLÜM 9 NORMAL DAĞILIM
 1 BÖLÜM 9 NORMAL DAĞILIM Normal dağılım; 'normal dağılım eğrisi (normaly distribution curve)' ile kavramlaştırılan hipotetik bir evren dağılımıdır. 'Gauss dağılımı' ya da 'Gauss eğrisi' olarak da bilinen
1 BÖLÜM 9 NORMAL DAĞILIM Normal dağılım; 'normal dağılım eğrisi (normaly distribution curve)' ile kavramlaştırılan hipotetik bir evren dağılımıdır. 'Gauss dağılımı' ya da 'Gauss eğrisi' olarak da bilinen
İSTATİSTİKSEL MERKEZİ EĞİLİM ÖLÇÜLERİ (DUYARSIZ ORTALAMALAR)
 SAÜ 5. BÖLÜM İSTATİSTİKSEL MERKEZİ EĞİLİM ÖLÇÜLERİ (DUYARSIZ ORTALAMALAR) PROF. DR. MUSTAFA AKAL İÇİNDEKİLER 1. HASSAS OLMAYAN ORTALAMALAR 1.1. Mod (Tepe Noktası) 1.1.1.1. Basit Serilerde Mod 1.1.1.2.
SAÜ 5. BÖLÜM İSTATİSTİKSEL MERKEZİ EĞİLİM ÖLÇÜLERİ (DUYARSIZ ORTALAMALAR) PROF. DR. MUSTAFA AKAL İÇİNDEKİLER 1. HASSAS OLMAYAN ORTALAMALAR 1.1. Mod (Tepe Noktası) 1.1.1.1. Basit Serilerde Mod 1.1.1.2.
İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği
 İSTATİSTİK E GİRİŞ TEMEL KAVRAMLAR İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği Elemanlarıl AMAÇ İstatistiğe
İSTATİSTİK E GİRİŞ TEMEL KAVRAMLAR İstatistik Nedir? İstatistiğin Önemi Nedir? Tanımlayıcı ve Çıkarımcı İstatistik ttitik Tanımlayıcı İstatistik Türleri Çıkarımcı İstatistiğin i iği Elemanlarıl AMAÇ İstatistiğe
SPSS UYGULAMALARI-II Dr. Seher Yalçın 1
 SPSS UYGULAMALARI-II 27.12.2016 Dr. Seher Yalçın 1 Normal Dağılım Varsayımının İncelenmesi Çarpıklık ve Basıklık Katsayısının İncelenmesi Analyze Descriptive Statistics Descriptives tıklanır. Açılan pencerede,
SPSS UYGULAMALARI-II 27.12.2016 Dr. Seher Yalçın 1 Normal Dağılım Varsayımının İncelenmesi Çarpıklık ve Basıklık Katsayısının İncelenmesi Analyze Descriptive Statistics Descriptives tıklanır. Açılan pencerede,
İSTATİSTİK EXCEL UYGULAMA
 İSTATİSTİK EXCEL UYGULAMA EXCEL UYGULAMA Bu bölümde Excel ile ilgili temel bilgiler sunulacak ve daha sonra İstatistiksel Uygulamalar hakkında bilgi verilecektir. İşlenecek Konular: Merkezi eğilim Ölçüleri
İSTATİSTİK EXCEL UYGULAMA EXCEL UYGULAMA Bu bölümde Excel ile ilgili temel bilgiler sunulacak ve daha sonra İstatistiksel Uygulamalar hakkında bilgi verilecektir. İşlenecek Konular: Merkezi eğilim Ölçüleri
DAĞILMA YADA DEĞİ KENLİK ÖLÇÜLERİ (MEASURE OF DISPERSION) Prof.Dr.A.KARACABEY Doç.Dr.F.GÖKGÖZ
 DAĞILMA YADA DEĞİ KENLİK ÖLÇÜLERİ (MEASURE OF DISPERSION) 1 AMAÇ... Mevcut veri seti için bulunan merkezi eğilim ölçüsünün yorumlamak Birden fazla veri seti için dağılımlar arası kıyaslama yapabilmek amaçlarıyla
DAĞILMA YADA DEĞİ KENLİK ÖLÇÜLERİ (MEASURE OF DISPERSION) 1 AMAÇ... Mevcut veri seti için bulunan merkezi eğilim ölçüsünün yorumlamak Birden fazla veri seti için dağılımlar arası kıyaslama yapabilmek amaçlarıyla
BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ
 BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ İŞTİRME Araştırma rma SüreciS 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ İŞTİRME Araştırma rma SüreciS 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
17/01/2015. PowerPoint Template. Dr. S.Nihat ŞAD LOGO. İnönü University. Company Logo
 PowerPoint Template LOGO Dr. S.Nihat ŞAD İnönü University www.thmemgallery.com Company Logo 1 Contents www.thmemgallery.com geliştirme süreci Birey hakkında bilgi toplama yolları lerin sınıflandırılması
PowerPoint Template LOGO Dr. S.Nihat ŞAD İnönü University www.thmemgallery.com Company Logo 1 Contents www.thmemgallery.com geliştirme süreci Birey hakkında bilgi toplama yolları lerin sınıflandırılması
Grafik üzerindeki bilgiler özetlenmiştir. Veriler arasındaki ilişkiler görünür haldedir.
 GRAFİK VE İSTATİSTİK Grafikler,verileri görsel hale getirerek,veriler üzerinde daha kolay işlem yapılmasına ve elde edilen sonuçları değerlendirerek üzerinde tahmin yapılmasına olanak sağlar. Grafik üzerindeki
GRAFİK VE İSTATİSTİK Grafikler,verileri görsel hale getirerek,veriler üzerinde daha kolay işlem yapılmasına ve elde edilen sonuçları değerlendirerek üzerinde tahmin yapılmasına olanak sağlar. Grafik üzerindeki
Ders 9: Kitle Ortalaması ve Varyansı için Tahmin
 Ders 9: Kitle Ortalaması ve Varyansı için Tahmin Kitle ve Örneklem Örneklem Dağılımı Nokta Tahmini Tahmin Edicilerin Özellikleri Kitle ortalaması için Aralık Tahmini Kitle Standart Sapması için Aralık
Ders 9: Kitle Ortalaması ve Varyansı için Tahmin Kitle ve Örneklem Örneklem Dağılımı Nokta Tahmini Tahmin Edicilerin Özellikleri Kitle ortalaması için Aralık Tahmini Kitle Standart Sapması için Aralık
H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS DERS NOTLARI I 5 Nisan 2012
 H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS DERS NOTLARI I 5 Nisan 2012 Aşağıdaki analizlerde http://yunus.hacettepe.edu.tr/~tonta/courses/spring2010/bby208/bby208
H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS DERS NOTLARI I 5 Nisan 2012 Aşağıdaki analizlerde http://yunus.hacettepe.edu.tr/~tonta/courses/spring2010/bby208/bby208
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
rasgele değişkeninin olasılık yoğunluk fonksiyonu,
 3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
Beklenti Anketi ne İlişkin Yöntemsel Açıklama
 Beklenti Anketi ne İlişkin Yöntemsel Açıklama İstatistik Genel Müdürlüğü Reel Sektör Verileri Müdürlüğü İçindekiler I- Amaç... 3 II- Kapsam... 3 III- Yöntem... 3 IV- Tanımlar ve Hesaplamalar... 3 V- Yayımlama...
Beklenti Anketi ne İlişkin Yöntemsel Açıklama İstatistik Genel Müdürlüğü Reel Sektör Verileri Müdürlüğü İçindekiler I- Amaç... 3 II- Kapsam... 3 III- Yöntem... 3 IV- Tanımlar ve Hesaplamalar... 3 V- Yayımlama...
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI. Yrd. Doç. Dr. Emre ATILGAN
 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
Veri Analizi. Isınma Hareketleri. Test İstatistikleri. b) En çok tekrar eden: 7 (mod) c) Açıklık = En büyük En küçük = 10 1 = 9. d)
 Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
İstatistiksel Yorumlama
 İstatistiksel Yorumlama Amaç, popülasyon hakkında yorumlamalar yapmaktadır. Populasyon Parametre Karar Vermek Örnek İstatistik Tahmin 1 Tahmin Olaylar hakkında tahminlerde bulunmak ve karar vermek zorundayız
İstatistiksel Yorumlama Amaç, popülasyon hakkında yorumlamalar yapmaktadır. Populasyon Parametre Karar Vermek Örnek İstatistik Tahmin 1 Tahmin Olaylar hakkında tahminlerde bulunmak ve karar vermek zorundayız
BİYOİSTATİSTİK. Ödev Çözümleri. Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Ödev Çözümleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr Ödev 1 Çözümleri 2 1. Bir sonucun
BİYOİSTATİSTİK Ödev Çözümleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr Ödev 1 Çözümleri 2 1. Bir sonucun
ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ
 ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ TEMEL KAVRAMLAR PARAMETRE: Populasyonun sayısal açıklayıcı bir ölçüsüdür ve anakütledeki tüm elemanlar dikkate alınarak hesaplanabilir. Ana kütledeki
ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ TEMEL KAVRAMLAR PARAMETRE: Populasyonun sayısal açıklayıcı bir ölçüsüdür ve anakütledeki tüm elemanlar dikkate alınarak hesaplanabilir. Ana kütledeki
İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014)
 İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014) S-1) Bir otoyol üzerinde radarla hız kontrolü yapan, polis ekipler tarafından tespit edilen tane aracın hızları aşağıdaki tabloda
İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014) S-1) Bir otoyol üzerinde radarla hız kontrolü yapan, polis ekipler tarafından tespit edilen tane aracın hızları aşağıdaki tabloda
BÖLÜM 13 HİPOTEZ TESTİ
 1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
[!] Sütun, çizgi ve daire grafikleri gerçek yaşamdan seçilmiş örnek etkinliklerle hatırlatılır.
![[!] Sütun, çizgi ve daire grafikleri gerçek yaşamdan seçilmiş örnek etkinliklerle hatırlatılır. [!] Sütun, çizgi ve daire grafikleri gerçek yaşamdan seçilmiş örnek etkinliklerle hatırlatılır.](/thumbs/56/39384679.jpg) : OLASILIK VE 2. BÖLÜM: PERMÜTASYON, KOMBİNASYON, OLASILIK VE ISTATISTIK 1. Verilen bir gerçek yaşam durumuna uygun serpilme grafiği ve kutu grafiği çizer ve bu grafikler üzerinden çıkarımlarda bulunur.
: OLASILIK VE 2. BÖLÜM: PERMÜTASYON, KOMBİNASYON, OLASILIK VE ISTATISTIK 1. Verilen bir gerçek yaşam durumuna uygun serpilme grafiği ve kutu grafiği çizer ve bu grafikler üzerinden çıkarımlarda bulunur.
Sıklık Tabloları ve Tek Değişkenli Grafikler
 Sıklık Tabloları ve Tek Değşkenl Grafkler Sıklık Tablosu Ver dzsnde yer alan değerlern tekrarlama sayılarını çeren tabloya sıklık tablosu denr. Sıklık Tabloları tek değşken çn marjnal tablo olarak adlandırılır.
Sıklık Tabloları ve Tek Değşkenl Grafkler Sıklık Tablosu Ver dzsnde yer alan değerlern tekrarlama sayılarını çeren tabloya sıklık tablosu denr. Sıklık Tabloları tek değşken çn marjnal tablo olarak adlandırılır.
