ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ YÜKSEK SICAKLIK SÜPERİLETKENLERDE FİZİKSEL ÖZELLİKLER. Erhan AKSU FİZİK ANABİLİM DALI
|
|
|
- Umut Tuncel
- 8 yıl önce
- İzleme sayısı:
Transkript
1 TR ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ YÜKSEK SICAKLIK SÜPERİLETKENLERDE FİZİKSEL ÖZELLİKLER Erhan AKSU FİZİK ANABİLİM DALI ANKARA 2003 Her hakkı saklıdır
2 Doç. Dr. Ali GENCER danışmanlığında, Erhan AKSU tarafından hazırlanan bu çalışma 23/10/2003 tarihinde aşağıdaki jüri tarafından Fizik Anabilim Dalı'nda doktora tezi olarak kabul edilmiştir. Başkan: Prof. Dr. Hüsnü ÖZKAN Prof. Dr. Abdullah VERÇİN Doç. Dr. Bora ALKAN Doç. Dr. Ali GENCER Doç. Dr. İman ASKERZADE Yukarıdaki sonucu onaylarım Prof. Dr. Metin OLGUN Enstitü Müdürü
3 ÖZET Doktora Tezi YÜKSEK SICAKLIK SÜPERİLETKENLERDE FİZİKSEL ÖZELLİKLER Erhan AKSU Ankara Üniversitesi Fen Bilimleri Enstitüsü Fizik Anabilim Dalı Danışman : Doç. Dr. Ali GENCER Bu tez çalışmasında, Bi ( ö Pb 04 Sr 2 Ca 2 Cu30,o, Bi1.g4Pbo.34Sr!.9iCa 2.o3Cu 2.o60ıo, Tl 2 Ba2Ca 2 Cu30ıo ve Bi /Ag kompozisyonlarına sahip yüksek sıcaklık süperiletken malzemelerin magnetik karakterizasyonıı, ac magnetik alınganlık ve elektriksel direnç ölçme teknikleri ile yapıldı. Bi.üPbo4Sr 2 Ca 2 Cu 3 Oı 0 ve Bi g 4 Pb 0 34Srı 9iCa 20 3Cu 2 o60ıo yüksek sıcaklık süperiletkenleri sıvı amonyum nitrat yöntemi ile Tl 2 Ba 2 Ca 2 Cu 3 O 0 süperiletkeni ise geleneksel katıhal reaksiyon metodu ile üretilmişlerdir. Bunların yanı sıra çok filamanlı Bi-2212/Ag süperiletkeni ise, tüp içerisinde toz tekniği kullanılarak üretildi. Yapısal karakterizasyonlar, X-ışını toz kırınım (XRD) deneyleri ve taramalı elektron mikroskop (SEM) çalışmaları ile incelendi. Tetragonal kristal yapıya sahip Bij 6Pbo.4Sr 2 Ca 2 Cu 3 0 o ve Tl 2 Ba 2 Ca 2 Cu30ıo yüksek sıcaklık süperiletkenlerinin birim hücre parametreleri sırasıyla, a=b= Â ve c= Â, a=b= Â ve c= Â olarak hesaplandı. Bulunan sonuçların literatürdeki sonuçlarla tutarlı olduğu görüldü. Bununla birlikte, SEM çalışması sonuçlan ile malzemelere ait faz yapısı ve tanecik büyüklükleri hakkında bilgi edinilmeye çalışıldı. Yüksek sıcaklık süperiletken malzemeler üzerinde temel ve yüksek mertebeden harmonık alınganlık +i ölçümleri X,, ~ X n -X n ( n==1 > 2 > 3 > 5 v e 7 )> 15 K-140 K sıcaklık aralığında, 8 A/m-1600 A/m alan genliklerinde ve 1 1 Hz Hz frekanslarda yapıldı. Tüm alınganlık ölçümleri uygulanan ac alana ve frekansa bağımlılık göstermektedir. Gözlenen bağımlılıklar Bean modeli kullanılarak analiz edildi. Sıcaklık ölçeği için sızma alanı H p =H a (l-t) (! formunda yarı-deneysel bir fonksiyon olarak bulundu Bi ûpbo^srjc^cı^oıo için en iyi parametre değerleri H a -= 3.3x10 4 A/m ve p=2.05 olarak elde edildi. Tek mertebeli harmonik alınganlık ölçümleri ile Bean modelinden elde edilen teorik sonuçların karşılaştırılması yapıldı. AC kayıplar Bean modeli ile hesaplandı ve deneysel verilerle karşılaştırıldı. Düşük sıcaklıklarda ve düşük alanlarda Bean modeli ile deneysel sonuçlar uyum içerisindedir. Bununla birlikte, Bean modeli yüksek sıcaklıklarda ve büyük alanlardaki davranışı açıklamakta yetersiz kalmaktadır. Son olarak çok filamanlı Bi-2212/Ag şerit süperiletken malzemesinde ac alan, filamanlara dik (DİK) ve paralel (PAR) bir şekilde uygulandı. Yapılan temel harmonik alınganlık ölçümlerinde alan ve frekans bağımlılığının olduğu gözlendi. Ayrıca, ac alınganlık ölçümlerinin malzemenin alana dik ve paralel yerleştirilmesine bağımlılık gösterdiği tespit edildi. 2003, 113 sayfa ANAHTAR KELİMELER : Süperiletkenlik, BSCCO, TBCCO, Bi-2212/Ag, Kritik sıcaklık, Bean Modeli, Kim Modeli, AC kayıp, Kritik akım yoğunluğu, Harmonik alınganlık
4 ABSTRACT Ph. D. Thesis PHYSICAL PROPERTIES OF HIGH TEMPERATURE SUPERCONDUCTORS Erhan AKSU Ankara University Graduate School of Nature! and Applied Sciences Department of Physics Supervisor : Assoc. Prof. Dr. Ali GENCER In this thesis, the magnetic characterization of some Bi, Pbo.4Sr2Ca2Cu 0, Bi 84Pb o.34srı Ca2o3Cu.cK;Oıo, Tİ2Ba Ca Cu30ıoand Bi-2212/Ag high temperature superconductors were given by ac magnetic susceptibility and electrical resistivity measuring techniques. Bi] Pb.4Sr2Ca Cu30io and Bi, Pb 34Srı 9 Ca2.o3Cu o60ıo high temperature superconductors were prepared by liquid ammonium 84 0 I 2 nitrate method, while conventional solid state reaction route was applied to make Tİ2Ba 2 Ca 2 Cu30ıo superconductor. On the other hand, Powder-In Tube (PIT) technique was used to make multi-filamentary Bi-2212/Ag tapes. Structural characterizations were carried out by X-ray powder diffraction (XRD) patterns and scanning electron microscopy (SEM). Unit cell parameters of Bi, Pb 4Sr Ca Cu30 o and Tl 2 Ba2Ca 2 Cıi30ıo high temperature superconductors which have tetragonal crystal structure were calculated as a=b= Â and c= Â, a=b= Â and c= Â respectively. The results are consistent with the literature. Some information with regards to the grain size and phase content were given by the SEM studies. Fundamental and high order ac susceptibilities, X n ~ X n "*" l X n ( I1= '> 2, 3, 5 ve 7) of the samples were measured for the temperature range 15 K-140 K, ac field range 8 A/m-1600 A/m and the frequency range 11 Hz-2110 Hz. All the susceptibilities exhibit field, frequency and temperature dependences. The observed dependences were analyzed using Bean model. For temperature scaling a function of the form H p =H a (l-t) p was found empirically. The best fitting parameters for the Bi, Pb 4Sr2Ca2Cu Oı ö superconductor were found as H a = 3.3xlO 4 A/m and P=2.O5. Odd-order harmonic susceptibilities were calculated from the Bean model to make comparison with the experiments. In addition, ac losses were also calculated from the Bean model to compare with the experimentally measured values. At low temperatures and fields, the Bean model is observed to account for the ac losses. However, some deviations from the model were seen for high temperature and high field values. Finally, the ac field was applied to parallel (PAR) and perpendicular (PER) to the multi-filamentary tapes of Bi-2212/Ag. The fundamental harmonic susceptibilities exhibit field and frequency dependences. The results were dependent on the orientation of the specimen which was placed parallel or perpendicular to the applied field. 2003, 113 pages Key Words : Superconductivity, BSCCO, TBCCO, Bi-2212/Ag, Critical temperature, Bean Model, Kim Model, AC loss, Critical current density, Harmonic susceptibility II
5 TEŞEKKÜR Doktora tez çalışmam süresince değerli bilgi birikim ve tecrübelerini benimle paylaşan, danışman hocam Sayın Doç. Dr. Ali GENCER' e teşekkür ederim. Tez çalışmalarım esnasında katkılarından dolayı Kırıkkale Üniversitesi Fen Edebiyat Fakültesi Fizik Bölümü Öğretim Üyesi, Sayın Doç. Dr. Saffet NEZİR' e, TAEK, ANAEM eski müdürü Sayın Doç. Dr. İsmail ERCAN'a, TAEK, Malzeme Araştırma Bölüm Başkanı Sayın Dr. Erdal Tan'a, SEM fotoğraflarını görüntüleyen Kırıkkale Üniversitesi Fen Edebiyat Fakültesindeki arkadaşlarım Sayın Yrd. Doç. Dr. Selçuk AKTÜRK ve çalışma arkadaşlarına, TAEK, ANAEM'deki çalışma arkadaşlarım Sayın Dr. Nurcan CALINLI, Dr. Selçuk KERVAN, Haluk KORALAY, Şükrü ÇAVDAR ve Muharrem BÜYÜM'e, TÜBİTAK-UME' de çalışan arkadaşım Fizik Yüksek Mühendisi Sayın Oğuz ÇELİKEL' e, A.Ü. Fen Fakültesi Fizik Bölümünde görevli arkadaşım Sayın Arş. Gör. Ahmet Kılıç'a ve arkadaşım Fizikçi Sayın İsmail TURGUT' a katkılarından dolayı çok teşekkür ederim. Doktora eğitimim süresince bana sağladıkları her türlü maddi ve manevi destek dolayısıyla canım Anneme, Babama, kardeşim Mürvet'e, biricik yeğenlerim Ceren Naz ile Çağn'ya ve sevgili nişanlım Yasemin'e sonsuz teşekkürlerimi sunarım. Bu çalışma, DPT tarafından (Proje no: 2002-K , Proje Yürütücüsü: Doç. Dr. Ali GENCER) ve Ankara Üniversitesi Bilimsel Araştırma Projelen Müdürlüğü (Proje no: , Proje Yürütücüsü: Doç. Dr. Alı GENCER) tarafından desteklenmiştir. Erhan AKSU Ankara, Ekim 2003 m
6 İÇİNDEKİLER ÖZET i ABSTRACT ii TEŞEKKÜR iii SİMGELER DİZİNİ vi ŞEKİLLER DİZİNİ viii ÇİZELGELER DİZİNİ xi 1. GİRİŞ 1 2. KURAMSAL TEMELLER Giriş Kusursuz iletkenlik Meissner Etkisi Kritik alan ve kritik sıcaklık Süperiletkenlerin Makroskopik Teorisi London denklemleri Ginzburg-Landau Teorisi Bardeen Cooper Scrieffer (BCS) teorisi AC/DC Direnç Kritik Durum Modelleri Giriş Anderson-Kim Modeli Basitleştirilmiş Kim Modeli Bean Modeli Mıknatıslanma ve alınganlık terimleri Yüksek Sıcaklık Süperiletkenleri Giriş Bi-Tabanlı Yüksek Sıcaklık Süperiletkenler Tl-Tabanlı Yüksek Sıcaklık Süperiletkenler Y-Tabanlı Yüksek Sıcaklık Süperiletkenler Yüksek Sıcaklık Süperiletkenlerin Elektromagnetik Özellikleri ve AC Kayıp Mekanizmaları Magnetık özellikler ve Ginzburg-Landau sonuçları Sızma derinliği ve uyum uzunluğu T c, J c> H cl, H c2 ve ölçmeleri Zayıf bağlar AC alınganlık Karışık durum ve tersinmezlik çizgisi Akı dinamikleri Faz dışı bileşen X\ de tepenin yorumlanması V/I karakteristikleri ve akı sürüklenmesi Akı akışı Kayıp Bileşenleri Histeresis kaybı Çiftlenme kaybı MATERYAL VE YÖNTEM Örneklerin Elde Edilmesi Bi.6Pbo.4Sr2Ca2Cu3C)ıo kompozisyonun hazırlanması 56 iv
7 Toz karışımının hazırlanması Kalsinasyon Presleme Sinterleme Bh.84Pbo 3*Srı 9iCa2 03Cu3 060ıo kompozisyonunun hazırlanması Tİ2Ba2Ca2Cu30ıo bileşiğinin hazırlanması Çok fılamanlı şerit Bi-2212/Ag süperiletkenin hazırlanması AC Alınganlık Ölçüm Sistemi Giriş Deneysel metod Magnetik alınganlık ölçümleri AC/DC Direnç Ölçüm Sistemi Taramalı Elekron Mikroskop Çalışması X-ışını Toz Kırınım Ölçümleri ARAŞTIRMA BULGULARI ve TARTIŞMA Bi t 84Pbo.34Srı 9iCa2.o3Cu3 OÖOIO Yüksek Sıcaklık Süperiletkeni Biı. 6 Pbo.4Sr2Ca 2 Cu30ıo Yüksek Sıcaklık Süperiletkeni Tİ2Ba 2 Ca 2 Cu3Oıo Yüksek Sıcaklık Süperiletkeni Şerit Bi-2212/Ag Yüksek Sıcaklık Süperiletkeni SONUÇ 105 KAYNAKLAR 108 ÖZGEÇMİŞ 114
8 SİMGELER DİZİNİ n s v / H H c H c ı H c2 B ıç I c X Süperelektron sayısı Dalga fonksiyonu Magnetik alan Kritik magnetik alan Alt kritik magnetik alan Üst kritik magnetik alan Malzeme içindeki yerel magnetik alan Kritik akım Magnetik alanın sızma derinliği E, Uyum uzunluğu 5 Ölçme parametresi p R oo u (j. o 7n T c H dc Özdirenç Direnç Açısal frekans Magnetik geçirgenlik Boşluğun magnetik geçirgenliği n. mertebeden harmonik alınganlık Kritik sıcaklık DC magnetik alan H ac AC magnetik alan T p Temel harmonik alınganlığın faz-dışı bileşenindeki tepenin oluşum sıcaklığı E Elektrik alan o İletkenlik J T J s E g s g n Akım yoğunluğu Sıcaklık Süperakım yoğunluğu Elektron yükü Süperiletken durumun serbest enerjisi Normal durumun serbest enerjisi VI
9 m A K <t>o Elektronun kütlesi Vektör potansiyeli Ginzburg-Landau parametresi Akı kuantumu J c Kritik akım yoğunluğu m* Elektronun etkin kütlesi ks Boltzman sabiti J n d H p M F p S P Q x Normal elektronların oluşturduğu akım yoğunluğu Akımın aktığı tabakanın kalınlığı Malzemenin merkezine sızması için gerekli minimum magnetik alan Mıknatıslanma Akı çizgilerinin perçinlenmesi için Lorentz kuvveti Poynting vektörü Güç AC kayıp Sönüm sabiti E a Aktivasyon enerjisi vıı
10 ŞEKİLLER DİZİNİ Şekil 2.1. (a) Silindir geometrisine sahip bir süperiletkenin kritik sıcaklık (T c ) üzerindeki sıcaklıklarda uygulanan düzgün magnetik alanda akı çizgilerinin süperiletken malzemeye sızması (b) Aynı süperiletken malzemenin kritik sıcaklığının altındaki bir sıcaklık değerinde uygulanan düzgün magnetik alan çizgilerinin malzemeden dışlanmasını göstermektedir 11 Şekil 2.2. Magnetik alanın süperiletkene sızması. B(x), süperiletken içerisindeki magnetik akının konuma göre değişimini ve belirli bir sızma derinliği sonrasında sıfır olduğunu göstermektedir 15 Şekil 2.3. Magnetik alandaki davranışlarına göre (a) I. tip süperiletkenler (b) II. tip süperiletkenler 18 Şekil 2.4. İletkenlerin özdirencinin sıcaklığa bağlı olarak değişimi 20 Şekil 2.5. Kim modeline göre alanın malzemeye parabolik olarak sızması. Kesikli çizgiler Bean modeline göre alanın malzemeye sızmasını göstermektedir. x o =O için alan malzemenin merkezine kadar sızmaktadır..24 Şekil 2.6. Basitleştirilmiş Kim modelinde dış alanın, (a) H a değerinden Hb değerine azalırken, (b) Hb değerinden H a değerine artarken malzemeye sızma profilleri 25 Şekil 2.7. Magnetik alanın "dilim" süperiletkene kısmi sızması (sol kolon) ve tam sızması (sağ kolon) durumları için -H 0 'dan H 0 'a kadar dış magnetik alanın artışında bir "dilim" içindeki magnetik alan ve akım profilleri 27 Şekil 2.8. Silindir geometrisine sahip bir süperiletkenin mıknatıslanma eğrisi 28 Şekil 2.9. Bean modeline göre temel harmonik alınganlığın (n=l) faz-içi X\ v e f az ~ dışı X\ bileşenlerinin H p /H m ' ye göre değişimi 3 1 Şekil Bean modeline göre 3. harmonik alınganlığın (n=3) faz-içi Xı Şekil Şekil dışı j 3 bileşenlerinin H p /H m ' ye göre değişimi 32 Bean modeline göre 5. harmonik alınganlığın (n=5) faz-içi Xs ve fazdışı^fğ bileşenlerinin H p /H m ' ye göre değişimi 33 Bean modeline göre 7. harmonik alınganlığın (n=7) faz-içi Xı dışı Xı bileşenlerinin H p /H m ' ye göre değişimi 34 Şekil Tanecikli bir süperiletkenin şematik modeli 43 Şekil H-T faz diyagramı ve tersinmezlik çizgisi 44 Şekil Yüksek sıcaklık süperiletkenin E-J karakteristiği 50 Şekil 3.1. AC alınganlık ölçüm sistemi şeması 62 Şekil 3.2. Bobinlerin şematik gösterimi 64 Şekil 3.3. DC direnç ölçüm sistemi şematik gösterimi 67 Şekil 4.1. Temel harmonik alınganlığın j,(7\// ûc ) ve x\(j.\h ac ) bileşenlerinin sıcaklığın fonksiyonu olarak farklı ac alan genliklerinde değişimi 70 v e v e f az ~ vııı
11 v e Şekil 4.2. Farklı sıcaklıklarda Şekil 1'den elde edilen Xı(H ac ) X\(^ac ) grafikleri 72 Şekil 4.3. Farklı 3 alan değeri için Bean modelinden hesaplanan xi(h ac ) sonuçları 73 Şekil 4.4. AC kayıpların ac alan genliğine bağlı olarak değişimleri 74 Şekil 4.5. AC alınganlığın faz-içi x\ v e faz-dışı x\ bileşenlerinin H ac =20 A/m, fmooo Hz frekansta ve H ac =20 A/m'lik alana ilave H dc =1520 A/m uygulandığında de alana bağımlılığı 75 Şekil harmonik alınganlığın H ac =20, 40, 80 ve 160 A/m, (a) f=125 Hz ve (b) f= 1000 Hz frekanslarda sıcaklığın fonksiyonu olarak değişimleri 77 Şekil 4.7. Bii84Pbo.34Sr191Ca203Cu3.06OK) süperiletkeninin kesit alanından elde edilen SEM fotoğrafı...78 Şekil 4.8. (a) Çeşitli ac alan genlikleri için temel harmonik alınganlığın faz-dışı %\ bileşeninden elde edilen tepe sıcaklıklarına karşı-sızma alanı H p. Eğri, 1 denklemi ile uyum sağlattırılarak düşük sıcaklıklara extrapolate edilmiştir, (a)'daki iç grafik faz-dışı^," bileşenin, (b) temel ac alınganlığın faz-içi X\ bileşenin deneysel ve teorik sonuçlarını göstermektedir. Noktalı çizgiler deneysel sonuçları, düz-siyah çizgiler teorik sonuçları göstermektedir 81 Şekil 4.9. Temel harmonik alınganlık bileşenleri, X\ I Xo 'nün X\ I Zo y e g re deneysel ve teorik gösterimleri 83 Şekil AC kayıpların ac alan genliğine bağlı olarak değişimleri 84 Şekil X n ~T eğrileri (n=3, 5 ve7) (a) deneysel ve (b) teorik 85 Şekil \lt p 'nin uygulanan dış magnetik alan frekansına göre değişimi 87 Şekil İkinci-mertebeden harmonik alınganlığın faz-içi Xı ve faz-dışı X2 bileşenlerinin f=1000 Hz frekanslı H ac =160 A/m ve H ac =320 A/m'lik ac alanlarda sıcaklığa göre değişimleri 88 Şekil Biı 6Pbo4Sr2Ca2Cu30ıo süperiletkeninin kesit alanından elde edilen SEM fotoğraf) 89 Şekil C de 150 saat sinterleme işlemine tabi tutularak üretilen Bi] 6Pbo4Sr 2 Ca2Cu 3 Oıo süperiletkeninin XRD deseni 90 Şekil AC direnç-sıcaklık grafiği 91 Şekil Temel harmonik alınganlığın farklı ac alan genliklerinde sıcaklığın fonksiyonu olarak değişimi 92 Şekil Tl 2 Ba2Ca2Cu30ıo malzemesinin özdirenç-sıcaklık grafiği 93 Şekil TBCCO-2223 yığın süperiletken malzemesinin tek-mertebeli (n=3, 5 ve 7) harmonik alınganlık ölçümleri a) deneysel sonuçlar, b) model sonuçları 94 Şekil Tİ2Ba2Ca2Cu30ıo süperiletkeninin kesit alanından elde edilen SEM fotoğrafı 95 Şekil C de sinterleme işlemine tabi tutularak üretilen Tl 2 Ba2Ca 2 Cu30ıo süperiletkeninin XRD deseni 96 Şekil Şerit Bi-2212/Ag süperiletkeninin şematik gösterimi 97 Şekil Farklı frekanslarda şerit Bi-2212/Ag süperiletken malzemesinin filamanlarına ac alan paralel uygulandığında temel harmonik alınganlığın sıcaklığa bağlı olarak değişimi 98 ıx
12 Şekil Farklı frekanslarda şerit Bi-2212/Ag süpeiletken malzemesinin filamanlanna ac alan genliği dik uygulandığında temel harmonik alınganlığın sıcaklığa bağlı olarak değişimi 99 Şekil Farklı ac alanlarda ve f=80 Hz frekansta şerit Bi-2212/Ag süperiletken malzemesinin filamanlanna ac alan paralel uygulandığında temel harmonik alınganlığın sıcaklığa bağlı olarak değişimi 100 Şekil Farklı ac alanlarda ve f=80 Hz frekansta şerit Bi-2212/Ag süperiletken malzemesinin filamanlanna ac alan dik uygulandığında temel harmonik alınganlığın sıcaklığa bağlı olarak değişimi 101 Şekil Uygulanan dış ac magnetik alana karşı ac kayıplar 101 Şekil AC alanın filamanlara paralel ve dik uygulanması sonucu temel harmonik alınganlığın faz-dışı %" x bileşenlerindeki tepe değerlerine karşı bu tepelerin ortaya çıktığı sıcaklık değerleri 102 Şekil Kritik akım yoğunluğu J c 'nin par ve dik konumları için sıcaklığın fonksiyonu olarak değişimi 103
13 ÇİZELGELER DİZİNİ Çizelge 2.1. Bazı süperiletken elementlerin kritik alan şiddetleri ve kritik sıcaklıkları...13 Çizelge 2.2. Kritik durum modelleri 23 Çizelge 4.1. Şerit Bi-2212/Ag malzemesinin Kim modeli kullanılarak bulunan süperüetkenlik parametreleri 104 xı
14 1.GİRİŞ Hollandalı fizikçi Heike Kamerling Onnes'in 1908 yılında Helyum'u sıvı hale dönüştürmeyi başarmasıyla 4.2 K' e kadar olan düşük sıcaklıklarda fiziksel özelliklerin araştırılması mümkün hale geldi. Metallerin elektriksel dirençlerinin bu düşük sıcaklık bölgelerindeki değişimi yine ilk olarak Onnes tarafından incelendi (Onnes 1911). Sıvı helyumun keşfinden 3 yıl sonra Kamerling Onnes, civa metalinde de elektriksel direncin kritik sıcaklık (T c ) diye adlandırdığı sıcaklık ve altındaki sıcaklıklarda ölçülemeyecek kadar küçük bir değere düştüğünü gözlemledi. Bu heyecan verici gözlem süperiletkenliğin keşfi olarak bilinmektedir. Bu çalışmasından dolayı Kamerling Onnes 1913 yılında Nobel Fizik ödülünü kazandı. Daha sonraki yıllarda yapılan çalışmalarda bu "sıfır direnç" durumunun kendine özgü fiziksel özellikleri olan yeni bir faz durumu olduğu anlaşıldı. Başka elementlerin ve bileşiklerin süperiletken olduğu zaman içerisinde anlaşıldı. Sıfır direnç durumunu tamamlayıcı bir özellik olan kusursuz diamagnetizma özelliği, keşfedilen süperiletkenler için ortak bir özelliktir. Kusursuz diamagnetizma özelliği ilk defa keşiften yaklaşık 22 yıl sonra W. Meissner" ve R. Ochsenfeld tarafından gözlendi (Meissner and Ochsenfeld 1933). Bu özellik Meissner etkisi olarak bilinmekte olup, bir süperiletkenin sıfır direnç özelliğinden sonra en belirgin özelliğidir. Elektromagnetizma açısından Meissner olayının ilk açıklaması London kardeşler tarafından yapılmıştır (London and London 1935). Böylece, süperiletkenliğin iki temel özelliği, klasik fizik açısından makroskopik düzeyde anlaşılabilir hale gelmiştir. Süperiletkenliğin kusursuz bir diamagnet gibi davranışı, süperiletken malzemenin elektriksel iletkenliğinin sonsuz büyümesi sonucu oluşur. Süperiletken malzeme magnetik alan içerisinde soğutulmuş ise, süperiletken hale geçer geçmez magnetik alan çizgileri malzeme içerisinden dışlanır (B 1Ç =O). London kardeşler 1935 yılında magnetik akıyı dışlayan akımın sadece yüzeyde akacağını önererek Meissner olayını açıklayabilmişlerdir. London kardeşlerin açıklamasına göre süperiletkende oluşan bu akımın gerçekte kuantum akımı formunda olduğu anlaşılmıştır. 1950'li yıllara gelindiğinde Ginzburg-Landau (GL), ikinci dereceden faz geçişi yapan bir sistemin fiziksel özelliklerindeki değişimleri termodinamik açıdan inceledi (Ginzburg and
15 Landau 1950). O yıllarda, süperiletkenliğin ne tür bir faz geçişi sergilediği bilinmiyordu. Mikroskopik anlamda süperiletkenliğin kuantum mekaniğine dayalı açıklaması 1957 yılında Bardeen, Cooper ve Schrieffer (BSC) tarafından yapıldı (Bardeen et al. 1957). Bu teori, Fermi enerji seviyesine yakın elektronların fononlar aracılığı ile çiftlenerek bir taban durumu oluşturduklarını ve bu taban durumun bir tek dalga fonksiyonu ile tanımlanabileceği gerçeğine dayanmaktadır. Aradan iki yıl geçtikten sonra Gorkov, Ginzburg-Landau denklemlerinin kritik sıcaklık civarında BCS denklemleri ile uyumlu olduğunu göstermiştir (Gorkov 1959). Bu bakımdan Ginzburg- Landau teorisinin süperiletkenliğe başarı ile uygulanması mümkün hale gelmiştir. Fenemolojik olan bu teori, bugün farklı tipte olan süperiletkenler için makroskopik özelliklerin açıklanmasında hala kullanılabilir durumdadır. Bu teoriye göre, çiftlenmiş elektronlar kritik sıcaklık yakınlarında makroskopik bir dalga fonksiyonu, ıj/ ile temsil edilebilirler ve tek bir kuantum düzeyinde çok sayıda elektron bulunabilir. Burada n s =M 2 çiftlenmiş elektronların yoğunluğudur. Dalga fonksiyonu \\ı, tek kuantum düzeyine girmiş çok sayıdaki parçacıktan dolayı tüm malzeme boyunca uzanmalı ve kararlı olmalıdır. BCS teorisinde çiftlenmenin fononlar vasıtası ile oluşması sonucu kritik sıcaklığın 35 K civarında olması gerektiği sonucunu doğurur yılları arasında, bileşiklerde yeni süperiletken malzemeler bulunmuştur. 1980'li yıllara gelindiğinde, BCS teorisindeki kritik sıcaklığa getirilen öngörünün deneysel olarak da doğrulanmış olması, süperiletkenlik çalışmalarında kritik sıcaklığın artık artırılamayacağı kanaatine sebep olmuş ve çalışmalar doyma noktasına gelmiştir. Ardından da 1986 yılında, Bednorz ve Müller'in La-Ba-Cu-O sisteminde yaklaşık 40 K'de süperiletkenlik gözlemeleri, çok önemli bir buluş olarak genel kabul görmüştür (Bednorz and Müler 1986). Bednorz ve Müller'in bu çalışmaları Nobel ödülüne layık görülmüş olup, yüksek sıcaklık süperiletkenler fiziğinin başlangıcı olmuştur. Daha sonra Wu ve arkadaşlarının La-Ba-Cu-O sistemindeki La'nın yerine daha küçük iyonik yarıçaplı Y ile yer değiştirmeleri sonucunda (YBCO-123), 92 K'de süperiletkenliğe geçiş gözlemelerine ve süperiletkenlik alanında büyük bir aşama kaydedilmesine yol açtı (Wu et al. 1987). Metal oksitlerden üretilen ve sıvı azot sıcaklığının üstünde kritik geçiş sıcaklığına sahip bu yeni malzemenin keşfinden sonra Maeda, 1988 yılında Bi-Sr- Ca-Cu-O bileşiğinde 110 K'de süperiletkenliği gözledi (Maeda et al. 1988). Aynı yıl Parkin et al. (1988), kritik geçiş sıcaklığı 125 K olan Tl-Ba-Ca-Cu-O bileşiğini ürettiler.
16 Şu anda en yüksek kritik sıcaklık Hg-bazlı süperiletkenlerde olup, 164 K (31 GPa basınç altında) civarındadır (Gatt et al. 1998). Bakır-oksit tabakası içeren süperiletkenlere yaygın olarak "Yüksek Sıcaklık Süperiletken" (YSS) veya yüksek T c 'li süperiletken denilmektedir ve teknolojik olarak büyük öneme sahiptirler. Çünkü, uygulamalarda geleneksel süperiletkenlerin aksine, YSS'leri sıvı azot sıcaklığında kullanılabilme potansiyeline sahiptirler. Teknolojik uygulamalar için, süperi letkenler ince ve kalın filmler, tel ve şerit halinde üretilmektedirler. Mühendislik uygulamaları açısından, bu malzemeler bugün Japonya, Avrupa ve Amerika Birleşik Devletlerinde geniş pazar payı potansiyeline sahip durumdadırlar. Çok yakın gelecekte, geleneksel süperiletkenlerin yerine YSS'lerin geçmesi ile, sıvı azot sıcaklığında uygulamaların yapılması muhtemel hale gelecektir. Magnetik davranışlarına göre süperiletkenler iki ayrı tipte bulunurlar. I. tip süperiletkenler genellikle elementlerden oluşurlar. Tek bir kritik magnetik alanları (H c ) mevcuttur. Malzeme H<H C alanlarında kusursuz diamagnet gibi davranır ve uygulanan dış magnetik alanı sızma derinliği haricinde dışlar. II. tip süperiletkenler ise, genellikle bileşiklerden oluşur ve iki adet kritik alanı vardır. Düşük kritik alan H C 'in altındaki magnetik alanlarda süperiletken I. tip süperiletkenlerde olduğu gibi kusursuz bir diamagnet gibi davranır. H c ı'den büyük alanlarda, magnetik alan malzemeye girebilmekte ve malzeme içinde net magnetik alan sıfırdan farklı olmaktadır (B.. ^0). Bu durum "karışık durum" olarak adlandırılmaktadır ve H C 2'ye kadar devam etmektedir. H C 2'den daha büyük alanlarda ise malzeme artık süperiletkenlik özelliğini yitirmektedir. Kritik akım (I c ), kritik alan (H c ), tersinmezlik çizgisi (T irr ), sızma derinliği (A) gibi kavramlar, magnetik ölçümlerle belirlenen niceliklerdendir. AC alınganlık ölçümleri, kritik sıcaklık ve sızma derinliği gibi fiziksel büyüklüklerin belirlenmesinde kullanılabilir. AC alınganlık tekniğinde, alanın frekansı ayarlanarak magnetik alanın malzemeye etki ettiği zaman aralığı değiştirilebilmektedir. Bu özellik, magnetik gevşeme ve akı dinamiklerinin incelenmesinde yararlıdır. YSS'lerin daha büyük miktarda akım taşıyabilmeleri yönünde çalışmalar mevcuttur (Sanchez 1991, Mikheenko and Kuzovlev 1993, Çelebi et al. 1997, Brandt 1998, Gömöry 2000, Lee et al. 2001). Süperiletkene karışık durumda sızan akı çizgilerinin
17 hareketi, süperiletkene istenmeyen bir direnç kazandırmaktadır. Bu nedenle, akı çizgilerinin hareketlerinin sınırlandırılması gerekir. Bu amaçla, süperiletken malzemelere suni perçinleme merkezleri oluşturulmakta ve akı çizgileri bu merkezlerde hareketsiz kalmalarının sağlanması amaçlanmaktadır. Böylece, kritik akım yoğunluğu artması beklenmektedir. Süperiletken bir malzemedeki perçinlenme kuvvetleri, genelde çok iyi anlaşılmamakla birlikte, perçinlenme mekanizmalarıyla ilgili literatürde yoğun çalışmalar bulunmaktadır (Glyde 1992, Schwartz 1994, Murakami 1997). Perçinlenme kuvveti F p, kısa mesafede bir akı çizgisinin hareketini engellemeye çalışan ve belli bir bölgede tutan kuvvettir. Süperiletkende perçinlenmeye; noktasal kusurlar, çatlaklar, vida tipi kusurlar, oksijen boşlukları, tane sınırları, ikizlenme düzlemleri, farklı fazlar, tanecik içi ve tanecikler arası süperiletken olmayan bölgeler katkıda bulunurlar. Malzemede bu tür perçinlenme merkezleri oluşturulması magnetik özelliklere de etki etmektedir. Süperiletkenlerin magnetik özelliklerini klasik elektrodinamik açıdan inceleyen modeller mevcuttur. Bunlardan ilki Bean modelidir ve ilk defa C. Bean tarafından 1962 yılında ortaya atılmıştır (Bean 1962). Bu model, II. tip süperiletkenlerde malzemeye sızan magnetik alanın rotasyonelinin kritik akım yoğunluğunu, J c, ürettiği gerçeğine dayanmaktadır. Model ilk olarak ortaya atıldığında sonsuz "dilim" veya "silindir" geometrisi için hesaplamalar yapılmıştır. Daha sonraki yıllarda, Kim modeli malzeme içerisine magnetik alanın sızması ile indüklenen kritik akım yoğunluğunun magnetik alanın bir fonksiyonu olacağını önerdi (Kim et al. 1963). YSS'lerin keşfinden sonra, kritik durum modellerine dayalı disk ve bar gibi sonlu geometriler için de yeni model hesaplamaları yapıldı (Goldfarb et al. 1991, Mıkheenko et al. 1993, Clem and Sanchez , Branth ). Bu modeller, YSS'lerin magnetik özelliklerinin anlaşılmasına katkıda bulunmaktadırlar. Ancak modellerin sonsuz geometriler için oluşu nicel bir inceleme imkanı sunmamaktaıdr. Ayrıca, YYS'lerin tanecikli yapıya sahip olmaları nicel karşılaştırma imkanını zora sokmaktadır. Bir süperiletkenin temel ve yüksek mertebeden ac alınganlığı, x n ~ X n + X,, ( n= ~': 2, 3,...) ifadesi ile verilir. Burada ilk terim, uygulanan alanla aynı fazda olan faz-içi bileşen (reel kısım), ikinci terim ise uygulanan alanla 90 derece faz farkında, faz-dışı bileşen (sanal kısım) olarak adlandırılır (Gioacchino et al , Yamamoto et al.
18 , Shatz et al , Gencer et al. 1996, Qin and Yao 1996-II, Zhang et al. 2001) ve uygulanan dış magnetik alana karşı süperiletkende indüklenen diamagnetik perdeleme akımlarının dinamiği ile incelenir. I. tip süperiletkenler için düşük magnetik alanlardaki (H<H C ) ac diamagnetik perdeleme akımları, Meissner durumundaki dağılım ile aynı dağılıma uyabilir. Bu durumda, diamagnetik etki iki akışkan modeli ve London denklemleri ile açıklanabilir. Fakat II. tip süperiletkenlerde uygulanan alan H c ı<h<h C 2 olduğunda, magnetik akı çizgilerinin varlığı ile perçinlenmesine etki eden faktörler perdeleme akımlarının dinamiğinin çok daha karmaşık olmasına neden olur. Bu durumda malzemede indüklenen akım hem alan genliğine hem de frekansa bağlılık gösterebilir. Bu nedenle malzemenin magnetik tepkisi artık doğrusal değildir. Bu da ac alınganlıkta yüksek harmoniklerin üretilmesine katkıda bulunur. YSS'lerin magnetik davranışının ac alana karşı doğrusal olmayan tepkisi (histeresis) bir çok deneysel ve teorik çalışmaya konu olmuştur (Gömöry and Lobotka 1988, Gencer et al. 1996, Shinde 1990, Goldfarb 1987). Doğrusal olmayan davranış, deneysel olarak magnetik tepki sinyalinde gözlenen harmonik bileşenlerin varlığı ile ilgilidir (Ishida and Goldfarb 1990, Xenikos and Lemberger 1990). Literatürde harmonik bileşenlerin varlığını açıklayan ilk model Bean modelidir. Ancak Bean modeli sadece tek mertebeli yüksek harmoniklerin (n=l, 3, 5, 7...) varlığını açıklayabilmektedir. Çift yüksek harmonikler bu modelde simetrik M-H eğrisinden dolayı sıfırdır. M-H eğrisindeki simetri, kritik akım yoğunluğuna bir alan bağımlılığı katıldığında bozulmaktadır. Kim-Anderson modelinde böylece çift mertebeli yüksek harmonik alınganlıklar (n=2, 4, 6,...) sıfırdan farklı olabilmektedirler. Ishida ve Mazak i tarafından önerilen (Ishida and Mazaki 1982) bir başka modelde ise, sadece tek mertebeli harmonik alınganlıkların varlığı bulunabilmiştir. Bu modelde, tanecikli yapıya sahip bir süperiletken için magnetik yapının, zayıf bağlantılı çoklu Josephson ağı şeklinde olduğu öngörülmektedir. Bu modelin öngörüsü de simetrik M-H eğrisine dayandığından çift mertebeli harmonik alınganlıklar üretilmemektedir. Yüksek sıcaklık süperiletkenler tanecikli yapıya sahiptirler. Tanecikli yapıya sahip bir süperiletken soğutulurken ac alınganlığı ölçüldüğünde, alınganlığın faz-içi bileşeni kritik sıcaklıkta küçük bir düşüş sergiler, bu düşüşe eşlik eden küçük bir tepecik faz-dışı
19 bileşende gözlenir. Alınganlıktaki bu değişimler öncelikle taneciklerin süperiletken oluşundan kaynaklanır. Sıcaklık daha da düşürülünce, tanecikler arası süperiletken akım akışı başlar. AC alınganlığın faz-içi bileşeni daha büyük bir değerle sıcaklıkla yavaşça değişen bir negatif düşme gösterir. Bu durum faz-dışı bileşende daha büyük bir tepe oluşmasına katkıda bulunacaktır. Sıcaklık daha da soğutulduğunda ise, faz-içi bileşen sabit bir değere asimptotik olarak yaklaşırken faz-dışı bileşende sıfır değerine ulaşır yılından itibaren süperiletkenlerin fiziksel özellikleri hakkında çok miktarda çalışma olmasına karşın, tezin amaçlan bakımından magnetik özelliklerle ilgili olanların önemli değişim noktalarını meydana getiren bazı çalışmaların özeti burada verilmektedir. Jeffries et al. (1989) tanecikli YBa2Cu3O7_ x 'de doğrusal olmayan magnetik davranışı incelediler. Tanecikler arası zayıf bağlanmanın Josepshon eklemlerine benzer bağlardan oluştuğunu önerdiler. Xenikos and Lemberger (1990) YBCO tek kristallerinde T c 'ye yakın sıcaklıklarda doğrusal olmayan magnetik davranışı gözlediler. Doğrusal olmayan magnetik davranışın ana kaynağının akı sürüklenmesi ile açıklanabileceğini önerdiler. Ji et al. (1989) kritik akımın alan bağımlılığını hesaba katarak Bean modelini geliştirdiler. Ayrıca basitleştirilmiş Kim-Modelini kullanarak, M-H eğrileri için analitik denklemler türettiler. Bu denklemlerin analitik olarak yazılması, alınganlık bileşenlerinin Fourier katsayıları gibi, basitçe integral alınarak bulunabilmesine yardımcı olmaktadır. Bu modelde kritik akım yoğunluğu, yerel alanla ters orantılıdır. Bu bağıntılardan x n 'i nümerik olarak hesaplayıp deneysel verilerle karşılaştırmasını yaptılar. Ishida and Goldfarb (1990), YBCO süperiletkeninde, harmonik alınganlıkların alan ve sıcaklık bağımlılıklarını ayrıntılı olarak incelediler ve deneyle teori arasında iyi bir uyum gözlediler. Fabbricatore et al. (1994-1) polikristal BSCCO süperiletkeninde temel ve yüksek mertebeden harmonik alınganlık ölçümlerini alanın farklı frekanslarında gerçekleştirerek sonuçların Bean ve Kim modeline göre incelemelerini yaptılar. Modeller ile deneysel sonuçlar arasında çıkan uyuşmazlıkların genellikle yüksek mertebeden harmonik alınganlık ölçüm sonuçlarında etkili olduğunu, bunun da akı dinamiklerinin güçlü bir şekilde frekansa bağlı olmasından kaynaklandığını gösterdiler. Shatz et al. ( ) çalışmalarında, kritik akımın alan bağımlılığını kullanarak bir model geliştirdiler. Kritik durum modeli yardımıyla, harmonik alınganlıklar için analitik denklemler türettiler. Bunun sonucunda harmonik
20 alınganlıkları, malzemeye uygulanan alternatif alanın sızma derinliği ile belirlenebilen 8 parametresinin fonksiyonu olarak tanımladılar. Shatz et al. ( ) teorik tartışmaları örneklemek için, süperiletken yüzeyine paralel kararlı bir Hd c alanı içerisinde bulunan sonlu bir süperiletken "dilim"i göz önüne aldılar. Harmonik alınganlıkları ölçmek için küçük bir H ac sin(cot) alternatif alanını, Hdc alanı ile aynı yönde uyguladılar. Buna göre H ac sin(cût) alanının, H dc alanını küçük bir pertürbeye uğratacağı düşünülebilir (H ac «Hd c )- Bu modelde Bean ve diğer kritik durum modellerinde olduğu gibi, magnetik özelliklerde gözlenen frekans bağımlılığını açıklamada yetersiz kalmaktadır. AC alınganlığın frekans bağımlılığı hakkında pek çok makale yayınlanmıştır. Takacs and Gömöry (1989), YSS'lerinde ac alınganlığın frekans bağımlılığı ile ilgili çalışmalarında kritik hal denklemindeki akım terimine büyük vîskoziteli akı akışı terimini ilave ettiler. Kritik hal denklemindeki akım yoğunluğu terimine akı sürüklenmesi terimi ilave edildiğinde, tanecikler-arası magnetik alan profilinde bir değişime neden olacağı ise, Müller tarafından gösterilmiştir (Müller 1990). Bu değişim, frekansı artırdığımızda, daha yüksek sıcaklığa doğru ac kayıp tepelerinin veya ac alınganlığın faz-dışı bileşeninin kayması şeklinde kendini göstermektedir. Lofland et al. (1992) farklı tanecik boyutuna sahip malzemelerde frekans ile tepe sıcaklığı T p 'nin değişiminin tanecik boyutları tarafından etkilendiğini gösteren bir çalışma yaptılar. Prozov et. al. (1992) magnetik durulma etkisini de içeren kritik durum modelleri çerçevesinde süperiletken malzemenin ac magnetik tepkisini analiz ettiler. Lee and Kao (1996), farklı yüksek sıcaklık süperiletkenlerde enerji kayıp tepelerinin frekans bağımlılığını incelemişler ve kritik durum modelinde akı sürüklenmesi etkilerini içeren bir modelle sonuçlarını analiz etmişlerdir. Qin et al. (1997, 1999) akı sürüklenmesi denklemini nümerik olarak çözmek suretiyle YSS'lerinin ac alınganlıklarının frekans bağımlılığını açıkladılar. Yukarıda YSS'lerin magnetik özelliklerinin anlaşılmasında yapılan çalışmaların bir özeti sunulmuşur. Çalışmaların çoğunluğu Bean modelinin modifiye edilmesini içermektedir. Bu sebeple, frekans etkileri dahil tanecik etkisinden dolayı diğer gözlenen fiziksel özelliklerin açıklanması hedeflenmiştir. Ancak, Bean modelinin çeşitli geometrilerdeki süperiletkenlere ve değişik süperiletken gruplarına sistematik olarak uygulanmasını hedefleyen çalışmalar literatürde bizim gözlemlerimiz dahilinde
Ankara Üniversitesi Fen Fakültesi Fizik Bölümü 7. Hafta. Aysuhan OZANSOY
 FİZ102 FİZİK-II Ankara Üniversitesi Fen Fakültesi Fizik Bölümü 7. Hafta Aysuhan OZANSOY Bölüm 6: Akım, Direnç ve Devreler 1. Elektrik Akımı ve Akım Yoğunluğu 2. Direnç ve Ohm Kanunu 3. Özdirenç 4. Elektromotor
FİZ102 FİZİK-II Ankara Üniversitesi Fen Fakültesi Fizik Bölümü 7. Hafta Aysuhan OZANSOY Bölüm 6: Akım, Direnç ve Devreler 1. Elektrik Akımı ve Akım Yoğunluğu 2. Direnç ve Ohm Kanunu 3. Özdirenç 4. Elektromotor
Akım ve Direnç. Bölüm 27. Elektrik Akımı Direnç ve Ohm Kanunu Direnç ve Sıcaklık Elektrik Enerjisi ve Güç
 Bölüm 27 Akım ve Direnç Elektrik Akımı Direnç ve Ohm Kanunu Direnç ve Sıcaklık Elektrik Enerjisi ve Güç Öğr. Gör. Dr. Mehmet Tarakçı http://kisi.deu.edu.tr/mehmet.tarakci/ Elektrik Akımı Elektrik yüklerinin
Bölüm 27 Akım ve Direnç Elektrik Akımı Direnç ve Ohm Kanunu Direnç ve Sıcaklık Elektrik Enerjisi ve Güç Öğr. Gör. Dr. Mehmet Tarakçı http://kisi.deu.edu.tr/mehmet.tarakci/ Elektrik Akımı Elektrik yüklerinin
4 ELEKTRİK AKIMLARI. Elektik Akımı ve Akım Yoğunluğu. Elektrik yüklerinin akışına elektrik akımı denir. Yük
 4 ELEKTRİK AKIMLARI Elektik Akımı ve Akım Yoğunluğu Elektrik yüklerinin akışına elektrik akımı denir. Yük topluluğu bir A alanı boyunca yüzeye dik olarak hareket etsin. Bu yüzeyden t zaman aralığında Q
4 ELEKTRİK AKIMLARI Elektik Akımı ve Akım Yoğunluğu Elektrik yüklerinin akışına elektrik akımı denir. Yük topluluğu bir A alanı boyunca yüzeye dik olarak hareket etsin. Bu yüzeyden t zaman aralığında Q
KARABÜK ÜNİVERSİTESİ Öğretim Üyesi: Doç.Dr. Tamila ANUTGAN 1
 KARABÜK ÜNİVERSİTESİ Öğretim Üyesi: Doç.Dr. Tamila ANUTGAN 1 Elektriksel olaylarla ilgili buraya kadar yaptığımız, tartışmalarımız, durgun yüklerle veya elektrostatikle sınırlı kalmıştır. Şimdi, elektrik
KARABÜK ÜNİVERSİTESİ Öğretim Üyesi: Doç.Dr. Tamila ANUTGAN 1 Elektriksel olaylarla ilgili buraya kadar yaptığımız, tartışmalarımız, durgun yüklerle veya elektrostatikle sınırlı kalmıştır. Şimdi, elektrik
YÜKSEK GEÇİŞ SICAKLIKLI SÜPERİLETKENLERDE KRİTİK DURUM MODELLERİNİN İNCELENMESİ * Investigation Of Critical State Models On High-T c Superconductors
 YÜKSEK GEÇİŞ SICAKLIKLI SÜPERİLETKENLERDE KRİTİK DURUM MODELLERİNİN İNCELENMESİ * Investigation Of Critical State Models On High-T c Superconductors Selda KILIÇ Yüksel UFUKTEPE Ahmet EKİCİBİL Fizik Anabilim
YÜKSEK GEÇİŞ SICAKLIKLI SÜPERİLETKENLERDE KRİTİK DURUM MODELLERİNİN İNCELENMESİ * Investigation Of Critical State Models On High-T c Superconductors Selda KILIÇ Yüksel UFUKTEPE Ahmet EKİCİBİL Fizik Anabilim
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-1 Diferansiyel Formda Maxwell Denklemleri İntegral Formda Maxwell Denklemleri Fazörlerin Kullanımı Zamanda Harmonik Alanlar Malzeme Ortamı Dalga Denklemleri Michael Faraday,
Elektromanyetik Dalga Teorisi Ders-1 Diferansiyel Formda Maxwell Denklemleri İntegral Formda Maxwell Denklemleri Fazörlerin Kullanımı Zamanda Harmonik Alanlar Malzeme Ortamı Dalga Denklemleri Michael Faraday,
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Magnetic Materials. 7. Ders: Ferromanyetizma. Numan Akdoğan.
 Magnetic Materials 7. Ders: Ferromanyetizma Numan Akdoğan akdogan@gyte.edu.tr Gebze Institute of Technology Department of Physics Nanomagnetism and Spintronic Research Center (NASAM) Moleküler Alan Teorisinin
Magnetic Materials 7. Ders: Ferromanyetizma Numan Akdoğan akdogan@gyte.edu.tr Gebze Institute of Technology Department of Physics Nanomagnetism and Spintronic Research Center (NASAM) Moleküler Alan Teorisinin
Elektrik ve Magnetizma
 Elektrik ve Magnetizma 1.1. Biot-Sawart yasası Üzerinden akım geçen, herhangi bir biçime sahip iletken bir tel tarafından bir P noktasında üretilen magnetik alan şiddeti H iletkeni oluşturan herbir parçanın
Elektrik ve Magnetizma 1.1. Biot-Sawart yasası Üzerinden akım geçen, herhangi bir biçime sahip iletken bir tel tarafından bir P noktasında üretilen magnetik alan şiddeti H iletkeni oluşturan herbir parçanın
İstatistiksel Mekanik I
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
Paslanmaz Çelik Gövde. Yalıtım Sargısı. Katalizör Yüzey Tabakası. Egzoz Emisyonları: Su Karbondioksit Azot
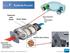 Paslanmaz Çelik Gövde Yalıtım Sargısı Egzoz Emisyonları: Su Karbondioksit Azot Katalizör Yüzey Tabakası Egzoz Gazları: Hidrokarbonlar Karbon Monoksit Azot Oksitleri Bu bölüme kadar, açıkça ifade edilmese
Paslanmaz Çelik Gövde Yalıtım Sargısı Egzoz Emisyonları: Su Karbondioksit Azot Katalizör Yüzey Tabakası Egzoz Gazları: Hidrokarbonlar Karbon Monoksit Azot Oksitleri Bu bölüme kadar, açıkça ifade edilmese
İÇİNDEKİLER -BÖLÜM / 1- -BÖLÜM / 2- -BÖLÜM / 3- GİRİŞ... 1 ÖZEL GÖRELİLİK KUANTUM FİZİĞİ ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ...
 İÇİNDEKİLER ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ... viii -BÖLÜM / 1- GİRİŞ... 1 -BÖLÜM / 2- ÖZEL GÖRELİLİK... 13 2.1. REFERANS SİSTEMLERİ VE GÖRELİLİK... 14 2.2. ÖZEL GÖRELİLİK TEORİSİ... 19 2.2.1. Zaman Ölçümü
İÇİNDEKİLER ÖNSÖZ... iii ŞEKİLLERİN LİSTESİ... viii -BÖLÜM / 1- GİRİŞ... 1 -BÖLÜM / 2- ÖZEL GÖRELİLİK... 13 2.1. REFERANS SİSTEMLERİ VE GÖRELİLİK... 14 2.2. ÖZEL GÖRELİLİK TEORİSİ... 19 2.2.1. Zaman Ölçümü
Şekilde görüldüğü gibi Gerilim/akım yoğunluğu karakteristik eğrisi dört nedenden dolayi meydana gelir.
 Bir fuel cell in teorik açık devre gerilimi: Formülüne göre 100 oc altinda yaklaşık 1.2 V dur. Fakat gerçekte bu değere hiçbir zaman ulaşılamaz. Şekil 3.1 de normal hava basıncında ve yaklaşık 70 oc da
Bir fuel cell in teorik açık devre gerilimi: Formülüne göre 100 oc altinda yaklaşık 1.2 V dur. Fakat gerçekte bu değere hiçbir zaman ulaşılamaz. Şekil 3.1 de normal hava basıncında ve yaklaşık 70 oc da
İÇİNDEKİLER 1: KRİSTALLERDE ATOMLAR...
 İÇİNDEKİLER Bölüm 1: KRİSTALLERDE ATOMLAR... 1 1.1 Katıhal... 1 1.1.1 Kristal Katılar... 1 1.1.2 Çoklu Kristal Katılar... 2 1.1.3 Kristal Olmayan (Amorf) Katılar... 2 1.2 Kristallerde Periyodiklik... 2
İÇİNDEKİLER Bölüm 1: KRİSTALLERDE ATOMLAR... 1 1.1 Katıhal... 1 1.1.1 Kristal Katılar... 1 1.1.2 Çoklu Kristal Katılar... 2 1.1.3 Kristal Olmayan (Amorf) Katılar... 2 1.2 Kristallerde Periyodiklik... 2
7 FARADAY IN İNDÜKSİYON KANUNU
 7 FARADAY IN İNDÜKİYON KANUNU Elektrik alanları durgun yüklerden manyetik alan ise hareketli yüklerden oluşur. Iletkenin üzerine bir elektrik alan uygulandığında akıma sebep olan bir manyetik alan üretir.
7 FARADAY IN İNDÜKİYON KANUNU Elektrik alanları durgun yüklerden manyetik alan ise hareketli yüklerden oluşur. Iletkenin üzerine bir elektrik alan uygulandığında akıma sebep olan bir manyetik alan üretir.
FZM 220. Malzeme Bilimine Giriş
 FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
FZM 220. Malzeme Bilimine Giriş
 FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Atomsal Yapı ve Atomlararası Bağ1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin
FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Atomsal Yapı ve Atomlararası Bağ1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin
TİTREŞİM VE DALGALAR BÖLÜM PERİYODİK HAREKET
 TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
engelsiz İki elektronun işbirliği!
 süperiletkenlik Süperiletkenlik Bir metali sert yaylar ile bağlanmış ve hareket edebilen pozitif iyonlardan oluşan bir kafes olarak düşünebiliriz. Kafeste hareket eden elektronlar elektrik akımı oluştururlar.
süperiletkenlik Süperiletkenlik Bir metali sert yaylar ile bağlanmış ve hareket edebilen pozitif iyonlardan oluşan bir kafes olarak düşünebiliriz. Kafeste hareket eden elektronlar elektrik akımı oluştururlar.
Fizik II Elektrik ve Manyetizma Akım, Direnç ve Elektromotor Kuvvet
 Ders Hakkında Fizik-II Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik ve manyetizmanın temel kanunlarını lisans düzeyinde öğretmektir. Dersin İçeriği Hafta
Ders Hakkında Fizik-II Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik ve manyetizmanın temel kanunlarını lisans düzeyinde öğretmektir. Dersin İçeriği Hafta
FZM 220. Malzeme Bilimine Giriş
 FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
MIT Açık Ders Malzemesi İstatistiksel Mekanik II: Alanların İstatistiksel Fiziği 2008 Bahar
 MIT Açık Ders Malzemesi http://ocw.mit.edu 8.334 İstatistiksel Mekanik II: Alanların İstatistiksel Fiziği 008 Bahar Bu malzemeye atıfta bulunmak ve Kullanım Şartlarımızla ilgili bilgi almak için http://ocw.mit.edu/terms
MIT Açık Ders Malzemesi http://ocw.mit.edu 8.334 İstatistiksel Mekanik II: Alanların İstatistiksel Fiziği 008 Bahar Bu malzemeye atıfta bulunmak ve Kullanım Şartlarımızla ilgili bilgi almak için http://ocw.mit.edu/terms
ÇEV-220 Hidrolik. Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT
 ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Türbülanslı Akış Mühendislik uygulamalarında akışların çoğu türbülanslıdır ve bu yüzden türbülansın
ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Türbülanslı Akış Mühendislik uygulamalarında akışların çoğu türbülanslıdır ve bu yüzden türbülansın
ENERJİ VERİMLİLİĞİ VE SÜPERİLETKEN MALZEMELER. Rıfkı Terzioğlu, Türker Fedai Çavuş Sakarya Üniversitesi Elektrik Elektronik Mühendisliği Bölümü
 ENERJİ VERİMLİLİĞİ VE SÜPERİLETKEN MALZEMELER Rıfkı Terzioğlu, Türker Fedai Çavuş Sakarya Üniversitesi Elektrik Elektronik Mühendisliği Bölümü İçerik Giriş İçerik Giriş Süperiletkenler ve temel özellikleri,
ENERJİ VERİMLİLİĞİ VE SÜPERİLETKEN MALZEMELER Rıfkı Terzioğlu, Türker Fedai Çavuş Sakarya Üniversitesi Elektrik Elektronik Mühendisliği Bölümü İçerik Giriş İçerik Giriş Süperiletkenler ve temel özellikleri,
FİZ4001 KATIHAL FİZİĞİ-I
 FİZ4001 KATIHAL FİZİĞİ-I Bölüm 3. Örgü Titreşimleri: Termal, Akustik ve Optik Özellikler Dr. Aytaç Gürhan GÖKÇE Katıhal Fiziği - I Dr. Aytaç Gürhan GÖKÇE 1 Bir Boyutlu İki Atomlu Örgü Titreşimleri M 2
FİZ4001 KATIHAL FİZİĞİ-I Bölüm 3. Örgü Titreşimleri: Termal, Akustik ve Optik Özellikler Dr. Aytaç Gürhan GÖKÇE Katıhal Fiziği - I Dr. Aytaç Gürhan GÖKÇE 1 Bir Boyutlu İki Atomlu Örgü Titreşimleri M 2
TAŞINIMIN FİZİKSEL MEKANİZMASI
 BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
Elektrostatik Elektrik Alan Elektrik Akı Kondansatör. Kaynak : Serway-Beichner Bölüm 23, 24, 26
 Elektrostatik Elektrik Alan Elektrik Akı Kondansatör Kaynak : Serway-Beichner Bölüm 23, 24, 26 İndüksiyon Nötr Maddenin indüksiyon yoluyla yüklenmesi (Bir yük türünün diğer yük türüne göre daha fazla olması)
Elektrostatik Elektrik Alan Elektrik Akı Kondansatör Kaynak : Serway-Beichner Bölüm 23, 24, 26 İndüksiyon Nötr Maddenin indüksiyon yoluyla yüklenmesi (Bir yük türünün diğer yük türüne göre daha fazla olması)
ATOM BİLGİSİ Atom Modelleri
 1. Atom Modelleri BÖLÜM2 Maddenin atom adı verilen bir takım taneciklerden oluştuğu fikri çok eskiye dayanmaktadır. Ancak, bilimsel bir (deneye dayalı) atom modeli ilk defa Dalton tarafından ileri sürülmüştür.
1. Atom Modelleri BÖLÜM2 Maddenin atom adı verilen bir takım taneciklerden oluştuğu fikri çok eskiye dayanmaktadır. Ancak, bilimsel bir (deneye dayalı) atom modeli ilk defa Dalton tarafından ileri sürülmüştür.
İletken Düzlemler Üstüne Yerleştirilmiş Antenler
 İletken Düzlemler Üstüne Yerleştirilmiş Antenler Buraya dek sınırsız ortamlarda tek başına bulunan antenlerin ışıma alanları incelendi. Anten yakınında bulunan başka bir ışınlayıcı ya da bir yansıtıcı,
İletken Düzlemler Üstüne Yerleştirilmiş Antenler Buraya dek sınırsız ortamlarda tek başına bulunan antenlerin ışıma alanları incelendi. Anten yakınında bulunan başka bir ışınlayıcı ya da bir yansıtıcı,
EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ. 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak.
 EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ AMAÇ: 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak. 2. Bu eş potansiyel çizgileri kullanarak elektrik alan çizgilerinin
EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ AMAÇ: 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak. 2. Bu eş potansiyel çizgileri kullanarak elektrik alan çizgilerinin
Aşağıda verilen özet bilginin ayrıntısını, ders kitabı. olarak önerilen, Erdik ve Sarıkaya nın Temel. Üniversitesi Kimyası" Kitabı ndan okuyunuz.
 KİMYASAL BAĞLAR Aşağıda verilen özet bilginin ayrıntısını, ders kitabı olarak önerilen, Erdik ve Sarıkaya nın Temel Üniversitesi Kimyası" Kitabı ndan okuyunuz. KİMYASAL BAĞLAR İki atom veya atom grubu
KİMYASAL BAĞLAR Aşağıda verilen özet bilginin ayrıntısını, ders kitabı olarak önerilen, Erdik ve Sarıkaya nın Temel Üniversitesi Kimyası" Kitabı ndan okuyunuz. KİMYASAL BAĞLAR İki atom veya atom grubu
Bi 1,6 Pb 0,4 Sr 2 Ca 2-x Sm x Cu 3 O y (x= 0,0 ve 1,0) SÜPERİLETKENLERİN ELEKTRİKSEL KARAKTERİZASYONU. Havva BOĞAZ
 Bi 1,6 Pb,4 Sr 2 Ca 2-x Sm x Cu 3 O y (x=, ve 1,) SÜPERİLETKENLERİN ELEKTRİKSEL KARAKTERİZASYONU Havva BOĞAZ YÜKSEK LİSANS TEZİ İLERİ TEKNOLOJİLER GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ HAZİRAN 26 ANKARA
Bi 1,6 Pb,4 Sr 2 Ca 2-x Sm x Cu 3 O y (x=, ve 1,) SÜPERİLETKENLERİN ELEKTRİKSEL KARAKTERİZASYONU Havva BOĞAZ YÜKSEK LİSANS TEZİ İLERİ TEKNOLOJİLER GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ HAZİRAN 26 ANKARA
MIT Açık Ders Malzemeleri Fizikokimya II 2008 Bahar
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
tayf kara cisim ışınımına
 13. ÇİZGİ OLUŞUMU Yıldızın iç kısımlarından atmosfere doğru akan ışınım, dalga boyunun yaklaşık olarak sürekli bir fonksiyonudur. Çünkü iç bölgede sıcaklık gradyenti (eğimi) küçüktür ve madde ile ışınım
13. ÇİZGİ OLUŞUMU Yıldızın iç kısımlarından atmosfere doğru akan ışınım, dalga boyunun yaklaşık olarak sürekli bir fonksiyonudur. Çünkü iç bölgede sıcaklık gradyenti (eğimi) küçüktür ve madde ile ışınım
Çukurova Üniversitesi Biyomedikal Mühendisliği
 Çukurova Üniversitesi Biyomedikal Mühendisliği BMM212 Elektronik-1 Laboratuvarı Deney Föyü Deney#8 Alan Etkili Transistör (FET) Karakteristikleri Arş. Gör. Mustafa İSTANBULLU Doç. Dr. Mutlu AVCI ADANA,
Çukurova Üniversitesi Biyomedikal Mühendisliği BMM212 Elektronik-1 Laboratuvarı Deney Föyü Deney#8 Alan Etkili Transistör (FET) Karakteristikleri Arş. Gör. Mustafa İSTANBULLU Doç. Dr. Mutlu AVCI ADANA,
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ Hakan GÜNDOĞMUŞ LAZER TEKNİĞİ İLE ÜRETİLEN KATKILI BSSCO SÜPERİLETKENLERİN FİZİKSEL ÖZELLİKLERİNİN ARAŞTIRILMASI FİZİK ANABİLİM DALI ADANA, 2013
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ Hakan GÜNDOĞMUŞ LAZER TEKNİĞİ İLE ÜRETİLEN KATKILI BSSCO SÜPERİLETKENLERİN FİZİKSEL ÖZELLİKLERİNİN ARAŞTIRILMASI FİZİK ANABİLİM DALI ADANA, 2013
5.111 Ders Özeti #12. Konular: I. Oktet kuralından sapmalar
 5.111 Ders Özeti #12 Bugün için okuma: Bölüm 2.9 (3. Baskıda 2.10), Bölüm 2.10 (3. Baskıda 2.11), Bölüm 2.11 (3. Baskıda 2.12), Bölüm 2.3 (3. Baskıda 2.1), Bölüm 2.12 (3. Baskıda 2.13). Ders #13 için okuma:
5.111 Ders Özeti #12 Bugün için okuma: Bölüm 2.9 (3. Baskıda 2.10), Bölüm 2.10 (3. Baskıda 2.11), Bölüm 2.11 (3. Baskıda 2.12), Bölüm 2.3 (3. Baskıda 2.1), Bölüm 2.12 (3. Baskıda 2.13). Ders #13 için okuma:
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM
 YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ
 EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ Giriş Isı değiştiricileri (eşanjör) değişik tiplerde olup farklı sıcaklıktaki iki akışkan arasında ısı alışverişini temin ederler. Isı değiştiricileri başlıca yüzeyli
EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ Giriş Isı değiştiricileri (eşanjör) değişik tiplerde olup farklı sıcaklıktaki iki akışkan arasında ısı alışverişini temin ederler. Isı değiştiricileri başlıca yüzeyli
Ankara Üniversitesi Fen Fakültesi Kimya Bölümü Bahar Yarıyılı Bölüm-6 Özeti Ankara Aysuhan OZANSOY
 FİZ102 FİZİK-II Ankara Üniversitesi Fen Fakültesi Kimya Bölümü 2014-2015 Bahar Yarıyılı Bölüm-6 Özeti 21.04.2015 Ankara Aysuhan OZANSOY Bölüm 6: Akım, Direnç ve Devreler 1. Elektrik Akımı ve Akım Yoğunluğu
FİZ102 FİZİK-II Ankara Üniversitesi Fen Fakültesi Kimya Bölümü 2014-2015 Bahar Yarıyılı Bölüm-6 Özeti 21.04.2015 Ankara Aysuhan OZANSOY Bölüm 6: Akım, Direnç ve Devreler 1. Elektrik Akımı ve Akım Yoğunluğu
NANO KURġUN ÜRETĠMĠ VE KARAKTERĠZASYONU
 NANO KURġUN ÜRETĠMĠ VE KARAKTERĠZASYONU AHMET GÜNGÖR MERSĠN ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ KĠMYA MÜHENDĠSLĠĞĠ ANA BĠLĠM DALI YÜKSEK LĠSANS TEZĠ MERSĠN TEMMUZ 2015 NANO KURġUN ÜRETĠMĠ VE KARAKTERĠZASYONU
NANO KURġUN ÜRETĠMĠ VE KARAKTERĠZASYONU AHMET GÜNGÖR MERSĠN ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ KĠMYA MÜHENDĠSLĠĞĠ ANA BĠLĠM DALI YÜKSEK LĠSANS TEZĠ MERSĠN TEMMUZ 2015 NANO KURġUN ÜRETĠMĠ VE KARAKTERĠZASYONU
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
ELEKTRİK AKIMI Elektrik Akım Şiddeti Bir İletkenin Direnci
 ELEKTRİK AKIMI Elektrikle yüklü ve potansiyelleri farklı olan iki iletken küreyi, iletken bir telle birleştirilirse, potansiyel farkından dolayı iletkende yük akışı meydana gelir. Bir iletkenden uzun süreli
ELEKTRİK AKIMI Elektrikle yüklü ve potansiyelleri farklı olan iki iletken küreyi, iletken bir telle birleştirilirse, potansiyel farkından dolayı iletkende yük akışı meydana gelir. Bir iletkenden uzun süreli
Bugün için Okuma: Bölüm 1.5 (3. Baskıda 1.3), Bölüm 1.6 (3. Baskıda 1.4 )
 5.111 Ders Özeti #4 Bugün için Okuma: Bölüm 1.5 (3. Baskıda 1.3), Bölüm 1.6 (3. Baskıda 1.4 ) Ders #5 için Okuma: Bölüm 1.3 (3. Baskıda 1.6 ) Atomik Spektrumlar, Bölüm 1.7 de eģitlik 9b ye kadar (3. Baskıda
5.111 Ders Özeti #4 Bugün için Okuma: Bölüm 1.5 (3. Baskıda 1.3), Bölüm 1.6 (3. Baskıda 1.4 ) Ders #5 için Okuma: Bölüm 1.3 (3. Baskıda 1.6 ) Atomik Spektrumlar, Bölüm 1.7 de eģitlik 9b ye kadar (3. Baskıda
Hareket halindeki elektrik yüklerinin oluşturduğu bir sistem düşünelim. Belirli bir bölgede net bir yük akışı olduğunda, akımın mevcut olduğu
 Akım ve Direnç Elektriksel olaylarla ilgili buraya kadar yaptığımız tartışmalar durgun yüklerle veya elektrostatikle sınırlı kalmıştır. Şimdi, elektrik yüklerinin hareket halinde olduğu durumları inceleyeceğiz.
Akım ve Direnç Elektriksel olaylarla ilgili buraya kadar yaptığımız tartışmalar durgun yüklerle veya elektrostatikle sınırlı kalmıştır. Şimdi, elektrik yüklerinin hareket halinde olduğu durumları inceleyeceğiz.
BÖLÜM 1: Matematiğe Genel Bakış 1. BÖLÜM:2 Fizik ve Ölçme 13. BÖLÜM 3: Bir Boyutta Hareket 20. BÖLÜM 4: Düzlemde Hareket 35
 BÖLÜM 1: Matematiğe Genel Bakış 1 1.1. Semboller, Bilimsel Gösterimler ve Anlamlı Rakamlar 1.2. Cebir 1.3. Geometri ve Trigometri 1.4. Vektörler 1.5. Seriler ve Yaklaşıklıklar 1.6. Matematik BÖLÜM:2 Fizik
BÖLÜM 1: Matematiğe Genel Bakış 1 1.1. Semboller, Bilimsel Gösterimler ve Anlamlı Rakamlar 1.2. Cebir 1.3. Geometri ve Trigometri 1.4. Vektörler 1.5. Seriler ve Yaklaşıklıklar 1.6. Matematik BÖLÜM:2 Fizik
Bölüm 24 Gauss Yasası
 Bölüm 24 Gauss Yasası Elektrik Akısı Gauss Yasası Gauss Yasasının Yüklü Yalıtkanlara Uygulanması Elektrostatik Dengedeki İletkenler Öğr. Gör. Dr. Mehmet Tarakçı http://kisi.deu.edu.tr/mehmet.tarakci/ Elektrik
Bölüm 24 Gauss Yasası Elektrik Akısı Gauss Yasası Gauss Yasasının Yüklü Yalıtkanlara Uygulanması Elektrostatik Dengedeki İletkenler Öğr. Gör. Dr. Mehmet Tarakçı http://kisi.deu.edu.tr/mehmet.tarakci/ Elektrik
8. ALTERNATİF AKIM VE SERİ RLC DEVRESİ
 8. ATENATİF AKIM E SEİ DEESİ AMAÇA 1. Alternatif akım ve gerilim ölçmeyi öğrenmek. Direnç, kondansatör ve indüktans oluşan seri bir alternatif akım devresini analiz etmek AAÇA oltmetre, ampermetre, kondansatör
8. ATENATİF AKIM E SEİ DEESİ AMAÇA 1. Alternatif akım ve gerilim ölçmeyi öğrenmek. Direnç, kondansatör ve indüktans oluşan seri bir alternatif akım devresini analiz etmek AAÇA oltmetre, ampermetre, kondansatör
Çukurova Üniversitesi Biyomedikal Mühendisliği
 Çukurova Üniversitesi Biyomedikal Mühendisliği BMM212 Elektronik-1 Laboratuvarı Deney Föyü Deney#8 Alan Etkili Transistör (FET) Karakteristikleri Doç. Dr. Mutlu AVCI Arş. Gör. Mustafa İSTANBULLU ADANA,
Çukurova Üniversitesi Biyomedikal Mühendisliği BMM212 Elektronik-1 Laboratuvarı Deney Föyü Deney#8 Alan Etkili Transistör (FET) Karakteristikleri Doç. Dr. Mutlu AVCI Arş. Gör. Mustafa İSTANBULLU ADANA,
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
Şekil-1. Doğru ve Alternatif Akım dalga şekilleri
 2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
MALZEME BİLGİSİ. Katı Eriyikler
 MALZEME BİLGİSİ Dr.- Ing. Rahmi ÜNAL Konu: Katı Eriyikler 1 Giriş Endüstriyel metaller çoğunlukla birden fazla tür eleman içerirler, çok azı arı halde kullanılır. Arı metallerin yüksek iletkenlik, korozyona
MALZEME BİLGİSİ Dr.- Ing. Rahmi ÜNAL Konu: Katı Eriyikler 1 Giriş Endüstriyel metaller çoğunlukla birden fazla tür eleman içerirler, çok azı arı halde kullanılır. Arı metallerin yüksek iletkenlik, korozyona
Termodinamik Termodinamik Süreçlerde İŞ ve ISI
 Termodinamik Süreçlerde İŞ ve ISI Termodinamik Hareketli bir pistonla bağlantılı bir silindirik kap içindeki gazı inceleyelim (Şekil e bakınız). Denge halinde iken, hacmi V olan gaz, silindir çeperlerine
Termodinamik Süreçlerde İŞ ve ISI Termodinamik Hareketli bir pistonla bağlantılı bir silindirik kap içindeki gazı inceleyelim (Şekil e bakınız). Denge halinde iken, hacmi V olan gaz, silindir çeperlerine
LİNEER DALGA TEORİSİ. Page 1
 LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
TERMODİNAMİĞİN ÜÇÜNCÜ YASASI
 Termodinamiğin Üçüncü Yasası: Mutlak Entropi Yalnızca entropi değişiminin hesaplanmasında kullanılan termodinamiğin ikinci yasasının ds = q tr /T şeklindeki matematiksel tanımından entropinin mutlak değerine
Termodinamiğin Üçüncü Yasası: Mutlak Entropi Yalnızca entropi değişiminin hesaplanmasında kullanılan termodinamiğin ikinci yasasının ds = q tr /T şeklindeki matematiksel tanımından entropinin mutlak değerine
KİNETİK GAZ KURAMI. Doç. Dr. Faruk GÖKMEŞE Kimya Bölümü Hitit Üniversitesi Fen Edebiyat Fakültesi 1
 Kinetik Gaz Kuramının Varsayımları Boyle, Gay-Lussac ve Avagadro deneyleri tüm ideal gazların aynı davrandığını göstermektedir ve bunları açıklamak üzere kinetik gaz kuramı ortaya atılmıştır. 1. Gazlar
Kinetik Gaz Kuramının Varsayımları Boyle, Gay-Lussac ve Avagadro deneyleri tüm ideal gazların aynı davrandığını göstermektedir ve bunları açıklamak üzere kinetik gaz kuramı ortaya atılmıştır. 1. Gazlar
Buna göre, bir devrede yük akışı olabilmesi için, üreteç ve pil gibi aygıtlara ihtiyaç vardır.
 ELEKTRİK AKIMI Potansiyelleri farklı olan iki iletken cisim birbirlerine dokundurulduğunda potansiyelleri eşit oluncaya kadar birinden diğerine elektrik yükü akışı olur. Potansiyeller eşitlendiğinde yani
ELEKTRİK AKIMI Potansiyelleri farklı olan iki iletken cisim birbirlerine dokundurulduğunda potansiyelleri eşit oluncaya kadar birinden diğerine elektrik yükü akışı olur. Potansiyeller eşitlendiğinde yani
1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları
 1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları Sol üstte yüzey seftleştirme işlemi uygulanmış bir çelik
1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları Sol üstte yüzey seftleştirme işlemi uygulanmış bir çelik
Dielektrik malzeme DİELEKTRİK ÖZELLİKLER. Elektriksel Kutuplaşma. Dielektrik malzemeler. Kutuplaşma Türleri 15.4.2015. Elektronik kutuplaşma
 Dielektrik malzeme DİELEKTRİK ÖZELLİKLER Dielektrik malzemeler; serbest elektron yoktur, yalıtkan malzemelerdir, uygulanan elektriksel alandan etkilenebilirler. 1 2 Dielektrik malzemeler Elektriksel alan
Dielektrik malzeme DİELEKTRİK ÖZELLİKLER Dielektrik malzemeler; serbest elektron yoktur, yalıtkan malzemelerdir, uygulanan elektriksel alandan etkilenebilirler. 1 2 Dielektrik malzemeler Elektriksel alan
Paylaşılan elektron ya da elektronlar, her iki çekirdek etrafında dolanacaklar, iki çekirdek arasındaki bölgede daha uzun süre bulundukları için bu
 4.Kimyasal Bağlar Kimyasal Bağlar Aynı ya da farklı cins atomları bir arada tutan kuvvetlere kimyasal bağlar denir. Pek çok madde farklı element atomlarının birleşmesiyle meydana gelmiştir. İyonik bağ
4.Kimyasal Bağlar Kimyasal Bağlar Aynı ya da farklı cins atomları bir arada tutan kuvvetlere kimyasal bağlar denir. Pek çok madde farklı element atomlarının birleşmesiyle meydana gelmiştir. İyonik bağ
Boya eklenmesi Kısmen karışma Homojenleşme
 DİFÜZYON 1 Katı içerisindeki atomların hareketi yüksek konsantrasyon bölgelerinden düşük konsantrasyon bölgelerine doğrudur. Kayma olayından farklıdır. Kaymada hareketli atom düzlemlerindeki bütün atomlar
DİFÜZYON 1 Katı içerisindeki atomların hareketi yüksek konsantrasyon bölgelerinden düşük konsantrasyon bölgelerine doğrudur. Kayma olayından farklıdır. Kaymada hareketli atom düzlemlerindeki bütün atomlar
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
ÇİNKO KATKILI ANTİBAKTERİYEL ÖZELLİKTE HİDROKSİAPATİT ÜRETİMİ VE KARAKTERİZASYONU
 ÇİNKO KATKILI ANTİBAKTERİYEL ÖZELLİKTE HİDROKSİAPATİT ÜRETİMİ VE KARAKTERİZASYONU SÜLEYMAN ÇINAR ÇAĞAN MERSİN ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MAKİNE MÜHENDİSLİĞİ ANA BİLİM DALI YÜKSEK LİSANS TEZİ
ÇİNKO KATKILI ANTİBAKTERİYEL ÖZELLİKTE HİDROKSİAPATİT ÜRETİMİ VE KARAKTERİZASYONU SÜLEYMAN ÇINAR ÇAĞAN MERSİN ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MAKİNE MÜHENDİSLİĞİ ANA BİLİM DALI YÜKSEK LİSANS TEZİ
Bölüm 1: Lagrange Kuramı... 1
 İÇİNDEKİLER Bölüm 1: Lagrange Kuramı... 1 1.1. Giriş... 1 1.2. Genelleştirilmiş Koordinatlar... 2 1.3. Koordinat Dönüşüm Denklemleri... 3 1.4. Mekanik Dizgelerin Bağ Koşulları... 4 1.5. Mekanik Dizgelerin
İÇİNDEKİLER Bölüm 1: Lagrange Kuramı... 1 1.1. Giriş... 1 1.2. Genelleştirilmiş Koordinatlar... 2 1.3. Koordinat Dönüşüm Denklemleri... 3 1.4. Mekanik Dizgelerin Bağ Koşulları... 4 1.5. Mekanik Dizgelerin
ELEKTROMANYETİK DALGALAR
 ELEKTROMANYETİK DALGALAR Hareket eden bir yük manyetik alan oluşturur. Yük sabit hızla hareket ederse, sabit bir akım ve sabit bir manyetik alan oluşturur. Yük osilasyon hareketi yaparsa değişken bir manyetik
ELEKTROMANYETİK DALGALAR Hareket eden bir yük manyetik alan oluşturur. Yük sabit hızla hareket ederse, sabit bir akım ve sabit bir manyetik alan oluşturur. Yük osilasyon hareketi yaparsa değişken bir manyetik
Sistem nedir? Başlıca Fiziksel Sistemler: Bir matematiksel teori;
 Sistem nedir? Birbirleriyle ilişkide olan elemanlar topluluğuna sistem denir. Yrd. Doç. Dr. Fatih KELEŞ Fiziksel sistemler, belirli bir görevi gerçekleştirmek üzere birbirlerine bağlanmış fiziksel eleman
Sistem nedir? Birbirleriyle ilişkide olan elemanlar topluluğuna sistem denir. Yrd. Doç. Dr. Fatih KELEŞ Fiziksel sistemler, belirli bir görevi gerçekleştirmek üzere birbirlerine bağlanmış fiziksel eleman
Akışkan Kinematiği 1
 Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
Kuantum Fiziğinin Gelişimi (Quantum Physics) 1900 den 1930 a
 Kuantum Fiziğinin Gelişimi (Quantum Physics) 1900 den 1930 a Kuantum Mekaniği Düşüncesinin Gelişimi Dalga Mekaniği Olarak da Adlandırılır Atom, Molekül ve Çekirdeği Açıklamada Oldukça Başarılıdır Kuantum
Kuantum Fiziğinin Gelişimi (Quantum Physics) 1900 den 1930 a Kuantum Mekaniği Düşüncesinin Gelişimi Dalga Mekaniği Olarak da Adlandırılır Atom, Molekül ve Çekirdeği Açıklamada Oldukça Başarılıdır Kuantum
İstatistiksel Mekanik I
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri
 Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
Elektromanyetik Işıma Electromagnetic Radiation (EMR)
 Elektromanyetik Işıma Electromagnetic Radiation (EMR) Elektromanyetik ışıma (ışık) bir enerji şeklidir. Işık, Elektrik (E) ve manyetik (H) alan bileşenlerine sahiptir. Light is a wave, made up of oscillating
Elektromanyetik Işıma Electromagnetic Radiation (EMR) Elektromanyetik ışıma (ışık) bir enerji şeklidir. Işık, Elektrik (E) ve manyetik (H) alan bileşenlerine sahiptir. Light is a wave, made up of oscillating
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ Duygu YAZICI TEK FAZLI BSCCO SÜPERİLETKEN MALZEME ÜRETİMİ VE MALZEMENİN FİZİKSEL ÖZELLİKLERİNİN ARAŞTIRILMASI FİZİK ANABİLİM DALI ADANA, 2010
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ Duygu YAZICI TEK FAZLI BSCCO SÜPERİLETKEN MALZEME ÜRETİMİ VE MALZEMENİN FİZİKSEL ÖZELLİKLERİNİN ARAŞTIRILMASI FİZİK ANABİLİM DALI ADANA, 2010
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
AKIŞKANLAR MEKANİĞİ-II
 AKIŞKANLAR MEKANİĞİ-II Şekil 1. Akışa bırakılan parçacıkların parçacık izlemeli hızölçer ile belirlenmiş cisim arkasındaki (iz bölgesi) yörüngeleri ve hızlarının zamana göre değişimi (renk skalası). Akış
AKIŞKANLAR MEKANİĞİ-II Şekil 1. Akışa bırakılan parçacıkların parçacık izlemeli hızölçer ile belirlenmiş cisim arkasındaki (iz bölgesi) yörüngeleri ve hızlarının zamana göre değişimi (renk skalası). Akış
4. Adveksiyon ve Difüzyon Süreçleri
 4. Adveksiyon ve Difüzyon Süreçleri ÇEV 3523 Çevresel Taşınım Süreçleri Prof.Dr. Alper ELÇİ Çevrede Taşınım Süreçleri Kirletici/madde taşınım süreçleri: 1. Adveksiyon 2. Difüzyon 3. Dispersiyon Adveksiyon
4. Adveksiyon ve Difüzyon Süreçleri ÇEV 3523 Çevresel Taşınım Süreçleri Prof.Dr. Alper ELÇİ Çevrede Taşınım Süreçleri Kirletici/madde taşınım süreçleri: 1. Adveksiyon 2. Difüzyon 3. Dispersiyon Adveksiyon
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SÜPERİLETKEN "RACETRACT" BOBİNLERDE VE BOBİN "STACK" YAPILARINDA ALTERNATİF AKIM KAYIPLARIN SONLU ELEMANLAR YÖNTEMİ İLE ARAŞTIRILMASI Meryem
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SÜPERİLETKEN "RACETRACT" BOBİNLERDE VE BOBİN "STACK" YAPILARINDA ALTERNATİF AKIM KAYIPLARIN SONLU ELEMANLAR YÖNTEMİ İLE ARAŞTIRILMASI Meryem
ELEKTRİK DEVRE TEMELLERİ
 ELEKTRİK DEVRE TEMELLERİ Dr. Cemile BARDAK Ders Gün ve Saatleri: Çarşamba (09:55-12.30) Ofis Gün ve Saatleri: Pazartesi / Çarşamba (13:00-14:00) 1 TEMEL KAVRAMLAR Bir atom, proton (+), elektron (-) ve
ELEKTRİK DEVRE TEMELLERİ Dr. Cemile BARDAK Ders Gün ve Saatleri: Çarşamba (09:55-12.30) Ofis Gün ve Saatleri: Pazartesi / Çarşamba (13:00-14:00) 1 TEMEL KAVRAMLAR Bir atom, proton (+), elektron (-) ve
 Geometriden kaynaklanan etkileri en aza indirmek için yük ve uzama, sırasıyla mühendislik gerilmesi ve mühendislik birim şekil değişimi parametreleri elde etmek üzere normalize edilir. Mühendislik gerilmesi
Geometriden kaynaklanan etkileri en aza indirmek için yük ve uzama, sırasıyla mühendislik gerilmesi ve mühendislik birim şekil değişimi parametreleri elde etmek üzere normalize edilir. Mühendislik gerilmesi
Fiziksel bir olayı incelemek için çeşitli yöntemler kullanılır. Bunlar; 1. Ampirik Bağıntılar 2. Boyut Analizi, Benzerlik Teorisi 3.
 Fiziksel bir olayı incelemek için çeşitli yöntemler kullanılır. Bunlar; 1. Ampirik Bağıntılar 2. Boyut Analizi, Benzerlik Teorisi 3. Benzetim Yöntemi (Analoji) 4. Analitik Yöntem 1. Ampirik Bağıntılar:
Fiziksel bir olayı incelemek için çeşitli yöntemler kullanılır. Bunlar; 1. Ampirik Bağıntılar 2. Boyut Analizi, Benzerlik Teorisi 3. Benzetim Yöntemi (Analoji) 4. Analitik Yöntem 1. Ampirik Bağıntılar:
FİZİK-II DERSİ LABORATUVARI ( FL 2 5 )
 FİZİK-II DERSİ LABORATUVARI ( FL 2 5 ) EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ AMAÇ: 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak. 2. Bu eş potansiyel çizgileri
FİZİK-II DERSİ LABORATUVARI ( FL 2 5 ) EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ AMAÇ: 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak. 2. Bu eş potansiyel çizgileri
Elektrik Akımı, Direnç ve Ohm Yasası
 1. Akım Şiddeti Elektrik akımı, elektrik yüklerinin hareketi sonucu oluşur. Ancak her hareketli yük akım yaratmaz. Belirli bir bölge ya da yüzeyden net bir elektrik yük akışı olduğu durumda elektrik akımından
1. Akım Şiddeti Elektrik akımı, elektrik yüklerinin hareketi sonucu oluşur. Ancak her hareketli yük akım yaratmaz. Belirli bir bölge ya da yüzeyden net bir elektrik yük akışı olduğu durumda elektrik akımından
Bölüm 9 ELEKTROMANYETİK İNDÜKSİYON. Copyright 2008 Pearson Education Inc., publishing as Pearson Addison-Wesley
 Bölüm 9 ELEKTROMANYETİK İNDÜKSİYON Hedef Öğretiler Faraday Kanunu Lenz kanunu Hareke bağlı EMK İndüksiyon Elektrik Alan Maxwell denklemleri ve uygulamaları Giriş Pratikte Mıknatısın hareketi akım oluşmasına
Bölüm 9 ELEKTROMANYETİK İNDÜKSİYON Hedef Öğretiler Faraday Kanunu Lenz kanunu Hareke bağlı EMK İndüksiyon Elektrik Alan Maxwell denklemleri ve uygulamaları Giriş Pratikte Mıknatısın hareketi akım oluşmasına
ELEKTROMANYETIK ALAN TEORISI
 ELEKTROMANYETIK ALAN TEORISI kaynaklar: 1) Electromagnetic Field Theory Fundamentals Guru&Hiziroglu 2) A Student s Guide to Maxwell s Equations Daniel Fleisch 3) Mühendislik Elektromanyetiğinin Temelleri
ELEKTROMANYETIK ALAN TEORISI kaynaklar: 1) Electromagnetic Field Theory Fundamentals Guru&Hiziroglu 2) A Student s Guide to Maxwell s Equations Daniel Fleisch 3) Mühendislik Elektromanyetiğinin Temelleri
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ
 BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METOTLAR II DOĞRUSAL ISI İLETİMİ DENEYİ 1.Deneyin Adı: Doğrusal ısı iletimi deneyi..
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METOTLAR II DOĞRUSAL ISI İLETİMİ DENEYİ 1.Deneyin Adı: Doğrusal ısı iletimi deneyi..
BÖLÜM 2. FOTOVOLTAİK GÜNEŞ ENERJİ SİSTEMLERİ (PV)
 BÖLÜM 2. FOTOOLTAİK GÜNEŞ ENERJİ SİSTEMLERİ (P) Fotovoltaik Etki: Fotovoltaik etki birbirinden farklı iki malzemenin ortak temas bölgesinin (common junction) foton radyasyonu ile aydınlatılması durumunda
BÖLÜM 2. FOTOOLTAİK GÜNEŞ ENERJİ SİSTEMLERİ (P) Fotovoltaik Etki: Fotovoltaik etki birbirinden farklı iki malzemenin ortak temas bölgesinin (common junction) foton radyasyonu ile aydınlatılması durumunda
Faraday Yasası. 31. Bölüm
 Faraday Yasası 31. Bölüm 1. Faraday İndüksiyon Yasası Faraday ve Henri: Değişen manyetik alanlar da emk (dolayısıyla akım) oluşturur. Şekilde görüldüğü gibi akım ile değişen manyetik alan arasında bir
Faraday Yasası 31. Bölüm 1. Faraday İndüksiyon Yasası Faraday ve Henri: Değişen manyetik alanlar da emk (dolayısıyla akım) oluşturur. Şekilde görüldüğü gibi akım ile değişen manyetik alan arasında bir
GÜNEŞ PİLLERİ (FOTOVOLTAİK PİLLER) I. BÖLÜM
 GÜNEŞ PİLLERİ (FOTOVOLTAİK PİLLER) I. BÖLÜM Prof. Dr. Olcay KINCAY Y. Doç. Dr. Nur BEKİROĞLU Y. Doç. Dr. Zehra YUMURTACI İ ç e r i k Genel bilgi ve çalışma ilkesi Güneş pili tipleri Güneş pilinin elektriksel
GÜNEŞ PİLLERİ (FOTOVOLTAİK PİLLER) I. BÖLÜM Prof. Dr. Olcay KINCAY Y. Doç. Dr. Nur BEKİROĞLU Y. Doç. Dr. Zehra YUMURTACI İ ç e r i k Genel bilgi ve çalışma ilkesi Güneş pili tipleri Güneş pilinin elektriksel
Selçuk Üniversitesi. Mühendislik-Mimarlık Fakültesi. Kimya Mühendisliği Bölümü. Kimya Mühendisliği Laboratuvarı. Venturimetre Deney Föyü
 Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Kimya Mühendisliği Bölümü Kimya Mühendisliği Laboratuvarı Venturimetre Deney Föyü Hazırlayan Arş.Gör. Orhan BAYTAR 1.GİRİŞ Genellikle herhangi bir akış
Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Kimya Mühendisliği Bölümü Kimya Mühendisliği Laboratuvarı Venturimetre Deney Föyü Hazırlayan Arş.Gör. Orhan BAYTAR 1.GİRİŞ Genellikle herhangi bir akış
8.04 Kuantum Fiziği Ders IV. Kırınım olayı olarak Heisenberg belirsizlik ilkesi. ise, parçacığın dalga fonksiyonu,
 Geçen Derste Kırınım olayı olarak Heisenberg belirsizlik ilkesi ΔxΔp x 2 Fourier ayrışımı Bugün φ(k) yı nasıl hesaplarız ψ(x) ve φ(k) ın yorumu: olasılık genliği ve olasılık yoğunluğu ölçüm φ ( k)veyahut
Geçen Derste Kırınım olayı olarak Heisenberg belirsizlik ilkesi ΔxΔp x 2 Fourier ayrışımı Bugün φ(k) yı nasıl hesaplarız ψ(x) ve φ(k) ın yorumu: olasılık genliği ve olasılık yoğunluğu ölçüm φ ( k)veyahut
Bölüm 7 ENTROPİ. Bölüm 7: Entropi
 Bölüm 7 ENTROPİ 1 Amaçlar Termodinamiğin ikinci kanununu hal değişimlerine uygulamak. İkinci yasa verimini ölçmek için entropi olarak adlandırılan özelliği tanımlamak. Entropinin artış ilkesinin ne olduğunu
Bölüm 7 ENTROPİ 1 Amaçlar Termodinamiğin ikinci kanununu hal değişimlerine uygulamak. İkinci yasa verimini ölçmek için entropi olarak adlandırılan özelliği tanımlamak. Entropinin artış ilkesinin ne olduğunu
1. HAFTA Giriş ve Temel Kavramlar
 1. HAFTA Giriş ve Temel Kavramlar TERMODİNAMİK VE ISI TRANSFERİ Isı: Sıcaklık farkının bir sonucu olarak bir sistemden diğerine transfer edilebilen bir enerji türüdür. Termodinamik: Bir sistem bir denge
1. HAFTA Giriş ve Temel Kavramlar TERMODİNAMİK VE ISI TRANSFERİ Isı: Sıcaklık farkının bir sonucu olarak bir sistemden diğerine transfer edilebilen bir enerji türüdür. Termodinamik: Bir sistem bir denge
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Bölüm 2. Bir boyutta hareket
 Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
Pb, Ag ve Sb KATKI ATOMLARIYLA HAZIRLANMIŞ YBaCuO SÜPERİLETKEN SİSTEMLERİN ELEKTRİKSEL PARAMETRELERİNİN SAPTANMASI
 DOKUZ EYLÜL ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ Pb, Ag ve Sb KATKI ATOMLARIYLA HAZIRLANMIŞ YBaCuO SÜPERİLETKEN SİSTEMLERİN ELEKTRİKSEL PARAMETRELERİNİN SAPTANMASI A. Gönül ÖZTÜRK Ekim, 2010 İZMİR Pb,
DOKUZ EYLÜL ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ Pb, Ag ve Sb KATKI ATOMLARIYLA HAZIRLANMIŞ YBaCuO SÜPERİLETKEN SİSTEMLERİN ELEKTRİKSEL PARAMETRELERİNİN SAPTANMASI A. Gönül ÖZTÜRK Ekim, 2010 İZMİR Pb,
AERODİNAMİK KUVVETLER
 AERODİNAMİK KUVVETLER Prof.Dr. Mustafa Cavcar Anadolu Üniversitesi, Sivil Havacılık Yüksekokulu, 26470 Eskişehir Bir uçak üzerinde meydana gelen aerodinamik kuvvetlerin bileşkesi ( ); uçağın etrafından
AERODİNAMİK KUVVETLER Prof.Dr. Mustafa Cavcar Anadolu Üniversitesi, Sivil Havacılık Yüksekokulu, 26470 Eskişehir Bir uçak üzerinde meydana gelen aerodinamik kuvvetlerin bileşkesi ( ); uçağın etrafından
ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ FİZİK II LABORATUVARI DENEY 2 TRANSFORMATÖRLER
 ELEKTRİK ELEKTROİK MÜHEDİSLİĞİ FİZİK LABORATUVAR DEEY TRASFORMATÖRLER . Amaç: Bu deneyde:. Transformatörler yüksüz durumdayken giriş ve çıkış gerilimleri gözlenecek,. Transformatörler yüklü durumdayken
ELEKTRİK ELEKTROİK MÜHEDİSLİĞİ FİZİK LABORATUVAR DEEY TRASFORMATÖRLER . Amaç: Bu deneyde:. Transformatörler yüksüz durumdayken giriş ve çıkış gerilimleri gözlenecek,. Transformatörler yüklü durumdayken
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
7. DİRENÇ SIĞA (RC) DEVRELERİ AMAÇ
 7. DİENÇ SIĞA (C) DEELEİ AMAÇ Seri bağlı direnç ve kondansatörden oluşan bir devrenin davranışını inceleyerek kondansatörün durulma ve yarı ömür zamanını bulmak. AAÇLA DC Güç kaynağı, kondansatör, direnç,
7. DİENÇ SIĞA (C) DEELEİ AMAÇ Seri bağlı direnç ve kondansatörden oluşan bir devrenin davranışını inceleyerek kondansatörün durulma ve yarı ömür zamanını bulmak. AAÇLA DC Güç kaynağı, kondansatör, direnç,
