2. SUYUN BORULARDAKİ AKIŞI
|
|
|
- Tülay Okyay
- 5 yıl önce
- İzleme sayısı:
Transkript
1 . SUYUN BORULARDAKİ AKIŞI.. Birim Sistemleri Diğer bilim dallarında olduğu gibi suyun borulardaki akış formüllerinde de çeşitli birim sistemleri kullanılabilir. Bunlar: a) MKS (Meter-Kilogram-Second), b) SI (International System of Units), c) CGS (Centimeter-Gram-Second) dır... Suyun Fiziksel Özellikleri... Kütle ve ağırlık Kütle, akışkanın madde miktarıyla ilgilidir ve akışkanın ağırlığının yerçekimi ivmesine bölümüne eşittir. Kütle skaler bir büyüklüktür; W m g... Özgül kütle Özgül kütle aşağıdaki gibi bulunabilir. m W g...3. Özgül ağırlık Birim hacimdeki akışkanın ağırlığına özgül ağırlık denir ve ile gösterilir. Özgül ağırlık bir başka tanımla bir akışkanın birim hacmine etki eden yerçekimi kuvvetidir. Özgül ağırlık; W ile hesaplanır. Burada: : Özgül ağırlık (kp/m 3 ), W : Ağırlık (kp), : Hacim (m 3 ) tür. Özgül ağırlık, özgül kütleyle de ilişkili olup, özgül kütleye bağlı olarak; 9
2 .g ile bulunur. Görüldüğü gibi özgül ağırlık özgül kütleyle, yerçekimi kuvvetinin çarpımıdır. Özgül ağırlık sıcaklığa bağlı olarak değişmektedir. Çizelge. de suyun sıcaklığa bağlı olarak bazı fiziksel özellikleri verilmiştir...4. Yoğunluk Akışkanın özgül kütlesinin +4 C o deki damıtık suyun özgül kütlesine oranına yoğunluk denir. Bir başka tanımlamayla akışkanın birim hacminin ağırlığının aynı hacimdeki ve +4 C o deki suyun ağırlığına oranına yoğunluk denmektedir. Görüldüğü gibi özgül kütle veya özgül ağırlığın oranı olması nedeniyle yoğunluk birimsiz olup SG ile gösterilebilmektedir. SG ak su Civanın yoğunluğu 3,6 olarak verildiğinde, bu belirli hacimdeki civanın aynı hacimdeki sudan 3,6 kat daha ağır olduğunu gösterir...5. iskozite iskozite, akışkanların akışa karşı gösterdikleri dirençtir. iskozitenin açıklanmasında Şekil. de görülen biri hareketli biri sabit iki plakadan yararlanılmaktadır. Şekilde hareketli plakanın alanı (A), hareketli plakaya etki eden kuvvet (F), sabit plaka ile hareketli plaka arasındaki akışkanın hız dağılımı dv (gradyenti), iki plaka arasındaki uzaklık (y) olarak alındığında ve hareketli dy plaka (F) kuvvetiyle çekildiğinde aşağıdaki ilişkinin oluştuğu görülmüştür. F A dv. dy Sabit plakada akışkan hızı sıfır olup, hareketli plakaya gidildikçe hız artmakta ve hareketli plakada hız maksimuma ulaşmaktadır. Eğer iki plaka arasındaki hız dağılımı homojen kabul edilirse yukarıdaki eşitlik, F A. y biçimine dönüşür. Buradaki µ (mü) ye dinamik (mutlak) viskozite veya yalnızca viskozite denir ve aşağıdaki şekilde formülize edilebilir; 0
3 F.y veya A. y. Sıvıların viskozitesi sıcaklığın artmasıyla azalırken gazların viskozitesi sıcaklığın artmasıyla artmaktadır. Teknikte, viskozite ölçme yöntemlerinde sıvının akma süresi viskozitesi yanında özgül kütlesine de bağlıdır. Özgül kütlesinin etkisini ortadan kaldırmak için kinematik viskozite adı verilen aşağıdaki tanımlama yapılmıştır. Burada: (nü) : Kinematik viskozite (m /s) dir, CGS sisteminde kinematik viskozitenin birimi cm /s olup stoke (st) olarak adlandırılır. Stok un yüzde biri centistoke olur ve cst ile gösterilir..3. Bernoulli Denklemi 738 yılında Daniel BERNOULLI tarafından ortaya konulmuştur. Bernoulli denklemi bir enerji eşitliğidir ve suyun akışının incelenmesini, genellikle akıştan ortaya çıkan sürtünme kayıplarını ve bunlarla ilgili konuları kapsar. P...z sabit ve ABCD kesitindeki enerji toplamı; P...z sabit olmaktadır. Buna göre borunun her noktasındaki enerji toplamları birbirine eşit alınabilmektedir. Yani; P...z P... z terimi yazılabilmektedir. Bu bağıntılardaki P terimi basınç enerjisini,.. kinetik enerjiyi ve z terimi de ağırlık kuvvetlerinin yaptığı işi göstermektedir. Bernoulli denklemi hem akım yönünde ve hem de akıma dik yönde yazılabilmektedir. Yukarıda akım yönündeki Bernoulli denklemi verilmiştir. Bu denklemin elde edilmesinde viskoz kuvvetler ihmal edilmiş, akım kararlı ve sıkıştırılamaz kabul edilmiştir. Sıvılar sıkıştırılamaz kabul edildiğinden bu denklem akım yönünde (akışkanın aktığı yönde) kolaylıkla kullanılabilmektedir.
4 Yukarıda verilen Bernoulli denkleminde basınç (P) birimleri (kp/m ), özgül kütle () birimi (kp.s /m 4 ), hız (v) birimi (m/s), özgül ağırlık () birimi (kp/m 3 ) ve referans düzlemine olan yükseklik (z) birimi de (m) alınacaktır. Ancak su çıkartma makinelerinde enerji birimi ve basınç birimi (mss) olarak kullanılacağından Bernoulli denkleminin birimini (m) ye dönüştürmek kullanım kolaylığı sağlayacaktır. Bu amaçla herbir terim özgül ağırlığa () bölündüğünde Bernoulli denkleminin en çok kullanılan aşağıdaki biçimi elde edilir. Bu denklemde; P z.g P z.g her terimin birimi (m) dir. Buradaki yükseklik terimi (z) akışkanın potansiyel enerjisiyle ilgilidir. Yani referans eksenine göre akışkanın sahip olduğu potansiyel enerjiyi verir ve potansiyel yük adını alır. Basınç terimine (P/) basınç yükü denir ve (P) basıncının elde edilmesi için gerekli olan akışkan yüksekliğini verir. Hız terimi ( /.g) ise hız yükü dür ve akışkanın () hızına ulaşmak için gerekli olan serbest düşme yüksekliğini verir. Bernoulli denklemi basınç yükü, hızı yükü ve potansiyel yükün toplamının, akışkanın akış yönünde sabit olduğunu göstermektedir..3.. Enerji ve hidrolik eğim çizgileri Bir önceki konuda Bernoulli denkleminin bir enerji eşitliği olduğunu, sürtünmesiz, sıkıştırılamaz, kararlı akım koşullarında akım çizgisi (akış yönünde) boyunca kullanılabileceği görülmüştü. Akışkan boru içerisinde bir yerden başka bir yere gittiğinde toplam enerjisi sabit kalmaktadır. Bernoulli eşitliği bir başka biçimde enerji (EÇ) ve hidrolik (HEÇ) eğim çizgisiyle de ifade edilebilir. Sürtünmesiz, sıkıştırılamaz ve kararlı akımda toplam enerji her yerde sabit kalmaktadır. Enerjiyi yük (yükseklik) olarak kabul ettiğimizde Bernoulli denklemi; P H z.g biçiminde yazılabilir. Buradaki H: toplam yük (yükseklik) olup basınç, hız ve potansiyel yükün toplamından oluşmaktadır..4. Süreklilik Denklemi Süreklilik denklemi hız, verdi ve kesit alanı arasındaki ilişkiyi gösterir. Bu üç terim birbiri ile ilgilidir ve her biri diğer ikisine bağlıdır. Borulardaki akışta verdi sabit kaldığı zaman boru kesit alanı hız ile ters orantılıdır. Kesit alanı azalırsa hız değerinin artması gerekir. Bu şu şekilde ifade edilebilir. Q Q veya A. = A. = sabit. bağıntısı elde edilir. (A) ve (A) herhangi iki kesit alanı olduğundan süreklilik denkleminin genel ifadesi, Q= A. şeklinde yazılabilir.
5 .5. Akım Tipleri ve Özellikleri Akışkanların borudaki akımı, Laminer ya da türbülans akım olarak incelenebilmektedir...d.d Re Reynolds sayısının birimi yoktur. Reynolds sayısı yaklaşık olarak 00 den küçükse Laminer ve 4000 den büyükse türbülans ve bu ikisi arasında ise geçiş akımı olarak kabul edilmiştir. Hesaplamalarda geçiş bölgesindeki akım Laminer da kabul edilebilir, türbülans da. Re 00 Laminer akım 00 < Re < 4000 Geçiş akımı. Re 4000 Türbülans akım Laminer akımda akışkan tanecikleri birbirine paralel olarak akım çizgisi boyunca hareket ederler. Doğrultu ve yönleri değişmez. Sürtünme (yük) kaybına etkili olan en önemli faktör akışkanın viskozitesidir. Borunun tipi ve iç yüzey pürüzlülüğü etkili değildir. Boru eksenindeki maksimum hız ortalama hızın katıdır (max= ort). Borunun iç yüzeyinde akışkan hızı sıfır kabul edilebilir. Laminer akımda sürtünme kaybı daha azdır. Hız değişimi paraboliktir..6. Borulardaki Sürtünme (yük) Kayıpları ve Hesaplanması Borulardaki yük kayıpları hesaplanırken akımın tipine göre farklı bağıntılar kullanılmaktadır. Konumuzla ilgili problemlerde akım tipi türbülans olduğundan özellikle bu akımdaki sürtünme kayıplarının hesaplanması üzerinde durulacaktır. Boru hatlarında oluşan sürtünme kaybı iki kısımda incelenmektedir. a) Düz borularda meydana gelen düz boru sürtünme (yük) kayıpları, b) Akışkanın yönünü ya da hızını değiştiren yardımcı boru parçalarında meydana gelen şekil (yersel) kayıpları..6.. Düz borularda sürtünme kayıplarının hesaplanması.6... Laminer akımda sürtünme kayıplarının hesaplanması Laminer akımda, yatay boruda meydana gelen sürtünme kaybını belirleyen faktör borunun iç yüzey pürüzlülüğü ve boru cinsi değil viskozitedir. Sürtünme kaybı; viskozite, boru uzunluğu ve akışkan hızı ile doğru, boru çapı ile ters orantılıdır. 3
6 h k L. 3.. g D Bu bağıntıda: 4 hk : Laminer akımda meydana gelen sürtünme kaybı (m), : Akışkanın kinematik viskozitesi (m /s), L : Boru uzunluğu (m), : Akışkanın hızı (m/s), D : Boru çapı (m) dir Türbülans akımda sürtünme kayıplarının hesaplanması Türbülans akımda düz borulardaki sürtünme kayıplarının hesaplanmasında teorik ve deneysel yollardan yararlanarak geliştirilen değişik eşitlikler kullanılmaktadır. Bu eşitlikler içinde en çok kullanılanlar; a) CHEZY, b) DARCY-WEISBACH, c) ÜSLÜ FORMÜLLER dir Chezy formülü ile sürtünme kayıplarının hesaplanması Chezy formülü bir hız eşitliği olup akışkan hızı, hidrolik eğim ve hidrolik yarıçap arasındaki ilişkiyi gösterir. C R. İ Bu bağıntıda; : Akışkanın ortalama hızı (m/s), C: Chezy katsayısı, R: Hidrolik yarıçap (m), İ : Hidrolik eğim (m/m) dir. Chezy formülünde (C) katsayısı için değişik eşitlikler vardır. Bunlardan birisi Ganguillet ve Kutter tarafından geliştirilen aşağıdaki eşitliktir. 0, C İ N N 0,055 0,5 R İ Burada; C: Chezy katsayısı, N: Boru pürüzlülük katsayısı, İ : Hidrolik eğim (m/m), R: Hidrolik yarıçap (m) tır.
7 .6... Darcy-Weisbach formülü ile sürtünme kayıplarının hesaplanması L. P.. D Bu formül yatay borular için geçerlidir ve yukarıda da söylediğimiz gibi Laminer akımda sürtünme katsayısı 64 / Re ye eşittir. Görüldüğü gibi sürtünme katsayısı Reynolds sayısına (Re) dolayısıyla da (Re) sayısını oluşturan viskozite, hız, boru çapı ve akışkanın özgül kütlesine bağlıdır. Türbülans akımda sürtünme katsayısı; yalnızca (Re) sayısının değil D aynı zamanda bağıl pürüzlülüğün de bir fonksiyonudur. Bağıl pürüzlülük k boru çapının boru iç yüzey pürüz yüksekliğine (mutlak pürüzlülük) oranıdır.. Re, D k Bir borunun iki noktası arasına Bernoulli eşitliğini uyguladığımızda bilindiği gibi aşağıdaki bağıntı elde edilir. P z.g P z.g h k Eğer boru çapının değişmediği yanı (D=D) ve dolayısıyla da (=) olduğunu, borunun yatay olduğunu (z=z) kabul ettiğimizde basınç düşümü (P); P P P. hk olur. Burada bulunan basınç düşümü yukarıda verilen Laminer akımdaki basınç düşümüyle birleştirilirse; L....h k elde edilir. D Buradan sürtünme kaybı aşağıdaki gibi yazılabilir. L hk.. D.g Bu eşitliğe Darcy-Weisbach eşitliği denir ve yatay boru ile eğimli borunun her ikisi için de geçerlidir. 5
8 Moody diyagramının kullanılmasında bazı özel formüller de bulunmaktadır. Örneğin pürüzsüz borularda k 0 D ve (Re) sayısının 0 5 den küçük olduğu koşullarda (Re0 5 ) aşağıdaki bağıntı sürtünme katsayısının hesaplanmasında kullanılabilir. 0,36 / 4 Re 6 k Yine bağıl pürüzlülük 0 0 ve Reynolds sayısı D Re 0 ise katsayısı şu bağıntıyla hesaplanabilir.,35 k 5,74 ln 3,7.D 0,9 Re Şekil.8 deki Moody diyagramını incelediğimizde, yatay eksende (Re) sayısı, düşey eksende D/k ve sürtünme katsayısı () vardır. Moody diyagramından yararlanmak için şu sıra izlenebilir. a) Boru cinsine göre mutlak pürüzlük çizelgeden alınır ve bağıl pürüzlülük (D/k) bulunur. b) Boru çapı ve verdiye göre hız belirlenir, suyun sıcaklığına göre viskozite seçilir ve (Re) sayısı hesaplanır. c) Moody diyagramında (Re) sayısı ekseninden dik çıkılıp, D/k eğrisiyle çakıştırılır. Çakışma noktasından yataya çizilen paralel düşey eksende sürtünme katsayısını () verir. Sürtünme katsayısı Darcy-Weisbach formülünde yerine konur ve sürtünme kaybı hesaplanır. Sürtünme katsayısının hesaplanmasında Moody diyagramı en çok kabul gören bir yöntemdir. Ancak farklı yöntemler de bulunmaktadır. Bu yöntemler, yöntemi bulan kişiye atıfta bulunularak aşağıdaki gibi özetlenebilir. Lang a göre sürtünme katsayısı; 0,008 a.d ile hesaplanmaktadır. Burada; a: Boru cinsine bağlı bir katsayı olup kayaklı çelik boru için a= 0,036, beton boru için a= 0,040, perçinli çelik boru için a= 0,093 alınabilir. : Ortalama hız (m/s) ve D: Boru çapı (m) dır. Darcy e göre: D: boru çapı (m) olmak üzere; 0,0005 0,0 D biçiminde hesaplanmaktadır. on Prandtl a göre; 6
9 0,3 λ 0,5 (k/d) bağıntısı sürtünme katsayısının belirlenmesinde kullanılabilir. Burada; k: mutlak pürüzlülük olup her boru tipine göre değişmektedir. Örneğin döküm borular için k= 0,005 alınabilmektedir. D: Boru çapı (m) dır. Weisbach tarafından geliştirilen aşağıdaki formül, : hız (m/s) olmak üzere, sürtünme katsayısının hesabında kullanılabilir. 0, ,0444 Son olarak Chezy, sürtünme katsayısını 8 g λ C şeklinde vermiştir. Burada; C: Chezy katsayısıdır Üslü formüllerle sürtünme kayıplarının hesaplanması Üslü formüller hız formülüdür ve aşağıdaki gibi yazılabilmektedir. = C.R a.i b Burada: : Ortalama su hızı (m/s), C : Katsayı, R : Hidrolik yarıçap (m), i : Hidrolik eğim (m/m), a ve b : Boru cinsine bağlı üs katsayılarıdır. Blair, formülleri kullanırken boruları 4 sınıfa ayırmıştır. İngiliz araştırmacı J.S. Blair in 949 yılında 4 sınıfa ayırdığı borular için C, a ve b katsayıları çizelge.7 de verilmiştir. Blair formülleri aşağıdaki gibi yazılabilir (Tezer 978) I. Sınıf borularda: = 94,4.R 0,7.İ 0,57 hk= 5, L.D -,46.,754 II. Sınıf borularda: = 54,.R 0,69.İ 0,55 hk= 6, L.D -,43.,80 7
10 III. Sınıf borularda: = 33,4.R 0,68.İ 0,54 hk= 6, L.D -,59.,85 I. Sınıf borularda: = 07,3.R 0,67.İ 0,5 hk= 7, L.D -,88.,93 Üslü formüllerden Blair formüllerinde, sadece boru sınıfının seçilerek hesaplama yapılması proje mühendislerine kolaylık sağlamaktadır. Darcy formülü ve Moody diyagramı ile yapılacak hesaplamalarda ise seçilen boru cinsinde mutlak pürüzlülük değerinin saptanması oldukça zordur. Ayrıca Blair formülleri, uygulamada karşılaşılan su iletim boru hatlarındaki problemlerin hemen hemen tümünü kapsamaktadır. Sürtünme kayıplarının üslü formüllerle hesaplanmasında grafiklerden de yararlanılmaktadır. Grafiklerle yapılan hesaplamalar çabuk ve kolaydır. Şekil.9... de Blair tarafından hazırlanan nomogramlar verilmiştir. Nomogramlarda iki eksen çifti vardır. Düşey eksen çiftinin birinde apsiste hidrolik eğim (İ= hk/l), ordinatta verdi (Q, L/min) değerleri logaritmik skalaya yerleştirilmiştir. İkinci eksen çiftinde apsiste hız (= m/s) değerleri ve ordinatta çap (D= cm) değerleri verilmiştir. erdi, hız, boru çapı ve hidrolik eğim değerlerinden ikisi bilindiğinde diğer ikisi kolaylıkla bulunabilir. Nomogramların kullanılmasına bir örnek verilirse, birinci sınıf boruda verdi, Q= 000 L/min ve boru çapı D= 3 cm ise hidrolik eğim i= 0,0 ve su hızı =,5 m/s bulunur. Nomogramda tüm eksenler logaritmik olduğundan ara değerlerin bulunmasında buna dikkat edilmelidir. Düz borulardaki yük kayıpları için, el kitaplarında kısa yoldan hesaplamayı sağlayan nomogram veya çizelgeler verilmektedir. Özellikle proje mühendisleri için uygulamada kısa sürede sonuç almak için yararlı olan bu tip nomogramlara bir örnek Şekil.3 de verilmiştir. Nomogramda iki eksen çifti kullanılmıştır. Birinci eksen çiftinde apsiste (m 3 /h) olarak verdi, ordinatta 00 m boru uzunluğundaki yük kaybı (mss) olarak verilmiştir. İkinci eksen çiftinde apsiste (m/s) olarak hız, ordinatta ise (mm) olarak boru anma çapları verilmiştir. Bu dört değerden herhangi ikisi bilinirse diğer ikisi kolayca saptanabilir (Nomogram aynı zamanda fps sisteminde de kullanılabilmektedir). Nomogram 00 m düz boru (metrik sistemde) için düzenlenmiştir. erilen değerler yeni durumda gri döküm boruları kapsamaktadır. Boru çapı mm ve verdi 0, m 3 /h sınırları arasında değişmektedir. Nomogram 8
11 .6.. Şekil (yersel) kayıplarının hesaplanması Şekil kayıpları genellikle hız yüksekliği ile ilgilidir ve aşağıdaki genel eşitlikle hesaplanır. h f k.. g Sürtünme kaybını basınç düşümü biçiminde yazarsak aşağıdaki bağıntı elde edilir.. P k Eşdeğer boru boyu ve toplam kayıp Boru hatlarında şekilli boru parçalarında oluşan yük kayıplarının hesabında eşdeğer boru boyunun kullanılması işlemleri kolaylaştırır. Bu nedenle şekil kayıpları bazen Eşdeğer boru boyu cinsinden belirtilebilir. Eşdeğer boru boyu, aynı yük kaybını meydana getirecek düz boru uzunluğuyla tanımlanır. Buna göre eşdeğer boru boyu boru parçası ile aynı ölçü ve malzemede ve belirli bir verdi değeri için oluşturacağı yük kaybına eşit değerde yük kaybı yaratan düz boru uzunluğudur. Eğer boru hattındaki çeşitli boru parçalarının cinsi ve boru boyları bilinirse, bu armatürler için eşdeğer boru boyları hesaplanır ve tesisteki düz boru boylarına eklenerek yük kaybı toplam boru boyundan hesaplanır. Herhangi bir boru parçasının yük kaybı v h f k.. g yarattığı kabul edilsin. Darcy-Weisbach formülüne göre (hf) değerine eşit yük kaybı yaratacak düz boru boyu hk= hf alınarak;. L eş. k. D. g. g ve k L eş. D ile tanımlanır. Eşdeğer boru boyu; şekil katsayısı ve boru çapıyla doğru, sürtünme katsayısı ile ters orantılıdır. 9
12 0
2. SUYUN BORULARDAKİ AKIŞI
 . SUYUN BORULARDAKİ AKIŞI Akışkanlar mekaniği, sıvı ve gaz akışkanların durgun ve hareket halindeki durumlarını inceler. Akışkanlar mekaniği sıvılara ve gazlara etki eden kuvvetleri ve bu kuvvetlerin meydana
. SUYUN BORULARDAKİ AKIŞI Akışkanlar mekaniği, sıvı ve gaz akışkanların durgun ve hareket halindeki durumlarını inceler. Akışkanlar mekaniği sıvılara ve gazlara etki eden kuvvetleri ve bu kuvvetlerin meydana
SU ÜRÜNLERİNDE MEKANİZASYON
 SU ÜRÜNLERİNDE MEKANİZASYON 8 Yrd.Doç.Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları & Teknolojileri Mühendisliği Bölümü Su Ürünleri Teknolojileri Su temini Boru parçaları
SU ÜRÜNLERİNDE MEKANİZASYON 8 Yrd.Doç.Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları & Teknolojileri Mühendisliği Bölümü Su Ürünleri Teknolojileri Su temini Boru parçaları
5. BORU HATLARI VE BORU BOYUTLARI
 h 1 h f h 2 1 5. BORU HATLARI VE BORU BOYUTLARI (Ref. e_makaleleri) Sıvılar Bernoulli teoremine göre, bir akışkanın bir borudan akabilmesi için, aşağıdaki şekilde şematik olarak gösterildiği gibi, 1 noktasındaki
h 1 h f h 2 1 5. BORU HATLARI VE BORU BOYUTLARI (Ref. e_makaleleri) Sıvılar Bernoulli teoremine göre, bir akışkanın bir borudan akabilmesi için, aşağıdaki şekilde şematik olarak gösterildiği gibi, 1 noktasındaki
Bölüm 8: Borularda sürtünmeli Akış
 Bölüm 8: Borularda sürtünmeli Akış Laminer ve Türbülanslı Akış Laminer Akış: Çalkantısız akışkan tabakaları ile karakterize edilen çok düzenli akışkan hareketi laminer akış olarak adlandırılır. Türbülanslı
Bölüm 8: Borularda sürtünmeli Akış Laminer ve Türbülanslı Akış Laminer Akış: Çalkantısız akışkan tabakaları ile karakterize edilen çok düzenli akışkan hareketi laminer akış olarak adlandırılır. Türbülanslı
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ
 BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METOTLAR-II BORU ve DİRSEKLERDE ENERJİ KAYBI DENEYİ 1.Deneyin Adı: Boru ve dirseklerde
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METOTLAR-II BORU ve DİRSEKLERDE ENERJİ KAYBI DENEYİ 1.Deneyin Adı: Boru ve dirseklerde
ÇÖZÜM 1) konumu mafsallı olup, buraya göre alınacak moment ile küçük pistona etkileyen kuvvet hesaplanır.
 SORU 1) Şekildeki (silindir+piston) düzeni vasıtası ile kolunda luk bir kuvvet elde edilmektedir. İki piston arasındaki hacimde yoğunluğu olan bir akışkan varıdr. Verilenlere göre büyük pistonun hareketi
SORU 1) Şekildeki (silindir+piston) düzeni vasıtası ile kolunda luk bir kuvvet elde edilmektedir. İki piston arasındaki hacimde yoğunluğu olan bir akışkan varıdr. Verilenlere göre büyük pistonun hareketi
HİDROLİK. Yrd. Doç. Dr. Fatih TOSUNOĞLU
 HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
5. BORULARDAKİ VİSKOZ (SÜRTÜNMELİ) AKIM
 5. BORULARDAKİ VİSKOZ (SÜRTÜNMELİ) AKIM 5.6. Moody Diyagramı Akışkanlar boru içerisinde iletilirken gerek viskoziteden ve gerekse sürtünmeden kaynaklanan bir basınç düşümü ya da yük kaybı meydana gelir.
5. BORULARDAKİ VİSKOZ (SÜRTÜNMELİ) AKIM 5.6. Moody Diyagramı Akışkanlar boru içerisinde iletilirken gerek viskoziteden ve gerekse sürtünmeden kaynaklanan bir basınç düşümü ya da yük kaybı meydana gelir.
Akışkanların Dinamiği
 Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
ZTM 431 HİDROLİK VE PNÖMATİK SİSTEMLER Prof. Dr. Metin Güner
 ZTM 431 HİDROLİK VE PNÖMATİK SİSTEMLER Prof. Dr. Metin Güner HİDROLİK SİSTEMLER 1.GIRİŞ İletim akışkanı olarak sıvı kullanan sistemlere hidrolik sistemler denir. Hidrolik kelimesi eski Yunanca da su anlamına
ZTM 431 HİDROLİK VE PNÖMATİK SİSTEMLER Prof. Dr. Metin Güner HİDROLİK SİSTEMLER 1.GIRİŞ İletim akışkanı olarak sıvı kullanan sistemlere hidrolik sistemler denir. Hidrolik kelimesi eski Yunanca da su anlamına
ÇEV-220 Hidrolik. Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT
 ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Türbülanslı Akış Mühendislik uygulamalarında akışların çoğu türbülanslıdır ve bu yüzden türbülansın
ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Türbülanslı Akış Mühendislik uygulamalarında akışların çoğu türbülanslıdır ve bu yüzden türbülansın
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
Akışkanların Dinamiği
 Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: SORULAR-CEVAPLAR
 MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: 1- (24 Puan) Şekildeki 5.08 cm çaplı 38.1 m uzunluğunda, 15.24 cm çaplı 22.86 m uzunluğunda ve 7.62 cm çaplı
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: 1- (24 Puan) Şekildeki 5.08 cm çaplı 38.1 m uzunluğunda, 15.24 cm çaplı 22.86 m uzunluğunda ve 7.62 cm çaplı
5. Boyut Analizi. 3) Bir deneysel tasarımda değişken sayısının azaltılması 4) Model tasarım prensiplerini belirlemek
 Boyut analizi, göz önüne alınan bir fiziksel olayı etkileyen deneysel değişkenlerin sayısını ve karmaşıklığını azaltmak için kullanılan bir yöntemdir. Akışkanlar mekaniğinin gelişimi ağırlıklı bir şekilde
Boyut analizi, göz önüne alınan bir fiziksel olayı etkileyen deneysel değişkenlerin sayısını ve karmaşıklığını azaltmak için kullanılan bir yöntemdir. Akışkanlar mekaniğinin gelişimi ağırlıklı bir şekilde
5. Boyut Analizi. 3) Bir deneysel tasarımda değişken sayısının azaltılması 4) Model tasarım prensiplerini belirlemek
 Boyut analizi, göz önüne alınan bir fiziksel olayı etkileyen deneysel değişkenlerin sayısını ve karmaşıklığını azaltmak için kullanılan bir yöntemdir. kışkanlar mekaniğinin gelişimi ağırlıklı bir şekilde
Boyut analizi, göz önüne alınan bir fiziksel olayı etkileyen deneysel değişkenlerin sayısını ve karmaşıklığını azaltmak için kullanılan bir yöntemdir. kışkanlar mekaniğinin gelişimi ağırlıklı bir şekilde
Pompa tarafından iletilen akışkanın birim ağırlığı başına verilen enerji (kg.m /kg), birim olarak uzunluk birimi (m) ile belirtilebilir.
 2.3.1. Pompalar Öteki sanayi kesimlerinde olduğu gibi, gıda sanayinde de çeşitli işlem aşamalarında, akışkanların iletiminde pompalar kullanılır. Örneğin; işlemlerde gerekli su, buhar, elde edilen sıvı
2.3.1. Pompalar Öteki sanayi kesimlerinde olduğu gibi, gıda sanayinde de çeşitli işlem aşamalarında, akışkanların iletiminde pompalar kullanılır. Örneğin; işlemlerde gerekli su, buhar, elde edilen sıvı
4.Sıkıştırılamayan Akışkanlarda Sürtünme Kayıpları
 4.Sıkıştırılamayan Akışkanlarda Sürtünme Kayıpları Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Sıkıştırılamayan bir akışkan olan suyun silindirik düz bir boru içerisinde akarken
4.Sıkıştırılamayan Akışkanlarda Sürtünme Kayıpları Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Sıkıştırılamayan bir akışkan olan suyun silindirik düz bir boru içerisinde akarken
elde edilir. Akışkan dinamiğinde değişik akım tipleri vardır. Bunlar aşağıdaki gibi tanımlanabilir (Ayyıldız 1983).
 3. AKIŞKAN DİNAMİĞİ 3.. Newton un İkinci Kanunu Bir akışkan taneciği bir noktadan başka bir noktaya giderken pozitif ya da negatif ivmeyle hareket etmekte ve bu süreçte, üzerine F m. a kuvveti etkimektedir.
3. AKIŞKAN DİNAMİĞİ 3.. Newton un İkinci Kanunu Bir akışkan taneciği bir noktadan başka bir noktaya giderken pozitif ya da negatif ivmeyle hareket etmekte ve bu süreçte, üzerine F m. a kuvveti etkimektedir.
Pürüzlü Cidar
 10.3.3. Pürüzlü Cidar Şimdiye kadar boru cidarını pürüzsüz kabul ettik ve bu tip cidarlara cilalı cidar denir. Yükseklikleri k s olan elemanları sık bir şekilde boru cidarına yapıştırılırsa, boru cidarını
10.3.3. Pürüzlü Cidar Şimdiye kadar boru cidarını pürüzsüz kabul ettik ve bu tip cidarlara cilalı cidar denir. Yükseklikleri k s olan elemanları sık bir şekilde boru cidarına yapıştırılırsa, boru cidarını
Selçuk Üniversitesi. Mühendislik-Mimarlık Fakültesi. Kimya Mühendisliği Bölümü. Kimya Mühendisliği Laboratuvarı. Venturimetre Deney Föyü
 Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Kimya Mühendisliği Bölümü Kimya Mühendisliği Laboratuvarı Venturimetre Deney Föyü Hazırlayan Arş.Gör. Orhan BAYTAR 1.GİRİŞ Genellikle herhangi bir akış
Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Kimya Mühendisliği Bölümü Kimya Mühendisliği Laboratuvarı Venturimetre Deney Föyü Hazırlayan Arş.Gör. Orhan BAYTAR 1.GİRİŞ Genellikle herhangi bir akış
NÖ-A NÖ-B. Şube. Alınan Puan. Adı- Soyadı: Fakülte No: 1. Aşağıda verilen fiziksel büyüklüklerin eşit olduğunu gösteriniz. 1/6
 Şube NÖ-A NÖ-B Adı- Soyadı: Fakülte No: Kimya Mühendisliği Bölümü, 2015/2016 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, Bütünleme Sınavı Soru ve Çözümleri 20.01.2016 Soru (puan) 1 (20) 2 (20) 3 (20)
Şube NÖ-A NÖ-B Adı- Soyadı: Fakülte No: Kimya Mühendisliği Bölümü, 2015/2016 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, Bütünleme Sınavı Soru ve Çözümleri 20.01.2016 Soru (puan) 1 (20) 2 (20) 3 (20)
Borularda Akış. Hesaplamalarda ortalama hız kullanılır.
 En yaygın karşılaşılan akış sistemi Su, petrol, doğal gaz, yağ, kan. Boru akışkan ile tam dolu (iç akış) Dairesel boru ve dikdörtgen kanallar Borularda Akış Dairesel borular içerisi ve dışarısı arasındaki
En yaygın karşılaşılan akış sistemi Su, petrol, doğal gaz, yağ, kan. Boru akışkan ile tam dolu (iç akış) Dairesel boru ve dikdörtgen kanallar Borularda Akış Dairesel borular içerisi ve dışarısı arasındaki
BORULARDA BASINÇ KAYBI VE SÜRTÜNME DENEYİ
 ONDOKUZ MAYIS ÜNİERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MM30 MAKİNA MÜHENDİSLİĞİ LABORATUARI DERSİ BORULARDA BASINÇ KAYBI E SÜRTÜNME DENEYİ Hazırlayan Yrd.Doç.Dr. Mustafa ÖZBEY SAMSUN
ONDOKUZ MAYIS ÜNİERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MM30 MAKİNA MÜHENDİSLİĞİ LABORATUARI DERSİ BORULARDA BASINÇ KAYBI E SÜRTÜNME DENEYİ Hazırlayan Yrd.Doç.Dr. Mustafa ÖZBEY SAMSUN
T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUVARI
 T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUVARI BORULARDA VE HİDROLİK ELEMANLARDA SÜRTÜNME KAYIPLARI DENEY FÖYÜ 1. DENEYİN AMACI Borularda
T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUVARI BORULARDA VE HİDROLİK ELEMANLARDA SÜRTÜNME KAYIPLARI DENEY FÖYÜ 1. DENEYİN AMACI Borularda
Su Debisi ve Boru Çapı Hesabı
 Su Debisi ve Boru Çapı Hesabı Su Debisi Hesabı Sıcak sulu ısıtma sistemleri, günümüzde bireysel ve bölgesel konut ısıtmasında, fabrika ve atölye, sera ısıtmasında, jeotermal enerjinin kullanıldığı ısıtma
Su Debisi ve Boru Çapı Hesabı Su Debisi Hesabı Sıcak sulu ısıtma sistemleri, günümüzde bireysel ve bölgesel konut ısıtmasında, fabrika ve atölye, sera ısıtmasında, jeotermal enerjinin kullanıldığı ısıtma
1. Aşağıda verilen fiziksel büyüklüklerin dönüşümünde? işareti yerine gelecek sayıyı bulunuz.
 Şube Adı- Soyadı: Fakülte No: NÖ-A NÖ-B Kimya Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, 2. Ara Sınavı Soruları 10.12.2016 Soru (puan) 1 (20) 2 (20) 3 (20) 4 (20) 5 (20)
Şube Adı- Soyadı: Fakülte No: NÖ-A NÖ-B Kimya Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, 2. Ara Sınavı Soruları 10.12.2016 Soru (puan) 1 (20) 2 (20) 3 (20) 4 (20) 5 (20)
ATIK SULARIN TERFİSİ VE TERFİ MERKEZİ
 ATIK SULARIN TERFİSİ VE TERFİ MERKEZİ Pompa; suya basınç sağlayan veya suyu aşağıdan yukarıya terfi ettiren (yükselten) makinedir. Terfi merkezi; atık suların, çamurun ve arıtılmış suların bir bölgeden
ATIK SULARIN TERFİSİ VE TERFİ MERKEZİ Pompa; suya basınç sağlayan veya suyu aşağıdan yukarıya terfi ettiren (yükselten) makinedir. Terfi merkezi; atık suların, çamurun ve arıtılmış suların bir bölgeden
ÇEV314 Yağmursuyu ve Kanalizasyon. KanalizasyonŞebekelerinde Hidrolik Hesaplar
 9.3.08 ÇE34 Yağmursuyu ve Kanalizasyon KanalizasyonŞebekelerinde Hidrolik Hesaplar r. Öğr. Üy. Özgür ZEYAN http://cevre.beun.edu.tr/zeydan/ Kanalizasyon İçinde Akışı Etkileyen Faktörler Eğim Akışın kesit
9.3.08 ÇE34 Yağmursuyu ve Kanalizasyon KanalizasyonŞebekelerinde Hidrolik Hesaplar r. Öğr. Üy. Özgür ZEYAN http://cevre.beun.edu.tr/zeydan/ Kanalizasyon İçinde Akışı Etkileyen Faktörler Eğim Akışın kesit
VENTURİMETRE DENEYİ 1. GİRİŞ
 VENTURİMETRE DENEYİ 1. GİRİŞ Genellikle herhangi bir akış esnasında akışkanın tabakaları farklı hızlarda hareket ederler ve akışkanın viskozitesi, uygulanan kuvvete karşı direnç gösteren tabakalar arasındaki
VENTURİMETRE DENEYİ 1. GİRİŞ Genellikle herhangi bir akış esnasında akışkanın tabakaları farklı hızlarda hareket ederler ve akışkanın viskozitesi, uygulanan kuvvete karşı direnç gösteren tabakalar arasındaki
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
TAŞINIMIN FİZİKSEL MEKANİZMASI
 BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
BÖLÜM 6 TAŞINIMIN FİZİKSEL MEKANİZMASI 2 or Taşınımla ısı transfer hızı sıcaklık farkıyla orantılı olduğu gözlenmiştir ve bu Newton un soğuma yasasıyla ifade edilir. Taşınımla ısı transferi dinamik viskosite
ÇEV-220 Hidrolik. Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT
 ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Akış Boru ve kanallardaki sıvı veya gaz akışından, yaygın olarak ısıtma soğutma uygulamaları ile akışkan
ÇEV-220 Hidrolik Çukurova Üniversitesi Çevre Mühendisliği Bölümü Yrd. Doç. Dr. Demet KALAT Borularda Akış Boru ve kanallardaki sıvı veya gaz akışından, yaygın olarak ısıtma soğutma uygulamaları ile akışkan
T. C. GÜMÜŞHANE ÜNİVERSİTESİ MÜHENDİSLİK VE DOĞA BİLİMLERİ FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE MÜHENDİSLİĞİ DENEYLER 2
 T. C. GÜMÜŞHANE ÜNİVERSİTESİ MÜHENDİSLİK VE DOĞA BİLİMLERİ FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE MÜHENDİSLİĞİ DENEYLER 2 DOĞAL VE ZORLANMIŞ TAŞINIMLA ISI TRANSFERİ DENEYİ ÖĞRENCİ NO: ADI SOYADI:
T. C. GÜMÜŞHANE ÜNİVERSİTESİ MÜHENDİSLİK VE DOĞA BİLİMLERİ FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE MÜHENDİSLİĞİ DENEYLER 2 DOĞAL VE ZORLANMIŞ TAŞINIMLA ISI TRANSFERİ DENEYİ ÖĞRENCİ NO: ADI SOYADI:
BÜLENT ECEVİT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK490 Makine Laboratuarı Dersi Akışkanlar Mekaniği Deneyi
 BÜLENT ECEVİT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK490 Makine Laboratuarı Dersi Akışkanlar Mekaniği Deneyi 1. Genel Bilgi Bazı akışlar oldukça çalkantılıyken bazıları düzgün ve düzenlidir. Düzgün
BÜLENT ECEVİT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK490 Makine Laboratuarı Dersi Akışkanlar Mekaniği Deneyi 1. Genel Bilgi Bazı akışlar oldukça çalkantılıyken bazıları düzgün ve düzenlidir. Düzgün
KBM0308 Kimya Mühendisliği Laboratuvarı I BERNOLLİ DENEYİ. Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1
 BERNOLLİ DENEYİ Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Yapılacak olan Bernoulli deneyinin temel amacı, akışkanlar mekaniğinin en önemli denklemlerinden olan, Bernoulli (enerjinin
BERNOLLİ DENEYİ Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Yapılacak olan Bernoulli deneyinin temel amacı, akışkanlar mekaniğinin en önemli denklemlerinden olan, Bernoulli (enerjinin
Taşınım Olayları II MEMM2009 Akışkanlar Mekaniği ve Isı Transferi bahar yy. borularda sürtünmeli akış. Prof. Dr.
 Taşınım Olayları II MEMM009 Akışkanlar Mekaniği ve Isı Transferi 07-08 bahar yy. borularda sürtünmeli akış Prof. Dr. Gökhan Orhan istanbul üniversitesi / metalurji ve malzeme mühendisliği bölümü Laminer
Taşınım Olayları II MEMM009 Akışkanlar Mekaniği ve Isı Transferi 07-08 bahar yy. borularda sürtünmeli akış Prof. Dr. Gökhan Orhan istanbul üniversitesi / metalurji ve malzeme mühendisliği bölümü Laminer
AKM 205 BÖLÜM 8 - UYGULAMA SORU VE ÇÖZÜMLERİ
 AKM 205 BÖLÜM 8 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Yoğunluğu 850 kg/m 3 ve kinematik viskozitesi 0.00062 m 2 /s olan yağ, çapı 5 mm ve uzunluğu 40
AKM 205 BÖLÜM 8 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Yoğunluğu 850 kg/m 3 ve kinematik viskozitesi 0.00062 m 2 /s olan yağ, çapı 5 mm ve uzunluğu 40
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB 305 KİMYA MÜHENDİSLİĞİ LABORATUVARI - 1
 ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB 305 KİMYA MÜHENDİSLİĞİ LABORATUVARI - 1 AKIŞKANLAR MEKANİĞİ DENEY FÖYÜ (BORULARDA SÜRTÜNME KAYIPLARI) Hazırlayan: Araş. Gör.
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB 305 KİMYA MÜHENDİSLİĞİ LABORATUVARI - 1 AKIŞKANLAR MEKANİĞİ DENEY FÖYÜ (BORULARDA SÜRTÜNME KAYIPLARI) Hazırlayan: Araş. Gör.
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ
 EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ Giriş Isı değiştiricileri (eşanjör) değişik tiplerde olup farklı sıcaklıktaki iki akışkan arasında ısı alışverişini temin ederler. Isı değiştiricileri başlıca yüzeyli
EŞANJÖR (ISI DEĞİŞTİRİCİSİ) DENEYİ FÖYÜ Giriş Isı değiştiricileri (eşanjör) değişik tiplerde olup farklı sıcaklıktaki iki akışkan arasında ısı alışverişini temin ederler. Isı değiştiricileri başlıca yüzeyli
HAVALANDIRMA DAĞITICI VE TOPLAYICI KANALLARIN HESAPLANMASI
 1.1.1. Temel Bilgiler a) Statik Basınç: Statik basınç, sıkıştırılmış havanın 1 m³ ünün serbest kalması halinde meydana çıkacak potansiyel enerjiyi gösterir. Ayrıca vantilatörlerde güç tecrübeleri kaidelerine
1.1.1. Temel Bilgiler a) Statik Basınç: Statik basınç, sıkıştırılmış havanın 1 m³ ünün serbest kalması halinde meydana çıkacak potansiyel enerjiyi gösterir. Ayrıca vantilatörlerde güç tecrübeleri kaidelerine
SORULAR - ÇÖZÜMLER. NOT: Toplam 5 (beş) soru çözünüz. Sınav süresi 90 dakikadır. 1. Aşağıdaki çizelgede boş bırakılan yerleri doldurunuz. Çözüm.1.
 SORULAR - ÇÖZÜMLER 1. Aşağıdaki çizelgede boş bırakılan yerleri doldurunuz. Çözüm.1. Gıda Mühendisliği Bölümü, 2014/2015 Öğretim Yılı, Bahar Yarıyılı 0216-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru
SORULAR - ÇÖZÜMLER 1. Aşağıdaki çizelgede boş bırakılan yerleri doldurunuz. Çözüm.1. Gıda Mühendisliği Bölümü, 2014/2015 Öğretim Yılı, Bahar Yarıyılı 0216-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ
 BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METODLAR -I BERNOULLİ DENEYİ FÖYÜ 2014 1. GENEL BİLGİLER Bernoulli denklemi basınç, hız
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METODLAR -I BERNOULLİ DENEYİ FÖYÜ 2014 1. GENEL BİLGİLER Bernoulli denklemi basınç, hız
ÖĞRENME ALANI : FİZİKSEL OLAYLAR ÜNİTE 2 : KUVVET VE HAREKET
 ÖĞRENME ALANI : FİZİKSEL OLAYLAR ÜNİTE 2 : KUVVET VE HAREKET A BASINÇ VE BASINÇ BİRİMLERİ (5 SAAT) Madde ve Özellikleri 2 Kütle 3 Eylemsizlik 4 Tanecikli Yapı 5 Hacim 6 Öz Kütle (Yoğunluk) 7 Ağırlık 8
ÖĞRENME ALANI : FİZİKSEL OLAYLAR ÜNİTE 2 : KUVVET VE HAREKET A BASINÇ VE BASINÇ BİRİMLERİ (5 SAAT) Madde ve Özellikleri 2 Kütle 3 Eylemsizlik 4 Tanecikli Yapı 5 Hacim 6 Öz Kütle (Yoğunluk) 7 Ağırlık 8
HİDROLİK MAKİNALAR YENİLENEBİLİR ENERJİ KAYNAKLARI
 HİDROLİK MAKİNALAR YENİLENEBİLİR ENERJİ KAYNAKLARI HİDROLİK TÜRBİN ANALİZ VE DİZAYN ESASLARI Hidrolik türbinler, su kaynaklarının yerçekimi potansiyelinden, akan suyun kinetik enerjisinden ya da her ikisinin
HİDROLİK MAKİNALAR YENİLENEBİLİR ENERJİ KAYNAKLARI HİDROLİK TÜRBİN ANALİZ VE DİZAYN ESASLARI Hidrolik türbinler, su kaynaklarının yerçekimi potansiyelinden, akan suyun kinetik enerjisinden ya da her ikisinin
İnşaat Mühendisliği Bölümü Uygulama VIII ÇÖZÜMLER
 Soru 1 : Şekildeki hazne boru sisteminde sıkışmaz ve ideal akışkanın (su) permanan bir akımı mevcuttur. Su yatay eksenli ABC borusu ile atmosfere boşalmaktadır. Mutlak atmosfer basıncını 9.81 N/cm 2 ve
Soru 1 : Şekildeki hazne boru sisteminde sıkışmaz ve ideal akışkanın (su) permanan bir akımı mevcuttur. Su yatay eksenli ABC borusu ile atmosfere boşalmaktadır. Mutlak atmosfer basıncını 9.81 N/cm 2 ve
SORU #1. (20 p) (İlişkili Olduğu / Ders Öğrenme Çıktısı: 1,5,6 Program Çıktısı: 1)
 Süre 90 dakikadır. T.C. SAKARYA ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ DERSİ 2015-2016 GÜZ FİNAL SINAVI (Prof.Dr. Tahsin ENGİN - Doç.Dr. Nedim Sözbir - Yrd.Doç.Dr. Yüksel KORKMAZ Yrd.Doç.Dr.
Süre 90 dakikadır. T.C. SAKARYA ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ DERSİ 2015-2016 GÜZ FİNAL SINAVI (Prof.Dr. Tahsin ENGİN - Doç.Dr. Nedim Sözbir - Yrd.Doç.Dr. Yüksel KORKMAZ Yrd.Doç.Dr.
3. AKIŞKANLARDA FAZ DEĞİŞİKLİĞİ OLMADAN ISI TRANSFERİ
 1 3. AKIŞKANLARDA FAZ DEĞİŞİKLİĞİ OLMADAN ISI TRANSFERİ (Ref. e_makaleleri) Isı değiştiricilerin büyük bir kısmında ısı transferi, akışkanlarda faz değişikliği olmadan gerçekleşir. Örneğin, sıcak bir petrol
1 3. AKIŞKANLARDA FAZ DEĞİŞİKLİĞİ OLMADAN ISI TRANSFERİ (Ref. e_makaleleri) Isı değiştiricilerin büyük bir kısmında ısı transferi, akışkanlarda faz değişikliği olmadan gerçekleşir. Örneğin, sıcak bir petrol
Alınan Puan NOT: Yalnızca 5 soru çözünüz, çözmediğiniz soruyu X ile işaretleyiniz. Sınav süresi 90 dakikadır. SORULAR ve ÇÖZÜMLER
 Gıda Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, Bahar yarıyılı 0216-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru Çözümleri 30.05.2017 Adı- Soyadı: Soru (puan) 1 (20) 2 (20) 3 (20) 4 (20) 5 (20)
Gıda Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, Bahar yarıyılı 0216-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru Çözümleri 30.05.2017 Adı- Soyadı: Soru (puan) 1 (20) 2 (20) 3 (20) 4 (20) 5 (20)
Ders Notları 3 Geçirimlilik Permeabilite
 Ders Notları 3 Geçirimlilik Permeabilite Zemindeki mühendislik problemleri, zeminin kendisinden değil, boşluklarında bulunan boşluk suyundan kaynaklanır. Su olmayan bir gezegende yaşıyor olsaydık, zemin
Ders Notları 3 Geçirimlilik Permeabilite Zemindeki mühendislik problemleri, zeminin kendisinden değil, boşluklarında bulunan boşluk suyundan kaynaklanır. Su olmayan bir gezegende yaşıyor olsaydık, zemin
DEN 322. Pompa Sistemleri Hesapları
 DEN 3 Pompa Sistemleri Hesapları Sistem karakteristiği B h S P P B Gözönüne alınan pompalama sisteminde, ve B noktalarına Genişletilmiş Bernoulli denklemi uygulanırsa: L f B B B h h z g v g P h z g v g
DEN 3 Pompa Sistemleri Hesapları Sistem karakteristiği B h S P P B Gözönüne alınan pompalama sisteminde, ve B noktalarına Genişletilmiş Bernoulli denklemi uygulanırsa: L f B B B h h z g v g P h z g v g
Makina Mühendisliği Bölümü Makine Laboratuarı
 Makina Mühendisliği Bölümü Makine Laboratuarı Reynolds Sayısı ve Akış Türleri Deneyi 1. Genel Bilgi Bazı akışlar oldukça çalkantılıyken bazıları düzgün ve düzenlidir. Düzgün akım çizgileriyle belirtilen
Makina Mühendisliği Bölümü Makine Laboratuarı Reynolds Sayısı ve Akış Türleri Deneyi 1. Genel Bilgi Bazı akışlar oldukça çalkantılıyken bazıları düzgün ve düzenlidir. Düzgün akım çizgileriyle belirtilen
POMPALAR 1. BORULARDA AKIŞ
 POMPALAR 1. BORULARDA AIŞ Borularda akış esnasında basınç düşmesi ve yük kaybı ile doğrudan ilişkili olan sürtünmeye özel önem göstermek gerekir. Çünkü bu basınç düşmesi pompalama gücü ihtiyacını belirlemek
POMPALAR 1. BORULARDA AIŞ Borularda akış esnasında basınç düşmesi ve yük kaybı ile doğrudan ilişkili olan sürtünmeye özel önem göstermek gerekir. Çünkü bu basınç düşmesi pompalama gücü ihtiyacını belirlemek
AKIŞ ÖLÇÜMLERİ. Kütlenin korunumu prensibine göre içerisinde üretim olmayan bir sistem için;
 ÖLÇME TEKNİĞİ DERS NOTLARI 2 AKIŞ ÖLÇÜMLERİ Akışkanın hareketi sırasındaki hızı ve debisi, bilim ve sanayinin pek çok yerinde ihtiyaç duyulan bilgilerdir. Bu verilerin ölçülmesi için pek çok cihaz geliştirilmiştir.
ÖLÇME TEKNİĞİ DERS NOTLARI 2 AKIŞ ÖLÇÜMLERİ Akışkanın hareketi sırasındaki hızı ve debisi, bilim ve sanayinin pek çok yerinde ihtiyaç duyulan bilgilerdir. Bu verilerin ölçülmesi için pek çok cihaz geliştirilmiştir.
Suyun bir yerden bir başka yere iletilmesi su mühendisliğinin ana ilgi konusunu oluşturur. İki temel iletim biçimi vardır:
 CE 307 Hidrolik 1. GİRİŞ Kapsam Suyun bir yerden bir başka yere iletilmesi su mühendisliğinin ana ilgi konusunu oluşturur. İki temel iletim biçimi vardır: 1. İçindeki akımın basınçlı olduğu kapalı sistemler.
CE 307 Hidrolik 1. GİRİŞ Kapsam Suyun bir yerden bir başka yere iletilmesi su mühendisliğinin ana ilgi konusunu oluşturur. İki temel iletim biçimi vardır: 1. İçindeki akımın basınçlı olduğu kapalı sistemler.
Fiziksel bir olayı incelemek için çeşitli yöntemler kullanılır. Bunlar; 1. Ampirik Bağıntılar 2. Boyut Analizi, Benzerlik Teorisi 3.
 Fiziksel bir olayı incelemek için çeşitli yöntemler kullanılır. Bunlar; 1. Ampirik Bağıntılar 2. Boyut Analizi, Benzerlik Teorisi 3. Benzetim Yöntemi (Analoji) 4. Analitik Yöntem 1. Ampirik Bağıntılar:
Fiziksel bir olayı incelemek için çeşitli yöntemler kullanılır. Bunlar; 1. Ampirik Bağıntılar 2. Boyut Analizi, Benzerlik Teorisi 3. Benzetim Yöntemi (Analoji) 4. Analitik Yöntem 1. Ampirik Bağıntılar:
2: MALZEME ÖZELLİKLERİ
 İÇİNDEKİLER Önsöz III Bölüm 1: TEMEL KAVRAMLAR 11 1.1.Mekanik, Tanımlar 12 1.1.1.Madde ve Özellikleri 12 1.2.Sayılar, Çevirmeler 13 1.2.1.Üslü Sayılarla İşlemler 13 1.2.2.Köklü Sayılarla İşlemler 16 1.2.3.İkinci
İÇİNDEKİLER Önsöz III Bölüm 1: TEMEL KAVRAMLAR 11 1.1.Mekanik, Tanımlar 12 1.1.1.Madde ve Özellikleri 12 1.2.Sayılar, Çevirmeler 13 1.2.1.Üslü Sayılarla İşlemler 13 1.2.2.Köklü Sayılarla İşlemler 16 1.2.3.İkinci
İnstagram:kimyaci_glcn_hoca GAZLAR-1.
 GAZLAR-1 Gazların Genel Özellikleri Maddenin en düzensiz hâlidir. Maddedeki molekül ve atomlar birbirinden uzaktır ve çok hızlı hareket eder. Tanecikleri arasında çekim kuvvetleri, katı ve sıvılarınkine
GAZLAR-1 Gazların Genel Özellikleri Maddenin en düzensiz hâlidir. Maddedeki molekül ve atomlar birbirinden uzaktır ve çok hızlı hareket eder. Tanecikleri arasında çekim kuvvetleri, katı ve sıvılarınkine
Soru No Puan Program Çıktısı 3, ,8 3,10 1,10
 Öğrenci Numarası Adı ve Soyadı İmzası: CEVAP ANAHTARI Açıklama: Sınavda ders notları ve dersle ilgili tablolar serbesttir. SORU. Tersinir ve tersinmez işlemi tanımlayınız. Gerçek işlemler nasıl işlemdir?
Öğrenci Numarası Adı ve Soyadı İmzası: CEVAP ANAHTARI Açıklama: Sınavda ders notları ve dersle ilgili tablolar serbesttir. SORU. Tersinir ve tersinmez işlemi tanımlayınız. Gerçek işlemler nasıl işlemdir?
ISI TEKNİĞİ PROF.DR.AHMET ÇOLAK PROF. DR. MUSA AYIK
 ISI TEKNİĞİ PROF.DR.AHMET ÇOLAK PROF. DR. MUSA AYIK 8. ISI TEKNİĞİ 8.1 Isı Geçişi Gıda teknolojisinin kapsamındaki bir çok işlemde, sistemler arasındaki, sistemle çevresi yada akışkanlar arasındaki ısı
ISI TEKNİĞİ PROF.DR.AHMET ÇOLAK PROF. DR. MUSA AYIK 8. ISI TEKNİĞİ 8.1 Isı Geçişi Gıda teknolojisinin kapsamındaki bir çok işlemde, sistemler arasındaki, sistemle çevresi yada akışkanlar arasındaki ısı
Akışkan Kinematiği 1
 Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
NÖ-A NÖ-B. Adı- Soyadı: Fakülte No:
 Şube Adı- Soyadı: Fakülte No: NÖ-A NÖ-B Kimya Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru ve Çözümleri 05.01.2017 Soru (puan) 1 (20) 2 (20) 3 (20)
Şube Adı- Soyadı: Fakülte No: NÖ-A NÖ-B Kimya Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru ve Çözümleri 05.01.2017 Soru (puan) 1 (20) 2 (20) 3 (20)
E = U + KE + KP = (kj) U = iç enerji, KE = kinetik enerji, KP = potansiyel enerji, m = kütle, V = hız, g = yerçekimi ivmesi, z = yükseklik
 Enerji (Energy) Enerji, iş yapabilme kabiliyetidir. Bir sistemin enerjisi, o sistemin yapabileceği azami iştir. İş, bir cisme, bir kuvvetin tesiri ile yol aldırma, yerini değiştirme şeklinde tarif edilir.
Enerji (Energy) Enerji, iş yapabilme kabiliyetidir. Bir sistemin enerjisi, o sistemin yapabileceği azami iştir. İş, bir cisme, bir kuvvetin tesiri ile yol aldırma, yerini değiştirme şeklinde tarif edilir.
İ çindekiler. xvii GİRİŞ 1 TEMEL AKIŞKANLAR DİNAMİĞİ BERNOULLİ DENKLEMİ 68 AKIŞKANLAR STATİĞİ 32. xvii
 Last A Head xvii İ çindekiler 1 GİRİŞ 1 1.1 Akışkanların Bazı Karakteristikleri 3 1.2 Boyutlar, Boyutsal Homojenlik ve Birimler 3 1.2.1 Birim Sistemleri 6 1.3 Akışkan Davranışı Analizi 9 1.4 Akışkan Kütle
Last A Head xvii İ çindekiler 1 GİRİŞ 1 1.1 Akışkanların Bazı Karakteristikleri 3 1.2 Boyutlar, Boyutsal Homojenlik ve Birimler 3 1.2.1 Birim Sistemleri 6 1.3 Akışkan Davranışı Analizi 9 1.4 Akışkan Kütle
DEÜ Makina Mühendisliği Bölümü MAK 4097
 ÇİFT BORULU BİR ISI EĞİŞTİRİCİSİNE ISI YÜKLERİNİN VE TOPLAM ISI TRANSFER KATSAYISININ BELİRLENMESİ üzenleyen: Prof. r. Serhan KÜÇÜKA r. Mehmet Akif EZAN eney Sorumlu: Prof. r. Serhan KÜÇÜKA Arş. Gör Ayşe
ÇİFT BORULU BİR ISI EĞİŞTİRİCİSİNE ISI YÜKLERİNİN VE TOPLAM ISI TRANSFER KATSAYISININ BELİRLENMESİ üzenleyen: Prof. r. Serhan KÜÇÜKA r. Mehmet Akif EZAN eney Sorumlu: Prof. r. Serhan KÜÇÜKA Arş. Gör Ayşe
Proses Tekniği 3.HAFTA YRD.DOÇ.DR. NEZAKET PARLAK
 Proses Tekniği 3.HAFTA 3.HAFTA YRD.DOÇ.DR. NEZAKET PARLAK Sürekli Akışlı Açık Sistemlerde Enerji Korunumu de = d dt Sistem dt eρdv + eρ V b n A Bu denklemde e = u + m + gz Q net,g + W net,g = d dt eρdv
Proses Tekniği 3.HAFTA 3.HAFTA YRD.DOÇ.DR. NEZAKET PARLAK Sürekli Akışlı Açık Sistemlerde Enerji Korunumu de = d dt Sistem dt eρdv + eρ V b n A Bu denklemde e = u + m + gz Q net,g + W net,g = d dt eρdv
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
Isı Kütle Transferi. Zorlanmış Dış Taşınım
 Isı Kütle Transferi Zorlanmış Dış Taşınım 1 İç ve dış akışı ayır etmek, AMAÇLAR Sürtünme direncini, basınç direncini, ortalama direnc değerlendirmesini ve dış akışta taşınım katsayısını, hesaplayabilmek
Isı Kütle Transferi Zorlanmış Dış Taşınım 1 İç ve dış akışı ayır etmek, AMAÇLAR Sürtünme direncini, basınç direncini, ortalama direnc değerlendirmesini ve dış akışta taşınım katsayısını, hesaplayabilmek
AKIġKANLAR MEKANĠĞĠ LABORATUARI 1
 AKIġKANLAR MEKANĠĞĠ LABORATUARI 1 Deney Sorumlusu ve Uyg. Öğr. El. Prof. Dr. İhsan DAĞTEKİN Prof. Dr. Haydar EREN Doç.Dr. Nevin ÇELİK ArĢ.Gör. Celal KISTAK DENEY NO:1 KONU: Su jeti deneyi. AMAÇ: Su jetinin
AKIġKANLAR MEKANĠĞĠ LABORATUARI 1 Deney Sorumlusu ve Uyg. Öğr. El. Prof. Dr. İhsan DAĞTEKİN Prof. Dr. Haydar EREN Doç.Dr. Nevin ÇELİK ArĢ.Gör. Celal KISTAK DENEY NO:1 KONU: Su jeti deneyi. AMAÇ: Su jetinin
YEREL KAYIPLAR. Borudaki yerel fiziki şekil değişimleri akımın yapısını mansaba doğru uzunca bir mesafe etkileyebilir.
 YEREL KAYIPLAR Bir boru hattı üzerinde akımı rahatsız edebilecek her çeşit yerel değişim bir miktar enerjinin kaybolmasına sebep olur. Örneğin boru birleşimleri, düğüm noktaları, çap değiştiren parçalar,
YEREL KAYIPLAR Bir boru hattı üzerinde akımı rahatsız edebilecek her çeşit yerel değişim bir miktar enerjinin kaybolmasına sebep olur. Örneğin boru birleşimleri, düğüm noktaları, çap değiştiren parçalar,
YILDIZ TEKNİK ÜNİVERSİTESİ
 YILDIZ TEKNİK ÜNİVERSİTESİ Makine Fakültesi Makine Mühendisliği Bölümü Termodinamik ve Isı Tekniği Anabilim Dalı Akışkanlar Mekaniği Genel Laboratuvar Föyü Güz Dönemi Öğrencinin Adı Soyadı : No : Grup
YILDIZ TEKNİK ÜNİVERSİTESİ Makine Fakültesi Makine Mühendisliği Bölümü Termodinamik ve Isı Tekniği Anabilim Dalı Akışkanlar Mekaniği Genel Laboratuvar Föyü Güz Dönemi Öğrencinin Adı Soyadı : No : Grup
AKIŞKANLAR MEKANİĞİ-II
 AKIŞKANLAR MEKANİĞİ-II Şekil 1. Akışa bırakılan parçacıkların parçacık izlemeli hızölçer ile belirlenmiş cisim arkasındaki (iz bölgesi) yörüngeleri ve hızlarının zamana göre değişimi (renk skalası). Akış
AKIŞKANLAR MEKANİĞİ-II Şekil 1. Akışa bırakılan parçacıkların parçacık izlemeli hızölçer ile belirlenmiş cisim arkasındaki (iz bölgesi) yörüngeleri ve hızlarının zamana göre değişimi (renk skalası). Akış
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM
 YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi
 Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi Akışkanlar dinamiğinde, sürtünmesiz akışkanlar için Bernoulli prensibi akımın hız arttıkça aynı anda
Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi Akışkanlar dinamiğinde, sürtünmesiz akışkanlar için Bernoulli prensibi akımın hız arttıkça aynı anda
LİNEER DALGA TEORİSİ. Page 1
 LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
SORU 1) ÇÖZÜM 1) UYGULAMALI AKIŞKANLAR MEKANİĞİ 1
 SORU 1) Şekildeki sistemde içteki mil dönmektedir. İki silindir arasında yağ filmi vardır. Sistemde sızdırmazlık sağlanarak yağ kaçağı önlenmiştir. Verilen değerlere göre sürtünme yolu ile harcanan sürtünme
SORU 1) Şekildeki sistemde içteki mil dönmektedir. İki silindir arasında yağ filmi vardır. Sistemde sızdırmazlık sağlanarak yağ kaçağı önlenmiştir. Verilen değerlere göre sürtünme yolu ile harcanan sürtünme
Orifis, Nozul ve Venturi Tip Akışölçerler
 Orifis, Nozul ve Venturi Tip Akışölçerler Bu tür akışölçerlerde, akışta kısıtlama yapılarak yaratılan basınç farkı (fark basınç), Bernoulli denkleminde işlenerek akış miktarı hesaplanır. Bernoulli denkleminin
Orifis, Nozul ve Venturi Tip Akışölçerler Bu tür akışölçerlerde, akışta kısıtlama yapılarak yaratılan basınç farkı (fark basınç), Bernoulli denkleminde işlenerek akış miktarı hesaplanır. Bernoulli denkleminin
BÖLÜM 6 PROSES DEĞİŞKENLERİNİN İNCELENMESİ
 BÖLÜM 6 PROSES DEĞİŞKENLERİNİN İNCELENMESİ Kimya Mühendisi, bir prosesin belirlenen koşullarda çalışıp çalışmadığını denetlemek için, sıcaklık, basınç, yoğunluk, derişim, akış hızı gibi proses değişkenlerini
BÖLÜM 6 PROSES DEĞİŞKENLERİNİN İNCELENMESİ Kimya Mühendisi, bir prosesin belirlenen koşullarda çalışıp çalışmadığını denetlemek için, sıcaklık, basınç, yoğunluk, derişim, akış hızı gibi proses değişkenlerini
7. BÖLÜMLE İLGİLİ ÖRNEK SORULAR
 7. BÖLÜMLE İLGİLİ ÖRNEK SORULAR 1) Denver, Colorao da (rakım 1610 m) yerel atmosfer basıncı 8.4 kpa dır. Bu basınçta ve 0 o C sıcaklıktaki hava, 120 o C sıcaklıkta ve 2.5m 8m boyutlarında düz bir plaka
7. BÖLÜMLE İLGİLİ ÖRNEK SORULAR 1) Denver, Colorao da (rakım 1610 m) yerel atmosfer basıncı 8.4 kpa dır. Bu basınçta ve 0 o C sıcaklıktaki hava, 120 o C sıcaklıkta ve 2.5m 8m boyutlarında düz bir plaka
İÇİNDEKİLER ÖNSÖZ Bölüm 1 DAİRESEL HAREKET Bölüm 2 İŞ, GÜÇ, ENERJİ ve MOMENTUM
 ÖNSÖZ İÇİNDEKİLER III Bölüm 1 DAİRESEL HAREKET 11 1.1. Dairesel Hareket 12 1.2. Açısal Yol 12 1.3. Açısal Hız 14 1.4. Açısal Hız ile Çizgisel Hız Arasındaki Bağıntı 15 1.5. Açısal İvme 16 1.6. Düzgün Dairesel
ÖNSÖZ İÇİNDEKİLER III Bölüm 1 DAİRESEL HAREKET 11 1.1. Dairesel Hareket 12 1.2. Açısal Yol 12 1.3. Açısal Hız 14 1.4. Açısal Hız ile Çizgisel Hız Arasındaki Bağıntı 15 1.5. Açısal İvme 16 1.6. Düzgün Dairesel
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 9 Ağırlık Merkezi ve Geometrik Merkez Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 9. Ağırlık
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 9 Ağırlık Merkezi ve Geometrik Merkez Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 9. Ağırlık
MANOMETRELER 3.1 PİEZOMETRE
 18 3 MANOMETRELER Düşük sıvı basınçlarını hassas olarak ölçmek için yaygın bir metot, bir veya birden fazla denge kolonu kullanan piezometre ve manometrelerin kullanılmasıdır. Burada çeşitli tipleri tartışılacaktır,
18 3 MANOMETRELER Düşük sıvı basınçlarını hassas olarak ölçmek için yaygın bir metot, bir veya birden fazla denge kolonu kullanan piezometre ve manometrelerin kullanılmasıdır. Burada çeşitli tipleri tartışılacaktır,
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB-305 KİMYA MÜHENDİSLİĞİ LABORATUVARI I
 ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB-305 KİMYA MÜHENDİSLİĞİ LABORATUVARI I DENEY 2 : BORULARDA BASINÇ KAYBI VE SÜRTÜNME DENEYİ (AKIŞKANLAR MEKANİĞİ) DENEYİN AMACI:
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB-305 KİMYA MÜHENDİSLİĞİ LABORATUVARI I DENEY 2 : BORULARDA BASINÇ KAYBI VE SÜRTÜNME DENEYİ (AKIŞKANLAR MEKANİĞİ) DENEYİN AMACI:
SORU #1. (20 p) (İlişkili Olduğu / Ders Öğrenme Çıktısı: 1,5,6 Program Çıktısı: 1)
 Süre 90 dakikadır. T.C. SAKARYA ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ DERSİ 015-016 GÜZ FİNAL SINAVI (Prof.Dr. Tahsin ENGİN - Doç.Dr. Nedim Sözbir - Yrd.Doç.Dr. Yüksel KORKMAZ Yrd.Doç.Dr.
Süre 90 dakikadır. T.C. SAKARYA ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ DERSİ 015-016 GÜZ FİNAL SINAVI (Prof.Dr. Tahsin ENGİN - Doç.Dr. Nedim Sözbir - Yrd.Doç.Dr. Yüksel KORKMAZ Yrd.Doç.Dr.
2. SUYUN BORULARDAKİ AKIŞI
 2. SUYUN BORULARDAKİ AKIŞI 2.6.4.4. Tesis yük kaybı eğrisinin değişik durumları Pompaj tesislerinde tesis yük kaybı eğrileri değişik alternatifler altında incelenebilir. Boru hatlarında kullanılan borular
2. SUYUN BORULARDAKİ AKIŞI 2.6.4.4. Tesis yük kaybı eğrisinin değişik durumları Pompaj tesislerinde tesis yük kaybı eğrileri değişik alternatifler altında incelenebilir. Boru hatlarında kullanılan borular
Hareket Kanunları Uygulamaları
 Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
BASMA DENEYİ MALZEME MÜHENDİSLİĞİ BÖLÜMÜ. 1. Basma Deneyinin Amacı
 1. Basma Deneyinin Amacı Mühendislik malzemelerinin çoğu, uygulanan gerilmeler altında biçimlerini kalıcı olarak değiştirirler, yani plastik şekil değişimine uğrarlar. Bu malzemelerin hangi koşullar altında
1. Basma Deneyinin Amacı Mühendislik malzemelerinin çoğu, uygulanan gerilmeler altında biçimlerini kalıcı olarak değiştirirler, yani plastik şekil değişimine uğrarlar. Bu malzemelerin hangi koşullar altında
AKIŞKAN STATİĞİNİN TEMEL PRENSİPLERİ
 8 AKIŞKAN STATİĞİNİN TEMEL PRENSİPLERİ 2 2.1 BİR NOKTADAKİ BASINÇ Sıvı içindeki bir noktaya bütün yönlerden benzer basınç uygulanır. Şekil 2.1 deki gibi bir sıvı parçacığını göz önüne alın. Anlaşıldığı
8 AKIŞKAN STATİĞİNİN TEMEL PRENSİPLERİ 2 2.1 BİR NOKTADAKİ BASINÇ Sıvı içindeki bir noktaya bütün yönlerden benzer basınç uygulanır. Şekil 2.1 deki gibi bir sıvı parçacığını göz önüne alın. Anlaşıldığı
GÜZ YARIYILI CEV3301 SU TEMİNİ DERSİ TERFİ MERKEZİ UYGULAMA NOTU
 2018-2019 GÜZ YARIYILI CEV3301 SU TEMİNİ DERSİ TERFİ MERKEZİ UYGULAMA NOTU Su alma kulesinin dip kısmında çıkılacak olan iletim borusuyla Q max 1,31 m 3 /sn olan su, kıyıdaki pompa istasyonuna getirilecektir.
2018-2019 GÜZ YARIYILI CEV3301 SU TEMİNİ DERSİ TERFİ MERKEZİ UYGULAMA NOTU Su alma kulesinin dip kısmında çıkılacak olan iletim borusuyla Q max 1,31 m 3 /sn olan su, kıyıdaki pompa istasyonuna getirilecektir.
Su seviyesi = ha Qin Kum dolu sütun Su seviyesi = h Qout
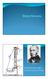 Su seviyesi = h a in Kum dolu sütun out Su seviyesi = h b 1803-1858 Modern hidrojeolojinin doğumu Henry Darcy nin deney seti (1856) 1 Darcy Kanunu Enerjinin yüksek olduğu yerlerden alçak olan yerlere doğru
Su seviyesi = h a in Kum dolu sütun out Su seviyesi = h b 1803-1858 Modern hidrojeolojinin doğumu Henry Darcy nin deney seti (1856) 1 Darcy Kanunu Enerjinin yüksek olduğu yerlerden alçak olan yerlere doğru
AKIġKAN BORUSU ve VANTĠLATÖR DENEYĠ
 AKIġKA BORUSU ve VATĠLATÖR DEEYĠ. DEEYĠ AMACI a) Lüle ile debi ölçmek, b) Dairesel kesitli bir borudaki türbülanslı akış şartlarında hız profili ve enerji kayıplarını deneysel olarak belirlemek ve literatürde
AKIġKA BORUSU ve VATĠLATÖR DEEYĠ. DEEYĠ AMACI a) Lüle ile debi ölçmek, b) Dairesel kesitli bir borudaki türbülanslı akış şartlarında hız profili ve enerji kayıplarını deneysel olarak belirlemek ve literatürde
Birimler. Giriş. - Ölçmenin tanımı. - Birim nedir? - Birim sistemleri. - Uluslararası (SI) birim sistemi
 Birimler Giriş - Ölçmenin tanımı - Birim nedir? - Birim sistemleri - Uluslararası (SI) birim sistemi 1 Ölçme: Değeri bilinmeyen bir büyüklüğün birim olarak isimlendirilen ve özelliği bilinen başka bir
Birimler Giriş - Ölçmenin tanımı - Birim nedir? - Birim sistemleri - Uluslararası (SI) birim sistemi 1 Ölçme: Değeri bilinmeyen bir büyüklüğün birim olarak isimlendirilen ve özelliği bilinen başka bir
P u, şekil kayıpları ise kanal şekline bağlı sürtünme katsayısı (k) ve ilgili dinamik basınç değerinden saptanır:
 2.2.2. Vantilatörler Vantilatörlerin görevi, belirli bir basınç farkı yaratarak istenilen debide havayı iletmektir. Vantilatörlerde işletme karakteristiklerini; toplam basınç (Pt), debi (Q) ve güç gereksinimi
2.2.2. Vantilatörler Vantilatörlerin görevi, belirli bir basınç farkı yaratarak istenilen debide havayı iletmektir. Vantilatörlerde işletme karakteristiklerini; toplam basınç (Pt), debi (Q) ve güç gereksinimi
DÜZENLİ AKIMLARDA ENERJİ DENKLEMİ VE UYGULAMALARI
 DÜZENLİ AKIMLARDA ENERJİ DENKLEMİ VE UYGULAMALARI, iş yapabilme yeteneği olarak tanımlanır(kg.m yada Kwh). Bir sıvının enerjisi, sıvı birim ağırlığının sahip olduğu iş yapabilme yeteneğidir. 1. Potansiyel
DÜZENLİ AKIMLARDA ENERJİ DENKLEMİ VE UYGULAMALARI, iş yapabilme yeteneği olarak tanımlanır(kg.m yada Kwh). Bir sıvının enerjisi, sıvı birim ağırlığının sahip olduğu iş yapabilme yeteneğidir. 1. Potansiyel
AÇIK KANAL AKIMI. Hopa Yukarı Sundura Deresi-ARTVİN
 AÇIK KANAL AKIMI Hopa Yukarı Sundura Deresi-ARTVİN AÇIK KANAL AKIMI (AKA) Açık kanal akımı serbest yüzeyli akımın olduğu bir akımdır. serbest yüzey hava ve su arasındaki ara yüzey @ serbest yüzeyli akımda
AÇIK KANAL AKIMI Hopa Yukarı Sundura Deresi-ARTVİN AÇIK KANAL AKIMI (AKA) Açık kanal akımı serbest yüzeyli akımın olduğu bir akımdır. serbest yüzey hava ve su arasındaki ara yüzey @ serbest yüzeyli akımda
BÖLÜM 1: TEMEL KAVRAMLAR
 BÖLÜM 1: TEMEL KAVRAMLAR Hal Değişkenleri Arasındaki Denklemler Aralarında sıfıra eşitlenebilen en az bir veya daha fazla denklem kurulabilen değişkenler birbirine bağımlıdır. Bu denklemlerden bilinen
BÖLÜM 1: TEMEL KAVRAMLAR Hal Değişkenleri Arasındaki Denklemler Aralarında sıfıra eşitlenebilen en az bir veya daha fazla denklem kurulabilen değişkenler birbirine bağımlıdır. Bu denklemlerden bilinen
AKM 205 BÖLÜM 3 - UYGULAMA SORU VE ÇÖZÜMLERİ. Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut
 AKM 205 BÖLÜM 3 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. 70 kg gelen bir bayanın 400 cm 2 toplam ayak tabanına sahip olduğunu göz önüne alınız. Bu bayan
AKM 205 BÖLÜM 3 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. 70 kg gelen bir bayanın 400 cm 2 toplam ayak tabanına sahip olduğunu göz önüne alınız. Bu bayan
