GPŞ Sistemi İle Şehir Nirengi Ağlarının Analizi
|
|
|
- Ilkin Derici
- 8 yıl önce
- İzleme sayısı:
Transkript
1
2
3 GPŞ Sistemi İle Şehir Nirengi Ağlarının Analizi Nihat ERSOY* ÖZET Şehir nirengi ağlarının değerlendirilmesinde, 1987 yılında klasik ölçme yöntemleri ile ülke nirengi ağına dayalı 3. derece bir yatay kontrol ağı olarak kurulan İstanbul Metropolitan Nirengi Ağının kontrolü ve analizi GPS yöntemi île yapılmıştır. Bu analizde yersel ağ, tüm bölgeyi kapsayacak şekilde seçilen 8 noktalık GPS kontrol ağı ile karşılaştırılmıştir. Bu çalışmanın amacı, metropolitan nirengi ağının öteleme, dönüklük ve ölçek parametreleri ile ağın iç doğruluğunu belirlemektir. Bu yöntemin ilk defa uygulanması ile değerlendirilen İstanbul Metropolitan Nirengi Ağının duyarlı ve güvenilir bir şekilde kontrolü yapılmıştır. 1. GİRİŞ İstanbul, Ankara, İzmir gibi çok hızlı gelişen büyük şehirlerin kendine özgü sorunları ancak etkin bir planlama ile çözülebilir. Etkin bir planlamanın ve uygulamanın altlığı ise, duyarlı ve güvenilir bir nirengi ağına dayalı içeriği doğru güncelleştirilebilen haritalardır. Bu haritalar kentlerin yerleşim, imar ve ulaşım planlan ile teknik alt yapı hizmetleri denen yol, su, elektrik gibi yapıların altlığını oluşturur (Koçak,74). Teknolojik gelişmelere parelel olarak amaçları, meteoroloji ve haberleşmeden uzaktan algılamaya, jeodezik konum belirlemesine kadar uzanan binlerce uydu uzaya yerleştirilmiştir. Yapay uydulardan en etkin yararlanılan disiplinlerin başında, jeodezi ve haritacılık gelmektedir. Ülke koordinat sisteminde koordinatları mevcut olan İstanbul Metropolitan Nirengi Ağının değerlendirilmesinde, uydu tekniklerinden GPS yönteminin kullanılması ile üretilen orjinal koordinatlar WGS-84 datumunda elde edilmektedir. Halbuki Ülkemizde Büyük Ölçekli Haritaların Yapım Yönetmeliğine göre, bu koordinatların ülke koordinat sisteminde elde edilmesi gerekmektedir. Bu nedenle iki datum arasında dönüşüm yapılmalıdır. Böylece her iki datumdaki ortak noktalar ile kurulan Bursa-Wolf modeli ile üç boyutlu dönüşüm yapılmış, ağdaki relatif şekil bozuklukları (ölçek faktörü), ötelemeler ve dönüklükler belirlenmiştir.dönüşüm sonucu belirlenen bu parametreler yardımı ile ülke datumuna indirgenen koordinatlar, klasik koordinatlar ile karşılaştırılmış ve aralarındaki farklar hesaplanmıştır. Ayrıca doğada değişmeyen büyüklüklerden eğik * Dr. (YTÜ) 6
4 uzunluklar ile uzay açılarının karşılaştırılması yapılmıştır. Bütün bu değerlendirmeler sonucunda İstanbul Metropolitan Nirengi Ağının kalitesini belirleyen duyarlığı ve güvenirliği hakkında sonuçlar ve öneriler ortaya konmuştur. 2. KOORDİNAT SİSTEMLERİ a. Yer Merkezli Koordinat Sistemieri Yeryüzünde yapılan gözlemlerin dayandığı merkezi yeryuvarının merkezinde ve bütün Dünya için geçerli olan, Greenwiçh sıfır meridyenine ve 1903 yılı ortalama CIO kutbuna göre tanımlanan bu koordinat sistemleri ikiye ayrılır. 1-) Dünya Dik Koordinat Sistemi Bu sistemin özel hali olan WGS-84 koordinat sistemine dayalı, uydu gözlemlerinin hesabı için referans yüzeyi olarak seçilen, WGS-84 datumunu oluşturan yer merkezli bir elipsoit olan WGS-84 elipsoidi tanımlanmıştır. WGS-84 Datumunu oluşturan WGS-84 Elipsoidini tanımlayan parametreler: Elipsoidin büyük yarı ekseni : a = m Elipsoidin basıklığı : f = 1 / Kutup eğrilik yarıçapı : c = m 2~) Jeodezik Elipsoidal Dik Koordinat Sistemi Bu sistemin ülkemizdeki özel hali olan ED-50 koordinat sistemine dayalı, uydu gözlemlerinin hesaplarının daha kolay yapılabildiği referans yüzeyi olarak seçilen, ED- 50 datumunu oluşturan uluslararası bir elipsoit olan ED-50 elîpsoiti (Hayford elipsoidi) tanımlanmıştır. ED-50 Datumunu oluşturan ED-50 Elipsoidini tanımlayan parametreler : Elipsoidin basıklığı : f = 1 / 297 Elipsoidin büyük yarı ekseni : a = m. Kutup eğrilik yarıçapı : c = m. WGS-84 datumunda uydu gözlemleri, global dik koordinatlar (X Y Z) ile belirlendiği gibi aynı datumda, elipsoidal eğri koordinatlar (B L h) ile de belirlenebilir. WGS- 84 datumunda belirlenen bu koordinatlar arasında, X = (N + h) cosb cosl Y = (N+h)cosBsinL Z= N(l-e 2 )+h]sinb 7
5 ilişkisi vardır. Bu eşitlikleri elipsoidal eğri koordinatlar cinsinden ifade edersek, tgb= öe7 y r Wî :^y^] iteratif olarak çözülebilir - Y h = (X 2 +Y 2 )secb-n (2) eşitlikleri ile ilişki kurularak dönüşüm yapılır (Hofmann, v.d.92. Leick,90). b. Düzlemsel Dik Koordinat Sistemleri Uydu teknikleri ile yapılan gözlemler sonucu elde edilen koordinatlar WGS-84 elipsoidinde hesaplanan WGS-84 datumunda belirlenirler. Bu belirlenen koordinatlar, ED- 50 datumuna dönüştürülür. Bu dönüşüm sonucu elde edilen jeodezîk koordinatları, ülke içinde bölgesel haritaların üretiminde ve pratik uygulamalarda kullanmak için, düzlemsel dik koordinatlara dönüştürmek gerekir. Bu şekilde dönüştürülen düzlemsel dik koordinatlara projeksiyon koordinatları da denir. Ülkemizde uygulamada kullanılan dilim genişliğine göre, düzlemsel dik koordinat sistemleri ülke datumunu oluşturan iki ayrı projeksiyon düzlemine ayrılır. 1-) UTM Projeksiyon Düzlemi Dilim genişliği 6 derece olan 1/25000 ve daha küçük ölçekli haritaları üretmek için kullanılır. 2-) Gauss-Kruger Projeksiyon Düzlemi Dilim genişliği 3 derece olan 1/5000 ve daha büyük ölçekli haritaları üretmek için kullanılır. Her iki projeksiyon düzleminde de dilim orta meridyeni x-eksenini, elipsoid ekvatoru ise y-eksenini oluşturur. (Ersoy,97). 8
6 Türkiye'de uygulamalarda kullanılan uydu tekniklerinden GPS yöntemi ile elde edilen koordinatların, ülke koordinatlarına dönüşürken izlediği yol aşağıdaki tabloda verilmiştir. Aynı şekilde bu dönüşümün terside mümkün olabilmektedir. Tablo-1: Koordinat Sistemleri Arasındaki Dönüşümler ile GPS Ölçülerinin Akış Diyagramı 3. DATUM BELİRLEME Matematiksel jeodezinin alanı içerisinde yeryüzünün tümünün veya bir parçasının fiziksel şeklini belirlemek amacı ile yeryüzünün ölçülmesi ve bir yüzeye izdüşürülmesi için, bir koordinat sisteminin tanımlanması ve fiziksel yeryüzünde bu sisteme göre tanımlanan nirengi noktalarının koordinatlarının bilinmesine ihtiyaç vardır. Fiziksel yeryüzünde ölçülen eğik uzunluklar ve doğrultu ölçüleri elipsoit yüzeyine indirgenirler (Ünal,81.Tuğluoğlu,75). Elipsoid yüzeyine indirgenen bu ölçülerin uzayda belli bir konuma yerleştirilmesi datum sorunu olarak bilinir. Ölçülerin hesaplandığı dönel elipsoitin parametreleri (a,f) ile jeodezik elipsoidal dik koordinat sistemine göre noktaların konumlarını belirleyen koordinatlar (x, y, z) jeodezik datumu oluşturur. Ülkemizde datum başlangıcı olarak Meşedağ noktası kullanılmıştır. Avrupa ülkeleri ile datum birliğini sağlamak amacı ile Türkiye yatay kontrol nirengi ağının, Avrupa datumu olarak bilinen ED-50 datumuna geçişi, Yunanistan ve Bulgaristan sınırındaki 8 nokta ile bağlantısı kurularak sağlanmıştır. 9
7 4. DÖNÜŞÜMLER Günümüzde uydu teknikleri ile yeryüzündeki noktaların konumlan belirlendiğinden, uygulamada en çok kullanılan global sistem ile ulusal sistem arasındaki üç boyutlu benzerlik dönüşümü açıklanacaktır. Üç boyutlu dönüşümün esası ; Uzayda uydu teknikleri ile WGS-84 koordinat sisteminde elde edilen noktaların koordinatları ile ulusal koordinatların elde edildiği ED-50 koordinat sistemi arasındaki ilişkiyi sağlayan eşlenik noktaların yardımıyla 7 parametreli bir benzerlik dönüşümünü gerçekleştirerek, sistemler arasındaki dönüşüm parametrelerini belirlemektir. Bu parametreler kullanılarak WGS-84 koordinat sisteminde elde edilen koordinatlar, ED-50 koordinat sistemine, 7 parametreli Bursa-Wolf Modeli ile üç boyutlu uzayda benzerlik dönüşümü yapılır. a. Bursa Wolf Modeli X Y Z : I. Sistemaeki koordinatlar ; I\. 1 \. T. : 3 öteleme parametresi xy 7. : II. Sistemdeki koordinatlar : \\\ \\\. \\\ : 3 dönüklük açısı 1+k : 1 ölçek faktörü şeklinde gösterilirse. X T x 1 w z -w y x Y = /;. + ( l + k) -w z 1 w x y 7 \ \ T -.\ [ w v " w x (3) eşitliği ile Bursa Wolf modeli kurulur ] J L Z J,, L o = F (X o ) ise. L = L,, - L,, = F (X,.) - L,. (4) 10
8 X X X w x w y w z k Zi (l+k) y,(l+k) x ı +w z y ı -v^z i z^l+k) 0 -x,(l+k) -w z x,+y ; +w x z, A= YiO+k) ^(1+k) O WyX.- WJı+Zi (5) eşitlikleri yardımı ile matematiksel model kurulur. L h + V = F (X () ) + A AX (6) Bu modelin En Küçük Kareler Yöntemine göre çözümü ile. A^= (A! A)-! A'L (7) V = A AX + L (8) eşitlikleri ile parametrelere ve koordinatlara gelen düzeltmeler hesaplanır (Uzel- Eren.95). II
9 Jeodezik elipsoidal dik koordinat sistemine dönüştürülen koordinatlar. Gauss Kruger Projeksiyon Düzlemindeki Koordinatlara : x = G + B 2 AA 2 + B 4 AA" +... y = B x AA + B, AA" + B, A/T +... (9) eşitlikleri ile dönüştürülür (Aksoy.87). 5. GPS SİSTEMİ ABD Savunma Bakanlığı tarafından geliştirilen hareketli cisimlerin zamana bağlı olarak konumlarının, izledikleri yolun doğrultusunun ve yönünün belirlenmesi diye tanımlanan navigasyon ve bu ihtiyaca yönelik olarak tasarlanan GPS sistemi ile. uydulardan yayınlanan radyo sinyalleri yardımıyla noktalar arası görüş olmaksızın her türlü hava koşullarında, gece ve gündüz, süratli, doğru ve ekonomik olarak üç boyutta konum belirlenir (Kınık.93). ' a. GPS'io Bölümleri 1-) Uzay Bölümü Yeryüzünden km yükseklikteki 25 adet aktif GPS uydusu bu bölümü oluşturur. 2-) Kontrol Bölümü GPS uydularının konumlarını belirlemeye yarıyan uydu izleme istasyonları bu bölümü oluşturur. Bu istasyonlardan, istatistik analizlerle önceden kestirilen uydu yörünge bilgileri, yayın efemerisi ve duyarlı efemeris olmak üzere iki ayrı efemeris altında yayınlanır. 3~) Kullanıcı Bölümü Yer kontrol noktalan üzerine konulan uygun donanımlı GPS alıcıları (receivers) ile noktaların konumları belirlenir. GPS ölçülerini elde etmede tek frekanslı ve çift frekanslı olmak üzere iki çeşit alıcı kullanılır (Lcick.90). 12
10
11 b. GPS Ölçme Yöntemleri Noktalar arasındaki baz uzunluklarına ve jeodezik ağların amaçlarına göre uygulamada en yaygın kullanılan 3 çeşit GPS ölçme yöntemi vardır. 1-) Statik Ölçme Yöntemi 20 km'den büyük bazlarda. 1 saat veya daha fazla süre ile eş zamanlı sinyallerin alınması bu yöntemin temelini oluşturur. Büyük mühendislik yapılarının deformasyonlarının belirlenmesinde, çok yüksek duyarlık gerektiren jeodinamik hareketlerin izlenmesinde ve ülke nirengi ağlarının yenilenmesinde kullanılır. 2-) Hızlı Statik Ölçme Yöntemi 20 km'nin altındaki bazlarda dakika süre ile eş zamanlı sinyallerin alınması bu yöntemin temelini oluşturur. Ülke nirengi ağlarının sıklaştırılmasında kullanılır. 3-) Kinematik Ölçme Yöntemi Kısa bazlarda saniye süre ile eş zamanlı sinyallerin alınması bu yöntemi oluşturur. Poligon noktalarının tesisinde ve Hidrografık ölçmelerde kullanılır. Her üç yöntemde de verilen ölçü süresine bağlı olarak ± (0.01-2) ppın arasında değişen doğrulukta noktaların konumları belirlenebilmektedir (Renıondi. 84). Elde edilen bu doğruluklar, klasik ölçme tekniklerine göre 10 ile 100 kez daha duyarlı olduğunu göstermiştir. 6. GPS BAZ VEKTÖRLERİNİN HESABI Jeodezik konum belirlenmesinde kullanılan taşıyıcı dalga faz farkı ölçüsünün genel denklemi A(» m p =<J) p (D-< )n.ü. n ) + N In p (l) (10) eşitliği ile verilen formülle ifade edilir. Bu eşitlikte. K/Cl) : tam sayı başlangıç faz bilinmeyeni m (Ln) alıcıda üretilen sinyalin alıcı tarafından ölçülen fazı (j) p ( T p ): uydudan gönderilen sinyalin alıcı tarafından ölçülen fazını gösterir. Bu ölçünün esası; gönderilen aynı uydu sinyalinin yerdeki alıcılarda kaydedilmesi ve alıcılarda üretilen aynı referans sinyalleri ile karşılaştırılarak faz farklarının ölçülmesidir. 14
12 Jeodezik amaçlı bağıl konum belirlemesi için. uygulamada kullanılan İkili fark ölçüleri ile oluşturulan denklemin: S»-^f/c)^+(f/cXpr-fC)a.-(f/cXpr-Pr)[b, + b I (t-ı I ) + b : (t-i ı ) J ] -(f/c)aa +AN«<l) (11) Bu eşitlikte. APS, - A P L - ApL ; PT - P. - P^1 AAS, - AAL - AAL ; p*" = p? - tf ANS,(1)-ANÎ M (1)-ANL(1) En Küçük Kareler yöntemine göre çözümü için. Lı, = S L o = F(X O ) sağ tarafı kapanma vektörü alınırsa. X () yaklaşık değerleri ile hesaplanan ( 1 1 ) eşitliğinin L = L (1 - Lı, veya L = FC^,) - Lı, (12) ^1) ' 0 g2). 0 P- ölçüleriuağırlık matrisi...m. 15
13 k ve m alıcılarından p ve q uydularına, n-epoğıı sayısı kadar ölçü yapıldığını varsayarsak. M sayısı kadar ikili fark ölçüsü elde edilir. Bu dununda oluşturulan A- olmak üzere. L.-F(X.) L b + V = F(X,) + AAX (14) eşitliği ile fonksiyonel model kurulur. Bu modelin çözülmesi ile. AX = -(A T PA)-'A T PL (15) eşitliği ile noktalar arasındaki baz vektörleri hesaplanır (Hofmann.v.d.92). 7. BAZ VEKTÖRLERİNİN DENGELENMESİ k ve m noktalan arasında hesaplanan baz vektörleri Lı,. bu noktalara karşılık gelen katsayılar matrisi A ve noktalar arasındaki yaklaşık koordinatlarla hesaplanan baz vektörleri L o ile gösterilirse. Fonksiyonel model : L a =L h +V = A AX + L O V = AAX + L (16) veya eşitliği ile kurulur. Hesaplanan baz vektörlerinin ağırlık katsayıları matrisi yardımı ile. 16
14 (17) Stokastik model kurulur. Kumlan matematiksel modellerin En Küçük Karelere göre dengelenmesi ile. AX = -(A T PA)-! A T PL (18) koordinat bilinmeyenlerinin yaklaşık değerlerine getirilecek düzeltmeler hesaplanır. Bu eşitlikten yararlanarak. X =X 0 +AX koordinat bilinme) enlerinin kesin değerleri (19) V=AAX+L (20) L rı = L h + V baz vektörlerine getirilen düzeltmeler baz vektörlerinin dengelenmiş kesin değerleri (21) eşitlikleri ile hesaplanır (Uzel-Ercn.95). dengeleme sonunda, birim ağırlıklı ölçünün varyansı (a poslriori \aryans) a o z ; eşitliği ile bulunur. cf = V T PV/n-u (22) Bulunan bu standart sapma a. ile ölçülerin ağırlık katsayıları matrisi Q. s>? = N' yararlanarak, koordinat bilinmeyenlerinin dengelenmiş değerlerinin ortalama hataları (standart sapmaları) n : ^ = q,(q # ) I/2 ; ">. = "o(q,>.)' 2 ; <\ = ^ ( q,,,, ) ' (23) : 17
15 noktaların konum hataları ise. koordinat bilinmeyenlerinin standart sapmaları yardımı ile. a p =(o;+ö;+a;) i2 (24) eşitliği ile hesaplanır (Hoşbaş.92). Eğer jeodezik eğri koordinatların model alınması ile çözüm gerçekleştirilirse. er,, ve o\ değerleri uzunluk birimine dönüştürüldükten sonra. <r p yine bu eşitlikle hesaplanabilir. Dengelenmiş koordinat bilinmeyenlerinin varvans-kovaryans matrisi S Xi, : 2 X;ı = cr;(a T PAr varyans-kovaryans matrisi Z, _ : ile hesaplanır (Uzcl-Eren.95). (25) Dengeli baz vektörü bileşenlerinin 2 U ı = a t> A ( A ' P A)"' A T = A 2 Xu A' (26) eşlilikleri a. Nokta Konum Doğruluklarının Hesabı Üç boyutlu uzayda, ölçülen GPS baz vektörlerinin dengelenmesi sonucunda elde edilen noktaların konum doğruluklarını tanımlayabilmek için. üç boyutlu Helmcrt hata elipsoidinden yararlanılır. Bunun için. hala clipsoitinin A. B. C yarı eksen a = -(qx*+q yy +q Z z) b = q xx + qyy + qzzqxx+qyyqzz - q^y - ql - q? z c =q xx qy Z +qyyql+qzzq^y - qxxqyyqzz - 2 qxyqx Z qyz p = b-(a 2 /3) q = c-(ab/3) + (2a 3 /27) Cos(3*) = i -~^ 2[-(p/3) 3 ] 18
16 (27) eşitlikleri yardımı ile. X A =2[-(p/3)]' 2 cos<l>-(a/3) X B =2[-(p/3)J 12 cos(( )+120 o )-(a/3) V =2[-(p/3)]' 2 cos(()) o )-(a/3) (2X) eşitlikleri ile  A.  h. Â,- değerleri hesaplanır. Bu değerlerin birim ağırlıklı ölçünün standart sapması rr () ile çarpılması sonucunda. A. B. C yarı eksen ıızunlııklan. A = a n (?, A ) 1-7 ; B = a ft (Â,,,) 12 ; C = a (! ( (.) i: (29) eşitlikleri ile hesaplanır. (27) eşitliklerinde geçen q NN. q yv. q z:,. q v. q«. q v, büyüklükleri, bilinmeyen noktaların jeodczik dik koordinatları (X Y Z) ile nıodcllcnmcsi dıırııınunda. dengeleme sonucunda elde edilen Q_^v, veya N bilinmeyenlerin ağırlık katsayıları matrisinin ilgili elemanlarıdır. Eğer bilinmeyen noktaların jeodezik eğri koordinatlar (ı ı /. h) ile modellcnmesi dunımıında ise. dengeleme sonucunda elde edilen Q,,> \eya N matrisinin. Q xy/ matrisine dönüştürülmesi gerekir (Şimşek. 94). b. Eğik U/unluklar ve Uzay Açılarının Hesabı Üç boyutlu iki farklı dadımda koordinatları belirlenen noktaların, konum doğruluklarını tanımlayan uzay açılan ile eğik uzunluklar arasındaki farkları veren formüller aşağıdaki şekilde hesaplanabilir. 19
olmak üzere 4 ayrı kütükte toplanan günlük GPS ölçüleri, baz vektörlerinin hesabı için bilgisayara aktarılmıştır (Ersoy.97).
 1-) GPS Ölçülerinin Yapılması Ölçülerin yapılacağı tarihlerde kısa bir süre gözlem yapılarak uydu efemerisi güncelleştirilmiştir. Bunun sonunda ölçü yapılacak bölgenin yaklaşık koordinatlarına göre, bir
1-) GPS Ölçülerinin Yapılması Ölçülerin yapılacağı tarihlerde kısa bir süre gözlem yapılarak uydu efemerisi güncelleştirilmiştir. Bunun sonunda ölçü yapılacak bölgenin yaklaşık koordinatlarına göre, bir
Harita Projeksiyonları ve Koordinat Sistemleri. Doç. Dr. Senem KOZAMAN
 Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
HARİTA DAİRESİ BAŞKANLIĞI. İSTANBUL TKBM HİZMET İÇİ EĞİTİM Temel Jeodezi ve GNSS
 HİZMET İÇİ EĞİTİM MART 2015 İSTANBUL TAPU VE KADASTRO II.BÖLGE MÜDÜRLÜĞÜ SUNUM PLANI 1- Jeodezi 2- Koordinat sistemleri 3- GNSS 3 JEODEZİ Jeodezi; Yeryuvarının şekil, boyut, ve gravite alanı ile zamana
HİZMET İÇİ EĞİTİM MART 2015 İSTANBUL TAPU VE KADASTRO II.BÖLGE MÜDÜRLÜĞÜ SUNUM PLANI 1- Jeodezi 2- Koordinat sistemleri 3- GNSS 3 JEODEZİ Jeodezi; Yeryuvarının şekil, boyut, ve gravite alanı ile zamana
GPS ağlarının dengelenmesinden önce ağın iç güvenirliğini artırmak ve hataları elimine etmek için aşağıda sıralanan analizler yapılır.
 13. GPS AĞLARININ DENGELENMESİ 13.1 GPS ÖLÇMELERİ GPS ( Global Positioning System ) alıcıları kullanılarak yer istasyonu ile uydu arasındaki uzunluklar ölçülür ve noktaların konumları belirlenir. GPS ile
13. GPS AĞLARININ DENGELENMESİ 13.1 GPS ÖLÇMELERİ GPS ( Global Positioning System ) alıcıları kullanılarak yer istasyonu ile uydu arasındaki uzunluklar ölçülür ve noktaların konumları belirlenir. GPS ile
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU. Yrd. Doç. Dr. Hüseyin KEMALDERE
 JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
31.10.2014. CEV 361 CBS ve UA. Koordinat ve Projeksiyon Sistemleri. Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli
 CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714 km
CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Öğr. Gör. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714 km
CEV 361 CBS ve UA. Koordinat ve Projeksiyon Sistemleri. Yrd. Doç. Dr. Özgür ZEYDAN Yerin Şekli
 CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Yrd. Doç. Dr. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714
CEV 361 CBS ve UA Koordinat ve Projeksiyon Sistemleri Yrd. Doç. Dr. Özgür ZEYDAN http://cevre.beun.edu.tr/zeydan/ Yerin Şekli 1 Yerin Şekli Ekvator çapı: 12756 km Kuzey kutuptan güney kutuba çap: 12714
Bağıl Konum Belirleme. GPS ile Konum Belirleme
 Mutlak Konum Belirleme Bağıl Konum Belirleme GPS ile Konum Belirleme büroda değerlendirme (post-prosessing) gerçek zamanlı (real-time) statik hızlı statik kinematik DGPS (kod) gerçek zamanlı kinematik
Mutlak Konum Belirleme Bağıl Konum Belirleme GPS ile Konum Belirleme büroda değerlendirme (post-prosessing) gerçek zamanlı (real-time) statik hızlı statik kinematik DGPS (kod) gerçek zamanlı kinematik
B = 2 f ρ. a 2. x A' σ =
 TÜRKİYE ULUSAL JEODEZİ KOMİSYONU (TUJK) 004 YILI BİLİMSEL TOPLANTISI MÜHENDİSLİK ÖLÇMELERİNDE JEODEZİK AĞLAR ÇALIŞTAYI JEODEZİK GPS AĞLARININ TASARIMINDA BİLGİSAYAR DESTEKLİ SİMÜLASYON YÖNTEMİNİN KULLANIMI
TÜRKİYE ULUSAL JEODEZİ KOMİSYONU (TUJK) 004 YILI BİLİMSEL TOPLANTISI MÜHENDİSLİK ÖLÇMELERİNDE JEODEZİK AĞLAR ÇALIŞTAYI JEODEZİK GPS AĞLARININ TASARIMINDA BİLGİSAYAR DESTEKLİ SİMÜLASYON YÖNTEMİNİN KULLANIMI
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
JEODEZİK ÖLÇMELER DERSİ. Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE
 JEODEZİK ÖLÇMELER DERSİ Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM 1. Hafta Ders Notları REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM Referans (Koordinat)
JEODEZİK ÖLÇMELER DERSİ Yrd. Doç. Dr. Hakan AKÇIN Yrd. Doç. Dr. Hüseyin KEMALDERE REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM 1. Hafta Ders Notları REFERANS (KOORDİNAT) SİSTEMLERİ VE DATUM Referans (Koordinat)
GPS YÖNTEMİ İLE HALİHAZIR HARİTA ÜRETİMİ
 GPS YÖNTEMİ İLE HALİHAZIR HARİTA ÜRETİMİ Nihat ERSOY*. ÖZET Ülkemizde sanayileşmenin getirdiği kentleşme toprak rantını da beraberinde getirmiştir. Böylece toprağın kullanımı, planlaması ülke menfaatleri
GPS YÖNTEMİ İLE HALİHAZIR HARİTA ÜRETİMİ Nihat ERSOY*. ÖZET Ülkemizde sanayileşmenin getirdiği kentleşme toprak rantını da beraberinde getirmiştir. Böylece toprağın kullanımı, planlaması ülke menfaatleri
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI
 SELÇUK TEKNİK ONLİNE DERGİSİ / ISSN 1302 6178 Volume 1, Number: 3 2001 İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI Doç Dr. Cevat İNAL S.Ü.
SELÇUK TEKNİK ONLİNE DERGİSİ / ISSN 1302 6178 Volume 1, Number: 3 2001 İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI Doç Dr. Cevat İNAL S.Ü.
Uygulamada Gauss-Kruger Projeksiyonu
 JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
Haritası yapılan bölge (dilim) Orta meridyen λ. Kuzey Kutbu. Güney Kutbu. Transversal silindir (projeksiyon yüzeyi) Yerin dönme ekseni
 1205321/1206321 Türkiye de Topografik Harita Yapımı Ölçek Büyük Ölçekli Haritalar 1:1000,1:5000 2005 tarihli BÖHHBYY ne göre değişik kamu kurumlarınca üretilirler. Datum: GRS80 Projeksiyon: Transverse
1205321/1206321 Türkiye de Topografik Harita Yapımı Ölçek Büyük Ölçekli Haritalar 1:1000,1:5000 2005 tarihli BÖHHBYY ne göre değişik kamu kurumlarınca üretilirler. Datum: GRS80 Projeksiyon: Transverse
Kuzey Kutbu. Yerin dönme ekseni
 1205321/1206321 Türkiye de Topoğrafik Harita Yapımı Ölçek Büyük Ölçekli Haritalar 1:1000,1:5000 2005 tarihli BÖHHBYY ne göre değişik kamu kurumlarınca üretilirler. Datum: GRS80 Projeksiyon: Transverse
1205321/1206321 Türkiye de Topoğrafik Harita Yapımı Ölçek Büyük Ölçekli Haritalar 1:1000,1:5000 2005 tarihli BÖHHBYY ne göre değişik kamu kurumlarınca üretilirler. Datum: GRS80 Projeksiyon: Transverse
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ
 KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI
 36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
CBS. Projeksiyon. CBS Projeksiyon. Prof.Dr. Emin Zeki BAŞKENT. Karadeniz Teknik Üniversitesi Orman Fakültesi 2010, EZB
 Prof.Dr. Emin Zeki BAŞKENT Karadeniz Teknik Üniversitesi Orman Fakültesi Elipsoid şeklindeki dünyanın bir düzlem üzerine indirilmesi ve koordinatlarının matematiksel dönüşümleridir. Harita üç şekilde projeksiyonu
Prof.Dr. Emin Zeki BAŞKENT Karadeniz Teknik Üniversitesi Orman Fakültesi Elipsoid şeklindeki dünyanın bir düzlem üzerine indirilmesi ve koordinatlarının matematiksel dönüşümleridir. Harita üç şekilde projeksiyonu
Jeodezide Yaklaşım Yöntemleri: Enterpolasyon ve Kollokasyon
 Jeodezide Yöntemleri: ve Lisansüstü Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Fen Bilimleri Enstitüsü e-posta: austun@selcuk.edu.tr Konya, 2007 A. Üstün yöntemleri 1 / 28 Bir soruyu ya
Jeodezide Yöntemleri: ve Lisansüstü Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Fen Bilimleri Enstitüsü e-posta: austun@selcuk.edu.tr Konya, 2007 A. Üstün yöntemleri 1 / 28 Bir soruyu ya
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
JEODEZİK AĞLARIN OPTİMİZASYONU
 JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
BEÜ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ
 BEÜ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT DÖNÜŞÜMÜ, DATUM TRANSFORMASYONU Prof.Dr.RASİM DENİZ MAYS 2014 ZONGULDAK KOORDİNAT DÖNÜŞÜMÜ,DATUM TRANSFORMASYONU 1-Genel Bilgiler Aynı datumdaki koordinatların
BEÜ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT DÖNÜŞÜMÜ, DATUM TRANSFORMASYONU Prof.Dr.RASİM DENİZ MAYS 2014 ZONGULDAK KOORDİNAT DÖNÜŞÜMÜ,DATUM TRANSFORMASYONU 1-Genel Bilgiler Aynı datumdaki koordinatların
JEOİD ve JEOİD BELİRLEME
 JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
Dünya nın şekli. Küre?
 Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
BÜLENT ECEVİT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT SİSTEMLERİ. Prof.Dr.Rasim Deniz
 BÜLENT ECEVİT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT SİSTEMLERİ Prof.Dr.Rasim Deniz Zonguldak, 2014 YERSEL KOORDİNAT SİSTEMLERİ 1-Genel Yer üzerindeki konumların belirlenmesi
BÜLENT ECEVİT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT SİSTEMLERİ Prof.Dr.Rasim Deniz Zonguldak, 2014 YERSEL KOORDİNAT SİSTEMLERİ 1-Genel Yer üzerindeki konumların belirlenmesi
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
TUSAGA-AKTİF İLE TG03 (ORTOMETRİK KOT) KULLANIMI
 Bilindiği gibi GNSS Cors ağlarında varsayılan yükseklik referansı olarak Elipsoit düzlemi kullanılmaktadır. Bu da cors yönteminde gerçek yükseklik bilgisi (ortometrik) olmadan, kullanıcının sadece elipsoidal
Bilindiği gibi GNSS Cors ağlarında varsayılan yükseklik referansı olarak Elipsoit düzlemi kullanılmaktadır. Bu da cors yönteminde gerçek yükseklik bilgisi (ortometrik) olmadan, kullanıcının sadece elipsoidal
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI
 ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
ULUSAL STANDART TOPOGRAFİK HARİTA PROJEKSİYONLARI Doç.Dr. Türkay GÖKGÖZ http://www.yarbis.yildiz.edu.tr/gokgoz İnşaat Fakültesi Harita Mühendisliği Bölümü Kartografya Anabilim Dalı BÜYÜK ÖLÇEKLİ HARİTA
YAŞAYAN : Son olarak benim sormadığım fakat sizin söylemek istediğiniz bir sözünüz veya mesajınız var mı?
 bir oda olduğumuz bilinsin, yaptığımız iş de zeminde görünsün istedik. Biz böyle bir imaj oluşturmaya çalıştık. Sanırım bunda da başarılı olduk. Bugün artık mesleğimizin böyle bir imaja ve tanıtıma ihtiyacı
bir oda olduğumuz bilinsin, yaptığımız iş de zeminde görünsün istedik. Biz böyle bir imaj oluşturmaya çalıştık. Sanırım bunda da başarılı olduk. Bugün artık mesleğimizin böyle bir imaja ve tanıtıma ihtiyacı
YERSEL YÖNTEMLERLE ÖLÇÜLEN JEODEZİK AĞLARIN ÜÇ BOYUTLU DENGELENMESİ
 23 YERSEL YÖNTEMLERLE ÖLÇÜLEN JEODEZİK AĞLARIN ÜÇ BOYUTLU DENGELENMESİ Veysel ATASOY İ, GİRİŞ Jeodezinin günümüzdeki tanımı, üç boyutlu ve zaman değişkenli bir uzayda yerin çekim alanını da kapsamak koşuluyla
23 YERSEL YÖNTEMLERLE ÖLÇÜLEN JEODEZİK AĞLARIN ÜÇ BOYUTLU DENGELENMESİ Veysel ATASOY İ, GİRİŞ Jeodezinin günümüzdeki tanımı, üç boyutlu ve zaman değişkenli bir uzayda yerin çekim alanını da kapsamak koşuluyla
Harita Projeksiyonları
 Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları
 JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
BÖLÜM 1 ÖLÇME BİLGİSİNE GİRİŞ
 BÖLÜM 1 ÖLÇME BİLGİSİNE GİRİŞ Kavramsal Kazanımlar: Yeryuvarının matematiksel ve fiziksel şekli, jeodezik metrolojinin konusu ve ölçü büyüklükleri, belirsizlik ve hata kavramı, koordinat sistemleri ve
BÖLÜM 1 ÖLÇME BİLGİSİNE GİRİŞ Kavramsal Kazanımlar: Yeryuvarının matematiksel ve fiziksel şekli, jeodezik metrolojinin konusu ve ölçü büyüklükleri, belirsizlik ve hata kavramı, koordinat sistemleri ve
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ
 HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Konuları_Ders# 5 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ JEODEZİ Yeryuvarının şekil,
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Konuları_Ders# 5 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ JEODEZİ Yeryuvarının şekil,
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Ağırlık ve Ters Ağırlık (Kofaktör) Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 016 AĞIRLIK
DENGELEME HESABI-I DERS NOTLARI Ağırlık ve Ters Ağırlık (Kofaktör) Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 016 AĞIRLIK
NİRENGİ ÂĞLARININ DEĞERLENDİRİLMESİ. Ergün ÖZTÜRK ÖZET
 NİRENGİ ÂĞLARININ DEĞERLENDİRİLMESİ ÖZET Ergün ÖZTÜRK Büyük ölçekli jeodezik çalışmaların tek bir birim sistemde hesaplanan nirengi ağlarına dayandırılmasında sayısız yararlar bulunmaktadır* Bu amaçla
NİRENGİ ÂĞLARININ DEĞERLENDİRİLMESİ ÖZET Ergün ÖZTÜRK Büyük ölçekli jeodezik çalışmaların tek bir birim sistemde hesaplanan nirengi ağlarına dayandırılmasında sayısız yararlar bulunmaktadır* Bu amaçla
Datum: Herhangi bir noktanın yatay ve düşey konumunu tanımlamak için başlangıç alınan referans yüzeyidir.
 İçindekiler Projeksiyon ve Dönüşümleri... 1 Dünyanın Şekli ve Referans Yüzeyler... 1 1. Projelsiyon Nedir?... 1 2. Koordinat Sistemleri... 1 3. Coğrafi Koordinat Sistemleri... 2 4. Projeksiyon Koordinat
İçindekiler Projeksiyon ve Dönüşümleri... 1 Dünyanın Şekli ve Referans Yüzeyler... 1 1. Projelsiyon Nedir?... 1 2. Koordinat Sistemleri... 1 3. Coğrafi Koordinat Sistemleri... 2 4. Projeksiyon Koordinat
Fotogrametride işlem adımları
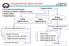 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
TUSAGA-AKTİF CORS İSTASYONLARININ YER DEĞİŞİKLİĞİNİN AĞ BAZLI RTK ÖLÇÜMLERİNE ETKİSİ. Sermet Öğütcü, İbrahim Kalaycı Necmettin Erbakan Üniversitesi
 TUSAGA-AKTİF CORS İSTASYONLARININ YER DEĞİŞİKLİĞİNİN AĞ BAZLI RTK ÖLÇÜMLERİNE ETKİSİ Sermet Öğütcü, İbrahim Kalaycı Necmettin Erbakan Üniversitesi ÇALIŞMA BÖLGESİ ÖLÇÜMLER Konya Aksaray-Cihanbeyli-Yunak
TUSAGA-AKTİF CORS İSTASYONLARININ YER DEĞİŞİKLİĞİNİN AĞ BAZLI RTK ÖLÇÜMLERİNE ETKİSİ Sermet Öğütcü, İbrahim Kalaycı Necmettin Erbakan Üniversitesi ÇALIŞMA BÖLGESİ ÖLÇÜMLER Konya Aksaray-Cihanbeyli-Yunak
Uzay Geriden Kestirme
 Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl
 İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
1. GLOBAL POSITONING SYSTEM HAKKINDA GENEL BİLGİLER
 1. GLOBAL POSITONING SYSTEM HAKKINDA GENEL BİLGİLER Global Positioning System (GPS), A.B.D. Savunma Dairesi tarafından geliştirilen, konumlama ve navigasyon amaçlı kulanılan uydular kümesidir. Bu uydu
1. GLOBAL POSITONING SYSTEM HAKKINDA GENEL BİLGİLER Global Positioning System (GPS), A.B.D. Savunma Dairesi tarafından geliştirilen, konumlama ve navigasyon amaçlı kulanılan uydular kümesidir. Bu uydu
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3351 3 4 3 0 0 DERSİN
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3351 3 4 3 0 0 DERSİN
Coğrafi Bilgi Sistemlerine Giriş. Ünite 3 - Coğrafi Konumlandırma
 Coğrafi Bilgi Sistemlerine Giriş Ünite 3 - Coğrafi Konumlandırma İçerik Giriş Yerkürenin matematiksel modeli Yerküre üzerinde haritalanacak bölgenin matematiksel modeli (datum) GİRİŞ Yeryüzündeki bir mekanın
Coğrafi Bilgi Sistemlerine Giriş Ünite 3 - Coğrafi Konumlandırma İçerik Giriş Yerkürenin matematiksel modeli Yerküre üzerinde haritalanacak bölgenin matematiksel modeli (datum) GİRİŞ Yeryüzündeki bir mekanın
T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA
 T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA ÇİFT STANDART DAİRELİ KONFORM LAMBERT PROJEKSİYONUNDA TÜRKİYE HARİTASININ YAPILMASI Hrt. Tğm. Soner ÖZDEMİR
T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA ÇİFT STANDART DAİRELİ KONFORM LAMBERT PROJEKSİYONUNDA TÜRKİYE HARİTASININ YAPILMASI Hrt. Tğm. Soner ÖZDEMİR
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
E.Ömür DEMİRKOL, Mehmet Ali GÜRDAL, Abdullah YILDIRIM
 AVRUPA DATUMU 1950 (EUROPEAN DATUM 1950: ED-50) İLE DÜNYA JEODEZİK SİSTEMİ 1984 (WORLD GEODETIC SYSTEM 1984: WGS84) ARASINDA DATUM (KOORDİNAT) DÖNÜŞÜMÜ VE ASKERİ UYGULAMALARI ÖZET E.Ömür DEMİRKOL, Mehmet
AVRUPA DATUMU 1950 (EUROPEAN DATUM 1950: ED-50) İLE DÜNYA JEODEZİK SİSTEMİ 1984 (WORLD GEODETIC SYSTEM 1984: WGS84) ARASINDA DATUM (KOORDİNAT) DÖNÜŞÜMÜ VE ASKERİ UYGULAMALARI ÖZET E.Ömür DEMİRKOL, Mehmet
JEODEZİK AĞLARIN TASARIMI (JEODEZİK AĞLARIN SINIFLANDIRILMASI, TÜRKİYE ULUSAL JEODEZİK AĞLARI)
 JEODEZİK AĞLARIN TASARIMI (JEODEZİK AĞLARIN SINIFLANDIRILMASI, TÜRKİYE ULUSAL JEODEZİK AĞLARI) 3.hafta, Ders 2 Prof. Dr. Mualla YALÇINKAYA, 2007 Yrd. Doç. Dr. Emine TANIR KAYIKÇI, 2017 Yeryüzünün bütününün
JEODEZİK AĞLARIN TASARIMI (JEODEZİK AĞLARIN SINIFLANDIRILMASI, TÜRKİYE ULUSAL JEODEZİK AĞLARI) 3.hafta, Ders 2 Prof. Dr. Mualla YALÇINKAYA, 2007 Yrd. Doç. Dr. Emine TANIR KAYIKÇI, 2017 Yeryüzünün bütününün
Uzaktan Algılama ve Coğrafi Bilgi Sistemlerinde Jeodezik Kavramlar
 Uzaktan Algılama ve Coğrafi Bilgi Sistemlerinde Jeodezik Kavramlar TASLAK DERS NOTU Doç.Dr. Niyazi Arslan Çukurova Üniversitesi, Harita Mühendisliği Bölümü, Ceyhan, Adana, 2014 İçindekiler Giriş Referans
Uzaktan Algılama ve Coğrafi Bilgi Sistemlerinde Jeodezik Kavramlar TASLAK DERS NOTU Doç.Dr. Niyazi Arslan Çukurova Üniversitesi, Harita Mühendisliği Bölümü, Ceyhan, Adana, 2014 İçindekiler Giriş Referans
GPS/INS Destekli Havai Nirengi
 GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
Küresel Konumlama Sistemi Yrd. Doç. Dr. Okan Yıldız Yrd. Doç. Dr. Mustafa Dihkan Öğr.Gör.Dr. Deniztan Ulutaş
 Küresel Konumlama Sistemi Yrd. Doç. Dr. Okan Yıldız Yrd. Doç. Dr. Mustafa Dihkan Öğr.Gör.Dr. Deniztan Ulutaş Ölçme Bilgisi Ders Notları 2015-2016 Bahar Yarıyılı Golabal Positioning System(GPS) Nedir? Küresel
Küresel Konumlama Sistemi Yrd. Doç. Dr. Okan Yıldız Yrd. Doç. Dr. Mustafa Dihkan Öğr.Gör.Dr. Deniztan Ulutaş Ölçme Bilgisi Ders Notları 2015-2016 Bahar Yarıyılı Golabal Positioning System(GPS) Nedir? Küresel
JEODEZİK GPS AĞLARINDA DUYARLIK ve
 I. ULUSAL MÜHENDİSLİK ÖLÇMELERİ SEMPOZYUMU JEODEZİK GPS AĞLARINDA DUYARLIK ve GÜVEN ANALİZİ Mualla YALÇINKAYA Kamil TEKE Temel BAYRAK mualla@ktu.edu.tr k_teke@ktu.edu.tr temelbayrak@hotmail.com ÇALIŞMANIN
I. ULUSAL MÜHENDİSLİK ÖLÇMELERİ SEMPOZYUMU JEODEZİK GPS AĞLARINDA DUYARLIK ve GÜVEN ANALİZİ Mualla YALÇINKAYA Kamil TEKE Temel BAYRAK mualla@ktu.edu.tr k_teke@ktu.edu.tr temelbayrak@hotmail.com ÇALIŞMANIN
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Dengeleme Hesabı Adımları, En Küçük Kareler İlkesine Giriş, Korelasyon Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita
DENGELEME HESABI-I DERS NOTLARI Dengeleme Hesabı Adımları, En Küçük Kareler İlkesine Giriş, Korelasyon Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita
UYDU JEODEZISI: ÖLÇME YÖNTEM VE TEKNIKLERI
 UYDU JEODEZISI: ÖLÇME YÖNTEM VE TEKNIKLERI Gözlem noktasına baglı yöntemler: Yerden uyduya Uydudan yer noktasına Uydudan uyduya Ölçünün cinsine baglı yöntemler: Dogrultu ölçmeleri (geometrik yöntem) Çift
UYDU JEODEZISI: ÖLÇME YÖNTEM VE TEKNIKLERI Gözlem noktasına baglı yöntemler: Yerden uyduya Uydudan yer noktasına Uydudan uyduya Ölçünün cinsine baglı yöntemler: Dogrultu ölçmeleri (geometrik yöntem) Çift
MADDESEL NOKTANIN EĞRİSEL HAREKETİ
 Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
TEMEL HARİTACILIK BİLGİLERİ. Erkan GÜLER Haziran 2018
 TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
İnşaat Mühendisliğine Giriş İNŞ-101. Yrd.Doç.Dr. Özgür Lütfi Ertuğrul
 İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
HARİTA PROJEKSİYONLARI
 1 HARİTA PROJEKSİYONLARI Haritacılık mesleğinin faaliyetlerinden birisi, yeryüzünün bütününün ya da bir parçasının haritasını yapmaktır. Harita denilen şey ise, basit anlamıyla, kapsadığı alandaki çeşitli
1 HARİTA PROJEKSİYONLARI Haritacılık mesleğinin faaliyetlerinden birisi, yeryüzünün bütününün ya da bir parçasının haritasını yapmaktır. Harita denilen şey ise, basit anlamıyla, kapsadığı alandaki çeşitli
Bölüm-4. İki Boyutta Hareket
 Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Dünyanın dönmesi: Yer sabit -> gök sistemleri arasındaki dönüşüm r gök = Qr yer-sabit Neden dünyanın dönmesi ile ilgileniyoruz?
 Dünyanın Dönmesi Dünyanın dönmesi: Yer sabit -> gök sistemleri arasındaki dönüşüm r gök = Qr yer-sabit Neden dünyanın dönmesi ile ilgileniyoruz? yer sistemi ve gök sistemini ilişkilendirmek istiyoruz quasarlar
Dünyanın Dönmesi Dünyanın dönmesi: Yer sabit -> gök sistemleri arasındaki dönüşüm r gök = Qr yer-sabit Neden dünyanın dönmesi ile ilgileniyoruz? yer sistemi ve gök sistemini ilişkilendirmek istiyoruz quasarlar
JEODEZİ DATUM KOORDİNAT SİSTEMLERİ HARİTA PROJEKSİYONLARI
 JEODEZİ DATUM KOORDİAT SİSTEMLERİ HARİTA PROJEKSİYOLARI Yer yüzeyi eredeyim? Deniz Elipsoid Geoid BÜ KRDAE JEODEZİ AABİLİM DALI Jeodezi; Yeryuvarının şekil, boyut, ve gravite alanı ile zamana bağlı değişimlerinin
JEODEZİ DATUM KOORDİAT SİSTEMLERİ HARİTA PROJEKSİYOLARI Yer yüzeyi eredeyim? Deniz Elipsoid Geoid BÜ KRDAE JEODEZİ AABİLİM DALI Jeodezi; Yeryuvarının şekil, boyut, ve gravite alanı ile zamana bağlı değişimlerinin
MEKANİZMA TEKNİĞİ (3. Hafta)
 MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
İÇİNDEKİLER. Ön Söz...2. Noktanın Analitik İncelenmesi...3. Doğrunun Analitiği Analitik Düzlemde Simetri...25
 İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Mühendislikte İstatistik Yöntemler
 .0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
.0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
CBS ALTLıK HARİTA BİLGİLERİ, HARİTALARıN SıNıFLANDıRMA - SıNıRLAMALARI
 CBS ALTLıK HARİTA BİLGİLERİ, HARİTALARıN SıNıFLANDıRMA - SıNıRLAMALARI Doç.Dr. Tolga ÇAN Çukurova Üniversitesi, Mühendislik fakültesi Jeoloji Mühendisliği Bölümü HARİTANIN TANIMI: Yeryüzünün tamamının
CBS ALTLıK HARİTA BİLGİLERİ, HARİTALARıN SıNıFLANDıRMA - SıNıRLAMALARI Doç.Dr. Tolga ÇAN Çukurova Üniversitesi, Mühendislik fakültesi Jeoloji Mühendisliği Bölümü HARİTANIN TANIMI: Yeryüzünün tamamının
T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.
![T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir. T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.](/thumbs/55/35591809.jpg) * = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
* = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
Veri toplama- Yersel Yöntemler Donanım
 Veri toplama- Yersel Yöntemler Donanım Data Doç. Dr. Saffet ERDOĞAN 1 Veri toplama -Yersel Yöntemler Optik kamera ve lazer tarayıcılı ölçme robotu Kameradan gerçek zamanlı veri Doç. Dr. Saffet ERDOĞAN
Veri toplama- Yersel Yöntemler Donanım Data Doç. Dr. Saffet ERDOĞAN 1 Veri toplama -Yersel Yöntemler Optik kamera ve lazer tarayıcılı ölçme robotu Kameradan gerçek zamanlı veri Doç. Dr. Saffet ERDOĞAN
AVRASYA ÜNİVERSİTESİ
 Ders Tanıtım Formu Dersin Adı Öğretim Dili MATEMATİK JEODEZİ Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x) Uzaktan Öğretim(
Ders Tanıtım Formu Dersin Adı Öğretim Dili MATEMATİK JEODEZİ Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x) Uzaktan Öğretim(
TRABZON İLİ İÇİN JEOİD ONDÜLASYONLARI BELİRLEME AMACIYLA ENTERPOLASYON YÖNTEMLERİNİN UYGULANMASI
 TMMOB Harita ve Kadastro Mühendisleri Odası, 15. Türkiye Harita Bilimsel ve Teknik Kurultayı, 25 28 Mart 2015, Ankara. TRABZON İLİ İÇİN JEOİD ONDÜLASYONLARI BELİRLEME AMACIYLA ENTERPOLASYON YÖNTEMLERİNİN
TMMOB Harita ve Kadastro Mühendisleri Odası, 15. Türkiye Harita Bilimsel ve Teknik Kurultayı, 25 28 Mart 2015, Ankara. TRABZON İLİ İÇİN JEOİD ONDÜLASYONLARI BELİRLEME AMACIYLA ENTERPOLASYON YÖNTEMLERİNİN
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON
 JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
JEODEZİ. Şekil1: Yerin şekli YERİN ŞEKLİ JEOİD
 JEODEZİ Jeodezi, üç boyutlu ve zaman değişkenli uzayda, çekim alanı ile birlikte, yeryuvarının ve öteki gök cisimlerinin ölçülmesi ve haritaya aktarılması ile uğraşan bilim dalıdır. Şekil1: Yerin şekli
JEODEZİ Jeodezi, üç boyutlu ve zaman değişkenli uzayda, çekim alanı ile birlikte, yeryuvarının ve öteki gök cisimlerinin ölçülmesi ve haritaya aktarılması ile uğraşan bilim dalıdır. Şekil1: Yerin şekli
GNSS Teknikleri ve Uygulamaları
 GNSS Teknikleri ve Uygulamaları Yrd. Doç. Dr. Sefa YALVAÇ Gümüşhane, 2017 Gümüşhane Üniversitesi, 2017 Versiyon: 2017.0 Bölüm-1 Tarihçe Tarih boyunca insanlar, Neredeyim? Nereye gidiyorum? sorularına cevap
GNSS Teknikleri ve Uygulamaları Yrd. Doç. Dr. Sefa YALVAÇ Gümüşhane, 2017 Gümüşhane Üniversitesi, 2017 Versiyon: 2017.0 Bölüm-1 Tarihçe Tarih boyunca insanlar, Neredeyim? Nereye gidiyorum? sorularına cevap
Manyetik Alanlar. Benzer bir durum hareketli yükler içinde geçerli olup bu yüklerin etrafını elektrik alana ek olarak bir manyetik alan sarmaktadır.
 Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
ARAZİ ÖLÇMELERİ. İki Boyutlu Koordinat sistemleri Arası Dönüşüm
 İki Boyutlu Koordinat sistemleri Arası Dönüşüm Amaç, bir koordinat sistemine göre elde edilmiş olan koordinatların, diğer bir koordinat sistemindeki koordinat değerlerini elde etmektir. İki haritanın koordinat
İki Boyutlu Koordinat sistemleri Arası Dönüşüm Amaç, bir koordinat sistemine göre elde edilmiş olan koordinatların, diğer bir koordinat sistemindeki koordinat değerlerini elde etmektir. İki haritanın koordinat
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ
 HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Kavramları_Ders#4 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ Çevre Düzeni Planı: Ülke ve
HRT 105 HARİTA MÜHENDİSLİĞİNE GİRİŞ Temel Haritacılık Kavramları_Ders#4 Yrd.Doç.Dr. H.Ebru ÇOLAK KTÜ. Mühendislik Fakültesi Harita Mühendisliği Bölümü TEMEL HARİTA BİLGİLERİ Çevre Düzeni Planı: Ülke ve
Hakan AKÇIN* SUNU Ali ihsan ŞEKERTEKİN
 AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
Koordinat Dönüşümleri (V )
 KOORDİNAT DÖNÜŞÜMLERİ ve FARKLI KOORDİNAT SİSTEMLERİ İLE ÇALIŞMA FieldGenius ile birden fazla koordinat sistemi arasında geçiş yaparak çalışmak mümkündür. Yaygın olarak kullanılan masaüstü harita ve CAD
KOORDİNAT DÖNÜŞÜMLERİ ve FARKLI KOORDİNAT SİSTEMLERİ İLE ÇALIŞMA FieldGenius ile birden fazla koordinat sistemi arasında geçiş yaparak çalışmak mümkündür. Yaygın olarak kullanılan masaüstü harita ve CAD
TOPOĞRAFYA. Ölçme Bilgisinin Konusu
 TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
HARİTA. Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir.
 HARİTA BİLGİSİ HARİTA Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir. ÇEŞİTLİ ÖLÇEKLİ HARİTALARIN NUMARALANMA SİSTEMİ
HARİTA BİLGİSİ HARİTA Harita,yeryüzünün bütününü yada bir parçasını tam tepeden görünüşe göre ve belli oranlarda küçültülmüş olarak gösteren çizimlerdir. ÇEŞİTLİ ÖLÇEKLİ HARİTALARIN NUMARALANMA SİSTEMİ
 hkm Jeodezi, Jeoinformasyon ve Arazi Yönetimi Dergisi 2005/2 Sayý 93 www.hkmo.org.tr Klasik Yöntemlerle Üretilmiþ Kontrol Noktalarýnýn (Poligon Noktalarýnýn) GPS Koordinatlarý ile Karþýlaþtýrýlmasýna Ýliþkin
hkm Jeodezi, Jeoinformasyon ve Arazi Yönetimi Dergisi 2005/2 Sayý 93 www.hkmo.org.tr Klasik Yöntemlerle Üretilmiþ Kontrol Noktalarýnýn (Poligon Noktalarýnýn) GPS Koordinatlarý ile Karþýlaþtýrýlmasýna Ýliþkin
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON
 JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
MESLEKİ HESAPLAMALAR
 MESLEKİ HESAPLAMALAR Jeodezi: Yer yuvarı şekil, boyut ve granite alanı ile zamana bağlı değişmelerin üç boyutlu bir koordinat sisteminde tanımlanmasını amaçlayan bir bilim dalıdır. Jeodezinin Bilimsel
MESLEKİ HESAPLAMALAR Jeodezi: Yer yuvarı şekil, boyut ve granite alanı ile zamana bağlı değişmelerin üç boyutlu bir koordinat sisteminde tanımlanmasını amaçlayan bir bilim dalıdır. Jeodezinin Bilimsel
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar
 Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Âna nirengi doğrultuları için p = 1 m 2 o Ara nirengi doğrultuları için p a =------------ m\
 4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
