Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
|
|
|
- Bora Ilkin
- 7 yıl önce
- İzleme sayısı:
Transkript
1 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu Öğretim Yılı Güz Dönemi
2 İzdüşüm merkezi(o): Kamera optik sisteminin merkezidir. İzdüşüm ışını: POP doğru parçasını oluşturan ışın. Asal uzaklık: Fotoğraf düzlemi ile izdüşüm merkezi arasında ki uzaklık (c).
3 Asal Nokta: Bu nokta aynı zaman da kamera ekseninin fotoğraf düzlemini ve nesne yüzeyini deldiği H ve H noktasıdır.
4 Ayak ucu (Nadir) Noktası (NN ): İzdüşüm merkezinden geçen çekül doğrusu fotoğraf ve araziyi ayak ucu noktasında keser.
5 Yaşayan,2011
6 1. Paralel izdüşüm: Bir d doğrusuna paralel izdüşüm doğruları çizerek izdüşüm düzlemini deldiği noktalar bulunur
7 2. Dik (Ortogonal) izdüşüm: Noktalardan izdüşüm düzlemine dikler inilir. Bu noktalar nesnenin izdüşüm noktasıdır. Harita, dik bir izdüşümdür. İzdüşüm düzlemi olarak yeryüzünün belirli bir noktasına teğet olan bir düzlem alınır. Genellikle bu düzey deniz yüzeyine paralel bir düzlemdir ve dik izdüşüm küçültülerek kâğıda aktarılır.
8 3. Merkezsel izdüşüm: Uzay noktaları izdüşüm düzlemi dışındaki bir O noktası ile birleştirilir. Bu doğruların düzlemi deldiği noktalar ilgili noktaların merkezsel izdüşümüdür. O noktası izdüşüm merkezidir. Merkezsel izdüflüm Pozitif konum Merkezsel izdüflüm negatif konum
9 3. Merkezsel izdüşüm: O izdüşüm merkezi şekildeki gibi, nesne noktaları ile izdüşüm düzlemi arasında da olabilir. Fotoğraf, merkezsel bir izdüşlümdür. O izdüşüm merkezi, kamera optik sisteminin merkezidir. Tüm izdüşüm ışınları bu noktadan geçer. Geometrik olarak bir harita ile düşey bir hava fotoğrafı arasında en önemli fark, farklı izdüşüm sonucu oluşmalarıdır. Merkezsel izdüflüm Pozitif konum Merkezsel izdüflüm negatif konum
10 Merkezsel izdüşümün Özellikleri Üç boyutlu uzayda bir A noktasına karşılık izdüşüm düzleminde tek bir A noktası vardır. İzdüşüm düzlemindeki A noktasına karşılık ise A O izdüşüm ışını üzerinde bulunan sonsuz sayıda nokta karşılık gelir. Ölçme noktalarının bulunduğu uzay, yani arazi üç boyutludur. Bu noktaların konumları A (X,Y,Z) koordinatları bir tek fotoğraftan elde edilemez. (ancak en az iki fotoğraftan elde edilebilir). Çifte oran özelliği: bir doğru üzerinde bulunan dört nokta için yazılacak bir çifte oran, merkezsel izdüşümde sabittir. Merkezsel İzdüşümün Özelliklerini Araştırın!
11 Üç boyutlu uzaydaki bir d doğrusuna karşılık izdüşüm düzleminde bir tek d' doğrusu vardır. İzdüşüm düzlemindeki bir d' doğrusuna d doğrusu ve O izdüşüm merkezinin belirlediği düzlem üzerinde sonsuz sayıda doğru parçası karşılık gelir. Uzayda birbirine paralel olan fakat izdüşüm düzlemine paralel olmayan doğruların izdüşümleri kesişir Merkezsel izdüşümde paralel doğrular
12 İzdüşüm düzlemine paralel olan birbirine paralel doğrular izdüşüm düzleminde de birbirine paralel kalır. Tek gözümüzde oluşan görüntü aslında merkezsel izdüşümdür ve çevremizdeki nesneleri gözlememizde her zaman perspektif kurallar geçerlidir.
13 Bir doğru üzerinde bulunan dört nokta için yazılacak bir çifte oran, merkezsel izdüşümde değişmez kalır. Buna çifte oran özelliği denir. Bilinen üç doğrultu yardımı ile fotoğrafta bulunan dördüncü bir doğrultunun nesne uzayındaki ya da haritadaki karflılığı bulunabilir.
14 Tek bir fotoğraftan ölçme uzayındaki noktaların X,Y,Z koordinatları elde edilemez. Ölçme uzayındaki noktalar bir düzlemde bulunuyorsa, ölçüm için bir tek fotoğraf yeterlidir. Ölçüm uzayındaki noktaların konumlarının, yani X,Y,Z koordinatlarının bulunması için başka bir noktadan çekilmiş ikinci bir fotoğraf gereklidir. Böylece aynı noktaya ait iki izdüşüm ışını nesne noktasında kesiştirilebilecektir.
15 MATEMATİK TEMELLER Fotogrametride Kullanılan Koordinat Sistemleri Fotoğraf Koordinat sistemi Fotoğraf koordinat sistemi eksenleri cisim koordinat sistemiyle aynı yönde olan ve sağ el koordinat sistemine uyan xyz koordinat sistemidir. Başlangıç noktası O izdüşüm merkezidir. xy düzlemi fotoğraf düzlemine paralel, z ekseni de kamera ekseni ile çakışıktır. x ekseni komşu fotoğrafın izdüşüm merkezi doğrultusundadır. Bu yön hava fotogrametrisinde, yaklaşık olarak uçuş çizgisi doğrultusudur. Noktaların z koordinatı sabit ve asal uzaklığa eşittir.
16 Uzay Koordinat Sistemi Fotogrametride nesne uzayındaki noktalar uzay koordinatları ile tanımlanır. Uzay koordinat sistemi, X ekseni pozitif yönü uçuş yönü doğrultusunda (hava fotogrametrisi için), Z ekseni XY düzlemine dik ve sağ el koordinat sistemine uyan dik bir XYZ koordinat sistemidir. Başlangıç noktasının seçimi serbesttir. Ancak Z (H) ekseni her durumda düşey doğrultuda, XY düzlemi de her zaman yatay bir düzlemdir
17 Matematik temeller Koordinat Dönüşümü İki boyutlu koordinat dönüşümü (Benzerlik dönüşümü)
18 İki boyutlu koordinat dönüşümü (Benzerlik dönüşümü) Başlangıçları farklı, aralarında α kadar dönüklük ve ölçek
19 Benzerlik dönüşümünde 1 ölçek, 1 dönüklük ve 2 öteleme parametresi İki koordinat sistemi arasındaki dönüşüm parametrelerinin bulunması için, her iki sistemde de koordinatları bilinen, ortak noktaya ihtiyaç duyulur.
20 Kaynak: Yaşayan, 2011 İki Boyutlu Affin Dönüşümü İki boyutlu Affin dönüşümü
21 Üç boyutlu koordinat dönüşümü Başlangıçları aynı olan iki üç boyutlu dik koordinat sistemi (kartezyen koordinat sistemi) arasındaki dönüşüm Bu iki koordinat sistemi arasında bir ölçek katsayısı ve öteleme varsa, genel bir üç boyutlu benzerlik dönüşümü formülü
22 Dönüşüm Matrisi (Ortogonal Matris) Dönüşüm formüllerindeki λa dönüşüm matrisi uzunlukları, λ katsayısı oranında değiştirilir. Ancak bu durumda şeklin benzerliği değişmez, açılar aynı kalır. Bu nedenle bu dönüşüme benzerlik dönüşümü denir. λ = 1 durumunda dönüşüm özel bir dönüşümdür ki buna ortogonal dönüşüm denir. Fotogrametride sembolik olarak tanımlanan A dönüşüm matrisi ortogonal bir matristir. Ortogonal matrisin özellikleri nelerdir?
23
24 Her eleman kendisinin kofaktörüne eşit ya da ters işaretlisidir. a11 için bu bağıntılar yazılırsa;
25 O izdüşüm merkezine paralel XYZ uzay koordinat sistemi ele alınsın Elde edilen xyz koordinat sistemi ve bu eksenler etrafında dönüklük açıları X-ekseni çevresindeki dönüklük v (omega ) Y-ekseni çevresindeki dönüklük ϕ ( fi ) Z-ekseni çevresindeki dönüklük k ( kappa )
26
27 Üç öteleme ve üç dönüklükten oluşan altı elemana bir fotoğrafın dış yöneltme elemanları denir. Bir fotoğrafın altı dış yöneltme elemanı: izdüşüm merkezinin üç koordinatı (Xo,Yo,Zo) ve fotoğraf koordinat sisteminin üç dönüklüğü (v, ϕ, k) dür.
28 Fotoğraf koordinat sisteminin arazi koordinat sistemine göre dönüklüğünü ifade eden A matrisi, her biri ortogonal olan ve düzlem dönüklükten elde edilen üç matrisin arka arkaya çarpılmaları ile elde edilen bir matristir. Av, Aϕ, Ak ya kısmi dönüklük matrisleri denir. Matris çarpımlarında sıra önemlidir.
29
30 Benzerlik dönüşüm formülleri A noktasının koordinat dönüşümü: B noktasının koordinat dönüşümü:
31 Dönüşüm parametrelerinin hesabı İki koordinat sistemi arasındaki dönüşüm parametrelerinin bulunması için, her iki sistemde de koordinatları bilinen, ortak noktaya ihtiyaç duyulur. P1 ve P2 noktalarının 1. koordinat sistemindeki koordinatları sırasıyla (x1, y1) ve (x2, y2), 2. koordinat sistemindeki koordinatlar (X1, Y1) ve (X2, Y2) olsun. P1 ve P2 noktaları için dönüşüm denklemleri aşağıdaki gibi yazılır.
32
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI
 FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI
 FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Parametrik doğru denklemleri 1
 Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Aycan M. MARANGOZ
 FOTOGRAMETRİ II GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
FOTOGRAMETRİ II GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
FOTOYORUMLAMA UZAKTAN ALGILAMA
 FOTOYORUMLAMA VE UZAKTAN ALGILAMA (Photointerpretation and Remote Sensing) 1 Ders İçeriği Hava fotoğrafının tanımı Fotogrametrinin geometrik ilkeleri Fotogrametride fotoğrafik temel ilkeler Stereoskopik
FOTOYORUMLAMA VE UZAKTAN ALGILAMA (Photointerpretation and Remote Sensing) 1 Ders İçeriği Hava fotoğrafının tanımı Fotogrametrinin geometrik ilkeleri Fotogrametride fotoğrafik temel ilkeler Stereoskopik
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur.
 Üç Boyutlu Geometri Nokta (Point,Vertex) Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur. Kartezyen Koordinat Sistemi Uzayda bir noktayı tanımlamak
Üç Boyutlu Geometri Nokta (Point,Vertex) Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur. Kartezyen Koordinat Sistemi Uzayda bir noktayı tanımlamak
Fotogrametride işlem adımları
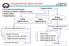 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
ARAZİ ÖLÇMELERİ Z P. O α X P. α = yatay açı. ω = düşey açı. µ =eğim açısı. ω + µ = 100 g
 Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI
 MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI SORU 1. Köşeleri (1,4) (3,0) (7,2) noktaları olan ABC üçgeninin bir ikizkenar dik üçgen (İpucu:, ve vektörlerinden yararlanın) SORU 2. Bir ABC üçgeninin
MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI SORU 1. Köşeleri (1,4) (3,0) (7,2) noktaları olan ABC üçgeninin bir ikizkenar dik üçgen (İpucu:, ve vektörlerinden yararlanın) SORU 2. Bir ABC üçgeninin
3. V, R 3 ün açık bir altkümesi olmak üzere, c R. p noktasında yüzeye dik olduğunu gösteriniz.(10
 Diferenisyel Geometri 2 Yazokulu 2010 AdıSoyadı: No : 1. ϕ (u, v) = ( u + 2v, v + 2u, u 2 v ) parametrizasyonu ile verilen M kümesinin bir regüler yüzey olduğunu gösteriniz. (15 puan) 3. V, R 3 ün açık
Diferenisyel Geometri 2 Yazokulu 2010 AdıSoyadı: No : 1. ϕ (u, v) = ( u + 2v, v + 2u, u 2 v ) parametrizasyonu ile verilen M kümesinin bir regüler yüzey olduğunu gösteriniz. (15 puan) 3. V, R 3 ün açık
TASARI GEOMETRİ SINAV SORULARI
 TASARI GEOMETRİ SINAV SORULARI 1. Alın iz düşümüne parelel veya çakışık olan doğrular profilde hangi ı verir? 9. Doğrunun düzlemi deldiği noktayı düzlem geçirme metodu ile bulunuz. A) Profil ve alınla
TASARI GEOMETRİ SINAV SORULARI 1. Alın iz düşümüne parelel veya çakışık olan doğrular profilde hangi ı verir? 9. Doğrunun düzlemi deldiği noktayı düzlem geçirme metodu ile bulunuz. A) Profil ve alınla
İÇİNDEKİLER. Ön Söz...2. Noktanın Analitik İncelenmesi...3. Doğrunun Analitiği Analitik Düzlemde Simetri...25
 İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
İÇİNDEKİLER Ön Söz...2 Noktanın Analitik İncelenmesi...3 Doğrunun Analitiği...11 Analitik Düzlemde Simetri...25 Analitik Sistemde Eşitsizlikler...34 Çemberin Analitik İncelenmesi...40 Elips...58 Hiperbol...70
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER
 BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
MHN 113 Teknik Resim ve Tasarı Geometri 2
 6. ÖLÜM İZDÜŞÜM MHN 113 Teknik Resim ve Tasarı Geometri 2 6. İZDÜŞÜM 6.1. GENEL İLGİLER Uzaydaki bir cisim, bir düzlem önünde tutulup bu cisme karşıdan bakılacak olursa, cismin düzlem üzerine bir görüntüsü
6. ÖLÜM İZDÜŞÜM MHN 113 Teknik Resim ve Tasarı Geometri 2 6. İZDÜŞÜM 6.1. GENEL İLGİLER Uzaydaki bir cisim, bir düzlem önünde tutulup bu cisme karşıdan bakılacak olursa, cismin düzlem üzerine bir görüntüsü
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Alan Hesapları. Şekil 14. Üç kenarı belli üçgen alanı
 lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Bölüm 3: Vektörler. Kavrama Soruları. Konu İçeriği. Sunuş. 3-1 Koordinat Sistemleri
 ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
Fotogrametride Koordinat Sistemleri
 Fotogrametride Koordinat Sistemleri Komparator koordinat sistemi, Resim koordinat sistemi / piksel koordinat sistemi, Model veya çekim koordinat sistemi, Jeodezik koordinat sistemi 08 Ocak 2014 Çarşamba
Fotogrametride Koordinat Sistemleri Komparator koordinat sistemi, Resim koordinat sistemi / piksel koordinat sistemi, Model veya çekim koordinat sistemi, Jeodezik koordinat sistemi 08 Ocak 2014 Çarşamba
Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme)
 FOTOGRAMETRİ FOTOGRAMETRİ Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme) Buna göre ışık yardımı ile ölçme (çizim yapabilme)
FOTOGRAMETRİ FOTOGRAMETRİ Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme) Buna göre ışık yardımı ile ölçme (çizim yapabilme)
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme. Yrd. Doç. Dr. Aycan M. MARANGOZ
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
ÖRNEK ÖRNEK ÖRNEK ÖRNEK
 Öteleme ve yansımanın birlikte kullanıldığı dönüşümlere ötelemeli yansıma denir. Düzlemde yansıma ve ötelemeli yansıma dönüşümlerinde uzaklıklar korunurken açıların yönleri değişir. Ötelemeli yansıma dönüşümünde
Öteleme ve yansımanın birlikte kullanıldığı dönüşümlere ötelemeli yansıma denir. Düzlemde yansıma ve ötelemeli yansıma dönüşümlerinde uzaklıklar korunurken açıların yönleri değişir. Ötelemeli yansıma dönüşümünde
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU. Yrd. Doç. Dr. Hüseyin KEMALDERE
 JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
İNS1101 MÜHENDİSLİK ÇİZİMİ. Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018
 İNS1101 MÜHENDİSLİK ÇİZİMİ Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 TEKNİK RESİM Teknik resim, teknik elemanların üretim yapabilmeleri için anlatmak istedikleri teknik özelliklerin biçim ve
İNS1101 MÜHENDİSLİK ÇİZİMİ Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 TEKNİK RESİM Teknik resim, teknik elemanların üretim yapabilmeleri için anlatmak istedikleri teknik özelliklerin biçim ve
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
2. KUVVET SİSTEMLERİ 2.1 Giriş
 2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
Perspektif: Bir cismin bir bakışta, genel olarak üç yüzünün birden görünecek şekilde çizilen resimlerine denir. PERSPEKTİF. Kavaliyer Kabinet Militer
 Perspektif Perspektifler Perspektif: Bir cismin bir bakışta, genel olarak üç yüzünün birden görünecek şekilde çizilen resimlerine denir. PERSPEKTİF ksonometrik perspektif Paralel perspektif Eğik perspektif
Perspektif Perspektifler Perspektif: Bir cismin bir bakışta, genel olarak üç yüzünün birden görünecek şekilde çizilen resimlerine denir. PERSPEKTİF ksonometrik perspektif Paralel perspektif Eğik perspektif
Üç Boyutlu Uzayda Koordinat sistemi
 Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
ARAZİ ÖLÇMELERİ. İki Boyutlu Koordinat sistemleri Arası Dönüşüm
 İki Boyutlu Koordinat sistemleri Arası Dönüşüm Amaç, bir koordinat sistemine göre elde edilmiş olan koordinatların, diğer bir koordinat sistemindeki koordinat değerlerini elde etmektir. İki haritanın koordinat
İki Boyutlu Koordinat sistemleri Arası Dönüşüm Amaç, bir koordinat sistemine göre elde edilmiş olan koordinatların, diğer bir koordinat sistemindeki koordinat değerlerini elde etmektir. İki haritanın koordinat
DÜZLEMDE GERİLME DÖNÜŞÜMLERİ
 3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
1. HAFTA. Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler.
 1. HAFTA Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler. Statikte üç temel büyüklük vardır. Uzay: Fiziksel olayların meydana geldiği geometrik bir bölgedir. İncelenen problemin
1. HAFTA Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler. Statikte üç temel büyüklük vardır. Uzay: Fiziksel olayların meydana geldiği geometrik bir bölgedir. İncelenen problemin
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
ARAZİ ÖLÇMELERİ Z P. O α X P. α = yatay açı. ω = düşey açı. µ =eğim açısı. ω + µ = 100 g
 Trigonometrik Fonksiyonlar ARAZİ ÖLÇMELERİ Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara
Trigonometrik Fonksiyonlar ARAZİ ÖLÇMELERİ Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT RESİM DEĞ. Analog ve Analitik Stereodeğerlendirme. Yrd. Doç. Dr. Aycan M. MARANGOZ
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT RESİM DEĞ. Analog ve Analitik Stereodeğerlendirme BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT RESİM DEĞ. Analog ve Analitik Stereodeğerlendirme BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Bölüm-4. İki Boyutta Hareket
 Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
TEMEL BAZI KAVRAMLAR. Uzay: İçinde yaşadığımız sonsuz boşluktur. Uzay, bir noktalar kümesidir. Uzay, bütün varlıkları içine alır.
 1 TEMEL ZI KVRMLR Nokta: Kalemin kâğıda, tebeşirin tahtaya bıraktığı ize nokta denir. Nokta boyutsuzdur. Yani; noktanın eni, boyu ve yüksekliği yoktur. ütün geometrik şekiller noktalardan oluşur. Noktalar
1 TEMEL ZI KVRMLR Nokta: Kalemin kâğıda, tebeşirin tahtaya bıraktığı ize nokta denir. Nokta boyutsuzdur. Yani; noktanın eni, boyu ve yüksekliği yoktur. ütün geometrik şekiller noktalardan oluşur. Noktalar
UZAYDA VEKTÖRLER ve DOĞRU DÜZLEM
 UD VEKTÖRLER ve DĞRU DÜLEM. ir küpün ayrıtlarını taşıyan doğrular kaç farklı doğrultu oluşturur? ) ) ) D) 7 E) 8. ir düzgün altıgenin en uzun köşegeni ile aynı doğrultuda kaç farklı kenar vardır?. şağıdaki
UD VEKTÖRLER ve DĞRU DÜLEM. ir küpün ayrıtlarını taşıyan doğrular kaç farklı doğrultu oluşturur? ) ) ) D) 7 E) 8. ir düzgün altıgenin en uzun köşegeni ile aynı doğrultuda kaç farklı kenar vardır?. şağıdaki
 LYS Y OĞRU MTMTİK TSTİ LYS-. u testte Matematik ile ilgili soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a ve b asal
LYS Y OĞRU MTMTİK TSTİ LYS-. u testte Matematik ile ilgili soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a ve b asal
TEMEL MEKANİK 5. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları
 JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
1. BÖLÜM uzayda Bir doğrunun vektörel ve parametrik denklemi... 71. 2. BÖLÜM uzayda düzlem denklemleri... 77
 UZAYDA DOĞRU VE DÜZLEM Sayfa No. BÖLÜM uzayda Bir doğrunun vektörel ve parametrik denklemi.............. 7. BÖLÜM uzayda düzlem denklemleri.......................................... 77. BÖLÜM uzayda Bir
UZAYDA DOĞRU VE DÜZLEM Sayfa No. BÖLÜM uzayda Bir doğrunun vektörel ve parametrik denklemi.............. 7. BÖLÜM uzayda düzlem denklemleri.......................................... 77. BÖLÜM uzayda Bir
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm : Azimutal Projeksiyonlar Prof.Dr. İ. Öztuğ BİLDİRİCİ Azimutal Projeksiyonlar Projeksiyon yüzeyi düzlemdir. Normal, transversal ve eğik konumlu olarak uygulanan azimutal projeksiyonlar,
Harita Projeksiyonları Bölüm : Azimutal Projeksiyonlar Prof.Dr. İ. Öztuğ BİLDİRİCİ Azimutal Projeksiyonlar Projeksiyon yüzeyi düzlemdir. Normal, transversal ve eğik konumlu olarak uygulanan azimutal projeksiyonlar,
7. BÖLÜM İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI .= 1 1 + + Genel: Vektörler bölümünde vektörel iç çarpım;
 İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
HARİTA PROJEKSİYONLARI
 1 HARİTA PROJEKSİYONLARI Haritacılık mesleğinin faaliyetlerinden birisi, yeryüzünün bütününün ya da bir parçasının haritasını yapmaktır. Harita denilen şey ise, basit anlamıyla, kapsadığı alandaki çeşitli
1 HARİTA PROJEKSİYONLARI Haritacılık mesleğinin faaliyetlerinden birisi, yeryüzünün bütününün ya da bir parçasının haritasını yapmaktır. Harita denilen şey ise, basit anlamıyla, kapsadığı alandaki çeşitli
HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR
 HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR Harita nedir? Yeryüzünün veya bir parçasının belli bir orana göre küçültülerek ve belirli işaretler kullanılarak yatay düzlem üzerinde gösterilmesine harita adı verilir.
HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR Harita nedir? Yeryüzünün veya bir parçasının belli bir orana göre küçültülerek ve belirli işaretler kullanılarak yatay düzlem üzerinde gösterilmesine harita adı verilir.
TOPOĞRAFYA Topoğrafya Aletleri ve Parçaları (Teodolit)
 TOPOĞRAFYA Topoğrafya Aletleri ve Parçaları (Teodolit) Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Topoğrafya Aletleri ve Parçaları (Teodolit) Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
KUTUPSAL KOORDİNATLAR
 KUTUPSAL KOORDİNATLAR Geometride, bir noktanın konumunu belirtmek için değişik yöntemler uygulanır. Örnek olarak çok kullanılan Kartezyen (Dik ) Koordinat sistemini anımsatarak çalışmamıza başlayalım.
KUTUPSAL KOORDİNATLAR Geometride, bir noktanın konumunu belirtmek için değişik yöntemler uygulanır. Örnek olarak çok kullanılan Kartezyen (Dik ) Koordinat sistemini anımsatarak çalışmamıza başlayalım.
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
TOPOĞRAFYA Takeometri
 TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Dik İzdüşüm Teorisi. Prof. Dr. Muammer Nalbant. Muammer Nalbant
 Dik İzdüşüm Teorisi Prof. Dr. Muammer Nalbant Muammer Nalbant 2017 1 Dik İzdüşüm Terminolojisi Bakış Noktası- 3 boyutlu uzayda bakılan nesneden sonsuz uzaktaki herhangi bir yer. Bakış Hattı- gözlemcinin
Dik İzdüşüm Teorisi Prof. Dr. Muammer Nalbant Muammer Nalbant 2017 1 Dik İzdüşüm Terminolojisi Bakış Noktası- 3 boyutlu uzayda bakılan nesneden sonsuz uzaktaki herhangi bir yer. Bakış Hattı- gözlemcinin
Bilgisayar Grafikleri
 Bilgisayar Grafikleri Konular: Cismin Tanımlanması Bilindiği gibi iki boyutta noktalar x ve y olmak üzere iki boyutun koordinatları şeklinde ifade edilirler. Üç boyutta da üçüncü boyut olan z ekseni üçücü
Bilgisayar Grafikleri Konular: Cismin Tanımlanması Bilindiği gibi iki boyutta noktalar x ve y olmak üzere iki boyutun koordinatları şeklinde ifade edilirler. Üç boyutta da üçüncü boyut olan z ekseni üçücü
3-1 Koordinat Sistemleri Bir cismin konumunu tanımlamak için bir yönteme gereksinim duyarız. Bu konum tanımlaması koordinat kullanımı ile sağlanır.
 Bölüm 3 VEKTÖRLER Bölüm 3: Vektörler Konu İçeriği Sunuş 3-1 Koordinat Sistemleri 3-2 Vektör ve Skaler nicelikler 3-3 Vektörlerin Bazı Özellikleri 3-4 Bir Vektörün Bileşenleri ve Birim Vektörler Sunuş Fizikte
Bölüm 3 VEKTÖRLER Bölüm 3: Vektörler Konu İçeriği Sunuş 3-1 Koordinat Sistemleri 3-2 Vektör ve Skaler nicelikler 3-3 Vektörlerin Bazı Özellikleri 3-4 Bir Vektörün Bileşenleri ve Birim Vektörler Sunuş Fizikte
TEKNİK RESİM. Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi. Perspektifler-2
 TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi Perspektifler-2 2/25 Perspektifler-2 Perspektifler-2 Perspektif Çeşitleri Dimetrik Perspektif Trimetrik Perspektif Eğik Perspektif
TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi Perspektifler-2 2/25 Perspektifler-2 Perspektifler-2 Perspektif Çeşitleri Dimetrik Perspektif Trimetrik Perspektif Eğik Perspektif
Uzayda Simetri. A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır.
![Uzayda Simetri. A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır. Uzayda Simetri. A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır.](/thumbs/55/36610671.jpg) Uzayda Simetri Hazırlayan Halit Çelik Matematik Öğretmeni Noktaya Göre Simetri: A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır. Buna göre şeklinde
Uzayda Simetri Hazırlayan Halit Çelik Matematik Öğretmeni Noktaya Göre Simetri: A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır. Buna göre şeklinde
Uzayda iki doğrunun ortak dikme doğrusunun denklemi
 Uzayda iki doğrunun ortak dikme doğrusunun denklemi Uzayda verilen d 1 ve d aykırı doğrularının ikisine birden dik olan doğruya ortak dikme doğrusu denir... olmak üzere bu iki doğru denkleminde değilse
Uzayda iki doğrunun ortak dikme doğrusunun denklemi Uzayda verilen d 1 ve d aykırı doğrularının ikisine birden dik olan doğruya ortak dikme doğrusu denir... olmak üzere bu iki doğru denkleminde değilse
GPS/INS Destekli Havai Nirengi
 GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
Harita Projeksiyonları ve Koordinat Sistemleri. Doç. Dr. Senem KOZAMAN
 Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Harita Projeksiyonları ve Koordinat Sistemleri Doç. Dr. Senem KOZAMAN Yeryüzü şekilleri ve ayrıntılarının düz bir yüzey üzerinde, belli bir ölçek ve semboller kullanarak, bir referans sisteme göre ifade
Ödev 1. Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N
 Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
Math 103 Lineer Cebir Dersi Final Sınavı
 Haliç Üniversitesi, Uygulamalı Matematik Bölümü Math 3 Lineer Cebir Dersi Final Sınavı 3 Araliık 7 Hazırlayan: Yamaç Pehlivan Başlama saati: : Bitiş Saati: 3:4 Toplam Süre: Dakika Lütfen adınızı ve soyadınızı
Haliç Üniversitesi, Uygulamalı Matematik Bölümü Math 3 Lineer Cebir Dersi Final Sınavı 3 Araliık 7 Hazırlayan: Yamaç Pehlivan Başlama saati: : Bitiş Saati: 3:4 Toplam Süre: Dakika Lütfen adınızı ve soyadınızı
NOKTA, ÇİZGİ VE DÜZLEMİN İZDÜŞÜMÜ
 NOKTA, ÇİZGİ VE DÜZLEMİN İZDÜŞÜMÜ Geometrik elemanlar Geometrik elemanlar noktalar, çizgiler, yüzeyler veya katılar biçiminde kategorize edilir. Nokta Teknik resimde nokta iki çizginin kesişme noktası
NOKTA, ÇİZGİ VE DÜZLEMİN İZDÜŞÜMÜ Geometrik elemanlar Geometrik elemanlar noktalar, çizgiler, yüzeyler veya katılar biçiminde kategorize edilir. Nokta Teknik resimde nokta iki çizginin kesişme noktası
( ) ( ) ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. Cevap D. Cevap C. noktası y ekseni üzerinde ise, a + 4 = 0 A 0, 5 = 1+
 ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. a+ = b 4. a = b 0+ a b a b = b a+ b = 0. A ( a + 4, a) noktası y ekseni üzerinde ise, ( + ) a + 4 = 0 A 0, 5 a = 4 B b, b 0 noktası x ekseni
ÖABT Analitik Geometri KONU TESTİ Noktanın Analitik İncelemesi. a+ = b 4. a = b 0+ a b a b = b a+ b = 0. A ( a + 4, a) noktası y ekseni üzerinde ise, ( + ) a + 4 = 0 A 0, 5 a = 4 B b, b 0 noktası x ekseni
GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Saygın Abdikan
 FOTOGRAMETRİ II GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Saygın Abdikan BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF 330/336 FOTOGRAMETRİ II DERSi NOTLARI
FOTOGRAMETRİ II GEOMETRİK, MATEMATİK, OPTİK ve FOTOĞRAFİK TEMELLER (HATIRLATMA) Yrd. Doç. Dr. Saygın Abdikan BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF 330/336 FOTOGRAMETRİ II DERSi NOTLARI
Doç. Dr. Bilge DORAN
 Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
UZAY KAVRAMI VE UZAYDA DOĞRULAR
 UZAY KAVRAMI VE UZAYDA DOĞRULAR Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusudur. Uzayda ise uzunluk ve genişliğin yanında
UZAY KAVRAMI VE UZAYDA DOĞRULAR Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusudur. Uzayda ise uzunluk ve genişliğin yanında
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları
 TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
3. KUVVET SİSTEMLERİ
 3. KUVVET SİSTEMLERİ F F W P P 3.1 KUVVET KAVRAMI VE ETKİLERİ Kuvvet, bir cisme etki eden yapısal yüklerdir. Kuvvet Şiddeti, yönü ve uygulama noktası olan vektörel bir büyüklüktür. Bir cismin üzerine uygulanan
3. KUVVET SİSTEMLERİ F F W P P 3.1 KUVVET KAVRAMI VE ETKİLERİ Kuvvet, bir cisme etki eden yapısal yüklerdir. Kuvvet Şiddeti, yönü ve uygulama noktası olan vektörel bir büyüklüktür. Bir cismin üzerine uygulanan
Harita Projeksiyonları
 Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
DOĞRUNUN ANALİTİK İNCELEMESİ
 Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
YÜKSEKLİK ÖLÇÜMÜ. Ölçme Bilgisi Ders Notları
 YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
Açı Ölçümü. Prof.Dr.Mustafa KARAŞAHİN
 Açı Ölçümü Prof.Dr.Mustafa KARAŞAHİN Açı Nedir? İki doğru arasındaki, doğrultu farkına açı adı verilir. Açılar, teodolit veya takeometre ile yapılır. Teodolit sadece açı ölçmede kullanılır iken, takeometreler
Açı Ölçümü Prof.Dr.Mustafa KARAŞAHİN Açı Nedir? İki doğru arasındaki, doğrultu farkına açı adı verilir. Açılar, teodolit veya takeometre ile yapılır. Teodolit sadece açı ölçmede kullanılır iken, takeometreler
2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ ALT ÖĞRENME. Örüntü ve Süslemeler
 2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE ÖĞRENME Ay Hafta D.Saati ALANI EYLÜL 2 Geometri 2 3 Geometri 2 Geometri 2 Olasılıkve ALT
2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE ÖĞRENME Ay Hafta D.Saati ALANI EYLÜL 2 Geometri 2 3 Geometri 2 Geometri 2 Olasılıkve ALT
= e DIŞ MERKEZLİK HAZİNE-1 HAZİNE-2
 HAZİNE-1 HAZİNE-2 Bir eksen üzerinde verilen noktadan geçen ve eksen ile belirli açı yaparak dönen doğrunun oluşturduğu yüzeye konik yüzey denir. Konik yüzeyin değişik düzlemler ile arakesit kümeleri çember,
HAZİNE-1 HAZİNE-2 Bir eksen üzerinde verilen noktadan geçen ve eksen ile belirli açı yaparak dönen doğrunun oluşturduğu yüzeye konik yüzey denir. Konik yüzeyin değişik düzlemler ile arakesit kümeleri çember,
MEKANİZMA TEKNİĞİ (3. Hafta)
 MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
TEKNİK RESİM. Ders Notları: Doç. Dr. Mehmet Çevik Celal Bayar Üniversitesi. İzdüşümler
 TEKNİK RESİM 5 2014 Ders Notları: Doç. Dr. Mehmet Çevik Celal Bayar Üniversitesi İzdüşümler 2/40 İzdüşümler İzdüşüm Nedir? İzdüşüm Çeşitleri Merkezi (Konik) İzdüşüm Paralel İzdüşüm Eğik İzdüşüm Dik İzdüşüm
TEKNİK RESİM 5 2014 Ders Notları: Doç. Dr. Mehmet Çevik Celal Bayar Üniversitesi İzdüşümler 2/40 İzdüşümler İzdüşüm Nedir? İzdüşüm Çeşitleri Merkezi (Konik) İzdüşüm Paralel İzdüşüm Eğik İzdüşüm Dik İzdüşüm
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
TOPOGRAFİK, JEOLOJİK HARİTALAR JEOLOJİK KESİTLER
 TOPOGRAFİK, JEOLOJİK HARİTALAR JEOLOJİK KESİTLER Dersin ipuçları Harita bilgisi Ölçek kavramı Topografya haritaları ve kesitleri Jeoloji haritaları ve kesitleri Jeolojik kesitlerin yorumları Harita, yeryüzünün
TOPOGRAFİK, JEOLOJİK HARİTALAR JEOLOJİK KESİTLER Dersin ipuçları Harita bilgisi Ölçek kavramı Topografya haritaları ve kesitleri Jeoloji haritaları ve kesitleri Jeolojik kesitlerin yorumları Harita, yeryüzünün
TEKNİK RESİM. Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi. Görünüşler - 2
 TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi Görünüşler - 2 2/23 Görünüşler-2 Görünüşler - 2 Eksik Verilmiş Görünüşler Yardımcı Görünüşler Kısmi Yardımcı Görünüş Özel Görünüşler
TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi Görünüşler - 2 2/23 Görünüşler-2 Görünüşler - 2 Eksik Verilmiş Görünüşler Yardımcı Görünüşler Kısmi Yardımcı Görünüş Özel Görünüşler
Akışkan Kinematiği 1
 Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ
 ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
ii) S 2LW 2WH 2LW 2WH S 2WH 2LW S 3( x 1) 5( x 2) 5 3x 3 5x x Maliye Bölümü EKON 103 Matematik I / Mart 2018 Proje 2 CEVAPLAR C.1) C.
 C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
ARAZİ ÖLÇMELERİ. Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) Dik İnmek. A Dik Çıkmak
 Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) P1 P2 Dik İnmek P3 P4 Dik Çıkmak Şekil 76 Şekil 76 da dik inme ve çıkmaya birer örnek gösterilmiştir. Dik çıkmadan anlaşılması gereken belirlenen bir
Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) P1 P2 Dik İnmek P3 P4 Dik Çıkmak Şekil 76 Şekil 76 da dik inme ve çıkmaya birer örnek gösterilmiştir. Dik çıkmadan anlaşılması gereken belirlenen bir
( m %n' m q >m q J > şekilde şematik olarak gösterilmiştir.
 Diğer Araştırmalar : Bir önceki bölümde açıklanan ilk araştırmaların teorik ve deneysel sonuçlarını sınamak amacı ile, seri halinde yeni teorik ve deneysel araştırmalar yapılmıştır. (Çizelge : IV) de belirtilen
Diğer Araştırmalar : Bir önceki bölümde açıklanan ilk araştırmaların teorik ve deneysel sonuçlarını sınamak amacı ile, seri halinde yeni teorik ve deneysel araştırmalar yapılmıştır. (Çizelge : IV) de belirtilen
İMÜ1109 TEKNİK RESİM. Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018
 İMÜ1109 TEKNİK RESİM Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 ANTET Bütün teknik resim yapraklarında mutlaka uygun ölçülerde bir çerçeve ve antet (baslık) bulunmalıdır. Antet, çizim kâğıdının
İMÜ1109 TEKNİK RESİM Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 ANTET Bütün teknik resim yapraklarında mutlaka uygun ölçülerde bir çerçeve ve antet (baslık) bulunmalıdır. Antet, çizim kâğıdının
