Bölüm-4. İki Boyutta Hareket
|
|
|
- Basak Şener
- 7 yıl önce
- İzleme sayısı:
Transkript
1 Bölüm-4 İki Boyutta Hareket
2 Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme Bu bölümde, bir boyutta türettiğimiz hareket denklemlerini iki boyutta hareket eden parçacık için genelleştireceğiz ve parçacığın hareketini düzlemde tanımlayacağız. Önce, iki boyutta (düzlemde) hareket eden bir cismin yer değiştirme, hız ve ivmesini tanımlayıp bu nicelikleri vektörel olarak ifade edeceğiz. Daha sonra düzlem üzerinde sabit ivme ile hareket eden cismin hareket denklemlerini ayrıntılı olarak yazıp, sabit ivmeli harekete güzel bir örnek olan eğik atış problemini inceleyeceğiz.
3 Yer değiştirme, Hız ve İvme Vektörleri Bir boyutta hareketi incelerken hareketli cismin bir boyutta yer değiştirmesini, hızını ve ivmesini bulmuştuk. Eğer cisim sadece bir boyutta hareket etmeyip bir düzlem üzerinde hareket ediyor ise yapacağımız iş, cismin hareketini dik koordinat sistemi kullanarak her bir eksen üzerinde (x ve y) ayrı ayrı incelemek ve hareketin her bir eksendeki izdüşümlerini kullanarak yer değiştirme, hız ve ivme niceliklerini vektörel olarak en genel bir şekilde ifade etmek olacaktır. Her bir eksen üzerindeki hareket diğer eksen üzerindeki hareketi etkilemeyeceği için eksenler üzerindeki izdüşümler birbirlerinden bağımsız olacaktır.
4 Bir ve iki boyuttaki harekete ilişkin fiziksel niceliklerimizi özetlersek:
5 İki Boyutta Sabit İvmeli Hareket Aşağıdaki şekilde noktasal bir parçacık düzlemsel bir yolda hareket etmektedir. Parçacık t i zamanda r i ile gösterilen ilk konumdadır ve t f zamanında ise parçacığın konumu son konum olan r f konumudur (Konum vektörlerinde yazılan i ve f alt indisleri ilk ve son konumlar anlamına gelmektedir). Bu parçacığın her hangi bir t anındaki konumu aşağıdaki gibi ifade edilebilir.
6 Parçacığın x- ve y-eksenlerindeki izdüşümleri, parçacığın hareketine bağlı olarak zaman içersinde değişir. Dolayısı ile konumun zamanla nasıl değiştiğine bakarsak cismin hızını bulabiliriz. Parçacığın hızını vektörel olarak aşağıdaki gibi tanımlayabiliriz; Buradaki v x ve v y parçacığın hızının x ve y eksenlerindeki izdüşümleridir (bileşenleridir). Aynı şekilde hızın zaman içeresindeki değişimine bakarsak hareketli cismin ivmesini vektörel olarak aşağıdaki gibi tanımlayabiliriz. a = a x i + a y j
7 Parçacığın ivmesi sabit olarak kabul edildiği için ivmenin a x ve a y bileşenleri de sabit olacaktır. Bu nedenle Bölüm 2 de türettiğimiz kinematik denklemlerini hız vektörünün hem x hem de y bileşenlerine uyarlayabiliriz. Hız v = v xf i + v yf j x-bileşeni v xf = v ix + a x t y-bileşeni v yf = v iy + a y t
8 Vektörel olarak yazarsak; Elde edilen bu ifadeye göre; sabit ivmeli düzlemsel hareket eden bir parçacığın belirli bir t anındaki hızı (v f ), ilk hızı (v i ) ile at nin toplamına eşittir.
9 Aynı şekilde sabit ivme ile hareket eden bir parçacığın x ve y konum denklemleri aşağıdaki gibi tanımlanmaktadır.
10
11 Eğik Atış Hareketi İki boyutta sabit ivmeli harekete en güzel örnek eğik atış problemidir. Serbest düşme bir boyutta olmasına rağmen eğik atış iki boyutta gerçekleşmektedir. Çünkü eğik atışta cisim sadece y-ekseni boyunca hareket etmeyip xy düzleminde hareket etmektedir. Dolayısı ile eğik atış problemini y-ekseni boyunca sabit ivmeli hareket (a y =-g) ve x-ekseni boyunca ivmenin sıfır olduğu ( a x =0) bir boyutlu iki hareketin bileşkesi olarak düşünebiliriz. Eğik atış problemini daha ayrıntılı olarak incelerken yapacağımız kabuller: a) Yerçekimi ivmesinin sabittir, b) Hava direncinin etkisi ihmal edilecektir. c) İvme değerleri a x =0 a y =-g d) t=0 başlangıç anında eğik atılan cismin konum değerleri x i = 0, y i = 0 dır.
12 Eğik atış problemlerinde kinematik denklemleri belirlemek için aşağıdaki şekilde gösterildiği gibi t = 0 başlangıç anında bir cismin v i hızıyla eğik atıldığını düşünüyoruz. v i hız vektörü yatayla θ i açısı yapmakta olup bu açıya atış açısı adı verilmektedir. Kosinüs ve sinüs fonksiyonlarının tanımından; dır Böylece, ilk hızın x ve y bileşenleri; ile tanımlanmaktadır.
13 x-ekseni boyunca alınan yol: (ekseni boyunca cismin ivmesi sıfır olacağından hızın x bileşeni (v ix ) zamanla değişmez)..1 y-ekseni boyunca alınan yol: (y-ekseni boyunca sabit ivmeli hareket (a y =-g) )..2 Eğik atış hareketinin yörüngesini nasıl olacağını öğrenmek istersek: Uçuş süresini 1. eşitlikten bulunup 2. eşitlikte yerine koyarsak elde ederiz
14 Görüldüğü gibi bu en genel olarak bu denklem y = ax bx 2 şeklinde tanımlanan bir parabol denklemidir. Yani eğik atışta cismin izlediği yol xy düzleminde her zaman bir parabol şeklindedir.
15 v ix = 20 m/sn, a x = 0 v iy = 40 m/sn, a y = 9,8 m/sn 2 Hız vektörünün; Top tam tepe noktasındaki iken hızın y bileşeni sıfır olduğundan hız vektörü aşağıdaki gibi yazılabilir. v x i + 0 j = v ix i + v iy j + (a x i + a y j)t Burada yatay hız (v x ) sabit olup değeri ilk hıza eşittir (v x =v ix ). Değerler yerine yazılır ve t çekilirse; 20 i + 0 j = 20 i + 40 j + 0 i 9,8 j t t = 40/9,8 = 4 saniye
16 Topun tepeye ulaşma zamanı 4 saniye olduğundan topun toplam uçuş zaman 4*2=8 saniyedir. t=8 saniye süresince x yer değiştirmesi: x f = 20 8 = 160 metre
17 Eğik atışta cismin menzili ve maksimum yüksekliği: Cismin şekildeki gibi, pozitif v iy bileşeniyle, t i = 0 anında orijinden atıldığını varsayalım. Şekilde gösterilen R uzaklığı cismin menzili, h uzunluğuna ise cismin maksimum yüksekliği denir. Tepe noktasında cismin yatay hız bileşeni sıfır olduğundan v ya = 0, cismin maksimum yüksekliğe ulaştığında geçen zamanı (t A ) aşağıdaki gibi bulabiliriz.
18 Eğik atış problemlerinde y-ekseni boyunca alınan yol aşağıdaki gibi tanımlanmaktaydı; Bu denklemde y f yerine maksimum yükseklik (h), t yerine ise biraz önce elde ettiğimiz maksimum yüksekliğe ulaşma süresini ( t A ) yazarsak, cismin maksimum yüksekliği aşağıdaki gibi elde ederiz.
19 Cismin R menzili, cismin tepe noktasına ulaşmak için geçen zamanın iki katında yani, t B = 2t A zamanı içinde alınan yatay uzaklıktır. Eğik atış problemlerinde x-ekseni boyunca alınan yol aşağıdaki gibi tanımlanmaktaydı; Bu denklemde x f yerine cismin menzili (R), t yerine ise biraz önce elde ettiğimiz maksimum yüksekliğe ulaşma süresinin 2 katını (2t A ) yazarsak, cismin R menzili aşağıdaki gibi elde ederiz.
20 sin2θ = 2sinθcosθ özdeşliği kullanılarak menzil ifadesi aşağıdaki gibi elde ifade edilebilir. Elde edilen maksimum yükseklik ve menzil denklemleri incelendiğinde sadece v i ve θ i değerlerinin bilinmesiyle hesaplanması istenilebilecek maksimum yükseklik ve menzil değerleri kolayca bulunabilir.
21 Örnek: Uzun atlama yapan bir sporcu, yatayla 20 açı altında 11 m/sn lik hızla fırlıyor. Sporcu ne kadar yatay uzaklığa sıçrayabilir? Sporcunu ulaştığı maksimum yükseklik nedir? Tepe noktasında sporcunun yatay hız bileşeni sıfır olduğundan v ya = 0, sporcunun maksimum yüksekliğe ulaştığında geçen zamanı ( t A ) aşağıdaki gibi bulabiliriz.
22 B noktasına ulaştığında geçen süre maksimum yüksekliğe ulaşılan sürenini iki katı olduğundan; Sporcu ulaşabileceği maksimum yatay uzaklık; Ulaşılan maksimum yükseklik ise; Not: Bu problemi elde edilen maksimum yükseklik ve menzil formülleriyle yeniden çözerek karşılaştırınız.
23 Örnek: Bir taş şekilde gösterildiği gibi, bir binanın tepesinden yatayla 30 derecelik bir açı altında ve 20 m/sn lik bir ilk hızla yukarıya doğru fırlatılmaktadır. Binanın yüksekliği 45 m ise, taş ne kadar sürede havada kalır? Zemine çarpmadan hemen önce taşın hızının büyüklüğü nedir? Çözüm: Taşın ne kadar sürede havada kaldığını bulmak için eğik atış problemlerinde y-ekseni boyunca alınan yol denklemini kullanabiliriz. *Çizilen koordinat sistemine göre y f değeri -45 metredir. 45 m = 20 m/sn sin30 t 1 2 9,8 t2 Bu ikinci dereceden denklemin pozitif kökü alınırsa; t=4,22 saniye elde edilir.
24 Taşın zemine çarpmadan hemen önce, hızının y bileşenini elde etmek için; v yf = v yi + a y = v i sinθ i + a y = 20 sin30 9,8 4,22 = 31,4 Taşın zemine çarpmadan hemen önce, hızının x bileşenini elde etmek için; v xf = v xi = v i cosθ i = 20 cos30 = 17,3
25
26 ÖDEV: Bir kayak sporcusu, kayak pistini şekildeki gibi 25 m/sn lik hızla yatay doğrultuda giderek terk eder. Aşağı inişinde 35 derecelik bir eğimle düşer. Sporcunun tepeden aşağıya nereye düştüğünü (x, y koordinatlarını) bulunuz.
27 Kaynak: Bu ders notları, R. A. Serway ve R. J. Beichner (Çeviri Editörü: K. Çolakoğlu), Fen ve Mühendislik için FİZİK-I (Mekanik), Palme Yayıncılık, kitabından derlenmiştir.
Bölüm 4: İki Boyutta Hareket
 Bölüm 4: İki Boyutta Hareket Kavrama Soruları 1- Yerden h yüksekliğinde, yere paralel tutulan bir silah ateşleniyor ve aynı anda silahın yanında başka bir kurşun aynı h yüksekliğinden serbest düşmeye bırakılıyor.
Bölüm 4: İki Boyutta Hareket Kavrama Soruları 1- Yerden h yüksekliğinde, yere paralel tutulan bir silah ateşleniyor ve aynı anda silahın yanında başka bir kurşun aynı h yüksekliğinden serbest düşmeye bırakılıyor.
V = g. t Y = ½ gt 2 V = 2gh. Serbest Düşme NOT:
 Havada serbest bırakılan cisimlerin aşağı doğru düşmesi etrafımızda her zaman gördüğümüz bir olaydır. Bu düşme hareketleri, cisimleri yerin merkezine doğru çeken bir kuvvetin varlığını gösterir. Daha önceki
Havada serbest bırakılan cisimlerin aşağı doğru düşmesi etrafımızda her zaman gördüğümüz bir olaydır. Bu düşme hareketleri, cisimleri yerin merkezine doğru çeken bir kuvvetin varlığını gösterir. Daha önceki
3-1 Koordinat Sistemleri Bir cismin konumunu tanımlamak için bir yönteme gereksinim duyarız. Bu konum tanımlaması koordinat kullanımı ile sağlanır.
 Bölüm 3 VEKTÖRLER Bölüm 3: Vektörler Konu İçeriği Sunuş 3-1 Koordinat Sistemleri 3-2 Vektör ve Skaler nicelikler 3-3 Vektörlerin Bazı Özellikleri 3-4 Bir Vektörün Bileşenleri ve Birim Vektörler Sunuş Fizikte
Bölüm 3 VEKTÖRLER Bölüm 3: Vektörler Konu İçeriği Sunuş 3-1 Koordinat Sistemleri 3-2 Vektör ve Skaler nicelikler 3-3 Vektörlerin Bazı Özellikleri 3-4 Bir Vektörün Bileşenleri ve Birim Vektörler Sunuş Fizikte
Bölüm 3: Vektörler. Kavrama Soruları. Konu İçeriği. Sunuş. 3-1 Koordinat Sistemleri
 ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Şekil 8.1: Cismin yatay ve dikey ivmesi
 Deney No : M7 Deneyin Adı : EĞİK ATIŞ Deneyin Amacı : 1. Topun ilk hızını belirlemek 2. Ölçülen menzille hesaplanan menzili karşılaştırmak 3. Bir düzlem üzerinde uygulanan eğik atışta açıyla menzil ve
Deney No : M7 Deneyin Adı : EĞİK ATIŞ Deneyin Amacı : 1. Topun ilk hızını belirlemek 2. Ölçülen menzille hesaplanan menzili karşılaştırmak 3. Bir düzlem üzerinde uygulanan eğik atışta açıyla menzil ve
Fizik 101-Fizik I 2013-2014. Nurdan Demirci Sankır Enerji Araştırmaları Laboratuarı- YDB Bodrum Kat Ofis: 325, Tel:4332. İçerik
 Fizik 101-Fizik I 2013-2014 İki Boyutta Hareket Nurdan Demirci Sankır Enerji Araştırmaları Laboratuarı- YDB Bodrum Kat Ofis: 325, Tel:4332 İçerik Yerdeğiştirme, hız ve ivme vektörleri Sabit ivmeli iki-boyutlu
Fizik 101-Fizik I 2013-2014 İki Boyutta Hareket Nurdan Demirci Sankır Enerji Araştırmaları Laboratuarı- YDB Bodrum Kat Ofis: 325, Tel:4332 İçerik Yerdeğiştirme, hız ve ivme vektörleri Sabit ivmeli iki-boyutlu
Bölüm 2. Bir boyutta hareket
 Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
Fizik Dr. Murat Aydemir
 Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
Bölüm 4. İki boyutta hareket
 Bölüm 4 İki boyutta hareket İki boyutta Hareket Burada konum, hız ve ivmenin vektör karakteri daha öne çıkacaktır. İlk olarak sabit ivmeli hareketler göz önünde bulundurulacak. Düzgün dairesel hareket
Bölüm 4 İki boyutta hareket İki boyutta Hareket Burada konum, hız ve ivmenin vektör karakteri daha öne çıkacaktır. İlk olarak sabit ivmeli hareketler göz önünde bulundurulacak. Düzgün dairesel hareket
TİTREŞİM VE DALGALAR BÖLÜM PERİYODİK HAREKET
 TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
r r s r i (1) = [x(t s ) x(t i )]î + [y(t s ) y(t i )]ĵ. (2) r s
![r r s r i (1) = [x(t s ) x(t i )]î + [y(t s ) y(t i )]ĵ. (2) r s r r s r i (1) = [x(t s ) x(t i )]î + [y(t s ) y(t i )]ĵ. (2) r s](/thumbs/55/37178256.jpg) Bölüm 4: İki-Boyutta Hareket(Özet) Bir-boyutta harekeçin geliştirilen tüm kavramlar iki-boyutta harekeçin genelleştirilebilir. Bunun için hareketli cismin(parçacığın) yer değiştirme vektörü xy-düzleminde
Bölüm 4: İki-Boyutta Hareket(Özet) Bir-boyutta harekeçin geliştirilen tüm kavramlar iki-boyutta harekeçin genelleştirilebilir. Bunun için hareketli cismin(parçacığın) yer değiştirme vektörü xy-düzleminde
DENİZLİ ANADOLU LİSESİ 2006-2007 EĞİTİM ve ÖĞRETİM YILI FİZİK DERSİ YILLIK ÖDEVİ
 DENİZLİ ANADOLU LİSESİ 2006-2007 EĞİTİM ve ÖĞRETİM YILI FİZİK DERSİ YILLIK ÖDEVİ Öğrencinin ; Adı : Özgür Soyadı : ATİK Numarası : 387 Sınıfı : 10F/J Ders Öğretmeninin ; Adı : Fahrettin Soyadı : KALE Ödevin
DENİZLİ ANADOLU LİSESİ 2006-2007 EĞİTİM ve ÖĞRETİM YILI FİZİK DERSİ YILLIK ÖDEVİ Öğrencinin ; Adı : Özgür Soyadı : ATİK Numarası : 387 Sınıfı : 10F/J Ders Öğretmeninin ; Adı : Fahrettin Soyadı : KALE Ödevin
Kuvvet. Kuvvet. Newton un 1.hareket yasası Fizik 1, Raymond A. Serway; Robert J. Beichner Editör: Kemal Çolakoğlu, Palme Yayınevi
 Kuvvet izik 1, Raymond A. Serway; Robert J. Beichner Editör: Kemal Çolakoğlu, Palme Yayınevi 2 Kuvvet Kuvvet ivmelenme kazandırır. Kuvvet vektörel bir niceliktir. Kuvvetler çift halinde bulunur. Kuvvet
Kuvvet izik 1, Raymond A. Serway; Robert J. Beichner Editör: Kemal Çolakoğlu, Palme Yayınevi 2 Kuvvet Kuvvet ivmelenme kazandırır. Kuvvet vektörel bir niceliktir. Kuvvetler çift halinde bulunur. Kuvvet
EĞİK ATIŞ Ankara 2008
 EĞİK ATIŞ Ankara 8 EĞİK ATIŞ: AMAÇ: 1. Topun ilk hızını belirlemek. Ölçülen menzille hesaplanan menzili karşılaştırmak 3. Bir düzlem üzerinde uygulanan eğik atışda açıyla menzil ve tepenoktası arasındaki
EĞİK ATIŞ Ankara 8 EĞİK ATIŞ: AMAÇ: 1. Topun ilk hızını belirlemek. Ölçülen menzille hesaplanan menzili karşılaştırmak 3. Bir düzlem üzerinde uygulanan eğik atışda açıyla menzil ve tepenoktası arasındaki
DİNAMİK (2.hafta) Yatay Hareket Formülleri: a x =0 olduğundan ilk hız ile yatay bileşende hareketine devam eder.
 EĞİK ATIŞ Bir merminin serbest uçuş hareketi iki dik bileşen şeklinde, yatay ve dikey hareket olarak incelenir. Bu harekette hava direnci ihmal edilerek çözüm yapılır. Hava direnci ihmal edilince yatay
EĞİK ATIŞ Bir merminin serbest uçuş hareketi iki dik bileşen şeklinde, yatay ve dikey hareket olarak incelenir. Bu harekette hava direnci ihmal edilerek çözüm yapılır. Hava direnci ihmal edilince yatay
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 13 Parçacık Kinetiği: Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 13 Parçacık
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 13 Parçacık Kinetiği: Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 13 Parçacık
Doç.Dr. Cesim ATAŞ MEKANİK ŞEKİL DEĞİŞTİREN CİSİMLER MEKANİĞİ DİNAMİK
 STATİK (Ders Notları) Kaynak: Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige, Wiley Yardımcı Kaynak: Mühendislik Mekaniği: Statik, R.C Hibbeler & S.C. Fan, Literatür
STATİK (Ders Notları) Kaynak: Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige, Wiley Yardımcı Kaynak: Mühendislik Mekaniği: Statik, R.C Hibbeler & S.C. Fan, Literatür
Kinematik. FİZ1011 : Ders 4. İki ve Üç Boyutta Hareket. Yerdeğiştirme, Hız ve İvme Vektörleri. Teğetsel ve Radyal İvme. Eğik Atış Hareketi
 FİZ1011 : Ders 4 Kinematik İki ve Üç Boyutta Hareket Yerdeğiştirme, Hız ve İvme Vektörleri Teğetsel ve Radyal İvme Eğik Atış Hareketi Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ İki
FİZ1011 : Ders 4 Kinematik İki ve Üç Boyutta Hareket Yerdeğiştirme, Hız ve İvme Vektörleri Teğetsel ve Radyal İvme Eğik Atış Hareketi Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ İki
1. STATİĞE GİRİŞ 1.1 TANIMLAR MEKANİK RİJİT CİSİMLER MEKANİĞİ ŞEKİL DEĞİŞTİREN CİSİMLER AKIŞKANLAR MEKANİĞİ DİNAMİK STATİK
 STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
HAREKETİN KİNEMATİK İNCELENMESİ
 HAREKETİN KİNEMATİK İNCELENMESİ Kinematik, cisimlerin hareketlerini, bu hareketlere neden olan ya da bu hareketler sonucunda oluşan kuvvetlerden bağımsız olarak inceleyen fizik dalıdır. Klasik mekaniğin
HAREKETİN KİNEMATİK İNCELENMESİ Kinematik, cisimlerin hareketlerini, bu hareketlere neden olan ya da bu hareketler sonucunda oluşan kuvvetlerden bağımsız olarak inceleyen fizik dalıdır. Klasik mekaniğin
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
HAREKET HAREKET KUVVET İLİŞKİSİ
 HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
Bölüm 9: Doğrusal momentum ve çarpışmalar
 Bölüm 9: Doğrusal momentum ve çarpışmalar v hızıyla hareket eden m kütleli bir parçacığın doğrusal momentumu kütle ve hızın çarpımına eşittir; p = mv Momentum vektörel bir niceliktir, yönü hız vektörü
Bölüm 9: Doğrusal momentum ve çarpışmalar v hızıyla hareket eden m kütleli bir parçacığın doğrusal momentumu kütle ve hızın çarpımına eşittir; p = mv Momentum vektörel bir niceliktir, yönü hız vektörü
MEKANİZMA TEKNİĞİ (3. Hafta)
 MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
Fiz Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi
 Fiz 1011 - Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi Açısal Yerdeğiştirme, Hız ve İvme Dönme Kinematiği: Sabit Açısal İvmeli Dönme Hareketi Açısal ve Doğrusal Nicelikler Dönme Enerjisi Eylemsizlik
Fiz 1011 - Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi Açısal Yerdeğiştirme, Hız ve İvme Dönme Kinematiği: Sabit Açısal İvmeli Dönme Hareketi Açısal ve Doğrusal Nicelikler Dönme Enerjisi Eylemsizlik
DİNAMİK MEKANİK. Şekil Değiştiren Cisimler Mekaniği. Mukavemet Elastisite Teorisi Sonlu Elemanlar Analizi PARÇACIĞIN KİNEMATİĞİ
 DİNAMİK Dinamik mühendislik mekaniği alanının bir alt grubudur: Mekanik: Cisimlerin dış yükler altındaki davranışını inceleyen mühendislik alanıdır. Aşağıdaki alt gruplara ayrılır: MEKANİK Rijit-Cisim
DİNAMİK Dinamik mühendislik mekaniği alanının bir alt grubudur: Mekanik: Cisimlerin dış yükler altındaki davranışını inceleyen mühendislik alanıdır. Aşağıdaki alt gruplara ayrılır: MEKANİK Rijit-Cisim
Bir boyutta sabit ivmeli hareket..
 Bir boyutta sabit ivmeli hareket.. İvme sabit olduğunda, ortalama ivme ani ivmeye eşit olur. Hız hareketin başından sonuna kadar aynı oranda artar veya azalır. a x = v xf v xi t ; t i = 0 ve t f = t alınmıştır
Bir boyutta sabit ivmeli hareket.. İvme sabit olduğunda, ortalama ivme ani ivmeye eşit olur. Hız hareketin başından sonuna kadar aynı oranda artar veya azalır. a x = v xf v xi t ; t i = 0 ve t f = t alınmıştır
2 TEK BOYUTTA HAREKET
 2 TEK BOYUTTA HAREKET 2.1 Konum, hız ve sürat 2.2 Anlık hız ve sürat 2.3 İvme 2.4 Hareket diyagramları 2.5 Tek boyutta sabit ivmeli hareket 2.6 Serbest düşen cisimler 2.7 Kinematik denklemlerin türetilmesi
2 TEK BOYUTTA HAREKET 2.1 Konum, hız ve sürat 2.2 Anlık hız ve sürat 2.3 İvme 2.4 Hareket diyagramları 2.5 Tek boyutta sabit ivmeli hareket 2.6 Serbest düşen cisimler 2.7 Kinematik denklemlerin türetilmesi
Newton un II. yasası. Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır.
 Newton un II. yasası Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır. Bir cisme F A, F B ve F C gibi çok sayıda kuvvet etkiyorsa, net kuvvet bunların
Newton un II. yasası Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır. Bir cisme F A, F B ve F C gibi çok sayıda kuvvet etkiyorsa, net kuvvet bunların
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 16 Rijit Cismin Düzlemsel Kinematiği Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 16 Rijit
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 16 Rijit Cismin Düzlemsel Kinematiği Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 16 Rijit
Bir cismin iki konumu arasındaki vektörel uzaklıktır. Başka bir ifadeyle son konum (x 2 ) ile ilk konum
 DOĞRUSAL ve BAĞIL HAREKET Hareket Maddelerin zamanla yer değiştirmesine hareket denir. Fakat cisimlerin nereye göre yer değiştirdiği ve nereye göre hareket ettiği belirtilmelidir. Örneğin at üstünde giden
DOĞRUSAL ve BAĞIL HAREKET Hareket Maddelerin zamanla yer değiştirmesine hareket denir. Fakat cisimlerin nereye göre yer değiştirdiği ve nereye göre hareket ettiği belirtilmelidir. Örneğin at üstünde giden
KOÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) Bölümü Dinamik Dersi (Türkçe Dilinde) 1. Çalişma Soruları / 24 Eylül 2017
 SORU-1) Dirençli bir ortamda doğrusal hareket yapan bir parçacığın ivmesi a=k V 3 olarak tanımlanmıştır. Burada k bir sabiti, V hızı, x konumu ve t zamanı sembolize etmektedir. Başlangıç koşulları x o
SORU-1) Dirençli bir ortamda doğrusal hareket yapan bir parçacığın ivmesi a=k V 3 olarak tanımlanmıştır. Burada k bir sabiti, V hızı, x konumu ve t zamanı sembolize etmektedir. Başlangıç koşulları x o
Manyetik Alanlar. Benzer bir durum hareketli yükler içinde geçerli olup bu yüklerin etrafını elektrik alana ek olarak bir manyetik alan sarmaktadır.
 Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
MADDESEL NOKTALARIN DİNAMİĞİ
 MÜHENDİSLİK MEKANİĞİ DİNAMİK MADDESEL NOKTALARIN DİNAMİĞİ DİNAMİK MADDESEL NOKTALARIN DİNAMİĞİ İÇİNDEKİLER 1. GİRİŞ - Konum, Hız ve İvme - Newton Kanunları 2. MADDESEL NOKTALARIN KİNEMATİĞİ - Doğrusal
MÜHENDİSLİK MEKANİĞİ DİNAMİK MADDESEL NOKTALARIN DİNAMİĞİ DİNAMİK MADDESEL NOKTALARIN DİNAMİĞİ İÇİNDEKİLER 1. GİRİŞ - Konum, Hız ve İvme - Newton Kanunları 2. MADDESEL NOKTALARIN KİNEMATİĞİ - Doğrusal
STATİĞİN TEMEL PRENSİPLERİ
 1.1. Temel Kavramlar ve Tanımlar Mühendislik mekaniği: Kuvvet etkisi altındaki cisimlerin denge veya hareket koşullarını inceleyen bilim dalı Genel olarak mühendislik mekaniği Sert (rijit) katı cisimlerin
1.1. Temel Kavramlar ve Tanımlar Mühendislik mekaniği: Kuvvet etkisi altındaki cisimlerin denge veya hareket koşullarını inceleyen bilim dalı Genel olarak mühendislik mekaniği Sert (rijit) katı cisimlerin
EĞRİSEL HAREKET : Silindirik Bileşenler
 EĞRİSEL HAREKET : Silindirik Bileşenler SİLİNDİRİK KOORDİNATLARDA (POLAR) HAREKET DENKLEMLERİ Bugünkü Konular: Silindirik koordinat takımı kullanılarak hareket denklemlerinin yazılması; hız ve ivme değerlerinin
EĞRİSEL HAREKET : Silindirik Bileşenler SİLİNDİRİK KOORDİNATLARDA (POLAR) HAREKET DENKLEMLERİ Bugünkü Konular: Silindirik koordinat takımı kullanılarak hareket denklemlerinin yazılması; hız ve ivme değerlerinin
Hareket Kanunları Uygulamaları
 Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
DİNAMİK TEKNOLOJİNİN BİLİMSEL İLKELERİ
 7 TEKNOLOJİNİN BİLİMSEL İLKELERİ Adem ÇALIŞKAN Hareket veya hareketteki değişmelerin sebeplerini araştırarak kuvvetle hareket arasındaki ilişkiyi inceleyen mekaniğin bölümüne dinamik denir. Hareket, bir
7 TEKNOLOJİNİN BİLİMSEL İLKELERİ Adem ÇALIŞKAN Hareket veya hareketteki değişmelerin sebeplerini araştırarak kuvvetle hareket arasındaki ilişkiyi inceleyen mekaniğin bölümüne dinamik denir. Hareket, bir
DENEY 2 SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET
 DENEY SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET AMAÇ: Sabit ivme ile düzgün doğrusal hareket çalışılıp analiz edilecek ve eğik durumda bulunan hava masasındaki diskin hareketi incelenecek
DENEY SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET AMAÇ: Sabit ivme ile düzgün doğrusal hareket çalışılıp analiz edilecek ve eğik durumda bulunan hava masasındaki diskin hareketi incelenecek
DENEY 2 SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET
 DENEY 2 SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET AMAÇ: Sabit ivme ile düzgün doğrusal hareket çalışılıp analiz edilecek ve eğik durumda bulunan hava masasındaki diskin hareketi incelenecek
DENEY 2 SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET AMAÇ: Sabit ivme ile düzgün doğrusal hareket çalışılıp analiz edilecek ve eğik durumda bulunan hava masasındaki diskin hareketi incelenecek
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
FIZ 1301 FİZİK-I LABORATUAR KILAVUZU
 FİZİK BÖLÜMÜ, MCBU, MANİSA, 2018 FIZ 1301 FİZİK-I LABORATUAR KILAVUZU İÇİNDEKİLER DENEY 1: Bir Boyutta Hareket (Düzgün Doğrusal Hareket)..2 DENEY 2: Eğik Atış.6 DENEY 3: Dinamik 15 DENEY 4: Momentum ve
FİZİK BÖLÜMÜ, MCBU, MANİSA, 2018 FIZ 1301 FİZİK-I LABORATUAR KILAVUZU İÇİNDEKİLER DENEY 1: Bir Boyutta Hareket (Düzgün Doğrusal Hareket)..2 DENEY 2: Eğik Atış.6 DENEY 3: Dinamik 15 DENEY 4: Momentum ve
Fizik 101-Fizik I 2013-2014. Dönme Hareketinin Dinamiği
 -Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
-Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
Fizik 101: Ders 18 Ajanda
 Fizik 101: Ders 18 Ajanda Özet Çoklu parçacıkların dinamiği Makara örneği Yuvarlanma ve kayma örneği Verilen bir eksen etrafında dönme: hokey topu Eğik düzlemde aşağı yuvarlanma Bowling topu: kayan ve
Fizik 101: Ders 18 Ajanda Özet Çoklu parçacıkların dinamiği Makara örneği Yuvarlanma ve kayma örneği Verilen bir eksen etrafında dönme: hokey topu Eğik düzlemde aşağı yuvarlanma Bowling topu: kayan ve
DENEY 1. İncelenmesi. Süleyman Demirel Üniversitesi Fen Edebiyat Fakültesi
 DENEY 1 Düzgün Doğrusal Hareketin İncelenmesi Süleyman Demirel Üniversitesi Fen Edebiyat Fakültesi Fizik Bölümü Isparta - 2018 Amaçlar 1. Tek boyutta hareket kavramının incelenmesi. 2. Yer değiştirme ve
DENEY 1 Düzgün Doğrusal Hareketin İncelenmesi Süleyman Demirel Üniversitesi Fen Edebiyat Fakültesi Fizik Bölümü Isparta - 2018 Amaçlar 1. Tek boyutta hareket kavramının incelenmesi. 2. Yer değiştirme ve
Bir cisme etki eden kuvvetlerin bileşkesi sıfır ise, cisim ya durur, ya da bir doğru boyunca sabit hızla hareketine devam eder.
 DİNAMİK Hareket veya hareketteki değişmelerin sebeplerini araştırarak kuvvetle hareket arasındaki ilişkiyi inceleyen mekaniğin bölümüne dinamik denir. Dinamiğin üç temel prensibi vardır. 1. Eylemsizlik
DİNAMİK Hareket veya hareketteki değişmelerin sebeplerini araştırarak kuvvetle hareket arasındaki ilişkiyi inceleyen mekaniğin bölümüne dinamik denir. Dinamiğin üç temel prensibi vardır. 1. Eylemsizlik
x ve y bileşenlerinin bağımsızlığı
 Fizik 11: Ders ugünün Konusu Hatırlatma: Sabit imeli 1-D hareket 1-D serbest düşme örnek Vektörler 3-D Kinematik Serbest atış (şut) e bileşenlerinin bağımsızlığı Sabit imeli harekette: t erine konduğunda:
Fizik 11: Ders ugünün Konusu Hatırlatma: Sabit imeli 1-D hareket 1-D serbest düşme örnek Vektörler 3-D Kinematik Serbest atış (şut) e bileşenlerinin bağımsızlığı Sabit imeli harekette: t erine konduğunda:
Noktasal Cismin Dengesi
 Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
İş, Güç ve Enerji. Fiz Ders 7. Sabit Bir Kuvvetin Yaptığı İş. Değişen Bir Kuvvetin Yaptığı İş. Güç. İş-Kinetik Enerji Teoremi
 Fiz 1011 - Ders 7 İş, Güç ve Enerji Sabit Bir Kuvvetin Yaptığı İş Değişen Bir Kuvvetin Yaptığı İş Güç İş-Kinetik Enerji Teoremi http://kisi.deu.edu.tr/mehmet.tarakci/ Günlük yaşamda iş kavramı bir çok
Fiz 1011 - Ders 7 İş, Güç ve Enerji Sabit Bir Kuvvetin Yaptığı İş Değişen Bir Kuvvetin Yaptığı İş Güç İş-Kinetik Enerji Teoremi http://kisi.deu.edu.tr/mehmet.tarakci/ Günlük yaşamda iş kavramı bir çok
Parametrik doğru denklemleri 1
 Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
TORK VE DENGE. İçindekiler TORK VE DENGE 01 TORK VE DENGE 02 TORK VE DENGE 03 TORK VE DENGE 04. Torkun Tanımı ve Yönü
 İçindekiler TORK VE DENGE TORK VE DENGE 01 Torkun Tanımı ve Yönü Torka Sebep Olan ve Olmayan Kuvvetler Tork Bulurken İzlenen Yöntemler Çubuğa Uygulanan Kuvvet Dik Değilse 1) Kuvveti bileşenlerine ayırma
İçindekiler TORK VE DENGE TORK VE DENGE 01 Torkun Tanımı ve Yönü Torka Sebep Olan ve Olmayan Kuvvetler Tork Bulurken İzlenen Yöntemler Çubuğa Uygulanan Kuvvet Dik Değilse 1) Kuvveti bileşenlerine ayırma
İçerik. Fizik 101-Fizik I
 Fizik 101-Fizik I 2013-2014 Nurdan Demirci Sankır Enerji Araştırmaları Laboratuarı- YDB Bodrum Kat Ofis: 325, Tel:4332-4392 İçerik Yerdeğiştirme, Hız ve Sürat Ani Hız ve Sürat İvme Hareket Diyagramları
Fizik 101-Fizik I 2013-2014 Nurdan Demirci Sankır Enerji Araştırmaları Laboratuarı- YDB Bodrum Kat Ofis: 325, Tel:4332-4392 İçerik Yerdeğiştirme, Hız ve Sürat Ani Hız ve Sürat İvme Hareket Diyagramları
VERİLER. Yer çekimi ivmesi : g=10 m/s 2
 VERİLER Yer çekimi ivmesi : g=10 m/s 2 Metrik Ön Takılar sin 45 = cos 45 = 0,7 Numara Ön Takı Simge sin 37 = cos 53 = 0,6 sin 53 = cos 37 = 0,8 10 9 giga G tan 37 = 0,75 10 6 mega M tan 53 = 1,33 10 3
VERİLER Yer çekimi ivmesi : g=10 m/s 2 Metrik Ön Takılar sin 45 = cos 45 = 0,7 Numara Ön Takı Simge sin 37 = cos 53 = 0,6 sin 53 = cos 37 = 0,8 10 9 giga G tan 37 = 0,75 10 6 mega M tan 53 = 1,33 10 3
Vektörler Bölüm Soruları 1. İki vektör eşit olmayan büyüklüklere sahiptir. Toplamları sıfır olabilir mi? Açıklayınız.
 Vektörler Bölüm Soruları 1. İki vektör eşit olmayan büyüklüklere sahiptir. Toplamları sıfır olabilir mi? Açıklayınız. 2. Bir parçacığın yerdeğiştirmesinin büyüklüğü, alınan yolun uzunluğundan daha büyük
Vektörler Bölüm Soruları 1. İki vektör eşit olmayan büyüklüklere sahiptir. Toplamları sıfır olabilir mi? Açıklayınız. 2. Bir parçacığın yerdeğiştirmesinin büyüklüğü, alınan yolun uzunluğundan daha büyük
SORULAR 1. Serbest düşmeye bırakılan bir cisim son iki saniyede 80 m yol almıştır.buna göre,cismin yere çarpma hızı nedir? a) 40 b) 50 c) 60 d) 70
 SORUAR 1. Serbest düşmeye bırakılan bir cisim son iki saniyede 80 m yol almıştır.buna göre,cismin yere çarpma ızı nedir? a) 40 b) 50 c) 60 d) 70 2. cismi v ızı ile ukarı atılıp, ise serbets bırakılıyor.
SORUAR 1. Serbest düşmeye bırakılan bir cisim son iki saniyede 80 m yol almıştır.buna göre,cismin yere çarpma ızı nedir? a) 40 b) 50 c) 60 d) 70 2. cismi v ızı ile ukarı atılıp, ise serbets bırakılıyor.
Düzgün olmayan dairesel hareket
 Düzgün olmayan dairesel hareket Dairesel harekette cisim üzerine etki eden net kuvvet merkeze doğru yönelmişse cismin hızı sabit kalır. Eğer net kuvvet merkeze doğru yönelmemişse, kuvvet teğetsel ve radyal
Düzgün olmayan dairesel hareket Dairesel harekette cisim üzerine etki eden net kuvvet merkeze doğru yönelmişse cismin hızı sabit kalır. Eğer net kuvvet merkeze doğru yönelmemişse, kuvvet teğetsel ve radyal
DİNAMİK. Ders_9. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 DİNAMİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ: ÖTELENME&DÖNME Bugünün
DİNAMİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ: ÖTELENME&DÖNME Bugünün
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü
 Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 7 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 7 Kasım 1999 Saat: 21.50 Problem 7.1 (Ohanian, sayfa 271, problem 55) Bu problem boyunca roket
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 7 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 7 Kasım 1999 Saat: 21.50 Problem 7.1 (Ohanian, sayfa 271, problem 55) Bu problem boyunca roket
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
MAK209 DİNAMİK ÖDEV 1 ÇÖZÜMÜ Dr. Nurdan Bilgin
 MAK09 DİNAMİK ÖDEV 1 ÇÖZÜMÜ Dr. Nurdan Bilgin SORULAR ve ÇÖZÜMLER Soru 1: Küçük çelik toplar durgun durumdayken sırayla 100 m yüksekliğindeki A açıklığından sırayla iki saniyede bir düşüyorlar. a.) Artarda
MAK09 DİNAMİK ÖDEV 1 ÇÖZÜMÜ Dr. Nurdan Bilgin SORULAR ve ÇÖZÜMLER Soru 1: Küçük çelik toplar durgun durumdayken sırayla 100 m yüksekliğindeki A açıklığından sırayla iki saniyede bir düşüyorlar. a.) Artarda
TEMEL MEKANİK 5. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ
 Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
KİNEMATİK TEKNOLOJİNİN BİLİMSEL İLKELERİ
 6 KİNEMATİK TEKNOLOJİNİN BİLİMSEL İLKELERİ Adem ÇALIŞKAN ( HAREKET BİLGİSİ ) Mekaniğin hareketi açıklayan koluna KĠNEMATĠK denir. Hareket, konumun sürekli değiģimidir. Hareket eden cismi, Ģekil değiģikliği
6 KİNEMATİK TEKNOLOJİNİN BİLİMSEL İLKELERİ Adem ÇALIŞKAN ( HAREKET BİLGİSİ ) Mekaniğin hareketi açıklayan koluna KĠNEMATĠK denir. Hareket, konumun sürekli değiģimidir. Hareket eden cismi, Ģekil değiģikliği
Öğr. Gör. Serkan AKSU
 Öğr. Gör. Serkan AKSU www.serkanaksu.net İki nokta arasındaki yerdeğiştirme, bir noktadan diğerine yönelen bir vektördür, ve bu vektörün büyüklüğü, bu iki nokta arasındaki doğrusal uzaklık olarak alınır.
Öğr. Gör. Serkan AKSU www.serkanaksu.net İki nokta arasındaki yerdeğiştirme, bir noktadan diğerine yönelen bir vektördür, ve bu vektörün büyüklüğü, bu iki nokta arasındaki doğrusal uzaklık olarak alınır.
G = mg bağıntısı ile bulunur.
 ATIŞLAR Havada serbest bırakılan cisimlerin aşağı doğru düşmesi etrafımızda her zaman gördüğümüz bir olaydır. Bu düşme hareketleri, cisimleri yerin merkezine doğru çeken bir kuvvetin varlığını gösterir.
ATIŞLAR Havada serbest bırakılan cisimlerin aşağı doğru düşmesi etrafımızda her zaman gördüğümüz bir olaydır. Bu düşme hareketleri, cisimleri yerin merkezine doğru çeken bir kuvvetin varlığını gösterir.
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
T.C. SAKARYA ÜNİVERSİTESİ FİZİK-1 LABORATUARI DENEY RAPORU. Deneyin yapılış amacının ne olabileceğini kendi cümlelerinizle yazınız.
 T.C. SAKARYA ÜNİVERSİTESİ FİZİK- LABORATUARI DENEY RAPORU Ad Soyad Numara Bölüm Grup Deney No Deneyin Adı Deneyin Amacı Teorik Bilgi Deneyin yapılış amacının ne olabileceğini kendi cümlelerinizle yazınız.
T.C. SAKARYA ÜNİVERSİTESİ FİZİK- LABORATUARI DENEY RAPORU Ad Soyad Numara Bölüm Grup Deney No Deneyin Adı Deneyin Amacı Teorik Bilgi Deneyin yapılış amacının ne olabileceğini kendi cümlelerinizle yazınız.
3.1 Vektör Tipleri 3.2 Vektörlerin Toplanması. 3.4 Poligon Kuralı 3.5 Bir Vektörün Skaler ile Çarpımı RİJİT CİSİMLER MEKANİĞİ
 1-STATİĞİN TEMEL İLKELERİ 1- BİRİMLER 2-TRİGONOMETRİ 3-VEKTÖRLER 3.1 Vektör Tipleri 3.2 Vektörlerin Toplanması 3.3 Vektörlerin uç-uca eklenerek toplanması 3.4 Poligon Kuralı 3.5 Bir Vektörün Skaler ile
1-STATİĞİN TEMEL İLKELERİ 1- BİRİMLER 2-TRİGONOMETRİ 3-VEKTÖRLER 3.1 Vektör Tipleri 3.2 Vektörlerin Toplanması 3.3 Vektörlerin uç-uca eklenerek toplanması 3.4 Poligon Kuralı 3.5 Bir Vektörün Skaler ile
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER
 BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 3 Parçacık Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 3 Parçacık Dengesi Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 3 Parçacık Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 3 Parçacık Dengesi Bu bölümde,
GÜZ YARIYILI FİZİK 1 DERSİ
 2015-2016 GÜZ YARIYILI FİZİK 1 DERSİ Yrd. Doç. Dr. Hakan YAKUT SAÜ Fen Edebiyat Fakültesi Fizik Bölümü Ofis: FEF A Blok, 812 nolu oda Tel.: +90 264 295 (6092) 1 Bölüm 3 İKİ BOYUTTA HAREKET 2 İçerik Yerdeğistirme,
2015-2016 GÜZ YARIYILI FİZİK 1 DERSİ Yrd. Doç. Dr. Hakan YAKUT SAÜ Fen Edebiyat Fakültesi Fizik Bölümü Ofis: FEF A Blok, 812 nolu oda Tel.: +90 264 295 (6092) 1 Bölüm 3 İKİ BOYUTTA HAREKET 2 İçerik Yerdeğistirme,
MAK 308 MAKİNA DİNAMİĞİ Bahar Dr. Nurdan Bilgin
 MAK 308 MAKİNA DİNAMİĞİ 2017-2018 Bahar Dr. Nurdan Bilgin Virtüel İş Yöntemi-Giriş Bu zamana kadar Newton yasaları ve D alambert prensibine dayanarak hareket özellikleri her konumda bilinen bir makinanın
MAK 308 MAKİNA DİNAMİĞİ 2017-2018 Bahar Dr. Nurdan Bilgin Virtüel İş Yöntemi-Giriş Bu zamana kadar Newton yasaları ve D alambert prensibine dayanarak hareket özellikleri her konumda bilinen bir makinanın
DİNAMİK Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi. Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
2. KUVVET SİSTEMLERİ 2.1 Giriş
 2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
İş-Kinetik Enerji, Potansiyel Enerji, Enerji Korunumu
 İş-Kinetik Enerji, Potansiyel Enerji, Enerji Korunumu 1. Kütlesi 7 kg olan motorsuz oyuncak bir araba, sürtünmesiz yatay bir düzlem üzerinde 4 m/s ilk hız ile gitmektedir. Araba daha sonra ilk hızı ile
İş-Kinetik Enerji, Potansiyel Enerji, Enerji Korunumu 1. Kütlesi 7 kg olan motorsuz oyuncak bir araba, sürtünmesiz yatay bir düzlem üzerinde 4 m/s ilk hız ile gitmektedir. Araba daha sonra ilk hızı ile
Vektörler. Skaler büyüklükler. Vektörlerin 2 ve 3 boyutta gösterimi. Vektörel büyüklükler. 1. Şekil I de A vektörü gösterilmiştir.
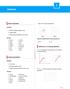 1 Vektörler Skaler büüklükler 1. de A vektörü gösterilmiştir. Özellikler: Sadece büüklüğü (şiddeti) vardır. Negatif olabilir. Skaler fiziksel büüklüklerin birimi vardır. Örnekler: Zaman Kütle Hacim Özkütle
1 Vektörler Skaler büüklükler 1. de A vektörü gösterilmiştir. Özellikler: Sadece büüklüğü (şiddeti) vardır. Negatif olabilir. Skaler fiziksel büüklüklerin birimi vardır. Örnekler: Zaman Kütle Hacim Özkütle
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 15 Parçacık Kinetiği: İmpuls ve Momentum Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 15 Parçacık
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 15 Parçacık Kinetiği: İmpuls ve Momentum Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 15 Parçacık
matematiksel eşitliğin her iki tarafındaki birim eşitliği kullanılarak a ve b sayılarına ulaşılır.
 Soru 1- Kuzey istikametinde 8m giden bir aracın, sonrasında 6m doğuya ve 10m güneye ilerlediği görülüyorsa, bu aracın hareketi boyunca aldığı toplam yol ve yerdeğiştirmesi kaç metredir? Cevap 1-8m Harekete
Soru 1- Kuzey istikametinde 8m giden bir aracın, sonrasında 6m doğuya ve 10m güneye ilerlediği görülüyorsa, bu aracın hareketi boyunca aldığı toplam yol ve yerdeğiştirmesi kaç metredir? Cevap 1-8m Harekete
İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine kuvveti görülmektedir. Parçacık A noktasından
 İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine etkiyen F kuvveti görülmektedir. Parçacık A noktasından r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve A dan A ne diferansiyel
İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine etkiyen F kuvveti görülmektedir. Parçacık A noktasından r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve A dan A ne diferansiyel
Newton un ikinci yasası: Bir cisim ivmesi cisim üzerine etki eden toplam kuvvet ile doğru orantılı cismin kütlesi ile ters orantılıdır.
 Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ÖLÇME VE BİRİM SİSTEMLERİ
 İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ÖLÇME VE BİRİM SİSTEMLERİ 1.1. FİZİKTE ÖLÇME VE BİRİMLERİN ÖNEMİ... 2 1.2. BİRİMLER VE BİRİM SİSTEMLERİ... 2 1.3. TEMEL BİRİMLERİN TANIMLARI... 3 1.3.1. Uzunluğun
İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ÖLÇME VE BİRİM SİSTEMLERİ 1.1. FİZİKTE ÖLÇME VE BİRİMLERİN ÖNEMİ... 2 1.2. BİRİMLER VE BİRİM SİSTEMLERİ... 2 1.3. TEMEL BİRİMLERİN TANIMLARI... 3 1.3.1. Uzunluğun
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
Fiz 1011 I. Vize UYGULAMA
 Fiz 1011 I. Vize UYGULAMA Bölüm 1. Fizik ve Ölçme 1. Aşağıdaki ölçme sonuçlarını 3 anlamlı rakamla gösteriniz. (a) 145,61 (b) 23457 (c) 2,4558 (d) 0,023001 (e) 0,12453 2. Farklı hasaslıkta aletler kullanılarak
Fiz 1011 I. Vize UYGULAMA Bölüm 1. Fizik ve Ölçme 1. Aşağıdaki ölçme sonuçlarını 3 anlamlı rakamla gösteriniz. (a) 145,61 (b) 23457 (c) 2,4558 (d) 0,023001 (e) 0,12453 2. Farklı hasaslıkta aletler kullanılarak
Gerilme Dönüşümü. Bölüm Hedefleri
 Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
Ankara Üniversitesi Fen Fakültesi Kimya Bölümü A Grubu 3. Bölüm (Doğrusal Hareket) Özet Aysuhan Ozansoy
 FİZ101 FİZİK-I Ankara Üniersitesi Fen Fakültesi Kimya Bölümü A Grubu 3. Bölüm (Doğrusal Hareket) Özet Aysuhan Ozansoy Bir şeyi basitçe açıklayamıyorsan onu tam olarak anlamamışsın demektir. Albert Einstein
FİZ101 FİZİK-I Ankara Üniersitesi Fen Fakültesi Kimya Bölümü A Grubu 3. Bölüm (Doğrusal Hareket) Özet Aysuhan Ozansoy Bir şeyi basitçe açıklayamıyorsan onu tam olarak anlamamışsın demektir. Albert Einstein
VEKTÖRLER SORULAR 1.) 3.) 4.) 2.)
 VETÖRER SORUR 1.) 3.) ynı düzlemde bulunan, ve vektörleri için verilen; I. = II. II = II III. = 2 Şekildeki aynı düzlemli vektörlerle tanımlanmış + + = D işleminin sonucunda elde edilen D vektörünün büyüklüğü
VETÖRER SORUR 1.) 3.) ynı düzlemde bulunan, ve vektörleri için verilen; I. = II. II = II III. = 2 Şekildeki aynı düzlemli vektörlerle tanımlanmış + + = D işleminin sonucunda elde edilen D vektörünün büyüklüğü
Matematikte karşılaştığınız güçlükler için endişe etmeyin. Emin olun benim karşılaştıklarım sizinkilerden daha büyüktür.
 - 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
- 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Fizik 101: Ders 17 Ajanda
 izik 101: Ders 17 Ajanda Dönme hareketi Yön ve sağ el kuralı Rotasyon dinamiği ve tork Örneklerle iş ve enerji Dönme ve Lineer Kinematik Karşılaştırma açısal α sabit 0 t 1 0 0t t lineer a sabit v v at
izik 101: Ders 17 Ajanda Dönme hareketi Yön ve sağ el kuralı Rotasyon dinamiği ve tork Örneklerle iş ve enerji Dönme ve Lineer Kinematik Karşılaştırma açısal α sabit 0 t 1 0 0t t lineer a sabit v v at
r r r F İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine kuvvetini göstermektedir. Parçacık A noktasından
 İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine etkiyenf r kuvvetini göstermektedir. Parçacık A noktasından r r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve d r A dan A ne
İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine etkiyenf r kuvvetini göstermektedir. Parçacık A noktasından r r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve d r A dan A ne
Fizik 101: Ders 6 Ajanda. Tekrar Problem problem problem!! ivme ölçer Eğik düzlem Dairesel hareket
 Fizik 101: Ders 6 Ajanda Tekrar Problem problem problem!! ivme ölçer Eğik düzlem Dairesel hareket Özet Dinamik. Newton un 3. yasası Serbest cisim diyagramları Problem çözmek için sahip olduğumuz gereçler:
Fizik 101: Ders 6 Ajanda Tekrar Problem problem problem!! ivme ölçer Eğik düzlem Dairesel hareket Özet Dinamik. Newton un 3. yasası Serbest cisim diyagramları Problem çözmek için sahip olduğumuz gereçler:
KKKKK VERİLER. Yer çekimi ivmesi : g=10 m/s 2. Metrik Ön Takılar sin 45 = cos 45 = 0,7
 VERİLER Yer çekimi ivmesi : g=10 m/s Metrik Ön Takılar sin = cos = 0, Numara Ön Takı Simge sin = cos = 0,6 sin = cos = 0,8 10 9 giga G tan = 0, 10 6 mega M sin 0 = cos 60 = -cos 10 = 0, 10 kilo k sin 60
VERİLER Yer çekimi ivmesi : g=10 m/s Metrik Ön Takılar sin = cos = 0, Numara Ön Takı Simge sin = cos = 0,6 sin = cos = 0,8 10 9 giga G tan = 0, 10 6 mega M sin 0 = cos 60 = -cos 10 = 0, 10 kilo k sin 60
11. SINIF KONU ANLATIMLI. 1. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM ETKİNLİK VE TEST ÇÖZÜMLERİ
 . SINIF KONU ANLATIMLI. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM ETKİNLİK VE TEST ÇÖZÜMLERİ 7 İtme ve Çizgisel Momentum. Ünite 7. Konu (İtme ve Çizgisel Momentum) A nın Çözümleri. Eğik
. SINIF KONU ANLATIMLI. ÜNİTE: KUVVET VE HAREKET 7. Konu İTME VE ÇİZGİSEL MOMENTUM ETKİNLİK VE TEST ÇÖZÜMLERİ 7 İtme ve Çizgisel Momentum. Ünite 7. Konu (İtme ve Çizgisel Momentum) A nın Çözümleri. Eğik
