KARŞI AKIŞLI SU SOĞUTMA KULESİ BOYUTLANIDIRILMASI
|
|
|
- Savas Birsen
- 8 yıl önce
- İzleme sayısı:
Transkript
1 KARŞI AKIŞI SU SOĞUTMA KUESİ BOYUTANIDIRIMASI Yrd. Doç. Dr. M. Turh Çob Ege Üiversitesi, Mühedislik Fkultesi Mkie Mühedisliği Bölümü Özet Bu yzımızd ters kışlı soğutm kulelerii boyut tyiie ve temel hesplrı bir giriş ypılmy çlışılmıştır.. 1. TERS AKIŞI SU SUĞUTMA KUESİ Soğutm kuleleri sistemleri soğutulmsı içi suyu buhrlşmsı sırsıd ısı lm temel presibii kull temel soğutm sistemleridir. Su soğutm kuleleride bir trft dış hv su soğutm kulesie girer. Diğer trft sistemde gele sıck su kuleye göderilir. Bu su dolgu ismii verdiğimiz ypılrı üzeride kıtılrk prçlır ve gire hvyl iyi bir tems yüzeyi sğlır. Bu yüzey boyuc suyu bir kısmı buhrlşır ve buhrlşırke ısı çeker. Buhrlş su hvy krışrk hvı su içeriğii rttırır. Bu yzımızd su kış yöüü ve hv kış yöüü birbirie ters olduğu (krşı kışlı) su soğutm kuleside kule temel boyutldırılmsıı ypılmsı verilecektir. Şekil 1 de krşı kışlı bir ve ısı değiştiricili bir soğutm kulesi gösterilmiştir. Şekil 1 Açık tip krşı kışlı soğutm kulesi
2 2. TERS AKIŞI SU SUĞUTMA KUESİ KUE KAREKTERİSTİĞİNİN TAYİNİ Bizim burd ilk olrk hesplmy çlışcğımız dolgu miktrı ve bu bğlı olrk soğutm kulesi boyutudur. Şekil 1 de krşı kışlı bir hv kuleside k suyu ve hvı dolgu üzerideki difersiyel kotrol hcmi görülmektedir. Şekil 1 hv kulesii difersiyel kotrol hcmi Şekildeki t su sıcklığı, hsu suyu etlpisi, yş hv giriş etlpisidir. su kütlesel debisi, G kuru hv kütlesel debisidir. Bu durumd difersiyel kotrol hcmi eerji deklemi : p dt dh su G d (1) Su dmlcığıı eerji trsferide 2 temel mekizm söz kousudur. Biricisi sıcklık frkıd dolyı ısı tşıımı diğeri ise kütle trsferide dolyı (dmlcık yüzeyide suyu belli bir kısmı buhrlşmktdır) oluş bizim mkie mühedisliğide gizli ısı dediğimiz eerji trsferi. (1) deklemii ısı ve kütle trsferi yöüde yzck olursk : p dt dh su h tşıım dv(t t ) + K dv (W - W )h fg (2) Burdki h tşıım tşıım ısı trsferi ktsyısı (W/m 2 K) K su hv tems yüzeyideki kütle trsferi ktsyısı dolgu mddesii birim hcmi bşı su ile hvı tems yüzeyi (m 2 ) p suyu özgül ısısı (KJ/kg K) h su suyu etlpisi (KJ/kg ) h fg h buhr h su suyu buhrlşm etlpisi W su sıcklığıdki doymuş hvı mutlk emi (kg su buhrı/kg kuru hv) W su sıcklığıdki doymuş hvı mutlk emi (kg su buhrı/kg kuru hv) Su hv tems yüzeyide eis dıı verdiğimiş bir bezeşim bğıtısı geellikle geçerlidir. Bu bğıtı K h tşıım / phv (3) bu bğıtıdki phv hvı sbit bsıçt su hv tems yüzeyideki özgül ısısıdır. Deklem (2) ve (3) ü bir ry getirirsek : p dt dh su K dv( phv t phv t + W h fg - W h fg ) (4) Deklemii elde ederiz. Yş hvı etlpisi phv t + W h fg (5) phv t + W h fg (6) Olduğu göz öüe lıırs deklemimiz p dt dh su K dv( + ) (7)
3 Formuu lır. Burd V 0 KdV p dt dhsu (8) KV p dt dhsu (9) deklemi elde edilir. Bu deklem Merkel deklemi dı ile ılır. Burdki KV terimi kule krekteristiği dıı lır. Kule dizyıd kule krekteristiği ısı değiştirici dizyıdki NTU gibi öemli bir prmetredir. Alm olrk t NTU y bezer. Diğer bir terimle çok büyük KV değerie ship ol bir kule gereğide büyüktür (yi çok KV phlıdır), çok küçük bir değeride ise gereğide küçüktür diyebiliriz. Deklem (9) litik olrk çözüme pek uygu bir deklem değildir. Syısl olrk çözülmesi çok dh kolydır. Syısl çözümde geel uygulm sıcklığı küçük stepler hlide değiştirilerek her step içi ol terimleri toplmsıdır. KV Δt Δh p su i 0 i 0 (10) hsug hsuc Δ t (11) vey Δ hsu (12) deklemleriyle verilir. Deklemdeki yş hv giriş etlpisii ilk değerii hv giriş yş hv sıcklığı ve kuru hv sıcklığıd (vey kuru hv sıcklığı ve bğıl emde) sptdıkt sor her stepteki değişimi deklem (1) de verdiğimiz eerji degesii kullrk hesplybiliriz. i+1 i + Δh G su i + G p Δt (13) Bu deklemi çözümüü ypmk içi jv progrmlm dilide bir progrm geliştirdik. Bu progrmı kullrk biri örek problemi irdeleyelim. Sıck su kuleye 45.0 de girmekte ve 30 de çıkmktdır. Kuru hv sıcklığı 34 ve yş hv sıcklığı 24 ise ve su hv debi orı (/G)1.3 ise kule krkteristik deklemii hesplylım : progrm çıktısı KV olrk buludu. Bu değeri elde etmek içi 40 stepli syısl itegrsyo kullıldı. er stepteki değerler Tblo 1 de verilmiştir. Tblo 1 örek problemdeki hespl etlpi değerleri T derece (kj/kg) (kj/kg) dhsu dt
4 Şekil 2 krşı kışlı hv kuleside etlpi değişimi grfiği
5 Bu değerleri grfik formud Şekil 2 de gösterilmiştir. Şekil 2 görsel olrkt bize u değişimii lieer olmdığıı göstermektedir. 3. TERS AKIŞI SU SUĞUTMA KUESİ KUE KÜTE TRANSFER KATSAYISININ VE DOGU BASINÇ DÜŞÜMÜNÜN TAYİNİ Soğutm edüstriside kullıl soğutm kuleleride geellikle plstik mlzemeler kullılır.
KAPALI ISI DEĞİŞTİRİCİLİ TERS VE DİK AKIŞLI SOĞUTMA KULELERİNİN ISI DEĞİŞİMİ MODELLENMESİ VE DİZAYNI
 X. UUSA TESİSAT ÜENDİSİĞİ KONGRESİ 3/6 NİSAN 0/İZİR _ 37 KAPAI ISI DEĞİŞTİRİCİİ TERS VE DİK AKIŞI SOĞUTA KUEERİNİN ISI DEĞİŞİİ ODEENESİ VE DİZAYNI ustf Turhn ÇOBAN ÖZET Soğutm kuleleri soğutm sistemlerinin
X. UUSA TESİSAT ÜENDİSİĞİ KONGRESİ 3/6 NİSAN 0/İZİR _ 37 KAPAI ISI DEĞİŞTİRİCİİ TERS VE DİK AKIŞI SOĞUTA KUEERİNİN ISI DEĞİŞİİ ODEENESİ VE DİZAYNI ustf Turhn ÇOBAN ÖZET Soğutm kuleleri soğutm sistemlerinin
Kesir Örnek Çözüm. 1. Yandaki şekilde bir TEST - 1. 1. Taralı alanı gösteren. bütün 8 eş parçaya bölünmüş ve bu parçalardan 3 tanesi
 Kesir.. Trlı lnı gösteren kesri bulunuz. kesrini ile genişlettiğimizde elde edilecek kesri bulunuz.. Yndki şekilde bir bütün 8 eş prçy bölünmüş ve bu prçlrdn tnesi trnmıştır. Trlı lnı gösteren kesir syısı
Kesir.. Trlı lnı gösteren kesri bulunuz. kesrini ile genişlettiğimizde elde edilecek kesri bulunuz.. Yndki şekilde bir bütün 8 eş prçy bölünmüş ve bu prçlrdn tnesi trnmıştır. Trlı lnı gösteren kesir syısı
ORAN ORANTI 2 1 3 - - 4 4 2 1 1 2 ÖYS. = = yazılabilir. veya ALIŞTIRMALAR
 YILLAR 00 003 00 00 006 00 008 009 00 0 3 - - ÖYS ORAN ORANTI ve t. t. t.e zılilir. f Or: E z iri sıfır frklı ı iste iki çokluğu ölümüe or eir. Or irimsizir. Ortı : iki ve h fzl orı eşitliğie ortı eir.
YILLAR 00 003 00 00 006 00 008 009 00 0 3 - - ÖYS ORAN ORANTI ve t. t. t.e zılilir. f Or: E z iri sıfır frklı ı iste iki çokluğu ölümüe or eir. Or irimsizir. Ortı : iki ve h fzl orı eşitliğie ortı eir.
PLAJLARDA ÇEVRE BİLİNÇLENDİRME PROJESİ. (19-22 Ağustos 2013 Akyaka)
 PLAJLARDA ÇEVRE BİLİNÇLENDİRME PROJESİ (19-22 Ağustos 213 Akyk) Pljlr Çevre Bilinçlenirme Projesi 19-22 Ağustos trihleri rsın TÜRÇEV Muğl Şuesi ve Akyk Beleiyesi iş irliği ile gerçekleştirili. Proje TÜRÇEV
PLAJLARDA ÇEVRE BİLİNÇLENDİRME PROJESİ (19-22 Ağustos 213 Akyk) Pljlr Çevre Bilinçlenirme Projesi 19-22 Ağustos trihleri rsın TÜRÇEV Muğl Şuesi ve Akyk Beleiyesi iş irliği ile gerçekleştirili. Proje TÜRÇEV
BİLİMSEL SÜREÇLERİN KAZANIMINA YÖNELİK BİR PROGRAM ÇALIŞMASI
 BİLİMSEL SÜREÇLERİN KAZANIMINA YÖNELİK BİR PROGRAM ÇALIŞMASI Dilek ARDAÇ, Ebru MUĞALOĞLU Boğziçi Üniversitesi, Eğitim Fkültesi, OFMA Eğitimi Bölümü, İSTANBUL ÖZET: Çlışm bilimsel süreçlerin kznımını mçlyn
BİLİMSEL SÜREÇLERİN KAZANIMINA YÖNELİK BİR PROGRAM ÇALIŞMASI Dilek ARDAÇ, Ebru MUĞALOĞLU Boğziçi Üniversitesi, Eğitim Fkültesi, OFMA Eğitimi Bölümü, İSTANBUL ÖZET: Çlışm bilimsel süreçlerin kznımını mçlyn
VORTEKS TÜPÜNDE AKIŞKAN OLARAK KULLANILAN HAVA İLE OKSİJENİN SOĞUTMA SICAKLIK PERFORMANSLARININ DENEYSEL İNCELENMESİ
 TEKNOLOJİ, Cilt 7, (24), Syı 3, 415-425 TEKNOLOJİ VORTEKS TÜPÜNDE AKIŞKAN OLARAK KULLANILAN HAVA İLE OKSİJENİN SOĞUTMA SICAKLIK PERFORMANSLARININ DENEYSEL İNCELENMESİ ÖZET Hüseyin USTA* Kevser DİNCER**
TEKNOLOJİ, Cilt 7, (24), Syı 3, 415-425 TEKNOLOJİ VORTEKS TÜPÜNDE AKIŞKAN OLARAK KULLANILAN HAVA İLE OKSİJENİN SOĞUTMA SICAKLIK PERFORMANSLARININ DENEYSEL İNCELENMESİ ÖZET Hüseyin USTA* Kevser DİNCER**
Ö rendiklerimizi Nerelerde Kullanabiliriz? Alan tahmin etmede kullanabiliriz.
 4.1 Aln Neler Ö renece iz? Geometrik flekillerin lnlr n hesplyc z. Ö rendiklerimizi Nerelerde Kullnbiliriz? Aln thmin etmede kullnbiliriz. Söz Vrl Prlelkenrsl bölge Bir y içinde yklfl k lt metre krelik
4.1 Aln Neler Ö renece iz? Geometrik flekillerin lnlr n hesplyc z. Ö rendiklerimizi Nerelerde Kullnbiliriz? Aln thmin etmede kullnbiliriz. Söz Vrl Prlelkenrsl bölge Bir y içinde yklfl k lt metre krelik
ege yayıncılık Oran Orant Özellikleri TEST : 91 a + 3b a b = 5 2 0,44 0,5 = 0,22 oldu una göre, a + b en az kaçt r? A) 3 B) 11 C) 14 D) 15 E) 16
 Orn Ornt Özellikleri TEST : 91 1. 0,44 0,5 = 0,22 5. + 3 = 5 2 2. 3. 4. oldu un göre, kçt r? A) 0,2 B) 0,25 C) 0,5 D) 0,6 E) 0,75 y = 3 4 + y oldu un göre, y orn kçt r? A) 7 B) 1 C) 1 D) 7 E) 10 oldu un
Orn Ornt Özellikleri TEST : 91 1. 0,44 0,5 = 0,22 5. + 3 = 5 2 2. 3. 4. oldu un göre, kçt r? A) 0,2 B) 0,25 C) 0,5 D) 0,6 E) 0,75 y = 3 4 + y oldu un göre, y orn kçt r? A) 7 B) 1 C) 1 D) 7 E) 10 oldu un
BÖLÜM II B. YENĐ ÇELĐK BĐNALARIN TASARIM ÖRNEKLERĐ ÖRNEK 6 ĐKĐ DOĞRULTUDA SÜNEKLĐK DÜZEYĐ YÜKSEK MERKEZĐ ÇAPRAZ PERDELĐ ÇELĐK BĐNANIN TASARIMI
 BÖLÜM II B. YENĐ ÇELĐK BĐNALARIN TASARIM ÖRNEKLERĐ ÖRNEK 6 ĐKĐ DOĞRULTUDA SÜNEKLĐK DÜZEYĐ YÜKSEK MERKEZĐ ÇAPRAZ PERDELĐ ÇELĐK BĐNANIN TASARIMI 6.1. SĐSTEM... 6/ 6.. YÜKLER... 6/4 6..1. Düşey Yükler...
BÖLÜM II B. YENĐ ÇELĐK BĐNALARIN TASARIM ÖRNEKLERĐ ÖRNEK 6 ĐKĐ DOĞRULTUDA SÜNEKLĐK DÜZEYĐ YÜKSEK MERKEZĐ ÇAPRAZ PERDELĐ ÇELĐK BĐNANIN TASARIMI 6.1. SĐSTEM... 6/ 6.. YÜKLER... 6/4 6..1. Düşey Yükler...
Komisyon. ALES EŞİT AĞRILIK ve SAYISAL ADAYLARA TAMAMI ÇÖZÜMLÜ 10 DENEME ISBN 978-605-364-214-5
 Komisyon LES EŞİT ĞRILIK ve SYISL DYLR TMMI ÇÖZÜMLÜ 10 DENEME ISBN 97-605-36-1-5 Kitpt yer ln ölümlerin tüm sorumluluğu yzrın ittir. Pegem kdemi Bu kitın sım, yyın ve stış hklrı Pegem kdemi Yy. Eğt. Dn.
Komisyon LES EŞİT ĞRILIK ve SYISL DYLR TMMI ÇÖZÜMLÜ 10 DENEME ISBN 97-605-36-1-5 Kitpt yer ln ölümlerin tüm sorumluluğu yzrın ittir. Pegem kdemi Bu kitın sım, yyın ve stış hklrı Pegem kdemi Yy. Eğt. Dn.
OKUL DENEYİMİ VE KAYNAŞTIRMA UYGULAMALARI
 OKUL DENEYİMİ VE KAYNAŞTIRMA UYGULAMALARI Uygulm Yönerge Kitpçığı 11.02.2015 ESOGÜ Eğitim Fkültesi Özel Eğitim Bölümü ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ EĞİTİM FAKÜLTESİ ÖZEL EĞİTİM BÖLÜMÜ 2014-2015 BAHAR
OKUL DENEYİMİ VE KAYNAŞTIRMA UYGULAMALARI Uygulm Yönerge Kitpçığı 11.02.2015 ESOGÜ Eğitim Fkültesi Özel Eğitim Bölümü ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ EĞİTİM FAKÜLTESİ ÖZEL EĞİTİM BÖLÜMÜ 2014-2015 BAHAR
BÖLÜM 5. MATRİS ve DETERMİNANTLAR 5.1. MATRİSLER. Taşkın, Çetin, Abdullayeva. reel sayılardan oluşan. olmak üzere tüm a.
 MTEMTİK BÖLÜM 5 Tşkın, Çetin, bdullyev MTRİS ve DETERMİNNTLR 5 MTRİSLER Tnım : mni,,, j + olmk üzere tüm ij reel syılrdn oluşn m m n n mn tblosun m x n tipinde bir mtrisi denir ve kısc şeklinde gösterilir
MTEMTİK BÖLÜM 5 Tşkın, Çetin, bdullyev MTRİS ve DETERMİNNTLR 5 MTRİSLER Tnım : mni,,, j + olmk üzere tüm ij reel syılrdn oluşn m m n n mn tblosun m x n tipinde bir mtrisi denir ve kısc şeklinde gösterilir
TEST - 1 KATI BASINCI. I. yarg do rudur. II. yarg yanl flt r. Buna göre, fiekil-i de K ve L cisimlerinin yere yapt klar bas nçlar eflit oldu una göre,
 TI BSINCI TEST - 1 1 1 π dir π Bun göre, 4 > 1 CEV B de ve cisimlerinin e ypt klr s nçlr eflit oldu un göre, SX S Z + 4 8 S Y I II III CEV B Tu llr n X, Y ve Z noktlr n ypt s nç, X S Y S Z S dir Bun göre,
TI BSINCI TEST - 1 1 1 π dir π Bun göre, 4 > 1 CEV B de ve cisimlerinin e ypt klr s nçlr eflit oldu un göre, SX S Z + 4 8 S Y I II III CEV B Tu llr n X, Y ve Z noktlr n ypt s nç, X S Y S Z S dir Bun göre,
DENEY 5 SOĞUTMA KULESİ PERFORMANSININ BELİRLENMESİ
 GAZİ ÜNİVERSİTESİ MÜHENDİSLİK-MİMARLIK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MM 410 MAKİNE MÜHENDİSLİĞİ LABORATUVARI II DENEY 5 SOĞUTMA KULESİ PERFORMANSININ BELİRLENMESİ 1. AMAÇ Soğutma kulesi performansının
GAZİ ÜNİVERSİTESİ MÜHENDİSLİK-MİMARLIK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MM 410 MAKİNE MÜHENDİSLİĞİ LABORATUVARI II DENEY 5 SOĞUTMA KULESİ PERFORMANSININ BELİRLENMESİ 1. AMAÇ Soğutma kulesi performansının
Kontak İbreli Termometreler
 E-mil: Fx: +49 661 6003-607 www.jumo.net www.jumo.co.uk www.jumo.us Veri Syfsı 608523 Syf 1/8 Kontk İbreli Termometreler Özellikler Pnel montj vey ek cihz gibi proses değeri göstergeli sıcklık kontrolörü
E-mil: Fx: +49 661 6003-607 www.jumo.net www.jumo.co.uk www.jumo.us Veri Syfsı 608523 Syf 1/8 Kontk İbreli Termometreler Özellikler Pnel montj vey ek cihz gibi proses değeri göstergeli sıcklık kontrolörü
Ölçme Hataları, Hata Hesapları. Ölçme Hataları, Hata Hesapları 2/22/2010. Ölçme... Ölçme... Yrd. Doç. Dr. Elif SERTEL sertele@itu.edu.
 //00 Ölçme Hataları, Hata Hesapları Ölçme Hataları, Hata Hesapları Yrd. Doç. Dr. Elif SERTEL sertele@itu.edu.tr Suu, Doç. Dr. Hade Demirel i ders otlarıda ve Ölçme Bilgisi kitabıda düzelemiştir. Ölçme...
//00 Ölçme Hataları, Hata Hesapları Ölçme Hataları, Hata Hesapları Yrd. Doç. Dr. Elif SERTEL sertele@itu.edu.tr Suu, Doç. Dr. Hade Demirel i ders otlarıda ve Ölçme Bilgisi kitabıda düzelemiştir. Ölçme...
JOVO STEFANOVSKİ NAUM CELAKOSKİ. Sekizyıllık İlköğretim
 JOVO STEFNOVSKİ NUM CELKOSKİ Sekizyıllık İlköğretim Syın Öğrenci! u kitp, ders proğrmınd öngörülen ders mlzemesini öğrenmek için yrdımcı olcktır. Vektörler, öteleme ve dönme hkkınd yeni ilginç bilgiler
JOVO STEFNOVSKİ NUM CELKOSKİ Sekizyıllık İlköğretim Syın Öğrenci! u kitp, ders proğrmınd öngörülen ders mlzemesini öğrenmek için yrdımcı olcktır. Vektörler, öteleme ve dönme hkkınd yeni ilginç bilgiler
12. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI
 12. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Progrmın öğrencilerde geliştirmeyi hedeflediği becerilerle 12. sınıf mtemtik öğretim progrmı ilişkisi Modelleme/Problem çözme Mtemtiksel Süreç Becerileri
12. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Progrmın öğrencilerde geliştirmeyi hedeflediği becerilerle 12. sınıf mtemtik öğretim progrmı ilişkisi Modelleme/Problem çözme Mtemtiksel Süreç Becerileri
Boru Çapının Soğutucu Akışkan Hızına ve Soğutma Yüküne Etkisi
 Süleymn Demirel Üniversitesi Fen Bilimleri Enstitüsü Derisi Suleymn Demirel University Journl of Nturl nd Applied Science 19(1), 9-18, 215 Boru Çpının Soğutucu Akışkn Hızın ve Soğutm Yüküne Etkisi Murt
Süleymn Demirel Üniversitesi Fen Bilimleri Enstitüsü Derisi Suleymn Demirel University Journl of Nturl nd Applied Science 19(1), 9-18, 215 Boru Çpının Soğutucu Akışkn Hızın ve Soğutm Yüküne Etkisi Murt
A A A A A TEMEL MATEMAT K TEST. + Bu bölümdeki cevaplar n z cevap ka d ndaki "TEMEL MATEMAT K TEST " bölümüne iflaretleyiniz. 4.
 TEMEL MTEMT K TEST KKT! + u bölümde cevplyc n z soru sy s 40 t r + u bölümdeki cevplr n z cevp k d ndki "TEMEL MTEMT K TEST " bölümüne iflretleyiniz.. ( + )y + = 0 (b ) + 4y 6 = 0 denklem sisteminin çözüm
TEMEL MTEMT K TEST KKT! + u bölümde cevplyc n z soru sy s 40 t r + u bölümdeki cevplr n z cevp k d ndki "TEMEL MTEMT K TEST " bölümüne iflretleyiniz.. ( + )y + = 0 (b ) + 4y 6 = 0 denklem sisteminin çözüm
TEKNOLOJİK ARAŞTIRMALAR
 www.teknolojikrstirmlr.com ISSN:- Mkine Teknolojileri Elektronik Dergisi 5 () - TEKNOLOJİK ARAŞTIRMALAR Kıs Mkle Sehim Ornın Bğlı Olrk Bir Mil Üzerinde Oluşn Sıcklık Dğılımının Arştırılmsı Vedt SAVAŞ,
www.teknolojikrstirmlr.com ISSN:- Mkine Teknolojileri Elektronik Dergisi 5 () - TEKNOLOJİK ARAŞTIRMALAR Kıs Mkle Sehim Ornın Bğlı Olrk Bir Mil Üzerinde Oluşn Sıcklık Dğılımının Arştırılmsı Vedt SAVAŞ,
 Ğ ü ü ç ş ş ğ ğ ğ ğ Ö ü ğ ş ğ ü ş Ç ş ş Ç ş ü ü ü ğ ç ç ş ü ş ş Ç ş ü ü ü ü ğ ş ş ü ü ş ş ş ü ü ğ ü üğü ş ç ü ü Ç ç ğ ü ü üğü ğ ü ç ş ş ş ş ğ ç ü ü ü ş ş ş Ç ş Ç ğ Ç ğ Ç Ç ü ş ş ü Öğ ü ş ş ğ ç Ç Ç ş Ç
Ğ ü ü ç ş ş ğ ğ ğ ğ Ö ü ğ ş ğ ü ş Ç ş ş Ç ş ü ü ü ğ ç ç ş ü ş ş Ç ş ü ü ü ü ğ ş ş ü ü ş ş ş ü ü ğ ü üğü ş ç ü ü Ç ç ğ ü ü üğü ğ ü ç ş ş ş ş ğ ç ü ü ü ş ş ş Ç ş Ç ğ Ç ğ Ç Ç ü ş ş ü Öğ ü ş ş ğ ç Ç Ç ş Ç
 Ü Ü Ğ Ş Ş Ş Ş Ş Ü Ğ ç Ş Ğ Ü Ü Ğ Ü Ş Ö ç ç Ğ Ğ Ü Ş Ü Ş Ş ç ç Ç Ü Ş Ç Ç Ü Ş Ş Ü Ü Ü Ü Ü Ü ç Ç ç ç ç ç ç ç ç ç ç ç ç ç Ç ç ç ç ç ç Ş Ğ Ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç Ş ç ç ç Ç ç ç ç ç ç ç Ç ç Ç ç ç ç
Ü Ü Ğ Ş Ş Ş Ş Ş Ü Ğ ç Ş Ğ Ü Ü Ğ Ü Ş Ö ç ç Ğ Ğ Ü Ş Ü Ş Ş ç ç Ç Ü Ş Ç Ç Ü Ş Ş Ü Ü Ü Ü Ü Ü ç Ç ç ç ç ç ç ç ç ç ç ç ç ç Ç ç ç ç ç ç Ş Ğ Ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç Ş ç ç ç Ç ç ç ç ç ç ç Ç ç Ç ç ç ç
 Ş İ İ ç İ İ İ İ ç Ş ü ü ü ü ç ü üç ü ü ü ç ü ü Ü İ Ğ Ş üç ü İ ü ü ü ç ü ç Ç ç İ ü üç ü Ç üç ü ç ç Ç ü Ç ç üç ü ç Ç ç ç ç ç Ğ Ğ ç İ ü ü ç ç ç ü ü ü Ü ç ç ü ç ç ü ü ü Ö ü ü ü ü Ü ü ü ç ü ç ç ü ü ü ü ç ü
Ş İ İ ç İ İ İ İ ç Ş ü ü ü ü ç ü üç ü ü ü ç ü ü Ü İ Ğ Ş üç ü İ ü ü ü ç ü ç Ç ç İ ü üç ü Ç üç ü ç ç Ç ü Ç ç üç ü ç Ç ç ç ç ç Ğ Ğ ç İ ü ü ç ç ç ü ü ü Ü ç ç ü ç ç ü ü ü Ö ü ü ü ü Ü ü ü ç ü ç ç ü ü ü ü ç ü
 ç ü ü ç ç ş İ Ç Ü ş İ Ç Ü ç ş ü İ Ç Ü ş ş ç ş ü Ö ü Ö İş ş ç İ Ç Ü ş ş ç ü ç ş ş İ Ç Ü ş ç Ü İ Ç Ü İ Ç Ü ü ç ş ş ş İ Ç Ü ç ü ş İ Ç Ü İş ş ş ü ş İ Ç Ü ş ü ş üç ü ş ş ş ç ü ü ç ş ş ş ş ü ş ü ü ş ç ü ç ç
ç ü ü ç ç ş İ Ç Ü ş İ Ç Ü ç ş ü İ Ç Ü ş ş ç ş ü Ö ü Ö İş ş ç İ Ç Ü ş ş ç ü ç ş ş İ Ç Ü ş ç Ü İ Ç Ü İ Ç Ü ü ç ş ş ş İ Ç Ü ç ü ş İ Ç Ü İş ş ş ü ş İ Ç Ü ş ü ş üç ü ş ş ş ç ü ü ç ş ş ş ş ü ş ü ü ş ç ü ç ç
 Ç Ü ğ Ç ç Ğ ç Ü ç ğ ç ğ ğ ç ğ ç ç ğ ç ç Ö Ş Ö ğ ç ğ Ç Ü Ç ğ Ç ğ Ü Ü Ç Ü ğ ğ Ü ğ ç Ç ğ Ü ç ç ğ Ğ Ğ ç ç ğ ğ ğ ğ ğ Ğ Ğ Ğ Ğ Ğ Ş Ş Ç Ö Ö ç Ç ğ ç ç ğ ç ğ ç ç ç ğ ç ç ç Ü ç ç ç ğ Ö Ü Ç Ş Ş ç Ö ç ğ ğ ğ ç ğ ğ ğ
Ç Ü ğ Ç ç Ğ ç Ü ç ğ ç ğ ğ ç ğ ç ç ğ ç ç Ö Ş Ö ğ ç ğ Ç Ü Ç ğ Ç ğ Ü Ü Ç Ü ğ ğ Ü ğ ç Ç ğ Ü ç ç ğ Ğ Ğ ç ç ğ ğ ğ ğ ğ Ğ Ğ Ğ Ğ Ğ Ş Ş Ç Ö Ö ç Ç ğ ç ç ğ ç ğ ç ç ç ğ ç ç ç Ü ç ç ç ğ Ö Ü Ç Ş Ş ç Ö ç ğ ğ ğ ç ğ ğ ğ
 Ü ş ğ ğ Ü ş Ç ğ ş ş Ç ğ ş Ü ğ Ü ş ğ Ü Ç ğ ğ Ü ğ ğ ğ ş ğ ğ ğ ş ş ğ ş ş ş Ç Ç Ö ş ğ ş ş ğ ş ğ ğ ş Ü Ç ğ ş ğ ş ş ğ Ü ğ ş ş ğ ş ş ş ş ş ş ğ ğ ş ş ş ş ş ş ş Ü ğ ş ş Ü Ç ğ Ç Ç ş ş ş ğ ş Ö ÇÜ Ö ş ğ Ö ş ş ğ ş
Ü ş ğ ğ Ü ş Ç ğ ş ş Ç ğ ş Ü ğ Ü ş ğ Ü Ç ğ ğ Ü ğ ğ ğ ş ğ ğ ğ ş ş ğ ş ş ş Ç Ç Ö ş ğ ş ş ğ ş ğ ğ ş Ü Ç ğ ş ğ ş ş ğ Ü ğ ş ş ğ ş ş ş ş ş ş ğ ğ ş ş ş ş ş ş ş Ü ğ ş ş Ü Ç ğ Ç Ç ş ş ş ğ ş Ö ÇÜ Ö ş ğ Ö ş ş ğ ş
 ç ğ ğ ğ ç ç ç ğ ç ğ ğ ç ğ ğ ç ğ ç ğ ğ ğ ç ğ ğ ç ğ ğ ç ç ğ ğ ğ Ü ç ğ ç ç ç ğ ç ç ğ ğ ğ ğ ğ ğ Ü ğ ğ ç ç ç ğ ç ğ ğ ç ğ ç ç ğ ğ ç ğ ğ ğ ğ ğ ç ğ ğ ğ ğ ç ğ ç ğ Ü ğ ğ ğ ç ç ğ ç ğ Ü ç ğ ğ ğ ç Ü ç ç ç ç ğ ç ğ ğ
ç ğ ğ ğ ç ç ç ğ ç ğ ğ ç ğ ğ ç ğ ç ğ ğ ğ ç ğ ğ ç ğ ğ ç ç ğ ğ ğ Ü ç ğ ç ç ç ğ ç ç ğ ğ ğ ğ ğ ğ Ü ğ ğ ç ç ç ğ ç ğ ğ ç ğ ç ç ğ ğ ç ğ ğ ğ ğ ğ ç ğ ğ ğ ğ ç ğ ç ğ Ü ğ ğ ğ ç ç ğ ç ğ Ü ç ğ ğ ğ ç Ü ç ç ç ç ğ ç ğ ğ
 Ü Ğ Ğ Ş Ö Ü Ü Ğ Ğ ü ü ü ü ü Ö Ü ü ü ü Ş ü ü Ş Ş ü ü ü ü üü ü Ş ü ü ü ü ü ü ü Ç ü ü ü ü ü ü ü üü ü ü ü üü ü ü ü ü ü ü ü ü Ş ü ü Ö ü ü ü ü ü ü ü ü Ç Ş Ç üü Ş ü ü ü ü üü ü ü ü ü ü ü ü ü ü ü Ş ü ü ü Ü ü ü
Ü Ğ Ğ Ş Ö Ü Ü Ğ Ğ ü ü ü ü ü Ö Ü ü ü ü Ş ü ü Ş Ş ü ü ü ü üü ü Ş ü ü ü ü ü ü ü Ç ü ü ü ü ü ü ü üü ü ü ü üü ü ü ü ü ü ü ü ü Ş ü ü Ö ü ü ü ü ü ü ü ü Ç Ş Ç üü Ş ü ü ü ü üü ü ü ü ü ü ü ü ü ü ü Ş ü ü ü Ü ü ü
 İ İ İ İ İ İ İ İ İ İ Ö İ İ İ İ İ Ü Ç İ Ş Ş İ İ Ü İ İ İ İ İ İÇİ Ö Ö Ç Ç Ç İ Ü Çİ İ Ü Ü İ İ İ İ İ İ İİ İ Ç Ş İ İ İ İ Ü Çİ Ö İ Ü Çİ İ İ Ü İİ İ Ç Ö İ Ö İ Ç Ç İ Ç Ö İ İ İİ İ Ç Ç Ç Ü İ Ç İ Ç İ Ş Ç İ Ğ İ İ İ İ
İ İ İ İ İ İ İ İ İ İ Ö İ İ İ İ İ Ü Ç İ Ş Ş İ İ Ü İ İ İ İ İ İÇİ Ö Ö Ç Ç Ç İ Ü Çİ İ Ü Ü İ İ İ İ İ İ İİ İ Ç Ş İ İ İ İ Ü Çİ Ö İ Ü Çİ İ İ Ü İİ İ Ç Ö İ Ö İ Ç Ç İ Ç Ö İ İ İİ İ Ç Ç Ç Ü İ Ç İ Ç İ Ş Ç İ Ğ İ İ İ İ
 İ Ç Ü ö üğü İ Ö ö üğü Ş ü öğ ü ç Ç ü ü ü Ç Ü ç ğ ç ğ Ğ ç Ş ğ ç ö ğ ğ ü ç Ü Ç ö üğü ö ü ü İİ Ç ğ ü ğ ç ğ ü ü ü ç ü ü Ş ü ğ ç ü ü ç ü ü ç ö Ö Ş Ö ğ ö ü ç ğ İ Ç Ü Ç ğ Ç ğ Ü Ü İ ü ç ğ ğ ğ ğ ğ ğ ç Ç ç ü ç Ş
İ Ç Ü ö üğü İ Ö ö üğü Ş ü öğ ü ç Ç ü ü ü Ç Ü ç ğ ç ğ Ğ ç Ş ğ ç ö ğ ğ ü ç Ü Ç ö üğü ö ü ü İİ Ç ğ ü ğ ç ğ ü ü ü ç ü ü Ş ü ğ ç ü ü ç ü ü ç ö Ö Ş Ö ğ ö ü ç ğ İ Ç Ü Ç ğ Ç ğ Ü Ü İ ü ç ğ ğ ğ ğ ğ ğ ç Ç ç ü ç Ş
 ü Ğ İ Ğ ü İ ç ü ü ü ç Ç ü ü ç Ç ü ü ç ü ü Ü Ç Ü ç ü ü ü ü ü ç Ç ü ü ç İ ü Ğ Ş İ İ ü Ğ İ Ğ ü İ Ö üçü ü Ö Ö ü Ö ü İ İ Ş Ğ İ İĞİ ü ü ü Ğİ İ Ğ İ Ğ ü Ö Ö Ü İĞİ ü Ü İ İ Ğİ ü ü Ğ İ İ İ İ İ İ ç ü ç ü ç ü ü ç ü
ü Ğ İ Ğ ü İ ç ü ü ü ç Ç ü ü ç Ç ü ü ç ü ü Ü Ç Ü ç ü ü ü ü ü ç Ç ü ü ç İ ü Ğ Ş İ İ ü Ğ İ Ğ ü İ Ö üçü ü Ö Ö ü Ö ü İ İ Ş Ğ İ İĞİ ü ü ü Ğİ İ Ğ İ Ğ ü Ö Ö Ü İĞİ ü Ü İ İ Ğİ ü ü Ğ İ İ İ İ İ İ ç ü ç ü ç ü ü ç ü
 İ İ İ Ğ İ İ İ İ Ğ Ğ Ş Ç Ş Ö Ş Ç İ Ç İ Ç Ş Ç Ü İ İ İ Ş Ş Ş Ş Ö Ç Ş Ş Ğ Ş Ç Ö Ş Ö Ö İ Ş Ç Ş Ş Ç Ş Ğ Ğ Ğ Ç İ Ğ Ş Ş Ç Ç Ş İ Ç Ş Ş Ş Ş İ Ğ Ö Ö Ş Ç Ş Ç Ş Ş Ş Ü Ö Ö Ö Ö Ö Ç Ç Ç Ö Ş Ç Ö Ö Ş İ İ Ç Ş Ş Ğ Ü Ş İ Ö
İ İ İ Ğ İ İ İ İ Ğ Ğ Ş Ç Ş Ö Ş Ç İ Ç İ Ç Ş Ç Ü İ İ İ Ş Ş Ş Ş Ö Ç Ş Ş Ğ Ş Ç Ö Ş Ö Ö İ Ş Ç Ş Ş Ç Ş Ğ Ğ Ğ Ç İ Ğ Ş Ş Ç Ç Ş İ Ç Ş Ş Ş Ş İ Ğ Ö Ö Ş Ç Ş Ç Ş Ş Ş Ü Ö Ö Ö Ö Ö Ç Ç Ç Ö Ş Ç Ö Ö Ş İ İ Ç Ş Ş Ğ Ü Ş İ Ö
 Ç Ç ç Ğ ç Ö Ğ Ş ç Ö Ö Ğ Ğ Ö Ö Ç Ü ç Ç Ü ç Ö ç ç ç ç Ğ ç ç Ç Ç ç Ç Ü ç ç Ç ç ç ç Ö ç Ö Ö ç ç ç ç ç ç ç ç ç ç ç Ö Ş ç ç ç ç ç ç ç ç Ü ç ç Ü ç ç ç ç ç ç ç Ö Ç ç ç ç ç ç ç ç ç ç ç Ö ç ç Ğ Ç Ü ç ç Ç Ü ç ç Ç
Ç Ç ç Ğ ç Ö Ğ Ş ç Ö Ö Ğ Ğ Ö Ö Ç Ü ç Ç Ü ç Ö ç ç ç ç Ğ ç ç Ç Ç ç Ç Ü ç ç Ç ç ç ç Ö ç Ö Ö ç ç ç ç ç ç ç ç ç ç ç Ö Ş ç ç ç ç ç ç ç ç Ü ç ç Ü ç ç ç ç ç ç ç Ö Ç ç ç ç ç ç ç ç ç ç ç Ö ç ç Ğ Ç Ü ç ç Ç Ü ç ç Ç
 İ Ç Ü ş ö üü ş ş ö üü Ü ü ü ö ü ç ü ü ü Ö Ü Ü Ö ç ç ş ş ç ç ü İ ü ç Ü ç ş ö üü ö ü ü ç ş ş ü ş ş ç ş ş ü ü ü ç ü ş ü ç Ş ü Ü ç ü ü ü ç ş ş ö ş Ö ş Ö ş ö ü ç ş Ç Ü Ç ş Ç İ Ü İ Ü Ş ş ü ş ö çü ü Ç Ü ü ö ş
İ Ç Ü ş ö üü ş ş ö üü Ü ü ü ö ü ç ü ü ü Ö Ü Ü Ö ç ç ş ş ç ç ü İ ü ç Ü ç ş ö üü ö ü ü ç ş ş ü ş ş ç ş ş ü ü ü ç ü ş ü ç Ş ü Ü ç ü ü ü ç ş ş ö ş Ö ş Ö ş ö ü ç ş Ç Ü Ç ş Ç İ Ü İ Ü Ş ş ü ş ö çü ü Ç Ü ü ö ş
 Ç Ç ü Ş ç Ü İ İ İ İ İ Ü İ İ Ş ğ ü Ö ç ç ü ç İ Ü ç İ İ ü ç ü ç İç ö ö ö ö ü ü ü ü ü ü ö Ü İ Ö İ ç ö ğ ü ö ç ç ö ç ö ü ğ ğ Ş ç Ç Ç Ş ü ö ç ğ ç ü ü ü ö ö ü ö ü ü ü ğ ğ ç ğ ğ ü ü ü ç ö ğ ç ğ ö ğ ğ ğ ç ü ü
Ç Ç ü Ş ç Ü İ İ İ İ İ Ü İ İ Ş ğ ü Ö ç ç ü ç İ Ü ç İ İ ü ç ü ç İç ö ö ö ö ü ü ü ü ü ü ö Ü İ Ö İ ç ö ğ ü ö ç ç ö ç ö ü ğ ğ Ş ç Ç Ç Ş ü ö ç ğ ç ü ü ü ö ö ü ö ü ü ü ğ ğ ç ğ ğ ü ü ü ç ö ğ ç ğ ö ğ ğ ğ ç ü ü
 Ş İ İ İ ç İ İ İ İ ç ç ç Ç ç ç ç ç İ Ö İ ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç Ç ç ç ç ç ç Ö Ö ç ç ç ç Ö ç Ö ç ç ç ç ç ç ç Ç ç ç ç Ç ç ç ç ç ç Ç ç Ö ç ç ç ç Ç ç Ö Ç ç ç Ş ç ç Ç Ş ç İ ç ç ç ç ç ç ç ç ç ç ç ç ç ç
Ş İ İ İ ç İ İ İ İ ç ç ç Ç ç ç ç ç İ Ö İ ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç Ç ç ç ç ç ç Ö Ö ç ç ç ç Ö ç Ö ç ç ç ç ç ç ç Ç ç ç ç Ç ç ç ç ç ç Ç ç Ö ç ç ç ç Ç ç Ö Ç ç ç Ş ç ç Ç Ş ç İ ç ç ç ç ç ç ç ç ç ç ç ç ç ç
 ç ç ö Ğ Ö Ş ö ü ü Ş ç ö ü ç ğ ü ç ç Ğ Ü Ü ÜĞÜ ç ö ö ü ç ü üç ç ğ ü ü Ş ğ ü ü üğü ç ö ö ü ç ü ö ç Ş Ş ü ü üğü Ğ Ğ Ş ü üğü Ğ ç ü ö ğ ü ö Ö Ü Ş ü ü ü Ğ ğ ü ö ğ ü ü üğü ğ Ö Ğ ğ ü ü ü ç ö ö ü ö ü ü ğ ç ç ö
ç ç ö Ğ Ö Ş ö ü ü Ş ç ö ü ç ğ ü ç ç Ğ Ü Ü ÜĞÜ ç ö ö ü ç ü üç ç ğ ü ü Ş ğ ü ü üğü ç ö ö ü ç ü ö ç Ş Ş ü ü üğü Ğ Ğ Ş ü üğü Ğ ç ü ö ğ ü ö Ö Ü Ş ü ü ü Ğ ğ ü ö ğ ü ü üğü ğ Ö Ğ ğ ü ü ü ç ö ö ü ö ü ü ğ ç ç ö
 ü ü üğü ğ Ö ü ö üş ö İ ü ü üğü ş ğ ç İ ç Ş ç ş ğ ş ş ğ ç ö ç ğ ş ş ş ö ü ğ ş ğ ü ü üğü ü ğ ö ü ü üğü ş ğ ş ş ş ö ü ç ğ ö ü ğ ö ü ü üğü ş ö ğ ç ğ ü ü üğü ü ğ ü ü üğü ü ü ü üğ ü ğ ö ü ğ ş ö üş ü ü üğü ü
ü ü üğü ğ Ö ü ö üş ö İ ü ü üğü ş ğ ç İ ç Ş ç ş ğ ş ş ğ ç ö ç ğ ş ş ş ö ü ğ ş ğ ü ü üğü ü ğ ö ü ü üğü ş ğ ş ş ş ö ü ç ğ ö ü ğ ö ü ü üğü ş ö ğ ç ğ ü ü üğü ü ğ ü ü üğü ü ü ü üğ ü ğ ö ü ğ ş ö üş ü ü üğü ü
 ü ü ü ö ü ü Ö Ö Ö öğ öğ ü ü İ ç ö ü ü ü Ü ü ö ü ü ö ö ö ö ö ç ö ö ü ö ü İ Ö Ü ü ü ü ü ö ü ö ü ü ü ü ü ç ü ö ç Ö ü ç ö ö ö ü ü ö ö ö ç ü ç ö ç ö ö ü ö ö ç ü ç ç ö ü ü ü ü ö ü ü ö ü Ö Ö ö ü ü Ö ö ö ö ü ü
ü ü ü ö ü ü Ö Ö Ö öğ öğ ü ü İ ç ö ü ü ü Ü ü ö ü ü ö ö ö ö ö ç ö ö ü ö ü İ Ö Ü ü ü ü ü ö ü ö ü ü ü ü ü ç ü ö ç Ö ü ç ö ö ö ü ü ö ö ö ç ü ç ö ç ö ö ü ö ö ç ü ç ç ö ü ü ü ü ö ü ü ö ü Ö Ö ö ü ü Ö ö ö ö ü ü
 ç Ğ Ü ç ö Ğ «ö ç ö ç ö ç ç ö ç ç ö ö ö ç ç ç ç ö ç ç ö ç ç ç ö ö ö ç ç ç Ç Ö Ü ç ç ç ç ç ç ç Ü ç ç ö ö ç ç ç ö ç ç ç ö ö ç ç ö Ç ç ö ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç Ç ç ç ç ç ç Ü ö ç ç ç ç ç Ç Ç ç ç Ç
ç Ğ Ü ç ö Ğ «ö ç ö ç ö ç ç ö ç ç ö ö ö ç ç ç ç ö ç ç ö ç ç ç ö ö ö ç ç ç Ç Ö Ü ç ç ç ç ç ç ç Ü ç ç ö ö ç ç ç ö ç ç ç ö ö ç ç ö Ç ç ö ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç Ç ç ç ç ç ç Ü ö ç ç ç ç ç Ç Ç ç ç Ç
 İ Ç Ü ö üğü İ ö üğü ü öğ ü ü ü ü Ö ği İ ü ö İ ğ Ğ Ü Ç ö üğü ö ü ü Ç ğ ü ğ Ş ğ ü ü ü ü ü ğ ö ü ü ü ü ü ö Ö Ş Ö ğ ö ü Ç ğ İ Ç Ü Ç ğ ğ Ü Ü ü «ü ö üğü İ Ü Ö Ü İ Ş İ Ü ü ö ü ö ğ ü İ «Ö ü ö ü İ ğ Ş ü Ş ö ö ü
İ Ç Ü ö üğü İ ö üğü ü öğ ü ü ü ü Ö ği İ ü ö İ ğ Ğ Ü Ç ö üğü ö ü ü Ç ğ ü ğ Ş ğ ü ü ü ü ü ğ ö ü ü ü ü ü ö Ö Ş Ö ğ ö ü Ç ğ İ Ç Ü Ç ğ ğ Ü Ü ü «ü ö üğü İ Ü Ö Ü İ Ş İ Ü ü ö ü ö ğ ü İ «Ö ü ö ü İ ğ Ş ü Ş ö ö ü
 Ç ö Ü ğ ö Ş ç ç Ş Ü Ö Ü Ü ö Ü ğ ğ ö ö ç ç Ü ğ ç ç ğ ğ ğ Ü ğ ö ö Ş ö ç ğ ö ç ç ğ ç ç ö Ş Ş ö ğ ç Ç ç ö ö ç Ç ö ğ Ü ö ğ ğ ç ö ç ğ ç ğ ö ç ö ö Üç ğ ö ç ö ç ö ç ğ ö ğ ö ç Ç ğ ç ç ğ ö ö ç ç ç ğ ğ ç ğ ç ğ ç
Ç ö Ü ğ ö Ş ç ç Ş Ü Ö Ü Ü ö Ü ğ ğ ö ö ç ç Ü ğ ç ç ğ ğ ğ Ü ğ ö ö Ş ö ç ğ ö ç ç ğ ç ç ö Ş Ş ö ğ ç Ç ç ö ö ç Ç ö ğ Ü ö ğ ğ ç ö ç ğ ç ğ ö ç ö ö Üç ğ ö ç ö ç ö ç ğ ö ğ ö ç Ç ğ ç ç ğ ö ö ç ç ç ğ ğ ç ğ ç ğ ç
 Ç Ü ö ö Ü ö ç Ö Ü ç ö ç ç Ğ ç ç ç ö ö ç ç Ü ç ö ö ç ç ç ç ç ç ö Ö Ş Ö ö ç Ç Ü Ç Ç Ü Ü ö ç ö ç ç ç ç ö ç ç ç ö ç ö ö ö ç ö ö Ü ç çö çö Ü ç çö Ö ö ö çö ç Ü ö ç ç ç çö ç ç ç ö ç çö çö ö ö ö ç Çö çö çö ö ç
Ç Ü ö ö Ü ö ç Ö Ü ç ö ç ç Ğ ç ç ç ö ö ç ç Ü ç ö ö ç ç ç ç ç ç ö Ö Ş Ö ö ç Ç Ü Ç Ç Ü Ü ö ç ö ç ç ç ç ö ç ç ç ö ç ö ö ö ç ö ö Ü ç çö çö Ü ç çö Ö ö ö çö ç Ü ö ç ç ç çö ç ç ç ö ç çö çö ö ö ö ç Çö çö çö ö ç
 Ü İ İ İ İ ö İ ö ğ ğ Ü ö Ş Ç ğ İç Ş Ç ğ Ü ö İ İ ğ Ü ö ğ Ü ö İ İ Ş Ç ğ İ İ ğ Ü ğ ğ ğ ç ç ö ğ ö ö ğ ğ ğ ö ç ç Ç Ç ö Ö ğ ğ ç ç Ş ğ ğ Üç Ç ğ ç ö Ş Ç ğ ğ Ş Ü ğ ğ Ş ğ ç ç ç ğ ö ö ğ ö ö İ ç ç ğ ğ Ü ö İ İ ğ Ş ğ
Ü İ İ İ İ ö İ ö ğ ğ Ü ö Ş Ç ğ İç Ş Ç ğ Ü ö İ İ ğ Ü ö ğ Ü ö İ İ Ş Ç ğ İ İ ğ Ü ğ ğ ğ ç ç ö ğ ö ö ğ ğ ğ ö ç ç Ç Ç ö Ö ğ ğ ç ç Ş ğ ğ Üç Ç ğ ç ö Ş Ç ğ ğ Ş Ü ğ ğ Ş ğ ç ç ç ğ ö ö ğ ö ö İ ç ç ğ ğ Ü ö İ İ ğ Ş ğ
 İ Ç Ü ş ö ğ ş ö ğ Ü öğ ç ş Ö Ü ğ ç ö ç ş ş ğ Ğ ç ç ğ ğ ö ş İ ç Ü ç ş ö ğ ö ç ç ş ş İ ğ ş ğ ş ç ş ğ ş ç ş ğ ç ç ş ş ö ş Ö Ş Ö ğ ş ö ç ş ğ Ç Ü Ç ğ ş Ç ğ İ Ü İ Ü ö ş ş ş ğ ç ş ö ğ çö ğ ş ş ç ö ş ş ş ğ ç ş
İ Ç Ü ş ö ğ ş ö ğ Ü öğ ç ş Ö Ü ğ ç ö ç ş ş ğ Ğ ç ç ğ ğ ö ş İ ç Ü ç ş ö ğ ö ç ç ş ş İ ğ ş ğ ş ç ş ğ ş ç ş ğ ç ç ş ş ö ş Ö Ş Ö ğ ş ö ç ş ğ Ç Ü Ç ğ ş Ç ğ İ Ü İ Ü ö ş ş ş ğ ç ş ö ğ çö ğ ş ş ç ö ş ş ş ğ ç ş
 ö Ü Ü ö Ö ğ ğ ğ ö Ü Ş ö Ü Ğ ö Ü ö Ü ö ğ ö ğ ö ö ğ ğ Ş Ü ğ ö ğ ğ ğ ğ ğ Ş Ş ğ ö ğ ğ ğ ğ ğ ö ö Ş ğ Ç ğ Ç Ş ö Ç ö ğ Ç ğ ö ğ ö ö ğ ö ğ ö Ş ğ Ç ğ Ç ğ ğ Ç Ş ö ö ö ğ Ç Ş Ç ö ö ğ ğ ğ ğ Ü Ü ö ğ «ğ ğ ğ ö ö «ö ğ ğ
ö Ü Ü ö Ö ğ ğ ğ ö Ü Ş ö Ü Ğ ö Ü ö Ü ö ğ ö ğ ö ö ğ ğ Ş Ü ğ ö ğ ğ ğ ğ ğ Ş Ş ğ ö ğ ğ ğ ğ ğ ö ö Ş ğ Ç ğ Ç Ş ö Ç ö ğ Ç ğ ö ğ ö ö ğ ö ğ ö Ş ğ Ç ğ Ç ğ ğ Ç Ş ö ö ö ğ Ç Ş Ç ö ö ğ ğ ğ ğ Ü Ü ö ğ «ğ ğ ğ ö ö «ö ğ ğ
 Ü Ö Ö ö ö Ü Ü Ö ö ç ç ö ç ö ç ç ö ö ö ö ö ç ö ö ç ç ç ç ç ç ö ö ö ö ç ç ö ç» ö ö ö ö ç ö ö ö ö ç ö ç ö ç ö ç ö ö ç ç ç ç ö ö ö ç ç ç ç ç ç ç ç ç ö ç ç ö ç ç ç ç ç ç ö ö ö ç ç ç ö ö ö ç ç ç ç ö ç ç ç ç
Ü Ö Ö ö ö Ü Ü Ö ö ç ç ö ç ö ç ç ö ö ö ö ö ç ö ö ç ç ç ç ç ç ö ö ö ö ç ç ö ç» ö ö ö ö ç ö ö ö ö ç ö ç ö ç ö ç ö ö ç ç ç ç ö ö ö ç ç ç ç ç ç ç ç ç ö ç ç ö ç ç ç ç ç ç ö ö ö ç ç ç ö ö ö ç ç ç ç ö ç ç ç ç
Sistem Dinamiği ve Modellemesi. Doğrusal Sistemlerin Sınıflandırılması Doğrusal Sistemlerin Zaman Davranışı
 Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
 İ» Ö İ İ ğ ğ İ ğ ğ ğ ğ ğ ğ ğ ğ İ ö ö ç ğ ğ ğ ğ ğ Ö Ü Ü ğ ğ ğ ö ğ ğ ğ ğ ö ğ ğ İ İ İ İ ğ ğ ğ ö İ ğ ğ ğ ğ ğ ö ğ ğ ö ö ğ öğ ğ ğ ğ İ ö ç ç ğ ö ö ç ğ ç ç ğ ç ğ ö ç ğ ğ ğ ğ ğ ğ İ Ü Ş İ ö İ ğ ğ İ İ ğ ğ ğ ç ğ ğ
İ» Ö İ İ ğ ğ İ ğ ğ ğ ğ ğ ğ ğ ğ İ ö ö ç ğ ğ ğ ğ ğ Ö Ü Ü ğ ğ ğ ö ğ ğ ğ ğ ö ğ ğ İ İ İ İ ğ ğ ğ ö İ ğ ğ ğ ğ ğ ö ğ ğ ö ö ğ öğ ğ ğ ğ İ ö ç ç ğ ö ö ç ğ ç ç ğ ç ğ ö ç ğ ğ ğ ğ ğ ğ İ Ü Ş İ ö İ ğ ğ İ İ ğ ğ ğ ç ğ ğ
 ğ Ş ğ ş ğ İ ö ç ö ö İ ğ ş ş ç ç ğ ç ğ ş ğ İ Ş Ü İş ö Ö ğ Öğ ş ğ ğ İ ö ö Çğ ö İ ö ç İ ş ş ş ç ş öğ ş Ş ğ ö ğ ş ö ğ İ ğ ö ş ş ş ğ ğ İ ş ğ çö ğ ğ ş ö öğ ç öği İ ğ ğ ğ ğ öğ ö ş ğ İ ç ş İ İ ğ ç İ İ Ö ÖĞ İ ğ
ğ Ş ğ ş ğ İ ö ç ö ö İ ğ ş ş ç ç ğ ç ğ ş ğ İ Ş Ü İş ö Ö ğ Öğ ş ğ ğ İ ö ö Çğ ö İ ö ç İ ş ş ş ç ş öğ ş Ş ğ ö ğ ş ö ğ İ ğ ö ş ş ş ğ ğ İ ş ğ çö ğ ğ ş ö öğ ç öği İ ğ ğ ğ ğ öğ ö ş ğ İ ç ş İ İ ğ ç İ İ Ö ÖĞ İ ğ
 Ğ Ğ Ü Ü Ö Ü Ö Ö Ö Ü Ö Ü Ü Ü Ü Ü İ İ Ü Ü Ö Ö Ü Ö Ü Ö Ü Ö İ Ü Ö Ö Ö Ö Ö Ö Ö Ö Ö Ö Ü Ö İ Ö Ü Ö İ Ö İ İ İ İ İ İ İ İ İ İ Ö Ö Ö Ö Ö Ö Ö İ Ü İ Ü İ İ İ İ İ İ İ Ö İ Ü İ İ İ Ö İ Ö Ö İ İ Ö Ö İ İ İ İ İ İ İ İ İ İ Ö
Ğ Ğ Ü Ü Ö Ü Ö Ö Ö Ü Ö Ü Ü Ü Ü Ü İ İ Ü Ü Ö Ö Ü Ö Ü Ö Ü Ö İ Ü Ö Ö Ö Ö Ö Ö Ö Ö Ö Ö Ü Ö İ Ö Ü Ö İ Ö İ İ İ İ İ İ İ İ İ İ Ö Ö Ö Ö Ö Ö Ö İ Ü İ Ü İ İ İ İ İ İ İ Ö İ Ü İ İ İ Ö İ Ö Ö İ İ Ö Ö İ İ İ İ İ İ İ İ İ İ Ö
ğ ğ Ö ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ Ö ğ ğ ğ ğ
 İ Ş Ş İ İ Ö İ ğ ğ ğ ğ ğ ğ ğ ğ ğ Ö ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ Ö ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ İ ğ ğ ğ ğ Ö Ö Ç ğ ğ ğ ğ ğ Ü ğ İ ğ ğ Ç İ ğ ğ Ç ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ Ş ğ ğ ğ Ü ğ ğ ğ ğ Ö ğ ğ Ö ğ ğ ğ
İ Ş Ş İ İ Ö İ ğ ğ ğ ğ ğ ğ ğ ğ ğ Ö ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ Ö ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ İ ğ ğ ğ ğ Ö Ö Ç ğ ğ ğ ğ ğ Ü ğ İ ğ ğ Ç İ ğ ğ Ç ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ ğ Ş ğ ğ ğ Ü ğ ğ ğ ğ Ö ğ ğ Ö ğ ğ ğ
İDEAL PERFORMANS DEĞERLENDİRME FORMU TASARIMINDA ANALİTİK HİYERARŞİ YÖNTEMİ YAKLAŞIMI
 Gzi Üniv Müh Mim Fk Der J Fc Eng Arch Gzi Univ Cilt 20, No 1, 95-106, 2005 Vol 20, No 1, 95-106, 2005 İDEAL PERFORMANS DEĞERLENDİRME FORMU TASARIMINDA ANALİTİK HİYERARŞİ YÖNTEMİ YAKLAŞIMI Ergün ERASLAN
Gzi Üniv Müh Mim Fk Der J Fc Eng Arch Gzi Univ Cilt 20, No 1, 95-106, 2005 Vol 20, No 1, 95-106, 2005 İDEAL PERFORMANS DEĞERLENDİRME FORMU TASARIMINDA ANALİTİK HİYERARŞİ YÖNTEMİ YAKLAŞIMI Ergün ERASLAN
 Ğ Ğ ö Ş Ş Ğ Ş Ş Ü Ş Ğ Ğ Ğ ö ö Ğ Ş Ş Ğ Ğ ö Ğ ö ö ö ö ö ö ö ö Ü Ş Ö Ö Ö Ş Ş Ç Ü ö Ü Ü Ğ ö «ö ö ö Ğ Ş ö ö ö ö ö ö ö ö ö ö ö Ş ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö Ö ö ö Ö Ö ö ö ö ö ö ö ö ö ö ö Ö Ö ö ö Ç Ö ö Ü ö
Ğ Ğ ö Ş Ş Ğ Ş Ş Ü Ş Ğ Ğ Ğ ö ö Ğ Ş Ş Ğ Ğ ö Ğ ö ö ö ö ö ö ö ö Ü Ş Ö Ö Ö Ş Ş Ç Ü ö Ü Ü Ğ ö «ö ö ö Ğ Ş ö ö ö ö ö ö ö ö ö ö ö Ş ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö Ö ö ö Ö Ö ö ö ö ö ö ö ö ö ö ö Ö Ö ö ö Ç Ö ö Ü ö
Yükseköğretime Geçiş Sınavı (Ygs) / 1 Nisan 2012. Matematik Soruları ve Çözümleri
 Yükseköğretime Geçiş Sınvı (Ygs) / Nisn 0 Mtemtik Sorulrı ve Çözümleri. 0,5, işleminin sonuu kçtır? 0,5 0, A) 5 B) 5,5 C) 6 D) 6,5 E) 7 Çözüm 0,5 0,5, 0, 05 50 5.5.4 5.5. 4 4 0 5 .. 4.6 6 işleminin sonuu
Yükseköğretime Geçiş Sınvı (Ygs) / Nisn 0 Mtemtik Sorulrı ve Çözümleri. 0,5, işleminin sonuu kçtır? 0,5 0, A) 5 B) 5,5 C) 6 D) 6,5 E) 7 Çözüm 0,5 0,5, 0, 05 50 5.5.4 5.5. 4 4 0 5 .. 4.6 6 işleminin sonuu
 Ğ Ğ Ö İ İĞİ» Çö İ İ İĞİ Ç İ İĞİ Ü İ İĞİ İ İ ö ö ö Ğ İ ç Ö Ö ö ö ö ç ç ö Ö ö ö ö ö ö Ö ç ç ç ç ç Ğ ç Ğ İ Çö öğ ö İ İ İ ç ö ö ç Ğ İ ö ö İ İĞİ İ İĞİ Ğ Ç Ğ ö ö ö Ğ ç Ö Ö ö ç ö Ö ö ö ç ö ö ö ç Ö ç ç ç ç ç Ğ
Ğ Ğ Ö İ İĞİ» Çö İ İ İĞİ Ç İ İĞİ Ü İ İĞİ İ İ ö ö ö Ğ İ ç Ö Ö ö ö ö ç ç ö Ö ö ö ö ö ö Ö ç ç ç ç ç Ğ ç Ğ İ Çö öğ ö İ İ İ ç ö ö ç Ğ İ ö ö İ İĞİ İ İĞİ Ğ Ç Ğ ö ö ö Ğ ç Ö Ö ö ç ö Ö ö ö ç ö ö ö ç Ö ç ç ç ç ç Ğ
 İ Ğ Ş İ» Ğ Ğ ö Ğ ö ö Ç ö Ç İ Ş ö ö ö ö ö ö ö ö ö ö ö Ç ö ö ö ö ö ö İ İ ö ö ö Ü ö ö ö ö ö ö ö Ş ö ö İ ö ö İ ö ö İ İ ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö Ç İ İ ö İ İ İ İ Ö İ Ç ö ö Ö Ç ö ö ö ö ö ö ö ö ö ö
İ Ğ Ş İ» Ğ Ğ ö Ğ ö ö Ç ö Ç İ Ş ö ö ö ö ö ö ö ö ö ö ö Ç ö ö ö ö ö ö İ İ ö ö ö Ü ö ö ö ö ö ö ö Ş ö ö İ ö ö İ ö ö İ İ ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö ö Ç İ İ ö İ İ İ İ Ö İ Ç ö ö Ö Ç ö ö ö ö ö ö ö ö ö ö
Veri, Sayma ve Olasılık. Test / 30. soru 1. soru 5. soru 2. soru 6. soru 3. soru 7. soru 8. soru 4
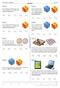 Test / 0 soru soru Bir zr t ld nd üste gelen sy n n tek oldu u ilindi ine göre, sy n n sl sy olm Bir çift zr t ld nd üste gelen sy lr n toplm n n 0 oldu u ilindi ine göre, zrlrdn irinin olm soru soru Bir
Test / 0 soru soru Bir zr t ld nd üste gelen sy n n tek oldu u ilindi ine göre, sy n n sl sy olm Bir çift zr t ld nd üste gelen sy lr n toplm n n 0 oldu u ilindi ine göre, zrlrdn irinin olm soru soru Bir
DOĞRUSAL PROGRAMLAMA PROBLEMLERİNİN EXCEL İLE ÇÖZÜMÜ
 C.Ü. İktisdi ve İdri Bilimler Dergisi, Cilt 5, Syı 5 DOĞRUSAL PROGRAMLAMA PROBLEMLERİNİN EXCEL İLE ÇÖZÜMÜ Öğr. Gör. Dr. Mehmet Ali ALAN Cumhuriyet Üiversitesi İktisdi ve İdri Bilimler Fkültesi Öğr. Gör.
C.Ü. İktisdi ve İdri Bilimler Dergisi, Cilt 5, Syı 5 DOĞRUSAL PROGRAMLAMA PROBLEMLERİNİN EXCEL İLE ÇÖZÜMÜ Öğr. Gör. Dr. Mehmet Ali ALAN Cumhuriyet Üiversitesi İktisdi ve İdri Bilimler Fkültesi Öğr. Gör.
DERS 1. Sayı Kümeleri ve Koordinatlar
 DERS Syı Kümeleri ve Koordintlr. Kümeler. Mtemtiğin temel kvrmlrındn biri küme kvrmıdır. Okuyucunun küme kvrmın ybncı olmyıp kümelerle ilgili temel işlemleri bildiğini kbul ediyoruz. Bununl berber, kümelerle
DERS Syı Kümeleri ve Koordintlr. Kümeler. Mtemtiğin temel kvrmlrındn biri küme kvrmıdır. Okuyucunun küme kvrmın ybncı olmyıp kümelerle ilgili temel işlemleri bildiğini kbul ediyoruz. Bununl berber, kümelerle
İKİNCİ BÖLÜM REEL SAYI DİZİLERİ
 Prof.Dr.Hüseyi ÇAKALLI İKİNCİ BÖLÜM REEL SAYI DİZİLERİ Bu ölümde dizileri, yi tım kümesi doğl syılr kümesi, değer kümesi, reel syılr kümesii ir lt kümesi ol foksiyolrı iceleyeceğiz... Ykısk Diziler. Öce
Prof.Dr.Hüseyi ÇAKALLI İKİNCİ BÖLÜM REEL SAYI DİZİLERİ Bu ölümde dizileri, yi tım kümesi doğl syılr kümesi, değer kümesi, reel syılr kümesii ir lt kümesi ol foksiyolrı iceleyeceğiz... Ykısk Diziler. Öce
DENKLEM ÇÖZME DENKLEM ÇÖZME. Birinci dereceden İki bilinmeyenli. 2x 2 + 5x + 2 = 0. 3x x 2 + 1 = 0. 5x + 3 = 0. x + 17 = 24.
 DENKLEM ÇÖZME + + = 0 + = 0 + = 0 + y = 0 İkinci dereceden ir ilinmeyenli denklemdir. İkinci dereceden ir ilinmeyenli denklemdir. Birinci dereceden ir ilinmeyenli denklemdir. Birinci dereceden İki ilinmeyenli
DENKLEM ÇÖZME + + = 0 + = 0 + = 0 + y = 0 İkinci dereceden ir ilinmeyenli denklemdir. İkinci dereceden ir ilinmeyenli denklemdir. Birinci dereceden ir ilinmeyenli denklemdir. Birinci dereceden İki ilinmeyenli
EKSTRÜZYONLA ŞEKİLLENDİRİLEN TİCARİ SAFLIKTAKİ ALÜMİNYUMUN SONLU ELEMANLAR METODUYLA MODELLENMESİ VE ANALİZİ
 5. Uluslrrsı İleri Teknolojiler Sempozyumu (IATS 09), 13-15 Myıs 2009, Krük, Türkiye EKSTRÜZYONLA ŞEKİLLENDİRİLEN TİCARİ SAFLIKTAKİ ALÜMİNYUMUN SONLU ELEMANLAR METODUYLA MODELLENMESİ VE ANALİZİ FINITE
5. Uluslrrsı İleri Teknolojiler Sempozyumu (IATS 09), 13-15 Myıs 2009, Krük, Türkiye EKSTRÜZYONLA ŞEKİLLENDİRİLEN TİCARİ SAFLIKTAKİ ALÜMİNYUMUN SONLU ELEMANLAR METODUYLA MODELLENMESİ VE ANALİZİ FINITE
Otomatik Kontrol Ulusal Toplantısı, TOK2013, 26-28 Eylül 2013, Malatya DİĞER KONULAR
 Oomik Korol Ulusl Toplısı, TOK, 6-8 Eylül, Mly DİĞER KONULAR 9 Oomik Korol Ulusl Toplısı, TOK, 6-8 Eylül, Mly Kesirli Türev içi Ypıl Tımlmlrı Eksiklikleri ve Yei Yklşım Ali KARCI Bilgisyr Müedisliği Bölümü
Oomik Korol Ulusl Toplısı, TOK, 6-8 Eylül, Mly DİĞER KONULAR 9 Oomik Korol Ulusl Toplısı, TOK, 6-8 Eylül, Mly Kesirli Türev içi Ypıl Tımlmlrı Eksiklikleri ve Yei Yklşım Ali KARCI Bilgisyr Müedisliği Bölümü



































